lesson 5 problem solving practice fundamental counting principle

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators
• Fundamental counting principle – Explanation & Examples

JUMP TO TOPIC

Fundamental Counting Principle definition

Fundamental counting principle formula, practice question:, fundamental counting principle – explanation & examples.

The fundamental counting principle is a mathematical rule that is extensively applied in the evaluation total number of possible arrangements of a set of objects. These calculations are essential for solving many probability problems.

The fundamental counting principle states that if one event can occur in $A$ different ways and a second event can occur in $B$ different ways, then the total number of ways in which both events can occur is $A \times B$.

After reading this article, you should understand:

• The Fundamental Counting Principle
• Difference Between the Rule of Sum and the Counting principle
• Examples of the Fundamental Counting Principle
• Applications of the Counting principle   

It is advisable to refresh the set theory to better understand the material discussed in this article.                                                        

What is the Fundamental Counting Principle

Let us consider the example of flipping a fair coin twice. When the coin is tossed the first time, we either get Heads or Tails, and the sample space can be written as $S = \{H, T\}$. When the coin is tossed the second time, the sample space we get is $S = \{HH, HT, TH, TT\}$. The first flip can result in two different outcomes, and so does the second flip. So, the total number of possible outcomes is $2 \times 2 =4$. The example is illustrated in the form of a tree diagram below:    

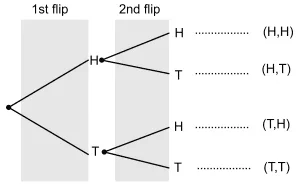
Let us take another simple example, James has to go to a party, and he has three different shirts and two different pants to choose from. The shirts are red, black and white in color while the pants are blue and green in color. How many possible outfits can James choose from? James can wear either of the two pants with each shirt.

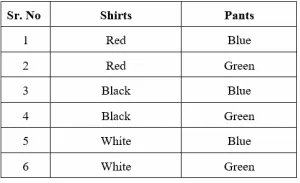
So, James can wear Red shirt with either Blue or Green pants. Similarly, Black and White shirts can be selected with either Blue or Green pants. As the table shows, there are six numbers of possible outfits. We can calculate it easily through the rule of counting principle. We had 3 different options for shirts and two different options for pants so, $3 \times 2=6$ possible outfits.

If there are $A$ different ways of selecting an object and $B$ different ways of selecting another object, then the total number of possible ways for selecting both objects together is $A\times B$.  

Example 1 : Harry went to a food restaurant, and he wants to order a combo deal that includes a pizza, drink, and dessert. The following choices are available:

Pizza : Chicken Fajita and Vegetable

Drink : Pepsi and 7-Up

Dessert : Ice-cream and Pie

We are given three different objects to choose from. There are three different types of pizza, four different types of drinks, and three different types of dessert. Let us draw a tree diagram.

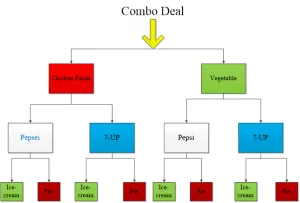
As the tree diagram shows, we can work out the possible arrangements for a combo deal.

Deal 1: Chicken fajita, Pepsi, and Ice-cream

Deal 2: Chicken fajita, Pepsi, and Pie

Deal 3: Chicken fajita, 7-UP, and Ice-cream

Deal 4: Chicken fajita, 7-UP, and Pie

Deal 5: Vegetable Pizza, Pepsi, and Ice-cream

Deal 6: Vegetable Pizza, Pepsi, and Pie

Deal 7: Vegetable Pizza, 7-UP and Ice-cream

Deal 8: Vegetable Pizza, 7-UP and Pie

Now solving it by counting principle, we have 2 options for pizza, 2 for drinks and 2 for desserts so, the total number of possible combo deals $= 2 \times 2 \times 2 =8$.

  Example 2 : Steve has to dress for a presentation. He has $3$ different shirts,$ 2$ different pants, and$ 3 $ different shoes available in his closet. Wearing the Tie is optional. Calculate the total number of possible outfits. 

There are three types of shirts, two types of pants and three types of shoes. While the tie is optional, the tie has two options, either “Yes” or “No.”

Total number of possible outfits $ = 3 \times 2 \times 3 \times 2= 36$.

  The Rule of Sum

The rule of sum states that if event $A$ can occur in $n$ different ways and event $B$ can occur in $m$ different ways. In contrast, both events $A$ and $B$ are mutually exclusive , then the total number of possible outcomes can be given as $n + m$. So, unlike the counting principle, we add both the events; however, it must be remembered that the condition for the rule of the sum is that the events must be mutually exclusive.         

Example 3 : Jessica has a jar of cookies. It has $3$ chocolate and $3$ peanut cookies in it. Jessica only wants to eat one cookie. How many possible options does Jessica have?

Since Jessica only wants one cookie, she has to choose only one cookie from 3 chocolate or 3 peanut cookies. The choices are mutually exclusives, so by applying the rule of sum, we have $3+3= 6$ possible options.

Example 4 : Ellie went to a dress shop to purchase a single blue dress. The shop has $14$ plain blue dresses, $13$ plain red dresses, 10 blue embroidered dresses, and $5$ red embroidered dresses. How many options does Ellie have?

Since Ellie wants to choose a blue dress so, we will eliminate all red dresses. She can choose from 14 plain blue dresses or 10 blue embroidered dresses. So, the total numbers of option are $14+10 = 24$

  The Counting Principle and Rule of Sum

We have discussed the problems related to the fundamental counting principle and the rule of sum. What if a problem has to be solved using both the rules? Let us discuss a few examples.

  Example 5 : Harris went to a shop to buy some items of clothing. He can choose a shirt from 3 different colors or a T-shirt from 2 different colors. Also, he can either get a pair of pants from 3 available colors or a pair of jeans from three available colors. How many possible outfits can Harris have?    

Harris can take one shirt from the given 3 colors or T-shirts from the available 2 colors. So number of available shirts $= 3+2 =5$.

Similarly, he can choose a pair of pants from either 3 options or a pair of jeans from three options. The number of available pairs of jeans/pants $3+3=6$.

So, we have $5$ different shirts and $6$ different pants, and the total number of possible outfits will be $5 \times 6= 30$.

Example 6 : Steve wants to go to a job interview in another city. He can choose from $4$ local bus services or $3$ taxi services to reach the other city. From there, he can choose from $3$ local bus services or $2$ taxi services to reach the place of his interview. How many possible routes/ways Steve can travel to his destination?  

Steve can choose to take either a local bus or a taxi to reach the other city. So, the possible numbers of vehicles that can be used to reach the city are $4+3 =7$. Similarly, Steve can either choose from $3$ local bus services or $2$ taxi services to reach the location of the interview from the city. Number of possible option $3+2=5$. Now, the total number of ways/vehicles Steve can use to reach his interview destination is $7 \times 5 = 35$.  

The basic formula for the fundamental counting principle is the same as its definition, i.e., if we have $A$ ways/options to do task-1 and $B$ ways to do task-2, then the total number of ways we can do task-1 and task-2 together are $A \times B$.

However, by applying the fundamental counting principle in questions related to possible arrangements of a given set of objects, we can derive formulae for permutations and combinations as discussed below:

Applications of the Counting Principle

Suppose $5$ boys $\textrm{A, B, C, D, and E}$ are to be seated on a couch in a row. Then in how many possible ways can they be seated? Suppose that $\textrm{Boy A} = \textrm{event A}$, $\textrm{Boy B} = \textrm{event B}$ and so on. So, for event $A$, we have five possible options, for the event $B$, we have four possible options, for the event $C$, we have three possible options, for the event $D$, we have two possible options and one option for the event $E$.

By the rule of counting principle to calculate the total number of ways, we multiply the possibilities of each event. In this case the total number of possible outcomes is $5 \times 4 \times 3 \times 2 \times 1= 120$. This is also known as permutation, and it is an application of the counting principle.  

Permutation

A permutation of $n$ different objects taken $r$ at a time where $r ≤ n$, then the arrangement of r objects can be represented by

$  P(n,r) = \frac{n!}{(n-r)!} $

Where $n! = n\times(n-1)\times(n-2)…..\times1$.

Example 7 : Calculate the number of ways in which digits from $0-9$ can be arranged.  

There are total numbers of $10$ digits. The number of ways in which the first digits can be arranged is 10. Similarly, for the second digit, we have 9 available options and so on for the rest of the digits. The total numbers of possible ways to arrange the digits

$10! = 10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 = 3628800$.  

Example 8 : Calculate the number of ways in which four digits can be selected from $0-9$.

There are total numbers of 10 digits, and we have to select only four from the available 10 digits. Here $n = 10$ while $r = 4$.

                                    $  P(n,r) = \frac{n!}{(n-r)!} $

                                    $  P(n,r) = \frac{10!}{(10-4)!} $

                                    $  P(n,r) = \frac{10!}{6!} $

                                    $  P(n,r) = \frac{2628800}{720} $

                                    $  P(n,r) = 5040 $.  

Just Like permutation, the combination is also an application of the counting principle.

Combination

The combination is a process of selecting objects from a set without giving importance to the order of arrangement. For instance, let’s suppose we have a class of four students; let’s call them $A$, $B$, $C$, and $D$. We wish to make a team of three students. How many different teams can we make?

In this case, note that the team $\{A,B,C\}$ is the same as the team $\{A,C,B\}$ or $\{B,A,C\}$. In other words, the order in which the team members are selected does not matter. Such arrangements in which order does not matter are called Combinations. We can use the fundamental counting principle to come up with a formula for finding the total number of combinations.

For instance, in the example discussed above, if we assume that order does matter, then as discussed in the previous section, by the counting principle, we will have $4 \times 3 \times 2 \times 1$ possible arrangements. Now for any given arrangement, let’s say $\{A, B, C\}$,  there are many possibilities such as $\{A, C, B\}$ or $\{B, A, C\}$ that result in the same combination. So, we need to figure out the total number of possibilities for any given arrangement that leads to the same team.

Since we have three slots and three members (i.e., $A$, $B$, $C$), so we can fill the first slot in three different ways, the second slot in 2 different ways, and the third slot in one different way. By the fundamental counting principle, we will have $3 \times 2 \times 1$ possibilities that lead to the same combination.

So the total number of unique combinations would be

$\large{\frac{4 \times 3 \times 2 \times 1}{3 \times 2 \times 1}}$

Generally, if we have $n$ objects and we choose $r$ objects to make a combination, the total number of combinations is denoted by $C(n,r)$ and is given as

$C(n,r) = \frac{n \times n-1 \times n-2 \times \cdots n-r}{r \times r-1 \times r-2 \times \cdots 1}$

Multiplying both numerator and denominator by $(n-r)!$ and using the factorial rule , we can simplify the formula as

$C(n,r) = \frac{n!}{r!(n-r)!}$

A locker is locked with a four-digit password. The password only contains numbers from $0-6$. How many different password options will you have if the order of numbers does that matter?

We have seven numbers to choose from and we have to make a $4$ digit password, hence $n=7$ and $r=4$, in this case. The total number of combinations is given as

$C(7,4) = \frac{7!}{4!(7-4)!}$

$C(7,4) = \frac{7 \times 6 \times 5 \times 4!}{4!3!}$

$C(7,4) = \frac{7 \times 6 \times 5}{3!} = 35$

1. We have a group of four people; let’s call those Jhon, Jill, Liz, and Tom. We wish to make the team consisting of three people using the available group. However, Liz must be included in every team. How many distinct teams can we make?

2. Kevin wants to buy a new Honda car. The car is available in 4 different models, and every model has 5 different colors. Calculate the total amount of choices.

3. A coin is flipped 3 times. Draw a tree diagram and calculate the total amount of possible outcomes using the counting principle

4. Freya went to an ice cream shop. The menu has 2 cones available Large and Small, and both the cones are available in 3 different shapes. Flavors available for large cones are Vanilla, Mango, Chocolate, and Strawberry, while small cones also include all the flavors except Mango. How many choices does Freya have?  

5.A restaurant has 6 different Appetizers, 5 different desserts, and 7 different meal options. Calculate the total number of options for given deals

a) Deal 1: It includes Appetizers and a meal.

b) Deal 2: Desserts and a meal.

c) Deal 3: Appetizers, a meal, and desserts.

2. The car is available in 4 different models and 5 different colors. So, by the rule of counting principle total number of choices are $ 4\times5 = 20$.

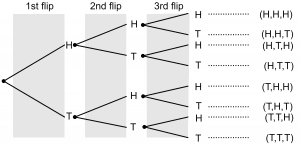
The first flip results in $2$ possible outcomes, so do the second and the third flip. Hence by the counting principle, the total possible outcomes will be $2 \times 2 \times 2 = 8$, which is also confirmed by the tree diagram.

Freya has two different cones available large and small, which are mutually exclusives and cannot happen together. So, we will calculate possible outcomes for each and then add them up.

Total number of options for large cone ice-cream:   $ 3\times4= 12$

Total number of options for small cone ice-cream: $ 3\times3 = 9$

Total number of possible options: $ 12+9 = 21$

a) Total number of options for deal 1 : $ 6\times7 = 42$.

b) Total number of options for deal 2: $ 5\times7= 35$.

c) Total number of options for deal 3: $ 6\times7\times5 = 210$.

Previous Lesson  |  Main Page | Next Lesson

You are using an outdated browser and it's not supported. Please upgrade your browser to improve your experience.

• LOGIN FOR PROGRAM PARTICIPANTS
• PROGRAM SUPPORT

Counting Rules—The Fundamental Counting Principle and Permutations

Description.

There may be cases when our downloadable resources contain hyperlinks to other websites. These hyperlinks lead to websites published or operated by third parties. UnboundEd and EngageNY are not responsible for the content, availability, or privacy policies of these websites.

• Precalculus Module 5, Topic A, Lesson 2: Student Version
• Precalculus Module 5, Topic A, Lesson 2: Teacher Version

Related Guides and Multimedia

Our professional learning resources include teaching guides, videos, and podcasts that build educators' knowledge of content related to the standards and their application in the classroom.

There are no related guides or videos. To see all our guides, please visit the Enhance Instruction section here .

Reset password New user? Sign up

Existing user? Log in

Fundamental Counting Principle

Already have an account? Log in here.

The fundamental counting principle is a rule used to count the total number of possible outcomes in a situation. It states that if there are \( n\) ways of doing something, and \( m\) ways of doing another thing after that, then there are \( n\times m\) ways to perform both of these actions. In other words, when choosing an option for \(n\) and an option for \(m\), there are \( n\times m\) different ways to do both actions.

Basic Examples

Intermediate examples, problem solving.

Lily is trying to decide what to wear. She has shirts in the following colors: red, purple, and blue, and she has pants in the following colors: black and white. How many different outfits can Lily choose from (assuming she selects one shirt and one pair of pants)? We know from the definition of the rule of product that if there are \(n\) options for doing one thing (like choosing a shirt), and \(m\) options for doing another thing (like choosing a pair of pants), then there are \(n \times m\) total combinations we can choose from. In this case, there are \(3\) options for choosing a shirt, and there are \(2\) options for choosing pants. Thus, there are \(3 \times 2 = 6\) total options. Here is a table where each row represents a possible outfit. Shirt Pants Red Black Blue Black Purple Black Red White Blue White Purple White As expected, there are \(6\) possible combinations. \(_\square\)

In the example above, there were two things to choose: a shirt and a pair of pants. However, the rule of product can extend to however many things to choose from. For example, if there are \(n\) choices for a shirt, \(m\) choices for a pair of pants, \(x\) choices for a pair of shoes, and \(y\) choices for a hat, the rule of product states that there are \(n \times m \times x \times y\) total possible combinations.

You go to check out three books at the library, and you want one history book, one science book, and one fantasy book.

The library has 50 history books, 95 fantasy novels, and 30 books about science. How many combinations of books do you have to choose from?

There are \(8\) daily newspapers and \(5\) weekly magazines published in Chicago. If Colin wants to subscribe to exactly one daily newspaper and one weekly magazine, how many different choices does he have? Colin has \(8\times5=40\) choices. \(_\square\)

Calvin wants to go to Milwaukee. He can choose from \(3\) bus services or \(2\) train services to head from home to downtown Chicago. From there, he can choose from 2 bus services or 3 train services to head to Milwaukee. How many ways are there for him to get to Milwaukee? Since Calvin can either take a bus or a train downtown , he has \( 3+2 =5\) ways to head downtown (Rule of sum). After which, he can either take a bus or a train to Milwaukee, and hence he has another \( 2+3=5\) ways to head to Milwaukee (Rule of sum). Thus in total, he has \( 5 \times 5 = 25\) ways to head from home to Milwaukee (Rule of product). \(_\square\)

Six friends Andy, Bandy, Candy, Dandy, Endy, and Fandy want to sit in a row at the cinema. If there are only six seats available, how many ways can we seat these friends? For the first seat, we have a choice of any of the 6 friends. After seating the first person, for the second seat, we have a choice of any of the remaining 5 friends. After seating the second person, for the third seat, we have a choice of any of the remaining 4 friends. After seating the third person, for the fourth seat, we have a choice of any of the remaining 3 friends. After seating the fourth person, for the fifth seat, we have a choice of any of the remaining 2 friends. After seating the fifth person, for the sixth seat, we have a choice of only 1 of the remaining friends. Hence, by the rule of product, there are \( 6 \times 5 \times 4 \times 3 \times 2 \times 1 = 720\) ways to seat these 6 people. More generally, this problem is known as a permutation . There are \( n! = n \times (n-1) \times (n-2) \times \cdots \times 1\) ways to seat \( n\) people in a row. \(_\square\)

My toy piano keyboard has 7 distinct white notes: letters A-G in English alphabet. I'm going to create a melody by playing three random notes. I am not allowed to repeat any notes and the melody cannot be ended with E, F or G. How many different melodies can I play?

• C G A is permitted.
• A F A isn't permitted because of repetition.
• A B E is not permitted because of last note rule.

How many positive divisors does \( 2000 = 2^4 5^3\) have? Any positive divisor of 2000 must have the form \( 2^a 5^b\), where \( a\) and \( b\) are integers satisfying \( 0 \leq a \leq 4, 0 \leq b \leq 3\). There are 5 possibilities for \( a\) and 4 possibilities for \( b\), hence there are \( 5 \times 4 = 20\) (rule of product) positive divisors of 2000 in all. \(_\square\)

• Problem solving
• Rule of Sum
• Permutations

Problem Loading...

Note Loading...

Set Loading...

Fundamental Counting Principle Calculator

What is the fundamental counting principle, fundamental counting principle examples, using the fundamental counting principle calculator.

Welcome to Omni's fundamental counting principle calculator , where we'll cover one of the basic counting rules for possible outcomes of several choices. In essence, it says that we can multiply (that's why we often call it the multiplication principle ) the number of options for one thing by the number of options for the other to obtain how many results we can find for the pair. Don't worry if the previous sentence sounds confusing; we'll see some real-life fundamental counting principle examples soon enough.

So what is the fundamental counting principle exactly?

Say that you have a new purchase in mind and are not yet sure which option to choose. You need to pick the company, the model, and the color. If every company has the same number of models to choose from, and every model has the same number of possible colors, then the fundamental counting principle is what we turn to .

Formally speaking, the fundamental counting principle (aka the multiplication principle) is one of the basic counting rules in mathematics that helps us compute the number of specific objects. Let's let the principle speak for itself.

💡 The fundamental counting principle says that if you have sets A and B with a and b elements, respectively, then there are a * b distinct pairs (x,y) with x from A and y from B .

It's worth mentioning that the multiplication principle extends to more than pairs . After all, using the notation from the box above, if we add a set C with c elements, then we can count triples (x,y,z) from A , B , and C , respectively, by saying that we have a * b choices for the pair (x,y) and c choices for z . All in all, this gives (a * b) * c = a * b * c possible triples.

Alright, we might have seen the formal side to it, but what is the fundamental counting principle when applied to real-life scenarios? Well, let's explain it in a few examples .

There are other counting methods, like the factorial, combinations, and permutations. You can read more about these at the factorial calculator , combination calculator , and the permutation and combination calculator . Take a look!

Suppose that you'd like to order pizza . You feel picky, so you decide to browse through all the options you have on offer. How many are there?

Suppose that there are 4 pizza places around you, and each offers its products in 3 different sizes. Coincidentally, each restaurant has 12 different pizzas to choose from and 4 side sauces.

Let's use the counting rules, i.e., the fundamental counting principle to see how many combinations we have here. In principle, we're choosing:

• The pizza itself; and
• The side sauce.

According to the data above, we have 4 choices for the pizza place, 3 possible sizes, 12 different sets of toppings, and 4 sauces to choose from. Note how it's important each place had the same number of sizes, pizzas, and sauces on offer. Therefore, if we apply the multiplication principle to our problem, we'll see that we have:

4 * 3 * 12 * 4 = 576

options. Now that's what we call diversity !

Observe how we can apply the same reasoning to many other life-like problems, e.g., buying a car (the company, the model, the color), choosing a movie for the evening (the platform, the genre), etc. We can apply to them the same counting rules as in the fundamental counting principle above, as long as for each variant of the first thing, we have the same number of options for the second thing , and so on.

Lastly, before we let you go for today, let's see how to use Omni's fundamental counting principle calculator to solve all such problems in the blink of an eye !

When you look at the fundamental counting principle calculator, you'll see two variable fields for the number of choices for the first and second things. The things in question can be pizza toppings, the color of a car, the score on dice when you roll it, or anything else of that sort. Check out the dice roller calculator to learn how to estimate the dice roll probability. However, every variant of the first characteristic must have the same number of options for the second (for instance, every car company must have the same number of colors available).

Although you first see only two variable fields, more will appear once you begin inputting data . In total, the fundamental counting principle calculator allows up to ten characteristics for the choice you're making! However, observe that the tool will already begin its calculations when you input two numbers. If you add new ones, the formula, and result will change accordingly.

That's all, folks! The fundamental counting principle calculator really is that simple, so make sure to play around with it and see how many options the world around you offers . Maybe we could calculate all possible pancake servings ? Thick or thin. With jam, with syrup, with cream. And from there, it's different pancakes every breakfast!

How do I use the fundamental counting principle?

To use the fundamental counting principle, you need to:

• Specify the number of choices for the first step.
• Repeat for all subsequent steps.
• Make sure the number of options at each step agrees for all choices.
• Multiply the number of choices at step 1, at step 2, etc.
• The result is the total number of choices you have.

Can permutations be solved by using the fundamental counting principle?

Yes. For instance, if you have 3 objects that you want to put in order (say, an apple, an orange, and a lemon), then the number of possibilities is the number of permutations of a 3-element set, i.e., 3! = 3 × 2 × 1 = 6 . Alternatively, we can use the fundamental counting principle to say that we have 3 choices for the first fruit, 2 choices for the second (after all, we've already chosen one to be the first), and 1 choice for the third (because we've already put the other two before). The fundamental counting principle then gives that, all in all, we have 3 × 2 × 1 = 6 choices.

Does order matter in the fundamental counting principle?

Yes. In the fundamental counting principle, we're numbering the steps in which we operate. For instance, if we're choosing ingredients for a pizza, but the first one we pick is the main one (i.e., there's more of it), then choosing pepperoni and onion gives a different one than picking onion and pepperoni: the second variant is more vegetarian than the first.

How are the fundamental counting principle, permutations, and combinations related?

Let's talk pizzas. Suppose we're choosing three toppings for a pizza, but the first will be the main one, and the other two will be secondary (there'll be less of it) and tertiary (even less), respectively.

• The fundamental counting principle counts how many choices we have for the main, secondary, and tertiary ingredients ( order matters ). Also, if we're feeling like it, we can allow the ingredients to repeat and have, for example, a super cheesy margherita with triple cheese.
• A permutation counts ordered triples of ingredients, but it doesn't allow them to repeat, so no margherita this time.
• A combination chooses three toppings and treats them equally, i.e., the order doesn't matter, and there's no main, secondary, or tertiary ingredient: there's the same amount of each. Usually, we count combinations without repetitions, but there are exceptions to this rule.

How do I know when to use the fundamental counting principle?

Before you use the fundamental counting principle, you need to:

• Make sure that the order of your choices matters.
• Calculate the number of options for the first step .
• Calculate the number of options for the second step .
• Make sure the number in point 3 doesn't depend on that from point 2.
• Repeat the reasoning for all consecutive steps.
• Unless the numbers don't agree at some point, you can use the principle .
• Least Common Multiple Calculator
• Absolute Value Calculator
• Least Common Denominator Calculator
• Null Space Calculator
• Unit Rate Calculator
• Exponential Function Calculator

BMR - Harris-Benedict equation

Significant figures, triangle angle.

• Biology (101)
• Chemistry (100)
• Construction (147)
• Conversion (295)
• Ecology (30)
• Everyday life (262)
• Finance (571)
• Health (440)
• Physics (511)
• Sports (106)
• Statistics (184)
• Other (183)
• Discover Omni (40)

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.1: The Fundamental Principle of Counting

• Last updated
• Save as PDF
• Page ID 40933

• Richard W. Beveridge
• Clatsop Community College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Combinatorics is a major area of what is generally known as "Discrete Mathematics." The word discrete refers to quantities that are individual, separate or distinct. This creates a major division in mathematics between "continuous mathematics" and "discrete mathematics." The difference between these two areas is that continuous mathematics considers and uses all parts of the number line whole numbers, rational numbers (fractions), irrational numbers and so forth. Discrete mathematics typically uses only the whole numbers.

Rather than limiting the possibilities in mathematics, this restriction actually opens amazing new areas of consideration. The binary codes that computers use are generally controlled and kept (mostly) error free through the use of discrete mathematics. Computer security for the simplest (checking your on-line bank balance) and the most complex (high level classified data) digital information is handled through encryption that relies on the concepts of discrete mathematics.

Any type of application in the sciences that involves choices and possibilities often uses the concepts of combinatorics. Combinatorial chemistry explores the results when a series of different chemical groups are added to the same basic chemical structure to investigate the qualities of the resulting compound. In addition, combinatorics is very important to the study of probability. In order to calculate the probability of an event, it is often necessary to calculate how many

different ways something can happen. The first major idea of combinatorics is the fundamental principle of counting. This is the idea that if two events occur in succession and there are \(m\) ways to do the first one and \(n\) ways to do the second (after the first has occurred), then there are \(m * n\) ways to complete the two tasks in succession.

All of the possibilities are listed out and can be constructed from the tree diagram. Here are some sample problems for using the fundamental principle of counting (also known as the multiplication principle). Example : An ice cream shop offers Vanilla, Chocolate, Strawberry, Boysenberry and Rocky Road ice cream. The ice cream comes with either a waffle cone, a sugar cone or a wafer cone and can be plain or with sprinkles. How many different ways are there to order a single scoop of ice cream?

With 5 different types of ice cream, 3 different cones and 2 choices for sprinkles, there would be \(5 * 3 * 2=30\) different possibilities. Example : In many states the license plates for automobiles consist of three letters followed three numbers. How many different possibilities are there: if repetition of letters and numbers is allowed? if repetition of letters and numbers is not allowed? There are six positions for letters and numbers that make up the license plate. The first three are to be letters and the second three numbers. There are 26 choices for the first three and 10 choices for the second three, so there are \(26 * 26 * 26 * 10 * 10 * 10=17,576,000\) possible license plates if repetition is allowed.

If repetition is not allowed then we have to discount whichever letter or number is chosen for a particular position. So, for the first letter there are 26 possibilities, but then only 25 for the second letter and 24 for the third. Likewise, with the numbers there are 10 choices initially, then 9 choices and then 8 So, the solution without repetition would be \(26 * 25 * 24 * 10 * 9 * 8=11,232,000\)

4) \(\quad\) A coin is flipped five times and the result each time is recorded. How many different possible outcomes are there? 5) \(\quad\) A coin is flipped and a six-sided die is rolled and the results are recorded. If this is done three times, how many possible outcomes are there? 6) \(\quad\) Two cards are chosen from a deck of 52 cards. If the first card is not replaced before the second card is chosen, how many ways are there to choose: a) \(\quad\) A spade first and a heart second? b) \(\quad\) Two spades? 7) \(\quad\) A company has 3000 employees. They plan to implement an employee ID numbering system that would consist of a letter followed by two digits. Is it possible to give each employee a different ID code under this plan? 8) \(\quad\) A baseball team has 7 pitchers and 3 catchers. How many different batteries (pitcher - catcher combinations) are possible? 9) \(\quad\) A string of five letters is created using the letters \(\mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D}\) and E. How many of these letter strings are possible if: \(\quad\) a) \(\quad\) No conditions are imposed \(\quad\) b) Repetition of the letter \(A\) is not allowed \(\quad\) c) Each letter string must begin with \(C\) \(\quad\) d) \(\quad\) B must be the middle letter \(\quad\) e) \(\quad\) \(A, B\) and \(C\) must be the middle letters in any order with no repetition For Part (e) please list all possibilities. 10) (\quad\) A combination lock is numbered from 0 to 30. Each combination consists of three numbers in succession. Successive numbers must be different, but the first and third can be the same. How many different combinations are possible?

FUNDAMENTAL PRINCIPLE OF COUNTING PROBLEMS WITH SOLUTION

Problem 1 :

A person went to a restaurant for dinner. In the menu card, the person saw 10 Indian and 7 Chinese food items. In how many ways the person can select either an Indian or a Chinese food?

Number of ways of selecting Chinese food items  =  7

Number of ways of selecting Indian food items  =  10

Here a person may choose any one food items, either an Indian or a Chinese food. So, we have to use "Addition" to find the total number of ways for selecting the food item.

Total number of selecting Indian or a Chinese food 

=  10 + 7  =  17 ways

Problem 2 :

There are 3 types of toy car and 2 types of toy train available in a shop. Find the number of ways a baby can buy a toy car and a toy train?

According to the given question, a baby wants to buy both toy car and toy train. So we have to use the binary operation "Multiplication" to find the total number of ways.

Types of car available in the shop  =  3

Types of car available in the shop  =  2

Total number of ways of buying a car  =  3 (2)  =  6

Problem 3 :

How many two-digit numbers can be formed using 1,2,3,4,5 without repetition of digits?

In order to form a two digit number, we have to select two numbers out of the given 5 numbers. 

___  ___

To fill up the first dash, we have 5 options.

To fill up the second dash, we have 4 options.

Number of two digit numbers formed using the above numbers  =  5 (4)  =  20.

Problem 4 :

Three persons enter in to a conference hall in which there are 10 seats. In how many ways they can take their seats?

1 st person may choose 1 seat out of 10 seats

2 nd person may choose 1 seat out of 9 seats

3 rd person may choose 1 seat out of 8 seats

Total number of ways of selecting seat  =  10 (9) (8)

  =  720 ways

Problem 5 :

In how many ways 5 persons can be seated in a row?

5 persons may sit in 5 seats.

1st person may sit any one of the 5 seats 

2nd person may sit any one of the 4 seats and so on.

Hence the total number of ways  =  5  ⋅ 4  ⋅ 3  ⋅ 2  ⋅ 1

 =  120 ways

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

Multiplying Matrices

Jun 07, 24 10:46 PM

SAT Math Videos (Part 3 - Calculator)

Jun 07, 24 05:28 PM

How to Convert Between Polar and Rectangular Coordinates

May 31, 24 08:11 PM

• Video Course Overview
• General GRE Info and Strategies - 7 videos (free)
• Quantitative Comparison - 7 videos (free)
• Arithmetic - 42 videos
• Powers and Roots - 43 videos
• Algebra and Equation Solving - 78 videos
• Word Problems - 54 videos
• Geometry - 48 videos
• Integer Properties - 34 videos
• Statistics - 28 videos
• Counting - 27 videos
• Probability - 25 videos
• Data Interpretation - 24 videos
• Analytical Writing - 9 videos (free)
• Sentence Equivalence - 39 videos (free)
• Text Completion - 51 videos
• Reading Comprehension - 16 videos
• New Study Guide
• Stage I: Required content
• Stage II: More practice
• Office Hours
• Free Flashcards, Word Lists and More
• Private Tutoring
• Quantitative diagnostic & tune-up package
• Extra Practice Questions
• Practice Tests
• Study Guide
• Record a Video Testimonial

Lesson: The Fundamental Counting Principle

Reinforcement Activities

• GRE practice question (difficulty level: 130 to 149) – GRE Prep Club
• GRE practice question (difficulty level: 130 to 149) – GRE Prep Club 
• GRE practice question (difficulty level: 150 to 159) – GRE Prep Club
• GRE practice question (difficulty level: 160 to 170) – GRE Prep Club
• GRE practice question (difficulty level: 160 to 170) – Greenlight Test Prep
• More basic practice applying the FCP - Khan Academy
• Need some extra help reaching your target scores? Brent (the creator of this website) offers online tutoring

Comment on The Fundamental Counting Principle

Thank you. very helpful..

Good point about electric

Good point!

This is the same diagram we

Very interesting!

Source: Princeton review

This is a very poorly-worded.

This is a VERY poorly-worded question.

To begin, what constitutes ONE "lunch order"? For example, if Sandy orders pasta and her husband orders steak, is that considered different from Sandy ordering steak and her husband ordering pasta? Or is it just considered ONE order of steak and pasta? The answer choice of 45 suggests that it's considered ONE order of steak and pasta. However, the answer choice of 720 suggests that this is NOT considered one order (with 3 people).

I suggest that you ignore this question.

Cheers, Brent

Hii, very helpful video, pls

Good question!

Positive 2-digit integers range from 10 to 99 inclusive.

Numbers with 0 in the tens position (01, 02, 03,...09) are not considered 2-digit numbers since the 0 in the tens position is not required. For example, 05 is the same as 5, and 08 is the same as 8.

In the second question ( https://gre.myprepclub.com/forum/number-of-two-digit-positive-integers-f... ), we're dealing with 2-digit numbers, so this means we must consider only 10 to 99 inclusive.

In the first question ( https://gre.myprepclub.com/forum/in-state-x-all-vehicle-license-plates-h... ), the last three spaces of the license plates must be one-digit numbers. In this case, each space can be filled with any of the 10 digits (0,1,2,3,4,5,6,7,8 or 9)

Thank you so much for this

You're not alone; most people.

You're not alone; most people struggle with counting questions. Glad you like the site!

Regarding this Kahn Academy

Great question.

Great question! Unfortunately, the word "combinations" here is misleading.

If we think about solving the question in STAGES, we can see that there's no duplication. Stage 1: Choose a couch. Stage 2: Choose a coffee table. Stage 3: Choose a recliner.

If we look at it this way, we are always choosing a couch first, a coffee table second and a recliner third. So, our strategy does now allow for duplication because we're choosing a DIFFERENT kind of furniture at each stage. That is, if we structure our solution this way, we can't choose a blue recliner first, then a red table, and then a green couch ----------------------

Now compare this to a SEEMINGLY similar question. Joe has 7 friends (A, B, C, D, E, F and G) want to invite 3 to his party. Stage 1: Choose a friend to invite. Stage 2: Choose a friend to invite. Stage 3: Choose a friend to invite.

In this case, we're drawing from the SAME GROUP of friends at each stage. So, in this solution, we'll have duplication.

Does that help?

Yes, that was very helpful.

Hello i am very confused on, when using the fundamental.

When using the Fundamental Counting Principle (aka the "slot method"), we must convince ourselves what each value in our product represents. For example, in my solution ( https://gre.myprepclub.com/forum/sets-with-odd-number-of-elements-15901.... ), the first stage is to determine whether element1 is included in the subset. Since element1 can be in the subset or not in the subset, there are TWO different ways to complete the first stage. So, 2 is the first value in my product.

In your solution, (35*34*33...), what does each value represent? For example, the first value suggests there are 35 different ways to complete the first stage. So, what's the first stage?

Six children ABCDEF and are

I agree that we can place b.

I agree that we can place B in 6 ways. However, there are more than 2 ways to place E. For example, if B sits in chair #1, then E can sit in chair #3, 4, 5 or 6 Similarly, if B sits in chair #2, then E can sit in chair #4, 5 or 6

You can continue with your approach. You'll just need to consider two cases: case i: B sits on one of the end chairs (chair #1 or 6) case ii: B sits on one of the non-end chairs (#2, 3, 4 or 5)

If you continue with that approach, you'll find that case i can be completed in 192 ways, and case ii can be completed in 288 ways, for a total of 480 ways.

https://gmatclub.com/forum/of

Question link: https:/.

Question link: https://gmatclub.com/forum/of-the-3-digit-positive-integers-greater-than...

I'm assuming that you examined three possible cases: - Integers in the form: same-same-different (e.g., 772) - 36 outcomes - Integers in the form: same-different-same(e.g., 858) - 36 outcomes - Integers in the form: different-same-same (e.g., 900) - 36 outcomes

However, the last set of outcomes includes the integer 600, which is not allowed, because we're told the integers must be greater than 600. So we must subtract that one outcome from our sum.

https://gre.myprepclub.com/forum

Question link: https://gre.myprepclub.com/forum/there-are-six-different-models-that-are...

Good idea, but we apply the Mississippi rule when some of the objects to be arranged are identical. For example, the four i's in Mississippi are all identical. In this case, there are two models from Europe, but those models are not identical. In fact, the question tells us that the six models are all different.

Have a question about this video?

Post your question in the Comment section below, and a GRE expert will answer it as fast as humanly possible.

Change Playback Speed

You have the option of watching the videos at various speeds (25% faster, 50% faster, etc). To change the playback speed, click the settings icon on the right side of the video status bar.

Let me Know

Have a suggestion to make the course even better? Email us today!

• Testimonials

© 2014 - 2024 Isla Verde Education Inc.

GRE® is a registered trademark of Educational Testing Service (ETS). This product is not endorsed or approved by ETS.

Free “Question of the Day” emails!

Sign up to receive daily emails with various GRE practice questions. Each email is jam-packed with free video lessons, insightful articles, and useful GRE strategies to help you improve your score!

Lesson Fundamental counting principle problems

9.5 Counting Principles

Learning objectives.

In this section, you will:

• Solve counting problems using the Addition Principle.
• Solve counting problems using the Multiplication Principle.
• Solve counting problems using permutations involving n distinct objects.
• Solve counting problems using combinations.
• Find the number of subsets of a given set.
• Solve counting problems using permutations involving n non-distinct objects.

A new company sells customizable cases for tablets and smartphones. Each case comes in a variety of colors and can be personalized for an additional fee with images or a monogram. A customer can choose not to personalize or could choose to have one, two, or three images or a monogram. The customer can choose the order of the images and the letters in the monogram. The company is working with an agency to develop a marketing campaign with a focus on the huge number of options they offer. Counting the possibilities is challenging!

We encounter a wide variety of counting problems every day. There is a branch of mathematics devoted to the study of counting problems such as this one. Other applications of counting include secure passwords, horse racing outcomes, and college scheduling choices. We will examine this type of mathematics in this section.

Using the Addition Principle

The company that sells customizable cases offers cases for tablets and smartphones. There are 3 supported tablet models and 5 supported smartphone models. The Addition Principle tells us that we can add the number of tablet options to the number of smartphone options to find the total number of options. By the Addition Principle, there are 8 total options, as we can see in Figure 1 .

The Addition Principle

According to the Addition Principle , if one event can occur in m m ways and a second event with no common outcomes can occur in n n ways, then the first or second event can occur in m + n m + n ways.

There are 2 vegetarian entrée options and 5 meat entrée options on a dinner menu. What is the total number of entrée options?

We can add the number of vegetarian options to the number of meat options to find the total number of entrée options.

There are 7 total options.

A student is shopping for a new computer. He is deciding among 3 desktop computers and 4 laptop computers. What is the total number of computer options?

Using the Multiplication Principle

The Multiplication Principle applies when we are making more than one selection. Suppose we are choosing an appetizer, an entrée, and a dessert. If there are 2 appetizer options, 3 entrée options, and 2 dessert options on a fixed-price dinner menu, there are a total of 12 possible choices of one each as shown in the tree diagram in Figure 2 .

The possible choices are:

• soup, chicken, cake
• soup, chicken, pudding
• soup, fish, cake
• soup, fish, pudding
• soup, steak, cake
• soup, steak, pudding
• salad, chicken, cake
• salad, chicken, pudding
• salad, fish, cake
• salad, fish, pudding
• salad, steak, cake
• salad, steak, pudding

We can also find the total number of possible dinners by multiplying.

We could also conclude that there are 12 possible dinner choices simply by applying the Multiplication Principle.

The Multiplication Principle

According to the Multiplication Principle , if one event can occur in m m ways and a second event can occur in n n ways after the first event has occurred, then the two events can occur in m × n m × n ways. This is also known as the Fundamental Counting Principle .

Diane packed 2 skirts, 4 blouses, and a sweater for her business trip. She will need to choose a skirt and a blouse for each outfit and decide whether to wear the sweater. Use the Multiplication Principle to find the total number of possible outfits.

To find the total number of outfits, find the product of the number of skirt options, the number of blouse options, and the number of sweater options.

There are 16 possible outfits.

A restaurant offers a breakfast special that includes a breakfast sandwich, a side dish, and a beverage. There are 3 types of breakfast sandwiches, 4 side dish options, and 5 beverage choices. Find the total number of possible breakfast specials.

Finding the Number of Permutations of n Distinct Objects

The Multiplication Principle can be used to solve a variety of problem types. One type of problem involves placing objects in order. We arrange letters into words and digits into numbers, line up for photographs, decorate rooms, and more. An ordering of objects is called a permutation .

Finding the Number of Permutations of n Distinct Objects Using the Multiplication Principle

To solve permutation problems, it is often helpful to draw line segments for each option. That enables us to determine the number of each option so we can multiply. For instance, suppose we have four paintings, and we want to find the number of ways we can hang three of the paintings in order on the wall. We can draw three lines to represent the three places on the wall.

There are four options for the first place, so we write a 4 on the first line.

After the first place has been filled, there are three options for the second place so we write a 3 on the second line.

After the second place has been filled, there are two options for the third place so we write a 2 on the third line. Finally, we find the product.

There are 24 possible permutations of the paintings.

Given n n distinct options, determine how many permutations there are.

• Determine how many options there are for the first situation.
• Determine how many options are left for the second situation.
• Continue until all of the spots are filled.
• Multiply the numbers together.

Finding the Number of Permutations Using the Multiplication Principle

At a swimming competition, nine swimmers compete in a race.

• ⓐ How many ways can they place first, second, and third?
• ⓑ How many ways can they place first, second, and third if a swimmer named Ariel wins first place? (Assume there is only one contestant named Ariel.)
• ⓒ How many ways can all nine swimmers line up for a photo?

There are 9 options for first place. Once someone has won first place, there are 8 remaining options for second place. Once first and second place have been won, there are 7 remaining options for third place.

Multiply to find that there are 504 ways for the swimmers to place.

We know Ariel must win first place, so there is only 1 option for first place. There are 8 remaining options for second place, and then 7 remaining options for third place.

Multiply to find that there are 56 ways for the swimmers to place if Ariel wins first.

Draw lines for describing each place in the photo.

There are 9 choices for the first spot, then 8 for the second, 7 for the third, 6 for the fourth, and so on until only 1 person remains for the last spot.

There are 362,880 possible permutations for the swimmers to line up.

Note that in part c, we found there were 9! ways for 9 people to line up. The number of permutations of n n distinct objects can always be found by n ! . n ! .

A family of five is having portraits taken. Use the Multiplication Principle to find the following.

How many ways can the family line up for the portrait?

How many ways can the photographer line up 3 family members?

How many ways can the family line up for the portrait if the parents are required to stand on each end?

Finding the Number of Permutations of n Distinct Objects Using a Formula

For some permutation problems, it is inconvenient to use the Multiplication Principle because there are so many numbers to multiply. Fortunately, we can solve these problems using a formula. Before we learn the formula, let’s look at two common notations for permutations. If we have a set of n n objects and we want to choose r r objects from the set in order, we write P ( n , r ) . P ( n , r ) . Another way to write this is n P r , n P r , a notation commonly seen on computers and calculators. To calculate P ( n , r ) , P ( n , r ) , we begin by finding n ! , n ! , the number of ways to line up all n n objects. We then divide by ( n − r ) ! ( n − r ) ! to cancel out the ( n − r ) ( n − r ) items that we do not wish to line up.

Let’s see how this works with a simple example. Imagine a club of six people. They need to elect a president, a vice president, and a treasurer. Six people can be elected president, any one of the five remaining people can be elected vice president, and any of the remaining four people could be elected treasurer. The number of ways this may be done is 6 × 5 × 4 = 120. 6 × 5 × 4 = 120. Using factorials, we get the same result.

There are 120 ways to select 3 officers in order from a club with 6 members. We refer to this as a permutation of 6 taken 3 at a time. The general formula is as follows.

Note that the formula stills works if we are choosing underline all end underline n n objects and placing them in order. In that case we would be dividing by ( n − n ) ! ( n − n ) ! or 0 ! , 0 ! , which we said earlier is equal to 1. So the number of permutations of n n objects taken n n at a time is n ! 1 n ! 1 or just n ! . n ! .

Formula for Permutations of n Distinct Objects

Given n n distinct objects, the number of ways to select r r objects from the set in order is

Given a word problem, evaluate the possible permutations.

• Identify n n from the given information.
• Identify r r from the given information.
• Replace n n and r r in the formula with the given values.

Finding the Number of Permutations Using the Formula

A professor is creating an exam of 9 questions from a test bank of 12 questions. How many ways can she select and arrange the questions?

Substitute n = 12 n = 12 and r = 9 r = 9 into the permutation formula and simplify.

There are 79,833,600 possible permutations of exam questions!

We can also use a calculator to find permutations. For this problem, we would enter 12, press the n P r n P r function, enter 9, and then press the equal sign. The n P r n P r function may be located under the MATH menu with probability commands.

Could we have solved Example 4 using the Multiplication Principle?

Yes. We could have multiplied 1 2 ⋅ 1 1 ⋅ 1 0 ⋅ 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 1 2 ⋅ 1 1 ⋅ 1 0 ⋅ 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 to find the same answer .

A play has a cast of 7 actors preparing to make their curtain call. Use the permutation formula to find the following.

How many ways can the 7 actors line up?

How many ways can 5 of the 7 actors be chosen to line up?

Find the Number of Combinations Using the Formula

So far, we have looked at problems asking us to put objects in order. There are many problems in which we want to select a few objects from a group of objects, but we do not care about the order. When we are selecting objects and the order does not matter, we are dealing with combinations . A selection of r r objects from a set of n n objects where the order does not matter can be written as C ( n , r ) . C ( n , r ) . Just as with permutations, C ( n , r ) C ( n , r ) can also be written as n C r . n C r . In this case, the general formula is as follows.

An earlier problem considered choosing 3 of 4 possible paintings to hang on a wall. We found that there were 24 ways to select 3 of the 4 paintings in order. But what if we did not care about the order? We would expect a smaller number because selecting paintings 1, 2, 3 would be the same as selecting paintings 2, 3, 1. To find the number of ways to select 3 of the 4 paintings, disregarding the order of the paintings, divide the number of permutations by the number of ways to order 3 paintings. There are 3 ! = 3 · 2 · 1 = 6 3 ! = 3 · 2 · 1 = 6 ways to order 3 paintings. There are 24 6 , 24 6 , or 4 ways to select 3 of the 4 paintings. This number makes sense because every time we are selecting 3 paintings, we are not selecting 1 painting. There are 4 paintings we could choose not to select, so there are 4 ways to select 3 of the 4 paintings.

Formula for Combinations of n Distinct Objects

Given n n distinct objects, the number of ways to select r r objects from the set is

Given a number of options, determine the possible number of combinations.

Finding the Number of Combinations Using the Formula

A fast food restaurant offers five side dish options. Your meal comes with two side dishes.

• ⓐ How many ways can you select your side dishes?
• ⓑ How many ways can you select 3 side dishes?
• ⓐ We want to choose 2 side dishes from 5 options. C ( 5 , 2 ) = 5 ! 2 ! ( 5 − 2 ) ! = 10 C ( 5 , 2 ) = 5 ! 2 ! ( 5 − 2 ) ! = 10
• ⓑ We want to choose 3 side dishes from 5 options. C ( 5 , 3 ) = 5 ! 3 ! ( 5 − 3 ) ! = 10 C ( 5 , 3 ) = 5 ! 3 ! ( 5 − 3 ) ! = 10

We can also use a graphing calculator to find combinations. Enter 5, then press n C r , n C r , enter 3, and then press the equal sign. The n C r , n C r , function may be located under the MATH menu with probability commands.

Is it a coincidence that parts (a) and (b) in Example 5 have the same answers?

No. When we choose r objects from n objects, we are not choosing ( n – r ) ( n – r ) objects. Therefore, C ( n , r ) = C ( n , n – r ) . C ( n , r ) = C ( n , n – r ) .

An ice cream shop offers 10 flavors of ice cream. How many ways are there to choose 3 flavors for a banana split?

Finding the Number of Subsets of a Set

We have looked only at combination problems in which we chose exactly r r objects. In some problems, we want to consider choosing every possible number of objects. Consider, for example, a pizza restaurant that offers 5 toppings. Any number of toppings can be ordered. How many different pizzas are possible?

To answer this question, we need to consider pizzas with any number of toppings. There is C ( 5 , 0 ) = 1 C ( 5 , 0 ) = 1 way to order a pizza with no toppings. There are C ( 5 , 1 ) = 5 C ( 5 , 1 ) = 5 ways to order a pizza with exactly one topping. If we continue this process, we get

There are 32 possible pizzas. This result is equal to 2 5 . 2 5 .

We are presented with a sequence of choices. For each of the n n objects we have two choices: include it in the subset or not. So for the whole subset we have made n n choices, each with two options. So there are a total of 2 · 2 · 2 · … · 2 2 · 2 · 2 · … · 2 possible resulting subsets, all the way from the empty subset, which we obtain when we say “no” each time, to the original set itself, which we obtain when we say “yes” each time.

Formula for the Number of Subsets of a Set

A set containing n distinct objects has 2 n 2 n subsets.

A restaurant offers butter, cheese, chives, and sour cream as toppings for a baked potato. How many different ways are there to order a potato?

We are looking for the number of subsets of a set with 4 objects. Substitute n = 4 n = 4 into the formula.

There are 16 possible ways to order a potato.

A sundae bar at a wedding has 6 toppings to choose from. Any number of toppings can be chosen. How many different sundaes are possible?

Finding the Number of Permutations of n Non-Distinct Objects

We have studied permutations where all of the objects involved were distinct. What happens if some of the objects are indistinguishable? For example, suppose there is a sheet of 12 stickers. If all of the stickers were distinct, there would be 12 ! 12 ! ways to order the stickers. However, 4 of the stickers are identical stars, and 3 are identical moons. Because all of the objects are not distinct, many of the 12 ! 12 ! permutations we counted are duplicates. The general formula for this situation is as follows.

In this example, we need to divide by the number of ways to order the 4 stars and the ways to order the 3 moons to find the number of unique permutations of the stickers. There are 4 ! 4 ! ways to order the stars and 3 ! 3 ! ways to order the moon.

There are 3,326,400 ways to order the sheet of stickers.

Formula for Finding the Number of Permutations of n Non-Distinct Objects

If there are n n elements in a set and r 1 r 1 are alike, r 2 r 2 are alike, r 3 r 3 are alike, and so on through r k , r k , the number of permutations can be found by

Find the number of rearrangements of the letters in the word DISTINCT.

There are 8 letters. Both I and T are repeated 2 times. Substitute n = 8 ,   r 1 = 2 ,   n = 8 ,   r 1 = 2 ,   and   r 2 = 2     r 2 = 2   into the formula.

There are 10,080 arrangements.

Find the number of rearrangements of the letters in the word CARRIER.

Access these online resources for additional instruction and practice with combinations and permutations.

• Combinations
• Permutations

9.5 Section Exercises

For the following exercises, assume that there are n n ways an event A A can happen, m m ways an event B B can happen, and that A and  B A and  B are non-overlapping.

Use the Addition Principle of counting to explain how many ways event A or  B A or  B can occur.

Use the Multiplication Principle of counting to explain how many ways event A and  B A and  B can occur.

Answer the following questions.

When given two separate events, how do we know whether to apply the Addition Principle or the Multiplication Principle when calculating possible outcomes? What conjunctions may help to determine which operations to use?

Describe how the permutation of n n objects differs from the permutation of choosing r r objects from a set of n n objects. Include how each is calculated.

What is the term for the arrangement that selects r r objects from a set of n n objects when the order of the r r objects is not important? What is the formula for calculating the number of possible outcomes for this type of arrangement?

For the following exercises, determine whether to use the Addition Principle or the Multiplication Principle. Then perform the calculations.

Let the set A = { − 5 , − 3 , − 1 , 2 , 3 , 4 , 5 , 6 } . A = { − 5 , − 3 , − 1 , 2 , 3 , 4 , 5 , 6 } . How many ways are there to choose a negative or an even number from A? A?

Let the set B = { − 23 , − 16 , − 7 , − 2 , 20 , 36 , 48 , 72 } . B = { − 23 , − 16 , − 7 , − 2 , 20 , 36 , 48 , 72 } . How many ways are there to choose a positive or an odd number from A ? A ?

How many ways are there to pick a red ace or a club from a standard card playing deck?

How many ways are there to pick a paint color from 5 shades of green, 4 shades of blue, or 7 shades of yellow?

How many outcomes are possible from tossing a pair of coins?

How many outcomes are possible from tossing a coin and rolling a 6-sided die?

How many two-letter strings—the first letter from A A and the second letter from B — B — can be formed from the sets A = { b , c , d } A = { b , c , d } and B = { a , e , i , o , u } ? B = { a , e , i , o , u } ?

How many ways are there to construct a string of 3 digits if numbers can be repeated?

How many ways are there to construct a string of 3 digits if numbers cannot be repeated?

For the following exercises, compute the value of the expression.

P ( 5 , 2 ) P ( 5 , 2 )

P ( 8 , 4 ) P ( 8 , 4 )

P ( 3 , 3 ) P ( 3 , 3 )

P ( 9 , 6 ) P ( 9 , 6 )

P ( 11 , 5 ) P ( 11 , 5 )

C ( 8 , 5 ) C ( 8 , 5 )

C ( 12 , 4 ) C ( 12 , 4 )

C ( 26 , 3 ) C ( 26 , 3 )

C ( 7 , 6 ) C ( 7 , 6 )

C ( 10 , 3 ) C ( 10 , 3 )

For the following exercises, find the number of subsets in each given set.

{ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 } { 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 }

{ a , b , c , … , z } { a , b , c , … , z }

A set containing 5 distinct numbers, 4 distinct letters, and 3 distinct symbols

The set of even numbers from 2 to 28

The set of two-digit numbers between 1 and 100 containing the digit 0

For the following exercises, find the distinct number of arrangements.

The letters in the word “juggernaut”

The letters in the word “academia”

The letters in the word “academia” that begin and end in “a”

The symbols in the string #,#,#,@,@,$,$,$,%,%,%,%

The symbols in the string #,#,#,@,@,$,$,$,%,%,%,% that begin and end with “%”

The set, S S consists of 900,000,000 900,000,000 whole numbers, each being the same number of digits long. How many digits long is a number from S ? S ? ( Hint: use the fact that a whole number cannot start with the digit 0.)

The number of 5-element subsets from a set containing n n elements is equal to the number of 6-element subsets from the same set. What is the value of n ? n ? ( Hint: the order in which the elements for the subsets are chosen is not important.)

Can C ( n , r ) C ( n , r ) ever equal P ( n , r ) ? P ( n , r ) ? Explain.

Suppose a set A A has 2,048 subsets. How many distinct objects are contained in A ? A ?

How many arrangements can be made from the letters of the word “mountains” if all the vowels must form a string?

Real-World Applications

A family consisting of 2 parents and 3 children is to pose for a picture with 2 family members in the front and 3 in the back.

• ⓐ How many arrangements are possible with no restrictions?
• ⓑ How many arrangements are possible if the parents must sit in the front?
• ⓒ How many arrangements are possible if the parents must be next to each other?

A cell phone company offers 6 different voice packages and 8 different data packages. Of those, 3 packages include both voice and data. How many ways are there to choose either voice or data, but not both?

In horse racing, a “trifecta” occurs when a bettor wins by selecting the first three finishers in the exact order (1st place, 2nd place, and 3rd place). How many different trifectas are possible if there are 14 horses in a race?

A wholesale T-shirt company offers sizes small, medium, large, and extra-large in organic or non-organic cotton and colors white, black, gray, blue, and red. How many different T-shirts are there to choose from?

Hector wants to place billboard advertisements throughout the county for his new business. How many ways can Hector choose 15 neighborhoods to advertise in if there are 30 neighborhoods in the county?

An art store has 4 brands of paint pens in 12 different colors and 3 types of ink. How many paint pens are there to choose from?

How many ways can a committee of 3 freshmen and 4 juniors be formed from a group of 8 8 freshmen and 11 11 juniors?

How many ways can a baseball coach arrange the order of 9 batters if there are 15 players on the team?

A conductor needs 5 cellists and 5 violinists to play at a diplomatic event. To do this, he ranks the orchestra’s 10 cellists and 16 violinists in order of musical proficiency. What is the ratio of the total cellist rankings possible to the total violinist rankings possible?

A motorcycle shop has 10 choppers, 6 bobbers, and 5 café racers—different types of vintage motorcycles. How many ways can the shop choose 3 choppers, 5 bobbers, and 2 café racers for a weekend showcase?

A skateboard shop stocks 10 types of board decks, 3 types of trucks, and 4 types of wheels. How many different skateboards can be constructed?

Just-For-Kicks Sneaker Company offers an online customizing service. How many ways are there to design a custom pair of Just-For-Kicks sneakers if a customer can choose from a basic shoe up to 11 customizable options?

A car wash offers the following optional services to the basic wash: clear coat wax, triple foam polish, undercarriage wash, rust inhibitor, wheel brightener, air freshener, and interior shampoo. How many washes are possible if any number of options can be added to the basic wash?

Suni bought 20 plants to arrange along the border of her garden. How many distinct arrangements can she make if the plants are comprised of 6 tulips, 6 roses, and 8 daisies?

How many unique ways can a string of Christmas lights be arranged from 9 red, 10 green, 6 white, and 12 gold color bulbs?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites

• Authors: Jay Abramson
• Publisher/website: OpenStax
• Book title: College Algebra 2e
• Publication date: Dec 21, 2021
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
• Section URL: https://openstax.org/books/college-algebra-2e/pages/9-5-counting-principles

© Jan 9, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Please log in to save materials. Log in

• 7th Grade Mathematics
• Independent and Dependent Events
• Probability

Education Standards

Maryland college and career ready math standards.

Learning Domain: Statistics and Probability

Standard: Find probabilities of compound events using organized lists, tables, tree diagrams, and simulation.

Standard: Understand that, just as with simple events, the probability of a compound event is the fraction of outcomes in the sample space for which the compound event occurs.

Standard: Represent sample spaces for compound events using methods such as organized lists, tables and tree diagrams. For an event described in everyday language (e.g., "rolling double sixes"ť), identify the outcomes in the sample space which compose the event.

Standard: Design and use a simulation to generate frequencies for compound events. For example, use random digits as a simulation tool to approximate the answer to the question: If 40% of donors have type A blood, what is the probability that it will take at least 4 donors to find one with type A blood?

Common Core State Standards Math

Cluster: Investigate chance processes and develop, use, and evaluate probability models

Standard: Represent sample spaces for compound events using methods such as organized lists, tables and tree diagrams. For an event described in everyday language (e.g., “rolling double sixes”), identify the outcomes in the sample space which compose the event.

Fundamental Counting Principle

Students will continue to apply their understanding of compound independent events. They will calculate probabilities and represent sample spaces with visual representations.

Key Concepts

• Students continue to solve problems with compound events. The formula for calculating the probability of independent events is introduced: P ( A and B ) = P ( A ) ⋅ P ( B )

Goals and Learning Objectives

• Deepen understanding of compound events using lists, tables, and tree diagrams.
• Learn about the Fundamental Counting Principle.

How Many Outfits?

Lesson guide.

Have students read the Opening question. Give students a few minutes to think about the question and then have them share their thoughts.

ELL: Be sure that your pace is appropriate when posing this question, especially when interacting with ELLs.

SWD: If students are not observing why there are 72 combinations for shirts and pants, thinking aloud is one strategy for making learning visible. When teachers think aloud, they are externalizing their internal thought processes. Doing so may provide students with insights into mathematical thinking and ways of tackling problems. It also helps to model accurate mathematical language.

Mathematics

Discuss student responses. Students will likely see that each of the 9 shirts can be paired with each of the 8 pants, making 72 combinations. Summarize the results from the previous lesson:

• Two coins: 2 outcomes for the first event, 2 for the second, 4 total outcomes
• One number cube and one coin: 6 outcomes for the first event, 2 for the second event, 12 total outcomes
• Two number cubes: 6 outcomes for the first event, 6 for the second, 36 total outcomes

Elicit from students that the number of outcomes for each event can be multiplied to find the total number of outcomes. Students may begin to see that the probability of each outcome can also be multiplied to find the probability of the compound event, although this idea is left for students to bring up and/or discover.

Mathematical Practices

Mathematical Practice 7: Look for and make use of structure.

• The Opening allows students to see the relationship between sample space diagrams and the total number of outcomes for compound events.

Bob has nine different shirts and eight different pairs of pants.

• How many different outfits can he wear (using one shirt and one pair of pants)?

Math Mission

Discuss the Math Mission. Students will find the probability of compound events.

Find the probability of compound events.

Students can work individually or with a partner.

Interventions

Student struggles to get started on the marble problem.

• How many outcomes are there for each event?
• If a marble is drawn, what are the outcomes for the second event?

Student has a solution but does not provide an explanation.

• Why did you approach the problem the way you did?
• Explain your strategy for solving the problem.

SWD: Struggling students may still need explicit instruction and guided scaffolding to recognize the relationships creating ratios to represent the probability and for multiplying fractions to find probability. Provide small group instruction to make sure that they can multiply fractions to find the probability accurately, and to convert fractions to decimals to percents.

List: B, B| B, B| B, R| B, R| B, R B, B| B, B| B, R| B, R| B, R R, B| R, B| R, R| R, R| R, R R, B| R, B| R, R| R, R| R, R R, B| R, B| R, R| R, R| R, R

• P (R then B) = 6 25 = 0.24 = 24%

You have a bag of three red marbles and two blue marbles. You draw one marble, replace it, and draw a second marble.

• Represent the sample space with a tree diagram, a list, or a table.
• What is the probability that you will draw a red marble and then draw a blue marble?

• How many marbles does the bag contain in all?
• What is the probability of selecting one red marble?
• Can you show the sample space in a tree diagram?

Student has an incorrect solution.

• Did you pair each of the first outcomes with each of the second outcomes?
• How many outcomes are favorable?
• How did you know that multiplying would work?
• P (Karen selects a 2 the first time) = 1 4 = 0.25 = 25%
• P (Karen selects a 2 the second time) = 1 4 = 0.25 = 25%

• P (Karen will select 2 both times) = 1 16 = 0.0625 = 6.25%

Karen has four cards numbered 1, 2, 3, and 4. She shuffles the cards face down, selects one randomly, and notes the number. Then she replaces the card, shuffles again, and selects a second card.

• What is the probability that Karen will select a 2 the first time she chooses a card?
• What is the probability that Karen will select a 2 the second time?
• Illustrate the sample space with a tree diagram, a list, or a table.
• What is the probability that Karen will select a 2 both times?
• How many cards does Karen have in all?
• If she selects a 2, how would she determine the probability of the next card she chooses?
• How can you use your representation of the sample space to help you solve the problem?

Prepare a Presentation

As students work, look for students who do not draw the sample space or use an abbreviated version. Some students will see the number of outcomes without the sample space, but will realize that they might still need the sample space to count all of the favorable outcomes. Some students will take the next step, thinking of ways they can find the favorable outcomes without drawing the sample space.

Mathematical Practice 1: Make sense of problems and persevere in solving them.

• Students continue to build their understanding and fluency by calculating the theoretical probability of events.

Mathematical Practice 2: Reason abstractly and quantitatively.

• The Challenge Problem provides students with the symbolic representation of the probability of compound independent events, and has them solve Work Time problems using it rather than more concrete representations.
• Presentations will vary. Presentations should compare methods and explain when and why one type might be better than another.

Challenge Problem

Marbles: P (draw red, then blue) = 3 5 ⋅ 2 5 = 6 25

Cards: P (Karen draws a 2, then draws 2) = 1 4 ⋅ 1 4 = 1 16

Compare the methods of using tree diagrams, tables, and organized lists to find the probability of compound independent events.

Karen says that compound probability of two independent events both occurring, then the probability is:

P ( A and B ) = P ( A ) • P ( B )

• Use the formula to calculate the probability you will draw a red marble and then draw a blue marble.
• Use the formula to calculate the probability that Karen will select a 2 both times.

Make Connections

Have student present their observations about different methods for representing sample spaces.

While students are presenting, ask:

• How did you find the sample space and the number of favorable outcomes?
• How did you determine the probability?

ELL: Call on ELLs and encourage them to participate, even if their pace is slower or they are reluctant to volunteer due to their weaker command of the language.

Performance Task

Ways of thinking: make connections.

Take notes about the approaches your classmates used to find the probability of compound independent events.

As your classmates present, ask questions such as:

• How does the diagram of the sample space help you solve the problem?
• Where do you see the probability in the diagram?
• Can you explain how you used the formula for finding the probability of a single event to find the probability of compound events?

Compound Events

A possible summary.

A compound event is two or more events that happen at the same time or one right after the other. Finding the probability is still the same: the ratio of the number of favorable outcomes to the total number of outcomes. Tree diagrams, systematic lists, and tables are tools used to find the sample space, which is a list of all possible outcomes. If the events of a compound event are independent, you can also find the probability of a compound event by multiplying together the probability of each event.

ELL: ELLs will understand more of what you say if you remember to modify your language as needed. Find subtle but effective ways to check that students have understood.

• Use shorter, less complex sentences for beginning ELLs.
• Avoid pronouns.
• Emphasize nouns and verbs.
• Use simple sentence structures.
• Use intonation, volume, and pauses to help make the meaning clear.
• Rephrase instead of repeating.
• Paraphrase important concepts and directions.

Formative Assessment

Summary of the math: compound events.

Write a summary about finding the probability of compound events using diagrams and a formula.

Check your summary:

• Do you explain how to determine the probability of compound independent events?

Reflect on Your Work

Have students write a brief reflection before the end of the class. Review the reflections to find out what students find confusing about compound events.

Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.

Some things about compound events that I am still not sure about are...

Fundamental Counting Principle

• The principle posits that if a task can be divided into stages, with each stage having a distinct number of ways it can be completed, the total number of ways to complete the entire task is the product of the ways each stage can be completed.
• Examples provided include calculating the number of possible meals from a set menu, the number of ways books can be arranged on a shelf, and the number of possible steering committees from a group of employees.
• The principle is foundational for understanding permutations and will be further explored with the introduction of factorials in subsequent lessons.
• Real-world applications of the principle demonstrate its utility in solving complex problems by breaking them down into simpler, sequential stages.
• The practice problem illustrates how quickly numbers can grow in combinatorial problems, highlighting the importance of mastering this principle for efficient problem-solving.

GMAT Quant: How to Count

Introduction to Counting

FCP with Restrictions

Factorial Notation

Counting What You Don't Want

Counting with Identical Items

Eliminating Repetition

Combinations

When to Use Combinations

Calculating Combinations

Permutations and Combinations

Case Counting

Counting Strategies