| Root 1: Root 2: Important Terms for Quadratic EquationsIn case you’re new, need a refresher, or appreciate the knowledge, here are some helpful terms and descriptions to assist your calculations. Quadratic EquationsA quadratic equation (also referred to as a quadratic function ) is a polynomial whose highest exponent is 2. The standard form of a quadratic equation looks like this: f (x) = ax² + bx + c When graphed on a coordinate plane, a quadratic equation creates a parabola , which is a u-shaped curve. When the leading coefficient is positive, the curve is oriented like the letter u, with the opening facing up. When the leading coefficient is negative, the curve is upside down, with the opening facing down. CoefficientsThe coefficient of x² is called the leading coefficient , and is represented by the variable a. In standard form, a, b, and c are all constants or numerical coefficients . One absolute rule is that the first constant, a, can never be equal to zero. The leading coefficient can tell you more than just the orientation of the parabola, it also determines how wide or skinny the u-curve is. This depends on the value of the leading coefficient. The closer to zero the value is, the wider the curve will be. The farther away from 0 the number is, the skinnier the curve will be. Structure of a GraphThe vertex of a parabola is the point at the bottom of the u curve. If you draw a vertical line through the vertex, you create the axis of symmetry , which is an imaginary line that cuts the parabola in half equally. The shape of the curve is reflected over this line. Quadratic FormulaThe quadratic formula is used to find the solution to a quadratic equation. The quadratic formula looks like this: For ax2 + bx + c = 0 where a ≠ 0: x= -b + √b2-4ac / 2a Every quadratic equation gives two values of the unknown variable (x) and these values are called roots of the equation. When you are asked to solve a quadratic equation, you are really being asked to find the roots (or solutions). The roots of a quadratic function are the x-intercepts, which are the points where the parabola crosses the x-axis. The y-coordinate of points lying on the x-axis is zero. Therefore, to find the roots of a quadratic function, we make f(x) = 0, and solve the equation. A quadratic equation has two roots which may be unequal real numbers, equal real numbers, or numbers which are not real. If a quadratic equation has two real equal roots, we say the equation has only one real solution. This occurs when the vertex is the parabola is the point that touches the x-axis. DiscriminantThe discriminant of a quadratic formula tells you about the nature of roots the equation has. For example: - b2−4ac = 0, one real solution
- b2−4ac > 0, two real solutions
- b2−4ac < 0, two imaginary solutions
If the discriminant is a perfect square, the roots are rational and when it is not a perfect square, the roots are irrational . Other Calculators Quadratic Formula CalculatorInstructions: This quadratic formula calculator will solve a quadratic equation for you, showing all the steps. Type the coefficients of the quadratic equation, and the solver will give you the roots, the y-intercept, the coordinates of the vertex showing all the work and it will plot the function.  The Quadratic Formula: How to Solve a Quadratic Equation?The quadratic equation is an equation of the form: with \( a \neq 0\). This is the main formula that determines a quadratic equation . Good news is that the above equation is not too hard to solve, which is a great thing considering that the quadratic equation appears literally everywhere in Algebra, Calculus and pretty much everywhere. The Quadratic Formula SolutionNow, the question is how to solve this quadratic formula. Fortunately, the answer simple and well-known: It has solutions of the form These are known as the roots of the quadratic equation (also known as solutions of the equation). In order to analyze the nature of the solution, the discriminant is defined as: Types of Solutions to the Quadratic FormulaBased on the value of the discriminant, the nature of the solutions is defined. In fact, when \(D > 0\), then there are two different real solutions, when \(D = 0\), there is one repeated real solution, and when \(D < 0\), there are two different imaginary solutions. This quadratic equation solver helps you make these calculations automatically. One of the neat things of this quadratic equation solver is that it will show the steps to compute the y-intercept, the coordinates of the vertex and it will plot the quadratic function  Quadratic Formula StepsThere are several steps you have to follow in order to successfully solve a quadratic equation: Step 1: Identify the coefficients. Examine the given equation of the form \(ax^2+bx+c\), and determine the coefficients \(a\), \(b\) and \(c\). The coefficient \(a\) is the coefficient that appears multiplying the quadratic term \(x^2\). The coefficient \(b\) is the coefficient that appears multiplying the linear term \(x\), and the coefficient \(c\) is the constant. Example: Suppose that you have the following expression: \(x^2+3x+1\). What are the coefficients? In this case \(a = 1\) (the coefficient multiplying the quadratic term \(x^2\)), \(b = 3\) (the coefficient multiplying the linear term \(x\)), and \(c = 1\) (the constant). Example: How about Suppose that you have the following expression: \(\frac{5}{4} + \frac{3}{4} x + \frac{1}{2} x^2\). What are the coefficients now? In this case \(a = \frac{1}{2}\) (the coefficient multiplying the quadratic term \(x^2\)), \(b = \frac{3}{4}\) (the coefficient multiplying the linear term \(x\)), and \(c = \frac{5}{4}\) (the constant). Example: What happens with following expression: \(-3 + \frac{1}{2} x\). In this case, we have that \(a = 0\), because the expression does not contain a quadratic term \(x^2\), so in this case, this is not a quadratic expression. Step 2: Plug the coefficients you found in the formula. The formula is quadratic formula is so you need to replace the value of the coefficients \(a\), \(b\) and \(c\). Example: If you have the equation: \(-3x^2 + 2x-1 = 0\), you find that \(a = -3\), \(b = 2\) and \(c = -1\). So, plugging this values in the formula we get: Step 3: Simplify the values in the equation, once you have plugged the values of \(a\), \(b\) and \(c\) . In the previous example, we would have Step 4: Look inside of the square root. If the value is positive, then the quadratic equation has two real roots. If the value is 0, then there is one real root, and if the value inside of the square root is negative, then there are two complex root. In the previous example, we have a -8 inside of the square root, so we have two complex solutions, as shown below: 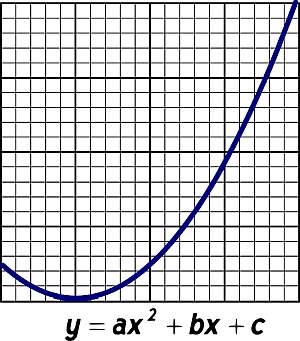 What is the Quadratic formula Used ForThe quadratic formula is one of the most ubiquitous formula in mathematics. It appears when you are solving all kind of geometric problems, such as when you are maximizing an area, given a fixed perimeter, or in numerous word problems. Lots of people wonder if there is any relationship between this quadratic equation formula and the method of completing the square . The answer is simple: you arrive the quadratic formula by solving the quadratic equation via completing the square. It is exactly the same idea, that derives to the quadratic formula that we all know. Observe that the solutions to the quadratic equation have a very interesting geometric property: when you compute the average of the solutions found, you get the x-coordinate of the vertex of the parabola, which helps you find the vertex form of a parabola, also known as the standard form, used in many applications, form example with conical sections. Quadratic Formula ExamplesCompute the roots of the following quadratic equation: \(3x^2 - 2x + 4 = 0\) The following equation needs to be solved: This corresponds to a quadratic equation. The following formula is used to find the solutions: Using the above formula, we get that: Hence, the solutions are: Therefore, there are two imaginary solutions \(x_1 = 0.333 - 1.106 i \) and \(x_2 = 0.333 + 1.106 i \). Also, the y-intercept occurs at \(y = 4\), which means that the coordinates of the y-intercept are \((0, 4)\). Finally, the coordinates of the vertex are: Related Calculators log in to your accountReset password. Quadratic Formula CalculatorEnter the equation you want to solve using the quadratic formula. The Quadratic Formula Calculator finds solutions to quadratic equations with real coefficients. For equations with real solutions, you can use the graphing tool to visualize the solutions. Quadratic Formula : x = − b ± b 2 − 4 a c 2 a Click the blue arrow to submit. Choose "Solve Using the Quadratic Formula" from the topic selector and click to see the result in our Algebra Calculator ! Solve Using the Quadratic Formula Apply the Quadratic Formula Popular ProblemsSolve Using the Quadratic Formula x 2 + 5 x + 6 = 0 Solve Using the Quadratic Formula x 2 - 9 = 0 Solve Using the Quadratic Formula 5 x 2 - 7 x - 3 = 0 Apply the Quadratic Formula x 2 - 14 x + 49 Apply the Quadratic Formula x 2 - 18 x - 4 Please ensure that your password is at least 8 characters and contains each of the following: - a special character: @$#!%*?&
Quadratic Formula CalculatorThe calculator below solves the quadratic equation of ax 2 + bx + c = 0 . | | | | Fractional values such as 3/4 can be used.
| In algebra, a quadratic equation is any polynomial equation of the second degree with the following form: ax 2 + bx + c = 0 where x is an unknown, a is referred to as the quadratic coefficient, b the linear coefficient, and c the constant. The numerals a , b , and c are coefficients of the equation, and they represent known numbers. For example, a cannot be 0, or the equation would be linear rather than quadratic. A quadratic equation can be solved in multiple ways, including factoring, using the quadratic formula, completing the square, or graphing. Only the use of the quadratic formula, as well as the basics of completing the square, will be discussed here (since the derivation of the formula involves completing the square). Below is the quadratic formula, as well as its derivation. 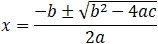 Derivation of the Quadratic Formula From this point, it is possible to complete the square using the relationship that: x 2 + bx + c = (x - h) 2 + k Continuing the derivation using this relationship:  Recall that the ± exists as a function of computing a square root, making both positive and negative roots solutions of the quadratic equation. The x values found through the quadratic formula are roots of the quadratic equation that represent the x values where any parabola crosses the x-axis. Furthermore, the quadratic formula also provides the axis of symmetry of the parabola. This is demonstrated by the graph provided below. Note that the quadratic formula actually has many real-world applications, such as calculating areas, projectile trajectories, and speed, among others.   Quadratic Formula Calculator & SolverCalculator for solutions to any quadratic equation.. The calculator uses the quadratic formula to find solutions to any quadratic equation .  The quadratic formula calculator below will solve any quadratic equation that you type in. Simply type in a number for 'a', 'b' and 'c' then hit the 'solve' button. Quadratic Formula Calculator and SolverThe Discriminant The Actual Solutions Parabola Animated GifsMore Quadratic Gifs The calculator on this page shows how the quadratic formula operates, but if you have access to a graphing calculator you should be able to solve quadratic equations, even ones with imaginary solutions. - Step 1) Most graphing calculators like the TI- 83 and others allow you to set the "Mode" to "a + bi" (Just click on 'mode' and select 'a+bi').
- If you can set your calculator's mode to a + bi you should be able to even calculate imaginary solutions.
- The rest of the steps just involve typing in a,b and c. Make sure that you divide the entire numerator by 2a, just use parentheses.
- Quadratic formula worksheets (several free printable pdfs with answer keys on the quadratic formula)
Create the graph of any Parabola Save Graph as Image to your desktop 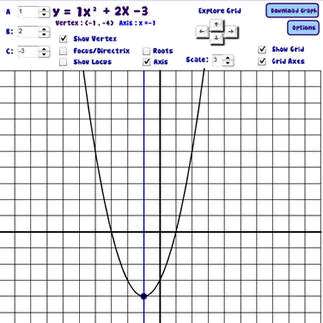 - Quadratic Equations
- Other Free Math Calculators
- All roots calculated
Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!Popular pages @ mathwarehouse.com.  Helping with Math Quadratic Formula CalculatorA Quadratic Formula Calculator is a tool that can be used to find the roots or solutions of a quadratic equation . Enter Information: What is the quadratic formula?The quadratic formula calculator is an online tool that is used to calculate the roots of a quadratic equation. The quadratic equation is a second-degree polynomial equation of the form ax^2 + bx + c = 0, where a, b, and c are constants and x is the variable. The quadratic formula is derived from the standard form of a quadratic equation, and it is given by: x = (-b ± √(b^2 – 4ac)) / 2a The quadratic formula calculator solves the quadratic equation using this formula and gives the two roots of the equation. What is the quadratic equation? The quadratic equation is a second-degree polynomial equation of the form ax^2 + bx + c = 0, where a, b, and c are constants and x is the variable. It is a fundamental concept in algebra and has numerous applications in science, engineering, economics, and many other fields. The quadratic equation can have either one or two real roots, or two complex roots, depending on the values of the coefficients a, b, and c. The quadratic formula is used to calculate the roots of the quadratic equation, and it is given by: The solutions to the quadratic equation can also be found by factoring, completing the square, or graphing the equation. Derivation of the quadratic formulaThe quadratic formula is used to solve the quadratic equation ax^2 + bx + c = 0, where a, b, and c are constants and x is the variable. The formula is given by: To derive this formula, we start by completing the square of the quadratic equation: ax^2 + bx + c = 0 ax^2 + bx = -c We now add and subtract (b/2a)^2 to the left-hand side of the equation: ax^2 + bx + (b/2a)^2 – (b/2a)^2 = -c The first three terms on the left-hand side can be factored as a perfect square: a(x + b/2a)^2 = -c + (b/2a)^2 We can now isolate x: (x + b/2a)^2 = (-c + (b/2a)^2) / a Taking the square root of both sides, we obtain: x + b/2a = ± √((-c + (b/2a)^2) / a) Subtracting b/2a from both sides gives: This is the quadratic formula, which can be used to find the solutions to any quadratic equation of the form ax^2 + bx + c = 0. How to use the Quadratic formula calculator?- Go to the Quadratic Formula Calculator website.
- Enter the values of a, b, and c in the input fields.
- Click on the “Calculate” button to get the solutions.
- The calculator will display the roots of the quadratic equation in the standard form (ax^2 + bx + c = 0).
Note: The calculator gives both the real and complex roots of the equation, if any. Suppose we have a quadratic equation: 2x^2 + 5x – 3 = 0 We can use the quadratic formula to find the roots of this equation. First, we identify the values of a, b, and c: a = 2 b = 5 c = -3 Next, we plug these values into the quadratic formula: x = (-5 ± √(5^2 – 4(2)(-3))) / 2(2) Simplifying the equation, we get: x = (-5 ± √49) / 4 x = (-5 ± 7) / 4 So the solutions are: x1 = (-5 + 7) / 4 = 1/2 x2 = (-5 – 7) / 4 = -3/2 Therefore, the roots of the equation 2x^2 + 5x – 3 = 0 are x1 = 1/2 and x2 = -3/2. Quadratic Equation SolverWe can help you solve an equation of the form " ax 2 + bx + c = 0 " Just enter the values of a, b and c below : Is it Quadratic?Only if it can be put in the form ax 2 + bx + c = 0 , and a is not zero . The name comes from "quad" meaning square, as the variable is squared (in other words x 2 ). These are all quadratic equations in disguise: | In disguise | In standard form | a, b and c | | = 3x -1 | - 3x + 1 = 0 | a=1, b=-3, c=1 | | - 2x) = 5 | - 4x - 5 = 0 | a=2, b=-4, c=-5 | | | - x - 3 = 0 | a=1, b=-1, c=-3 | | = 0 | + x - 1 = 0 | a=5, b=1, c=-1 | How Does this Work?The solution(s) to a quadratic equation can be calculated using the Quadratic Formula : The "±" means we need to do a plus AND a minus, so there are normally TWO solutions ! The blue part ( b 2 - 4ac ) is called the "discriminant", because it can "discriminate" between the possible types of answer: - when it is positive, we get two real solutions,
- when it is zero we get just ONE solution,
- when it is negative we get complex solutions.
Learn more at Quadratic Equations  - Math Lessons
- Math Formulas
- Calculators
Math Calculators, Lessons and Formulas It is time to solve your math problem - HW Help (paid service)
- Solving Equations
- Quadratic Equation Solver
Quadratic equation solver This step-by-step calculator solves quadratic equations using three different methods: the quadratic formula method , completing the square , and the factoring method . Calculator shows all the work and provides detailed explanation on how to solve an equation. | Factoring | | Completing the square | | Quadratic formula | - Factoring Polynomials
- Polynomial Roots
- Synthetic Division
- Polynomial Operations
- Graphing Polynomials
- Simplify Polynomials
- Generate From Roots
- Simplify Expression
- Multiplication / Division
- Addition / Subtraction
- Rationalize Denominator
- Simplifying
- Quadratic Equations Solver
- Polynomial Equations
- Solving Equations - With Steps
- Solving (with steps)
- Quadratic Plotter
- Factoring Trinomials
- Equilateral Triangle
- Right Triangle
- Oblique Triangle
- Square Calculator
- Rectangle Calculator
- Circle Calculator
- Hexagon Calculator
- Rhombus Calculator
- Trapezoid Calculator
- Triangular Prism
- Distance calculator
- Midpoint Calculator
- Triangle Calculator
- Graphing Lines
- Lines Intersection
- Two Point Form
- Line-Point Distance
- Parallel/Perpendicular
- Circle Equation
- Circle From 3 Points
- Circle-line Intersection
- Modulus, inverse, polar form
- Vectors (2D & 3D)
- Add, Subtract, Multiply
- Determinant Calculator
- Matrix Inverse
- Characteristic Polynomial
- Eigenvalues
- Eigenvectors
- Matrix Decomposition
- Limit Calculator
- Derivative Calculator
- Integral Calculator
- Arithmetic Sequences
- Geometric Sequences
- Find n th Term
- Degrees to Radians
- Trig. Equations
- Long Division
- Evaluate Expressions
- Fraction Calculator
- Greatest Common Divisor GCD
- Least Common Multiple LCM
- Prime Factorization
- Scientific Notation
- Percentage Calculator
- Dec / Bin / Hex
- Probability Calculator
- Probability Distributions
- Descriptive Statistics
- Standard Deviation
- Z - score Calculator
- Normal Distribution
- T-Test Calculator
- Correlation & Regression
- Simple Interest
- Compound Interest
- Amortization Calculator
- Annuity Calculator
- Work Problems
Hire MATHPORTAL experts to do math homework for you. Prices start at $3 per problem. How to use this calculatorThe most commonly used methods for solving quadratic equations are: 1 . Factoring method 2 . Solving quadratic equations by completing the square 3 . Using quadratic formula In the following sections, we'll go over these methods. Method 1A : Factoring methodIf a quadratic trinomial can be factored, this is the best solving method. We often use this method when the leading coefficient is equal to 1 or -1. If this is not the case, then it is better to use some other method. Example 01: Solve $ x^2 \color{red}{-8}x \color{blue}{+ 15} = 0 $ by factoring. Here we see that the leading coefficient is 1, so the factoring method is our first choice. To factor this equation, we must find two numbers ( $ a $ and $ b $ ) with a sum is $ a + b = \color{red}{8} $ and a product of $ a \cdot b = \color{blue}{15} $. After some trials and errors, we see that $ a = 3 $ and $ b = 5 $. Now we use formula $ x^2 - 8x + 15 = (x - a)(x - b) $ to get factored form: Divide the factored form into two linear equations to get solutions. Method 1B : Factoring - special casesExample 02: Solve $ x^2 -8x = 0 $ by factoring. In this case, (when the coefficient c = 0 ) we can factor out $ \color{blue}{x} $ out of $ x^2 - 8x $. Example 03: Solve $ x^2 - 16 = 0 $ by factoring. In this case, ( when the middle term is equal 0) we can use the difference of squares formula. Method 3 : Solve using quadratic formulaThis method solves all types of quadratic equations. It works best when solutions contain some radicals or complex numbers. Example 05: Solve equation $ 2x^2 + 3x - 2 = 0$ by using quadratic formula. Step 1 : Read the values of $a$, $b$, and $c$ from the quadratic equation. ( $a$ is the number in front of $x^2$ , $b$ is the number in front of $x$ and $c$ is the number at the end) Step 2 :Plug the values for a, b, and c into the quadratic formula and simplify. Step 3 : Solve for $x_1$ and $x_2$ Number Line- x^4-5x^2+4=0
- \sqrt{x-1}-x=-7
- \left|3x+1\right|=4
- \log _2(x+1)=\log _3(27)
- 3^x=9^{x+5}
- What is the completing square method?
- Completing the square method is a technique for find the solutions of a quadratic equation of the form ax^2 + bx + c = 0. This method involves completing the square of the quadratic expression to the form (x + d)^2 = e, where d and e are constants.
- What is the golden rule for solving equations?
- The golden rule for solving equations is to keep both sides of the equation balanced so that they are always equal.
- How do you simplify equations?
- To simplify equations, combine like terms, remove parethesis, use the order of operations.
- How do you solve linear equations?
- To solve a linear equation, get the variable on one side of the equation by using inverse operations.
| 🌐 Languages | EN, ES, PT & more | | 🏆 Practice | Improve your math skills | |
| 😍 Step by step | In depth solution steps | | ⭐️ Rating | based on 20924 reviews | equation-calculator - High School Math Solutions – Radical Equation Calculator Radical equations are equations involving radicals of any order. We will show examples of square roots; higher...
Please add a message. Message received. Thanks for the feedback. Quadratic Equation Solver A quadratic equation solver is a free step by step solver for solving the quadratic equation to find the values of the variable. With the help of this solver, we can find the roots of the quadratic equation given by, ax 2 + bx + c = 0, where the variable x has two roots. The solution is obtained using the quadratic formula ;  where a, b and c are the real numbers and a ≠ 0. If a = 0, then the equation becomes linear. We can call it a linear equation. The quadratic equation is of three types namely, - Standard form
- Factored form
- Vertex form
Generally, there are four different methods to solve the quadratic equation. Those methods are: - Using square roots
- Completing the squares
- Using quadratic formula
In this, quadratic equation solver page, we will use the quadratic formula to solve the quadratic equation. How does the Quadratic Equation Solver Work?A quadratic equation is nothing but a polynomial of degree 2. The roots of polynomials give the solution of the equation. Here we have to solve an equation in the form of ax 2 + bx + c = 0. The quadratic equation solver uses the quadratic formula to find the roots of the given quadratic equation. The procedure to use the quadratic equation solver is as follows: Step 1: Enter the coefficients of the quadratic equation “a”, “b” and “c” in the input fields. Step 2: Now, click the button “Solve the Quadratic Equation” to get the roots. Step 3: Finally, the discriminant and the roots of the given quadratic equation will be displayed in the output fields. Enter the values of a, b and c in the solver given below to solve any given quadratic equation. Q u a d r a t i c E q u a t i o n : a x 2 + b x + c = 0 Enter the value of a : Enter the value of b : Enter the value of c : Discriminant (D) : x 1 : x 2 : where x 1 and x 2 are root 1 and root 2. If an input is given, it easily shows the solution of the given equation. Use the quadratic solver to check your answers. Use it as a reference when you are finding the unknown values of a variable. When you are numerically solving the quadratic equations, you can check it with the solver whether your answer is correct or incorrect. Once you find that your answers are correct, then you are on the right path to solve the algebraic equations. But, if you find that your answers are incorrect, you should figure out the area of mistakes that you had done. The quadratic equation online solver helps to find out the exact solution of a quadratic equation. Sometimes, the solutions for the quadratic equation are not rational, and hence, it cannot be obtained using the factoring method. It means that the simple quadratic equations with rational roots can be solved easily with the help of the factorization method. Steps to Solve Quadratic EquationThe input for the quadratic equation solver is of the form ax 2 + bx + c = 0 Where a is not zero, a ≠ 0 If the value of a is zero, then the equation is not a quadratic equation. The quadratic equation solution is obtained using the quadratic formula: Normally, we get two solutions, because of a plus or minus symbol “ ± ”. You need to do both the addition and subtraction operation. The part of an equation “ b 2 -4ac “ is called the “ discriminant ” and it produces the different types of possible solutions. Some of the possible solutions are - Case 1: When a discriminant part is positive, you get two real solutions
- Case 2: When a discriminant part is zero, it gives only one solution
- Case 3: When a discriminant part is negative, you get complex solutions
Quadratic solver level helps the students of class 10 to clearly know about the different cases involved in the discriminant producing different solutions. Here are some of the quadratic equation examples Quadratic Formula ExamplesExample 1: Consider an example x 2 – 3x – 10 = 0 Given data : a =1, b = -3 and c = -10 b 2 – 4ac = (-3) 2 – 4 (1)(-10) = 9 +40 = 49 b 2 – 4ac= 49 >0 Therefore, we get two real solutions The general quadratic formula is given as; x= 10/2 , -4/2 Therefore, the solutions are 5 and -2 Example 2: Consider an example 9x 2 +12x + 4 = 0 Given data : a =9, b = 12 and c = 4 b 2 – 4ac = (12) 2 – 4 (9)(4) = 144 – 144= 0 b 2 – 4ac= 0 Therefore, we get only one distinct solution The general quadratic formula is given as x= -6/9 = -2/3 Therefore, the solution is -2 / 3 Example 3: Consider an example x 2 + x + 12= 0 Given data : a =1, b = 1 and c = 12 b 2 – 4ac = (1) 2 – 4 (1)(12) = 1 – 48 = -47 b 2 – 4ac= -47 < 0 Therefore, we get complex solutions Therefore, the solutions are Frequently Asked Questions on Quadratic Equation SolverWhat is meant by the quadratic equation. In Maths, the quadratic equation is defined as an algebraic equation of degree 2, and it should be in the form of ax 2 + bx + c = 0. Here, a, b, and c are the coefficients of the variable x, and the value of “a” should not be equal to 0. (i.e., a≠ 0). The solutions of the quadratic equation are called the roots of the equation. What are the four different methods to solve the quadratic equation?The different methods to solve the quadratic equation are: Factoring Completing the squares Using the square root method Quadratic formula What is discriminant?The discriminant D = b 2 – 4ac reveals the nature of the roots that the equation has. It is determined from the coefficients of the equation. If D = 0, the roots are equal, real and rational If D > 0, and also a perfect square, the roots are real, distinct and rational If D > 0, but not a perfect square, the roots are real, distinct and irrational What is the standard form of the quadratic equation?The standard form to represent the quadratic equation is Ax 2 + Bx + C = 0 Here A, B and C are the known values, and A should not be equal to 0. X is a variable. Mention the applications of quadratic equations.The quadratic equations are used in everyday life activities such as finding the profit of the product, calculating the area of the room, athletics, finding the speed of the object, and so on.  Leave a Comment Cancel replyYour Mobile number and Email id will not be published. Required fields are marked * Request OTP on Voice Call Post My Comment  Register with BYJU'S & Download Free PDFsRegister with byju's & watch live videos.  - Solve equations and inequalities
- Simplify expressions
- Factor polynomials
- Graph equations and inequalities
- Advanced solvers
- All solvers
- Arithmetics
- Determinant
- Percentages
- Scientific Notation
- Inequalities
 Quadratic EquationsSolving equations is the central theme of algebra. All skills learned lead eventually to the ability to solve equations and simplify the solutions. In previous chapters we have solved equations of the first degree. You now have the necessary skills to solve equations of the second degree, which are known as quadratic equations . QUADRATICS SOLVED BY FACTORING- Identify a quadratic equation.
- Place a quadratic equation in standard form.
- Solve a quadratic equation by factoring.
A quadratic equation is a polynomial equation that contains the second degree, but no higher degree, of the variable. The standard form of a quadratic equation is ax 2 + bx + c = 0 when a ≠ 0 and a, b, and c are real numbers. All quadratic equations can be put in standard form, and any equation that can be put in standard form is a quadratic equation. In other words, the standard form represents all quadratic equations. The solution to an equation is sometimes referred to as the root of the equation. An important theorem, which cannot be proved at the level of this text, states "Every polynomial equation of degree n has exactly n roots." Using this fact tells us that quadratic equations will always have two solutions. It is possible that the two solutions are equal. The simplest method of solving quadratics is by factoring. This method cannot always be used, because not all polynomials are factorable, but it is used whenever factoring is possible. The method of solving by factoring is based on a simple theorem. If AB = 0, then either A = 0 or B = 0. We will not attempt to prove this theorem but note carefully what it states. We can never multiply two numbers and obtain an answer of zero unless at least one of the numbers is zero. Of course, both of the numbers can be zero since (0)(0) = 0. 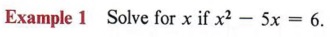 Solution Step 1 Put the equation in standard form. 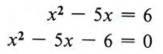 Step 2 Factor completely. 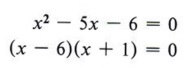 Step 3 Set each factor equal to zero and solve for x. Since we have (x - 6)(x + 1) = 0, we know that x - 6 = 0 or x + 1 = 0, in which case x = 6 or x = - 1. Step 4 Check the solution in the original equation. If x = 6, then x 2 - 5x = 6 becomes 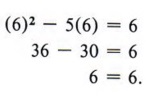 Therefore, x = 6 is a solution. If x = - 1, then x 2 - 5x = 6 becomes 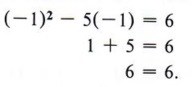 Therefore, - 1 is a solution. The solutions can be indicated either by writing x = 6 and x = - 1 or by using set notation and writing {6, - 1}, which we read "the solution set for x is 6 and - 1." In this text we will use set notation. 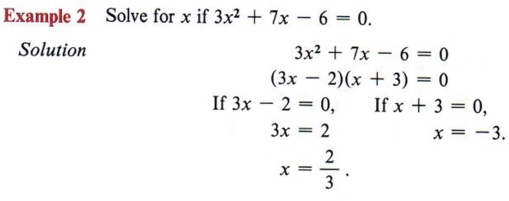 | are also called roots of the equation. |  Check the solutions in the original equation.  INCOMPLETE QUADRATICS- Identify an incomplete quadratic equation.
- Solve an incomplete quadratic equation.
If, when an equation is placed in standard form ax 2 + bx + c = 0, either b = 0 or c = 0, the equation is an incomplete quadratic . 5x 2 - 10 = 0 is an incomplete quadratic, since the middle term is missing and therefore b = 0. When you encounter an incomplete quadratic with c - 0 (third term missing), it can still be solved by factoring. 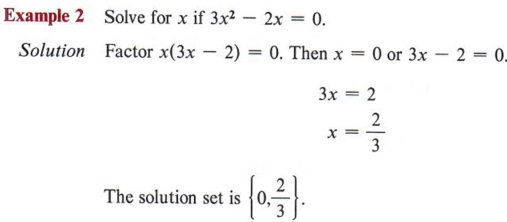 Notice that if the c term is missing, you can always factor x from the other terms. This means that in all such equations, zero will be one of the solutions. An incomplete quadratic with the b term missing must be solved by another method, since factoring will be possible only in special cases. Example 3 Solve for x if x 2 - 12 = 0. Solution Since x 2 - 12 has no common factor and is not the difference of squares, it cannot be factored into rational factors. But, from previous observations, we have the following theorem.  Using this theorem, we have  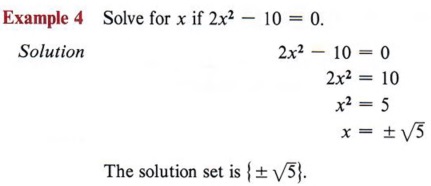 Note that in this example we have the square of a number equal to a negative number. This can never be true in the real number system and, therefore, we have no real solution. COMPLETING THE SQUARE- Identify a perfect square trinomial.
- Complete the third term to make a perfect square trinomial.
- Solve a quadratic equation by completing the square.
From your experience in factoring you already realize that not all polynomials are factorable. Therefore, we need a method for solving quadratics that are not factorable. The method needed is called "completing the square." First let us review the meaning of "perfect square trinomial." When we square a binomial we obtain a perfect square trinomial. The general form is (a + b) 2 = a 2 + 2ab + b 2 . 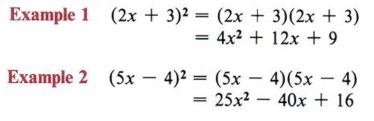 - The other term is either plus or minus two times the product of the square roots of the other two terms.
 The -7 term immediately says this cannot be a perfect square trinomial. The task in completing the square is to find a number to replace the -7 such that there will be a perfect square. Consider this problem: Fill in the blank so that "x 2 + 6x + _______" will be a perfect square trinomial. From the two conditions for a perfect square trinomial we know that the blank must contain a perfect square and that 6x must be twice the product of the square root of x 2 and the number in the blank. Since x is already present in 6x and is a square root of x 2 , then 6 must be twice the square root of the number we place in the blank. In other words, if we first take half of 6 and then square that result, we will obtain the necessary number for the blank. 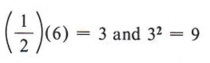 Therefore x 2 + 6x + 9 is a perfect square trinomial. 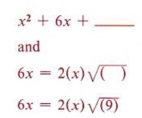 Now let's consider how we can use completing the square to solve quadratic equations. Example 5 Solve x 2 + 6x - 7 = 0 by completing the square. Solution First we notice that the -7 term must be replaced if we are to have a perfect square trinomial, so we will rewrite the equation, leaving a blank for the needed number. 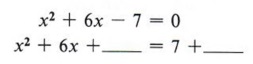 At this point, be careful not to violate any rules of algebra. For instance, note that the second form came from adding +7 to both sides of the equation. Never add something to one side without adding the same thing to the other side. Now we find half of 6 = 3 and 3 2 = 9, to give us the number for the blank. Again, if we place a 9 in the blank we must also add 9 to the right side as well. 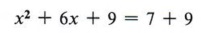 Now factor the perfect square trinomial, which gives 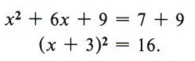 | + 6x + 9 may be written as (x + 3) . |  Example 6 Solve 2x 2 + 12x - 4 = 0 by completing the square. Solution This problem brings in another difficulty. The first term, 2x 2 , is not a perfect square. We will correct this by dividing all terms of the equation by 2 and obtain 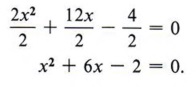 We now add 2 to both sides, giving 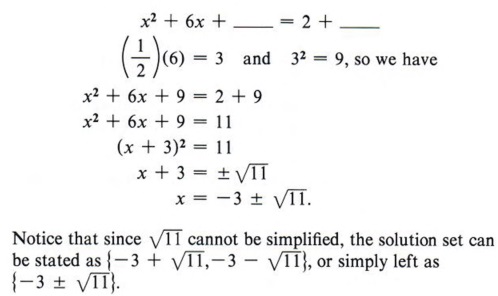
Again, this is more concise. | Example 7 Solve 3x 2 + 7x - 9 = 0 by completing the square. Solution Step 1 Divide all terms by 3.  Step 2 Rewrite the equation, leaving a blank for the term necessary to complete the square. 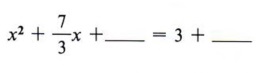 Step 3 Find the square of half of the coefficient of x and add to both sides. 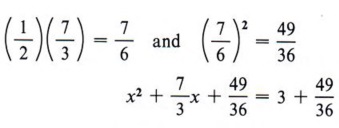 Step 4 Factor the completed square. 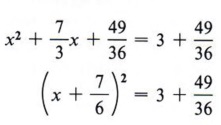 Step 5 Take the square root of each side of the equation. 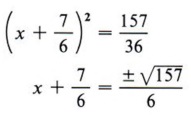 Step 6 Solve for x (two values). 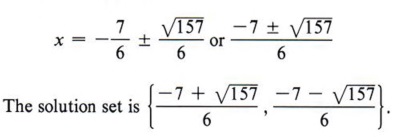 cannot be simplified. We could also write the solution to this problem in a more condensed form as
| 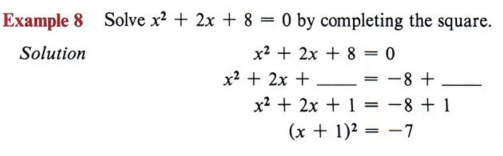 Follow the steps in the previous computation and then note especially the last ine. What is the conclusion when the square of a quantity is equal to a negative number? "No real solution." In summary, to solve a quadratic equation by completing the square, follow this step-by-step method. Step 1 If the coefficient of x2 is not 1, divide all terms by that coefficient. Step 2 Rewrite the equation in the form of x2 + bx + _______ = c + _______. Step 3 Find the square of one-half of the coefficient of the x term and add this quantity to both sides of the equation. Step 4 Factor the completed square and combine the numbers on the right-hand side of the equation. Step 5 Find the square root of each side of the equation. Step 6 Solve for x and simplify. If step 5 is not possible, then the equation has no real solution. THE QUADRATIC FORMULA- Solve the general quadratic equation by completing the square.
- Solve any quadratic equation by using the quadratic formula.
The standard form of a quadratic equation is ax 2 + bx + c = 0. This means that every quadratic equation can be put in this form. In a sense then ax 2 + bx + c = 0 represents all quadratics. If you can solve this equation, you will have the solution to all quadratic equations. We will solve the general quadratic equation by the method of completing the square. 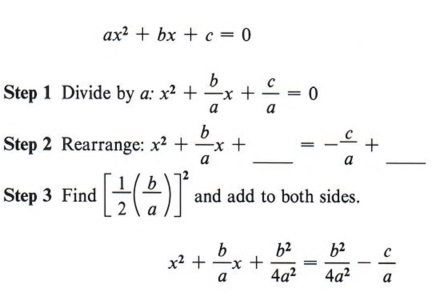 term with a coefficient of 1.
This we did in the previous section many times. |  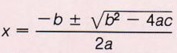 To use the quadratic formula you must identify a, b, and c. To do this the given equation must always be placed in standard form.  Not every quadratic equation will have a real solution. 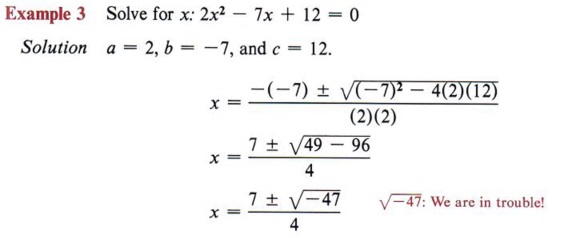 There is no real solution since -47 has no real square root. 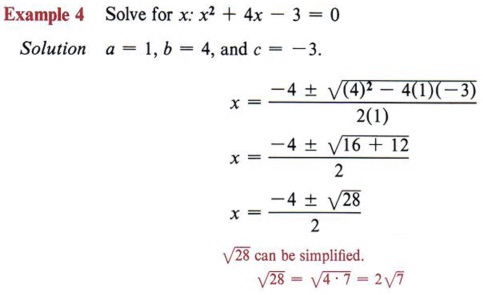 This solution should now be simplified. 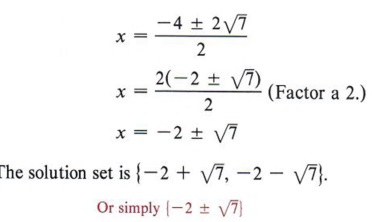 WORD PROBLEMS- Identify word problems that require a quadratic equation for their solution.
- Solve word problems involving quadratic equations.
Certain types of word problems can be solved by quadratic equations. The process of outlining and setting up the problem is the same as taught in chapter 5, but with problems solved by quadratics you must be very careful to check the solutions in the problem itself. The physical restrictions within the problem can eliminate one or both of the solutions. Example 1 If the length of a rectangle is 1 unit more than twice the width, and the area is 55 square units, find the length and width. Solution The formula for the area of a rectangle is Area = Length X Width. Let x = width, 2x + 1 = length.  At this point, you can see that the solution x = -11/2 is not valid since x represents a measurement of the width and negative numbers are not used for such measurements. Therefore, the solution is width = x = 5, length = 2x + 1 = 11.  .
Remember LCD means lowest common denominator.
Every term must be multiplied by 10x.
Again, this quadratic can be factored. | 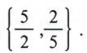 Example 3 If a certain integer is subtracted from 6 times its square, the result is 15. Find the integer. Solution Let x = the integer. Then 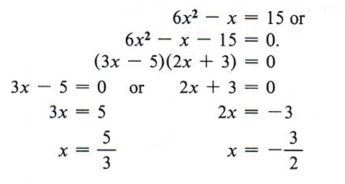 Since neither solution is an integer, the problem has no solution. Example 4 A farm manager has 200 meters of fence on hand and wishes to enclose a rectangular field so that it will contain 2,400 square meters in area. What should the dimensions of the field be? Solution Here there are two formulas involved. P = 2l + 2w for the perimeter and A = lw for the area. First using P = 2l + 2w, we get 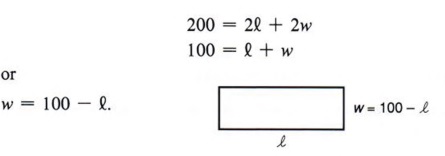 We can now use the formula A = lw and substitute (100 - l) for w, giving 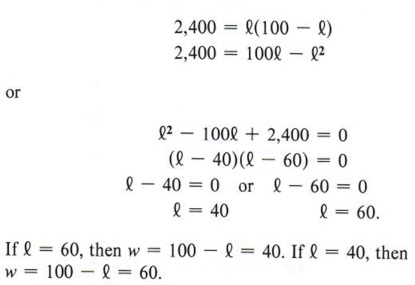 The field must be 40 meters wide by 60 meters long. Note that in this problem we actually use a system of equations P = 2 l + 2 w A = l w. In general, a system of equations in which a quadratic is involved will be solved by the substitution method. (See chapter 6.) - A quadratic equation is a polynomial equation in one unknown that contains the second degree, but no higher degree, of the variable.
- The standard form of a quadratic equation is ax 2 + bx + c = 0, when a ≠ 0.
- An incomplete quadratic equation is of the form ax 2 + bx + c = 0, and either b = 0 or c = 0.
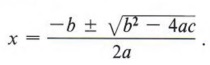 - The most direct and generally easiest method of finding the solutions to a quadratic equation is factoring. This method is based on the theorem: if AB = 0, then A = 0 or B = 0. To use this theorem we put the equation in standard form, factor, and set each factor equal to zero.
- To solve a quadratic equation by completing the square, follow these steps: Step 1 If the coefficient of x 2 is not 1, divide all terms by that coefficient. Step 2 Rewrite the equation in the form of x 2 + bx +_____ = c + _____ Step 3 Find the square of one-half of the coefficient of the x term and add this quantity to both sides of the equation. Step 4 Factor the completed square and combine the numbers on the right-hand side of the equation. Step 5 Find the square root of each side of the equation. Step 6 Solve for x and simplify.
- The method of completing the square is used to derive the quadratic formula.
- To use the quadratic formula write the equation in standard form, identify a, b, and c, and substitute these values into the formula. All solutions should be simplified.
Math TopicsMore solvers. - Add Fractions
- Simplify Fractions
Quadratic equation calculator - Calculators
- triangle ΔABC
- percentage %
- prime factors
- complex numbers
- combinatorics
- ... all maths calculators
- Add to Home
- TigerMilk.Education GmbH
- Privacy policy
- Terms of service
Copyright Ⓒ 2013-2024 tiger-algebra.com This site is best viewed with Javascript. If you are unable to turn on Javascript, please click here . Solution - Adding, subtracting and finding the least common multipleOther Ways to Solve Step by Step SolutionRearrange the equation by subtracting what is to the right of the equal sign from both sides of the equation : 2/x^2+1-(3/x)=0 Step by step solution :Step 1 :, equation at the end of step 1 :, step 2 :, equation at the end of step 2 :, step 3 :, rewriting the whole as an equivalent fraction :. 3.1 Adding a whole to a fraction Rewrite the whole as a fraction using x 2 as the denominator : Equivalent fraction : The fraction thus generated looks different but has the same value as the whole Common denominator : The equivalent fraction and the other fraction involved in the calculation share the same denominator Adding fractions that have a common denominator : 3.2 Adding up the two equivalent fractions Add the two equivalent fractions which now have a common denominator Combine the numerators together, put the sum or difference over the common denominator then reduce to lowest terms if possible: Equation at the end of step 3 :Step 4 :, polynomial roots calculator :. 4.1 Find roots (zeroes) of : F(x) = x 2 +2 Polynomial Roots Calculator is a set of methods aimed at finding values of x for which F(x)=0 Rational Roots Test is one of the above mentioned tools. It would only find Rational Roots that is numbers x which can be expressed as the quotient of two integers The Rational Root Theorem states that if a polynomial zeroes for a rational number P/Q then P is a factor of the Trailing Constant and Q is a factor of the Leading Coefficient In this case, the Leading Coefficient is 1 and the Trailing Constant is 2. The factor(s) are: of the Leading Coefficient : 1 of the Trailing Constant : 1 ,2 Let us test .... | | P | | Q | | P/Q | | F(P/Q) | | Divisor |
|---|
| | -1 | | 1 | | -1.00 | | 3.00 | | | | | -2 | | 1 | | -2.00 | | 6.00 | | | | | 1 | | 1 | | 1.00 | | 3.00 | | | | | 2 | | 1 | | 2.00 | | 6.00 | | |
Polynomial Roots Calculator found no rational roots Calculating the Least Common Multiple : 4.2 Find the Least Common Multiple The left denominator is : x 2 The right denominator is : x Number of times each Algebraic Factor
appears in the factorization of: Algebraic
Factor | Left
Denominator | Right
Denominator | L.C.M = Max
{Left,Right} |
|---|
| x | 2 | 1 | 2 | Least Common Multiple: x 2 Calculating Multipliers : 4.3 Calculate multipliers for the two fractions Denote the Least Common Multiple by L.C.M Denote the Left Multiplier by Left_M Denote the Right Multiplier by Right_M Denote the Left Deniminator by L_Deno Denote the Right Multiplier by R_Deno Left_M = L.C.M / L_Deno = 1 Right_M = L.C.M / R_Deno = x Making Equivalent Fractions : 4.4 Rewrite the two fractions into equivalent fractions Two fractions are called equivalent if they have the same numeric value. For example : 1/2 and 2/4 are equivalent, y/(y+1) 2 and (y 2 +y)/(y+1) 3 are equivalent as well. To calculate equivalent fraction , multiply the Numerator of each fraction, by its respective Multiplier. 4.5 Adding up the two equivalent fractions Trying to factor by splitting the middle term 4.6 Factoring x 2 - 3x + 2 The first term is, x 2 its coefficient is 1 . The middle term is, -3x its coefficient is -3 . The last term, "the constant", is +2 Step-1 : Multiply the coefficient of the first term by the constant 1 • 2 = 2 Step-2 : Find two factors of 2 whose sum equals the coefficient of the middle term, which is -3 . Step-3 : Rewrite the polynomial splitting the middle term using the two factors found in step 2 above, -2 and -1 x 2 - 2x - 1x - 2 Step-4 : Add up the first 2 terms, pulling out like factors : x • (x-2) Add up the last 2 terms, pulling out common factors : 1 • (x-2) Step-5 : Add up the four terms of step 4 : (x-1) • (x-2) Which is the desired factorization Equation at the end of step 4 :Step 5 :, when a fraction equals zero :. Where a fraction equals zero, its numerator, the part which is above the fraction line, must equal zero. Now,to get rid of the denominator, Tiger multiplys both sides of the equation by the denominator. Here's how: Now, on the left hand side, the x 2 cancels out the denominator, while, on the right hand side, zero times anything is still zero. The equation now takes the shape : (x-1) • (x-2) = 0 Theory - Roots of a product : 5.2 A product of several terms equals zero. When a product of two or more terms equals zero, then at least one of the terms must be zero. We shall now solve each term = 0 separately In other words, we are going to solve as many equations as there are terms in the product Any solution of term = 0 solves product = 0 as well. Solving a Single Variable Equation : 5.3 Solve : x-1 = 0 Add 1 to both sides of the equation : x = 1 5.4 Solve : x-2 = 0 Add 2 to both sides of the equation : x = 2 Supplement : Solving Quadratic Equation DirectlyEarlier we factored this polynomial by splitting the middle term. let us now solve the equation by Completing The Square and by using the Quadratic Formula Parabola, Finding the Vertex : 6.1 Find the Vertex of y = x 2 -3x+2 Parabolas have a highest or a lowest point called the Vertex . Our parabola opens up and accordingly has a lowest point (AKA absolute minimum) . We know this even before plotting "y" because the coefficient of the first term, 1 , is positive (greater than zero). Each parabola has a vertical line of symmetry that passes through its vertex. Because of this symmetry, the line of symmetry would, for example, pass through the midpoint of the two x -intercepts (roots or solutions) of the parabola. That is, if the parabola has indeed two real solutions. Parabolas can model many real life situations, such as the height above ground, of an object thrown upward, after some period of time. The vertex of the parabola can provide us with information, such as the maximum height that object, thrown upwards, can reach. For this reason we want to be able to find the coordinates of the vertex. For any parabola, Ax 2 +Bx+C, the x -coordinate of the vertex is given by -B/(2A) . In our case the x coordinate is 1.5000 Plugging into the parabola formula 1.5000 for x we can calculate the y -coordinate : y = 1.0 * 1.50 * 1.50 - 3.0 * 1.50 + 2.0 or y = -0.250 Parabola, Graphing Vertex and X-Intercepts :Solve quadratic equation by completing the square. 6.2 Solving x 2 -3x+2 = 0 by Completing The Square . Subtract 2 from both side of the equation : x 2 -3x = -2 Now the clever bit: Take the coefficient of x , which is 3 , divide by two, giving 3/2 , and finally square it giving 9/4 Add 9/4 to both sides of the equation : On the right hand side we have : -2 + 9/4 or, (-2/1)+(9/4) The common denominator of the two fractions is 4 Adding (-8/4)+(9/4) gives 1/4 So adding to both sides we finally get : x 2 -3x+(9/4) = 1/4 Adding 9/4 has completed the left hand side into a perfect square : x 2 -3x+(9/4) = (x-(3/2)) • (x-(3/2)) = (x-(3/2)) 2 Things which are equal to the same thing are also equal to one another. Since x 2 -3x+(9/4) = 1/4 and x 2 -3x+(9/4) = (x-(3/2)) 2 then, according to the law of transitivity, (x-(3/2)) 2 = 1/4 We'll refer to this Equation as Eq. #6.2.1 The Square Root Principle says that When two things are equal, their square roots are equal. Note that the square root of (x-(3/2)) 2 is (x-(3/2)) 2/2 = (x-(3/2)) 1 = x-(3/2) Now, applying the Square Root Principle to Eq. #6.2.1 we get: x-(3/2) = √ 1/4 Add 3/2 to both sides to obtain: x = 3/2 + √ 1/4 Since a square root has two values, one positive and the other negative x 2 - 3x + 2 = 0 has two solutions: x = 3/2 + √ 1/4 or x = 3/2 - √ 1/4 Note that √ 1/4 can be written as √ 1 / √ 4 which is 1 / 2 Solve Quadratic Equation using the Quadratic Formula 6.3 Solving x 2 -3x+2 = 0 by the Quadratic Formula . According to the Quadratic Formula, x , the solution for Ax 2 +Bx+C = 0 , where A, B and C are numbers, often called coefficients, is given by : - B ± √ B 2 -4AC x = ———————— 2A In our case, A = 1 B = -3 C = 2 Accordingly, B 2 - 4AC = 9 - 8 = 1 Applying the quadratic formula : 3 ± √ 1 x = ———— 2 So now we are looking at: x = ( 3 ± 1) / 2 Two real solutions: x =(3+√ 1 )/2= 2.000 or: x =(3-√ 1 )/2= 1.000 Two solutions were found :How did we do? Why learn thisTerms and topics. - Operations with fractions
- Reducing fractions to lowest terms
Related linksLatest related drills solved.  Online Quadratic Formula CalculatorApply the quadratic formula using wolfram|alpha, a useful tool for finding the solutions to quadratic equations. 2 + b x + c = 0 . In doing so, Wolfram|Alpha finds both the real and complex roots of these equations. It can also utilize other methods helpful to solving quadratic equations, such as completing the square, factoring and graphing.  Learn more about: Tips for entering queriesEnter your queries using plain English. To avoid ambiguous queries, make sure to use parentheses where necessary. Here are some examples illustrating how to ask about finding roots of quadratic equations. - quadratic formula 4x^2 + 4 x - 8
- quadratic formula a = 1, b = -1, c = 2
- solve x^2 - x - 4 = 0
- solve x^2 - 3x - 4 = 0
- View more examples
Access instant learning toolsGet immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator  - Step-by-step solutions
- Wolfram Problem Generator
What are quadratic equations, and what is the quadratic formula?A quadratic is a polynomial of degree two.. Quadratic equations form parabolas when graphed, and have a wide variety of applications across many disciplines. In physics, for example, they are used to model the trajectory of masses falling with the acceleration due to gravity. Situations arise frequently in algebra when it is necessary to find the values at which a quadratic is zero. In other words, it is necessary to find the zeros or roots of a quadratic, or the solutions to the quadratic equation. Relating to the example of physics, these zeros, or roots, are the points at which a thrown ball departs from and returns to ground level. b 2 - 4 a c 2 a , determines the one or two solutions to any given quadratic. Sometimes, one or both solutions will be complex valued. Discovered in ancient times, the quadratic formula has accumulated various derivations, proofs and intuitions explaining it over the years since its conception. Some involve geometric approaches. Others involve analysis of extrema. There are also many others. Those listed and more are often topics of study for students learning the process of solving quadratic equations and finding roots of equations in general. Alternative methods for solving quadratic equations do exist. Completing the square, factoring and graphing are some of many, and they have use cases—but because the quadratic formula is a generally fast and dependable means of solving quadratic equations, it is frequently chosen over the other methods. Quadratic EquationQuadratic equations are second-degree algebraic expressions and are of the form ax 2 + bx + c = 0. The term "quadratic" comes from the Latin word "quadratus" meaning square, which refers to the fact that the variable x is squared in the equation. In other words, a quadratic equation is an “equation of degree 2.” There are many scenarios where a quadratic equation is used. Did you know that when a rocket is launched, its path is described by a quadratic equation? Further, a quadratic equation has numerous applications in physics, engineering, astronomy, etc. Quadratic equations have maximum of two solutions, which can be real or complex numbers. These two solutions (values of x) are also called the roots of the quadratic equations and are designated as (α, β). We shall learn more about the roots of a quadratic equation in the below content. | 1. | | | 2. | | | 3. | | | 4. | | | 5. | | | 6. | | | 7. | | | 8. | | | 9. | | | 10. | | | 11. | | | 12. | | What is Quadratic Equation?A quadratic equation is an algebraic equation of the second degree in x. The quadratic equation in its standard form is ax 2 + bx + c = 0, where a and b are the coefficients, x is the variable, and c is the constant term. The important condition for an equation to be a quadratic equation is the coefficient of x 2 is a non-zero term (a ≠ 0). For writing a quadratic equation in standard form, the x 2 term is written first, followed by the x term, and finally, the constant term is written. 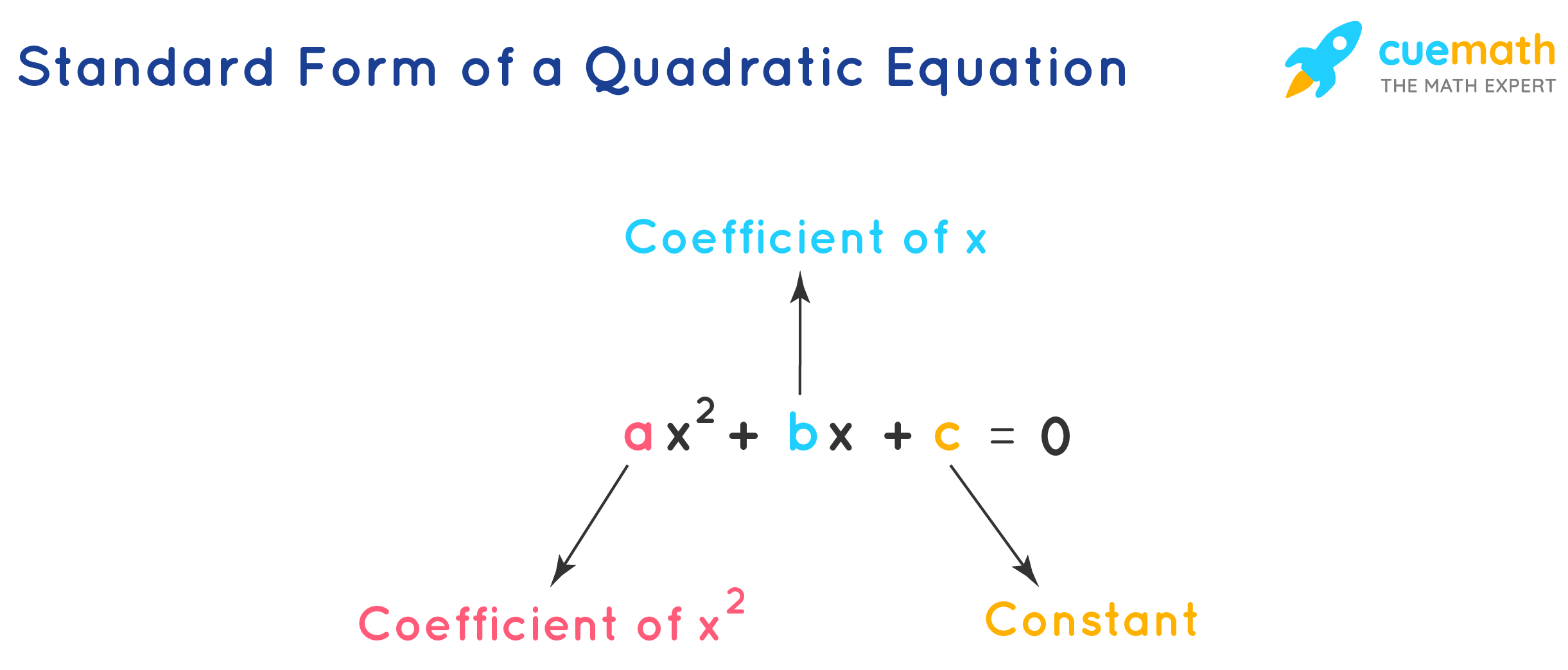 Further, in real math problems the quadratic equations are presented in different forms: (x - 1)(x + 2) = 0, -x 2 = -3x + 1, 5x(x + 3) = 12x, x 3 = x(x 2 + x - 3). All of these equations need to be transformed into standard form of the quadratic equation before performing further operations. Roots of a Quadratic EquationThe roots of a quadratic equation are the two values of x, which are obtained by solving the quadratic equation. These roots of the quadratic equation are also called the zeros of the equation. For example, the roots of the equation x 2 - 3x - 4 = 0 are x = -1 and x = 4 because each of them satisfies the equation. i.e., - At x = -1, (-1) 2 - 3(-1) - 4 = 1 + 3 - 4 = 0
- At x = 4, (4) 2 - 3(4) - 4 = 16 - 12 - 4 = 0
There are various methods to find the roots of a quadratic equation. The usage of the quadratic formula is one of them. Quadratic FormulaQuadratic formula is the simplest way to find the roots of a quadratic equation . There are certain quadratic equations that cannot be easily factorized, and here we can conveniently use this quadratic formula to find the roots in the quickest possible way. The two roots in the quadratic formula are presented as a single expression. The positive sign and the negative sign can be alternatively used to obtain the two distinct roots of the equation. Quadratic Formula: The roots of a quadratic equation ax 2 + bx + c = 0 are given by x = [-b ± √(b 2 - 4ac)]/2a. 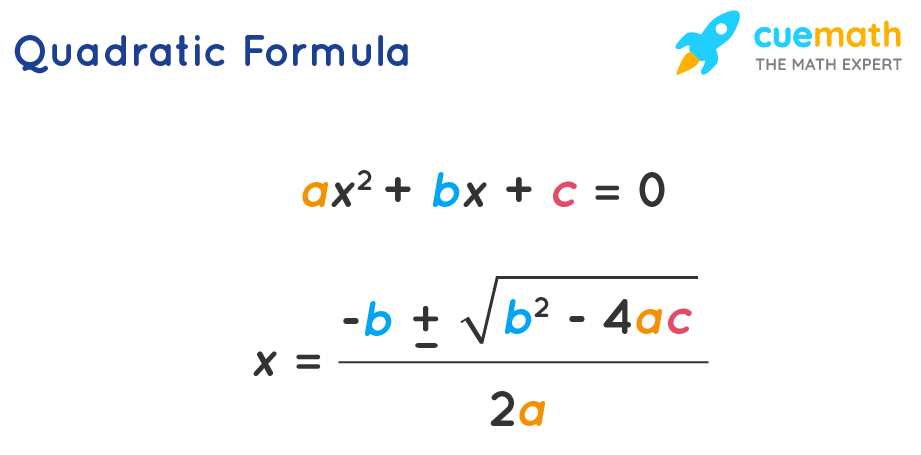 This formula is also known as the Sridharacharya formula . Example: Let us find the roots of the same equation that was mentioned in the earlier section x 2 - 3x - 4 = 0 using the quadratic formula. a = 1, b = -3, and c = -4. x = [-b ± √(b 2 - 4ac)]/2a = [-(-3) ± √((-3) 2 - 4(1)(-4))]/2(1) = [3 ± √25] / 2 = [3 ± 5] / 2 = (3 + 5)/2 or (3 - 5)/2 = 8/2 or -2/2 = 4 or -1 are the roots. Proof of Quadratic FormulaConsider an arbitrary quadratic equation: ax 2 + bx + c = 0, a ≠ 0 To determine the roots of this equation, we proceed as follows: ax 2 + bx = -c ⇒ x 2 + bx/a = -c/a Now, we express the left-hand side as a perfect square , by introducing a new term (b/2a) 2 on both sides: - x 2 + bx/a + (b/2a) 2 = -c/a + (b/2a) 2
The left-hand side is now a perfect square: (x + b/2a) 2 = -c/a + b 2 /4a 2 ⇒ (x + b/2a) 2 = (b 2 - 4ac)/4a 2 This is good for us, because now we can take square roots to obtain: x + b/2a = ±√(b 2 - 4ac)/2a x = (-b ± √(b 2 - 4ac))/2a Thus, by completing the squares, we were able to isolate x and obtain the two roots of the equation. Nature of Roots of the Quadratic EquationThe roots of a quadratic equation are usually represented to by the symbols alpha (α), and beta (β). Here we shall learn more about how to find the nature of roots of a quadratic equation without actually finding the roots of the equation. The nature of roots of a quadratic equation can be found without actually finding the roots (α, β) of the equation. This is possible by taking the discriminant value, which is part of the formula to solve the quadratic equation. The value b 2 - 4ac is called the discriminant of a quadratic equation and is designated as 'D'. Based on the discriminant value the nature of the roots of the quadratic equation can be predicted. Discriminant: D = b 2 - 4ac- D > 0, the roots are real and distinct
- D = 0, the roots are real and equal.
- D < 0, the roots do not exist or the roots are imaginary .
 Now, check out the formulas to find the sum and the product of the roots of the equation. Sum and Product of Roots of Quadratic EquationThe coefficient of x 2 , x term, and the constant term of the quadratic equation ax 2 + bx + c = 0 are useful in determining the sum and product of the roots of the quadratic equation. The sum and product of the roots of a quadratic equation can be directly calculated from the equation, without actually finding the roots of the quadratic equation. For a quadratic equation ax 2 + bx + c = 0, the sum and product of the roots are as follows. - Sum of the Roots: α + β = -b/a = - Coefficient of x/ Coefficient of x 2
- Product of the Roots: αβ = c/a = Constant term/ Coefficient of x 2
Writing Quadratic Equations Using RootsThe quadratic equation can also be formed for the given roots of the equation. If α, β, are the roots of the quadratic equation, then the quadratic equation is as follows. x 2 - (α + β)x + αβ = 0 Example: What is the quadratic equation whose roots are 4 and -1? Solution: It is given that α = 4 and β = -1. The corresponding quadratic equation is found by: x 2 - (α + β)x + αβ = 0 x 2 - (α + β)x + αβ = 0 x 2 - (4 - 1)x + (4)(-1) = 0 x 2 - 3x - 4 = 0 Formulas Related to Quadratic EquationsThe following list of important formulas is helpful to solve quadratic equations. - The quadratic equation in its standard form is ax 2 + bx + c = 0
- For D > 0 the roots are real and distinct.
- For D = 0 the roots are real and equal.
- For D < 0 the real roots do not exist, or the roots are imaginary.
- The formula to find the roots of the quadratic equation is x = [-b ± √(b 2 - 4ac)]/2a.
- The sum of the roots of a quadratic equation is α + β = -b/a.
- The product of the Root of the quadratic equation is αβ = c/a.
- The quadratic equation whose roots are α, β, is x 2 - (α + β)x + αβ = 0.
- The condition for the quadratic equations a 1 x 2 + b 1 x + c 1 = 0, and a 2 x 2 + b 2 x + c 2 = 0 having the same roots is (a 1 b 2 - a 2 b 1 ) (b 1 c 2 - b 2 c 1 ) = (a 2 c 1 - a 1 c 2 ) 2 .
- When a > 0, the quadratic expression f(x) = ax 2 + bx + c has a minimum value at x = -b/2a.
- When a < 0, the quadratic expression f(x) = ax 2 + bx + c has a maximum value at x = -b/2a.
- The domain of any quadratic function is the set of all real numbers.
Methods to Solve Quadratic EquationsA quadratic equation can be solved to obtain two values of x or the two roots of the equation. There are four different methods to find the roots of the quadratic equation. The four methods of solving the quadratic equations are as follows. - Factorizing of Quadratic Equation
- Using quadratic formula (which we have seen already)
Method of Completing the Square- Graphing Method to Find the Roots
Let us look in detail at each of the above methods to understand how to use these methods, their applications, and their uses. Solving Quadratic Equations by FactorizationFactorization of quadratic equation follows a sequence of steps. For a general form of the quadratic equation ax 2 + bx + c = 0, we need to first split the middle term into two terms, such that the product of the terms is equal to the constant term. Further, we can take the common terms from the available term, to finally obtain the required factors as follows: - x 2 + (a + b)x + ab = 0
- x 2 + ax + bx + ab = 0
- x(x + a) + b(x + a)
- (x + a)(x + b) = 0
Here is an example to understand the factorization process. - x 2 + 5x + 6 = 0
- x 2 + 2x + 3x + 6 = 0
- x(x + 2) + 3(x + 2) = 0
- (x + 2)(x + 3) = 0
Thus the two obtained factors of the quadratic equation are (x + 2) and (x + 3). To find its roots, just set each factor to zero and solve for x. i.e., x + 2 = 0 and x + 3 = 0 which gives x = -2 and x = -3. Thus, x = -2 and x = -3 are the roots of x 2 + 5x + 6 = 0. Further, there is another important method of solving a quadratic equation. The method of completing the square for a quadratic equation is also useful to find the roots of the equation. The method of completing the square in a quadratic equation is to algebraically square and simplify, to obtain the required roots of the equation. Consider a quadratic equation ax 2 + bx + c = 0, a ≠ 0. To determine the roots of this equation, we simplify it as follows: - ax 2 + bx + c = 0
- ax 2 + bx = -c
- x 2 + bx/a = -c/a
Now, we express the left-hand side as a perfect square, by introducing a new term (b/2a) 2 on both sides: - (x + b/2a) 2 = -c/a + b 2 /4a 2
- (x + b/2a) 2 = (b 2 - 4ac)/4a 2
- x + b/2a = + √(b 2 - 4ac)/2a
- x = - b/2a + √(b 2 - 4ac)/2a
- x = [-b ± √(b 2 - 4ac)]/2a
Here the '+' sign gives one root and the '-' sign gives another root of the quadratic equation. Generally, this detailed method is avoided, and only the quadratic formula is used to obtain the required roots. Graphing a Quadratic Equation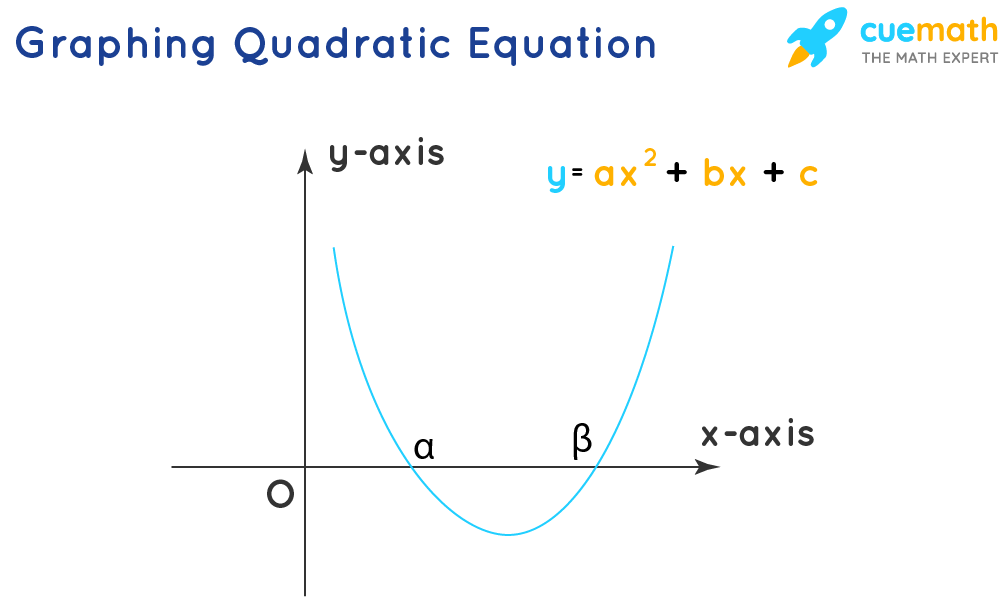 The point(s) where the graph cuts the horizontal x-axis (typically the x-intercepts ) is the solution of the quadratic equation. These points can also be algebraically obtained by equalizing the y value to 0 in the function y = ax 2 + bx + c and solving for x. Quadratic Equations Having Common RootsConsider two quadratic equations having common roots a 1 x 2 + b 1 x + c 1 = 0, and a 2 x 2 + b 2 x + c 2 = 0. Let us solve these two equations to find the conditions for which these equations have a common root. The two equations are solved for x 2 and x respectively. (x 2 )(b 1 c 2 - b 2 c 1 ) = (-x)/(a 1 c 2 - a 2 c 1 ) = 1/(a 1 b 2 - a 2 b 1 ) x 2 = (b 1 c 2 - b 2 c 1 ) / (a 1 b 2 - a 2 b 1 ) x = (a 2 c 1 - a 1 c 2 ) / (a 1 b 2 - a 2 b 1 ) Hence, by simplifying the above two expressions we have the following condition for the two equations having the common root. (a 1 b 2 - a 2 b 1 ) (b 1 c 2 - b 2 c 1 ) = (a 2 c 1 - a 1 c 2 ) 2 Maximum and Minimum Value of Quadratic Expression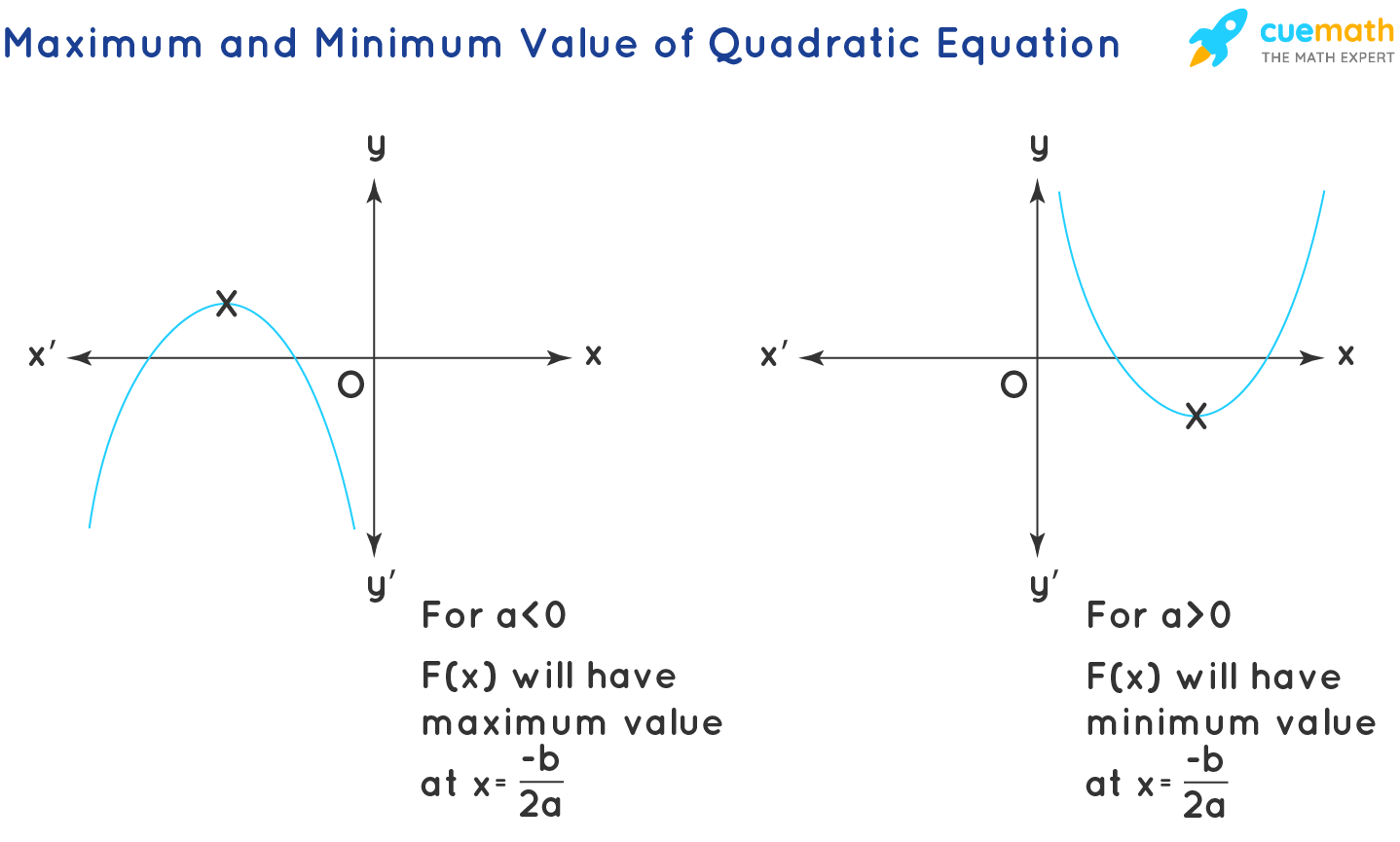 The maximum and minimum values of the quadratic expressions are of further help to find the range of the quadratic expression: The range of the quadratic expressions also depends on the value of a. For positive values of a( a > 0), the range is [ F(-b/2a), ∞), and for negative values of a ( a < 0), the range is (-∞, F(-b/2a)]. - For a > 0, Range: [ f(-b/2a), ∞)
- For a < 0, Range: (-∞, f(-b/2a)]
Note that the domain of a quadratic function is the set of all real numbers, i.e., (-∞, ∞). Tips and Tricks on Quadratic Equation: Some of the below-given tips and tricks on quadratic equations are helpful to more easily solve quadratic equations. - The quadratic equations are generally solved through factorization. But in instances when it cannot be solved by factorization, the quadratic formula is used.
- The roots of a quadratic equation are also called the zeroes of the equation.
- For quadratic equations having negative discriminant values, the roots are represented by complex numbers.
- The sum and product of the roots of a quadratic equation can be used to find higher algebraic expressions involving these roots.
☛Related Topics: - Roots Calculator
- Quadratic Factoring Calculator
- Roots of Quadratic Equation Calculator
Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12 . Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs. Quadratic Equations ExamplesExample 1: James is a fitness enthusiast and goes for a jog every morning. The park where he jogs is rectangular in shape and measures 12m × 8m. An environmentalist group plans to revamp the park and decides to build a pathway surrounding the park. This would increase the total area to 140 sq m. What will be the width of the pathway? Let’s denote the width of the pathway by x. Then, the length and breadth of the outer rectangle is (12+2x) m and (8+2x) m. Given that, area = 140 (12 + 2x)(8 + 2x) = 140 2(6 + x) 2(4 + x) = 140 (6 + x)(4 + x) = 35 24 + 6x + 4x + x 2 = 35 x 2 + 10x -11 = 0 x 2 + 11x - x - 11 = 0 x(x + 11) - 1(x + 11) = 0 (x + 11)(x - 1) = 0 (x + 11) =0 and (x - 1) = 0 x = -11 and x = 1 Since length can’t be negative, we take x = 1. Answer: Therefore the width of the pathway is 1 m. Example 2: Rita throws a ball upwards from a platform that is 20m above the ground. The height of the ball from the ground at a time 't', is denoted by 'h'. Suppose h = -4t 2 + 16t + 20. Find the maximum height attained by the ball. We can rearrange the terms of the quadratic equation h = -4t 2 + 16t + 20 in such a way that it is easy to find the maximum value of this equation. = -4t 2 + 16t + 20 = -4(t 2 - 4t - 5) = -4((t - 2) 2 - 9) = -4(t - 2) 2 + 36 We should keep the value of (t - 2) 2 minimum in order to find the maximum value of h. So, the minimum value (t - 2) 2 can take is 0. Answer: Therefore the maximum height attained is 36m. Example 3: Find the quadratic equation having the roots 5 and 8 respectively. The quadratic equation having the roots α, β, is x 2 - (α + β)x + αβ = 0. Given α = 5, and β = 8. Therefore the quadratic equation is: x 2 - (5 + 8)x + 5×8 = 0 x 2 - 13x + 40 = 0 Answer: Hence the required quadratic equation is x 2 - 13x + 40 = 0 Example 4: The quad equation 2x 2 + 9x + 7 = 0 has roots α, β. Find the quadratic equation having the roots 1/α, and 1/β. The quadratic equation having roots that are reciprocal to the roots of the equation ax 2 + bx + c = 0, is cx 2 + bx + a = 0. The given quadratic equation is 2x 2 + 9x + 7 = 0. Hence the required equation having reciprocal roots is 7x 2 + 9x + 2 = 0. Method 2: From the given equation, α + β = -9/2 and α β = 2/7. The new equation should have its roots to be 1/α and 1/β. Their sum = 1/α + 1/β = (α + β) / α β = -9/7 Their product = 1/α β = 2/7 Thus, the required equation is, x 2 - (1/α + 1/β)x + 1/α β = 0 x 2 - (-9/7)x + 2/7 = 0 Multiplying both sides by 7, 7x 2 + 9x + 2 = 0 Answer: Therefore the equation is 7x 2 + 9x + 2 = 0. go to slide go to slide go to slide go to slide  Book a Free Trial Class Practice Questions on Quadratic Equationgo to slide go to slide FAQs on Quadratic EquationWhat is the definition of a quadratic equation. A quadratic equation in math is a second-degree equation of the form ax 2 + bx + c = 0. Here a and b are the coefficients, c is the constant term, and x is the variable. Since the variable x is of the second degree, there are two roots or answers for this quadratic equation. The roots of the quadratic equation can be found by either solving by factorizing or through the use of the quadratic formula. What is the Quadratic Formula?The quadratic equation formula to solve the equation ax 2 + bx + c = 0 is x = [-b ± √(b 2 - 4ac)]/2a. Here we obtain the two values of x, by applying the plus and minus symbols in this formula. Hence the two possible values of x are [-b + √(b 2 - 4ac)]/2a, and [-b - √(b 2 - 4ac)]/2a. How do You Solve a Quadratic Equation?There are several methods to solve quadratic equations, but the most common ones are factoring, using the quadratic formula, and completing the square. - Factoring involves finding two numbers that multiply to equal the constant term, c, and add up to the coefficient of x, b.
- The quadratic formula is used when factoring is not possible, and it is given by x = [-b ± √(b 2 - 4ac)]/2a.
- Completing the square involves rewriting the quadratic equation in a different form that allows you to easily solve for x.
What is Determinant in Quadratic Formula?The value b 2 - 4ac is called the discriminant and is designated as D. The discriminant is part of the quadratic formula. The discriminants help us to find the nature of the roots of the quadratic equation, without actually finding the roots of the quadratic equation. What are Some Real-Life Applications of Quadratic Equations?Quadratic equations are used to find the zeroes of the parabola and its axis of symmetry . There are many real-world applications of quadratic equations. - They can be used in running time problems to evaluate the speed, distance or time while traveling by car, train or plane.
- Quadratic equations describe the relationship between quantity and the price of a commodity.
- Similarly, demand and cost calculations are also considered quadratic equation problems.
- It can also be noted that a satellite dish or a reflecting telescope has a shape that is defined by a quadratic equation.
How are Quadratic Equations Different From Linear Equations?A linear degree is an equation of a single degree and one variable, and a quadratic equation is an equation in two degrees and a single variable. A linear equation is of the the form ax + b = 0 and a quadratic equation is of the form ax 2 + bx + c = 0. A linear equation has a single root and a quadratic equation has two roots or two answers. Also, a quadratic equation is a product of two linear equations. What Are the 4 Ways To Solve A Quadratic Equation?The four ways of solving a quadratic equation are as follows. - Factorizing method
- Roots of Quadratic Equation Formula Method
- Method of Completing Squares
- Graphing Method
How to Solve a Quadratic Equation by Completing the Square?The quadratic equation is solved by the method of completing the square and it uses the formula (a + b)^2 = a 2 + 2ab + b 2 (or) (a - b)^2 = a 2 - 2ab + b 2 . How to Find the Value of the Discriminant?The value of the discriminant in a quadratic equation can be found from the variables and constant terms of the standard form of the quadratic equation ax 2 + bx + c = 0. The value of the discriminant is D = b 2 - 4ac, and it helps to predict the nature of roots of the quadratic equation, without actually finding the roots of the equation. How Do You Solve Quadratic Equations With Graphing?The quadratic equation can be solved similarly to a linear equal by graphing. Let us take the quadratic equation ax 2 + bx + c = 0 as y = ax 2 + bx + c . Here we take the set of values of x and y and plot the graph. The two points where this graph meets the x-axis, are the solutions of this quadratic equation. How Important Is the Discriminant of a Quadratic Equation?The discriminant is very much needed to easily find the nature of the roots of the quadratic equation. Without the discriminant, finding the nature of the roots of the equation is a long process, as we first need to solve the equation to find both the roots. Hence the discriminant is an important and needed quantity, which helps to easily find the nature of the roots of the quadratic equation. Where Can I Find Quadratic Equation Solver?To get the quadratic equation solver, click here . Here, we can enter the values of a, b, and c for the quadratic equation ax 2 + bx + c = 0, then it will give you the roots along with a step-by-step procedure. What is the Use of Discriminants in Quadratic Formula?The discriminant (D = b 2 - 4ac) is useful to predict the nature of the roots of the quadratic equation. For D > 0, the roots are real and distinct, for D = 0 the roots are real and equal, and for D < 0, the roots do not exist or the roots are imaginary complex numbers . With the help of this discriminant and with the least calculations, we can find the nature of the roots of the quadratic equation. How do you Solve a Quadratic Equation without Using the Quadratic Formula?There are two alternative methods to the quadratic formula. One method is to solve the quadratic equation through factorization, and another method is by completing the squares. In total there are three methods to find the roots of a quadratic equation. How to Derive Quadratic Formula?The algebra formula (a + b) 2 = a 2 + 2ab + b 2 is used to solve the quadratic equation and derive the quadratic formula. This algebraic formula is used to manipulate the quadratic equation and derive the quadratic formula to find the roots of the equation. For what value of k are the roots of the quadratic equation 3x² 2kx 27/0 real and equal?For the values k = 9 and k = -9 the roots of the quadratic equation 3x²+ 2kx + 27 = 0 real and equal . What is quadratic equation? Any equation in algebra that can be rearranged in standard form as : [tex]ax^2 + bx + c = 0[/tex] is known as a quadratic equation (from the Latin quadratus, " square "). where a ≠ 0 and a, b, and c are known numbers, x is an unknown value, and a. The equation is linear, not quadratic , if a = 0 and b ≠ 0. The coefficients of the equation, denoted by the numbers a, b, and c, are the quadratic coefficient, linear coefficient, and constant or free term, respectively. The given equation is, [tex]3x^2 + 2kx + 27 = 0[/tex] ⇒ a = 3, b = 2k, c = 27 It is given that roots are real and equal. [tex]b^2 - 4ac = 0[/tex] Plug the values of a, b, c in the above equation. [tex](2k)^2 - 4(3)(27) = 0\\4k^2 - 324=0\\4k^2 = 324\\k^2 = 81[/tex] Hence, for the values k = 9 and k = -9 the roots of the quadratic equation 3x²+ 2kx + 27 = 0 real and equal . To know more about quadratic equation , click on the link https://brainly.com/question/1214333 Related QuestionsHow do you prove the transitive property of similarity? We can prove the transitive property of similarity as following. To prove the transitive property of similarity, you need to show that if two figures are similar to a third figure , then they are also similar to each other. Here's one way to prove it: Let's say we have three figures: A, B, and C. We want to prove that if A is similar to B, and B is similar to C, then A is similar to C. First, we need to show that A is similar to B. We can do this by showing that the corresponding angles of A and B are congruent, and the ratios of the lengths of the corresponding sides of A and B are equal. Next, we need to show that B is similar to C. We can do this in the same way by showing that the corresponding angles of B and C are congruent, and the ratios of the lengths of the corresponding sides of B and C are equal. Finally, we can use the property of transitive relations to conclude that A is similar to C. This is because if A is related to B, and B is related to C, then A must also be related to C. In other words, if A is similar to B and B is similar to C, then A must also be similar to C because similarity is a transitive relation. To learn more about transitive property of similarity, visit; brainly.com/question/2547884 there are 195 people in a movie theater 117 of them people are eating popcorn what the percentage of the people that are eating popcorn is Answer: 60% Step-by-step explanation: you just have to divide the amount eating the popcorn by the total amount of people… so 117/195 which is 0.6 or 60%. Hope this helps!! Is the unit circle a formula? No, the unit circle is a visual representation of a mathematical concept , not a formula. The unit circle is a visual representation of a mathematical concept, not a formula. It is a circle with a radius of 1, centered at the origin of a coordinate plane. The unit circle is commonly used to represent the trigonometric functions sine, cosine, and tangent. It is used to model periodic functions, such as waveforms and graphs of sine and cosine, and can be used to find the angles of a triangle given the lengths of its sides. It can also be used to solve equations involving angles in a right triangle and to find the area of a sector in a circle. Learn more about circle here https://brainly.com/question/11878555 For items 7-10, use the figure shown. Find the coordinates of the specified vertex after the given sequence of transformations. Quadrilateral Q R S T plotted on a coordinate plane with vertices at, Q, (1, 3), R, (3, negative 3), S, (zero, negative 2), and T, (negative 2, 1). a translation 2 units right, then a reflection across x = 0 Q' = ( , ) The coordinates of the specified vertex after the given sequence of transformations is given by; Q' = (3, -3). In Mathematics, the translation of a geometric figure to the right simply means adding a digit to the value on the x-coordinate (x-axis) of the pre-image of a function while a geometric figure that is translated up simply means adding a digit to the value on the y-coordinate (y-axis) of the pre-image or parent function. Mathematically, a horizontal translation to the right is modeled by this mathematical expression g(x) = f(x + N) while a vertical translation to the positive y-direction (upward) is modeled by this mathematical expression g(x) = f(x) + N. By translating the coordinate Q (1, 3) two (2) units to the right , we have the following: Coordinate Q (1, 3) → Coordinate Q' (1 + 2, 3) = Q (3, 3) In Mathematics, a reflection across the x-axis would maintain the same x-coordinate while the sign of the y-coordinate would change from positive to negative. Therefore, a reflection over the x-axis is given by this transformation rule: (x, y) → (x, -y) Coordinate Q' (3, 3) → (3, -3). Read more on reflection here: brainly.com/question/10260342 Why does AAA similarity work? AAA similarity works because it compares the angles between three points in space and determines whether they are congruent. According to the Angle-Angle-Angle (AAA) criterion, "if in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio (or proportion), and hence the two triangles are identical." AAA similarity is a way to determine whether or not three shapes are similar, meaning that they have the same shape but may be different sizes. This is significant because it allows us to make predictions about the relationships between the sides and angles of the shapes, which can be useful in a variety of contexts such as solving geometry problems or comparing the shapes of objects in the real world. AAA similarity works because it compares the angles between three points in space and determines whether they are congruent. Congruent angles have the same measure, so if the three angles in two different shapes are congruent, it follows that the shapes are similar. Think about the triangles ABC and DEF as an illustration. The triangles are comparable if we can demonstrate that the angles at A, B, and C are congruent to the angles at D, E, and F, respectively. We would need to calculate and compare each triangle's angles in order to accomplish this. According to the AAA similarity criterion, the triangles are similar if they are all equal. To learn more about AAA similarity visit: https://brainly.com/question/29887944 if 23 37 = 60, does 23 + 37 + 9 = 60 + 9 Yes or no, Multiply f(x) = (x + 2)(x + 3)(x − 1)(x − 3 Answer: [tex]x^{4}[/tex] + [tex]x^{3}[/tex] −11 [tex]x^{2}[/tex] −9x+18−f(x)=0 Step-by-step explanation: Solve for f(x) by simplifying both sides of the equation, then isolating the variable. Dr fisher is researching the growth culture of bacteria. He records the count of bacteria, y, after x hours. He wants to determine whether there is a relationship between the amount of time passed and the count of bacteria. He finds that the linear model that best fits the data is y= -143+51x The correct answer is option D . Because the residuals do not form a pattern, there is a linear relationship between the amount of time and the count of bacteria as demonstrated by y= -143+51x. Residuals are the differences between the observed values and the predicted values of a variable , and they are used to assess the fit of a statistical model. If the residuals form a random , non-patterned distribution , this suggests that the model is a good fit for the data and that there is a linear relationship between the variables being modeled. On the other hand, if the residuals form a pattern, this suggests that the model is not a good fit for the data and that there may be other factors influencing the relationship between the variables being modeled. Read more about the Linear model function : brainly.com/question/28033207 Error Analysis A garderer plans to extend the length of a rectangular garden by 4 feet. Let x represent the garden's original length. The expression 8(x + 4) represents the area of the garden, where 8 is the width, in feet, and (x + 4) represents the extended length, in feet, of the garden. When asked for the area of the extended portion, the gardener incorrectly said it was 12 square feet. Expand the expression to find the area of the extension. Then describe an error the gardener might have made. The correct Area of extended portion will be 28 square feet A rectangle in the Euclidean plane is a quadrilateral with four right angles . Other names for it include a parallelogram with a right angle and an equiangular quadrilateral , where equiangular means that all of its angles are equal. Four equally long sides make to a square, which is a rectangle. Area of original garden=length*breadth=4 × x=4x square feet Area of extended garden=4 × 7=28 sq. feet Total area (including the extended portion)=4x+28= 4(x+7) square feet The mistake made by gardener is that he added 4+7=11 square feet But correct area of extended portion= length*breadth=4 × 7=28 square feet. Learn more about Area : brainly.com/question/11952845 A sociologist recorded the number of contacts entered in a cell phone and the number of texts sent in a week for 20 cell phone users. The resulting data were used to conduct a hypothesis test to investigate whether there is a linear relationship between the number of contacts and the number of texts sent. What are the correct hypothesis for the test The correct hypothesis for the test would be the Null hypothesis (H0): There is no linear relationship between the number of contacts and the number of texts sent. Alternative hypothesis (H1): There is a linear relationship between the number of contacts and the number of texts sent. The null hypothesis is the default assumption that there is no relationship between the two variables being studied. The alternative hypothesis is the hypothesis that the researcher hopes to prove through the study. In this case, the sociologist is attempting to determine if there is a linear relationship between the number of contacts and the number of texts sent in a week for cell phone users. To learn more about the linear relationship , visit: brainly.com/question/29066440 what is the answer???? (3[tex]\sqrt{3x}[/tex])/3x+2, x can not be -2/3 You basically divide the two functions. (I hope it's correct) Which table could represent a proportional relationship? For A, y=1,300x what does it mean for the relationship between the variables when the correlation is positive in this situation? When the correlation between two variables is positive, it means that there is a direct relationship between the two variables, meaning that as one variable increases, the other variable also increases , and as one variable decreases, the other variable also decreases . A positive correlation coefficient ranges between 0 and 1, and it suggests that the two variables have a direct relationship, meaning that if one variable increases, the other variable will also increase. In other words, the two variables tend to move in the same direction. A positive correlation suggests that there is a perfect positive correlation, meaning that the two variables move exactly in the same direction. For example, if you were studying the relationship between the number of hours studied and the grade obtained, a positive correlation would mean that the more hours one study, the higher the grade will be, and the fewer hours one studies the lower the grade will be. Learn more about positive correlation here: https://brainly.com/question/28093573 How many solutions we get in parallel? We get no solutions in Parallel lines . What are parallel lines? Two lines in the same plane that are equally spaced apart and never cross each other are said to be parallel lines in geometry . Both horizontal and vertical lines are possible. The two lines existing simultaneously beside each other at a specified distance without crossing each other are parallel lines . Let us consider two equations of parallel lines - 2x+3y=1... eq (1) 4x+6y=4... eq (2) When two linear equations are parallel , the following outcome is obtained - a1/a2=b1/b2[tex]\neq[/tex]c1/c2 [No Solution] Simplifying the two equations - 2/4=3/6[tex]\neq[/tex]1/4 Therefore, the parallel lines give no solution. To learn more about parallel lines from the given link https://brainly.com/question/16742265 Is 3 a domain or range? The terms domain and range are not applicable for the given function x = 3. What is the domain and range of the function? The domain of a function is the set of all input values that the function is defined for. The range of a function is the set of all possible output values of the function. A function is a mapping of values from one set, called the domain, into another set, called the range, with the provision that no single value in the domain can map into more than one value in the range. x=3 is not a function in the normal sense. Hence, the terms domain and range are not applicable for the given function x = 3. To learn more about the domain and range of the function , visit: https://brainly.com/question/17021809 Given the function f(x) = 3x 1 and the linear function g(x), which function has a greater slope? positive linear function increasing through 2 comma 3 and 3 comma 7 f(x) has a greater slope. g(x) has a greater slope. the slopes of f(x) and g(x) are the same. the slope of g(x) is undefined. The correct option is f(x) is greater than g(x).Because we get the new function by putting value of x. we get by performing f first and then performing g. A linear function is a function that has either one or two variables without exponents.Linear functions has a graph in a straight line.The slope of linear function is always constant because the slope of a straight line is always constant. The function f with g is (f∘g)(x)=f(g(x)) and is read f of g of x . It means that wherever there is an x in the function f , it is replaced with the function g(x).we can find f(x) and g(x) by adding value of x in the function. Now we have when x=3 we get f(x)= 3(3) +1 Similarly from graph of g(x) f(3) > g(3) Hence proved that f(x) is greater than g(x). To learn more about function of f(x) and g(x) visit; https://brainly.com/question/20317632 Solve for X. 4(5+x)/3 = 2x + 2 [tex]\frac{4(5+x)}{3}[/tex] = 2x + 2 Multiply both sides by 3 ([tex]\frac{3}{1}[/tex])[tex]\frac{4(5+x)}{3}[/tex] = 3(2x + 2) Distribute the 3 4(5+x) = 6x + 6 Distribute the 4 20 + 4x = 6x + 6 Subtract 4x from both sides 20 + 4x - 4x + 6x -4x + 6 20 = 2x + 6 Subtract 6 from both sides 20 - 6 = 2x + 6 -6 14 = 2x Divide both sides by 2 What is the area, in square feet, of the shape below? Express your answer as a fraction in simplest form. The area of the triangle is 2/25 ft² The entire area that is bounded by a triangle's three sides is referred to as the triangle's area . The formula for the area of a triangle is given by Here we have Triangle From the given figure, => Base of the triangle = 4/5 ft => Height of the triangle = 1/5 ft Area of triangle = (1/2)×base × height => Area of the triangle = [tex]\frac{1}{2} \times (\frac{1}{5} )\times (\frac{4}{5} )[/tex] = [tex]\frac{1}{1} \times (\frac{1}{5} )\times (\frac{2}{5} )[/tex] = [tex]\frac{2}{25}[/tex] Learn more about the Area of the triangle is https://brainly.com/question/29156501 The sum of integers from (-20) to 15 is p . What will be the sum of integers from (-22) to 17? Enter the number in the blank space to complete the answer. The answer will be (p-10) -20-19-18-...-1+ 0 +... +14 + 15=p. So sum of integers from -22 to 17. -22-21+p+16+ 17. =-43+p+33. =-10+p = p-10 (And) Answer: To find the sum of the integers from -22 to 17, we can first find the sum of the integers from -20 to 15 and then add or subtract the appropriate values to get the sum of the integers from -22 to 17. Step-by-step explanation: The sum of the integers from -20 to 15 can be found using the formula for the sum of an arithmetic series : Sum = (number of terms) * (average of the first and last term) In this case, the number of terms is 36 (because there are 36 integers from -20 to 15, inclusive), and the average of the first and last term is -20 + 15 = -5 / 2 = -2.5 . Plugging these values into the formula, we get: Sum = 36 * (-2.5) = -90 To find the sum of the integers from -22 to 17, we need to add the values -22 and -21 to this sum and subtract the value 16. This gives us a final sum of -90 + (-22) + (-21) - 16 = -109. Therefore, the sum of the integers from -22 to 17 is -109. Read more about integers https://brainly.com/question/929808 solving systems by substitution x+y=10 4x-3y=12 Times the first equation by three and solve 3x + 3y = 30 4x - 3y = 12 Then put 6 back in to solve for y 4(6) - 3y = 12 24 - 3y = 12 Let's check So, my answer is correct! assume you are asked to create a model that predicts the number of new babies born per period according to the size of the stork population. in this case, the number of babies is multiple choice an outcome. a feature. an observation. a target. The number of babies in this problem is classified as an: For each student, we have an input variable and an output variable, given as follows: For this problem, we have that the number of babies is predicted according to the size of the stork population, hence the variables are given as follows: This means that the number of babies can be classified as either the target variable or the outcome, as it is the output of the study, and then either the first and the last options are correct. More can be learned about target variables at https://brainly.com/question/13813326 What is the vertical asymptote of f/x )= log5x? The required vertical asymptote of the function f(x )= log5x is x=0. A vertical line that appears to coincide with a function's graph but never actually does so is known as a vertical asymptote. When graphing a function, a function's vertical asymptote is crucial. Set ax + b to 0 and do a numerical analysis of x to determine the vertical asymptotes of the logarithmic function f(x) = log (ax + b). given, f(x )= log(5x) => x=0/5 = 0 Thus, the vertical asymptote of f(x )= log5x is x=0. To learn more about the vertical asymptote visit: brainly.com/question/4138300 Rectangle a b c d is rotated around line m. line m bisects the rectangle and splits side a b into 2, 6 inch pieces. sides a d and b d are 5 inches. what solid will be produced if rectangle abcd is rotated around line m? assume that the line bisects both sides it intersects. what will the dimensions of the three-dimensional solid be? rectangular prism; length = 12 in.; width = 6 in.; height = 5 in. triangular prism; length = 12 in.; width = 6 in.; height = 5 in. cylinder; radius = 12 in.; height = 5 in. cylinder; radius = 6 in.; height = 5 in. A cylinder with a radius of 6 inches and a height of 5 inches is produced if rectangle ABCD is rotated around line m. A solid figure is a 3-dimensional shape (length, width, and height) so that it has a volume inside. Examples of solid figures are prism , cylinder , cone , pyramid , and so on. From the question we get the following information: - rectangle ABCD - line m divides side AB into 2, each 6 inches - the length of side AD and BD is 5 inches So, when we rotate rectangle ABCD around line m, it will produce a cylinder, with: - cylinder height = AD = BD = 5 inches - cylinder diameter = 1/2 AB = 6 inches To get the best illustration of the problem, we can draw rectangle ABCD and line m. So the solid figure produces if we rotate rectangle ABCD around line m is a cylinder with a radius of 6 inches and a height of 5 inches. To learn more about solid figures , click here: https://brainly.com/question/16054481 Answer: D) cylinder; radius = 6 in.; height = 5 in. How do you solve unknown angle problems in algebra? To find any unknown angle in algebra we use the different properties of the angles. Some of the properties of angle include alternate interior angle, corresponding angles, exterior angle as well as sum of the angles. Suppose we have a quadrilateral having three angles as 75°, 85° and 95° and we need to find the unknown angle. We know that the sum of all the interior angles of quadrilateral is equal to 360°. So we assume that the unknown angle is x°. By using the property we write the algebraic expression as x° + 75° + 85° + 95° = 360° x° + 255° = 360° x° = 360° - 255° Thus the unknown angle is determined by using geometry as well as algebra. Learn more about Quadrilateral at: brainly.com/question/23935806 What is a sphere Grade 5? A sphere is a three-dimensional shape that looks like a ball. It is made up of all points that are the same distance from the center point. A sphere has no edges or corners and all points on its surface are the same distance from the center. A sphere is a three-dimensional shape that looks like a ball. It is made up of all points that are the same distance from the center point. This makes it a very strong shape as all points on its surface are the same distance from the center, meaning it can withstand a lot of force in different directions. It has no edges or corners, making it a smooth and round shape. The mathematical formula for the area of a sphere is 4πr2, where r is the radius of the sphere. Spheres are often used in sports and games, such as soccer balls and billiard balls, due to their perfectly round shape. Spheres are also used in engineering and architecture for their strength, as well as for aesthetic reasons. Spheres have many applications in everyday life and can be found in a variety of shapes and sizes. Learn more about distance here https://brainly.com/question/28956738 Use the Distributive Property to solve the equation below. 40 - (3c + 4) = 2(c + 6) + c 40-3c-4c=2c+12+c 40-7c=3c+12 40-12=3c+7c A bus traveling at 40 m/s accelerates at a constant rate of 3. 5 m/s2 over a distance of 50 m. What is its speed after accelerating? The speed after accelerating is 44 m/s The given parameters are The initial speed of the bus is 40m/s The acceleration of the bus = 3.5m/s²² The distance covered by the bus = 50 m We can find the final speed of the bus using the formula ⇒V= ⇒40 +3.5*5/4 Note that t=d/s t= 50/40 = 5/4 This means that V= 40+ (3.5*5)/4 V=40 + 4.375 Velocity = 44.375m/s In conclusion, the speed of the bus after accelerating is 44m/s Learn more about speed on https://brainly.com/question/28224010 Patricia wants to solve the system using linear combination by eliminating the x - terms first. multiple the first equation by -5 -10x + 45y = 40 multiple the second equation by 2 10x + 2y = -40 47y = 0 The x's dropped out. Greg swims at a steady rate of 8 miles per hour. Determine the constant of proportionality. When Greg swims at a steady rate of 8 miles per hour, the constant of proportionality is 8. The ratio connecting two given values in what is known as a proportional relationship is the constant of proportionality. The constant of proportionality may also be referred to as the constant ratio, constant rate, unit rate, constant of variation, or even the rate of change. For direct proportion, in order to find the value of 'k' in a direct proportionality , use the formula b = ka. From this formula k = b/a. For indirect proportion: To determine the value of 'k' in indirect proportionality, use the formula b = k/a. Since Greg swims at a steady rate of 8 miles per hour, the constant is 8. Learn more about constant on: https://brainly.com/question/924976 A farmer is plowing his cornfields. The relationship _ between , the driving the plow, and , the number of rows of corn plowed, is shown in the graph at the right. a. What does the point represent? b. Choose an ordered pair to find the constant of proportionality. c. Write an equation to represent the situation. TIME ( ) r asked to determine if the statements below represent the graph. a) The point (0,0) represents the fact that at zero hours, the farmer has not plowed any row. b) The ordered pair that gives the constant of proportionality is of: (4,60). c) The equation is of: y = 15x. A proportional relationship is defined as follows: Meaning that it is a special case of a linear function, with intercept of zero, meaning that it always passes through the origin, and the constant of proportionality k represents the slope. From the graph given by the image at the end of the answer, one ordered pair is given as follows: Then the constant of proportionality is calculated as follows: Then the equation that represents the relationship is: The problem is given by the image shown at the end of the answer. More can be learned about proportional relationships at brainly.com/question/10424180  | 

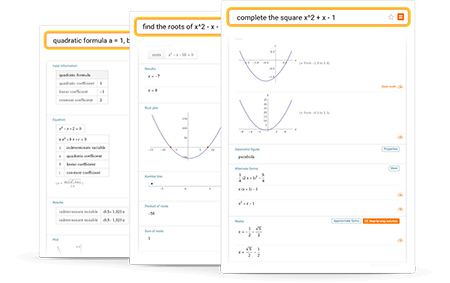


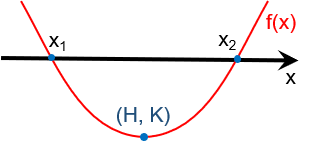













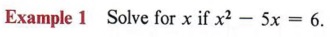
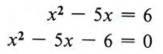
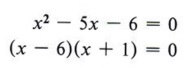
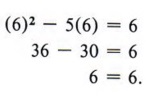
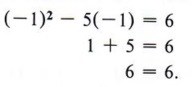
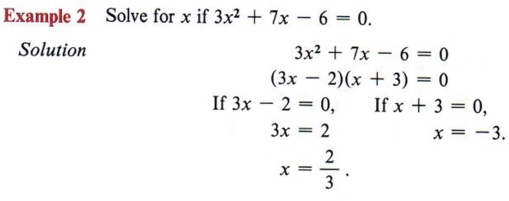


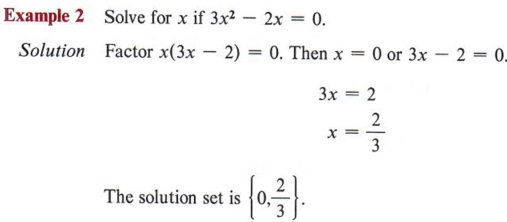


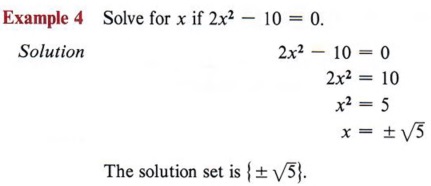
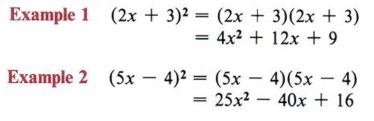

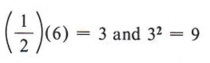
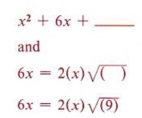
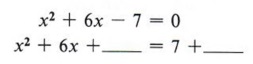
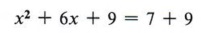
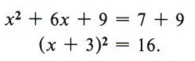

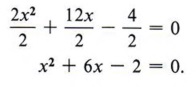
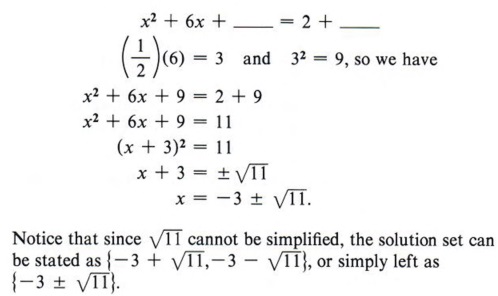

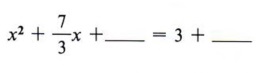
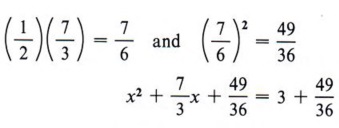
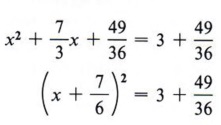
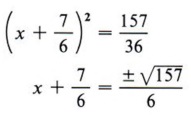
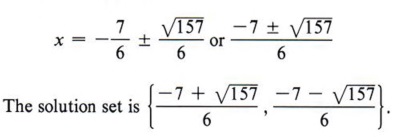
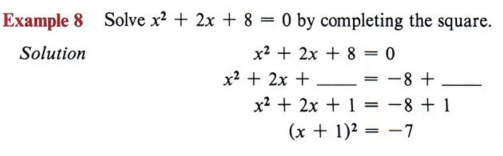
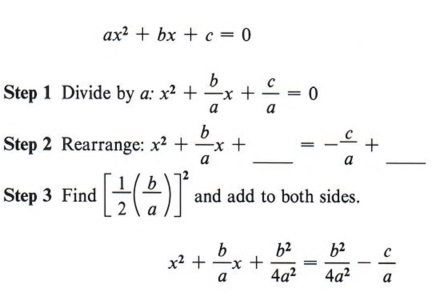

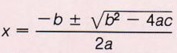

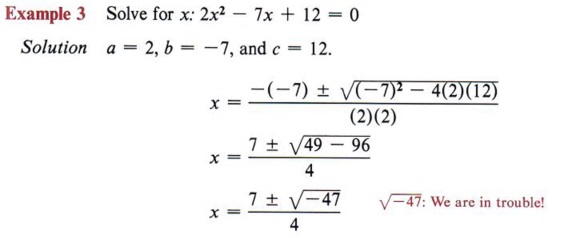
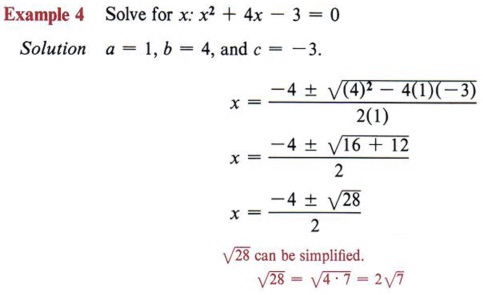
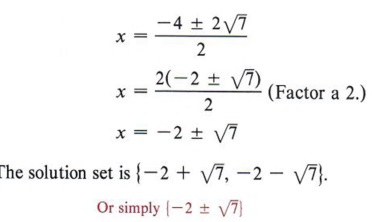


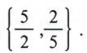
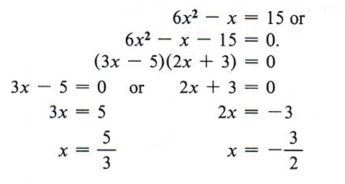

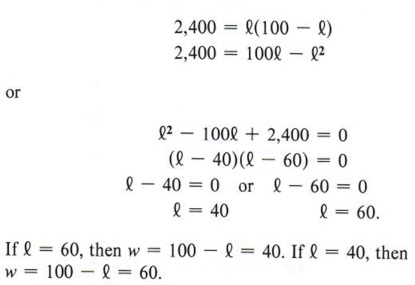
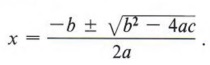





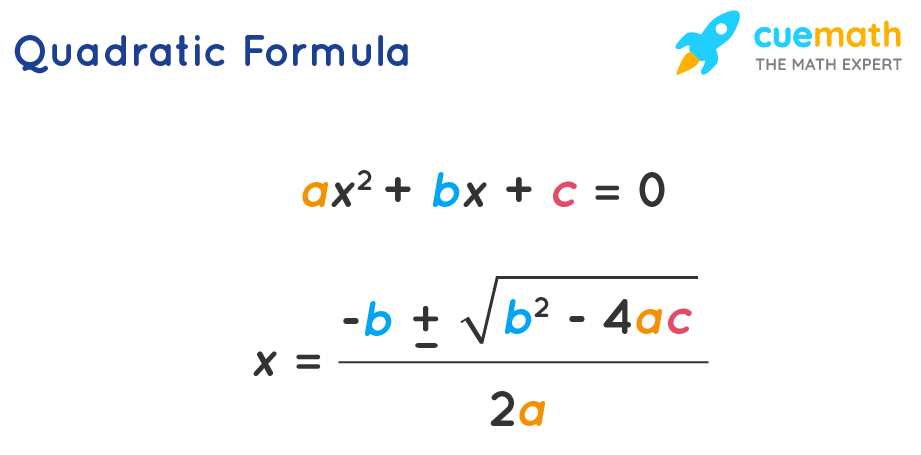




IMAGES
VIDEO
COMMENTS
Free Equation Given Roots Calculator - Find equations given their roots step-by-step
The calculator solution will show work using the quadratic formula to solve the entered equation for real and complex roots. Calculator determines whether the discriminant \( (b^2 - 4ac) \) is less than, greater than or equal to 0. When \( b^2 - 4ac = 0 \) there is one real root. When \( b^2 - 4ac > 0 \) there are two real roots. When \( b^2 ...
A useful tool for finding the solutions to quadratic equations. Wolfram|Alpha can apply the quadratic formula to solve equations coercible into the form ax 2 + bx + c = 0. In doing so, Wolfram|Alpha finds both the real and complex roots of these equations. It can also utilize other methods helpful to solving quadratic equations, such as ...
Example: 3x^2-2x-1=0 (After you click the example, change the Method to 'Solve By Completing the Square'.) Take the Square Root. Example: 2x^2=18. Quadratic Formula. Example: 4x^2-2x-1=0. About quadratic equations Quadratic equations have an x^2 term, and can be rewritten to have the form: a x 2 + b x + c = 0. Need more problem types?
A quadratic is a second degree polynomial of the form: ax2 + bx + c = 0 where a ≠ 0. To solve an equation using the online calculator, simply enter the math problem in the text area provided. Hit the calculate button to get the roots. A quadratic equation has two roots or zeroes namely; Root1 and Root2.
The quadratic formula is the solution of a second-degree polynomial equation of the following form: Ax² + Bx + C = 0. If you can rewrite your equation in this form, it means that it can be solved with the quadratic formula. A solution to this equation is also called a root of an equation. The quadratic formula is as follows: x = (-B ± √Δ ...
Quadratic Formula. The calculator uses the following formula: x = (-b ± √ D) / 2a, where D = b 2 - 4ac. This formula calculates the solution of quadratic equations (ax 2 +bx+c=0) where x is unknown, a is the quadratic coefficient (a ≠ 0), b is the linear coefficient and c represents the equation's constant. The letters a, b and c are known numbers and are the quadratic equation's ...
The results will appear in the boxes labeled Root 1 and Root 2. For example, for the quadratic equation below, you would enter 1, 5 and 6. After pressing Solve, your resulting roots would be -2 and -3. Click Reset to clear the calculator and enter new values. x 2 + 5x + 6 = 0. Enter the coefficient of x 2 here. Enter the coefficient of x here.
Quadratic Formula Steps. There are several steps you have to follow in order to successfully solve a quadratic equation: Step 1: Identify the coefficients. Examine the given equation of the form \ (ax^2+bx+c\), and determine the coefficients \ (a\), \ (b\) and \ (c\). The coefficient \ (a\) is the coefficient that appears multiplying the ...
Step 1: Enter the equation you want to solve using the quadratic formula. The Quadratic Formula Calculator finds solutions to quadratic equations with real coefficients. For equations with real solutions, you can use the graphing tool to visualize the solutions. Quadratic Formula: x = −b±√b2 −4ac 2a x = − b ± b 2 − 4 a c 2 a.
In algebra, a quadratic equation is any polynomial equation of the second degree with the following form: ax 2 + bx + c = 0. where x is an unknown, a is referred to as the quadratic coefficient, b the linear coefficient, and c the constant. The numerals a, b, and c are coefficients of the equation, and they represent known numbers. For example, a cannot be 0, or the equation would be linear ...
The calculator on this page shows how the quadratic formula operates, but if you have access to a graphing calculator you should be able to solve quadratic equations, even ones with imaginary solutions.. Step 1) Most graphing calculators like the TI- 83 and others allow you to set the "Mode" to "a + bi" (Just click on 'mode' and select 'a+bi').
Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Quadratic Equation Solver. Save Copy. Log InorSign Up "Change the coefficients of your quadratic equation useing the sliders below. ... Roots. 18. 68. powered by. powered by "x" x "y" y "a" squared a 2 "a ...
The quadratic equation can have either one or two real roots, or two complex roots, depending on the values of the coefficients a, b, and c. The quadratic formula is used to calculate the roots of the quadratic equation, and it is given by: x = (-b ± √ (b^2 - 4ac)) / 2a. The solutions to the quadratic equation can also be found by ...
The solution (s) to a quadratic equation can be calculated using the Quadratic Formula: The "±" means we need to do a plus AND a minus, so there are normally TWO solutions ! The blue part ( b2 - 4ac) is called the "discriminant", because it can "discriminate" between the possible types of answer: when it is negative we get complex solutions.
This method can be used to solve all types of quadratic equations, although it can be complicated for some types of equations. The method involves seven steps. Example 04: Solve equation $ 2x^2 + 8x - 10= 0$ by completing the square. Step 1: Divide the equation by the number in front of the square term.
Free equations calculator - solve linear, quadratic, polynomial, radical, exponential and logarithmic equations with all the steps. Type in any equation to get the solution, steps and graph
A quadratic equation solver is a free step by step solver for solving the quadratic equation to find the values of the variable. With the help of this solver, we can find the roots of the quadratic equation given by, ax 2 + bx + c = 0, where the variable x has two roots. The solution is obtained using the quadratic formula;. where a, b and c are the real numbers and a ≠ 0.
SolutionStep 1 Put the equation in standard form. We must subtract 6 from both sides. Step 2 Factor completely. Recall how to factor trinomials. Step 3 Set each factor equal to zero and solve for x. Since we have (x - 6) (x + 1) = 0, we know that x - 6 = 0 or x + 1 = 0, in which case x = 6 or x = - 1.
Quadratic equation calculator. Quadratic equation has the basic form: ax2 + bx+ c = 0. Enter the quadratic equation's coefficients a, b, and c of its basic standardized form. A solution of quadratic equations is usually two different real or complex roots or one double root — the calculation using the discriminant. a =.
The quadratic formula says the roots of a quadratic equation ax 2 + bx + c = 0 are given by x = (-b ± √ (b 2 - 4ac)) /2a. To solve any quadratic equation, convert it into standard form ax 2 + bx + c = 0, find the values of a, b, and c, substitute them in the roots of quadratic equation formula and simplify.
Solve Quadratic Equation using the Quadratic Formula 6.3 Solving x 2-3x+2 = 0 by the Quadratic Formula . According to the Quadratic Formula, x , the solution for Ax 2 +Bx+C = 0 , where A, B and C are numbers, often called coefficients, is given by : - B ± √ B 2-4AC x = ————————
A useful tool for finding the solutions to quadratic equations. Wolfram|Alpha can apply the quadratic formula to solve equations coercible into the form ax2 +bx+c= 0 a x 2 + b x + c = 0. In doing so, Wolfram|Alpha finds both the real and complex roots of these equations. It can also utilize other methods helpful to solving quadratic equations ...
The two roots in the quadratic formula are presented as a single expression. The positive sign and the negative sign can be alternatively used to obtain the two distinct roots of the equation. Quadratic Formula: The roots of a quadratic equation ax 2 + bx + c = 0 are given by x = [-b ± √(b 2 - 4ac)]/2a.
For the values k = 9 and k = -9 the roots of the quadratic equation . 3x²+ 2kx + 27 = 0 real and equal.. What is quadratic equation? Any equation in algebra that can be rearranged in standard form as: [tex]ax^2 + bx + c = 0[/tex] is known as a quadratic equation (from the Latin quadratus, "square").. where a ≠ 0 and a, b, and c are known numbers, x is an unknown value, and a.