solution of the following initial value problems

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators

Solve Initial Value Problem-Definition, Application and Examples

JUMP TO TOPIC

Existence and Uniqueness

Continuity and differentiability, dependence on initial conditions, local vs. global solutions, higher order odes, boundary behavior, particular and general solutions, engineering, biology and medicine, economics and finance, environmental science, computer science, control systems.

Solving initial value problems (IVPs) is an important concept in differential equations . Like the unique key that opens a specific door, an initial condition can unlock a unique solution to a differential equation.

As we dive into this article, we aim to unravel the mysterious process of solving initial value problems in differential equations . This article offers an immersive experience to newcomers intrigued by calculus’s wonders and experienced mathematicians looking for a comprehensive refresher.

Solving the Initial Value Problem 

To solve an initial value problem , integrate the given differential equation to find the general solution. Then, use the initial conditions provided to determine the specific constants of integration.

An initial value problem (IVP) is a specific problem in differential equations . Here is the formal definition. An initial value problem is a differential equation with a specified value of the unknown function at a given point in the domain of the solution.

More concretely, an initial value problem is typically written in the following form:

dy/dt = f(t, y) with y(t₀) = y₀

• dy/dt = f(t, y) is the differential equation , which describes the rate of change of the function y with respect to the variable t .
• t₀ is the given point in the domain , often time in many physical problems .
• y(t₀) = y₀ is the initial condition , which specifies the value of the function y at the point t₀.

An initial value problem aims to find the function y(t) that satisfies both the differential equation and the initial condition . The solution y(t) to the IVP is not just any solution to the differential equation , but specifically, the one which passes through the point (t₀, y₀) on the (t, y) plane.

Because the solution of a differential equation is a family of functions, the initial condition is used to find the particular solution that satisfies this condition. This differentiates an initial value problem from a boundary value problem , where conditions are specified at multiple points or boundaries.

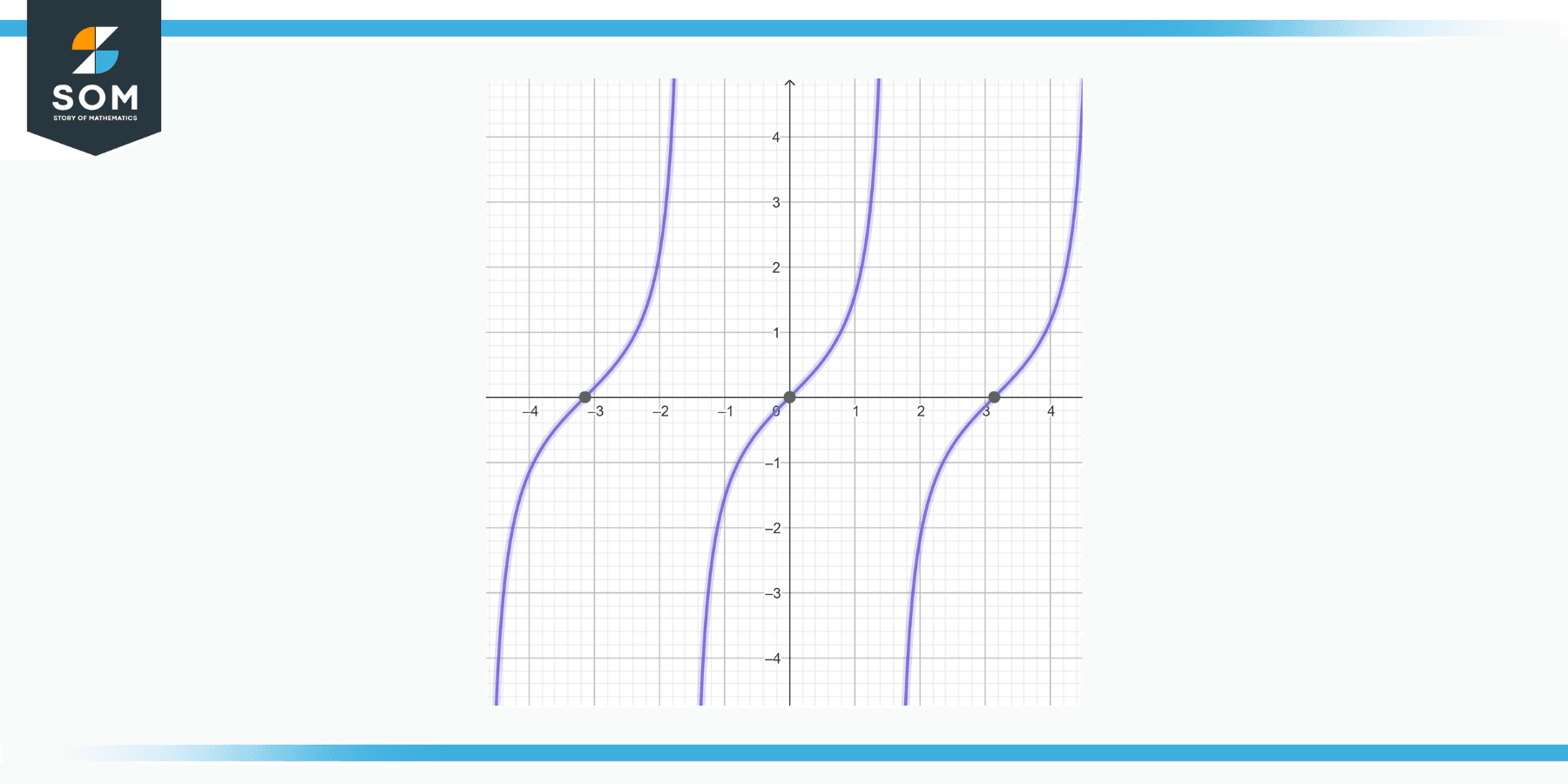
Solve the IVP y’ = 1 + y^2, y(0) = 0 .

This is a standard form of a first-order non-linear differential equation known as the Riccati equation. The general solution is y = tan(t + C) .

Applying the initial condition y(0) = 0, we get:

0 = tan(0 + C)

The solution to the IVP is then y = tan(t) .

According to the Existence and Uniqueness Theorem for ordinary differential equations (ODEs) , if the function f and its partial derivative with respect to y are continuous in some region of the (t, y) -plane that includes the initial condition (t₀, y₀) , then there exists a unique solution y(t) to the IVP in some interval about t = t₀ .

In other words, given certain conditions, we are guaranteed to find exactly one solution to the IVP that satisfies both the differential equation and the initial condition .

If a solution exists, it will be a function that is at least once differentiable (since it must satisfy the given ODE ) and, therefore, continuous . The solution will also be differentiable as many times as the order of the ODE .

Small changes in the initial conditions can result in drastically different solutions to an IVP . This is often called “ sensitive dependence on initial conditions ,” a characteristic feature of chaotic systems .

The Existence and Uniqueness Theorem only guarantees a solution in a small interval around the initial point t₀ . This is called a local solution . However, under certain circumstances, a solution might extend to all real numbers, providing a global solution . The nature of the function f and the differential equation itself can limit the interval of the solution.

For higher-order ODEs , you will have more than one initial condition. For an n-th order ODE , you’ll need n initial conditions to find a unique solution.

The solution to an IVP may behave differently as it approaches the boundaries of its validity interval. For example, it might diverge to infinity , converge to a finite value , oscillate , or exhibit other behaviors.

The general solution of an ODE is a family of functions that represent all solutions to the ODE . By applying the initial condition(s), we narrow this family down to one solution that satisfies the IVP .

Applications 

Solving initial value problems (IVPs) is fundamental in many fields, from pure mathematics to physics , engineering , economics , and beyond. Finding a specific solution to a differential equation given initial conditions is essential in modeling and understanding various systems and phenomena. Here are some examples:

IVPs are used extensively in physics . For example, in classical mechanics , the motion of an object under a force is determined by solving an IVP using Newton’s second law ( F=ma , a second-order differential equation). The initial position and velocity (the initial conditions) are used to find a unique solution that describes the object’s motion .

IVPs appear in many engineering problems. For instance, in electrical engineering , they are used to describe the behavior of circuits containing capacitors and inductors . In civil engineering , they are used to model the stress and strain in structures over time.

In biology , IVPs are used to model populations’ growth and decay , the spread of diseases , and various biological processes such as drug dosage and response in pharmacokinetics .

Differential equations model various economic processes , such as capital growth over time. Solving the accompanying IVP gives a specific solution that models a particular scenario, given the initial economic conditions.

IVPs are used to model the change in populations of species , pollution levels in a particular area, and the diffusion of heat in the atmosphere and oceans.

In computer graphics, IVPs are used in physics-based animation to make objects move realistically. They’re also used in machine learning algorithms, like neural differential equations , to optimize parameters.

In control theory , IVPs describe the time evolution of systems. Given an initial state , control inputs are designed to achieve a desired state.

Solve the IVP y’ = 2y, y(0) = 1 .

The given differential equation is separable. Separating variables and integrating, we get:

∫dy/y = ∫2 dt

ln|y| = 2t + C

y = $e^{(2t+C)}$

= $e^C  * e^{(2t)}$

Now, apply the initial condition y(0) = 1 :

1 = $e^C * e^{(2*0)}$

The solution to the IVP is y = e^(2t) .

Solve the IVP y’ = -3y, y(0) = 2 .

The general solution is y = Ce^(-3t) . Apply the initial condition y(0) = 2 to get:

2 = C $e^{(-3*0)}$

2 = C $e^0$

So, C = 2, and the solution to the IVP is y = 2e^(-3t) .

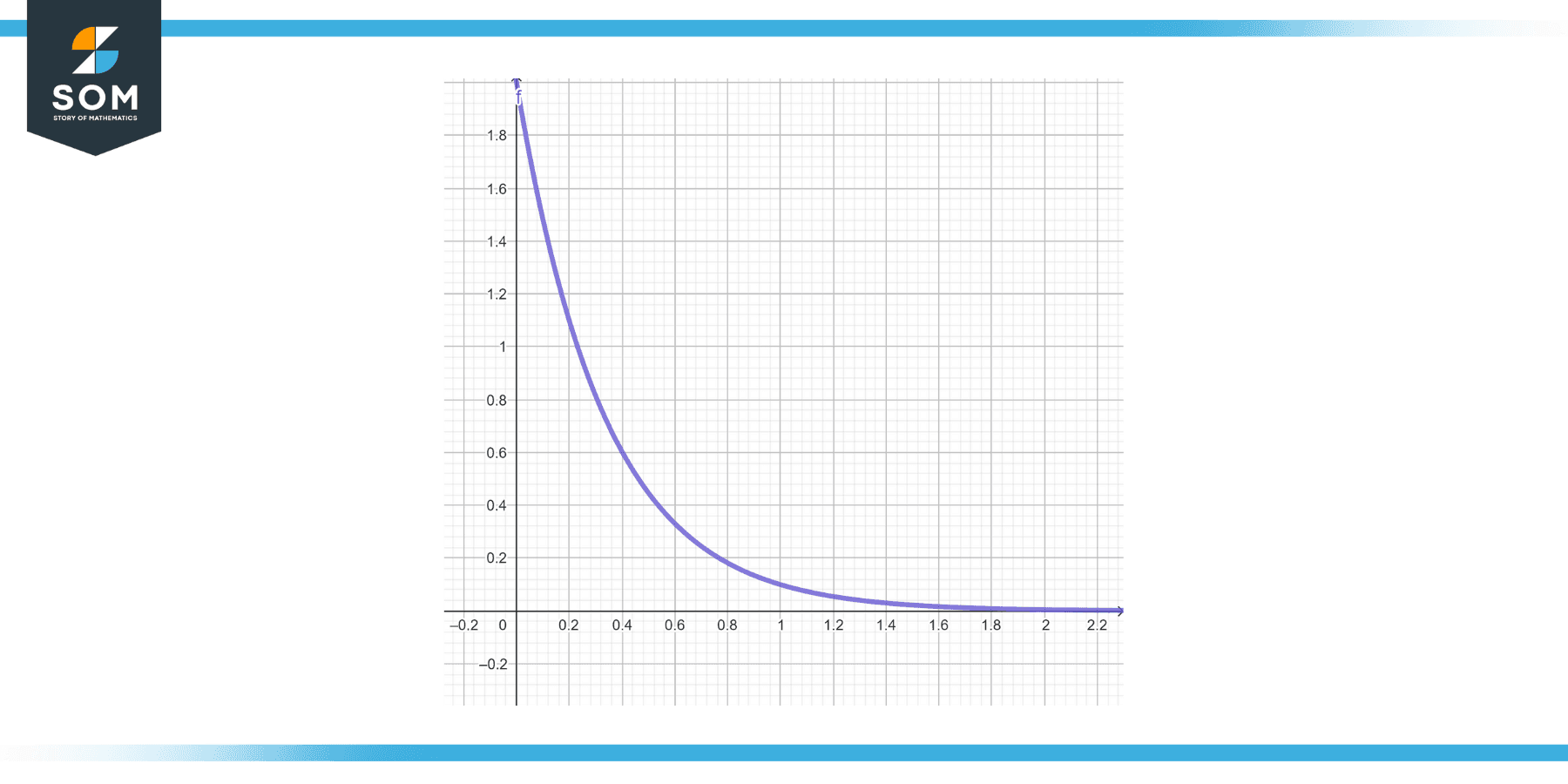
Solve the IVP y’ = y^2, y(1) = 1 .

This is also a separable differential equation. We separate variables and integrate them to get:

∫$dy/y^2$ = ∫dt,

1/y = t + C.

Applying the initial condition y(1) = 1, we find C = -1. So the solution to the IVP is -1/y = t – 1 , or y = -1/(t – 1).

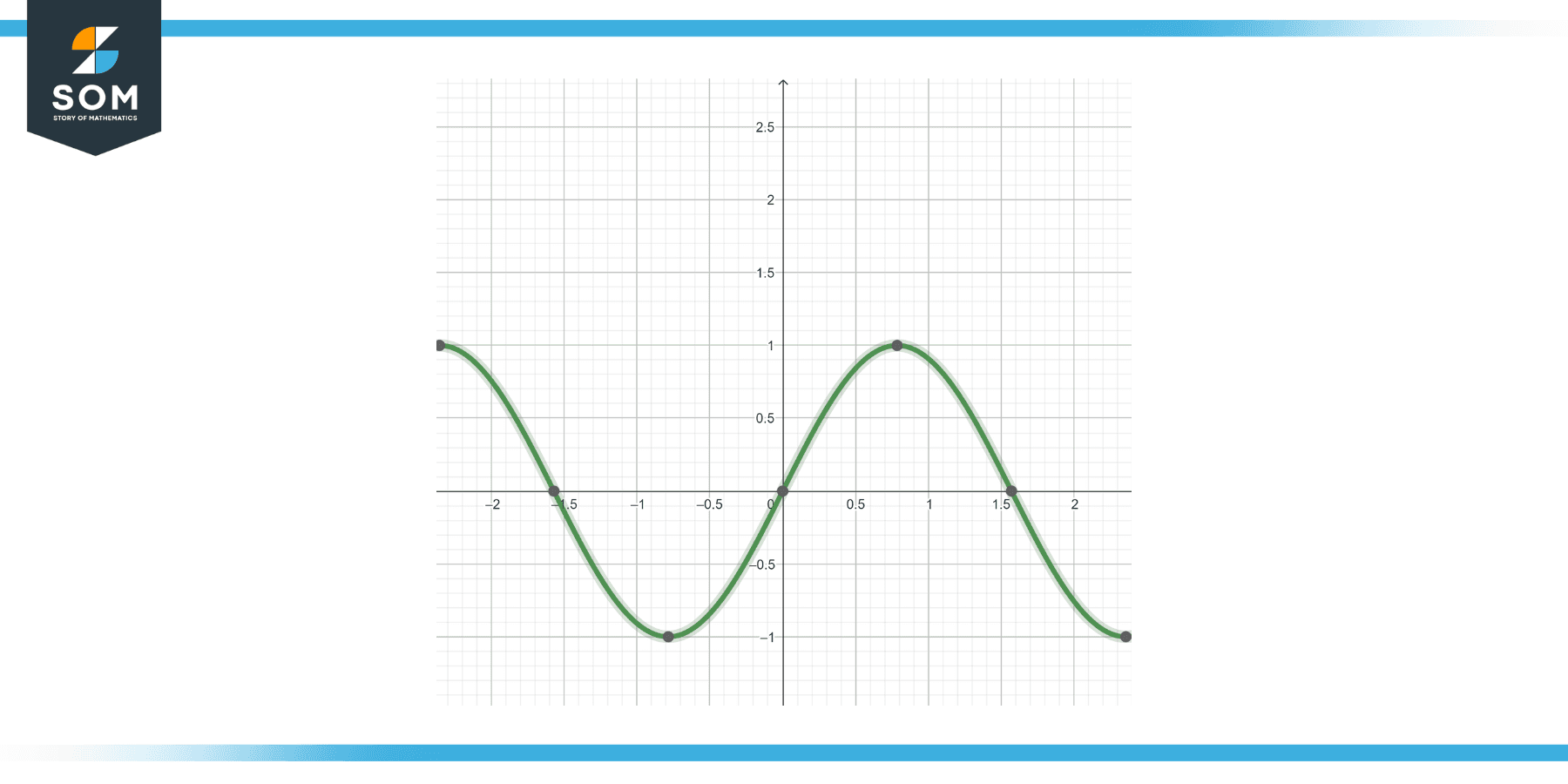
Solve the IVP y” – y = 0, y(0) = 0, y'(0) = 1 .

This is a second-order linear differential equation. The general solution is y = A sin(t) + B cos(t) .

The first initial condition y(0) = 0 gives us:

0 = A 0 + B 1

The second initial condition y'(0) = 1 gives us:

1 = A cos(0) + B*0

The solution to the IVP is y = sin(t) .

Solve the IVP y” + y = 0, y(0) = 1, y'(0) = 0 .

This is also a second-order linear differential equation. The general solution is y = A sin(t) + B cos(t) .

The first initial condition y(0) = 1 gives us:

1 = A 0 + B 1

The second initial condition y'(0) = 0 gives us:

0 = A cos(0) – B*0

The solution to the IVP is y = cos(t) .

Solve the IVP y” = 9y, y(0) = 1, y'(0) = 3.

The differential equation can be rewritten as y” – 9y = 0. The general solution is y = A $ e^{(3t)} + B e^{(-3t)}$ .

1 = A $e^{(30)}$ + B $e^{(-30)}$

So, A + B = 1.

The second initial condition y'(0) = 3 gives us:

3 = 3A $e^{30} $ – 3B $e^{-30}$

= 3A – 3B

So, A – B = 1.

We get A = 1 and B = 0 to solve these two simultaneous equations. So, the solution to the IVP is y = $e^{(3t)}$ .

Solve the IVP y” + 4y = 0, y(0) = 0, y'(0) = 2 .

The differential equation is a standard form of a second-order homogeneous differential equation. The general solution is y = A sin(2t) + B cos(2t) .

The second initial condition y'(0) = 2 gives us:

2 = 2A cos(0) – B*0

The solution to the IVP is y = sin(2t) .

• Pre Calculus
• Probability
• Sets & Set Theory
• Trigonometry

Calcworkshop

Solving Initial Value Problems (IVPs) A Comprehensive Guide

// Last Updated: April 17, 2023 - Watch Video //

Did you know that when you solve a differential equation with a specific condition, you’re tackling an initial value problem ?

Jenn, Founder Calcworkshop ® , 15+ Years Experience (Licensed & Certified Teacher)

In simpler terms, you’re looking for a solution that meets certain requirements to find a unique answer .

In a previous lesson, you learned about Ordinary Differential Equations . Now, you’ll dive deeper to explore n-parameter family of solutions and use an initial condition (IC) to figure out the constants in that family.

Understanding n-parameter Family of Solutions

So, what’s an n-parameter family?

Well, a first-order differential equation \(F\left(x, y, y^{\prime}\right)=0\) typically has a single arbitrary constant called a parameter \(\mathrm{c}\), whereas a second-order differential equation \(F\left(x, y, y^{\prime}, y^{\prime \prime}\right)=0\) usually has two arbitrary constants, denoted \(c_{1}\) and \(c_{2}\).

One Two Three Parameter —  Solution Formulas

Therefore, a single differential equation can possess an infinite number of solutions corresponding to the unlimited number of choices for the parameters.

So, an n-parameter family of solutions of a given nth-order differential equation represents the set of all solutions of the equation. And we typically refer to an \(n\)-parameter family of solutions as the general solution – it’s easier to say!

Consequently, if we assign arbitrary constants to the differential equation, referred to as initial conditions, our general solution is called a particular solution because it represents a specific answer for some particular constraint.

It should also be noted that solutions of an \(\mathrm{n}\)-th order differential equation that are not included in the general solution are called singular solutions.

Example: Verifying and Finding Solutions to Initial Value Problems

Let’s look at an example of how we will verify and find a solution to an initial value problem given an ordinary differential equation.

Verify that the function \(y=c_{1} e^{2 x}+c_{2} e^{-2 x}\) is a solution of the differential equation \(y^{\prime \prime}-4 y=0\).

Then find a solution of the second-order IVP consisting of the differential equation that satisfies the initial conditions \(y(0)=1\) and \(y^{\prime}(0)=2\).

First, we will verify that the function is a solution by noticing that we are given a two-parameter family of solutions because we have a second-order differential equation. Therefore, we need to find the second derivative of our function.

\begin{align*} \begin{aligned} & y=c_{1} e^{2 x}+c_{2} e^{-2 x} \\ & y^{\prime}=2 c_{1} e^{2 x}-2 c_{2} e^{-2 x} \\ & y^{\prime \prime}=4 c_{1} e^{2 x}+4 c_{2} e^{-2 x} \end{aligned} \end{align*}

Now, we will substitute our derivatives into the ODE and verify that the left-hand side equals the right-hand side.

\begin{equation} \begin{aligned} & y^{\prime \prime}-4 y=0 \\ & \left(4 c_1 e^{2 x}+4 c_2 e^{-2 x}\right)-4\left(c_1 e^{2 x}+c_2 e^{-2 x}\right)=0 \\ & 4 c_1 e^{2 x}+4 c_2 e^{-2 x}-4 c_1 e^{2 x}-4 c_2 e^{-2 x}=0 \\ & 0=0 \end{aligned} \end{equation}

Now, we will find a solution to the second-order IVP by substituting the initial conditions into their corresponding functions.

\begin{equation} \text { If } y=c_1 e^{2 x}+c_2 e^{-2 x} \text { and } y(0)=1, \text { then } \end{equation}

\begin{align*} 1=c_{1} e^{2(0)}+c_{2} e^{-2(0)} \Rightarrow 1=c_{1}(1)+c_{2}(1) \Rightarrow 1=c_{1}+c_{2} \end{align*}

\begin{equation} \text { If } y^{\prime}=2 c_1 e^{2 x}-2 c_2 e^{-2 x} \text { and } y^{\prime}(0)=2 \text {, then } \end{equation}

\begin{align*} 2=2 c_{1} e^{2(0)}-2 c_{2} e^{-2(0)} \Rightarrow 2=2 c_{1}(1)-2(1) \Rightarrow 2=2 c_{1}-2 c_{2} \end{align*}

Next, we will solve the resulting system for \(c_{1}\) and \(c_{2}\).

\begin{align*} \left\{\begin{array} { c } { 1 = c _ { 1 } + c _ { 2 } } \\ { 2 = 2 c _ { 1 } – 2 c _ { 2 } } \end{array} \Rightarrow \left\{\begin{array}{c} c_{1}+c_{2}=1 \\ c_{1}-c_{2}=1 \end{array} \Rightarrow c_{1}=1 \quad \text { and } \quad c_{2}=0\right.\right. \end{align*}

Therefore, the particular solution for the IVP given the initial condition is:

\begin{equation} \begin{aligned} & y=(1) e^{2 x}+(0) e^{-2 x} \\ & y=e^{2 x} \end{aligned} \end{equation}

I find that it’s helpful to remember that Initial condition(s) are values of the solution and/or its derivative(s) at specific points. Which means, according to Paul’s Online Notes that solutions to “nice enough” differential equations are unique; hence, only one solution will meet the given conditions.

The Game-Changing Existence and Uniqueness Theorem

But how do we know there will be a solution to the differential equation?

The Existence of a Unique Solution Theorem is a key concept in this course. It provides specific conditions that ensure a unique solution exists for an Initial Value Problem (IVP).

Definition: The existence-unique solution theorem says that if we let \(\mathrm{R}\) be a rectangular region in the \(x y-\) plane defined by \(a \leq x \leq b, c \leq y \leq d\) that contains the point \(\left(x_{0}, y_{0}\right)\) in its interior. And if \(f(x, y)\) and \(\frac{\partial f}{\partial y}\) are continuous on \(\mathrm{R}\), then there exists some interval \(\left(x_{0}-h, x_{0}+h\right), h>0\), contained in \([a, b]\), and a unique function \(y(x)\), defined on \(I_{0}\), that is a solution of the initial value problem.

That’s pretty “mathy” right?!

In *sorta* simpler terms, the existence-unique solution theorem essentially states that under specific conditions, there is a unique solution for an initial value problem. If a point (x₀, y₀) is within a rectangular region R in the xy-plane, and both the function f(x, y) and its partial derivative with respect to y are continuous in R , then there is an interval (x₀-h, x₀+h), with h>0, contained within the range [a, b]. Within this interval, a unique function y(x) exists as a solution to the initial value problem.

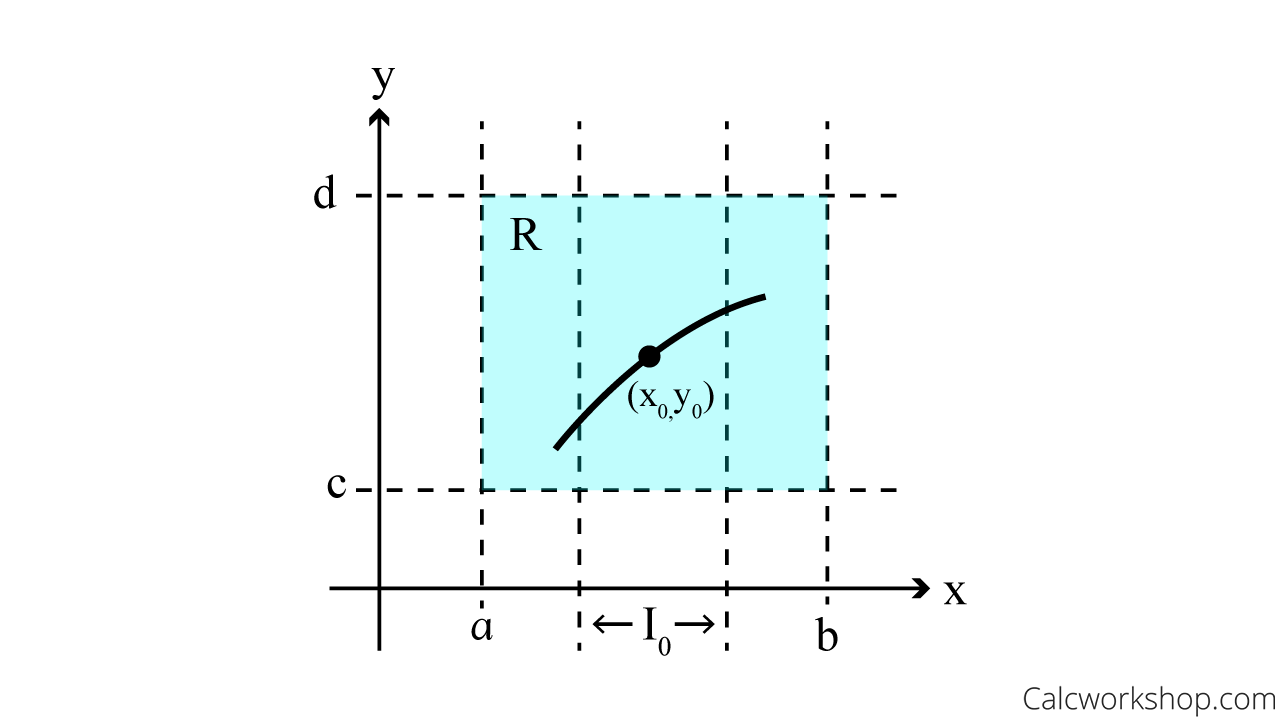
Existence Uniqueness Theorem — Graphical

Example: Solving an IVP with Given Initial Conditions

Let’s break this down into easy-to-understand steps by working an example.

Determine whether the existence-uniqueness theorem implies the given initial value problem has a unique solution through the given point.

\begin{equation} y^{\prime}=y^{2 / 3},(8,4) \end{equation}

First, we will verify that our ODE is continuous by letting \(f(x, y)=y^{\prime}\) and graphing the curve.

\begin{equation} f(x, y)=y^{2 / 3} \end{equation}

ODE — 3D Graph

So, \(f(x, y)\) is continuous for all real numbers.

Next, we will take the partial derivative with respect to \(\mathrm{y}\) and determine if the partial derivative is also continuous.

\begin{align*} \frac{\partial f}{\partial y}=f_{y}=\frac{2}{3} y^{-1 / 3}=\frac{2}{3}\left(\frac{1}{\sqrt[3]{y}}\right) \end{align*}

This indicates that a unique solution exists when \(y>0\).

Therefore, we can safely conclude that our given point \((8,4)\) will provide a unique solution because our \(y\)-value is greater than zero.

Going forward…

So, together we will dive into the world of n-th parameter family of solutions, find solutions for initial value problems, and determine the existence of a solution and whether a differential equation contains a unique solution through a given point.

Let’s jump right in.

Video Tutorial w/ Full Lesson & Detailed Examples

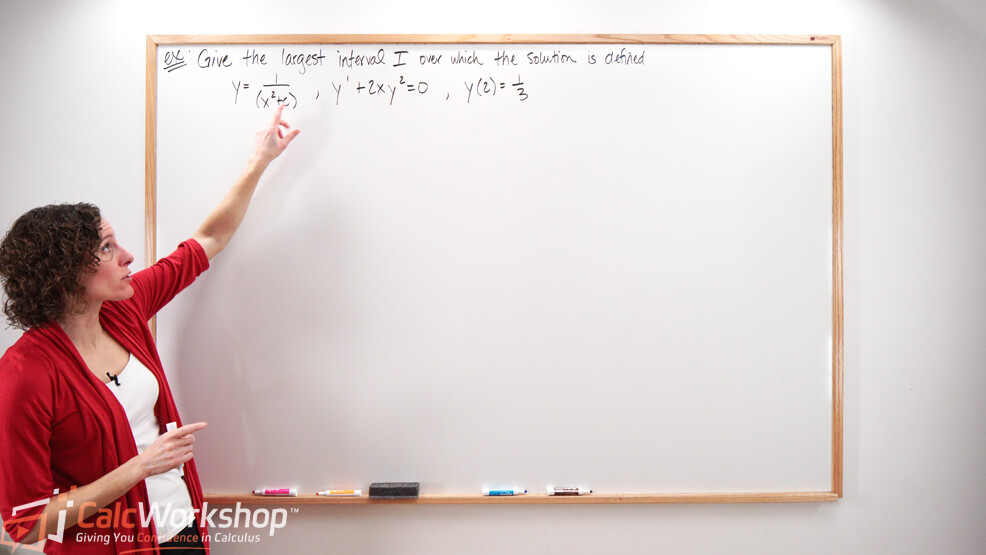
Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

Get My Subscription Now

Still wondering if CalcWorkshop is right for you? Take a Tour and find out how a membership can take the struggle out of learning math.

Module 7: Second-Order Differential Equations

Initial-value problems and boundary-value problems, learning objectives.

• Solve initial-value and boundary-value problems involving linear differential equations.

So far, we have been finding general solutions to differential equations. However, differential equations are often used to describe physical systems, and the person studying that physical system usually knows something about the state of that system at one or more points in time. For example, if a constant-coefficient differential equation is representing how far a motorcycle shock absorber is compressed, we might know that the rider is sitting still on his motorcycle at the start of a race, time [latex]t=t_0[/latex]. This means the system is at equilibrium, so [latex]y(t_0)=0[/latex], and the compression of the shock absorber is not changing, so [latex]y'(t_0)=0[/latex]. With these two initial conditions and the general solution to the differential equation, we can find the  specific  solution to the differential equation that satisfies both initial conditions. This process is known as  solving an initial-value problem . (Recall that we discussed  initial-value problems  in  Introduction to Differential Equations .) Note that second-order equations have two arbitrary constants in the general solution, and therefore we require two initial conditions to find the solution to the initial-value problem.

Sometimes we know the condition of the system at two different times. For example, we might know [latex]y(t_0)=y_0[/latex] and [latex]y(t_1)=y_1[/latex]. These conditions are called  boundary conditions , and finding the solution to the differential equation that satisfies the boundary conditions is called solving a  boundary-value problem .

Mathematicians, scientists, and engineers are interested in understanding the conditions under which an initial-value problem or a boundary-value problem has a unique solution. Although a complete treatment of this topic is beyond the scope of this text, it is useful to know that, within the context of constant-coefficient, second-order equations, initial-value problems are guaranteed to have a unique solution as long as two initial conditions are provided. Boundary-value problems, however, are not as well behaved. Even when two boundary conditions are known, we may encounter boundary-value problems with unique solutions, many solutions, or no solution at all.

Example: solving an initial-value problem

Solve the following initial-value problem: [latex]y''+3y'-4y=0[/latex], [latex]y(0)=1[/latex], [latex]y'(0)=-9[/latex].

We already solved this differential equation in Example “Solving Second-Order Equations with Constant Coefficients” part a. and found the general solution to be

[latex]y(x)=c_1e^{-4x}+c_2e^x[/latex].

[latex]y^\prime=-4c_1e^{-4x}+c_2e^x[/latex].

When [latex]x=0[/latex], we have [latex]y(0)=c_1+c_2[/latex] and [latex]y^\prime(0)=-4c_1+c_2[/latex]. Applying the initial conditions, we have

[latex]\begin{aligned} c_1+c_2&=1 \\ -4c_1+c_2&=-9 \end{aligned}[/latex].

Then [latex]c_1=1-c_2[/latex]. Substituting this expression into the second equation, we see that

[latex]\begin{aligned} -4(1-c_2)+c_2&=-9 \\ -4+4c_2+c_2&=-9 \\ 5c_2&=-5 \\ c_2&=-1 \end{aligned}[/latex].

So, [latex]c_1=2[/latex] and the solution to the initial-value problem is

[latex]y(x)=2e^{-4x}-e^x[/latex].

Solve the initial-value problem [latex]y''-3y'-10y=0[/latex], [latex]y(0)=0[/latex], [latex]y'(0)=7[/latex].

[latex]y(x)=-e^{-2x}+e^{-5x}[/latex].

Watch the following video to see the worked solution to the above Try It

Example: solving an initial-value problem and graphing the solution

Solve the following initial-value problem and graph the solution:

[latex]y^{\prime\prime}+6y^\prime+13y=0, \ y(0)=0, \ y^\prime(0)=2[/latex].

We already solved this differential equation in Example “Solving Second-Order Equations with Constant Coefficients” part b. and found the general solution to be

[latex]y(x)=e^{-3x}(c_1\cos2x+c_2\sin2x)[/latex].

[latex]y^\prime(x)=e^{-3x}(-2c_1\sin2x+2c_2\cos2x)-3e^{-3x}(c_1\cos2x+c_2\sin2x)[/latex].

When [latex]x=0[/latex], we have [latex]y(0)=c_1[/latex] and [latex]y^\prime(0)=2c_2-3c_1[/latex]. Applying the initial conditions, we obtain

[latex]\begin{aligned} c_1&=0 \\ -3c_1+2c_2&= 2 \end{aligned}[/latex].

Therefore, [latex]c_1=0[/latex], [latex]c_2=1[/latex], and the solution to the initial value problem is shown in the following graph.

[latex]y=e^{-3x}\sin2x[/latex]

Solve the following initial-value problem and graph the solution: [latex]y''-2y'+10y=10=0[/latex], [latex]y(0)=2[/latex], [latex]y'(0)=-1[/latex].

[latex]y(x)=e^{x}(2\cos3x-\sin3x)[/latex]

Figure 2. Graph of [latex]y(x)=e^{x}(2\cos3x-\sin3x)[/latex].

Example: initial-value problem representing a spring-mass system

The following initial-value problem models the position of an object with mass attached to a spring. Spring-mass systems are examined in detail in  Applications . The solution to the differential equation gives the position of the mass with respect to a neutral (equilibrium) position (in meters) at any given time. (Note that for spring-mass systems of this type, it is customary to define the downward direction as positive.)

[latex]y^{\prime\prime}+2y^\prime+y=0, \ y(0)=1, \ y^\prime(0)=0[/latex]

Solve the initial-value problem and graph the solution. What is the position of the mass at time [latex]t=2[/latex] sec? How fast is the mass moving at time [latex]t=1[/latex] sec? In what direction?

In Example “Solving Second-Order Equations with Constant Coefficients” part c. we found the general solution to this differential equation to be

[latex]y(t)=c_1e^{-t}+c_2te^{-t}[/latex].

[latex]y^\prime(t)=-c_1e^{-t}+c_2(-te^{-t}+e^{-t})[/latex].

When [latex]t=0[/latex], we have [latex]y(0)=c_1[/latex] and [latex]y'(0)=-c_1+c_2[/latex]. Applying the initial conditions, we obtain

[latex]\begin{aligned} c_1&=1 \\ -c_1+c_2&= 0 \end{aligned}[/latex].

Thus, [latex]c_1=1[/latex], [latex]c_2=1[/latex], and the solution to the initial value problem is

[latex]y(t)=e^{-t}+te^{-t}[/latex].

This solution is represented in the following graph. At time [latex]t=2[/latex], the mass is at position [latex]y(2)=e^{-2}+2e^{-2}=3e^{-2}\approx0.406[/latex] [latex]m[/latex] below equilibrium.

To calculate the velocity at time [latex]t=1[/latex], we need to find the derivative. We have [latex]y(t)=e^{-t}+te^{-t}[/latex], so

[latex]y^\prime(t)=-e^{-t}+e^{-t}-te^{-t}=-te^{-t}[/latex].

Then [latex]y^\prime(1)=e^{-1}\approx-0.3679[/latex]. At time [latex]t=1[/latex], the mass is moving upward at [latex]0.3679[/latex] m/sec.

Suppose the following initial-value problem models the position (in feet) of a mass in a spring-mass system at any given time. Solve the initial-value problem and graph the solution. What is the position of the mass at time [latex]t=0.3[/latex] sec? How fast is it moving at time [latex]t=0.1[/latex] sec? In what direction?

[latex]y^{\prime\prime}+14y^\prime+49y=0, \ y(0)=0, \ y^\prime(0)=1[/latex]

[latex]y(t)=te^{-7t}[/latex]

At time [latex]t=0.3[/latex], [latex]y(0.3)=0.3^{(-7*0.3)}=0.3e^{-2.1}\approx0.0367[/latex]. The mass is [latex]0.0367[/latex] ft below equilibrium. At time [latex]t=0.1[/latex], [latex]y^\prime(0.1)=0.3e^{-0.7}\approx0.1490[/latex]. The mass is moving downward at a speed of [latex]0.1490[/latex] ft/sec.

Example: solving a boundary-value problem

In Example “Solving Second-Order Equations with Constant Coefficients” part f. we solved the differential equation [latex]y''+16y=0[/latex] and found the general solution to be [latex]y(t)=c_1\cos4t+c_2\sin4t[/latex]. If possible, solve the boundary-value problem if the boundary conditions are the following:

• [latex]y(0)=0[/latex], [latex]y\left(\frac{\pi}4\right)=0[/latex]
• [latex]y(0)=1[/latex], [latex]y\left(\frac{\pi}8\right)=0[/latex]
• [latex]y\left(\frac{\pi}8\right)=0[/latex], [latex]y\left(\frac{3\pi}8\right)=0[/latex]

[latex]y(x)=c_1\cos{4t}+c_2\sin{4t}[/latex]

• Applying the first boundary condition given here, we get [latex]y(0)=c_1=0[/latex]. So the solution is of the form [latex]y(t)=c_2\sin4t[/latex]. When we apply the second boundary condition, though, we get [latex]y\left(\frac{\pi}4\right)=c_2\sin\left(4\left(\frac{\pi}4\right)\right)=c_2\sin\pi=0[/latex] for all values of [latex]c_2[/latex]. The boundary conditions are not sufficient to determine a value for [latex]c_2[/latex], so this boundary-value problem has infinitely many solutions. Thus, [latex]y(t)=c_2\sin4t[/latex] is a solution for any value of [latex]c_2[/latex].
• Applying the first boundary condition given here, we get [latex]y(0)=c_1=1[/latex]. Applying the second boundary condition gives[latex]y(\frac{\pi}{8})=c_2=0[/latex], so [latex]c_2=0[/latex]. In this case, we have a unique solution: [latex]y(t)=\cos 4t[/latex].
• Applying the first boundary condition given here, we get [latex]y\left(\frac{\pi}8\right)=c_2=0[/latex]. However, applying the second boundary condition gives [latex]y\left(\frac{3\pi}8\right)=-c_2=2[/latex], so [latex]c_2=-2[/latex]. We cannot have [latex]c_2=0=-2[/latex] so this boundary value problem has no solution.
• CP 7.7. Authored by : Ryan Melton. License : CC BY: Attribution
• Calculus Volume 3. Authored by : Gilbert Strang, Edwin (Jed) Herman. Provided by : OpenStax. Located at : https://openstax.org/books/calculus-volume-3/pages/1-introduction . License : CC BY-NC-SA: Attribution-NonCommercial-ShareAlike . License Terms : Access for free at https://openstax.org/books/calculus-volume-3/pages/1-introduction

Privacy Policy

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Laplace Transform

4.4 Solving Initial Value Problems

Having explored the Laplace Transform, its inverse, and its properties, we are now equipped to solve initial value problems (IVP) for linear differential equations. Our focus will be on second-order linear differential equations with constant coefficients.

Method of Laplace Transform for IVP

General Approach:

1. Apply the Laplace Transform to each term of the differential equation. Use the properties of the Laplace Transform listed in Tables 4.1 and 4.2 to obtain an equation in terms of [asciimath]Y(s)[/asciimath] . The Laplace Transform of the derivatives are

  [asciimath]\mathcal{L}{f'(t)} = sF(s) - f(0)[/asciimath]

  [asciimath]\mathcal{L}{f''(t)\} = s^2F(s) - s f(0) - f'(0)[/asciimath]

2. The transforms of derivatives involve initial conditions at [asciimath]t=0[/asciimath] . Apply the initial conditions.

3. Simplify the transformed equation to isolate  [asciimath]Y(s)[/asciimath] .

4. If needed, use partial fraction decomposition to break down  [asciimath]Y(s)[/asciimath] into simpler components.

5. Determine the inverse Laplace Transform using the tables and linearity property to find [asciimath]y(t)[/asciimath] .

Shortcut Approach:

1. Find the characteristic polynomial of the differential equation [asciimath]p(s)=as^2+bs+c[/asciimath] .

2. Substitute [asciimath]p(s)[/asciimath] , [asciimath]F(s)=\mathcal{L}{f(t)}[/asciimath] , and the initial conditions into the equation

  [asciimath]Y(s)=(F(s)+a(y'(0)+sy(0))+b y(0) )/(p(s))[/asciimath]   (4.4.1)

3. If needed, use partial fraction decomposition to break down [asciimath]Y(s)[/asciimath] into simpler components.

4. Determine the inverse Laplace transform of [asciimath]Y(s)[/asciimath] using the tables and linearity property to find [asciimath]y(t)[/asciimath] .

Solve the initial value problem.

  [asciimath]y''-5y'+6y=4e^(-2t)\ ;[/asciimath]      [asciimath]y(0)=-1, \ y'(0)=2[/asciimath]

Using the General Approach

1. Take the Laplace Transform of both sides of the equation

  [asciimath]\mathcal{L}^-1{ y''}-5\mathcal{L}^-1{ y'}+6\mathcal{L}^-1{y}=4\mathcal{L}^-1{ e^(-2t)}[/asciimath]

Letting [asciimath]Y(s)=\mathcal{L}^-1{y}[/asciimath] , we get

  [asciimath]s^2Y(s)-sy(0)-y'(0)-5(sY(s)-y(0))+6Y(s)=4(1/(s+2))[/asciimath]

2. Plugging in the initial conditions gives

  [asciimath]s^2Y(s)+s-2-5(sY(s)+1)+6Y(s)=4(1/(s+2))[/asciimath]

3. Collecting like terms and isolating [asciimath]Y(s)[/asciimath] , we get

  [asciimath](s^2-5s+6)Y(s)=4/(s+2)-s+7[/asciimath]

  [asciimath]Y(s)[/asciimath]   [asciimath]=(4//(s+2)-s+7)/(s^2-5s+6)[/asciimath]

Multiplying both the denominator and numerator by [asciimath](s+2)[/asciimath] and factoring the denominator yields

  [asciimath]Y(s)=(-s^2+5s+18)/((s+2)(s-3)(s-2))[/asciimath]

4. Using partial fraction expansion, we get

  [asciimath]Y(s)=1/5 (1/(s+2))+24/5 (1/(s-3))-6 (1/(s-2))[/asciimath]

5. From Table 4.1 , we see that

  [asciimath]1/(s-a)[/asciimath]      [asciimath]harr \ \e^(at)[/asciimath]

Taking the inverse, we obtain the solution of the equation

  [asciimath]y(t)=\mathcal{L}^-1{Y(s)}[/asciimath]   [asciimath]=1/5 \ e^(-2t) +24/5 e^(3t)-6 e^(2t)[/asciimath]

  [asciimath]y''+4y=3sin(t) \ ;[/asciimath]      [asciimath]y(0)=1, \ y'(0)=-1[/asciimath]

Using the Shortcut Approach

1. The characteristic polynomial is

  [asciimath]p(s)=s^2+4[/asciimath]

  [asciimath]F(s)=\mathcal{L}^-1{3sin(t)}[/asciimath]   [asciimath]=3/(s^2+1)[/asciimath]

2. Substituting them together with the initial values into Equation 4.4.1 , we obtain

  [asciimath]Y(s)=(3//(s^2+1)+(-1+s(1)))/(s^2+4)[/asciimath] [asciimath]=(3//(s^2+1)+s-1)/(s^2+4)[/asciimath]

Multiplying both the denominator and numerator by [asciimath](s^2+1)[/asciimath]  yields

  [asciimath]Y(s)=(s^3-s^2+s+2)/((s^2+1)(s^2+4))[/asciimath]

3. Using partial fraction expansion, we get

  [asciimath]Y(s)=1/(s^2+1)+(s-2)/(s^2+4)[/asciimath]

[asciimath]\ =1/(s^2+1)+s/(s^2+4)- 2/(s^2+4)[/asciimath]

4. From Table 4.1 ,

  [asciimath]sin(bt)\ harr\ b/(s^2+b^2)[/asciimath]      and    [asciimath]cos(bt)\ harr\ s/(s^2+b^2)[/asciimath]

  [asciimath]y(t)=\mathcal{L}^-1{Y(s)}[/asciimath]   [asciimath]=sin(t)+cos(2t)-sin(2t)[/asciimath]

Section 4.4 Exercises

  [asciimath]y'' +3 y' -10 y = 0, \ quad y(0) = -1, \ quad y'(0) = 2[/asciimath]

[asciimath]y(t)=-3/7 e^(2t)-4/7 e^(-5t)[/asciimath]

  [asciimath]y'' +6 y' + 13 y = 0, \ quad y(0) = 2, \ quad y'(0) = 0[/asciimath]

[asciimath]y(t)=e^(-3t)(2cos(2t)+3sin(2t))[/asciimath]

  [asciimath]y'' - 8 y' +16 y = 0, \ quad y(0) = 1, \ quad y'(0) = -1[/asciimath]

  [asciimath]y(t)=e^(4t)(1-5t)[/asciimath]

Differential Equations Copyright © 2024 by Amir Tavangar is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

Stack Exchange Network

Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.

Q&A for work

Connect and share knowledge within a single location that is structured and easy to search.

Find the solution of each of the following initial value problems

Find the solution of each of the following initial value problems:

$$a) y''-5y'+6y=0 \space \space \space \space \space \space y(1)=e^2 \space \space y'(1)=3e^2$$

$$b) y''-6y'+9y=0 \space \space \space \space \space \space y(0)=0 \space \space y'(0)=5$$

$$c) y''+4y'+5y=0 \space \space \space \space \space \space y(0)=1 \space \space y'(0)=0$$

I can easily find the general solution for each $a)$ , $b)$ and $c)$, but I'm not entirely sure what to do, or how I use the initial value.

What I have so far, for part $a)$:

$$ y''-5y'+6y=0$$ $$r^2-5r+6=0$$ $$(r-3)(r-2)=0$$ So, the general solution is: $$y=Ae^{2x}+Be^{3x}$$

For part $b)$:

$$ y''-6y'+9y=0$$ $$r^2-6r+9=0$$ $$(r-3)^2=0$$ So, the general solution is: $$y=Ae^{3x}+Bxe^{3x}$$

For part $c)$:

$$r^2+4r+5=0$$ $$\frac{-4 \pm \sqrt{16-4*1*5}}{2}$$ $$-2 \pm i$$ So, the general solution is:

$$Ae^{-2x}cos(x)+Be^{-2x}sin(x)$$

• ordinary-differential-equations

Take problem a): Plug the initial values into the general solution to get 2 equations in 2 unknowns, A and B. Solve them for A and B. Proceed the same way for the other problems.

You must log in to answer this question.

Not the answer you're looking for browse other questions tagged calculus ordinary-differential-equations ..

• Featured on Meta
• We spent a sprint addressing your requests — here’s how it went
• Upcoming initiatives on Stack Overflow and across the Stack Exchange network...

Hot Network Questions

• Books using the axiomatic method
• y / p does not paste all yanked lines
• mirrorlist.centos.org no longer resolve?
• How does Magic Item creation cost differ between Sorcerer and Wizard?
• Why should I meet my advisor even if I have nothing to report?
• Don't make noise. OR Don't make a noise
• Identify rear derailleur (Shimano 105 - medium or short)
• Position where last x halfmoves are determined
• Is there a drawback to using Heart's blood rote repeatedly?
• Is it possible to arrange the free n-minoes of orders 2, 3, 4 and 5 into a rectangle?
• Line from Song KÄMPFERHERZ
• Orange marks on ceiling underneath bathroom
• How to osacompile a script containing `tell Application` and NSAppleScriptEnabled without activating it
• exploded pie chart, circumscribing arc, and text labels
• Graphics tablet pressure not working in blender (Blender 4.0 / XP-Pen Deco01V2 / MacBook M1 Pro 2021)
• What does it mean if Deutsche Bahn say that a train is cancelled between two instances of the same stop?
• All sections & plugins gone after local reinstall - help!
• Why does independent research from people without formal academic qualifications generally turn out to be a complete waste of time?
• What's the point of Dream Chaser?
• Will 2.1" schwalbe MTB tire in 25mm rim become wider that 2.25" in 19mm rim?
• Why would a plane be allowed to fly to LAX but not Maui?
• Acts 13:43 and the grace of God
• Are all Starship/Super Heavy "cylinders" 4mm thick?
• openssh-client/openssh-server show different version than ssh -V

HIGH SCHOOL

• ACT Tutoring
• SAT Tutoring
• PSAT Tutoring
• ASPIRE Tutoring
• SHSAT Tutoring
• STAAR Tutoring

GRADUATE SCHOOL

• MCAT Tutoring
• GRE Tutoring
• LSAT Tutoring
• GMAT Tutoring
• AIMS Tutoring
• HSPT Tutoring
• ISAT Tutoring
• SSAT Tutoring

Search 50+ Tests

Loading Page

math tutoring

• Elementary Math
• Pre-Calculus
• Trigonometry

science tutoring

Foreign languages.

• Mandarin Chinese

elementary tutoring

• Computer Science

Search 350+ Subjects

• Video Overview
• Tutor Selection Process
• Online Tutoring
• Mobile Tutoring
• Instant Tutoring
• How We Operate
• Our Guarantee
• Impact of Tutoring
• Reviews & Testimonials
• About Varsity Tutors

Differential Equations : Initial-Value Problems

Study concepts, example questions & explanations for differential equations, all differential equations resources, example questions, example question #1 : initial value problems.

First identify what is known.

The general function is,

The initial value is six in mathematical terms is,

So this is a separable differential equation, but it is also subject to an initial condition. This means that you have enough information so that there should not be a constant in the final answer.

You start off by getting all of the like terms on their respective sides, and then taking the anti-derivative. Your pre anti-derivative equation will look like:

Then taking the anti-derivative, you include a C value:

Then, using the initial condition given, we can solve for the value of C:

Solving for C, we get 

So this is a separable differential equation with a given initial value.

To start off, gather all of the like variables on separate sides.

Then integrate, and make sure to add a constant at the end

Plug in the initial condition to get:

Solve the separable differential equation

none of these answers

To start off, gather all of the like variables on separate sides. 

Notice that when you divide sec(y) to the other side, it will just be cos(y),

and the csc(x) on the bottom is equal to sin(x) on the top. 

In order to solve for y, we just need to take the arcsin of both sides:

Solve the differential equation

Then, after the anti-derivative, make sure to add the constant C:

Solve for y

None of these answers

Taking the anti-derivative once, we get:

we get the final answer of:

Example Question #8 : Initial Value Problems

Solve the differential equation for y

subject to the initial condition:

Solving for C:

Then taking the square root to solve for y, we get:

Example Question #10 : Initial Value Problems

Report an issue with this question

If you've found an issue with this question, please let us know. With the help of the community we can continue to improve our educational resources.

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC 101 S. Hanley Rd, Suite 300 St. Louis, MO 63105

Or fill out the form below:

Number Line

The Calculus Calculator is a powerful online tool designed to assist users in solving various calculus problems efficiently. Here's how to make the most of its capabilities:

• Begin by entering your mathematical expression into the above input field, or scanning it with your camera.
• Choose the specific calculus operation you want to perform, such as differentiation, integration, or finding limits.
• Once you've entered the function and selected the operation, click the 'Go' button to generate the result.
• The calculator will instantly provide the solution to your calculus problem, saving you time and effort.
• \lim_{x\to 3}(\frac{5x^2-8x-13}{x^2-5})
• \lim _{x\to \:0}(\frac{\sin (x)}{x})
• \int e^x\cos (x)dx
• \int \cos^3(x)\sin (x)dx
• \int_{0}^{\pi}\sin(x)dx
• \frac{d}{dx}(\frac{3x+9}{2-x})
• \frac{d^2}{dx^2}(\frac{3x+9}{2-x})
• implicit\:derivative\:\frac{dy}{dx},\:(x-y)^2=x+y-1
• \sum_{n=0}^{\infty}\frac{3}{2^n}
• tangent\:of\:f(x)=\frac{1}{x^2},\:(-1,\:1)

calculus-calculator

initial value problem

• The Art of Convergence Tests Infinite series can be very useful for computation and problem solving but it is often one of the most difficult...

Please add a message.

Message received. Thanks for the feedback.

Use Laplace transforms to solve the following initial value problem. x" + x = 8 cos 7t, x(0) = 1, x'(0) = 0 Click the icon to view the table of Laplace transforms. The solution is x(t) = (Type an expression using t as the variable. Type an exact answer.)

The solution to the given initial value problem using Laplace transforms is x(t) = (8/65)cos(7t) + (57/65)sin(7t).

To solve the given initial value problem using Laplace transforms, we first take the Laplace transform of the differential equation and apply the initial conditions.

Applying the Laplace transform to the differential equation x" + x = 8cos(7t), we get:

s^2X(s) + X(s) = 8/(s^2 + 49)

Now, substituting the initial conditions x(0) = 1 and x'(0) = 0, we can solve for X(s):

Simplifying the equations, we find:

X(s) = (8/(s^2 + 49)) / (s^2 + 1)

Using partial fraction decomposition , we can express X(s) as:

X(s) = (8/65) * (1 / (s^2 + 1)) + (57/65) * (s / (s^2 + 1))

Taking the inverse Laplace transform, we obtain the solution:

x(t) = (8/65)cos(7t) + (57/65)sin(7t)

Thus, the solution to the given initial value problem is x(t) = (8/65)cos(7t) + (57/65)sin(7t).

To learn more about “ Laplace transform ” refer to the https://brainly.com/question/29583725

Related Questions

please answer all questions B. Use the matrix method or otherwise to solve the following system of simultaneous equations: i. x + 2y + 3z = -5 ii. 3x + y - 3z = 4 iii. - 3x + 4y + 7z=-7 (15 marks)

The solution to the system of simultaneous equations is x = 34/7, y = -13/7, z = -9/7.

To solve the system of simultaneous equations :

i. x + 2y + 3z = -5

ii. 3x + y - 3z = 4

iii. -3x + 4y + 7z = -7

We can use the matrix method or the augmented matrix to solve the equations. Let's use the augmented matrix method:

-3 4 7 | -7

We'll perform row operations to transform the matrix into row-echelon form:

R2 = R2 - 3R1

R3 = R3 + 3R1

0 -5 -12 | 19

0 10 16 | 4

R3 = R3 + 2R2

0 1 12/5 | -19/5

0 0 56/5 | -36/5

R3 = (5/56)R3

0 0 1 | -9/7

R2 = R2 - (12/5)R3

R1 = R1 - 3R3

1 2 0 | 8/7

0 1 0 | -13/7

R1 = R1 - 2R2

1 0 0 | 34/7

The row-echelon form of the augmented matrix is obtained. Now, we can read off the solution to the system of equations:

Therefore, the solution to the system of simultaneous equations is x = 34/7, y = -13/7, z = -9/7.

Read more about matrices here:

brainly.com/question/1279486

in exercises 79, 80, 81, 82, 83 and 84, determine the value(s) of such that the system of linear equations has the indicated number of solutions.

The required answers are:

Exercise 79: No solution for all values of "k".

Exercise 80: Exactly one solution for all values of "k".

Exercise 81: Infinitely many solutions for all values of "k".

Exercise 82: No solution for all values of "k".

Exercise 83: Infinitely many solutions for all values of "k".

Exercise 84: Infinitely many solutions for all values of "k".

Using the concept of the system of linear equations , we can determine the number of solutions for each exercise:

No solution:

Equations: x + ky = 2, kx + y = 4

For a unique solution , the slopes of the two lines formed by the equations should be different. In this case, the slopes are k and 1, respectively. Since a1/b1 = k/1 is not equal to a2/b2 = 1/k, there is no common slope. Therefore, for exercise 79, there is no solution for all values of "k".

Exactly one solution:

Equations: x + ky = 0, kx + y = 0

For exactly one solution , the slopes of the two lines formed by the equations should be different. In this case, the slopes are k and 1, respectively. Since a1/b1 = k/1 is not equal to a2/b2 = 1/k, the slopes are different. Therefore, for exercise 80, there is exactly one solution for all values of "k".

Infinitely many solutions :

Equations: kx + 2ky + 3kz = 4k, x + y + z = 0, 2x - y + z = 1

For infinitely many solutions , the slopes of the planes formed by the equations should be equal. In this case, a1/b1 = a2/b2 = 1/2 = c1/c2. Therefore, for exercise 81, there are infinitely many solutions for all values of "k".

Equations: x + 2y + kz = 6, 3x + 6y + 8z = 4

For a unique solution , the slopes of the planes formed by the equations should be different. In this case, a1/b1 = 1/2 is not equal to a2/b2 = 3/6 = 1/2. Therefore, for exercise 82, there is no solution for all values of "k".

Infinitely many solutions:

Equations: 4x + ky = 6, kx + y = -3

For infinitely many solutions , the slopes of the lines formed by the equations should be equal. In this case, a1/b1 = 4/k is equal to a2/b2 = k/1. Therefore, for exercise 83, there are infinitely many solutions for all values of "k".

Equations: kx + y = 16, 3x - 4y = -64

For infinitely many solutions , the slopes of the lines formed by the equations should be equal. In this case, a1/b1 = k/1 is equal to a2/b2 = 3/-4 = -3/4. Therefore, for exercise 84, there are infinitely many solutions for all values of "k".

Thus, the required answers are:

Learn more about systems of linear equations   here:

https://brainly.com/question/29208263

Determine the volume of the wedge above the xy-plane formed when cylinder is cut by planes z = 0 and y = -z.

The volume of the wedge above the xy-plane formed by the cylinder x² + y² = 4 and the planes z = 0 and y = -z is (22/3)π cubic units.

To determine the volume of the wedge above the xy-plane formed when the cylinder x² + y² = 4 is cut by the planes z = 0 and y = -z, we need to find the intersection points of the cylinder with the planes and then calculate the volume within that region.

First, let's find the intersection points of the cylinder x² + y² = 4 with the plane z = 0. Setting z = 0, we have:

Substituting y = 0 into the equation of the cylinder, we get:

x² + 0² = 4

So the intersection points of the cylinder with the plane z = 0 are (2, 0, 0) and (-2, 0, 0).

Now, let's find the intersection points of the cylinder with the plane y = -z. Substituting y = -z into the equation of the cylinder, we get:

x² + (-z)² = 4

x² + z² = 4

This equation represents a circle in the xz-plane centered at the origin with a radius of 2. Thus, the intersection points lie on this circle.

The volume of the wedge can be found by integrating the area of the cross-sections perpendicular to the z-axis. Since the cross-sections are circular, we can use the formula for the volume of a cylinder.

The radius of the cross-section circle is given by the distance from the z-axis to the circle, which is equal to the x-coordinate of the points on the circle. Thus, the radius is given by |x|.

The height of the cylinder is the difference between the z-values of the two planes, which is 0 - (-z) = z.

Integrating over the region, the volume V is given by:

V = ∫[from z = 0 to z = 2] π|x|² dz

Using symmetry, we can integrate from z = 0 to z = 1 and multiply the result by 2 to get the total volume:

V = 2 * ∫[from z = 0 to z = 1] πx² dz

Substituting x² = 4 - y², we have:

V = 2 * ∫[from z = 0 to z = 1] π(4 - y²) dz

Since y = -z, we can substitute y = -z in the integral:

V = 2 * ∫[from z = 0 to z = 1] π(4 - (-z)²) dz

= 2 * ∫[from z = 0 to z = 1] π(4 - z²) dz

Evaluating the integral, we get:

V = 2 * π * [4z - (z³/3)] |[from z = 0 to z = 1]

= 2 * π * [(4 - (1/3)) - (0 - 0)]

= 2 * π * (11/3)

The complete question is:

Determine the volume of the wedge above the xy-plane formed when cylinder x²+y²=4 is cut by planes z = 0 and y = -z.

To know more about volume:

https://brainly.com/question/28058531

The present value of the following cash flow stream is $6,770 when discounted at 12 percent annually. Cash Flow year 1= $850, Cash Flow year 2=?, Cash Flow year 3-$1,150 & Cash Flow year 4 = $1,750. What is the value of the missing cash flow? A) $3,987.99 B) $3,070 C) $4,728.96 D) $5,118.41 E) $4,921.97 11) A loan where the horrower receives money today and renave a sinele lump sum on a future date is called a

a. The value of the missing cash flow is  $5,118.41. The correct answer is

b. A loan where the borrower receives money today and renave a sinele lump sum on a future date is called a Balloon Loan

a. To find the missing cash flow in year 2, we can use the present value formula:

PV = CF / (1 + r)^n

PV = Present Value

CF = Cash Flow

r = Interest rate

n = Number of years

Present Value = $6,770

Cash Flow in year 1 = $850

Cash Flow in year 3 = $1,150

Cash Flow in year 4 = $1,750

Interest rate = 12% = 0.12

Now, we can solve for the missing cash flow in year 2:

$6,770 = $850 / (1 + 0.12)^1 + X / (1 + 0.12)^2 + $1,150 / (1 + 0.12)^3 + $1,750 / (1 + 0.12)^4

Simplifying the equation:

$6,770 = $850 / 1.12 + X / 1.2544 + $1,150 / 1.4049 + $1,750 / 1.5735

$6,770 = $759.82 + 0.7974X + $818.97 + $1,111.69

$6,770 = $2,690.48 + 0.7974X

Subtracting $2,690.48 from both sides:

$6,770 - $2,690.48 = 0.7974X

$4,079.52 = 0.7974X

Dividing by 0.7974:

X = $4,079.52 / 0.7974

X ≈ $5,118.41

Therefore, the value of the missing cash flow in year 2 is approximately $5,118.41.

Hence, the correct option is D) $5,118.41.

b. Regarding the second question, a loan where the borrower receives money today and repays a single lump sum on a future date is called a "Balloon Loan."

Learn more about cash flow at:

brainly.com/question/30450133

9) A carpenter went to a discount hardware store to buy hammers, screwdrivers, and large nails. and large nails cost 50 cents each. The carpenter Hammers cost $10 each, screwdrivers cost $7 each, bought exactly 100 items and spent $150. How many of each item did he buy?

Step-by-step explanation:

To solve this problem, we can use a system of equations. Let’s use the variables h, s, and n to represent the number of hammers, screwdrivers, and nails that the carpenter bought, respectively.

From the problem statement, we know that:

h + s + n = 100 (the carpenter bought exactly 100 items) 10h + 7s + 0.5n = 150 (the carpenter spent $150)

We can use the first equation to solve for n:

n = 100 - h - s

We can then substitute this expression for n into the second equation:

10h + 7s + 0.5(100 - h - s) = 150

Simplifying this equation gives:

9.5h + 6.5s = 100

We can multiply both sides of this equation by 2 to eliminate the decimals:

19h + 13s = 200

Now we have two equations with two variables:

h + s + n = 100 19h + 13s = 200

We can solve for one variable in terms of the other using either equation. Let’s solve for h in terms of s using the second equation:

h = (200 - 13s)/19

We know that h must be a whole number since it represents the number of hammers that the carpenter bought. Therefore, we can try different values of s until we find a whole number value for h.

Let’s start by trying s = 1:

h = (200 - 13(1))/19 = 9.21

This is not a whole number, so let’s try s = 2:

h = (200 - 13(2))/19 = 8.84

This is also not a whole number, so let’s try s = 3:

h = (200 - 13(3))/19 = 8.47

This is still not a whole number, so let’s try s = 4:

h = (200 - 13(4))/19 = 8.11

This is a whole number! Therefore, the carpenter bought 8 hammers, 4 screwdrivers, and 88 nails.

I hope this helps! Let me know if you have any other questions.

Make t the subject of the formula 2(d-t) = 4t+7

2(d-t)=4t+7

I don't know

Group like terms

[tex] \frac{2 d- 7 } 6t= \frac{6t}{6t} [/tex]

[tex]t = \frac{2d - 7}{6t} [/tex]

Solve the following system of equations using matrix inverse. 4x + 5y = 14 3x - 2y = -1

The solution to the system of equations is:x = -3 and y = 2.

To solve the following system of equations using matrix inverse:4x + 5y = 143x - 2y = -1

Using the matrix inverse , we can rewrite the system of equations into a matrix equation:

where A is the coefficient matrix, X is the variable matrix, and B is the constant matrix.

The variable matrix X can be found by multiplying the inverse of A to the constant matrix B, which is:X = A⁻¹B

To use matrix inverse, let us first obtain the coefficient matrix A, constant matrix B, and inverse of matrix A.

Then we will use these matrices to obtain the variable matrix X.

A = [4 5; 3 -2]

B = [14; -1]

A⁻¹ = (1/22) [-2 -5; -3 4]

X = A⁻¹BX = (1/22)[-2 -5; -3 4][14; -1]= [-3; 2]

Learn more about matrix at

https://brainly.com/question/32268282

15%-IN Determine the productivity growth (in percentage %) of a carpeting company after they use a mechanized carpeting compared to manual process: (a) manual process: 8 workers is able to complete the carpeting of 471 square meter area in a day. (b) mechanized carpeting: Using machine the 8 workers complete 627 square meter area in a day. Enter the final answer without the % symbol. Answer: T

After considering the given data we conclude that the productivity growth of the carpeting company after they apply mechanized carpeting compared to manual process is approximately 33.10. To evaluate the productivity growth (in percentage %) of a carpeting company after they use a mechanized carpeting compared to manual process, we can apply the following formula: [tex]Productivity growth = ((New productivity - Old productivity) / Old productivity) * 100\%[/tex] where: Old productivity is the area of carpeting completed by 8 workers in a day applying manual process. New productivity is the area of carpeting completed by 8 workers in a day using mechanized carpeting. Given that: Old productivity = 471 square meters per day New productivity = 627 square meters per day We are applying substitution of these values into the formula and evaluate the productivity growth as follows: [tex]Productivity growth = ((627 - 471) / 471) * 100\%[/tex] [tex]Productivity growth = (156 / 471)*100\%[/tex] Productivity growth ≈ 33.10 percent To learn more about productivity growth https://brainly.com/question/28475735 #SPJ4

Explain what is wrong with the following use of the power rule 5 3 3 Choose the correct answer below O A The power rule was applied to the numerator rather than the entire integrand OB. The power rule for derivatives was used instead of the power rule for integrals 31 OC. The arbitrwy constant is not required when the power rule is used OD. The power rule was applied to the denominator other than the entire integrand

The correct answer is: OB. The power rule for derivatives was used instead of the power rule for integrals.

The power rule states that when differentiating a function of the form [tex]x^n[/tex], where n is a constant, the derivative is given by[tex]nx^(^n^-^1^)[/tex]. However, when integrating a function, the power rule for integrals states that the integral of x^n dx, where n is a constant, is equal to [tex](1/(n+1))x^(^n^+^1^)[/tex]+ C, where C is the constant of integration .

In the given question, the power rule was applied incorrectly. The expression "5 3 3" suggests that the integrand is [tex]5x^3^3[/tex], where the superscript 3 is mistakenly applied to the numerator instead of the entire integrand. The power rule for derivatives was then applied, resulting in a derivative instead of an integral. This is incorrect because the power rule for derivatives and the power rule for integrals have different formulas and purposes.

To solve the integral correctly using the power rule for integrals, the exponent in the integrand should be reduced by 1 and then divided by the new exponent plus 1. Applying the power rule for integrals to the expression would yield [tex](1/4)x^4[/tex]+ C, where C is the constant of integration.

In summary, the mistake in the given use of the power rule is that the power rule for derivatives was used instead of the power rule for integrals. The correct application of the power rule for integrals would lead to a different result.

Learn more about Power rule

brainly.com/question/30226066

1. Provide example of one qualitative and one mixed research question. 2. Explain how you will select your sample, collect, and analyse data. 3. Discuss the advantages and challenges of the research method. 4. Examples used in this reflection should be different from the research question submitted in your proposal. 5. One page for each method (Qualitative / Mixed Method)

1.Qualitative Research: How do individuals perceive and experience job satisfaction in remote work settings? Mixed Research: What is the impact of a nutrition education program on the dietary habits and health outcomes of school children? 2. The sample will be selected using purposive sampling to ensure representation from different industries and job roles. 3. Qualitative research can generate new insights and hypotheses for further investigation. Qualitative research may be time-consuming due to the extensive data collection and analysis process. 4. Using different examples in the reflection than those presented in the research proposal enhances the depth and breadth of analysis. It allows for a broader exploration of the topic, promotes critical thinking, and demonstrates a comprehensive understanding of the subject matter beyond the initial research question. 5.Qualitative Method: Involves collecting and analyzing non-numerical data to gain an in-depth understanding of phenomena . Mixed Method: Combines both qualitative and quantitative approaches to research.

Sample Selection: The sample will be selected using purposive sampling to ensure representation from different industries and job roles. Participants will be recruited through online platforms and professional networks, targeting individuals who have experience with remote work. Approximately 15-20 participants will be chosen based on their willingness to participate and their diversity in terms of age, gender, and job characteristics.

Data Collection: Semi-structured interviews will be conducted with the participants to explore their perceptions and experiences of job satisfaction in remote work settings. The interviews will be audio-recorded with participants' consent, transcribed verbatim, and supplemented with field notes.

Data Analysis: Thematic analysis will be employed to identify patterns and themes within the qualitative data. The transcripts and field notes will be coded and analyzed using a qualitative data analysis software. The researcher will immerse themselves in the data, identify emerging themes, and refine them through a process of constant comparison.

Advantages: Qualitative research allows for in-depth exploration of individuals' perceptions and experiences, providing rich and detailed data. It allows for flexibility and adaptability in data collection, enabling the researcher to probe deeper into participants' responses.

Challenges: Qualitative research may be time-consuming due to the extensive data collection and analysis process. The findings may be subjective and not easily generalizable due to the small sample size and potential researcher bias. Maintaining confidentiality and anonymity can also be challenging when dealing with sensitive topics.

Sample Selection: A mixed methods sequential explanatory design will be employed. Initially, a purposive sampling strategy will be used to select a diverse group of schools (both urban and rural) to participate in the study. From each selected school, a random sample of students will be chosen to participate in the program, ensuring representation across grade levels .

Data Collection: Quantitative data will be collected using pre- and post-intervention surveys to assess changes in dietary habits and health outcomes. Qualitative data will be collected through focus group interviews with students to gain a deeper understanding of their experiences and perceptions of the program.

Data Analysis: The quantitative data will be analyzed using descriptive statistics and inferential tests (e.g., t-tests) to examine changes in dietary habits and health outcomes. The qualitative data from the focus groups will be transcribed and analyzed thematically to identify common themes and patterns.

Advantages: Mixed methods research combines the strengths of both qualitative and quantitative approaches, allowing for a comprehensive understanding of the research question. It provides a more holistic view of the topic by capturing both numerical data and participants' perspectives.

Challenges: Implementing a mixed methods design requires careful planning and coordination between the qualitative and quantitative components. The data collection process can be time-consuming, particularly when conducting interviews and administering surveys to a large sample.

Qualitative Method: Involves collecting and analyzing non-numerical data to gain an in-depth understanding of phenomena, often using techniques like interviews, observations, and thematic analysis.

Mixed Method: Combines both qualitative and quantitative approaches to research, allowing for a comprehensive understanding of a phenomenon by integrating the

strengths of both methods.

Learn more about data analysis here:

https://brainly.com/question/31940698

Convert the spherical coordinates to rectangular coordinates. [1 point e a) (8,-,-) 6 4, [2 points Write the equations in spherical coordinates. a) x² + y² + z² = 9 b) x² - y²z² = 4 V Find the volume of the solid that lies above the cone z = √√√x² + y² and below the sphere x² + y² + z² = 4. [4 points]

The rectangular coordinates for the spherical coordinates (8, π/6, π/3) are (2, 2√3, 4√3),a)ρ² = 9,b)ρ² =4,The volume V integrating the function 1   region in spherical coordinates V = ∭ dV.

To convert spherical coordinates to rectangular coordinates, we use the following formulas:

x = r × sin(θ) × cos(φ)

y = r × sin(θ) × sin(φ)

z = r ×cos(θ)

For the given spherical coordinates (ρ, θ, φ),

a) (8, π/6, π/3)

Using the formulas, convert these spherical coordinates to rectangular coordinates as follows:

x = 8 × sin(π/6) × cos(π/3) = 8 × (1/2) × (1/2) = 2

y = 8 × sin(π/6) × sin(π/3) = 8 × (1/2) × (√3/2) = 2√3

z = 8 × cos(π/6) = 8 × (√3/2) = 4√3

Regarding the equations in spherical coordinates:

a) x² + y² + z² = 9

In spherical coordinates, this equation can be written as:

b) x² - y²z² = 4

(ρ × sin(θ) × cos(φ))² - (ρ × sin(θ) × sin(φ))² × (ρ × cos(θ))² = 4

For the volume of the solid that lies above the cone z = √√√(x² + y²) and below the sphere x² + y² + z² = 4, use triple integration in spherical coordinates.

dV is the differential volume element in spherical coordinates.

To know more about rectangular here

https://brainly.com/question/32444543

The total amount due for Lim's electricity bill, including 10% GST, is $348.85. Calculate the GST charged.

Answer: $34.885

Explanation:

$348.85 /  10 = $34.885

for any group elements a and x, prove that |xax1||a|. this exercise is referred to in chapter 24.

For any group elements a and x, |xax⁻¹| = |a| is true.

The given statement for any group elements a and x, we will use the properties of groups and the definition of the absolute value of an element in a group.

Let G be a group with the operation denoted by multiplication (·). We want to prove that |xax⁻¹| = |a|.

First, let's define the absolute value of an element in a group. For any group element g in G, the absolute value |g| is defined as the smallest positive integer n such that gⁿ = e, where e is the identity element of the group.

Now, let's proceed with the proof:

Start with the expression |xax⁻¹|.

Multiply and divide by |x⁻¹|. This does not change the value of the expression since we are multiplying and dividing by the same element.

|xax⁻¹| = |x⁻¹xax⁻¹| × |x⁻¹|.

Rearrange the expression using the associative property of the group operation.

|x⁻¹xax⁻¹| = |x⁻¹xax⁻¹| × |x⁻¹|.

Apply the cancellation law for group elements. Since xx⁻¹ = e (identity element), we can cancel it out.

|x⁻¹xax⁻¹| = |ax⁻¹| × |x⁻¹|.

|ax⁻¹| × |x⁻¹| = |a| × |x⁻¹|.

Since |x⁻¹| is a positive integer (as it is the absolute value of an element in a group), we can multiply both sides of the equation by |x⁻¹| without changing the inequality.

|ax⁻¹| × |x⁻¹| = |a| × |x⁻¹| × |x⁻¹|.

Simplify the expression.

|a| × |x⁻¹| × |x⁻¹| = |a|.

Finally, we have shown that |xax⁻¹| = |a|.

Hence, we have proved that for any group elements a and x, |xax⁻¹| = |a|.

To know more about group elements click here :

https://brainly.com/question/30910436

a pair of dice are tossed. what is the probability that doubles are rolled, given that the sum on the two dice is less than 12? (round your answer to three decimal places.)

The probability of rolling doubles given that the sum on the two dice is less than 12 is 0.171.

We need to consider the favorable outcomes (rolling doubles) and the total possible outcomes (sum less than 12).

Favorable outcomes:

There are six possible doubles when rolling a pair of dice: (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6).

Total possible outcomes:

The total number of outcomes when rolling a pair of dice is 6× 6 = 36. Since we want to consider only the cases where the sum is less than 12, we need to exclude the outcome (6, 6), as its sum is 12.

Therefore, the total possible outcomes are 36 - 1 = 35.

Now we can calculate the probability :

Probability = (Number of favorable outcomes) / (Number of total possible outcomes)

Probability = 0.171

To learn more on probability click:

https://brainly.com/question/11234923

3. Solve the following equations: (a) 3x (b) 14 x+y 4y + + 1 = 0; 3 -= 5; x-y 1 + 5x 2y 21 2 x+y x-y 15 = 1​

you add the ×'s

Find the area of the region bounded by the curve y=f(x) = x3-4x + 1 and the tangent line to the curve y =fx) at (-1,4). You get: O 27 4 4 31 4 O 8.25 6.25

The area of the region bounded by the curve y = f(x) = x³ - 4x + 1 and the tangent line to the curve at (-1, 4) = 8.25.

To calculate the area of the region bounded by the curve y = f(x) = x³ - 4x + 1 and the tangent line to the curve at (-1, 4), we need to obtain the points of intersection between the curve and the tangent line.

First, let's find the equation of the tangent line .

We know that the tangent line to a curve at a given point has the same slope as the curve at that point.

Taking the derivative of f(x), we get:

f'(x) = 3x^2 - 4

Evaluating the derivative at x = -1 to obtain the slope at that point:

f'(-1) = 3(-1)^2 - 4 = -1

So, the slope of the tangent line at (-1, 4) is -1.

Using the point-slope form of a linear equation, we have:

y - 4 = -1(x - (-1))

y - 4 = -1(x + 1)

y - 4 = -x - 1

Now, let's obtain the points of intersection between the curve and the tangent line.

We equate the two equations:

x^3 - 4x + 1 = -x + 3

Rearranging the equation:

x^3 - 3x + 4x - 2 = 0

x^3 + x - 2 = 0

Now, we integrate the difference between the curve and the tangent line from x = -1 to x = 1.328 to obtain the area of the region:

Area = ∫[from -1 to 1.328] (f(x) - (-x + 3)) dx

Evaluating this integral, we get the area as approximately 8.25.

Therefore, the correct answer is O 8.25.

To know more about region bounded by the curve refer here:

https://brainly.com/question/32386889#

Say whether the given function has limit at the point (0,0). If the limit exists, then find it. (a) f(x, y) = 5ry² 3x² + y² (Hint: the parabola z = - y²); (b) f2(x, y) = Vel+V sin(y). (Hint: [√x + √] × [√ √U] ...). [2,3]

(a) The function f(x, y) does not have a limit at (0,0). (b) No information is provided to determine the limit for f2(x, y).

(a) For the function f(x, y) = 5ry²/(3x² + y²), we can analyze the behavior as (x, y) approaches (0,0). Since the denominator 3x² + y² becomes zero as (x, y) approaches (0,0), we cannot directly evaluate the function at this point. However, by considering the parabola z = -y², we can observe that the function does not approach a specific value and thus does not have a limit at (0,0).

(b) The function f2(x, y) = Vel + Vsin(y) is not well-defined as no information or context is provided for the variables Vel, V, and U. Without this information, it is not possible to determine the limit of the function at (0,0) or any other point.

Therefore, for (a), the function f(x, y) does not have a limit at (0,0), and for (b), no information is given to determine the limit for f2(x, y).

To learn more about “ variable ” refer to the https://brainly.com/question/28248724

1. The base of a solid is the region in the first quadrant bounded by the y-axis, the graph of y = -1x, the horizontal line y = 3 and the vertical line x = 1. For this solid, each cross section perpendicular to the x-axis is a square. What is the volume of the solid? 2. The region bounded by the graph of y = 2x −x2 and the x-axis is the base of a solid. For this solid, each cross section perpendicular to the x-axis is an equilateral triangle. What is the volume of the solid? 3. The base of a solid is a region in the first quadrant bounded by the x-axis, the y-axis, and the line x + 2y = 8, as shown in the figure. If cross sections of the solid perpendicular to the xaxis are semicircles, what is the volume of the solid?

1. The volume of the given solid is ∫[0,1] (3 - tan^(-1)(-x))² dx. 2. The volume of the given solid is (√3/4) × (b - a)³. 3. The volume of the given solid is (π/12) × [(8 - b)³ - (8 - a)³].

1. To find the volume of the solid with square cross sections, we need to integrate the area of the square cross sections over the interval from x = 0 to x = 1.

The equation y = tan⁻¹(-x) bounds the upper side of the square, while the line y = 3 bounds the lower side. Since each cross section is a square, the side length of the square is given by the difference between these two y-values.

The height of the square cross section is dx, as the cross sections are perpendicular to the x-axis.

Therefore, the volume (V) of the solid can be calculated by integrating the area of the square cross sections:

V = ∫[0,1] (3 - tan⁻¹(-x))² dx

Simplifying the integral is not straightforward, and there isn't a closed-form solution. However, you can approximate the integral using numerical methods such as the trapezoidal rule or Simpson's rule.

2. To find the volume of the solid with equilateral triangle cross sections, we need to integrate the area of the equilateral triangles over the given region.

The equation y = 2x - x² bounds the upper side of the equilateral triangle, while the x-axis bounds the lower side. The height of the equilateral triangle is the y-value of the curve at a given x.

The base of the equilateral triangle is given by the difference between the x-values of the region.

Therefore, the volume (V) of the solid can be calculated by integrating the area of the equilateral triangle cross sections:

V = ∫[a,b] [(side length)² × (√3)/4] dx

The side length of the equilateral triangle can be determined by taking the difference between the x-values of the region

side length = b - a

Substituting the values into the equation, we have:

V = ∫[a,b] [(b - a)² × (√3)/4] dx

= (√3/4) × (b - a)² × (b - a)

Therefore, the volume of the solid is (√3/4) × (b - a)³ cubic units.

3. Since the cross sections perpendicular to the x-axis are semicircles, the volume of the solid can be calculated by integrating the area of the semicircle cross sections over the given region.

The equation x + 2y = 8 can be rewritten as y = (8 - x)/2, which represents the upper boundary of the semicircle.

The x-axis represents the lower boundary of the semicircle.

The radius of the semicircle at a given x is given by the y-value of the upper boundary.

Therefore, the volume (V) of the solid can be calculated by integrating the area of the semicircle cross sections:

V = ∫[a,b] [(π × r²)/2] dx

The radius of the semicircle can be determined by taking the y-value of the upper boundary:

r = (8 - x)/2

V = ∫[a,b] [(π × (8 - x)²)/4] dx = (π/4) × [(8 - x)³/3] evaluated from a to b = (π/4) × [(8 - b)³/3 - (8 - a)³/3]

Therefore, the volume of the solid is (π/12) × [(8 - b)³ - (8 - a)³] cubic units.

To know more about volume here

https://brainly.com/question/30167677

-- The given question is incomplete, the complete question is

= -é 6t and Determine the second derivative of the parametrically defined curve represented by the equations x(t) y(t) = e2t . = Sorry, that's incorrect. Try again? dạy dx2

The second derivative of the parametrically defined curve represented by the equations [tex]x(t) = -e^{(-6t)[/tex] and [tex]y(t) = e^{(2t)[/tex] is:

[tex]d^2x/dt^2 = -36e^{(-6t)\\d^2y/dt^2 = 4e^{(2t)[/tex]

To find the second derivative of the parametrically defined curve represented by the equations [tex]x(t) = -e^{(-6t)[/tex] and [tex]y(t) = e^{(2t)[/tex], we need to differentiate each component twice with respect to t.

First, let's find the first derivative of x(t):

dx/dt = d/dt [tex](-e^{(-6t)})[/tex]

To differentiate [tex]-e^{(-6t)[/tex], we use the chain rule:

dx/dt = (-1)(d/dt)([tex]e^{(-6t)[/tex]) = -(-6[tex]e^{(-6t)[/tex]) = 6[tex]e^{(-6t)[/tex]

Now, let's find the second derivative of x(t):

d²x/dt² = d/dt(dx/dt) = d/dt(6[tex]e^{(-6t)[/tex])

Using the chain rule again:

d²x/dt² = 6(d/dt)([tex]e^{(-6t)[/tex]) = 6(-6[tex]e^{(-6t)[/tex]) = -36[tex]e^{(-6t)[/tex]

Next, let's find the first derivative of y(t):

dy/dt = d/dt([tex]e^{(2t)[/tex]) = 2[tex]e^{(2t)[/tex]

Now, let's find the second derivative of y(t):

d²y/dt² = d/dt(dy/dt) = d/dt(2[tex]e^{(2t)[/tex]) = 4[tex]e^{(2t)[/tex]

Therefore, the second derivative of the parametrically defined curve represented by the equations x(t) = [tex]-e^{(-6t)[/tex] and y(t) = [tex]e^{(2t)[/tex] is:

Learn more about Chain Rule at

brainly.com/question/31585086

Complete Question:

Determine The Second Derivative Of The Parametrically Defined Curve Represented By The Equations [tex]X(T)= -e^{-6t[/tex] And [tex]Y(T)=e^{2t.[/tex]

Can you please help me with this? Thank you so much.

Check the picture below.

[tex]0.24(d-85525)+14605.5 \\\\[-0.35em] ~\dotfill\\\\ \stackrel{ \textit{\LARGE Noam} }{0.24(90000-85525)+14605.5}\implies 0.24(4475)+14605.5\implies 15679.5 \\\\\\ \stackrel{ \textit{\LARGE Betty} }{0.24(120000-85525)+14605.5}\implies 0.24(34475)+14605.5\implies 22879.5 \\\\[-0.35em] ~\dotfill\\\\ 22879.5~~ - ~~15679.5\implies \text{\LARGE 7200}[/tex]

Question number 7. Carefully show he substitution steps for this equation.

By algebraic substitution , the integral of the rational function is - (2 / 7) · (7 · x² + 3) + C.

In this problem we find the case of a rational function, whose integral must be found. This can be done by means of algebraic substitution which simplifies the expression and gives a quicker solution. First, write the entire expression:

∫ [x / (7 · x² + 3)⁵] dx

Second, use the following algebraic substitution to simplify the expression:

u = 7 · x² + 3

du = 14 · x dx

(1 / 14) ∫ [du / u⁵]

(1 / 14) ∫ u⁻⁵ du

Third, solve the resulting expression:

- (4 / 14) · u⁻⁴ + C

- (2 / 7) · u⁻⁴ + C

Fourth, revert the substitution:

- (2 / 7) · (7 · x² + 3) + C

To learn more on indefinite integrals : https://brainly.com/question/28036871

evaluate 4g-124g−124, g, minus, 12 when g=5g=5g, equals, 5.

When g = 5, the Value of the expression 4g - 124g - 124 is -724.

To evaluate the expression 4g - 124g - 124 when g = 5, we substitute the value of g into the expression and perform the necessary calculations. Let's proceed step by step:

Step 1: Substitute g = 5 into the expression:

4(5) - 124(5) - 124

Step 2: Simplify the expression using the order of operations (PEMDAS):

20 - 620 - 124

Step 3: Perform subtraction from left to right:

Step 4: Calculate the final result:

Therefore, when g = 5, the value of the expression 4g - 124g - 124 is -724.

For more questions on Value .

https://brainly.com/question/843074

A standing inspector picks up 20 lb castings from a pallet the floor and lift it 50 inches high with a horizontal distance of 20 inches for first visual inspection. He then puts the casting on a work area 25 inches from the floor and closer to the body (a minimum horizontal distance) for second inspection. Assume a frequency of 1 lift per minute over 8 hours (multiplier=0.75) and a poor coupling multiplier (0.90). This led to the following calculations RWLorg = 51 (10/20) (1 - .0075/50-30) (82 +1.8/50) (1 -.0032 (0)) (0.75) (0.90) = 12.52 RWLdest = 51 (10/10) (1 - .0075/25-30) (.82 + 1.8/25) (1 -.0032 (0)) (0.75) (0.90) = 29.56 LI = 20/12.03 -1.66 LI = 20/29.56 = 0.68 1.1 Which lift is acceptable according to the NIOSH guidelines? (2) You were requested to investigate the above situation and recommend changes to the layout to get the Ll value below a value of 1 (company policy). Shortly discuss what changes you will make and then show the calculated results of your suggested changes proving that LI will be below 1 using formulas provided. (10) 1 RWL = 51 (10/H) (1 -.0075 V-301) (.82 +1.8/D) (1 -.0032A) (FM) (CM) LI = load weight/RWL

According to the NIOSH guidelines, a lifting index (LI) value below 1 is considered acceptable, indicating a low risk of developing work-related musculoskeletal disorders.

In the given scenario, the LI values for the two lifts are calculated as follows:

For the first lift:

LI = 20/12.52 = 1.60

For the second lift:

LI = 20/29.56 = 0.68

Based on these calculations, the second lift with an LI value of 0.68 is acceptable according to the NIOSH guidelines since it is below the threshold of 1.

To reduce the LI value below 1, several changes can be made to the layout and lifting procedure:

Reduce the weight of the castings: If it is possible to use lighter castings, it would decrease the load weight, resulting in a lower LI value.

Modify the work area height: Adjusting the work area height to a lower level, closer to the inspector's body, would decrease the vertical distance of the lift and consequently lower the LI value.

Optimize the horizontal distance: If feasible, reposition the work area closer to the inspector's body to reduce the horizontal distance of the lift, which would contribute to a lower LI value.

By implementing these changes, the new LI values can be calculated using the provided formulas to ensure compliance with the company policy of maintaining an LI value below 1.

Learn more about weight here:

https://brainly.com/question/31659519

If you toss a coin 4 times, what is the probability of getting at least 3 tails? Show your work. what is the probability of getting exactly 3 tails? Show your work.

Therefore, the probability of getting at least 3 tails is 1/16 + 1/4 = 5/16 or 0.3125.

The probability of getting exactly 3 tails is just 1/4, as we calculated above.

To find the probability of getting at least 3 tails when tossing a coin 4 times, we need to add the probabilities of getting 3 tails and 4 tails.

The probability of getting a tail on one toss is 1/2, and the probability of getting a head is also 1/2.

The probability of getting 4 tails is (1/2)^4 = 1/16 because there is a 1/2 chance of getting a tail on each toss, and the events are independent, so we multiply the probabilities together.

The probability of getting 3 tails is (4 choose 3) * (1/2)^4 = 4/16 = 1/4 because we need to choose which 3 tosses will be tails (this can be done in (4 choose 3) = 4 ways), and there is a 1/2 chance of each of those tosses being a tail, with a 1/2 chance of the last toss being a head.

Use complex exponentials to express the function f(x) = cos^3x as a real linear combination of trigonometric function:s 1, cos x, sin x, cos 2x, sin 2x, cos 3x, sin 3a , . .

the answer is - we have expressed the function [tex]$f(x)$[/tex] as a real linear combination of the trigonometric functions 1, [tex]$\cos(x)$, $\sin(x)$, $\cos(2x)$, $\sin(2x)$, $\cos(3x)$ and $\sin(3x)$[/tex], as required.

The given function is[tex]$f(x) = \cos^3(x)$.[/tex]

We know that [tex]$\cos(3x) = 4 \cos^3(x) - 3 \cos(x)$,[/tex] thus [tex]$4\cos^3(x) = \frac{3}{4} \cos(3x) + \frac{1}{4}\cos(x)$.[/tex]

So, [tex]$f(x) = \cos^3(x) = \frac{3}{4}\cos(x)\cos(3x) + \frac{1}{4} \cos^3(x)$.[/tex]

We can express [tex]$\cos(x)$[/tex]in terms of exponentials as: [tex]$\cos(x) = \frac{e^{ix}+e^{-ix}}{2}$.[/tex]

Similarly, we can write [tex]$\cos(3x)$[/tex] in terms of exponentials as:[tex]$\cos(3x) = \frac{e^{i3x}+e^{-i3x}}{2}$.[/tex]

Using these identities, we can express [tex]$f(x)$[/tex] as a linear combination of real trigonometric functions as: [tex]f(x) = $\frac{3}{8}(e^{ix}+e^{-ix}) (e^{i3x}+e^{-i3x}) + \frac{1}{8}(e^{ix}+e^{-ix})^3$[/tex]

Expanding the last term, we get[tex]$f(x) = \frac{1}{8}(e^{i3x}+e^{-i3x}) + \frac{3}{4}(e^{ix}+e^{-ix})\cos^2(x)$[/tex]

Using the identity [tex]$\cos^2(x) = \frac{1}{2} (1+\cos(2x))$,[/tex]

we can write[tex]$f(x) = \frac{1}{8}(e^{i3x}+e^{-i3x}) + \frac{3}{8}(e^{ix}+e^{-ix}) + \frac{3}{8}(e^{ix+2ix}+e^{-ix-2ix})[/tex]

[tex]$$f(x) = \frac{1}{8}(e^{i3x}+e^{-i3x}) + \frac{3}{8}(e^{ix}+e^{-ix}) + \frac{3}{16}(e^{3ix}+e^{-3ix}) + \frac{3}{16}(e^{ix}+e^{-ix})$[/tex]

Thus, we have expressed the function [tex]$f(x)$[/tex] as a real linear combination of the trigonometric functions 1, [tex]$\cos(x)$, $\sin(x)$, $\cos(2x)$, $\sin(2x)$, $\cos(3x)$ and $\sin(3x)$,[/tex] as required.

know more about trigonometric functions

https://brainly.com/question/29090818

Suppose 67 percent of the public support T-cell research. In a simple random sample of eight people, what is the probability more than half support T-cell research? Plass)= b. .252 e. .272 d. .748 e. .915 .167 .67

The probability more than half of the people from the simple random sample support T-cell research is 0.748.

To calculate the probability that more than half out of eight people in the simple random sample support T -cell research , we will use the binomial distribution, where:n = 8 (number of trials)

P = 0.67 (probability of success in one trial)q = 1 - P = 1 - 0.67 = 0.33 (probability of failure in one trial)r > 4 (number of successes)

The required probability is P(r > 4).

We will use the complement of this probability, i.e. P(r ≤ 4) and calculate it using the binomial probability formula :

[tex]P(r ≤ 4) = ∑ nCr P^r q {}^{(n-r)} [/tex]

where r varies from 0 to 4.

P(r ≤ 4) = C(8, 0) (0.67)⁰ (0.33)⁸ + C(8, 1) (0.67)¹ (0.33)⁷ + C(8, 2) (0.67)² (0.33)⁶+ C(8, 3) (0.67)³ (0.33)⁵ + C(8, 4) (0.67)⁴ (0.33)⁴= 0.000456 + 0.00715 + 0.045 + 0.168 + 0.312= 0.533

So, P(r > 4) = 1 - P(r ≤ 4) = 1 - 0.533 = 0.467 ≈ 0.748

Learn more about the probability at

https://brainly.com/question/14065987

I need help with this one !

use as a expression

What is the volume of the prism? All angles are right angles.

The volume of the given prism is 168 cubic meters. It's important to note that the units of the measurements provided (m) are in meters. So the resulting volume is in cubic meters (m³).

To find the volume of a prism, we need to multiply the area of the base by the height. In this case, the given prism has a base that measures 7 m by 4 m and a height of 6 m.

Step 1: Calculate the area of the base. The base of the prism is a rectangle, so the area is found by multiplying the length (7 m) by the width (4 m).

Area of the base = length × width

              = 7 m × 4 m

              = 28 m²

Step 2: Multiply the area of the base by the height of the prism to find the volume.

Volume of the prism = Area of the base × height

                  = 28 m² × 6 m

                  = 168 m³

Therefore, the volume of the given prism is 168 cubic meters .

It's important to note that the units of the measurements provided (m) are in meters. So the resulting volume is in cubic meters (m³). The volume represents the amount of space enclosed by the prism. In this case, the prism has a length of 7 m, width of 4 m, and height of 6 m, resulting in a volume of 168 cubic meters.

Remember to always include the appropriate unit of measurement when expressing the volume or any other quantity.

for more such question on measurements visit

https://brainly.com/question/27233632

How do I do these question? Please answer a and b. not mix them together. Please help!

b) subtract 4 from right

a) If we double the number of counters on the left side, to maintain the balance, we should double the number of counters on the left side .

b) 14 oranges = 2 packs and 4 oranges

From this we can conclude that 10 oranges are equal to the weight of 2 packs. So, 5 oranges are equal to 1 pack.

Suppose if we subtract four counters from left side, subtract 4 counters (oranges) from the right side .

So, left side will have 2 packs and right side will have 10 counters(oranges).

7. A box contains ten marbles on which the numbers 1,2,…,9,10 are written. Consider experiments in which you select marbles one at a time with replacement. (a) Suppose you choose three marbles. Find the probability that exactly two marbles show a number greater than 7. (b) Let X represent the number of marbles you must choose until you obtain one that shows a number divisible by 5 . Evaluate P(X=4).

a) Probability of exactly two marbles showing a number greater than 7: 237/1000.

(b) Probability of obtaining a marble divisible by 5 on the fourth draw: 1/5.

(a) To find the probability that exactly two marbles show a number greater than 7 out of three chosen marbles, we need to consider the possible combinations. There are three cases:

Case 1: Selecting two marbles with numbers greater than 7 and one marble with a number less than or equal to 7.

The probability of selecting a marble with a number greater than 7 is 3/10, and the probability of selecting a marble with a number less than or equal to 7 is 7/10. Since there are three positions for the marble with a number less than or equal to 7, the probability for this case is (3/10) × (3/10) × (7/10) = 63/1000.

Case 2: Selecting one marble with a number greater than 7 and two marbles with numbers less than or equal to 7.

The probability of selecting a marble with a number greater than 7 is 3/10, and the probability of selecting a marble with a number less than or equal to 7 is 7/10. Since there are three positions for the marble with a number greater than 7, the probability for this case is (3/10) × (7/10) × (7/10) = 147/1000.

Case 3: Selecting three marbles with numbers greater than 7.

The probability of selecting a marble with a number greater than 7 is 3/10. Since all three marbles should have numbers greater than 7, the probability for this case is (3/10) × (3/10) × (3/10) = 27/1000.

Adding up the probabilities for the three cases, we get (63 + 147 + 27)/1000 = 237/1000.

Therefore, the probability of exactly two marbles showing a number greater than 7 is 237/1000.

(b) To evaluate P(X=4), where X represents the number of marbles chosen until obtaining one that shows a number divisible by 5, we need to consider the sequence of events leading up to this outcome.

The first three marbles chosen can have any numbers, so the probability is (10/10) × (10/10) × (10/10) = 1.

The fourth marble must be divisible by 5, which includes the numbers 5 and 10. So the probability for this event is 2/10 = 1/5.

Therefore, P(X=4) = 1 × (1/5) = 1/5.

Read more on Probability here: https://brainly.com/question/13604758

Information

• Author Services

Initiatives

You are accessing a machine-readable page. In order to be human-readable, please install an RSS reader.

All articles published by MDPI are made immediately available worldwide under an open access license. No special permission is required to reuse all or part of the article published by MDPI, including figures and tables. For articles published under an open access Creative Common CC BY license, any part of the article may be reused without permission provided that the original article is clearly cited. For more information, please refer to https://www.mdpi.com/openaccess .

Feature papers represent the most advanced research with significant potential for high impact in the field. A Feature Paper should be a substantial original Article that involves several techniques or approaches, provides an outlook for future research directions and describes possible research applications.

Feature papers are submitted upon individual invitation or recommendation by the scientific editors and must receive positive feedback from the reviewers.

Editor’s Choice articles are based on recommendations by the scientific editors of MDPI journals from around the world. Editors select a small number of articles recently published in the journal that they believe will be particularly interesting to readers, or important in the respective research area. The aim is to provide a snapshot of some of the most exciting work published in the various research areas of the journal.

Original Submission Date Received: .

• Active Journals
• Find a Journal
• Proceedings Series
• For Authors
• For Reviewers
• For Editors
• For Librarians
• For Publishers
• For Societies
• For Conference Organizers
• Open Access Policy
• Institutional Open Access Program
• Special Issues Guidelines
• Editorial Process
• Research and Publication Ethics
• Article Processing Charges
• Testimonials
• Preprints.org
• SciProfiles
• Encyclopedia

Article Menu

• Subscribe SciFeed
• Recommended Articles
• Google Scholar
• on Google Scholar
• Table of Contents

Find support for a specific problem in the support section of our website.

Please let us know what you think of our products and services.

Visit our dedicated information section to learn more about MDPI.

JSmol Viewer

On a local and nonlocal second-order boundary value problem with in-homogeneous cauchy–neumann boundary conditions—applications in engineering and industry.

Share and Cite

Barbu, T.; Miranville, A.; Moroşanu, C. On a Local and Nonlocal Second-Order Boundary Value Problem with In-Homogeneous Cauchy–Neumann Boundary Conditions—Applications in Engineering and Industry. Mathematics 2024 , 12 , 2050. https://doi.org/10.3390/math12132050

Barbu T, Miranville A, Moroşanu C. On a Local and Nonlocal Second-Order Boundary Value Problem with In-Homogeneous Cauchy–Neumann Boundary Conditions—Applications in Engineering and Industry. Mathematics . 2024; 12(13):2050. https://doi.org/10.3390/math12132050

Barbu, Tudor, Alain Miranville, and Costică Moroşanu. 2024. "On a Local and Nonlocal Second-Order Boundary Value Problem with In-Homogeneous Cauchy–Neumann Boundary Conditions—Applications in Engineering and Industry" Mathematics 12, no. 13: 2050. https://doi.org/10.3390/math12132050

Article Metrics

Article access statistics, further information, mdpi initiatives, follow mdpi.

Subscribe to receive issue release notifications and newsletters from MDPI journals

• Advanced Search

Existence results for a class of four point nonlinear singular BVP arising in thermal explosion in a spherical vessel

New citation alert added.

This alert has been successfully added and will be sent to:

You will be notified whenever a record that you have chosen has been cited.

To manage your alert preferences, click on the button below.

New Citation Alert!

Please log in to your account

Information & Contributors

Bibliometrics & citations, view options, recommendations, a class of boundary value problems for first-order impulsive integro-differential equations with deviating arguments.

This paper is concerned with a class of boundary value problems for nonlinear mixed impulsive integro-differential equations with deviating arguments. We establish a new comparison principle and use the method of upper and lower solutions together with ...

Singular perturbations of third-order nonlinear differential equations with full nonlinear boundary conditions

In this paper, we discuss singular perturbations of third-order nonlinear ordinary differential equations with full nonlinear boundary conditions. The emphasis here is that the nonlinear term depends on the first, second order derivatives and the ...

A new superconvergent method for systems of nonlinear singular boundary value problems

A new superconvergent method based on a sextic spline is described and analysed for the solution of systems of nonlinear singular two-point boundary value problems BVPs. It is well known that the optimal orders of convergence could not be achieved using ...

Information

Published in.

Elsevier Science Publishers B. V.

Netherlands

Publication History

Author tags.

• Monotone iterative technique
• Upper and lower solutions
• Green’s function
• Research-article

Contributors

Other metrics, bibliometrics, article metrics.

• 0 Total Citations
• 0 Total Downloads
• Downloads (Last 12 months) 0
• Downloads (Last 6 weeks) 0

View options

Login options.

Check if you have access through your login credentials or your institution to get full access on this article.

Full Access

Share this publication link.

Copying failed.

Share on social media

Affiliations, export citations.

• Please download or close your previous search result export first before starting a new bulk export. Preview is not available. By clicking download, a status dialog will open to start the export process. The process may take a few minutes but once it finishes a file will be downloadable from your browser. You may continue to browse the DL while the export process is in progress. Download
• Download citation
• Copy citation

We are preparing your search results for download ...

We will inform you here when the file is ready.

Your file of search results citations is now ready.

Your search export query has expired. Please try again.

If we’re all so busy, why isn’t anything getting done?

Have you ever asked why it’s so difficult to get things done in business today—despite seemingly endless meetings and emails? Why it takes so long to make decisions—and even then not necessarily the right ones? You’re not the first to think there must be a better way. Many organizations address these problems by redesigning boxes and lines: who does what and who reports to whom. This exercise tends to focus almost obsessively on vertical command relationships and rarely solves for what, in our experience, is the underlying disease: the poor design and execution of collaborative interactions.

About the authors

This article is a collaborative effort by Aaron De Smet , Caitlin Hewes, Mengwei Luo, J.R. Maxwell , and Patrick Simon , representing views from McKinsey’s People & Organizational Performance Practice.

In our efforts to connect across our organizations, we’re drowning in real-time virtual interaction technology, from Zoom to Slack to Teams, plus group texting, WeChat, WhatsApp, and everything in between. There’s seemingly no excuse to not collaborate. The problem? Interacting is easier than ever, but true, productive, value-creating collaboration is not. And what’s more, where engagement is occurring, its quality is deteriorating. This wastes valuable resources, because every minute spent on a low-value interaction eats into time that could be used for important, creative, and powerful activities.

It’s no wonder a recent McKinsey survey  found 80 percent of executives were considering or already implementing changes in meeting structure and cadence in response to the evolution in how people work due to the COVID-19 pandemic. Indeed, most executives say they frequently find themselves spending way too much time on pointless interactions that drain their energy and produce information overload.

Most executives say they frequently find themselves spending way too much time on pointless interactions.

Three critical collaborative interactions

What can be done? We’ve found it’s possible to quickly improve collaborative interactions by categorizing them by type and making a few shifts accordingly. We’ve observed three broad categories of collaborative interactions (exhibit):

• Decision making, including complex or uncertain decisions (for example, investment decisions) and cross-cutting routine decisions (such as quarterly business reviews)
• Creative solutions and coordination, including innovation sessions (for example, developing new products) and routine working sessions (such as daily check-ins)
• Information sharing, including one-way communication (video, for instance) and two-way communication (such as town halls with Q&As)

Below we describe the key shifts required to improve each category of collaborative interaction, as well as tools you can use to pinpoint problems in the moment and take corrective action.

Decision making: Determining decision rights

When you’re told you’re “responsible” for a decision, does that mean you get to decide? What if you’re told you’re “accountable”? Do you cast the deciding vote, or does the person responsible? What about those who must be “consulted”? Sometimes they are told their input will be reflected in the final answer—can they veto a decision if they feel their input was not fully considered?

It’s no wonder one of the key factors for fast, high-quality decisions is to clarify exactly who makes them. Consider a success story at a renewable-energy company. To foster accountability and transparency, the company developed a 30-minute “role card” conversation for managers to have with their direct reports. As part of this conversation, managers explicitly laid out the decision rights and accountability metrics for each direct report. The result? Role clarity enabled easier navigation for employees, sped up decision making, and resulted in decisions that were much more customer focused.

How to define decision rights

We recommend a simple yet comprehensive approach for defining decision rights. We call it DARE, which stands for deciders, advisers, recommenders, and executors:

Deciders are the only ones with a vote (unlike the RACI model, which helps determine who is responsible, accountable, consulted, and informed). If the deciders get stuck, they should jointly agree on how to escalate the decision or figure out a way to move the process along, even if it means agreeing to “disagree and commit.”

Advisers have input and help shape the decision. They have an outsize voice in setting the context of the decision and have a big stake in its outcome—for example, it may affect their profit-and-loss statements—but they don’t get a vote.

Recommenders conduct the analyses, explore the alternatives, illuminate the pros and cons, and ultimately recommend a course of action to advisers and deciders. They see the day-to-day implications of the decision but also have no vote. Best-in-class recommenders offer multiple options and sometimes invite others to suggest more if doing so may lead to better outcomes. A common mistake of recommenders, though, is coming in with only one recommendation (often the status quo) and trying to convince everyone it’s the best path forward. In general, the more recommenders, the better the process—but not in the decision meeting itself.

Executers don’t give input but are deeply involved in implementing the decision. For speed, clarity, and alignment, executers need to be in the room when the decision is made so they can ask clarifying questions and spot flaws that might hinder implementation. Notably, the number of executers doesn’t necessarily depend on the importance of the decision. An M&A decision, for example, might have just two executors: the CFO and a business-unit head.

To make this shift, ensure everyone is crystal clear about who has a voice but no vote or veto. Our research indicates while it is often helpful to involve more people in decision making, not all of them should be deciders—in many cases, just one individual should be the decider (see sidebar “How to define decision rights”). Don’t underestimate the difficulty of implementing this. It often goes against our risk-averse instinct to ensure everyone is “happy” with a decision, particularly our superiors and major stakeholders. Executing and sustaining this change takes real courage and leadership.

Creative solutions and coordination: Open innovation

Routine working sessions are fairly straightforward. What many organizations struggle with is finding innovative ways to identify and drive toward solutions. How often do you tell your teams what to do versus empowering them to come up with solutions? While they may solve the immediate need to “get stuff done,” bureaucracies and micromanagement are a recipe for disaster. They slow down the organizational response to the market and customers, prevent leaders from focusing on strategic priorities, and harm employee engagement. Our research suggests  key success factors in winning organizations are empowering employees  and spending more time on high-quality coaching interactions.

How microenterprises empower employees to drive innovative solutions

Haier, a Chinese appliance maker, created more than 4,000 microenterprises (MEs) that share common approaches but operate independently. Haier has three types of microenterprises:

• Market-facing MEs have roots in Haier’s legacy appliance business, reinvented for today’s customer-centric, web-enabled world. They are expected to grow revenue and profit ten times faster than the industry average.
• Incubating MEs focus on emerging markets such as e-gaming or wrapping new business models around familiar products. They currently account for more than 10 percent of Haier’s market capitalization.
• “Node” MEs sell market-facing ME products and services such as design, manufacturing, and human-resources support.

Take Haier. The Chinese appliance maker divided itself into more than 4,000 microenterprises with ten to 15 employees each, organized in an open ecosystem of users, inventors, and partners (see sidebar “How microenterprises empower employees to drive innovative solutions”). This shift turned employees into energetic entrepreneurs who were directly accountable for customers. Haier’s microenterprises are free to form and evolve with little central direction, but they share the same approach to target setting, internal contracting, and cross-unit coordination. Empowering employees to drive innovative solutions has taken the company from innovation-phobic to entrepreneurial at scale. Since 2015, revenue from Haier Smart Home, the company’s listed home-appliance business, has grown by more than 18 percent a year, topping 209 billion renminbi ($32 billion) in 2020. The company has also made a string of acquisitions, including the 2016 purchase of GE Appliances, with new ventures creating more than $2 billion in market value.

Empowering others doesn’t mean leaving them alone. Successful empowerment, counterintuitively, doesn’t mean leaving employees alone. Empowerment requires leaders to give employees both the tools and the right level of guidance and involvement. Leaders should play what we call the coach role: coaches don’t tell people what to do but instead provide guidance and guardrails and ensure accountability, while stepping back and allowing others to come up with solutions.

Haier was able to use a variety of tools—including objectives and key results (OKRs) and common problem statements—to foster an agile way of working across the enterprise that focuses innovative organizational energy on the most important topics. Not all companies can do this, and some will never be ready for enterprise agility. But every organization can take steps to improve the speed and quality of decisions made by empowered individuals.

Managers who are great coaches, for example, have typically benefited from years of investment by mentors, sponsors, and organizations. We think all organizations should do more to improve the coaching skills of managers and help them to create the space and time to coach teams, as opposed to filling out reports, presenting in meetings, and other activities that take time away from driving impact through the work of their teams.

But while great coaches take time to develop, something as simple as a daily stand-up or check-in can drive horizontal connectivity, creating the space for teams to understand what others are doing and where they need help to drive work forward without having to specifically task anyone in a hierarchical way. You may also consider how you are driving a focus on outcomes over activities on a near-term and long-term basis. Whether it’s OKRs or something else, how is your organization proactively communicating a focus on impact and results over tasks and activities? What do you measure? How is it tracked? How is the performance of your people and your teams managed against it? Over what time horizons?

The importance of psychological safety. As you start this journey, be sure to take a close look at psychological safety. If employees don’t feel psychologically safe, it will be nearly impossible for leaders and managers to break through disempowering behaviors like constant escalation, hiding problems or risks, and being afraid to ask questions—no matter how skilled they are as coaches.

Employers should be on the lookout for common problems indicating that significant challenges to psychological safety lurk underneath the surface. Consider asking yourself and your teams questions to test the degree of psychological safety you have cultivated: Do employees have space to bring up concerns or dissent? Do they feel that if they make a mistake it will be held against them? Do they feel they can take risks or ask for help? Do they feel others may undermine them? Do employees feel valued for their unique skills and talents? If the answer to any of these is not a clear-cut “yes,” the organization likely has room for improvement on psychological safety and relatedness as a foundation to high-quality interactions within and between teams.

Information sharing: Fit-for-purpose interactions

Do any of these scenarios sound familiar? You spend a significant amount of time in meetings every day but feel like nothing has been accomplished. You jump from one meeting to another and don’t get to think on your own until 7 p.m. You wonder why you need to attend a series of meetings where the same materials are presented over and over again. You’re exhausted.

An increasing number of organizations have begun to realize the urgency of driving ruthless meeting efficiency and of questioning whether meetings are truly required at all to share information. Live interactions can be useful for information sharing, particularly when there is an interpretive lens required to understand the information, when that information is particularly sensitive, or when leaders want to ensure there’s ample time to process it and ask questions. That said, most of us would say that most meetings are not particularly useful and often don’t accomplish their intended objective.

We have observed that many companies are moving to shorter meetings (15 to 30 minutes) rather than the standard default of one-hour meetings in an effort to drive focus and productivity. For example, Netflix launched a redesign effort to drastically improve meeting efficiency, resulting in a tightly controlled meeting protocol. Meetings cannot go beyond 30 minutes. Meetings for one-way information sharing must be canceled in favor of other mechanisms such as a memo, podcast, or vlog. Two-way information sharing during meetings is limited by having attendees review materials in advance, replacing presentations with Q&As. Early data show Netflix has been able to reduce the number of meetings by more than 65 percent, and more than 85 percent of employees favor the approach.

Making meeting time a scarce resource is another strategy organizations are using to improve the quality of information sharing and other types of interactions occurring in a meeting setting. Some companies have implemented no-meeting days. In Japan, Microsoft’s “Work Life Choice Challenge” adopted a four-day workweek, reduced the time employees spend in meetings—and boosted productivity by 40 percent. 1 Bill Chappell, “4-day workweek boosted workers’ productivity by 40%, Microsoft Japan says,” NPR, November 4, 2019, npr.org. Similarly, Shopify uses “No Meeting Wednesdays” to enable employees to devote time to projects they are passionate about and to promote creative thinking. 2 Amy Elisa Jackson, “Feedback & meeting-free Wednesdays: How Shopify beats the competition,” Glassdoor, December 5, 2018, glassdoor.com. And Moveline’s product team dedicates every Tuesday to “Maker Day,” an opportunity to create and solve complex problems without the distraction of meetings. 3 Rebecca Greenfield, “Why your office needs a maker day,” Fast Company , April 17, 2014, fastcompany.com.

Finally, no meeting could be considered well scoped without considering who should participate, as there are real financial and transaction costs to meeting participation. Leaders should treat time spent in meetings as seriously as companies treat financial capital. Every leader in every organization should ask the following questions before attending any meeting: What’s this meeting for? What’s my role? Can I shorten this meeting by limiting live information sharing and focusing on discussion and decision making? We encourage you to excuse yourself from meetings if you don’t have a role in influencing the outcome and to instead get a quick update over email. If you are not essential, the meeting will still be successful (possibly more so!) without your presence. Try it and see what happens.

High-quality, focused interactions can improve productivity, speed, and innovation within any organization—and drive better business performance. We hope the above insights have inspired you to try some new techniques to improve the effectiveness and efficiency of collaboration within your organization.

Aaron De Smet is a senior partner in McKinsey’s New Jersey office; Caitlin Hewes is a consultant in the Atlanta office; Mengwei Luo is an associate partner in the New York office; J.R. Maxwell is a partner in the Washington, DC, office; and Patrick Simon is a partner in the Munich office.

Explore a career with us

Related articles.

Author Talks: Beyond collaboration overload

Battling burnout: A conversation with resiliency expert Dr. Amit Sood

Author Talks: Why burnout is an epidemic—and what to do about it