Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.

Solving a minimization problem using a Simplex method
There is a method of solving a minimization problem using the simplex method where you just need to multiply the objective function by -ve sign and then solve it using the simplex method. All you need to do is to multiply the max value found again by -ve sign to get the required max value of the original minimization problem. My question is there is any condition that must be satisfied on the constraints of the optimization problem to use this method?
- linear-programming
- $\begingroup$ Would you be able to edit your question to include an example of your objective function in algebraic terms? $\endgroup$ – danielcharters Commented Apr 10, 2020 at 7:45
- $\begingroup$ @danielcharters many thanks for ur reply. please see my edit I mean is there are any conditions that must be satisfied on the constrains inequality equations to use this method? Sorry about that. $\endgroup$ – John adams Commented Apr 10, 2020 at 7:49
- $\begingroup$ @Johnadams, To solve the optimization problem using the simplex method, it needs to be interpreted as a standard form , in which all of the model constraints are equal. (To do that, adding slack/surplus/artificial variables.). $\endgroup$ – A.Omidi Commented Apr 10, 2020 at 9:33
- $\begingroup$ @A.Omidi but there is no constrain on the inequality itself to use the above-mentioned method? I mean the constrain should be <= or >= to use the above-mentioned method or whatever the inequality is I can use this method? $\endgroup$ – John adams Commented Apr 10, 2020 at 9:43
- $\begingroup$ @Johnadams, for both inequality you mentioned, $<=$ or $>=$, you could use the simplex method. In the $<=$ you need slack variables and in the $>=$ you need surplus and even artificial variables. If your problem has many variables I recommended using optimization software to do that automatically. $\endgroup$ – A.Omidi Commented Apr 10, 2020 at 9:48
2 Answers 2
It has nothing to do even with linear programming. It's a simple mathematical fact:
$$\min \left( f \left( x \right) \right) = - \max \left( -f \left( x \right) \right)$$
which still holds when you restrict the domain of the function by the constraints (actually to a convex polyhedron in case of LP).
- 1 $\begingroup$ "Convex cone" should probably be "convex polytope" (or polyhedron), but the mathematical statement is correct. $\endgroup$ – prubin ♦ Commented Apr 10, 2020 at 19:38
The only requirements for the constraints, that I am aware of, when using the simplex algorithm to solve a minimization (and maximization) problem is to include the slack and surplus variables where needed, and the decision variables have to be non-negative. Below is an example to illustrate how to formulate a problem to be solved using the simplex algorithm and how to include slack and surplus variables into your formulation. \begin{align}\min&\quad z = 2x_1 - 3x_2\\\text{s.t.}&\quad x_1+x_2 \leq 4\\&\quad x_1-x_2 \geq 6\\&\quad x_1,x_2 \geq 0\end{align}
The optimal solution to this would be where $ z = 2x_1-3x_2$ is the smallest, but equivalently it can be said that the optimal solution would be where $ -z = -2x_1+3x_2$ is the largest. This is done as the simplex algorithm is used to solve maximization problems, and the formulation now becomes \begin{align}\max&\quad-z = -2x_1 + 3x_2\\\text{s.t.}&\quad x_1+x_2 \leq 4\\&\quad x_1-x_2 \geq 6\\&\quad x_1,x_2 \geq 0\end{align}
We add a slack variable $s_1$ to the first constraint, which now becomes $x_1 +x_2 +s_1 = 4$ . Similarly for the second constraint, we add the surplus variable $s_2$ , and the constraint now becomes $x_1-x_2 + s_2= 6$ .
The formulation, which is now in standard form to be solved using the simplex algorithm, is as follows: \begin{align}\max&\quad-z = -2x_1 + 3x_2\\\text{s.t.}&\quad x_1 +x_2 +s_1 = 4\\&\quad x_1-x_2 + s_2= 6\\&\quad x_1,x_2 \geq 0\\&\quad s_1,s_2 \geq 0.\end{align}
Your Answer
Sign up or log in, post as a guest.
Required, but never shown
By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .
Not the answer you're looking for? Browse other questions tagged linear-programming simplex or ask your own question .
- Featured on Meta
- Announcing a change to the data-dump process
- Upcoming initiatives on Stack Overflow and across the Stack Exchange network...
- We spent a sprint addressing your requests — here’s how it went
Hot Network Questions
- Seatstay eyelet cracked on carbon frame
- My result is accepted in a journal as an errata, but the editors want to change the authorship
- Why doesn't sed have a j command?
- vi (an old AIX vi, not vim): map: I can search, move, yank, or dd, but cannot paste
- To what degree are we expected to identify/fix others' mistakes?
- Calculate sum of self-exponentation
- In the travel industry, why is the "business" term coined in for luxury or premium services?
- Problems recording music from Yamaha keyboard to PC
- Which civil aircraft use fly-by-wire without mechanical backup?
- Why do the Fourier components of a piano note shift away from the harmonic series?
- The use of Bio-weapons as a deterrent?
- How can I write a std::apply on a std::expected?
- What side-effects, if any, are okay when importing a python module?
- Draw a Regular Reuleaux Polygon
- Is this "continuous" function really continuous?
- Older brother licking younger sister's legs
- How can I get rid of/ smooth out weird/ sharp edges like this?
- RegionPlot does not work appropriately
- Possessive pronoun
- What does impedance seen from input/output mean?
- Pattern on a PCB
- How does anyone know for sure who the Prime Minister is?
- Iterating over the contents of a file
- Continued calibration of atomic clocks
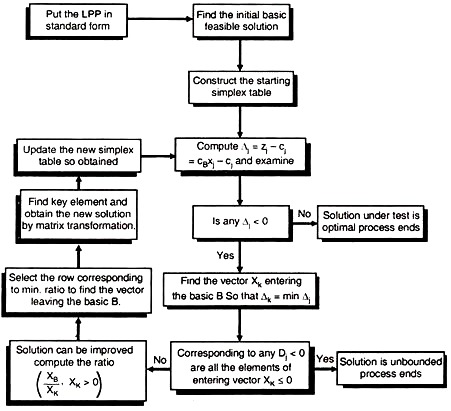
Simplex Method for Solution of L.P.P (With Examples) | Operation Research
After reading this article you will learn about:- 1. Introduction to the Simplex Method 2. Principle of Simplex Method 3. Computational Procedure 4. Flow Chart.
Introduction to the Simplex Method :
Simplex method also called simplex technique or simplex algorithm was developed by G.B. Dantzeg, An American mathematician. Simplex method is suitable for solving linear programming problems with a large number of variable. The method through an iterative process progressively approaches and ultimately reaches to the maximum or minimum values of the objective function.
Principle of Simplex Method :
It has not been possible to obtain the graphical solution to the LP problem of more than two variables. For these reasons mathematical iterative procedure known as ‘Simplex Method’ was developed. The simplex method is applicable to any problem that can be formulated in-terms of linear objective function subject to a set of linear constraints.
ADVERTISEMENTS:
The simplex method provides an algorithm which is based on the fundamental theorem of linear programming. This states that “the optimal solution to a linear programming problem if it exists, always occurs at one of the corner points of the feasible solution space.”
The simplex method provides a systematic algorithm which consist of moving from one basic feasible solution to another in a prescribed manner such that the value of the objective function is improved. The procedure of jumping from vertex to the vertex is repeated. The simplex algorithm is an iterative procedure for solving LP problems.
It consists of:
(i) Having a trial basic feasible solution to constraints equation,
(ii) Testing whether it is an optimal solution,
(iii) Improving the first trial solution by repeating the process till an optimal solution is obtained.
Computational Procedure of Simplex Method :
The computational aspect of the simplex procedure is best explained by a simple example.
Consider the linear programming problem:
Maximize z = 3x 1 + 2x 2
Subject to x 1 + x 2 , ≤ 4
x 1 – x 2 , ≤ 2
x 1 , x 2 , ≥ 4
< 2 x v x 2 > 0
The steps in simplex algorithm are as follows:
Formulation of the mathematical model:
(i) Formulate the mathematical model of given LPP.
(ii) If objective function is of minimisation type then convert it into one of maximisation by following relationship
Minimise Z = – Maximise Z*
When Z* = -Z
(iii) Ensure all b i values [all the right side constants of constraints] are positive. If not, it can be changed into positive value on multiplying both side of the constraints by-1.
In this example, all the b i (height side constants) are already positive.
(iv) Next convert the inequality constraints to equation by introducing the non-negative slack or surplus variable. The coefficients of slack or surplus variables are zero in the objective function.
In this example, the inequality constraints being ‘≤’ only slack variables s 1 and s 2 are needed.
Therefore given problem now becomes:

The first row in table indicates the coefficient c j of variables in objective function, which remain same in successive tables. These values represent cost or profit per unit of objective function of each of the variables.
The second row gives major column headings for the simple table. Column C B gives the coefficients of the current basic variables in the objective function. Column x B gives the current values of the corresponding variables in the basic.
Number a ij represent the rate at which resource (i- 1, 2- m) is consumed by each unit of an activity j (j = 1,2 … n).
The values z j represents the amount by which the value of objective function Z would be decreased or increased if one unit of given variable is added to the new solution.
It should be remembered that values of non-basic variables are always zero at each iteration.
So x 1 = x 2 = 0 here, column x B gives the values of basic variables in the first column.
So 5, = 4, s 2 = 2, here; The complete starting feasible solution can be immediately read from table 2 as s 1 = 4, s 2 , x, = 0, x 2 = 0 and the value of the objective function is zero.

Flow Chart of Simplex Method :

Wolfram|Alpha Widgets Overview Tour Gallery Sign In
Share this page.
- StumbleUpon
- Google Buzz
Output Type
Output width, output height.
To embed this widget in a post, install the Wolfram|Alpha Widget Shortcode Plugin and copy and paste the shortcode above into the HTML source.
To embed a widget in your blog's sidebar, install the Wolfram|Alpha Widget Sidebar Plugin , and copy and paste the Widget ID below into the "id" field:
Save to My Widgets
Build a new widget.
We appreciate your interest in Wolfram|Alpha and will be in touch soon.

Simplex Method Calculator – Two Phase Online 🥇
Simplex method calculator - free version, members-only content, do you already have a membership, get membership.
The free version of the calculator shows you each of the intermediate tableaus that are generated in each iteration of the simplex method, so you can check the results you obtained when solving the problem manually.
Advanced Functions of the simplex method online calculator – Two-Phase
Let's face it, the simplex method is characterized by being a meticulous and impractical procedure, because if you fail in an intermediate calculation you can compromise the final solution of the problem. In that sense, it is important for the student to know the step by step procedure to obtain each of the values in the iterations. Thus, in PM Calculators we have improved our application to include a complete step-by-step explanation of the calculations of the method. You can access this tool and others (such as the big m calculator and the graphical linear programming calculator ) by becoming a member of our membership .
Within the functionality that this application counts we have:
- Ability to solve exercises with up to 20 variables and 50 constraints.
- Explanation of how to determine the optimality condition.
- Explanation of the criteria to establish the feasibility condition.
- Detail of the calculations performed to obtain the vector of reduced costs, the pivot row and the other rows of the table.
- For exercises with artificial variables it becomes a two-phase method calculator .
- Explanation of the special cases such as unbounded and infeasible solutions.
You can find complete examples of how the application works in this link .
How to use the simplex method online calculator
To use our tool you must perform the following steps:
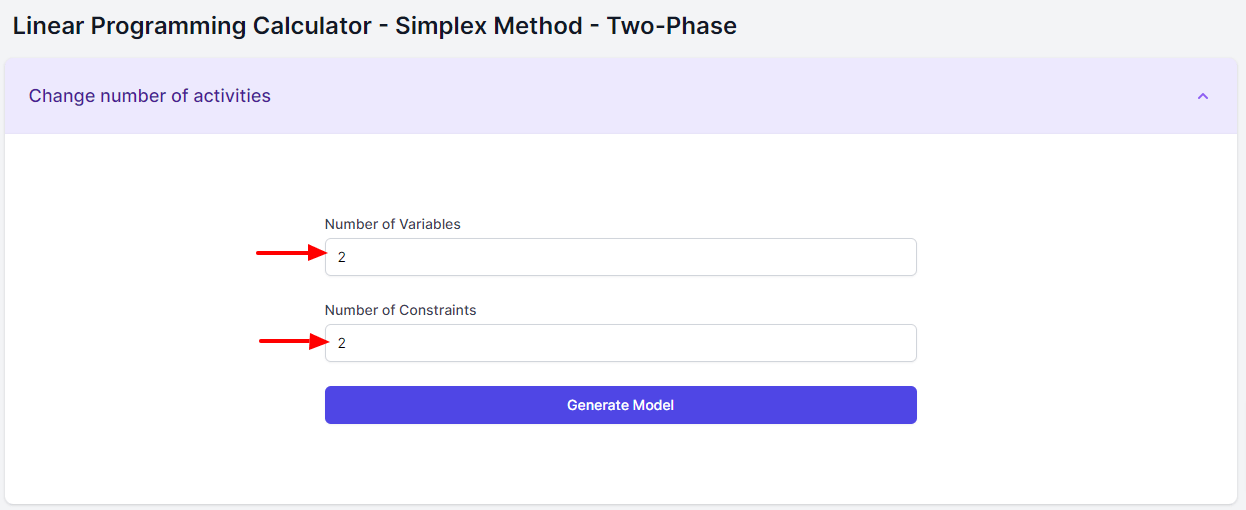
- Enter the number of variables and constraints of the problem.
- Select the type of problem: maximize or minimize .
- Enter the coefficients in the objective function and the constraints. You can enter negative numbers, fractions, and decimals (with point).
- Click on “Solve”.
- The online software will adapt the entered values to the standard form of the simplex algorithm and create the first tableau .
- Depending on the sign of the constraints, the normal simplex algorithm or the two phase method is used.
- We can see step by step the iterations and tableaus of the simplex method calculator.
- In the last part will show the results of the problem.
We have considered for our application to solve problems with a maximum of 20 variables and 50 restrictions; this is because exercises with a greater number of variables would make it difficult to follow the steps using the simplex method. For problems with more variables, we recommend using other method.
Below we show some reference images of the step by step and the result of the following example:
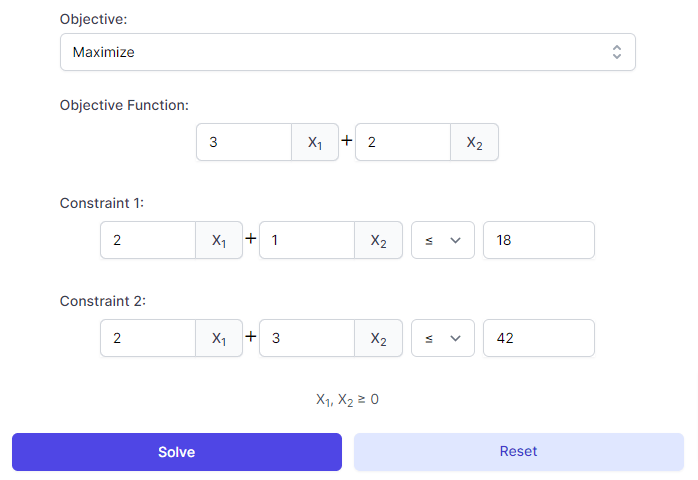
The following problem is required to be maximized:
Objective Function Z = 3X 1 + 2X 2
Subject to the following restrictions
2X 1 + X 2 ≤ 18 2X 1 + 3X 2 ≤ 42 X 1 , X 2 ≥ 0
We enter the number of variables and constraints:
Enter the coefficients of the equations / inequalities of the problem and click on Solve:
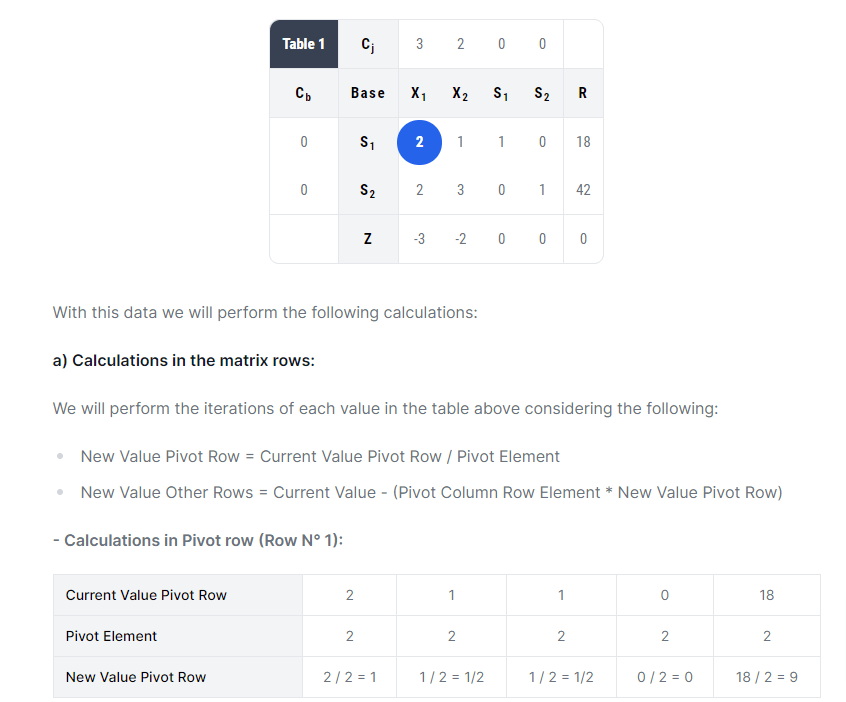
Next you will see the step by step in obtaining the solution as well as the calculation of the vector of reduced costs:

The calculation of the values of the pivot row:
Until the final result:

Final reflection
Our free simplex minimizing and maximizing calculator is being used by thousands of students every month and has become one of the most popular online Simplex method calculators available. In addition, our full version has been helping hundreds of students study and do their homework faster and giving them more time to devote to their personal activities.
If you have questions about it or find an error in our application, we will appreciate if you can write to us on our contact page .
Solved Exercise of Minimization of 2 variables with the Big M Method Example of Linear Programming - Big M Method
Problem data.
We want to Minimize the following problem:
- X 1 + X 2 ≥ 2
- - X 1 + X 2 ≥ 1
- 0 X 1 + X 2 ≤ 3
X 1 , X 2 ≥ 0
To solve the problem, the iterations of the simplex method will be performed until the optimal solution is found.
Next, the problem will be adapted to the standard linear programming model, adding the slack, excess and/or artificial variables in each of the constraints and converting the inequalities into equalities:
- Constraint 1 : It has sign “ ≥ ” (greatest equal), therefore the excess variable S 1 will be subtracted and the artificial variable A 1 will be added. In the initial matrix, A 1 will be in the base.
- Constraint 2 : It has sign “ ≥ ” (greatest equal), therefore the excess variable S 2 will be subtracted and the artificial variable A 2 will be added. In the initial matrix, A 2 will be in the base.
- Constraint 3 : It has sign “ ≤ ” (least equal), therefore the slack variable S 3 . This variable will be placed at the base in the initial matrix.
Now we will show the problem in the standard form. We will place the coefficient 0 (zero) where appropriate to create our initial matrix:
Objective Function:
Minimize Z = X 1 - 2 X 2 + 0 S 1 + 0 S 2 + 0 S 3 + M A 1 + M A 2
Subject to:
- X 1 + X 2 - S 1 + 0 S 2 + 0 S 3 + A 1 + 0 A 2 = 2
- - X 1 + X 2 + 0 S 1 - S 2 + 0 S 3 + 0 A 1 + A 2 = 1
- 0 X 1 + X 2 + 0 S 1 + 0 S 2 + S 3 + 0 A 1 + 0 A 2 = 3
Initial Matrix
We will use the coefficients of the equations to elaborate our first table:
| Table | C | 1 | -2 | 0 | 0 | 0 | M | M | |
|---|---|---|---|---|---|---|---|---|---|
| C | Base | X | X | S | S | S | A | A | R |
| M | A | 1 | 1 | -1 | 0 | 0 | 1 | 0 | 2 |
| M | A | -1 | 1 | 0 | -1 | 0 | 0 | 1 | 1 |
| 0 | S | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 3 |
| Z | -1 | 2M + 2 | -M | -M | 0 | 0 | 0 | 3M |
a ) Reduced Cost Vector Calculation (Z):
The values recorded in row Z were obtained as follows:
- Z 1 = (C b, 1 × X 1 , 1 ) + (C b, 2 × X 1 , 2 ) + (C b, 3 × X 1 , 3 ) - C j, 1 = ( M × 1 ) + ( M × -1 ) + ( 0 × 0 ) - ( 1 ) = -1
- Z 2 = (C b, 1 × X 2 , 1 ) + (C b, 2 × X 2 , 2 ) + (C b, 3 × X 2 , 3 ) - C j, 2 = ( M × 1 ) + ( M × 1 ) + ( 0 × 1 ) - ( -2 ) = 2M + 2
- Z 3 = (C b, 1 × S 1 , 1 ) + (C b, 2 × S 1 , 2 ) + (C b, 3 × S 1 , 3 ) - C j, 3 = ( M × -1 ) + ( M × 0 ) + ( 0 × 0 ) - ( 0 ) = -M
- Z 4 = (C b, 1 × S 2 , 1 ) + (C b, 2 × S 2 , 2 ) + (C b, 3 × S 2 , 3 ) - C j, 4 = ( M × 0 ) + ( M × -1 ) + ( 0 × 0 ) - ( 0 ) = -M
- Z 5 = (C b, 1 × S 3 , 1 ) + (C b, 2 × S 3 , 2 ) + (C b, 3 × S 3 , 3 ) - C j, 5 = ( M × 0 ) + ( M × 0 ) + ( 0 × 1 ) - ( 0 ) = 0
- Z 6 = (C b, 1 × A 1 , 1 ) + (C b, 2 × A 1 , 2 ) + (C b, 3 × A 1 , 3 ) - C j, 6 = ( M × 1 ) + ( M × 0 ) + ( 0 × 0 ) - ( M ) = 0
- Z 7 = (C b, 1 × A 2 , 1 ) + (C b, 2 × A 2 , 2 ) + (C b, 3 × A 2 , 3 ) - C j, 7 = ( M × 0 ) + ( M × 1 ) + ( 0 × 0 ) - ( M ) = 0
- Z 8 = (C b, 1 × R 1 ) + (C b, 2 × R 2 ) + (C b, 3 × R 3 ) = ( M × 2 ) + ( M × 1 ) + ( 0 × 3 ) = 3M
b ) Optimality Condition (Incoming Variable):
In the reduced cost vector (Z) we have positive values, so we must select the highest value for the pivot column ( minimization ).
In the vector Z (excluding the last value), we have the following numbers: [ -1, 2M + 2, -M, -M, 0, 0, 0 ] . The highest value is = 2M + 2 which corresponds to the X 2 variable. This variable will enter the base and its values in the table will form our pivot column.
Note: To check the chosen value, simply replace the variable M by a large number (e.g. M = 1000000) in the vector of reduced costs.
d ) Feasibility Condition (Outgoing Variable):
The feasibility condition will be verified by dividing the values of column R by the pivot column X 2 . To process the division, the denominator must be strictly positive (If it's negative or zero, it'll display N/A = Not applicable). The lowest value will define the variable that will exit from the base:
- Row A 1 → R 1 / X 2 , 1 = 2 / 1 = 2
- Row A 2 → R 2 / X 2 , 2 = 1 / 1 = 1 (The Lowest Value)
- Row S 3 → R 3 / X 2 , 3 = 3 / 1 = 3
The lowest value corresponds to the A 2 row. This variable will come from the base. The pivot element corresponds to the value that crosses the X 2 column and the A 2 row = 1 .
Enter the variable X 2 and the variable A 2 leaves the base. The pivot element is 1
Learn with step-by-step explanations
At PM Calculators we strive to help you overcome those tricky subjects in an easier way.
With access to our membership you will have access to 13 applications to learn projects, linear programming, statistics, among others.
What calculators are included?
Critical Path PERT and CPM
Linear Programming Methods
Normal Distribution
Break-even and more
Purchase our monthly subscription from
Learn more and save with semi-annual, annual and lifetime plans.

IMAGES
VIDEO
COMMENTS
In this section, we will solve the standard linear programming minimization problems using the simplex method. Once again, we remind the reader that in the standard minimization problems all constraints are of the form \(ax + by ≥ c\). The procedure to solve these problems was developed by Dr. John Von Neuman.
Simplex method is an approach to solving linear programming models by hand using slack variables, tableaus, and pivot variables as a means to finding the optimal solution of an optimization problem.
SECTION 4.3 PROBLEM SET: MINIMIZATION BY THE SIMPLEX METHOD. In problems 3-4, convert each minimization problem into a maximization problem, the dual, and then solve by the simplex method. Minimize subject to z = 4x1 + 3x2 x1 +x2 ≥ 10 3x1 + 2x2 ≥ 24 x1,x2 ≥ 0 Minimize z = 4 x 1 + 3 x 2 subject to x 1 + x 2 ≥ 10 3 x 1 + 2 x 2 ≥ 24 x 1 ...
4.3: Minimization By The Simplex Method In this section, we will solve the standard linear programming minimization problems using the simplex method. The procedure to solve these problems involves solving an associated problem called the dual problem. The solution of the dual problem is used to find the solution of the original problem.
solving linear equations, it is customary to drop the variables and perform Gaussian elimination on a matrix of coefficients. The technique used in the previous section to maximize the function xˆ, called the simplex method, is also typically performed on a matrix of coefficients, usually referred to (in this context) as a tableau. The
A systematic procedure for solving linear programs - the simplex method. 4. §Proceeds by moving from one feasible solution to another, at each step improving the value of the objective function. §Terminates after a finite number of such transitions. §Two important characteristics of the simplex method: •The method is robust.
Welcome to our illuminating YouTube video, your guide to conquering Operations Research Linear Programming Problems (LPP) using the sophisticated Simplex Met...
Chapter 6: The Simplex Method 1 Minimization Problem (§6.5) We can solve minimization problems by transforming it into a maximization problem. Another way is to change the selection rule for entering variable. Since we want to minimize z, we would now choose a reduced cost c¯ k that is negative, so that increasing the nonbasic variable x
9.3: Minimization By The Simplex Method In this section, we will solve the standard linear programming minimization problems using the simplex method. The procedure to solve these problems involves solving an associated problem called the dual problem. The solution of the dual problem is used to find the solution of the original problem.
Examples and standard form Fundamental theorem Simplex algorithm Simplex method I Simplex method is first proposed by G.B. Dantzig in 1947. I Simply searching for all of the basic solution is not applicable because the whole number is Cm n. I Basic idea of simplex: Give a rule to transfer from one extreme point to another such that the objective function is decreased.
Simplex Method itself to solve the Phase I LP problem for which a starting BFS is known, and for which an optimal basic solution is a BFS for the original LP problem if it's feasible. For example, for the standard equality form with the right-hand-side nonnegative, the Phase-I problem is min z 1 +z 2+…+z m, s.t. Ax+z=b, (x,z) ≥0.
Solving a standard minimization problem using the Simplex Method by create the dual problem. First half of the problem.
1 The basic steps of the simplex algorithm Step 1: Write the linear programming problem in standard form Linear programming (the name is historical, a more descriptive term would be linear optimization) refers to the problem of optimizing a linear objective function of several variables subject to a set of linear equality or inequality constraints.
There is a method of solving a minimization problem using the simplex method where you just need to multiply the objective function by -ve sign and then solve it using the simplex method. All you need to do is to multiply the max value found again by -ve sign to get the required max value of the original minimization problem.
The simplex method provides an algorithm which is based on the fundamental theorem of linear programming. This states that "the optimal solution to a linear programming problem if it exists, always occurs at one of the corner points of the feasible solution space.". The simplex method provides a systematic algorithm which consist of moving from one basic feasible solution to another in a ...
Minimization linear programming problems are solved in much the same way as the maximization problems. For the standard minimization linear program, the constraints are of the form \(ax + by ≥ c\), as opposed to the form \(ax + by ≤ c\) for the standard maximization problem.As a result, the feasible solution extends indefinitely to the upper right of the first quadrant, and is unbounded.
In Section 9.3, we applied the simplex method only to linear programming problems in standard form where the objective function was to be maximized. In this section, we extend this procedure to linear programming problems in which the objective function is to be min-imized. A minimization problem is in standard formif the objective function
In this section, we will solve the standard linear programming minimization problems using the simplex method. Once again, we remind the reader that in the standard minimization problems all constraints are of the form \(ax + by ≥ c\). The procedure to solve these problems was developed by Dr. John Von Neuman.
Here is the video about LPP using simplex method (Minimization) with three variables, in that we have discussed that how to solve the simplex method minimiza...
Linear Programming Solver. Linear programming solver with up to 9 variables. New constraints could be added by using commas to separate them. Get the free "Linear Programming Solver" widget for your website, blog, Wordpress, Blogger, or iGoogle. Find more Mathematics widgets in Wolfram|Alpha.
Click on "Solve". The online software will adapt the entered values to the standard form of the simplex algorithm and create the first tableau. Depending on the sign of the constraints, the normal simplex algorithm or the two phase method is used. We can see step by step the iterations and tableaus of the simplex method calculator.
Solution. In solving this problem, we will follow the algorithm listed above. STEP 1. Set up the problem. Write the objective function and the constraints. Since the simplex method is used for problems that consist of many variables, it is not practical to use the variables \ (x\), \ (y\), \ (z\) etc.
In the reduced cost vector (Z) we have positive values, so we must select the highest value for the pivot column ( minimization ). In the vector Z (excluding the last value), we have the following numbers: [-1, 2M + 2, -M, -M, 0, 0, 0]. The highest value is = 2M + 2 which corresponds to the X2 variable. This variable will enter the base and its ...