linear programming sample problems with solutions

Linear Programming

Linear programming is a process that is used to determine the best outcome of a linear function. It is the best method to perform linear optimization by making a few simple assumptions. The linear function is known as the objective function. Real-world relationships can be extremely complicated. However, linear programming can be used to depict such relationships, thus, making it easier to analyze them.

Linear programming is used in many industries such as energy, telecommunication, transportation, and manufacturing. This article sheds light on the various aspects of linear programming such as the definition, formula, methods to solve problems using this technique, and associated linear programming examples.

What is Linear Programming?

Linear programming, also abbreviated as LP, is a simple method that is used to depict complicated real-world relationships by using a linear function . The elements in the mathematical model so obtained have a linear relationship with each other. Linear programming is used to perform linear optimization so as to achieve the best outcome.

Linear Programming Definition

Linear programming can be defined as a technique that is used for optimizing a linear function in order to reach the best outcome. This linear function or objective function consists of linear equality and inequality constraints. We obtain the best outcome by minimizing or maximizing the objective function .

Linear Programming Examples

Suppose a postman has to deliver 6 letters in a day from the post office (located at A) to different houses (U, V, W, Y, Z). The distance between the houses is indicated on the lines as given in the image. If the postman wants to find the shortest route that will enable him to deliver the letters as well as save on fuel then it becomes a linear programming problem. Thus, LP will be used to get the optimal solution which will be the shortest route in this example.

Linear Programming Formula

A linear programming problem will consist of decision variables , an objective function, constraints, and non-negative restrictions. The decision variables, x, and y, decide the output of the LP problem and represent the final solution. The objective function, Z, is the linear function that needs to be optimized (maximized or minimized) to get the solution. The constraints are the restrictions that are imposed on the decision variables to limit their value. The decision variables must always have a non-negative value which is given by the non-negative restrictions. The general formula of a linear programming problem is given below:

• Objective Function: Z = ax + by
• Constraints: cx + dy ≤ e, fx + gy ≤ h. The inequalities can also be "≥"
• Non-negative restrictions: x ≥ 0, y ≥ 0

How to Solve Linear Programming Problems?

The most important part of solving linear programming problem is to first formulate the problem using the given data. The steps to solve linear programming problems are given below:

• Step 1: Identify the decision variables.
• Step 2: Formulate the objective function. Check whether the function needs to be minimized or maximized.
• Step 3: Write down the constraints.
• Step 4: Ensure that the decision variables are greater than or equal to 0. (Non-negative restraint)
• Step 5: Solve the linear programming problem using either the simplex or graphical method.

Let us study about these methods in detail in the following sections.

Linear Programming Methods

There are two main methods available for solving linear programming problem. These are the simplex method and the graphical method. Given below are the steps to solve a linear programming problem using both methods.

Linear Programming by Simplex Method

The simplex method in lpp can be applied to problems with two or more decision variables. Suppose the objective function Z = 40\(x_{1}\) + 30\(x_{2}\) needs to be maximized and the constraints are given as follows:

\(x_{1}\) + \(x_{2}\) ≤ 12

2\(x_{1}\) + \(x_{2}\) ≤ 16

\(x_{1}\) ≥ 0, \(x_{2}\) ≥ 0

Step 1: Add another variable, known as the slack variable, to convert the inequalities into equations. Also, rewrite the objective function as an equation .

- 40\(x_{1}\) - 30\(x_{2}\) + Z = 0

\(x_{1}\) + \(x_{2}\) + \(y_{1}\) =12

2\(x_{1}\) + \(x_{2}\) + \(y_{2}\) =16

\(y_{1}\) and \(y_{2}\) are the slack variables.

Step 2: Construct the initial simplex matrix as follows:

\(\begin{bmatrix} x_{1} & x_{2} &y_{1} & y_{2} & Z & \\ 1&1 &1 &0 &0 &12 \\ 2& 1 & 0& 1 & 0 & 16 \\ -40&-30&0&0&1&0 \end{bmatrix}\)

Step 3: Identify the column with the highest negative entry. This is called the pivot column. As -40 is the highest negative entry, thus, column 1 will be the pivot column.

Step 4: Divide the entries in the rightmost column by the entries in the pivot column. We exclude the entries in the bottom-most row.

12 / 1 = 12

The row containing the smallest quotient is identified to get the pivot row. As 8 is the smaller quotient as compared to 12 thus, row 2 becomes the pivot row. The intersection of the pivot row and the pivot column gives the pivot element.

Thus, pivot element = 2.

Step 5: With the help of the pivot element perform pivoting, using matrix properties , to make all other entries in the pivot column 0.

Using the elementary operations divide row 2 by 2 (\(R_{2}\) / 2)

\(\begin{bmatrix} x_{1} & x_{2} &y_{1} & y_{2} & Z & \\ 1&1 &1 &0 &0 &12 \\ 1& 1/2 & 0& 1/2 & 0 & 8 \\ -40&-30&0&0&1&0 \end{bmatrix}\)

Now apply \(R_{1}\) = \(R_{1}\) - \(R_{2}\)

\(\begin{bmatrix} x_{1} & x_{2} &y_{1} & y_{2} & Z & \\ 0&1/2 &1 &-1/2 &0 &4 \\ 1& 1/2 & 0& 1/2 & 0 & 8 \\ -40&-30&0&0&1&0 \end{bmatrix}\)

Finally \(R_{3}\) = \(R_{3}\) + 40\(R_{2}\) to get the required matrix.

\(\begin{bmatrix} x_{1} & x_{2} &y_{1} & y_{2} & Z & \\ 0&1/2 &1 &-1/2 &0 &4 \\ 1& 1/2 & 0& 1/2 & 0 & 8 \\ 0&-10&0&20&1&320 \end{bmatrix}\)

Step 6: Check if the bottom-most row has negative entries. If no, then the optimal solution has been determined. If yes, then go back to step 3 and repeat the process. -10 is a negative entry in the matrix thus, the process needs to be repeated. We get the following matrix.

\(\begin{bmatrix} x_{1} & x_{2} &y_{1} & y_{2} & Z & \\ 0&1 &2 &-1 &0 &8 \\ 1& 0 & -1& 1 & 0 & 4 \\ 0&0&20&10&1&400 \end{bmatrix}\)

Writing the bottom row in the form of an equation we get Z = 400 - 20\(y_{1}\) - 10\(y_{2}\). Thus, 400 is the highest value that Z can achieve when both \(y_{1}\) and \(y_{2}\) are 0.

Also, when \(x_{1}\) = 4 and \(x_{2}\) = 8 then value of Z = 400

Thus, \(x_{1}\) = 4 and \(x_{2}\) = 8 are the optimal points and the solution to our linear programming problem.

Linear Programming by Graphical Method

If there are two decision variables in a linear programming problem then the graphical method can be used to solve such a problem easily.

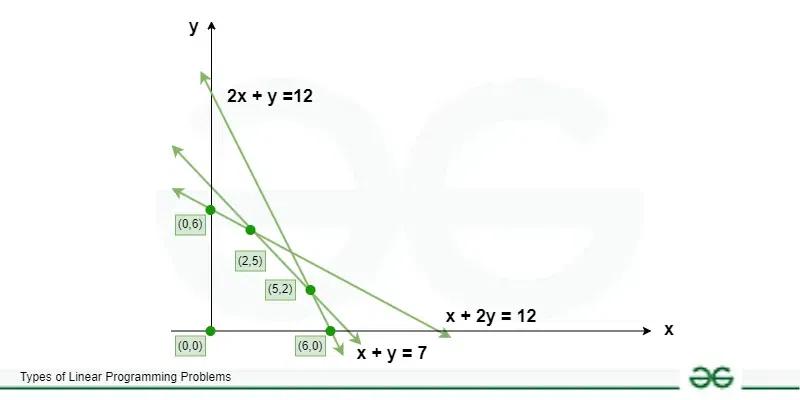
Suppose we have to maximize Z = 2x + 5y.

The constraints are x + 4y ≤ 24, 3x + y ≤ 21 and x + y ≤ 9

where, x ≥ 0 and y ≥ 0.

To solve this problem using the graphical method the steps are as follows.

Step 1: Write all inequality constraints in the form of equations.

x + 4y = 24

3x + y = 21

Step 2: Plot these lines on a graph by identifying test points.

x + 4y = 24 is a line passing through (0, 6) and (24, 0). [By substituting x = 0 the point (0, 6) is obtained. Similarly, when y = 0 the point (24, 0) is determined.]

3x + y = 21 passes through (0, 21) and (7, 0).

x + y = 9 passes through (9, 0) and (0, 9).

Step 3: Identify the feasible region. The feasible region can be defined as the area that is bounded by a set of coordinates that can satisfy some particular system of inequalities.

Any point that lies on or below the line x + 4y = 24 will satisfy the constraint x + 4y ≤ 24.

Similarly, a point that lies on or below 3x + y = 21 satisfies 3x + y ≤ 21.

Also, a point lying on or below the line x + y = 9 satisfies x + y ≤ 9.

The feasible region is represented by OABCD as it satisfies all the above-mentioned three restrictions.

Step 4: Determine the coordinates of the corner points. The corner points are the vertices of the feasible region.

B = (6, 3). B is the intersection of the two lines 3x + y = 21 and x + y = 9. Thus, by substituting y = 9 - x in 3x + y = 21 we can determine the point of intersection.

C = (4, 5) formed by the intersection of x + 4y = 24 and x + y = 9

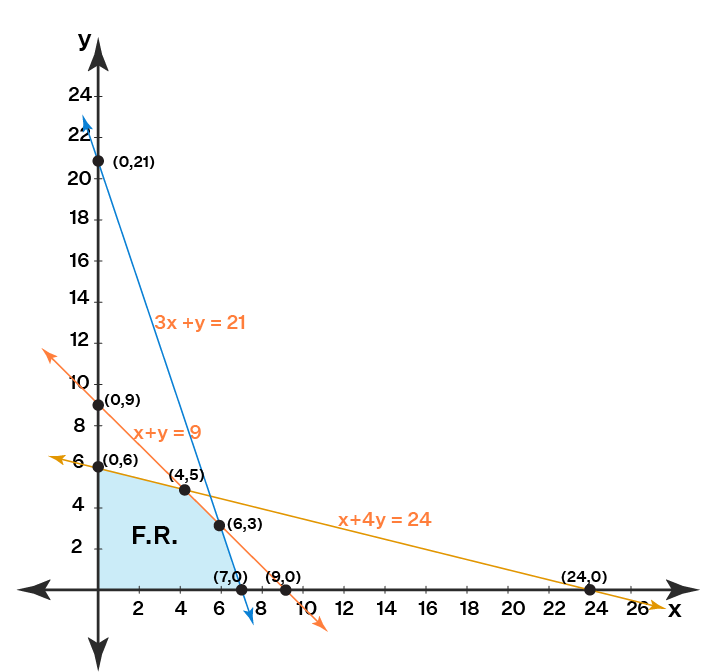
Step 5: Substitute each corner point in the objective function. The point that gives the greatest (maximizing) or smallest (minimizing) value of the objective function will be the optimal point.

33 is the maximum value of Z and it occurs at C. Thus, the solution is x = 4 and y = 5.

Applications of Linear Programming

Linear programming is used in several real-world applications. It is used as the basis for creating mathematical models to denote real-world relationships. Some applications of LP are listed below:

• Manufacturing companies make widespread use of linear programming to plan and schedule production.
• Delivery services use linear programming to decide the shortest route in order to minimize time and fuel consumption.
• Financial institutions use linear programming to determine the portfolio of financial products that can be offered to clients.

Related Articles:

• Introduction to Graphing
• Linear Equations in Two Variables
• Solutions of a Linear Equation
• Mathematical Induction

Important Notes on Linear Programming

• Linear programming is a technique that is used to determine the optimal solution of a linear objective function.
• The simplex method in lpp and the graphical method can be used to solve a linear programming problem.
• In a linear programming problem, the variables will always be greater than or equal to 0.

As the minimum value of Z is 127, thus, B (3, 28) gives the optimal solution. Answer: The minimum value of Z is 127 and the optimal solution is (3, 28)

• Example 3: Using the simplex method in lpp solve the linear programming problem Minimize Z = \(x_{1}\) + 2\(x_{2}\) + 3\(x_{3}\) \(x_{1}\) + \(x_{2}\) + \(x_{3}\) ≤ 12 2\(x_{1}\) + \(x_{2}\) + 3\(x_{3}\) ≤ 18 \(x_{1}\), \(x_{2}\), \(x_{3}\) ≥ 0 Solution: Convert all inequalities to equations by introducing slack variables. -\(x_{1}\) - 2\(x_{2}\) - 3\(x_{3}\) + Z = 0 \(x_{1}\) + \(x_{2}\) + \(x_{3}\) + \(y_{1}\) = 12 2\(x_{1}\) + \(x_{2}\) + 3\(x_{3}\) + \(y_{2}\) = 18 Expressing this as a matrix we get, \(\begin{bmatrix} x_{1} & x_{2} & x_{3} & y_{1} & y_{2} & Z & \\ 1 & 1 & 1 & 1 & 0 & 0 & 12\\ 2 & 1 & 3 & 0 & 1 & 0 & 18\\ -1 & -2 & -3 & 0 & 0 & 1 & 0 \end{bmatrix}\) As -3 is the greatest negative value thus, column 3 is the pivot column. 12 / 1 = 12 18 / 3 = 6 As 6 is the smaller quotient thus, row 2 is the pivot row and 3 is the pivot element. By applying matrix operations we get, \(\begin{bmatrix} x_{1} & x_{2} & x_{3} & y_{1} & y_{2} & Z & \\ 0.33 & 0.667 & 0 & 1 & -0.33 & 0 & 6\\ 0.667 & 0.33 & 1 & 0 & 0.33 & 0 & 6\\ 1 & -1 & 0 & 0 & 1 & 1 & 18 \end{bmatrix}\) Now -1 needs to be eliminated. Thus, by repreating the steps the matrix so obtained is as follows \(\begin{bmatrix} x_{1} & x_{2} & x_{3} & y_{1} & y_{2} & Z & \\ 0.5 & 1 & 0 & 1.5 & 0.5 & 0 & 9\\ 0.5 & 0 & 1 & -0.5 & 0.5 & 0 & 3\\ 1.5 & 0 & 0 & 1.5 & 0.5 & 1 & 27 \end{bmatrix}\) We get the maximum value of Z = 27 at \(x_{1}\) = 0, \(x_{2}\) = 9 \(x_{3}\) = 3 Answer: Maximum value of Z = 27 and optimal solution (0, 9, 3)

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Linear Programming

go to slide go to slide

FAQs on Linear Programming

What is meant by linear programming.

Linear programming is a technique that is used to identify the optimal solution of a function wherein the elements have a linear relationship.

What is Linear Programming Formula?

The general formula for a linear programming problem is given as follows:

What is the Objective Function in Linear Programming Problems?

The objective function is the linear function that needs to be maximized or minimized and is subject to certain constraints. It is of the form Z = ax + by.

How to Formulate a Linear Programming Model?

The steps to formulate a linear programming model are given as follows:

• Identify the decision variables.
• Formulate the objective function.
• Identify the constraints.
• Solve the obtained model using the simplex or the graphical method.

How to Find Optimal Solution in Linear Programming?

We can find the optimal solution in a linear programming problem by using either the simplex method or the graphical method. The simplex method in lpp can be applied to problems with two or more variables while the graphical method can be applied to problems containing 2 variables only.

How to Find Feasible Region in Linear Programming?

To find the feasible region in a linear programming problem the steps are as follows:

• Draw the straight lines of the linear inequalities of the constraints.
• Use the "≤" and "≥" signs to denote the feasible region of each constraint.
• The region common to all constraints will be the feasible region for the linear programming problem.

What are Linear Programming Uses?

Linear programming is widely used in many industries such as delivery services, transportation industries, manufacturing companies, and financial institutions. The linear program is solved through linear optimization method, and it is used to determine the best outcome in a given scenerio.

Linear Programming

In these lessons, we will learn about linear programming and how to use linear programming to solve word problems.

Related Pages Linear Programming Graphing Linear Inequalities Systems of Linear Inequalities

Many problems in real life are concerned with obtaining the best result within given constraints. In the business world, people would like to maximize profits and minimize loss; in production, people are interested in maximizing productivity and minimizing cost. However, there are constraints like the budget, number of workers, production capacity, space, etc. Linear programming deals with this type of problems using inequalities and graphical solution method.

Example: On the graph below, R is the region of feasible solutions defined by inequalities y > 2, y = x + 1 and 5y + 8x < 92. Find the greatest value of 2y + x which satisfies the set of inequalities, where x and y are integers.

Solution: We are looking for integer values of x and y in the region R where 2y + x has the greatest value. We could substitute all the possible (x , y) values in R into 2y + x to get the largest value but that would be too long and tedious.

A better method would be to find the line 2y + x = c where x and y are in R and c has the largest possible value. In this case, the equation 2y + x = c is known as the linear objective function .

Solving Linear Programming Problems

Now, we have all the steps that we need for solving linear programming problems, which are:

Step 1: Interpret the given situations or constraints into inequalities.

Step 2: Plot the inequalities graphically and identify the feasible region.

Step 3: Determine the gradient for the line representing the solution (the linear objective function).

Step 4: Construct parallel lines within the feasible region to find the solution.

Example: Joanne wants to buy x oranges and y peaches from the store. She must buy at least 5 oranges and the number of oranges must be less than twice the number of peaches. An orange weighs 150 grams and a peach weighs 100 grams. Joanne can carry not more than 3.6 kg of fruits home. a) Write 3 inequalities to represent the information given above. b) Plot the inequalities on the Cartesian grid and show the region that satisfies all the inequalities. Label the region S. c) Oranges cost $0.70 each and peaches cost $0.90 each. Find the maximum that Joanne can spend buying the fruits.

Solution: a) at least 5 oranges: x ≥ 5 oranges less than twice of peaches: x < 2y not more than 3.6 kg: 150x + 100y ≤ 3600 ⇒ 3x + 2y ≤ 72

The maximum value is found at (5,28) i.e. 5 oranges and 28 peaches. Therefore, the maximum that Joanne can spend on the fruits is: 70  × 5 + 90 × 28 = 2870 cents = $28.70.

It also possible to test the vertices of the feasible region to find the minimum or maximum values, instead of using the linear objective function. The following videos gives examples of linear programming problems and how to test the vertices.

Linear Programming Example:

Maximize C = x + y given the constraints, y ≥ 0 x ≥ 0 4x + 2y ≤ 8 2x − y ≤ 0

Solving for Maxima-Minima

Maximize C = x + y given the constraints, − 3x + 2y ≤ 6 3x + y ≤ 3 y ≥ 0

Linear Programming Steps and Example

• Graph the inequalities and find the vertices.
• Compute the function at the vertices. Largest = Max, Smallest = Min.

Problem: Constraints are 240 acres of land. Profit $40/acre corn, $30/acre oats. Have 320 hrs available. Corn takes 2 hrs of labor per acre, oats requires 1 hr. How many acres of each should be planted to maximize profits?

How to solve a word problem using linear programming?

First, find the equation that needs to be maximized or minimized as well as create the corresponding inequalities and then solve.

Example: A rancher is mixing two types of food, Brand X and Brand Y, for his cattle. If each serving is required to have 60 grams of protein and 30 grams of fat, where Brand X has 15 grams of protein and 10 grams of fat and costs 80 cents per unit, and Brand Y contains 20 grams of protein and 5 grams of fat and costs 50 cents per unit, how much of each type should be used to minimize cost to the rancher?

Linear Programming Word Problem

Example: A refinery produces both gasoline and fuel oil, and sells gasoline for $1 per gallon and fuel oil for $0.90 per gallon. The refinery can produce at most 600,000 gallons a day, but must produce at least two gallons of fuel oil for every gallon of gasoline. At least 150,000 gallons of fuel oil must be produce each day to meet current demands. How much of each type of fuel should be produced to maximize daily profits?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

High school math (India)

Course: high school math (india)   >   unit 7, linear programming 12.1.

• Linear programming 12.2
• Your answer should be
• an integer, like 6 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍  
• an exact decimal, like 0.75 ‍  
• a multiple of pi, like 12   pi ‍   or 2 / 3   pi ‍  

Linear Programming Problems and Questions

How are linear programming problems and word problems solved? Below are links to many examples on how to formulate and solve optimization problems in linear programming.

• Solve Inequalities with Two Variables .
• Solve Systems of Inequalities with Two Variables .
• Linear Programming and Optimization .
• Linear Programming: Word Problems and Applications .

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators
• Linear Programming – Explanation & Examples

JUMP TO TOPIC

What is Linear Programming?

Identifying variables, identify the objective function, the solution, example 1 solution, example 2 solution, example 3 solution, example 4 solution, example 5 solution, practice questions, linear programming – explanation and examples.

How to Solve Linear Programming Problems

• Identify the variables and the constraints.
• Find the objective function.
• Graph the constraints and identify the vertices of the polygon.
• Test the values of the vertices in the objective function.

• What are the inequalities that define this function?
• If the objective function is 3x+2y=P, what is the maximum value of P?
• If the objective function is 3x+2y=P, what is the minimum value of P

Constraints

The objective function.

Finding the Maximum

The Vertices

Finding the minimum, the feasible region.

Alternative Solution?

Previous Lesson  |  Main Page | Next Lesson

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

Linear Programming Word Problems

Intro How-To Word Problems More Examples Four Variables

What are the constraints they "forget" to mention?

When you are doing a linear programming word problem, you are dealing with a (pretend) real-world situation. In this context, you will need to remember the understood (and thus usually omitted) constraints; namely, that you can't (generally) have negative amounts of inputs.

Content Continues Below

MathHelp.com

This omitted fact requires that you remember to add non-negativity constraints for each of your graphing variables; namely, x  ≥ 0 and y  ≥ 0 .

• A calculator company produces a scientific calculator and a graphing calculator. Long-term projections indicate an expected demand of at least 100 scientific and 80 graphing calculators each day. Because of limitations on production capacity, no more than 200 scientific and 170 graphing calculators can be made daily. To satisfy a shipping contract, a total of at least 200 calculators much be shipped each day.   If each scientific calculator sold results in a $2 loss, but each graphing calculator produces a $5 profit, how many of each type should be made daily to maximize net profits?

The question asks for the optimal number of calculators, so my variables will stand for numbers of calculators:

x : number of scientific calculators produced

y : number of graphing calculators produced

Advertisement

Since they can't produce negative numbers of calculators, I have my first two constraints; namely, x  ≥ 0 and y  ≥ 0 . However, as it turns out, I can ignore these constraints in this particular exercise, because they've already given me minimums:

The exercise also gives maximums:

The minimum shipping requirement gives me another constraint:

x + y ≥ 200

For graphing purposes, I'll restate this constraint as:

y ≥ − x + 200

The profit relation will be my optimization equation:

P = −2 x + 5 y

So my entire system is:

P = 2 x + 5 y , subject to:

100 ≤ x ≤ 200

80 ≤ y ≤ 170

The feasibility region graphs as:

The corner points are at (100, 170) , (200, 170) , (200, 80) , (120, 80) , and (100, 100) . When you test these points in the optimization equation, you should obtain the maximum value of profit P  = 650 at ( x ,  y ) = (100, 170) . Interpreting this within the context of the original word problem, the solution will be " 100 scientific calculators and 170 graphing calculators".

(Yes, you can also find the answer just using logic: If the one kind loses you money and the other makes you money, obviously you'll want to maximize production of what makes you money.)

• You need to buy some filing cabinets. You know that Cabinet X costs $10 per unit, requires six square feet of floor space, and holds eight cubic feet of files. Cabinet Y costs $20 per unit, requires eight square feet of floor space, and holds twelve cubic feet of files. You have been given $140 for this purchase, though you don't have to spend that much. The office has room for no more than 72 square feet of cabinets. How many of which model should you buy, in order to maximize storage volume?

The question ask for the number of cabinets I need to buy, so my variables will stand for that:

x : number of model X cabinets purchased y : number of model Y cabinets purchased

Naturally, x  ≥ 0 and y  ≥ 0 . I have to consider the costs and the floor space (that is, the footprint of each unit), while maximizing the storage volume, so costs and floor space will be my constraints, while volume will be my optimization equation.

cost: 10 x + 20 y ≤ 140 , or y ≤ −(½) x + 7

space: 6 x + 8 y ≤ 72 , or y ≤ −(¾) x + 9

volume: V = 8 x + 12 y

This system (along with the first two constraints) graphs as:

The corner points are at (0, 0) , (8, 3) , (0, 7) , and (12, 0) . When you plug them into the optimization equation, you should obtain a maximal volume of 100 cubic feet by buying eight of model X and three of model Y.

URL: https://www.purplemath.com/modules/linprog3.htm

Page 1 Page 2 Page 3 Page 4 Page 5

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• Privacy / Cookies
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles

• Math Article

Linear Programming

In Mathematics, linear programming is a method of optimising operations with some constraints. The main objective of linear programming is to maximize or minimize the numerical value. It consists of linear functions which are subjected to the constraints in the form of linear equations or in the form of inequalities.  Linear programming is considered an important technique that is used to find the optimum resource utilisation. The term “linear programming” consists of two words as linear and programming. The word “linear” defines the relationship between multiple variables with degree one. The word “programming” defines the process of selecting the best solution from various alternatives.

Linear Programming is widely used in Mathematics and some other fields such as economics, business, telecommunication, and manufacturing fields. In this article, let us discuss the definition of linear programming, its components, and different methods to solve linear programming problems.

Table of Contents:

• Characteristics
• Linear programming Problems
• Simplex Method

Graphical Method

• Applications
• Practice Problems

What is Linear Programming?

Linear programming (LP)   or Linear Optimisation may be defined as the problem of maximizing or minimizing a linear function that is subjected to linear constraints. The constraints may be equalities or inequalities. The optimisation problems involve the calculation of profit and loss.   Linear programming problems  are an important class of optimisation problems, that helps to find the feasible region and optimise the solution in order to have the highest or lowest value of the function.

In other words, linear programming is considered as an optimization method to maximize or minimize the objective function of the given mathematical model with the set of some requirements which are represented in the linear relationship. The main aim of the linear programming problem is to find the optimal solution.

Linear programming is the method of considering different inequalities relevant to a situation and calculating the best value that is required to be obtained in those conditions.  Some of the assumptions taken while working with linear programming are:

• The number of constraints should be expressed in the quantitative terms
• The relationship between the constraints and the objective function should be linear
• The linear function (i.e., objective function) is to be optimised

Components of Linear Programming

The basic components of the LP are as follows:

• Decision Variables
• Constraints
• Objective Functions

Characteristics of Linear Programming

The following are the five characteristics of the linear programming problem:

Constraints – The limitations should be expressed in the mathematical form, regarding the resource.

Objective Function – In a problem, the objective function should be specified in a quantitative way.

Linearity – The relationship between two or more variables in the function must be linear. It means that the degree of the variable is one.

Finiteness –  There should be finite and infinite input and output numbers. In case, if the function has infinite factors, the optimal solution is not feasible. 

Non-negativity – The variable value should be positive or zero. It should not be a negative value.

Decision Variables – The decision variable will decide the output. It gives the ultimate solution of the problem. For any problem, the first step is to identify the decision variables.

Linear Programming Problems

The Linear Programming Problems (LPP) is a problem that is concerned with finding the optimal value of the given linear function. The optimal value can be either maximum value or minimum value. Here, the given linear function is considered an objective function. The objective function can contain several variables, which are subjected to the conditions and it has to satisfy the set of linear inequalities called linear constraints. The linear programming problems can be used to get the optimal solution for the following scenarios, such as manufacturing problems, diet problems, transportation problems, allocation problems and so on.

Methods to Solve Linear Programming Problems

The linear programming problem can be solved using different methods, such as the graphical method, simplex method, or by using tools such as R, open solver etc. Here, we will discuss the two most important techniques called the simplex method and graphical method in detail.

Linear Programming Simplex Method

The simplex method is one of the most popular methods to solve linear programming problems. It is an iterative process to get the feasible optimal solution. In this method, the value of the basic variable keeps transforming to obtain the maximum value for the objective function. The algorithm for linear programming simplex method is provided below:

Step 1 : Establish a given problem. (i.e.,) write the inequality constraints and objective function.

Step 2: Convert the given inequalities to equations by adding the slack variable to each inequality expression.

Step 3 : Create the initial simplex tableau. Write the objective function at the bottom row. Here, each inequality constraint appears in its own row. Now, we can represent the problem in the form of an augmented matrix, which is called the initial simplex tableau.

Step 4 : Identify the greatest negative entry in the bottom row, which helps to identify the pivot column. The greatest negative entry in the bottom row defines the largest coefficient in the objective function, which will help us to increase the value of the objective function as fastest as possible.

Step 5 : Compute the quotients. To calculate the quotient, we need to divide the entries in the far right column by the entries in the first column, excluding the bottom row. The smallest quotient identifies the row. The row identified in this step and the element identified in the step will be taken as the pivot element.

Step 6: Carry out pivoting to make all other entries in column is zero.

Step 7: If there are no negative entries in the bottom row, end the process. Otherwise, start from step 4.

Step 8: Finally, determine the solution associated with the final simplex tableau.

The graphical method is used to optimize the two-variable linear programming. If the problem has two decision variables, a graphical method is the best method to find the optimal solution. In this method, the set of inequalities are subjected to constraints. Then the inequalities are plotted in the XY plane. Once, all the inequalities are plotted in the XY graph, the intersecting region will help to decide the feasible region. The feasible region will provide the optimal solution as well as explains what all values our model can take.  Let us see an example here and understand the concept of linear programming in a better way.

Calculate the maximal and minimal value of z = 5x + 3y for the following constraints.

x + 2y ≤ 14

3x – y ≥ 0

x – y ≤ 2

The three inequalities indicate the constraints. The area of the plane that will be marked is the feasible region.

The optimisation equation (z) = 5x + 3y. You have to find the (x,y) corner points that give the largest and smallest values of z.

To begin with, first solve each inequality.

x + 2y ≤ 14 ⇒  y ≤ -(1/2)x + 7

3x – y ≥ 0 ⇒  y ≤ 3x

x – y ≤ 2 ⇒ y  ≥ x – 2

Here is the graph for the above equations.

Now pair the lines to form a system of linear equations to find the corner points.

y = -(½) x + 7

Solving the above equations, we get the corner points as (2, 6)

y = -1/2 x + 7

y = x – 2

Solving the above equations, we get the corner points as (6, 4)

Solving the above equations, we get the corner points as (-1, -3)

For linear systems, the maximum and minimum values of the optimisation equation lie on the corners of the feasibility region. Therefore, to find the optimum solution, you only need to plug these three points in z = 3x + 4y

z = 5(2) + 3(6) = 10 + 18 = 28

z = 5(6) + 3(4) = 30 + 12 = 42

z = 5(-1) + 3(-3) = -5 -9 = -14

Hence, the maximum of z = 42 lies at (6, 4) and the minimum of z = -14 lies at (-1, -3)

Linear Programming Applications

A real-time example would be considering the limitations of labours and materials and finding the best production levels for maximum profit in particular circumstances. It is part of a vital area of mathematics known as optimisation techniques. The applications of LP in some other fields are

• Engineering – It solves design and manufacturing problems as it is helpful for doing shape optimisation
• Efficient Manufacturing – To maximise profit, companies use linear expressions
• Energy Industry – It provides methods to optimise the electric power system.
• Transportation Optimisation – For cost and time efficiency.

Importance of Linear Programming

Linear programming is broadly applied in the field of optimisation for many reasons. Many functional problems in operations analysis can be represented as linear programming problems. Some special problems of linear programming are such as network flow queries and multi-commodity flow queries are deemed to be important to have produced much research on functional algorithms for their solution.

Linear Programming Video Lesson

Linear programming problem.

Linear Programming Practice Problems

Solve the following linear programming problems:

• A doctor wishes to mix two types of foods in such a way that the vitamin contents of the mixture contain at least 8 units of vitamin A and 10 units of vitamin C. Food ‘I’ contains 2 units/kg of vitamin A and 1 unit/kg of vitamin C. Food ‘II’ contains 1 unit/kg of vitamin A and 2 units/kg of vitamin C. It costs Rs 50 per kg to purchase Food ‘I’ and Rs 70 per kg to purchase Food ‘II’. Formulate this problem as a linear programming problem to minimise the cost of such a mixture
• One kind of cake requires 200g of flour and 25g of fat, and another kind of cake requires 100g of flour and 50g of fat.  Formulate this problem as a linear programming problem to find the maximum number of cakes that can be made from 5kg of flour and 1 kg of fat assuming that there is no shortage of the other ingredients used in making the cakes.

Frequently Asked Questions on Linear Programming

Linear programming is a process of optimising the problems which are subjected to certain constraints. It means that it is the process of maximising or minimizing the linear functions under linear inequality constraints. The problem of solving linear programs is considered as the easiest one.

Mention the different types of linear programming.

The different types of linear programming are: Solving linear programming by Simplex method Solving linear programming using R Solving linear programming by graphical method Solving linear programming with the use of an open solver.

What are the requirements of linear programming?

The five basic requirements of linear programming are: Objective function Constraints Linearity Non-negativity Finiteness

Mention the advantages of Linear programming

The advantages of linear programming are: Linear programming provides insights to the business problems It helps to solve multi-dimensional problems According to the condition change, LP helps in making the adjustments By calculating the cost and profit of various things, LP helps to take the best optimal solution

What is meant by linear programming problems?

The linear programming problems (LPP) helps to find the best optimal solution of a linear function (also, known as the objective function) which are placed under certain constraints (set of linear inequality constraints)

To learn all concepts in Maths in a more engaging way, register at BYJU’S. Also, watch interesting videos on various Maths topics by downloading BYJU’S– The Learning App.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Thank you so much for clearly explained notes. I benefited a lot from them

Thank you very much for this material.

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

• School Guide
• Mathematics
• Number System and Arithmetic
• Trigonometry
• Probability
• Mensuration
• Maths Formulas
• Class 8 Maths Notes
• Class 9 Maths Notes
• Class 10 Maths Notes
• Class 11 Maths Notes
• Class 12 Maths Notes
• Graphical Solution of Linear Programming Problems
• Linear Programming
• Solving Linear Inequalities Word Problems
• Stars and Bars Algorithms for Competitive Programming
• Python | Linear search on list or tuples
• Top 50 Dynamic Programming Coding Problems for Interviews
• Dynamic Programming (DP) Tutorial with Problems
• Program to find all types of Matrix
• Dynamic Programming | High-effort vs. Low-effort Tasks Problem
• Python | Linear Programming in Pulp
• C++ Program for the Fractional Knapsack Problem
• Transportation Problem | Set 1 (Introduction)
• Algorithms | Dynamic Programming | Question 7
• Algorithms | Dynamic Programming | Question 4
• Algorithms | Dynamic Programming | Question 3
• Algorithms | Dynamic Programming | Question 2
• How to begin with Competitive Programming?
• Dynamic Programming (DP) on Grids
• Knuth's Optimization in Dynamic Programming

Types of Linear Programming Problems

Linear programming is a mathematical technique for optimizing operations under a given set of constraints. The basic goal of linear programming is to maximize or minimize the total numerical value. It is regarded as one of the most essential strategies for determining optimum resource utilization. Linear programming challenges include a variety of problems involving cost minimization and profit maximization, among others. They will be briefly discussed in this article.

The purpose of this article is to provide students with a comprehensive understanding of the different types of linear programming problems and their solutions.

What is Linear Programming?

Linear programming (LP) is a mathematical optimization technique used to maximize or minimize a linear objective function, subject to a set of linear equality and inequality constraints. It is widely used in various fields such as economics, engineering, operations research, and management science to find the best possible outcome given limited resources.

Components of Linear Programming

Components of linear programming include:

• Objective Function: This is a linear function that needs to be optimized (maximized or minimized). It represents the quantity to be maximized or minimized, such as profit, cost, time, etc.
• Decision Variables: These are the variables that represent the choices or decisions to be made. They are the unknown quantities that the optimization process seeks to determine. Decision variables must be continuous and can take any real value within a specified range.
• Constraints: These are restrictions or limitations on the decision variables that must be satisfied. Constraints can be expressed as linear equations or inequalities. They represent the limitations imposed by available resources, capacity constraints, demand requirements, etc.
• Feasible Region: The feasible region is the set of all possible combinations of decision variables that satisfy all constraints. It is defined by the intersection of the constraint boundaries.
• Optimal Solution: This is the best possible solution that maximizes or minimizes the objective function while satisfying all constraints. In graphical terms, it is the point within the feasible region that maximizes or minimizes the objective function.

Linear programming provides a systematic and efficient approach to decision-making in situations where resources are limited and objectives need to be optimized.

Different Types of Linear Programming Problems

The following are the types of linear programming problems:

• Manufacturing problems
• Diet problems
• Transportation problems
• Optimal alignment problem

Let’s discuss more about each of them.

Manufacturing Problems

In these problems, we evaluate the number of units of various items that should be produced and sold by a company when each product requires a given number of workforce, machine hours, labour hours per unit of product, warehouse space per unit of output, and so on, to maximize profit.

Manufacturing problems involve maximizing the production rate or net profits of manufactured products, which might measure the available workspace, the number of workers, machine hours, packing materials used, raw materials required, the product’s market value, and other factors. These are commonly used in the industrial sector to anticipate a company’s future capital increase over time.

Diet Problems

In these challenges, we assess how many components or nutrients a diet should contain in order to lower the cost of the desired diet while guaranteeing the minimal amount of each vitamin.

As the name suggests, diet-related problems can be resolved by eating more particular foods that are rich in essential nutrients and can support the adoption of a particular diet plan. Finding a set of meals that will satisfy a set of daily nutritional demands for the least amount of money is the aim of a diet problem.

Transportation Problems

In these problems , we create a transportation schedule to discover the most cost-effective method of carrying a product from various plants/factories to various markets.

The study of transportation routes or how items from diverse production sources are transported to various markets to minimize the total transportation cost is linked to transportation difficulties. Analyzing such challenges is crucial for large firms with several production units and a broad customer base.

Optimal Assignment Problems

This problem addresses a company’s completion of a given task/assignment by selecting a specific number of employees to complete the assignment within the required timeframe, assuming that each person works on only one job. Event planning and management in major organizations, for example, are examples of such problems.

Constraints and Objective Function of Each Linear Programming Problem

Steps for solving linear programming problems.

Step 1: Identify the decision variables : The first step is to determine which choice factors control the behaviour of the objective function. A function that needs to be optimised is an objective function. Determine the decision variables and designate them with X, Y, and Z symbols.

Step 2: Form an objective function : Using the decision variables, write out an algebraic expression that displays the quantity we aim to maximize.

Step 3: Identify the constraints : Choose and write the given linear inequalities from the data.

Step 4: Draw the graph for the given data : Construct the graph by using constraints for solving the linear programming problem.

Step 5: Draw the feasible region : Every constraint on the problem is satisfied by this portion of the graph. Anywhere in the feasible zone is a viable solution for the objective function.

Step 6: Choosing the optimal point : Choose the point for which the given function has maximum or minimum values.

Solved Problems of Linear Programming Problems

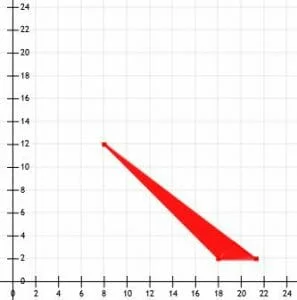
Question 1. A factory manufactures two types of gadgets, regular and premium. Each gadget requires the use of two operations, assembly and finishing, and there are at most 12 hours available for each operation. A regular gadget requires 1 hour of assembly and 2 hours of finishing, while a premium gadget needs 2 hours of assembly and 1 hour of finishing. Due to other restrictions, the company can make at most 7 gadgets a day. If a profit of $20 is realized for each regular gadget and $30 for a premium gadget, how many of each should be manufactured to maximize profit?

We define our unknowns:

Let the number of regular gadgets manufactured each day = x

and the number of premium gadgets manufactured each day = y

The objective function is

P = 20x + 30y

We now write the constraints. The fourth sentence states that the company can make at most 7 gadgets a day. This translates as

Since the regular gadget requires one hour of assembly and the premium gadget requires two hours of assembly, and there are at most 12 hours available for this operation, we get

x + 2y ≤ 12

Similarly, the regular gadget requires two hours of finishing and the premium gadget one hour. Again, there are at most 12 hours available for finishing. This gives us the following constraint.

2x + y ≤ 12

The fact that x and y can never be negative is represented by the following two constraints:

x ≥ 0, and y ≥ 0.

We have formulated the problem as follows :

Maximize P=20x + 30y Subject to : x + y ≤ 7, x + 2y ≤ 122, x + y ≤ 12, x ≥ 0, y ≥ 0

In order to solve the problem, we next graph the constraints and feasible region.

Again, we have shaded the feasible region, where all constraints are satisfied.

Since the extreme value of the objective function always takes place at the vertices of the feasible region, we identify all the critical points. They are listed as (0, 0), (0, 6), (2, 5), (5, 2), and (6, 0). To maximize profit, we will substitute these points in the objective function to see which point gives us the maximum profit each day. The results are listed below.

FAQ on Linear programming

How many methods are there in lpp.

There are different methods to solve a linear programming problem. Such as Graphical method, Simplex method, Ellipsoid method, Interior point methods.

What are the four 4 special cases in linear programming?

Four special cases and difficulties arise at times when using the graphical approach to solving LP problems: (1) infeasibility, (2) unboundedness, (3) redundancy, and (4) alternate optimal solutions.

What are the 3 components of linear programming?

The basic components of the LP are as follows: Decision Variables. Constraints. Objective Functions.

What are the applications of LPP?

LPP applications may include production scheduling, inventory policies, investment portfolio, allocation of advertising budget, construction of warehouses, etc.

What are the limitations of LPP?

Constraints (limitations) should be expressed in mathematical form. Relationships between two or more variables should be linear. The values of the variables should always be non-negative or zero. There should always be finite and infinite inputs and output numbers.

Please Login to comment...

Similar reads.

• Maths-Class-12
• School Learning

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4: Linear Programming - The Simplex Method

• Last updated
• Save as PDF
• Page ID 37816

• Rupinder Sekhon and Roberta Bloom
• De Anza College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

In this chapter, you will:

• Investigate real world applications of linear programming and related methods.
• Solve linear programming maximization problems using the simplex method.
• Solve linear programming minimization problems using the simplex method.
• 4.1: Introduction to Linear Programming Applications in Business, Finance, Medicine, and Social Science In this section, you will learn about real world applications of linear programming and related methods.
• 4.2.1: Maximization By The Simplex Method (Exercises)
• 4.3.1: Minimization By The Simplex Method (Exercises)
• 4.4: Chapter Review

Thumbnail: Polyhedron of simplex algorithm in 3D. (CC BY-SA 3.0; Sdo via Wikipedia)

Lesson LINEAR PROGRAMMING PROBLEMS AND SOLUTIONS 1