problem solving graph

• Solve equations and inequalities
• Simplify expressions
• Factor polynomials
• Graph equations and inequalities
• Advanced solvers
• All solvers
• Arithmetics
• Determinant
• Percentages
• Scientific Notation
• Inequalities

FIRST-DEGREE EQUATIONS AND INEQUALITIES IN TWO VARIABLES

The language of mathematics is particularly effective in representing relationships between two or more variables. As an example, let us consider the distance traveled in a certain length of time by a car moving at a constant speed of 40 miles per hour. We can represent this relationship by

We have already used word sentences and equations to describe such relationships; in this chapter, we will deal with tabular and graphical representations.

7.1 SOLVING EQUATIONS IN TWO VARIABLES

ORDERED PAIRS

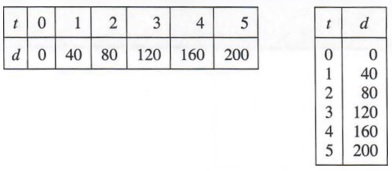
The equation d = 40f pairs a distance d for each time t. For example,

if t = 1, then d = 40 if t = 2, then d = 80 if t = 3, then d = 120

The pair of numbers 1 and 40, considered together, is called a solution of the equation d = 40r because when we substitute 1 for t and 40 for d in the equation, we get a true statement. If we agree to refer to the paired numbers in a specified order in which the first number refers to time and the second number refers to distance, we can abbreviate the above solutions as (1, 40), (2, 80), (3, 120), and so on. We call such pairs of numbers ordered pairs, and we refer to the first and second numbers in the pairs as components. With this agreement, solutions of the equation d - 40t are ordered pairs (t, d) whose components satisfy the equation. Some ordered pairs for t equal to 0, 1, 2, 3, 4, and 5 are

(0,0), (1,40), (2,80), (3,120), (4,160), and (5,200)

Such pairings are sometimes shown in one of the following tabular forms.

In any particular equation involving two variables, when we assign a value to one of the variables, the value for the other variable is determined and therefore dependent on the first. It is convenient to speak of the variable associated with the first component of an ordered pair as the independent variable and the variable associated with the second component of an ordered pair as the dependent variable. If the variables x and y are used in an equation, it is understood that replace- ments for x are first components and hence x is the independent variable and replacements for y are second components and hence y is the dependent variable. For example, we can obtain pairings for equation

by substituting a particular value of one variable into Equation (1) and solving for the other variable.

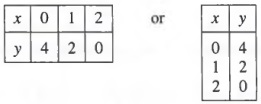
Find the missing component so that the ordered pair is a solution to

if x = 0, then 2(0) + y = 4 y = 4

if x = 1, then 2(1) + y = 4 y = 2

if x = 2, then 2(2) + y = 4 y = 0

The three pairings can now be displayed as the three ordered pairs

(0,4), (1,2), and (2,0)

or in the tabular forms

EXPRESSING A VARIABLE EXPLICITLY

We can add -2x to both members of 2x + y = 4 to get

-2x + 2x + y = -2x + 4 y = -2x + 4

In Equation (2), where y is by itself, we say that y is expressed explicitly in terms of x. It is often easier to obtain solutions if equations are first expressed in such form because the dependent variable is expressed explicitly in terms of the independent variable.

For example, in Equation (2) above,

if x = 0, then y = -2(0) + 4 = 4 if x = 1, then y = -2(1) + 4 = 2 if x = 2 then y = -2(2) + 4 = 0

We get the same pairings that we obtained using Equation (1)

We obtained Equation (2) by adding the same quantity, -2x, to each member of Equation (1), in that way getting y by itself. In general, we can write equivalent equations in two variables by using the properties we introduced in Chapter 3, where we solved first-degree equations in one variable.

Equations are equivalent if:

Solve 2y - 3x = 4 explicitly for y in terms of x and obtain solutions for x = 0, x = 1, and x = 2.

Solution First, adding 3x to each member we get

2y - 3x + 3x = 4 + 3x 2y = 4 + 3x (continued)

Now, dividing each member by 2, we obtain

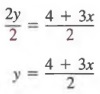
In this form, we obtain values of y for given values of x as follows:

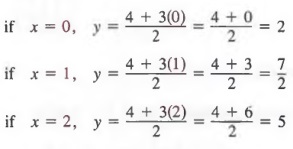
In this case, three solutions are (0, 2), (1, 7/2), and (2, 5).

FUNCTION NOTATION

Sometimes, we use a special notation to name the second component of an ordered pair that is paired with a specified first component. The symbol f(x), which is often used to name an algebraic expression in the variable x, can also be used to denote the value of the expression for specific values of x. For example, if

f(x) = -2x + 4

where f{x) is playing the same role as y in Equation (2) on page 285, then f(1) represents the value of the expression -2x + 4 when x is replaced by 1

f(l) = -2(1) + 4 = 2

f(0) = -2(0) + 4 = 4

f(2) = -2(2) + 4 = 0

The symbol f(x) is commonly referred to as function notation.

If f(x) = -3x + 2, find f(-2) and f(2).

Replace x with -2 to obtain f(-2) = -3(-2) + 2 = 8

Replace x with 2 to obtain f(2) = -3(2) + 2 = -4

7.2 GRAPHS OF ORDERED PAIRS

In Section 1.1, we saw that every number corresponds to a point in a line. Simi- larly, every ordered pair of numbers (x, y) corresponds to a point in a plane. To graph an ordered pair of numbers, we begin by constructing a pair of perpendicular number lines, called axes. The horizontal axis is called the x-axis, the vertical axis is called the y-axis, and their point of intersection is called the origin. These axes divide the plane into four quadrants, as shown in Figure 7.1.

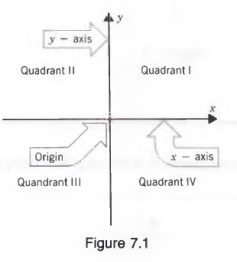
Now we can assign an ordered pair of numbers to a point in the plane by referring to the perpendicular distance of the point from each of the axes. If the first component is positive, the point lies to the right of the vertical axis; if negative, it lies to the left. If the second component is positive, the point lies above the horizontal axis; if negative, it lies below.

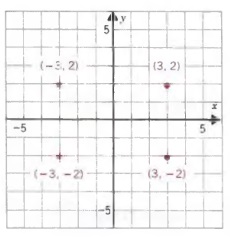
Graph (3, 2), (-3, 2), (-3, -2), and (3, -2) on a rectangular coordinate system.

Solution The graph of (3, 2) lies 3 units to the right of the y-axis and 2 units above the x-axis; the graph of (-3,2) lies 3 units to the left of the y-axis and 2 units above the x-axis; the graph of (-3, -2) lies 3 units to the left of the y-axis and 2 units below the x-axis; the graph of (3, -2) lies 3 units to the right of the y-axis and 2 units below the x-axis.

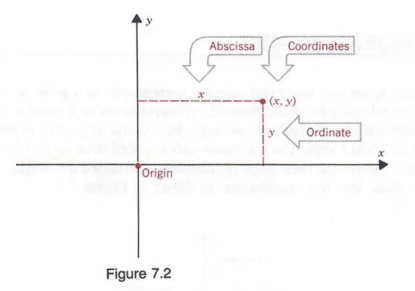
The distance y that the point is located from the x-axis is called the ordinate of the point, and the distance x that the point is located from the y-axis is called the abscissa of the point. The abscissa and ordinate together are called the rectan- gular or Cartesian coordinates of the point (see Figure 7.2).

7.3 GRAPHING FIRST-DEGREE EQUATIONS

In Section 7.1, we saw that a solution of an equation in two variables is an ordered pair. In Section 7.2, we saw that the components of an ordered pair are the coordinates of a point in a plane. Thus, to graph an equation in two variables, we graph the set of ordered pairs that are solutions to the equation. For example, we can find some solutions to the first-degree equation

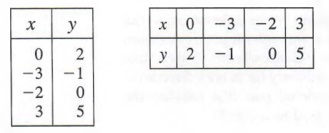
by letting x equal 0, -3, -2, and 3. Then,

for x = 0, y=0+2=2 for x = 0, y = -3 + 2 = -1 for x = -2, y = -2 + 2 - 0 for x = 3, y = 3 + 2 = 5

and we obtain the solutions

(0,2), (-3,-1), (-2,0), and (3,5)

which can be displayed in a tabular form as shown below.

If we graph the points determined by these ordered pairs and pass a straight line through them, we obtain the graph of all solutions of y = x + 2, as shown in Figure 7.3. That is, every solution of y = x + 2 lies on the line, and every point on the line is a solution of y = x + 2.

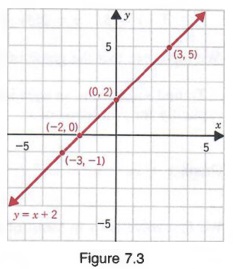
The graphs of first-degree equations in two variables are always straight lines; therefore, such equations are also referred to as linear equations.

In the above example, the values we used for x were chosen at random; we could have used any values of x to find solutions to the equation. The graphs of any other ordered pairs that are solutions of the equation would also be on the line shown in Figure 7.3. In fact, each linear equation in two variables has an infinite number of solutions whose graph lies on a line. However, we only need to find two solutions because only two points are necessary to determine a straight line. A third point can be obtained as a check.

To graph a first-degree equation:

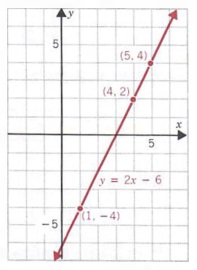
Graph the equation y = 2x - 6.

Solution We first select any two values of x to find the associated values of y. We will use 1 and 4 for x. If x = 1, y = 2(1) - 6 = -4 if x = 4, y = 2(4) - 6 = 2 Thus, two solutions of the equation are (1, -4) and (4, 2). Next, we graph these ordered pairs and draw a straight line through the points as shown in the figure. We use arrowheads to show that the line extends infinitely far in both directions. Any third ordered pair that satisfies the equation can be used as a check: if x = 5, y = 2(5) -6 = 4 We then note that the graph of (5, 4) also lies on the line To find solutions to an equation, as we have noted it is often easiest to first solve explicitly for y in terms of x.

Graph x + 2y = 4.

Solution We first solve for y in terms of x to get

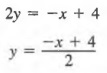
We now select any two values of x to find the associated values of y. We will use 2 and 0 for x.

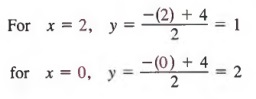
Thus, two solutions of the equation are (2, 1) and (0, 2).

Next, we graph these ordered pairs and pass a straight line through the points, as shown in the figure.

Any third ordered pair that satisfies the equation can be used as a check:

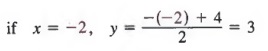
We then note that the graph of (-2, 3) also lies on the line.

SPECIAL CASES OF LINEAR EQUATIONS

The equation y = 2 can be written as

and can be considered a linear equation in two variables where the coefficient of x is 0. Some solutions of 0x + y = 2 are

(1,2), (-1,2), and (4,2)

In fact, any ordered pair of the form (x, 2) is a solution of (1). Graphing the solutions yields a horizontal line as shown in Figure 7.4.

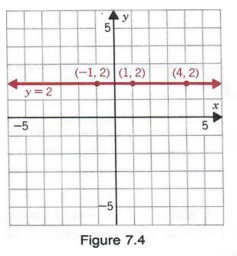
Similarly, an equation such as x = -3 can be written as

x + 0y = -3

and can be considered a linear equation in two variables where the coefficient of y is 0.

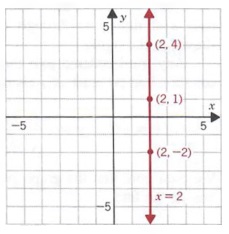
Some solutions of x + 0y = -3 are (-3, 5), (-3, 1), and (-3, -2). In fact, any ordered pair of the form (-3, y) is a solution of (2). Graphing the solutions yields a vertical line as shown in Figure 7.5.

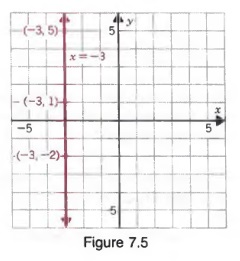
a. y = 3 b. x=2

Solution a. We may write y = 3 as Ox + y =3. Some solutions are (1, 3), (2,3), and (5, 3).

b. We may write x = 2 as x + Oy = 2. Some solutions are (2, 4), (2, 1), and (2, -2).

7.4 INTERCEPT METHOD OF GRAPHING

In Section 7.3, we assigned values to x in equations in two variables to find the corresponding values of y. The solutions of an equation in two variables that are generally easiest to find are those in which either the first or second component is 0. For example, if we substitute 0 for x in the equation

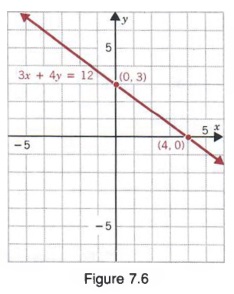
3x + 4y = 12

3(0) + 4y = 12 y = 3

Thus, a solution of Equation (1) is (0, 3). We can also find ordered pairs that are solutions of equations in two variables by assigning values to y and determining the corresponding values of x. In particular, if we substitute 0 for y in Equation (1), we get

3x + 4(0) = 12 x = 4

and a second solution of the equation is (4, 0). We can now use the ordered pairs (0, 3) and (4, 0) to graph Equation (1). The graph is shown in Figure 7.6. Notice that the line crosses the x-axis at 4 and the y-axis at 3. For this reason, the number 4 is called the x-intercept of the graph, and the number 3 is called the y-intercept.

This method of drawing the graph of a linear equation is called the intercept method of graphing. Note that when we use this method of graphing a linear equation, there is no advantage in first expressing y explicitly in terms of x.

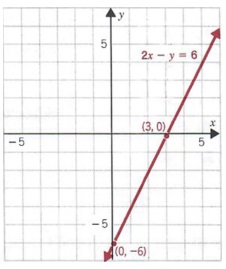
Graph 2x - y = 6 by the intercept method.

Solution We find the x-intercept by substituting 0 for y in the equation to obtain

2x - (0) = 6 2x = 6 x = 3

Now, we find the y-intercept by substituting for x in the equation to get

2(0) - y = 6 -y = 6 y = -6

The ordered pairs (3, 0) and (0, -6) are solutions of 2x - y = 6. Graphing these points and connecting them with a straight line give us the graph of 2x - y = 6. If the graph intersects the axes at or near the origin, the intercept method is not satisfactory. We must then graph an ordered pair that is a solution of the equation and whose graph is not the origin or is not too close to the origin.

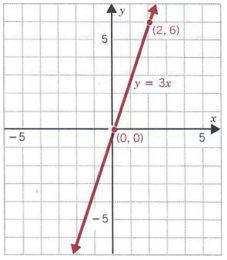
Graph y = 3x.

Solution We can substitute 0 for x and find y = 3(0) = 0 Similarly, substituting 0 for y, we get 0 = 3.x, x = 0 Thus, 0 is both the x-intercept and the y-intercept.

Since one point is not sufficient to graphy = 3x, we resort to the methods outlined in Section 7.3. Choosing any other value for x,say 2, we get

y = 3(2) = 6

Thus, (0, 0) and (2, 6) are solutions to the equation. The graph of y = 3x is shown at the right.

7.5 SLOPE OF A LINE

SLOPE FORMULA

In this section, we will study an important property of a line. We will assign a number to a line, which we call slope, that will give us a measure of the "steepness" or "direction" of the line.

It is often convenient to use a special notation to distinguish between the rectan- gular coordinates of two different points. We can designate one pair of coordinates by (x 1 , y 1 (read "x sub one, y sub one"), associated with a point P 1 , and a second pair of coordinates by (x 2 , y 2 ), associated with a second point P 2 , as shown in Figure 7.7. Note in Figure 7.7 that when going from P 1 to P 2 , the vertical change (or vertical distance) between the two points is y 2 - y 1 and the horizontal change (or horizontal distance) is x 2 - x 1 .

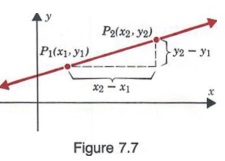
The ratio of the vertical change to the horizontal change is called the slope of the line containing the points P 1 and P 2 . This ratio is usually designated by m. Thus,

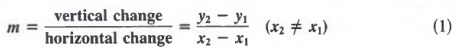
Solution We designate (3, 5) as (x 2 , y 2 ) and (-4, 2) as (x 1 , y 1 ). Substituting into Equation (1) yields

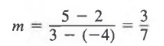
Note that we get the same result if we subsitute -4 and 2 for x 2 and y 2 and 3 and 5 for x 1 and y 1

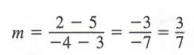
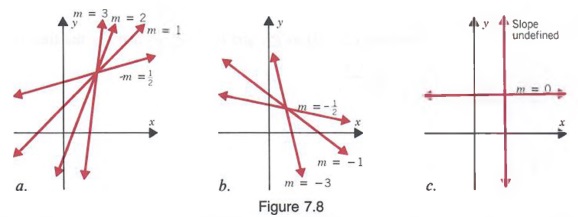
Lines with various slopes are shown in Figure 7.8 below. Slopes of the lines that go up to the right are positive (Figure 7.8a) and the slopes of lines that go down to the right are negative (Figure 7.8b). And note (Figure 7.8c) that because all points on a horizontal line have the same y value, y 2 - y 1 equals zero for any two points and the slope of the line is simply

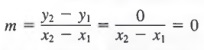
Also note (Figure 7.8c) that since all points on a vertical have the same x value, x 2 - x 1 equals zero for any two points. However,

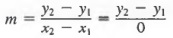
is undefined, so that a vertical line does not have a slope.

PARALLEL AND PERPENDICULAR LINES

Consider the lines shown in Figure 7.9. Line l 1 has slope m 1 = 3, and line l 2 has slope m 2 = 3. In this case,

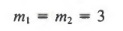
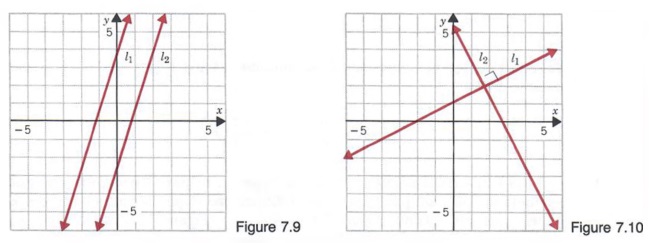
These lines will never intersect and are called parallel lines. Now consider the lines shown in Figure 7.10. Line l 1 , has slope m 1 = 1/2 and line l 2 has slope m 2 = -2. In this case,

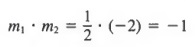
These lines meet to form a right angle and are called perpendicular lines.

In general, if two lines have slopes and m2: a. The lines are parallel if they have the same slope, that is, if m 1 = m 2 . b. The lines are perpendicular If the product of their slopes is -1, that is, if m 1 * m 2 = -1.

7.6 EQUATIONS OF STRAIGHT LINES

POINT-SLOPE FORM

In Section 7.5, we found the slope of a straight line by using the formula

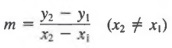
Let us say we know that a line goes through the point (2, 3) and has a slope of 2. If we denote any other point on the line as P(x, y) (See Figure 7.1 la), by the slope formula

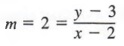
Thus, Equation (1) is the equation of the line that goes through the point (2, 3) and has a slope of 2.

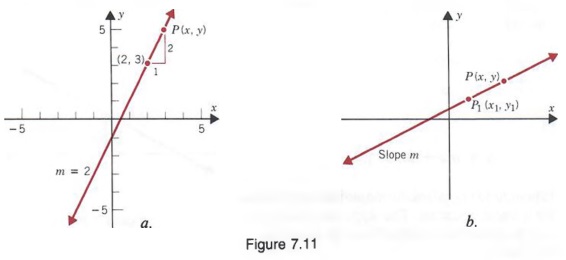
In general let us say we know a line passes through a point P 1 (x 1 , y 1 and has slope m. If we denote any other point on the line as P(x, y) (see Figure 7.11 b), by the slope formula

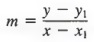
Equation (2) is called the point-slope form for a linear equation. In Equation (2), m, x 1 and y 1 are known and x and y are variables that represent the coordinates of any point on the line. Thus, whenever we know the slope of a line and a point on the line, we can find the equation of the line by using Equation (2).

A line has slope -2 and passes through point (2, 4). Find the equation of the line.

Solution Substitute -2 for m and (2, 4) for (x 1 , y 1 ) in Equation (2)

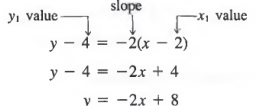
Thus, a line with slope -2 that passes through the point (2, 4) has the equation y = -2x + 8. We could also write the equation in equivalent forms y + 2x = 8, 2x + y = 8, or 2x + y - 8 = 0.

SLOPE-INTERCEPT FORM

Now consider the equation of a line with slope m and y-intercept b as shown in Figure 7.12. Substituting 0 for x 1 and b for y 1 in the point-slope form of a linear equation, we have

y - b = m(x - 0) y - b = mx

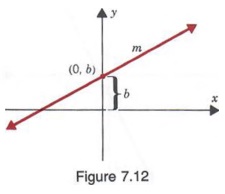
Equation (3) is called the slope-intercept form for a linear equation. The slope and y-intercept can be obtained directly from an equation in this form.

Example 2 If a line has the equation

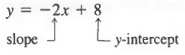
then the slope of the line must be -2 and the y-intercept must be 8. Similarly, the graph of

y = -3x + 4

has a slope -3 and a y-intercept 4; and the graph of

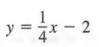
has a slope 1/4 and a y-intercept -2.

If an equation is not written in x = mx + b form and we want to know the slope and/or the y-intercept, we rewrite the equation by solving for y in terms of x.

Find the slope and y-intercept of 2x - 3y = 6.

Solution We first solve for y in terms of x by adding -2x to each member.

2x - 3y - 2x = 6 - 2x - 3y = 6 - 2x

Now dividing each member by -3, we have

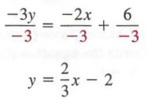
Comparing this equation with the form y = mx + b, we note that the slope m (the coefficient of x) equals 2/3, and the y-intercept equals -2.

7.7 DIRECT VARIATION

A special case of a first-degree equation in two variables is given by

y = kx (k is a constant)

Such a relationship is called a direct variation. We say that the variable y varies directly as x.

We know that the pressure P in a liquid varies directly as the depth d below the surface of the liquid. We can state this relationship in symbols as

In a direct variation, if we know a set of conditions on the two variables, and if we further know another value for one of the variables, we can find the value of the second variable for this new set of conditions.

In the above example, we can solve for the constant k to obtain

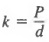
Since the ratio P/d is constant for each set of conditions, we can use a proportion to solve problems involving direct variation.

If pressure P varies directly as depth d, and P = 40 when d = 10, find P when d = 15.

Solution Since the ratio P/d is constant, we can substitute values for P and d and obtain the proportion

Thus, P = 60 when d = 15.

7.8 INEQUALITIES IN TWO VARIABLES

In Sections 7.3 and 7.4, we graphed equations in two variables. In this section we will graph inequalities in two variables. For example, consider the inequality

y ≤ -x + 6

The solutions are ordered pairs of numbers that "satisfy" the inequality. That is, (a, b) is a solution of the inequality if the inequality is a true statement after we substitute a for x and b for y.

Determine if the given ordered pair is a solution of y = -x + 6.

a. (1, 1) b. (2, 5)

Solution The ordered pair (1, 1) is a solution because, when 1 is substituted for x and 1 is substituted for y, we get

(1) = -(1) + 6, or 1 = 5

which is a true statement. On the other hand, (2, 5) is not a solution because when 2 is substituted for x and 5 is substituted for y, we obtain

(5) = -(2) + 6, or 5 = 4

which is a false statement.

To graph the inequality y = -x + 6, we first graph the equation y = -x + 6 shown in Figure 7.13. Notice that (3, 3), (3, 2), (3, 1), (3, 0), and so on, associated with the points that are on or below the line, are all solutions of the inequality y = -x + 6, whereas (3,4), (3, 5), and (3,6), associated with points above the line are not solutions of the inequality. In fact, all ordered pairs associated with points on or below the line are solutions of y = - x + 6. Thus, every point on or below the line is in the graph. We represent this by shading the region below the line (see Figure 7.14).

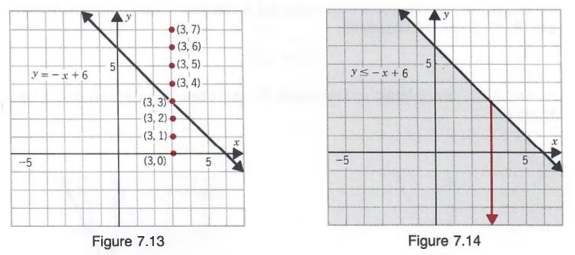
In general, to graph a first-degree inequality in two variables of the form Ax + By = C or Ax + By = C, we first graph the equation Ax + By = C and then determine which half-plane (a region above or below the line) contains the solutions. We then shade this half-plane. We can always determine which half- plane to shade by selecting a point (not on the line of the equation Ax + By = C) and testing to see if the ordered pair associated with the point is a solution of the given inequality. If so, we shade the half-plane containing the test point; otherwise, we shade the other half-plane. Often, (0, 0) is a convenient test point.

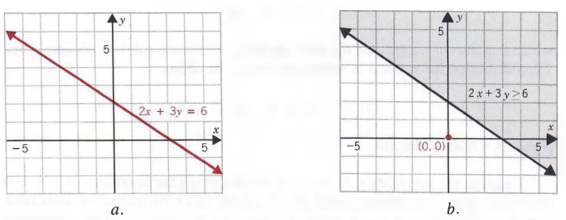
Graph 2x+3y = 6

Solution We first graph the line 2x + 3y = 6 (see graph a). Using the origin as a test point, we determine whether (0, 0) is a solution of 2x + 3y ≥ 6. Since the statement

2(0) + 3(0) = 6

is false, (0, 0) is not a solution and we shade the half-plane that does not contain the origin (see graph b).

When the line Ax + By = C passes through the origin, (0, 0) is not a valid test point since it is on the line.

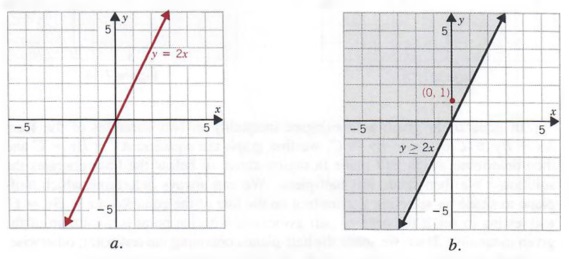
Graph y = 2x.

Solution We begin by graphing the line y = 2x (see graph a). Since the line passes through the origin, we must choose another point not on the line as our test point. We will use (0, 1). Since the statement

is true, (0, 1) is a solution and we shade the half-plane that contains (0, 1) (see graph b).

If the inequality symbol is ' , the points on the graph of Ax + By = C are not solutions of the inequality. We then use a dashed line for the graph of Ax + By = C.

CHAPTER SUMMARY

A solution of an equation in two variables is an ordered pair of numbers. In the ordered pair (x, y), x is called the first component and y is called the second component. For an equation in two variables, the variable associated with the first component of a solution is called the independent variable and the variable associated with the second component is called the dependent variable. Function notation f(x) is used to name an algebraic expression in x. When x in the symbol f(x) is replaced by a particular value, the symbol represents the value of the expression for that value of x.

The intersection of the two perpendicular axes in a coordinate systemis called the origin of the system, and each of the four regions into which the plane is divided is called a quadrant. The components of an ordered pair (x, y) associated with a point in the plane are called the coordinates of the point; x is called the abscissa of the point and y is called the ordinate of the point.

The graph of a first-degree equation in two variables is a straight line. That is, every ordered pair that is a solution of the equation has a graph that lies in a line, and every point in the line is associated with an ordered pair that is a solution of the equation.

The graphs of any two solutions of an equation in two variables can be used to obtain the graph of the equation. However, the two solutions of an equation in two variables that are generally easiest to find are those in which either the first or second component is 0. The x-coordinate of the point where a line crosses the x-axis is called the x-intercept of the line, and the y-coordinate of the point where a line crosses the y-axis is called they-intercept of the line. Using the intercepts to graph an equation is called the intercept method of graphing.

The slope of a line containing the points P 1 (x 1 , y 1 ) and P 2 (x 2 , y 2 ) is given by

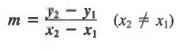
Two lines are parallel if they have the same slope (m 1 = m 2 ).

Two lines are perpendicular if the product of their slopes is - l(m 1 * m 2 = -1).

The point-slope form of a line with slope m and passing through the point (x 1 , y 1 ) is

y - y 1 - m(x - x 1 )

The slope-intercept form of a line with slope m and y-intercept b is

A relationship determined by an equation of the form

y = kx (k a constant)

is called a direct variation.

A solution of an inequality in two variables is an ordered pair of numbers that, when substituted into the inequality, makes the inequality a true statement. The graph of a linear inequality in two variables is a half-plane. The symbols introduced in this chapter appear on the inside front covers.

Math Topics

More solvers.

• Add Fractions
• Simplify Fractions

The Definitive Guide to Graph Problems

Do you want to learn how to solve graph problems? Are you preparing for a coding interview? Do you want to polish your problem-solving skills? In this article I will try to answer these questions and more, and you will learn the patterns necessary to deal with these problems.

What is a Graph?

A Graph is a data structure consisting of Nodes (or vertices) and Edges . This data structure is often use as a way to represent distances or different connections.

For example the distances between cities, with arbitrary distances.

With a graph you can know things like, the distance from New York to Paris, and from Paris to Tokyo, also, thanks to the graph you know that if you can go from New York to Paris and from Paris to Tokyo, you can go from New York to Tokyo.

• Nodes: a node (normally the circles in the graph) can have a value, for example a letter or a number, or have not value at all.
• Edges: the edges (or arrows) are the lines that connect one node with another one. An edge can have a value, this value may represent some sort o distance.

More formally a Graph is composed of a set of Nodes(N) and a set of edges(E).

Graph in the context of coding interviews

During technical interviews you are often asked to solve coding challenges. And you must have a good understanding of graph algorithms if you want to do well in these challenges.

Graph are often a topic present in coding interviews, so here I want to show you how to tackle these problems and the different patterns that you need to know or be aware of.

I recommend reading the topics in this article in order, as we will develop the subject progressively and the understanding of the first exercises are the basis for the following ones.

Problem solutions

All the solutions to the problems presented in this article can be found in this GitHub Repository

How do you traverse a graph?

When traversing a graph there are two main techniques, known as Breadth-First-Search and Depth-First-Search , this is the fundamental block that you will use in most graph problems.

Breadth-First-Search (BFS)

Breadth-First-Search (BFS) is an algorithm for searching a tree data structure for a node that satisfies a given property. It starts at the tree root (or the node that you want) and explores all nodes at the present depth prior to moving on to the nodes at the next depth level.

Extra memory, usually a queue , is needed to keep track of the child nodes that were encountered but not yet explored.

The result of the BFS algorithm will be –> 1, 2, 3, 4, 5, 6.

To implement a BFS algorithm, you have to follow the next steps:

• Declare a queue and insert the starting node.
• While the queue is not empty you remove the first node of the queue.
• Insert all the neighbors of the node into the queue.

All of the algorithms will be presented in python, feel free to implement them in your favorite language

BFS Code implementation

Time and space complexity.

Time Complexity of BFS: O(V+E) where V is vertices (nodes) and E is edges, since you must go through all the nodes and edges of the graph

Space Complexity of BFS: O(V) where V is vertices (nodes), since the queue will have at most V elements

Depth-First-Search (DFS)

Depth-First-Search (DFS) is an algorithm for traversing or searching tree or graph data structures.

The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking.

Extra memory, usually a stack , is needed to keep track of the nodes discovered so far along a specified branch which helps in backtracking of the graph.

The result of the DFS algorithm will be –> 1, 3, 6, 5, 2, 4.

To implement a DFS algorithm, you have to follow the next steps:

For the iterative solution :

• Declare a stack and insert the starting node.
• While the stack is not empty you remove the last node of the stack.

For the recursive solution :

• Create a recursive function that takes in the graph and the starting node.
• Create your base cases.
• Traverse all the neighboring nodes and call the recursive function with the index of the neighboring node.

DFS Code implementation, Iterative

Dfs code implementation, recursion.

Time Complexity of DFS: O(V+E) where V is vertices (nodes) and E is edges, since you must go through all the nodes and edges of the graph

Space Complexity of DFS: O(V) where V is vertices (nodes), since the stack will have at most V elements

Adjacency List as my Graph representation

Sometimes we may be given an input that is not what we expect, or that is difficult to work with. One of the easiest ways to work with graphs is with an adjacency list .

Suppose we have an input like the one below.

Where the first element of the array, [“1”, “2”] , reads as, node one connects to node 2, and node 2 connects to node 1. To transform this input into an adjacency list we can create a function like create_graph , to transform the array into an adjacency list that is easier to work with.

And the output is:

In this way we can deal with these problems without having to worry about the shape of the input.

Let’s practice the traversal

Now we need to put into practice what we have learned with an exercise.

We are going to write a function has_path that takes a dictionary or object representing the adjacency list of a graph, and the parameters will be (starting_node, destination) . The function must return a True value whether there is a directed path between the source node and the destination node, otherwise we should return False

This is the input graph

Has path Code implementation

We are going to implement the solution using BFS and DFS (recursively and iteratively).

The process is quite straightforward, we need to implement the same algorithm we implemented above, but searching for the destination node. Feel free to give it a try on your own before jump into the solution 😋.

BFS Iterative Solution

Dfs iterative solution.

As we can see, this is essentially the same code, except with an stack instead of a queue data structure.

DFS Recursive Solution

Here we are going to implement the DFS algorithm using a recursive approach.

Undirected Graph and the Visited Pattern

So far we have seen directed graph , that is, from one node to another node there is only one direction, consider the next example:

In this example you can go from New York to Paris, but not the other way around.

An undirected graph is a graph, where all the edges are bidirectional.

In this example 👆, you can go from New York to Paris, and from Paris to New York.

But what is the Visited Pattern ?

As you can imagine, now we need to find some way to know which nodes we visit and which we don’t, so we can avoid infinite loops.

Generally a solution to this is to use a set , which allows us to have constant lookups, that is access to an element in constant time.

Let’s practice some exercises.

Here we will practice some exercises using BFS and DFS, and we will implement the visited pattern. Again, feel free to try to solve these exercises on your own before jump into the code.

I will explain in the code the new lines that we need to solve the problem and potential gotchas.

Find a path Between node A and B in a undirected Graph

This problem is similar to the Has Path problem presented above, but with the difference that we have an undirected node, so we have to pay attention to the nodes we visit, in order not to fall into an infinite loop.

Our input graph is the following:

The new concepts to keep in mind are the following:

• We need to create a data structure to keep track of the visited node, typically a set .
• When we loop through the neighbors of our current node, we need to ask if that node has already been visited.
• If the node has been visited, we skip the node (this may depend of the problem).
• After we check that our node has not been visited yet, we mark it as visited.

BFS Solution - Has Path - Undirected Graph

We implement the BFS algorithm as we have seen before, but we add a new element, the visited set, to keep track of our visited nodes.

DFS Iterative Solution - Has Path - Undirected Graph

This solution is similar to the BFS approach, but using an stack instead of a queue.

DFS Recursive Solution - Has Path - Undirected Graph - Variation # 1

We implement a recursive approach to look for the visited nodes, we also add a new parameter to our function, a set, to keep track of the node that we have seen.

DFS Recursive Solution - Has Path - Undirected Graph - Variation # 2

This is a slight variation of the recursive DFS recursive approach. The main difference is that we check if the node has been visited when we loop the neighbors of our current node.

Count Components

In this exercise we will have to count the components that are connected. For instance, that a look at the example below 👇. As you see, there are 3 components. So our objective consists of counts how many components our graph has.

We need to write a function connected_components_counts(graph) that takes in a graph as a parameter, and it must return the number of components that the graph has, or zero if it has none.

This problem has the particularity that we have to iterate through all the nodes of the graph, because if not, we will not know if they are all connected, or if we are missing any of them.

BFS Solution - Count Components

Here we implement our now classic BFS traversal, we iterate through our graph, and asking if the node has been visited or not. We also need a way to count the components, to do so, we create a count variable, to count our components.

We have to take into account the following in order to solve this problem

We count as + 1 component, when our queue is empty, because when we’re traversing on the first node of a component and we add an element to the queue, and when the queue happened to be empty that means that we have visited all the nodes related to the first node of our for loop

On the next element of our for loop, if that element has been visited we skip it, if the next element of our for loop is a node that has not been visited, that means that we found a new component and we need to search for its neighbors and add them to the queue.

DFS Iterative Solution - Count Components

The way to solve the count components problem using a DFS algorithm is similar to the BFS version, except that we use a stack instead of a queue .

DFS Recursive Solution - Count Components

The recursive solution at first glance seems different from what we have been implementing.

The difference is that now we use a for loop, to iterate through all the nodes of the graph and then we call the function traverse_graph to do our classic DFS algorithm. We still need to keep track of the nodes we visit.

Now our recursive function is going to return True or False , if it is True it means that we traversed all the nodes of a component, and we add + 1 to our count variable.

Largest Component

IIn this exercise we have to calculate the size of the largest component, this gives us the idea that we should initialize a variable, to keep track of the largest component so far, and that is exactly what we are going to do.

We need to write a function get_largests_component that takes in a graph as a parameter, and it must return the the size of the largest component.

For example, the graph we are going to take as an example is the one below, we can see that the maximum size of the component is 6, which is the component on the left.

BFS Solution - Largest Component

Dfs iterative solution - largest component.

As always, the difference between DFS and BFS is the use of a stack instead of a queue.

DFS Recursive Solution - Largest Component - Variation #1

Here we will look at two variations using recursion. The first is to pass the parameter size to the recursive function and increment it one by one, and then compare it with the maximum value obtained from all the functions.

DFS Recursive Solution - Largest Component - Variation #2

The difference with this variation with respect to the previous one is that now we have a base case, where if the node is visited we return zero, otherwise, the size is 1 and we add the results of the other recursive functions.

Shortest Path

In this exercise we must find the shortest path in an undirected graph, between two nodes. For example consider the example below, where we can see that there are several paths to get from node 1 to node 6, these paths can be:

• 1, 2, 4, 5, 6
• 1, 2, 4, 5, 3, 6

But we must consider the shortest one, we need a notion of length/distance , for our case, we consider that the distance between each node is 1, that is, the distance is the amount of “Edges”, for example the route (1, 2, 4, 5, 6) consists of 4 edges, therefore the distance is 4.

In the example below we can see the correct shortest path, although there may be several.

The difficulty of these exercises is that now we need to keep track, not only the nodes we visited, but also the distance from the previous node to the current one.

For example, we can start from node A, saying that the distance is 0, but when adding an element to the queue or stack, we will have to add not only the neighboring node, but also the current distance, which is zero, plus 1.

Write a function, shortest_path , that receives an undirected graph and two nodes, (source, destination) . The function should return the length of the shortest path between Source and Destination. Consider the length as the number of edges in the path, not the number of nodes. If there is no path between A and B, then return -1.

BFS Iterative Solution - Shortest Path

If you think about it for a moment you may ask yourself, what is the best way to traverse the graph, if you look at a Depth First Search approach, it will try to traverse the graph from the beginning to the end in a single direction, where this may not be the most convenient. On the other hand, BFS, will try to expand by extending one by one the distances to the surroundings of the node, finding the solution faster.

A particularity of these exercises is that we add to the queue or stack, the node and the distance, in our case it is in the form of a tuple, that is to say (node, distance_so_far) , as we are doing BFS, at the moment we find the destination node, it means that we find the shortest distance,

Graph with cycles

Now we are going to look at how to deal with problems of finding cycles in graphs, although the graphs we were looking at previously had cycles, we did not try to determine whether they contained them or not, but rather avoided them, using the visited pattern .

Let’s refresh the concepts a bit

A cycle graph is a graph consisting of a single cycle, or in other words, a certain number of nodes connected in a closed chain.

For example, if we look at the image below, we can see that node 3 has a cycle, since from node 3 we can go to node 3 an infinite number of times, thus forming a closed chain.

The graph below also contains a cycle, as we can go from 1 to 2 and from 2 to 1 many times, but we can also go from node 1, to node 4, from 4 to 5 and from 5 to 2 and back to 1 again.

How to find a cycle?

You might be imagining that finding a cycle is a trivial task, since you can use the visited variable we’ve been using and determine that if the new node is visited it means we’ve found a cycle.

But that solution has a problem, we may be presented with a graph like the following.

In this graph, we have explored nodes 1, 2 and 3, but node 4 has not yet been explored, when we start exploring node 4, we will arrive at node 2, and this node has been visited, but as you can see in the image, this graph does not present a cycle, so our solution would be incorrect.

The solution is to use an additional variable, which we will call it currently_in_stack , to keep track of the nodes we explored from our first node.

Once we have explored a path with a node, we remove it from the stack, while keeping track of the nodes visited in our visited variable.

As a way of illustration, suppose we explore these nodes, the value of our variables would be:

• Visited: 1, 2, 3
• Currently_in_stack: 1, 2, 3

Now we need to explore node 4, so what we do is empty the currently_in_stack variable, and the visited variable is left unchanged.

So when we go from node 4 to node 2, we will ask if node 2 is in the variable currently_in_stack , and if it is not, it means that we have not found a cycle yet. To find a cycle, what should have happened is that the node we explore must be in the variable currently_in_stack.

Has a cycle?

This exercise consists of finding out whether the graph has a cycle or not.

Write a function cycle_in_graph that has a graph as a parameter, and returns True if the graph contains a cycle or false if it does not have a cycle.

Feel free to try it out for yourself before jumping into the solution.

Has a cycle solution

In this solution we use a combination of iteration with recursion to find whether the graph has a cycle or not.

Matrix as a graph

You may not always get the nodes and edges of a graph, you may get a grid , in which case it is still possible to think of a problem with a grid as if it were a graph.

For example we can, think of the position of a cell (row, col), as if it were the node, and we can consider that a node can move, up , down , left , right , i.e. it has at most 4 neighbors.

For example consider the grid below, the node would be, with index zero, row 3 and column 2, that is (3, 2), and the neighbors would be the arrows.

The problem with these grids is that when finding our neighbors, we must consider not to go out of the grid.

If our position is (row, col), our neighbors would be:

• Up: (row - 1, col)
• Down: (row + 1, col)
• Right: (row, col + 1)
• Left: (row, col - 1)

Problems with islands 🏝

Now we are going to look at two typical grid problems, which consist of counting the islands and finding the largest island. I will start by first explaining how to count the islands.

Count the islands

This problem consists of counting how many islands there are in the grid. The water will be represented in blue and the land in yellow, the idea is to consider an island as any set of yellow cells that are next to each other. If we look at the grid below, we will see that there are 4 islands, but how do we solve this problem?

The input parameter of our problem will be a grid of the following style:

You have probably noticed that what we have to do is to iterate this grid to access the cells, and then ask if it is water, we do nothing, and if it is a land, we must mark it as visited.

As we find land, we must also find the neighboring nodes, through BFS or DFS, we must also ask if the neighboring nodes are water or land, and if they are land, we must explore their neighbors and so on.

It is important to mark neighboring nodes as visited, so that in the next iteration of our for loop, we ask if the current cell is water or the land has been visited, if that is the case, we skip them.

The problem statement is as follows:

Write a function, island_count , that takes in a grid containing Ws and Ls. W represents water and L represents land. The function should return the number of island on the grid. An island is a vertically or horizontally connected region of land

BFS Iterative Solution - Count the islands

Here we are going to use a BFS algorithm to solve the problem, the difference with the previous exercises is that we are going to have an additional loop to iterate through the grid, then we will ask if the cell is water or land, if it is water we do nothing, or if we already visited it we do nothing.

Another difference is that we are going to store in the variable visited the position of the cell, as a tuple (row, col) , but feel free to use whatever you want, it could also be an array [row, col] .

We also create an additional function called get_neighbors , to get the neighboring nodes to the current cell, being careful not to get an out of bounds error.

DFS Recursive Solution - Count the islands

The recursive solution has the particularity that it will have more base cases, where it will check not to have an out of bound situation.

Also, the recursive function will take care of adding the neighboring nodes as visited.

Largest Island

This problem is similar to the previous one, with the particularity that we must slightly change our function to keep track of the largest island we have found.

Write a function, largest_island , that takes in a grid containing Ws and Ls. W represents water and L, represents Land. The function should return the size of the largest island. An island is a vertically or horizontally connected region of land.

BFS Iterative Solution - Largest Island

The iterative BFS solution is similar to the previous one, with the main difference being that we count the length of the island in the explore_land function , and then compare it to our max_island variable.

DFS Recursive Solution - Largest Island

The main difference between the solution of counting the islands and getting the largest island by recursion, is that now we have to add up the sizes of the islands we find, and then compare them with our max_size variable.

If you have reached this point, it means that you have learnt the following:

• How to explore a graph using Breadth-First-Search.
• How to explore a graph using Depth-First-Search.
• You learned not to fall into infinite loops by using the visited pattern.
• You know how to tackle problems with grids as if they were graphs.
• You know how to apply recursive and iterative solutions.

Congratulations you have learned the basic building blocks to tackle any problem with graphs, I wish you all the best in your future coding interviews 😉.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: Algebra 2   >   Unit 10

• Solving equations by graphing
• Solving equations by graphing: intro
• Solving equations graphically: intro
• Solving equations by graphing: graphing calculator
• Solving equations graphically: graphing calculator
• Solving equations by graphing: word problems

Solving equations graphically: word problems

• Equations: FAQ
• Your answer should be
• an integer, like 6 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍  
• an exact decimal, like 0.75 ‍  
• a multiple of pi, like 12   pi ‍   or 2 / 3   pi ‍