solving problems involving rational equations

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.5: Solving Rational Equations

• Last updated
• Save as PDF
• Page ID 18372

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Solve rational equations.
• Solve literal equations, or formulas, involving rational expressions.

Solving Rational Equations

A rational equation is an equation containing at least one rational expression. Rational expressions typically contain a variable in the denominator. For this reason, we will take care to ensure that the denominator is not 0 by making note of restrictions and checking our solutions.

Solve rational equations by clearing the fractions by multiplying both sides of the equation by the least common denominator (LCD).

Example \(\PageIndex{1}\)

\(\frac{5}{x}-\frac{1}{3} = \frac{1}{x}\)

We first make a note that \(x≠0\) and then multiply both sides by the LCD, \(3x\):

Check your answer by substituting 12 for x to see if you obtain a true statement.

\(\begin{aligned} \frac{5}{x}-\frac{1}{3} &=\frac{1}{x} \\ \color{black}{\frac{5}{\color{OliveGreen}{12}}}-\frac{1}{3} &=\color{black}{\frac{1}{\color{OliveGreen}{12}}} \\ \frac{5}{12}-\frac{4}{12} &=\frac{1}{12} \\ \frac{1}{12} &=\frac{1}{12}\quad\color{Cerulean}{ \checkmark} \end{aligned}\)

The solution is 12.

After multiplying both sides of the previous example by the LCD, we were left with a linear equation to solve. This is not always the case; sometimes we will be left with a quadratic equation.

Example \(\PageIndex{2}\)

\(2-\frac{1}{x(x+1)}=\frac{3}{x+1}\)

In this example, there are two restrictions, \(x≠0\) and \(x≠−1\). Begin by multiplying both sides by the LCD, \(x(x+1)\).

After distributing and dividing out the common factors, a quadratic equation remains. To solve it, rewrite it in standard form, factor, and then set each factor equal to 0.

\(\begin{array}{rlrl}{2 x+1} & {=0} & {\text { or }} & {x-1=0} \\ {2 x} & {=-1} && {x=1} \\ {x} & {=-\frac{1}{2}}\end{array}\)

Check to see if these values solve the original equation.

\(\begin{array}{c|c}{Check\:x=-\frac{1}{2}}&{Check\:x=1}\\{2-\frac{1}{\color{Cerulean}{(-\frac{1}{2})}\color{black}{(\color{Cerulean}{(-\frac{1}{2})}\color{black}{+1)}}}=\frac{3}{\color{Cerulean}{(-\frac{1}{2})}\color{black}{+1}}}&{2-\frac{1}{\color{Cerulean}{1}\color{black}{(\color{Cerulean}{1}\color{black}{+1)}}=}\frac{3}{\color{Cerulean}{1}\color{black}{+1}}}\\{2-\frac{1}{(-\frac{1}{4})}=\frac{3}{\frac{1}{2}}}&{\frac{4}{2}-\frac{1}{2}=\frac{3}{2}}\\{2+1\cdot\frac{4}{1}=3\cdot\frac{2}{1}}&{\frac{3}{2}=\frac{3}{2}}\quad\color{Cerulean}{\checkmark}\\{2+4=6}\\{6=6}\quad\color{Cerulean}{\checkmark} \end{array}\)

The solutions are \(-\frac{1}{2}\) and \(1\).

Up to this point, all of the possible solutions have solved the original equation. However, this may not always be the case. Multiplying both sides of an equation by variable factors may lead to extraneous solutions, which are solutions that do not solve the original equation. A complete list of steps for solving a rational equation is outlined in the following example.

Example \(\PageIndex{3}\)

\(\frac{x}{x+2}+\frac{2}{x^{2}+5 x+6}=\frac{5}{x+3}\)

Step 1 : Factor all denominators and determine the LCD.

\(\begin{aligned} \frac{x}{x+2}+\frac{2}{x^{2}+5 x+6} &=\frac{5}{x+3} \\ \frac{x}{(x+2)}+\frac{2}{(x+2)(x+3)} &=\frac{5}{(x+3)} \end{aligned}\)

The LCD is \((x+2)(x+3)\).

Step 2 : Identify the restrictions. In this case, they are \(x≠−2\) and \(x≠−3\).

Step 3 : Multiply both sides of the equation by the LCD. Distribute carefully and then simplify.

\(\begin{aligned}\color{Cerulean}{(x+2)(x+3)}\color{black}{\cdot}\left(\frac{x}{(x+2)}+\frac{2}{(x+2)(x+3)} \right)&=\color{Cerulean}{(x+2)(x+3)}\color{black}{\cdot\frac{5}{(x+3)}}\\ \frac{x\cdot\color{Cerulean}{\cancel{(x+2)}(x+3)}}{\color{Cerulean}{\cancel{\color{black}{(x+2)}}}}\color{black}{+}\frac{2\cdot\color{Cerulean}{\cancel{(x+2)}\cancel{(x+3)}}}{\color{Cerulean}{\cancel{\color{black}{(x+2)}}\cancel{\color{black}{(x+3)}}}}&\color{black}{=}\frac{5\cdot\color{Cerulean}{(x+2)\cancel{(x+3)}}}{\color{Cerulean}{\cancel{\color{black}{(x+3)}}}}\\x(x+3)+2&=5(x+2)\\x^{2}+3x+2&=5x+10 \end{aligned}\)

Step 4 : Solve the resulting equation. Here the result is a quadratic equation. Rewrite it in standard form, factor, and then set each factor equal to \(0\).

\(\begin{array}{cc}{x+2=0} & {\text { or } \quad x-4=0} \\ {x=-2} & {x=4}\end{array}\)

Step 5 : Check for extraneous solutions. Always substitute into the original equation, or the factored equivalent. In this case, choose the factored equivalent to check:

\(\frac{x}{(x+2)}+\frac{2}{(x+2)(x+3)}=\frac{5}{(x+3)}\)

\(\begin{array}{c|c}{Check\:x=-2}&{Check\:x=4}\\{\frac{-2}{(\color{Cerulean}{-2}\color{black}{+2)}}+\frac{2}{(\color{Cerulean}{-2}\color{black}{+2)(}\color{Cerulean}{-2}\color{black}{+3)}}=\frac{5}{(\color{Cerulean}{-2}\color{black}{+3)}}}&{\frac{4}{(\color{Cerulean}{4}\color{black}{+2)}}+\frac{2}{(\color{Cerulean}{4}\color{black}{+2)(}\color{Cerulean}{4}\color{black}{+3)}}=\frac{5}{(\color{Cerulean}{4}\color{black}{+3)}}}\\{-\frac{2}{0}+\frac{2}{0(1)}=\frac{5}{1}\quad\color{red}{x}}&{\frac{4}{6}+\frac{2}{6\cdot7}=\frac{5}{7}}\\{Undefined\:terms!}&{\frac{2}{3}+\frac{1}{21}=\frac{5}{7}}\\{}&{\frac{14}{21}+\frac{1}{21}=\frac{5}{7}}\\{}&{\frac{15}{21}=\frac{5}{7}}\\{}&{\frac{5}{7}=\frac{5}{7}\quad\color{Cerulean}{\checkmark}} \end{array}\)

Here \(−2\) is an extraneous solution and is not included in the solution set. It is important to note that \(−2\) is a restriction.

The solution is \(4\).

If this process produces a solution that happens to be a restriction, then disregard it as an extraneous solution.

Exercise \(\PageIndex{1}\)

Sometimes all potential solutions are extraneous, in which case we say that there is no solution to the original equation. In the next two examples, we demonstrate two ways in which a rational equation can have no solutions.

Example \(\PageIndex{4}\)

\(\frac{3 x}{x^{2}-4}-\frac{2}{x+2}=\frac{1}{x+2}\)

To identify the LCD, first factor the denominators.

\(\begin{aligned} \frac{3 x}{x^{2}-4}-\frac{2}{x+2} &=\frac{1}{x+2} \\ \frac{3 x}{(x+2)(x-2)}-\frac{2}{(x+2)} &=\frac{1}{(x+2)} \end{aligned}\)

Multiply both sides by the least common denominator (LCD), \((x+2)(x−2)\), distributing carefully.

The equation is a contradiction and thus has no solution.

No solution, \(∅\)

Example \(\PageIndex{5}\)

\(\frac{x}{x-4}-\frac{4}{x+5}=\frac{36}{x^{2}+x-20}\)

First, factor the denominators.

\(\frac{x}{(x-4)}-\frac{4}{(x+5)}=\frac{36}{(x-4)(x+5)}\)

Take note that the restrictions are \(x≠4\) and \(x≠−5\). To clear the fractions, multiply by the LCD, \((x−4)(x+5)\).

\(\begin{array}{cc}{x-4=0}&{ \text { or } }&{ x+5=0} \\ {x=4} && {x=-5}\end{array}\)

Both of these values are restrictions of the original equation; hence both are extraneous.

No solution, \(\emptyset\)

Exercise \(\PageIndex{2}\)

\(\emptyset\)

It is important to point out that this technique for clearing algebraic fractions only works for equations. Do not try to clear algebraic fractions when simplifying expressions. As a reminder, we have

\(\begin{array}{cc} {\color{Cerulean}{Expression}}&{\color{Cerulean}{Equation}}\\{\frac{1}{x}+\frac{x}{2 x+1}}&{\frac{1}{x}+\frac{x}{2 x+1}=0} \end{array}\)

Expressions are to be simplified and equations are to be solved. If we multiply the expression by the LCD, \(x(2x+1)\), we obtain another expression that is not equivalent.

\(\begin{array}{c|c}{\color{red}{Incorrect}}&{\color{Cerulean}{Correct}}\\{\frac{1}{x}+\frac{x}{2x+1}}&{\frac{1}{x}+\frac{x}{2x+1}=0}\\{\neq\color{red}{x(2x+1)}\color{black}{\cdot\left(\frac{1}{x}+\frac{x}{2x+1} \right) }}&{\color{Cerulean}{x(2x+1)}\color{black}{\cdot\left(\frac{1}{x}+\frac{x}{2x+1} \right)}\color{black}{=}\color{Cerulean}{x(2x+1)}\color{black}{\cdot 0}}\\{=2x+1+x^{2}\quad\color{red}{x}}&{2x+1+x^{2}=0}\\{}&{x^{2}+2x+1=0\quad\color{Cerulean}{\checkmark}}\end{array}\)

Literal Equations

Literal equations, or formulas, are often rational equations. Hence the techniques described in this section can be used to solve for particular variables. Assume that all variable expressions in the denominator are nonzero.

Example \(\PageIndex{6}\)

Solve for \(x\):

\(x=\frac{x-5}{y}\)

The goal is to isolate x . Assuming that y is nonzero, multiply both sides by y and then add \(5\) to both sides.

\(x=y z+5\)

Example \(\PageIndex{7}\)

Solve for \(c\):

\(\frac{1}{c}=\frac{1}{a}+\frac{1}{b}\)

In this example, the goal is to isolate \(c\). We begin by multiplying both sides by the LCD, \(a⋅b⋅c\), distributing carefully.

\(\begin{aligned} \frac{1}{c} &=\frac{1}{a}+\frac{1}{b} \\ \color{Cerulean}{a b c}\color{black}{ \cdot \frac{1}{c}} &\color{black}{=}\color{Cerulean}{a b c}\color{black}{ \cdot \frac{1}{a}+}\color{Cerulean}{a b c}\color{black}{ \cdot \frac{1}{b}} \\ a b &=b c+a c \end{aligned}\)

On the right side of the equation, factor out \(c\).

\(a b=c(b+a)\)

Next, divide both sides of the equation by the quantity \((b+a)\).

\(\begin{array}{c}{\frac{a b}{\color{Cerulean}{(b+a)}}\color{black}{=\frac{c(b+a)}{\color{Cerulean}{(b+a)}}}} \\ {\frac{a b}{b+a}=c}\end{array}\)

\(c=\frac{a b}{b+a}\)

Exercise \(\PageIndex{3}\)

Solve for \(y\):

\(x=\frac{y+1}{y−1}\)

\(y=\frac{1+x}{x-1}\)

Key Takeaways

• Begin solving rational equations by multiplying both sides by the LCD. The resulting equivalent equation can be solved using the techniques learned up to this point.
• Multiplying both sides of a rational equation by a variable expression introduces the possibility of extraneous solutions. Therefore, we must check the solutions against the set of restrictions. If a solution is a restriction, then it is not part of the domain and is extraneous.
• When multiplying both sides of an equation by an expression, distribute carefully and multiply each term by that expression.
• If all of the resulting solutions are extraneous, then the original equation has no solutions.

Exercise \(\PageIndex{4}\) Rational Equations

• \(\frac{1}{2}+\frac{1}{x}=\frac{1}{8}\)
• \(\frac{1}{3}−\frac{1}{x}=\frac{2}{9}\)
• \(\frac{1}{3x}−\frac{2}{3}=\frac{1}{x}\)
• \(\frac{2}{5x}−\frac{1}{x}=\frac{3}{10}\)
• \(\frac{1}{2 x+1}=5\)
• \(\frac{3}{3x−1}+4=5\)
• \(\frac{2 x-3}{x+5}=\frac{2}{x+5}\)
• \(\frac{5x}{2x−1}=\frac{x−1}{2x−1}\)
• \(\frac{5}{x−7}=\frac{6}{x−9}\)
• \(\frac{5}{x+5}=\frac{3}{x+1}\)
• \(\frac{x}{6}-\frac{6}{x}=0\)
• \(\frac{5x+x}{5}=−2\)
• \(\frac{x}{x+12}=\frac{2}{x}\)
• \(\frac{2x}{x+5}=\frac{1}{6−x}\)
• \(\frac{1}{x}+\frac{x}{2x+1}=0\)
• \(\frac{9x}{3x−1}−\frac{4}{x}=0\)
• \(1−\frac{2}{x}=\frac{48}{x^{2}}\)
• \(2−\frac{9}{x}=\frac{5}{x^{2}}\)
• \(1+\frac{12}{x}=\frac{12}{x-2}\)
• \(1−\frac{3x−5}{x(3x−4)}=−\frac{1}{x}\)
• \(\frac{x}{2}=\frac{14}{x+3}\)
• \(\frac{3x}{2}=\frac{x+1}{3−x}\)
• \(6=\frac{−3x+3}{x−1}\)
• \(\frac{1}{2x−2}=2+\frac{6(4−x)}{x−2}\)
• \(2+\frac{2x}{x−3}=\frac{3(x−1)}{x−3}\)
• \(\frac{x}{x−1}+\frac{1}{6x−1}=\frac{x(x−1)}{(6x−1)}\)
• \(\frac{12}{x^{2}−81}=\frac{1}{x+9}−\frac{2}{x−9}\)
• \(\frac{14}{x^{2}−49}=\frac{2}{x−7}−\frac{3}{x+7}\)
• \(\frac{6x}{x+3}+\frac{4}{x−3}=\frac{3x}{x^{2}−9}\)
• \(\frac{3x}{x+2}−\frac{17}{x−2}=−\frac{48}{x^{2}−4}\)
• \(x^{-1}+3=0\)
• \(4^{−y}−1=0\)
• \(y^{−2}−4=0\)
• \(9 x^{-2}-1=0\)
• \(3(x−1)^{−1}+5=0\)
• \(5−2(3x+1)^{−1}=0\)
• \(3+2x^{−3}=2x^{−3}\)
• \(\frac{1}{x}=\frac{1}{x+1}\)
• \(\frac{x}{x+1}=\frac{x+1}{x}\)
• \(\frac{3x−1}{3x}=\frac{x}{x+3}\)
• \(\frac{4x−7}{x−5}=\frac{3x−2}{x−5}\)
• \(\frac{x}{x^{2}−9}=\frac{1}{x−3}\)
• \(\frac{3x+4}{x−8}−\frac{2}{8−x}=1\)
• \(\frac{1}{x}=\frac{6}{x(x+3)}\)
• \(\frac{3}{x}=\frac{1}{x+1}+\frac{13}{x(x+1)}\)
• \(\frac{x}{x−1}−\frac{3}{4x−1}=\frac{9x}{(4x-1)(x−1)}\)
• \(\frac{1}{x−4}+\frac{x}{x−2}=2x^{2}−6x+8 \)
• \(\frac{x}{x−5}+\frac{x−1}{x^{2}−11x+30}=\frac{5}{x−6}\)
• \(\frac{x}{x+1}−\frac{6}{5x^{2}+4x−1}=−\frac{5}{5x−1}\)
• \(\frac{−8x^{2}−4}{x−12}+\frac{2(x+2)}{x^{2}+4x−60}=\frac{1}{x+2}\)
• \(\frac{x}{x+2}-\frac{20}{x^{2}-6-x}=\frac{-4}{x-3}\)
• \(\frac{x+7}{x−1}+\frac{x−1}{x+1}=\frac{4}{x^{2}−1}\)
• \(\frac{x−1}{x−3}+\frac{x−3}{x−1}=−\frac{x+5}{x−3}\)
• \(\frac{x−2}{x−5}−\frac{x−5}{x−2}=\frac{8−x}{x−5}\)
• \(\frac{x+7}{x−2}−\frac{81}{x^{2}+5x−14}=\frac{9}{x+7}\)
• \(\frac{x}{x−6}+1=\frac{5x+30}{36−x^{2}}\)
• \(\frac{2x}{x+1}−\frac{4}{4x−3}=−\frac{7}{4x^{2}+x−3}\)
• \(\frac{x−5}{x−10}+\frac{5}{x−5}=−\frac{5x}{x^{2}−15x+50}\)
• \(\frac{5}{x^{2}+5 x+4}+\frac{x+1}{x^{2}+3 x-4}=\frac{5}{x^{2}-1}\)
• \(\frac{1}{x^{2}−2x−63}+\frac{x−9x^{2}+10}{x+21}=\frac{1}{x^{2}−6x−27}\)
• \(\frac{4}{x^{2}-4}+\frac{2(x-2)}{x^{2}-4 x-12}=\frac{x+2}{x^{2}-8 x+12}\)
• \(\frac{x+2}{x^{2}−5x+4}+\frac{x+2}{x^{2}+x−2}=\frac{x−1}{x^{2}−2x−8}\)
• \(\frac{6 x}{x-1}-\frac{11 x+1}{2 x^{2}-x-1}=\frac{6 x}{2 x+1}\)
• \(\frac{8x}{2x−3}+\frac{4x^{2}}{x^{2}−7x+6}=\frac{1}{x−2}\)

1. \(−\frac{8}{3}\)

3. \(−1\)

5. \(−\frac{2}{5}\)

7. \(\frac{5}{2}\)

9. \(−3\)

11. \(-6, 6\)

13. \(−4, 6\)

15. \(−1\)

17. \(−6, 8\)

19. \(−4, 6\)

21. \(−7, 4\)

23. \(∅\)

25. \(∅\)

27. \(−39\)

29. \(\frac{4}{3}, \frac{3}{2}\)

31. \(−\frac{1}{3}\)

33. \(−\frac{1}{2}, \frac{1}{2}\)

35. \(\frac{2}{5}\)

37. \(∅\)

39. \(−\frac{1}{2}\)

41. \(∅\)

43. \(−7\)

47. \(−1\)

49. \(∅\)

51. \(−4\)

53. \(\frac{5}{3}\)

55. \(∅\)

57. \(\frac{1}{2}\)

59. \(−6, 4\)

63. \(\frac{1}{3}\)

Exercise \(\PageIndex{5}\) Literal Equations

Solve for the indicated variable.

• Solve for \(r\): \(t=\frac{D}{r}\)
• Solve for \(b\): \(h=\frac{2A}{b}\)
• Solve for \(P\): \(t=\frac{I}{Pr}\)
• Solve for \(π\): \(r=\frac{C}{2π}\)
• Solve for \(c\): \(\frac{1}{a}=\frac{1}{b}+\frac{1}{c}\)
• Solve for \(y\): \(m=\frac{y−y_{1}}{x−x_{1}}\)
• Solve for \(w\): \(P=2(l+w)\)
• Solve for \(t\): \(A=P(1+rt)\)
• Solve for \(m\): \(s=\frac{1}{n+m}\)
• Solve for \(S\): \(h=S2πr−r\)
• Solve for \(x\): \(y=\frac{x}{x+2}\)
• Solve for \(x\): \(y=2x+15x\)
• Solve for \(R\): \(\frac{1}{R}=\frac{1}{R_{1}}+\frac{1}{R_{2}}\)
• Solve for \(S_{1}\): \(\frac{1}{f}=\frac{1}{S_{1}}+\frac{1}{S_{2}}\)

1. \(r=\frac{D}{t}\)

3. \(P=\frac{I}{tr}\)

5. \(c=\frac{ab}{b−a}\)

7. \(w=\frac{P}{2}-l\)

9. \(m=\frac{1}{s}-n\)

11. \(x=-\frac{2y}{y-1}\)

13. \(R=\frac{R_{1}R_{2}}{R_{1}+R_{2}}\)

Exercise \(\PageIndex{6}\) Discussion Board

• Explain why multiplying both sides of an equation by the LCD sometimes produces extraneous solutions.
• Explain the connection between the technique of cross multiplication and multiplying both sides of a rational equation by the LCD.
• Explain how we can tell the difference between a rational expression and a rational equation. How do we treat them differently?

1. Answers may vary

3. Answers may vary

7.4 Solve Rational Equations

Learning objectives.

By the end of this section, you will be able to:

• Solve rational equations
• Use rational functions
• Solve a rational equation for a specific variable

Be Prepared 7.10

Before you get started, take this readiness quiz.

Solve: 1 6 x + 1 2 = 1 3 . 1 6 x + 1 2 = 1 3 . If you missed this problem, review Example 2.9 .

Be Prepared 7.11

Solve: n 2 − 5 n − 36 = 0 . n 2 − 5 n − 36 = 0 . If you missed this problem, review Example 6.45 .

Be Prepared 7.12

Solve the formula 5 x + 2 y = 10 5 x + 2 y = 10 for y . y . If you missed this problem, review Example 2.31 .

After defining the terms ‘expression’ and ‘equation’ earlier, we have used them throughout this book. We have simplified many kinds of expressions and solved many kinds of equations . We have simplified many rational expressions so far in this chapter. Now we will solve a rational equation .

Rational Equation

A rational equation is an equation that contains a rational expression.

You must make sure to know the difference between rational expressions and rational equations. The equation contains an equal sign.

Solve Rational Equations

We have already solved linear equations that contained fractions. We found the LCD of all the fractions in the equation and then multiplied both sides of the equation by the LCD to “clear” the fractions.

We will use the same strategy to solve rational equations. We will multiply both sides of the equation by the LCD. Then, we will have an equation that does not contain rational expressions and thus is much easier for us to solve. But because the original equation may have a variable in a denominator, we must be careful that we don’t end up with a solution that would make a denominator equal to zero.

So before we begin solving a rational equation, we examine it first to find the values that would make any denominators zero. That way, when we solve a rational equation we will know if there are any algebraic solutions we must discard.

An algebraic solution to a rational equation that would cause any of the rational expressions to be undefined is called an extraneous solution to a rational equation .

Extraneous Solution to a Rational Equation

An extraneous solution to a rational equation is an algebraic solution that would cause any of the expressions in the original equation to be undefined.

We note any possible extraneous solutions, c , by writing x ≠ c x ≠ c next to the equation.

Example 7.33

How to solve a rational equation.

Solve: 1 x + 1 3 = 5 6 . 1 x + 1 3 = 5 6 .

Try It 7.65

Solve: 1 y + 2 3 = 1 5 . 1 y + 2 3 = 1 5 .

Try It 7.66

Solve: 2 3 + 1 5 = 1 x . 2 3 + 1 5 = 1 x .

The steps of this method are shown.

Solve equations with rational expressions.

• Step 1. Note any value of the variable that would make any denominator zero.
• Step 2. Find the least common denominator of all denominators in the equation.
• Step 3. Clear the fractions by multiplying both sides of the equation by the LCD.
• Step 4. Solve the resulting equation.
• If any values found in Step 1 are algebraic solutions, discard them.
• Check any remaining solutions in the original equation.

We always start by noting the values that would cause any denominators to be zero.

Example 7.34

How to solve a rational equation using the zero product property.

Solve: 1 − 5 y = − 6 y 2 . 1 − 5 y = − 6 y 2 .

Try It 7.67

Solve: 1 − 2 x = 15 x 2 . 1 − 2 x = 15 x 2 .

Try It 7.68

Solve: 1 − 4 y = 12 y 2 . 1 − 4 y = 12 y 2 .

In the next example, the last denominators is a difference of squares. Remember to factor it first to find the LCD.

Example 7.35

Solve: 2 x + 2 + 4 x − 2 = x − 1 x 2 − 4 . 2 x + 2 + 4 x − 2 = x − 1 x 2 − 4 .

Try It 7.69

Solve: 2 x + 1 + 1 x − 1 = 1 x 2 − 1 . 2 x + 1 + 1 x − 1 = 1 x 2 − 1 .

Try It 7.70

Solve: 5 y + 3 + 2 y − 3 = 5 y 2 − 9 . 5 y + 3 + 2 y − 3 = 5 y 2 − 9 .

In the next example, the first denominator is a trinomial . Remember to factor it first to find the LCD.

Example 7.36

Solve: m + 11 m 2 − 5 m + 4 = 5 m − 4 − 3 m − 1 . m + 11 m 2 − 5 m + 4 = 5 m − 4 − 3 m − 1 .

Try It 7.71

Solve: x + 13 x 2 − 7 x + 10 = 6 x − 5 − 4 x − 2 . x + 13 x 2 − 7 x + 10 = 6 x − 5 − 4 x − 2 .

Try It 7.72

Solve: y − 6 y 2 + 3 y − 4 = 2 y + 4 + 7 y − 1 . y − 6 y 2 + 3 y − 4 = 2 y + 4 + 7 y − 1 .

The equation we solved in the previous example had only one algebraic solution, but it was an extraneous solution. That left us with no solution to the equation. In the next example we get two algebraic solutions. Here one or both could be extraneous solutions.

Example 7.37

Solve: y y + 6 = 72 y 2 − 36 + 4 . y y + 6 = 72 y 2 − 36 + 4 .

Try It 7.73

Solve: x x + 4 = 32 x 2 − 16 + 5 . x x + 4 = 32 x 2 − 16 + 5 .

Try It 7.74

Solve: y y + 8 = 128 y 2 − 64 + 9 . y y + 8 = 128 y 2 − 64 + 9 .

In some cases, all the algebraic solutions are extraneous.

Example 7.38

Solve: x 2 x − 2 − 2 3 x + 3 = 5 x 2 − 2 x + 9 12 x 2 − 12 . x 2 x − 2 − 2 3 x + 3 = 5 x 2 − 2 x + 9 12 x 2 − 12 .

Try It 7.75

Solve: y 5 y − 10 − 5 3 y + 6 = 2 y 2 − 19 y + 54 15 y 2 − 60 . y 5 y − 10 − 5 3 y + 6 = 2 y 2 − 19 y + 54 15 y 2 − 60 .

Try It 7.76

Solve: z 2 z + 8 − 3 4 z − 8 = 3 z 2 − 16 z − 16 8 z 2 + 16 z − 64 . z 2 z + 8 − 3 4 z − 8 = 3 z 2 − 16 z − 16 8 z 2 + 16 z − 64 .

Example 7.39

Solve: 4 3 x 2 − 10 x + 3 + 3 3 x 2 + 2 x − 1 = 2 x 2 − 2 x − 3 . 4 3 x 2 − 10 x + 3 + 3 3 x 2 + 2 x − 1 = 2 x 2 − 2 x − 3 .

Try It 7.77

Solve: 15 x 2 + x − 6 − 3 x − 2 = 2 x + 3 . 15 x 2 + x − 6 − 3 x − 2 = 2 x + 3 .

Try It 7.78

Solve: 5 x 2 + 2 x − 3 − 3 x 2 + x − 2 = 1 x 2 + 5 x + 6 . 5 x 2 + 2 x − 3 − 3 x 2 + x − 2 = 1 x 2 + 5 x + 6 .

Use Rational Functions

Working with functions that are defined by rational expressions often lead to rational equations. Again, we use the same techniques to solve them.

Example 7.40

For rational function, f ( x ) = 2 x − 6 x 2 − 8 x + 15 , f ( x ) = 2 x − 6 x 2 − 8 x + 15 , ⓐ find the domain of the function, ⓑ solve f ( x ) = 1 , f ( x ) = 1 , and ⓒ find the points on the graph at this function value.

ⓐ The domain of a rational function is all real numbers except those that make the rational expression undefined. So to find them, we will set the denominator equal to zero and solve.

However, x = 3 x = 3 is outside the domain of this function, so we discard that root as extraneous.

ⓒ The value of the function is 1 when x = 7 . x = 7 . So the points on the graph of this function when f ( x ) = 1 f ( x ) = 1 is ( 7 , 1 ) ) ( 7 , 1 ) )

Try It 7.79

For rational function, f ( x ) = 8 − x x 2 − 7 x + 12 , f ( x ) = 8 − x x 2 − 7 x + 12 , ⓐ find the domain of the function ⓑ solve f ( x ) = 3 f ( x ) = 3 ⓒ find the points on the graph at this function value.

Try It 7.80

For rational function, f ( x ) = x − 1 x 2 − 6 x + 5 , f ( x ) = x − 1 x 2 − 6 x + 5 , ⓐ find the domain of the function ⓑ solve f ( x ) = 4 f ( x ) = 4 ⓒ find the points on the graph at this function value.

Solve a Rational Equation for a Specific Variable

When we solved linear equations, we learned how to solve a formula for a specific variable. Many formulas used in business, science, economics, and other fields use rational equations to model the relation between two or more variables. We will now see how to solve a rational equation for a specific variable.

When we developed the point-slope formula from our slope formula, we cleared the fractions by multiplying by the LCD.

m = y − y 1 x − x 1 Multiply both sides of the equation by x − x 1 . m ( x − x 1 ) = ( y − y 1 x − x 1 ) ( x − x 1 ) Simplify. m ( x − x 1 ) = y − y 1 Rewrite the equation with the y terms on the left. y − y 1 = m ( x − x 1 ) m = y − y 1 x − x 1 Multiply both sides of the equation by x − x 1 . m ( x − x 1 ) = ( y − y 1 x − x 1 ) ( x − x 1 ) Simplify. m ( x − x 1 ) = y − y 1 Rewrite the equation with the y terms on the left. y − y 1 = m ( x − x 1 )

In the next example, we will use the same technique with the formula for slope that we used to get the point-slope form of an equation of a line through the point ( 2 , 3 ) . ( 2 , 3 ) . We will add one more step to solve for y .

Example 7.41

Solve: m = y − 2 x − 3 m = y − 2 x − 3 for y . y .

Try It 7.81

Solve: m = y − 5 x − 4 m = y − 5 x − 4 for y . y .

Try It 7.82

Solve: m = y − 1 x + 5 m = y − 1 x + 5 for y . y .

Remember to multiply both sides by the LCD in the next example.

Example 7.42

Solve: 1 c + 1 m = 1 1 c + 1 m = 1 for c .

Try It 7.83

Solve: 1 a + 1 b = c 1 a + 1 b = c for a .

Try It 7.84

Solve: 2 x + 1 3 = 1 y 2 x + 1 3 = 1 y for y .

Access this online resource for additional instruction and practice with equations with rational expressions.

• Equations with Rational Expressions

Section 7.4 Exercises

Practice makes perfect.

In the following exercises, solve each rational equation.

1 a + 2 5 = 1 2 1 a + 2 5 = 1 2

6 3 − 2 d = 4 9 6 3 − 2 d = 4 9

4 5 + 1 4 = 2 v 4 5 + 1 4 = 2 v

3 8 + 2 y = 1 4 3 8 + 2 y = 1 4

1 − 2 m = 8 m 2 1 − 2 m = 8 m 2

1 + 4 n = 21 n 2 1 + 4 n = 21 n 2

1 + 9 p = −20 p 2 1 + 9 p = −20 p 2

1 − 7 q = −6 q 2 1 − 7 q = −6 q 2

5 3 v − 2 = 7 4 v 5 3 v − 2 = 7 4 v

8 2 w + 1 = 3 w 8 2 w + 1 = 3 w

3 x + 4 + 7 x − 4 = 8 x 2 − 16 3 x + 4 + 7 x − 4 = 8 x 2 − 16

5 y − 9 + 1 y + 9 = 18 y 2 − 81 5 y − 9 + 1 y + 9 = 18 y 2 − 81

8 z − 10 − 7 z + 10 = 5 z 2 − 100 8 z − 10 − 7 z + 10 = 5 z 2 − 100

9 a + 11 − 6 a − 11 = 6 a 2 − 121 9 a + 11 − 6 a − 11 = 6 a 2 − 121

−10 q − 2 − 7 q + 4 = 1 −10 q − 2 − 7 q + 4 = 1

2 s + 7 − 3 s − 3 = 1 2 s + 7 − 3 s − 3 = 1

v − 10 v 2 − 5 v + 4 = 3 v − 1 − 6 v − 4 v − 10 v 2 − 5 v + 4 = 3 v − 1 − 6 v − 4

w + 8 w 2 − 11 w + 28 = 5 w − 7 + 2 w − 4 w + 8 w 2 − 11 w + 28 = 5 w − 7 + 2 w − 4

x − 10 x 2 + 8 x + 12 = 3 x + 2 + 4 x + 6 x − 10 x 2 + 8 x + 12 = 3 x + 2 + 4 x + 6

y − 5 y 2 − 4 y − 5 = 1 y + 1 + 1 y − 5 y − 5 y 2 − 4 y − 5 = 1 y + 1 + 1 y − 5

b + 3 3 b + b 24 = 1 b b + 3 3 b + b 24 = 1 b

c + 3 12 c + c 36 = 1 4 c c + 3 12 c + c 36 = 1 4 c

d d + 3 = 18 d 2 − 9 + 4 d d + 3 = 18 d 2 − 9 + 4

m m + 5 = 50 m 2 − 25 + 6 m m + 5 = 50 m 2 − 25 + 6

n n + 2 − 3 = 8 n 2 − 4 n n + 2 − 3 = 8 n 2 − 4

p p + 7 − 8 = 98 p 2 − 49 p p + 7 − 8 = 98 p 2 − 49

q 3 q − 9 − 3 4 q + 12 = 7 q 2 + 6 q + 63 24 q 2 − 216 q 3 q − 9 − 3 4 q + 12 = 7 q 2 + 6 q + 63 24 q 2 − 216

r 3 r − 15 − 1 4 r + 20 = 3 r 2 + 17 r + 40 12 r 2 − 300 r 3 r − 15 − 1 4 r + 20 = 3 r 2 + 17 r + 40 12 r 2 − 300

s 2 s + 6 − 2 5 s + 5 = 5 s 2 − 3 s − 7 10 s 2 + 40 s + 30 s 2 s + 6 − 2 5 s + 5 = 5 s 2 − 3 s − 7 10 s 2 + 40 s + 30

t 6 t − 12 − 5 2 t + 10 = t 2 − 23 t + 70 12 t 2 + 36 t − 120 t 6 t − 12 − 5 2 t + 10 = t 2 − 23 t + 70 12 t 2 + 36 t − 120

2 x 2 + 2 x − 8 − 1 x 2 + 9 x + 20 = 4 x 2 + 3 x − 10 2 x 2 + 2 x − 8 − 1 x 2 + 9 x + 20 = 4 x 2 + 3 x − 10

5 x 2 + 4 x + 3 + 2 x 2 + x − 6 = 3 x 2 − x − 2 5 x 2 + 4 x + 3 + 2 x 2 + x − 6 = 3 x 2 − x − 2

3 x 2 − 5 x − 6 + 3 x 2 − 7 x + 6 = 6 x 2 − 1 3 x 2 − 5 x − 6 + 3 x 2 − 7 x + 6 = 6 x 2 − 1

2 x 2 + 2 x − 3 + 3 x 2 + 4 x + 3 = 6 x 2 − 1 2 x 2 + 2 x − 3 + 3 x 2 + 4 x + 3 = 6 x 2 − 1

Solve Rational Equations that Involve Functions

For rational function, f ( x ) = x − 2 x 2 + 6 x + 8 , f ( x ) = x − 2 x 2 + 6 x + 8 , ⓐ find the domain of the function ⓑ solve f ( x ) = 5 f ( x ) = 5 ⓒ find the points on the graph at this function value.

For rational function, f ( x ) = x + 1 x 2 − 2 x − 3 , f ( x ) = x + 1 x 2 − 2 x − 3 , ⓐ find the domain of the function ⓑ solve f ( x ) = 1 f ( x ) = 1 ⓒ find the points on the graph at this function value.

For rational function, f ( x ) = 2 − x x 2 − 7 x + 10 , f ( x ) = 2 − x x 2 − 7 x + 10 , ⓐ find the domain of the function ⓑ solve f ( x ) = 2 f ( x ) = 2 ⓒ find the points on the graph at this function value.

For rational function, f ( x ) = 5 − x x 2 + 5 x + 6 , f ( x ) = 5 − x x 2 + 5 x + 6 , ⓐ find the domain of the function ⓑ solve f ( x ) = 3 f ( x ) = 3 ⓒ the points on the graph at this function value.

In the following exercises, solve.

C r = 2 π C r = 2 π for r . r .

I r = P I r = P for r . r .

v + 3 w − 1 = 1 2 v + 3 w − 1 = 1 2 for w . w .

x + 5 2 − y = 4 3 x + 5 2 − y = 4 3 for y . y .

a = b + 3 c − 2 a = b + 3 c − 2 for c . c .

m = n 2 − n m = n 2 − n for n . n .

1 p + 2 q = 4 1 p + 2 q = 4 for p . p .

3 s + 1 t = 2 3 s + 1 t = 2 for s . s .

2 v + 1 5 = 3 w 2 v + 1 5 = 3 w for w . w .

6 x + 2 3 = 1 y 6 x + 2 3 = 1 y for y . y .

m + 3 n − 2 = 4 5 m + 3 n − 2 = 4 5 for n . n .

r = s 3 − t r = s 3 − t for t . t .

E c = m 2 E c = m 2 for c . c .

R T = W R T = W for T . T .

3 x − 5 y = 1 4 3 x − 5 y = 1 4 for y . y .

c = 2 a + b 5 c = 2 a + b 5 for a . a .

Writing Exercises

Your class mate is having trouble in this section. Write down the steps you would use to explain how to solve a rational equation.

Alek thinks the equation y y + 6 = 72 y 2 − 36 + 4 y y + 6 = 72 y 2 − 36 + 4 has two solutions, y = −6 y = −6 and y = 4 . y = 4 . Explain why Alek is wrong.

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ On a scale of 1 − 10 , 1 − 10 , how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction

• Authors: Lynn Marecek, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Intermediate Algebra 2e
• Publication date: May 6, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/intermediate-algebra-2e/pages/7-4-solve-rational-equations

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Solving Rational Equations · Examples

Listen up, fraction fans! In today’s lesson, you will learn and practice solving rational equations. As you will see, these are any equation involving a fraction, also known as a rational number in math talk!

By the end, you will know the difference between rational and irrational numbers and have two tricks for solving rational equations.

You could even tackle one of the tricky challenges to form a rational equation using the Pythagorean theorem , or to simplify an expression involving some radicals!

What is a Rational Equation? How to Solve Rational Equations Step 1: Eliminate the Denominators Step 2: Simplify the Equation Step 3: Solve the Equation Step 4: Check Solutions Practice & Challenges Question 1 Question 2 Challenge 1 Challenge 2 Worksheet To Sum Up (Pun Intended!)

What is a Rational Equation?

A rational equation is simply an equation involving a rational number.

A ratio -nal number can be written as a ratio of two integers – an irratio -nal number cannot.

Most of the numbers you know and love such as \(\Large\frac{2}{7}\), \(\Large\frac{1}{2}\) and \(-\Large\frac{20817}{43}\) are rational. Some common irrational numbers are π, \(\sqrt{2}\) and Euler’s number, e. These cannot be written as a fraction of integers.

Numberphile has an interesting video about All the Numbers , which categorizes number types, including rational and irrational numbers .

Technically speaking, basic equations like x+2=5 are rational because each term is a rational number. However, the rational equations you will solve today won’t be so easy!

An example of what you will more likely see in an exam is something like this:

Each term is shown as a fraction.

Rational equations can also include radicals:

Or other operations such as division:

Luckily, the technique you learn now will work for every type of rational equation!

How to Solve Rational Equations

The method to solve these equations is pretty much the same for every type of rational equation. You’ll see questions of varying difficulty in this lesson; don’t be afraid to tackle the challenges later on!

Step 1: The Denominator Elimination Round!

First, you need to deal with the elephant in the room: what should you do with the denominators!?

Solving rational equations is just like solving any other equation once you complete this step.

If it’s a simple case, where you have one fraction being equal to one other fraction, you can cross multiply .

Multiply both sides by the values of both denominators. In this example, both sides are multiplied by 3, then 5.

The 3 cancels with the left denominator and the 5 cancels with the right denominator, leaving you with 5(x+4)=3×2.

See why it’s called cross multiplying?

The product of the left denominator and right numerator equals the product of the right denominator and left numerator !

The more general way to deal with the denominators is to find their lowest common multiple (LCM) . This is the smallest number which all denominators divide neatly, leaving no remainder.

If you cannot find the LCM by inspection – if you cannot “just see it” – you need to factor every denominator like you would with a polynomial.

If you have more than one constant term, you may need to find their prime factors.

The LCM is the smallest combination of each denominator’s factors.

You’ll now see a worked example to illustrate!

Remember, you can only cross multiply when each side has only one fraction, so in this case, your first step is to find the LCM.

The only factors of 3x you know for certain are 3 and x. The only factor you know of x is just x, and 4 is a constant so you can use it as it is.

Write down each denominator’s polynomial factors into rows, with similar terms lined up in the same column.

You need to include both 3 and 4 because neither is a factor of the other. You don’t need both copies of x because x is a factor of itself! So the LCM is 12x.

You might find another example of finding the LCM with the same technique helpful.

You’re now ready to eliminate the denominators by multiplying both sides by the LCM.

Step 2: Simplify the Equation

Multiply each term by the LCM. Continuing from the last example, you have:

You now have a regular equation with no fractions, which should be familiar ground!

Step 3: Solve the Equation

Solving rational equations usually produces a simple polynomial equation. Hopefully, you’ve solved lots of these before!

You could complete the square, factor the terms by inspection, or use the quadratic formula.

This example can be solved by factoring the polynomial, having found that x+2 and x+4 are factors.

You could also solve the equation by completing the square:

Or by using the quadratic formula with a=1, b=6 and c=8:

Each way of solving the simplified rational equation is valid, but you will find that some are quicker than others!

Step 4: Check Every Solution

It is important to check that your solutions are complete, meaning you’ve found all of them and that they don’t give any weird numbers when substituted into the original equation.

In the worked example, you were left with a quadratic equation and found two distinct roots.

Quadratic equations either have two distinct solutions, one repeated solution, or no real solution so the solution x=-2 or x=-4 is complete.

You must be careful that none of the rational terms in the original equation have a zero in the denominator.

Do this by going back to the beginning and substituting your answers into the denominators!

The denominators in the worked example are 3x, x, and 4. Replacing x with -2 or -4 doesn’t give you zero in any of them, so you’re safe here!

A solution that gives a zero-denominator is not allowed. That’s because dividing by zero is “illegal” in math!

Any number divided by zero gives an error on a calculator. Ever wondered why that is?

This is your time to shine – try solving rational equations for yourself and, if you’re feeling confident, tackle the challenges too.

As they say, practice makes perfect! Use the worked example for guidance if you get stuck.

Find x in the following rational equation:

The equation is two equal fractions so you can cross-multiply. You could also simplify \(\Large\frac{15}{3}\normalsize\) to 5, but this does not change the final answer.

Each term is divisible by 9. Simplify the equation by dividing both sides by 9:

This form is called the difference of two squares because it can be factored like this:

So the solution is x=±3.

These must be all the solutions because quadratic equations have a maximum of two distinct real roots.

Neither denominator in the original rational equation has an x term, so substituting any value for x makes no difference to their values – there is no chance of them being zero!

This means the solutions x=3 and x=-3 are valid.

Solve the following rational equation:

There are three fractions so you cannot cross-multiply.

See that the second denominator is the difference of two squares?

Multiply each term by the LCM and simplify.

So its solution is -5, right?… STOP RIGHT THERE! Don’t forget, we can’t divide by zero!

If you put x=±5 into the original equation, at least one of the denominators is always zero, so the original equation has no solutions.

Challenge 1

Can you spot the mistake in the following example? Hint: there has been some cheating with radicals!

If you need a refresher on radicals , check out our lesson on multiplying them. That will get you on the right track!

The mistake is that radicals cannot be subtracted like normal terms.

Instead, you must square both sides of the equation to remove the radical. Similar terms can then be combined as usual.

Still confused? You can find lots of interactive questions on Lumen Learning . Radicals often pop up in rational equations, so getting comfortable with radicals is super helpful for exam success!

Challenge 2

Find the value of x, by using the Pythagorean theorem on the following right-angled triangle:

If you need a refresher on the Pythagorean theorem or are interested in the man himself, check out our lesson. Do the worksheets and you’ll be acing triangle questions in no time !

The Pythagorean theorem states that:

Where c is the length of the hypotenuse, and a and b are the other side lengths.

This gives the rational equation:

Simplifying, you find:

The LCM is 36 so the denominators are removed by dividing each term by this:

It’s always fun when different areas of math link together!

To Sum Up (Pun Intended!)

In today’s lesson on solving rational equations, you first saw the difference between rational and irrational numbers.

Rational numbers are “nice” because they can be written as a fraction of integers. Remember that all integers are rational because they can be written with a denominator of 1!

Irrational numbers are a little more abstract. They include weird but incredibly beautiful numbers like π and e, which cannot be written as a fraction of integers.

Rational equations are solved by eliminating the denominator in every term, then simplifying and solving as normal.

Denominators can be removed by cross-multiplication if there is only one fraction on either side or by finding the LCM if the equation is more complicated.

Don’t be shy, leave a comment below if you have any questions or need help!

Still curious about rational numbers, or eager for an extra challenge? Check out our lesson on the rational root theorem , which combines algebra and equation solving.

Number Line

• \frac{5}{x-7}=\frac{2}{x-2}
• \frac{7x+5}{x-4}-\frac{6x-1}{x-3}-\frac{1}{x^{2}-7x+12}=1
• \frac{7}{x-3}-\frac{10}{x-2}-\frac{6}{x-1}=0
• \frac{x-3}{3-x}=2

rational-equation-calculator

• High School Math Solutions – Exponential Equation Calculator Solving exponential equations is pretty straightforward; there are basically two techniques: <ul> If the exponents...

Please add a message.

Message received. Thanks for the feedback.

Rational Equations Word Problems Lesson

• Demonstrate an understanding of how to solve a word problem
• Demonstrate an understanding of how to solve an equation with rational expressions
• Learn how to solve word problems that involve rational equations

How to Solve a Word Problem with Rational Equations

Six-step method for solving word problems with rational expressions.

• Read the problem carefully and determine what you are asked to find
• Assign a variable to represent the unknown
• Write out an equation that describes the given situation
• Solve the equation
• State the answer using a nice clear sentence
• Check the result by reading back through the problem

Solving a Proportion Problem

Motion word problems with rational expressions, rate of work word problems, skills check:.

Solve each word problem.

Working alone, it takes Steve 11 hours to complete a restoration project on a truck. Jacob can perform the same task in 110 hours. How long would it take if they worked together?

Please choose the best answer.

Jamie’s hot tub has an outlet pipe that can empty the hot tub in 6 minutes. Additionally, her hot tub has an inlet pipe that can fill the hot tub in 3 minutes. If both pipes were turned on, how long would it take to fill a completely empty hot tub?

On her drive from Port Smith to Maryland, Stephanie averaged 51 miles per hour. If she had been able to average 60 miles per hour, she would have reached Maryland 3 hours earlier. What is the driving distance between Port Smith and Maryland?

Congrats, Your Score is 100 %

Better Luck Next Time, Your Score is %

Ready for more? Watch the Step by Step Video Lesson   |   Take the Practice Test

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Precalculus

Course: precalculus   >   unit 4.

• Analyzing structure word problem: pet store (1 of 2)
• Analyzing structure word problem: pet store (2 of 2)
• Combining mixtures example
• Rational equations word problem: combined rates

Rational equations word problem: combined rates (example 2)

• Mixtures and combined rates word problems
• Rational equations word problem: eliminating solutions
• Reasoning about unknown variables
• Reasoning about unknown variables: divisibility
• Structure in rational expression

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

Module 5: Polynomial and Rational Functions

Applications of rational equations, learning objectives.

• Define and write a proportion
• Solve proportional problems involving scale drawings
• Solve a rational formula for a specified variable
• Solve work problems
• Solve motion problem
• Define and solve an equation that represents the concentration of a mixture

Matryoshka, or nesting dolls.

A proportion is a statement that two ratios are equal to each other.  There are many things that can be represented with ratios, including the actual distance on the earth that is represented on a map.  In fact, you probably use proportional reasoning on a regular basis and don’t realize it.  For example, say you have volunteered to provide drinks for a community event.  You are asked to bring enough drinks for 35-40 people.  At the store  you see that drinks come in packages of 12. You multiply 12 by 3 and get 36 – this may not be enough if 40 people show up, so you decide to buy 4 packages of drinks just to be sure.

This process can also be expressed as a proportional equation and solved using mathematical principles. First, we can express the number of drinks in a package as a ratio:

[latex]\frac{12\text{ drinks }}{1\text{ package }}[/latex]

Then we express the number of people who we are buying drinks for as a ratio with the unknown number of packages we need. We will use the maximum so we have enough.

[latex]\frac{40\text{ people }}{x\text{ packages }}[/latex]

We can find out how many packages to purchase by setting the expressions equal to each other:

[latex]\frac{12\text{ drinks }}{1\text{ package }}=\frac{40\text{ people }}{x\text{ packages }}[/latex]

To solve for x, we can use techniques for solving linear equations, or we can cross multiply as a shortcut.

[latex]\begin{array}{l}\,\,\,\,\,\,\,\frac{12\text{ drinks }}{1\text{ package }}=\frac{40\text{ people }}{x\text{ packages }}\\\text{}\\x\cdot\frac{12\text{ drinks }}{1\text{ package }}=\frac{40\text{ people }}{x\text{ packages }}\cdot{x}\\\text{}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,12x=40\\\text{}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x=\frac{40}{12}=\frac{10}{3}=3.33\end{array}[/latex]

We can round up  to 4 since it doesn’t make sense to by 0.33 of a package of drinks.  Of course, you don’t write out your thinking this way when you are in the grocery store, but doing so helps you to be able to apply the concepts to less obvious problems.  In the following example we will show how to use a proportion to find the number of people on the planet who don’t have access to a toilet. Because, why not?

As of March, 2016 the world’s population was estimated at 7.4 billion.  [1] .  According to water.org , 1 out of every 3 people on the planet lives without access to a toilet.  Find the number of people on the planet that do not have access to a toilet.

We can use a proportion to find the unknown number of people who live without a toilet since we are given that 1 in 3 don’t have access, and we are given the population of the planet.

We know that 1 out of every 3 people don’t have access, so we can write that as a ratio (fraction)

[latex]\frac{1}{3}[/latex].

Let the number of people without access to a toilet be x. The ratio of people with and without toilets is then

[latex]\frac{x}{7.4\text{ billion }}[/latex]

Equate the two ratios since they are representing the same fractional amount of the population.

[latex]\frac{1}{3}=\frac{x}{7.4\text{ billion }}[/latex]

[latex]\begin{array}{l}\frac{1}{3}=\frac{x}{7.4}\\\text{}\\7.4\cdot\frac{1}{3}=\frac{x}{7.4}\cdot{7.4}\\\text{}\\2.46=x\end{array}[/latex]

The original units were billions of people, so our answer is [latex]2.46[/latex] billion people don’t have access to a toilet.  Wow, that’s a lot of people.

2.46 billion people don’t have access to a toilet.

In the next example, we will use the length of a person’t femur to estimate their height.  This process is used in forensic science and anthropology, and has been found in many scientific studies to be a very good estimate.

It has been shown that a person’s height is proportional to the length of their femur  [2] . Given that a person who is 71 inches tall has a femur length of 17.75 inches, how tall is someone with a femur length of 16 inches?

Height and femur length are proportional for everyone, so we can define a ratio with the given height and femur length.  We can then use this to write a proportion to find the unknown height.

Let x be the unknown height.  Define the ratio of femur length and height for both people using the given measurements.

Person 1:  [latex]\frac{\text{femur length}}{\text{height}}=\frac{17.75\text{inches}}{71\text{inches}}[/latex]

Person 2:  [latex]\frac{\text{femur length}}{\text{height}}=\frac{16\text{inches}}{x\text{inches}}[/latex]

Equate the ratios, since we are assuming height and femur length are proportional for everyone.

[latex]\frac{17.75\text{inches}}{71\text{inches}}=\frac{16\text{inches}}{x\text{inches}}[/latex]

 Solve by using the common denominator to clear fractions.  The common denominator is [latex]71x[/latex]

[latex]\begin{array}{c}\frac{17.75}{71}=\frac{16}{x}\\\\71x\cdot\frac{17.75}{71}=\frac{16}{x}\cdot{71x}\\\\17.75\cdot{x}=16\cdot{71}\\\\x=\frac{16\cdot{71}}{17.75}=64\end{array}[/latex]

The unknown height of person 2 is 64 inches. In general, we can reduce the fraction [latex]\frac{17.75}{71}=0.25=\frac{1}{4}[/latex] to find a general rule for everyone.  This would translate to sayinga person’s height is 4 times the length of their femur.

Another way to describe the ratio of femur length to height that we found in the last example is to say there’s a 1:4 ratio between femur length and height, or 1 to 4.

Ratios are also used in scale drawings. Scale drawings are enlarged or reduced drawings of objects, buildings, roads, and maps. Maps are smaller than what they represent and a drawing of dendritic cells in your brain is most likely larger than what it represents. The scale of the drawing is a ratio that represents a comparison of the length of the actual object and it’s representation in the drawing. The image below shows a map of the us with a scale of 1 inch representing 557 miles. We could write the scale factor as a fraction [latex]\frac{1}{557}[/latex] or as we did with the femur-height relationship, 1:557.

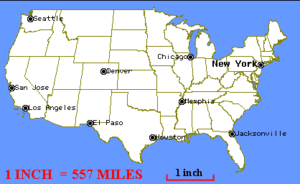
Map with scale factor

In the next example we will use the scale factor given in the image above to find the distance between Seattle Washington and San Jose California.

Given a scale factor of 1:557 on a map of the US, if the distance from Seattle, WA to San Jose, CA is 1.5 inches on the map,  define a proportion to find the actual distance between them.

We need to define a proportion to solve for the unknown distance between Seattle and San Jose.

 T he scale factor is 1:557, and we will call the unknown distance x. The ratio of inches to miles is [latex]\frac{1}{557}[/latex].

We know inches between the two cities, but we don’t know miles, so the ratio that describes the distance between them is [latex]\frac{1.5}{x}[/latex].

The proportion that will help us solve this problem is [latex]\frac{1}{557}=\frac{1.5}{x}[/latex].

Solve using the common denominator [latex]557x[/latex] to clear fractions.

[latex]\begin{array}{ccc}\frac{1}{557}=\frac{1.5}{x}\\557x\cdot\frac{1}{557}=\frac{1.5}{x}\cdot{557x}\\x=1.5\cdot{557}=835.5\end{array}[/latex]

We used the scale factor 1:557 to find an unknown distance between Seattle and San Jose. We also checked our answer of 835.5 miles with Google maps, and found that the distance is 839.9 miles, so we did pretty well!

In the next example, we will find a scale factor given the length between two cities on a map, and their actual distance from each other.

Two cities are 2.5 inches apart on a map.  Their actual distance from each other is 325 miles.  Write a proportion to represent and solve for the scale factor for one inch of the map.

We know that for each 2.5 inches on the map, it represents 325 actual miles. We are looking for the scale factor for one inch of the map.

The ratio we want is [latex]\frac{1}{x}[/latex] where x is the actual distance represented by one inch on the map.  We know that for every 2.5 inches, there are 325 actual miles, so we can define that relationship as [latex]\frac{2.5}{325}[/latex]

We can use a proportion to equate the two ratios and solve for the unknown distance.

[latex]\begin{array}{ccc}\frac{1}{x}=\frac{2.5}{325}\\325x\cdot\frac{1}{x}=\frac{2.5}{325}\cdot{325x}\\325=2.5x\\x=130\end{array}[/latex]

The scale factor for one inch on the map is 1:130, or for every inch of map there are 130 actual miles.

In the video that follows, we present an example of using proportions to obtain the correct amount of medication for a patient, as well as finding a desired mixture of coffees.

Rational formulas

Rational formulas can be useful tools for representing real-life situations and for finding answers to real problems. Equations representing direct, inverse, and joint variation are examples of rational formulas that can model many real-life situations. As you will see, if you can find a formula, you can usually make sense of a situation.

When solving problems using rational formulas, it is often helpful to first solve the formula for the specified variable. For example, work problems ask you to calculate how long it will take different people working at different speeds to finish a task. The algebraic models of such situations often involve rational equations derived from the work formula, [latex]W=rt[/latex]. The amount of work done ( W ) is the product of the rate of work ( r ) and the time spent working ( t ). Using algebra, you can write the work formula 3 ways:

[latex]W=rt[/latex]

Find the time (t): [latex] t=\frac{W}{r}[/latex] (divide both sides by r)

Find the rate (r): [latex] r=\frac{W}{t}[/latex] (divide both sides by t)

The formula for finding the density of an object is [latex] D=\frac{m}{v}[/latex], where D is the density, m is the mass of the object and v is the volume of the object. Rearrange the formula to solve for the mass ( m ) and then for the volume ( v ).

[latex] D=\frac{m}{v}[/latex]

Multiply both side of the equation by v to isolate m.

[latex] v\cdot D=\frac{m}{v}\cdot v[/latex]

Simplify and rewrite the equation, solving for m .

[latex]\begin{array}{l}v\cdot D=m\cdot \frac{v}{v}\\v\cdot D=m\cdot 1\\v\cdot D=m\end{array}[/latex]

To solve the equation [latex] D=\frac{m}{v}[/latex] in terms of v , you will need do the same steps to this point, and then divide both sides by D .

[latex]\begin{array}{r}\frac{v\cdot D}{D}=\frac{m}{D}\\\\\frac{D}{D}\cdot v=\frac{m}{D}\\\\1\cdot v=\frac{m}{D}\\\\v=\frac{m}{D}\end{array}[/latex]

[latex] m=D\cdot v[/latex] and [latex] v=\frac{m}{D}[/latex]

Now let’s look at an example using the formula for the volume of a cylinder.

The formula for finding the volume of a cylinder is [latex]V=\pi{r^{2}}h[/latex], where V is the volume, r is the radius and h is the height of the cylinder. Rearrange the formula to solve for the height ( h ).

[latex] V=\pi{{r}^{2}}h[/latex]

Divide both sides by [latex] \pi {{r}^{2}}[/latex] to isolate h.

[latex] \frac{V}{\pi {{r}^{2}}}=\frac{\pi {{r}^{2}}h}{\pi {{r}^{2}}}[/latex]

Simplify. You find the height, h , is equal to [latex] \frac{V}{\pi {{r}^{2}}}[/latex].

[latex] \frac{V}{\pi {{r}^{2}}}=h[/latex]

[latex] h=\frac{V}{\pi {{r}^{2}}}[/latex]

In the following video we give another example of solving for a variable in a formula, or as they are also called, a literal equation.

Rational equations can be used to solve a variety of problems that involve rates, times and work. Using rational expressions and equations can help you answer questions about how to combine workers or machines to complete a job on schedule.

A Good Day’s Work

A “work problem” is an example of a real life situation that can be modeled and solved using a rational equation. Work problems often ask you to calculate how long it will take different people working at different speeds to finish a task. The algebraic models of such situations often involve rational equations derived from the work formula, [latex]W=rt[/latex]. (Notice that the work formula is very similar to the relationship between distance, rate, and time, or [latex]d=rt[/latex].) The amount of work done ( W ) is the product of the rate of work ( r ) and the time spent working ( t ). The work formula has 3 versions.

[latex]\begin{array}{l}W=rt\\\\\,\,\,\,\,t=\frac{W}{r}\\\\\,\,\,\,\,r=\frac{W}{t}\end{array}[/latex]

Some work problems include multiple machines or people working on a project together for the same amount of time but at different rates. In that case, you can add their individual work rates together to get a total work rate. Let’s look at an example.

Myra takes 2 hours to plant 50 flower bulbs. Francis takes 3 hours to plant 45 flower bulbs. Working together, how long should it take them to plant 150 bulbs?

Myra: [latex] \frac{50\,\,\text{bulbs}}{2\,\,\text{hours}}[/latex], or [latex] \frac{25\,\,\text{bulbs}}{1\,\,\text{hour}}[/latex]

Francis: [latex] \frac{45\,\,\text{bulbs}}{3\,\,\text{hours}}[/latex], or [latex] \frac{15\,\,\text{bulbs}}{1\,\,\text{hour}}[/latex]

Combine their hourly rates to determine the rate they work together.

Myra and Francis together:

[latex] \frac{25\,\,\text{bulbs}}{1\,\,\text{hour}}+\frac{15\,\,\text{bulbs}}{1\,\,\text{hour}}=\frac{40\,\,\text{bulbs}}{1\,\,\text{hour}}[/latex]

Use one of the work formulas to write a rational equation, for example [latex] r=\frac{W}{t}[/latex]. You know r , the combined work rate, and you know W , the amount of work that must be done. What you don’t know is how much time it will take to do the required work at the designated rate.

[latex] \frac{40}{1}=\frac{150}{t}[/latex]

Solve the equation by multiplying both sides by the common denominator, then isolating t .

[latex]\begin{array}{c}\frac{40}{1}\cdot 1t=\frac{150}{t}\cdot 1t\\\\40t=150\\\\t=\frac{150}{40}=\frac{15}{4}\\\\t=3\frac{3}{4}\text{hours}\end{array}[/latex]

It should take 3 hours 45 minutes for Myra and Francis to plant 150 bulbs together.

Other work problems go the other way. You can calculate how long it will take one person to do a job alone when you know how long it takes people working together to complete the job.

Joe and John are planning to paint a house together. John thinks that if he worked alone, it would take him 3 times as long as it would take Joe to paint the entire house. Working together, they can complete the job in 24 hours. How long would it take each of them, working alone, to complete the job?

Let x = time it takes Joe to complete the job

3 x = time it takes John to complete the job

The work is painting 1 house or 1. Write an expression to represent each person’s rate using the formula [latex] r=\frac{W}{t}[/latex] .

Joe’s rate: [latex] \frac{1}{x}[/latex]

John’s rate: [latex] \frac{1}{3x}[/latex]

Their combined rate is the sum of their individual rates. Use this rate to write a new equation using the formula [latex]W=rt[/latex].

combined rate: [latex] \frac{1}{x}+\frac{1}{3x}[/latex]

The problem states that it takes them 24 hours together to paint a house, so if you multiply their combined hourly rate [latex] \left( \frac{1}{x}+\frac{1}{3x} \right)[/latex] by 24, you will get 1, which is the number of houses they can paint in 24 hours.

[latex] \begin{array}{l}1=\left( \frac{1}{x}+\frac{1}{3x} \right)24\\\\1=\frac{24}{x}+\frac{24}{3x}\end{array}[/latex]

Now solve the equation for x . (Remember that x represents the number of hours it will take Joe to finish the job.)

[latex]\begin{array}{l}\,\,\,1=\frac{3}{3}\cdot \frac{24}{x}+\frac{24}{3x}\\\\\,\,\,1=\frac{3\cdot 24}{3x}+\frac{24}{3x}\\\\\,\,\,1=\frac{72}{3x}+\frac{24}{3x}\\\\\,\,\,1=\frac{72+24}{3x}\\\\\,\,\,1=\frac{96}{3x}\\\\3x=96\\\\\,\,\,x=32\end{array}[/latex]

Check the solutions in the original equation.

[latex]\begin{array}{l}1=\left( \frac{1}{x}+\frac{1}{3x} \right)24\\\\1=\left[ \frac{\text{1}}{\text{32}}+\frac{1}{3\text{(32})} \right]24\\\\1=\frac{24}{\text{32}}+\frac{24}{3\text{(32})}\\\\1=\frac{24}{\text{32}}+\frac{24}{96}\\\\1=\frac{3}{3}\cdot \frac{24}{\text{32}}+\frac{24}{96}\\\\1=\frac{72}{96}+\frac{24}{96}[\end{array}[/latex]

The solution checks. Since [latex]x=32[/latex], it takes Joe 32 hours to paint the house by himself. John’s time is 3 x , so it would take him 96 hours to do the same amount of work.

It takes 32 hours for Joe to paint the house by himself and 96 hours for John the paint the house himself.

In the video that follows, we show another example of finding one person’s work rate given a combined work rate.

As shown above, many work problems can be represented by the equation [latex] \frac{t}{a}+\frac{t}{b}=1[/latex], where t is the time to do the job together, a is the time it takes person A to do the job, and b is the time it takes person B to do the job. The 1 refers to the total work done—in this case, the work was to paint 1 house.

The key idea here is to figure out each worker’s individual rate of work. Then, once those rates are identified, add them together, multiply by the time t , set it equal to the amount of work done, and solve the rational equation.

We present another example of two people painting at different rates in the following video.

We have solved uniform motion problems using the formula [latex]D = rt[/latex] in previous chapters. We used a table like the one below to organize the information and lead us to the equation.

[latex]\begin{array}{|c|c|c|c|} \hline & \,\text{rate}\,&\,\text{time}\,&\,\text{distance}\\ \hline \,\text{First}\,&\,&\,&\\ \hline \,\text{Second}\,&\,&\,&\\ \hline \end{array} [/latex]

The formula [latex]D=rt[/latex] assumes we know [latex]r[/latex] and  [latex]t[/latex] and use them to find  [latex]D[/latex]. If we know  [latex]D[/latex] and [latex]r[/latex] and need to find  [latex]t[/latex], we would solve the equation for  [latex]t[/latex] and get the formula [latex]\displaystyle t=\frac{D}{r}[/latex].

Greg went to a conference in a city 120 miles away. On the way back, due to road construction he had to drive 10 mph slower which resulted in the return trip taking 2 hours longer. How fast did he drive on the way to the conference?

[latex]\begin{eqnarray*} \begin{array}{|c|c|c|c|} \hline & \,\text{rate}\,& \,\text{time}\,& \,\text{distance}\\ \hline \,\text{There}\,& r & t & 120\\ \hline \,\text{Back}\,& & & \\ \hline \end{array}\,& & \begin{array}{l} \,\text{We}\,\,\text{do}\,\,\text{not}\,\,\text{know}\,\,\text{rate}, r, \,\text{or} \,\text{time}, t \,\text{he}\,\,\text{traveled}\\ \,\text{on}\,\,\text{the}\,\,\text{way}\,\,\text{to}\,\,\text{the}\,\,\text{conference}\,. \,\text{But}\,\,\text{we}\,\,\text{do}\,\,\text{know}\\ \,\text{the}\,\,\text{distance}\,\,\text{was}\,120 \,\text{miles}\,. \end{array}\\ & & \\ \begin{array}{|c|c|c|c|} \hline & \,\text{rate}\,& \,\text{time}\,& \,\text{distance}\\ \hline \,\text{There}\,& r & t & 120\\ \hline \,\text{Back}\,& r - 10 & t + 2 & 120\\ \hline \end{array}& & \begin{array}{l} \,\text{Coming}\,\,\text{back}\,\,\text{he}\,\,\text{drove}\,10 \,\text{mph} \,\text{slower}\,(r - 10)\\ \,\text{and}\,\,\text{took}\,2 \,\text{hours}\,\,\text{longer}\,(t + 2) . \,\text{The} \,\text{distance}\\ \,\text{was}\,\,\text{still}\,120 \,\text{miles}\,. \end{array}\\ & & \\ r t = 120 & & \,\text{Equations}\,\,\text{are}\,\,\text{product}\,\,\text{of} \,\text{rate}\,\,\text{and}\,\,\text{time}\\ (r - 10) (t + 2) = 120 & & \,\text{We}\,\,\text{have}\,\,\text{simultaneous} \,\text{product}\,\,\text{equations}\\ & & \\ t = \frac{120}{r}\,\,\text{and}\,t + 2 = \frac{120}{r - 10} & & \,\text{Solving}\,\,\text{for}\,\,\text{rate}, \,\text{divide}\,\,\text{by}\,r \,\text{and}\,r - 10\\ & & \\ \frac{120}{r}\,+ 2 = \frac{120}{r - 10}& & \,\text{Substitute} \frac{120}{r} \,\text{for}\,t \,\text{in}\,\,\text{the}\,\,\text{second} \,\text{equation}\\ & & \\ \frac{120 r (r - 10)}{r} + 2 r (r - 10) = \frac{120 r (r - 10)}{r - 10} & & \,\text{Multiply}\,\,\text{each}\,\,\text{term}\,\,\text{by}\,\,\text{LCD}\,: r (r - 10)\\ & & \\ 120 (r - 10) + 2 r^2 - 20 r = 120 r & & \,\text{Reduce}\,\,\text{each} \,\text{fraction}\\ 120 r - 1200 + 2 r^2 - 20 r = 120 r & & \,\text{Distribute}\\ 2 r^2 + 100 r - 1200 = 120 r & & \,\text{Combine}\,\,\text{like} \,\text{terms}\\ \underline{- 120 r - 120 r} & & \,\text{Make}\,\,\text{equation}\,\,\text{equal} \,\text{to}\,\,\text{zero}\\ 2 r^2 - 20 r - 1200 = 0 & & \,\text{Divide}\,\,\text{each}\,\,\text{term} \,\text{by}\,2\\ r^2 - 10 r - 600 = 0 & & \,\text{Factor}\\ (r - 30) (r + 20) = 0 & & \,\text{Set}\,\,\text{each}\,\,\text{factor} \,\text{equal}\,\,\text{to}\,\,\text{zero}\\ r - 30 = 0 \,\text{and}\,r + 20 = 0 & & \,\text{Solve}\,\,\text{each} \,\text{equation}\\ \underline{+ 30 + 30} \underline{- 20 - 20} & & \\ r = 30 \,\text{and}\,r = - 20 & & \,\text{Can}' t \,\text{have}\,a \,\text{negative}\,\,\text{rate}\\ 30 \,\text{mph}\,& & \,\text{Our}\,\,\text{Solution} \end{eqnarray*}[/latex]

A man rows down stream for 30 miles then turns around and returns to his original location, the total trip took 8 hours. If the current flows at 2 miles per hour, how fast would the man row in still water?

Mixtures are made of ratios of different substances that may include chemicals, foods, water, or gases. There are many different situations where mixtures may occur both in nature and as a means to produce a desired product or outcome.  For example, chemical spills, manufacturing and even biochemical reactions involve mixtures.  The thing that can make mixtures interesting mathematically is when components of the mixture are added at different rates and concentrations. In our last example we will define an equation that models the concentration  – or ratio of sugar to water – in a large mixing tank over time. You are asked whether the final concentration of sugar is greater than the concentration at the beginning.

A large mixing tank currently contains 100 gallons of water into which 5 pounds of sugar have been mixed. A tap will open pouring 10 gallons per minute of water into the tank at the same time sugar is poured into the tank at a rate of 1 pound per minute. Find the concentration (pounds per gallon) of sugar in the tank after 12 minutes. Is that a greater concentration than at the beginning?

Let t  be the number of minutes since the tap opened. Since the water increases at 10 gallons per minute, and the sugar increases at 1 pound per minute, these are constant rates of change. This tells us the amount of water in the tank is a linear equation, as is the amount of sugar in the tank. We can write an equation independently for each:

The concentration, C , will be the ratio of pounds of sugar to gallons of water

The concentration after 12 minutes is given by evaluating [latex]C\left(t\right)\\[/latex] at [latex]t=\text{ }12\\[/latex].

This means the concentration is 17 pounds of sugar to 220 gallons of water.

At the beginning, the concentration is

Since [latex]\frac{17}{220}\approx 0.08>\frac{1}{20}=0.05\\[/latex], the concentration is greater after 12 minutes than at the beginning.

In the following video, we show another example of how to use rational functions to model mixing.

• "Current World Population." World Population Clock: 7.4 Billion People (2016). Accessed June 21, 2016. http://www.worldometers.info/world-population/ . "Current World Population." World Population Clock: 7.4 Billion People (2016). Accessed June 21, 2016. http://www.worldometers.info/world-population/ . "Current World Population." World Population Clock: 7.4 Billion People (2016). Accessed June 21, 2016. http://www.worldometers.info/world-population/ . ↵
• Obialor, Ambrose, Churchill Ihentuge, and Frank Akapuaka. "Determination of Height Using Femur Length in Adult Population of Oguta Local Government Area of Imo State Nigeria." Federation of American Societies for Experimental Biology, April 2015. Accessed June 22, 2016. http://www.fasebj.org/content/29/1_Supplement/LB19.short . ↵
• Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
• Solve Basic Rational Equations. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/R9y2D9VFw0I . License : CC BY: Attribution
• Solve Rational Equations with Like Denominators. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/gGA-dF_aQQQ . License : CC BY: Attribution
• Screenshot: map with scale factor. Provided by : Lumen Learning. License : CC BY: Attribution
• Screenshot: so many cars, so many tires. Provided by : Lumen Learning. License : CC BY: Attribution
• Screenshot: Water temperature in the ocean varies inversely with depth. Located at : http://Lumen%20Learning . License : CC BY: Attribution
• Ex: Direct Variation Application - Aluminum Can Usage. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/DLPKiMD_ZZw . License : CC BY: Attribution
• Ex: Inverse Variation Application - Number of Workers and Job Time. Provided by : Lumen Learning. Located at : https://youtu.be/y9wqI6Uo6_M . License : CC BY: Attribution
• Joint Variation: Determine the Variation Constant (Volume of a Cone). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/JREPATMScbM . License : CC BY: Attribution
• Screenshot: A Good Day's Work. Provided by : Lumen Learning. License : Public Domain: No Known Copyright
• Ex 1: Rational Equation Application - Painting Together. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/SzSasnDF7Ms . License : CC BY: Attribution
• Rational Function Application - Concentration of a Mixture. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/GD6H7BE_0EI . License : CC BY: Attribution
• Unit 15: Rational Expressions, from Developmental Math: An Open Program. Provided by : Monterey Institute of Technology and Education. License : CC BY: Attribution
• Ex 2: Solve a Literal Equation for a Variable. Authored by : James Sousa (Mathispower4u.com). Located at : https://www.youtube.com/watch?v=ecEUUbRLDQs&feature=youtu.be . License : CC BY: Attribution
• Screenshot: Matroyshka, or nesting dolls.. Provided by : Lumen Learning. License : CC BY: Attribution
• Ex: Proportion Applications - Mixtures . Authored by : James Sousa (Mathispower4u.com) . Located at : https://youtu.be/yGid1a_x38g . License : CC BY: Attribution
• Ex: Rational Equation App - Find Individual Working Time Given Time Working Together. Authored by : James Sousa (Mathispower4u.com) . Located at : https://www.youtube.com/watch?v=kbRSYb8UYqU&feature=youtu.be . License : CC BY: Attribution
• College Algebra: Mixture Problem. Authored by : Abramson, Jay et al.. Located at : http://cnx.org/contents/[email protected]:1/Preface . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]:1/Preface
• Quadratics - Revenue and Distance - Motion Examples. Authored by : Tyler Wallace. Located at : http://www.wallace.ccfaculty.org/book/book.html . Project : Beginning and Intermediate Algebra. License : CC BY: Attribution

Privacy Policy

Snapsolve any problem by taking a picture. Try it in the Numerade app?