Math Worksheets Land
Math Worksheets For All Ages
- Math Topics
- Grade Levels

Scientific Notation Multiplication and Division
When it comes to these two operations, students often get intimidated by before even seeing a single demonstration of how to solve these types of problems. Once they do, they figure out it is a cinch. You treat the decimal part of the operation as would normally. The magic comes in when you concerned with the base ten section. When multiplying, you simply add the powers that are present. Division, being the counter operation to multiplication, you do the opposite and subtract them. That is all there is to it. It really just comes down to understanding the operation that is taking place. These worksheets show students how to find the outcome of quotients and products of values that are expressed in scientific notation.
Aligned Standard: 8.EE.A.4
- Multiplying Scientific Notation Step-by-Step Lesson - I love how you can just add the powers of ten. The first person to figure that out must have been floored.
- Guided Lesson - We add two quotients in here to get more practice in. Remember to pay attention to the exponents.
- Guided Lesson Explanation - Finding quotients is very similar to finding products when working with this form of notation.
- Practice Worksheet - When we multiply forms of scientific notation you get some interesting products in here.
- Matching Worksheet - The answers to these are not as obvious as you would think.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
The top half of all the worksheets is filled with multiplication. The bottom portions of the sheets are where you will be processing division problems.
- Homework 1 - Separate the problem into its two components and then break the pieces into parts.
- Homework 2 - Writing the number in proper scientific form. You will practice with both operations in here.
- Homework 3 - Find the quotient of the powers of ten by subtracting. This is tricky at first.
Practice Worksheets
A good idea is to get in the habit of circling and rewriting the exponents immediately.
- Practice 1 - Separate the problem into its two components. a) Constants b) Powers of ten
- Practice 2 - A sample problem that you will be working with here: (1.17 × 10 3 ) (2.11 × 10 3 )
- Practice 3 - The important part is following the sections of the notation before you start to multiply or divide it.
Math Skill Quizzes
I used a larger font for the numbers that forces kids to rewrite the problem. This is a good thing!
- Quiz 1 - Rearrange the problem to put the constants and powers of ten together.
- Quiz 2 - We follow the same exact strategy we need to. See how you are doing with this skill.
- Quiz 3 - Complete all the problems to get them all headed in the right direction.
How to Multiply and Divide Values in Scientific Notation
Multiplying and dividing values with scientific notations is easier since the values have the same base 10 in them. Let us solve both of them separately with the help of examples.
Multiplication Example - (5.6 × 10 5 ) × (2.4 × 10 5 ).
Here we will first have to separate the decimal number and the base 10 number and multiply them.
(5.6 × 2.4) × (10 5 × 10 5 )
The exponential numbers have the same base (i.e., 10), so according to the multiplicative property, the powers are added. 10 5 × 10 5 = 10 10 . Now the decimal numbers will have a result of 13.44 (5.6 × 2.4).
The resulting value would be: (13.44 × 10 10 ).
Division Example - ((5.6 × 10 5 )/(4.3 × 10 4 )).
Here, similar to the multiplication operations, we can use an exponential property of division to divide the notation by subtracting the powers that are present: ((5.6 × 10 (5-4) ) / (4.3 ))
Now, you can divide the decimal numbers (5.6 / 4.3) to get an answer of 1.3, and the answer becomes:
1.3 × 10 1 = 13
When Would You Find Yourself Multiplying and Dividing Scientific Notation?
As the name implies, scientific notation is form of display numeric values that the science community gravitates towards. This is because they are constantly studying and researching things that are either very large or very small. Chemist will often use this number expression form to indicate the amount of a substance that they use to create a reaction. When they need to calculate how much of the substance is needed to be present in order for the reaction to take place, they will need to either multiply or divide those values that are stated in scientific notation. There is an example of using operations with scientific notation when the values are ridiculously small, and another example would be Microbiologists that study the effects of a drug on cells. They will often place the remnants of the drug on a plate with bacterial cells to see how they react to the drug. After some time, they will come back and evaluate the number of bacteria that survived the drug treatment. To determine the mortality rate of the drug they will often divide the surviving population by the starting population in scientific notation. Astronomers work with numbers that are in the opposite spectrum, they are really big numbers. They will often use these distances to measure the size of stars or solar systems. To determine the relative distances of solar systems between one another they will often multiply and divide their distances in scientific notation.
Get Access to Answers, Tests, and Worksheets
Become a paid member and get:
- Answer keys to everything
- Unlimited access - All Grades
- 64,000 printable Common Core worksheets, quizzes, and tests
- Used by 1000s of teachers!
Worksheets By Email:
Get Our Free Email Now!
We send out a monthly email of all our new free worksheets. Just tell us your email above. We hate spam! We will never sell or rent your email.
Thanks and Don't Forget To Tell Your Friends!
I would appreciate everyone letting me know if you find any errors. I'm getting a little older these days and my eyes are going. Please contact me, to let me know. I'll fix it ASAP.
- Privacy Policy
- Other Education Resource
© MathWorksheetsLand.com, All Rights Reserved
- + ACCUPLACER Mathematics
- + ACT Mathematics
- + AFOQT Mathematics
- + ALEKS Tests
- + ASVAB Mathematics
- + ATI TEAS Math Tests
- + Common Core Math
- + DAT Math Tests
- + FSA Tests
- + FTCE Math
- + GED Mathematics
- + Georgia Milestones Assessment
- + GRE Quantitative Reasoning
- + HiSET Math Exam
- + HSPT Math
- + ISEE Mathematics
- + PARCC Tests
- + Praxis Math
- + PSAT Math Tests
- + PSSA Tests
- + SAT Math Tests
- + SBAC Tests
- + SIFT Math
- + SSAT Math Tests
- + STAAR Tests
- + TABE Tests
- + TASC Math
- + TSI Mathematics
- + ACT Math Worksheets
- + Accuplacer Math Worksheets
- + AFOQT Math Worksheets
- + ALEKS Math Worksheets
- + ASVAB Math Worksheets
- + ATI TEAS 6 Math Worksheets
- + FTCE General Math Worksheets
- + GED Math Worksheets
- + 3rd Grade Mathematics Worksheets
- + 4th Grade Mathematics Worksheets
- + 5th Grade Mathematics Worksheets
- + 6th Grade Math Worksheets
- + 7th Grade Mathematics Worksheets
- + 8th Grade Mathematics Worksheets
- + 9th Grade Math Worksheets
- + HiSET Math Worksheets
- + HSPT Math Worksheets
- + ISEE Middle-Level Math Worksheets
- + PERT Math Worksheets
- + Praxis Math Worksheets
- + PSAT Math Worksheets
- + SAT Math Worksheets
- + SIFT Math Worksheets
- + SSAT Middle Level Math Worksheets
- + 7th Grade STAAR Math Worksheets
- + 8th Grade STAAR Math Worksheets
- + THEA Math Worksheets
- + TABE Math Worksheets
- + TASC Math Worksheets
- + TSI Math Worksheets
- + AFOQT Math Course
- + ALEKS Math Course
- + ASVAB Math Course
- + ATI TEAS 6 Math Course
- + CHSPE Math Course
- + FTCE General Knowledge Course
- + GED Math Course
- + HiSET Math Course
- + HSPT Math Course
- + ISEE Upper Level Math Course
- + SHSAT Math Course
- + SSAT Upper-Level Math Course
- + PERT Math Course
- + Praxis Core Math Course
- + SIFT Math Course
- + 8th Grade STAAR Math Course
- + TABE Math Course
- + TASC Math Course
- + TSI Math Course
- + Number Properties Puzzles
- + Algebra Puzzles
- + Geometry Puzzles
- + Intelligent Math Puzzles
- + Ratio, Proportion & Percentages Puzzles
- + Other Math Puzzles
How to Multiply and Divide in Scientific Notation? (+FREE Worksheet!)
This article teaches you how to Multiply and Divide Scientific Notations into a few simple steps.

Related Topics
- How to Round Decimals
- How to Multiply and Divide Decimals
- How to Add and Subtract Decimals
- How to Compare Decimals
Step by step guide to Multiply and Divide Scientific Notations
Multiplying numbers that are in the form of a scientific notation is relatively simple because multiplying by coefficients of ten is simple.
To multiply two numbers in scientific notation:
- Step 1: Multiply their coefficients which may be a decimal number or an integer.
- Step 2: Multiply the two exponential numbers (with a base of \(10\)) by adding their powers together.
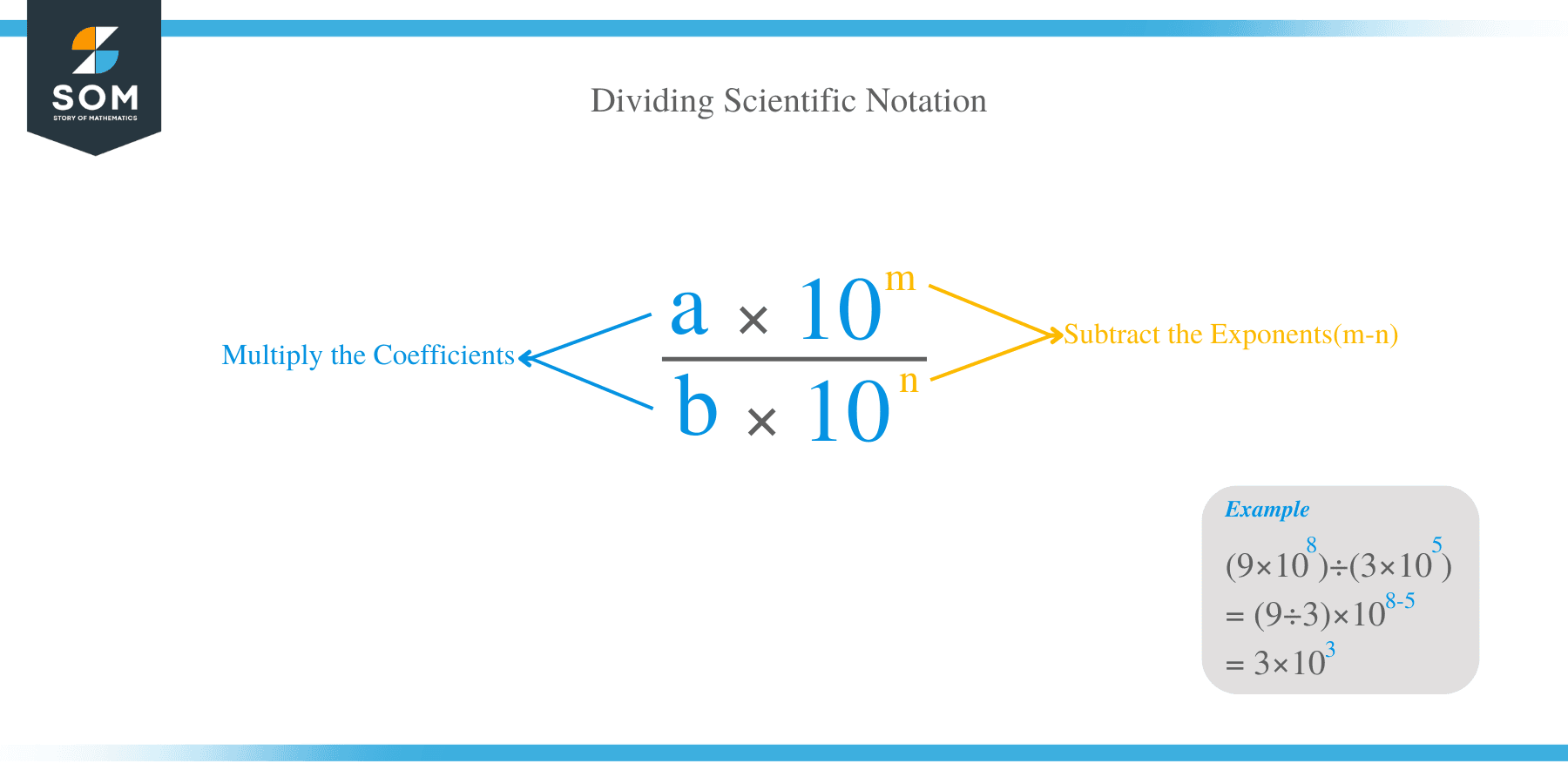
To divide two numbers in scientific notation:
- Step 1: divide their coefficients which may be a decimal number or an integer.
- Step 2: divide the two exponential numbers (with a base of \(10\)) by subtracting their powers from each other.
The answer must be converted to scientific notation.
Multiplication and Division in Scientific Notation – Example 1:
Write the answers in scientific notation. \((2.2\times 10^6) (4\times 10^{ \ -3})=\)
First, multiply the coefficients: \(2.2\times 4=8.8\)
Add the powers of \(10\): \(10^6\times 10^{ \ -3}=10^{6+(-3)}= 10^ {6-3}= 10^3\)
Then: \((2.2\times 10^6) (4\times 10^{ \ -3})=8.8\times 10^3\)
Multiplication and Division in Scientific Notation – Example 2:
Write the answers in scientific notation. \(\frac{7.5\times 10^9}{1.5\times 10^5}\)
First, divide the coefficients: \(\frac{7.5}{1.5}=5\)
Subtract the power of the exponent in the denominator from the exponent in the numerator: \(\frac{10^9}{10^5}=10^{9-5}=10^4\)
Then: \(\frac{7.5\times 10^9}{1.5\times 10^5}=5\times 10^4\)
Multiplication and Division in Scientific Notation – Example 3:
Write the answers in scientific notation. \((1.1\times 10^9) (9\times 10^{ \ -4})=\)
First, multiply the coefficients: \(1.1\times 9=9.9\)
Add the powers of \(10\): \(10^9\times 10^{ \ -4}=10^ { 9+(-4)}=10^ {9-4} = 10^5\)
Then: \((1.1\times 10^9) (9\times 10^{ \ -4})=9.9\times 10^5\)
Multiplication and Division in Scientific Notation – Example 4:
Write the answers in scientific notation. \(\frac{4.5\times 10^{-7}}{5\times 10^2}\)
First, divide the coefficients: \(\frac{4.5}{5}=0.9\)
Subtract the power of the exponent in the denominator from the exponent in the numerator: \(\frac{10^{-7}}{10^2}=10^{-7-2}=10^{-9}\)
Then: \(\frac{4.5\times 10^{-7}}{5\times 10^2}=0.9\times 10^{-9}\)
Now, convert the answer to scientific notation: \(0.9\times 10^{-9}=9\times 10^{-10}\)
Exercises for Multiplying and Dividing Scientific Notations
Write the answers in scientific notation. .
- \(\color{blue}{(4.2\times 10^6) (3\times 10^{ \ -9})=}\)
- \(\color{blue}{(5\times 10^8) (3.6\times 10^{ \ -6})=}\)
- \(\color{blue}{(4.9\times 10^7) (2\times 10^{ \ -5})=}\)
- \(\color{blue}{\frac{6.3\times 10^{-9}}{9\times 10^5}}\)
- \(\color{blue}{\frac{8.8\times 10^9}{4\times 10^2}}\)
- \(\color{blue}{\frac{9.6\times 10^{-5}}{3\times 10^4}}\)
- \(\color{blue}{1.26\times 10^{-2}}\)
- \(\color{blue}{1.8\times 10^3}\)
- \(\color{blue}{9.8\times 10^2}\)
- \(\color{blue}{7\times 10^{-15}}\)
- \(\color{blue}{2.2\times 10^7}\)
- \(\color{blue}{3.2\times 10^{-9}}\)
by: Effortless Math Team about 3 years ago (category: Articles , Free Math Worksheets )
Effortless Math Team
Related to this article, more math articles.
- How to Solve Point-Slope Form of Equations?
- How to Use Area Models to Find Equivalent Fractions
- How to Find Adjacent Angles
- How Do Secant-Tangent and Tangent-Tangent Angles Work? A Complete Guide
- How to Find Similarity and Ratios? (+FREE Worksheet!)
- Full-Length 7th Grade Common Core Math Practice Test
- What Skills Do I Need for the ACCUPLACER Math Test?
- How to Prepare for the CLEP College Mathematics Test?
- 4th Grade Common Core Math FREE Sample Practice Questions
- A Deep Dive into the Chapters of the Book: Pre-Algebra for Beginners
What people say about "How to Multiply and Divide in Scientific Notation? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.
Leave a Reply Cancel reply
You must be logged in to post a comment.
CBEST Math Worksheets A Comprehensive Review of CBEST Math Test
Dat quantitative reasoning worksheets a comprehensive review of dat quantitative reasoning test, sat math worksheets a comprehensive review of sat math test, psat math worksheets a comprehensive review of psat math test, parapro math worksheets a comprehensive review of parapro math test, hspt math worksheets a comprehensive review of hspt math test, ftce general knowledge math worksheets a comprehensive review of ftce math test, act math worksheets a comprehensive review of act math test, afoqt math worksheets a comprehensive review of afoqt math test, aleks math worksheets a comprehensive review of aleks math test, asvab math worksheets a comprehensive review of asvab math test, ati teas 7 math worksheets a comprehensive review of ati teas 7 math test, 10 full length kap algebra i practice tests the practice you need to ace the kap algebra i test, 10 full length istep+ algebra i practice tests the practice you need to ace the istep+ algebra i test, 10 full length nm-mssa algebra i practice tests the practice you need to ace the nm-mssa algebra i test.
- ATI TEAS 6 Math
- ISEE Upper Level Math
- SSAT Upper-Level Math
- Praxis Core Math
- 8th Grade STAAR Math
Limited time only!
Save Over 45 %
It was $89.99 now it is $49.99
Login and use all of our services.
Effortless Math services are waiting for you. login faster!
Register Fast!
Password will be generated automatically and sent to your email.
After registration you can change your password if you want.
- Math Worksheets
- Math Courses
- Math Topics
- Math Puzzles
- Math eBooks
- GED Math Books
- HiSET Math Books
- ACT Math Books
- ISEE Math Books
- ACCUPLACER Books
- Premium Membership
- Youtube Videos
Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.
- Bulk Orders
- Refund Policy
Module 1: Exponents and Radicals
Multiplying and dividing numbers in scientific notation, learning outcomes.
- Multiply numbers expressed in scientific notation
- Divide numbers expressed in scientific notation
Multiplying Numbers Expressed in Scientific Notation
Numbers that are written in scientific notation can be multiplied and divided rather simply by taking advantage of the properties of numbers and the rules of exponents that you may recall. To multiply numbers in scientific notation, first multiply the numbers that aren’t powers of 10 (the a in [latex]a\times10^{n}[/latex]). Then multiply the powers of ten by adding the exponents.
This will produce a new number times a different power of [latex]10[/latex]. All you have to do is check to make sure this new value is in scientific notation. If it isn’t, you convert it.
Let’s look at some examples.
[latex]\left(3\times10^{8}\right)\left(6.8\times10^{-13}\right)[/latex]
[latex]\left(3\times6.8\right)\left(10^{8}\times10^{-13}\right)[/latex]
Multiply the coefficients.
[latex]\left(20.4\right)\left(10^{8}\times10^{-13}\right)[/latex]
Multiply the powers of [latex]10[/latex] using the Product Rule. Add the exponents.
[latex]20.4\times10^{-5}[/latex]
Convert [latex]20.4[/latex] into scientific notation by moving the decimal point one place to the left and multiplying by [latex]10^{1}[/latex].
[latex]\left(2.04\times10^{1}\right)\times10^{-5}[/latex]
Group the powers of [latex]10[/latex] using the associative property of multiplication.
[latex]2.04\times\left(10^{1}\times10^{-5}\right)[/latex]
Multiply using the Product Rule—add the exponents.
[latex]2.04\times10^{1+\left(-5\right)}[/latex]
[latex]\left(3\times10^{8}\right)\left(6.8\times10^{-13}\right)=2.04\times10^{-4}[/latex]
[latex]\left(8.2\times10^{6}\right)\left(1.5\times10^{-3}\right)\left(1.9\times10^{-7}\right)[/latex]
[latex]\left(8.2\times1.5\times1.9\right)\left(10^{6}\times10^{-3}\times10^{-7}\right)[/latex]
Multiply the numbers.
[latex]\left(23.37\right)\left(10^{6}\times10^{-3}\times10^{-7}\right)[/latex]
Multiply the powers of [latex]10[/latex] using the Product Rule—add the exponents.
[latex]23.37\times10^{-4}[/latex]
Convert [latex]23.37[/latex] into scientific notation by moving the decimal point one place to the left and multiplying by [latex]10^{1}[/latex].
[latex]\left(2.337\times10^{1}\right)\times10^{-4}[/latex]
[latex]2.337\times\left(10^{1}\times10^{-4}\right)[/latex]
Multiply using the Product Rule and add the exponents.
[latex]2.337\times10^{1+\left(-4\right)}[/latex]
[latex]\left(8.2\times10^{6}\right)\left(1.5\times10^{-3}\right)\left(1.9\times10^{-7}\right)=2.337\times10^{-3}[/latex]
Multiply. Write answers in decimal form: [latex]\left(4\times {10}^{5}\right)\left(2\times {10}^{-7}\right)[/latex].
| [latex]\left(4\times {10}^{5}\right)\left(2\times {10}^{-7}\right)[/latex] | |
| Use the Commutative Property to rearrange the factors. | [latex]4\cdot 2\cdot {10}^{5}\cdot {10}^{-7}[/latex] |
| Multiply [latex]4[/latex] by [latex]2[/latex] and use the Product Property to multiply [latex]{10}^{5}[/latex] by [latex]{10}^{-7}[/latex]. | [latex]8\times {10}^{-2}[/latex] |
| Change to decimal form by moving the decimal two places left. | [latex]{\Large\frac{8}{100}} = 0.08[/latex] |
In the following video you will see an example of how to multiply tow numbers that are written in scientific notation.
Dividing Numbers Expressed in Scientific Notation
In order to divide numbers in scientific notation, you once again apply the properties of numbers and the rules of exponents. You begin by dividing the numbers that aren’t powers of [latex]10[/latex] (the a in [latex]a\times10^{n}[/latex]. Then you divide the powers of ten by subtracting the exponents.
This will produce a new number times a different power of 10. If it isn’t already in scientific notation, you convert it, and then you’re done.
[latex] \displaystyle \frac{2.829\times 1{{0}^{-9}}}{3.45\times 1{{0}^{-3}}}[/latex]
[latex] \displaystyle \left( \frac{2.829}{3.45} \right)\left( \frac{{{10}^{-9}}}{{{10}^{-3}}} \right)[/latex]
Divide the coefficients.
[latex] \displaystyle \left(0.82\right)\left( \frac{{{10}^{-9}}}{{{10}^{-3}}} \right)[/latex]
Divide the powers of [latex]10[/latex] using the Quotient Rule. Subtract the exponents.
[latex]\begin{array}{l}0.82\times10^{-9-\left(-3\right)}\\0.82\times10^{-6}\end{array}[/latex]
Convert [latex]0.82[/latex] into scientific notation by moving the decimal point one place to the right and multiplying by [latex]10^{-1}[/latex].
[latex]\left(8.2\times10^{-1}\right)\times10^{-6}[/latex]
Group the powers of [latex]10[/latex] together using the associative property.
[latex]8.2\times\left(10^{-1}\times10^{-6}\right)[/latex]
[latex]8.2\times10^{-1+\left(-6\right)}[/latex]
[latex] \displaystyle \frac{2.829\times {{10}^{-9}}}{3.45\times {{10}^{-3}}}=8.2\times {{10}^{-7}}[/latex]
[latex] \displaystyle \frac{\left(1.37\times10^{4}\right)\left(9.85\times10^{6}\right)}{5.0\times10^{12}}[/latex]
[latex] \displaystyle \frac{\left( 1.37\times 9.85 \right)\left( {{10}^{6}}\times {{10}^{4}} \right)}{5.0\times {{10}^{12}}}[/latex]
[latex] \displaystyle \frac{13.4945\times {{10}^{10}}}{5.0\times {{10}^{12}}}[/latex]
Regroup using the associative property.
[latex] \displaystyle \left( \frac{13.4945}{5.0} \right)\left( \frac{{{10}^{10}}}{{{10}^{12}}} \right)[/latex]
Divide the numbers.
[latex] \displaystyle \left(2.6989\right)\left(\frac{10^{10}}{10^{12}}\right)[/latex]
Divide the powers of [latex]10[/latex] using the Quotient Rule—subtract the exponents.
[latex] \displaystyle \begin{array}{c}\left(2.6989 \right)\left( {{10}^{10-12}} \right)\\2.6989\times {{10}^{-2}}\end{array}[/latex]
[latex] \displaystyle \frac{\left( 1.37\times {{10}^{4}} \right)\left( 9.85\times {{10}^{6}} \right)}{5.0\times {{10}^{12}}}=2.6989\times {{10}^{-2}}[/latex]
Divide. Write answers in decimal form: [latex]{\Large\frac{9\times {10}^{3}}{3\times {10}^{-2}}}[/latex].
| [latex]{\Large\frac{9\times {10}^{3}}{3\times {10}^{-2}}}[/latex] | |
| Separate the factors. | [latex]{\Large\frac{9}{3}}\times {\Large\frac{{10}^{3}}{{10}^{-2}}}[/latex] |
| Divide [latex]9[/latex] by [latex]3[/latex] and use the Quotient Property to divide [latex]{10}^{3}[/latex] by [latex]{10}^{-2}[/latex] . | [latex]3\times {10}^{5}[/latex] |
| Change to decimal form by moving the decimal five places right. | [latex]300,000[/latex] |
Notice that when you divide exponential terms, you subtract the exponent in the denominator from the exponent in the numerator. You will see another example of dividing numbers written in scientific notation in the following video.
The following video is a mini-lesson on how to convert decimals to scientific notation, and back to a decimal. Additionally, you will see more examples of how to multiply and divide numbers given in scientific notation.
Contribute!
Improve this page Learn More
- Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
- Unit 11: Exponents and Polynomials, from Developmental Math: An Open Program. Provided by : Monterey Institute of Technology and Education. Located at : http://nrocnetwork.org/resources/downloads/nroc-math-open-textbook-units-1-12-pdf-and-word-formats/ . License : CC BY: Attribution
- Examples: Dividing Numbers Written in Scientific Notation. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/RlZck2W5pO4 . License : CC BY: Attribution
- Examples: Multiplying Numbers Written in Scientific Notation. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/5ZAY4OCkp7U . License : CC BY: Attribution
How to Multiply & Divide in Scientific Notation - Quiz & Worksheet
- Quiz & Worksheet - Multiplying & Dividing in Scientific Notation Quiz
Choose an answer and hit 'next'. You will receive your score and answers at the end.
Which is the digit term in 5.6 x 10^-15?
As a member, you'll also get unlimited access to over 88,000 lessons in math, English, science, history, and more. Plus, get practice tests, quizzes, and personalized coaching to help you succeed.
Already registered? Log in here for access
1. which is the exponent term in 4.29 x 10^17, 2. what is the result of (3.4 x 10^15) x (2.1 x 10^4).
5.5 x 10^60
5.5 x 10^19
7.14 x 10^60
7.14 x 10^19
About This Quiz & Worksheet
Scientific notation is a shorthand way to write small or large numbers and is often used in science and mathematics. This quiz and worksheet will help guide your understanding of how to multiply and divide numbers in scientific notation, and questions will ask about format and mathematical operations.

Quiz & Worksheet Goals
This quiz will test you on:
- Exponent term
- Multiplying in scientific notation
- Dividing in scientific notation
Skills Practiced
Students will test the following skills in this quiz and worksheet combo:
- Reading comprehension - ensure that you draw the most important information from the related lesson about scientific notation
- Distinguishing differences - compare and contrast topics from the lesson, such as exponent term and digit term
- Problem solving - use acquired knowledge to solve practice problems involving multiplication and division
- Knowledge application - use your knowledge to answer questions about the format of scientific notation and how to perform mathematical operations using it
Additional Learning
For additional learning about how to multiply or divide numbers in scientific notation, look over the accompanying less entitled How to Multiply & Divide in Scientific Notation. Objectives covered by the lesson include:
- Define scientific notation
- Identify components of scientific notation, such as the exponent and digit terms
- Learn how to multiply and divide using numbers in scientific notation
- Solve practice problems using information from the lesson
34 chapters | 191 quizzes
- Scientific Notation | Definition, Conversion & Examples Quiz
- Comparing Numbers Written in Scientific Notation Quiz
Previous Lesson

- Converting Numbers to Scientific Notation Quiz
Current Lesson

- How to Multiply & Divide in Scientific Notation Quiz
Next Lesson

- Multiplying by Powers of 10 | Explanation & Examples Quiz
Explore our library of over 88,000 lessons
- Foreign Language
- Social Science
- See All College Courses
- Common Core
- High School
- See All High School Courses
- College & Career Guidance Courses
- College Placement Exams
- Entrance Exams
- General Test Prep
- K-8 Courses
- Skills Courses
- Teacher Certification Exams
- See All Other Courses
- Create a Goal
- Create custom courses
- Get your questions answered
- PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
- EDIT Edit this Article
- EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
- Browse Articles
- Learn Something New
- Quizzes Hot
- This Or That Game
- Train Your Brain
- Explore More
- Support wikiHow
- About wikiHow
- Log in / Sign up
- Education and Communications
- Mathematics
How to Divide Scientific Notation
Last Updated: October 25, 2022 Fact Checked
This article was co-authored by Jake Adams and by wikiHow staff writer, Hannah Madden . Jake Adams is an academic tutor and the owner of Simplifi EDU, a Santa Monica, California based online tutoring business offering learning resources and online tutors for academic subjects K-College, SAT & ACT prep, and college admissions applications. With over 14 years of professional tutoring experience, Jake is dedicated to providing his clients the very best online tutoring experience and access to a network of excellent undergraduate and graduate-level tutors from top colleges all over the nation. Jake holds a BS in International Business and Marketing from Pepperdine University. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 16,057 times.
When you’re learning about scientific notation, you’ll probably come across a division question sooner or later. Fortunately, since numbers with the same base can be divided easily, dividing scientific notation only takes a few extra steps. In this article, we’ll walk you through dividing scientific notation and give you some helpful examples along the way.
Things You Should Know
- Divide the whole numbers, then use the rule of exponents to divide the bases.
- If the new coefficient is a whole number, multiply the number by the new power of 10 to get your solution.
- If the new coefficient is not a whole number, convert it to scientific notation before multiplying it by the new power of 10.
Divide the coefficients.

Divide the bases.

Multiply whole numbers by the new power of 10.

Convert the coefficient to scientific notation if needed.

Expert Q&A
You might also like.

- ↑ https://janus.astro.umd.edu/astro/scinote/help.html
- ↑ https://www.edinformatics.com/math_science/division-in-scientific-notation.html
- ↑ https://flexbooks.ck12.org/cbook/ck-12-interactive-middle-school-math-8-for-ccss/section/9.8/primary/lesson/multiplying-dividing-numbers-in-scientific-notation-msm8-ccss/
About This Article

- Send fan mail to authors
Reader Success Stories
Chris Anthony
Dec 7, 2022
Did this article help you?
Featured Articles

Trending Articles

Watch Articles

- Terms of Use
- Privacy Policy
- Do Not Sell or Share My Info
- Not Selling Info
Don’t miss out! Sign up for
wikiHow’s newsletter
- Inspiration
Search Functionality Update!
To optimize your search experience, please refresh the page.
Windows: Press Ctrl + F5
Mac: Use Command + Shift+ R or Command + Option + R
Mobile: Tap and hold the refresh icon, then select "Hard Refresh" or "Reload Without Cache" for an instant upgrade!
- Child Login
- Number Sense
- Measurement
- Pre Algebra
- Figurative Language
- Reading Comprehension
- Reading and Writing
- Science Worksheets
- Social Studies Worksheets
- Math Worksheets
- ELA Worksheets
- Online Worksheets
Browse By Grade
- Become a Member

- Kindergarten

- Skip Counting
- Place Value
- Number Lines
- Subtraction
- Multiplication
- Word Problems
- Comparing Numbers
- Ordering Numbers
- Odd and Even Numbers
- Prime and Composite Numbers
- Roman Numerals
- Ordinal Numbers

- Big vs Small
- Long vs Short
- Tall vs Short
- Heavy vs Light
- Full, Half-Full, or Empty
- Metric Unit Conversion
- Customary Unit Conversion
- Temperature
- Tally Marks
- Mean, Median, Mode, Range
- Mean Absolute Deviation
- Stem and Leaf Plot
- Box and Whisker Plot
- Permutations
- Combinations

- Lines, Rays, and Line Segments
- Points, Lines, and Planes
- Transformation
- Ordered Pairs
- Midpoint Formula
- Distance Formula
- Parallel and Perpendicular Lines
- Surface Area
- Pythagorean Theorem

- Significant Figures
- Proportions
- Direct and Inverse Variation
- Order of Operations
- Scientific Notation
- Absolute Value

- Translating Algebraic Phrases
- Simplifying Algebraic Expressions
- Evaluating Algebraic Expressions
- Systems of Equations
- Slope of a Line
- Equation of a Line
- Quadratic Equations
- Polynomials
- Inequalities
- Determinants
- Arithmetic Sequence
- Arithmetic Series
- Geometric Sequence
- Complex Numbers
- Trigonometry
Multiplication and Division with Scientific Notation Worksheets
- Pre-Algebra >
- Scientific Notation >
- Multiplication and Division
Ferret out the practice in our free, printable multiplication and division with scientific notation worksheets, and flaunt your flair for very big or very small numbers. Draw on your dexterity in simplifying and deciphering small or large numerals in convenient forms, while diligently applying the principles of multiplication and division.
Our multiplication and division with scientific notation worksheet pdfs are perfect for 8th grade students.
Multiply and Divide Numbers with Positive Powers in Scientific Notation
These printable worksheets will take math enthusiasts of grade 8 on a trip through multiplication and division of scientific notation with positive powers.

Multiplying and Dividing Numbers in Scientific Notation
Stay a step ahead of your 8th grade peers with these pdf worksheets on multiplying and dividing numbers in scientific notation, that feature both positive and negative powers.

Multiplying and Dividing Decimals in Scientific Notation
Lock in great practice of scientific notation calculations on decimals using our printable multiplication and division with scientific notation worksheets.

Operations with Scientific Notation Worksheets | Mixed Review
Race to the finish line with these pdf worksheets containing problems on scientific notation where children practice all four basic mathematical operations.

Related Printable Worksheets
▶ Addition and Subtraction with Scientific Notation
▶ Scientific Notation of Large Numbers
▶ Scientific Notation of Small Numbers
Tutoringhour
What we offer, information.
- Membership Benefits
- How to Use Online Worksheets
- How to Use Printable Worksheets
- Printing Help
- Testimonial
- Privacy Policy
- Refund Policy
Copyright © 2024 - Tutoringhour
You must be a member to unlock this feature!
Sign up now for only $29.95/year — that's just 8 cents a day!
Printable Worksheets
- 20,000+ Worksheets Across All Subjects
- Access to Answer Key
- Add Worksheets to "My Collections"
- Create Custom Workbooks
Digitally Fillable Worksheets
- 1100+ Math and ELA Worksheets
- Preview and Assign Worksheets
- Create Groups and Add Children
- Track Progress

- Mathematicians
- Math Lessons
- Square Roots
- Math Calculators
- Dividing Numbers in Scientific Notation – Technique & Examples
Dividing Numbers in Scientific Notation – Methods & Examples

This type of notation is easier and more concise to express quantities that are too big or small. For example, the number 125,000,000,000 can be represented as 1.25 x 10 11 .
How to Divide Scientific Notation?
This article illustrates how you can perform division of numbers expressed in scientific notation.
To divide two numbers written in scientific notation, follow the steps below:
- Separately divide the coefficients and exponents.
- For the division of bases, use the division rule of exponents, where the exponents are subtracted.
- Combine the result of coefficients by the new power of 10.
- If the quotient from division of coefficients is not less than 10 and greater than 1, convert it to scientific notation and multiply it by the new power of 10.
- Note that when you dividing exponential terms, always subtract the denominator from the numerator.
Let us take a look at a few examples to help you understand the above procedures better.
Divide and express the answer in scientific notation: 9 x 10 8 / 3 x 10 5 .
Explanation
- Start by dividing the coefficients: (9 ÷ 3) = 3
- Now, divide the bases using the division rule of exponents: (10 8 ÷ 10 5 ) = 10 8 – 5 =10 3
- The coefficient is less than 10 and greater than 1, therefore multiply it by the new power of 10.
(2.8 x 10 10 ) / (2 x 10 20 )
Divide the coefficients and bases separately:
= (2.8/2) x (10 10 /10 20 )
= 1.4 x 10 10- 20
= 1.4 x 10 -10
(6.4 x 10 6 )/ (8.9 x 10 2 )
Divide the coefficients and powers of 10 separately;
= (6.4)/ (8.9) x 10 (6-2)
= 0.719 x 10 4 The new coefficient is less than 1, therefore convert the number to scientific notation and multiply by the power of 10.
= 7.19 x 10 3
(3.2 x 10 3 )/ (5.7 x 10 – 2 )
Divide the coefficients and bases separately
= (3.2)/ (5.7) x 10 3 – ( – 2)
= 0.561 x 10 5
The coefficient is less than 1, therefore convert the number to scientific notation by moving the decimal point one step to the right.
= 5.61 x 10 4
(2 x 10 3 ) / (4 x 10 -8 )
= (2/4) x (10 3 /10 -8 )
= 0.5 x 10 3 – (-8)
= 0.5 x 10 11
Since the new coefficient is less than 1; convert it to scientific notation:
= 0.5 = 5 x 10 -1
Now multiply the coefficient by the new power of 10;
= (5 x 10 -1 ) x (10 11 )
= 5 x 10 10
Evaluate and express your answer in scientific notation:
(2.688 x 10 6 ) / (1.2 x 10 2 )
= (2.688 / 1.2) x (10 6 / 10 2 )
= (2.24) x (10 6-2 )
= 2.24 x 10 4
Practice Questions
Previous lesson | main page | next lesson.
Have an account?

Multiplying & Dividing in Scientific Not...
Mathematics.
Multiplying & Dividing in Scientific Notation Practice
24 questions

Introducing new Paper mode
No student devices needed. Know more
- 1. Multiple Choice Edit 45 seconds 1 pt When dividing numbers in scientific notation, what do you do to the exponents? For example: (4×10⁵) ∕ (3×10²) Add them Subtract them Keep them the same Divide them
- 2. Multiple Choice Edit 45 seconds 1 pt In what types of problems do you have to make sure the exponents are the same before beginning to compute? Adding and Subtracting Multiplying and Dividing Subtracting and Dividing Adding and Multiplying
- 3. Multiple Choice Edit 45 seconds 1 pt When multiplying numbers in scientific notation, what do you do to the leading numbers? For example: (4×10⁵)(3×10⁻²) Keep them the same Divide them Add them Multiply them
- 4. Multiple Choice Edit 2 minutes 1 pt Evaluate. Leave your answer in scientific notation. (3.4×10⁴)(2×10⁴) 6.8×10⁴ 5.4×10⁴ 6.8×10⁸ 5.4×10⁸
- 5. Multiple Choice Edit 2 minutes 1 pt Evaluate. Leave your answer in scientific notation. (9.6×10⁸) ⁄ (3×10⁴) (hint - it's division...) 6.6×10² 3.2×10¹² 3.2×10⁴ 6.6×10⁴
- 6. Multiple Choice Edit 2 minutes 1 pt Order from least to greatest... a) 4.5×10⁻³ b) 0.000045 c) 3.1×10⁻³ d) -45 D , B , C, A B , C , D , A C , A , D , B A , C , D , B
- 7. Multiple Choice Edit 1 minute 1 pt Which inequality sign should be placed between these numbers to make it a true/correct statement? 7.6×10⁴ ? 0.00076 < > =
- 8. Multiple Choice Edit 1 minute 1 pt Determine the missing value. (5.4×10 ? )(3.2×10³) = 17.28×10 15 12 8 18 5
- 10. Multiple Choice Edit 2 minutes 1 pt Multiply: (9.4 x 10 6 )(3.2 x 10 5 ) 30.08 x 10 11 3.8 x 10 1 3.008 x 10 12 2.9375 x 10 1
- 11. Multiple Choice Edit 3 minutes 1 pt (9.6×10 3 ) × (6.7×10 2 ) 64.32×10 5 6.432×10 6 64.32×10 6 64.32×10 5
- 12. Multiple Choice Edit 2 minutes 1 pt Solve: (6 x 10 6 ) / (2 x 10 3 ) 12 x 10 3 3 x 10 9 1.2 x 10 4 3 x 10 3
- 13. Multiple Choice Edit 5 minutes 1 pt (2 x 10 9 )(4 x 10 -4 ) 8 x 10 13 8 x 10 36 8 x 10 5 8 x 10 -36
- 14. Multiple Choice Edit 5 minutes 1 pt (5 x 10 6 )(5 x 10 7 ) 2.5 x 10 12 2.5 x 10 14 25 x 10 12 25 x 10 13
(20 x 10 50 ) / (4 x 10 15 )
2.4 x 10 51
Write 7.113 x 10 7 in standard form.
0.0000007113
- 17. Multiple Choice Edit 45 seconds 1 pt Write 0.00000707 in scientific notation. 7.07 x 10 -6 7.07 x 10 6 707 x 10 8 707 x 10 -8
- 18. Multiple Choice Edit 30 seconds 1 pt Write 7.8 x 10 -3 in standard form. 0.0078 7,800 78 0.078
- 19. Multiple Choice Edit 30 seconds 1 pt Write 2.08 x 10 2 in standard form. 208 0.0208 20,800 0.208
- 20. Multiple Choice Edit 30 seconds 1 pt UNDERSTANDING If the exponent is a negative number... you will get a large number you will get a small number
- 21. Multiple Choice Edit 30 seconds 1 pt UNDERSTANDING: The first number in scientific notation must be... between and including 0 and 10 between and including 1 and 9.9999 between and including 0 and 9.999 between and including 1 and 10
- 22. Multiple Choice Edit 45 seconds 1 pt Which of the following is correct scientific notation? 20.35 x 10 4 .2035 x 10 4 2035 4 2.035 x10 4
- 23. Multiple Choice Edit 30 seconds 1 pt Which is the smallest? 1.3 x 10 20 2.9 x 10 21 9.5 x 10 32 8.4 x 10 19 1.3 x 10 20 2.9 x 10 21 9.5 x 10 32 8.4 x 10 19
- 24. Multiple Choice Edit 2 minutes 1 pt ANY number raised to a power of 0 will be.... 10 itself 1 0
Explore all questions with a free account

Continue with email
Continue with phone
Multiply And Divide In Scientific Notation (Word Problems) Problems
# 1 of 8 : mild.
Multiply and divide in scientific notation (word problems)
# 2 of 8 : Medium
# 3 of 8 : medium, # 4 of 8 : medium, # 5 of 8 : medium, # 6 of 8 : spicy, # 7 of 8 : spicy, # 8 of 8 : spicy.
Scientific notations are used when there is an involvement of very large numbers or very small numbers. Scientific notations are also known as the standard form. All the numbers that are represented in this form have the base of 10. Normally, scientific notations are used by scientists and physicists who perform calculations that involve very large or very small numbers. For example, the weight of the Sun is generally written in scientific notation.
Share this fun and amazing multiplying and dividing scientific notation word problems with yo...
What teachers are saying about Bytelearn What teachers are saying

Add And Subtract In Scientific Notation Convert Standard Form To Scientific Notation Multiply And Divide In Scientific Notation Convert Scientific Notation To Standard Form
Scientific Notation Quiz

This online quiz is intended to give you extra practice in converting between scientific notation and decimal notation.
Select your preferences below and click 'Start' to give it a try!

| Number of problems: | |
| Type of questions: | |
| Count sig figs: | |
| Question format: | |
| Display quiz as: | • • • |
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Course: 8th grade > Unit 1
- Multiplying & dividing in scientific notation
- Multiplying three numbers in scientific notation
- Subtracting in scientific notation
Adding & subtracting in scientific notation
- Simplifying in scientific notation challenge
Multiplying Scientific Notation — Examples & Practice - Expii

IMAGES
VIDEO
COMMENTS
Multiplying & dividing in scientific notation. Calculate the quotient below and give your answer in scientific notation. 2.40 × 10 2 3.0 × 10 − 1 = ? Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a ...
In order to simplify multiplication and division using scientific notation, you should multiply and divide numbers with the same base, and add or subtract the exponents. Through this process, complex expressions can be simplified into a single value multiplied with 10 to a certain power. As an example, 7 times 10 to the fifth over 2 times 10 to ...
Practice Worksheets. A good idea is to get in the habit of circling and rewriting the exponents immediately. Practice 1 - Separate the problem into its two components. a) Constants b) Powers of ten. Practice 3 - The important part is following the sections of the notation before you start to multiply or divide it.
For these problems, our numerator and denominator will be in scientific notation. Then we want our final answer to be in scientific notation as well. (3×102) (6×105) Like multiplication, we can divide the constants and then divide the powers of 10. (36)× (102105) When dividing powers with the same base, you can just subtract the exponents.
To divide two numbers in scientific notation: Step 1: divide their coefficients which may be a decimal number or an integer. Step 2: divide the two exponential numbers (with a base of \(10\)) by subtracting their powers from each other. The answer must be converted to scientific notation. Multiplication and Division in Scientific Notation ...
You begin by dividing the numbers that aren't powers of \displaystyle 10 10 (the a in \displaystyle a\times10^ {n} a × 10n. Then you divide the powers of ten by subtracting the exponents. This will produce a new number times a different power of 10. If it isn't already in scientific notation, you convert it, and then you're done.
Identify components of scientific notation, such as the exponent and digit terms Learn how to multiply and divide using numbers in scientific notation Solve practice problems using information ...
Things You Should Know. Divide the whole numbers, then use the rule of exponents to divide the bases. If the new coefficient is a whole number, multiply the number by the new power of 10 to get your solution. If the new coefficient is not a whole number, convert it to scientific notation before multiplying it by the new power of 10.
Multiplying and Dividing Using Scientific Notation Simplify. Write each answer in scientific notation . 1) (8.18 × 10−6)(1.15 × 10−5) 2) (5.8 × 10−6)(2 × 104) 3) (0.8 × 104)(1.28 × 106) 4) (3.8 × 10−6)(2.37 × 10−3) 5) (1.9 × 10−3)(2 × 104) 6) (9.2 × 105)(4 × 10−3) 7) 7.8 × 104 8 × 101 8) 5.3 × 103 7.65 × 105 9) 4.6 ...
©m m2G0 u1B28 uK1u stPa j BScohf Otjw 1a Er1e c CLeL RCN. Q R EAVl4l1 CrTitg Ohvt su yrIe Usgezr3v me0d O.v T rMEaNdceO NwniVtNhs bICn1fTi3n0i QtJeI 2AolWgBeub 8r7ai k1V.d Worksheet by Kuta Software LLC
Skill plans. IXL plans. Virginia state standards. Textbooks. Test prep. Awards. Multiplying and dividing numbers in scientific notation. Share lesson:
Multiplication and Division. Ferret out the practice in our free, printable multiplication and division with scientific notation worksheets, and flaunt your flair for very big or very small numbers. Draw on your dexterity in simplifying and deciphering small or large numerals in convenient forms, while diligently applying the principles of ...
Let us take a look at a few examples to help you understand the above procedures better. Example 1. Divide and express the answer in scientific notation: 9 x 10 8 / 3 x 10 5. Explanation. Start by dividing the coefficients: (9 ÷ 3) = 3. Now, divide the bases using the division rule of exponents: (10 8 ÷ 10 5) = 10 8 - 5 =10 3.
Express this number in scientific notation. 0.3643. Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class education for anyone, anywhere.
Multiplying and Dividing in Scientific Notation (Word Problems) 1. Multiple Choice. A factory can make 3 x 10 4 t-shirts per day, how many t-shirts will it make in 2.5 x 10 2 days? 2. Multiple Choice. The US spends on average 10,200 dollars on each student per year. There are about 77,000,000 students in the United States.
11. Summarize Multiplying and Dividing Numbers in Scientific Notation, Attachment F. Instruct students to complete a graphic organizer which compares multiplying and dividing numbers in scientific notation. If students are not familiar with using graphic organizers in mathematics, model the use and discuss the structure of the organizer.
Multiplying & Dividing in Scientific Notation Practice quiz for 8th grade students. Find other quizzes for Mathematics and more on Quizizz for free!
Normally, scientific notations are used by scientists and physicists who perform calculations that involve very large or very small numbers. For example, the weight of the Sun is generally written in scientific notation. Share this fun and amazing multiplying and dividing scientific notation word problems with yo...
Scientific Notation Quiz. Dark mode. This online quiz is intended to give you extra practice in converting between scientific notation and decimal notation. Select your preferences below and click 'Start' to give it a try! Number of problems: 1. 5. 10.
Multiplying & dividing in scientific notation. Subtracting in scientific notation. Adding & subtracting in scientific notation. Simplifying in scientific notation challenge. Math > 8th grade > ... Report a problem. Loading... Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history ...
Multiplying Scientific Notation — Examples & Practice - Expii ... Multiplying and Dividing Scientific Notation. ... Let's jump right in with a problem: (2×103)⋅(4×1020) The order in which you multiply doesn't matter. We start by multiplying the constants, and then the powers of 10. (2⋅4)×(103⋅1020) When multiplying powers with the ...