

Free Mathematics Tutorials

Normal Distribution Problems with Solutions
Problems and applications on normal distributions are presented. The solutions to these problems are at the bottom of the page. An online normal probability calculator and an inverse normal probability calculator may be useful to check your answers.
Problems with Solutions
- X is a normally distributed variable with mean μ = 30 and standard deviation σ = 4. Find the probabilities a) P(X < 40) b) P(X > 21) c) P(30 < X < 35)
- A radar unit is used to measure the speeds of cars on a motorway. The speeds are normally distributed with a mean of 90 km/hr and a standard deviation of 10 km/hr. What is the probability that a car picked at random is traveling at more than 100 km/hr?
- For certain types of computers, the length of time between charges of the battery is normally distributed with a mean of 50 hours and a standard deviation of 15 hours. John owns one of these computers and wants to know the probability that the length of time will be between 50 and 70 hours.
- Entry to a certain University is determined by a national test. The scores on this test are normally distributed with a mean of 500 and a standard deviation of 100. Tom wants to be admitted to this university and he knows that he must score better than at least 70% of the students who took the test. Tom takes the test and scores 585. Will he be admitted to this university?
- The length of similar components produced by a company is approximated by a normal distribution model with a mean of 5 cm and a standard deviation of 0.02 cm. If a component is chosen at random a) what is the probability that the length of this component is between 4.98 and 5.02 cm? b) What is the probability that the length of this component is between 4.96 and 5.04 cm?
- The length of life of an instrument produced by a machine has a normal distribution with a mean of 12 months and a standard deviation of 2 months. Find the probability that an instrument produced by this machine will last a) less than 7 months. b) between 7 and 12 months.
- The time taken to assemble a car in a certain plant is a random variable having a normal distribution of 20 hours and a standard deviation of 2 hours. What is the probability that a car can be assembled at this plant in a period of time a) less than 19.5 hours? b) between 20 and 22 hours?
- A large group of students took a test in Physics and the final grades have a mean of 70 and a standard deviation of 10. If we can approximate the distribution of these grades by a normal distribution, what percent of the students a) scored higher than 80? b) Should pass the test (grades≥60)? c) Should fail the test (grades<60)?
- The annual salaries of employees in a large company are approximately normally distributed with a mean of $50,000 and a standard deviation of $20,000. a) What percent of people earn less than $40,000? b) What percent of people earn between $45,000 and $65,000? c) What percent of people earn more than $70,000?
Solutions to the Above Problems
- Note: What is meant here by area is the area under the standard normal curve. a) For x = 40, the z-value z = (40 - 30) / 4 = 2.5 Hence P(x < 40) = P(z < 2.5) = [area to the left of 2.5] = 0.9938 b) For x = 21, z = (21 - 30) / 4 = -2.25 Hence P(x > 21) = P(z > -2.25) = [total area] - [area to the left of -2.25] = 1 - 0.0122 = 0.9878 c) For x = 30 , z = (30 - 30) / 4 = 0 and for x = 35, z = (35 - 30) / 4 = 1.25 Hence P(30 < x < 35) = P(0 < z < 1.25) = [area to the left of z = 1.25] - [area to the left of 0] = 0.8944 - 0.5 = 0.3944
- Let x be the random variable that represents the speed of cars. x has μ = 90 and σ = 10. We have to find the probability that x is higher than 100 or P(x > 100) For x = 100 , z = (100 - 90) / 10 = 1 P(x > 90) = P(z > 1) = [total area] - [area to the left of z = 1] = 1 - 0.8413 = 0.1587 The probability that a car selected at random has a speed greater than 100 km/hr is equal to 0.1587
- Let x be the random variable that represents the length of time. It has a mean of 50 and a standard deviation of 15. We have to find the probability that x is between 50 and 70 or P( 50< x < 70) For x = 50 , z = (50 - 50) / 15 = 0 For x = 70 , z = (70 - 50) / 15 = 1.33 (rounded to 2 decimal places) P( 50< x < 70) = P( 0< z < 1.33) = [area to the left of z = 1.33] - [area to the left of z = 0] = 0.9082 - 0.5 = 0.4082 The probability that John's computer has a length of time between 50 and 70 hours is equal to 0.4082.
- Let x be the random variable that represents the scores. x is normally distributed with a mean of 500 and a standard deviation of 100. The total area under the normal curve represents the total number of students who took the test. If we multiply the values of the areas under the curve by 100, we obtain percentages. For x = 585 , z = (585 - 500) / 100 = 0.85 The proportion P of students who scored below 585 is given by P = [area to the left of z = 0.85] = 0.8023 = 80.23% Tom scored better than 80.23% of the students who took the test and he will be admitted to this University.
- a) P(4.98 < x < 5.02) = P(-1 < z < 1) = 0.6826 b) P(4.96 < x < 5.04) = P(-2 < z < 2) = 0.9544
- a) P(x < 7) = P(z < -2.5) = 0.0062 b) P(7 < x < 12) = P(-2.5 < z < 0) = 0.4938
- a) P(x < 19.5) = P(z < -0.25) = 0.4013 b) P(20 < x < 22) = P(0 < z < 1) = 0.3413
- a) For x = 80, z = 1 Area to the right (higher than) z = 1 is equal to 0.1586 = 15.87% scored more that 80. b) For x = 60, z = -1 The area to the right of z = -1 is equal to 0.8413 = 84.13% should pass the test. c) 100% - 84.13% = 15.87% should fail the test.
- a) For x = 40000, z = -0.5 The area to the left (less than) of z = -0.5 is equal to 0.3085 = 30.85% earn less than $40,000. b) For x = 45000 , z = -0.25 and for x = 65000, z = 0.75 The area between z = -0.25 and z = 0.75 is equal to 0.3720 = 37.20 earning between $45,000 and $65,000. c) For x = 70000, z = 1 The area to the right (higher) of z = 1 is equal to 0.1586 = 15.86% earning more than $70,000.
More References and links
- Normal Distribution Definition
- Elementary statistics and probabilities
Popular Pages
- Normal Distribution Probability Calculator
- Probability Questions with Solutions
- Elementary Statistics and Probability Tutorials and Problems
- Introduction to Probability
- Mean and Standard deviation - Problems with Solutions
Stay In Touch
- Privacy Policy
Normal distribution - practice problems
Number of problems found: 54.
- all math problems 18832
- statistics 781
- normal distribution 54
- standard deviation 15
- probability 9
- comparing 6
- binomial distribution 6
- percentages 6
- algebra 5561
- arithmetic 4234
- basic functions 5936
- combinatorics 1007
- geometry 3072
- goniometry and trigonometry 563
- numbers 6250
- physical quantity 6396
- planimetrics 3407
- solid geometry 2292
- themes, topics 3031

- New math problems
- Popular math problems
- Harder math problems
- The easiest word problems

Normal Distribution
In these lessons, we learn the characteristics of the normal distribution and its applications.
Related Pages Normal Distribution Normal Distribution: Probability Standard Deviation More Lessons for Statistics Math Worksheets
What is the Normal Distribution? Probably the most widely known and used of all distributions is the normal distribution. It fits many human characteristics, such as height, weight, speed etc. Many living things in nature, such as trees, animals and insects have many characteristics that are normally distributed. Many variables in business and industry are also normally distributed.
Discovery of the normal curve is generally credited to Karl Gauss (1777 – 1855), who recognized that the errors of repeated measurement of objects are often normally distributed. Sometimes, the normal distribution is also called the Gaussian distribution.
The normal distribution has the following characteristics:
- It is a continuous distribution
- It is symmetrical about the mean. Each half of the distribution is a mirror image of the other half.
- It is asymptotic to the horizontal axis. That is, it does not touch the x -axis and it goes on forever in each direction.
- It is unimodal. The normal curve is sometimes called a bell-shaped curve. All the values are “bunched up” in only one portion of the graph – the center of the curve.
- It is a family of curves. Every unique value of the mean and every unique value of the standard deviation result in a different normal curve.
- The area under the curve is 1. The area under the curve yields the probabilities, so the total of all probabilities for a normal distribution is 1. Since the distribution is symmetric, the area of the distribution on each side of the mean is 0.5.
What is the Probability density function of the normal distribution? The normal distribution is described by two parameters: the mean, μ, and the standard deviation, σ. We write X - N(μ, σ 2 ).
The following diagram shows the formula for Normal Distribution. Scroll down the page for more examples and solutions on using the normal distribution formula.

Since the formula is so complex, using it to determine area under the curve is cumbersome and time consuming. Instead, tables and software are used to find the probabilities for the normal distribution. This will be discussed in the lesson on Z-Score .
Normal Distribution The 68-95-99.7 Rule
- Approximately 68% of the data falls ±1 standard deviation from the mean.
- Approximately 95% of the data falls ±2 standard deviation from the mean.
- Approximately 99.7% of the data falls ±3 standard deviation from the mean.
In a call center, the distribution of the number of phone calls answered each day by each of the 12 receptionists is bell-shaped and has a mean of 63 and a standard deviation of 3. Use the empirical rule, what is the approximate percentage of daily phone calls numbering between 60 and 66?
The scores of a midterm are normally distributed with a mean of 85% and a standard deviation of 6%. Find the percentage of the class that score above and below the given score. Use the 68-95-99.7 rule from the text. a) Score: 91% b) Score: 73%
The following video explores the normal distribution
Presentation on spreadsheet to show that the normal distribution approximates the binomial distribution for a large number of trials.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
Normal Distribution Word Problems
What is frequency, frequency distribution, what is probability, probability distribution, types of distributions, normal distribution.

When people think about modern statistics, they often think about the immense advancements in the realm of machine learning and artificial intelligence. While self-driving cars and robots are incredible uses of science and maths, the majority of the statistics that are used on a daily basis are really quite simple. Frequency, a descriptive statistic, is one example of this.
Frequency is defined as the number of times something occurs. Take a look at some examples below.
As you can see above, the frequency is calculated by simply counting the number of times something occurs. The information displayed in the chart above would normally be summarised as in the table below.
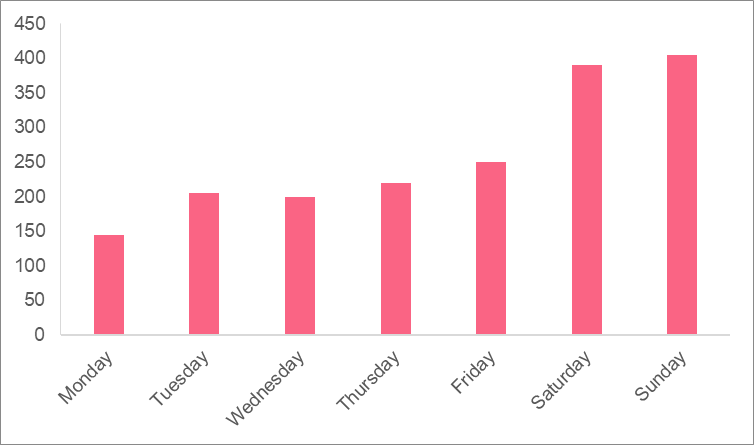
While a frequency distribution can be a formula, a frequency distribution is most often a visual representation of the frequency. Regardless of how its displayed, a frequency distribution helps us get a better understanding of how a variable is distributed, or how a variable looks like. The following table gives the number of passengers riding the bus for every day of the week.
While having this information in a table is very handy, it can often be difficult to understand in plain numbers. Showing the frequency distribution is an easy way to present the frequency in a more understandable manner.
In order to define probability, there are a couple of basic definitions you must understand first. These definitions, along with examples, are listed below.
Probability is defined as the chance, or likelihood, of an event occurring. Continuing the table above:
A probability distribution is a visualization that allows you to see all possible values a random variable can take on along with the probability of each value occurring. While this can sound like a strange concept, we can think about it in terms of the heights of people in the population.
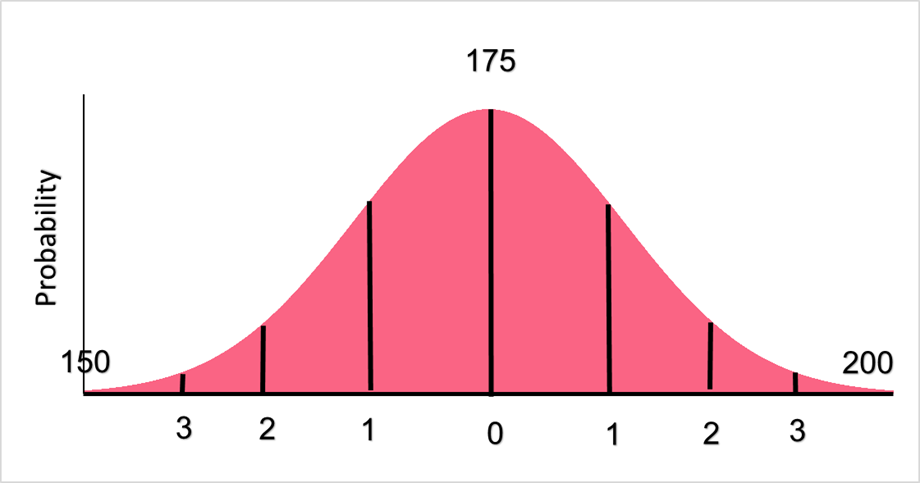
The image above is an example of a probability distribution for heights, where the average height is 175 cm. The distribution shows us that heights that are on the lower and upper end, such as 150 or 200 cm, are much less common in the population. In other words, it is less probable that someone’s height be at either of these ends.
As you can guess, different variables have different distributions. Knowing the distribution of a variable allows us to be able to calculate probabilities. This is because each distribution has a probability equation.
The table above shows the three most common probability distributions. The standard normal distribution is quite special. One major difference is that it’s probability can only be found along with a z-table.
A normal distribution is a continuous probability distribution that is symmetric and has a bell shape. A standard normal distribution is similar to a normal one. Instead of having the variable of interest on the x-axis as a raw score, or a plain number, a standard normal distribution shows each value of the random variable in terms of the standard deviation. Each value is standardized using the equation in the table above, resulting in what is known as a z-score.
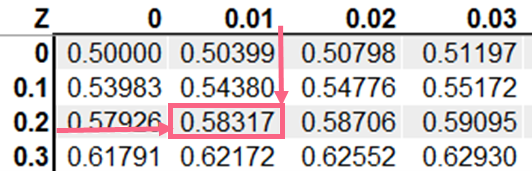
The table above shows an example of a z-table. The image below shows how to look up a z-score on a z-table.
We are interested in knowing how likely it is for one type of tree to grow to a certain length. The length of these trees exhibit a normal distribution. The tree that you measure is 120 cm. Given the following information, do you think this tree length is uncommon for this type of tree?
- Standard deviation: 10

In order to solve this problem, we first need to understand what this distribution will look like. Remember that a standard normal distribution has the mean at the center, with a z-score of 0. The image below represents the mean and the distribution of the tree heights.
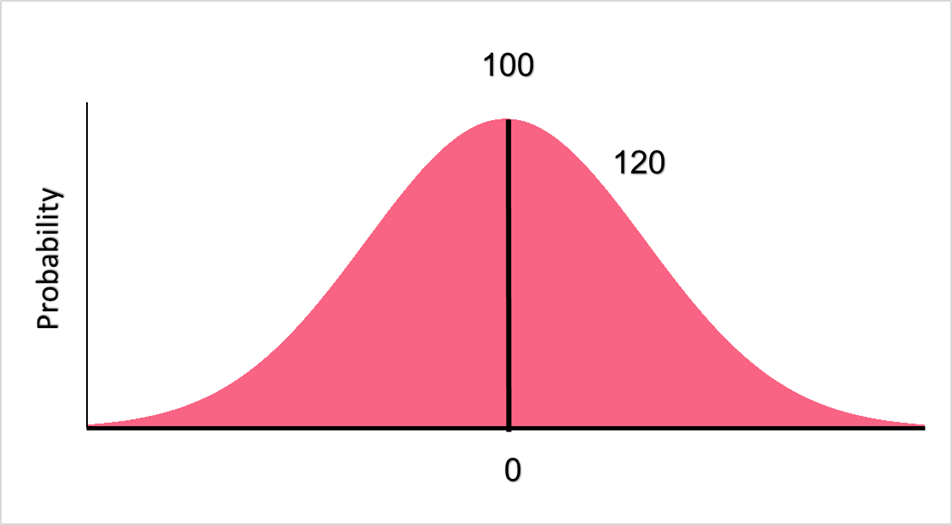
For now, we know that 120cm is located to the right of 100 on the distribution. In order to find its exact location, we need to find the z-score of 120.
z-score = \frac{120-100}{10} = 2
The z-score is 2, which means that the height of 120 is 2 standard deviations above the mean height of 100. Next, we can find this z-score on a z-table.
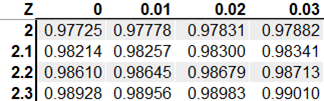
This gives us a probability 0.9772, which is very likely.
You are interested in how uniform the lengths of socks are that are produced at a factory. You measure the distribution and see that there is a normal distribution for the length of the socks. Given the following information, how likely is it that a sock is above 25 cm.
- Standard deviation: 10.5
This time, we want to know how likely it is for a sock to have a length at and above 25 cm. This means that we are looking for a right tail probability instead of a left tail probability. Looking at the distribution will help you understand why.
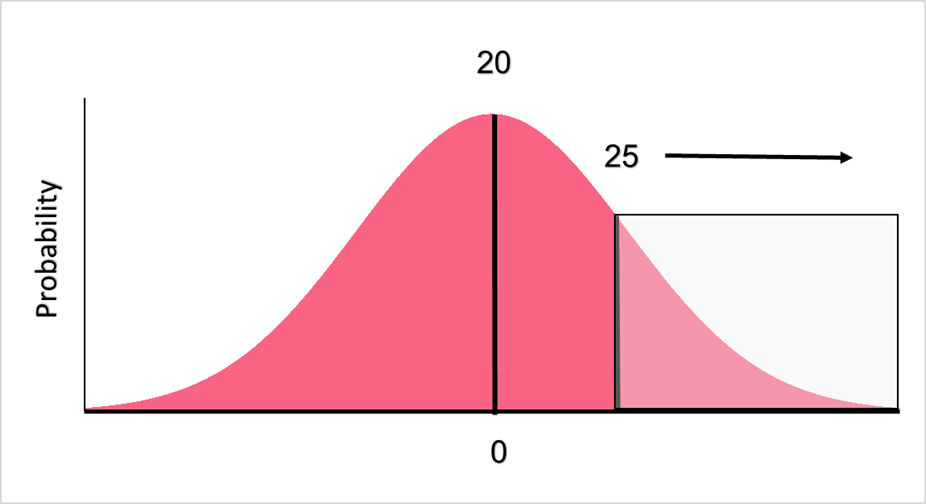
First we find the z-score.
z-score = \frac{20-25}{1.5} = 3.33
Next, we look at the z-table to find the probability.
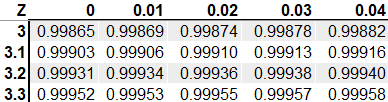
This gives us a probability of 0.0004, which is highly unlikely.
Did you like this article? Rate it!

I am passionate about travelling and currently live and work in Paris. I like to spend my time reading, gardening, running, learning languages and exploring new places.
Solved Problem of Probabilty 8
Measures of central tendency, position and dispersion, solved problems of simple and compound probability, solved problems of conditional probability, confidence interval, solved problem of probabilty 1, solved problem of probabilty 13, solved problem of probabilty 15, confidence interval for the mean, contingency tables, multiplication rule, standard normal table, solved problem of probabilty 10, solved problem of probabilty 14, solved problem of probabilty 6, combinatorics and probability, confidence interval for the proportion, percentiles, conditional probability word problems, using the z table, normal approximation, probability properties, solved problem of probability 18, solved problem of probabilty 5, solved problem of probability 2, tree diagrams, probability theory, bayes’ theorem, conditional probability, standard normal distribution, law of total probability, solved problems of probability 4, solved problems of probability 11, solved problems of probability 17, solved problems of probability 16, solved problems of probability 3, solved problem of probabilty 9, s1 and s2 distributions cheat sheet, probability formulas, arithmetic mean worksheet, confidence interval problems, arithmetic mean problems, median worksheet, mode worksheet, standard deviation problems, probability worksheet, probability word problems, cancel reply.
Your comment
Current ye@r *
Leave this field empty
Using facebook account,conduct a survey on the number of sport related activities your friends are involvedin.construct a probability distribution andbcompute the mean variance and standard deviation.indicate the number of your friends you surveyed
this page has a lot of advantage, those student who are going to be statitian
I’m a junior high school,500 students were randomly selected.240 liked ice cream,200 liked milk tea and 180 liked both ice cream and milktea
A box of Ping pong balls has many different colors in it. There is a 22% chance of getting a blue colored ball. What is the probability that exactly 6 balls are blue out of 15?
Where is the answer??
ere is a 60% chance that a final years student would throw a party before leaving school ,taken over 50 student from a total of 150 .calculate for the mean and the variance
There are 4 white balls and 30 blue balls in the basket. If you draw 7 balls from the basket without replacement, what is the probability that exactly 4 of the balls are white?
Normal Distribution & Probability Problems

If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Statistics and probability
Course: statistics and probability > unit 4, normal distribution problem: z-scores (from ck12.org).
- Comparing with z-scores
- Calculating z-scores
- Z-scores review
Want to join the conversation?
- Upvote Button navigates to signup page
- Downvote Button navigates to signup page
- Flag Button navigates to signup page

Video transcript

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

6.3: Finding Probabilities for the Normal Distribution
- Last updated
- Save as PDF
- Page ID 16356

- Kathryn Kozak
- Coconino Community College
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
The Empirical Rule is just an approximation and only works for certain values. What if you want to find the probability for x values that are not integer multiples of the standard deviation? The probability is the area under the curve. To find areas under the curve, you need calculus. Before technology, you needed to convert every x value to a standardized number, called the z-score or z-value or simply just z . The z-score is a measure of how many standard deviations an x value is from the mean. To convert from a normally distributed x value to a z-score, you use the following formula.
Definition \(\PageIndex{1}\): z-score
\[z=\dfrac{x-\mu}{\sigma} \label{z-score}\]
where \(\mu\)= mean of the population of the x value and \(\sigma\)= standard deviation for the population of the x value
The z-score is normally distributed, with a mean of 0 and a standard deviation of 1. It is known as the standard normal curve. Once you have the z-score, you can look up the z-score in the standard normal distribution table.
Definition \(\PageIndex{2}\): standard normal distribution
The standard normal distribution , z, has a mean of \(\mu =0\) and a standard deviation of \(\sigma =1\).
.png?revision=1)
Luckily, these days technology can find probabilities for you without converting to the zscore and looking the probabilities up in a table. There are many programs available that will calculate the probability for a normal curve including Excel and the TI-83/84. There are also online sites available. The following examples show how to do the calculation on the TI-83/84 and with R. The command on the TI-83/84 is in the DISTR menu and is normalcdf(. You then type in the lower limit, upper limit, mean, standard deviation in that order and including the commas.
Example \(\PageIndex{1}\) general normal distribution
The length of a human pregnancy is normally distributed with a mean of 272 days with a standard deviation of 9 days (Bhat & Kushtagi, 2006).
- State the random variable.
- Find the probability of a pregnancy lasting more than 280 days.
- Find the probability of a pregnancy lasting less than 250 days.
- Find the probability that a pregnancy lasts between 265 and 280 days.
- Find the length of pregnancy that 10% of all pregnancies last less than.
- Suppose you meet a woman who says that she was pregnant for less than 250 days. Would this be unusual and what might you think?
a. x = length of a human pregnancy
b. First translate the statement into a mathematical statement.
P (x>280)
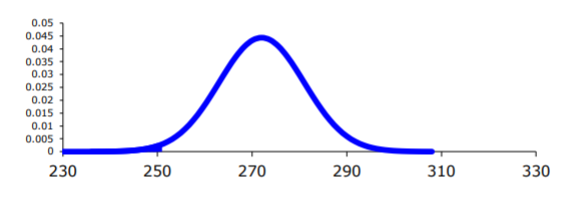
Now, draw a picture. Remember the center of this normal curve is 272.
.png?revision=1)
To find the probability on the TI-83/84, looking at the picture you realize the lower limit is 280. The upper limit is infinity. The calculator doesn’t have infinity on it, so you need to put in a really big number. Some people like to put in 1000, but if you are working with numbers that are bigger than 1000, then you would have to remember to change the upper limit. The safest number to use is \(1 \times 10^{99}\), which you put in the calculator as 1E99 (where E is the EE button on the calculator). The command looks like:
\(\text{normalcdf}(280,1 E 99,272,9)\)
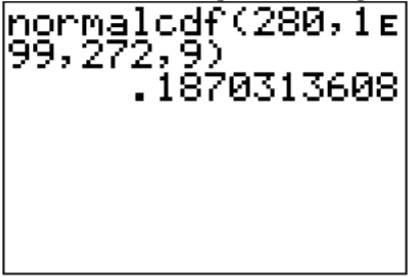.png?revision=1)
Thus 18.7% of all pregnancies last more than 280 days. This is not unusual since the probability is greater than 5%.
c. First translate the statement into a mathematical statement.
P (x<250)
.png?revision=1)
To find the probability on the TI-83/84, looking at the picture, though it is hard to see in this case, the lower limit is negative infinity. Again, the calculator doesn’t have this on it, put in a really small number, such as \(-1 \times 10^{99}=-1 E 99\) on the calculator.
.png?revision=1)
\(P(x<250)=\text { normalcdf }(-1 E 99,250,272,9)=0.0073\)
Thus 0.73% of all pregnancies last less than 250 days. This is unusual since the probability is less than 5%.
d. First translate the statement into a mathematical statement.
\(P(265<x<280)\)
.png?revision=1)
In this case, the lower limit is 265 and the upper limit is 280.
Using the calculator
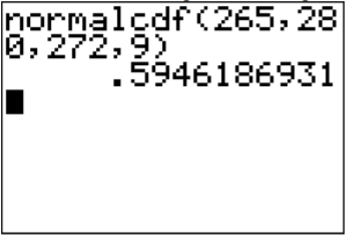.png?revision=1)
\(P(265<x<280)=\text { normalcdf }(265,280,272,9)=0.595\)
Many software programs always give you the area to the left. So \(P(x<280)\) is the area to the left of 280 and \(P(x<265)\) is the area to the left of 265. So the area is between the two would be the bigger one minus the smaller one. So, \(P(265<x<280)= P(x<280) - P(x<265) =0.595\). Thus 59.5% of all pregnancies last between 265 and 280 days.
e. This problem is asking you to find an x value from a probability. You want to find the x value that has 10% of the length of pregnancies to the left of it. On the TI-83/84, the command is in the DISTR menu and is called invNorm(. The invNorm( command needs the area to the left. In this case, that is the area you are given. For the command on the calculator, once you have invNorm( on the main screen you type in the probability to the left, mean, standard deviation, in that order with the commas.
.png?revision=1)
Thus 10% of all pregnancies last less than approximately 260 days.
f. From part (c) you found the probability that a pregnancy lasts less than 250 days is 0.73%. Since this is less than 5%, it is very unusual. You would think that either the woman had a premature baby, or that she may be wrong about when she actually became pregnant.
Example \(\PageIndex{2}\) general normal distribution
The mean mathematics SAT score in 2012 was 514 with a standard deviation of 117 ("Total group profile," 2012). Assume the mathematics SAT score is normally distributed.
- Find the probability that a person has a mathematics SAT score over 700.
- Find the probability that a person has a mathematics SAT score of less than 400.
- Find the probability that a person has a mathematics SAT score between a 500 and a 650.
- Find the mathematics SAT score that represents the top 1% of all scores.
a. x = mathematics SAT score
P (x>700)
Now, draw a picture. Remember the center of this normal curve is 514.
.png?revision=1)
On TI-83/84: \(P(x>700)=\text { normalcdf }(700,1 E 99,514,117) \approx 0.056\)
On R: \(P(x>700)=1-\text { pnorm }(700,514,117) \approx 0.056\)
There is a 5.6% chance that a person scored above a 700 on the mathematics SAT test. This is not unusual.
P (x<400)
.png?revision=1)
On TI-83/84: \(P(x<400)=\text { normalcdf }(-1 E 99,400,514,117) \approx 0.165\)
On R: \(P(x<400)=\operatorname{pnorm}(400,514,117) \approx 0.165\)
So, there is a 16.5% chance that a person scores less than a 400 on the mathematics part of the SAT.
P (500<x<650)
.png?revision=1)
On TI-83/84: \(P(500<x<650)=\text { normalcdf }(500,650,514,117) \approx 0.425\)
On R: \(P(500<x<650)=\text { pnorm }(650,514,117)-\text { pnorm }(500,514,117) \approx 0.425\)
So, there is a 42.5% chance that a person has a mathematical SAT score between 500 and 650.
e. This problem is asking you to find an x value from a probability. You want to find the x value that has 1% of the mathematics SAT scores to the right of it. Remember, the calculator and R always need the area to the left, you need to find the area to the left by 1 - 0.01 = 0.99.
On TI-83/84: \(\text{invNorm}(.99,514,117) \approx 786\)
On R: \(\text{qnorm}(.99,514,117) \approx 786\)
So, 1% of all people who took the SAT scored over about 786 points on the mathematics SAT.
Exercise \(\PageIndex{1}\)
- P (z<2.36)
- P (z>0.67)
- P (0<z<2.11)
- P (-2.78<z<1.97)
- The area to the left of z is 15%.
- The area to the right of z is 65%.
- The area to the left of z is 10%.
- The area to the right of z is 5%.
- The area between -z and z is 95%. (Hint draw a picture and figure out the area to the left of the -z.)
- The area between -z and z is 99%.
- Find the probability that a person in China has blood pressure of 135 mmHg or more.
- Find the probability that a person in China has blood pressure of 141 mmHg or less.
- Find the probability that a person in China has blood pressure between 120 and 125 mmHg.
- Is it unusual for a person in China to have a blood pressure of 135 mmHg? Why or why not?
- What blood pressure do 90% of all people in China have less than?
- Find the probability that an Atlantic cod has a length less than 52 cm.
- Find the probability that an Atlantic cod has a length of more than 74 cm.
- Find the probability that an Atlantic cod has a length between 40.5 and 57.5 cm.
- If you found an Atlantic cod to have a length of more than 74 cm, what could you conclude?
- What length are 15% of all Atlantic cod longer than?
- Find the probability that a woman age 45-59 in Ghana, Nigeria, or Seychelles has a cholesterol level above 6.2 mmol/l (considered a high level).
- Find the probability that a woman age 45-59 in Ghana, Nigeria, or Seychelles has a cholesterol level below 5.2 mmol/l (considered a normal level).
- Find the probability that a woman age 45-59 in Ghana, Nigeria, or Seychelles has a cholesterol level between 5.2 and 6.2 mmol/l (considered borderline high).
- If you found a woman age 45-59 in Ghana, Nigeria, or Seychelles having a cholesterol level above 6.2 mmol/l, what could you conclude?
- What value do 5% of all woman ages 45-59 in Ghana, Nigeria, or Seychelles have a cholesterol level less than?
- Find the probability that a man age 40-49 in the U.S. eats more than 110 g of fat every day.
- Find the probability that a man age 40-49 in the U.S. eats less than 93 g of fat every day.
- Find the probability that a man age 40-49 in the U.S. eats less than 65 g of fat every day.
- If you found a man age 40-49 in the U.S. who says he eats less than 65 g of fat every day, would you believe him? Why or why not?
- What daily fat level do 5% of all men age 40-49 in the U.S. eat more than?
- Find the probability that a dishwasher will last more than 15 years.
- Find the probability that a dishwasher will last less than 6 years.
- Find the probability that a dishwasher will last between 8 and 10 years.
- If you found a dishwasher that lasted less than 6 years, would you think that you have a problem with the manufacturing process? Why or why not?
- A manufacturer of dishwashers only wants to replace free of charge 5% of all dishwashers. How long should the manufacturer make the warranty period?
- Find the probability that a starting nurse will make more than $80,000.
- Find the probability that a starting nurse will make less than $60,000.
- Find the probability that a starting nurse will make between $55,000 and $72,000.
- If a nurse made less than $50,000, would you think the nurse was under paid? Why or why not?
- What salary do 30% of all nurses make more than?
- Find the probability that the yearly rainfall is less than 100 mm.
- Find the probability that the yearly rainfall is more than 240 mm.
- Find the probability that the yearly rainfall is between 140 and 250 mm.
- If a year has a rainfall less than 100mm, does that mean it is an unusually dry year? Why or why not?
- What rainfall amount are 90% of all yearly rainfalls more than?
1. a. \(P(z<2.36)=0.9909\), b. \(P(z>0.67)=0.2514\), c. \(P(0<z<2.11)=0.4826\), d. \(P(-2.78<z<1.97)=0.9729\)
3. a. -0.6667, b. -2.6667, c. -2, d. 6.6667
5. a. See solutions, b. \(P(x<52 \mathrm{cm})=0.7128\), c. \(P(x>74 \mathrm{cm})=5.852 \times 10^{-11}\), d. \(P(40.5 \mathrm{cm}<x<57.5 \mathrm{cm})=0.9729\), e. See solutions, f. 53.8 cm
7. a. See solutions, b. \(P(x>110 \mathrm{g})=0.0551\) c. \(P(x<93 \mathrm{g})=0.0097\), d. \(P(x<65 \mathrm{g}) \approx 0\) or \(5.57 \times 10^{-19}\), e. See solutions, f. 110.2 g
9. a. See solutions, b. \(P(x>\$ 80,000)=0.1168\), c. \(P(x>\$ 80,000)=0.2283\), d. \(P(\$ 55,000<x<\$ 72,000)=0.5519\), e. See solutions, f. $73,112

IMAGES
VIDEO
COMMENTS
Word problems with normal distribution: "Between": Steps. Step 1: Identify the parts of the word problem. The word problem will identify: The mean (average or μ). Standard deviation (σ). Number selected (i.e. "choose one at random" or "select ten at random"). X: the numbers associated with "between" (i.e. "between $5,000 and ...
Problems with Solutions. X is a normally distributed variable with mean μ = 30 and standard deviation σ = 4. Find the probabilities. a) P (X < 40) b) P (X > 21) c) P (30 < X < 35) A radar unit is used to measure the speeds of cars on a motorway. The speeds are normally distributed with a mean of 90 km/hr and a standard deviation of 10 km/hr.
This calculus video tutorial provides a basic introduction into normal distribution and probability. It explains how to solve normal distribution problems u...
This video shows how to calculate probabilities for word problems using the normal distribution.
Solution: Step 1: Sketch a normal distribution with a mean of μ = 150 cm and a standard deviation of σ = 30 cm . Step 2: The diameter of 120 cm is one standard deviation below the mean. Shade below that point. Step 3: Add the percentages in the shaded area: 0.15 % + 2.35 % + 13.5 % = 16 %.
General steps for solving normal probability practice problems: Use the equation above to find a z-score. If you don't know how to look up z-scores (or if you want more practice, see this z-score article for videos and step-by-step instructions. Look up the z-score in the z-table and find the area. Convert the area to a percentage.
This is a great review of the Normal Distribution curve. This video assumes you know the basics. In this video I provide a few problems with the solutions...
Step 5. From the 0.5th and 99.5th percentiles of the standard normal distribution, solve for the corresponding values of the normal distribution that has mean=100 and sd=14. Tip - Notice that the 0.5th and 99.5th percentiles are -2.57 and +2.57, symmetric about zero. So, really, we only needed to solve for one of them.
Normal distribution - practice problems. It is used for random variables that are the sum of a large number of independent or only weakly dependent values. The probability distribution has a bell-shaped Gaussian curve. It is symmetric around the mean value μ, both median and mode.
STATS 113 Problem Sessions Normal Distribution/Empirical Rule/Z-Scores Word Problems 1. The average playing time of CDs in a large collection is 35 minutes, and the standard deviation is ... The red blood cell count for a population of adult males can be approximated by a normal distribution, with a mean of 5.4 million cells per microliter and ...
Transcript. The empirical rule (also called the "68-95-99.7 rule") is a guideline for how data is distributed in a normal distribution. The rule states that (approximately): - 68% of the data points will fall within one standard deviation of the mean. - 95% of the data points will fall within two standard deviations of the mean. - 99.7% of the ...
The scores of a midterm are normally distributed with a mean of 85% and a standard deviation of 6%. Find the percentage of the class that score above and below the given score. Use the 68-95-99.7 rule from the text. a) Score: 91%. b) Score: 73%. Show Video Lesson. The following video explores the normal distribution.
Solution 1. In order to solve this problem, we first need to understand what this distribution will look like. Remember that a standard normal distribution has the mean at the center, with a z-score of 0. The image below represents the mean and the distribution of the tree heights.
Normal Distribution Word Problem with Z-score. This video shows how to calculate probabilities for word problems using the normal distribution. Normal distri...
Step 1: Write the probability desired in probability notation in terms of the raw score, x. Note both the mean, μ, and standard deviation of the distribution of raw scores. Step 2: Standardized ...
What is a normal distribution and how to use it in statistics? Learn the definition, formulas, examples, and applications of this common data pattern. Find out how to calculate the mean, standard deviation, and z-scores of a normal distribution, and how to compare it with other distributions. Scribbr offers clear and concise explanations, diagrams, and calculators to help you master this topic.
One standard deviation above the mean is 37 hours. The bell curve of a normal distribution puts the mean at 50%. One standard deviation in either direction is 34% away from the mean. So, one standard deviation is 84% of the employees. Since 84% of the employees work 37 hours, 16% work more than 37 hours. 16% of 450 employees = 72. No trick.
It explains how to solve normal distribution problems using a simple chart and using calculus by evaluating the definite integral of the probability density function for a bell shaped curve or normal distribution curve. This video contains 1 practice problem in the form of a word problem with many parts giving you plenty of examples to master ...
The grades on a statistics midterm for a high school are normally distributed with a mean of 81 and a standard deviation of 6.3. All right. Calculate the z-scores for each of the following exam grades. Draw and label a sketch for each example. We can probably do it all on the same example.
Wonder how to estimate and calculate a normal distribution problem? This video will show you how.
Normal Probabilites Practice Solution.doc. Normal Probabilities Practice Problems Solution. 5. The average number of acres burned by forest and range fires in a large New Mexico county is 4,300 acres per year, with a standard deviation of 750 acres. The distribution of the number of acres burned is normal.
To convert from a normally distributed x value to a z-score, you use the following formula. Definition 6.3.1 6.3. 1: z-score. z = x − μ σ (6.3.1) (6.3.1) z = x − μ σ. where μ μ = mean of the population of the x value and σ σ = standard deviation for the population of the x value.
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features NFL Sunday Ticket Press Copyright ...