problem solving draw a picture and write an equation 2 9

• Grades 6-12
• School Leaders

Free end-of-year letter templates to your students 📝!

Teaching Math Word Problems with Pictures

Help your students visualize their answers.

If you google word problem jokes, this one will pop up a lot:

“If you have 4 pencils and I have 7 apples, how many pancakes will fit on the roof?

Purple, because aliens don’t wear hats.”

It’s hilarious because it’s true! Many of our students see nonsense in word problems. They not only have to figure out what the word problem is asking them to do, but then they have to actually solve it. It’s a process. However, if we want them to internalize the concept, not just the numbers, pictures can help! Visuals can help students comprehend meaning when the words aren’t making sense to them. Don’t underestimate the power of teaching word problems with pictures. Here are a few easy ways to incorporate visuals into everyday math:

The power of “acting it out”

Before you go from manipulatives to drawing, try having students act out problems. If the problems involve eating, bring in food and have a student actually act like they are in the story problem. If the problem involves a specific number of boys and girls, have that many students get up and show the class what is going on in the problem. Taking this step will help students visualize the problem and think about the actions rather than just guessing if they should add, subtract, multiply, or divide.

[contextly_auto_sidebar]

Getting ready to draw

When you’re ready to start solving word problems with pictures, follow Jan Rowe’s steps :

• Read the entire problem: Get all the facts and underline keywords.
• Answer the question: What am I looking for?
• Draw a picture or diagram: Visualize as a real-world situation.
• Solve the problem: Set up the equation and solve.
• Check your solution: Is this answer reasonable?

Drawing as a step of the process

Visual representations are a good starting point for word problems because it is an intermediate step between language-as-text and the symbolic language of math . Drawing lowers the affective filter because it can be less stressful. We aren’t stepping straight into that equation; we are just drawing to figure out what the question is actually asking us. Remind students that we are not in art class. It is perfectly OK for your math pictures to be just scribbles as long as you know what they represent. Another great perk of the “Draw a Picture” strategy is that you, as a teacher, can really step inside the student’s brain to see how their mathematical brain works. Encourage labeling so that you can catch misconceptions right away. These drawings can lead to great math talk conversations, which build that academic language that we all want to hear.

Jayden had two boxes of books with twelve books in each box. He gave four books to his sister. How many books did Jayden keep for himself?

Draw a picture:

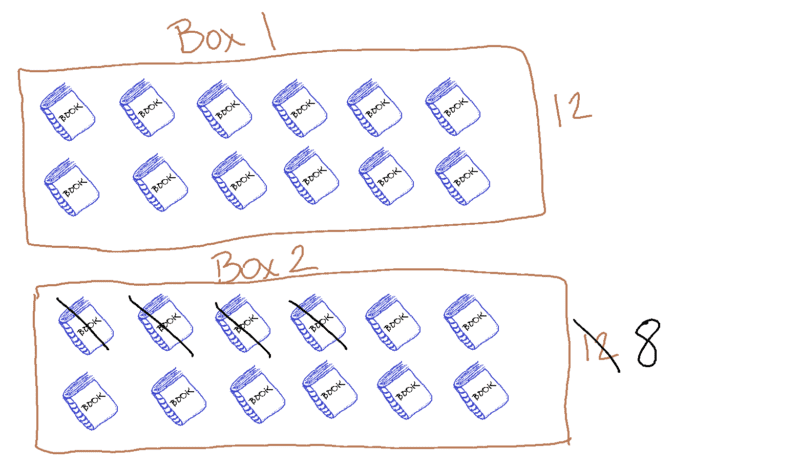
Try photography instead of drawing

Story problems are grounded in reading. Photograph Math is an activity that can help visual learners grasp the math skill first, then add in the language. All you’ll need is a camera (or phone) to take pictures. Here’s how it works:

• Students brainstorm the ways in which, and the places where, they use math.
• They stage a photograph representing one of these ideas.
• Students write their own real-life word problems to go with their posed photograph(s).
• Students take a photograph of the menu inside the cafeteria. They write problems that help them figure out how much money they need to get specific lunches, snacks, or drinks. Extension: Think about how much you would need to get a snack every day, for a week, etc.
• Someone might take a photo of a number on a library book. Then try to figure out what value that number would have based on the number of digits and round the number to the nearest whole, tenths, or hundredth.
• Students take a photo of your stash of whiteboards markers. They could write problems about the amount of each color you have. They may choose to think about what happens if another teacher borrows a certain number of markers, etc.

Photograph math can help students to start thinking like a mathematician in all aspects of life. If students begin to see the math around them, then they can truly begin to comprehend the story problems that we present to them in class.

Read a math picture book

Remember when I said story problems are grounded in reading? Why not use actual stories? Children’s picture books can provide a rich context from which to begin mathematical investigations . As students see math concepts play out in stories and illustrations, they are engaged and better able to construct meaning. Seeing the problem-solving process in action through a book can serve as a model for students when they go off on their own to solve problems. Here is a list of 16 picture books about math .

Assign math as picture prompts

Consider starting each week with a relevant picture prompt. Sometimes, the picture is of a mathematical error we came across in real life. The challenge to students is to figure out the mistake. Other times, we simply provide an image and challenge students to come up with a story problem to accompany it. Giving students ownership of these problems can strengthen and extend their comprehension of story problems.

• Put up a sign of a price mistake in a store. Then write on the board: “Ms. Caudill saw this sign at Walmart this weekend and laughed. Why? How might you fix it?”
• Show students the following prompt: Write a story problem using the photo and the following word bank: apples, tomatoes, sweet potatoes, pound, gallon, farmer’s market.

The truth is, story problems are challenging for all students. We have to find ways to make the story problems relative to students’ lives if we want them to succeed.

How do you teach word problems with pictures? Share in the comments below.

Want even more strategies for teaching word problems check out 14 effective ways to help your students conquer math word problems ., want more articles like this make sure to sign up for my weekly newsletter for third grade teachers .

You Might Also Like

14 Effective Ways to Help Your Students Conquer Math Word Problems

If a train leaving Minneapolis is traveling at 87 miles an hour... Continue Reading

Copyright © 2024. All rights reserved. 5335 Gate Parkway, Jacksonville, FL 32256

Get step-by-step solutions to your math problems

Try Math Solver

Get step-by-step explanations

Graph your math problems

Practice, practice, practice

Graphing Calculator

Generating pdf....

Please add a message.

Message received. Thanks for the feedback.

2-9 Problem Solving: Draw A Picture And Write An Equation

By m seelhorst on feb 19, 2016.

About FAQ Contact Terms Privacy © 2024 Educreations, Inc.

• Try for free

Problem Solving: Draw a Picture

Problem-solving is a critical 21st Century and social-emotional skill

Looking for more resources on 21st Century skills and social-emotional learning? Find them in our FutureFit resources center .

What Is It?

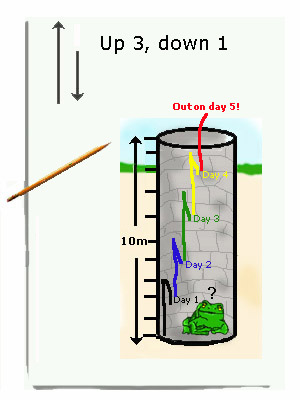
The draw a picture strategy is a problem-solving technique in which students make a visual representation of the problem. For example, the following problem could be solved by drawing a picture:

A frog is at the bottom of a 10-meter well. Each day he climbs up 3 meters. Each night he slides down 1 meter. On what day will he reach the top of the well and escape?

Why Is It Important?

Drawing a diagram or other type of visual representation is often a good starting point for solving all kinds of word problems . It is an intermediate step between language-as-text and the symbolic language of mathematics. By representing units of measurement and other objects visually, students can begin to think about the problem mathematically . Pictures and diagrams are also good ways of describing solutions to problems; therefore they are an important part of mathematical communication.

How Can You Make It Happen?

Encourage students to draw pictures of problems at the very beginning of their mathematical education. Promote and reinforce the strategy at all subsequent stages. Most students will naturally draw pictures if given the slightest encouragement.

Introduce a problem to students that will require them to draw a picture to solve. For example:

Marah is putting up a tent for a family reunion. The tent is 16 feet by 5 feet. Each 4-foot section of tent needs a post except the sides that are 5 feet. How many posts will she need?

Demonstrate that the first step to solving the problem is understanding it. This involves finding the key pieces of information needed to figure out the answer. This may require students reading the problem several times or putting the problem into their own words.

16 feet by 5 feet 1 post every 4 feet, including 1 at each corner No posts on the short sides

Choose a Strategy

Most often, students use the draw a picture strategy to solve problems involving space or organization, but it can be applied to almost all math problems. Also students use this strategy when working with new concepts such as equivalent fractions or the basic operations of multiplication and division.

In This Article:

Featured high school resources.

Related Resources

About the author

TeacherVision Editorial Staff

The TeacherVision editorial team is comprised of teachers, experts, and content professionals dedicated to bringing you the most accurate and relevant information in the teaching space.

Standards Alignment

Assessments, professional learning, family engagement, case studies.

NEW EUREKA MATH 2 ® PILOT PACKAGE

Are you looking for new ways to advance equity and build knowledge in your math classroom with high-quality instructional materials? EdReports recently reviewed Eureka Math 2 . Scan the QR code or access the final report .

Check out our special pilot package for only $10 per student.

Shop Online

SEE THE SCIENCE OF READING IN ACTION

At Great Minds ® , we’re committed to ensuring our curricula are aligned to the latest research on how students best learn to read, write, and build knowledge.

Explore webinars, blogs, research briefs, and more to discover how we incorporate this important body of research.

FREE CLASSROOM PRINTABLES

At Great Minds®, we’re committed to supporting educators with high-quality curricula and resources.

Explore resources designed to aid students in science and engineering and spark classroom conversation.

Webinar Library

Instructional resources, trending topics, knowledge-building, the science of reading, lesson design, universal design for learning (udl), background knowledge.

Palm Springs, CA

Houston, TX

New Orleans, LA

Topics: Featured Math Concepts Conceptual Understanding Eureka Math Squared

From Read-Draw-Write (RDW) to Modeling–How Students Experience Problem Solving in Eureka Math²

by Great Minds

every child is capable of greatness.

Posted in: Aha! Blog > Eureka Math Blog > Math Concepts Conceptual Understanding Eureka Math Squared > From Read-Draw-Write (RDW) to Modeling–How Students Experience Problem Solving in Eureka Math²

Coherence is a key feature of the Eureka Math 2 ® curriculum. The problem-solving process employed in Grade Levels K–9 is a major part of that coherence. In Grade Levels K–5, students know it as the Read–Draw–Write (RDW) process. Starting in Grade Level 6 the process advances to Read, Represent, Solve, Summarize (RRSS) while maintaining the same foundational approach. Word problems become accessible as students cycle through reading and representing parts of a word problem to make sense of it. The process is simple, memorable, and powerful enough to support all students with language demands, sense-making, and algebraic thinking. This paper outlines the progression of problem-solving in Eureka Math 2 . We invite you to discover where your students fit into this progression, how you can support them with the work of prior grades, and build the foundation needed to problem-solve in subsequent grades.

Grade Levels K–2

The Read–Draw–Write process for solving word problems is introduced and intentionally taught step-by-step in Grade Levels K–2. You may not always recognize the developmental progression of this problem-solving process. After all, the first piece of the process is Read, a skill many of our youngest students have not learned yet. Let’s follow the journey our students take to problem-solving.

Kindergarten

One of the first experiences students have with problem-solving is counting. In the kindergarten Module 1, Topic G, Lesson 33, students use 10-frames and other problem-solving tools. Young students sometimes employ the Read-Draw-Write process without knowing it.

Are they counting a large set of objects or a small set?

Are the objects movable, or are they part of a picture?

Can they group the objects to count?

Even before students can technically read, they take in information and understand the task to get started.

The next step is Drawing. How can students organize the information they took in during the Read phase to solve the problem? For our young students, this may look like crossing out or drawing objects, it may be writing an equation or making tally marks, or it may be simply using their fingers to track their counting. Finally, students Write: they state or write the answer they have arrived at after contextualizing the problem. “There are 9 buttons!” or “I counted 25 erasers. I made 2 groups of ten and had five ones.”

Kindergarten students progress to more traditional problem-solving scenarios later in the year. In Grade Level Kindergarten Module 5 Topic A Lesson 2, students represent a math story by using pictures, number bonds, and number sentences.

There are some pigeons on our playground. Then, some more pigeons land on our playground. What could this math story look like?

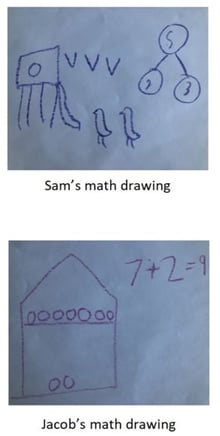
The title Read–Draw–Write may be misleading. Understanding and recognizing the more subtle instances of this powerful problem-solving strategy when reading, drawing, and writing may not be applicable in the literal sense is important.

Grade Level 1

In Grade Level 1, RDW expands to include all addition and subtraction problem types. Most problems students were presented with in kindergarten were the dark-shaded problem types shown in the chart. Grade Level 1 signals the transition to working with all the problem types in the chart, including the more challenging types shown in white.

As students’ problem-solving development progresses, it is important to spend time crafting the problems. Problems should be varied in type, and the numbers in the problems need to be high enough so that RDW is necessary to find the answer. For example, in Grade Level 1, Module 2, Lesson 8, students see a Change Unknown problem.

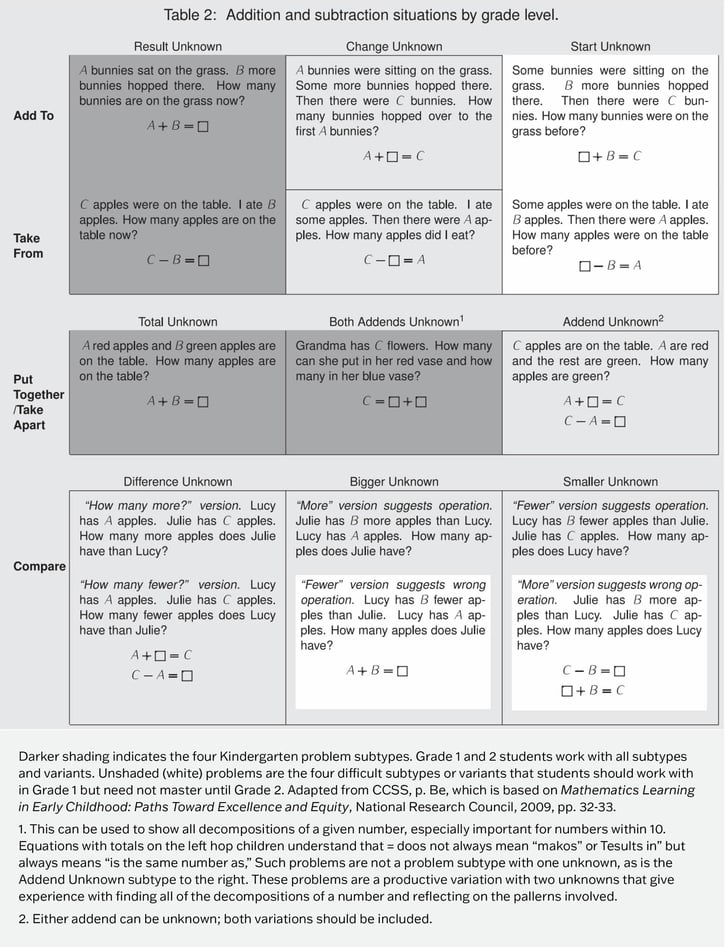
The numbers in this problem are large enough to make mental math more challenging, and the problem type lends itself to drawing to understand what the question is asking. If we ask students to use RDW with a problem that is too “easy,” for example:

Kit is coloring a rainbow.

She has 3 markers and she gets 4 more.

How many markers does she have?

Students won’t see the value in problem-solving with RDW because they could do mental math or count on their fingers, which we want them to do in circumstances like this. Teaching first-grade students to discern when to use RDW is important, and asking them to “show your work” may not always be appropriate.

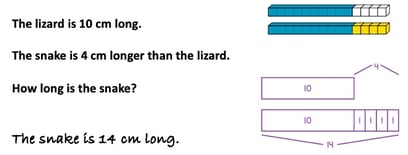
Comparison problem types frequently provide the productive struggle that leads to students seeing the need to use RDW. In Module 4, the tape diagram is taught and explored in the context of measurement. It begins with concrete cube trains (read) and moves to a tape diagram, a pictorial recording (draw), and then an equation and a statement (write).

Grade Level 2

With these added problem-solving complexities, Grade Level 2 students will find the part between reading and drawing the most challenging. Drawing a model that shows what is being asked in the problem and what helps students solve the problem needs to be the focus in this teaching. For example, in Module 4 Lesson 3, this problem requires two-steps to solve it. First, a student must understand that they need to find the total number of cars and trucks. Second, they must understand that they are only solving for the number of trucks. The round numbers in this problem are intentional because we want students to attend to the set-up of the problem rather than worrying about the calculations.

Further along in the Module, the numbers and the problem types increase in complexity. The focus remains on drawing or representing the problem, so students perform the correct operation with the correct numbers. Too often, students look at the numbers presented in a word problem and guess whether they should add or subtract them to get an answer. We hope to prevent that by teaching the RDW problem-solving process, as shown below.

Grade Levels 3–5

In Grade Levels 3–5, students use the RDW process to solve word problems involving all operations and to build multi-step problems. Lessons emphasize students developing strategies to address newer complexities of multiplication, division, and working with fractions in word problems.

Beginning in Grade Level 3, students are introduced to division through the context of word problems and encounter two types of division. In a partitive division problem, the number of groups and the total are known, but the number in each group is unknown. Partitive division asks, “How many are in each group?” In measurement division, the total and number in each group are known, but the number of groups is unknown. Measurement division asks the question, “How many groups are there?” Using the RDW process, students create a drawing that accurately represents the known and unknown number of groups and the number in each group to reveal the solution path.

In Grade Level 3, Module 1, Topic B, Lesson 9, students solve a partitive and measurement division problem using the RDW process. As they read and draw, they discern and represent what is known. Then, they identify the unknown and use division to solve it. In the problem shown here involving 24 desks, the number of groups is known. One approach is to begin by drawing 6 circles to represent the groups, then sharing the 24 desks between the groups. There is flexibility in the RDW process for students to draw and solve in a way that makes sense. In this case, a second student starts by drawing the 24 desks and knows they must form 6 equal groups. They can determine that forming six equal groups will result in 4 desks in each group.

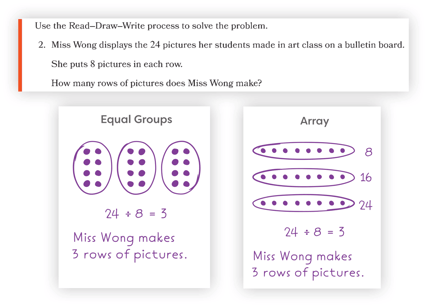
How does thinking about what is known and unknown help you solve division word problems? Thinking about what is known helps me know if I should draw the number of groups or the number in each group. If the unknown is the number of groups, I can count the number of groups in my drawing to solve the problem. If the unknown is the number in each group, I can look at the number in each group in my drawing to solve the problem.

Later, in Lesson 18, students represent partitive and measurement division word problems with tape diagrams, rather than with equal groups. As a built-in feature of the RDW process, the teacher asks consistent questions: What is known? What is unknown? and How is it represented in the tape diagram? Students can consider those questions and rely on the familiar process of reading and representing the problem in chunks until identifying a path to solve it, even with the more abstract tape diagram. That process also reveals the difference between partitive and measurement division problems and deepens students’ understanding of problem-solving.

In Grade Level 4, word problem contexts expand to include multiplicative comparisons. There are multiple variations of the language in a problem that students encounter. Reading and drawing to represent the parts of the problem helps students distinguish between the known and unknown. In multiplicative comparison problems, the relationship between two quantities is often stated as “___ times as many as ___”, in other contexts, it is stated as “___ times as much as ___”, or even more specifically, “___times as heavy/long/tall as ___”. Both quantities may be given, and the total is unknown, or the total and one quantity are known, and the second quantity is unknown. Depending on the known and unknown quantities in the problems, students use multiplication or division to solve.

The RDW process supports students as they learn to interpret and evaluate multiplicative comparisons within word problems. For example, in the problem from Grade Level 4, Module 1, Topic A, Lesson 2 shown, students first Read and encounter comparison language in the phrase “4 times as many books.” Students typically represent the quantities with two separate tapes. The first tape shows 1 unit, the books that Ray reads. The second tape shows 4 units, or 4 times as many as Ray, the number of books Jayla reads. As part of the Draw step in the RDW process, students look at the tape diagram they’ve drawn and consider what it’s showing, what is known and unknown. This leads students to determine how to solve the problem. In this example, students recognize that they know the total of 4 units, so they can divide to find the unknown value of 1 unit.

How do you decide when to rename a product that Is a fraction greater than 1 as a mixed number? If it’s a word problem, thinking about what the product represents helps me decide when I should rename fractions greater than 1 as mixed numbers. If the answer doesn’t make sense as a fraction greater than 1, then I can rename it as a mixed number. Sometimes the question in the word problem helps me think about whether I should rename the fraction greater than 1 as a mixed number. When there isn’t a word problem or directions to write the answer as a mixed number, we can leave the product as a fraction greater than 1.

In Grade Level 4, Module 4, Lesson 33, students solve the problem: A kitten weighs 4 ⁄ 5 kilograms. A puppy is 6 times as heavy as the kitten. How many kilograms does the puppy weigh? Again, students can read the problem in chunks and draw a tape diagram to represent the weights of the kitten and puppy. The same process of reading and representing the problem supports problem-solving, even when one of the values is a fraction. However, with a fractional value, students consider whether to state their answer as a fraction greater than one or a mixed number. In the Write step, students return to the word problem to write an accurate solution statement and use the problem’s context to decide which number type makes sense to answer the question posed. As students engage in that decision-making process, they are reasoning abstractly and quantitatively and engaging in Standard for Mathematical Practice 2 (MP2). The Debrief discussion shown here emphasizes the role of the RDW process in deciding how to record an answer.

As the repertoire of problem types continues to expand along with number types, RDW continues to be a supportive process students use to read and understand a problem, create a drawing that clarifies the known, unknown, and solution path, and to state the answer in a way that makes sense.

In Grade Level 5, the complexity of word problems advances to multi-step (3+ steps) word problems. Students reiterate the RDW steps of reading a chunk and representing the information in a drawing multiple times. Students practice refining this process to create an accurate drawing and to use the RDW process efficiently in Module 3, Lessons 20 and 21.

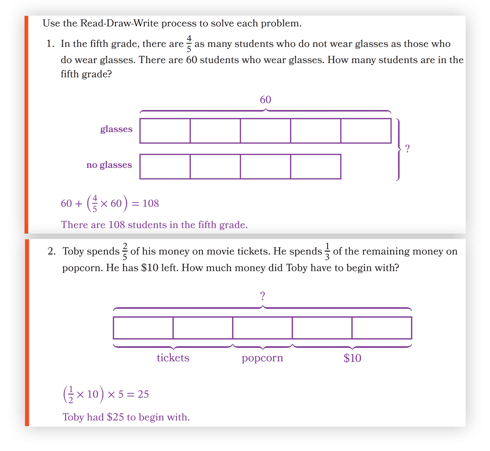
In Lesson 20, through the RDW process, students explore multiple ways fractional amounts can be represented in tape diagrams. In reading and understanding the language of the problem, students determine whether it is a comparison problem, which helps them decide how many tapes to draw. Students also represent fractional amounts such as “ 2 ⁄ 5 of his money” and “ 1 ⁄ 3 of the remaining money.” When students draw step by step as they read, they first partition the tape diagram into 5 parts and label 2 parts to represent 2 ⁄ 5 . This leaves 3 parts unlabeled and 1 ⁄ 3 is simpler to identify.

Does the Read-Draw-Write process help us solve multI-step word problems Involving fractions? How? Yes. We read, draw, and write in chunks.When we learn new information, we pause to draw and then go back to reading and draw when we learn something new. We can write expressions or equations as we realize which operations we can use to find unknown information. Yes. The model I draw helps me decide which operation to use to find an unknown value. Each time we find new information by evaluating an expression, we can compare it to our model and ask, Does that make sense based on what I see in the model?

In Lesson 21, students encounter additional multi-step word problems with fractional amounts and take on more responsibility in determining how to represent and solve. When students use a self-selected method to solve a comparison word problem involving fractions, they model with mathematics and practice Standard for Mathematical Practice 4 (MP4). The key question of the lesson: Does the Read–Draw–Write process help us solve multi-step word problems? How? has them reflecting on the process throughout the lesson and finally in the Debrief, as shown. The flexibility of the process supports students as they read and return to modify their drawings multiple times. RDW also continues to aid students in identifying the known and unknown information and a solution path.

Representing comparisons and fractional amounts in Grade Levels 4 and 5 prepares students to visually represent ratios in Grade Levels 6 and beyond. The number choices and problem types continue to grow in complexity over the years. However, the RDW process remains a foundational tool for solving word problems.

Grade Levels 6–Algebra I

Much of the progression of mathematics in the middle school years includes algebraic understanding and representation, and the RDW routine progresses similarly. Instead of using drawing as the main problem-solving strategy, Eureka Math 2 Story of Ratios uses algebraic thinking as the main strategy. RDW progresses to RRSS: Read, Represent, Solve, Summarize. The representation can still be a drawing, but it could also be an equation with variables representing the unknown.

The Read portion of the routine is used to find the same information as in RDW, to identify what the problem is asking us to find and what we know. In the Represent portion of the routine, students choose the representation that makes the most sense to them, such as tape diagrams, a double number line, a table, or a graph, and then they share their representations with one another. Pairs then use their representation to solve the problem. After completing the problem, the teacher directs students to summarize their findings by asking questions such as, “Does my answer make sense?” and “Does my result answer the question?”

Have groups work to solve problem 3. Circulate as students work, and observe the strategies groups use as they read, represent, solve, and summarize. Encourage students to return to problems 1 and 2 if necessary, and ask the following questions to advance their thinking:

• What is the problem asking you to find? What do you know that is given in the problem? What do you know based on your chosen method of travel?
• What tool can you use to represent the problem?
• Does your model show what is known and whot is unknown? How can you improve your model?
• What units do you need to consider in the problem?
• Does your answer make sense?
• Does your result answer the question?

To continue practicing the routine, students choose from a list of transportation methods and determine how long it will take for that method to transport them to the moon. The teacher is given a list of possible questions to advance students’ use of the RRSS routine. Beyond the Read portion of the routine, questions such as “What tool can you use to represent the problem?” and “Does your model show what is known and what is unknown?” gently guide students through the Represent portion of the routine.

This lesson that specifies the use of the RRSS routine is rare. Generally, the routine is not called out in the problem prompts or lesson structures. Instead, the tool is part of the students’ toolkit, and students reach for it when they deem it appropriate. Because of this, teachers will likely need to post the steps to the routine, say the steps during think-alouds, and remind students during problem-solving activities. Consider using the advancing questions from Lesson 21 in other problem-solving situations.

The first instance of the routine in Grade Level 7 is in Module 1, Lesson 11, when students are further encouraged to represent the problem “…by using a tape diagram, an equation, a graph, a table, or any other model.” Advancing students’ thinking toward an algebraic representation, students use a double number line, then a graph, and finally an equation for the distance formula,  d=rt , in subsequent problems in the lesson. The RRSS routine is mentioned in Launch and in a Teacher Note but not called out further in the lesson guidance. Encouraging students to use RRSS as a tool in their kit will again be important for Grade Level 7 teachers.

There are many instances in Grade Level 8 when using the RRSS routine would aid students in problem-solving. However, the routine is not called out by name until Module 4, Lesson 10. In this Grade Level 8 lesson, students use linear equations to solve real-world problems. Students begin working with the routine as a class. Then, they use the routine with a partner and eventually work with it independently. While other representations may help students write the linear equation, representation of the problem with a linear equation is a specific task requirement. Students analyze the number of solutions to the equation in the context of the situation as they summarize the solution in the last step of the routine. Students recognize that the solution to the equation does not always answer the question from the problem, an additional complexity to problem-solving at this level.

The work with Read–Draw–Write and Read–Represent–Solve–Summarize engages students in many of the mathematical practices, but ultimately leads to the final goal, success with the modeling cycle (MP4) for problem-solving in high school mathematics. Math Practice 4 begins with, “Mathematically proficient students can apply the mathematics they know to solve problems arising in everyday life, society, and the workplace.” 1 There are many ways to model the process of mathematical problem-solving. Most start with a real-world problem, iterate, formulating a solution strategy, performing some computations, interpreting the results, ensuring those results are accurate, and then reporting final results if they are validated.

The Algebra I Eureka Math 2 curriculum takes the modeling cycle to its fruition, giving students multiple experiences with real-world problems. The first instance is in Module 1, Lesson 7 titled Printing Presses. Students work in groups to find an entry point for solving a problem about printing presses. Students analyze a variety of solution paths, building connections between quantitative reasoning and the process of writing and solving an equation in one variable. Connections are made to the RDW and RRSS routines when the teacher asks, “What assumptions can be made? What information do we know remains constant?” and “What are the important quantities? How are these quantities related?” The answers to all of these questions result in ways to read and represent the information from the problem.

In Module 2, students watch a video showing a “regular” showerhead and a low-flow showerhead. To further develop the modeling cycle, instead of giving students the problem, students explore questions related to the problem before narrowing their focus to one question. Information is withheld to allow students to independently determine what is required to answer the question. Additional information is provided only after students decide what assumptions need to be made during the formulation and computation stages of the modeling cycle. Students eventually connect different solution paths to a system of linear equations and explore the effects of changing the assumptions within the context as groups interpret and verify their results.

In other lessons, Algebra I students analyze falling objects and projectile motion, maximize area, and determine how a search and rescue helicopter relates quadratic functions to the real world. Connecting linear and exponential functions to the real world involves lessons in which students work with world populations, temperatures of objects cooling over time, and invasive species populations. The final Module of Algebra I brings all the years’ learning together as students use the modeling cycle to analyze paint splatters, reflect on the role of a city planner, consider a financial deal proposed by a business owner, plan a three-dimensional model of the solar system, and plan a fundraiser that maximizes profit.

Download the Article as a Free PDF

Great Minds

Great Minds PBC is a public benefit corporation and a subsidiary of Great Minds, a nonprofit organization. A group of education leaders founded Great Minds® in 2007 to advocate for a more content-rich, comprehensive education for all children. In pursuit of that mission, Great Minds brings together teachers and scholars to create exemplary instructional materials that provide joyful rigor to learning, spark and reward curiosity, and impart knowledge with equal parts delight.

Get the Latest Great Minds Updates

Stay informed of simple yet crucial implementation support tips, curriculum updates, new resources, professional development opportunities, and more for math, science, and ELA.

Looking for a hybrid learning resource?

Discover the benefits of  Great Minds in Sync ™. A collection of digital and print resources for  Eureka Math ®,  Wit & Wisdom ® and  PhD Science ®.

More blogs on Featured:

Response to Intervention with Eureka Math²

K–5 Eureka Math² in Summer School

Math Manipulatives: A Student-Centered Approach to Teaching Mathematics

Eureka Math²® Earns Top Ratings from EdReports

Sign up for Eureka Math Blog updates

Every child is capable of greatness.

• Job Openings
• Digital Support
• Print Support
• Media Inquiries

Let’s Connect

• Terms of Service
• Privacy Policy
• System Status
• CA Residents: Do Not Sell My Info

• Kindergarten
• Greater Than Less Than
• Measurement
• Multiplication
• Place Value
• Subtraction
• Punctuation
• 1st Grade Reading
• 2nd Grade Reading
• 3rd Grade Reading
• Cursive Writing

Problem Solving Draw A Picture And Write An Equation

Problem Solving Draw A Picture And Write An Equation - Displaying top 8 worksheets found for this concept.

Some of the worksheets for this concept are Polyas problem solving techniques, Solving linear equations using pictures by tiffany bryant, Problem solving strategies guess and check work backward, Multiplication arrays word problems, Algebra tiles and equation solving, Polyas problem solving techniques, Grade 3 supplement, K 12.

Found worksheet you are looking for? To download/print, click on pop-out icon or print icon to worksheet to print or download. Worksheet will open in a new window. You can & download or print using the browser document reader options.

1. Polyas Problem Solving Techniques

2. solving linear equations using pictures by tiffany bryant ..., 3. problem-solving strategies: guess and check, work backward, 4. multiplication arrays (word problems), 5. algebra tiles and equation solving, 6. polyas problem solving techniques, 7. grade 3 supplement.

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

10.1: George Polya's Four Step Problem Solving Process

• Last updated
• Save as PDF
• Page ID 72365

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Step 1: Understand the Problem

• Do you understand all the words?
• Can you restate the problem in your own words?
• Do you know what is given?
• Do you know what the goal is?
• Is there enough information?
• Is there extraneous information?
• Is this problem similar to another problem you have solved?

Step 2: Devise a Plan: Below are some strategies one might use to solve a problem. Can one (or more) of the following strategies be used? (A strategy is defined as an artful means to an end.)

draw a picture and write an equation

All Formats

Resource types, all resource types.

• Rating Count
• Price (Ascending)
• Price (Descending)
• Most Recent

Draw a picture and write an equation

Word Problems - Addition and Subtraction within 10

1st Grade Word Problems Addition & Subtraction Within 20 Story Problems FREE

• Easel Activity

Addition Word Problems (within 10 and within 20)

Winter Math Word Problems Within 20 Story Problem Worksheets & Math Journal Page

Addition and Subtraction Word Problems Bundle | Distance Learning

Area and Perimeter Minecraft Building | Activity Packet | No Prep! | 5th Grade

Story Problems FREEBIE: Addition and Subtraction Within 20

Addition & Subtraction Word Problems Christmas Themed

Addition & Subtraction Word Problems Winter Themed

Addition and Subtraction Word Problems Back to School Theme

Simple Word Problem Worksheets Using Addition and Subtraction Facts Up to 20

Simple Addition and Subtraction Story Problem {Word Problem} Practice Sheets

NGSS 1OA.1: Word Problems Using Decodable Passages/Printable & TPT Digital

2.NBT.B.6 Add Up to Four 2 Digit Numbers Practice Pages and Assessment

Addition and Subtraction within 20 Word Problems Worksheets First Grade

Simple Word Problem Worksheets Using Addition and Subtraction Facts 1-10

Addition & Subtraction Word Problem Worksheets within 20-Math Numbers-50 pages

Place Value Tens and Ones

Math Strategies Visual Posters | Addition & Subtraction Strategies | Primary

Addition and Subtraction Word Problems Worksheets

Solving Addition and Subraction Word Problems Within 20 Worksheet Packet

Decodable Word Problems for K-1st Grade - Addition and Subtraction Within 10

Halloween Single Digit Addition & Subtraction Book {FREEBIE}

Perimeter and Area Word Problems, Notebook Pages, and Problem Solving Strategy

• We're hiring
• Help & FAQ
• Privacy policy
• Student privacy
• Terms of service
• Tell us what you think

Online Mathematics Editor a fast way to write and share mathematics 100k + users registered, 450k + documents created

Desktop (offline) version, built for your privacy