solving real life problems using trigonometric ratios involving right triangles

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.4: Solving Right Triangles

• Last updated
• Save as PDF
• Page ID 61221

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Solve right triangles.
• Find the area of any triangle using trigonometry.
• Solve real-world problems using right triangles.
• Find the measure of an angle using inverse trig functions.

Inverse Trigonometric Ratios

In mathematics, the word inverse means “undo.” For example, addition and subtraction are inverses of each other because one undoes the other. When we use the inverse trigonometric ratios, we can find acute angle measures as long as we are given two sides.

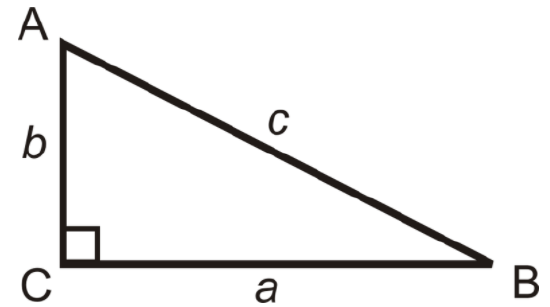
Inverse Tangent : Labeled \(\tan ^{-1}\), the “-1” means inverse.

\(\tan ^{-1} \left(\dfrac{b}{a}\right)=m\angle B\) and \(\tan ^{-1} \left(\dfrac{a}{b}\right)=m\angle A.\)

Inverse Sine : Labeled \(\sin ^{-1}\).

\(\sin ^{-1} \left(\dfrac{b}{c}\right)=m\angle B\) and \(\sin ^{-1} \left(\dfrac{a}{c}\right)=m\angle A.\)

Inverse Cosine : Labeled \(\cos ^{-1}\).

\(\cos ^{-1} \left(\dfrac{a}{c}\right)=m\angle B\) and \(\cos ^{-1} \left(\dfrac{b}{c}\right)=m\angle A.\)

In most problems, to find the measure of the angles you will need to use your calculator. On most scientific and graphing calculators, the buttons look like \([\sin ^{-1}]\), \([\cos ^{-1}]\), and \([\(\tan ^{-1}]\). You might also have to hit a shift or 2nd button to access these functions.

Now that you know both the trig ratios and the inverse trig ratios you can solve a right triangle. To solve a right triangle, you need to find all sides and angles in it. You will usually use sine, cosine, or tangent; inverse sine, inverse cosine, or inverse tangent; or the Pythagorean Theorem .

What if you were told the tangent of \(\angle Z\) is 0.6494? How could you find the measure of \(\angle Z\)?

Example \(\PageIndex{1}\)

Solve the right triangle.

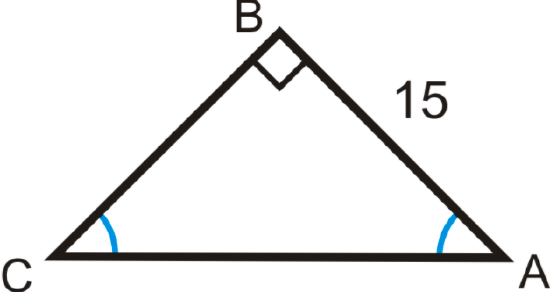
The two acute angles are congruent, making them both \(45^{\circ}\). This is a 45-45-90 triangle. You can use the trigonometric ratios or the special right triangle ratios.

Trigonometric Ratios

\(\begin{array}{rlrl} \tan 45^{\circ} & =\dfrac{15}{B C} & \sin 45^{\circ} & =\dfrac{15}{A C} \\ B C & =\dfrac{15}{\tan 45^{\circ}}=15 & A C & =\dfrac{15}{\sin 45^{\circ}} \approx 21.21 \end{array}\)

45-45-90 Triangle Ratios

\(BC=AB=15 \text{, } AC=15\sqrt{2} \approx 21.21\)

Example \(\PageIndex{2}\)

Use the sides of the triangle and your calculator to find the value of \(\angle A\). Round your answer to the nearest tenth of a degree.

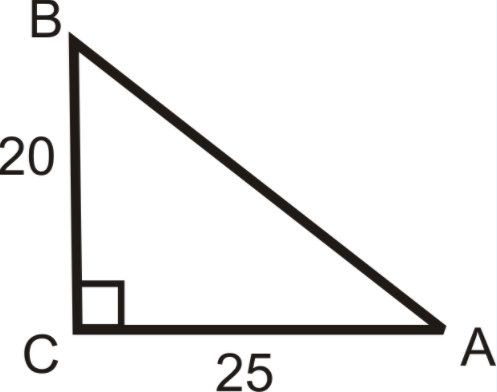
In reference to \(\angle A\), we are given the opposite leg and the adjacent leg. This means we should use the tangent ratio.

\(\tan A=\dfrac{20}{25}=\dfrac{4}{5}\). So, \(\tan ^{-1} \dfrac{4}{5}=m\angle A\). Now, use your calculator.

If you are using a TI-83 or 84, the keystrokes would be: [2nd][TAN](\(\dfrac{4}{5}\)) [ENTER] and the screen looks like:

Figure \(\PageIndex{4}\)

\(m\angle A \approx 38.7^{\circ}\)

Example \(\PageIndex{3}\)

\angle A is an acute angle in a right triangle. Find \(m\angle A\) to the nearest tenth of a degree for \(\sin A=0.68\), \(\cos A=0.85\), and \(\tan A=0.34\).

\(\begin{aligned} m\angle A&=\sin ^{-1} 0.68\approx 42.8^{\circ} \\ m\angle A&=\cos ^{-1} 0.85\approx 31.8^{\circ} \\ m\angle A&=\tan ^{-1} 0.34\approx 18.8^{\circ} \end{aligned}\)

Example \(\PageIndex{4}\)

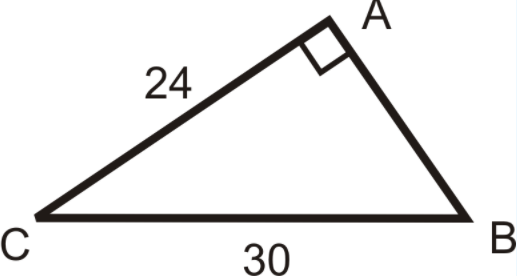
Figure \(\PageIndex{5}\)

To solve this right triangle, we need to find \(AB\), \(m\angle C\) and \(m\angle B\). Use only the values you are given.

\(\underline{AB}: \text{ Use the Pythagorean Theorem.}

\(\begin{aligned} 24^2+AB^2&=30^2 \\ 576+AB^2&=900 \\ AB^2&=324 \\ AB&=\sqrt{324}=18 \end{aligned}\)

\(\underline{m\angle B} : \text{ Use the inverse sine ratio.}\)

\(\begin{aligned} \sin B &=\dfrac{24}{30}=\dfrac{4}{5} \\ \sin ^{-1} (45) &\approx 53.1^{\circ} =m\angle B\end{aligned}\)

\(\underline{m\angle C} : \text{ Use the inverse cosine ratio.}\)

\(\cos C=\dfrac{24}{30}=\dfrac{4}{5} \rightarrow \cos ^{-1} (\dfrac{4}{5})\approx 36.9^{\circ} =m\angle C\)

Example \(\PageIndex{5}\)

When would you use sin and when would you use \(\sin ^{-1}\) ?

You would use sin when you are given an angle and you are solving for a missing side. You would use \(\sin ^{-1} \)when you are given sides and you are solving for a missing angle.

Solving the following right triangles. Find all missing sides and angles. Round any decimal answers to the nearest tenth.

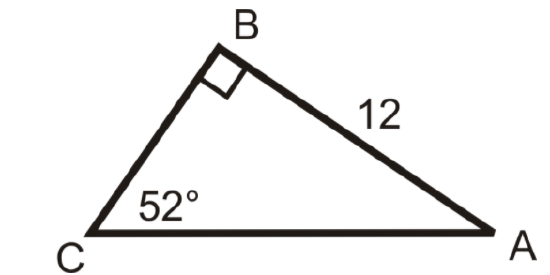
Additional Resources

Interactive Element

Video: Introduction to Inverse Trigonometric Functions

Activities: Inverse Trigonometric Ratios Discussion Questions

Study Aids: Trigonometric Ratios Study Guide

Practice: Solve Right Triangles

Angles of Elevation and Depression

You can use right triangles to find distances, if you know an angle of elevation or an angle of depression .

The figure below shows each of these kinds of angles.

The angle of elevation is the angle between the horizontal line of sight and the line of sight up to an object. For example, if you are standing on the ground looking up at the top of a mountain, you could measure the angle of elevation. The angle of depression is the angle between the horizontal line of sight and the line of sight down to an object. For example, if you were standing on top of a hill or a building, looking down at an object, you could measure the angle of depression. You can measure these angles using a clinometer or a theodolite. People tend to use clinometers or theodolites to measure the height of trees and other tall objects. Here we will solve several problems involving these angles and distances.

Finding the angle of elevation

You are standing 20 feet away from a tree, and you measure the angle of elevation to be \(38^{\circ}\). How tall is the tree?

The solution depends on your height, as you measure the angle of elevation from your line of sight. Assume that you are 5 feet tall.

The figure shows us that once we find the value of \(T\), we have to add 5 feet to this value to find the total height of the triangle. To find \(T\), we should use the tangent value:

\(\begin{aligned} tan38^{\circ}&=\dfrac{\text{opposite}}{\text{adjacent}}=\dfrac{T}{20} \\ tan38^{\circ}&=\dfrac{T}{20}\\ T&=20tan38^{\circ}\approx 15.63\\ \text{Height of tree}&\approx 20.63 \text{ ft}\end{aligned}\)

You are standing on top of a building, looking at a park in the distance. The angle of depression is 53^{\circ} . If the building you are standing on is 100 feet tall, how far away is the park? Does your height matter?

Finding the angle of depression

If we ignore the height of the person, we solve the following triangle:

Given the angle of depression is \(53^{\circ}\), \(\angle A\) in the figure above is \(37^{\circ}\). We can use the tangent function to find the distance from the building to the park:

\(\begin{aligned} tan 37^{\circ}=\dfrac{\text{opposite}}{\text{adjacent}}=\dfrac{d}{100}\\ tan37^{\circ} &=\dfrac{d}{100}\\d&=100 tan37^{\circ} \approx 75.36\text{ ft} \end{aligned}\)

If we take into account the height if the person, this will change the value of the adjacent side. For example, if the person is 5 feet tall, we have a different triangle:

\(\begin{aligned} tan37^{\circ}=&\dfrac{\text{opposite}}{\text{adjacent}}=\dfrac{d}{105} \\ tan37^{\circ} &=\dfrac{d}{105} \\ d&=105 tan37^{\circ} \approx 79.12\text{ ft}\end{aligned}\)

If you are only looking to estimate a distance, then you can ignore the height of the person taking the measurements. However, the height of the person will matter more in situations where the distances or lengths involved are smaller. For example, the height of the person will influence the result more in the tree height problem than in the building problem, as the tree is closer in height to the person than the building is.

Real-World Application: The Horizon

You are on a long trip through the desert. In the distance you can see mountains, and a quick measurement tells you that the angle between the mountaintop and the ground is \(13.4^{\circ}\). From your studies, you know that one way to define a mountain is as a pile of land having a height of at least 2,500 meters. If you assume the mountain is the minimum possible height, how far are you away from the center of the mountain?

\(\begin{aligned} tan 13.4^{\circ}&=\dfrac{\text{opposite}}{\text{adjacent}}=\dfrac{2500}{d}\\ tan 13.4^{\circ} &=\dfrac{2500}{d} \\ d&=\dfrac{2500}{tan13.4^{\circ}} \approx 10,494 meters \end{aligned}\)

Example \(\PageIndex{6}\)

You are six feet tall and measure the angle between the horizontal and a bird in the sky to be 40^{\circ} . You can see that the shadow of the bird is directly beneath the bird, and 200 feet away from you on the ground. How high is the bird in the sky?

We can use the tangent function to find out how high the bird is in the sky:

\(\begin{aligned} tan40^{\circ} =\dfrac{height}{200} \\ height&=200 tan40^{\circ} \\ height&=(200)(.839) \\height&=167.8\end{aligned}\)

We then need to add your height to the solution for the triangle. Since you are six feet tall, the total height of the bird in the sky is 173.8 feet.

Example \(\PageIndex{7}\)

While out swimming one day you spot a coin at the bottom of the pool. The pool is ten feet deep, and the angle between the top of the water and the coin is \(15^{\circ}\). How far away is the coin from you along the bottom of the pool?

Since the distance along the bottom of the pool to the coin is the same as the distance along the top of the pool to the coin, we can use the tangent function to solve for the distance to the coin:

\(\begin{aligned} tan15^{\circ}&=\dfrac{\text{opposite}}{\text{adjacent}} \\ tan 15^{\circ} =\dfrac{10}{x} \\ x&=\dfrac{10}{tan15^{\circ}} \\ x&\approx 37.32^{\circ}\end{aligned}\)

Example \(\PageIndex{8}\)

You are hiking and come to a cliff at the edge of a ravine. In the distance you can see your campsite at the base of the cliff, on the other side of the ravine. You know that the distance across the ravine is 500 meters, and the angle between your horizontal line of sight and your campsite is \(25^{\circ}\). How high is the cliff? (Assume you are five feet tall.)

Using the information given, we can construct a solution:

\(\begin{aligned} tan 25^{\circ} =\dfrac{\text{opposite}}{\text{adjacent}}\\ tan25^{\circ}&=\dfrac{height}{500} \\ height&=\dfrac{500}{tan25^{\circ}}\\ height&=(500)(.466) \\ height&=233\text{ meters}\end{aligned}\)

This is the total height from the bottom of the ravine to your horizontal line of sight. Therefore, to get the height of the ravine, you should take away five feet for your height, which gives an answer of 228 meters.

• A 70 foot building casts an 50 foot shadow. What is the angle that the sun hits the building?
• You are standing 10 feet away from a tree, and you measure the angle of elevation to be \(65^{\circ}\). How tall is the tree? Assume you are 5 feet tall up to your eyes.
• Kaitlyn is swimming in the ocean and notices a coral reef below her. The angle of depression is \(35^{\circ}\) and the depth of the ocean, at that point is 350 feet. How far away is she from the reef?
• The angle of depression from the top of a building to the base of a car is \(60^{\circ}\). If the building is 78 ft tall, how far away is the car?

Video: Example: Determine What Trig Function Relates Specific Sides of a Right Triangle

Practice: Angles of Elevation and Depression

Want Better Math Grades?

✅ Unlimited Solutions

✅ Step-by-Step Answers

✅ Available 24/7

➕ Free Bonuses ($1085 value!)

On this page

• Trigonometric Functions
• 2. Sine, Cosine, Tangent & Reciprocals
• 3. Values of Trigonometric Functions

4. The Right Triangle and Applications

• 4a. Trigonometry Revision Summary
• 5. Signs of the Trigonometric Functions
• 6. Trigonometric Functions of Any Angle
• 8. Applications of Radian Measure
• 8a. Pulleys
• 9. Radians and the Trigonometric Ratios

Related Sections

Math Tutoring

Need help? Chat with a tutor anytime, 24/7.

Online Trigonometry Solver

Solve your trigonometry problem step by step!

IntMath Forum

Get help with your math queries:

Many problems involve right triangles. We often need to use the trigonometric ratios to solve such problems.

Example 1 - Finding the Height

Find h for the given triangle.

Triangle with unknown height h.

`sin 15.70^"o" = h/2.500`

`h = 2.500\ sin 15.70^"o"`

`= 0.6765\ "km"`

Example 2 - Solving Triangles

Solve the triangle ABC, given that `A = 35°` and `c = 15.67`.

Triangle sides a,b,c and angles A,B,C.

To "solve" a triangle means to find the unknown sides and angles.

We have, for the values given:

In this example, we need to find side lengths a and b and angle B . Note C = 90 o .

`sin 35^"o" = a/c = a/15.67`

So a = 15.67 sin 35 o = 8.99

`cos 35^"o"=b/c=b/15.67`

So b = 15.67 cos 35 o = 12.84

Angle B = 90 o − 35 o = 55 o .

So a = 8.99, b = 12.84 and B = 55 o . We have found all the unknowns.

Angles of Elevation and Depression

In surveying, the angle of elevation is the angle from the horizontal looking up to some object:

The angle of depression is the angle from the horizontal looking down to some object:

The angle of elevation of an aeroplane is `23°`. If the aeroplane's altitude is `2500\ "m"`, how far away is it?

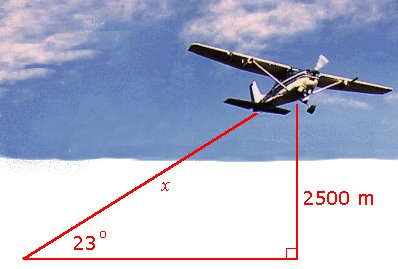
Let the distance be x . Then `sin 23^"o"=2500/x`

`x=2500/(sin 23^"o")=6400\ "m"`

You can walk across the Sydney Harbour Bridge and take a photo of the Opera House from about the same height as top of the highest sail.

This photo was taken from a point about `500\ "m"` horizontally from the Opera House and we observe the waterline below the highest sail as having an angle of depression of `8°`. How high above sea level is the highest sail of the Opera House?

This is a simple tan ratio problem.

`tan 8^"o" = h/500`

`h= 500\ tan 8° = 70.27\ "m"`.

So the height of the tallest point is around `70\ "m"`.

[The actual height is `67.4\ "m"`.]

Tips, tricks, lessons, and tutoring to help reduce test anxiety and move to the top of the class.

Email Address Sign Up

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

5. Trigonometry

5.2 Solve Applications: Sine, Cosine and Tangent Ratios.

Learning Objectives

By the end of this section it is expected that you will be able to

• Find missing side of a right triangle using sine, cosine, or tangent ratios
• Find missing angle of a right triangle using sine, cosine, or tangent ratios
• Solve applications using right angle trigonometry

Sine, Cosine, and Tangent Ratios

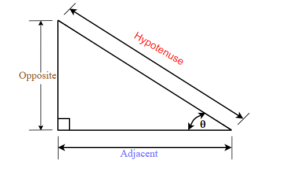
We know that any right triangle has three sides and a right angle. The side opposite to the right angle is called the hypotenuse. The other two angles in a right triangle are acute angles (with a measure less than 90 degrees). One of those angles we call reference angle and we use θ (theta) to represent it.

The hypotenuse is always the longest side of a right triangle. The other two sides are called opposite side and adjacent side. The names of those sides depends on which of the two acute angles is being used as a reference angle.

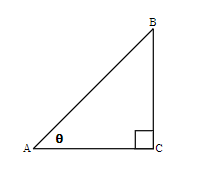
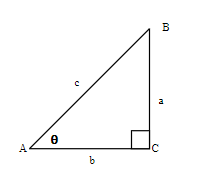
In the right triangle each side is labeled with a lowercase letter to match the uppercase letter of the opposite vertex.

Label the sides of the triangle and find the hypotenuse, opposite, and adjacent.

We labeled  the sides with a lowercase letter to match the uppercase letter of the opposite vertex.

c is hypotenuse

a is opposite

b is adjacent

Label the sides of the triangle and find the hypotenuse, opposite and adjacent.

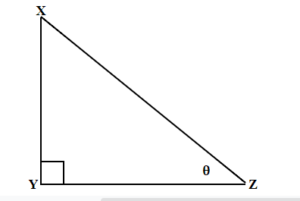
y is hypotenuse

z is opposite

x is adjacent

Trigonometric Ratios

Trigonometric ratios are the ratios of the sides in the right triangle. For any right triangle we can define three basic trigonometric ratios: sine, cosine, and tangent.

Let us refer to Figure 1 and define the three basic trigonometric ratios as:

Three Basic Trigonometric Ratios

Where θ is the measure of a reference angle measured in degrees.

Very often we use the abbreviations for sine, cosine, and tangent ratios.

Some people remember the definition of the trigonometric ratios as SOH CAH TOA.

For the given triangle find the sine, cosine and tangent ratio.

For the given triangle find the sine cosine and tangent ratio.

When calculating we will usually round the ratios to four decimal places and at the end our final answer to one decimal place unless stated otherwise.

For the given triangle find the sine, cosine and tangent ratios. If necessary round to four decimal places.

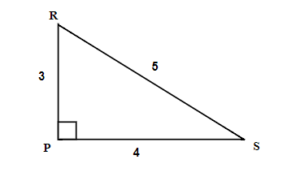
We have two possible reference angles: R an S.

Using the definitions, the trigonometric ratios for angle R are:

Using the definitions, the trigonometric ratios for angle S:

For the given triangle find the sine, cosine, and tangent ratios. If necessary round to four decimal places.

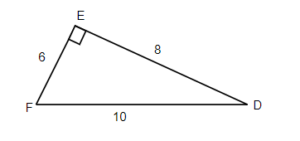
Now, let us use a scientific calculator to find the trigonometric ratios.  Can you find the sin, cos, and tan buttons on your calculator? To find the trigonometric ratios make sure your calculator is in Degree Mode.

Using a calculator find the trigonometric ratios. If necessary, round to 4 decimal places.

Make sure your calculator is in Degree Mode.

a)  Using a calculator find that sin 30° = 0.5

b)  Using a calculator find that cos 45° = 0.7071 Rounded to 4 decimal places.

c)  Using a calculator find that tan 60° = 1.7321 Rounded to 4 decimal places.

Find the trigonometric ratios. If necessary, round to 4 decimal places.

a)  sin 60°

b)  cos 30°

c)  tan 45°

a)   sin 60° = 0.8660

b)   cos 30° = 0.8660

c)   tan 45° = 1

Finding Missing Sides of a Right Triangle

In this section you will be using trigonometric ratios to solve right triangle problems. We will adapt our problem solving strategy for trigonometry applications. In addition, since those problems will involve the right triangle, it is helpful to draw it (if the drawing is not given) and label it with the given information.We will include this in the first step of the problem solving strategy for trigonometry applications.

HOW TO: Solve Trigonometry Applications

• Read the problem and make sure all the words and ideas are understood. Draw the right triangle and label the given parts.
• Identify what we are looking for.
• Label what we are looking for by choosing a variable to represent it.
• Find the required trigonometric ratio.
• Solve the ratio using good algebra techniques.
• Check the answer by substituting it back into the ratio in step 4 and by making sure it makes sense in the context of the problem.
• Answer the question with a complete sentence.

In the next few examples, having given the measure of one acute angle and the length of one side of the right triangle, we will solve the right triangle for the missing sides.

 Find the missing sides. Round  your final answer to two decimal places

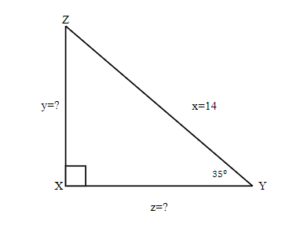
 Find the missing sides. Round  your final answer to one decimal place.

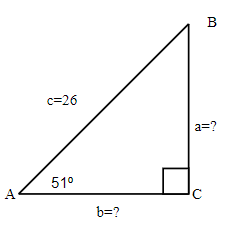
Find the hypotenuse. Round your final answer to one decimal place.

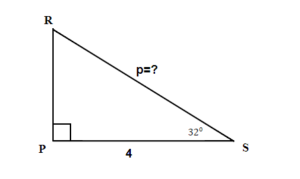
Finding Missing Angles of a Right Triangle

Sometimes we have a right triangle with only the sides given. How can we find the missing angles? To find the missing angles, we use the inverse of the trigonometric ratios. The inverse buttons sin -1 , cos -1 , and tan -1 are on your scientific calculator.

Find the angles. Round your final answer to one decimal place.

a)  sin A = 0.5

b)  cos B = 0.9735

c)  tan C = 2.89358

Use your calculator and press the 2nd FUNCTION key and then press the SIN, COS, or TAN key

a)  A = sin -1 0.5

b)  B = cos -1 0.9735

c) C = tan -1 2.89358

a)  sin X = 1

b)  cos Y = 0.375

c)  tan Z = 1.676767

In the example below we have a right triangle with two sides given. Our acute angles are missing. Let us see what the steps are to find the missing angles.

Find the missing angle X. Round your final answer to one decimal place.

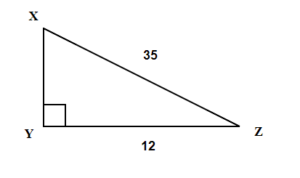
Find the missing angle A. Round your final answer to one decimal place.

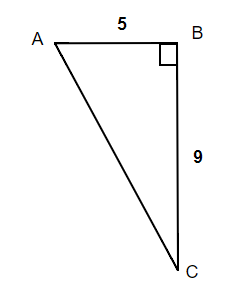
Find the missing angle C. Round your final answer to one decimal place.

Solving a Right Triangle

From the section before we know that any triangle has three sides and three interior angles. In a right triangle, when all six parts of the triangle are known, we say that the right triangle is solved.

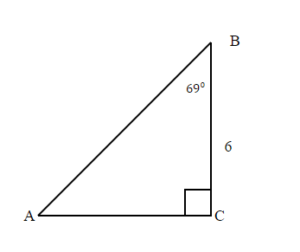
Solve the right triangle. Round your final answer to one decimal place.

Since the sum of angles in any triangle is 180°, the measure of angle B can be easy calculated.

We solved the right triangle

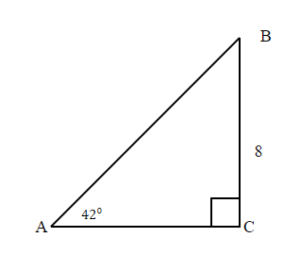
Solve the right triangle. Round to two decimal places.

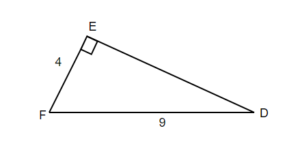
The missing angle F = 180° – 90° – 26.39° = 63.64°

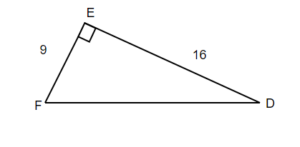
Solve the right triangle. Round to one decimal place.

Solve Applications Using Trigonometric Ratios

In the previous examples we were able to find missing sides and missing angles of a right triangle. Now, let’s use the trigonometric ratios to solve real-life  problems.

Many applications of trigonometric ratios involve understanding of an angle of elevation or angle of depression.

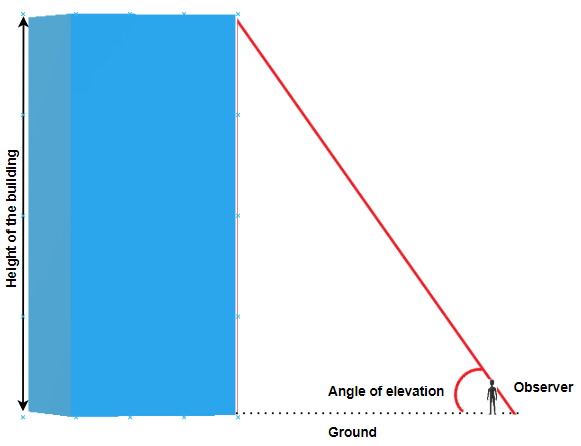
The angle of elevation is an angle between the horizontal line (ground) and the observer’s line of sight.

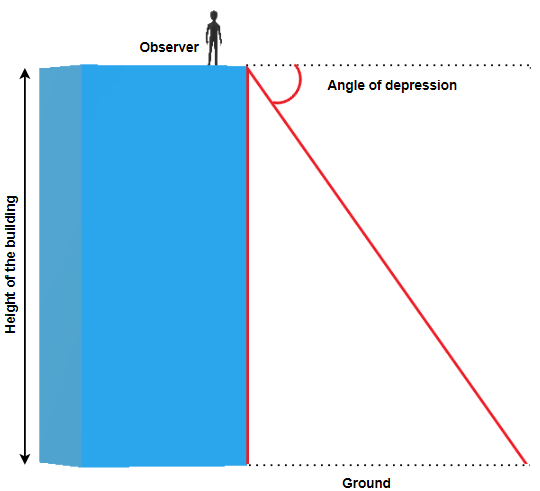
The angle of depression is the angle between horizontal line (that is parallel to the ground) and the observer’s line of sight.

James is standing 31 metres away from the base of the Harbour Centre in Vancouver. He looks up to the top of the building at a 78° angle. How tall is the Harbour Centre?

Marta is standing 23 metres away from the base of the tallest apartment building in Prince George and looks at the top of the building at a 62° angle. How tall is the building?

43.3 metres

Thomas is standing at the top of the building that is 45 metres high and looks at her friend that is standing on the ground, 22 metres from the base of the building. What is the angle of depression?

Hemanth is standing on the top of a cliff 250 feet above the ground and looks at his friend that is standing on the ground, 40 feet from the base of the cliff. What is the angle of depression?

Key Concepts

• Read the problem and make sure all the words and ideas are understood. Draw the right triangle and label  the given parts.
• Check the answer by substituting it back into the ratio solved in step 5 and by making sure it makes sense in the context of the problem.

5.2 Exercise Set

Label the sides of the triangle.

• If the reference angle in Question 1 is B, Find the adjacent ?
• If the reference angle in Question 2 is Z, find the opposite?

Use your calculator to find the given ratios. Round to four decimal places if necessary:

For the given triangles, find the sine, cosine and tangent of the θ.

For the given triangles, find the missing side. Round it to one decimal place.

For the given triangles, find the missing sides. Round it to one decimal place.

Solve the triangles. Round to one decimal place.

• Kim stands 75 metres from the bottom of a tree and looks up at the top of the tree at a 48° angle. How tall is the tree?
• A tree makes a shadow that is 6 metres long when the angle of elevation to the sun is 52°. How tall is the tree?
• A ladder that is 15 feet is leaning against a house and makes a 45° angle with the ground. How far is the base of the ladder from the house?
• Roxanne is flying a kite and has let out 100 feet of string. The angle of elevation with the ground is 38°. How high is her kite above the ground?
• Marta is flying a kite and has let out 28 metres of string. If the kite is 10 metres above the ground, what is the angle of elevation?
• An airplane takes off from the ground at the angle of 25°. If the airplane traveled 200 kilometres, how high above the ground is it?

• y = 19.3, z = 8.2

Attribution:

This chapter has been adapted from “Solve Applications: Sine, Cosine and Tangent Ratios” in Introductory Algebra  by Izabela Mazur, which is under a CC BY 4.0 Licence . See the Adaptation Statement for more information.

Business/Technical Mathematics Copyright © 2021 by Izabela Mazur and Kim Moshenko is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

Chapter 2: Trigonometric Ratios

2.3 Solving Right Triangles

Algebra refresher.

1. [latex]\:\sqrt{2}\sqrt{2}[/latex]

2. [latex]\:\dfrac{3}{\sqrt{3}}[/latex]

3. [latex]\:\sqrt{8}[/latex]

4. [latex]\:\sqrt{\dfrac{3}{4}}[/latex]

Rationalize the denominator.

5. [latex]\:\dfrac{1}{\sqrt{2}}[/latex]

6. [latex]\:\dfrac{2}{\sqrt{3}}[/latex]

7. [latex]\:\dfrac{6}{\sqrt{3}}[/latex]

8. [latex]\:\dfrac{4}{\sqrt{8}}[/latex]

[latex]\underline{\qquad\qquad\qquad\qquad}[/latex]

• [latex]\displaystyle 2\vphantom{\dfrac{\sqrt{3}}{2}}[/latex]
• [latex]\displaystyle \sqrt{3}\vphantom{\vphantom{\dfrac{\sqrt{3}}{2}}}[/latex]
• [latex]\displaystyle 2\sqrt{2}\vphantom{\dfrac{\sqrt{3}}{2}}[/latex]
• [latex]\displaystyle \dfrac{\sqrt{3}}{2}[/latex]
• [latex]\displaystyle \dfrac{\sqrt{2}}{2}[/latex]
• [latex]\displaystyle \dfrac{2\sqrt{3}}{3}[/latex]
• [latex]\displaystyle 2\sqrt{3}\vphantom{\dfrac{\sqrt{3}}{2}}[/latex]
• [latex]\displaystyle \sqrt{2}\vphantom{\dfrac{\sqrt{3}}{2}}[/latex]

Learning Objectives

• Solve a right triangle
• Use inverse trig ratio notation
• Use trig ratios to find an angle
• Solve problems involving right triangles
• Know the trig ratios for the special angles

Introduction

A triangle has six parts: three sides and three angles. In a right triangle, we know that one of the angles is [latex]90 {^o}\text{.}[/latex] If we know three parts of a right triangle, including one of the sides, we can use trigonometry to find all the other unknown parts. This is called solving the triangle.

Example 2.31.

The hypotenuse of a right triangle is 150 feet long, and one of the angles is [latex]35 {^o}\text{,}[/latex] as shown in the figure. Solve the triangle.

We can find the side opposite the 35° angle by using the sine ratio. [latex]\begin{align*} \sin 35 {^o} = \dfrac {\text{opposite}}{\text{hypotenuse}}\\ 0.5736 = \dfrac{a}{150}\\ a = 150(0.5736) = 86.04 \end{align*}[/latex] The opposite side is about 86 feet long. To find side [latex]b[/latex], we could use the Pythagorean theorem now, but it is better to use given information, rather than values we have calculated, to find the other unknown parts. We will use the cosine ratio. [latex]\begin{align*} \cos 35 {^o} = \dfrac {\text{adjacent}}{\text{hypotenuse}}\\ 0.8192 = \dfrac{b}{150}\\ b = 150(0.8192) = 122.89 \end{align*}[/latex] The adjacent side is about [latex]123[/latex] feet long. Finally, the unknown angle is the complement of [latex]35 {^o}\text{,}[/latex] or [latex]55 {^o}\text{.}[/latex]

Checkpoint 2.32.

Sketch a right triangle with

• one angle of [latex]37 {^o}\text{,}[/latex] and
• the side adjacent to that angle of length 5 centimeters.

Without doing the calculations, list the steps you would use to solve the triangle.

Use tan [latex]37{^o}[/latex] to find the opposite side. Use cos [latex]37{^o}[/latex] to find the hypotenuse. Subtract [latex]37{^o}[/latex] from [latex]90{^o}[/latex] to find the third angle.

Finding an Angle

While watching her niece at the playground, Francine wonders how steep the slide is. She happens to have a tape measure and her calculator with her and finds that the slide is 77 inches high and covers a horizontal distance of 136 inches, as shown below.

Francine knows that one way to describe the steepness of an incline is to calculate its slope, which in this case is [latex]\begin{equation*} \dfrac {\Delta y}{\Delta x} = \dfrac{77}{136} = 0.5662 \end{equation*}[/latex] However, Francine would really like to know what angle the slide makes with the horizontal. She realizes that the slope she has just calculated is also the tangent of the angle she wants.

If we know the tangent of an angle, can we find the angle? Yes, we can: locate the key labeled [latex]\boxed{\text{TAN}^{-1}}[/latex] on your calculator; it is probably the second function above the TAN key. Enter [latex]\qquad\qquad\qquad[/latex] 2nd TAN 0.5662

and you should find that [latex]\begin{equation*} \text{tan}^{-1} 0.5662 = 29.52 {^o}\text{.} \end{equation*}[/latex] This means that [latex]29.52 {^o}[/latex] is the angle whose tangent is [latex]0.5662\text{.}[/latex] We read the notation as “ inverse tangent of [latex]0.5662[/latex] is [latex]29.52[/latex] degrees.”

When we find [latex]\tan^{-1}[/latex] of a number, we are finding an angle whose tangent is that number. Similarly, [latex]\sin^{-1}[/latex] and [latex]cos^{-1}[/latex] are read as “inverse sine” and “inverse cosine.” They find an angle with the given sine or cosine.

Example 2.33.

Find the angle whose sine is [latex]0.6834\text{.}[/latex]

Enter 2nd SIN 0.6834 into your calculator to find [latex]\begin{equation*} \sin^{-1} 0.6834 = 43.11{^o} \end{equation*}[/latex] So [latex]43.11{^o}[/latex] is the angle whose sine is [latex]0.6834\text{.}[/latex] Or we can say that [latex]\begin{equation*} \sin 43.11{^o} = 0.6834 \end{equation*}[/latex] You can check the last equation on your calculator.

In the last example, the two equations:

[latex]\begin{equation*} \sin 43.11{^o} = 0.6834\end{equation*}[/latex]

[latex]\begin{equation*} \sin^{-1} 0.6834 = 43.11{^o}\end{equation*}[/latex]

say the same thing in different ways.

Caution 2.35.

The notation [latex]\sin^{-1} x[/latex] does not mean [latex]\dfrac{1}{\sin x}\text{.}[/latex] It is true that we use negative exponents to indicate reciprocals of numbers; for example, [latex]a^{-1} = \dfrac{1}{a}[/latex] and [latex]3^{-1} = \dfrac{1}{3}\text{.}[/latex] But “sin” by itself is not a variable.

• [latex]\sin^{-1} x[/latex] means “the angle whose sine is [latex]x[/latex]”
• [latex]\dfrac{1}{\sin x}[/latex] means “the reciprocal of the sine of angle [latex]x[/latex]”

(You may recall that [latex]f^{-1}(x)[/latex] denotes the inverse function for [latex]f(x)\text{.}[/latex] We will study trigonometric functions in Chapter 4.)

Checkpoint 2.36.

Write the following fact in two different ways: [latex]68{^o}[/latex] is the angle whose cosine is [latex]0.3746\text{.}[/latex]

[latex]\cos 68{^o} = 0.3746[/latex] or [latex]\cos^{-1}(0.3746) = 68{^o}[/latex]

Example 2.37.

Find the angle of inclination of a hill if you gain [latex]400[/latex] feet in elevation while traveling half a mile.

A sketch of the hill is shown at right. (Recall that [latex]1[/latex] mile [latex]= 5280[/latex] feet.)

[latex]\begin{align*} \sin \theta = \dfrac {400}{2640} = 0.\overline{15}\\ \theta = \sin^{-1} 0.\overline{15} = 8.71{^o} \end{align*}[/latex]

The angle of inclination of the hill is about [latex]8.7{^o}\text{.}[/latex]

Checkpoint 2.38.

The tallest living tree is a coastal redwood named Hyperion, at 378.1 feet tall. If you stand 100 feet from the base of the tree, what is the angle of elevation of your line of sight to the top of the tree? Round your answer to the nearest degree.

[latex]75{^o}[/latex]

The Special Angles

The trigonometric ratios for most angles are irrational numbers, but there are a few angles whose trig ratios are “nice” values. You already know one of these values: the sine of [latex]30{^o}\text{.}[/latex] Because the sides of a right triangle are related by the Pythagorean theorem, if we know any one of the trig ratios for an angle, we can find the others. Recall that the side opposite a [latex]30{^o}[/latex] angle is half the length of the hypotenuse, so [latex]\sin 30{^o} = \dfrac{1}{2}\text{.}[/latex]

The figure at right shows a 30-60-90 triangle with hypotenuse of length [latex]2[/latex]. The opposite side has length 1, and we can calculate the length of the adjacent side. [latex]\begin{align*} 1^2 + b^2 = 2^2 \\ b^2 = 2^2 - 1^2 = 3\\ b = \sqrt{3} \end{align*}[/latex]

Now we know the cosine and tangent of [latex]30{^o}\text{.}[/latex] [latex]\begin{equation*} \cos 30{^o} = \dfrac {\text{adjacent}}{\text{hypotenuse}} = \dfrac{\sqrt{3}}{2} \qquad \tan 30{^o} = \dfrac {\text{opposite}}{\text{adjacent}} = \dfrac{1}{\sqrt{3}} \end{equation*}[/latex]

These are exact values for the trig ratios, but we can also find decimal approximations. Use your calculator to verify the following approximate values. [latex]\begin{align*} \ \ {\text{exact value}} \ \ {\text{approximation}}\\ \cos 30{^o} = \dfrac{\sqrt{3}}{2} \approx 0.8660\\ \tan 30{^o} = \dfrac{1}{\sqrt{3}} \approx 0.5774 \end{align*}[/latex]

Caution 2.39.

It is important for you to understand the difference between exact and approximate values. These decimal approximations, like nearly all the other trig values your calculator gives you, are rounded off. Even if your calculator shows you ten or twelve digits, the values are not exactly correct — although they are quite adequate for most practical calculations!

The angles [latex]30{^o}\text{,}[/latex] [latex]60{^o}\text{,}[/latex] and [latex]45{^o}[/latex] are “special” because we can easily find exact values for their trig ratios and use those exact values to find exact lengths for the sides of triangles with those angles.

Example 2.40.

The sides of an equilateral triangle are [latex]8[/latex] centimeters long. Find the exact length of the triangle’s altitude, [latex]h\text{.}[/latex]

The altitude divides the triangle into two 30-60-90 right triangles as shown in the figure. The altitude is adjacent to the [latex]30{^o}[/latex] angle, and the hypotenuse of the right triangle is 8 centimeters. Thus,

[latex]\begin{align*} \cos 35 {^o} = \dfrac {\text{adjacent}}{\text{hypotenuse}} \ \ {\text{Fill in the values.}}\\ \dfrac{\sqrt{3}}{2} = \dfrac{h}{8} \ \ {\text{Multiply both sides by 8.}}\\ h = 8\left(\dfrac{\sqrt{3}}{2}\right) = 4\sqrt{3} \end{align*}[/latex] The altitude is exactly [latex]4\sqrt{3}[/latex] centimeters long.

From this exact answer, we can find approximations to any degree of accuracy we like. You can check that [latex]4\sqrt{3} \approx6.9282\text{,}[/latex] so the altitude is approximately 6.9 centimeters long.

Checkpoint 2.41.

Use the figure in the previous example to find exact values for the sine, cosine, and tangent of [latex]60{^o}\text{.}[/latex]

[latex]\sin 60{^o} = \dfrac{\sqrt{3}}{2}\text{,}[/latex] [latex]\cos 60{^o} = \dfrac{1}{2}\text{,}[/latex] [latex]\tan 60{^o} = \sqrt{3}[/latex]

There is one more special angle: [latex]45{^o}\text{.}[/latex] We find the trig ratios for this angle using an isosceles right triangle. Because the base angles of an isosceles triangle are equal, they must both be [latex]45{^o}\text{.}[/latex] The figure shows an isosceles right triangle with equal sides of length 1. You can use the Pythagorean theorem to show that the hypotenuse has length [latex]\sqrt{2}\text{,}[/latex] so the trig ratios for [latex]45{^o}[/latex] are[latex]\begin{align*} \sin 45{^o} = \dfrac {\text{opposite}}{\text{hypotenuse}} = \dfrac{1}{\sqrt{2}} \approx 0.7071\\ \cos 45{^o} = \dfrac {\text{adjacent}}{\text{hypotenuse}} = \dfrac{1}{\sqrt{2}} \approx 0.7071\\ \tan 45{^o} = \dfrac {\text{opposite}}{\text{adjacent}} = 1 \end{align*}[/latex]

The Trigonometric Ratios for the Special Angles

Here is a summary of the trig ratios for the special angles.

You should memorize the exact values for these trig ratios. A good way to remember them is to know the two special triangles shown below. From these triangles, you can always write down the three trig ratios for the special angles.

You should also be able to recognize their decimal approximations.

We can use the special angles as benchmarks for estimating and mental calculation. For example, we know that [latex]60{^o} \approx 0.8660\text{,}[/latex] so if sin [latex]\theta = 0.95[/latex] for some unknown angle [latex]\theta\text{,}[/latex] we know that [latex]\theta \gt 60{^o}\text{,}[/latex] because as [latex]\theta[/latex] increases, the sine of [latex]\theta[/latex] increases also.

Example 2.43.

If [latex]\cos \alpha \gt \dfrac{\sqrt{3}}{2}\text{,}[/latex] what can we say about [latex]\alpha\text{?}[/latex]

As an angle increases from [latex]0{^o}[/latex] to [latex]90{^o}\text{,}[/latex] its cosine decreases. Now, [latex]\cos 30{^o} = \dfrac{\sqrt{3}}{2}\text{,}[/latex] so if [latex]\cos \alpha \gt \dfrac{\sqrt{3}}{2}\text{,}[/latex] then [latex]\alpha[/latex] must be less than [latex]30{^o}\text{.}[/latex]

Checkpoint 2.44.

If [latex]1 \lt \tan \beta \lt \sqrt{3}\text{,}[/latex] what can we say about [latex]\beta\text{?}[/latex]

[latex]45{^o} \lt \beta \lt 60{^o}[/latex]

Section 2.3 Summary

• Solve a triangle
• Inverse sine
• Inverse cosine
• Inverse tangent
• Special angles
• Exact value
• Decimal approximation
• If we know one of the sides of a right triangle and any one of the other four parts, we can use trigonometry to find all the other unknown parts.
• If we know one of the trigonometric ratios of an acute angle, we can find the angle using the inverse trig key on a calculator.
• For the trigonometric ratios of most angles, your calculator gives approximations, not exact values.

Study Questions

• How many parts of a right triangle (including the right angle) do you need to know in order to solve the triangle?
• Why is it better to use the given values, rather than values you have calculated, when solving a triangle?
• What is the [latex]\sin^{-1}[/latex] (or [latex]\cos^{-1}[/latex] or [latex]\tan^{-1}[/latex]) button on the calculator used for?
• Which are the “special” angles, and why are they special?

If we know three parts of a right triangle, including one of the sides, we can use trigonometry to find all the other unknown parts. This is called solving the triangle.

The inverse sine (arcsine) of a value is the angle whose sine is equal to that value.

The inverse cosine (arccosine) of a value is the angle whose sine is equal to that value.

The inverse tangent (arctangent) of a value is the angle whose sine is equal to that value.

Special angles in trigonometry are angles whose sine, cosine, and tangent values can be calculated exactly without the use of a calculator.

An exact value for a trigonometric function is a value that can be represented as a finite combination of integers, radicals, and/or known mathematical constants without the use of a calculator or approximations.

A decimal approximation for a trigonometric function is an estimation of its value expressed as a finite string of decimal digits, usually rounded to a certain number of decimal places, and obtained through the use of a calculator or other computational tool.

Trigonometry Copyright © 2024 by Bimal Kunwor; Donna Densmore; Jared Eusea; and Yi Zhen. All Rights Reserved.

Share This Book

To use this resource a subscription to Go Teach Maths is required. A subscription gives you access to every resource on the website!

Individual Subscription

School subscription.

• Comprehensive topic coverage
• Over 7000 classroom resources
• GCSE & IGCSE coverage

A subscription to Go Teach Maths gives you access to every resource on the website!

Log in to your individual or school account

Or subscribe from only £25 per year!

Reset your password

Please enter the registered email address for your individual or school subscription.

Solving Real-Life Problems Using Trigonometry

Teacher-Led Activities

2-Minute Feedback Form

[email protected]

• About Go Teach Maths
• What Do Teachers Say About GTM?
• Terms & Conditions

© Go Teach Maths

Privacy Overview

Solve Problems Using Trigonometric Ratios

Calculus ETF 6e

Solve real-life problems involving right triangles

If you are in need of technical support, have a question about advertising opportunities, or have a general question, please contact us by phone or submit a message through the form below.

General Inquiry

Articles From Math Journals

MathArticles.com provides relevant articles from renowned math journals. The articles are coordinated to the topics of Larson Calculus. Visit MathArticles.com to access articles from:

Advertisement

Trig Identities: A Crash Course in Complex Math Concepts

• Share Content on Facebook
• Share Content on LinkedIn
• Share Content on Flipboard
• Share Content on Reddit
• Share Content via Email

Fundamental trigonometric identities, aka trig identities or trigo identities, are equations involving trigonometric functions that hold true for any value you substitute into their variables.

These identities are essential tools if you want to solve trigonometric equations and perform complex calculations in mathematics, physics or engineering . Understanding all the trigonometric identities can help you simplify seemingly complicated problems, especially in geometry and calculus.

The Foundation of Trigonometry

Fundamental trigonometric identities, double angle trigonometric identities, triple angle trigonometric identities, half angle identities, sum and difference identities.

Trigonometry is a branch of mathematics . At the heart of trigonometry lie the trigonometric functions, which relate the angles of a triangle to the ratios of its sides.

The most basic trigonometric functions are sine, cosine and tangent, which instructors often teach using the mnemonic SOH-CAH-TOA in right-angled triangles.

From these basic trig functions, we derive other crucial functions, such as secant, cosecant and cotangent, all of which play vital roles in further developing trigonometric theory.

You might hear people refer to sine, cosine, tangent, secant, cosecant and cotangent as the six trigonometric ratios , or trig ratios.

Trigonometric identities form a cornerstone of higher mathematics. They encapsulate all the trigonometric ratios and relationships in a framework that enhances the solving of equations and understanding of geometric and algebraic concepts.

Trigonometric identities encompass a wide range of formulas, but people generally group them into categories based on their specific applications and forms.

There are three main categories comprising eight fundamental trigonometric identities. These categories include reciprocal identities, Pythagorean identities and quotient identities.

Reciprocal Identities

These identities express the basic trigonometric functions in terms of their reciprocal functions:

• Sine and cosecant : csc( θ ) = 1/sin( θ )
• Cosine and secant : sec( θ ) = 1/cos( θ )
• Tangent and cotangent : cot( θ ) = 1/tan( θ )

Pythagorean Identities

The Pythagorean trigonometric identities stem from the Pythagorean theorem , also known as the Pythagoras theorem, after the Greek scholar who came up with the mathematical statement.

The trig identities based on the Pythagorean theorem are fundamental to connecting the squares of the primary trigonometric functions:

• Basic Pythagorean identity : sin 2 ( θ ) + cos 2 ( θ ) = 1
• Derived for tangent : 1 + tan 2 ( θ ) = sec 2 ( θ )
• Derived for cotangent : cot 2 ( θ ) + 1 = csc 2 ( θ )

Quotient Identities

These identities relate the functions through division:

• Tangent as a quotient : tan( θ ) = sin( θ )/cos( θ )
• Cotangent as a quotient : cot( θ ) = cos( θ )/sin( θ )

Of course, there are many more trigonometric identities beyond just these core identities that have applications in specific scenarios, such as double angle, triple angle, half angle and sum and difference identities.

The double angle formulas are trigonometric identities that express trigonometric functions of double angles — that is, angles of the form 2 θ — in terms of trigonometric functions of single angles ( θ ).

These formulas are crucial in various mathematical computations and transformations, particularly in calculus, geometry and solving trigonometric equations.

The primary double angle formulas include those for sine, cosine and tangent.

Cosine Double Angle Formula

The cosine double angle formula is:

cos(2 θ ) = cos 2 ( θ ) – sin 2 ( θ )

You can also represent this in two alternative forms using the Pythagorean identity sin 2 ( θ ) + cos 2 ( θ ) = 1 :

Sine Double Angle Formula

The sine double angle formula is:

This formula is derived from the sum identities and is useful for solving problems involving products of sine and cosine.

Tangent Double Angle Formula

The tangent double angle formula is:

This expression arises from dividing the sine double angle formula by the cosine double angle formula and simplifying using the definition of tangent.

Triple angle formulas, while less commonly used, offer shortcuts in specific scenarios, such as in certain integrals and polynomial equations. These are identities that allow the calculation of the sine, cosine and tangent of three times a given angle (3θ) using the trigonometric functions of the angle itself (θ).

For example, the sine triple angle formula is:

This formula is derived by using the sine double angle formula and the angle sum identity.

Triple angle formulas can be derived from double angle and sum identities and are useful in specific mathematical and engineering contexts, such as simplifying complex trigonometric expressions or solving higher-degree trigonometric equations.

Half angle identities are trigonometric formulas that allow you to prove trigonometric identities for the sine, cosine and tangent of half of a given angle.

Half angle formulas are particularly useful in solving trigonometric equations, integrating trigonometric functions, and simplifying expressions when the angle involved is halved. Half angle formulas are derived from the double angle identities and other fundamental trigonometric identities.

The half angle identities for sine, cosine and tangent use the following half angle formulas:

• Sine half angle identity : sin⁡( θ /2) = ±√((1 – cos θ )/2)
• Cosine half angle identity : cos⁡( θ /2) = ±√((1 + cos θ ​​)/2)
• Tangent half angle identity : tan( θ /2) = sin( θ )/(1 + cos( θ )) = 1 – (cos( θ )/sin( θ ))

In the case of the sine and cosine half angle formulas, the sign depends on the quadrant in which θ /2​ resides. The tangent half angle formula you can also express in terms of sine and cosine directly.

These identities are derived by manipulating the double angle identities. For example, the cosine double angle identity cos(2 θ ) = 2cos 2 ( θ ) can be rearranged to express cos 2 ( θ ) in terms of cos(2 θ ) , and then taking the square root (and adjusting for sign based on the angle's quadrant) gives the half angle formula for cosine.

Half angle identities are crucial for simplifying the integration of trigonometric functions, particularly when integral limits involve pi (π) or when integrating periodic functions. They also play a vital role in various fields of science and engineering where wave functions and oscillations are analyzed.

Sum identities in trigonometry are essential formulas that allow for the calculation of the sine, cosine and tangent of the sum of two angles. Conversely, difference formulas allow you to calculate the sine, cosine and tangent of the difference between two angles.

These identities are incredibly useful for simplifying expressions, solving trigonometric equations and performing complex calculations.

We created this article in conjunction with AI technology, then made sure it was fact-checked and edited by a HowStuffWorks editor.

Please copy/paste the following text to properly cite this HowStuffWorks.com article:

Precalculus with Limits 3e

Solve real-life problems involving right triangles

If you are in need of technical support, have a question about advertising opportunities, or have a general question, please contact us by phone or submit a message through the form below.

Articles From Math Journals

MathArticles.com provides relevant articles from renowned math journals. The articles are coordinated to the topics of Larson Calculus. Visit MathArticles.com to access articles from: