hardest math problems ever solved

13 World’s Hardest Math Problems | With Solutions

For decades, mathematics has been a fascinating and challenging topic. People have been interested in learning and getting good at math from ancient Greeks to modern mathematicians. But have you ever wondered which math problem is the most challenging?

What could be so tricky and complicated that only some of the brightest mathematicians have been able to solve it? This article will look at 13 of the hardest math problems and how mathematicians have tried to solve them.

Continue reading the article to explore the world’s hardest math problems, listed below.

The Poincaré Conjecture

The prime number theorem, fermat’s last theorem, the reimann hypothesis, classification of finite simple groups, four color theorem, goldbach’s conjecture.

• Inscribed Square Problem

Twin Prime Conjecture

The continuum hypothesis, collatz conjecture, birch and swinnerton-dyer conjecture, the kissing number problem.

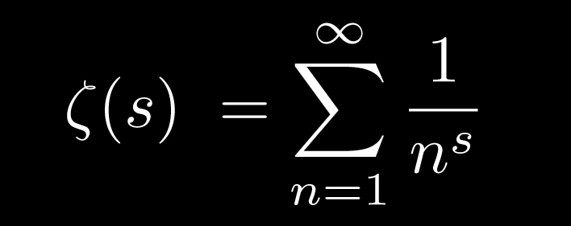
Mathematicians struggled for about a century with the Poincaré conjecture, which was put forth by Henri Poincaré in 1904.

According to this theory,

every closed, connected three-dimensional space is topologically identical to a three-dimensional sphere (S3).

We must explore the field of topology to comprehend what this entails. The study of properties of objects that hold after being stretched, bent, or otherwise distorted is known as topology. In other words, topologists are fascinated by how things can change without rupturing or being torn.

The topology of three-dimensional spaces is the subject of the Poincaré conjecture. A space volume with three dimensions—length, breadth, and height—is a three-dimensional space. A three-dimensional object called a sphere has a round and curved surface.

According to the Poincaré Conjecture, a three-sphere (S3), or the collection of points in four dimensions that are all at a fixed distance from a given point, is topologically identical to every simply-connected, closed, three-dimensional space (i.e., one that has no gaps or voids) and edges. 

Although it would appear easy, it took more than a century to confirm the conjecture thoroughly.

• Poincaré expanded his hypothesis to include any dimension (n-sphere). 
• Stephen Smale, an American mathematician, proved the conjecture to be true for n = 5 in 1961.
• Freedman, another American mathematician, proved the conjecture to be true for n = 4 in 1983. 
• Grigori Perelman, a Russian mathematician, then proved the conjecture to be true for n = 3 in 2002, completing the solution.
• Perelman eventually addressed the problem by combining topology and geometry. One of the highest awards in mathematics, the Fields Medal, was given to all three mathematicians. Perelman rejected the Fields Medal. He was also given a $1 million prize by the Clay Mathematics Institute (CMI) of Cambridge, Massachusetts, for resolving one of the seven Millennium Problems, considered one of the world’s most challenging mathematical puzzles. However, he turned it down as well.

The prime number theorem (PNT) explains how prime numbers asymptotically distribute among positive integers. It shows how fast primes become less common as numbers get bigger.

The prime number theorem states that the number of primes below a given natural number N is roughly N/log(N), with the word “approximately” carrying the typical statistical connotations.

• Two mathematicians, Jacques Hadamard and Charles Jean de la Vallée Poussin, independently proved the Prime Number Theorem in 1896. Since then, the proof has frequently been the subject of rewrites, receiving numerous updates and simplifications. However, the theorem’s influence has only increased.

French lawyer and mathematician Pierre de Fermat lived in the 17th century. Fermat was one of the best mathematicians in history. He talked about many of his theorems in everyday conversation because math was more of a hobby for him.

He made claims without proof, leaving it to other mathematicians decades or even centuries later to prove them. The hardest of them is now referred to as Fermat’s Last Theorem.

Fermat’s last theorem states that;

there are no positive integers a, b, and c that satisfy the equation an + bn = cn for any integer value of n greater than 2.

• In 1993, British mathematician Sir Andrew Wiles solved one of history’s longest mysteries. As a result of his efforts, Wiles was knighted by Queen Elizabeth II and given a special honorary plaque rather than the Fields Medal because he was old enough to qualify.
• Wiles synthesized recent findings from many distinct mathematics disciplines to find answers to Fermat’s well-known number theory query.
• Many people think Fermat never had proof of his Last Theorem because Elliptic Curves were utterly unknown in Fermat’s time.

Mathematicians have been baffled by the Riemann Hypothesis for more than 150 years. It was put forth by the German mathematician Bernhard Riemann in 1859. According to Riemann’s Hypothesis

Every Riemann zeta function nontrivial zero has a real component of ½.

The distribution of prime numbers can be described using the Riemann zeta function. Prime numbers, such as 2, 3, 5, 7, and 11, can only be divided by themselves and by one. Mathematicians have long been fascinated by the distribution of prime numbers because figuring out their patterns and relationships can provide fresh perspectives on number theory and other subject areas.

Riemann’s hypothesis says there is a link between how prime numbers are spread out and how the zeros of the Riemann zeta function are set up. If this relationship is accurate, it could significantly impact number theory and help us understand other parts of mathematics in new ways.

• The Riemann Hypothesis is still unproven, despite being one of mathematics’ most significant unsolved issues.
• Michael Atiyah, a mathematician, proclaimed in 2002 that he had proved the Riemann Hypothesis, although the mathematical community still needs to acknowledge his claim formally.
• The Clay Institute has assigned the hypothesis as one of the seven Millennium Prize Problems. A $1 million prize is up for anyone who can prove the Riemann hypothesis to be true or false.

Abstract algebra can be used to do many different things, like solve the Rubik’s cube or show a body-swapping fact in Futurama. Algebraic groups follow a few basic rules, like having an “identity element” that adds up to 0. Groups can be infinite or finite, and depending on your choice of n, it can be challenging to describe what a group of a particular size n looks like.

There is one possible way that the group can look at whether n is 2 or 3. There are two possibilities when n equals 4. Mathematicians intuitively wanted a complete list of all feasible groups for each given size.

• The categorization of finite simple groups, arguably the most significant mathematical undertaking of the 20th century, was planned by Harvard mathematician Daniel Gorenstein, who presented the incredibly intricate scheme in 1972.
• By 1985, the project was almost finished, but it had consumed so many pages and publications that peer review by a single person was impossible. The proof’s numerous components were eventually reviewed one by one, and the classification’s completeness was verified.
• The proof was acknowledged mainly by the 1990s. Verification was later streamlined to make it more manageable, and that project is still active today.

According to four color theorem

Any map in a plane can be given a four-color coloring utilizing the rule that no two regions sharing a border (aside from a single point) should have the same color.

• Two mathematicians at the University of Illinois at Urbana-Champaign, Kenneth Appel and Wolfgang Hakan identified a vast, finite number of examples to simplify the proof. They thoroughly examined the over 2,000 cases with the aid of computers, arriving at an unheard-of proof style.
• The proof by Appel and Hakan was initially debatable because a computer generated it, but most mathematicians ultimately accepted it. Since then, there has been a noticeable increase in the usage of computer-verified components in proofs, as Appel and Hakan set the standard.

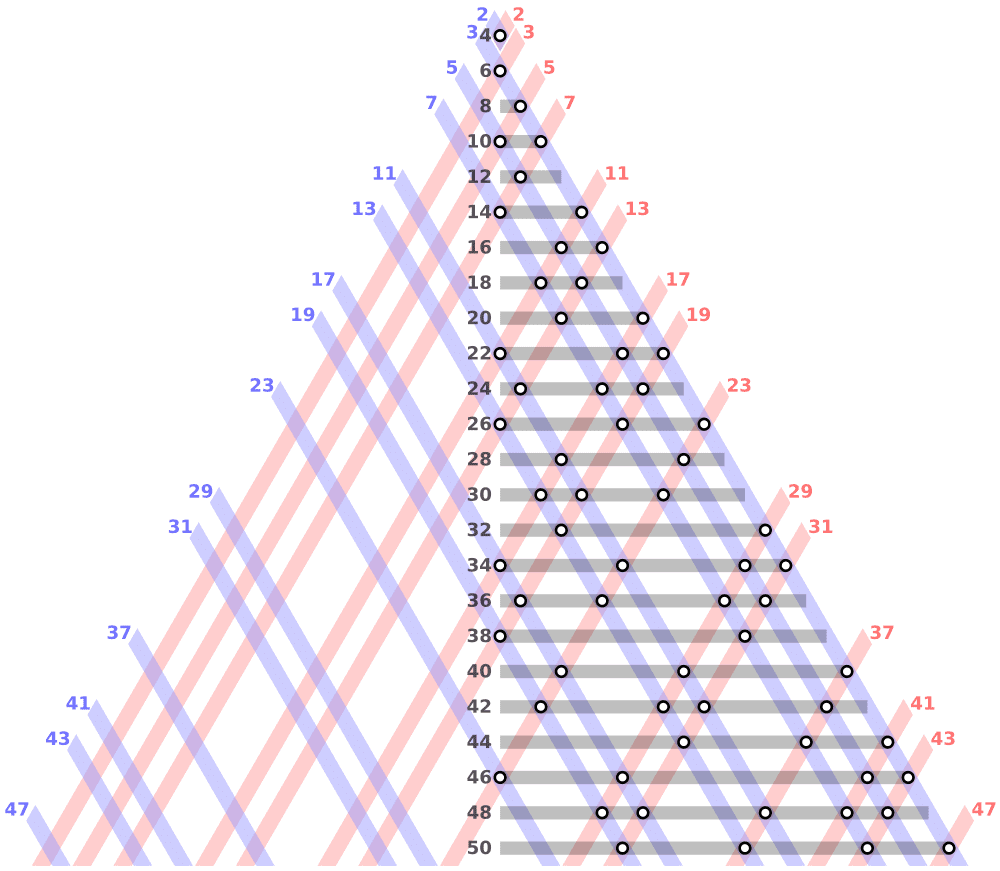
According to Goldbach’s conjecture, every even number (higher than two) is the sum of two primes. You mentally double-check the following for small numbers: 18 is 13 + 5, and 42 is 23 + 19. Computers have tested the conjecture for numbers up to a certain magnitude. But for all natural numbers, we need proof.

Goldbach’s conjecture resulted from correspondence between Swiss mathematician Leonhard Euler and German mathematician Christian Goldbach in 1742.

• Euler is regarded as one of the finest mathematicians in history. Although I cannot prove it, in the words of Euler, “I regard [it] as a totally certain theorem.”
• Euler might have understood why it is conversely tricky to resolve this problem. More significant numbers have more methods than smaller ones to be expressed as sums of primes. In the same way that only 3+5 can split eight into two prime numbers, 42 can be divided into 5+37, 11+31, 13+29, and 19+23. Therefore, for vast numbers, Goldbach’s Conjecture is an understatement.
• The Goldbach conjecture has been confirmed for all integers up to 4*1018, but an analytical proof has yet to be found.
• Many talented mathematicians have attempted to prove it but have yet to succeed.

Inscribed Sq uare Problem

Another complex geometric puzzle is the “square peg problem,” also known as the “inscribed square problem” or the “Toeplitz conjecture.” The Inscribe Square Problem Hypothesis asks:

Does every simple closed curve have an inscribed square?

In other words, it states, ” For any curve, you could draw on a flat page whose ends meet (closed), but lines never cross (simple); we can fit a square whose four corners touch the curve somewhere.

• The inscribed square problem is unsolved in geometry.
• It bears the names of mathematicians Bryan John Birch and Peter Swinnerton-Dyer, who established the conjecture using automated calculation in the first half of the 1960s.
• Only specific instances of the hypothesis have been proven as of 2023.

The Twin Prime Conjecture is one of many prime number-related number theory puzzles. Twin primes are two primes that differ from each other by two. The twin prime examples include 11 and 13 and 599 and 601. Given that there are an unlimited number of prime numbers, according to number theory, there should also be an endless number of twin primes.

The Twin Prime Conjecture asserts that there are limitless numbers of twin primes.

• In 2013, Yitang Zhang did groundbreaking work to solve the twin prime conjecture.
• However, the twin prime conjecture still needs to be solved.

Infinities are everywhere across modern mathematics. There are infinite positive whole numbers (1, 2, 3, 4, etc.) and infinite lines, triangles, spheres, cubes, polygons, etc. It has also been proven by modern mathematics that there are many sizes of infinity.

If the elements of a set can be arranged in a 1-to-1 correspondence with the positive whole numbers, we say the set of elements is countably infinite. Therefore, the set of whole numbers and rational numbers are countable infinities.

Georg Cantor found that the set of real numbers is uncountable. In other words, even if we used all the whole numbers, we would never be able to go through and provide a positive whole number to every real number. Uncountable infinities might be seen as “larger” than countable infinities.

• According to the continuum hypothesis, there must be a set of numbers whose magnitude strictly falls between countably infinite and uncountably infinite. The continuum hypothesis differs from the other problems in this list in that it is impossible to solve or at least impossible to address using present mathematical methods.
• As a result, even though we have yet to determine whether the continuum hypothesis is accurate, we do know that it cannot be supported by the tools of modern set theory either. It would be necessary to develop a new framework for set theory, which has yet to be done, to resolve the continuum hypothesis.

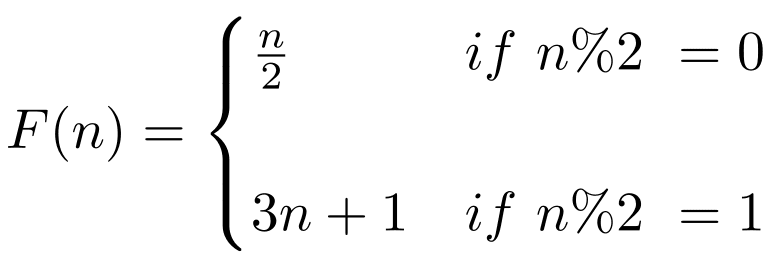
To understand Collatz’s conjecture, try to understand the following example. First, you have to pick a positive number, n. Then, from the last number, create the following sequence:

If the number is even, divide by 2. If it’s odd, multiply by 3 and then add 1. The objective is to keep going through this sequence until you reach 1. Let’s try this sequence with the number 12 as an example. Starting with number 12, we get: 12, 6, 3, 10, 5, 16, 8, 4, 2, 1

Starting at 19, we obtain the following: 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1

According to the Collatz conjecture, this sequence will always end in 1, regardless of the value of n you started with. This speculation has been tested for all values of n up to 87,260, but no proof has been found.

• Collatz’s conjecture has been unsolved up till now.
• Mathematical problem-solver Paul Erdree once said of the Collatz Conjecture, “Mathematics may not be ready for such problems.”

Two British mathematicians, Bryan Birch and Peter Swinnerton-Dyer formulated their hypotheses in the 1960s. The Birch and Swinnerton-Dyer conjecture in mathematics describes rational answers to the equations defining an elliptic curve.

This hypothesis states explicitly that there are an infinite number of rational points (solutions) if ζ(1) equals 0 and that there are only a finite number of such places if ζ(1) is not equal to 0.

• For Birch and Swinnerton-Dyer’s conjecture, Euclid provided a comprehensive solution, but this becomes very challenging for problems with more complex solutions.
• Yu. V. Matiyasevich demonstrated in 1970 that Hilbert’s tenth problem could not be solved, saying there is no mechanism for identifying when such equations have a whole number solution.
• As of 2023, only a few cases have been solved.

Each sphere has a Kissing Number, the number of other spheres it is kissing, when a group of spheres is packed together in one area. For example, your kissing number is six if you touch six nearby spheres. Nothing difficult.

Mathematically, the condition can be described by the average kissing number of a tightly packed group of spheres. However, a fundamental query regarding the kissing number remains unsolved.

First, you must learn about dimensions to understand the kissing number problem. In mathematics, dimensions have a special meaning as independent coordinate axes. The two dimensions of a coordinate plane are represented by the x- and y-axes. 

A line is a two-dimensional object, whereas a plane is a three-dimensional object. Mathematicians have established the highest possible kissing number for spheres with those few dimensions for these low numbers. On a 1-D line, there are two spheres—one to your left and the other to your right.

• The Kissing Problem is generally unsolved in dimensions beyond three.
• A complete solution for the kissing problem number faces many obstacles, including computational constraints. The debate continued to solve this problem.

The Bottom Line

When it comes to pushing the boundaries of the enormous human ability to comprehend and problem-solving skills, the world’s hardest math problems are unquestionably the best. These issues, which range from the evasive Continuum Hypothesis to the perplexing Riemann Hypothesis, continue to puzzle even the sharpest mathematicians.

But regardless of how challenging they are, these problems keep mathematicians inspired and driven to explore new frontiers. Whether or not these problems ever get resolved, they illustrate the enormous ability of the human intellect.

Even though some of these issues might never fully be resolved, they continue to motivate and inspire advancement within the field of mathematics and reflects how broad and enigmatic this subject is!

Let us know out of these 13 problems which problem you find the hardest!

Related Posts

I want to be prodigy genius?

• June 5, 2024 | Starliner’s Stellar Liftoff: NASA Astronauts Embark on Historic Journey to ISS
• June 5, 2024 | How a Single Gram of Salt Can Aggravate Your Eczema
• June 5, 2024 | Unlocking Parental Powers in the Digital Battle With Tweens
• June 5, 2024 | Bone Medications Transform Into Fungal Fighters in Groundbreaking Study
• June 5, 2024 | New “Cost-Effective” Plan Could Reduce CO2 Emissions by 20% – However, It Still Costs Billions of Dollars

This Math Problem Stumped Scientists for Almost a Century – Two Mathematicians Have Finally Solved It

By University of California - San Diego April 11, 2024

Jacques Verstraete and Sam Mattheus, researchers at the University of California, San Diego, have made a significant breakthrough in Ramsey theory by solving the r(4,t) problem, a challenge that has eluded mathematicians for decades.

Mathematicians at UC San Diego have discovered the secret behind Ramsey numbers.

We’ve all been there: staring at a math test with a problem that seems impossible to solve. What if finding the solution to a problem took almost a century? For mathematicians who dabble in Ramsey theory, this is very much the case. In fact, little progress had been made in solving Ramsey problems since the 1930s.

Now, University of California San Diego researchers Jacques Verstraete and Sam Mattheus have found the answer to r(4,t), a longstanding Ramsey problem that has perplexed the math world for decades.

What was Ramsey’s problem, anyway?

In mathematical parlance, a graph is a series of points and the lines in between those points. Ramsey theory suggests that if the graph is large enough, you’re guaranteed to find some kind of order within it — either a set of points with no lines between them or a set of points with all possible lines between them (these sets are called “cliques”). This is written as r(s,t) where s are the points with lines and t are the points without lines.

To those of us who don’t deal in graph theory, the most well-known Ramsey problem, r(3,3), is sometimes called “the theorem on friends and strangers” and is explained by way of a party: in a group of six people, you will find at least three people who all know each other or three people who all don’t know each other. The answer to r(3,3) is six.

Ramsey problems, such as r(4,5) are simple to state, but as shown in this graph, the possible solutions are nearly endless, making them very difficult to solve. Credit: Jacques Verstraete

“It’s a fact of nature, an absolute truth,” Verstraete states. “It doesn’t matter what the situation is or which six people you pick — you will find three people who all know each other or three people who all don’t know each other. You may be able to find more, but you are guaranteed that there will be at least three in one clique or the other.”

What happened after mathematicians found that r(3,3) = 6? Naturally, they wanted to know r(4,4), r(5,5), and r(4,t) where the number of points that are not connected is variable. The solution to r(4,4) is 18 and is proved using a theorem created by Paul Erdös and George Szekeres in the 1930s.

Currently, r(5,5) is still unknown.

A good problem fights back

Why is something so simple to state so hard to solve? It turns out to be more complicated than it appears. Let’s say you knew the solution to r(5,5) was somewhere between 40-50. If you started with 45 points, there would be more than 10 234 graphs to consider!

“Because these numbers are so notoriously difficult to find, mathematicians look for estimations,” Verstraete explained. “This is what Sam and I have achieved in our recent work. How do we find not the exact answer, but the best estimates for what these Ramsey numbers might be?”

Math students learn about Ramsey problems early on, so r(4,t) has been on Verstraete’s radar for most of his professional career. In fact, he first saw the problem in print in Erdös on Graphs: His Legacy of Unsolved Problems, written by two UC San Diego professors, Fan Chung and the late Ron Graham. The problem is a conjecture from Erdös, who offered $250 to the first person who could solve it.

“Many people have thought about r(4,t) — it’s been an open problem for over 90 years,” Verstraete said. “But it wasn’t something that was at the forefront of my research. Everybody knows it’s hard and everyone’s tried to figure it out, so unless you have a new idea, you’re not likely to get anywhere.”

Then about four years ago, Verstraete was working on a different Ramsey problem with a mathematician at the University of Illinois-Chicago, Dhruv Mubayi. Together they discovered that pseudorandom graphs could advance the current knowledge on these old problems.

In 1937, Erdös discovered that using random graphs could give good lower bounds on Ramsey problems. What Verstraete and Mubayi discovered was that sampling from pseudo random graphs frequently gives better bounds on Ramsey numbers than random graphs. These bounds — upper and lower limits on the possible answer — tightened the range of estimations they could make. In other words, they were getting closer to the truth.

In 2019, to the delight of the math world, Verstraete and Mubayi used pseudorandom graphs to solve r(3,t). However, Verstraete struggled to build a pseudorandom graph that could help solve r(4,t).

He began pulling in different areas of math outside of combinatorics, including finite geometry, algebra, and probability. Eventually, he joined forces with Mattheus, a postdoctoral scholar in his group whose background was in finite geometry.

“It turned out that the pseudorandom graph we needed could be found in finite geometry,” Verstraete stated. “Sam was the perfect person to come along and help build what we needed.”

Once they had the pseudorandom graph in place, they still had to puzzle out several pieces of math. It took almost a year, but eventually, they realized they had a solution: r(4,t) is close to a cubic function of t . If you want a party where there will always be four people who all know each other or t people who all don’t know each other, you will need roughly t 3 people present. There is a small asterisk (actually an o) because, remember, this is an estimate, not an exact answer. But t 3 is very close to the exact answer.

The findings are currently under review with the Annals of Mathematics .

“It really did take us years to solve,” Verstraete stated. “And there were many times where we were stuck and wondered if we’d be able to solve it at all. But one should never give up, no matter how long it takes.”

Verstraete emphasizes the importance of perseverance — something he reminds his students of often. “If you find that the problem is hard and you’re stuck, that means it’s a good problem. Fan Chung said a good problem fights back. You can’t expect it just to reveal itself.”

Verstraete knows such dogged determination is well-rewarded: “I got a call from Fan saying she owes me $250.”

Reference: “The asymptotics of r(4,t)” by Sam Mattheus and Jacques Verstraete, 5 March 2024, Annals of Mathematics . DOI: 10.4007/annals.2024.199.2.8

More on SciTechDaily

Scientists Develop Stronger, Stretchier, Self-Healing Plastic

Cells May Use “Fingers” to Communicate Instructions for Wound Closure

From Big Bang to Big Picture: A Comprehensive New View of All Objects in the Universe

Modernizing planetary protection: less restrictive “bioburden” rules would make mars missions simpler.

Transparent Solar Panels for Windows Hit New Efficiency Record – Could Help Enable Skyscrapers to Serve As Power Sources

Redefining Physics: Plasma Jets With Unexpected X-Ray Emissions

Flexible Robot Designed to “Grow” Like a Plant Snakes Through Tight Spaces, Lifts Heavy Loads [Video]

NASA’s Perseverance Rover Discovers Possible Organic Compounds in Mars Crater Rocks

Be the first to comment on "this math problem stumped scientists for almost a century – two mathematicians have finally solved it", leave a comment cancel reply.

Email address is optional. If provided, your email will not be published or shared.

Save my name, email, and website in this browser for the next time I comment.

Advertisement

5 of the world’s toughest unsolved maths problems

The Open Problems in Mathematical Physics is a list of the most monstrous maths riddles in physics. Here are five of the top problems that remain unsolved

By Benjamin Skuse

7 February 2019

Mike Dunning/Getty

1. Separatrix Separation

A pendulum in motion can either swing from side to side or turn in a continuous circle. The point at which it goes from one type of motion to the other is called the separatrix, and this can be calculated in most simple situations. When the pendulum is prodded at an almost constant rate though, the mathematics falls apart. Is there an equation that can describe that kind of separatrix?

Science History Images / Alamy Stock Photo

2. Navier–Stokes

The Navier-Stokes equations, developed in 1822, are used to describe the motion of viscous fluid. Things like air passing over an aircraft wing or water flowing out of a tap. But there are certain situations in which it is unclear whether the equations fail or give no answer at all. Many mathematicians have tried – and failed – to resolve the matter, including Mukhtarbay Otelbaev of the Eurasian National University in Astana, Kazakhstan. In 2014, he claimed a solution, but later retracted it. This is one problem that is worth more than just prestige. It is also one of the Millennium Prize Problems , which means anyone who solves it can claim $1 million in prize money.

Read more: The baffling quantum maths solution it took 10 years to understand

Cecile Lavabre/Getty

3. Exponents and dimensions

Imagine a squirt of perfume diffusing across a room. The movement of each molecule is random, a process called Brownian motion, even if the way the gas wafts overall is predictable. There is a mathematical language that can describe things like this, but not perfectly. It can provide exact solutions by bending its own rules or it can remain strict, but never quite arrive at the exact solution. Could it ever tick both boxes? That is what the exponents and dimensions problem asks. Apart from the quantum Hall conductance problem , this is the only one on the list that is at least partially solved. In 2000, Gregory Lawler, Oded Schramm and Wendelin Werner proved that exact solutions to two problems in Brownian motion can be found without bending the rules. It earned them a Fields medal, the maths equivalent of a Nobel prize. More recently, Stanislav Smirnov at the University of Geneva in Switzerland solved a related problem, which resulted in him being awarded the Fields medal in 2010.

Godong / Alamy Stock Photo

4. Impossibility theorems

There are plenty of mathematical expressions that have no exact solution. Take one of the most famous numbers ever, pi, which is the ratio of a circle’s circumference to its diameter. Proving that it was impossible for pi’s digits after the decimal point to ever end was one of the greatest contributions to maths. Physicists similarly say that it is impossible to find solutions to certain problems, like finding the exact energies of electrons orbiting a helium atom. But can we prove that impossibility?

Tetra Images/Getty

5. Spin glass

To understand this problem, you need to know about spin, a quantum mechanical property of atoms and particles like electrons, which underlies magnetism. You can think of it like an arrow that can point up or down. Electrons inside blocks of materials are happiest if they sit next to electrons that have the opposite spin, but there are some arrangements where that isn’t possible. In these frustrated magnets, spins often flip around randomly in a way that, it turns out, is a useful model of other disordered systems including financial markets. But we have limited ways of mathematically describing how systems like this behave. This spin glass question asks if we can find a good way of doing it.

• See the full list of unsolved problems:  Open Problems in Mathematical Physics  

• mathematics /

Sign up to our weekly newsletter

Receive a weekly dose of discovery in your inbox! We'll also keep you up to date with New Scientist events and special offers.

More from New Scientist

Explore the latest news, articles and features

How the weird and powerful pull of black holes made me a physicist

Subscriber-only

Mathematics

The monty hall problem shows how tricky judging the odds can be, some metals actually grow more resilient when hot, x-ray laser fires most powerful pulse ever recorded, popular articles.

Trending New Scientist articles

Reset password New user? Sign up

Existing user? Log in

Millennium Prize Problems

Already have an account? Log in here.

The Millennium Prize Problems are seven of the most well-known and important unsolved problems in mathematics. The Clay Mathematics Institute, a private nonprofit foundation devoted to mathematical research, famously challenged the mathematical community in 2000 to solve these seven problems, and established a US $1,000,000 reward for the solvers of each. One of the seven problems has been solved, and the other six are the subject of a great deal of current research.

The timing of the announcement of the Millennium Prize Problems at the turn of the century was an homage to a famous speech of David Hilbert to the International Congress of Mathematicians in Paris in 1900. The 23 unsolved problems posed by Hilbert were studied by countless \(20^\text{th}\) century mathematicians, which led not only to solutions to some of the problems, but also to the development of new ideas and new research topics. Some of Hilbert's problems remain open--indeed, the most famous of Hilbert's problems, the Riemann hypothesis , is one of the seven Millennium Prize Problems as well.

The problems encompass a diverse group of topics, including theoretical computer science and physics, as well as pure mathematical areas such as number theory, algebraic geometry, and topology.

Poincare Conjecture

Hodge conjecture, riemann hypothesis, yang-mills existence and mass gap, navier-stokes existence and smoothness, birch-swinnerton-dyer conjecture.

The only Millennium Problem that has been solved to date is the Poincare conjecture, a problem posed in 1904 about the topology of objects called manifolds .

A manifold of dimension \(n\) is a geometric object equipped with a topological structure such that every point has a neighborhood that looks like (is homeomorphic to) \(n\)-dimensional Euclidean space, for some \( n.\) The standard example is a sphere, the surface of a ball embedded in three-dimensional space. An ant on the surface of a sphere thinks that he is standing on flat ground, as the curvature of the sphere is not observable locally. So a sphere is a \(2\)-manifold; the flat ground looks like \(2\)-dimensional Euclidean space.

Another example of a \(2\)-manifold is a (one-holed) torus .

Two manifolds are considered to be different if one cannot be continuously deformed into the other. One way to see that the torus is different from the \(2\)-sphere is that loops on the sphere can all be contracted on the sphere to a point (imagine a rubber band on the surface of a sphere--it can be pulled to the top of the sphere without breaking the band or leaving the sphere), but loops on a torus cannot (e.g. the loop on the top of the torus, or one of the black loops in the picture).

A fundamental question in the theory of manifolds is the classification problem : is there a way to characterize when two manifolds are the same, without having to explicitly write down the map that identifies them? That is, is there a set of properties such that any two manifolds that share all these properties must be the same?

The Poincare conjecture states that any closed (boundaryless) \( n\)-manifold which is homotopy equivalent to the \(n\)-sphere must be the \(n\)-sphere. (Homotopy equivalence is a notion that is strictly weaker than being the same, in general.) This is relatively easy for \(n=1,2.\) It was proved for \( n\ge 5\) by Stephen Smale in the 1960s, and for \( n=4 \) by Michael Freedman in 1982. Both mathematicians were given Fields Medals, the highest honor a mathematician can receive.

The case \(n=3\) is equivalent to the following statement:

Any simply connected, closed 3-manifold is the same as the 3-sphere.

Here simply connected means intuitively that the manifold has no holes; a loop on its surface can always be contracted to a point. As \(n=3\) was the only case left to be proved, this was the statement of the Poincare conjecture when it was posed as a Millennium Problem.

The conjecture was proved in 2003 by the Russian mathematician Grigori Perelman, using ideas of Richard Hamilton from the early 1980s. Hamilton suggested using a vector field flow called the Ricci flow to solve the problem, and demonstrated its efficacy by proving special cases of Poincare's conjecture. Perelman announced his solution of the problem in a series of papers in 2002 and 2003. Peer review confirmed that his proof was correct, and in 2006 he was offered the Fields Medal for his work.

Perelman turned down the Fields Medal and also refused to accept the Clay Millennium Prize when it was officially offered to him in 2010, saying that his contributions were no more significant than Hamilton's. His work is by all accounts quite original and accomplished; despite his apparent modesty and shunning of the spotlight, his proof of the Poincare conjecture will be famous for a very long time.

Main article: P vs. NP

The problem of determining whether \({\mathbf P} = \mathbf{NP}\) is the most important open problem in theoretical computer science. The question asks whether computational problems whose solutions can be verified quickly can also be solved quickly. The consensus of most experts in the field is that this is not true in general, i.e. \( {\mathbf P}\ne \mathbf{NP},\) but there is very little progress toward a proof.

The class of problems in \( \mathbf P\) is the set of problems for which a solution can be found in polynomial time. That is, the problem depends on a positive integer \(n \) which represents the number of inputs (more formally, the information in the problem can be translated into a string of length \( n\)), and it is in \( \mathbf P\) if there is an algorithm that takes the problem as an input and returns a valid solution, such that the running time of the algorithm is less than \( cn^k \) for some positive numbers \( c,k\) which are independent of \( n.\)

The problem of computing the greatest common divisor of two integers \( a,b\) is in \( \mathbf P;\) in fact the Euclidean algorithm runs in time \( \le 5n,\) where \(n\) is the number of decimal digits of either of the integers.

Note that the constants \( c\) and \(k\) in the definition of polynomial time given above might be forbiddingly large in practice. For instance, the primality testing problem was shown quite recently to be in \( {\mathbf P}\); the proof exhibited an explicit algorithm, but the algorithm is not the fastest algorithm for practical purposes.

The class of problems in \( \mathbf{NP}\) is the set of problems for which a solution can be verified in polynomial time. That is, the problem depends on a positive integer \(n \) which represents the number of inputs (more formally, the information in the problem and the prospective solution can be translated into a string of length \( n\)), and it is in \( \mathbf{NP}\) if there is an algorithm that takes the prospective solution as input and returns "yes" or "no" depending on whether the prospective solution is in fact a solution to the problem, such that the running time of the algorithm is less than \( cn^k\) for some positive numbers \( c,k\) which are independent of \( n.\)

The problem of determining whether there is a Hamiltonian path on a given graph is in \( \mathbf{NP}.\) That is, it is quite easy to check whether a particular path on a graph is Hamiltonian; simply check whether it passes through each vertex exactly once. However, the problem of finding a Hamiltonian path is (conjecturally) much harder. Even the problem of determining whether a Hamiltonian path exists is in a class of problems known as \( \mathbf{NP}\)-complete problems; that is, any problem in \( \mathbf{NP}\) can be reduced in polynomial time to the Hamiltonian path problem. So if the Hamiltonian path problem is in \( \mathbf P,\) it follows that \( \mathbf{P}=\mathbf{NP}.\) An extension of the Hamiltonian path problem is the famous traveling salesperson problem .

A proof that \( {\mathbf P} = {\mathbf{NP}} \) would have far-reaching implications, as it would show that many problems thought to be hard, including problems on which many cryptosystems are based, can be solved in polynomial time. Many problems in theoretical mathematics are in \({\mathbf{NP}}\) as well, so \( {\mathbf P} = {\mathbf{NP}} \) would imply that they could be proved or disproved "mechanically" in polynomial time. It should be noted that this does not necessarily mean that these solutions would be practical, and in fact a proof that \( {\mathbf P} = {\mathbf{NP}} \) might be non-constructive; that is, it might be provable that these problems could be solved in polynomial time, via a proof that does not give any indication of the construction of an explicit algorithm that accomplishes this.

The Hodge conjecture is a statement about geometric shapes cut out by polynomial equations over the complex numbers. These are called complex algebraic varieties . An extremely useful tool in the study of these varieties was the construction of groups called cohomology groups , which contained information about the structure of the varieties. The groups are constructed quite abstractly, but have many useful relationships: for instance, a map between varieties corresponds to maps between cohomology groups. Since computations on groups are often more straightforward than computations on varieties, this gives a way to classify and study properties of complex algebraic varieties.

Some elements of these cohomology groups can be written down explicitly from geometric information about the variety, in particular subvarieties of the variety.

The unit sphere \(x^2+y^2+z^2=1\) in complex 3-space contains a curve cut out by \( z=0,\) namely the unit circle \( x^2+y^2=1\) in the \(xy\)-plane. This is the equator of the sphere, and is a subvariety.

The Hodge conjecture states that certain cohomology groups studied by Hodge over certain nice complex varieties are generated by the classes of subvarieties. The cohomology groups in question are often called the groups of Hodge classes, and classes generated by subvarieties are often called algebraic. So in these terms, the conjecture becomes

Every Hodge class on a projective complex manifold is algebraic.

The conjecture was formulated by Hodge in 1950. It is known for varieties of dimension \( \le 3,\) and certain other special cases are known. A successful proof would give a useful indication of the interplay between algebra and geometry. Correspondences between geometric structures (varieties) and algebraic structures (groups) often yield very powerful results: for another example of this phenomenon, see Wiles' proof of Fermat's last theorem , which used the Taniyama-Shimura conjecture relating elliptic curves to modular forms.

The Riemann hypothesis is perhaps the most famous unsolved problem in mathematics. It concerns the nontrivial zeroes of the Riemann zeta function , which is defined for \( \text{Re } s > 1 \) by the infinite sum \[ \zeta(s) = \sum_{n=1}^\infty \frac1{n^s}. \] It can be shown that \( \zeta \) can be analytically continued to a function which is defined and differentiable everywhere in the complex plane, except for a simple pole at \( s=1.\) This function has trivial zeroes on the negative real line, at \( s=-2,-4,-6,\ldots.\) The location of its other zeroes is more mysterious; the conjecture is that

The nontrivial zeroes of the zeta function lie on the line \( \text{Re }s=\frac12.\)

The beauty of the Riemann hypothesis is that it has strong implications about the distribution of primes . In particular, it implies strong bounds on the error term in the prime number theorem , as well as many other results from number theory . For instance, the Riemann hypothesis is equivalent to any of the following three statements:

(1) \( \sigma(n) < e^{\gamma} n \log \log n\) for all \( n > 5040,\) where \( \sigma(n) \) is the sum of divisors of \(n\) and \( \gamma\) is the Euler-Mascheroni constant .

(2) \( \sigma(n) < H_n + e^{H_n} \log(H_n)\) for all \( n \ge 2,\) where \( H_n\) is the \(n^\text{th}\) harmonic number .

(3) \( \sum\limits_{n\le x} \mu(n) = O\big(x^{\frac12 + \epsilon}\big)\) for any \( \epsilon > 0,\) where \(\mu\) is the Möbius function . (See the wiki on big O notation for an explanation of the right side of the equation.)

The generalized Riemann hypothesis is a statement about the zeroes of certain functions known as \( L\)-functions, defined by Dirichlet series , which are generalizations of the Riemann zeta function. The generalized Riemann hypothesis can be used to prove many open questions in number theory, including Artin's conjecture on primitive roots and the so-called weak Goldbach conjecture that every odd prime greater than 5 is the sum of three odd primes.

There are some known results about nontrivial zeroes; they all lie in the critical strip \( 0 < \text{Re } s < 1;\) infinitely many of them lie on the critical line \( \text{Re } s = \frac12;\) the first \( 10^{13} \) nontrivial zeroes, ordered by size of imaginary part, are all on the critical line. The Riemann hypothesis itself still appears to be quite difficult to attack in any meaningful way.

A Yang-Mills theory in quantum physics is a generalization of Maxwell's work on electromagnetic forces to the strong and weak nuclear forces. It is a key ingredient in the so-called Standard Model of particle physics. The Standard Model provides a framework for explaining electromagnetic and nuclear forces and classifying subatomic particles. It has so far proved to be consistent with experimental evidence, but questions remain about its internal consistency.

In particular, successful applications of the theory to experiments and simplified models have involved a "mass gap," which is formally defined as the difference between the default energy in a vacuum and the next lowest energy state. So this quantity is the mass of the lightest particle in the theory. A solution of the Millennium Problem will include both a set of formal axioms that characterize the theory and show that it is internally logically consistent, as well as a proof that there is some strictly positive lower bound on the masses of particles predicted by the theory.

Generally speaking, the current state of the problem is that researchers are successfully obtaining results consistent with experimental evidence by using ideas and models that come from Yang-Mills theory, but there is no rigorous, axiomatized theory that coherently explains the experimental data and successfully predicts results about nuclear forces. There does not appear to be a compelling reason to believe that the problem will be solved soon, but it is of great interest to the physics and mathematics community at large, and will be the subject of extensive research in the coming decades.

The Navier-Stokes equations are partial differential equations modeling the motion of liquids or gases. The fluid is acted on by forces including pressure \( p({\mathbb x},t),\) viscous stress \( \nu,\) and a specified external force. The Navier-Stokes equations are the result of writing down Newton's second law for the fluid with respect to these forces, in terms of partial derivatives of the velocity \(v({\mathbf x},t)\) of the fluid as a function of position and time. The Millennium Problem has two parts; there are existence and smoothness questions for solutions in \( {\mathbb R}^3,\) and existence and smoothness questions for solutions in \( \frac{{\mathbb R}^3}{{\mathbb Z}^3},\) a three-dimensional torus--this is the so-called periodic case. One common explanation for why the problem is so difficult is that solutions to these equations include turbulence, which is a little-understood area of fluid dynamics.

The problem is

Given any initial condition \( v_0 = v({\mathbf x},0)\), a vector field on \( {\mathbb R}^3, \) is there a velocity vector function \( v({\mathbf x},t) \) and a pressure function \( p({\mathbf x},t) \) that satisfy the equations? Is there a smooth solution if \( v_0\) is smooth?

In the non-periodic case, some extra requirements are also imposed on the initial condition and the solution so that they do not grow too large as the length of the position vector in \( {\mathbb R}^3 \) tends to infinity.

Not very much seems to be known about the answer to this question. Smooth solutions exist for the analogous problem in two dimensions (known since the 1960s), but this does not give much of a clue about how to proceed in three dimensions. In three dimensions, smooth solutions are known to exist if \( v_0 \) is "small" in a certain sense, and it is known that smooth solutions exist in general defined for values of the time parameter \( t \) in \( [0,T),\) where \( T\) is a finite time depending on \( v_0\) called the "blowup time." The problem asks for solutions defined for all \( t \in [0,\infty),\) which is more stringent.

There has been some progress on weak solutions to the equation, which are velocity functions \( v({\mathbf x},t) \) that satisfy the equations "on average," rather than for all points \( {\mathbf x}.\) But this has yet to lead to a convincing program to find solutions to the general equations.

The Birch-Swinnerton-Dyer conjecture concerns the rational points (points with all coordinates rational numbers ) on elliptic curves . Elliptic curves are, from a Diophantine perspective, the most interesting curves by far. Associated to every plane curve is a nonnegative integer called the genus. Genus-0 curves are well-understood, and their points are easily parameterized. Curves of genus \( \ge 2 \) have only finitely many rational points, by an extremely deep theorem from the 1980s due to Faltings. Curves of genus 1 with a rational point are precisely the elliptic curves, which have a myriad of applications and a very interesting structure on their sets of rational points. See the elliptic curves wiki for details.

In particular, it is a fact that, given an elliptic curve \( E,\) there is a nonnegative integer \( n\) and a set of rational points \( P_1,\ldots,P_n\) on \( E\) such that every rational point on \(E\) can be written uniquely as an integer linear combination of the \( P_i \) plus a torsion point \( T.\) The torsion points are the points of finite order , and there are finitely many of them. Here the linear combination involves the group law on the elliptic curve, which is nontrivial to write down explicitly (but note that it is not the same thing as coordinate-wise addition). The integer \( n\) is called the rank of \( E,\) and half of the Birch-Swinnerton-Dyer conjecture concerns the computation of that rank.

There is a function \( L(E,s)\) defined by a certain Dirichlet series , which is similar to the Riemann zeta function . The order of vanishing of \( L(E,s) \) at \( s=1\) is called the analytic rank of \( E,\) and the first half of the Birch-Swinnerton-Dyer conjecture is that

The rank of \( E\) equals its analytic rank.

The second half of the conjecture is more technical; it involves the coefficient of \( (s-1)^r \) in the Taylor series for \( L(E,s)\) around \( s=1.\) This coefficient is conjecturally equal to an expression involving products and quotients of several fundamental constants relating to the elliptic curve (for instance, one of them is the number of torsion points).

The first half of the conjecture has been proved in the case when the analytic rank is \( 0 \) or \( 1.\) The second half has been proved for certain special classes of elliptic curves with analytic rank \( 0.\) There is quite a lot of computational evidence for the conjecture (some of which dates back to computer computations done by Birch and Swinnerton-Dyer in the 1960s), but there is not very much progress toward a general proof. Establishing the conjecture would help with theoretical results about the structure of points on elliptic curves, as well as practical applications including finding generators \( P_1,\ldots,P_n\) of the set of rational points.

Problem Loading...

Note Loading...

Set Loading...

• Today's news
• Reviews and deals
• Climate change
• 2024 election
• Fall allergies
• Health news
• Mental health
• Sexual health
• Family health
• So mini ways
• Unapologetically
• Buying guides

Entertainment

• How to Watch
• My watchlist
• Stock market
• Biden economy
• Personal finance
• Stocks: most active
• Stocks: gainers
• Stocks: losers
• Trending tickers
• World indices
• US Treasury bonds
• Top mutual funds
• Highest open interest
• Highest implied volatility
• Currency converter
• Basic materials
• Communication services
• Consumer cyclical
• Consumer defensive
• Financial services
• Industrials
• Real estate
• Mutual funds
• Credit cards
• Balance transfer cards
• Cash back cards
• Rewards cards
• Travel cards
• Online checking
• High-yield savings
• Money market
• Home equity loan
• Personal loans
• Student loans
• Options pit
• Fantasy football
• Pro Pick 'Em
• College Pick 'Em
• Fantasy baseball
• Fantasy hockey
• Fantasy basketball
• Download the app
• Daily fantasy
• Scores and schedules
• GameChannel
• World Baseball Classic
• Premier League
• CONCACAF League
• Champions League
• Motorsports
• Horse racing
• Newsletters

New on Yahoo

• Privacy Dashboard

These Are the 7 Hardest Math Problems Ever Solved — Good Luck in Advance

On the surface, it seems easy. Can you think of the integers for x, y, and z so that x³+y³+z³=8? Sure. One answer is x = 1, y = -1, and z = 2. But what about the integers for x, y, and z so that x³+y³+z³=42?

That turned out to be much harder—as in, no one was able to solve for those integers for 65 years until a supercomputer finally came up with the solution to 42. (For the record: x = -80538738812075974, y = 80435758145817515, and z = 12602123297335631. Obviously.)

That’s the beauty of math: There’s always an answer for everything, even if takes years, decades, or even centuries to find it. So here are seven more brutally difficult math problems that once seemed impossible until mathematicians found a breakthrough.

Henri Poincaré was a French mathematician who, around the turn of the 20th century, did foundational work in what we now call topology. Here’s the idea: Topologists want mathematical tools for distinguishing abstract shapes. For shapes in 3D space, like a ball or a donut, it wasn’t very hard to classify them all . In some significant sense, a ball is the simplest of these shapes.

Poincaré then went up to 4-dimensional stuff, and asked an equivalent question. After some revisions and developments, the conjecture took the form of “Every simply-connected, closed 3-manifold is homeomorphic to S^3,” which essentially says “the simplest 4D shape is the 4D equivalent of a sphere.”

Still with us?

A century later, in 2003, a Russian mathematician named Grigori Perelman posted a proof of Poincaré’s conjecture on the modern open math forum arXiv. Perelman’s proof had some small gaps, and drew directly from research by American mathematician Richard Hamilton. It was groundbreaking, yet modest.

After the math world spent a few years verifying the details of Perelman’s work, the awards began . Perelman was offered the million-dollar Millennium Prize, as well as the Fields Medal, often called the Nobel Prize of Math. Perelman rejected both. He said his work was for the benefit of mathematics, not personal gain, and also that Hamilton, who laid the foundations for his proof, was at least as deserving of the prizes.

It’s a simple one to write. There are many trios of integers (x,y,z) that satisfy x²+y²=z². These are known as the Pythagorean Triples, like (3,4,5) and (5,12,13). Now, do any trios (x,y,z) satisfy x³+y³=z³? The answer is no, and that’s Fermat’s Last Theorem.

Fermat famously wrote the Last Theorem by hand in the margin of a textbook, along with the comment that he had a proof, but could not fit it in the margin. For centuries, the math world has been left wondering if Fermat really had a valid proof in mind.

Flash forward 330 years after Fermat’s death to 1995, when British mathematician Sir Andrew Wiles finally cracked one of history’s oldest open problems . For his efforts, Wiles was knighted by Queen Elizabeth II and was awarded a unique honorary plaque in lieu of the Fields Medal, since he was just above the official age cutoff to receive a Fields Medal.

Wiles managed to combine new research in very different branches of math in order to solve Fermat’s classic number theory question. One of these topics, Elliptic Curves, was completely undiscovered in Fermat’s time, leading many to believe Fermat never really had a proof of his Last Theorem.

Grab any map and four crayons. It’s possible to color each state (or country) on the map, following one rule: No states that share a border get the same color.

The fact that any map can be colored with five colors—the Five Color Theorem —was proven in the 19th century. But getting that down to four took until 1976.

Two mathematicians at the University of Illinois, Urbana-Champaign, Kenneth Appel and Wolfgang Hakan, found a way to reduce the proof to a large, finite number of cases . With computer assistance, they exhaustively checked the nearly 2,000 cases, and ended up with an unprecedented style of proof.

Arguably controversial since it was partially conceived in the mind of a machine, Appel and Hakan’s proof was eventually accepted by most mathematicians. It has since become far more common for proofs to have computer-verified parts, but Appel and Hakan blazed the trail.

Cantor proved that the set of real numbers is larger than the set of natural numbers, which we write as |ℝ|>|ℕ|. It was easy to establish that the size of the natural numbers, |ℕ|, is the first infinite size; no infinite set is smaller than ℕ.

Now, the real numbers are larger, but are they the second infinite size? This turned out to be a much harder question, known as The Continuum Hypothesis (CH) .

If CH is true, then |ℝ| is the second infinite size, and no infinite sets are smaller than ℝ, yet larger than ℕ. And if CH is false, then there is at least one size in between.

So what’s the answer? This is where things take a turn.

CH has been proven independent, relative to the baseline axioms of math. It can be true, and no logical contradictions follow, but it can also be false, and no logical contradictions will follow.

It’s a weird state of affairs, but not completely uncommon in modern math. You may have heard of the Axiom of Choice, another independent statement. The proof of this outcome spanned decades and, naturally, split into two major parts: the proof that CH is consistent, and the proof that the negation of CH is consistent.

The first half is thanks to Kurt Gödel, the legendary Austro-Hungarian logician. His 1938 mathematical construction, known as Gödel’s Constructible Universe , proved CH compatible with the baseline axioms, and is still a cornerstone of Set Theory classes. The second half was pursued for two more decades until Paul Cohen, a mathematician at Stanford, solved it by inventing an entire method of proof in Model Theory known as “forcing.”

Gödel’s and Cohen’s halves of the proof each take a graduate level of Set Theory to approach, so it’s no wonder this unique story has been esoteric outside mathematical circles.

The Prime Number Theorem is more subtle; it describes the distribution of prime numbers along the number line. More precisely, it says that, given a natural number N, the number of primes below N is approximately N/log(N) ... with the usual statistical subtleties to the word “approximately” there.

Drawing on mid-19th-century ideas, two mathematicians, Jacques Hadamard and Charles Jean de la Vallée Poussin, independently proved the Prime Number Theorem in 1898. Since then, the proof has been a popular target for rewrites, enjoying many cosmetic revisions and simplifications. But the impact of the theorem has only grown.

The usefulness of the Prime Number Theorem is huge. Modern computer programs that deal with prime numbers rely on it. It’s fundamental to primality testing methods, and all the cryptology that goes with that.

Now, if we go up to ax³+bx²+cx+d=0, a closed form for “x=” is possible to find, although it’s much bulkier than the quadratic version. It’s also possible, yet ugly, to do this for degree 4 polynomials ax⁴+bx³+cx²+dx+f=0.

The goal of doing this for polynomials of any degree was noted as early as the 15th century. But from degree 5 on, a closed form is not possible. Writing the forms when they’re possible is one thing, but how did mathematicians prove it’s not possible from 5 up?

The world was only starting to comprehend the brilliance of French mathematician Evariste Galois when he died at the age of 20 in 1832. His life included months spent in prison, where he was punished for his political activism, writing ingenious, yet unrefined mathematics to scholars, and it ended in a fatal duel.

Galois’ ideas took decades after his death to be fully understood, but eventually they developed into an entire theory now called Galois Theory . A major theorem in this theory gives exact conditions for when a polynomial can be “solved by radicals,” meaning it has a closed form like the quadratic formula. All polynomials up to degree 4 satisfy these conditions, but starting at degree 5, some don’t, and so there’s no general form for a solution for any degree higher than 4.

The Ancient Greeks wondered about constructing lines and shapes in various ratios, using the tools of an unmarked compass and straightedge. If someone draws an angle on some paper in front of you, and gives you an unmarked ruler, a basic compass, and a pen, it’s possible for you to draw the line that cuts that angle exactly in half. It’s a quick four steps, nicely illustrated like this , and the Greeks knew it two millennia ago.

What eluded them was cutting an angle in thirds. It stayed elusive for literally 15 centuries, with hundreds of attempts in vain to find a construction. It turns out such a construction is impossible.

Modern math students learn the angle trisection problem—and how to prove it’s not possible—in their Galois Theory classes. But, given the aforementioned period of time it took the math world to process Galois’ work, the first proof of the problem was due to another French mathematician, Pierre Wantzel . He published his work in 1837, 16 years after the death of Galois, but nine years before most of Galois’ work was published.

Either way, their insights are similar, casting the construction question into one about properties of certain representative polynomials. Many other ancient construction questions became approachable with these methods, closing off some of the oldest open math questions in history.

So if you ever time-travel to ancient Greece, you can tell them their attempts at the angle trisection problem are futile.

In 2019, mathematicians finally solved a math puzzle that had stumped them for decades. It’s called a Diophantine Equation, and it’s sometimes known as the “summing of three cubes”: Find x, y, and z such that x³+y³+z³=k, for each k from one to 100.

These ten brutally difficult math problems once seemed impossible until mathematicians eventually solved them—even if it took them years, decades, or centuries.

Recommended Stories

Angel reese's 'weak' ejection from sky-liberty game draws attention, offer from bulls' lonzo ball.

Reese was ejected after two very quick whistles from referee Charles Watson.

Sparks rookie Cameron Brink: 'There's a privilege' for WNBA's younger white players

The Sparks rookie had plenty to say about her WNBA rookie class, headlined by Caitlin Clark.

Paul Skenes blows away Shohei Ohtani, who returns the favor in his next at-bat

The Dodgers-Pirates matchup lived up to its billing.

Sky's Chennedy Carter has 'no regrets' about foul on Caitlin Clark; Angel Reese will 'take the bad guy role'

The Sky have broken their silence about the flagrant foul on Caitlin Clark, and they had a lot to say.

Larry Allen, Cowboys legend and Pro Football Hall of Famer, dies at 52

Allen was a seven-time first-team All-Pro and part of the Cowboys' Super Bowl XXX winning team.

Emma Hayes' first big USWNT conundrum: Olympic roster cuts

At least two players who started for the USWNT over the past week will have to be cut for the Olympics. Might Alex Morgan or Rose Lavelle be on the roster bubble?

Chicago Sky players report harassment at team hotel after Chennedy Carter's hard foul on Caitlin Clark

Chennedy Carter's flagrant foul on Caitlin Clark has become something bigger.

Chiefs' Harrison Butker may be removed from kickoffs due to new NFL rules

Kansas City Chiefs special teams coach Dave Toub said kicker Harrison Butker may be removed from kickoffs. But not because of Butker's recent controversial remarks.

Opposing players aren't fond of Caitlin Clark ... which should be good for the WNBA

Watching Clark fight through adversity and rack up rivals will only bring more eyeballs to the league.

Beware the retirement savings 'time bomb,' tax expert warns

Taxes are the "retirement time bomb," according to one tax expert. Here's what you can do now.