how to solve sequence problems

Number Sequences

Related Pages Linear Sequences Geometric Sequences Quadratic and Cubic Sequences

Number sequences are ordered lists of numbers that follow a particular pattern or rule. These sequences can be either finite or infinite, and can have different types of patterns. Some number sequences have a simple pattern, such as adding a fixed number to each term, while others may have more complex patterns that are not immediately obvious.

In these lessons, we will look at various types of number sequences and how to solve problems related to number sequences. In another set of lessons, we have some examples of Integer Word Problems that involve two unknowns .

Arithmetic and geometric sequences are two common types of number sequences that follow specific patterns.

An arithmetic sequence is a sequence in which each term is obtained by adding a fixed number to the previous term. For example, 2, 4, 6, 8, 10, 12, … is an arithmetic sequence, where each term is obtained by adding 2 to the previous term. The fixed number that is added to each term is called the common difference.

A geometric sequence, on the other hand, is a sequence in which each term is obtained by multiplying the previous term by a fixed number. For example, 2, 4, 8, 16, 32, 64, … is a geometric sequence, where each term is obtained by multiplying the previous term by 2. The fixed number that is multiplied by each term is called the common ratio.

How To Find The Next Term In A Number Sequence?

A number sequence is a list of numbers arranged in a row. Let us look at two examples below. (i) 4, 6, 1, 10, 14, 5, … (ii) 4, 7, 10, 13, ….

Number sequence (i) is a list of numbers without order or pattern. You cannot tell what number comes after 5.

Number sequence (ii) has a pattern. Do you observe that each number is obtained by adding 3 to the preceding number (i.e. the number just before it)?

In these lesson, we will only study number sequences with patterns.

Some other examples of number sequences are:

How To Complete Missing Terms In A Number Sequence?

Each of the number in the sequence is called a term . In order to find the missing terms in a number sequence, we must first find the pattern of the number sequence.

Example: Find the missing terms in the following sequence: 8, ______, 16, ______, 24, 28, 32

Solution: To find the pattern, look closely at 24, 28 and 32. Each term in the number sequence is formed by adding 4 to the preceding number. So, the missing terms are 8 + 4 = 12 and 16 + 4 = 20. Check that the pattern is correct for the whole sequence from 8 to 32.

Example: What is the value of n in the following number sequence?

Solution: We find that the number pattern of the sequence is “add 5” to the preceding number. So, n = 21 + 5 = 26

The following video shows some examples of how to determine the next term in a number sequence.

Examples: Find the next number

• 1, 8, 15, 22, …
• 1, 8, 64, 512, …
• 1, 8, 27, 64, …
• 1, 8, 16, 15, …

How To Find The nth Term Of An Arithmetic Sequence

Example: 7, 9, 11, 13, 15, …

How To Find The nth Term Of A Geometric Sequence

Example: 5, 10, 20, 40, …

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

You can read a gentle introduction to Sequences in Common Number Patterns .

What is a Sequence?

A Sequence is a list of things (usually numbers) that are in order.

Infinite or Finite

When the sequence goes on forever it is called an infinite sequence , otherwise it is a finite sequence

{1, 2, 3, 4, ...} is a very simple sequence (and it is an infinite sequence )

{20, 25, 30, 35, ...} is also an infinite sequence

{1, 3, 5, 7} is the sequence of the first 4 odd numbers (and is a finite sequence )

{4, 3, 2, 1} is 4 to 1 backwards

{1, 2, 4, 8, 16, 32, ...} is an infinite sequence where every term doubles

{a, b, c, d, e} is the sequence of the first 5 letters alphabetically

{f, r, e, d} is the sequence of letters in the name "fred"

{0, 1, 0, 1, 0, 1, ...} is the sequence of alternating 0s and 1s (yes they are in order, it is an alternating order in this case)

When we say the terms are "in order", we are free to define what order that is ! They could go forwards, backwards ... or they could alternate ... or any type of order we want!

A Sequence is like a Set , except:

• the terms are in order (with Sets the order does not matter)
• the same value can appear many times (only once in Sets)

Example: {0, 1, 0, 1, 0, 1, ...} is the sequence of alternating 0s and 1s.

The set is just {0,1}

Sequences also use the same notation as sets:

The curly brackets { } are sometimes called "set brackets" or "braces".

A Sequence usually has a Rule , which is a way to find the value of each term.

Example: the sequence {3, 5, 7, 9, ...} starts at 3 and jumps 2 every time:

As a Formula

Saying " starts at 3 and jumps 2 every time " is fine, but it doesn't help us calculate the:

• 10 th term,
• 100 th term, or
• n th term, where n could be any term number we want.

So, we want a formula with " n " in it (where n is any term number).

So, What Can A Rule For {3, 5, 7, 9, ...} Be?

Firstly, we can see the sequence goes up 2 every time, so we can guess that a Rule is something like "2 times n" (where "n" is the term number). Let's test it out:

Test Rule: 2n

That nearly worked ... but it is too low by 1 every time, so let us try changing it to:

Test Rule: 2n+1

That Works!

So instead of saying "starts at 3 and jumps 2 every time" we write this:

Now we can calculate, for example, the 100th term :

2 × 100 + 1 = 201

But mathematics is so powerful we can find more than one Rule that works for any sequence.

Example: the sequence {3, 5, 7, 9, ...}

We have just shown a Rule for {3, 5, 7, 9, ...} is: 2n+1

And so we get: {3, 5, 7, 9, 11, 13, ...}

But can we find another rule?

How about "odd numbers without a 1 in them" :

And we get: {3, 5, 7, 9, 23, 25, ...}

A completely different sequence!

And we could find more rules that match {3, 5, 7, 9, ...} . Really we could.

So it is best to say "A Rule" rather than "The Rule" (unless we know it is the right Rule).

To make it easier to use rules, we often use this special style:

Example: to mention the "5th term" we write: x 5

So a rule for {3, 5, 7, 9, ...} can be written as an equation like this:

And to calculate the 10th term we can write:

x 10 = 2 n +1 = 2× 10 +1 = 21

Can you calculate x 50 (the 50th term) doing this?

Here is another example:

{a n } = { (-1/n) n }

Calculations:

• a 1 = (-1/1) 1 = -1
• a 2 = (-1/2) 2 = 1/4
• a 3 = (-1/3) 3 = -1/27
• a 4 = (-1/4) 4 = 1/256

{a n } = { -1, 1/4, -1/27, 1/256, ... }

Special Sequences

Now let's look at some special sequences, and their rules.

Arithmetic Sequences

In an Arithmetic Sequence the difference between one term and the next is a constant .

In other words, we just add some value each time ... on to infinity.

This sequence has a difference of 3 between each number. Its Rule is x n = 3n-2

In General we can write an arithmetic sequence like this:

{a, a+d, a+2d, a+3d, ... }

• a is the first term, and
• d is the difference between the terms (called the "common difference" )

And we can make the rule:

x n = a + d(n-1)

(We use "n-1" because d is not used in the 1st term).

Geometric Sequences

In a Geometric Sequence each term is found by multiplying the previous term by a constant .

This sequence has a factor of 2 between each number. Its Rule is x n = 2 n

In General we can write a geometric sequence like this:

{a, ar, ar 2 , ar 3 , ... }

• r is the factor between the terms (called the "common ratio" )

Note: r should not be 0.

• When r=0 , we get the sequence {a,0,0,...} which is not geometric

And the rule is:

x n = ar (n-1)

(We use "n-1" because ar 0 is the 1st term)

Triangular Numbers

The Triangular Number Sequence is generated from a pattern of dots which form a triangle:

By adding another row of dots and counting all the dots we can find the next number of the sequence.

But it is easier to use this Rule:

x n = n(n+1)/2

• the 5th Triangular Number is x 5 = 5(5+1)/2 = 15 ,
• and the sixth is x 6 = 6(6+1)/2 = 21

Square Numbers

The next number is made by squaring where it is in the pattern.

Cube Numbers

The next number is made by cubing where it is in the pattern.

Fibonacci Sequence

This is the Fibonacci Sequence

The next number is found by adding the two numbers before it together:

• The 2 is found by adding the two numbers before it (1+1)
• The 21 is found by adding the two numbers before it (8+13)

x n = x n-1 + x n-2

That rule is interesting because it depends on the values of the previous two terms.

Rules like that are called recursive formulas.

The Fibonacci Sequence is numbered from 0 onwards like this:

Example: term "6" is calculated like this:

x 6 = x 6-1 + x 6-2 = x 5 + x 4 = 5 + 3 = 8

Series and Partial Sums

Now you know about sequences, the next thing to learn about is how to sum them up. Read our page on Partial Sums .

When we sum up just part of a sequence it is called a Partial Sum .

But a sum of an infinite sequence it is called a "Series" (it sounds like another name for sequence, but it is actually a sum). See Infinite Series .

Example: Odd numbers

Sequence: {1, 3, 5, 7, ...}

Series: 1 + 3 + 5 + 7 + ...

Partial Sum of first 3 terms: 1 + 3 + 5

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators

Arithmetic Sequence Problems with Solutions – Mastering Series Challenges

JUMP TO TOPIC

Arithmetic Sequences Practice Problems and Solutions

Calculating terms in an arithmetic sequence, solving problems involving arithmetic sequences.

An arithmetic sequence is a series where each term increases by a constant amount, known as the common difference . I’ve always been fascinated by how this simple pattern appears in many mathematical problems and real-world situations alike.

Understanding this concept is fundamental for students as it not only enhances their problem-solving skills but also introduces them to the systematic approach of sequences in math .

The first term of an arithmetic sequence sets the stage, while the common difference dictates the incremental steps that each subsequent term will follow. This can be mathematically expressed as $a_n = a_1 + (n – 1)d$.

Whether I’m calculating the nth term or the sum of terms within a sequence , these formulas are the tools that uncover solutions to countless arithmetic sequence problems. Join me in unraveling the beauty and simplicity of arithmetic sequences ; together, we might just discover why they’re considered the building blocks in the world of mathematics .

When I work with arithmetic sequences , I always keep in mind that they have a unique feature: each term is derived by adding a constant value, known as the common difference , to the previous term. Let’s explore this concept through a few examples and problems.

Example 1: Finding a Term in the Sequence

Given the first term, $a_1$ of an arithmetic sequence is 5 and the common difference ( d ) is 3, what is the 10th term $a_{10}$?

Here’s how I determine it: $a_{10} = a_1 + (10 – 1)d ] [ a_{10} = 5 + 9 \times 3 ] [ a_{10} = 5 + 27 ] [ a_{10} = 32$

So, the 10th term is 32.

Sequence A: If $a_1 = 2 $and ( d = 4 ), find $a_5$.

Sequence B: For $a_3 = 7 $ and $a_7 = 19$, calculate the common difference ( d ).

I calculate $a_5$ by using the formula: $a_n = a_1 + (n – 1)d $ $ a_5 = 2 + (5 – 1) \times 4 $ $a_5 = 2 + 16 $ $a_5 = 18$

To find ( d ), I use the formula: $a_n = a_1 + (n – 1)d$ Solving for ( d ), I rearrange the terms from $a_3$ and $a_7$: $d = \frac{a_7 – a_3}{7 – 3}$ $d = \frac{19 – 7}{4}$ $d = \frac{12}{4}$ [ d = 3 ]

Here’s a quick reference table summarizing the properties of arithmetic sequences :

Remember these properties to solve any arithmetic sequence problem effectively!

In an arithmetic sequence , each term after the first is found by adding a constant, known as the common difference ( d ), to the previous term. I find that a clear understanding of the formula helps immensely:

$a_n = a_1 + (n – 1)d$

Here, $a_n$ represents the $n^{th}$term, $a_1$ is the first term, and ( n ) is the term number.

Let’s say we need to calculate the fourth and fifth terms of a sequence where the first term $a_1 $ is 8 and the common difference ( d ) is 2. The explicit formula for this sequence would be $ a_n = 8 + (n – 1)(2) $.

To calculate the fourth term $a_4 $: $a_4 = 8 + (4 – 1)(2) = 8 + 6 = 14$

For the fifth term ( a_5 ), just add the common difference to the fourth term: $a_5 = a_4 + d = 14 + 2 = 16$

Here’s a table to illustrate these calculations:

Remember, the formula provides a direct way to calculate any term in the sequence, known as the explicit or general term formula. Just insert the term number ( n ) and you’ll get the value for $a_n$. I find this methodical approach simplifies the process and avoids confusion.

When I approach arithmetic sequences , I find it helpful to remember that they’re essentially lists of numbers where each term is found by adding a constant to the previous term. This constant is called the common difference, denoted as ( d ). For example, in the sequence 3, 7, 11, 15, …, the common difference is ( d = 4 ).

To articulate the ( n )th term of an arithmetic sequence, $a_n $, I use the fundamental formula:

$a_n = a_1 + (n – 1)d $

In this expression, $a_1$ represents the first term of the sequence.

If I’m solving a specific problem—let’s call it Example 1—I might be given $a_1 = 5 $and ( d = 3 ), and asked to find $a_4 $. I’d calculate it as follows:

$a_4 = 5 + (4 – 1) \times 3 = 5 + 9 = 14$

In applications involving arithmetic series, such as financial planning or scheduling tasks over weeks, the sum of the first ( n ) terms often comes into play. To calculate this sum, ( S_n ), I rely on the formula:

$S_n = \frac{n}{2}(a_1 + a_n)$

Now, if I’m asked to work through Example 3, where I need the sum of the first 10 terms of the sequence starting with 2 and having a common difference of 5, the process looks like this:

$a_{10} = 2 + (10 – 1) \times 5 = 47$ $S_{10} = \frac{10}{2}(2 + 47) = 5 \times 49 = 245$

Linear functions and systems of equations sometimes bear a resemblance to arithmetic sequences, such as when I need to find the intersection of sequence A and sequence B. This would involve setting the nth terms equal to each other and solving the resulting linear equation.

Occasionally, arithmetic sequences can be mistaken for geometric sequences , where each term is found by multiplying by a constant. It’s important to differentiate between them based on their definitions.

For exercises, it’s beneficial to practice finding nth terms, and sums , and even constructing sequences from given scenarios. This ensures a robust understanding when faced with a variety of problems involving arithmetic sequences .

In exploring the realm of arithmetic sequences , I’ve delved into numerous problems and their corresponding solutions. The patterns in these sequences—where the difference between consecutive terms remains constant—allow for straightforward and satisfying problem-solving experiences.

For a sequence with an initial term of $a_1 $ and a common difference of ( d ), the $n^{th}$term is given by $a_n = a_1 + (n – 1)d $.

I’ve found that this formula not only assists in identifying individual terms but also in predicting future ones. Whether calculating the $50^{th}$term or determining the sum of the first several terms, the process remains consistent and is rooted in this foundational equation.

In educational settings, arithmetic sequences serve as an excellent tool for reinforcing the core concepts of algebra and functions. Complexity varies from basic to advanced problems, catering to a range of skill levels. These sequences also reflect practical real-world applications, such as financial modeling and computer algorithms, highlighting the relevance beyond classroom walls.

Through practicing these problems, the elegance and power of arithmetic sequences in mathematical analysis become increasingly apparent. They exemplify the harmony of structure and progression in mathematics —a reminder of how simple rules can generate infinitely complex and fascinating patterns.

• Pre Calculus
• Probability
• Sets & Set Theory
• Trigonometry

Arithmetic Sequences Problems with Solutions

Arithmetic sequences are used throughout mathematics and applied to engineering, sciences, computer sciences, biology and finance problems. A set of problems and exercises involving arithmetic sequences, along with detailed solutions are presented.

Review of Arithmetic Sequences

The formula for the n th term a n of an arithmetic sequence with a common difference d and a first term a 1 is given by \[ a_n = a_1 + (n - 1) d \] The sum s n of the first n terms of an arithmetic sequence is defined by \[ s_n = a_1 + a_2 + a_3 + ... + a_n \] and is is given by \[ s_n = \dfrac{n (a_1 + a_n)}{2} \] Arithmetic Series Online Calculator . An online calculator to calculate the sum of the terms in an arithmetic sequence.

Problems with Solutions

The first term of an arithmetic sequence is equal to 6 and the common difference is equal to 3. Find a formula for the n th term and the value of the 50 th term Solution to Problem 1: Use the value of the common difference d = 3 and the first term a 1 = 6 in the formula for the n th term given above \( a_n = a_1 + (n - 1) d \\ = 6 + 3 (n - 1) \\ = 3 n + 3 \) The 50 th term is found by setting n = 50 in the above formula. \[ a_{50} = 3 (50) + 3 = 153 \]

The first term of an arithmetic sequence is equal to 200 and the common difference is equal to -10. Find the value of the 20 th term Solution to Problem 2: Use the value of the common difference d = -10 and the first term a 1 = 200 in the formula for the n th term given above and then apply it to the 20 th term a 20 = 200 + (-10) (20 - 1 ) = 10

An arithmetic sequence has a common difference equal to 10 and its 6 th term is equal to 52. Find its 15 th term. Solution to Problem 3: We use the n th term formula for the 6 th term, which is known, to write a 6 = 52 = a 1 + 10 (6 - 1 ) The above equation allows us to calculate a 1 . a 1 = 2 Now that we know the first term and the common difference, we use the n th term formula to find the 15 th term as follows. a 15 = 2 + 10 (15 - 1) = 142

An arithmetic sequence has a its 5 th term equal to 22 and its 15 th term equal to 62. Find its 100 th term. Solution to Problem 4: We use the n th term formula for the 5 th and 15 th terms to write a 5 = a 1 + (5 - 1 ) d = 22 a 15 = a 1 + (15 - 1 ) d = 62 We obtain a system of 2 linear equations where the unknown are a 1 and d. Subtract the right and left term of the two equations to obtain 62 - 22 = 14 d - 4 d Solve for d. d = 4 Now use the value of d in one of the equations to find a 1 . a 1 + (5 - 1 ) 4 = 22 Solve for a 1 to obtain. a 1 = 6 Now that we have calculated a 1 and d we use them in the n th term formula to find the 100 th formula. a 100 = 6 + 4 (100 - 1 )= 402

Find the sum of all the integers from 1 to 1000. Solution to Problem 5: The sequence of integers starting from 1 to 1000 is given by 1 , 2 , 3 , 4 , ... , 1000 The above sequence has 1000 terms. The first term is 1 and the last term is 1000 and the common difference is equal to 1. We have the formula that gives the sum of the first n terms of an arithmetic sequence knowing the first and last term of the sequence and the number of terms (see formula above). s 1000 = 1000 (1 + 1000) / 2 = 500500

Find the sum of the first 50 even positive integers. Solution to Problem 6: The sequence of the first 50 even positive integers is given by 2 , 4 , 6 , ... The above sequence has a first term equal to 2 and a common difference d = 2. We use the n th term formula to find the 50 th term a 50 = 2 + 2 (50 - 1) = 100 We now the first term and last term and the number of terms in the sequence, we now find the sum of the first 50 terms s 50 = 50 (2 + 100) / 2 = 2550

Find the sum of all positive integers, from 5 to 1555 inclusive, that are divisible by 5. Solution to Problem 7: The first few terms of a sequence of positive integers divisible by 5 is given by 5 , 10 , 15 , ... The above sequence has a first term equal to 5 and a common difference d = 5. We need to know the rank of the term 1555. We use the formula for the n th term as follows 1555 = a 1 + (n - 1 )d Substitute a 1 and d by their values 1555 = 5 + 5(n - 1 ) Solve for n to obtain n = 311 We now know that 1555 is the 311 th term, we can use the formula for the sum as follows s 311 = 311 (5 + 1555) / 2 = 242580

Find the sum S defined by \[ S = \sum_{n=1}^{10} (2n + 1 / 2) \] Solution to Problem 8: Let us first decompose this sum as follows \( S = \sum_{n=1}^{10} (2n + 1 / 2) \) \( = 2 \sum_{n=1}^{10} n + \sum_{n=1}^{10} (1/2) \) The term ∑ n is the sum of the first 10 positive integers. The 10 first positive integers make an arirhmetic sequence with first term equal to 1, it has n = 10 terms and its 10 th term is equal to 10. This sum is obtained using the formula s n = n (a 1 + a n ) / 2 as follows 10(1+10)/2 = 55 The term ∑ (1 / 2) is the addition of a constant term 10 times and is given by 10(1/2) = 5 The sum S is given by S = 2(55) + 5 = 115

Answer the following questions related to arithmetic sequences: a) Find a 20 given that a 3 = 9 and a 8 = 24 b) Find a 30 given that the first few terms of an arithmetic sequence are given by 6,12,18,... c) Find d given that a 1 = 10 and a 20 = 466 d) Find s 30 given that a 10 = 28 and a 20 = 58 e) Find the sum S defined by \[ S = \sum_{n=1}^{20}(3n - 1 / 2) \] f) Find the sum S defined by \[ S = \sum_{n=1}^{20}0.2 n + \sum_{j=21}^{40} 0.4 j \]

Solutions to Above Exercises

a) a 20 = 60 b) a 30 = 180 c) d = 24 d) s 30 = 1335 e) 1380 f) 286

More References and links

• Geometric Sequences Problems with Solutions
• math problems with detailed solutions
• Math Tutorials and Problems

• IIT JEE Study Material

Sequence and Series Problems

Introduction to sequence and series.

In Mathematics, a sequence is a group of numbers in an ordered way following a pattern. The numbers are the terms, and the index is the position of the term denoted by a i . In this article, you will learn sequence and series problems along with the solutions.

A series is the summation of a sequence. It is given by S N = a 1 + a 2 + a 3 + a 4 +……. + a n .

Types of Sequence and Series

The following are the types of sequence and series.

In a finite series, a finite number of terms are present, whereas an infinite series consists of infinite terms.

Some common sequences are as follows:

• Finite and Infinite Sequence : A finite sequence is one with finite terms, whereas an infinite sequence is with never-ending terms or is infinite in the count.
• Arithmetic Sequence: A sequence where the sum or difference between any two consecutive terms is a constant, termed a common difference.
• Geometric Sequence: A sequence where every term is obtained by multiplying or dividing a certain number by the preceding term.
• Harmonic Sequence: A sequence obtained by the reciprocals of the elements of an arithmetic sequence.
• Fibonacci Sequence: A sequence where the sum of the two preceding terms will give the succeeding term.

Important Formulas

The formulae for sequence and series are as follows:

• The n th term of the arithmetic sequence or arithmetic progression (A.P) is given by a n = a + (n – 1) d
• The arithmetic mean [AM] between a and b is AM = [a + b] / 2
• The n th term an of the geometric sequence or geometric progression [GP] is a n = a * r n–1
• The geometric mean between a and b is \(\begin{array}{l}GM = \pm \sqrt{ab}\end{array} \)
• The n th term a n of the harmonic progression is a n = 1 / [a + (n – 1) d]
• The harmonic mean between a and b is HM = 2ab / [a + b]
• Series of AP: S n = [n / 2] (a + l), S n = (n / 2) [2a + (n – 1) d], where S n is the sum to n terms of AP.
• The sum of ‘n’ AM between a and b is AM = [n (a + b)] / 2
• Series of GP: S n = [a (1 – r n )] / [1 – r], where S n is the sum to n terms of GP.
• The sum ‘S’ of infinite geometric series is S = a / 1–r.

Also, Read:

• Arithmetic Progression for IIT JEE
• Arithmetic Progression Solved Examples
• Geometric Progression Solved Examples

Top Questions of Sequence and Series for JEE Advanced

Solved Examples on Sequence and Series

Example 1: In a GP, the second term is 12, and the sixth term is 192. Find the 11 th term.

Given second term, ar = 12 ..(1)

Sixth term, ar 5 = 192 …(2)

Dividing (2) by (1), we get ar 5 / ar = 192/12

Substitute r in (1), we get a ×2 = 12

⇒ a = 12/2 = 6

11 the  term is given by ar 10  = 6 ×2 10 = 6144

Hence, the required answer is 6144.

Example 2: If S n denotes the sum of the first n terms of an AP and [S 3n − S n−1 ] / [S 2n −S 2n−1 ] = 31, then the value of n is __________.

= a (2n + 1) + d (4n 2 − 1)

S 2n − S 2n−1 = T 2n = a +(2n − 1) d

⇒ S 3n  − S n − S 2n −S 2n−1  = (2n + 1)

Given, ⇒ [S 3n − S n−1 ] / [S 2n − S 2n−1 ] = 31

Example 3: If the sum of n terms of an AP is (c*n) (n – 1), where c ≠ 0, then the sum of the squares of this term is __________.

If t r is the r th term of the AP, then

t r = S r − S r−1 = cr (r − 1) − c (r − 1) (r − 2) = c (r − 1) (r − r + 2) = 2c (r − 1)

We have, t 1 2 + t 2 2 +……..+t n 2 = 4c 2 (o 2 + 1 2 + 2 2 … + (n − 1) 2 )

= [2 / 3] c 2 n (n − 1) (2n − 1)

Example 4: The largest term common to the sequences 1, 11, 21, 31,…. to 100 terms and 31, 36, 41, 46,………to 100 terms is ___________.

100 th term of 1, 11, 21, 31, …………. is 1+ (100 – 1) 10 = 991.

100 th term of 31, 36, 41, 46, ………… is 31 + (100 – 1) 5 = 526.

Let the largest common term be 526.

Then, 526 = 31 + (n – 1) 10

Or n = 50.5

But n is an integer, so n = 50.

Hence, the largest common terms are 31 + (n – 1) 10 = 521.

Example 5: Find the sum of the series 1 + 1 / [4 * 2!] + 1 / [16 * 4!] + 1 / [64 * 6!]+……….

We know that e x = 1 + x / 1! + x 2 / 2! + x 3 / 3! + x 4 / 4! + …….. ∞ ——— (i)

∴ [e x + e −x ] / 2 = 1 + x 2 / 2! + x 3 / 3! + x 4 / 4………..∞ ————-(ii)

On adding equations (i) and (ii),

We get e x + e −x = 2x + 2x 2 / 2! + 2x 4 / 4!+…∞

∴ [e x + e −x ] / 2 = 1 + x 2 / 2! + x 4 / 4 + x 6 / 6!+ ……………

Putting x = 1 / 2, we get

e + 1 / 2√ e = 1 + 1 / [4 * 2!] + 1 / [16 * 4!] + 1 / [64 * 6!]+……….

Example 6: If a, b, and c are in AP, p, q, and r are in HP, and ap, bq, and cr are in GP, then [p / r] + [r / p] is equal to ______________.

p / r + r / p = [p 2 + r 2 ] / [pr]  

= (p + r) 2  − ([2pr] / [pr])  

= [(4p 2 r 2  / q 2 ) − 2pr] / [pr] 

[p, q, r are in HP. Therefore, q = 2pr / [p + r]] 

= [4pr / q 2 ] − [2]

= [4b  / ac] − [2]                    

[ap, bq, cr are in A.P ⇒ b 2 q 2 = ac * pr] 

= [(a + c) 2  / ac] − [2]            

[a, b, c are in A.P ⇒ 2b = a + c] 

= [a / c] + [c / a]. 

Example 7: If x, 2y, 3z are in AP, where the distinct numbers x, y, z are in GP, then the common ratio of the GP is ___________.

x, y and z are in GP.

Hence, Y= xr, zy = xr, x = xr 2

Also, x, 2y, and 3z are in AP.

Hence, 4y = x + 3z ⇒4xr = x + 3xr 2

⇒ 3r 2 − 4r + 1 = 0

⇒ (3r − 1) (r − 1) = 0

Example 8: Consider the ten numbers ar, ar 2 , ar 3 ,…, ar 10 . If their sum is 18 and the sum of the reciprocals is 6, then the product of these ten numbers is __________. A) 81                    

C) 343                 

Given \(\begin{array}{l}\frac{ar({{r}^{10}}-1)}{r-1}=18 \rightarrow (1)\end{array} \)

\(\begin{array}{l}\frac{\frac{1}{ar}\left( 1-\frac{1}{{{r}^{10}}} \right)}{1-\frac{1}{r}}=6 \\ \frac{1}{a{{r}^{11}}}.\frac{({{r}^{10}}-1)r}{r-1}=6\\ \frac{1}{{{a}^{2}}{{r}^{11}}}.\frac{ar({{r}^{10}}-1)}{r-1}=6 \rightarrow (2)\end{array} \)

From (1) and (2),

\(\begin{array}{l}\frac{1}{{{a}^{2}}{{r}^{11}}}.\times 18=6\\ {{a}^{2}}{{r}^{11}}=3\\ \text Now \ P={{a}^{10}}{{r}^{11}}={{({{a}^{2}}{{r}^{11}})}^{5}}={{3}^{5}}=243\end{array} \) .

Example 9: If S n denotes the sum of the first n terms of an AP, whose first term is a and S nx /S x is independent of x, then S p  =

\(\begin{array}{l}A) {{p}^{3}}\\ B) {{p}^{2}}a\\ C) p{{a}^{2}}\\ D) {{a}^{3}}\end{array} \) .

\(\begin{array}{l}\frac{{{S}_{nx}}}{{{S}_{x}}}=\frac{\frac{nx}{2}[2a+(nx-1)d]}{\frac{x}{2}[2a+(x-1)d]}=\frac{n[(2a-d)+nxd]}{(2a-d)+xd}\end{array} \)

For S nx /S x to be independent of x, 

2a – d = 0 or 

\(\begin{array}{l}{{S}_{p}}=\frac{p}{2}[2a+(p-1)d]={{p}^{2}}a\end{array} \)

Example 10: If a 1 , a 2 , a 3 , …., a n are in H.P. and \(\begin{array}{l}f(k)=\left( \sum\limits_{r=1}^{n}{{{a}_{r}}} \right)-{{a}_{k}}\ \text{then}\ \frac{{{a}_{1}}}{f(1)},\frac{{{a}_{2}}}{f(2)},\frac{{{a}_{3}}}{f(3)},…\frac{{{a}_{n}}}{f(n)}\ \text{are in}\end{array} \)  

A) AP                  

C) HP                 

D) none of these

\(\begin{array}{l}f(k)+{{a}_{k}}=\sum\limits_{r=1}^{n}{{{a}_{r}}}=\lambda \,(\text \ say)\\ f(k)=\lambda -{{a}_{k}}\\ \Rightarrow \frac{{{f}_{(k)}}}{{{a}_{k}}}=\frac{\lambda }{{{a}_{k}}}-1\\ \frac{f(1)}{{{a}_{1}}},\frac{f(2)}{{{a}_{2}}},…,\frac{f(n)}{{{a}_{n}}}\end{array} \) are in A.P. 

So \(\begin{array}{l}\frac{{{a}_{1}}}{f(1)},\frac{{{a}_{2}}}{f(2)},…\frac{{{a}_{n}}}{f(n)}\end{array} \) are in H.P.

Example 11: If x 1 , x 2 ,…., x 20 are in HP and x 1 , 2, x 20 are in GP, then \(\begin{array}{l}\sum\limits_{r=1}^{19}{{{x}_{r}}{{x}_{r+1}}}=\end{array} \)

\(\begin{array}{l}\frac{1}{{{x}_{1}}},\frac{1}{{{x}_{2}}},…\frac{1}{{{x}_{20}}}\end{array} \) will be in A.P. Hence,

\(\begin{array}{l}\frac{1}{{{x}_{2}}}-\frac{1}{{{x}_{1}}}=\frac{1}{{{x}_{3}}}-\frac{1}{{{x}_{2}}}=…=\frac{1}{{{x}_{r+1}}}-\frac{1}{{{x}_{r}}}=…\lambda (\text{say})\\ \Rightarrow \frac{{{x}_{r}}-{{x}_{r+1}}}{{{x}_{1}}{{x}_{r+1}}}=\lambda \\ {{x}_{r}}{{x}_{r+1}}=-\frac{1}{\lambda }({{x}_{r+1}}-{{x}_{r}})\\ \Rightarrow \sum\limits_{r=1}^{19}{{{x}_{r}}{{x}_{r+1}}=-\frac{1}{\lambda }\sum\limits_{r=1}^{19}{({{x}_{r+1}}-{{x}_{r}})}}\\ =-\frac{1}{\lambda }({{x}_{20}}-{{x}_{1}})\end{array} \)

\(\begin{array}{l}\frac{1}{{{x}_{20}}}=\frac{1}{{{x}_{1}}}+19\lambda\\ \frac{{{x}_{1}}-{{x}_{20}}}{{{x}_{1}}{{x}_{20}}}=19\lambda \\ \Rightarrow \sum\limits_{r=1}^{19}{{{x}_{r}}{{x}_{r+1}}=19{{x}_{1}}{{x}_{20}}=19\times 4=76}\end{array} \)

Sequence and Series – Revision Video

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all JEE related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

• Share Share

Register with Aakash BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

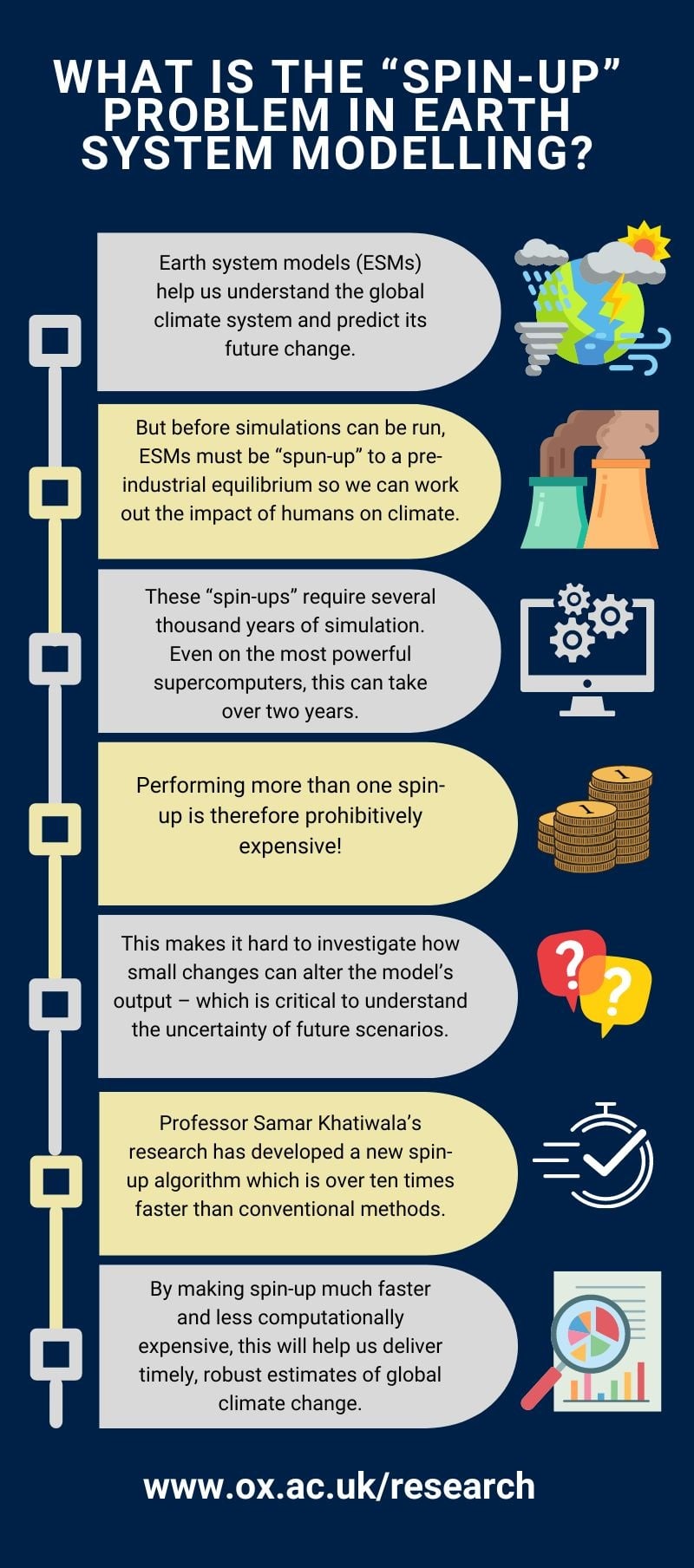
New algorithm supercharges climate models and could lead to better predictions of future climate change

Professor Samar Khatiwala , from the University of Oxford’s Department of Earth Sciences, has led a major advance to solve a critical issue in modelling future climate change. The findings have been published in Science Advances .

Minimising model drift at a much lower cost in time and energy is obviously critical for climate change simulations, but perhaps the greatest value of this research may ultimately be to policy makers who need to know how reliable climate projections are. Study author Professor Samar Khatiwala , Department of Earth Sciences, University of Oxford

Earth System Models – complex computer models which describe Earth processes and how they interact – are critical for predicting future climate change. By simulating the response of our land, oceans, and atmosphere to manmade greenhouse gas emissions, these models form the foundation for predictions of future extreme weather and climate event scenarios, including those issued by the UN Intergovernmental Panel on Climate Change (IPCC).

However, climate modellers have long faced a major problem. Because Earth System Models integrate many complicated processes, they cannot immediately run a simulation; they must first ensure that it has reached a stable equilibrium representative of real-world conditions before the industrial revolution. Without this initial settling period – referred to as the “spin-up” phase – the model can “drift”, simulating changes that may be erroneously attributed to manmade factors.

Unfortunately, this process is extremely slow as it requires running the model for many thousands of model years which, for IPCC simulations, can take as much as two years on some of the world’s most powerful supercomputers.

Spin-up has always been prohibitively expensive in terms of computational cost and time. The new approaches developed by Professor Khatiwala have the promise to break this logjam and deliver a quantum leap in the efficiency of spinning up such complex models and, as a consequence, greatly increase our ability to deliver timely, robust estimates of global climate change. Professor Colin Jones Head of the NERC/Met Office sponsored UK Earth system modelling, commenting on the findings

However, a new study published in Science Advances by a University of Oxford scientist funded through the Agile Initiative describes a new computer algorithm which can be applied to Earth System Models to drastically reduce spin-up time. During tests on models used in IPCC simulations, the algorithm was on average 10 times faster at spinning up the model than currently-used approaches, reducing the time taken to achieve equilibrium from many months to under a week.

Study author Samar Khatiwala , Professor of Earth Sciences at the University of Oxford’s Department of Earth Sciences, who devised the algorithm, said: ‘Minimising model drift at a much lower cost in time and energy is obviously critical for climate change simulations, but perhaps the greatest value of this research may ultimately be to policy makers who need to know how reliable climate projections are.’

Currently, the lengthy spin-up time of many IPCC models prevents climate researchers from running their model at a higher resolution and defining uncertainty through carrying out repeat simulations. By drastically reducing the spin-up time, the new algorithm will enable researchers to investigate how subtle changes to the model parameters can alter the output – which is critical for defining the uncertainty of future emission scenarios.

Policymakers rely on climate projections to inform negotiations as the world tries to meet the Paris Agreement. This work is a step towards reducing the time it takes to produce those critical climate projections. Professor Helene Hewitt OBE, Co-chair for the Coupled Model Intercomparison Project (CMIP) Panel, which will inform the next IPCC report, commenting on the findings

Professor Khatiwala’s new algorithm employs a mathematical approach known as sequence acceleration, which has its roots with the famous mathematician Euler. In the 1960s this idea was applied by D. G. Anderson to speed-up the solution of Schrödinger’s equation, which predicts how matter behaves at the microscopic level. So important is this problem that more than half the world’s supercomputing power is currently devoted to solving it, and ‘Anderson Acceleration’, as it is now known, is one of the most commonly used algorithms employed for it.

Professor Khatiwala realised that Anderson Acceleration might also be able to reduce model spin-up time since both problems are of an iterative nature: an output is generated and then fed back into the model many times over. By retaining previous outputs and combining them into a single input using Anderson’s scheme, the final solution is achieved much more quickly.

Not only does this make the spin-up process much faster and less computationally expensive, but the concept can be applied to the huge variety of different models that are used to investigate, and inform policy on, issues ranging from ocean acidification to biodiversity loss. With research groups around the world beginning to spin-up their models for the next IPCC report, due in 2029, Professor Khatiwala is working with a number of them, including the UK Met Office, to trial his approach and software in their models.

The study ‘Efficient spin-up of Earth System Models using sequence acceleration’ has been published in the journal Science Advances .

DISCOVER MORE

• Support Oxford's research
• Partner with Oxford on research
• Study at Oxford
• Research jobs at Oxford

You can view all news or browse by category