key words in math problem solving

Over 6,200 homeschool resources and growing!

Teaching Math Word Problem Key Words (Free Cheat Sheet)

Published: November 20, 2023

Contributor: Jeannette Tuionetoa

Disclosure: This post may contain affiliate links, meaning if you decide to make a purchase via my links, I may earn a commission at no additional cost to you. See my disclosure for more info.

Tackling word problems in math can be challenging for kids to learn. We called them story problems when I was in school. If your kids are learning math key words so they can solve word problems, they you’ll find these free cheat sheets and worksheets for word problem key words helpful. 

Math Word Problem Key Words

There is no doubt that mathematical operations using words are difficult for kids. They go from counting numbers to doing math equations with numbers.

Then all of a sudden… there are words, just words . All of a sudden algebraic expressions and mathematical operations are POOF – words.

The lack of numbers and shift in mindset can completely throw off a lot of students. If kids have difficulty with reading, then that is yet another struggle for kids as they try to learn basic problems in math.

Teaching students about challenging math keywords just got easier! Be sure to download our free math key words cheat sheet at the end of this post. 

Why do some kids struggle with word problems?

A key proponent in different operations in math is learning the key words that prompt kids to understand which operation skill they need to use to solve the problem.

This means that they should master regular math problems first and be able to read with comprehension. You will shortly find that if these two skills aren’t somewhat mastered first, then word problems will become an issue.

Many times math is a subject best taught in sequential order. If one step is missed, then the future steps falter. This is much like how it is when teaching word problems.

The best thing for your children is for them to first:

• Be able to read well.
• Understand math concepts and phrases.
• Know to not rush, but focus on math key words, identify relevant information, and understand the text.
• Get to know the keywords for math word problems

What are keywords for math word problems?

Key words in mathematical word operations are the words or phrases that will signal or show a student which type of math operation to choose in order to solve the math word problem.

The keywords for math word problems used in operations are a strategy that helps the math problem make sense and draw connections to how it can be answered.

Basically, when using key words, students must decipher whether they need to solve the math equation via addition, subtraction, multiplication, or division.

What are the common keywords for math word problems?

Thankfully, there are math key words that our children can learn that help them work through their word problems. They are prompts that point them in the right direction.

Just like a different language needs words translated for comprehension, students translate the words… into math .

Keywords for Math Word Problems

Learning these math keywords will help with problem solving:

Addition Math Key Words:

• increased by
• larger than
• in addition to
• how much in all

Subtraction Math Key Words:

• how many more
• how many less
• shorter than
• smaller than

Key Words for Multiplication Word Problems:

• multiplied by
• double/twice

Key Words used for Division Word Problems:

• equal group
• how many in each

You can print off a free math key words cheat sheet that has the above math key words for word problems and add it to your homeschool binder . Find the download link at the bottom of this post. 

How can we help kids learn keywords for solving numberless word problems?

Teach kids steps for solving word problems until it becomes a habit or they get comfortable with the steps. First, they can look for the important information and write those down. (Read the problem carefully). Next, kids need to define or find the variables in the math equation.

From the keywords, kids can now determine what math operation to use. Translate the words to math. Then, kids can solve the math equation. This is where the skills of solving numbered equations are important.

Finally, students have to put their answers in the form of a word sentence. NOTE: Many times kids think after solving the equation they are done. However, the key to making sure they understand that word problems need word answers.

Different Strategies to Familiarize Keywords in Word Operations

You can use some of these keywords for math word problems as vocabulary words in your homeschool.

Students can display subtraction, addition, multiplication, and multiplication handy reference posters on a bulletin board in your homeschool area. Students can also just list them on dry erase boards . These are perfect visual reminders for what keywords go with what math word problems.

Your students can also keep their keywords for math word problems with them as they study. They can place the list of keywords in a math folder or in an anchor chart – and then in their math folder.

Kids can keep the keyword poster sets in their math notebooks or keep them in a word problem journal .

Their strategy for learning word problem keywords all depends on how they best absorb information.

Students may do well using a combination of these methods. Either way, all of these different strategies can be used to get them comfortable in identifying the route to solve math word equations.

Math Word Problem Keywords Cheat Sheets & Teaching Aids:

We created a free pdf download Word Problem Key Words Cheat Sheet that you can find at the bottom of this post. It’s great to use as a reference for math word problems.

Word Problem Clue Words

Get a Clue Free Download – Check out these word problem clue word handouts and posters to help your students with word problems. There 5 pages in all that will be handy for your kids in trying to find the correct answer while using the correct operation.

Addition and Subtraction Word Problem Keywords

Subtraction Keywords/Addition Keywords – Until your kids memorize keywords and what they mean, this freebie can help. Grab these simple black and white printable signs. They will help kids look for keywords like larger numbers for subtraction word problems or addition keywords like in addition to . 

Story Problem Key Words

Words to Math – Keywords in math problems are essentially turning words into math. This graphic organizer printable is a quick reference for your students to use with numberless math word problems. Place them in a notebook chart or your homeschool classroom wall as a visual reminder.

Word Problem Key Words Poster

Key Word Posters for Math Problems – Grab these word problem keyword handy reference posters for subtraction, addition, division, and multiplication. Each poster has its specific theme and specific words to solve all problem types. Kids will enjoy having practiced with these math key words posters.

Word Problem Key Words Worksheets

Fun Key Word Sorting Activity – Your kids have now studied some keywords for math word problems helpful for problem solving in mathematical operations. Use this word problem sorting activity to test their knowledge in a fun engaging way. Add this fun activity to your test prep materials.

World Problems Worksheets with Key Words – These word problems worksheets use key phrases to help your students identify the phrases that will help them determine which math operation to use.

Word Problem Key Words for Math

Math word problems are probably the first opportunity students get to understand how math relates to real world situations. The applications can be relevant in their real life experiences like going to the market.

However, the benefit to word problems doesn’t stop there…

With word problems, students develop their higher-order thinking and critical thinking skills.

Different types of word problems guide your students to applying math various math concepts at the same time. They have to know basic number sense, basic algebra skills, and even geometry when they attempt multiplication word problems.

If we do it the right way, kids won’t see word problems as a dreadful experience in math. Understanding word problems is a learning curve and doesn’t come easily to kids.

Identify Learning Gaps

Another important aspect of word problems is that they tell a parent/teacher if a child needs help in areas like reading comprehension or math number operations skills. This type of word math is a great evaluation of your student’s thinking processes.

We can, however, help make it a better experience for them by teaching it the right way.

Free Math Key Words Cheat Sheet Instant Download

You won’t want to miss our free Word Problem Key Words Cheat Sheet PDF download for different ways kids see keywords in various types of problems in mathematics. This math tool is everything your student needs and the perfect resource to reference keywords in math operations.

Includes the keywords that will help your children solve and recognize word problems for:

• Subtraction
• Multiplication

Instant Download: Math Word Problems Keywords Cheat Sheet

Jeannette tuionetoa.

Jeannette is a wife, mother and homeschooling mom. She has been mightily, saved by grace and is grateful for God’s sovereignty throughout her life’s journey. She has a Bachelor in English Education and her MBA. Jeannette is bi-lingual and currently lives in the Tongan Islands of the South Pacific. She posts daily freebies for homeschoolers!

Related resources

23 Math Life of Fred Books in Order (K-12 Series)

Printable Number Playdough Mats 1-10 (Free Download)

Free Writing Numbers 1-20 Tracing Numbers for Preschool

Using Living Books to Teach Math Lessons & Review

Free Times Table Test Printables & PDF Worksheets

Printable Number Coloring Pages for Early Learners

"Key Words and Catch Phrases" for Word Problems

Addition Words

2. Altogether

Subtraction Words

1. Difference

3. How many more

4. How much more

6. Less: Debra bought apples for $3.20 and oranges for $4.23. How much less did the apples cost?

10. Subtract

10. Words ending with "er"; higher, longer, faster, heavier, larger, shorter, slower, farther, etc. Example: Jean's apple weighs 100 grams, and Karen's apple weighs 80 grams. How much heavier is Jean's apple?

Multiplication Words

1. Times : Maria ran around the track 5 times. It took her 5 minutes to run around the track. How many minutes did she run?

2. Every : Kim buys 2 apples everyday . How many apples does she buy in a week?

3. At this rate: Ed reads 25 words per minute. At this rate , how many words does he read in one hour?

Division Words

1. Each: Ken has 75 pencils and 15 boxes. How many pencils should he pack in each box so each customer gets the same number of pencils?

How do you solve word problems in math?

Master word problems with eight simple steps from a math tutor!

Author Amber Watkins

Published April 2024

• Key takeaways
• Students who struggle with reading, tend to struggle with understanding and solving word problems. So the best way to solve word problems in math is to become a better reader!
• Mastery of word problems relies on your child’s knowledge of keywords for word problems in math and knowing what to do with them.
• There are 8 simple steps each child can use to solve word problems- let’s go over these together.

Table of contents

• How to solve word problems

Lesson credits

As a tutor who has seen countless math worksheets in almost every grade – I’ll tell you this: every child is going to encounter word problems in math. The key to mastery lies in how you solve them! So then, how do you solve word problems in math?

In this guide, I’ll share eight steps to solving word problems in math.

How to solve word problems in math in 8 steps

Step 1: read the word problem aloud.

For a child to understand a word problem, it needs to be read with accuracy and fluency! That is why, when I tutor children with word problems, I always emphasize the importance of reading properly.

Mastering step 1 looks like this:

• Allow your child to read the word problem aloud to you. 
• Don’t let your child skip over or mispronounce any words. 
• If necessary, model how to read the word problem, then allow your child to read it again. Only after the word problem is read accurately, should you move on to step 2.

Step 2: Highlight the keywords in the word problem

The keywords for word problems in math indicate what math action should be taken. Teach your child to highlight or underline the keywords in every word problem. 

Here are some of the most common keywords in math word problems: 

• Subtraction words – less than, minus, take away
• Addition words – more than, altogether, plus, perimeter
• Multiplication words – Each, per person, per item, times, area 
• Division words – divided by, into
• Total words – in all, total, altogether

Let’s practice. Read the following word problem with your child and help them highlight or underline the main keyword, then decide which math action should be taken.

Michael has ten baseball cards. James has four baseball cards less than Michael. How many total baseball cards does James have? 

The words “less than” are the keywords and they tell us to use subtraction .

Step 3: Make math symbols above keywords to decode the word problem

As I help students with word problems, I write math symbols and numbers above the keywords. This helps them to understand what the word problem is asking.

Let’s practice. Observe what I write over the keywords in the following word problem and think about how you would create a math sentence using them:

Step 4: Create a math sentence to represent the word problem

Using the previous example, let’s write a math sentence. Looking at the math symbols and numbers written above the word problem, our math sentence should be: 10 – 5 = 5 ! 

Each time you practice a word problem with your child, highlight keywords and write the math symbols above them. Then have your child create a math sentence to solve. 

Step 5: Draw a picture to help illustrate the word problem

Pictures can be very helpful for problems that are more difficult to understand. They also are extremely helpful when the word problem involves calculating time , comparing fractions , or measurements . 

Step 6: Always show your work

Help your child get into the habit of always showing their work. As a tutor, I’ve found many reasons why having students show their work is helpful:

• By showing their work, they are writing the math steps repeatedly, which aids in memory
• If they make any mistakes they can track where they happened
• Their teacher can assess how much they understand by reviewing their work
• They can participate in class discussions about their work

Step 7: When solving word problems, make sure there is always a word in your answer!

If the word problem asks: How many peaches did Lisa buy? Your child’s answer should be: Lisa bought 10 peaches .

If the word problem asks: How far did Kyle run? Your child’s answer should be: Kyle ran 20 miles .

So how do you solve a word problem in math?

Together we reviewed the eight simple steps to solve word problems. These steps included identifying keywords for word problems in math, drawing pictures, and learning to explain our answers. 

Is your child ready to put these new skills to the test? Check out the best math app for some fun math word problem practice.

Parents, sign up for a DoodleMath subscription and see your child become a math wizard!

Amber Watkins

Amber is an education specialist with a degree in Early Childhood Education. She has over 12 years of experience teaching and tutoring elementary through college level math. "Knowing that my work in math education makes such an impact leaves me with an indescribable feeling of pride and joy!"

What we offer

Quick links

All rights reserved. 

Are you a parent, teacher or student?

Get started for free!

Maths information pack

We ask for your contact info so we can send our info pack directly to your inbox for your convenience, exam prep information pack, case studies information pack.

Book a chat with our team

I’m new to Doodle

My school is already using Doodle

Information pack

We ask for your contact info so that our education consultants can get in touch with you and let you know a bit more about doodle., student login, which programme would you like to use.

DoodleMaths

DoodleTables

DoodleEnglish

DoodleSpell

If you’d like to use Doodle’s browser version, please visit this page on a desktop.

To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here:

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Free ready-to-use math resources

Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth

20 Effective Math Strategies To Approach Problem-Solving 

Katie Keeton

Math strategies for problem-solving help students use a range of approaches to solve many different types of problems. It involves identifying the problem and carrying out a plan of action to find the answer to mathematical problems.  

Problem-solving skills are essential to math in the general classroom and real-life. They require logical reasoning and critical thinking skills. Students must be equipped with strategies to help them find solutions to problems.

This article explores mathematical problem solving strategies, logical reasoning and critical thinking skills to help learners with solving math word problems independently in real-life situations. 

What are problem-solving strategies?

Problem-solving strategies in math are methods students can use to figure out solutions to math problems. Some problem-solving strategies: 

• Draw a model
• Use different approaches
• Check the inverse to make sure the answer is correct

Students need to have a toolkit of math problem-solving strategies at their disposal to provide different ways to approach math problems. This makes it easier to find solutions and understand math better. 

Strategies can help guide students to the solution when it is difficult ot know when to start.

The ultimate guide to problem solving techniques

Download these ready-to-go problem solving techniques that every student should know. Includes printable tasks for students including challenges, short explanations for teachers with questioning prompts.

20 Math Strategies For Problem-Solving

Different problem-solving math strategies are required for different parts of the problem. It is unlikely that students will use the same strategy to understand and solve the problem. 

Here are 20 strategies to help students develop their problem-solving skills. 

Strategies to understand the problem

Strategies that help students understand the problem before solving it helps ensure they understand: 

• The context
• What the key information is
• How to form a plan to solve it

Following these steps leads students to the correct solution and makes the math word problem easier .

Here are five strategies to help students understand the content of the problem and identify key information. 

1. Read the problem aloud

Read a word problem aloud to help understand it. Hearing the words engages auditory processing. This can make it easier to process and comprehend the context of the situation.

2. Highlight keywords 

When keywords are highlighted in a word problem, it helps the student focus on the essential information needed to solve it. Some important keywords help determine which operation is needed.  For example, if the word problem asks how many are left, the problem likely requires subtraction.  Ensure students highlight the keywords carefully and do not highlight every number or keyword. There is likely irrelevant information in the word problem.

3. Summarize the information

Read the problem aloud, highlight the key information and then summarize the information. Students can do this in their heads or write down a quick summary.  Summaries should include only the important information and be in simple terms that help contextualize the problem.

4. Determine the unknown

A common problem that students have when solving a word problem is misunderstanding what they are solving. Determine what the unknown information is before finding the answer.  Often, a word problem contains a question where you can find the unknown information you need to solve. For example, in the question ‘How many apples are left?’ students need to find the number of apples left over.

5. Make a plan

Once students understand the context of the word problem, have dentified the important information and determined the unknown, they can make a plan to solve it.  The plan will depend on the type of problem. Some problems involve more than one step to solve them as some require more than one answer.  Encourage students to make a list of each step they need to take to solve the problem before getting started.

Strategies for solving the problem 

1. draw a model or diagram.

Students may find it useful to draw a model, picture, diagram, or other visual aid to help with the problem solving process.  It can help to visualize the problem to understand the relationships between the numbers in the problem. In turn, this helps students see the solution.

Similarly, you could draw a model to represent the objects in the problem:

2. Act it out

This particular strategy is applicable at any grade level but is especially helpful in math investigation in elementary school . It involves a physical demonstration or students acting out the problem using movements, concrete resources and math manipulatives .  When students act out a problem, they can visualize and contectualize the word problem in another way and secure an understanding of the math concepts.  The examples below show how 1st-grade students could “act out” an addition and subtraction problem:

3. Work backwards

Working backwards is a popular problem-solving strategy. It involves starting with a possible solution and deciding what steps to take to arrive at that solution.  This strategy can be particularly helpful when students solve math word problems involving multiple steps. They can start at the end and think carefully about each step taken as opposed to jumping to the end of the problem and missing steps in between.

For example,

To solve this problem working backwards, start with the final condition, which is Sam’s grandmother’s age (71) and work backwards to find Sam’s age. Subtract 20 from the grandmother’s age, which is 71.  Then, divide the result by 3 to get Sam’s age. 71 – 20 = 51 51 ÷ 3 = 17 Sam is 17 years old.

4. Write a number sentence

When faced with a word problem, encourage students to write a number sentence based on the information. This helps translate the information in the word problem into a math equation or expression, which is more easily solved.  It is important to fully understand the context of the word problem and what students need to solve before writing an equation to represent it.

5. Use a formula

Specific formulas help solve many math problems. For example, if a problem asks students to find the area of a rug, they would use the area formula (area = length × width) to solve.   Make sure students know the important mathematical formulas they will need in tests and real-life. It can help to display these around the classroom or, for those who need more support, on students’ desks.

Strategies for checking the solution 

Once the problem is solved using an appropriate strategy, it is equally important to check the solution to ensure it is correct and makes sense. 

There are many strategies to check the solution. The strategy for a specific problem is dependent on the problem type and math content involved.

Here are five strategies to help students check their solutions. 

1. Use the Inverse Operation

For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7. As good practice, encourage students to use the inverse operation routinely to check their work. 

2. Estimate to check for reasonableness

Once students reach an answer, they can use estimation or rounding to see if the answer is reasonable.  Round each number in the equation to a number that’s close and easy to work with, usually a multiple of ten.  For example, if the question was 216 ÷ 18 and the quotient was 12, students might round 216 to 200 and round 18 to 20. Then use mental math to solve 200 ÷ 20, which is 10.  When the estimate is clear the two numbers are close. This means your answer is reasonable. 

3. Plug-In Method

This method is particularly useful for algebraic equations. Specifically when working with variables.  To use the plug-in method, students solve the problem as asked and arrive at an answer. They can then plug the answer into the original equation to see if it works. If it does, the answer is correct.

If students use the equation 20m+80=300 to solve this problem and find that m = 11, they can plug that value back into the equation to see if it is correct. 20m + 80 = 300 20 (11) + 80 = 300 220 + 80 = 300 300 = 300 ✓

4. Peer Review

Peer review is a great tool to use at any grade level as it promotes critical thinking and collaboration between students. The reviewers can look at the problem from a different view as they check to see if the problem was solved correctly.   Problem solvers receive immediate feedback and the opportunity to discuss their thinking with their peers. This strategy is effective with mixed-ability partners or similar-ability partners. In mixed-ability groups, the partner with stronger skills provides guidance and support to the partner with weaker skills, while reinforcing their own understanding of the content and communication skills.  If partners have comparable ability levels and problem-solving skills, they may find that they approach problems differently or have unique insights to offer each other about the problem-solving process.

5. Use a Calculator

A calculator can be introduced at any grade level but may be best for older students who already have a foundational understanding of basic math operations. Provide students with a calculator to allow them to check their solutions independently, accurately, and quickly. Since calculators are so readily available on smartphones and tablets, they allow students to develop practical skills that apply to real-world situations.  

Step-by-step problem-solving processes for your classroom

In his book, How to Solve It , published in 1945, mathematician George Polya introduced a 4-step process to solve problems. 

Polya’s 4 steps include:

• Understand the problem
• Devise a plan
• Carry out the plan

Today, in the style of George Polya, many problem-solving strategies use various acronyms and steps to help students recall. 

Many teachers create posters and anchor charts of their chosen process to display in their classrooms. They can be implemented in any elementary, middle school or high school classroom. 

Here are 5 problem-solving strategies to introduce to students and use in the classroom.

How Third Space Learning improves problem-solving 

Resources .

Third Space Learning offers a free resource library is filled with hundreds of high-quality resources. A team of experienced math experts carefully created each resource to develop students mental arithmetic, problem solving and critical thinking. 

Explore the range of problem solving resources for 2nd to 8th grade students. 

One-on-one tutoring 

Third Space Learning offers one-on-one math tutoring to help students improve their math skills. Highly qualified tutors deliver high-quality lessons aligned to state standards. 

Former teachers and math experts write all of Third Space Learning’s tutoring lessons. Expertly designed lessons follow a “my turn, follow me, your turn” pedagogy to help students move from guided instruction and problem-solving to independent practice. 

Throughout each lesson, tutors ask higher-level thinking questions to promote critical thinking and ensure students are developing a deep understanding of the content and problem-solving skills.

Problem-solving

Educators can use many different strategies to teach problem-solving and help students develop and carry out a plan when solving math problems. Incorporate these math strategies into any math program and use them with a variety of math concepts, from whole numbers and fractions to algebra. 

Teaching students how to choose and implement problem-solving strategies helps them develop mathematical reasoning skills and critical thinking they can apply to real-life problem-solving.

READ MORE : 8 Common Core math examples

There are many different strategies for problem-solving; Here are 5 problem-solving strategies: • draw a model  • act it out  • work backwards  • write a number sentence • use a formula

Here are 10 strategies of problem-solving: • Read the problem aloud • Highlight keywords • Summarize the information • Determine the unknown • Make a plan • Draw a model  • Act it out  • Work backwards  • Write a number sentence • Use a formula

1. Understand the problem 2. Devise a plan 3. Carry out the plan 4. Look back

Some strategies you can use to solve challenging math problems are: breaking the problem into smaller parts, using diagrams or models, applying logical reasoning, and trying different approaches.

Related articles

Why Student Centered Learning Is Important: A Guide For Educators

13 Effective Learning Strategies: A Guide to Using them in your Math Classroom

Differentiated Instruction: 9 Differentiated Curriculum And Instruction Strategies For Teachers 

5 Math Mastery Strategies To Incorporate Into Your 4th and 5th Grade Classrooms

Ultimate Guide to Metacognition [FREE]

Looking for a summary on metacognition in relation to math teaching and learning?

Check out this guide featuring practical examples, tips and strategies to successfully embed metacognition across your school to accelerate math growth.

Privacy Overview

Solving Word Questions

With LOTS of examples!

In Algebra we often have word questions like:

Example: Sam and Alex play tennis.

On the weekend Sam played 4 more games than Alex did, and together they played 12 games.

How many games did Alex play?

How do we solve them?

The trick is to break the solution into two parts:

Turn the English into Algebra.

Then use Algebra to solve.

Turning English into Algebra

To turn the English into Algebra it helps to:

• Read the whole thing first
• Do a sketch if possible
• Assign letters for the values
• Find or work out formulas

You should also write down what is actually being asked for , so you know where you are going and when you have arrived!

Also look for key words:

Thinking Clearly

Some wording can be tricky, making it hard to think "the right way around", such as:

Example: Sam has 2 dollars less than Alex. How do we write this as an equation?

• Let S = dollars Sam has
• Let A = dollars Alex has

Now ... is that: S − 2 = A

or should it be: S = A − 2

or should it be: S = 2 − A

The correct answer is S = A − 2

( S − 2 = A is a common mistake, as the question is written "Sam ... 2 less ... Alex")

Example: on our street there are twice as many dogs as cats. How do we write this as an equation?

• Let D = number of dogs
• Let C = number of cats

Now ... is that: 2D = C

or should it be: D = 2C

Think carefully now!

The correct answer is D = 2C

( 2D = C is a common mistake, as the question is written "twice ... dogs ... cats")

Let's start with a really simple example so we see how it's done:

Example: A rectangular garden is 12m by 5m, what is its area ?

Turn the English into Algebra:

• Use w for width of rectangle: w = 12m
• Use h for height of rectangle: h = 5m

Formula for Area of a Rectangle : A = w × h

We are being asked for the Area.

A = w × h = 12 × 5 = 60 m 2

The area is 60 square meters .

Now let's try the example from the top of the page:

Example: Sam and Alex play Tennis. On the weekend Sam played 4 more games than Alex did, and together they played 12 games. How many games did Alex play?

• Use S for how many games Sam played
• Use A for how many games Alex played

We know that Sam played 4 more games than Alex, so: S = A + 4

And we know that together they played 12 games: S + A = 12

We are being asked for how many games Alex played: A

Which means that Alex played 4 games of tennis.

Check: Sam played 4 more games than Alex, so Sam played 8 games. Together they played 8 + 4 = 12 games. Yes!

A slightly harder example:

Example: Alex and Sam also build tables. Together they make 10 tables in 12 days. Alex working alone can make 10 in 30 days. How long would it take Sam working alone to make 10 tables?

• Use a for Alex's work rate
• Use s for Sam's work rate

12 days of Alex and Sam is 10 tables, so: 12a + 12s = 10

30 days of Alex alone is also 10 tables: 30a = 10

We are being asked how long it would take Sam to make 10 tables.

30a = 10 , so Alex's rate (tables per day) is: a = 10/30 = 1/3

Which means that Sam's rate is half a table a day (faster than Alex!)

So 10 tables would take Sam just 20 days.

Should Sam be paid more I wonder?

And another "substitution" example:

Example: Jenna is training hard to qualify for the National Games. She has a regular weekly routine, training for five hours a day on some days and 3 hours a day on the other days. She trains altogether 27 hours in a seven day week. On how many days does she train for five hours?

• The number of "5 hour" days: d
• The number of "3 hour" days: e

We know there are seven days in the week, so: d + e = 7

And she trains 27 hours in a week, with d 5 hour days and e 3 hour days: 5d + 3e = 27

We are being asked for how many days she trains for 5 hours: d

The number of "5 hour" days is 3

Check : She trains for 5 hours on 3 days a week, so she must train for 3 hours a day on the other 4 days of the week.

3 × 5 hours = 15 hours, plus 4 × 3 hours = 12 hours gives a total of 27 hours

Some examples from Geometry:

Example: A circle has an area of 12 mm 2 , what is its radius?

• Use A for Area: A = 12 mm 2
• Use r for radius

And the formula for Area is: A = π r 2

We are being asked for the radius.

We need to rearrange the formula to find the area

Example: A cube has a volume of 125 mm 3 , what is its surface area?

Make a quick sketch:

• Use V for Volume
• Use A for Area
• Use s for side length of cube
• Volume of a cube: V = s 3
• Surface area of a cube: A = 6s 2

We are being asked for the surface area.

First work out s using the volume formula:

Now we can calculate surface area:

An example about Money:

Example: Joel works at the local pizza parlor. When he works overtime he earns 1¼ times the normal rate. One week Joel worked for 40 hours at the normal rate of pay and also worked 12 hours overtime. If Joel earned $660 altogether in that week, what is his normal rate of pay?

• Joel's normal rate of pay: $N per hour
• Joel works for 40 hours at $N per hour = $40N
• When Joel does overtime he earns 1¼ times the normal rate = $1.25N per hour
• Joel works for 12 hours at $1.25N per hour = $(12 × 1¼N) = $15N
• And together he earned $660, so:

$40N + $(12 × 1¼N) = $660

We are being asked for Joel's normal rate of pay $N.

So Joel’s normal rate of pay is $12 per hour

Joel’s normal rate of pay is $12 per hour, so his overtime rate is 1¼ × $12 per hour = $15 per hour. So his normal pay of 40 × $12 = $480, plus his overtime pay of 12 × $15 = $180 gives us a total of $660

More about Money, with these two examples involving Compound Interest

Example: Alex puts $2000 in the bank at an annual compound interest of 11%. How much will it be worth in 3 years?

This is the compound interest formula:

So we will use these letters:

• Present Value PV = $2,000
• Interest Rate (as a decimal): r = 0.11
• Number of Periods: n = 3
• Future Value (the value we want): FV

We are being asked for the Future Value: FV

Example: Roger deposited $1,000 into a savings account. The money earned interest compounded annually at the same rate. After nine years Roger's deposit has grown to $1,551.33 What was the annual rate of interest for the savings account?

The compound interest formula:

• Present Value PV = $1,000
• Interest Rate (the value we want): r
• Number of Periods: n = 9
• Future Value: FV = $1,551.33

We are being asked for the Interest Rate: r

So the annual rate of interest is 5%

Check : $1,000 × (1.05) 9 = $1,000 × 1.55133 = $1,551.33

And an example of a Ratio question:

Example: At the start of the year the ratio of boys to girls in a class is 2 : 1 But now, half a year later, four boys have left the class and there are two new girls. The ratio of boys to girls is now 4 : 3 How many students are there altogether now?

• Number of boys now: b
• Number of girls now: g

The current ratio is 4 : 3

Which can be rearranged to 3b = 4g

At the start of the year there was (b + 4) boys and (g − 2) girls, and the ratio was 2 : 1

b + 4 g − 2 = 2 1

Which can be rearranged to b + 4 = 2(g − 2)

We are being asked for how many students there are altogether now: b + g

There are 12 girls !

And 3b = 4g , so b = 4g/3 = 4 × 12 / 3 = 16 , so there are 16 boys

So there are now 12 girls and 16 boys in the class, making 28 students altogether .

There are now 16 boys and 12 girls, so the ratio of boys to girls is 16 : 12 = 4 : 3 At the start of the year there were 20 boys and 10 girls, so the ratio was 20 : 10 = 2 : 1

And now for some Quadratic Equations :

Example: The product of two consecutive even integers is 168. What are the integers?

Consecutive means one after the other. And they are even , so they could be 2 and 4, or 4 and 6, etc.

We will call the smaller integer n , and so the larger integer must be n+2

And we are told the product (what we get after multiplying) is 168, so we know:

n(n + 2) = 168

We are being asked for the integers

That is a Quadratic Equation , and there are many ways to solve it. Using the Quadratic Equation Solver we get −14 and 12.

Check −14: −14(−14 + 2) = (−14)×(−12) = 168 YES

Check 12: 12(12 + 2) = 12×14 = 168 YES

So there are two solutions: −14 and −12 is one, 12 and 14 is the other.

Note: we could have also tried "guess and check":

• We could try, say, n=10: 10(12) = 120 NO (too small)
• Next we could try n=12: 12(14) = 168 YES

But unless we remember that multiplying two negatives make a positive we might overlook the other solution of (−14)×(−12).

Example: You are an Architect. Your client wants a room twice as long as it is wide. They also want a 3m wide veranda along the long side. Your client has 56 square meters of beautiful marble tiles to cover the whole area. What should the length of the room be?

Let's first make a sketch so we get things right!:

• the length of the room: L
• the width of the room: W
• the total Area including veranda: A
• the width of the room is half its length: W = ½L
• the total area is the (room width + 3) times the length: A = (W+3) × L = 56

We are being asked for the length of the room: L

This is a quadratic equation , there are many ways to solve it, this time let's use factoring :

And so L = 8 or −14

There are two solutions to the quadratic equation, but only one of them is possible since the length of the room cannot be negative!

So the length of the room is 8 m

L = 8, so W = ½L = 4

So the area of the rectangle = (W+3) × L = 7 × 8 = 56

There we are ...

... I hope these examples will help you get the idea of how to handle word questions. Now how about some practice?

• ELEMENTARY TEACHING , MATH

Elementary Math Word Problem Key Words and Their Limitations

When you tell your students you will be working on word problems, do you hear a chorus of groans? If so, you are not alone! Teaching students how to solve math word problems tends to not be the most exciting math exercise in an elementary math curriculum (especially not learning about word problem key words and how they can be used to solve problems). They also tend to be very challenging for students. No wonder many students don’t like them!

In order for students to become proficient in mathematics, however, they need to apply their math learning to real life situations , which can be achieved through word problems. This experience should not be about following rote procedures and computing correct responses. When solving these types of problems, it is important for students to apply multiple strategies to make sense of the problem and solve it. These experiences should be grounded in strategy application and problem solving, rather than simply computation.

Identifying word problem key words is one of many strategies elementary students can use to help them solve single and multi-step word problems. Additionally, students need access to anchor charts, tools, and manipulatives that will equip them with the resources they need for these problem solving experiences. Using keywords for math word problems is just one piece of the puzzle!

This blog post will answer the following questions:

• What are word problem key words?
• What are some examples of keywords for addition word problems?
• Can you share some examples of keywords for subtraction word problems?
• What are some examples of keywords for multiplication word problems?
• Can you share some examples of keywords for division word problems?
• What are the limitations of using keywords to solve word problems?
• Is using word problem keywords an effective strategy?

What are Word Problem Key Words?

Word problem key words are words or phrases that signal which operations (addition, subtraction, multiplication, or division) are needed in order to solve a math word problem.

Using keywords for math word problems (often referred to as clue words and phrases) is a strategy to make sense of and solve word problems. It is the idea of training the brain to look for specific words and phrases to determine what mathematical operations are needed. Here is an example of this strategy in practice:

Erin reads the problem: Pat has 3 red shirts. He has 2 blue shirts. How many red and blue shirts does he have in all? After reading through the problem once, Erin rereads the problem but this time she is looking specifically for the clue words and phrases she has learned. She highlights or underlines the phrase “in all.” She has learned in class that “in all” signals to the reader that they need to add. This strategy has helped her make sense of the problem (which in this case means that the addition operation is needed), set up an equation (3 + 2 = ?), and solve for the answer (5 shirts).

Common Math Word Problem Key Words and Phrases

Below is a list of key words and phrases that students can use to solve addition, subtraction, multiplication, and division word problems. If you teach the younger grades, you’ll find the list of addition and subtraction key words helpful. If you teach the older grades, you’ll find those helpful, as well as the multiplication and division key words.

Addition Key Words

Here are some examples of addition key words :

• increased by
• larger than
• longer than

Subtraction Key Words

Here are some examples of subtraction key words :

• How many more…?
• How many less…?
• shorter than
• smaller than

Multiplication Key Words

Here are some examples of multiplication key words :

Division Key Words

Here are some examples of division key words :

• equal group

Limitations of Using Keywords to Solve Word Problems

When students are learning how to solve word problems, it is beneficial for them to be exposed to, directly taught, and given practice with key words (also sometimes written as word problem keywords or keywords for math word problems). However, students need to understand that problems can be solved in many different ways. This is just one tool in their toolkit.  It is not always the most effective strategy to solve a given word problem. For example, students should not be trained to always subtract when they see the word less because they could use a missing addend from addition to solve.  This strategy should be used along with other strategies (e.g. visualization). As students progress through their math education and come across more challenging word problems, this strategy will become less effective. As a result, your students need to be equipped with an abundance of diverse strategies.

Math Resources for 1st-5th Grade Teachers

If you need printable and digital math resources for your classroom, then check out my time and money-saving math collections below!

Free Elementary Math Resources

We would love for you to try these word problem resources with your students. It offers them opportunities to practice applying word problem key words strategies, as well as other problem solving strategies. You can download word problem worksheets specific to your grade level (along with lots of other math freebies) in our free printable math resources bundle using this link: free printable math activities for elementary teachers .

Check out my monthly word problem resources !

• 1st Grade Word Problems
• 2nd Grade Word Problems
• 3rd Grade Word Problems
• 4th Grade Word Problems
• 5th Grade Word Problems

You might also like...

Increasing Parent Participation in Elementary Math (Grades 1-5)

100+ Math Accommodations for Elementary Teachers

Vertical Alignment Curriculum in Math Education (Grades 1-5)

Join the newsletter.

• CLUTTER-FREE TEACHER CLUB
• FACEBOOK GROUPS
• EMAIL COMMUNITY
• OUR TEACHER STORE
• ALL-ACCESS MEMBERSHIPS
• OUR TPT SHOP
• JODI & COMPANY
• TERMS OF USE
• Privacy Policy

Get a collection of FREE MATH RESOURCES for your grade level!

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

Translating Word Problems: Keywords

Keywords Examples

The hardest thing about doing word problems is using the part where you need to take the English words and translate them into mathematics. Usually, once you get the math equation, you're fine; the actual math involved is often fairly simple. But figuring out the actual equation can seem nearly impossible. What follows is a list of hints and helps. Be advised, however: To really learn "how to do" word problems, you will need to practice, practice, practice.

How do I convert word problems into math?

• Read the entire exercise.
• Work in an organized manner.
• Look for the keywords.
• Apply your knowledge of "the real world".

Content Continues Below

MathHelp.com

Algebra Word Problems

Step 1 in effectively translating and solving word problems is to read the problem entirely. Don't start trying to solve anything when you've only read half a sentence. Try first to get a feel for the whole problem; try first to see what information you have, and then figure out what you still need.

Step 2 is to work in an organized manner. Figure out what you need but don't have. Name things. Pick variables to stand for the unknows, clearly labelling these variables with what they stand for. Draw and label pictures neatly. Explain your reasoning as you go along. And make sure you know just exactly what the problem is actually asking for. You need to do this for two reasons:

• Working clearly will help you think clearly, and
• figuring out what you need will help you translate your final answer back into English.

Regarding point (a) above:

It can be really frustrating (and embarassing) to spend fifteen minutes solving a word problem on a test, only to realize at the end that you no longer have any idea what " x " stands for, so you have to do the whole problem over again. I did this on a calculus test — thank heavens it was a short test! — and, trust me, you don't want to do this to yourself. Taking fifteen seconds to label things is a better use of your time than spending fifteen minutes reworking the entire exercise!

Step 3 is to look for "key" words. Certain words indicate certain mathematica operations. Some of those words are easy. If an exercise says that one person "added" her marbles to the pile belonging to somebody else, and asks for how many marbles are now in the pile, you know that you'll be adding two numbers.

What are common keywords for word problems?

The following is a listing of most of the more-common keywords for word problems:

increased by more than combined, together total of sum, plus added to comparatives ("greater than", etc)

Subtraction:

decreased by minus, less difference between/of less than, fewer than left, left over, after save (old-fashioned term) comparatives ("smaller than", etc)

Multiplication:

of times, multiplied by product of increased/decreased by a factor of (this last type can involve both addition or subtraction and multiplication!) twice, triple, etc each ("they got three each", etc)

per, a out of ratio of, quotient of percent (divide by 100) equal pieces, split average

is, are, was, were, will be gives, yields sold for, cost

Note that "per", in "Division", means "divided by", as in "I drove 90 miles on three gallons of gas, so I got 30 miles per gallon". Also, "a" sometimes means "divided by", as in "When I tanked up, I paid $12.36 for three gallons, so the gas was $4.12 a gallon".

Warning: The "less than" construction, in "Subtraction", is backwards in the English from what it is in the math. If you need, for instance, to translate " 1.5 less than x ", the temptation is to write " 1.5 −  x ". Do not do this!

You can see how this is wrong by using this construction in a "real world" situation: Consider the statement, "He makes $1.50 an hour less than me." You do not figure his wage by subtracting your wage from $1.50 . Instead, you subtract $1.50 from your wage. So remember: the "less than" construction is backwards.

(Technically, the "greater than" construction, in "Addition", is also backwards in the math from the English. But the order in addition doesn't matter, so it's okay to add backwards, because the result will be the same either way.)

Also note that order is important in the "quotient/ratio of" and "difference between/of" constructions. If a problems says "the ratio of x and y ", it means " x divided by y ", not " y divided by x ". If the problem says "the difference of x and y ", it means " x  −  y ", not " y  −  x ".

Advertisement

Some times, you'll be expected to bring your "real world" knowledge to an exercise. For instance, suppose you're told that "Shelby worked eight hours MTThF and six hours WSat". You would be expected to understand that this meant that she worked eight hours for each of the four days Monday, Tuesday, Thursday, and Friday; and six hours for each of the two days Wednesday and Saturday. Suppose you're told that Shelby earns "time and a half" for any hours she works over forty for a given week. You would be expected to know that "time and a half" means 1.5 times her base rate of pay; if her base rate is twelve dollars an hour, then she'd get 1.5 × 12 = 18 dollars for every over-time hour.

You'll be expected to know that a "dozen" is twelve; you may be expected to know that a "score" is twenty. You'll be expected to know the number of days in a year, the number of hours in a day, and other basic units of measure.

Probably the greatest source of error, though, is the use of variables without definitions. When you pick a letter to stand for something, write down explicitly what that latter is meant to stand for. Does " S " stand for "Shelby" or for "hours Shelby worked"? If the former, what does this mean, in practical terms? (And, if you can't think of any meaningful definition, then maybe you need to slow down and think a little more about what's going on in the word problem.)

In all cases, don't be shy about using your "real world" knowledge. Sometimes you'll not feel sure of your translation of the English into a mathematical expression or equation. In these cases, try plugging in numbers. For instance, if you're not sure if you should be dividing or multiplying, try the process each way with regular numbers. For instance, suppose you're not sure if "half of (the unknown amount)" should be represented by multiplying by one-half, or by dividing by one-half. If you use numbers, you can be sure. Pick an easy number, like ten. Half of ten is five, so we're looking for the operation (that is, multiplication or division) that gives us an answer of 5 . First, let's try division:

ten divided by one-half:

10/(1/2) = (10/1)×(2/1) = 20

Well, that's clearly wrong. How about going the other way?

ten multiplied by one-half:

(10)×(1/2) = 10 ÷ 2 = 5

That's more like it! You know that half of ten is five, and now you can see which mathematical operations gets you the right value. So now you'd know that the expression you're wanting is definitely " (1/2) x ".

You have experience and knowledge; don't be afraid to apply your skills to this new context!

URL: https://www.purplemath.com/modules/translat.htm

Page 1 Page 2

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles

• Math for Kids
• Parenting Resources
• ELA for Kids
• Teaching Resources

How to Teach Number Formation in 5 Easy Steps

13 Best Resources for Math Videos for Kids: Math Made Fun

How to Teach Skip Counting to Kids in 9 Easy Steps

10 Best Math Intervention Strategies for Struggling Students

How to Teach Division to Kids in 11 Easy Steps

How to Cope With Test Anxiety in 12 Easy Ways

Developmental Milestones for 4 Year Olds: The Ultimate Guide

Simple & Stress-Free After School Schedule for Kids of All Ages

When Do Kids Start Preschool: Age & Readiness Skills

Kindergarten Readiness Checklist: A Guide for Parents

How to Teach Letter Formation to Kids in 9 Easy Steps

15 Best Literacy Activities for Preschoolers in 2024

12 Best Poems About Teachers Who Change Lives

6 Effective Ways to Improve Writing Skills

40 Four Letter Words That Start With A

60 Fun Animal Facts for Kids

12 Best Behavior Management Techniques for the Classroom

13 Best Online Teaching Tips for Teachers

How to Teach Kids to Write in 9 Easy Steps

13 Challenges for Teachers and How to Address Them

10 Best Strategies for Solving Math Word Problems

1. Understand the Problem by Paraphrasing

2. identify key information and variables, 3. translate words into mathematical symbols, 4. break down the problem into manageable parts, 5. draw diagrams or visual representations, 6. use estimation to predict answers, 7. apply logical reasoning for unknown variables, 8. leverage similar problems as templates, 9. check answers in the context of the problem, 10. reflect and learn from mistakes.

Have you ever observed the look of confusion on a student’s face when they encounter a math word problem ? It’s a common sight in classrooms worldwide, underscoring the need for effective strategies for solving math word problems . The main hurdle in solving math word problems is not just the math itself but understanding how to translate the words into mathematical equations that can be solved.

SplashLearn: Most Comprehensive Learning Program for PreK-5

SplashLearn inspires lifelong curiosity with its game-based PreK-5 learning program loved by over 40 million children. With over 4,000 fun games and activities, it’s the perfect balance of learning and play for your little one.

Generic advice like “read the problem carefully” or “practice more” often falls short in addressing students’ specific difficulties with word problems. Students need targeted math word problem strategies that address the root of their struggles head-on. 

A Guide on Steps to Solving Word Problems: 10 Strategies 

One of the first steps in tackling a math word problem is to make sure your students understand what the problem is asking. Encourage them to paraphrase the problem in their own words. This means they rewrite the problem using simpler language or break it down into more digestible parts. Paraphrasing helps students grasp the concept and focus on the problem’s core elements without getting lost in the complex wording.

Original Problem: “If a farmer has 15 apples and gives away 8, how many does he have left?”

Paraphrased: “A farmer had some apples. He gave some away. Now, how many apples does he have?”

This paraphrasing helps students identify the main action (giving away apples) and what they need to find out (how many apples are left).

Play these subtraction word problem games in the classroom for free:

Students often get overwhelmed by the details in word problems. Teach them to identify key information and variables essential for solving the problem. This includes numbers , operations ( addition , subtraction , multiplication , division ), and what the question is asking them to find. Highlighting or underlining can be very effective here. This visual differentiation can help students focus on what’s important, ignoring irrelevant details.

• Encourage students to underline numbers and circle keywords that indicate operations (like ‘total’ for addition and ‘left’ for subtraction).
• Teach them to write down what they’re solving for, such as “Find: Total apples left.”

Problem: “A classroom has 24 students. If 6 more students joined the class, how many students are there in total?”

Key Information:

• Original number of students (24)
• Students joined (6)
• Looking for the total number of students

Here are some fun addition word problems that your students can play for free:

The transition from the language of word problems to the language of mathematics is a critical skill. Teach your students to convert words into mathematical symbols and equations. This step is about recognizing keywords and phrases corresponding to mathematical operations and expressions .

Common Translations:

• “Total,” “sum,” “combined” → Addition (+)
• “Difference,” “less than,” “remain” → Subtraction (−)
• “Times,” “product of” → Multiplication (×)
• “Divided by,” “quotient of” → Division (÷)
• “Equals” → Equals sign (=)

Problem: “If one book costs $5, how much would 4 books cost?”

Translation: The word “costs” indicates a multiplication operation because we find the total cost of multiple items. Therefore, the equation is 4 × 5 = $20

Complex math word problems can often overwhelm students. Incorporating math strategies for problem solving, such as teaching them to break down the problem into smaller, more manageable parts, is a powerful approach to overcome this challenge. This means looking at the problem step by step rather than simultaneously trying to solve it. Breaking it down helps students focus on one aspect of the problem at a time, making finding the solution more straightforward.

Problem: “John has twice as many apples as Sarah. If Sarah has 5 apples, how many apples do they have together?”

Steps to Break Down the Problem:

Find out how many apples John has: Since John has twice as many apples as Sarah, and Sarah has 5, John has 5 × 2 = 10

Calculate the total number of apples: Add Sarah’s apples to John’s to find the total,  5 + 10 = 15

By splitting the problem into two parts, students can solve it without getting confused by all the details at once.

Explore these fun multiplication word problem games:

Diagrams and visual representations can be incredibly helpful for students, especially when dealing with spatial or quantity relationships in word problems. Encourage students to draw simple sketches or diagrams to represent the problem visually. This can include drawing bars for comparison, shapes for geometry problems, or even a simple distribution to better understand division or multiplication problems .

Problem: “A garden is 3 times as long as it is wide. If the width is 4 meters, how long is the garden?”

Visual Representation: Draw a rectangle and label the width as 4 meters. Then, sketch the length to represent it as three times the width visually, helping students see that the length is 4 × 3 = 12

Estimation is a valuable skill in solving math word problems, as it allows students to predict the answer’s ballpark figure before solving it precisely. Teaching students to use estimation can help them check their answers for reasonableness and avoid common mistakes.

Problem: “If a book costs $4.95 and you buy 3 books, approximately how much will you spend?”

Estimation Strategy: Round $4.95 to the nearest dollar ($5) and multiply by the number of books (3), so 5 × 3 = 15. Hence, the estimated total cost is about $15.

Estimation helps students understand whether their final answer is plausible, providing a quick way to check their work against a rough calculation.

Check out these fun estimation and prediction word problem worksheets that can be of great help:

When students encounter problems with unknown variables, it’s crucial to introduce them to logical reasoning. This strategy involves using the information in the problem to deduce the value of unknown variables logically. One of the most effective strategies for solving math word problems is working backward from the desired outcome. This means starting with the result and thinking about the steps leading to that result, which can be particularly useful in algebraic problems.

Problem: “A number added to three times itself equals 32. What is the number?”

Working Backward:

Let the unknown number be x.

The equation based on the problem is  x + 3x = 32

Solve for x by simplifying the equation to 4x=32, then dividing by 4 to find x=8.

By working backward, students can more easily connect the dots between the unknown variable and the information provided.

Practicing problems of similar structure can help students recognize patterns and apply known strategies to new situations. Encourage them to leverage similar problems as templates, analyzing how a solved problem’s strategy can apply to a new one. Creating a personal “problem bank”—a collection of solved problems—can be a valuable reference tool, helping students see the commonalities between different problems and reinforcing the strategies that work.

Suppose students have solved a problem about dividing a set of items among a group of people. In that case, they can use that strategy when encountering a similar problem, even if it’s about dividing money or sharing work equally.

It’s essential for students to learn the habit of checking their answers within the context of the problem to ensure their solutions make sense. This step involves going back to the original problem statement after solving it to verify that the answer fits logically with the given information. Providing a checklist for this process can help students systematically review their answers.

Checklist for Reviewing Answers:

• Re-read the problem: Ensure the question was understood correctly.
• Compare with the original problem: Does the answer make sense given the scenario?
• Use estimation: Does the precise answer align with an earlier estimation?
• Substitute back: If applicable, plug the answer into the problem to see if it works.

Problem: “If you divide 24 apples among 4 children, how many apples does each child get?”

After solving, students should check that they understood the problem (dividing apples equally).

Their answer (6 apples per child) fits logically with the number of apples and children.

Their estimation aligns with the actual calculation.

Substituting back 4×6=24 confirms the answer is correct.

Teaching students to apply logical reasoning, leverage solved problems as templates, and check their answers in context equips them with a robust toolkit for tackling math word problems efficiently and effectively.

One of the most effective ways for students to improve their problem-solving skills is by reflecting on their errors, especially with math word problems. Using word problem worksheets is one of the most effective strategies for solving word problems, and practicing word problems as it fosters a more thoughtful and reflective approach to problem-solving

These worksheets can provide a variety of problems that challenge students in different ways, allowing them to encounter and work through common pitfalls in a controlled setting. After completing a worksheet, students can review their answers, identify any mistakes, and then reflect on them in their mistake journal. This practice reinforces mathematical concepts and improves their math problem solving strategies over time.

3 Additional Tips for Enhancing Word Problem-Solving Skills

Before we dive into the importance of reflecting on mistakes, here are a few impactful tips to enhance students’ word problem-solving skills further:

1. Utilize Online Word Problem Games

Incorporate online games that focus on math word problems into your teaching. These interactive platforms make learning fun and engaging, allowing students to practice in a dynamic environment. Games can offer instant feedback and adaptive challenges, catering to individual learning speeds and styles.

Here are some word problem games that you can use for free:

2. Practice Regularly with Diverse Problems

Consistent practice with a wide range of word problems helps students become familiar with different questions and mathematical concepts. This exposure is crucial for building confidence and proficiency.

Start Practicing Word Problems with these Printable Word Problem Worksheets:

3. Encourage Group Work

Solving word problems in groups allows students to share strategies and learn from each other. A collaborative approach is one of the best strategies for solving math word problems that can unveil multiple methods for tackling the same problem, enriching students’ problem-solving toolkit.

Conclusion 

Mastering math word problems is a journey of small steps. Encourage your students to practice regularly, stay curious, and learn from their mistakes. These strategies for solving math word problems are stepping stones to turning challenges into achievements. Keep it simple, and watch your students grow their confidence and skills, one problem at a time.

Frequently Asked Questions (FAQs)

How can i help my students stay motivated when solving math word problems.

Encourage small victories and use engaging tools like online games to make practice fun and rewarding.

What's the best way to teach beginners word problems?

Begin with simple problems that integrate everyday scenarios to make the connection between math and real-life clear and relatable.

How often should students practice math word problems?

Regular, daily practice with various problems helps build confidence and problem-solving skills over time.

• Pre-Kindergarten
• Kindergarten

Most Popular

15 Best Report Card Comments Samples

117 Best Riddles for Kids (With Answers)

40 best good vibes quotes to brighten your day, recent posts.

What is World  Homeschooling & how To Start [Full Guide]

15 Best Movement Activities for Preschoolers in 2024

10 Best Online Homeschool Programs

Math & ela | prek to grade 5, kids see fun., you see real learning outcomes..

Watch your kids fall in love with math & reading through our scientifically designed curriculum.

Parents, try for free Teachers, use for free

• Games for Kids
• Worksheets for Kids
• Math Worksheets
• ELA Worksheets
• Math Vocabulary
• Number Games
• Addition Games
• Subtraction Games
• Multiplication Games
• Division Games
• Addition Worksheets
• Subtraction Worksheets
• Multiplication Worksheets
• Division Worksheets
• Times Tables Worksheets
• Reading Games
• Writing Games
• Phonics Games
• Sight Words Games
• Letter Tracing Games
• Reading Worksheets
• Writing Worksheets
• Phonics Worksheets
• Sight Words Worksheets
• Letter Tracing Worksheets
• Prime Number
• Order of Operations
• Long multiplication
• Place value
• Parallelogram
• SplashLearn Success Stories
• SplashLearn Apps
• [email protected]

© Copyright - SplashLearn

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free

Maths with Mum

Be your child's best tutor

Addition and Subtraction Word Problem Keywords

• Each word problem contains numbers which should be written down.
• Keywords in the word problem can help us to decide whether to add or subtract these numbers.
• The list above contains some common addition and subtraction keywords.
• If you see these words in the word problem, they may help you to decide whether to add or subtract the numbers that you have already written down.

• Phoebe has 12 cm of ribbon and Jack has 23 cm of ribbon.
• How much ribbon do they have altogether?
• The word ‘altogether’ tells us to add the two numbers to make a total.
• We can write the numbers of 12 and 23 with their digits above each other.
• Adding the units column, 2 + 3 = 5.
• Adding the tens column, 1 + 2 = 3.
• 12 + 23 = 35 and so, there is 35 cm of ribbon in total.

• Number Bonds to 20
• 2-Digit Column Addition
• Column Subtraction without Borrowing / Regrouping

Mixed Addition and Subtraction Word Problems Worksheets and Answers

Mixed Addition and Subtraction Word Problems

Addition and subtraction keywords.

• Together / Altogether
• Less / Fewer than
• How many are left / remain?
• Change – in money questions
• Words ending in ‘er’, such as shorter, longer, faster.

Share this:

• Click to share on Twitter (Opens in new window)
• Click to share on Facebook (Opens in new window)
• Click to share on WhatsApp (Opens in new window)
• Click to share on Pinterest (Opens in new window)
• Click to email a link to a friend (Opens in new window)
• Click to print (Opens in new window)
• Click to share on Tumblr (Opens in new window)
• Click to share on Pocket (Opens in new window)
• Click to share on Telegram (Opens in new window)
• Click to share on Skype (Opens in new window)

• HOW IT WORKS
• INSTITUTIONAL SALES

Creating key word flash cards:

• Have a student count out the number of index cards that the class determined in the warm up problem and distribute four cards to each student.
• Direct students to create four flash cards — one for each of the four mathematical operations. On the blank side of each card, they should boldly write an operation and its symbol (i.e., +, -, x, where is the division symbol?), and on the reverse, lined sign they should list the key words associated with that operation. (Students should base these flash cards on the table you created on the front board.)

Playing the role of "math coach":

• Organize the class into small groups of no more than three to four students in each group, and explain that they will be using their new flash cards as visual aids in math coaching!
• Distribute a "Solving Word Problems through Key Words" sheet to a student in each group and explain that the student with the sheet will act as the reader and recorder during the first round. The reader and recorder's job is to read a word problem aloud and to allow his fellow "math coaches" to advise him on which mathematical operation to follow in solving the problem.
• Advise the math coaches in the class to listen to the word problem closely, to advise the reader and recorder to underline any key words in the problem that they detect, and to follow the flash card mathematical operation that they decide to "flash."
• Direct groups to complete the "Solving Word Problems through Key Words" sheet, alternating the role of reader and recorder so that each student has at least one or two turns in that role.

Sharing word problem answers and strategies:

• Invite students to the front of the classroom to explain their group's word problem strategies and how key words led to determining which mathematical operations to use in each problem.
• For homework, assign students the task of writing some of their own word problems containing some of the key words discussed in class but not previously used on the "Solving Word Problems through Key Words" sheet.

Extending the Lesson:

• To further challenge students, you could give them additional word problems that challenge them to interpret the same key words in somewhat confusing contexts (e.g., "I have eight jelly beans, which is three fewer than my brother has. How many jelly beans does my brother have?") Or, you could also introduce word problems involving multiple mathematical operations  (e.g., "A 6000 seat stadium is divided into 3 sections. There are 2000 seats in Section 1, and there are 1500 more seats in Section 2 than in Section 3. How many seats are in Section 2?")

Assessment:

• Check whether or not groups accurately solved each of the ten word problems and underlined appropriate key words in the "Solving Word Problems through Key Words" sheet.
• Assess students' original word problems to see if they appropriately incorporated key words to indicate specific mathematical operations.

Educational Standards :

Benchmarks for Mathematics

Standard 1.     Uses a variety of strategies in the problem-solving process

Level II (Grades 3-5) 1. Uses a variety of strategies to understand problem situations (e.g., discussing with peers, stating problems in own words, modeling problem with diagrams or physical objects, identifying a pattern)  2. Represents problems situations in a variety of forms (e.g., translates from a diagram to a number or symbolic expression) 3. Understands that some ways of representing a problem are more helpful than others 4. Uses trial and error and the process of elimination to solve problems 5. Knows the difference between pertinent and irrelevant information when solving problems  6. Understands the basic language of logic in mathematical situations (e.g., "and," "or," "not")  7. Uses explanations of the methods and reasoning behind the problem solution to determine reasonableness of and to verify results with respect to the original problem  Level III (Grades 6-8) 1. Understands how to break a complex problem into simpler parts or use a similar problem type to solve a problem 2. Uses a variety of strategies to understand problem-solving situations and processes (e.g., considers different strategies and approaches to a problem, restates problem from various perspectives)  3. Understands that there is no one right way to solve mathematical problems but that different methods (e.g., working backward from a solution, using a similar problem type, identifying a pattern) have different advantages and disadvantages 4. Formulates a problem, determines information required to solve the problem, chooses methods for obtaining this information, and sets limits for acceptable solutions  5. Represents problem situations in and translates among oral, written, concrete, pictorial, and graphical forms  6. Generalizes from a pattern of observations made in particular cases, makes conjectures, and provides supporting arguments for these conjectures (i.e., uses inductive reasoning)  7. Constructs informal logical arguments to justify reasoning processes and methods of solutions to problems (i.e., uses informal deductive methods)  8. Understands the role of written symbols in representing mathematical ideas and the use of precise language in conjunction with the special symbols of mathematics

Article Topics:

Keywords for Word Problems

With our Keywords for Word Problems lesson plan, students learn how to identify keywords in word problems that refer to specific mathematic operations (multiplication, division, addition, and subtraction) in order to help them decide how to solve word problems.

Description

Additional information.

Our Keywords for Word Problems lesson plan teaches students strategies for recognizing important keywords in word problems. During this lesson, students are asked to work collaboratively with a partner to write their own word problems that use some of the keywords introduced in this lesson. Students are also asked to solve practice word problems that contain these keywords, demonstrating their understanding of the lesson material and which keywords refer to which operations (multiplication, division, addition, and subtraction).

At the end of the lesson, students will be able to identify keywords in word problems.

State Educational Standards: LB.Math.Content.1.OA.A.2, LB.Math.Content.2.OA.A.1, LB.Math.Content.3.OA.D.8

Thank you for submitting a review!

Your input is very much appreciated. Share it with your friends so they can enjoy it too!

Great Resource!

It was exactly what I needed

This item was very useful to teach students words to look for when determining whether to add, subtract, multiply, or divide. Word problems are very difficult at times and this tool will make the process easier!

This lesson plan was excellent in helping my 2nd grader understand keywords used in solving math problems!

The lesson and materials provided assisted my students who were struggling to recognize key words to determine which operation was used. Thank you

Related products

Rosie the Riveter

Careers: Computer Programmer

Make your life easier with our lesson plans, stay up-to-date with new lessons.

• Lesson Plans
• For Teachers

© 2024 Learn Bright. All rights reserved. Terms and Conditions. Privacy Policy.

• Sign Up for Free

MAKE WAVES WITH THIS FREE WEEKLONG VOCABULARY UNIT!

Strategies for Solving Word Problems – Math

It’s one thing to solve a math equation when all of the numbers are given to you but with word problems, when you start adding reading to the mix, that’s when it gets especially tricky.

The simple addition of those words ramps up the difficulty (and sometimes the math anxiety) by about 100!

How can you help your students become confident word problem solvers? By teaching your students to solve word problems in a step by step, organized way, you will give them the tools they need to solve word problems in a much more effective way.

Here are the seven strategies I use to help students solve word problems.

1. read the entire word problem.

Before students look for keywords and try to figure out what to do, they need to slow down a bit and read the whole word problem once (and even better, twice). This helps kids get the bigger picture to be able to understand it a little better too.

2. Think About the Word Problem

Students need to ask themselves three questions every time they are faced with a word problem. These questions will help them to set up a plan for solving the problem.

Here are the questions:

A. what exactly is the question.

What is the problem asking? Often times, curriculum writers include extra information in the problem for seemingly no good reason, except maybe to train kids to ignore that extraneous information (grrrr!). Students need to be able to stay focused, ignore those extra details, and find out what the real question is in a particular problem.

B. What do I need in order to find the answer?

Students need to narrow it down, even more, to figure out what is needed to solve the problem, whether it’s adding, subtracting, multiplying, dividing, or some combination of those. They’ll need a general idea of which information will be used (or not used) and what they’ll be doing.

This is where key words become very helpful. When students learn to recognize that certain words mean to add (like in all, altogether, combined ), while others mean to subtract, multiply, or to divide, it helps them decide how to proceed a little better

Here’s a Key Words Chart I like to use for teaching word problems. The handout could be copied at a smaller size and glued into interactive math notebooks. It could be placed in math folders or in binders under the math section if your students use binders.

One year I made huge math signs (addition, subtraction, multiplication, and divide symbols) and wrote the keywords around the symbols. These served as a permanent reminder of keywords for word problems in the classroom.

If you’d like to download this FREE Key Words handout, click here:

C. What information do I already have?

This is where students will focus in on the numbers which will be used to solve the problem.

3. Write on the Word Problem

This step reinforces the thinking which took place in step number two. Students use a pencil or colored pencils to notate information on worksheets (not books of course, unless they’re consumable). There are lots of ways to do this, but here’s what I like to do:

• Circle any numbers you’ll use.
• Lightly cross out any information you don’t need.
• Underline the phrase or sentence which tells exactly what you’ll need to find.

4. Draw a Simple Picture and Label It

Drawing pictures using simple shapes like squares, circles, and rectangles help students visualize problems. Adding numbers or names as labels help too.

For example, if the word problem says that there were five boxes and each box had 4 apples in it, kids can draw five squares with the number four in each square. Instantly, kids can see the answer so much more easily!

5. Estimate the Answer Before Solving

Having a general idea of a ballpark answer for the problem lets students know if their actual answer is reasonable or not. This quick, rough estimate is a good math habit to get into. It helps students really think about their answer’s accuracy when the problem is finally solved.

6. Check Your Work When Done

This strategy goes along with the fifth strategy. One of the phrases I constantly use during math time is, Is your answer reasonable ? I want students to do more than to be number crunchers but to really think about what those numbers mean.

Also, when students get into the habit of checking work, they are more apt to catch careless mistakes, which are often the root of incorrect answers.

7. Practice Word Problems Often

Just like it takes practice to learn to play the clarinet, to dribble a ball in soccer, and to draw realistically, it takes practice to become a master word problem solver.

When students practice word problems, often several things happen. Word problems become less scary (no, really).

They start to notice similarities in types of problems and are able to more quickly understand how to solve them. They will gain confidence even when dealing with new types of word problems, knowing that they have successfully solved many word problems in the past.

If you’re looking for some word problem task cards, I have quite a few of them for 3rd – 5th graders.

This 3rd grade math task cards bundle has word problems in almost every one of its 30 task card sets..

There are also specific sets that are dedicated to word problems and two-step word problems too. I love these because there’s a task card set for every standard.

CLICK HERE to take a look at 3rd grade:

This 4th Grade Math Task Cards Bundle also has lots of word problems in almost every single of its 30 task card sets. These cards are perfect for centers, whole class, and for one on one.

CLICK HERE to see 4th grade:

This 5th Grade Math Task Cards Bundle is also loaded with word problems to give your students focused practice.

CLICK HERE to take a look at 5th grade:

Want to try a FREE set of math task cards to see what you think?

3rd Grade: Rounding Whole Numbers Task Cards

4th Grade: Convert Fractions and Decimals Task Cards

5th Grade: Read, Write, and Compare Decimals Task Cards

Thanks so much for stopping by!

• Read more about: Math

You might also like...

Fraction Activities Students Love – Math

Fractions can be tough! While it takes time and repeated exposure with fractions for students to have a real understanding of them, there are lots

Math Games Using Dice

Games are an important part of math class, in my opinion. Not only are kids able to practice the skills that we have been focusing

Math Games Using Dominoes

Math games have always been part of our math time. I love the fact that any time I introduce a math game, I know I’ll

Hi, I’m Jenn, CEO and owner of The Teacher Next Door!

I know that you strive to be an effective upper elementary teacher while maintaining a healthy work-life balance.

In order to do that, you need resources that are impactful, yet simple .

The problem is that most resources and curriculums out there are far from simple. The pages upon pages of daily lesson plans are just plain overwhelming .

At TTND, we believe teachers should be living their lives outside of the classroom, and not spend hours lesson planning and searching for resources.

We understand that now, more than ever, teachers need space to be themselves which is why we create and support teachers with timesaving tips and standards-aligned resources.

Want access to TTND's Free Resource Library? Sign up for our newsletter and we'll email you the exclusive password!

Trending posts.

SEARCH BY TOPIC

• Classroom Ideas
• Holidays and Seasonal
• Mentor Texts
• Reading Block
• Uncategorized
• Writing & Grammar

POPULAR RESOURCES

Facebook Group

Teachers Pay Teachers

Free Resource Library

💌 Contact Us

Disclosures

Privacy Policy

Refund Policy

Purchase Orders

Your Downloads

Reward Points

©  The Teacher Next Door, LLC. All rights reserved.

* Please note: If your school has strong email filters, you may wish to use your personal email to ensure access.

No More Keywords for Math Word Problems

• Content and Standards

The use of math keywords focuses on looking at the words of a word problem in isolation and not in the context of the problem. In this post, I share four reasons why using keywords for math word problems fail students .

There are 125 sheep and 5 dogs in a flock. How old is the shepherd?  

1st Student: “I can’t solve this because it doesn’t say anything about the shepherd.” 

2nd Student: “120 years old because 125 minus the 5 dogs in a flock.” 

3rd Student: “25.” [The student’s work shows 125 divided by 5].

4th Student: “25” [The student’s work shows 125 divided by 5].

5th Student: “25” [The student’s work shows 125 divided by 5].

6th Student: “It doesn’t tell you.” 

7th Student: “130” [The student’s work shows the sum of 125 and 5.]

8th Student: “65” [The student’s work shows (125 + 5) ÷ 2.]

9th Student: “25.” When asked to explain her solution, the student responded, “Because it doesn’t say the difference, or the sum, or the product.” 

Of the 32 eighth-grade students asked to solve this problem, only 8 of them were able to give a response indicating they were able to read the problem, make sense of it, and determine there was not enough information to solve it.   

While the results of this scenario are quite shocking, this kind of formulaic thinking when it comes to solving word problems is all too common. 

In fact, when another mathematics educator tried a similar activity with her first graders, her results were just as astounding. (See the original post and video here . )

So, what’s the problem?

Using Keywords For Math Word Problems

Our students have been trained to look for math keywords, or clues, to what operation they are expected to perform to solve a math word problem. While I completely understand that teachers have perfected the use of keywords over the years in order to provide a strategy that would prove successful both in the classroom and on standardized tests, the use of keywords does not require students to think critically about a problem or allow them to make sense of the situation.

On a recent search in Pinterest, I was not surprised to find a plethora of pins related to using keywords for math word problems. The picture below shows a list of all the keywords that I found– many of which, I disagree with the placement or inclusion of.

As a teacher, I can’t imagine what it would feel like to help my students memorize all of these terms. How are they going to learn them– with a weekly quiz?

I think not.

Why Not Keywords?

But using keywords for math word problems works just fine for me you say?

Van de Walle and Lovin (2006) and Van de Walle, Karp, and Bay-Williams (2012) offer four reasons to remove the use of keywords from our work with students:

1. Keywords can be Dangerous!

Many authors and resource creators use keywords in ways that differ from the way students expect them to be used which leads students to an incorrect solution strategy pathway. Add to that the use of multiple-meaning words and our students can become quickly overwhelmed and confused.

Consider the following problem: Julie left $9 on the table. Her brother left $6 on the table. How much money was left on the table? Use of the word “left” might indicate to some that the solution to this problem is obtained with subtraction; however, this is an addition situation because two quantities are being joined together. 

(Find more “Keyword Fails” here .)

2. Use of Keywords Misses the Big Picture

The use of math keywords focuses on looking at the words in isolation and not in the context of the problem.

“Mathematics is about reasoning and making sense of situations” (Van de Walle & Lovin, 2006, p. 70); therefore, students should analyze the structure of the problems in the context not just dissect them for keywords.

When students begin to view problem situations in this way, they can identify the bigger picture and make connections between problem situations and the necessary solution strategy required to solve the problem.

3. What If There’s No Keyword?

Many problems, especially as students begin to advance to more sophisticated work, have no keywords.

Consider the following problem: Dominique had 10 flower petals. Four were green and the rest were orange. How many orange flower petals does Dominique have?  

Because this problem does not contain keywords, students who rely on this approach will not have a strategy on which to rely, which will most likely result in a new word, like “rest” being added to the subtraction word list.

4. Will Keywords Support Students Long-Term?

While teachers in the younger grades claim to have great success using keywords for math word problems, the use of keywords does not work with more advanced problems or those with more than one step.

Therefore, students who do not attend to the meaning of a problem while solving it will be unsuccessful in completing the problem because they will miss the intermediate steps needed to lead to the final result.

Making Sense of Problems

The first Mathematical Practice Standard of the Common Core State Standards for Math describe mathematically proficient students as those who can: 

• Explain the meaning of a problem
• Plan a solution pathway rather than jumping to a solution
• Continually check for reasonableness and ask, “Does this make sense?” 

These three skills are essential to solving math word problems successfully.

But, how do we help students develop them?

Using Tricks To Replace Thinking

Tina Cardone, the author of Nix the Tricks , a guide to avoiding non-conceptually developmental short-cuts, suggests having students think about the words of the problem as a whole and focus on what is happening in the problem in context.

Students can accomplish this by visualizing the situation and creating a mental picture of the actions that are taking place. Once they understand the actions, students can then connect the actions to symbols.

After students have experience with a variety of problem situations, some patterns will begin to emerge as students begin to recognize recurring themes, such as joining, part-part-whole, separating, comparing, equal groups, sharing, and measuring.

Throughout the year, teachers can record the different situations students encounter on an anchor chart. Then replace that old, out-dated math keywords poster with the brand-spanking-new operation situations poster.

Want to know more about the operation situations and strategies to help with math word problems ?

Download the free poster above using the form below and click here to learn more about strategies to help with math word problems.

What strategies do you use to emphasize making sense of word problems with your students? Share your ideas in the comments section below. 

• Common Core State Standards for Math
• https://gfletchy.com/2015/01/12/teaching-keywords-forget-about-it/
• http://nixthetricks.com/
• http://tjzager.com/2014/10/18/making-sense/
• Van de Wall, J. A., Karp, K. S., & Bay-Williams, J. M. (2012). Elementary and middle school mathematics: Teaching developmentally. Boston, MA: Pearson.
• Van de Wall, J. A. and Lovin, L. H. (2006). Teaching student-centered mathematics: Grades 3 – 5. Boston, MA: Pearson.

Shametria Routt Banks

• Assessment Tools
• Critical Thinking
• Differentiation
• Math & Literature
• Math & Technology
• Math Routines
• Math Stations
• Virtual Learning
• Writing in Math

You may also like...

8 Responses

Love the Analyzing Word Problems poster!

Thank you SOOOOO very much. I always thought that lists of key words were incomplete and had so much crossover … and needed to be used in context. You have combined all of this in a clear and concise way. LOVE IT!

Hi Patricia!

I’m so glad you found the post useful!

~ Shametria

Hi. As a non math teacher,I really like this approach. Word problems were the hated vegetable that went with a main course I hated and couldn’t cut. I was disappointed, though,that so many links didn’t work. I’m not sure how old the post is, so that may be the problem. But thanks for teaching me to teach them.

I’m so glad you found the post helpful! I went through the post and all the links work; however, you may have read it at a time when I was updating the connecting posts and they were in draft form. My apologies about that. All the links do work though, so I encourage you to take another look. If you have any questions, please contact me at [email protected] . Thank you!

What about EL learners? I have third grade newcomers who have zero language and have to work through word problems.

Interesting concept and makes sense… I tell my students to think about the action that is taking place to help them determine the operation needed.

Hi LaChone! Love that you don’t focus on keywords– such a gamechanger!

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed .

©2024 The Routty Math Teacher.   All Rights Reserved.  Designed by Ashley Hughes.

Privacy overview.

Choose Your Test

Sat / act prep online guides and tips, the complete guide to sat math word problems.

About 25% of your total SAT Math section will be word problems, meaning you will have to create your own visuals and equations to solve for your answers. Though the actual math topics can vary, SAT word problems share a few commonalities, and we’re here to walk you through how to best solve them.

This post will be your complete guide to SAT Math word problems. We'll cover how to translate word problems into equations and diagrams, the different types of math word problems you’ll see on the test, and how to go about solving your word problems on test day.

Feature Image: Antonio Litterio /Wikimedia

What Are SAT Math Word Problems?

A word problem is any math problem based mostly or entirely on a written description. You will not be provided with an equation, diagram, or graph on a word problem and must instead use your reading skills to translate the words of the question into a workable math problem. Once you do this, you can then solve it.

You will be given word problems on the SAT Math section for a variety of reasons. For one, word problems test your reading comprehension and your ability to visualize information.

Secondly, these types of questions allow test makers to ask questions that'd be impossible to ask with just a diagram or an equation. For instance, if a math question asks you to fit as many small objects into a larger one as is possible, it'd be difficult to demonstrate and ask this with only a diagram.

Translating Math Word Problems Into Equations or Drawings

In order to translate your SAT word problems into actionable math equations you can solve, you’ll need to understand and know how to utilize some key math terms. Whenever you see these words, you can translate them into the proper mathematical action.

For instance, the word "sum" means the value when two or more items are added together. So if you need to find the sum of a and b , you’ll need to set up your equation like this: a+b.

Also, note that many mathematical actions have more than one term attached, which can be used interchangeably.

Here is a chart with all the key terms and symbols you should know for SAT Math word problems:

Now, let's look at these math terms in action using a few official examples:

We can solve this problem by translating the information we're given into algebra. We know the individual price of each salad and drink, and the total revenue made from selling 209 salads and drinks combined. So let's write this out in algebraic form.

We'll say that the number of salads sold = S , and the number of drinks sold = D . The problem tells us that 209 salads and drinks have been sold, which we can think of as this:

S + D = 209

Finally, we've been told that a certain number of S and D have been sold and have brought in a total revenue of 836 dollars and 50 cents. We don't know the exact numbers of S and D , but we do know how much each unit costs. Therefore, we can write this equation:

6.50 S + 2 D = 836.5

We now have two equations with the same variables ( S and D ). Since we want to know how many salads were sold, we'll need to solve for D so that we can use this information to solve for S . The first equation tells us what S and D equal when added together, but we can rearrange this to tell us what just D equals in terms of S :

Now, just subtract S from both sides to get what D equals:

D = 209 − S

Finally, plug this expression in for D into our other equation, and then solve for S :

6.50 S + 2(209 − S ) = 836.5

6.50 S + 418 − 2 S = 836.5

6.50 S − 2 S = 418.5

4.5 S = 418.5

The correct answer choice is (B) 93.

This word problem asks us to solve for one possible solution (it asks for "a possible amount"), so we know right away that there will be multiple correct answers.

Wyatt can husk at least 12 dozen ears of corn and at most 18 dozen ears of corn per hour. If he husks 72 dozen at a rate of 12 dozen an hour, this is equal to 72 / 12 = 6 hours. You could therefore write 6 as your final answer.

If Wyatt husks 72 dozen at a rate of 18 dozen an hour (the highest rate possible he can do), this comes out to 72 / 18 = 4 hours. You could write 4 as your final answer.

Since the minimum time it takes Wyatt is 4 hours and the maximum time is 6 hours, any number from 4 to 6 would be correct.

Though the hardest SAT word problems might look like Latin to you right now, practice and study will soon have you translating them into workable questions.

Typical SAT Word Problems

Word problems on the SAT can be grouped into three major categories:

• Word problems for which you must simply set up an equation
• Word problems for which you must solve for a specific value
• Word problems for which you must define the meaning of a value or variable

Below, we look at each world problem type and give you examples.

Word Problem Type 1: Setting Up an Equation

This is a fairly uncommon type of SAT word problem, but you’ll generally see it at least once on the Math section. You'll also most likely see it first on the section.

For these problems, you must use the information you’re given and then set up the equation. No need to solve for the missing variable—this is as far as you need to go.

Almost always, you’ll see this type of question in the first four questions on the SAT Math section, meaning that the College Board consider these questions easy. This is due to the fact that you only have to provide the setup and not the execution.

To solve this problem, we'll need to know both Armand's and Tyrone's situations, so let's look at them separately:

Armand: Armand sent m text messages each hour for 5 hours, so we can write this as 5m —the number of texts he sent per hour multiplied by the total number of hours he texted.

Tyrone: Tyrone sent p text messages each hour for 4 hours, so we can write this as 4 p —the number of texts he sent per hour multiplied by the total number of hours he texted.

We now know that Armand's situation can be written algebraically as 5m , and Tyrone's can be written as 4 p . Since we're being asked for the expression that represents the total number of texts sent by Armand and Tyrone, we must add together the two expressions:

The correct answer is choice (C) 5m + 4 p

Word Problem Type 2: Solving for a Missing Value

The vast majority of SAT Math word problem questions will fall into this category. For these questions, you must both set up your equation and solve for a specific piece of information.

Most (though not all) word problem questions of this type will be scenarios or stories covering all sorts of SAT Math topics , such as averages , single-variable equations , and ratios . You almost always must have a solid understanding of the math topic in question in order to solve the word problem on the topic.

Let's try to think about this problem in terms of x . If Type A trees produced 20% more pears than Type B did, we can write this as an expression:

x + 0.2 x = 1.2 x = # of pears produced by Type A

In this equation, x is the number of pears produced by Type B trees. If we add 20% of x (0.2 x ) to x , we get the number of pears produced by Type A trees.

The problem tells us that Type A trees produced a total of 144 pears. Since we know that 1.2 x is equal to the number of pears produced by Type A, we can write the following equation:

1.2 x = 144

Now, all we have to do is divide both sides by 1.2 to find the number of pears produced by Type B trees:

x = 144 / 1.2

The correct answer choice is (B) 120.

You might also get a geometry problem as a word problem, which might or might not be set up with a scenario, too. Geometry questions will be presented as word problems typically because the test makers felt the problem would be too easy to solve had you been given a diagram, or because the problem would be impossible to show with a diagram. (Note that geometry makes up a very small percentage of SAT Math . )

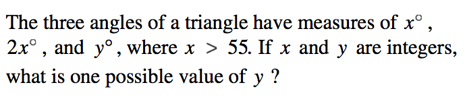
This is a case of a problem that is difficult to show visually, since x is not a set degree value but rather a value greater than 55; thus, it must be presented as a word problem.

Since we know that x must be an integer degree value greater than 55, let us assign it a value. In this case, let us call x 56°. (Why 56? There are other values x could be, but 56 is guaranteed to work since it's the smallest integer larger than 55. Basically, it's a safe bet!)

Now, because x = 56, the next angle in the triangle—2 x —must measure the following:

Let's make a rough (not to scale) sketch of what we know so far:

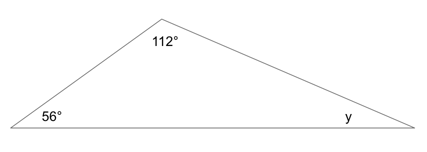
Now, we know that there are 180° in a triangle , so we can find the value of y by saying this:

y = 180 − 112 − 56

One possible value for y is 12. (Other possible values are 3, 6, and 9. )

Word Problem Type 3: Explaining the Meaning of a Variable or Value

This type of problem will show up at least once. It asks you to define part of an equation provided by the word problem—generally the meaning of a specific variable or number.

This question might sound tricky at first, but it's actually quite simple.

We know tha t P is the number of phones Kathy has left to fix, and d is the number of days she has worked in a week. If she's worked 0 days (i.e., if we plug 0 into the equation), here's what we get:

P = 108 − 23(0)

This means that, without working any days of the week, Kathy has 108 phones to repair. The correct answer choice, therefore, is (B) Kathy starts each week with 108 phones to fix.

To help juggle all the various SAT word problems, let's look at the math strategies and tips at our disposal.

Ready to go beyond just reading about the SAT? Then you'll love the free five-day trial for our SAT Complete Prep program . Designed and written by PrepScholar SAT experts , our SAT program customizes to your skill level in over 40 subskills so that you can focus your studying on what will get you the biggest score gains.

Click on the button below to try it out!

SAT Math Strategies for Word Problems

Though you’ll see word problems on the SAT Math section on a variety of math topics, there are still a few techniques you can apply to solve word problems as a whole.

#1: Draw It Out

Whether your problem is a geometry problem or an algebra problem, sometimes making a quick sketch of the scene can help you understand what exactly you're working with. For instance, let's look at how a picture can help you solve a word problem about a circle (specifically, a pizza):

If you often have trouble visualizing problems such as these, draw it out. We know that we're dealing with a circle since our focus is a pizza. We also know that the pizza weighs 3 pounds.

Because we'll need to solve the weight of each slice in ounces, let's first convert the total weight of our pizza from pounds into ounces. We're given the conversion (1 pound = 16 ounces), so all we have to do is multiply our 3-pound pizza by 16 to get our answer:

3 * 16 = 48 ounces (for whole pizza)

Now, let's draw a picture. First, the pizza is divided in half (not drawn to scale):

We now have two equal-sized pieces. Let's continue drawing. The problem then says that we divide each half into three equal pieces (again, not drawn to scale):

This gives us a total of six equal-sized pieces. Since we know the total weight of the pizza is 48 ounces, all we have to do is divide by 6 (the number of pieces) to get the weight (in ounces) per piece of pizza:

48 / 6 = 8 ounces per piece

The correct answer choice is (C) 8.

As for geometry problems, remember that you might get a geometry word problem written as a word problem. In this case, make your own drawing of the scene. Even a rough sketch can help you visualize the math problem and keep all your information in order.

#2: Memorize Key Terms

If you’re not used to translating English words and descriptions into mathematical equations, then SAT word problems might be difficult to wrap your head around at first. Look at the chart we gave you above so you can learn how to translate keywords into their math equivalents. This way, you can understand exactly what a problem is asking you to find and how you’re supposed to find it.

There are free SAT Math questions available online , so memorize your terms and then practice on realistic SAT word problems to make sure you’ve got your definitions down and can apply them to the actual test.

#3: Underline and/or Write Out Important Information

The key to solving a word problem is to bring together all the key pieces of given information and put them in the right places. Make sure you write out all these givens on the diagram you’ve drawn (if the problem calls for a diagram) so that all your moving pieces are in order.

One of the best ways to keep all your pieces straight is to underline your key information in the problem, and then write them out yourself before you set up your equation. So take a moment to perform this step before you zero in on solving the question.

#4: Pay Close Attention to What's Being Asked

It can be infuriating to find yourself solving for the wrong variable or writing in your given values in the wrong places. And yet this is entirely too easy to do when working with math word problems.

Make sure you pay strict attention to exactly what you’re meant to be solving for and exactly what pieces of information go where. Are you looking for the area or the perimeter? The value of x, 2x, or y?

It’s always better to double-check what you’re supposed to find before you start than to realize two minutes down the line that you have to begin solving the problem all over again.

#5: Brush Up on Any Specific Math Topic You Feel Weak In

You're likely to see both a diagram/equation problem and a word problem for almost every SAT Math topic on the test. This is why there are so many different types of word problems and why you’ll need to know the ins and outs of every SAT Math topic in order to be able to solve a word problem about it.

For example, if you don’t know how to find an average given a set of numbers, you certainly won’t know how to solve a word problem that deals with averages!

Understand that solving an SAT Math word problem is a two-step process: it requires you to both understand how word problems work and to understand the math topic in question. If you have any areas of mathematical weakness, now's a good time to brush up on them—or else SAT word problems might be trickier than you were expecting!

All set? Let's go!

Test Your SAT Math Word Problem Knowledge

Finally, it's time to test your word problem know-how against real SAT Math problems:

Word Problems

1. No Calculator

2. Calculator OK

3. Calculator OK

4. Calculator OK

Answers: C, B, A, 1160

Answer Explanations

1. For this problem, we have to use the information we're given to set up an equation.

We know that Ken spent x dollars, and Paul spent 1 dollar more than Ken did. Therefore, we can write the following equation for Paul:

Ken and Paul split the bill evenly. This means that we'll have to solve for the total amount of both their sandwiches and then divide it by 2. Since Ken's sandwich cost x dollars and Paul's cost x + 1, here's what our equation looks like when we combine the two expressions:

Now, we can divide this expression by 2 to get the price each person paid:

(2 x + 1) / 2

But we're not finished yet. We know that both Ken and Paul also paid a 20% tip on their bills. As a result, we have to multiply the total cost of one bill by 0.2, and then add this tip to the bill. Algebraically, this looks like this:

( x + 0.5) + 0.2( x + 0.5)

x + 0.5 + 0.2 x + 0.1

1.2 x + 0.6

The correct answer choice is (C) 1.2 x + 0.6

2. You'll have to be familiar with statistics in order to understand what this question is asking.

Since Nick surveyed a random sample of his freshman class, we can say that this sample will accurately reflect the opinion (and thus the same percentages) as the entire freshman class.

Of the 90 freshmen sampled, 25.6% said that they wanted the Fall Festival held in October. All we have to do now is find this percentage of the entire freshmen class (which consists of 225 students) to determine how many total freshmen would prefer an October festival:

225 * 0.256 = 57.6

Since the question is asking "about how many students"—and since we obviously can't have a fraction of a person!—we'll have to round this number to the nearest answer choice available, which is 60, or answer choice (B).

3. This is one of those problems that is asking you to define a value in the equation given. It might look confusing, but don't be scared—it's actually not as difficult as it appears!

First off, we know that t represents the number of seconds passed after an object is launched upward. But what if no time has passed yet? This would mean that t = 0. Here's what happens to the equation when we plug in 0 for t :

h (0) = -16(0)2 + 110(0) + 72

h (0) = 0 + 0 + 72

As we can see, before the object is even launched, it has a height of 72 feet. This means that 72 must represent the initial height, in feet, of the object, or answer choice (A).

4. You might be tempted to draw a diagram for this problem since it's talking about a pool (rectangle), but it's actually quicker to just look at the numbers given and work from there.

We know that the pool currently holds 600 gallons of water and that water has been hosed into it at a rate of 8 gallons a minute for a total of 70 minutes.

To find the amount of water in the pool now, we'll have to first solve for the amount of water added to the pool by hose. We know that 8 gallons were added each minute for 70 minutes, so all we have to do is multiply 8 by 70:

8 * 70 = 560 gallons

This tells us that 560 gallons of water were added to our already-filled, 600-gallon pool. To find the total amount of water, then, we simply add these two numbers together:

560 + 600 = 1160

The correct answer is 1160.

Aaaaaaaaaaand time for a nap.

Key Takeaways: Making Sense of SAT Math Word Problems

Word problems make up a significant portion of the SAT Math section, so it’s a good idea to understand how they work and how to translate the words on the page into a proper expression or equation. But this is still only half the battle.

Though you won’t know how to solve a word problem if you don’t know what a product is or how to draw a right triangle, you also won’t know how to solve a word problem about ratios if you don’t know how ratios work.

Therefore, be sure to learn not only how to approach math word problems as a whole, but also how to narrow your focus on any SAT Math topics you need help with. You can find links to all of our SAT Math topic guides here to help you in your studies.

What’s Next?

Want to brush up on SAT Math topics? Check out our individual math guides to get an overview of each and every topic on SAT Math . From polygons and slopes to probabilities and sequences , we've got you covered!

Running out of time on the SAT Math section? We have the know-how to help you beat the clock and maximize your score .

Been procrastinating on your SAT studying? Learn how you can overcome your desire to procrastinate and make a well-balanced prep plan.

Trying to get a perfect SAT score? Take a look at our guide to getting a perfect 800 on SAT Math , written by a perfect scorer.

Want to improve your SAT score by 160 points?

Check out our best-in-class online SAT prep program . We guarantee your money back if you don't improve your SAT score by 160 points or more.

Our program is entirely online, and it customizes what you study to your strengths and weaknesses . If you liked this Math strategy guide, you'll love our program. Along with more detailed lessons, you'll get thousands of practice problems organized by individual skills so you learn most effectively. We'll also give you a step-by-step program to follow so you'll never be confused about what to study next.

Check out our 5-day free trial:

Courtney scored in the 99th percentile on the SAT in high school and went on to graduate from Stanford University with a degree in Cultural and Social Anthropology. She is passionate about bringing education and the tools to succeed to students from all backgrounds and walks of life, as she believes open education is one of the great societal equalizers. She has years of tutoring experience and writes creative works in her free time.

Ask a Question Below

Have any questions about this article or other topics? Ask below and we'll reply!

Improve With Our Famous Guides

• For All Students

The 5 Strategies You Must Be Using to Improve 160+ SAT Points

How to Get a Perfect 1600, by a Perfect Scorer

Series: How to Get 800 on Each SAT Section:

Score 800 on SAT Math

Score 800 on SAT Reading

Score 800 on SAT Writing

Series: How to Get to 600 on Each SAT Section:

Score 600 on SAT Math

Score 600 on SAT Reading

Score 600 on SAT Writing

Free Complete Official SAT Practice Tests

What SAT Target Score Should You Be Aiming For?

15 Strategies to Improve Your SAT Essay

The 5 Strategies You Must Be Using to Improve 4+ ACT Points

How to Get a Perfect 36 ACT, by a Perfect Scorer

Series: How to Get 36 on Each ACT Section:

36 on ACT English

36 on ACT Math

36 on ACT Reading

36 on ACT Science

Series: How to Get to 24 on Each ACT Section:

24 on ACT English

24 on ACT Math

24 on ACT Reading

24 on ACT Science

What ACT target score should you be aiming for?

ACT Vocabulary You Must Know

ACT Writing: 15 Tips to Raise Your Essay Score

How to Get Into Harvard and the Ivy League

How to Get a Perfect 4.0 GPA

How to Write an Amazing College Essay

What Exactly Are Colleges Looking For?

Is the ACT easier than the SAT? A Comprehensive Guide

Should you retake your SAT or ACT?

When should you take the SAT or ACT?

Stay Informed

Get the latest articles and test prep tips!

Looking for Graduate School Test Prep?

Check out our top-rated graduate blogs here:

GRE Online Prep Blog

GMAT Online Prep Blog

TOEFL Online Prep Blog

Holly R. "I am absolutely overjoyed and cannot thank you enough for helping me!”

math problem solving key words

All Formats

Resource types, all resource types.

• Rating Count
• Price (Ascending)
• Price (Descending)
• Most Recent

Math problem solving key words

Math Vocabulary Problem Solving Key Words Anchor Chart 2nd 3rd 4th 5th Grade ESL

Math CUBES Problem Solving & Math Key Words Bulletin Board Posters

Key Words to Problem Solve ? Math Basic Operations Posters

Math Problem Solving Key Words

Identify Keywords Math Problem Solving BUNDLE

Math Word Problems for 3rd grade using Math Key Words for Problem Solving

Math : Problem Solving - Key Word Anchor Chart and Bookmarks

Keywords , Steps, and Strategies for Solving Math Word Problems

Spanish Math Strategies and Key Words for Problem Solving

CUBES Problem Solving and Math Key Words Reference Bulletin Board

Math Problem Solving Key Words Posters

Key Words for Solving Math Word Problems

Math Problem Solving Key Word Posters

Quiz, Quiz, Trade: Key Words In Math Problem Solving

Math Code/ Key Words - Using key words for math problem solving

Math Problem Solving Key Words Posters with worksheets for ESL Smaller size

Math Word Problem Anchor Chart - Key Words for Problem Solving for 4 Operations

Problem Solving - Key Words to Solve Math Problems

Key Words to Solve Math Problems Word Sort & Practice

Superhero Math BUNDLE- Problem Solving Mats & Key Words & Skip Counting Posters

Giant Posters - Key Words for Math Problem Solving (b&w spiral)

• Google Slides™

Giant Posters - Key Words for Math Problem Solving (yellow with black dots)

Giant Posters - Key Words for Math Problem Solving (rainbow stripes)

Giant Posters - Key Words for Math Problem Solving (patriotic)

• We're hiring
• Help & FAQ
• Privacy policy
• Student privacy
• Terms of service
• Tell us what you think

Watch CBS News

How two high school students solved a 2,000-year-old math puzzle

By Bill Whitaker , Aliza Chasan , Sara Kuzmarov, Mariah Campbell

May 5, 2024 / 7:00 PM EDT / CBS News

A high school math teacher at St. Mary's Academy in New Orleans, Michelle Blouin Williams, was looking for ingenuity when she and her colleagues set a school-wide math contest with a challenging bonus question. That bonus question asked students to create a new proof for the Pythagorean Theorem, a fundamental principle of geometry, using trigonometry. The teachers weren't necessarily expecting anyone to solve it, as proofs of the Pythagorean Theorem using trigonometry were believed to be impossible for nearly 2,000 years.

But then, in December 2022, Calcea Johnson and Ne'Kiya Jackson, seniors at St. Mary's Academy, stepped up to the challenge. The $500 prize money was a motivating factor.

After months of work, they submitted their innovative proofs to their teachers. With the contest behind them, their teachers encouraged the students to present at a mathematics conference, and then to seek to publish their work. And even today, they're not done. Now in college, they've been working on further proofs of the Pythagorean Theorem and believe they have found five more proofs. Amazingly, despite their impressive achievements, they insist they're not math geniuses.

"I think that's a stretch," Calcea said.

The St. Mary's math contest

When the pair started working on the math contest they were familiar with the Pythagorean Theorem's equation: A² + B² = C², which explains that by knowing the length of two sides of a right triangle, it's possible to figure out the length of the third side.

When Calcea and Ne'Kiya set out to create a new Pythagorean Theorem proof, they didn't know that for thousands of years, one using trigonometry was thought to be impossible.  In 2009, mathematician Jason Zimba submitted one, and now Calcea and Ne'Kiya are adding to the canon.

Calcea and Ne'Kiya had studied geometry and some trigonometry when they started working on their proofs, but said they didn't feel math was easy. As the contest went on, they spent almost all their free time developing their ideas.

"The garbage can was full of papers, which she would, you know, work out the problems and if that didn't work, she would ball it up, throw it in the trash," Cal Johnson, Calcea's dad, said.

Neliska Jackson, Ne'Kiya's mother, says lightheartedly, that most of the time, her daughter's work was beyond her. 

To document Calcea and Ne'Kiya's work, math teachers at St. Mary's submitted their proofs to an American Mathematical Society conference in Atlanta in March 2023.

"Well, our teacher approached us and was like, 'Hey, you might be able to actually present this,'" Ne'Kiya said. "I was like, 'Are you joking?' But she wasn't. So we went. I got up there. We presented and it went well, and it blew up."

Why Calcea' and Ne'kiya's work "blew up"

The reaction was insane and unexpected, Calcea said. News of their accomplishment spread around the world. The pair got a write-up in South Korea and a shoutout from former first lady Michelle Obama. They got a commendation from the governor and keys to the city of New Orleans. 

Calcea and Ne'Kiya said they think there's several reasons why people found their work so impressive. 

"Probably because we're African American, one," Ne'Kiya said. "And we're also women. So I think-- oh, and our age. Of course our ages probably played a big part."

Ne'Kiya said she'd like their accomplishment to be celebrated for what it is: "a great mathematical achievement."

In spite of the community's celebration of the students' work, St. Mary's Academy president and interim principal Pamela Rogers said that with recognition came racist calls and comments. 

"[People said] 'they could not have done it. African Americans don't have the brains to do it.' Of course, we sheltered our girls from that," Rogers said. "But we absolutely did not expect it to come in the volume that it came."

Rogers said too often society has a vision of who can be successful.

"To some people, it is not always an African American female," Rogers said. "And to us, it's always an African American female."

Success at St. Marys 

St. Mary's, a private Catholic elementary and high school, was started for young Black women just after the Civil War. Ne'Kiya and Calcea follow a long line of barrier-breaking graduates. Leah Chase , the late queen of Creole cuisine, was an alum. So was Michelle Woodfork, the first African American female New Orleans police chief, and Dana Douglas, a judge for the Fifth Circuit Court of Appeals. 

Math teacher Michelle Blouin Williams, who initiated the math contest, said Calcea and Ne'Kiya are typical St. Mary's students. She said if they're "unicorns," then every student who's matriculated through the school is a "beautiful, Black unicorn."

Students hear that message from the moment they walk in the door, Rogers said. 

"We believe all students can succeed, all students can learn," the principal said. "It does not matter the environment that you live in."

About half the students at St. Mary's get scholarships, subsidized by fundraising to defray the $8,000 a year tuition. There's no test to get in, but expectations are high and rules are strict: cellphones are not allowed and modest skirts and hair in its natural color are required. 

Students said they appreciate the rules and rigor.

"Especially the standards that they set for us," junior Rayah Siddiq said. "They're very high. And I don't think that's ever going to change." 

What's next for Ne'Kiya and Calcea

Last year when Ne'Kiya and Calcea graduated, all their classmates were accepted into college and received scholarship offers. The school has had a 100% graduation rate and a 100% college acceptance rate for 17 years, according to Rogers.

Ne'Kiya got a full ride in the pharmacy department at Xavier University in New Orleans. Calcea, the class valedictorian, is studying environmental engineering at Louisiana State University. Neither one is pursuing a career in math, though Calcea said she may minor in math.

"People might expect too much out of me if I become a mathematician," Ne'Kiya said wryly. 

Bill Whitaker is an award-winning journalist and 60 Minutes correspondent who has covered major news stories, domestically and across the globe, for more than four decades with CBS News.

More from CBS News

Reporting on the battle with Hezbollah in Metula, Israel

Veteran faces charges after he says he tried to help North Koreans defect

U.S., Israel "drifting apart," former head of Israeli army intelligence says

Transborder students who crossed from Mexico to U.S. set to graduate

Help | Advanced Search

Mathematics > Optimization and Control

Title: solving maximally comonotone inclusion problems via an implicit newton-like inertial dynamical system and its discretization.

Abstract: This paper deals with an implicit Newton-like inertial dynamical system governed by a maximally comonotone inclusion problem in a Hilbert space. Under suitable conditions, we establish not only pointwise estimates and integral estimates for the velocity and the value of the associated Yosida regularization operator along the trajectory of the system, but also the weak convergence of the trajectory to a zero of the maximally comonotone operator. Moreover, a new inertial algorithm is developed via a time discretization of the proposed system. Our analysis reveals that the resulting discrete algorithm exhibits fast convergence properties matching the ones of the continuous time counterpart. Finally, the theoretical results are illustrated by numerical experiments.

Submission history

Access paper:.

• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

History Daily

New Orleans teens solve 2,000-year-old math problem

Posted: May 11, 2024 | Last updated: May 11, 2024

Some ingenuity

Teacher Michelle Blouin Williams initiated a math competition with a bonus question tasking students to develop a new proof for the Pythagorean theorem using trigonometry, without anticipating that anyone would successfully tackle the challenge.  

She said, “I was just looking for some ingenuity.”   

Williams' expectations

Calcea Johnson and Ne’Kiya Jackson exceeded Williams' expectations by successfully solving the challenge in 2023.   

St. Mary's Academy

These two teenagers, who were seniors at St. Mary's Academy in New Orleans, a renowned Catholic school for girls with impressive college acceptance and graduation rates, were featured on CBS News' "60 Minutes" to discuss their accomplishment.   

$500 reward

Initially enticed by the math competition's $500 reward, their determination to complete the task intensified as they delved into the complex bonus question.   

Over a period of two months, these high school seniors dedicated themselves to completing their proof.  

Pages and pages

During an interview with "60 Minutes," CeCe Johnson, the mother of Calcea, said “It was pages and pages and pages of, like, over 20 or 30 pages for this one problem.”  

The garbage can

Her father, Cal Johnson, added, “Yeah, the garbage can was full of papers, which she would, you know, work out the problems and — if that didn’t work she would ball it up, throw it in the trash.”  

Upon completion

Upon completion, the teachers at St. Mary's Academy acknowledged the significance of Calcea and Ne'Kiya's achievement and submitted their proof to the American Mathematical Society for recognition at a conference in March 2023, where the students presented their findings.  

The Pythagorean theorem

The Pythagorean theorem, at its core, states that knowing the lengths of two sides of a right triangle allows you to determine the length of the third side using the formula a² + b² = c².   

While commonly attributed to the Greek mathematician Pythagoras, historical evidence suggests its existence in Babylon and Iron Age India. This theorem finds practical applications in construction, architecture, navigation, and surveying.  

A mathematical proof

A mathematical proof is a logical argument that demonstrates the truth of a mathematical theorem. American mathematician Daniel Kane likens proofs to essays, but rooted in mathematical concepts.  

Using trigonometry

As per the "60 Minutes" segment, “there had been more than 300 documented proofs of the Pythagorean Theorem using algebra and geometry, but for 2,000 years a proof using trigonometry was thought to be impossible.”  

Mathematician Elisha Loomis

Back in 1927, mathematician Elisha Loomis made a statement in his book "The Pythagorean Proposition." Loomis contended that a trigonometric proof of the theorem was impossible as it would create a circular argument.  

Stuart Anderson

Stuart Anderson, a retired mathematics professor from Texas A&M University-Commerce, mentioned to Scientific American, “A lot of the basic trig ‘identities’ are nothing more than Pythagoras’ theorem.”  

Trigonometric functions

Loomis contended that attempting to use trigonometric functions to prove the Pythagorean theorem would result in a circular reasoning loop, as the functions themselves are built upon the theorem. This, according to Loomis, would constitute a fundamental mathematical mistake.  

The law of sines

As reported by Scientific American, the teenagers challenged this notion during their presentation in 2023 and stated that “a trigonometric identity called the law of sines didn’t depend on the Pythagorean theorem and that they could use it to prove the theorem.”  

Final peer review

Calcea and Ne'Kiya are now part of a select few who have achieved a similar milestone, such as mathematician Jason Zimba, who developed a new proof in 2009. They submitted their proof for the final peer review earlier this year and are actively working on crafting additional proofs.  

In recognition

In recognition of their accomplishment, the teenagers were honored with the keys to the city of New Orleans and received commendations from the governor of Louisiana, along with other public acknowledgments.  

Widespread recognition

Despite the widespread recognition of their accomplishment which “blew up,” as Ne'Kiya expressed it, the two students maintain their humility and even chuckled at being labeled as geniuses.  

Surprised and skeptical

Upon the revelation of their achievement, there were individuals who appeared surprised and skeptical, dismissing the news as untrue, as mentioned by St. Mary's president Pamela Rogers during the interview.  

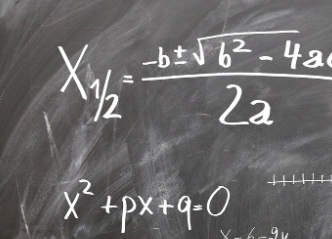
African Americans

“They were saying, ‘Oh, they could not have done it. African Americans don’t have the brains to do it.’ ... People — have a vision of who can be successful. And — to some people, it is not always an African American female. And to us, it’s always an African American female.”  

The significant reaction

When questioned by interviewer Bill Whitaker about their thoughts on the significant reaction, Ne’Kiya said, “Probably because we’re African American, one. And we’re also women. So I think — oh, and our age. Of course our ages probably played a big part.”  

Great mathematical achievement

“I’d like to actually be celebrated for what it is. Like, it’s a great mathematical achievement,” she continued.  

More for You

The dog breed that has attacked the most people, based on data. Plus, see the rest of the top 20.

7 Ways People Destroy the Value of Their Homes, According to a Real Estate Agent

Trump's Wildwood, NJ rally was 'truly stunning': Joe Concha

Only Murders in the Building Star to Return in Season 4 Despite Character's Death

A Photo of Pedro Pascal and Dakota Johnson Kissing Passionately on the Street Has Gone Viral

10 Reasons Hybrids Are Worse Than All-Electric Cars

The food your state is best known for

Millions of Americans are set to lose a popular 401(k) benefit — are you one of them? Here's what it is and what it means for you

Surprising Misconceptions About Early Humans

Hillary Clinton slammed by fellow Democrat for 'dismissive' remarks about anti-Israel protesters

Broncos quarterback Bo Nix is off to a good start at rookie minicamp

10 Natural Ways To Reduce Anxiety

20 Best Sandwiches in America You Need to Try At Least Once

Best Normal Pokémon of All Time Ranked

Russia Suffers Highest Daily Casualties of War So Far: Kyiv

Saying goodbye to "Young Sheldon"

24-year-old earns $50,000 a year living in a town of 121—how she spends her time and money

Top Gun Tech: 5 Incredible Features Inside Modern Fighter Jets

Garfield by Jim Davis

6 Food Dishes That Are Absolute Symbols of Arkansas