solution to brachistochrone problem

Brachistochrone Problem

The brachistochrone problem was one of the earliest problems posed in the calculus of variations . Newton was challenged to solve the problem in 1696, and did so the very next day (Boyer and Merzbach 1991, p. 405). In fact, the solution, which is a segment of a cycloid , was found by Leibniz, L'Hospital, Newton, and the two Bernoullis. Johann Bernoulli solved the problem using the analogous one of considering the path of light refracted by transparent layers of varying density (Mach 1893, Gardner 1984, Courant and Robbins 1996). Actually, Johann Bernoulli had originally found an incorrect proof that the curve is a cycloid, and challenged his brother Jakob to find the required curve. When Jakob correctly did so, Johann tried to substitute the proof for his own (Boyer and Merzbach 1991, p. 417).

In the solution, the bead may actually travel uphill along the cycloid for a distance, but the path is nonetheless faster than a straight line (or any other line).

Plugging this into (◇) together with the identity

The function to be varied is thus

To proceed, one would normally have to apply the full-blown Euler-Lagrange differential equation

Squaring both sides and rearranging slightly results in

which are--lo and behold--the equations of a cycloid .

If kinetic friction is included, the problem can also be solved analytically, although the solution is significantly messier. In that case, terms corresponding to the normal component of weight and the normal component of the acceleration (present because of path curvature ) must be included. Including both terms requires a constrained variational technique (Ashby et al. 1975), but including the normal component of weight only gives an approximate solution. The tangent and normal vectors are

gravity and friction are then

and the components along the curve are

so Newton's Second Law gives

Using the Euler-Lagrange differential equation gives

This can be reduced to

Now letting

the solution is

Explore with Wolfram|Alpha

More things to try:

• continued fraction sqrt(1+x^2)
• Legendre P(10,x)

Referenced on Wolfram|Alpha

Cite this as:.

Weisstein, Eric W. "Brachistochrone Problem." From MathWorld --A Wolfram Web Resource. https://mathworld.wolfram.com/BrachistochroneProblem.html

Subject classifications

 MacTutor

The brachistochrone problem.

I, Johann Bernoulli , address the most brilliant mathematicians in the world. Nothing is more attractive to intelligent people than an honest, challenging problem, whose possible solution will bestow fame and remain as a lasting monument. Following the example set by Pascal , Fermat , etc., I hope to gain the gratitude of the whole scientific community by placing before the finest mathematicians of our time a problem which will test their methods and the strength of their intellect. If someone communicates to me the solution of the proposed problem, I shall publicly declare him worthy of praise.

Given two points A and B in a vertical plane, what is the curve traced out by a point acted on only by gravity, which starts at A and reaches B in the shortest time.

...there are fewer who are likely to solve our excellent problems, aye, fewer even among the very mathematicians who boast that [ they ] ... have wonderfully extended its bounds by means of the golden theorems which ( they thought ) were known to no one, but which in fact had long previously been published by others.

... in the midst of the hurry of the great recoinage, did not come home till four ( in the afternoon ) from the Tower very much tired, but did not sleep till he had solved it, which was by four in the morning.

I do not love to be dunned [ pestered ] and teased by foreigners about mathematical things ...

Problem . It is required to find the curve ADB in which a weight, by the force of its gravity, shall descend most swiftly from any given point A to any given point B. Solution . From the given point A let there be drawn an unlimited straight line APCZ parallel to the horizontal, and on it let there be described an arbitrary cycloid AQP meeting the straight line AB ( assumed drawn and produced if necessary ) in the point Q, and further a second cycloid ADC whose base and height are to the base and height of the former as AB is to AQ respectively. This last cycloid will pass through the point B, and it will be that curve along which a weight, by the force of its gravity, shall descend most swiftly from the point A to the point B.

... my elder brother made up the fourth of these, that the three great nations, Germany, England, France, each one of their own to unite with myself in such a beautiful search, all finding the same truth.

Before I end I must voice once more the admiration I feel for the unexpected identity of Huygens ' tautochrone and my brachistochrone. I consider it especially remarkable that this coincidence can take place only under the hypothesis of Galileo , so that we even obtain from this a proof of its correctness. Nature always tends to act in the simplest way, and so it here lets one curve serve two different functions, while under any other hypothesis we should need two curves ...

Given a starting point and a vertical line, of all the cycloids from the starting point with the same horizontal base, which will allow the point subjected only to uniform gravity, to reach the vertical line most quickly.

The first problem of this type [ calculus of variations ] which mathematicians solved was that of the brachistochrone, or the curve of fastest descent, which Johann Bernoulli proposed towards the end of the last century. The solution was found by considering special cases, and it was only some time later, in research isoperimetric curves, that the great mathematician of whom we speak and his famous brother Jacob Bernoulli gave some general rules for solving several other problems of the same type. Since, however, the rules were not sufficiently general, the famous Euler undertook the task of reducing all such investigations to a general method which he gave in the work "Essay on a new method of determining the maxima and minima of indefinite integral formulas"; an original work in which the profound science of the calculus shines through. Even so, while the method is ingenious and rich, one must admit that it is not as simple as one might hope in a work of pure analysis ....

... a method which only requires a straightforward use of the principles if the differential and integral calculus; but I must strongly emphasise that since my method requires that a quantity be allowed to vary in two different ways, so as not to confuse these different variations, I have introduced a new symbol δ into my calculations. In this way δz expresses a difference of z which is different from dz, but which, however, will satisfy the same rules; such that where we have for any equation dz = m dx, we can equally have δz = mδx, and likewise in other cases.

References ( show )

• P Costabel and J Peiffer ( eds. ) , Bernoulli, Johann I Der Briefwechsel von Johann I Bernoulli. Band 2 : Der Briefwechsel mit Pierre Varignon : Erster Teil : 1692 - 1702 , Die Gesammelten Werke der Mathematiker und Physiker der Familie Bernoulli ( Basel, 1988) .
• M de Icaza Herrera, Galileo, Bernoulli, Leibniz and Newton around the brachistochrone problem, Rev. Mexicana Fis. 40 (3) (1994) , 459 - 475 .
• P Dietz, Die Ursprünge der Variationsrechnung bei Jakob Bernoulli, Verh. Naturf. Ges. Basel 70 (1959) , 81 - 146 .
• H Erlichson, Johann Bernoulli's brachistochrone solution using Fermat's principle of least time, European J. Phys. 20 (5) (1999) , 299 - 304 .
• T Koetsier, The story of the creation of the calculus of variations : the contributions of Jakob Bernoulli, Johann Bernoulli and Leonhard Euler ( Dutch ) , in 1985 holiday course : calculus of variations ( Amsterdam, 1985) , 1 - 25 .
• K Pedersen and K M Pedersen, The early history of the calculus of variations ( Danish ) , Nordisk Mat. Tidskr. 19 (1971) , 61 - 74 ; 108 .
• J Peiffer, Le problème de la brachystochrone à travers les relations de Jean I Bernoulli avec L'Hôpital et Varignon, in Der Ausbau des Calculus durch Leibniz und die Brüder Bernoulli, Basel, 1987 , Studia Leibnitiana Sonderheft 17 ( Wiesbaden, 1989) .
• B Singh and R Kumar, Brachistochrone problem in nonuniform gravity, Indian J. Pure Appl. Math. 19 (6) (1988) , 575 - 585 .
• G J Tee, Isochrones and brachistochrones, Neural Parallel Sci. Comput. 7 (3) (1999) , 311 - 341 .
• R Thiele, Das Zerwürfnis Johann Bernoullis mit seinem Bruder Jakob, Natur, Mathematik und Geschichte, Acta Hist. Leopold. No. 27 (1997) , 257 - 276 .
• G Wanner, Les équations différentielles ont 350 ans, Enseign. Math. (2) 34 (3 - 4) (1988) , 365 - 385 .
• F Williamson, Jr., An historical note on the finite element method, Internat. J. Numer. Methods Engrg. 15 (6) (1980) , 930 - 934 .

Additional Resources ( show )

Other pages about Brachistochrone problem:

• The cycloid

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

2.12: The Brachistochrone

• Last updated
• Save as PDF
• Page ID 29952

• Michael Fowler
• University of Virginia

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Suppose you have two points, A and B, B is below A, but not directly below. You have some smooth, let’s say frictionless, wire, and a bead that slides on the wire. The problem is to curve the wire from A down to B in such a way that the bead makes the trip as quickly as possible.

This optimal curve is called the “brachistochrone”, which is just the Greek for “shortest time”.

But what, exactly, is this curve, that is, what is \(\begin{equation} y(x) \end{equation}\) in the obvious notation?

This was the challenge problem posed by Johann Bernoulli to the mathematicians of Europe in a Journal run by Leibniz in June 1696. Isaac Newton was working fulltime running the Royal Mint, recoining England, and hanging counterfeiters. Nevertheless, ending a full day’s work at 4 pm, and finding the problem delivered to him, he solved it by 4am the next morning, and sent the solution anonymously to Bernoulli. Bernoulli remarked of the anonymous solution “I recognize the lion by his clawmark”.

This was the beginning of the Calculus of Variations.

Here’s how to solve the problem: we’ll take the starting point A to be the origin, and for convenience measure the y -axis positive downwards . This means the velocity at any point on the path is given by

\begin{equation} \dfrac{1}{2} m v^{2}=m g y, \quad v=\sqrt{2 g y} \end{equation}

So measuring length along the path as \(ds\) as usual, the time is given by

\begin{equation} T=\int_{A}^{B} \dfrac{d s}{v}=\int_{A}^{B} \dfrac{d s}{\sqrt{2 g y}}=\int_{0}^{X} \dfrac{\sqrt{1+y^{\prime 2}} d x}{\sqrt{2 g y}} \end{equation}

Notice that this has the same form as the catenary equation, the only difference being that \(y\) is replaced by \(\begin{equation} 1 / \sqrt{2 g y} \end{equation}\) the integrand does not depend on \(x\), so we have the first integral:

\begin{equation} y^{\prime} \dfrac{\partial f}{\partial y^{\prime}}-f=\text { constant }, \quad f=\sqrt{\dfrac{1+y^{\prime 2}}{2 g y}} \end{equation}

\begin{equation} \dfrac{y^{\prime 2}}{\sqrt{\left(1+y^{\prime 2}\right) 2 g y}}-\sqrt{\dfrac{1+y^{\prime 2}}{2 g y}}=-\dfrac{1}{\sqrt{\left(1+y^{\prime 2}\right) 2 g y}}=\text { constant } \end{equation}

\begin{equation} \left(\dfrac{d y}{d x}\right)^{2}+1=\dfrac{2 a}{y} \end{equation}

\(2a\) being a constant of integration (the 2 proves convenient).

Recalling that the curve starts at the origin A, it must begin by going vertically downward, since \(\begin{equation} y=0 \end{equation}\). For small enough \(y\), we can approximate by ignoring the 1, so \(\begin{equation} \sqrt{2 a} d x \cong \sqrt{y} d y, \sqrt{2 a} x \cong 2 /{ }_{3} y^{3 / 2} \end{equation}\). The curve must however become horizontal if it gets as far down as \(\begin{equation} y=2 a \end{equation}\), and it cannot go below that level.

Rearranging in order to integrate,

\begin{equation} d x=\dfrac{d y}{\sqrt{\dfrac{2 a}{y}-1}}=\sqrt{\dfrac{y}{2 a-y}} d y \end{equation}

This is not a very appealing integrand. It looks a little nicer on writing \(\begin{equation} y=a-a z \end{equation}\)

\begin{equation} d x=-a \sqrt{\dfrac{1-z}{1+z}} d z \end{equation}

Now what? We’d prefer for the expression inside the square root to be a perfect square, of course. You may remember from high school trig that \(\begin{equation} 1+\cos \theta=2 \cos ^{2}(\theta / 2), \quad 1-\cos \theta=2 \sin ^{2}(\theta / 2) \end{equation}\). This gives immediately that

\begin{equation} \dfrac{1-\cos \theta}{1+\cos \theta}=\tan ^{2} \dfrac{\theta}{2} \end{equation}

so the substitution \(\begin{equation} z=\cos \theta \end{equation}\) is what we need.

Then \(\begin{equation} d z=-\sin \theta d \theta=-2 \sin (\theta / 2) \cos (\theta / 2) d \theta \end{equation}\)

\begin{equation} d x=-a \tan \dfrac{\theta}{2} d z=2 a \tan \dfrac{\theta}{2} \sin \dfrac{\theta}{2} \cos \dfrac{\theta}{2} d \theta=2 a \sin ^{2} \dfrac{\theta}{2} d \theta=a(1-\cos \theta) d \theta \end{equation}

This integrates to give

\begin{equation} \begin{array}{l} x=a(\theta-\sin \theta) \\ y=a(1-\cos \theta) \end{array} \end{equation}

where we’ve fixed the constant of integration so that the curve goes through the origin \(\begin{equation} (\text { at } \theta=0) \end{equation}\)

To see what this curve looks like, first ignore the \(\theta\) terms in \(x\), leaving \(\begin{equation} x=-a \sin \theta, y=-a \cos \theta \end{equation}\). Evidently as \(\theta\) increases from zero, the point \(\begin{equation} (x, y) \end{equation}\) goes anticlockwise around a circle of radius \(a\) centered at \(\begin{equation} (0,-a) \end{equation}\) that is, touching the x -axis at the origin.

Now adding the \(\theta\) back in, this circular motion move steadily to the right, in such a way that the initial direction of the path is vertically down. \(\begin{equation} \text { (For very small } \left.\theta, y \sim \theta^{2} \gg x \sim \theta^{3}\right) \end{equation}\)

Visualizing the total motion as \(\theta\) steadily increases, the center moves from its original position at \(\begin{equation} (0,-a) \end{equation}\) to the right at a speed \(a\theta\). Meanwhile, the point is moving round the circle anticlockwise at this same speed. Putting together the center’s linear velocity with the corresponding angular velocity, we see the motion \(\begin{equation} (x(\theta), y(\theta)) \end{equation}\) is the path of a point on the rim of a wheel rolling without sliding along a road (upside down in our case, of course). This is a cycloid .

• This Website
• Chapter 1: Introduction
• Additional Problems
• Additional Examples
• Additional Notes

The Brachistochrone problem

Posted by: christian on 30 mar 2017.

( 6 comments )

The Brachistochrone problem asks the question "what is the shape of the curve down which a bead sliding from rest and accelerated by gravity will slip, without friction, from one fixed point, $P_1$ to another $P_2$ in the least time?"

Its solution is well-known and given in various forms in many places on the internet, but is given in outline at the bottom of this post.

Paths between $P_1 = (0,0)$ and $P_2 = (1, 0.65)$:

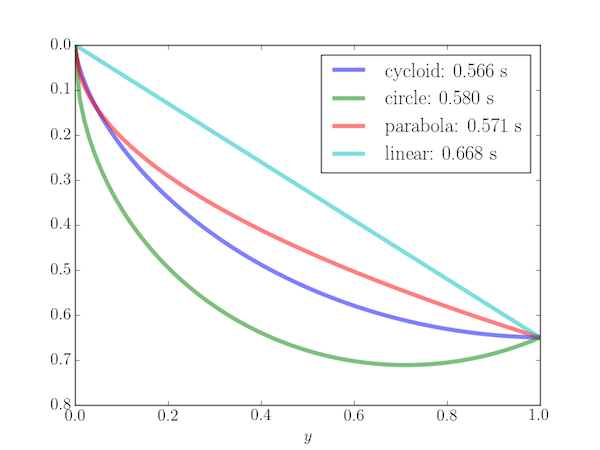
Note that the path giving the shortest time (the cycloid) is not the shortest distance between the points and may have a minimum ( i.e. the bead slides down and then up before reaching $P_2$, as shown by the following example for $P_2 = (1, 0.3)$.

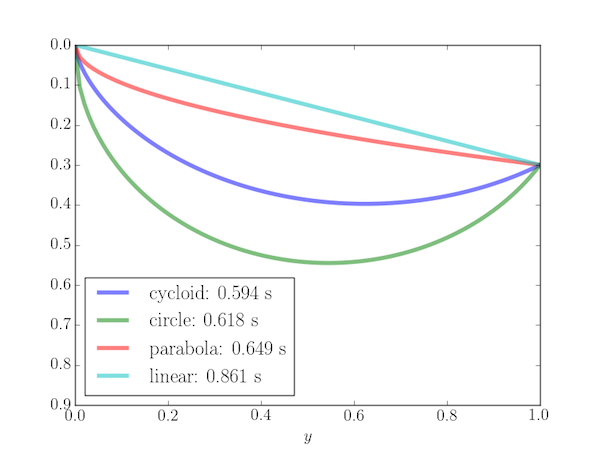
The following Python program plots the Brachistochrone curve (an arc of a cycloid) and calculates the time of travel. It is also compared with three other paths: (i) a straight line, (ii) a circular path with a vertical tangent at $P_1$ and (iii) a parabola with vertical tangent at $P_1$.

Appendix A: Solution the the Brachistochrone problem

We choose $P_1 = (0,0)$ and set $P_2 = (x_2, y_2)$, with the $y-$axis pointing in the same direction as the acceleration due to gravity, $\boldsymbol{g}$. Then we seek to minimize $$ T = \int_{P_1}^{P_2}\frac{\mathrm{d}s}{v}, $$ where the arc length element along the curve we seek is $\mathrm{d}s = \sqrt{\mathrm{d}x^2 + \mathrm{d}y^2}$ and the speed along the curve, $v$ satisfies $\frac{1}{2}mv^2 = mgy$ by conservation of energy. Then the functional to be minimized is $$ T = \int_{P_1}^{P_2}\sqrt{\frac{1+y'^2}{2gy}}\,\mathrm{d}x, $$ where $y' = \mathrm{d}y/\mathrm{d}x$. The function to be varied in this minimization, $$ F(x,y,y') = \sqrt{\frac{1+y'^2}{2gy}} $$ does not explicitly depend on $x$ so the Beltrami identity applies: $$ F - y'\frac{\partial F}{\partial y'} = C = \mathrm{constant}. $$ Now, $$ \frac{\partial F}{\partial y'} = \frac{y'}{\sqrt{2gy}\sqrt{1+y'^2}} $$ and substitution into the Beltrami identity gives $$ y(1+y'^2) = \frac{1}{2gC^2} = 2R. $$ This differential equation has a parametric solution in the form of a cycloid : \begin{align*} x(\theta) &= R(\theta - \sin\theta),\\ y(\theta) &= R(1 - \cos\theta). \end{align*} The parameter $\theta$ varies from $0$ at $P_1 = (0,0)$ to $\theta_2$ at $P_2 = (x_2, y_2)$ which may be found numerically as the solution to $$ \frac{y_2}{x_2} = \frac{1-\cos\theta_2}{\theta_2 - \sin\theta_2} $$ Substitution back into the second parametric equation then gives $$ R = \frac{y_2}{1-\cos\theta_2}. $$

Appendix B: Paths and times for other curves

Straight line.

The straight line between $P_1 = (0,0)$ and $P_2 = (x_2,y_2)$ has the equation $y = mx$ with $m=y_2/x_2$. The time taken is $$ T = \int_{P_1}^{P_2}\sqrt{\frac{1+y'^2}{2gy}}\,\mathrm{d}x = \int_0^{x_2} \sqrt{\frac{1+m^2}{2gmx}}\,\mathrm{d}x = \sqrt{\frac{(1+m^2)x_2}{gm}}. $$

Circular arc

The circle through $P_1 = (0,0)$ and $P_2 = (x_2,y_2)$ with vertical tangent at $P_1$ has the formula $y^2 = r^2 - (x-r)^2$ with radius $$ r = \frac{x_2^2 + y_2^2}{2x_2}. $$ The integral giving $T$ may be evaluated numerically using $y = \sqrt{2xr-x^2}$ and $y' = (r-x)/y$.

Parabolic arc

The parabola through $P_1 = (0,0)$ and $P_2 = (x_2,y_2)$ with vertical tangent at $P_1$ has the formula $y = \sqrt{cx}$ with $c = (y_2/x_2)^2$. The integral giving $T$ may be evaluated numerically using this and $y' = c/(2y)$.

• ← Solving word wheels
• Making word wheels →

Comments are pre-moderated. Please be patient and your comment will appear soon.

Matt 5 years, 10 months ago

Wonderful. Thanks for sharing this. I'm very happy to have found your website. If y2 > x2 is a brachistochrone still a tautochrone as Vsauce says here, https://youtu.be/skvnj67YGmw?t=1090 ? Keep up the good work!

required (not published)

christian 5 years, 10 months ago

I'm glad you enjoyed it. As far as I know, a brachistochrone is still a tautocrone for y2 > x2. Wikipedia has some proofs here: https://en.wikipedia.org/wiki/Tautochrone_curve and taking e.g. Abel's solution, I don't see why this condition should invalidate the proof.

Thanks for the reply. It occurred to me that when y2 >> x2 say, y2 = 1 and x2 = 0.01, the curve approaches a vertical drop. And a vertical drop is not a tautochrone: objects dropped from different heights reach the ground (end point) at different times. However, a not-quite-a-vertical-drop could still be described by the equation to a brachistochrone (one with a large cycloid radius), but presumably not fulfill the definition of a tautochrone. I'm curious to know the parameters whereby the brachistochrone ceases to be a tautochrone. Trying to do this with Python, I hit a wall about here, x2, y2 = 0.26173,1 ...where slightly smaller values for x2 give, scipy\optimize\zeros.py:173: RuntimeWarning: Tolerance of 4.76539196989e+27 reached In my web-search for an answer, this excellent post appears to completely contradict my earlier statement, “So it is easy to break the Brachistochrone condition while keeping the isochrone [tautochrone] condition satisfied.” - https://physics.stackexchange.com/questions/16819/is-there-an-intuitive-reason-the-brachistochrone-and-the-tautochrone-are-the-sam Do you think the brachistochrone is a general solution to the tautochrone or vice versa or are they perhaps mutually exclusive under certain circumstances?

christian 5 years, 9 months ago

I think the brachistochrone has to include the cusp of the cycloid (where the acceleration is greatest) and the tautochrone must end at its minimum. There's more on this here: https://math.stackexchange.com/a/2853385/126411

Anathnath Ghosh 3 years, 5 months ago

Fantastic works. hats off to you sir

Joaquín Herreros 2 years, 7 months ago

I have been playing with this curves for unitary radius (for aplying it to skateboard slides), and I have found a pretty good cartesian approximation (0<x<pi/2): y(x) = cos^2(sqrt(5/2)+pi^2/2*{[log(2)]^(1/8)-[log(pi/x)]^(1/8)}) Is not too complicated and its fits very well. I hope it helps you too. Best regards.

New Comment

• WolframAlpha.com
• WolframCloud.com
• All Sites & Public Resources...

• Wolfram|One
• Mathematica
• Wolfram|Alpha Notebook Edition
• Finance Platform
• System Modeler
• Wolfram Player
• Wolfram Engine
• WolframScript
• Enterprise Private Cloud
• Application Server
• Enterprise Mathematica
• Wolfram|Alpha Appliance
• Corporate Consulting
• Technical Consulting
• Wolfram|Alpha Business Solutions
• Data Repository
• Neural Net Repository
• Function Repository
• Wolfram|Alpha Pro
• Problem Generator
• Products for Education
• Wolfram Cloud App
• Wolfram|Alpha for Mobile
• Wolfram|Alpha-Powered Apps
• Paid Project Support
• Summer Programs
• All Products & Services »
• Wolfram Language Revolutionary knowledge-based programming language. Wolfram Cloud Central infrastructure for Wolfram's cloud products & services. Wolfram Science Technology-enabling science of the computational universe. Wolfram Notebooks The preeminent environment for any technical workflows. Wolfram Engine Software engine implementing the Wolfram Language. Wolfram Natural Language Understanding System Knowledge-based broadly deployed natural language. Wolfram Data Framework Semantic framework for real-world data. Wolfram Universal Deployment System Instant deployment across cloud, desktop, mobile, and more. Wolfram Knowledgebase Curated computable knowledge powering Wolfram|Alpha.
• All Technologies »
• Aerospace & Defense
• Chemical Engineering
• Control Systems
• Electrical Engineering
• Image Processing
• Industrial Engineering
• Mechanical Engineering
• Operations Research
• Actuarial Sciences
• Bioinformatics
• Data Science
• Econometrics
• Financial Risk Management
• All Solutions for Education
• Machine Learning
• Multiparadigm Data Science
• High-Performance Computing
• Quantum Computation Framework
• Software Development
• Authoring & Publishing
• Interface Development
• Web Development
• All Solutions »
• Wolfram Language Documentation
• Fast Introduction for Programmers
• Videos & Screencasts
• Wolfram Language Introductory Book
• Webinars & Training
• Support FAQ
• Wolfram Community
• Contact Support
• All Learning & Support »
• Company Background
• Wolfram Blog
• Careers at Wolfram
• Internships
• Other Wolfram Language Jobs
• Wolfram Foundation
• Computer-Based Math
• A New Kind of Science
• Wolfram Technology for Hackathons
• Student Ambassador Program
• Wolfram for Startups
• Demonstrations Project
• Wolfram Innovator Awards
• Wolfram + Raspberry Pi
• All Company »

• Wolfram|Alpha Notebook Edition
• Mobile Apps
• Wolfram Workbench
• Volume & Site Licensing
• View all...
• For Customers
• Online Store
• Product Registration
• Product Downloads
• Service Plans Benefits
• User Portal
• Your Account
• Customer Service
• Get Started with Wolfram
• Fast Introduction for Math Students
• Public Resources
• Wolfram|Alpha
• Resource System
• Connected Devices Project
• Wolfram Data Drop
• Wolfram Science
• Computational Thinking
• Announcements
• About Wolfram
• Legal & Privacy Policy