solve geometric problems with angles and triangles

Solving Triangles

"Solving" means finding missing sides and angles.

Six Different Types

If you need to solve a triangle right now choose one of the six options below:

Which Sides or Angles do you know already? (Click on the image or link)

... or read on to find out how you can become an expert triangle solver :

Your Solving Toolbox

Want to learn to solve triangles?

Imagine you are " The Solver " ... ... the one they ask for when a triangle needs solving!

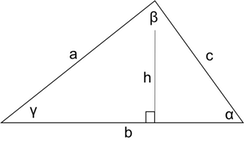
In your solving toolbox (along with your pen, paper and calculator) you have these 3 equations:

1. Angles Add to 180° :

A + B + C = 180°

When you know two angles you can find the third.

2. Law of Sines (the Sine Rule):

When there is an angle opposite a side, this equation comes to the rescue.

Note: angle A is opposite side a, B is opposite b, and C is opposite c.

3. Law of Cosines (the Cosine Rule):

This is the hardest to use (and remember) but it is sometimes needed to get you out of difficult situations.

It is an enhanced version of the Pythagoras Theorem that works on any triangle.

Six Different Types (More Detail)

There are SIX different types of puzzles you may need to solve. Get familiar with them:

This means we are given all three angles of a triangle, but no sides.

AAA triangles are impossible to solve further since there are is nothing to show us size ... we know the shape but not how big it is.

We need to know at least one side to go further. See Solving "AAA" Triangles .

This mean we are given two angles of a triangle and one side, which is not the side adjacent to the two given angles.

Such a triangle can be solved by using Angles of a Triangle to find the other angle, and The Law of Sines to find each of the other two sides. See Solving "AAS" Triangles .

This means we are given two angles of a triangle and one side, which is the side adjacent to the two given angles.

In this case we find the third angle by using Angles of a Triangle , then use The Law of Sines to find each of the other two sides. See Solving "ASA" Triangles .

This means we are given two sides and the included angle.

For this type of triangle, we must use The Law of Cosines first to calculate the third side of the triangle; then we can use The Law of Sines to find one of the other two angles, and finally use Angles of a Triangle to find the last angle. See Solving "SAS" Triangles .

This means we are given two sides and one angle that is not the included angle.

In this case, use The Law of Sines first to find either one of the other two angles, then use Angles of a Triangle to find the third angle, then The Law of Sines again to find the final side. See Solving "SSA" Triangles .

This means we are given all three sides of a triangle, but no angles.

In this case, we have no choice. We must use The Law of Cosines first to find any one of the three angles, then we can use The Law of Sines (or use The Law of Cosines again) to find a second angle, and finally Angles of a Triangle to find the third angle. See Solving "SSS" Triangles .

Tips to Solving

Here is some simple advice:

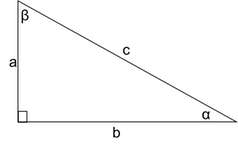
When the triangle has a right angle, then use it, that is usually much simpler.

When two angles are known, work out the third using Angles of a Triangle Add to 180° .

Try The Law of Sines before the The Law of Cosines as it is easier to use.

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Straight angle

Angles in polygons

Angles of a triangle

Here you will learn about angles of a triangle including what the sum of both interior and exterior angles of a triangle are, how to find missing angles, and how to use this alongside other angle facts to form and solve equations.

Students will first learn about angles of a triangle as a part of geometry in 8 th grade and will extend their knowledge throughout high school geometry.

What are angles of a triangle?

Angles of a triangle refer to the sum of the angles of a triangle, found at each vertex in a triangle.

A triangle has both interior angles and exterior angles.

Interior angles of a triangle

Interior angles of a triangle are angles that are formed inside a triangle by its three sides. Each interior angle is formed by two adjacent sides of the triangle.

The sum of the interior angles of a triangle is \bf{180}^{\circ}.

For example,

Exterior angles of a triangle

The exterior angles of a triangle are angles that are formed on the outside of the triangle when its sides are extended.

The sum of exterior angles of a triangle is \bf360^{\circ}.

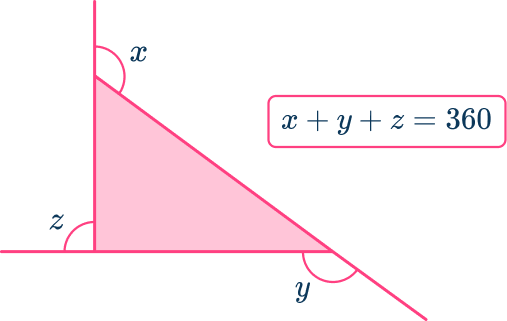
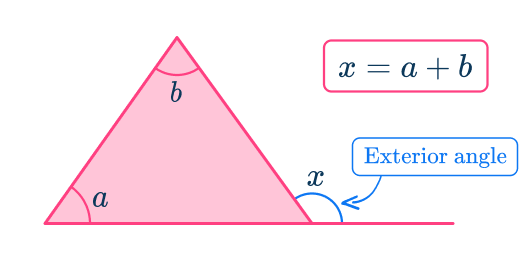
The exterior angle is also equal to the sum of the two opposite interior angles. Each exterior angle is supplementary to its adjacent interior angle.

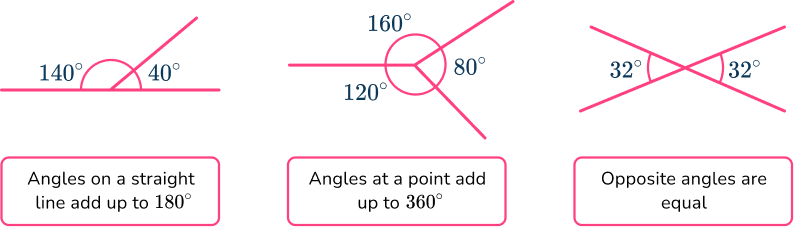
Other angle facts

Sometimes the problem will involve using other angle facts. Let’s recap some of the other important angle facts:

Common Core State Standards

How does this relate to 8 th grade math and high school math?

• Grade 8: Geometry (8.G.A.5) Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles. For example, arrange three copies of the same triangle so that the sum of the three angles appears to form a line, and give an argument in terms of transversals why this is so.
• High school: Geometry (HS.G.CO.C.10) Prove theorems about triangles. Theorems include: measures of interior angles of a triangle sum to 180^{\circ}; base angles of isosceles triangles are congruent; the segment joining midpoints of two sides of a triangle is parallel to the third side and half the length; the medians of a triangle meet at a point.

[FREE] Angles Worksheet (Grade 4)

Use this quiz to check your grade 4 students’ understanding of angles. 10+ questions with answers covering a range of 4th grade angles topics to identify areas of strength and support!

How to find a missing angle of a triangle

In order to find the measure of a missing angle of a triangle:

Add up the angles that are given within the triangle.

Subtract this total from \bf{180}^{\circ}.

Angles of a triangle examples

Example 1: scalene triangle.

Find the measure of the unknown angle labeled a in the following triangle:

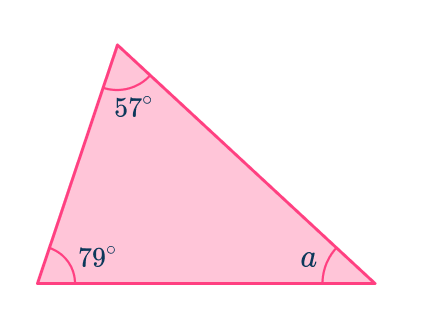
The angles 57^{\circ} and 79^{\circ} are given. Add these together:

2 Subtract this total from \bf{180}^{\circ}.

Subtract 136^{\circ} from 180^{\circ} \text{:}

Example 2: right triangle

Find the measure of the unknown angle labeled b in the following triangle:

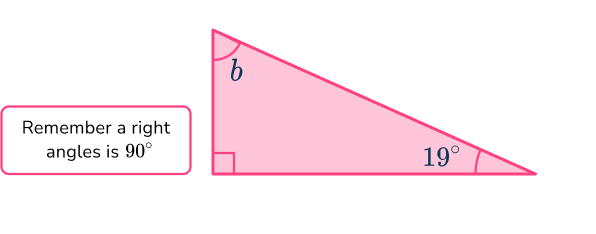
The angles 90^{\circ} and 19^{\circ} are given. Add these together:

90+19=109^{\circ}

Subtract 109^{\circ} from 180^{\circ} \text{:}

\begin{aligned}& 180-109=71^{\circ} \\\\ & b=71^{\circ}\end{aligned}

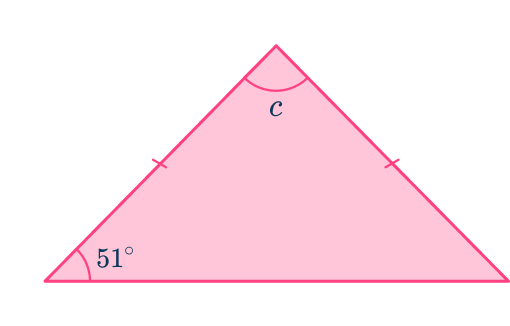
Example 3: isosceles triangle

Find the measure of the unknown angle labeled c in the following triangle:

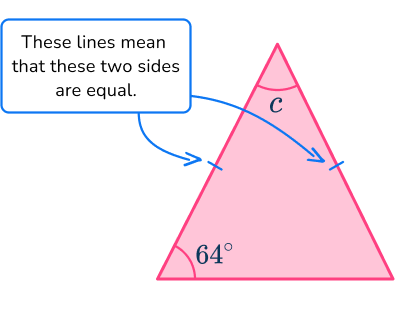
When two sides of a triangle are equal, the angles at the ends of those sides will also be equal.

The angle 64^{\circ} is given. This is an isosceles triangle (two equal length sides and two equal angles), so the other angle at the bottom will also be 64^{\circ}.

64+64=128^{\circ}

Subtract 128^{\circ} from 180^{\circ} \text{:}

\begin{aligned}& 180-128=52^{\circ} \\\\ & c=52^{\circ}\end{aligned}

How to find a missing angle of a triangle using other angle facts

In order to find the missing angle of a triangle using other angle facts:

Use angle facts to identify all possible angles.

Calculate the missing angles in the triangle.

Example 4: using angles at a point

Find the measure of the angle labeled e \text{:}

Angles at a point add up to 360^{\circ}, so you can subtract the known exterior angle from 360^{\circ}.

360-310=50^{\circ}

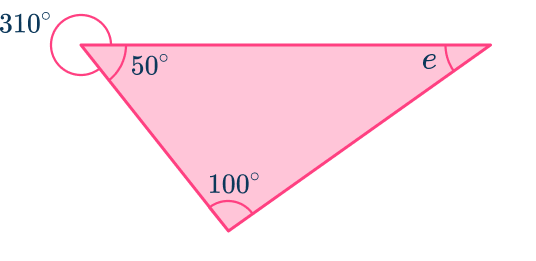
With the measure of two angles within the triangle, you can find the missing angle:

\begin{aligned}& 100+50=150 \\\\ & 180-150=30^{\circ} \\\\ & e=30^{\circ}\end{aligned}

Example 5: using opposite angles

Find the measure of the angle labeled f \text{:}

You are given two of the angles in the triangle, so start by finding the third angle:

\begin{aligned}& 90+61=151 \\\\ & 180-151=29^{\circ}\end{aligned}

Use the fact that opposite angles are equal to find f.

f=29^{\circ}

Example 6: two different triangles

Find the measure of the angle labeled g \text{:}

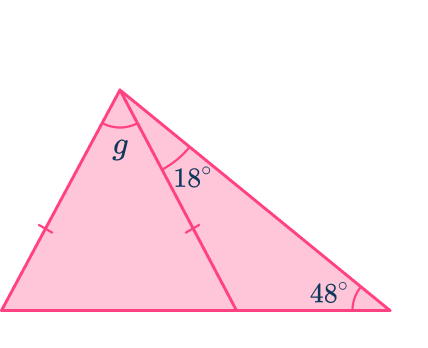
You know two of the angles in the triangle on the right, so now calculate the third.

\begin{aligned}& 48+18=66 \\\\ & 180-66=114^{\circ}\end{aligned}

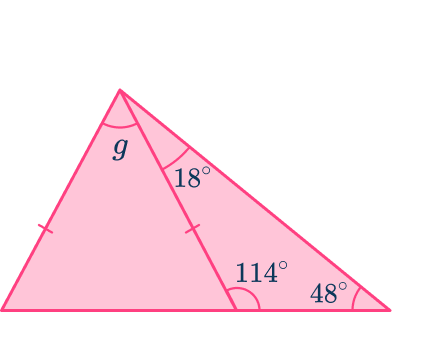
You can use the fact that angles on a straight line add up to 180^{\circ}.

180-114=66^{\circ}

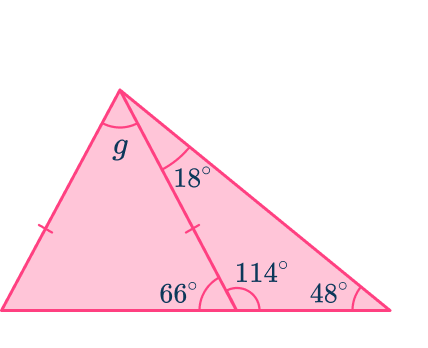
Since the sides of the triangle are equal, the triangle on the left is an isosceles triangle and the two angles at the bottom of the triangle are equal. Therefore you can find the third angle.

Teaching tips for angles of a triangle

• Visual aids, such as diagrams, and hands-on activities allow students to explore the properties of triangles in a different way.
• Allow students to work in pairs or small groups while working through practice problems on worksheets. This encourages discussions about math between peers, which allows for students to share their personal insights and strategies used.
• Provide real-time feedback to students as they are working through practice problems to clarify any misunderstandings as they arise. The use of a triangle calculator can support this, without having to take any additional time from you.

Easy mistakes to make

• Mixing up the sum of interior angles and exterior angles Students may use 360^{\circ} instead of 180^{\circ} for the sum of the interior angles of the triangle and vice versa.

Related angles in polygons lessons

• Interior and exterior angles of polygons
• Quadrilateral angles
• Interior angles of a polygon
• Sum of exterior angles of a polygon
• Angles of a hexagon

Angles in a triangle practice questions

1. Find the measure of the angle b in the following triangle:

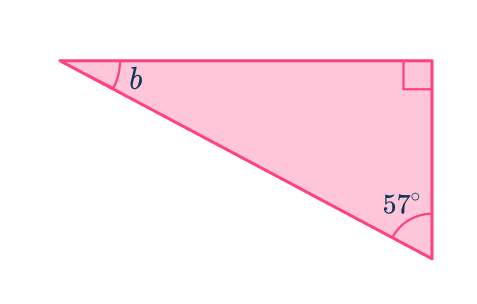
2. Find the measure of the angle c \text{:}

This is an isosceles triangle and the two angles at the bottom of the triangle are equal.

3. Find the measure of angle x in the following triangle:

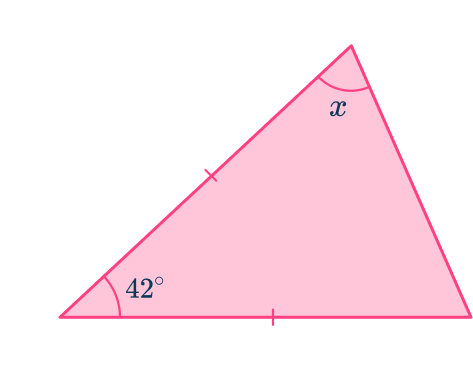
This is an isosceles triangle and the two angles on the right are equal.

4. What is the size of each angle in an equilateral triangle?

An equilateral triangle has three equal sides so

5. Find the measure of the angle labeled w in the following triangle:

The angle opposite 24^{\circ} is also 24^{\circ} since vertically opposite angles are equal. The triangle is an isosceles triangle and the two angles on the left are the same size.

6. Find the measure of the angle labeled v \text{:}

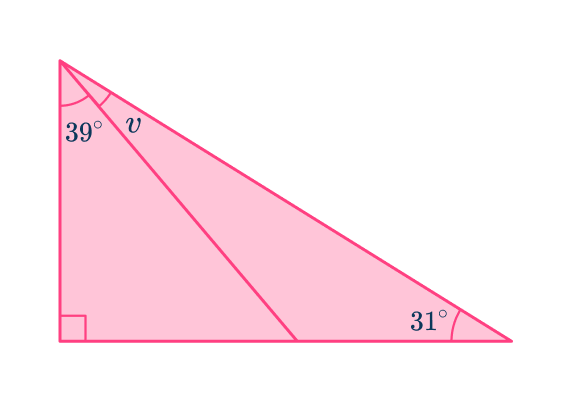
Let’s find the missing angle in the triangle on the left first,

Then use the fact that angles on a straight line add up to 180^{\circ} to find the unlabeled angle in the right hand triangle.

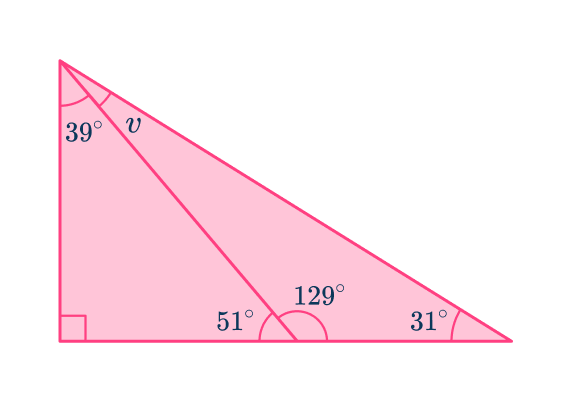
Now, find angle v \text{:}

Angles of a triangle FAQs

No, the interior angles within a triangle can vary depending on the triangle. However, all of the measures of angles within a triangle will always equal 180 degrees.

Each exterior angle of a triangle is supplementary to its adjacent interior angle. The sum of each exterior angle and its adjacent interior angle will equal 180 degrees.

The Law of Sines is a principle in trigonometry that relates the side lengths of a triangle to the sines of its angles. It states that in any triangle, the ration of the length of a side to the sine of its opposite angle is constant for all three sides. It can be expressed as: \cfrac{a}{\sin (A)}=\cfrac{b}{\sin (B)}=\cfrac{c}{\sin (C)}.

The next lessons are

• Congruence and similarity
• Transformations
• Mathematical proofs
• Trigonometry

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (Grades 3 to 6)

Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.

40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!

Triangles Calculator

Calculate area, perimeter, sides and angles for triangles step-by-step.

• Basic (Linear)
• Biquadratic
• Logarithmic
• Exponential
• Solve For x
• Scientific Calculator
• Scientific Notation Arithmetics
• Complex Numbers
• Cartesian to Polar
• Polar to Cartesian
• System of Inequalities
• Partial Fractions
• Periodicity
• Y Intercept
• X Intercepts
• Point Slope Form
• Step Functions
• Arithmetics
• Start Point
• Area & Perimeter
• Sides & Angles

Law of Sines

Law of cosines.

• Width & Length
• Volume & Surface
• Edges & Diagonal
• Volume & Radius
• Surface Area
• Radius & Diameter
• Volume & Height
• Circumference
• Eccentricity
• Trigonometric Equations
• Evaluate Functions

Equilateral

Isosceles Triangle

Right Angled

triangles-calculator

Related Symbolab blog posts

Please add a message.

Message received. Thanks for the feedback.

3.4 Solve Geometry Applications: Triangles, Rectangles, and the Pythagorean Theorem

Learning objectives.

By the end of this section, you will be able to:

• Solve applications using properties of triangles

Use the Pythagorean Theorem

• Solve applications using rectangle properties

Be Prepared 3.12

Before you get started, take this readiness quiz.

Simplify: 1 2 ( 6 h ) . 1 2 ( 6 h ) . If you missed this problem, review Example 1.122 .

Be Prepared 3.13

The length of a rectangle is three less than the width. Let w represent the width. Write an expression for the length of the rectangle. If you missed this problem, review Example 1.26 .

Be Prepared 3.14

Solve: A = 1 2 b h A = 1 2 b h for b when A = 260 A = 260 and h = 52 . h = 52 . If you missed this problem, review Example 2.61 .

Be Prepared 3.15

Simplify: 144 . 144 . If you missed this problem, review Example 1.111 .

Solve Applications Using Properties of Triangles

In this section we will use some common geometry formulas. We will adapt our problem-solving strategy so that we can solve geometry applications. The geometry formula will name the variables and give us the equation to solve. In addition, since these applications will all involve shapes of some sort, most people find it helpful to draw a figure and label it with the given information. We will include this in the first step of the problem solving strategy for geometry applications.

Solve Geometry Applications.

• Step 1. Read the problem and make sure all the words and ideas are understood. Draw the figure and label it with the given information.
• Step 2. Identify what we are looking for.
• Step 3. Label what we are looking for by choosing a variable to represent it.
• Step 4. Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
• Step 5. Solve the equation using good algebra techniques.
• Step 6. Check the answer by substituting it back into the equation solved in step 5 and by making sure it makes sense in the context of the problem.
• Step 7. Answer the question with a complete sentence.

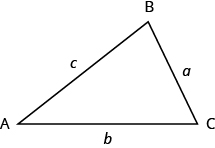
We will start geometry applications by looking at the properties of triangles. Let’s review some basic facts about triangles. Triangles have three sides and three interior angles. Usually each side is labeled with a lowercase letter to match the uppercase letter of the opposite vertex.

The plural of the word vertex is vertices . All triangles have three vertices . Triangles are named by their vertices: The triangle in Figure 3.4 is called △ A B C . △ A B C .

The three angles of a triangle are related in a special way. The sum of their measures is 180 ° . 180 ° . Note that we read m ∠ A m ∠ A as “the measure of angle A.” So in △ A B C △ A B C in Figure 3.4 ,

Because the perimeter of a figure is the length of its boundary, the perimeter of △ A B C △ A B C is the sum of the lengths of its three sides.

To find the area of a triangle, we need to know its base and height. The height is a line that connects the base to the opposite vertex and makes a 90 ° 90 ° angle with the base. We will draw △ A B C △ A B C again, and now show the height, h . See Figure 3.5 .

Triangle Properties

For △ A B C △ A B C

Angle measures:

• The sum of the measures of the angles of a triangle is 180 ° . 180 ° .
• The perimeter is the sum of the lengths of the sides of the triangle.
• The area of a triangle is one-half the base times the height.

Example 3.34

The measures of two angles of a triangle are 55 and 82 degrees. Find the measure of the third angle.

Try It 3.67

The measures of two angles of a triangle are 31 and 128 degrees. Find the measure of the third angle.

Try It 3.68

The measures of two angles of a triangle are 49 and 75 degrees. Find the measure of the third angle.

Example 3.35

The perimeter of a triangular garden is 24 feet. The lengths of two sides are four feet and nine feet. How long is the third side?

Try It 3.69

The perimeter of a triangular garden is 48 feet. The lengths of two sides are 18 feet and 22 feet. How long is the third side?

Try It 3.70

The lengths of two sides of a triangular window are seven feet and five feet. The perimeter is 18 feet. How long is the third side?

Example 3.36

The area of a triangular church window is 90 square meters. The base of the window is 15 meters. What is the window’s height?

Try It 3.71

The area of a triangular painting is 126 square inches. The base is 18 inches. What is the height?

Try It 3.72

A triangular tent door has an area of 15 square feet. The height is five feet. What is the base?

The triangle properties we used so far apply to all triangles. Now we will look at one specific type of triangle—a right triangle. A right triangle has one 90 ° 90 ° angle, which we usually mark with a small square in the corner.

Right Triangle

A right triangle has one 90 ° 90 ° angle, which is often marked with a square at the vertex.

Example 3.37

One angle of a right triangle measures 28 ° . 28 ° . What is the measure of the third angle?

Try It 3.73

One angle of a right triangle measures 56 ° . 56 ° . What is the measure of the other small angle?

Try It 3.74

One angle of a right triangle measures 45 ° . 45 ° . What is the measure of the other small angle?

In the examples we have seen so far, we could draw a figure and label it directly after reading the problem. In the next example, we will have to define one angle in terms of another. We will wait to draw the figure until we write expressions for all the angles we are looking for.

Example 3.38

The measure of one angle of a right triangle is 20 degrees more than the measure of the smallest angle. Find the measures of all three angles.

Try It 3.75

The measure of one angle of a right triangle is 50° more than the measure of the smallest angle. Find the measures of all three angles.

Try It 3.76

The measure of one angle of a right triangle is 30° more than the measure of the smallest angle. Find the measures of all three angles.

We have learned how the measures of the angles of a triangle relate to each other. Now, we will learn how the lengths of the sides relate to each other. An important property that describes the relationship among the lengths of the three sides of a right triangle is called the Pythagorean Theorem . This theorem has been used around the world since ancient times. It is named after the Greek philosopher and mathematician, Pythagoras, who lived around 500 BC.

Before we state the Pythagorean Theorem, we need to introduce some terms for the sides of a triangle. Remember that a right triangle has a 90 ° 90 ° angle, marked with a small square in the corner. The side of the triangle opposite the 90 ° 90 ° angle is called the hypotenuse and each of the other sides are called legs .

The Pythagorean Theorem tells how the lengths of the three sides of a right triangle relate to each other. It states that in any right triangle, the sum of the squares of the lengths of the two legs equals the square of the length of the hypotenuse. In symbols we say: in any right triangle, a 2 + b 2 = c 2 , a 2 + b 2 = c 2 , where a and b a and b are the lengths of the legs and c c is the length of the hypotenuse.

Writing the formula in every exercise and saying it aloud as you write it, may help you remember the Pythagorean Theorem.

The Pythagorean Theorem

In any right triangle, a 2 + b 2 = c 2 . a 2 + b 2 = c 2 .

where a and b are the lengths of the legs, c is the length of the hypotenuse.

To solve exercises that use the Pythagorean Theorem, we will need to find square roots. We have used the notation m m and the definition:

If m = n 2 , m = n 2 , then m = n , m = n , for n ≥ 0 . n ≥ 0 .

For example, we found that 25 25 is 5 because 25 = 5 2 . 25 = 5 2 .

Because the Pythagorean Theorem contains variables that are squared, to solve for the length of a side in a right triangle, we will have to use square roots.

Example 3.39

Use the Pythagorean Theorem to find the length of the hypotenuse shown below.

Try It 3.77

Use the Pythagorean Theorem to find the length of the hypotenuse in the triangle shown below.

Try It 3.78

Example 3.40.

Use the Pythagorean Theorem to find the length of the leg shown below.

Try It 3.79

Use the Pythagorean Theorem to find the length of the leg in the triangle shown below.

Try It 3.80

Example 3.41.

Kelvin is building a gazebo and wants to brace each corner by placing a 10 ″ 10 ″ piece of wood diagonally as shown above.

If he fastens the wood so that the ends of the brace are the same distance from the corner, what is the length of the legs of the right triangle formed? Approximate to the nearest tenth of an inch.

Try It 3.81

John puts the base of a 13-foot ladder five feet from the wall of his house as shown below. How far up the wall does the ladder reach?

Try It 3.82

Randy wants to attach a 17 foot string of lights to the top of the 15 foot mast of his sailboat, as shown below. How far from the base of the mast should he attach the end of the light string?

Solve Applications Using Rectangle Properties

You may already be familiar with the properties of rectangles. Rectangles have four sides and four right ( 90 ° ) ( 90 ° ) angles. The opposite sides of a rectangle are the same length. We refer to one side of the rectangle as the length, L , and its adjacent side as the width, W .

The distance around this rectangle is L + W + L + W , L + W + L + W , or 2 L + 2 W . 2 L + 2 W . This is the perimeter , P , of the rectangle.

What about the area of a rectangle? Imagine a rectangular rug that is 2-feet long by 3-feet wide. Its area is 6 square feet. There are six squares in the figure.

The area is the length times the width.

The formula for the area of a rectangle is A = L W . A = L W .

Properties of Rectangles

Rectangles have four sides and four right ( 90 ° ) ( 90 ° ) angles.

The lengths of opposite sides are equal.

The perimeter of a rectangle is the sum of twice the length and twice the width.

The area of a rectangle is the product of the length and the width.

Example 3.42

The length of a rectangle is 32 meters and the width is 20 meters. What is the perimeter?

Try It 3.83

The length of a rectangle is 120 yards and the width is 50 yards. What is the perimeter?

Try It 3.84

The length of a rectangle is 62 feet and the width is 48 feet. What is the perimeter?

Example 3.43

The area of a rectangular room is 168 square feet. The length is 14 feet. What is the width?

Try It 3.85

The area of a rectangle is 598 square feet. The length is 23 feet. What is the width?

Try It 3.86

The width of a rectangle is 21 meters. The area is 609 square meters. What is the length?

Example 3.44

Find the length of a rectangle with perimeter 50 inches and width 10 inches.

Try It 3.87

Find the length of a rectangle with: perimeter 80 and width 25.

Try It 3.88

Find the length of a rectangle with: perimeter 30 and width 6.

We have solved problems where either the length or width was given, along with the perimeter or area; now we will learn how to solve problems in which the width is defined in terms of the length. We will wait to draw the figure until we write an expression for the width so that we can label one side with that expression.

Example 3.45

The width of a rectangle is two feet less than the length. The perimeter is 52 feet. Find the length and width.

Try It 3.89

The width of a rectangle is seven meters less than the length. The perimeter is 58 meters. Find the length and width.

Try It 3.90

The length of a rectangle is eight feet more than the width. The perimeter is 60 feet. Find the length and width.

Example 3.46

The length of a rectangle is four centimeters more than twice the width. The perimeter is 32 centimeters. Find the length and width.

Try It 3.91

The length of a rectangle is eight more than twice the width. The perimeter is 64. Find the length and width.

Try It 3.92

The width of a rectangle is six less than twice the length. The perimeter is 18. Find the length and width.

Example 3.47

The perimeter of a rectangular swimming pool is 150 feet. The length is 15 feet more than the width. Find the length and width.

Try It 3.93

The perimeter of a rectangular swimming pool is 200 feet. The length is 40 feet more than the width. Find the length and width.

Try It 3.94

The length of a rectangular garden is 30 yards more than the width. The perimeter is 300 yards. Find the length and width.

Section 3.4 Exercises

Practice makes perfect.

Solving Applications Using Triangle Properties

In the following exercises, solve using triangle properties.

The measures of two angles of a triangle are 26 and 98 degrees. Find the measure of the third angle.

The measures of two angles of a triangle are 61 and 84 degrees. Find the measure of the third angle.

The measures of two angles of a triangle are 105 and 31 degrees. Find the measure of the third angle.

The measures of two angles of a triangle are 47 and 72 degrees. Find the measure of the third angle.

The perimeter of a triangular pool is 36 yards. The lengths of two sides are 10 yards and 15 yards. How long is the third side?

A triangular courtyard has perimeter 120 meters. The lengths of two sides are 30 meters and 50 meters. How long is the third side?

If a triangle has sides 6 feet and 9 feet and the perimeter is 23 feet, how long is the third side?

If a triangle has sides 14 centimeters and 18 centimeters and the perimeter is 49 centimeters, how long is the third side?

A triangular flag has base one foot and height 1.5 foot. What is its area?

A triangular window has base eight feet and height six feet. What is its area?

What is the base of a triangle with area 207 square inches and height 18 inches?

What is the height of a triangle with area 893 square inches and base 38 inches?

One angle of a right triangle measures 33 degrees. What is the measure of the other small angle?

One angle of a right triangle measures 51 degrees. What is the measure of the other small angle?

One angle of a right triangle measures 22.5 degrees. What is the measure of the other small angle?

One angle of a right triangle measures 36.5 degrees. What is the measure of the other small angle?

The perimeter of a triangle is 39 feet. One side of the triangle is one foot longer than the second side. The third side is two feet longer than the second side. Find the length of each side.

The perimeter of a triangle is 35 feet. One side of the triangle is five feet longer than the second side. The third side is three feet longer than the second side. Find the length of each side.

One side of a triangle is twice the shortest side. The third side is five feet more than the shortest side. The perimeter is 17 feet. Find the lengths of all three sides.

One side of a triangle is three times the shortest side. The third side is three feet more than the shortest side. The perimeter is 13 feet. Find the lengths of all three sides.

The two smaller angles of a right triangle have equal measures. Find the measures of all three angles.

The measure of the smallest angle of a right triangle is 20° less than the measure of the next larger angle. Find the measures of all three angles.

The angles in a triangle are such that one angle is twice the smallest angle, while the third angle is three times as large as the smallest angle. Find the measures of all three angles.

The angles in a triangle are such that one angle is 20° more than the smallest angle, while the third angle is three times as large as the smallest angle. Find the measures of all three angles.

In the following exercises, use the Pythagorean Theorem to find the length of the hypotenuse.

In the following exercises, use the Pythagorean Theorem to find the length of the leg. Round to the nearest tenth, if necessary.

In the following exercises, solve using the Pythagorean Theorem. Approximate to the nearest tenth, if necessary.

A 13-foot string of lights will be attached to the top of a 12-foot pole for a holiday display, as shown below. How far from the base of the pole should the end of the string of lights be anchored?

Pam wants to put a banner across her garage door, as shown below, to congratulate her son for his college graduation. The garage door is 12 feet high and 16 feet wide. How long should the banner be to fit the garage door?

Chi is planning to put a path of paving stones through her flower garden, as shown below. The flower garden is a square with side 10 feet. What will the length of the path be?

Brian borrowed a 20 foot extension ladder to use when he paints his house. If he sets the base of the ladder 6 feet from the house, as shown below, how far up will the top of the ladder reach?

In the following exercises, solve using rectangle properties.

The length of a rectangle is 85 feet and the width is 45 feet. What is the perimeter?

The length of a rectangle is 26 inches and the width is 58 inches. What is the perimeter?

A rectangular room is 15 feet wide by 14 feet long. What is its perimeter?

A driveway is in the shape of a rectangle 20 feet wide by 35 feet long. What is its perimeter?

The area of a rectangle is 414 square meters. The length is 18 meters. What is the width?

The area of a rectangle is 782 square centimeters. The width is 17 centimeters. What is the length?

The width of a rectangular window is 24 inches. The area is 624 square inches. What is the length?

The length of a rectangular poster is 28 inches. The area is 1316 square inches. What is the width?

Find the length of a rectangle with perimeter 124 and width 38.

Find the width of a rectangle with perimeter 92 and length 19.

Find the width of a rectangle with perimeter 16.2 and length 3.2.

Find the length of a rectangle with perimeter 20.2 and width 7.8.

The length of a rectangle is nine inches more than the width. The perimeter is 46 inches. Find the length and the width.

The width of a rectangle is eight inches more than the length. The perimeter is 52 inches. Find the length and the width.

The perimeter of a rectangle is 58 meters. The width of the rectangle is five meters less than the length. Find the length and the width of the rectangle.

The perimeter of a rectangle is 62 feet. The width is seven feet less than the length. Find the length and the width.

The width of the rectangle is 0.7 meters less than the length. The perimeter of a rectangle is 52.6 meters. Find the dimensions of the rectangle.

The length of the rectangle is 1.1 meters less than the width. The perimeter of a rectangle is 49.4 meters. Find the dimensions of the rectangle.

The perimeter of a rectangle is 150 feet. The length of the rectangle is twice the width. Find the length and width of the rectangle.

The length of a rectangle is three times the width. The perimeter of the rectangle is 72 feet. Find the length and width of the rectangle.

The length of a rectangle is three meters less than twice the width. The perimeter of the rectangle is 36 meters. Find the dimensions of the rectangle.

The length of a rectangle is five inches more than twice the width. The perimeter is 34 inches. Find the length and width.

The perimeter of a rectangular field is 560 yards. The length is 40 yards more than the width. Find the length and width of the field.

The perimeter of a rectangular atrium is 160 feet. The length is 16 feet more than the width. Find the length and width of the atrium.

A rectangular parking lot has perimeter 250 feet. The length is five feet more than twice the width. Find the length and width of the parking lot.

A rectangular rug has perimeter 240 inches. The length is 12 inches more than twice the width. Find the length and width of the rug.

Everyday Math

Christa wants to put a fence around her triangular flowerbed. The sides of the flowerbed are six feet, eight feet and 10 feet. How many feet of fencing will she need to enclose her flowerbed?

Jose just removed the children’s playset from his back yard to make room for a rectangular garden. He wants to put a fence around the garden to keep out the dog. He has a 50 foot roll of fence in his garage that he plans to use. To fit in the backyard, the width of the garden must be 10 feet. How long can he make the other length?

Writing Exercises

If you need to put tile on your kitchen floor, do you need to know the perimeter or the area of the kitchen? Explain your reasoning.

If you need to put a fence around your backyard, do you need to know the perimeter or the area of the backyard? Explain your reasoning.

Look at the two figures below.

• ⓐ Which figure looks like it has the larger area?
• ⓑ Which looks like it has the larger perimeter?
• ⓒ Now calculate the area and perimeter of each figure.
• ⓓ Which has the larger area?
• ⓔ Which has the larger perimeter?

Write a geometry word problem that relates to your life experience, then solve it and explain all your steps.

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/elementary-algebra-2e/pages/1-introduction

• Authors: Lynn Marecek, MaryAnne Anthony-Smith, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Elementary Algebra 2e
• Publication date: Apr 22, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/elementary-algebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/elementary-algebra-2e/pages/3-4-solve-geometry-applications-triangles-rectangles-and-the-pythagorean-theorem

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Appendix B: Geometry

Using the properties of triangles to solve problems, learning outcomes.

• Given the measures of two angles of a triangle, find the third
• Use properties of similar triangles to find unknown lengths of triangles

What do you already know about triangles? Triangle have three sides and three angles. Triangles are named by their vertices. The triangle below is called [latex]\Delta ABC[/latex], read ‘triangle [latex]\text{ABC}[/latex] ’. We label each side with a lower case letter to match the upper case letter of the opposite vertex.

[latex]\Delta ABC[/latex] has vertices [latex]A,B,\text{ and }C[/latex] and sides [latex]a,b,\text{ and }c\text{.}[/latex]

[latex]m\angle A+m\angle B+m\angle C=\text{180}^ \circ[/latex]

Sum of the Measures of the Angles of a Triangle

For any [latex]\Delta ABC[/latex], the sum of the measures of the angles is [latex]\text{180}^ \circ[/latex].

The measures of two angles of a triangle are [latex]55^\circ [/latex] and [latex]82^\circ [/latex]. Find the measure of the third angle.

In the following video we show an example of how to find the measure of an unknown angle in a triangle. In this example, we have two triangles who share a common side, and find two unknown interior angles.

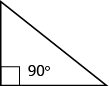
Right Triangles

Some triangles have special names. We will look first at the right triangle. A right triangle has one [latex]90^\circ[/latex] angle, which is often marked with the symbol shown in the triangle below.

One angle of a right triangle measures [latex]28^\circ [/latex]. What is the measure of the third angle?

In the examples so far, we could draw a figure and label it directly after reading the problem. In the next example, we will have to define one angle in terms of another. So we will wait to draw the figure until we write expressions for all the angles we are looking for.

The measure of one angle of a right triangle is [latex]20^\circ [/latex] more than the measure of the smallest angle. Find the measures of all three angles.

Similar Triangles

When we use a map to plan a trip, a sketch to build a bookcase, or a pattern to sew a dress, we are working with similar figures. In geometry, if two figures have exactly the same shape but different sizes, we say they are similar figures. One is a scale model of the other. The corresponding sides of the two figures have the same ratio, and all their corresponding angles are have the same measures.

The two triangles below are similar. Each side of [latex]\Delta ABC[/latex] is four times the length of the corresponding side of [latex]\Delta XYZ[/latex] and their corresponding angles have equal measures.

[latex]\Delta ABC[/latex] and [latex]\Delta XYZ[/latex] are similar triangles. Their corresponding sides have the same ratio and the corresponding angles have the same measure.

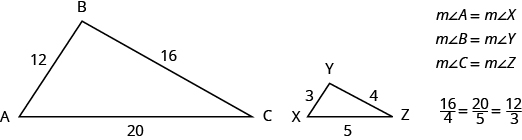
Properties of Similar Triangles

If two triangles are similar, then their corresponding angle measures are equal and their corresponding side lengths are in the same ratio.

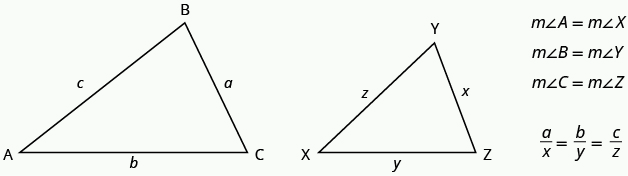
The length of a side of a triangle may be referred to by its endpoints, two vertices of the triangle. For example, in [latex]\Delta ABC\text{:}[/latex]

[latex]\begin{array}{c}\text{the length }a\text{can also be written}BC\hfill \\ \text{the length}b\text{ can also be written }AC\hfill \\ \text{the length }c\text{ can also be written }AB\hfill \end{array}[/latex]

We will often use this notation when we solve similar triangles because it will help us match up the corresponding side lengths.

[latex]\Delta ABC[/latex] and [latex]\Delta XYZ[/latex] are similar triangles. The lengths of two sides of each triangle are shown. Find the lengths of the third side of each triangle.

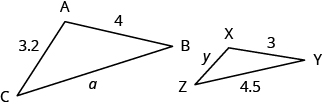
In the video below we show an example of how to find the missing sides of two triangles that are similar.  Note that the measures of the sides in this example are whole numbers, and we use a cross product to solve the resulting proportions.

• Question ID 146912, 146498, 146499, 146500. Authored by : Lumen Learning. License : CC BY: Attribution
• Ex 2B: Find the Measure of an Interior Angle of a Triangle. Authored by : James Sousa (mathispower4u.com). Located at : https://youtu.be/3kRLkbU6-cI . License : CC BY: Attribution
• Prealgebra. Provided by : OpenStax. License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]

Algebra: Geometry Word Problems

In these lessons, we look at geometry word problems, which involves geometric figures and angles described in words. You would need to be familiar with the formulas in geometry .

Related Pages Perimeter and Area of Polygons Nets Of 3D Shapes Surface Area Formulas Volume Formulas More Geometry Lessons

Making a sketch of the geometric figure is often helpful.

You can see how to solve geometry word problems in the following examples: Problems involving Perimeter Problems involving Area Problems involving Angles

There is also an example of a geometry word problem that uses similar triangles.

Geometry Word Problems Involving Perimeter

Example 1: A triangle has a perimeter of 50. If 2 of its sides are equal and the third side is 5 more than the equal sides, what is the length of the third side?

Solution: Step 1: Assign variables: Let x = length of the equal side. Sketch the figure.

Step 2: Write out the formula for perimeter of triangle . P = sum of the three sides

Step 3: Plug in the values from the question and from the sketch. 50 = x + x + x + 5

Combine like terms 50 = 3x + 5

Isolate variable x 3x = 50 – 5 3x = 45 x =15

Be careful! The question requires the length of the third side. The length of third side = 15 + 5 =20

Answer: The length of third side is 20

Example 2: Writing an equation and finding the dimensions of a rectangle knowing the perimeter and some information about the about the length and width. The width of a rectangle is 3 feet less than its length. The perimeter of the rectangle is 110 feet. Find its dimensions.

Geometry Word Problems Involving Area

Example 1: A rectangle is 4 times as long as it is wide. If the length is increased by 4 inches and the width is decreased by 1 inch, the area will be 60 square inches. What were the dimensions of the original rectangle?

Step 1: Assign variables: Let x = original width of rectangle

Step 2: Write out the formula for area of rectangle. A = lw

Step 3: Plug in the values from the question and from the sketch. 60 = (4x + 4)(x –1)

Use distributive property to remove brackets 60 = 4x 2 – 4x + 4x – 4

Put in Quadratic Form 4x 2 – 4 – 60 = 0 4x 2 – 64 = 0

This quadratic can be rewritten as a difference of two squares (2x) 2 – (8) 2 = 0

Factorize difference of two squares "> (2x) 2 – (8) 2 = 0 (2x – 8)(2x + 8) = 0

Since x is a dimension, it would be positive. So, we take x = 4

The question requires the dimensions of the original rectangle. The width of the original rectangle is 4. The length is 4 times the width = 4 × 4 = 16

Answer: The dimensions of the original rectangle are 4 and 16.

Example 2: This is a geometry word problem that we can solve by writing an equation and factoring. The height of a triangle is 4 inches more than twice the length of the base. The area of the triangle is 35 square inches. Find the height of the triangle.

Geometry Word Problems involving Angles

Example 1: In a quadrilateral two angles are equal. The third angle is equal to the sum of the two equal angles. The fourth angle is 60° less than twice the sum of the other three angles. Find the measures of the angles in the quadrilateral.

Step 1: Assign variables: Let x = size of one of the two equal angles Sketch the figure

Step 2: Write down the sum of angles in quadrilateral . The sum of angles in a quadrilateral is 360°

Step 3: Plug in the values from the question and from the sketch. 360 = x + x + (x + x) + 2(x + x + x + x) – 60

Combine like terms 360 = 4x + 2(4x) – 60 360 = 4x + 8x – 60 360 = 12x – 60

Isolate variable x 12x = 420 x = 35

The question requires the values of all the angles. Substituting x for 35, you will get: 35, 35, 70, 220

Answer: The values of the angles are 35°, 35°, 70° and 220°.

Example 2: The sum of the supplement and the complement of an angle is 130 degrees. Find the measure of the angle.

Geometry Word Problems involving Similar Triangles

Indirect Measurement Using Similar Triangles

This video illustrates how to use the properties of similar triangles to determine the height of a tree.

How to solve problems involving Similar Triangles and Proportions?

Given that triangle ABC is similar to triangle DEF, solve for x and y.

The extendable ramp shown below is used to move crates of fruit to loading docks of different heights. When the horizontal distance AB is 4 feet, the height of the loading dock, BC, is 2 feet. What is the height of the loading dock, DE?

Triangles ABC and A’B’C' are similar figures. Find the length AB.

How to use similar triangles to solve a geometry word problem?

Examples: Raul is 6 ft tall and he notices that he casts a shadow that’s 5 ft long. He then measures that the shadow cast by his school building is 30 ft long. How tall is the building?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Choose Your Test

Sat / act prep online guides and tips, triangles on sat math: geometry strategies and practice problems.

Triangle questions account for less than 10% of all SAT math questions. That being said, you still want to get those questions right, so you should be prepared to know every kind of triangle: right triangles, isosceles triangles, isosceles right triangles—the SAT could test you on any one of them. Since triangle problems only account for a small percent of the SAT math questions, you shouldn’t spend all of your study time on triangles.

This article should be all you need to prepare you to tackle SAT triangle questions. I'll let you know the types of triangles that will show up on the SAT, their formulas, and the strategies you’ll need to apply when approaching a triangle question. I’ll also break down SAT math practice questions and explain how to knock triangle questions out of the park.

What Are Triangles?

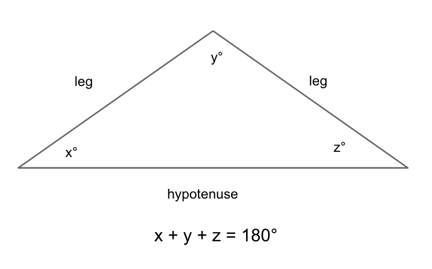
First, let’s talk basics. A triangle is a flat figure made up of three straight lines that connect together at three angles. The sum of these angles is 180°.

Each of the three sides of a triangle is called a “leg” of the triangle, and the longest leg of a right triangle is called the “hypotenuse.” The angle opposite the hypotenuse will always be 90°, the largest of the three angles.

Special Triangles

There are several different kinds of special triangles, all of which commonly appear on the SAT.

In this section, we will define and describe all the different kinds of triangles you’ll see on the test. In the next section, we will go through all the formulas you’ll need to know for your SAT triangle problems, as well as how to use them.

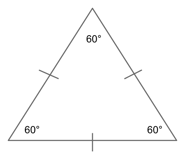
Equilateral Triangles

An equilateral triangle is a triangle that has three equal legs and three equal angles. Though the leg measurements can be anything (so long as they are all equal), the angle measurements must all equal 60°. Why? Because a triangle’s angles must always total 180°, and ${180}/{3}=60$.

In the figure above, triangle ABC is inscribed in the circle with center O and diameter AC. If $\ov{AB}=\ov{AO}$, what is the degree measure of∠ABO?

Answer Explanation: We are told that two of the side lengths of the circle are equal, and we must find an unknown angle, ∠ABO. If you are familiar with your circles , then you know that any and all radii of a circle are equal.

Lines $\ov{AO}$ and $\ov{OB}$ are both radii of the circle, so they must be equal.

This means that all three legs of the circle BOA—lines $\ov {AO}$, $\ov {OB}$, and $\ov {BA}$—are equal. And we know that having three equal legs of a triangle means we have an equilateral triangle.

We also know that equilateral triangles have three equal inner angles, all of which are 60 degrees. This means that angle ABO is 60 degrees.

Our final answer is D, 60°.

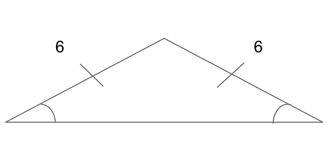
Isosceles Triangles

An isosceles triangle is a triangle in which two sides and two angles are equal.

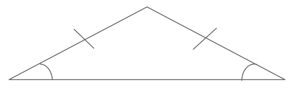
The sides opposite equal angles will always be equal, and the angles opposite equal sides will always be equal. This knowledge will often lead you to the correct answers for many SAT questions in which it seems you are given very little information.

Answer Explanation: Since the question tells you that $180−z=2y$ and $y=75$, we know that $180−z=(2)(75)$ and solving that gives you $z=30$. If $z=30$, then each of the base angles of the isosceles triangle on the right must measure 75°(${180−30}/{2}$). Therefore, the angle marked $x°$ is $180°−75°=105°$, and so the value of $x$ is 105. The answer is 105.

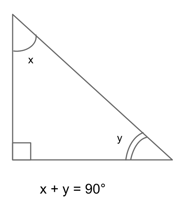
Right Triangles

A right triangle is a triangle in which one of the angles measures 90° (90° is a right angle). This means that the sum of the other two angles must be 90° as well since a triangle’s angles always add up to 180°.

Special Right Triangles

There are many different kinds of right triangles and some are considered “special.” These are triangles that have set angles or side lengths and formulas to correspond with them. Understanding these types of triangles (and their formulas) will save you a significant amount of time on triangle questions.

We'll go through the formulas that correspond to these types of triangles in the next section, but for now, let’s go through their definitions.

Isosceles Right Triangle

An isosceles right triangle is just what it sounds like—a right triangle in which two sides and two angles are equal.

Though the side measurements may change, an isosceles triangle will always have one 90° angle and two 45° angles. (Why? Because a right triangle has to have one 90° angle by definition and the other two angles must add up to 90°. So ${90}/{2}=45$.

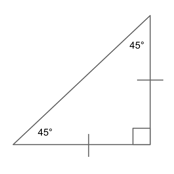
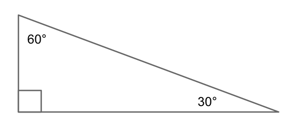
30-60-90 Triangles

A 30-60-90 triangle is a special right triangle defined by its angles. It is a right triangle due to its 90° angle, and the other two angles must be 30° and 60°.

It's also half of an equilateral triangle. As I mentioned earlier, an equilateral triangle has three equal angles all measuring 60°. If you attached another 30-60-90 triangle to this one (along the leg opposite the 60°), you'd have an equilateral triangle with all angles measuring 60°.

3-4-5, and 5-12-13 Right Triangles

3-4-5 and 5-12-13 triangles are special right triangles defined by their side lengths. The numbers 3-4-5 and 5-12-13 describe the lengths of the triangle’s legs, meaning that, when you have a right triangle with one leg length 4 and with a hypotenuse length 5, then you automatically know that the third leg equals 3.

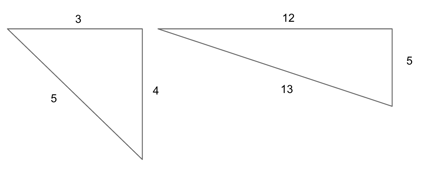
Any consistent multiples of these numbers will also work the same way. So a right triangle could have leg lengths of:

3(1)-4(1)-5(1) => 3-4-5

3(2)-4(2)-5(2) => 6-8-10

3(3)-4(3)-5(3) => 9-12-15

These are considered “special” right triangles because all of their sides are integers.

Recognize this handsome fellow? Because Pythagoras is here to impart his triangle wisdom.

Triangle Formulas

Now that you know what all your triangles will look like, let’s go through how to find missing variables and information about them.

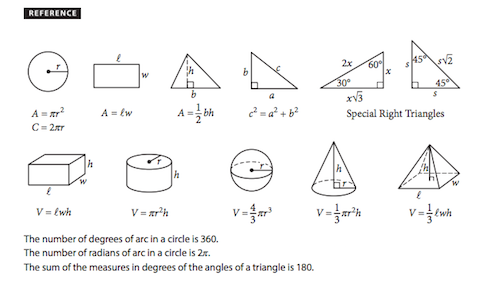
This is the box of formulas you will be given on every SAT math section. Though all the formulas you’ll need to know for triangles are all included, you must understand how and why these formulas work as well as when to use them. It will also save you time and effort to memorize these rather than flipping back and forth between the problem and the formula box.

So memorize your formulas if possible and read below to see what these formulas mean and how to use them. All the formula boxes in the world aren’t worth the paper they’re printed on if you don’t know how to apply them when solving your problems.

All Triangles

Some formulas apply to all triangles while other formulas only apply to special triangles. So let's first look at the triangle formulas that apply to any and all types of triangles.

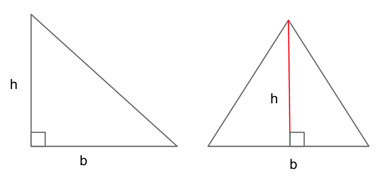
$$a= {1}/{2}bh$$

$b$ is the base of the triangle, which is the length of any one of the triangle’s legs.

$h$ is the height of a triangle, found by drawing a straight line (at a 90° angle) from the base of the triangle to the opposite angle from the base.

This means that, in a right triangle, the height is the length of the leg that meets at a 90° angle to the base. In a non-right triangle, you must create a new line for your height.

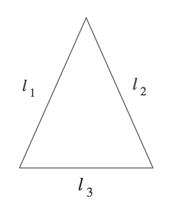
p=l 1 +l 2 +l 3

Just like with any other kind of plane geometry figure, the perimeter of a triangle is the sum of its outer sides (the triangle’s three legs).

There are also formulas that apply to right triangles and to specific types of right triangles. Let's take a look.

Pythagorean Theorem

a 2 +b 2 =c 2

The Pythagorean theorem allows you to find the side lengths of a right triangle by using the lengths of its other sides. a and b signify the shorter legs of the triangle while c is always the leg opposite the 90° angle (the hypotenuse).

3-4-5 and 5-12-13 triangles (and their multiples) are special because you do not need to work through the Pythagorean Theorem in order to find the side measures of the third length (though, of course, you always can). Remember, if one side of a right triangle is 8 and its hypoteneuse is 10, then you automatically know the third side is 6.

Trigonometric Formulas: Sine and Cosine

Trigonometry makes up less than 5% of all math questions, but you won't be able to answer any trigonometry questions correctly without knowing trigonometry formulas. Check out our trigonometry guide to learn all the formulas you need to know and to learn how to apply the formulas to SAT math questions.

Though you can find the missing side lengths of an isosceles triangle using the Pythagorean theorem, you can also take a shortcut and say that the equal side lengths are each x, and the hypotenuse is $x√2$.

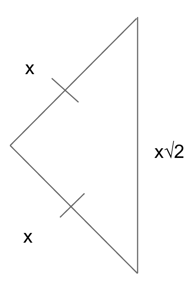
Why does this work? Well, think about an isosceles triangle with a leg length of 6.

We know the second leg must also equal 6 because the two legs are equal in an isosceles triangle. And we can also find the hypotenuse using the Pythagorean theorem because it is a right triangle. So:

6 2 +6 2 =c 2

$$c = √72$$

$c = √36 * √2$ (Why were we able to split up our root this way? Check out our guide to SAT advanced integers and its section on roots if this process is unfamiliar to you.)

So, we are left with side lengths of 6, 6, and $6√2$. Or, in other words, our side lengths are x,x, and $x√2$.

30-60-90 Triangle

$$x, x√3, 2x$$

Just like with an isosceles right triangle, a 30-60-90 triangle has side lengths that are dictated by a set of rules. Again, you can find these lengths with the Pythagorean theorem, but you can also always find them using the rule: $x, x√3, 2x$, where $x$ is the side opposite 30°, $x√3$ is the side opposite 60°, and $2x$ is the side opposite 90°.

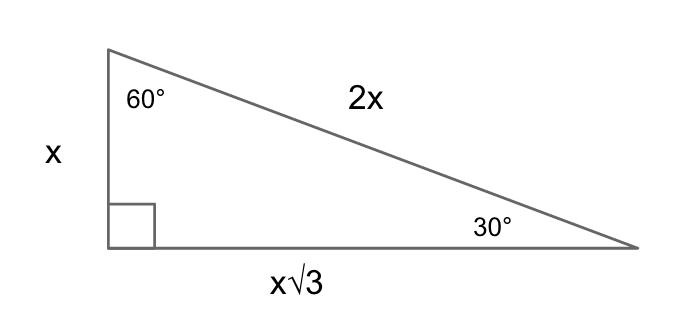
This knowledge can help you find the lengths of sides when given a more complex triangle problem.

Typical Triangle Questions

Let’s look at some of the standard types of question in each category. NOTE: the question examples provided are not from official SAT tests since the newly redesigned SAT doesn't start until March 2016. These questions have been taken from College Board new SAT practice tests or adapted from other College Board study materials for the new SAT.

#1: Finding Missing Values

Most triangle problems will fall into this category—you will be asked to find a missing angle, an area, a perimeter, or a side length (among other things) based on given information.

Some of these questions will be more complicated than others, but the SAT will always provide you will enough information to solve a problem, so it’s up to you to put the clues together.

Let’s walk through an example question of this type:

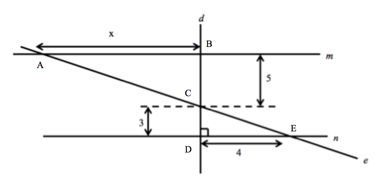
In the figure above, line m is parallel to line n , line d  is perpendicular to line n , and line e intersects line m and line n . What is the length of x?

Answer Explanation: Since line d and line e intersect at C, >ACB and ∠DCE are vertical angles , and therefore they are equal in measure. Since line m is parallel to line n , ∠DEC and ∠CAB are alternate interior angles of parallel lines cut by a transversal, and so the measures of ∠DEC and ∠CAB are equal. By the angle-angle theorem , triangle ABC is similar to triangle EDC with vertices A, B, and C corresponding to vertices E, D, and C, respectively.

Also, triangle EDC is a right triangle, so you can use either the Pythagorean theorem or your knowledge of 3-4-5 right triangles to find that the hypotenuse is 5.

Since triangle ABC is similar to triangle EDC, the ratios of the lengths of corresponding sides of the two triangles are the same so ${CD}/{BC}={3}/{5}={DE}/{AB}={4}/{x}$.

Solving for $x$, we get $3x=20$. Therefore, $x={20}/{3}$.

#2: Ratios and (In)Equalities

These kinds of questions will generally ask you to either find the ratios between parts of different triangles or will ask you whether or not certain sides or angles of triangles are equal or unequal.

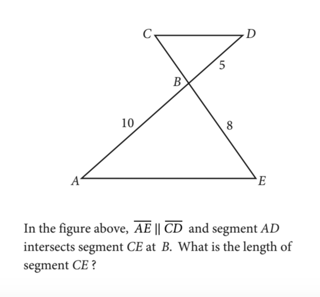
Answer Explanation: Angles ABE and DBC are vertical angles (meaning they are pairs of opposite angles made by two intersecting lines), and, therefore, they have the same measure. Since segment AE is parallel to segment CD, angles A and D are of the same measure by the alternate interior angle theorem . Since all angles are equal in triangles ABE and DBC, triangle ABE is similar to triangle DBC, with vertices A, B, and E matching up to vertices D, B, and C, respectively. Therefore,

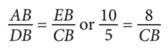
#3: Multi-Shape or Shapes Within Shapes

As you can see from earlier examples, some of the triangle problems on the SAT will involve multiple triangles (or other geometric shapes) combined together. This technique for presenting problems is designed to challenge your understanding of lines and angles as well as triangles.

For these types of problems, you must use the information you are given and solve for more information down the line until you find exactly what you need. It’s essentially a domino effect of problem-solving.

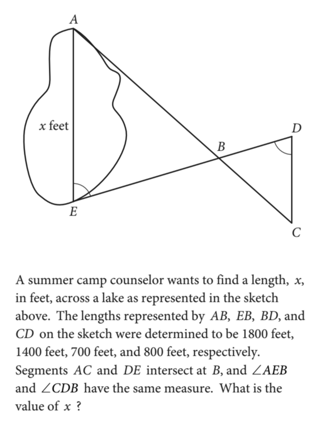
Answer Explanation: The question tells you that ∠AEB and ∠CDB have the same measure. Since ∠ABE and ∠CBD are vertical angles (meaning they are pairs of opposite angles made by two intersecting lines), they have the same measure. Triangle EAB is similar to triangle DCB because the triangles have two pairs of congruent corresponding angles ( angle-angle criterion for similarity of triangles ). Since the triangles are similar, the corresponding sides are in the same proportion:

$${CD}/{x}={BD}/{EB}$$

Substituting the given values of 800 for CD, 700 for BD, and 1400 for EB in ${CD}/{x}={BD}/{EB}$ gives ${800}/{x}={700}/{1400}$

Therefore, $x={(800)(1400)}/{700}=1600$.

The final answer is 1600.

#4: Variables and Combination Variables

Finally, triangle problems that involve multiple variables (or only variables) in both the problem and the answer are usually located somewhere in the last three questions of any SAT math section. This means they are some of the most challenging types of math problems for the majority of students.

The good news is that there are many different ways to solve these types of problems and that a little time, organization, and creativity will almost always get you to your correct answer.

Considering these kinds of problems involve multiple variables, it is probably a good idea to check out the strategy of plugging in numbers if you haven’t done so already. This is a great technique to use if you are hesitant about the geometry and/or the algebra, or simply if multiple integers bother you.

Let’s take a look at an example problem of this type and the various methods of solving it.

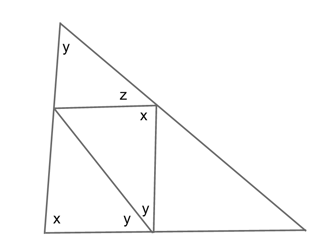
Which of the following expresses $z$ in terms of $x$ and $y$?

(A) $2x+3y−180$

(B) $x+2y−180$

(C) $180−x−y$

(D) $360−2x−3y$

As you can see, this is a triangle problem that uses multiple variables and so is a bit complicated. Let’s look at all our options for solving the question:

Solving Method 1: Plug in our own numbers

On most any occasion in which you are given several variables in the question or in the answer options, a sure-fire technique you can use is the one of plugging in your own numbers. (For more on this strategy, check out our guide to plugging in numbers .)

We are given the variables $x$ and $y$ and told to find $z$. So let us choose some values for $x$ and $y$ that seem appropriate and use them to find $z$.

Let us just say that $x=60$ and $y=70$. Why those numbers? Why not!

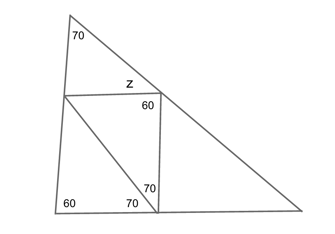
Because the angles of a triangle always add up to 180°, we can find the missing values in our two bottom triangles by saying:

$$180−60−70=50$$

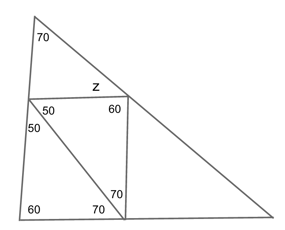
This means we can also find the value of the missing angle in our top triangle because we know that a straight line must also equal 180°. So:

$$180−50−50=80$$

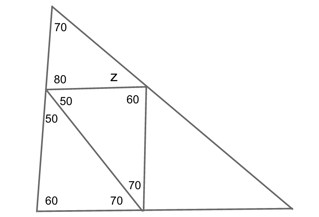
Which means we can finally find the value of z by saying that:

$$z=180−80−70$$

Now, let us use the same values for $x$ and $y$ that we used in our problem to find which answer choice (or choices) gets us $z=30$.

Answer choice A gives us:

$$2x+3y−180$$

Which, when we replace our variables, is:

$$2(60)+3(70)−180$$

$$120+210−180$$

We are looking for an answer to match $z=30$, so this is far too large. We can eliminate answer choice A.

Let us try answer choice B:

$$x+2y−180$$

$$60+2(70)−180$$

$$60+140−180$$

This answer still does not equal 30, so we can eliminate answer choice B.

Answer choice C says:

$$180−x−y$$

But we already know that this is 50 and not 30, as we used this equation to find the missing components of our triangles earlier (180−60−70). We can eliminate choice C.

By process of elimination, answer choice D must be correct. But let us double-check to be sure.

$$360−2x−3y$$

$$360−2(60)−3(70)$$

$$360−120−210$$

Success! We have found an answer choice (and only one answer choice) that matches what we found for $z$.

Our final answer is D.

Solving Method 2: Algebraic approach

Alternatively, we could have found our answer using pure algebra and the properties of triangles, instead of filling in our own numbers. To do so, we would essentially be repeating the process we used to find our missing variables from above, but keeping the variables intact.

Each of the three triangles we are focusing on would all add up to 180°. We have three different triangles and three missing angles, so their equations would look like:

$$180−y−z$$

We know that all of those equations will find us one of the three unmarked angles. We also know that those three angles add up to 180°. (Why? Because they lie on a straight line, and a straight line equals 180°.)

So when we add the equations together and set them equal to 180°, we get:

$$(180−x−y)+(180−x−y)+(180−y−z)=180$$

$$540−2x−3y−z=180$$

$$−2x−3y−z=−360$$

$$−z=−360+2x+3y$$

$$z=360−2x−3y$$

So again, our final answer is D.

(Note: there is a third—and even faster—way to solve this problem that involves quadrilaterals. Check out our guide to SAT polygons for more info!)

How to Solve a Triangle Question

Triangle questions are as numerous (comprising nearly 10% of the entire SAT math section) as they are varied. Because of this, it is difficult to break down one exact path for problem-solving triangle questions.

That said, your greatest assets and strategies when solving triangle problems will be to:

#1: Use Your Formulas (and Take Your Short-Cuts)

Using your formulas is the absolute most crucial step for any triangle problem. And, considering that most of your formulas essentially act as short-cuts (why bother solving with the Pythagorean theorem when you know that the legs of a 30-60-90 triangle are $x, x√3, 2x$?), you will save yourself a great deal of time and energy when you can keep your formulas on hand and in order.

#2: When Working With Multi-Shapes, Break It into Small Steps

Remember that dealing with a multi-shape triangle problem is like working with dominoes. Each successive piece of information makes way for finding the next piece of information.

Don’t get intimidated by the idea that you don’t have enough information or that there are too many shapes or lines to deal with. You will always have enough data to go on—just focus on finding one shape and one piece of information at a time, and the dominoes will fall into place.

#3: Draw It Out

Draw your own diagrams if you are given none. Draw on top of your diagrams when you are given pictures. Write in your givens and all the measurements you find along the way to your missing variable (or variables), and mark congruent lines and angles.

The more you can clarify your diagrams, the less likely you’ll be to make careless errors in misplacing or confusing your numbers and equalities.

#4: Plug in Your Own Numbers Whenever Possible

Finally, give yourself a break from dealing with variables and complex algebra if you need to. It can be far too easy to make a mistake when dealing with variables alone, so if you have the time to spare, go for plugging in your own numbers!

Test Your Knowledge

Now let's test your triangle knowledge on more, SAT math problems. NOTE: these questions are not official SAT math section questions (since the newly redesigned SAT debuts in March 2016). These questions were taken from College Board practice tests for the new SAT or adapted from other new SAT practice questions and old SAT questions.

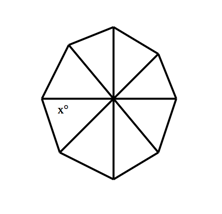
Note: Figure not drawn to scale.

In the figure above, a regular polygon with 8 sides has been divided into 8 congruent isosceles triangles by line segments drawn from the center of the polygon to its vertices. What is the value of $x$?

Answer Explanation: The sum of the measures of the angles around a point is 360°. Since the 8 triangles are congruent, the measures of each of the 8 angles are the same. Therefore, the measure of each is ${360°}/{8}=45°$. In any triangle, the measure of the interior angles is 180°. So in each triangle, the sum of the measures of the remaining two angles is $180°-45°=135°$. Since the triangles are isosceles, the measures of the two angles are the same. Therefore, the measure of each of these angles is ${135°}/{2}=67.5°$.

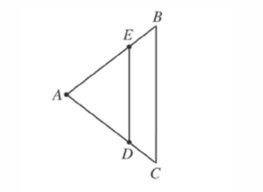
In triangle ABC above, $AB=AC$, E is the midpoint of $\ov{AB}$, and D is the midpoint of $\ov{AC}$. If $AE = x$, and $ED = 4$, what is the length of $\ov{BC}$?

Answer Explanation: As always, let us first fill in our given information.

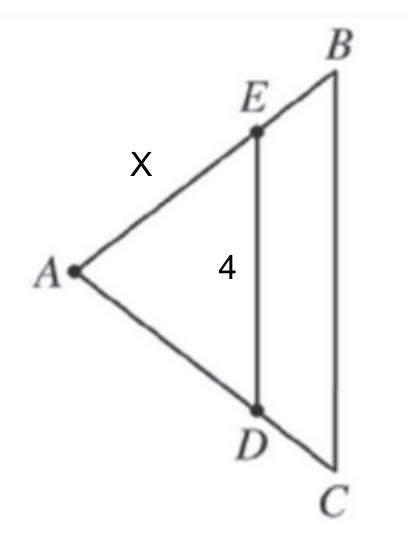
Now, though it may not look it, we are told that E is the midpoint of line AB. This means that, if segment AE is worth $x$, then segment EB is also worth $x$. This also means that the entire length AB will, therefore, be worth $x+x=2x$.

So let us set up a proportion.

Leg AE will be to its base, ED, as the leg AB will be to its base, BC. So:

$${AE}/{ED}:{AB}/{BC}$$

$${x}/{4}:{2x}/{BC}$$

Our final answer is B, BC = 8.

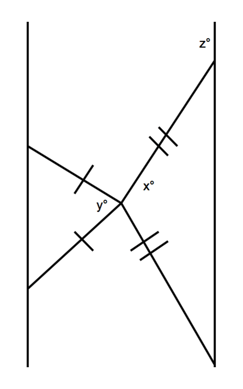
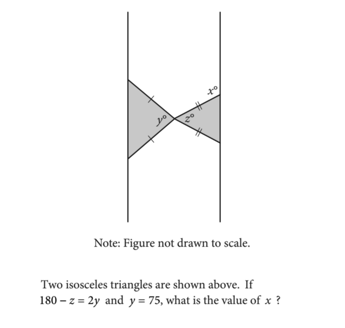
Two isosceles triangles are shown above. If $180−x=3y$ and $y=20$, what is the value of z?

Answer Explanation: Since the question tells you that $180−x=3y$ and $y=20$, then $180−x=3y=60$, and solving that gives you $x=120$. If $x=120$, then each of the base angles of the isosceles triangle on the right must measure 30° (${180−120}/{2}$). Therefore, the angle marked $z°$ is $180°−30°=150°$, and so the value of z is 150. The answer is 150.

We think you've earned a break, don't you?

The Take-Aways

Triangles will show up, without fail, at least a few times on every single SAT (usually in about 1 to 3 problems). The good news is that you will be given multiple formulas to aid you through these types of questions, but the drawback is that the test is timed, and so you should only waste time going to your formula box if you are all out of options.

Know your definitions, try to memorize your formulas, and do your best to keep a clear head as you go through your test. And, as always, practice, practice, practice! The more experience you get in solving the variety of triangle questions the SAT can think to put in front of you, the better off you’ll be in slaying those triangle problems.

What’s Next?

Now that you've done your paces on your triangles, it's time to make sure you are prepared for all the math topics you'll see on the SAT. All of our math guides will take you through strategies and practice problems for all the topics covered on the math section, from integers , to ratios , circles to polygons (and more!). 

Feeling anxious about test day? Make sure you know exactly what to do and bring to ease your mind and settle your nerves before it's time to take your SAT.

Running out of time on the SAT math section? Look no further than our guide to help you beat the clock and maximize your SAT math score.

Angling to get a perfect score? Check out our guide to getting a perfect 800 , written by a perfect-scorer.

Courtney scored in the 99th percentile on the SAT in high school and went on to graduate from Stanford University with a degree in Cultural and Social Anthropology. She is passionate about bringing education and the tools to succeed to students from all backgrounds and walks of life, as she believes open education is one of the great societal equalizers. She has years of tutoring experience and writes creative works in her free time.

Ask a Question Below

Have any questions about this article or other topics? Ask below and we'll reply!

Improve With Our Famous Guides

• For All Students

The 5 Strategies You Must Be Using to Improve 160+ SAT Points

How to Get a Perfect 1600, by a Perfect Scorer

Series: How to Get 800 on Each SAT Section:

Score 800 on SAT Math

Score 800 on SAT Reading

Score 800 on SAT Writing

Series: How to Get to 600 on Each SAT Section:

Score 600 on SAT Math

Score 600 on SAT Reading

Score 600 on SAT Writing

Free Complete Official SAT Practice Tests

What SAT Target Score Should You Be Aiming For?

15 Strategies to Improve Your SAT Essay

The 5 Strategies You Must Be Using to Improve 4+ ACT Points

How to Get a Perfect 36 ACT, by a Perfect Scorer

Series: How to Get 36 on Each ACT Section:

36 on ACT English

36 on ACT Math

36 on ACT Reading

36 on ACT Science

Series: How to Get to 24 on Each ACT Section:

24 on ACT English

24 on ACT Math

24 on ACT Reading

24 on ACT Science

What ACT target score should you be aiming for?

ACT Vocabulary You Must Know

ACT Writing: 15 Tips to Raise Your Essay Score

How to Get Into Harvard and the Ivy League

How to Get a Perfect 4.0 GPA

How to Write an Amazing College Essay

What Exactly Are Colleges Looking For?

Is the ACT easier than the SAT? A Comprehensive Guide

Should you retake your SAT or ACT?

When should you take the SAT or ACT?

Stay Informed

Get the latest articles and test prep tips!

Looking for Graduate School Test Prep?

Check out our top-rated graduate blogs here:

GRE Online Prep Blog

GMAT Online Prep Blog

TOEFL Online Prep Blog

Holly R. "I am absolutely overjoyed and cannot thank you enough for helping me!”

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: 7th grade   >   Unit 9

• Find measure of vertical angles
• Finding missing angles
• Find measure of angles word problem
• Equation practice with complementary angles
• Equation practice with supplementary angles
• Equation practice with vertical angles
• Create equations to solve for missing angles

Unknown angle problems (with algebra)

• Your answer should be
• an integer, like 6 ‍  
• an exact decimal, like 0.75 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍