solving problems involving rational inequalities

• Parallelogram
• Quadrilateral
• Parallelepiped
• Tetrahedron
• Dodecahedron
• Fraction Calculator
• Mixed Fraction Calculator
• Greatest Common Factor Calulator
• Decimal to Fraction Calculator
• Whole Numbers
• Rational Numbers
• Place Value
• Irrational Numbers
• Natural Numbers
• Binary Operation
• Numerator and Denominator
• Order of Operations (PEMDAS)
• Scientific Notation

Table of Contents

Last modified on April 19th, 2024

#ezw_tco-2 .ez-toc-title{ font-size: 120%; ; ; } #ezw_tco-2 .ez-toc-widget-container ul.ez-toc-list li.active{ background-color: #ededed; } chapter outline

Rational inequalities.

A rational inequality is a rational expression with an inequality sign and a fraction in either the numerator, denominator, or both.

${\dfrac{12}{x}\leq -4}$, ${\dfrac{2+x}{-7+x} >0}$, and ${\dfrac{3}{2-5x}\geq 8}$ are some examples of rational inequalities.

General Forms

If f(x) is a rational function, the four general forms of rational inequalities are:

• f(x) < 0

While solving rational inequalities, we follow most of the steps we use in linear inequalities. We first write them in the general form and then find the critical values (or the zeros of both the numerator and the denominator). The solution is then plotted on the number line to verify the interval that satisfies the given inequality. 

Additionally, we must remember that when multiplying and dividing by a negative number, the inequality sign reverses. Also, we must find the value(s), which might make the expression undefined.

Let us solve the rational inequality ${\dfrac{12}{x}\leq -4}$

Step 1: Converting into the General form

${\dfrac{12}{x}+4\leq 0}$

⇒ ${\dfrac{12+4x}{x}\leq 0}$ …..(i)

Step 2: Finding the Zeros of the Numerator and Denominator

Separating each factor equals to zero, we get

For the numerator , 

12 + 4x = 0 

⇒ 4x = -12 

⇒ x = -3 

For the denominator ,

Step 3: Dividing the Intervals and Verifying 

This step involves choosing a number from each interval and substituting it with the original rational inequality to check its validity. If the result is true, the interval is part of the solution set. Otherwise, it is not.

Here, we picked up the numbers within the interval to check whether they satisfy the given inequality.

On verifying,

At x = -3, ${\dfrac{12+4\left( -3\right) }{-3}=\dfrac{12-12}{-3}=0}$, holds true.

At x = 0, ${\dfrac{12+4\left( 0\right) }{0}}$, which is undefined.

Step 4: Determining the Solution

Thus, the solution is -3 ≤ x < 0 or x Є [-3, 0) (in the interval notation) 

Solved Examples

Solve the rational inequality: ${\dfrac{2+x}{x-7} >0}$

Step 1: Converting into the General form Here, the rational inequality ${\dfrac{2+x}{-7+x} >0}$ is already in its general form. Step 2: Finding the Zeros of the Numerator and Denominator For the numerator and denominator, we get x + 2 = 0 and x – 7 = 0 ⇒ x = -2 and x = 7 Step 3: Dividing the Intervals and Verifying  Now, verifying the intervals between the above critical points on the number line, we get On verifying the given inequality at the critical points, we get At x = -2, ${\dfrac{-2+2}{-2-7}=0}$, which means the result does not follow the inequality. At x = 7, ${\dfrac{7+2}{7-7}}$, undefined. Step 4: Determining the Solution Thus, the solution is x Є (-∞, -2) ⋃ (7, ∞) (also written as x < -2 or x > 7)

 Find the solution of the rational inequality ${\dfrac{x^{2}+2x-15}{\left( x+1\right) }\leq 0}$

Here, ${\dfrac{x^{2}+2x-15}{\left( x+1\right) }\leq 0}$ Step 1: Converting into the General form The given rational inequality is already in its general form. Further simplifying the given inequality, we get ${\dfrac{x^{2}+5x-3x-15}{\left( x+1\right) }\leq 0}$ ⇒ ${\dfrac{\left( x+5\right) \left( x-3\right) }{\left( x+1\right) }\leq 0}$ Step 2: Finding the Zeros of the Numerator and Denominator For the numerator and denominator, we get x + 5 = 0, x – 3 = 0, and x + 1 = 0 ⇒ x = -5, x = 3, and x = -1 Step 3: Dividing the Intervals and Verifying  Now, verifying the intervals between the above critical points on the number line, we get On verifying the general form of the given inequality at the critical points, we get At x = -5, ${\dfrac{\left( -5+5\right) \left( -5-3\right) }{\left( -5+1\right) }=0}$, holds true At x = -1, ${\dfrac{\left( -1+5\right) \left( -1-3\right) }{\left( -1+1\right) }}$, undefined At x = 3, ${\dfrac{\left( 3+5\right) \left( 3-3\right) }{\left( 3+1\right) }=0}$, holds true Step 4: Determining the Solution Thus, the solution is either x ≤ -5 or -1 < x ≤ 3

Solve the rational inequality ${\dfrac{x^{2}-3x-4}{x^{2}-16}\geq 0}$

Here, ${\dfrac{x^{2}-3x-4}{x^{2}-16}\geq 0}$ Step 1: Converting into the General form The given rational inequality is already in its general form. Further simplifying the given inequality, we get ${\dfrac{\left( x+1\right) \left( x-4\right) }{\left( x+4\right) \left( x-4\right) }\geq 0}$ Step 2: Finding the Zeros of the Numerator and Denominator For the numerator, we get x + 1 = 0 and x – 4 = 0 ⇒ x = -1 and 4 For the denominator, we get x + 4 = 0 and x – 4 = 0 ⇒ x = -4 and 4 Step 3: Dividing the Intervals and Verifying  Now, verifying the intervals between the above critical points on the number line, we get On verifying the general form of the given inequality at the critical points, we get At x = -4, ${\dfrac{\left( -4+1\right) \left( -4-4\right) }{\left( -4+4\right) \left( -4-4\right) }}$, undefined. At x = -1, ${\dfrac{\left( -1+1\right) \left( -1-4\right) }{\left( -1+4\right) \left( -1-4\right) }=0}$, holds true. At x = 4, ${\dfrac{\left( 4+1\right) \left( 4-4\right) }{\left( 4+4\right) \left( 4-4\right) }}$, undefined. Step 4: Determining the Solution Thus, the solution is either x < -4 or -1 ≤ x < 4 or x > 4, which implies (-∞, -4) ⋃ [-1, 4) ⋃ (4, ∞)

Solve: ${\dfrac{8x+14}{x} <-x-1}$

Here, ${\dfrac{8x+14}{x} <-x-1}$ Step 1: Converting into the General form On adding ‘x’ and 1 to both sides of the inequality, we get ${\dfrac{8x+14}{x}+x+1 <-x-1+x+1}$ ⇒ ${\dfrac{8x+14+x^{2}+x}{x} <0}$ Further simplifying, we get ${\dfrac{x^{2}+9x+14}{x} <0}$ ⇒ ${\dfrac{\left( x+2\right) \left( x+7\right) }{x} <0}$ Step 2: Finding the Zeros of the Numerator and Denominator For the numerator and denominator, we get x + 2 = 0, x + 7 = 0, and x = 0 ⇒ x = -2, -7, and 0 Step 3: Dividing the Intervals and Verifying  Now, verifying the intervals between the above critical points on the number line, we get On verifying the general form of the given inequality at the critical points, we get At x = -7, ${\dfrac{\left( -7+2\right) \left( -7+7\right) }{-7}=0}$, holds true. At x = -2, ${\dfrac{\left( -2+2\right) \left( -2+7\right) }{-2}=0}$, holds true. At x = 0, ${\dfrac{\left( 0+2\right) \left( 0+7\right) }{0}}$, undefined. Step 4: Determining the Solution Thus, the solution is either x ≤ -7 or -2 ≤ x < 0

• Privacy Policy
• Trigonometry

Join Our Newsletter

© 2024 Mathmonks.com . All rights reserved. Reproduction in whole or in part without permission is prohibited.

7.6 Solve Rational Inequalities

Learning objectives.

By the end of this section, you will be able to:

• Solve rational inequalities
• Solve an inequality with rational functions

Be Prepared 7.16

Before you get started, take this readiness quiz.

Find the value of x − 5 x − 5 when ⓐ x = 6 x = 6 ⓑ x = −3 x = −3 ⓒ x = 5 . x = 5 . If you missed this problem, review Example 1.6 .

Be Prepared 7.17

Solve: 8 − 2 x < 12 . 8 − 2 x < 12 . If you missed this problem, review Example 2.52 .

Be Prepared 7.18

Write in interval notation: −3 ≤ x < 5 . −3 ≤ x < 5 . If you missed this problem, review Example 2.49 .

Solve Rational Inequalities

We learned to solve linear inequalities after learning to solve linear equations. The techniques were very much the same with one major exception. When we multiplied or divided by a negative number, the inequality sign reversed.

Having just learned to solve rational equations we are now ready to solve rational inequalities. A rational inequality is an inequality that contains a rational expression.

Rational Inequality

A rational inequality is an inequality that contains a rational expression.

Inequalities such as 3 2 x > 1 , 2 x x − 3 < 4 , 2 x − 3 x − 6 ≥ x , 3 2 x > 1 , 2 x x − 3 < 4 , 2 x − 3 x − 6 ≥ x , and 1 4 − 2 x 2 ≤ 3 x 1 4 − 2 x 2 ≤ 3 x are rational inequalities as they each contain a rational expression.

When we solve a rational inequality, we will use many of the techniques we used solving linear inequalities. We especially must remember that when we multiply or divide by a negative number, the inequality sign must reverse.

Another difference is that we must carefully consider what value might make the rational expression undefined and so must be excluded.

When we solve an equation and the result is x = 3 , x = 3 , we know there is one solution, which is 3.

When we solve an inequality and the result is x > 3 , x > 3 , we know there are many solutions. We graph the result to better help show all the solutions, and we start with 3. Three becomes a critical point and then we decide whether to shade to the left or right of it. The numbers to the right of 3 are larger than 3, so we shade to the right.

To solve a rational inequality, we first must write the inequality with only one quotient on the left and 0 on the right.

Next we determine the critical points to use to divide the number line into intervals. A critical point is a number which make the rational expression zero or undefined.

We then will evaluate the factors of the numerator and denominator, and find the quotient in each interval. This will identify the interval, or intervals, that contains all the solutions of the rational inequality.

We write the solution in interval notation being careful to determine whether the endpoints are included.

Example 7.54

Solve and write the solution in interval notation: x − 1 x + 3 ≥ 0 . x − 1 x + 3 ≥ 0 .

• Step 1. Write the inequality as one quotient on the left and zero on the right.

Our inequality is in this form. x − 1 x + 3 ≥ 0 x − 1 x + 3 ≥ 0

Step 2. Determine the critical points—the points where the rational expression will be zero or undefined.

The rational expression will be zero when the numerator is zero. Since x − 1 = 0 x − 1 = 0 when x = 1 , x = 1 , then 1 1 is a critical point.

The rational expression will be undefined when the denominator is zero. Since x + 3 = 0 x + 3 = 0 when x = −3 , x = −3 , then −3 −3 is a critical point.

The critical points are 1 and −3 . −3 .

• Step 3. Use the critical points to divide the number line into intervals.

The number line is divided into three intervals:

( − ∞ , −3 ) ( −3 , 1 ) ( 1 , ∞ ) ( − ∞ , −3 ) ( −3 , 1 ) ( 1 , ∞ )

Step 4. Test a value in each interval. Above the number line show the sign of each factor of the rational expression in each interval. Below the number line show the sign of the quotient.

To find the sign of each factor in an interval, we choose any point in that interval and use it as a test point. Any point in the interval will give the expression the same sign, so we can choose any point in the interval.

The number −4 −4 is in the interval ( − ∞ , −3 ) . ( − ∞ , −3 ) . Test x = −4 x = −4 in the expression in the numerator and the denominator.

Above the number line, mark the factor x − 1 x − 1 negative and mark the factor x + 3 x + 3 negative.

Since a negative divided by a negative is positive, mark the quotient positive in the interval ( − ∞ , −3 ) . ( − ∞ , −3 ) .

The number 0 is in the interval ( −3 , 1 ) . ( −3 , 1 ) . Test x = 0 . x = 0 .

Above the number line, mark the factor x − 1 x − 1 negative and mark x + 3 x + 3 positive.

Since a negative divided by a positive is negative, the quotient is marked negative in the interval ( −3 , 1 ) . ( −3 , 1 ) .

The number 2 is in the interval ( 1 , ∞ ) . ( 1 , ∞ ) . Test x = 2 . x = 2 .

Above the number line, mark the factor x − 1 x − 1 positive and mark x + 3 x + 3 positive.

Since a positive divided by a positive is positive, mark the quotient positive in the interval ( 1 , ∞ ) . ( 1 , ∞ ) .

• Step 5. Determine the intervals where the inequality is correct. Write the solution in interval notation.

We want the quotient to be greater than or equal to zero, so the numbers in the intervals ( − ∞ , −3 ) ( − ∞ , −3 ) and ( 1 , ∞ ) ( 1 , ∞ ) are solutions.

But what about the critical points?

The critical point x = −3 x = −3 makes the denominator 0, so it must be excluded from the solution and we mark it with a parenthesis.

The critical point x = 1 x = 1 makes the whole rational expression 0. The inequality requires that the rational expression be greater than or equal to 0. So, 1 is part of the solution and we will mark it with a bracket.

Recall that when we have a solution made up of more than one interval we use the union symbol, ∪ , ∪ , to connect the two intervals. The solution in interval notation is ( − ∞ , −3 ) ∪ [ 1 , ∞ ) . ( − ∞ , −3 ) ∪ [ 1 , ∞ ) .

Try It 7.107

Solve and write the solution in interval notation: x − 2 x + 4 ≥ 0 . x − 2 x + 4 ≥ 0 .

Try It 7.108

Solve and write the solution in interval notation: x + 2 x − 4 ≥ 0 . x + 2 x − 4 ≥ 0 .

We summarize the steps for easy reference.

Solve a rational inequality.

• Step 2. Determine the critical points–the points where the rational expression will be zero or undefined.
• Step 4. Test a value in each interval. Above the number line show the sign of each factor of the numerator and denominator in each interval. Below the number line show the sign of the quotient.

The next example requires that we first get the rational inequality into the correct form.

Example 7.55

Solve and write the solution in interval notation: 4 x x − 6 < 1 . 4 x x − 6 < 1 .

Try It 7.109

Solve and write the solution in interval notation: 3 x x − 3 < 1 . 3 x x − 3 < 1 .

Try It 7.110

Solve and write the solution in interval notation: 3 x x − 4 < 2 . 3 x x − 4 < 2 .

In the next example, the numerator is always positive, so the sign of the rational expression depends on the sign of the denominator.

Example 7.56

Solve and write the solution in interval notation: 5 x 2 − 2 x − 15 > 0 . 5 x 2 − 2 x − 15 > 0 .

Try It 7.111

Solve and write the solution in interval notation: 1 x 2 + 2 x − 8 > 0 . 1 x 2 + 2 x − 8 > 0 .

Try It 7.112

Solve and write the solution in interval notation: 3 x 2 + x − 12 > 0 . 3 x 2 + x − 12 > 0 .

The next example requires some work to get it into the needed form.

Example 7.57

Solve and write the solution in interval notation: 1 3 − 2 x 2 < 5 3 x . 1 3 − 2 x 2 < 5 3 x .

Try It 7.113

Solve and write the solution in interval notation: 1 2 + 4 x 2 < 3 x . 1 2 + 4 x 2 < 3 x .

Try It 7.114

Solve and write the solution in interval notation: 1 3 + 6 x 2 < 3 x . 1 3 + 6 x 2 < 3 x .

Solve an Inequality with Rational Functions

When working with rational functions, it is sometimes useful to know when the function is greater than or less than a particular value. This leads to a rational inequality.

Example 7.58

Given the function R ( x ) = x + 3 x − 5 , R ( x ) = x + 3 x − 5 , find the values of x that make the function less than or equal to 0.

We want the function to be less than or equal to 0.

Try It 7.115

Given the function R ( x ) = x − 2 x + 4 , R ( x ) = x − 2 x + 4 , find the values of x that make the function less than or equal to 0.

Try It 7.116

Given the function R ( x ) = x + 1 x − 4 , R ( x ) = x + 1 x − 4 , find the values of x that make the function less than or equal to 0.

In economics, the function C ( x ) C ( x ) is used to represent the cost of producing x units of a commodity. The average cost per unit can be found by dividing C ( x ) C ( x ) by the number of items x . x . Then, the average cost per unit is c ( x ) = C ( x ) x . c ( x ) = C ( x ) x .

Example 7.59

The function C ( x ) = 10 x + 3000 C ( x ) = 10 x + 3000 represents the cost to produce x , x , number of items. Find ⓐ the average cost function, c ( x ) c ( x ) ⓑ how many items should be produced so that the average cost is less than $40.

More than 100 items must be produced to keep the average cost below $40 per item.

Try It 7.117

The function C ( x ) = 20 x + 6000 C ( x ) = 20 x + 6000 represents the cost to produce x , x , number of items. Find ⓐ the average cost function, c ( x ) c ( x ) ⓑ how many items should be produced so that the average cost is less than $60?

Try It 7.118

The function C ( x ) = 5 x + 900 C ( x ) = 5 x + 900 represents the cost to produce x , x , number of items. Find ⓐ the average cost function, c ( x ) c ( x ) ⓑ how many items should be produced so that the average cost is less than $20?

Section 7.6 Exercises

Practice makes perfect.

In the following exercises, solve each rational inequality and write the solution in interval notation.

x − 3 x + 4 ≥ 0 x − 3 x + 4 ≥ 0

x + 6 x − 5 ≥ 0 x + 6 x − 5 ≥ 0

x + 1 x − 3 ≤ 0 x + 1 x − 3 ≤ 0

x − 4 x + 2 ≤ 0 x − 4 x + 2 ≤ 0

x − 7 x − 1 > 0 x − 7 x − 1 > 0

x + 8 x + 3 > 0 x + 8 x + 3 > 0

x − 6 x + 5 < 0 x − 6 x + 5 < 0

x + 5 x − 2 < 0 x + 5 x − 2 < 0

3 x x − 5 < 1 3 x x − 5 < 1

5 x x − 2 < 1 5 x x − 2 < 1

6 x x − 6 > 2 6 x x − 6 > 2

3 x x − 4 > 2 3 x x − 4 > 2

2 x + 3 x − 6 ≤ 1 2 x + 3 x − 6 ≤ 1

4 x − 1 x − 4 ≤ 1 4 x − 1 x − 4 ≤ 1

3 x − 2 x − 4 ≥ 2 3 x − 2 x − 4 ≥ 2

4 x − 3 x − 3 ≥ 2 4 x − 3 x − 3 ≥ 2

1 x 2 + 7 x + 12 > 0 1 x 2 + 7 x + 12 > 0

1 x 2 − 4 x − 12 > 0 1 x 2 − 4 x − 12 > 0

3 x 2 − 5 x + 4 < 0 3 x 2 − 5 x + 4 < 0

4 x 2 + 7 x + 12 < 0 4 x 2 + 7 x + 12 < 0

2 2 x 2 + x − 15 ≥ 0 2 2 x 2 + x − 15 ≥ 0

6 3 x 2 − 2 x − 5 ≥ 0 6 3 x 2 − 2 x − 5 ≥ 0

−2 6 x 2 − 13 x + 6 ≤ 0 −2 6 x 2 − 13 x + 6 ≤ 0

−1 10 x 2 + 11 x − 6 ≤ 0 −1 10 x 2 + 11 x − 6 ≤ 0

1 2 + 12 x 2 > 5 x 1 2 + 12 x 2 > 5 x

1 3 + 1 x 2 > 4 3 x 1 3 + 1 x 2 > 4 3 x

1 2 − 4 x 2 ≤ 1 x 1 2 − 4 x 2 ≤ 1 x

1 2 − 3 2 x 2 ≥ 1 x 1 2 − 3 2 x 2 ≥ 1 x

1 x 2 − 16 < 0 1 x 2 − 16 < 0

4 x 2 − 25 > 0 4 x 2 − 25 > 0

4 x − 2 ≥ 3 x + 1 4 x − 2 ≥ 3 x + 1

5 x − 1 ≤ 4 x + 2 5 x − 1 ≤ 4 x + 2

In the following exercises, solve each rational function inequality and write the solution in interval notation.

Given the function R ( x ) = x − 5 x − 2 , R ( x ) = x − 5 x − 2 , find the values of x x that make the function less than or equal to 0.

Given the function R ( x ) = x + 1 x + 3 , R ( x ) = x + 1 x + 3 , find the values of x x that make the function greater than or equal to 0.

Given the function R ( x ) = x − 6 x + 2 R ( x ) = x − 6 x + 2 , find the values of x that make the function less than or equal to 0.

Writing Exercises

Write the steps you would use to explain solving rational inequalities to your little brother.

Create a rational inequality whose solution is ( − ∞ , −2 ] ∪ [ 4 , ∞ ) . ( − ∞ , −2 ] ∪ [ 4 , ∞ ) .

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ After reviewing this checklist, what will you do to become confident for all objectives?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction

• Authors: Lynn Marecek, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Intermediate Algebra 2e
• Publication date: May 6, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/intermediate-algebra-2e/pages/7-6-solve-rational-inequalities

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Rational Expressions and Functions

Solve Rational Inequalities

Learning Objectives

By the end of this section, you will be able to:

• Solve rational inequalities
• Solve an inequality with rational functions

Before you get started, take this readiness quiz.

We learned to solve linear inequalities after learning to solve linear equations. The techniques were very much the same with one major exception. When we multiplied or divided by a negative number, the inequality sign reversed.

Having just learned to solve rational equations we are now ready to solve rational inequalities. A rational inequality is an inequality that contains a rational expression.

A rational inequality is an inequality that contains a rational expression.

When we solve a rational inequality, we will use many of the techniques we used solving linear inequalities. We especially must remember that when we multiply or divide by a negative number, the inequality sign must reverse.

Another difference is that we must carefully consider what value might make the rational expression undefined and so must be excluded.

To solve a rational inequality, we first must write the inequality with only one quotient on the left and 0 on the right.

Next we determine the critical points to use to divide the number line into intervals. A critical point is a number which make the rational expression zero or undefined.

We then will evaluate the factors of the numerator and denominator, and find the quotient in each interval. This will identify the interval, or intervals, that contains all the solutions of the rational inequality.

We write the solution in interval notation being careful to determine whether the endpoints are included.

Step 1. Write the inequality as one quotient on the left and zero on the right.

Step 2. Determine the critical points—the points where the rational expression will be zero or undefined.

Step 3. Use the critical points to divide the number line into intervals.

The number line is divided into three intervals:

Step 4. Test a value in each interval. Above the number line show the sign of each factor of the rational expression in each interval. Below the number line show the sign of the quotient.

To find the sign of each factor in an interval, we choose any point in that interval and use it as a test point. Any point in the interval will give the expression the same sign, so we can choose any point in the interval.

Step 5. Determine the intervals where the inequality is correct. Write the solution in interval notation.

But what about the critical points?

We summarize the steps for easy reference.

• Write the inequality as one quotient on the left and zero on the right.
• Determine the critical points–the points where the rational expression will be zero or undefined.
• Use the critical points to divide the number line into intervals.
• Test a value in each interval. Above the number line show the sign of each factor of the numerator and denominator in each interval. Below the number line show the sign of the quotient.
• Determine the intervals where the inequality is correct. Write the solution in interval notation.

The next example requires that we first get the rational inequality into the correct form.

In the next example, the numerator is always positive, so the sign of the rational expression depends on the sign of the denominator.

The next example requires some work to get it into the needed form.

Solve an Inequality with Rational Functions

When working with rational functions, it is sometimes useful to know when the function is greater than or less than a particular value. This leads to a rational inequality.

We want the function to be less than or equal to 0.

More than 100 items must be produced to keep the average cost below ?40 per item.

Key Concepts

• Test a value in each interval. Above the number line show the sign of each factor of the rational expression in each interval. Below the number line show the sign of the quotient.

Section Exercises

Practice makes perfect.

In the following exercises, solve each rational inequality and write the solution in interval notation.

In the following exercises, solve each rational function inequality and write the solution in interval notation.

Writing Exercises

Write the steps you would use to explain solving rational inequalities to your little brother.

Answers will vary.

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ After reviewing this checklist, what will you do to become confident for all objectives?

Chapter Review Exercises

Simplify, multiply, and divide rational expressions.

Determine the Values for Which a Rational Expression is Undefined

In the following exercises, determine the values for which the rational expression is undefined.

Simplify Rational Expressions

In the following exercises, simplify.

Multiply Rational Expressions

In the following exercises, multiply.

Divide Rational Expressions

In the following exercises, divide.

Multiply and Divide Rational Functions

Add and Subtract Rational Expressions

Add and Subtract Rational Expressions with a Common Denominator

In the following exercises, perform the indicated operations.

Add and Subtract Rational Expressions Whose Denominators Are Opposites

In the following exercises, add and subtract.

Find the Least Common Denominator of Rational Expressions

In the following exercises, find the LCD.

Add and Subtract Rational Expressions with Unlike Denominators

Add and Subtract Rational Functions

Simplify Complex Rational Expressions

Simplify a Complex Rational Expression by Writing It as Division

Simplify a Complex Rational Expression by Using the LCD

7.4 Solve Rational Equations

Solve Rational Equations

In the following exercises, solve.

no solution

Solve Rational Equations that Involve Functions

Solve a Rational Equation for a Specific Variable

In the following exercises, solve for the indicated variable.

Solve Applications with Rational Equations

Solve Proportions

Solve Using Proportions

Rachael had a 21-ounce strawberry shake that has 739 calories. How many calories are there in a 32-ounce shake?

Leo went to Mexico over Christmas break and changed ?525 dollars into Mexican pesos. At that time, the exchange rate had ?1 US is equal to 16.25 Mexican pesos. How many Mexican pesos did he get for his trip?

Solve Similar Figure Applications

On a map of Europe, Paris, Rome, and Vienna form a triangle whose sides are shown in the figure below. If the actual distance from Rome to Vienna is 700 miles, find the distance from

ⓐ Paris to Rome

ⓑ Paris to Vienna

Francesca is 5.75 feet tall. Late one afternoon, her shadow was 8 feet long. At the same time, the shadow of a nearby tree was 32 feet long. Find the height of the tree.

The height of a lighthouse in Pensacola, Florida is 150 feet. Standing next to the statue, 5.5-foot-tall Natasha cast a 1.1-foot shadow. How long would the shadow of the lighthouse be?

Solve Uniform Motion Applications

When making the 5-hour drive home from visiting her parents, Lolo ran into bad weather. She was able to drive 176 miles while the weather was good, but then driving 10 mph slower, went 81 miles when it turned bad. How fast did she drive when the weather was bad?

Mark is riding on a plane that can fly 490 miles with a tailwind of 20 mph in the same time that it can fly 350 miles against a tailwind of 20 mph. What is the speed of the plane?

Josue can ride his bicycle 8 mph faster than Arjun can ride his bike. It takes Luke 3 hours longer than Josue to ride 48 miles. How fast can John ride his bike?

Curtis was training for a triathlon. He ran 8 kilometers and biked 32 kilometers in a total of 3 hours. His running speed was 8 kilometers per hour less than his biking speed. What was his running speed?

Solve Work Applications

Brandy can frame a room in 1 hour, while Jake takes 4 hours. How long could they frame a room working together?

Prem takes 3 hours to mow the lawn while her cousin, Barb, takes 2 hours. How long will it take them working together?

Jeffrey can paint a house in 6 days, but if he gets a helper he can do it in 4 days. How long would it take the helper to paint the house alone?

Marta and Deb work together writing a book that takes them 90 days. If Sue worked alone it would take her 120 days. How long would it take Deb to write the book alone?

Solve Direct Variation Problems

If the cost of a pizza varies directly with its diameter, and if an 8” diameter pizza costs ?12, how much would a 6” diameter pizza cost?

The distance to stop a car varies directly with the square of its speed. It takes 200 feet to stop a car going 50 mph. How many feet would it take to stop a car going 60 mph?

Solve Inverse Variation Problems

The number of tickets for a music fundraiser varies inversely with the price of the tickets. If Madelyn has just enough money to purchase 12 tickets for ?6, how many tickets can Madelyn afford to buy if the price increased to ?8?

On a string instrument, the length of a string varies inversely with the frequency of its vibrations. If an 11-inch string on a violin has a frequency of 360 cycles per second, what frequency does a 12-inch string have?

In the following exercises, solve each rational function inequality and write the solution in interval notation

The function

Practice Test

In the following exercises, perform the indicated operation and simplify.

In the following exercises, solve each equation.

Given the function,

Matheus can ride his bike for 30 miles with the wind in the same amount of time that he can go 21 miles against the wind. If the wind’s speed is 6 mph, what is Matheus’ speed on his bike?

Oliver can split a truckload of logs in 8 hours, but working with his dad they can get it done in 3 hours. How long would it take Oliver’s dad working alone to split the logs?

The volume of a gas in a container varies inversely with the pressure on the gas. If a container of nitrogen has a volume of 29.5 liters with 2000 psi, what is the volume if the tank has a 14.7 psi rating? Round to the nearest whole number.

The cities of Dayton, Columbus, and Cincinnati form a triangle in southern Ohio. The diagram gives the map distances between these cities in inches.

The actual distance from Dayton to Cincinnati is 48 miles. What is the actual distance between Dayton and Columbus?

The distance between Dayton and Columbus is 64 miles.

Intermediate Algebra Copyright © 2017 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

Solve Rational Inequalities Examples With Solutions

Rational Inequalities are solved in the examples below. Knowing that the sign of an algebraic expression changes at its zeros of odd multiplicity, solving an inequality may be reduced to finding the sign of an algebraic expression within intervals defined by the zeros of the expression in question.

Solve the following inequalities

References and links.

Solving Inequality Word Questions

(You might like to read Introduction to Inequalities and Solving Inequalities first.)

In Algebra we have "inequality" questions like:

Sam and Alex play in the same soccer team. Last Saturday Alex scored 3 more goals than Sam, but together they scored less than 9 goals. What are the possible number of goals Alex scored?

How do we solve them?

The trick is to break the solution into two parts:

Turn the English into Algebra.

Then use Algebra to solve.

Turning English into Algebra

To turn the English into Algebra it helps to:

• Read the whole thing first
• Do a sketch if needed
• Assign letters for the values
• Find or work out formulas

We should also write down what is actually being asked for , so we know where we are going and when we have arrived!

The best way to learn this is by example, so let's try our first example:

Assign Letters:

• the number of goals Alex scored: A
• the number of goals Sam scored: S

We know that Alex scored 3 more goals than Sam did, so: A = S + 3

And we know that together they scored less than 9 goals: S + A < 9

We are being asked for how many goals Alex might have scored: A

Sam scored less than 3 goals, which means that Sam could have scored 0, 1 or 2 goals.

Alex scored 3 more goals than Sam did, so Alex could have scored 3, 4, or 5 goals .

• When S = 0, then A = 3 and S + A = 3, and 3 < 9 is correct
• When S = 1, then A = 4 and S + A = 5, and 5 < 9 is correct
• When S = 2, then A = 5 and S + A = 7, and 7 < 9 is correct
• (But when S = 3, then A = 6 and S + A = 9, and 9 < 9 is incorrect)

Lots More Examples!

Example: Of 8 pups, there are more girls than boys. How many girl pups could there be?

• the number of girls: g
• the number of boys: b

We know that there are 8 pups, so: g + b = 8, which can be rearranged to

We also know there are more girls than boys, so:

We are being asked for the number of girl pups: g

So there could be 5, 6, 7 or 8 girl pups.

Could there be 8 girl pups? Then there would be no boys at all, and the question isn't clear on that point (sometimes questions are like that).

• When g = 8, then b = 0 and g > b is correct (but is b = 0 allowed?)
• When g = 7, then b = 1 and g > b is correct
• When g = 6, then b = 2 and g > b is correct
• When g = 5, then b = 3 and g > b is correct
• (But if g = 4, then b = 4 and g > b is incorrect)

A speedy example:

Example: Joe enters a race where he has to cycle and run. He cycles a distance of 25 km, and then runs for 20 km. His average running speed is half of his average cycling speed. Joe completes the race in less than 2½ hours, what can we say about his average speeds?

• Average running speed: s
• So average cycling speed: 2s
• Speed = Distance Time
• Which can be rearranged to: Time = Distance Speed

We are being asked for his average speeds: s and 2s

The race is divided into two parts:

• Distance = 25 km
• Average speed = 2s km/h
• So Time = Distance Average Speed = 25 2s hours
• Distance = 20 km
• Average speed = s km/h
• So Time = Distance Average Speed = 20 s hours

Joe completes the race in less than 2½ hours

• The total time < 2½
• 25 2s + 20 s < 2½

So his average speed running is greater than 13 km/h and his average speed cycling is greater than 26 km/h

In this example we get to use two inequalities at once:

Example: The velocity v m/s of a ball thrown directly up in the air is given by v = 20 − 10t , where t is the time in seconds. At what times will the velocity be between 10 m/s and 15 m/s?

• velocity in m/s: v
• the time in seconds: t
• v = 20 − 10t

We are being asked for the time t when v is between 5 and 15 m/s:

So the velocity is between 10 m/s and 15 m/s between 0.5 and 1 second after.

And a reasonably hard example to finish with:

Example: A rectangular room fits at least 7 tables that each have 1 square meter of surface area. The perimeter of the room is 16 m. What could the width and length of the room be?

Make a sketch: we don't know the size of the tables, only their area, they may fit perfectly or not!

• the length of the room: L
• the width of the room: W

The formula for the perimeter is 2(W + L) , and we know it is 16 m

• 2(W + L) = 16
• L = 8 − W

We also know the area of a rectangle is the width times the length: Area = W × L

And the area must be greater than or equal to 7:

• W × L ≥ 7

We are being asked for the possible values of W and L

Let's solve:

So the width must be between 1 m and 7 m (inclusive) and the length is 8−width .

• Say W = 1, then L = 8−1 = 7, and A = 1 x 7 = 7 m 2 (fits exactly 7 tables)
• Say W = 0.9 (less than 1), then L = 7.1, and A = 0.9 x 7.1 = 6.39 m 2 (7 won't fit)
• Say W = 1.1 (just above 1), then L = 6.9, and A = 1.1 x 6.9 = 7.59 m 2 (7 fit easily)
• Likewise for W around 7 m

You are about to erase your work on this activity. Are you sure you want to do this?

Updated Version Available

There is an updated version of this activity. If you update to the most recent version of this activity, then your current progress on this activity will be erased. Regardless, your record of completion will remain. How would you like to proceed?

Mathematical Expression Editor

Equations and inequalities with Rational Functions

Rational equations and inequalities

To solve equations involving rational expressions, we have the freedom to clear out fractions before proceeding. After multiplying both sides by the common denominator, we are left with a polynomial equation.

Inequalities

When faced with nonlinear inequalities, such as those involving general rational functions, we make use of a sign chart. The inequality in the following example is not given in factored form, so we have some work to do.

Now that the inequality is in a better form for us to work with, we’ll build a sign chart like we did in the last example.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.8: Polynomial and Rational Inequalities

• Last updated
• Save as PDF
• Page ID 44357

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Skills to Develop

• Solve polynomial inequalities.
• Solve rational inequalities.

Solving Polynomial Inequalities

A polynomial inequality  is a mathematical statement that relates a polynomial expression as either less than or greater than another. We can use sign charts to solve polynomial inequalities with one variable.

Graphs are helpful in providing a visualization to the solutions of polynomial inequalities. Examine the graph below to see the relationship between a graph of a polynomial and its corresponding sign chart.

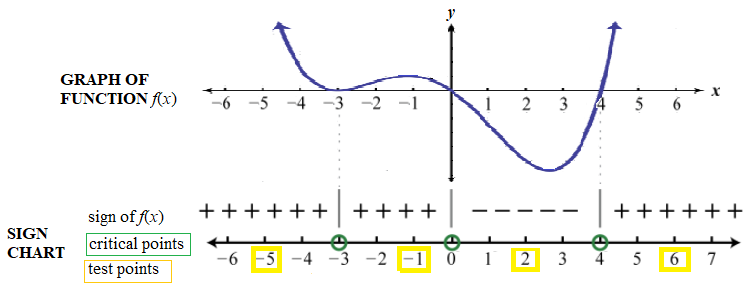
In this graph, the \(x\)-intercepts, -3, 0 and 4, are critical points , which are the only places where the graph may possibly change from being above the \(x\)-axis (where we say that \(f(x) > 0) \) ), to below the \(x\)-axis (where we say that \(f(x) < 0) \).  Within each interval between two adjacent critical points, the graph is either always above the \(x\)-axis, or always below the \(x\)-axis. Thus, finding the critical points of a polynomial inequality plays a fundamental role in solving a polynomial inequality.

• Step 1 : Rewrite the inequality so there is a zero on the right side of the inequality. The expression on the left side designate as \(f(x)\).
• Step 2 : Find the critical numbers . Critical numbers for polynomial functions are the real number solutions to \( f(x) = 0 \). Draw a number line with the critical numbers labelled. Draw an open circle at each critical number if the inequality uses "<" or ">"; draw a filled in circle at each critical number if the inequality uses " \( \le \)" or "\( \ge \)".
• Step 3 : Create a sign chart .  The critical numbers partition the number line into regions. Choose a test value for each region, including one to the left of all the critical values and one  to the right of all the critical values. For each test value, \(v\), determine if \(f(v)\) is positive or negative and record the result on the sign chart for each region.
• Step 4 : Use the sign chart to find the set of all values of \(x\) for which the inequality is true. Write the answer in interval notation.

Example \(\PageIndex{1}\)

Solve \(x(x+3)^{2}(x-4)<0\).

Step 2 . Begin by finding the critical numbers. For a polynomial inequality in standard form, with zero on one side, the critical numbers are the roots. Because \(f (x) = x(x + 3)^{2} (x − 4)\) is given in its factored form the roots are apparent. Here the roots are: \(0, −3\), and \(4\). Because of the strict inequality, plot them using open dots on a number line.

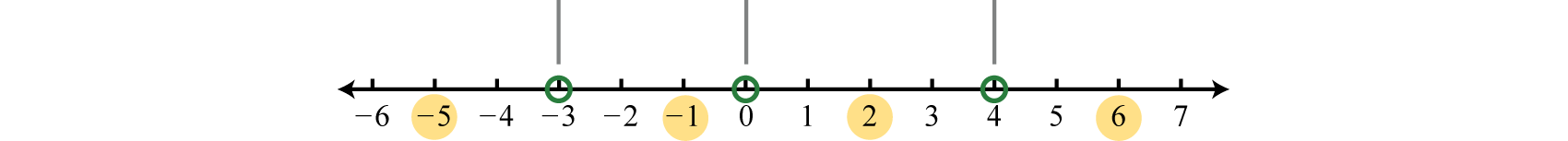
Step 3 . In this case, the critical numbers partition the number line into four regions. Test values in each region to determine if \(f\) is positive or negative. Here we choose test values \(−5, −1, 2\), and \(6\). Remember that we are only concerned with the sign \((+\) or \(−)\) of the result.

\(\begin{aligned} f(\color{OliveGreen}{-5}\color{black}{)}&=(\color{OliveGreen}{-5}\color{black}{)}(\color{OliveGreen}{-5}\color{black}{+}3)^{2}(\color{OliveGreen}{-5}\color{black}{-}4) =(-)(-)^{2}(-)&=+\color{Cerulean} { Positive} \\ f(\color{OliveGreen}{-1}\color{black}{)}&=(\color{OliveGreen}{-1}\color{black}{)}(\color{OliveGreen}{-1}\color{black}{+}3)^{2}(\color{OliveGreen}{-1}\color{black}{-}4) =(-)(+)^{2}(-)&=+\color{Cerulean} { Positive } \\ f(\color{OliveGreen}{2}\color{black}{)}&=(\color{OliveGreen}{2}\color{black}{)}(\color{OliveGreen}{2}\color{black}{+}3)^{2}(\color{OliveGreen}{2}\color{black}{-}4) =(+)(+)^{2}(-)&=-\color{Cerulean} { Negative } \\ f(\color{OliveGreen}{6}\color{black}{)}&=(\color{OliveGreen}{6}\color{black}{)}(\color{OliveGreen}{6}\color{black}{+}3)^{2}(\color{OliveGreen}{6}\color{black}{-}4) =(+)(+)^{2}(+)&=+\color{Cerulean} { Positive } \end{aligned}\)

After testing values we can complete a sign chart.

Step 4 . The question asks us to find the values where \(f (x) < 0\), or where the function is negative. From the sign chart we can see that the function is negative for \(x\)-values in between \(0\) and \(4\).

We can express this solution set in two ways:

\(\begin{aligned}\{x | 0<&x<4\} &\color{Cerulean} { Set\: notation } \\ (0,&4) &\color{Cerulean} { Interval\: notation }\end{aligned}\)

In this sectionwe will continue to present solution sets using interval notation.  Answer : \((0,4)\)

Graphs can help us to visualize solutions of polynomial inequalities. Below is the graph of the function in the above example. Compare the graph to its corresponding sign chart. Notice that the sign chart is positive when the graph is above the \(x\)-axis and negative when the graph is below the \(x\)-axis. The graph crosses or touches the \(x\)-axis at the critical points.

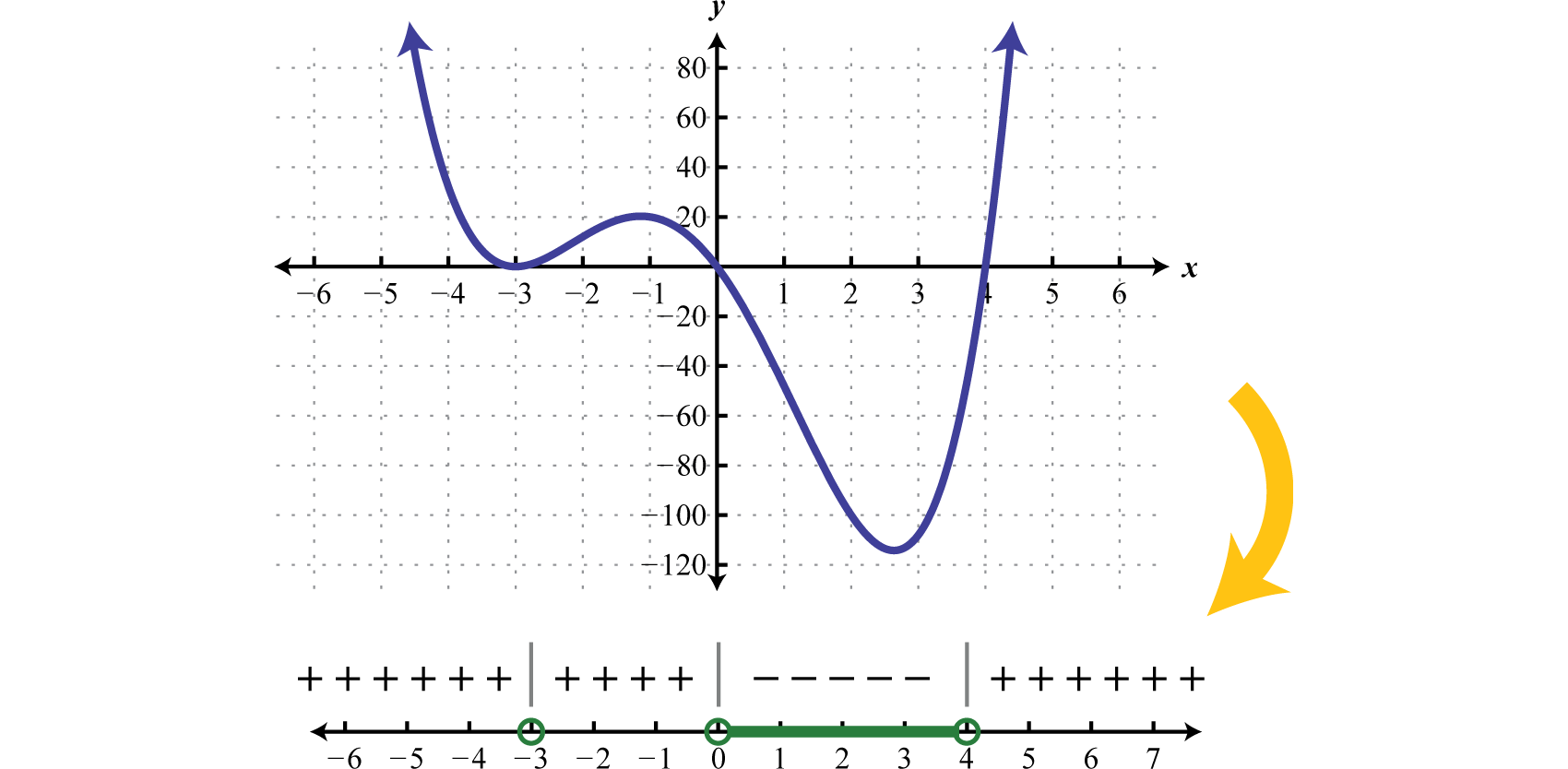
Certainly it may not be the case that the polynomial is factored nor that it has zero on one side of the inequality. To model a function using a sign chart, all of the terms should be on one side and zero on the other. The general steps for solving a polynomial inequality are listed in the following example.

Example \(\PageIndex{2}\)

Solve: \(2 x^{4}>3 x^{3}+9 x^{2} \).

Step 1 : Obtain zero on one side of the inequality. In this case, subtract to obtain a polynomial on the left side in standard form.

\(\begin{aligned}2 x^{4}&>3 x^{3}+9 x^{2} \\ 2 x^{4}-3 x^{3}-9 x^{2}&>0\end{aligned}\)

Step 2 : Find the critical numbers. Here we can find the zeros by factoring.

\(2 x^{4}-3 x^{3}-9 x^{2}=0 \) \(x^{2}\left(2 x^{2}-3 x-9\right)=0 \) \(x^{2}(2 x+3)(x-3)=0 \)

There are three solutions, hence, three critical numbers \(−\frac{3}{2}, 0\), and \(3\). The strict inequality indicates that we should use open dots.

Step 3 : Create a sign chart. In this case use \(f (x) = x^{2} (2x + 3) (x − 3) \) and test values \(−2, −1, 1\), and \(4\) to determine the sign of the function in each interval.

\(\begin{aligned} f(\color{OliveGreen}{-2}\color{black}{)} &=(\color{OliveGreen}{-2}\color{black}{)}^{2}[2(\color{OliveGreen}{-2}\color{black}{)}+3](\color{OliveGreen}{-2}\color{black}{-}3)&=(-)^{2}(-)(-)=+\\ f(\color{OliveGreen}{-1}\color{black}{)} &=(\color{OliveGreen}{-1}\color{black}{)}^{2}[2(\color{OliveGreen}{-1}\color{black}{)}+3](\color{OliveGreen}{-1}\color{black}{-}3)&=(-)^{2}(+)(-)=-\\ f(\color{OliveGreen}{1}\color{black}{)} &=(\color{OliveGreen}{1}\color{black}{)}^{2}[2(\color{OliveGreen}{1}\color{black}{)}+3](\color{OliveGreen}{1}\color{black}{-}3) &=(+)^{2}(+)(-)=-\\ f(\color{OliveGreen}{4}\color{black}{)} &=(\color{OliveGreen}{4}\color{black}{)}^{2}[2(\color{OliveGreen}{4}\color{black}{)}+3](\color{OliveGreen}{4}\color{black}{-}3) &=(+)^{2}(+)(+)=+\end{aligned}\)

With this information we can complete the sign chart.

Step 4 : Use the sign chart to answer the question. Here the solution consists of all values for which \(f (x) > 0\). Shade in the values that produce positive results and then express this set in interval notation.

Answer : \(\left(-\infty,-\frac{3}{2}\right) \cup(3, \infty)\)

Example \(\PageIndex{3}\)

Solve: \(x^{3}+x^{2} \leq 4(x+1)\).

Step 1 . Begin by rewriting the inequality in standard form, with zero on one side.

\(\begin{aligned}x^{3}+x^{2} &\leq 4(x+1) \\ x^{3}+x^{2} &\leq 4 x+4 \\ x^{3}+x^{2}-4 x-4 &\leq 0\end{aligned}\)

Step 2 . Next find the critical numbers of \(f(x)=x^{3}+x^{2}-4 x-4\):

\(\begin{aligned} x^{3}+x^{2}-4 x-4 &=0 \quad\color{Cerulean} { Factor\: by\: grouping.} \\ x^{2}(x+1)-4(x+1) &=0 \\(x+1)\left(x^{2}-4\right) &=0 \\(x+1)(x+2)(x-2) &=0 \end{aligned}\)

The critical numbers are \(−2, −1\), and \(2\). Because of the inclusive inequality \((≤)\) we will plot them using closed dots.

Step 3 . Use test values, \(-3\), \(-\frac{3}{2}\), \(0\), and \(3\) to create a sign chart.

\(\begin{aligned} f(\color{OliveGreen}{-3}\color{black}{)}&=(\color{OliveGreen}{-3}\color{black}{+}1)(\color{OliveGreen}{-3}\color{black}{+}2)(\color{OliveGreen}{-3}\color{black}{-}2) &=(-)(-)(-)=- \\ f(\color{OliveGreen}{-\frac{3}{2}}\color{black}{)}&=(\color{OliveGreen}{-\frac{3}{2}}\color{black}{+}1)(\color{OliveGreen}{-\frac{3}{2}}\color{black}{+}2)(\color{OliveGreen}{-\frac{3}{2}}\color{black}{-}2) &=(-)(+)(-)=+\\ f(\color{OliveGreen}{0}\color{black}{)}&=(\color{OliveGreen}{0}\color{black}{+}1)(\color{OliveGreen}{0}\color{black}{+}2)(\color{OliveGreen}{0}\color{black}{-}2)&=(+)(+)(-)=- \\ f(\color{OliveGreen}{3}\color{black}{)}&=(\color{OliveGreen}{3}\color{black}{+}1)(\color{OliveGreen}{3}\color{black}{+}2)(\color{OliveGreen}{3}\color{black}{-}2)&=(+)(+)(+)=+\end{aligned}\)

And we have

Step 4 . Use the sign chart to shade in the values that have negative results \((f (x) ≤ 0)\).

Answer:  \((-\infty,-2] \cup[-1,2]\)

Solve \(-3 x^{4}+12 x^{3}-9 x^{2}>0\).

Solving Rational Inequalities

A rational inequality  is a mathematical statement that relates a rational expression as either less than or greater than another. Because rational functions have restrictions to the domain we must take care when solving rational inequalities. In addition to the zeros, we will include the restrictions to the domain of the function in the set of critical numbers.

Graphs are helpful in providing a visualization to the solutions of rational inequalities. Examine the graph below to see the relationship between a graph of a rational function and its corresponding sign chart . It is very similar to the sign chart for polynomials except additionally, vertical asymptotes are included in the list of critical points.

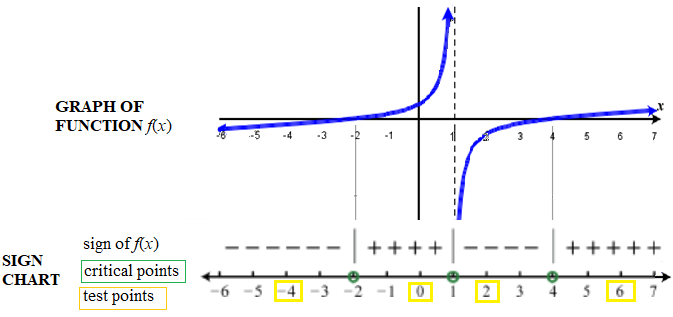
Both the x- intercepts, -2 and 4, and the vertical asymptote \(x=1\) are critical points . The vertical asymptote occurs at \(x=1\) because that is the value that makes the denominator zero, and thus makes the rational expression undefined. Again, these critical points are the only places where the graph may possibly change from being above the \(x\)-axis (where \(f(x) > 0) \) ), to below the \(x\)-axis (where  \(f(x) < 0) \).  Within each interval between two adjacent critical points, the graph is either always above the \(x\)-axis, or always below the \(x\)-axis. Thus, finding the critical points of a rational inequality plays a fundamental role in solving it.

• Step 1 : Rewrite the inequality so there is a zero on the right side of the inequality. Write the expression on the left as a single algebraic fraction. Designate this fraction as \(f(x)\). 
• Solve \(f((x)=0\). Find values that make the numerator of \(f(x)\) zero. These critical points are the \(x\)-intercepts. If the inequality uses "<" or ">", draw an open circle at each of these critical numbers; if the inequality uses " \( \le \)" or "\( \ge \)", draw a filled in circle at each of these critical numbers .
• Solve \(f((x)=undefined\). Find values that make the denominator of \(f(x)\) zero. These critical points are where the vertical asymptotes are. These values are not part of the domain of \(f(x)\). Therefore these critical values are never part of the solution set. Always draw an open circle at each of these critical numbers.
• Step 3 : Create a sign chart.  The critical numbers partition the number line into regions. Choose a test value for each region, including one to the left of all the critical values and one to the right of all the critical values. For each test value, \(v\), determine if \(f(v)\) is positive or negative and record the result on the sign chart for each region.

Example \(\PageIndex{4}\)

Solve: \(\dfrac{(x-4)(x+2)}{(x-1)} \geq 0\)

Step 2 . The zeros of a rational function occur when the numerator is zero and the values that produce zero in the denominator are the restrictions. In this case,

\(\begin{array}{c | c}{\text { Roots (Numerator) }} & {\text{Restriction(Denominator)}} \\ {x-4=0 \text { or } x+2=0} & {x-1=0} \\ { x=4 \quad\quad\quad x=-2}& {x=1}\end{array}\)

Therefore the critical numbers are \(−2, 1\), and \(4\). Because of the inclusive inequality \((≥)\) use a closed dot for the roots \({−2, 4}\) and always use an open dot for restrictions \({1}\). Restrictions are never included in the solution set.

Step 3 . Use test values \(x = −4, 0, 2, 6\).

\(\begin{aligned} f(\color{OliveGreen}{-4}\color{black}{)} &=\frac{(\color{OliveGreen}{-4}\color{black}{-}4)(\color{OliveGreen}{-4}\color{black}{+}2)}{(\color{OliveGreen}{-4}\color{black}{-}1)}&=\frac{(-)(-)}{(-)}=-\\ f(\color{OliveGreen}{0}\color{black}{)} &=\frac{(\color{OliveGreen}{0}\color{black}{-}4)(\color{OliveGreen}{0}\color{black}{+}2)}{(\color{OliveGreen}{0}\color{black}{-}1)}&=\frac{(-)(+)}{(-)}=+\\ f(\color{OliveGreen}{2}\color{black}{)} &=\frac{(\color{OliveGreen}{2}\color{black}{-}4)(\color{OliveGreen}{2}\color{black}{+}2)}{(\color{OliveGreen}{2}\color{black}{-}1)}&=\frac{(-)(+)}{(+)}=-\\ f(\color{OliveGreen}{6}\color{black}{)} &=\frac{(\color{OliveGreen}{6}\color{black}{-}4)(\color{OliveGreen}{6}\color{black}{+}2)}{(\color{OliveGreen}{6}\color{black}{-}1)}&=\frac{(+)(+)}{(+)}=+\end{aligned}\)

And then complete the sign chart.

Step 4 . The question asks us to find the values for which \(f (x) ≥ 0\), in other words, positive or zero. Shade in the appropriate regions and present the solution set in interval notation.

Answer:  \([-2,1) \cup[4, \infty)\)

Once again the graph of this function below provides a visualization of what the sign chart means. As in the case with the polynomial inequality, the sign chart is positive when the graph is above the \(x\)-axis and negative when the graph is below the \(x\)-axis.  The graph (potentially) changes from being above the \(x\)-axis to below the \(x\)-axis at the critical values. Unlike the polynomial, where critical values are only where the graph crosses or touches the \(x\)-axis, for rational functions, critical values also exist at the vertical asymptotes of the graph.

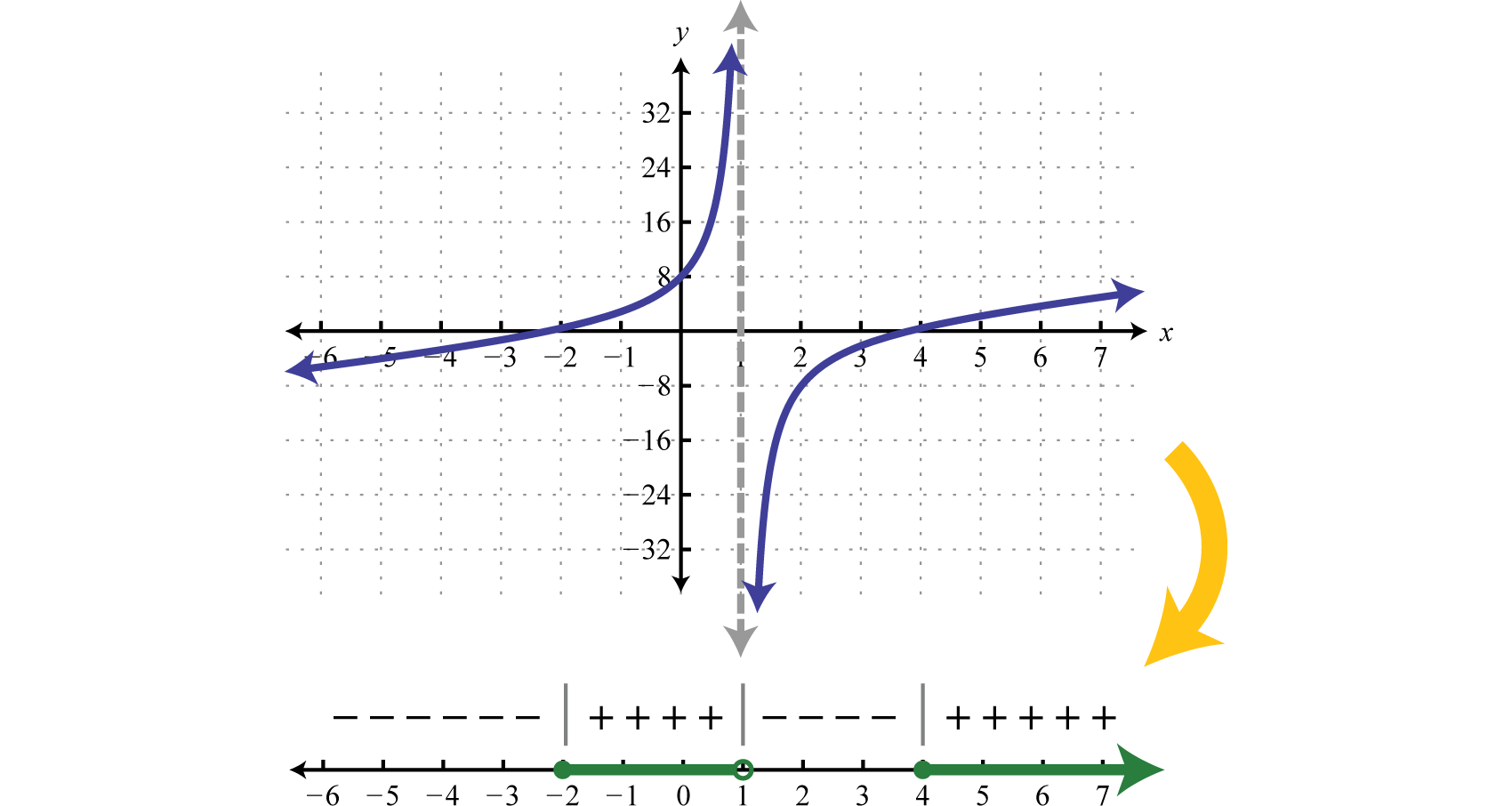
Figure 3.7.14 Rational Function with Sign Chart and Solution Set

Notice that the restriction \(x = 1\) corresponds to a vertical asymptote which bounds regions where the function changes from positive to negative. While not included in the solution set, the restriction is a critical number. Before creating a sign chart we must ensure the inequality has a zero on one side. The general steps for solving a rational inequality are outlined in the following example.

Example \(\PageIndex{5}\)

Solve \(\dfrac{7}{x+3}<2\).

Step 1 : Begin by obtaining zero on the right side.

\(\begin{aligned}\frac{7}{x+3}&<2 \\ \frac{7}{x+3}-2&<0\end{aligned}\)

Step 2 : Determine the critical numbers. The critical numbers are the zeros and restrictions. Begin by simplifying to a single algebraic fraction.

\(\begin{aligned}\frac{7}{x+3}-\frac{2}{1}&<0 \\ \frac{7-2(x+3)}{x+3}&<0 \\ \frac{7-2 x-6}{x+3}&<0 \\ \frac{-2 x+1}{x+3}&<0\end{aligned}\)

Next find the critical numbers. Set the numerator and denominator equal to zero and solve.

\(\begin{array}{c|c} {\text{Root}}&{\text{Restriction}}\\ {-2x+1=0}\\{-2x=-1}&{x+3=0}\\{x=\frac{1}{2}}&\quad\quad\:\:{x=-3} \end{array}\)

In this case, the strict inequality indicates that we should use an open dot for the root. Any restriction always uses an open dot.

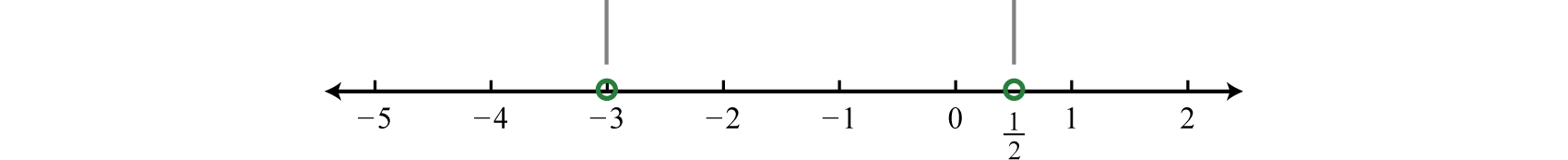
Step 3 : Create a sign chart. Choose test values \(−4, 0\), and \(1\).

\(\begin{aligned} f(\color{OliveGreen}{-4}\color{black}{)} &=\frac{-2(\color{OliveGreen}{-4}\color{black}{)}+1}{\color{OliveGreen}{-4}\color{black}{+}3}&=\frac{+}{-}=-\\ f(\color{OliveGreen}{0}\color{black}{)} &=\frac{-2(\color{OliveGreen}{0}\color{black}{)}+1}{\color{OliveGreen}{0}\color{black}{+}3}&=\frac{+}{+}=+\\ f(\color{OliveGreen}{1}\color{black}{)} &=\frac{-2(\color{OliveGreen}{1}\color{black}{)}+1}{\color{OliveGreen}{1}\color{black}{+}3}&=\frac{-}{+}=-\end{aligned}\)

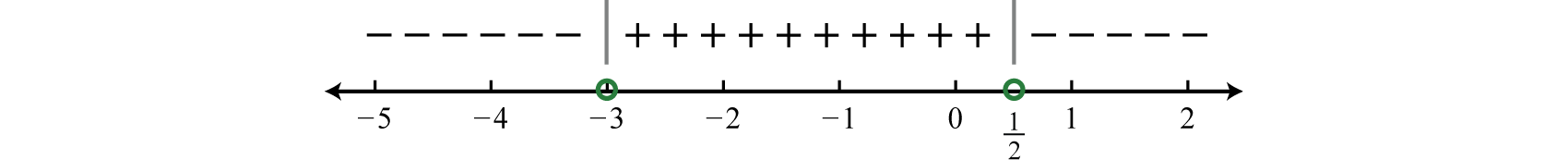
Step 4 : Use the sign chart to answer the question. In this example we are looking for the values for which the function is negative, \(f (x) < 0\). Shade the appropriate values and then present your answer using interval notation.

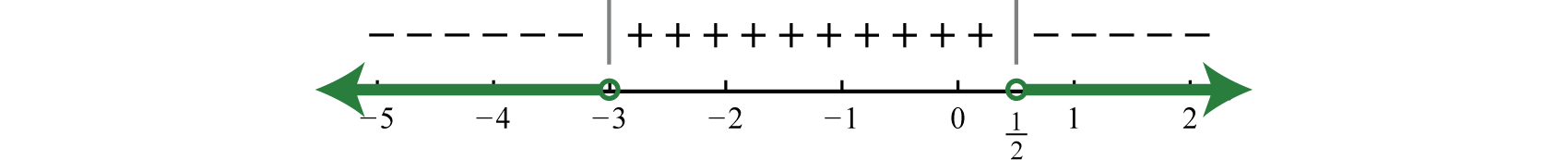
\((-\infty,-3) \cup\left(\frac{1}{2}, \infty\right)\)

Example \(\PageIndex{6}\)

Solve: \(\dfrac{1}{x^{2}-4} \leq \dfrac{1}{2-x}\).

Step 1 . Begin by obtaining zero on the right side.

\(\begin{aligned}\frac{1}{x^{2}-4} &\leq \frac{1}{2-x} \\ \frac{1}{x^{2}-4}-\frac{1}{2-x} &\leq 0\end{aligned}\)

Step 2 . Next simplify the left side to a single algebraic fraction.

\(\begin{array}{r}{\dfrac{1}{x^{2}-4}-\dfrac{1}{2-x} \leq 0} \\ {\dfrac{1}{(x+2)(x-2)}-\dfrac{1}{-(x-2)} \leq 0} \\ {\frac{1}{(x+2)(x-2)}+\frac{1\color{Cerulean}{(x+2)}}{\color{black}{(x-2)}\color{Cerulean}{(x+2)}}\color{black}{ \leq} 0} \\ {\dfrac{1+x+2}{(x+2)(x-2)} \leq 0} \\ \boxed{{f(x) = \dfrac{x+3}{(x+2)(x-2)}} \leq 0}\end{array}\)

The critical numbers are \(−3, −2\), and \(2\). Note that \(±2\) are restrictions and thus we will use open dots when plotting them on a number line. Because of the inclusive inequality we will use a closed dot at the root \(−3\).

Step 3 . Choose test values \(-4, -2\frac{1}{2} = -\frac{5}{2}, 0\), and \(3\).

\(\begin{aligned}f(\color{OliveGreen}{-4}\color{black}{)}&= \frac{\color{OliveGreen}{-4}\color{black}{+}3}{(\color{OliveGreen}{-4}\color{black}{+}2)(\color{OliveGreen}{-4}\color{black}{-}2)}&=\frac{(-)}{(-)(-)}=- \\ f(\color{OliveGreen}{-\frac{5}{2}}\color{black}{)} &= \frac{\color{OliveGreen}{-\frac{5}{2}}\color{black}{+}3}{(\color{OliveGreen}{-\frac{5}{2}}\color{black}{+}2)(\color{OliveGreen}{-\frac{5}{2}}\color{black}{-}2)}&=\frac{(+)}{(-)(-)}=+\\ f(\color{OliveGreen}{0}\color{black}{)}&=\frac{\color{OliveGreen}{0}\color{black}{+}3}{(\color{OliveGreen}{0}\color{black}{+}2)(\color{OliveGreen}{0}\color{black}{-}2)}&=\frac{(+)}{(+)(-)}=- \\ f(\color{OliveGreen}{3}\color{black}{)}&=\frac{\color{OliveGreen}{3}\color{black}{+}3}{(\color{OliveGreen}{3}\color{black}{+}2)(\color{OliveGreen}{3}\color{black}{-}2)} &=\frac{(+)}{(+)(+)}=+\end{aligned}\)

Construct a sign chart.

Step 4 . Answer the question; in this case, find \(x\) where \(f(x) \leq 0\).

Answer:  \((-\infty,-3] \cup(-2,2)\)

Solve \(\dfrac{2 x^{2}}{2 x^{2}+7 x-4} \geq \dfrac{x}{x+4}\).

\((-4,0] \cup\left(\frac{1}{2}, \infty\right)\)

Key Takeaways

• When a polynomial inequality is in standard form, with zero on one side, the roots of the polynomial are the critical numbers. Create a sign chart that models the function and then use it to answer the question.
• When a rational inequality is written as a single algebraic fraction, with zero on one side, the roots as well as the restrictions are the critical numbers. The values that produce zero in the numerator are the roots, and the values that produce zero in the denominator are the restrictions. Always use open dots for restrictions, regardless of the given inequality, because restrictions are not part of the domain. Create a sign chart that models the function and then use it to answer the question.