solving quadratic equations graphically worksheet

Solving Quadratic Equations: Worksheets with Answers

Whether you want a homework, some cover work, or a lovely bit of extra practise, this is the place for you. And best of all they all (well, most!) come with answers.

Mathster keyboard_arrow_up Back to Top

Mathster is a fantastic resource for creating online and paper-based assessments and homeworks. They have kindly allowed me to create 3 editable versions of each worksheet, complete with answers.

Corbett Maths keyboard_arrow_up Back to Top

Corbett Maths offers outstanding, original exam style questions on any topic, as well as videos, past papers and 5-a-day. It really is one of the very best websites around.

Solving Quadratics Graphically Textbook Exercise

Click here for questions, gcse revision cards.

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

In order to access this I need to be confident with:

This topic is relevant for:

Solving Quadratic Equations Graphically

Here we will learn about solving quadratic equations graphically including how to find the roots of a quadratic function from a graph, how to use this method to solve any quadratic equation by drawing a graph, and then how to solve a quadratic equation from a graph that is already drawn for you.

There are also quadratic graphs worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is solving quadratic equations graphically?

Solving quadratic equations graphically is a useful way to find estimated solutions or roots for quadratic equations or functions.

Solve x^2=6 graphically

If we plot the quadratic function y=x^{2} and the linear function y=6 on the same graph, the intersection points of the line and the curve are the solutions to the quadratic equation x^{2}=6 .

The solutions to the quadratic equation (to 1 dp) are x=-2.5, \; x=2.5 .

You can see from the graph that these intersection points aren’t at exactly x=-2.5, \; x=2.5.

These solutions are estimates. This is the main disadvantage of the graphical method – for exact solutions, we would need to use the quadratic formula or completing the square and leave answers in surd form.

Step-by-step guide: Quadratic formula

Step-by-step guide: Completing the square

What are the roots of a quadratic?

The roots of a quadratic function are the values of the x -coordinates where the function crosses the x -axis. They are sometimes called the x -intercepts.

A quadratic function will have zero, one (repeated), or two real roots.

When you solve a quadratic equation in the form ax^2+bx+c=0 , with the right-hand side equal to zero, you are finding the roots.

On this page we will look at finding roots, and then finding other solutions, using a graph.

How to solve quadratic equations graphically

In order to find the solutions of a quadratic equation using a graph:

Rearrange the equation so that one side = 0 (if necessary).

• Draw the graph of the quadratic function.

Read off the x -coordinate(s) of the point(s) where the curve crosses the x -axis.

Explain how to solve quadratic equations graphically

Quadratic graphs worksheet

Get your free quadratic graphs worksheet of 20+ questions and answers. Includes reasoning and applied questions.

Related lessons on quadratic graphs

Solving quadratic equations graphically is part of our series of lessons to support revision on types of graphs . You may find it helpful to start with the main quadratic graphs lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

• Types of graphs
• Quadratic graphs
• Sketching quadratic graphs
• Plotting quadratic graphs

Solve quadratic equations graphically examples

Example 1: a simple quadratic.

Find the solutions of the equation x^{2}-4=0 graphically

Rearrange the equation so that one side = 0 (if necessary) .

No rearrangement needed in this case.

2 Draw the graph of the quadratic function .

Write y=x^2-4 and draw the graph.

3 Read off the x -coordinate(s) of the point(s) where the curve crosses the x -axis .

The roots are x=-2 and x=2 . 

These are the solutions to the equation x^{2}-4=0

Example 2: a trinomial quadratic

Find the solutions of the equation x^{2}+6x+9=0 graphically.

Draw the graph of the quadratic function .

Write y=x^{2}+6x+9 and draw the graph.

Here we have one (repeated) root at x=-3 .

The solution to the equation x^{2}+6 x+9=0 is x=-3 .

Example 3: no real roots

Find the solutions of the equation x^{2}-2x+4=0 graphically.

Write y=x^{2}-2x+4 and draw the graph.

Step by step guide : Plotting quadratic graphs (Example 5)

This quadratic function does not cross or touch the x -axis; there are no (real) roots and therefore the equation x^{2}-2x+4=0   has no (real) solutions.

If you tried to solve the equation x^{2}-2x+4=0 using the quadratic formula, this would result in a ‘maths error’ when entered into your calculator.

You will see “no real roots” written because these equations can be solved using techniques studied in A Level Further Mathematics, so it’s not correct just to write “there are no roots”. 

Example 4: a rearrangement

Find the solutions of the equation 12+x=x^{2} graphically.

Bring the x^2 to the LHS to give 12+x-x^{2}=0

Write y=12+x-x^{2} and draw the graph.

Read off the x -coordinate(s) of the point(s) where the curve crosses the x -axis .

The roots are x=-3 and x=4 . .

These are the solutions to the equation 12+x=x^{2} .

Example 5: a rearrangement

Find the solutions (to 1 decimal place) of the equation 3-2x^{2}=4x graphically.

Bring the 4x to the LHS to give 3-2x^{2}-4x=0

Draw the graph of the quadratic function

Write y=3-2x^{2}-4x and draw the graph.

Step by step guide: Plotting quadratic graphs (Example 7)

Here, the curve doesn’t cross at integer or easy-to-read values. Give the roots as estimates; you shouldn’t try to be any more accurate than one decimal place.

The roots are x=-2.6 and x=0.6 . 

These are approximate solutions to the equation 3-2x^{2}=4x , correct to one decimal place.

Solving a quadratic equation when a graph is given

The method detailed above will always work, for any quadratic equation – you can rearrange so that one side equals 0 , plot the points and find the roots.

However, sometimes you may already have drawn a particular graph or had this given to you – this is usually the case in exam questions. In these situations, this alternative method is quicker.

In order to find solutions to a quadratic equation using a graph:

• Rearrange so that one side of the equation matches the graphed function.
• Write y = the other side of the equation and plot this function.

At the intersection points, draw vertical lines down to the x -axis to find the solutions.

Example 6: a quadratic and a horizontal line

Here is the graph of the function y=x^{2} .

Use this graph to find the solutions of the equation x^{2}=3 .

Rearrange so that one side of the equation matches the graphed function .

The equation is x^{2}=3 and the graph we’re given is of the function y=x^{2} . The LHS of the original equation already matches the RHS of the function on the graph. In this case, we don’t need to rearrange.

Write y = the other side of the equation and plot this function .

Write y=3 and plot this.

It is a horizontal line through the y -axis at 3 :

At the intersection points, draw vertical lines down to the x -axis to find the solutions .

Find the two points where the line and curve meet; we draw vertical lines down to the x -axis and read off the x -coordinate values.

These values aren’t particularly easy to read off. Give the roots as estimates; you shouldn’t try to be any more accurate than one decimal place.

We have solutions x=-1.7, \; x=1.7 , correct to 1 decimal place.

Example 7: a quadratic and line with non-zero gradient

Here is the graph of the function y=x^{2}-2x+4 .

(This is the same graph we used in Example 3).

Find the solutions of the equation x^{2}-2x+4=2x+4 graphically.

The equation is x^{2}-2x+4=2x+4 and the graph we’re given is of the function y=x^{2}-2x+4 .

The LHS of the original equation already matches the RHS of the function on the graph. In this case, we don’t need to rearrange.

Write y=2x+4 and plot this.

It is a straight line with y -intercept (0,4) and gradient 2 .

Step by step guide: Plotting linear graphs (coming soon)

We have solutions x=0, \; x=4 .

Example 8: rearrangement required

This is an example of the sort of question favoured in exams; the graph of one function is pre-drawn, and you will have to manipulate the algebra in some way in order to be able to use the graph. 

Here is the graph of the function y=x^{2}+3x+2 .

Find the solutions of the equation x^{2}+3x=-1 graphically, to 1 decimal place.

The equation is x^{2}+3x=-1 and the graph we’re given is of the function y=x^{2}+3x+2 .

These look similar; there’s an x^2 and a +3x term in both, but we need to rearrange so that the constant term is also the same, and the LHS of the equation matches the RHS of the function.

We need a +2 on the LHS of the equation, so we add 2 to both sides of the equation:

Write y=1 and plot this.

It is a horizontal line through the y -axis at 1 :

We have (estimated) solutions x=-2.6, \; x=-0.4 .

These are the solutions to the original equation, x^{2}+3x=-1 , correct to 1 decimal place.

Common misconceptions

• Drawing a pointy vertex

Make sure that the vertex of the graph is a smooth curve, not pointed:

• Forgetting to rearrange when necessary

In order to solve when you haven’t been given a graph , rearrange so that one size equals 0 , then find the roots. In order to solve when you have been given a graph , rearrange so that one side of the equation matches the function that’s been graphed.

Practice solving quadratic equations graphically questions

1. Find the solutions of the equation x^{2}-9=0 graphically.

The RHS is already 0 , so plot the function on a graph and find the roots.

2. Find the solutions of the equation x^{2}+5x+4=0 graphically.

3. Find the solutions of the equation 3 x-x^{2}+2=0 graphically to 1 decimal place.

These solutions are estimates, so give them carefully to 1 decimal place.

4. Find the solutions of the equation x^{2}-2x=5 graphically.

Rearrange so that RHS = 0 , and plot the graph of y=x^{2}-2x-5 . Give solutions to 1 decimal place.

5. Here is the graph of y=x^{2}+4 x-3 .

Use the graph to find the solutions of the equation x^{2}+4x=4 to 1 decimal place.

Rearrange the equation to get x^{2}+4x-3=1 , then draw the line y=1 on the graph given.

Read off solutions to 1 decimal place.

6. Here is the graph of y=7x-2x^{2} .

Use the graph to find the solutions of the equation 7x=2x^{2} to 1 decimal place.

Rearrange the equation to get 7x-2x^{2}=0 .

Because RHS = 0 , you can just read off the roots on the x -axis.

7. Here is the graph of y=2x^{2}+x-3 .

Use the graph to find the solutions of the equation 2x^{2}-x=10 to 1 decimal place.

Rearrange the equation to get x^{2}+x-3=2 x+7 .

Read off the x values where the line and curve intersect.

Solving quadratic equations graphically GCSE questions

1. Here is the graph of y=6x-x^{2}

(a) Use the graph to write down the roots of the equation 6x-x^{2}=0

(b) Use the graph to find the solutions of the equation 6x-x^{2}=3 , correct to 1 decimal place.

Indication of reading x -intercept values/roots

x=0, \; x=6

Line y=3 drawn on graph

Indication of reading coordinates of intersection points

x=0.6, \; x=5.5

2. Here is the graph of y=x^{2}-4x+2

Use the graph to find approximate roots of the equation x^{2}+2=4x

Indication of reading x -intercept values

x=0.6,\; x=3.4

3.    (a) Complete the table of values for y=x^{2}+2x-6

(b) On the grid draw the graph of y=x^{2}+2x-6 for values of x from -4 to 2 .

(c) Use the graph to find estimates of the solutions to the equation -2=x^{2}+2x-6 .

(d) Use the graph to find solutions to the equation x^{2}+2x=3 .

Points plotted correctly ft. pt (a)

Points joined with a smooth curve

Line y=-2 drawn on graph

x=-3.2, \; x=1.2

Rearrange x^{2}+2 x=3 to x^{2}+2 x-6=-3

Line y=-3 drawn on graph

x=-3, \; x=1

Learning checklist

You have now learned how to:

• Find the roots of a quadratic function graphically
• Find approximate solutions to quadratic equations using a graph

The next lessons are:

• Factorising
• Solving equations

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Privacy Overview

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

10.5: Graphing Quadratic Equations

• Last updated
• Save as PDF
• Page ID 15196

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

By the end of this section, you will be able to:

• Recognize the graph of a quadratic equation in two variables
• Find the axis of symmetry and vertex of a parabola
• Find the intercepts of a parabola
• Graph quadratic equations in two variables
• Solve maximum and minimum applications

Be Prepared

Before you get started, take this readiness quiz.

• Graph the equation \(y=3x−5\) by plotting points. If you missed this problem, review [link] .
• Evaluate \(2x^2+4x−1\)when \(x=−3\) If you missed this problem, review [link] .
• Evaluate \(−\frac{b}{2a}\) when \(a=13\) and b=\(\frac{5}{6}\) If you missed this problem, review [link] .

Recognize the Graph of a Quadratic Equation in Two Variables

We have graphed equations of the form \(Ax+By=C\). We called equations like this linear equations because their graphs are straight lines.

Now, we will graph equations of the form \(y=ax^2+bx+c\). We call this kind of equation a quadratic equation in two variables .

definition: QUADRATIC EQUATION IN TWO VARIABLES

A quadratic equation in two variables , where a,b,and c are real numbers and \(a\neq 0\), is an equation of the form \[y=ax^2+bx+c \nonumber\]

Just like we started graphing linear equations by plotting points, we will do the same for quadratic equations.

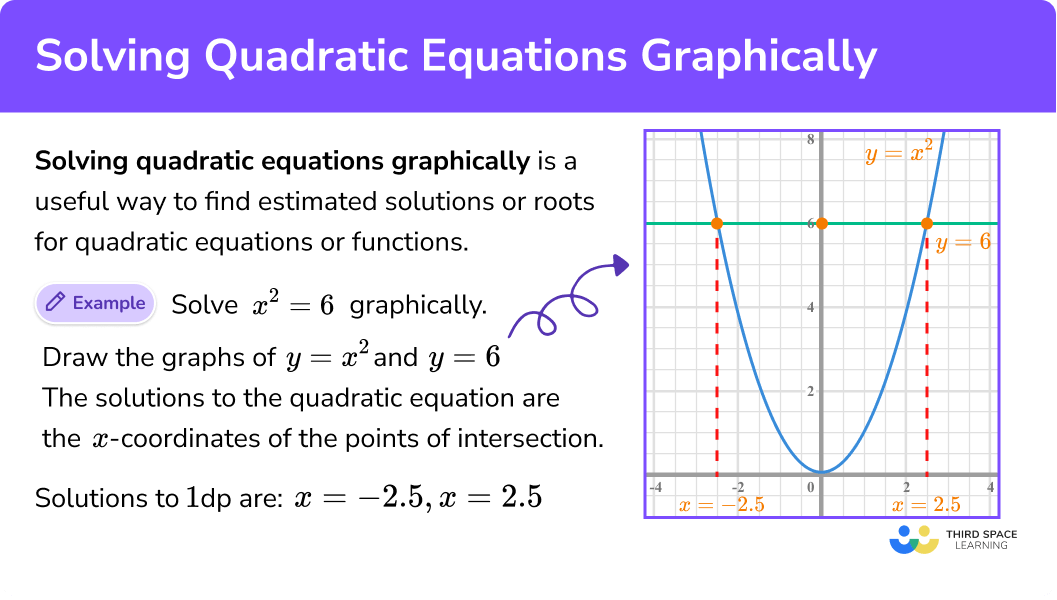
Let’s look first at graphing the quadratic equation \(y=x^2\). We will choose integer values of x between −2 and 2 and find their y values. See Table .

Notice when we let \(x=1\) and \(x=−1\), we got the same value for y.

\[\begin{array} {ll} {y=x^2} &{y=x^2} \\ {y=1^2} &{y=(−1)^2} \\ {y=1} &{y=1} \\ \nonumber \end{array}\]

The same thing happened when we let \(x=2\) and \(x=−2\).

Now, we will plot the points to show the graph of \(y=x^2\). See Figure .

The graph is not a line. This figure is called a parabola . Every quadratic equation has a graph that looks like this.

In Example you will practice graphing a parabola by plotting a few points.

Example \(\PageIndex{1}\)

\(y=x^2-1\)

We will graph the equation by plotting points.

Example \(\PageIndex{2}\)

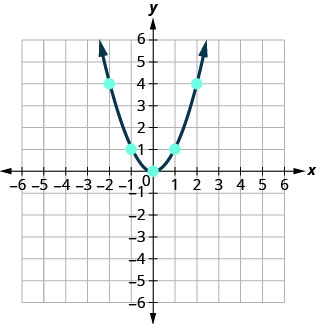
Graph \(y=−x^2\).

Example \(\PageIndex{3}\)

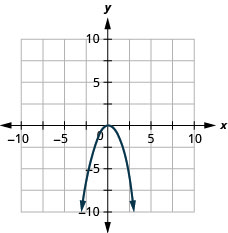
Graph \(y=x^2+1\).

How do the equations \(y=x^2\) and \(y=x^2−1\) differ? What is the difference between their graphs? How are their graphs the same?

All parabolas of the form \(y=ax^2+bx+c\) open upwards or downwards. See Figure .

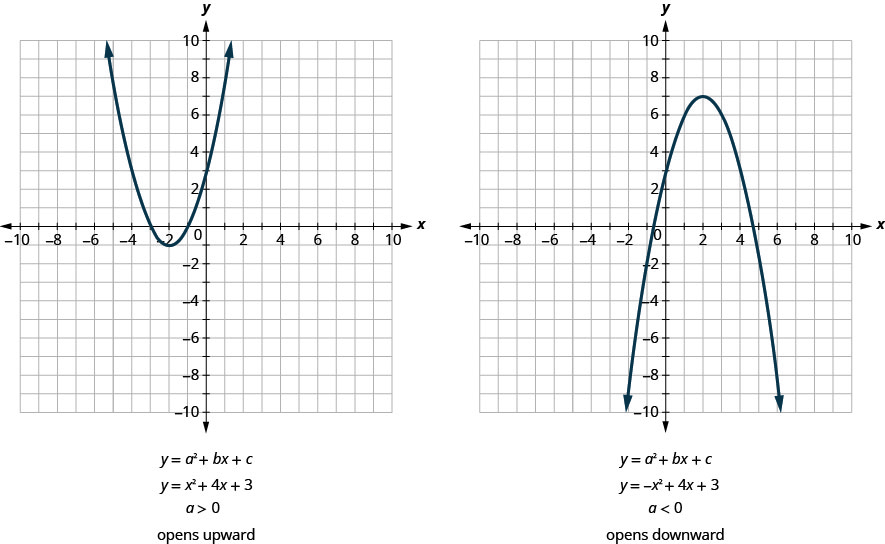
Notice that the only difference in the two equations is the negative sign before the \(x^2\) in the equation of the second graph in Figure . When the \(x^2\) term is positive, the parabola opens upward, and when the \(x^2\) term is negative, the parabola opens downward.

Definition: PARABOLA ORIENTATION

For the quadratic equation \(y=ax^2+bx+c\), if:

Example\(\PageIndex{4}\)

Determine whether each parabola opens upward or downward:

• \(y=−3x^2+2x−4\)
• \( y=6x^2+7x−9\)

Example\(\PageIndex{5}\)

• \(y=2x^2+5x−2\)
• \(y=−3x^2−4x+7\)

Example \(\PageIndex{6}\)

• \(y=−2x^2−2x−3\)
• \(y=5x^2−2x−1\)

Find the Axis of Symmetry and Vertex of a Parabola

Look again at Figure . Do you see that we could fold each parabola in half and that one side would lie on top of the other? The ‘fold line’ is a line of symmetry. We call it the axis of symmetry of the parabola.

We show the same two graphs again with the axis of symmetry in red. See Figure .

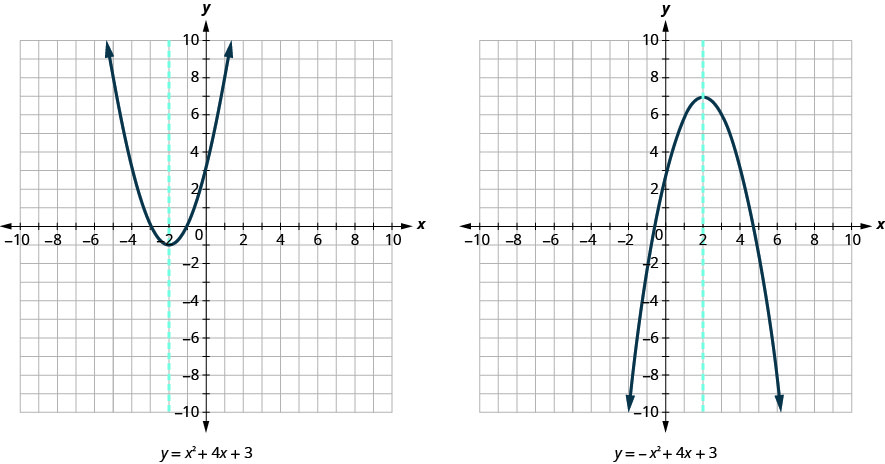
The equation of the axis of symmetry can be derived by using the Quadratic Formula. We will omit the derivation here and proceed directly to using the result. The equation of the axis of symmetry of the graph of \(y=ax^2+bx+c\) is x=\(−\frac{b}{2a}\).

So, to find the equation of symmetry of each of the parabolas we graphed above, we will substitute into the formula x=\(−\frac{b}{2a}\).

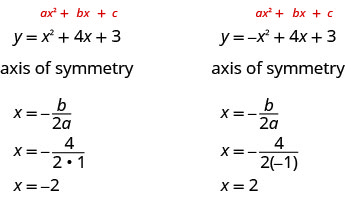
The point on the parabola that is on the axis of symmetry is the lowest or highest point on the parabola, depending on whether the parabola opens upwards or downwards. This point is called the vertex of the parabola.

We can easily find the coordinates of the vertex, because we know it is on the axis of symmetry. This means its x -coordinate is \(−\frac{b}{2a}\). To find the y -coordinate of the vertex, we substitute the value of the x -coordinate into the quadratic equation.

Definition: AXIS OF SYMMETRY AND VERTEX OF A PARABOLA

For a parabola with equation \(y=ax^2+bx+c\):

• The axis of symmetry of a parabola is the line x=\(−\frac{b}{2a}\).
• The vertex is on the axis of symmetry, so its x -coordinate is \(−\frac{b}{2a}\).

To find the y -coordinate of the vertex, we substitute x=\(−\frac{b}{2a}\) into the quadratic equation.

Example\(\PageIndex{7}\)

For the parabola \(y=3x^2−6x+2\) find:

• the axis of symmetry and
• the vertex.

Example \(\PageIndex{8}\)

For the parabola \(y=2x^2−8x+1\) find:

• (2,−7)

Example \(\PageIndex{9}\)

For the parabola \(y=2x^2−4x−3\) find:

• (1,−5)

Find the Intercepts of a Parabola

When we graphed linear equations, we often used the x - and y -intercepts to help us graph the lines. Finding the coordinates of the intercepts will help us to graph parabolas, too.

Remember, at the y -intercept the value of x is zero. So, to find the y -intercept, we substitute x=0 into the equation.

Let’s find the y -intercepts of the two parabolas shown in the figure below.

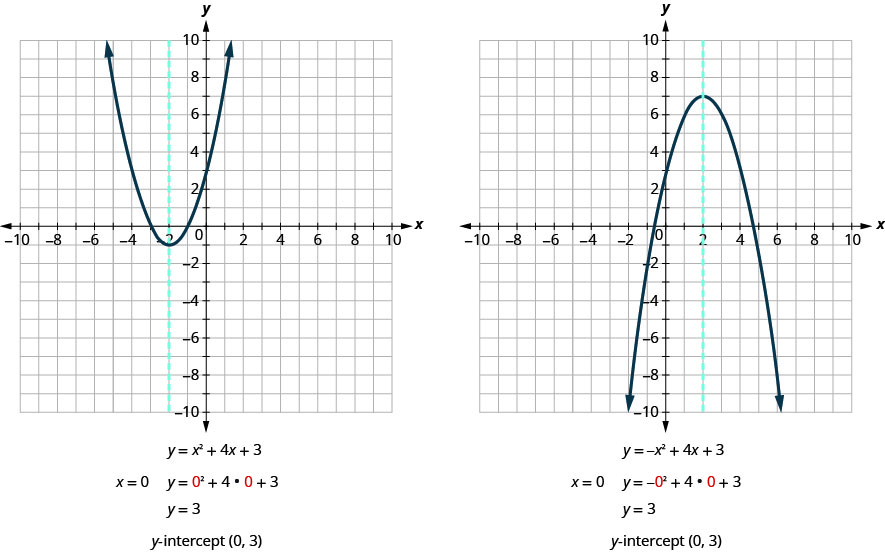
At an x -intercept , the value of y is zero. To find an x -intercept, we substitute \(y=0\) into the equation. In other words, we will need to solve the equation \(0=ax^2+bx+c\) for x.

\[\begin{array} {ll} {y=ax^2+bx+c} \\ {0=ax^2+bx+c} \\ \nonumber \end{array}\]

But solving quadratic equations like this is exactly what we have done earlier in this chapter.

We can now find the x -intercepts of the two parabolas shown in Figure .

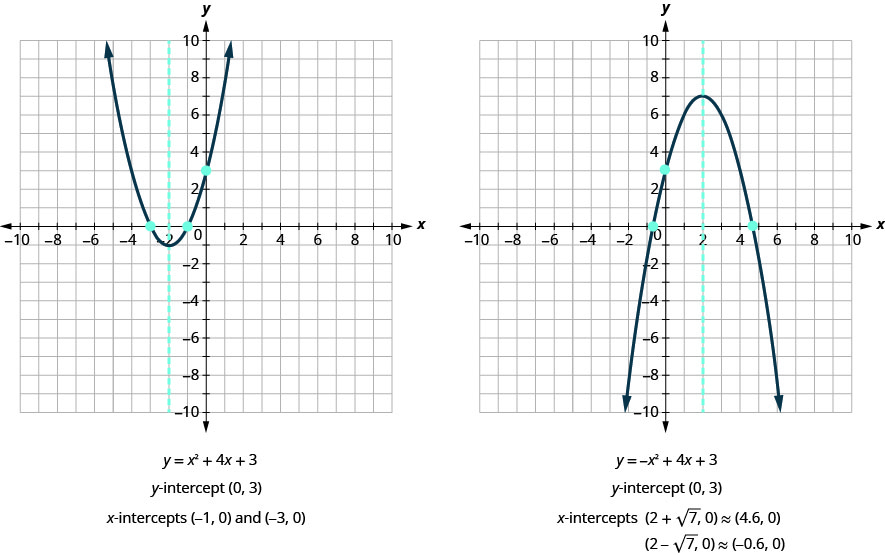
First, we will find the x -intercepts of a parabola with equation \(y=x^2+4x+3\).

Now, we will find the x -intercepts of the parabola with equation \(y=−x^2+4x+3\).

We will use the decimal approximations of the x-intercepts, so that we can locate these points on the graph.

\[\begin{array} {l} {(2+\sqrt{7},0) \approx (4.6,0)} & {(2−\sqrt{7},0) \approx (-0.6,0)}\\ \nonumber \end{array}\]

Do these results agree with our graphs? See Figure .

Definition: FIND THE INTERCEPTS OF A PARABOLA

To find the intercepts of a parabola with equation \(y=ax^2+bx+c\):

\[\begin{array}{ll} {\textbf{y-intercept}}& {\textbf{x-intercept}}\\ {\text{Let} x=0 \text{and solve the y}}& {\text{Let} y=0 \text{and solve the x}}\\ \nonumber \end{array}\]

Example \(\PageIndex{10}\)

Find the intercepts of the parabola \(y=x^2−2x−8\).

Example \(\PageIndex{11}\)

Find the intercepts of the parabola \(y=x^2+2x−8\).

y:(0,−8); x:(−4,0), (2,0)

Example \(\PageIndex{12}\)

Find the intercepts of the parabola \(y=x^2−4x−12\).

y:(0,−12); x:(6,0), (−2,0)

In this chapter, we have been solving quadratic equations of the form \(ax^2+bx+c=0\). We solved for xx and the results were the solutions to the equation.

We are now looking at quadratic equations in two variables of the form \(y=ax^2+bx+c\). The graphs of these equations are parabolas. The x -intercepts of the parabolas occur where y=0.

For example:

\[\begin{array}{cc} {\textbf{Quadratic equation}}&{\textbf{Quadratic equation in two variable}}\\ {}&{y=x^2−2x−15}\\ {x^2−2x−15}&{\text{Let} y=0, 0=x^2−2x−15}\\ {(x−5)(x+3)=0}&{0=(x−5)(x+3)}\\ {x−5=0, x+3=0}&{x−5=0, x+3=0}\\ {x=5, x=−3}&{x=5, x=−3}\\ {}&{(5,0) \text{and} (−3,0)}\\ {}&{\text{x-intercepts}}\\ \end{array}\]

The solutions of the quadratic equation are the x values of the x -intercepts.

Earlier, we saw that quadratic equations have 2, 1, or 0 solutions. The graphs below show examples of parabolas for these three cases. Since the solutions of the equations give the x -intercepts of the graphs, the number of x -intercepts is the same as the number of solutions.

Previously, we used the discriminant to determine the number of solutions of a quadratic equation of the form \(ax^2+bx+c=0\). Now, we can use the discriminant to tell us how many x -intercepts there are on the graph.

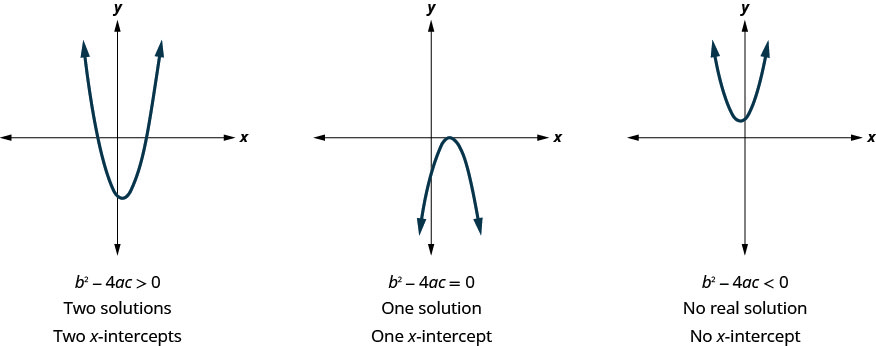
Before you start solving the quadratic equation to find the values of the x -intercepts, you may want to evaluate the discriminant so you know how many solutions to expect.

Example \(\PageIndex{13}\)

Find the intercepts of the parabola \(y=5x^2+x+4\).

Example \(\PageIndex{14}\)

Find the intercepts of the parabola \(y=3x^2+4x+4\).

y:(0,4); x:none

Example \(\PageIndex{15}\)

Find the intercepts of the parabola \(y=x^2−4x−5\).

y:(0,−5); x:(5,0)(−1,0)

Example \(\PageIndex{16}\)

Find the intercepts of the parabola \(y=4x^2−12x+9\).

Example \(\PageIndex{17}\)

Find the intercepts of the parabola \(y=−x^2−12x−36.\).

y:(0,−36); x:(−6,0)

Example \(\PageIndex{18}\)

Find the intercepts of the parabola \(y=9x^2+12x+4\).

y:(0,4); x:\((−\frac{2}{3},0)\)

Graph Quadratic Equations in Two Variables

Now, we have all the pieces we need in order to graph a quadratic equation in two variables. We just need to put them together. In the next example, we will see how to do this.

How To Graph a Quadratic Equation in Two Variables

Example \(\PageIndex{19}\)

Graph \(y=x2−6x+8\).

Example \(\PageIndex{20}\)

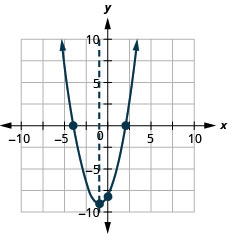
Graph the parabola \(y=x^2+2x−8\).

y:(0,−8); x:(2,0),(−4,0); axis: x=−1; vertex: (−1,−9);

Example \(\PageIndex{21}\)

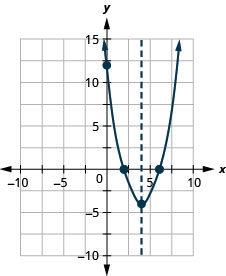
Graph the parabola \(y=x^2−8x+12\).

y:(0,12); x:(2,0),(6,0); axis: x=4; vertex:(4,−4);

Definition: GRAPH A QUADRATIC EQUATION IN TWO VARIABLES.

• Write the quadratic equation with yy on one side.
• Determine whether the parabola opens upward or downward.
• Find the axis of symmetry.
• Find the vertex.
• Find the y -intercept. Find the point symmetric to the y -intercept across the axis of symmetry.
• Find the x -intercepts.
• Graph the parabola.

We were able to find the x -intercepts in the last example by factoring. We find the x -intercepts in the next example by factoring, too.

Example \(\PageIndex{22}\)

Graph \(y=−x^2+6x−9\).

Example \(\PageIndex{23}\)

Graph the parabola \(y=−3x^2+12x−12\).

y:(0,−12); x:(2,0); axis: x=2; vertex:(2,0);

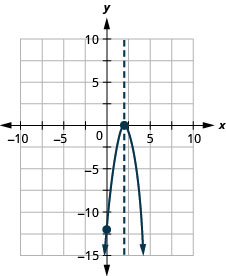
Example \(\PageIndex{24}\)

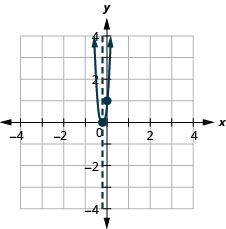
Graph the parabola \(y=25x^2+10x+1\).

y:(0,1); x:(−15,0); axis: x=−15; vertex:(−15,0);

For the graph of \(y=−x^2+6x−9\) the vertex and the x -intercept were the same point. Remember how the discriminant determines the number of solutions of a quadratic equation? The discriminant of the equation \(0=−x^2+6x−9\) is 0, so there is only one solution. That means there is only one x -intercept, and it is the vertex of the parabola.

How many x -intercepts would you expect to see on the graph of \(y=x^2+4x+5\)?

Example \(\PageIndex{25}\)

Graph \(y=x^2+4x+5\).

Example \(\PageIndex{26}\)

Graph the parabola \(y=2x^2−6x+5\).

y:(0,5); x:none; axis: \(x=\frac{3}{2}\); vertex:\((\frac{3}{2},\frac{1}{2})\);

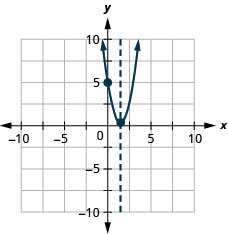
Example \(\PageIndex{27}\)

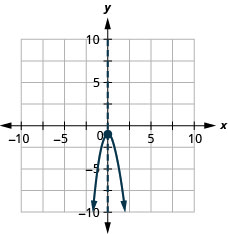
Graph the parabola \(y=−2x^2−1\).

y:(0,−1); x:none; axis: x=0; vertex:(0,−1);

Finding the y -intercept by substituting x=0 into the equation is easy, isn’t it? But we needed to use the Quadratic Formula to find the x -intercepts in Example . We will use the Quadratic Formula again in the next example.

Example \(\PageIndex{28}\)

Graph \(y=2x^2−4x−3\).

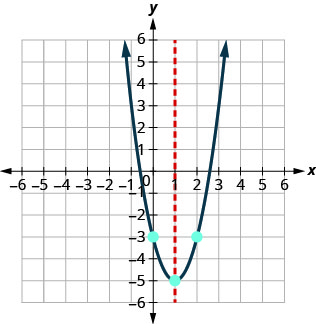
Example \(\PageIndex{29}\)

Graph the parabola \(y=5x^2+10x+3\).

y:(0,3); x:(−1.6,0),(−0.4,0); axis: x=−1; vertex:(−1,−2);

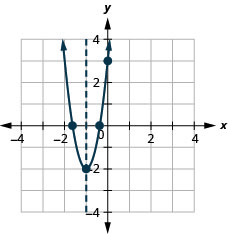
Example \(\PageIndex{30}\)

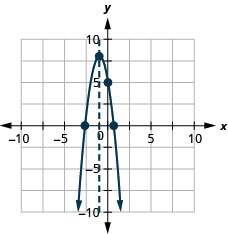
Graph the parabola \(y=−3x^2−6x+5\).

y:(0,5); x:(0.6,0),(−2.6,0); axis: x=−1; vertex:(−1,8);

Solve Maximum and Minimum Applications

Knowing that the vertex of a parabola is the lowest or highest point of the parabola gives us an easy way to determine the minimum or maximum value of a quadratic equation. The y -coordinate of the vertex is the minimum y -value of a parabola that opens upward. It is the maximum y -value of a parabola that opens downward. See Figure .

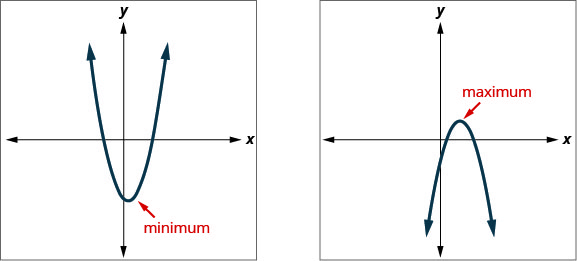
Definition: MINIMUM OR MAXIMUM VALUES OF A QUADRATIC EQUATION

The y -coordinate of the vertex of the graph of a quadratic equation is the

• minimum value of the quadratic equation if the parabola opens upward.
• maximum value of the quadratic equation if the parabola opens downward.

Example \(\PageIndex{31}\)

Find the minimum value of the quadratic equation \(y=x^2+2x−8\).

Example \(\PageIndex{32}\)

Find the maximum or minimum value of the quadratic equation \(y=x^2−8x+12\).

The minimum value is −4 when x=4.

Example \(\PageIndex{33}\)

Find the maximum or minimum value of the quadratic equation \(y=−4x^2+16x−11\).

The maximum value is 5 when x=2.

We have used the formula

\[\begin{array} {l} {h=−16t^2+v_{0}t+h_{0}}\\ \nonumber \end{array}\]

to calculate the height in feet, h, of an object shot upwards into the air with initial velocity, \(v_{0}\), after t seconds.

This formula is a quadratic equation in the variable tt, so its graph is a parabola. By solving for the coordinates of the vertex, we can find how long it will take the object to reach its maximum height. Then, we can calculate the maximum height.

Example \(\PageIndex{34}\)

The quadratic equation \(h=−16t^2+v_{0}t+h_{0}\) models the height of a volleyball hit straight upwards with velocity 176 feet per second from a height of 4 feet.

• How many seconds will it take the volleyball to reach its maximum height?
• Find the maximum height of the volleyball.

\(h=−16t^2+176t+4\)

Since a is negative, the parabola opens downward.

The quadratic equation has a maximum.

1. \[\begin{array} {ll} {}&{t=−\frac{b}{2a}}\\ {\text{Find the axis of symmetry.}}& {t=−\frac{176}{2(−16)}}\\ {}&{t=5.5}\\ {}&{\text{The axis of symmetry is} t = 5.5}\\ {\text{The vertex is on the line} t=5.5}& {\text{The maximum occurs when} t =5.5 \text{seconds.}}\\ \nonumber \end{array}\]

Example \(\PageIndex{35}\)

The quadratic equation \(h=−16t^2+128t+32\) is used to find the height of a stone thrown upward from a height of 32 feet at a rate of 128 ft/sec. How long will it take for the stone to reach its maximum height? What is the maximum height? Round answers to the nearest tenth.

It will take 4 seconds to reach the maximum height of 288 feet.

Example \(\PageIndex{36}\)

A toy rocket shot upward from the ground at a rate of 208 ft/sec has the quadratic equation of \(h=−16t^2+208t\). When will the rocket reach its maximum height? What will be the maximum height? Round answers to the nearest tenth.

It will take 6.5 seconds to reach the maximum height of 676 feet.

• Graphing Quadratic Functions
• How do you graph a quadratic function?
• Graphing Quadratic Equations

Key Concepts

• The graph of every quadratic equation is a parabola.
• a>0, the parabola opens upward.
• a<0, the parabola opens downward.
• The axis of symmetry of a parabola is the line \(x=−\frac{b}{2a}\).
• To find the y -coordinate of the vertex we substitute \(x=−\frac{b}{2a}\) into the quadratic equation.
• Find the Intercepts of a Parabola To find the intercepts of a parabola with equation \(y=ax^2+bx+c\): \[\begin{array} {ll} {\textbf{y-intercept}}&{\textbf{x-intercepts}}\\ {\text{Let} x=0 \text{and solve for y}}&{\text{Let} y=0 \text{and solve for x}}\\ \nonumber \end{array}\]
• The y - coordinate of the vertex of the graph of a quadratic equation is the

Graphing Quadratic Functions Worksheets

Graphing quadratic functions is an important concept from a mathematical point of view. Just as linear equations are represented by a straight line, quadratic equations are represented by a parabola on the graph. The nature of the parabola can give us a lot of information regarding the particular quadratic equation, like the number of real roots it has, the range of values it can take, etc. The graphing quadratic functions worksheets developed by Cuemath is one of the best resources one can have to clarify this concept.

Benefits of Graphing Quadratic Functions Worksheets

Cuemath experts developed a set of graphing quadratic functions worksheets that contain many solved examples as well as questions. Students will know how to plot parabolic graphs of quadratic equations and extract information from them.

Download Graphing Quadratic Functions Worksheet PDFs

These math worksheets should be practiced regularly and are free to download in PDF formats.

Child Login

• Kindergarten
• Number charts
• Skip Counting
• Place Value
• Number Lines
• Subtraction
• Multiplication
• Word Problems
• Comparing Numbers
• Ordering Numbers
• Odd and Even
• Prime and Composite
• Roman Numerals
• Ordinal Numbers
• In and Out Boxes
• Number System Conversions
• More Number Sense Worksheets
• Size Comparison
• Measuring Length
• Metric Unit Conversion
• Customary Unit Conversion
• Temperature
• More Measurement Worksheets
• Writing Checks
• Profit and Loss
• Simple Interest
• Compound Interest
• Tally Marks
• Mean, Median, Mode, Range
• Mean Absolute Deviation
• Stem-and-leaf Plot
• Box-and-whisker Plot
• Permutation and Combination
• Probability
• Venn Diagram
• More Statistics Worksheets
• Shapes - 2D
• Shapes - 3D
• Lines, Rays and Line Segments
• Points, Lines and Planes
• Transformation
• Quadrilateral
• Ordered Pairs
• Midpoint Formula
• Distance Formula
• Parallel, Perpendicular and Intersecting Lines
• Scale Factor
• Surface Area
• Pythagorean Theorem
• More Geometry Worksheets
• Converting between Fractions and Decimals
• Significant Figures
• Convert between Fractions, Decimals, and Percents
• Proportions
• Direct and Inverse Variation
• Order of Operations
• Squaring Numbers
• Square Roots
• Scientific Notations
• Speed, Distance, and Time
• Absolute Value
• More Pre-Algebra Worksheets
• Translating Algebraic Phrases
• Evaluating Algebraic Expressions
• Simplifying Algebraic Expressions
• Algebraic Identities
• Quadratic Equations
• Systems of Equations
• Polynomials
• Inequalities
• Sequence and Series
• Complex Numbers
• More Algebra Worksheets
• Trigonometry
• Math Workbooks
• English Language Arts
• Summer Review Packets
• Social Studies
• Holidays and Events
• Worksheets >
• Algebra >
• Functions >
• Quadratic >

Graphing Quadratic Function Worksheets

Use this ensemble of printable worksheets to assess student's cognition of Graphing Quadratic Functions. This webpage comprises a variety of topics like identifying zeros from the graph, writing quadratic function of the parabola, graphing quadratic function by completing the function table, identifying various properties of a parabola, and a plethora of MCQs. This forms an excellent resource for students of high school. Access some of these worksheets for free!

Printing Help - Please do not print graphing quadratic function worksheets directly from the browser. Kindly download them and print.

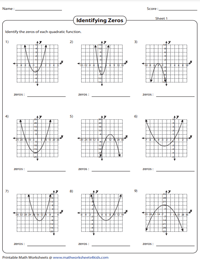
Identifying Zeros

Each pdf worksheet has nine problems identifying zeros from the graph. Read the parabola and locate the x-intercepts. x-intercepts of a parabola are the zeros of the quadratic function.

• Download the set

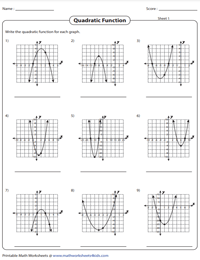
Write the Quadratic Functions

This set of printable worksheets requires high school students to write the quadratic function using the information provided in the graph. If the x-intercepts are known from the graph, apply intercept form to find the quadratic function. If the vertex and a point on the parabola are known, apply vertex form.

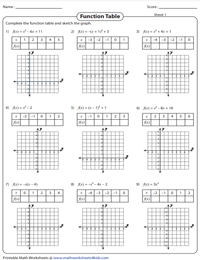
Graphing Quadratic Function: Function Tables

Complete each function table by substituting the values of x in the given quadratic function to find f(x). Plot the points on the grid and graph the quadratic function. The graph results in a curve called a parabola; that may be either U-shaped or inverted.

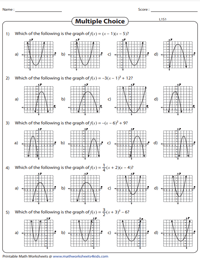
Graph of a Quadratic Function: MCQs | Level 1

Gain a competitive edge over your peers by solving this set of multiple-choice questions, where learners are required to identify the correct graph that represents the given quadratic function provided in vertex form or intercept form.

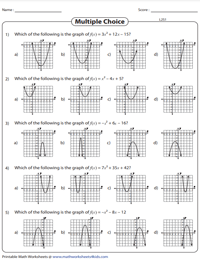
Graph of a Quadratic Function: MCQs | Level 2

Stocked with 15 MCQs, this resource is designed by math experts to seamlessly align with CCSS. Get students to convert the standard form of a quadratic function to vertex form or intercept form using factorization or completing the square method and then choose the correct graph from the given options.

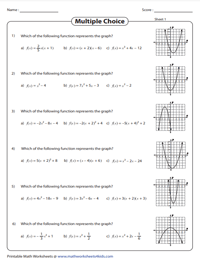
Quadratic Function of the Graph: MCQs

These high school pdf worksheets are based on identifying the correct quadratic function for the given graph. Students should collect the necessary information like zeros, y-intercept, vertex etc. From the graph to identify the quadratic function.

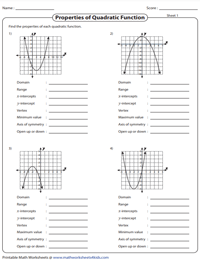
Properties of Quadratic Function From the Graph

Read each graph and list down the properties of quadratic function. Algebra learners are required to find the domain, range, x-intercepts, y-intercept, vertex, minimum or maximum value, axis of symmetry and open up or down. There are four graphs in each worksheet.

Related Worksheets

» Quadratic Transformation

» Graphing Linear Function

» Graphs

Become a Member

Membership Information

Privacy Policy

What's New?

Printing Help

Testimonial

Copyright © 2024 - Math Worksheets 4 Kids

This is a members-only feature!

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: Algebra 1   >   Unit 14

• Finding the vertex of a parabola in standard form

Graphing quadratics: standard form

• Graph quadratics in standard form
• Quadratic word problem: ball
• Quadratic word problems (standard form)

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

Quadratic Equation Worksheets (pdfs)

Free worksheets with answer keys.

Enjoy these free sheets. Each one has model problems worked out step by step, practice problems, as well as challenge questions at the sheets end. Plus each one comes with an answer key.

• Solve Quadratic Equations by Factoring
• Solve Quadratic Equations by Completing the Square
• Quadratic Formula Worksheet (real solutions)
• Quadratic Formula Worksheet (complex solutions)
• Quadratic Formula Worksheet (both real and complex solutions)
• Discriminant Worksheet
• Sum and Product of Roots
• Radical Equations Worksheet

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

• International
• Schools directory
• Resources Jobs Schools directory News Search

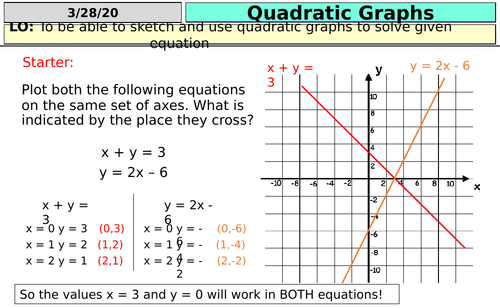
Quadratic Graphs (KS4)

Subject: Mathematics

Age range: 14-16

Resource type: Lesson (complete)

Last updated

28 March 2020

• Share through email
• Share through twitter
• Share through linkedin
• Share through facebook
• Share through pinterest

I made the presentation made using different sources. Slides template is inspired by https://www.tes.com/teaching-resources/shop/cparkinson3

Worksheets are not mine and are from another author https://www.tes.com/member/mariomonte40

Creative Commons "Sharealike"

Your rating is required to reflect your happiness.

It's good to leave some feedback.

Something went wrong, please try again later.

cparkinson3

Excellent resource. Thank you for crediting on the slide template. Not many do and just freely copy and brand as their own. It is appreciated!

Empty reply does not make any sense for the end user

Very good! Thank you.

Super!!!! Thank so much.

Nellyprasad

very good resources. thank you

nazish_khaalid

Thanks for the feedback :)

Report this resource to let us know if it violates our terms and conditions. Our customer service team will review your report and will be in touch.

Not quite what you were looking for? Search by keyword to find the right resource: