taylor and laurent series solved problems

Laurent’s Series

In Mathematics, Laurent’s series expansion is considered to be an essential tool in complex analysis. Laurent’s series helps us to work around the singularities of the complex function. In this article, let us discuss the definition, formulas, difference between the Taylor series and Laurent’s series with solved examples in detail.

Table of Contents:

• Convergence

Difference Between Taylor and Laurent Series

What is laurent’s series.

Laurent’s series, also known as Laurent’s expansion, of a complex function f(z) is defined as a representation of that function in terms of power series that includes the terms of negative degree. Laurent’s series was first published by Pierre Alphonse Laurent in 1843.

Laurent’s Series Formula

Assume that f(z) is analytic on the annulus (i.e.,) A: r 1 < | z- z 0 | < r 2 , then f(z) is expressed in terms of series is:

Here the coefficients a n and b n have the following formulas:

γ can be any circle | w – z 0 | = r, inside the annulus. It means, r 1 < r < r 2 .

From the series, we can also say,

• \(\begin{array}{l}\sum_{n=0}^{\infty }a_{n}(z-z_{0})^{n} \text{ converges to the analytic function, when} |z-z_{0}| < r_{2}.\end{array} \)
• \(\begin{array}{l}\sum_{n=1}^{\infty }\frac{b_{n}}{(z-z_{0})^{n}}\text{ converges to the analytic function, when} |z-z_{0}| > r_{1}.\end{array} \)

Thus, together both series converges on the annulus (A), where f is analytic.

Note: It should be noted that as f(z) may not be analytic (even defined) at z 0 , there exists no such formulas for the coefficients using derivatives.

The below diagram represents the contour used to prove the formulas of Laurent’s series:

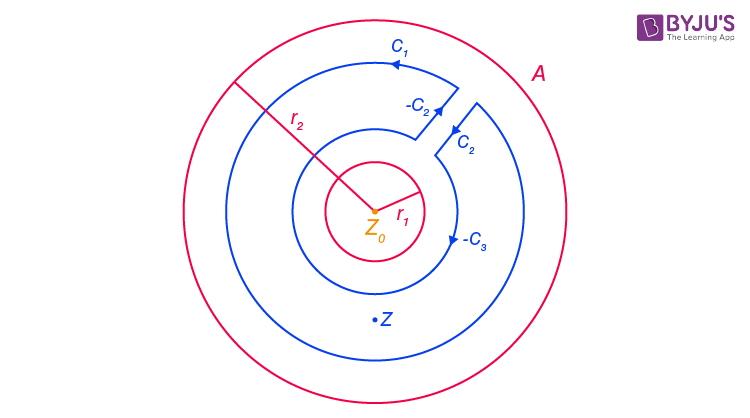
Laurent’s Series Convergence

The Laurent’s series converges on the open annulus A ≡ {z : r 1 < |z − z 0 | < r 2 }. In other words, the Laurent series converges, when both the positive and negative degree of the power series converges. Also, the Laurent series convergence should be uniform for compact sets. Hence, we can say that the convergent series will define the holomorphic function on open annulus.

The following are the major differences between Taylor and Laurent Series:

Laurent Series Solved Examples

Determine the Laurent series for the function, f(z) = (z+1)/z around z 0 = 0. Also, define the region where the function is valid.

Given function, f(z) = (z+1)/z

The given function can be written as:

f(z) = (z/z) + (1/z)

f(z) = 1+(1/z)

Hence, f(z) = 1+ (1/z) is the Laurent series, which is valid on the infinite region 0 < |z| < ∞.

Compute the Laurent series for the function f(z) = z / [z 2 + 1] around z 0 = i. Give the region where the function is valid. Also, determine the principal part of the Laurent series.

Using the partial fraction, the above function can be written as:

As 1/(z+i) is analytic at z = i, it should have Taylor expansion and it can be found using the geometric series.

Therefore, the Laurent series is

As we know, the principal part is given by the first term.

And, the region of convergence is 0 < |z − i| < 2.

Note: The function f(z) on the region 2 < |z − i| < ∞ will produce a different Laurent series.

Frequently Asked Questions on Laurent’s Series

Laurent’s Series is used to express the complex function when the Taylor series cannot be applied. Laurent’s series can be used if a function f(z) is not analytic at a point, but the function is analytic around neighbourhood.

Are Laurent’s series and Taylor’s series the same?

The power series which consists of only positive power terms is called the Taylor series, whereas the power series containing the negative power terms is called Laurent’s series.

Which portion is considered to be the principal part of Laurent’s series?

In Laurent’s series, the portion that consists of terms with the negative degree is called the singular or the principal part of Laurent’s series.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

HIGH SCHOOL

• ACT Tutoring
• SAT Tutoring
• PSAT Tutoring
• ASPIRE Tutoring
• SHSAT Tutoring
• STAAR Tutoring

GRADUATE SCHOOL

• MCAT Tutoring
• GRE Tutoring
• LSAT Tutoring
• GMAT Tutoring
• AIMS Tutoring
• HSPT Tutoring
• ISAT Tutoring
• SSAT Tutoring

Search 50+ Tests

Loading Page

math tutoring

• Elementary Math
• Pre-Calculus
• Trigonometry

science tutoring

Foreign languages.

• Mandarin Chinese

elementary tutoring

• Computer Science

Search 350+ Subjects

• Video Overview
• Tutor Selection Process
• Online Tutoring
• Mobile Tutoring
• Instant Tutoring
• How We Operate
• Our Guarantee
• Impact of Tutoring
• Reviews & Testimonials
• Media Coverage
• About Varsity Tutors

Complex Analysis : Taylor and Laurent Series

Study concepts, example questions & explanations for complex analysis, all complex analysis resources, example questions, example question #1 : taylor and laurent series.

It is well known (can be shown by the definition) that that

Making the appropriate substitutions

Shifting the index of summation gives us

Taylor Series expansion of the numerator and the denominator seperately gives us

A term by term multiplication gives us

Combining like terms 

Report an issue with this question

If you've found an issue with this question, please let us know. With the help of the community we can continue to improve our educational resources.

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC 101 S. Hanley Rd, Suite 300 St. Louis, MO 63105

Or fill out the form below:

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• x^{2}-x-6=0
• -x+3\gt 2x+1
• line\:(1,\:2),\:(3,\:1)
• prove\:\tan^2(x)-\sin^2(x)=\tan^2(x)\sin^2(x)
• \frac{d}{dx}(\frac{3x+9}{2-x})
• (\sin^2(\theta))'
• \lim _{x\to 0}(x\ln (x))
• \int e^x\cos (x)dx
• \int_{0}^{\pi}\sin(x)dx
• \sum_{n=0}^{\infty}\frac{3}{2^n}

step-by-step

laurent series

• My Notebook, the Symbolab way Math notebooks have been around for hundreds of years. You write down problems, solutions and notes to go back...

Please add a message.

Message received. Thanks for the feedback.

Power Series: Problem Sets

Problem set: taylor and maclaurin series.

In the following exercises, find the Taylor polynomials of degree two approximating the given function centered at the given point.

2.  [latex]f\left(x\right)=1+x+{x}^{2}[/latex] at [latex]a=-1[/latex]

Show Solution

4.  [latex]f\left(x\right)=\sin\left(2x\right)[/latex] at [latex]a=\frac{\pi }{2}[/latex]

6.  [latex]f\left(x\right)=\text{ln}x[/latex] at [latex]a=1[/latex]

8.  [latex]f\left(x\right)={e}^{x}[/latex] at [latex]a=1[/latex]

In the following exercises, verify that the given choice of n in the remainder estimate [latex]|{R}_{n}|\le \frac{M}{\left(n+1\right)\text{!}}{\left(x-a\right)}^{n+1}[/latex], where M is the maximum value of [latex]|{f}^{\left(n+1\right)}\left(z\right)|[/latex] on the interval between a and the indicated point, yields [latex]|{R}_{n}|\le \frac{1}{1000}[/latex]. Find the value of the Taylor polynomial p n of [latex]f[/latex] at the indicated point.

10. [T] [latex]{\left(28\right)}^{\frac{1}{3}};a=27,n=1[/latex]

12. [T] e 2 ; [latex]a=0,n=9[/latex]

13. [T] [latex]\cos\left(\frac{\pi }{5}\right);a=0,n=4[/latex]

14. [T] [latex]\text{ln}\left(2\right);a=1,n=1000[/latex]

16.  Integrate the approximation [latex]{e}^{x}\approx 1+x+\frac{{x}^{2}}{2}+\cdots+\frac{{x}^{6}}{720}[/latex] evaluated at − x 2 to approximate [latex]{\displaystyle\int }_{0}^{1}{e}^{\text{-}{x}^{2}}dx[/latex].

[latex]=1-\frac{{1}^{3}}{3}+\frac{{1}^{5}}{10}-\frac{{1}^{7}}{42}+\frac{{1}^{9}}{9\cdot 24}-\frac{{1}^{11}}{120\cdot 11}+\frac{{1}^{13}}{720\cdot 13}\approx 0.74683[/latex] whereas [latex]{\displaystyle\int }_{0}^{1}{e}^{\text{-}{x}^{2}}dx\approx 0.74682[/latex].

In the following exercises, find the smallest value of n such that the remainder estimate [latex]|{R}_{n}|\le \frac{M}{\left(n+1\right)\text{!}}{\left(x-a\right)}^{n+1}[/latex], where M is the maximum value of [latex]|{f}^{\left(n+1\right)}\left(z\right)|[/latex] on the interval between a and the indicated point, yields [latex]|{R}_{n}|\le \frac{1}{1000}[/latex] on the indicated interval.

18.  [latex]f\left(x\right)=\cos{x}[/latex] on [latex]\left[-\frac{\pi }{2},\frac{\pi }{2}\right],a=0[/latex]

20.  [latex]f\left(x\right)={e}^{\text{-}x}[/latex] on [latex]\left[-3,3\right],a=0[/latex]

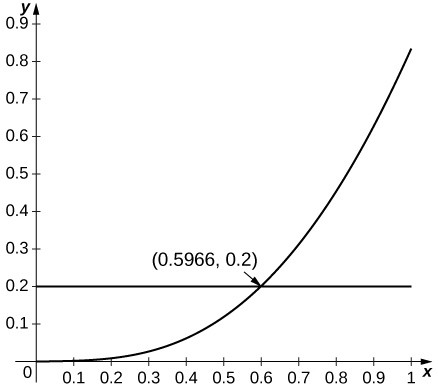
In the following exercises, the maximum of the right-hand side of the remainder estimate [latex]|{R}_{1}|\le \frac{\text{max}|f\text{''}\left(z\right)|}{2}{R}^{2}[/latex] on [latex]\left[a-R,a+R\right][/latex] occurs at a or [latex]a\pm R[/latex]. Estimate the maximum value of R such that [latex]\frac{\text{max}|f\text{''}\left(z\right)|}{2}{R}^{2}\le 0.1[/latex] on [latex]\left[a-R,a+R\right][/latex] by plotting this maximum as a function of R .

22. [T] [latex]\sin{x}[/latex] approximated by x , [latex]a=0[/latex]

24. [T] [latex]\cos{x}[/latex] approximated by [latex]1,a=0[/latex]

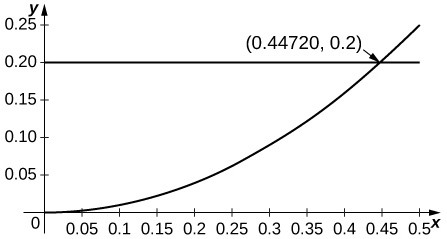
In the following exercises, find the Taylor series of the given function centered at the indicated point.

26.  [latex]1+x+{x}^{2}+{x}^{3}[/latex] at [latex]a=-1[/latex]

28.  [latex]\cos{x}[/latex] at [latex]a=2\pi [/latex]

30.  [latex]\cos{x}[/latex] at [latex]x=\frac{\pi }{2}[/latex]

32.  [latex]{e}^{x}[/latex] at [latex]a=1[/latex]

34.  [latex]\frac{1}{{\left(x - 1\right)}^{3}}[/latex] at [latex]a=0[/latex]

In the following exercises, compute the Taylor series of each function around [latex]x=1[/latex].

36.  [latex]f\left(x\right)=2-x[/latex]

38.  [latex]f\left(x\right)={\left(x - 2\right)}^{2}[/latex]

40.  [latex]f\left(x\right)=\frac{1}{x}[/latex]

42.  [latex]f\left(x\right)=\frac{x}{4x - 2{x}^{2}-1}[/latex]

44.  [latex]f\left(x\right)={e}^{2x}[/latex]

[T] In the following exercises, identify the value of x such that the given series [latex]\displaystyle\sum _{n=0}^{\infty }{a}_{n}[/latex] is the value of the Maclaurin series of [latex]f\left(x\right)[/latex] at [latex]x[/latex]. Approximate the value of [latex]f\left(x\right)[/latex] using [latex]{S}_{10}=\displaystyle\sum _{n=0}^{10}{a}_{n}[/latex].

46.  [latex]\displaystyle\sum _{n=0}^{\infty }\frac{{2}^{n}}{n\text{!}}[/latex]

48.  [latex]\displaystyle\sum _{n=0}^{\infty }\frac{{\left(-1\right)}^{n}{\left(2\pi \right)}^{2n+1}}{\left(2n+1\right)\text{!}}[/latex]

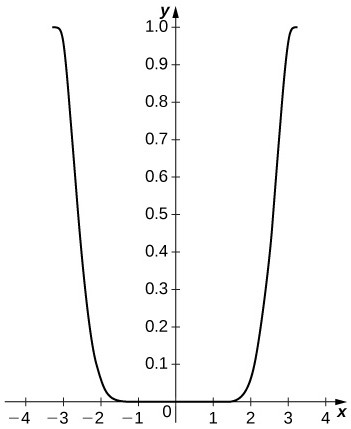
The following exercises make use of the functions [latex]{S}_{5}\left(x\right)=x-\frac{{x}^{3}}{6}+\frac{{x}^{5}}{120}[/latex] and [latex]{C}_{4}\left(x\right)=1-\frac{{x}^{2}}{2}+\frac{{x}^{4}}{24}[/latex] on [latex]\left[\text{-}\pi ,\pi \right][/latex].

50. [T] Plot [latex]{\cos}^{2}x-{\left({C}_{4}\left(x\right)\right)}^{2}[/latex] on [latex]\left[\text{-}\pi ,\pi \right][/latex]. Compare the maximum difference with the square of the Taylor remainder estimate for [latex]\cos{x}[/latex].

52. [T] Compare [latex]\frac{{S}_{5}\left(x\right)}{{C}_{4}\left(x\right)}[/latex] on [latex]\left[-1,1\right][/latex] to [latex]\tan{x}[/latex]. Compare this with the Taylor remainder estimate for the approximation of [latex]\tan{x}[/latex] by [latex]x+\frac{{x}^{3}}{3}+\frac{2{x}^{5}}{15}[/latex].

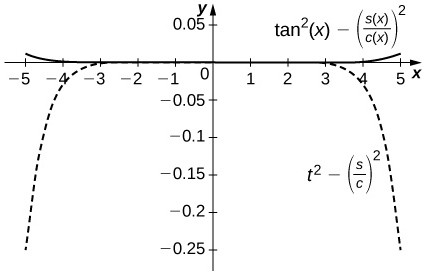
54.  (Taylor approximations and root finding.) Recall that Newton’s method [latex]{x}_{n+1}={x}_{n}-\frac{f\left({x}_{n}\right)}{f\prime \left({x}_{n}\right)}[/latex] approximates solutions of [latex]f\left(x\right)=0[/latex] near the input [latex]{x}_{0}[/latex].

• If [latex]f[/latex] and [latex]g[/latex] are inverse functions, explain why a solution of [latex]g\left(x\right)=a[/latex] is the value [latex]f\left(a\right)\text{of}f[/latex].
• Let [latex]{p}_{N}\left(x\right)[/latex] be the [latex]N\text{th}[/latex] degree Maclaurin polynomial of [latex]{e}^{x}[/latex]. Use Newton’s method to approximate solutions of [latex]{p}_{N}\left(x\right)-2=0[/latex] for [latex]N=4,5,6[/latex].
• Explain why the approximate roots of [latex]{p}_{N}\left(x\right)-2=0[/latex] are approximate values of [latex]\text{ln}\left(2\right)[/latex].

In the following exercises, use the fact that if [latex]q\left(x\right)=\displaystyle\sum _{n=1}^{\infty }{a}_{n}{\left(x-c\right)}^{n}[/latex] converges in an interval containing [latex]c[/latex], then [latex]\underset{x\to c}{\text{lim}}q\left(x\right)={a}_{0}^{}[/latex] to evaluate each limit using Taylor series.

56.  [latex]\underset{x\to 0}{\text{lim}}\frac{\text{ln}\left(1-{x}^{2}\right)}{{x}^{2}}[/latex]

58.  [latex]\underset{x\to {0}^{+}}{\text{lim}}\frac{\cos\left(\sqrt{x}\right)-1}{2x}[/latex]

• Calculus Volume 2. Authored by : Gilbert Strang, Edwin (Jed) Herman. Provided by : OpenStax. Located at : https://openstax.org/books/calculus-volume-2/pages/1-introduction . License : CC BY-NC-SA: Attribution-NonCommercial-ShareAlike . License Terms : Access for free at https://openstax.org/books/calculus-volume-2/pages/1-introduction

Privacy Policy

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.4: Taylor and Maclaurin Series

• Last updated
• Save as PDF
• Page ID 42137

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Describe the procedure for finding a Taylor polynomial of a given order for a function.
• Explain the meaning and significance of Taylor’s theorem with remainder.
• Estimate the remainder for a Taylor series approximation of a given function.

In the previous two sections we discussed how to find power series representations for certain types of functions––specifically, functions related to geometric series. Here we discuss power series representations for other types of functions. In particular, we address the following questions: Which functions can be represented by power series and how do we find such representations? If we can find a power series representation for a particular function \(f\) and the series converges on some interval, how do we prove that the series actually converges to \(f\)?

Overview of Taylor/Maclaurin Series

Consider a function \(f\) that has a power series representation at \(x=a\). Then the series has the form

\[\sum_{n=0}^∞c_n(x−a)^n=c_0+c_1(x−a)+c_2(x−a)^2+ \dots. \label{eq1} \]

What should the coefficients be? For now, we ignore issues of convergence, but instead focus on what the series should be, if one exists. We return to discuss convergence later in this section. If the series Equation \ref{eq1} is a representation for \(f\) at \(x=a\), we certainly want the series to equal \(f(a)\) at \(x=a\). Evaluating the series at \(x=a\), we see that

\[\sum_{n=0}^∞c_n(x−a)^n=c_0+c_1(a−a)+c_2(a−a)^2+\dots=c_0.\label{eq2} \]

Thus, the series equals \(f(a)\) if the coefficient \(c_0=f(a)\). In addition, we would like the first derivative of the power series to equal \(f′(a)\) at \(x=a\). Differentiating Equation \ref{eq2} term-by-term, we see that

\[\dfrac{d}{dx}\left( \sum_{n=0}^∞c_n(x−a)^n \right)=c_1+2c_2(x−a)+3c_3(x−a)^2+\dots.\label{eq3} \]

Therefore, at \(x=a,\) the derivative is

\[\dfrac{d}{dx}\left( \sum_{n=0}^∞c_n(x−a)^n \right)=c_1+2c_2(a−a)+3c_3(a−a)^2+\dots=c_1.\label{eq4} \]

Therefore, the derivative of the series equals \(f′(a)\) if the coefficient \(c_1=f′(a).\) Continuing in this way, we look for coefficients \(c_n\) such that all the derivatives of the power series Equation \ref{eq4} will agree with all the corresponding derivatives of \(f\) at \(x=a\). The second and third derivatives of Equation \ref{eq3} are given by

\[\dfrac{d^2}{dx^2} \left(\sum_{n=0}^∞c_n(x−a)^n \right)=2c_2+3⋅2c_3(x−a)+4⋅3c_4(x−a)^2+\dots\label{eq5} \]

\[\dfrac{d^3}{dx^3} \left( \sum_{n=0}^∞c_n(x−a)^n \right)=3⋅2c_3+4⋅3⋅2c_4(x−a)+5⋅4⋅3c_5(x−a)^2+⋯.\label{eq6} \]

Therefore, at \(x=a\), the second and third derivatives

\[\dfrac{d^2}{dx^2} \left(\sum_{n=0}^∞c_n(x−a)^n\right)=2c_2+3⋅2c_3(a−a)+4⋅3c_4(a−a)^2+\dots=2c_2\label{eq7} \]

\[\dfrac{d^3}{dx^3} \left(\sum_{n=0}^∞c_n(x−a)^n\right)=3⋅2c_3+4⋅3⋅2c_4(a−a)+5⋅4⋅3c_5(a−a)^2+\dots =3⋅2c_3\label{eq8} \]

equal \(f''(a)\) and \(f'''(a)\), respectively, if \(c_2=\dfrac{f''(a)}{2}\) and \(c_3=\dfrac{f'''(a)}{3⋅2}\). More generally, we see that if \(f\) has a power series representation at \(x=a\), then the coefficients should be given by \(c_n=\dfrac{f^{(n)}(a)}{n!}\). That is, the series should be

\[\sum_{n=0}^∞\dfrac{f^{(n)}(a)}{n!}(x−a)^n=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+\dfrac{f'''(a)}{3!}(x−a)^3+⋯ \nonumber \]

This power series for \(f\) is known as the Taylor series for \(f\) at \(a.\) If \(x=0\), then this series is known as the Maclaurin series for \(f\).

Definition \(\PageIndex{1}\): Maclaurin and Taylor series

If \(f\) has derivatives of all orders at \(x=a\), then the Taylor series for the function \(f\) at \(a\) is

\[\sum_{n=0}^∞\dfrac{f^{(n)}(a)}{n!}(x−a)^n=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n+⋯ \nonumber \]

The Taylor series for \(f\) at 0 is known as the Maclaurin series for \(f\).

Later in this section, we will show examples of finding Taylor series and discuss conditions under which the Taylor series for a function will converge to that function. Here, we state an important result. Recall that power series representations are unique. Therefore, if a function \(f\) has a power series at \(a\), then it must be the Taylor series for \(f\) at \(a\).

Uniqueness of Taylor Series

If a function \(f\) has a power series at a that converges to \(f\) on some open interval containing \(a\), then that power series is the Taylor series for \(f\) at \(a\).

The proof follows directly from that discussed previously.

To determine if a Taylor series converges, we need to look at its sequence of partial sums. These partial sums are finite polynomials, known as Taylor polynomials.

Taylor Polynomials

The \(n^{\text{th}}\) partial sum of the Taylor series for a function \(f\) at \(a\) is known as the \(n^{\text{th}}\)-degree Taylor polynomial. For example, the 0 th , 1 st , 2 nd , and 3 rd partial sums of the Taylor series are given by

\[\begin{align*} p_0(x) &=f(a) \\[4pt] p_1(x) &=f(a)+f′(a)(x−a) \\[4pt]p_2(x) &=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2\ \\[4pt]p_3(x) &=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+\dfrac{f'''(a)}{3!}(x−a)^3 \end{align*}\]

respectively. These partial sums are known as the 0 th , 1 st , 2 nd , and 3 rd degree Taylor polynomials of \(f\) at \(a\), respectively. If \(x=a\), then these polynomials are known as Maclaurin polynomials for \(f\). We now provide a formal definition of Taylor and Maclaurin polynomials for a function \(f\).

Definition \(\PageIndex{2}\): Maclaurin polynomial

If \(f\) has \(n\) derivatives at \(x=a\), then the \(n^{\text{th}}\)-degree Taylor polynomial of \(f\) at \(a\) is

\[p_n(x)=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+\dfrac{f'''(a)}{3!}(x−a)^3+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n. \nonumber \]

The \(n^{\text{th}}\)-degree Taylor polynomial for \(f\) at \(0\) is known as the \(n^{\text{th}}\)-degree Maclaurin polynomial for \(f\).

We now show how to use this definition to find several Taylor polynomials for \(f(x)=\ln x\) at \(x=1\).

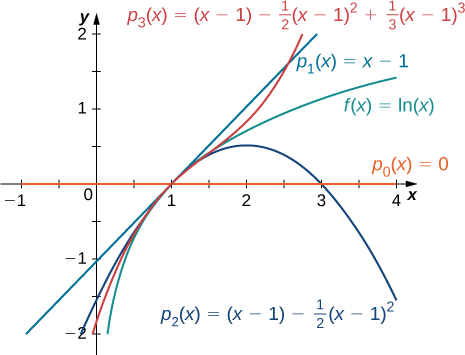
Example \(\PageIndex{1}\): Finding Taylor Polynomials

Find the Taylor polynomials \(p_0,p_1,p_2\) and \(p_3\) for \(f(x)=\ln x\) at \(x=1\). Use a graphing utility to compare the graph of \(f\) with the graphs of \(p_0,p_1,p_2\) and \(p_3\).

To find these Taylor polynomials, we need to evaluate \(f\) and its first three derivatives at \(x=1\).

\[\begin{align*} f(x)&=\ln x & f(1)&=0\\[5pt] f′(x)&=\dfrac{1}{x} & f′(1)&=1\\[5pt] f''(x)&=−\dfrac{1}{x^2} & f''(1)&=−1\\[5pt] f'''(x)&=\dfrac{2}{x^3} & f'''(1)&=2\end{align*}\]

\[\begin{align*} p_0(x) &= f(1)=0,\\[4pt]p_1(x) &=f(1)+f′(1)(x−1) =x−1,\\[4pt]p_2(x) &=f(1)+f′(1)(x−1)+\dfrac{f''(1)}{2}(x−1)^2 = (x−1)−\dfrac{1}{2}(x−1)^2 \\[4pt]p_3(x) &=f(1)+f′(1)(x−1)+\dfrac{f''(1)}{2}(x−1)^2+\dfrac{f'''(1)}{3!}(x−1)^3=(x−1)−\dfrac{1}{2}(x−1)^2+\dfrac{1}{3}(x−1)^3 \end{align*}\]

The graphs of \(y=f(x)\) and the first three Taylor polynomials are shown in Figure \(\PageIndex{1}\).

Exercise \(\PageIndex{1}\)

Find the Taylor polynomials \(p_0,p_1,p_2\) and \(p_3\) for \(f(x)=\dfrac{1}{x^2}\) at \(x=1\).

Find the first three derivatives of \(f\) and evaluate them at \(x=1.\)

\[ \begin{align*} p_0(x)&=1\\[5pt] p_1(x)&=1−2(x−1)\\[5pt] p_2(x)&=1−2(x−1)+3(x−1)^2\\[5pt] p_3(x)&=1−2(x−1)+3(x−1)^2−4(x−1)^3\end{align*}\]

We now show how to find Maclaurin polynomials for \(e^x, \sin x,\) and \(\cos x\). As stated above, Maclaurin polynomials are Taylor polynomials centered at zero.

Example \(\PageIndex{2}\): Finding Maclaurin Polynomials

For each of the following functions, find formulas for the Maclaurin polynomials \(p_0,p_1,p_2\) and \(p_3\). Find a formula for the \(n^{\text{th}}\)-degree Maclaurin polynomial and write it using sigma notation. Use a graphing utility to compare the graphs of \(p_0,p_1,p_2\) and \(p_3\) with \(f\).

• \(f(x)=e^x\)
• \(f(x)=\sin x\)
• \(f(x)=\cos x\)

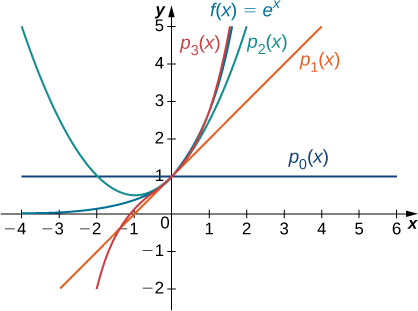
Since \(f(x)=e^x\),we know that \(f(x)=f′(x)=f''(x)=⋯=f^{(n)}(x)=e^x\) for all positive integers \(n\). Therefore,

\[f(0)=f′(0)=f''(0)=⋯=f^{(n)}(0)=1 \nonumber \]

for all positive integers \(n\). Therefore, we have

\(\begin{align*} p_0(x)&=f(0)=1,\\[5pt] p_1(x)&=f(0)+f′(0)x=1+x,\\[5pt] p_2(x)&=f(0)+f′(0)x+\dfrac{f''(0)}{2!}x^2=1+x+\dfrac{1}{2}x^2,\\[5pt] p_3(x)&=f(0)+f′(0)x+\dfrac{f''(0)}{2}x^2+\dfrac{f'''(0)}{3!}x^3=1+x+\dfrac{1}{2}x^2+\dfrac{1}{3!}x^3,\end{align*}\)

\(\displaystyle \begin{align*} p_n(x)&=f(0)+f′(0)x+\dfrac{f''(0)}{2}x^2+\dfrac{f'''(0)}{3!}x^3+⋯+\dfrac{f^{(n)}(0)}{n!}x^n\\[5pt] &=1+x+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+⋯+\dfrac{x^n}{n!}\\[5pt] &=\sum_{k=0}^n\dfrac{x^k}{k!}\end{align*}\).

The function and the first three Maclaurin polynomials are shown in Figure \(\PageIndex{2}\).

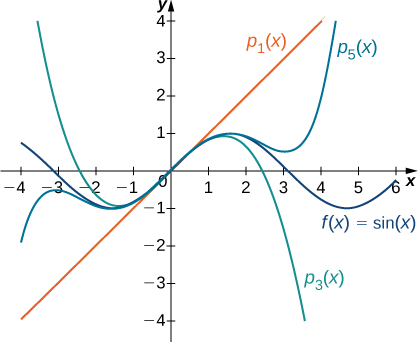
b. For \(f(x)=\sin x\), the values of the function and its first four derivatives at \(x=0\) are given as follows:

\[\begin{align*} f(x)&=\sin x & f(0)&=0\\[5pt] f′(x)&=\cos x & f′(0)&=1\\[5pt] f''(x)&=−\sin x & f''(0)&=0\\[5pt] f'''(x)&=−\cos x & f'''(0)&=−1\\[5pt] f^{(4)}(x)&=\sin x & f^{(4)}(0)&=0.\end{align*}\]

Since the fourth derivative is \(\sin x,\) the pattern repeats. That is, \(f^{(2m)}(0)=0\) and \(f^{(2m+1)}(0)=(−1)^m\) for \(m≥0.\) Thus, we have

\(\begin{align*} p_0(x)&=0,\\[5pt] p_1(x)&=0+x=x,\\[5pt] p_2(x)&=0+x+0=x,\\[5pt] p_3(x)&=0+x+0−\dfrac{1}{3!}x^3=x−\dfrac{x^3}{3!},\\[5pt] p_4(x)&=0+x+0−\dfrac{1}{3!}x^3+0=x−\dfrac{x^3}{3!},\\[5pt] p_5(x)&=0+x+0−\dfrac{1}{3!}x^3+0+\dfrac{1}{5!}x^5=x−\dfrac{x^3}{3!}+\dfrac{x^5}{5!},\end{align*}\)

and for \(m≥0\),

\[\begin{align*} p_{2m+1}(x)=p_{2m+2}(x)&=x−\dfrac{x^3}{3!}+\dfrac{x^5}{5!}−⋯+(−1)^m\dfrac{x^{2m+1}}{(2m+1)!}\\[5pt] &=\sum_{k=0}^m(−1)^k\dfrac{x^{2k+1}}{(2k+1)!}.\end{align*}\]

Graphs of the function and its Maclaurin polynomials are shown in Figure \(\PageIndex{3}\).

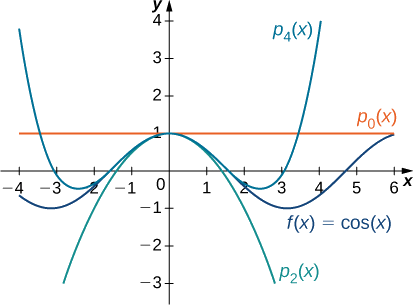
c. For \(f(x)=\cos x\), the values of the function and its first four derivatives at \(x=0\) are given as follows:

\[\begin{align*} f(x)&=\cos x & f(0)&=1\\[5pt] f′(x)&=−\sin x & f′(0)&=0\\[5pt] f''(x)&=−\cos x & f''(0)&=−1\\[5pt] f'''(x)&=\sin x & f'''(0)&=0\\[5pt] f^{(4)}(x)&=\cos x & f^{(4)}(0)&=1.\end{align*}\]

Since the fourth derivative is \(\sin x\), the pattern repeats. In other words, \(f^{(2m)}(0)=(−1)^m\) and \(f^{(2m+1)}=0\) for \(m≥0\). Therefore,

\(\begin{align*} p_0(x)&=1,\\[5pt] p_1(x)&=1+0=1,\\[5pt] p_2(x)&=1+0−\dfrac{1}{2!}x^2=1−\dfrac{x^2}{2!},\\[5pt] p_3(x)&=1+0−\dfrac{1}{2!}x^2+0=1−\dfrac{x^2}{2!},\\[5pt] p_4(x)&=1+0−\dfrac{1}{2!}x^2+0+\dfrac{1}{4!}x^4=1−\dfrac{x^2}{2!}+\dfrac{x^4}{4!},\\[5pt] p_5(x)&=1+0−\dfrac{1}{2!}x^2+0+\dfrac{1}{4!}x^4+0=1−\dfrac{x^2}{2!}+\dfrac{x^4}{4!},\end{align*}\)

and for \(n≥0\),

\[\begin{align*} p_{2m}(x)&=p_{2m+1}(x)\\[5pt] &=1−\dfrac{x^2}{2!}+\dfrac{x^4}{4!}−⋯+(−1)^m\dfrac{x^{2m}}{(2m)!}\\[5pt] &=\sum_{k=0}^m(−1)^k\dfrac{x^{2k}}{(2k)!}.\end{align*}\]

Graphs of the function and the Maclaurin polynomials appear in Figure \(\PageIndex{4}\).

Exercise \(\PageIndex{2}\)

Find formulas for the Maclaurin polynomials \(p_0,\,p_1,\,p_2\) and \(p_3\) for \(f(x)=\dfrac{1}{1+x}\).

Find a formula for the \(n^{\text{th}}\)-degree Maclaurin polynomial. Write your answer using sigma notation.

Evaluate the first four derivatives of \(f\) and look for a pattern.

\(\displaystyle p_0(x)=1;\;p_1(x)=1−x;\;p_2(x)=1−x+x^2;\;p_3(x)=1−x+x^2−x^3;\;p_n(x)=1−x+x^2−x^3+⋯+(−1)^nx^n=\sum_{k=0}^n(−1)^kx^k\)

Taylor’s Theorem with Remainder

Recall that the \(n^{\text{th}}\)-degree Taylor polynomial for a function \(f\) at \(a\) is the \(n^{\text{th}}\) partial sum of the Taylor series for \(f\) at \(a\). Therefore, to determine if the Taylor series converges, we need to determine whether the sequence of Taylor polynomials \({p_n}\) converges. However, not only do we want to know if the sequence of Taylor polynomials converges, we want to know if it converges to \(f\). To answer this question, we define the remainder \(R_n(x)\) as

\[R_n(x)=f(x)−p_n(x). \nonumber \]

For the sequence of Taylor polynomials to converge to \(f\), we need the remainder \(R_n\) to converge to zero. To determine if \(R_n\) converges to zero, we introduce Taylor’s theorem with remainder . Not only is this theorem useful in proving that a Taylor series converges to its related function, but it will also allow us to quantify how well the \(n^{\text{th}}\)-degree Taylor polynomial approximates the function.

Here we look for a bound on \(|R_n|.\) Consider the simplest case: \(n=0\). Let \(p_0\) be the 0 th Taylor polynomial at \(a\) for a function \(f\). The remainder \(R_0\) satisfies

\(R_0(x)=f(x)−p_0(x)=f(x)−f(a).\)

If \(f\) is differentiable on an interval \(I\) containing \(a\) and \(x\), then by the Mean Value Theorem there exists a real number \(c\) between \(a\) and \(x\) such that \(f(x)−f(a)=f′(c)(x−a)\). Therefore,

\[R_0(x)=f′(c)(x−a). \nonumber \]

Using the Mean Value Theorem in a similar argument, we can show that if \(f\) is \(n\) times differentiable on an interval \(I\) containing \(a\) and \(x\), then the \(n^{\text{th}}\) remainder \(R_n\) satisfies

\[R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}(x−a)^{n+1} \nonumber \]

for some real number \(c\) between \(a\) and \(x\). It is important to note that the value \(c\) in the numerator above is not the center \(a\), but rather an unknown value \(c\) between \(a\) and \(x\). This formula allows us to get a bound on the remainder \(R_n\). If we happen to know that \(∣f^{(n+1)}(x)∣\) is bounded by some real number \(M\) on this interval \(I\), then

\[|R_n(x)|≤\dfrac{M}{(n+1)!}|x−a|^{n+1} \nonumber \]

for all \(x\) in the interval \(I\).

We now state Taylor’s theorem, which provides the formal relationship between a function \(f\) and its \(n^{\text{th}}\)-degree Taylor polynomial \(p_n(x)\). This theorem allows us to bound the error when using a Taylor polynomial to approximate a function value, and will be important in proving that a Taylor series for \(f\) converges to \(f\).

Let \(f\) be a function that can be differentiated \(n+1\) times on an interval \(I\) containing the real number \(a\). Let \(p_n\) be the \(n^{\text{th}}\)-degree Taylor polynomial of \(f\) at \(a\) and let

\[R_n(x)=f(x)−p_n(x) \nonumber \]

be the \(n^{\text{th}}\) remainder. Then for each \(x\) in the interval \(I\), there exists a real number \(c\) between \(a\) and \(x\) such that

\[R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}(x−a)^{n+1} \nonumber \].

If there exists a real number \(M\) such that \(∣f^{(n+1)}(x)∣≤M\) for all \(x∈I\), then

for all \(x\) in \(I\).

Fix a point \(x∈I\) and introduce the function \(g\) such that

\[g(t)=f(x)−f(t)−f′(t)(x−t)−\dfrac{f''(t)}{2!}(x−t)^2−⋯−\dfrac{f^{(n)}(t)}{n!}(x−t)^n−R_n(x)\dfrac{(x−t)^{n+1}}{(x−a)^{n+1}}. \nonumber \]

We claim that \(g\) satisfies the criteria of Rolle’s theorem. Since \(g\) is a polynomial function (in \(t\)), it is a differentiable function. Also, \(g\) is zero at \(t=a\) and \(t=x\) because

\[ \begin{align*} g(a) &=f(x)−f(a)−f′(a)(x−a)−\dfrac{f''(a)}{2!}(x−a)^2+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n−R_n(x) \\[4pt] &=f(x)−p_n(x)−R_n(x) \\[4pt] &=0, \\[4pt] g(x) &=f(x)−f(x)−0−⋯−0 \\[4pt] &=0. \end{align*}\]

Therefore, \(g\) satisfies Rolle’s theorem, and consequently, there exists \(c\) between \(a\) and \(x\) such that \(g′(c)=0.\) We now calculate \(g′\). Using the product rule, we note that

\[\dfrac{d}{dt}\left[\dfrac{f^{(n)}(t)}{n!}(x−t)^n\right]=−\dfrac{f^{(n)}(t)}{(n−1)!}(x−t)^{n−1}+\dfrac{f^{(n+1)}(t)}{n!}(x−t)^n. \nonumber \]

Consequently,

\[\begin{align} g′(t)&=−f′(t)+[f′(t)−f''(t)(x−t)]+\left[f''(t)(x−t)−\dfrac{f'''(t)}{2!}(x−t)^2\right]+⋯ \nonumber\\ &\quad+\left[\dfrac{f^{(n)}(t)}{(n−1)!}(x−t)^{n−1}−\dfrac{f^{(n+1)}(t)}{n!}(x−t)^n\right]+(n+1)R_n(x)\dfrac{(x−t)^n}{(x−a)^{n+1}}\end{align} \nonumber \].

Notice that there is a telescoping effect. Therefore,

\[g'(t)=−\dfrac{f^{(n+1)}(t)}{n!}(x−t)^n+(n+1)R_n(x)\dfrac{(x−t)^n}{(x−a)^{n+1}} \nonumber \].

By Rolle’s theorem, we conclude that there exists a number \(c\) between \(a\) and \(x\) such that \(g′(c)=0.\) Since

\[g′(c)=−\dfrac{f^{(n+1})(c)}{n!}(x−c)^n+(n+1)R_n(x)\dfrac{(x−c)^n}{(x−a)^{n+1}} \nonumber \]

we conclude that

\[−\dfrac{f^{(n+1)}(c)}{n!}(x−c)^n+(n+1)R_n(x)\dfrac{(x−c)^n}{(x−a)^{n+1}}=0. \nonumber \]

Adding the first term on the left-hand side to both sides of the equation and dividing both sides of the equation by \(n+1,\) we conclude that

as desired. From this fact, it follows that if there exists \(M\) such that \(∣f^{(n+1)}(x)∣≤M\) for all \(x\) in \(I\), then

\[|R_n(x)|≤\dfrac{M}{(n+1)!}|x−a|^{n+1} \nonumber \].

Not only does Taylor’s theorem allow us to prove that a Taylor series converges to a function, but it also allows us to estimate the accuracy of Taylor polynomials in approximating function values. We begin by looking at linear and quadratic approximations of \(f(x)=\sqrt[3]{x}\) at \(x=8\) and determine how accurate these approximations are at estimating \(\sqrt[3]{11}\).

Example \(\PageIndex{3}\): Using Linear and Quadratic Approximations to Estimate Function Values

Consider the function \(f(x)=\sqrt[3]{x}\).

• Find the first and second Taylor polynomials for \(f\) at \(x=8\). Use a graphing utility to compare these polynomials with \(f\) near \(x=8.\)
• Use these two polynomials to estimate \(\sqrt[3]{11}\).
• Use Taylor’s theorem to bound the error.

a. For \(f(x)=\sqrt[3]{x}\), the values of the function and its first two derivatives at \(x=8\) are as follows:

\[\begin{align*} f(x)&=\sqrt[3]{x}, & f(8)&=2\\[5pt] f′(x)&=\dfrac{1}{3x^{2/3}}, & f′(8)&=\dfrac{1}{12}\\[5pt] f''(x)&=\dfrac{−2}{9x^{5/3}}, & f''(8)&=−\dfrac{1}{144.}\end{align*}\]

Thus, the first and second Taylor polynomials at \(x=8\) are given by

\(\begin{align*} p_1(x)&=f(8)+f′(8)(x−8)\\[5pt] &=2+\dfrac{1}{12}(x−8)\end{align*}\)

\(\begin{align*} p_2(x)&=f(8)+f′(8)(x−8)+\dfrac{f''(8)}{2!}(x−8)^2\\[5pt] &=2+\dfrac{1}{12}(x−8)−\dfrac{1}{288}(x−8)^2.\end{align*}\)

The function and the Taylor polynomials are shown in Figure \(\PageIndex{5}\).

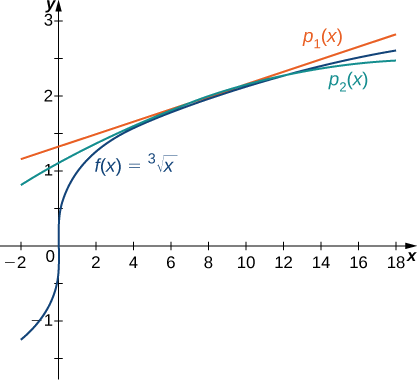
b. Using the first Taylor polynomial at \(x=8\), we can estimate

\[\sqrt[3]{11}≈p_1(11)=2+\dfrac{1}{12}(11−8)=2.25. \nonumber \]

Using the second Taylor polynomial at \(x=8\), we obtain

\[\sqrt[3]{11}≈p_2(11)=2+\dfrac{1}{12}(11−8)−\dfrac{1}{288}(11−8)^2=2.21875. \nonumber \]

c. By Note, there exists a c in the interval \((8,11)\) such that the remainder when approximating \(\sqrt[3]{11}\) by the first Taylor polynomial satisfies

\[R_1(11)=\dfrac{f''(c)}{2!}(11−8)^2. \nonumber \]

We do not know the exact value of \(c,\) so we find an upper bound on \(R_1(11)\) by determining the maximum value of \(f''\) on the interval \((8,11)\). Since \(f''(x)=−\dfrac{2}{9x^{5/3}}\), the largest value for \(|f''(x)|\) on that interval occurs at \(x=8\). Using the fact that \(f''(8)=−\dfrac{1}{144}\), we obtain

\(|R_1(11)|≤\dfrac{1}{144⋅2!}(11−8)^2=0.03125.\)

Similarly, to estimate \(R_2(11)\), we use the fact that

\(R_2(11)=\dfrac{f'''(c)}{3!}(11−8)^3\).

Since \(f'''(x)=\dfrac{10}{27x^{8/3}}\), the maximum value of \(f'''\) on the interval \((8,11)\) is \(f'''(8)≈0.0014468\). Therefore, we have

\(|R_2(11)|≤\dfrac{0.0011468}{3!}(11−8)^3≈0.0065104.\)

Exercise \(\PageIndex{3}\):

Find the first and second Taylor polynomials for \(f(x)=\sqrt{x}\) at \(x=4\). Use these polynomials to estimate \(\sqrt{6}\). Use Taylor’s theorem to bound the error.

Evaluate \(f(4),f′(4),\) and \(f''(4).\)

\(p_1(x)=2+\dfrac{1}{4}(x−4);p_2(x)=2+\dfrac{1}{4}(x−4)−\dfrac{1}{64}(x−4)^2;p_1(6)=2.5;p_2(6)=2.4375;\)

\(|R_1(6)|≤0.0625;|R_2(6)|≤0.015625\)

Example \(\PageIndex{4}\): Approximating \(\sin x\) Using Maclaurin Polynomials

From Example \(\PageIndex{2b}\) , the Maclaurin polynomials for \(\sin x\) are given by

\[p_{2m+1}(x)=p_{2m+2}(x)=x−\dfrac{x^3}{3!}+\dfrac{x^5}{5!}−\dfrac{x^7}{7!}+⋯+(−1)^m\dfrac{x^{2m+1}}{(2m+1)!} \nonumber \]

for \(m=0,1,2,….\)

• Use the fifth Maclaurin polynomial for \(\sin x\) to approximate \(\sin\left(\dfrac{π}{18}\right)\) and bound the error.
• For what values of \(x\) does the fifth Maclaurin polynomial approximate \(\sin x\) to within \(0.0001\)?

The fifth Maclaurin polynomial is

\[p_5(x)=x−\dfrac{x^3}{3!}+\dfrac{x^5}{5!} \nonumber \].

Using this polynomial, we can estimate as follows:

\[\sin\left(\dfrac{π}{18}\right)≈p_5\left(\dfrac{π}{18}\right)=\dfrac{π}{18}−\dfrac{1}{3!}\left(\dfrac{π}{18}\right)^3+\dfrac{1}{5!}\left(\dfrac{π}{18}\right)^5≈0.173648. \nonumber \]

To estimate the error, use the fact that the sixth Maclaurin polynomial is \(p_6(x)=p_5(x)\) and calculate a bound on \(R_6(\dfrac{π}{18})\). By Note, the remainder is

\[R_6\left(\dfrac{π}{18}\right)=\dfrac{f^{(7)}(c)}{7!}\left(\dfrac{π}{18}\right)^7 \nonumber \]

for some \(c\) between 0 and \(\dfrac{π}{18}\). Using the fact that \(∣f^{(7)}(x)∣≤1\) for all \(x\), we find that the magnitude of the error is at most

\[\dfrac{1}{7!}⋅\left(\dfrac{π}{18}\right)^7≤9.8×10^{−10}. \nonumber \]

We need to find the values of \(x\) such that

\[\dfrac{1}{7!}|x|^7≤0.0001. \nonumber \]

Solving this inequality for \(x\), we have that the fifth Maclaurin polynomial gives an estimate to within \(0.0001\) as long as \(|x|<0.907.\)

Exercise \(\PageIndex{4}\)

Use the fourth Maclaurin polynomial for \(\cos x\) to approximate \(\cos\left(\dfrac{π}{12}\right).\)

The fourth Maclaurin polynomial is \(p_4(x)=1−\dfrac{x^2}{2!}+\dfrac{x^4}{4!}\).

Now that we are able to bound the remainder \(R_n(x)\), we can use this bound to prove that a Taylor series for \(f\) at a converges to \(f\).

Representing Functions with Taylor and Maclaurin Series

We now discuss issues of convergence for Taylor series. We begin by showing how to find a Taylor series for a function, and how to find its interval of convergence.

Example \(\PageIndex{5}\): Finding a Taylor Series

Find the Taylor series for \(f(x)=\dfrac{1}{x}\) at \(x=1\). Determine the interval of convergence.

For \(f(x)=\dfrac{1}{x},\) the values of the function and its first four derivatives at \(x=1\) are

\[\begin{align*} f(x)&=\dfrac{1}{x} & f(1)&=1\\[5pt] f′(x)&=−\dfrac{1}{x^2} & f′(1)&=−1\\[5pt] f''(x)&=\dfrac{2}{x^3} & f''(1)&=2!\\[5pt] f'''(x)&=−\dfrac{3⋅2}{x^4} & f'''(1)&=−3!\\[5pt] f^{(4)}(x)&=\dfrac{4⋅3⋅2}{x^5} & f^{(4)}(1)&=4!.\end{align*}\]

That is, we have \(f^{(n)}(1)=(−1)^nn!\) for all \(n≥0\). Therefore, the Taylor series for \(f\) at \(x=1\) is given by

\(\displaystyle \sum_{n=0}^∞\dfrac{f^{(n)}(1)}{n!}(x−1)^n=\sum_{n=0}^∞(−1)^n(x−1)^n\).

To find the interval of convergence, we use the ratio test. We find that

\(\dfrac{|a_{n+1}|}{|a_n|}=\dfrac{∣(−1)^{n+1}(x−1)n^{+1}∣}{|(−1)^n(x−1)^n|}=|x−1|\).

Thus, the series converges if \(|x−1|<1.\) That is, the series converges for \(0<x<2\). Next, we need to check the endpoints. At \(x=2\), we see that

\(\displaystyle \sum_{n=0}^∞(−1)^n(2−1)^n=\sum_{n=0}^∞(−1)^n\)

diverges by the divergence test. Similarly, at \(x=0,\)

\(\displaystyle \sum_{n=0}^∞(−1)^n(0−1)^n=\sum_{n=0}^∞(−1)^{2n}=\sum_{n=0}^∞1\)

diverges. Therefore, the interval of convergence is \((0,2)\).

Exercise \(\PageIndex{5}\)

Find the Taylor series for \(f(x)=\dfrac{1}{2}\) at \(x=2\) and determine its interval of convergence.

\(f^{(n)}(2)=\dfrac{(−1)^nn!}{2^{n+1}}\)

\(\dfrac{1}{2}\displaystyle \sum_{n=0}^∞\left(\dfrac{2−x}{2}\right)^n\). The interval of convergence is \((0,4)\).

We know that the Taylor series found in this example converges on the interval \((0,2)\), but how do we know it actually converges to \(f\)? We consider this question in more generality in a moment, but for this example, we can answer this question by writing

\[ f(x)=\dfrac{1}{x}=\dfrac{1}{1−(1−x)}. \nonumber \]

That is, \(f\) can be represented by the geometric series \(\displaystyle \sum_{n=0}^∞(1−x)^n\). Since this is a geometric series, it converges to \(\dfrac{1}{x}\) as long as \(|1−x|<1.\) Therefore, the Taylor series found in Example does converge to \(f(x)=\dfrac{1}{x}\) on \((0,2).\)

We now consider the more general question: if a Taylor series for a function \(f\) converges on some interval, how can we determine if it actually converges to \(f\)? To answer this question, recall that a series converges to a particular value if and only if its sequence of partial sums converges to that value. Given a Taylor series for \(f\) at \(a\), the \(n^{\text{th}}\) partial sum is given by the \(n^{\text{th}}\)-degree Taylor polynomial \(p_n\). Therefore, to determine if the Taylor series converges to \(f\), we need to determine whether

\(\displaystyle \lim_{n→∞}p_n(x)=f(x)\).

Since the remainder \(R_n(x)=f(x)−p_n(x)\), the Taylor series converges to \(f\) if and only if

\(\displaystyle \lim_{n→∞}R_n(x)=0.\)

We now state this theorem formally.

Convergence of Taylor Series

Suppose that \(f\) has derivatives of all orders on an interval \(I\) containing \(a\). Then the Taylor series

\[\sum_{n=0}^∞\dfrac{f^{(n)}(a)}{n!}(x−a)^n \nonumber \]

converges to \(f(x)\) for all \(x\) in \(I\) if and only if

\[\lim_{n→∞}R_n(x)=0 \nonumber \]

for all \(x\) in \(I\) .

With this theorem, we can prove that a Taylor series for \(f\) at a converges to \(f\) if we can prove that the remainder \(R_n(x)→0\). To prove that \(R_n(x)→0\), we typically use the bound

from Taylor’s theorem with remainder.

In the next example, we find the Maclaurin series for \(e^x\) and \(\sin x\) and show that these series converge to the corresponding functions for all real numbers by proving that the remainders \(R_n(x)→0\) for all real numbers \(x\).

Example \(\PageIndex{6}\): Finding Maclaurin Series

For each of the following functions, find the Maclaurin series and its interval of convergence. Use Note to prove that the Maclaurin series for \(f\) converges to \(f\) on that interval.

a. Using the \(n^{\text{th}}\)-degree Maclaurin polynomial for \(e^x\) found in Example a., we find that the Maclaurin series for \(e^x\) is given by

\(\displaystyle \sum_{n=0}^∞\dfrac{x^n}{n!}\).

To determine the interval of convergence, we use the ratio test. Since

\(\dfrac{|a_{n+1}|}{|a_n|}=\dfrac{|x|^{n+1}}{(n+1)!}⋅\dfrac{n!}{|x|^n}=\dfrac{|x|}{n+1}\),

\(\displaystyle \lim_{n→∞}\dfrac{|a_{n+1}|}{|a_n|}=\lim_{n→∞}\dfrac{|x|}{n+1}=0\)

for all \(x\). Therefore, the series converges absolutely for all \(x\), and thus, the interval of convergence is \((−∞,∞)\). To show that the series converges to \(e^x\) for all \(x\), we use the fact that \(f^{(n)}(x)=e^x\) for all \(n≥0\) and \(e^x\) is an increasing function on \((−∞,∞)\). Therefore, for any real number \(b\), the maximum value of \(e^x\) for all \(|x|≤b\) is \(e^b\). Thus,

\(|R_n(x)|≤\dfrac{e^b}{(n+1)!}|x|^{n+1}\).

Since we just showed that

\(\displaystyle \sum_{n=0}^∞\dfrac{|x|^n}{n!}\)

converges for all \(x\), by the divergence test, we know that

\(\displaystyle \lim_{n→∞}\dfrac{|x|^{n+1}}{(n+1)!}=0\)

for any real number \(x\). By combining this fact with the squeeze theorem, the result is \(\displaystyle \lim_{n→∞}R_n(x)=0.\)

b. Using the \(n^{\text{th}}\)-degree Maclaurin polynomial for \(\sin x\) found in Example b., we find that the Maclaurin series for \(\sin x\) is given by

\(\displaystyle \sum_{n=0}^∞(−1)^n\dfrac{x^{2n+1}}{(2n+1)!}\).

In order to apply the ratio test, consider

\[\begin{align*} \dfrac{|a_{n+1}|}{|a_n|}&=\dfrac{|x|^{2n+3}}{(2n+3)!}⋅\dfrac{(2n+1)!}{|x|^{2n+1}}\\[5pt] &=\dfrac{|x|^2}{(2n+3)(2n+2)}\end{align*}. \nonumber \]

\(\displaystyle \lim_{n→∞}\dfrac{|x|^2}{(2n+3)(2n+2)}=0\)

for all \(x\), we obtain the interval of convergence as \((−∞,∞).\) To show that the Maclaurin series converges to \(\sin x\), look at \(R_n(x)\). For each \(x\) there exists a real number \(c\) between \(0\) and \(x\) such that

\(R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}x^{n+1}\).

Since \(∣f^{(n+1)}(c)∣≤1\) for all integers \(n\) and all real numbers \(c\), we have

\(|R_n(x)|≤\dfrac{|x|^{n+1}}{(n+1)!}\)

for all real numbers \(x\). Using the same idea as in part a., the result is \(\displaystyle \lim_{n→∞}R_n(x)=0\) for all \(x\), and therefore, the Maclaurin series for \(\sin x\) converges to \(\sin x\) for all real \(x\).

Exercise \(\PageIndex{6}\)

Find the Maclaurin series for \(f(x)=\cos x\). Use the ratio test to show that the interval of convergence is \((−∞,∞)\). Show that the Maclaurin series converges to \(\cos x\) for all real numbers \(x\).

Use the Maclaurin polynomials for \(\cos x.\)

\(\displaystyle \sum_{n=0}^∞\dfrac{(−1)^nx^{2n}}{(2n)!}\)

By the ratio test, the interval of convergence is \((−∞,∞).\) Since \(|R_n(x)|≤\dfrac{|x|^{n+1}}{(n+1)!}\), the series converges to \(\cos x\) for all real \(x\).

Proving that \(e\) is Irrational

In this project, we use the Maclaurin polynomials for \(e^x\) to prove that \(e\) is irrational. The proof relies on supposing that \(e\) is rational and arriving at a contradiction. Therefore, in the following steps, we suppose \(e=r/s\) for some integers \(r\) and \(s\) where \(s≠0.\)

• Write the Maclaurin polynomials \(p_0(x),p_1(x),p_2(x),p_3(x),p_4(x)\) for \(e^x\). Evaluate \(p_0(1),p_1(1),p_2(1),p_3(1),p_4(1)\) to estimate \(e\).
• Let \(R_n(x)\) denote the remainder when using \(p_n(x)\) to estimate \(e^x\). Therefore, \(R_n(x)=e^x−p_n(x)\), and \(R_n(1)=e−p_n(1)\). Assuming that \(e=\dfrac{r}{s}\) for integers \(r\) and \(s\), evaluate \(R_0(1),R_1(1),R_2(1),R_3(1),R_4(1).\)
• Using the results from part 2, show that for each remainder \(R_0(1),R_1(1),R_2(1),R_3(1),R_4(1),\) we can find an integer \(k\) such that \(kR_n(1)\) is an integer for \(n=0,1,2,3,4.\)
• Write down the formula for the \(n^{\text{th}}\)-degree Maclaurin polynomial \(p_n(x)\) for \(e^x\) and the corresponding remainder \(R_n(x).\) Show that \(sn!R_n(1)\) is an integer.
• Use Taylor’s theorem to write down an explicit formula for \(R_n(1)\). Conclude that \(R_n(1)≠0\), and therefore, \(sn!R_n(1)≠0\).
• Use Taylor’s theorem to find an estimate on \(R_n(1)\). Use this estimate combined with the result from part 5 to show that \(|sn!R_n(1)|<\dfrac{se}{n+1}\). Conclude that if \(n\) is large enough, then \(|sn!R_n(1)|<1\). Therefore, \(sn!R_n(1)\) is an integer with magnitude less than 1. Thus, \(sn!R_n(1)=0\). But from part 5, we know that \(sn!R_n(1)≠0\). We have arrived at a contradiction, and consequently, the original supposition that e is rational must be false.

Key Concepts

• Taylor polynomials are used to approximate functions near a value \(x=a\). Maclaurin polynomials are Taylor polynomials at \(x=0\).
• The \(n^{\text{th}}\)-degree Taylor polynomials for a function \(f\) are the partial sums of the Taylor series for \(f\).
• If a function \(f\) has a power series representation at \(x=a\), then it is given by its Taylor series at \(x=a\).
• A Taylor series for \(f\) converges to \(f\) if and only if \(\displaystyle \lim_{n→∞}R_n(x)=0\) where \(R_n(x)=f(x)−p_n(x)\).
• The Taylor series for \(e^x, \sin x\), and \(\cos x\) converge to the respective functions for all real x.

Key Equations

• Taylor series for the function \(f\) at the point \(x=a\)

\(\displaystyle \sum_{n=0}^∞\dfrac{f^{(n)}(a)}{n!}(x−a)^n=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n+⋯\)

for a function \(f\) and the \(n^{\text{th}}\)-degree Taylor polynomial for \(f\) at \(x=a\), the remainder \(R_n(x)=f(x)−p_n(x)\) satisfies \(R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}(x−a)^{n+1}\)

for some\(c\) between \(x\) and \(a\); if there exists an interval \(I\) containing \(a\) and a real number \(M\) such that \(∣f^{(n+1)}(x)∣≤M\) for all \(x\) in \(I\), then \(|R_n(x)|≤\dfrac{M}{(n+1)!}|x−a|^{n+1}\)