thevenin theorem solved problems

Thevenin’s Theorem with solved problem

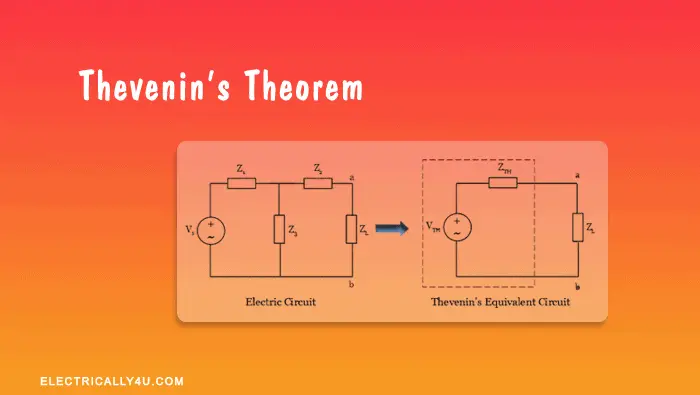
Thevenin’s theorem is used to solve the complex circuits consisting of several sources and impedances by converting them into a simple equivalent circuit called Thevenin’s equivalent circuit. Now let’s look at the statement.

Thevenin’s Theorem states that

“ Any linear bilateral circuit containing several voltage sources and impedance s can be replaced with an equivalent circuit consisting of single Thevenin’s voltage source in series with a Thevenin’s impedance connected across the load impedance“.

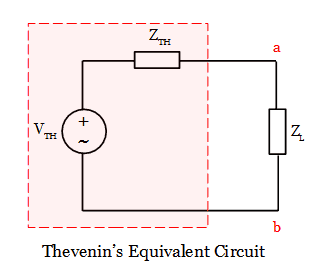
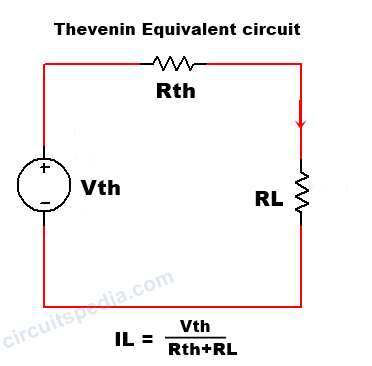
The Thevenin’s equivalent circuit has a single voltage source called Thevenin’s voltage source(V TH ), equivalent impedance called Thevenin’s equivalent impedance Z TH and a load impedance Z L .

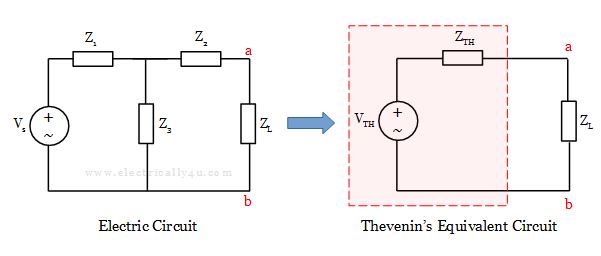
In the above equivalent circuit, the Thevenin’s voltage V TH is nothing but an open-circuit voltage, which is obtained by removing the load impedance Z L . The Thevenin’s equivalent impedance Z TH is obtained by short-circuiting all the voltage sources and open circuiting all the current sources in the circuit.

Now, let us look at the step-by-step procedure to determine the V TH and Z TH in the above circuit.

Procedure to determine Thevenin’s equivalent circuit

Step 1 – determination of thevenin’s voltage.

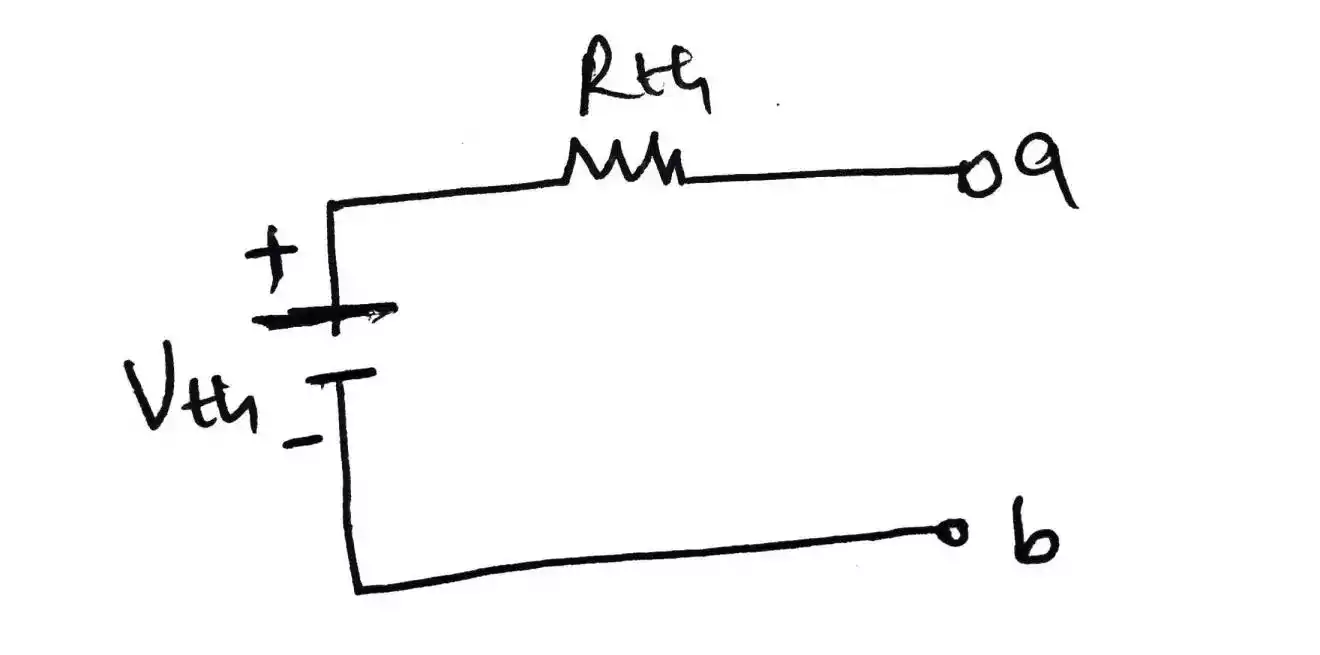
Remove the load impedance Z L in the above electric circuit, by open circuiting the terminal ab as shown in the below figure.

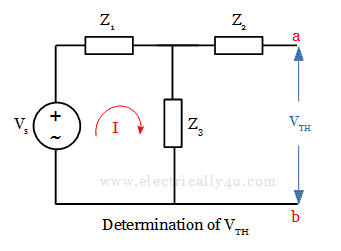
In this circuit, there exists a loop, through which the current I flows. Apply KVL to the loop and find the current I.

$I.Z_1 + I.Z_3 = V_s$

Solving the above equation, we will get the value of current. Then Thevenin’s voltage is obtained for the circuit as,

$V_{TH} = I.Z_3$

Step 2 – Determination of Thevenin’s Impedance

Since there is only one voltage source is available in the circuit, remove the voltage source and short circuit the terminals and remove the load impedance, as shown in the figure below.

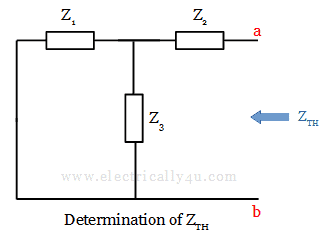
The Thevenin’s equivalent impedance is obtained from terminal ab using the formula,

$Z_{TH} = \frac{Z_1 . Z_3}{Z_1 + Z_3} + Z_2$

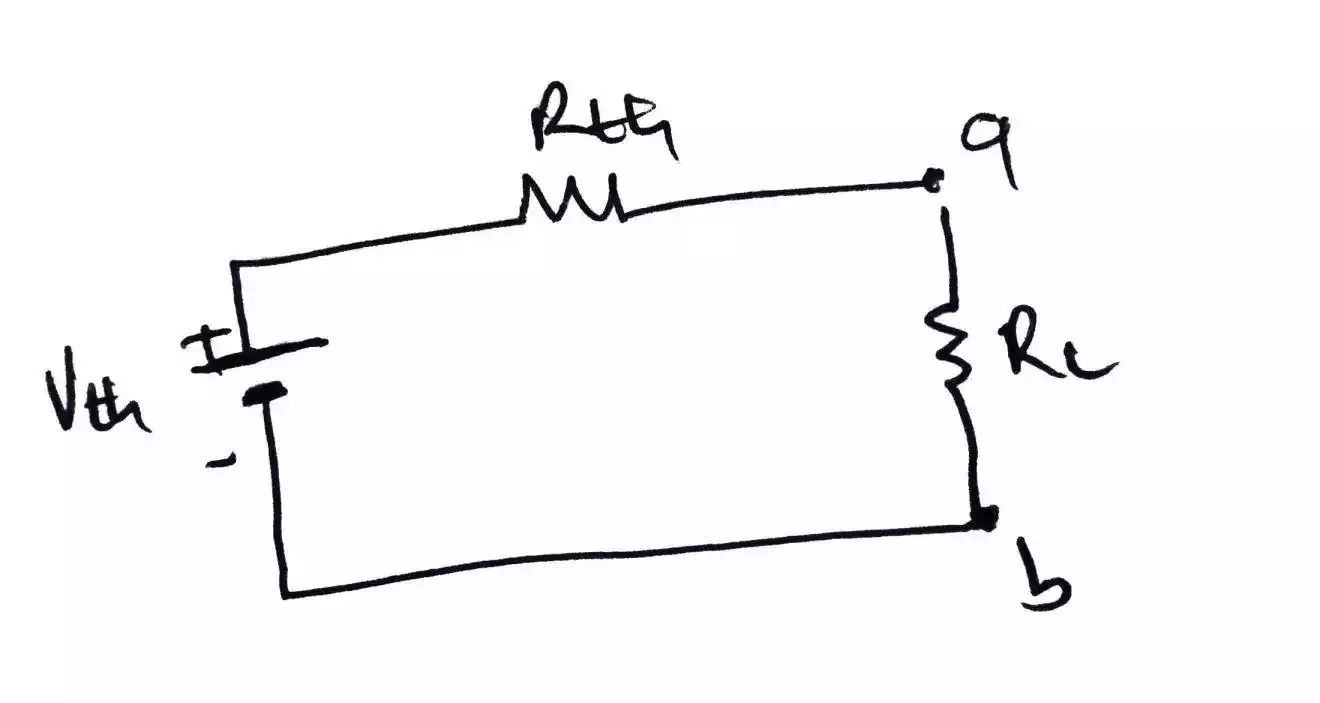
Step 3 – Formation of Thevenin’s equivalent circuit

Using the obtained values of V TH and Z TH , the equivalent circuit is drawn as below. This circuit is called Thevenin’s equivalent circuit.

From this circuit, we can obtain the current flowing through the load, using the formula

$I_L = \frac{V_TH}{Z_TH + Z_L}$

Solved Problem 1

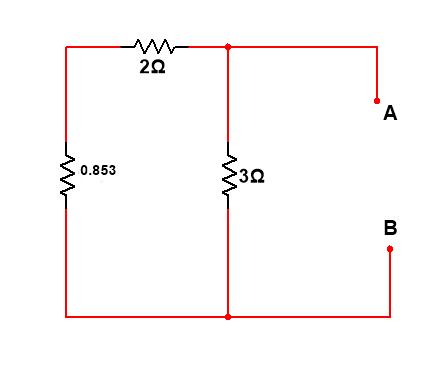
Solve the given circuit to find the current through 10 Ω using Thevenin’s Theorem.

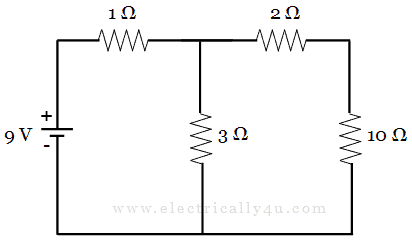
First, let us consider 10 Ω as the load resistor.

(a) To find Thevenin’s voltage , Remove the load resistor(10 Ω) and the circuit is redrawn as below.

Thevenin’s Theorem - Problem_1 solution_1

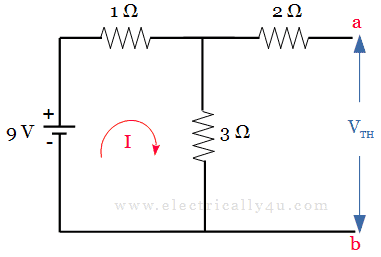
Now the circuit is open-circuited. From the drawn circuit, Thevenin’s voltage is calculated between a and b. Since no current flows through 2 Ω, V TH is equal to the voltage across 3 Ω resistor.

To find the voltage across the 3 Ω resistor, we need to know the current flowing through it.

The total resistance in the circuit, R = 1 Ω + 3 Ω = 4 Ω .

By Ohm’s law,

$I = \frac{V}{R} = \frac{9}{4} = 2.25 A$

Thus, the voltage across 3 Ω resistor(or Thevenin’s voltage V TH ) is given by,

$V_{ab} = V_{TH} = I * R = 2.25 * 3 = 6.75 V$

(b)To find Thevenin’s resistance, Remove the load resistor, short the voltage source and circuit is redrawn as below.

Thevenin’s Theorem - Problem_1 solution_2

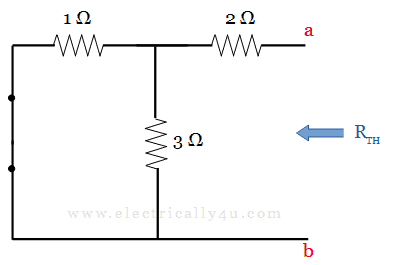
In this circuit, we can observe that the 2 Ω resistor is in series with the parallel combination of 1 Ω and 3 Ω resistors. Thus the equivalent value of resistance is obtained as,

$R_{TH} = 2 + \frac{1 * 3}{1 + 3} = 2.75 \Omega$

[ Learn how to find the equivalent resistance of resistor when they are connected in series and parallel. ]

(c)Thevenin’s Equivalent Circuit. It is drawn by connecting the Thevenin’s voltage V TH , Thevenin’s resistance R TH and load resistor in series, as shown below

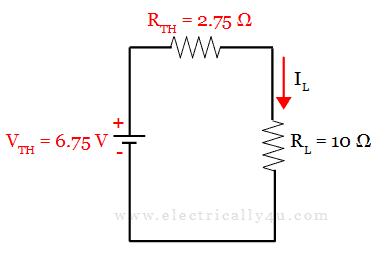
From this circuit, I L is the current flowing through the load of 10 Ω resistance.

$I_L = \frac{V_{TH}}{R_{TH} + R_L} = \frac{6.75}{2.75 + 10} = 0.529 A$

Please enable JavaScript

Solved Problem 2

Solve the given circuit to find the current through 15 Ω using Thevenin’s Theorem.

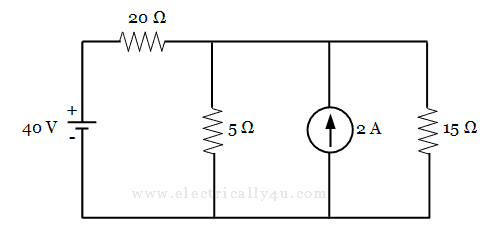
In this problem, let us consider 15 Ω resistor as the load.

(a) To find Thevenin’s voltage , Remove the load resistor(15 Ω). Also when observing the circuit, it has 2A current source in parallel with the 5 Ω resistor.

By source transformation , let us convert this current source into its equivalent voltage source in series with 5 Ω resistor.

Thevenin’s Theorem - Problem_2 solution_1

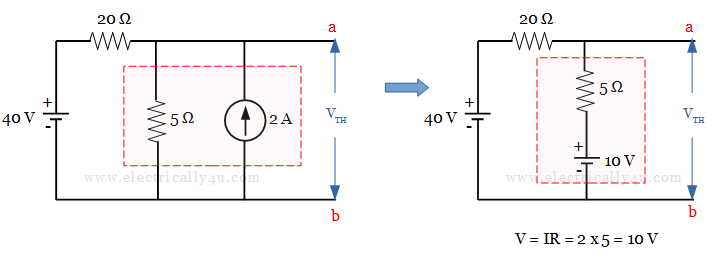
Now we have the following circuit, for which we have to find the Thevenin’s voltage V TH . You can observe a loop in this circuit. [ Learn how to solve a circuit using mesh analysis . ]

Thevenin’s Theorem - Problem_2 solution_2

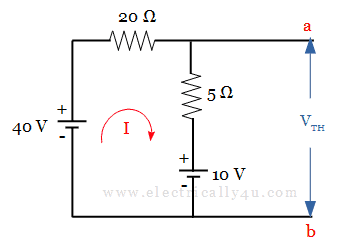
Let us apply Kirchoff’s Voltage Law to this loop and find the value of loop current.

Applying KVL, 20I + 5I +10 – 40 = 0

V TH = 10 + (5 * 1.2) = 16 v

(b)To find Thevenin’s resistance, Remove the load resistor, short the voltage source and the circuit is redrawn as below.

Thevenin’s Theorem - Problem_2 solution_3

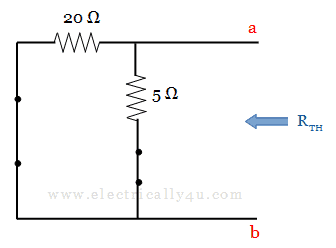
When you observe the circuit between points a and b, the 5 Ω resistor looks parallel to the 20 Ω resistor. Thus the equivalent value of resistance is obtained as,

$R_{TH} = \frac{5 * 20}{5 + 20} = 4 \Omega$

Sharing is Caring

An Assistant Professor in the Department of Electrical and Electronics Engineering, Certified Energy Manager, Photoshop designer, a blogger and Founder of Electrically4u.

Subscribe to Electrically4u..!

Enter your Email Address to get all our updates about new articles to your inbox.

Switch skin

Home > Circuit Analysis > Thevenin’s Theorem. Step by Step Procedure with Solved Example

Thevenin’s Theorem. Step by Step Procedure with Solved Example

Thevenin’s Theorem in DC Circuit Analysis

A French engineer, M.L Thevenin , made one of these quantum leaps in 1893. Thevenin’s Theorem (also known as Helmholtz–Thévenin Theorem ) is not by itself an analysis tool, but the basis for a very useful method of simplifying active circuits and complex networks . This theorem is useful to quickly and easily solve complex linear circuits and networks, especially electric circuits and electronic networks.

Thevenin’s Theorem may be stated below:

Any linear electric network or a complex circuit with current and voltage sources can be replaced by an equivalent circuit containing a single independent voltage source V TH and a Series Resistance R TH .

V TH = Thevenin’s Voltage
R TH = Thevenin’s Resistance

Related Post: Norton’s Theorem. Easy Step by Step Procedure with Example (Pictorial Views)

Steps to Analyze an Electric Circuit using Thevenin’s Theorem

Open the load resistor.
Calculate / measure the open circuit voltage. This is the Thevenin Voltage (V TH ) .
Open current sources and short voltage sources.
Calculate /measure the Open Circuit Resistance. This is the Thevenin Resistance (R TH ) .
Now, redraw the circuit with measured open circuit Voltage (V TH ) in Step (2) as voltage source and measured open circuit resistance (R TH ) in step (4) as a series resistance and connect the load resistor which we had removed in Step (1). This is the equivalent Thevenin circuit of that linear electric network or complex circuit which had to be simplified and analyzed by Thevenin’s Theorem . You have done it.
Now find the Total current flowing through the load resistor by using the Ohm’s Law : I T = V TH / (R TH + R L ).

Related Post: SUPERMESH Circuit Analysis | Step by Step with Solved Example

Solved Example by Thevenin’s Theorem:

Thevenin's Theorem. Easy Step by Step Procedure with Example (Pictorial Views)

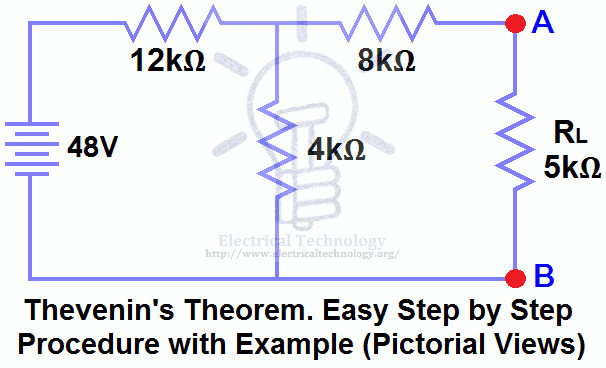
Calculate / measure the open circuit voltage. This is the Thevenin Voltage (V TH ) . Fig (3).

We have already removed the load resistor in figure 1, so the circuit became an open circuit as shown in fig 2. Now we have to calculate the Thevenin’s Voltage. Since 3mA current flows in both 12kΩ and 4kΩ resistors as this is a series circuit and current will not flow in the 8kΩ resistor as it is open.

This way, 12V (3mA x 4kΩ) will appear across the 4kΩ resistor . We also know that current is not flowing through the 8kΩ resistor as it is an open circuit, but the 8kΩ resistor is in parallel with 4k resistor . So the same voltage i.e. 12V will appear across the 8kΩ resistor as well as 4kΩ resistor. Therefore 12V will appear across the AB terminals. i.e,

Open current sources and short voltage sources as shown below. Fig (4)

Calculate / measure the open circuit resistance . This is the Thevenin Resistance (R TH )

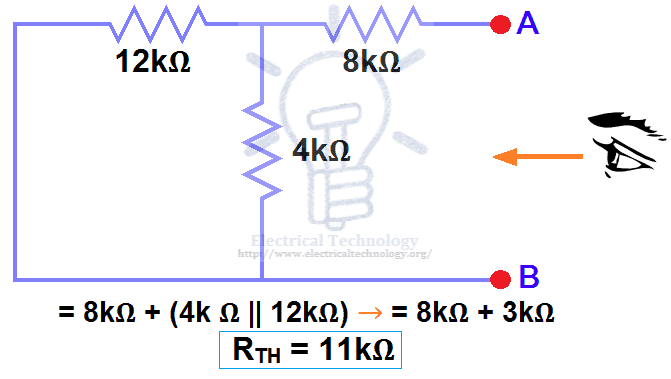
We have removed the 48V DC source to zero as equivalent i.e. 48V DC source has been replaced with a short in step 3 (as shown in figure 3). We can see that 8kΩ resistor is in series with a parallel connection of 4kΩ resistor and 12k Ω resistor. i.e.:

8kΩ + (4k Ω || 12kΩ) ….. (|| = in parallel with)

R TH = 8kΩ + [(4kΩ x 12kΩ) / (4kΩ + 12kΩ)]

R TH = 8kΩ + 3kΩ

R TH = 11kΩ

Connect the R TH in series with Voltage Source V TH and re-connect the load resistor. This is shown in fig (6) i.e. Thevenin circuit with load resistor. This the Thevenin’s equivalent circuit .

Now apply the last step i.e Ohm’s law . Calculate the total load current and load voltage as shown in fig 6.

I L = V TH / (R TH + R L )

I L = 12V / (11kΩ + 5kΩ) → = 12/16kΩ

I L = 0.75mA

V L = I L x R L

V L = 0.75mA x 5kΩ

V L = 3.75V

thevenin's theorem examples thevenin's theorem solved problems

Now compare this simple circuit with the original circuit shown in figure 1. Do you see how much easier it will be to measure and calculate the load current in complex circuit and network for different load resistors by Thevenin’s Theorem ? Yes and only yes.

Good to know: Both Thevenin’s and Norton’s theorems can be applied to both AC and DC circuits containing difference components such as resistors , inductors and capacitors etc. Keep in mind that the Thevenin’s voltage “V TH ” in AC circuit is expressed in complex number (polar form) whereas, the Thevenin’s resistance “R TH ” is stated in rectangular form.

Maximum Power Transfer Theorem for AC & DC Circuits
Kirchhoff’s Current & Voltage Law (KCL & KVL) | Solved Example
Compensation Theorem – Proof, Explanation and Solved Examples
Substitution Theorem – Step by Step Guide with Solved Example
Millman’s Theorem – Analyzing AC & DC Circuits – Examples
Superposition Theorem – Circuit Analysis with Solved Example
Tellegen’s Theorem – Solved Examples & MATLAB Simulation
SUPERNODE Circuit Analysis | Step by Step with Solved Example
SUPERMESH Circuit Analysis | Step by Step with Solved Example
Voltage Divider Rule (VDR) – Solved Examples for R, L and C Circuits
Current Divider Rule (CDR) – Solved Examples for AC and DC Circuits
Star to Delta & Delta to Star Conversion. Y-Δ Transformation

Electrical Technology

How to Size a Single Phase and Three Phase Transformer in kVA? Calculator

Battery Charging Current and Battery Charging Time formula with 120Ah battery solved examples

How to Calculate the Battery Charging Time & Battery Charging Current – Example

How To Calculate Your Electricity Bill Simple Calculation.

How To Calculate Your Electricity Bill. Electric Bill Calculator with Examples

How to Find The Suitable Size of Cable & Wire for Electrical Wiring Installation (Solved Examples in British and SI System)

How to Find the Proper Size of Wire & Cable: Metric & Imperial Systems

Dark Detector Circuit for Automatic Street Light Control using BC547 Transistor and LDR

Automatic Street Light Control Circuit using LDR & Transistor BC 547

Emergency LED Light Schematic - DP-716 Emergency 30 LED's Light Circuit Diagram

Emergency LED Light Circuit – DP-716 Rechargeable 30 LED’s Lights Schematic

108 comments.

thanks, good easy to understand.but the voltage source have more than one. how to do it.

It is simple example for ref & explanation purpose only…Wait for upcoming posts….Thanks

Surely when the load resistor is replaced the circuit changes and the 8k and 5k are in parallel with the 4k causing the cu

Surely when the load resistor is replaced the circuit changes and the 8k and 5k are in parallel with the 4k causing the current and voltage to change oops just figured it out the long way and the 5k gets 3.75 out of the 9.75 volts across that part of the circuit your way of showing thevenin is better thank you

Thanks for your kind words…

If the voltage source is more than one you calculate two components of Nortons current that is I’ and I”, add them to get the total Nortons current and repeat the procedure explained above.

Admin. You are doing great work. Your posts related to electricals are easy to learn. . . Keep updating. . .

Thanks for appreciation…

Thevenin's Theorem is not very intuitive for a newbie, good to have this nice easy to follow explanation.

simple and good steps for easy understanding

Good one for basic understanding of theorems :)

How did u get 3mA?

I = V / R … = 48V / (12kΩ + 4kΩ ) = 3mA So 3mA Current will flow in both 12kΩ and 4kΩ resistors as this is a series circuit because current will not flow in the 8kΩ resistor as it is open

If the rounded off value of 3mA is used to find Vth you get 12V. If the less rounded off value of 3.273mA is used we’d get 13V.

when the load terminals are open then all the current passes through only first circuit and the current is from v=i/r can be calculated

1st of all find req than by v=ir , i=v/r we can get the value of current

Thanku. What happens when there is 2 voltage sources?

Use Kirchhoff law

i am proud that u can make this subject such intresting.. hope many teachers of ur kind should be there.. i am learning this during my job period ..if it was during my college it would have been a big deal for me.. anyway thanks!!

hope many teachers of ur kind should be there.. i am learning this during my job period ..if it was during my college it would have been a big deal for me.. anyway thanks!!

Dhuurrrrrr!!

tq admin..mechanical stdent frm malaysia :)

Most welcome dear….

How can I find you in Facebook?

Here is the official Facebook Page of Electrical Technology .

step by step process is easy way for students to understand the problem

Great job there, sometimes is easy to understand through other source.

thank you sir…. this is really a helpful information..

thank u very much sir……

plesae provide telligan’s theorem

Thanks for your very informative post. I had a very bad going with this topic, but now I can assure keep my hands dirty on complex circuits related to this phenomenon by using your idea.

outstanding sir

it is very easy to understand the concept,but if more than one voltage sources are present then how will be the solution and procedure

It is too much easy

boss i love this your tutorials its the best i have ever seen you simplified the sturf to the last five star 4 u *****

best tutors site

Thank you…

sir this is awesome sir i had clarify my doubts succesfully

it is soo easy to understand

Thank you very much!!!

could you give another exercise with 2 suppliers? and show steps

Thumps up to yo tutorials,now I understand the theorem way better than I previously did.Thanx so Much

Thanks for appreciation….

why you solve 12 and 4 as parallel?

If you see in step 4, 8kΩ resistor is in series with a parallel connection of 4kΩ resistor and 12k Ω resistor. i.e. If you solve for the parallel connection of 4kΩ resistor and 12k Ω, It becomes in Series with 8kΩ.

In step 2, The Circuit is Open, Hence, Current will not flow in 8kΩ, Therefore, That’s Why it is in parallel with 4kΩ.

will you please add step by step procedure for dual loops that will help alot Thanx in advance

Great job. you make the determination of thevenin’s voltage is very very easy. Thank you…

I could not solve even a single problem .But this helped me a lot .Thank u

Glad it helps You….

Thanks…

can i get more relevant problems using thevinin’s theorem & may i know that thevinin’s theorem can use for AC supplied circuits.

Yes…. It can be used on both AC and DC Circuits,,, We will post about Thevinin’s theorem about AC Circuits in coming days… Thanks

Told how to solve thevinins them in ac by using kvl.

please inform more and more about electrical and electronics

sir I have a confusion when you calculate Rth because I dont think that Rth=8+4||12. But It should be Rth=12+4||8. Am I wrong Sir ?, if so then please guide me. Thanks Ankit

As mentioned above that We can see that 8kΩ resistor is in series with a parallel connection of 4kΩ resistor and 12k Ω resistor. i.e.: 8kΩ + (4k Ω || 12kΩ)

Saqib Javeed is Right…. Thanks

let me know if you want to know more… Thanks

simply superb

Thank you very much, this was the best explanation available on the internet

Thanks for appreciation …

Was very helpful…thanks a billion times ?

Most Welcome….

Awesome explanation. It’s very useful to us, Thank you!!

Most welcome… And thanks for appreciation….

have we already been provided with 3Am or you have solved it? if you have solved it how have you done it?? a ain’t sure if I have followed you on that one

It is not provided. In Step 2, You may see that this is an Open Circuit, I.e. Current will not flow in the 8kΩ. So the circuit of 48V, 4kΩ and 12kΩ becomes a series circuit. By using Ohms Law, (I = V/R), We found the value of current as 3mA. Thanks

what will be total R in the circuit if 4k shud the load resistance in revolving towards the source

You may just change the value of the resistance and solve again same as above…. No Difficulties…. :)

you said 8k resistor is parallel to 4k resistor in step 2.in step 4 you said 8k resistor is sereis to 4k.why?

Yes Dear…. If you see in step 4, 8kΩ resistor is in series with a parallel connection of 4kΩ resistor and 12k Ω resistor. i.e. If you solve for the parallel connection of 4kΩ resistor and 12k Ω, It becomes in Series with 8kΩ.

In step 2, The Circuit is Open, Hence, Current will not flow in 8kΩ, Therefore, That’s Why it is in parallel with 4kΩ. Thanks. let me know if you want to know more… Thanks

wow. thank you. now i understand. :)

thank you for this. but how about 3 sources using this theorem?

Please how was the 3mA current gotten ?

can you explain to me about how did you get 12V as it is 48V?

IT IS GOOD BUT I WILL LIKE IT IF IT SOLVED USING SMALL NUMBERS LIKE 3,4,2 TO MAKE IT LOOK MORE SIMPLER

Thevenin made simply. thanks dear.

A/C to my point of view, Its very simple and easy method for understanding..

Simplified example…great work

if I find current across 5 ohm resister there is a greater value then the total load current that is 0.75 can anyone answer

thanks for the example.

thank you dear

A really Understanding work!

Thanks for keeping the simplicity in the explination I thoroughly understood the conpect.

Thanks soooooo much, it really help me out.

Thank you so much to help me in easy way

And if there is an ammeter in parallel with the resistance, then what to do

Really good

If there are a voltage or current source between A & B terminals or in the place of load resistor, Then how can i solve this????????

VERY SIMPLY AND THOROUGHLY EXPLAINED THE CONCEPT OF THEVENINS THEOREM. PLEASE INCLUDE THE NOTES OF TWO POLE NETWORKS ALSO

Am happy for the steps of thevenins i cam now calculate but following the steps

sir please tell me….is this the right and only method to solve problems by thevenin’s theorem?

Yes! But you can analyze the same problem by different methods as well.

can you please tell me the different methods sir?

please respond quick!!

Very good explanation. I tend to solve complex circuits using Kirchoff’s laws…Are there particular cases when one method is favourably used instead of the other? ( I have not read all posts…maybe you have already gone into this)

how did u get 3mA

3mA current will flows in both 12kΩ and 4kΩ resistors as it is a series circuit because current will not flow in the 8kΩ resistor as it is open (Fig 2)

thankyou its help full. request.. how can I calculate if there are voltage source in the circuit?

thank u so much

Where does the load resistor come from? Can any load resistor be used?

Hi Admin If point A and point B are at 4kohm, how to get V(TH) and R(TH)? Thanks

Sir RL=5kom kese find ?

It is the given data in the first circuit (fig 1).

Sr i need more explanation on how you get 12v

Inspiring lessons, Thanks so much

Thevenin theorem statement

Thevenin theorem definition, related posts:.

Thevenin’s theorem is very important in point of view to Simplify the Network and Reduction of Network complexity in any circuit. This is also a very important theorem for Engineering and diploma students in basic Electrical.

According to Thevenin’s theorem, any linear bilateral network irrespective of its complexities can be reduced into a Thevenin’s equivalent circuit having the thevenins’ open circuit voltage Vth in series with the Thevenin equivalent resistance Rth along with load resistance RL .

This theorem is named Thevenin’s theorem on the name of scientist Thevenin, he fist apply this theorem to the analysis of a circuit. By using this theorem we can reduce the complexity of any circuit network and can simplify if only two criteria are fulfilled 1st the network is linear and 2nd is bilateral. We see two elements in the simplified network 1st are Thevenin equivalent voltage Vth this is also called open-circuit voltage (Voc) , a series resistance Rth connected with this vth, this series resistance Rth is called Thevenin equivalent resistance. all of them are connected in series with a load resistance RL.

We can find the current IL which is flowing through the load resistance RL in any Thevenin equivalent circuit.

IL=Vth/Rth+RL

This identity is nothing But Ohm’s law {I=V/R} . Here RL is the load resistance which to say that finds the value in any question.

Now we go to steps that help us to solve the numerical question of Thevenin theorem. There are following steps required to solve the Thevenin’s theorem questions.

Identify the load resistance value of RL
Remove the load resistance and calculate the open circuit potential across the two open ends. This will be equivalent to Thevenin voltage Vth.- If I require the potential of load resistance then we need to remove the load resistance because after the removing of load resistance, there will create the Two points and at that point where we can find the potential difference, and this potential is called Thevenin equivalent Thevenin voltage. The reason behind removing the load resistance is to we need to find the voltage, If we need to find the current then I can short-circuit on that. So we remove the RL and Leave that point open and the potential difference between two points is our Vth or Voc(It is also said that open-circuit voltage).
Again remove the load resistance and replace all active sources with their internal resistance and find Rth – If we find the equivalent resistance then there is no need of any active sources. We required only the internal resistance of those active sources.
Calculate the equivalent resistance across the open ends. – This will we the Thevenin equivalent resistance Rth.
Draw the Thevenin equivalent network.
Calculate the Load current IL using this identity IL=Vth/Rth+RL

Thevenin’s theorem problems

Q. Find the value of current through 1Ω Resistor in the given circuit using Thevenin’s theorem.

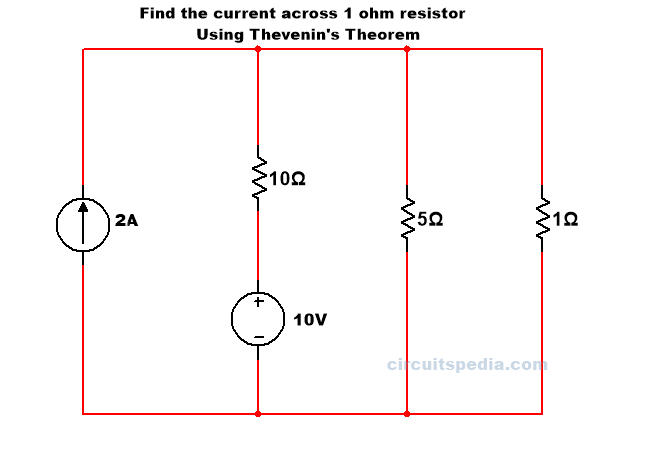
Solution – First we have to remember that the IL Load current is current flow across the resistor which value says to find in question. So here IL is the current of the resistor of 1Ω and this is also here the load resistor RL. In question value across which resistor asks that is Load resistor RL.

According to step 1 find the value of RL- Here Value of RL = 1Ω

In 2nd step remove the Load resistance and calculate the open circuit Vth for the two open ends.

We can calculate the voltage at pint a and b using Kirchoff’s law (KCL AND KVL). so we use here KVL , first, we need a path between point a and b that completes a circuit between these. we need All elements to convert into voltage. So we have the shortest path between A and B through the 5Ω resistor. If we have the value of current across 5Ω resistor then I can calculate the voltage across 5Ω using Ohm’s law.

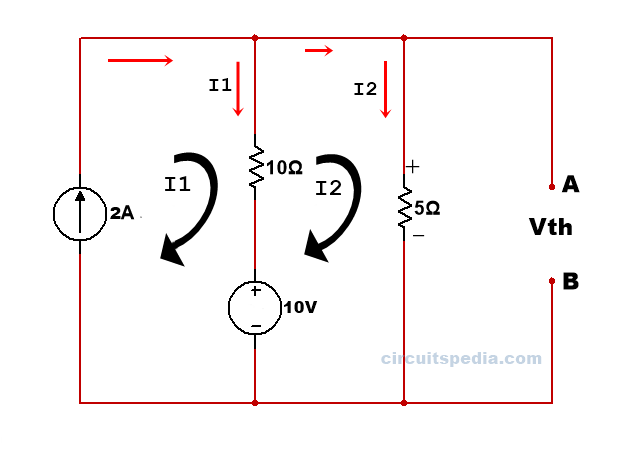
Applying KVL in All meshes.

10-10(I2-I1)-5I2=0 -15I2=10I1=-10 -15I2=-10-20=-30 -15I2=-30 I2=30/15=2A

The voltage across the 5Ω resistor is V=I*R=2*5=10Ω

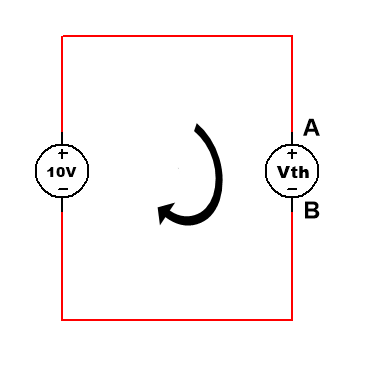
and we consider point A and b is a voltage source of Vth, then the voltage of Vth is

Now we replace all active voltage and current sources with their internal resistance

If any circuit there is internal resistance as given below

[Voltage – if not given internal resistance of voltage source in any circuit means 0Ω=short circuit

Current – α(Infinite)= Open circuit)]

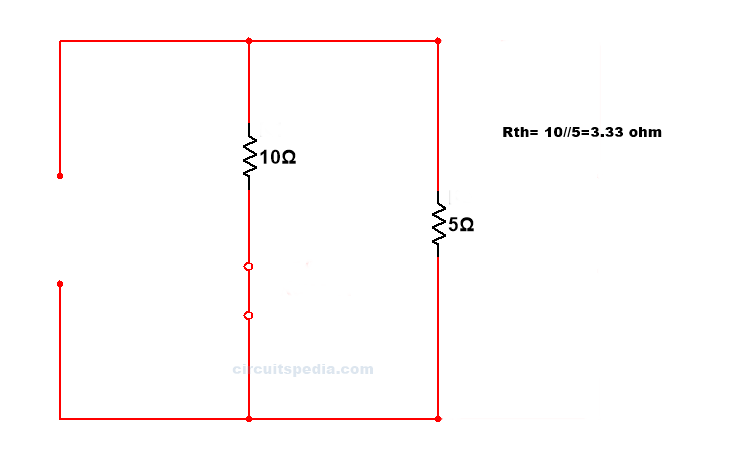
step 3 Remove again load resistance and replace all sources with their internal resistance, Then circuit will as below

Rth= 1/10+1/5 =3.33Ω

IL= Vth/Rth+RL=10/3.33+1

Q.2 Find the value of current across resistor 6Ω resistor using Thevenin’s Theorem.

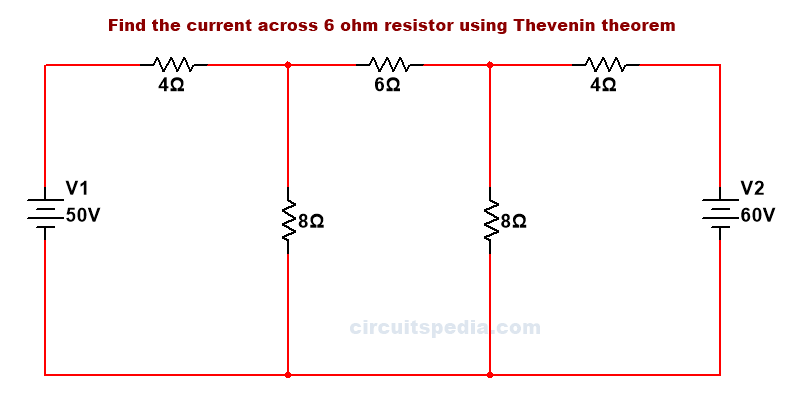
solution –

The formula is IL= Vth/Rth+RL

RL is given in all circuits because the value of current across which resistor asked in the question, is Load resistor RL.

First, we remove the load resistance RL and make it open at that point.

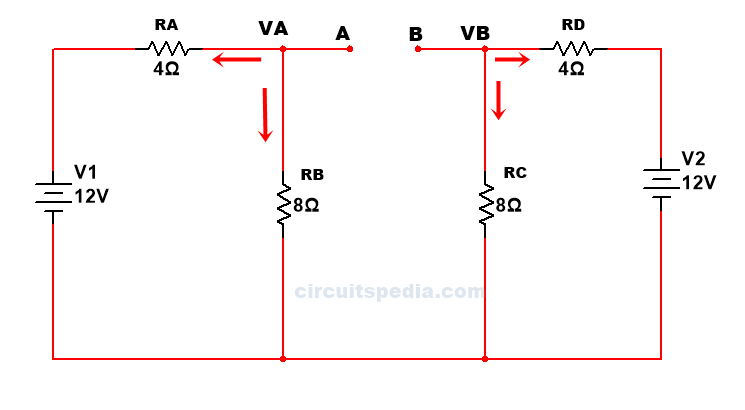
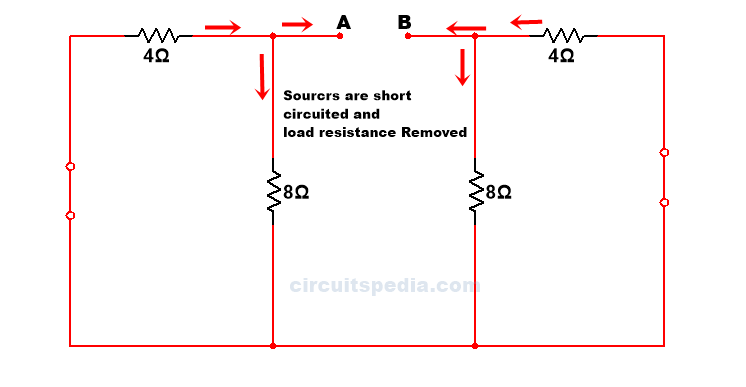
After that replace all active sources with their internal resistance. Now, here no any internal resistance is given in sources.so, we assume that the internal resistance of all sources have 0Ω . Then sources are short circuits.

Q.3 Find the value of current across 5Ω resistor using the Thevenin’s Theorem

solution –

First, we remove the load resistor 5Ω from the circuit.

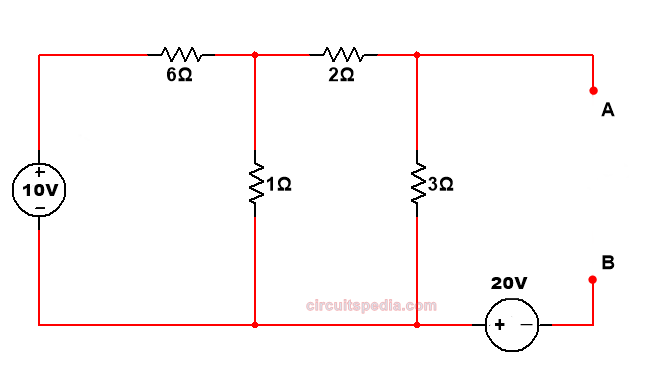
Replacing the sources with their internal resistance.

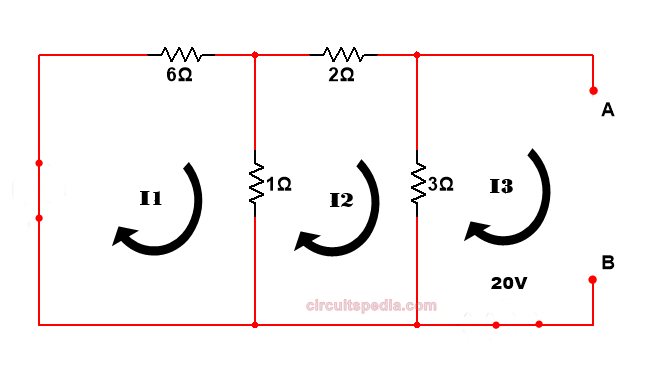
We find the current equation in all meshes using KVL

7I1-I2 =10 ——eq.1

-I1+6I2=0 ——eq 2.

by solving eq1 and 2 ——-eq.1

Applying KVL in mesh 3

-3(I3-I2)-Vth-20=0

-I3+3I1-Vth+20=0

3I2-Vth+20=0

I3=0 (because this mesh is open)

3(0.2434)+20=Vth

Vth=20.73170v

Rth = 2.857//3=1.4637

Draw the Thevenin equivalent circuit and calculate the value of current using ohm’s law

=3.20756A Ans.

Kirchoff’s law (kcl, kvl)

Norton’s theorem, how capacitor block dc current, logic gates, semiconductor p-n diode | p-n junction, related posts.

Automatic DC FAN controller circuit

220v 50W Low Power Inverter Circuit

What is NOT gate (Inverter)

Simple LED Flasher Circuit with 555 timer

Simple 2 led blinking flasher circuit.

Simple 5 LED Blinker/Flasher circuit

Best Low power Mic Amplifier circuit using LM386

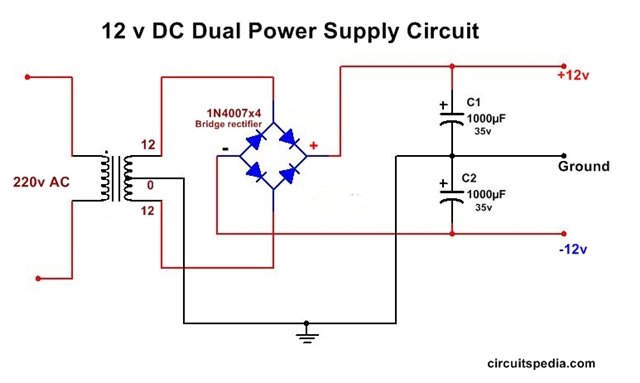
Dual Power Supply Circuit

Thevenin’s Theorem -explanation, equivalent circuit & examples

Circuits can contain many power sources and power dissipation elements. It is common that any one of the elements in the circuit is a variable while all others are fixed. Thevenin’s theorem is applied in order to simplify complex circuits with a single varying load. Confused? Let us discuss a very common example:

Imagine the utility socket in your home. Each appliance in your home has a different impedance. So, every time you plug in an appliance to the socket the load added to the circuit is different. Whereas the other circuit remaining parameters such as wire resistance remain constant at normal temperature. Hence, the circuit needs to be analyzed each time a different appliance is plugged in.

To avoid this problem, Léon Charles Thévenin came up with a new approach of circuit analysis, by which the fixed elements of the circuit can be replaced by their equivalent.

Thevenin’s theorem statement

Solved examples

How to find thevenin’s resistance?
How to find thevenin’s voltage?
Steps to calculate Thevenin’s equivalent circuit

Thevenin’s theorem

Thevenin’s theorem states that any linear network having a number of voltage sources and resistances can be replaced by a simple equivalent circuit consisting of a single voltage source (V TH ) in series with a resistance (R TH ), where V TH is the open-circuit voltage at the terminals of the load and R TH is the equivalent resistance measured across the terminals while independent sources are turned off.

Simply, Thevenin’s theorem states that any linear network with several power sources, resistances and a variable load can be represented in a much simpler circuit containing a single voltage source (V TH ) (known as Thevenin’s equivalent voltage) in series with a resistance (R TH ) (known as Thevenin’s equivalent resistance) and the variable load, where V TH is the open-circuit voltage at the terminals of the load and R TH is the equivalent resistance measured across the terminals while independent sources are turned off. See the below figure for better understanding.

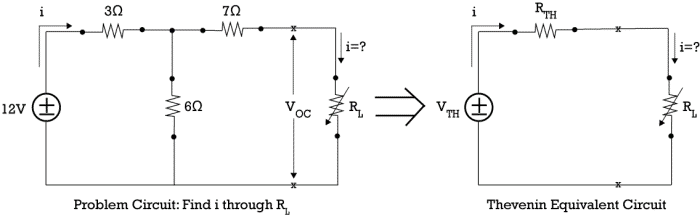
Thevenin’s theorem can be better understood from the below example:

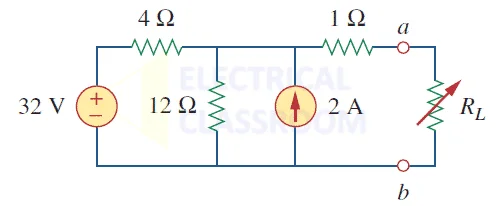
Problem : Let’s find the Thevenin’s equivalent circuit for the above circuit.

In the above circuit, we have a voltage source (32V) and another current source (2A).

Step 1: Find Thevenin’s resistance

While calculating the thevenin’s equivalent resistance, all voltage sources must be turned off, meaning it acts like a short circuit and all current sources act like an open circuit, as shown in the figure below:

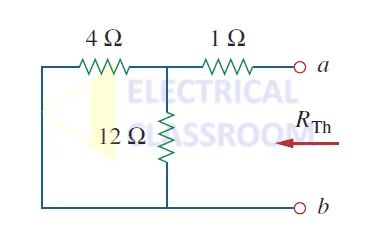
Let us calculate the thevenin’s resistance for the above circuit:

Thevenin’s resistance , R th = 4 || 12 +1 = 4 x 12 / 16 + 1 = 4 ohms

Step 2: Find Thevenin’s voltage

Let’s perform mesh analysis to find Thevenin’s voltage:

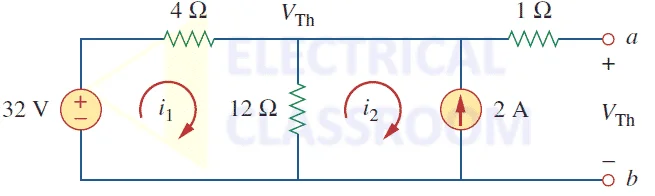
4i 1 + 12(i 1 – i 2 ) = 32V, i 2 = -2A

Solving the above equations, we get i 1 = 0.5A

Therefore V th = 12(i 1 – i 2 ) = 12(0.5 + 2) = 30V

Step 3: Draw equivalent circuit

The equivalent Thevenin’s circuit is shown in the figure below:

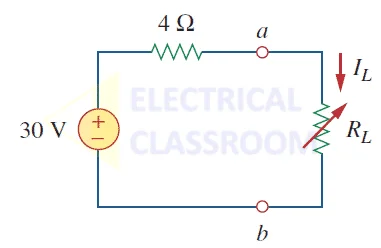
Steps to calculate Thevenin’s equivalent circuit.

Remove the load resistance.
After short circuiting all the voltage sources and open circuiting all current sources, find the equivalent resistance (R th ) of the circuit, seeing from the load end.
Now, find V th by usual circuit analysis.
Draw Thevenin’s equivalent circuit with V th , R th and load. From this circuit we can calculate I L for different values of load resistance.

Thevenin’s theorem is very important in circuit analysis, power system analysis, short circuit calculations and is a key tool for circuit design. Thevenin’s circuit is a simplified form of a large circuit containing multiple power sources and resistances. The simplified circuit contains a voltage source (equivalent to the voltage measured across the terminals of the load) and an equivalent resistance in series with the variable load.

6 thoughts on “Thevenin’s Theorem -explanation, equivalent circuit & examples”

What about situations where there are three other resistors on the loop the Vth is on the circuit?

Good job, well done!

Thevenin's Theorem

Most commonly, we use Ohm’s law, Kirchhoff’s law to solve complex electrical circuits, but we must also be aware that there are many circuit analysis theorems using which we can calculate the current and voltage at any given point in a circuit. Among the various circuit theorems, Thevenin’s theorem is most commonly used. In this article, let us learn about Thevenin’s theorem in detail.

Thevenin’s Theorem Explanation

Thevenin’s theorem states that it is possible to simplify any linear circuit, irrespective of how complex it is, to an equivalent circuit with a single voltage source and a series resistance.

A Thevenin equivalent circuit is shown in the image. In the image, we see that multiple resistive circuit elements are replaced by a single equivalent resistance R s and multiple energy sources by an equivalent voltage source V s .

Thevenin’s Theorem Example

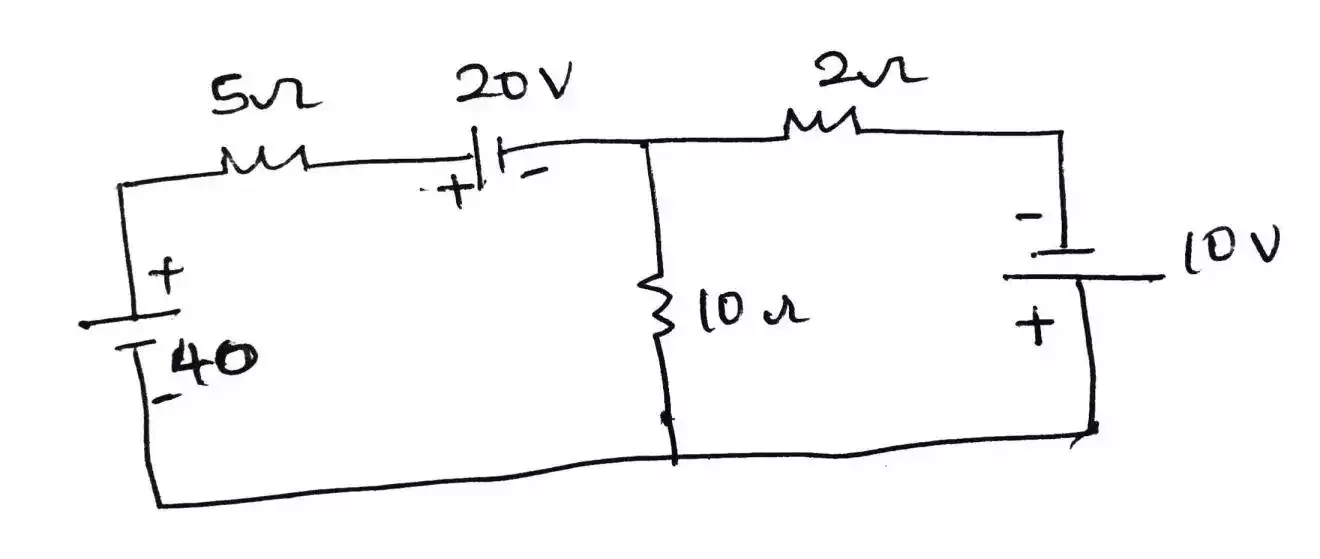
Let us understand Thevenin’s Theorem with the help of an example.

Step 1: For the analysis of the above circuit using Thevenin’s theorem, firstly remove the load resistance at the centre, in this case, 40 Ω.

Step 2: Remove the voltage sources’ internal resistance by shorting all the voltage sources connected to the circuit, i.e. v = 0. If current sources are present in the circuit, then remove the internal resistance by open circuiting the sources. This step is done to have an ideal voltage source or an ideal current source for the analysis.

Step 3: Find the equivalent resistance. In the example, the equivalent resistance of the circuit is calculated as follows:

With the load resistance removed and the voltage sources shorted, the equivalent resistance of the circuit is calculated as follows:

The resistor 10 Ω is parallel to 20 Ω, therefore the equivalent resistance of the circuit is:

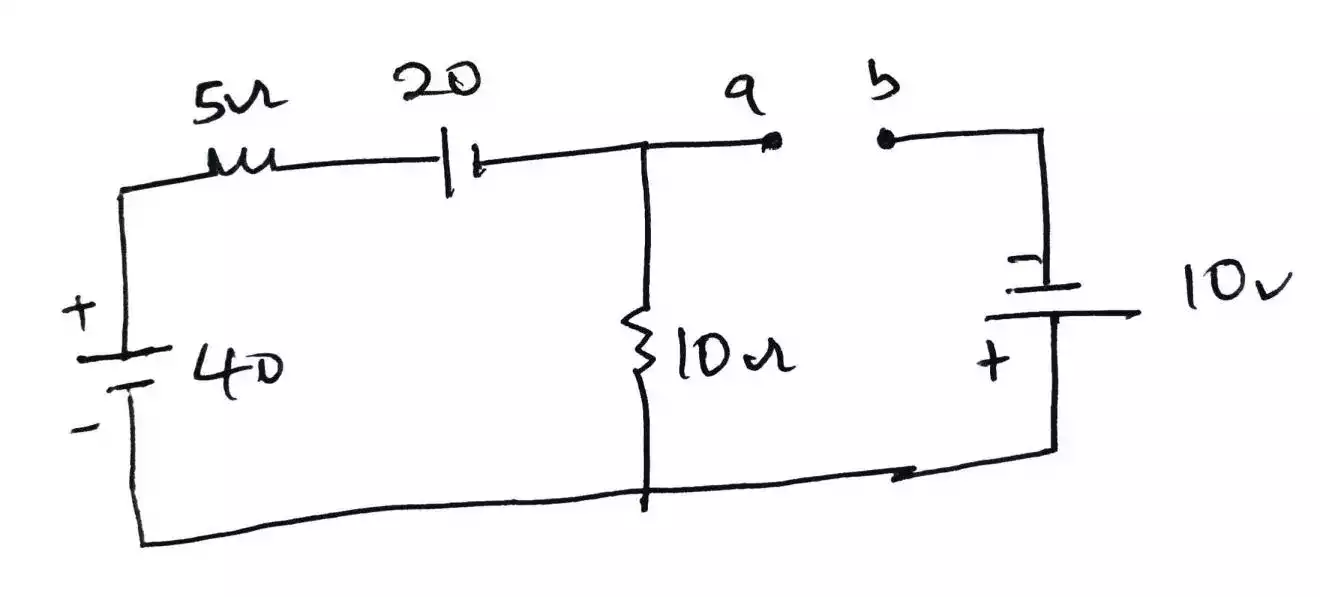
Step 4: Find the equivalent voltage.

To calculate the equivalent voltage, reconnect the voltage sources back into the circuit. V s = V AB , therefore the current flowing around the loop is calculated as follows:

The calculated current is common to both resistors, so the voltage drop across the resistors can be calculated as follows:

V AB = 20 – (20 Ω x 0.33 A) = 13.33 V

V AB = 10 + (10 Ω x 0.33 A) = 13.33 V

The voltage drop across both resistors is the same.

Step 5: Draw the Thevenin’s equivalent circuit. The Thevenin’s equivalent circuit consists of a series resistance of 6.67 Ω and a voltage source of 13.33 V.

The current flowing in the circuit is calculated using the formula below:

Thevenin’s theorem can be applied to both AC and DC circuits. But it should be noted that this method can only be applied to AC circuits consisting of linear elements like resistors, inductors, capacitors. Like Thevenin’s equivalent resistance, Thevenin’s equivalent impedance is obtained by replacing all voltage sources with their internal impedances.

Thevenin’s Theorem Solved Example

Find V TH , R TH and the load current I L flowing through and load voltage across the load resistor in the circuit below using Thevenin’s Theorem.

Step 1: Remove the 5 kΩ from the circuit.

Step 2: Measure the open-circuit voltage. This will give you the Thevenin’s voltage (V TH ).

Step 3: We calculate Thevenin’s voltage by determining the current that flows through 12 kΩ and 4 kΩ resistors.

As both the resistors are in series, the current that flows across them can be calculated as follows:

I = 48 V /( 12 kΩ + 4 kΩ) = 3 mA

The voltage across the 4 kΩ resistors can be calculated as follows:

3 mA x 4 kΩ = 12 V

As there is no current flowing through the 8 kΩ resistor, so there is no voltage drop across it and hence the voltage across the terminals AB is same as the voltage across the 4 kΩ resistor. Therefore, 12 V will appear across the AB terminals. Hence, the Thevenin’s voltage, V TH = 12 V.

Step 4: Short the voltage sources as shown in the figure below:

Step 5: Calculate the Thevenin’s Resistance

By measuring the open circuit resistance, we can measure Thevenin’s resistance.

We notice that the 8 kΩ resistor is in series with the parallel connection of 12 kΩ and 4 kΩ resistors. Therefore, the equivalent resistance or the Thevenin’s resistance is calculated as follows:

8kΩ + (4k Ω || 12kΩ)

R TH = 8 kΩ + 3 kΩ

R TH = 11 kΩ

Step 6: Now, connect the R TH in series with Voltage Source V TH and the load resistor as shown in the figure.

Step 7: For the last step, calculate the load voltage and load current using Ohm’s law as follows:

I L = V TH / (R TH + R L )

I L = 12 V / (11 kΩ + 5 kΩ) = 12 V/16 kΩ = 0.75 mA

The load voltage is determined as follows:

V L = 0.75 mA x 5 kΩ = 3.75 V

Thevenin Theorem Applications

Thevenin’s theorem is used in the analysis of power systems.

Thevenin’s theorem is used in source modelling and resistance measurement using the Wheatstone bridge.

Thevenin Theorem Limitations

Thevenin’s theorem is used only in the analysis of linear circuits.
The power dissipation of the Thevenin equivalent is not identical to the power dissipation of the real system.

Frequently Asked Questions – FAQs

What is thevenin’s theorem.

Thevenin’s theorem states that it is possible to simplify any linear circuit, irrespective of how complex it is, to an equivalent circuit with a single voltage source and a series resistance.

What is Thevenin Voltage?

The open-circuit voltage that appears across the two terminals is the Thevenin voltage.

Where is Thevenin’s Theorem used?

Is thevenin’s theorem applicable to non-linear circuits.

No, Thevenin’s Theorem is not applicable to non-linear circuits.

Is Thevenin’s Theorem applicable to AC circuits?

Yes, Thevenin’s theorem applies to AC circuits.

Stay tuned to BYJU’S and Fall in Love with Learning !

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Physics related queries and study materials

Your result is as below

Request OTP on Voice Call

Register with BYJU'S & Download Free PDFs

Thevenin’s Theorem | Thevenin’s Equivalent Circuit

What is the thevenin’s theorem.

Thevenin’s Theorem states that any two-terminal linear network containing resistances and voltage sources and/or current sources may be replaced by single voltage source in series with a single resistance. The emf of the voltage source is the open circuit emf at the network terminals, and the series resistance is the thevenin’s equivalent resistance between the network terminals when sources are set to zero.

Suppose we are given an arbitrary circuit containing any or all of the following elements: resistors, voltage sources, current sources (the source can be dependent as well as independent). Let us identify a pair of nodes, say node a and b, such that the circuit can be partitioned into two parts as shown in figure 1.

Figure.1: Circuit partitioned into two parts

Furthermore, suppose that circuit A contains no dependent source that is dependent on a variable in circuit B and vice versa. Then, we can model circuit A by an appropriate independent voltage source, call it V oc that is connected in series with an appropriate resistance, call it R TH . This series combination of a voltage source and a resistance is called the Thevenin’s equivalent of circuit A. in other words, circuit A in figure 1 and the circuit in the shaded box in figure 2 have the same effect on circuit B. This result is known as Thevenin’s theorem and is one of the most useful and significant concepts in circuit theory.

Figure.2: Thevenin’s Equivalent Circuit

Circuit B (which is often called a load) may consist of many circuit elements, a single element (a load resistor), or no element.

You May Also Read: Norton’s Theorem with Solved Examples

How to Find the Equivalent Voltage of a Thevenin Circuit?

To obtain the voltage V oc – called the open circuit voltage- remove circuit B from circuit A, and determine the voltage between node a and b ( where the + is at node a). This voltage, as shown in figure 3(a), is V oc .

Figure.3 (a): How to Find the Equivalent Voltage of a Thevenin Circuit

How to Find the Equivalent Resistance in Thevenin’s Theorem?

There are several ways to find the Thevenin’s equivalent resistance, which are given below: 1. To obtain the resistance R TH – called the Thevenin’s equivalent resistance of circuit A: i) Remove circuit B from circuit A. ii) Set all independent sources in circuit A to zero. (A zero voltage source is equivalent to a short circuit, and zero current source is equivalent to an open circuit). iii) Determine the resistance between nodes a and b- this is R TH – as shown in figure 3(b).

Figure.3 (b): Determination of Thevenin’s Equivalent Resistance R TH

2. Short-circuit the terminals a and b then find the short-circuit current I sc . The Thevenin equivalent resistance is given by

\[{{\text{R}}_{\text{th}}}\text{= }{{\text{V}}_{\text{oc}}}\text{/}{{\text{I}}_{\text{sc}}}\text{= }{{\text{V}}_{\text{th}}}\text{/}{{\text{I}}_{\text{sc}}}\]

3. When the source network has a ladder structure and contains no controlled (dependent) sources, R TH is easily found by series-parallel reduction of the dead network.

When the source network contains controlled sources , the Thevenin’s resistance can be found using the method represented by figure 4.

Figure.4: How to Find the Thevenin’s Equivalent Resistance

Here, the dead source network has been connected to an external test source. This test source may be any independent voltage or current source that establishes v o at the terminals. Since the dead network contains only resistors and controlled sources, and since R TH equals the equivalent resistance of the dead network, the equivalent resistance theorem tells us that

\[{{R}_{TH}}={{v}_{o}}/{{i}_{o}}\]

Thevenin’s Theorem Solved Example with Voltage Source

Find Thevenin equivalent circuit of the following network.

By applying nodal voltage method,

$\frac{{{V}_{1}}-25}{5}+\frac{{{V}_{1}}}{20}-3=0$

${{V}_{1}}=32~V$

${{V}_{th}}=32V$

To find short circuit current, we short-circuited terminals a and b as shown in the following figure:

Again using nodal voltage method ,

$\frac{{{V}_{2}}-25}{5}+\frac{{{V}_{2}}}{20}-3+\frac{{{V}_{2}}}{4}=0$

${{V}_{2}}=16~V$

${{I}_{sc}}=\frac{{{V}_{2}}}{4}=\frac{16}{4}=4A$

${{R}_{th}}=\frac{{{V}_{th}}}{{{I}_{sc}}}=\frac{32}{4}$

${{R}_{th}}=8~\Omega $

Now, we have following equivalent circuit:

Thevenin’s Theorem Solved Problem with Dependent Sources

Consider a circuit shown in the following figure. We will determine V th and R th across terminals a and b of the circuit.

Applying KCL at node 1:

\[\begin{matrix} \frac{{{V}_{1}}-5}{2000}+\frac{{{V}_{1}}}{6000}+\frac{{{V}_{1}}-{{V}_{2}}}{1000}=0 & \cdots & (1) \\\end{matrix}\]

Multiply (1) by 6000 yields

\[3{{V}_{1}}\text{- }15\text{ }+\text{ }{{V}_{1}}+\text{ }6{{V}_{1}}\text{ -}6{{V}_{2}}=\text{ }0\]

\[10{{V}_{1}}=\text{ }6{{V}_{2}}+\text{ }15\]

\[{{V}_{1}}=\text{ }0.6{{V}_{2}}+\text{ }1.5\]

Applying KCL at node 2:

\[\begin{matrix} \frac{{{V}_{2}}-{{V}_{1}}}{1000}+0.0005{{V}_{1}}+\frac{{{V}_{2}}}{10000}=0 & \cdots & (2) \\\end{matrix}\]

Multiply (2) by 10000 yields

\[10{{V}_{2}}\text{ -}10{{V}_{1}}+\text{ }5{{V}_{1}}+\text{ }{{V}_{2}}=\text{ }0\]

\[11{{V}_{2}}\text{ -}5{{V}_{1}}=\text{ }0\]

\[11{{V}_{2}}\text{- }5(0.6{{V}_{2}}+\text{ }1.5)\text{ }=\text{ }0\]

\[8{{V}_{2}}=\text{ }7.5\]

Finally we have

\[{{V}_{th}}=\text{ }{{V}_{oc}}=\text{ }{{V}_{2}}=\text{ }7.5/8\text{ }=\text{ }0.9375\text{ }V\]

Now, we have dependent source, so method 1 cannot be used for finding Thevenin’s Equivalent resistance Rth. Either Method 2 or Method 3 can be utilized here. We will prefer to employ second method. Terminals a and b are to be shorted as shown in the following figure and V 2 = 0.

\[\begin{matrix} \frac{{{V}_{1}}-5}{2000}+\frac{{{V}_{1}}}{6000}+\frac{{{V}_{1}}}{1000}=0 & \cdots & (3) \\\end{matrix}\]

Multiplying (3) by 6000 yields:

\[3{{V}_{1}}\text{- }15\text{ }+\text{ }{{V}_{1}}+\text{ }6{{V}_{1}}=\text{ }0\]

\[10{{V}_{1}}=\text{ }15\]

\[{{V}_{1}}=\text{ }1.5\text{ }V\to \text{ }v\text{ }=\text{ }{{V}_{1}}=\text{ }1.5\text{ }V\]

The current through R 3 (⟶) is given by

\[{{I}_{{{R}_{3}}}}=\text{ }{{V}_{1}}/{{R}_{3}}=~1.5\text{ }V/1k\Omega =\text{ }1.5mA\]

The current through VCCS (↓) is given by

\[{{I}_{VCCS}}=\text{ }0.0005{{V}_{1}}=~0.0005*1.5\text{ }A\text{ }=\text{ }0.75mA\]

Now, short-circuit current would be

\[{{I}_{sc}}=\text{ }{{I}_{{{R}_{3}}}}\text{ -}{{I}_{VCCS}}=\text{ }1.5mA\text{ -}0.75mA=\text{ }0.75mA\]

And Thevenin’s equivalent resistance is

\[{{R}_{th}}={{V}_{th}}/{{I}_{sc}}=\text{ }0.9675\text{ }V/0.75mA=\text{ }1.25\text{ }k\Omega \]

Thevenin’s Theorem Steps

Following steps are being used to determine Thevenin’s equivalent circuit.

The portion of circuit considered as load is removed
The open circuit voltage V oc is calculated at terminals.
To calculate R th
Short circuit all independent voltage sources.
Open circuit all independent current sources.
Draw equivalent circuit, connect the load and determine load current.

1 thought on “Thevenin’s Theorem | Thevenin’s Equivalent Circuit”

Pingback: Norton Theorem and Norton Equivalent Circuit | Electrical Academia

Thevenin’s Theorem

Thevenin theorem is an analytical method used to change a complex circuit into a simple equivalent circuit consisting of a single resistance in series with a source voltage

In the previous three tutorials we have looked at solving complex electrical circuits using Kirchhoff’s Circuit Laws, Mesh Analysis and finally Nodal Analysis. But there are many more “Circuit Analysis Theorems” available to choose from which can calculate the currents and voltages at any point in a circuit. In this tutorial we will look at one of the more common circuit analysis theorems (next to Kirchhoff´s) that has been developed, Thevenins Theorem .

Thevenin’s Theorem states that “ Any linear circuit containing several voltages and resistances can be replaced by just one single voltage in series with a single resistance connected across the load “. In other words, it is possible to simplify any electrical circuit, no matter how complex, to an equivalent two-terminal circuit with just a single constant voltage source in series with a resistance (or impedance) connected to a load as shown below.

Thevenins Theorem is especially useful in the circuit analysis of power or battery systems and other interconnected resistive circuits where it will have an effect on the adjoining part of the circuit.

Thevenins Theorem Equivalent Circuit

As far as the load resistor R L is concerned, any complex “one-port” network consisting of multiple resistive circuit elements and energy sources can be replaced by one single equivalent resistance Rs and one single equivalent voltage Vs . Rs is the source resistance value looking back into the circuit and Vs is the open circuit voltage at the terminals.

For example, consider the circuit from the previous tutorials.

Firstly, to analyse the circuit we have to remove the centre 40Ω load resistor connected across the terminals A-B , and remove any internal resistance associated with the voltage source(s). This is done by shorting out all the voltage sources connected to the circuit, that is v = 0 , or open circuit any connected current sources making i = 0 . The reason for this is that we want to have an ideal voltage source or an ideal current source for the circuit analysis.

The value of the equivalent resistance, Rs is found by calculating the total resistance looking back from the terminals A and B with all the voltage sources shorted. We then get the following circuit.

Find the Equivalent Resistance (Rs)

The voltage Vs is defined as the total voltage across the terminals A and B when there is an open circuit between them. That is without the load resistor R L connected.

Find the Equivalent Voltage (Vs)

We now need to reconnect the two voltages back into the circuit, and as V S = V AB the current flowing around the loop is calculated as:

This current of 0.33 amperes (330mA) is common to both resistors so the voltage drop across the 20Ω resistor or the 10Ω resistor can be calculated as:

V AB = 20 – (20Ω x 0.33amps) = 13.33 volts.

V AB = 10 + (10Ω x 0.33amps) = 13.33 volts , the same.

Then the Thevenin’s Equivalent circuit would consist or a series resistance of 6.67Ω and a voltage source of 13.33v . With the 40Ω resistor connected back into the circuit we get:

and from this the current flowing around the circuit is given as:

which again, is the same value of 0.286 amps , we found using Kirchhoff’s circuit law in the previous circuit analysis tutorial.

Thevenins theorem can be used as another type of circuit analysis method and is particularly useful in the analysis of complicated circuits consisting of one or more voltage or current source and resistors that are arranged in the usual parallel and series connections.

While Thevenin’s circuit theorem can be described mathematically in terms of current and voltage, it is not as powerful as Mesh Current Analysis or Nodal Voltage Analysis in larger networks because the use of Mesh or Nodal analysis is usually necessary in any Thevenin exercise, so it might as well be used from the start. However, Thevenin’s equivalent circuits of Transistors, Voltage Sources such as batteries etc, are very useful in circuit design.

Thevenins Theorem Summary

We have seen here that Thevenins theorem is another type of circuit analysis tool that can be used to reduce any complicated electrical network into a simple circuit consisting of a single voltage source, Vs in series with a single resistor, Rs .

When looking back from terminals A and B , this single circuit behaves in exactly the same way electrically as the complex circuit it replaces. That is the i-v relationships at terminals A-B are identical.

The basic procedure for solving a circuit using Thevenin’s Theorem is as follows:

1. Remove the load resistor R L or component concerned.
2. Find R S by shorting all voltage sources or by open circuiting all the current sources.
3. Find V S by the usual circuit analysis methods.
4. Find the current flowing through the load resistor R L .

In the next tutorial we will look at Nortons Theorem which allows a network consisting of linear resistors and sources to be represented by an equivalent circuit with a single current source in parallel with a single source resistance.

348 Comments

Notify me of follow-up comments by email.

This lesson has improved my mind thank you

I enjoyed the tutorial

The tutoria is so nicely

Electrical and Electronic Engineering courses question

Write your comment here we go physics

Wow so amazing thanks for the tutorial it is well understood now

I can’t understand 😩

since we cut open the circuit at points a and b, why 10 and 20Ω resistances are added as in parallel and not as in series connection?

Because they are parallel connected

I’m join the conversation

Thanks a lot…very nicely explained..

Electrical engineer problem

Please thanks for the tutorials, it benefits me a lot. Here is my whatsAp number (+237), like communicating with you. Thanks Ngale Raymond.

Very good learning staff.

Thevinns theorem

Using Thevenin’s theorem, find the current through load Resistor (RL=10 kΩ) for the circuit shown in Figure 5 and power dissipated in the load resistor.

very nice explanation

Great brief analysis

I really appropriate

Privacy Policy
Terms of Use
Contact Sales
Media Guide Request
Electronic Products
Power Electronics News
Planet Analog
ElectroSchematics
Datasheets.com
Electronics Know How
The Channelist
EE Times Asia
EE Times China
EE Times India
EE Times Japan
EE Times Taiwan

Thevenin's Theorem Explained With Solved Examples

Mohammad Jamiu

Circuit Analysis

Read Time 🕠 - 4mins

Thevenin theorem is a theorem used to model complex circuits into a simple circuit with an equivalent voltage source and resistance.

As the theorem states that;

‘any two terminals of a network can be replaced by an equivalent voltage source and an equivalent series resistance.

The voltage source is the voltage across the two terminals with load, if any, removed.

The series resistance is the resistance of the network measured between two terminals with load removed and constant voltage source being replaced by its internal resistance (or if it is not given with zero resistance, i.e., short circuit) and constant current source replaced by infinite resistance, i.e., open circuit.’

But why do we need this theorem

Because it is not like mesh analysis or nodal analysis which we use to analyze circuit but rather it is a technique that makes engineers unique (to my opinion). Here’s is what I mean, if two engineers are tasked to design a circuit each with an output of (5V and 1A).

The first engineer let’s say MR X decided to design his own circuit with 2 resistors and a 20V battery as shown below while MR Y decided to design his own circuit with just one resistor and a 9V battery as shown below also.

As you can see, both circuit gives the required output but what both circuits contain are different and this is what makes the thevenin theorem helpful as it lets us to approximately guess what another engineer has designed even if one does not know what is inside the box containing the circuit just as our home charger.

There are different variations but at the end of the day, the output of those charger are quite same.

Steps to solve circuit problem using thevenin theorem

If there is a load resistor R L then you need to remove it.

Find the thevenin voltage V th across the terminal of interest. The V th can be found by finding the open circuit voltage across the terminal

Find the short circuit current I sc between terminal a → b

With the short circuit current known, the thevenin resistance can be found by dividing V th by I sc

To solve for V th , you can use whatever technique you are most comfortable with or that suit the problem at hand maybe mesh analysis, nodal analysis or source transform.

After finding the V th and R th then you need to sketch your circuit as shown below.

Also if there is R L then, you need to replace the open terminal a → b with R L as shown below and lastly find the current that flow through R L as the current that flows through it is not I sc .

Lets solve some examples to understand the concept better.

Example problem on thevenin’s theorem

Ex.1 – find the current through the 2Ω resistor using thevenin theorem?

Remove the 2Ω resistor and leave the terminal open.

Using mesh analysis, lets analyse the circuit. Since there is only one loop as the terminal a → b has made the second loop to no longer be a loop.

The equation gotten is :

40-5i-20-10i = 0

I=20/15 = 1.33A.

Now to find the open terminal voltage V th , we need to add the voltage across the 10Ω resistor and the 10V battery.

Thus, the voltage across the 10Ω is V 10Ω = 10 * 1.33 = 13.3v

Hence, V th = 13.3 + 10 = 23.3v

To find I sc we need to short circuit the a → b terminal.

Now since short circuiting of the circuit has cause the loop to be two as oppose to one that we previously did.

So equation for loop I :

40- 51 1 -20-10(1 1 -1 2 ) =0;

40-51 1 -20-101 1 +101 2 =0; by expanding the bracket

20-151 1 +101 2 = 0;

151 1 -101 2 =20 ………(1)

-10(1 2 -1 1 )+10 =0;

-101 2 +101 1 +10 =0;

101 1 -101 2 =-10……………..(2)

By solving the simultaneous equation, we get

But I sc = 1 2 = 7A

hence, R th = V th /I sc = 23.3/7 = 3.33Ω

now replacing the 2Ω resistor we removed earlier then the circuit becomes this;

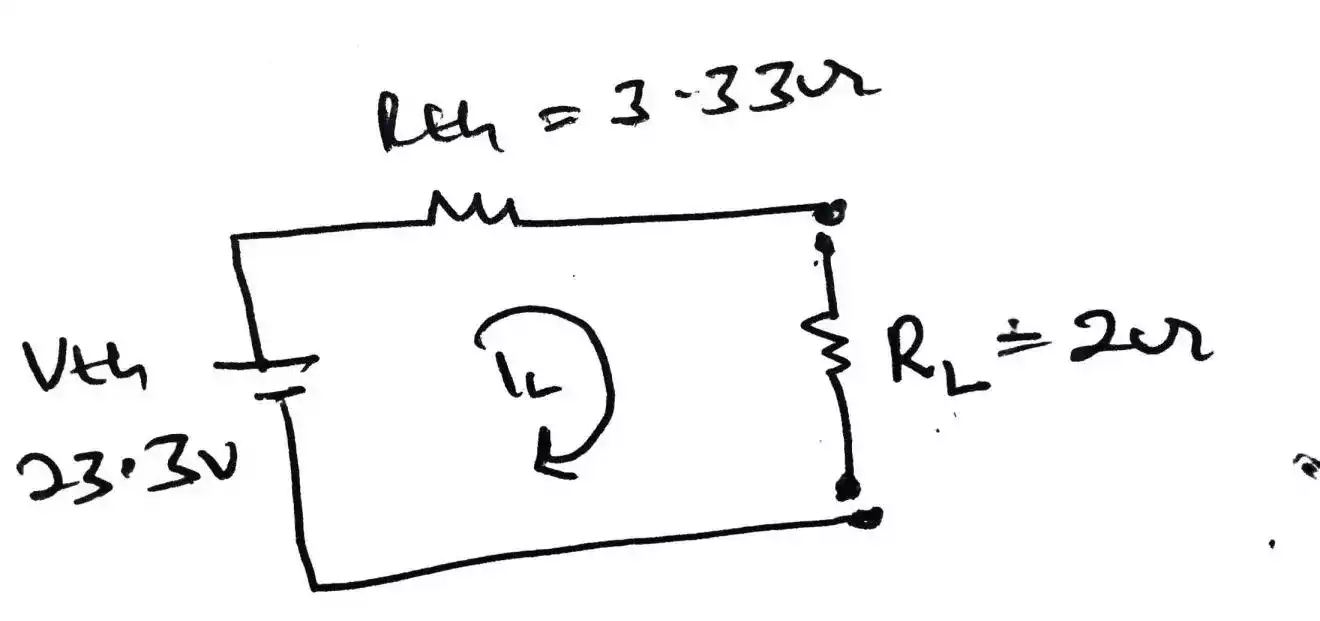
but we need to calculate for the current that flows through the load resistor (2Ω),

I L = V th / (R th + R L ) = 23.3/(3.33 +2) =23.3/(5.33) = 4.37A

More For You ☄

Thevenin theorem with solved problems

What is thevenin's theorem, thevenin theorem statements.

Thevenin's equivalent circuit

Solved problems by Thevenin's Theorem

Share on Facebook
Share on Twitter

Contact Form

+91-7507585950

eeGATE - Free EE gate tutorials and Solved Numericals

Free EE gate Solved Problems and tutorials

Solved problems on Thevenin’s Theorem

Home Blog Basic Electrical Engineering Solved problems on Thevenin&#8...

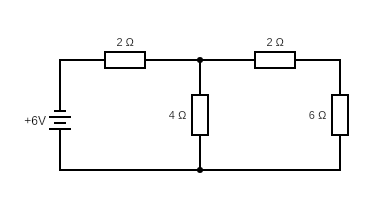
1) Find current flowing through 1 \Omega resistor.

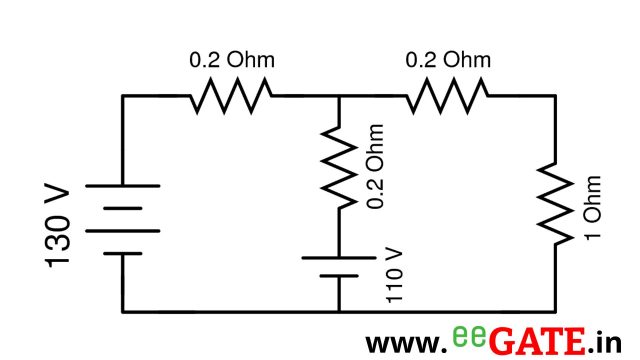
Calculate V_{th}

130-0.2I-0.2I-110 = 0

-0.4I = -20

-V_{th} + 110 +0.2I = 0

V_{th} = 120 V

Calculate R_{th}

0.2 || 0.2 = 0.1 \Omega

0.1 + 0.2 = 0.3 \Omega

R_{th} = 0.3 \Omega

Thevenin’s equivalent circuit.

I_{1\Omega} = \dfrac{V_{th}}{R_{th} + R_L} = \dfrac{120}{0.3+1} = 92.3076 A

One Response

Tutoria helpfull

Add a Comment Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons
Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

4.4: Thévenin's Theorem

Last updated
Save as PDF
Page ID 98420

James M. Fiore
Mohawk Valley Community College

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

Thévenin's theorem, named after Léon Charles Thévenin, is a powerful analysis tool. For DC, it states:

\[\text{Any single port linear network can be reduced to a simple voltage source, } E_{th}, \text{in series with an internal resistance, } R_{th}. \nonumber \]

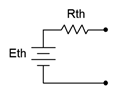
Figure 6.4.1 : Thévenin equivalent circuit.

An example is shown in Figure 6.4.1 . The phrase “single port network” means that the circuit is cut in such a way that only two connections exist to the remainder of the circuit (two connection points makes up one port). The remainder of the circuit may be a single component or a large multi-component sub-circuit. As there are many ways to cut a typical circuit, there are many possible Thévenin equivalents. The important thing is that there are only two connection points between the two portions of the circuit and neither point has to be ground.

Figure 6.4.2 : Example circuit.

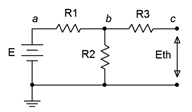
Figure 6.4.3 : Finding $E_{th}$..

Consider the circuit shown in Figure 6.4.2 . Suppose we cut the circuit immediately to the left of $R_4$. That is, we will find the Thévenin equivalent that drives $R_4$. The first step is to make the cut, removing the remainder of the circuit (in this case, just $R_4$). We then determine the open circuit output voltage. This is the maximum voltage that could appear between the cut points and is called the Thévenin voltage, $E_{th}$. This is shown in Figure 6.4.3 . In a circuit such as this, basic series-parallel analysis may be used to find $E_{th}$. This process turns out to be quite straightforward in this particular circuit. Due to the open, no current flows through $R_3$, thus no voltage is developed across $R_3$, and therefore $E_{th}$ must equal the voltage developed across $R_2$ which may be obtained via a voltage divider with resistor $R_1$ and source $E$.

The second part is finding the Thévenin resistance, $R_{th}$. Beginning with the “cut” circuit, replace all sources with their ideal internal resistance (thus shorting voltage sources and opening current sources). From the perspective of the cut point, look back into the circuit and simplify by making appropriate series and parallel combinations to determine its equivalent resistance. This is shown in Figure 6.4.4 . Looking in from where the cut was made (right-to-left here), we find that $R_1$ and $R_2$ are in parallel, and this combination is then in series with $R_3$. Thus, $R_{th} = R_3 + (R_1 || R_2)$. A common error is to determine the equivalent resistance that the source drives. Remember, everything is determined from the vantage point of the cut or port.

Thévenin equivalents are not limited to single source circuits. It is possible to find the equivalent of a network with several sources. Finding the open circuit output voltage will undoubtedly require some extra work, for example the use of superposition of source conversions. Finding the Thévenin resistance is unchanged, just remember to replace every source with its ideal internal resistance before simplifying the network.

As noted earlier, the original circuit could be cut in a number of different ways. We might, for example, want to determine the Thévenin equivalent that drives $R_2$ in the circuit of Figure 6.4.2 . This cut appears in Figure 6.4.5 . Clearly, this will result in different values for both $E_{th}$ and $R_{th}$. For example, $R_{th}$ is now $R_1 || (R_3 + R_4)$.

Figure 6.4.4 : Finding $R_{th}$.

Finding Thévenin Equivalents in Lab

The procedure for experimentally determining an equivalent in the laboratory mimics the analytical approach. The first step is to figuratively cut the circuit and isolate the section that is to be converted. At this point we have the open circuit version of the circuit and all we need do is connect a multimeter to the open port to determine $E_{th}$.

There are two methods for determining $R_{th}$. The first method works well for simple circuits that use only resistors and current and/or voltage sources. The second method is more generally applicable and will work for circuits with active devices such as transistors. To use the first method, the sources are physically removed from the circuit and replaced with their ideal internal resistance. Thus voltage sources are replaced with a shorting wire and current sources are left as opens. Do not simply place shorting wires across the terminals of voltage sources as doing so will cause an overload and potentially damage the sources. Once this is completed, a multimeter is placed at the open port and set to read resistance. The indicated value is $R_{th}$.

Figure 6.4.5 : An alternate cut or port location.

The second method uses a variable resistance, namely either a rheostat or a decade box, and exploits the voltage divider rule. In this version, the sources are left active (powered up) and are not replaced with opens or shorts. Once $E_{th}$ is measured, the variable resistor is placed across the port connections. This resistance is adjusted until the port voltage drops to exactly half of $E_{th}$. In the equivalent circuit, there are only two resistances of concern, $R_{th}$ and this variable load resistance, and they are in series. Consequently, if the load voltage is now half of the open circuit voltage ($E_{th}$), then the other half of the voltage must be dropping across the equivalent internal resistance ($R_{th}$). For this to be true in a series circuit, the two resistances must have the same value. Thus, we simply remove the rheostat from the circuit and use a multimeter to determine its precise value. If a decade box is used instead, the value is determined directly by reading the knob settings.

Whether determined analytically or empirically, the Thévenin equivalent circuit can replace the original single port network regardless of what the original was connected to. The same voltages and currents will be seen in this other portion, and it won't matter if the other portion is comprised of a single resistor, multiple resistors, multiple resistors and multiple sources, or even multiple resistors and sources wired to a selection of piquant cheeses. The Thévenin equivalent is a true functional equivalent and can be used on any linear bilateral network.

Example 6.4.1

Determine the Thévenin equivalent of the circuit driving the 1 k$\Omega$ in Figure 6.4.6 . Verify that the equivalent produces the same voltage across this resistor as the original circuit.

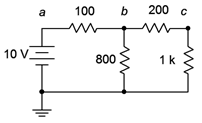
Figure 6.4.6 : Circuit for Example 6.4.1 .

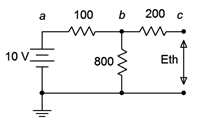
Figure 6.4.7 : Finding $E_{th}$.

First, we'll redraw the circuit showing the portion to be Théveninized, as shown in Figure 6.4.7 . The open circuit output voltage will be the voltage across the 800 $\Omega$ resistor as there will be no voltage drop across the 200 $\Omega$ resistor (as no current flows through it into the open). This is found via a simple voltage divider.

\[E_{th} = E \frac{R_x}{R_x+R_y} \nonumber \]

\[E_{th} = 10 V \frac{800 \Omega}{800\Omega +100 \Omega} \nonumber \]

\[E_{th} \approx 8.889 V \nonumber \]

The equivalent resistance is found by shorting the voltage source and then simplifying the circuit. The result is 200 $\Omega$ in series with the parallel combination of the 100 $\Omega$ and 800 $\Omega$. $200 + 100 || 800 \approx 288.89 \Omega$.

To determine Vc, we can use a voltage divider between the 1 k$\Omega$ and the 288.89 $\Omega$ along with the equivalent source voltage of 8.889 volts.

\[V_c = E_{th} \frac{R_L}{R_L+R_{th}} \nonumber \]

\[V_c = 8.889V \frac{1k \Omega}{ 1 k\Omega +288.89\Omega} \nonumber \]

\[V_c \approx 6.897V \nonumber \]

Now let's determine $V_c$ in the original circuit using series-parallel analysis techniques. Perhaps the quickest approach is a pair of voltage dividers. $V_b$ is found via a divider between the parallel combination of the 1 k$\Omega$ + 200 $\Omega$ and the 800 $\Omega$, against the 100 $\Omega$. $V_c$ is is then found using that voltage with a divider between the 1 k$\Omega$ and 200 $\Omega$. Using this approach, $V_b$ is approximately 8.276 volts and $V_c$ is approximately 6.897 volts, providing an excellent match.

It might seem that the Thévenin method is the “long way home” in this example, and it is, but it has the advantage of being more efficient if several different loads are being considered. For example, suppose we decided to determine the output voltage not just for the 1 k$\Omega$, but for a group of a half dozen different resistors. The double voltage divider would have to be determined for each load resistor using the straight series-parallel method but only a single divider needs to be computed for each load when using the Thévenin method. The Thévenin method is also of great use when determining maximum power transfer, as we shall see a later in this chapter.

Computer Simulation

To verify the results of Example 6.4.1 , the original circuit is recreated in a simulator along its Thévenin equivalent, as shown in Figure 6.4.8 .

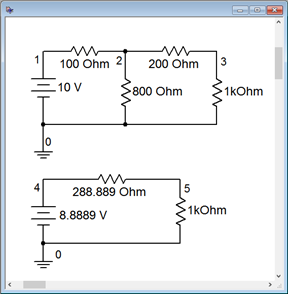
Figure 6.4.8 : The original circuit of Example 6.4.1 in a simulator along with the equivalent.

A DC operating point analysis is performed and the results are shown in Figure 6.4.9 . Note that the voltages across the identical 1 k$\Omega$ loads (nodes 3 and 5) are virtually the same, indicating functional equivalence between the two. The slight deviation is due to the rounding of the Thévenin voltage and resistance.

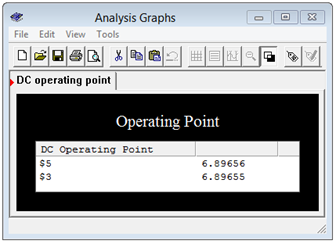
Figure 6.4.9 : Results of the simulation showing equivalence.

As a further check, the simulation is run again, but this time using an alternate load resistor value. The value chosen is the Thévenin resistance value. By matching the resistances, this should produce a 50/50 voltage divider and the load voltage should equal half of the Thévenin source voltage, or approximately 4.444 volts. That is precisely what we find, as seen in Figure 6.4.10 .

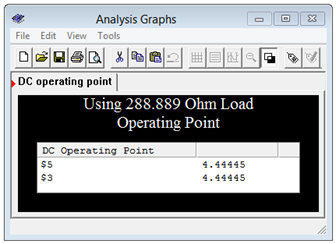
Figure 6.4.10 : Results of the simulation for matched resistance.

As mentioned previously, Thévenin's theorem can be applied to much more complex multi-source circuits, and the item being driven need not be just a single resistor. This is illustrated in the next example.

Example 6.4.2

Determine the Thévenin equivalent of the circuit driving the resistor/voltage source combo in Figure 6.4.11 . Verify that the equivalent produces the same voltage across this resistor as the original circuit.

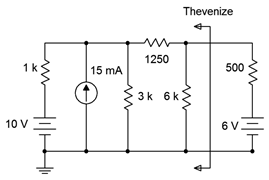
Figure 6.4.11 : Circuit for Example 6.4.2 .

Determining $R_{th}$ is not particularly difficult here. After shorting the 10 volt source and open the current source, it can be seen that the 1 k$\Omega$ and 3 k$\Omega$ are in parallel, yielding 750 $\Omega$. This is in series with the 1250 $\Omega$ for a total of 2 k$\Omega$, which is in turn in parallel with the 6 k$\Omega$. The final result is 1.5 k$\Omega$.

Finding $E_{th}$ is a little more involved. One possibility is to use a source conversion on the 10 volt source as that will leave us with two parallel current sources that may be combined directly. The converted source will be 10 V/ 1k$\Omega$, or 10 mA, in parallel with 1 k$\Omega$. This results in a total of 25 mA feeding upwards with 1 k$\Omega$ $||$ 3 k$\Omega$, or 750 $\Omega$. We can use the current divider rule to determine the current flowing through the 1250 $\Omega$ plus 6 k$\Omega$ branch, and then use Ohm's law to find the open circuit voltage (i.e., the voltage across the 6 k$\Omega$).

\[I_{6k} = I_S \frac{R_x}{R_x+R_y} \nonumber \]

\[I_{6k} = 25 mA \frac{750\Omega}{ 750\Omega +7250\Omega} \nonumber \]

\[I_{6k} = 2.34375 mA \nonumber \]

\[E_{th} = I_{6k} \times R_{6k} \nonumber \]

\[E_{th} = 2.34375 mA \times 6 k \Omega \nonumber \]

\[E_{th} = 14.0625V \nonumber \]

Another approach to determine this value would be to use superposition. This is left as an additional exercise.

Turning our attention to the voltage produced across the 6 volt with 500 $\Omega$ sub-circuit, we have a simple series loop with $E_{th}$ opposing this 6 volt source, leaving 8.0625 volts to produce a clockwise current through $R_{th}$ in series with the 500 $\Omega$ (a total of 2 k$\Omega$). That current will be 8.0625 V / 2 k$\Omega$, or 4.03125 mA. This will produce a drop across the 500 $\Omega$ of 2.015625 volts with a polarity of + to − from top to bottom. This will add to the 6 volt source resulting in a final potential of 8.015625 volts. The results are verified via the simulation technique used previously. The node voltages for both the original and equivalent circuits are shown in Figure 6.4.12 .

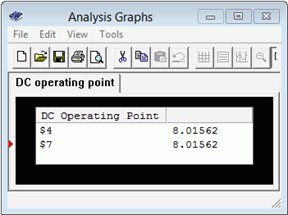
Figure 6.4.12 : Results of the simulation using the original and equivalent circuits.

Trending Now
Foundational Courses
Data Science
Practice Problem
Machine Learning
System Design
DevOps Tutorial
Lami's Theorem
Liouville’s Theorem
Real Life Application of Rolle's Theorem
Maximum Power Transfer Theorem
Basic Proportionality Theorem (BPT) | Proof and Examples
Some important mathematical proofs
Rolle's Mean Value Theorem
Some Basic Theorems on Trees
Lagrange's Mean Value Theorem
Mean Value Theorem
Cauchy's Mean Value Theorem
Consensus Theorem in Digital Logic
Information Security - Return To LIBC
C | Operators | Question 8
C | Operators | Question 7
C | Operators | Question 9
C | Operators | Question 27
C | Operators | Question 21
C | Operators | Question 13
Norton’s Theorem

Electrical engineering widely uses different theorems and laws to simplify the circuits involved in this field. One such theorem is known as Norton’s Theorem which is used for analysing linear circuits in electrical engineering. In this article, we will study what is Norton’s Theorem, what is the statement of this theorem, and what the circuit implementation of this theorem looks like. We will also study the step-by-step Procedure for applying Norton’s theorem to our circuit and see how it can determine IN or ISC.

Once we have successfully discussed the advantages and applications of this theorem, we will proceed to see the limitations of this theorem. Some solved examples have been solved for a better understanding of the theorem. The article concludes with some frequently asked questions that readers can refer to.

Table of Content

Circuit Diagram

Step-by-Step Procedure

Norton’s Theorem Formula

Disadvantages
Applications
Solved Example

What is Norton’s Theorem?

Norton’s theorem is a popular theorem used for simplifying linear circuits that use multiple independent and dependent sources. It is used to replace circuit elements by Norton’s current source which is in parallel with Norton’s resistance. Basic circuit equations are then written to find the current in different elements of the circuit. It is important to note that the theorem does not apply to non-linear circuits since these circuits don’t follow Ohm’s law .

Norton’s Theorem Statement

Let us look at the official statement of Norton’s Theorem

Norton’s theorem states that any linear circuit can be simplified to an equivalent circuit consisting of a single current source and parallel resistance that is connected to a load.

Now we will study the meaning of this statement through some circuit diagrams.

Norton’s Theorem Circuit Diagram

Here is the circuit diagram for Norton’s Theorem

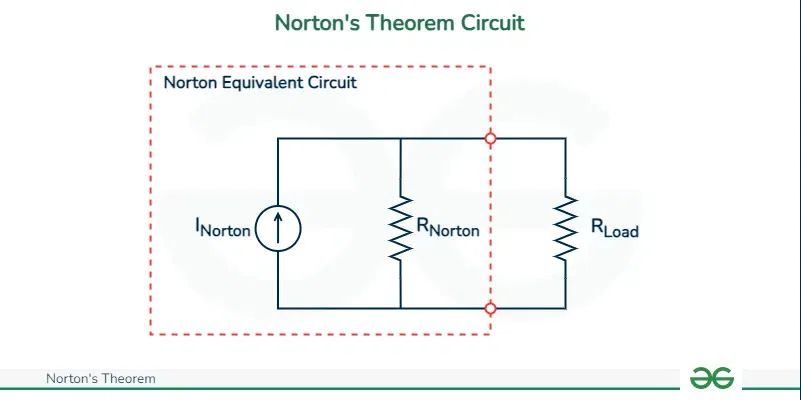
Norton’s theorem circuit

I norton : Norton’s current source R norton : Norton’s resistance

This circuit is a general simplification of a complex circuit which is done using Norton’s Theorem. If you carefully observe, the circuit has been reduced to have one current source and one resistance known as Norton’s current source and Norton’s resistance. This new circuit is used for calculating the voltage and current developed across the load resistance. Note that the equivalent circuit will depend on the type of load and the circuit elements. The basic circuit has been made by short circuiting the voltage sources and open circuiting all the independent current elements which are then replaced by Norton’s equivalent of these values. The steps for determining the current and voltage after the equivalent circuit is made have been explained below.

Norton’s Theorem Step-by-Step Procedure

Here are the steps to be followed for applying Norton’s Theorem

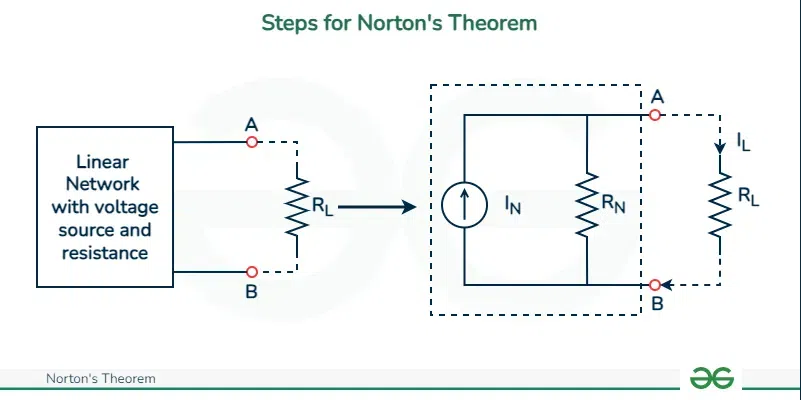
Steps for Norton’s Theorem

Step 1: Observe all the voltage sources and short them resulting in plain wires. After that observe all the current sources and open-circuit them which will give you all the internal resistances of the circuit.

Step 2: We consider a network shown above to apply Norton’s theorem. We will short circuit all the voltages. The circuit after short circuit has been given and we can calculate current I N across the terminals AB

Calculating I N: The whole circuit is replaced by an equivalent resistance R L to replace the short circuit . Now since we replaced the shorted element with Norton’s equivalent, the short circuit current I SC will be equal to the Norton current I N . The formula for calculating the Norton’s current has been explained in the later section.

Calculating I SC : The final circuit network is displayed in the figure and the left side of terminal AB is replaced by Thevenin’s equivalent resistance R TH . Let us see the formula that will be used for calculating the values of I sc , I N and thevenin voltage. The formula for the Norton’s current or short circuit current will be given by

I sc = I N = V th / R th

The derivation will be shown in the later parts.

From our previous derivations, we can write down the formula as

V Th = R 2 /(R 1 +R 2 ). V and R Th = R 3 + (R 1 .R 2 )/(R 1 +R 2 )

Now, we can calculate the short circuit current as

I SC = V Th / R Th

When Norton’s theorem is applied to any general circuit, the current source is in parallel with resistance and we can write the current across the load as

I L = I N . R N /(R N +R L )

Advantages of Norton’s Theorem

Let us see some advantages of Norton’s Theorem

Norton’s theorem simplifies the overall complexity of the circuit and makes circuit solving an easy process.
Norton’s theorem reduces the size of the circuit by replacing the different current sources with Norton’s resistance and Norton’s voltage.
Norton’s theorem can be used to find current and voltage across a single element in the network without caring about other elements in a linear circuit.
Norton’s Theorem can be useful for studying the nature of circuits and understanding how internal resistance is dependent on other resistances.
Norton’s Theorem along with Thevenin’s theorem is used by engineers to solve complex circuits.

Limitations of Norton’s Theorem

Let us see some limitations of Norton’s Theorem

Norton’s theorem can only be applied to linear circuit elements and it fails for non linear circuits.
Circuits that deal with magnetic fields can affect the resistance of the overall circuit so Norton’s theorem can’t be applied to such magnetic circuits .
Using Norton’s Theorem for the analysis of complex circuits can be a difficult task due to the enumerable mathematical calculations.
Norton’s Theorem is based on certain assumptions which make the results of Norton’s Theorem inaccurate in real world due to introduction of real world parameters.
Norton’s Theorem focuses on current carrying elements therefore we have to use Thevenin Theorem to study the voltage distribution.

Applications of Norton’s Theorem

Let us see some Applications of Norton’s Theorem

The ease of application of Norton’s Theorem makes it a suitable concept to be taught to high school students so it is used for educational purposes.
Telecommunication engineering employs the use of Norton’s Theorem to study network models and optimize the process of communication.
Norton’s Theorem can be used for load matching where Norton’s Theorem is used to calculate the value of load to minimize power loss.
Norton’s Theorem is commonly used by engineers for circuit analysis by replacing the complex circuit with simpler components.
Norton’s Theorem can also be used for finding faults in circuits by simplifying the circuit at every step and identifying the potential cause of error.

Norton’s Theorem Solved Example

Q.Solve the value of current and voltage across the load branch in the given circuit using Norton’s Theorem.

We will calculate Norton’s resistance by shorting the load resistance branch. The circuit will now look like this

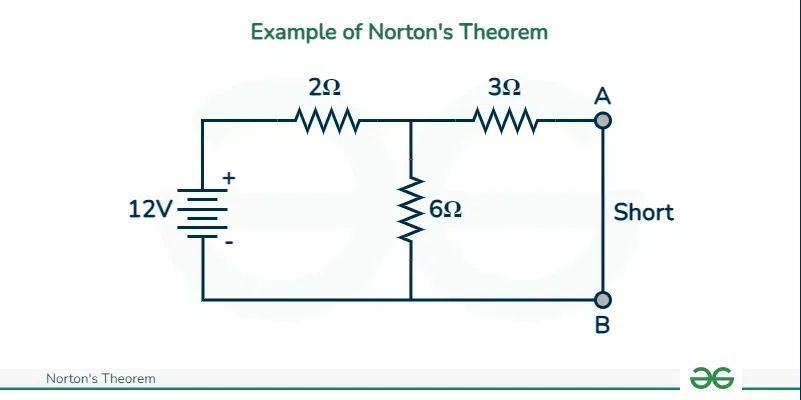
The total resistance for the given circuit is

R eq = 2 + 3×6/(3+6) ∴ R eq = 4 ohm ∴ R T = 4 ohm

We will calculate current using ohm’s law

I Th = V/R Th ∴ I th = 12/4 = 3A

Using current divider rule, we will calculate the current across the load element

I sc = I N ∴ I sc = 3×6/(3+6) ∴ I sc = 2A

Now we will calculate the Norton’s resistance by open circuiting the current sources. The 12 V voltage will become 0 and be replaced by a short. Here is the circuit

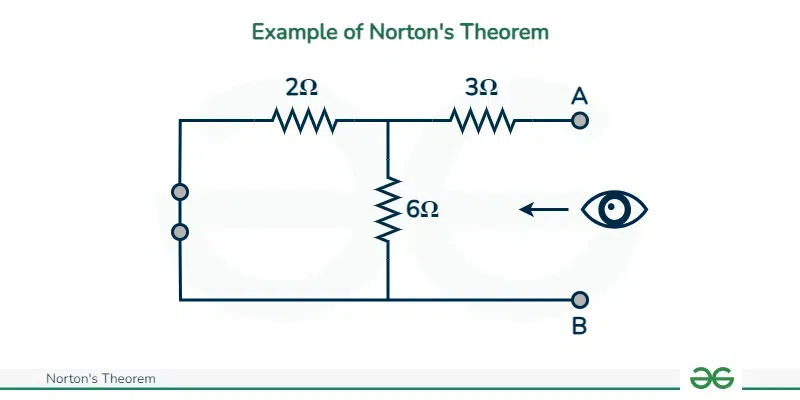
The equivalent voltage will be given by

R eq = 3 + 6×2/(2+6) ∴ R eq = 3 + 1.5 ∴ R eq = 4.5 ohm

We will calculate thevenin voltage by applying Norton’s resistance across the current source. Therefore, using ohms law

I L = I n x [R n ÷ (R n + R L )] ∴ I L = 2A x (4.5Ω /( 4.5Ω + 1.5Ω)) ∴ I L = 1.5A

We can give voltage across load resistance by

V L = I L x R L ∴ V L = 1.5A x 1.5Ω ∴ V L = 2.25V

Q.Solve the value of current across the load branch in the given circuit using Norton’s Theorem.

Circuit diagram

We will calculate Norton’s resistance by shorting the load resistance branch. The circuit will now look like this after removing 5 ohm resistance.

Let us calculate the equivalent resistance of the circuit using series and parallel method.

R = (5+5)Ω+(10Ω||(4+6)Ω) ∴ R =10+10×10/(10+10) ∴ R =10+5=15Ω

The total current can be calculated from ohm’s law

I=V/R ∴ I=30/15=2A

The Norton’s current can be calculated by current divider rule

I sc = I N = I×10/(10+4+6) ∴ I N = 2×(10/20)=1A

Now we need to calculate Norton’s resistance so we short circuit the voltage source, the circuit will look like

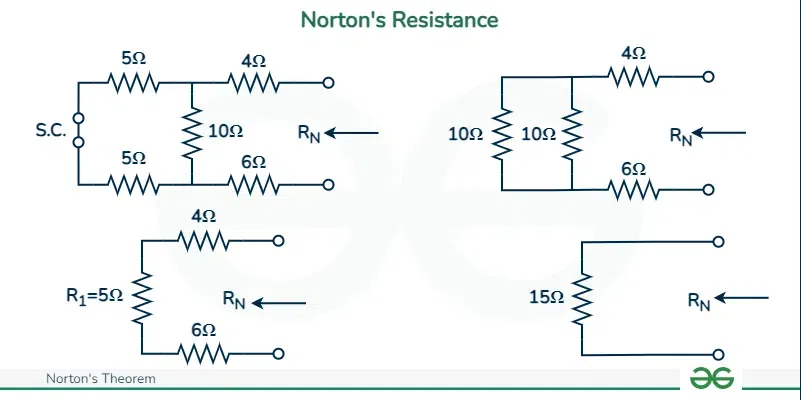
Norton’s resistance

R 1 =10Ω||10Ω ∴ R 1 =10×10/(10+10)=5Ω ∴ R n =R AB =4+R 1 +6 ∴ R 1 = 4+5+6 = 15Ω

Now we will make Norton’s equivalent circuit by adding Norton’s equivalents in the circuit.

R L =5Ω ∴ I L =I N .R N /(R N +R L ) ∴ I L =1×15/(15+5) ∴ I L = 15/20=0.75

We have seen how we can use Norton’s Theorem to simplify the linear circuits and find the current distribution in the circuit. The derivation of Norton’s voltage and resistance has been explained and some solved examples have been provided to build better concepts. We have seen how Norton’s Theorem is a useful tool that finds its application in fields like circuit analysis. Despite the advantages offered by Norton’s Theorem, there are some limitations associated with it which have been discussed briefly. Frequently asked questions have been provided below.

Norton’s Theorem – FAQs

What are linear circuits.

Linear circuits are the circuits that obey superposition principle making the output proportional to the input fed to the circuit.

Why can’t we use Norton’s Theorem in non linear circuits?

The reason why we can’t use Norton’s Theorem in non linear circuits is that non linear circuit elements don’t follow superposition principle and KCL and KVL used in Norton’s theorem become inapplicable.

How is Norton’s Theorem related to Thevenin’s theorem?

Thevenin’s Theorem deals with a voltage source and Norton’s Theorem uses a current source. The Thevenin voltage is calculated by multiplying Norton’s resistance and Norton’s current.

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

IMAGES

Thevenin's Theorem Problems and Solution With Example -
Thevenin’s Theorem
SOLUTION: Thevenin theorem with examples
Thévenin's Theorem
Thevenin's Theorem problem with dependent source
Thevenin's Theorem (Problem 1)

VIDEO

Thevenin theorem math
Thevenin's Theorem Solved Example (Easy Problem)
Thevenin's Theorem Problems |Thevenin's Theorem Problem IV
Thevenin's Theorem
Ep 27: Solved Problems on Thevenin's theorem
Thévenin's Theorem

COMMENTS

Thevenin's Theorem with solved problem
Solved Problem 1. Solve the given circuit to find the current through 10 Ω using Thevenin's Theorem. First, let us consider 10 Ω as the load resistor. (a) To find Thevenin's voltage, Remove the load resistor (10 Ω) and the circuit is redrawn as below. Now the circuit is open-circuited.
Thevenin's Theorem
Thevenin's Theorem in DC Circuit Analysis. A French engineer, M.L Thevenin, made one of these quantum leaps in 1893.Thevenin's Theorem (also known as Helmholtz-Thévenin Theorem) is not by itself an analysis tool, but the basis for a very useful method of simplifying active circuits and complex networks.This theorem is useful to quickly and easily solve complex linear circuits and ...
Thevenin Theorem
Example 1. Q. Find the value of current through 1Ω Resistor in the given circuit using Thevenin's theorem. Solution - First we have to remember that the IL Load current is current flow across the resistor which value says to find in question. So here IL is the current of the resistor of 1Ω and this is also here the load resistor RL.
Thevenin's Theorem made easy with circuits & examples
Problem: Let's find the Thevenin's equivalent circuit for the above circuit.. Solution. In the above circuit, we have a voltage source (32V) and another current source (2A). Step 1: Find Thevenin's resistance. While calculating the thevenin's equivalent resistance, all voltage sources must be turned off, meaning it acts like a short circuit and all current sources act like an open ...
Thevenin's Theorem
Learn how to simplify complex electrical circuits using Thevenin's theorem, which states that any circuit can be reduced to an equivalent circuit with a single voltage source and a series resistance. See solved examples, applications and limitations of this circuit analysis method.
Thevenin's Theorem: Statement, Equivalent Circuit, Solved Examples
Thevenin's Theorem Solved Examples. Example 1: Obtain thevenin's equivalent circuit with respect to the terminals of AB of the network shown in the circuit. Solution 1: The Thevenin's equivalent circuit at the ends of AB can be obtained by. Transforming the circuit. Fig: Circuit to determine the VTh and RTh.
4.4: Thévenin's Theorem
4.4: Thévenin's Theorem. Thévenin's theorem, named after Léon Charles Thévenin, is a powerful analysis tool. For DC, it states: Any single port linear network can be reduced to a simple voltage source, Eth, in series with an internal resistance, Rth. Any single port linear network can be reduced to a simple voltage source, E t h, in series ...
5.4: Thévenin's and Norton's Theorems
1. Figure 5.4.1 5.4. 1: Generic Thévenin equivalent circuit. The phrase "single port network" means that the original circuit is cut in such a way that only two connections exist to the remainder of the circuit. That remainder may be a single component or a large multi-component sub-circuit.
How to Use Thevenin's Theorem
Thevenin's theorem states that all linear circuits can be simplified to an equivalent circuit with a single voltage source in series with a single resistor connected to a load. Step 1: Remove the load resistor and replace it with an open circuit. Step 2: Calculate the Thevenin voltage—the voltage across the open circuit.
Thevenin's Theorem Tutorial
To obtain the resistance RTH- called the Thevenin's equivalent resistance of circuit A: i) Remove circuit B from circuit A. ii) Set all independent sources in circuit A to zero. (A zero voltage source is equivalent to a short circuit, and zero current source is equivalent to an open circuit). iii) Determine the resistance between nodes a ...
Solved Examples on Thevenin's Theorem -- Tutorial 1
Thevenin's Theorem Explained with lot of solved examples to help you guys understand real quick without difficulty. ##[email protected] a co...
Thevenin's Theorem
This video explains how to calculate the current flowing through a load resistor using thevenin's theorem.Schematic Diagrams & Symbols: https://www....
Thevenins Theorem Tutorial for DC Circuits
The basic procedure for solving a circuit using Thevenin's Theorem is as follows: 1. Remove the load resistor RL or component concerned. 2. Find RS by shorting all voltage sources or by open circuiting all the current sources. 3. Find VS by the usual circuit analysis methods. 4.
Learn About Thevenin Theorem and Dependent Source Circuits
Thevenin's theorem states that any linear, two-terminal portion of a network can be replaced by a Thevenin equivalent circuit. ... Now to apply this theory to an example problem. Figure 2. Solving for R Th first, redraw the circuit with the 12V source as a short circuit. Then excite the circuit using either a 1A current source or 1V voltage ...
18
18 - Thevenin's Theorem - Concept with Solved Examples #knustIn this video we are going to learn how to solve circuit problems using Thevenin's theorem.Theve...
Thevenin's Theorem Explained With Solved Examples
Steps to solve circuit problem using thevenin theorem. If there is a load resistor R L then you need to remove it. Find the thevenin voltage V th across the terminal of interest. The V th can be found by finding the open circuit voltage across the terminal. Find the short circuit current I sc between terminal a → b
PDF Thevenin's and Norton's Theorems
Find Vo using Thevenin's theorem. Problems - In class. Find Io using Thevenin's or Norton's theorem. Problems - In class. Problems - In class. Problem 5: Find the Thevenin equivalent circuit for the following circuit with respect to the terminals AB (Irwin - Example 5.8) Problems - In class. Problem 6: Find the Thevenin ...
Thevenin theorem with solved problems
Steps to follow for solving problems by Thevenin's Theorem. Identify the load (R L ). Step 2 : Remove the load and calculate the open-circuit voltage (V TH ). Step 3 : To calculate Thevenin's impedance (R TH ), replace the sources with their internal impedance. Step 4 :
PDF Thévenin's Theorem -Circuit with Two Independent Sources
A Source of Free Solved Problems www.solved-problems.com Thévenin's Theorem - Circuit with Two Independent Sources Use Thévenin's theorem to determine . Solution Lets break the circuit at the load as shown in Fig. (1-27-2). Now, we should ﬁnd an equivalent circuit that contains only an independent voltage source in Notes IO 3Ω
Solved problems on Thevenin's Theorem
Solved problems on Thevenin's Theorem; Solved Problems on Superposition Theorem; Single Phase Transformer Solved Problems; solved problems on electrostatics; KVL problems with solutions / Solved problems on Kirchhoff's Voltage Law (KVL) / Mesh Analysis; Categories. Basic Electrical Engineering; Electrical Machine; HTML and CSS; Power System
4.4: Thévenin's Theorem
Example 6.4.2. Thévenin's theorem, named after Léon Charles Thévenin, is a powerful analysis tool. For DC, it states: Any single port linear network can be reduced to a simple voltage source, Eth, in series with an internal resistance, Rth. Any single port linear network can be reduced to a simple voltage source, E t h, in series with an ...
Norton's Theorem and Thevenin's Theorem
This electronics video tutorial on electrical circuit analysis provides a basic introduction into Norton's theorem and touches on Thevenin's theorem. It exp...
Norton's Theorem
Norton's theorem is a popular theorem used for simplifying linear circuits that use multiple independent and dependent sources. It is used to replace circuit elements by Norton's current source which is in parallel with Norton's resistance. Basic circuit equations are then written to find the current in different elements of the circuit.

Thevenin’s Theorem with solved problem

Procedure to determine Thevenin’s equivalent circuit

Step 2 – Determination of Thevenin’s Impedance

Step 3 – Formation of Thevenin’s equivalent circuit

Solved Problem 1

Solved Problem 2

Related Posts

Leave a Reply Cancel reply

Subscribe to Electrically4u..!

Thevenin’s Theorem. Step by Step Procedure with Solved Example

Steps to Analyze an Electric Circuit using Thevenin’s Theorem

Solved Example by Thevenin’s Theorem:

Electrical Technology

How to Size a Single Phase and Three Phase Transformer in kVA? Calculator

How to Calculate the Battery Charging Time & Battery Charging Current – Example

How To Calculate Your Electricity Bill. Electric Bill Calculator with Examples

How to Find the Proper Size of Wire & Cable: Metric & Imperial Systems

Automatic Street Light Control Circuit using LDR & Transistor BC 547

Emergency LED Light Circuit – DP-716 Rechargeable 30 LED’s Lights Schematic

Leave a Reply Cancel reply

Thevenin theorem statement

Thevenin’s theorem problems

Kirchoff’s law (kcl, kvl)

Automatic DC FAN controller circuit

220v 50W Low Power Inverter Circuit

What is NOT gate (Inverter)

Simple LED Flasher Circuit with 555 timer

Simple 5 LED Blinker/Flasher circuit

Best Low power Mic Amplifier circuit using LM386

Dual Power Supply Circuit

Thevenin’s Theorem -explanation, equivalent circuit & examples

Solved examples

Thevenin’s theorem

Step 1: Find Thevenin’s resistance

Step 2: Find Thevenin’s voltage

Step 3: Draw equivalent circuit

Steps to calculate Thevenin’s equivalent circuit.

6 thoughts on “Thevenin’s Theorem -explanation, equivalent circuit & examples”

Leave a Comment Cancel reply

Thevenin's Theorem

Thevenin’s Theorem Explanation

Thevenin’s Theorem Example

Thevenin’s Theorem Solved Example

Thevenin Theorem Applications

Thevenin Theorem Limitations

Frequently Asked Questions – FAQs

What is Thevenin Voltage?

Where is Thevenin’s Theorem used?

Is Thevenin’s Theorem applicable to AC circuits?

Leave a Comment Cancel reply

Register with BYJU'S & Download Free PDFs

Thevenin’s Theorem | Thevenin’s Equivalent Circuit

How to Find the Equivalent Voltage of a Thevenin Circuit?

How to Find the Equivalent Resistance in Thevenin’s Theorem?

Thevenin’s Theorem Solved Example with Voltage Source

Thevenin’s Theorem Solved Problem with Dependent Sources

Thevenin’s Theorem Steps

1 thought on “Thevenin’s Theorem | Thevenin’s Equivalent Circuit”

Leave a Comment Cancel reply

Thevenin’s Theorem

Thevenins Theorem Equivalent Circuit

Find the Equivalent Resistance (Rs)

Find the Equivalent Voltage (Vs)

Thevenins Theorem Summary

Read more Tutorials inDC Circuits

348 Comments

Thevenin's Theorem Explained With Solved Examples

But why do we need this theorem

Steps to solve circuit problem using thevenin theorem

Example problem on thevenin’s theorem

More For You ☄

Thevenin theorem with solved problems

Thevenin's equivalent circuit

Solved problems by Thevenin's Theorem

Contact Form

eeGATE - Free EE gate tutorials and Solved Numericals

Solved problems on Thevenin’s Theorem

One Response

Add a Comment Cancel reply

4.4: Thévenin's Theorem