how to find domain and range word problems

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: Algebra 1   >   Unit 8

• Determining whether values are in domain of function
• Identifying values in the domain
• Examples finding the domain of functions
• Determine the domain of functions
• Worked example: determining domain word problem (real numbers)
• Worked example: determining domain word problem (positive integers)
• Worked example: determining domain word problem (all integers)

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• \mathrm{Lauren's\:age\:is\:half\:of\:Joe's\:age.\:Emma\:is\:four\:years\:older\:than\:Joe.\:The\:sum\:of\:Lauren,\:Emma,\:and\:Joe's\:age\:is\:54.\:How\:old\:is\:Joe?}
• \mathrm{Kira\:went\:for\:a\:drive\:in\:her\:new\:car.\:She\:drove\:for\:142.5\:miles\:at\:a\:speed\:of\:57\:mph.\:For\:how\:many\:hours\:did\:she\:drive?}
• \mathrm{The\:sum\:of\:two\:numbers\:is\:249\:.\:Twice\:the\:larger\:number\:plus\:three\:times\:the\:smaller\:number\:is\:591\:.\:Find\:the\:numbers.}
• \mathrm{If\:2\:tacos\:and\:3\:drinks\:cost\:12\:and\:3\:tacos\:and\:2\:drinks\:cost\:13\:how\:much\:does\:a\:taco\:cost?}
• \mathrm{You\:deposit\:3000\:in\:an\:account\:earning\:2\%\:interest\:compounded\:monthly.\:How\:much\:will\:you\:have\:in\:the\:account\:in\:15\:years?}

word-problems-calculator

Domain and range of linear functions: word problems

• High School Math Solutions – Inequalities Calculator, Exponential Inequalities Last post, we talked about how to solve logarithmic inequalities. This post, we will learn how to solve exponential...

Please add a message.

Message received. Thanks for the feedback.

3.2 Domain and Range

Learning objectives.

In this section, you will:

• Find the domain of a function defined by an equation.
• Graph piecewise-defined functions.

Horror and thriller movies are both popular and, very often, extremely profitable. When big-budget actors, shooting locations, and special effects are included, however, studios count on even more viewership to be successful. Consider five major thriller/horror entries from the early 2000s— I am Legend , Hannibal , The Ring , The Grudge , and The Conjuring . Figure 1 shows the amount, in dollars, each of those movies grossed when they were released as well as the ticket sales for horror movies in general by year. Notice that we can use the data to create a function of the amount each movie earned or the total ticket sales for all horror movies by year. In creating various functions using the data, we can identify different independent and dependent variables, and we can analyze the data and the functions to determine the domain and range. In this section, we will investigate methods for determining the domain and range of functions such as these.

Finding the Domain of a Function Defined by an Equation

In Functions and Function Notation , we were introduced to the concepts of domain and range . In this section, we will practice determining domains and ranges for specific functions. Keep in mind that, in determining domains and ranges, we need to consider what is physically possible or meaningful in real-world examples, such as tickets sales and year in the horror movie example above. We also need to consider what is mathematically permitted. For example, we cannot include any input value that leads us to take an even root of a negative number if the domain and range consist of real numbers. Or in a function expressed as a formula, we cannot include any input value in the domain that would lead us to divide by 0.

We can visualize the domain as a “holding area” that contains “raw materials” for a “function machine” and the range as another “holding area” for the machine’s products. See Figure 2 .

We can write the domain and range in interval notation , which uses values within brackets to describe a set of numbers. In interval notation, we use a square bracket [ when the set includes the endpoint and a parenthesis ( to indicate that the endpoint is either not included or the interval is unbounded. For example, if a person has $100 to spend, they would need to express the interval that is more than 0 and less than or equal to 100 and write ( 0 , 100 ] . ( 0 , 100 ] . We will discuss interval notation in greater detail later.

Let’s turn our attention to finding the domain of a function whose equation is provided. Oftentimes, finding the domain of such functions involves remembering three different forms. First, if the function has no denominator or an odd root, consider whether the domain could be all real numbers. Second, if there is a denominator in the function’s equation, exclude values in the domain that force the denominator to be zero. Third, if there is an even root, consider excluding values that would make the radicand negative.

Before we begin, let us review the conventions of interval notation:

• The smallest number from the interval is written first.
• The largest number in the interval is written second, following a comma.
• Parentheses, ( or ), are used to signify that an endpoint value is not included, called exclusive.
• Brackets, [ or ], are used to indicate that an endpoint value is included, called inclusive.

See Figure 3 for a summary of interval notation.

Finding the Domain of a Function as a Set of Ordered Pairs

Find the domain of the following function: { ( 2 , 10 ) , ( 3 , 10 ) , ( 4 , 20 ) , ( 5 , 30 ) , ( 6 , 40 ) } { ( 2 , 10 ) , ( 3 , 10 ) , ( 4 , 20 ) , ( 5 , 30 ) , ( 6 , 40 ) } .

First identify the input values. The input value is the first coordinate in an ordered pair . There are no restrictions, as the ordered pairs are simply listed. The domain is the set of the first coordinates of the ordered pairs.

Find the domain of the function:

{ ( −5 , 4 ) , ( 0 , 0 ) , ( 5 , −4 ) , ( 10 , −8 ) , ( 15 , −12 ) } { ( −5 , 4 ) , ( 0 , 0 ) , ( 5 , −4 ) , ( 10 , −8 ) , ( 15 , −12 ) }

Given a function written in equation form, find the domain.

• Identify the input values.
• Identify any restrictions on the input and exclude those values from the domain.
• Write the domain in interval form, if possible.

Finding the Domain of a Function

Find the domain of the function f ( x ) = x 2 − 1. f ( x ) = x 2 − 1.

The input value, shown by the variable x x in the equation, is squared and then the result is lowered by one. Any real number may be squared and then be lowered by one, so there are no restrictions on the domain of this function. The domain is the set of real numbers.

In interval form, the domain of f f is ( − ∞ , ∞ ) . ( − ∞ , ∞ ) .

Find the domain of the function: f ( x ) = 5 − x + x 3 . f ( x ) = 5 − x + x 3 .

Given a function written in an equation form that includes a fraction, find the domain.

• Identify any restrictions on the input. If there is a denominator in the function’s formula, set the denominator equal to zero and solve for x x . If the function’s formula contains an even root, set the radicand greater than or equal to 0, and then solve.
• Write the domain in interval form, making sure to exclude any restricted values from the domain.

Finding the Domain of a Function Involving a Denominator

Find the domain of the function f ( x ) = x + 1 2 − x . f ( x ) = x + 1 2 − x .

When there is a denominator, we want to include only values of the input that do not force the denominator to be zero. So, we will set the denominator equal to 0 and solve for x . x .

Now, we will exclude 2 from the domain. The answers are all real numbers where x < 2 x < 2 or x > 2 x > 2 as shown in Figure 4 . We can use a symbol known as the union, ∪ , ∪ , to combine the two sets. In interval notation, we write the solution: ( −∞ , 2 ) ∪ ( 2 , ∞ ) . ( −∞ , 2 ) ∪ ( 2 , ∞ ) .

Find the domain of the function: f ( x ) = 1 + 4 x 2 x − 1 . f ( x ) = 1 + 4 x 2 x − 1 .

Given a function written in equation form including an even root, find the domain.

• Since there is an even root, exclude any real numbers that result in a negative number in the radicand. Set the radicand greater than or equal to zero and solve for x . x .
• The solution(s) are the domain of the function. If possible, write the answer in interval form.

Finding the Domain of a Function with an Even Root

Find the domain of the function f ( x ) = 7 − x . f ( x ) = 7 − x .

When there is an even root in the formula, we exclude any real numbers that result in a negative number in the radicand.

Set the radicand greater than or equal to zero and solve for x . x .

Now, we will exclude any number greater than 7 from the domain. The answers are all real numbers less than or equal to 7 , 7 , or ( − ∞ , 7 ] . ( − ∞ , 7 ] .

Find the domain of the function f ( x ) = 5 + 2 x . f ( x ) = 5 + 2 x .

Can there be functions in which the domain and range do not intersect at all?

Yes. For example, the function f ( x ) = − 1 x f ( x ) = − 1 x has the set of all positive real numbers as its domain but the set of all negative real numbers as its range. As a more extreme example, a function’s inputs and outputs can be completely different categories (for example, names of weekdays as inputs and numbers as outputs, as on an attendance chart), in such cases the domain and range have no elements in common.

Using Notations to Specify Domain and Range

In the previous examples, we used inequalities and lists to describe the domain of functions. We can also use inequalities, or other statements that might define sets of values or data, to describe the behavior of the variable in set-builder notation . For example, { x | 10 ≤ x < 30 } { x | 10 ≤ x < 30 } describes the behavior of x x in set-builder notation. The braces { } { } are read as “the set of,” and the vertical bar | is read as “such that,” so we would read { x | 10 ≤ x < 30 } { x | 10 ≤ x < 30 } as “the set of x -values such that 10 is less than or equal to x , x , and x x is less than 30.”

Figure 5 compares inequality notation, set-builder notation, and interval notation.

To combine two intervals using inequality notation or set-builder notation, we use the word “or.” As we saw in earlier examples, we use the union symbol, ∪ , ∪ , to combine two unconnected intervals. For example, the union of the sets { 2 , 3 , 5 } { 2 , 3 , 5 } and { 4 , 6 } { 4 , 6 } is the set { 2 , 3 , 4 , 5 , 6 } . { 2 , 3 , 4 , 5 , 6 } . It is the set of all elements that belong to one or the other (or both) of the original two sets. For sets with a finite number of elements like these, the elements do not have to be listed in ascending order of numerical value. If the original two sets have some elements in common, those elements should be listed only once in the union set. For sets of real numbers on intervals, another example of a union is

Set-Builder Notation and Interval Notation

Set-builder notation is a method of specifying a set of elements that satisfy a certain condition. It takes the form { x | statement about  x } { x | statement about  x } which is read as, “the set of all x x such that the statement about x x is true.” For example,

Interval notation is a way of describing sets that include all real numbers between a lower limit that may or may not be included and an upper limit that may or may not be included. The endpoint values are listed between brackets or parentheses. A square bracket indicates inclusion in the set, and a parenthesis indicates exclusion from the set. For example,

Given a line graph, describe the set of values using interval notation.

• Identify the intervals to be included in the set by determining where the heavy line overlays the real line.
• At the left end of each interval, use [ with each end value to be included in the set (solid dot) or ( for each excluded end value (open dot).
• At the right end of each interval, use ] with each end value to be included in the set (filled dot) or ) for each excluded end value (open dot).
• Use the union symbol ∪ ∪ to combine all intervals into one set.

Describing Sets on the Real-Number Line

Describe the intervals of values shown in Figure 6 using inequality notation, set-builder notation, and interval notation.

To describe the values, x , x , included in the intervals shown, we would say, “ x x is a real number greater than or equal to 1 and less than or equal to 3, or a real number greater than 5.”

Remember that, when writing or reading interval notation, using a square bracket means the boundary is included in the set. Using a parenthesis means the boundary is not included in the set.

Given Figure 7 , specify the graphed set in

• ⓑ set-builder notation
• ⓒ interval notation

Finding Domain and Range from Graphs

Another way to identify the domain and range of functions is by using graphs. Because the domain refers to the set of possible input values, the domain of a graph consists of all the input values shown on the x -axis. The range is the set of possible output values, which are shown on the y -axis. Keep in mind that if the graph continues beyond the portion of the graph we can see, the domain and range may be greater than the visible values. See Figure 8 .

We can observe that the graph extends horizontally from −5 −5 to the right without bound, so the domain is [ −5 , ∞ ) . [ −5 , ∞ ) . The vertical extent of the graph is all range values 5 5 and below, so the range is ( −∞ , 5 ] . ( −∞ , 5 ] . Note that the domain and range are always written from smaller to larger values, or from left to right for domain, and from the bottom of the graph to the top of the graph for range.

Finding Domain and Range from a Graph

Find the domain and range of the function f f whose graph is shown in Figure 9 .

We can observe that the horizontal extent of the graph is –3 to 1, so the domain of f f is ( − 3 , 1 ] . ( − 3 , 1 ] .

The vertical extent of the graph is 0 to –4, so the range is [ − 4 , 0 ] . [ − 4 , 0 ] . See Figure 10 .

Finding Domain and Range from a Graph of Oil Production

Find the domain and range of the function f f whose graph is shown in Figure 11 .

The input quantity along the horizontal axis is “years,” which we represent with the variable t t for time. The output quantity is “thousands of barrels of oil per day,” which we represent with the variable b b for barrels. The graph may continue to the left and right beyond what is viewed, but based on the portion of the graph that is visible, we can determine the domain as 1973 ≤ t ≤ 2008 1973 ≤ t ≤ 2008 and the range as approximately 180 ≤ b ≤ 2010. 180 ≤ b ≤ 2010.

In interval notation, the domain is [1973, 2008], and the range is about [180, 2010]. For the domain and the range, we approximate the smallest and largest values since they do not fall exactly on the grid lines.

Given Figure 12 , identify the domain and range using interval notation.

Can a function’s domain and range be the same?

Yes. For example, the domain and range of the cube root function are both the set of all real numbers.

Finding Domains and Ranges of the Toolkit Functions

We will now return to our set of toolkit functions to determine the domain and range of each.

Given the formula for a function, determine the domain and range.

• Exclude from the domain any input values that result in division by zero.
• Exclude from the domain any input values that have nonreal (or undefined) number outputs.
• Use the valid input values to determine the range of the output values.
• Look at the function graph and table values to confirm the actual function behavior.

Finding the Domain and Range Using Toolkit Functions

Find the domain and range of f ( x ) = 2 x 3 − x . f ( x ) = 2 x 3 − x .

There are no restrictions on the domain, as any real number may be cubed and then subtracted from the result.

The domain is ( − ∞ , ∞ ) ( − ∞ , ∞ ) and the range is also ( − ∞ , ∞ ) . ( − ∞ , ∞ ) .

Finding the Domain and Range

Find the domain and range of f ( x ) = 2 x + 1 . f ( x ) = 2 x + 1 .

We cannot evaluate the function at −1 −1 because division by zero is undefined. The domain is ( − ∞ , −1 ) ∪ ( −1 , ∞ ) . ( − ∞ , −1 ) ∪ ( −1 , ∞ ) . Because the function is never zero, we exclude 0 from the range. The range is ( − ∞ , 0 ) ∪ ( 0 , ∞ ) . ( − ∞ , 0 ) ∪ ( 0 , ∞ ) .

Find the domain and range of f ( x ) = 2 x + 4 . f ( x ) = 2 x + 4 .

We cannot take the square root of a negative number, so the value inside the radical must be nonnegative.

The domain of f ( x ) f ( x ) is [ − 4 , ∞ ) . [ − 4 , ∞ ) .

We then find the range. We know that f ( − 4 ) = 0 , f ( − 4 ) = 0 , and the function value increases as x x increases without any upper limit. We conclude that the range of f f is [ 0 , ∞ ) . [ 0 , ∞ ) .

Figure 22 represents the function f . f .

Find the domain and range of f ( x ) = − 2 − x . f ( x ) = − 2 − x .

Graphing Piecewise-Defined Functions

Sometimes, we come across a function that requires more than one formula in order to obtain the given output. For example, in the toolkit functions, we introduced the absolute value function f ( x ) = | x | . f ( x ) = | x | . With a domain of all real numbers and a range of values greater than or equal to 0, absolute value can be defined as the magnitude , or modulus , of a real number value regardless of sign. It is the distance from 0 on the number line. All of these definitions require the output to be greater than or equal to 0.

If we input 0, or a positive value, the output is the same as the input.

If we input a negative value, the output is the opposite of the input.

Because this requires two different processes or pieces, the absolute value function is an example of a piecewise function. A piecewise function is a function in which more than one formula is used to define the output over different pieces of the domain.

We use piecewise functions to describe situations in which a rule or relationship changes as the input value crosses certain “boundaries.” For example, we often encounter situations in business for which the cost per piece of a certain item is discounted once the number ordered exceeds a certain value. Tax brackets are another real-world example of piecewise functions. For example, consider a simple tax system in which incomes up to $10,000 are taxed at 10%, and any additional income is taxed at 20%. The tax on a total income S S would be 0.1 S 0.1 S if S ≤ $ 10 , 000 S ≤ $ 10 , 000 and $ 1000 + 0.2 ( S − $ 10 , 000 ) $ 1000 + 0.2 ( S − $ 10 , 000 ) if S > $ 10 , 000. S > $ 10 , 000.

Piecewise Function

A piecewise function is a function in which more than one formula is used to define the output. Each formula has its own domain, and the domain of the function is the union of all these smaller domains. We notate this idea like this:

In piecewise notation, the absolute value function is

Given a piecewise function, write the formula and identify the domain for each interval.

• Identify the intervals for which different rules apply.
• Determine formulas that describe how to calculate an output from an input in each interval.
• Use braces and if-statements to write the function.

Writing a Piecewise Function

A museum charges $5 per person for a guided tour with a group of 1 to 9 people or a fixed $50 fee for a group of 10 or more people. Write a function relating the number of people, n , n , to the cost, C . C .

Two different formulas will be needed. For n -values under 10, C = 5 n . C = 5 n . For values of n n that are 10 or greater, C = 50. C = 50.

The function is represented in Figure 23 . The graph is a diagonal line from n = 0 n = 0 to n = 10 n = 10 and a constant after that. In this example, the two formulas agree at the meeting point where n = 10 , n = 10 , but not all piecewise functions have this property.

Working with a Piecewise Function

A cell phone company uses the function below to determine the cost, C , C , in dollars for g g gigabytes of data transfer.

Find the cost of using 1.5 gigabytes of data and the cost of using 4 gigabytes of data.

To find the cost of using 1.5 gigabytes of data, C ( 1.5 ) , C ( 1.5 ) , we first look to see which part of the domain our input falls in. Because 1.5 is less than 2, we use the first formula.

To find the cost of using 4 gigabytes of data, C ( 4 ) , C ( 4 ) , we see that our input of 4 is greater than 2, so we use the second formula.

The function is represented in Figure 24 . We can see where the function changes from a constant to a shifted and stretched identity at g = 2. g = 2. We plot the graphs for the different formulas on a common set of axes, making sure each formula is applied on its proper domain.

Given a piecewise function, sketch a graph.

• Indicate on the x -axis the boundaries defined by the intervals on each piece of the domain.
• For each piece of the domain, graph on that interval using the corresponding equation pertaining to that piece. Do not graph two functions over one interval because it would violate the criteria of a function.

Graphing a Piecewise Function

Sketch a graph of the function.

Each of the component functions is from our library of toolkit functions, so we know their shapes. We can imagine graphing each function and then limiting the graph to the indicated domain. At the endpoints of the domain, we draw open circles to indicate where the endpoint is not included because of a less-than or greater-than inequality; we draw a closed circle where the endpoint is included because of a less-than-or-equal-to or greater-than-or-equal-to inequality.

Figure 25 shows the three components of the piecewise function graphed on separate coordinate systems.

Now that we have sketched each piece individually, we combine them in the same coordinate plane. See Figure 26 .

Note that the graph does pass the vertical line test even at x = 1 x = 1 and x = 2 x = 2 because the points ( 1 , 3 ) ( 1 , 3 ) and ( 2 , 2 ) ( 2 , 2 ) are not part of the graph of the function, though ( 1 , 1 ) ( 1 , 1 ) and ( 2 , 3 ) ( 2 , 3 ) are.

Graph the following piecewise function.

Can more than one formula from a piecewise function be applied to a value in the domain?

No. Each value corresponds to one equation in a piecewise formula.

Access these online resources for additional instruction and practice with domain and range.

• Domain and Range of Square Root Functions
• Determining Domain and Range
• Find Domain and Range Given the Graph
• Find Domain and Range Given a Table
• Find Domain and Range Given Points on a Coordinate Plane

3.2 Section Exercises

Why does the domain differ for different functions?

How do we determine the domain of a function defined by an equation?

Explain why the domain of f ( x ) = x 3 f ( x ) = x 3 is different from the domain of f ( x ) = x . f ( x ) = x .

When describing sets of numbers using interval notation, when do you use a parenthesis and when do you use a bracket?

How do you graph a piecewise function?

For the following exercises, find the domain of each function using interval notation.

f ( x ) = − 2 x ( x − 1 ) ( x − 2 ) f ( x ) = − 2 x ( x − 1 ) ( x − 2 )

f ( x ) = 5 − 2 x 2 f ( x ) = 5 − 2 x 2

f ( x ) = 3 x − 2 f ( x ) = 3 x − 2

f ( x ) = 3 − 6 − 2 x f ( x ) = 3 − 6 − 2 x

f ( x ) = 4 − 3 x f ( x ) = 4 − 3 x

f ( x ) = x 2 + 4 f ( x ) = x 2 + 4

f ( x ) = 1 − 2 x 3 f ( x ) = 1 − 2 x 3

f ( x ) = x − 1 3 f ( x ) = x − 1 3

f ( x ) = 9 x − 6 f ( x ) = 9 x − 6

f ( x ) = 3 x + 1 4 x + 2 f ( x ) = 3 x + 1 4 x + 2

f ( x ) = x + 4 x − 4 f ( x ) = x + 4 x − 4

f ( x ) = x − 3 x 2 + 9 x − 22 f ( x ) = x − 3 x 2 + 9 x − 22

f ( x ) = 1 x 2 − x − 6 f ( x ) = 1 x 2 − x − 6

f ( x ) = 2 x 3 − 250 x 2 − 2 x − 15 f ( x ) = 2 x 3 − 250 x 2 − 2 x − 15

f ( x ) = 5 x − 3 f ( x ) = 5 x − 3

f ( x ) = 2 x + 1 5 − x f ( x ) = 2 x + 1 5 − x

f ( x ) = x − 4 x − 6 f ( x ) = x − 4 x − 6

f ( x ) = x − 6 x − 4 f ( x ) = x − 6 x − 4

f ( x ) = x x f ( x ) = x x

f ( x ) = x 2 − 9 x x 2 − 81 f ( x ) = x 2 − 9 x x 2 − 81

Find the domain of the function f ( x ) = 2 x 3 − 50 x f ( x ) = 2 x 3 − 50 x by:

• ⓐ using algebra.
• ⓑ graphing the function in the radicand and determining intervals on the x -axis for which the radicand is nonnegative.

For the following exercises, write the domain and range of each function using interval notation.

For the following exercises, sketch a graph of the piecewise function. Write the domain in interval notation.

f ( x ) = { x + 1 if x < − 2 − 2 x − 3 if x ≥ − 2 f ( x ) = { x + 1 if x < − 2 − 2 x − 3 if x ≥ − 2

f ( x ) = { 2 x − 1 if x < 1 1 + x if x ≥ 1 f ( x ) = { 2 x − 1 if x < 1 1 + x if x ≥ 1

f ( x ) = { x + 1 if x < 0 x − 1 if x > 0 f ( x ) = { x + 1 if x < 0 x − 1 if x > 0

f ( x ) = { 3 if x < 0 x if x ≥ 0 f ( x ) = { 3 if x < 0 x if x ≥ 0

f ( x ) = { x 2      if  x < 0 1 − x  if  x > 0 f ( x ) = { x 2      if  x < 0 1 − x  if  x > 0

f ( x ) = { x 2 x + 2 if x < 0 if x ≥ 0 f ( x ) = { x 2 x + 2 if x < 0 if x ≥ 0

f ( x ) = { x + 1 if x < 1 x 3 if x ≥ 1 f ( x ) = { x + 1 if x < 1 x 3 if x ≥ 1

f ( x ) = { | x | 1 if x < 2 if x ≥ 2 f ( x ) = { | x | 1 if x < 2 if x ≥ 2

For the following exercises, given each function f , f , evaluate f ( −3 ) , f ( −2 ) , f ( −1 ) , f ( −3 ) , f ( −2 ) , f ( −1 ) , and f ( 0 ) . f ( 0 ) .

f ( x ) = { 1 if  x ≤ − 3 0 if  x > − 3 f ( x ) = { 1 if  x ≤ − 3 0 if  x > − 3

f ( x ) = { − 2 x 2 + 3 if  x ≤ − 1 5 x − 7 if  x > − 1 f ( x ) = { − 2 x 2 + 3 if  x ≤ − 1 5 x − 7 if  x > − 1

For the following exercises, given each function f , f , evaluate f ( −1 ) , f ( 0 ) , f ( 2 ) , f ( −1 ) , f ( 0 ) , f ( 2 ) , and f ( 4 ) . f ( 4 ) .

f ( x ) = { 7 x + 3 if x < 0 7 x + 6 if x ≥ 0 f ( x ) = { 7 x + 3 if x < 0 7 x + 6 if x ≥ 0

f ( x ) = { x 2 − 2 if x < 2 4 + | x − 5 | if x ≥ 2 f ( x ) = { x 2 − 2 if x < 2 4 + | x − 5 | if x ≥ 2

f ( x ) = { 5 x if x < 0 3 if 0 ≤ x ≤ 3 x 2 if x > 3 f ( x ) = { 5 x if x < 0 3 if 0 ≤ x ≤ 3 x 2 if x > 3

For the following exercises, write the domain for the piecewise function in interval notation.

f ( x ) = { x 2 − 2 if x < 1 − x 2 + 2 if x > 1 f ( x ) = { x 2 − 2 if x < 1 − x 2 + 2 if x > 1

f ( x ) = { 2 x − 3 − 3 x 2 if x < 0 if x ≥ 2 f ( x ) = { 2 x − 3 − 3 x 2 if x < 0 if x ≥ 2

Graph y = 1 x 2 y = 1 x 2 on the viewing window [ −0.5 , −0.1 ] [ −0.5 , −0.1 ] and [ 0.1 , 0.5 ] . [ 0.1 , 0.5 ] . Determine the corresponding range for the viewing window. Show the graphs.

Graph y = 1 x y = 1 x on the viewing window [ −0.5 , −0.1 ] [ −0.5 , −0.1 ] and [ 0.1 , 0.5 ] . [ 0.1 , 0.5 ] . Determine the corresponding range for the viewing window. Show the graphs.

Suppose the range of a function f f is [ −5 , 8 ] . [ −5 , 8 ] . What is the range of | f ( x ) | ? | f ( x ) | ?

Create a function in which the range is all nonnegative real numbers.

Create a function in which the domain is x > 2. x > 2.

Real-World Applications

The height h h of a projectile is a function of the time t t it is in the air. The height in feet for t t seconds is given by the function h ( t ) = −16 t 2 + 96 t . h ( t ) = −16 t 2 + 96 t . What is the domain of the function? What does the domain mean in the context of the problem?

The cost in dollars of making x x items is given by the function C ( x ) = 10 x + 500. C ( x ) = 10 x + 500.

• ⓐ The fixed cost is determined when zero items are produced. Find the fixed cost for this item.
• ⓑ What is the cost of making 25 items?
• ⓒ Suppose the maximum cost allowed is $1500. What are the domain and range of the cost function, C ( x ) ? C ( x ) ?
• 3 The Numbers: Where Data and the Movie Business Meet. “Box Office History for Horror Movies.” http://www.the-numbers.com/market/genre/Horror. Accessed 3/24/2014
• 4 http://www.eia.gov/dnav/pet/hist/LeafHandler.ashx?n=PET&s=MCRFPAK2&f=A.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites

• Authors: Jay Abramson
• Publisher/website: OpenStax
• Book title: College Algebra 2e
• Publication date: Dec 21, 2021
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
• Section URL: https://openstax.org/books/college-algebra-2e/pages/3-2-domain-and-range

© Jan 9, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.2: Domain and Range

• Last updated
• Save as PDF
• Page ID 67093

• David Lippman & Melonie Rasmussen
• The OpenTextBookStore

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

One of our main goals in mathematics is to model the real world with mathematical functions. In doing so, it is important to keep in mind the limitations of those models we create.

This table shows a relationship between circumference and height of a tree as it grows.

While there is a strong relationship between the two, it would certainly be ridiculous to talk about a tree with a circumference of -3 feet, or a height of 3000 feet. When we identify limitations on the inputs and outputs of a function, we are determining the domain and range of the function.

Definitions: Domain and Range

• Domain: The set of possible input values to a function
• Range: The set of possible output values of a function

Example \(\PageIndex{1}\)

Using the tree table above, determine a reasonable domain and range.

We could combine the data provided with our own experiences and reason to approximate the domain and range of the function \(h = f(c)\). For the domain, possible values for the input circumference \(c\), it doesn’t make sense to have negative values, so \(c > 0\). We could make an educated guess at a maximum reasonable value, or look up that the maximum circumference measured is about 119 feet. With this information, we would say a reasonable domain is \(0< c \le 119\) feet.

Similarly for the range, it doesn’t make sense to have negative heights, and the maximum height of a tree could be looked up to be 379 feet, so a reasonable range is \(0 < h \le 379\) feet.

Example \(\PageIndex{2}\)

When sending a letter through the United States Postal Service, the price depends upon the weight of the letter ( https://pe.usps.com/text/dmm300/Notice123.htm , retrieved August 6, 2018), as shown in the table below. Determine the domain and range.

Suppose we notate Weight by \(w\) and Price by \(p\), and set up a function named \(P\), where Price, \(p\) is a function of Weight, \(w. p = P(w).\)

Since acceptable weights are 3.5 ounces or less, and negative weights don’t make sense, the domain would be \(0< w \le 3.5\). Technically 0 could be included in the domain, but logically it would mean we are mailing nothing, so it doesn’t hurt to leave it out.

Since possible prices are from a limited set of values, we can only define the range of this function by listing the possible values. The range is \(p\) = $0.50, $0.71, $0.92, or $1.13.

The population of a small town in the year 1960 was 100 people. Since then the population has grown to 1400 people reported during the 2010 census. Choose descriptive variables for your input and output and use interval notation to write the domain and range.

Domain; \(y =\) years [1960, 2010]

Range, \(p =\) population, [100, 1400]

In the previous examples, we used inequalities to describe the domain and range of the functions. This is one way to describe intervals of input and output values, but is not the only way. Let us take a moment to discuss notation for domain and range.

Using inequalities, such as \(0 < c \le 163\), \(0 < w \le 3.5\), and \(0 < h \le 379\) imply that we are interested in all values between the low and high values, including the high values in these examples.

However, occasionally we are interested in a specific list of numbers like the range for the price to send letters, \(p\) = $0.44, $0.61, $0.78, or $0.95. These numbers represent a set of specific values: {0.44, 0.61, 0.78, 0.95}

Representing values as a set, or giving instructions on how a set is built, leads us to another type of notation to describe the domain and range.

Suppose we want to describe the values for a variable x that are 10 or greater, but less than 30. In inequalities, we would write \(10 \le x < 30\).

When describing domains and ranges, we sometimes extend this into set-builder notation , which would look like this: \(\{x\ |\ 10 \le x < 30\}\). The curly brackets {} are read as “the set of”, and the vertical bar is read as “such that”, so altogether we would read \(\{x\ |\ 10 \le x < 30\}\) as “the set of x -values such that 10 is less than or equal to \(x\) and \(x\) is less than 30.”

When describing ranges in set-builder notation, we could similarly write something like \(\{f(x)\ |\ 0 < f(x) < 30\}\), or if the output had its own variable, we could use it. So for our tree height example above, we could write for the range \(\{h\ |\ 0 < h \le 379\}\). In set-builder notation, if a domain or range is not limited, we could write {\(t\) | \(t\) is a real number}, or \(\{t\ |\ t \in \mathbb{R}\}\), read as “the set of t -values such that \(t\) is an element of the set of real numbers.

A more compact alternative to set-builder notation is interval notation , in which intervals of values are referred to by the starting and ending values. Curved parentheses are used for “strictly less than,” and square brackets are used for “less than or equal to.” Since infinity is not a number, we can’t include it in the interval, so we always use curved parentheses with \(\infty\) and - \(\infty\). The table below will help you see how inequalities correspond to set-builder notation and interval notation:

To combine two intervals together, using inequalities or set-builder notation we can use the word “or”. In interval notation, we use the union symbol, \(\cup\), to combine two unconnected intervals together.

Example \(\PageIndex{3}\)

Describe the intervals of values shown on the line graph below using set builder and interval notations.

To describe the values, \(x\), that lie in the intervals shown above we would say, “ x is a real number greater than or equal to 1 and less than or equal to 3, or a real number greater than 5.”

• As an inequality it is: \[1 \le x \le 3\quad \text{or} \quad x > 5 \nonumber\]
• In set builder notation: \[\{x|1 \le x \le 3 \quad \text{or} \quad x > 5\} \nonumber\]
• In interval notation: \[[1,3] \cup (5, \infty ) \nonumber\]

Remember when writing or reading interval notation:

Using a square bracket [ means the start value is included in the set;

Using a parenthesis ( means the start value is not included in the set.

Given the following interval, write its meaning in words, set builder notation, and interval notation.

a. Values that are less than or equal to -2, or values that are greater than or equal to -1 and less than 3

b. \(\{x\ |\ x \le -2\ or \ -1 \le x < 3\}\)

c. \((-\infty, -2] \cup [-1, 3)\)

Domain and Range from Graphs

We can also talk about domain and range based on graphs. Since domain refers to the set of possible input values, the domain of a graph consists of all the input values shown on the graph. Remember that input values are almost always shown along the horizontal axis of the graph. Likewise, since range is the set of possible output values, the range of a graph we can see from the possible values along the vertical axis of the graph.

Be careful – if the graph continues beyond the window on which we can see the graph, the domain and range might be larger than the values we can see.

Example \(\PageIndex{4}\)

Determine the domain and range of the graph below.

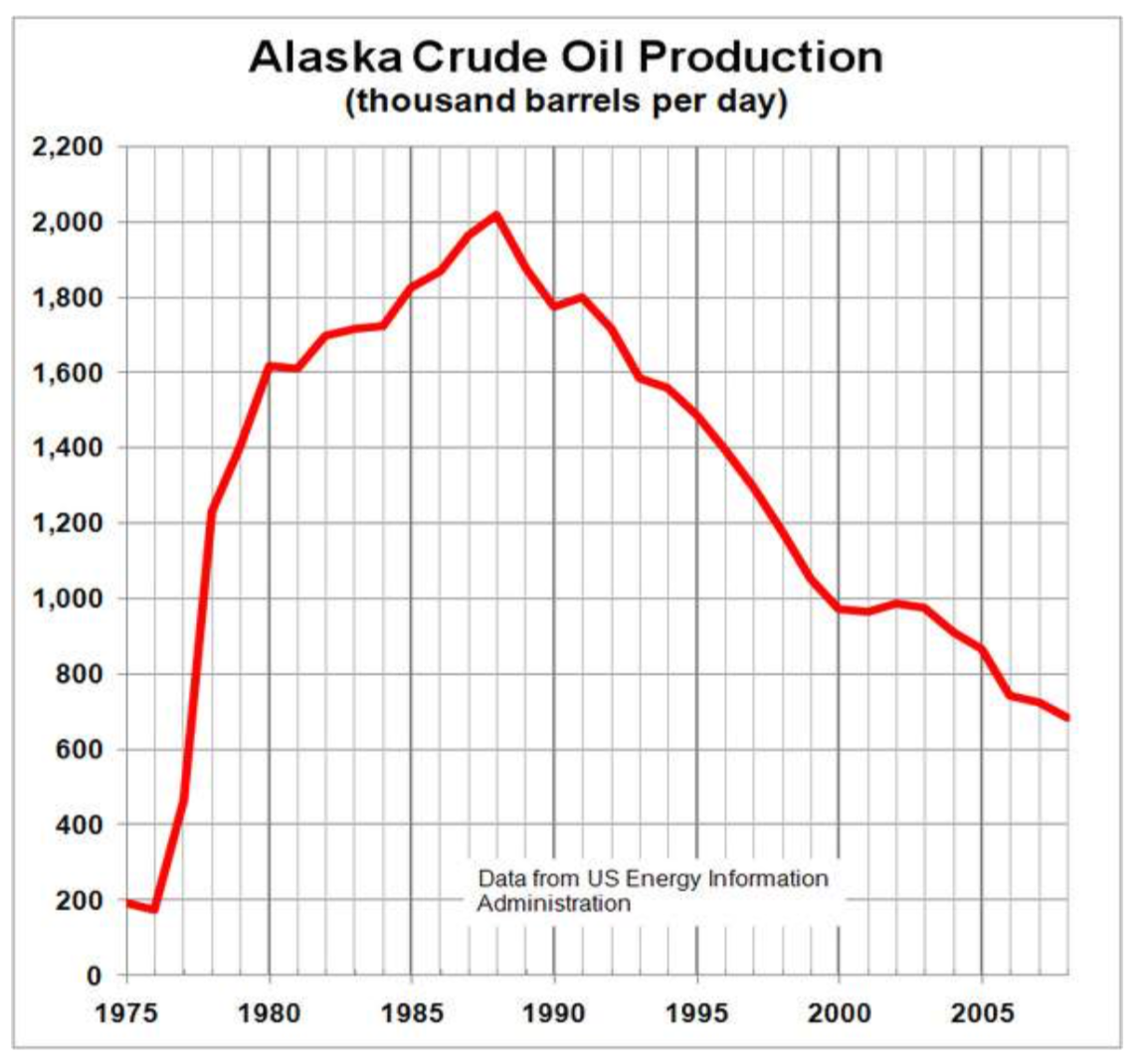
In the graph above ( http://commons.wikimedia.org/wiki/Fi...Production.PNG , CC-BY-SA, July 19, 2010), the input quantity along the horizontal axis appears to be “year”, which we could notate with the variable y . The output is “thousands of barrels of oil per day”, which we might notate with the variable b , for barrels. The graph would likely continue to the left and right beyond what is shown, but based on the portion of the graph that is shown to us, we can determine the domain is \(1975\le y\le 2008\), and the range is approximately \(180\le b\le 2010\).

In interval notation, the domain would be [1975, 2008] and the range would be about [180, 2010]. For the range, we have to approximate the smallest and largest outputs since they don’t fall exactly on the grid lines.

Remember that, as in the previous example, x and y are not always the input and output variables. Using descriptive variables is an important tool to remembering the context of the problem.

Given the graph below write the domain and range in interval notation

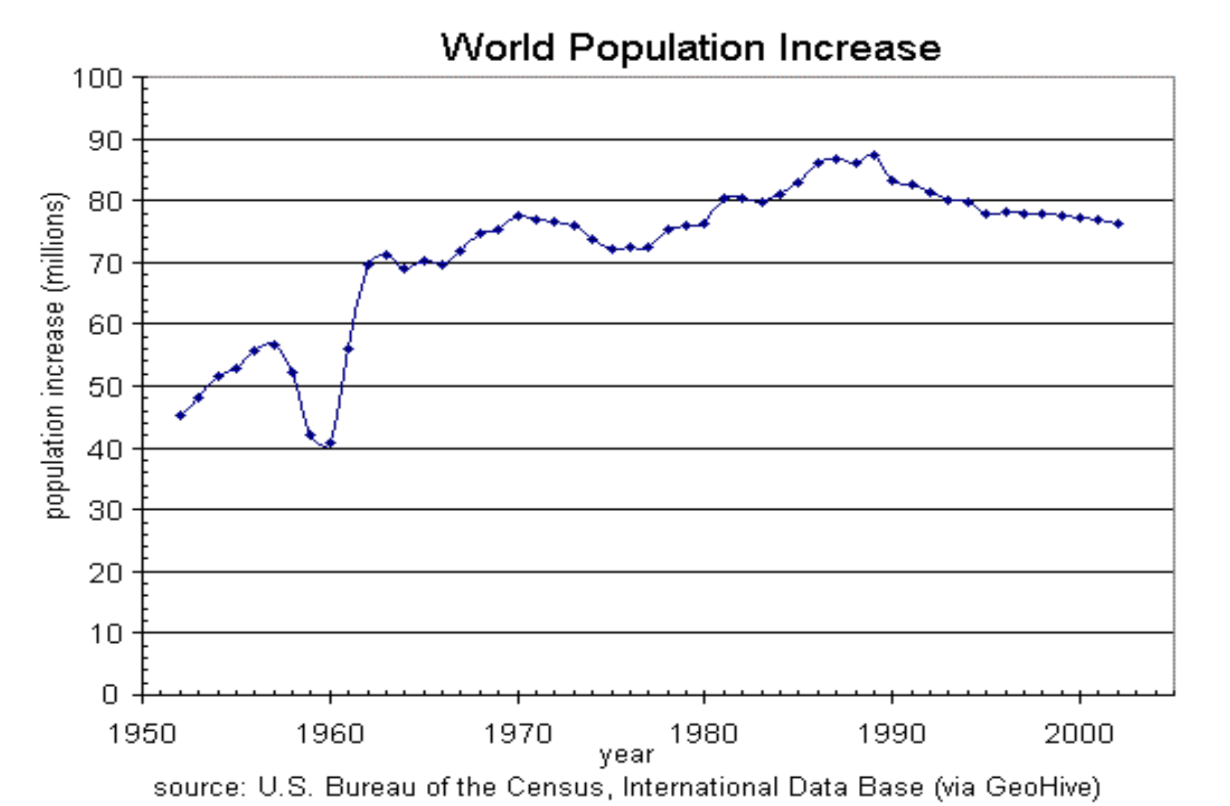
Domain; \(y =\) years, [1952, 2002]; Range, \(p =\) population in millions, [40, 88]

Domains and Range from Formulas

Most basic formulas can be evaluated at an input.  Two common restrictions are:

• The square root of negative values is non-real.
• We cannot divide by zero.

Example \(\PageIndex{5}\)

Find the domain of each function:

• \(f(x)=2\sqrt{x+4}\)
• \(g(x)=\dfrac{3}{6-3x}\)

a) Since we cannot take the square root of a negative number, we need the inside of the square root to be non-negative.

\(x + 4 \ge 0\) when \(x \ge -4\).

The domain of \(f(x)\) is \([-4, \infty)\).

b) We cannot divide by zero, so we need the denominator to be non-zero.

\(6 - 3x = 0\) when x = 2, so we must exclude 2 from the domain.

The domain of g(x) is \((-\infty , 2) \cup (2, \infty)\).

Piecewise Functions

Some functions cannot be described by a single formula. 

Definition: Piecewise Function

A piecewise function is a function in which the formula used depends upon the domain the input lies in. We notate this idea like:

\[f(x) = \begin{cases} \text{formula 1 if domain to use formula 1} \\ \text{formula 2 if domain to use formula 2} \\ \text{formula 3 if domain to use formula 3} \end{cases}\nonumber \]

Example \(\PageIndex{6}\)

A museum charges $5 per person for a guided tour with a group of 1 to 9 people, or a fixed $50 fee for 10 or more people in the group. Set up a function relating the number of people, \(n\), to the cost, \(C\).

To set up this function, two different formulas would be needed. C = 5 n would work for n values under 10, and C = 50 would work for values of n ten or greater. Notating this:

\[C(n) = \begin{cases} 5n & if & 0 < n < 10 \\ 50 & if & n \ge 10 \end{cases}\nonumber \]

Example \(\PageIndex{7}\)

A cell phone company uses the function below to determine the cost, C , in dollars for g gigabytes of data transfer.

\[C(g)=\left\{\begin{array}{ccc} {25} & {if} & {0<g<2} \\ {25+10(g-2)} & {if} & {g\ge 2} \end{array}\right.\nonumber \]

Find the cost of using 1.5 gigabytes of data, and the cost of using 4 gigabytes of data.

To find the cost of using 1.5 gigabytes of data, \(C(1.5)\), we first look to see which piece of domain our input falls in. Since 1.5 is less than 2, we use the first formula, giving \(C(1.5)\) = $25.

The find the cost of using 4 gigabytes of data, \(C(4)\), we see that our input of 4 is greater than 2, so we’ll use the second formula. \(C(4)\) = 25 + 10(4 - 2) = $45.

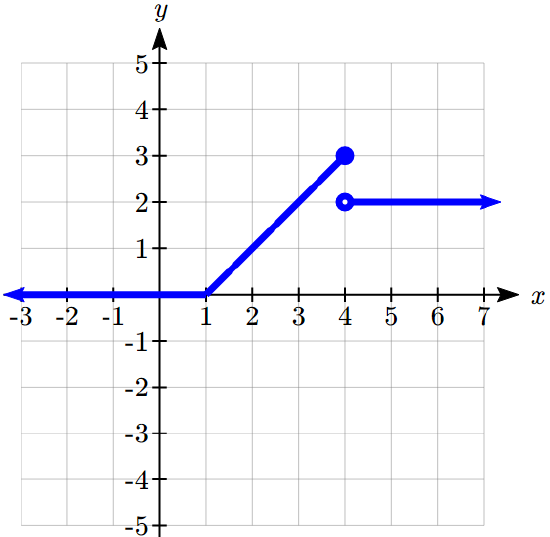
Sketch a graph of the function

\[f(x) = \left\{ {\begin{array}{*{20}{c}} 0&{if}&{x \leqslant 1} \\ {x - 1}&{if}&{1 < x \leqslant 4} \\ 2&{if}&{x > 4}\end{array}} \right.\nonumber\]

We can imagine graphing each function, then limiting the graph to the indicated domain.  At the endpoints of the domain, we put open circles to indicate where the endpoint is not included, due to a strictly-less-than inequality, and a closed circle where the endpoint is included, due to a less-than-or-equal-to inequality.  The first and last parts are constant functions, where the output is the same for all inputs.  The middle part we might recognize as a line, and could graph by evaluating the function at a couple inputs and connecting the points with a line.

Now that we have each piece individually, we combine them onto the same graph.  When the first and second parts meet at x = 1, we can imagine the closed dot filling in the open dot.  Since there is no break in the graph, there is no need to show the dot.

At Pierce College during the 2009-2010 school year tuition rates for in-state residents were $89.50 per credit for the first 10 credits, $33 per credit for credits 11-18, and for over 18 credits the rate is $73 per credit (www.pierce.ctc.edu/dist/tuit...ition_rate.pdf, retrieved August 6, 2010). Write a piecewise defined function for the total tuition, \(T\), at Pierce College during 2009-2010 as a function of the number of credits taken, \(c\). Be sure to consider a reasonable domain and range

\(T(c) = \begin{cases} 89.5c & if & c \le 10 \\ 895 + 33(c - 10) & if & 10 < c \le 18 \\ 1159 + 73(c - 18) & if & c > 18 \end{cases}\) Tuition, \(T\), as a function of credits, \(c\).

Reasonable domain should be whole numbers 0 to (answers may vary), e.g. [0, 23]

Reasonable range should be $0 – (answers may vary), e.g. [0,1524]

Important Topics of this Section

• Definition of domain
• Definition of range
• Inequalities
• Interval notation
• Set builder notation
• Domain and Range from graphs
• Domain and Range of toolkit functions
• Piecewise defined functions

PRACTICE PROBLEMS ON FINDING DOMAIN AND RANGE OF A FUNCTION

Find the domain and range of following modulus function

1)   f(x)  =  |x - 3|

2)   f(x)  =  1 - |x - 2|

3)   f(x)  =  |x - 4|/(x - 4)

1)    Domain :  |x - 3|, Range :  [0 , ∞)

2)  Domain :  All the real values R, Range :  ( - ∞, 1]

3)  Domain :    R - {0}, Range :  [-1, 1]

Find the domain of the following rational functions

1)  f(x)  =  (x - 1)/(x - 3)

2)  f(x)  =  (2x - 3)/(x 2  - 3x + 2)

3)     √(x - 2)

4)   f(x)  =   √(4 - x) + (1/ √(x 2  - 1))

5)   f(x)  =  (2x + 1)/(x 2  - 9)

6)   f(x)  =  x/(1 + x 2 )

7)   f(x)  =  3/(2 - x 2 )

1)  Domain :    R - {3}

2)  Domain :  R - {1, 2}

3)  Domain :  [2,  ∞)

4)  Domain :  (- ∞, -1) U (1, 4]

5)  Domain :  R - [-3, 3]

6)  Domain : All the real values R, Range :  [-1/2, 1/2]

7)  Domain :  R - { ±  √2}, Range :  (- ∞, 0) U  [3/2,  ∞)

Find the domain of the following radical function

Find the domain of the following square root function

1)   f(x)   =   √(x - 2)

2)   f(x)   = 1/  √(1 - x)

3)   f(x)   =  √(4 - x 2 )

4)   f(x)   =  √(4 - x) + 1/ √(x 2  - 1)

Find the domain and range of the following trigonometric function

1)   f(x)  =  1/(2 - sin 3x)

2)   f(x)  =  1/(1 - 2 cos x) 

1) Domain :  All the real values, Range :   [1/3, 1]

2)  Range :  [-1, 1/3]

Find the domain and range of the following quadratic function

1)   y   =  x 2  + 5x + 6

2)   y   =  -2x 2  + 5x - 7

1)  Domain :  {x │ x Є R}, Range :  {y │ y ≥ -0.25}

2)    Domain :  {x │ x Є R}, Range :  {y │ y ≤ -3.875}

Apart from the stuff given above ,    if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

SAT Math Videos (Part 2 - No Calculator)

May 25, 24 05:35 AM

SAT Math Videos (Part 1 - No Calculator)

May 25, 24 05:07 AM

Simplifying Algebraic Expressions with Fractional Coefficients

May 17, 24 08:12 AM

Domain and range word problem

1 expert answer.

Andrew M. answered • 01/17/18

Mathematics - Algebra a Specialty / F.I.T. Grad - B.S. w/Honors

Still looking for help? Get the right answer, fast.

Get a free answer to a quick problem. Most questions answered within 4 hours.

Choose an expert and meet online. No packages or subscriptions, pay only for the time you need.

RELATED TOPICS

Related questions, f(x)= square root x + 2 - 3.

Answers · 2

how to find the range and domain of y=-18x^2+300x+100

Answers · 1

what is the range if the domain is (-5,2,7) in the equation y=-2/3x+4

What is the domain and range of a function (in general terms), y=-4-10 for all prime # less than 15, recommended tutors.

find an online tutor

• Algebra 2 tutors
• Algebra tutors
• College Algebra tutors
• Precalculus tutors
• Calculus tutors
• Geometry tutors
• Business Calculus tutors
• Linear Programming tutors

related lessons

• Need help with something else? Try one of our lessons.
• Need help with something else? Try searching for a tutor.

How To : Solve word problems involving domain and range

See how to find the domain and range of a function implied by a word problem with this free video math lesson. From Ramanujan to calculus co-creator Gottfried Leibniz, many of the world's best and brightest mathematical minds have belonged to autodidacts. And, thanks to the Internet, it's easier than ever to follow in their footsteps (or just finish your homework or study for that next big test). With this installment from Internet pedagogical superstar Salman Khan's series of free math tutorials, you'll learn how to solve word problems that ask you to solve for the domain and range of a function.

Just updated your iPhone? You'll find new features for Podcasts, News, Books, and TV, as well as important security improvements and fresh wallpapers. Find out what's new and changed on your iPhone with the iOS 17.5 update.

Be the First to Comment

Share your thoughts, how to : find the equation of a circle given: center & tangent, how to : remember "greater than" & "less than" symbols, how to : find the perimeter & area of a complex figure, how to : write a sum/difference of logarithms as a logarithm, how to : use ">" (greater than) and "<" (less than) symbols, how to : calculate faster than a calculator, how to : find the circumference of a circle, how to : factor & simplify different algebraic expressions, how to : figure out a tip without a calculator, how to : prove the log a + log b = log ab logarithm property, how to : solve word problems involving the pythagorean theorem, how to : find the volue and surface area of a cylinder, how to : find standard deviation, how to : find a number given its percent, how to : prove a triangle inscribed in a circle is right angled, how to : find extra points for a parabola (quadractic equation), how to : find a slope of a straight line with: ax + by + c = 0, how to : divide small numbers by big numbers, how to : solve a 2x2 system of linear equations with inverses, how to : find the volume of a cone quickly.

• All Features
• All Hot Posts

Determining the Domain and Range for Quadratic Functions

Let's get started.

Given a situation that can be modeled by a quadratic function or the graph of a quadratic function, determine the domain and range of the function.

TEKS Standards and Student Expectations

A(6) Quadratic functions and equations. The student applies the mathematical process standards when using properties of quadratic functions to write and represent in multiple ways, with and without technology, quadratic equations. The student is expected to:

A(6)(A)  determine the domain and range of quadratic functions and represent the  domain and range using inequalities

Resource Objective(s)

To determine the domain and range of a quadratic function when given a statement or graph.

Essential Questions

How do you determine the domain and range of a quadratic function when given its graph?

How do you determine the domain and range of a quadratic function when given a verbal statement? Vocabulary

• Quadratic Equation

Investigating Domain and Range Using Graphs

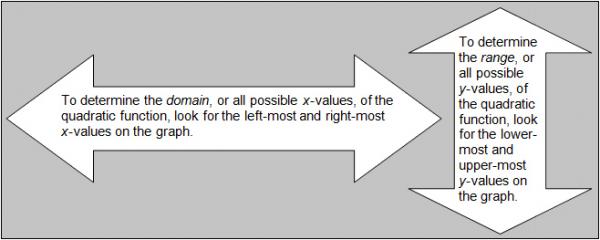
We're going to explore different representations of quadratic functions, including graphs, verbal descriptions, and tables. We'll determine the domain and range of the quadratic function with these representations.

Let's first examine graphs of quadratic functions, and learn how to determine the domain and range of a quadratic function from the graph.

A quadratic equation  is any equation/function with a degree of 2 that can be written in the form y = a x 2 + b x + c, where a, b, and c are real numbers, and a does not equal 0. Its graph is called a parabola. The constants a, b, and c are called the parameters of the equation. The values of a, b, and c determine the shape and position of the parabola.

The domain  of a function is the set of all real values  of x that will give real values for y . The range of a function is the set of all real values of y that you can get by plugging real numbers into x.

The quadratic parent function is y = x 2 . The graph of this function is shown below.

The graph of  y = - x 2 + 5 is shown below. Determine the domain and range of the function, and check to see if you interpreted the graph correctly.

The graph of  y = 25 x 2 + 4 is shown below. Determine the domain and range of this function. Drag the appropriate values into the boxes below the graph.

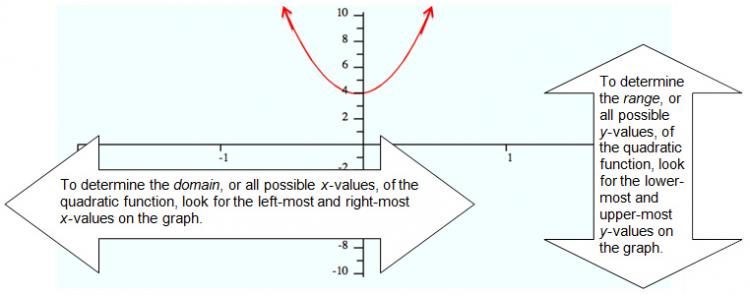
Practice Activity—Quadratic Function Explorer

1. Using the interactive link above, move the sliders to adjust the values of the coefficients: a, b, and c. Observe how the graph changes when you move these sliders.

2. Continue to adjust the values of the coefficients until the graph satisfies the domain and range values listed below. Record the function and its corresponding domain and range in your notes.

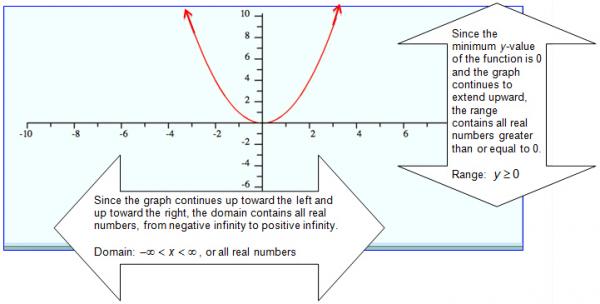
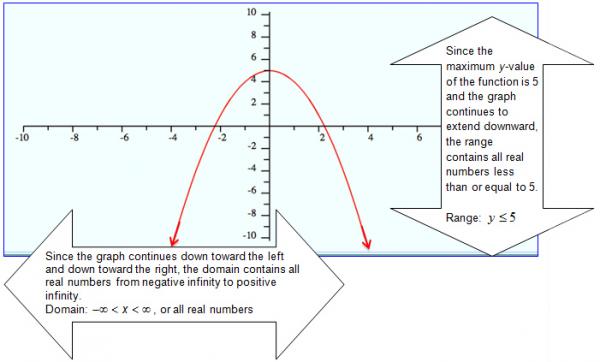
Domain: –∞ < x < ∞, Range: y ≥ 0 Domain: –∞ < x < ∞, Range: y ≤ -5 Domain: –∞ < x < ∞, Range: y ≥ 2

Investigating Domain and Range Using Verbal Descriptions

Sometimes you will be presented a problem in verbal form, rather than in symbolic form. In order to determine the domain and range of a quadratic function from the verbal statement it is often easier to use the verbal representation—or word problem—to generate a graph. By using this word problem, you can more conveniently find the domain and range from the graph.

Click on the image to access the video and follow the instructions:

• Watch the video. When asked to identify the true statement regarding the independent and dependent variable, choose A, B, or C.
• Record the example problem and the table of values for t and h .
• After the graph is drawn, identify the domain and range for the function, and record it in your notes. Estimate the maximum value of t for the domain.

Use your graphing calculator or an online graphing calculator  for the following examples. Graph the functions to determine the domain and range of the quadratic function.

A bird is building a nest in a tree 36 feet above the ground. The bird drops a stick from the nest. The function f( x ) = -16 x 2 + 36 describes the height of the stick in feet after x seconds. The graph of this function is shown below. Identify the domain and range of this function using the drag and drop activity below.

The DeWind family lives in a rectangular-shaped home with a length of 45 feet and a width of 35 feet. Mr. DeWind plans to install carpet in every room of the house, with the exception of the square kitchen. The kitchen has a side length of  x feet. The function  y = 1575 - x 2 describes the area of the home in square feet, without the kitchen. Identify the domain and range of this function. 

Vocabulary Activity

Journal activity.

Copy and paste the link code above.

Related Items

Have an account?

Domain and range from word problems

Mathematics.

7 questions

Introducing new   Paper mode

No student devices needed.   Know more

• 6. Multiple Choice Edit 5 minutes 1 pt Mario has and iTunes gift card worth $20.00. He uses the formula    y=0.99x to determine y, the total cost for x number of songs. What is the domain for the situation? All integers between 0 and 20 All real numbers between 0 and 19.80 All integers greater than 0 All integers between 0 and 250
• 7. Multiple Choice Edit 5 minutes 1 pt Hanna is measuring the height in inches of her roses over time. She discovers the formula y=5+0.25x, where x represents the number of days. If she measures between 4 and 8 days, what is the range of this situation? All integers between 4 and 8 All real numbers between 6 and 7 All integers between 0 and 8 All real numbers between 0 and 10

Explore all questions with a free account

Continue with email

Continue with phone