- IIT JEE Study Material
- System Of Linear Equations Using Determinants

System of Linear Equations Using Determinants
A system of linear equations having two and three variables can be easily solved using determinants . Here, the formulas and steps to find the solution of a system of linear equations are given along with practice problems. Cramer’s rule is well explained, along with a diagram, below:

How to Solve a Linear Equation System Using Determinants?
1. system of linear equations with two variables.
Let the equations be a 1 x + b 1 y + c 1 = 0 and a 2 x + b 2 y + c 2 = 0
The solution to a system of equations having 2 variables is given by:
2. System of Linear Equations Involving Three Variables
\(\begin{array}{l}{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}z={{d}_{1}} \;\;and\;\;{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}z={{d}_{2}} \;\;and\;{{a}_{3}}x+{{b}_{3}}y+{{c}_{3}}z={{d}_{3}}\end{array} \)
To solve this system, we need to first define the following determinants:
Now, the following algorithm is used to solve the system ( CRITERION FOR CONSISTENCY )

This method of finding a solution to a system of equations is called Cramer’s rule.
Conditions for Infinite and No Solutions
(a) If Δ = 0 and Δ 1 = Δ 2 = Δ 3 = 0, then the system of the equation may or may not be consistent:
(i) If the value of x, y and z in terms of t satisfy the third equation, then the system is said to be consistent and will have infinite solutions.
(ii) If the values of x, y, and z don’t satisfy the third equation, the system is said to be inconsistent and will have no solution.
(b) If d 1 = d 2 = d 3 = 0, then the system of linear equations is known as Homogeneous linear equations, which always possess at least one solution, i.e. (0, 0, 0). This is called a trivial solution for homogeneous linear equations .
(c) If the system of homogeneous linear equations possesses non-zero/nontrivial solutions, and Δ = 0, the given system has infinite solutions.
We can also solve these solutions using the matrix inversion method.
We can write the linear equations in the matrix form as AX = B, where
Now, the solution set is obtained by solving X = A -1 B. Hence, the solution set exists only if the inverse of A exists.
Some Important Results
Condition for the consistency of three simultaneous linear equations in 2 variables
(a) \(\begin{array}{l}a{{x}^{2}}+2hxy+b{{y}^{2}}+2gx+2fy+c=0\end{array} \) represents a pair of straight lines if
If D = 0, then the three points are collinear.
(d) If each element of any row (or column) can be expressed as a sum of two terms, then the determinant can be expressed as the sum of the determinants.
It should be noted that while applying operations on determinants, at least one row (or column) must remain unchanged, i.e. the maximum number of simultaneous operations = order of determinant – 1.
Practice Problems on System of Linear Equations Using Determinants
Here, in this problem, define the determinants Δ 1 , Δ 2 , and Δ 3 and find out their value by using the invariance property and then by using Cramer’s rule, we can get the values of x, y and z.
⇒ \(\begin{array}{l}{{\Delta }_{1}}=\left| \begin{matrix} 9 & 2 & 1 \\ 52 & 12 & 7 \\ 0 & 0 & -1 \\ \end{matrix} \right|=-1\left( 108-104 \right)=-4;\,\,{{\Delta }_{2}}=\left| \begin{matrix} 1 & 9 & 1 \\ 2 & 52 & 7 \\ 2 & 0 & -1 \\ \end{matrix} \right|\; (Applying \;{{C}_{1}}\to {{C}_{1}}+2{{C}_{3}})\end{array} \) ,
. x=1,y=3,z=5
Then by using Cramer’s rule, we can get the values of x and y.
Let us put \(\begin{array}{l}\Delta ,\frac{1}{x+5}=a\; and \;\frac{1}{y+7}=b\end{array} \) , then the 2 linear equations become
4a + 3b = -1 … (i)
And 6a – 6b = -5 … (ii);
Using Cramer’s rule, we get,
\(\begin{array}{l}b=\frac{1}{3}\,\,\,\Rightarrow \frac{1}{y+7}=\frac{1}{3} \;\;\;\Rightarrow \,\,\,3=y+7\,\,\,\Rightarrow \,\,y=-4\end{array} \)
Illustration: For what value of k will the following system of equations possess nontrivial solutions? Also, find all the solutions of the system for that value of k.
x+y-kz = 0; 3x-y-2z = 0; x-y+2z = 0.
In this problem, first, define Δ. As we know, for a non-trivial solution, Δ = 0.
So, by using the invariance property, we can solve Δ = 0 and will get the value of k.
For non-trivial solution, Δ = 0
Putting the value of k in the given equation, we get,
x+y-6z=0 … (i)
3x-y-2z=0 … (ii)
x-y+2z=0 … (iii)
Putting the value of z in (i), we get x+y-3x = 0
Thus when k = 6, the solution of the given system of equations will be \(\begin{array}{l}x=t,y=2t,z=\frac{t}{2},\end{array} \) , when t is an arbitrary number.
Illustration: Solve the following equations by matrix inversion.
2x + y + 2z = 0, 2x – y + z = 10, x + 3y – z = 5
By writing the given equations into the form of AX = D and then multiplying both sides by A -1 , we will get the required value of x, y and z.
Related Topics:
- Introduction to Determinants
- Minors and Cofactors
- Properties of Determinants
- Linear Equations
- Differentiation and Integration of Determinants
- Standard Determinants
Frequently Asked Questions
Give the condition that a system of linear equations has an infinite solution..
If a 1 /a 2 = b 1 /b 2 = c 1 /c 2 , then the system of equations has an infinite solution.
Give the condition that a system of linear equations has no solution.
If a 1 /a 2 = b 1 /b 2 ≠ c 1 /c 2 , then the system of equations has no solution.
How to check whether the 3 points are collinear?
Three points are collinear if the value of the area of the triangle formed by the three points is zero.
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
Register with Aakash BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
7.8 Solving Systems with Cramer's Rule
Learning objectives.
In this section, you will:
- Evaluate 2 × 2 determinants.
- Use Cramer’s Rule to solve a system of equations in two variables.
- Evaluate 3 × 3 determinants.
- Use Cramer’s Rule to solve a system of three equations in three variables.
- Know the properties of determinants.
We have learned how to solve systems of equations in two variables and three variables, and by multiple methods: substitution, addition, Gaussian elimination, using the inverse of a matrix, and graphing. Some of these methods are easier to apply than others and are more appropriate in certain situations. In this section, we will study two more strategies for solving systems of equations.
Evaluating the Determinant of a 2×2 Matrix
A determinant is a real number that can be very useful in mathematics because it has multiple applications, such as calculating area, volume, and other quantities. Here, we will use determinants to reveal whether a matrix is invertible by using the entries of a square matrix to determine whether there is a solution to the system of equations. Perhaps one of the more interesting applications, however, is their use in cryptography. Secure signals or messages are sometimes sent encoded in a matrix. The data can only be decrypted with an invertible matrix and the determinant. For our purposes, we focus on the determinant as an indication of the invertibility of the matrix. Calculating the determinant of a matrix involves following the specific patterns that are outlined in this section.
Find the Determinant of a 2 × 2 Matrix
The determinant of a 2 × 2 2 × 2 matrix, given
is defined as
Notice the change in notation. There are several ways to indicate the determinant, including det ( A ) det ( A ) and replacing the brackets in a matrix with straight lines, | A | . | A | .
Finding the Determinant of a 2 × 2 Matrix
Find the determinant of the given matrix.
Using Cramer’s Rule to Solve a System of Two Equations in Two Variables
We will now introduce a final method for solving systems of equations that uses determinants. Known as Cramer’s Rule , this technique dates back to the middle of the 18th century and is named for its innovator, the Swiss mathematician Gabriel Cramer (1704-1752), who introduced it in 1750 in Introduction à l'Analyse des lignes Courbes algébriques . Cramer’s Rule is a viable and efficient method for finding solutions to systems with an arbitrary number of unknowns, provided that we have the same number of equations as unknowns.
Cramer’s Rule will give us the unique solution to a system of equations, if it exists. However, if the system has no solution or an infinite number of solutions, this will be indicated by a determinant of zero. To find out if the system is inconsistent or dependent, another method, such as elimination, will have to be used.
To understand Cramer’s Rule, let’s look closely at how we solve systems of linear equations using basic row operations. Consider a system of two equations in two variables.
We eliminate one variable using row operations and solve for the other. Say that we wish to solve for x . x . If equation (2) is multiplied by the opposite of the coefficient of y y in equation (1), equation (1) is multiplied by the coefficient of y y in equation (2), and we add the two equations, the variable y y will be eliminated.
Now, solve for x . x .
Similarly, to solve for y , y , we will eliminate x . x .
Solving for y y gives
Notice that the denominator for both x x and y y is the determinant of the coefficient matrix.
We can use these formulas to solve for x x and y , y , but Cramer’s Rule also introduces new notation:
- D : D : determinant of the coefficient matrix
- D x : D x : determinant of the numerator in the solution of x x x = D x D x = D x D
- D y : D y : determinant of the numerator in the solution of y y y = D y D y = D y D
The key to Cramer’s Rule is replacing the variable column of interest with the constant column and calculating the determinants. We can then express x x and y y as a quotient of two determinants.
Cramer’s Rule for 2×2 Systems
Cramer’s Rule is a method that uses determinants to solve systems of equations that have the same number of equations as variables.
Consider a system of two linear equations in two variables.
The solution using Cramer’s Rule is given as
If we are solving for x , x , the x x column is replaced with the constant column. If we are solving for y , y , the y y column is replaced with the constant column.
Using Cramer’s Rule to Solve a 2 × 2 System
Solve the following 2 × 2 2 × 2 system using Cramer’s Rule.
Solve for x . x .
Solve for y . y .
The solution is ( 2 , −3 ) . ( 2 , −3 ) .
Use Cramer’s Rule to solve the 2 × 2 system of equations.
Evaluating the Determinant of a 3 × 3 Matrix
Finding the determinant of a 2×2 matrix is straightforward, but finding the determinant of a 3×3 matrix is more complicated. One method is to augment the 3×3 matrix with a repetition of the first two columns, giving a 3×5 matrix. Then we calculate the sum of the products of entries down each of the three diagonals (upper left to lower right), and subtract the products of entries up each of the three diagonals (lower left to upper right). This is more easily understood with a visual and an example.
Find the determinant of the 3×3 matrix.
- Augment A A with the first two columns. det ( A ) = | a 1 b 1 c 1 a 2 b 2 c 2 a 3 b 3 c 3 | a 1 a 2 a 3 b 1 b 2 b 3 | det ( A ) = | a 1 b 1 c 1 a 2 b 2 c 2 a 3 b 3 c 3 | a 1 a 2 a 3 b 1 b 2 b 3 |
- From upper left to lower right: Multiply the entries down the first diagonal. Add the result to the product of entries down the second diagonal. Add this result to the product of the entries down the third diagonal.
- From lower left to upper right: Subtract the product of entries up the first diagonal. From this result subtract the product of entries up the second diagonal. From this result, subtract the product of entries up the third diagonal.
The algebra is as follows:
Finding the Determinant of a 3 × 3 Matrix
Find the determinant of the 3 × 3 matrix given
Augment the matrix with the first two columns and then follow the formula. Thus,
Find the determinant of the 3 × 3 matrix.
Can we use the same method to find the determinant of a larger matrix?
No, this method only works for 2 × 2 2 × 2 and 3 × 3 3 × 3 matrices. For larger matrices it is best to use a graphing utility or computer software.
Using Cramer’s Rule to Solve a System of Three Equations in Three Variables
Now that we can find the determinant of a 3 × 3 matrix, we can apply Cramer’s Rule to solve a system of three equations in three variables . Cramer’s Rule is straightforward, following a pattern consistent with Cramer’s Rule for 2 × 2 matrices. As the order of the matrix increases to 3 × 3, however, there are many more calculations required.
When we calculate the determinant to be zero, Cramer’s Rule gives no indication as to whether the system has no solution or an infinite number of solutions. To find out, we have to perform elimination on the system.
Consider a 3 × 3 system of equations.
If we are writing the determinant D x , D x , we replace the x x column with the constant column. If we are writing the determinant D y , D y , we replace the y y column with the constant column. If we are writing the determinant D z , D z , we replace the z z column with the constant column. Always check the answer.
Solving a 3 × 3 System Using Cramer’s Rule
Find the solution to the given 3 × 3 system using Cramer’s Rule.
Use Cramer’s Rule.
The solution is ( 1 , 3 , −2 ) . ( 1 , 3 , −2 ) .
Use Cramer’s Rule to solve the 3 × 3 matrix.
Using Cramer’s Rule to Solve an Inconsistent System
Solve the system of equations using Cramer’s Rule.
We begin by finding the determinants D , D x , and D y . D , D x , and D y .
We know that a determinant of zero means that either the system has no solution or it has an infinite number of solutions. To see which one, we use the process of elimination. Our goal is to eliminate one of the variables.
- Multiply equation (1) by −2. −2.
- Add the result to equation ( 2 ) . ( 2 ) .
We obtain the equation 0 = −8 , 0 = −8 , which is false. Therefore, the system has no solution. Graphing the system reveals two parallel lines. See Figure 1 .
Use Cramer’s Rule to Solve a Dependent System
Solve the system with an infinite number of solutions.
Let’s find the determinant first. Set up a matrix augmented by the first two columns.
As the determinant equals zero, there is either no solution or an infinite number of solutions. We have to perform elimination to find out.
- Multiply equation (1) by −2 −2 and add the result to equation (3): − 2 x + 4 y − 6 z = 0 2 x − 4 y + 6 z = 0 0 = 0 − 2 x + 4 y − 6 z = 0 2 x − 4 y + 6 z = 0 0 = 0
- Obtaining an answer of 0 = 0 , 0 = 0 , a statement that is always true, means that the system has an infinite number of solutions. Graphing the system, we can see that two of the planes are the same and they both intersect the third plane on a line. See Figure 2 .
Understanding Properties of Determinants
There are many properties of determinants . Listed here are some properties that may be helpful in calculating the determinant of a matrix.
Properties of Determinants
- If the matrix is in upper triangular form, the determinant equals the product of entries down the main diagonal.
- When two rows are interchanged, the determinant changes sign.
- If either two rows or two columns are identical, the determinant equals zero.
- If a matrix contains either a row of zeros or a column of zeros, the determinant equals zero.
- The determinant of an inverse matrix A − 1 A − 1 is the reciprocal of the determinant of the matrix A . A .
- If any row or column is multiplied by a constant, the determinant is multiplied by the same factor.
Illustrating Properties of Determinants
Illustrate each of the properties of determinants.
Property 1 states that if the matrix is in upper triangular form, the determinant is the product of the entries down the main diagonal.
Augment A A with the first two columns.
Property 2 states that interchanging rows changes the sign. Given
Property 3 states that if two rows or two columns are identical, the determinant equals zero.
Property 4 states that if a row or column equals zero, the determinant equals zero. Thus,
Property 5 states that the determinant of an inverse matrix A − 1 A − 1 is the reciprocal of the determinant A . A . Thus,
Property 6 states that if any row or column of a matrix is multiplied by a constant, the determinant is multiplied by the same factor. Thus,
Using Cramer’s Rule and Determinant Properties to Solve a System
Find the solution to the given 3 × 3 system.
Using Cramer’s Rule , we have
Notice that the second and third columns are identical. According to Property 3, the determinant will be zero, so there is either no solution or an infinite number of solutions. We have to perform elimination to find out.
- Multiply equation (3) by –2 and add the result to equation (1). − 2 x − 4 y − 4 x = − 8 2 x + 4 y + 4 z = 2 0 = − 6 − 2 x − 4 y − 4 x = − 8 2 x + 4 y + 4 z = 2 0 = − 6
Obtaining a statement that is a contradiction means that the system has no solution.
Access these online resources for additional instruction and practice with Cramer’s Rule.
- Solve a System of Two Equations Using Cramer's Rule
- Solve a Systems of Three Equations using Cramer's Rule
7.8 Section Exercises
Explain why we can always evaluate the determinant of a square matrix.
Examining Cramer’s Rule, explain why there is no unique solution to the system when the determinant of your matrix is 0. For simplicity, use a 2 × 2 2 × 2 matrix.
Explain what it means in terms of an inverse for a matrix to have a 0 determinant.
The determinant of 2 × 2 2 × 2 matrix A A is 3. If you switch the rows and multiply the first row by 6 and the second row by 2, explain how to find the determinant and provide the answer.
For the following exercises, find the determinant.
| 1 2 3 4 | | 1 2 3 4 |
| − 1 2 3 − 4 | | − 1 2 3 − 4 |
| 2 − 5 − 1 6 | | 2 − 5 − 1 6 |
| − 8 4 − 1 5 | | − 8 4 − 1 5 |
| 1 0 3 − 4 | | 1 0 3 − 4 |
| 10 20 0 − 10 | | 10 20 0 − 10 |
| 10 0.2 5 0.1 | | 10 0.2 5 0.1 |
| 6 − 3 8 4 | | 6 − 3 8 4 |
| − 2 − 3 3.1 4 , 000 | | − 2 − 3 3.1 4 , 000 |
| − 1.1 0.6 7.2 − 0.5 | | − 1.1 0.6 7.2 − 0.5 |
| − 1 0 0 0 1 0 0 0 − 3 | | − 1 0 0 0 1 0 0 0 − 3 |
| − 1 4 0 0 2 3 0 0 − 3 | | − 1 4 0 0 2 3 0 0 − 3 |
| 1 0 1 0 1 0 1 0 0 | | 1 0 1 0 1 0 1 0 0 |
| 2 − 3 1 3 − 4 1 − 5 6 1 | | 2 − 3 1 3 − 4 1 − 5 6 1 |
| − 2 1 4 − 4 2 − 8 2 − 8 − 3 | | − 2 1 4 − 4 2 − 8 2 − 8 − 3 |
| 6 − 1 2 − 4 − 3 5 1 9 − 1 | | 6 − 1 2 − 4 − 3 5 1 9 − 1 |
| 5 1 − 1 2 3 1 3 − 6 − 3 | | 5 1 − 1 2 3 1 3 − 6 − 3 |
| 1.1 2 − 1 − 4 0 0 4.1 − 0.4 2.5 | | 1.1 2 − 1 − 4 0 0 4.1 − 0.4 2.5 |
| 2 − 1.6 3.1 1.1 3 − 8 − 9.3 0 2 | | 2 − 1.6 3.1 1.1 3 − 8 − 9.3 0 2 |
| − 1 2 1 3 1 4 1 5 − 1 6 1 7 0 0 1 8 | | − 1 2 1 3 1 4 1 5 − 1 6 1 7 0 0 1 8 |
For the following exercises, solve the system of linear equations using Cramer’s Rule.
2 x − 3 y = −1 4 x + 5 y = 9 2 x − 3 y = −1 4 x + 5 y = 9
5 x − 4 y = 2 − 4 x + 7 y = 6 5 x − 4 y = 2 − 4 x + 7 y = 6
6 x − 3 y = 2 − 8 x + 9 y = −1 6 x − 3 y = 2 − 8 x + 9 y = −1
2 x + 6 y = 12 5 x − 2 y = 13 2 x + 6 y = 12 5 x − 2 y = 13
4 x + 3 y = 23 2 x − y = −1 4 x + 3 y = 23 2 x − y = −1
10 x − 6 y = 2 − 5 x + 8 y = −1 10 x − 6 y = 2 − 5 x + 8 y = −1
4 x − 3 y = −3 2 x + 6 y = −4 4 x − 3 y = −3 2 x + 6 y = −4
4 x − 5 y = 7 − 3 x + 9 y = 0 4 x − 5 y = 7 − 3 x + 9 y = 0
4 x + 10 y = 180 − 3 x − 5 y = −105 4 x + 10 y = 180 − 3 x − 5 y = −105
8 x − 2 y = −3 − 4 x + 6 y = 4 8 x − 2 y = −3 − 4 x + 6 y = 4
x + 2 y − 4 z = − 1 7 x + 3 y + 5 z = 26 − 2 x − 6 y + 7 z = − 6 x + 2 y − 4 z = − 1 7 x + 3 y + 5 z = 26 − 2 x − 6 y + 7 z = − 6
− 5 x + 2 y − 4 z = − 47 4 x − 3 y − z = − 94 3 x − 3 y + 2 z = 94 − 5 x + 2 y − 4 z = − 47 4 x − 3 y − z = − 94 3 x − 3 y + 2 z = 94
4 x + 5 y − z = −7 −2 x − 9 y + 2 z = 8 5 y + 7 z = 21 4 x + 5 y − z = −7 −2 x − 9 y + 2 z = 8 5 y + 7 z = 21
4 x − 3 y + 4 z = 10 5 x − 2 z = − 2 3 x + 2 y − 5 z = − 9 4 x − 3 y + 4 z = 10 5 x − 2 z = − 2 3 x + 2 y − 5 z = − 9
4 x − 2 y + 3 z = 6 − 6 x + y = − 2 2 x + 7 y + 8 z = 24 4 x − 2 y + 3 z = 6 − 6 x + y = − 2 2 x + 7 y + 8 z = 24
5 x + 2 y − z = 1 − 7 x − 8 y + 3 z = 1.5 6 x − 12 y + z = 7 5 x + 2 y − z = 1 − 7 x − 8 y + 3 z = 1.5 6 x − 12 y + z = 7
13 x − 17 y + 16 z = 73 − 11 x + 15 y + 17 z = 61 46 x + 10 y − 30 z = − 18 13 x − 17 y + 16 z = 73 − 11 x + 15 y + 17 z = 61 46 x + 10 y − 30 z = − 18
− 4 x − 3 y − 8 z = − 7 2 x − 9 y + 5 z = 0.5 5 x − 6 y − 5 z = − 2 − 4 x − 3 y − 8 z = − 7 2 x − 9 y + 5 z = 0.5 5 x − 6 y − 5 z = − 2
4 x − 6 y + 8 z = 10 − 2 x + 3 y − 4 z = − 5 x + y + z = 1 4 x − 6 y + 8 z = 10 − 2 x + 3 y − 4 z = − 5 x + y + z = 1
4 x − 6 y + 8 z = 10 − 2 x + 3 y − 4 z = − 5 12 x + 18 y − 24 z = − 30 4 x − 6 y + 8 z = 10 − 2 x + 3 y − 4 z = − 5 12 x + 18 y − 24 z = − 30
For the following exercises, use the determinant function on a graphing utility.
| 1 0 8 9 0 2 1 0 1 0 3 0 0 2 4 3 | | 1 0 8 9 0 2 1 0 1 0 3 0 0 2 4 3 |
| 1 0 2 1 0 −9 1 3 3 0 −2 −1 0 1 1 −2 | | 1 0 2 1 0 −9 1 3 3 0 −2 −1 0 1 1 −2 |
| 1 2 1 7 4 0 1 2 100 5 0 0 2 2,000 0 0 0 2 | | 1 2 1 7 4 0 1 2 100 5 0 0 2 2,000 0 0 0 2 |
| 1 0 0 0 2 3 0 0 4 5 6 0 7 8 9 0 | | 1 0 0 0 2 3 0 0 4 5 6 0 7 8 9 0 |
Real-World Applications
For the following exercises, create a system of linear equations to describe the behavior. Then, calculate the determinant. Will there be a unique solution? If so, find the unique solution.
Two numbers add up to 56. One number is 20 less than the other.
Two numbers add up to 104. If you add two times the first number plus two times the second number, your total is 208
Three numbers add up to 106. The first number is 3 less than the second number. The third number is 4 more than the first number.
Three numbers add to 216. The sum of the first two numbers is 112. The third number is 8 less than the first two numbers combined.
For the following exercises, create a system of linear equations to describe the behavior. Then, solve the system for all solutions using Cramer’s Rule.
You invest $10,000 into two accounts, which receive 8% interest and 5% interest. At the end of a year, you had $10,710 in your combined accounts. How much was invested in each account?
You invest $80,000 into two accounts, $22,000 in one account, and $58,000 in the other account. At the end of one year, assuming simple interest, you have earned $2,470 in interest. The second account receives half a percent less than twice the interest on the first account. What are the interest rates for your accounts?
A theater needs to know how many adult tickets and children tickets were sold out of the 1,200 total tickets. If children’s tickets are $5.95, adult tickets are $11.15, and the total amount of revenue was $12,756, how many children’s tickets and adult tickets were sold?
A concert venue sells single tickets for $40 each and couple’s tickets for $65. If the total revenue was $18,090 and the 321 tickets were sold, how many single tickets and how many couple’s tickets were sold?
You decide to paint your kitchen green. You create the color of paint by mixing yellow and blue paints. You cannot remember how many gallons of each color went into your mix, but you know there were 10 gal total. Additionally, you kept your receipt, and know the total amount spent was $29.50. If each gallon of yellow costs $2.59, and each gallon of blue costs $3.19, how many gallons of each color go into your green mix?
You sold two types of scarves at a farmers’ market and would like to know which one was more popular. The total number of scarves sold was 56, the yellow scarf cost $10, and the purple scarf cost $11. If you had total revenue of $583, how many yellow scarves and how many purple scarves were sold?
Your garden produced two types of tomatoes, one green and one red. The red weigh 10 oz, and the green weigh 4 oz. You have 30 tomatoes, and a total weight of 13 lb, 14 oz. How many of each type of tomato do you have?
At a market, the three most popular vegetables make up 53% of vegetable sales. Corn has 4% higher sales than broccoli, which has 5% more sales than onions. What percentage does each vegetable have in the market share?
At the same market, the three most popular fruits make up 37% of the total fruit sold. Strawberries sell twice as much as oranges, and kiwis sell one more percentage point than oranges. For each fruit, find the percentage of total fruit sold.
Three artists performed at a concert venue. The first one charged $15 per ticket, the second artist charged $45 per ticket, and the final one charged $22 per ticket. There were 510 tickets sold, for a total of $12,700. If the first band had 40 more audience members than the second band, how many tickets were sold for each band?
A movie theatre sold tickets to three movies. The tickets to the first movie were $5, the tickets to the second movie were $11, and the third movie was $12. 100 tickets were sold to the first movie. The total number of tickets sold was 642, for a total revenue of $6,774. How many tickets for each movie were sold?
For the following exercises, use this scenario: A health-conscious company decides to make a trail mix out of almonds, dried cranberries, and chocolate-covered cashews. The nutritional information for these items is shown in Table 1 .
| Fat (g) | Protein (g) | Carbohydrates (g) | |
|---|---|---|---|
| 6 | 2 | 3 | |
| 0.02 | 0 | 8 | |
| 7 | 3.5 | 5.5 |
For the special “low-carb”trail mix, there are 1,000 pieces of mix. The total number of carbohydrates is 425 g, and the total amount of fat is 570.2 g. If there are 200 more pieces of cashews than cranberries, how many of each item is in the trail mix?
For the “hiking” mix, there are 1,000 pieces in the mix, containing 390.8 g of fat, and 165 g of protein. If there is the same amount of almonds as cashews, how many of each item is in the trail mix?
For the “energy-booster” mix, there are 1,000 pieces in the mix, containing 145 g of protein and 625 g of carbohydrates. If the number of almonds and cashews summed together is equivalent to the amount of cranberries, how many of each item is in the trail mix?
As an Amazon Associate we earn from qualifying purchases.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
- Authors: Jay Abramson
- Publisher/website: OpenStax
- Book title: College Algebra 2e
- Publication date: Dec 21, 2021
- Location: Houston, Texas
- Book URL: https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
- Section URL: https://openstax.org/books/college-algebra-2e/pages/7-8-solving-systems-with-cramers-rule
© Jan 9, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

- $ 0.00 0 items
Solve Systems of Equations Using Determinants
4.6 solve systems of equations using determinants.
Topics covered in this section are:
- Evaluate the determinant of a $2 \times 2$ matrix
- Evaluate the determinant of a $3 \times 3$ matrix
- Use Cramer’s Rule to solve systems of equations
- Solve applications using determinants
In this section we will learn of another method to solve systems of linear equations called Cramer’s rule. Before we can begin to use the rule, we need to learn some new definitions and notation.
4.6.1 Evaluate the Determinant of a $2 \times 2$ Matrix
If a matrix has the same number of rows and columns, we call it a square matrix . Each square matrix has a real number associated with it called its determinant . To find the determinant of the square matrix $\begin{bmatrix} a&b\\c&d \end{bmatrix}$ , we first write it as $\begin{vmatrix} a & b \\ c& d \end{vmatrix}$. To get the real number value of the determinate we subtract the products of the diagonals, as shown.
DETERMINANT
The determinant of any square matrix $\begin{bmatrix} a&b\\c&d \end{bmatrix}$, where $a$, $b$, $c$, and $d$ are real numbers, is
$\begin{vmatrix} a&b \\ c&d \end{vmatrix} = ad-bc$
Evaluate the determinant of:
- $\begin{bmatrix} 4&-2 \\ 3&1 \end{bmatrix}$
- $\begin{bmatrix} -3&-4 \\ -2&0 \end{bmatrix}$
| $\begin{bmatrix} 4&-2 \\ 3&-1 \end{bmatrix}$ | |
| Write the determinant. | |
| Subtract the products of the diagonals. | $4(-1)-3(-2)$ |
| Simplify. | $-4+6$ |
| Simplify. | $2$ |
| $\begin{bmatrix} -3&-4 \\ -2&0 \end{bmatrix}$ | |
| Write the determinant. | |
| Subtract the products of the diagonals. | $-3(0)-(-2)(-4)$ |
| Simplify. | $0-8$ |
| Simplify. | $-8$ |
4.6.2 Evaluate the Determinant of a $3 \times 3$ Matrix
To evaluate the determinant of a $3 \times 3$ matrix, we have to be able to evaluate the minor of an entry in the determinant. The minor of an entry is the $2 \times 2$ determinant found by eliminating the row and column in the $3 \times 3$ determinant that contains the entry.
MINOR OF AN ENTRY IN $3 \times 3$ A DETERMINANT
The minor of an entry in a $3 \times 3$ determinant is the $2 \times 2$ determinant found by eliminating the row and column in the $3 \times 3$ determinant that contains the entry.
To find the minor of entry $a_1$ we eliminate the row and column which contain it. So we eliminate the first row and first column. Then we write the $2 \times 2$ determinant that remains.

To find the minor of entry $b_2$, we eliminate the row and column that contain it. So we eliminate the $2^{\text{nd}}$ row and $2^{\text{nd}}$ column. Then we write the $2 \times 2$ determinant that remains.

For the determinant $\begin{vmatrix} 4&-2&3 \\ 1&0&-3 \\ -2&-4&2 \end{vmatrix}$, find and then evaluate the minor of:
| $\begin{vmatrix} 4&-2&3 \\ 1&0&-3 \\ -2&-4&2 \end{vmatrix}$ | |
| Eliminate the row and column that contains $a_1$. | |
| Write the $2 \times 2$ determinant that remains. | minor of $a_1$, $\begin{vmatrix}0&-3 \\ -4&2 \end{vmatrix}$ |
| Evaluate. | $0(2)-(-3)(-4)$ |
| Simplify. | $-12$ |
| $\begin{vmatrix} 4&-2&3 \\ 1&0&-3 \\ -2&-4&2 \end{vmatrix}$ | |
| Eliminate the row and column that contains $b_3$. | |
| Write the $2 \times 2$ determinant that remains. | minor of $b_3$, $\begin{vmatrix}4&3 \\ 1&-3 \end{vmatrix}$ |
| Evaluate. | $4(-3)-(1)(3)$ |
| Simplify. | $-15$ |
| $\begin{vmatrix} 4&-2&3 \\ 1&0&-3 \\ -2&-4&2 \end{vmatrix}$ | |
| Eliminate the row and column that contains $c_2$. | |
| Write the $2 \times 2$ determinant that remains. | minor of $c_2$, $\begin{vmatrix}4&-2 \\ -2&-4 \end{vmatrix}$ |
| Evaluate. | $4(-4)-(-2)(-2)$ |
| Simplify. | $-20$ |
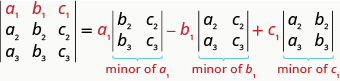
We are now ready to evaluate a $3 \times 3$ determinant. To do this we expand by minors, which allows us to evaluate the $3 \times 3$ determinant using $2 \times 2$ determinants—which we already know how to evaluate!
To evaluate a $3 \times 3$ determinant by expanding by minors along the first row, we use the following pattern:

Remember, to find the minor of an entry we eliminate the row and column that contains the entry.
EXPANDING BY MINORS ALONG THE FIRST ROW TO EVALUATE A $3 \times 3$ DETERMINANT
To evaluate a $3 \times 3$ determinant by expanding by minors along the first row , the following pattern:

Evaluate the determinant $\begin{vmatrix} 2&-3&-1 \\ 3&2&0 \\ -1&-1&-2 \end{vmatrix}$ by expanding by minors along the first row.
| $\begin{vmatrix} \textcolor{red}{2}&\textcolor{red}{-3}&\textcolor{red}{-1} \\ 3&2&0 \\ -1&-1&-2 \end{vmatrix}$ | |
| Expand by minors along the first row. | |
| Evaluate each determinant. | $\textcolor{red}{2}(-4-0)+\textcolor{red}{3}(-6-0)-\textcolor{red}{1}(-3-(-2))$ |
| Simplify. | $2(-4)+3(-6)-1(-1)$ |
| Simplify. | $-8-18+1$ |
| Simplify. | $-25$ |
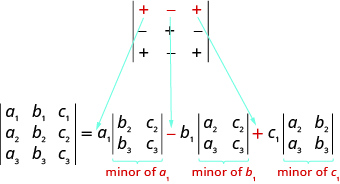
To evaluate a $3 \times 3$ determinant we can expand by minors using any row or column. Choosing a row or column other than the first row sometimes makes the work easier.
When we expand by any row or column, we must be careful about the sign of the terms in the expansion. To determine the sign of the terms, we use the following sign pattern chart.
$\begin{vmatrix} +&-&+ \\ -&+&- \\ +&-&+ \end{vmatrix}$
SIGN PATTERN
When expanding by minors using a row or column, the sign of the terms in the expansion follow the following pattern.
$\begin{vmatrix} +&-&+ \\ -&+&- \\ +&-&= \end{vmatrix}$
Notice that the sign pattern in the first row matches the signs between the terms in the expansion by the first row.

Since we can expand by any row or column, how do we decide which row or column to use? Usually we try to pick a row or column that will make our calculation easier. If the determinant contains a $0$, using the row or column that contains the $0$ will make the calculations easier.
Evaluate the determinant $\begin{vmatrix} 4&-1&-3 \\ 3&0&2 \\ 5&-4&-3 \end{vmatrix}$ by expanding minors.
To expand by minors, we look for a row or column that will make our calculations easier. Since 0 is in the second row and second column, expanding by either of those is a good choice. Since the second row has fewer negatives than the second column, we will expand by the second row.
| $\begin{vmatrix} 4&-1&-3 \\ 3&0&2 \\ \textcolor{red}{5}&\textcolor{red}{-4}&\textcolor{red}{-3} \end{vmatrix}$ | |
| Expand using the second row. | |
| Be careful of the signs. | |
| Evaluate each determinant. | $-3(3-12)+0(-12-(-15))-2(-16-(-5))$ |
| Simplify. | $-3(-9)+0-2(-11)$ |
| Simplify. | $27+0+22$ |
| Add. | $49$ |
4.6.3 Use Cramer’s Rule to Solve Systems of Equations
Cramer’s Rule is a method of solving systems of equations using determinants. It can be derived by solving the general form of the systems of equations by elimination. Here we will demonstrate the rule for both systems of two equations with two variables and for systems of three equations with three variables.
Let’s start with the systems of two equations with two variables.
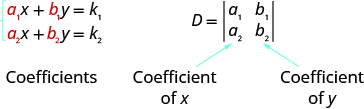
CRAMER’S RULE FOR SOLVING A SYSTEM OF TWO EQUATIONS
For the system of equations $\Bigg\{ \begin{align*} a_1x+b_1y&=k_1 \\ a_2x+b_2y&=k_2 \end{align*}$, the solution $(x, y)$ can be determined by

Notice that to form the determinant $D$, we use take the coefficients of the variables.

Notice that to form the determinant $D_x$ and $D_y$ we substitute the constants for the coefficients of the variable we are finding.

Solve using Cramer’s Rule: $\Bigg\{ \begin{align*} 2x+y&=-4 \\ 3x-2y&=-6 \end{align*}$
| Evaluate the determinant $D$, using the coefficients of the variables. | $\Bigg\{ \begin{align*} 2x+y&=-4 \\ 3x-2y&=-6 \end{align*}$ $D=\begin{vmatrix}2&1 \\ 3&-2 \end{vmatrix}$ $D=-4-3$ $D=-7$ | |
| Evaluate the determinant $D_x$. Use the constants in place of the $x$ coefficients. | We replace the coefficients of $x$, $2$ and $3$ with the constants, $-4$ and $-6$. | $D_x=\begin{vmatrix}-4&1 \\ -6&-2 \end{vmatrix}$ $D_x=8-(-6)$ $D_x=14$ |
| Evaluate the determinant $D_y$. Use the constants in place of the $y$ coefficients. | We replace the coefficients of $y$, $1$ and $2$ with the constants, $-4$ and $-6$. | $D_y=\begin{vmatrix}2&-4 \\ 3&-6 \end{vmatrix}$ $D_y=-12-(-12)$ $D_y=0$ |
| Find $x$ and $y$. | Substitute in the values of $D$, $D_x$, and $D_y$. | $x=\frac{D_x}{D} \text{ and } y=\frac{D_y}{D}$ $x=\frac{14}{-7} \text{ and } y=\frac{0}{-7}$ $x=-2 \text{ and } y=0$ |
| Write the solution as an ordered pair. | The ordered pair is $(x, y)$. | $(-2, 0)$ |
| Check that the ordered pair is a solution to original equations. | Substitute $x=-2$ and $y=0$ into both equations and make sure they are both true. | $(2, 0)$ is the solution to the system. |
HOW TO: Solve a system of two equations using Cramer’s rule.
- Evaluate the determinant $D$, using the coefficients of the variables.
- Evaluate the determinant $D_x$. Use the constants in place of the $x$ coefficients.
- Evaluate the determinant $D_y$. Use the constants in place of the $y$ coefficients.
- Find $x$ and $y$. $x=\frac{D_x}{D}$, $y=\frac{D_y}{D}$
- Write the solution as an ordered pair.
- Check that the ordered pair is a solution to both original equations.
To solve a system of three equations with three variables with Cramer’s Rule, we basically do what we did for a system of two equations. However, we now have to solve for three variables to get the solution. The determinants are also going to be $3 \times 3$ which will make our work more interesting!
CRAMER’S RULE FOR SOLVING A SYSTEM OF THREE EQUATIONS
For the system of equations $\Bigg\{ \begin{align*} a_1x+b_1y+c_1z&=k_1 \\ a_2x+b_2y+c_2z&=k_2 \\ a_3x+b_3y+c_3z&=k_3 \end{align*}$, the solution $(x, y, z)$ can be determined by

Solve the system of equations using Cramer’s Rule: $\Bigg\{ \begin{align*} 3x-5y+&4z=5 \\ 5x+2y+&z=0 \\ 2x+3y-&2z=3 \end{align*}$
| Evaluate the determinant $D$. | $D=\begin{vmatrix} \textcolor{red}{3}&-5&4 \\ \textcolor{red}{5}&2&1 \\ \textcolor{red}{2}&3&-2 \end{vmatrix}$ |
| Expand by minors using column 1. | |
| Be careful of the signs. $\begin{vmatrix} \textcolor{red}{+}&-&+ \\ \textcolor{red}{-}&+&- \\ \textcolor{red}{+}&-&+ \end{vmatrix}$ | $D=\textcolor{red}{3}\begin{vmatrix} 2&1 \\ 3&-2 \end{vmatrix} – \textcolor{red}{5}\begin{vmatrix} -5&4 \\ 3&-2 \end{vmatrix} +\textcolor{red}{2}\begin{vmatrix} -5&4 \\ 2&1 \end{vmatrix}$ |
| Evaluate the determinants. | $D=\textcolor{red}{3}(-4-3)-\textcolor{red}{5}(10-12)+\textcolor{red}{2}(-5-8)$ |
| Simplify. | $D=3(-7)-5(-2)+2(-13)$ $D=-21+10-26$ $D=-37$ |
| Evaluate the determinant $D_x$. Use the constants to replace the coefficients of $x$. | $D_x=\begin{vmatrix} \textcolor{red}{5}&-5&4 \\ \textcolor{red}{0}&2&1 \\ \textcolor{red}{3}&3&-2 \end{vmatrix}$ |
| Expand by minors using column 1. | $D_x=\textcolor{red}{5}\begin{vmatrix} 2&1 \\ 3&-2 \end{vmatrix} – \textcolor{red}{0}\begin{vmatrix} -5&4 \\ 3&-2 \end{vmatrix} +\textcolor{red}{3}\begin{vmatrix} -5&4 \\ 2&1 \end{vmatrix}$ |
| Evaluate the determinants. | $D_x=\textcolor{red}{5}(-4-3)-\textcolor{red}{0}(10-12)+\textcolor{red}{3}(-5-8)$ |
| Simplify. | $D_x=5(-7)-0+3(-13)$ $D_x=-35+0-39$ $D_x=-74$ |
| Evaluate the determinant $D_y$. Use the constants to replace the coefficients of $y$. | $D_y=\begin{vmatrix} 3&\textcolor{red}{5}&4 \\ 5&\textcolor{red}{0}&1 \\ 2&\textcolor{red}{3}&-2 \end{vmatrix}$ |
| Expand by minors using column 2. Be careful of the signs. $\begin{vmatrix} +&\textcolor{red}{-}&+ \\ -&\textcolor{red}{+}&- \\ +&\textcolor{red}{-}&+ \end{vmatrix}$ | $D_y=\textcolor{red}{-5}\begin{vmatrix} 5&1 \\ 2&-2 \end{vmatrix} + \textcolor{red}{0}\begin{vmatrix} 5&4 \\ 3&-2 \end{vmatrix} -\textcolor{red}{3}\begin{vmatrix} 3&4 \\ 5&1 \end{vmatrix}$ |
| Evaluate the determinants. | $D_y=-\textcolor{red}{5}(-10-2)+\textcolor{red}{0}(-10-12)-\textcolor{red}{3}(3-20)$ |
| Simplify. | $D_y=-5(-12)+0-3(-17)$ $D_y=60+0+51$ $D_y=111$ |
| Evaluate the determinant $D_z$. Use the constants to replace the coefficients of $z$. | $D_z=\begin{vmatrix} 3&-5&\textcolor{red}{5} \\ 5&2&\textcolor{red}{0} \\ 2&3&\textcolor{red}{3} \end{vmatrix}$ |
| Expand by minors using column 3. Be careful of the signs. $\begin{vmatrix} +&-&\textcolor{red}{+} \\ -&+&\textcolor{red}{-} \\ +&-&\textcolor{red}{+} \end{vmatrix}$ | $D_z=\textcolor{red}{5}\begin{vmatrix} 5&2 \\ 2&3 \end{vmatrix} – \textcolor{red}{0}\begin{vmatrix} 3&-5 \\ 2&3 \end{vmatrix} +\textcolor{red}{3}\begin{vmatrix} 3&-5 \\ 5&2 \end{vmatrix}$ |
| Evaluate the determinants. | $D_z=\textcolor{red}{5}(15-4)-\textcolor{red}{0}(9-(-10))+\textcolor{red}{3}(6-(-25))$ |
| Simplify. | $D_z=5(11)-0+3(31)$ $D_z=55-0+93$ $D_z=148$ |
| Find $x$, $y$, and $z$. | $x=\frac{D_x}{D}, y=\frac{D_y}{D}, \text{ and } z=\frac{D_z}{D}$ |
| Substitute in the values. | $x=\frac{-74}{-37}, y=\frac{111}{-37}, \text{ and } z=\frac{148}{-37}$ |
| Simplify. | $x=2, y=-3, \text{ and } z=-4$ |
| Write the solution as an ordered triple. | $(2, -3, -4)$ |
| Check that the ordered triple is a solution to original equations. | We leave the check to you. |
| The solution is $(2, -3, -4)$. |
Cramer’s rule does not work when the value of the $D$ determinant is $0$, as this would mean we would be dividing by $0$. But when $D=0$, the system is either inconsistent or dependent.
When the value of $D=0$ and $D_x$, $D_y$ and $D_z$ are all zero, the system is consistent and dependent and there are infinitely many solutions.
When the value of $D=0$ and $D_x$, $D_y$ and $D_z$ are not all zero, the system is inconsistent and there is no solution.
DEPENDENT AND INCONSISTENT SYSTEMS OF EQUATIONS
For any system of equations, where the value of the determinant $D=0$,
| $D=0$ and $D_x$, $D_y$, and $D_z$ are all zero | consistent and dependent |
| $D=0$ and $D_x$, $D_y$, and $D_z$ are all not zero | inconsistent |
In the next example, we will use the values of the determinants to find the solution of the system.
Solve the system of equations using Cramer’s rule: $\Bigg\{ \begin{align*} x+3y&=4 \\ -2x-6y&=3 \end{align*}$.
| $\Bigg\{ \begin{align*} x+3y&=4 \\ -2x-6y&=3 \end{align*}$. | |
| Evaluate the determinant $D$, using the coefficients of the variables. | $D=\begin{vmatrix} 1&3 \\ -2&-6 \end{vmatrix}$ $D=-6-(-6)$ $D=0$ |
We cannot use Cramer’s Rule to solve this system. But by looking at the value of the determinants $D_x$ and $D_y$, we can determine whether the system is dependent or inconsistent.
| Evaluate the determinant $D_x$. | $D_x=\begin{vmatrix} 4&3 \\ 3&-6 \end{vmatrix}$ $D_x=-24-9$ $D_x=-33$ |
Since all the determinants are not zero, the system is inconsistent. There is no solution.
4.6.4 Solve Applications using Determinants
An interesting application of determinants allows us to test if points are collinear. Three points $(x_1, y_1)$, $(x_2, y_2)$ and $(x_3, y_3)$ are collinear if and only if the determinant below is zero.
$\begin{vmatrix} x_1&y_1&1 \\ x_2&y_2&1 \\ x_3&y_3&1 \end{vmatrix} = 0$
TEST FOR COLLINEAR POINTS
Three points $(x_1, y_1)$, $(x_2, y_2)$ and $(x_3, y_3)$ are collinear if and only if
We will use this property in the next example.
Determine whether the points $(5, −5)$, $(4, −3)$, and $(3, −1)$ are collinear.
| $\begin{vmatrix} x_1&y_1&1 \\ x_2&y_2&1 \\ x_3&y_3&1 \end{vmatrix}$ | |
| Substitute the values into the determinant. $(5, -5)$, $(4, -3)$, and $(3, -1)$. | $\begin{vmatrix} 5&-5&1 \\ 4&-3&1 \\ 3&-1&1 \end{vmatrix}$ |
| Calculate the determinant by expanding by minors using column 3. | $D=\textcolor{red}{1} \begin{vmatrix} 4&-3 \\ 3&-1 \end{vmatrix} – \textcolor{red}{1} \begin{vmatrix} 5&-5 \\ 3&-1 \end{vmatrix}+\textcolor{red}{1} \begin{vmatrix} 5&-5 \\ 4&-3 \end{vmatrix}$ |
| Evaluate the determinants. | $D=1(-4-(-9))-1(-5-(-15))+1(-15-(-20))$ |
| Simplify. | $D=1(5)-1(10)+1(5)$ $D=5-10+5$ $D=0$ |
| The value of the determinant is $0$, so the points are collinear. |
CC Licensed Content, Original
- Revision and Adaption. Provided by: Minute Math. License: CC BY 4.0
CC Licensed Content, Shared Previously
- Marecek, L., & Mathis, A. H. (2020). Solve Systems of Equations Using Determinants. In Intermediate Algebra 2e. OpenStax. https://openstax.org/books/intermediate-algebra-2e/pages/4-6-solve-systems-of-equations-using-determinants . License: CC BY 4.0 . Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
Share this:
- No products in the cart.

- Français
- Preparatory
Question Video: Solving a System of Three Equations Using Determinants Mathematics • First Year of Secondary School
Join nagwa classes.
Attend live Mathematics sessions on Nagwa Classes to learn more about this topic from an expert teacher!

- Remaining Seats: 11
Use determinants to solve the system 5𝑥 = −2𝑦 − 5 + 3𝑧, −3𝑥 − 𝑦 + 1 = 2𝑧, 2𝑦 − 𝑧 = −5𝑥 + 3.
Video Transcript
Use determinants to solve the system five 𝑥 equals negative two 𝑦 minus five plus three 𝑧, negative three 𝑥 minus 𝑦 plus one equals two 𝑧, and two 𝑦 minus 𝑧 equals negative five 𝑥 plus three.
So, in a problem like this, the first thing we want to do is actually rearrange our equations so that we have our variables on the left-hand side. And then we have our answers on the right-hand side, which are numerical values or constants. So our first equation rearranged is gonna be five 𝑥 plus two 𝑦 minus three 𝑧 equals negative five. Then, for the second equation, we’re gonna have negative three 𝑥 minus 𝑦 minus two 𝑧 equals negative one. And then finally, five 𝑥 plus two 𝑦 minus 𝑧 equals three.
Okay, great. We’ve got it like this, but why do we want it in this form? We want it in this form so we can set up a matrix equation. And when we do, what we get is the matrix five, two, negative three, negative three, negative one, negative two, five, two, negative one multiplied by the matrix for our variables, which is 𝑥, 𝑦, 𝑧. Then this is equal to our answer matrix negative five, negative one, three. Okay, great. But how does this help us meet our objective, which is to solve the system of equations using determinants? Well, what we’re gonna do is use Cramer’s rule. And what Cramer’s rule tells us is that we can find the variables or solutions to our system of equations using, for example, 𝑥 is equal to, then we’ve got the determinant of the matrix Δ sub 𝑥 over the determinant of the matrix Δ. And then this pattern continues for 𝑦 and 𝑧.
Okay, to use this then, what we need to do is work out our determinants. The first determinant we’re gonna work out is the determinant of Δ, which is gonna be our coefficient matrix. So what we’re gonna do is find out the determinant of the matrix five, two, negative three, negative three, negative one, negative two, five, two, negative one. So this is gonna be equal to five multiplied by the determinant of the submatrix negative one, negative two, two, negative one minus two multiplied by the submatrix negative three, negative two, five, negative one minus three multiplied by the submatrix negative three, negative one, five, two, remembering that when we find the determinants, the coefficients go positive, negative, positive. And to find our submatrices, we delete the column and row that our coefficient is in.
Okay, great. So now, we calculate this. And then remembering that when we work out determinants of two-by-two matrices, what we do is cross multiply and then subtract, we’re gonna get five multiplied by one plus four minus two multiplied by three plus 10 minus three multiplied by negative six plus five which is equal to two. So this is great cause it also tells us that the matrix is nonsingular. So therefore, we know that there is not gonna be an infinite number of solutions. And that’s because if there was, then the determinant would be equal to zero. So now, what we’re gonna do is clear a space and work out the other determinants we need to find.
So next, what we want to do is find the determinant of Δ sub 𝑥. And the way we do that is by substituting in the answer matrix values for the coefficient of 𝑥-value, so the first column in our matrix. So now what we’re gonna want to do is find the determinant of this matrix. And to do that, what we’re gonna do is to use the same methods as we used for the previous determinant, which is gonna give us a determinant value of negative 42. And you can see the working there. Okay, great. So once again, we’re gonna clear a bit of space and look at our next determinant.
So now what we’re gonna find is the determinant of the matrix Δ sub 𝑦. And this is gonna be where we substitute in our answer matrix for the 𝑦-coefficients in the matrix. So then once again, using the same method to find the determinant, we’re gonna have a determinant of 112. And again, the working is shown here. So once again, what we’re gonna do is clear a space for the final determinant. So for the final one, it’s gonna be the determinant of the matrix Δ sub 𝑧. So then once again, we go through the same method to find the determinant of our three-by-three matrix. And what it gives us is a value of eight.
So now what we have are all the determinants we need to use Cramer’s rule to find out our variables 𝑥, 𝑦, and 𝑧. So, first of all, we’re gonna start with 𝑥, which is gonna be equal to negative 42 over two. And we get that because it’s the determinant of Δ sub 𝑥 over the determinant of Δ. So this is gonna give us a value of 𝑥 equals negative 21. And then for 𝑦, we’re gonna have 112 over two which is gonna give us a 𝑦-value of 56. And then finally, we’re gonna get 𝑧 is equal to eight over two, and this is gonna give us 𝑧 is equal four. So therefore, we can say the solutions to our systems of equation are 𝑥 equals negative 21, 𝑦 equals 56, and 𝑧 equals four.
Attend live sessions on Nagwa Classes to boost your learning with guidance and advice from an expert teacher!
- Interactive Sessions
- Chat & Messaging
- Realistic Exam Questions

Nagwa uses cookies to ensure you get the best experience on our website. Learn more about our Privacy Policy

Cramer’s Rule for 3×3 System
Cramer’s rule for a 3×3 system (with three variables).
In our previous lesson, we studied how to use Cramer’s Rule with two variables . Our goal here is to expand the application of Cramer’s Rule to three variables usually in terms of [latex]\large{x}[/latex], [latex]\large{y}[/latex], and [latex]\large{z}[/latex]. I will go over five (5) worked examples to help you get familiar with this concept.
To do well on this topic, you need to have an idea of how to find the determinant of a 3⨉3 matrix . So, this is what we are going to do first. Ready?
Formula to Find the Determinant of a 3⨉3 Matrix
- Given a 3⨉3 matrix
- Its determinant can be calculated using the following formula.
Let’s do a quick example of this.
Find the determinant of matrix A
Solution: Make sure that you follow the formula on how to find the determinant of a 3×3 matrix carefully, as shown above. More so, don’t rush when you perform the required arithmetic operations in every step. This is where common errors usually occur, but it can be prevented. When you do it right, your solution should be similar to the one below.
Now, it’s time to go over the procedure on how to use Cramer’s Rule in a linear system involving three variables.
Cramer’s Rules for Systems of Linear Equations with Three Variables
- Given a linear system
- Labeling each of the four matrices
coefficient matrix:
X – matrix:
Y – matrix:
Z – matrix:
- To solve for [latex]x[/latex]:
- To solve for [latex]y[/latex]:
- To solve for [latex]z[/latex]:
Things to observe from the setup above:
1) The coefficients of variables [latex]x[/latex], [latex]y[/latex], and [latex]z[/latex] make use of subscripted [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex], respectively. While the constant terms use subscripted [latex]d[/latex].
2) The denominators to find the values of [latex]x[/latex], [latex]y[/latex], and [latex]z[/latex] are all the same which is the determinant of the coefficient matrix (coefficients coming from the columns of [latex]x[/latex], [latex]y[/latex], and [latex]z[/latex]).
3) To solve for [latex]x[/latex], the coefficients of the [latex]x-[/latex]column is replaced by the constant column ( in red ) .
4) To solve for [latex]y[/latex], the coefficients of the [latex]y-[/latex]column is replaced by the constant column ( in red ).
5) In the same manner, to solve for [latex]z[/latex], the coefficients of the [latex]z-[/latex]column is replaced by the constant column ( in red ) .
Examples of How to Solve Systems of Linear Equations with Three Variables using Cramer’s Rule
Example 1 : Solve the system with three variables by Cramer’s Rule.
From the given system of linear equations, I will construct the four matrices that will be used to solve for the values of [latex]\large{\color{green}x}[/latex], [latex]\large{\color{green}y}[/latex], and [latex]\large{\color{green}z}[/latex].
Use the guide above to correctly set up these special matrices.
- coefficient matrix
- X – matrix
- Y – matrix
- Z – matrix
Next, I will solve for the determinant of each matrix. To do this, I can manually solve the determinant of each matrix on paper using the formula provided above. It can be tedious, but it’s okay since good math skills are developed by doing lots of problems.
The values of the determinants are listed below.
Determinants of each matrix:
The final answers or solutions are easily computed or calculated once all the required determinants are found.
Solved values for [latex]\large{\color{green}x}[/latex], [latex]\large{\color{green}y}[/latex], and [latex]\large{\color{green}z}[/latex].
The final answer written in point notation is [latex]\color{blue}\left( {x,y,z} \right) = \left( { – 1,1, – 2} \right)[/latex].
Example 2 : Solve the system with three variables by Cramer’s Rule.
I actually consider the coefficient matrix as the “primary” matrix because the other three matrices are derived from it. For instance, the [latex]x-[/latex]matrix is just the “primary” matrix with the [latex]x-[/latex]column replaced by the constant column (in red). You can observe that the same pattern is applied in constructing the other matrices: [latex]y[/latex] and [latex]z[/latex].
After solving the determinant of each matrix, I have them all written down.
The values for [latex]x[/latex], [latex]y[/latex] and [latex]z[/latex] are calculated as follows. Notice that [latex]x[/latex] is obtained by taking the determinant of the [latex]x-[/latex]matrix divided by the determinant of the coefficient matrix. This rule holds for the rest.
Our final answer is [latex]\color{blue}\left( {x,y,z} \right) = \left( { – \,4,2,1} \right)[/latex].
Example 3 : Solve the system with three variables by Cramer’s Rule.
This problem is much easier than the first two examples because of the presence of zero entries in the [latex]x[/latex], [latex]y[/latex], and constant columns. Do you see it? When we have zero entries in a matrix, the calculation of its determination is dramatically simplified.
In fact, as you increase the number of zeroes in a square matrix, the work done to find its determinant is greatly reduced.
Here are the matrices extracted from the system of linear equations.
Solving for their determinants, I got the following values.
This leads us to easily set up and calculate the final answers.
The final answer is [latex]\color{blue}\left( {x,y,z} \right) = \left( { – \,1,6,1} \right)[/latex].
Example 4 : Solve the system with three variables by Cramer’s Rule
Write down the four special matrices.
Evaluate each matrix to find its determinant.
These are the determinants of each matrix:
Use the Cramer’s Rule to get the following solutions.
The final answer is [latex]\color{blue}\left( {x,y,z} \right) = \left( { – \,1,2,0} \right)[/latex].
Example 5 : Solve the system with three variables by Cramer’s Rule
Let’s do one final example! I hope that at this point, you have had enough practice on how to solve systems with three variables using Cramer’s Rule.
I suggest that you solve this on paper first and then come back to compare your answer. When you are ready, scroll down to see the solution.

Construct the four special matrices.
Find the determinant of each square matrix.
Determinants of each matrix
Solve for [latex]x[/latex], [latex]y[/latex] and [latex]z[/latex] using the given formula.
Done! The final answer in point form is [latex]\color{blue}\left( {x,y,z} \right) = {\large{\left( { – \,3, – {4 \over 5},{3 \over 5}} \right)}}[/latex].
You may also be interested in these related math lessons or tutorials:
Cramer’s Rule 2×2
Determinant of a 2×2 Matrix
Determinant of a 3×3 Matrix
Solve Systems of Equations Using Determinants
By the end of this section, you will be able to:
- Use Cramer’s Rule to solve systems of equations
- Solve applications using determinants
Before you get started, take this readiness quiz.
If you missed this problem, review [link] .
In this section we will learn of another method to solve systems of linear equations called Cramer’s rule. Before we can begin to use the rule, we need to learn some new definitions and notation.
Evaluate the Determinant of a 2 × 2
If a matrix has the same number of rows and columns, we call it a square matrix . Each square matrix has a real number associated with it called its determinant . To find the determinant of the square matrix [ a b c d ] ,
we first write it as \| a b c d \| .
To get the real number value of the determinate we subtract the products of the diagonals, as shown.
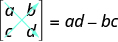
The determinant of any square matrix [ a b c d ] ,
where a, b, c, and d are real numbers, is
</div>
Evaluate the determinate of ⓐ [ 4 −2 3 −1 ]
ⓑ [ −3 −4 −2 0 ] .
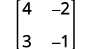
Evaluate the determinate of ⓐ [ 5 −3 2 −4 ]
ⓑ [ −4 −6 0 7 ] .
Evaluate the determinate of ⓐ [ −1 3 −2 4 ]
ⓑ [ −7 −3 −5 0 ] .
Evaluate the Determinant of a 3 × 3
To evaluate the determinant of a 3 × 3
matrix, we have to be able to evaluate the minor of an entry in the determinant. The minor of an entry is the 2 × 2
determinant found by eliminating the row and column in the 3 × 3
determinant that contains the entry.
The minor of an entry in a 3 × 3
determinant is the 2 × 2
To find the minor of entry a 1 ,
we eliminate the row and column which contain it. So we eliminate the first row and first column. Then we write the 2 × 2
determinant that remains.

we eliminate the row and column that contain it. So we eliminate the 2 nd row and 2 nd column. Then we write the 2 × 2

For the determinant \| 4 −2 3 1 0 −3 −2 −4 2 \| ,
find and then evaluate the minor of ⓐ a 1
| {: valign=”top”} | Eliminate the row and column that contains |
| {: valign=”top”} | Write the |
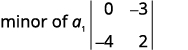
| Eliminate the row and column that contains |
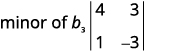
For the determinant \| 1 −1 4 0 2 −1 −2 −3 3 \| ,
ⓐ 3 ⓑ 11 ⓒ 2
For the determinant \| −2 −1 0 3 0 −1 −1 −2 3 \| ,
find and then evaluate the minor of ⓐ a 2
We are now ready to evaluate a 3 × 3
determinant. To do this we expand by minors, which allows us to evaluate the 3 × 3
determinant using 2 × 2
determinants—which we already know how to evaluate!
To evaluate a 3 × 3
determinant by expanding by minors along the first row, we use the following pattern:
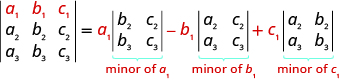
determinant by expanding by minors along the first row , the following pattern:
Evaluate the determinant \| 2 −3 −1 3 2 0 −1 −1 −2 \|
by expanding by minors along the first row.

Evaluate the determinant \| 3 −2 4 0 −1 −2 2 3 −1 \| ,
Evaluate the determinant \| 3 −2 −2 2 −1 4 −1 0 −3 \| ,
determinant we can expand by minors using any row or column. Choosing a row or column other than the first row sometimes makes the work easier.
When we expand by any row or column, we must be careful about the sign of the terms in the expansion. To determine the sign of the terms, we use the following sign pattern chart.
When expanding by minors using a row or column, the sign of the terms in the expansion follow the following pattern.
Notice that the sign pattern in the first row matches the signs between the terms in the expansion by the first row.
Evaluate the determinant \| 4 −1 −3 3 0 2 5 −4 −3 \|
by expanding by minors.
To expand by minors, we look for a row or column that will make our calculations easier. Since 0 is in the second row and second column, expanding by either of those is a good choice. Since the second row has fewer negatives than the second column, we will expand by the second row.

Evaluate the determinant \| 2 −1 −3 0 3 −4 3 −4 −3 \|
Evaluate the determinant \| −2 −1 −3 −1 2 2 4 −4 0 \|
Use Cramer’s Rule to Solve Systems of Equations
Cramer’s Rule is a method of solving systems of equations using determinants. It can be derived by solving the general form of the systems of equations by elimination. Here we will demonstrate the rule for both systems of two equations with two variables and for systems of three equations with three variables.
Let’s start with the systems of two equations with two variables.
For the system of equations { a 1 x + b 1 y = k 1 a 2 x + b 2 y = k 2 ,
the solution ( x , y )
can be determined by

Notice that to form the determinant D , we use take the coefficients of the variables.
we substitute the constants for the coefficients of the variable we are finding.
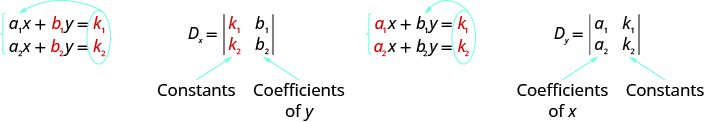
Solve using Cramer’s Rule: { 2 x + y = −4 3 x − 2 y = −6 .
Solve using Cramer’s rule: { 3 x + y = −3 2 x + 3 y = 6 .
Solve using Cramer’s rule: { − x + y = 2 2 x + y = −4 .
- Evaluate the determinant D , using the coefficients of the variables.
Use the constants in place of the x coefficients.
Use the constants in place of the y coefficients.
- Find x and y . x = D x D , y = D y D
- Write the solution as an ordered pair.
- Check that the ordered pair is a solution to both original equations.
To solve a system of three equations with three variables with Cramer’s Rule, we basically do what we did for a system of two equations. However, we now have to solve for three variables to get the solution. The determinants are also going to be 3 × 3
which will make our work more interesting!
For the system of equations { a 1 x + b 1 y + c 1 z = k 1 a 2 x + b 2 y + c 2 z = k 2 a 3 x + b 3 y + c 3 z = k 3 ,
the solution ( x , y , z )

Solve the system of equations using Cramer’s Rule: { 3 x − 5 y + 4 z = 5 5 x + 2 y + z = 0 2 x + 3 y − 2 z = 3 .
| Evaluate the determinant . | |
| Expand by minors using column 1. | |
| Evaluate the determinants. | |
| Simplify. | |
| Simplify. | |
| Simplify. | |
| Evaluate the determinant Use the . | |
| Expand by minors using column 1. | |
| Evaluate the determinants. | |
| Simplify. | |
| Simplify. | |
| Evaluate the determinant Use the . | |
| Evaluate the determinants. | |
| Simplify. | |
| Simplify. | |
| Simplify. | |
| Evaluate the determinant Use the . | |
| Evaluate the determinants. | |
| Simplify. | |
| Simplify. | |
| Simplify. | |
| Find , , and . | |
| Substitute in the values. | |
| Simplify. | |
| Write the solution as an ordered triple. | |
| Check that the ordered triple is a solution original equations. | We leave the check to you. |
| The solution is |
Solve the system of equations using Cramer’s Rule: { 3 x + 8 y + 2 z = −5 2 x + 5 y − 3 z = 0 x + 2 y − 2 z = −1 .
Solve the system of equations using Cramer’s Rule: { 3 x + y − 6 z = −3 2 x + 6 y + 3 z = 0 3 x + 2 y − 3 z = −6 .
Cramer’s rule does not work when the value of the D determinant is 0, as this would mean we would be dividing by 0. But when D = 0 ,
the system is either inconsistent or dependent.
When the value of D = 0
and D x , D y
are all zero, the system is consistent and dependent and there are infinitely many solutions.
are not all zero, the system is inconsistent and there is no solution.
For any system of equations, where the value of the determinant D = 0 ,
In the next example, we will use the values of the determinants to find the solution of the system.
Solve the system of equations using Cramer’s rule : { x + 3 y = 4 −2 x − 6 y = 3 .
We cannot use Cramer’s Rule to solve this system. But by looking at the value of the determinants D x
we can determine whether the system is dependent or inconsistent.
Since all the determinants are not zero, the system is inconsistent. There is no solution.
Solve the system of equations using Cramer’s rule: { 4 x − 3 y = 8 8 x − 6 y = 14 .
no solution
Solve the system of equations using Cramer’s rule: { x = −3 y + 4 2 x + 6 y = 8 .
infinite solutions
Solve Applications using Determinants
An interesting application of determinants allows us to test if points are collinear. Three points ( x 1 , y 1 ) ,
and ( x 3 , y 3 )
are collinear if and only if the determinant below is zero.
Three points ( x 1 , y 1 ) ,
are collinear if and only if
We will use this property in the next example.
Determine whether the points ( 5 , −5 ) ,
and ( 3 , −1 )
are collinear.
| Substitute the values into the determinant. and | |
| Evaluate the determinant by expanding | |
| Evaluate the determinants. | |
| Simplify. | |
| Simplify. | |
| The value of the determinate is 0, so the |
Determine whether the points ( 3 , −2 ) ,
and ( 1 , −1 )
Determine whether the points ( −4 , −1 ) ,
and ( −2 , −4 )
Access these online resources for additional instruction and practice with solving systems of linear inequalities by graphing.
- Solving Systems of Linear Inequalities by Graphing
- Systems of Linear Inequalities
Key Concepts
determinant by expanding by minors along the first row, the following pattern:
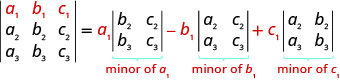
- Sign Pattern: When expanding by minors using a row or column, the sign of the terms in the expansion follow the following pattern. \| + − + − + − + − + \|
the solution

- Find x and y . x = D x D , y = D y D .
- Dependent and Inconsistent Systems of Equations: For any system of equations, where the value of the determinant D = 0 , Value of determinants Type of system Solution D = 0 and D x , D y and D z are all zero consistent and dependent infinitely many solutions D = 0 and D x , D y and D z are not all zero inconsistent no solution
Practice Makes Perfect
Evaluate the Determinant of a 2 × 2 Matrix
In the following exercises, evaluate the determinate of each square matrix.
Evaluate the Determinant of a 3 × 3 Matrix
In the following exercises, find and then evaluate the indicated minors.
Find the minor ⓐ a 1
Find the minor ⓐ a 2
Find the minor ⓐ a 3
In the following exercises, evaluate each determinant by expanding by minors along the first row.
In the following exercises, evaluate each determinant by expanding by minors.
In the following exercises, solve each system of equations using Cramer’s Rule.
infinitely many solutions
inconsistent
Solve Applications Using Determinants
In the following exercises, determine whether the given points are collinear.
and ( −2 , 2 ) .
and ( 2 , −8 ) .
and ( 2 , −2 ) .
and ( 0 , −2 ) .
Writing Exercises
Explain the difference between a square matrix and its determinant. Give an example of each.
Explain what is meant by the minor of an entry in a square matrix.
Answers will vary.
Explain how to decide which row or column you will use to expand a 3 × 3
determinant.
Explain the steps for solving a system of equations using Cramer’s rule.
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
minor of an entry in a 3 × 3
determinant is the
determinant found by eliminating the row and column in the

You can also download for free at http://cnx.org/contents/[email protected]
Attribution:
- For questions regarding this license, please contact [email protected] .
- If you use this textbook as a bibliographic reference, then you should cite it as follows: OpenStax College, Intermediate Algebra. OpenStax CNX. http://cnx.org/contents/[email protected] .
- If you redistribute this textbook in a print format, then you must include on every physical page the following attribution: "Download for free at http://cnx.org/contents/[email protected] ."
- If you redistribute part of this textbook, then you must retain in every digital format page view (including but not limited to EPUB, PDF, and HTML) and on every physical printed page the following attribution: "Download for free at http://cnx.org/contents/[email protected] ."
Systems of Equations and Inequalities
Solving systems with cramer’s rule, learning objectives.
In this section, you will:
- Evaluate 2 × 2 determinants.
- Use Cramer’s Rule to solve a system of equations in two variables.
- Evaluate 3 × 3 determinants.
- Use Cramer’s Rule to solve a system of three equations in three variables.
- Know the properties of determinants.
We have learned how to solve systems of equations in two variables and three variables, and by multiple methods: substitution, addition, Gaussian elimination, using the inverse of a matrix, and graphing. Some of these methods are easier to apply than others and are more appropriate in certain situations. In this section, we will study two more strategies for solving systems of equations.
Evaluating the Determinant of a 2×2 Matrix
A determinant is a real number that can be very useful in mathematics because it has multiple applications, such as calculating area, volume, and other quantities. Here, we will use determinants to reveal whether a matrix is invertible by using the entries of a square matrix to determine whether there is a solution to the system of equations. Perhaps one of the more interesting applications, however, is their use in cryptography. Secure signals or messages are sometimes sent encoded in a matrix. The data can only be decrypted with an invertible matrix and the determinant. For our purposes, we focus on the determinant as an indication of the invertibility of the matrix. Calculating the determinant of a matrix involves following the specific patterns that are outlined in this section.

Find the Determinant of a 2 × 2 Matrix
The determinant of a[latex]\,2\text{ }×\text{ }2\,[/latex]matrix, given
is defined as

Notice the change in notation. There are several ways to indicate the determinant, including[latex]\,\mathrm{det}\left(A\right)\,[/latex]and replacing the brackets in a matrix with straight lines,[latex]\,|A|.[/latex]
Finding the Determinant of a 2 × 2 Matrix
Find the determinant of the given matrix.
Using Cramer’s Rule to Solve a System of Two Equations in Two Variables
We will now introduce a final method for solving systems of equations that uses determinants. Known as Cramer’s Rule , this technique dates back to the middle of the 18th century and is named for its innovator, the Swiss mathematician Gabriel Cramer (1704-1752), who introduced it in 1750 in Introduction à l’Analyse des lignes Courbes algébriques. Cramer’s Rule is a viable and efficient method for finding solutions to systems with an arbitrary number of unknowns, provided that we have the same number of equations as unknowns.
Cramer’s Rule will give us the unique solution to a system of equations, if it exists. However, if the system has no solution or an infinite number of solutions, this will be indicated by a determinant of zero. To find out if the system is inconsistent or dependent, another method, such as elimination, will have to be used.
To understand Cramer’s Rule, let’s look closely at how we solve systems of linear equations using basic row operations. Consider a system of two equations in two variables.
We eliminate one variable using row operations and solve for the other. Say that we wish to solve for[latex]\,x.\,[/latex]If equation (2) is multiplied by the opposite of the coefficient of[latex]\,y\,[/latex]in equation (1), equation (1) is multiplied by the coefficient of[latex]\,y\,[/latex]in equation (2), and we add the two equations, the variable[latex]\,y\,[/latex]will be eliminated.
Now, solve for[latex]\,x.[/latex]
Similarly, to solve for[latex]\,y,[/latex]we will eliminate[latex]\,x.[/latex]
Solving for[latex]\,y\,[/latex]gives
Notice that the denominator for both[latex]\,x\,[/latex]and[latex]\,y\,[/latex]is the determinant of the coefficient matrix.
We can use these formulas to solve for[latex]\,x\,[/latex]and[latex]\,y,\,[/latex]but Cramer’s Rule also introduces new notation:
- [latex]\,\,D:[/latex]determinant of the coefficient matrix
- [latex]{D}_{x}:[/latex]determinant of the numerator in the solution of[latex]x[/latex] [latex]x=\frac{{D}_{x}}{D}[/latex]
- [latex]{D}_{y}:[/latex]determinant of the numerator in the solution of[latex]\,y[/latex] [latex]y=\frac{{D}_{y}}{D}[/latex]
The key to Cramer’s Rule is replacing the variable column of interest with the constant column and calculating the determinants. We can then express[latex]\,x\,[/latex]and[latex]\,y\,[/latex]as a quotient of two determinants.
Cramer’s Rule for 2×2 Systems
Cramer’s Rule is a method that uses determinants to solve systems of equations that have the same number of equations as variables.
Consider a system of two linear equations in two variables.
The solution using Cramer’s Rule is given as
If we are solving for[latex]\,x,\,[/latex]the[latex]\,x\,[/latex]column is replaced with the constant column. If we are solving for[latex]\,y,\,[/latex]the[latex]\,y\,[/latex]column is replaced with the constant column.
Using Cramer’s Rule to Solve a 2 × 2 System
Solve the following[latex]\,2\text{ }×\text{ }2\,[/latex]system using Cramer’s Rule.
Solve for[latex]\,x.[/latex]
Solve for[latex]\,y.[/latex]
Use Cramer’s Rule to solve the 2 × 2 system of equations.
[latex]\left(3,-7\right)[/latex]
Evaluating the Determinant of a 3 × 3 Matrix
Finding the determinant of a 2×2 matrix is straightforward, but finding the determinant of a 3×3 matrix is more complicated. One method is to augment the 3×3 matrix with a repetition of the first two columns, giving a 3×5 matrix. Then we calculate the sum of the products of entries down each of the three diagonals (upper left to lower right), and subtract the products of entries up each of the three diagonals (lower left to upper right). This is more easily understood with a visual and an example.
Find the determinant of the 3×3 matrix.
- Augment[latex]\,A\,[/latex]with the first two columns. [latex]\mathrm{det}\left(A\right)=|\begin{array}{ccc}{a}_{1}& {b}_{1}& {c}_{1}\\ {a}_{2}& {b}_{2}& {c}_{2}\\ {a}_{3}& {b}_{3}& {c}_{3}\end{array}\,\,\,|\,\,\,\begin{array}{c}{a}_{1}\\ {a}_{2}\\ {a}_{3}\end{array}\,\,\,\,\begin{array}{c}{b}_{1}\\ {b}_{2}\\ {b}_{3}\end{array}|[/latex]
- From upper left to lower right: Multiply the entries down the first diagonal. Add the result to the product of entries down the second diagonal. Add this result to the product of the entries down the third diagonal.
- From lower left to upper right: Subtract the product of entries up the first diagonal. From this result subtract the product of entries up the second diagonal. From this result, subtract the product of entries up the third diagonal.

The algebra is as follows:
Finding the Determinant of a 3 × 3 Matrix
Find the determinant of the 3 × 3 matrix given
Augment the matrix with the first two columns and then follow the formula. Thus,
Find the determinant of the 3 × 3 matrix.
[latex]-10[/latex]
Can we use the same method to find the determinant of a larger matrix?
No, this method only works for[latex]\,2\text{ }×\text{ }2\,[/latex]and[latex]\,\text{3}\text{ }×\text{ }3\,[/latex]matrices. For larger matrices it is best to use a graphing utility or computer software.
Using Cramer’s Rule to Solve a System of Three Equations in Three Variables
Now that we can find the determinant of a 3 × 3 matrix, we can apply Cramer’s Rule to solve a system of three equations in three variables . Cramer’s Rule is straightforward, following a pattern consistent with Cramer’s Rule for 2 × 2 matrices. As the order of the matrix increases to 3 × 3, however, there are many more calculations required.
When we calculate the determinant to be zero, Cramer’s Rule gives no indication as to whether the system has no solution or an infinite number of solutions. To find out, we have to perform elimination on the system.
Consider a 3 × 3 system of equations.

If we are writing the determinant[latex]\,{D}_{x},[/latex]we replace the[latex]\,x\,[/latex]column with the constant column. If we are writing the determinant[latex]{D}_{y},[/latex]we replace the[latex]\,y\,[/latex]column with the constant column. If we are writing the determinant[latex]\,{D}_{z},[/latex]we replace the[latex]\,z\,[/latex]column with the constant column. Always check the answer.
Solving a 3 × 3 System Using Cramer’s Rule
Find the solution to the given 3 × 3 system using Cramer’s Rule.
Use Cramer’s Rule.
Use Cramer’s Rule to solve the 3 × 3 matrix.
[latex]\left(-2,\frac{3}{5},\frac{12}{5}\right)[/latex]
Using Cramer’s Rule to Solve an Inconsistent System
Solve the system of equations using Cramer’s Rule.
We begin by finding the determinants[latex]\,D,{D}_{x},\text{and }{D}_{y}.[/latex]
We know that a determinant of zero means that either the system has no solution or it has an infinite number of solutions. To see which one, we use the process of elimination. Our goal is to eliminate one of the variables.
- Multiply equation (1) by[latex]\,-2.[/latex]
- Add the result to equation[latex]\,\left(2\right).[/latex]
We obtain the equation[latex]\,0=-8,\,[/latex]which is false. Therefore, the system has no solution. Graphing the system reveals two parallel lines. See (Figure) .

Use Cramer’s Rule to Solve a Dependent System
Solve the system with an infinite number of solutions.
Let’s find the determinant first. Set up a matrix augmented by the first two columns.
As the determinant equals zero, there is either no solution or an infinite number of solutions. We have to perform elimination to find out.
- Multiply equation (1) by[latex]\,-2\,[/latex]and add the result to equation (3): [latex]\frac{\begin{array}{r}\hfill -2x+4y-6x=0\\ \hfill 2x-4y+6z=0\end{array}}{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0=0}[/latex]

Understanding Properties of Determinants
There are many properties of determinants . Listed here are some properties that may be helpful in calculating the determinant of a matrix.
Properties of Determinants
- If the matrix is in upper triangular form, the determinant equals the product of entries down the main diagonal.
- When two rows are interchanged, the determinant changes sign.
- If either two rows or two columns are identical, the determinant equals zero.
- If a matrix contains either a row of zeros or a column of zeros, the determinant equals zero.
- The determinant of an inverse matrix[latex]\,{A}^{-1}\,[/latex]is the reciprocal of the determinant of the matrix[latex]\,A.[/latex]
- If any row or column is multiplied by a constant, the determinant is multiplied by the same factor.
Illustrating Properties of Determinants
Illustrate each of the properties of determinants.
Property 1 states that if the matrix is in upper triangular form, the determinant is the product of the entries down the main diagonal.
Augment[latex]\,A\,[/latex]with the first two columns.
Property 2 states that interchanging rows changes the sign. Given
Property 3 states that if two rows or two columns are identical, the determinant equals zero.
Property 4 states that if a row or column equals zero, the determinant equals zero. Thus,
Property 5 states that the determinant of an inverse matrix[latex]\,{A}^{-1}\,[/latex]is the reciprocal of the determinant[latex]\,A.\,[/latex]Thus,
Property 6 states that if any row or column of a matrix is multiplied by a constant, the determinant is multiplied by the same factor. Thus,
Using Cramer’s Rule and Determinant Properties to Solve a System
Find the solution to the given 3 × 3 system.
Using Cramer’s Rule , we have
Notice that the second and third columns are identical. According to Property 3, the determinant will be zero, so there is either no solution or an infinite number of solutions. We have to perform elimination to find out.
- Multiply equation (3) by –2 and add the result to equation (1). [latex]\frac{\begin{array}{l}-2x-4y-4x=-8\hfill \\ \text{ }2x+4y+4z=2\,\,\,\,\,\hfill \end{array}}{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0=-6}[/latex]
Access these online resources for additional instruction and practice with Cramer’s Rule.
- Solve a System of Two Equations Using Cramer’s Rule
- Solve a Systems of Three Equations using Cramer’s Rule
Key Concepts
- The determinant for[latex]\,\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\,[/latex]is[latex]\,ad-bc.\,[/latex]See (Figure) .
- Cramer’s Rule replaces a variable column with the constant column. Solutions are[latex]\,x=\frac{{D}_{x}}{D},y=\frac{{D}_{y}}{D}.\,[/latex]See (Figure) .
- To find the determinant of a 3×3 matrix, augment with the first two columns. Add the three diagonal entries (upper left to lower right) and subtract the three diagonal entries (lower left to upper right). See (Figure) .
- To solve a system of three equations in three variables using Cramer’s Rule, replace a variable column with the constant column for each desired solution:[latex]\,x=\frac{{D}_{x}}{D},y=\frac{{D}_{y}}{D},z=\frac{{D}_{z}}{D}.\,[/latex]See (Figure) .
- Cramer’s Rule is also useful for finding the solution of a system of equations with no solution or infinite solutions. See (Figure) and (Figure) .
- If any row or column is multiplied by a constant, the determinant is multiplied by the same factor. See (Figure) and (Figure) .
Section Exercises
Explain why we can always evaluate the determinant of a square matrix.
A determinant is the sum and products of the entries in the matrix, so you can always evaluate that product—even if it does end up being 0.
Examining Cramer’s Rule, explain why there is no unique solution to the system when the determinant of your matrix is 0. For simplicity, use a[latex]\,2\,×\,2\,[/latex]matrix.
Explain what it means in terms of an inverse for a matrix to have a 0 determinant.
The inverse does not exist.
The determinant of[latex]\,2\,×\,2\,[/latex]matrix[latex]\,A\,[/latex]is 3. If you switch the rows and multiply the first row by 6 and the second row by 2, explain how to find the determinant and provide the answer.
For the following exercises, find the determinant.
[latex]|\begin{array}{cc}1& 2\\ 3& 4\end{array}|[/latex]
[latex]-2[/latex]
[latex]|\begin{array}{rr}\hfill -1& \hfill 2\\ \hfill 3& \hfill -4\end{array}|[/latex]
[latex]|\begin{array}{rr}\hfill 2& \hfill -5\\ \hfill -1& \hfill 6\end{array}|[/latex]
[latex]7[/latex]
[latex]|\begin{array}{cc}-8& 4\\ -1& 5\end{array}|[/latex]
[latex]|\begin{array}{rr}\hfill 1& \hfill 0\\ \hfill 3& \hfill -4\end{array}|[/latex]
[latex]-4[/latex]
[latex]|\begin{array}{rr}\hfill 10& \hfill 20\\ \hfill 0& \hfill -10\end{array}|[/latex]
[latex]|\begin{array}{cc}10& 0.2\\ 5& 0.1\end{array}|[/latex]
[latex]0[/latex]
[latex]|\begin{array}{rr}\hfill 6& \hfill -3\\ \hfill 8& \hfill 4\end{array}|[/latex]
[latex]|\begin{array}{rr}\hfill -2& \hfill -3\\ \hfill 3.1& \hfill 4,000\end{array}|[/latex]
[latex]-7,990.7[/latex]
[latex]|\begin{array}{rrr}\hfill -1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 1& \hfill 0\\ \hfill 0& \hfill 0& \hfill -3\end{array}|[/latex]
[latex]3[/latex]
[latex]|\begin{array}{rrr}\hfill -1& \hfill 4& \hfill 0\\ \hfill 0& \hfill 2& \hfill 3\\ \hfill 0& \hfill 0& \hfill -3\end{array}|[/latex]
[latex]|\begin{array}{ccc}1& 0& 1\\ 0& 1& 0\\ 1& 0& 0\end{array}|[/latex]
[latex]-1[/latex]
[latex]|\begin{array}{rrr}\hfill 2& \hfill -3& \hfill 1\\ \hfill 3& \hfill -4& \hfill 1\\ \hfill -5& \hfill 6& \hfill 1\end{array}|[/latex]
[latex]|\begin{array}{rrr}\hfill -2& \hfill 1& \hfill 4\\ \hfill -4& \hfill 2& \hfill -8\\ \hfill 2& \hfill -8& \hfill -3\end{array}|[/latex]
[latex]224[/latex]
[latex]|\begin{array}{rrr}\hfill 6& \hfill -1& \hfill 2\\ \hfill -4& \hfill -3& \hfill 5\\ \hfill 1& \hfill 9& \hfill -1\end{array}|[/latex]
[latex]|\begin{array}{rrr}\hfill 5& \hfill 1& \hfill -1\\ \hfill 2& \hfill 3& \hfill 1\\ \hfill 3& \hfill -6& \hfill -3\end{array}|[/latex]
[latex]15[/latex]
[latex]|\begin{array}{rrr}\hfill 1.1& \hfill 2& \hfill -1\\ \hfill -4& \hfill 0& \hfill 0\\ \hfill 4.1& \hfill -0.4& \hfill 2.5\end{array}|[/latex]
[latex]|\begin{array}{rrr}\hfill 2& \hfill -1.6& \hfill 3.1\\ \hfill 1.1& \hfill 3& \hfill -8\\ \hfill -9.3& \hfill 0& \hfill 2\end{array}|[/latex]
[latex]-17.03[/latex]
[latex]|\begin{array}{ccc}-\frac{1}{2}& \frac{1}{3}& \frac{1}{4}\\ \frac{1}{5}& -\frac{1}{6}& \frac{1}{7}\\ 0& 0& \frac{1}{8}\end{array}|[/latex]
For the following exercises, solve the system of linear equations using Cramer’s Rule.
[latex]\begin{array}{l}2x-3y=-1\\ 4x+5y=9\end{array}[/latex]
[latex]\left(1,1\right)[/latex]
[latex]\begin{array}{r}5x-4y=2\\ -4x+7y=6\end{array}[/latex]
[latex]\begin{array}{l}\text{ }6x-3y=2\,\,\,\,\,\hfill \\ -8x+9y=-1\hfill \end{array}[/latex]
[latex]\left(\frac{1}{2},\frac{1}{3}\right)[/latex]
[latex]\begin{array}{l}2x+6y=12\\ 5x-2y=13\end{array}[/latex]
[latex]\begin{array}{l}4x+3y=23\,\,\hfill \\ \text{ }2x-y=-1\hfill \end{array}[/latex]
[latex]\left(2,5\right)[/latex]
[latex]\begin{array}{l}10x-6y=2\,\,\,\,\hfill \\ -5x+8y=-1\hfill \end{array}[/latex]
[latex]\begin{array}{l}4x-3y=-3\\ 2x+6y=-4\end{array}[/latex]
[latex]\left(-1,-\frac{1}{3}\right)[/latex]
[latex]\begin{array}{r}4x-5y=7\\ -3x+9y=0\end{array}[/latex]
[latex]\begin{array}{l}4x+10y=180\,\,\,\,\hfill \\ -3x-5y=-105\hfill \end{array}[/latex]
[latex]\left(15,12\right)[/latex]
[latex]\begin{array}{l}\text{ }8x-2y=-3\hfill \\ -4x+6y=4\,\,\,\,\hfill \end{array}[/latex]
[latex]\left(1,3,2\right)[/latex]
[latex]\begin{array}{l}-5x+2y-4z=-47\hfill \\ \text{ }4x-3y-z=-94\hfill \\ \text{ }3x-3y+2z=94\,\,\,\,\hfill \end{array}[/latex]
[latex]\begin{array}{l}\text{ }4x+5y-z=-7\hfill \\ -2x-9y+2z=8\,\,\,\,\hfill \\ \text{ }5y+7z=21\,\hfill \end{array}[/latex]
[latex]\left(-1,0,3\right)[/latex]
[latex]\begin{array}{r}4x-3y+4z=10\\ 5x-2z=-2\\ 3x+2y-5z=-9\end{array}[/latex]
[latex]\begin{array}{l}4x-2y+3z=6\,\,\,\hfill \\ \text{ }-6x+y=-2\hfill \\ 2x+7y+8z=24\hfill \end{array}[/latex]
[latex]\left(\frac{1}{2},1,2\right)[/latex]
[latex]\begin{array}{r}\hfill 5x+2y-z=1\,\,\,\,\,\\ \hfill -7x-8y+3z=1.5\\ \hfill 6x-12y+z=7\,\,\,\,\end{array}[/latex]
[latex]\begin{array}{l}\text{ }13x-17y+16z=73\,\,\,\,\hfill \\ -11x+15y+17z=61\,\,\,\,\hfill \\ \text{ }46x+10y-30z=-18\hfill \end{array}[/latex]
[latex]\begin{array}{l}\begin{array}{l}\hfill \\ -4x-3y-8z=-7\hfill \end{array}\hfill \\ \text{ }2x-9y+5z=0.5\hfill \\ \text{ }5x-6y-5z=-2\hfill \end{array}[/latex]
[latex]\begin{array}{l}\text{ }4x-6y+8z=10\,\,\hfill \\ -2x+3y-4z=-5\hfill \\ \text{ }x+y+z=1\,\,\,\,\,\hfill \end{array}[/latex]
Infinite solutions
[latex]\begin{array}{r}\hfill 4x-6y+8z=10\,\,\,\,\,\\ \hfill -2x+3y-4z=-5\,\,\,\\ \hfill 12x+18y-24z=-30\end{array}[/latex]
For the following exercises, use the determinant function on a graphing utility.
[latex]24[/latex]
[latex]|\begin{array}{rrrr}\hfill 1& \hfill 0& \hfill 2& \hfill 1\\ \hfill 0& \hfill -9& \hfill 1& \hfill 3\\ \hfill 3& \hfill 0& \hfill -2& \hfill -1\\ \hfill 0& \hfill 1& \hfill 1& \hfill -2\end{array}|[/latex]
[latex]|\begin{array}{rrrr}\hfill \frac{1}{2}& \hfill 1& \hfill 7& \hfill 4\\ \hfill 0& \hfill \frac{1}{2}& \hfill 100& \hfill 5\\ \hfill 0& \hfill 0& \hfill 2& \hfill 2,000\\ \hfill 0& \hfill 0& \hfill 0& \hfill 2\end{array}|[/latex]
[latex]1[/latex]
[latex]|\begin{array}{rrrr}\hfill 1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 2& \hfill 3& \hfill 0& \hfill 0\\ \hfill 4& \hfill 5& \hfill 6& \hfill 0\\ \hfill 7& \hfill 8& \hfill 9& \hfill 0\end{array}|[/latex]
Real-World Applications
For the following exercises, create a system of linear equations to describe the behavior. Then, calculate the determinant. Will there be a unique solution? If so, find the unique solution.
Two numbers add up to 56. One number is 20 less than the other.
Yes; 18, 38
Two numbers add up to 104. If you add two times the first number plus two times the second number, your total is 208
Three numbers add up to 106. The first number is 3 less than the second number. The third number is 4 more than the first number.
Yes; 33, 36, 37
Three numbers add to 216. The sum of the first two numbers is 112. The third number is 8 less than the first two numbers combined.
For the following exercises, create a system of linear equations to describe the behavior. Then, solve the system for all solutions using Cramer’s Rule.
You invest $10,000 into two accounts, which receive 8% interest and 5% interest. At the end of a year, you had $10,710 in your combined accounts. How much was invested in each account?
$7,000 in first account, $3,000 in second account.
You invest $80,000 into two accounts, $22,000 in one account, and $58,000 in the other account. At the end of one year, assuming simple interest, you have earned $2,470 in interest. The second account receives half a percent less than twice the interest on the first account. What are the interest rates for your accounts?
A movie theater needs to know how many adult tickets and children tickets were sold out of the 1,200 total tickets. If children’s tickets are $5.95, adult tickets are $11.15, and the total amount of revenue was $12,756, how many children’s tickets and adult tickets were sold?
120 children, 1,080 adult
A concert venue sells single tickets for $40 each and couple’s tickets for $65. If the total revenue was $18,090 and the 321 tickets were sold, how many single tickets and how many couple’s tickets were sold?
You decide to paint your kitchen green. You create the color of paint by mixing yellow and blue paints. You cannot remember how many gallons of each color went into your mix, but you know there were 10 gal total. Additionally, you kept your receipt, and know the total amount spent was $29.50. If each gallon of yellow costs $2.59, and each gallon of blue costs $3.19, how many gallons of each color go into your green mix?
4 gal yellow, 6 gal blue
You sold two types of scarves at a farmers’ market and would like to know which one was more popular. The total number of scarves sold was 56, the yellow scarf cost $10, and the purple scarf cost $11. If you had total revenue of $583, how many yellow scarves and how many purple scarves were sold?
Your garden produced two types of tomatoes, one green and one red. The red weigh 10 oz, and the green weigh 4 oz. You have 30 tomatoes, and a total weight of 13 lb, 14 oz. How many of each type of tomato do you have?
13 green tomatoes, 17 red tomatoes
At a market, the three most popular vegetables make up 53% of vegetable sales. Corn has 4% higher sales than broccoli, which has 5% more sales than onions. What percentage does each vegetable have in the market share?
At the same market, the three most popular fruits make up 37% of the total fruit sold. Strawberries sell twice as much as oranges, and kiwis sell one more percentage point than oranges. For each fruit, find the percentage of total fruit sold.
Strawberries 18%, oranges 9%, kiwi 10%
Three bands performed at a concert venue. The first band charged $15 per ticket, the second band charged $45 per ticket, and the final band charged $22 per ticket. There were 510 tickets sold, for a total of $12,700. If the first band had 40 more audience members than the second band, how many tickets were sold for each band?
A movie theatre sold tickets to three movies. The tickets to the first movie were $5, the tickets to the second movie were $11, and the third movie was $12. 100 tickets were sold to the first movie. The total number of tickets sold was 642, for a total revenue of $6,774. How many tickets for each movie were sold?
100 for movie 1, 230 for movie 2, 312 for movie 3
Men aged 20–29, 30–39, and 40–49 made up 78% of the population at a prison last year. This year, the same age groups made up 82.08% of the population. The 20–29 age group increased by 20%, the 30–39 age group increased by 2%, and the 40–49 age group decreased to[latex]\,\frac{3}{4}\,[/latex]of their previous population. Originally, the 30–39 age group had 2% more prisoners than the 20–29 age group. Determine the prison population percentage for each age group last year.
At a women’s prison down the road, the total number of inmates aged 20–49 totaled 5,525. This year, the 20–29 age group increased by 10%, the 30–39 age group decreased by 20%, and the 40–49 age group doubled. There are now 6,040 prisoners. Originally, there were 500 more in the 30–39 age group than the 20–29 age group. Determine the prison population for each age group last year.
20–29: 2,100, 30–39: 2,600, 40–49: 825
For the following exercises, use this scenario: A health-conscious company decides to make a trail mix out of almonds, dried cranberries, and chocolate-covered cashews. The nutritional information for these items is shown in (Figure) .
| Fat (g) | Protein (g) | Carbohydrates (g) | |
|---|---|---|---|
| 6 | 2 | 3 | |
| 0.02 | 0 | 8 | |
| 7 | 3.5 | 5.5 |
For the special “low-carb”trail mix, there are 1,000 pieces of mix. The total number of carbohydrates is 425 g, and the total amount of fat is 570.2 g. If there are 200 more pieces of cashews than cranberries, how many of each item is in the trail mix?
For the “hiking” mix, there are 1,000 pieces in the mix, containing 390.8 g of fat, and 165 g of protein. If there is the same amount of almonds as cashews, how many of each item is in the trail mix?
300 almonds, 400 cranberries, 300 cashews
For the “energy-booster” mix, there are 1,000 pieces in the mix, containing 145 g of protein and 625 g of carbohydrates. If the number of almonds and cashews summed together is equivalent to the amount of cranberries, how many of each item is in the trail mix?
Review Exercises
Systems of linear equations: two variables.
For the following exercises, determine whether the ordered pair is a solution to the system of equations.
[latex]\begin{array}{l}3x-y=4\\ x+4y=-3\,\end{array}[/latex]and[latex]\,\left(-1,1\right)[/latex]
[latex]\begin{array}{l}6x-2y=24\\ -3x+3y=18\,\end{array}[/latex]and[latex]\,\left(9,15\right)[/latex]
For the following exercises, use substitution to solve the system of equations.
[latex]\begin{array}{l}10x+5y=-5\hfill \\ \,\,\,3x-2y=-12\hfill \end{array}[/latex]
[latex]\left(-2,3\right)[/latex]
[latex]\begin{array}{l}\frac{4}{7}x+\frac{1}{5}y=\frac{43}{70}\\ \frac{5}{6}x-\frac{1}{3}y=-\frac{2}{3}\end{array}[/latex]
[latex]\begin{array}{l}5x+6y=14\\ 4x+8y=8\end{array}[/latex]
[latex]\left(4,-1\right)[/latex]
For the following exercises, use addition to solve the system of equations.
[latex]\begin{array}{l}3x+2y=-7\\ 2x+4y=6\end{array}[/latex]
[latex]\begin{array}{r}3x+4y=2\\ 9x+12y=3\end{array}[/latex]
No solutions exist.
[latex]\begin{array}{l}8x+4y=2\\ 6x-5y=0.7\end{array}[/latex]
For the following exercises, write a system of equations to solve each problem. Solve the system of equations.
A factory has a cost of production[latex]\,C\left(x\right)=150x+15\text{,}000\,[/latex]and a revenue function[latex]\,R\left(x\right)=200x.\,[/latex]What is the break-even point?
[latex]\left(300,60,000\right)[/latex]
A performer charges[latex]\,C\left(x\right)=50x+10\text{,}000,\,[/latex]where[latex]\,x\,[/latex]is the total number of attendees at a show. The venue charges $75 per ticket. After how many people buy tickets does the venue break even, and what is the value of the total tickets sold at that point?
[latex]\left(400,30,000\right)[/latex]
Systems of Linear Equations: Three Variables
For the following exercises, solve the system of three equations using substitution or addition.
[latex]\begin{array}{l}\text{ }0.5x-0.5y=10\hfill \\ \text{ }-0.2y+0.2x=4\hfill \\ \text{ }0.1x+0.1z=2\hfill \end{array}[/latex]
[latex]\left(10,-10,10\right)[/latex]
[latex]\begin{array}{r}\hfill 5x+3y-z=5\,\,\,\\ \hfill 3x-2y+4z=13\\ \hfill 4x+3y+5z=22\end{array}[/latex]
[latex]\begin{array}{r}x+y+z=1\\ 2x+2y+2z=1\\ 3x+3y=2\end{array}[/latex]
[latex]\begin{array}{l}\text{ }2x-3y+z=-1\hfill \\ \text{ }x+y+z=-4\hfill \\ \text{ }4x+2y-3z=33\hfill \end{array}[/latex]
[latex]\begin{array}{l}\,\,3x+2y-z=-10\hfill \\ \,\,\,\,x-y+2z=7\hfill \\ -x+3y+z=-2\hfill \end{array}[/latex]
[latex]\left(-1,-2,3\right)[/latex]
[latex]\begin{array}{r}\hfill 3x+4z=-11\\ \hfill x-2y=5\,\,\,\,\,\,\,\\ \hfill 4y-z=-10\end{array}[/latex]
[latex]\begin{array}{r}2x-3y+z=0\\ 2x+4y-3z=0\\ 6x-2y-z=0\end{array}[/latex]
[latex]\left(x,\frac{8x}{5},\frac{14x}{5}\right)[/latex]
[latex]\begin{array}{r}6x-4y-2z=2\\ 3x+2y-5z=4\\ 6y-7z=5\end{array}[/latex]
Three odd numbers sum up to 61. The smaller is one-third the larger and the middle number is 16 less than the larger. What are the three numbers?
A local theatre sells out for their show. They sell all 500 tickets for a total purse of $8,070.00. The tickets were priced at $15 for students, $12 for children, and $18 for adults. If the band sold three times as many adult tickets as children’s tickets, how many of each type was sold?
Systems of Nonlinear Equations and Inequalities: Two Variables
For the following exercises, solve the system of nonlinear equations.
[latex]\begin{array}{l}\begin{array}{l}\\ y={x}^{2}-7\end{array}\hfill \\ y=5x-13\hfill \end{array}[/latex]
[latex]\left(2,-3\right),\left(3,2\right)[/latex]
[latex]\begin{array}{l}\begin{array}{l}\\ y={x}^{2}-4\end{array}\hfill \\ y=5x+10\hfill \end{array}[/latex]
[latex]\begin{array}{l}{x}^{2}+{y}^{2}=16\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,y=x-8\hfill \end{array}[/latex]
No solution
[latex]\begin{array}{l}{x}^{2}+{y}^{2}=25\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,y={x}^{2}+5\hfill \end{array}[/latex]
[latex]\begin{array}{r}{x}^{2}+{y}^{2}=4\\ y-{x}^{2}=3\end{array}[/latex]
For the following exercises, graph the inequality.
[latex]y>{x}^{2}-1[/latex]
[latex]\frac{1}{4}{x}^{2}+{y}^{2}<4[/latex]

For the following exercises, graph the system of inequalities.
[latex]\begin{array}{l}{x}^{2}+{y}^{2}+2x<3\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,y>-{x}^{2}-3\hfill \end{array}[/latex]
[latex]\begin{array}{l}{x}^{2}-2x+{y}^{2}-4x<4\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,y<-x+4\hfill \end{array}[/latex]

[latex]\begin{array}{l}{x}^{2}+{y}^{2}<1\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,{y}^{2}<x\hfill \end{array}[/latex]
Partial Fractions
For the following exercises, decompose into partial fractions.
[latex]\frac{-2x+6}{{x}^{2}+3x+2}[/latex]
[latex]\frac{2}{x+2},\frac{-4}{x+1}[/latex]
[latex]\frac{10x+2}{4{x}^{2}+4x+1}[/latex]
[latex]\frac{7x+20}{{x}^{2}+10x+25}[/latex]
[latex]\frac{7}{x+5},\frac{-15}{{\left(x+5\right)}^{2}}[/latex]
[latex]\frac{x-18}{{x}^{2}-12x+36}[/latex]
[latex]\frac{-{x}^{2}+36x+70}{{x}^{3}-125}[/latex]
[latex]\frac{3}{x-5},\frac{-4x+1}{{x}^{2}+5x+25}[/latex]
[latex]\frac{-5{x}^{2}+6x-2}{{x}^{3}+27}[/latex]
[latex]\frac{{x}^{3}-4{x}^{2}+3x+11}{{\left({x}^{2}-2\right)}^{2}}[/latex]
[latex]\frac{x-4}{\left({x}^{2}-2\right)},\frac{5x+3}{{\left({x}^{2}-2\right)}^{2}}[/latex]
[latex]\frac{4{x}^{4}-2{x}^{3}+22{x}^{2}-6x+48}{x{\left({x}^{2}+4\right)}^{2}}[/latex]
Matrices and Matrix Operations
For the following exercises, perform the requested operations on the given matrices.
[latex]-4A[/latex]
[latex]\left[\begin{array}{cc}-16& 8\\ -4& -12\end{array}\right][/latex]
[latex]10D-6E[/latex]
[latex]B+C[/latex]
undefined; dimensions do not match
[latex]AB[/latex]
[latex]BA[/latex]
undefined; inner dimensions do not match
[latex]BC[/latex]
[latex]CB[/latex]
[latex]\left[\begin{array}{ccc}113& 28& 10\\ 44& 81& -41\\ 84& 98& -42\end{array}\right][/latex]
[latex]DE[/latex]
[latex]ED[/latex]
[latex]\left[\begin{array}{ccc}-127& -74& 176\\ -2& 11& 40\\ 28& 77& 38\end{array}\right][/latex]
[latex]EC[/latex]
[latex]CE[/latex]
[latex]{A}^{3}[/latex]
Solving Systems with Gaussian Elimination
For the following exercises, write the system of linear equations from the augmented matrix. Indicate whether there will be a unique solution.
[latex]\left[\begin{array}{rrr}\hfill 1& \hfill 0& \hfill -3\\ \hfill 0& \hfill 1& \hfill 2\\ \hfill 0& \hfill 0& \hfill 0\end{array}\text{ }|\text{ }\begin{array}{r}\hfill 7\\ \hfill -5\\ \hfill 0\end{array}\right][/latex]
[latex]\begin{array}{l}x-3z=7\\ y+2z=-5\,\end{array}[/latex]with infinite solutions
[latex]\left[\begin{array}{rrr}\hfill 1& \hfill 0& \hfill 5\\ \hfill 0& \hfill 1& \hfill -2\\ \hfill 0& \hfill 0& \hfill 0\end{array}\text{ }|\text{ }\begin{array}{r}\hfill -9\\ \hfill 4\\ \hfill 3\end{array}\right][/latex]
For the following exercises, write the augmented matrix from the system of linear equations.
[latex]\begin{array}{l}\\ \begin{array}{r}\hfill -2x+2y+z=7\\ \hfill 2x-8y+5z=0\\ \hfill 19x-10y+22z=3\end{array}\end{array}[/latex]
[latex]\left[\begin{array}{rrr}\hfill -2& \hfill 2& \hfill 1\\ \hfill 2& \hfill -8& \hfill 5\\ \hfill 19& \hfill -10& \hfill 22\end{array}\text{ }|\text{ }\begin{array}{r}\hfill 7\\ \hfill 0\\ \hfill 3\end{array}\right][/latex]
[latex]\begin{array}{l}\,\,\,\,\,4x+2y-3z=14\hfill \\ -12x+3y+z=100\hfill \\ \,\,\,\,\,9x-6y+2z=31\hfill \end{array}[/latex]
[latex]\begin{array}{r}\hfill x+3z=12\,\\ \hfill -x+4y=0\,\,\,\,\\ \hfill y+2z=-7\end{array}[/latex]
[latex]\left[\begin{array}{rrr}\hfill 1& \hfill 0& \hfill 3\\ \hfill -1& \hfill 4& \hfill 0\\ \hfill 0& \hfill 1& \hfill 2\end{array}\text{ }|\text{ }\begin{array}{r}\hfill 12\\ \hfill 0\\ \hfill -7\end{array}\right][/latex]
For the following exercises, solve the system of linear equations using Gaussian elimination.
[latex]\begin{array}{r}3x-4y=-7\\ -6x+8y=14\end{array}[/latex]
[latex]\begin{array}{r}3x-4y=1\\ -6x+8y=6\end{array}[/latex]
[latex]\begin{array}{l}\begin{array}{l}\\ -1.1x-2.3y=6.2\end{array}\hfill \\ -5.2x-4.1y=4.3\hfill \end{array}[/latex]
[latex]\begin{array}{r}\hfill 2x+3y+2z=1\,\,\,\,\,\\ \hfill -4x-6y-4z=-2\\ \hfill 10x+15y+10z=0\,\,\,\,\,\end{array}[/latex]
[latex]\begin{array}{r}\hfill -x+2y-4z=8\,\,\,\,\\ \hfill 3y+8z=-4\\ \hfill -7x+y+2z=1\,\,\,\,\end{array}[/latex]
Solving Systems with Inverses
For the following exercises, find the inverse of the matrix.
[latex]\left[\begin{array}{rr}\hfill -0.2& \hfill 1.4\\ \hfill 1.2& \hfill -0.4\end{array}\right][/latex]
[latex]\frac{1}{8}\left[\begin{array}{cc}2& 7\\ 6& 1\end{array}\right][/latex]
[latex]\left[\begin{array}{rr}\hfill \frac{1}{2}& \hfill -\frac{1}{2}\\ \hfill -\frac{1}{4}& \hfill \frac{3}{4}\end{array}\right][/latex]
[latex]\left[\begin{array}{ccc}12& 9& -6\\ -1& 3& 2\\ -4& -3& 2\end{array}\right][/latex]
No inverse exists.
[latex]\left[\begin{array}{ccc}2& 1& 3\\ 1& 2& 3\\ 3& 2& 1\end{array}\right][/latex]
For the following exercises, find the solutions by computing the inverse of the matrix.
[latex]\begin{array}{l}\,\,\,\,0.3x-0.1y=-10\hfill \\ -0.1x+0.3y=14\hfill \end{array}[/latex]
[latex]\left(-20,40\right)[/latex]
[latex]\begin{array}{l}\,\,\,\,\,\,\,\,0.4x-0.2y=-0.6\hfill \\ -0.1x+0.05y=0.3\hfill \end{array}[/latex]
[latex]\begin{array}{r}4x+3y-3z=-4.3\\ 5x-4y-z=-6.1\\ x+z=-0.7\end{array}[/latex]
[latex]\left(-1,0.2,0.3\right)[/latex]
[latex]\begin{array}{r}\hfill \begin{array}{l}\\ -2x-3y+2z=3\end{array}\\ \hfill -x+2y+4z=-5\\ \hfill -2y+5z=-3\end{array}[/latex]
Students were asked to bring their favorite fruit to class. 90% of the fruits consisted of banana, apple, and oranges. If oranges were half as popular as bananas and apples were 5% more popular than bananas, what are the percentages of each individual fruit?
17% oranges, 34% bananas, 39% apples
A sorority held a bake sale to raise money and sold brownies and chocolate chip cookies. They priced the brownies at $2 and the chocolate chip cookies at $1. They raised $250 and sold 175 items. How many brownies and how many cookies were sold?
[latex]|\begin{array}{cc}100& 0\\ 0& 0\end{array}|[/latex]
[latex]|\begin{array}{cc}0.2& -0.6\\ 0.7& -1.1\end{array}|[/latex]
[latex]|\begin{array}{ccc}-1& 4& 3\\ 0& 2& 3\\ 0& 0& -3\end{array}|[/latex]
[latex]|\begin{array}{ccc}\sqrt{2}& 0& 0\\ 0& \sqrt{2}& 0\\ 0& 0& \sqrt{2}\end{array}|[/latex]
For the following exercises, use Cramer’s Rule to solve the linear systems of equations.
[latex]\begin{array}{r}\hfill 4x-2y=23\,\,\,\,\\ \hfill -5x-10y=-35\end{array}[/latex]
[latex]\left(6,\frac{1}{2}\right)[/latex]
[latex]\begin{array}{l}0.2x-0.1y=0\\ -0.3x+0.3y=2.5\end{array}[/latex]
[latex]\begin{array}{r}\hfill -0.5x+0.1y=0.3\,\,\,\\ \hfill -0.25x+0.05y=0.15\end{array}[/latex]
( x , 5 x + 3)
[latex]\begin{array}{l}x+6y+3z=4\\ 2x+y+2z=3\\ 3x-2y+z=0\end{array}[/latex]
[latex]\begin{array}{r}\hfill 4x-3y+5z=-\frac{5}{2}\\ \hfill 7x-9y-3z=\frac{3}{2}\,\,\,\,\\ \hfill x-5y-5z=\frac{5}{2}\,\,\,\,\end{array}[/latex]
[latex]\left(0,0,-\frac{1}{2}\right)[/latex]
[latex]\begin{array}{r}\frac{3}{10}x-\frac{1}{5}y-\frac{3}{10}z=-\frac{1}{50}\\ \frac{1}{10}x-\frac{1}{10}y-\frac{1}{2}z=-\frac{9}{50}\\ \frac{2}{5}x-\frac{1}{2}y-\frac{3}{5}z=-\frac{1}{5}\end{array}[/latex]
Practice Test
Is the following ordered pair a solution to the system of equations?
[latex]\begin{array}{l}\\ \begin{array}{l}-5x-y=12\,\hfill \\ x+4y=9\hfill \end{array}\end{array}[/latex]with[latex]\,\left(-3,3\right)[/latex]
For the following exercises, solve the systems of linear and nonlinear equations using substitution or elimination. Indicate if no solution exists.
[latex]\begin{array}{r}\frac{1}{2}x-\frac{1}{3}y=4\\ \frac{3}{2}x-y=0\end{array}[/latex]
[latex]\begin{array}{r}\hfill \begin{array}{l}\\ -\frac{1}{2}x-4y=4\end{array}\\ \hfill 2x+16y=2\end{array}[/latex]
[latex]\begin{array}{r}\hfill 5x-y=1\,\,\,\,\\ \hfill -10x+2y=-2\end{array}[/latex]
[latex]\begin{array}{l}4x-6y-2z=\frac{1}{10}\hfill \\ \,\,\,x-7y+5z=-\frac{1}{4}\hfill \\ 3x+6y-9z=\frac{6}{5}\hfill \end{array}[/latex]
[latex]\frac{1}{20}\left(10,5,4\right)[/latex]
[latex]\begin{array}{r}x+z=20\\ x+y+z=20\\ x+2y+z=10\end{array}[/latex]
[latex]\begin{array}{r}5x-4y-3z=0\\ 2x+y+2z=0\\ x-6y-7z=0\end{array}[/latex]
[latex]\left(x,\frac{16x}{5}-\frac{13x}{5}\right)[/latex]
[latex]\begin{array}{l}y={x}^{2}+2x-3\\ y=x-1\end{array}[/latex]
[latex]\begin{array}{l}{y}^{2}+{x}^{2}=25\\ {y}^{2}-2{x}^{2}=1\end{array}[/latex]
[latex]\left(-2\sqrt{2},-\sqrt{17}\right),\left(-2\sqrt{2},\sqrt{17}\right),\left(2\sqrt{2},-\sqrt{17}\right),\left(2\sqrt{2},\sqrt{17}\right)[/latex]
For the following exercises, graph the following inequalities.
[latex]y<{x}^{2}+9[/latex]
[latex]\begin{array}{l}{x}^{2}+{y}^{2}>4\\ y<{x}^{2}+1\end{array}[/latex]

For the following exercises, write the partial fraction decomposition.
[latex]\frac{-8x-30}{{x}^{2}+10x+25}[/latex]
[latex]\frac{13x+2}{{\left(3x+1\right)}^{2}}[/latex]
[latex]\frac{5}{3x+1}-\frac{2x+3}{{\left(3x+1\right)}^{2}}[/latex]
[latex]\frac{{x}^{4}-{x}^{3}+2x-1}{x{\left({x}^{2}+1\right)}^{2}}[/latex]
For the following exercises, perform the given matrix operations.
[latex]5\left[\begin{array}{cc}4& 9\\ -2& 3\end{array}\right]+\frac{1}{2}\left[\begin{array}{cc}-6& 12\\ 4& -8\end{array}\right][/latex]
[latex]\left[\begin{array}{cc}17& 51\\ -8& 11\end{array}\right][/latex]
[latex]\left[\begin{array}{rrr}\hfill 1& \hfill 4& \hfill -7\\ \hfill -2& \hfill 9& \hfill 5\\ \hfill 12& \hfill 0& \hfill -4\end{array}\right]\text{ }\left[\begin{array}{cc}3& -4\\ 1& 3\\ 5& 10\end{array}\right][/latex]
[latex]{\left[\begin{array}{rr}\hfill \frac{1}{2}& \hfill \frac{1}{3}\\ \hfill \frac{1}{4}& \hfill \frac{1}{5}\end{array}\right]}^{-1}[/latex]
[latex]\left[\begin{array}{cc}12& -20\\ -15& 30\end{array}\right][/latex]
[latex]\mathrm{det}|\begin{array}{cc}0& 0\\ 400& 4\text{,}000\end{array}|[/latex]
[latex]\mathrm{det}|\begin{array}{rrr}\hfill \frac{1}{2}& \hfill -\frac{1}{2}& \hfill 0\\ \hfill -\frac{1}{2}& \hfill 0& \hfill \frac{1}{2}\\ \hfill 0& \hfill \frac{1}{2}& \hfill 0\end{array}|[/latex]
[latex]-\frac{1}{8}[/latex]
If[latex]\,\mathrm{det}\left(A\right)=-6,\,[/latex] what would be the determinant if you switched rows 1 and 3, multiplied the second row by 12, and took the inverse?
Rewrite the system of linear equations as an augmented matrix.
[latex]\left[\begin{array}{rrr}\hfill 14& \hfill -2& \hfill 13\\ \hfill -2& \hfill 3& \hfill -6\\ \hfill 1& \hfill -5& \hfill 12\end{array}\text{ }|\text{ }\begin{array}{r}\hfill 140\\ \hfill -1\\ \hfill 11\end{array}\right][/latex]
Rewrite the augmented matrix as a system of linear equations.
For the following exercises, use Gaussian elimination to solve the systems of equations.
[latex]\begin{array}{r}x-6y=4\\ 2x-12y=0\end{array}[/latex]
[latex]\begin{array}{r}\hfill 2x+y+z=-3\\ \hfill x-2y+3z=6\,\,\,\,\\ \hfill x-y-z=6\,\,\,\,\end{array}[/latex]
For the following exercises, use the inverse of a matrix to solve the systems of equations.
[latex]\begin{array}{r}\hfill 4x-5y=-50\\ \hfill -x+2y=80\,\,\,\,\end{array}[/latex]
[latex]\left(100,90\right)[/latex]
[latex]\begin{array}{r}\hfill \frac{1}{100}x-\frac{3}{100}y+\frac{1}{20}z=-49\\ \hfill \frac{3}{100}x-\frac{7}{100}y-\frac{1}{100}z=13\,\,\,\,\\ \hfill \frac{9}{100}x-\frac{9}{100}y-\frac{9}{100}z=99\,\,\,\,\end{array}[/latex]
For the following exercises, use Cramer’s Rule to solve the systems of equations.
[latex]\begin{array}{l}200x-300y=2\\ 400x+715y=4\end{array}[/latex]
[latex]\left(\frac{1}{100},0\right)[/latex]
[latex]\begin{array}{l}0.1x+0.1y-0.1z=-1.2\\ 0.1x-0.2y+0.4z=-1.2\\ 0.5x-0.3y+0.8z=-5.9\end{array}[/latex]
For the following exercises, solve using a system of linear equations.
A factory producing cell phones has the following cost and revenue functions:[latex]\,C\left(x\right)={x}^{2}+75x+2\text{,}688\,[/latex]and[latex]\,R\left(x\right)={x}^{2}+160x.\,[/latex]What is the range of cell phones they should produce each day so there is profit? Round to the nearest number that generates profit.
32 or more cell phones per day
A small fair charges $1.50 for students, $1 for children, and $2 for adults. In one day, three times as many children as adults attended. A total of 800 tickets were sold for a total revenue of $1,050. How many of each type of ticket was sold?
- Algebra and Trigonometry. Authored by : Jay Abramson, et. al. Provided by : OpenStax CNX. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]

Privacy Policy

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
Chapter 1.10: Solving Systems with Cramer’s Rule
Learning objectives.
In this section, you will:
- Evaluate 2 × 2 determinants.
- Use Cramer’s Rule to solve a system of equations in two variables.
- Evaluate 3 × 3 determinants.
- Use Cramer’s Rule to solve a system of three equations in three variables.
- Know the properties of determinants.
We have learned how to solve systems of equations in two variables and three variables, and by multiple methods: substitution, addition, Gaussian elimination, using the inverse of a matrix, and graphing. Some of these methods are easier to apply than others and are more appropriate in certain situations. In this section, we will study two more strategies for solving systems of equations.
Evaluating the Determinant of a 2×2 Matrix
A determinant is a real number that can be very useful in mathematics because it has multiple applications, such as calculating area, volume, and other quantities. Here, we will use determinants to reveal whether a matrix is invertible by using the entries of a square matrix to determine whether there is a solution to the system of equations. Perhaps one of the more interesting applications, however, is their use in cryptography. Secure signals or messages are sometimes sent encoded in a matrix. The data can only be decrypted with an invertible matrix and the determinant. For our purposes, we focus on the determinant as an indication of the invertibility of the matrix. Calculating the determinant of a matrix involves following the specific patterns that are outlined in this section.
Find the Determinant of a 2 × 2 Matrix
is defined as

Finding the Determinant of a 2 × 2 Matrix
Find the determinant of the given matrix.
Using Cramer’s Rule to Solve a System of Two Equations in Two Variables
We will now introduce a final method for solving systems of equations that uses determinants. Known as Cramer’s Rule , this technique dates back to the middle of the 18th century and is named for its innovator, the Swiss mathematician Gabriel Cramer (1704-1752), who introduced it in 1750 in Introduction à l’Analyse des lignes Courbes algébriques. Cramer’s Rule is a viable and efficient method for finding solutions to systems with an arbitrary number of unknowns, provided that we have the same number of equations as unknowns.
Cramer’s Rule will give us the unique solution to a system of equations, if it exists. However, if the system has no solution or an infinite number of solutions, this will be indicated by a determinant of zero. To find out if the system is inconsistent or dependent, another method, such as elimination, will have to be used.
To understand Cramer’s Rule, let’s look closely at how we solve systems of linear equations using basic row operations. Consider a system of two equations in two variables.
Cramer’s Rule for 2×2 Systems
Cramer’s Rule is a method that uses determinants to solve systems of equations that have the same number of equations as variables.
Consider a system of two linear equations in two variables.
The solution using Cramer’s Rule is given as
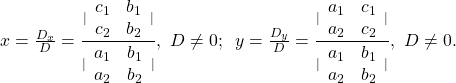
Using Cramer’s Rule to Solve a 2 × 2 System
Use Cramer’s Rule to solve the 2 × 2 system of equations.
Evaluating the Determinant of a 3 × 3 Matrix
Finding the determinant of a 2×2 matrix is straightforward, but finding the determinant of a 3×3 matrix is more complicated. One method is to augment the 3×3 matrix with a repetition of the first two columns, giving a 3×5 matrix. Then we calculate the sum of the products of entries down each of the three diagonals (upper left to lower right), and subtract the products of entries up each of the three diagonals (lower left to upper right). This is more easily understood with a visual and an example.
Find the determinant of the 3×3 matrix.
![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc}{a}_{1}& {b}_{1}& {c}_{1}\\ {a}_{2}& {b}_{2}& {c}_{2}\\ {a}_{3}& {b}_{3}& {c}_{3}\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-725f7f0d021ae716834add6a84be6bcd_l3.png)
- From upper left to lower right: Multiply the entries down the first diagonal. Add the result to the product of entries down the second diagonal. Add this result to the product of the entries down the third diagonal.
- From lower left to upper right: Subtract the product of entries up the first diagonal. From this result subtract the product of entries up the second diagonal. From this result, subtract the product of entries up the third diagonal.

The algebra is as follows:
Finding the Determinant of a 3 × 3 Matrix
Find the determinant of the 3 × 3 matrix given
![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc}0& 2& 1\\ 3& -1& 1\\ 4& 0& 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-630cb2890f5874537b6a0e743621a2ee_l3.png)
Augment the matrix with the first two columns and then follow the formula. Thus,
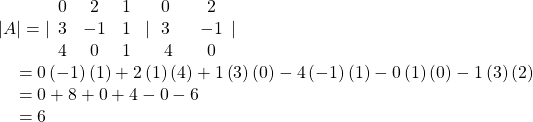
Find the determinant of the 3 × 3 matrix.
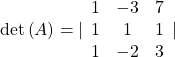
Can we use the same method to find the determinant of a larger matrix?
Using Cramer’s Rule to Solve a System of Three Equations in Three Variables
Now that we can find the determinant of a 3 × 3 matrix, we can apply Cramer’s Rule to solve a system of three equations in three variables . Cramer’s Rule is straightforward, following a pattern consistent with Cramer’s Rule for 2 × 2 matrices. As the order of the matrix increases to 3 × 3, however, there are many more calculations required.
When we calculate the determinant to be zero, Cramer’s Rule gives no indication as to whether the system has no solution or an infinite number of solutions. To find out, we have to perform elimination on the system.
Consider a 3 × 3 system of equations.

Solving a 3 × 3 System Using Cramer’s Rule
Find the solution to the given 3 × 3 system using Cramer’s Rule.
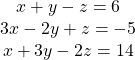
Use Cramer’s Rule.

Use Cramer’s Rule to solve the 3 × 3 matrix.
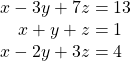
Using Cramer’s Rule to Solve an Inconsistent System
Solve the system of equations using Cramer’s Rule.
We know that a determinant of zero means that either the system has no solution or it has an infinite number of solutions. To see which one, we use the process of elimination. Our goal is to eliminate one of the variables.
Use Cramer’s Rule to Solve a Dependent System
Solve the system with an infinite number of solutions.
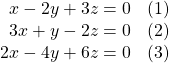
Let’s find the determinant first. Set up a matrix augmented by the first two columns.
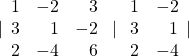
As the determinant equals zero, there is either no solution or an infinite number of solutions. We have to perform elimination to find out.
Understanding Properties of Determinants
There are many properties of determinants . Listed here are some properties that may be helpful in calculating the determinant of a matrix.
Properties of Determinants
- If the matrix is in upper triangular form, the determinant equals the product of entries down the main diagonal.
- When two rows are interchanged, the determinant changes sign.
- If either two rows or two columns are identical, the determinant equals zero.
- If a matrix contains either a row of zeros or a column of zeros, the determinant equals zero.
- If any row or column is multiplied by a constant, the determinant is multiplied by the same factor.
Illustrating Properties of Determinants
Illustrate each of the properties of determinants.
Property 1 states that if the matrix is in upper triangular form, the determinant is the product of the entries down the main diagonal.
![Rendered by QuickLaTeX.com A=\left[\begin{array}{rrr}\hfill 1& \hfill \,\,2& \hfill 3\\ \hfill 0& \hfill \,\,2& \hfill 1\\ \hfill 0& \hfill \,\,0& \hfill -1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-fb103557ac6c17c832786e57b1b3798d_l3.png)
Property 2 states that interchanging rows changes the sign. Given
![Rendered by QuickLaTeX.com \begin{array}{l}\begin{array}{l}\\ A=\left[\begin{array}{cc}-1& 5\\ 4& -3\end{array}\right],\,\,\mathrm{det}\left(A\right)=\left(-1\right)\left(-3\right)-\left(4\right)\left(5\right)=3-20=-17\end{array}\hfill \\ \hfill \\ B=\left[\begin{array}{cc}4& -3\\ -1& 5\end{array}\right],\,\,\mathrm{det}\left(B\right)=\left(4\right)\left(5\right)-\left(-1\right)\left(-3\right)=20-3=17\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-a5d094644da416ccb00d98e7ccdb2369_l3.png)
Property 3 states that if two rows or two columns are identical, the determinant equals zero.
![Rendered by QuickLaTeX.com \begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,A=\left[\begin{array}{ccc}1& 2& 2\\ 2& 2& 2\\ -1& 2& 2\end{array}\text{ }|\text{ }\begin{array}{c}1\\ 2\\ -1\end{array} \begin{array}{c}2\\ 2\\ 2\end{array}\right]\hfill \\ \hfill \\ \mathrm{det}\left(A\right)=1\left(2\right)\left(2\right)+2\left(2\right)\left(-1\right)+2\left(2\right)\left(2\right)+1\left(2\right)\left(2\right)-2\left(2\right)\left(1\right)-2\left(2\right)\left(2\right)\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=4-4+8+4-4-8=0\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-958c9ed766c2fe2e13afb8811b845c56_l3.png)
Property 4 states that if a row or column equals zero, the determinant equals zero. Thus,
Property 6 states that if any row or column of a matrix is multiplied by a constant, the determinant is multiplied by the same factor. Thus,
![Rendered by QuickLaTeX.com \begin{array}{l}A=\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right],\mathrm{det}\left(A\right)=1\left(4\right)-2\left(3\right)=-2\hfill \\ \hfill \\ B=\left[\begin{array}{cc}2\left(1\right)& 2\left(2\right)\\ 3& 4\end{array}\right],\mathrm{det}\left(B\right)=2\left(4\right)-3\left(4\right)=-4\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-3cf26f2f303b96680a7c8885242b9e3b_l3.png)
Using Cramer’s Rule and Determinant Properties to Solve a System
Find the solution to the given 3 × 3 system.

Using Cramer’s Rule , we have
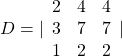
Notice that the second and third columns are identical. According to Property 3, the determinant will be zero, so there is either no solution or an infinite number of solutions. We have to perform elimination to find out.
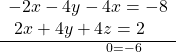
Obtaining a statement that is a contradiction means that the system has no solution.
Access these online resources for additional instruction and practice with Cramer’s Rule.
- Solve a System of Two Equations Using Cramer’s Rule
- Solve a Systems of Three Equations using Cramer’s Rule
Key Concepts
- To find the determinant of a 3×3 matrix, augment with the first two columns. Add the three diagonal entries (upper left to lower right) and subtract the three diagonal entries (lower left to upper right). See (Figure) .
- Cramer’s Rule is also useful for finding the solution of a system of equations with no solution or infinite solutions. See (Figure) and (Figure) .
- If any row or column is multiplied by a constant, the determinant is multiplied by the same factor. See (Figure) and (Figure) .
Section Exercises
1. Explain why we can always evaluate the determinant of a square matrix.
A determinant is the sum and products of the entries in the matrix, so you can always evaluate that product—even if it does end up being 0.
3. Explain what it means in terms of an inverse for a matrix to have a 0 determinant.
The inverse does not exist.
For the following exercises, find the determinant.
For the following exercises, solve the system of linear equations using Cramer’s Rule.
Infinite solutions
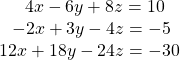
For the following exercises, use the determinant function on a graphing utility.

Real-World Applications
For the following exercises, create a system of linear equations to describe the behavior. Then, calculate the determinant. Will there be a unique solution? If so, find the unique solution.
49. Two numbers add up to 56. One number is 20 less than the other.
Yes; 18, 38
50. Two numbers add up to 104. If you add two times the first number plus two times the second number, your total is 208
51. Three numbers add up to 106. The first number is 3 less than the second number. The third number is 4 more than the first number.
Yes; 33, 36, 37
52. Three numbers add to 216. The sum of the first two numbers is 112. The third number is 8 less than the first two numbers combined.
For the following exercises, create a system of linear equations to describe the behavior. Then, solve the system for all solutions using Cramer’s Rule.
53. You invest $10,000 into two accounts, which receive 8% interest and 5% interest. At the end of a year, you had $10,710 in your combined accounts. How much was invested in each account?
$7,000 in first account, $3,000 in second account.
54. You invest $80,000 into two accounts, $22,000 in one account, and $58,000 in the other account. At the end of one year, assuming simple interest, you have earned $2,470 in interest. The second account receives half a percent less than twice the interest on the first account. What are the interest rates for your accounts?
55. A movie theater needs to know how many adult tickets and children tickets were sold out of the 1,200 total tickets. If children’s tickets are $5.95, adult tickets are $11.15, and the total amount of revenue was $12,756, how many children’s tickets and adult tickets were sold?
120 children, 1,080 adult
56. A concert venue sells single tickets for $40 each and couple’s tickets for $65. If the total revenue was $18,090 and the 321 tickets were sold, how many single tickets and how many couple’s tickets were sold?
57. You decide to paint your kitchen green. You create the color of paint by mixing yellow and blue paints. You cannot remember how many gallons of each color went into your mix, but you know there were 10 gal total. Additionally, you kept your receipt, and know the total amount spent was $29.50. If each gallon of yellow costs $2.59, and each gallon of blue costs $3.19, how many gallons of each color go into your green mix?
4 gal yellow, 6 gal blue
58. You sold two types of scarves at a farmers’ market and would like to know which one was more popular. The total number of scarves sold was 56, the yellow scarf cost $10, and the purple scarf cost $11. If you had total revenue of $583, how many yellow scarves and how many purple scarves were sold?
59. Your garden produced two types of tomatoes, one green and one red. The red weigh 10 oz, and the green weigh 4 oz. You have 30 tomatoes, and a total weight of 13 lb, 14 oz. How many of each type of tomato do you have?
13 green tomatoes, 17 red tomatoes
60. At a market, the three most popular vegetables make up 53% of vegetable sales. Corn has 4% higher sales than broccoli, which has 5% more sales than onions. What percentage does each vegetable have in the market share?
61. At the same market, the three most popular fruits make up 37% of the total fruit sold. Strawberries sell twice as much as oranges, and kiwis sell one more percentage point than oranges. For each fruit, find the percentage of total fruit sold.
Strawberries 18%, oranges 9%, kiwi 10%
62. Three bands performed at a concert venue. The first band charged $15 per ticket, the second band charged $45 per ticket, and the final band charged $22 per ticket. There were 510 tickets sold, for a total of $12,700. If the first band had 40 more audience members than the second band, how many tickets were sold for each band?
63. A movie theatre sold tickets to three movies. The tickets to the first movie were $5, the tickets to the second movie were $11, and the third movie was $12. 100 tickets were sold to the first movie. The total number of tickets sold was 642, for a total revenue of $6,774. How many tickets for each movie were sold?
100 for movie 1, 230 for movie 2, 312 for movie 3
65. At a women’s prison down the road, the total number of inmates aged 20–49 totaled 5,525. This year, the 20–29 age group increased by 10%, the 30–39 age group decreased by 20%, and the 40–49 age group doubled. There are now 6,040 prisoners. Originally, there were 500 more in the 30–39 age group than the 20–29 age group. Determine the prison population for each age group last year.
20–29: 2,100, 30–39: 2,600, 40–49: 825
For the following exercises, use this scenario: A health-conscious company decides to make a trail mix out of almonds, dried cranberries, and chocolate-covered cashews. The nutritional information for these items is shown in (Figure) .
| Fat (g) | Protein (g) | Carbohydrates (g) | |
|---|---|---|---|
| 6 | 2 | 3 | |
| 0.02 | 0 | 8 | |
| 7 | 3.5 | 5.5 |
66. For the special “low-carb”trail mix, there are 1,000 pieces of mix. The total number of carbohydrates is 425 g, and the total amount of fat is 570.2 g. If there are 200 more pieces of cashews than cranberries, how many of each item is in the trail mix?
67. For the “hiking” mix, there are 1,000 pieces in the mix, containing 390.8 g of fat, and 165 g of protein. If there is the same amount of almonds as cashews, how many of each item is in the trail mix?
300 almonds, 400 cranberries, 300 cashews
68. For the “energy-booster” mix, there are 1,000 pieces in the mix, containing 145 g of protein and 625 g of carbohydrates. If the number of almonds and cashews summed together is equivalent to the amount of cranberries, how many of each item is in the trail mix?
Differential Calculus Copyright © 2022 by Mike LePine is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book

In order to continue enjoying our site, we ask that you confirm your identity as a human. Thank you very much for your cooperation.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
40 Solve Systems of Equations Using Determinants
Learning objectives.
By the end of this section, you will be able to:
- Use Cramer’s Rule to solve systems of equations
- Solve applications using determinants
Before you get started, take this readiness quiz.
In this section we will learn of another method to solve systems of linear equations called Cramer’s rule. Before we can begin to use the rule, we need to learn some new definitions and notation.
Evaluate the Determinant of a Matrix
| Write the determinant. | |
| Subtract the products of the diagonals. | |
| Simplify. | |
| Simplify. |
| Write the determinant. | |
| Subtract the products of the diagonals. | |
| Simplify. | |
| Simplify. |
| Eliminate the row and column that contains | |
| Write the | |
| Evaluate. | |
| Simplify. |
| Eliminate the row and column that contains | |
| Write the | |
| Evaluate. | |
| Simplify. |
| Eliminate the row and column that contains | |
| Write the | |
| Evaluate. | |
| Simplify. |

ⓐ 3 ⓑ 11 ⓒ 2

Remember, to find the minor of an entry we eliminate the row and column that contains the entry.

| Expand by minors along the first row | |
| Evaluate each determinant. | |
| Simplify. | |
| Simplify. | |
| Simplify. |

When we expand by any row or column, we must be careful about the sign of the terms in the expansion. To determine the sign of the terms, we use the following sign pattern chart.

When expanding by minors using a row or column, the sign of the terms in the expansion follow the following pattern.
Notice that the sign pattern in the first row matches the signs between the terms in the expansion by the first row.

Since we can expand by any row or column, how do we decide which row or column to use? Usually we try to pick a row or column that will make our calculation easier. If the determinant contains a 0, using the row or column that contains the 0 will make the calculations easier.

To expand by minors, we look for a row or column that will make our calculations easier. Since 0 is in the second row and second column, expanding by either of those is a good choice. Since the second row has fewer negatives than the second column, we will expand by the second row.
| Expand using the second row. | |
| Be careful of the signs. | |
| Evaluate each determinant. | |
| Simplify. | |
| Simplify. | |
| Add. |

Use Cramer’s Rule to Solve Systems of Equations
Cramer’s Rule is a method of solving systems of equations using determinants. It can be derived by solving the general form of the systems of equations by elimination. Here we will demonstrate the rule for both systems of two equations with two variables and for systems of three equations with three variables.
Let’s start with the systems of two equations with two variables.
Notice that to form the determinant D , we use take the coefficients of the variables.

- Evaluate the determinant D , using the coefficients of the variables.
- Write the solution as an ordered pair.
- Check that the ordered pair is a solution to both original equations.

| Evaluate the determinant . | |
| Expand by minors using column 1. | |
| Evaluate the determinants. | |
| Simplify. | |
| Simplify. | |
| Simplify. | |
| Evaluate the determinant constants to replace the coefficients of . | |
| Expand by minors using column 1. | |
| Evaluate the determinants. | |
| Simplify. | |
| Simplify. | |
| Evaluate the determinant constants to replace the coefficients of . | |
| Evaluate the determinants. | |
| Simplify. | |
| Simplify. | |
| Simplify. | |
| Evaluate the determinant constants to replace the coefficients of . | |
| Evaluate the determinants. | |
| Simplify. | |
| Simplify. | |
| Simplify. | |
| Find , , and . | |
| Substitute in the values. | |
| Simplify. | |
| Write the solution as an ordered triple. | |
| Check that the ordered triple is a solution to original equations. | We leave the check to you. |
| The solution is |

In the next example, we will use the values of the determinants to find the solution of the system.
Since all the determinants are not zero, the system is inconsistent. There is no solution.
no solution
infinite solutions
Solve Applications using Determinants
We will use this property in the next example.
| Substitute the values into the determinant.
| |
| Evaluate the determinant by expanding by minors using column 3. | |
| Evaluate the determinants. | |
| Simplify. | |
| Simplify. | |
| The value of the determinate is 0, so the points are collinear. |
Access these online resources for additional instruction and practice with solving systems of linear inequalities by graphing.
- Solving Systems of Linear Inequalities by Graphing
- Systems of Linear Inequalities
Key Concepts

Practice Makes Perfect
Evaluate the Determinant of a 2 × 2 Matrix
In the following exercises, evaluate the determinate of each square matrix.
Evaluate the Determinant of a 3 × 3 Matrix
In the following exercises, find and then evaluate the indicated minors.

In the following exercises, evaluate each determinant by expanding by minors along the first row.

In the following exercises, evaluate each determinant by expanding by minors.

In the following exercises, solve each system of equations using Cramer’s Rule.
infinitely many solutions
inconsistent

Solve Applications Using Determinants
In the following exercises, determine whether the given points are collinear.
Writing Exercises
Explain the difference between a square matrix and its determinant. Give an example of each.
Explain what is meant by the minor of an entry in a square matrix.
Answers will vary.
Explain the steps for solving a system of equations using Cramer’s rule.
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ After reviewing this checklist, what will you do to become confident for all objectives?
Intermediate Algebra but cloned this time not imported Copyright © 2017 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.
Share This Book

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
3.5 Determinants and Cramer’s Rule
We have learned how to solve systems of equations in two variables and three variables, and by multiple methods: substitution, addition, Gaussian elimination, using the inverse of a matrix, and graphing. Some of these methods are easier to apply than others and are more appropriate in certain situations. In this section, we will study two more strategies for solving systems of equations.
Evaluating the Determinant of a 2×2 Matrix
A determinant is a real number that can be very useful in mathematics because it has multiple applications, such as calculating area, volume, and other quantities. Here, we will use determinants to reveal whether a matrix is invertible by using the entries of a square matrix to determine whether there is a solution to the system of equations. Perhaps one of the more interesting applications, however, is their use in cryptography. Secure signals or messages are sometimes sent encoded in a matrix. The data can only be decrypted with an invertible matrix and the determinant. For our purposes, we focus on the determinant as an indication of the invertibility of the matrix. Calculating the determinant of a matrix involves following the specific patterns that are outlined in this section.
is defined as:
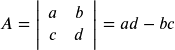
Find the determinant of the given matrix
Using Cramer’s Rule to Solve a System of Two Equations in Two Variables
We will now introduce a final method for solving systems of equations that uses determinants. Known as Cramer’s rule, this technique dates back to the middle 18th century and is named for its innovator, the Swiss mathematician Gabriel Cramer (1704-1752), who introduced it in 1750. Cramer’s Rule is a viable and efficient method for finding solutions to systems with any number of unknowns, provided that we have the same number of equations as unknowns.
To see how and why Cramer’s Rule works, we will direct you to the source material at OpenStax College Algebra .
In short, Cramer’s rule begins with a system of equations, such as:
and we can show that
![Rendered by QuickLaTeX.com \[x=\dfrac{\left| \begin{array}{cc} c_1&b_1\\ c_2&b_2 \end{array} \right|}{\left| \begin{array}{cc} a_1&b_1\\ a_2&b_2 \end{array} \right| } \; \textsf{and} \; y=\dfrac{\left| \begin{array}{cc} a_1&c_1\\ a_2&c_2 \end{array} \right|}{\left| \begin{array}{cc} a_1&b_1\\ a_2&b_2 \end{array} \right|} \]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-c007976eac0715c68a6f1ef234003db2_l3.png)
Cramer’s Rule is a method that uses determinants to solve systems of equations that have the same number of equations as variables.
Consider a system of two linear equations in two variables.
The solution using Cramer’s Rule is given as:
![Rendered by QuickLaTeX.com \[x=\dfrac{D_x}{D}=\dfrac{\left| \begin{array}{cc} c_1&b_1\\ c_2&b_2 \end{array} \right|}{\left| \begin{array}{cc} a_1&b_1\\ a_2&b_2 \end{array} \right| } \; \textsf{and} \; y=\dfrac{D_y}{D}=\dfrac{\left| \begin{array}{cc} a_1&c_1\\ a_2&c_2 \end{array} \right|}{\left| \begin{array}{cc} a_1&b_1\\ a_2&b_2 \end{array} \right|} \]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-bb57a55d197e1ce7ace8611719934aa4_l3.png)
Example Using Cramer’s Rule to Solve a System
Solve the following system using Cramer’s Rule
The solution is (2,-3).
Try it Now 1
Evaluating the Determinant of a Matrix
The algebra is as follows:
Augment the matrix with the first two columns and then follow the formula. Thus,
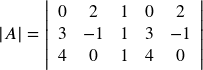
Determinants can also be found using technology. Once a matrix is entered into your calculator. Going to MATRIX – MATH and det and calling up the matrix in question will provide the determinant for a matrix. In Excel, =mdeterm will find the determinant of a matrix as well. The methods mentioned in this section only work for the specified size. For larger matrices, it is recommended to use a calculator, Excel, or another program.
Try it Now 2
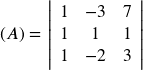
Using Cramer’s Rule to Solve a System of Three Equations in Three Variables
Consider the system:
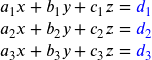
Solve the following system using Cramer’s Rule.
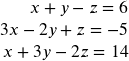
Use Cramer’s Rule.
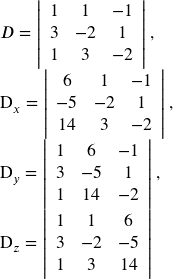
The solution is (1,3,-2).
Try it Now 3
Use Cramer’s Rule to solve the system:
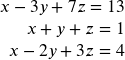
Examples of Cramer’s Rule when D = 0
a. Solve the system of equations (if possible) using Cramer’s Rule.
We begin by finding determinants:
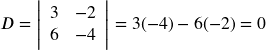
Now we know that it is either dependent or inconsistent. Let’s see one of the other determinants.
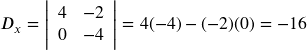
Since -16 \neq 0, we have an inconsistent solution.
b. Solve the following system of equations (if possible, or give general solution if dependent).
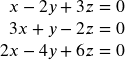
Let’s find D using technology, via calculator or Excel.
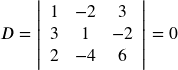
We know that this is a dependent or inconsistent system. We could find all three of the other determinants to see if it is dependent and if it is, we’d then have to use rref in a calculator to find a general solution. For this reason, it’s faster to simply use rref now. There is an online version by planetcalc .
The reduced row echelon form of the matrix is:
![Rendered by QuickLaTeX.com \left[\begin{array}{cccc} 1&0&-\frac{1}{7}&0\\ 0&1&-\frac{11}{7}&0\\ 0&0&0&0 \end{array} \right]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-b051dc2fc220acdba8d0be44d79f99dd_l3.png)
As equations, these are:
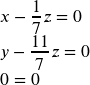
Properties of Determinants
Here are few properties that may make find determinants quicker and easier.
- If the matrix is in the upper triangular form (the bottom triangle below the diagonal is all 0’s), then the determinant equals the product of the entries down the main diagonal.
- When two rows are interchanged, the determinant changes sign.
- If either two rows or two columns are identical, the determinant is zero.
- If a matrix contains either a row or column of 0’s, the determinant is 0.
- If any row or column is multiplied by a constant, the determinant is multiplied by the same factor.
Try it Now Answers
Media Attributions
- takenote is licensed under a Public Domain license
- This section adapted from OpenStax College Algebra by Jay Abramson, Arizona State University, et. al. under a Creative Commons License 4.0 CC-BY ↵
College Algebra for the Managerial Sciences Copyright © by Terri Manthey is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book
Pardon Our Interruption
As you were browsing something about your browser made us think you were a bot. There are a few reasons this might happen:
- You've disabled JavaScript in your web browser.
- You're a power user moving through this website with super-human speed.
- You've disabled cookies in your web browser.
- A third-party browser plugin, such as Ghostery or NoScript, is preventing JavaScript from running. Additional information is available in this support article .
To regain access, please make sure that cookies and JavaScript are enabled before reloading the page.

IMAGES
VIDEO
COMMENTS
A system of linear equations having two and three variables can be easily solved using determinants. Here, the formulas and steps to find the solution of a system of linear equations are given along with practice problems. Cramer's rule is well explained, along with a diagram, below: How to Solve a Linear Equation System Using Determinants? 1.
The solution is. To use determinants to solve a system of three equations with three variables (Cramer's Rule), say x, y, and z, four determinants must be formed following this procedure: Write all equations in standard form. Create the denominator determinant, D, by using the coefficients of x, y, and z from the equations and evaluate it.
Example 4.7.18. Solve the system of equations using Cramer's Rule: {3x + y − 6z = − 3 2x + 6y + 3z = 0 3x + 2y − 3z = − 6. Answer. Cramer's rule does not work when the value of the D determinant is 0, as this would mean we would be dividing by 0. But when D = 0, the system is either inconsistent or dependent.
To solve a system of three equations with three variables with Cramer's Rule, we basically do what we did for a system of two equations. However, we now have to solve for three variables to get the solution. The determinants are also going to be 3 × 3 3 × 3 which will make our work more interesting!
Systems of three equations in three variables are useful for solving many different types of real-world problems. See Example \(\PageIndex{3}\). A system of equations in three variables is inconsistent if no solution exists. After performing elimination operations, the result is a contradiction. See Example \(\PageIndex{4}\).
Cramer's Rule is a method that uses determinants to solve systems of equations that have the same number of equations as variables. Consider a system of two linear equations in two variables. a1x + b1y = c1 a2x + b2y = c2. The solution using Cramer's Rule is given as. x = Dx D = [c1 b1 c2 b2] [a1 b1 a2 b2], D ≠ 0 y = Dy D = [a1 c1 a2 c2 ...
Solve a System of Linear Equations with Three Variables. To solve a system of linear equations with three variables, we basically use the same techniques we used with systems that had two variables. We start with two pairs of equations and in each pair we eliminate the same variable.
Three times the determinant of these numbers minus two times the determinant of these numbers plus one times the determinant of these numbers. So after evaluating, now we need to multiply and simplify, and we get 63. And 63 divided by negative three is negative 21. So after solving this system using determinants, 𝑥 equals three, 𝑦 equals ...
And we can recall to use determinants to solve a system of equations, we need to use Cramer's rule. So let's start by recalling the shortened version of Cramer's rule for a system of three equations in three unknowns. This tells us if the determinant of the matrix of coefficients is nonzero, then 𝑥 is equal to sub 𝑥 over , 𝑦 is ...
Using Cramer's Rule to Solve a System of Three Equations in Three Variables. Now that we can find the determinant of a 3 × 3 matrix, we can apply Cramer's Rule to solve a system of three equations in three variables. Cramer's Rule is straightforward, following a pattern consistent with Cramer's Rule for 2 × 2 matrices.
Example 6. Solve the system of equations using Cramer's Rule: { 3 x − 5 y + 4 z = 5 5 x + 2 y + z = 0 2 x + 3 y − 2 z = 3. Cramer's rule does not work when the value of the D determinant is 0, as this would mean we would be dividing by 0. But when D = 0 , the system is either inconsistent or dependent.
Use determinants to solve the system 5푥 = −2푦 − 5 + 3푧, −3푥 − 푦 + 1 = 2푧, 2푦 − 푧 = −5푥 + 3. ... Solving a System of Three Equations Using Determinants Mathematics • First Year of Secondary School ... the first thing we want to do is actually rearrange our equations so that we have our variables on the left-hand ...
Next, I will solve for the determinant of each matrix. To do this, I can manually solve the determinant of each matrix on paper using the formula provided above. It can be tedious, but it's okay since good math skills are developed by doing lots of problems. The values of the determinants are listed below. Determinants of each matrix:
How to solve a system of two equations using Cramer's rule. Evaluate the determinant D, using the coefficients of the variables. Evaluate the determinant Use the constants in place of the x coefficients. Evaluate the determinant Use the constants in place of the y coefficients. Find x and y. Write the solution as an ordered pair.
Cramer's Rule for Solving a System of Two Equations. For the system of equations {a1x +b1y = k1 a2x +b2y = k2, { a 1 x + b 1 y = k 1 a 2 x + b 2 y = k 2, the solution (x, y) ( x, y) can be determined by. Notice that to form the determinant D, we use take the coefficients of the variables.
Solve the system of equations using Cramer's Rule: { 3x + y − 6z = −3 2x + 6y + 3z = 0 3x + 2y − 3z = −6. Cramer's rule does not work when the value of the D determinant is 0, as this would mean we would be dividing by 0. But when D = 0, the system is either inconsistent or dependent. When the value of D = 0.
Using Cramer's Rule to Solve a System of Three Equations in Three Variables. Now that we can find the determinant of a 3 × 3 matrix, we can apply Cramer's Rule to solve a system of three equations in three variables. Cramer's Rule is straightforward, following a pattern consistent with Cramer's Rule for 2 × 2 matrices.
Cramer's Rule is a method that uses determinants to solve systems of equations that have the same number of equations as variables. Consider a system of two linear equations in two variables. The solution using Cramer's Rule is given as. If we are solving for the column is replaced with the constant column.
We will use Cramer's rule. This rule allows us to find the solution by just using the determinants. The main determinant is that of the coefficient matrix. We call this determinant, D. Then we ...
How to solve a system of two equations using Cramer's rule. Evaluate the determinant D, using the coefficients of the variables. Evaluate the determinant Use the constants in place of the x coefficients. Evaluate the determinant Use the constants in place of the y coefficients. Find x and y. Write the solution as an ordered pair.
3.5 Determinants and Cramer's Rule. [1] We have learned how to solve systems of equations in two variables and three variables, and by multiple methods: substitution, addition, Gaussian elimination, using the inverse of a matrix, and graphing. Some of these methods are easier to apply than others and are more appropriate in certain situations.
The solution is x = 2, y = 1, z = 3. Example 2. Solve the following system of equations, using matrices. Put the equations in matrix form. Eliminate the x ‐coefficient below row 1. Eliminate the y‐ coefficient below row 5. Reinserting the variables, the system is now: Equation (9) can be solved for z. Substitute into equation (8) and solve ...