quadratic equation solver with letters

Quadratic Equation Solver

What do you want to calculate.

• Solve for Variable
• Practice Mode
• Step-By-Step

Step-By-Step Example

Example (click to try), choose your method, solve by factoring.

Example: 3x^2-2x-1=0

Complete The Square

Example: 3x^2-2x-1=0 (After you click the example, change the Method to 'Solve By Completing the Square'.)

Take the Square Root

Example: 2x^2=18

Quadratic Formula

Example: 4x^2-2x-1=0

About quadratic equations

Need more problem types? Try MathPapa Algebra Calculator

Clear Quadratic Equation Solver »

Quadratic Formula Calculator

Enter the equation you want to solve using the quadratic formula.

The Quadratic Formula Calculator finds solutions to quadratic equations with real coefficients. For equations with real solutions, you can use the graphing tool to visualize the solutions.

Quadratic Formula : x = − b ± b 2 − 4 a c 2 a

Click the blue arrow to submit. Choose "Solve Using the Quadratic Formula" from the topic selector and click to see the result in our Algebra Calculator !

Solve Using the Quadratic Formula Apply the Quadratic Formula

Popular Problems

Solve Using the Quadratic Formula x 2 + 5 x + 6 = 0 Solve Using the Quadratic Formula x 2 - 9 = 0 Solve Using the Quadratic Formula 5 x 2 - 7 x - 3 = 0 Apply the Quadratic Formula x 2 - 14 x + 49 Apply the Quadratic Formula x 2 - 18 x - 4

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

Game Central

• Solve equations and inequalities
• Simplify expressions
• Factor polynomials
• Graph equations and inequalities
• Advanced solvers
• All solvers
• Arithmetics
• Determinant
• Percentages
• Scientific Notation
• Inequalities

Quadratic Equations

Solving equations is the central theme of algebra. All skills learned lead eventually to the ability to solve equations and simplify the solutions. In previous chapters we have solved equations of the first degree. You now have the necessary skills to solve equations of the second degree, which are known as quadratic equations .

QUADRATICS SOLVED BY FACTORING

• Identify a quadratic equation.
• Place a quadratic equation in standard form.
• Solve a quadratic equation by factoring.

A quadratic equation is a polynomial equation that contains the second degree, but no higher degree, of the variable.

The standard form of a quadratic equation is ax 2 + bx + c = 0 when a ≠ 0 and a, b, and c are real numbers.

All quadratic equations can be put in standard form, and any equation that can be put in standard form is a quadratic equation. In other words, the standard form represents all quadratic equations.

The solution to an equation is sometimes referred to as the root of the equation.

An important theorem, which cannot be proved at the level of this text, states "Every polynomial equation of degree n has exactly n roots." Using this fact tells us that quadratic equations will always have two solutions. It is possible that the two solutions are equal.

The simplest method of solving quadratics is by factoring. This method cannot always be used, because not all polynomials are factorable, but it is used whenever factoring is possible.

The method of solving by factoring is based on a simple theorem.

If AB = 0, then either A = 0 or B = 0.

We will not attempt to prove this theorem but note carefully what it states. We can never multiply two numbers and obtain an answer of zero unless at least one of the numbers is zero. Of course, both of the numbers can be zero since (0)(0) = 0.

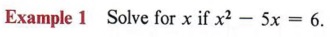
Solution Step 1 Put the equation in standard form.

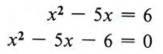
Step 2 Factor completely.

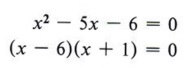
Step 3 Set each factor equal to zero and solve for x. Since we have (x - 6)(x + 1) = 0, we know that x - 6 = 0 or x + 1 = 0, in which case x = 6 or x = - 1.

Step 4 Check the solution in the original equation. If x = 6, then x 2 - 5x = 6 becomes

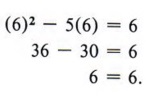
Therefore, x = 6 is a solution. If x = - 1, then x 2 - 5x = 6 becomes

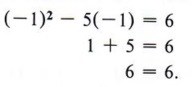
Therefore, - 1 is a solution.

The solutions can be indicated either by writing x = 6 and x = - 1 or by using set notation and writing {6, - 1}, which we read "the solution set for x is 6 and - 1." In this text we will use set notation.

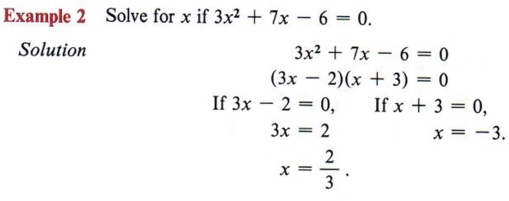
Check the solutions in the original equation.

INCOMPLETE QUADRATICS

• Identify an incomplete quadratic equation.
• Solve an incomplete quadratic equation.

If, when an equation is placed in standard form ax 2 + bx + c = 0, either b = 0 or c = 0, the equation is an incomplete quadratic .

5x 2 - 10 = 0 is an incomplete quadratic, since the middle term is missing and therefore b = 0.

When you encounter an incomplete quadratic with c - 0 (third term missing), it can still be solved by factoring.

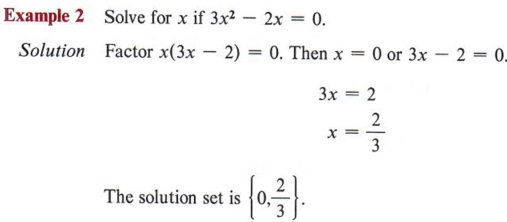
Notice that if the c term is missing, you can always factor x from the other terms. This means that in all such equations, zero will be one of the solutions. An incomplete quadratic with the b term missing must be solved by another method, since factoring will be possible only in special cases.

Example 3 Solve for x if x 2 - 12 = 0.

Solution Since x 2 - 12 has no common factor and is not the difference of squares, it cannot be factored into rational factors. But, from previous observations, we have the following theorem.

Using this theorem, we have

Note that in this example we have the square of a number equal to a negative number. This can never be true in the real number system and, therefore, we have no real solution.

COMPLETING THE SQUARE

• Identify a perfect square trinomial.
• Complete the third term to make a perfect square trinomial.
• Solve a quadratic equation by completing the square.

From your experience in factoring you already realize that not all polynomials are factorable. Therefore, we need a method for solving quadratics that are not factorable. The method needed is called "completing the square."

First let us review the meaning of "perfect square trinomial." When we square a binomial we obtain a perfect square trinomial. The general form is (a + b) 2 = a 2 + 2ab + b 2 .

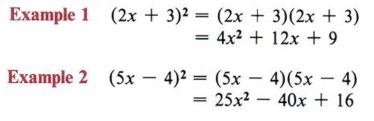
• The other term is either plus or minus two times the product of the square roots of the other two terms.

The -7 term immediately says this cannot be a perfect square trinomial. The task in completing the square is to find a number to replace the -7 such that there will be a perfect square.

Consider this problem: Fill in the blank so that "x 2 + 6x + _______" will be a perfect square trinomial. From the two conditions for a perfect square trinomial we know that the blank must contain a perfect square and that 6x must be twice the product of the square root of x 2 and the number in the blank. Since x is already present in 6x and is a square root of x 2 , then 6 must be twice the square root of the number we place in the blank. In other words, if we first take half of 6 and then square that result, we will obtain the necessary number for the blank.

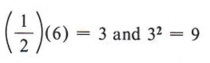
Therefore x 2 + 6x + 9 is a perfect square trinomial.

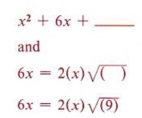
Now let's consider how we can use completing the square to solve quadratic equations.

Example 5 Solve x 2 + 6x - 7 = 0 by completing the square.

Solution First we notice that the -7 term must be replaced if we are to have a perfect square trinomial, so we will rewrite the equation, leaving a blank for the needed number.

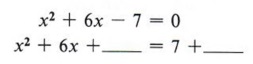
At this point, be careful not to violate any rules of algebra. For instance, note that the second form came from adding +7 to both sides of the equation. Never add something to one side without adding the same thing to the other side.

Now we find half of 6 = 3 and 3 2 = 9, to give us the number for the blank. Again, if we place a 9 in the blank we must also add 9 to the right side as well.

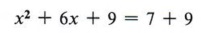
Now factor the perfect square trinomial, which gives

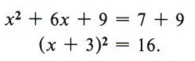
Example 6 Solve 2x 2 + 12x - 4 = 0 by completing the square.

Solution This problem brings in another difficulty. The first term, 2x 2 , is not a perfect square. We will correct this by dividing all terms of the equation by 2 and obtain

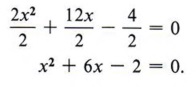
We now add 2 to both sides, giving

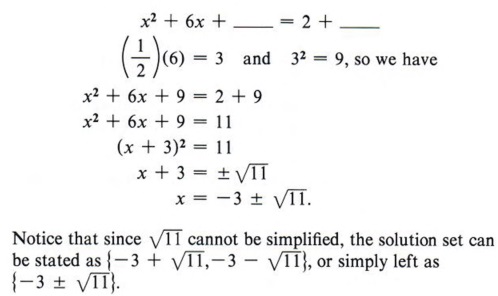
Example 7 Solve 3x 2 + 7x - 9 = 0 by completing the square.

Solution Step 1 Divide all terms by 3.

Step 2 Rewrite the equation, leaving a blank for the term necessary to complete the square.

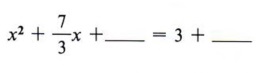
Step 3 Find the square of half of the coefficient of x and add to both sides.

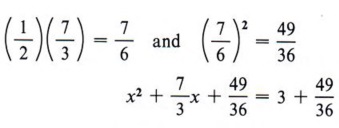
Step 4 Factor the completed square.

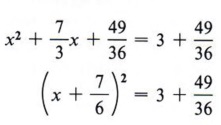
Step 5 Take the square root of each side of the equation.

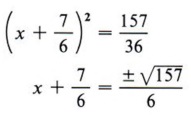
Step 6 Solve for x (two values).

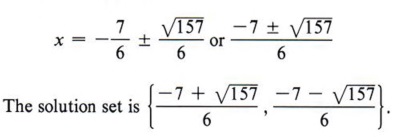
Follow the steps in the previous computation and then note especially the last ine. What is the conclusion when the square of a quantity is equal to a negative number? "No real solution."

In summary, to solve a quadratic equation by completing the square, follow this step-by-step method.

Step 1 If the coefficient of x2 is not 1, divide all terms by that coefficient. Step 2 Rewrite the equation in the form of x2 + bx + _______ = c + _______. Step 3 Find the square of one-half of the coefficient of the x term and add this quantity to both sides of the equation. Step 4 Factor the completed square and combine the numbers on the right-hand side of the equation. Step 5 Find the square root of each side of the equation. Step 6 Solve for x and simplify. If step 5 is not possible, then the equation has no real solution.

THE QUADRATIC FORMULA

• Solve the general quadratic equation by completing the square.
• Solve any quadratic equation by using the quadratic formula.

The standard form of a quadratic equation is ax 2 + bx + c = 0. This means that every quadratic equation can be put in this form. In a sense then ax 2 + bx + c = 0 represents all quadratics. If you can solve this equation, you will have the solution to all quadratic equations.

We will solve the general quadratic equation by the method of completing the square.

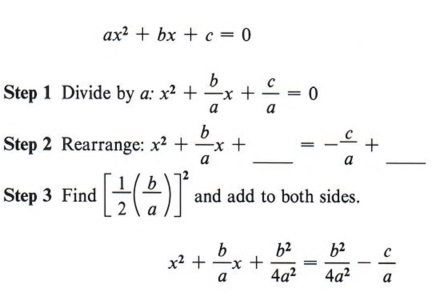
To use the quadratic formula you must identify a, b, and c. To do this the given equation must always be placed in standard form.

Not every quadratic equation will have a real solution.

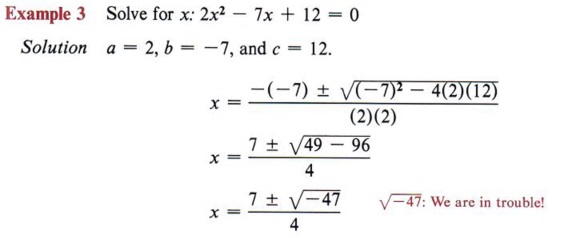
There is no real solution since -47 has no real square root.

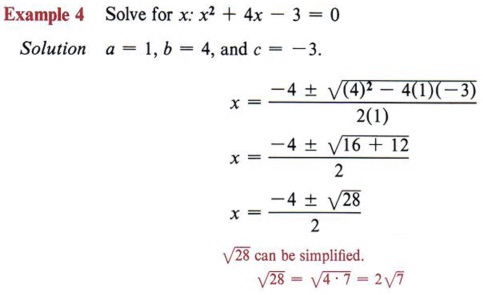
This solution should now be simplified.

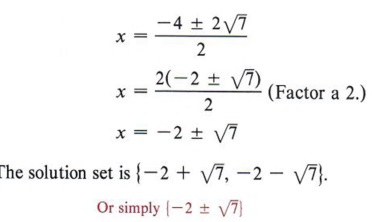
WORD PROBLEMS

• Identify word problems that require a quadratic equation for their solution.
• Solve word problems involving quadratic equations.

Certain types of word problems can be solved by quadratic equations. The process of outlining and setting up the problem is the same as taught in chapter 5, but with problems solved by quadratics you must be very careful to check the solutions in the problem itself. The physical restrictions within the problem can eliminate one or both of the solutions.

Example 1 If the length of a rectangle is 1 unit more than twice the width, and the area is 55 square units, find the length and width.

Solution The formula for the area of a rectangle is Area = Length X Width. Let x = width, 2x + 1 = length.

At this point, you can see that the solution x = -11/2 is not valid since x represents a measurement of the width and negative numbers are not used for such measurements. Therefore, the solution is

width = x = 5, length = 2x + 1 = 11.

Example 3 If a certain integer is subtracted from 6 times its square, the result is 15. Find the integer.

Solution Let x = the integer. Then

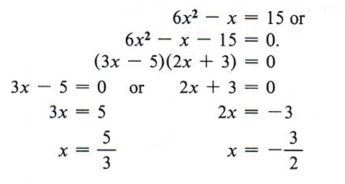
Since neither solution is an integer, the problem has no solution.

Example 4 A farm manager has 200 meters of fence on hand and wishes to enclose a rectangular field so that it will contain 2,400 square meters in area. What should the dimensions of the field be?

Solution Here there are two formulas involved. P = 2l + 2w for the perimeter and A = lw for the area. First using P = 2l + 2w, we get

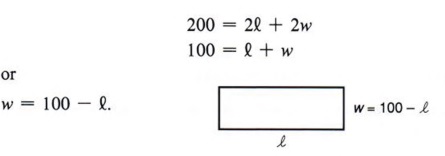
We can now use the formula A = lw and substitute (100 - l) for w, giving

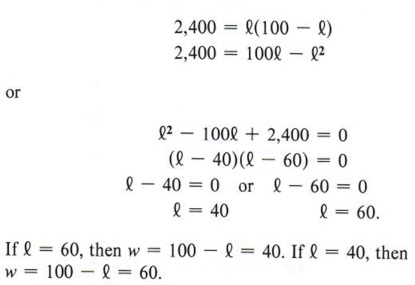
The field must be 40 meters wide by 60 meters long.

Note that in this problem we actually use a system of equations

P = 2 l + 2 w A = l w.

In general, a system of equations in which a quadratic is involved will be solved by the substitution method. (See chapter 6.)

• A quadratic equation is a polynomial equation in one unknown that contains the second degree, but no higher degree, of the variable.
• The standard form of a quadratic equation is ax 2 + bx + c = 0, when a ≠ 0.
• An incomplete quadratic equation is of the form ax 2 + bx + c = 0, and either b = 0 or c = 0.

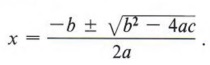
• The most direct and generally easiest method of finding the solutions to a quadratic equation is factoring. This method is based on the theorem: if AB = 0, then A = 0 or B = 0. To use this theorem we put the equation in standard form, factor, and set each factor equal to zero.
• To solve a quadratic equation by completing the square, follow these steps: Step 1 If the coefficient of x 2 is not 1, divide all terms by that coefficient. Step 2 Rewrite the equation in the form of x 2 + bx +_____ = c + _____ Step 3 Find the square of one-half of the coefficient of the x term and add this quantity to both sides of the equation. Step 4 Factor the completed square and combine the numbers on the right-hand side of the equation. Step 5 Find the square root of each side of the equation. Step 6 Solve for x and simplify.
• The method of completing the square is used to derive the quadratic formula.
• To use the quadratic formula write the equation in standard form, identify a, b, and c, and substitute these values into the formula. All solutions should be simplified.

Math Topics

More solvers.

• Add Fractions
• Simplify Fractions

Quadratic Equations

An example of a Quadratic Equation :

The function can make nice curves like this one:

The name Quadratic comes from "quad" meaning square, because the variable gets squared (like x 2 ).

It is also called an "Equation of Degree 2" (because of the "2" on the x )

Standard Form

The Standard Form of a Quadratic Equation looks like this:

• a , b and c are known values. a can't be 0
• x is the variable or unknown (we don't know it yet)

Here are some examples:

Have a Play With It

Play with the Quadratic Equation Explorer so you can see:

• the function's graph, and
• the solutions (called "roots").

Hidden Quadratic Equations!

As we saw before, the Standard Form of a Quadratic Equation is

But sometimes a quadratic equation does not look like that!

For example:

How To Solve Them?

The " solutions " to the Quadratic Equation are where it is equal to zero .

They are also called " roots ", or sometimes " zeros "

There are usually 2 solutions (as shown in this graph).

And there are a few different ways to find the solutions:

Just plug in the values of a, b and c, and do the calculations.

We will look at this method in more detail now.

About the Quadratic Formula

First of all what is that plus/minus thing that looks like ± ?

The ± means there are TWO answers:

x = −b + √(b 2 − 4ac) 2a

x = −b − √(b 2 − 4ac) 2a

Here is an example with two answers:

But it does not always work out like that!

• Imagine if the curve "just touches" the x-axis.
• Or imagine the curve is so high it doesn't even cross the x-axis!

This is where the "Discriminant" helps us ...

Discriminant

Do you see b 2 − 4ac in the formula above? It is called the Discriminant , because it can "discriminate" between the possible types of answer:

• when b 2 − 4ac is positive, we get two Real solutions
• when it is zero we get just ONE real solution (both answers are the same)
• when it is negative we get a pair of Complex solutions

Complex solutions? Let's talk about them after we see how to use the formula.

Using the Quadratic Formula

Just put the values of a, b and c into the Quadratic Formula, and do the calculations.

Example: Solve 5x 2 + 6x + 1 = 0

Answer: x = −0.2 or x = −1

Let's check the answers:

Remembering The Formula

A kind reader suggested singing it to "Pop Goes the Weasel":

Try singing it a few times and it will get stuck in your head!

Or you can remember this story:

x = −b ± √(b 2 − 4ac) 2a

"A negative boy was thinking yes or no about going to a party, at the party he talked to a square boy but not to the 4 awesome chicks. It was all over at 2 am. "

Complex Solutions?

When the Discriminant (the value b 2 − 4ac ) is negative we get a pair of Complex solutions ... what does that mean?

It means our answer will include Imaginary Numbers . Wow!

Example: Solve 5x 2 + 2x + 1 = 0

Answer: x = −0.2 ± 0.4 i

The graph does not cross the x-axis. That is why we ended up with complex numbers.

In a way it is easier: we don't need more calculation, we leave it as −0.2 ± 0.4 i .

Example: Solve x 2 − 4x + 6.25 = 0

Answer: x = 2 ± 1.5 i

BUT an upside-down mirror image of our equation does cross the x-axis at 2 ± 1.5 (note: missing the i ).

Just an interesting fact for you!

• Quadratic Equation in Standard Form: ax 2 + bx + c = 0
• Quadratic Equations can be factored
• Quadratic Formula: x = −b ± √(b 2 − 4ac) 2a
• positive, there are 2 real solutions
• zero, there is one real solution
• negative, there are 2 complex solutions

The Quadratic Formula

What it is, what it does, and how to use it

What is the Quadratic Formula?

The quadratic formula is:

What does this formula tell us?

The quadratic formula calculates the solutions of any quadratic equation.

What is a quadratic equation?

A quadratic equation is an equation that can be written as ax ² + bx + c where a ≠ 0 . In other words, a quadratic equation must have a squared term as its highest power.

Examples of quadratic equations

$$ y = 5x^2 + 2x + 5 \\ y = 11x^2 + 22 \\ y = x^2 - 4x +5 \\ y = -x^2 + + 5 $$

Non Examples

$$ y = 11x + 22 \\ y = x^3 -x^2 +5x +5 \\ y = 2x^3 -4x^2 \\ y = -x^4 + 5 $$

Ok, but what is a 'solution'?

Well a solution can be thought in two ways:

Example of the quadratic formula to solve an equation

Use the formula to solve theQuadratic Equation: $$ y = x^2 + 2x + 1 $$ .

Just substitute a,b, and c into the general formula:

$$ a = 1 \\ b = 2 \\ c = 1 $$

Below is a picture representing the graph of y = x² + 2x + 1 and its solution.

Quadratic Formula Song

A catchy way to remember the quadratic formula is this song (pop goes the weasel).

Practice Problems

Use the quadratic formula to find the solutions to the following equation: y = x² − 2x + 1 and its solution.

• b = − 2

Use the quadratic formula to find the solutions to the following equation: y = x² − x − 2 and its solution .

In this quadratic equation, y = x² − x − 2 and its solution:

• b = − 1
• c = − 2

Use the quadratic formula to find the solutions to the following equation: y = x² − 1 and its solution.

In this quadratic equation, y = x² − 1 and its solution:

• c = −1

Calculate the solutions of the the quadratic equation below by using the quadratic formula : y = x² + 2x − 3 and its solution.

In this quadratic equation, y = x² + 2x − 3 and its solution:

• c = −3

Below is a picture of the graph of the quadratic equation and its two solutions.

Use the quadratic formula to find the solutions to the following equation: y = x² + 4x − 5 and its solution.

In this quadratic equation, y = x² + 4x − 5 and its solution:

• c = −5

Use the quadratic formula to find the solutions to the following equation: y = x² − 4x + 5 and its solution.

In this quadratic equation, y = x² − 4x + 5 and its solution:

• b = −4

Below is a picture of this quadratic's graph.

• Solving Quadratic Equations

• Discriminant
• Completing the Square in Math

Completing The Square Calculator

Solves Equation and lets you print image to Desktop!

• Quadratic Formula Calculator
• Formula for Sum and Product of Roots

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

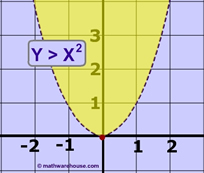
Quadratic Equation

Quadratic equations are second-degree algebraic expressions and are of the form ax 2 + bx + c = 0. The term "quadratic" comes from the Latin word "quadratus" meaning square, which refers to the fact that the variable x is squared in the equation. In other words, a quadratic equation is an “equation of degree 2.” There are many scenarios where a quadratic equation is used. Did you know that when a rocket is launched, its path is described by a quadratic equation? Further, a quadratic equation has numerous applications in physics, engineering, astronomy, etc.

Quadratic equations have maximum of two solutions, which can be real or complex numbers. These two solutions (values of x) are also called the roots of the quadratic equations and are designated as (α, β). We shall learn more about the roots of a quadratic equation in the below content.

What is Quadratic Equation?

A quadratic equation is an algebraic equation of the second degree in x. The quadratic equation in its standard form is ax 2 + bx + c = 0, where a and b are the coefficients, x is the variable, and c is the constant term. The important condition for an equation to be a quadratic equation is the coefficient of x 2 is a non-zero term (a ≠ 0). For writing a quadratic equation in standard form, the x 2 term is written first, followed by the x term, and finally, the constant term is written.

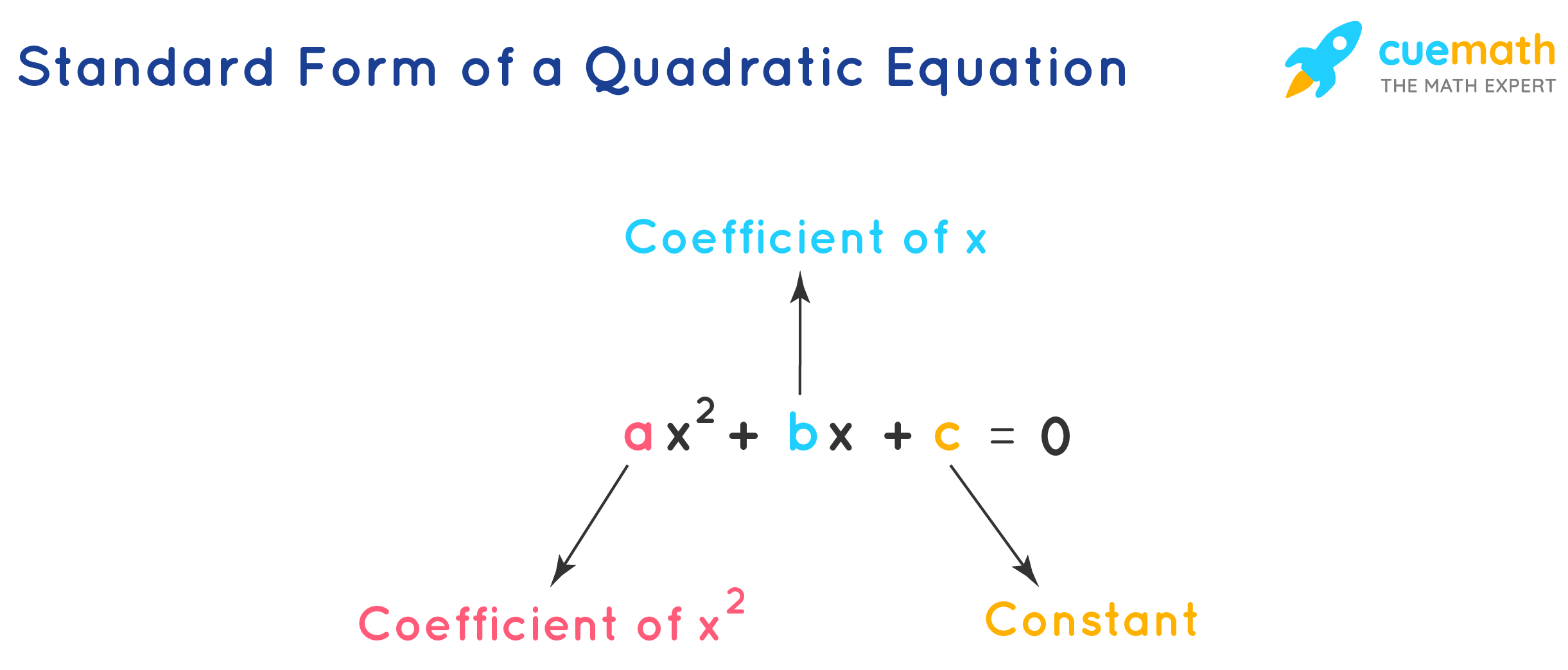
Further, in real math problems the quadratic equations are presented in different forms: (x - 1)(x + 2) = 0, -x 2 = -3x + 1, 5x(x + 3) = 12x, x 3 = x(x 2 + x - 3). All of these equations need to be transformed into standard form of the quadratic equation before performing further operations.

Roots of a Quadratic Equation

The roots of a quadratic equation are the two values of x, which are obtained by solving the quadratic equation. These roots of the quadratic equation are also called the zeros of the equation. For example, the roots of the equation x 2 - 3x - 4 = 0 are x = -1 and x = 4 because each of them satisfies the equation. i.e.,

• At x = -1, (-1) 2 - 3(-1) - 4 = 1 + 3 - 4 = 0
• At x = 4, (4) 2 - 3(4) - 4 = 16 - 12 - 4 = 0

There are various methods to find the roots of a quadratic equation. The usage of the quadratic formula is one of them.

Quadratic Formula

Quadratic formula is the simplest way to find the roots of a quadratic equation . There are certain quadratic equations that cannot be easily factorized, and here we can conveniently use this quadratic formula to find the roots in the quickest possible way. The two roots in the quadratic formula are presented as a single expression. The positive sign and the negative sign can be alternatively used to obtain the two distinct roots of the equation.

Quadratic Formula: The roots of a quadratic equation ax 2 + bx + c = 0 are given by x = [-b ± √(b 2 - 4ac)]/2a.

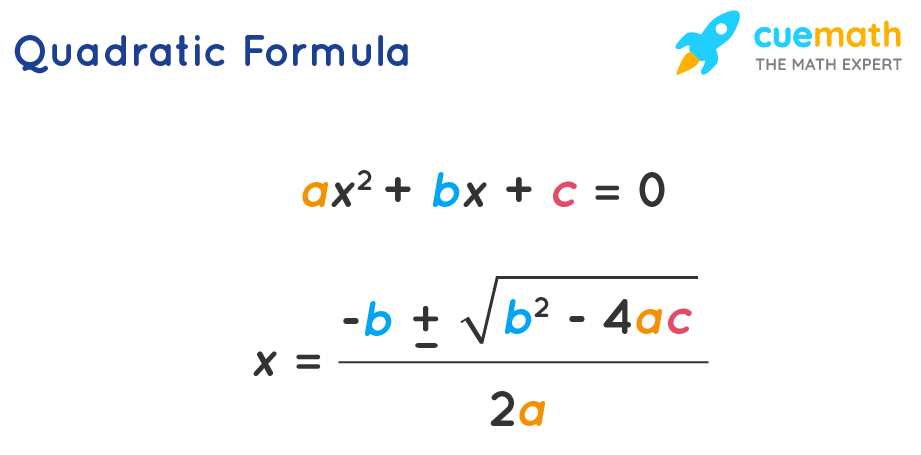
This formula is also known as the Sridharacharya formula .

Example: Let us find the roots of the same equation that was mentioned in the earlier section x 2 - 3x - 4 = 0 using the quadratic formula.

a = 1, b = -3, and c = -4.

x = [-b ± √(b 2 - 4ac)]/2a = [-(-3) ± √((-3) 2 - 4(1)(-4))]/2(1) = [3 ± √25] / 2 = [3 ± 5] / 2 = (3 + 5)/2 or (3 - 5)/2 = 8/2 or -2/2 = 4 or -1 are the roots.

Proof of Quadratic Formula

Consider an arbitrary quadratic equation: ax 2 + bx + c = 0, a ≠ 0

To determine the roots of this equation, we proceed as follows:

ax 2 + bx = -c ⇒ x 2 + bx/a = -c/a

Now, we express the left-hand side as a perfect square , by introducing a new term (b/2a) 2 on both sides:

• x 2 + bx/a + (b/2a) 2 = -c/a + (b/2a) 2

The left-hand side is now a perfect square:

(x + b/2a) 2 = -c/a + b 2 /4a 2 ⇒ (x + b/2a) 2 = (b 2 - 4ac)/4a 2

This is good for us, because now we can take square roots to obtain:

x + b/2a = ±√(b 2 - 4ac)/2a

x = (-b ± √(b 2 - 4ac))/2a

Thus, by completing the squares, we were able to isolate x and obtain the two roots of the equation.

Nature of Roots of the Quadratic Equation

The roots of a quadratic equation are usually represented to by the symbols alpha (α), and beta (β). Here we shall learn more about how to find the nature of roots of a quadratic equation without actually finding the roots of the equation.

The nature of roots of a quadratic equation can be found without actually finding the roots (α, β) of the equation. This is possible by taking the discriminant value, which is part of the formula to solve the quadratic equation. The value b 2 - 4ac is called the discriminant of a quadratic equation and is designated as 'D'. Based on the discriminant value the nature of the roots of the quadratic equation can be predicted.

Discriminant: D = b 2 - 4ac

• D > 0, the roots are real and distinct
• D = 0, the roots are real and equal.
• D < 0, the roots do not exist or the roots are imaginary .

Now, check out the formulas to find the sum and the product of the roots of the equation.

Sum and Product of Roots of Quadratic Equation

The coefficient of x 2 , x term, and the constant term of the quadratic equation ax 2 + bx + c = 0 are useful in determining the sum and product of the roots of the quadratic equation. The sum and product of the roots of a quadratic equation can be directly calculated from the equation, without actually finding the roots of the quadratic equation. For a quadratic equation ax 2 + bx + c = 0, the sum and product of the roots are as follows.

• Sum of the Roots: α + β = -b/a = - Coefficient of x/ Coefficient of x 2
• Product of the Roots: αβ = c/a = Constant term/ Coefficient of x 2

Writing Quadratic Equations Using Roots

The quadratic equation can also be formed for the given roots of the equation. If α, β, are the roots of the quadratic equation, then the quadratic equation is as follows.

x 2 - (α + β)x + αβ = 0

Example: What is the quadratic equation whose roots are 4 and -1?

Solution: It is given that α = 4 and β = -1. The corresponding quadratic equation is found by:

x 2 - (α + β)x + αβ = 0 x 2 - (α + β)x + αβ = 0 x 2 - (4 - 1)x + (4)(-1) = 0 x 2 - 3x - 4 = 0

Formulas Related to Quadratic Equations

The following list of important formulas is helpful to solve quadratic equations.

• The quadratic equation in its standard form is ax 2 + bx + c = 0
• For D > 0 the roots are real and distinct.
• For D = 0 the roots are real and equal.
• For D < 0 the real roots do not exist, or the roots are imaginary.
• The formula to find the roots of the quadratic equation is x = [-b ± √(b 2 - 4ac)]/2a.
• The sum of the roots of a quadratic equation is α + β = -b/a.
• The product of the Root of the quadratic equation is αβ = c/a.
• The quadratic equation whose roots are α, β, is x 2 - (α + β)x + αβ = 0.
• The condition for the quadratic equations a 1 x 2 + b 1 x + c 1 = 0, and a 2 x 2 + b 2 x + c 2 = 0 having the same roots is (a 1 b 2 - a 2 b 1 ) (b 1 c 2 - b 2 c 1 ) = (a 2 c 1 - a 1 c 2 ) 2 .
• When a > 0, the quadratic expression f(x) = ax 2 + bx + c has a minimum value at x = -b/2a.
• When a < 0, the quadratic expression f(x) = ax 2 + bx + c has a maximum value at x = -b/2a.
• The domain of any quadratic function is the set of all real numbers.

Methods to Solve Quadratic Equations

A quadratic equation can be solved to obtain two values of x or the two roots of the equation. There are four different methods to find the roots of the quadratic equation. The four methods of solving the quadratic equations are as follows.

• Factorizing of Quadratic Equation
• Using quadratic formula (which we have seen already)

Method of Completing the Square

• Graphing Method to Find the Roots

Let us look in detail at each of the above methods to understand how to use these methods, their applications, and their uses.

Solving Quadratic Equations by Factorization

Factorization of quadratic equation follows a sequence of steps. For a general form of the quadratic equation ax 2 + bx + c = 0, we need to first split the middle term into two terms, such that the product of the terms is equal to the constant term. Further, we can take the common terms from the available term, to finally obtain the required factors as follows:

• x 2 + (a + b)x + ab = 0
• x 2 + ax + bx + ab = 0
• x(x + a) + b(x + a)
• (x + a)(x + b) = 0

Here is an example to understand the factorization process.

• x 2 + 5x + 6 = 0
• x 2 + 2x + 3x + 6 = 0
• x(x + 2) + 3(x + 2) = 0
• (x + 2)(x + 3) = 0

Thus the two obtained factors of the quadratic equation are (x + 2) and (x + 3). To find its roots, just set each factor to zero and solve for x. i.e., x + 2 = 0 and x + 3 = 0 which gives x = -2 and x = -3. Thus, x = -2 and x = -3 are the roots of x 2 + 5x + 6 = 0.

Further, there is another important method of solving a quadratic equation. The method of completing the square for a quadratic equation is also useful to find the roots of the equation.

The method of completing the square in a quadratic equation is to algebraically square and simplify, to obtain the required roots of the equation. Consider a quadratic equation ax 2 + bx + c = 0, a ≠ 0. To determine the roots of this equation, we simplify it as follows:

• ax 2 + bx + c = 0
• ax 2 + bx = -c
• x 2 + bx/a = -c/a

Now, we express the left-hand side as a perfect square, by introducing a new term (b/2a) 2 on both sides:

• (x + b/2a) 2 = -c/a + b 2 /4a 2
• (x + b/2a) 2 = (b 2 - 4ac)/4a 2
• x + b/2a = + √(b 2 - 4ac)/2a
• x = - b/2a + √(b 2 - 4ac)/2a
• x = [-b ± √(b 2 - 4ac)]/2a

Here the '+' sign gives one root and the '-' sign gives another root of the quadratic equation. Generally, this detailed method is avoided, and only the quadratic formula is used to obtain the required roots.

Graphing a Quadratic Equation

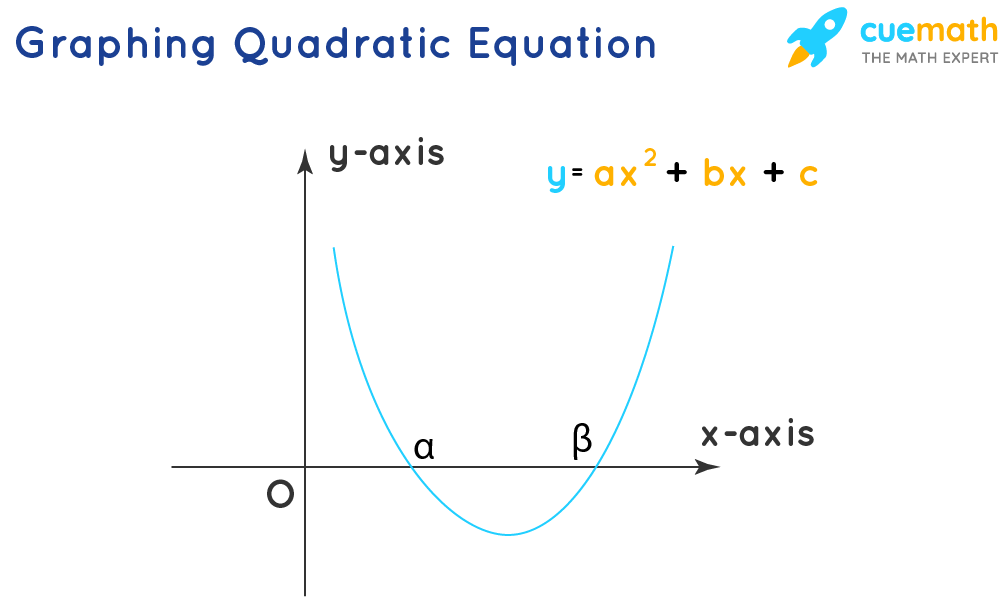
The point(s) where the graph cuts the horizontal x-axis (typically the x-intercepts ) is the solution of the quadratic equation. These points can also be algebraically obtained by equalizing the y value to 0 in the function y = ax 2 + bx + c and solving for x.

Quadratic Equations Having Common Roots

Consider two quadratic equations having common roots a 1 x 2 + b 1 x + c 1 = 0, and a 2 x 2 + b 2 x + c 2 = 0. Let us solve these two equations to find the conditions for which these equations have a common root. The two equations are solved for x 2 and x respectively.

(x 2 )(b 1 c 2 - b 2 c 1 ) = (-x)/(a 1 c 2 - a 2 c 1 ) = 1/(a 1 b 2 - a 2 b 1 )

x 2 = (b 1 c 2 - b 2 c 1 ) / (a 1 b 2 - a 2 b 1 )

x = (a 2 c 1 - a 1 c 2 ) / (a 1 b 2 - a 2 b 1 )

Hence, by simplifying the above two expressions we have the following condition for the two equations having the common root.

(a 1 b 2 - a 2 b 1 ) (b 1 c 2 - b 2 c 1 ) = (a 2 c 1 - a 1 c 2 ) 2

Maximum and Minimum Value of Quadratic Expression

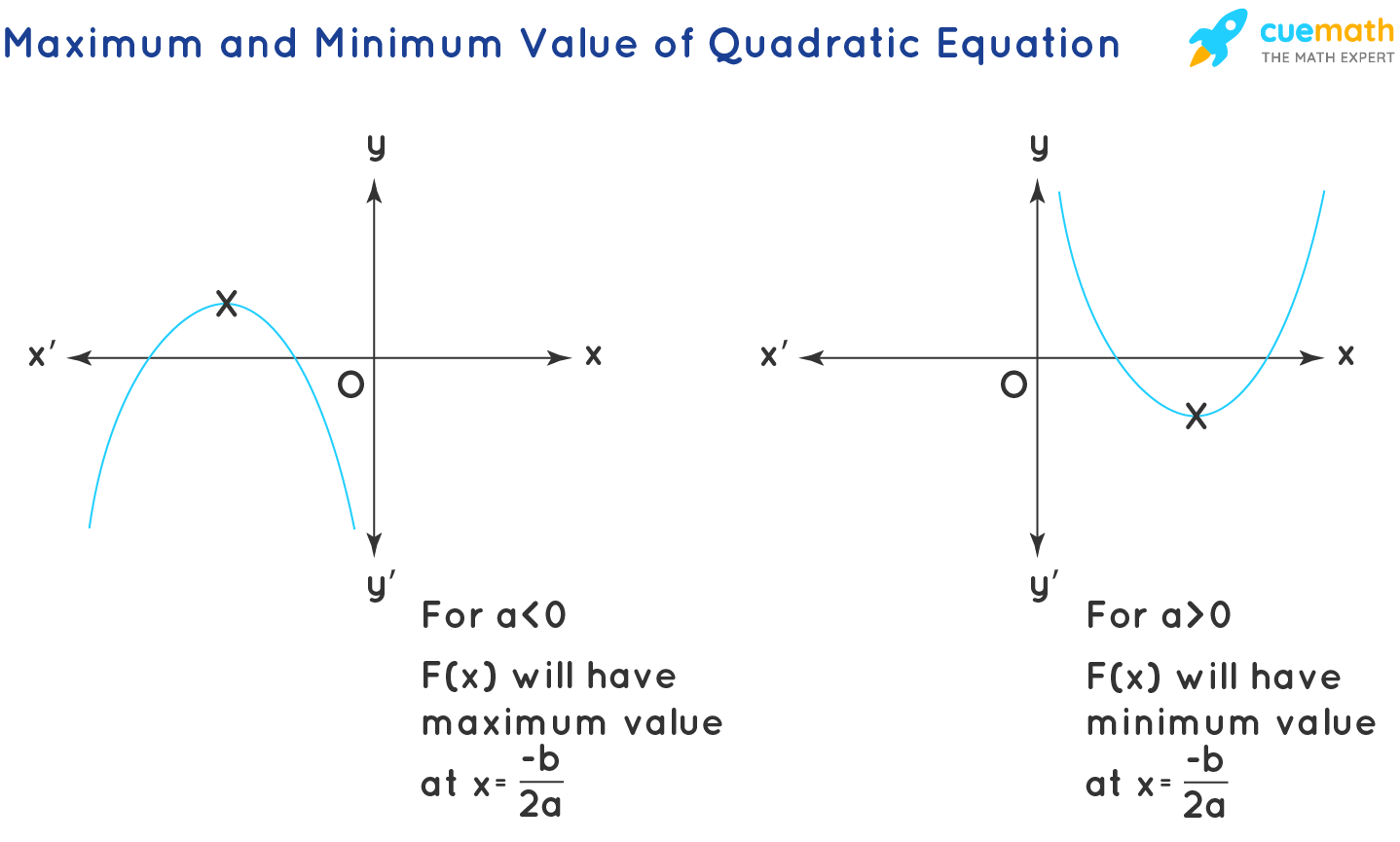
The maximum and minimum values of the quadratic expressions are of further help to find the range of the quadratic expression: The range of the quadratic expressions also depends on the value of a. For positive values of a( a > 0), the range is [ F(-b/2a), ∞), and for negative values of a ( a < 0), the range is (-∞, F(-b/2a)].

• For a > 0, Range: [ f(-b/2a), ∞)
• For a < 0, Range: (-∞, f(-b/2a)]

Note that the domain of a quadratic function is the set of all real numbers, i.e., (-∞, ∞).

Tips and Tricks on Quadratic Equation:

Some of the below-given tips and tricks on quadratic equations are helpful to more easily solve quadratic equations.

• The quadratic equations are generally solved through factorization. But in instances when it cannot be solved by factorization, the quadratic formula is used.
• The roots of a quadratic equation are also called the zeroes of the equation.
• For quadratic equations having negative discriminant values, the roots are represented by complex numbers.
• The sum and product of the roots of a quadratic equation can be used to find higher algebraic expressions involving these roots.

☛Related Topics:

• Roots Calculator
• Quadratic Factoring Calculator
• Roots of Quadratic Equation Calculator

Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12 . Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.

Quadratic Equations Examples

Example 1: James is a fitness enthusiast and goes for a jog every morning. The park where he jogs is rectangular in shape and measures 12m × 8m. An environmentalist group plans to revamp the park and decides to build a pathway surrounding the park. This would increase the total area to 140 sq m. What will be the width of the pathway?

Let’s denote the width of the pathway by x.

Then, the length and breadth of the outer rectangle is (12+2x) m and (8+2x) m.

Given that, area = 140

(12 + 2x)(8 + 2x) = 140

2(6 + x) 2(4 + x) = 140

(6 + x)(4 + x) = 35

24 + 6x + 4x + x 2 = 35

x 2 + 10x -11 = 0

x 2 + 11x - x - 11 = 0

x(x + 11) - 1(x + 11) = 0

(x + 11)(x - 1) = 0

(x + 11) =0 and (x - 1) = 0

x = -11 and x = 1

Since length can’t be negative, we take x = 1.

Answer: Therefore the width of the pathway is 1 m.

Example 2: Rita throws a ball upwards from a platform that is 20m above the ground. The height of the ball from the ground at a time 't', is denoted by 'h'. Suppose h = -4t 2 + 16t + 20. Find the maximum height attained by the ball.

We can rearrange the terms of the quadratic equation

h = -4t 2 + 16t + 20

in such a way that it is easy to find the maximum value of this equation.

= -4t 2 + 16t + 20

= -4(t 2 - 4t - 5)

= -4((t - 2) 2 - 9)

= -4(t - 2) 2 + 36

We should keep the value of (t - 2) 2 minimum in order to find the maximum value of h.

So, the minimum value (t - 2) 2 can take is 0.

Answer: Therefore the maximum height attained is 36m.

Example 3: Find the quadratic equation having the roots 5 and 8 respectively.

The quadratic equation having the roots α, β, is x 2 - (α + β)x + αβ = 0.

Given α = 5, and β = 8.

Therefore the quadratic equation is:

x 2 - (5 + 8)x + 5×8 = 0

x 2 - 13x + 40 = 0

Answer: Hence the required quadratic equation is x 2 - 13x + 40 = 0

Example 4: The quad equation 2x 2 + 9x + 7 = 0 has roots α, β. Find the quadratic equation having the roots 1/α, and 1/β.

The quadratic equation having roots that are reciprocal to the roots of the equation ax 2 + bx + c = 0, is cx 2 + bx + a = 0.

The given quadratic equation is 2x 2 + 9x + 7 = 0.

Hence the required equation having reciprocal roots is 7x 2 + 9x + 2 = 0.

Method 2: From the given equation,

α + β = -9/2 and α β = 2/7.

The new equation should have its roots to be 1/α and 1/β.

Their sum = 1/α + 1/β = (α + β) / α β = -9/7 Their product = 1/α β = 2/7 Thus, the required equation is, x 2 - (1/α + 1/β)x + 1/α β = 0 x 2 - (-9/7)x + 2/7 = 0 Multiplying both sides by 7, 7x 2 + 9x + 2 = 0

Answer: Therefore the equation is 7x 2 + 9x + 2 = 0.

go to slide go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Quadratic Equation

go to slide go to slide

FAQs on Quadratic Equation

What is the definition of a quadratic equation.

A quadratic equation in math is a second-degree equation of the form ax 2 + bx + c = 0. Here a and b are the coefficients, c is the constant term, and x is the variable. Since the variable x is of the second degree, there are two roots or answers for this quadratic equation. The roots of the quadratic equation can be found by either solving by factorizing or through the use of the quadratic formula.

What is the Quadratic Formula?

The quadratic equation formula to solve the equation ax 2 + bx + c = 0 is x = [-b ± √(b 2 - 4ac)]/2a. Here we obtain the two values of x, by applying the plus and minus symbols in this formula. Hence the two possible values of x are [-b + √(b 2 - 4ac)]/2a, and [-b - √(b 2 - 4ac)]/2a.

How do You Solve a Quadratic Equation?

There are several methods to solve quadratic equations, but the most common ones are factoring, using the quadratic formula, and completing the square.

• Factoring involves finding two numbers that multiply to equal the constant term, c, and add up to the coefficient of x, b.
• The quadratic formula is used when factoring is not possible, and it is given by x = [-b ± √(b 2 - 4ac)]/2a.
• Completing the square involves rewriting the quadratic equation in a different form that allows you to easily solve for x.

What is Determinant in Quadratic Formula?

The value b 2 - 4ac is called the discriminant and is designated as D. The discriminant is part of the quadratic formula. The discriminants help us to find the nature of the roots of the quadratic equation, without actually finding the roots of the quadratic equation.

What are Some Real-Life Applications of Quadratic Equations?

Quadratic equations are used to find the zeroes of the parabola and its axis of symmetry . There are many real-world applications of quadratic equations.

• They can be used in running time problems to evaluate the speed, distance or time while traveling by car, train or plane.
• Quadratic equations describe the relationship between quantity and the price of a commodity.
• Similarly, demand and cost calculations are also considered quadratic equation problems.
• It can also be noted that a satellite dish or a reflecting telescope has a shape that is defined by a quadratic equation.

How are Quadratic Equations Different From Linear Equations?

A linear degree is an equation of a single degree and one variable, and a quadratic equation is an equation in two degrees and a single variable. A linear equation is of the the form ax + b = 0 and a quadratic equation is of the form ax 2 + bx + c = 0. A linear equation has a single root and a quadratic equation has two roots or two answers. Also, a quadratic equation is a product of two linear equations.

What Are the 4 Ways To Solve A Quadratic Equation?

The four ways of solving a quadratic equation are as follows.

• Factorizing method
• Roots of Quadratic Equation Formula Method
• Method of Completing Squares
• Graphing Method

How to Solve a Quadratic Equation by Completing the Square?

The quadratic equation is solved by the method of completing the square and it uses the formula (a + b)^2 = a 2 + 2ab + b 2 (or) (a - b)^2 = a 2 - 2ab + b 2 .

How to Find the Value of the Discriminant?

The value of the discriminant in a quadratic equation can be found from the variables and constant terms of the standard form of the quadratic equation ax 2 + bx + c = 0. The value of the discriminant is D = b 2 - 4ac, and it helps to predict the nature of roots of the quadratic equation, without actually finding the roots of the equation.

How Do You Solve Quadratic Equations With Graphing?

The quadratic equation can be solved similarly to a linear equal by graphing. Let us take the quadratic equation ax 2 + bx + c = 0 as y = ax 2 + bx + c . Here we take the set of values of x and y and plot the graph. The two points where this graph meets the x-axis, are the solutions of this quadratic equation.

How Important Is the Discriminant of a Quadratic Equation?

The discriminant is very much needed to easily find the nature of the roots of the quadratic equation. Without the discriminant, finding the nature of the roots of the equation is a long process, as we first need to solve the equation to find both the roots. Hence the discriminant is an important and needed quantity, which helps to easily find the nature of the roots of the quadratic equation.

Where Can I Find Quadratic Equation Solver?

To get the quadratic equation solver, click here . Here, we can enter the values of a, b, and c for the quadratic equation ax 2 + bx + c = 0, then it will give you the roots along with a step-by-step procedure.

What is the Use of Discriminants in Quadratic Formula?

The discriminant (D = b 2 - 4ac) is useful to predict the nature of the roots of the quadratic equation. For D > 0, the roots are real and distinct, for D = 0 the roots are real and equal, and for D < 0, the roots do not exist or the roots are imaginary complex numbers . With the help of this discriminant and with the least calculations, we can find the nature of the roots of the quadratic equation.

How do you Solve a Quadratic Equation without Using the Quadratic Formula?

There are two alternative methods to the quadratic formula. One method is to solve the quadratic equation through factorization, and another method is by completing the squares. In total there are three methods to find the roots of a quadratic equation.

How to Derive Quadratic Formula?

The algebra formula (a + b) 2 = a 2 + 2ab + b 2 is used to solve the quadratic equation and derive the quadratic formula. This algebraic formula is used to manipulate the quadratic equation and derive the quadratic formula to find the roots of the equation.

• Math Article

Quadratics or Quadratic Equations

Quadratics   can be defined as a polynomial equation of a second degree, which implies that it comprises a minimum of one term that is squared. It is also called quadratic equations . The general form of the quadratic equation is: 

ax² + bx + c = 0

where x is an unknown variable and a, b, c are numerical coefficients. For example, x 2 + 2x +1 is a quadratic or quadratic equation. Here, a ≠ 0 because if it equals zero then the equation will not remain quadratic anymore and it will become a linear equation, such as: 

Thus, this equation cannot be called a quadratic equation.

The terms a, b and c are also called quadratic coefficients. 

The solutions to the quadratic equation are the values of the unknown variable x, which satisfy the equation. These solutions are called roots or zeros of quadratic equations . The roots of any polynomial are the solutions for the given equation.

What is Quadratic Equation?

The polynomial equation whose highest degree is two is called a quadratic equation or sometimes just quadratics. It is expressed in the form of:

where x is the unknown variable and a, b and c are the constant terms.

Standard Form of Quadratic Equation

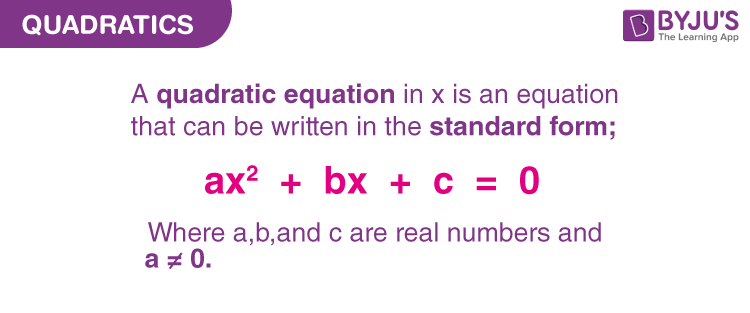
Since the quadratic includes only one unknown term or variable, thus it is called univariate. The power of variable x is always non-negative integers. Hence the equation is a polynomial equation with the highest power as 2.

The solution for this equation is the values of x, which are also called zeros. Zeros of the polynomial are the solution for which the equation is satisfied. In the case of quadratics, there are two roots or zeros of the equation. And if we put the values of roots or x on the left-hand side of the equation, it will equal to zero. Therefore, they are called zeros.

Quadratics Formula

The formula for a quadratic equation is used to find the roots of the equation. Since quadratics have a degree equal to two, therefore there will be two solutions for the equation. Suppose ax² + bx + c = 0 is the quadratic equation, then the formula to find the roots of this equation will be:

x = [-b±√(b 2 -4ac)]/2a

The sign of plus/minus indicates there will be two solutions for x. Learn in detail the quadratic formula here.

Examples of Quadratics

Beneath are the illustrations of quadratic equations of the form (ax² + bx + c = 0)

• x² –x – 9 = 0
• 5x² – 2x – 6 = 0
• 3x² + 4x + 8 = 0
• -x² +6x + 12 = 0

Examples of a quadratic equation with the absence of a ‘ C ‘- a constant term.

• -x² – 9x = 0
• x² + 2x = 0
• -6x² – 3x = 0
• -5x² + x = 0
• -12x² + 13x = 0
• 11x² – 27x = 0

Following are the examples of a quadratic equation in factored form

• (x – 6)(x + 1) = 0  [ result obtained after solving is x² – 5x – 6 = 0]
• –3(x – 4)(2x + 3) = 0  [result obtained after solving is -6x² + 15x + 36 = 0]
• (x − 5)(x + 3) = 0  [result obtained after solving is x² − 2x − 15 = 0]
• (x – 5)(x + 2) = 0  [ result obtained after solving is x² – 3x – 10 = 0]
• (x – 4)(x + 2) = 0  [result obtained after solving is x² – 2x – 8 = 0]
• (2x+3)(3x – 2) = 0  [result obtained after solving is 6x² + 5x – 6]

Below are the examples of a quadratic equation with an absence of linear co – efficient ‘ bx’

• 2x² – 64 = 0
• x² – 16 = 0
• 9x² + 49 = 0
• -2x² – 4 = 0
• 4x² + 81 = 0
• -x² – 9 = 0

How to Solve Quadratic Equations?

There are basically four methods of solving quadratic equations. They are:

• Completing the square

Using Quadratic Formula

• Taking the square root

Factoring of Quadratics

• Begin with a equation of the form ax² + bx + c = 0
• Ensure that it is set to adequate zero.
• Factor the left-hand side of the equation by assuming zero on the right-hand side of the equation.
• Assign each factor equal to zero.
• Now solve the equation in order to determine the values of x.

Suppose if the main coefficient is not equal to one then deliberately, you have to follow a methodology in the arrangement of the factors.

(2x+3)(x-2)=0

Learn more about the factorization of quadratic equations here.

Completing the Square Method

Let us learn this method with example.

Example: Solve 2x 2 – x – 1 = 0.

First, move the constant term to the other side of the equation.

2x 2 – x = 1

Dividing both sides by 2.

x 2 – x/2 = ½

Add the square of half of the coefficient of x, (b/2a) 2 , on both the sides, i.e., 1/16

x 2 – x/2 + 1/16 = ½ + 1/16

Now we can factor the right side,

(x-¼) 2 = 9/16 = (¾) 2

Taking root on both sides;

X – ¼ = ±3/4

Add ¼ on both sides

X = ¼ + ¾ = 4/4 = 1

X = ¼ – ¾ = -2/4 = -½ 

To learn more about completing the square method, click here .

For the given Quadratic equation of the form, ax² + bx + c = 0

Therefore the roots of the given equation can be found by:

\(\begin{array}{l}x = \frac{-b \pm \sqrt{b^{2}-4ac}}{2a}\end{array} \)

where ± (one plus and one minus) represent two distinct roots of the given equation.

Taking the Square Root

We can use this method for the equations such as:

x 2 + a 2 = 0

Example: Solve x 2 – 50 = 0.

x 2 – 50 = 0

Taking the roots both sides

√x 2 = ±√50

x = ±√(2 x 5 x 5)

Thus, we got the required solution.

Related Articles

Video lesson on quadratic equations, range of quadratic equations.

Solved Problems on Quadratic Equations

Applications of quadratic equations.

Many real-life word problems can be solved using quadratic equations. While solving word problems, some common quadratic equation applications include speed problems and Geometry area problems.

• Solving the problems related to finding the area of quadrilateral such as rectangle, parallelogram and so on
• Solving Word Problems involving Distance, speed, and time, etc.,

Example: Find the width of a rectangle of area 336 cm2 if its length is equal to the 4 more than twice its width. Solution: Let x cm be the width of the rectangle. Length = (2x + 4) cm We know that Area of rectangle = Length x Width x(2x + 4) = 336 2x 2 + 4x – 336 = 0 x 2 + 2x – 168 = 0 x 2 + 14x – 12x – 168 = 0 x(x + 14) – 12(x + 14) = 0 (x + 14)(x – 12) = 0 x = -14, x = 12 Measurement cannot be negative. Therefore, Width of the rectangle = x = 12 cm

Practice Questions

• Solve x 2 + 2 x + 1 = 0.
• Solve 5x 2 + 6x + 1 = 0
• Solve 2x 2 + 3 x + 2 = 0.
• Solve x 2 − 4x + 6.25 = 0

Frequently Asked Questions on Quadratics

What is a quadratic equation, what are the methods to solve a quadratic equation, is x 2 – 1 a quadratic equation, what is the solution of x 2 + 4 = 0, write the quadratic equation in the form of sum and product of roots., leave a comment cancel reply.

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Thanks a lot ,This was very useful for me

x=√9 Squaring both the sides, x^2 = 9 x^2 – 9 = 0 It is a quadratic equation.

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

In order to access this I need to be confident with:

This topic is relevant for:

Quadratic Formula

Here we will learn about the quadratic formula and how we can use it to solve quadratic equations.

There are also solving quadratic equations worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is the quadratic formula?

The quadratic formula is a formula that provides the solutions to quadratic equations.

This is the quadratic formula:

By using the general form of a quadratic equation:

we can substitute the values of a, b and c into the quadratic formula to work out x .

We need to memorise the quadratic formula.

The ± in front of the square root means ‘plus or minus’

Quadratic equations normally have two solutions, so we need to use the formula twice, once with a + and once with a −.

The solutions to quadratic equations could involve fractions, decimals or integers.

Quadratic formula worksheet

Get your free quadratic formula worksheet of 20+ questions and answers. Includes reasoning and applied questions.

Related lessons on quadratic equations

Quadratic formula  is part of our series of lessons to support revision on  quadratic equations and solving equations . You may find it helpful to start with the main solving equations lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

• Solving equations
• Quadratic equations
• Solving quadratic equations by factorising
• Completing the square

How to use the quadratic formula

In order to solve a quadratic equation by using the quadratic formula, it is a good idea to simplify it and make sure it is in the form of the general quadratic equation.

We must ensure the quadratic equation is equal to 0 , rearranging it if necessary.

Step by step guide: 

• Identify the value of  a , b and c .
• Substitute these values into the quadratic formula.
• Use a calculator to solve the equation with a + and then with a −.

Step-by-step guide: Substitution

Explain how to use the quadratic formula in 3 steps

Quadratic formula examples

Example 1: with a = 1.

• Identify the a, b and c .

2 Substitute these values into the quadratic formula .

Using brackets will help to make the calculation clear.

3 Use a calculator to solve the equation with a +, and then with a − .

When we plot the graph of the quadratic equation we get a special ‘U’ shaped curve called a parabola.

By using graphing techniques such as this we can see that the roots of the quadratic equation are where the quadratic graph crosses the x -axis .

We can check that our solution is correct by substituting it back into the quadratic function.

Example 2: with a > 1

Identify the a, b and c .

Substitute these values into the quadratic formula .

Use a calculator to solve the equation with a +, and then with a − .

We can see the roots of the quadratic equation are where the quadratic graph crosses the x -axis .

We can check that our solution is correct by substituting it into the original equation.

Common misconceptions

• When to use the quadratic formula

We can use the quadratic formula to solve quadratic equations regardless of whether the factorising (sometimes called factoring) method will work.

• Not including the sign in front of a , b and c

When writing the coefficients of the variables for the values of a, b and c , we need to include the sign in front but not the variable.

 So here b = − 8 , NOT 8 or − 8x

• Typing into calculator

Mistakes can be made when typing into a calculator. 

E.g. for 

Use the fraction button and brackets to carefully type into the calculator.

Use the arrow buttons to change the + on the top left of the calculation to a − to work out the second solution. 

• Sometimes there are no real roots to a quadratic equation

We can see that there are no values of x that give a y value of 0.

The graph does not cross the x -axis.

Not needed at GCSE but very interesting!

There is an easy way to find out how many real roots a quadratic equation has by using the expression under the square root in the quadratic formula:

This is called the discriminant :

this means there are two solutions (these are real numbers).

this means there is one solution (which is a real number).

this means there are no real solutions , here the solutions will be imaginary numbers.

Practice quadratic formula questions

We can use the quadratic formula with a=1, b=4 and c=3 . Make sure you find both solutions using the formula.

We can use the quadratic formula with a=1, b=3 and c=-18 . Make sure you find both solutions using the formula.

We can use the quadratic formula with a=2, b=-3 and c=-2 . Make sure you find both solutions using the formula.

We can use the quadratic formula with a=3, b=-4 and c=-5 . Make sure you find both solutions using the formula.

Quadratic formula GCSE questions

Give your answer to 2.d.p

Substitution into the quadratic formula

x=1.24 (2.d.p)

x=-3.24 (2.d.p)

Substitution into the quadratic formula or an attempt to factorise

x=\frac{1}{2} \quad

3 x^{2}+6 x-2=0

x=0.29 (2.d.p)

x=-2.29 (2.d.p)

Did you know?

• Did you know that Al-Khwarizmi (Abu Ja’far Muhammad ibn Musa al-Khwarizmi ) was one of the first people in history to write about algebra? He lived in Baghdad around 780 to 850 AD and his book “Hisab Al-jabr w’al-muqabala” is where we get the word ‘ algebra’ (meaning ‘restoration of broken parts’).

• Did you know the ancient Babylonians could solve quadratic equations using a method equivalent to the quadratic formula , despite not using algebraic notation! The history of mathematics is amazing!

Learning checklist

• Solve quadratic equations algebraically by using the quadratic formula (H)
• Solve quadratic equations by finding approximate solutions using a graph

The next lessons are

• Factorising
• Simultaneous equations
• Rearranging equations

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Privacy Overview

• Math Lessons
• Math Formulas
• Calculators

Math Calculators, Lessons and Formulas

It is time to solve your math problem

• HW Help (paid service)
• Radical expressions calculators
• Simplifying radical expressions

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line, algebra calculator.

The Algebra Calculator is a versatile online tool designed to simplify algebraic problem-solving for users of all levels. Here's how to make the most of it:

• Begin by typing your algebraic expression into the above input field, or scanning the problem with your camera.
• After entering the equation, click the 'Go' button to generate instant solutions.
• The calculator provides detailed step-by-step solutions, aiding in understanding the underlying concepts.
• -x+3\gt 2x+1
• (x+5)(x-5)\gt 0
• 10^{1-x}=10^4
• \sqrt{3+x}=-2
• 6+11x+6x^2+x^3=0
• factor\:x^{2}-5x+6
• simplify\:\frac{2}{3}-\frac{3}{2}+\frac{1}{4}
• x+2y=2x-5,\:x-y=3
• How do you solve algebraic expressions?
• To solve an algebraic expression, simplify the expression by combining like terms, isolate the variable on one side of the equation by using inverse operations. Then, solve the equation by finding the value of the variable that makes the equation true.
• What are the basics of algebra?
• The basics of algebra are the commutative, associative, and distributive laws.
• What are the 3 rules of algebra?
• The basic rules of algebra are the commutative, associative, and distributive laws.
• What is the golden rule of algebra?
• The golden rule of algebra states Do unto one side of the equation what you do to others. Meaning, whatever operation is being used on one side of equation, the same will be used on the other side too.
• What are the 5 basic laws of algebra?
• The basic laws of algebra are the Commutative Law For Addition, Commutative Law For Multiplication, Associative Law For Addition, Associative Law For Multiplication, and the Distributive Law.

algebra-calculator

• Middle School Math Solutions – Equation Calculator Welcome to our new "Getting Started" math solutions series. Over the next few weeks, we'll be showing how Symbolab...

Please add a message.

Message received. Thanks for the feedback.