solving systems of equations with three variables practice problems

4.4 Solve Systems of Equations with Three Variables

Learning objectives.

By the end of this section, you will be able to:

Determine whether an ordered triple is a solution of a system of three linear equations with three variables
Solve a system of linear equations with three variables
Solve applications using systems of linear equations with three variables

Be Prepared 4.10

Before you get started, take this readiness quiz.

Evaluate 5 x − 2 y + 3 z 5 x − 2 y + 3 z when x = −2 , x = −2 , y = −4 , y = −4 , and z = 3 . z = 3 . If you missed this problem, review Example 1.21 .

Be Prepared 4.11

Classify the equations as a conditional equation, an identity, or a contradiction and then state the solution. { − 2 x + y = −11 x + 3 y = 9 . { − 2 x + y = −11 x + 3 y = 9 . If you missed this problem, review Example 2.6 .

Be Prepared 4.12

Classify the equations as a conditional equation, an identity, or a contradiction and then state the solution. { 7 x + 8 y = 4 3 x − 5 y = 27 . { 7 x + 8 y = 4 3 x − 5 y = 27 . If you missed this problem, review Example 2.8 .

Determine Whether an Ordered Triple is a Solution of a System of Three Linear Equations with Three Variables

In this section, we will extend our work of solving a system of linear equations. So far we have worked with systems of equations with two equations and two variables. Now we will work with systems of three equations with three variables. But first let's review what we already know about solving equations and systems involving up to two variables.

We learned earlier that the graph of a linear equation , a x + b y = c , a x + b y = c , is a line. Each point on the line, an ordered pair ( x , y ) , ( x , y ) , is a solution to the equation. For a system of two equations with two variables, we graph two lines. Then we can see that all the points that are solutions to each equation form a line. And, by finding what the lines have in common, we’ll find the solution to the system.

Most linear equations in one variable have one solution, but we saw that some equations, called contradictions, have no solutions and for other equations, called identities, all numbers are solutions

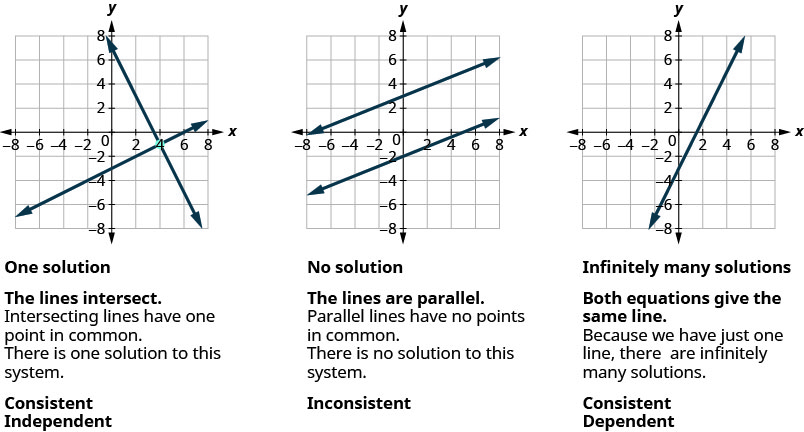
We know when we solve a system of two linear equations represented by a graph of two lines in the same plane, there are three possible cases, as shown.

Similarly, for a linear equation with three variables a x + b y + c z = d , a x + b y + c z = d , every solution to the equation is an ordered triple, ( x , y , z ) ( x , y , z ) , that makes the equation true.

Linear Equation in Three Variables

A linear equation with three variables, where a, b, c, and d are real numbers and a, b , and c are not all 0, is of the form

Every solution to the equation is an ordered triple, ( x , y , z ) ( x , y , z ) that makes the equation true.

All the points that are solutions to one equation form a plane in three-dimensional space. And, by finding what the planes have in common, we’ll find the solution to the system.

When we solve a system of three linear equations represented by a graph of three planes in space, there are three possible cases.

To solve a system of three linear equations, we want to find the values of the variables that are solutions to all three equations. In other words, we are looking for the ordered triple ( x , y , z ) ( x , y , z ) that makes all three equations true. These are called the solutions of the system of three linear equations with three variables .

Solutions of a System of Linear Equations with Three Variables

Solutions of a system of equations are the values of the variables that make all the equations true. A solution is represented by an ordered triple ( x , y , z ) . ( x , y , z ) .

To determine if an ordered triple is a solution to a system of three equations, we substitute the values of the variables into each equation. If the ordered triple makes all three equations true, it is a solution to the system.

Example 4.31

Determine whether the ordered triple is a solution to the system: { x − y + z = 2 2 x − y − z = −6 2 x + 2 y + z = −3 . { x − y + z = 2 2 x − y − z = −6 2 x + 2 y + z = −3 .

ⓐ ( −2 , −1 , 3 ) ( −2 , −1 , 3 ) ⓑ ( −4 , −3 , 4 ) ( −4 , −3 , 4 )

Try It 4.61

Determine whether the ordered triple is a solution to the system: { 3 x + y + z = 2 x + 2 y + z = −3 3 x + y + 2 z = 4 . { 3 x + y + z = 2 x + 2 y + z = −3 3 x + y + 2 z = 4 .

ⓐ ( 1 , −3 , 2 ) ( 1 , −3 , 2 ) ⓑ ( 4 , −1 , −5 ) ( 4 , −1 , −5 )

Try It 4.62

Determine whether the ordered triple is a solution to the system: { x − 3 y + z = −5 − 3 x − y − z = 1 2 x − 2 y + 3 z = 1 . { x − 3 y + z = −5 − 3 x − y − z = 1 2 x − 2 y + 3 z = 1 .

ⓐ ( 2 , −2 , 3 ) ( 2 , −2 , 3 ) ⓑ ( −2 , 2 , 3 ) ( −2 , 2 , 3 )

Solve a System of Linear Equations with Three Variables

To solve a system of linear equations with three variables, we basically use the same techniques we used with systems that had two variables. We start with two pairs of equations and in each pair we eliminate the same variable. This will then give us a system of equations with only two variables and then we know how to solve that system!

Next, we use the values of the two variables we just found to go back to the original equation and find the third variable. We write our answer as an ordered triple and then check our results.

Example 4.32

How to solve a system of equations with three variables by elimination.

Solve the system by elimination: { x − 2 y + z = 3 2 x + y + z = 4 3 x + 4 y + 3 z = −1 . { x − 2 y + z = 3 2 x + y + z = 4 3 x + 4 y + 3 z = −1 .

Try It 4.63

Solve the system by elimination: { 3 x + y − z = 2 2 x − 3 y − 2 z = 1 4 x − y − 3 z = 0 . { 3 x + y − z = 2 2 x − 3 y − 2 z = 1 4 x − y − 3 z = 0 .

Try It 4.64

Solve the system by elimination: { 4 x + y + z = −1 − 2 x − 2 y + z = 2 2 x + 3 y − z = 1 . { 4 x + y + z = −1 − 2 x − 2 y + z = 2 2 x + 3 y − z = 1 .

The steps are summarized here.

Solve a system of linear equations with three variables.

If any coefficients are fractions, clear them.
Decide which variable you will eliminate.
Work with a pair of equations to eliminate the chosen variable.
Multiply one or both equations so that the coefficients of that variable are opposites.
Add the equations resulting from Step 2 to eliminate one variable
Step 3. Repeat Step 2 using two other equations and eliminate the same variable as in Step 2.
Step 4. The two new equations form a system of two equations with two variables. Solve this system.
Step 5. Use the values of the two variables found in Step 4 to find the third variable.
Step 6. Write the solution as an ordered triple.
Step 7. Check that the ordered triple is a solution to all three original equations.

Example 4.33

Solve: { 3 x − 4 z = 0 3 y + 2 z = −3 2 x + 3 y = −5 . { 3 x − 4 z = 0 3 y + 2 z = −3 2 x + 3 y = −5 .

We can eliminate z z from equations (1) and (2) by multiplying equation (2) by 2 and then adding the resulting equations.

Notice that equations (3) and (4) both have the variables x x and y y . We will solve this new system for x x and y y .

To solve for y , we substitute x = −4 x = −4 into equation (3).

We now have x = −4 x = −4 and y = 1 . y = 1 . We need to solve for z . We can substitute x = −4 x = −4 into equation (1) to find z .

We write the solution as an ordered triple. ( −4 , 1 , −3 ) ( −4 , 1 , −3 )

We check that the solution makes all three equations true.

3 x − 4 z = 0 ( 1 ) 3 ( −4 ) − 4 ( −3 ) = ? 0 0 = 0 ✓ 3 y + 2 z = −3 ( 2 ) 3 ( 1 ) + 2 ( −3 ) = ? − 3 −3 = −3 ✓ 2 x + 3 y = −5 ( 3 ) 2 ( −4 ) + 3 ( 1 ) = ? − 5 −5 = −5 ✓ The solution is ( −4 , 1 , −3 ) . 3 x − 4 z = 0 ( 1 ) 3 ( −4 ) − 4 ( −3 ) = ? 0 0 = 0 ✓ 3 y + 2 z = −3 ( 2 ) 3 ( 1 ) + 2 ( −3 ) = ? − 3 −3 = −3 ✓ 2 x + 3 y = −5 ( 3 ) 2 ( −4 ) + 3 ( 1 ) = ? − 5 −5 = −5 ✓ The solution is ( −4 , 1 , −3 ) .

Try It 4.65

Solve: { 3 x − 4 z = −1 2 y + 3 z = 2 2 x + 3 y = 6 . { 3 x − 4 z = −1 2 y + 3 z = 2 2 x + 3 y = 6 .

Try It 4.66

Solve: { 4 x − 3 z = −5 3 y + 2 z = 7 3 x + 4 y = 6 . { 4 x − 3 z = −5 3 y + 2 z = 7 3 x + 4 y = 6 .

When we solve a system and end up with no variables and a false statement, we know there are no solutions and that the system is inconsistent. The next example shows a system of equations that is inconsistent.

Example 4.34

Solve the system of equations: { x + 2 y − 3 z = −1 x − 3 y + z = 1 2 x − y − 2 z = 2 . { x + 2 y − 3 z = −1 x − 3 y + z = 1 2 x − y − 2 z = 2 .

Use equation (1) and (2) to eliminate z .

Use (2) and (3) to eliminate z z again.

Use (4) and (5) to eliminate a variable.

There is no solution.

We are left with a false statement and this tells us the system is inconsistent and has no solution.

Try It 4.67

Solve the system of equations: { x + 2 y + 6 z = 5 − x + y − 2 z = 3 x − 4 y − 2 z = 1 . { x + 2 y + 6 z = 5 − x + y − 2 z = 3 x − 4 y − 2 z = 1 .

Try It 4.68

Solve the system of equations: { 2 x − 2 y + 3 z = 6 4 x − 3 y + 2 z = 0 − 2 x + 3 y − 7 z = 1 . { 2 x − 2 y + 3 z = 6 4 x − 3 y + 2 z = 0 − 2 x + 3 y − 7 z = 1 .

When we solve a system and end up with no variables but a true statement, we know there are infinitely many solutions. The system is consistent with dependent equations. Our solution will show how two of the variables depend on the third.

Example 4.35

Solve the system of equations: { x + 2 y − z = 1 2 x + 7 y + 4 z = 11 x + 3 y + z = 4 . { x + 2 y − z = 1 2 x + 7 y + 4 z = 11 x + 3 y + z = 4 .

Use equation (1) and (3) to eliminate x .

Use equation (1) and (2) to eliminate x again.

Use equation (4) and (5) to eliminate y y .

	There are infinitely many solutions.
Solve equation (4) for .	Represent the solution showing how and are dependent on .
Use equation (1) to solve for .
Substitute

The true statement 0 = 0 0 = 0 tells us that this is a dependent system that has infinitely many solutions. The solutions are of the form ( x , y , z ) ( x , y , z ) where x = 5 z − 5 ; y = −2 z + 3 x = 5 z − 5 ; y = −2 z + 3 and z is any real number.

Try It 4.69

Solve the system by equations: { x + y − z = 0 2 x + 4 y − 2 z = 6 3 x + 6 y − 3 z = 9 . { x + y − z = 0 2 x + 4 y − 2 z = 6 3 x + 6 y − 3 z = 9 .

Try It 4.70

Solve the system by equations: { x − y − z = 1 − x + 2 y − 3 z = −4 3 x − 2 y − 7 z = 0 . { x − y − z = 1 − x + 2 y − 3 z = −4 3 x − 2 y − 7 z = 0 .

Solve Applications using Systems of Linear Equations with Three Variables

Applications that are modeled by a systems of equations can be solved using the same techniques we used to solve the systems. Many of the application are just extensions to three variables of the types we have solved earlier.

Example 4.36

The community college theater department sold three kinds of tickets to its latest play production. The adult tickets sold for $15, the student tickets for $10 and the child tickets for $8. The theater department was thrilled to have sold 250 tickets and brought in $2,825 in one night. The number of student tickets sold is twice the number of adult tickets sold. How many of each type did the department sell?

We will use a chart to organize the information.
Number of students is twice number of adults.
Rewrite the equation in standard form.

Use equations (1) and (2) to eliminate .

Use (3) and (4) to eliminate

Solve for .	adult tickets
Use equation (3) to find .
Substitute
Use equation (1) to find .
Substitute in the values
Write the solution.	The theater department sold 75 adult tickets, 150 student tickets, and 25 child tickets.

Try It 4.71

The community college fine arts department sold three kinds of tickets to its latest dance presentation. The adult tickets sold for $20, the student tickets for $12 and the child tickets for $10.The fine arts department was thrilled to have sold 350 tickets and brought in $4,650 in one night. The number of child tickets sold is the same as the number of adult tickets sold. How many of each type did the department sell?

Try It 4.72

The community college soccer team sold three kinds of tickets to its latest game. The adult tickets sold for $10, the student tickets for $8 and the child tickets for $5. The soccer team was thrilled to have sold 600 tickets and brought in $4,900 for one game. The number of adult tickets is twice the number of child tickets. How many of each type did the soccer team sell?

Access this online resource for additional instruction and practice with solving a linear system in three variables with no or infinite solutions.

Solving a Linear System in Three Variables with No or Infinite Solutions
3 Variable Application

Section 4.4 Exercises

Practice makes perfect.

In the following exercises, determine whether the ordered triple is a solution to the system.

{ 2 x − 6 y + z = 3 3 x − 4 y − 3 z = 2 2 x + 3 y − 2 z = 3 { 2 x − 6 y + z = 3 3 x − 4 y − 3 z = 2 2 x + 3 y − 2 z = 3

ⓐ ( 3 , 1 , 3 ) ( 3 , 1 , 3 ) ⓑ ( 4 , 3 , 7 ) ( 4 , 3 , 7 )

{ − 3 x + y + z = −4 − x + 2 y − 2 z = 1 2 x − y − z = −1 { − 3 x + y + z = −4 − x + 2 y − 2 z = 1 2 x − y − z = −1

ⓐ ( −5 , −7 , 4 ) ( −5 , −7 , 4 ) ⓑ ( 5 , 7 , 4 ) ( 5 , 7 , 4 )

{ y − 10 z = −8 2 x − y = 2 x − 5 z = 3 { y − 10 z = −8 2 x − y = 2 x − 5 z = 3

ⓐ ( 7 , 12 , 2 ) ( 7 , 12 , 2 ) ⓑ ( 2 , 2 , 1 ) ( 2 , 2 , 1 )

{ x + 3 y − z = 15 y = 2 3 x − 2 x − 3 y + z = −2 { x + 3 y − z = 15 y = 2 3 x − 2 x − 3 y + z = −2

ⓐ ( −6 , 5 , 1 2 ) ( −6 , 5 , 1 2 ) ⓑ ( 5 , 4 3 , −3 ) ( 5 , 4 3 , −3 )

In the following exercises, solve the system of equations.

{ 5 x + 2 y + z = 5 − 3 x − y + 2 z = 6 2 x + 3 y − 3 z = 5 { 5 x + 2 y + z = 5 − 3 x − y + 2 z = 6 2 x + 3 y − 3 z = 5

{ 6 x − 5 y + 2 z = 3 2 x + y − 4 z = 5 3 x − 3 y + z = −1 { 6 x − 5 y + 2 z = 3 2 x + y − 4 z = 5 3 x − 3 y + z = −1

{ 2 x − 5 y + 3 z = 8 3 x − y + 4 z = 7 x + 3 y + 2 z = −3 { 2 x − 5 y + 3 z = 8 3 x − y + 4 z = 7 x + 3 y + 2 z = −3

{ 5 x − 3 y + 2 z = −5 2 x − y − z = 4 3 x − 2 y + 2 z = −7 { 5 x − 3 y + 2 z = −5 2 x − y − z = 4 3 x − 2 y + 2 z = −7

{ 3 x − 5 y + 4 z = 5 5 x + 2 y + z = 0 2 x + 3 y − 2 z = 3 { 3 x − 5 y + 4 z = 5 5 x + 2 y + z = 0 2 x + 3 y − 2 z = 3

{ 4 x − 3 y + z = 7 2 x − 5 y − 4 z = 3 3 x − 2 y − 2 z = −7 { 4 x − 3 y + z = 7 2 x − 5 y − 4 z = 3 3 x − 2 y − 2 z = −7

{ 3 x + 8 y + 2 z = −5 2 x + 5 y − 3 z = 0 x + 2 y − 2 z = −1 { 3 x + 8 y + 2 z = −5 2 x + 5 y − 3 z = 0 x + 2 y − 2 z = −1

{ 11 x + 9 y + 2 z = −9 7 x + 5 y + 3 z = −7 4 x + 3 y + z = −3 { 11 x + 9 y + 2 z = −9 7 x + 5 y + 3 z = −7 4 x + 3 y + z = −3

{ 1 3 x − y − z = 1 x + 5 2 y + z = −2 2 x + 2 y + 1 2 z = −4 { 1 3 x − y − z = 1 x + 5 2 y + z = −2 2 x + 2 y + 1 2 z = −4

{ x + 1 2 y + 1 2 z = 0 1 5 x − 1 5 y + z = 0 1 3 x − 1 3 y + 2 z = −1 { x + 1 2 y + 1 2 z = 0 1 5 x − 1 5 y + z = 0 1 3 x − 1 3 y + 2 z = −1

{ x + 1 3 y − 2 z = −1 1 3 x + y + 1 2 z = 0 1 2 x + 1 3 y − 1 2 z = −1 { x + 1 3 y − 2 z = −1 1 3 x + y + 1 2 z = 0 1 2 x + 1 3 y − 1 2 z = −1

{ 1 3 x − y + 1 2 z = 4 2 3 x + 5 2 y − 4 z = 0 x − 1 2 y + 3 2 z = 2 { 1 3 x − y + 1 2 z = 4 2 3 x + 5 2 y − 4 z = 0 x − 1 2 y + 3 2 z = 2

{ x + 2 z = 0 4 y + 3 z = −2 2 x − 5 y = 3 { x + 2 z = 0 4 y + 3 z = −2 2 x − 5 y = 3

{ 2 x + 5 y = 4 3 y − z = 3 4 x + 3 z = −3 { 2 x + 5 y = 4 3 y − z = 3 4 x + 3 z = −3

{ 2 y + 3 z = −1 5 x + 3 y = −6 7 x + z = 1 { 2 y + 3 z = −1 5 x + 3 y = −6 7 x + z = 1

{ 3 x − z = −3 5 y + 2 z = −6 4 x + 3 y = −8 { 3 x − z = −3 5 y + 2 z = −6 4 x + 3 y = −8

{ 4 x − 3 y + 2 z = 0 − 2 x + 3 y − 7 z = 1 2 x − 2 y + 3 z = 6 { 4 x − 3 y + 2 z = 0 − 2 x + 3 y − 7 z = 1 2 x − 2 y + 3 z = 6

{ x − 2 y + 2 z = 1 − 2 x + y − z = 2 x − y + z = 5 { x − 2 y + 2 z = 1 − 2 x + y − z = 2 x − y + z = 5

{ 2 x + 3 y + z = 12 x + y + z = 9 3 x + 4 y + 2 z = 20 { 2 x + 3 y + z = 12 x + y + z = 9 3 x + 4 y + 2 z = 20

{ x + 4 y + z = −8 4 x − y + 3 z = 9 2 x + 7 y + z = 0 { x + 4 y + z = −8 4 x − y + 3 z = 9 2 x + 7 y + z = 0

{ x + 2 y + z = 4 x + y − 2 z = 3 − 2 x − 3 y + z = −7 { x + 2 y + z = 4 x + y − 2 z = 3 − 2 x − 3 y + z = −7

{ x + y − 2 z = 3 − 2 x − 3 y + z = −7 x + 2 y + z = 4 { x + y − 2 z = 3 − 2 x − 3 y + z = −7 x + 2 y + z = 4

{ x + y − 3 z = −1 y − z = 0 − x + 2 y = 1 { x + y − 3 z = −1 y − z = 0 − x + 2 y = 1

{ x − 2 y + 3 z = 1 x + y − 3 z = 7 3 x − 4 y + 5 z = 7 { x − 2 y + 3 z = 1 x + y − 3 z = 7 3 x − 4 y + 5 z = 7

In the following exercises, solve the given problem.

The sum of the measures of the angles of a triangle is 180. The sum of the measures of the second and third angles is twice the measure of the first angle. The third angle is twelve more than the second. Find the measures of the three angles.

The sum of the measures of the angles of a triangle is 180. The sum of the measures of the second and third angles is three times the measure of the first angle. The third angle is fifteen more than the second. Find the measures of the three angles.

After watching a major musical production at the theater, the patrons can purchase souvenirs. If a family purchases 4 t-shirts, the video, and 1 stuffed animal, their total is $135.

A couple buys 2 t-shirts, the video, and 3 stuffed animals for their nieces and spends $115. Another couple buys 2 t-shirts, the video, and 1 stuffed animal and their total is $85. What is the cost of each item?

The church youth group is selling snacks to raise money to attend their convention. Amy sold 2 pounds of candy, 3 boxes of cookies and 1 can of popcorn for a total sales of $65. Brian sold 4 pounds of candy, 6 boxes of cookies and 3 cans of popcorn for a total sales of $140. Paulina sold 8 pounds of candy, 8 boxes of cookies and 5 cans of popcorn for a total sales of $250. What is the cost of each item?

Writing Exercises

In your own words explain the steps to solve a system of linear equations with three variables by elimination.

How can you tell when a system of three linear equations with three variables has no solution? Infinitely many solutions?

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ On a scale of 1-10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction

Authors: Lynn Marecek, Andrea Honeycutt Mathis
Publisher/website: OpenStax
Book title: Intermediate Algebra 2e
Publication date: May 6, 2020
Location: Houston, Texas
Book URL: https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
Section URL: https://openstax.org/books/intermediate-algebra-2e/pages/4-4-solve-systems-of-equations-with-three-variables

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Site Navigation


Unless it is given, translate the problem into a of 3 equations using 3 variables. Solve the and answer the question.

Marina had $24,500 to invest. She divided the money into three different accounts. At the end of the year, she had made $1,300 in interest. The annual on each of the three accounts was 4%, 5.5%, and 6%. If the amount of money in the 4% account was four times the amount of money in the 5.5% account, how much had she placed in each account?

The currents running through an electrical are given by the following of equations. The three currents, I1, I2, and I3, are measured in amps. Solve the to find the currents in this circuit. + 2I - I = 0.425
3I - I + 2I = 2.225
5I + I + 2I = 3.775

Find the of the parabola,y = ax + bx + c, that passes through the following three points:
(-2, 40), (1, 7), (3, 15).

Billy’s Restaurant ordered 200 flowers for Mother’s Day. They ordered carnations at $1.50 each, roses at $5.75 each, and daisies at $2.60 each. They ordered mostly carnations, and 20 fewer roses than daisies. The total order came to $589.50. How many of each type of flower was ordered?

The Arcadium arcade in Lynchburg, Tennessee uses 3 different colored tokens for their game machines. For $20 you can purchase any of the following mixtures of tokens: 14 gold, 20 silver, and 24 bronze; OR, 20 gold, 15 silver, and 19 bronze; OR, 30 gold, 5 silver, and 13 bronze. What is the monetary value of each token?

In the position for vertical height, s(t) = ½at + v t + s , s(t)represents in meters and t represents time in seconds.

(a) Find the position for a volleyball served at an initial of one meter, with of 6.275 meters ½ second after serve, and of 9.1 meters one second after serve.
(b) How long until the ball hits the ground on the other of the if everyone on that team completely misses it?

Last Tuesday, Regal Cinemas sold a total of 8500 movie tickets. Proceeds totaled $64,600. Tickets can be bought in one of 3 ways: a matinee admission costs $5, student admission is $6 all day, and regular admissions are $8.50. How many of each type of ticket was sold if twice as many student tickets were sold as matinee tickets?

   Catharine H. Colwell
Application Programmers
   Jeremy R. Blawn
   Mark Acton
Copyright © 2003-2024
All rights reserved.

Child Login

Kindergarten
Number charts
Skip Counting
Place Value
Number Lines
Subtraction
Multiplication
Word Problems
Comparing Numbers
Ordering Numbers
Odd and Even
Prime and Composite
Roman Numerals
Ordinal Numbers
In and Out Boxes
Number System Conversions
More Number Sense Worksheets
Size Comparison
Measuring Length
Metric Unit Conversion
Customary Unit Conversion
Temperature
More Measurement Worksheets
Writing Checks
Profit and Loss
Simple Interest
Compound Interest
Tally Marks
Mean, Median, Mode, Range
Mean Absolute Deviation
Stem-and-leaf Plot
Box-and-whisker Plot
Permutation and Combination
Probability
Venn Diagram
More Statistics Worksheets
Shapes - 2D
Shapes - 3D
Lines, Rays and Line Segments
Points, Lines and Planes
Transformation
Quadrilateral
Ordered Pairs
Midpoint Formula
Distance Formula
Parallel, Perpendicular and Intersecting Lines
Scale Factor
Surface Area
Pythagorean Theorem
More Geometry Worksheets
Converting between Fractions and Decimals
Significant Figures
Convert between Fractions, Decimals, and Percents
Proportions
Direct and Inverse Variation
Order of Operations
Squaring Numbers
Square Roots
Scientific Notations
Speed, Distance, and Time
Absolute Value
More Pre-Algebra Worksheets
Translating Algebraic Phrases
Evaluating Algebraic Expressions
Simplifying Algebraic Expressions
Algebraic Identities
Quadratic Equations
Systems of Equations
Polynomials
Inequalities
Sequence and Series
Complex Numbers
More Algebra Worksheets
Trigonometry
Math Workbooks
English Language Arts
Summer Review Packets
Social Studies
Holidays and Events
Worksheets >
Algebra >
Equations >
Systems of Equations >
Three Variables

Systems of Equations with Three Variables Worksheets

Focusing on solving systems of equations with three variables, this assemblage of printable worksheets provides immense practice to high school students. Featured here are simultaneous equations to be solved using the substitution method, the elimination method, Cramer's rule, and involves reciprocal equations as well. Included here is a review section allowing students to use a method of their choice. Click on our free worksheets and kick-start practice!

Substitution Method

Express one variable in terms of the other and substitute until one equation with one variable is left. Solve for the variable and perform back substitution to find the value of the other two, in this batch of pdf worksheets.

Download the set

Elimination Method

Pair-up the linear equations to eliminate one variable and form two new equations of 2 variables each. Find the value of one variable by eliminating the other. Substitute and find the other two unknown variables in each system of equations.

Cramer's Rule

Extract the coefficient, x, y and z matrices from the systems of equations. Find the determinant of each 3 x 3 matrix. Divide the determinant of the x, y and z matrices with the coefficient matrix to find the solution to each system of equations with 3 variables.

Solve using Any Method

Each printable worksheet in this unit of solving systems of equations offers eight sets of equations. High school students use their discretion to choose from the substitution method, elimination method or the Cramer's Rule to find the solution to the systems of equations involving 3 variables.

Solving Reciprocal Equations

Replace each fraction in the equation with a variable to convert the reciprocal equations into standard equations. Apply any method of your choice and determine the solution.

Related Worksheets

» Systems of Equations with Two Variables

» Rearranging Equations

» One-step Equation

» Two-Step Equation

» Multi-Step Equation

Become a Member

Membership Information

What's New?

Printing Help

Testimonial

This is a members-only feature!

Parallelogram
Quadrilateral
Parallelepiped
Tetrahedron
Dodecahedron
Fraction Calculator
Mixed Fraction Calculator
Greatest Common Factor Calulator
Decimal to Fraction Calculator
Whole Numbers
Rational Numbers
Place Value
Irrational Numbers
Natural Numbers
Binary Operation
Numerator and Denominator
Order of Operations (PEMDAS)
Scientific Notation

By Subjects

Trigonometry

3 Variable System of Equations Worksheets

While most of the worksheets of this post contain problems with 3 variable systems of equations, there are a few that have word problems for solving using 3-variable systems of equations that you need to formulate yourself.

solving systems of equations with three variables practice problems

Join Our Newsletter

How to solve systems of 3 variable equations

Using Elimination

Types of solutions for systems of planes (3 variable equations)

What is a solution of system of equations with 3 variables.

Solution for system of lines

Just as the solution system of lines is where those lines meet, a solution for a system of 3 variable equations (planes), is again, just where these planes meet.

Why 3 planes?

If you want to solve a linear equation with 2 variables, you need 2 equations.

You can's solve $$ x + y = 1$$ , right? That's because you need equations to solve for 2 variables.

Similarly, if you have an equation with 3 variables, ( graphically represented by 3 planes), you're going to need 3 equations to solve it.

Two important terms

Means that there is at least 1 intersection (solutions).

Means that there are no intersections (solutions).

Ok, so how do we find that point of intersection?

Before attempting to solve systems of three variable equations using elimination, you should probably be comfortable solving 2 variable systems of linear equations using elimination .

Video Tutorial on using Elimination

Example of how to solve a system of three variable equations using elimination.

Practice Problems

Use elimination to solve the following system of three variable equations.

A) 4x + 2y – 2z = 10
B) 2x + 8y + 4z = 32
C) 30x + 12y – 4z = 24

steps to solve 3 variable system by elimination

A) x - y + z = -1
B) x + y + z = 3
C) 4x + 2y + z = 8
A) 2x + 2y + 2z = -4

Although you can indeed solve 3 variable systems using elimination and substitution as shown on this page, you may have noticed that this method is quite tedious. The most efficient method is to use matrices or, of course, you can use this online system of equations solver . ( all of our pictures on this topic )

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

Course Enrichment Unit

Solve systems of three equations in three variables, learning outcomes.

Determine whether an ordered triple is a solution to a system of three equations.
Use back substitution to find a solution to a system of three equations.
Write the equations for a system given a scenario, and solve.

In order to solve systems of equations in three variables, known as three-by-three systems, the primary goal is to eliminate one variable at a time to achieve back-substitution. A solution to a system of three equations in three variables [latex]\left(x,y,z\right),\text{}[/latex] is called an ordered triple .

To find a solution, we can perform the following operations:

Interchange the order of any two equations.
Multiply both sides of an equation by a nonzero constant.
Add a nonzero multiple of one equation to another equation.

Graphically, the ordered triple defines the point that is the intersection of three planes in space. You can visualize such an intersection by imagining any corner in a rectangular room. A corner is defined by three planes: two adjoining walls and the floor (or ceiling). Any point where two walls and the floor meet represents the intersection of three planes.

A General Note: Number of Possible Solutions

The planes illustrate possible solution scenarios for three-by-three systems.

Systems that have a single solution are those which, after elimination, result in a solution set consisting of an ordered triple [latex]\left\{\left(x,y,z\right)\right\}[/latex]. Graphically, the ordered triple defines a point that is the intersection of three planes in space.
Systems that have an infinite number of solutions are those which, after elimination, result in an expression that is always true, such as [latex]0=0[/latex]. Graphically, an infinite number of solutions represents a line or coincident plane that serves as the intersection of three planes in space.
Systems that have no solution are those that, after elimination, result in a statement that is a contradiction, such as [latex]3=0[/latex]. Graphically, a system with no solution is represented by three planes with no point in common.

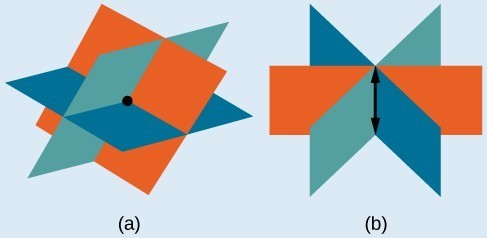
(a)Three planes intersect at a single point, representing a three-by-three system with a single solution. (b) Three planes intersect in a line, representing a three-by-three system with infinite solutions.

Example: Determining Whether an Ordered Triple Is a Solution to a System

Determine whether the ordered triple [latex]\left(3,-2,1\right)[/latex] is a solution to the system.

[latex]\begin{array}{l}\text{ }x+y+z=2\hfill \\ 6x - 4y+5z=31\hfill \\ 5x+2y+2z=13\hfill \end{array}[/latex]

We will check each equation by substituting in the values of the ordered triple for [latex]x,y[/latex], and [latex]z[/latex].

[latex]\begin{align} x+y+z=2\\ \left(3\right)+\left(-2\right)+\left(1\right)=2\\ \text{True}\end{align}\hspace{5mm}[/latex] [latex]\hspace{5mm}\begin{align} 6x - 4y+5z=31\\ 6\left(3\right)-4\left(-2\right)+5\left(1\right)=31\\ 18+8+5=31\\ \text{True}\end{align}\hspace{5mm}[/latex] [latex]\hspace{5mm}\begin{align}5x+2y+2z=13\\ 5\left(3\right)+2\left(-2\right)+2\left(1\right)=13\\ 15 - 4+2=13\\ \text{True}\end{align}[/latex]

The ordered triple [latex]\left(3,-2,1\right)[/latex] is indeed a solution to the system.

How To: Given a linear system of three equations, solve for three unknowns.

Pick any pair of equations and solve for one variable.
Pick another pair of equations and solve for the same variable.
You have created a system of two equations in two unknowns. Solve the resulting two-by-two system.
Back-substitute known variables into any one of the original equations and solve for the missing variable.

tip for success

Work through the following examples on paper in the order given. They slowly build up the technique of solving a three-by-three system in stages. Then you will have an opportunity to practice the 4-step process given in the How To box above.

Solving a system with three variables is very similar to solving one with two variables. It is important to keep track of your work as the addition of one more equation creates more steps in the solution process.

We’ll take the steps slowly in the following few examples. First, we’ll look just at the last step in the process: back-substitution. Then, we’ll look at an example that requires the addition (elimination) method to reach the first solution. Then we’ll see some video examples that illustrate some of the different kinds of situations you may encounter when solving three-by-three systems. Finally, you’ll have the opportunity to practice applying the complete process.

In the example that follows, we will solve the system by using back-substitution.

Solve the given system.

[latex]\displaystyle\begin{cases}x-\dfrac{1}{3}y+\dfrac{1}{2}z=1\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,y-\dfrac{1}{2}z=4\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,z=-1\end{cases}[/latex]

The third equation states that [latex]z = −1[/latex], so we substitute this into the second equation to obtain a solution for [latex]y[/latex].

[latex]\begin{array}{l}y-\dfrac{1}{2}(-1)=4\\y+\dfrac{1}{2}=4\\y=4-\dfrac{1}{2}\\y=\dfrac{8}{2}-\dfrac{1}{2}\\y=\dfrac{7}{2}\end{array}[/latex]

Now we have two of our solutions, and we can substitute them both into the first equation to solve for [latex]x[/latex].

[latex]\begin{array}{l}x-\dfrac{1}{3}\left(\dfrac{7}{2}\right)+\dfrac{1}{2}\left(-1\right)=1\\x-\dfrac{7}{6}-\dfrac{1}{2}=1\\x-\dfrac{7}{6}-\dfrac{3}{6}=1\\x-\dfrac{10}{6}=1\\x=1+\dfrac{10}{6}\\x=\dfrac{6}{6}+\dfrac{10}{6}\\x=\dfrac{16}{6}=\dfrac{8}{3}\end{array}[/latex]

Now we have our ordered triple; remember to place each variable solution in order.

[latex](x,y,z)=\left(\dfrac{8}{3},\dfrac{7}{2},-1\right)[/latex]

Analysis of the Solution: Each of the lines in the system above represents a plane (think about a sheet of paper). If you imagine three sheets of notebook paper each representing a portion of these planes, you will start to see the complexities involved in how three such planes can intersect. Below is a sketch of the three planes. It turns out that any two of these planes intersect in a line, so our intersection point is where all three of these lines meet.

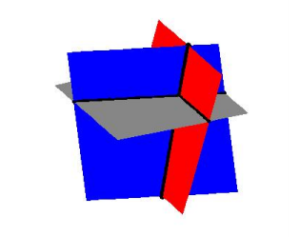
Three planes intersecting.

In the following video, we show another example of using back-substitution to solve a system in three variables.

In the next example we’ll need to use the addition method (elimination) to find our first solution.

Find a solution to the following system:

We labeled the equations this time to be able to keep track of things a little more easily. The most obvious first step here is to eliminate [latex]y[/latex] by adding equations (2) and (3).

Now we can substitute the value for [latex]z[/latex] that we obtained into equation [latex](2)[/latex].

[latex]\begin{array}{rrr}-2y+(6)=6\\-2y=6-6\\-2y=0\\\,\,\,\,y=0\end{array}[/latex]

Be careful here not to get confused with a solution of [latex]y = 0[/latex] and an inconsistent solution. It is ok for variables to equal [latex]0[/latex].

Now we can substitute [latex]z = 6[/latex] and [latex]y = 0[/latex] back into the first equation.

[latex]\begin{array}{rrr}x-y+z=5\\x-0+6=5\\x+6=5\\x=5-6\\x=-1\end{array}[/latex]

[latex](x,y,z)=(-1,0,6)[/latex]

Watch the following videos for more examples of the algebra you may encounter when solving systems with three variables.

Now, try the example and problems that follow to see if the process is becoming familiar to you. Solving three-by-three systems involves both creativity and careful, well-organized work. It will take some practice before it begins to feel natural.

Example: Solving a System of Three Equations in Three Variables by Elimination

[latex]\begin{align}x - 2y+3z=9& &\text{(1)} \\ -x+3y-z=-6& &\text{(2)} \\ 2x - 5y+5z=17& &\text{(3)} \end{align}[/latex]

There will always be several choices as to where to begin, but the most obvious first step here is to eliminate [latex]x[/latex] by adding equations (1) and (2).

[latex]\begin{align}x - 2y+3z&=9\\ -x+3y-z&=-6 \\ \hline y+2z&=3 \end{align}[/latex][latex]\hspace{5mm}\begin{gathered}\text{(1})\\ \text{(2)}\\ \text{(4)}\end{gathered}[/latex]

The second step is multiplying equation (1) by [latex]-2[/latex] and adding the result to equation (3). These two steps will eliminate the variable [latex]x[/latex].

[latex]\begin{align}−2x+4y−6z&=−18 \\ 2x−5y+5z&=17 \\ \hline −y−z&=−1\end{align}[/latex][latex]\hspace{5mm}\begin{align}&\text{(2) multiplied by }−2\\&\left(3\right)\\&(5)\end{align}[/latex]

In equations (4) and (5), we have created a new two-by-two system. We can solve for [latex]z[/latex] by adding the two equations.

[latex]\begin{align}y+2z&=3 \\ -y-z&=-1 \\ \hline z&=2 \end{align}[/latex][latex]\hspace{5mm}\begin{align}(4)\\(5)\\(6)\end{align}[/latex]

Choosing one equation from each new system, we obtain the upper triangular form:

[latex]\begin{align}x - 2y+3z&=9 && \left(1\right) \\ y+2z&=3 && \left(4\right) \\ z&=2 && \left(6\right) \end{align}[/latex]

Next, we back-substitute [latex]z=2[/latex] into equation (4) and solve for [latex]y[/latex].

[latex]\begin{align}y+2\left(2\right)&=3 \\ y+4&=3 \\ y&=-1 \end{align}[/latex]

Finally, we can back-substitute [latex]z=2[/latex] and [latex]y=-1[/latex] into equation (1). This will yield the solution for [latex]x[/latex].

[latex]\begin{align} x - 2\left(-1\right)+3\left(2\right)&=9\\ x+2+6&=9\\ x&=1\end{align}[/latex]

The solution is the ordered triple [latex]\left(1,-1,2\right)[/latex].

Three planes intersect at 1, negative 1, 2. The light blue plane's equation is x=1. The dark blue plane's equation is z=2. The orange plane's equation is y=negative 2.

Solve the system of equations in three variables.

[latex]\begin{array}{l}2x+y - 2z=-1\hfill \\ 3x - 3y-z=5\hfill \\ x - 2y+3z=6\hfill \end{array}[/latex]

[latex]\left(1,-1,1\right)[/latex]

https://ohm.lumenlearning.com/multiembedq.php?id=23765&theme=oea&iframe_resize_id=mom1

In the following video, you will see a visual representation of the three possible outcomes for solutions to a system of equations in three variables. There is also a worked example of solving a system using elimination.

Applications of Systems of Three Equations in Three Variables

Now we are ready to handle the problem we encountered as we began this section by using what we know about linear equations to translate the situation into a system of three equations. Then, we’ll use our new understanding of three-by-three systems to find the solution.

Tip for success

Applications of three-by-three systems are complicated. Work through each of the examples below perhaps more than once or twice. Don’t be discouraged if you don’t understand the process right away. It will take time and practice to become familiar with it.

Example: Solving a Real-World Problem Using a System of Three Equations in Three Variables

In the problem posed at the beginning of the section, John invested his inheritance of $12,000 in three different funds: part in a money-market fund paying 3% interest annually; part in municipal bonds paying 4% annually; and the rest in mutual funds paying 7% annually. John invested $4,000 more in mutual funds than he invested in municipal bonds. The total interest earned in one year was $670. How much did he invest in each type of fund?

To solve this problem, we use all of the information given and set up three equations. First, we assign a variable to each of the three investment amounts:

[latex]\begin{align}&x=\text{amount invested in money-market fund} \\ &y=\text{amount invested in municipal bonds} \\ z&=\text{amount invested in mutual funds} \end{align}[/latex]

The first equation indicates that the sum of the three principal amounts is $12,000.

[latex]x+y+z=12{,}000[/latex]

We form the second equation according to the information that John invested $4,000 more in mutual funds than he invested in municipal bonds.

[latex]z=y+4{,}000[/latex]

The third equation shows that the total amount of interest earned from each fund equals $670.

[latex]0.03x+0.04y+0.07z=670[/latex]

Then, we write the three equations as a system.

[latex]\begin{align}x+y+z=12{,}000 \\ -y+z=4{,}000 \\ 0.03x+0.04y+0.07z=670 \end{align}[/latex]

To make the calculations simpler, we can multiply the third equation by 100. Thus,

[latex]\begin{align}x+y+z=12{,}000 \hspace{5mm} \left(1\right) \\ -y+z=4{,}000 \hspace{5mm} \left(2\right) \\ 3x+4y+7z=67{,}000 \hspace{5mm} \left(3\right) \end{align}[/latex]

Step 1. Interchange equation (2) and equation (3) so that the two equations with three variables will line up.

[latex]\begin{align}x+y+z=12{,}000\hfill \\ 3x+4y +7z=67{,}000 \\ -y+z=4{,}000 \end{align}[/latex]

Step 2. Multiply equation (1) by [latex]-3[/latex] and add to equation (2). Write the result as row 2.

[latex]\begin{align}x+y+z=12{,}000 \\ y+4z=31{,}000 \\ -y+z=4{,}000 \end{align}[/latex]

Step 3. Add equation (2) to equation (3) and write the result as equation (3).

[latex]\begin{align}x+y+z=12{,}000 \\ y+4z=31{,}000 \\ 5z=35{,}000 \end{align}[/latex]

Step 4. Solve for [latex]z[/latex] in equation (3). Back-substitute that value in equation (2) and solve for [latex]y[/latex]. Then, back-substitute the values for [latex]z[/latex] and [latex]y[/latex] into equation (1) and solve for [latex]x[/latex].

[latex]\begin{align}&5z=35{,}000 \\ &z=7{,}000 \\ \\ &y+4\left(7{,}000\right)=31{,}000 \\ &y=3{,}000 \\ \\ &x+3{,}000+7{,}000=12{,}000 \\ &x=2{,}000 \end{align}[/latex]

John invested $2,000 in a money-market fund, $3,000 in municipal bonds, and $7,000 in mutual funds.

https://ohm.lumenlearning.com/multiembedq.php?id=19353&theme=oea&iframe_resize_id=mom10

Systems of three equations in three variables apply to other types of real-world situations as well.

In this example, we will write three equations that model sales at an art fair to learn how many prints should be sold to break even for the cost of the booth rental.

Andrea sells photographs at art fairs. She prices the photos according to size: small photos cost [latex]$10[/latex], medium photos cost [latex]$15[/latex], and large photos cost [latex]$40[/latex]. She usually sells as many small photos as medium and large photos combined. She also sells twice as many medium photos as large. A booth at the art fair costs [latex]$300[/latex].

If her sales go as usual, how many of each size photo must she sell to pay for the booth?

To set up the system, first choose the variables. In this case the unknown values are the number of small, medium, and large photos.

S = number of small photos sold

M = number of medium photos sold

L = number of large photos sold

The total of her sales must be [latex]$300[/latex] to pay for the booth. We can find the total by multiplying the cost for each size by the number of that size sold.

[latex]10[/latex] S = money received for small photos

[latex]15[/latex] M = money received for medium photos

[latex]40[/latex] L = money received for large photos

Total Sales:[latex]10[/latex] S +[latex]15[/latex] M +[latex]40[/latex] L =[latex]300[/latex]

The number of small photos is the same as the total of medium and large photos combined.

She sells twice as many medium photos as large photos.

M =[latex]2[/latex]L

To make things easier, rewrite the equations to be in the same format, with all variables on the left side of the equal sign and only a constant number on the right.

[latex]\begin{cases}10S+15M+40L=300\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,S–M–L=0\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,M–2L=0\end{cases}[/latex]

Now solve the system.

Step 1: First choose two equations and eliminate a variable. Since one equation has no S variable, it may be helpful to use the other two equations and eliminate the S variable from them. Multiply both sides of the second equation by [latex]−10[/latex].

[latex]\begin{array}{l}-10(S–M–L)=-10(0)\\-10s+10M+10L=0\end{array}[/latex]

Now add this modified equation with the first equation in the original list of equation.

[latex]\begin{array}{ccc}10S+15M+40L=300\\\underline{+(-10s+10M+10L=0)}\\25M+50L=300\end{array}[/latex]

Step 2: The other equation for our two-variable system will be the remaining equation (that has no S variable). Eliminate a second variable using the equation from step [latex]1[/latex]. While you could multiply the third of the original equations by [latex]25[/latex] to eliminate L , the numbers will stay nicer if you divide the resulting equation from step [latex]1[/latex] by [latex]25[/latex]. Do not forget to be careful of the signs!

Divide first:

[latex]\begin{array}{ccc}\dfrac{25}{25}M+\dfrac{50}{25}L=\dfrac{300}{25}\\M+2L=12\end{array}[/latex]

Now eliminate L by adding M-2L=0 to this new equation.

[latex]\begin{array}{l}M+2L=12\\\underline{M–2L=0}\\2M=12\\M=\dfrac{12}{2}=6\end{array}[/latex]

Step 3: Use M=[latex]6[/latex] and one of the equations containing just two variables to solve for the second variable. It is best to use one of the original equation in case an error was made in multiplication.

[latex]\begin{array}{ccc}M-2L=0\\6-2L=0\\-2L=-6\\L=3\end{array}[/latex]

Step 4: Use the two found values and one of the original equations to solve for the third variable.

[latex]\begin{array}{ccc}S–M–L=0\\S-6-3=0\\S-9=0\\S=9\end{array}[/latex]

Step 5: Check your answer . With application problems, it is sometimes easier (and better) to use the original wording of the problem rather than the equations you write.

She usually sells as many small photos as medium and large photos combined.

Medium and large photos combined: [latex]6 + 3 = 9[/latex], which is the number of small photos.

She also sells twice as many medium photos as large.

Medium photos is [latex]6[/latex], which is twice the number of large photos [latex](3)[/latex].

A booth at the art fair costs [latex]$300[/latex].

Andrea receives [latex]$10(9)[/latex] or [latex]$90[/latex] for the [latex]9[/latex] small photos, [latex]$15(6)[/latex] or [latex]$90[/latex] for the [latex]6[/latex] medium photos, and [latex]$40(3)[/latex] or [latex]$120[/latex] for the large photos. [latex]$90 + $90 + $120 = $300[/latex].

If Andrea sells [latex]9[/latex] small photos, [latex]6[/latex] medium photos, and [latex]3[/latex] large photos, she will receive exactly the amount of money needed to pay for the booth.

In the following video example, we show how to define a system of three equations in three variables that represents a mixture needed by a chemist.

Our last example shows you how to write a system of three equations that represents ticket sales for a theater that has three different prices for tickets.

Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
College Algebra. Authored by : Abramson, Jay et al.. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
Question ID 23765. Authored by : Shahbazian,Roy. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
Systems of Equations in Three Variables: Part 1 of 2 . Authored by : Sousa, James (Mathispower4u.com). Located at : https://youtu.be/wIE8KSpb-E8 . License : CC BY: Attribution
System of 3 Equations with 3 Unknowns Application - Concentration Problem. Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/612Ad0W9ZeY . License : CC BY: Attribution
System of 3 Equations with 3 Unknowns Application - Ticket Sales. Authored by : James Sousa (Mathispower4u.com) . Located at : https://youtu.be/Wg_v5R7BFo0 . License : CC BY: Attribution

Get step-by-step solutions to your math problems

$qr code$

Try Math Solver

Get step-by-step explanations

$Graph your math problems$

Graph your math problems

$Practice, practice, practice$

Practice, practice, practice

$Get math help in your language$

Get math help in your language

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

4.5: Solve Systems of Equations with Three Variables

Last updated
Save as PDF
Page ID 5141

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

Learning Objectives

By the end of this section, you will be able to:

Determine whether an ordered triple is a solution of a system of three linear equations with three variables
Solve a system of linear equations with three variables
Solve applications using systems of linear equations with three variables

Before you get started, take this readiness quiz.

Evaluate $5x−2y+3z$ when $x=−2, y=−4,$ and $z=3.$ If you missed this problem, review [link] .
Classify the equations as a conditional equation, an identity, or a contradiction and then state the solution. $ \left\{ \begin{array} {l} −2x+y=−11 \\ x+3y=9 \end{array} \right. $ If you missed this problem, review [link] .
Classify the equations as a conditional equation, an identity, or a contradiction and then state the solution. $\left\{ \begin{array} {l} 7x+8y=4 \\ 3x−5y=27 \end{array} \right. $ If you missed this problem, review [link] .

Determine Whether an Ordered Triple is a Solution of a System of Three Linear Equations with Three Variables

We learned earlier that the graph of a linear equation , $ax+by=c$, is a line. Each point on the line, an ordered pair $(x,y)$, is a solution to the equation. For a system of two equations with two variables, we graph two lines. Then we can see that all the points that are solutions to each equation form a line. And, by finding what the lines have in common, we’ll find the solution to the system.

Most linear equations in one variable have one solution, but we saw that some equations, called contradictions, have no solutions and for other equations, called identities, all numbers are solutions

We know when we solve a system of two linear equations represented by a graph of two lines in the same plane, there are three possible cases, as shown.

$Figure shows three graphs. In the first one, two lines intersect. Intersecting lines have one point in common. There is one solution to this system. The graph is labeled Consistent Independent. In the second graph, two lines are parallel. Parallel lines have no points in common. There is no solution to this system. The graph is labeled inconsistent. In the third graph, there is just one line. Both equations give the same line. Because we have just one line, there are infinitely many solutions. It is labeled consistent dependent.$

Similarly, for a linear equation with three variables ax+by+cz=d,ax+by+cz=d, every solution to the equation is an ordered triple, (x,y,z)(x,y,z)that makes the equation true.

LINEAR EQUATION IN THREE VARIABLES

A linear equation with three variables, where a, b, c, and d are real numbers and a, b , and c are not all 0, is of the form

\[ ax+by+cz=d\nonumber \]

Every solution to the equation is an ordered triple, $(x,y,z)$ that makes the equation true.

All the points that are solutions to one equation form a plane in three-dimensional space. And, by finding what the planes have in common, we’ll find the solution to the system.

When we solve a system of three linear equations represented by a graph of three planes in space, there are three possible cases.

$Eight figures are shown. The first one shows three intersecting planes with one point in common. It is labeled Consistent system and Independent equations. The second figure has three parallel planes with no points in common. It is labeled Inconsistent system. In the third figure two planes are coincident and parallel to the third plane. The planes have no points in common. In the fourth figure, two planes are parallel and each intersects the third plane. The planes have no points in common. In the fifth figure, each plane intersects the other two, but all three share no points. The planes have no points in common. In the sixth figure, three planes intersect in one line. There is just one line, so there are infinitely many solutions. In the seventh figure, two planes are coincident and intersect the third plane in a line. There is just one line, so there are infinitely many solutions. In the last figure, three planes are coincident. There is just one plane, so there are infinitely many solutions.$

To solve a system of three linear equations, we want to find the values of the variables that are solutions to all three equations. In other words, we are looking for the ordered triple $(x,y,z)$ that makes all three equations true. These are called the solutions of the system of three linear equations with three variables .

SolutionS OF A SYSTEM OF LINEAR EQUATIONS WITH THREE VARIABLES

Solutions of a system of equations are the values of the variables that make all the equations true. A solution is represented by an ordered triple $(x,y,z)$.

Example $\PageIndex{1}$

Determine whether the ordered triple is a solution to the system: $ \left\{ \begin{array} {l} x−y+z=2 \\ 2x−y−z=−6 \\ 2x+2y+z=−3 \end{array} \right. $

ⓐ $(−2,−1,3)$ ⓑ $(−4,−3,4)$

$The equations are x minus y plus z equals 2, 2x minus y minus z equals minus 6 and 2x plus 2y plus z equals minus 3. Substituting minus 2 for x, minus 1 for y and 3 for z into all three equations, we find that all three hold true. Hence, minus 2, minus 1, 3 is a solution.$

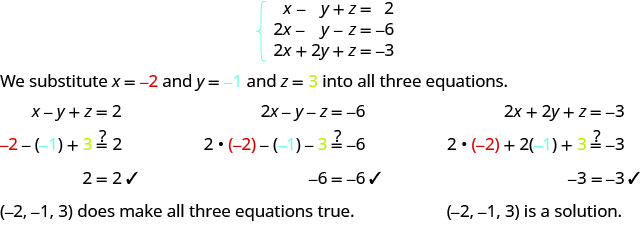
Example $\PageIndex{2}$

Determine whether the ordered triple is a solution to the system: $ \left\{ \begin{array} {l} 3x+y+z=2 \\ x+2y+z=−3 \\ 3x+y+2z=4 \end{array} \right. $

ⓐ $(1,−3,2)$ ⓑ $(4,−1,−5)$

ⓐ yes ⓑ no

Example $\PageIndex{3}$

Determine whether the ordered triple is a solution to the system: $ \left\{ \begin{array} {l} x−3y+z=−5 \\ −3x−y−z=1 \\ 2x−2y+3z=1 \end{array} \right. $

ⓐ $(2,−2,3)$ ⓑ $(−2,2,3)$

ⓐ no ⓑ yes

Solve a System of Linear Equations with Three Variables

Next, we use the values of the two variables we just found to go back to the original equation and find the third variable. We write our answer as an ordered triple and then check our results.

Example $\PageIndex{4}$: How to Solve a System of Equations With Three Variables by Elimination

Solve the system by elimination: $ \left\{ \begin{array} {l} x−2y+z=3 \\ 2x+y+z=4 \\ 3x+4y+3z=−1 \end{array} \right. $

$The equations are x minus 2y plus z equals 3, 2x plus y plus z equals 4 and 3x plus 4y plus 3z equals minus 1. Step 1 is to write the equations in standard form. They are. If any coefficients are fractions, clear them. There are none.$

Example $\PageIndex{5}$

Solve the system by elimination: $ \left\{ \begin{array} {l} 3x+y−z=2 \\ 2x−3y−2z=1 \\ 4x−y−3z=0 \end{array} \right.$

$(2,−1,3)$

Example $\PageIndex{6}$

Solve the system by elimination: $ \left\{ \begin{array} {l} 4x+y+z=−1 \\ −2x−2y+z=2 \\ 2x+3y−z=1 \end{array} \right. $

$(−2,3,4)$

The steps are summarized here.

SOLVE A SYSTEM OF LINEAR EQUATIONS WITH THREE VARIABLES.

If any coefficients are fractions, clear them.
Decide which variable you will eliminate.
Work with a pair of equations to eliminate the chosen variable.
Multiply one or both equations so that the coefficients of that variable are opposites.
Add the equations resulting from Step 2 to eliminate one variable
Repeat Step 2 using two other equations and eliminate the same variable as in Step 2.
The two new equations form a system of two equations with two variables. Solve this system.
Use the values of the two variables found in Step 4 to find the third variable.
Write the solution as an ordered triple.
Check that the ordered triple is a solution to all three original equations.

Example $\PageIndex{7}$

Solve: $ \left\{ \begin{array} {l} 3x−4z=0 \\ 3y+2z=−3 \\ 2x+3y=−5 \end{array} \right. $

\[ \left\{ \begin{array} {ll} 3x−4z=0 &(1) \\ 3y+2z=−3 &(2) \\ 2x+3y=−5 &(3) \end{array} \right. \nonumber \]

We can eliminate $z$ from equations (1) and (2) by multiplying equation (2) by 2 and then adding the resulting equations.

$The equations are 3 x minus 4 equals 0, 3y plus 2 z equals minus 3 and 2 x plus 3 y equals minus 5. Multiply equation 2 by 2 and add to equation 1. We get 3 x plus 6 y equals minus 6.$

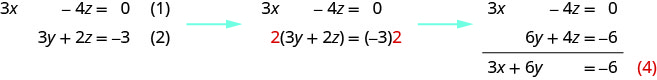
Notice that equations (3) and (4) both have the variables $x$ and $y$. We will solve this new system for $x$ and $y$.

$Multiply equation 3 by minus 2 and add that to equation 4. We get x equal to minus 4.$

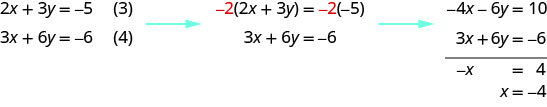
To solve for y , we substitute $x=−4$ into equation (3).

$Substitute minus 4 into equation 3 and solve for y. We get y equal to 1.$

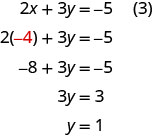
We now have $x=−4$ and $y=1$. We need to solve for z . We can substitute $x=−4$ into equation (1) to find z .

$Substituting minus 4 into equation 1 for x, we get z equal to minus 3.$

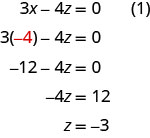
We write the solution as an ordered triple. $(−4,1,−3)$

We check that the solution makes all three equations true.

$\begin{array} {lll} {3x-4z=0 \space (1)} &{3y+2z=−3 \space (2)} &{2x+3y=−5 \space (3)} \\ {3(−4)−4(−3)\overset{?}{=} 0} &{3(1)+2(−3)\overset{?}{=} −3} &{2(−4)+3(1)\overset{?}{=} −5} \\ {0=0 \checkmark} &{−3=−3 \checkmark} &{−5=−5 \checkmark} \\ {} &{} &{\text{The solution is }(−4,1,−3)} \end{array}$

Example $\PageIndex{8}$

Solve: $ \left\{ \begin{array} {l} 3x−4z=−1 \\ 2y+3z=2 \\ 2x+3y=6 \end{array} \right. $

$(−3,4,−2)$

Example $\PageIndex{9}$

Solve: $ \left\{ \begin{array} {l} 4x−3z=−5 \\ 3y+2z=7 \\ 3x+4y=6 \end{array} \right. $

$(−2,3,−1)$

Example $\PageIndex{10}$

Solve the system of equations: $ \left\{ \begin{array} {l} x+2y−3z=−1 \\ x−3y+z=1 \\ 2x−y−2z=2 \end{array} \right. $

\[\left\{ \begin{array} {ll} x+2y−3z=−1 &(1) \\ x−3y+z=1 &(2) \\ 2x−y−2z=2 &(3) \end{array} \right.\nonumber \]

Use equation (1) and (2) to eliminate z .

$The equations are x plus 2y minus 3z equals minus 1, x minus 3y plus z equals 1 and 2x minus y minus 2z equals 2.$

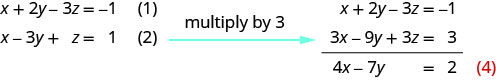
Use (2) and (3) to eliminate $z$ again.

$Multiplying equation 2 by 3 and adding it to equation 1, we get equation 4, 4x minus 7y equals 2. Multiplying equation 2 by 2 and adding it to equation 3, we get equation 5, 4x minus 7y equals 4.$

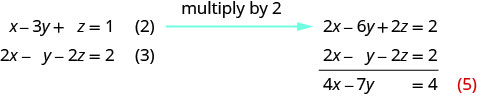
Use (4) and (5) to eliminate a variable.

$Equations 4 and 5 both have 2 variables. Multiply equation 5 by minus 1 and add it to equation 4. We get 0 equal to minus 2, which is false.$

There is no solution.

We are left with a false statement and this tells us the system is inconsistent and has no solution.

Example $\PageIndex{11}$

Solve the system of equations: $ \left\{ \begin{array} {l} x+2y+6z=5 \\ −x+y−2z=3 \\ x−4y−2z=1 \end{array} \right. $

no solution

Example $\PageIndex{12}$

Solve the system of equations: $ \left\{ \begin{array} {l} 2x−2y+3z=6 \\ 4x−3y+2z=0 \\ −2x+3y−7z=1 \end{array} \right. $

Example $\PageIndex{13}$

Solve the system of equations: $ \left\{ \begin{array} {l} x+2y−z=1 \\ 2x+7y+4z=11 \\ x+3y+z=4 \end{array} \right. $

\[\left\{ \begin{array} {ll} x+2y−z=1 &(1) \\ 2x+7y+4z=11 &(2) \\ x+3y+z=4 &(3) \end{array} \right.\nonumber \]

Use equation (1) and (3) to eliminate x .

$The equations are x plus 2y minus z equals 1, 2x plus 7y plus 4z equals 11 and x plus 3y plus z equals 4. Multiply equation 1 with minus 1 and add it to equation 3. We get equation 4, y plus 2z equals 3.$

Use equation (1) and (2) to eliminate x again.

$Multiply equation 1 with minus 2 and add it to equation 2. We get equation 5, 3y plus 6z equals 9.$

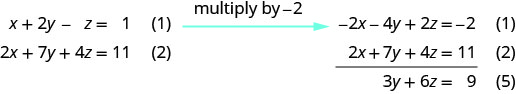
Use equation (4) and (5) to eliminate $y$.

$Multiply equation 4 with minus 3 and add it to equation 5. We get 0 equal to 0. There are infinite many solutions. Solving equation 4 for y, we get y equal to minus 2z plus 3. Substituting this into equation 1, we get x equal to 5z minus 5. The true statement 0 equal to 0 tells us that this is a dependent system that has infinitely many solutions. The solutions are of the form x, y, z where x is 5z minus 5, y is minus 2z plus 3 and z is any real number.$

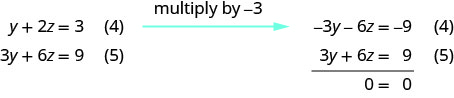
	There are infinitely many solutions.
Solve equation (4) for .	Represent the solution showing how and are dependent on . $ \begin{aligned} y+2z &= 3 \\ y &= −2z+3 \end{aligned} $
Use equation (1) to solve for .	$ x+2y−z=1$
Substitute $y=−2z+3$.	$ \begin{aligned} x+2(−2z+3)−z &= 1 \\ x−4z+6−z &= 1 \\ x−5z+6 &= 1 \\ x &= 5z−5 \end{aligned} $

The true statement $0=0$ tells us that this is a dependent system that has infinitely many solutions. The solutions are of the form (x,y,z)(x,y,z) where $x=5z−5;\space y=−2z+3$ and z is any real number.

Example $\PageIndex{14}$

Solve the system by equations: $ \left\{ \begin{array} {l} x+y−z=0 \\ 2x+4y−2z=6 \\ 3x+6y−3z=9 \end{array} \right. $

infinitely many solutions $(x,3,z)$ where $x=z−3;\space y=3;\space z$ is any real number

Example $\PageIndex{15}$

Solve the system by equations: $ \left\{ \begin{array} {l} x−y−z=1 \\ −x+2y−3z=−4 \\ 3x−2y−7z=0 \end{array} \right. $

infinitely many solutions $(x,y,z)$ where $x=5z−2;\space y=4z−3;\space z$ is any real number

Solve Applications using Systems of Linear Equations with Three Variables

Example $\PageIndex{16}$

We will use a chart to organize the information.
Number of students is twice number of adults.
Rewrite the equation in standard form.	$\begin{aligned} y &= 2x \\ 2x−y &= 0 \end{aligned} $

Use equations (1) and (2) to eliminate .

Use (3) and (4) to eliminate $y$.

Solve for .	$x=75 $ adult tickets
Use equation (3) to find .	$−2x+y=0$
Substitute $x=75$.	$\begin{aligned} −2(75)+y &= 0 \\ −150+y &= 0 \\ y &= 150\text{ student tickets}\end{aligned} $
Use equation (1) to find .	$x+y+z=250$
Substitute in the values $x=75, \space y=150.$	$\begin{aligned} 75+150+z &= 250 \\ 225+z &= 250 \\ z &= 25\text{ child tickets} \end{aligned} $
Write the solution.	The theater department sold 75 adult tickets, 150 student tickets, and 25 child tickets.

Example $\PageIndex{17}$

The fine arts department sold 75 adult tickets, 200 student tickets, and 75 child tickets.

Example $\PageIndex{18}$

The soccer team sold 200 adult tickets, 300 student tickets, and 100 child tickets.

Access this online resource for additional instruction and practice with solving a linear system in three variables with no or infinite solutions.

Solving a Linear System in Three Variables with No or Infinite Solutions
3 Variable Application

Key Concepts

\[ax+by+cz=d\nonumber \]

Write the equations in standard form If any coefficients are fractions, clear them.
Eliminate the same variable from two equations. Decide which variable you will eliminate. Work with a pair of equations to eliminate the chosen variable. Multiply one or both equations so that the coefficients of that variable are opposites. Add the equations resulting from Step 2 to eliminate one variable

Inspiration

$Texas flag$

IXL's high school skills will be aligned to the Texas Essential Knowledge and Skills (TEKS) soon! Until then, you can view a complete list of high school standards below.

Standards are in black and IXL math skills are in dark green. Hold your mouse over the name of a skill to view a sample question. Click on the name of a skill to practice that skill.

Show alignments for:

College and Career Readiness Standards College and Career Readiness Standards
Texas Essential Knowledge and Skills (TEKS): 111.47 Statistics Texas Essential Knowledge and Skills (TEKS): 111.47 Statistics
Texas Essential Knowledge and Skills (TEKS): 111.48 Algebraic Reasoning Texas Essential Knowledge and Skills (TEKS): 111.48 Algebraic Reasoning
State of Texas Assessments of Academic Readiness (STAAR) State of Texas Assessments of Academic Readiness (STAAR)
Texas Essential Knowledge and Skills (TEKS): Algebra 1 Texas Essential Knowledge and Skills (TEKS): Algebra 1
Texas Essential Knowledge and Skills (TEKS): Algebra 2 Texas Essential Knowledge and Skills (TEKS): Algebra 2
Texas Essential Knowledge and Skills (TEKS): Geometry Texas Essential Knowledge and Skills (TEKS): Geometry
Texas Essential Knowledge and Skills (TEKS): Mathematical processes Texas Essential Knowledge and Skills (TEKS): Mathematical processes
Texas Essential Knowledge and Skills (TEKS): Precalculus Texas Essential Knowledge and Skills (TEKS): Precalculus
Texas College and Career Readiness Standards: Grades: 9-12 Texas College and Career Readiness Standards: Grades: 9-12
Print standards

2-5 Linear functions, equations, and inequalities

2 the student applies the mathematical process standards when using properties of linear functions to write and represent in multiple ways, with and without technology, linear equations, inequalities, and systems of equations., a determine the domain and range of a linear function in mathematical problems; determine reasonable domain and range values for real-world situations, both continuous and discrete; and represent domain and range using inequalities;.

Domain and range of relations ( A1-M.2 )
Domain and range of linear functions: graphs ( A1-N. )
Domain and range of linear functions: word problems ( A1-N.7 )

B write linear equations in two variables in various forms, including y = mx + b, Ax + By = C, and y - y 1 = m(x - x 1 ), given one point and the slope and given two points;

Slope-intercept form: write an equation ( A1-L.6 )
Write linear equations in standard form ( A1-L.9 )
Point-slope form: write an equation ( A1-L.15 )
Write equations for lines of best fit ( A1-JJ.5 )

C write linear equations in two variables given a table of values, a graph, and a verbal description;

Slope-intercept form: write an equation from a graph ( A1-L.5 )
Slope-intercept form: write an equation from a table ( A1-L.7 )
Point-slope form: write an equation from a graph ( A1-L.16 )
Write a linear function: word problems ( A1-N.6 )

D write and solve equations involving direct variation;

Find the constant of variation ( A1-J.1 )
Write direct variation equations ( A1-J.2 )
Write and solve direct variation equations ( A1-J.3 )

E write the equation of a line that contains a given point and is parallel to a given line;

Slopes of parallel and perpendicular lines ( A1-L.18 )
Write an equation for a parallel or perpendicular line ( A1-L.19 )

F write the equation of a line that contains a given point and is perpendicular to a given line;

G write an equation of a line that is parallel or perpendicular to the x or y axis and determine whether the slope of the line is zero or undefined;.

Equations of horizontal and vertical lines ( A1-L.12 )

H write linear inequalities in two variables given a table of values, a graph, and a verbal description; and

Write a linear inequality from a graph ( A1-P.4 )
Write two-variable inequalities: word problems ( A1-P.5 )

I write systems of two linear equations given a table of values, a graph, and a verbal description.

Solve a system of equations by graphing: word problems ( A1-O.3 )
Solve a system of equations using substitution: word problems ( A1-O.9 )
Solve a system of equations using elimination: word problems ( A1-O.11 )
Solve a system of equations using any method: word problems ( A1-O.15 )
Write a system of equations given a graph ( A1 )

Checkpoint opportunity

Checkpoint: Linear equations ( A1 )
Checkpoint: Parallel and perpendicular lines ( A1 )

3 The student applies the mathematical process standards when using graphs of linear functions, key features, and related transformations to represent in multiple ways and solve, with and without technology, equations, inequalities, and systems of equations.

A determine the slope of a line given a table of values, a graph, two points on the line, and an equation written in various forms, including y = mx + b, ax + by = c 1 and y - y 1 = m(x - x 1 );.

Find the slope of a graph ( A1-K.1 )
Find the slope from two points ( A1-K.2 )
Find the slope from a table ( A1-K.3 )
Slope-intercept form: find the slope and y-intercept ( A1-L.3 )
Find the slope from an equation ( A1 )

B calculate the rate of change of a linear function represented tabularly, graphically, or algebraically in context of mathematical and real-world problems;

Interpret the slope and y-intercept of a linear function ( A1-N.5 )

C graph linear functions on the coordinate plane and identify key features, including x-intercept, y-intercept, zeros, and slope, in mathematical and real-world problems;

Slope-intercept form: graph an equation ( A1-L.4 )
Standard form: find x- and y-intercepts ( A1-L.10 )
Standard form: graph a line from an equation ( A1-L.11 )
Graph a horizontal or vertical line ( A1-L.13 )
Point-slope form: graph an equation ( A1-L.14 )
Complete a table and graph a linear function ( A1-N.3 )
Compare linear functions: graphs and equations ( A1-N.8 )
Graph a proportional relationship ( A1 )

D graph the solution set of linear inequalities in two variables on the coordinate plane;

Does (x, y) satisfy the inequality? ( A1-P.1 )
Graph a two-variable linear inequality ( A1-P.3 )

E determine the effects on the graph of the parent function f(x) = x when f(x) is replaced by af(x), f(x) + d, f(x - c), f(bx) for specific values of a, b, c, and d;

Transformations of linear functions ( A1-N.10 )

F graph systems of two linear equations in two variables on the coordinate plane and determine the solutions if they exist;

Solve a system of equations by graphing ( A1-O.2 )
Find the number of solutions to a system of equations by graphing ( A1-O.4 )

G estimate graphically the solutions to systems of two linear equations with two variables in real-world problems; and

H graph the solution set of systems of two linear inequalities in two variables on the coordinate plane..

Is (x, y) a solution to the system of linear inequalities? ( A1-P.6 )
Solve systems of linear inequalities by graphing ( A1-P.7 )
Checkpoint: Slope and rate of change ( A1 )
Checkpoint: Graphs and transformations of linear functions ( A1 )
Checkpoint: Linear inequalities ( A1 )

4 The student applies the mathematical process standards to formulate statistical relationships and evaluate their reasonableness based on real-world data.

A calculate, using technology, the correlation coefficient between two quantitative variables and interpret this quantity as a measure of the strength of the linear association;.

Match correlation coefficients to scatter plots ( A1-JJ.3 )
Calculate correlation coefficients ( A1-JJ.4 )

B compare and contrast association and causation in real-world problems; and

Correlation and causation ( A1-JJ.9 )

C write, with and without technology, linear functions that provide a reasonable fit to data to estimate solutions and make predictions for real-world problems.

Interpret lines of best fit: word problems ( A1-JJ. )
Find the equation of a regression line ( A1-JJ.6 )
Interpret regression lines ( A1-JJ.7 )
Analyze a regression line of a data set ( A1-JJ.8 )
Checkpoint: Linear modeling ( A1 )

5 The student applies the mathematical process standards to solve, with and without technology, linear equations and evaluate the reasonableness of their solutions.

A solve linear equations in one variable, including those for which the application of the distributive property is necessary and for which variables are included on both sides;.

Model and solve linear equations using algebra tiles ( A1-C.6 )
Solve one-step linear equations ( A1-C.7 )
Solve two-step linear equations ( A1-C.8 )
Solve one-step and two-step linear equations: word problems ( A1-C.9 )
Solve multi-step linear equations ( A1-C.10 )
Solve linear equations with variables on both sides ( A1-C.12 )
Solve linear equations: complete the solution ( A1-C.13 )
Find the number of solutions to a linear equation ( A1-C.14 )
Solve linear equations with variables on both sides: word problems ( A1-C.16 )
Solve linear equations: mixed review ( A1-C.17 )

B solve linear inequalities in one variable, including those for which the application of the distributive property is necessary and for which variables are included on both sides; and

Solve one-step linear inequalities: addition and subtraction ( A1-F.4 )
Solve one-step linear inequalities: multiplication and division ( A1-F.5 )
Solve one-step linear inequalities ( A1-F.6 )
Graph solutions to one-step linear inequalities ( A1-F.7 )
Solve two-step linear inequalities ( A1-F.8 )
Graph solutions to two-step linear inequalities ( A1-F.9 )
Solve advanced linear inequalities ( A1-F.10 )
Graph solutions to advanced linear inequalities ( A1-F.11 )

C solve systems of two linear equations with two variables for mathematical and real-world problems.

Find the number of solutions to a system of equations ( A1-O.5 )
Solve a system of equations using substitution ( A1-O.8 )
Solve a system of equations using elimination ( A1-O.10 )
Solve a system of equations using any method ( A1-O.14 )
Checkpoint: Solve linear equations and inequalities ( A1 )
Checkpoint: Systems of equations and inequalities ( A1 )

6-8 Quadratic functions and equations

6 the student applies the mathematical process standards when using properties of quadratic functions to write and represent in multiple ways, with and without technology, quadratic equations., a determine the domain and range of quadratic functions and represent the domain and range using inequalities;.

Domain and range of quadratic functions: graphs ( A1-Y.9 )
Domain and range of quadratic functions: equations ( A1-Y.10 )

B write equations of quadratic functions given the vertex and another point on the graph, write the equation in vertex form (f(x) = a(x - h)²+ k), and rewrite the equation from vertex form to standard form (f(x) = ax²+ bx + c); and

Write a quadratic function from its vertex and another point ( A1-Y.11 )

C write quadratic functions when given real solutions and graphs of their related equations.

Match quadratic functions and graphs ( A1-Y.8 )
Write a quadratic function from its x-intercepts and another point ( A1-Y. )

7 The student applies the mathematical process standards when using graphs of quadratic functions and their related transformations to represent in multiple ways and determine, with and without technology, the solutions to equations.

A graph quadratic functions on the coordinate plane and use the graph to identify key attributes, if possible, including x-intercept, y-intercept, zeros, maximum value, minimum values, vertex, and the equation of the axis of symmetry;.

Characteristics of quadratic functions: graphs ( A1-Y.1 )
Characteristics of quadratic functions: equations ( A1-Y.2 )
Graph quadratic functions in vertex form ( A1-Y.5 )
Graph quadratic functions in standard form ( A1-Y.7 )

B describe the relationship between the linear factors of quadratic expressions and the zeros of their associated quadratic functions; and

Solve a quadratic equation using the zero product property ( A1-Z.2 )
Solve a quadratic equation by factoring ( A1-Z.3 )

C determine the effects on the graph of the parent function f(x) = x² when f(x) is replaced by af(x), f(x) + d, f(x - c), f(bx) for specific values of a, b, c, and d.

Transformations of quadratic functions ( A1-Y.4 )
Checkpoint: Graphs and transformations of quadratic functions ( A1 )

8 The student applies the mathematical process standards to solve, with and without technology, quadratic equations and evaluate the reasonableness of their solutions. The student formulates statistical relationships and evaluates their reasonableness based on real-world data.

A solve quadratic equations having real solutions by factoring, taking square roots, completing the square, and applying the quadratic formula; and.

Solve a quadratic equation using square roots ( A1-Z.1 )
Complete the square ( A1-Z.4 )
Solve a quadratic equation by completing the square ( A1-Z.5 )
Solve a quadratic equation using the quadratic formula ( A1-Z.6 )
Solve quadratic equations: word problems ( A1-Z.7 )
Using the discriminant ( A1-Z.8 )

B write, using technology, quadratic functions that provide a reasonable fit to data to estimate solutions and make predictions for real-world problems.

Checkpoint: Write quadratic functions ( A1 )
Checkpoint: Solve quadratic equations ( A1 )

9 Exponential functions and equations

9 the student applies the mathematical process standards when using properties of exponential functions and their related transformations to write, graph, and represent in multiple ways exponential equations and evaluate, with and without technology, the reasonableness of their solutions. the student formulates statistical relationships and evaluates their reasonableness based on real-world data., a determine the domain and range of exponential functions of the form f(x) = ab to the x power and represent the domain and range using inequalities;.

Domain and range of exponential functions: graphs ( A1 )
Domain and range of exponential functions: equations ( A1 )

B interpret the meaning of the values of a and b in exponential functions of the form f(x) = ab to the x power in real-world problems;

Exponential growth and decay: word problems ( A1-V.8 )

C write exponential functions in the form f(x) = ab to the x power (where b is a rational number) to describe problems arising from mathematical and real-world situations, including growth and decay;

Write exponential functions: word problems ( A1-V.7 )

D graph exponential functions that model growth and decay and identify key features, including y-intercept and asymptote, in mathematical and real-world problems; and

Graph exponential functions ( A1-V.2 )
Match exponential functions and graphs I ( A1-V.3 )
Match exponential functions and graphs II ( A1-V.4 )

E write, using technology, exponential functions that provide a reasonable fit to data and make predictions for real-world problems.

Checkpoint: Exponential functions ( A1 )

10-12 Number and algebraic methods

10 the student applies the mathematical process standards and algebraic methods to rewrite in equivalent forms and perform operations on polynomial expressions., a add and subtract polynomials of degree one and degree two;.

Add and subtract polynomials using algebra tiles ( A1-W.3 )
Add polynomials to find perimeter ( A1-W.5 )
Add and subtract polynomials ( A1 )

B multiply polynomials of degree one and degree two;

Multiply a polynomial by a monomial ( A1-W.6 )
Multiply two binomials using algebra tiles ( A1-W.7 )
Multiply two binomials ( A1-W.8 )
Multiply two binomials: special cases ( A1-W.9 )
Multiply polynomials using area models ( A1-W.10 )
Multiply polynomials ( A1-W.11 )

C determine the quotient of a polynomial of degree one and polynomial of degree two when divided by a polynomial of degree one and polynomial of degree two when the degree of the divisor does not exceed the degree of the dividend;

Divide polynomials by monomials ( A1 )
Divide polynomials using long division ( A1 )

D rewrite polynomial expressions of degree one and degree two in equivalent forms using the distributive property;

Distributive property ( A1-B.6 )

E factor, if possible, trinomials with real factors in the form ax² + bx + c, including perfect square trinomials of degree two; and

Factor quadratics using algebra tiles ( A1-X.3 )
Factor quadratics with leading coefficient 1 ( A1-X.4 )
Factor quadratics with other leading coefficients ( A1-X.5 )
Factor quadratics: special cases ( A1-X.6 )

F decide if a binomial can be written as the difference of two squares and, if possible, use the structure of a difference of two squares to rewrite the binomial.

Checkpoint: Polynomial operations ( A1 )

11 The student applies the mathematical process standards and algebraic methods to rewrite algebraic expressions into equivalent forms.

A simplify numerical radical expressions involving square roots; and.

Simplify radical expressions ( A1-EE.1 )
Add and subtract radical expressions ( A1-EE.5 )
Simplify radical expressions using the distributive property ( A1-EE.6 )
Simplify radical expressions using conjugates ( A1-EE.7 )
Simplify radicals with fractions ( A1 )
Multiply radicals ( A1 )

B simplify numeric and algebraic expressions using the laws of exponents, including integral and rational exponents.

Powers with integer bases ( A1-R.1 )
Powers with decimal and fractional bases ( A1-R.2 )
Negative exponents ( A1-R.3 )
Multiplication rule for exponents ( A1-R.4 )
Division rule for exponents ( A1-R.5 )
Power rule for exponents ( A1-R.6 )
Simplify exponential expressions using the multiplication rule ( A1-R.7 )
Simplify exponential expressions using the division rule ( A1-R.8 )
Simplify exponential expressions using the multiplication and division rules ( A1-R.9 )
Simplify exponential expressions using the power rule ( A1-R.10 )
Evaluate expressions using exponent rules ( A1-R.12 )
Identify equivalent exponential expressions I ( A1-R.13 )
Identify equivalent exponential expressions II ( A1-R.14 )
Evaluate integers raised to positive rational exponents ( A1-S.1 )
Evaluate integers raised to rational exponents ( A1-S.2 )
Multiplication with rational exponents ( A1-S.3 )
Division with rational exponents ( A1-S.4 )
Power rule with rational exponents ( A1-S.5 )
Simplify expressions involving rational exponents ( A1-S.6 )
Checkpoint: Exponents and radicals ( A1 )

12 The student applies the mathematical process standards and algebraic methods to write, solve, analyze, and evaluate equations, relations, and functions.

A decide whether relations represented verbally, tabularly, graphically, and symbolically define a function;.

Identify functions ( A1-M.4 )
Identify functions: vertical line test ( A1-M.5 )

B evaluate functions, expressed in function notation, given one or more elements in their domains;

Evaluate a function ( A1-M.7 )
Complete a function table from an equation ( A1-M.10 )
Evaluate piecewise-defined functions ( A1-Q.1 )
Evaluate an exponential function ( A1-V.1 )
Complete a function table: quadratic functions ( A1-Y.3 )

C identify terms of arithmetic and geometric sequences when the sequences are given in function form using recursive processes;

Evaluate variable expressions for number sequences ( A1-U.4 )
Evaluate recursive formulas for sequences ( A1-U.5 )
Write a formula for a recursive sequence ( A1-U.9 )

D write a formula for the nth term of arithmetic and geometric sequences, given the value of several of their terms; and

Write variable expressions for arithmetic sequences ( A1-U.7 )
Write variable expressions for geometric sequences ( A1-U.8 )

E solve mathematic and scientific formulas, and other literal equations, for a specified variable.

Rearrange multi-variable equations ( A1-C.18 )
Linear equations: solve for y ( A1-L.8 )
Checkpoint: Sequences ( A1 )
Checkpoint: Function concepts ( A1 )

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Want additional help with Algebra 2?

Number Line

The Algebra Calculator is a versatile online tool designed to simplify algebraic problem-solving for users of all levels. Here's how to make the most of it:

Begin by typing your algebraic expression into the above input field, or scanning the problem with your camera.
After entering the equation, click the 'Go' button to generate instant solutions.
The calculator provides detailed step-by-step solutions, aiding in understanding the underlying concepts.
-x+3\gt 2x+1
(x+5)(x-5)\gt 0
10^{1-x}=10^4
\sqrt{3+x}=-2
6+11x+6x^2+x^3=0
factor\:x^{2}-5x+6
simplify\:\frac{2}{3}-\frac{3}{2}+\frac{1}{4}
x+2y=2x-5,\:x-y=3
How do you solve algebraic expressions?
To solve an algebraic expression, simplify the expression by combining like terms, isolate the variable on one side of the equation by using inverse operations. Then, solve the equation by finding the value of the variable that makes the equation true.
What are the basics of algebra?
The basics of algebra are the commutative, associative, and distributive laws.
What are the 3 rules of algebra?
The basic rules of algebra are the commutative, associative, and distributive laws.
What is the golden rule of algebra?
The golden rule of algebra states Do unto one side of the equation what you do to others. Meaning, whatever operation is being used on one side of equation, the same will be used on the other side too.
What are the 5 basic laws of algebra?
The basic laws of algebra are the Commutative Law For Addition, Commutative Law For Multiplication, Associative Law For Addition, Associative Law For Multiplication, and the Distributive Law.

🌐 Languages	EN, ES, PT & more
🏆 Practice	Improve your math skills
😍 Step by step	In depth solution steps
⭐️ Rating	based on 20924 reviews

algebra-calculator

Middle School Math Solutions – Simultaneous Equations Calculator Solving simultaneous equations is one small algebra step further on from simple equations. Symbolab math solutions...

Please add a message.

Message received. Thanks for the feedback.

Game Central

Reciprocals, related concepts.

IMAGES

3 Variable System of Equations Worksheets
Systems Of Equations With 3 Variables Worksheets
3 Variable System of Equations Worksheets
How to solve systems of 3 variable equations using elimination, step by
Solving Systems Of Equations With 3 Variables Word Problems
How to Solve Solving Systems of 3x3 equations part I three variables

VIDEO

Solving a 3x3 system of linear equations: Problem type 1
Solve System Of Three Equations With Three Variables
Solving 3 Variables with 3 Equations
Math 114 U3 O8 Solving Systems of Equations Three Variables
Systems of Linear Equations
Solving a Linear System in Three Variables

COMMENTS

4.4 Solve Systems of Equations with Three Variables
Step 3. Repeat Step 2 using two other equations and eliminate the same variable as in Step 2. Step 4. The two new equations form a system of two equations with two variables. Solve this system. Step 5. Use the values of the two variables found in Step 4 to find the third variable. Step 6.
7.3: Systems of Linear Equations with Three Variables
Systems of three equations in three variables are useful for solving many different types of real-world problems. See Example $\PageIndex{3}$. A system of equations in three variables is inconsistent if no solution exists. After performing elimination operations, the result is a contradiction. See Example $\PageIndex{4}$.
PDF Systems of Three Equations Elimination
Critical thinking question: 17) Write a system of equations with the solution. Many answers. Ex: x + y + z = 3, 2 x + y + z = 5, x + 2 y − z = 4. Create your own worksheets like this one with Infinite Algebra 2. Free trial available at KutaSoftware.com.
3.4: Solving Linear Systems with Three Variables
Solve: {3x + 2y − z = − 7 (1) 6x − y + 3z = − 4 (2) x + 10y − 2z = 2 (3) Solution. All three equations are in standard form. If this were not the case, it would be a best practice to rewrite the equations in standard form before beginning this process. Step 1: Choose any two of the equations and eliminate a variable.
6.5: Solve Systems of Equations with Three Variables
The two new equations form a system of two equations with two variables. Solve this system. Use the values of the two variables found in Step 4 to find the third variable. Write the solution as an ordered triple. Check that the ordered triple is a solution to all three original equations.
Solving linear systems with 3 variables (video)
Here are the steps. 1. Turn on your graphing calculator. (It needs to be a TI-83 or better) 2. click 2nd, matrix. 3. click to the right until you are on the setting, EDIT. 4. select 1 of the matrices. It will bring up the matrix size on the top row and the matrix at the bottom. 5. change the matrix size to 3 x 4.
Solving Systems of Three Equations in Three Variables
A General Note: Number of Possible Solutions Figure 2 and Figure 3 illustrate possible solution scenarios for three-by-three systems. Systems that have a single solution are those which, after elimination, result in a solution set consisting of an ordered triple [latex]\left\{\left(x,y,z\right)\right\}[/latex]. Graphically, the ordered triple defines a point that is the intersection of three ...
Study Guide
A solution of a system of equations in three variables is an ordered triple (x, y, z) (x,y,z), and describes a point where three planes intersect in space. There are three possible solution scenarios for systems of three equations in three variables: Independent systems have a single solution. Solving the system by elimination results in a ...
PDF 4.4 Systems of Equations
To reduce from three variables down to two it is very important to keep the work ogranized. We will use addition with two equations to eliminate one variable. This new equation we will call (A). Then we will use a different pair of equations and use addition to eliminate the same variable. This second new equation we will call (B).
Word Problem Exercises: Applications of 3 Equations with 3 Variables
1. The currents running through an electrical system are given by the following system of equations. The three currents, I1, I2, and I3, are measured in amps. Solve the system to find the currents in this circuit. I 1 + 2I 2 - I 3 = 0.425. 3I 1 - I 2 + 2I 3 = 2.225. 5I 1 + I 2 + 2I 3 = 3.775.
Solving Systems of Equations Worksheets with Three Variables
Solve using Any Method. Each printable worksheet in this unit of solving systems of equations offers eight sets of equations. High school students use their discretion to choose from the substitution method, elimination method or the Cramer's Rule to find the solution to the systems of equations involving 3 variables. Download the set.
Solve Systems of Three Equations in Three Variables
In order to solve systems of equations in three variables, known as three-by-three systems, the primary goal is to eliminate one variable at a time to achieve back-substitution. A solution to a system of three equations in three variables [latex]\left(x,y,z\right),\text{}[/latex] is called an ordered triple. To find a solution, we can perform ...
IXL
IXL plans. Virginia state standards. Textbooks. Test prep. Improve your math knowledge with free questions in "Solve a system of equations in three variables using elimination" and thousands of other math skills.
3 Variable System of Equations Worksheets
3 Variable System of Equations Worksheets. Tags: 7th Grade 8th Grade. While most of the worksheets of this post contain problems with 3 variable systems of equations, there are a few that have word problems for solving using 3-variable systems of equations that you need to formulate yourself. Download PDF.
PDF Solving Systems of Equations with Three Variables
Using a Matrix to Solve a System of Equations. Step 1: Write the coefficients in a matrix using a vertical line to represent equals signs. Step 2: Find the inverse of the matrix that's left of the equals signs. Step 3: Multiply the inverse matrix by the part of the matrix that is right of the equals sign.
How to solve systems of 3 variable equations
Practice Problems. Problem 1. Use elimination to solve the following system of three variable equations. A) 4x + 2y - 2z = 10. B) 2x + 8y + 4z = 32. C) 30x + 12y - 4z = 24. Solution. Problem 2. Use elimination to solve the following system of three variable equations.
Solve Systems of Three Equations in Three Variables
A solution to a system of three equations in three variables (x, y, z), is called an ordered triple. To find a solution, we can perform the following operations: Interchange the order of any two equations. Multiply both sides of an equation by a nonzero constant. Add a nonzero multiple of one equation to another equation.
Writing linear equations word problems
Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class education for anyone, anywhere.
Algebra 1
The Algebra 1 course, often taught in the 9th grade, covers Linear equations, inequalities, functions, and graphs; Systems of equations and inequalities; Extension of the concept of a function; Exponential models; and Quadratic equations, functions, and graphs. Khan Academy's Algebra 1 course is built to deliver a comprehensive, illuminating, engaging, and Common Core aligned experience!
IXL
Solve a system of equations in three variables using substitution 13. Solve a system of equations in three variables using elimination ... Solve quadratic equations: word problems 13. Using the discriminant 14. Write a quadratic function in vertex form 15. Match quadratic functions and graphs 16. Domain and range of quadratic functions: graphs ...
Microsoft Math Solver
Online math solver with free step by step solutions to algebra, calculus, and other math problems. Get help on the web or with our math app.
Algebra Basics
Two-step equations word problems; Equations with variables on both sides; ... Coordinate plane: Graphing lines and slope Solutions to two-variable linear equations: ... Solving systems of equations with elimination. Community questions. Our mission is to provide a free, world-class education to anyone, anywhere. ...
4.5: Solve Systems of Equations with Three Variables
The two new equations form a system of two equations with two variables. Solve this system. Use the values of the two variables found in Step 4 to find the third variable. Write the solution as an ordered triple. Check that the ordered triple is a solution to all three original equations.
IXL
Write two-variable inequalities: word problems (A1-P.5) I write systems of two linear equations given a table of values, a graph, and a verbal description. Solve a system of equations by graphing: word problems (A1-O.3) Solve a system of equations using substitution: word problems (A1-O.9)
Equation Calculator
Free equations calculator - solve linear, quadratic, polynomial, radical, exponential and logarithmic equations with all the steps. Type in any equation to get the solution, steps and graph
Algebra Calculator
Systems of Equations. ... Type a math problem Related Concepts. Polynomial. In mathematics, a polynomial is a mathematical expression consisting of indeterminates and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. ... A quadratic equation always has two roots ...
Algebra 2
The Algebra 2 course, often taught in the 11th grade, covers Polynomials; Complex Numbers; Rational Exponents; Exponential and Logarithmic Functions; Trigonometric Functions; Transformations of Functions; Rational Functions; and continuing the work with Equations and Modeling from previous grades. Khan Academy's Algebra 2 course is built to deliver a comprehensive, illuminating, engaging, and ...
Algebra Calculator
The Algebra Calculator is a versatile online tool designed to simplify algebraic problem-solving for users of all levels. Here's how to make the most of it: Begin by typing your algebraic expression into the above input field, or scanning the problem with your camera. After entering the equation, click the 'Go' button to generate instant solutions.
Trigonometry Calculator
Solve for a Variable. Factor. Expand. Evaluate Fractions. Linear Equations. Quadratic Equations. Inequalities. Systems of Equations. Matrices ... Type a math problem. Related Concepts. Trigonometry. Trigonometry is a branch of mathematics concerned with relationships between angles and side lengths of triangles. ...

	There are infinitely many solutions.
Solve equation (4) for .	Represent the solution showing how and are dependent on . \( \begin{aligned} y+2z &= 3 \\ y &= −2z+3 \end{aligned} \)
Use equation (1) to solve for .	\( x+2y−z=1\)
Substitute \(y=−2z+3\).	\( \begin{aligned} x+2(−2z+3)−z &= 1 \\ x−4z+6−z &= 1 \\ x−5z+6 &= 1 \\ x &= 5z−5 \end{aligned} \)

4.4 Solve Systems of Equations with Three Variables

Be Prepared 4.10

Be Prepared 4.11

Be Prepared 4.12

Linear Equation in Three Variables

Solutions of a System of Linear Equations with Three Variables

Example 4.31

Try It 4.61

Try It 4.62

Example 4.32

Try It 4.63

Try It 4.64

Solve a system of linear equations with three variables.

Example 4.33

Try It 4.65

Try It 4.66

Example 4.34

Try It 4.67

Try It 4.68

Example 4.35

Try It 4.69

Try It 4.70

Example 4.36

Try It 4.71

Try It 4.72

Section 4.4 Exercises

Writing Exercises

Systems of Equations with Three Variables Worksheets

By Subjects

3 Variable System of Equations Worksheets

Join Our Newsletter

How to solve systems of 3 variable equations

Types of solutions for systems of planes (3 variable equations)

Why 3 planes?

Two important terms

Ok, so how do we find that point of intersection?

Video Tutorial on using Elimination

Practice Problems

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Course Enrichment Unit

A General Note: Number of Possible Solutions

Example: Determining Whether an Ordered Triple Is a Solution to a System

How To: Given a linear system of three equations, solve for three unknowns.

tip for success

Example: Solving a System of Three Equations in Three Variables by Elimination

Applications of Systems of Three Equations in Three Variables

Tip for success

Example: Solving a Real-World Problem Using a System of Three Equations in Three Variables

Get step-by-step solutions to your math problems

Try Math Solver

Get step-by-step explanations

Graph your math problems

Practice, practice, practice

Get math help in your language

Margin Size

4.5: Solve Systems of Equations with Three Variables

Learning Objectives

Determine Whether an Ordered Triple is a Solution of a System of Three Linear Equations with Three Variables

LINEAR EQUATION IN THREE VARIABLES

SolutionS OF A SYSTEM OF LINEAR EQUATIONS WITH THREE VARIABLES

Example \(\PageIndex{1}\)

Example \(\PageIndex{2}\)

Example \(\PageIndex{3}\)

Solve a System of Linear Equations with Three Variables

Example \(\PageIndex{4}\): How to Solve a System of Equations With Three Variables by Elimination

Example \(\PageIndex{5}\)

Example \(\PageIndex{6}\)

SOLVE A SYSTEM OF LINEAR EQUATIONS WITH THREE VARIABLES.

Example \(\PageIndex{7}\)

Example \(\PageIndex{8}\)

Example \(\PageIndex{9}\)

Example \(\PageIndex{10}\)

Example \(\PageIndex{11}\)

Example \(\PageIndex{12}\)

Example \(\PageIndex{13}\)

Example \(\PageIndex{14}\)

Example \(\PageIndex{15}\)

Solve Applications using Systems of Linear Equations with Three Variables

Example \(\PageIndex{16}\)

Example \(\PageIndex{17}\)