explain the graphical method of solving linear programming problem

Talk to our experts

1800-120-456-456

• Graphical Method Linear Programming

Graphical Method of Solving Linear Programming Problems

It is not hidden that the simplex method is a well-studied and widely used method for solving Linear Programming problems. But as far as non-Linear Programming is concerned, such a universal method does not exist. With graphical methods, any optimization programming problems consisting of only two variables can easily be solved. These variables can be referred as x₁ and x₂ and with the help of these variables, most of the analysis can be done on a two-dimensional graph. Although we cannot generalize a large number of variables using a graphical approach, the basic concepts of Linear Programming in a two-variable context can be easily demonstrated. We can always turn to two-variable problems if the problems seem to be complicated and we find ourselves in a pool of questions. And we can always search for answers in a two-variable case using graphs, that is solving Linear Programming problems graphically. 

The graphical approach wraps itself with another advantage and that is its visual nature. It provides us with a picture to get along with the algebra of Linear Programming. This picture can quench our thirst for understanding the basic definitions and possibilities. These reasons are proof that the graphical approach works smoothly with Linear Programming concepts.

Now, for solving Linear Programming problems graphically, we must two things:

Inequality constraints

And the objective function.

The Graphical Method of Solving Linear Programming problems is based on a well-defined set of logical steps. With the help of these steps, we can master the graphical solution of Linear Programming problems.

Methods used for Solving Linear Programming

Following two methods used for Graphical Method of Solving Linear Programming:

Extreme point solution method 

Iso-profit (cost) performance line method to find the perfect solution to the LP problem.

Important Points

A set of variable values ​​xj (j = 1, 2,3..., N) that satisfies the issues of the LP problem is said to form the solution to that LP problem.

Potential Solution Set of variable values ​​xj (j = 1, 2,3.., N) that satisfies all the barriers and non-negative conditions of the LP problem at the same time is said to form a possible solution to that LP problem.

Unlikely solution A set of variable values ​​xj (j = 1, 2,3..., N) that do not satisfy all the barriers and non-negative conditions of the LP problem at one time is said to form an impossible solution for that. LP problem.

With an m-group of simultaneous n (n> m) variables in the LP problem, the solution obtained by placing (n - m) zero-equal variables and solving the remaining m-variables of m is called the basic solution. of that LP problem. Variables (n - m) whose value did not appear in the basic solution are called non-core variables and the remaining variables of m are called the base variables.

A possible basic solution A possible solution to the LP problem and a basic solution is called a possible basic solution. That is, all basic changes take non-negative values. 

The Basic Solution is two Types

Degenerate A basic solution that is possible is called degenerate if the value of at least one basic element is zero. 

Non-degradable The basic practical solution is called non-degenerate if the value of all the basic variables is zero and positive.

Ways to Solve the LP Problem Law

Point Method

To resolve the issue using the existing point method you need to follow these steps:

Step 1: Create statistical design from a given problem. If not provided.

Step 2: Now plan the graph using the given obstacles and find a region that you can use.

Step 3: Find the possible location links (vertices) that we found in step 2.

Step 4: Now check the objective function in each of the possible location areas. Assume that N and n represent the largest and smallest values ​​in these points.

Step 5: If the possible region is bound then N and n are the maximum and minimum values of the objective function. Or if the area is likely to have no boundaries then:

N is the highest value of the target function if the open half system is obtained with an ax + by> N without a common point in the possible area. If not, purpose work has no solution.

n a small amount of objective work if the open half system is found by the ax + by <n does not have a common point in the probable location. If not, purpose work has no solution. 

Iso-Cost Method

The term iso-cost or iso-profit method provides a combination of points that produce the same cost/profit as any other combination in the same line. This is done by arranging the lines corresponding to the slope of the equation.

Follow the following steps for the Iso-cost method solution:

Step 1: Create a statistical design from a given problem. If not provided.

Step 3: Now find the possible location links we found in step 2.

Step 4: Find the correct Z (objective function) and draw a line for this objective activity.

Step 5: If the objective function is high type, draw a line corresponding to the objective performance line and this line is farther from the root and has only one common point in the possible area. Or if the target function is a small type then draw a line that corresponds to the target performance line and this line is very close to the source and has one common point in the possible position.

Step 6: Now find the links to the common point we find in step 5. Now, this point is used to find the right solution and the amount of objective work.

Information for the Wooden Tables and Chairs Linear Programming Problem

Table 1 gives us the information for the Linear Programming problem. We can go step-by-step for solving the Linear Programming problems graphically.

Step 1) The aforementioned table can help us to formulate the problem. The bottom row will serve the objective function. The objective function of the company is to maximize unit profit. The woods and the laborers are the constraint set. The nonnegativity conditions are also stated.

Maximize Z = 6x 2 +8x 2 (is the objective function)

Subject to: 30x 1 +20x 2 ≤ 300      (300 bf available) 

5x 1 +10x 2 ≤ 110        (110 hours available)

x 1 +x 2 ≥ 0                (non - negative conditions)

The two variables (wood and labor) in this problem, can be solved graphically. 

Step 2) This is the graph plotting step. With the x-axis as the number of tables and y-axis as the number of chairs, we can find the two constraint lines. This can be found if we find the x and y-intercepts for the two constraint equations. But before that, we have to rewrite the constraint inequalities as equalities. 

30x 1 +20x 2 = 300 

Setting x₂ = 0 to solve x₁         

30x₁ = 300   

x₁ =300/30 = 10 tables      (Wood used to make tables) 

Next: 

Setting x₁ = 0 to solve x₂  

20x₂ = 300  

x₂ =300/20  = 15 chairs (Wood used to make chairs)

50x 1 +10x 2 = 110

Setting x₂ = 0 to solve x₁

x₁ = 110/5= 22 tables(labors used to make tables)

Setting x₁ = 0 to solve x₂ 

x₂ = 110/10= 11 chairs (labors used to make chairs)

Now, plot the wood constraint line (x 1 = 10 and x 2 =15) and labor constraint line (x 1 =22

and x 2 =11)

(Image will be uploaded soon)

Step 3) To check the valid side for both constraint lines use the origin (0,0).

30(0) + 20(0) < 300 is the valid side of the wood constraint line. In the same way  5(0) + 10(0) < 110 also is a valid side of the labor constraint line. Now, draw the arrows indicating the valid side of each constraint line. 

Step 4) Identify the feasible region which is the area on the valid side of both constraint lines. 

Step 5) Find x 1 and x 2 using Z = 48 and 72.

In the first case, the values will be x 1 = 8 and x2= 12

In the second case, the values will be x 1 = 6 and x 2 = 9

Plot the objective function lines when Z = 48 and Z = 72.

The two objective function lines move away from the origin (0,0), Z increases.

Step 6) Find the most attractive corner. 

Step 7) Calculate the coordinates and find the values of x and y. 

Therefore, according to the company’s optimal solution four tables and nine chairs can be manufactured.

Step 8) finally, determine the value of the objective function for the optimal solution by plugging in the number of tables and chairs and solve for Z: 

Z = $ 6(4) + $ 8(9) = $ 96 

Thus, by producing four tables and nine chairs we can achieve the maximum profit of $ 96.

FAQs on Graphical Method Linear Programming

1. How does the graphical approach solve successive planning problems?

Graphical approach solution stepwise

Step 1: Create a LP (Linear Programming) problem. ...

Step 2: Create a graph and edit the blocking lines. ...

Step 3: Find the right side of each boundary line. ...

Step 4: Locate the potential solution. ...

Step 5: Arrange the objective activity on the graph. ...

Step 6: Identify the best point.

2. What is the problem with the editing line for example?

The oldest example of a consecutive planning problem is related to a company that has to allocate its time and money to create two separate products. Products require different amounts of time and money, which are limited resources, and are sold at different prices.

3. If you are using a graphic solution to a line editing problem the right solution would be in a place known as?

Consecutive planning problems are solved using graphic representations of all given barrier functions. A potential region is found in the crosshairs of all issues and the right solution is within the Feasible range.

4. What is the graphical approach to performance research?

Graphical method represents an efficient algorithm for problem solving a line system that contains two resolutions (x 1 and x 2 ). It is one of the most popular ways to solve simple system line problems.

5. What is the graphical approach to measurement techniques?

The Linear Programming (LPP) problem-solving method helps to see the process more clearly. It is also helpful to understand the different terms associated with the LPP solution. Linear editing problems with two variants can be represented and solved with drawings easily.

6. What is the Use of the Graphical Method?

A graphical method of Linear Programming is used for solving the problems by finding out the maximum or minimum point of the intersection between the objective function line and the feasible region on a graph.

7. What are Graphical Methods?

Graph is a powerful tool for data evaluation as they provide us with quick and visual summaries of essential data characteristics. Examples of graphs can be a box plot or a histogram. Graphical methods are basically used for qualitative statistical evaluations.

8. What is Linear Programming Used for?

Linear Programming is used for analyzing the supplies in the manufacturing industries. It is used for shelf space optimization. Linear Programming is also used for optimizing daily routes. It is used in machine learning.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

4.2 Graphical Solutions of Linear Programming

Wouldn’t it be nice if we could simply produce and sell infinitely many units of a product and thus make a never-ending amount of money? In business (and in day-to-day living) we know that some things are just unreasonable or impossible. Instead, our hope is to maximize or minimize some quantity, given a set of constraints.

In order to have a linear programming problem, we must have:

• Constraints, represented as inequalities
• An  objective function , which is a function whose value we either want to be a large as possible (want to maximize it) or as small as possible (want to minimize it).

Let’s consider an extension of the example from the end of the last section:

Example of Linear Programming

A company produces a basic and premium version of its product.  The basic version requires 20 minutes of assembly and 15 minutes of painting.  The premium version requires 30 minutes of assembly and 30 minutes of painting.  If the company has staffing for 3,900 minutes of assembly and 3,300 minutes of painting each week.  They sell the basic products for a profit of $30 and the premium products for a profit of $40.  How many of each version should be produced to maximize profit?

In the last section, the example developed our constraints. Together, these define our linear programming problem:

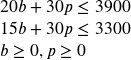
In this section, we will approach this type of problem graphically. We start by graphing the constraints to determine the feasible region – the set of possible solutions. Just showing the solution set where the four inequalities overlap, we see a clear region.

Notice that all the constant-profit lines are parallel, and that in general the profit increases as we move up to upper right. Notice also that for a profit of $5000 there are some production levels inside the feasible region for that profit level, but some are outside. That means we could feasibly make $5000 profit by producing, for example, 167 basic items and no premium items, but we can’t make $5000 by producing 125 premium items and no basic items because that falls outside our constraints.

The solution to our linear programming problem will be the largest possible profit that is still feasible. Graphically, that means the line furthest to the upper-right that still touches the feasible region on at least point. That solution is the one below:

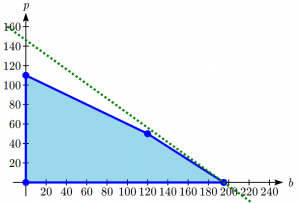
The objective function along with the four corner points above forms a bounded linear programming problem. That is, imagine you are looking at three fence posts connected by fencing (black point and lines, respectively). If you were to put your dog in the middle, you could be sure it would not escape (assuming the fence is tall enough). If this is the case, then you have a bounded linear programming problem. If the dog could walk infinitely in any one direction, then the problem is unbounded.

In the past example, you can see that the line of maximum profit will always touch the boundary of the feasible region. That observation inspires the fundamental theorem of linear programming.

Fundamental Theorem of Linear Programming

• If a solution exists to a bounded linear programming problem, then it occurs at one of the corner points.
• If a feasible region is unbounded, then a maximum value for the objective function does not exist.
• If a feasible region is unbounded, and the objective function has only positive coefficients, then a minimum value exists.

In the last example we solve the problem somewhat intuitively by “sliding” the profit line up.  Typically we use a more procedural approach.

Solving a Linear Programming Problem Graphically

• Define the variables
• Define the variable to be optimized. The question asked is a good indicator as to what this will be: Profit, Revenue, Cost are popular choices.
• Write the objective function, as a mathematical equation, like P=10x+15y or C=200a+300b.
• Write the constraints as a system of mathematical inequalities
• Graph the constraint system of inequalities and shade the feasible region
• Identify the corner point by solving systems of linear equation whose intersection represents a corner point.
• Test each corner point in the objective function. The “winning” point is the point that optimizes the objective function (greatest if maximizing, least if minimizing.)

Try it Now 1

Another Linear Programming Example

A health-food business would like to create a high-potassium blend of dried fruit in the form of a box of 10 fruit bars. It decides to use dried apricots, which have 407 mg of potassium per serving, and dried dates, which have 271 mg of potassium per serving. The company can purchase its fruit through in bulk for a reasonable price. Dried apricots cost $9.99/lb. (about 3 servings) and dried dates cost $7.99/lb. (about 4 servings). The company would like the box of bars to have at least the recommended daily potassium intake of about 4700 mg, and contain at least 1 serving of each fruit. In order to minimize cost, how many servings of each dried fruit should go into the box of bars?

Step 2: We next work on the objective function.

• There just be at least 1 serving of each fruit
• The product must contain at least 4700 mg of potassium

Mathematically,

Thus, we have,

Subject to:

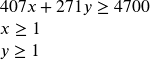
Step 5: We graph the constraints and shade the feasible region:

Step 6: The region is unbounded, but we will be able to find a minimum still. We can see there are two corner points.

Step 7: Testing the objective function at each of these corner points:

The company can minimize cost by using 1 serving of apricots and 15.8 servings of dates.

Try it Now 2

A company makes two products.  Product A requires 3 hours of manufacturing and 1 hour of assembly.  Product B requires 4 hours of manufacturing and 2 hours of assembly.  There are a total of 84 hours of manufacturing and 32 hours of assembly available.  Determine the production to maximize profit if the profit on product A is $50 and the profit on product B is $60.

Yet another Example of Linear Programming

We begin by defining the variables. Let c  = number of chairs made t = number of tables made

The profit, P , will be P = 20 c + 30 t .

There are five corner points for this region.

Point 1:  In the lower left, where t = 0 crosses c = 0.    Point: (0, 0)

Testing the objective function at each of these corner points:

The profit will be maximized by producing 10 chairs and 15 tables.

Graphing is not the only way to do Linear Programming and Optimization. There is another method, called The Simplex Method . It is included in the source material for this chapter. Most people use technology for these problems as well and many can be found online. While this books gives only an introduction to Linear Programming, it is used in many business applications.

Try it Now Answers

Graphing the feasible region, we see there are three corner points of potential interest: (0, 9), (5, 0), and the intersection of the two lines at (3, 6). We then evaluate the objective function at each corner point.

2. Let a be the number of product A produced, and b be the number of product B.

Evaluating the objective function at each of these points:

Profit will be maximized by producing 28 units of product A and 0 units of product B.

Media Attributions

• linearprogexample1
• linearprogexample2
• linearprogexample3
• takenote is licensed under a Public Domain license
• linearprogexample4
• linearprogexample5

College Algebra for the Managerial Sciences Copyright © by Terri Manthey is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.3: Graphical Solutions

• Last updated
• Save as PDF
• Page ID 67113

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Wouldn’t it be nice if we could simply produce and sell infinitely many units of a product and thus make a never-ending amount of money? In business (and in day-to-day living) we know that some things are just unreasonable or impossible. Instead, our hope is to maximize or minimize some quantity, given a set of constraints.

In order to have a linear programming problem, we must have:

• Constraints, represented as inequalities
• An objective function , that is, a function whose value we either want to be as large as possible (want to maximize it) or as small as possible (want to minimize it).

Consider this extension of the example from the end of the last section.

Example \(\PageIndex{1}\)

A company produces a basic and premium version of its product.  The basic version requires 20 minutes of assembly and 15 minutes of painting.  The premium version requires 30 minutes of assembly and 30 minutes of painting.  If the company has staffing for 3,900 minutes of assembly and 3,300 minutes of painting each week.  They sell the basic products for a profit of $30 and the premium products for a profit of $40.  How many of each version should be produced to maximize profit?

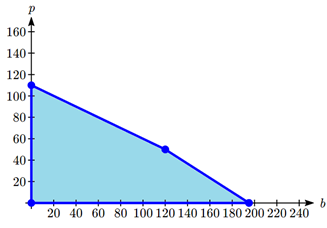
Let \(b-\) the number of basic products made, and \(p=\) the number of premium products made.  Our objective function is what we’re trying to maximize or minimize.  In this case, we’re trying to maximize profit.  The total profit, \(P\), is

\[P = 30b + 40p\nonumber \]

In the last section, the example developed our constraints.  Together, these define our linear programming problem:

Objective function: \[P = 30b + 40p\nonumber \]

Constraints:

\[\begin{array}{*{20}{c}}  20b + 30p \leq 3900 \\ 15b + 30p \leq 3300 \end{array}\nonumber \]

\[b \geq 0, \quad p \geq 0\nonumber \]

In this section, we will approach this type of problem graphically.  We start by graphing the constraints to determine the feasible region – the set of possible solutions.  Just showing the solution set where the four inequalities overlap, we see a clear region.

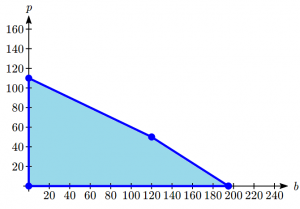
To consider how the objective function connects, suppose we considered all the possible production combinations that gave a profit of \(P = \$3000\), so that \(3000 = 30b + 40p\). That set of combinations would form a line in the graph.  Doing the same for a profit of $5000 and $6500 would give additional lines.  Graphing those on top of our feasible region, we see a pattern:

Notice that all the constant-profit lines are parallel, and that in general the profit increases as we move up to upper right.  Notice also that for a profit of $5000 there are some production levels inside the feasible region for that profit level, but some are outside.  That means we could feasibly make $5000 profit by producing, for example, 167 basic items and no premium items, but we can’t make $5000 by producing 125 premium items and no basic items because that falls outside our constraints. 

The solution to our linear programming problem will be the largest possible profit that is still feasible.  Graphically, that means the line furthest to the upper-right that still touches the feasible region on at least point.  That solution is the one below:

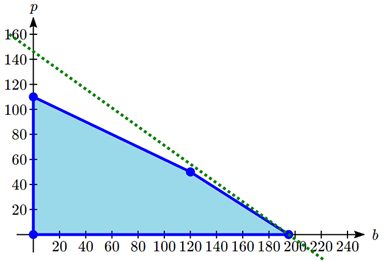
This profit line touches the feasible region where \(b = 195\) and \(p = 0\), giving a profit of

\[P = 30(195) + 40(0) = \$ 5850. \nonumber \]

Notice that this is slightly larger than the profit that would be made by completely utilizing all staffing at \(b = 120, p = 50\), where the profit would be $5600.

The objective function along with the four corner points above forms a bounded linear programming problem. That is, imagine you are looking at three fence posts connected by fencing (black point and lines, respectively). If you were to put your dog in the middle, you could be sure it would not escape (assuming the fence is tall enough). If this is the case, then you have a bounded linear programming problem. If the dog could walk infinitely in any one direction, then the problem is unbounded.

In the past example, you can see that the line of maximum profit will always touch the boundary of the feasible region.  That observation inspires the fundamental theorem of linear programming.

Fundamental Theorem of Linear Programming

• If a solution exists to a bounded linear programming problem, then it occurs at one of the corner points.
• If a feasible region is unbounded, then a maximum value for the objective function does not exist.
• If a feasible region is unbounded, and the objective function has only positive coefficients, then a minimum value exists.

In the last example we solve the problem somewhat intuitively by “sliding” the profit line up.  Typically we use a more procedural approach.

Solving a Linear Programming Problem Graphically

• Define the variables to be optimized. The question asked is a good indicator as to what these will be.
• Write the objective function, first in words, then convert to a mathematical equation
• Write the constraints, first in words, then convert to mathematical inequalities
• Graph the constraints inequalities, and shade the feasible region
• Identify the corner points by solving systems of linear equations whose intersection represents a corner point.
• Test all corner points in the objective function. The “winning” point is the point that optimizes the objective function (biggest if maximizing, smallest if minimizing)

Exercise \(\PageIndex{1}\)

Maximize \(P = 14x + 9y\nonumber \) subject to the constraints:

 \[\begin{align*}  x + y &\leq 9  \\  3x + y &\leq 15  \\  x \geq 0, & \; y \geq 0  \\ \end{align*} \nonumber \]

Graphing the feasible region, we see there are three corner points of potential interest:  (0, 9), (5, 0), and the intersection of the two lines at (3, 6).  We then evaluate the objective function at each corner point.

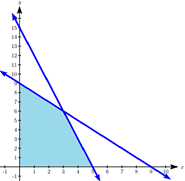
\(P\) is maximized when \(x = 3, y = 6\).

Example \(\PageIndex{2}\)

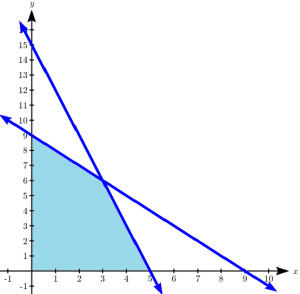
A health-food business would like to create a high-potassium blend of dried fruit in the form of a box of 10 fruit bars. It decides to use dried apricots, which have 407 mg of potassium per serving, and dried dates, which have 271 mg of potassium per serving. The company can purchase its fruit through in bulk for a reasonable price. Dried apricots cost $9.99/lb. (about 3 servings) and dried dates cost $7.99/lb. (about 4 servings). The company would like the box of bars to have at least the recommended daily potassium intake of about 4700 mg, and contain at least 1 serving of each fruit. In order to minimize cost, how many servings of each dried fruit should go into the box of bars?

We begin by defining the variables. Let

\(x =\) number of servings of dried apricots

\(y =\) number of servings of dried dates

We next work on the objective function.

For apricots, there are 3 servings in one pound. This means that the cost per serving is $9.99/3 = $3.33. The cost for \(x\) servings would thus be 3.33\(x\).

For dates, there are 4 servings per pound. This means that the cost per serving is \(\$ 7.99 / 4=\$ 2.00 .\) The cost for \(y\) servings would thus be \(2.00 y.\)

The total cost, \(C\), for apricots and dates would be

\[C=3.33 x+2.00 y \nonumber\]

Normally we would have constraints \(x \geq 0\) and \(y \geq 0\) since negative servings can't be used. But in this case, we re further restricted. In words:

• There must be at least 1 serving of each fruit
• The product must contain at least \(4700 \mathrm{mg}\) of potassium

Mathematically,

• Since there must be at least 1 serving of each fruit, \(x \geq 1\) and \(v \geq 1\)
• There are \(407 x\) mg of potassium in \(x\) servings of apricots and \(271 y\) mg of potassium in \(y\) servings of dates. The sum should be greater than or equal to \(4700 \mathrm{mg}\) of potassium, or \(407 x+271 y \geq 4700\)

Thus we have.

Objective function:

\[\begin{align*}407 x+271 y \geq 4700 \\ x \geq 1, \quad y \geq 1\end{align*}\]

We graph the constraints and shade the feasible region:

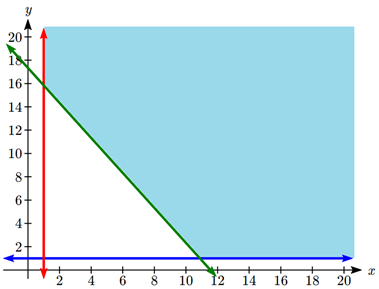
The region is unbounded, but we will be able to find a minimum still.  We can see there are two corner points.

The one in the upper left is the intersection of the lines \(407x + 271y = 4700\) and \(x=1\).  Solving for the intersection using substitution:

\[\begin{align*} 407(1) + 271y &= 4700  \\ y &\approx 15.8  \\ \end{align*} \nonumber \]

Point:  \((1, 15.8)\)

The one in the lower right is the intersection of the lines \(407x + 271y = 4700\) and \(y = 1\). 

\[\begin{align*}  407x + 271(1) &= 4700  \\ x &\approx 10.9 \end{align*}  \]

Point:  \((10.9, 1)\)

Testing the objective function at each of these corner points:

The company can minimize cost by using 1 serving of apricots and 15.8 servings of dates.

Exercise \(\PageIndex{2}\)

A company makes two products.  Product A requires 3 hours of manufacturing and 1 hour of assembly.  Product B requires 4 hours of manufacturing and 2 hours of assembly.  There are a total of 84 hours of manufacturing and 32 hours of assembly available.  Determine the production to maximize profit if the profit on product A is $50 and the profit on product B is $60.

Let \(a\) be the number of product A produced, and \(b\) be the number of product B.

Our goal is to maximize profit:  \(P = 50a + 60b\).

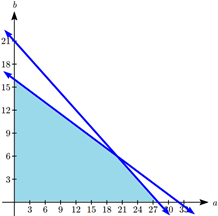
From manufacturing we get the constraint:

\[3a + 4b \leq 84\nonumber \]

From assembly we get the constraint:

\[1a + 2b \leq 32\nonumber \]

We have corner points at (0, 16), (28, 0).  The third is at the intersection of the two lines.  To find that we could multiply the second equation by -2 and add:

\[\begin{array}{rc} 3a + 4b &= 84 \\ - 2a - 4b &=  - 64 \\ \hline  a&= 20  \end{array} \nonumber \]

The third corner point is at (20, 6).

Evaluating the objective function at each of these points:

Profit will be maximized by producing 28 units of product A and 0 units of product B.

Example \(\PageIndex{3}\)

A factory manufactures chairs and tables, each requiring the use of three operations: Cutting, Assembly, and Finishing. The first operation can be used at most 40 hours; the second at most 42 hours; and the third at most 25 hours. A chair requires 1 hour of cutting, 2 hours of assembly, and 1 hour of finishing; a table needs 2 hours of cutting, 1 hour of assembly, and 1 hour of finishing.  If the profit is $20 per unit for a chair and $30 for a table, how many units of each should be manufactured to maximize profit?

\(c  =\) number of chairs made

\(t =\) number of tables made

The profit, \(P\), will be \(P = 20c + 30t\).

For cutting, \(c\) chairs will require \(1c\) hours and \(t\) tables will require \(2t\) hours.  We can use at most 40 hours, so

\[c + 2t \leq 40\nonumber \].

For assembly, \(c\) chairs will require \(2c\) hours and t tables will require \(1t\) hours.  We can use at most 42 hours, so

\[2c + t \leq 42\nonumber \].

For finishing, c chairs will require \(1c\) hours and \(t\) tables will require \(1t\) hours.  We can use at most 25 hours, so

\[c + t \leq 25\nonumber \].

Since we can’t produce negative items, \(c \geq 0,\quad t \geq 0\).

Graphing the constraints, we can see the feasible region.

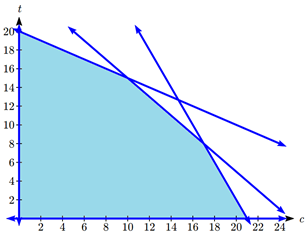
There are five corner points for this region.

Point 1 : 

In the lower left, where \(t = 0\) crosses \(c = 0\).    Point: (0, 0)

Point 2 : 

In the upper left, where \(c = 0\) crosses \(c + 2t = 40 \).   

Using substitution, \(0 + 2t = 40 \), so \(t = 20\).

Point: \((0, 20)\)

Point 3 : 

In the lower right, where \(t = 0\) crosses \(2c + t = 42 \).   

Using substitution, \(2c + 0 = 42 \), so \(c = 21\).

Point: \((21, 0)\)

Point 4 : 

Where \(c + 2t = 40\) crosses \(c + t = 25\).

We can solve this as a system using any techniques we know. We could solve the second equation for \(c\), giving \(c = 25 - t\), then substitute into the first equation:

\[\begin{align*} (25 - t) + 2t &= 40  \\ 25 + t &= 40  \\ t &= 15  \end{align*} \nonumber \]

Then \(c = 25 – 15 = 10\).

Point:  \((10, 15)\)

Point 5 : 

Where \(2c + t = 42\) crosses \(c + t = 25\).

We can solve this as a system using any techniques we know.  Using a different technique this time, we could multiply the bottom equation by -1 then add it to the first:

\[\begin{array}{rc}  2c + t &= 42  \\  - c - t &=  - 25  \\ \hline c = 17 \end{array} \nonumber \]

Then using \(c + t = 25 \), we have \(17 + t = 25\), so \(t = 8\).

Point:  \((17, 8)\)

The profit will be maximized by producing 10 chairs and 15 tables.

Important Topics of this Section

Objective function

Constraint equations

Feasible region

Corner points

Solving a linear programming problem using a graph

Linear Programming

Linear programming is a process that is used to determine the best outcome of a linear function. It is the best method to perform linear optimization by making a few simple assumptions. The linear function is known as the objective function. Real-world relationships can be extremely complicated. However, linear programming can be used to depict such relationships, thus, making it easier to analyze them.

Linear programming is used in many industries such as energy, telecommunication, transportation, and manufacturing. This article sheds light on the various aspects of linear programming such as the definition, formula, methods to solve problems using this technique, and associated linear programming examples.

What is Linear Programming?

Linear programming, also abbreviated as LP, is a simple method that is used to depict complicated real-world relationships by using a linear function . The elements in the mathematical model so obtained have a linear relationship with each other. Linear programming is used to perform linear optimization so as to achieve the best outcome.

Linear Programming Definition

Linear programming can be defined as a technique that is used for optimizing a linear function in order to reach the best outcome. This linear function or objective function consists of linear equality and inequality constraints. We obtain the best outcome by minimizing or maximizing the objective function .

Linear Programming Examples

Suppose a postman has to deliver 6 letters in a day from the post office (located at A) to different houses (U, V, W, Y, Z). The distance between the houses is indicated on the lines as given in the image. If the postman wants to find the shortest route that will enable him to deliver the letters as well as save on fuel then it becomes a linear programming problem. Thus, LP will be used to get the optimal solution which will be the shortest route in this example.

Linear Programming Formula

A linear programming problem will consist of decision variables , an objective function, constraints, and non-negative restrictions. The decision variables, x, and y, decide the output of the LP problem and represent the final solution. The objective function, Z, is the linear function that needs to be optimized (maximized or minimized) to get the solution. The constraints are the restrictions that are imposed on the decision variables to limit their value. The decision variables must always have a non-negative value which is given by the non-negative restrictions. The general formula of a linear programming problem is given below:

• Objective Function: Z = ax + by
• Constraints: cx + dy ≤ e, fx + gy ≤ h. The inequalities can also be "≥"
• Non-negative restrictions: x ≥ 0, y ≥ 0

How to Solve Linear Programming Problems?

The most important part of solving linear programming problem is to first formulate the problem using the given data. The steps to solve linear programming problems are given below:

• Step 1: Identify the decision variables.
• Step 2: Formulate the objective function. Check whether the function needs to be minimized or maximized.
• Step 3: Write down the constraints.
• Step 4: Ensure that the decision variables are greater than or equal to 0. (Non-negative restraint)
• Step 5: Solve the linear programming problem using either the simplex or graphical method.

Let us study about these methods in detail in the following sections.

Linear Programming Methods

There are two main methods available for solving linear programming problem. These are the simplex method and the graphical method. Given below are the steps to solve a linear programming problem using both methods.

Linear Programming by Simplex Method

The simplex method in lpp can be applied to problems with two or more decision variables. Suppose the objective function Z = 40\(x_{1}\) + 30\(x_{2}\) needs to be maximized and the constraints are given as follows:

\(x_{1}\) + \(x_{2}\) ≤ 12

2\(x_{1}\) + \(x_{2}\) ≤ 16

\(x_{1}\) ≥ 0, \(x_{2}\) ≥ 0

Step 1: Add another variable, known as the slack variable, to convert the inequalities into equations. Also, rewrite the objective function as an equation .

- 40\(x_{1}\) - 30\(x_{2}\) + Z = 0

\(x_{1}\) + \(x_{2}\) + \(y_{1}\) =12

2\(x_{1}\) + \(x_{2}\) + \(y_{2}\) =16

\(y_{1}\) and \(y_{2}\) are the slack variables.

Step 2: Construct the initial simplex matrix as follows:

\(\begin{bmatrix} x_{1} & x_{2} &y_{1} & y_{2} & Z & \\ 1&1 &1 &0 &0 &12 \\ 2& 1 & 0& 1 & 0 & 16 \\ -40&-30&0&0&1&0 \end{bmatrix}\)

Step 3: Identify the column with the highest negative entry. This is called the pivot column. As -40 is the highest negative entry, thus, column 1 will be the pivot column.

Step 4: Divide the entries in the rightmost column by the entries in the pivot column. We exclude the entries in the bottom-most row.

12 / 1 = 12

The row containing the smallest quotient is identified to get the pivot row. As 8 is the smaller quotient as compared to 12 thus, row 2 becomes the pivot row. The intersection of the pivot row and the pivot column gives the pivot element.

Thus, pivot element = 2.

Step 5: With the help of the pivot element perform pivoting, using matrix properties , to make all other entries in the pivot column 0.

Using the elementary operations divide row 2 by 2 (\(R_{2}\) / 2)

\(\begin{bmatrix} x_{1} & x_{2} &y_{1} & y_{2} & Z & \\ 1&1 &1 &0 &0 &12 \\ 1& 1/2 & 0& 1/2 & 0 & 8 \\ -40&-30&0&0&1&0 \end{bmatrix}\)

Now apply \(R_{1}\) = \(R_{1}\) - \(R_{2}\)

\(\begin{bmatrix} x_{1} & x_{2} &y_{1} & y_{2} & Z & \\ 0&1/2 &1 &-1/2 &0 &4 \\ 1& 1/2 & 0& 1/2 & 0 & 8 \\ -40&-30&0&0&1&0 \end{bmatrix}\)

Finally \(R_{3}\) = \(R_{3}\) + 40\(R_{2}\) to get the required matrix.

\(\begin{bmatrix} x_{1} & x_{2} &y_{1} & y_{2} & Z & \\ 0&1/2 &1 &-1/2 &0 &4 \\ 1& 1/2 & 0& 1/2 & 0 & 8 \\ 0&-10&0&20&1&320 \end{bmatrix}\)

Step 6: Check if the bottom-most row has negative entries. If no, then the optimal solution has been determined. If yes, then go back to step 3 and repeat the process. -10 is a negative entry in the matrix thus, the process needs to be repeated. We get the following matrix.

\(\begin{bmatrix} x_{1} & x_{2} &y_{1} & y_{2} & Z & \\ 0&1 &2 &-1 &0 &8 \\ 1& 0 & -1& 1 & 0 & 4 \\ 0&0&20&10&1&400 \end{bmatrix}\)

Writing the bottom row in the form of an equation we get Z = 400 - 20\(y_{1}\) - 10\(y_{2}\). Thus, 400 is the highest value that Z can achieve when both \(y_{1}\) and \(y_{2}\) are 0.

Also, when \(x_{1}\) = 4 and \(x_{2}\) = 8 then value of Z = 400

Thus, \(x_{1}\) = 4 and \(x_{2}\) = 8 are the optimal points and the solution to our linear programming problem.

Linear Programming by Graphical Method

If there are two decision variables in a linear programming problem then the graphical method can be used to solve such a problem easily.

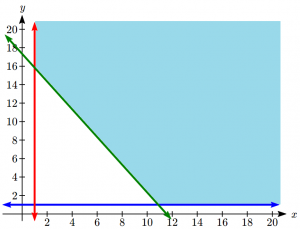
Suppose we have to maximize Z = 2x + 5y.

The constraints are x + 4y ≤ 24, 3x + y ≤ 21 and x + y ≤ 9

where, x ≥ 0 and y ≥ 0.

To solve this problem using the graphical method the steps are as follows.

Step 1: Write all inequality constraints in the form of equations.

x + 4y = 24

3x + y = 21

Step 2: Plot these lines on a graph by identifying test points.

x + 4y = 24 is a line passing through (0, 6) and (24, 0). [By substituting x = 0 the point (0, 6) is obtained. Similarly, when y = 0 the point (24, 0) is determined.]

3x + y = 21 passes through (0, 21) and (7, 0).

x + y = 9 passes through (9, 0) and (0, 9).

Step 3: Identify the feasible region. The feasible region can be defined as the area that is bounded by a set of coordinates that can satisfy some particular system of inequalities.

Any point that lies on or below the line x + 4y = 24 will satisfy the constraint x + 4y ≤ 24.

Similarly, a point that lies on or below 3x + y = 21 satisfies 3x + y ≤ 21.

Also, a point lying on or below the line x + y = 9 satisfies x + y ≤ 9.

The feasible region is represented by OABCD as it satisfies all the above-mentioned three restrictions.

Step 4: Determine the coordinates of the corner points. The corner points are the vertices of the feasible region.

B = (6, 3). B is the intersection of the two lines 3x + y = 21 and x + y = 9. Thus, by substituting y = 9 - x in 3x + y = 21 we can determine the point of intersection.

C = (4, 5) formed by the intersection of x + 4y = 24 and x + y = 9

Step 5: Substitute each corner point in the objective function. The point that gives the greatest (maximizing) or smallest (minimizing) value of the objective function will be the optimal point.

33 is the maximum value of Z and it occurs at C. Thus, the solution is x = 4 and y = 5.

Applications of Linear Programming

Linear programming is used in several real-world applications. It is used as the basis for creating mathematical models to denote real-world relationships. Some applications of LP are listed below:

• Manufacturing companies make widespread use of linear programming to plan and schedule production.
• Delivery services use linear programming to decide the shortest route in order to minimize time and fuel consumption.
• Financial institutions use linear programming to determine the portfolio of financial products that can be offered to clients.

Related Articles:

• Introduction to Graphing
• Linear Equations in Two Variables
• Solutions of a Linear Equation
• Mathematical Induction

Important Notes on Linear Programming

• Linear programming is a technique that is used to determine the optimal solution of a linear objective function.
• The simplex method in lpp and the graphical method can be used to solve a linear programming problem.
• In a linear programming problem, the variables will always be greater than or equal to 0.

As the minimum value of Z is 127, thus, B (3, 28) gives the optimal solution. Answer: The minimum value of Z is 127 and the optimal solution is (3, 28)

• Example 3: Using the simplex method in lpp solve the linear programming problem Minimize Z = \(x_{1}\) + 2\(x_{2}\) + 3\(x_{3}\) \(x_{1}\) + \(x_{2}\) + \(x_{3}\) ≤ 12 2\(x_{1}\) + \(x_{2}\) + 3\(x_{3}\) ≤ 18 \(x_{1}\), \(x_{2}\), \(x_{3}\) ≥ 0 Solution: Convert all inequalities to equations by introducing slack variables. -\(x_{1}\) - 2\(x_{2}\) - 3\(x_{3}\) + Z = 0 \(x_{1}\) + \(x_{2}\) + \(x_{3}\) + \(y_{1}\) = 12 2\(x_{1}\) + \(x_{2}\) + 3\(x_{3}\) + \(y_{2}\) = 18 Expressing this as a matrix we get, \(\begin{bmatrix} x_{1} & x_{2} & x_{3} & y_{1} & y_{2} & Z & \\ 1 & 1 & 1 & 1 & 0 & 0 & 12\\ 2 & 1 & 3 & 0 & 1 & 0 & 18\\ -1 & -2 & -3 & 0 & 0 & 1 & 0 \end{bmatrix}\) As -3 is the greatest negative value thus, column 3 is the pivot column. 12 / 1 = 12 18 / 3 = 6 As 6 is the smaller quotient thus, row 2 is the pivot row and 3 is the pivot element. By applying matrix operations we get, \(\begin{bmatrix} x_{1} & x_{2} & x_{3} & y_{1} & y_{2} & Z & \\ 0.33 & 0.667 & 0 & 1 & -0.33 & 0 & 6\\ 0.667 & 0.33 & 1 & 0 & 0.33 & 0 & 6\\ 1 & -1 & 0 & 0 & 1 & 1 & 18 \end{bmatrix}\) Now -1 needs to be eliminated. Thus, by repreating the steps the matrix so obtained is as follows \(\begin{bmatrix} x_{1} & x_{2} & x_{3} & y_{1} & y_{2} & Z & \\ 0.5 & 1 & 0 & 1.5 & 0.5 & 0 & 9\\ 0.5 & 0 & 1 & -0.5 & 0.5 & 0 & 3\\ 1.5 & 0 & 0 & 1.5 & 0.5 & 1 & 27 \end{bmatrix}\) We get the maximum value of Z = 27 at \(x_{1}\) = 0, \(x_{2}\) = 9 \(x_{3}\) = 3 Answer: Maximum value of Z = 27 and optimal solution (0, 9, 3)

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Linear Programming

go to slide go to slide

FAQs on Linear Programming

What is meant by linear programming.

Linear programming is a technique that is used to identify the optimal solution of a function wherein the elements have a linear relationship.

What is Linear Programming Formula?

The general formula for a linear programming problem is given as follows:

What is the Objective Function in Linear Programming Problems?

The objective function is the linear function that needs to be maximized or minimized and is subject to certain constraints. It is of the form Z = ax + by.

How to Formulate a Linear Programming Model?

The steps to formulate a linear programming model are given as follows:

• Identify the decision variables.
• Formulate the objective function.
• Identify the constraints.
• Solve the obtained model using the simplex or the graphical method.

How to Find Optimal Solution in Linear Programming?

We can find the optimal solution in a linear programming problem by using either the simplex method or the graphical method. The simplex method in lpp can be applied to problems with two or more variables while the graphical method can be applied to problems containing 2 variables only.

How to Find Feasible Region in Linear Programming?

To find the feasible region in a linear programming problem the steps are as follows:

• Draw the straight lines of the linear inequalities of the constraints.
• Use the "≤" and "≥" signs to denote the feasible region of each constraint.
• The region common to all constraints will be the feasible region for the linear programming problem.

What are Linear Programming Uses?

Linear programming is widely used in many industries such as delivery services, transportation industries, manufacturing companies, and financial institutions. The linear program is solved through linear optimization method, and it is used to determine the best outcome in a given scenerio.

• School Guide
• Mathematics
• Number System and Arithmetic
• Trigonometry
• Probability
• Mensuration
• Maths Formulas
• Integration Formulas
• Differentiation Formulas
• Trigonometry Formulas
• Algebra Formulas
• Mensuration Formula
• Statistics Formulas
• Trigonometric Table
• CBSE Class 12 Maths Notes: Chapter Wise Notes PDF 2024

Chapter 1: Relations and Functions

• Types of Functions
• Composite functions - Relations and functions
• Invertible Functions
• Composition of Functions
• Inverse Functions
• Verifying Inverse Functions by Composition

Chapter 2: Inverse Trigonometric Functions

• Inverse Trigonometric Functions
• Graphs of Inverse Trigonometric Functions - Trigonometry | Class 12 Maths
• Properties of Inverse Trigonometric Functions
• Inverse Trigonometric Identities

Chapter 3: Matrices

• Types of Matrices
• Matrix Operations
• Matrix Addition
• Matrix Multiplication - How to Multiply Matrices, Methods, Examples
• Transpose of a Matrix
• Symmetric and Skew Symmetric Matrices
• Elementary Operations on Matrices
• Inverse of a Matrix by Elementary Operations - Matrices | Class 12 Maths
• Invertible Matrix

Chapter 4: Determinants

• Determinant of a Matrix with Solved Examples
• Properties of Determinants
• Area of a Triangle using Determinants
• Minors and Cofactors
• Adjoint of a Matrix
• Applications of Matrices and Determinants

Chapter 5: Continuity and Differentiability

• Continuity and Discontinuity in Calculus - Class 12 CBSE
• Differentiability of a Function | Class 12 Maths
• Derivatives of Inverse Functions
• Derivatives of Implicit Functions - Continuity and Differentiability | Class 12 Maths
• Derivatives of Composite Functions
• Derivatives of Inverse Trigonometric Functions | Class 12 Maths
• Derivative of Exponential Functions
• Logarithmic Differentiation - Continuity and Differentiability
• Proofs for the derivatives of eˣ and ln(x) - Advanced differentiation
• Rolle's Theorem and Lagrange's Mean Value Theorem
• Derivative of Functions in Parametric Forms
• Second Order Derivatives: Rules , Formula and Examples (Class 12 Maths)
• Mean Value Theorem
• Algebra of Continuous Functions - Continuity and Differentiability | Class 12 Maths

Chapter 6: Applications of Derivatives

• Critical Points
• Derivatives as Rate of Change
• Increasing and Decreasing Functions
• Increasing and Decreasing Intervals
• Tangents and Normals
• Equation of Tangents and Normals
• Relative Minima and Maxima
• Absolute Minima and Maxima
• Concave Function
• Inflection Point
• Curve Sketching
• Approximations & Maxima and Minima - Application of Derivatives | Class 12 Maths
• Higher Order Derivatives

Chapter 7: Integrals

• Integration by Substitution Method
• Integration by Partial Fractions
• Integration by Parts
• Integration of Trigonometric Functions
• Functions Defined by Integrals
• Definite Integral
• Computing Definite Integrals
• Fundamental Theorem of Calculus
• Finding Derivative with Fundamental Theorem of Calculus
• Evaluating Definite Integrals
• Properties of Definite Integrals
• Definite Integrals of Piecewise Functions
• Improper Integrals
• Riemann Sum
• Riemann Sums in Summation Notation
• Trapezoidal Rule
• Definite Integral as the Limit of a Riemann Sum
• Antiderivatives
• Indefinite Integrals
• Particular Solutions to Differential Equations
• Integration by U-substitution
• Reverse Chain Rule
• Partial Fraction Expansion
• Trigonometric Substitution: Method, Formula and Solved Examples

Chapter 8: Applications of Integrals

• Area under Simple Curves
• Area Between Two Curves - Calculus
• Area between Polar Curves
• Area as Definite Integral

Chapter 9: Differential Equations

• Differential Equations
• Homogeneous Differential Equations
• Separable Differential Equations
• Exact Equations and Integrating Factors
• Implicit Differentiation
• Implicit differentiation - Advanced Examples
• Advanced Differentiation
• Disguised Derivatives - Advanced differentiation | Class 12 Maths
• Derivative of Inverse Trig Functions
• Logarithmic Differentiation

Chapter 10: Vector Algebra

• Vector Algebra
• Dot and Cross Products on Vectors
• How to Find the Angle Between Two Vectors?
• Section Formula - Vector Algebra

Chapter 11: Three-dimensional Geometry

• Direction Cosines and Direction Ratios
• Equation of a Line in 3D
• Angles Between two Lines in 3D Space: Solved Examples
• Shortest Distance Between Two Lines in 3D Space | Class 12 Maths
• Points, Lines and Planes

Chapter 12: Linear Programming

Linear programming.

• Graphical Solution of Linear Programming Problems

Chapter 13: Probability

• Conditional Probability and Independence - Probability | Class 12 Maths
• Multiplication Theorem
• Dependent and Independent Events
• Bayes' Theorem
• Probability Distribution - Function, Formula, Table
• Binomial Distribution in Probability
• Binomial Mean and Standard Deviation - Probability | Class 12 Maths
• Bernoulli Trials and Binomial Distribution
• Discrete Random Variable
• Expected Value
• NCERT Solution for Class 12 Math PDF 2024-25
• RD Sharma Class 12 Solutions for Maths

Linear programming is a mathematical concept that is used to find the optimal solution of the linear function. This method uses simple assumptions for optimizing the given function. Linear Programming has a huge real-world application and it is used to solve various types of problems.

Linear programming is used in various industries such as shipping industries, manufacturing industries, transportation industries, telecommunications, and others.

Term “linear programming” consists of two words linear and programming, the word linear tells the relation between various types of variables of degree one used in a problem and the word programming tells us the step-by-step procedure to solve these problems.

In this article, we will learn about linear programming, its examples, formulas, and other concepts in detail.

Table of Content

What is Linear Programming? 

Components of linear programming, linear programming examples, linear programming problems, types of linear programming problems, linear programming formula, how to solve linear programming problems, linear programming methods, linear programming simplex method, linear programming graphical method, linear programming applications, importance of linear programming, up-to-date applications of linear programming, linear programming in operations research, simplex method.

Linear programming or Linear optimization is a technique that helps us to find the optimum solution for a given problem, an optimum solution is a solution that is the best possible outcome of a given particular problem.

In simple terms, it is the method to find out how to do something in the best possible way. With limited resources, you need to do the optimum utilization of resources and achieve the best possible result in a particular objective such as least cost, highest margin, or least time. 

The situation that requires a search for the best values of the variables subject to certain constraints is where we use linear programming problems. These situations cannot be handled by the usual calculus and numerical techniques.

Linear Programming Definition

Linear programming is the technique used for optimizing a particular scenario. Using linear programming provides us with the best possible outcome in a given situation. It uses all the available resources in a manner such that they produce the optimum result.

The basic components of a linear programming(LP) problem are:

• Decision Variables: Variables you want to determine to achieve the optimal solution.
• Objective Function: M athematical equation that represents the goal you want to achieve
• Constraints: Limitations or restrictions that your decision variables must follow.
• Non-Negativity Restrictions: In some real-world scenarios, decision variables cannot be negative

Additional Characteristics of Linear Programming

• Finiteness: The number of decision variables and constraints in an LP problem are finite.
• Linearity: The objective function and all constraints must be linear functions of the decision variables . It means the degree of variables should be one.

We can understand the situations in which Linear programming is applied with the help of the example discussed below,

Suppose a delivery man has to deliver 8 packets in a day to the different locations of a city. He has to pick all the packets from A and has to deliver them to points P, Q, R, S, T, U, V, and W. The distance between them is indicated using the lines as shown in the image below. The shortest path followed by the delivery man is calculated using the concept of Linear Programming.

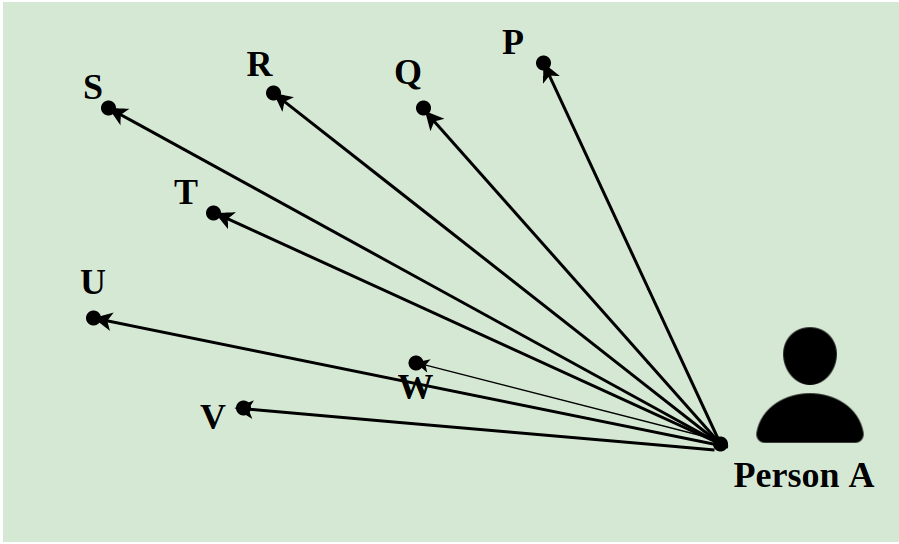
Linear Programming Problems (LPP) involve optimizing a linear function to find the optimal value solution for the function. The optimal value can be either the maximum value or the minimum value.

In LPP, the linear functions are called objective functions. An objective function can have multiple variables, which are subjected to conditions and have to satisfy the linear constraints .

There are many different linear programming problems(LPP) but we will deal with three major linear programming problems in this article.

Manufacturing Problems

Manufacturing problems are a problem that deals with the number of units that should be produced or sold to maximize profits when each product requires fixed manpower, machine hours, and raw materials.

Diet Problems

It is used to calculate the number of different kinds of constituents to be included in the diet to get the minimum cost, subject to the availability of food and their prices.

Transportation Problems

It is used to determine the transportation schedule to find the cheapest way of transporting a product from plants /factories situated at different locations to different markets.

A linear programming problem consists of,

• Decision variables
• Objective function
• Constraints
• Non-Negative restrictions

Decision variables are the variables x, and y, which decide the output of the linear programming problem and represent the final solution. 

The objective function , generally represented by Z, is the linear function that needs to be optimized according to the given condition to get the final solution. 

The restrictions imposed on decision variables that limit their values are called constraints.

Now, the general formula of a linear programming problem is,

Objective Function : Z = ax + by

Constraints: cx + dy ≥ e, px + qy ≤ r

Non-Negative restrictions: x ≥ 0, y ≥ 0

In the above condition x, and y are the decision variables.

Before solving the linear programming problems first we have to formulate the problems according to the standard parameters. The steps for solving linear programming problems are,

Step 1: Mark the decision variables in the problem. Step 2: Build the objective function of the problem and check if the function needs to be minimized or maximized. Step 3: Write down all the constraints of the linear problems. Step 4: Ensure non-negative restrictions of the decision variables. Step 5: Now solve the linear programming problem using any method generally we use either the simplex or graphical method.

We use various methods for solving linear programming problems. The two most common methods used are,

• Graphical Method

Let’s learn about these two methods in detail in this article,

One of the most common methods to solve the linear programming problem is the simplex method. In this method, we repeat a specific condition ‘n’ a number of times until an optimum solution is achieved.

The steps required to solve linear programming problems using the simplex method are,

Step 1: Formulate the linear programming problems based on the given constraints. Step 2: Convert all the given inequalities to equations or equalities of the linear programming problems by adding the slack variable to each inequality where ever required. Step 3: Construct the initial simplex table. By representing each constraint equation in a row and writing the objective function at the bottom row. The table so obtained is called the Simplex table. Step 4: Identify the greatest negative entry in the bottom row the column of the element with the highest negative entry is called the pivot column Step 5: Divide the entries of the right-most column with the entries of the respective pivot column, excluding the entries of the bottommost row. Now the row containing the least entry is called the pivot row. The pivot element is obtained by the intersection of the pivot row and the pivot column. Step 6: Using matrix operation and with the help of the pivot element make all the entries in the pivot column to be zero. Step 7: Check for the non-negative entries in the bottommost row if there are no negative entries in the bottom row, end the process else start the process again from step 4. Step 8: The final simplex table so obtained gives the solution to our problem.

Graphical Method is another method than the Simplex method which is used to solve linear programming problems. As the name suggests this method uses graphs to solve the given linear programming problems. This is the best method to solve linear programming problems and requires less effort than the simplex method. 

While using this method we plot all the inequalities that are subjected to constraints in the given linear programming problems. As soon as all the inequalities of the given LPP are plotted in the XY graph the common region of all the inequalities gives the optimum solution. All the corner points of the feasible region are calculated and the value of the objective function at all those points is calculated then comparing these values we get the optimum solution of the LPP.

Example: Find the maximal and minimal value of z = 6x + 9y when the constraint conditions are,

• 2x + 3y ≤ 12
• x and y ≥ 0

Step 1 : First convert the inequations into normal equations. Hence the equations will be 2x+3y = 0, x = 0, y = 0 and x + y = 5. Step 2 : Find the points at which 2x + 3y and x + y = 5 cut the x-axis and y-axis. To find the point of intersection of the x-axis put y = 0 in the respective equation and find the point. Similarly for y-axis intersection points put x = 0 in the respective equation. Step 3 : Draw the two lines cutting the x-axis and y-axis. We find that the two axes cut each other at (3,2). Step 4 : For x ≥ 0 and y ≥ 0, we find that both inequations are followed. Hence the region will include an area region enclosed by two axes and both lines including the origin. The plotted region is shown below in the figure. Step 5 : Find Z for each point and maxima and minima. Coordinates Z = 6x + 9y (0,5) Z = 45 (0,4) Z = 36 (5,0) Z = 30 (6,0) Z = 36 (3,2) Z = 36 Hence, we find that Z = 6x + 9y is maximum at (0,5) and minimum at (5,0).

Linear Programming has applications in various fields. It is used to find the minimum cost of a process when all the constraints of the problems are given. It is used to optimize the transportation cost of the vehicle, etc. Various applications of Linear Programming are

Engineering Industries

Engineering Industries use linear programming to solve design and manufacturing problems and to get the maximum output from a given condition.

Manufacturing Industries

Manufacturing Industries use linear programming to maximize the profit of the companies and to reduce the manufacturing cost.

Energy Industries

Energy companies use linear programming to optimize their production output.

Transportation Industries

Linear programming is also used in transportation industries to find the path to minimize the cost of transportation.

Linear Programming has huge importance in various industries it maximizes the output value while minimizing the input values according to various constraints.

LP is highly applicable when we have multiple conditions while solving a problem and we have to optimize the output of the problem i.e. either we have to find the minimum or the maximum value according to a given condition.

Linear Inequalities Algebraic Solution of Linear Inequalities

Problem 1: A company manufactures and sells two types of products and the cost of production of each unit a and b is rupees 200 and 150 respectively each unit of product yields a profit of 20 rupees and each unit of product b yields a profit of 15 rupees on selling. The company estimates the monthly demand of A and B to be at a maximum of the harvested unit in all the production budget for the month is set at rupees 50000. How many units should the company manufacture to earn maximum profit from its monthly sales from a and b?

Let x = number of units of type A y = Number of units of type B Maximize Z = 40x + 50y Subject to the constraints 3x + y ≤ 9 x + 2y ≤ 8 and x, y ≥ 0 Consider the equation, 3x + y = 9 x = 3 y = 0 and x + 2y = 8 x = 8 y = 0 Now, we can determine the maximum value of Z by evaluating the value of Z at the four points (vertices) is shown below Vertices Z = 40x + 50y (0, 0) Z = 40 × 0 + 50 × 0 = Rs. 0 (3, 0) Z = 40 × 3 + 50 × 0 = Rs. 120 (0, 4)  Z = 40 × 0 + 50 × 4 = Rs. 200 (2, 3) Z = 40 × 2 + 50 × 3 = Rs. 230 Maximum profit, Z = Rs. 230 ∴ Number of units of type A is 2 and the number of units of type B is 3.

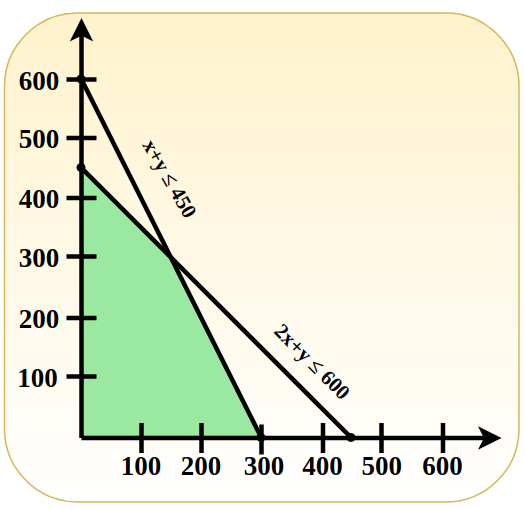
Problem 2: Maximize Z = 3x + 4y.

Subject to constraints , x + y ≤ 450, 2x + y ≤ 600 and x, y ≤ 0.

We have from the given Constraints (1) X + Y = 450 Putting x = 0, ⇒ 0 + y = 450 ⇒ y = 450 Putting y = 0, ⇒ x + 0 = 450 ⇒ x = 450 From, Constraints (2) 2x + y = 600 Putting x = 0, ⇒ 0 + y = 600 ⇒ y = 600 Putting  y = 0, ⇒ 2x + 0 = 600 ⇒ x = 300 Now, we have the points co-ordinate Z = 3x + 4y

Therefore, the optimal solution maximum Z = 1800 at co-ordinate x = 0 and y = 450. The graph is given below.

Linear programming, a powerful mathematical technique, is used to solve optimization problems in various industries. Here are some modern applications:

• Supply Chain Optimization : Linear programming helps companies minimize costs and maximize efficiency in their supply chains. It’s used for determining the most cost-effective transportation routes, warehouse operations, and inventory management strategies.
• Energy Management : In the energy sector, linear programming is utilized to optimize the mix of energy production methods. This includes balancing traditional energy sources with renewable ones to reduce costs and environmental impact while meeting demand.
• Telecommunications Network Design : Linear programming aids in designing efficient telecommunications networks. It helps in allocating bandwidth, designing network layouts, and optimizing the flow of data to ensure high-speed communication at lower costs.
• Financial Planning : Businesses and financial analysts use linear programming for portfolio optimization, risk management, and capital budgeting. It helps in making investment decisions that maximize returns while minimizing risk.
• Healthcare Logistics : In healthcare, linear programming is applied to optimize the allocation of resources, such as hospital beds, medical staff, and equipment. It’s crucial for improving patient care, reducing wait times, and managing costs effectively.
• Manufacturing Process Optimization : Linear programming is used to determine the optimal production levels for multiple products within a manufacturing facility, considering constraints like labor, materials, and machine availability.
• Agricultural Planning : Farmers and agricultural planners use linear programming to decide on crop selection, land use, and resource allocation to maximize yields and profits while conserving resources.
• Airline Crew Scheduling : Airlines employ linear programming to schedule crews efficiently, ensuring that flights are staffed in compliance with regulations and minimizing operational costs.

These applications demonstrate the versatility and power of linear programming in solving complex optimization problems across various sectors, showcasing its relevance in today’s data-driven world.

• Core Tool : Linear programming is a foundational tool in operations research for optimizing resources.
• Decision Making : Helps in making the best decisions regarding resource allocation, maximizing profits, or minimizing costs.
• Wide Applications : Used in various fields such as logistics, manufacturing, finance, and healthcare for solving complex problems.
• Modeling Real-World Problems : Transforms real-world problems into mathematical models to find the most efficient solutions.
• Optimization Algorithm : The Simplex Method is a powerful algorithm used in linear programming to find the optimal solution to linear inequalities.
• Step-by-Step Approach : It iteratively moves towards the best solution by navigating the edges of the feasible region defined by constraints.
• Efficiency : Known for its efficiency in solving large-scale linear programming problems.
• Versatility : Applicable in various domains like diet planning, network flows, production scheduling, and more, showcasing its versatility.

Linear Programming – FAQs

What is linear programming.

Linear programming is a mathematical concept which is used to optimize a given linear problem which has a variety of constraints. Using linear programming we the optimum output of the given problem

What are Linear Programming Problems?

Linear Programming Problems (LPP) are the problems which give the optimum solution to the given conditions.

What is Linear Programming Formula?

General Linear Programming Formulas are, Objective Function: Z = ax + by Constraints: px + qy ≤ r, sx + ty ≤ u Non-Negative Restrictions: x ≥ 0, y ≥ 0

What are the different types of Linear Programming?

Different types of linear programming methods are, Linear Programming by Simplex Method Linear Programming by R Method Linear Programming by Graphical Method

What are requirements of Linear Programming?

Various requirements of linear programming problems are, Linearity Objective Function Constraints Non-negativity

What are the advantages of Linear Programming?

Various advantages of linear programming are, It provides the optimal solution to any given linear problem. It is easy to use and always gives consistent results It helps to maximize profits and to reduce the input cost.

Please Login to comment...

Similar reads.

• Math-Concepts
• Maths-Class-12
• Technical Scripter 2020
• School Learning
• Technical Scripter

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Graphical and Simplex Methods

Graphical Method

Simplex method, big m method.

Graphical method of linear programming is used to solve problems by finding the highest or lowest point of intersection between the objective function line and the feasible region on a graph.

The graphical method can be broken down into the following 7 steps:

Step 1 : Define Constraints

Step 2 : Define the Objective Function

Step 3 : Plot the constraints on a graph paper

Step 4 : Highlight the feasible region on the g

Step 5 : Plot the objective function on the graph

Step 6 : Find the optimum point

Step 7 : Find the coordinates of the optimum point

Step 1 : Insert slack variables and find slack equations.

Step 2 : Rewrite the objective function and put it below the slack equations.

Step 3 : Write the initial simplex tableau.

Step 4 : Find the pivot element by finding the most negative indicator in last row and using the smallest quotient rule.

Step 5 : Perform the pivot operation.

Step 6 : Are there any more negative indicators in the last row? If Yes, Go to Step 4 , Else the maximum has been reached.

1) Use graphical method to solve the linear programming problem. Maximize \(Z=3x_1+2x_2\) subject to \(x_1-x_2\geq 1\), \(x_1+x_2\geq 3\) and \(x_1,x_2,x_3\geq 0\)

[2019, 10M]

2) Using graphical method, find the maximum value of

\(4x+3y \leq 12\) \(4x+y \leq 8\) \(4x-y \leq 8\) \(x, y \geq 0\)

[2017, 10M]

3) Find the maximum value of

with constraints

\(x+2y \geq 1\), \(2x+y \leq 1\) \(x \geq 0\) and \(y \geq 0\)

by graphical method.

[2016, 10M]

4) Maximize

\(2x_1+x_2+x_3 \leq 5\) \(3x_2+2x_3 \leq 6\) \(x_1 \geq 0\), \(x_2 \geq 0\), \(x_3 \geq 0\)

Is the optimal solution unique? Justify your answer.

[2016, 20M]

5) Solve graphically:

Maximize \(Z=6 x_{1}+5 x_{2}\), subject to: \(2 x_{1}+ x_{2} \leq 216\) \(x_{1}+x_{2} \leq 11\) \(x_{1} + 2x_{2} \geq 6\) \(5x_{1} + 6x_{2} \leq 90\) \(x_{1} x_{2} \geq 0\)

[2014, 10M]

6) Maximize \(z=2x_1+3x_2-5x_3\),

subject to \(x_1+x_2+x_3=7\)

and \(2x_1-5x_2+x_3 \geq 10\), \(x_i \geq 0\)

[2013, 10M]

7) Minimize \(z=5x_1-4x_2+56x_3-8x_4\),

subject to the constraints

\(4x_1-2x_2+x_3 -x_4 \leq 10\),

[2013, 30M]

8) For each hour per day that Ashok studies mathematics, it yields him 10 marks and for eaach hour that he studies physics, it yields him 5 marks. He can study at most 14 hours a day and he must get at least 40 marks in each. Determine graphically how many hours a day he should study mathematics and physics each, in order to maximize his marks?

[2012, 12M]

9) Maximize: \(Z=3x_1+5x_2+4x_3\) subject to:

\(2x_1+3x_2 \leq 8\), \(3x_1+2x_2+4x_3 \leq 15\), \(2x_2+5x_3 \leq 10\), \(x_i \geq 0\)

[2009, 30M]

1) Solve the linear programming problem using Simplex method. Maximize $Z=x_1+2x_2-3x_3-2x_4$ subject to \(x_1+2x_2-3x_3+x_4=4\), \(x_1+2x_2+x_3+2x_4=4\) and \(x_1\), \(x_2\), \(x_3\), \(x_4\geq 0\)

[2019, 15M]

2) Solve the following linear programming problem by simplex method. Maximize \(z=3 x_{1}+5 x_{2}+4 x_{3}\), subject to: \(2 x_{2}+3 x_{2} \leq 8\) \(2 x_{1}+5 x_{2} \leq 10\) \(3 x_{1}+2 x_{2}+4 x_{3} \leq 15 x_{3}\) \(x_{1}, x_{2}, x_{3} \geq 0\)

[2017, 20M]

3) Find the initial basic feasible solution of the following transportation problem using Vogel’s approximation methods and find the cost. \(Destinations\) \(\begin{array}{|c|c|c|c|c|c|} \hline { }&{D_{1}} & {D_{2}} & {D_{3}} & {D_{4}} & {D_{5}} \\ \hline O_{1} & {4} & {7} & {0} & {3} & {6}& {14}\\ \hline O_{2} & {1} & {2} & {-3} & {3} & {8}&{9}\\ \hline {O_{3}} & {3} & {-1} & {4} & {0} & {5} & {17} \\ \hline { }&{8} & {3} & {8} & {13} & {8} \\ \hline \end{array}\)

[2017, 15M]

4) Solve the following linear programming problem by the simplex method. Write its dual. Also, write the optimal solution of the dual from the optimal table of the given problem: Maximize \(Z=2 x_{1}-4 x_{2}+5 x_{3}\),

subject to:

\(x_{1}+4 x_{2}-2 x_{3} \leq 2\) \(-x_{1}+2 x_{2}+3 x_{3} \leq 1\) \(\qquad x_{1}, x_{2}, x_{3} \geq 0\)

[2015, 20M]

5) Find all optimal solutions of the following linear programming problem by the simplex method. Maximize \(Z=30 x_{1}+24 x_{2}\), subject to: \(5 x_{1}+4 x_{2} \leq 200\) \(x_{1} \leq 32\) \(x_{2} \leq 40\) \(x_{1} x_{2} \geq 0\)

[2014, 20M]

6) Solve by simplex method. Maximize \(Z=5 x_{1}+x_{2}\), subject to constraints: \(3 x_{1}+5 x_{2} \leq 15\) \(5 x_{1}+2 x_{2} \leq 10\) \(x_{1}\), \(x_{2} \geq 0\)

[2011, 12M]

7) Put the following in slack form and describe which of the variables are 0 at each of the vertices of the constraint set and hence determine the vertices algebraically:

Maximize \(Z=4x+3y\), subject to: \(x+y \leq 4\) \(-x+y \leq 2\) \(x, y \leq 0\)

[2007, 12M]

8) Solve the following by Simplex method: Maximize \(u=x+y\), subject to: \(-x+y \leq 1\) \(x-2 y \leq 4\) \(x, y \geq 0\)

[2007, 30M]

9) Use the simplex method to solve the problem. Maximize \(u=2x+3y\), subject to: \(-2x+3y \leq 2\) \(3 x+2 y \leq 5\) \(x, y \geq 0\)

[2006, 30M]

10) Use the simplex method to solve the problem. Maximize \(Z=5 x_{1}+2 x_{2}\), subject to: \(6 x_{1}+x_{2} \geq 12\) \(4 x_{1}+3 x_{2} \geq 12\) \(x_{1}+2 x_{2} \geq 4\) \(x_{1}\), \(x_{2} \geq 0\)

[2005, 30M]

11) Use simplex method to solve the linear programming problem. Maximize \(Z=3 x_{1}+2 x_{2}\), subject to: \(x_{1}+x_{2} \leq 4\) \(x_{1}-x_{2} \leq 2\) \(x_{1}\), \(x_{2} \geq 0\)

[2004, 12M]

12) An animal feed company must produce 200 \(\mathrm{kg}\) of a mixture consisting of ingredients \(X_{1}\) and \(X_{2}\) daily. \(X_{1}\) costs Rs 3 per Kg and \(X_2\) costs Rs 8 per Kg. No more than 80 Kg of \(X_1\) can be used, and at least 60 Kg of \(X_2\) must be used. Formulate a linear programming model of the problem and use Simplex method to determine the ingredients \(X_{1}\) and \(X_{2}\) to be used to minimize cost.

[2003, 15M]

13) Using Simplex method, Maximize \(Z=45 x_{1}+80 x_{2}\), subject to: \(5 x_{1}+20 x_{2} \leq 400\) \(10 x_{1}+15 x_{2} \leq 450\) \(x_{1}\), \(x_{2} \geq 0\)

[2002, 12M]

14) Using simplex method, Maximize \(Z=5 x_{1}+3 x_{2}\), subject to: \(x_{1}+x_{2} \leq 2\) \(5 x_{1}+2 x_{2} \leq 10\) \(3 x_{1}+8 x_{2} \leq 12\) \(x_{1}\), \(x_{2} \geq 0\)

[2002, 15M]

1) Solve the following linear programming problem by Big M-method and show that the problem has finite optimal solutions. Also, find the value of the objective function: Minimize \(z=3x_1+5x_2\) subject to \(x_1+2x_2\geq 8\) \(3x_1+2x_2\geq 12\), \(5x_1+6x_2\geq 60\), \(x_1,x_2\geq 0\)

[2018, 20M]

Linear Programming: Graphic Solution

• Post last modified: 22 July 2022
• Reading time: 13 mins read
• Post category: Operations Research

In the previous article, you studied that linear programming is a method of achieving the optimum outcome for a maximum or a mini- mum equation with linear constraints.

Once the mathematical model of a linear programming problem has been formulated, the next phase in applying linear programming to a decision-making problem is to find the solution of the model.

An LP problem can be solved by using multiple methods, with graphical and simplex methods being the most popular. An LP problem that involves two variables in a linear relationship can be easily solved with the help of graphical method. When there are only two variables in the problem, most of the analysis can be performed on a two-dimensional graph.

Table of Content

• 1.1 Graphical Method
• 2.1 Extreme Point Enumeration Approach
• 2.2 ISO-profit (Cost) Function Line Approach
• 3 Important Terms of Linear Programming for Graphic Solution

Graphical method helps in showing all the feasible solutions that are present within the feasible area on the graph. The feasible area’s corner points are tested by putting these values in the objective function for determining the optimal solution.

A major advantage of using the graphical approach is its visual nature. It helps us gain a visual representation of the algebra of LP, which in turn supports our understanding of the key concepts. But when an LP problem involves three or more variables, trying to solve the problem by drawing its graph is very difficult. In such cases, the simplex method developed the simplex method is used, developed by G.B. Dantzig is used.

Methods for Solving Linear Programming Problems

As you might recall from the last article, a linear programming problem is one where you need to optimise (maximise or minimise) a linear objective function, subject to constraints in the form of linear inequalities or equations. In this section of the article, you are going to discuss how you can solve such LP problems.

Graphical Method

The graphical method is used to solve a linear program involving only two decision variables that can be represented on a graph of two dimensions. While it is not impossible to graph LP models with three decision variables in three dimensions, it is a very difficult and complicated task to perform, and LP models with four or more decision variables are impossible to graph at all. Despite the limitation of being useful for only two decision variables, the graphical method is still very valuable as it enables the visualisation of the algebra of LP and how a solution is obtained in LP.

When the graphical method is used to determine the optimal solution to the LP problem, the fundamental theorem of linear programming is applied, which states that:

• The set of all feasible solutions to an LP problem is represented by a convex polygon whose extreme points correspond to the basic feasible solutions. In case this, a convex polygon is a convex polyhedron, then at least one of the extreme points gives an optimal solution.
• The number of basic feasible solutions within the feasible area is finite.
• If more than one extreme point corresponds to the optimal solution, then the value of the objective function will be the same for all these extreme points.
• The maximum value for the objective function does not exist for an unbounded feasible region.
• A minimum value for an unbounded feasible region exists if the objective function has only positive coefficients.

For LP problems involving more than two variables or those involving a large number of constraints, graphical methods are not suited. In such cases, solution methods that are adaptable to computers are more appropriate.

The simplex method is one such approach. This method presents a systematic approach for evaluating the vertices of a feasible region, which then allows you to figure out the optimal value of the objective function. You will study more about the simplex method in the next article.

Graphical Solution of a Linear Programming Problem

The graphical solution of an LP problem involves the following steps:

• Represent the problem in a mathematical form by formulating the mathematical model. For this, decode the given situations or constraints into equations or inequalities.
• Draw x1 and x2 axes. The values of x1 and x2 variables can only lie in the first quadrant because of the non-negativity constraints x1 ≥ 0 and x2 ≥ 0. Infeasible alternatives that lie in the 2nd, 3rd and 4th quadrants are thus removed.
• Plot each of the problem constraints, whether equations or inequalities, as equations on the graph. For each of the constraints, obtain the value of one variable by assigning an arbitrary value to the other variable. Then, assign a different arbitrary value to the first variable and obtain the value of the other variable. Now plot these two points and join them with a straight line. Each constraint is thus plotted as a line in the first quadrant.
• Identify the feasible solution area that satisfies all the constraints simultaneously. The feasible region is the area common to all the constraints and is usually depicted as a shaded region. Any point that lies within or on the boundary of this shaded region depicts a feasible solution. The feasible region is a convex polygon formed by the intersection of a finite number of half-planes.
• Plot the objective function by assuming Z = 0. This is a line passing through the origin. Increasing the value of Z moves the line parallelly to the right. For a maximisation problem, draw a line parallel to this line till it is farthest from the origin. For a minimisation problem, draw a line parallel to this line till the line is closest to the origin. The optimal point is the point where this line passes through the feasible region.

Now, you know the basic steps of the graphical method to solve an LP problem. Know that graphical methods can be classified into two types as

Extreme Point Enumeration Approach

Iso-profit (cost) function line approach.

An extreme point or vertex is a unique point where a hyperplane inter- sects. The extreme point enumeration approach of graphically solving an LP problem is based on the principle of extreme value theorem which states that if f is a continuous function over a closed, bounded interval, then there is a point in the interval at which f has an absolute maximum and there is also a point at which f has an absolute minimum value.

The various steps involved in this approach are as follows:

• Identify the decision variables, constraints and objective of the problem.
• Formulate the mathematical model of the problem.
• Plot each of the problem constraints as an equation on the graph Each one will geometrically represent a straight line.
• Identify the common region that satisfies all the constraints simultaneously. It is a convex polygon formed by the intersection of a finite number of half-planes.
• Determine the vertices of the convex polygon. These vertices are called the extreme points of the feasible region.
• Find the coordinates of each extreme point/vertex of the feasible region. Determine the values of the objective function at each extreme point. The optimal point is the extreme point at which the value of the objective function is optimum (maximum or mini- mum) and its coordinates give us the optimal solution.

The Iso-profit (cost) function line method is another approach to find the optimum point in a graphic linear programming problem. After graphing the feasible region, the point lying in the feasible region that produces the highest profit is the optimal solution to the problem. The term Iso-profit (cost) implies that any combination of points generates the same profit (cost) as any other combination on the same line.

• Plot a graph taking in all the constraint equations of the problem and identify the feasible region. The feasible region is the intersection of the regions satisfying all the constraints. As you read earlier, it is restricted to the first quadrant only. The feasible region obtained in this step may be bounded or unbounded.
• Determine the corner points of the feasible region.
• Calculate the coordinates of all the corner points of the feasible region.
• Give a suitable value k to the objective function Z and draw the corresponding straight line in the xy plane so that it lies within the feasible region. This is the iso-profit (iso-cost) function line.
• Draw the iso-profit (iso-cost) function line parallel to itself till the line is farthest from the origin (for highest possible profit) or closest to the origin (for lowest possible cost). Each such line for which the value of the objective function remains the same is called an iso-profit line for maximisation problems, or an iso-cost line for minimisation problems.
• Determine the optimum solution with the coordinates of the point where the highest possible iso-profit or lowest possible cost line passes on the feasible region.

Important Terms of Linear Programming for Graphic Solution

• Solution of LPP : The solution of the LPP is a set of values of the variables xl, x2…., xn that satisfies the constraints.
• Basic feasible solution: A basic feasible solution is a set of values of the variables xl, x2…., xn that satisfies all constraints along with the non-negativity restrictions.
• Optimum basic feasible solution: A basic feasible solution becomes optimum if it also optimises the objective function.
• Feasible region : The region in the graph that satisfies all the constraints is known as the feasible region.
• Corner point: A corner point is a point that falls along the corner of a feasible region.
• Bounded set: A set which consists of a boundary around the feasible set is referred as the bounded set. An LP problem (with a bounded set) always has an optimal solution. In other words, a bounded set has a maximum value as well as a minimum value.
• Unbounded set: A set that has no boundary and continues indefinitely is known as an unbounded set. An optimal solution for an LP problem with an unbounded set may or may not be possible, but in case an optimal solution does exist, it occurs at a corner point.
• Unbounded solution : Those solutions where the objective function’s value can be increased or decreased indefinitely are called unbounded solutions.
• Fundamental extreme point theorem : The fundamental extreme point theorem states that if an optimum solution for an LP problem exists, it occurs at one of the extreme points or corner points of the convex polygon of the set of all feasible solutions.
• If there is a solution to a bounded LP problem, it occurs at one of the corner points of the convex polygon of the set of all feasible solutions.

Business Ethics

( Click on Topic to Read )

• What is Ethics?
• What is Business Ethics?
• Values, Norms, Beliefs and Standards in Business Ethics
• Indian Ethos in Management
• Ethical Issues in Marketing
• Ethical Issues in HRM
• Ethical Issues in IT
• Ethical Issues in Production and Operations Management
• Ethical Issues in Finance and Accounting
• What is Corporate Governance?
• What is Ownership Concentration?
• What is Ownership Composition?
• Types of Companies in India
• Internal Corporate Governance
• External Corporate Governance
• Corporate Governance in India
• What is Enterprise Risk Management (ERM)?
• What is Assessment of Risk?
• What is Risk Register?
• Risk Management Committee

Corporate social responsibility (CSR)

• Theories of CSR
• Arguments Against CSR
• Business Case for CSR
• Importance of CSR in India
• Drivers of Corporate Social Responsibility
• Developing a CSR Strategy
• Implement CSR Commitments
• CSR Marketplace
• CSR at Workplace
• Environmental CSR
• CSR with Communities and in Supply Chain
• Community Interventions
• CSR Monitoring
• CSR Reporting
• Voluntary Codes in CSR
• What is Corporate Ethics?

Lean Six Sigma

• What is Six Sigma?
• What is Lean Six Sigma?
• Value and Waste in Lean Six Sigma
• Six Sigma Team
• MAIC Six Sigma
• Six Sigma in Supply Chains
• What is Binomial, Poisson, Normal Distribution?
• What is Sigma Level?
• What is DMAIC in Six Sigma?
• What is DMADV in Six Sigma?
• Six Sigma Project Charter
• Project Decomposition in Six Sigma
• Critical to Quality (CTQ) Six Sigma
• Process Mapping Six Sigma
• Flowchart and SIPOC
• Gage Repeatability and Reproducibility
• Statistical Diagram
• Lean Techniques for Optimisation Flow
• Failure Modes and Effects Analysis (FMEA)
• What is Process Audits?
• Six Sigma Implementation at Ford
• IBM Uses Six Sigma to Drive Behaviour Change
• Research Methodology
• What is Research?
• What is Hypothesis?
• Sampling Method
• Research Methods
• Data Collection in Research
• Methods of Collecting Data
• Application of Business Research
• Levels of Measurement
• What is Sampling?
• Hypothesis Testing
• Research Report
• What is Management?
• Planning in Management
• Decision Making in Management
• What is Controlling?
• What is Coordination?
• What is Staffing?
• Organization Structure
• What is Departmentation?
• Span of Control
• What is Authority?
• Centralization vs Decentralization
• Organizing in Management
• Schools of Management Thought
• Classical Management Approach
• Is Management an Art or Science?
• Who is a Manager?

Operations Research

• What is Operations Research?
• Operation Research Models
• Linear Programming
• Linear Programming Graphic Solution
• Linear Programming Simplex Method
• Linear Programming Artificial Variable Technique

Duality in Linear Programming

• Transportation Problem Initial Basic Feasible Solution
• Transportation Problem Finding Optimal Solution
• Project Network Analysis with Critical Path Method

Project Network Analysis Methods

Project evaluation and review technique (pert), simulation in operation research, replacement models in operation research.

Operation Management

• What is Strategy?
• What is Operations Strategy?
• Operations Competitive Dimensions
• Operations Strategy Formulation Process
• What is Strategic Fit?
• Strategic Design Process
• Focused Operations Strategy
• Corporate Level Strategy
• Expansion Strategies
• Stability Strategies
• Retrenchment Strategies
• Competitive Advantage
• Strategic Choice and Strategic Alternatives
• What is Production Process?
• What is Process Technology?
• What is Process Improvement?
• Strategic Capacity Management
• Production and Logistics Strategy
• Taxonomy of Supply Chain Strategies
• Factors Considered in Supply Chain Planning
• Operational and Strategic Issues in Global Logistics
• Logistics Outsourcing Strategy
• What is Supply Chain Mapping?
• Supply Chain Process Restructuring
• Points of Differentiation
• Re-engineering Improvement in SCM
• What is Supply Chain Drivers?
• Supply Chain Operations Reference (SCOR) Model
• Customer Service and Cost Trade Off
• Internal and External Performance Measures
• Linking Supply Chain and Business Performance
• Netflix’s Niche Focused Strategy
• Disney and Pixar Merger
• Process Planning at Mcdonald’s

Service Operations Management

• What is Service?
• What is Service Operations Management?
• What is Service Design?
• Service Design Process
• Service Delivery
• What is Service Quality?
• Gap Model of Service Quality
• Juran Trilogy
• Service Performance Measurement
• Service Decoupling
• IT Service Operation
• Service Operations Management in Different Sector

Procurement Management

• What is Procurement Management?
• Procurement Negotiation
• Types of Requisition
• RFX in Procurement
• What is Purchasing Cycle?
• Vendor Managed Inventory
• Internal Conflict During Purchasing Operation
• Spend Analysis in Procurement
• Sourcing in Procurement
• Supplier Evaluation and Selection in Procurement
• Blacklisting of Suppliers in Procurement
• Total Cost of Ownership in Procurement
• Incoterms in Procurement
• Documents Used in International Procurement
• Transportation and Logistics Strategy
• What is Capital Equipment?
• Procurement Process of Capital Equipment
• Acquisition of Technology in Procurement
• What is E-Procurement?
• E-marketplace and Online Catalogues
• Fixed Price and Cost Reimbursement Contracts
• Contract Cancellation in Procurement
• Ethics in Procurement
• Legal Aspects of Procurement
• Global Sourcing in Procurement
• Intermediaries and Countertrade in Procurement

Strategic Management

• What is Strategic Management?
• What is Value Chain Analysis?
• Mission Statement
• Business Level Strategy
• What is SWOT Analysis?
• What is Competitive Advantage?
• What is Vision?
• What is Ansoff Matrix?
• Prahalad and Gary Hammel
• Strategic Management In Global Environment
• Competitor Analysis Framework
• Competitive Rivalry Analysis
• Competitive Dynamics
• What is Competitive Rivalry?
• Five Competitive Forces That Shape Strategy
• What is PESTLE Analysis?
• Fragmentation and Consolidation Of Industries
• What is Technology Life Cycle?
• What is Diversification Strategy?
• What is Corporate Restructuring Strategy?
• Resources and Capabilities of Organization
• Role of Leaders In Functional-Level Strategic Management
• Functional Structure In Functional Level Strategy Formulation
• Information And Control System
• What is Strategy Gap Analysis?
• Issues In Strategy Implementation
• Matrix Organizational Structure
• What is Strategic Management Process?

Supply Chain

• What is Supply Chain Management?
• Supply Chain Planning and Measuring Strategy Performance
• What is Warehousing?
• What is Packaging?
• What is Inventory Management?
• What is Material Handling?
• What is Order Picking?
• Receiving and Dispatch, Processes
• What is Warehouse Design?
• What is Warehousing Costs?

You Might Also Like

Project network analysis with critical path method, what is linear programming assumptions, properties, advantages, disadvantages, what is operations research (or) definition, concept, characteristics, tools, advantages, limitations, applications and uses, linear programming: simplex method, operation research models and modelling, transportation problem: finding an optimal solution, linear programming: artificial variable technique, leave a reply cancel reply.

You must be logged in to post a comment.

World's Best Online Courses at One Place

We’ve spent the time in finding, so you can spend your time in learning

Digital Marketing

Personal growth.

Development

Linear Programming

Linear programming is the method used in mathematics to optimize the outcome of a function. It is widely used in the fields of Mathematics, Economics and Statistics. In this chapter, we will learn about different types of Linear Programming Problems and the methods to solve them.

• Different Types of Linear Programming Problems
• Graphical Method of Solving Linear Programming Problems
• Linear Programming Problem and Its Mathematical Formulation

FAQs on Linear Programming

Question 1: Explain the use of linear programming?

Answer: Linear programming is useful in obtaining the most optimal solution for a specific problem with specific constraints. Here, formulation of a real-life problem into a mathematical model takes place. It involves an objective function, linear inequalities with subject to constraints.

Question 2: Explain the components of linear programming?

Answer: The components of linear programming are as follows:

• Decision variables represent quantities whose determination has to take place.
• The objective function shows how the decision variables will impact the cost or value whose optimization has to take place.
• Constraints explain how the decision variables utilize resources that are limited.
• Data quantifies the relationships that are represented in the constraints and the objective function.

Question 3: Give the disadvantages of linear programming?

Answer: The disadvantages of linear programming are as follows:

• It takes place only with the variables that are linear.
• It does not consider change of variables.
• It cannot solve the nonlinear function.
• Impossible to solve a problem that has more than two variables in the graphical method.

Question 4: What are the various characteristics of linear programming?

Customize your course in 30 seconds

• Math Article

Linear Programming

In Mathematics, linear programming is a method of optimising operations with some constraints. The main objective of linear programming is to maximize or minimize the numerical value. It consists of linear functions which are subjected to the constraints in the form of linear equations or in the form of inequalities.  Linear programming is considered an important technique that is used to find the optimum resource utilisation. The term “linear programming” consists of two words as linear and programming. The word “linear” defines the relationship between multiple variables with degree one. The word “programming” defines the process of selecting the best solution from various alternatives.

Linear Programming is widely used in Mathematics and some other fields such as economics, business, telecommunication, and manufacturing fields. In this article, let us discuss the definition of linear programming, its components, and different methods to solve linear programming problems.

Table of Contents:

• Characteristics
• Linear programming Problems
• Simplex Method

Graphical Method

• Applications
• Practice Problems

What is Linear Programming?

Linear programming (LP)   or Linear Optimisation may be defined as the problem of maximizing or minimizing a linear function that is subjected to linear constraints. The constraints may be equalities or inequalities. The optimisation problems involve the calculation of profit and loss.   Linear programming problems  are an important class of optimisation problems, that helps to find the feasible region and optimise the solution in order to have the highest or lowest value of the function.

In other words, linear programming is considered as an optimization method to maximize or minimize the objective function of the given mathematical model with the set of some requirements which are represented in the linear relationship. The main aim of the linear programming problem is to find the optimal solution.

Linear programming is the method of considering different inequalities relevant to a situation and calculating the best value that is required to be obtained in those conditions.  Some of the assumptions taken while working with linear programming are:

• The number of constraints should be expressed in the quantitative terms
• The relationship between the constraints and the objective function should be linear
• The linear function (i.e., objective function) is to be optimised

Components of Linear Programming

The basic components of the LP are as follows:

• Decision Variables
• Constraints
• Objective Functions

Characteristics of Linear Programming

The following are the five characteristics of the linear programming problem:

Constraints – The limitations should be expressed in the mathematical form, regarding the resource.

Objective Function – In a problem, the objective function should be specified in a quantitative way.

Linearity – The relationship between two or more variables in the function must be linear. It means that the degree of the variable is one.

Finiteness –  There should be finite and infinite input and output numbers. In case, if the function has infinite factors, the optimal solution is not feasible. 

Non-negativity – The variable value should be positive or zero. It should not be a negative value.

Decision Variables – The decision variable will decide the output. It gives the ultimate solution of the problem. For any problem, the first step is to identify the decision variables.

Linear Programming Problems

The Linear Programming Problems (LPP) is a problem that is concerned with finding the optimal value of the given linear function. The optimal value can be either maximum value or minimum value. Here, the given linear function is considered an objective function. The objective function can contain several variables, which are subjected to the conditions and it has to satisfy the set of linear inequalities called linear constraints. The linear programming problems can be used to get the optimal solution for the following scenarios, such as manufacturing problems, diet problems, transportation problems, allocation problems and so on.

Methods to Solve Linear Programming Problems

The linear programming problem can be solved using different methods, such as the graphical method, simplex method, or by using tools such as R, open solver etc. Here, we will discuss the two most important techniques called the simplex method and graphical method in detail.

Linear Programming Simplex Method

The simplex method is one of the most popular methods to solve linear programming problems. It is an iterative process to get the feasible optimal solution. In this method, the value of the basic variable keeps transforming to obtain the maximum value for the objective function. The algorithm for linear programming simplex method is provided below:

Step 1 : Establish a given problem. (i.e.,) write the inequality constraints and objective function.

Step 2: Convert the given inequalities to equations by adding the slack variable to each inequality expression.

Step 3 : Create the initial simplex tableau. Write the objective function at the bottom row. Here, each inequality constraint appears in its own row. Now, we can represent the problem in the form of an augmented matrix, which is called the initial simplex tableau.

Step 4 : Identify the greatest negative entry in the bottom row, which helps to identify the pivot column. The greatest negative entry in the bottom row defines the largest coefficient in the objective function, which will help us to increase the value of the objective function as fastest as possible.

Step 5 : Compute the quotients. To calculate the quotient, we need to divide the entries in the far right column by the entries in the first column, excluding the bottom row. The smallest quotient identifies the row. The row identified in this step and the element identified in the step will be taken as the pivot element.

Step 6: Carry out pivoting to make all other entries in column is zero.

Step 7: If there are no negative entries in the bottom row, end the process. Otherwise, start from step 4.

Step 8: Finally, determine the solution associated with the final simplex tableau.

The graphical method is used to optimize the two-variable linear programming. If the problem has two decision variables, a graphical method is the best method to find the optimal solution. In this method, the set of inequalities are subjected to constraints. Then the inequalities are plotted in the XY plane. Once, all the inequalities are plotted in the XY graph, the intersecting region will help to decide the feasible region. The feasible region will provide the optimal solution as well as explains what all values our model can take.  Let us see an example here and understand the concept of linear programming in a better way.

Calculate the maximal and minimal value of z = 5x + 3y for the following constraints.

x + 2y ≤ 14

3x – y ≥ 0

x – y ≤ 2

The three inequalities indicate the constraints. The area of the plane that will be marked is the feasible region.

The optimisation equation (z) = 5x + 3y. You have to find the (x,y) corner points that give the largest and smallest values of z.

To begin with, first solve each inequality.

x + 2y ≤ 14 ⇒  y ≤ -(1/2)x + 7

3x – y ≥ 0 ⇒  y ≤ 3x

x – y ≤ 2 ⇒ y  ≥ x – 2

Here is the graph for the above equations.

Now pair the lines to form a system of linear equations to find the corner points.

y = -(½) x + 7

Solving the above equations, we get the corner points as (2, 6)

y = -1/2 x + 7

y = x – 2

Solving the above equations, we get the corner points as (6, 4)

Solving the above equations, we get the corner points as (-1, -3)

For linear systems, the maximum and minimum values of the optimisation equation lie on the corners of the feasibility region. Therefore, to find the optimum solution, you only need to plug these three points in z = 3x + 4y

z = 5(2) + 3(6) = 10 + 18 = 28

z = 5(6) + 3(4) = 30 + 12 = 42

z = 5(-1) + 3(-3) = -5 -9 = -14

Hence, the maximum of z = 42 lies at (6, 4) and the minimum of z = -14 lies at (-1, -3)

Linear Programming Applications

A real-time example would be considering the limitations of labours and materials and finding the best production levels for maximum profit in particular circumstances. It is part of a vital area of mathematics known as optimisation techniques. The applications of LP in some other fields are

• Engineering – It solves design and manufacturing problems as it is helpful for doing shape optimisation
• Efficient Manufacturing – To maximise profit, companies use linear expressions
• Energy Industry – It provides methods to optimise the electric power system.
• Transportation Optimisation – For cost and time efficiency.

Importance of Linear Programming

Linear programming is broadly applied in the field of optimisation for many reasons. Many functional problems in operations analysis can be represented as linear programming problems. Some special problems of linear programming are such as network flow queries and multi-commodity flow queries are deemed to be important to have produced much research on functional algorithms for their solution.

Linear Programming Video Lesson

Linear programming problem.

Linear Programming Practice Problems

Solve the following linear programming problems:

• A doctor wishes to mix two types of foods in such a way that the vitamin contents of the mixture contain at least 8 units of vitamin A and 10 units of vitamin C. Food ‘I’ contains 2 units/kg of vitamin A and 1 unit/kg of vitamin C. Food ‘II’ contains 1 unit/kg of vitamin A and 2 units/kg of vitamin C. It costs Rs 50 per kg to purchase Food ‘I’ and Rs 70 per kg to purchase Food ‘II’. Formulate this problem as a linear programming problem to minimise the cost of such a mixture
• One kind of cake requires 200g of flour and 25g of fat, and another kind of cake requires 100g of flour and 50g of fat.  Formulate this problem as a linear programming problem to find the maximum number of cakes that can be made from 5kg of flour and 1 kg of fat assuming that there is no shortage of the other ingredients used in making the cakes.

Frequently Asked Questions on Linear Programming

Linear programming is a process of optimising the problems which are subjected to certain constraints. It means that it is the process of maximising or minimizing the linear functions under linear inequality constraints. The problem of solving linear programs is considered as the easiest one.

Mention the different types of linear programming.

The different types of linear programming are: Solving linear programming by Simplex method Solving linear programming using R Solving linear programming by graphical method Solving linear programming with the use of an open solver.

What are the requirements of linear programming?

The five basic requirements of linear programming are: Objective function Constraints Linearity Non-negativity Finiteness

Mention the advantages of Linear programming

The advantages of linear programming are: Linear programming provides insights to the business problems It helps to solve multi-dimensional problems According to the condition change, LP helps in making the adjustments By calculating the cost and profit of various things, LP helps to take the best optimal solution

What is meant by linear programming problems?

The linear programming problems (LPP) helps to find the best optimal solution of a linear function (also, known as the objective function) which are placed under certain constraints (set of linear inequality constraints)

To learn all concepts in Maths in a more engaging way, register at BYJU’S. Also, watch interesting videos on various Maths topics by downloading BYJU’S– The Learning App.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Thank you so much for clearly explained notes. I benefited a lot from them

Thank you very much for this material.

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Graphical Method Calculator – Linear Programming 🥇

Do you often find yourself confused by linear programming problems that you can't solve? Maybe it's time to get some help. Well… You're in luck! Solving optimization exercises with the graphical method will be easier with our graphical method calculator for linear programming problems.

Graphical Method Calculator - Linear Programming

Objective function:, constraints.

Constraint 1:

Constraint 2:

X 1 , X 2 ≥ 0

Members-Only Content

Do you already have a membership, get membership.

The above application is a simplified version of our graphing method calculator available to students who have a membership with us; however, it has all the basic functionality required to graph most linear programming exercises in your school.

This free version, like other available free linear programming calculators, only shows the final result (optimal solution and graph) of the problem. Since many students cannot adequately understand how the graphs were generated, we have developed a version with detailed step-by-step explanations of the solution of the problem.

Advanced Functions of the Graphical Method of Linear Programming Calculator

Our membership aims to help you improve your problem solving skills and perform better in your school. That is why we include a series of online resources, where linear programming is a must. In this application you will find the following:

• Calculation of the intersections with the axes to graph each constraint.
• Explanation of the area to shade depending on the type of inequality.
• Determination of the feasible region.
• Location of the objective function on the graph, if applicable.
• Determination of special cases such as unbounded, unbounded or infeasible solutions.
• Solve exercises with inequalities or equations.
• You can enter a maximum of 10 restrictions and 2 variables.

You can find complete examples of how the application works in this link .

How to use the Online Graphical Method Calculator

The use of our calculator is very simple and intuitive, however, we will explain its use step by step:

• Before starting, you must have made the approach of the model to be optimized. Remember that for the graphical method we normally work with 2 decision variables.
• You must enter the coefficients of the objective function and the constraints. You can enter integer values, fractions and decimals. Likewise, you must also select the sign of the inequalities.
• To enter the coefficients of the objective function and the constraints, you can use integer values as well as fractions and decimals. You must also select the sign of the inequalities.
• Click on “Solve / Graph” .
• If you are in the free version, you will immediately get the final graph and results. In the full version, you will be able to see the step by step from the creation of the graphs to the final result.

Next we will see some images of the operation of the calculator:

This calculator facilitates your learning of the graphical method and combines well with our simplex method application (two phases) and our Big M Method calculator .

Final Reflection

We know that the best way to learn something is to have the right tools to do it. At PM Calculators we are working to bring you the best tools gathered in one place. If you have any recommendation to improve our calculator, write us to our contact form.