how to solve sum of subset problem

• [email protected]

What’s New ?

The Top 10 favtutor Features You Might Have Overlooked

• Don’t have an account Yet? Sign Up

Remember me Forgot your password?

• Already have an Account? Sign In

Lost your password? Please enter your email address. You will receive a link to create a new password.

Back to log-in

By Signing up for Favtutor, you agree to our Terms of Service & Privacy Policy.

Subset Sum Problem Explained (Dynamic Programming)

• Nov 15, 2022
• 7 Minutes Read
• Why Trust Us We uphold a strict editorial policy that emphasizes factual accuracy, relevance, and impartiality. Our content is crafted by top technical writers with deep knowledge in the fields of computer science and data science, ensuring each piece is meticulously reviewed by a team of seasoned editors to guarantee compliance with the highest standards in educational content creation and publishing.
• By Manvi Saxena

With thousands of students preparing for jobs in the technology industry, the best way for you to stand out is to practice as many questions as you can. Sometimes even complex questions can be solved very easily with just a little trick and sometimes the interviewer is not looking for an optimal solution but just the right approach.

So, in today's blog, we present to you a question that is commonly asked by tech giants like Microsoft and Amazon. Yes, we're talking about the Subset Sum Problem! 

We understand that code can be pasted from anywhere, the right thing to build in today's engineering students is the intuition and approach behind the question. We'll walk you through the question and give you awesome tricks to solve it.

From naive solutions to solving questions using advanced concepts like Dynamic Programming, we're going to do it with you! 

What is the Subset Sum Problem?

Let's look at the problem statement: " You are given an array of non-negative numbers and a value 'sum'. You have to find out whether a subset of the given array is present whose sum is equal to the given value. "

Let's look at an example:

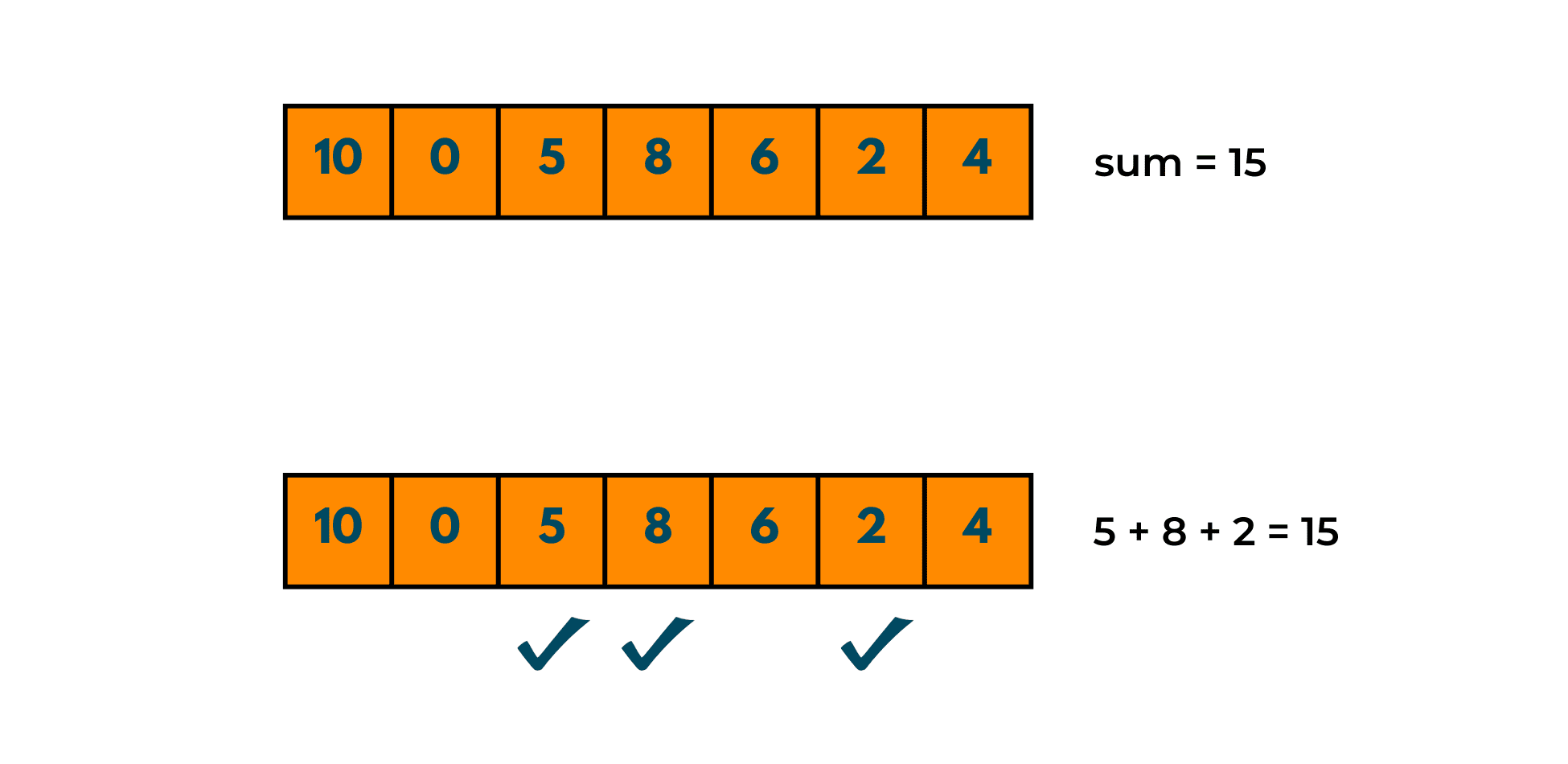
Input:  {10, 0, 5, 8, 6, 2, 4}, 15

Output:  True

Explanation:  The sum of the subset {5,8,2} gives the sum as 15. Therefore, the answer comes out to be true. 

Let's take a look at another example for your clarification. 

Input:  {10, 0, 5, 8, 6, 2, 4}, 3

Output:  False

Explanation:  There is no subset whose sum is equal to the given value. Hence, the output is false.

Understanding the Problem

Before moving towards any method, you need to make sure whether you understood the Subset Sum Problem correctly or not. In interviews also, even if you do not know the whole code, you can still conquer it by moving in the right direction and following the right approach. So, what exactly is being asked over here?

If you are familiar with the concepts of subset then this question is not that difficult for you to understand. What is a subset? A subset is a set that contains the elements of a previously defined set. For eg. {a, b} is a subset of {a,b,c,e,f}. In this question also, you have to find a subset or the set of numbers from the given array that amount to the given value in the input. 

Now that you have understood the problem, let's move on to some methods with which you can solve the problem. 

How to Solve the Sum of Subset Problem?

Let's look at 3 best methods to solve it:

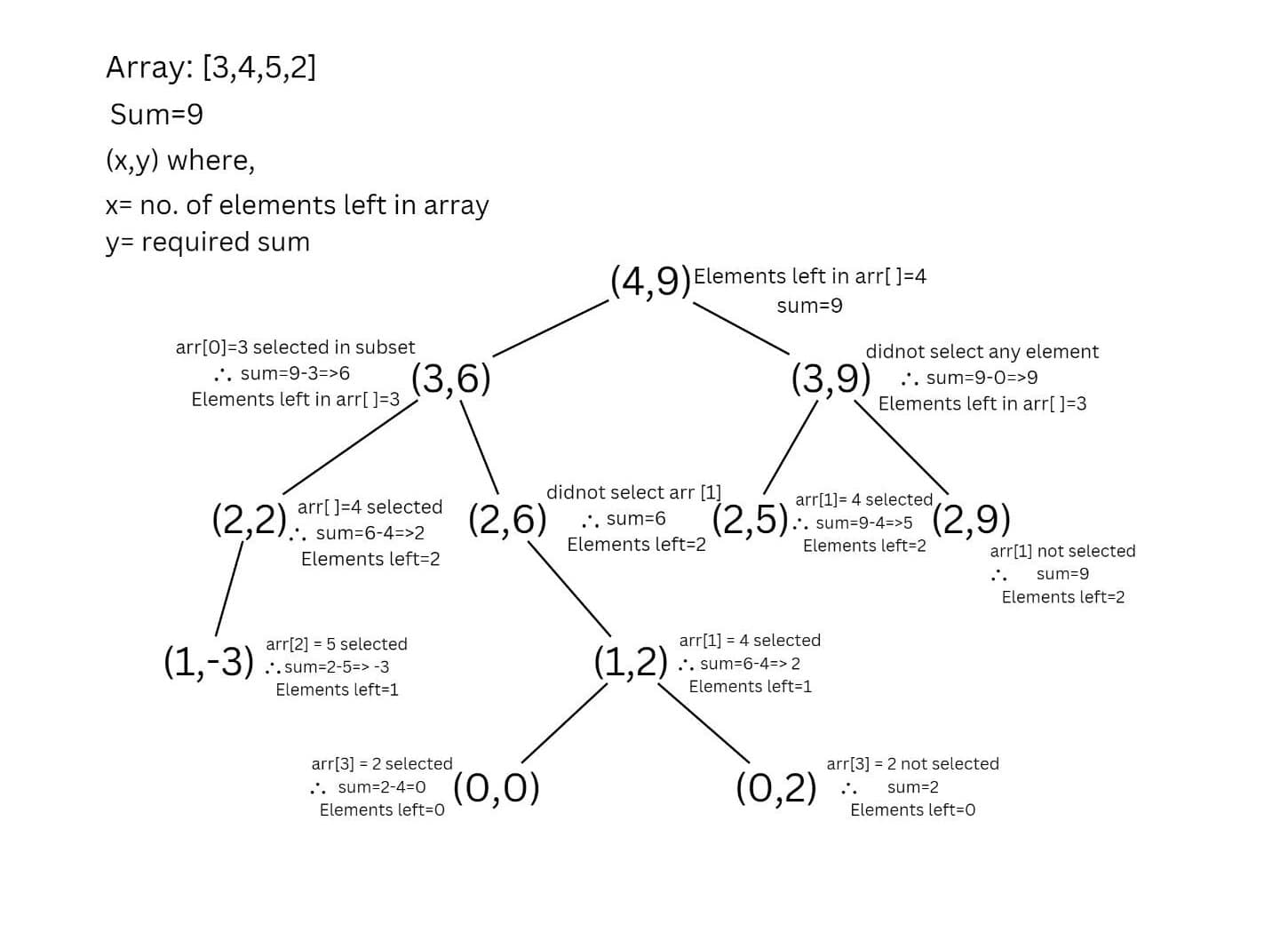
Method 01) Recursion

Recursion is a widely known concept and is majorly famous in questions where you need to process the same data again and again till you hit the base condition. So, in this method, we'll be using recursion only. Let's understand the algorithm and try to decode the question with some illustrations. 

• Take input of the array and the value 'sum'.
• Find the size of the array.
• Create a function whose return type is boolean so that it returns True if the sum is found otherwise False.
• In this function, check whether the last element of the array is greater than the 'sum' or not.
• If it is greater then skip to the next element and if not, consider it in the subset.
• Keep decreasing the value of the sum by subtracting the value of the last element (if considered).
• Keep the base condition to be true till the elements are present and till the given sum is not equal to 0.

Recursive Formula and Base Cases for the Code:

Take a look at the given illustration as well!

Method 02) Dynamic Programming

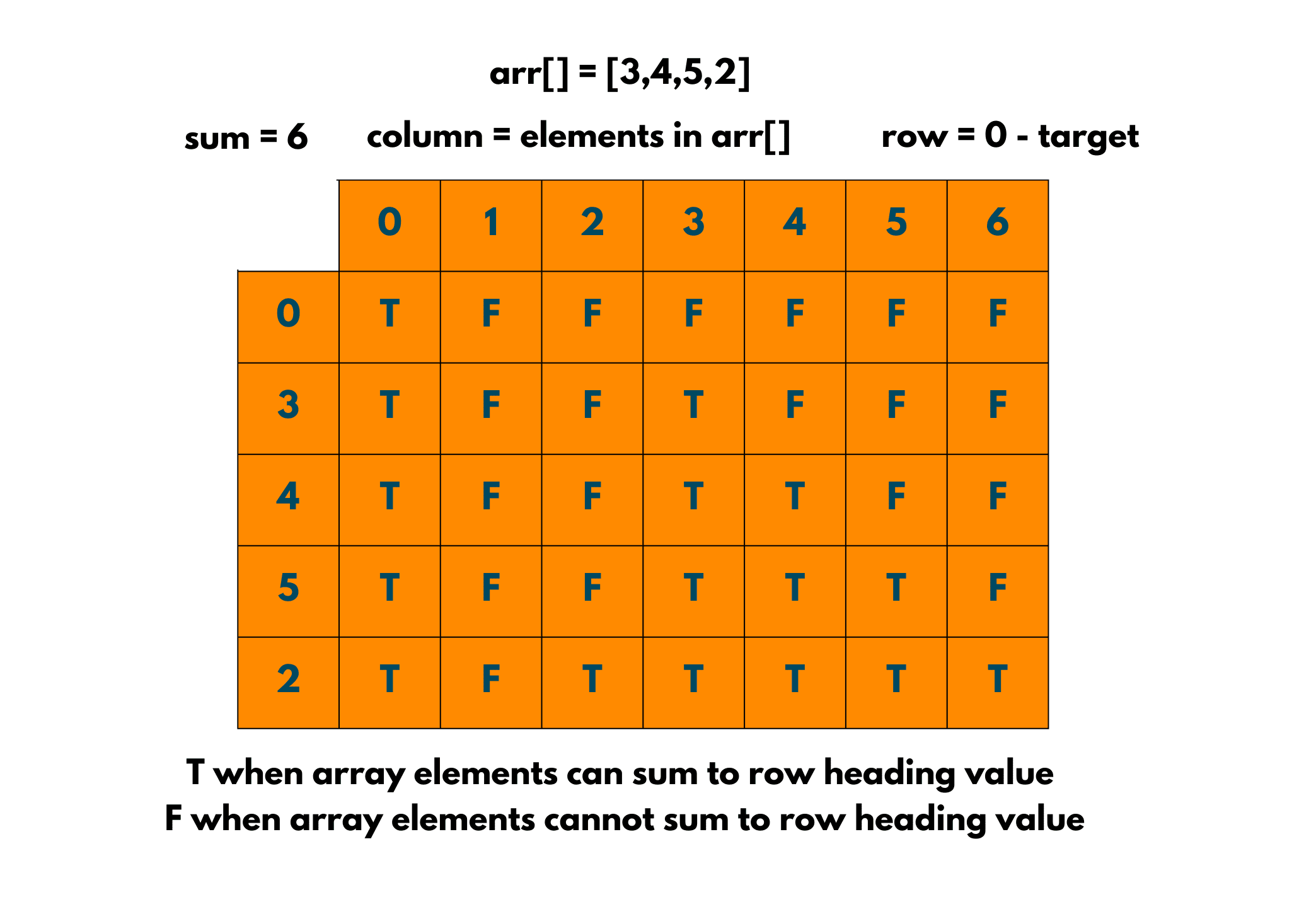
Using a Recursive technique to solve this question is good, but with Dynamic Programming , the time complexity of the solution can be improved by manifolds. The time complexity of the recursive solution is exponential, therefore, the need to come up with a better solution arises. So, look at the given solution that uses the top-down approach to Dynamic Programming. 

• Create a 2d array of size(size+1)*(target+1)
• Now, this state of the 2d array will be true if the subset of the given sum is found else, it will be false.
• While traversing the array, if the current element has a value greater than the ‘current sum value’ it will be copied for previous cases.
• If the current sum value is greater than the ‘ith’ element, we'll observe whether the previous states have experienced the sum=j.

The formula used in the method:

Method 03) Memoization Technique

The Dynamic Programming method solves the question in polynomial time, but what if your interviewer asks you to optimize it further? Well, we got you covered! Using this Memoization Technique, your interviewer will definitely get impressed. Although this method also uses recursion, we optimize it further using the memoization technique. 

• Create a function whose return type is boolean so that it returns True if sum is found otherwise False.
• Create a 2d matrix and initialize it with -1 or any other negative number.
• Using the same recursive method as in 1st method, but storing the value of the previous call.

Code Implementation with C++

Here is the C++ code to solve the Subset Sum Problem:

Code Implementation with Java

Here is the Java code to solve this problem:

Comparative Study of Complexity Analysis

Here are the time complexities for all ways to solve the Subset Sum Problem:

With the above 3 methods, we are sure that you'll be able to analyze and solve the Subset Sum Problem with wonderful time complexity. After reading this tech blog we are sure, you'll have a basic understanding of memoization as well as Dynamic Programming technique.

We'll keep bringing great and informative articles to FavTutor for your betterment. 

FavTutor - 24x7 Live Coding Help from Expert Tutors!

About The Author

Manvi Saxena

More by favtutor blogs, monte carlo simulations in r (with examples), aarthi juryala.

The unlist() Function in R (with Examples)

Paired Sample T-Test using R (with Examples)

• Interview Q

DAA Tutorial

Asymptotic analysis, analysis of sorting, divide and conquer, lower bound theory, sorting in linear time, binary search trees, red black tree, dynamic programming, greedy algorithm, backtracking, shortest path, all-pairs shortest paths, maximum flow, sorting networks, complexity theory, approximation algo, string matching.

Interview Questions

• Send your Feedback to [email protected]

Help Others, Please Share

Learn Latest Tutorials

Transact-SQL

Reinforcement Learning

R Programming

React Native

Python Design Patterns

Python Pillow

Python Turtle

Preparation

Verbal Ability

Company Questions

Trending Technologies

Artificial Intelligence

Cloud Computing

Data Science

Machine Learning

B.Tech / MCA

Data Structures

Operating System

Computer Network

Compiler Design

Computer Organization

Discrete Mathematics

Ethical Hacking

Computer Graphics

Software Engineering

Web Technology

Cyber Security

C Programming

Control System

Data Mining

Data Warehouse

• Coding Problems
• Subset Sum Problem

Problem Statement

Recursive approach, c implementation of recursive approach, java implementation of recursive approach, python implementation of recursive approach, dynamic programming approach, c implementation for subset sum, java implementation for subset sum, python implementation for subset sum, practice questions, frequently asked questions.

Given an array of non-negative integers and an integer sum. We have to tell whether there exists any subset in an array whose sum is equal to the given integer sum.

Input: arr[] = {3, 34, 4, 12, 3, 2}, sum = 7 Output: True Explanation: There is a subset (4, 3) with sum 7.

Confused about your next job?

Input: arr[] = {2, 2, 2, 3, 2, 2}, sum = 10 Output: True Explanation:

For this approach, we have two cases. 

• Let’s take the last element and now the sum = target sum – value of ‘last’ element and elements remaining = size of array – 1.
• Now  don’t take the ‘last’ element and now the  sum = target sum and elements remaining = size of array – 1.

Dry Run of the Approach:

Suppose n is the size of the array.

isThereSubsetSum(arr, n, sum) = false, if sum > 0 and n == 0 isThereSubsetSum(arr, n, sum) = true, if sum == 0

Time complexity: The above approach may try all the possible subsets of a given array in the worst case. Therefore the time complexity of the above approach is exponential.

In this approach, we will make a 2D array of size equal to (size of array + 1) * (target sum + 1) of boolean type. The state dp[i][j] will be true if there is a subset of elements from A[0….i] with a sum value equal to j .

• We make a boolean dp[][] and fill it in a top-down manner.
• The value of dp[i][j] will be true if there exists a subset of dp[0..i] with a sum equal to j ., otherwise false
• Finally, we return dp[n][sum]

Time Complexity: O(N * sum) where N is the size of the array. Space Complexity: O(N * sum) where N is the size of the array.

Minimum Difference Subsets Subset Sum Problem Equal Average Partition Dynamic Programming

What subset sum problem gives a suitable example? The Subset-Sum Problem is to find a subset’ of the given array A = (A1 A2 A3…An) where the elements of the array A are n positive integers in such a way that a’∈A and summation of the elements of that subsets is equal to some positive integer S.

Is the subset sum problem NP-hard? Yes, it is an NP-hard problem.

Is subset-sum an optimization problem? Yes, subset-sum is an optimization problem because it has a variety of algorithms for tackling it.

How do you solve subsets? Subsets can be solved using backtracking and dynamic programming with efficient time complexity.

• Dynamic Programming

Previous Post

Find the missing number, difference between artificial intelligence and machine learning.

• Data Structures & Algorithms
• DSA - Overview
• DSA - Environment Setup
• DSA - Algorithms Basics
• DSA - Asymptotic Analysis
• Data Structures
• DSA - Data Structure Basics
• DSA - Data Structures and Types
• DSA - Array Data Structure
• Linked Lists
• DSA - Linked List Data Structure
• DSA - Doubly Linked List Data Structure
• DSA - Circular Linked List Data Structure
• Stack & Queue
• DSA - Stack Data Structure
• DSA - Expression Parsing
• DSA - Queue Data Structure
• Searching Algorithms
• DSA - Searching Algorithms
• DSA - Linear Search Algorithm
• DSA - Binary Search Algorithm
• DSA - Interpolation Search
• DSA - Jump Search Algorithm
• DSA - Exponential Search
• DSA - Fibonacci Search
• DSA - Sublist Search
• DSA - Hash Table
• Sorting Algorithms
• DSA - Sorting Algorithms
• DSA - Bubble Sort Algorithm
• DSA - Insertion Sort Algorithm
• DSA - Selection Sort Algorithm
• DSA - Merge Sort Algorithm
• DSA - Shell Sort Algorithm
• DSA - Heap Sort
• DSA - Bucket Sort Algorithm
• DSA - Counting Sort Algorithm
• DSA - Radix Sort Algorithm
• DSA - Quick Sort Algorithm
• Graph Data Structure
• DSA - Graph Data Structure
• DSA - Depth First Traversal
• DSA - Breadth First Traversal
• DSA - Spanning Tree
• Tree Data Structure
• DSA - Tree Data Structure
• DSA - Tree Traversal
• DSA - Binary Search Tree
• DSA - AVL Tree
• DSA - Red Black Trees
• DSA - B Trees
• DSA - B+ Trees
• DSA - Splay Trees
• DSA - Tries
• DSA - Heap Data Structure
• DSA - Recursion Algorithms
• DSA - Tower of Hanoi Using Recursion
• DSA - Fibonacci Series Using Recursion
• Divide and Conquer
• DSA - Divide and Conquer
• DSA - Max-Min Problem
• DSA - Strassen's Matrix Multiplication
• DSA - Karatsuba Algorithm
• Greedy Algorithms
• DSA - Greedy Algorithms
• DSA - Travelling Salesman Problem (Greedy Approach)
• DSA - Prim's Minimal Spanning Tree
• DSA - Kruskal's Minimal Spanning Tree
• DSA - Dijkstra's Shortest Path Algorithm
• DSA - Map Colouring Algorithm
• DSA - Fractional Knapsack Problem
• DSA - Job Sequencing with Deadline
• DSA - Optimal Merge Pattern Algorithm
• Dynamic Programming
• DSA - Dynamic Programming
• DSA - Matrix Chain Multiplication
• DSA - Floyd Warshall Algorithm
• DSA - 0-1 Knapsack Problem
• DSA - Longest Common Subsequence Algorithm
• DSA - Travelling Salesman Problem (Dynamic Approach)
• Approximation Algorithms
• DSA - Approximation Algorithms
• DSA - Vertex Cover Algorithm
• DSA - Set Cover Problem
• DSA - Travelling Salesman Problem (Approximation Approach)
• Randomized Algorithms
• DSA - Randomized Algorithms
• DSA - Randomized Quick Sort Algorithm
• DSA - Karger’s Minimum Cut Algorithm
• DSA - Fisher-Yates Shuffle Algorithm
• DSA Useful Resources
• DSA - Questions and Answers
• DSA - Quick Guide
• DSA - Useful Resources
• DSA - Discussion
• Selected Reading
• UPSC IAS Exams Notes
• Developer's Best Practices
• Questions and Answers
• Effective Resume Writing
• HR Interview Questions
• Computer Glossary

Subset Sum Problem

In the sum of subsets problem , there is a given set with some non-negative integer elements. And another sum value is also provided, our task is to find all possible subsets of the given set whose sum is the same as the given sum value.

Set: In mathematical terms, a set is defined as a collection of similar types of objects. The entities or objects of a set must be related to each other through the same rule. Subset: Suppose there are two sets namely set P and set Q. The set P is said to be a subset of set Q, only if all the elements of set P also belong to the set Q and vice-versa need not be true.

Input Output Scenario

Suppose the given set and sum value is −

All possible subsets of the given set, where sum of each element for every subset is the same as the given sum value are given below −

Backtracking Approach to solve Subset Sum Problem

In the naive method to solve a subset sum problem, the algorithm generates all the possible permutations and then checks for a valid solution one by one. Whenever a solution satisfies the constraints, mark it as a part of the solution.

In solving the subset sum problem, the backtracking approach is used for selecting a valid subset. When an item is not valid, we will backtrack to get the previous subset and add another element to get the solution.

In the worst-case scenario, backtracking approach may generate all combinations, however, in general, it performs better than the naive approach.

Follow the below steps to solve subset sum problem using the backtracking approach −

First, take an empty subset.

Include the next element, which is at index 0 to the empty set.

If the subset is equal to the sum value, mark it as a part of the solution.

If the subset is not a solution and it is less than the sum value, add next element to the subset until a valid solution is found.

Now, move to the next element in the set and check for another solution until all combinations have been tried.

In this example, we are illustrating how to solve the subset sum problem in various programming languages.

To Continue Learning Please Login

Ace your Coding Interview

• DSA Problems
• Binary Tree
• Binary Search Tree
• Dynamic Programming
• Divide and Conquer
• Linked List
• Backtracking

Subset Sum Problem – Dynamic Programming Solution

Given a set of positive integers and an integer k , check if there is any non-empty subset that sums to k .

For example,

Practice this problem

A naive solution would be to cycle through all subsets of n numbers and, for every one of them, check if the subset sums to the right number. The running time is of order O(2 n .n) since there are 2 n subsets, and to check each subset, we need to sum at most n elements.

  A better exponential-time algorithm uses recursion . Subset sum can also be thought of as a special case of the 0–1 Knapsack problem . For each item, there are two possibilities:

• Include the current item in the subset and recur for the remaining items with the remaining total.
• Exclude the current item from the subset and recur for the remaining items.

Finally, return true if we get a subset by including or excluding the current item; otherwise, return false. The recursion’s base case would be when no items are left, or the sum becomes negative. Return true when the sum becomes 0, i.e., the subset is found.

  Following is the C++, Java, and Python implementation of the idea:

Download    Run Code

Output: Subsequence with the given sum exists

The time complexity of the above solution is exponential and occupies space in the call stack.

  The problem has an optimal substructure . That means the problem can be broken down into smaller, simple “subproblems”, which can further be divided into yet simpler, smaller subproblems until the solution becomes trivial. The above solution also exhibits overlapping subproblems . If we draw the solution’s recursion tree, we can see that the same subproblems are getting computed repeatedly.

We know that problems with optimal substructure and overlapping subproblems can be solved using dynamic programming, where subproblem solutions are memo ized rather than computed again and again. Following is the memo ized implementation in C++, Java, and Python, which follows the top-down approach since we first break the problem into subproblems and then calculate and store values.

The time complexity of the above solution is O(n × sum) and requires O(n × sum) extra space, where n is the size of the input and sum is the sum of all elements in the input.

  We can also solve this problem in a bottom-up manner. In the bottom-up approach, we solve smaller subproblems first, then solve larger subproblems from them. The following bottom-up approach computes T[i][j] , for each 1 <= i <= n and 1 <= j <= sum , which is true if subset with sum j can be found using items up to first i items. It uses the value of smaller values i and j already computed. It has the same asymptotic runtime as Memoization but no recursion overhead.

Following is the C++, Java, and Python implementation of the idea:

Partition Problem using Dynamic Programming

K–Partition Problem | Printing all partitions

3–Partition Problem

Rate this post

Average rating 4.79 /5. Vote count: 147

No votes so far! Be the first to rate this post.

We are sorry that this post was not useful for you!

Tell us how we can improve this post?

Thanks for reading.

To share your code in the comments, please use our online compiler that supports C, C++, Java, Python, JavaScript, C#, PHP, and many more popular programming languages.

Like us? Refer us to your friends and support our growth. Happy coding :)

Subset Sum Problem using Backtracking

Summary : In this post, we will learn what the Subset Sum Problem is and how to solve the Subset Sum Problem using the backtracking algorithm in C++ and Java.

What is Subset Sum Problem?

Given a set of elements and a sum value. We need to find all possible subsets of the elements with a sum equal to the sum value.

• Set: {10, 7, 5, 18, 12, 20, 15}
• Output: [ {10, 5, 15}, {10, 20}, {7, 5, 18}, {18, 12} ]

There are two ways to solve the Subset Sum Problem:

• Brute Force – Slow
• Backtracking – Fast

In the Bruteforce approach, we usually test every combination starting from one, then two, then three, and so on for the required sum.

Using Backtracking we can reduce its time complexity up to a great extent. Let’s see how.

Subset Sum Problem Solution using Backtracking Algorithm

The main idea is to add the number to the stack and track the sum of stack values.

Add a number to the stack, and check if the sum of all elements is equal to the sum. If yes then print the stack, else if the stack elements are less than the sum then repeat the step by adding the next element to the stack.

If the sum of stack elements exceeds the sum value then pop the last inserted element (top value) and repeat the process by adding the next available element.

In order to pop an element we need to backtrack, therefore we will use recursion.

The solution for the subset-sum is similar to the solution of N Queen Problem using Backtracking .

Recommeded: What is Backtracking Algorithm?

Let’s see the algorithm to solve sum of subset problems in code.

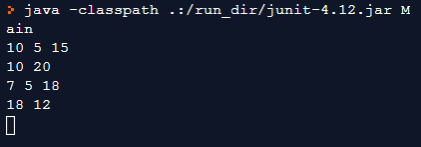
In the program, we add the set element to s by recursively passing the s+set[i] argument to the solve(int s, int idx) method.

Whenever the sum of stack elements equals the sum i.e. s==sum, we output the stack elements and deliberately return to look for more possible solutions.

If the stack sum exceeds sum i.e. s>sum , we return to the last recursive call to backtrack (i.e. to pop an element from the stack and push another element if available).

The displaySolutionSet() display stack elements whenever a solution has been found.

If there is no solution the value of the hasSolution remains false otherwise we update it to true .

In this tutorial, we learned what is subset sum problem and the solution for the subset sum problem using backtracking in C++ and Java programming languages.

You May Also Like:

• N Queen Problem
• Sudoku using Backtracking
• Print all Combinations of Factors using Backtracking
• Shortest Path in Maze using Backtracking

Leave a Reply Cancel reply

Save my name, email, and website in this browser for the next time I comment.

Subset Sum Problem

Greedy algorithms for combinatorial problems: subset sum problem.

In the world of algorithms and problem-solving, greedy algorithms are fascinating approaches that often provide efficient solutions to various combinatorial problems. In this tutorial, we will dive into the concept of greedy algorithms and explore how they can be applied to solve the Subset Sum Problem.

Introduction to Greedy Algorithms

Greedy algorithms are algorithms that make locally optimal choices at each step, with the hope that such choices will eventually lead to a globally optimal solution. Unlike other algorithmic approaches that make use of exhaustive searches or dynamic programming, greedy algorithms tackle problems by selecting the best option at each decision point.

The key idea behind greedy algorithms is that, at every step, they choose the optimal choice based on the current information available, without considering the bigger picture or potential future consequences. This inherent simplicity and efficiency make them particularly useful in solving combinatorial problems.

The Subset Sum Problem

The Subset Sum Problem is a classic example of a combinatorial problem that can be solved using greedy algorithms. Given a set of integers and a target sum, the problem asks whether any subset of the given set adds up to the target sum.

Here's a formal definition of the problem: Given a set of integers S and a target sum T , determine if there exists a subset X ⊆ S such that the sum of elements in X equals T . It can be restated as a decision problem, where the answer is either "yes" or "no" based on whether a valid subset exists.

Greedy Algorithm for the Subset Sum Problem

To solve the Subset Sum Problem using a greedy algorithm, we can follow a simple approach that iteratively builds a solution. Let's outline the steps involved:

• Sort the given set of integers in non-decreasing order.
• Initialize a variable current_sum to track the sum of the elements in the current subset. Set it to 0 initially.
• Iterate through the sorted set of integers from left to right.
• At each step, add the current element to current_sum .
• If current_sum exceeds the target sum T , remove the previous element and backtrack to the previous step.
• If current_sum equals the target sum T , we have found a valid subset, and we can terminate the algorithm.
• If we reach the end of the sorted set without finding a valid subset, such a subset does not exist.

Let's illustrate the algorithm with an example:

Suppose we have the set of integers {2, 7, 4, 1, 5} and the target sum is 10.

• Sorting the set gives us {1, 2, 4, 5, 7}.
• Start with an empty subset and current_sum = 0 .
• Add 1 to current_sum , resulting in current_sum = 1 .
• Add 2 to current_sum , resulting in current_sum = 3 .
• Add 4 to current_sum , resulting in current_sum = 7 .
• Add 5 to current_sum , resulting in current_sum = 12 , which exceeds the target sum.
• Backtrack and remove 5 from the subset.
• Add 7 to current_sum , resulting in current_sum = 14 , which exceeds the target sum.
• Backtrack and remove 7 from the subset.
• Continue with the remaining elements, but the sum will keep exceeding the target sum.
• Since no valid subset is found, the algorithm terminates, and the answer is "no."

Code Implementation

Here's a Python implementation of the greedy algorithm for the Subset Sum Problem:

The above code snippet demonstrates the implementation of the greedy algorithm for the Subset Sum Problem using Python.

In this tutorial, we have explored the concept of greedy algorithms for combinatorial problems, specifically focusing on the Subset Sum Problem. Greedy algorithms offer an elegant and efficient approach to problem-solving, with the Subset Sum Problem being just one of many examples.

By following the outlined steps and examining the code snippet, you should now have a good understanding of how greedy algorithms can be utilized to solve combinatorial problems. Remember to adapt and modify the algorithm as per the specific requirements of your problem.

Keep exploring more combinatorial problems and experimenting with various algorithmic approaches to broaden your knowledge and problem-solving skills as a programmer. Happy coding!

Hi, I'm Ada, your personal AI tutor. I can help you with any coding tutorial. Go ahead and ask me anything.

I have a question about this topic

Give more examples

Subset Sum (The Subset-Sum Problem)

• 1 Description
• 2 Parameters
• 3 Table of Algorithms
• 4 Time Complexity Graph
• 5 Reductions FROM Problem

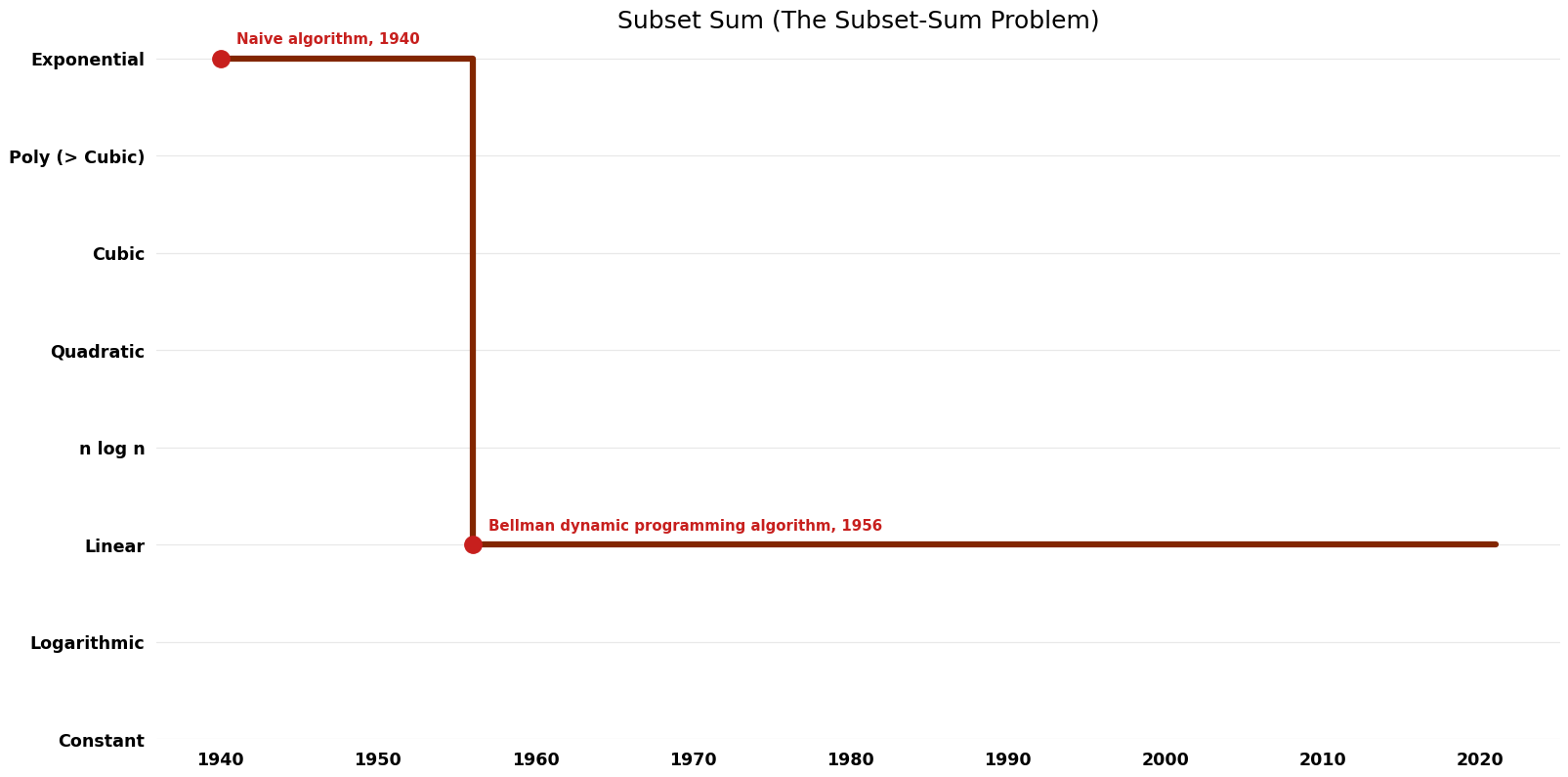
Description

Given a set $S$ of integers and a target sum $t$, determine whether there is a subset of $S$ that sum to $t$.

$S$: the set of integers

$n$: the number of integers in the set

$n'$: the number of distinct elements in the set

$t$: the target sum

$\sigma$: sum of elements in the set

Table of Algorithms

Time complexity graph.

Reductions FROM Problem

Navigation menu.

Subset Sum Problem

There are two problems commonly known as the subset sum problem.

so the sum appearing most often is 3, which occurs twice, and the number of different sums is 7.

(Borwein and Bailey 2003, p. 21).

Explore with Wolfram|Alpha

More things to try:

• subset sum problem proof date
• subset sum problem status
• independent set problem, subset sum problem status

Referenced on Wolfram|Alpha

Cite this as:.

Weisstein, Eric W. "Subset Sum Problem." From MathWorld --A Wolfram Web Resource. https://mathworld.wolfram.com/SubsetSumProblem.html

Subject classifications

Search anything:

Subset Sum Problem solved using Backtracking approach 【O(2^N) time complexity】

Algorithms backtracking subset sum problem.

Open-Source Internship opportunity by OpenGenus for programmers. Apply now.

Reading time: 30 minutes | Coding time: 10 minutes

In this article, we will solve Subset Sum problem using a backtracking approach which will take O(2^N) time complexity but is significantly faster than the recursive approach which take exponential time as well.

Subset sum problem is the problem of finding a subset such that the sum of elements equal a given number. The backtracking approach generates all permutations in the worst case but in general, performs better than the recursive approach towards subset sum problem.

A subset A of n positive integers and a value sum is given, find whether or not there exists any subset of the given set, the sum of whose elements is equal to the given value of sum.

Given the following set of positive numbers:

We need to find if there is a subset for a given sum say 4:

For another value say 5, there is another subset:

Similarly, for 6, we have {2, 1, 3} as the subset.

For 7, there is no subset where the sum of elements equal to 7.

This problem can be solved using following algorithms:

• Recursive method

Backtracking

• Dynamic Programing

In this article, we will solve this using Backtracking approach

In Backtracking algorithm as we go down along depth of tree we add elements so far, and if the added sum is satisfying explicit constraints, we will continue to generate child nodes further. Whenever the constraints are not met, we stop further generation of sub-trees of that node, and backtrack to previous node to explore the nodes not yet explored.We need to explore the nodes along the breadth and depth of the tree. Generating nodes along breadth is controlled by loop and nodes along the depth are generated using recursion (post order traversal).

• Start with an empty set
• Add the next element from the list to the set
• If the subset is having sum M, then stop with that subset as solution.
• If the subset is not feasible or if we have reached the end of the set, then backtrack through the subset until we find the most suitable value.
• If the subset is feasible (sum of seubset < M) then go to step 2.
• If we have visited all the elements without finding a suitable subset and if no backtracking is possible then stop without solution.

Consider the following array/ list of integers:

We want to find if there is a subset with sum 3.

Note that there are two such subsets {1, 2} and {3} . We will follow our backtracking approach.

Consider our empty set {}

We add 1 to it {1} (sum = 1, 1 < 3)

We add 2 to it {1, 3} (sum = 3, 3 == 3, found)

We remove 3 from it {1} (sum = 1, 1 < 3)

We add 2 to it {1, 2} (sum = 3, 3 == 3, found)

We remove 2 and see that all elements have been considered.

Following diagram captures the idea:

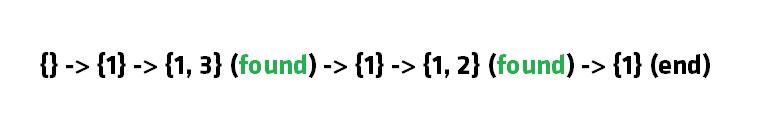
Implementations in Java and C++

Following is the implementation of the backtracking approach in Java :

Following is the implementation in C++ :

Worst case time complexity: Θ(2^n)

Space complexity: Θ(1)

• Python Basics
• Interview Questions
• Python Quiz
• Popular Packages
• Python Projects
• Practice Python
• AI With Python
• Learn Python3
• Python Automation
• Python Web Dev
• DSA with Python
• Python OOPs
• Dictionaries
• Subset Sum Problem

Subset sum in Different languages

Python program for subset sum problem | dp-25.

• Java Program for Subset Sum Problem | DP-25
• C Program for Subset Sum Problem | DP-25
• PHP Program for Subset Sum Problem | DP-25
• C# Program for Subset Sum Problem | DP-25
• Subset Sum Problem using Backtracking
• Perfect Sum Problem (Print all subsets with given sum)
• Subset Sum Problem in O(sum) space
• Subset Sum is NP Complete
• Minimum Subset sum difference problem with Subset partitioning
• Maximum subset sum such that no two elements in set have same digit in them
• Find all distinct subset (or subsequence) sums of an array
• Subset sum problem where Array sum is at most N
• Find the smallest positive integer value that cannot be represented as sum of any subset of a given array
• Count of subsets with sum equal to X | Set-2
• Number of subsets with sum divisible by m
• Size of the smallest subset with maximum Bitwise OR
• Sum of subset differences

Write a Python program for a given set of non-negative integers and a value sum , the task is to check if there is a subset of the given set whose sum is equal to the given sum.

Input: set[] = {3, 34, 4, 12, 5, 2}, sum = 9 Output: True Explanation: There is a subset (4, 5) with sum 9. Input: set[] = {3, 34, 4, 12, 5, 2}, sum = 30 Output: False Explanation: There is no subset that adds up to 30.

Recommended: Please solve it on “ PRACTICE ” first, before moving on to the solution.

Python program for subset sum problem using recursion :.

For the recursive approach, there will be two cases. Consider the ‘last’ element to be a part of the subset. Now the new required sum = required sum – value of ‘last’ element . Don’t include the ‘last’ element in the subset. Then the new required sum = old required sum . In both cases, the number of available elements decreases by 1.

Step-by-step approach:

• Build a recursive function and pass the index to be considered (here gradually moving from the last end) and the remaining sum amount.
• For each index check the base cases and utilize the above recursive call.
• If the answer is true for any recursion call, then there exists such a subset. Otherwise, no such subset exists.

Below is the implementation of the above approach.

Time Complexity:  O(2 n ) Auxiliary space : O(n)

Python Program for Subset Sum Problem using Memoization :

As seen in the previous recursion method, each state of the solution can be uniquely identified using two variables – the index and the remaining sum. So create a 2D array to store the value of each state to avoid recalculation of the same state.

Below is the implementation of the above approach:

Time Complexity : O(sum*n) Auxiliary space : O(n)

Python Program for Subset Sum Problem using Dynamic Programming :

We can solve the problem in Pseudo-polynomial time we can use the Dynamic programming approach.

So we will create a 2D array of size (n + 1) * (sum + 1) of type boolean . The state dp[i][j] will be true if there exists a subset of elements from set[0 . . . i] with sum value = ‘j’. The dynamic programming relation is as follows: if (A[i-1] > j) dp[i][j] = dp[i-1][j] else dp[i][j] = dp[i-1][j] OR dp[i-1][j-set[i-1]]

Time Complexity : O(sum * n), where n is the size of the array. Auxiliary Space : O(sum*n), as the size of the 2-D array is sum*n .

Python Program for Subset Sum Problem using  Dynamic Programming  with space optimization to linear:

In previous approach of dynamic programming we have derive the relation between states as given below: if (A[i-1] > j) dp[i][j] = dp[i-1][j] else dp[i][j] = dp[i-1][j] OR dp[i-1][j-set[i-1]] If we observe that for calculating current dp[i][j] state we only need previous row dp[i-1][j] or dp[i-1][j-set[i-1]]. There is no need to store all the previous states just one previous state is used to compute result.

• Define two arrays  prev  and  curr  of size  Sum+1  to store the just previous row result and current row result respectively.
• Once  curr  array is calculated then  curr  becomes our  prev  for the next row.
• When all rows are processed the answer is stored in  prev  array.

Time Complexity: O(sum * n), where n is the size of the array. Auxiliary Space : O(sum), as the size of the 1-D array is sum+1 .

Please refer complete article on Subset Sum Problem | DP-25 for more details!

Please Login to comment...

Similar reads.

• Python Programs

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Tutorial Playlist

Data structure tutorial, arrays in data structures: a guide with examples, all you need to know about two-dimensional arrays, all you need to know about a linked list in a data structure, the complete guide to implement a singly linked list, the ultimate guide to implement a doubly linked list, the fundamentals for understanding circular linked list, the ultimate guide to understand the differences between stack and queue.

Implementing Stacks in Data Structures

Your One-Stop Solution for Stack Implementation Using Array

Your one-stop solution for queue implementation using array, your one-stop solution to learn depth-first search(dfs) algorithm from scratch, your one-stop solution for stack implementation using linked-list, the definitive guide to understand stack vs heap memory allocation, all you need to know about linear search algorithm, all you need to know about breadth-first search algorithm, a one-stop solution for using binary search trees in data structure, the best tutorial to understand trees in data structure, a complete guide to implement binary tree in data structure, a holistic look at using avl trees in data structures, all you need to know about tree traversal in data structure, the best and easiest way to understand an algorithm, the best guide you’ll ever need to understand b-tree in data structure, the best guide you'll ever need to understand spanning tree in data structure, a one-stop solution guide to understand data structure and algorithm complexity, your one-stop solution to understand shell sort algorithm, your one-stop solution to quick sort algorithm, the most useful guide to learn selection sort algorithm, everything you need to know about radix sort algorithm, everything you need to know about the counting sort algorithm, everything you need to know about the merge sort algorithm, insertion sort algorithm: one-stop solution that will help you understand insertion sort, everything you need to know about the bubble sort algorithm, the best guide you’ll ever need to understand bucket sort algorithm, your one-stop solution to understand recursive algorithm in programming, the definitive guide to understanding greedy algorithm, your one-stop solution to understand backtracking algorithm, the fundamentals of the bellman-ford algorithm, your one-stop solution for graphs in data structures, the best guide to understand and implement solutions for tower of hanoi puzzle, a simplified and complete guide to learn space and time complexity, all you need to know about the knapsack problem : your complete guide, the fibonacci series: mathematical and programming interpretation, the holistic look at longest common subsequence problem, the best article to understand what is dynamic programming, a guide to implement longest increasing subsequence using dynamic programming, a holistic guide to learn stop solution using dynamic programming, one stop solution to all the dynamic programming problems, understanding the fundamentals of binomial distribution, here’s all you need to know about minimum spanning tree in data structures, understanding the difference between array and linked list, the best article out there to understand the b+ tree in data structure, a comprehensive look at queue in data structure, your one-stop solution to understand coin change problem, the best way to understand the matrix chain multiplication problem, your one-stop solution to learn floyd-warshall algorithm for using dynamic programming, the best tutorial you'll ever need for queue implementation using linked list, how to create a fake news detection system, all you need to know about how to create a react js portfolio project, a complete guide on the role of ai in healthcare, the best guide to learn how to make a wireframe: what is a wireframe, the best dsa projects for your resume, the best guide to understanding the working and implementation of selective repeat arq, one stop guide to understanding network layer in the osi model, the working and implementation of data-link layer in the osi model, top 5 best coding books you must read, the working and implementation of physical layer in the osi model, how to create an instagram clone using react, reactjs vs vuejs, subset sum problem: dynamic programming & recursion based solution.

Lesson 46 of 68

Table of Contents

Most of the time, dynamic programming is just a faster way to do things with recursion. You use dynamic programming to optimize any recursive solution that makes use of the same inputs repeatedly. Subproblem results will be stored, so they do not have to be recomputed in the future as needed. This straightforward optimization decreases the time complexity from exponential to polynomial levels.

By the end of this tutorial, you will better understand the recursion and dynamic programming approach to the subset sum problem with all the necessary details and practical implementations.

Here's How to Land a Top Software Developer Job

What Is the Problem Statement for the Subset Sum Problem?

You will be given a set of non-negative integers and a value of variable sum, and you must determine if there is a subset of the given set with a sum equal to a given sum.

Now, look at the recursive solution to solve the subset sum problem.

What Is the Recursion Based Solution to the Subset Sum Problem?

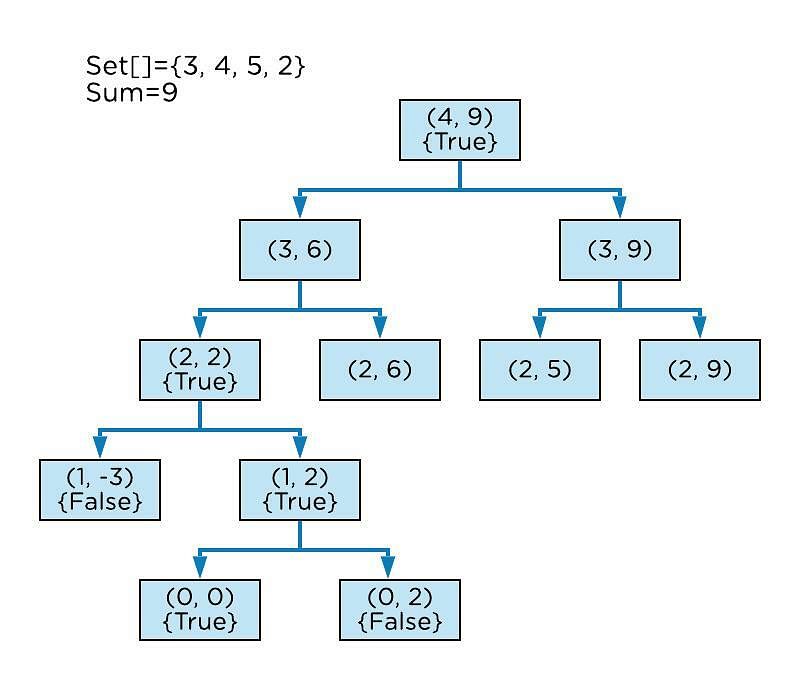
For the recursion based approach, you will look at two scenarios:

• Start with the last element and work your way up to the goal sum by subtracting the value of the 'last' element from the total number of elements.
• 'Final' element will be removed, and the required sum will equal the target sum, with the number of elements equal to the total elements minus 1.

And this is how you solve the subset sum problem using recursion. Now, implement this solution through a simple C++ code.

How Do You Implement the Recursion-Based Solution of the Subset Sum Problem?

You will be provided with a set with elements {10, 7, 8, 9, 1, 5}. You are to find a subset whose sum must be equal to 16, which is set {7, 9}.

// A c++ program to illustrate recursion based solution

#include <bits/stdc++.h>

using namespace std;

//It will return true if subset of set[] 

//has sum equal to given sum; false otherwise

bool is_subset_sum(int set[], int n, int sum)

// Base Cases

if (sum == 0)

return true;

if (n == 0)

return false;

// If last element is greater than sum,

// then we will ignore it

if (set[n - 1] > sum)

return is_subset_sum(set, n - 1, sum);

/* otherwise,we will check if the sum can be obtained by any

of the following:

(a) including the last element

(b) excluding the last element */

return is_subset_sum(set, n - 1, sum)

|| is_subset_sum(set, n - 1, sum - set[n - 1]);

// Driver code

int set[] = { 10, 7, 8, 9, 1, 5 };

int sum = 16;

int n = sizeof(set) / sizeof(set[0]);

if (is_subset_sum(set, n, sum) == true)

cout <<"Found a subset with given sum";

cout <<"No subset with given sum was found";

You have now explored the recursive approach to the subset sum problem with a code. Now, look at the dynamic programming-based solution to this problem.

Basics to Advanced - Learn It All!

What Is the Dynamic Programming Based Solution to the Subset Sum Problem?

You use dynamic programming to solve the problem in pseudo-polynomial time,

• Make a boolean-type 2D array of size (arr.size() + 1) * (target + 1).
• If there is a subset of elements from A[0....i] with sum value = 'j,' the state DP[i][j] is true.
• To avoid duplicating previous cases' answers, you will have to ensure that the current element has a value greater than the "current sum value."
• So, check if any prior states have already encountered the sum='j' OR have previously experienced the value 'j – A[i], which will help you achieve your purpose if it is bigger than the current total value.

And this is how you solve this problem using dynamic programming. Now implement this solution through a simple C++ code.

How Do You Implement the Dynamic Programming Based Solution of the Subset Sum Problem?

You will be given a set with elements as {10, 7, 8, 4, 1, 6}. You have to find a subset whose sum must be equal to 16, which is set {10, 6}.

// A C++ program to demonstrate Dynamic Programming 

//approach to solve this problem

bool is_subset_sum(int set[], int n, int target_sum)

//If set[0..j-1] has a subset with 

//target_sum equal to i then the 

//value of sub_set[i][j] will be true.

bool sub_set[n + 1][target_sum + 1];

// If target_sum is 0, then answer is true

for (int i = 0; i <= n; i++)

sub_set[i][0] = true;

// If target_sum is not 0 and set is empty,

// then answer is false

for (int i = 1; i <= target_sum; i++)

sub_set[0][i] = false;

// we will now fill the subset table in bottom up manner

for (int i = 1; i <= n; i++) {

for (int j = 1; j <= target_sum; j++) {

if (j < set[i - 1])

sub_set[i][j] = sub_set[i - 1][j];

if (j >= set[i - 1])

sub_set[i][j] = sub_set[i-1][j]

|| sub_set[i - 1][j - set[i - 1]];

/* // we can uncomment this code to print table

for (int j = 0; j <= target_sum; j++)

printf ("%4d", sub_set[i][j]);

cout <<"\n";

return sub_set[n][target_sum];

int set[] = { 10, 7, 8, 4, 1, 6 };

int target_sum = 16;

if (is_subset_sum(set, n, target_sum) == true)

cout <<"Found a subset with given sum = "<<target_sum;

cout <<"No subset found with given sum = "<<target_sum;

With this, you have come to an end of this tutorial. You will now look at what could be your next steps to conquer dynamic programming problems.

Advance your career as a MEAN stack developer with the  Full Stack Web Developer - MEAN Stack Master's Program . Enroll now!

Your next stop in mastering dynamic programming problems should be matrix chain multiplication. Given a list of matrices, you must find the most efficient way to multiply a set of matrices together. The issue isn't whether or not to multiply, but rather which multiplications to perform first.

If you're searching for a more in-depth understanding of software development that can help you carve out a successful career in the field, look no further. If that's the case, consider Simplilearn's Postgraduate Program in Full Stack Web Development , which is offered in collaboration with Caltech CTME, the world's largest technology education institution. This Post-Graduate Program will teach you how to master both front-end and back-end Java technologies , beginning with the fundamentals and progressing to the more advanced aspects of Full Stack Web Development. In this web development course, you'll study Angular, Spring Boot, Hibernate , JSPs, and MVC , which will help you get started as a full-stack developer. 

If you have any questions or require clarification on this "Subset Sum Problem" tutorial, please leave them in the comments section below. Our expert team will review them and respond as soon as possible.

Find our Full Stack Java Developer Online Bootcamp in top cities:

About the author.

Vaibhav Khandelwal is a proactive tech geek who's always on the edge of learning new technologies. He is well versed in competitive programming and possess sound knowledge of web development. He likes to read fictional and sci-fi novels and likes to play strategy games like chess.

Recommended Programs

Full Stack Java Developer

Full Stack Web Developer - MEAN Stack

Automation Testing Masters Program

*Lifetime access to high-quality, self-paced e-learning content.

Recommended Resources

Blockchain Career Guide: A Comprehensive Playbook To Becoming A Blockchain Developer

Introducing Simplilearn’s Full Stack Java Developer Master’s Program

How To Become a Pro MERN Stack Developer in 2024

What is Java: A Beginners Guide To Java

Free eBook: Salesforce Developer Salary Report

• PMP, PMI, PMBOK, CAPM, PgMP, PfMP, ACP, PBA, RMP, SP, and OPM3 are registered marks of the Project Management Institute, Inc.

Solution: Partition Equal Subset Sum

Let's solve the Partition Equal Subset Sum problem using the Dynamic Programming pattern.

Naive approach

• Solution summary
• Time complexity
• Space complexity
• Can we do better?

Given a non-empty array of positive integers, determine if the array can be divided into two subsets so that the sum of both subsets is equal.

Constraints:

• 1 ≤ 1 \leq 1 ≤ nums.Length ≤ 200 \leq 200 ≤ 200
• 1 ≤ 1 \leq 1 ≤ nums[i] ≤ 100 \leq 100 ≤ 100

So far, you’ve probably brainstormed some approaches and have an idea of how to solve this problem. Let’s explore some of these approaches and figure out which one to follow based on considerations such as time complexity and any implementation constraints.

We can solve this problem with the following two steps:

• First, we calculate the sum of the array. If the sum of the array is odd, there can’t be two subsets with an equal sum, so we return FALSE.
• If the sum is even, we calculate s u m / 2 sum/2 s u m /2 and find a subset of the array with a sum equal to s u m / 2 sum/2 s u m /2 .

The naive approach is to solve the second step using recursion. In this approach, we calculate the result repeatedly every time. For example, consider an array, [1, 6, 20, 7, 8] , which can be partitioned into [1, 20] and [6, 7, 8] with the sum 21 . While computing the sum, we encounter 21 twice: once in the first subset ( 6 + 7 = 13, 13 + 8 = 21 ) and once in the second subset ( 1 + 20 = 21 ). However, since we’re not storing these sums, it is computed twice.

The time complexity of this approach is O ( 2 n ) O(2^n) O ( 2 n ) . In the worst case, for each element in an array, this solution tests two possibilities, i.e., whether to include or exclude it. We can avoid the repeated work done in the naive approach by storing the result calculated at each step. We store all the values in a lookup table.

Optimized approach using dynamic programming

We use the bottom-up approach of dynamic programming, also known as the tabulation technique . In this approach, the smallest problem is solved, the result is saved, and larger subproblems are computed based on the evaluated results. The problem is divided into subproblems, which are dependent on each other. We start by initializing a lookup table and setting up the values of the base cases. For every subsequent, larger subproblem, we fetch the results of the required preceding smaller subproblems and use them to get the solution to the current subproblem.

Here is how we implement this algorithm:

First, we calculate the sum of the array, nums . If the sum of the array is odd, there can’t be two subsets with an equal sum, so we return FALSE.

Create a lookup table, dp , of size ( ( ( s / 2 ) + 1 ) × ( n + 1 ) ) (((s/2)+1) \times (n+1)) ((( s /2 ) + 1 ) × ( n + 1 )) , where s s s is the sum, and n n n is the size of the array. The dp[0][0] represents that the sum is 0 0 0 , and none of the elements is included in the sum. Therefore, ( s / 2 + 1 ) (s/2+1) ( s /2 + 1 ) rows and ( n + 1 ) (n+1) ( n + 1 ) columns are needed. Initialize all cells of dp with FALSE.

Since each element in the array is a positive number, therefore the sum of elements can’t be 0 0 0 . Hence, each element of the first row in dp is set to TRUE to represent the solution of the smallest sub-problem.

The FALSE in the first column except [ 0 ] [ 0 ] [0][0] [ 0 ] [ 0 ] location indicates that an empty array has no subset whose sum is greater than 0 0 0 .

Fill the table in a bottom-up approach where [i][j] represents the current row and column entry.

If the j t h ^{th} t h element of the array is greater than i , it will make the sum greater than i , which means we cannot include this element in our subset. Therefore, we copy the previous column’s value, which is dp[i][j-1] , into dp[i][j] .

If the j t h ^{th} t h element of the array is less than or equal to i , we have two choices: either include it in our subset or exclude it. Here, we want to find out if it is possible to form a subset with a sum of i using the first j elements of the array.

In the first choice, we need to find a subset that adds up to i - nums[j-1] using the first j-1 elements of the nums array. That means we are looking at the value of dp[i - nums[j - 1]][j - 1] .

In the second choice, we exclude the j t h ^{th} t h element from our subset and find a subset that adds up to i using the first j-1 elements of the nums array. This means we are looking at the value of dp[i][j - 1] .

Finally, we set dp[i][j] to the logical OR of these two choices: dp[i][j] = dp[i - nums[j - 1]][j - 1] OR dp[i][j - 1] .

Return the value present at the last row and last column of the dp , which denotes whether the array can be partitioned or not.

• If we get TRUE, then the array can be partitioned.
• If we get FALSE, then the array can not be partitioned.

Here’s the demonstration of the steps above:

Level up your interview prep. Join Educative to access 80+ hands-on prep courses.

Distributed algorithm for solving variational inequalities over time-varying unbalanced digraphs

• Research Article
• Published: 31 May 2024

Cite this article

• Yichen Zhang 1 ,
• Yutao Tang 1 ,
• Zhipeng Tu 2 &
• Yiguang Hong 3 , 4  

In this paper, we study a distributed model to cooperatively compute variational inequalities over time-varying directed graphs. Here, each agent has access to a part of the full mapping and holds a local view of the global set constraint. By virtue of an auxiliary vector to compensate the graph imbalance, we propose a consensus-based distributed projection algorithm relying on local computation and communication at each agent. We show the convergence of this algorithm over uniformly jointly strongly connected unbalanced digraphs with nonidentical local constraints. We also provide a numerical example to illustrate the effectiveness of our algorithm.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Facchinei, F., & Pang, J.-S. (2003). Finite-dimensional Variational Inequalities and Complementarity Problems . New York: Springer.

Google Scholar  

Ansari, Q. H., Lalitha, C., & Mehta, M. (2013). Generalized Convexity, Nonsmooth Variational Inequalities, and Nonsmooth Optimization . Boca Raton, FL: CRC Press.

Book   Google Scholar  

Bertsekas, D. P., & Tsitsiklis, J. N. (1989). Parallel and Distributed Computation: Numerical Methods . Englewood Cliffs, NJ: Prentice-Hall.

Koshal, J., Nedić, A., & Shanbhag, U. V. (2011). Multiuser optimization: Distributed algorithms and error analysis. SIAM Journal on Optimization, 21 (3), 1046–1081.

Article   MathSciNet   Google Scholar  

Yang, T., Yi, X., Wu, J., Yuan, Y., Wu, D., Meng, Z., Hong, Y., Wang, H., Lin, Z., & Johansson, K. H. (2019). A survey of distributed optimization. Annual Reviews in Control, 47 , 278–305.

Beznosikov, A., Dvurechenskii, P., Koloskova, A., Samokhin, V., Stich, S. U., & Gasnikov, A. (2022). Decentralized local stochastic extra-gradient for variational inequalities. Advances in Neural Information Processing Systems, 35 , 38116–38133.

Beznosikov, A., Richtárik, P., Diskin, M., Ryabinin, M., & Gasnikov, A. (2022). Distributed methods with compressed communication for solving variational inequalities, with theoretical guarantees. Advances in Neural Information Processing Systems, 35 , 14013–14029.

Tu, Z. (2023). Research on communication-efficient distributed optimization algorithms . Ph.D. thesis. Beijing: University of Chinese Academy of Sciences.

Salehisadaghiani, F., & Pavel, L. (2016). Distributed nash equilibrium seeking: A gossip-based algorithm. Automatica, 72 , 209–216.

Scutari, G., Palomar, D. P., Facchinei, F., & Pang, J.-S. (2010). Convex optimization, game theory, and variational inequality theory. IEEE Signal Processing Magazine, 27 (3), 35–49.

Article   Google Scholar  

Liang, S., Yi, P., & Hong, Y. (2017). Distributed nash equilibrium seeking for aggregative games with coupled constraints. Automatica, 85 , 179–185.

Parise, F., & Ozdaglar, A. (2019). A variational inequality framework for network games: Existence, uniqueness, convergence and sensitivity analysis. Games and Economic Behavior, 114 , 47–82.

Yi, P., & Pavel, L. (2019). An operator splitting approach for distributed generalized nash equilibria computation. Automatica, 102 , 111–121.

Tatarenko, T., Shi, W., & Nedić, A. (2021). Geometric convergence of gradient play algorithms for distributed nash equilibrium seeking. IEEE Transactions on Automatic Control, 66 (11), 5342–5353.

Belgioioso, G., Nedic, A., & Grammatico, S. (2021). Distributed generalized nash equilibrium seeking in aggregative games on time-varying networks. IEEE Transactions on Automatic Control, 66 (5), 2061–2075.

Bianchi, M., & Grammatico, S. (2021). Fully distributed nash equilibrium seeking over time-varying communication networks with linear convergence rate. IEEE Control Systems Letters, 5 (2), 499–504.

Tang, Y., Yi, P., Zhang, Y., & Liu, D. (2022). Nash equilibrium seeking over directed graphs. Autonomous Intelligent Systems, 2 (1), 7.

Lin, P., Ren, W., & Song, Y. (2016). Distributed multi-agent optimization subject to nonidentical constraints and communication delays. Automatica, 65 , 120–131.

Gadjov, D., & Pavel, L. (2019). A passivity-based approach to nash equilibrium seeking over networks. IEEE Transactions on Automatic Control, 64 (3), 1077–1092.

Lou, Y., Hong, Y., Xie, L., Shi, G., & Johansson, K. H. (2016). Nash equilibrium computation in subnetwork zero-sum games with switching communications. IEEE Transactions on Automatic Control, 61 (10), 2920–2935.

Zhu, Y., Yu, W., Wen, G., & Chen, G. (2021). Distributed nash equilibrium seeking in an aggregative game on a directed graph. IEEE Transactions on Automatic Control, 66 (6), 2746–2753.

Li, H., Lü, Q., & Huang, T. (2018). Distributed projection subgradient algorithm over time-varying general unbalanced directed graphs. IEEE Transactions on Automatic Control, 64 (3), 1309–1316.

Nedic, A., Ozdaglar, A., & Parrilo, P. A. (2010). Constrained consensus and optimization in multi-agent networks. IEEE Transactions on Automatic Control, 55 (4), 922–938.

Bauschke, H. H., & Combettes, P. L. (2011). Convex Analysis and Monotone Operator Theory in Hilbert Spaces . New York: Springer.

Arefizadeh, S., Nedić, A. (2022). A distributed algorithm for aggregative games on directed communication graphs . In: Proceedings of IEEE 61st Conference on Decision and Control (CDC) , pp. 6407–6412. IEEE

Nguyen, D.T.A., Nguyen, D.T., Nedić, A. (2023). Distributed Nash equilibrium seeking over time-varying directed communication networks. arXiv:2201.02323

Mou, S., Liu, J., & Morse, A. S. (2015). A distributed algorithm for solving a linear algebraic equation. IEEE Transactions on Automatic Control, 60 (11), 2863–2878.

Wang, P., Ren, W., & Duan, Z. (2018). Distributed algorithm to solve a system of linear equations with unique or multiple solutions from arbitrary initializations. IEEE Transactions on Control of Network Systems, 6 (1), 82–93.

Zeng, X., Liang, S., Hong, Y., & Chen, J. (2018). Distributed computation of linear matrix equations: An optimization perspective. IEEE Transactions on Automatic Control, 64 (5), 1858–1873.

Liu, Y., Lageman, C., Anderson, B. D., & Shi, G. (2019). An Arrow-Hurwicz-Uzawa type flow as least squares solver for network linear equations. Automatica, 100 , 187–193.

Tang, Y., Zhang, Y., Li, R., & Wang, X. (2023). On measurement disturbances in distributed least squares solvers for linear equations. arXiv:2305.05512

Wang, L., Fullmer, D., & Morse, A.S. (2016). A distributed algorithm with an arbitrary initialization for solving a linear algebraic equation. In: 2016 American Control Conference (ACC), pp. 1078–1081. IEEE

Krawczyk, J. B., & Uryasev, S. (2000). Relaxation algorithms to find nash equilibria with economic applications. Environmental Modeling and Assessment, 5 , 63–73.

Download references

Author information

Authors and affiliations.

School of Artificial Intelligence, Beijing University of Posts and Telecommunications, Beijing, 100876, China

Yichen Zhang & Yutao Tang

Network Technology Laboratory, Huawei Technologies Co., Ltd., Beijing, 100095, China

Department of Control Science and Engineering, Tongji University, Shanghai, 200092, China

Yiguang Hong

Shanghai Research Institute for Intelligent Autonomous Systems, Tongji University, Shanghai, 200092, China

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Yutao Tang .

Additional information

This work was supported by the National Natural Science Foundation of China (No. 61973043) and Shanghai Municipal Science and Technology Major Project (No. 2021SHZDZX0100).

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Zhang, Y., Tang, Y., Tu, Z. et al. Distributed algorithm for solving variational inequalities over time-varying unbalanced digraphs. Control Theory Technol. (2024). https://doi.org/10.1007/s11768-024-00223-9

Download citation

Received : 24 September 2023

Revised : 12 December 2023

Accepted : 13 December 2023

Published : 31 May 2024

DOI : https://doi.org/10.1007/s11768-024-00223-9

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Variational inequality
• Distributed computation
• Multi-agent system
• Weight-unbalanced graph
• Find a journal
• Publish with us
• Track your research