problem solving involving polynomial equations learning task 1

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 10: Polynomial expressions, equations, & functions

About this unit.

This topic covers:

• Adding, subtracting, and multiplying polynomial expressions
• Factoring polynomial expressions as the product of linear factors
• Dividing polynomial expressions
• Proving polynomials identities
• Solving polynomial equations & finding the zeros of polynomial functions
• Graphing polynomial functions
• Symmetry of functions

Intro to polynomials

• Polynomials intro (Opens a modal)
• The parts of polynomial expressions (Opens a modal)
• Evaluating polynomials (Opens a modal)
• Simplifying polynomials (Opens a modal)
• Polynomials intro 4 questions Practice

Adding & subtracting polynomials

• Adding polynomials (Opens a modal)
• Subtracting polynomials (Opens a modal)
• Polynomial subtraction (Opens a modal)
• Adding & subtracting multiple polynomials (Opens a modal)
• Adding polynomials (old) (Opens a modal)
• Adding and subtracting polynomials review (Opens a modal)
• Add polynomials (intro) 4 questions Practice
• Subtract polynomials (intro) 4 questions Practice
• Add & subtract polynomials 4 questions Practice

Adding & subtracting polynomials: two variables

• Adding polynomials: two variables (intro) (Opens a modal)
• Subtracting polynomials: two variables (intro) (Opens a modal)
• Subtracting polynomials: two variables (Opens a modal)
• Finding an error in polynomial subtraction (Opens a modal)
• Polynomials review (Opens a modal)
• Adding and subtracting polynomials with two variables review (Opens a modal)
• Add & subtract polynomials: two variables (intro) 4 questions Practice
• Add & subtract polynomials: two variables 4 questions Practice
• Add & subtract polynomials: find the error 4 questions Practice

Multiplying monomials

• Multiplying monomials (Opens a modal)
• Multiplying monomials to find area: two variables (Opens a modal)
• Multiplying monomials to find area (Opens a modal)
• Multiplying monomials challenge (Opens a modal)
• Multiplying monomials review (Opens a modal)
• Multiply monomials 4 questions Practice
• Multiply monomials (advanced) 4 questions Practice

Multiplying monomials by polynomials

• Multiplying monomials by polynomials: area model (Opens a modal)
• Multiplying monomials by polynomials (Opens a modal)
• Multiplying monomials by polynomials challenge (Opens a modal)
• Multiplying monomials by polynomials review (Opens a modal)
• Multiply monomials by polynomials: area model 4 questions Practice
• Multiply monomials by polynomials 4 questions Practice
• Multiply monomials by polynomials challenge 4 questions Practice

Multiplying binomials

• Multiplying binomials: area model (Opens a modal)
• Multiplying binomials intro (Opens a modal)
• Multiplying binomials (Opens a modal)
• Multiplying binomials review (Opens a modal)
• Multiply binomials: area model 4 questions Practice
• Warmup: multiplying binomials intro 4 questions Practice
• Multiply binomials intro 4 questions Practice
• Multiply binomials 4 questions Practice

Special products of binomials

• Special products of the form (x+a)(x-a) (Opens a modal)
• Squaring binomials of the form (x+a)² (Opens a modal)
• Special products of the form (ax+b)(ax-b) (Opens a modal)
• Squaring binomials of the form (ax+b)² (Opens a modal)
• Special products of binomials: two variables (Opens a modal)
• More examples of special products (Opens a modal)
• Squaring a binomial (old) (Opens a modal)
• Binomial special products review (Opens a modal)
• Multiply difference of squares 4 questions Practice
• Polynomial special products: perfect square 4 questions Practice

Multiplying binomials by polynomials

• Multiplying binomials by polynomials (Opens a modal)
• Multiplying binomials by polynomials: area model (Opens a modal)
• Multiplying binomials by polynomials challenge (Opens a modal)
• Multiplying binomials by polynomials review (Opens a modal)
• Multiplying binomials by polynomials (old) (Opens a modal)
• Multiplying binomials with radicals (old) (Opens a modal)
• Multiply binomials by polynomials 4 questions Practice

Polynomials word problems

• Polynomial multiplication word problem (Opens a modal)
• Polynomial word problem: rectangle and circle area (Opens a modal)
• Polynomial word problem: total value of bills (Opens a modal)
• Polynomial word problem: area of a window (Opens a modal)

Introduction to factorization

• Intro to factors & divisibility (Opens a modal)
• Factors & divisibility 4 questions Practice

Factoring monomials

• Which monomial factorization is correct? (Opens a modal)
• Factoring monomials (Opens a modal)
• Worked example: finding the missing monomial factor (Opens a modal)
• Worked example: finding missing monomial side in area model (Opens a modal)
• Greatest common factor of monomials (Opens a modal)
• Factor monomials 4 questions Practice
• Greatest common factor of monomials 4 questions Practice

Factoring polynomials by taking common factors

• Factoring with the distributive property (Opens a modal)
• Factoring polynomials by taking a common factor (Opens a modal)
• Taking common factor from binomial (Opens a modal)
• Taking common factor from trinomial (Opens a modal)
• Taking common factor: area model (Opens a modal)
• Factoring polynomials: common binomial factor (Opens a modal)
• Factoring by common factor review (Opens a modal)
• Factoring polynomials: common factor (old) (Opens a modal)
• Factor polynomials: common factor 4 questions Practice

Evaluating expressions with unknown variables

• Worked example: evaluating expressions using structure (Opens a modal)
• Worked example: evaluating expressions using structure (more examples) (Opens a modal)
• Evaluate expressions using structure 4 questions Practice

Factoring quadratics intro

• Factoring quadratics as (x+a)(x+b) (Opens a modal)
• Factoring quadratics: leading coefficient = 1 (Opens a modal)
• Factoring quadratics as (x+a)(x+b) (example 2) (Opens a modal)
• More examples of factoring quadratics as (x+a)(x+b) (Opens a modal)
• Factoring simple quadratics review (Opens a modal)
• Warmup: factoring quadratics intro 4 questions Practice
• Factoring quadratics intro 4 questions Practice

Factoring quadratics by grouping

• Intro to grouping (Opens a modal)
• Factoring by grouping (Opens a modal)
• Factoring quadratics by grouping (Opens a modal)
• Factoring quadratics: leading coefficient ≠ 1 (Opens a modal)
• Factor quadratics by grouping 4 questions Practice

Factoring polynomials with quadratic forms

• Factoring quadratics: common factor + grouping (Opens a modal)
• Factoring quadratics: negative common factor + grouping (Opens a modal)
• Factoring two-variable quadratics (Opens a modal)
• Factoring two-variable quadratics: rearranging (Opens a modal)
• Factoring two-variable quadratics: grouping (Opens a modal)
• Factoring quadratics with common factor (old) (Opens a modal)
• Factor polynomials: quadratic methods 4 questions Practice
• Factor polynomials: quadratic methods (challenge) 4 questions Practice

Factoring quadratics: Difference of squares

• Difference of squares intro (Opens a modal)
• Factoring quadratics: Difference of squares (Opens a modal)
• Factoring difference of squares: leading coefficient ≠ 1 (Opens a modal)
• Factoring difference of squares: analyzing factorization (Opens a modal)
• Factoring difference of squares: missing values (Opens a modal)
• Factoring difference of squares: shared factors (Opens a modal)
• Difference of squares intro 4 questions Practice
• Difference of squares 4 questions Practice

Factoring quadratics: Perfect squares

• Perfect square factorization intro (Opens a modal)
• Factoring quadratics: Perfect squares (Opens a modal)
• Factoring perfect squares (Opens a modal)
• Identifying perfect square form (Opens a modal)
• Factoring higher-degree polynomials: Common factor (Opens a modal)
• Factoring perfect squares: negative common factor (Opens a modal)
• Factoring perfect squares: missing values (Opens a modal)
• Factoring perfect squares: shared factors (Opens a modal)
• Perfect squares intro 4 questions Practice
• Perfect squares 4 questions Practice

Strategy in factoring quadratics

• Strategy in factoring quadratics (part 1 of 2) (Opens a modal)
• Strategy in factoring quadratics (part 2 of 2) (Opens a modal)
• Factoring quadratics in any form (Opens a modal)

Factoring polynomials with special product forms

• Factoring using the perfect square pattern (Opens a modal)
• Factoring using the difference of squares pattern (Opens a modal)
• Factoring difference of squares: two variables (example 2) (Opens a modal)
• Factor polynomials using structure 4 questions Practice

Long division of polynomials

• Intro to long division of polynomials (Opens a modal)
• Dividing polynomials: long division (Opens a modal)

Synthetic division of polynomials

• Intro to polynomial synthetic division (Opens a modal)
• Dividing polynomials: synthetic division (Opens a modal)
• Why synthetic division works (Opens a modal)

Practice dividing polynomials with remainders

• Divide polynomials by x (with remainders) (Opens a modal)
• Divide polynomials by monomials (with remainders) (Opens a modal)
• Dividing polynomials with remainders (Opens a modal)
• Divide polynomials by monomials (with remainders) 4 questions Practice
• Divide polynomials by linear expressions 4 questions Practice
• Divide polynomials with remainders 4 questions Practice

Polynomial Remainder Theorem

• Intro to the Polynomial Remainder Theorem (Opens a modal)
• Remainder theorem: finding remainder from equation (Opens a modal)
• Remainder theorem: checking factors (Opens a modal)
• Remainder theorem: finding coefficients (Opens a modal)
• Proof of the Polynomial Remainder Theorem (Opens a modal)
• Remainder theorem 4 questions Practice

Binomial theorem

• Intro to the Binomial Theorem (Opens a modal)
• Pascal's triangle and binomial expansion (Opens a modal)
• Expanding binomials (Opens a modal)
• Expanding binomials w/o Pascal's triangle (Opens a modal)
• Expand binomials 4 questions Practice

Understanding the binomial theorem

• Binomial expansion & combinatorics (Opens a modal)
• Pascal's triangle & combinatorics (Opens a modal)
• Binomial expansion & combinatorics (old) (Opens a modal)

Advanced polynomial factorization methods

• Factoring higher-degree polynomials (Opens a modal)
• Factoring sum of cubes (Opens a modal)
• Factoring difference of cubes (Opens a modal)

Proving polynomial identities

• Analyzing polynomial identities (Opens a modal)
• Polynomial identities 4 questions Practice

Polynomial identities with complex numbers

• Complex numbers & sum of squares factorization (Opens a modal)
• Factoring sum of squares (Opens a modal)
• Factor polynomials: complex numbers 4 questions Practice

Quadratic equations with complex numbers

• Solving quadratic equations: complex roots (Opens a modal)
• Solve quadratic equations: complex solutions 4 questions Practice

Fundamental Theorem of Algebra

• The Fundamental theorem of Algebra (Opens a modal)
• Quadratics & the Fundamental Theorem of Algebra (Opens a modal)
• Number of possible real roots of a polynomial (Opens a modal)

Finding zeros of polynomials

• Finding zeros of polynomials (1 of 2) (Opens a modal)
• Finding zeros of polynomials (2 of 2) (Opens a modal)
• Finding zeros of polynomials (example 2) (Opens a modal)
• Zeros of polynomials (with factoring) 4 questions Practice

Zeros of polynomials and their graphs

• Zeros of polynomials & their graphs (Opens a modal)
• Positive & negative intervals of polynomials (Opens a modal)
• Zeros of polynomials (factored form) 4 questions Practice
• Positive & negative intervals of polynomials 4 questions Practice

End behavior of polynomial functions

• Intro to end behavior of polynomials (Opens a modal)
• End behavior of polynomials (Opens a modal)
• End behavior of functions & their graphs (Opens a modal)
• End behavior of polynomials 4 questions Practice

Graphs of polynomials

• Graphs of polynomials (Opens a modal)
• Graphs of polynomials: Challenge problems (Opens a modal)

Introduction to symmetry of functions

• Function symmetry introduction (Opens a modal)
• Even and odd functions: Graphs (Opens a modal)
• Even/odd functions & numbers (Opens a modal)
• Even and odd functions: Graphs and tables 4 questions Practice

Symmetry of polynomial functions

• Even & odd polynomials (Opens a modal)
• Symmetry of polynomials (Opens a modal)
• Even & odd functions: Equations 4 questions Practice

Polynomial Equation Word Problems (Mixed Operations)

These lessons help Algebra students learn how to write and solve polynomial equations for algebra word problems.

Related Pages Solving Challenging Word Problems Math Word Problems More Algebra Lessons

How To Solve Polynomial Equation Word Problem?

Example: A tree is supported by a wire anchored in the ground 5 feet from its base. The wire is 1 foot longer than the height that it reaches on the tree. Find the length of the wire.

Polynomial Equation Word Problem

Example: A gymnast dismounts the uneven parallel bars. Her height, h, depends on the time, t, that she is in the air as follows: h = -16t 2 + 8t + 8 a) How long will it take the gymnast to reach the ground? b) When will the gymnast be 8 feet above the ground?

How To Solve Word Problems With Polynomial Equations?

• The sum of a number and its square is 72. Find the number.
• The area of a triangle is 44m 2 . Find the lengths of the legs if one of the legs is 3m longer than the other leg.
• The top of a 15-foot ladder is 3 feet farther up a wall than the foo is from the bottom of the wall. How far is the ladder from the bottom of the wall?
• A projectile is launched upward from ground level with an initial speed of 98m/s. How high will it go? When will it return to the ground?

How To Write Polynomials For Word Problems?

Learn to write a polynomial for Word problems involving perimeter and area of rectangles and circles.

Learn How To Write And Solve Polynomial Equations

Learn to write and solve polynomial equations for special integers, consecutive integers.

Example 1: Find a number that is 56 less than its square. Let n be the number. Example 2: Find two consecutive odd integers whose sum is 130.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Module 7: Polynomials and Polynomial Functions

7.5 – polynomial equations and applications, learning objectives.

• The principle of zero products
• Projectile motion
• Using the Pythagorean theorem to find the lengths of a right triangle

Geometric Applications

• Cost, revenue, and profit polynomials

(7.5.1) – Solving polynomial equations

Not all of the techniques we use for solving linear equations will apply to solving polynomial equations. In this section we will introduce a method for solving polynomial equations that combines factoring and the zero product principle.

The Principle of Zero Products

What if we told you that we multiplied two numbers together and got an answer of zero? What could you say about the two numbers? Could they be 2 and 5? Could they be 9 and 1? No! When the result (answer) from multiplying two numbers is zero, that means that one of them  had  to be zero. This idea is called the zero product principle, and it is useful for solving polynomial equations that can be factored.

Principle of Zero Products

The Principle of Zero Products states that if the product of two numbers is 0, then at least one of the factors is 0. If [latex]ab=0[/latex], then either [latex]a=0[/latex] or [latex]b=0[/latex], or both [latex]a[/latex] and [latex]b[/latex] are 0.

Let’s start with a simple example.  We will factor a GCF from a binomial and apply the principle of zero products to solve a polynomial equation.

[latex]-t^2+t=0[/latex]

Each term has a common factor of [latex]t[/latex], so we can factor and use the zero product principle. Rewrite each term as the product of the GCF and the remaining terms.

[latex]\begin{array}{c}-t^2=t\left(-t\right)\\t=t\left(1\right)\end{array}[/latex]

Rewrite the polynomial equation using the factored terms in place of the original terms.

[latex]\begin{array}{c}-t^2+t=0\\t\left(-t\right)+t\left(1\right)\\t\left(-t+1\right)=0\end{array}[/latex]

Now we have a product on one side and zero on the other, so we can set each factor equal to zero using the zero product principle.

[latex]\begin{array}{c}t=0\,\,\,\,\,\,\,\,\text{ OR }\,\,\,\,\,\,\,\,\,\,\,-t+1=0\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{-1}\,\,\,\underline{-1}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-t=-1\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{-t}{-1}=\frac{-1}{-1}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,t=1\end{array}[/latex]

[latex]t=0\text{ OR }t=1[/latex]

In the following video we show two more examples of using both factoring and the principle of zero products to solve a polynomial equation.

In the next video we show that you can factor a trinomial using methods previously learned to solve a quadratic equation.

You and I both know that it is rare to be given an equation to solve that has zero on one side, so let’s try another one.

Solve: [latex]s^2-4s=5[/latex]

First, move all the terms to one side.  The goal is to try and see if we can use the zero product principle, since that is the only tool we know for solving polynomial equations.

[latex]\begin{array}{c}\,\,\,\,\,\,\,s^2-4s=5\\\,\,\,\,\,\,\,s^2-4s-5=0\\\end{array}[/latex]

We now have all the terms on the left side, and zero on the other side. The polynomial [latex]s^2-4s-5[/latex] factors nicely, which makes this equation a good candidate for the zero product principle. (imagine that)

[latex]\begin{array}{c}s^2-4s-5=0\\\left(s+1\right)\left(s-5\right)=0\end{array}[/latex]

We separate our factors into two linear equations using the principle of zero products.

[latex]\begin{array}{c}\left(s-5\right)=0\\s-5=0\\\,\,\,\,\,\,\,\,\,s=5\end{array}[/latex]

[latex]\begin{array}{c}\left(s+1\right)=0\\s+1=0\\s=-1\end{array}[/latex]

[latex]s=-1\text{ OR }s=5[/latex]

We will work through one more example that is similar to the one above, except this example has fractions.

Solve [latex]y^2-5=-\frac{7}{2}y+\frac{5}{2}[/latex]

Start by multiplying the whole equation by 2 to eliminate fractions:

[latex]\begin{array}{ccc}2\left(y^2-5=-\frac{7}{2}y+\frac{5}{2}\right)\\\,\,\,\,\,\,2(y^2)+2(-5)=2\left(-\frac{7}{2}\right)+2\left(-\frac{5}{2}\right)\\2y^2-10=-7y+5\end{array}[/latex]

Now we can move all the terms to one side and see if this will factor so we can use the principle of zero products.

[latex]\begin{array}{c}2y^2-10=-7y-5\\2y^2-10+7y-5=0\\2y^2-15+7y=0\\2y^2+7y-15=0\end{array}[/latex]

We can now check whether this polynomial will factor, using a table we can list factors until we find two numbers with a product of [latex]2\cdot-15=-30[/latex] and a sum of 7.

We have found the factors that will produce the middle term we want,[latex]-3,10[/latex]. We need to place the factors in a way that will lead to a term of [latex]10y[/latex]:

[latex]\left(2y-3\right)\left(y+5\right)=0[/latex]

Now we can set each factor equal to zero and solve:

[latex]\begin{array}{ccc}\left(2y-3\right)=0\text{ OR }\left(y+5\right)=0\\2y=3\text{ OR }y=-5\\y=\frac{3}{2}\text{ OR }y=-5\end{array}[/latex]

You can always check your work to make sure your solutions are correct:

Check [latex]y=\frac{3}{2}[/latex]

[latex]\begin{array}{ccc}\left(\frac{3}{2}\right)^2-5=-\frac{7}{2}\left(\frac{3}{2}\right)+\frac{5}{2}\\\frac{9}{4}-5=-\frac{21}{4}+\frac{5}{2}\\\text{ common denominator = 4}\\\frac{9}{4}-\frac{20}{4}=-\frac{21}{4}+\frac{10}{4}\\-\frac{11}{4}=-\frac{11}{4}\end{array}[/latex]

[latex]y=\frac{3}{2}[/latex] is indeed a solution, now check [latex]y=-5[/latex]

[latex]\begin{array}{ccc}\left(-5\right)^2-5=-\frac{7}{2}\left(-5\right)+\frac{5}{2}\\25-5=\frac{35}{2}+\frac{5}{2}\\20=\frac{40}{2}\\20=20\end{array}[/latex]

[latex]y=-5[/latex] is also a solution, so we must have done something right!

[latex]y=\frac{3}{2}\text{ OR }y=-5[/latex]

In our last video, we show how to solve another quadratic equation that contains fractions.

(7.5.2) – Applications of polynomial equations

Projectile motion.

Projectile motion happens when you throw a ball into the air and it comes back down because of gravity.  A projectile will follow a curved path that behaves in a predictable way.  This predictable motion has been studied for centuries, and in simple cases it’s height from the ground at a given time, [latex]t[/latex], can be modeled with a polynomial function of the form [latex]h(t)=at^2+bt+c[/latex], where h(t) = height of an object at a given time, [latex]t[/latex].  Projectile motion is also called a parabolic trajectory because of the shape of the path of a projectile’s motion, as in the image of water in the fountain below.

Parabolic WaterTrajectory

Parabolic motion and it’s related functions allow us to launch satellites for telecommunications, and rockets for space exploration. Recently, police departments have even begun using projectiles with GPS to track fleeing suspects in vehicles, rather than pursuing them by high-speed chase  [1] .

In this section we will use polynomial functions to answer questions about the parabolic motion of a projectile. The real mathematical model for the path of a rocket or a police GPS projectile may have different coefficients or more variables, but the concept remains the same. We will also learn to interpret the meaning of the variables in a polynomial function that models projectile motion.

A small toy rocket is launched from a 4-foot pedestal. The height ([latex]h[/latex] , in feet) of the rocket [latex]t[/latex] seconds after taking off is given by the function [latex]h(t)=−2t^{2}+7t+4[/latex]. How long will it take the rocket to hit the ground?

  The rocket will be on the ground when the [latex]h(t)=0[/latex]. We want to know how long, [latex]t[/latex],  the rocket is in the air.

[latex]\begin{array}{l}h(t)=−2t^{2}+7t+4=0\\0=−2t^{2}+7t+4\end{array}[/latex]

We can factor the polynomial [latex]−2t^{2}+7t+4[/latex] more easily by first factoring out a [latex]-1[/latex]

[latex]\begin{array}{c}0=-1(2t^{2}-7t-4)\\0=-1\left(2t+1\right)\left(t-4\right)\end{array}[/latex]

Use the Zero Product Property. There is no need to set the constant factor [latex]-1[/latex] to zero, because [latex]-1[/latex] will never equal zero.

[latex]2t+1=0\,\,\,\,\,\,\text{or}\,\,\,\,\,\,t-4=0[/latex]

Solve each equation.

[latex]t=-\frac{1}{2}\,\,\,\,\,\,\text{or}\,\,\,\,\,\,t=4[/latex]

Interpret the answer. Since t represents time, it cannot be a negative number; only [latex]t=4[/latex] makes sense in this context.

[latex]t=4[/latex]

We can check our answer: [latex]\begin{array}{c}h(4)=−2(4)^{2}+7(4)+4=0\\h(4)=-2(16)+28+4=0\\h(4)-32+32=0\\h(4)=0\end{array}[/latex]

The rocket will hit the ground 4 seconds after being launched.

In the next example we will solve for the time that the rocket is at a given height other than zero.

Use the formula for the height of the rocket in the previous example to find the time when the rocket is 4 feet from hitting the ground on it’s way back down.  Refer to the image.

[latex]h(t)=−2t^{2}+7t+4[/latex]

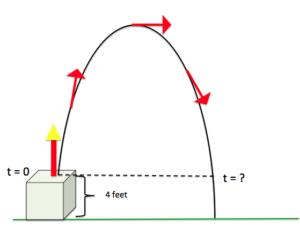
We are given that the height of the rocket is 4 feet from the ground on it’s way back down. We want to know how long it has taken the rocket to get to that point in it’s path, we are going to solve for [latex]t[/latex].

Substitute [latex]h(t) = 4[/latex] into the formula for height, and try to get zero on one side since we know we can use the zero product principle to solve polynomials.

Write and Solve:

[latex]\begin{array}{l}h(t)=4=−2t^{2}+7t+4\\4=-2t^2+7t+4\\\underline{-4}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{-4}\\0=-2t^2+7t\end{array}[/latex]

Now we can factor out a [latex]t[/latex] from each term:

[latex]0=t\left(-2t+7\right)[/latex]

Solve each equation for [latex]t[/latex] using the zero product principle:

[latex]\begin{array}{l}t=0\text{ OR }-2t+7=0\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{-7}\,\,\,\,\,\,\,\underline{-7}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{-2t}{-2}=\frac{-7}{-2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,t=\frac{7}{2}=3.5\end{array}[/latex]

It doesn’t make sense for us to choose [latex]t=0[/latex] because we are interested in the amount of time that has passed when the projectile is 4 feet from hitting the ground on it’s way back down. We will choose [latex]t=3.5[/latex]

Check the answer on your own for practice.

[latex]t=3.5\text{ seconds }[/latex]

In the following video we show another example of how to find the time when a object following a parabolic trajectory hits the ground.

In this section we introduced the concept of projectile motion, and showed that it can be modeled with polynomial function.  While the models used in these examples are simple, the concepts and interpretations are the same as what would happen in “real life”.

Pythagorean Theorem

The Pythagorean theorem or Pythagoras’s theorem is a statement about the sides of a right triangle. One of the angles of a right triangle is always equal to 90 degrees. This angle is the right angle. The two sides next to the right angle are called the legs and the other side is called the hypotenuse. The hypotenuse is the side opposite to the right angle, and it is always the longest side. The image above shows four common kinds of triangle, including a right triangle.

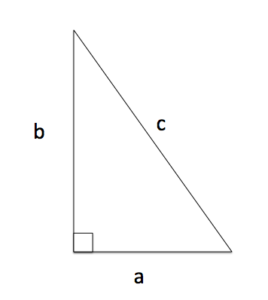
Right Triangle Labeled

The Pythagorean theorem is often used to find unknown lengths of the sides of right triangles. If the longest leg of a right triangle is labeled c, and the other two a, and b as in the image on teh left,  The Pythagorean Theorem states that

[latex]a^2+b^2=c^2[/latex]

Given enough information, we can solve for an unknown length.  This relationship has been used for many, many years for things such as celestial navigation and early civil engineering projects. We now have digital GPS and survey equipment that have been programmed to do the calculations for us.

In the next example we will combine the power of the Pythagorean theorem and what we know about solving quadratic equations to find unknown lengths of right triangles.

A right triangle has one leg with length [latex]x[/latex], another whose length is greater by two, and the length of the hypotenuse is greater by four.  Find the lengths of the sides of the triangle. Use the image below.

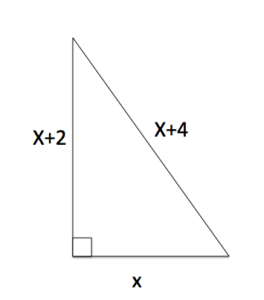
Read and understand:  We know the lengths of all the sides of a triangle in terms of one side. We also know that the Pythagorean theorem will give us a relationship between the side lengths of a right triangle.

Translate: 

[latex]\begin{array}{l}a^2+b^2=c^2\\x^2+\left(x+2\right)^2=\left(x+4\right)^2\end{array}[/latex]

Solve:   If we can move all the terms to one side and factor, we can use the zero product principle to solve.  Since this is the only method we know – let’s hope it works!

First, multiply the binomials and simplify so we can see what we are working with.

[latex]\begin{array}{l}x^2+\left(x+2\right)^2=\left(x+4\right)^2\\x^2+x^2+4x+4=x^2+8x+16\\2x^2+4x+4=x^2+8x+16\end{array}[/latex]

Now move all the terms to one side and see if we can factor.

[latex]\begin{array}{l}2x^2+4x+4=x^2+8x+16\\\underline{-x^2}\,\,\,\underline{-8x}\,\,\,\underline{-16}\,\,\,\,\,\underline{-x^2}\,\,\,\underline{-8x}\,\,\,\underline{-16}\\x^2-4x-12=0\end{array}[/latex]

This went from a messy looking problem to something promising. We can factor using the shortcut:

[latex]-6\cdot{2}=-12,\text{ and }-6+2=-4[/latex]

So we can build our binomial factors with -6 and 2:

[latex]\left(x-6\right)\left(x+2\right)=0[/latex]

Set each factor equal to zero:

[latex]x-6=0, x=6[/latex]

[latex]x+2=0, x=-2[/latex]

Interpret:  Ok, it doesn’t make sense to have a length equal to -2, so we can safely throw that solution out.  The lengths of the sides are as follows:

[latex]x=6[/latex]

[latex]x+2=6+2=8[/latex]

[latex]x+4=6+4=10[/latex]

Check:  Since we know the relationship between the sides of a right triangle we can check that we are correct. Sometimes it helps to draw a picture

We know that [latex]a^2+b^2=c^2[/latex], so we can substitute the values we found:

[latex]\begin{array}{l}6^2+8^2=10^2\\36+64=100\\100=100\end{array}[/latex]

Our solution checks out.

The lengths of the sides of the right triangle are 6, 8, and 10

This video example shows another way a quadratic equation can be used to find and unknown length of a right triangle.

In this section we will explore ways that polynomials are used in applications of area problems.

The length of a rectangle is 3 more than the width. If the area is 40 square inches, what are the dimensions?

[latex]\begin{eqnarray*} x & & \text{ We} \text{ do} \text{ not} \text{ know} \text{ the} \text{ width}, x.\\ x + 3 & & \text{ Length} \text{ is}\, 3 \text{ more}, \text{ or}\, x + 3, \text{ and} \text{ area} \text{ is}\, 40.\\ x (x + 3) = 40 & & \text{ Multiply} \text{ length} \text{ by} \text{ width} \text{ to} \text{ get} \text{ area}\\ x^2 + 3 x = 40 & & \text{ Distribute}\\ \underline{- 40 - 40} & & \text{ Make} \text{ equation} \text{ equal} \text{ zero}\\ x^2 + 3 x - 40 = 0 & & \text{ Factor}\\ (x - 5) (x + 8) = 0 & & \text{ Set} \text{ each} \text{ factor} \text{ equal} \text{ to} \text{ zero}\\ x - 5 = 0 \text{ or}\, x + 8 = 0 & & \text{ Solve} \text{ each} \text{ equation}\\ x = 5 \text{ or}\, x = - 8 & & \text{ Our}\, x \text{ is} a \text{ width}, \text{ cannot} \text{ be} \text{ negative} .\\ (5) + 3 = 8 & & \text{ Length} \text{ is}\, x + 3, \text{ substitute} 5 \text{ for}\, x \text{ to} \text{ find} \text{ length}\\ 5 \text{ in} \text{ by}\, 8 \text{ in} & & \text{ Our} \text{ Solution} \end{eqnarray*}[/latex]

The dimensions of the rectangle are 5 inches by 8 inches.

In the following video you are shown how to find the dimensions of a border around a rectangle.

Cost, Revenue, and Profit Polynomials

In the systems of linear equations section, we discussed how a company’s cost and revenue can be modeled with two linear equations. We found that the profit region for a company was the area between the two lines where the company would make money based on how much was produced. In this section, we will see that sometimes polynomials are used to describe cost and revenue.

Profit is typically defined in business as the difference between the amount of money earned (revenue) by producing a certain number of items and the amount of money it takes to produce that number of items. When you are in business, you definitely want to see profit, so it is important to know what your cost and revenue is.

Cell Phones

For example, let’s say that the cost to a manufacturer to produce a certain number of things is C and the revenue generated by selling those things is R.  The profit, P, can then be defined as

The example we will work with is a hypothetical cell phone manufacturer whose cost to manufacture x number of phones is [latex]C=2000x+750,000[/latex], and the Revenue generated from manufacturing x number of cell phones is [latex]R=-0.09x^2+7000x[/latex].

Define a Profit polynomial for the hypothetical cell phone manufacturer.

Read and Understand: Profit is the difference between revenue and cost, so we will need to define P = R – C for the company.

Define and Translate:  [latex]\begin{array}{c}R=-0.09x^2+7000x\\C=2000x+750,000\end{array}[/latex]

Write and Solve:  Substitute the expressions for R and C into the Profit equation.

[latex]\begin{array}{c}P=R-C\\=-0.09x^2+7000x-\left(2000x+750,000\right)\\=-0.09x^2+7000x-2000x-750,000\\=-0.09x^2+5000x-750,000\end{array}[/latex]

Remember that when you subtract a polynomial, you have to subtract every term of the polynomial.

[latex]P=-0.09x^2+5000x-750,000[/latex]

Mathematical models are great when you use them to learn important information.  The cell phone manufacturing company can use the profit equation to find out how much profit they will make given [latex]x[/latex] number of phones are manufactured.  In the next example, we will explore some profit values for this company.

Given the following numbers of cell phones manufactured, find the profit for the cell phone manufacturer:

• x = 100 phones
• x = 25,000 phones
• x=60,000 phones

Interpret your results.

Read and Understand:  The profit polynomial defined in the previous example,[latex]P=-0.09x^2+5000x-750,000[/latex], gives profit based on x number of phones manufactured.  We need to substitute the given numbers of phones manufactured into the equation, then try to understand what our answer means in terms of profit and number of phones manufactured.

We will move straight into write and solve since we already have our polynomial. It is probably easiest to use a calculator since the numbers in this problem are so large.

Write and Solve: 

Substitute [latex]x = 100[/latex]

[latex]\begin{array}{c}P=-0.09x^2+5000x-750,000\\=-0.09\left(100\right)^2+5000\left(100\right)-750,000\\=-900+500,000-750,000\\=-250,900\end{array}[/latex]

Interpret:  When the number of phones manufactured is 100, the profit for the business is $-250,000.  This is not what we want!  The company must produce more than 100 phones to make a profit.

Substitute [latex]x = 25,000[/latex]

[latex]\begin{array}{c}P=-0.09x^2+5000x-750,000\\=-0.09\left(25000\right)^2+5000\left(25000\right)-750,000\\=-6120000+125,000,000-750,000\\=118,130,000\end{array}[/latex]

Interpret:  When the number of phones manufactured is 25,000, the profit for the business is $118,130,000.  This is more like it!  If the company makes 25,000 phones it will make a profit after it pays all it’s bills.

 If this is true, then the company should make even more phones so it can make even more money, right?  Actually, something different happens as the number of items manufactured increases without bound.

Substitute [latex]x = 60,000[/latex]

[latex]\begin{array}{c}P=-0.09x^2+5000x-750,000\\=-0.09\left(60000\right)^2+5000\left(60000\right)-750,000\\=-324,000,000+300,000,000-750,000\\=-24,750,000\end{array}[/latex]

Interpret:  When the number of phones manufactured is 60,000, the profit for the business is $-24,750,000.  Wait a minute! If the company makes 60,000 phones it will lose money, what happened? At some point, the cost to manufacture the phones will overcome the amount of profit that the business can make.  If this is interesting to you, you may enjoy reading about Economics and Business models.

In the video that follows, we present another example of finding a polynomial profit equation.

• "Cops' Latest Tool in High-speed Chases: GPS Projectiles." CBSNews . CBS Interactive, n.d. Web. 14 June 2016. ↵
• Solve a Quadratic Equations with Fractions by Factoring (a not 1). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/kDj_qdKW-ls . License : CC BY: Attribution
• Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
• Parabolic motion description and example. Provided by : Lumen Learning. License : CC BY: Attribution
• Factoring Application - Find the Time When a Projectile Hits and Ground. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/hsWSzu3KcPU . License : CC BY: Attribution
• Pythagorean Theorem, Description and Examples. Provided by : Lumen Learning. License : CC BY: Attribution
• Screenshot: Thumbsdown. Provided by : Lumen Learning. License : CC BY: Attribution
• Screenshot PI. Provided by : Lumen Learning. License : CC BY: Attribution
• Polynomial Multiplication Application - Volume of a Cylinder. . Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/g-g_nSsfGs4 . License : CC BY: Attribution
• Polynomial Subtracton App - Profit Equation from Revene and Cost.. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning.. Located at : https://youtu.be/-TWjDC4g9dU . License : CC BY: Attribution
• Screenshot: Cell Phones.. Authored by : Lumen Learning. License : CC BY: Attribution
• Profit Polynomial Examples. Provided by : Lumen Learning. License : CC BY: Attribution
• Ex: Factor and Solve Quadratic Equation - Greatest Common Factor Only. Authored by : James Sousa (Mathispower4u.com) . Located at : https://youtu.be/gIwMkTAclw8 . License : CC BY: Attribution
• Ex: Factor and Solve Quadratic Equations When A equals 1. Authored by : James Sousa (Mathispower4u.com) . Located at : https://youtu.be/bi7i_RuIGl0 . License : CC BY: Attribution
• Unit 12: Factoring, from Developmental Math: An Open Program. Provided by : Monterey Institute of Technology. Located at : http://nrocnetwork.org/dm-opentext . License : CC BY: Attribution
• Parabolic water trajectory. Authored by : By GuidoB. Located at : https://commons.wikimedia.org/w/index.php?curid=8015696 . License : CC BY-SA: Attribution-ShareAlike
• Pythagorean Theorem. Provided by : Wikipedia. Located at : https://en.wikipedia.org/wiki/Pythagorean_theorem . License : CC BY-SA: Attribution-ShareAlike
• Ex: Polynomial Addition Application - Perimeter.. Authored by : James Sousa (Mathispower4u.com). . Located at : . License : CC BY: Attribution
• Ex: Find the Area of a Rectangle Using a Polynomial.. Authored by : James Sousa (Mathispower4u.com) .. Located at : . License : CC BY: Attribution
• Unit 11: Exponents and Polynomials, from Developmental Math: An Open Program. . Provided by : Monterey Institute of Technology and Education. Located at : http://nrocnetwork.org/dm-opentext . License : CC BY: Attribution
• Applied Optimization Problems. Provided by : OpenStax. Located at : http://cnx.org/contents/svyieFe9@2/Applied-Optimization-Problems . License : CC BY-NC-SA: Attribution-NonCommercial-ShareAlike . License Terms : Download for free at http://cnx.org/contents/b2fca278-57bd-421d-aa85-21f539b4cc6f@2
• Applications of Quadratic Equations. Authored by : James Sousa. Located at : http://www.youtube.com/watch?v=AlIoxXQ-V50 . License : CC BY: Attribution
• Quadratics - Rectangle. Authored by : Tyler Wallace. Located at : http://wallace.ccfaculty.org/book/book.html . Project : Beginning and Intermediate Algebra. License : Public Domain: No Known Copyright
• Question ID#74417. Authored by : Nearing,Daniel. License : CC BY: Attribution
• Celestial Navigation Math. Authored by : TabletClass Math. Located at : https://www.youtube.com/watch?v=XWLZKmPU17M . License : All Rights Reserved . License Terms : Standard YouTube License

PRACTICE PROBLEMS ON SOLVING POLYNOMIAL EQUATIONS

(1)  Solve the cubic equation : 2x 3 − x 2 −18x + 9 = 0, if sum of two of its roots vanishes         Solution

(2)   Solve the equation 9x 3 − 36x 2 + 44x −16 = 0 if the roots form an arithmetic progression.         Solution

(3)  Solve the equation 3x 3  − 26x 2  + 52x − 24 = 0 if its roots form a geometric progression.         Solution

(4)  Determine k and solve the equation 2x 3  − 6x 2  + 3x + k = 0 if one of its roots is twice the sum of the other two  roots.         Solution

(5)  Find all zeros of the polynomial x 6  − 3x 5  − 5x 4  + 22x 3  − 39x 2  − 39x + 135, if it is known that 1 + 2i an d  √ 3 are two of its zeros.              Solution

(6)   Solve the cubic equation

(i) 2x 3  − 9x 2  +10x = 3

(ii)  8x 3  − 2x 2  − 7x + 3 = 0.        Solution

(7)  Solve the equation x 4  −14x 2  + 45 = 0    Solution

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

Simplifying Algebraic Expressions with Fractional Coefficients

May 17, 24 08:12 AM

The Mean Value Theorem Worksheet

May 14, 24 08:53 AM

Mean Value Theorem

May 14, 24 02:48 AM

• No category

A Detailed Lesson Plan in MATH 10

Related documents

Add this document to collection(s)

You can add this document to your study collection(s)

Add this document to saved

You can add this document to your saved list

Suggest us how to improve StudyLib

(For complaints, use another form )

Input it if you want to receive answer

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.4: Problem Solving

• Last updated
• Save as PDF
• Page ID 51442

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Translate words into algebraic expressions and equations
• Define a process for solving word problems
• Apply the steps for solving word problems to distance, rate, and time problems
• Apply the steps for solving word problems to interest rate problems
• Evaluate a formula using substitution
• Rearrange formulas to isolate specific variables
• Identify an unknown given a formula
• Apply the steps for solving word problems to geometry problems
• Use the formula for converting between Fahrenheit and Celsius

Define a Process for Problem Solving

Word problems can be tricky. Often it takes a bit of practice to convert an English sentence into a mathematical sentence, which is one of the first steps to solving word problems. In the table below, words or phrases commonly associated with mathematical operators are categorized. Word problems often contain these or similar words, so it’s good to see what mathematical operators are associated with them.

Some examples follow:

• Three more than a number becomes \(x+3\)
• Four less than a number becomes \(x-4\)
• Double the cost becomes \(2\cdot\text{ cost }\)
• Groceries and gas together for the week cost $250 means \(\text{ groceries }+\text{ gas }=250\)
• The difference of 9 and a number becomes \(9-x\). Notice how 9 is first in the sentence and the expression

Let’s practice translating a few more English phrases into algebraic expressions.

Translate the table into algebraic expressions:

[reveal-answer q=”790402″]Show Solution[/reveal-answer]

[hidden-answer a=”790402″]

[/hidden-answer]

In this example video, we show how to translate more words into mathematical expressions.

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=50

The power of algebra is how it can help you model real situations in order to answer questions about them.

Here are some steps to translate problem situations into algebraic equations you can solve. Not every word problem fits perfectly into these steps, but they will help you get started.

• Read and understand the problem.
• Determine the constants and variables in the problem.
• Translate words into algebraic expressions and equations.
• Write an equation to represent the problem.
• Solve the equation.
• Check and interpret your answer. Sometimes writing a sentence helps.

Twenty-eight less than five times a certain number is 232. What is the number?

[reveal-answer q=”720402″]Show Solution[/reveal-answer]

[hidden-answer a=”720402″]

Following the steps provided:

• Read and understand: we are looking for a number.
• Constants and variables: 28 and 232 are constants, “a certain number” is our variable because we don’t know its value, and we are asked to find it. We will call it x.
• Translate: five times a certain number translates to \(5x-28\) because subtraction is built backward. is 232 translates to \(=232\) because “is” is associated with equals.
• Write an equation: \(5x-28=232\)

\(\begin{array}{r}5x-28=232\\5x=260\\x=52\,\,\,\end{array}\)

\(\begin{array}{r}5\left(52\right)-28=232\\5\left(52\right)=260\\260=260\end{array}\).

In the video that follows, we show another example of how to translate a sentence into a mathematical expression using a problem solving method.

Another type of number problem involves consecutive numbers. Consecutive numbers are numbers that come one after the other, such as 3, 4, 5. If we are looking for several consecutive numbers it is important to first identify what they look like with variables before we set up the equation.

For example, let’s say I want to know the next consecutive integer after 4. In mathematical terms, we would add 1 to 4 to get 5. We can generalize this idea as follows: the consecutive integer of any number, x , is \(x+1\). If we continue this pattern we can define any number of consecutive integers from any starting point. The following table shows how to describe four consecutive integers using algebraic notation.

We apply the idea of consecutive integers to solving a word problem in the following example.

The sum of three consecutive integers is 93. What are the integers?

[reveal-answer q=”120402″]Show Solution[/reveal-answer]

[hidden-answer a=”120402″] Following the steps provided:

• Read and understand: We are looking for three numbers, and we know they are consecutive integers.
• Constants and Variables: 93 is a constant. The first integer we will call x . Second: \(x+2\)
• Translate: The sum of three consecutive integers translates to \(=93\) because is is associated with equals.
• Write an equation: \(x+\left(x+1\right)+\left(x+2\right)=93\)

\(\begin{array}{r}x+x+1+x+2=93\\3x+3 = 93\\\underline{-3\,\,\,\,\,-3}\\3x=90\\\frac{3x}{3}=\frac{90}{3}\\x=30\end{array}\)

• Check and Interpret: Okay, we have found a value for x . We were asked to find the value of three consecutive integers, so we need to do a couple more steps. Remember how we defined our variables: The first integer we will call \(x=30\) Second: \(30+1=31\) Third: \(30+2=32\) The three consecutive integers whose sum is \(30\text{, }31\text{, and }32\)

In the following video we show another example of a consecutive integer problem.

There is often a well-known formula or relationship that applies to a word problem. For example, if you were to plan a road trip, you would want to know how long it would take you to reach your destination. \(d=rt\) is a well-known relationship that associates distance traveled, the rate at which you travel, and how long the travel takes.

Distance, Rate, and Time

If you know two of the quantities in the relationship \(30\frac{\text{ miles }}{\text{ hour }}\) for 2 hours, you can find the distance you would travel by multiplying rate times time or \(\left(30\frac{\text{ miles }}{\text{ hour }}\right)\left(2\text{ hours }\right)=60\text{ miles }\).

We can generalize this idea depending on what information we are given and what we are looking for. For example, if we need to find time, we could solve the \(d=rt\) equation for t using division:

\(d=rt\\\frac{d}{r}=t\)

Likewise, if we want to find rate, we can isolate r using division:

\(d=rt\\\frac{d}{t}=r\)

In the following examples you will see how this formula is applied to answer questions about ultra marathon running.

Ultra marathon running (defined as anything longer than 26.2 miles) is becoming very popular among women even though it remains a male-dominated niche sport. Ann Trason has broken twenty world records in her career. One such record was the American River 50-mile Endurance Run which begins in Sacramento, California, and ends in Auburn, California. [1] In 1993 Trason finished the run with a time of 6:09:08. The men’s record for the same course was set in 1994 by Tom Johnson who finished the course with a time of 5:33:21. [2]

In the next examples we will use the \(d=rt\) formula to answer the following questions about the two runners.

• What was each runner’s rate for their record-setting runs?
• By the time Johnson had finished, how many more miles did Trason have to run?

How much further could Johnson have run if he had run as long as Trason?

What was each runner’s time for running one mile?

To make answering the questions easier, we will round the two runners’ times to 6 hours and 5.5 hours.

What was each runner’s rate for their record-setting runs? [reveal-answer q=”55589″]Show Solution[/reveal-answer] [hidden-answer a=”55589″]

Read and Understand: We are looking for rate and we know distance and time, so we can use the idea: \(d=rt\\\frac{d}{t}=r\)

Define and Translate: Because there are two runners, making a table to organize this information helps. Note how we keep units to help us keep track of what how all the terms are related to each other.

Write and Solve:

Trason’s rate:

\(\begin{array}{c}d=rt\\\\50\text{ miles }=\text{r}\left(6\text{ hours }\right)\\\frac{50\text{ miles }}{6\text{ hours }}=\frac{8.33\text{ miles }}{\text{ hour }}\end{array}\).

(rounded to two decimal places)

Johnson’s rate:

\(\begin{array}{c}d=rt\\\\,\,\,\,\,\,\,50\text{ miles }=\text{r}\left(5.5\text{ hours }\right)\\\frac{50\text{ miles }}{6\text{ hours }}=\frac{9.1\text{ miles }}{\text{ hour }}\end{array}\)

Check and Interpret:

We can fill in our table with this information.

Now that we know each runner’s rate we can answer the second question.

By the time Johnson had finished, how many more miles did Trason have to run? [reveal-answer q=”747303″]Show Solution[/reveal-answer] [hidden-answer a=”747303″]

Here is the table we created for reference:

Read and Understand: We are looking for how many miles Trason still had on the trail when Johnson had finished after 5.5 hours. This is a distance, and we know rate and time.

Define and Translate: We can use the formula \(d=rt\) again. This time the unknown is d , and the time Trason had run is 5.5 hours.

\(\begin{array}{l}d=rt\\\\d=8.33\frac{\text{ miles }}{\text{ hour }}\left(5.5\text{ hours }\right)\\\\d=45.82\text{ miles }\end{array}\).

Have we answered the question? We were asked to find how many more miles she had to run after 5.5 hours. What we have found is how long she had run after 5.5 hours. We need to subtract \(d=45.82\text{ miles }\) from the total distance of the course.

\(50\text{ miles }-45.82\text{ miles }=1.48\text{ miles }\)

The third question is similar to the second. Now that we know each runner’s rate, we can answer questions about individual distances or times.

[reveal-answer q=”757303″]Show Solution[/reveal-answer] [hidden-answer a=”757303″]

Read and Understand: The word further implies we are looking for a distance.

Define and Translate: We can use the formula \(9.1\frac{\text{ miles }}{\text{ hour }}\)

\(\begin{array}{l}d=rt\\\\d=9.1\frac{\text{ miles }}{\text{ hour }}\left(6\text{ hours }\right)\\\\d=54.6\text{ miles }\end{array}\).

Have we answered the question? We were asked to find how many more miles Johnson would have run if he had run at his rate of \(9.1\frac{\text{ miles }}{\text{ hour }}\) for 6 hours.

Johnson would have run 54.6 miles, so that’s 4.6 more miles than than he ran for the race.

Now we will tackle the last question where we are asked to find a time for each runner.

[reveal-answer q=”757309″]Show Solution[/reveal-answer] [hidden-answer a=”757309″]

Read and Understand: we are looking for time, and this time our distance has changed from 50 miles to 1 mile, so we can use

Define and Translate: we can use the formula \(d=rt\) again. This time the unknown is t , the distance is 1 mile, and we know each runner’s rate. It may help to create a new table:

We will need to divide to isolate time.

\(\begin{array}{c}d=rt\\\\1\text{ mile }=8.33\frac{\text{ miles }}{\text{ hour }}\left(t\text{ hours }\right)\\\\\frac{1\text{ mile }}{\frac{8.33\text{ miles }}{\text{ hour }}}=t\text{ hours }\\\\0.12\text{ hours }=t\end{array}\).

0.12 hours is about 7.2 minutes, so Trason’s time for running one mile was about 7.2 minutes. WOW! She did that for 6 hours!

\(\begin{array}{c}d=rt\\\\1\text{ mile }=9.1\frac{\text{ miles }}{\text{ hour }}\left(t\text{ hours }\right)\\\\\frac{1\text{ mile }}{\frac{9.1\text{ miles }}{\text{ hour }}}=t\text{ hours }\\\\0.11\text{ hours }=t\end{array}\).

0.11 hours is about 6.6 minutes, so Johnson’s time for running one mile was about 6.6 minutes. WOW! He did that for 5.5 hours!

Have we answered the question? We were asked to find how long it took each runner to run one mile given the rate at which they ran the whole 50-mile course. Yes, we answered our question.

Trason’s mile time was \(6.6\frac{\text{minutes}}{\text{mile}}\)

In the following video, we show another example of answering many rate questions given distance and time.

Simple Interest

In order to entice customers to invest their money, many banks will offer interest-bearing accounts. The accounts work like this: a customer deposits a certain amount of money (called the Principal, or P ), which then grows slowly according to the interest rate ( R , measured in percent) and the length of time ( T , usually measured in months) that the money stays in the account. The amount earned over time is called the interest ( I ), which is then given to the customer.

The simplest way to calculate interest earned on an account is through the formula \(\displaystyle I=P\,\cdot \,R\,\cdot \,T\).

If we know any of the three amounts related to this equation, we can find the fourth. For example, if we want to find the time it will take to accrue a specific amount of interest, we can solve for T using division:

\(\displaystyle\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,I=P\,\cdot \,R\,\cdot \,T\\\\ \frac{I}{{P}\,\cdot \,R}=\frac{P\cdot\,R\,\cdot \,T}{\,P\,\cdot \,R}\\\\\,\,\,\,\,\,\,\,\,\,\,{T}=\frac{I}{\,R\,\cdot \,T}\end{array}\)

Below is a table showing the result of solving for each individual variable in the formula.

In the next examples, we will show how to substitute given values into the simple interest formula, and decipher which variable to solve for.

If a customer deposits a principal of $2000 at a monthly rate of 0.7%, what is the total amount that she has after 24 months?

[reveal-answer q=”57640″] Show Solution [/reveal-answer] [hidden-answer a=”57640″]

Substitute in the values given for the Principal, Rate, and Time.

\(\displaystyle\begin{array}{l}I=P\,\cdot \,R\,\cdot \,T\\I=2000\cdot 0.7\%\cdot 24\end{array}\)

Rewrite 0.7% as the decimal 0.007, then multiply.

\(\begin{array}{l}I=2000\cdot 0.007\cdot 24\\I=336\end{array}\)

Add the interest and the original principal amount to get the total amount in her account.

\(\displaystyle 2000+336=2336\)

She has $2336 after 24 months.[/hidden-answer]

The following video shows another example of finding an account balance after a given amount of time, principal invested, and a rate.

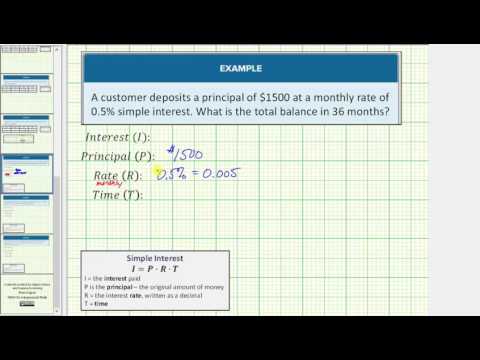
In the following example you will see why it is important to make sure the units of the interest rate match the units of time when using the simple interest formula.

Alex invests $600 at 3.25% monthly interest for 3 years. What amount of interest has Alex earned?

[reveal-answer q=”97640″]Show Solution[/reveal-answer] [hidden-answer a=”97640″]

Read and Understand: The question asks for an amount, so we can substitute what we are given into the simple interest formula \(I=P\,\cdot \,R\,\cdot \,T\)

Define and Translate: we know P, R, and T so we can use substitution. R = 0.0325, P = $600, and T = 3 years. We have to be careful! R is in months, and T is in years. We need to change T into months because we can’t change the rate—it is set by the bank.

\({T}=3\text{ years }\cdot12\frac{\text{ months }}{ year }=36\text{ months }\)

Substitute the given values into the formula.

\(\begin{array}{l} I=P\,\cdot \,R\,\cdot \,T\\\\I=600\,\cdot \,0.035\,\cdot \,36\\\\{I}=756\end{array}\)

We were asked what amount Alex earned, which is the amount provided by the formula. In the previous example we were asked the total amount in the account, which included the principal and interest earned.

Alex has earned $756.

In the following video we show another example of how to find the amount of interest earned after an investment has been sitting for a given monthly interest.

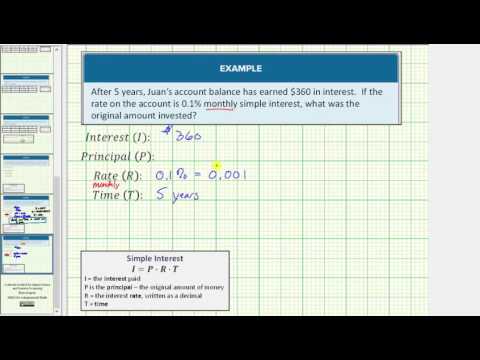
After 10 years, Jodi’s account balance has earned $1080 in interest. The rate on the account is 0.09% monthly. What was the original amount she invested in the account?

[reveal-answer q=”97641″]Show Solution[/reveal-answer] [hidden-answer a=”97641″]

Read and Understand: The question asks for the original amount invested, the principal. We are given a length of time in years, and an interest rate in months, and the amount of interest earned.

Define and Translate: we know I = $1080, R = 0.009, and T = 10 years so we can use \({P}=\frac{I}{{R}\,\cdot \,T}\)

We also need to make sure the units on the interest rate and the length of time match, and they do not. We need to change time into months again.

\({T}=10\text{ years }\cdot12\frac{\text{ months }}{ year }=120\text{ months }\)

Substitute the given values into the formula

\(\begin{array}{l}{P}=\frac{I}{{R}\,\cdot \,T}\\\\{P}=\frac{1080}{{0.009}\,\cdot \,120}\\\\{P}=\frac{1080}{1.08}=1000\end{array}\)

We were asked to find the principal given the amount of interest earned on an account. If we substitute P = $1000 into the formula \(I=P\,\cdot \,R\,\cdot \,T\) we get

\(I=1000\,\cdot \,0.009\,\cdot \,120\\I=1080\)

Our solution checks out. Jodi invested $1000.

The last video shows another example of finding the principle amount invested based on simple interest.

In the next section we will apply our problem-solving method to problems involving dimensions of geometric shapes.

Further Applications of Linear Equations

Formulas come up in many different areas of life. We have seen the formula that relates distance, rate, and time and the formula for simple interest on an investment. In this section we will look further at formulas and see examples of formulas for dimensions of geometric shapes as well as the formula for converting temperature between Fahrenheit and Celsius.

There are many geometric shapes that have been well studied over the years. We know quite a bit about circles, rectangles, and triangles. Mathematicians have proven many formulas that describe the dimensions of geometric shapes including area, perimeter, surface area, and volume.

Perimeter is the distance around an object. For example, consider a rectangle with a length of 8 and a width of 3. There are two lengths and two widths in a rectangle (opposite sides), so we add \({P}=2\left({L}\right)+2\left({W}\right)\) where

In the following example, we will use the problem-solving method we developed to find an unknown width using the formula for the perimeter of a rectangle. By substituting the dimensions we know into the formula, we will be able to isolate the unknown width and find our solution.

You want to make another garden box the same size as the one you already have. You write down the dimensions of the box and go to the lumber store to buy some boards. When you get there you realize you didn’t write down the width dimension—only the perimeter and length. You want the exact dimensions so you can have the store cut the lumber for you.

Here is what you have written down:

Perimeter = 16.4 feet Length = 4.7 feet

Can you find the dimensions you need to have your boards cut at the lumber store? If so, how many boards do you need and what lengths should they be?

[reveal-answer q=”719712″]Show Solution[/reveal-answer] [hidden-answer a=”719712″]

Read and Understand: We know perimeter = 16.4 feet and length = 4.7 feet, and we want to find width.

Define and Translate:

Define the known and unknown dimensions:

First we will substitute the dimensions we know into the formula for perimeter:

\(\begin{array}{l}\,\,\,\,\,P=2{W}+2{L}\\\\16.4=2\left(w\right)+2\left(4.7\right)\end{array}\)

Then we will isolate w to find the unknown width.

\(\begin{array}{l}16.4=2\left(w\right)+2\left(4.7\right)\\16.4=2{w}+9.4\\\underline{-9.4\,\,\,\,\,\,\,\,\,\,\,\,\,-9.4}\\\,\,\,\,\,\,\,7=2\left(w\right)\\\,\,\,\,\,\,\,\frac{7}{2}=\frac{2\left(w\right)}{2}\\\,\,\,\,3.5=w\end{array}\)

Write the width as a decimal to make cutting the boards easier and replace the units on the measurement, or you won’t get the right size of board!

If we replace the width we found, \(w=3.5\text{ feet }\) into the formula for perimeter with the dimensions we wrote down, we can check our work:

\(\begin{array}{l}\,\,\,\,\,{P}=2\left({L}\right)+2\left({W}\right)\\\\{16.4}=2\left({4.7}\right)+2\left({3.5}\right)\\\\{16.4}=9.4+7\\\\{16.4}=16.4\end{array}\)

Our calculation for width checks out. We need to ask for 2 boards cut to 3.5 feet and 2 boards cut to 4.7 feet so we can make the new garden box.

This video shows a similar garden box problem.

We could have isolated the w in the formula for perimeter before we solved the equation, and if we were going to use the formula many times, it could save a lot of time. The next example shows how to isolate a variable in a formula before substituting known dimensions or values into the formula.

Isolate the term containing the variable, w, from the formula for the perimeter of a rectangle :

\({P}=2\left({L}\right)+2\left({W}\right)\).

[reveal-answer q=”967601″]Show Solution[/reveal-answer] [hidden-answer a=”967601″]

First, isolate the term with w by subtracting 2 l from both sides of the equation.

\(\displaystyle \begin{array}{l}\,\,\,\,\,\,\,\,\,\,p\,=\,\,\,\,2l+2w\\\underline{\,\,\,\,\,-2l\,\,\,\,\,-2l\,\,\,\,\,\,\,\,\,\,\,}\\p-2l=\,\,\,\,\,\,\,\,\,\,\,\,\,2w\end{array}\)

Next, clear the coefficient of w by dividing both sides of the equation by 2.

\(\displaystyle \begin{array}{l}\underline{p-2l}=\underline{2w}\\\,\,\,\,\,\,2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2\\ \,\,\,\frac{p-2l}{2}\,\,=\,\,w\\\,\,\,\,\,\,\,\,\,\,\,w=\frac{p-2l}{2}\end{array}\)

You can rewrite the equation so the isolated variable is on the left side.

\(w=\frac{p-2l}{2}\)

The area of a triangle is given by \(A=\frac{1}{2}bh\) where

A = area b = the length of the base h = the height of the triangle

Remember that when two variables or a number and a variable are sitting next to each other without a mathematical operator between them, you can assume they are being multiplied. This can seem frustrating, but you can think of it like mathematical slang. Over the years, people who use math frequently have just made that shortcut enough that it has been adopted as convention.

In the next example we will use the formula for area of a triangle to find a missing dimension, as well as use substitution to solve for the base of a triangle given the area and height.

Find the base ( b) of a triangle with an area ( A ) of 20 square feet and a height ( h) of 8 feet. [reveal-answer q=”698967″]Show Solution[/reveal-answer] [hidden-answer a=”698967″]

Use the formula for the area of a triangle, \({A}=\frac12{bh}\) .

Substitute the given lengths into the formula and solve for b.

\(\displaystyle \begin{array}{l}\,\,A=\frac{1}{2}bh\\\\20=\frac{1}{2}b\cdot 8\\\\20=\frac{8}{2}b\\\\20=4b\\\\\frac{20}{4}=\frac{4b}{4}\\\\ \,\,\,5=b\end{array}\)

The base of the triangle measures 5 feet.[/hidden-answer]

We can rewrite the formula in terms of b or h as we did with perimeter previously. This probably seems abstract, but it can help you develop your equation-solving skills, as well as help you get more comfortable with working with all kinds of variables, not just x .

Use the multiplication and division properties of equality to isolate the variable b .

[reveal-answer q=”291790″]Show Solution[/reveal-answer] [hidden-answer a=”291790″]

\(\begin{array}{l}\,\,\,\,\,\,\,\,A=\frac{1}{2}bh\\\\\left(2\right)A=\left(2\right)\frac{1}{2}bh\\\\\,\,\,\,\,\,2A=bh\\\\\,\,\,\,\,\,\,\frac{2A}{h}=\frac{bh}{h}\\\\\,\,\,\,\,\,\,\,\frac{2A}{h}=\frac{b\cancel{h}}{\cancel{h}}\end{array}\)

Write the equation with the desired variable on the left-hand side as a matter of convention:

\(b=\frac{2A}{h}\) [/hidden-answer]

Use the multiplication and division properties of equality to isolate the variable h . [reveal-answer q=”595790″]Show Solution[/reveal-answer] [hidden-answer a=”595790″]

\(\begin{array}{l}\,\,\,\,\,\,\,\,A=\frac{1}{2}bh\\\\\left(2\right)A=\left(2\right)\frac{1}{2}bh\\\\\,\,\,\,\,\,2A=bh\\\\\,\,\,\,\,\,\,\frac{2A}{b}=\frac{bh}{b}\\\\\,\,\,\,\,\,\,\,\frac{2A}{b}=\frac{h\cancel{b}}{\cancel{b}}\end{array}\)

\(h=\frac{2A}{b}\) [/hidden-answer]

The following video shows another example of finding the base of a triangle given area and height.

Temperature

Let’s look at another formula that includes parentheses and fractions, the formula for converting from the Fahrenheit temperature scale to the Celsius scale.

\(C=\left(F--32\right)\cdot \frac{5}{9}\)

Given a temperature of \({}^{\circ}{F}\). [reveal-answer q=”594254″]Show Solution[/reveal-answer] [hidden-answer a=”594254″]

Substitute the given temperature in\({}^{\circ}{C}\) into the conversion formula:

\(12=\left(F-32\right)\cdot \frac{5}{9}\)

Isolate the variable F to obtain the equivalent temperature.

\(\begin{array}{r}12=\left(F-32\right)\cdot \frac{5}{9}\\\\\left(\frac{9}{5}\right)12=F-32\,\,\,\,\,\,\,\,\,\,\,\,\,\\\\\left(\frac{108}{5}\right)12=F-32\,\,\,\,\,\,\,\,\,\,\,\,\,\\\\21.6=F-32\,\,\,\,\,\,\,\,\,\,\,\,\,\\\underline{+32\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+32}\,\,\,\,\,\,\,\,\,\,\,\,\\\\53.6={}^{\circ}{F}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}\)

As with the other formulas we have worked with, we could have isolated the variable F first, then substituted in the given temperature in Celsius.

Solve the formula shown below for converting from the Fahrenheit scale to the Celsius scale for F.

[reveal-answer q=”591790″]Show Solution[/reveal-answer] [hidden-answer a=”591790″]

To isolate the variable F, it would be best to clear the fraction involving F first. Multiply both sides of the equation by \(\displaystyle \frac{9}{5}\).

\(\begin{array}{l}\\\,\,\,\,\left(\frac{9}{5}\right)C=\left(F-32\right)\left(\frac{5}{9}\right)\left(\frac{9}{5}\right)\\\\\,\,\,\,\,\,\,\,\,\,\,\,\frac{9}{5}C=F-32\end{array}\)

Add 32 to both sides.

\(\begin{array}{l}\frac{9}{5}\,C+32=F-32+32\\\\\frac{9}{5}\,C+32=F\end{array}\)

\(F=\frac{9}{5}C+32\)[/hidden-answer]

Think About It

Express the formula for the surface area of a cylinder, \(s=2\pi rh+2\pi r^{2}\), in terms of the height, h .

In this example, the variable h is buried pretty deeply in the formula for surface area of a cylinder. Using the order of operations, it can be isolated. Before you look at the solution, use the box below to write down what you think is the best first step to take to isolate h .

[practice-area rows=”1″][/practice-area] [reveal-answer q=”194805″]Show Solution[/reveal-answer] [hidden-answer a=”194805″] Isolate the term containing the variable, h , by subtracting \(2\pi r^{2}\)from both sides.

\(\begin{array}{r}S\,\,=2\pi rh+2\pi r^{2} \\ \underline{-2\pi r^{2}\,\,\,\,\,\,\,\,\,\,\,\,\,-2\pi r^{2}}\\S-2\pi r^{2}\,\,\,\,=\,\,\,\,2\pi rh\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}\)

Next, isolate the variable h by dividing both sides of the equation by \(2\pi r\).

\(\begin{array}{r}\frac{S-2\pi r^{2}}{2\pi r}=\frac{2\pi rh}{2\pi r} \\\\ \frac{S-2\pi r^{2}}{2\pi r}=h\,\,\,\,\,\,\,\,\,\,\end{array}\)

\(h=\frac{S-2\pi r^{2}}{2\pi r}\)[/hidden-answer]

In the last video, we show how to convert from celsius to fahrenheit.

• "Ann Trason." Wikipedia. Accessed May 05, 2016. https://en.Wikipedia.org/wiki/Ann_Trason . ↵
• "American River 50 Mile Endurance Run." Wikipedia. Accessed May 05, 2016. https://en.Wikipedia.org/wiki/American_River_50_Mile_Endurance_Run . ↵
• Writing Algebraic Expressions. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/uD_V5t-6Kzs . License : CC BY: Attribution
• Write and Solve a Linear Equations to Solve a Number Problem (1). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/izIIqOztUyI . License : CC BY: Attribution
• Write and Solve a Linear Equations to Solve a Number Problem (Consecutive Integers). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/S5HZy3jKodg . License : CC BY: Attribution
• Screenshot: Ann Trason Trail Running. Authored by : Lumen Learning. License : CC BY: Attribution
• Problem Solving Using Distance, Rate, Time (Running). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/3WLp5mY1FhU . License : CC BY: Attribution
• Simple Interest - Determine Account Balance (Monthly Interest). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/XkGgEEMR_00 . License : CC BY: Attribution
• Simple Interest - Determine Interest Balance (Monthly Interest). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/mRV5ljj32Rg . License : CC BY: Attribution
• Simple Interest - Determine Principal Balance (Monthly Interest). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/vbMqN6lVoOM . License : CC BY: Attribution
• Find the Width of a Rectangle Given the Perimeter / Literal Equation. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/jlxPgKQfhQs . License : CC BY: Attribution
• Find the Base of a Triangle Given Area / Literal Equation. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/VQZQvJ3rXYg . License : CC BY: Attribution
• Convert Celsius to Fahrenheit / Literal Equation. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/DRydX8V-JwY . License : CC BY: Attribution
• Ann Trason. Provided by : Wikipedia. Located at : https://en.Wikipedia.org/wiki/Ann_Trason . License : CC BY-SA: Attribution-ShareAlike
• American River 50 Mile Endurance Run. Provided by : Wikipedia. Located at : https://en.Wikipedia.org/wiki/American_River_50_Mile_Endurance_Run . License : CC BY-SA: Attribution-ShareAlike