reasoning and problem solving maths

Is mathematical reasoning important to study?

Table of Contents

January 18, 2021

Reading Time: 9 minutes

Introduction

The purpose of mathematics is not just to earn grades. Students who wish to aim high in life need to figure out their purpose. Broadly speaking, Mathematics is implemented in every sphere of life. Nowadays, organizations require measurable input and output for performance assessment, and career outcomes are not based on qualitative or verbal feedback.

Students need to gear up and prepare for a future that will depend solely on mathematics. The evolution of newer technologies like data science will bring a renewed emphasis on Mathematics.   

Mathematical reasoning, on the other hand, helps individuals build mathematical critical thinking and logical reasoning. A lack of mathematical reasoning skills may reflect not just in mathematics performance but also in Physics, Chemistry, or Economics.

In the subsequent sections, we will try to understand What is Mathematical reasoning and what are the basic terms used in mathematical reasoning. We will also have a look at different types of mathematical reasoning and go through mathematical reasoning questions and answers.

Later in the article, we will look at a few Frequently Asked Questions with solutions to solidify the idea behind learning mathematical reasoning.

• The importance of developing mathematical thinking in children
• Logical Reasoning: Topics, Examples, Syllabus, Questions
• Slow Learners

Here is a downloadable PDF. After downloading, you will be able to read 'Mathematical Reasoning’ offline at your convenience and as many times as you want. Click on the download button to explore them.

What is Mathematical Reasoning?

Mathematical reasoning is a critical skill that enables students to analyze a given hypothesis without any reference to a particular context or meaning. In layman's words, when a scientific inquiry or statement is examined, the reasoning is not based on an individual's opinion. Derivations and proofs require a factual and scientific basis. 

Mathematical critical thinking and logical reasoning are important skills that are required to solve maths reasoning questions. 

When we learn literature, we follow certain rules of grammar. Likewise, there are certain rules and parts of a scientific hypothesis. It is important to note that most books and texts written on mathematical reasoning follow scientific grammar or relevant terminologies and notations.

What are the basic terms used in Mathematical Reasoning?

In this section, the basic terminologies associated with Mathematical reasoning are discussed.

Any sentence in mathematics which follows the following rules is a statement.

A sentence needs to be either true or false but not both to be considered a mathematically accepted statement.

Any sentence which is either imperative or interrogative or exclamatory cannot be considered a mathematically validated statement. 

A Sentence containing one or many variables is termed an open statement. An open statement can become a statement if the variables present in the sentence are replaced by definite values

Example: The distance from the center of a circle to any point on the circumference of the circle is equal. 

Conjunction and Disjunction

Whenever statements are joined to make a new statement and all the conditions need to be fulfilled, it is a Conjunction. ‘And’, ‘with’ are commonly used to join such statements.

Whenever statements are joined to make a new statement and only one of the conditions needs to be fulfilled, it is a Disjunction. ‘Or’, ‘But’ are commonly used to join such statements.

The conjunction is true only if the original statements are found to be true. The conjunction is false if the original statement or statements are found to be false.

The conjunction is true if only one statement is found to be true. The conjunction is false if none of the original statements are found to be true.

Example: Square is a polygon and a parallelogram can also be a square.

These are a few mathematical terminologies that will help you comprehend and apply mathematical reasoning. These terms will also help you solve and understand reasoning questions.

What are the types of mathematical reasoning?

Inductive reasoning.

Inductive reasoning is based on observations and not any hypothesis. If any phenomena are observed for n number of times, it can be generalized. This generalization is based on observation and therefore it may be false. Inductive reasoning is a logical guess which can be backed up by using valid reasons.

This type of reasoning is not used in geometry, for instance, one may observe a few right triangles and conclude all triangles to be right triangles. Therefore, other mathematical tools are used to prove geometrical results. An example of inductive reasoning will help elucidate the concept.

Example of Inductive Reasoning:

Statement:  I picked a ball from the bag and it happens to be a red ball. I picked a second red ball. A third ball from the bag is also red. Therefore, all the balls in the bag are red.

Reasoning : All the balls picked up from the bag are red. Therefore, we can say all the balls are red. This is an example of inductive reasoning where existing data is analyzed to come to a general conclusion.

Deductive Reasoning

Deductive reasoning is based on the exact opposite principles of induction. Unlike Inductive reasoning, Deductive reasoning is not based on simple generalizations. A Hypothesis is required or a statement that has to be true under specified conditions for deductive reasoning to be valid. In the case of Inductive reasoning, the conclusion may be false but Deductive reasoning is true in all cases.

Therefore, Deductive reading is used for geometrical and mathematical proofs. The following example will simplify the concepts discussed in this section.

Example of Deductive Reasoning:

Statement:  The sum of angles in a triangle is always equal to 180° and ABC is a Triangle.

Reasoning:  Here in the given statement we are considering two hypotheses, where the sum of angles in a triangle is said to be 180° and ABC is a triangle. Based on the given hypotheses we deduce that the sum of angles of ABC is 180°.

Abductive Reasoning

Abductive reasoning is a modified version of Inductive Reasoning and takes a more practical approach. In the case of inductive reasoning, the data or observation is complete but in real situations, most of the data is not available at the time of making a decision.

So based on the data and its availability, the conclusion may vary and reasoning may change.   

Example of Abductive Reasoning:

Statement: The heights of four students studying in a class were found to be 160cm, 162cm, 163 cm, 167 cm respectively. The measuring scale available had the least count of 1cm. 

Reasoning : As per the data and hypotheses available at the time of observation, the average height comes out to be 163cm. But once a new measuring scale was installed the least count was found to be 0.1 cm and the recorded height of students changed. This also impacted the Average height which came to be 63.8 cm. 

As discussed in this section, reasoning techniques are categorized in three major sections. An understanding of Inductive, Abductive and Deductive reasoning will help you solve any reasoning question. It is important to identify the reasoning technique which has to be used to solve a question from examination point of view. 

What are the types of reasoning statements?

Reasoning statements in mathematics are broadly classified into three types:

Simple Statements

Compound Statements

If-Then Statements

We will look into each type of reasoning statement along with their examples.

If the truth value of a statement or proposition does not directly depend on another statement, it is a simple statement. In other words, a simple statement should not be composed of simpler statements.

Therefore a simple statement can never be broken down into simpler statements. It is easiest to work with simple statements and direct reasoning approach can be implemented. A few examples have been provided to clear the concept of simple statements. 

Example 1: Square is a parallelogram.   

Reasoning: There are no modifiers in the given statement. Therefore we can say that the given statement is simple. 

Compound Statement

In simple words, the combination of simple statements is a compound statement. Therefore, such statements are made of either two or more simple statements joined together by connectives like 'and', 'or'.

A variety of connectives can be used instead of the two connectives as mentioned. These statements are crucial for Deduction reasoning in Mathematics. Have a look at the detailed example below for a better understanding:

Example 1: We have taken two simple statements that can be joined together by the use of a connector.

Statement 1:  Parallel lines do not intersect.

Statement 2: Transversal lines make equal alternate angles with parallel lines

Compound Statement:  Parallel lines do not intersect and Transversal lines make equal alternate angles with parallel lines.

Example 2: In this example, a compound statement is being dissected into its simple statement components. 

Compound Statement:  Triangle has three sides and the square has four sides.

The Simple Statements for this statement is:

Statement 1:  Triangle has three sides.

Statement 2:  The square has four sides. 

If-then Statement

Conditional statements where a hypothesis is followed by a conclusion are known as the If-then statement. If the hypothesis is true and the conclusion is false then the conditional statement is false. Likewise, if the hypothesis is false the whole statement is false.

Example 1: If 40% population is female then 60% population is male.

Reasoning: Here the 40% female is the hypothesis and if that condition is met then the conclusion is satisfying.

Sample Mathematical Reasoning Questions With Answers

Now that we have an understanding of Mathematical Reasoning and the various terminologies and reasoning associated, we will go through two sample questions with an explanation to understand maths and reasoning in depth.

Q1. Look at this series: 12, 10, 13, 11, 14, 12, … What number should come next?

A. 15 B. 16 C. 13 D. 10

Answer: Option D.

Explanation: First, 2 is subtracted, then 3 is added therefore when 3 is added to 12 it becomes 15. This is an example of an alternating number of subtraction series.

Q2. SQUARE:PERIMETER::CIRCLE :?

A.RADIUS B. CHORD C. SECTOR D. CIRCUMFERENCE

Answer: D.CIRCUMFERENCE. 

Explanation:  The boundary of a square is given by its perimeter just as the boundary of a circle is given by circumference.

Most kids study mathematics for the sake of grades. That will improve grades temporarily but cause great damage in the longer run. Kids need to ask questions to understand how a particular concept is being used. If children do not understand the concepts in their initial days, they will struggle at a later stage.

Practice Proofs

Proofs will help Children Ideate their own set of techniques to understand complex problems. Students need to focus on Geometry Proofs, results, and maths reasoning questions.

Cuemath Activities

Some kids do need additional support and tools. Sometimes kids underperform in mathematics due to stress and fear of bad grades. Such kids are unable to ask questions in class and eventually start lagging. Cuemath provides a customized learning journey for such kids.

The most basic concepts are cleared and corrected. Individual attention by professional Mathematics Teachers helps them cope better. Once a child gains confidence, mathematics is a cakewalk. 

Begin teaching mathematical reasoning at an early age to avoid struggling with it at a later stage. Children need to understand the principles of mathematics rather than mugging up proofs and theorems.

This will help them solve higher-order problems and develop mathematical aptitude. Over time you will find your child solving complex problems on their own without much intervention or assistance. 

About Cuemath

Cuemath, a student-friendly mathematics and coding platform, conducts regular  Online Classes  for academics and skill-development, and their Mental Math App, on both  iOS  and  Android , is a one-stop solution for kids to develop multiple skills. Understand the Cuemath fee structure and sign up for a free trial.

Frequently asked questions (FAQs)

What is a fallacy in mathematical reasoning.

Fallacy refers to errors in hypotheses caused due to logical inaccuracy.

Why is mathematical reasoning important?

Students have the potential to solve higher-order thinking questions which are frequently asked in competitive examinations. But a lack of mathematical reasoning skills may render their potential. Encouragement is needed to develop a student's natural inclination to strive for purpose and meaning.

The reasoning is the most fundamental and essential tool of mathematics. It helps one understand and justify mathematical theorems. A good grip in reasoning will help students apply the concepts they learn in the classroom. 

What are the two types of fallacy?

The two types of fallacies are as follows:

Formal fallacy: When the relationship between premises and conclusion is not valid or when premises are unsound, Formal fallacies are created.

Informal Fallacy: Misuse of language and evidence is classified as an Informal fallacy.

Mathematical Fundamentals

Learn the essential tools for mastering algebra, logic, and number theory.

Algebra was never meant to be memorized. Learn a new way to see.

Rewrite, Rethink, Redraw

Explore fractal patterns and compound interest in the mathematics of fractions.

Thinking Forwards and Backwards

To solve new problems, you need to be able to think in several directions.

End of Unit 1

Complete all lessons above to reach this milestone.

0 of 3 lessons complete

Reasoning from Results to Cause

You can't trust everything you hear, but you'll always have logic.

Werewolves of London

Werewolves are predictably treacherous creatures. But they make for great puzzles.

Eliminating the Impossible

Once you eliminate the impossible, whatever remains must be the truth.

A Treasure Hunt

The real treasures are the truths we find along the way.

Mad Hatter Puzzles

You'll need to keep track of what other people might think you are thinking.

Repairing Broken Puzzles

These puzzles can't be solved — until you fix them.

End of Unit 2

0 of 6 lessons complete

Strategic Arithmetic

Learn to sum 100 numbers at a glance with this one simple trick.

Dissecting Numbers

See the composition of numbers in a brand new light.

Divisible by 3

Dividing numbers in clever ways is the first step towards number theory.

Building Numbers to Spec

Bring your divisibility rules, because not just any numbers will do.

Numerical Logic

Learn how to track down all the information you'll need from a problem.

End of Unit 3

0 of 5 lessons complete

Compare the Pair

Find the best deals in town by breaking down these problems.

Understanding Fractions

A high-stakes Segway race puts you on the fast lane to comparing rates and ratios.

Probability

The Lumps has hit Flatland. Can you use probabilities to separate fact from fiction?

Compound Interest

Questionable business practices and multiplying fractions greater than one are quick ways to get exponential growth.

End of Unit 4

0 of 4 lessons complete

Magical Variables

Writing down equations is often the easiest way to organize information and solve problems.

Reverse Engineering Arithmetic

Find the patterns and you'll be able to solve these problems.

Sums and Symmetry

Algebra is all about maintaining symmetry and balance.

How Much Altogether?

Mix, match, and compare unknown values – then put them to work.

Cryptogram Challenges

These problems are tough, but you have all the skills you'll need.

End of Unit 5

Pythagoras' Theorem

A visual proof of the most famous theorem in all of mathematics.

• The Distributive Property

If you replace algebra with geometry, you'll never need to factor again.

Difference of Squares

This isn't how you learned this identity at school.

Difference of Squares Challenges

Put all your learnings to the test.

The Quadratic Formula

Use visual intuition and algebra to solve every quadratic ever.

End of Unit 6

Course description.

In this course, we'll introduce the foundational ideas of algebra, number theory, and logic that come up in nearly every topic across STEM. This course is ideal for anyone who's either starting or re-starting their math education. You'll learn many essential problem solving techniques and you'll need to think creatively and strategically to solve each challenge. Each exploration is designed to push your mathematical skills to the next level. Math isn't about memorizing formulas, it's about problem solving. It's about looking at patterns and predicting the future of those patterns, and it's about solving complex problems by using deductive reasoning to turn them into simple ones.

Topics covered

• Algebraic Expressions
• Arithmetic Operators
• Cryptogram Puzzles
• Discount Finance
• Divisibility
• Divisibility Rules
• Logic Fundamentals
• Rates and Ratios

Prerequisites and next steps

This course is for anyone who remembers middle school math (basic algebra and fractions), and is ready for a refresher and new challenges on core mathematical concepts.

• Computer Science Fundamentals

Reasoning Skills

Developing opportunities and ensuring progression in the development of reasoning skills

Achieving the aims of the new National Curriculum:

Developing opportunities and ensuring progression in the development of reasoning skills.

The aims of the National Curriculum are to develop fluency and the ability to reason mathematically and solve problems. Reasoning is not only important in its own right but impacts on the other two aims. Reasoning about what is already known in order to work out what is unknown will improve fluency; for example if I know what 12 × 12 is, I can apply reasoning to work out 12 × 13. The ability to reason also supports the application of mathematics and an ability to solve problems set in unfamiliar contexts.

Research by Nunes (2009) identified the ability to reason mathematically as the most important factor in a pupil’s success in mathematics. It is therefore crucial that opportunities to develop mathematical reasoning skills are integrated fully into the curriculum. Such skills support deep and sustainable learning and enable pupils to make connections in mathematics.

This resource is designed to highlight opportunities and strategies that develop aspects of reasoning throughout the National Curriculum programmes of study. The intention is to offer suggestions of how to enable pupils to become more proficient at reasoning throughout all of their mathematics learning rather than just at the end of a particular unit or topic.

We take the Progression Map for each of the National Curriculum topics, and augment it with a variety of reasoning activities (shaded sections) underneath the relevant programme of study statements for each year group. The overall aim is to support progression in reasoning skills. The activities also offer the opportunity for children to demonstrate depth of understanding, and you might choose to use them for assessment purposes as well as regular classroom activities.

Place Value Reasoning

Addition and subtraction reasoning, multiplication and division reasoning, fractions reasoning, ratio and proportion reasoning, measurement reasoning, geometry - properties of shapes reasoning, geometry - position direction and movement reasoning, statistics reasoning, algebra reasoning.

The strategies embedded in the activities are easily adaptable and can be integrated into your classroom routines. They have been gathered from a range of sources including real lessons, past questions, children’s work and other classroom practice.

Strategies include:

• Spot the mistake / Which is correct?
• True or false?
• What comes next?
• Do, then explain
• Make up an example / Write more statements / Create a question / Another and another
• Possible answers / Other possibilities
• What do you notice?
• Continue the pattern
• Missing numbers / Missing symbols / Missing information/Connected calculations
• Working backwards / Use the inverse / Undoing / Unpicking
• Hard and easy questions
• What else do you know? / Use a fact
• Fact families
• Convince me / Prove it / Generalising / Explain thinking
• Make an estimate / Size of an answer
• Always, sometimes, never
• Making links / Application
• Can you find?
• What’s the same, what’s different?
• Odd one out
• Complete the pattern / Continue the pattern
• Another and another
• Testing conditions
• The answer is…
• Visualising

These strategies are a very powerful way of developing pupils’ reasoning skills and can be used flexibly. Many are transferable to different areas of mathematics and can be differentiated through the choice of different numbers and examples.

Nunes, T. (2009) Development of maths capabilities and confidence in primary school, Research Report DCSF-RR118 (PDF)

Is there anything wrong with this page?

Subscribe to our newsletter

The resources on this page will hopefully help you teach AO2 and AO3 of the new GCSE specification - problem solving and reasoning.

This brief lesson is designed to lead students into thinking about how to solve mathematical problems. It features ideas of strategies to use, clear steps to follow and plenty of opportunities for discussion.

The PixiMaths problem solving booklets are aimed at "crossover" marks (questions that will be on both higher and foundation) so will be accessed by most students. The booklets are collated Edexcel exam questions; you may well recognise them from elsewhere. Each booklet has 70 marks worth of questions and will probably last two lessons, including time to go through answers with your students. There is one for each area of the new GCSE specification and they are designed to complement the PixiMaths year 11 SOL.

These problem solving starter packs are great to support students with problem solving skills. I've used them this year for two out of four lessons each week, then used Numeracy Ninjas as starters for the other two lessons.  When I first introduced the booklets, I encouraged my students to use scaffolds like those mentioned here , then gradually weaned them off the scaffolds. I give students some time to work independently, then time to discuss with their peers, then we go through it as a class. The levels correspond very roughly to the new GCSE grades.

Some of my favourite websites have plenty of other excellent resources to support you and your students in these assessment objectives.

@TessMaths has written some great stuff for BBC Bitesize.

There are some intersting though-provoking problems at Open Middle.

I'm sure you've seen it before, but if not, check it out now! Nrich is where it's at if your want to provide enrichment and problem solving in your lessons.

MathsBot  by @StudyMaths has everything, and if you scroll to the bottom of the homepage you'll find puzzles and problem solving too.

I may be a little biased because I love Edexcel, but these question packs are really useful.

The UKMT has a mentoring scheme that provides fantastic problem solving resources , all complete with answers.

I have only recently been shown Maths Problem Solving and it is awesome - there are links to problem solving resources for all areas of maths, as well as plenty of general problem solving too. Definitely worth exploring!

• Mathematics proficiencies

Introduction

The Australian Curriculum: Mathematics aims to be relevant and applicable to the 21st century. The inclusion of the proficiencies of understanding, fluency, problem-solving and reasoning in the curriculum is to ensure that student learning and student independence are at the centre of the curriculum. The curriculum focuses on developing increasingly sophisticated and refined mathematical understanding, fluency, reasoning, and problem-solving skills. These proficiencies enable students to respond to familiar and unfamiliar situations by employing mathematical strategies to make informed decisions and solve problems efficiently.

The proficiency strands describe the actions in which students can engage when learning and using the content of the Australian Curriculum: Mathematics.

Understanding

Students build a robust knowledge of adaptable and transferable mathematical concepts. They make connections between related concepts and progressively apply the familiar to develop new ideas. They develop an understanding of the relationship between the ‘why’ and the ‘how’ of mathematics. Students build understanding when they connect related ideas, when they represent concepts in different ways, when they identify commonalities and differences between aspects of content, when they describe their thinking mathematically and when they interpret mathematical information

Students develop skills in choosing appropriate procedures; carrying out procedures flexibly, accurately, efficiently and appropriately; and recalling factual knowledge and concepts readily. Students are fluent when they calculate answers efficiently, when they recognise robust ways of answering questions, when they choose appropriate methods and approximations, when they recall definitions and regularly use facts, and when they can manipulate expressions and equations to find solutions.

Problem-Solving

Students develop the ability to make choices, interpret, formulate, model and investigate problem situations, and communicate solutions effectively. Students formulate and solve problems when they use mathematics to represent unfamiliar or meaningful situations, when they design investigations and plan their approaches, when they apply their existing strategies to seek solutions, and when they verify that their answers are reasonable.

Students develop an increasingly sophisticated capacity for logical thought and actions, such as analysing, proving, evaluating, explaining, inferring, justifying and generalising. Students are reasoning mathematically when they explain their thinking, when they deduce and justify strategies used and conclusions reached, when they adapt the known to the unknown, when they transfer learning from one context to another, when they prove that something is true or false, and when they compare and contrast related ideas and explain their choices.

Useful Links

• Australian Curriculum: Mathematics F–10
• Review by Kaye Stacey of 'Adding it up: helping children learn mathematics' report
• Peter Sullivan presentation: Designing learning experiences to exemplify the proficiencies
• Peter Sullivan presentation: Create your own lessons
• Peter Sullivan paper: Using the proficiencies to enrich mathematics teaching and assessment

Explore Mathematics proficiencies portfolios and illustrations

• Future Students
• Current Students
• Faculty/Staff

News and Media

• News & Media Home
• Research Stories
• School's In
• In the Media

You are here

Softening the sharp edges in mathematics.

For everyone whose relationship with mathematics is distant or broken, Jo Boaler , a professor at Stanford Graduate School of Education (GSE), has ideas for repairing it. She particularly wants young people to feel comfortable with numbers from the start — to approach the subject with playfulness and curiosity, not anxiety or dread.

“Most people have only ever experienced what I call narrow mathematics — a set of procedures they need to follow, at speed,” Boaler says. “Mathematics should be flexible, conceptual, a place where we play with ideas and make connections. If we open it up and invite more creativity, more diverse thinking, we can completely transform the experience.”

“Mathematics should be flexible, conceptual, a place where we play with ideas and make connections," says Professor Jo Boaler. (Photo: Robert Houser Photography)

Boaler, the Nomellini and Olivier Professor of Education at the GSE, is the co-founder and faculty director of Youcubed , a Stanford research center that provides resources for math learning that has reached more than 230 million students in over 140 countries. In 2013 Boaler, a former high school math teacher, produced “How to Learn Math,” the first massive open online course (MOOC) on mathematics education. She leads workshops and leadership summits for teachers and administrators, and her online courses have been taken by over a million users. 

In her new book, Math-ish: Finding Creativity, Diversity, and Meaning in Mathematics , Boaler argues for a broad, inclusive approach to math education, offering strategies and activities for learners at any age. We spoke with her about why creativity is an important part of mathematics, the impact of representing numbers visually and physically, and how what she calls “ishing” a math problem can help students make better sense of the answer. 

What do you mean by “math-ish” thinking?

It’s a way of thinking about numbers in the real world, which are usually imprecise estimates. If someone asks how old you are, how warm it is outside, how long it takes to drive to the airport – these are generally answered with what I call “ish” numbers, and that’s very different from the way we use and learn numbers in school.

In the book I share an example of a multiple-choice question from a nationwide exam where students are asked to estimate the sum of two fractions: 12/13 + 7/8. They’re given four choices for the closest answer: 1, 2, 19, or 21. Each of the fractions in the question is very close to 1, so the answer would be 2 — but the most common answer 13-year-olds gave was 19. The second most common was 21. 

I’m not surprised, because when students learn fractions, they often don’t learn to think conceptually or to consider the relationship between the numerator or denominator. They learn rules about creating common denominators and adding or subtracting the numerators, without making sense of the fraction as a whole. But stepping back and judging whether a calculation is reasonable might be the most valuable mathematical skill a person can develop.

But don’t you also risk sending the message that mathematical precision isn’t important? 

I’m not saying precision isn’t important. What I’m suggesting is that we ask students to estimate before they calculate, so when they come up with a precise answer, they’ll have a real sense for whether it makes sense. This also helps students learn how to move between big-picture and focused thinking, which are two different but equally important modes of reasoning.

Some people ask me, “Isn’t ‘ishing’ just estimating?” It is, but when we ask students to estimate, they often groan, thinking it’s yet another mathematical method. But when we ask them to “ish” a number, they're more willing to offer their thinking.

Ishing helps students develop a sense for numbers and shapes. It can help soften the sharp edges in mathematics, making it easier for kids to jump in and engage. It can buffer students against the dangers of perfectionism, which we know can be a damaging mind-set. I think we all need a little more ish in our lives. 

You also argue that mathematics should be taught in more visual ways. What do you mean by that? 

For most people, mathematics is an almost entirely symbolic, numerical experience. Any visuals are usually sterile images in a textbook, showing bisecting angles, or circles divided into slices. But the way we function in life is by developing models of things in our minds. Take a stapler: Knowing what it looks like, what it feels and sounds like, how to interact with it, how it changes things — all of that contributes to our understanding of how it works. 

There’s an activity we do with middle-school students where we show them an image of a 4 x 4 x 4 cm cube made up of smaller 1 cm cubes, like a Rubik’s Cube. The larger cube is dipped into a can of blue paint, and we ask the students, if they could take apart the little cubes, how many sides would be painted blue? Sometimes we give the students sugar cubes and have them physically build a larger 4 x 4 x 4 cube. This is an activity that leads into algebraic thinking. 

Some years back we were interviewing students a year after they’d done that activity in our summer camp and asked what had stayed with them. One student said, ‘I’m in geometry class now, and I still remember that  sugar cube, what it looked like and felt like.’ His class had been asked to estimate the volume of their shoes, and he said he’d imagined his shoes filled with 1 cm sugar cubes in order to solve that question. He had built a mental model of a cube.

When we learn about cubes, most of us don’t get to see and manipulate them. When we learn about square roots, we don’t take squares and look at their diagonals. We just manipulate numbers.

I wonder if people consider the physical representations more appropriate for younger kids.

That’s the thing — elementary school teachers are amazing at giving kids those experiences, but it dies out in middle school, and by high school it’s all symbolic. There’s a myth that there’s a hierarchy of sophistication where you start out with visual and physical representations and then build up to the symbolic. But so much of high-level mathematical work now is visual. Here in Silicon Valley, if you look at Tesla engineers, they're drawing, they're sketching, they're building models, and nobody says that's elementary mathematics.

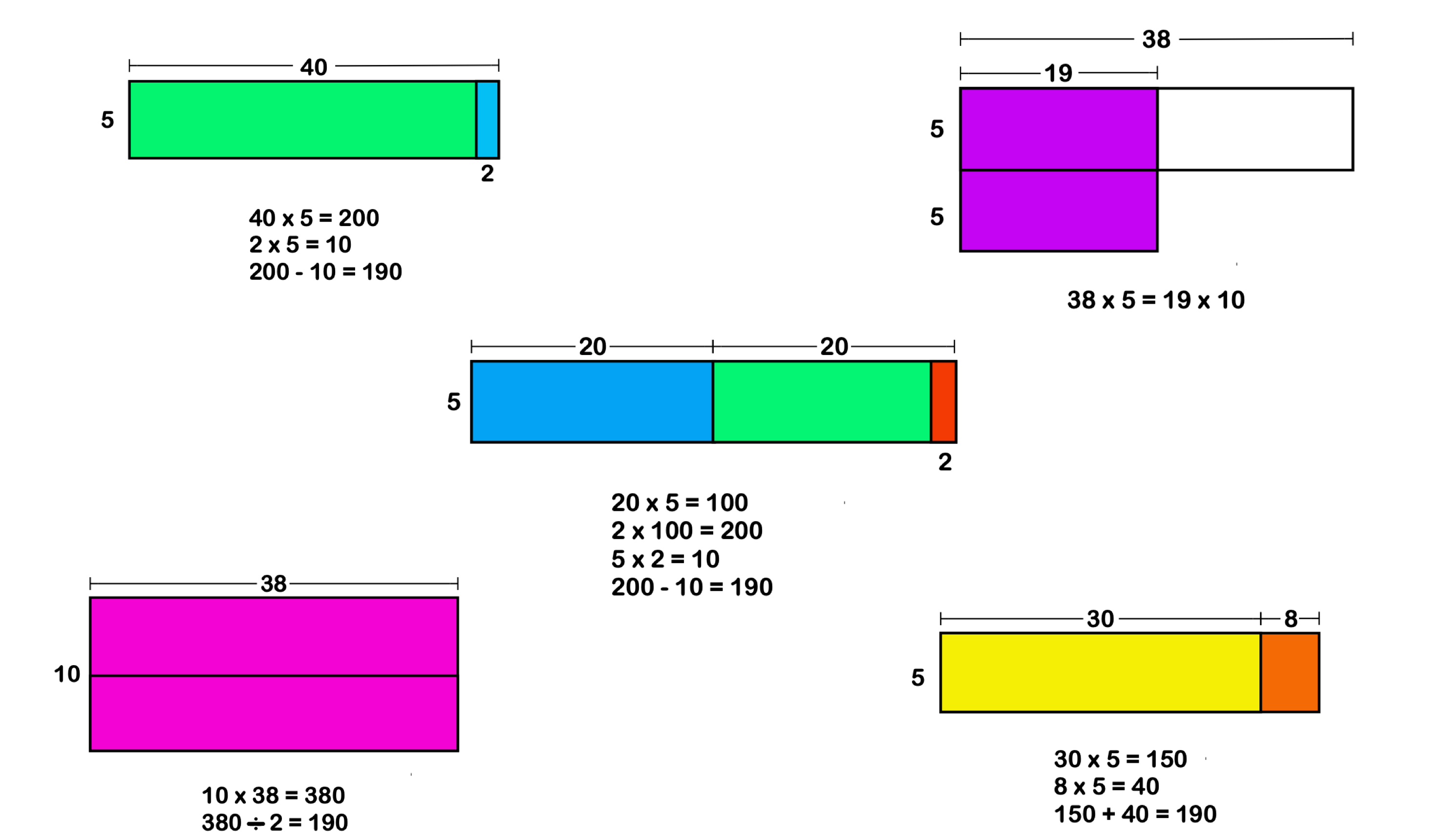
Click to enlarge: A depiction of various ways to calculate 38 x 5, numerically and visually. (Image: Courtesy of Jo Boaler)

There’s an example in the book where you’ve asked students how they would calculate 38 x 5 in their heads, and they come up with several different ways of arriving at the same answer. The creativity is fascinating, but wouldn’t it be easier to teach students one standard method?

That narrow, rigid version of mathematics where there’s only one right approach is what most students experience, and it’s a big part of why people have such math trauma. It keeps them from realizing the full range and power of mathematics. When you only have students blindly memorizing math facts, they’re not developing number sense. They don’t learn how to use numbers flexibly in different situations. It also makes students who think differently believe there’s something wrong with them. 

When we open mathematics to acknowledge the different ways a concept or problem can be viewed, we also open the subject to many more students. Mathematical diversity, to me, is a concept that includes both the value of diversity in people and the diverse ways we can see and learn mathematics. When we bring those forms of diversity together, it’s powerful. If we want to value different ways of thinking and problem-solving in the world, we need to embrace mathematical diversity.

More Stories

⟵ Go to all Research Stories

Get the Educator

Subscribe to our monthly newsletter.

Stanford Graduate School of Education

482 Galvez Mall Stanford, CA 94305-3096 Tel: (650) 723-2109

• Contact Admissions
• GSE Leadership
• Site Feedback
• Web Accessibility
• Career Resources
• Faculty Open Positions
• Explore Courses
• Academic Calendar
• Office of the Registrar
• Cubberley Library
• StanfordWho
• StanfordYou

Improving lives through learning

• Stanford Home
• Maps & Directions
• Search Stanford
• Emergency Info
• Terms of Use
• Non-Discrimination
• Accessibility

© Stanford University , Stanford , California 94305 .

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Reasoning: Identifying Opportunities (Article)   Age 5 to 11

Reasoning: Identifying Opportunities (Selection of Tasks)   Age 5 to 11

Reasoning: the Journey from Novice to Expert (Article)   Age 5 to 11

Reasoning: The Journey from Novice to Expert (Selection of Tasks)   Age 5 to 11

• Reasoning and Convincing at KS1 - Primary Teachers
• Reasoning and Convincing at KS2 - Primary Teachers
• Improving Reasoning: Analysing Alternative Approaches
• Primary Proof?
• Take One Example

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• 14 May 2024

Why mathematics is set to be revolutionized by AI

• Thomas Fink 0

Thomas Fink is the director of the London Institute for Mathematical Sciences, UK.

You can also search for this author in PubMed   Google Scholar

You have full access to this article via your institution.

Giving birth to a conjecture — a proposition that is suspected to be true, but needs definitive proof — can feel to a mathematician like a moment of divine inspiration. Mathematical conjectures are not merely educated guesses. Formulating them requires a combination of genius, intuition and experience. Even a mathematician can struggle to explain their own discovery process. Yet, counter-intuitively, I think that this is the realm in which machine intelligence will initially be most transformative.

In 2017, researchers at the London Institute for Mathematical Sciences, of which I am director, began applying machine learning to mathematical data as a hobby. During the COVID-19 pandemic, they discovered that simple artificial intelligence (AI) classifiers can predict an elliptic curve’s rank 1 — a measure of its complexity. Elliptic curves are fundamental to number theory, and understanding their underlying statistics is a crucial step towards solving one of the seven Millennium Problems, which are selected by the Clay Mathematics Institute in Providence, Rhode Island, and carry a prize of US$1 million each. Few expected AI to make a dent in this high-stakes arena.

AI now beats humans at basic tasks — new benchmarks are needed, says major report

AI has made inroads in other areas, too. A few years ago, a computer program called the Ramanujan Machine produced new formulae for fundamental constants 2 , such as π and e . It did so by exhaustively searching through families of continued fractions — a fraction whose denominator is a number plus a fraction whose denominator is also a number plus a fraction and so on. Some of these conjectures have since been proved, whereas others remain open problems.

Another example pertains to knot theory, a branch of topology in which a hypothetical piece of string is tangled up before the ends are glued together. Researchers at Google DeepMind, based in London, trained a neural network on data for many different knots and discovered an unexpected relationship between their algebraic and geometric structures 3 .

How has AI made a difference in areas of mathematics in which human creativity was thought to be essential?

First, there are no coincidences in maths. In real-world experiments, false negatives and false positives abound. But in maths, a single counterexample leaves a conjecture dead in the water. For example, the Pólya conjecture states that most integers below any given integer have an odd number of prime factors. But in 1960, it was found that the conjecture does not hold for the number 906,180,359. In one fell swoop, the conjecture was falsified.

Second, mathematical data — on which AI can be trained — are cheap. Primes, knots and many other types of mathematical object are abundant. The On-Line Encyclopedia of Integer Sequences (OEIS) contains almost 375,000 sequences — from the familiar Fibonacci sequence (1, 1, 2, 3, 5, 8, 13, ...) to the formidable Busy Beaver sequence (0, 1, 4, 6, 13, …), which grows faster than any computable function. Scientists are already using machine-learning tools to search the OEIS database to find unanticipated relationships.

DeepMind AI outdoes human mathematicians on unsolved problem

AI can help us to spot patterns and form conjectures. But not all conjectures are created equal. They also need to advance our understanding of mathematics. In his 1940 essay A Mathematician’s Apology , G. H. Hardy explains that a good theorem “should be one which is a constituent in many mathematical constructs, which is used in the proof of theorems of many different kinds”. In other words, the best theorems increase the likelihood of discovering new theorems. Conjectures that help us to reach new mathematical frontiers are better than those that yield fewer insights. But distinguishing between them requires an intuition for how the field itself will evolve. This grasp of the broader context will remain out of AI’s reach for a long time — so the technology will struggle to spot important conjectures.

But despite the caveats, there are many upsides to wider adoption of AI tools in the maths community. AI can provide a decisive edge and open up new avenues for research.

Mainstream mathematics journals should also publish more conjectures. Some of the most significant problems in maths — such as Fermat’s Last Theorem, the Riemann hypothesis, Hilbert’s 23 problems and Ramanujan’s many identities — and countless less-famous conjectures have shaped the course of the field. Conjectures speed up research by pointing us in the right direction. Journal articles about conjectures, backed up by data or heuristic arguments, will accelerate discovery.

Last year, researchers at Google DeepMind predicted 2.2 million new crystal structures 4 . But it remains to be seen how many of these potential new materials are stable, can be synthesized and have practical applications. For now, this is largely a task for human researchers, who have a grasp of the broad context of materials science.

Similarly, the imagination and intuition of mathematicians will be required to make sense of the output of AI tools. Thus, AI will act only as a catalyst of human ingenuity, rather than a substitute for it.

Nature 629 , 505 (2024)

doi: https://doi.org/10.1038/d41586-024-01413-w

He, Y.-H., Lee, K.-H., Oliver, T. & Pozdnyakov, A. Preprint at arXiv https://doi.org/10.48550/arXiv.2204.10140 (2024).

Raayoni, G. et al. Nature 590 , 67–73 (2021).

Article   PubMed   Google Scholar  

Davies, A. et al. Nature 600 , 70–74 (2021).

Merchant, A. et al. Nature 624 , 80–85 (2023).

Download references

Reprints and permissions

Competing Interests

The author declares no competing interests.

Related Articles

• Machine learning
• Mathematics and computing

How does ChatGPT ‘think’? Psychology and neuroscience crack open AI large language models

News Feature 14 MAY 24

The US Congress is taking on AI — this computer scientist is helping

News Q&A 09 MAY 24

Accurate structure prediction of biomolecular interactions with AlphaFold 3

Article 08 MAY 24

The dream of electronic newspapers becomes a reality — in 1974

News & Views 07 MAY 24

3D genomic mapping reveals multifocality of human pancreatic precancers

Article 01 MAY 24

AI’s keen diagnostic eye

Outlook 18 APR 24

Faculty Positions& Postdoctoral Research Fellow, School of Optical and Electronic Information, HUST

Job Opportunities: Leading talents, young talents, overseas outstanding young scholars, postdoctoral researchers.

Wuhan, Hubei, China

School of Optical and Electronic Information, Huazhong University of Science and Technology

Postdoc in CRISPR Meta-Analytics and AI for Therapeutic Target Discovery and Priotisation (OT Grant)

APPLICATION CLOSING DATE: 14/06/2024 Human Technopole (HT) is a new interdisciplinary life science research institute created and supported by the...

Human Technopole

Research Associate - Metabolism

Houston, Texas (US)

Baylor College of Medicine (BCM)

Postdoc Fellowships

Train with world-renowned cancer researchers at NIH? Consider joining the Center for Cancer Research (CCR) at the National Cancer Institute

Bethesda, Maryland

NIH National Cancer Institute (NCI)

Faculty Recruitment, Westlake University School of Medicine

Faculty positions are open at four distinct ranks: Assistant Professor, Associate Professor, Full Professor, and Chair Professor.

Hangzhou, Zhejiang, China

Westlake University

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

• International
• Schools directory
• Resources Jobs Schools directory News Search

Outstanding Maths Lesson for Interview/Lesson Observation Problem Solving - Years 5 and 6

Subject: Mathematics

Age range: 7-11

Resource type: Lesson (complete)

Last updated

10 May 2024

• Share through email
• Share through twitter
• Share through linkedin
• Share through facebook
• Share through pinterest

An exceptional maths problem solving lesson, complete with written lesson plan and interactive slides. Crafted to engage and challenge high-ability Year 5/6 students, this lesson offers a rich tapestry of activities and tasks designed to ignite mathematical thinking.

Perfect for a lesson observation or job interview, these comprehensive materials will impress all observers and demonstrate your expertise in delivering high-quality maths education.

Tes paid licence How can I reuse this?

Your rating is required to reflect your happiness.

It's good to leave some feedback.

Something went wrong, please try again later.

This resource hasn't been reviewed yet

To ensure quality for our reviews, only customers who have purchased this resource can review it

Report this resource to let us know if it violates our terms and conditions. Our customer service team will review your report and will be in touch.

Not quite what you were looking for? Search by keyword to find the right resource:

SATs Tutoring Programme

"Seeing our 2023 maths results has highlighted what I already knew about the impact - it's brilliant!"

Hundreds of FREE maths SATs resources!

SATs practice papers, SATs revision packs, SATs intervention lessons and more!

35 SATs Maths Questions And Answers With Worked Examples: Essential Maths Reasoning Practice For Year 6 [FREE]

Anantha Anilkumar

For Year 6, the toughest of their SATs maths questions are the reasoning questions. 

No matter how good pupils’ subject knowledge is or how effective your SATs revision lessons are, the examiners always manage to come up with maths questions that can baffle and flummox even the hardiest year 6 pupil.

To mitigate against this for SATs 2024 your pupils need plenty of exam practice and more specifically exam question practice to be familiar with both the types of SATs reasoning questions that can come up and the skills needed to answer them.

So to make life easy for you we’ve put together here a comprehensive collection of 35 SATs maths questions, organised by the sorts of question that pupils can expect to encounter.

All these practice SATs questions have been based on a mix of questions from past SATs papers , our own free year 6 maths SATs papers , and our collections of year 6 reasoning questions from the Rapid Reasoning resource collection. The answers are all taken from the answer sheets we provide for each test paper.

Other useful SATs revision resources

Before we get into the year 6 maths questions you might find it helpful to know that we have hundreds of other free KS2 SATs revision resources, including free SATs papers , and SATs intervention packs for those wanting to use the Year 6 SATs revision lessons we use in one to one tutoring in their own boosters.

You should also make sure you’re up to date with the latest analysis on the 20 most ‘valuable’ topics to study for SATs this year and also this analysis of the KS2 SATs Maths Papers Question Breakdown in 2023 .

You may also wish to read this guide to SATs first to give you some background information about the tests.

Why the focus on maths reasoning questions for SATs? 

Ever since the new national curriculum Key Stage 2 SATs in 2016, the emphasis in the all SATs papers has been very much on SATs reasoning questions. While there is one arithmetic paper, there are two reasoning papers; and the variety, breadth and level of challenge in the reasoning paper continues to impress us.

Most Year 6 pupils find the reasoning SATs maths questions the hardest part of these maths papers. Unsurprisingly! We teach thousands of pupils every week in the run up to SATs, and teaching them maths reasoning skills at KS2 is a big part of what we do.

We even recently took the decision to restructure our SATs lessons to introduce maths reasoning questions earlier in the learning journey as the level of challenge just at the end of the lesson was too high. So we feel the Year 6 teacher’s pain!

Whatever level pupils go on to perform at in maths, maths reasoning questions and numerical reasoning tests (such as those used by grammar and private schools) are likely to be a part of the practice they require.

If you find you have children in your class with much further to catch-up than the others then we we would be happy to support them with some personalised online one to one maths tuition .

35 SATs maths questions for KS2 year 6 SATs

For the KS2 SATs tests, there are 7 types of maths reasoning question that are likely to come up:

• Single step worded problems
• Multiple step worded problems
• Problems involving measures
• Problems involving drawing
• Explanation questions
• Sequence questions
• Ordering questions

For each of these types we’ll examine an example SATs maths question from a previous SATs paper, looking at the question, the correct answer, and how to go about answering this question.

We’ll also look at further examples of each type of maths reasoning questions and answers from Third Space’s Rapid Reasoning resource, again with worked examples and an explanation of how to answer each.

Finally, at the end of this article we provide links to further Year 6 maths questions, assessments and other SATs papers that you may find useful including plenty of arithmetic practice too.

Our aim is to provide you as part of your SATs practice with a sample of the types of KS2 SATs questions pupils can expect in the reasoning papers and how to teach the reasoning and problem solving  skills they’ll need to answer them.

For more word problems like this, check out our collection of 2-step and multi-step word problems for you as well as tips on how to use the bar model to answer Year 6 word problems . For advice on how to teach children to solve problems like this, check out these maths problem solving strategies.

SATs Maths Question Type 1: Single step worded problems

The simplest type of reasoning question pupils are likely to encounter in the reasoning papers, single step problems are exactly that: pupils are asked to interpret a written question and carry out a single mathematical step to solve it.

Have a look at the question below:

Reasoning Question 1

Answer: 65p

A relatively easy question to interpret and solve – the first step is to recognise £2 and £1.35 as equivalent to 200 and 135. From here the simple mathematical step is subtraction i.e. 200-135=65.

The most crucial skill for primary school pupils in this question is a solid understanding of money as relating to place value. If this understanding is present, the mathematical step itself is quite easy.

Below are several more examples, taken from Third Space Learning’s Rapid Reasoning resources:

Reasoning Question 2

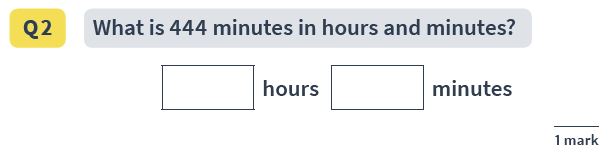
Answer : 7 hours 24 minutes

Pupils need to understand that one hour is equal to 60 minutes. From here the single mathematical step is short division: 444/60, with a remainder.

Reasoning Question 3

Answer : 48 cm 3

Pupils must calculate length by breadth by height, using the figures provided by the question.

Reasoning Question 4

Answer : 124 cm

A simple enough calculation (doubling) if pupils are aware that the diameter is twice the radius.

Reasoning Question 5

Answer : 7,590

A single, relatively simple rounding problem – pupils should recognise that ’94’ is the operative part of this figure.

SATs Maths Question Type 2: Multiple step worded problems

A more complex version of the single step worded problem, multi-step problems require pupils to interpret a written problem, but solving it then requires the use of two or three maths skills,

For example, consider this question from the 2019 KS2 maths SATs:

Reasoning Question 6

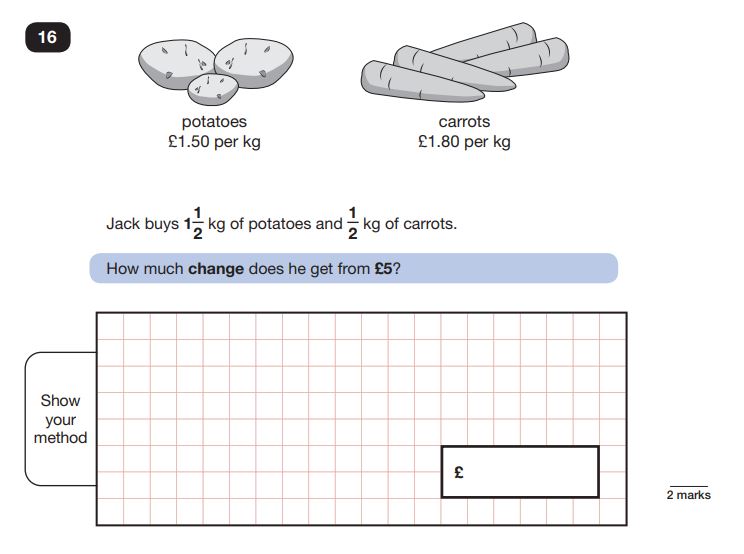
Answer: £1.85

This question encompasses three different maths skills: multiplying (and dividing) mixed numbers, addition and subtraction. Pupils can choose to work out the multiplication or division first, but must complete both before moving on.

Once these values have been worked out the next steps are relatively simple – adding the two values together, and subtracting the total from £5.

Multi-step problems are particularly valuable to include in practice tests because they require children to apply their knowledge of maths language and their reasoning skills several times across the course of a single question, usually in slightly different contexts.

More examples:

Reasoning Question 7

Answer : £5,520

There are two steps to this problem, but both are multiplications. The first is to work out how much money is made per day – 92 x £15. This sum is then multiplied by 4 – the number of days – to get to the solution.

Reasoning Question 8

Answer : 2,160 km

Another two step problem. The first step is to work out 10% of 5400 km. Then multiply this by 4 to solve 40%.

Reasoning Question 9

Answer : £43.50

There are three steps involved in solving this problem: multiplication (doubling £51 and £36 to find the cost of two adult and two child tickets), addition (putting the two costs together) and division (dividing the total by four to obtain the mean cost).

Given the number of steps involved it can be easy for pupils to make arithmetic mistakes, and the mark scheme accounts for this by allowing for one mistake – but no more.

Read more: Mean median mode

Reasoning question 10.

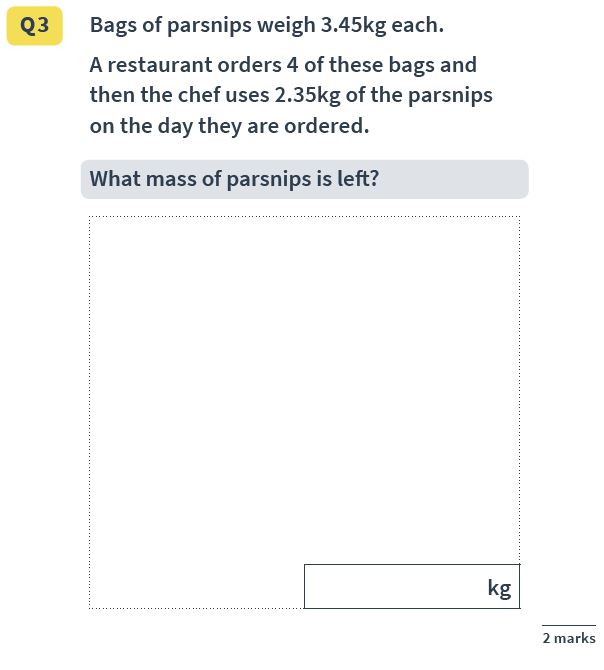
Answer : 11.45 kg

A two-step problem again: multiplying 3.45 kg by 4, then subtracting 2.35 kg from the total. As with the previous problem, the mark scheme again allows for at most one arithmetic error, assuming the method is correct.

Year 6 Rapid Reasoning (Weeks 1-6)

Download 6 weeks of Rapid Reasoning slides for your Year 6 pupils and help them get a head start on preparing for the SATs reasoning papers.

SATs Maths Question Type 3: Problems involving measures

As their name suggests, these questions ask pupils to solve a problem that includes one or more units of measurement.

Take a look at this question from 2018’s Reasoning Paper 3:

Reasoning Question 1 1

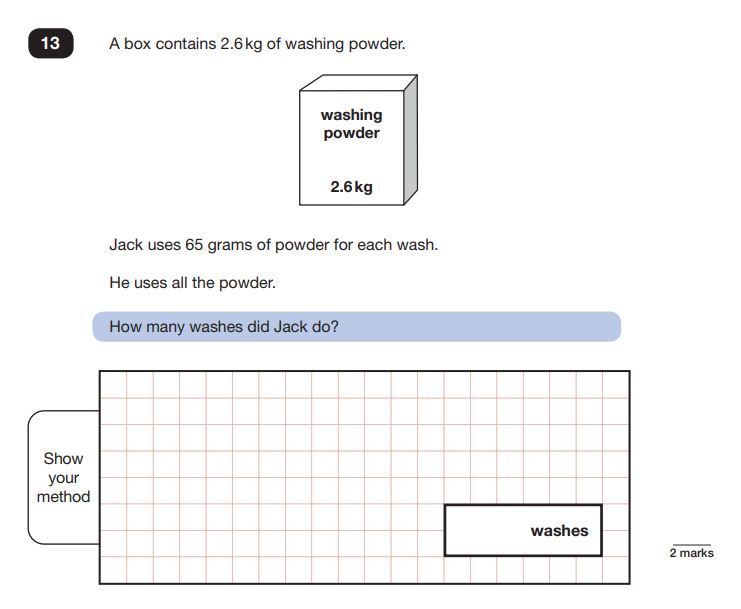
Answer: 40 washes

This is a two step problem; pupils must first be able to read and convert kilograms to grams (and therefore know the relationship between the two units), then divide 2600 by 65 to work out the number of washes possible.

Questions involving measures tend to be few in number in the KS2 exam papers, but they often provide an excellent way to couch key maths skills such as the four operations.

Further examples:

Reasoning Question 12

Answer : 50g

A relatively simple division problem, relying on pupils having knowledge that 200g is one fifth of a kilogram.

Reasoning Question 13

Answer : 1.1kg

Another three step problem – multiplying 500 by 4 to get the total mass of the four melons, multiplying 300 by 3 to get the total mass of the remaining three melons, and then subtracting 2000 from 900 to obtain the mass of the fourth melon.

It’s worth noting that the mark scheme allows either 1.1kg or 1,100g as acceptable answers – the units of measurement are not as important as obtaining the current figure.

Reasoning Question 14

Answer : 216cm

Interesting to note that in this problem (unlike the previous example), the units for the answer are specified – an answer given in metres will be marked as wrong, since cm is specified in the answer box. This is why we encourage pupils to keep an eye on whether units are provided in the answer box.

Reasoning Question 15

Answer : 170g

As with the melon question there are three steps involved to solve this problem: working out the mass of the four cars (4 x 80), working out the mass of the remaining three cars (3 x 50) and subtracting 150 from 320 to get the mass of the fourth car.

SATs Maths Question Type 4: Problems involving drawing

Problems involving drawing require pupils to construct an  accurate  drawing by following a set of instructions, or through reflection, translation, or scaling.   

This type of question is quite rare, but there are some notable exceptions, such as the infamous Question 21 in Paper 2 of the 2019 Reasoning SATs:

Reasoning Question 1 6

Answer: Any pair of lines that make a square of 4 units, a rectangle of 6 units, and a square of 25 units.

This question is considerably more complex than it appears, and incorporates aspects of multiplication as well as spatial awareness. One potential solution is to work out the area of the card (35), then work out the possible square numbers that will fit in (understanding that square numbers produce a square when drawn out as on a grid), and which then leave a single rectangle behind.

A lot of work for a single mark!

Some further examples:

Reasoning Question 17

Answer : Any quadrilateral made by joining the dots that has 3 acute angles e.g. an arrowhead shape.

Reasoning Question 18

Answer : An accurately drawn angle.

The mark scheme here allows some room for error – “between 34 and 36 degrees” is acceptable .

Reasoning Question 19

As with the question above, a small amount of room for error is given – “between 139 and 141 degrees”.

Reasoning Question 20

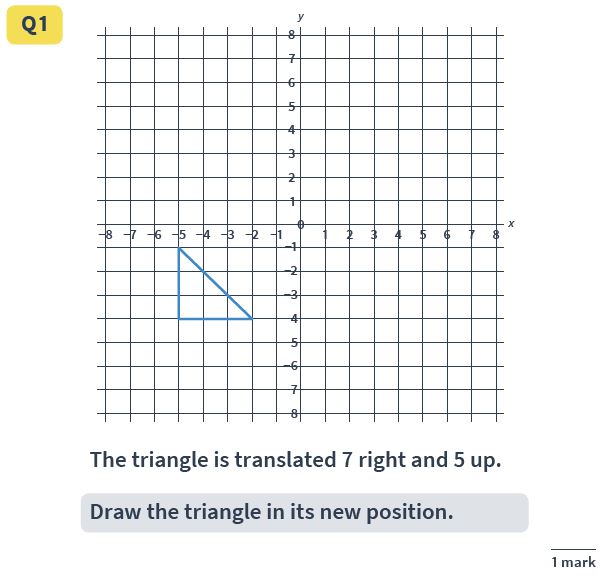
Answer : a new triangle drawn with points at (2,1), (5,1) and (2,4).

Translation can be tricky for pupils. Encourage them to look at the triangle as three points, and to translate each point separately rather than trying to move ‘the whole triangle’.

SATs Maths Question Type 5: Explanation questions

An early form of the ‘Prove X’ questions that come up in GCSEs, these problems ask children to explain a mathematical statement or error.

As an example:

Reasoning Question 21

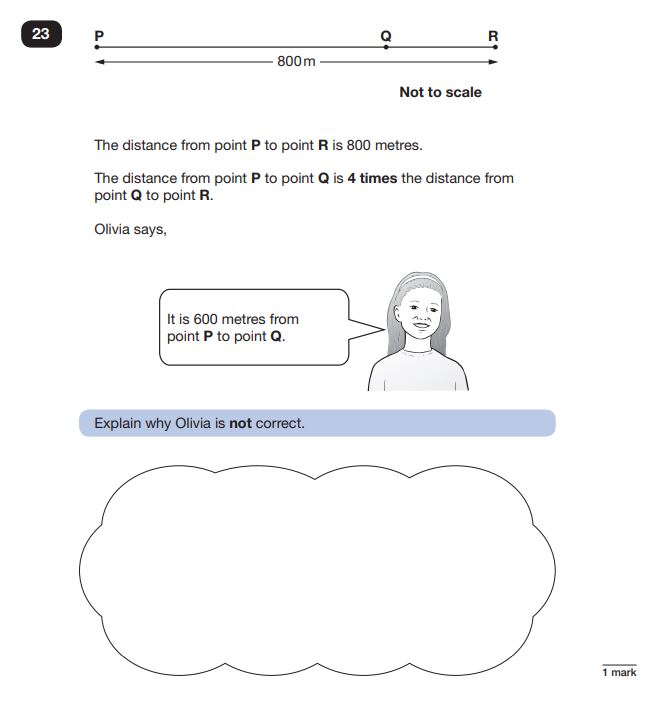
Answer: If the distance from P to R is 800m and the distance from P to Q is (Q -> R x 4), it must be 4/5 of 800 = 640m. Therefore Olivia is wrong.

More than most problems, this type requires pupils to actively demonstrate their  reasoning skills  as well as their mathematical ones. Here pupils must articulate either in words or (where possible) numerically that they understand that Q to R is 1/5 of the total, that therefore P to Q is 4/5 of the total distance, and then calculate what this is via division and multiplication.

Further examples from TSL’s Rapid Reasoning resources:

Reasoning Question 22

Answer : No; 20/100 is the same as 20 divided by 100, which equals 0.2.

Reasoning Question 23

Answer : No; multiplication and division have the same priority, so in a problem like 40 x 6 ÷2, you would carry out the multiplication first as it occurs first.

The mark scheme notes that vague answers or any answers with a mathematical error are unacceptable.

Reasoning Question 24

Answer : No

Any explanation that provides a counter-example is acceptable e.g. “Not if the number is 1”, “Not for 0” etc.

Reasoning Question 25

Answer : Any answer that refers to the fact that there is a 5 in the hundreds place, AND a 9 in the thousands place, so that the number has to be rounded up as far as the ten-thousands place.

SATs Maths Question Type 6: Sequence questions

Another relatively simple kind of reasoning question, sequence problems involve pupils completing mathematical sequences.

Consider this example:

Reasoning Question 26

Answer:   35 , 42, 49,  56 , 63,  70

Number sequence questions, particularly those that involve linear sequences or (as in this case) times tables, come up relatively frequently in the SATs maths tests. The question’s instructions point clearly to the solution: work out what the increase between numbers is, then apply this via addition or subtraction to find the missing numbers.

Higher attaining pupils might quickly pick up that this is in fact the 7 times table and rely on their knowledge of multiplication facts to obtain the answer – this should be encouraged so long as they then check their answer in the normal method to ensure they haven’t made a mistake.

Reasoning Question 2 7

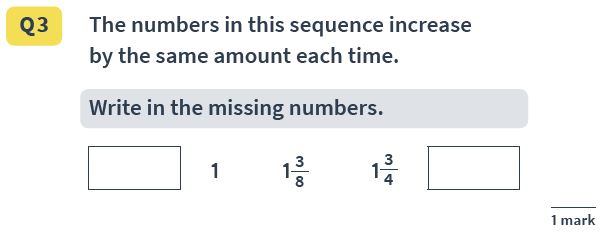
Answer(s) : 5/8 and 2 1/8 (OR 17/8)

Both answers must be correct to receive the mark. Pupils must recognise that 3/4 is the same as 6/8, so the following number must be three eighths higher.

Reasoning Question 28

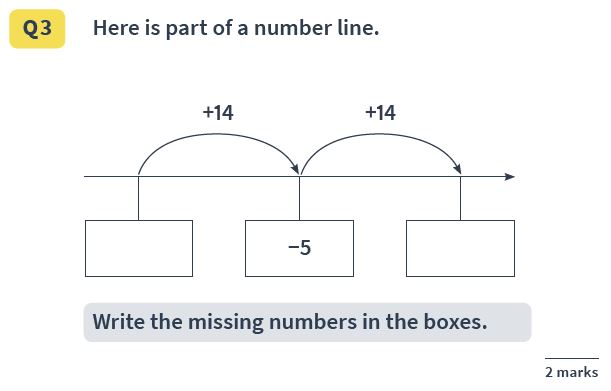
Answer(s) : -19 and 9

Reasoning Question 29

Answer(s) : 128, 135 and 156.

Reasoning Question 30

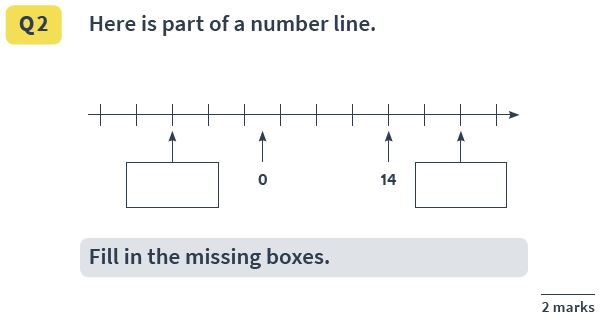
Answer(s) : -10 and 22

This question can be a little tricky; pupils need to work out that the marks on the line represent increments of 4, and count backwards and forwards in 4s to obtain the missing numbers.

SATs Maths Question Type 7: Ordering questions

A slightly more complex variation of the sequence question, ordering problems require pupils to put a set of numbers, fractions or measures in the correct order.

A good example is this question from Paper 2 of the 2018 SATs:

Reasoning Question 31

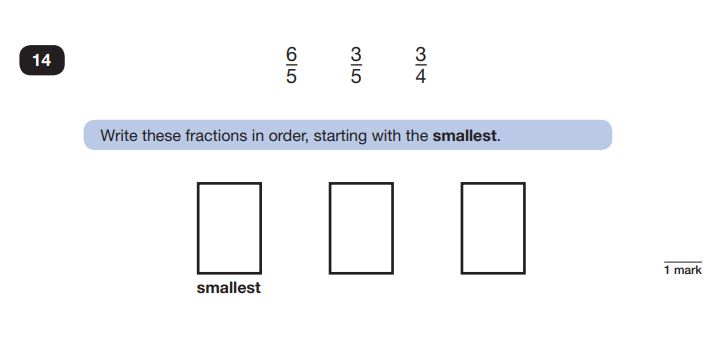
Answer: 3/5, 3/4, 6/5

This question throws a stick in the wheels by including an improper fraction, but this is hardly unusual. These sorts of questions are just the place to find other ‘curveballs’ such as equivalent fractions, mixed numbers and decimals and fractions combined.

A good knowledge of the fundamentals of fractions is essential here: pupils must understand what a larger denominator means, and the significance of a fraction with a numerator greater than its denominator.

Reasoning Question 32

Answer : D,C,A,B

Encourage pupils to convert all the fractions to one denominator value to make ordering easier.

Reasoning Question 33

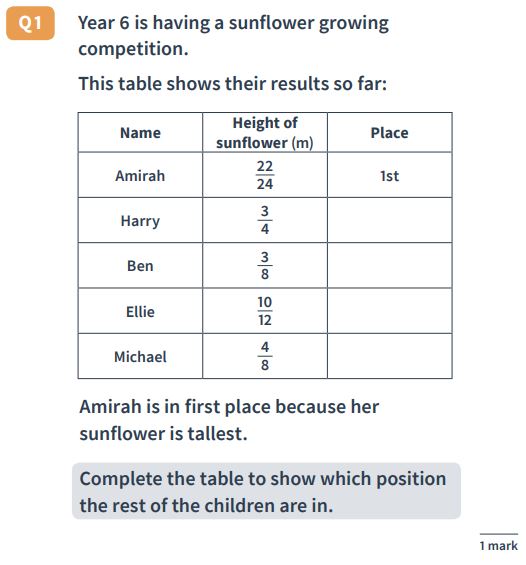
Answer : (descending down the ‘Place’ column) 3rd, 5th, 2nd, 4th

As with the example above, pupils should be encouraged to convert the fractions to make it easier to order them.

Reasoning Question 34

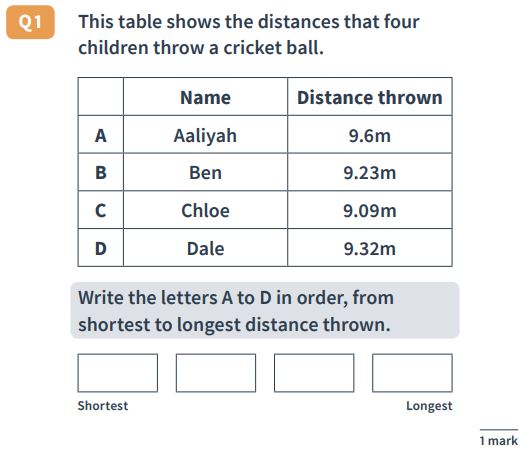
Answer : C, B, D, A

Reasoning Question 35

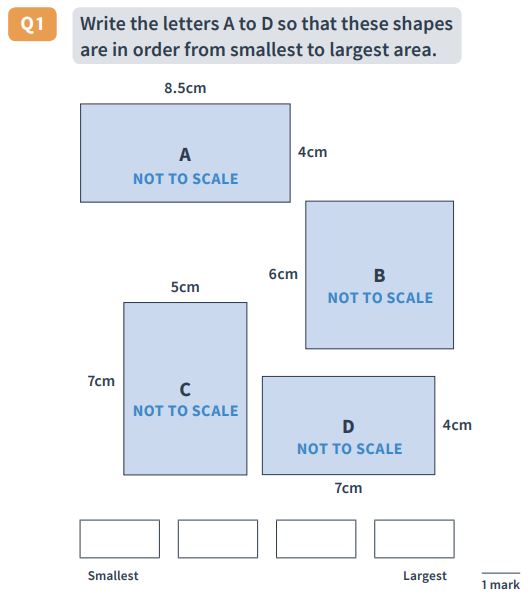
Answer : D, A, C, B

7 top tips for answering SATs questions

Now that we’ve covered how to answer some specific types of reasoning questions, here are some more generic tips for success in the reasoning papers. They may not all be applicable to every single question type, but will apply to at least two, usually more.

• Get pupils in the habit for any practice paper of identifying what information they’re given in a question, and what they need to know to solve the problem. This helps them start to form the steps needed to find the solution.
• Ask pupils to ‘spot the maths’ in a question – which calculations or skills do they actually need to use to solve the problem? This is useful even for arithmetic questions – it’s no surprise how often children can misread a question.
• Check the units! Especially in questions involving multiple measures, it can be easy to give the answer in the wrong one. The answer box might give a specific unit of measurement, so pupils should work to give their answer in that unit.
• In a similar vein, remind pupils to convert different units of measurement in a question into the same unit to make calculations easier e.g. kg to g.
• Encourage numerical answers where possible. Even in explanation questions demonstrating the mathematical calculation is a better explanation than trying to write it out.
• The bar model can be a useful way of visualising many different types of questions, and might make it easier to spot the ‘steps’ needed for the solution.
• Check your working out! Even if the working is ultimately irrelevant to the question, you can lose marks if it is wrong.

More free SATs questions (all with answers)

• 75 KS2 SATs maths questions Reasoning and Arithmetic practice questions by topic – includes fractions, decimals, percentages; place value; addition and subtraction.
• 250+ SATs questions
• Year 6 algebra questions
• Year 6 arithmetic questions
• Year 6 ratio questions
• Year 6 fractions questions
• Free year 6 maths test

If you’re looking for even more free and premium maths resources join 80,000 teachers using the resources in the Third Space Learning Mathshub (free to sign up).

Online 1-to-1 maths lessons trusted by schools and teachers Every week Third Space Learning’s maths specialist tutors support thousands of pupils across hundreds of schools with weekly online 1-to-1 lessons and  maths interventions  designed to plug gaps and boost progress. Since 2013 we’ve helped over 80,000 primary and secondary school pupils become more confident, able mathematicians.  Learn more  or  request a personalised quote  to speak to us about your school’s needs and how we can help.

DO YOU HAVE PUPILS WHO NEED MORE SUPPORT IN MATHS?

Every week Third Space Learning’s specialist primary maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.

Since 2013 these personalised one to 1 lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.

Learn about the SATs revision programme or request a personalised quote from your school to speak to us about your school’s needs and how we can help.

Related articles

Review Of Maths SATs 2024: Results Of Our Teacher Survey! What Do You Think?

25 Year 6  Algebra Questions And Answers: KS2 Assessment Preparation

20 Year 6 Ratio Questions And Answers: From Easy To Hard

Year 6 Arithmetic Questions: 36 SATs-Style Questions and Answers

FREE Year 6 Survival Pack

A selection of fun activities to use with your Year 6 class after SATs plus our most downloaded free SATs resources to support next year's cohort.

Includes KS2 maths games and investigations and our most popular resource, Fluent in Five!

Privacy Overview