solve eigenvalue problem

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.1: The Eigenvalue Problem

• Last updated
• Save as PDF
• Page ID 96166

• Jeffrey R. Chasnov
• Hong Kong University of Science and Technology

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

View The Eigenvalue Problem on Youtube

View Finding Eigenvalue and Eigenvectors (Part 1) on Youtube

View Finding Eigenvalue and Eigenvectors (Part 2) on Youtube

Let A be an \(n\) -by- \(n\) matrix, \(x\) an \(n\) -by- 1 column vector, and \(\lambda\) a scalar. The eigenvalue problem for a given matrix A solves

\[A x=\lambda x \nonumber \]

for \(n\) eigenvalues \(\lambda_{i}\) with corresponding eigenvectors \(\mathrm{x}_{i}\) . Since \(\mathrm{Ix}=\mathrm{x}\) , where \(\mathrm{I}\) is the \(n\) -by- \(n\) identity matrix, we can rewrite the eigenvalue equation Equation \ref{5.1} as

\[(\mathrm{A}-\lambda \mathrm{I}) \mathrm{x}=0 . \nonumber \]

The trivial solution to this equation is \(x=0\) , and for nontrivial solutions to exist, the \(n\) -by- \(n\) matrix A \(-\lambda I\) , which is the matrix A with \(\lambda\) subtracted from its diagonal, must be singular. Hence, to determine the nontrivial solutions, we must require that

\[\operatorname{det}(\mathrm{A}-\lambda \mathrm{I})=0 . \nonumber \]

Using the big formula for the determinant, one can see that Equation \ref{5.3} is an \(n\) -th order polynomial equation in \(\lambda\) , and is called the characteristic equation of A. The characteristic equation can be solved for the eigenvalues, and for each eigenvalue, a corresponding eigenvector can be determined directly from Equation \ref{5.2}.

We can demonstrate how to find the eigenvalues of a general 2-by-2 matrix given by

\[A=\left(\begin{array}{ll} a & b \\ c & d \end{array}\right) \text {. } \nonumber \]

\[\begin{aligned} 0 &=\operatorname{det}(\mathrm{A}-\lambda \mathrm{I}) \\ &=\left|\begin{array}{cc} a-\lambda & b \\ c & d-\lambda \end{array}\right| \\ &=(a-\lambda)(d-\lambda)-b c \\ &=\lambda^{2}-(a+d) \lambda+(a d-b c), \end{aligned} \nonumber \]

which can be more generally written as

\[\lambda^{2}-\operatorname{Tr} \mathrm{A} \lambda+\operatorname{det} \mathrm{A}=0 \nonumber \]

where \(\operatorname{Tr} \mathrm{A}\) is the trace, or sum of the diagonal elements, of the matrix \(\mathrm{A}\) .

Since the characteristic equation of a two-by-two matrix is a quadratic equation, it can have either (i) two distinct real roots; (ii) two distinct complex conjugate roots; or (iii) one degenerate real root. That is, eigenvalues and eigenvectors can be real or complex, and that for certain defective matrices, there may be less than \(n\) distinct eigenvalues and eigenvectors.

If \(\lambda_{1}\) is an eigenvalue of our 2-by-2 matrix \(A\) , then the corresponding eigenvector \(\mathrm{x}_{1}\) may be found by solving

\[\left(\begin{array}{cc} a-\lambda_{1} & b \\ c & d-\lambda_{1} \end{array}\right)\left(\begin{array}{l} x_{11} \\ x_{21} \end{array}\right)=0 \nonumber \]

where the equation of the second row will always be a multiple of the equation of the first row because the determinant of the matrix on the left-hand-side is zero. The eigenvector \(\mathrm{x}_{1}\) can be multiplied by any nonzero constant and still be an eigenvector. We could normalize \(x_{1}\) , for instance, by taking \(x_{11}=1\) or \(\left|x_{1}\right|=1\) , or whatever, depending on our needs.

The equation from the first row of Equation \ref{5.5} is

\[\left(a-\lambda_{1}\right) x_{11}+b x_{21}=0, \nonumber \]

and we could take \(x_{11}=1\) to find \(x_{21}=\left(\lambda_{1}-a\right) / b\) . These results are usually derived as needed when given specific matrices.

Example: Find the eigenvalues and eigenvectors of the following matrices:

\[\left(\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right) \text { and }\left(\begin{array}{ll} 3 & 1 \\ 1 & 3 \end{array}\right) \nonumber \]

\[\mathrm{A}=\left(\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right) \nonumber \]

the characteristic equation is

\[\lambda^{2}-1=0, \nonumber \]

with solutions \(\lambda_{1}=1\) and \(\lambda_{2}=-1\) . The first eigenvector is found by solving \(\left(\mathrm{A}-\lambda_{1} \mathrm{I}\right) \mathrm{x}_{1}=0\) , or

\[\left(\begin{array}{rr} -1 & 1 \\ 1 & -1 \end{array}\right)\left(\begin{array}{l} x_{11} \\ x_{21} \end{array}\right)=0, \nonumber \]

so that \(x_{21}=x_{11}\) . The second eigenvector is found by solving \(\left(\mathrm{A}-\lambda_{2} \mathrm{I}\right) \mathrm{x}_{2}=0\) , or

\[\left(\begin{array}{ll} 1 & 1 \\ 1 & 1 \end{array}\right)\left(\begin{array}{l} x_{12} \\ x_{22} \end{array}\right)=0, \nonumber \]

so that \(x_{22}=-x_{12}\) . The eigenvalues and eigenvectors are therefore given by

\[\lambda_{1}=1, \mathrm{x}_{1}=\left(\begin{array}{l} 1 \\ 1 \end{array}\right) ; \quad \lambda_{2}=-1, \mathrm{x}_{2}=\left(\begin{array}{r} 1 \\ -1 \end{array}\right) \nonumber \]

To find the eigenvalues and eigenvectors of the second matrix we can follow this same procedure. Or better yet, we can take a shortcut. Let

\[A=\left(\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right) \quad \text { and } \quad B=\left(\begin{array}{ll} 3 & 1 \\ 1 & 3 \end{array}\right) \nonumber \]

We know the eigenvalues and eigenvectors of \(\mathrm{A}\) and that \(\mathrm{B}=\mathrm{A}+3 \mathrm{I}\) . Therefore, with \(\lambda_{\mathrm{B}}\) representing the eigenvalues of \(\mathrm{B}\) , and \(\lambda_{\mathrm{A}}\) representing the eigenvalues of \(A\) , we have

\[0=\operatorname{det}\left(\mathrm{B}-\lambda_{\mathrm{B}} \mathrm{I}\right)=\operatorname{det}\left(\mathrm{A}+3 \mathrm{I}-\lambda_{\mathrm{B}} \mathrm{I}\right)=\operatorname{det}\left(\mathrm{A}-\left(\lambda_{\mathrm{B}}-3\right) \mathrm{I}\right)=\operatorname{det}\left(\mathrm{A}-\lambda_{\mathrm{A}} \mathrm{I}\right) \nonumber \]

Therefore, \(\lambda_{\mathrm{B}}=\lambda_{\mathrm{A}}+3\) and the eigenvalues of \(\mathrm{B}\) are 4 and 2. The eigenvectors remain the same.

It is useful to notice that \(\lambda_{1}+\lambda_{2}=\operatorname{Tr} \mathrm{A}\) and that \(\lambda_{1} \lambda_{2}=\operatorname{det} \mathrm{A}\) . The analogous result for \(n\) -by- \(n\) matrices is also true and worthwhile to remember. In particular, summing the eigenvalues and comparing to the trace of the matrix provides a rapid check on your algebra.

\[\left(\begin{array}{rr} 0 & -1 \\ 1 & 0 \end{array}\right) \text { and }\left(\begin{array}{ll} 0 & 1 \\ 0 & 0 \end{array}\right) \nonumber \]

\[A=\left(\begin{array}{rr} 0 & -1 \\ 1 & 0 \end{array}\right) \nonumber \]

\[\lambda^{2}+1=0 \nonumber \]

with solutions \(i\) and \(-i\) . Notice that if the matrix \(A\) is real, then the complex conjugate of the eigenvalue equation \(A x=\lambda x\) is \(A \bar{x}=\bar{\lambda} \bar{x}\) . So if \(\lambda\) and \(x\) is an eigenvalue and eigenvector of a real matrix \(A\) then so is the complex conjugates \(\bar{\lambda}\) and \(\bar{x}\) . Eigenvalues and eigenvectors of a real matrix appear as complex conjugate pairs.

The eigenvector associated with \(\lambda=i\) is determined from \((\mathrm{A}-i \mathrm{I}) \mathrm{x}=0\) , or

\[\left(\begin{array}{rr} -i & -1 \\ 1 & -i \end{array}\right)\left(\begin{array}{l} x_{1} \\ x_{2} \end{array}\right)=0 \nonumber \]

or \(x_{1}=i x_{2}\) . The eigenvectors and eigenvectors of \(\mathrm{A}\) are therefore given by

\[\lambda=i, \quad \mathbf{X}=\left(\begin{array}{l} i \\ 1 \end{array}\right) ; \quad \bar{\lambda}=-i, \quad \overline{\mathrm{X}}=\left(\begin{array}{r} -i \\ 1 \end{array}\right) \nonumber \]

\[B=\left(\begin{array}{ll} 0 & 1 \\ 0 & 0 \end{array}\right) \nonumber \]

\[\lambda^{2}=0, \nonumber \]

so that there is a degenerate eigenvalue of zero. The eigenvector associated with the zero eigenvalue if found from \(\mathrm{Bx}=0\) and has zero second component. Therefore, this matrix is defective and has only one eigenvalue and eigenvector given by

\[\lambda=0, \quad \mathrm{x}=\left(\begin{array}{l} 1 \\ 0 \end{array}\right) \nonumber \]

Example: Find the eigenvalues and eigenvectors of the rotation matrix:

\[R=\left(\begin{array}{rr} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right) \nonumber \]

The characteristic equation is given by

\[\lambda^{2}-2 \cos \theta \lambda+1=0, \nonumber \]

with solution

\[\lambda_{\pm}=\cos \theta \pm \sqrt{\cos ^{2} \theta-1}=\cos \theta \pm i \sin \theta=e^{\pm i \theta} \nonumber \]

The eigenvector corresponding to \(\lambda=e^{i \theta}\) is found from

\[-i \sin \theta x_{1}-\sin \theta x_{2}=0, \nonumber \]

or \(x_{2}=-i x_{1}\) . Therefore, the eigenvalues and eigenvectors are

\[\lambda=e^{i \theta}, \quad x=\left(\begin{array}{r} 1 \\ -i \end{array}\right) \nonumber \]

and their complex conjugates.

Eigenvector and Eigenvalue

They have many uses!

A simple example is that an eigenvector does not change direction in a transformation:

How do we find that vector?

The Mathematics Of It

For a square matrix A , an Eigenvector and Eigenvalue make this equation true:

Let us see it in action:

Let's do some matrix multiplies to see if that is true.

Av gives us:

λv gives us :

Yes they are equal!

So we get Av = λv as promised.

Notice how we multiply a matrix by a vector and get the same result as when we multiply a scalar (just a number) by that vector .

How do we find these eigen things?

We start by finding the eigenvalue . We know this equation must be true:

Next we put in an identity matrix so we are dealing with matrix-vs-matrix:

Bring all to left hand side:

Av − λIv = 0

If v is non-zero then we can (hopefully) solve for λ using just the determinant :

| A − λI | = 0

Let's try that equation on our previous example:

Example: Solve for λ

Start with | A − λI | = 0

Calculating that determinant gets:

(−6−λ)(5−λ) − 3×4 = 0

Which simplifies to this Quadratic Equation :

λ 2 + λ − 42 = 0

And solving it gets:

λ = −7 or 6

And yes, there are two possible eigenvalues.

Now we know eigenvalues , let us find their matching eigenvectors .

Example (continued): Find the Eigenvector for the Eigenvalue λ = 6 :

Start with:

After multiplying we get these two equations:

Bringing all to left hand side:

Either equation reveals that y = 4x , so the eigenvector is any non-zero multiple of this:

And we get the solution shown at the top of the page:

... and also ...

So Av = λv , and we have success!

Now it is your turn to find the eigenvector for the other eigenvalue of −7

What is the purpose of these?

One of the cool things is we can use matrices to do transformations in space, which is used a lot in computer graphics.

In that case the eigenvector is "the direction that doesn't change direction" !

And the eigenvalue is the scale of the stretch:

• 1 means no change,
• 2 means doubling in length,
• −1 means pointing backwards along the eigenvector's direction

There are also many applications in physics, etc.

Why "Eigen"

Eigen is a German word meaning "own" or "typical"

"das ist ihnen eigen " is German for "that is typical of them"

Sometimes in English we use the word "characteristic", so an eigenvector can be called a "characteristic vector".

Not Just Two Dimensions

Eigenvectors work perfectly well in 3 and higher dimensions.

First calculate A − λI :

Now the determinant should equal zero:

(2−λ) [ (4−λ)(3−λ) − 5×4 ] = 0

This ends up being a cubic equation, but just looking at it here we see one of the roots is 2 (because of 2−λ), and the part inside the square brackets is Quadratic, with roots of −1 and 8 .

So the Eigenvalues are −1 , 2 and 8

Example (continued): find the Eigenvector that matches the Eigenvalue −1

Put in the values we know:

After multiplying we get these equations:

So x = 0 , and y = −z and so the eigenvector is any non-zero multiple of this:

So Av = λv , yay!

(You can try your hand at the eigenvalues of 2 and 8 )

Back in the 2D world again, this matrix will do a rotation by θ:

Example: Rotate by 30°

cos(30°) = √3 2 and sin(30°) = 1 2 , so:

But if we rotate all points , what is the "direction that doesn't change direction"?

Let us work through the mathematics to find out:

( √3 2 −λ)( √3 2 −λ) − ( −1 2 )( 1 2 ) = 0

Which becomes this Quadratic Equation:

λ 2 − (√3)λ + 1 = 0

Whose roots are:

λ = √3 2 ± i 2

The eigenvalues are complex!

I don't know how to show you that on a graph, but we still get a solution.

Eigenvector

So, what is an eigenvector that matches, say, the √3 2 + i 2 root?

√3 2 x − 1 2 y = √3 2 x + i 2 x

1 2 x + √3 2 y = √3 2 y + i 2 y

Which simplify to:

And the solution is any non-zero multiple of:

Wow, such a simple answer!

Is this just because we chose 30°? Or does it work for any rotation matrix? I will let you work that out! Try another angle, or better still use "cos(θ)" and "sin(θ)".

Oh, and let us check at least one of those solutions:

Does it match this?

Oh yes it does!

Online Eigenvalue Calculator

Compute eigenvalues with wolfram|alpha.

• Natural Language

More than just an online eigenvalue calculator

Wolfram|Alpha is a great resource for finding the eigenvalues of matrices. You can also explore eigenvectors, characteristic polynomials, invertible matrices, diagonalization and many other matrix-related topics.

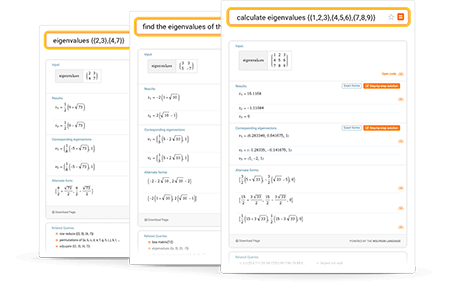
Learn more about:

• Eigenvalues

Tips for entering queries

Use plain English or common mathematical syntax to enter your queries. To enter a matrix, separate elements with commas and rows with curly braces, brackets or parentheses.

• eigenvalues {{2,3},{4,7}}
• calculate eigenvalues {{1,2,3},{4,5,6},{7,8,9}}
• find the eigenvalues of the matrix ((3,3),(5,-7))
• [[2,3],[5,6]] eigenvalues
• View more examples

Access instant learning tools

Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator

• Step-by-step solutions
• Wolfram Problem Generator

Eigenvalues

We come up with the terms eigenvalues and eigenvectors when we study the linear transformations. Some vectors change almost by their scale factors when some linear transformation (matrix) is applied to it. Such vectors are known as eigenvectors and the corresponding scale factors are known as eigenvalues of matrix.

Let us learn more about the eigenvalues of matrix along with their properties and examples.

What are Eigenvalues of Matrix?

The eigenvalues of matrix are scalars by which some vectors (eigenvectors) change when the matrix (transformation) is applied to it. In other words, if A is a square matrix of order n x n and v is a non-zero column vector of order n x 1 such that Av = λv (it means that the product of A and v is just a scalar multiple of v ), then the scalar (real number) λ is called an eigenvalue of the matrix A that corresponds to the eigenvector v .

The word "eigen" is from the German language and it means "characteristic", "proper", or "own". Thus, eigenvalues are also known as "characteristic values" (or) "characteristic roots" (or) "proper values", etc. The mathematical definition of eigenvalues is as shown below.

How to Find Eigenvalues?

From the definition of eigenvalues, if λ is an eigenvalue of a square matrix A, then

If I is the identity matrix of the same order as A, then we can write the above equation as

A v = λ (I v ) (because v = I v )

A v - λ (I v ) = 0

Taking v as common factor,

v (A - λI) = 0

This represents a homogeneous system of linear equations and it has a non-trivial solution only when the determinant of the coefficient matrix is 0.

i.e., |A - λI| = 0

This equation is called the characteristic equation (where |A - λI| is called the characteristic polynomial) and by solving this for λ, we get the eigenvalues. Here is the step-by-step process used to find the eigenvalues of a square matrix A.

• Take the identity matrix I whose order is the same as A.
• Multiply every element of I by λ to get λI.
• Subtract λI from A to get A - λI.
• Find its determinant .
• Set the determinant to zero and solve for λ.

Let us apply these steps to find the eigenvalues of matrices of different orders.

Eigenvalues of a 2x2 Matrix

Let us see the process of finding the eigenvalues of a 2x2 matrix with an example where we will find the eigenvalues of A = \(\begin{equation} \left[\begin{array}{ll} 5 & 4 \\ \\ 1 & 2 \end{array}\right] \end{equation}\). Let λ represents its eigenvalue(s). The identity matrix of order 2x2 is, I = \(\begin{equation} \left[\begin{array}{ll} 1 & 0 \\ \\ 0 & 1 \end{array}\right] \end{equation}\). Then

λI = λ \(\begin{equation} \left[\begin{array}{ll} 1 & 0 \\ \\ 0 & 1 \end{array}\right] \end{equation}\) = \(\begin{equation} \left[\begin{array}{ll} λ & 0 \\ \\ 0 & λ \end{array}\right] \end{equation}\)

A - λI = \(\begin{equation} \left[\begin{array}{ll} 5 & 4 \\ \\ 1 & 2 \end{array}\right] \end{equation}\) - \(\begin{equation} \left[\begin{array}{ll} λ & 0 \\ \\ 0 & λ \end{array}\right] \end{equation}\)

= \(\begin{equation} \left[\begin{array}{ll} 5 -λ& 4 \\ \\ 1 & 2 - λ \end{array}\right] \end{equation}\)

Its determinant is,

|A - λI| = (5 - λ) (2 - λ) - (1)(4)

= 10 - 5λ - 2λ + λ 2 - 4

= λ 2 - 7λ + 6

The characteristic equation is,

|A - λI| = 0

λ 2 - 7λ + 6 = 0

(λ - 6)(λ - 1) = 0

λ - 6 = 0; λ - 1 = 0

λ = 6; λ = 1

Thus, the eigenvalues of matrix A are 1 and 6.

Eigenvalues of a 3x3 Matrix

Let us just observe the result of A - λI in the previous section. Isn't it just the matrix obtained by subtracting λ from all diagonal elements of A? Yes, so we will use this fact here and find the eigenvalues of 3x3 matrix A = \(\begin{equation} \left[\begin{array}{lll} 3 & 1 & 1 \\ 2 & 4 & 2 \\ 1 & 1 & 3 \end{array}\right] \end{equation}\).

\(\begin{equation} \left|\begin{array}{lll} 3 - λ & 1 & 1 \\ 2 & 4 - λ & 2 \\ 1 & 1 & 3 - λ \end{array}\right| \end{equation}\) = 0

(3 - λ) [(4 - λ)(3 - λ) - 2(1) ] - 1 [ 2(3 - λ) - 2(1) ] + 1 [2 (1) - 1 (4 - λ) ] = 0

(3 - λ) [12 - 4λ - 3λ + λ 2 - 2] - 6 + 2λ + 2 + 2 - 4 + λ = 0

(3 - λ) [10 - 7λ + λ 2 ] - 6 + 3λ = 0

30 - 21λ + 3λ 2 - 10λ + 7λ 2 - λ 3 - 6 + 3λ = 0

-λ 3 + 10λ 2 - 28λ + 24 = 0

Multiplying both sides by -1,

λ 3 - 10λ 2 + 28λ - 24 = 0

This is a cubic equation . We will find one of its roots by trial and error and the other roots by synthetic division. By trial and error, we can see that λ = 2 satisfies the above equation (substitute and check whether we get 0 = 0). Now, using synthetic division ,

Set the quotient equal to 0.

λ 2 - 8λ + 12 = 0

(λ - 6)(λ - 2) = 0

λ = 6; λ = 2

Thus, the eigenvalues of the given 3x3 matrix are 2, 2, and 6.

Properties of Eigenvalues

• A square matrix of order n has at most n eigenvalues.
• An identity matrix has only one eigenvalue which is 1.
• The eigenvalues of triangular matrices and diagonal matrices are nothing but the elements of their principal diagonal.
• The sum of eigenvalues of matrix A is equal to the sum of its diagonal elements.
• The product of eigenvalues of matrix A is equal to its determinant .
• The eigenvalues of hermitian and symmetric matrices are real.
• The eigenvalues of skew hermitian and skew-symmetric matrices are either zeros are purely imaginary numbers .
• A matrix and its transpose have the same eigenvalues.
• If A and B are two square matrices of the same order, then AB and BA have the same eigenvalues.
• The eigenvalues of an orthogonal matrix are 1 and -1.
• If λ is an eigenvalue of A, then kλ is an eigenvalue of kA, where 'k' is a scalar.
• If λ is an eigenvalue of A, then λ k is an eigenvalue of A k .
• If λ is an eigenvalue of A, then 1/λ is an eigenvalue of A -1 (if the inverse of A exists).
• If λ is an eigenvalue of A, then |A| / λ is an eigenvalue of the adjoint of A.

Apart from these properties, we have another theorem related to eigenvalues called the " Caley-Hamilton Theorem " . It says, "every square matrix satisfies its characteristic equation". i.e., if A is a square matrix then it satisfies |A - λI| = 0. For example, if λ 2 - 8λ + 12 = 0 is the characteristic equation of a square matrix A, then A 2 - 8A + 12 = 0.

Applications of Eigenvalues

• Eigenvalues are used in electric circuits, quantum mechanics, control theory, etc.
• They are used in the design of car stereo systems.
• They are also used to design bridges.
• It is not surprising to know that eigenvalues are also used in determining Google's page rank.
• They are used in geometric transformations.

Examples of Eigenvalues

Example 1: Find the eigenvalues of the matrix \(\begin{equation} \left[\begin{array}{lll} 3 & 0 & 0 \\ -1 & 2 & 0 \\ 2 & 0 & -3 \end{array}\right] \end{equation}\).

The given matrix is a lower triangular matrix. Hence its eigenvalues are nothing but its diagonal elements which are 3, 2, and -3.

The characteristic equation of the given matrix is:

\(\begin{equation} \left|\begin{array}{lll} 3 - λ & 0 & 0 \\ -1 & 2 - λ& 0 \\ 2 & 0 & -3 - λ \end{array}\right| \end{equation}\) = 0

Expanding the determinant using the first row:

(3 - λ)(2 - λ)(-3 - λ) = 0

3 - λ = 0; 2 - λ = 0; -3 - λ = 0

λ = 3; λ = 2; λ = -3

Answer: 3, 2, and -3.

Example 2: Prove that the eigenvalues of the 2x2 matrix \(\begin{equation} \left[\begin{array}{ll} 0 & -1 \\ \\ 1 & 0 \end{array}\right] \end{equation}\)

\(\begin{equation} \left|\begin{array}{ll} 0 - λ & -1 \\ \\ 1 & 0 - λ \end{array}\right| \end{equation}\) = 0

\(\begin{equation} \left|\begin{array}{ll} -λ & -1 \\ \\ 1 & - λ \end{array}\right| \end{equation}\) = 0

λ 2 + 1 = 0

λ = ± √(-1) = ± i

But eigenvalues should be real numbers .

Answer: The given matrix has no eigenvalues.

Example 3: Find the eigenvalues of \(\begin{equation} \left|\begin{array}{lll} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array}\right| \end{equation}\).

\(\begin{equation} \left[\begin{array}{lll} 1- λ & 1 & 1 \\ 1 & 1- λ & 1 \\ 1 & 1 & 1- λ \end{array}\right] \end{equation}\)

(1 - λ) [ (1 - λ)(1 - λ) - 1 ] - 1 (1 - λ - 1) + 1 (1 - 1 + λ) = 0

(1 - λ) (1 - 2λ + λ 2 - 1) + λ + λ = 0

(1 - λ) (λ 2 -2λ) + 2λ = 0

λ 2 - 2λ - λ 3 + 2λ 2 + 2λ = 0

-λ 3 + 3λ 2 = 0

λ 2 (-λ + 3) = 0

λ 2 = 0; -λ + 3 = 0

λ = 0, 0, 3

Answer: 0, 0, 3.

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Eigenvalues

go to slide go to slide

FAQs on Eigenvalues

What is the definition of eigenvalues.

Eigenvalues of a matrix are scalars by which eigenvectors change when the matrix or transformation is applied to it. Mathematically, if A v = λ v , then

• λ is called the eigenvalue
• v is called the corresponding eigenvector

How can We Find the Eigenvalues of Matrix?

To find the eigenvalues of a square matrix A:

• Find its characteristic equation using |A - λI| = 0, where I is the identity matrix of same order A.
• Solve it for λ and the solutions would give the eigenvalues.

What are the Eigenvalues of a Diagonal Matrix?

We know that all the elements of a diagonal matrix other than its diagonal elements are zeros. Hence, the eigen values of a diagonal matrix are just its diagonal elements.

How to Find Eigenvalues and Eigenvectors?

For any square matrix A:

• Solve |A - λI| = 0 for λ to find eigenvalues.
• Solve (A - λI) v = 0 for v to get corresponding eigenvectors.

Where Can We Find Eigenvalue Calculator?

We can find the eigenvalue calculator by clicking here . Here, you can enter any 2x2 matrix, then it will show you the eigenvalues along with steps.

What is Characteristic Equation For Finding Eigenvalues?

If A is a square matrix and λ represents its eigenvalues then |A - λI| = 0 represents its characteristic equation and by solving this would result in the eigenvalues.

What are the Eigenvalues of an Upper Triangular Matrix?

Since in upper triangular matrix , all elements under the principal diagonal are zeros, the eigenvalues are nothing but the diagonal elements of the matrix.

What are the Eigenvalues of a Unitary Matrix?

A unitary matrix is a complex matrix such that its inverse is equal to its conjugate transpose. The eigenvalues of a unitary matrix are -1 and 1.

• IIT JEE Study Material

Eigenvalues and Eigenvectors Problems and Solutions

Introduction to eigenvalues and eigenvectors.

A rectangular arrangement of numbers in the form of rows and columns is known as a matrix. In this article, we will discuss Eigenvalues and Eigenvectors Problems and Solutions .

Download Complete Chapter Notes of Matrices & Determinants Download Now

Consider a square matrix n × n. If X is the non-trivial column vector solution of the matrix equation AX = λX, where λ is a scalar, then X is the eigenvector of matrix A, and the corresponding value of λ is the eigenvalue of matrix A.

Suppose the matrix equation is written as A X – λ X = 0. Let I be the n × n identity matrix.

If I X is substituted by X in the equation above, we obtain

A X – λ I X = 0.

The equation is rewritten as (A – λ I) X = 0.

The equation above consists of non-trivial solutions if and only if the determinant value of the matrix is 0. The characteristic equation of A is Det (A – λ I) = 0. ‘A’ being an n × n matrix, if (A – λ I) is expanded, (A – λ I) will be the characteristic polynomial of A because its degree is n.

Properties of Eigenvalues

Let A be a matrix with eigenvalues λ 1 , λ 2 ,…., λ n .

The following are the properties of eigenvalues.

(1) The trace of A, defined as the sum of its diagonal elements, is also the sum of all eigenvalues,

\(\begin{array}{l}{\displaystyle {tr} (A)=\sum _{i=1}^{n}a_{ii}=\sum _{i=1}^{n}\lambda _{i}=\lambda _{1}+\lambda _{2}+\cdots +\lambda _{n}.}\end{array} \)

(2) The determinant of A is the product of all its eigenvalues, \(\begin{array}{l}{\displaystyle \det(A)=\prod _{i=1}^{n}\lambda _{i}=\lambda _{1}\lambda _{2}\cdots \lambda _{n}.}\end{array} \)

(3) The eigenvalues of the k th power of A, that is, the eigenvalues of A k , for any positive integer k, are \(\begin{array}{l}{\displaystyle \lambda _{1}^{k},…,\lambda _{n}^{k}}.\end{array} \) .

(4) The matrix A is invertible if and only if every eigenvalue is nonzero.

(5) If A is invertible, then the eigenvalues of A -1 are \(\begin{array}{l}{\displaystyle {\frac {1}{\lambda _{1}}},…,{\frac {1}{\lambda _{n}}}}\end{array} \) and each eigenvalue’s geometric multiplicity coincide. The characteristic polynomial of the inverse is the reciprocal polynomial of the original, the eigenvalues share the same algebraic multiplicity.

(6) If A is equal to its conjugate transpose, or equivalently if A is Hermitian, then every eigenvalue is real. The same is true for any real symmetric matrix.

(7) If A is not only Hermitian but also positive-definite, positive-semidefinite, negative-definite, or negative-semidefinite, then every eigenvalue is positive, non-negative, negative, or non-positive, respectively.

(8) If A is unitary, every eigenvalue has absolute value |λ i | = 1.

(9) If A is a n×n matrix and {λ 1 , λ 2 ,…., λ k } are its eigenvalues, then the eigenvalues of the matrix I + A (where I is the identity matrix) are {λ 1 + 1, λ 2 +1,…., λ k +1}.

Also, Read:

Eigenvectors of a Matrix

Adjoint and Inverse of a Matrix

Normalized and Decomposition of Eigenvectors

Eigenvalues and Eigenvectors Solved Problems

Example 1: Find the eigenvalues and eigenvectors of the following matrix.

Example 2: Find all eigenvalues and corresponding eigenvectors for the matrix A if

\(\begin{array}{l}\begin{pmatrix}2&-3&0\\ \:\:2&-5&0\\ \:\:0&0&3\end{pmatrix}\end{array} \)

Solution:  

\(\begin{array}{l}\det \left(\begin{pmatrix}2&-3&0\\ 2&-5&0\\ 0&0&3\end{pmatrix}-λ\begin{pmatrix}1&0&0\\ 0&1&0\\ 0&0&1\end{pmatrix}\right)\\\begin{pmatrix}2&-3&0\\ 2&-5&0\\ 0&0&3\end{pmatrix}-λ\begin{pmatrix}1&0&0\\ 0&1&0\\ 0&0&1\end{pmatrix}\\λ\begin{pmatrix}1&0&0\\ 0&1&0\\ 0&0&1\end{pmatrix}=\begin{pmatrix}λ&0&0\\ 0&λ&0\\ 0&0&λ\end{pmatrix}\\=\begin{pmatrix}2&-3&0\\ 2&-5&0\\ 0&0&3\end{pmatrix}-\begin{pmatrix}λ&0&0\\ 0&λ&0\\ 0&0&λ\end{pmatrix}\\=\begin{pmatrix}2-λ&-3&0\\ 2&-5-λ&0\\ 0&0&3-λ\end{pmatrix}\\=\det \begin{pmatrix}2-λ&-3&0\\ 2&-5-λ&0\\ 0&0&3-λ\end{pmatrix}\\=\left(2-λ\right)\det \begin{pmatrix}-5-λ&0\\ 0&3-λ\end{pmatrix}-\left(-3\right)\det \begin{pmatrix}2&0\\ 0&3-λ\end{pmatrix}+0\cdot \det \begin{pmatrix}2&-5-λ\\ 0&0\end{pmatrix}\\=\left(2-λ\right)\left(λ^2+2λ-15\right)-\left(-3\right)\cdot \:2\left(-λ+3\right)+0\cdot \:0\\=-λ^3+13λ-12\\-λ^3+13λ-12=0\\-\left(λ-1\right)\left(λ-3\right)\left(λ+4\right)=0\\\mathrm{The\:eigenvalues\:are:}\\λ=1,\:λ=3,\:λ=-4\\\mathrm{Eigenvectors\:for\:}λ=1\\\begin{pmatrix}2&-3&0\\ 2&-5&0\\ 0&0&3\end{pmatrix}-1\cdot \begin{pmatrix}1&0&0\\ 0&1&0\\ 0&0&1\end{pmatrix}=\begin{pmatrix}1&-3&0\\ 2&-6&0\\ 0&0&2\end{pmatrix}\\\left(A-1I\right)\begin{pmatrix}x\\ y\\ z\end{pmatrix}=\begin{pmatrix}1&-3&0\\ 0&0&1\\ 0&0&0\end{pmatrix}\begin{pmatrix}x\\ y\\ z\end{pmatrix}=\begin{pmatrix}0\\ 0\\ 0\end{pmatrix}\\\begin{Bmatrix}x-3y=0\\ z=0\end{Bmatrix}\\Isolate\\\begin{Bmatrix}z=0\\ x=3y\end{Bmatrix}\\\mathrm{Plug\:into\:}\begin{pmatrix}x\\ y\\ z\end{pmatrix}\\η=\begin{pmatrix}3y\\ y\\ 0\end{pmatrix}\space\space\:y\ne \:0\\\mathrm{Let\:}y=1\\\begin{pmatrix}3\\ 1\\ 0\end{pmatrix}\\Similarly\\\mathrm{Eigenvectors\:for\:}λ=3:\quad \begin{pmatrix}0\\ 0\\ 1\end{pmatrix}\\\mathrm{Eigenvectors\:for\:}λ=-4:\quad \begin{pmatrix}1\\ 2\\ 0\end{pmatrix}\\\mathrm{The\:eigenvectors\:for\:}\begin{pmatrix}2&-3&0\\ 2&-5&0\\ 0&0&3\end{pmatrix}\\=\begin{pmatrix}3\\ 1\\ 0\end{pmatrix},\:\begin{pmatrix}0\\ 0\\ 1\end{pmatrix},\:\begin{pmatrix}1\\ 2\\ 0\end{pmatrix}\\\end{array} \)

Example 3: Consider the matrix

for some variable ‘a’. Find all values of ‘a’, which will prove that A has eigenvalues 0, 3, and −3.

Let p (t) be the characteristic polynomial of A, i.e. let p (t) = det (A − tI) = 0. By expanding along the second column of A − tI, we can obtain the equation

= (3 − t) (2 + t + 2t + t 2 −4) + 2 (−2a − ta + 5)

= (3 − t) (t 2 + 3t − 2) + (−4a −2ta + 10)

= 3t 2 + 9t − 6 − t 3 − 3t 2 + 2t − 4a − 2ta + 10

= −t 3 + 11t − 2ta + 4 − 4a

= −t 3 + (11 − 2a) t + 4 − 4a

For the eigenvalues of A to be 0, 3 and −3, the characteristic polynomial p (t) must have roots at t = 0, 3, −3. This implies p (t) = –t (t − 3) (t + 3) =–t(t 2 − 9) = –t 3 + 9t.

Therefore, −t 3 + (11 − 2a) t + 4 − 4a = −t 3 + 9t.

For this equation to hold, the constant terms on the left and right-hand sides of the above equation must be equal. This means that 4 − 4a = 0, which implies a = 1.

Hence, A has eigenvalues 0, 3, and −3 precisely when a = 1.

Example 4: Find the eigenvalues and eigenvectors of \(\begin{array}{l}\begin{pmatrix}2&0&0\\ \:0&3&4\\ \:0&4&9\end{pmatrix}\end{array} \)

Frequently Asked Questions

What do you mean by eigenvalues.

Eigenvalues are the special set of scalar values associated with the set of linear equations in the matrix equations.

Can the eigenvalue be zero?

Yes, the eigenvalue can be zero.

Can a singular matrix have eigenvalues?

Every singular matrix has a 0 eigenvalue.

How to find the eigenvalues of a square matrix A?

Use the equation det(A-λI) = 0 and solve for λ. Determine all the possible values of λ, which are the required eigenvalues of matrix A.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

• Share Share

Register with Aakash BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Help Center Help Center

• Help Center
• Trial Software
• Product Updates
• Documentation

Eigenvalues and eigenvectors

Description

e = eig( A ) returns a column vector containing the eigenvalues of square matrix A .

[ V , D ] = eig( A ) returns diagonal matrix D of eigenvalues and matrix V whose columns are the corresponding right eigenvectors, so that A*V = V*D .

[ V , D , W ] = eig( A ) also returns full matrix W whose columns are the corresponding left eigenvectors, so that W'*A = D*W' .

The eigenvalue problem is to determine the solution to the equation A v = λ v , where A is an n -by- n matrix, v is a column vector of length n , and λ is a scalar. The values of λ that satisfy the equation are the eigenvalues. The corresponding values of v that satisfy the equation are the right eigenvectors. The left eigenvectors, w , satisfy the equation w ’ A = λ w ’.

e = eig( A , B ) returns a column vector containing the generalized eigenvalues of square matrices A and B .

[ V , D ] = eig( A , B ) returns diagonal matrix D of generalized eigenvalues and full matrix V whose columns are the corresponding right eigenvectors, so that A*V = B*V*D .

[ V , D , W ] = eig( A , B ) also returns full matrix W whose columns are the corresponding left eigenvectors, so that W'*A = D*W'*B .

The generalized eigenvalue problem is to determine the solution to the equation A v = λ B v , where A and B are n -by- n matrices, v is a column vector of length n , and λ is a scalar. The values of λ that satisfy the equation are the generalized eigenvalues. The corresponding values of v are the generalized right eigenvectors. The left eigenvectors, w , satisfy the equation w ’ A = λ w ’ B .

[ ___ ] = eig( A , balanceOption ) , where balanceOption is "nobalance" , disables the preliminary balancing step in the algorithm. The default for balanceOption is "balance" , which enables balancing. The eig function can return any of the output arguments in previous syntaxes.

[ ___ ] = eig( A , B , algorithm ) , where algorithm is "chol" , uses the Cholesky factorization of B to compute the generalized eigenvalues. The default for algorithm depends on the properties of A and B , but is "qz" , which uses the QZ algorithm, when A or B are not symmetric.

[ ___ ] = eig( ___ , outputForm ) returns the eigenvalues in the form specified by outputForm using any of the input or output arguments in previous syntaxes. Specify outputForm as "vector" to return the eigenvalues in a column vector or as "matrix" to return the eigenvalues in a diagonal matrix.

collapse all

Eigenvalues of Matrix

Use gallery to create a symmetric positive definite matrix.

Calculate the eigenvalues of A . The result is a column vector.

Alternatively, use outputForm to return the eigenvalues in a diagonal matrix.

Eigenvalues and Eigenvectors of Matrix

Use gallery to create a circulant matrix.

Calculate the eigenvalues and right eigenvectors of A .

Verify that the results satisfy A*V = V*D .

Ideally, the eigenvalue decomposition satisfies the relationship. Since eig performs the decomposition using floating-point computations, then A*V can, at best, approach V*D . In other words, A*V - V*D is close to, but not exactly, 0 .

Sorted Eigenvalues and Eigenvectors

By default eig does not always return the eigenvalues and eigenvectors in sorted order. Use the sort function to put the eigenvalues in ascending order and reorder the corresponding eigenvectors.

Calculate the eigenvalues and eigenvectors of a 5-by-5 magic square matrix.

The eigenvalues of A are on the diagonal of D . However, the eigenvalues are unsorted.

Extract the eigenvalues from the diagonal of D using diag(D) , then sort the resulting vector in ascending order. The second output from sort returns a permutation vector of indices.

Use ind to reorder the diagonal elements of D . Since the eigenvalues in D correspond to the eigenvectors in the columns of V , you must also reorder the columns of V using the same indices.

Both (V,D) and (Vs,Ds) produce the eigenvalue decomposition of A . The results of A*V-V*D and A*Vs-Vs*Ds agree, up to round-off error.

Left Eigenvectors

Create a 3-by-3 matrix.

Calculate the right eigenvectors, V , the eigenvalues, D , and the left eigenvectors, W .

Verify that the results satisfy W'*A = D*W' .

Ideally, the eigenvalue decomposition satisfies the relationship. Since eig performs the decomposition using floating-point computations, then W'*A can, at best, approach D*W' . In other words, W'*A - D*W' is close to, but not exactly, 0 .

Eigenvalues of Nondiagonalizable (Defective) Matrix

A has repeated eigenvalues and the eigenvectors are not independent. This means that A is not diagonalizable and is, therefore, defective.

Verify that V and D satisfy the equation, A*V = V*D , even though A is defective.

Generalized Eigenvalues

Create two matrices, A and B , then solve the generalized eigenvalue problem for the eigenvalues and right eigenvectors of the pair (A,B) .

Verify that the results satisfy A*V = B*V*D .

The residual error A*V - B*V*D is exactly zero.

Generalized Eigenvalues Using QZ Algorithm for Badly Conditioned Matrices

Create a badly conditioned symmetric matrix containing values close to machine precision.

Calculate the generalized eigenvalues and a set of right eigenvectors using the default algorithm. In this case, the default algorithm is "chol" .

Now, calculate the generalized eigenvalues and a set of right eigenvectors using the "qz" algorithm.

Check how well the "chol" result satisfies A*V1 = A*V1*D1 .

Now, check how well the "qz" result satisfies A*V2 = A*V2*D2 .

When both matrices are symmetric, eig uses the "chol" algorithm by default. In this case, the QZ algorithm returns more accurate results.

Generalized Eigenvalues Where One Matrix Is Singular

Create a 2-by-2 identity matrix, A , and a singular matrix, B .

If you attempt to calculate the generalized eigenvalues of the matrix B - 1 A with the command [V,D] = eig(B\A) , then MATLAB® returns an error because B\A produces Inf values.

Instead, calculate the generalized eigenvalues and right eigenvectors by passing both matrices to the eig function.

It is better to pass both matrices separately, and let eig choose the best algorithm to solve the problem. In this case, eig(A,B) returns a set of eigenvectors and at least one real eigenvalue, even though B is not invertible.

Verify A v = λ B v for the first eigenvalue and the first eigenvector.

Ideally, the eigenvalue decomposition satisfies the relationship. Since the decomposition is performed using floating-point computations, then A*eigvec can, at best, approach eigval*B*eigvec , as it does in this case.

Input Arguments

A — input matrix square matrix.

Input matrix, specified as a real or complex square matrix.

Data Types: double | single Complex Number Support: Yes

B — Generalized eigenvalue problem input matrix square matrix

Generalized eigenvalue problem input matrix, specified as a square matrix of real or complex values. B must be the same size as A .

balanceOption — Balance option "balance" (default) | "nobalance"

Balance option, specified as: "balance" , which enables a preliminary balancing step, or "nobalance" which disables it. In most cases, the balancing step improves the conditioning of A to produce more accurate results. However, there are cases in which balancing produces incorrect results. Specify "nobalance" when A contains values whose scale differs dramatically. For example, if A contains nonzero integers, as well as very small (near zero) values, then the balancing step might scale the small values to make them as significant as the integers and produce inaccurate results.

"balance" is the default behavior. For more information about balancing, see balance .

algorithm — Generalized eigenvalue algorithm "chol" (default) | "qz"

Generalized eigenvalue algorithm, specified as "chol" or "qz" , which selects the algorithm to use for calculating the generalized eigenvalues of a pair.

In general, the two algorithms return the same result. The QZ algorithm can be more stable for certain problems, such as those involving badly conditioned matrices.

Regardless of the algorithm you specify, the eig function always uses the QZ algorithm when A or B are not symmetric.

outputForm — Output format of eigenvalues "vector" | "matrix"

Output format of eigenvalues, specified as "vector" or "matrix" . This option allows you to specify whether the eigenvalues are returned in a column vector or a diagonal matrix. The default behavior varies according to the number of outputs specified:

If you specify one output, such as e = eig(A) , then the eigenvalues are returned as a column vector by default.

If you specify two or three outputs, such as [V,D] = eig(A) , then the eigenvalues are returned as a diagonal matrix, D , by default.

Example: D = eig(A,"matrix") returns a diagonal matrix of eigenvalues with the one output syntax.

Output Arguments

E — eigenvalues (returned as vector) column vector.

Eigenvalues, returned as a column vector containing the eigenvalues (or generalized eigenvalues of a pair) with multiplicity. Each eigenvalue e(k) corresponds with the right eigenvector V(:,k) and the left eigenvector W(:,k) .

When A is real symmetric or complex Hermitian , the values of e that satisfy A v = λ v are real.

When A is real skew-symmetric or complex skew-Hermitian , the values of e that satisfy A v = λ v are imaginary.

V — Right eigenvectors square matrix

Right eigenvectors, returned as a square matrix whose columns are the right eigenvectors of A or generalized right eigenvectors of the pair, (A,B) . The form and normalization of V depends on the combination of input arguments:

[V,D] = eig(A) returns matrix V , whose columns are the right eigenvectors of A such that A*V = V*D . The eigenvectors in V are normalized so that the 2-norm of each is 1.

If A is real symmetric , Hermitian , or skew-Hermitian , then the right eigenvectors V are orthonormal.

[V,D] = eig(A,"nobalance") also returns matrix V . However, the 2-norm of each eigenvector is not necessarily 1.

[V,D] = eig(A,B) and [V,D] = eig(A,B,algorithm) return V as a matrix whose columns are the generalized right eigenvectors that satisfy A*V = B*V*D . The 2-norm of each eigenvector is not necessarily 1. In this case, D contains the generalized eigenvalues of the pair, (A,B) , along the main diagonal.

When eig uses the "chol" algorithm with symmetric (Hermitian) A and symmetric (Hermitian) positive definite B , it normalizes the eigenvectors in V so that the B -norm of each is 1.

Different machines and releases of MATLAB ® can produce different eigenvectors that are still numerically accurate:

For real eigenvectors, the sign of the eigenvectors can change.

For complex eigenvectors, the eigenvectors can be multiplied by any complex number of magnitude 1.

For a multiple eigenvalue, its eigenvectors can be recombined through linear combinations. For example, if A x = λ x and A y = λ y , then A ( x + y ) = λ ( x + y ) , so x + y also is an eigenvector of A .

D — Eigenvalues (returned as matrix) diagonal matrix

Eigenvalues, returned as a diagonal matrix with the eigenvalues of A on the main diagonal or the eigenvalues of the pair, (A,B) , with multiplicity, on the main diagonal. Each eigenvalue D(k,k) corresponds with the right eigenvector V(:,k) and the left eigenvector W(:,k) .

When A is real symmetric or complex Hermitian , the values of D that satisfy A v = λ v are real.

When A is real skew-symmetric or complex skew-Hermitian , the values of D that satisfy A v = λ v are imaginary.

W — Left eigenvectors square matrix

Left eigenvectors, returned as a square matrix whose columns are the left eigenvectors of A or generalized left eigenvectors of the pair, (A,B) . The form and normalization of W depends on the combination of input arguments:

[V,D,W] = eig(A) returns matrix W , whose columns are the left eigenvectors of A such that W'*A = D*W' . The eigenvectors in W are normalized so that the 2-norm of each is 1. If A is symmetric , then W is the same as V .

[V,D,W] = eig(A,"nobalance") also returns matrix W . However, the 2-norm of each eigenvector is not necessarily 1.

[V,D,W] = eig(A,B) and [V,D,W] = eig(A,B,algorithm) returns W as a matrix whose columns are the generalized left eigenvectors that satisfy W'*A = D*W'*B . The 2-norm of each eigenvector is not necessarily 1. In this case, D contains the generalized eigenvalues of the pair, (A,B) , along the main diagonal.

If A and B are symmetric , then W is the same as V .

Different machines and releases of MATLAB can produce different eigenvectors that are still numerically accurate:

Symmetric Matrix

A square matrix, A , is symmetric if it is equal to its nonconjugate transpose, A = A.' .

In terms of the matrix elements, this means that

a i ,   j = a j ,   i     .

Since real matrices are unaffected by complex conjugation, a real matrix that is symmetric is also Hermitian. For example, the matrix

A = [ 1 0 0 2 1 0 1 0 1 ]

is both symmetric and Hermitian.

Skew-Symmetric Matrix

A square matrix, A , is skew-symmetric if it is equal to the negation of its nonconjugate transpose, A = -A.' .

a i ,   j = − a j ,   i     .

Since real matrices are unaffected by complex conjugation, a real matrix that is skew-symmetric is also skew-Hermitian. For example, the matrix

A = [ 0 − 1 1       0 ]

is both skew-symmetric and skew-Hermitian.

Hermitian Matrix

A square matrix, A , is Hermitian if it is equal to its complex conjugate transpose, A = A' .

In terms of the matrix elements,

a i ,   j = a ¯ j ,   i     .

The entries on the diagonal of a Hermitian matrix are always real. Because real matrices are unaffected by complex conjugation, a real matrix that is symmetric is also Hermitian. For example, this matrix is both symmetric and Hermitian.

The eigenvalues of a Hermitian matrix are real.

Skew-Hermitian Matrix

A square matrix, A , is skew-Hermitian if it is equal to the negation of its complex conjugate transpose, A = -A' .

a i ,   j = − a ¯ j ,   i     .

The entries on the diagonal of a skew-Hermitian matrix are always pure imaginary or zero. Since real matrices are unaffected by complex conjugation, a real matrix that is skew-symmetric is also skew-Hermitian. For example, the matrix

is both skew-Hermitian and skew-symmetric.

The eigenvalues of a skew-Hermitian matrix are purely imaginary or zero.

The eig function can calculate the eigenvalues of sparse matrices that are real and symmetric. To calculate the eigenvectors of a sparse matrix, or to calculate the eigenvalues of a sparse matrix that is not real and symmetric, use the eigs function.

Extended Capabilities

C/c++ code generation generate c and c++ code using matlab® coder™..

Usage notes and limitations:

V might represent a different basis of eigenvectors. This representation means that the eigenvector calculated by the generated code might be different in C and C++ code than in MATLAB. The eigenvalues in D might not be in the same order as in MATLAB. You can verify the V and D values by using the eigenvalue problem equation A*V = V*D .

If you specify the LAPACK library callback class, then the code generator supports these options:

The computation of left eigenvectors.

Outputs are complex.

Code generation does not support sparse matrix inputs for this function.

Thread-Based Environment Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool .

This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment .

GPU Arrays Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

The eig function partially supports GPU arrays. Some syntaxes of the function run on a GPU when you specify the input data as a gpuArray (Parallel Computing Toolbox) . Usage notes and limitations:

For the generalized case, eig(A,B) , A and B must be real symmetric or complex Hermitian. Additionally, B must be positive definite.

The QZ algorithm, eig(A,B,"qz") , is not supported.

For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox) .

Distributed Arrays Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.

These syntaxes are not supported for full distributed arrays:

[__] = eig(A,B,"qz")

[V,D,W] = eig(A,B)

For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox) .

Version History

R2021b: eig returns nan for nonfinite inputs.

eig returns NaN values when the input contains nonfinite values ( Inf or NaN ). Previously, eig threw an error when the input contained nonfinite values.

R2021a: Improved algorithm for skew-Hermitian matrices

The algorithm for input matrices that are skew-Hermitian was improved. With the function call [V,D] = eig(A) , where A is skew-Hermitian, eig now guarantees that the matrix of eigenvectors V is unitary and the diagonal matrix of eigenvalues D is purely imaginary.

eigs | polyeig | balance | condeig | cdf2rdf | hess | schur | qz

• Eigenvalues

MATLAB Command

You clicked a link that corresponds to this MATLAB command:

Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site

Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .

• Switzerland (English)
• Switzerland (Deutsch)
• Switzerland (Français)
• 中国 (English)

You can also select a web site from the following list:

How to Get Best Site Performance

Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.

• América Latina (Español)
• Canada (English)
• United States (English)
• Belgium (English)
• Denmark (English)
• Deutschland (Deutsch)
• España (Español)
• Finland (English)
• France (Français)
• Ireland (English)
• Italia (Italiano)
• Luxembourg (English)
• Netherlands (English)
• Norway (English)
• Österreich (Deutsch)
• Portugal (English)
• Sweden (English)
• United Kingdom (English)

Asia Pacific

• Australia (English)
• India (English)
• New Zealand (English)

Contact your local office

Python Numerical Methods

This notebook contains an excerpt from the Python Programming and Numerical Methods - A Guide for Engineers and Scientists , the content is also available at Berkeley Python Numerical Methods .

The copyright of the book belongs to Elsevier. We also have this interactive book online for a better learning experience. The code is released under the MIT license . If you find this content useful, please consider supporting the work on Elsevier or Amazon !

< 15.3 The QR Method | Contents | 15.5 Summary and Problems >

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Pre Calculus
• Linear Algebra
• Add, Subtract
• Multiply, Power
• Determinant
• Minors & Cofactors
• Characteristic Polynomial
• Gauss Jordan (RREF)
• Row Echelon
• LU Decomposition
• Eigenvalues
• Eigenvectors
• Diagonalization
• Exponential
• Scalar Multiplication
• Dot Product
• Cross Product
• Scalar Projection
• Orthogonal Projection
• Gram-Schmidt
• Trigonometry
• Conversions

Most Used Actions

Number line.

• eigenvalues\:\begin{pmatrix}6&-1\\2&3\end{pmatrix}
• eigenvalues\:\begin{pmatrix}1&-2\\-2&0\end{pmatrix}
• eigenvalues\:\begin{pmatrix}2&0&0\\1&2&1\\-1&0&1\end{pmatrix}
• eigenvalues\:\begin{pmatrix}1&2&1\\6&-1&0\\-1&-2&-1\end{pmatrix}

matrix-eigenvalues-calculator

• The Matrix… Symbolab Version Matrix, the one with numbers, arranged with rows and columns, is extremely useful in most scientific fields. There...

Please add a message.

Message received. Thanks for the feedback.

An Ulm-like algorithm for generalized inverse eigenvalue problems

• Original Paper
• Published: 09 May 2024

Cite this article

• Yusong Luo 1 &
• Weiping Shen 1  

29 Accesses

Explore all metrics

In this paper, we study the numerical solutions of the generalized inverse eigenvalue problem (for short, GIEP). Motivated by Ulm’s method for solving general nonlinear equations and the algorithm of Aishima (J. Comput. Appl. Math. 367 , 112485 2020 ) for the GIEP, we propose here an Ulm-like algorithm for the GIEP. Compared with other existing methods for the GIEP, the proposed algorithm avoids solving the (approximate) Jacobian equations and so it seems more stable. Assuming that the relative generalized Jacobian matrices at a solution are nonsingular, we prove the quadratic convergence property of the proposed algorithm. Incidentally, we extend the work of Luo et al. (J. Nonlinear Convex Anal. 24 , 2309–2328 2023 ) for the inverse eigenvalue problem (for short, IEP) to the GIEP. Some numerical examples are provided and comparisons with other algorithms are made.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Similar content being viewed by others

Riemannian inexact Newton method for structured inverse eigenvalue and singular value problems

Disguised and new quasi-Newton methods for nonlinear eigenvalue problems

Solving an abstract nonlinear eigenvalue problem by the inverse iteration method, data availability.

No datasets were generated or analysed during the current study.

Code Availability

Not applicable.

Aishima, K.: A quadratically convergent algorithm based on matrix equations for inverse eigenvalue problems. Linear Algebra Appl. 542 , 310–333 (2018)

Article   MathSciNet   Google Scholar  

Aishima, K.: A quadratically convergent algorithm for inverse eigenvalue problems with multiple eigenvalues. Linear Algebra Appl. 549 , 30–52 (2018)

Aishima, K.: A quadratically convergent algorithm for inverse generalized eigenvalue problems. J. Comput. Appl. Math. 367 , 112485 (2020)

Arela-Pérez, S., Lozano, C., Nina, H., Pickmann-Soto, H., Rodríguez, J.: The new inverse eigenvalue problems for periodic and generalized periodic Jacobi matrices from their extremal spectral data. Linear Algebra Appl. 659 , 55–72 (2023)

Bai, Z.J., Chan, R.H., Morini, B.: An inexact Cayley transform method for inverse eigenvalue problems. Inverse Probl. 20 , 1675–1689 (2004)

Bai, Z.J., Jin, X.Q.: A note on the Ulm-like method for inverse eigenvalue problems. Recent Advances in Scientific Computing and Matrix Analysis, 1–7 (2011)

Behera, K.K.: A generalized inverse eigenvalue problem and m-functions. Linear Algebra Appl. 622 , 46–65 (2021)

Cai, J., Chen, J.: Iterative solutions of generalized inverse eigenvalue problem for partially bisymmetric matrices. Linear Multilinear A. 65 , 1643–1654 (2017)

Chan, R.H., Chung, H.L., Xu, S.F.: The inexact Newton-like method for inverse eigenvalue problem. BIT Numer. Math. 43 , 7–20 (2003)

Chu, M.T., Golub, G.H.: Structured inverse eigenvalue problems. Acta Numer. 11 , 1–71 (2002)

Dai, H.: An algorithm for symmetric generalized inverse eigenvalue problems. Linear Algebra Appl. 296 , 79–98 (1999)

Dai, H., Lancaster, P.: Newton’s method for a generalized inverse eigenvalue problem. Numer. Linear Algebra Appl. 4 , 1–21 (1997)

Dai, H., Bai, Z.Z., Wei, Y.: On the solvability condition and numerical algorithm for the parameterized generalized inverse eigenvalue problem. SIAM J. Matrix Anal. Appl. 36 , 707–726 (2015)

Dalvand, Z., Hajarian, M.: Newton-like and inexact Newton-like methods for a parameterized generalized inverse eigenvalue problem. Math. Methods Appl. Sci. 44 , 4217–4234 (2021)

Dalvand, Z., Hajarian, M., Roman, J.E.: An extension of the Cayley transform method for a parameterized generalized inverse eigenvalue problem. Numer. Linear Algebra Appl. 27 , e2327 (2020)

Ezquerro, J.A., Hernández, M.A.: The Ulm method under mild differentiability conditions. Numer. Math. 109 , 193–207 (2008)

Friedland, S., Nocedal, J., Overton, M.L.: The formulation and analysis of numerical methods for inverse eigenvalue problems. SIAM J. Numer. Anal. 24 , 634–667 (1987)

Gajewski, A., Zyczkowski, M.: Optimal structural design under stability constraints. Kluwer Academic, Dordrecht, The Natherlands (1988)

Book   Google Scholar  

Galperin, A., Waksman, Z.: Ulm’s method under regular smoothness. Numer. Funct. Anal. Optim. 19 , 285–307 (1998)

Ghanbari, K.: A survey on inverse and generalized inverse eigenvalue problems for Jacobi matrices. Appl. Math. Comput. 195 , 355–363 (2008)

MathSciNet   Google Scholar  

Ghanbari, K.: m-functions and inverse generalized eigenvalue problem. Inverse Probl. 17 , 211 (2001)

Golub, G.H., Van Loan, C.F.: Matrix Computations, 3rd edn. Johns Hopkins University Press, Baltimore (1996)

Google Scholar  

Grandhi, R.: Structural optimization with frequency constraints-Areview. AIAA J. 31 , 2296–2303 (1993)

Article   Google Scholar  

Gutiérrez, J.M., Hernández, M.A., Romero, N.: A note on a modification of Moser’s method. J. Complex. 24 , 185–197 (2008)

Hald, O.: On discrete and numerical Sturm-Liouville problems. New York University, New York (1972)

Hald, O.: On a Newton-Moser type method. Numer. Math. 23 , 411–426 (1975)

Harman, H.: Modern factor analysis. University of Chicago Press, Chicago (1976)

Joseph, K.T.: Inverse eigenvalue problem in structural design. AIAA J. 30 , 2890–2896 (1992)

Li, R.C.: A perturbation bound for definite pencils. Linear Algebra Appl. 179 , 191–202 (1993)

Luo, Y.S., Shen, W.P., Luo, E.P.: A quadratically convergent algorithm for inverse eigenvalue problems. J. Nonlinear Convex Anal. 24 , 2309–2328 (2023)

Ma, W.: Two-step Ulm-Chebyshev-like Cayley transform method for inverse eigenvalue problems. Int. J. of Comput. Math. 99 , 391–406 (2022)

Shen, W.P., Li, C., Jin, X.Q.: A Ulm-like method for inverse eigenvalue problems. Appl. Numer. Math. 61 , 356–367 (2011)

Shen, W.P., Li, C., Jin, X.Q.: An inexact Cayley transform method for inverse eigenvalue problems with multiple eigenvalues. Inverse Probl. 31 , 085007 (2015)

Shen, W.P., Li, C., Jin, X.Q.: An Ulm-like Cayley transform method for inverse eigenvalue problems with multiple eigenvalues. Numer. Math. -Theory Me. 9 , 664–685 (2016)

Sivan, D.D., Ram, Y.M.: Mass and stiffness modifications to achieve desired natural frequencies. Commun. Numer. Methods Engrg. 12 , 531–542 (1996)

Sun, D., Sun, J.: Strong semismoothness of eigenvalues of symmetric matrices and its application to inverse eigenvalue problems. SIAM J. Numer. Anal. 40 , 2352–2367 (2002)

Sun, J.G.: Multiple eigenvalue sensitivity analysis. Linear Algebra Appl. 137 , 183–211 (1990)

Ulm, S.: On iterative methods with successive approximation of the inverse operator. Izv. Akad. Nauk Est. SSR 16 , 403–411 (1967)

Wen, C.T., Chen, X.S., Sun, H.W.: A two-step inexact Newton-Chebyshev-like method for inverse eigenvalue problems. Linear Algebra Appl. 585 , 241–262 (2020)

Xie, H.Q., Dai, H.: Inverse eigenvalue problem in structural dynamics design. Number. Math. J. Chinese Univ. 15 , 97–106 (2006)

Zehnder, E.J.: A remark about Newton’s method, Commun. Pure. Appl. Math. 27 , 361–366 (1974)

Zhang, H., Yuan, Y.: Generalized inverse eigenvalue problems for Hermitian and J-Hamiltonian/skew-Hamiltonian matrices. Appl. Math. Comput. 361 , 609–616 (2019)

Download references

Acknowledgements

We would like to thank the anonymous referees for their helpful and valuable comments which lead to the improvement of this paper.

This work was supported in part by the National Natural Science Foundation of China (grant 12071441).

Author information

Authors and affiliations.

School of Mathematical Sciences, Zhejiang Normal University, Jinhua, 321004, People’s Republic of China

Yusong Luo & Weiping Shen

You can also search for this author in PubMed   Google Scholar

Contributions

Yusong Luo and Weiping Shen wrote the main manuscript text. Both authors reviewed the manuscript.

Corresponding author

Correspondence to Weiping Shen .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Ethics approval

Consent to participate.

All authors participated.

Consent for publication

All authors agreed to publish.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Luo, Y., Shen, W. An Ulm-like algorithm for generalized inverse eigenvalue problems. Numer Algor (2024). https://doi.org/10.1007/s11075-024-01845-5

Download citation

Received : 29 November 2023

Accepted : 29 April 2024

Published : 09 May 2024

DOI : https://doi.org/10.1007/s11075-024-01845-5

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Generalized inverse eigenvalue problem
• Newton’s method
• Ulm’s method
• Quadratic convergence

Mathematics Subject Classification (2010)

• Find a journal
• Publish with us
• Track your research

Help | Advanced Search

Mathematics > Optimization and Control

Title: adversarial neural network methods for topology optimization of eigenvalue problems.

Abstract: This research presents a novel method using an adversarial neural network to solve the eigenvalue topology optimization problems. The study focuses on optimizing the first eigenvalues of second-order elliptic and fourth-order biharmonic operators subject to geometry constraints. These models are usually solved with topology optimization algorithms based on sensitivity analysis, in which it is expensive to repeatedly solve the nonlinear constrained eigenvalue problem with traditional numerical methods such as finite elements or finite differences. In contrast, our method leverages automatic differentiation within the deep learning framework. Furthermore, the adversarial neural networks enable different neural networks to train independently, which improves the training efficiency and achieve satisfactory optimization results. Numerical results are presented to verify effectiveness of the algorithms for maximizing and minimizing the first eigenvalues.

Submission history

Access paper:.

• HTML (experimental)
• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .