solving an initial value problem

Module 4: Applications of Derivatives

Initial-value problems, learning outcomes.

• Use antidifferentiation to solve simple initial-value problems

We look at techniques for integrating a large variety of functions involving products, quotients, and compositions later in the text. Here we turn to one common use for antiderivatives that arises often in many applications: solving differential equations.

A differential equation is an equation that relates an unknown function and one or more of its derivatives. The equation

is a simple example of a differential equation. Solving this equation means finding a function [latex]y[/latex] with a derivative [latex]f[/latex]. Therefore, the solutions of [latex]\frac{dy}{dx}[/latex] are the antiderivatives of [latex]f[/latex]. If [latex]F[/latex] is one antiderivative of [latex]f[/latex], every function of the form [latex]y=F(x)+C[/latex] is a solution of that differential equation. For example, the solutions of

are given by

Sometimes we are interested in determining whether a particular solution curve passes through a certain point [latex](x_0,y_0)[/latex]—that is, [latex]y(x_0)=y_0[/latex]. The problem of finding a function [latex]y[/latex] that satisfies a differential equation

with the additional condition

is an example of an initial-value problem . The condition [latex]y(x_0)=y_0[/latex] is known as an initial condition . For example, looking for a function [latex]y[/latex] that satisfies the differential equation

and the initial condition

is an example of an initial-value problem. Since the solutions of the differential equation are [latex]y=2x^3+C[/latex], to find a function [latex]y[/latex] that also satisfies the initial condition, we need to find [latex]C[/latex] such that [latex]y(1)=2(1)^3+C=5[/latex]. From this equation, we see that [latex]C=3[/latex], and we conclude that [latex]y=2x^3+3[/latex] is the solution of this initial-value problem as shown in the following graph.

Figure 2. Some of the solution curves of the differential equation [latex]\frac{dy}{dx}=6x^2[/latex] are displayed. The function [latex]y=2x^3+3[/latex] satisfies the differential equation and the initial condition [latex]y(1)=5[/latex].

Example: Solving an Initial-Value Problem

Solve the initial-value problem

First we need to solve the differential equation. If [latex]\frac{dy}{dx}= \sin x,[/latex] then

Next we need to look for a solution [latex]y[/latex] that satisfies the initial condition. The initial condition [latex]y(0)=5[/latex] means we need a constant [latex]C[/latex] such that [latex]− \cos x+C=5[/latex]. Therefore,

The solution of the initial-value problem is [latex]y=− \cos x+6[/latex].

Solve the initial value problem [latex]\frac{dy}{dx}=3x^{-2}, \,\,\, y(1)=2[/latex].

Find all antiderivatives of [latex]f(x)=3x^{-2}[/latex].

[latex]y=-\frac{3}{x}+5[/latex]

Watch the following video to see the worked solution to Example: Solving an Initial-Value Problem and the above Try It.

Initial-value problems arise in many applications. Next we consider a problem in which a driver applies the brakes in a car. We are interested in how long it takes for the car to stop. Recall that the velocity function [latex]v(t)[/latex] is the derivative of a position function [latex]s(t)[/latex], and the acceleration [latex]a(t)[/latex] is the derivative of the velocity function. In earlier examples in the text, we could calculate the velocity from the position and then compute the acceleration from the velocity. In the next example, we work the other way around. Given an acceleration function, we calculate the velocity function. We then use the velocity function to determine the position function.

Number Line

• x^{2}-x-6=0
• -x+3\gt 2x+1
• line\:(1,\:2),\:(3,\:1)
• prove\:\tan^2(x)-\sin^2(x)=\tan^2(x)\sin^2(x)
• \frac{d}{dx}(\frac{3x+9}{2-x})
• (\sin^2(\theta))'
• \lim _{x\to 0}(x\ln (x))
• \int e^x\cos (x)dx
• \int_{0}^{\pi}\sin(x)dx
• \sum_{n=0}^{\infty}\frac{3}{2^n}

step-by-step

initial value problem

• Practice Makes Perfect Learning math takes practice, lots of practice. Just like running, it takes practice and dedication. If you want...

Please add a message.

Message received. Thanks for the feedback.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Laplace Transform

4.4 Solving Initial Value Problems

Having explored the Laplace Transform, its inverse, and its properties, we are now equipped to solve initial value problems (IVP) for linear differential equations. Our focus will be on second-order linear differential equations with constant coefficients.

Method of Laplace Transform for IVP

General Approach:

1. Apply the Laplace Transform to each term of the differential equation. Use the properties of the Laplace Transform listed in Tables 4.1 and 4.2 to obtain an equation in terms of [asciimath]Y(s)[/asciimath] . The Laplace Transform of the derivatives are

  [asciimath]\mathcal{L}{f'(t)} = sF(s) - f(0)[/asciimath]

  [asciimath]\mathcal{L}{f''(t)\} = s^2F(s) - s f(0) - f'(0)[/asciimath]

2. The transforms of derivatives involve initial conditions at [asciimath]t=0[/asciimath] . Apply the initial conditions.

3. Simplify the transformed equation to isolate  [asciimath]Y(s)[/asciimath] .

4. If needed, use partial fraction decomposition to break down  [asciimath]Y(s)[/asciimath] into simpler components.

5. Determine the inverse Laplace Transform using the tables and linearity property to find [asciimath]y(t)[/asciimath] .

Shortcut Approach:

1. Find the characteristic polynomial of the differential equation [asciimath]p(s)=as^2+bs+c[/asciimath] .

2. Substitute [asciimath]p(s)[/asciimath] , [asciimath]F(s)=\mathcal{L}{f(t)}[/asciimath] , and the initial conditions into the equation

  [asciimath]Y(s)=(F(s)+a(y'(0)+sy(0))+b y(0) )/(p(s))[/asciimath]   (4.4.1)

3. If needed, use partial fraction decomposition to break down [asciimath]Y(s)[/asciimath] into simpler components.

4. Determine the inverse Laplace transform of [asciimath]Y(s)[/asciimath] using the tables and linearity property to find [asciimath]y(t)[/asciimath] .

Solve the initial value problem.

  [asciimath]y''-5y'+6y=4e^(-2t)\ ;[/asciimath]      [asciimath]y(0)=-1, \ y'(0)=2[/asciimath]

Using the General Approach

1. Take the Laplace Transform of both sides of the equation

  [asciimath]\mathcal{L}^-1{ y''}-5\mathcal{L}^-1{ y'}+6\mathcal{L}^-1{y}=4\mathcal{L}^-1{ e^(-2t)}[/asciimath]

Letting [asciimath]Y(s)=\mathcal{L}^-1{y}[/asciimath] , we get

  [asciimath]s^2Y(s)-sy(0)-y'(0)-5(sY(s)-y(0))+6Y(s)=4(1/(s+2))[/asciimath]

2. Plugging in the initial conditions gives

  [asciimath]s^2Y(s)+s-2-5(sY(s)+1)+6Y(s)=4(1/(s+2))[/asciimath]

3. Collecting like terms and isolating [asciimath]Y(s)[/asciimath] , we get

  [asciimath](s^2-5s+6)Y(s)=4/(s+2)-s+7[/asciimath]

  [asciimath]Y(s)[/asciimath]   [asciimath]=(4//(s+2)-s+7)/(s^2-5s+6)[/asciimath]

Multiplying both the denominator and numerator by [asciimath](s+2)[/asciimath] and factoring the denominator yields

  [asciimath]Y(s)=(-s^2+5s+18)/((s+2)(s-3)(s-2))[/asciimath]

4. Using partial fraction expansion, we get

  [asciimath]Y(s)=1/5 (1/(s+2))+24/5 (1/(s-3))-6 (1/(s-2))[/asciimath]

5. From Table 4.1 , we see that

  [asciimath]1/(s-a)[/asciimath]      [asciimath]harr \ \e^(at)[/asciimath]

Taking the inverse, we obtain the solution of the equation

  [asciimath]y(t)=\mathcal{L}^-1{Y(s)}[/asciimath]   [asciimath]=1/5 \ e^(-2t) +24/5 e^(3t)-6 e^(2t)[/asciimath]

  [asciimath]y''+4y=3sin(t) \ ;[/asciimath]      [asciimath]y(0)=1, \ y'(0)=-1[/asciimath]

Using the Shortcut Approach

1. The characteristic polynomial is

  [asciimath]p(s)=s^2+4[/asciimath]

  [asciimath]F(s)=\mathcal{L}^-1{3sin(t)}[/asciimath]   [asciimath]=3/(s^2+1)[/asciimath]

2. Substituting them together with the initial values into Equation 4.4.1 , we obtain

  [asciimath]Y(s)=(3//(s^2+1)+(-1+s(1)))/(s^2+4)[/asciimath] [asciimath]=(3//(s^2+1)+s-1)/(s^2+4)[/asciimath]

Multiplying both the denominator and numerator by [asciimath](s^2+1)[/asciimath]  yields

  [asciimath]Y(s)=(s^3-s^2+s+2)/((s^2+1)(s^2+4))[/asciimath]

3. Using partial fraction expansion, we get

  [asciimath]Y(s)=1/(s^2+1)+(s-2)/(s^2+4)[/asciimath]

[asciimath]\ =1/(s^2+1)+s/(s^2+4)- 2/(s^2+4)[/asciimath]

4. From Table 4.1 ,

  [asciimath]sin(bt)\ harr\ b/(s^2+b^2)[/asciimath]      and    [asciimath]cos(bt)\ harr\ s/(s^2+b^2)[/asciimath]

  [asciimath]y(t)=\mathcal{L}^-1{Y(s)}[/asciimath]   [asciimath]=sin(t)+cos(2t)-sin(2t)[/asciimath]

Section 4.4 Exercises

  [asciimath]y'' +3 y' -10 y = 0, \ quad y(0) = -1, \ quad y'(0) = 2[/asciimath]

[asciimath]y(t)=-3/7 e^(2t)-4/7 e^(-5t)[/asciimath]

  [asciimath]y'' +6 y' + 13 y = 0, \ quad y(0) = 2, \ quad y'(0) = 0[/asciimath]

[asciimath]y(t)=e^(-3t)(2cos(2t)+3sin(2t))[/asciimath]

  [asciimath]y'' - 8 y' +16 y = 0, \ quad y(0) = 1, \ quad y'(0) = -1[/asciimath]

  [asciimath]y(t)=e^(4t)(1-5t)[/asciimath]

Differential Equations Copyright © 2024 by Amir Tavangar is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

Calcworkshop

Solving Initial Value Problems (IVPs) A Comprehensive Guide

// Last Updated: April 17, 2023 - Watch Video //

Did you know that when you solve a differential equation with a specific condition, you’re tackling an initial value problem ?

Jenn, Founder Calcworkshop ® , 15+ Years Experience (Licensed & Certified Teacher)

In simpler terms, you’re looking for a solution that meets certain requirements to find a unique answer .

In a previous lesson, you learned about Ordinary Differential Equations . Now, you’ll dive deeper to explore n-parameter family of solutions and use an initial condition (IC) to figure out the constants in that family.

Understanding n-parameter Family of Solutions

So, what’s an n-parameter family?

Well, a first-order differential equation \(F\left(x, y, y^{\prime}\right)=0\) typically has a single arbitrary constant called a parameter \(\mathrm{c}\), whereas a second-order differential equation \(F\left(x, y, y^{\prime}, y^{\prime \prime}\right)=0\) usually has two arbitrary constants, denoted \(c_{1}\) and \(c_{2}\).

One Two Three Parameter —  Solution Formulas

Therefore, a single differential equation can possess an infinite number of solutions corresponding to the unlimited number of choices for the parameters.

So, an n-parameter family of solutions of a given nth-order differential equation represents the set of all solutions of the equation. And we typically refer to an \(n\)-parameter family of solutions as the general solution – it’s easier to say!

Consequently, if we assign arbitrary constants to the differential equation, referred to as initial conditions, our general solution is called a particular solution because it represents a specific answer for some particular constraint.

It should also be noted that solutions of an \(\mathrm{n}\)-th order differential equation that are not included in the general solution are called singular solutions.

Example: Verifying and Finding Solutions to Initial Value Problems

Let’s look at an example of how we will verify and find a solution to an initial value problem given an ordinary differential equation.

Verify that the function \(y=c_{1} e^{2 x}+c_{2} e^{-2 x}\) is a solution of the differential equation \(y^{\prime \prime}-4 y=0\).

Then find a solution of the second-order IVP consisting of the differential equation that satisfies the initial conditions \(y(0)=1\) and \(y^{\prime}(0)=2\).

First, we will verify that the function is a solution by noticing that we are given a two-parameter family of solutions because we have a second-order differential equation. Therefore, we need to find the second derivative of our function.

\begin{align*} \begin{aligned} & y=c_{1} e^{2 x}+c_{2} e^{-2 x} \\ & y^{\prime}=2 c_{1} e^{2 x}-2 c_{2} e^{-2 x} \\ & y^{\prime \prime}=4 c_{1} e^{2 x}+4 c_{2} e^{-2 x} \end{aligned} \end{align*}

Now, we will substitute our derivatives into the ODE and verify that the left-hand side equals the right-hand side.

\begin{equation} \begin{aligned} & y^{\prime \prime}-4 y=0 \\ & \left(4 c_1 e^{2 x}+4 c_2 e^{-2 x}\right)-4\left(c_1 e^{2 x}+c_2 e^{-2 x}\right)=0 \\ & 4 c_1 e^{2 x}+4 c_2 e^{-2 x}-4 c_1 e^{2 x}-4 c_2 e^{-2 x}=0 \\ & 0=0 \end{aligned} \end{equation}

Now, we will find a solution to the second-order IVP by substituting the initial conditions into their corresponding functions.

\begin{equation} \text { If } y=c_1 e^{2 x}+c_2 e^{-2 x} \text { and } y(0)=1, \text { then } \end{equation}

\begin{align*} 1=c_{1} e^{2(0)}+c_{2} e^{-2(0)} \Rightarrow 1=c_{1}(1)+c_{2}(1) \Rightarrow 1=c_{1}+c_{2} \end{align*}

\begin{equation} \text { If } y^{\prime}=2 c_1 e^{2 x}-2 c_2 e^{-2 x} \text { and } y^{\prime}(0)=2 \text {, then } \end{equation}

\begin{align*} 2=2 c_{1} e^{2(0)}-2 c_{2} e^{-2(0)} \Rightarrow 2=2 c_{1}(1)-2(1) \Rightarrow 2=2 c_{1}-2 c_{2} \end{align*}

Next, we will solve the resulting system for \(c_{1}\) and \(c_{2}\).

\begin{align*} \left\{\begin{array} { c } { 1 = c _ { 1 } + c _ { 2 } } \\ { 2 = 2 c _ { 1 } – 2 c _ { 2 } } \end{array} \Rightarrow \left\{\begin{array}{c} c_{1}+c_{2}=1 \\ c_{1}-c_{2}=1 \end{array} \Rightarrow c_{1}=1 \quad \text { and } \quad c_{2}=0\right.\right. \end{align*}

Therefore, the particular solution for the IVP given the initial condition is:

\begin{equation} \begin{aligned} & y=(1) e^{2 x}+(0) e^{-2 x} \\ & y=e^{2 x} \end{aligned} \end{equation}

I find that it’s helpful to remember that Initial condition(s) are values of the solution and/or its derivative(s) at specific points. Which means, according to Paul’s Online Notes that solutions to “nice enough” differential equations are unique; hence, only one solution will meet the given conditions.

The Game-Changing Existence and Uniqueness Theorem

But how do we know there will be a solution to the differential equation?

The Existence of a Unique Solution Theorem is a key concept in this course. It provides specific conditions that ensure a unique solution exists for an Initial Value Problem (IVP).

Definition: The existence-unique solution theorem says that if we let \(\mathrm{R}\) be a rectangular region in the \(x y-\) plane defined by \(a \leq x \leq b, c \leq y \leq d\) that contains the point \(\left(x_{0}, y_{0}\right)\) in its interior. And if \(f(x, y)\) and \(\frac{\partial f}{\partial y}\) are continuous on \(\mathrm{R}\), then there exists some interval \(\left(x_{0}-h, x_{0}+h\right), h>0\), contained in \([a, b]\), and a unique function \(y(x)\), defined on \(I_{0}\), that is a solution of the initial value problem.

That’s pretty “mathy” right?!

In *sorta* simpler terms, the existence-unique solution theorem essentially states that under specific conditions, there is a unique solution for an initial value problem. If a point (x₀, y₀) is within a rectangular region R in the xy-plane, and both the function f(x, y) and its partial derivative with respect to y are continuous in R , then there is an interval (x₀-h, x₀+h), with h>0, contained within the range [a, b]. Within this interval, a unique function y(x) exists as a solution to the initial value problem.

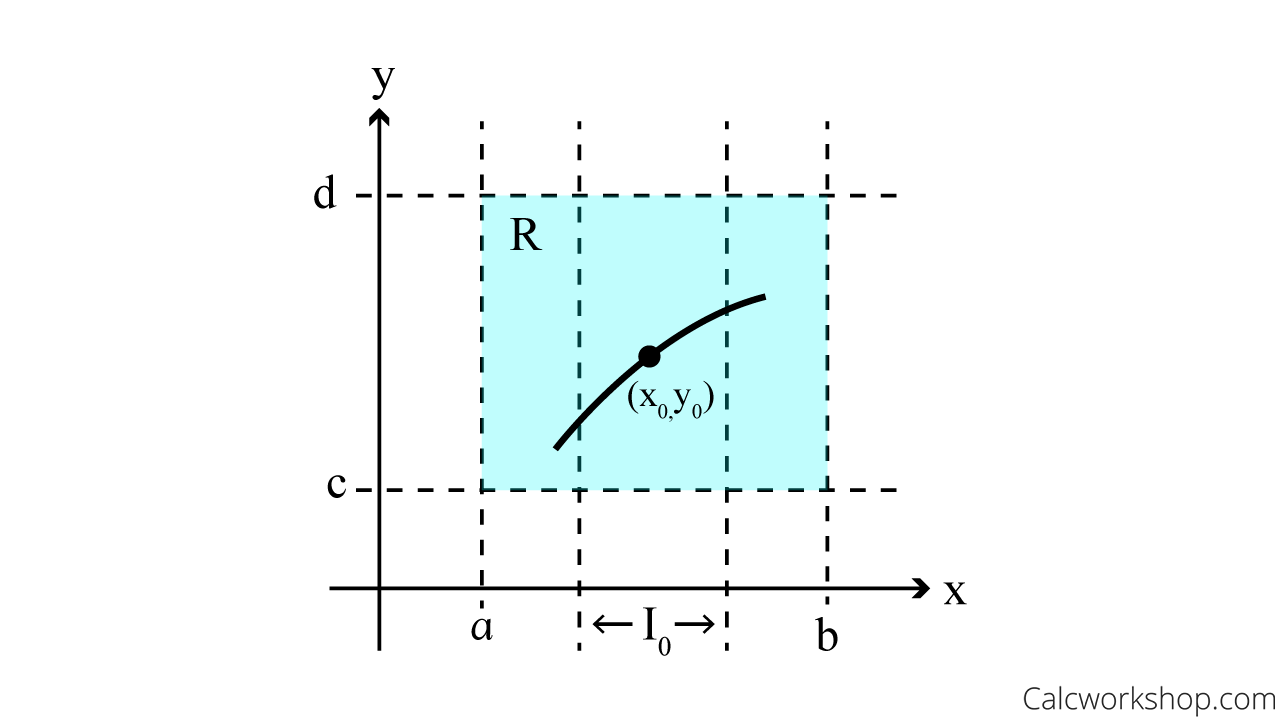
Existence Uniqueness Theorem — Graphical

Example: Solving an IVP with Given Initial Conditions

Let’s break this down into easy-to-understand steps by working an example.

Determine whether the existence-uniqueness theorem implies the given initial value problem has a unique solution through the given point.

\begin{equation} y^{\prime}=y^{2 / 3},(8,4) \end{equation}

First, we will verify that our ODE is continuous by letting \(f(x, y)=y^{\prime}\) and graphing the curve.

\begin{equation} f(x, y)=y^{2 / 3} \end{equation}

ODE — 3D Graph

So, \(f(x, y)\) is continuous for all real numbers.

Next, we will take the partial derivative with respect to \(\mathrm{y}\) and determine if the partial derivative is also continuous.

\begin{align*} \frac{\partial f}{\partial y}=f_{y}=\frac{2}{3} y^{-1 / 3}=\frac{2}{3}\left(\frac{1}{\sqrt[3]{y}}\right) \end{align*}

This indicates that a unique solution exists when \(y>0\).

Therefore, we can safely conclude that our given point \((8,4)\) will provide a unique solution because our \(y\)-value is greater than zero.

Going forward…

So, together we will dive into the world of n-th parameter family of solutions, find solutions for initial value problems, and determine the existence of a solution and whether a differential equation contains a unique solution through a given point.

Let’s jump right in.

Video Tutorial w/ Full Lesson & Detailed Examples

Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

Get My Subscription Now

Still wondering if CalcWorkshop is right for you? Take a Tour and find out how a membership can take the struggle out of learning math.

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators

Solve Initial Value Problem-Definition, Application and Examples

JUMP TO TOPIC

Existence and Uniqueness

Continuity and differentiability, dependence on initial conditions, local vs. global solutions, higher order odes, boundary behavior, particular and general solutions, engineering, biology and medicine, economics and finance, environmental science, computer science, control systems.

Solving initial value problems (IVPs) is an important concept in differential equations . Like the unique key that opens a specific door, an initial condition can unlock a unique solution to a differential equation.

As we dive into this article, we aim to unravel the mysterious process of solving initial value problems in differential equations . This article offers an immersive experience to newcomers intrigued by calculus’s wonders and experienced mathematicians looking for a comprehensive refresher.

Solving the Initial Value Problem 

To solve an initial value problem , integrate the given differential equation to find the general solution. Then, use the initial conditions provided to determine the specific constants of integration.

An initial value problem (IVP) is a specific problem in differential equations . Here is the formal definition. An initial value problem is a differential equation with a specified value of the unknown function at a given point in the domain of the solution.

More concretely, an initial value problem is typically written in the following form:

dy/dt = f(t, y) with y(t₀) = y₀

• dy/dt = f(t, y) is the differential equation , which describes the rate of change of the function y with respect to the variable t .
• t₀ is the given point in the domain , often time in many physical problems .
• y(t₀) = y₀ is the initial condition , which specifies the value of the function y at the point t₀.

An initial value problem aims to find the function y(t) that satisfies both the differential equation and the initial condition . The solution y(t) to the IVP is not just any solution to the differential equation , but specifically, the one which passes through the point (t₀, y₀) on the (t, y) plane.

Because the solution of a differential equation is a family of functions, the initial condition is used to find the particular solution that satisfies this condition. This differentiates an initial value problem from a boundary value problem , where conditions are specified at multiple points or boundaries.

Solve the IVP y’ = 1 + y^2, y(0) = 0 .

This is a standard form of a first-order non-linear differential equation known as the Riccati equation. The general solution is y = tan(t + C) .

Applying the initial condition y(0) = 0, we get:

0 = tan(0 + C)

The solution to the IVP is then y = tan(t) .

According to the Existence and Uniqueness Theorem for ordinary differential equations (ODEs) , if the function f and its partial derivative with respect to y are continuous in some region of the (t, y) -plane that includes the initial condition (t₀, y₀) , then there exists a unique solution y(t) to the IVP in some interval about t = t₀ .

In other words, given certain conditions, we are guaranteed to find exactly one solution to the IVP that satisfies both the differential equation and the initial condition .

If a solution exists, it will be a function that is at least once differentiable (since it must satisfy the given ODE ) and, therefore, continuous . The solution will also be differentiable as many times as the order of the ODE .

Small changes in the initial conditions can result in drastically different solutions to an IVP . This is often called “ sensitive dependence on initial conditions ,” a characteristic feature of chaotic systems .

The Existence and Uniqueness Theorem only guarantees a solution in a small interval around the initial point t₀ . This is called a local solution . However, under certain circumstances, a solution might extend to all real numbers, providing a global solution . The nature of the function f and the differential equation itself can limit the interval of the solution.

For higher-order ODEs , you will have more than one initial condition. For an n-th order ODE , you’ll need n initial conditions to find a unique solution.

The solution to an IVP may behave differently as it approaches the boundaries of its validity interval. For example, it might diverge to infinity , converge to a finite value , oscillate , or exhibit other behaviors.

The general solution of an ODE is a family of functions that represent all solutions to the ODE . By applying the initial condition(s), we narrow this family down to one solution that satisfies the IVP .

Applications 

Solving initial value problems (IVPs) is fundamental in many fields, from pure mathematics to physics , engineering , economics , and beyond. Finding a specific solution to a differential equation given initial conditions is essential in modeling and understanding various systems and phenomena. Here are some examples:

IVPs are used extensively in physics . For example, in classical mechanics , the motion of an object under a force is determined by solving an IVP using Newton’s second law ( F=ma , a second-order differential equation). The initial position and velocity (the initial conditions) are used to find a unique solution that describes the object’s motion .

IVPs appear in many engineering problems. For instance, in electrical engineering , they are used to describe the behavior of circuits containing capacitors and inductors . In civil engineering , they are used to model the stress and strain in structures over time.

In biology , IVPs are used to model populations’ growth and decay , the spread of diseases , and various biological processes such as drug dosage and response in pharmacokinetics .

Differential equations model various economic processes , such as capital growth over time. Solving the accompanying IVP gives a specific solution that models a particular scenario, given the initial economic conditions.

IVPs are used to model the change in populations of species , pollution levels in a particular area, and the diffusion of heat in the atmosphere and oceans.

In computer graphics, IVPs are used in physics-based animation to make objects move realistically. They’re also used in machine learning algorithms, like neural differential equations , to optimize parameters.

In control theory , IVPs describe the time evolution of systems. Given an initial state , control inputs are designed to achieve a desired state.

Solve the IVP y’ = 2y, y(0) = 1 .

The given differential equation is separable. Separating variables and integrating, we get:

∫dy/y = ∫2 dt

ln|y| = 2t + C

y = $e^{(2t+C)}$

= $e^C  * e^{(2t)}$

Now, apply the initial condition y(0) = 1 :

1 = $e^C * e^{(2*0)}$

The solution to the IVP is y = e^(2t) .

Solve the IVP y’ = -3y, y(0) = 2 .

The general solution is y = Ce^(-3t) . Apply the initial condition y(0) = 2 to get:

2 = C $e^{(-3*0)}$

2 = C $e^0$

So, C = 2, and the solution to the IVP is y = 2e^(-3t) .

Solve the IVP y’ = y^2, y(1) = 1 .

This is also a separable differential equation. We separate variables and integrate them to get:

∫$dy/y^2$ = ∫dt,

1/y = t + C.

Applying the initial condition y(1) = 1, we find C = -1. So the solution to the IVP is -1/y = t – 1 , or y = -1/(t – 1).

Solve the IVP y” – y = 0, y(0) = 0, y'(0) = 1 .

This is a second-order linear differential equation. The general solution is y = A sin(t) + B cos(t) .

The first initial condition y(0) = 0 gives us:

0 = A 0 + B 1

The second initial condition y'(0) = 1 gives us:

1 = A cos(0) + B*0

The solution to the IVP is y = sin(t) .

Solve the IVP y” + y = 0, y(0) = 1, y'(0) = 0 .

This is also a second-order linear differential equation. The general solution is y = A sin(t) + B cos(t) .

The first initial condition y(0) = 1 gives us:

1 = A 0 + B 1

The second initial condition y'(0) = 0 gives us:

0 = A cos(0) – B*0

The solution to the IVP is y = cos(t) .

Solve the IVP y” = 9y, y(0) = 1, y'(0) = 3.

The differential equation can be rewritten as y” – 9y = 0. The general solution is y = A $ e^{(3t)} + B e^{(-3t)}$ .

1 = A $e^{(30)}$ + B $e^{(-30)}$

So, A + B = 1.

The second initial condition y'(0) = 3 gives us:

3 = 3A $e^{30} $ – 3B $e^{-30}$

= 3A – 3B

So, A – B = 1.

We get A = 1 and B = 0 to solve these two simultaneous equations. So, the solution to the IVP is y = $e^{(3t)}$ .

Solve the IVP y” + 4y = 0, y(0) = 0, y'(0) = 2 .

The differential equation is a standard form of a second-order homogeneous differential equation. The general solution is y = A sin(2t) + B cos(2t) .

The second initial condition y'(0) = 2 gives us:

2 = 2A cos(0) – B*0

The solution to the IVP is y = sin(2t) .

• Pre Calculus
• Probability
• Sets & Set Theory
• Trigonometry

Initial and Boundary Value Problems

Overview of initial (ivps) and boundary value problems (bvps).

DSolve can be used for finding the general solution to a differential equation or system of differential equations. The general solution gives information about the structure of the complete solution space for the problem. However, in practice, one is often interested only in particular solutions that satisfy some conditions related to the area of application. These conditions are usually of two types.

The symbolic solution of both IVPs and BVPs requires knowledge of the general solution for the problem. The final step, in which the particular solution is obtained using the initial or boundary values, involves mostly algebraic operations, and is similar for IVPs and for BVPs.

IVPs and BVPs for linear differential equations are solved rather easily since the final algebraic step involves the solution of linear equations. However, if the underlying equations are nonlinear , the solution could have several branches, or the arbitrary constants from the general solution could occur in different arguments of transcendental functions. As a result, it is not always possible to complete the final algebraic step for nonlinear problems. Finally, if the underlying equations have piecewise (that is, discontinuous) coefficients, an IVP naturally breaks up into simpler IVPs over the regions in which the coefficients are continuous.

Linear IVPs and BVPs

To begin, consider an initial value problem for a linear first-order ODE.

It should be noted that, in contrast to initial value problems, there are no general existence or uniqueness theorems when boundary values are prescribed, and there may be no solution in some cases.

The previous discussion of linear equations generalizes to the case of higher-order linear ODEs and linear systems of ODEs.

Nonlinear IVPs and BVPs

Many real-world applications require the solution of IVPs and BVPs for nonlinear ODEs. For example, consider the logistic equation, which occurs in population dynamics.

It may not always be possible to obtain a symbolic solution to an IVP or BVP for a nonlinear equation. Numerical methods may be necessary in such cases.

IVPs with Piecewise Coefficients

The differential equations that arise in modern applications often have discontinuous coefficients. DSolve can handle a wide variety of such ODEs with piecewise coefficients. Some of the functions used in these equations are UnitStep , Max , Min , Sign , and Abs . These functions and combinations of them can be converted into Piecewise objects.

A piecewise ODE can be thought of as a collection of ODEs over disjoint intervals such that the expressions for the coefficients and the boundary conditions change from one interval to another. Thus, different intervals have different solutions, and the final solution for the ODE is obtained by patching together the solutions over the different intervals.

If there are a large number of discontinuities in a problem, it is convenient to use Piecewise directly in the formulation of the problem.

Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

Arbitrary High Order ADER-DG Method with Local DG Predictor for Solutions of Initial Value Problems for Systems of First-Order Ordinary Differential Equations

• Published: 04 June 2024
• Volume 100 , article number  22 , ( 2024 )

Cite this article

• Ivan S. Popov   ORCID: orcid.org/0000-0003-2686-0124 1  

An adaptation of the arbitrary high order ADER-DG numerical method with local DG predictor for solving the IVP for a first-order non-linear ODE system is proposed. The proposed numerical method is a completely one-step ODE solver with uniform steps, and is simple in algorithmic and software implementations. It was shown that the proposed version of the ADER-DG numerical method is A -stable and L -stable. The ADER-DG numerical method demonstrates superconvergence with convergence order \({\varvec{2N}}+\textbf{1}\) for the solution at grid nodes, while the local solution obtained using the local DG predictor has convergence order \({\varvec{N}}+\textbf{1}\) . It was demonstrated that an important applied feature of this implementation of the numerical method is the possibility of using the local solution as a solution with a subgrid resolution, which makes it possible to obtain a detailed solution even on very coarse coordinate grids. The scale of the error of the local solution, when calculating using standard representations of single or double precision floating point numbers, using large values of the degree N , practically does not differ from the error of the solution at the grid nodes. The capabilities of the ADER-DG method for solving stiff ODE systems characterized by extreme stiffness are demonstrated. Estimates of the computational costs of the ADER-DG numerical method are obtained.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Data availability

The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.

Butcher, J.C.: Numerical Methods for Ordinary Differential Equations. Wiley, Chichester (2016)

Book   Google Scholar  

Hairer, E., Nørsett, S.P., Wanner, G.: Solving Ordinary Differential Equations I: Nonstiff Problems. Springer, Berlin (1993)

Google Scholar  

Hairer, E., Wanner, G.: Solving Ordinary Differential Equations II: Stiff and Differential-Algebraic Problems. Springer, Berlin (1996)

Babuška, I., Strouboulis, T.: The Finite Element Method and Its Reliability. Numerical Mathematics and Scientific Computation. Clarendon Press, Oxford (2001)

Wahlbin, L.: Superconvergence in Galerkin Finite Element Methods. Springer, Verlag Berlin Heidelberg (1995)

Baccouch, M.: Analysis of optimal superconvergence of the local discontinuous Galerkin method for nonlinear fourth-order boundary value problems. Numer. Algor. 86 , 1615–1650 (2021)

Article   MathSciNet   Google Scholar  

Baccouch, M.: The discontinuous Galerkin method for general nonlinear third-order ordinary differential equations. Appl. Numer. Math. 162 , 331–350 (2021)

Baccouch, M.: Superconvergence of an ultra-weak discontinuous Galerkin method for nonlinear second-order initial-value problems. Int. J. Comput. Methods 20 (2), 2250042 (2023)

Reed, W.H., Hill, T.R.: Triangular mesh methods for the neutron transport equation. Technical Report LA-UR-73-479, Los Alamos Scientific Laboratory (1973)

Delfour, M., Hager, W., Trochu, F.: Discontinuous Galerkin methods for ordinary differential equations. Math. Comput. 36 , 455–473 (1981)

Cockburn, B., Shu, C.-W.: TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws. II. General framework. Math. Comp. 52 , 411–435 (1989)

MathSciNet   Google Scholar  

Cockburn, B., Lin, S.-Y., Shu, C.-W.: TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws III: one-dimensional systems. J. Comput. Phys. 84 , 90–113 (1989)

Cockburn, B., Hou, S., Shu, C.-W.: TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws. IV. The multidimensional case. Math. Comput. 54 , 545–581 (1990)

Cockburn, B., Shu, C.-W.: TVB Runge-Kutta local projection discontinuous Galerkin method for conservation laws V: multidimensional systems. J. Comput. Phys. 141 , 199–224 (1998)

Cockburn, B., Shu, C.-W.: The Runge-Kutta local projection \(P^1\) -discontinuous-Galerkin finite element method for scalar conservation laws. ESAIM M2AN 25 , 337–361 (1991)

Article   Google Scholar  

Baccouch, M.: Analysis of a posteriori error estimates of the discontinuous Galerkin method for nonlinear ordinary differential equations. Appl. Numer. Math. 106 , 129–153 (2016)

Baccouch, M.: A posteriori error estimates and adaptivity for the discontinuous Galerkin solutions of nonlinear second-order initial-value problems. Appl. Numer. Math. 121 , 18–37 (2017)

Baccouch, M.: Superconvergence of the discontinuous Galerkin method for nonlinear second-order initial-value problems for ordinary differential equations. Appl. Numer. Math. 115 , 160–179 (2017)

Baccouch, M.: A superconvergent ultra-weak local discontinuous Galerkin method for nonlinear fourth-order boundary-value problems. Numer. Algorithms 92 (4), 1983–2023 (2023)

Baccouch, M.: A superconvergent ultra-weak discontinuous Galerkin method for nonlinear second-order two-point boundary-value problems. J. Appl. Math. Comput. 69 (2), 1507–1539 (2023)

Baccouch, M., Johnson, B.: A high-order discontinuous Galerkin method for Ito stochastic ordinary differential equations. J. Comput. Appl. Math. 308 , 138–165 (2016)

Baccouch, M., Temimi, H., Ben-Romdhane, M.: A discontinuous Galerkin method for systems of stochastic differential equations with applications to population biology, finance, and physics. J. Comput. Appl. Math. 388 , 113297 (2021)

Zanotti, O., Fambri, F., Dumbser, M., Hidalgo, A.: Space-time adaptive ADER discontinuous Galerkin finite element schemes with a posteriori sub-cell finite volume limiting. Comput. Fluids 118 , 204 (2015)

Fambri, F., Dumbser, M., Zanotti, O.: Space-time adaptive ADER-DG schemes for dissipative flows: compressible Navier-Stokes and resistive MHD equations. Comput. Phys. Commun. 220 , 297 (2017)

Boscheri, W., Dumbser, M.: Arbitrary-Lagrangian-Eulerian discontinuous Galerkin schemes with a posteriori subcell finite volume limiting on moving unstructured meshes. J. Comput. Phys. 346 , 449 (2017)

Fambri, F., Dumbser, M., Koppel, S., Rezzolla, L., Zanotti, O.: ADER discontinuous Galerkin schemes for general-relativistic ideal magnetohydrodynamics. MNRAS 477 , 4543 (2018)

Dumbser, M., Guercilena, F., Koppel, S., Rezzolla, L., Zanotti, O.: Conformal and covariant Z4 formulation of the Einstein equations: strongly hyperbolic first-order reduction and solution with discontinuous Galerkin schemes. Phys. Rev. D 97 , 084053 (2018)

Dumbser, M., Zanotti, O., Gaburro, E., Peshkov, I.: A well-balanced discontinuous Galerkin method for the first-order Z4 formulation of the Einstein-Euler system. J. Comp. Phys. 504 , 112875 (2024)

Dumbser, M., Loubère, R.: A simple robust and accurate a posteriori sub-cell finite volume limiter for the discontinuous Galerkin method on unstructured meshes. J. Comput. Phys. 319 , 163 (2016)

Gaburro, E., Dumbser, M.: A posteriori subcell finite volume limiter for general \(P_N P_M\) schemes: applications from gas dynamics to relativistic magnetohydrodynamics. J. Sci. Comput. 86 , 37 (2021)

Busto, S., Chiocchetti, S., Dumbser, M., Gaburro, E., Peshkov, I.: High order ADER schemes for continuum mechanics. Front. Phys. 32 , 8 (2020)

Dumbser, M., Fambri, F., Tavelli, M., Bader, M., Weinzierl, T.: Efficient implementation of ADER discontinuous Galerkin schemes for a scalable hyperbolic PDE engine. Axioms 7 (3), 63 (2018)

Reinarz, A., Charrier, D.E., Bader, M., Bovard, L., Dumbser, M., Duru, K., Fambri, F., Gabriel, A.-A., Gallard, G.-M., Koppel, S., Krenz, L., Rannabauer, L., Rezzolla, L., Samfass, P., Tavelli, M., Weinzierl, T.: ExaHyPE: An engine for parallel dynamically adaptive simulations of wave problems. Comput. Phys. Commun. 254 , 107251 (2020)

Dumbser, M., Zanotti, O.: Very high order PNPM schemes on unstructured meshes for the resistive relativistic MHD equations. J. Comput. Phys. 228 , 6991 (2009)

Dumbser, M., Enaux, C., Toro, E.F.: Finite volume schemes of very high order of accuracy for stiff hyperbolic balance laws. J. Comput. Phys. 227 , 3971 (2008)

Titarev, V.A., Toro, E.F.: ADER: arbitrary high order Godunov approach. J. Sci. Comput. 17 , 609 (2002)

Titarev, V.A., Toro, E.F.: ADER schemes for three-dimensional nonlinear hyperbolic systems. J. Comput. Phys. 204 , 715 (2005)

Hidalgo, A., Dumbser, M.: ADER schemes for nonlinear systems of stiff advection-diffusion-reaction equations. J. Sci. Comput. 48 , 173 (2011)

Dumbser, M.: Arbitrary high order PNPM schemes on unstructured meshes for the compressible Navier–Stokes equations. Comput. Fluids 39 , 60–76 (2010)

Han Veiga, M., Offner, P., Torlo, D.: DeC and ADER: similarities, differences and a unified framework. J. Sci. Comput. 87 , 2 (2021)

Daniel, J.W., Pereyra, V., Schumaker, L.L.: Iterated deferred corrections for initial value problems. Acta Ci. Venezolana 19 , 128–135 (1968)

Dutt, A., Greengard, L., Rokhlin, V.: Spectral deferred correction methods for ordinary differential equations. BIT Numer. Math. 40 , 241–266 (2000)

Abgrall, R., Bacigaluppi, P., Tokareva, S.: Semi-implicit spectral deferred correction methods for ordinary differential equations. Commun. Math. Sci. 1 , 471–500 (2003)

Liu, Y., Shu, C.-W., Zhang, M.: Strong stability preserving property of the deferred correction time discretization. J. Comput. Math. 26 , 633–656 (2008)

Abgrall, R.: High order schemes for hyperbolic problems using globally continuous approximation and avoiding mass matrices. J. Sci. Comput. 73 , 461–494 (2017)

Abgrall, R., Bacigaluppi, P., Tokareva, S.: High-order residual distribution scheme for the time-dependent Euler equations of fluid dynamics. Comput. Math. Appl. 78 , 274–297 (2019)

Baeza, A., Boscarino, S., Mulet, P., Russo, G., Zorio, D.: Approximate Taylor methods for ODEs. Comput. Fluids 159 , 156–166 (2017)

Jorba, A., Zou, M.: A software package for the numerical integration of ODEs by means of high-order Taylor methods. Exp. Math. 14 , 99–117 (2005)

Dumbser, M., Zanotti, O., Hidalgo, A., Balsara, D.S.: ADER-WENO finite volume schemes with space-time adaptive mesh refinement. J. Comput. Phys. 248 , 257 (2013)

Dumbser, M., Hidalgo, A., Zanotti, O.: High order space-time adaptive ADER-WENO finite volume schemes for non-conservative hyperbolic systems. Comput. Methods Appl. Mech. Engrg. 268 , 359 (2014)

Dumbser, M., Zanotti, O., Loubère, R., Diot, S.: A posteriori subcell limiting of the discontinuous Galerkin finite element method for hyperbolic conservation laws. J. Comput. Phys. 278 , 47 (2014)

Zanotti, O., Dumbser, M.: A high order special relativistic hydrodynamic and magnetohydrodynamic code with space-time adaptive mesh refinement. Comput. Phys. Commun. 188 , 110 (2015)

Ketcheson, D., Waheed, U.: A comparison of high-order explicit Runge-Kutta, extrapolation, and deferred correction methods in serial and parallel. Commun. Appl. Math. Comput. Sci. 9 , 175–200 (2014)

Jackson, H.: On the eigenvalues of the ADER-WENO Galerkin predictor. J. Comput. Phys. 333 , 409 (2017)

Popov, I.S.: Space-time adaptive ADER-DG finite element method with LST-DG predictor and a posteriori sub-cell WENO finite-volume limiting for simulation of non-stationary compressible multicomponent reactive flows. J. Sci. Comput. 95 , 44 (2023)

Nechita, M.: Revisiting a flame problem. Remarks on some non-standard finite difference schemes. Didactica Math. 34 , 51–56 (2016)

Abelman, S., Patidar, K.C.: Comparison of some recent numerical methods for initial-value problems for stiff ordinary differential equations. Comput. Math. Appl. 55 , 733–744 (2008)

Shampine, L.F., Gladwell, I., Thompson, S.: Solving ODEs with Matlab. Cambridge University Press, Cambridge (2003)

O’Malley, R.E.: Singular Perturbation Methods for Ordinary Differential Equations. Springer, New York (1991)

Reiss, E.L.: A new asymptotic method for jump phenomena. SIAM J. Appl. Math. 39 , 440–455 (1980)

Owren, B., Zennaro, M.: Derivation of efficient, continuous, explicit Runge-Kutta methods. SIAM J. Sci. Stat. Comput. 13 , 1488–1501 (1992)

Gassner, G., Dumbser, M., Hindenlang, F., Munz, C.: Explicit one-step time discretizations for discontinuous Galerkin and finite volume schemes based on local predictors. J. Comput. Phys. 230 , 4232–42471 (2011)

Bogacki, P., Shampine, L.W.: A 3(2) pair of Runge-Kutta formulas. Appl. Math. Lett. 2 , 321–325 (1989)

Dormand, J.R., Prince, P.J.: A family of embedded Runge-Kutta formulae. J. Comput. Appl. Math. 6 , 19–26 (1980)

Shampine, L.W.: Some practical Runge-Kutta formulas. Math. Comput. 46 , 135–150 (1986)

Download references

Acknowledgements

The reported study was supported by the Russian Science Foundation grant No. 21-71-00118 https://rscf.ru/en/project/21-71-00118/ . The author would like to thank the anonymous reviewers for their encouraging comments and remarks that helped to improve the quality and readability of this paper. The author would like to thank Popova A.P. for help in correcting the English text.

The reported study was supported by the Russian Science Foundation grant No. 21-71-00118 https://rscf.ru/en/project/21-71-00118/ .

Author information

Authors and affiliations.

Department of Theoretical Physics, Dostoevsky Omsk State University, Mira prospekt, Omsk, Russia, 644077

Ivan S. Popov

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Ivan S. Popov .

Ethics declarations

Conflict of interest.

The author declares that he has no Conflict of interest.

Competing interest

The author declares that he has no Competing interest.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Popov, I.S. Arbitrary High Order ADER-DG Method with Local DG Predictor for Solutions of Initial Value Problems for Systems of First-Order Ordinary Differential Equations. J Sci Comput 100 , 22 (2024). https://doi.org/10.1007/s10915-024-02578-2

Download citation

Received : 09 August 2023

Revised : 14 May 2024

Accepted : 18 May 2024

Published : 04 June 2024

DOI : https://doi.org/10.1007/s10915-024-02578-2

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Discontinuous Galerkin method
• ADER-DG method
• Local DG predictor
• First-order ODE systems
• Superconvergence

Mathematics Subject Classification

• Find a journal
• Publish with us
• Track your research

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

6.3: Solution of Initial Value Problems

• Last updated
• Save as PDF
• Page ID 153691

• William F. Trench
• Trinity University

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Laplace Transforms of Derivatives

In the rest of this chapter we’ll use the Laplace transform to solve initial value problems for constant coefficient second order equations. To do this, we must know how the Laplace transform of \(f'\) is related to the Laplace transform of \(f\). The next theorem answers this question.

Theorem 8.3.1

Suppose \(f\) is continuous on \([0,\infty)\) and of exponential order \(s_0\), and \(f'\) is piecewise continuous on \([0,\infty).\) Then \(f\) and \(f'\) have Laplace transforms for \(s > s_0,\) and

\[\label{eq:8.3.1} {\cal L}(f')=s {\cal L}(f)-f(0).\]

We know from Theorem 8.1.6 that \({\cal L}(f)\) is defined for \(s>s_0\). We first consider the case where \(f'\) is continuous on \([0,\infty)\). Integration by parts yields

\[ \begin{align} \int^T_0 e^{-st}f'(t)\,dt &= e^{-st}f(t)\Big|^T_0+s \int^T_0e^{-st}f(t)\,dt \nonumber \\[4pt] &= e^{-sT}f(T)-f(0)+s\int^T_0 e^{-st}f(t)\,dt \label{eq:8.3.2} \end{align} \]

for any \(T>0\). Since \(f\) is of exponential order \(s_0\), \(\displaystyle \lim_{T\to \infty}e^{-sT}f(T)=0\) and the integral in on the right side of Equation \ref{eq:8.3.2} converges as \(T\to\infty\) if \(s> s_0\). Therefore

\[\begin{aligned} \int^\infty_0 e^{-st}f'(t)\,dt&=-f(0)+s\int^\infty_0 e^{-st}f(t)\,dt\\ &=-f(0)+s{\cal L}(f),\end{aligned}\nonumber \]

which proves Equation \ref{eq:8.3.1}.

Suppose \(T>0\) and \(f'\) is only piecewise continuous on \([0,T]\), with discontinuities at \(t_1 < t_2 <\cdots < t_{n-1}\). For convenience, let \(t_0=0\) and \(t_n=T\). Integrating by parts yields

\[\begin{aligned} \int^{t_i}_{t_{i-1}}e^{-st}f'(t)\,dt &= e^{-st}f(t)\Big|^{t_i}_{t_{i-1}}+s\int^{t_i}_{t_{i-1}}e^{-st}f(t)\,dt\\ &= e^{-st_i} f(t_i)- e^{-st_{i-1}}f(t_{i-1})+s\int^{t_i}_{t_{i-1}}e^{-st}f(t)\,dt.\end{aligned}\nonumber\]

Summing both sides of this equation from \(i=1\) to \(n\) and noting that

\[\left(e^{-st_1}f(t_1)-e^{-st_0}f(t_0)\right)+\left(e^{-st_2} f(t_2)-e^{-st_1}f(t_1)\right) +\cdots+\left(e^{-st_N}f(t_N)-e^{-st_{N-1}}f(t_{N-1})\right) \nonumber\]

\[=e^{-st_N}f(t_N)-e^{-st_0}f(t_0)=e^{-sT}f(T)-f(0) \nonumber\]

yields Equation \ref{eq:8.3.2}, so Equation \ref{eq:8.3.1} follows as before.

Example 8.3.1

In Example 8.1.4 we saw that

\[{\cal L}(\cos\omega t)={s\over s^2+\omega^2}. \nonumber\]

Applying Equation \ref{eq:8.3.1} with \(f(t)=\cos\omega t\) shows that

\[{\cal L}(-\omega\sin\omega t)=s {s\over s^2+\omega^2}-1=- {\omega^2\over s^2+\omega^2}.\nonumber\]

\[{\cal L}(\sin\omega t)={\omega\over s^2+\omega^2},\nonumber\]

which agrees with the corresponding result obtained in 8.1.4.

In Section 2.1 we showed that the solution of the initial value problem

\[\label{eq:8.3.3} y'=ay, \quad y(0)=y_0,\]

is \(y=y_0e^{at}\). We’ll now obtain this result by using the Laplace transform.

Let \(Y(s)={\cal L}(y)\) be the Laplace transform of the unknown solution of Equation \ref{eq:8.3.3}. Taking Laplace transforms of both sides of Equation \ref{eq:8.3.3} yields

\[{\cal L}(y')={\cal L}(ay),\nonumber\]

which, by Theorem 8.3.1 , can be rewritten as

\[s{\cal L}(y)-y(0)=a{\cal L}(y),\nonumber\]

\[sY(s)-y_0=aY(s).\nonumber\]

Solving for \(Y(s)\) yields

\[Y(s)={y_0\over s-a},\nonumber\]

\[y={\cal L}^{-1}(Y(s))={\cal L}^{-1}\left({y_0\over s-a}\right)=y_0{\cal L}^{-1}\left({1\over s-a}\right)=y_0e^{at},\nonumber\]

which agrees with the known result.

We need the next theorem to solve second order differential equations using the Laplace transform.

Theorem 8.3.2

Suppose \(f\) and \(f'\) are continuous on \([0,\infty)\) and of exponential order \(s_0,\) and that \(f''\) is piecewise continuous on \([0,\infty).\) Then \(f\), \(f'\), and \(f''\) have Laplace transforms for \(s > s_0\),

\[\label{eq:8.3.4} {\cal L}(f')=s {\cal L}(f)-f(0),\]

\[\label{eq:8.3.5} {\cal L}(f'')=s^2{\cal L}(f)-f'(0)-sf(0).\]

Theorem 8.3.1 implies that \({\cal L}(f')\) exists and satisfies Equation \ref{eq:8.3.4} for \(s>s_0\). To prove that \({\cal L}(f'')\) exists and satisfies Equation \ref{eq:8.3.5} for \(s>s_0\), we first apply Theorem 8.3.1 to \(g=f'\). Since \(g\) satisfies the hypotheses of Theorem 8.3.1 , we conclude that \({\cal L}(g')\) is defined and satisfies

\[{\cal L}(g')=s{\cal L}(g)-g(0)\nonumber\]

for \(s>s_0\). However, since \(g'=f''\), this can be rewritten as

\[{\cal L}(f'')=s{\cal L}(f')-f'(0).\nonumber\]

Substituting Equation \ref{eq:8.3.4} into this yields Equation \ref{eq:8.3.5}.

Solving Second Order Equations with the Laplace Transform

We’ll now use the Laplace transform to solve initial value problems for second order equations.

Example 8.3.2

Use the Laplace transform to solve the initial value problem

\[\label{eq:8.3.6} y''-6y'+5y=3e^{2t},\quad y(0)=2, \quad y'(0)=3.\]

Taking Laplace transforms of both sides of the differential equation in Equation \ref{eq:8.3.6} yields

\[{\cal L}(y''-6y'+5y)={\cal L}\left(3e^{2t}\right)={3\over s-2},\nonumber\]

which we rewrite as

\[\label{eq:8.3.7} {\cal L}(y'')-6{\cal L}(y')+5{\cal L}(y)={3\over s-2}.\]

Now denote \({\cal L}(y)=Y(s)\). Theorem 8.3.2 and the initial conditions in Equation \ref{eq:8.3.6} imply that

\[{\cal L}(y')=sY(s)-y(0)=sY(s)-2\nonumber\]

\[{\cal L}(y'')=s^2Y(s)-y'(0)-sy(0)=s^2Y(s)-3-2s.\nonumber\]

Substituting from the last two equations into Equation \ref{eq:8.3.7} yields

\[\left(s^2Y(s)-3-2s\right)-6\left(sY(s)-2\right)+5Y(s)={3\over s-2}.\nonumber\]

\[\label{eq:8.3.8} (s^2-6s+5)Y(s)={3\over s-2}+(3+2s)+6(-2),\]

\[(s-5)(s-1)Y(s)={3+(s-2)(2s-9)\over s-2},\nonumber\]

\[Y(s)={3+(s-2)(2s-9)\over(s-2)(s-5)(s-1)}.\nonumber\]

Heaviside’s method yields the partial fraction expansion

\[Y(s)=-{1\over s-2}+{1\over2}{1\over s-5}+{5\over2}{1\over s-1},\nonumber\]

and taking the inverse transform of this yields

\[y=-e^{2t}+{1\over2}e^{5t}+{5\over2}e^t \nonumber\]

as the solution of Equation \ref{eq:8.3.6}.

It isn’t necessary to write all the steps that we used to obtain Equation \ref{eq:8.3.8}. To see how to avoid this, let’s apply the method of Example 8.3.2 to the general initial value problem

\[\label{eq:8.3.9} ay''+by'+cy=f(t), \quad y(0)=k_0,\quad y'(0)=k_1.\]

Taking Laplace transforms of both sides of the differential equation in Equation \ref{eq:8.3.9} yields

\[\label{eq:8.3.10} a{\cal L}(y'')+b{\cal L}(y')+c{\cal L}(y)=F(s).\]

Now let \(Y(s)={\cal L}(y)\). Theorem 8.3.2 and the initial conditions in Equation \ref{eq:8.3.9} imply that

\[{\cal L}(y')=sY(s)-k_0\quad \text{and} \quad {\cal L}(y'')=s^2Y(s)-k_1-k_0s.\nonumber\]

Substituting these into Equation \ref{eq:8.3.10} yields

\[\label{eq:8.3.11} a\left(s^2Y(s)-k_1-k_0s\right)+b\left(sY(s)-k_0\right)+cY(s)=F(s).\]

The coefficient of \(Y(s)\) on the left is the characteristic polynomial

\[p(s)=as^2+bs+c\nonumber\]

of the complementary equation for Equation \ref{eq:8.3.9}. Using this and moving the terms involving \(k_0\) and \(k_1\) to the right side of Equation \ref{eq:8.3.11} yields

\[\label{eq:8.3.12} p(s)Y(s)=F(s)+a(k_1+k_0s)+bk_0.\]

This equation corresponds to Equation \ref{eq:8.3.8} of Example 8.3.2 . Having established the form of this equation in the general case, it is preferable to go directly from the initial value problem to this equation. You may find it easier to remember Equation \ref{eq:8.3.12} rewritten as

\[\label{eq:8.3.13} p(s)Y(s)=F(s)+a\left(y'(0)+sy(0)\right)+by(0).\]

Example 8.3.3

\[\label{eq:8.3.14} 2y''+3y'+y=8e^{-2t}, \quad y(0)=-4,\; y'(0)=2.\]

The characteristic polynomial is

\[p(s)=2s^2+3s+1=(2s+1)(s+1)\nonumber\]

\[F(s)={\cal L}(8e^{-2t})={8\over s+2},\nonumber\]

so Equation \ref{eq:8.3.13} becomes

\[(2s+1)(s+1)Y(s)={8\over s+2}+2(2-4s)+3(-4).\nonumber\]

\[Y(s)={4\left(1-(s+2)(s+1)\right)\over (s+1/2)(s+1)(s+2)}.\nonumber\]

\[Y(s)={4\over3}{1\over s+1/2}-{8\over s+1}+{8\over3}{1\over s+2},\nonumber\]

so the solution of Equation \ref{eq:8.3.14} is

\[y={\cal L}^{-1}(Y(s))={4\over3}e^{-t/2}-8e^{-t}+{8\over3}e^{-2t}\nonumber\]

(Figure 8.3.1 ).

Example 8.3.4

Solve the initial value problem

\[\label{eq:8.3.15} y''+2y'+2y=1, \quad y(0)=-3,\; y'(0)=1.\]

\[p(s)=s^2+2s+2=(s+1)^2+1\nonumber\]

\[F(s)={\cal L}(1)={1\over s},\nonumber\]

\[\left[(s+1)^2+1\right] Y(s)={1\over s}+1\cdot(1-3s)+2(-3).\nonumber\]

\[Y(s)={1-s(5+3s)\over s\left[(s+1)^2+1\right]}.\nonumber\]

In Example 8.2.8 we found the inverse transform of this function to be

\[y={1\over2}-{7\over2}e^{-t}\cos t-{5\over2}e^{-t}\sin t \nonumber\]

(Figure 8.3.2 ), which is therefore the solution of Equation \ref{eq:8.3.15}.

In our examples we applied Theorems 8.3.1 and 8.3.2 without verifying that the unknown function \(y\) satisfies their hypotheses. This is characteristic of the formal manipulative way in which the Laplace transform is used to solve differential equations. Any doubts about the validity of the method for solving a given equation can be resolved by verifying that the resulting function \(y\) is the solution of the given problem.