solving arithmetic progression problems

Reset password New user? Sign up

Existing user? Log in

Arithmetic and Geometric Progressions Problem Solving

Already have an account? Log in here.

Recommended Course

Algebra through puzzles.

Supercharge your algebraic intuition and problem solving skills!

• Vilakshan Gupta
• Andres Gonzalez

To solve problems on this page, you should be familiar with

• arithmetic progressions
• geometric progressions
• arithmetic-geometric progressions .

You can boost up your problem solving on arithmetic and geometric progressions through this wiki. Make sure you hit all the problems listed in this page.

Problem Solving - Basic

Problem solving - intermediate, problem solving - advanced.

This section contains basic problems based on the notions of arithmetic and geometric progressions. Starting with an example, we will head into the problems to solve.

I have an arithmetic progression such that the initial term is 5 and the common difference is 10. What is minimum value of \(n\) such that the \(n^\text{th}\) term is larger than 100? We can just start by listing out the numbers: \[ 5,15,25,35,45,55,65,75,85, 95,105. \] We can clearly see that the \(11^\text{th}\) number is larger than 100, and thus \(n=11.\) However, note that this will become impractical if the common difference becomes smaller and/or the number we are looking for becomes larger. A practical way to solve it is via applying the \(n^\text{th}\) term formula. With \(a = 5, d = 10\), we have \( T_n = a + (n-1) d > 100 \). Then \(5 + (n-1) \cdot 10 > 100 \). Solving for \(n\) yields \(n > 10.5\). So the \(11^\text{th}\) term is the smallest term that satisfies the condition. \(_\square\)

Here comes the problems for you to solve.

The average of the first 100 positive integers is \(\text{__________}.\)

If \(A, B, C, D \) are consecutive terms in an arithmetic progression, what is the value of

\[ \frac{ D^2 - A^2 } { C^2 - B^2} ? \]

Assume \( C^2 - B^2 \neq 0.\)

\[ 54+51+48+45+ \cdots\]

You are given the sum of an arithmetic progression of a finite number of terms, as shown above.

What is the minimum number of terms used to make a total value of 513?

One side of an equilateral triangle is 24 cm. The midpoints of its sides are joined to form another triangle whose midpoints, in turn, are joined to form still another triangle. This process continues indefinitely.

Find the sum of the perimeters of all these triangles that are defined above.

Once a man did a favor to a king that made the king very happy. Out of joy the king told the man to wish for anything and he would be granted. The man wanted to ask for the whole kingdom which was worth 1500 trillion dollars, but obviously that would make the king mad and he would never be granted that wish.

The man who happened to be a mathematician thought a little bit and said the following:

"Bring in a big piece of rug with an \(8\times 8\) grid in it. Starting from the top left square, put one dollar in that square. Put two dollars in the square next to it and then double of that, four dollars, in the next square and so on. When you reach the end of the first row, continue on to the next row, doubling the amount every time as you move to the next square, all the way until the \(64^\text{th}\) square at the bottom right."

The king thought for a second. The first square will take one dollar, the second two dollars, the third, four dollars, and next 8 dollars, and then 16 dollars, and then 32 dollars, 64 dollars, 128 dollars, 256 dollars, and so on. That's not too bad. I can do it.

The king agreed. What happened next?

\[1+2 \cdot 2+ 3 \cdot 2^2 + 4 \cdot 2^3 + \cdots+ 100 \cdot 2^{99}= \, ?\]

This section contains a bit harder problems than the previous section. But all these can be solved using arithmetic and geometric problems. Here we go:

Real numbers \(a_1,a_2,\ldots,a_{99}\) form an arithmetic progression.

Suppose that \[ a_2+a_5+a_8+\cdots+a_{98}=205.\] Find the value of \( \displaystyle \sum_{k=1}^{99} a_k\).

The value of \(\displaystyle \sum_{n=1}^ \infty \frac{ 2n}{ 3^n } \) can be expressed in the form \( \frac{a}{b} \), where \(a\) and \(b\) are coprime positive integers. Find \( a - b \).

Let \(a,b,c\) be positive integers such that \(\frac{b}{a}\) is an integer. If \(a,b,c\) are in geometric progression and the arithmetic mean of \(a,b,c\) is \(b+2,\) find the value of

\[\dfrac{a^2+a-14}{a+1}.\]

If an infinite GP of real numbers has second term \(x\) and sum \(4,\) where does \(x\) belong?

4 positive integers form an arithmetic progression.

If we subtract \(2,6,7\) and \(2,\) respectively, from the 4 numbers, it forms a geometric progression.

What is the sum of these 4 numbers?

Let \(a, b \in R^{+}.\)

\(a, A_{1}, A_{2}, b\) is an arithmetic progression. \(a, G_{1}, G_{2}, b\) is a geometric progression.

Which of the following must be true?

We have three numbers in an arithmetic progression, and another three numbers in a geometric progression. Adding the corresponding terms of the two series, we get \( 120 , 116 , 130 \). If the sum of all the terms in the geometric progression is \( 342 \), what is the largest term in the geometric progression?

\(\) Details and Assumptions:

• If the terms of the AP are A, B, C, and the terms of the GP are X, Y, Z, then adding the corresponding terms will give us A+X, B+Y, C+Z.

This section has problems which need advanced understanding of the notions and generally get solved on using multiple notions at a time. Let's give these problems an attempt.

\[(1-x)(1-2x)(1-4x)\cdots \left(1-2^{101}x\right)\]

What is the coefficient of \(x^{101} \) in the expansion of the above?

\[ \frac {2+6}{4^{100}} + \frac {2+2 \times 6}{4^{99}} + \frac {2+ 3 \times 6}{4^{98}} + \cdots + \frac {2+ 100 \times 6}{4} \]

Evaluate the above expression.

In JEE examination the paper consists of 90 questions. The marks are awarded in such a way that if a person gets a question correct, he gets \(+4\) marks; if he does it wrong, he gets \(-2\) marks; if he leaves the question unanswered, he gets \(0\) marks (as per 2015). Find the sum of all possible marks that a student can get in JEE.

Let \(A=\{a_1, a_2, \ldots, a_n\}\) be a set of the first \(n\) terms of an arithmetic progression. Similarly, let \(B=\{b_1, b_2, \ldots, b_n\}\) be a set of the first \(n\) terms of a geometric progression.

If a new set \(C=A+B=\{a_1+b_1, a_2+b_2, \ldots, a_n+b_n\}\) and the first four terms of \(C\) are \(\{0, 0, 1, 0\},\) what is the \(11^\text{th}\) term of \(C?\)

A linear function \(f(x)=bx+a\) has the property that \(f\big(f(x)\big)=dx+c\) is another linear function such that \(a,b,c,d\) are integers that are consecutive terms in an arithmetic sequence. Find the last three digits of the sum of all possible values of \(f(2013)\).

\[ \begin{eqnarray} &\displaystyle\sum_{n=0}^{7}\log_{3}(x_{n}) &= 308 \\ 56 \leq & \log_{3}\left ( \sum_{n=0}^{7}x_{n}\right )& \leq 57 \\ \end{eqnarray} \]

The increasing geometric sequence \(x_{0},x_{1},x_{2},\ldots\) consists entirely of integral powers of 3. If they satisfy the two conditions above, find \(\log_{3}(x_{14}).\)

Suppose \(2015\) people of different heights are arranged in a straight line from shortest to tallest such that

(i) the tops of their heads are collinear, and

(ii) for any two successive people, the horizontal distance between them is equal to the height of the shorter of the two people.

If the shortest person is \(49\) inches tall and the tallest is \(81\) inches tall, then how tall is the person at the middle of the line, (in inches)?

Given that \(a_1,a_2,a_3\) is an arithmetic progression in that order so that \(a_1+a_2+a_3=15\) and \(b_1,b_2,b_3\) is a geometric progression in that order so that \(b_1b_2b_3=27\).

If \(a_1+b_1, a_2+b_2, a_3+b_3\) are positive integers and form a geometric progression in that order, determine the maximum possible value of \(a_3\).

The answer is of the form \(\dfrac{a+b\sqrt{c}}{d}\), where \(a\), \(b\), \(c\), and \(d\) are positive integers and the fraction is in its simplest form and \(c\) is square free. Submit the value of \( a + b + c + d \).

Telescoping Series - Sum and Telescoping Series - Product

Limits of Sequences

Master concepts like these

Learn more in our Algebra through Puzzles course, built by experts for you.

Problem Loading...

Note Loading...

Set Loading...

Arithmetic Progression

An arithmetic progression (AP) is a sequence where the differences between every two consecutive terms are the same. For example, the sequence 2, 6, 10, 14, … is an arithmetic progression (AP) because it follows a pattern where each number is obtained by adding 4 to the previous term. A real-life example of an AP is the sequence formed by the annual income of an employee whose income increases by a fixed amount of $5000 every year.

In this article, we will explore the concept of arithmetic progression, the AP formulas to find its n th term, common difference, and the sum of n terms of an AP. We will solve various examples based on the arithmetic progression formula for a better understanding of the concept.

What is Arithmetic Progression?

An arithmetic progression (AP) is a sequence of numbers where the differences between every two consecutive terms are the same. In this progression, each term, except the first term, is obtained by adding a fixed number to its previous term. This fixed number is known as the common difference and is denoted by 'd'. The first term of an arithmetic progression is usually denoted by 'a' or 'a 1 '.

For example, 1, 5, 9, 13, 17, 21, 25, 29, 33, ... is an arithmetic progression as the differences between every two consecutive terms are the same (as 4). i.e., 5 - 1 = 9 - 5 = 13 - 9 = 17 - 13 = 21 - 17 = 25 - 21 = 29 - 25 = 33 - 29 = ... = 4. We can also notice that every term (except the first term) of this AP is obtained by adding 4 to its previous term. In this arithmetic progression:

• a = 1 (the first term)
• d = 4 (the "common difference" between terms)

Thus, an arithmetic progression, in general, can be written as: {a, a + d, a + 2d, a + 3d, ... }.

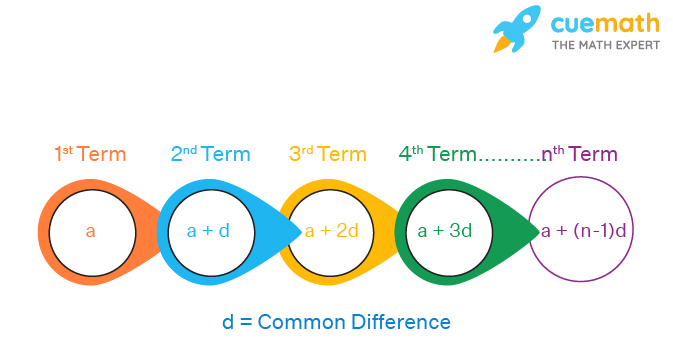
In the above example we have: {a, a + d, a + 2d, a + 3d, ... } = {1, 1 + 4, 1 + 2 × 4, 1 + 3 × 4, ... } = {1, 5, 9, 13, ... }

Arithmetic Progression Formula (AP Formulas)

For the first term 'a' of an AP and common difference 'd', given below is a list of arithmetic progression formulas that are commonly used to solve various problems related to AP:

• Common difference of an AP: d = a 2 - a 1 = a 3 - a 2 = a 4 - a 3 = ... = a n - a n-1
• n th term of an AP: a n = a + (n - 1)d
• Sum of n terms of an AP: S n = n/2 (2a + (n - 1) d) = n/2 (a + l), where l is the last term of the arithmetic progression.

The following image comprehends all AP formulas.

Common Terms Used in Arithmetic Progression

From now on, we will abbreviate arithmetic progression as AP. An AP generally is shown as follows: a 1 , a 2 , a 3 , . . . It involves the following terminology.

First Term of Arithmetic Progression:

As the name suggests, the first term of an AP is the first number of the progression. It is usually represented by a 1 (or) a. For example, in the sequence 6, 13, 20, 27, 34, . . . . the first term is 6. i.e., a 1 = 6 (or) a = 6.

Common Difference of Arithmetic Progression:

We know that an AP is a sequence where each term, except the first term, is obtained by adding a fixed number to its previous term. Here, the “fixed number” is called the “ common difference ” and is denoted by 'd' i.e., if the first term is a 1 , then: the second term is a 1 + d, the third term is a 1 + d + d = a 1 + 2d, and the fourth term is a 1 + 2d + d= a 1 + 3d and so on. For example, in the sequence 6, 13, 20, 27, 34,. . . , each term, except the first term, is obtained by the addition of 7 to its previous term. Thus, the common difference is, d=7. In general, the common difference is the difference between every two successive terms of an AP. Thus, the formula for calculating the common difference of an AP is: d = a n - a n-1 .

Here are some AP examples with their first term and common difference.

• 6, 13, 20, 27, 34, . . . . is an AP with the first term 6 and common difference 7.
• 91, 81, 71, 61, 51, . . . . is an AP with the first term 91 and common difference -10.
• π, 2π, 3π, 4π, 5π,… is an AP with the first term π and common difference π.
• -√3, −2√3, −3√3, −4√3, −5√3,… is an AP with the first term -√3 and common difference -√3.

Nth Term of Arithmetic Progression

The general term (or) n th term of an AP whose first term is 'a' and the common difference is 'd' is given by the formula a n = a + (n - 1) d. For example, to find the general term (or) n th term of the progression 6, 13, 20, 27, 34,. . . ., we substitute the first term, a 1 = 6, and the common difference, d = 7 in the formula for the n th term formula. Then we get, a n = a + (n - 1) d = 6 + (n - 1) 7 = 6 + 7n - 7 = 7n -1. Thus, the general term (or) n th term of this AP is: a n = 7n - 1. But what is the use of finding the general term of an AP? Let us see.

Use of AP Formula for General Term

We know that to find a term, we can add 'd' to its previous term. For example, if we have to find the 6 th term of 6, 13, 20, 27, 34, . . ., we can just add d = 7 to the 5 th term which is 34. Then 6 th term = 5 th term + 7 = 34 + 7 = 41. But what if we have to find the 102 nd term? Isn’t it difficult to calculate it manually? In this case, we can just substitute n = 102 (and also a = 6 and d = 7 in the formula of the n th term of an AP). Then we get:

a n = a + (n - 1) d

a 102 = 6 + (102 - 1) 7 = 6 + (101) 7 = 713

Therefore, the 102 nd term of the given AP 6, 13, 20, 27, 34, .... is 713. Thus, the general term (or) n th term of an AP is referred to as the arithmetic sequence explicit formula and can be used to find any term of the AP without finding its previous term.

The following table shows some AP examples and the first term, the common difference, and the general term in each case.

Sum of Arithmetic Progression

Consider an arithmetic progression (AP) whose first term is a 1 (or) a and the common difference is d.

• The sum of first n terms of an arithmetic progression when the n th term is NOT known is S n = (n/2) [2a + (n - 1) d]
• The sum of first n terms of an arithmetic progression when the n th term(a n ) is known is S n = n/2[a 1 + a n ]

Example: Mr. Kevin earns $400,000 per annum and his salary increases by $50,000 per annum. Then how much does he earn at the end of the first 3 years?

Solution: The amount earned by Mr. Kevin for the first year is, a = 4,00,000. The increment per annum is, d = 50,000. We have to calculate his earnings in the 3 years. So n = 3.

Substituting these values in the AP sum formula,

S n = n/2 [2a + (n - 1) d]

S n = 3/2(2(400000) + (3 - 1)(50000))

= 3/2 (800000 + 100000)

= 3/2 (900000)

He earned $1,350,000 in 3 years.

We can get the same answer by general thinking also as follows: The amount earned in 3 years = 400000 + 450000 + 500000 = 1350000. This could be calculated manually as n is a smaller value. But the above formulas are useful when n is a larger value.

Derivation of AP Sum Formula

Let us consider the first n terms of an arithmetic progression a 1 , a 1 + d, a 1 + 2d, ...., a 1 + (n - 1) d. Assume that the sum of these n terms is S n . Then

S n = a 1 + (a 1 + d) + (a 1 + 2d) + … + [a 1 + (n–1)d].

We can also start with the n th term and successively subtract the common difference, so,

S n = a n + (a n – d) + (a n – 2d) + … + [a n – (n–1)d].

Thus the sum of the arithmetic progression could be found in either of the ways. However, on adding those two equations together, we get

S n = a 1 + (a 1 + d) + (a 1 + 2d) + … + [a 1 + (n–1)d]

S n = a n + (a n – d) + (a n – 2d) + … + [a n – (n–1)d]

_________________________________________

2S n = (a 1 + a n ) + (a 1 + a n ) + (a 1 + a n ) + … + (a 1 + a n ).

____________________________________________

Notice all the d terms are cancelled out. So,

2S n = n (a 1 + a n )

⇒ S n = [n(a 1 + a n )]/2 --- (1)

By substituting a n = a 1 + (n – 1)d into the last formula, we have

S n = n/2 [a 1 + a 1 + (n – 1)d] ...Simplifying

S n = n/2 [2a 1 + (n – 1)d] --- (2)

These two formulas (1) and (2) help us to find the sum of an arithmetic series quickly.

Differences Between Arithmetic Progression and Geometric Progression

The following table explains the differences between arithmetic and geometric progression :

Important Notes on Arithmetic Progression:

• An AP is a list of numbers in which each term is obtained by adding a fixed number to the preceding number.
• a is represented as the first term, d is a common difference, a n as the n th term, and n as the number of terms.
• In general, AP can be represented as a, a + d, a + 2d, a + 3d, ...
• The n th term of an AP can be obtained by a n = a + (n − 1)d
• The sum of an AP can be obtained by s n = n/2 [2a + (n − 1) d]
• The graph of an AP is a straight line with the slope as the common difference.
• The common difference doesn't need to be positive always. For example, in the progression, 16, 8, 0, −8, −16, ... the common difference is negative (d = 8 - 16 = 0 - 8 = -8 - 0 = -16 - (-8) =... = -8).

☛ Related Articles:

• Arithmetic Sequence Calculator
• Sum of Arithmetic Sequence Calculator
• Sequence Calculator

Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12 . Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.

Arithmetic Progression Examples

Example 1: Find the general term of the arithmetic progression -3, -(1/2), 2…

The given progression is -3, -(1/2),2…

Here, the first term is a = -3, and the common difference is, d = -(1/2) - (-3) = -(1/2) + 3 = 5/2

By AP formulas , the general term of an AP is calculated by the formula:

a n = -3 + (n - 1) 5/2

= -3 + (5/2)n - 5/2

= 5n/2 - 11/2

Therefore, the general term of the given AP is:

Answer: a n = 5n/2 - 11/2

Example 2: Which term of the AP 3, 8, 13, 18,... is 78?

The given progression is 3,8,13,18,...

Here the first term is a = 3, and the common difference is, d = 8 - 3= 13 - 8 = ... = 5

Let us assume that the n th term is,

Substitute all these values in the general term of an arithmetic progression:

a n = a+(n - 1)d

78 = 3 +(n - 1)5

78 = 3 + 5n - 5

78 = 5n - 2

Answer: ∴ 78 is the 16 th term.

Example 3: Find the sum of the first 5 terms of the arithmetic progression whose first term is 3 and 5 th term is 11.

Solution: We have a 1 = a = 3 and a 5 = 11 and n = 5.

Using the AP formula for the sum of n terms, we have

S n = (n/2) (a + a n )

⇒ S 5 = (5/2) (3 + 11)

= (5/2) × 14

Answer: The required sum of the first 5 terms is 35.

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Arithmetic Progression

go to slide go to slide

FAQs on Arithmetic Progression

What is the meaning of arithmetic progression in maths.

A sequence of numbers where each term (other than the first term) is obtained by adding a fixed number to its previous term is called an arithmetic progression (A.P.). For example, is 3, 6, 9, 12, 15, 18, 21, … is an A.P. In simple words, we can say that an arithmetic progression is a sequence of numbers where the difference between each consecutive term is the same.

What is AP formula?

Here are the AP formulas corresponding to the AP a, a + d, a + 2d, a + 3d, . . . a + (n - 1)d:

• The formula to find the n th term is: a n = a + (n – 1) × d
• The formula to find the sum of n terms is S n = n/2 [2a + (n − 1) × d]

What are the Explicit Formula and Recursive Formula of AP?

For an AP a, a + d, a + 2d, ...

• the explicit formula to find the n th term is, a n = a + (n - 1) d
• the recursive formula to find the n th term is, a n = a n - 1 + d

How to Find the Sum of Arithmetic Progression?

To find the sum of arithmetic progression , we have to know the first term (a), the number of terms(n), and the common difference (d) between consecutive terms. Then substitute the values in the formula S n = n/2[2a + (n − 1) × d].

How to Find Number of Terms in Arithmetic Progression?

The number of terms in an arithmetic progression can be simply found by the division of the difference between the last and first terms by the common difference, and then adding 1.

What is the Sum of N Terms of the Arithmetic Progression Formula?

The sum of first n terms of an arithmetic progression can be calculated using one of the following two formulas:

• S n = n/2 [2a + (n - 1)d]
• S n = n/2 [a 1 + a n ].

How to Find Common Difference in Arithmetic Progression?

The common difference is the difference between every two consecutive terms in an arithmetic progression. Therefore, you can say that the formula to find the common difference of an arithmetic sequence is: d = a n - a n - 1 , where a n is the n th term in the progression, and a n - 1 is the previous term.

How to Find First Term in Arithmetic Progression?

If we know ‘d'(common difference) and any term (n th term) in the progression then we can find ‘a' (first term). If 5 th term is 10 and d = 2, then a 5 = a + 4d; 10 = a + 4(2); 10 = a + 8; a = 2.

What is the Difference Between Arithmetic Series and Arithmetic Progression?

Arithmetic progression is a progression in which the difference between every two consecutive terms is a constant whereas an arithmetic series is the sum of the elements of Arithmetic Progression.

What are the Types of Progressions in Maths?

There are three types of progressions in Maths. They are:

• Arithmetic Progression (AP)
• Geometric Progression (GP)
• Harmonic Progression (HP)

How do you Solve Arithmetic Progression Problems?

The following formulas help to solve arithmetic progression problems:

• Common difference of an AP: d = a n - a n-1 .
• Sum of n terms of an AP: S n = n/2 (2a + (n - 1)d)

Where is Arithmetic Progression Used?

A real-life application of arithmetic progression is seen when you take a taxi. Once you ride a taxi you will be charged an initial rate and then a per-mile or per-kilometre charge. This shows an arithmetic progression that for every kilometre you will be charged a certain fixed (constant) rate plus the initial rate.

What is Infinite Arithmetic Progression?

When the number of terms in an AP is infinite, we call it an infinite arithmetic progression. For example, 2, 4, 6, 8, 10, ... is an infinite AP; etc. The sum of an infinite arithmetic progression doesn't exist.

What is Nth Term in Arithmetic Progression?

The 'n th ' term in an AP is a formula with 'n' in it which enables you to find any term of a progression without having to go up from one term to the next. 'n' stands for the term number so to find the 50 th term we would just substitute 50 in the formula a n = a+ (n - 1)d in place of 'n'.

How to Find d in Arithmetic Progression?

To find d in an arithmetic progression, we take the difference between any two consecutive terms of the AP. It is always a term minus its previous term. An alternative way to find the common difference is just to see how much each term is getting added to get the next term.

Arithmetic Progression Questions

The Arithmetic Progression questions and answers are given here for students to help them better grasp the concept. Arithmetic Progressions (AP) is one of the most important concepts in Maths and it is included in higher education. NCERT standards will be followed for preparing these questions. The problems given here will cover both the basics and more complex topics, for students of all levels. Students can practise the arithmetic progression questions, and can then cross verify their answers with the provided solutions. To learn more about Arithmetic progression, click here .

Here, we have provided the Arithmetic Progression questions and answers with complete explanations.

Arithmetic Progression Questions with Solutions

1. Find the common difference for the following AP: 10, 20, 30, 40, 50.

Given AP: 10, 20, 30, 40, 50

Common difference:

d = 20 – 10 = 10

d = 30 – 20 = 10

d = 40 – 30 = 10

d = 50 – 40 = 10.

Hence, the common difference for the sequence, 10, 20, 30, 40, 50 is 10.

2. Is a, 2a, 3a, 4a, … an arithmetic progression?

Given sequence: a, 2a, 3a, 4a, …

To check whether the given sequence is AP or not, we have to find the common difference.

Hence, d = 2a – a = a

d = 3a – 2a = a

d = 4a – 3a = a

Hence, the common difference is “a”.

Therefore, the sequence a, 2a, 3a, 4a,… is an arithmetic progression.

3. Prove that 7, 11, 15, 19, 23 is an AP.

Given sequence: 7, 11, 15, 19, 23.

To prove that the sequence is AP, find the common difference between two consecutive terms.

d = 11 – 7 = 4

d = 15 – 11 = 4

d = 19 – 15 = 4

d = 23 – 19 = 4

Hence, 7, 11, 15, 19, 23 is an AP with a common difference of 4.

4. The sequence 28, 22, x, y, 4 is an AP. Find the values of x and y.

Given AP: 28, 22, x, y, 4

Here, first term, a = 28

Common difference, d = 22 – 28 = -6

Hence, x = 22 – 6 = 16

y = 16 – 6 = 10.

Hence, the values of x and y are 16 and 10, respectively.

5. What is the nth term of an AP 9, 13, 17, 21, 25, …?

Given AP: 9, 13, 17, 21, 25, …

Here, a = 9

d = 13 – 9 = 4

The formula to find the nth term of an AP is a + (n-1)d.

The nth term of an AP = 9 + (n-1)4

= 9 + 4n -4

Hence, the nth term of AP 9, 13, 17, 21, 25, … is 4n+5.

6. Find the 5th term of the arithmetic progression 1, 4, 7, ….

Given AP: 1, 4, 7, …

d = 4 – 1 = 3

As we know,

The nth term of AP = a + (n-1)d

Hence, 5th term of AP = 1 + (5-1)3

Hence, the 5th term of AP is 13.

Also, check: Arithmetic Progression Class 10 Notes .

7. Find the 17th term of AP 4, 9, 14, …

Given AP: 4, 9, 14, …

Here, a = 4

d = 9 – 4 = 5

Now, substitute the values in the formula a+(n-1)d,

17th term of AP = 4+(17-1)5

= 4+80 = 84

Hence, the 17th term of AP is 84.

8. If the first, second and last terms of the AP are 5, 9, 101, respectively, find the total number of terms in the AP.

Given: First term, a = 5

Common difference, d = 9 – 5 = 4

Last term, a n = 101

Now, we have to find the value of “n”.

Hence, a n = a+(n-1)d

Substituting the values, we get

5+(n-1)4 = 101

5+4n-4 = 101

n=100/4 = 25

Hence, the number of terms in the AP is 25.

9. What is the general term of the series, 4, 7, 10, 13, …?

Given sequence is 4, 7, 10, 13, …

d = 7-4 = 3

The general term of an AP is:

a n = a+(n-1)d

a n = 4 +(n-1)3

a n = 4 + 3n-3

Therefore, the general term of the series 4, 7, 10, 13 is 3n+1.

10. Which term of AP 27, 24, 21, … is 0?

Given AP: 27, 24, 21, …

Here, a = 27

d = 24 – 27 = -3.

Also given that a n = 0

Now, we have to find the value of n.

0 = 27 +(n-1)(-3)

0 = 27 -3n +3

0 = 30 – 3n

Hence, n = 10

Therefore, the 10th term of AP is 0.

Practice Questions

• The sequence 12b, 8b, 4b is in AP. Find the sum of the first 18 terms.
• The first three terms of a sequence are 8, y, 18. Find the value of y so that the sequence becomes an Arithmetic progression.
• In an Arithmetic progression, the ratio of the 7th term to the 10th term is -1. If the 16th term is -15, find the 3rd term.

Visit BYJU’S – The Learning App, and download the app to learn all Maths-related concepts easily by exploring more videos.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

• Math Lessons
• Math Formulas
• Calculators

Math Calculators, Lessons and Formulas

It is time to solve your math problem

• HW Help (paid service)
• Progressions

Arithmetic Progressions

Definition:

By an arithmetic progression of $m$ terms, we mean a finite sequence of the form

The real number $a$ is called the first term of the arithmetic progression, and the real number $d$ is called the difference of the arithmetic progression.

Consider the sequence of numbers

The property of this sequence is that the difference between successive terms is constant and equal to 2.

Here we have: $a = 1$; $d = 2$.

Consider the sequence of numbers:

The property of this sequence is that the difference between successive terms is constant and equal to 3.

Here we have: $a = 2$; $d = 3$.

• Roots and Radicals Simplify Expression Adding and Subtracting Multiplying and Dividing
• Complex Numbers Arithmetic Polar representation
• Polynomials Multiplying Polynomials Division of Polynomials Zeros of Polynomials
• Rational Expressions Simplifying Multiplying and Dividing Adding and Subtracting
• Solving Equations Linear Equations Absolute Value Equations Quadratic Equation Equations with Radicals
• Systems of Equations Substitution Method Elimination Method Row Reduction Cramers Rule Inverse Matrix Method
• Exponential Functions Introduction Exponential Equations Logarithmic Functions
• Trigonometry Trigonometric Formulas Trigonometric Equations Law of Cosines
• Progressions Arithmetic Progressions Geometric Progressions
• Differentiation Common formulas Product and Quotient Rule Chain Rule
• Limits Properties of Limits Rational Function Irrational Functions Trigonometric Functions L'Hospital's Rule
• Integrals Integration Formulas Exercises
• Integral techniques Substitution Integration by Parts Integrals with Trig. Functions Trigonometric Substitutions
• Integral Applications Area Volume Arc Length

Analytic geometry

• Analytic Geometry 2D Basic Concepts Lines Parallel and Perpendicular Lines Polar Coordinates
• Conic Sections Circle Ellipse Hyperbola
• Analytic Geometry 3D Line in 3D Planes

Linear Algebra

• Matrices Definitions Addition and Multiplication Gauss-Jordan elimination
• Determinants Introduction to Determinants Applications of Determinants
• Vectors Basic Operations Dot Product Cross Product

Random Quote

There are things which seem incredible to most men who have not studied Mathematics.

Archimedes of Syracus

Go down deep enough into anything and you will find mathematics.

Dean Schlicter

Welcome to MathPortal. This website's owner is mathematician Miloš Petrović. I designed this website and wrote all the calculators, lessons, and formulas .

If you want to contact me, probably have some questions, write me using the contact form or email me on [email protected]

Email (optional)

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.2: Problem Solving with Arithmetic Sequences

• Last updated
• Save as PDF
• Page ID 83159

• Jennifer Freidenreich
• Diablo Valley College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Arithmetic sequences, introduced in Section 8.1, have many applications in mathematics and everyday life. This section explores those applications.

Example 8.2.1

A water tank develops a leak. Each week, the tank loses \(5\) gallons of water due to the leak. Initially, the tank is full and contains \(1500\) gallons.

• How many gallons are in the tank \(20\) weeks later?
• How many weeks until the tank is half-full?
• How many weeks until the tank is empty?

This problem can be viewed as either a linear function or as an arithmetic sequence. The table of values give us a few clues towards a formula.

The problem allows us to begin the sequence at whatever \(n\)−value we wish. It’s most convenient to begin at \(n = 0\) and set \(a_0 = 1500\).

Therefore, \(a_n = −5n + 1500\)

Since the leak is first noticed in week one, \(20\) weeks after the initial week corresponds with \(n = 20\). Use the formula where \(\textcolor{red}{n = 20}\):

\(a_{20} = −5(\textcolor{red}{20}) + 1500 = −100 + 1500 = 1400\)

Therefore, \(20\) weeks later, the tank contains \(1400\) gallons of water.

• How many weeks until the tank is half-full? A half-full tank would be \(750\) gallons. We need to find \(n\) when \(\textcolor{red}{a_n = 750}\).

\(\begin{array} &750 &= −5n + 1500 &\text{Substitute \(a_n = 750\) into the general term.} \\ 750 − 1500 &= −5n + 1505 − 1500 &\text{Subtract \(1500\) from each side of the equation.} \\ −750 &= −5n &\text{Simplify each side of the equation.} \\ \dfrac{−750}{−5} &= \dfrac{−5n}{−5} &\text{Divide both sides by \(−5\).} \\ 150 &= n & \end{array}\)

Since \(n\) is the week-number, this answer tells us that on week \(150\), the tank is half full. However, most people would better understand the answer if stated in the following way, “The tank is half full after 150 weeks.” This answer sounds more natural and is preferred.

• How many weeks until the tank is empty? The tank is empty when \(a_n = 0\) gallons. Find \(n\) such that \(\textcolor{red}{a_n = 0}\).

\(\begin{array}& 0 &= −5n + 1500 &\text{Substitute \(a_n=0\) into the general term.} \\ 0 − 1500 &= −5n + 1500 − 1500 &\text{Subtract \(1500\) from each side of the equation.} \\ −1500 &= −5n &\text{Simplify.} \\ \dfrac{−1500}{−5} &= \dfrac{−5n}{−5} &\text{Divide both sides by \(−5\).} \\ 300 &= n & \end{array}\)

Since \(n\) is the week-number, this answer tells us that on week \(300\), the tank is empty. However, most people would better understand the answer if stated in the following way, “ The tank is empty after 300 weeks. ” This answer sounds more natural and is preferred.

Example 8.2.2

Three stages of a pattern are shown below, using matchsticks. Each stage requires a certain number of matchsticks. If we keep up the pattern…

• How many matchsticks are required to make the figure in stage \(34\)?
• What stage would require \(220\) matchsticks?

Let’s create a table of values. Let \(n =\) stage number, and let \(a_n =\) the number of matchsticks used in that stage. Then note the common difference.

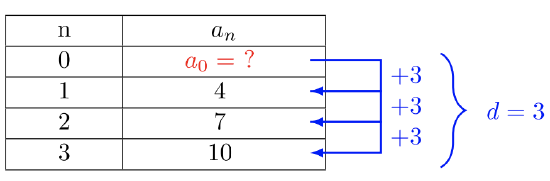
Find the value \(a_0\):

\(\begin{array} &a_0 + 3 &= 4 \\ a_0 + 3 − 3 &= 4 − 3 \\ a_0 &= 1 \end{array}\)

The general term of the sequence is:

\(a_n = 3n + 1\)

• Compute \(a_{34}\) to find the number of matchsticks in stage \(34\):

\(a_{34} = 3(\textcolor{red}{34}) + 1 = 103\).

There are \(103\) matchsticks in stage \(34\).

• What stage would require \(220\) matchsticks? We are looking for the stage-number, given the number of matchsticks. Find \(n\) if \(a_n = 220\).

\(\begin{array} &220 &= 3n + 1 \\ 219 &= 3n \\ 73 &= n \end{array}\)

Answer Stage \(73\) would require \(220\) matchsticks.

Example 8.2.3

Cory buys \(5\) items at the grocery store with prices \(a_1\), \(a_2\), \(a_3\), \(a_4\), \(a_5\) which is an arithmetic sequence. The least expensive item is \($1.89\), while the total cost of the \(5\) items is \($12.95\). What is the cost of each item?

Put the \(5\) items in order of expense: least to most and left to right. Because it is an arithmetic sequence, each item is \(d\) more dollars than the previous item. Each item’s price can be written in terms of the price of the least expensive item, \(a_1\), and \(a_1 = $1.89\).

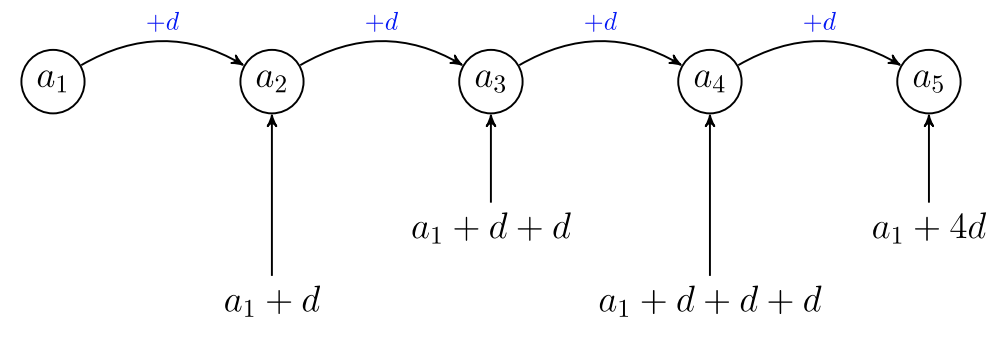
The diagram above gives \(5\) expressions for the costs of the \(5\) items in terms of \(a_1\) and the common difference is \(d\).

\(\begin{array} &a_1 + a_2 + a_3 + a_4 + a_5 &= 12.95 &\text{Total cost of \(5\) items is \($12.95\).} \\ a_1 + (a_1 + d) + (a_1 + 2d) + (a_1 + 3d) + (a_1 + 4d) &= 12.95 &\text{See diagram for substitutions.} \\ 5s_1 + 10d &= 12.95 &\text{Gather like terms.} \\ 5(1.89) + 10d &= 12.95 &a_1 = 1.89. \\ 9.45 + 10d &= 12.95 &\text{Simplify.} \\ 9.45 + 10d − 9.45 &= 12.95 − 9.45 &\text{Subtract \(9.45\) from each side of equation.} \\ 10d &= 3.50 &\text{Simplify. Then divide both sides by \(10\).} \\ d &= 0.35 &\text{The common difference is \($0.35\).} \end{array}\)

Now that we know the common difference, \(d = $0.35\), we can answer the question.

The price of each item is as follows: \($1.89, $2.24, $2.59, $2.94, $3.29\).

Try It! (Exercises)

1. ZKonnect cable company requires customers sign a \(2\)-year contract to use their services. The following describes the penalty for breaking contract: Your services are subject to a minimum term agreement of \(24\) months. If the contract is terminated before the end of the \(24\)-month contract, an early termination fee is assessed in the following manner: \($230\) termination fee is assessed if contract is terminated in the first \(30\) days of service. Thereafter, the termination fee decreases by \($10\) per month of contract.

• If Jack enters contract with ZKonnect on April 1 st of \(2021\), but terminates the service on January 10 th of \(2022\), what are Jack’s early termination fees?
• The general term \(a_n\) describes the termination fees for the stated contract. Describe the meaning of the variable \(n\) in the context of this problem. Find the general term \(a_n\).
• Is the early termination fee a finite sequence or an infinite sequence? Explain.
• Find the value of \(a_{13}\) and interpret its meaning in words.

2. A drug company has manufactured \(4\) million doses of a vaccine to date. They promise additional production at a rate of \(1.2\) million doses/month over the next year.

• How many doses of the vaccine, in total, will have been produced after a year?
• The general term \(a_n\) describes the total number of doses of the vaccine produced. Describe the meaning of the variable \(n\) in the context of this problem. Find the general term\(a_n\).
• Find the value of \(a_8\) and interpret its meaning in words.

3. The theater shown at right has \(22\) seats in the first row of the “A Center” section. Each row behind the first row gains two additional seats.

• Let \(a_n = 22 + 2n\), starting with \(n = 0\). Give the first \(10\) values of this sequence.
• Using \(a_n = 22 + 2n\), Find the value of \(a_{10}\) and interpret its meaning in words in the context of this problem. Careful! Does \(n=\) row number?
• How many seats, in total, are in “A Center” section if there are \(12\) rows in the section?

4) Logs are stacked in a pile with \(48\) logs on the bottom row and \(24\) on the top row. Each row decreases by three logs.

• The stack, as described, has how many rows of logs?
• Write the general term \(a_n\) to describe the number of logs in a row in two different ways. Each general term should produce the same sequence, regardless of its starting \(n\)-value.

i. Start with \(n = 0\).

ii. Start with \(n = 1\).

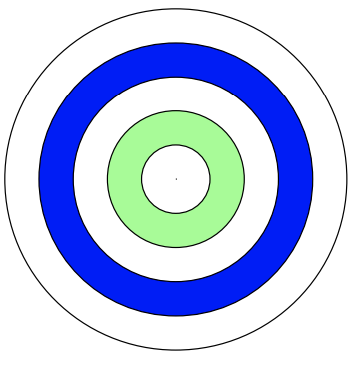
5) The radii of the target circle are an arithmetic sequence. If the area of the innermost circle is \(\pi \text{un}^2\) and the area of the entire target is \(49 \pi \text{un}^2\), what is the area of the blue ring? [The formula for area of a circle is \(A = \pi r^2\)].

6) Three stages of a pattern are shown below, using matchsticks. Each stage adds another triangle and requires a certain number of matchsticks. If we keep up the pattern…

• What stage would require \(325\) matchsticks?

7) Three stages of a pattern are shown below, using matchsticks. Each stage requires a certain number of matchsticks. If we keep up the pattern…

• How many matchsticks are required to make the figure in stage \(22\)?
• What stage would require \(424\) matchsticks?

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators

Arithmetic Sequence Problems with Solutions – Mastering Series Challenges

JUMP TO TOPIC

Arithmetic Sequences Practice Problems and Solutions

Calculating terms in an arithmetic sequence, solving problems involving arithmetic sequences.

An arithmetic sequence is a series where each term increases by a constant amount, known as the common difference . I’ve always been fascinated by how this simple pattern appears in many mathematical problems and real-world situations alike.

Understanding this concept is fundamental for students as it not only enhances their problem-solving skills but also introduces them to the systematic approach of sequences in math .

The first term of an arithmetic sequence sets the stage, while the common difference dictates the incremental steps that each subsequent term will follow. This can be mathematically expressed as $a_n = a_1 + (n – 1)d$.

Whether I’m calculating the nth term or the sum of terms within a sequence , these formulas are the tools that uncover solutions to countless arithmetic sequence problems. Join me in unraveling the beauty and simplicity of arithmetic sequences ; together, we might just discover why they’re considered the building blocks in the world of mathematics .

When I work with arithmetic sequences , I always keep in mind that they have a unique feature: each term is derived by adding a constant value, known as the common difference , to the previous term. Let’s explore this concept through a few examples and problems.

Example 1: Finding a Term in the Sequence

Given the first term, $a_1$ of an arithmetic sequence is 5 and the common difference ( d ) is 3, what is the 10th term $a_{10}$?

Here’s how I determine it: $a_{10} = a_1 + (10 – 1)d ] [ a_{10} = 5 + 9 \times 3 ] [ a_{10} = 5 + 27 ] [ a_{10} = 32$

So, the 10th term is 32.

Sequence A: If $a_1 = 2 $and ( d = 4 ), find $a_5$.

Sequence B: For $a_3 = 7 $ and $a_7 = 19$, calculate the common difference ( d ).

I calculate $a_5$ by using the formula: $a_n = a_1 + (n – 1)d $ $ a_5 = 2 + (5 – 1) \times 4 $ $a_5 = 2 + 16 $ $a_5 = 18$

To find ( d ), I use the formula: $a_n = a_1 + (n – 1)d$ Solving for ( d ), I rearrange the terms from $a_3$ and $a_7$: $d = \frac{a_7 – a_3}{7 – 3}$ $d = \frac{19 – 7}{4}$ $d = \frac{12}{4}$ [ d = 3 ]

Here’s a quick reference table summarizing the properties of arithmetic sequences :

Remember these properties to solve any arithmetic sequence problem effectively!

In an arithmetic sequence , each term after the first is found by adding a constant, known as the common difference ( d ), to the previous term. I find that a clear understanding of the formula helps immensely:

$a_n = a_1 + (n – 1)d$

Here, $a_n$ represents the $n^{th}$term, $a_1$ is the first term, and ( n ) is the term number.

Let’s say we need to calculate the fourth and fifth terms of a sequence where the first term $a_1 $ is 8 and the common difference ( d ) is 2. The explicit formula for this sequence would be $ a_n = 8 + (n – 1)(2) $.

To calculate the fourth term $a_4 $: $a_4 = 8 + (4 – 1)(2) = 8 + 6 = 14$

For the fifth term ( a_5 ), just add the common difference to the fourth term: $a_5 = a_4 + d = 14 + 2 = 16$

Here’s a table to illustrate these calculations:

Remember, the formula provides a direct way to calculate any term in the sequence, known as the explicit or general term formula. Just insert the term number ( n ) and you’ll get the value for $a_n$. I find this methodical approach simplifies the process and avoids confusion.

When I approach arithmetic sequences , I find it helpful to remember that they’re essentially lists of numbers where each term is found by adding a constant to the previous term. This constant is called the common difference, denoted as ( d ). For example, in the sequence 3, 7, 11, 15, …, the common difference is ( d = 4 ).

To articulate the ( n )th term of an arithmetic sequence, $a_n $, I use the fundamental formula:

$a_n = a_1 + (n – 1)d $

In this expression, $a_1$ represents the first term of the sequence.

If I’m solving a specific problem—let’s call it Example 1—I might be given $a_1 = 5 $and ( d = 3 ), and asked to find $a_4 $. I’d calculate it as follows:

$a_4 = 5 + (4 – 1) \times 3 = 5 + 9 = 14$

In applications involving arithmetic series, such as financial planning or scheduling tasks over weeks, the sum of the first ( n ) terms often comes into play. To calculate this sum, ( S_n ), I rely on the formula:

$S_n = \frac{n}{2}(a_1 + a_n)$

Now, if I’m asked to work through Example 3, where I need the sum of the first 10 terms of the sequence starting with 2 and having a common difference of 5, the process looks like this:

$a_{10} = 2 + (10 – 1) \times 5 = 47$ $S_{10} = \frac{10}{2}(2 + 47) = 5 \times 49 = 245$

Linear functions and systems of equations sometimes bear a resemblance to arithmetic sequences, such as when I need to find the intersection of sequence A and sequence B. This would involve setting the nth terms equal to each other and solving the resulting linear equation.

Occasionally, arithmetic sequences can be mistaken for geometric sequences , where each term is found by multiplying by a constant. It’s important to differentiate between them based on their definitions.

For exercises, it’s beneficial to practice finding nth terms, and sums , and even constructing sequences from given scenarios. This ensures a robust understanding when faced with a variety of problems involving arithmetic sequences .

In exploring the realm of arithmetic sequences , I’ve delved into numerous problems and their corresponding solutions. The patterns in these sequences—where the difference between consecutive terms remains constant—allow for straightforward and satisfying problem-solving experiences.

For a sequence with an initial term of $a_1 $ and a common difference of ( d ), the $n^{th}$term is given by $a_n = a_1 + (n – 1)d $.

I’ve found that this formula not only assists in identifying individual terms but also in predicting future ones. Whether calculating the $50^{th}$term or determining the sum of the first several terms, the process remains consistent and is rooted in this foundational equation.

In educational settings, arithmetic sequences serve as an excellent tool for reinforcing the core concepts of algebra and functions. Complexity varies from basic to advanced problems, catering to a range of skill levels. These sequences also reflect practical real-world applications, such as financial modeling and computer algorithms, highlighting the relevance beyond classroom walls.

Through practicing these problems, the elegance and power of arithmetic sequences in mathematical analysis become increasingly apparent. They exemplify the harmony of structure and progression in mathematics —a reminder of how simple rules can generate infinitely complex and fascinating patterns.

• Pre Calculus
• Probability
• Sets & Set Theory
• Trigonometry

Arithmetic Sequences and Sums

A Sequence is a set of things (usually numbers) that are in order.

Each number in the sequence is called a term (or sometimes "element" or "member"), read Sequences and Series for more details.

Arithmetic Sequence

In an Arithmetic Sequence the difference between one term and the next is a constant .

In other words, we just add the same value each time ... infinitely.

Example: 1, 4, 7, 10, 13, 16, 19, 22, 25, ...

This sequence has a difference of 3 between each number. The pattern is continued by adding 3 to the last number each time, like this:

In General we could write an arithmetic sequence like this:

{a, a+d, a+2d, a+3d, ... }

• a is the first term, and
• d is the difference between the terms (called the "common difference" )

Example (continued): 1, 4, 7, 10, 13, 16, 19, 22, 25, ...

• a = 1 (the first term)
• d = 3 (the "common difference" between terms)

And we get:

{1, 1+3, 1+2×3, 1+3×3, ... }

{1, 4, 7, 10, ... }

We can write an Arithmetic Sequence as a rule :

x n = a + d(n−1)

(We use "n−1" because d is not used in the 1st term).

Example: Write a rule, and calculate the 9th term, for this Arithmetic Sequence:

3, 8, 13, 18, 23, 28, 33, 38, ...

This sequence has a difference of 5 between each number.

The values of a and d are:

• a = 3 (the first term)
• d = 5 (the "common difference")

Using the Arithmetic Sequence rule:

So the 9 th term is:

x 9 = 5× 9 − 2 = 43

Is that right? Check for yourself!

Arithmetic Sequences are sometimes called Arithmetic Progressions (A.P.’s)

Advanced Topic : Summing an Arithmetic Series

To sum up the terms of this arithmetic sequence:

a + (a+d) + (a+2d) + (a+3d) + ...

use this formula:

What is that funny symbol? It is called Sigma Notation

And below and above it are shown the starting and ending values:

It says "Sum up n where n goes from 1 to 4. Answer= 10

Here is how to use it:

Example: Add up the first 10 terms of the arithmetic sequence:

{ 1, 4, 7, 10, 13, ... }

The values of a , d and n are:

• n = 10 (how many terms to add up)

= 5(2+9·3) = 5(29) = 145

Check: why don't you add up the terms yourself, and see if it comes to 145

Footnote: Why Does the Formula Work?

Let's see why the formula works, because we get to use an interesting "trick" which is worth knowing.

First , we will call the whole sum "S" :

Next , rewrite S in reverse order:

Now add those two, term by term:

Each term is the same! And there are "n" of them so ...

Now, just divide by 2 and we get:

S = n 2 (2a + (n−1)d)

Which is our formula:

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 9: Sequences

About this unit.

Sequences are a special type of function that are useful for describing patterns. In this unit, we'll see how sequences let us jump forwards or backwards in patterns to solve problems.

Introduction to arithmetic sequences

• Sequences intro (Opens a modal)
• Intro to arithmetic sequences (Opens a modal)
• Extending arithmetic sequences (Opens a modal)
• Using arithmetic sequences formulas (Opens a modal)
• Intro to arithmetic sequence formulas (Opens a modal)
• Worked example: using recursive formula for arithmetic sequence (Opens a modal)
• Extend arithmetic sequences Get 3 of 4 questions to level up!
• Use arithmetic sequence formulas Get 5 of 7 questions to level up!

Constructing arithmetic sequences

• Recursive formulas for arithmetic sequences (Opens a modal)
• Explicit formulas for arithmetic sequences (Opens a modal)
• Arithmetic sequence problem (Opens a modal)
• Converting recursive & explicit forms of arithmetic sequences (Opens a modal)
• Arithmetic sequences review (Opens a modal)
• Recursive formulas for arithmetic sequences Get 3 of 4 questions to level up!
• Explicit formulas for arithmetic sequences Get 3 of 4 questions to level up!
• Converting recursive & explicit forms of arithmetic sequences Get 3 of 4 questions to level up!

Introduction to geometric sequences

• Intro to geometric sequences (Opens a modal)
• Extending geometric sequences (Opens a modal)
• Using explicit formulas of geometric sequences (Opens a modal)
• Using recursive formulas of geometric sequences (Opens a modal)
• Extend geometric sequences Get 3 of 4 questions to level up!
• Extend geometric sequences: negatives & fractions Get 3 of 4 questions to level up!
• Use geometric sequence formulas Get 3 of 4 questions to level up!

Constructing geometric sequences

• Explicit & recursive formulas for geometric sequences (Opens a modal)
• Converting recursive & explicit forms of geometric sequences (Opens a modal)
• Geometric sequences review (Opens a modal)
• Recursive formulas for geometric sequences Get 3 of 4 questions to level up!
• Explicit formulas for geometric sequences Get 3 of 4 questions to level up!
• Converting recursive & explicit forms of geometric sequences Get 3 of 4 questions to level up!

Modeling with sequences

• Sequences word problems (Opens a modal)
• Sequences word problems Get 3 of 4 questions to level up!

General sequences

• Evaluating sequences in recursive form (Opens a modal)
• Sequences and domain (Opens a modal)
• Sequences: FAQ (Opens a modal)
• Evaluate sequences in recursive form Get 3 of 4 questions to level up!
• Sequences and domain Get 3 of 4 questions to level up!