solving problems using complex number

Study Guides > Boundless Algebra

Complex numbers, introduction to complex numbers, learning objectives, key takeaways.

A complex number is a number that can be expressed in the form [latex]a+bi[/latex], where [latex]a[/latex] and [latex]b[/latex] are real numbers and [latex]i[/latex] is the imaginary unit.
The real number [latex]a[/latex] is called the real part of the complex number [latex]z=a+bi[/latex] and is denoted [latex]\text{Re}\{a+bi\}=a[/latex]. The real number [latex]b[/latex] is called the imaginary part of [latex]z=a+bi[/latex] and is denoted [latex]\text{Im}\{a+bi\}=b[/latex].
real number : An element of the set of real numbers. The set of real numbers include the rational numbers and the irrational numbers, but not all complex numbers.
imaginary number : a number of the form [latex]ai[/latex], where [latex]a[/latex] is a real number and [latex]i[/latex] the imaginary unit
complex : a number, of the form [latex]a+bi[/latex], where [latex]a[/latex] and [latex]b[/latex] are real numbers and [latex]i[/latex] is the square root of [latex]-1[/latex].

The Complex Number System

Addition and Subtraction of Complex Numbers

Complex numbers can be added and subtracted to produce other complex numbers. This is done by adding the corresponding real parts and the corresponding imaginary parts.
It is possible for two non-real complex numbers to add to a real number. However, two real numbers can never add to be a non-real complex number.

Sums of Complex Numbers

Differences (subtraction) of complex numbers, multiplication of complex numbers.

The imaginary unit [latex]i[/latex] has the property that [latex]i^2=-1[/latex]
Complex numbers can be multiplied using the FOIL algorithm

The Square of the Imaginary Unit [latex]i[/latex]

Multiplying complex numbers, complex numbers and the binomial theorem.

The binomial theorem can be used to compute powers of complex numbers. To compute [latex](a+bi)^n[/latex] we consider the expression [latex](x+y)^n [/latex] where [latex]x=a[/latex] and [latex]y=bi[/latex].
The powers of [latex]i[/latex] are [latex]i^2=-1[/latex], [latex]i^3=-i[/latex], [latex]i^4=1[/latex], and [latex]i^5=i[/latex], etc.

The Powers of [latex]i[/latex]

Computing powers of complex numbers, complex conjugates.

The complex conjugate of [latex]a+bi[/latex] is [latex]a-bi[/latex], and vice versa.
Two complex conjugates multiply together to be the square of the length of the complex number.
If a complex number is a root of a polynomial equation, then its complex conjugate is a root as well.
modulus : The length of a complex number, [latex]\sqrt{a^2+b^2}[/latex]
complex conjugate : For the number [latex]a + bi[/latex], this is [latex]a-bi[/latex].

The Product of Two Conjugates

The x-axis is the real axis and the imaginary axis is the y-axis. The point a + bi is in the first quadrant in this image, with x (real) coordinate a and y (imaginary) coordinate b.

Complex Roots Come in Conjugate Pairs

Division of complex numbers.

Division of complex numbers is accomplished by multiplying by the multiplicative inverse of the denominator.
The multiplicative inverse of the complex number [latex]z[/latex] is [latex]\frac{\overline{z}}{|z|^2}[/latex]
If [latex]w[/latex] and [latex]z[/latex] are complex numbers, we have [latex]\frac{w}{z} = w \cdot \frac{\overline{z}}{|z|^2}[/latex]

Multiplicative Inverses of Complex Numbers

Complex numbers in polar coordinates.

The complex number [latex]z=a+bi[/latex] can be written [latex]z=re^{i\phi}[/latex] where [latex]r=\sqrt{a^2+b^2}[/latex] is the modulus of [latex]z[/latex], and [latex]\phi[/latex] is the angle that the line segment from the origin to [latex]z[/latex] makes with the horizontal.
Using polar coordinates, it becomes easier to multiply and divide complex numbers, using the geometric interpretation as a guide.

Multiplying Complex Numbers in Polar Coordinates

Dividing complex numbers in polar coordinates, licenses & attributions, cc licensed content, shared previously.

Curation and Revision. Authored by: Boundless.com. License: Public Domain: No Known Copyright .

CC licensed content, Specific attribution

Complex number. Provided by: Wikipedia Located at: https://en.wikipedia.org/wiki/Complex_number. License: CC BY-SA: Attribution-ShareAlike .
real number. Provided by: Wiktionary License: CC BY-SA: Attribution-ShareAlike .
complex. Provided by: Wiktionary License: CC BY-SA: Attribution-ShareAlike .
imaginary number. Provided by: Wiktionary License: CC BY-SA: Attribution-ShareAlike .
CNX_Precalc_Figure_03_01_002.jpg. Provided by: OpenStax Located at: https://cnx.org/contents/9AFg5Sd0@11/Complex-Numbers. License: Public Domain: No Known Copyright .
440px-Complex_number_illustration.svg.png. Provided by: Wikipedia License: Public Domain: No Known Copyright .
Complex_number_illustration_modarg.svg. Provided by: Wikipedia License: Public Domain: No Known Copyright .

Please add a message.

Message received. Thanks for the feedback.

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons
Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

9.6: Introduction to Complex Numbers and Complex Solutions

Last updated
Save as PDF
Page ID 18387

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

Learning Objectives

Perform operations with complex numbers.
Solve quadratic equations with complex solutions.

Introduction to Complex Numbers

Up to this point, the square root of a negative number has been left undefined. For example, we know that $\sqrt{−9}$ is not a real a number.

$\sqrt{-9}=\color{Cerulean}{?} \quad \color{black}{\text { or} } \quad(\color{Cerulean}{?}\color{black}{)}^{2}=-9$

There is no real number that when squared results in a negative number. We begin the resolution of this issue by defining the imaginary unit, i, as the square root of −1.

\[i=\sqrt{-1} \quad \text { and } \quad i^{2}=-1\]

To express a square root of a negative number in terms of the imaginary unit i , we use the following property, where a represents any nonnegative real number:

With this we can write

If $\sqrt{-9}=3i$, then we would expect that 3 i squared equals: -9:

Therefore, the square root of any negative real number can be written in terms of the imaginary unit. Such numbers are often called imaginary numbers.

Example $\PageIndex{1}$

Rewrite in terms of the imaginary unit i .

$\sqrt{-4}$
$\sqrt{-5}$
$\sqrt{-8}$

a. $\sqrt{-4}=\sqrt{-1\cdot 4} = \sqrt{-1}\cdot\sqrt{4}=i\cdot 2 = 2i$

b. $\sqrt{-5}=\sqrt{-1\cdot 5} = \sqrt{-1}\cdot\sqrt{5}=i\cdot\sqrt{5} = i\sqrt{5}$

c. $\sqrt{-8}=\sqrt{-1\cdot 4\cdot 2} = \sqrt{-1}\cdot\sqrt{4}\sqrt{2} = i\cdot 2\cdot \sqrt{2} = 2i\sqrt{2}$

When an imaginary number involves a radical, place i in front of the radical. Consider the following:

$2i\sqrt{2} = 2\sqrt{2}i$

Since multiplication is commutative, these numbers are equivalent. However, in the form $2\sqrt{2}i$, the imaginary unit i is often misinterpreted to be part of the radicand. To avoid this confusion, it is a best practice to place the i in front of the radical and use $2i\sqrt{2}$.

A complex number is any number of the form

where a and b are real numbers. Here a is called the real part and b is called the imaginary part. For example, $3−4i$ is a complex number with a real part, 3, and an imaginary part, −4. It is important to note that any real number is also a complex number. For example, the real number 5 is also a complex number because it can be written as $5+0i$ with a real part of 5 and an imaginary part of 0. Hence the set of real numbers, denoted R , is a subset of the set of complex numbers, denoted C .

Adding and subtracting complex numbers is similar to adding and subtracting like terms. Add or subtract the real parts and then the imaginary parts.

Example $\PageIndex{2}$

$(3−4i)+(2+5i)$

Add the real parts and then add the imaginary parts.

To subtract complex numbers, subtract the real parts and subtract the imaginary parts. This is consistent with the use of the distributive property.

Example $\PageIndex{3}$

$(3−4i)−(2+5i)$

Distribute the negative one and then combine like terms

The distributive property also applies when multiplying complex numbers. Make use of the fact that $i^{2}=−1$ to resolve the result into standard form: $a+bi$.

Example $\PageIndex{4}$

$5i(3−4i)$

Begin by applying the distributive property.

Example $\PageIndex{5}$

$(3−4i)(4+5i)$

Given a complex number $a+bi$, its complex conjugate is $a−bi$. We next explore the product of complex conjugates.

Example $\PageIndex{6}$

$(3−4i)(3+4i)$

In general, the product of complex conjugates follows:

$\begin{aligned}(a+b i)(a-b i) &=a^{2}-a \cdot b i+b i \cdot a-b^{2} i^{2} \\ &=a^{2}-a b i+a b i-b^{2}(-1) \\ &=a^{2}+b^{2} \end{aligned}$

Note that the result does not involve the imaginary unit; hence the result is real. This leads us to the very useful property:

\[(a+b i)(a-b i)=a^{2}+b^{2}\]

To divide complex numbers, we apply the technique used to rationalize the denominator. Multiply the numerator and denominator (dividend and divisor) by the conjugate of the denominator. The result can then be resolved into standard form, $a+bi$.

Example $\PageIndex{7}$

$\frac{1}{1-2i}$

In this example, the conjugate of the denominator is $1+2i$. Multiply by 1 in the form $\frac{(1+2i)}{(1+2i)}$.

To express this complex number in standard form, write each term over the common denominator 5.

$\begin{aligned} \frac{1+2 i}{5} &=\frac{1}{5}+\frac{2 i}{5} \\ &=\frac{1}{5}+\frac{2}{5} i \end{aligned}$

$\frac{1}{5}+\frac{2}{5} i$

Example $\PageIndex{8}$

$\frac{3−4i}{3+2i}$.

$\frac{1}{13}-\frac{18}{13} i$

Exercise $\PageIndex{1}$

$\frac{5+5i}{1-3i}$

Quadratic Equations with Complex Solutions

Now that complex numbers are defined, we can complete our study of solutions to quadratic equations. Often solutions to quadratic equations are not real.

Example $\PageIndex{9}$

Solve using the quadratic formula:

$x^{2}−2x+5=0$

Begin by identifying a , b , and c . Here

Substitute these values into the quadratic formula and then simplify.

Check these solutions by substituting them into the original equation.

$\begin{array}{r|r}{Check \:x=1-2i}&{Check\:x=1+2i}\\ {x^{2}-2x+5=0}&{x^{2}-2x+5=0}\\{(\color{OliveGreen}{1-2i}\color{black}{)}^{2}-2(\color{OliveGreen}{1-2i}\color{black}{)}+5=0}&{(\color{OliveGreen}{1+2i}\color{black}{)}^{2}-2(\color{OliveGreen}{1+2i}\color{black}{)}+5=0}\\{1-4i+4i^{2}-2+4i+5=0}&{1+4i+4i^{2}-2-4i+5=0}\\{4i^{2}+4=0}&{4i^{2}+4=0} \\{4-1+4=0}&{4-1+4=0}\\{-4+4=0\:\:\color{Cerulean}{\checkmark}}&{-4+4=0\:\:\color{Cerulean}{\checkmark}} \end{array}$

The solutions are $1−2i$ and $1+2i$.

The equation may not be given in standard form. The general steps for solving using the quadratic formula are outlined in the following example.

Example $\PageIndex{10}$

$(2x+1)(x−3)=x−8$

Step 1 : Write the quadratic equation in standard form.

Step 2 : Identify a , b , and c for use in the quadratic formula. Here

Step 3 : Substitute the appropriate values into the quadratic formula and then simplify.

The solution is $\frac{3}{2} \pm \frac{1}{2} i$. The check is optional.

Example $\PageIndex{11}$

$x(x+2)=−19$

Begin by rewriting the equation in standard form.

Here a=1 , b=2 , and c=19 . Substitute these values into the quadratic formula.

The solutions are $-1 - 3 i \sqrt{2}$ and $-1 + 3 i \sqrt{2}$.

Consider the following:

Both numbers are equivalent and $-1+ 3\sqrt{2}i$ is in standard form, where the real part is −1 and the imaginary part is $3\sqrt{2}$. However, this number is often expressed as $-1 + 3 i \sqrt{2} $, even though this expression is not in standard form. Again, this is done to avoid the possibility of misinterpreting the imaginary unit as part of the radicand.

Exercise $\PageIndex{2}$

$(2x+3)(x+5)=5x+4$

$-4\pm6i\sqrt{2} = -2\pmi \sqrt{\frac{3}{2}}$

Key Takeaways

The result of adding, subtracting, multiplying, and dividing complex numbers is a complex number.
Use complex numbers to describe solutions to quadratic equations that are not real.

Exercise $\PageIndex{3}$ introduction to complex numbers

Rewrite in terms of i .

$\sqrt{-64}$
$\sqrt{-81}$
$\sqrt{-20}$
$\sqrt{-18}$
$\sqrt{-50}$
$\sqrt{-48}$
$\sqrt{-45}$
$\sqrt{-14}$
$\sqrt{-29}$

3. $2i\sqrt{5}$

5. $5i\sqrt{2}$

7. $-3i\sqrt{5}$

9. $i\sqrt{14}$

Exercise $\PageIndex{4}$ introduction to complex numbers

Perform the operations.

$(3+5i)+(7−4i)$
$(6−7i)+(−5−2i)$
$(−8−3i)+(5+2i)$
$(−10+15i)+(15−20i)$
$(12+34i)+(16−18i)$
$(25 −16 i ) + (110 −32 i )$
$( 5 + 2 i)−( 8 − 3 i )$
$( 7 − i)−(− 6 − 9 i )$
$(− 9 − 5 i)−( 8 +12 i )$
$(−11 + 2 i)−(13 − 7 i )$
$(114 +32 i ) − (47 −34 i )$
$(38 −13 i ) − (12 −12 i )$
$2 i ( 7 − 4 i )$
$6 i ( 1 − 2 i )$
$− 2 i ( 3 − 4 i )$
$− 5 i ( 2 − i )$
$( 2 + i)( 2 − 3 i )$
$( 3 − 5 i)( 1 − 2 i )$
$( 1 − i)( 8 − 9 i )$
$( 1 + 5 i)( 5 + 2 i )$
$( 4 + 3 i )^{2}$
$( 2 − 5 i )^{2}$
$( 4 − 2 i)( 4 + 2 i )$
$( 6 + 5 i)( 6 − 5 i )$
$(12 +23 i)(13 −12 i )$
$(23 −13 i)(12 −32 i )$
$15 + 4 i$
$13 − 4 i$
$\frac{20 i}{ 1 − 3 i}$
$\frac{10 i}{ 1 − 2 i}$
$\frac{10 − 5 i}{ 3 − i}$
$\frac{4 − 2 i}{ 2 − 2 i}$
$\frac{5 +10 i}{ 3 + 4 i}$
$\frac{2 − 4 i}{ 5 + 3 i}$
$\frac{1+2i}{2−3i}$
$\frac{3−i}{4−5i}$

1. $10+i$

3. $−3−i$

5. $28+16i$

7. $−3+5i$

9. $−17−17i$

11. $67+66i$

13. $8+14i$

15. $−8−6i$

17. $7−4i$

19. $−1−17i$

21. $7+24i$

25. $-140-892i$

27. $15+4i$

29. $−6+2i$

31. $\frac{7-i}{2}$

33. $\frac{11+2i}{5}$

35. $\frac{−4+7i}{13}$

Exercise $\PageIndex{5}$ complex roots

Solve by extracting the roots and then solve by using the quadratic formula. Check answers.

$x^{2}+9=0$
$x^{2}+1=0$
$4t^{2}+25=0$
$9t^{2}+4=0$
$4y^{2}+3=0$
$9y^{2}+5=0$
$3x^{2}+2=0$
$5x^{2}+3=0$
$(x+1)^{2}+4=0$
$(x+3)^{2}+9=0$

1. $±3i$

3. $±\frac{5}{2}i$

5. $±i\frac{\sqrt{3}}{2}$

7. \(±i\sqrt{\frac{2}{3}}

9. $−1±2i$

Exercise $\PageIndex{6}$ complex roots

Solve using the quadratic formula.

$x^{2}−2x+10=0$
$x^{2}−4x+13=0$
$x^{2}+4x+6=0$
$x^{2}+2x+9=0$
$y^{2}−6y+17=0$
$y^{2}−2y+19=0$
$t^{2}−5t+10=0$
$t^{2}+3t+4=0$
$−x^{2}+10x−29=0$
$−x^{2}+6x−10=0$
$−y^{2}−y−2=0$
$−y^{2}+3y−5=0$
$−2x^{2}+10x−17=0$
$−8x^{2}+20x−13=0$
$3y^{2}−2y+4=0$
$5y^{2}−4y+3=0$
$2x^{2}+3x+2=0$
$4x^{2}+2x+1=0$
$2x^{2}−12x+14=0$
$3x^{2}−23x+13=0$
$2x(x−1)=−1$
$x(2x+5)=3x−5$
$3t(t−2)+4=0$
$5t(t−1)=t−4$
$(2x+3)^{2}=16x+4$
$(2y+5)^{2}−12(y+1)=0$
$−3(y+3)(y−5)=5y+46$
$−2(y−4)(y+1)=3y+10$
$9x(x−1)+3(x+2)=1$
$5x(x+2)−6(2x−1)=5$
$3(t−1)−2t(t−2)=6t$
$3(t−3)−t(t−5)=7t$
$(2x+3)(2x−3)−5(x^{2}+1)=−9$
$5(x+1)(x−1)−3x^{2}=−8$

1. $1±3i$

3. $−2±i\sqrt{2}$

5. $3±2\sqrt{2}i$

7. $\frac{5}{2}±i\frac{\sqrt{15}}{2}$

9. $5±2i$

11. $\frac{−1}{2}±i\frac{\sqrt{7}}{2}$

13. $\frac{5}{2}±i\frac{3}{2}$

15. $\frac{1}{3}±i\frac{\sqrt{11}}{3}$

17. $\frac{−3}{4}±i\frac{\sqrt{7}}{4}$

19. $3\pm\sqrt{2}$

21. $\frac{1}{2}±i\frac{1}{2}$

23. $1±i\frac{\sqrt{3}}{3}$

25. $\frac{1}{2}±i$

27. $\frac{1}{6}±i\frac{\sqrt{11}}{6}$

29. $\frac{1}{3}±i\frac{2}{3}$

31. $\frac{1}{4}±i\frac{\sqrt{23}}{4}$

33. $±i\sqrt{\frac{3}{2}}$

Exercise $\PageIndex{7}$ discussion board

Explore the powers of i . Share your discoveries on the discussion board.
Research and discuss the rich history of imaginary numbers.
Research and discuss real-world applications involving complex numbers.

1. Answers may vary

3. Answers may vary

Complex Numbers

A Complex Number is a combination of a Real Number and an Imaginary Number

Real Numbers are numbers like:

Nearly any number you can think of is a Real Number!

Imaginary Numbers when squared give a negative result.

Normally this doesn't happen, because:

when we square a positive number we get a positive result, and
when we square a negative number we also get a positive result (because a negative times a negative gives a positive ), for example −2 × −2 = +4

But just imagine such numbers exist, because we want them.

Let's talk some more about imaginary numbers ...

The "unit" imaginary number (like 1 for Real Numbers) is i , which is the square root of −1

When we square i we get −1

Examples of Imaginary Numbers:

And we keep that little "i" there to remind us we still need to multiply by √−1

When we combine a Real Number and an Imaginary Number we get a Complex Number :

Can a Number be a Combination of Two Numbers?

Can we make a number from two other numbers? Sure we can!

We do it with fractions all the time. The fraction 3 / 8 is a number made up of a 3 and an 8. We know it means "3 of 8 equal parts".

Well, a Complex Number is just two numbers added together (a Real and an Imaginary Number).

Either Part Can Be Zero

So, a Complex Number has a real part and an imaginary part.

But either part can be 0 , so all Real Numbers and Imaginary Numbers are also Complex Numbers .

Complicated?

Complex does not mean complicated.

It means the two types of numbers, real and imaginary, together form a complex , just like a building complex (buildings joined together).

A Visual Explanation

You know how the number line goes left-right ?

Well let's have the imaginary numbers go up-down :

A complex number can now be shown as a point:

The letter z is often used for a complex number:

z is a Complex Number
a and b are Real Numbers
i is the unit imaginary number = √−1

we refer to the real part and imaginary part using Re and Im like this:

Re(z) = a Im(z) = b

The conjugate (it changes the sign in the middle) of z is shown with a star:

z * = a − bi

We can also use angle and distance like this (called polar form ):

So the complex number 3 + 4i can also be shown as distance 5 and angle 0.927 radians . To convert from one form to the other use Cartesian to Polar conversion .

The magnitude of z is:

|z| = √(a 2 + b 2 )

And the angle of z , also called Arg(z) is:

Arg(z) = tan -1 (b/a) (for a>0)

Example: z = 3 + 4i

3 and 4 are Real Numbers
|z| = √(3 2 + 4 2 ) = 5
Arg(z) = tan -1 (4/3) = 0.927... radians
z * = 3 − 4i

To add two complex numbers we add each part separately:

(a+b i ) + (c+d i ) = (a+c) + (b+d) i

Example: add the complex numbers 3 + 2 i and 1 + 7 i

add the real numbers, and
add the imaginary numbers:

(3 + 2 i ) + (1 + 7 i ) = 3 + 1 + (2 + 7) i = 4 + 9 i

Let's try another:

Example: add the complex numbers 3 + 5 i and 4 − 3 i

(3 + 5 i ) + (4 − 3 i ) = 3 + 4 + (5 − 3) i = 7 + 2 i

On the complex plane it is:

Multiplying

To multiply complex numbers:

Each part of the first complex number gets multiplied by each part of the second complex number

Just use "FOIL", which stands for " F irsts, O uters, I nners, L asts" (see Binomial Multiplication for more details):

Example: (3 + 2 i )(1 + 7 i )

Example: (1 + i ) 2, but there is a quicker way.

Use this rule:

(a+b i )(c+d i ) = (ac−bd) + (ad+bc) i

Example: (3 + 2 i )(1 + 7 i ) = (3×1 − 2×7) + (3×7 + 2×1) i = −11 + 23 i

Why Does That Rule Work?

It is just the "FOIL" method after a little work:

And there we have the (ac − bd) + (ad + bc) i pattern.

This rule is certainly faster, but if you forget it, just remember the FOIL method.

Let us try i 2

Just for fun, let's use the method to calculate i 2

Example: i 2

We can write i with a real and imaginary part as 0 + i

And that agrees nicely with the definition that i 2 = −1

So it all works wonderfully!

Learn more at Complex Number Multiplication .

We will need to use conjugates in a minute!

A conjugate is where we change the sign in the middle like this:

A conjugate can be shown with a little star, or with a bar over it:

5 − 3 i = 5 + 3 i

The conjugate is used to help complex division.

The trick is to multiply both top and bottom by the conjugate of the bottom .

Example: Do this Division:

2 + 3 i 4 − 5 i

Multiply top and bottom by the conjugate of 4 − 5 i :

2 + 3 i 4 − 5 i × 4 + 5 i 4 + 5 i = 8 + 10 i + 12 i + 15 i 2 16 + 20 i − 20 i − 25 i 2

Now remember that i 2 = −1 , so:

= 8 + 10 i + 12 i − 15 16 + 20 i − 20 i + 25

Add Like Terms (and notice how on the bottom 20 i − 20 i cancels out!):

= −7 + 22 i 41

Lastly we should put the answer back into a + b i form:

= −7 41 + 22 41 i

Yes, there is a bit of calculation to do. But it can be done.

Multiplying By the Conjugate

There is a faster way though.

In the previous example, what happened on the bottom was interesting:

(4 − 5 i )(4 + 5 i ) = 16 + 20 i − 20 i − 25 i 2

The middle terms (20 i − 20 i ) cancel out:

(4 − 5 i )(4 + 5 i ) = 16 − 25 i 2

Also i 2 = −1 :

(4 − 5 i )(4 + 5 i ) = 16 + 25

And 16 and 25 are (magically) squares of the 4 and 5:

(4 − 5 i )(4 + 5 i ) = 4 2 + 5 2

Which is really quite a simple result. The general rule is:

(a + b i )(a − b i ) = a 2 + b 2

That can save us time when we do division, like this:

Example: Let's try this again

2 + 3 i 4 − 5 i × 4 + 5 i 4 + 5 i = 8 + 10 i + 12 i + 15 i 2 16 + 25

And then back into a + b i form:

We often use z for a complex number. And Re() for the real part and Im() for the imaginary part, like this:

Which looks like this on the complex plane:

The Mandelbrot Set

Complex Numbers to Solve Equations

By making use of the imaginary number i we can solve equations that involve the square roots of negative numbers.

Complex numbers enable us to solve equations that we wouldn't be able to otherwise solve. Examine the following example:

$ x^2 = -11 \\ x = \sqrt{ \red - 11} \\ \sqrt{ 11 \cdot \red - 1} = \sqrt{11} \cdot i \\ i \sqrt{11} $

Without the ability to take the square root of a negative number we would not be able to solve these kinds of problems.

Imaginary number
Complex numbers
Solving equations with complex numbers

Practice Problems Solving Equations

Use imaginary numbers to solve this practice equation:

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

Free Mathematics Tutorials

Complex Numbers Problems with Solutions and Answers - Grade 12

Complex numbers are important in applied mathematics. Problems and questions on complex numbers with detailed solutions are presented.

If (x + yi) / i = ( 7 + 9i ) , where x and y are real, what is the value of (x + yi)(x - yi)?
P(z) = z 4 + a z 3 + b z 2 + c z + d is a polynomial where a, b, c and d are real numbers. Find a, b, c and d if two zeros of polynomial P are the following complex numbers: 2 - i and 1 - i.

Solutions to the Above Questions

a) -5 + 7i b) -6 - 22i c) -4 + 2i d) -7/15 - 4i/15
(x + yi) / i = ( 7 + 9i ) (x + yi) = i(7 + 9i) = -9 + 7i (x + yi)(x - yi) = (-9 + 7i)(-9 - 7i) = 81 + 49 = 130
Let z = a + bi , z' = a - bi ; a and b real numbers. Substituting z and z' in the given equation obtain a + bi + 3*(a - bi) = 5 - 6i a + 3a + (b - 3b) i = 5 - 6i 4a = 5 and -2b = -6 a = 5/4 and b = 3 z = 5/4 + 3i
z z' = (a + bi)(a - bi) = a 2 + b 2 = 25 a + b = 7 gives b = 7 - a Substitute above in the equation a 2 + b 2 = 25 a 2 + (7 - a) 2 = 25 Solve the above quadratic function for a and use b = 7 - a to find b. a = 4 and b = 3 or a = 3 and b = 4 z = 4 + 3i and z = 3 + 4i have the property z z' = 25.
a) Substitute solution in equation: (2 + 4i) 2 + b(2 + 4i) + c = 0 Expand terms in equation and rewrite as: (-12 + 2b + c) + (16 + 4b)i = 0 Real part and imaginary part equal zero. -12 + 2b + c = 0 and 16 + 4b = 0 Solve for b: b = -4 , substitute and solve for c: c = 20 b) Since the given equation has real numbers, the second root is the complex conjugate of the given root: 2 - 4i is the second solution. Check: (2 - 4i) 2 - 4 (2 - 4i) + 20 (Expand) = 4 - 16 - 16i - 8 + 16i + 20 = (4 - 16 - 8 + 20) + (-16 + 16)i = 0
Let z = a + bi Substitute into given equation: (a + bi) 2 = -1 + 2 sqrt(6) i Expand: a 2 - b 2 + 2 ab i = - 1 + 2 sqrt(6) i Real part and imaginary parts must be equal. a 2 - b 2 = - 1 and 2 ab = 2 sqrt(6) Equation 2 ab = 2 sqrt(6) gives: b = sqrt(6) / a Substitute: a 2 - ( sqrt(6) / a ) 2 ) = - 1 a 4 - 6 = - a 2 Solve above equation and select only real roots: a = sqrt(2) and a = - sqrt(2) Substitute to find b and write the two complex numbers that satisfies the given equation. z1 = sqrt(2) + sqrt(3) i , z2 = - sqrt(2) - sqrt(3) i
Let z = a + bi where a and b are real numbers. The complex conjugate z' is written in terms of a and b as follows: z'= a - bi. Substitute z and z' in the given equation (4 + 2i)(a + bi) + (8 - 2i)(a - bi) = -2 + 10i Expand and separate real and imaginary parts. (4a - 2b + 8a - 2b) + (4b + 2a - 8b - 2a )i = -2 + 10i Two complex numbers are equal if their real parts and imaginary parts are equal. Group like terms. 12a - 4b = -2 and - 4b = 10 Solve the system of the unknown a and b to find: b = -5/2 and a = -1 z = -1 - (5/2)i
Since z = -2 + 7i is a root to the equation and all the coefficients in the terms of the equation are real numbers, then z' the complex conjugate of z is also a solution. Hence z 3 + 6 z 2 + 61 z + 106 = (z - (-2 + 7i))(z - (-2 - 7i)) q(z) = (z 2 + 4z + 53) q(z) q(z) = [ z 3 + 6 z 2 + 61 z + 106 ] / [ z 2 + 4z + 53 ] = z + 2 Z + 2 is a factor of z 3 + 6 z 2 + 61 z + 106 and therefore z = -2 is the real root of the given equation.
a) (2i) 4 + (2i) 3 + 2 (2i) 2 + 4 (2i) - 8 = 16 - 8i - 8 + 8i - 8 = 0 b) 2i is a root -2i is also a root (complex conjugate because all coefficients are real). z 4 + z 3 + 2 z 2 + 4 z - 8 = (z - 2i)(z + 2i) q(z) = (z 2 + 4)q(z) q(z) = z 2 + z - 2 The other two roots of the equation are the roots of q(z): z = 1 and z = -2.
Since all coefficients of polynomial P are real, the complex conjugate to the given zeros are also zeros of P. Hence P(z) = (z - (2 - i))(z - (2 + i))(z - (1 - i))(z - (1 + i)) = = z 4 - 6 z 3 + 15 z 2 - 18 z + 10 Hence: a = -6, b = 15, c = -18 and d = 10.

Get In Touch

HW Guidelines
Study Skills Quiz
Find Local Tutors
Demo MathHelp.com
Join MathHelp.com

Select a Course Below

ACCUPLACER Math
Math Placement Test
PRAXIS Math
+ more tests
5th Grade Math
6th Grade Math
Pre-Algebra
College Pre-Algebra
Introductory Algebra
Intermediate Algebra
College Algebra

Complex Numbers and the Quadratic Formula

The Imaginary Complexes Quadratic Formula

For the time being, you will probably be using complex numbers only in the context of solving quadratic equations for their zeroes. (There are many other practical uses for complexes, but you'll have to wait for more interesting classes like "Engineering 201" to get to the good stuff.) So let's refresh on the topic.

The Quadratic Formula takes the generic quadratic equation, stated as:

a x 2 + b x + c = 0

Content Continues Below

MathHelp.com

...and provides the solution values of the variable x by plugging the values a , b , and c of the numerical coefficients into the following formula:

Previously, when the Formula gave you a negative value inside the square root (that is, inside the "discriminant"), you would have responded that the equation under question had "no solutions". Were you to graph the quadratic equation (setting the quadratic equal to y instead of to 0 ), your graph would not cross the horizontal axis.

Now, with complex numbers, when the Formula gives you a negative inside the root, you now can simplify that solution by using the imaginary and respond that the equation under question has no real-valued solution, but it does have a complex-valued solution. Were you to graph the quadratic equation, your graph will still not cross the horizontal axis.

The difference now is that you have solutions (from the Quadratic Formula) to the equation which are not graphable. "Solutions", "roots", and "zeroes" of a given quadratic equation are now no longer necessarily also " x -intercepts".

The values on the x , y -plane are real numbers, so the complex-valued solutions of the equation cannot be seen on the x -axis. Your complex-valued answer is still a valid "zero" or "root" or "solution" for that quadratic equation, because, if you plug the answer value back into the quadratic equation, you'll get zero after you simplify. (This is the definition of a "solution"; it is a value that solves the equation, making it true.) However, this complex-valued answer will not be a graphable x -intercept of the graph.

What is the connection between the Quadratic Formula, complex numbers, and graphing?

The connection between the Quadratic Formula, complex numbers, and graphing is illustrated in the table below:

In the discussion above, I repeatedly pointed out that complex solutions to a quadratic equation are not graphable in the x , y -plane, because all points on the x , y are pairs of real numbers. However, if we change what the axes stand for, we can plot complex numbers.

How can you graph complex numbers?

To graph a complex number, you:

Draw the regular x , y -plane.
using the regular x and y labels
using the regular x for the horizontal axis, but use yi for the vertical axis
using "Re" for the horizontal axis having real-number values, and using "Im" for the vertical axis having imaginary-number values
Convert the complex number from " a + bi " summing (that is, additive) form to " ( a , b ) coordinate form
Plot the point just as you would a coordinate point on the coordinate plane

For instance, you would plot the complex number 3 − 2 i by converting the complex number into coordinate-point form (that is, into (3, −2) form), and then graphing in the usual way: starting at the origin, moving three units to the right along the x -axis, moving two units down parallel to the y -axis, and drawing a dot. Here's what it looks like:

This graphability of complex numbers leads somewhere interesting.

When you learned about regular (that is, about "real") numbers, you also learned about their order on the number line. But x , y -points don't come in any particular order. You can't say that one point "comes after" another point in the same way that you can say that one number comes after another number; you can't say that (4, 5) "comes after" (4, 3) in the way that you can say that 5 comes after 3 .

Pretty much all you can do is compare the "sizes" of the different points, and, for complex numbers as for regular x , y -points, "size" means "how far from the origin". To find a point's size, you use the Distance Formula . Complexes that are closer to the origin will have smaller sizes; complexes further away will have larger values.

This "size" concept is called "the modulus" of a complex-valued point. For instance, the modulus of the above-graphed point (denoted by absolute-value bars around the absolute-value bars) is computed by using the Distance Formula:

Now, isn't that interesting? 😎

URL: https://www.purplemath.com/modules/complex3.htm

You can use the Mathway widget below to practice finding the magnitude (or modulus or "size") of complex numbers. Try the entered exercise, or type in your own exercise. Then click the button to compare your answer to Mathway's.

Please accept "preferences" cookies in order to enable this widget.

(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)

Page 1 Page 2 Page 3

Standardized Test Prep

College math, homeschool math, share this page.

Terms of Use
Privacy / Cookies
About Purplemath
About the Author
Tutoring from PM
Advertising
Linking to PM
Site licencing

Visit Our Profiles

Complex Number Calculator

Enter the equation for which you want to find all complex solutions.

The Complex Number Calculator solves complex equations and gives real and imaginary solutions.

Click the blue arrow to submit. Choose "Find All Complex Number Solutions" from the topic selector and click to see the result in our Algebra Calculator !

Find All Complex Number Solutions Find All Complex Number Solutions

Solving Complex Analysis Assignments: A Student's Survival Guide

Complex analysis, a captivating yet demanding branch of mathematics, delves into the intricate realm of complex numbers and functions. The mastery of this discipline is deemed indispensable for students pursuing mathematics or related fields. However, the journey through complex analysis assignments presents a formidable challenge. This comprehensive guide endeavors to unravel the complexities, offering an exploration of diverse strategies and insightful tips to empower students in effectively navigating through their complex analysis assignments. If you need help with your complex analysis assignment , we're here to provide guidance and support throughout your academic journey. As the bedrock, a solid understanding of fundamental concepts, including the elusive nature of complex numbers and functions, sets the stage for a deeper comprehension of more advanced topics. The aim is not merely to unravel the mysteries of abstract mathematical constructs but to provide students with practical tools for solving intricate problems that characterize this field. From the foundational elements to the nuances of analytic functions, this survival guide seeks to be an invaluable resource, offering clarity and guidance to those striving for success in the realm of complex analysis. Visualization techniques play a pivotal role, as the ability to envisage complex functions and regions within the complex plane enhances problem-solving skills. In the contemporary landscape, technology becomes an ally, with software tools such as Mathematica and MATLAB offering a helping hand in navigating through complex mathematical landscapes.

Solving Complex Analysis Assignments- A Student's Survival Guide

Yet, no guide is complete without the crucible of practice, and this guide includes a curated set of problems, spanning the spectrum from basic to advanced, complemented by detailed solutions. Recognizing that challenges are inevitable, this guide addresses common conceptual hurdles and provides strategies for effective time management. It encourages students to discern when seeking help is imperative, introducing them to an array of resources, from textbooks to online forums and the guidance of professors. As the journey advances into advanced topics, the guide sheds light on the potent Residue Theorem and the transformative power of Conformal Mapping. The Residue Theorem emerges as a formidable tool, unlocking the ability to solve complex integrals with finesse. Conformal mapping, with its applications in diverse fields, underscores the real-world relevance of complex analysis. In summation, this survival guide not only equips students with the requisite knowledge and problem-solving strategies but also fosters resilience and determination. It is a beacon for those navigating the challenging waters of complex analysis, emphasizing that, with perseverance and practice, success is not just an aspiration but an attainable reality in this fascinating mathematical discipline.

Fundamentals of Complex Analysis

The fundamentals of complex analysis serve as the bedrock upon which a student's understanding of this intricate mathematical discipline is built. At its core lies the concept of complex numbers, where the imaginary unit "i" plays a pivotal role in defining numbers beyond the realm of real values. This exploration paves the way for delving into analytic functions, a key aspect of complex analysis that involves functions expressible as power series. Understanding the properties and behaviors of these functions provides a solid foundation for tackling more advanced topics. Moving forward, the study of contour integrals introduces students to the intricate world of integration along paths in the complex plane. The importance of contour integrals becomes evident in their applications, making them a fundamental tool in problem-solving. As students navigate through these initial concepts, they not only grasp the theoretical underpinnings of complex analysis but also begin to appreciate its real-world implications. This section lays the groundwork for a deeper exploration of the subject, emphasizing the importance of a strong foundation in the fundamentals to tackle the challenges that lie ahead in the realm of complex analysis assignments.

1. Definition of Complex Numbers

Complex analysis begins with a solid grasp of complex numbers, where the imaginary unit "i" interacts with real numbers. Mastering this fundamental concept sets the stage for delving into the intricacies of complex analysis, providing a foundation for further exploration of advanced topics.

2. Analytic Functions

At the heart of complex analysis lies the concept of analytic functions. These functions, expressible as power series, possess properties critical to advancing one's comprehension of complex analysis. Delving into the intricacies of analytic functions opens the door to a deeper exploration of this mathematical discipline.

3. Contour Integrals

Contour integrals are central to complex analysis, serving as powerful tools for problem-solving. This section explores the nuances of contour integration, delving into key theorems and practical applications. Understanding how to navigate through complex integrals using contour integrals is essential for students to excel in solving complex analysis problems.

Strategies for Problem Solving

We delve into essential strategies for effective problem-solving in the realm of complex analysis. Visualization techniques play a pivotal role, offering students a powerful tool to understand and interpret complex functions geometrically. By mastering mapping and contour plotting, students can gain an intuitive grasp of intricate concepts, paving the way for more confident problem-solving. Additionally, the integration of software tools such as Mathematica and MATLAB is explored. Embracing these technologies enhances efficiency in solving complex analysis problems, allowing students to focus on the core mathematical concepts rather than getting bogged down by tedious computations. A curated set of practice problem sets is presented, ranging from foundational to advanced levels. These problem sets, accompanied by detailed solutions, serve as invaluable resources for honing problem-solving skills through consistent and targeted practice. Emphasizing the importance of practice, this section empowers students to apply theoretical knowledge to real-world problems. Furthermore, the guide advocates for a balanced approach to time management, acknowledging the challenges of juggling complex analysis assignments with other academic and personal responsibilities. By adopting these strategies, students can navigate the intricate landscape of complex analysis problem-solving with confidence and competence, ultimately fortifying their foundation in this challenging mathematical discipline.

1. Visualization Techniques

Visualization techniques play a pivotal role in mastering complex analysis, particularly when dealing with geometric interpretations. Developing the ability to visualize complex functions and regions within the complex plane enhances problem-solving skills. Methods such as mapping and contour plotting are invaluable tools for students seeking a deeper understanding of the abstract concepts in complex analysis.

2. Utilizing Software Tools

In the contemporary landscape, embracing technology is essential for effective learning. Complex analysis can be made more manageable with the assistance of software tools like Mathematica and MATLAB. These tools facilitate efficient problem-solving, visualization, and exploration of complex mathematical concepts, empowering students to navigate assignments with precision.

3. Practice Problem Sets

Rigorous practice is the cornerstone of mastering complex analysis. To strengthen problem-solving skills, this guide offers a curated set of practice problems ranging from basic to advanced levels. Each problem comes with detailed solutions, providing students with the opportunity to apply theoretical knowledge to practical scenarios. Regular engagement with these problem sets not only reinforces understanding but also builds confidence in approaching complex analysis assignments.

Common Challenges and How to Overcome Them

We delve into the common challenges encountered by students in the realm of complex analysis and propose effective strategies to overcome these hurdles. Conceptual barriers often impede progress in understanding abstract topics; however, this guide addresses prevalent misconceptions head-on, providing lucid explanations to enhance comprehension. Time management emerges as a formidable challenge, as students grapple with the demands of complex analysis assignments alongside other academic and personal commitments. To address this, we explore practical time management strategies, ensuring students can allocate sufficient time to tackle assignments without succumbing to overwhelming pressures. Moreover, recognizing the threshold for seeking help is crucial, and this section guides students on leveraging resources such as textbooks, online forums, and seeking guidance from professors when faced with intricate problems. By empowering students to navigate conceptual intricacies, manage their time effectively, and seek assistance when needed, this guide aims to transform common challenges into stepping stones for success in the complex and rewarding field of complex analysis. Remember, embracing challenges as opportunities for growth is fundamental to mastering this mathematical discipline.

1. Overcoming Conceptual Hurdles

Students often encounter conceptual challenges when delving into abstract topics in complex analysis. Common misconceptions can hinder understanding, making it essential to address these hurdles head-on. This section aims to provide clarity by identifying prevalent misconceptions and offering detailed explanations. By tackling conceptual difficulties, students can build a stronger foundation and approach complex analysis assignments with increased confidence.

2. Time Management Strategies

Balancing the demands of complex analysis assignments with other academic and personal commitments requires effective time management. In this section, we explore various strategies to help students optimize their time effectively. From setting priorities to creating a study schedule, these strategies aim to empower students to efficiently allocate time for complex analysis studies without compromising on other essential aspects of their academic and personal lives.

3. Seeking Help When Needed

Recognizing when to seek assistance is crucial when facing the challenges of complex analysis assignments. This section provides insights into the importance of seeking help, be it through consulting textbooks, participating in online forums, or seeking guidance from professors. Understanding the available resources and having the initiative to seek help when needed are essential aspects of overcoming obstacles and ensuring a successful journey through complex analysis studies.

Advanced Topics and Applications

We delve into advanced topics and applications that elevate the study of complex analysis to a more sophisticated level. The Residue Theorem takes center stage, emerging as a powerful tool with wide-ranging applications. By understanding the intricacies of this theorem, students gain the ability to elegantly evaluate complex integrals that might otherwise seem insurmountable. The detailed exploration of the Residue Theorem in this section equips students with the knowledge needed to confidently navigate through intricate calculations, demonstrating the theorem's utility in various mathematical scenarios. Moving beyond, Conformal Mapping emerges as another advanced topic of paramount importance. We unravel the principles of Conformal Mapping, shedding light on its significance and diverse applications across different disciplines. The transformative nature of conformal maps not only provides a deeper understanding of complex functions but also unveils their real-world relevance. By guiding students through the intricacies of conformal mapping, this section aims to empower them to apply this concept in solving practical problems, be it in physics, engineering, or other fields. Together, these advanced topics not only enrich the understanding of complex analysis but also showcase its immense applicability, emphasizing the interdisciplinary nature of this mathematical discipline. In essence, Section 4 serves as a gateway to the advanced realms of complex analysis, unveiling the beauty and versatility that lie within its intricate concepts and their real-world implications.

1. Residue Theorem

The residue theorem stands as a cornerstone in complex analysis, offering a potent method for evaluating complex integrals. This theorem facilitates the computation of challenging integrals through the identification and calculation of residues, which are the residues of functions at singular points within a closed contour. Understanding the residue theorem empowers students to elegantly handle complex integrations, providing a valuable tool in problem-solving across various mathematical and scientific domains.

2. Conformal Mapping

Delving into the advanced realms of complex analysis, conformal mapping emerges as a pivotal concept with broad applications. This technique involves transforming complex functions to preserve angles, providing a powerful tool for mapping one complex domain onto another. Conformal mapping finds relevance in diverse fields such as fluid dynamics, electrostatics, and cartography. By grasping the principles of conformal mapping, students gain insight into how complex functions can be manipulated to simplify problem-solving and address real-world scenarios, showcasing the profound practicality and versatility of complex analysis in applied mathematics.

In conclusion, navigating the intricate realm of complex analysis demands a multifaceted approach that combines a strong grasp of fundamental concepts with strategic problem-solving skills. By immersing oneself in the understanding of complex numbers, analytic functions, and contour integrals, students lay the groundwork for tackling more sophisticated challenges. Visualization techniques and the integration of software tools further enhance the student's ability to decipher complex functions and regions within the intricate landscape of the complex plane. However, the journey is not without its hurdles, and addressing conceptual difficulties, managing time effectively, and recognizing the importance of seeking assistance when needed are integral aspects of a student's survival guide. Practice problem sets, ranging from basic to advanced, serve as the crucible for refining problem-solving skills, providing the necessary muscle memory to face more intricate assignments. Delving into advanced topics such as the Residue Theorem and Conformal Mapping opens doors to powerful tools with real-world applications, marking the transition from theoretical understanding to practical problem-solving proficiency. In this comprehensive guide, the emphasis has been on empowering students with the knowledge, strategies, and resources to not only survive but thrive in the complex analysis landscape. Remember, as students persist in their studies with determination and practice, they pave the way for mastering the complexities of this captivating mathematical discipline, fostering not just academic success but a profound appreciation for the elegance inherent in the world of complex analysis.

Understanding Fire and Rescue Service Practices Through Problems and Problem-Solving Networks: An Analysis of a Critical Incident

Open access
Published: 10 May 2024

Cite this article

You have full access to this open access article

Lotta Vylund ORCID: orcid.org/0000-0002-7222-798X 1 , 2 ,
Tove Frykmer ORCID: orcid.org/0000-0002-4122-8437 3 ,
Margaret McNamee 4 &
Kerstin Eriksson ORCID: orcid.org/0000-0002-0494-0089 1

31 Accesses

Explore all metrics

This study explores how the Fire and Rescue Service can better prepare for solving complex problems in emergencies by using the concept of problems and problem-solving networks. Primary and secondary data from an extensive fire incident were analysed, including semi-structured interviews and incident assessment reports. Complex problems that arise during emergencies can be challenging to define, and solutions can be difficult to identify. However, this study demonstrates that breaking down complex problems into sub-problems can facilitate the identification of what kind of problem-solving network is needed to be able to solve problems in emergencies. Overall, this study contributes to a deeper understanding of the rationale behind problem-solving network in emergency situations and highlights the importance of relationships in problem-solving network to address complex problems during emergencies.

Avoid common mistakes on your manuscript.

1 Introduction

Emergency situations are often complex and dynamic events that require quick and effective responses to mitigate potential harm to individuals and societies. While many definitions of emergency exist (see e.g. [ 1 , 2 , 3 , 4 , 5 ]) in this paper we define emergency as situations characterised by a high level of uncertainty, unpredictability, and ambiguity. Under such conditions societal response challenges the ability of the Fire and Rescue Services (FRS), and other stakeholders, to solve the myriad of problems that can occur, e.g., fires, explosions, vehicle accidents, shootings. Problems that arise in emergencies often center around complex, or wicked, problems, i.e. those that are ambiguous, open-ended and, in some way, require the flexible adaptation of existing routines as part of their response [ 6 , 7 ]. These problems are difficult to define, and solutions can be hard to identify [ 8 , 9 ].

Solving complex problems requires a diversity of perspectives, skills, and knowledge and, therefore, a need for different emergency actors to come together and work towards a common goal [ 10 , 11 , 12 ]. This collaboration between emergency actors can be seen as taking place through networks, which can be helpful to quickly identify and access resources, share information, and coordinate efforts [ 13 , 14 , 15 , 16 , 17 , 18 , 19 ]. A network of inter-organisational relationships with the primary purpose of solving problems in a coordinated fashion can be defined as a Problem-Solving Network (PSN) [ 20 ]. Although previous studies have mentioned PSN, their usefulness in emergencies has only been briefly touched upon, as was confirmed by a search in the database Scopus. General research on emergency management networks describes a lack of knowledge of what the driving forces are behind network formation and development [ 15 ]. Therefore, studying the rationale behind the network formation and development can be important to fully understand the importance of PSN in emergencies and what drives the networks to form.

In this paper, the aim is to explore how problems and sub-problems can be used as a means to understand the rationale behind PSNs. Although complex problems present challenges in understanding and analysis, Head and Alford [ 6 ] posit that it is possible in most cases to break the complex problems down into sub-problems that could be easier to understand. The analysis of an emergency in terms of problems and sub-problems, and their associated PSN fits well with the idea of problem-solving in emergencies [ 21 ]. Further, such understanding can help the FRS to better prepare for complex problems by understanding what kind of sub-problems could be encountered and which network could or should be mobilised to solve those problems. In other words, we maintain that it is possible for the FRS to improve their ability to solve problems during incident response, by analysing and understanding how PSN are formed during specific events and learning from such analysis. To this end, we have performed a case study of a major explosion in Gothenburg, Sweden in 2021 [ 22 ]. The study involved identifying problems and sub-problems encountered during emergency response, along with the PSN formed around these sub-problems. To evaluate the incident and why the PSN was formed we have used a conceptual framework based on complexity theory.

2 Conceptual Framework

Problem-solving in emergencies are dependent on collective efforts where organisations need to work together to solve the problems that appear [ 10 , 11 , 21 , 23 ]. Similarly, Moynihan [ 13 ] argues that to identify and apply effective problem-solving when faced with complex problems, such as in emergencies, networks of actors may be required. There are many different ways to describe how actors collectively respond to problems in emergencies, e.g. through teamwork [ 24 , 25 ], interteam work [ 26 ], or social networks [ 16 ]. While teamwork is often discussed in terms of how two or more people cooperate, coordinate and communicate towards a common goal, network formation and development is often studied in wider terms drawing on organisational, contextual, inter-organisational or structural factors [ 15 ]. Collaborating in networks is a well-known feature in emergency management literature (see e.g. [ 13 , 14 , 27 ]). Milward and Provan [ 20 ] denote networks created to facilitate collective problem-solving in emergencies as Problem Solving Networks (PSN), which is at the centre of this paper.

To further understand how networks are formed and developed in emergencies, this paper focuses on networks which arise in direct response to the problems that are identified. They will therefore specifically be identified as PSN to differentiate them from networks which could exist to foster connections without the immediate desire to find solutions to specific problems. Milward and Provan [ 20 ] define a PSN as a set of interorganisational relationships that are shaped by an imminent problem that requires immediate attention and response. This paper has adapted this definition by including the interpretation that the purpose of the PSN is to solve a particular problem, which could be extinguishing a fire or rescuing people from a flooded area, and include components and relationships needed to find solutions to the problem at hand without limiting the network to only interorganisational relationships. In other words, we adopt a view that networks are connected to general system theory [ 28 ], where networks that solve a particular problem are interpreted as a collection of interconnected nodes that allow for the exchange, transfer, or flow of information, resources, or entities between the nodes. Nodes in this sense is not limited to people or organisations, instead it includes anything that could be a part of solving the problem at hand. Such PSNs could leverage existing professional networks or develop entirely new connections.

To better understand the rationale behind PSN formation and development in emergencies, this paper explores the concepts of problems and sub-problems. In much of the problem-solving literature, there is considerable agreement that a problem means that there is an undesirable current state, a desired future state with no direct, obvious way to move from the given state to the goal state [ 29 , 30 , 31 ].

In emergencies, problems often centre around complex problems. Also called wicked [ 32 ], ill-defined [ 33 , 34 ] or unstructured-unbounded [ 35 ]. These types of problems are ambiguous, unconstrained and there are no objective solutions to be found. Current states and goal states are difficult to define, and, in fact, whether there is a problem or not is highly subjective [ 8 , 9 ], and how to reach the goal might not be agreed upon [ 36 ]. In addition, these types of problems cannot be separated from the environment, i.e., they are difficult to place boundaries around, and they appear to have an infinite number of solutions, where one often has to make to with a “good enough” solution.

How humans solve problems has been the subject of lively debate and there are many ways to present the diverse area of problem-solving. A related concept to problem-solving is decision-making and, frequently, the different terms are used interchangeably [ 37 , 38 , 39 ]. Theories related to decision making are important to understanding problem-solving. For example, the Recognition Primed Decision model [ 40 ] or the simplification of cognitive processes through the use of heuristics (see e.g. [ 41 , 42 , 43 ]) are used to understand problem-solving in the FRS. However, these theories are used to understand individual processes and actions whereas the focus in this paper is on collective problem-solving within a network context. In this paper, problem-solving is viewed as a search process using actions to reduce or eliminate the difference between the goal state and the undesired current state [ 30 , 44 ]. This search process can be illustrated through Newell and Simon [ 30 ] problem space , see Fig. 1 . Here, the nodes represent the current state, the goal state, and possible solution steps along the way. There may be several ways to reach the goal state and selecting a suitable strategy is crucial.

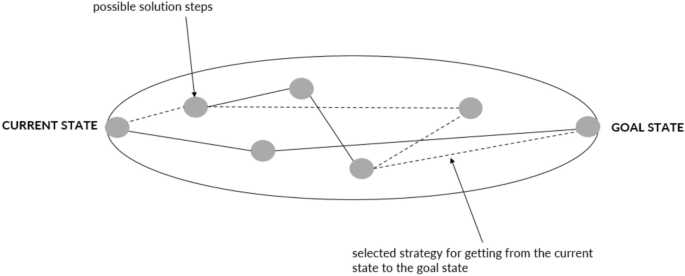
The problem space with the current state, goal state, possible solution steps and the selected strategy. Based on Newell and Simon [ 30 ]

During an emergency, at a given moment in time, some problems are known, and some can be envisaged as possible future problems. New problems, foreseen or unforeseen, appear over time. The situation resembles a dynamic system of problems, similar to Ackoff [ 45 ] messes , i.e., situations consisting of complex systems of problems that are changing and interacting with each other and are difficult to define. These complex systems demonstrate characteristics such as non-linear interactions, openness to the surrounding and internal adaptiveness, and the system as a whole cannot be understood entirely by looking at its parts in isolation [ 46 , 47 ]. Despite this latter aspect, in emergencies where important values are at stake and there is a need for swift action, it can nevertheless be useful to analyse the present situation by help of the perspective of sub-problems [ 6 ]. Here, we acknowledge the risk of losing the holistic understanding of the situation, but we view the breakdown of complex problems into sub-problems as a necessary first step in dealing with a complex emergency situation.

Figure 2 illustrates the perspective of a complex system of problems in emergencies, using Newell and Simon’s problem space [ 30 ]. The emergency event represents the main problem, which is the reason for the responding actors to be active in the first place. Within the main problem are sub-problems, some of which are known, and some are future, potential problems that may appear. Sub-problems and future, potential problems must often be solved before progress can be made toward the main problem's goal state. Distinguishing one solution strategy from another is virtually impossible due to the non-linear interactions between problems and the dynamic properties of the system. This means that it is possible to identify numerous possible sub-problems, and the strategy for moving between them, as well as towards the main goal state, will vary depending on the participants in the process and the situation itself.

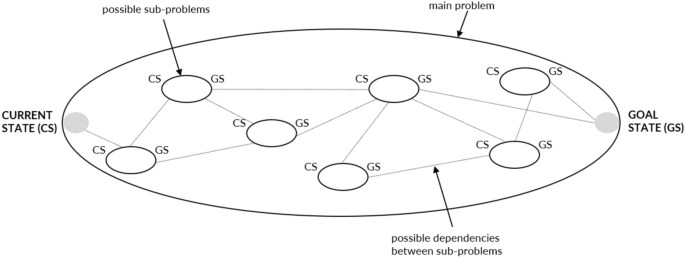
Illustration of the problem space as containing main problem and sub-problems in emergencies (adapted from Newell & Simon [ 30 ])

Using the concepts of problem space explained above, we investigate the rationale behind PSN formation and development, by applying the Complexity Framework brought forward by Bergström et al. [ 48 ]. The framework facilitates an analysis of the complex combination of components needed to address problem-solving in emergency management by systematically exploring sub-problems, components and activities that are needed to find solutions to the problems at hand.

Originally brought forward for studying how emergency response systems achieve direction and coordination, the framework presents how a complex understanding of emergency response management can be generated. The framework is rooted in Cilliers’ approach to complexity [ 47 ] which implies the need to analyse multiple interpretations of complex systems, make transparent analytical choices, and be modest by making clear that additional interpretations will always be possible. The framework is based on constructing multiple system interpretations where each interpretation is based on analytical choices according to three system aspects: dimension, scope and resolution.

System dimension refers to the types of components the system comprises and the types of relationships that bind these components together. Components are, for example, humans, artefacts or functions. Relationships could be, e.g., a flow of information or resources, power, or trust. System scope represents the boundary around what components and relationships that are to be included in the interpretation. It usually represents a spatial or functional/organisational delineation, for example, humans present in a certain geographical area, or in a specific organisation. In this study, scope denotes relevant problems that the FRS is trying to solve during a response operation. This will be further described in the data analysis section. System resolution concerns the level of detail at which the components of the system are observed, e.g., at single, group or organisational level. A high degree of detail means high system resolution and vice versa.

3 Methodology

Identification of problems, sub-problems and PSN is based on analysis of a single case study [ 49 ] of a large-scale incident which occurred in Gothenburg, Sweden in 2021. This section presents the methodology in more detail as a backdrop for the later analysis of both primary and secondary data sources.

The primary data consisted of semi-structured interviews with nine interview participants, see Table 1 . The focus of the study was on the FRS and how they collaborate in a wider PSN to solve problems, i.e., the sample was chosen to get the FRS perspective. The single non-FRS participant was from the insurance industry, but this participant had extensive experience of the FRS having worked for over 20 years in the FRS.

The sampling procedure started with identifying persons in the FRS who were involved in the incident in a variety of ways based on a combination of the following:

Recommendations from the FRS accident investigators,

Recommendations from those involved in initial interviews, and

Availability to participate in the interviews.

The secondary data used in this study included the incident assessment report created on behalf of the Swedish Civil Contingencies Agency (MSB) [ 22 ], the local FRS assessment report [ 50 ], an educational video developed by MSB [ 51 ], and various media articles. See Table 1 for a summary of primary and secondary data used to develop the empirical data for analysis.

3.2 Data Collection

An interview guide was created for the semi-structured interviews, see supplementary material file 1. All individuals identified for interviews were contacted, received information about the study and, after informed consent, were given the opportunity to participate in an interview. Two researchers participated in each interview; the first author was present in all interviews while one of the other authors was an observer. The observer was specifically given the opportunity to ask follow-up questions that the primary interviewer may have missed at the end of each interview. All interviews were conducted in a hybrid setting where the person leading the interview was in-person and the observer was virtual. The interviews were all conducted over approximately 1 h. All interviews were transcribed. All interviews were confidential, and handling of personal details was in accordance with Lund University and RISE Research Institutes of Sweden policy for personal data handling.

3.3 Data Analysis

The primary and secondary data collected as part of this study were analysed using the perspective of the problem space, including identification of the main problem and sub-problems, and application of the complexity framework described in Sect. 2. A PSN was defined as a network that arose in direct response to identified problems [ 20 ]. Breaking the main problem into sub-problems was viewed as a first step in dealing with this complex system of problems. Therefore, when analysing the rationale behind PSN using the complexity framework, we defined the scope in terms of what sub-problems were to be solved during the response operation (main problem). Thereby, the analytic boundary was drawn around what components and relationships were involved in solving those sub-problems (defined as dimension in the complexity framework), and the corresponding level of analysis (defined as resolution in the complexity framework). Consequently, the data were entered into NVivo 12 and coded according to the sub-problems ( scope ) together with relationships ( dimensions ) and a chosen level of detail ( resolution ).

During this coding process, two of the authors coded a small number of interviews independently and then compared their coding to ensure that these were similar. After this comparison the first author conducted the remaining coding independently while the analysis involved all authors. To gain a deeper understanding of the selected case study, secondary data was identified and included in NVivo for coding in the same way as the interview material. The results of the coding were discussed between the authors until agreement concerning the interpretation of the data was reached. Illuminating quotes are presented to clarify how the empirical data supports the results. Note that all quotes have been translated from Swedish to English by the authors.

4 Case Description

In the early morning of September 28, 2021, an explosion occurred in an apartment building in central Gothenburg, resulting in a fire with extensive smoke spread [ 22 ]. Gothenburg is the second largest city in Sweden and their FRS is a local federation which, in 2021, included six municipalities over the region surrounding Gothenburg. The area encompassed around 850 000 residents and had a total area of 3300 square kilometres [ 52 ].

In the part of the city where the explosion occurred, most buildings contain private residences (apartments) in the upper floors, with different types of businesses in the lower floors. The explosion occurred in the basement and was so powerful that several fire cell boundaries were compromised, and entrance doors were pushed out by the pressure wave, which allowed the fire smoke to be dispersed throughout almost the whole building. The potential threat to building stability resulting from the explosion was quickly disregarded because the building was deemed capable of withstanding this type of explosions. Additionally, the risk of subsequent explosions was thought minimal, leading the FRS to immediately commence evacuation and firefighting efforts. An illustration of the affected building is given in Fig. 3 .

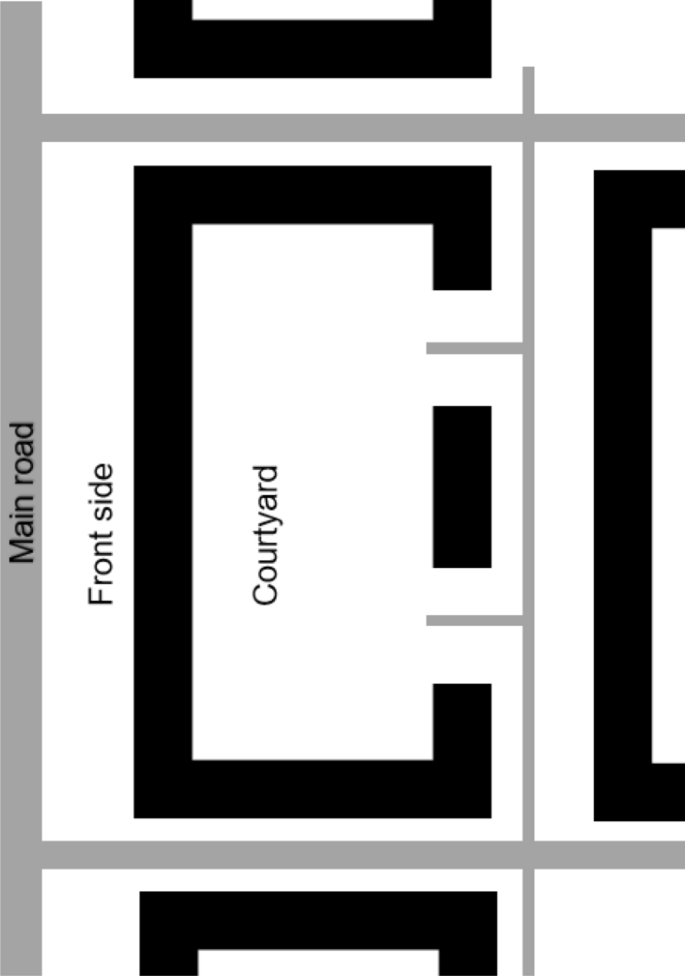
Conceptual illustration of the affected building

A large number of units from the FRS were called to the scene Upon arrival the FRS observed smoke from windows and balcony doors of various apartments, and about fifty people calling for help. The initial evacuation of approximately 60 apartments was carried out from the courtyard side of the building, during the first two hours. In all, three stairwells and associated apartments were affected. One person died due to injuries resulting from the fire and several people had to be taken to hospital for observation. All injured were removed from the scene by ambulance or bus. Residents who were evacuated but not injured, were referred to the nearby church where additional practical help was available, e.g. insurance company contacts, social support and sustenance [ 22 ].

The smoke dispersing in the building lead to the initial assessment that multiple fires had broken out and fire identification and firefighting was carried out during the first two hours on both sides of the building, but after the initial evacuation was completed, these activities were intensified at the front side of the building. Almost four hours into the incident response, the FRS realised that the explosion had compromised the fire cell boundaries, and that smoke was crossing these boundaries causing them to initially overestimate the number of individual fires distributed throughout the building. The seat of the fire could ultimately be localised to the storage room in the basement, although the fire had also spread to an adjacent store on the same floor. In the afternoon, the fire was under control, and approximately 24h hours after the explosion, the rescue operation was ended [ 22 ]. The approximate timeline of the event is shown in Fig. 4 , focusing on the first hours of the incident. Apart from evacuation, identification of the fire and fighting the fire, other problems of a more indirect nature included, e.g. traffic congestion due to the building's central location in the city and anxiety among the public, resulting in an inflow of media requests to the FRS [ 22 ].

Approximate timeline of event from start of the incident at approximately 5 am day 1 to end of operations at approximately 11 am day 2. The start and close are from the FRS perspective

5 Results and Analysis

To understand the rationale behind PSN from an FRS perspective, the conceptual framework described above, including the concept of problem space and the complexity framework, was applied to the case. Relevant sub-problems were identified for analysis (see Sect. 5.1). Thereafter, the resulting PSN were developed for each selected sub-problem.

5.1 Sub-Problems Used to Analyse PSN

Upon arrival, the FRS identified the current state of the main problem as a burning building with residents in danger, and the goal state as having extinguished the fire and ensured the safety of the residents [ 22 ].

Beyond the main problem, the data revealed a complex system of problems that could be further defined through different sub-problems. Respondents described the situation as complex due to the building construction and location in the central city. They further described the situation as chaotic and dramatic due to the large number of residents in need of evacuation and expressed that this incident was different from other incidents that they had encountered due to its chaotic nature and complexity. Due to the extensive resource demand, the respondents described problems of handling the personnel management both on site and in terms of being prepared for other incidents. The chaotic situation also created problems in understanding the situation, both on site and in the command centre. Handling documentation was also described as a problem, along with concerns regarding building stability, informing other actors and taking care of residents after the evacuation. These aspects were described by several respondents as well as in incident reports [ 22 , 50 ]. The main problem and examples of sub-problems from the FRS perspective is illustrated in Fig. 5 using the concept of problem space previously presented. Potential dependencies between the difference sub-problems have not been investigated in this paper.

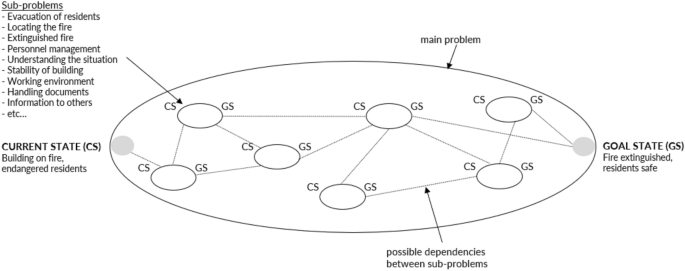
The main problem and example of sub-problems as revealed in the data

Despite the complexity of the situation, data indicated that the focus of the FRS was initially on the evacuation of residents and locating the seat of the fire. Therefore, these two sub-problems were chosen for further analysis in terms of which PSN were formed to solve these problems. Connected to the complexity framework, these sub-problems make up the scope of the two analytic interpretations. These scopes, together with relevant dimension and resolution (see Sect. 5.2 and 5.3), are summarised in Table 2 .

5.2 The PSN for Initial Evacuation of Residents

The FRS prioritised the initial evacuation of approximately 60 apartments across three stairwells during the first two hours of the incident. All injured residents were taken from the scene by ambulance or bus, while uninjured residents were directed to a nearby church where their needs were addressed [ 22 ]. The PSN which formed to deal with the initial evacuation is illustrated in Fig. 6 . Applying the complexity framework, this PSN consists of humans connected by relationships of coordination and different kinds of support (dimension). The resolution is on group level to illustrate that actions from the FRS, police, ambulance, and residents were executed in teams.

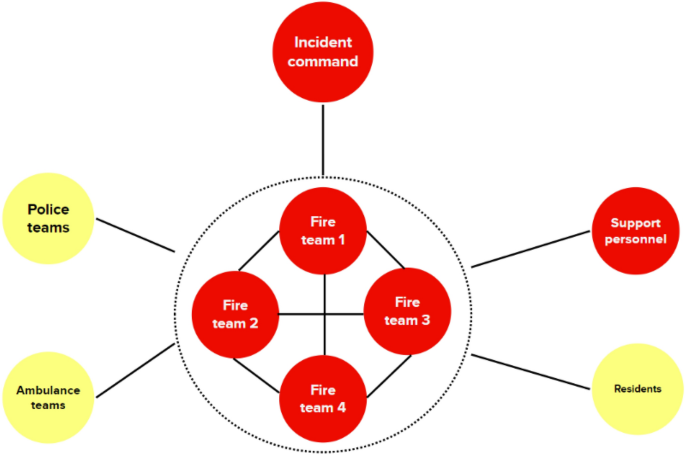
SN for the initial evacuation of residents. Red colour symbolizes the groups from FRS

The evacuation activities were mainly performed by four fire teams, as shown in the middle of Fig. 6 . The relationship between these fire teams concerns coordination of activities. In terms of relationships of support, the Incident Command relieved the fire teams by undertaking tasks of a more comprehensive nature, such as overall organisation and information to other actors [ 22 ]. At the same time, however, one respondent from a fire team mentioned that “ [The Incident Command] became very absent in relation to what we are used to [in this type of incident]. Therefore, there was some form of self-organisation at the scene .” Thus, in a sense, the four fire teams acted as one unit, which is why they are depicted with a dashed circle surrounding them.

The relationship of support between the fire teams and the other groups is demonstrated by the ambulance teams taking care of first aid and transportation of injured residents to local hospitals; police teams registering and redirecting residents after evacuation, provided they did not need medical assistance. These types of support allowed the fire teams to focus on searching the apartments rather than taking care of residents after evacuation. This means that the skill sets of the various organisations could be applied to solving problems for their particular skill sets. The fire teams were further supported by support personnel from FRS responsible for logistical matters such as equipment and water [ 22 ]. In addition to professional first responders, especially in the start-up phase, two residents offered support by providing their knowledge of the building, including familiarity with the building layout and keys to unlock gates blocking the passage to the building entrance. One of these residents (an off-duty firefighter) also spoke to residents on balconies to prevent them from jumping [ 53 ].

The FRS and the other first responders (police and ambulance) encountered a, for them, clear and known problem (apartment fires are common incidents). In some respect, the FRS fell into habitual patterns [ 22 ] as exemplified by one respondent: “ … what experience do we have? So, references around past events are a big part of my thinking ”. The fact that the residents were standing on their balconies surrounded by smoke made it clear to the FRS that the most urgent problem was evacuation, and it was also clear which resources were needed to solve this problem. As one respondent stated “ It was quite obvious. It's so clear that lifesaving is our priority ”. Similarly, one respondent identified the most important supporting partners by stating “ I want the police's support here with parts of evacuation and registration of it. And ambulance is very important here…[taking care of injured residents] ”. Previous experiences between the FRS, police and ambulance teams enabled the team members to comprehend each other's roles and responsibilities, facilitating the formation of the PSN. This is also described by one respondent as a capability of the PSN members to identify the right context for each actor in a particular moment.

On the other hand, while evacuation is something the FRS train for and are experienced with, the situation was nevertheless perceived as different from what they typically deal with, as exemplified by one of the respondents “ In this case, the conditions for self-evacuation were eliminated and the situation was overwhelming for both the residents and for us at the same time ”. Therefore, the outcome was a shift towards a PSN with self-organisation among the fire teams, as opposed to the traditional hierarchical command structure with the Incident Command at the top. One team member experienced that they had to establish a more comprehensive level of communication between themselves compared to in other incidents. In other words, they needed to work as a team of teams rather than as individual teams. This resulted in fire team members experiencing a PSN that was larger than usual and required more collaboration on the part of team leaders. The respondent described that the team leaders needed to take control of on-site activities without waiting for instructions from the Incident Commander. It was also mentioned that this self-organisation between the fire teams was a result of previous training with the police. One firefighter involved in the incident, who was not interviewed in this study, expressed this in an educational video that was developed after the fire [ 51 ]: “ … education has given us the ability to work independently, you understand that you need to make many decisions yourself [and not wait for instructions from a higher Incident Commander] ”.

Despite the unique scale of the incident, as described both in primary and secondary data, it could be noted that the Incident Command had confidence in the fire teams’ abilities to autonomously manage the on-site operations and that detailed management was neither necessary nor desirable. This assessment is reinforced by another respondent who noted that " In this context, if there had been detailed management, top management, central management, then it would have been very unfortunate. Here, it is important to have control over the right things further up”. The MSB incident report [ 22 ] established that there was an insufficient number of firefighters involved in the initial evacuation. Despite the Fire Chief's communication to the on-site Incident Commander that additional resources were available to assist the teams, it was not perceived that additional resources were needed, leading to a shared perception among the fire teams on-site in the courtyard that no further assistance could be expected. Therefore, the PSN was not developed further even if there was a need for it.

5.3 PSN for Locating the Fire

Locating the seat of the fire is a crucial prerequisite for effective suppression by the FRS. In this case, the fire was caused by an explosion in the basement and during the whole incident the fire was mainly contained within the basement and an adjacent store. However, the process of locating the fire was problematic due to two reasons, leading to a delay of almost four hours before the FRS could understand where the fire was and how it was developing. Firstly, FRS needed to prioritise evacuation of residents in the initial stages of the response and could not focus on locating the fire. Secondly, the explosion that caused the fire breached multiple fire cell boundaries which resulted in the dispersion of smoke throughout almost the entire building. This ultimately lead to the perception of multiple fires and, therefore, the FRS searched for several fires in different locations in the building [ 22 ]. Figure 7 present a visual representation of the proposed PSN that emerged to solve the problem of locating the fire. This PSN consists of both artefacts, i.e., floorplans and smoke emerging from the building, and humans, i.e., fire teams, residents, representatives from businesses and the building owner as components, connected by relationships of information flow. The resolution is both at single and group level as the actions needed to solve the problem involve both single components and groups of components.

PSN for locating the fire. Red colour symbolizes components connected to the FRS

Locating the fire was centred around the Incident Command which was responsible for the overall situation understanding and for coordinating the FRS overall response [ 22 ]. The figure indicates two important processes where the Incident Command needed to create a flow of information between different components (both artefacts and humans) in order to solve the problem of locating the fire. The two processes were to locate the fire by dispatching fire teams to report on potential fire locations and contacting different actors to gather information about the building [ 22 ].

Finding information about the building is one process which is shown in the upper part of Fig. 7 . This included different components e.g., the FRS command centre, with help from the municipality, provided information about the building layout by finding technical drawings. The property owner, found through the insurance representative, was able to provide further insights regarding the building layout. Moreover, since the building had undergone renovation, it was imperative to contact the relevant parties involved in the renovation process for input on changes relative to the technical drawings [ 22 ].

The lower part in Fig. 7 shows the other process, where the information flow included evaluating each presumed location of the fire within the building. First, smoke was observed emanating from multiple apartments in the courtyard side of the building. Although the primary focus for the fire teams was on initial evacuation, they also attempted to locate the source of the fire in the apartments. The dashed line in Fig. 7 illustrates the lack of information between Incident Command on the front side and the fire teams in the courtyard as exemplified by one respondent “ We had no idea there was a fire on the front side…We wondered why our extinction efforts didn’t have expected effect…It was the lack of this information [that it was a fire in the basement] that would have been of value to us .”

Early in the incident, a crackling sound was identified from the basement by a person walking by (named individual in the figure), and a fire team was sent to evaluate the sound. The fire team found a fire in the basement but was unable to extinguish it. Later, a person in the Incident Command observed smoke from a store located next to the basement. Subsequently, a fire team was dispatched to the location, whereupon they successfully located that the fire in the basement had spread to this location. After a couple of hours into the incident, the Incident Commander discovered smoke from the roof which prompted the FRS to prepare for a possible attic fire, but this risk was soon dismissed due to effective communication between the UAV (Unmanned Aerial Vehicle), fire teams and Incident Command [ 22 ].

The PSN developed to locate the assumed fires was formed because of the need to obtain a better understanding of the unusual smoke dispersion and the complicated building layout. Although the incident was atypical and did not conform to previously encountered scenarios [ 22 ], the Incident Command handled the incident as usual and predicted that where there is smoke, there should be a fire. Two respondents sum this up well: “ it seemed that there were several apartment fires going on together with maybe some type of fire in the basement so that you are very focused on finding these apartment fires at the beginning then. But then after a while you realise that you are inside these apartments and there is no fire but just smoke from somewhere else… ” and, “ the whole house was leaking smoke in a way that it normally shouldn't ”. The complicated building layout is exemplified by the following quote: “ It's a tricky building… If it had been a normal Swedish apartment building with three staircases and four floors, that we could have run around with ease, then we would have understood the incident almost immediately ”.

This PSN indicates that artifacts can be integral components and can have an impact on the problem-solving process. It seems especially important to obtain an understanding of the building through visual observations, which include on-site inspections and the examination of the building layout and UAV images. Furthermore, the visual dispersion of smoke played a critical role in shaping the network, as shown by the network's formation.

The rationale behind this PSN could be a case of how the FRS try to solve problems by focusing on different sub-problems in both time and space. One respondent describes this way of working through: “ I fly with a drone in my head, I zoom in to the firefighter to think about whether they have the right conditions at the sharp end, then I zoom back and zoom in on Incident Command if they have the capacity, then I zoom out further to see which other actors we have. Then I jump forward in time and think about what it looks like if we continue with the same tactics and what it looks like if we were to do nothing ”.

6 Discussion

This section discusses how the conceptual framework can be used to understand the rationale behind PSN and how the use of evaluating FRS practice from the perspective of problems and PSN better can help FRS to prepare for solving complex problems in emergencies.

6.1 Using the Concept of Problem Space to Understand the Rationale Behind PSN

The purpose of a PSN is to solve a particular problem. In this paper, we have shown that the FRS develop PSN by breaking down complex problems into manageable sub-problems. In these sub-problems, components and relationships within the PSN can be found more easily. Dividing complex problems into sub-problems is a way to match the situation to previous experience and to more easily identify which actions to take. Actions in this context can be interpreted as the FRS searching for which resources (or components in the network) are needed to solve the problem. Our results indicate that the matching with previous experience [ 54 ] will affect the formation and development of PSN, e.g. in the context of locating the fire where the layout of the building and the dispersion of smoke presented a challenge. The Incident Command created a PSN by dividing the problem into several known sub-problem, finding resources that could assist in understanding the building layout and sending resources to investigate each location emitting smoke. This is consistent with previous studies where it is argued that it is possible to divide complex problems into more manageable sub-problems [ 6 ] and manage the sub-problems through sub-networks that operate within the larger response network [ 13 , 16 , 55 ]. Even though the initial interpretation of the fire location was incorrect, the use of sub-problems allowed the ultimate outcome of the fire location.

6.2 The Rationale for PSN Formation and Development Exists in Relationships Between Components

The results indicate that the rationale behind the PSN could not be found in the main problem itself, nor the sub-problems per se, but rather in the relationships which contribute to the process of using actions to reduce or eliminate the difference between the current state and goal state. For instance, in the context of the initial evacuation, a clear problem for those directly involved, and the corresponding PSN, was developed based on previous experience. The fire team knew which support they needed and the PSN was formed around the relationships associated with this support. Similarly, the need for coordinated actions between the fire team and the lack of support from the Incident Command shaped the PSN, with the relationship of coordination between the fire teams and surrounding support functions at the heart of the PSN formation. In the context of locating the fire, the incident command function needed different types of information to understand the fire behaviour within the building. This in turn led to the creation of the PSN for the purpose of gathering information, thereby establishing relationships of information flows between different components. An understanding of network relationships can be beneficial to FRS organisations, as it enables them to identify the key actors to approach for information, personnel support, and collaboration on tasks [ 15 ].

6.3 The Practical Contributions of this Study

The main practical contribution of the present study is the application of the conceptual framework in the context of learning from incidents.

When it comes to learning from incidents, Frykmer [ 23 ] has noted that emergency evaluations often lead to conclusions that are too broad or general to be readily operationalised. Conversely, by applying the conceptual framework in this study and zooming in on different sub-problems in an incident, organisations can identify important components and types of relationships needed to solve the problems and use this as an input to their learning process. The learning outcome from this incident can be summarized in four main lessons learned:

Breaking down a complex problem into more manageable sub-problems makes the problem clear and easier to identify which resources are needed to solve the problem in hand. A downside of this approach is potentially the risk of losing the overall holistic understanding of the situation, as illustrated by the initial inability of the FRS to locate the fire. The perception of multiple fires was a result of incorrectly decomposing the main problem into (incorrect) sub-problems. This identifies the value of experienced FRS personnel with the ability to quickly reanalyse and redraft their understanding of a given situation .

Informal contacts are important to be able to solve problems at the scene of an accident. This is exemplified by the support provided by the local resident with firefighting experience and local knowledge of the building and the building owner providing timely structural drawings of the building. Not all buildings have a resident firefighter but building owners can provide detailed building specific information on short notice. Establishing contacts between the FRS and such stakeholders provides significant support as part of a PSN.

Comprehension of different roles and responsibilities facilitates rapid problem-solving. This is illustrated in the initial evacuation where established routines and contacts between the FRS, police and ambulance personnel facilitated rapid deployment of the PSN and effective evacuation of all residents. This emphasizes the importance of continuous networking and common professional terminology.

Problem solving is not only affected by the people and organisations involved in the incident, but artifacts are also an integral component of the PSN.

This is illustrated in the case of locating the fire where artifacts such as building drawings affected how the problems was ultimately identified and solved. This emphasizes the need to train FRS to include such artifacts in their PSN.

By identifying relationships and components needed to solve problems, the FRS could plan and exercise for important components for problem-solving during emergencies [ 13 ]. Using the relevant sub-problems to determine related parameters based on the chosen scope, dimension and resolution [ 48 ] can improve the learning potential in an exercise [ 56 ]. This approach could also assist the FRS in managing relationships as vital resources, and better comprehending the efficacy of different relationships in addressing emergency challenges [ 15 ].

6.4 The Theoretical Contributions of this Study

This study contains several theoretical contributions. First, we have addressed the call for more knowledge of what lies in the relationships within a network (as presented in Hu, Yeo [ 15 ]). We see the relationships within a PSN as tools for reducing or eliminating the difference between the current state and goal state [ 30 , 44 ]. For example, this study has illustrated that the relationships can consist of different types of support, information flow and coordination, that are used to solve the specific problems.

Second, we have contributed to the literature on PSN, as exemplified with Milward and Provan [ 20 ]. We argue that it is not only inter-organisational relationships that could explain the rationale behind PSN (as in the current definition by Milward and Provan [ 20 ]) instead we should include all components and relationships that affect the process of finding a solution to the sub-problem. To obtain a better understanding of the purpose of a PSN in emergencies, we suggest that the definition of a PSN is expanded to include not only organisations and humans within organisations, but also different artifacts relevant for reducing the difference between the current state and the goal state.

Third, the study contributes to developing the complexity framework by Bergström et al. [ 48 ] We believe that the framework can be expanded to incorporate multiple levels of resolution within the same scope, such as components on single and group level. For example, the resolution needed for analysing the PSN in the case of locating the fire contained system components at both single and group level to ensure that interactions between the Incident Command and various components could be captured. The study has also introduced an additional view on scope that can be applied in the framework; that of problems and sub-problems.

6.5 Reflecting on the Research Quality

The perception of a given situation or circumstance can vary widely between individuals due to their unique experiences, biases or role in a specific emergency situation. This implies that what one individual considers to be a problem, another may not [ 8 , 9 ]. Therefore, the problems identified in this study would most likely have been impacted if more or other respondents had been interviewed.

Moreover, it should be noted that the PSN depicted in this study constitutes a condensed representation. The dynamic nature of a PSN implies that its configuration is in a constant state of change, and a particular representation of the PSN is only applicable within specific temporal and spatial limitations [ 48 ], which is a limitation in our study.

In our work, we used two different interpretations of sub-problems. We acknowledge that there will always be additional interpretations. We however maintain that these interpretations captured the most important sub-problems perceived by the respondents and were thus the main problems to cover.

Last, our findings are based on a single case. While the findings may not be directly generalisable, they have contributed valuable insight into how the conceptual framework can be used to gain a more comprehensive understanding of FRS practices through problems and problem-solving networks.

6.6 Further Research

Collaboration in networks has been widely investigated by numerous researchers (e.g., [ 13 , 14 , 15 , 16 , 17 , 18 ]. In this paper, we have taken a first step of going beyond collaboration relationships in networks. Our study can be seen as a first step towards developing a better understanding of what network relationships actually mean in problem solving networks. This is relevant for other kinds of network research as previously stated by Hu et al. [ 15 ]. Further research could focus on the deeper understanding of the constituents of the relationships, to gain a more profound understanding of the rationale behind the PSN.

In this paper, we have seen how PSN are formed by both formal and informal relationships between the components. Examples are formal relationships between the FRS and other first responders and informal relationships between the fire teams and the off-duty firefighter in the case of initial evacuation. Further research could be conducted to examine whether PSN exhibit formal or informal characteristics. Such research would serve to evaluate the significance of formal organisational structures or prior experience in shaping effective incident management practices.

Finally, investigating the dynamic nature of PSN can provide important insight into how these networks develop over time. Such insight can, for example, be useful for understanding which components and relationships might be valuable at what time during an emergency, to further improve the solving of complex problems in this context.

7 Conclusions

This study has explored the rationale behind problem-solving networks (PSN) in emergency management and how these networks are developed in relation to complex problems that arise in an emergency. It has focused on the FRS and their role in a PSN relative to other actors. The findings indicate that the FRS practice could be understood as breaking down complex problems into manageable sub-problems, which facilitate the identification of components and relationships needed within the PSN. Components includes both people, organisations and artifacts and both formal and informal relationships is important to be able to solve problems at the scene of an accident. Accordingly, the rationale behind PSN in emergencies lies in the relationships that contribute to solve the sub-problems. The conceptual framework used in this paper can assist the FRS in effectively preparing for future complex problems in emergencies by identifying the essential components and relationships required in the PSN to transition from the current state to the goal state of the present complex system of problems.

Quarantelli EL, Boin A, Lagadec P (2018) Studying future disasters and crises: a heuristic approach. In: Rodriquez H, Donner W, Trainor E (eds) Handbooks of sociology and social research. Springer, Cham, pp 61–83

Google Scholar

Quarantelli EL, Lagadec P, Boin A (2007) A Heuristic Approach to Future Disasters and Crises: New, Old, and In-Between Types. In: Rodriquez H, Quarantelli EL, Dynes RR (eds) Handbooks of Sociology and Social Research. Springer, New York, New York, pp 16–41

Lagadec P (2007) Crisis management in the Twenty-First Century: “unthinkable” events in “inconceivable” contexts. In: Rodríguez H, Quarantelli EL, Dynes RR (eds) Handbook of disaster research. Edward Elgar, Cheltenham, pp 489–507

Chapter Google Scholar

Quarantelli EL, Ten, (1997) criteria for evaluating the management of community disasters. Disasters 21(1):39–56

Article Google Scholar

Quarantelli EL (1988) Disaster crisis management: a summary of research findings. J Manag Stud 25(4):373–385

Head BW, Alford J (2015) Wicked problems: implications for public policy and management. Adm Society 47(6):711–739

Gustavsson J, Carlsson G, McNamee MS (2021) Barriers and facilitators for implementation of individualized fire safety (IFS) in Sweden. Fire Technol 57(5):2707–2736

Hart P, Boin A (2001) Between crisis and normalcy: The long shadow of post-crisis politics. In: Rosenthal U, Boin A, Comfort LK (eds) Managing crises: Threats, dilemmas, opportunities. Charles C Thomas Publisher, Springfield, pp 28–46

Smith GF (1992) Towards a theory of managerial problem solving. Decis Support Syst 8(1):29–40

Waugh WL Jr, Streib G (2006) Collaboration and leadership for effective emergency management. Public Adm Rev 66:131–140

Nohrstedt D (2016) Explaining mobilization and performance of collaborations in routine emergency management. Adm Soc 48(2):135–162

Ford JK, Schmidt AM (2000) Emergency response training: strategies for enhancing real-world performance. J Hazard Mater 75(2–3):195–215

Moynihan DP (2009) The network governance of crisis response: Case studies of incident command systems. J Public Adm Res Theory 19(4):895–915

Kapucu N, Arslan T, Collins ML (2010) Examining intergovernmental and interorganizational response to catastrophic disasters: toward a network-centered approach. Adm Soc 42(2):222–247

Hu Q, Yeo J, Kapucu N (2022) A systematic review of empirical emergency management network research: formation and development, properties, and performance. Am Rev Public Adm 52(4):280–297

Bodin Ö, Nohrstedt D (2016) Formation and performance of collaborative disaster management networks: evidence from a Swedish wildfire response. Glob Environ Chang 41:183–194

Provan KG, Kenis P (2008) Modes of network governance: structure, management, and effectiveness. J Public Adm Res Theory 18(2):229–252

Hu Q, Kapucu N (2016) Information communication technology utilization for effective emergency management networks. Public Manag Rev 18(3):323–348

Sparf J, Petridou E (2018) Collaborations in routine emergency management: lessons from Sweden. Procedia Eng 212:302–308

Milward HB, Provan KG (2006) A manager’s guide to choosing and using collaborative networks. vol. 8, IBM Center for the Business of Government Washington, DC

Frykmer T (2021) Improving emergency and disaster response management performance: a problem-solving perspective. Lund University, Lund

MSB (2022) Olycksutredning - Explosion och brand i flerbostadshus Göteborg, 28 Sept 2021

Frykmer T (2020) “ What’s the problem?”-Toward a framework for collective problem representation in emergency response management. J Emerg Manag 18(6):511–524

Schraagen JM, Veld MHIT, de Koning L (2010) Information sharing during crisis management in hierarchical vs. network teams. J Contingencies Crisis Manag 18(2):117–127

Jouanne E et al (2017) Correlates of team effectiveness: an exploratory study of firefighter’s operations during emergency situations. Appl Ergon 61:69–77

Power N (2018) Extreme teams: toward a greater understanding of multiagency teamwork during major emergencies and disasters. Am Psychol 73(4):478

Kapucu N, Garayev V (2016) Structure and network performance: horizontal and vertical networks in emergency management. Administration & Society 48(8):931–961

Skyttner L (1996) General systems theory: origin and hallmarks. Kybernetes 25(6):16–22

Duncker K, Lees LS (1945) On problem-solving. Psychol Monogr 58(5):i

Newell A, Simon HA (1972) Human problem solving, vol 104. Prentice Hall Englewood Cliffs, New Jersey

Mayer RE (1992) Thinking, problem solving, cognition. WH Freeman/Times Books/Henry Holt & Co, New York

Rittel HW, Webber MM (1973) Dilemmas in a general theory of planning. Policy Sci 4(2):155–169

Reitman WR (1964) Heuristic decision procedures, open constraints, and the structure of ill-defined problems. Human Judgm Optim 282:283–315

Simon HA (1973) The structure of ill structured problems. Artif Intell 4(3–4):181–201

Mitroff I, Linstone H (1992) The unbounded mind. Oxford University Press, New York

Klein GA (1998) Sources of power: How people make decisions. MIT press, Cambridge

Smith GF (2008) Teaching decision making

Dery D (1983) Decision-making, problem-solving and organizational learning. Omega 11(4):321–328

Greiff S, Wüstenberg S, Funke J (2012) Dynamic problem solving: a new assessment perspective. Appl Psychol Meas 36(3):189–213

Klein GA (1993) A recognition-primed decision (RPD) model of rapid decision making. Decis Mak Action: Models Methods 5(4):138–147

Kahneman D (2011) Thinking, Fast and Slow, (ed) SAG. Farrar. New York: Farrar, Strauss and Giroux

Kahneman D (2021) Noise. Harper Collins Publishers, London

Kahneman D, Tversky A (1979) Prospect theory: an analysis of decision under risk. Econometrica 47(2):363–391

Article MathSciNet Google Scholar

Simon HA (1997) The sciences of the artificial, (third edition): By Herbert A. Simon. MIT Press, Cambridge, MA (1996), 231 pages, $14.50. Comput Math Appl 33(5):130

Ackoff RL (1979) Resurrecting the future of operational research. J Oper Res Soc 30(3):189–199

Kauffman SA (1993) The origins of order: self-organization and selection in evolution. Oxford University Press, Oxford

Book Google Scholar

Cilliers P (2005) Complexity, deconstruction and relativism. Theory Cult Soc 22(5):255–267

Bergström J, Uhr C, Frykmer T (2016) A complexity framework for studying disaster response management. J Contingencies Crisis Manag 24(3):124–135

Yin RK (2003) Design and methods. Case Study Res 3(92):84

RSG Olycksutredning: Brand och explosion i byggnad, flerfamiljshus Övre Husargatan, Göteborg 2021–09–28. 2022, Räddningstjänsten Storgöteborg (RSG).

MSB Explosin-Brand Göteborg, in 90 sekunder play. 2022: Sweden. p. 14:25.

RSG Handlingsprogram 2020–2023 enligt lag (2003:778) om skydd mot olyckor . 2020, Räddningstjänstförbundet Storgöteborg

Ivarsson K (2021) Explosionen på Övre husargatan. Sveriges Radio: https://sverigesradio.se/artikel/ny-podd-om-explosionen-pa-ovre-husargatan

Klein G (2008) Naturalistic decision making. Hum Factors 50(3):456–460

Kapucu N, Arslan T, Demiroz F (2010) Collaborative emergency management and national emergency management network. Disaster Prev Manag Int J 19(4):452–468

Borell J, Eriksson K (2013) Learning effectiveness of discussion-based crisis management exercises. Int J Disaster Risk Reduct 5:28–37

Download references

Acknowledgements

The research for this paper was financially supported by NordForsk within the project Nordic Fire and Rescue Services in the Twenty First Century, No. 97830.

Open access funding provided by RISE Research Institutes of Sweden.

Author information

Authors and affiliations.

Division of Safety and Transport, RISE Research Institute of Sweden, Brinellgatan 4, Box 857, 501 15, Borås, Sweden

Lotta Vylund & Kerstin Eriksson

Greater Gothenburg Fire and Rescue Service, Goteburg, Sweden

Lotta Vylund

Division of Risk Management and Societal Safety, Lund University, Lund, Sweden

Tove Frykmer

Division of Fire Safety Engineering, Lund University, Lund, Sweden

Margaret McNamee

You can also search for this author in PubMed Google Scholar

Contributions

All authors contributed to the study conception and design. LV was responsible for the data collection and coding of the data. TF was responsible for the conceptual framework. The analysis was performed by LV, TF, MM and KE. LV wrote the first draft and all authors contributed to the development of the final manuscript for submission.

Corresponding author

Correspondence to Lotta Vylund .

Ethics declarations

Conflict of interest.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Interview guide

The interview guide that was created for the semi-structured interviews is presented below. Note that the questions have been translated from Swedish to English by the authors.

Could you describe the response to the explosion in Gothenburg in 2021

In what way were you involved in the incident?

What needs could you identify in the accident?

How did you identify the needs?

What did you need to understand what had happened and what was about to happen?

How did you identify what actions were needed to meet the identified needs?

Are there any aids that were most important to you in dealing with this accident? What would happen if you didn't have access to these?

How has your organization prepared for this type of event? For example. emergency plans/instructions/practices/resources/materials etc.?

With the experiences from the accident that you have today, would you have done anything differently? Would you have prepared differently?

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Vylund, L., Frykmer, T., McNamee, M. et al. Understanding Fire and Rescue Service Practices Through Problems and Problem-Solving Networks: An Analysis of a Critical Incident. Fire Technol (2024). https://doi.org/10.1007/s10694-024-01582-0

Download citation

Received : 18 June 2023

Accepted : 02 April 2024

Published : 10 May 2024

DOI : https://doi.org/10.1007/s10694-024-01582-0

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Problem-solving network
Complex problem
Complexity framework
Sub-problems
Problem space
Fire and rescue service
Find a journal
Publish with us
Track your research

Novel quantum algorithm proposed for high-quality solutions to combinatorial optimization problems

C ombinatorial optimization problems (COPs) have applications in many different fields such as logistics, supply chain management, machine learning, material design and drug discovery, among others, for finding the optimal solution to complex problems. These problems are usually very computationally intensive using classical computers and thus solving COPs using quantum computers has attracted significant attention from both academia and industry.

Quantum computers take advantage of the quantum property of superposition, using specialized qubits, that can exist in an infinite yet contained number of states of 0 or 1 or any combination of the two, to quickly solve large problems. However, when COPs involve constraints, conventional quantum algorithms like adiabatic quantum annealing struggle to obtain a near-optimal solution within the operation time of quantum computers.

Recent advances in quantum technology have led to devices such as quantum annealers and gate-type quantum devices that provide suitable platforms for solving COPs. Unfortunately, they are susceptible to noise, which limits their applicability to quantum algorithms with low computational costs.

To address this challenge, Assistant Professor Tatsuhiko Shirai and Professor Nozomu Togawa from the Department of Computer Science and Communications Engineering at Waseda University in Japan have recently developed a post-processing variationally scheduled quantum algorithm (pVSQA). Their study was published in the journal IEEE Transactions on Quantum Engineering .

"The two main methods for solving COPs with quantum devices are variational scheduling and post-processing. Our algorithm combines variational scheduling with a post-processing method that transforms infeasible solutions into feasible ones, allowing us to achieve near-optimal solutions for constrained COPs on both quantum annealers and gate-based quantum computers," explains Dr. Shirai.

The innovative pVSQA algorithm uses a quantum device to first generate a variational quantum state via quantum computation. This is then used to generate a probability distribution function which consists of all the feasible and infeasible solutions that are within the constraints of the COP.

Next, the post-processing method transforms the infeasible solutions into feasible ones, leaving the probability distribution with only feasible solutions. A classical computer is then used to calculate an energy expectation value of the cost function using this new probability distribution. Repeating this calculation results in a near-optimal solution.

The researchers analyzed the performance of this algorithm using both a simulator and real quantum devices such as a quantum annealer and a gate-type quantum device. The experiments revealed that pVSQA achieves a near-optimal performance within a predetermined time on the simulator and outperforms conventional quantum algorithms without post-processing on real quantum devices.

Dr. Shirai said, "Drastic social transformations are urgently needed to address various social issues. Examples include the realization of a carbon-neutral society to solve climate change issues and the realization of sustainable development goals to address issues such as increased energy demand and food shortage.

"Efficiently solving combinatorial optimization problems is at the heart of achieving these transformations. Our new method will play a significant role in realizing these long-term social transformations."

In conclusion, this study marks a significant step forward for using quantum computers for solving COPs, holding promise for addressing complex real-world problems across various domains.

More information: Tatsuhiko Shirai et al, Post-Processing Variationally Scheduled Quantum Algorithm for Constrained Combinatorial Optimization Problems, IEEE Transactions on Quantum Engineering (2024). DOI: 10.1109/TQE.2024.3376721

Provided by Waseda University

The proposed algorithm combines variational scheduling with post-processing to achieve near-optimal solutions to combinatorial optimization problems with constraints within the operation time of quantum computers. Credit: Tatsuhiko Shirai / Waseda University

Sine waves problems

Hello devs, I’ve recently been messing around with sine waves and ran into a bit of a problem. I’ve been trying to create a bobbing effect that can smoothly transition from one speed to another, but I can’t figure out exactly how

Lets say im trying to create a buoy bounce up and down using:

To speed it up, im lerping Frequency from one number to another, but this causes jittering as the sine wave expands from the origin, meaning the Y value would appear to slow down or even reverse. For example:

To swtich from Red to blue at tick() = 2, the Y value would switch from going down to going up.

My best guess as to solve this problem is to set the phase of sinewave to some number so that the point of expansion is on tick(), but that might just cause the motion to freeze until it reaches its target frequency, I don’t know. How would you smoothly translate from one frequency to another?

are both waves a whole different formula? or is it the same equation with different values?

they are both sine waves, just have different terms.

you want it like this la is it? :

You could try doing this instead.

There is of course a better way to do this but I hope this makes sense. You increment the frequency slowly to make it go faster, this should in theory prevent weird jittery effects and whatnot.

Yea, that’s exactly what i’m looking for.

This won’t help because there is nothing to compensate for the change in frequency. Just to be clear, the phase is an offset in a sine wave and also the b in:

The idea behind it is that you increase the offset every step to smoothly interpolate from slow to fast.

If you interpolate from a low frequency to a high frequency, the 2 individual sine waves will mix. I suggest you try this code I provided on a part first and increase the offset per tick to see what happens.

I’ve had this problem before and you have to add a single offset to the phase, you can figure it out using some algebra and the two wave functions’ frequencies

Thank you so much!

The problem was instead of changing the sine wave to be smooth on a fixed x-interval, change the x interval itself to the wanted speed.

SUGGESTED TOPICS
The Magazine
Newsletters
Managing Yourself
Managing Teams
Work-life Balance
The Big Idea
Data & Visuals
Reading Lists
Case Selections
HBR Learning
Topic Feeds
Account Settings
Email Preferences

AI’s Trust Problem

Bhaskar Chakravorti

As AI becomes more powerful, it faces a major trust problem. Consider 12 leading concerns: disinformation, safety and security, the black box problem, ethical concerns, bias, instability, hallucinations in LLMs, unknown unknowns, potential job losses and social inequalities, environmental impact, industry concentration, and state overreach. Each of these issues is complex — and not easy to solve. But there is one consistent approach to addressing the trust gap: training, empowering, and including humans to manage AI tools.

Twelve persistent risks of AI that are driving skepticism.

With tens of billions invested in AI last year and leading players such as OpenAI looking for trillions more, the tech industry is racing to add to the pileup of generative AI models. The goal is to steadily demonstrate better performance and, in doing so, close the gap between what humans can do and what can be accomplished with AI.

Bhaskar Chakravorti is the Dean of Global Business at The Fletcher School at Tufts University and founding Executive Director of Fletcher’s Institute for Business in the Global Context . He is the author of The Slow Pace of Fast Change .

Partner Center

IMAGES

Complex numbers: Solving Equations (with example)
Solving Equations With Complex Numbers
A Quick Problem To Solve
Solutions of Problems Based on Complex Numbers || Solving Complex
Complex Numbers
Simplifying Complex Numbers Worksheet

VIDEO

Using Complex Number for Integration !!!
Complex Numbers
Complex FRACTION Practice Problem
How to find solutions of the questions based on the complex numbers? || Part 2
How To Find The Complex Solutions Of An Equation
Mechanism Analysis course Lecture 8 Velocity Analysis Calculus and Vector Methods

COMMENTS

Complex numbers
Test your understanding of Complex numbers with these NaN questions. Start test. This topic covers: - Adding, subtracting, multiplying, & dividing complex numbers - Complex plane - Absolute value & angle of complex numbers - Polar coordinates of complex numbers.
Complex Numbers Calculator
A complex number is a number that can be expressed in the form a + bi, where a and b are real numbers and i is the imaginary unit, which is defined as the square root of -1. The number a is called the real part of the complex number, and the number bi is called the imaginary part.
5.7: Complex Numbers and Their Operations
Solution. Add the real parts and then add the imaginary parts. (5 − 2i) + (7 + 3i) = 5 − 2i + 7 + 3i = 5 + 7 − 2i + 3i = 12 + i. Answer. 12 + i. To subtract complex numbers, we subtract the real parts and subtract the imaginary parts. This is consistent with the use of the distributive property. Example 5.7.3:
Study Guide
This extension makes it possible to solve certain problems that can't be solved within the realm of the set of real numbers. Complex numbers are used in many scientific fields, including engineering, electromagnetism, quantum physics, and applied mathematics, such as chaos theory. ... Using polar coordinates, it becomes easier to multiply and ...
Complex Numbers, Defined, with examples and practice problems
A complex number can be written in the form a + b i where a and b are real numbers (including 0) and i is an imaginary number. Therefore a complex number contains two 'parts': one that is real. and another part that is imaginary. note: Even though complex have an imaginary part, there are actually many real life applications of these "imaginary ...
Complex number
The absolute value (or modulus or magnitude) of a complex number is the distance from the complex number to the origin. It is denoted by . The argument of a complex number is the angle formed between the line drawn from the complex number to the origin and the positive real axis on the complex coordinate plane. It is denoted by .
9.6: Introduction to Complex Numbers and Complex Solutions
Answer: 1 − 9i 1 − 9 i. The distributive property also applies when multiplying complex numbers. Make use of the fact that i2 = −1 i 2 = − 1 to resolve the result into standard form: a + bi a + b i. Example 9.6.4 9.6. 4. Multiply: 5i(3 − 4i) 5 i ( 3 − 4 i) Solution: Begin by applying the distributive property.
Complex Numbers
And we get the Complex Plane. A complex number can now be shown as a point: The complex number 3 + 4i. Properties. The letter z is often used for a complex number: z = a + bi. z is a Complex Number; a and b are Real Numbers; i is the unit imaginary number = √−1; we refer to the real part and imaginary part using Re and Im like this: Re(z ...
Solving equations using complex numbers.
By making use of the imaginary number i we can solve equations that involve the square roots of negative numbers. Complex numbers enable us to solve equations that we wouldn't be able to otherwise solve. Examine the following example: x2 = −11 x = −11− −−−√ 11 ⋅ −1− −−−−−√ = 11−−√ ⋅ i i 11−−√ x 2 ...
Complex Numbers
Examples and questions with detailed solutions on using De Moivre's theorem to find powers and roots of complex numbers. . Complex Numbers - Basic Operations. A tutorial on how to find the conjugate of a complex number and add, subtract, multiply, divide complex numbers supported by online calculators. Complex Numbers Problems with Solutions ...
Complex Numbers Problems with Solutions and Answers
The complex number 2 + 4i is one of the root to the quadratic equation x 2 + bx + c = 0, where b and c are real numbers. a) Find b and c b) Write down the second root and check it. Find all complex numbers z such that z 2 = -1 + 2 sqrt(6) i. Find all complex numbers z such that (4 + 2i)z + (8 - 2i)z' = -2 + 10i, where z' is the complex ...
Complex Numbers Solver
With its user-friendly interface and accurate results, the MathCrave Fractions Calculator takes the hassle out of dealing with fractions and ensures you get the correct answers every time. Say goodbye to manual calculations and hello to a faster, more efficient way of working with fractions. Solve complex numbers problems with MathCrave complex ...
Complex numbers
Unit test. Humans expand our number system when we find new questions to answer. For finding distances in construction, we opened up to irrational numbers. For solutions for more quadratics, we unveiled complex numbers. The good news is, complex numbers follow most of the same patterns as the numbers that came before.
Complex Numbers: Problems with Solutions
Problem 22. Let \displaystyle s s be the sum of the complex numbers. \displaystyle z=2+3i z = 2 +3i and \displaystyle w=1-4i w = 1−4i and let \displaystyle r r be the subtraction of the same numbers. Find the midpoint of \displaystyle s,r s,r. \displaystyle 4+6i 4 +6i.
PDF Complex Numbers
MA.912.NSO.2.1 Extend previous understanding of the real number system to include the complex number system. Add, subtract, multiply and divide complex numbers. Algebraic Reasoning MA.912.AR.3.2 Given a mathematical or real-world context, write and solve one-variable quadratic equations over the GO DIGITAL real and complex number systems.
Complex Numbers and the Quadratic Formula
Your complex-valued answer is still a valid "zero" or "root" or "solution" for that quadratic equation, because, if you plug the answer value back into the quadratic equation, you'll get zero after you simplify. (This is the definition of a "solution"; it is a value that solves the equation, making it true.) However, this complex-valued answer ...
Complex Number Calculator
Find All Complex Solutions 7x2 +3x+8 = 0 7 x 2 + 3 x + 8 = 0. Free complex number calculator - step-by-step solutions to help find the complex factors of the quadratic expressions, find all the complex number solutions, find the magnitude of complex number and find trigonometric form of a complex number.
Solving Complex Analysis Assignments: A Student's Survival Guide
1. Visualization Techniques. Visualization techniques play a pivotal role in mastering complex analysis, particularly when dealing with geometric interpretations. Developing the ability to visualize complex functions and regions within the complex plane enhances problem-solving skills.
Understanding Fire and Rescue Service Practices Through Problems and
This study explores how the Fire and Rescue Service can better prepare for solving complex problems in emergencies by using the concept of problems and problem-solving networks. Primary and secondary data from an extensive fire incident were analysed, including semi-structured interviews and incident assessment reports. Complex problems that arise during emergencies can be challenging to ...
Novel quantum algorithm proposed for high-quality solutions to ...
In conclusion, this study marks a significant step forward for using quantum computers for solving COPs, holding promise for addressing complex real-world problems across various domains.
Sine waves problems
Hello devs, I've recently been messing around with sine waves and ran into a bit of a problem. I've been trying to create a bobbing effect that can smoothly transition from one speed to another, but I can't figure out exactly how Lets say im trying to create a buoy bounce up and down using: --psuedocode local Frequency = 1 local Phase = 0 Bouy.Position.Y= math.sin(time() * frequency ...
Solving quadratic equations: complex roots (video)
Solving quadratic equations can lead to complex solutions. Listen to Sal break down the process using the quadratic formula and standard form. Then, learn how to verify these complex solutions, ensuring you've got the right answer. It's all about turning tricky problems into solvable equations!
AI's Trust Problem
As AI becomes more powerful, it faces a major trust problem. Consider 12 leading concerns: disinformation, safety and security, the black box problem, ethical concerns, bias, instability ...