Compound Interest
You may wish to read Introduction to Interest first
With Compound Interest, we work out the interest for the first period, add it to the total, and then calculate the interest for the next period, and so on ..., like this:
It grows faster and faster like this:
Here are the calculations for 5 Years at 10%:
Those calculations are done one step at a time:
- Calculate the Interest (= "Loan at Start" × Interest Rate)
- Add the Interest to the "Loan at Start" to get the "Loan at End" of the year
- The "Loan at End" of the year is the "Loan at Start" of the next year
A simple job, with lots of calculations.
But there are quicker ways, using some clever mathematics.

Make A Formula
Let us make a formula for the above ... just looking at the first year to begin with:
$1,000.00 + ($1,000.00 × 10%) = $1,100.00
We can rearrange it like this:
So, adding 10% interest is the same as multiplying by 1.10
| $1,000 + ($1,000 x 10%) = $1,000 + $100 = | ||
| $1,000 × 1.10 = |
Note: the Interest Rate was turned into a decimal by dividing by 100:
10% = 10/100 = 0.10
Read Percentages to learn more, but in practice just move the decimal point 2 places, like this:
10% → 1.0 → 0.10
6% → 0.6 → 0.06
The result is that we can do a year in one step:
Now, here is the magic ...
... the same formula works for any year!
- We could do the next year like this: $1,100 × 1.10 = $1,210
- And then continue to the following year: $1,210 × 1.10 = $1,331
So it works like this:
In fact we could go from the start straight to Year 5, if we multiply 5 times :
$1,000 × 1.10 × 1.10 × 1.10 × 1.10 × 1.10 = $1,610.51
And a series of multiplies can be done using Exponents (or Powers) like this:
This does all the calculations in the top table in one go. Wow.
The Formula
We have been using a real example, but let's be more general by using letters instead of numbers , like this:
(This is the same as above, but with PV = $1,000, r = 0.10, n = 5, and FV = $1,610.51)
Here it is written with "FV" first:
FV = PV × (1+r) n
where FV = Future Value PV = Present Value r = annual interest rate n = number of periods

This is the basic formula for Compound Interest. Remember it, as it is very useful.
How about some examples ... ... what if the loan went for 15 Years ? Change the "n" value like this:
... and what if the loan was for 5 years, but the interest rate was only 6%? Here:
| Did you see how we just put the 6% into its place like this: |
... and what if the loan was for 20 years at 8%? Your turn to work it out!
Going "Backwards" to Work Out the Present Value
Let's say your goal is to have $2,000 in 5 Years. You can get 10%, so how much should you start with ?
In other words, you know a Future Value, and want to know a Present Value .
We know that multiplying a Present Value (PV) by (1+r) n gives us the Future Value (FV), so we can go backwards by dividing , like this:
So the Formula is:
PV = FV (1+r) n
Now we can calculate the answer:
In other words, $1,241.84 will grow to $2,000 if you invest it at 10% for 5 years.
Another Example: How much do you need to invest now, to get $10,000 in 10 years at 8% interest rate?
So, $4,631.93 invested at 8% for 10 Years grows to $10,000
Compounding Periods
Compound Interest is not always calculated per year, it could be per month, per day, etc. But if it isn't per year it should say so!
Example: you take out a $1,000 loan for 12 months and it says " 1% per month ", how much do you pay back?
Just use the Future Value formula with "n" being the number of months:
And it is also possible to have yearly interest but with several compoundings within the year , which is called Periodic Compounding .
Example, 6% interest with " monthly compounding " does not mean 6% per month, it means 0.5% per month (6% divided by 12 months), and is worked out like this:
This is equal to a 6.168% ($1,000 grew to $1,061.68) for the whole year.
So be careful to understand what is meant!
Because it is easy for loan ads to be confusing (sometimes on purpose!), the " APR " is often used.
APR means " Annual Percentage Rate ": it shows how much you will actually be paying for the year (including compounding, fees, etc).
Here are some examples:
Example 1: " 1% per month " actually works out to be 12.683% APR (if no fees) .
Example 2: " 6% interest with monthly compounding " works out to be 6.168% APR (if no fees) .
If you are shopping around, ask for the APR.
Break Time!
So far we have looked at using (1+r) n to go from a Present Value (PV) to a Future Value (FV) and back again, plus some of the tricky things that can happen to a loan.
Now is a good time to have a break before we look at two more topics:
- How to work out the Interest Rate if we know PV, FV and the Number of Periods.
- How to work out the Number of Periods if we know PV, FV and the Interest Rate
Working Out The Interest Rate
We can calculate the Interest Rate if we know a Present Value, a Future Value and how many Periods.
Example: you have $1,000, and want it to grow to $2,000 in 5 Years, what interest rate do you need?
The formula is:
r = ( FV / PV ) 1/n − 1
Note: the little "1/n" is a Fractional Exponent , first calculate 1/n, then use that as the exponent on your calculator.
For example 2 0.2 is entered as 2, "x^y", 0, ., 2, =
Now we can "plug in" the values to get the result:
And 0.1487 as a percentage is 14.87% ,
So you need 14.87% interest rate to turn $1,000 into $2,000 in 5 years.
Another Example: What interest rate do you need to turn $1,000 into $5,000 in 20 Years?
And 0.0838 as a percentage is 8.38% .
So 8.38% will turn $1,000 into $5,000 in 20 Years.
Working Out How Many Periods
We can calculate how many Periods if we know a Future Value, a Present Value and the Interest Rate.
Example: you want to know how many periods it will take to turn $1,000 into $2,000 at 10% interest.
This is the formula (note: it uses the natural logarithm function ln ):
n = ln (FV / PV) / ln (1 + r)
The " ln" function should be on a good calculator.
You could also use log , just don't mix the two.
Anyway, let's "plug in" the values:
Magic! It will need 7.27 years to turn $1,000 into $2,000 at 10% interest.
Example: How many years to turn $1,000 into $10,000 at 5% interest?
47 Years! But we are talking about a 10-fold increase, at only 5% interest.
| I also made a that uses these formulas. |
The basic formula for Compound Interest is:
FV = PV (1+r) n
Finds the Future Value , where:
- FV = Future Value,
- PV = Present Value,
- r = Interest Rate (as a decimal value), and
- n = Number of Periods
And by rearranging that formula (see Compound Interest Formula Derivation ) we can find any value when we know the other three:
Find the Present Value when we know a Future Value, the Interest Rate and number of Periods:
Find the Interest Rate when we know the Present Value, Future Value and number of Periods:
Find the number of Periods when we know the Present Value, Future Value and Interest Rate (note: ln is the logarithm function):
We have covered what happens to a value as time goes by ... but what if we have a series of values , like regular loan payments or yearly investments ? That is covered in the topic of Annuities .
Compound Interest Formula
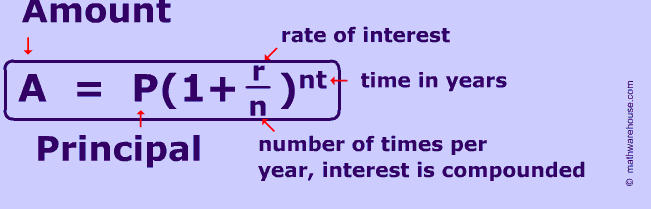
Compound interest is interest that is calculated on both the money deposited and the interest earned from that deposit.
The formula for compound interest is \(A=P(1+\frac{r}{n})^{nt}\), where \(A\) represents the final balance after the interest has been calculated for the time, \(t\), in years, on a principal amount, \(P\), at an annual interest rate, \(r\). The number of times in the year that the interest is compounded is \(n\).
Jasmine deposits $520 into a savings account that has a 3.5% interest rate compounded monthly. What will be the balance of Jasmine’s savings account after two years?
To find the balance after two years, \(A\), we need to use the formula, \(A=P(1+\frac{r}{n})^{nt}\). The principal, \(P\), in this situation is the amount Jasmine used to start her account, $520. The rate, \(r\), as stated in the problem, is 3.5% (or 0.35 as a decimal) and compounded monthly, so \(n=12\). Since we are looking for the balance of the account after two years, 2, is the time, \(t\).
\(A=520(1+\frac{0.035}{12})^{12(2)}\) \(A=557.65\)
The balance of Jasmine’s account after 2 years is $557.65.
Lex has $1,780.80 in his savings account that he opened 6 years ago. His account has an annual interest rate of 6.8% compounded annually. How much money did Lex use to open his savings account?
To find the principal, \(P\) we can use the same formula, \(A=P(1+\frac{r}{n})^{nt}\). We have the balance of the account, \(A\), after 6 years, which is $1,780.80. The interest rate, \(r\), is 6.8% (or 0.68 as a decimal) and is compounded annually, so \(n=1\). The time, \(t\), is 6, since we know he opened his account 6 years ago. Plug in the known values into the formula and solve for the missing variable, \(P\).
\(1{,}780.80=P(1+\frac{0.068}{1})^{1(6)}\) \(1{,}780.80=1.484P\) \(1{,}200=P\)
The principal amount Lex used to open his account 6 years ago is $1,200.

Compound Interest Sample Questions
A teacher wants to invest $30,000 into an account that compounds annually. The interest rate at this bank is 1.8%. How much money will be in the account after 6 years?
Use the compound interest formula to solve this problem.
\(A=P(1+\frac{r}{n})^{nt}\) From here, simply plug in each value and simplify in order to isolate the variable \(A\).
\(A=30{,}000(1+\frac{0.018}{1})^{1×6}\) \(A=30{,}000(1.018)^6\) \(A=$33{,}389.35\)
An investment earns 3% each year and is compounded monthly. Calculate the total value after 6 years from an initial investment of $5,000.
Once again, use the compound interest formula to solve this problem.
\(A=5,000(1+\frac{0.03}{12}^{12×6}\) \(A=5,000(1.36)^{72}\) \(A=$5{,}984.74\)
Kristen wants to have $2,000,000 for retirement in 45 years. She invests in a mutual fund and pays 8.5% each year, compounded quarterly. How much should she deposit into the mutual fund initially?
\(A=P(1+\frac{r}{n}^{nt}\) From here, simply plug in each value and simplify in order to isolate the variable \(P\).
\(2,000,000=P(1+\frac{0.085}{4})^{4×45}\) \(2,000,000=P(1.02125)^{180}\) \(P=$45{,}421.08\)
Sean invests $50,000 into an index annuity that averages 6.5% per year, compounded semi-annually. After 9 years how much will be in his account?
\(A=50{,}000(1+\frac{0.065}{2})^{2×9}\) \(A=50{,}000(1.0325)^{18}\) \(A=$88{,}918.29\)
Calculate the interest rate for an account that started with $5,000 and now has $13,000 and has been compounded annually for the past 12 years.
\(A=P(1+\frac{r}{n})^{nt}\) From here, simply plug in each value and simplify in order to isolate the variable \(r\).
\(13{,}000=5{,}000(1+\frac{r}{1})^{1×12}\) \(13{,}000=5{,}000(1+\frac{r}{1})^{12}\) \(2.6=(1+\frac{r}{1})^{12}\)
To get rid of the exponent 12, find the 12th root of both sides. This means raising both sides of the equation to the power of 112.
\(2.6^{\frac{1}{12}}=((1+\frac{r}{1})^{12})^{\frac{1}{12}}\) \(1.08288=1+r\)
Subtract 1 from both sides.
\(r=0.08288\) (as a decimal) \(r=8.288\%\) (as a percent)
Return to Math Sample Questions
by Mometrix Test Preparation | Last Updated: February 16, 2024

Calculate Compound Interest
Formula for Compound Interest
Compound interest is a great thing when you are earning it! Compound interest is when a bank pays interest on both the principal (the original amount of money)and the interest an account has already earned.
To calculate compound interest use the formula below. In the formula, A represents the final amount in the account after t years compounded 'n' times at interest rate 'r' with starting amount 'p' .
This page focuses on understanding the formula for compound interest ; if you're interested in taking a deeper dive into how compound interest works and exploring some real world examples, please read our article here .
Practice Problems
If you have a bank account whose principal = $1,000, and your bank compounds the interest twice a year at an interest rate of 5%, how much money do you have in your account at the year's end?

If you start a bank account with $10,000 and your bank compounds the interest quarterly at an interest rate of 8%, how much money do you have at the year's end? (assume that you do not add or withdraw any money from the account)

The first credit card that you got charges 12.49% interest to its customers and compounds that interest monthly. Within one day of getting your first credit card, you max out the credit limit by spending $1,200.00. If you do not buy anything else on the card and you do not make any payments, how much money would you owe the company after 6 months?
Note: since the duration of time is half of a year, the value of t is ½.

You win the lottery and get $1,000,000. You decide that you want to invest all of the money in a savings account. However, your bank has two different plans.
The bank gives you a 6% interest rate and compounds the interest each month.
The bank gives you a 12% interest rate and compounds the interest every 2 months .
Question: In 5 years from now, which plan will provide you with more money.
- FHA Mortgage Calculator
- Continuously Compounded Interest
- Exponential Growth
- How Credit Card Companies Use Compound Interest
- Real World Compound Interest Stories
Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!
Popular pages @ mathwarehouse.com.

- Compound Interest
- Compound Interest (Daily)
- Amortization Calculator
- APY Calculator
- Boat Loan Calculator
- CAGR Calculator
- Car Loan Calculator
- Credit Card Repayment
- Currency Converter
- Forex Compounding
- How Long to Save
- How Long Will Money Last
- Interest Rate Calculator
- IRR Calculator
- Loan Calculator
- Loan Payoff Calculator
- Margin Calculator
- Million to Billion Converter
- Money Counter
- Mortgage Calculator
- Mortgage Refinance
- Price Per Square Foot
- Retirement Planning
- Savings Calculators
- Savings Goals
- Simple Interest Calculator
- SIP Calculator
- Hourly to Salary Calc
- Overtime Calculator
- Pay Raise Calculator
- Salary to Hourly Calc
- Time and a Half Calculator
- Centimeters to feet
- Centimeters to inches
- Feet to inches
- Feet to meters
- Inches to centimeters
- Inches to feet
- Meters to feet & inches
- mm to inches
- Grams to pounds
- Kilos to stone & lb
- Kilos to pounds
- Micrograms to mg
- Micrograms to grams
- Milligrams to grams
- Ounces to pounds
- Stone to pounds
- Cubic feet to gallons
- Gallons to ounces
- Liters to gallons
- Liters to ounces
- Cubic yards to tons
- Gallons to pounds
- Liters to tons
- Inch-pounds to ft-lb
- Newton-Meters to ft lb
- Square ft and acres
- Square meters to square ft
- Square feet to cubic feet
- Square feet to cubic yds
- Amps to watts
- Hertz to seconds
- Lumens to Watts
- Watts to amps
- Acceleration
- Data Storage
- Data Transfer Rate
- Fuel Consumption
- Gold Weight
- Length and Distance
- Liquid Volume
- Mass and Weight
- Temperature
- Water Weight
- Weight to Volume
- Cubic Feet Calculator
- Cubic Meters Calculator
- Cubic Yards Calculator
- Electricity Cost Calculator
- Gravel Calculator
- How Much Flooring
- LED Savings Calculator
- MPGe Calculator
- Mulch Calculator
- Square Footage
- Birthday Calculator
- Roman Numerals
- Scientific Calculator
- Final Grade Calculator
- Uni Grade Calculator
- Age Calculator
- Age Difference Calculator
- Chronological Age
- Date Calculator
- Days Between Dates
- Days From Today
- Days Until...
- Generation Calculator
- Decimal to Fraction
- Density Calculator
- Fractions Calculators
- Hex to Decimal
- Percentage Calculator
- Percentage Change
- Baking Conversions
- Butter Converter
- Cooking Converter
- Cups to Grams
- Cups to Ounces
- Cups to Tablespoons
- Grams to Cups
- Grams to Ounces
- Grams to Tablespoons
- Grams to Teaspoons
- mL to Grams
- Ounces to mL
- Ounces to Grams
- Oven Temperatures
- Pints to Cups
- Pounds and Cups
- Quarts to Cups
- Tablespoons to Teaspoons
- Teaspoons to Grams
- Teaspoons to mL
- BMI Calculator
- BMR Calculator
- How Long to Walk a Mile
- How Many Steps in a Mile
- Kilojoules to Calories
- Miles to Steps
- Pregnancy Calculator
- Sobriety Calculator
- Steps to Calories
- Steps to Km
- Steps to Miles
- WHR Calculator
Compound Interest Formula With Examples
Compound interest, or 'interest on interest', is calculated using the compound interest formula A = P*(1+r/n)^(nt) , where P is the principal balance, r is the interest rate (as a decimal), n represents the number of times interest is compounded per year and t is the number of years.
- How to use the formula
To better understand the formula, let's create a simple example. We'll say that you invest $10,000 into a savings account for 20 years at an annual interest rate of 6%, compounded monthly . Here's how our calculation looks:
- r = 6/100 = 0.06 (decimal)
Plugging those figures into the formula, we can calculate as follows:
- A = 10000 × (1 + 0.06 / 12)^(12 × 20)
- A = 10000 × (1 + 0.005)^240
- A = 10000 × 3.310204
- A = 33,102.04
The investment balance after 20 years is therefore $33,102.04 . Checking this figure against our compound interest calculator , we can see that we have calculated correctly.
Keep scrolling to see variations of the formula for annual, quarterly, monthly and daily compounding, a step-by-step explanation of how to use the formula, and some information on how to integrate it within a spreadsheet...
- Table of contents:
Formula variations
Monthly compound interest formula, how to use the formula in excel or google sheets, example calculation, interactive compound interest formula.
- Formula for calculating interest rate (%)
- Formula for calculating principal
- Formula for calculating time factor
Monthly contributions formula
To assist those looking for a convenient formula reference, I've included a concise list of compound interest formula variations applicable to common compounding intervals. Later in the article, we will delve into each variation separately for a comprehensive understanding.
| Calculation | Formula |
|---|---|
| Annual compounding (1x compound per year) | A = P(1 + r)^t |
| Quarterly compounding | A = P(1 + r/4)^4t |
| Monthly compounding | A = P(1 + r/12)^12t |
| Daily compounding | A = P(1 + r/365)^365t |
| Calculate principal (P) based upon future value | P = A / (1 + r/n)^nt |
| Calculate interest rate % (R) | R = n[(A/P)^(1/nt)-1] × 100 |
| Calculate time factor (t) | t = ln(A/P) / n[ln(1 + r/n)] |
- A = future value of the investment/loan
- P = principal amount
- r = annual interest rate (decimal)
- R = annual interest rate (percentage)
- n = number of times interest is compounded per year
- t = time in years
- ^ = ... to the power of ...
- ln = the natural logarithm
How to use the compound interest formula
In order to use the compound interest formula you will require specific values for your initial balance (principal), annual interest rate (expressed as a decimal), the number of compounds per year and the number of years you wish to calculate for. Let's take a look at how we put these into our formula...
How to calculate compound interest using the formula
Start by multiply your initial balance by one plus the annual interest rate (expressed as a decimal) divided by the number of compounds per year. Next, raise the result to the power of the number of compounds per year multiplied by the number of years. Subtract the initial balance from the result if you want to see only the interest earned.
The above set out as a formula is:
A = P(1 + r/n)^nt
- P = principal investment or loan amount
It's worth noting that this formula gives you the future value of an investment or loan, which is compound interest plus the principal. Should you wish to calculate the compound interest only, you need to deduct the principal from the result. So, your formula looks like this:
Earned interest only (without principal) Interest = P(1 + r/n)^nt - P
Let's look at how we can use this formula for monthly compounding, and we can then go through an example calculation...
The formula for calculating compound interest with monthly compounding is:
A = P(1 + r/12)^12t
- A = future value of the investment
- P = principal investment amount
If you're using Excel, Google Sheets or Numbers, you can copy and paste the following into your spreadsheet and adjust your figures for the first four rows as you see fit. This example shows monthly compounding (12 compounds per year) with a 5% interest rate.
| Principal | 10,000 |
| Interest rate (%) | 5 |
| Compounds per year | 12 |
| Years | 10 |
| Future value | = ROUND(INDIRECT(ADDRESS(ROW()-4,COLUMN())) * (1+(INDIRECT(ADDRESS(ROW()-3,COLUMN())) / 100)/INDIRECT(ADDRESS(ROW()-2,COLUMN()))) ^ (INDIRECT(ADDRESS(ROW()-2,COLUMN())) * INDIRECT(ADDRESS(ROW()-1,COLUMN()))),2) |
Here's how it will look in Excel or Google Sheets...
Now that we've looked at how to use the formula for calculations in Excel, let's go through a step-by-step example to demonstrate how to make a manual calculation using the formula...
If an amount of $10,000 is deposited into a savings account at an annual interest rate of 3%, compounded monthly , the value of the investment after 10 years can be calculated as follows...
- r = 3/100 = 0.03 (decimal)
If we plug those figures into the formula, we get the following:
A = 10000 × (1 + 0.03 / 12)^(12 * 10) = 13493.54.
So, the investment balance after 10 years is $13,493.54.
Formula methodology
Let's go through, step-by-step, how we get the 13493.54 result. Our methodology revolves around the PEMDAS order of operations . That is to say that we have to perform operations such as multiplication and addition in the right order.
Let's start off with our equation again:
A = 10000 (1 + 0.03 / 12) ^ (12(10))
(note that ^ means 'to the power of')
Using the order of operations we work out the totals in the brackets first.
Within the first set of brackets, you need to do the division first and then the addition (division and multiplication should be carried out before addition and subtraction). We can also work out the 12(10), which is 12 × 10. This gives us...
A = 10000 (1 + 0.0025)^120
A = 10000 (1.0025)^120
The exponent goes next. So, we calculate 1.0025^120.
This means we end up with:
10000 × 1.34935355
= 13,493.54.
The benefits of compound interest
I think it's worth taking a moment to mention the monetary gain that interest compounding can offer.
Looking back at our example, with simple interest (no compounding) , your investment balance at the end of the term would be $13,000, with $3,000 interest. With regular interest compounding, however, you would stand to gain an additional $493.54 on top.
Interest for $10,000 at 3% for 10 years:
- With simple interest : $3,000
- With compound interest : $3,493.54
Interest for $10,000 at 5% for 10 years:
- With simple interest : $5,000
- With compound interest : $6,470.09
I created the calculator below to show you the formula and resulting accrued investment/loan value (A) for the figures that you enter.
It may be that you want to manipulate the compound interest formula to work out the interest rate for IRR or CAGR , or a principal investment/loan figure. Here are the formulae you need.
Formula for calculating interest rate (r)
This formula can help you work out the yearly interest rate you're getting on your savings, investment or loan. Note that you should multiply your result by 100 to get a percentage figure (%) .
r = n[(A/P)^(1/nt)-1]
- r = interest rate (decimal)
Formula for calculating principal (P)
This formula is useful if you want to work backwards and calculate how much your starting balance would need to be in order to achieve a future monetary value.
P = A / (1 + r/n)^nt
Example: Let's say your goal is to end up with $10,000 in 5 years, and you can get an 8% interest rate on your savings, compounded monthly. Your calculation would be: P = 10000 / (1 + 0.08/12)^(12×5) = $6712.10. So, you would need to start off with $6712.10 to achieve your goal.
Formula for calculating time factor (t)
This variation of the formula works for calculating time (t), by using natural logarithms. You can use it to calculate how long it might take you to reach your savings target , based upon an initial balance and interest rate. You can see how this formula was worked out by reading this explanation on algebra.com .
t = ln(A/P) / n[ln(1 + r/n)]
- A = value of the accrued investment/loan
I've received a lot of requests over the years to provide a formula for compound interest with monthly contributions . So, let's go over how we do this.
In order to work out calculations involving regular contributions, you will need to combine two formulae: our original compound interest formula — P(1+r/n)^(nt) — plus the future value of a series formula for the monthly deposits.
These formulae assume that your frequency of compounding is the same as the periodic payment interval (monthly compounding, monthly contributions, etc).
If the additional deposits are made at the END of the period (end of month, year, etc), here are the two formulae you need:
Compound interest for principal:
P(1+r/n)^(nt)
Future value of a series:
PMT × {[(1 + r/n)^(nt) - 1] / (r/n)}
If the additional deposits are made at the BEGINNING of the period (beginning of year, etc), here are the two formulae you need:
PMT × {[(1 + r/n)^(nt) - 1] / (r/n)} × (1+r/n)
- PMT = monthly payment amount
If an amount of $5,000 is deposited into a savings account at an annual interest rate of 3%, compounded monthly, with additional deposits of $100 per month (made at the end of each month). The value of the investment after 10 years can be calculated as follows...
P = 5000. PMT = 100. r = 3/100 = 0.03 (decimal). n = 12. t = 10.
Let's plug those figures into our formulae and use our PEMDAS order of operations to create our calculation...
- Total = [ Compound interest for principal ] + [ Future value of a series ]
- Total = [ P(1+r/n)^(nt) ] + [ PMT × (((1 + r/n)^(nt) - 1) / (r/n)) ]
- Total = [ 5000 × (1 + 0.03 / 12)^(12 × 10) ] + [ 100 × (((1 + 0.03 / 12)^(12 × 10) - 1) / (0.03 / 12)) ]
- Total = [ 5000 × (1 + 0.0025)^(12 × 10) ] + [ 100 × (((1 + 0.0025)^(12 × 10) - 1) / (0.0025)) ]
- Total = [ 5000 × (1.0025)^120 ] + [ 100 × (((1.0025^120) - 1) / 0.0025) ]
- Total = [ 6746.77 ] + [ 100 × (0.34935354719 / 0.0025) ]
- Total = [ 6746.77 ] + [ 13974.14 ]
- Total = [ $20,720.91 ]
Our investment balance after 10 years therefore works out at $20,720.91.
To conclude
This article about the compound interest formula has expanded and evolved based upon your requests for adapted formulae and examples. So, I appreciate it's now quite long and detailed. That said, I hope you've found it useful. Please feel free to share any thoughts in the comments section below.
Should you need any help with checking your calculations, please make use of our popular compound interest calculator and daily compounding calculator .
Disclaimer: Whilst every effort has been made in building our calculator tools, we are not to be held liable for any damages or monetary losses arising out of or in connection with their use. Full disclaimer .
- Discounting and compounding . John A. Dutton e-Education Institute.
Your comments
If you have any problems using our calculator tool, please contact us .
Finance features
- Compound Interest Calculator
- The Compound Interest Formula
- How Long Will it Take to Save?
- How Much is a TRILLION?
Calculate percentage additions and deductions with our handy calculator.
Discover the number one song and movie on the day you were born.
Home & Garden
- + ACCUPLACER Mathematics
- + ACT Mathematics
- + AFOQT Mathematics
- + ALEKS Tests
- + ASVAB Mathematics
- + ATI TEAS Math Tests
- + Common Core Math
- + DAT Math Tests
- + FSA Tests
- + FTCE Math
- + GED Mathematics
- + Georgia Milestones Assessment
- + GRE Quantitative Reasoning
- + HiSET Math Exam
- + HSPT Math
- + ISEE Mathematics
- + PARCC Tests
- + Praxis Math
- + PSAT Math Tests
- + PSSA Tests
- + SAT Math Tests
- + SBAC Tests
- + SIFT Math
- + SSAT Math Tests
- + STAAR Tests
- + TABE Tests
- + TASC Math
- + TSI Mathematics
- + ACT Math Worksheets
- + Accuplacer Math Worksheets
- + AFOQT Math Worksheets
- + ALEKS Math Worksheets
- + ASVAB Math Worksheets
- + ATI TEAS 6 Math Worksheets
- + FTCE General Math Worksheets
- + GED Math Worksheets
- + 3rd Grade Mathematics Worksheets
- + 4th Grade Mathematics Worksheets
- + 5th Grade Mathematics Worksheets
- + 6th Grade Math Worksheets
- + 7th Grade Mathematics Worksheets
- + 8th Grade Mathematics Worksheets
- + 9th Grade Math Worksheets
- + HiSET Math Worksheets
- + HSPT Math Worksheets
- + ISEE Middle-Level Math Worksheets
- + PERT Math Worksheets
- + Praxis Math Worksheets
- + PSAT Math Worksheets
- + SAT Math Worksheets
- + SIFT Math Worksheets
- + SSAT Middle Level Math Worksheets
- + 7th Grade STAAR Math Worksheets
- + 8th Grade STAAR Math Worksheets
- + THEA Math Worksheets
- + TABE Math Worksheets
- + TASC Math Worksheets
- + TSI Math Worksheets
- + AFOQT Math Course
- + ALEKS Math Course
- + ASVAB Math Course
- + ATI TEAS 6 Math Course
- + CHSPE Math Course
- + FTCE General Knowledge Course
- + GED Math Course
- + HiSET Math Course
- + HSPT Math Course
- + ISEE Upper Level Math Course
- + SHSAT Math Course
- + SSAT Upper-Level Math Course
- + PERT Math Course
- + Praxis Core Math Course
- + SIFT Math Course
- + 8th Grade STAAR Math Course
- + TABE Math Course
- + TASC Math Course
- + TSI Math Course
- + Number Properties Puzzles
- + Algebra Puzzles
- + Geometry Puzzles
- + Intelligent Math Puzzles
- + Ratio, Proportion & Percentages Puzzles
- + Other Math Puzzles
How to Solve Compound Interest Problems?
Compound interest is an interest that is accumulated on the principal and interest together over a given time. In this article, let's familiarize ourselves with solving compound interest problems.

Simple interest is interest that is paid only on the principal of money, while compound interest is interest that is paid on principal and compound interest at regular intervals.
Related Topics
- How to Solve Simple Interest Problems
A step-by-step guide to solving compound interest problems
Compound interest is the interest paid on principal and interest that is combined at regular intervals. At regular intervals, the interest so far accumulated is added to the existing principal amount and then the interest is calculated for the new principal. The new principal is equal to the sum of the Initial principal, and the interest accumulated so far.
Compound interest \(=\) interest on principal \(+\) compounded interest at regular intervals
The compound interest is calculated at regular intervals like annually( yearly), semi-annually, quarterly, monthly, etc.
Compound interest formula
The compound interest is calculated after calculating the total amount over some time, based on the interest rate and the initial principle. For an initial principal of \(P\), rate of interest per annum of \(r\), period \(t\) in years, frequency of the number of times the interest is compounded annually \(n\), the formula for calculation of amount is as follows.
\(\color{blue}{A=P\left(1+\frac{r}{n}\right)^{nt}}\)
The above formula represents the total amount at the end of the period and includes compound interest and principal. In addition, we can calculate the compound interest by subtracting the principal from this amount. The formula for calculating compound interest is as follows:
\(\color{blue}{CI=P\left(1+\frac{r}{n}\right)^{nt}-P}\)
In the above expression:
- \(P\) is the principal amount
- \(r\) is the rate of interest (decimal)
- \(n\) is the frequency or no. of times the interest is compounded annually
- \(t\) is the overall tenure.
It should be noted that the above formula is a general formula when the principal is compounded \(n\) several times in a year. If the given principal is compounded annually, the amount after the period at the percent rate of interest, \(r\), is given as:
\(\color{blue}{A=P\left(1+\frac{r}{100}\right)^t}\)
\(\color{blue}{C.I.=P\left(1+\frac{r}{100}\right)^t-P}\)
Compound interest formula for different periods
The compound interest for a given principle can be calculated for different periods using different formulas.
Compound interest formula – quarterly
If the period for calculating the interest is quarterly, the profit is calculated every three months and the amount is combined \(4\) times a year. The formula to calculate the compound interest when the principal is compounded quarterly is given:
\(\color{blue}{C.I.=P\left(1+\frac{\frac{r}{4}}{100}\right)^{4t}-P}\)
Here the compound interest is calculated for the quarterly period, so the interest rate r is divided by \(4\) and the period is quadrupled. The formula to calculate the amount when the principal is compounded quarterly is given:
\(\color{blue}{A=P\left(1+\frac{\frac{r}{4}}{100}\right)^{4t}}\)
In the above expression,
- \(A\) is the amount at the end of the period
- \(P\) is the initial principal value, \(r\) is the rate of interest per annum
- \(t\) is the period
- \(C.I.\) is the compound interest.
Compound interest formula – half-yearly
Profit for compound interest varies based on the calculation period. If the profit calculation period is half-yearly, the profit is calculated once every six months and is combined twice a year. The formula for calculating compound interest if the principal is compounded semi-annually or half-yearly is given as:
\(\color{blue}{C.I.=P\left(1+\frac{\frac{r}{2}}{100}\right)^{2t}-P}\)
Here the compound interest is calculated for six months, so the interest rate \(r\) is divided by \(2\) and the period is doubled. The formula to calculate the amount when the principal is compounded semi-annually or half-yearly is given:
\(\color{blue}{A=P\left(1+\frac{\frac{r}{2}}{100}\right)^{2t}}\)
Compound Interest – Example 1:
Davide lends \($3,000\) to John at an interest rate of \(10%\) per annum, compounded half-yearly for \(2\) years. Can you help him find out how much amount he gets after \(2\) years from John?
The principal amount \(P\) is \($3,000\). The rate of interest \(r\) is \(10%\) per annum. Conversion period \(=\) Half-year, Rate of interest per half-year \(= \frac{10%}{2}= 5%\). The time period \(t\) is \(2\) years. The compounding frequency \(n\) is \(2\).
Now, substitute the given data in the compound interest formula: \(A\:=\:P\left(1+\frac{\frac{r}{2}}{100}\right)^{2n}\)
\(A=3,000\left(1+\frac{\frac{10}{2}}{100}\right)^{2\times 2}\)
\(=3646.51\)
Exercises for Solving Compound Interest Problems
- What interest rate do you need to turn \($1,000\) into \($5,000\) in \(20\) Years?
- If you deposit \($5,000\) into an account paying \(6%\) annual interest compounded monthly, how long until there is \($8,000\) in the account?
- \(\color{blue}{8.38%}\)
- \(\color{blue}{7.9}\)
by: Effortless Math Team about 2 years ago (category: Articles )
Effortless Math Team
Related to this article, more math articles.
- How to Solve Linear Inequalities?
- 5th Grade PARCC Math Worksheets: FREE & Printable
- How to Use a Venn Diagram to Classify Rational Numbers?
- 5th Grade TNReady Math Worksheets: FREE & Printable
- Top 10 Tips to Create the CLEP College Algebra Study Plan
- Unraveling the Mysteries of Math: How to Solve Word Problems Involving Percent of Change
- 7th Grade MAP Math Worksheets: FREE & Printable
- Quadratic Function
- How Right Triangles Demonstrate Similarity
- The Best Keyboards For Online Teaching
What people say about "How to Solve Compound Interest Problems? - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.
Leave a Reply Cancel reply
You must be logged in to post a comment.
Mastering Grade 6 Math Word Problems The Ultimate Guide to Tackling 6th Grade Math Word Problems
Mastering grade 5 math word problems the ultimate guide to tackling 5th grade math word problems, mastering grade 7 math word problems the ultimate guide to tackling 7th grade math word problems, mastering grade 2 math word problems the ultimate guide to tackling 2nd grade math word problems, mastering grade 8 math word problems the ultimate guide to tackling 8th grade math word problems, mastering grade 4 math word problems the ultimate guide to tackling 4th grade math word problems, mastering grade 3 math word problems the ultimate guide to tackling 3rd grade math word problems.
- ATI TEAS 6 Math
- ISEE Upper Level Math
- SSAT Upper-Level Math
- Praxis Core Math
- 8th Grade STAAR Math
Limited time only!
Save Over 45 %
It was $89.99 now it is $49.99
Login and use all of our services.
Effortless Math services are waiting for you. login faster!
Register Fast!
Password will be generated automatically and sent to your email.
After registration you can change your password if you want.
- Math Worksheets
- Math Courses
- Math Topics
- Math Puzzles
- Math eBooks
- GED Math Books
- HiSET Math Books
- ACT Math Books
- ISEE Math Books
- ACCUPLACER Books
- Premium Membership
- Youtube Videos
Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.
- Bulk Orders
- Refund Policy
- Pre-algebra lessons
- Pre-algebra word problems
- Algebra lessons
- Algebra word problems
- Algebra proofs
- Advanced algebra
- Geometry lessons
- Geometry word problems
- Geometry proofs
- Trigonometry lessons
- Consumer math
- Baseball math
- Math for nurses
- Statistics made easy
- High school physics
- Basic mathematics store
- SAT Math Prep
- Math skills by grade level
- Ask an expert
- Other websites
- K-12 worksheets
- Worksheets generator
- Algebra worksheets
- Geometry worksheets
- Free math problem solver
- Pre-algebra calculators
- Algebra Calculators
- Geometry Calculators
- Math puzzles
- Math tricks
- Member login
Compound interest word problems
We will use the compound interest formula to solve these compound interest word problems.
Example #1 A deposit of $3000 earns 2% interest compounded semiannually. How much money is in the bank after for 4 years? Solution B = P( 1 + r) n P = $3000 r = 2% annual interest rate / 2 interest periods = 1% semiannual interest rate n = number of payment periods = number of interest periods times number of years
n = 2 times 4 = 8
B = 3000( 1 + 1%) 8 = 3000(1 + 0.01) 8 = 3000(1.01) 8 B = 3000(1.082856) B = 3248.57
After four years, there will be 3248.57 dollars in the bank account.
Example #2 A deposit of $2150 earns 6% interest compounded quarterly. How much money is in the bank after for 6 years? Solution B = P( 1 + r) n P = $2150 r = 6% annual interest rate / 4 interest periods = 1.5% quarterly interest rate n = number of payment periods = number of interest periods times number of years
n = 4 times 6 = 24
B = 2150( 1 + 1.5%) 24 = 2150(1 + 0.015) 24 = 2150(1.015) 24 B = 2150(1.4295) B = 3073.425
After 6 years, there will be 3073.425 dollars in the bank account.
Example #3 A deposit of $495 earns 3% interest compounded annually. How much money is in the bank after for 3 years? Solution B = P( 1 + r) n P = $495 r = 3% annual interest rate / 1 interest period = 3% annual interest rate n = number of payment periods = number of interest periods times number of years
n = 1 times 3 = 3
B = 495( 1 + 3%) 3 = 495(1 + 0.03) 3 = 495(1.03) 3 B = 495(1.092727) B = 540.89
After 3 years, there will be 540.89 dollars in the bank account.
Compound interest
Recent Articles
How to divide any number by 5 in 2 seconds.
Feb 28, 24 11:07 AM
Math Trick to Square Numbers from 50 to 59
Feb 23, 24 04:46 AM
Sum of Consecutive Odd Numbers
Feb 22, 24 10:07 AM
100 Tough Algebra Word Problems. If you can solve these problems with no help, you must be a genius!

Recommended
About me :: Privacy policy :: Disclaimer :: Donate Careers in mathematics
Copyright © 2008-2021. Basic-mathematics.com. All right reserved
MathBootCamps
Compound interest formula and examples.
Compound interest is when interest is earned not only on the initial amount invested, but also on any interest. In other words, interest is earned on top of interest and thus “compounds”. The compound interest formula can be used to calculate the value of such an investment after a given amount of time, or to calculate things like the doubling time of an investment. We will see examples of this below. [adsenseWide]
Examples of finding the future value with the compound interest formula
First, we will look at the simplest case where we are using the compound interest formula to calculate the value of an investment after some set amount of time. This is called the future value of the investment and is calculated with the following formula.

An investment earns 3% compounded monthly. Find the value of an initial investment of $5,000 after 6 years.
Determine what values are given and what values you need to find.
- Earns 3% compounded monthly: the rate is \(r = 0.03\) and the number of times compounded each year is \(m = 12\)
- Initial investment of $5,000: the initial amount is the principal, \(P = 5000\)
You are trying to find \(A\), the future value (the value after 6 years). Now apply the formula with the known values:
\(\begin{align}A &= P\left(1 + \dfrac{r}{m}\right)^{mt} \\ &= 5000\left(1 + \dfrac{0.03}{12}\right)^{12 \times 6} \\ &\approx \bbox[border: 1px solid black; padding: 2px]{5984.74}\end{align}\)
Answer: The value after 6 years will be $5,984.74.
Important! Be careful about rounding within the formula. You should do as much work as possible in your calculator and not round until the very end. Otherwise your answer may be off by a few dollars.
Let’s try one more example like this before we try some more difficult types of problems.
What is the value of an investment of $3,500 after 2 years if it earns 1.5% compounded quarterly?
As before, we are finding the future value, A. In this example, we are given:
- Value after 2 years: \(t = 2\)
- Earns 3% compounded quarterly: \(r = 0.015\) and \(m = 4\) since compounded quarterly means 4 times a year
- Principal: \(P = 3500\)
Applying the formula:
\(\begin{align}A &= P\left(1 + \dfrac{r}{m}\right)^{mt} \\ &= 3500\left(1 + \dfrac{0.015}{4}\right)^{4 \times 2}\\ &\approx \bbox[border: 1px solid black; padding: 2px]{3606.39}\end{align}\)
Answer : The value after 2 years will be $3,606.39.
There are other types of questions that can be answered using the compound interest formula. Most of these require some algebra, and the level of algebra required depends on which variable you need to solve for. We will look at some different possibilities below.
Example of finding the rate given other values
Suppose you were given the future value, the time, and the number of compounding periods, but you were asked to calculate the rate earned. This could be used in a situation where you are taking the amount of home sold for and determining the rate earned, if it is viewed as an investment. Consider the following example.
Mrs. Jefferson purchased an antique statue for $450. Ten years later, she sold this statue for $750. If the statue is viewed as an investment, what annual rate did she earn?
If we view this as an investment of \(P = $450\), then we know that the future value is \(A = $750\). This was after \(t = 10\) years. Finally, if we assume an annual rate, we will use \(m = 1\) and have:
\(A = P\left(1 + \dfrac{r}{m}\right)^{mt}\)
\(750 = 450\left(1 + \dfrac{r}{1}\right)^{1 \times 10}\)
This is the same as:
\(750 = 450\left(1 + r\right)^{10}\)
We are solving for the rate, \(r\). We will do this using the following steps.
Divide both sides by 450.
\(\dfrac{750}{450} = \left(1 + r\right)^{10}\)
Simplify on the left-hand side. But, we need to be careful about rounding, so we will keep the fraction for now.
\(\dfrac{5}{3} = \left(1 + r\right)^{10}\)
Take the left-hand side to the 1/10th power to clear the power of 10 on the right.
\(\left(\dfrac{5}{3}\right)^{\dfrac{1}{10}} = 1 + r\)
Calculate the value on the left and solve for \(r\).
\(\begin{align}1.0524 &= 1 + r \\1.0524 – 1 &= r \\ \bbox[border: 1px solid black; padding: 2px] {0.0524} &= r\end{align}\)
Therefore, Mrs. Jefferson earned an annual rate of 5.24%. Not bad! But there was definitely some more complicated algebra involved. In some cases, you may even have to make use of logarithms. A common situation where you might see this is when calculating the doubling time of an investment at a given rate.

Calculating the doubling time of an investment using the compound interest formula
Regardless of the amount initially invested, you can find the doubling time of an investment as long as you are given the rate and the number of compounding periods. Let’s look at an example and see how this could be done.
How many years will it take for an investment to double in value if it earns 5% compounded annually?
It may seem tough to decide where to start here, as we are only given the rate, \(r = 0.05\), and the number of compounding periods, \(m = 1\). Note that we are trying to find the time, \(t\).
Since we do not know the initial investment, we can simply call it \(P\). For this to double, its value would be \(2P\) and, using the compound interest formula, we would have:
\(2P = P\left(1 + \dfrac{0.05}{1}\right)^{t}\)
This could be written as:
\(2P = P\left(1.05\right)^{t}\)
Remember that this would only make sense if the amount invested is not zero, so we can divide both side by \(P\). This gives:
\(2 = \left(1.05\right)^{t}\)
To solve for t, we will take the natural log, ln, of both sides. By the laws of logarithms, this will allow us to bring the exponent to the front.
\(\ln(2) = t\ln\left(1.05\right)\)
Finally, we can divide and then use our calculators to find t.
\(\begin{align}t &= \dfrac{\ln(2)}{\ln\left(1.05\right)}\\ &\approx \bbox[border: 1px solid black; padding: 2px]{14.2 \text{ years}}\end{align}\)
Answer : It will take a little more than 14 years before the investment will double in value.
The same process could be used to determine when an investment would triple or even quadruple. You would just use a different multiple of \(P\) in the first part of the formula.
[adsenseLargeRectangle]
The compound interest formula is used when an investment earns interest on the principal and the previously-earned interest. Investments like this grow quickly; how quickly depends on the rate and the number of compounding periods. When working with a compound interest formula question, always make note of what values are known and what values need to be found so that you stay organized with your work.
Now that you have studied compound interest, you should also review simple interest and how it is different .
Share this:
- Click to share on Twitter (Opens in new window)
- Click to share on Facebook (Opens in new window)
Using a compound interest calculator
The basics of a compound interest calculator, the power of compound interest, how compound interest works, the impact of compounding frequencies, common mistakes to avoid, compound interest calculator.
Affiliate links for the products on this page are from partners that compensate us and terms apply to offers listed (see our advertiser disclosure with our list of partners for more details). However, our opinions are our own. See how we rate banking products to write unbiased product reviews.
- Compound interest is commonly described as "interest earned on interest."
- Compound interest can work to your advantage as your investments grow over time, but against you if you're paying off debt, like credit cards.
- A calculator can help predict how much money compound interest will earn over time.
Most people only think of interest in terms of how high or low a rate is. But understanding how interest is calculated — or how it compounds — is important, too. Using our compound interest calculator can help you understand how compound interest factors into your investments, savings, and debts.
Knowing how compound interest works can help you avoid expensive mistakes and make the most of your money, whether you're planning to save money , invest, borrow, or spend.
Use our compound interest calculator to see how your initial investment will grow over time. We also let you change your compounding frequency, so if you need a daily compound interest calculator, a monthly compound interest calculator, or an annual compound interest calculator, we have you covered.
Compound Interest Calculator
Step-by-step guide.
When using our compound interest calculator, you'll want to use the key components we talked about earlier: principal amount, interest rate, compounding frequency, time period, and, optionally, any regular contributions you're making. Just enter that information into the calculator, and it will give you how much money you'll have at the end of the given time period.
You can also press the "show details" button to see the breakdown of how much money you started with, how much extra money you contributed over time, and the total interest you earned.
If you're interested in compound interest savings, or how much money you're saving by using savings or investment accounts that offer compound interest, we can help you. As such, you can also use our calculator if you're interested in using an investment growth calculator, a future value calculator, a retirement savings calculator , or a wealth accumulation calculator.
If you're looking for a loan interest calculator to see how much interest you'll accrue while you're paying your loan off, our calculator can also help with that.
Our calculator uses the following compound interest formula to figure out how much you'll be left with at the end of the period:
As an example of how this works, let's say you decide to deposit your $10,000 annual bonus into a 5-year certificate of deposit (CD) . You leave that money in the CD for the full five years, and it earns a 4% annual rate of interest that's compounded daily. The numbers you'd plug into each variable are as follows:
- P = $10,000
The formula gives you $12,213.89 for A. That's the total amount of money you'd have in your CD at the end of five years. This means you earned $2,213.89 in interest.
Tips for maximizing returns
The best way to take advantage of compound interest is through saving and investing. If you're borrowing money , you want the lowest interest rate possible, compounded as infrequently as possible.
It's worth noting that the interest rates on even the best high-yield savings accounts barely outpace inflation, so they're best for short-term savings. If you want to build long-term wealth, whether that's saving for retirement or a goal that's years away, investing your money will really get it working for you.
When comparing loans, credit card APRs , savings account APYs, or other securities' returns — check the frequency at which the interest compounds, and make sure you're comparing like to like. Two interest rates can be nominally the same, but if they compound at different speeds, it can make a difference.
Ultimately, whether earning it or paying it, the nature of compound interest means that getting on top of it early on is exponentially better for your wallet and budget .
Key components of a compound interest calculator
When using a compound interest calculator, there are several pieces of information you'll need to know ahead of time. These are the principal amount (the amount of money you start with), the interest rate you're earning, the compounding frequency, and the time period you're interested in using for your calculations.
Principal amount
The principal amount is the money that you start off with. For savings accounts, this is generally the money you open the account with. For investments, this is the money you start the investment with. And for loans, such as a personal loan , this is the initial amount of money you get from the loan.
Interest rate
The interest rate is what you're earning or paying on top of your initial principal. For investments, this is also sometimes called the rate of return. The interest rate generally does not include compounding interest in its calculations; for example, if you have a CD rate of 4.50% and the CD compounds interest daily, you'll actually be earning slightly more than 4.50% in interest over the course of a year.
You might also see people talk about annual percent yields or annual percentage rates. Both APYs and APRs take compounding interest into account; because of that, they tend to be slightly higher. They are a better representation of how much money you'll actually earn or owe at the end of the time period you're interested in. This can also be called the annual effective rate, and you can use an effective annual rate (EAR) calculator to find out what yours is.
Compounding frequency
The compound frequency is how often interest is calculated and added to your principal amount. Your interest can compound daily, weekly, monthly, quarterly, or yearly. If you're earning money, whether through a high-yield savings account offered by an online bank or through an investment, you'll want a quick compounding frequency, since interest builds up faster with shorter compounding times.
If you're borrowing money, whether for a mortgage, car loan, credit card, or something else, you want a slow compounding frequency, as that will cost you less money over time.
Time period
The time period is the amount of time you want to measure compound interest across. For example, if you want to see how much interest you'll earn in five years with a 5-year CD , you'll enter five years as the time period.
While it's not required, you might want to include regular contributions in your calculations. Regular contributions are additional amounts of money you add to your investment or savings. This does not include the money you use to open the savings account or investment account. You'll want to know how much you've added, as well as how frequently you add it, if you're using regular contributions as part of your calculations.
Compound interest is a kind of interest based on adding the original principal with the accumulated interest from previous periods. In other words, with compound interest, you earn interest on previously earned interest. Because of this, compounding interest makes the principal grow exponentially, meaning as interest accrues and the quantity of money increases, the rate of growth becomes faster. This can help you reach savings goals more quickly.
How quickly your money grows with compound interest depends on the interest rate and the frequency of compounding. Interest can be compounded daily, monthly, quarterly, or annually. The more frequently it's compounded, the faster it accumulates.
Daily vs. monthly vs. annually
If you're the one earning money off the interest, daily or monthly compounding is preferable to yearly. Since money is put into your account more frequently, more interest is counted when compounds happen. As an example, let's say you put $5,000 in an account offering a 10% rate of return for one year. If your interest compounds annually, no interest will be added to your principal amount, so you'd get $500 added to your account by the end of the year. This is the same amount you'd get if the account offered simple interest , since the interest only compounded once.
Comparatively, if your interest compounds monthly, some of the interest you make in that year will earn its own interest. In this case, you'll end up with $5,524 at the end of the year. With daily compounding interest, you'll have $5,526 at the end of the year.
While these differences may seem small, they get much bigger when the dollar amount you're working with increases, or if you let the interest build up longer. You could end up with hundreds or thousands of dollars more if you choose daily or monthly compounding interest over yearly.
On the other hand, if you're being charged interest, like with a mortgage , monthly or yearly compounding will save you money compared to daily.
Overlooking compounding frequency
It can be easy to overlook compounding frequency when choosing things like bank accounts or loans, but it can make a big difference. If you're comparing offers that list similar interest rates, make sure to check if interest compounds daily, monthly, quarterly, or yearly. If one offers daily compounding and another offers yearly compounding, you could end up earning or owing very different amounts of money.
Ignoring tax implications
Keep in mind that you will need to pay taxes on interest you earn from your savings account or CD, including compound interest. Since you're earning more money in a year if your investment or bank account uses compound interest, you might have to pay more in taxes than you expect.
Make sure to plan ahead so you aren't surprised come tax season. Using financial planning tools can help you stay aware of exactly how much money you're making in interest.
Similarly, tax software may help you to remember to include your interest earnings when the time comes to pay your taxes.
FAQs on compound interest calculators
A compound interest calculator is an online tool that helps you figure out how much interest you'll earn on an investment, bank account, or loan that uses compound interest. This means it uses both your principal amount and the interest you get on that principal over time in its calculations.
You need a few pieces of information when using a compound interest calculator: the principal amount, the interest rate, the compounding frequency, and the time period that the money is invested, saved, or borrowed. Once you give the calculator that information, it will provide you with the total amount that will be accumulated at the end of the given period.
The compounding frequency is how often the interest is calculated and added to the principal amount. Common compounding frequencies are daily, weekly, monthly, quarterly, and yearly. The more frequently your interest compounds, the more you earn or pay in the long run.
Yes, many compound interest calculators let you include regular contributions in your compound interest calculations. You'll need to enter the additional contribution amount and the frequency of your contributions if you want them to be included.
Different calculators might use slightly different formulas and rounding methods. They also might assume different things about when contributions are made (at the beginning or end of compounding periods) and how the final interest is calculated.
- Certificates of deposit
- Savings accounts
- Checking accounts
- Bank reviews
- Main content
Compound Interest Questions

Compound interest questions are provided here to help the students understand the applications of compound interest in our daily existence. As we know, compound interest is one of the important mathematical concepts that can be applied in many financial transactions.
Below are some situations where we can use the formula of CI to calculate the required results.
- Increase or decrease in population
- The growth of a bacteria (when the rate of growth is known)
- The value of an item, if its price increases or decreases in the intermediate years
What is Compound Interest?
Interest is the additional money paid by organisations like banks or post offices on money deposited (kept) with them. Interest is also paid by people when they borrow money. When the interest is calculated on the previous year’s amount, the interest is called compounded or Compound Interest (C.I.).
The formula for finding the amount on compound interest is given by:
A = P[1 +(R/100)] n
This is the amount when interest is compounded annually.
Compound interest (CI) = A – P
Read more: Compound interest
Compound Interest Questions and Answers
1. Find the compound interest (CI) on Rs. 12,600 for 2 years at 10% per annum compounded annually.
Principal (P) = Rs. 12,600
Rate (R) = 10
Number of years (n) = 2
= 12600[1 + (10/100)] 2
= 12600[1 + (1/10)] 2
= 12600 [(10 + 1)/10] 2
= 12600 × (11/10) × (11/10)
= 126 × 121
Total amount, A = Rs. 15,246
= Rs. 15,246 – Rs. 12,600
2. At what rate of compound interest per annum, a sum of Rs. 1200 becomes Rs. 1348.32 in 2 years?
Let R% be the rate of interest per annum.
Principal (P) = Rs. 1200
Total amount after 2 years (A) = Rs. 1348.32
We know that,
A = P[1 + (R/100)] n
Rs. 1348.32 = Rs. 1200[1 + (R/100)] 2
1348.32/1200 = [1 + (R/100)] 2
1 + (R/100) = 53/50
R/100 = (53/50) – 1
R/100 = (53 – 50)/50
Hence, the rate of interest is 6%.
| Amount, when interest is compounded half-yearly, is A = P[1 + (R/200)] Here, R/200 = half-yearly rate 2n = the number of half years |
3. A TV was bought for Rs. 21,000. The value of the TV was depreciated by 5% per annum. Find the value of the TV after 3 years. (Depreciation means the reduction of value due to use and age of the item)
Principal (P) = Rs. 21,000
Rate of depreciation (R) = 5%
Using the formula of CI for depreciation,
A = P[1 – (R/100)] n
A = Rs. 21,000[1 (5/100)] 3
= Rs. 21,000[1 – (1/20)] 3
= Rs. 21,000[(20 – 1)/20] 3
= Rs. 21,000 × (19/20) × (19/20) × (19/20)
= Rs. 18,004.875
Therefore, the value of the TV after 3 years = Rs. 18,004.875.
4. Find the compound interest on Rs 48,000 for one year at 8% per annum when compounded half-yearly.
Principal (P) = Rs 48,000
Rate (R) = 8% p.a.
Time (n) = 1 year
Also, the interest is compounded half-yearly.
So, A = P[1 + (R/200)] 2n
= Rs. 48000[1 + (8/200)] 2(1)
= Rs. 48000[1 + (1/25)] 2
= Rs. 48000[(25 + 1)/25] 2
= Rs. 48,000 × (26/25) × (26/25)
= Rs. 76.8 × 26 × 26
= Rs 51,916.80
Therefore, the compound interest = A – P
= Rs (519,16.80 – 48,000)
= Rs 3,916.80
5. Find the compound interest on Rs. 8000 at 15% per annum for 2 years 4 months, compounded annually.
Principal (P) = Rs. 8000
Rate of interest (R) = 15% p.a
Time (n) = 2 years 4 months
4 months = 4/12 years = 1/3 years
= Rs. 8000 × (23/20) × (23/20) × (21/20)
= Rs. 11,109
Therefore, the compound interest = A – P = Rs. 11,109 – Rs. 8000 = Rs. 3109
6. If principal = Rs 1,00,000. rate of interest = 10% compounded half-yearly. Find
(i) Interest for 6 months.
(ii) Amount after 6 months.
(iii) Interest for the next 6 months.
(iv) Amount after one year.
P = Rs 1,00,000
(i) A = P[1 + (R/200)] 2n
Here, 2n is the number of half years.
Let us find the interest compounded half-yearly for 6 months, i.e., one half year.
So, A = Rs. 1,00,000 [1 + (10/200)] 1
= Rs. 1,00,000 × 21/20
= Rs. 1,05,000
Compounded interest for 6 months = Rs. 1,05,000 – Rs. 1,00,000 = Rs. 5000
(ii) Amount after 6 months = Rs. 1,05,000
(iii) To find the interest for the next 6 months, we should consider the principal amount as Rs. 1,05,000.
Thus, A = Rs. 1,05,000 [1 + (10/200)] 1
= Rs. 1,05,000 × (21/20)
= Rs. 1,10,250
Compound interest for next 6 months = Rs. 1,10,250 – Rs. 1,05,000 = Rs. 5250
(iv) Amount after one year = Rs. 1,10,250
7. The population of a place increased to 54,000 in 2003 at a rate of 5% per annum.
(i) Find the population in 2001.
(ii) What would be its population in 2005?
(i) Let P be the population in the year 2001.
Thus, population in the year 2003 = A = 54000 (given)
Also, n = 2
54000 = P[1 + (5/100)] 2
54000 = P[1 + (1/20)] 2
54000 = P × [(20 + 1)/20] 2
54000 = P × (21/20) × (21/20)
P = 54000 × (20/21) × (20/21)
P = 48979.6
The population in 2001 = 48980 (approx.)
(ii) Given that the population in the year 2003 = P = 54000
= 54000[1 + (5/100)] 2
= 54000[1 + (1/20)] 2
= 54000 × [(20 + 1)/20] 2
= 54000 × (21/20) × (21/20)
Therefore, the population in 2005 = 59535
| Amount, when interest is compounded quarterly, is A = P[1 + (R/400)] Here, R/400 = Quarterly rate 4n = The number of quarters |
8. What is the difference between the compound interests on Rs. 5000 for 1 ½ year at 4% per annum compounded yearly and half-yearly?
P = Rs. 5000
Time (n) = 1 ½ years
When the interest is compounded yearly,
= Rs. 5000 × (26/25) × (51/50)
CI = A – P = Rs. 5304 – Rs. 5000 = Rs. 304
When the interest is compounded half-yearly,
n = 1 ½ years = 3 half-years
A = P[1 + (R/200)] 2n
Here, 2n = 3
A = Rs. 5000 [1 + (4/200)] 3
= Rs. 5000 [1 + (1/50)] 3
= Rs. 5000 [(50 + 1)/50] 3
= Rs. 5000 × (51/50) × (51/50) × (51/50)
= Rs. 5306.04
CI = A – P = Rs. 5306.04 – Rs. 5000 = Rs. 306.04
Difference between compound interest = Rs. 306.04 – Rs. 304 = Rs. 2.04
9. The population of a town decreased every year due to migration, poverty and unemployment. The present population of the town is 6,31,680. Last year the migration was 4%, and the year before last, it was 6%. What was the population two years ago?
The present population of the town (A) = 631680
Last year migration rate was 4%, and the year before, the previous migration rate was 6%.
Let P be the population of a town, two years ago.
Thus, R 1 = 4%
According to the given situation, the total population is:
631680 = P × (24/25) × (47/50)
P = 631680 × (25/24) × (50/47)
Therefore, the population of the town, two years ago = 700000
10. Find the amount and the compound interest on Rs. 1,00,000 compounded quarterly for 9 months at the rate of 4% per annum.
P = Rs. 1,00,000
Time = 9 months
A = P[1 + (R/400)] 4n
Here, R/400 is the quarterly interest rate.
4n = 9 months = 3 quarters
So, A = Rs. 1,00,000 [1 + (4/400)] 3
= Rs. 1,00,000 [1 + (1/100)] 3
= Rs. 1,00,000 [(100 + 1)/100] 3
= Rs. 1,00,000 × (101/100) × (101/100) × (101/100)
= Rs. 103030.10
Practice Questions on Compound Interest
- The population of a city was 20,000 in the year 1997. It increased at the rate of 5% p.a. Find the population at the end of the year 2000.
- Find the compound interest on Rs. 16,000 at 20% per annum for 9 months, compounded quarterly.
- Vasudevan invested Rs. 60,000 at an interest rate of 12% per annum, compounded half-yearly. What amount would he get- (i) after 6 months? (ii) after 1 year?
- Kamala borrowed Rs. 26,400 from a bank to buy a scooter at a rate of 15% p.a., compounded yearly. What amount will she pay at the end of 2 years and 4 months to clear the loan?
- Find CI paid when a sum of Rs. 10,000 is invested for 1 year and 3 months at 8 1/2 % per annum, compounded annually.
| MATHS Related Links | |
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
- Search Search Please fill out this field.
What Is Compounding?
Understanding compounding, formula for compound interest, increased compounding periods.
- Compounding on Savings and Debt
The Bottom Line
- Dividend Stocks
Compounding Interest: Formulas and Examples
James Chen, CMT is an expert trader, investment adviser, and global market strategist.
:max_bytes(150000):strip_icc():format(webp)/photo__james_chen-5bfc26144cedfd0026c00af8.jpeg)
Gordon Scott has been an active investor and technical analyst or 20+ years. He is a Chartered Market Technician (CMT).
:max_bytes(150000):strip_icc():format(webp)/gordonscottphoto-5bfc26c446e0fb00265b0ed4.jpg)
Compounding is the process in which an asset’s earnings, from either capital gains or interest , are reinvested to generate additional earnings over time. This growth, calculated using exponential functions, occurs because the investment will generate earnings from both its initial principal and the accumulated earnings from preceding periods.
Compounding, therefore, differs from linear growth, where only the principal earns interest each period.
Key Takeaways
- Compounding is the process whereby interest is credited to an existing principal amount as well as to interest already paid.
- Compounding thus can be construed as interest on interest—the effect of which is to magnify returns to interest over time, the so-called “miracle of compounding.”
- When banks or financial institutions credit compound interest, they will use a compounding period such as annual, monthly, or daily.
- Compounding may occur on investments in which savings grow more quickly or on debt where the amount owed may grow even if payments are being made.
- Compounding naturally occurs in savings accounts; some investments that yield dividends may also benefit from compounding.
Sydney Saporito / Investopedia
Compounding typically refers to the increasing value of an asset due to the interest earned on both a principal and an accumulated interest. This phenomenon, which is a direct realization of the time value of money (TMV) concept, is also known as compound interest.
Compounding is crucial in finance , and the gains attributable to its effects are the motivation behind many investing strategies. For example, many corporations offer dividend reinvestment plans (DRIPs) that allow investors to reinvest their cash dividends to purchase additional shares of stock . Reinvesting in more of these dividend-paying shares compounds investor returns because the increased number of shares will consistently increase future income from dividend payouts, assuming steady dividends.
Investing in dividend growth stocks on top of reinvesting dividends adds another layer of compounding to this strategy that some investors refer to as double compounding. In this case, not only are dividends being reinvested to buy more shares, but these dividend growth stocks are also increasing their per-share payouts.
The formula for the future value (FV) of a current asset relies on the concept of compound interest. It takes into account the present value of an asset, the annual interest rate, the frequency of compounding (or the number of compounding periods) per year, and the total number of years. The generalized formula for compound interest is:
F V = P V × ( 1 + i n ) n t where: F V = Future value P V = Present value i = Annual interest rate n = Number of compounding periods per time period t = The time period \begin{aligned}&FV = PV \times \Big (1 + \frac{ i }{ n } \Big ) ^ {nt} \\&\textbf{where:} \\&FV = \text{Future value} \\&PV = \text{Present value} \\&i = \text{Annual interest rate} \\&n = \text{Number of compounding periods per time period} \\&t = \text{The time period} \\\end{aligned} F V = P V × ( 1 + n i ) n t where: F V = Future value P V = Present value i = Annual interest rate n = Number of compounding periods per time period t = The time period
This formula assumes that no additional changes outside of interest are made to the original principal balance.
536,870,912
Curious what 100% daily compounding looks like? “One Grain of Rice,” the folk tale by Demi, is centered around a reward where a single grain of rice is awarded on the first day and the number of grains of rice awarded each day is doubled over 30 days. At the end of the month, over 536 million grains of rice would be awarded on the last day.
The effects of compounding strengthen as the frequency of compounding increases. Assume a one-year time period. The more compounding periods throughout this one year, the higher the future value of the investment; naturally, two compounding periods per year are better than one, and four compounding periods per year are better than two.
To illustrate this effect, consider the following example given the above formula. Assume that an investment of $1 million earns 20% per year. The resulting future value, based on a varying number of compounding periods, is:
- Annual compounding (n = 1) : FV = $1,000,000 × [1 + (20%/1)] (1 x 1) = $1,200,000
- Semiannual compounding (n = 2) : FV = $1,000,000 × [1 + (20%/2)] (2 x 1) = $1,210,000
- Quarterly compounding (n = 4) : FV = $1,000,000 × [1 + (20%/4)] (4 x 1) = $1,215,506
- Monthly compounding (n = 12) : FV = $1,000,000 × [1 + (20%/12)] (12 x 1) = $1,219,391
- Weekly compounding (n = 52) : FV = $1,000,000 × [1 + (20%/52)] (52 x 1) = $1,220,934
- Daily compounding (n = 365) : FV = $1,000,000 × [1 + (20%/365)] (365 x 1) = $1,221,336
As evident, the future value increases by a smaller margin even as the number of compounding periods per year increases significantly. The frequency of compounding over a set length of time has a limited effect on an investment’s growth. This limit, based on calculus, is known as continuous compounding and can be calculated using the formula:
F V = P × e r t where: e = Irrational number 2.7183 r = Interest rate t = Time \begin{aligned}&FV=P\times e^{rt}\\&\textbf{where:}\\&e=\text{Irrational number 2.7183}\\&r=\text{Interest rate}\\&t=\text{Time}\end{aligned} F V = P × e r t where: e = Irrational number 2.7183 r = Interest rate t = Time
In the above example, the future value with continuous compounding equals: FV = $1,000,000 × 2.7183 (0.2 x 1) = $1,221,404.
Compounding is an example of “the snowball effect,” where a situation of small significance builds upon itself into a larger, more serious state.
Compounding on Investments and Debt
Compound interest works on both assets and liabilities. While compounding boosts the value of an asset more rapidly, it can also increase the amount of money owed on a loan, as interest accumulates on the unpaid principal and previous interest charges. Even if you make loan payments, compounding interest may result in the amount of money you owe being greater in future periods.
The concept of compounding is especially problematic for credit card balances. Not only is the interest rate on credit card debt high, but the interest charges also may be added to the principal balance and incur interest assessments on itself in the future. For this reason, the concept of compounding is not necessarily “good” or “bad.” The effects of compounding may work for or against an investor depending on their specific financial situation.
Example of Compounding
To illustrate how compounding works, suppose $10,000 is held in an account that pays 5% interest annually. After the first year or compounding period, the total in the account has risen to $10,500, a simple reflection of $500 in interest being added to the $10,000 principal . In year two, the account realizes 5% growth on both the original principal and the $500 of first-year interest, resulting in a second-year gain of $525 and a balance of $11,025.
| Example of Compounding | |||
|---|---|---|---|
| 1 | $10,000.00 | $500.00 | $10,500.00 |
| 2 | $10,500.00 | $525.00 | $11,025.00 |
| 3 | $11,025.00 | $551.25 | $11,576.25 |
| 4 | $11,576.25 | $578.81 | $12,155.06 |
| 5 | $12,155.06 | $607.75 | $12,762.82 |
| 6 | $12,762.82 | $638.14 | $13,400.96 |
| 7 | $13,400.96 | $670.05 | $14,071.00 |
| 8 | $14,071.00 | $703.55 | $14,774.55 |
| 9 | $14,774.55 | $738.73 | $15,513.28 |
| 10 | $15,513.28 | $775.66 | $16,288.95 |
After 10 years, assuming no withdrawals and a steady 5% interest rate, the account would grow to $16,288.95. Without having added or removed anything from our principal balance except for interest, the impact of compounding has increased the change in balance from $500 in Period 1 to $775.66 in Period 10.
In addition, without having added new investments on our own, our investment has grown $6,288.95 in 10 years. Had the investment only paid simple interest (5% on the original investment only), annual interest would have only been $5,000 ($500 per year for 10 years).
What Is the Rule of 72?
The Rule of 72 is a heuristic used to estimate how long an investment or savings will double in value if there is compound interest (or compounding returns). The rule states that the number of years it will take to double is 72 divided by the interest rate. If the interest rate is 5% with compounding, it would take around 14 years and five months to double.
What Is the Difference Between Simple Interest and Compound Interest?
Simple interest pays interest only on the amount of principal invested or deposited. For instance, if $1,000 is deposited with 5% simple interest, it would earn $50 each year. Compound interest, however, pays “interest on interest,” so in the first year, you would receive $50, but in the second year, you would receive $52.5 ($1,050 × 0.05), and so on.
How Do I Compound My Money?
In addition to compound interest, investors can receive compounding returns by reinvesting dividends . This means taking the cash received from dividend payments to purchase additional shares in the company—which will, themselves, pay out dividends in the future.
Which Type of Average Is Best Suited to Compounding?
There are different types of average ( mean ) calculations used in finance. When computing the average returns of an investment or savings account that has compounding, it is best to use the geometric average . In finance, this is sometimes known as the time-weighted average return or the compound annual growth rate (CAGR) .
What Is the Best Example of Compounding?
High-yield savings accounts are a great example of compounding. Let’s say you deposit $1,000 in a savings account . In the first year, you will earn a given amount of interest. If you never spend any money in the account and the interest rate at least stays the same as the year before, the amount of interest you earn in the second year will be higher. This is because savings accounts add interest earned to the cash balance that is eligible to earn interest.
Compounding and compound interest play a very important part in shaping the financial success of investors. If you take advantage of compounding, you’ll earn more money faster. If you take on compounding debt, you’ll be stuck in a growing debt balance longer. By compounding interest, financial balances are able to exponentially grow faster than straight-line interest.
Donna Kirk et al. “ Contemporary Mathematics: 6.4 Compound Interest .” OpenStax, 2023.
Barnes & Noble. “ One Grain of Rice: a Mathematical Folktale .”
Gilbert Strang et al. “ Calculus Volume 1: 1.5 Exponential and Logarithmic Functions .” OpenStax, 2016.
Investor.gov. “ What Is Compound Interest? ”
:max_bytes(150000):strip_icc():format(webp)/investing20-5bfc2b8f46e0fb00517be081.jpg)
- Terms of Service
- Editorial Policy
- Privacy Policy
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Finance and capital markets
Course: finance and capital markets > unit 1.
- 𝑒 and compound interest
- 𝑒 as a limit
Formula for continuously compounding interest
Want to join the conversation?
- Upvote Button navigates to signup page
- Downvote Button navigates to signup page
- Flag Button navigates to signup page

Video transcript
- Toggle navigation
Mathematics Department Course Hub
- Project Profile
- Course Outline
- Official Textbooks
- Video resources
- Faculty Announcements
- Course Coordination
- WeBWorK – Faculty Resources
- Training and Support
- STEM Applications
- Lesson 27: Properties of Logarithms & Compound Interest
Hi Everyone!
On this page you will find some material about Lesson 27. Read through the material below, watch the videos, and follow up with your instructor if you have questions.
Table of Contents
In this section you will find some important information about the specific resources related to this lesson:
- the learning outcomes,
- the section in the textbook,
- the WeBWorK homework sets,
- a link to the pdf of the lesson notes,
- a link to a video lesson.
Learning Outcomes.
- Simplify a logarithmic expression.
- Expand a logarithmic expression using the properties.
- Rewrite a logarithmic expression as a single logarithm using the properties.
- Use the change-of-base formula.
- Solve compound interest problems.
Topic . This lesson covers
Section 8.5: Properties of Logarithms, and
Section 8.6: The Irrational Number $e$ and Change of Base.
WeBWorK . There are two WeBWorK assignments on today’s material:
LogarithmicProperties
CompoundInterest
Lesson Notes.
These notes are used in Lessons 25-27. Today’s lesson starts on Properties on page 3 through page 5.
These notes are used in Lessons 27 and 28. Today’s lesson starts on Application on page 2 through page 4, not including the Example.
Video Lessons.
Video Lesson 27 – part 1 (based on Lesson 27 Notes -part 1)
This video is used in Lessons 25-27. For today’s lesson, watch from [11:39] to [22:24].
Video Lesson 27 – part 2 (based on Lesson 27 Notes – part 2)
This video is used in Lessons 27 and 28. For today’s lesson, watch from [5:23] to [9:16].
Warmup Questions
These are questions on fundamental concepts that you need to know before you can embark on this lesson. Don’t skip them! Take your time to do them, and check your answer by clicking on the “Show Answer” tab.
Warmup Question 1
Find $\log_7\sqrt[3]7.$
Show Answer 1
$7^{1/3}=\sqrt[3]7$, so $\log_7(\sqrt[3]7)=1/3$.
Warmup Question 2
Find $\log_88.$
Show Answer 2
$8^1=8$, so $\log_88=1$.
Warmup Question 3
Find $\log_{15}1.$
Show Answer 3
$15^{0}= 1$, so $\log_{15}1=0$.
Warmup Question 4
Find $\log_aa^3.$
Show Answer 4
$\log_aa^3=3$
If you are not comfortable with the Warmup Questions, don’t give up! Click on the indicated lesson for a quick catchup. A brief review will help you boost your confidence to start the new lesson, and that’s perfectly fine.
Need a review? Check Lesson 26 .
Quick Intro I
This is like a mini-lesson with an overview of the main objects of study. It will often contain a list of key words, definitions and properties – all that is new in this lesson. We will use this opportunity to make connections with other concepts. It can be also used as a review of the lesson.
A Quick Intro to Properties of Logarithm s
Key Words. Logarithmic expression, properties of logarithms, change-of-base formula.
In the Warmup Questions 2-4, we saw that
$$\log_88=1,$$
$$\log_{15}1=0,$$
$$\log_aa^3=3.$$
These logarithms can be generalized. Say that $b>0$ and $b\neq 1$. Think about what the following logarithms are. Do you see the pattern with the above logarithms?
$$\log_bb$$
$$\log_{b}1$$
$$\log_bb^p$$
Below we give the answers, and provide a few more useful properties.
Properties of Logarithms
Suppose $a, b,x,y>0$ and $a, b\neq 1$.
- $\log_bb=1$
- $\log_{b}1=0$
- $\log_bb^p=p$
- $b^{\log_bx}=x$
- $\log_{b}(xy) = \log_bx+\log_by$
- $\log_{b}\left(\dfrac{x}{y}\right) = \log_bx-\log_by$
- $\log_bx^p=p\log_bx$
- Change-of-Base Formula: $\log_bx=\dfrac{\log_ax}{\log_ab}$
These properties are used to simplify a logarithmic expression as you will see in the video. They are also used to solve logarithmic equations as we will see in Lesson 28 .
Video Lesson I
Many times the mini-lesson will not be enough for you to start working on the problems. You need to see someone explaining the material to you. In the video you will find a variety of examples, solved step-by-step – starting from a simple one to a more complex one. Feel free to play them as many times as you need. Pause, rewind, replay, stop… follow your pace!
Video Lesson 1
A description of the video
In this video you will see the logarithmic expressions:
- $\log_b\sqrt{xy}z^2$
- $\log_{7}\left(\dfrac{x^2y}{zw^2}\right)$
- $\log_2x-2\log_2y+\dfrac{1}{2}\left(\log_2z-\log_2w)-1$
Try Questions I
Now that you have read the material and watched the video, it is your turn to put in practice what you have learned. We encourage you to try the Try Questions on your own. When you are done, click on the “Show answer” tab to see if you got the correct answer.
Try Question 1
Suppose $x,y>0$. Expand $\log\left(\dfrac{\sqrt{10x}}{y^2}\right)$.
$$\log\left(\dfrac{\sqrt{10x}}{y^2}\right)= \log\left(\sqrt{10x}\right)-\log y^2$$
$$=\log\left(10x\right)^{1/2}-\log y^2 $$
$$ = \dfrac{1}{2}\log\left(10x\right)-2\log y$$
$$=\dfrac{1}{2}\left(\log 10+\log x\right)-2\log y $$
$$=\dfrac{1}{2}\left(1+\log x\right)-2\log y $$
$$=\dfrac{1}{2}+\dfrac{\log x}{2}-2\log y$$
Try Question 2
Rewrite the expression as a single logarithm and simplify.
$$\log_7{x}-3\log_7y+6\log_7z$$
$$\log_7{x}-3\log_7y+6\log_7z = \log_7x- \log_7y^3+\log_7z^6$$
$$= \log_7x+\log_7z^6- \log_7y^3 $$
$$= \log_7(xz^6)-\log_7y^3$$
$$=\log_7\left(\dfrac{xz^6}{y^3}\right)$$
Try Question 3
Calculate $\log_{100}5$. Round your answer to the nearest thousandth.
$$\log_{100}5 = \dfrac{\log 5}{\log 100} = \dfrac{0.69897}{2}\approx 0.349$$
You should now be ready to start working on the WeBWorK problems. Doing the homework is an essential part of learning. It will help you practice the lesson and reinforce your knowledge.
It is time to do the homework on WeBWork:
When you are done, come back to this page for the Exit Questions.
Exit Questions I
After doing the WeBWorK problems, come back to this page. The Exit Questions include vocabulary checking and conceptual questions. Knowing the vocabulary accurately is important for us to communicate. You will also find one last problem. All these questions will give you an idea as to whether or not you have mastered the material. Remember: the “Show Answer” tab is there for you to check your work!
Exit Questions
- In $3^x=4$, does the base of the logarithm used when solve that equation matter?
- How do the properties of logarithms correspond to properties of exponents?
$\bigstar$ (a) Assuming that $x,y,z>0$, combine to an expression with one logarithm only.
$$\dfrac{2}{3}\log_5 x – 5\log_5 y-3\log_5z$$
$\bigstar$ (b) Assuming that $x,y>0$, expand $$\log_6\left(\dfrac{\sqrt[5]{x^2}}{36y^3}\right) .$$
Show Answer
(a) $$\dfrac{2}{3}\log_5 x – 5\log_5 y-3\log_5z=\log_5 x^{2/3}-\log_5y^5-\log_5z^3$$
$$ = \log_5\sqrt[3]{x^2}-(\log_5y^5+\log_5z^3) $$
$$= \log_5\sqrt[3]{x^2}-\log_5(y^5z^3)$$
$$= \log_5\left(\dfrac{\sqrt[3]{x^2}}{y^5z^3}\right)$$
(b) $$\log_6\left(\dfrac{\sqrt[5]{x^2}}{36y^3}\right) = \log_6\sqrt[5]{x^2}-\log_6(36y^3)$$
$$=\dfrac{2}{5}\log_6x-(\log_6{36}+\log_6y^3) $$
$$= \dfrac{2}{5}\log_6x-(2+\log_6y^3) $$
$$=\dfrac{2}{5}\log_6x-\log_6y^3-2$$
Lessons Menu
- Lesson 1: Properties of Integer Exponents & Addition and Subtraction of Rational Expressions
- Lesson 2: Complex Fractions
- Lesson 3: Solving Rational Equations
- Lesson 4: Roots and Rational Exponents
- Lesson 5: Simplifying Radical Expressions & Addition and Subtraction of Radicals
- Lesson 6: Multiplication of Radicals
- Lesson 7: Division of Radicals and Rationalization
- Lesson 8: Solving Radical Equations
- Lesson 9: Complex Numbers
- Lesson 10: Solving Equations by Using the Zero Product Rule
- Lesson 11: Square Root Property and Completing the Square & Quadratic Formula
- Lesson 12: Applications of Quadratic Equations
- Lesson 13: Graphs of Quadratic Functions & Vertex of a Parabola
- Lesson 14: Distance Formula, Midpoint Formula, and Circles & Perpendicular Bisector
- Lesson 1: Systems of Linear Equations With Three Variables
- Lesson 16: Nonlinear Systems of Equations in Two Variables
- Lesson 17: Angle Measure and Special Triangles & The Trigonometry of Right Triangles
- Lesson 18: Solving Right Triangles & Applications of Static Trigonometry
- Lesson 19: Angle Measure in Radian & Trigonometry and the Coordinate Plane
- Lesson 20: Unit Circles
- Lesson 21: Graphs of Sine and Cosine
- Lesson 22: Fundamental Identities and Families of Identities
- Lesson 23: Trigonometric Equations
- Lesson 24: Oblique Triangles and The Law of Sines & The Law of Cosines
- Lesson 25: Exponential Expressions
- Lesson 26: Logarithmic Expressions
- Lesson 28: Logarithmic and Exponential Equations

Unless otherwise noted, this site by Ariane Masuda and Jonas Reitz has a Creative Commons Attribution-NonCommercial-ShareAlike (CC BY-NC-SA) license. Learn more.
© 2024 MAT 1275 Course Hub
Theme by Anders Noren — Up ↑
The OpenLab at City Tech: A place to learn, work, and share
The OpenLab is an open-source, digital platform designed to support teaching and learning at City Tech (New York City College of Technology), and to promote student and faculty engagement in the intellectual and social life of the college community.

New York City College of Technology | City University of New York
Accessibility
Our goal is to make the OpenLab accessible for all users.
Learn more about accessibility on the OpenLab
Creative Commons
- - Attribution
- - NonCommercial
- - ShareAlike

© New York City College of Technology | City University of New York

IMAGES
VIDEO
COMMENTS
Do you want to learn how to solve compound interest problems using the formula A = P(1 + r/n)^(nt)? Watch this video from Khan Academy, a free online learning platform that offers courses in math, science, and more. You will see a step-by-step explanation of the concept and an example problem with solution.
Let's say this is a different reality here. We have 7% compounding annual interest. Then after one year we would have 100 times, instead of 1.1, it would be 100% plus 7%, or 1.07. Let's go to 3 years. After 3 years, I could do 2 in between, it would be 100 times 1.07 to the 3rd power, or 1.07 times itself 3 times.
Thousands of practice questions and explanation videos at:http://www.acemymathcourse.com
The basic formula for Compound Interest is: FV = PV (1+r) n. Finds the Future Value, where: FV = Future Value, PV = Present Value, r = Interest Rate (as a decimal value), and; n = Number of Periods; And by rearranging that formula (see Compound Interest Formula Derivation) we can find any value when we know the other three:
This algebra & precalculus video tutorial explains how to use the compound interest formula to solve investment word problems. Logarithms - The Easy Way! ...
Compound interest is interest that is calculated on both the money deposited and the interest earned from that deposit. The formula for compound interest is \ (A=P (1+\frac {r} {n})^ {nt}\), where \ (A\) represents the final balance after the interest has been calculated for the time, \ (t\), in years, on a principal amount, \ (P\), at an ...
Compound interest is when a bank pays interest on both the principal (the original amount of money)and the interest an account has already earned. To calculate compound interest use the formula below. In the formula, A represents the final amount in the account after t years compounded 'n' times at interest rate 'r' with starting amount 'p' .
I had a weird homework question where I was allowed to use a calculator and I eventually solved it, but I didn't understand. Sally had a credit card with $5,500 and 17% compounded annually. She wanted to pay off a loan within 5 years, and they wanted us to find the interest she paid off. I am unaware of where the loan comes in or why the answer ...
Compound Interest Formula With Examples By Alastair Hazell. Reviewed by Chris Hindle.. Compound interest, or 'interest on interest', is calculated using the compound interest formula A = P*(1+r/n)^(nt), where P is the principal balance, r is the interest rate (as a decimal), n represents the number of times interest is compounded per year and t is the number of years.
Interest rates are usually given as an annual percentage rate (APR) - the total interest that will be paid in the year. If the interest is paid in smaller time increments, the APR will be divided up. For example, a 6% 6 % APR paid monthly would be divided into twelve 0.5% 0.5 % payments. A 4% 4 % annual rate paid quarterly would be divided ...
A step-by-step guide to solving compound interest problems. Compound interest is the interest paid on principal and interest that is combined at regular intervals. At regular intervals, the interest so far accumulated is added to the existing principal amount and then the interest is calculated for the new principal. The new principal is equal ...
Compound Interest Word Problems. Question 1: A sum of Rs.10000 is borrowed by Akshit for 2 years at an interest of 10% compounded annually. Find the compound interest and amount he has to pay at the end of 2 years. Solution: Given, Principal/ Sum = Rs. 10000, Rate = 10%, and Time = 2 years.
Learn the Compound Interest Formula in this free math video by Mario's Math Tutoring.0:05 Formula for Calculating Compound Interest0:38 Example 1 $5000 at 8%...
SECTION 6.2 PROBLEM SET: COMPOUND INTEREST. Do the following compound interest problems involving a lump-sum amount. 1) What will the final amount be in 4 years if $8,000 is invested at 9.2% compounded monthly.? 2) How much should be invested at 10.3% for it.
We will use the compound interest formula to solve these compound interest word problems. Example #1. A deposit of $3000 earns 2% interest compounded semiannually. How much money is in the bank after for 4 years? Solution. B = P ( 1 + r) n. P = $3000. r = 2% annual interest rate / 2 interest periods = 1% semiannual interest rate.
Solution. Determine what values are given and what values you need to find. Earns 3% compounded monthly: the rate is \ (r = 0.03\) and the number of times compounded each year is \ (m = 12\) Initial investment of $5,000: the initial amount is the principal, \ (P = 5000\) 6 years: \ (t = 6\)
Step-by-step guide. When using our compound interest calculator, you'll want to use the key components we talked about earlier: principal amount, interest rate, compounding frequency, time period ...
When the interest is calculated on the previous year's amount, the interest is called compounded or Compound Interest (C.I.). The formula for finding the amount on compound interest is given by: A = P[1 +(R/100)] n. This is the amount when interest is compounded annually. Compound interest (CI) = A - P. Read more: Compound interest
This finance video tutorial explains how to calculate the compound interest on an annual, quarterly, and monthly basis.Logarithms - The Easy Way! ...
Compounding is the process where the value of an investment increases because the earnings on an investment, both capital gains and interest, earn interest as time passes. This exponential growth ...
It's then raised to the 4th power because it compounds every period.If you do the above math you'll find (1+0.10/4)^4 = 1.1038, which we could round to 1.10, which ends up at your 10% rate. So the example's fancy compounding rate every 3 months effectively amounts to the same thing as a 10% rate for a year's loan.
STEP 3: Convert the percentages to decimals by dividing by 100. On the bottom bar, change the 105% label to 1.05 and change the 5% label to 0.05. Label the end of the original bottom bar 1. Image ...
This algebra video tutorial explains how to solve the compound interest word problem, population growth, and the bacterial growth word problems using basic p...
Lesson 27 Notes - part 1 Download. These notes are used in Lessons 25-27. Today's lesson starts on Properties on page 3 through page 5. Lesson 27 Notes - part 2 Download. These notes are used in Lessons 27 and 28. Today's lesson starts on Application on page 2 through page 4, not including the Example. Video Lessons.