Solving Systems Of Equations With Fractions Or Decimals
In these lessons, we help Algebra 1 students learn to solve systems of linear equations with fractions.
Related Pages Solving Systems of Equations or Simultaneous Equations using algebra Solving Simultaneous Equations Using Matrices More Lessons On Matrices Algebra Lessons

How To Solve Systems Of Equations With Fractions?
When a system includes an equation with fractions as coefficients: Step 1. Eliminate the fractions by multiplying each side of the equation by a common denominator. Step 2: Solve the resulting system using the addition method, elimination method, or the substitution method.
The following diagrams show how to solve systems of equations using the Substitution Method and the Elimination Method.

Systems of Equations with Fractions
Students learn to solve systems of linear equations that involve fractions. Students also learn to solve linear systems of equations by the method of their choice using the following rules: if one of the variables cancels out when the equations are added together, then use addition, and if a variable is already isolated in one of the equations, then use substitution.
Example: Solve the following systems of equations y = 1/3 x - 1 3x - 2y = 4
Solving a System Involving Fractions with Substitution
How to solve a system of 2 equations with 2 variables involving fractions using substitution?
Example: y = -3/4 x + 12 y = 1/3 x - 2
Solving a System Involving Fractions with Elimination
How to solve a linear system by the process of elimination where the equations contain fractions?
Example: x/2 + y/8 = 4 x/3 - y/2 = -2
Solving systems of linear equations involving decimals and fractions
- Scale the system so that integer coefficients exist.
- Use elimination to solve for the solutions, if they exist.
Examples: System 1 0.05x - 0.03y = 0.21 0.07x + 0.02y = 0.16
System 2 x/4 + y/6 = 1 x - y = 3
System 3 (x + 3)/4 + (y - 1)/3 = 1 2x - y = 1
Solving System Of Linear Equations by Adding (with decimals)
Examples: 3.5x + 2.5y = 17 -1.5x - 7.5y = -33
Solving Systems of Linear Equations with Fractions
Solve a system of linear equations using multiplication with addition or subtraction.
Examples: x/2 + y/3 = -4 x/5 + y/5 = -2

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
5.3 Solve Systems of Equations by Elimination
Learning objectives.
By the end of this section, you will be able to:
- Solve a system of equations by elimination
- Solve applications of systems of equations by elimination
- Choose the most convenient method to solve a system of linear equations
Be Prepared 5.8
Before you get started, take this readiness quiz.
Simplify −5 ( 6 − 3 a ) −5 ( 6 − 3 a ) . If you missed this problem, review Example 1.136 .
Be Prepared 5.9
Solve the equation 1 3 x + 5 8 = 31 24 1 3 x + 5 8 = 31 24 . If you missed this problem, review Example 2.48 .
We have solved systems of linear equations by graphing and by substitution. Graphing works well when the variable coefficients are small and the solution has integer values. Substitution works well when we can easily solve one equation for one of the variables and not have too many fractions in the resulting expression.
The third method of solving systems of linear equations is called the Elimination Method. When we solved a system by substitution, we started with two equations and two variables and reduced it to one equation with one variable. This is what we’ll do with the elimination method, too, but we’ll have a different way to get there.
Solve a System of Equations by Elimination
The Elimination Method is based on the Addition Property of Equality. The Addition Property of Equality says that when you add the same quantity to both sides of an equation, you still have equality. We will extend the Addition Property of Equality to say that when you add equal quantities to both sides of an equation, the results are equal.
For any expressions a , b , c , and d ,
To solve a system of equations by elimination, we start with both equations in standard form. Then we decide which variable will be easiest to eliminate. How do we decide? We want to have the coefficients of one variable be opposites, so that we can add the equations together and eliminate that variable.
Notice how that works when we add these two equations together:
The y ’s add to zero and we have one equation with one variable.
Let’s try another one:
This time we don’t see a variable that can be immediately eliminated if we add the equations.
But if we multiply the first equation by −2, we will make the coefficients of x opposites. We must multiply every term on both sides of the equation by −2.
Now we see that the coefficients of the x terms are opposites, so x will be eliminated when we add these two equations.
Add the equations yourself—the result should be −3 y = −6. And that looks easy to solve, doesn’t it? Here is what it would look like.
We’ll do one more:
It doesn’t appear that we can get the coefficients of one variable to be opposites by multiplying one of the equations by a constant, unless we use fractions. So instead, we’ll have to multiply both equations by a constant.
We can make the coefficients of x be opposites if we multiply the first equation by 3 and the second by −4, so we get 12 x and −12 x .
This gives us these two new equations:
When we add these equations,
the x ’s are eliminated and we just have −29 y = 58.
Once we get an equation with just one variable, we solve it. Then we substitute that value into one of the original equations to solve for the remaining variable. And, as always, we check our answer to make sure it is a solution to both of the original equations.
Now we’ll see how to use elimination to solve the same system of equations we solved by graphing and by substitution.
Example 5.25
How to solve a system of equations by elimination.
Solve the system by elimination. { 2 x + y = 7 x − 2 y = 6 { 2 x + y = 7 x − 2 y = 6
Try It 5.49
Solve the system by elimination. { 3 x + y = 5 2 x − 3 y = 7 { 3 x + y = 5 2 x − 3 y = 7
Try It 5.50
Solve the system by elimination. { 4 x + y = −5 −2 x − 2 y = −2 { 4 x + y = −5 −2 x − 2 y = −2
The steps are listed below for easy reference.
How to solve a system of equations by elimination.
- Step 1. Write both equations in standard form. If any coefficients are fractions, clear them.
- Decide which variable you will eliminate.
- Multiply one or both equations so that the coefficients of that variable are opposites.
- Step 3. Add the equations resulting from Step 2 to eliminate one variable.
- Step 4. Solve for the remaining variable.
- Step 5. Substitute the solution from Step 4 into one of the original equations. Then solve for the other variable.
- Step 6. Write the solution as an ordered pair.
- Step 7. Check that the ordered pair is a solution to both original equations.
First we’ll do an example where we can eliminate one variable right away.
Example 5.26
Solve the system by elimination. { x + y = 10 x − y = 12 { x + y = 10 x − y = 12
| Both equations are in standard form. | |
| The coefficients of are already opposites. | |
| Add the two equations to eliminate . The resulting equation has only 1 variable, . | |
| Solve for , the remaining variable. Substitute = 11 into one of the original equations. | |
| Solve for the other variable, . | |
| Write the solution as an ordered pair. | The ordered pair is (11, −1). |
| Check that the ordered pair is a solution to original equations. | |
| The solution is (11, −1). |
Try It 5.51
Solve the system by elimination. { 2 x + y = 5 x − y = 4 { 2 x + y = 5 x − y = 4
Try It 5.52
Solve the system by elimination. { x + y = 3 −2 x − y = −1 { x + y = 3 −2 x − y = −1
In Example 5.27 , we will be able to make the coefficients of one variable opposites by multiplying one equation by a constant.
Example 5.27
Solve the system by elimination. { 3 x − 2 y = −2 5 x − 6 y = 10 { 3 x − 2 y = −2 5 x − 6 y = 10
| Both equations are in standard form. | |
| None of the coefficients are opposites. | |
| We can make the coefficients of opposites by multiplying the first equation by −3. | |
| Simplify. | |
| Add the two equations to eliminate . | |
| Solve for the remaining variable, . Substitute = −4 into one of the original equations. | |
| Solve for . | |
| Write the solution as an ordered pair. | The ordered pair is (−4, −5). |
| Check that the ordered pair is a solution to both original equations. | |
| The solution is (−4, −5). |
Try It 5.53
Solve the system by elimination. { 4 x − 3 y = 1 5 x − 9 y = −4 { 4 x − 3 y = 1 5 x − 9 y = −4
Try It 5.54
Solve the system by elimination. { 3 x + 2 y = 2 6 x + 5 y = 8 { 3 x + 2 y = 2 6 x + 5 y = 8
Now we’ll do an example where we need to multiply both equations by constants in order to make the coefficients of one variable opposites.
Example 5.28
Solve the system by elimination. { 4 x − 3 y = 9 7 x + 2 y = −6 { 4 x − 3 y = 9 7 x + 2 y = −6
In this example, we cannot multiply just one equation by any constant to get opposite coefficients. So we will strategically multiply both equations by a constant to get the opposites.
| Both equations are in standard form. To get opposite coefficients of , we will multiply the first equation by 2 and the second equation by 3. | |
| Simplify. | |
| Add the two equations to eliminate . | |
| Solve for . Substitute = 0 into one of the original equations. | |
| Solve for . | |
| Write the solution as an ordered pair. | The ordered pair is (0, −3). |
| Check that the ordered pair is a solution to original equations. | |
| The solution is (0, −3). |
What other constants could we have chosen to eliminate one of the variables? Would the solution be the same?
Try It 5.55
Solve the system by elimination. { 3 x − 4 y = −9 5 x + 3 y = 14 { 3 x − 4 y = −9 5 x + 3 y = 14
Try It 5.56
Solve the system by elimination. { 7 x + 8 y = 4 3 x − 5 y = 27 { 7 x + 8 y = 4 3 x − 5 y = 27
When the system of equations contains fractions, we will first clear the fractions by multiplying each equation by its LCD.
Example 5.29
Solve the system by elimination. { x + 1 2 y = 6 3 2 x + 2 3 y = 17 2 { x + 1 2 y = 6 3 2 x + 2 3 y = 17 2
In this example, both equations have fractions. Our first step will be to multiply each equation by its LCD to clear the fractions.
| To clear the fractions, multiply each equation by its LCD. | |
| Simplify. | |
| Now we are ready to eliminate one of the variables. Notice that both equations are in standard form. | |
| We can eliminate multiplying the top equation by −4. | |
| Simplify and add. Substitute = 3 into one of the original equations. | |
| Solve for . | |
| Write the solution as an ordered pair. | The ordered pair is (3, 6). |
| Check that the ordered pair is a solution to original equations. | |
| The solution is (3, 6). |
Try It 5.57
Solve the system by elimination. { 1 3 x − 1 2 y = 1 3 4 x − y = 5 2 { 1 3 x − 1 2 y = 1 3 4 x − y = 5 2
Try It 5.58
Solve the system by elimination. { x + 3 5 y = − 1 5 − 1 2 x − 2 3 y = 5 6 { x + 3 5 y = − 1 5 − 1 2 x − 2 3 y = 5 6
In the Solving Systems of Equations by Graphing we saw that not all systems of linear equations have a single ordered pair as a solution. When the two equations were really the same line, there were infinitely many solutions. We called that a consistent system. When the two equations described parallel lines, there was no solution. We called that an inconsistent system.
Example 5.30
Solve the system by elimination. { 3 x + 4 y = 12 y = 3 − 3 4 x { 3 x + 4 y = 12 y = 3 − 3 4 x
| Write the second equation in standard form. | |
| Clear the fractions by multiplying the second equation by 4. | |
| Simplify. | |
| To eliminate a variable, we multiply the second equation by . Simplify and add. |
This is a true statement. The equations are consistent but dependent. Their graphs would be the same line. The system has infinitely many solutions.
After we cleared the fractions in the second equation, did you notice that the two equations were the same? That means we have coincident lines.
Try It 5.59
Solve the system by elimination. { 5 x − 3 y = 15 y = −5 + 5 3 x { 5 x − 3 y = 15 y = −5 + 5 3 x
Try It 5.60
Solve the system by elimination. { x + 2 y = 6 y = − 1 2 x + 3 { x + 2 y = 6 y = − 1 2 x + 3
Example 5.31
Solve the system by elimination. { −6 x + 15 y = 10 2 x − 5 y = −5 { −6 x + 15 y = 10 2 x − 5 y = −5
| The equations are in standard form. | |
| Multiply the second equation by 3 to eliminate a variable. | |
| Simplify and add. |
This statement is false. The equations are inconsistent and so their graphs would be parallel lines.
The system does not have a solution.
Try It 5.61
Solve the system by elimination. { −3 x + 2 y = 8 9 x − 6 y = 13 { −3 x + 2 y = 8 9 x − 6 y = 13
Try It 5.62
Solve the system by elimination. { 7 x − 3 y = − 2 −14 x + 6 y = 8 { 7 x − 3 y = − 2 −14 x + 6 y = 8
Solve Applications of Systems of Equations by Elimination
Some applications problems translate directly into equations in standard form, so we will use the elimination method to solve them. As before, we use our Problem Solving Strategy to help us stay focused and organized.
Example 5.32
The sum of two numbers is 39. Their difference is 9. Find the numbers.
| the problem. | |
| what we are looking for. | We are looking for two numbers. |
| what we are looking for. Choose a variable to represent that quantity. | Let the first number. the second number. |
| into a system of equations. The system is: | The sum of two numbers is 39. Their difference is 9. |
| the system of equations. To solve the system of equations, use elimination. The equations are in standard form and the coefficients of are opposites. Add. Solve for . Substitute into one of the original equations and solve for . | |
| the answer. | Since and , the answers check. |
| the question. | The numbers are 24 and 15. |
Try It 5.63
The sum of two numbers is 42. Their difference is 8. Find the numbers.
Try It 5.64
The sum of two numbers is −15. Their difference is −35. Find the numbers.
Example 5.33
Joe stops at a burger restaurant every day on his way to work. Monday he had one order of medium fries and two small sodas, which had a total of 620 calories. Tuesday he had two orders of medium fries and one small soda, for a total of 820 calories. How many calories are there in one order of medium fries? How many calories in one small soda?
| the problem. | |
| what we are looking for. | We are looking for the number of calories in one order of medium fries and in one small soda. |
| what we are looking for. | Let = the number of calories in 1 order of medium fries. = the number of calories in 1 small soda. |
| into a system of equations: | one medium fries and two small sodas had a total of 620 calories |
| two medium fries and one small soda had a total of 820 calories. | |
| Our system is: | |
| the system of equations. To solve the system of equations, use elimination. The equations are in standard form. To get opposite coefficients of , multiply the top equation by −2. | |
| Simplify and add. | |
| Solve for . | |
| Substitute = 140 into one of the original equations and then solve for . | |
| the answer. | Verify that these numbers make sense in the problem and that they are solutions to both equations. We leave this to you! |
| the question. | The small soda has 140 calories and the fries have 340 calories. |
Try It 5.65
Malik stops at the grocery store to buy a bag of diapers and 2 cans of formula. He spends a total of $37. The next week he stops and buys 2 bags of diapers and 5 cans of formula for a total of $87. How much does a bag of diapers cost? How much is one can of formula?
Try It 5.66
To get her daily intake of fruit for the day, Sasha eats a banana and 8 strawberries on Wednesday for a calorie count of 145. On the following Wednesday, she eats two bananas and 5 strawberries for a total of 235 calories for the fruit. How many calories are there in a banana? How many calories are in a strawberry?
Choose the Most Convenient Method to Solve a System of Linear Equations
When you will have to solve a system of linear equations in a later math class, you will usually not be told which method to use. You will need to make that decision yourself. So you’ll want to choose the method that is easiest to do and minimizes your chance of making mistakes.
Example 5.34
For each system of linear equations decide whether it would be more convenient to solve it by substitution or elimination. Explain your answer.
ⓐ { 3 x + 8 y = 40 7 x − 4 y = −32 { 3 x + 8 y = 40 7 x − 4 y = −32 ⓑ { 5 x + 6 y = 12 y = 2 3 x − 1 { 5 x + 6 y = 12 y = 2 3 x − 1
- ⓐ { 3 x + 8 y = 40 7 x − 4 y = −32 { 3 x + 8 y = 40 7 x − 4 y = −32 Since both equations are in standard form, using elimination will be most convenient.
- ⓑ { 5 x + 6 y = 12 y = 2 3 x − 1 { 5 x + 6 y = 12 y = 2 3 x − 1
>Since one equation is already solved for y , using substitution will be most convenient.
Try It 5.67
For each system of linear equations, decide whether it would be more convenient to solve it by substitution or elimination. Explain your answer.
ⓐ { 4 x − 5 y = −32 3 x + 2 y = −1 { 4 x − 5 y = −32 3 x + 2 y = −1 ⓑ { x = 2 y − 1 3 x − 5 y = − 7 { x = 2 y − 1 3 x − 5 y = − 7
Try It 5.68
ⓐ { y = 2 x − 1 3 x − 4 y = − 6 { y = 2 x − 1 3 x − 4 y = − 6 ⓑ { 6 x − 2 y = 12 3 x + 7 y = −13 { 6 x − 2 y = 12 3 x + 7 y = −13
Access these online resources for additional instruction and practice with solving systems of linear equations by elimination.
- Instructional Video-Solving Systems of Equations by Elimination
- Instructional Video-Solving by Elimination
- Instructional Video-Solving Systems by Elimination
Section 5.3 Exercises
Practice makes perfect.
In the following exercises, solve the systems of equations by elimination.
{ 5 x + 2 y = 2 −3 x − y = 0 { 5 x + 2 y = 2 −3 x − y = 0
{ −3 x + y = −9 x − 2 y = −12 { −3 x + y = −9 x − 2 y = −12
{ 6 x − 5 y = −1 2 x + y = 13 { 6 x − 5 y = −1 2 x + y = 13
{ 3 x − y = −7 4 x + 2 y = −6 { 3 x − y = −7 4 x + 2 y = −6
{ x + y = −1 x − y = −5 { x + y = −1 x − y = −5
{ x + y = −8 x − y = −6 { x + y = −8 x − y = −6
{ 3 x − 2 y = 1 − x + 2 y = 9 { 3 x − 2 y = 1 − x + 2 y = 9
{ −7 x + 6 y = −10 x − 6 y = 22 { −7 x + 6 y = −10 x − 6 y = 22
{ 3 x + 2 y = −3 − x − 2 y = −19 { 3 x + 2 y = −3 − x − 2 y = −19
{ 5 x + 2 y = 1 −5 x − 4 y = −7 { 5 x + 2 y = 1 −5 x − 4 y = −7
{ 6 x + 4 y = −4 −6 x − 5 y = 8 { 6 x + 4 y = −4 −6 x − 5 y = 8
{ 3 x − 4 y = −11 x − 2 y = −5 { 3 x − 4 y = −11 x − 2 y = −5
{ 5 x − 7 y = 29 x + 3 y = −3 { 5 x − 7 y = 29 x + 3 y = −3
{ 6 x − 5 y = −75 − x − 2 y = −13 { 6 x − 5 y = −75 − x − 2 y = −13
{ − x + 4 y = 8 3 x + 5 y = 10 { − x + 4 y = 8 3 x + 5 y = 10
{ 2 x − 5 y = 7 3 x − y = 17 { 2 x − 5 y = 7 3 x − y = 17
{ 5 x − 3 y = −1 2 x − y = 2 { 5 x − 3 y = −1 2 x − y = 2
{ 7 x + y = −4 13 x + 3 y = 4 { 7 x + y = −4 13 x + 3 y = 4
{ −3 x + 5 y = −13 2 x + y = −26 { −3 x + 5 y = −13 2 x + y = −26
{ 3 x − 5 y = −9 5 x + 2 y = 16 { 3 x − 5 y = −9 5 x + 2 y = 16
{ 4 x − 3 y = 3 2 x + 5 y = −31 { 4 x − 3 y = 3 2 x + 5 y = −31
{ 4 x + 7 y = 14 −2 x + 3 y = 32 { 4 x + 7 y = 14 −2 x + 3 y = 32
{ 5 x + 2 y = 21 7 x − 4 y = 9 { 5 x + 2 y = 21 7 x − 4 y = 9
{ 3 x + 8 y = −3 2 x + 5 y = −3 { 3 x + 8 y = −3 2 x + 5 y = −3
{ 11 x + 9 y = −5 7 x + 5 y = −1 { 11 x + 9 y = −5 7 x + 5 y = −1
{ 3 x + 8 y = 67 5 x + 3 y = 60 { 3 x + 8 y = 67 5 x + 3 y = 60
{ 2 x + 9 y = −4 3 x + 13 y = −7 { 2 x + 9 y = −4 3 x + 13 y = −7
{ 1 3 x − y = −3 x + 5 2 y = 2 { 1 3 x − y = −3 x + 5 2 y = 2
{ x + 1 2 y = 3 2 1 5 x − 1 5 y = 3 { x + 1 2 y = 3 2 1 5 x − 1 5 y = 3
{ x + 1 3 y = −1 1 2 x − 1 3 y = −2 { x + 1 3 y = −1 1 2 x − 1 3 y = −2
{ 1 3 x − y = −3 2 3 x + 5 2 y = 3 { 1 3 x − y = −3 2 3 x + 5 2 y = 3
{ 2 x + y = 3 6 x + 3 y = 9 { 2 x + y = 3 6 x + 3 y = 9
{ x − 4 y = −1 −3 x + 12 y = 3 { x − 4 y = −1 −3 x + 12 y = 3
{ −3 x − y = 8 6 x + 2 y = −16 { −3 x − y = 8 6 x + 2 y = −16
{ 4 x + 3 y = 2 20 x + 15 y = 10 { 4 x + 3 y = 2 20 x + 15 y = 10
{ 3 x + 2 y = 6 −6 x − 4 y = −12 { 3 x + 2 y = 6 −6 x − 4 y = −12
{ 5 x − 8 y = 12 10 x − 16 y = 20 { 5 x − 8 y = 12 10 x − 16 y = 20
{ −11 x + 12 y = 60 −22 x + 24 y = 90 { −11 x + 12 y = 60 −22 x + 24 y = 90
{ 7 x − 9 y = 16 −21 x + 27 y = −24 { 7 x − 9 y = 16 −21 x + 27 y = −24
{ 5 x − 3 y = 15 y = 5 3 x − 2 { 5 x − 3 y = 15 y = 5 3 x − 2
{ 2 x + 4 y = 7 y = − 1 2 x − 4 { 2 x + 4 y = 7 y = − 1 2 x − 4
In the following exercises, translate to a system of equations and solve.
The sum of two numbers is 65. Their difference is 25. Find the numbers.
The sum of two numbers is 37. Their difference is 9. Find the numbers.
The sum of two numbers is −27. Their difference is −59. Find the numbers.
The sum of two numbers is −45. Their difference is −89. Find the numbers.
Andrea is buying some new shirts and sweaters. She is able to buy 3 shirts and 2 sweaters for $114 or she is able to buy 2 shirts and 4 sweaters for $164. How much does a shirt cost? How much does a sweater cost?
Peter is buying office supplies. He is able to buy 3 packages of paper and 4 staplers for $40 or he is able to buy 5 packages of paper and 6 staplers for $62. How much does a package of paper cost? How much does a stapler cost?
The total amount of sodium in 2 hot dogs and 3 cups of cottage cheese is 4720 mg. The total amount of sodium in 5 hot dogs and 2 cups of cottage cheese is 6300 mg. How much sodium is in a hot dog? How much sodium is in a cup of cottage cheese?
The total number of calories in 2 hot dogs and 3 cups of cottage cheese is 960 calories. The total number of calories in 5 hot dogs and 2 cups of cottage cheese is 1190 calories. How many calories are in a hot dog? How many calories are in a cup of cottage cheese?
In the following exercises, decide whether it would be more convenient to solve the system of equations by substitution or elimination.
ⓐ { 8 x − 15 y = −32 6 x + 3 y = −5 { 8 x − 15 y = −32 6 x + 3 y = −5 ⓑ { x = 4 y − 3 4 x − 2 y = −6 { x = 4 y − 3 4 x − 2 y = −6
ⓐ { y = 7 x − 5 3 x − 2 y = 16 { y = 7 x − 5 3 x − 2 y = 16 ⓑ { 12 x − 5 y = −42 3 x + 7 y = −15 { 12 x − 5 y = −42 3 x + 7 y = −15
ⓐ { y = 4 x + 9 5 x − 2 y = −21 { y = 4 x + 9 5 x − 2 y = −21 ⓑ { 9 x − 4 y = 24 3 x + 5 y = −14 { 9 x − 4 y = 24 3 x + 5 y = −14
ⓐ { 14 x − 15 y = −30 7 x + 2 y = 10 { 14 x − 15 y = −30 7 x + 2 y = 10 ⓑ { x = 9 y − 11 2 x − 7 y = −27 { x = 9 y − 11 2 x − 7 y = −27
Everyday Math
Norris can row 3 miles upstream against the current in 1 hour, the same amount of time it takes him to row 5 miles downstream, with the current. Solve the system. { r − c = 3 r + c = 5 { r − c = 3 r + c = 5
- ⓐ for r r , his rowing speed in still water.
- ⓑ Then solve for c c , the speed of the river current.
Josie wants to make 10 pounds of trail mix using nuts and raisins, and she wants the total cost of the trail mix to be $54. Nuts cost $6 per pound and raisins cost $3 per pound. Solve the system { n + r = 10 6 n + 3 r = 54 { n + r = 10 6 n + 3 r = 54 to find n n , the number of pounds of nuts, and r r , the number of pounds of raisins she should use.
Writing Exercises
Solve the system { x + y = 10 5 x + 8 y = 56 { x + y = 10 5 x + 8 y = 56
ⓐ by substitution ⓑ by graphing ⓒ Which method do you prefer? Why?
Solve the system { x + y = −12 y = 4 − 1 2 x { x + y = −12 y = 4 − 1 2 x
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?
As an Amazon Associate we earn from qualifying purchases.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/elementary-algebra-2e/pages/1-introduction
- Authors: Lynn Marecek, MaryAnne Anthony-Smith, Andrea Honeycutt Mathis
- Publisher/website: OpenStax
- Book title: Elementary Algebra 2e
- Publication date: Apr 22, 2020
- Location: Houston, Texas
- Book URL: https://openstax.org/books/elementary-algebra-2e/pages/1-introduction
- Section URL: https://openstax.org/books/elementary-algebra-2e/pages/5-3-solve-systems-of-equations-by-elimination
© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
OpenAlgebra.com
- Videos & Interactives
- Algebra Worksheets
Solving Linear Systems by Elimination



Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
4. Systems of Equations

4.3 Solve Systems of Equations by Elimination
Lynn Marecek and MaryAnne Anthony-Smith
Learning Objectives
By the end of this section it is expected that you will be able to:
- Solve a system of equations by elimination
- Solve applications of systems of equations by elimination
- Choose the most convenient method to solve a system of linear equations
We have solved systems of linear equations by graphing and by substitution. Graphing works well when the variable coefficients are small and the solution has integer values. Substitution works well when we can easily solve one equation for one of the variables and not have too many fractions in the resulting expression.
The third method of solving systems of linear equations is called the Elimination Method. When we solved a system by substitution, we started with two equations and two variables and reduced it to one equation with one variable. This is what we’ll do with the elimination method, too, but we’ll have a different way to get there.
Solve a System of Equations by Elimination
The Elimination Method is based on the Addition Property of Equality. The Addition Property of Equality says that when you add the same quantity to both sides of an equation, you still have equality. We will extend the Addition Property of Equality to say that when you add equal quantities to both sides of an equation, the results are equal.
For any expressions a , b , c , and d ,
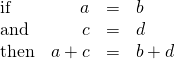
To solve a system of equations by elimination, we start with both equations in standard form. Then we decide which variable will be easiest to eliminate. How do we decide? We want to have the coefficients of one variable be opposites, so that we can add the equations together and eliminate that variable.
Notice how that works when we add these two equations together:
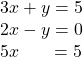
Let’s try another one:
This time we don’t see a variable that can be immediately eliminated if we add the equations.
But if we multiply the first equation by −2, we will make the coefficients of x opposites. We must multiply every term on both sides of the equation by −2.
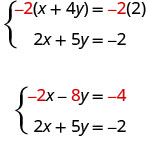
Now we see that the coefficients of the x terms are opposites, so x will be eliminated when we add these two equations.
Add the equations yourself—the result should be −3 y = −6. And that looks easy to solve, doesn’t it? Here is what it would look like.
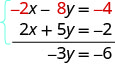
We’ll do one more:
It doesn’t appear that we can get the coefficients of one variable to be opposites by multiplying one of the equations by a constant, unless we use fractions. So instead, we’ll have to multiply both equations by a constant.
We can make the coefficients of x be opposites if we multiply the first equation by 3 and the second by −4, so we get 12 x and −12 x .
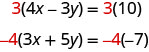
This gives us these two new equations:
When we add these equations,
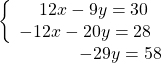
the x ’s are eliminated and we just have −29 y = 58.
Once we get an equation with just one variable, we solve it. Then we substitute that value into one of the original equations to solve for the remaining variable. And, as always, we check our answer to make sure it is a solution to both of the original equations.
Now we’ll see how to use elimination to solve the same system of equations we solved by graphing and by substitution.
The steps are listed below for easy reference.
How to solve a system of equations by elimination.
- Write both equations in standard form. If any coefficients are fractions, clear them.
- Decide which variable you will eliminate.
- Multiply one or both equations so that the coefficients of that variable are opposites.
- Add the equations resulting from Step 2 to eliminate one variable.
- Solve for the remaining variable.
- Substitute the solution from Step 4 into one of the original equations. Then solve for the other variable.
- Write the solution as an ordered pair.
- Check that the ordered pair is a solution to both original equations.
First we’ll do an example where we can eliminate one variable right away.
| Both equations are in standard form. | |
| The coefficients of are already opposites. | |
| Add the two equations to eliminate . The resulting equation has only 1 variable, . | |
| Solve for , the remaining variable. Substitute = 11 into one of the original equations. | |
| Solve for the other variable, . | |
| Write the solution as an ordered pair. | The ordered pair is (11, −1). |
| Check that the ordered pair is a solution to original equations. | |
| The solution is (11, −1). |
In the next example, we will be able to make the coefficients of one variable opposites by multiplying one equation by a constant.
| Both equations are in standard form. | |
| None of the coefficients are opposites. | |
| We can make the coefficients of opposites by multiplying the first equation by −3. | |
| Simplify. | |
| Add the two equations to eliminate . | |
| Solve for the remaining variable, . Substitute = −4 into one of the original equations. | |
| Solve for . | |
| Write the solution as an ordered pair. | The ordered pair is (−4, −5). |
| Check that the ordered pair is a solution to both original equations. | |
| The solution is (−4, −5). |
Now we’ll do an example where we need to multiply both equations by constants in order to make the coefficients of one variable opposites.
In this example, we cannot multiply just one equation by any constant to get opposite coefficients. So we will strategically multiply both equations by a constant to get the opposites.
| Both equations are in standard form. To get opposite coefficients of , we will multiply the first equation by 2 and the second equation by 3. | |
| Simplify. | |
| Add the two equations to eliminate . | |
| Solve for . Substitute = 0 into one of the original equations. | |
| Solve for . | |
| Write the solution as an ordered pair. | The ordered pair is (0, −3). |
| Check that the ordered pair is a solution to original equations. | |
| The solution is (0, −3). |
What other constants could we have chosen to eliminate one of the variables? Would the solution be the same?
When the system of equations contains fractions, we will first clear the fractions by multiplying each equation by its LCD.
In this example, both equations have fractions. Our first step will be to multiply each equation by its LCD to clear the fractions.
| To clear the fractions, multiply each equation by its LCD. | |
| Simplify. | |
| Now we are ready to eliminate one of the variables. Notice that both equations are in standard form. | |
| We can eliminate multiplying the top equation by −4. | |
| Simplify and add. Substitute = 3 into one of the original equations. | |
| Solve for . | |
| Write the solution as an ordered pair. | The ordered pair is (3, 6). |
| Check that the ordered pair is a solution to original equations. | |
| The solution is (3, 6). |
When we were solving systems of linear equations by graphing, we saw that not all systems of linear equations have a single ordered pair as a solution. When the two equations were really the same line, there were infinitely many solutions. We called that a consistent system. When the two equations described parallel lines, there was no solution. We called that an inconsistent system.
Solve the system by elimination:
| a) | |
| Write the second equation in standard form. | |
| Clear the fractions by multiplying the second equation by 4. | |
| Simplify. | |
| To eliminate a variable, we multiply the second equation by Simplify and add. | |
| This is a true statement. The equations are consistent but dependent. Their graphs would be the same line. The system has infinitely many solutions. | |
| After we cleared the fractions in the second equation, did you notice that the two equations were the same? That means we have coincident lines. |
| b) | |
| infinitely many solutions |
| c) | |
| infinitely many solutions |
| d) | |
| The equations are in standard form. | |
| Multiply the second equation by 3 to eliminate a variable. | |
| Simplify and add. | |
| This statement is false. The equations are inconsistent and so their graphs would be parallel lines. | |
| The system does not have a solution. |
no solution
Solve Applications of Systems of Equations by Elimination
Some applications problems translate directly into equations in standard form, so we will use the elimination method to solve them. As before, we use our Problem Solving Strategy to help us stay focused and organized.
The sum of two numbers is 39. Their difference is 9. Find the numbers.
| the problem. | |
| what we are looking for. | We are looking for two numbers. |
| what we are looking for. Choose a variable to represent that quantity. | Let |
| into a system of equations. The system is: | The sum of two numbers is 39. Their difference is 9. |
| the system of equations. To solve the system of equations, use elimination. The equations are in standard form and the coefficients of Solve for Substitute | |
| the answer. | Since |
| the question. | The numbers are 24 and 15. |
The sum of two numbers is 42. Their difference is 8. Find the numbers.
The numbers are 25 and 17.
Joe stops at a burger restaurant every day on his way to work. Monday he had one order of medium fries and two small sodas, which had a total of 620 calories. Tuesday he had two orders of medium fries and one small soda, for a total of 820 calories. How many calories are there in one order of medium fries? How many calories in one small soda?
| the problem. | |
| what we are looking for. | We are looking for the number of calories in one order of medium fries and in one small soda. |
| what we are looking for. | Let = the number of calories in 1 order of medium fries. = the number of calories in 1 small soda. |
| into a system of equations: | one medium fries and two small sodas had a total of 620 calories |
| two medium fries and one small soda had a total of 820 calories. | |
| Our system is: | |
| the system of equations. To solve the system of equations, use elimination. The equations are in standard form. To get opposite coefficients of , multiply the top equation by −2. | |
| Simplify and add. | |
| Solve for . | |
| Substitute = 140 into one of the original equations and then solve for . | |
| the answer. | Verify that these numbers make sense in the problem and that they are solutions to both equations. We leave this to you! |
| the question. | The small soda has 140 calories and the fries have 340 calories. |
Malik stops at the grocery store to buy a bag of diapers and 2 cans of formula. He spends a total of $37. The next week he stops and buys 2 bags of diapers and 5 cans of formula for a total of $87. How much does a bag of diapers cost? How much is one can of formula?
The bag of diapers costs ?11 and the can of formula costs ?13.
Choose the Most Convenient Method to Solve a System of Linear Equations
When you will have to solve a system of linear equations in a later math class, you will usually not be told which method to use. You will need to make that decision yourself. So you’ll want to choose the method that is easiest to do and minimizes your chance of making mistakes.

For each system of linear equations decide whether it would be more convenient to solve it by substitution or elimination. Explain your answer.
For each system of linear equations, decide whether it would be more convenient to solve it by substitution or elimination. Explain your answer.
a) Since both equations are in standard form, using elimination will be most convenient.
Access these online resources for additional instruction and practice with solving systems of linear equations by elimination.
- Instructional Video-Solving Systems of Equations by Elimination
- Instructional Video-Solving by Elimination
- Instructional Video-Solving Systems by Elimination
Key Concepts
4.3 exercise set.
In the following exercises, solve the systems of equations by elimination.
In the following exercises, translate to a system of equations and solve.
- The sum of two numbers is 65. Their difference is 25. Find the numbers .
- The sum of two numbers is −27. Their difference is −59. Find the numbers.
- Andrea is buying some new shirts and sweaters. She is able to buy 3 shirts and 2 sweaters for $114 or she is able to buy 2 shirts and 4 sweaters for $164. How much does a shirt cost? How much does a sweater cost?
- The total amount of sodium in 2 hot dogs and 3 cups of cottage cheese is 4720 mg. The total amount of sodium in 5 hot dogs and 2 cups of cottage cheese is 6300 mg. How much sodium is in a hot dog? How much sodium is in a cup of cottage cheese?
In the following exercises, decide whether it would be more convenient to solve the system of equations by substitution or elimination.
- infinitely many solutions
- inconsistent, no solution
- The numbers are 20 and 45.
- The numbers are 16 and −43.
- A shirt costs $16 and a sweater costs $33.
- There are 860 mg in a hot dog. There are 1,000 mg in a cup of cottage cheese.
- elimination
- substitution
Business/Technical Mathematics Copyright © 2021 by Lynn Marecek and MaryAnne Anthony-Smith is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.
Share This Book

How to solve systems of equations by Elimination
Step by step tutorial for systems of linear equations (in 2 variables)
Video on Solving by Elimination
What is the Elimination Method?
It is one way to solve a system of equations.
The basic idea is if you have 2 equations, you can sometimes do a single operation and then add the 2 equations in a way that eleiminates 1 of the 2 variables as the example that follows shows.

Elimination Example 1
$$ y = x + 1 \\ y = -x $$

Practice Problems
Ultimate math solver (free) free algebra solver ... type anything in there, popular pages @ mathwarehouse.com.


Elimination Method
Elimination method (systems of linear equations).
The main concept behind the elimination method is to create terms with opposite coefficients because they cancel each other when added. In the end, we should deal with a simple linear equation to solve, like a one-step equation in [latex]x[/latex] or in [latex]y[/latex].
Two Ideal Cases of the Elimination Method
I can summarize the “big” ideas about the elimination method when solving systems of linear equations using the illustrations below. Here I present two ideal cases that I want to achieve during the solving process. Take a look at them and hopefully, it makes sense. Otherwise, go directly to the six (6) worked examples to see how actual problems are being solved.
Case 1 : By Adding the Two Equations, the Variable “[latex]x[/latex]” is Eliminated
The coefficients of variable [latex]x[/latex] are opposites.
Case 2 : By Adding the Two Equations, the Variable “[latex]y[/latex]” is Eliminated
The coefficients of variable [latex]y[/latex] are opposites.
Examples of Solving Systems of Linear Equations by Elimination Method
Example 1: Solve the system of linear equations by elimination method.
I have observed that adding the [latex]x[/latex]-column will not eliminate the variable [latex]x[/latex]. However, if I add the [latex]y[/latex]-column the variable [latex]y[/latex] disappears. This happens because the coefficients of [latex]y[/latex] are opposite of each other in terms of signs. Now, I will proceed with the second option.
After doing so, I end up with an easy equation.
I divide both sides by the coefficient of [latex]x[/latex] which gives the answer of [latex]x = 4[/latex].
The next step is to find the corresponding value of [latex]y[/latex]. This is easy to find since I already know what [latex]x[/latex] is. I will pick any of the two original equations, which in this case, I chose the top equation. Then, I will plug in the value of [latex]x = 4[/latex] to get [latex]y[/latex]. The process or procedure of solving for [latex]y[/latex] should be similar below.
Here I get [latex]y = – \,4[/latex]. The final answer in point notation is shown below.
Graphically, the solution looks like this.
Example 2: Solve the system of linear equations by elimination method.
This is quite interesting because no variables will cancel when added. What I want is to introduce a multiplier to one of the equations, or both, and then observe if I arrive at some coefficients that only differ in signs.
There are a few ways to do just that. However, looking at the [latex]x[/latex]-column, I can easily make the [latex]− 3[/latex] into [latex]− 12[/latex] by multiplying the top equation by [latex]+ 4[/latex]. At this point, I can proceed with the addition of [latex]x[/latex]-column.
Multiplying the entire equation by any nonzero number does not change its original meaning. What will change is just its form. I call this process, equation “revision” or “modification”.
This is a one-step equation so I solve [latex]y[/latex] by dividing both sides by its coefficient.
Great! I obtained the value [latex]y = 2[/latex]. Next, I will solve [latex]x[/latex] using back substitution using either of the original equations. For this, I will utilize the top equation because it is less complicated.
I obtained the value [latex]x = – 1[/latex]. I can now write the final answer as the ordered pair written below.
The graph below verifies that our solution is correct.
Example 3: Use the method of elimination or linear combination to solve.
There’s some twist on this problem because the coefficients of [latex]x[/latex] variables are exactly the same, both [latex]- 2[/latex]. The only thing I need to fix here is to make one of them positive. Now, I decided to multiply the top equation by [latex]− 1[/latex]. It should also work just fine if I multiply the bottom by [latex]− 1[/latex].
You should see that the plan works since adding the [latex]x[/latex]-column results to the cancellation of [latex]x[/latex].
I solved the value of [latex]y[/latex] by dividing both sides by [latex]− 17[/latex] which results to [latex]y = 3[/latex]. This time, I will back solve the value of [latex]x[/latex] using the bottom equation because I know what [latex]y[/latex] is.
After a few steps in solving the equation above, I arrive at [latex]x = 2[/latex]. The final answer as an ordered pair is shown below.
Indeed, the two lines intersect at the point that we found in our calculations.
Example 4: Use the method of elimination or linear combination to solve.
This example follows along the line of example 3 where we have exactly the same coefficients. I see that variable [latex]y[/latex] both have coefficients of [latex]8[/latex]. So, I will need to tweak it a bit in order to make their signs opposite. I now have two options on how to proceed. I can multiply the top equation by [latex]− 1[/latex] or the bottom by [latex]− 1[/latex] as well. For this exercise, I choose to do the latter.
Applying the [latex]− 1[/latex] multiplier on the bottom equation and adding them together results to [latex]y[/latex] going away.
Solve the simple equation that arises from it.
I got [latex]x = 4[/latex] by dividing both sides by [latex]− 9[/latex]. The next obvious step is to solve for the other variable [latex]y[/latex] using back substitution. Pick any of the original equations, plug [latex]x = 4[/latex], and you will get [latex]y[/latex] in no time.
The answer is [latex]y = – \,1[/latex]. The final answer in the ordered pair form is shown below.
The graphical solution looks like this.
Example 5: Use the method of elimination or linear combination to solve.
This type of problem requires us to simultaneously multiply both the top and bottom equations by some number in order to generate coefficients with opposite signs.
If I decide to eliminate [latex]x[/latex], I can multiply the top equation by [latex]− 2[/latex] and the bottom by [latex]9[/latex]. By doing so, I should end up with [latex]x[/latex] terms, [latex]18x[/latex] and [latex] – 18x[/latex], respectively, which would cancel when added together.
For this exercise, I want to eliminate [latex]y[/latex]. Therefore, I will multiply the top by [latex]5[/latex] and the bottom by [latex]3[/latex].
As predicted, I was able to get rid of [latex]y[/latex] which leaves us with a simple equation to deal with.
You should arrive at [latex]x = 1[/latex]. Proceed on solving the other variable which is [latex]y[/latex]. Plug in [latex]x = 1[/latex] then solve for [latex]y[/latex].
I got [latex]y = – \,2[/latex]. Putting it together, our final answer is the ordered pair below .
The graphical representation of the two lines intersecting at the solved point is…
Example 6: Use the method of elimination or linear combination to solve.
This last example is very similar to the previous one. As it stands, no variables will be eliminated after adding the columns of [latex]x[/latex] and [latex]y[/latex]. However, I can eliminate the [latex]x[/latex] variables by multiplying the first equation by [latex]5[/latex] and the second by [latex]− 4[/latex], and then add them together. The rest is history!
I will end up solving a simple equation as shown.
I now have [latex]y = 5[/latex] after dividing both sides by [latex]8[/latex]. I will then substitute this value of [latex]y[/latex] to any of the original equations to solve for the corresponding [latex]x[/latex]-value.
This yields an answer of [latex]x = – \,6[/latex]. The final answer should be [latex]\left( {x,y} \right) = \left( { – \,6,5} \right)[/latex] .
This point is where the two lines intersect, as shown below.
You may also be interested in these related math lessons or tutorials:
Substitution Method (Systems of Linear Equations)
Systems of Non-Linear Equations
- Math Lessons
- Math Formulas
- Calculators
Math Calculators, Lessons and Formulas
It is time to solve your math problem
- HW Help (paid service)
- Solving System of Linear Equations
Elimination Method
| Substitution Method |
The elimination method of solving systems of equations is also called the addition method. To solve a system of equations by elimination we transform the system such that one variable "cancels out".
Example 1: Solve the system of equations by elimination
In this example we will "cancel out" the y term. To do so, we can add the equations together.
Now we can find: $x = 2$
In order to solve for y, take the value for x and substitute it back into either one of the original equations.
The solution is $(x, y) = (2, 1)$.
Example 2: Solve the system using elimination
Look at the x - coefficients. Multiply the first equation by -4, to set up the x-coefficients to cancel.
Now we can find: $y = -2$
Take the value for y and substitute it back into either one of the original equations.
The solution is $(x, y) = (1, -2)$.
Example 3: Solve the system using elimination method
In this example, we will multiply the first row by -3 and the second row by 2 ; then we will add down as before.
Now we can find: y = -1
Substitute y = -1 back into first equation:
The solution is $(x, y) = (3, -1)$.
Exercise: Solve the following systems using elimination method
| $$ \color{blue}{x + y = 4}\\\color{blue}{2x - 3y = 18} $$ | $ ( x , y ) = ( 6 , 2 ) $ | |
| $ ( x , y ) = ( -6 , 2 ) $ | ||
| $ ( x , y ) = ( 6 , -2 ) $ | ||
| $ ( x , y ) = ( -6 , -2 ) $ |
| $$ \color{blue}{3x + 5y = -2}\\\color{blue}{2x - y = 3} $$ | $ ( x , y ) = ( 1 , -1 ) $ | |
| $ ( x , y ) = ( -1 , -1 ) $ | ||
| $ ( x , y ) = ( 1 , 1 ) $ | ||
| $ ( x , y ) = ( -1 , 1 ) $ |
- Roots and Radicals Simplify Expression Adding and Subtracting Multiplying and Dividing
- Complex Numbers Arithmetic Polar representation
- Polynomials Multiplying Polynomials Division of Polynomials Zeros of Polynomials
- Rational Expressions Simplifying Multiplying and Dividing Adding and Subtracting
- Solving Equations Linear Equations Absolute Value Equations Quadratic Equation Equations with Radicals
- Systems of Equations Substitution Method Elimination Method Row Reduction Cramers Rule Inverse Matrix Method
- Exponential Functions Introduction Exponential Equations Logarithmic Functions
- Trigonometry Trigonometric Formulas Trigonometric Equations Law of Cosines
- Progressions Arithmetic Progressions Geometric Progressions
- Differentiation Common formulas Product and Quotient Rule Chain Rule
- Limits Properties of Limits Rational Function Irrational Functions Trigonometric Functions L'Hospital's Rule
- Integrals Integration Formulas Exercises
- Integral techniques Substitution Integration by Parts Integrals with Trig. Functions Trigonometric Substitutions
- Integral Applications Area Volume Arc Length
Analytic geometry
- Analytic Geometry 2D Basic Concepts Lines Parallel and Perpendicular Lines Polar Coordinates
- Conic Sections Circle Ellipse Hyperbola
- Analytic Geometry 3D Line in 3D Planes
Linear Algebra
- Matrices Definitions Addition and Multiplication Gauss-Jordan elimination
- Determinants Introduction to Determinants Applications of Determinants
- Vectors Basic Operations Dot Product Cross Product
Random Quote
Creative mathematicians now, as in the past, are inspired by the art of mathematics rather than by any prospect of ultimate usefulness.
Eric Temple Bell
The essence of mathematics is not to make simple things complicated, but to make complicated things simple.
Welcome to MathPortal. This website's owner is mathematician Miloš Petrović. I designed this website and wrote all the calculators, lessons, and formulas .
If you want to contact me, probably have some questions, write me using the contact form or email me on [email protected]
Email (optional)
This is “Solving Linear Systems by Elimination”, section 4.3 from the book Beginning Algebra (v. 1.0). For details on it (including licensing), click here .
This book is licensed under a Creative Commons by-nc-sa 3.0 license. See the license for more details, but that basically means you can share this book as long as you credit the author (but see below), don't make money from it, and do make it available to everyone else under the same terms.
This content was accessible as of December 29, 2012, and it was downloaded then by Andy Schmitz in an effort to preserve the availability of this book.
Normally, the author and publisher would be credited here. However, the publisher has asked for the customary Creative Commons attribution to the original publisher, authors, title, and book URI to be removed. Additionally, per the publisher's request, their name has been removed in some passages. More information is available on this project's attribution page .
For more information on the source of this book, or why it is available for free, please see the project's home page . You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here .

4.3 Solving Linear Systems by Elimination
Learning objectives.
- Solve linear systems using the elimination method.
- Solve linear systems with fractions and decimals.
- Identify the weaknesses and strengths of each method for solving linear systems.
The Elimination Method
In this section, the goal is to develop another completely algebraic method for solving a system of linear equations. We begin by defining what it means to add equations together. In the following example, notice that if we add the expressions on both sides of the equal sign, we obtain another true statement.

This is true in general: if A , B , C , and D are algebraic expressions, then we have the following addition property of equations If A , B , C , and D are algebraic expressions, where A = B and C = D , then A + C = B + D . :

For the system

we add the two equations together:

The sum of y and − y is zero and that term is eliminated. This leaves us with a linear equation with one variable that can be easily solved:

At this point, we have the x coordinate of the simultaneous solution, so all that is left to do is back substitute to find the corresponding y -value.

Hence the solution to the system is (3, 2). This process describes the elimination (or addition) method A means of solving a system by adding equivalent equations in such a way as to eliminate a variable. for solving linear systems. Of course, the variable is not always so easily eliminated. Typically, we have to find an equivalent system by applying the multiplication property of equality to one or both of the equations as a means to line up one of the variables to eliminate. The goal is to arrange that either the x terms or the y terms are opposites, so that when the equations are added, the terms eliminate. The steps for the elimination method are outlined in the following example.
Example 1: Solve by elimination: { 2 x + y = 7 3 x − 2 y = − 7 .
Step 1: Multiply one, or both, of the equations to set up the elimination of one of the variables. In this example, we will eliminate the variable y by multiplying both sides of the first equation by 2. Take care to distribute.

This leaves us with an equivalent system where the variable y is lined up to eliminate.

Step 2: Add the equations together to eliminate one of the variables.

Step 3: Solve for the remaining variable.

Step 3: Back substitute into either equation or its equivalent equation.

Step 4: Check. Remember that the solution must solve both of the original equations.

Answer: (1, 5)
Occasionally, we will have to multiply both equations to line up one of the variables to eliminate. We want the resulting equivalent equations to have terms with opposite coefficients.
Example 2: Solve by elimination: { 5 x − 3 y = − 1 3 x + 2 y = 7 .
Solution: We choose to eliminate the terms with variable y because the coefficients have different signs. To do this, we first determine the least common multiple of the coefficients; in this case, the LCM(3, 2) is 6. Therefore, multiply both sides of both equations by the appropriate values to obtain coefficients of −6 and 6.

This results in the following equivalent system:

The y terms are now lined up to eliminate.

Back substitute.

Answer: (1, 2)
Sometimes linear systems are not given in standard form. When this is the case, it is best to first rearrange the equations before beginning the steps to solve by elimination.
Example 3: Solve by elimination: { 5 x + 12 y = 11 3 y = 4 x + 1 .
Solution: First, rewrite the second equation in standard form.

This results in the following equivalent system where like terms are aligned in columns:

We can eliminate the term with variable y if we multiply the second equation by −4.

Next, we add the equations together,

Answer: (1/3, 7/9)
Try this! Solve by elimination: { 2 x + y = − 3 − 3 x − 2 y = 4 .
Answer: (−2, 1)
Video Solution
At this point, we explore what happens when solving dependent and inconsistent systems using the elimination method.
Example 4: Solve by elimination: { 3 x − y = 7 6 x − 2 y = 14 .
Solution: To eliminate the variable x , we could multiply the first equation by −2.

Now adding the equations we have

A true statement indicates that this is a dependent system. The lines coincide, and we need y in terms of x to present the solution set in the form ( x , m x + b ) . Choose one of the original equations and solve for y . Since the equations are equivalent, it does not matter which one we choose.

Answer: ( x , 3 x − 7 )
Example 5: Solve by elimination: { − x + 3 y = 9 2 x − 6 y = 12 .
Solution: We can eliminate x by multiplying the first equation by 2.

A false statement indicates that the system is inconsistent. The lines are parallel and do not intersect.
Answer: No solution, ∅
Try this! Solve by elimination: { 3 x + 15 y = − 15 2 x + 10 y = 30 .
Clearing Fractions and Decimals
Given a linear system where the equations have fractional coefficients, it is usually best to clear the fractions before beginning the elimination method.
Example 6: Solve: { − 1 10 x + 1 2 y = 4 5 1 7 x + 1 3 y = − 2 21 .
Solution: Recall that we can clear fractions by multiplying both sides of an equation by the least common denominator (LCD). Take care to distribute and then simplify.

This results in an equivalent system where the equations have integer coefficients,

Solve using the elimination method.

Answer: (−3, 1)
We can use a similar technique to clear decimals before solving.
Example 7: Solve: { 3 x − 0.6 y = − 0.9 − 0.5 x + 0.12 y = 0.16 .
Solution: Multiply each equation by the lowest power of 10 necessary to result in integer coefficients. In this case, multiply the first equation by 10 and the second equation by 100.

This results in an equivalent system where the equations have integer coefficients:

Answer: (−0.2, 0.5)
Try this! Solve using elimination: { 1 3 x − 2 3 y = 3 1 3 x − 1 2 y = 8 3 .
Answer: (5, −2)
Summary of the Methods for Solving Linear Systems
We have developed three methods for solving linear systems of two equations with two variables. In this section, we summarize the strengths and weaknesses of each method.
The graphing method is useful for understanding what a system of equations is and what the solutions must look like. When the equations of a system are graphed on the same set of axes, we can see that the solution is the point where the graphs intersect. The graphing is made easy when the equations are in slope-intercept form. For example,

The simultaneous solution (−1, 10) corresponds to the point of intersection. One drawback of this method is that it is very inaccurate. When the coordinates of the solution are not integers, the method is practically unusable. If we have a choice, we typically avoid this method in favor of the more accurate algebraic techniques.
The substitution method, on the other hand, is a completely algebraic method. It requires you to solve for one of the variables and substitute the result into the other equation. The resulting equation has one variable for which you can solve. This method is particularly useful when there is a variable within the system with coefficient of 1. For example,

In this case, it is easy to solve for y in the first equation and then substitute the result into the other equation. One drawback of this method is that it often leads to equivalent equations with fractional coefficients, which are tedious to work with. If there is not a coefficient of 1, then it usually is best to choose the elimination method.
The elimination method is a completely algebraic method that makes use of the addition property of equations. We multiply one or both of the equations to obtain equivalent equations where one of the variables is eliminated if we add them together. For example,

Here we multiply both sides of the first equation by 5 and both sides of the second equation by −2. This results in an equivalent system where the variable x is eliminated when we add the equations together. Of course, there are other combinations of numbers that achieve the same result. We could even choose to eliminate the variable y . No matter which variable is eliminated first, the solution will be the same. Note that the substitution method, in this case, would require tedious calculations with fractional coefficients. One weakness of the elimination method, as we will see later in our study of algebra, is that it does not always work for nonlinear systems.
Key Takeaways
- The elimination method is a completely algebraic method for solving a system of equations.
- Multiply one or both of the equations in a system by certain numbers to obtain an equivalent system consisting of like terms with opposite coefficients. Adding these equivalent equations together eliminates a variable, and the resulting equation has one variable for which you can solve.
- It is a good practice to first rewrite the equations in standard form before beginning the elimination method.
- When the value of one of the variables is determined, back substitute into one of the original equations, or their equivalent equations, and determine the corresponding value of the other variable.
Topic Exercises
Part A: Elimination Method
Solve by elimination.
1. { x + y = 3 2 x − y = 9
2. { x − y = − 6 5 x + y = − 18
3. { x + 3 y = 5 − x − 2 y = 0
4. { − x + 4 y = 4 x − y = − 7
5. { − x + y = 2 x − y = − 3
6. { 3 x − y = − 2 6 x + 4 y = 2
7. { 5 x + 2 y = − 3 10 x − y = 4
8. { − 2 x + 14 y = 28 x − 7 y = 21
9. { − 2 x + y = 4 12 x − 6 y = − 24
10. { x + 8 y = 3 3 x + 12 y = 6
11. { 2 x − 3 y = 15 4 x + 10 y = 14
12. { 4 x + 3 y = − 10 3 x − 9 y = 15
13. { − 4 x − 5 y = − 3 8 x + 3 y = − 15
14. { − 2 x + 7 y = 56 4 x − 2 y = − 112
15. { − 9 x − 15 y = − 15 3 x + 5 y = − 10
16. { 6 x − 7 y = 4 2 x + 6 y = − 7
17. { 4 x + 2 y = 4 − 5 x − 3 y = − 7
18. { 5 x − 3 y = − 1 3 x + 2 y = 7
19. { 7 x + 3 y = 9 2 x + 5 y = − 14
20. { 9 x − 3 y = 3 7 x + 2 y = − 15
21. { 5 x − 3 y = − 7 − 7 x + 6 y = 11
22. { 2 x + 9 y = 8 3 x + 7 y = − 1
23. { 2 x + 2 y = 5 3 x + 3 y = − 5
24. { − 3 x + 6 y = − 12 2 x − 4 y = 8
25. { 25 x + 15 y = − 1 15 x + 10 y = − 1
26. { 2 x − 3 y = 2 18 x − 12 y = 5
27. { y = − 2 x − 3 − 3 x − 2 y = 4
28. { 28 x + 6 y = 9 6 y = 4 x − 15
29. { y = 5 x + 15 y = − 5 x + 5
30. { 2 x − 3 y = 9 5 x − 8 y = − 16
31. { 1 2 x − 1 3 y = 1 6 5 2 x + y = 7 2
32. { 1 4 x − 1 9 y = 1 x + y = 3 4
33. { 1 2 x − 1 4 y = 1 3 1 4 x + 1 2 y = − 19 6
34. { − 14 3 x + 2 y = 4 − 1 3 x + 1 7 y = 4 21
35. { 0.025 x + 0.1 y = 0.5 0.11 x + 0.04 y = − 0.2
36. { 1.3 x + 0.1 y = 0.35 0.5 x + y = − 2.75
37. { x + y = 5 0.02 x + 0.03 y = 0.125
38. { x + y = 30 0.05 x + 0.1 y = 2.4
Set up a linear system and solve it using the elimination method.
39. The sum of two numbers is 14. The larger number is 1 less than two times the smaller.
40. The sum of two numbers is 30. The larger is 2 more than three times the smaller.
41. The difference of two numbers is 13 and their sum is 11.
42. The difference of two numbers is 2 and their sum is −12.
Part B: Mixed Exercises
Solve using any method.
43. { y = 2 x − 3 3 x + y = 12
44. { x + 3 y = − 5 y = 1 3 x + 5
45. { x = − 1 y = 3
46. { y = 1 2 x + 9 = 0
47. { y = x − x + y = 1
48. { y = 5 x y = − 10
49. { 3 y = 2 x − 24 3 x + 4 y = 2
50. { y = − 3 2 x + 1 − 2 y + 2 = 3 x
51. { 7 y = − 2 x − 1 7 x = 2 y + 23
52. { 5 x + 9 y − 14 = 0 3 x + 2 y − 5 = 0
53. { y = − 5 16 x + 10 y = 5 16 x − 10
54. { y = − 6 5 x + 12 x = 6
55. { 2 ( x − 3 ) + y = 0 3 ( 2 x + y − 1 ) = 15
56. { 3 − 2 ( x − y ) = − 3 4 x − 3 ( y + 1 ) = 8
57. { 2 ( x + 1 ) = 3 ( 2 y − 1 ) − 21 3 ( x + 2 ) = 1 − ( 3 y − 2 )
58. { x 2 − y 3 = − 7 x 3 − y 2 = − 8
59. { x 4 − y 2 = 3 4 x 3 + y 6 = 1 6
60. { 1 3 x − 2 3 y = 3 1 3 x − 1 2 y = 8 3
61. { − 1 10 x + 1 2 y = 4 5 1 7 x + 1 3 y = − 2 21
62. { y = − 5 3 x + 1 2 1 3 x + 1 5 y = 1 10
63. { − 1 7 x + y = − 2 3 − 1 14 x + 1 2 y = 1 3
64. { 1 15 x − 1 12 y = 1 3 − 3 10 x + 3 8 y = − 3 2
65. { x + y = 4,200 0.03 x + 0.0525 y = 193.5
66. { x + y = 350 0.2 x + 0.1 y = 52.5
67. { 0.2 x − 0.05 y = 0.43 0.3 x + 0.1 y = − 0.3
68. { 0.1 x + 0.3 y = 0.3 0.05 x − 0.5 y = − 0.63
69. { 0.15 x − 0.25 y = − 0.3 − 0.75 x + 1.25 y = − 4
70. { − 0.15 x + 1.25 y = 0.4 − 0.03 x + 0.25 y = 0.08
Part C: Discussion Board Topics
71. How do we choose the best method for solving a linear system?
72. What does it mean for a system to be dependent? How can we tell if a given system is dependent?
3: (−10, 5)
7: (1/5, −2)
9: ( x , 2 x + 4 )
11: (6, −1)
13: (−3, 3)
17: (−1, 4)
19: (3, −4)
21: (−1, 2/3)
25: (1/5, −2/5)
27: (−2, 1)
29: (−1, 10)
33: (−2, −16/3)
35: (−4, 6)
37: (2.5, 2.5)
39: The two numbers are 5 and 9.
41: The two numbers are 12 and −1.
45: (−1, 3)
49: (6, −4)
51: (3, −1)
53: (32, 0)
55: ( x , − 2 x + 6 )
57: (−4, 3)
59: (1, −1)
61: (−3, 1)
65: (1,200, 3,000)
67: (0.8, −5.4)

- HW Guidelines
- Study Skills Quiz
- Find Local Tutors
- Demo MathHelp.com
- Join MathHelp.com
Select a Course Below
- ACCUPLACER Math
- Math Placement Test
- PRAXIS Math
- + more tests
- 5th Grade Math
- 6th Grade Math
- Pre-Algebra
- College Pre-Algebra
- Introductory Algebra
- Intermediate Algebra
- College Algebra
Systems of Linear Equations: Solving by Addition / Elimination
Definitions Graphing Special Cases Substitution Elimination/Addition Gaussian Elimination More Examples
The "addition" method of solving systems of linear equations is also called the "elimination" method. Under either name, this method is similar to the method you probably used when you were first learning how to solve one-variable linear equations .
Suppose, back in the day, they'd given you the equation " x + 6 = 11 ". To solve this, you would probably have subtracted the six to the other side of the "equals" sign by putting a " −6 " under either side of the equation. Then you'd have drawn a horizontal line underneath (representing an "equals" line) and "added down" to get " x = 5 " as the solution.
Content Continues Below
MathHelp.com
Solving Systems by Addition
Your work would probably have looked something like this:
x + 6 = 11 −6 −6 x = 5
You'll do something very similar when you solve systems of linear equations using the addition method. I'll demonstrate with some examples.
- Solve the following system using addition.
2 x + y = 9 3 x − y = 16
Advertisement
When I was solving one-variable linear equations, back in the day, I would "cancel out" an unwanted number by adding its opposite. (In the example above, this would have been the −6 that was added in the second line, in order to cancel out the +6 .) Then I'd draw a horizontal "equals" line under what I'd added to both sides of the original equation, and I'd add down. This would get the variable by itself on one side of the "equals" sign.
I want to do something similar here. I know how to solve linear equations with one variable. Here I've got two. Can I get rid of one of these variables in the system, just as I'd have gotten rid of the −6 in the equation?
Looking at the system of equations they've given me, I see that I've got a + y in the first line, and a − y in the second line. If I added these, they'd cancel out, leaving me with just the variable x . In other words, if I add down, I should end up with a linear equation with just one variable, and I know how to solve those. So let's do that!
I write down the two equations, draw an "equals" bar under them, and add down:
2 x + y = 9 3 x − y = 16 5 x = 25
Now I have a one-variable linear equation that I already know how to solve. I divide through on both sides by 5 to get x = 5 . This is half of the solution to this system.
(By the way, this adding of the two equations, or two "rows", is called a "row operation".)
To find the other half (that is, to find the y -value), I can plug this x -value back into either one of the original equations, and simplify for the value of y . (This process — of taking a partial solution and plugging it back in to some portion of the original exercise to find the rest of the solution — is called "back-solving".)
I can use either of the original equations to back-solve and find the value of y . The first equation has smaller numbers (and I'm lazy), so I'll back-solve in that one:
2(5) + y = 9 10 + y = 9 y = −1
This gives me the other half of the solution, so my answer is:
( x , y ) = (5, −1)
In case you're wondering how I knew which was the "right" equation to use for the backsolving, I didn't. Because it doesn't matter. Solutions to systems are intersection points; intersection points will, by definition, be on both of the lines; so either equation will work just fine. You'll get the same answer either way.
Check it out: if I'd have used the other equation for the back-solving, here would be my working:
3(5) − y = 16 15 − y = 16 − y = 1 y = −1
...which is the same result as before.
x − 2 y = −9 x + 3 y = 16
Note that the x -terms would cancel out if only they'd had opposite signs. But I can create this opposite-sign cancellation by multiplying either one of the equations by −1 , and then adding down as usual. It doesn't matter which equation I choose, as long as I am careful to multiply the −1 through the entire equation. (That means both sides of the "equals" sign!)
I flipped a coin; I'll multiply the second equation.
(The " −1 R 2 " notation over the arrow in the above image indicates that I multiplied row 2 by −1 . This " R n " notation, indicating that you're doing something with the n -th row, is standard. And this multiplying of a row by a numerical value is another "row operation".)
By setting up the x -terms to cancel out when the equations are added together, I have eliminated that variable. Now I can solve the resulting one-variable equation " −5 y = −25 " to get y = 5 .
To find the corresponding value of x , I plug this y -value back into either of the original equations. Back-solving in the first equation, I get:
x − 2(5) = −9 x − 10 = −9 x = 1
This gives me the other coordinate of the solution point, so my answer is:
( x , y ) = (1, 5)
A very common temptation is to write the solution to a system of equations in the form "(first number I found, second number I found)". Sometimes, though, as in this case, you find the y -value first and then the x -value second, and of course in points the x -value comes first. So just be careful to write the coordinates for your solutions correctly.
2 x − y = 9 3 x + 4 y = −14
Nothing cancels here, but I can multiply to create a cancellation. (As long as I multiply both sides of the equation by the same value, I won't have changed anything in mathematical terms. But I may be able to change things in practical terms, to create a cancellation.) If I multiply the first equation by 4 , this will set up the y -terms to cancel.
Solving this, I get that x = 2 . I'll use the first equation for backsolving, because the coefficients are smaller (and I'm lazy).
2(2) − y = 9 4 − y = 9 − y = 5 y = −5
Now I have the two coordinates of the solution point:
( x , y ) = (2, −5)
4 x − 3 y = 25 −3 x + 8 y = 10
Hmm... As the system stands, nothing cancels. But I know that I can multiply to create a cancellation.
In this case, neither variable is an obvious choice for cancellation, so I'll consider the least common multiples of the coefficients. I can multiply the equations (by 3 and 4 , respectively) to convert the x -terms to 12 x 's, or I can multiply them (by 8 and 3 , respectively) to convert the y -terms to 24 y 's. Since I'm lazy and 12 is smaller than 24 , I'll multiply to cancel the x -terms.
(I would get the same answer in the end if I set up the y -terms to cancel. It's not that how I'm doing it is "the right way"; it was just my choice. You could make a different choice, and your choice would be just as correct as mine.)
I will multiply the first row by 3 and the second row by 4 ; then I'll add down and solve.
Solving, I get that y = 5 . Neither equation looks particularly better than the other for back-solving, so I'll flip a coin and use the first equation.
4 x − 3(5) = 25 4 x − 15 = 25 4 x = 40 x = 10
Remembering to put the x -coordinate first in the solution, I get:
( x , y ) = (10, 5)

Usually when you are solving "by addition", you will need to create the cancellation. Warning: The most common mistake is to forget to multiply all the way through the equation, multiplying on both sides of the "equals" sign. Be careful of this; always multiply through the entire equation.
- Solve the following using addition.
12 x − 13 y = 2 −6 x + 6.5 y = −2
I think I'll multiply the second equation by 2 ; this will at least get rid of the decimal place.
Oops! This result isn't true! Zero is never equal to −2 !
All of my steps were correct, but I ended up with garbage. This tells me that my original assumption (being that the system had a solution) must have been wrong. So this is an inconsistent system (that i s, one that graphs as two parallel lines) with no solution (that is, having no intersection point).
no solution: inconsistent system
12 x − 3 y = 6 4 x − y = 2
I think it'll be simplest to cancel off the y -terms, so I'll multiply the second row by −3 .
Well, yes, zero does equal zero, but...?
I already knew that zero equals zero. This information doesn't add anything to my store of knowledge. In particular, it doesn't help me narrow down my answer to one solution point. All my math was correct, so the issue lies elsewhere.
Then I remember: If the two equations are really the same one equation, then this "zero equals zero" result is the sort of thing I should expect. In fact, this result tells me that this system is a dependent system (that is, one that graphs as just one line) and, solving either of the original equations for " y = ", I find that the solution is the equation of the whole line, namely:
y = 4 x − 2
(Your text may format the answer as " ( s , 4 s − 2) ", or something like that.)
Remember the difference: a nonsense answer (like " 0 = −2 " in the exercise before the last one above) means that you have an inconsistent system with no solution; a useless-but-true answer (like " 0 = 0 " in the last exercise above) means that you have a dependent system where the set of all the points on the whole line is the solution.
Note: Some books use only " x " and " y " for their variables in systems of two equations, but many will also use additional variables. When you write the solution for an x , y -point, you know that the x -coordinate goes first and the y -coordinate goes second. When you are dealing with other variables, assume (unless explicitly told otherwise) that those variables, when used as coordinates of a point, are written in alphabetical order. For instance, if the variables in a given system are a and b , the solution point would be ( a , b ) ; it would not be ( b , a ) . Remember: Unless otherwise specified, the variables are always written in alphabetical order.
URL: https://www.purplemath.com/modules/systlin5.htm
You can use the Mathway widget below to practice solving systems of equations by addition/elimination (or skip the widget and proceed to the next page ). Try the entered exercise, or type in your own exercise. Then click on the arrow and select "Solve by Addition/Elimination" from the menu to compare your answer to Mathway's.
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
Page 1 Page 2 Page 3 Page 4 Page 5 Page 6 Page 7
Standardized Test Prep
College math, homeschool math, share this page.
- Terms of Use
- Privacy / Cookies
- About Purplemath
- About the Author
- Tutoring from PM
- Advertising
- Linking to PM
- Site licencing
Visit Our Profiles
A free service from Mattecentrum
The elimination method for solving linear systems
- Solve the system IV
- Solve the system V
Another way of solving a linear system is to use the elimination method. In the elimination method you either add or subtract the equations to get an equation in one variable.
When the coefficients of one variable are opposites you add the equations to eliminate a variable and when the coefficients of one variable are equal you subtract the equations to eliminate a variable.
\begin{cases} 3y+2x=6\\ 5y-2x=10 \end{cases}
We can eliminate the \(x\)-variable by addition of the two equations.
\begin{cases} 3y+2x=6 \\ \underline{+\: 5y-2x=10} \end{cases}
$$=8y\: \: \: \: \; \; \; \; =16$$
$$\begin{matrix} \: \: \: y\: \: \: \: \: \; \; \; \; \; =2 \end{matrix}$$
The value of \(y\) can now be substituted into either of the original equations to find the value of \(x\)
$$3y+2x=6$$
$$3\cdot {\color{green} 2}+2x=6$$
The solution of the linear system is \((0, 2)\).
To avoid errors make sure that all like terms and equal signs are in the same columns before beginning the elimination.
If you don't have equations where you can eliminate a variable by addition or subtraction you directly you can begin by multiplying one or both of the equations with a constant to obtain an equivalent linear system where you can eliminate one of the variables by addition or subtraction.
\begin{cases} 3x+y=9\\ 5x+4y=22 \end{cases}
Begin by multiplying the first equation by \(-4\) so that the coefficients of \(y\) are opposites
\begin{cases} \color{green}{-4} \cdot (3x + y) = \color{green}{-4} \cdot 9\\ 5x + 4y = 22 \end{cases}
$$\Rightarrow$$
\begin{cases}-12x-4y=-36 \\ \underline{+5x+4y=22 }\end{cases}
$$=-7x\: \: \: \: \: \: \: \: \: \: =-14$$
$$\begin{matrix} \: \:\; \:\: x\: \: \: \: \: \: \: \: \: \: \:=2 \end{matrix}$$
Substitute \(x\) in either of the original equations to get the value of \(y\)
$$3\cdot {\color{green} 2}+y=9$$
The solution of the linear system is \((2, 3)\)
Video lesson
Solve the following linear system using the elimination method
\begin{cases} 2y - 4x = 2 \\ y = -x + 4 \end{cases}
- Properties of exponents
- Scientific notation
- Exponential growth functions
- Monomials and polynomials
- Special products of polynomials
- Polynomial equations in factored form
- Use graphing to solve quadratic equations
- Completing the square
- The quadratic formula
- The graph of a radical function
- Simplify radical expressions
- Radical equations
- The Pythagorean Theorem
- The distance and midpoint formulas
- Simplify rational expression
- Multiply rational expressions
- Division of polynomials
- Add and subtract rational expressions
- Solving rational equations
- Algebra 2 Overview
- Geometry Overview
- SAT Overview
- ACT Overview
- Anatomy & Physiology
- Astrophysics
- Earth Science
- Environmental Science
- Organic Chemistry
- Precalculus
- Trigonometry
- English Grammar
- U.S. History
- World History
... and beyond
- Socratic Meta
- Featured Answers

How do you solve by elimination with fractions?

Elimination Calculator
gives you step-by-step help on solving systems by elimination.
What do you want to calculate?
- Solve for Variable
- Practice Mode
- Step-By-Step
Example (Click to try)
- Enter your equations separated by a comma in the box, and press Calculate!
- Or click the example.
About Elimination
Need more problem types? Try MathPapa Algebra Calculator
Clear Elimination Calculator »

COMMENTS
When a system includes an equation with fractions as coefficients: Step 1. Eliminate the fractions by multiplying each side of the equation by a common denominator. Step 2: Solve the resulting system using the addition method, elimination method, or the substitution method. The following diagrams show how to solve systems of equations using the ...
How to solve a linear system with two equations and two unknowns with fractions.Notes on solving linear systems of two equations and two unknowns using the e...
Example 4.3.1. Solve by elimination: { 2x + y = 7 3x − 2y = − 7. Solution: Step 1: Multiply one, or both, of the equations to set up the elimination of one of the variables. In this example, we will eliminate the variable y by multiplying both sides of the first equation by 2. Take care to distribute.
Example 1. We're asked to solve this system of equations: 2 y + 7 x = − 5 5 y − 7 x = 12. We notice that the first equation has a 7 x term and the second equation has a − 7 x term. These terms will cancel if we add the equations together—that is, we'll eliminate the x terms: 2 y + 7 x = − 5 + 5 y − 7 x = 12 7 y + 0 = 7. Solving for ...
👉Learn how to solve a system (of equations) by elimination. A system of equations is a set of equations which are collectively satisfied by one solution of ...
2.5 Solve Equations with Fractions or Decimals; 2.6 Solve a Formula for a Specific Variable; ... The third method of solving systems of linear equations is called the Elimination Method. When we solved a system by substitution, we started with two equations and two variables and reduced it to one equation with one variable. ... Now we'll see ...
Substitution works well when we can easily solve one equation for one of the variables and not have too many fractions in the resulting expression. The third method of solving systems of linear equations is called the Elimination Method. When we solved a system by substitution, we started with two equations and two variables and reduced it to ...
Elimination method review (systems of linear equations) Equivalent systems of equations review. Math > Algebra ... Let's explore a few more methods for solving systems of equations. Let's say I have the equation, 3x plus 4y is equal to 2.5. ... We're going to stay in the fraction world. So this is going to be 21 over 2 plus 4y is equal to 5/2 ...
Section 5.3 Solving Systems of Linear Equations by Elimination 213 EXAMPLE 2 Solving a System of Linear Equations by Elimination Solve the system by elimination. −6x + 5y = 25 Equation 1 −2x − 4y = 14 Equation 2 Step 1: Notice that no pairs of like terms have the same or opposite coeffi cients. One way to solve by elimination is to multiply Equation 2 by 3 so that the x-terms have a ...
Solving Linear Systems Playlist on YouTube. Solve the system using the elimination method: Step 1: Multiply one or both of the equations by factors that will line up one variable to eliminate. Step 2: Add the equations together. Step 3: Back substitute and present the answer as an ordered pair. Tip: If you multiply an equation by any number ...
How to solve a system of equations by elimination. Write both equations in standard form. If any coefficients are fractions, clear them. Make the coefficients of one variable opposites. Decide which variable you will eliminate. Multiply one or both equations so that the coefficients of that variable are opposites.
What is the Elimination Method? It is one way to solve a system of equations.. The basic idea is if you have 2 equations, you can sometimes do a single operation and then add the 2 equations in a way that eleiminates 1 of the 2 variables as the example that follows shows.
Elimination Method. Elimination Method (Systems of Linear Equations) The main concept behind the elimination methodis to create terms with opposite coefficientsbecause they cancel each other when added. In the end, we should deal with a simple linear equation to solve, like a one-step equation in [latex]x[/latex] or in [latex]y[/latex].
Example 2: Solve the system using elimination. Solution: Look at the x - coefficients. Multiply the first equation by -4, to set up the x-coefficients to cancel. Now we can find: Take the value for y and substitute it back into either one of the original equations. The solution is . Example 3: Solve the system using elimination method.
Hence the solution to the system is (3, 2). This process describes the elimination (or addition) method A means of solving a system by adding equivalent equations in such a way as to eliminate a variable. for solving linear systems. Of course, the variable is not always so easily eliminated. Typically, we have to find an equivalent system by applying the multiplication property of equality to ...
Infinite number of solutions. 23) −14 =. 24) (2, 0) (−1, 1) Create your own worksheets like this one with Infinite Algebra 1. Free trial available at KutaSoftware.com. ©q R2h041222 cK7uitqaL ASPovfPthwEanrQed vLOLrCy.6 w AAVlXl9 wrxivgghCtUsC xrmeAsfeGrivpe9du.Q Q iMwaHdMeB GwSijtZht xIrnOfNiRnFiotLeH 1AAlSgheWb4r0aG X1K.J.
If there was a number in front of the y I would need to divide and that would cause fractions. So I will take the equation 3x - y =11 and solve for y. You will get y = 3x - 11. Now we need to substitute this into the other equation for y: − 2 x + 5 (3 x − 11 ) = − 16 Now solve for x. 2 x + 15 x −. 13 x − 55 = −.
The "addition" method of solving systems of linear equations is also called the "elimination" method. Under either name, this method is similar to the method you probably used when you were first learning how to solve one-variable linear equations. Suppose, back in the day, they'd given you the equation " x + 6 = 11 ".
Another way of solving a linear system is to use the elimination method. In the elimination method you either add or subtract the equations to get an equation in one variable. ... Solve the following linear system using the elimination method \begin{cases} 2y - 4x = 2 \\ y = -x + 4 \end{cases} Do excercises Show all 2 exercises. Solve the system IV
A good start would be to multiply each equation by the least common multiple (LCM) of the denominator. If you multiply all parts of the equation by the LCM, it does not affect the solution. This would eliminate the fractions and you could go forth and solve the system by elimination. Here is an example: #-1/10x + 1/2y = 4/5# #1/7x + 1/3y = -2/21#
About Elimination. Use elimination when you are solving a system of equations and you can quickly eliminate one variable by adding or subtracting your equations together. You can use this Elimination Calculator to practice solving systems. Need more problem types?