lesson 3 4 direct variation practice and problem solving a/b

Direct Variation Lesson

• Demonstrate an understanding of linear equations in two variables
• Learn how to solve a direct variation problem
• Learn how to solve a direct variation as a power problem
• Learn how to solve a word problem that involves direct variation

How to Solve a Direct Variation Problem

Solving a direct variation problem.

• Write the variation equation: y = kx or k = y/x
• Substitute in for the given values and find the value of k
• Rewrite the variation equation: y = kx with the known value of k
• Substitute the remaining values and find the unknown

Study Guides > College Algebra CoRequisite Course

Direct variation, learning outcomes.

• Solve a direct variation problem
• Use a constant of variation to describe the relationship between two variables

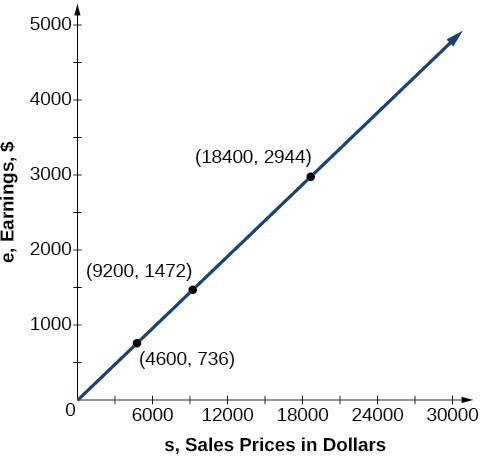
A General Note: Direct Variation

[latex]y=k{x}^{n}[/latex] then we say that the relationship is direct variation and [latex]y[/latex]  varies directly with the [latex]n[/latex]th power of [latex]x[/latex]. In direct variation relationships, there is a nonzero constant ratio [latex]k=\dfrac{y}{{x}^{n}}[/latex], where [latex]k[/latex] is called the constant of variation , which help defines the relationship between the variables.

recall isolating a variable in a formula

How to: given a description of a direct variation problem, solve for an unknown..

• Identify the input, [latex]x[/latex], and the output, [latex]y[/latex].
• Determine the constant of variation. You may need to divide [latex]y[/latex] by the specified power of [latex]x[/latex] to determine the constant of variation.
• Use the constant of variation to write an equation for the relationship.
• Substitute known values into the equation to find the unknown.

Example: Solving a Direct Variation Problem

[latex]\begin{align} k&=\dfrac{y}{{x}^{3}} \\[1mm] &=\dfrac{25}{{2}^{3}}\\[1mm] &=\dfrac{25}{8}\end{align}[/latex] Now use the constant to write an equation that represents this relationship.

[latex]y=\dfrac{25}{8}{x}^{3}[/latex] Substitute [latex]x=6[/latex] and solve for [latex]y[/latex].

Analysis of the Solution

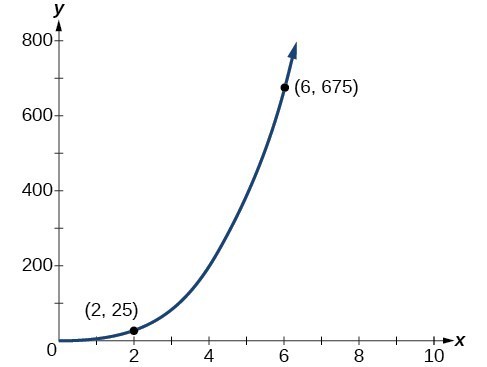
Answer: [latex-display]\dfrac{128}{3}[/latex-display]

Licenses & Attributions

Cc licensed content, original.

• Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution .

CC licensed content, Shared previously

• Question ID 91391. Authored by: Jenck, Michael. License: CC BY: Attribution . License terms: IMathAS Community License CC-BY + GPL.
• College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution . License terms: Download for free at http://cnx.org/contents/ [email protected] .
• Direct Variation Applications . Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution .

Please add a message.

Message received. Thanks for the feedback.

Direct Variation: Definition, Formula, Equation, Examples, FAQs

What is direct variation in math, what is a direct variation equation (direct variation formula), difference between direct variation and inverse variation, solved examples of direct variation, practice problems on direct variation, frequently asked questions about direct variation.

Direct variation is a type of proportionality in which one quantity directly varies with respect to a change in another quantity, by the same factor. 

This means that an increase in one quantity results in a proportionate increase in the other quantity. Similarly, a decrease in one quantity results in a proportionate decrease in the other quantity. There will be a proportionate increase or decrease.

Note that the ratio between two quantities that are in direct proportion or direct variation always remains the same. 

In direct variation, the variable that represents the cause of the relationship is called the independent variable, generally denoted by x. The other variable depends on the value of the independent variable; it is called the dependent variable, generally denoted by y. 

( Note: It’s important to note that the roles of independent and dependent variables vary depending on the specific context and the relationship between the defined variables. It is always better to first understand the relationship between two quantities in comparison.)

Direct variation real-life example:

Suppose you are working on an hourly pay basis. In this case, the number of hours you work is directly proportional to your earnings. The more you work, the more you earn. You can earn double by working twice as many hours.  

Here, $x =$ Number of hours you work and $y =$ The amount of money you earn

Direct Variation Definition

Direct variation or direct proportionality is a mathematical relationship between two variables where one variable varies in direct proportion with respect to the other variable.

Direct Variation Symbol

Suppose that a variable y is directly proportional to x. In other words, y varies directly as x.

We can write this mathematically as

$y \propto x$

Symbol “$\propto$” stands for “is proportional to.”

The relationship between two variables x and y, which are in direct variation, can be represented by an equation

$k = \frac{y}{x}$ is the constant of variation representing the constant ratio between the two variables.

Here, k is a non-zero real constant. The value of k can be both positive or negative.

The above equation can be decoded as “y varies directly with x” or “y varies directly as x.” The equation can be used to derive different formulas according to the requirements of a solution. 

Different forms of the direct variation formula are as follows:

• To solve for the constant of variation, k, we can shuffle the formula.

$k = \frac{y}{x}$ and $x \neq 0$

• To solve for one of the variables (x or y), we can shuffle the formula.

$x = \frac{y}{k}$

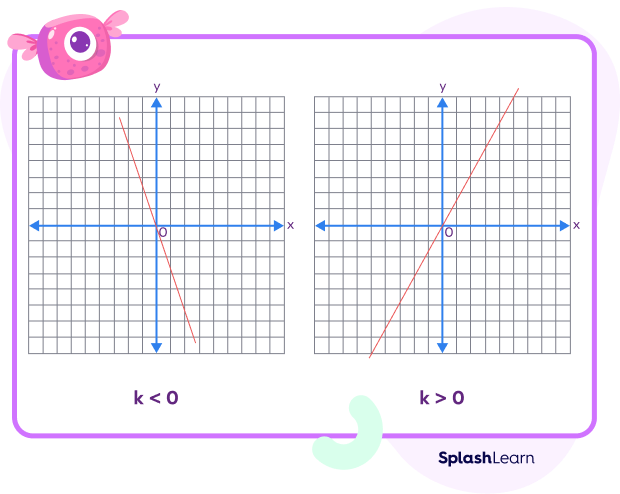
Direct Variation on a Graph

Note that the graph of the direct variation linear equation $y = kx$ is a straight line passing through the origin.

• If k is positive, then the line will rise from left to right, passing through the origin.
• If k is negative, then the line will fall from left to right, passing through the origin.

The slope of the line represents the constant of variation in a direct variation. It indicates how much the dependent variable changes for each unit increase in the independent variable.

So, to understand how to graph direct variation, we will identify the plot points satisfying the equation $y = kx$.

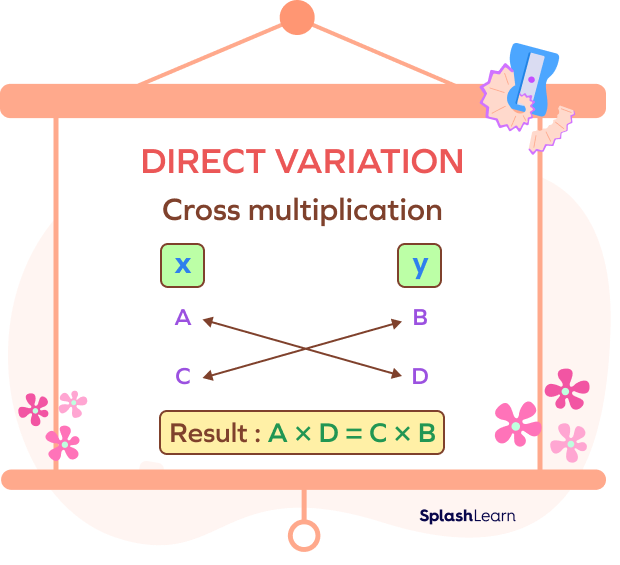
Cross Multiplication Method to Solve Direct Variation Problems

We can easily solve direct variation problems using the cross multiplication method. Consider two variables, x and y, in direct variation. 

Let y = B for x = A.

Let y = D for x = C.

Since x and y are in direct variation, we can write the proportion as

$\frac{A}{B} = \frac{C}{D}$ 

By cross multiplication, we get

Thus, $A \times D = B \times C$

We can find any missing value using this method.

In a direct variation, the variables change in proportion to each other, while in an inverse variation, the variables change in inverse proportion to each other.

See this comparison table that shows the difference between Direct and Inverse variations:

Facts on Direct Variation

• The constant of variation (k) is the fixed ratio that does not change even if the values of x and y change.
• The graph line passes through the origin (0,0) because the direct variation equation always includes the term y = 0 when x = 0.
• The constant of variation (k) gets bigger with a rise in the steepness of the slope of the line.
• A horizontal graph line indicates that the variable y is constant and does not change with x; hence, it does not have direct variation.
• A vertical graph line indicates that the variable x is constant and does not change with y; hence, it does not have direct variation.

Okay, so we now have a clear idea of the concepts relating to direct variation, including direct variation function, definition, graph, differences, and much more. Let us now look at some examples and practice problems to boost our understanding of the concept.

1. The cost of printing 100 pages is $50. What will be the cost of printing 150 pages?

Cost $\propto$ Number of pages

Cost $= k \times$ Number of pages

$k = \frac{y}{x} = \frac{cost}{Number \;of \;pages}$

$k = \frac{50}{100} = 0.5$

Now, the cost of 150 pages can be calculated by a direct variation equation.

Cost $= 0.5 \times $Number of pages

Cost $= 0.5 \times 150$

Cost $= 75$

Therefore, $\$75$ is the cost of printing 150 pages.

Another method:

$\$50 \times 150 = 100 \times$ ?

?$ = \frac{\$7500}{100}$

2. If the number and cost of notebooks have a direct variation, what will be the cost of 15 notebooks if 5 notebooks cost $\$10$ ?

As the cost varies directly with the number of notebooks, we can solve it by setting up the proportions.

5 notebooks cost $\$10$.

Let the cost of 15 notebooks to be x.

The proportion can be written as

$\frac{5}{10} = \frac{15}{x}$

Cross multiply.

$5 \times x = 10 \times 15$

Solve for x

Therefore, $\$30$ is the cost of 15 notebooks.

3. If a car covers 240 miles in 4 hours time. How many miles will it travel in 6 hours?

Solution:  

We know that the distance covered is directly proportional to the time taken. So, we can solve this question accordingly.

240 miles$\times 6 =$ ?$\times 4$ hours

?$= 360$ miles

Therefore, the car will cover 360 miles in 6 hours.

4. A company produces 100 units of a product per day. How many units will it produce in 5 days?

The number of units produced are directly proportional to the number of days.

Suppose that the company produces y units in 5 days.

$y = 100 \times 5$

Therefore, 500 units can be produced in 5 days.

5. Find the constant of direct variation where the cost of 4 dozen oranges is $\$24$ . Also, find the cost of 8 dozen oranges.

Assume the cost of 8 dozen oranges to be y. 

As we can see that the cost of oranges varies directly with the number of dozens. So, we can set up a proportion as

$\frac{4}{24} = 8y$

Isolate y on one side by cross-multiplying both sides

$4y = 24 \times 8$

Simplify it

Therefore, 8 dozen oranges will cost $48.

Now, let us find the constant of direct variation by using the equation y = kx

where 

y = the cost,

x = the number of dozens, and

k = the constant of variation

$k = \frac{1}{6}$

Therefore, $\frac{1}{6}$ or 0.1667 (approx) is the constant of direct variation.

Attend this quiz & Test your knowledge.

What will be the cost of 10 donuts if 4 donuts cost $\$2$?

If it takes 2 hours to mow a 1 acre lawn, how many hours will it take to mow a lawn that is $\frac{1}{4}$ an acre, if a car can go 30 miles with one gallon of gas, then how far can it go with 6 gallons of gas, 5 pounds of apples cost $\$10$. what will be the cost of 8.5 pounds of apples, which equation represents a direct variation.

Are the terms direct variation and direct proportion the same?

Yes, the terms direct variation and direct proportion are used interchangeably, but mean the same thing.

How can you identify direct variation?

In direct variation, the ratio of two quantities is always constant. As one variable increases, the other variable also increases. Also, if one variable decreases, the other variable also decreases.

Can the constant of proportionality be negative?

Yes, it can be positive or negative. It can never be 0. When we study the positive rate of change, we only consider positive values of k.

Are direct variations always linear?

We mostly study direct variations that are linear, but they do not have to be linear. We can say that linear equations are a specific type of direct variation, but not all direct variations follow a linear relationship. In direct variation, the ratio between the two variables remains constant, regardless of the type of relationship they exhibit.

RELATED POSTS

• Difference between Square and Rectangle – Definition, Examples, FAQs
• Onto Function: Definition, Formula, Properties, Graph, Examples
• Octagon Formula For Area and Perimeter With Derivation
• Area of Triangle in Determinant Form – Definition, Examples
• Convert MM to Inches Formula – Examples, FAQs, How to Convert

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.8e: Exercises - Variation

• Last updated
• Save as PDF
• Page ID 59374

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

A:  Translate Words into a Formula

Exercise \(\PageIndex{A}\) 

\( \bigstar\)  Translate each of the following sentences into a mathematical formula.

1. The distance \(D\) an automobile can travel is directly proportional to the time \(t\) that it travels at a constant speed.

2. The extension of a hanging spring \(d\) is directly proportional to the weight \(w\) attached to it.

3. An automobile’s braking distance \(d\) is directly proportional to the square of the automobile’s speed \(v\).

4. The volume \(V\) of a sphere varies directly as the cube of its radius \(r\).

5. The volume \(V\) of a given mass of gas is inversely proportional to the pressure \(p\) exerted on it.

6. Every particle of matter in the universe attracts every other particle with a force \(F\) that is directly proportional to the product of the masses \(m_{1}\) and \(m_{2}\) of the particles, and it is inversely proportional to the square of the distance d between them.

7. Simple interest \(I\) is jointly proportional to the annual interest rate \(r\) and the time \(t\) in years a fixed amount of money is invested.

8. The time \(t\) it takes an object to fall is directly proportional to the square root of the distance \(d\) it falls.

B:  Translate Words and Find a Formula

Exercise \(\PageIndex{B}\) 

\( \bigstar\)   Construct a mathematical model given the following:

9. \(y\) varies directly as \(x\), and \(y=30\) when \(x=6\).

10. \(y\) varies directly as \(x\), and \(y=52\) when \(x=4\).

11. \(y\) is directly proportional to \(x\), and \(y=12\) when \(x=3\).

12. \(y\) is directly proportional to \(x\), and \(y=120\) when \(x=20\).

13. \(y\) is directly proportional to \(x\), and \(y=3\) when \(x=9\).

14. \(y\) is directly proportional to \(x\), and \(y=21\) when \(x=3\).

15. \(y\) varies inversely as \(x\), and \(y=2\) when \(x=\frac{1}{8}\).

16. \(y\) varies inversely as \(x\), and \(y=\frac{3}{2}\) when \(x=\frac{1}{9}\).

17. \(y\) is jointly proportional to \(x\) and \(z\), where \(y=2\) when \(x=1\) and \(z=3\).

18. \(y\) is jointly proportional to \(x\) and \(z\), where \(y=15\) when \(x=3\) and \(z=7\).

19. \(y\) varies jointly as \(x\) and \(z\), where \(y=\frac{2}{3}\) when \(x=\frac{1}{2}\) and \(z=12\).

20. \(y\) varies jointly as \(x\) and \(z\), where \(y=5\) when \(x=\frac{3}{2}\) and \(z=\frac{2}{9}\).

21. \(y\) varies directly as the square of \(x\), where \(y=45\) when \(x=3\).

22. \(y\) varies directly as the square of \(x\), where \(y=3\) when \(x=\frac{1}{2}\).

23. \(y\) is inversely proportional to the square of \(x\), where \(y=27\) when \(x=\frac{1}{3}\).

24. \(y\) is inversely proportional to the square of \(x\), where \(y=9\) when \(x=\frac{2}{3}\).

25. \(y\) varies jointly as \(x\) and the square of \(z\), where \(y=6\) when \(x=\frac{1}{4}\) and \(z=\frac{2}{3}\).

26. \(y\) varies jointly as \(x\) and \(z\) and inversely as the square of \(w\), where \(y=5\) when \(z=1, z=3\), and \(w=\frac{1}{2}\).

27. \(y\) varies directly as the square root of \(x\) and inversely as the square of \(z\), where \(y=15\) when \(x=25\) and \(z=2\).

28. \(y\) varies directly as the square of \(x\) and inversely as \(z\) and the square root of \(w\), where \(y=14\) when \(x=4, w=9\) and \(z=2\).

C:  Direct variation problems

Exercise \(\PageIndex{C}\): Direct variation problems

\( \bigstar\)   Solve applications involving variation.

29. Revenue in dollars is directly proportional to the number of branded sweatshirts sold. The revenue earned from selling \(25\) sweatshirts is \($318.75\). Determine the revenue if \(30\) sweatshirts are sold.

30. The sales tax on the purchase of a new car varies directly as the price of the car. If an \($18,000\) new car is purchased, then the sales tax is \($1,350\). How much sales tax is charged if the new car is priced at \($22,000\)?

31. The price of a share of common stock in a company is directly proportional to the earnings per share (EPS) of the previous \(12\) months. If the price of a share of common stock in a company is $22.55, and the EPS is published to be \($1.10\), determine the value of the stock if the EPS increases by \($0.20\).

32. The distance traveled on a road trip varies directly with the time spent on the road. If a \(126\)-mile trip can be made in \(3\) hours, then what distance can be traveled in \(4\) hours?

33. The circumference of a circle is directly proportional to its radius. The circumference of a circle with radius \(7\) centimeters is measured as \(14π\) centimeters. What is the constant of proportionality?

34. The area of circle varies directly as the square of its radius. The area of a circle with radius \(7\) centimeters is determined to be \(49π\) square centimeters. What is the constant of proportionality?

35. The surface area of a sphere varies directly as the square of its radius. When the radius of a sphere measures \(2\) meters, the surface area measures \(16π\) square meters. Find the surface area of a sphere with radius \(3\) meters.

36. The volume of a sphere varies directly as the cube of its radius. When the radius of a sphere measures \(3\) meters, the volume is \(36π\) cubic meters. Find the volume of a sphere with radius \(1\) meter.

37. With a fixed height, the volume of a cone is directly proportional to the square of the radius at the base. When the radius at the base measures \(10\) centimeters, the volume is \(200\) cubic centimeters. Determine the volume of the cone if the radius of the base is halved.

38. The distance \(d\) an object in free fall drops varies directly with the square of the time \(t\) that it has been falling. If an object in free fall drops \(36\) feet in \(1.5\) seconds, then how far will it have fallen in \(3\) seconds?

39. A hanging spring is stretched \(5\) inches when a \(20\)-pound weight is attached to it. Determine its spring constant.

40. A hanging spring is stretched \(3\) centimeters when a \(2\)-kilogram weight is attached to it. Determine the spring constant.

41. If a hanging spring is stretched \(3\) inches when a \(2\)-pound weight is attached, how far will it stretch with a \(5\)-pound weight attached?

42. If a hanging spring is stretched \(6\) centimeters when a \(4\)-kilogram weight is attached to it, how far will it stretch with a \(2\)-kilogram weight attached?

\( \bigstar\)  The braking distance of an automobile is directly proportional to the square of its speed.

43. It takes \(36\) feet to stop a particular automobile moving at a speed of \(30\) miles per hour. How much breaking distance is required if the speed is \(35\) miles per hour?

44. After an accident, it was determined that it took a driver \(80\) feet to stop his car. In an experiment under similar conditions, it takes \(45\) feet to stop the car moving at a speed of \(30\) miles per hour. Estimate how fast the driver was moving before the accident.

45. The period \(T\) of a pendulum is directly proportional to the square root of its length \(L\). If the length of a pendulum is \(1\) meter, then the period is approximately \(2\) seconds. Approximate the period of a pendulum that is \(0.5\) meter in length.

46. The time \(t\) it takes an object to fall is directly proportional to the square root of the distance \(d\) it falls. An object dropped from \(4\) feet will take \(\frac{1}{2}\) second to hit the ground. How long will it take an object dropped from \(16\) feet to hit the ground?

D:  Inverse Variation Problems

Exercise \(\PageIndex{D}\)

47. To balance a seesaw, the distance from the fulcrum that a person must sit is inversely proportional to his weight. If a \(72\)-pound boy is sitting \(3\) feet from the fulcrum, how far from the fulcrum must a \(54\)-pound boy sit to balance the seesaw?

48. The current \(I\) in an electrical conductor is inversely proportional to its resistance \(R\). If the current is \(\frac{1}{4}\) ampere when the resistance is \(100\) ohms, what is the current when the resistance is \(150\) ohms?

49. The amount of illumination \(I\) is inversely proportional to the square of the distance \(d\) from a light source. If \(70\) foot-candles of illumination is measured \(2\) feet away from a lamp, what level of illumination might we expect \(\frac{1}{2}\) foot away from the lamp?

50. The amount of illumination \(I\) is inversely proportional to the square of the distance \(d\) from a light source. If \(40\) foot-candles of illumination is measured \(3\) feet away from a lamp, at what distance can we expect \(10\) foot-candles of illumination?

51. A balloon is filled to a volume of \(216\) cubic inches on a diving boat under \(1\) atmosphere of pressure. If the balloon is taken underwater approximately \(33\) feet, where the pressure measures \(2\) atmospheres, then what is the volume of the balloon?

52. A balloon is filled to \(216\) cubic inches under a pressure of \(3\) atmospheres at a depth of \(66\) feet. What would the volume be at the surface, where the pressure is \(1\) atmosphere?

E:  Joint and Combined Variation

Exercise \(\PageIndex{E}\) 

53.  The number of men, represented by \(y\), needed to lay a cobblestone driveway is directly proportional to the area \(A\) of the driveway and inversely proportional to the amount of time \(t\) allowed to complete the job. Typically, \(3\) men can lay \(1,200\) square feet of cobblestone in \(4\) hours. How many men will be required to lay \(2,400\) square feet of cobblestone in \(6\) hours?

54. The volume of a right circular cylinder varies jointly as the square of its radius and its height. A right circular cylinder with a \(3\)-centimeter radius and a height of \(4\) centimeters has a volume of \(36π\) cubic centimeters. Find a formula for the volume of a right circular cylinder in terms of its radius and height.

55. If two objects with masses \(50\) kilograms and \(100\) kilograms are \(\frac{1}{2}\) meter apart, then they produce approximately \(1.34 × 10^{−6}\) newtons (N) of force. Calculate the gravitational constant.

56. Use the gravitational constant from the previous exercise to write a formula that approximates the force \(F\) in newtons between two masses \(m_{1}\) and \(m_{2}\), expressed in kilograms, given the distance \(d\) between them in meters.

57. Calculate the force in newtons between Earth and the Moon, given that the mass of the Moon is approximately \(7.3 × 10^{22}\) kilograms, the mass of Earth is approximately \(6.0 × 10^{24}\) kilograms, and the distance between them is on average \(1.5 × 10^{11}\) meters.

58. Calculate the force in newtons between Earth and the Sun, given that the mass of the Sun is approximately \(2.0 × 10^{30}\) kilograms, the mass of Earth is approximately \(6.0 × 10^{24}\) kilograms, and the distance between them is on average \(3.85 × 10^{8}\) meters.

59. If \(y\) varies directly as the square of \(x\), then how does \(y\) change if \(x\) is doubled?

60. If \(y\) varies inversely as square of \(t\), then how does \(y\) change if \(t\) is doubled?

61. If \(y\) varies directly as the square of \(x\) and inversely as the square of \(t\), then how does \(y\) change if both \(x\) and \(t\) are doubled?

F: More Variation Problems

Exercise \(\PageIndex{F}\) 

\( \bigstar\)  Solve the following variation problems.

71. The number of calories, c , burned varies directly with the amount of time, t, spent exercising. Arnold burned 312 calories in 65 minutes exercising. How many calories would he burn if he exercises for 90 minutes?

72. The number of gallons of gas a car uses varies directly with the number of miles driven. Driving 469.8 miles used 14.5 gallons of gas.  How many gallons of gas would the car use if driven 1000 miles?

73. The weight of a liquid varies directly as its volume. A liquid that weighs 24 pounds has a volume of 4 gallons.  If a liquid has volume 13 gallons, what is its weight?

74. The maximum load a beam will support varies directly with the square of the diagonal of the beam’s cross-section. A beam with diagonal 4” will support a maximum load of 75 pounds.  What is the maximum load that can be supported by a beam with diagonal 8”?

75. The area of a circle varies directly as the square of the radius. A circular pizza with a radius of 6 inches has an area of 113.1 square inches.  What is the area of a pizza with a radius of 9 inches?

76. The fuel consumption (mpg) of a car varies inversely with its weight. A car that weighs 3100 pounds gets 26 mpg on the highway.  What would be the fuel consumption of a car that weighs 4030 pounds?

77. A car’s value varies inversely with its age. If a two-year-old car is worth $20,000, what will be the value of the car when it is 5 years old? 

78. The number of hours it takes for ice to melt varies inversely with the air temperature. Suppose a block of ice melts in 2 hours when the temperature is 65 degrees.  How many hours would it take for the same block of ice to melt if the temperature was 78 degrees?

79.  The force needed to break a board varies inversely with its length. Richard uses 24 pounds of pressure to break a 2-foot long board.  How many pounds of pressure is needed to break a 5-foot long board?

80. For people with roughly the same build, the weight of the person varies as the cube of their height. If a person 65 inches high weighs 125 pounds, how much would a person 75 inches high with a similar build be expected to weigh?

81. The fuel consumption (mpg) of a car varies inversely with its weight. A Ford Focus weighs 3000 pounds and gets 28.7 mpg on the highway. What would the fuel consumption be for a Ford Expedition that weighs 5,500 pounds? Round to the nearest tenth.

82. A person's BMI (body mass index) varies directly as their weight and inversely as the square of their height. Given a person who weighs 180 pounds and is 60 inches tall has a BMI of 35.2, what is the BMI for  someone who is 150 pounds and 68 inches tall?

83. The maximum load \(L\) that a cylindrical column with a circular cross section can hold varies directly as the fourth power of the diameter \(d\) and inversely as the square of the height \(h\). If an 8.0 m column that is 2.0 m in diameter will support 64 tons, how many tons can be supported by a column 12.0 m high and 3.0 m in diameter?

84. The heat loss per hour through a glass window varies directly  with the difference in temperature between the inside and outside temperatures and inversely as the thickness of the glass. A 0.3 cm thick window loses 2.4 BTU per hour when the outside temperature is 50 degrees Fahrenheit and the inside temperature is 70 degrees Fahrenheit. What will the heat loss be for a 1.5 cm thick window when the outside temperature is 30 degrees Fahrenheit and the inside temperature is 70 degrees Fahrenheit?

85. The heat loss of a glass window varies jointly as the window's area and the difference between the outside and inside temperatures. A window 3 feet wide by 6 feet long loses 1200 Btu per hour when the temperature outside is 20 degrees colder than the temperature inside. Find the heat loss through a glass window that is 6 feet wide by 9 feet long when the temperature outside is 10 degrees colder that the temperature inside.

86. Sound intensity varies inversely as the square root of the distance from the sound source. If you are in a movie theater and you change your seat to one that is twice as far from the speakers, how does the new sound intensity compare to that of your original seat?

87. The number of hours \(h\) that it takes \(p\) people to assemble \(m\) machines varies directly as the number of machines and inversely as the number of people. If four people can assemble 12 machines in four hours, how many people are needed to assemble 36 machines in eight hours?

88. The amount of time  t  needed to build a wall varies directly as the number of bricks  b need and inversely as the number of workers  w.  If it takes 18 hours for six workers to make a wall composed of 2400 bricks, how long would it take to build a wall of 4500 bricks with  10 workers? 

Chapter 9, Lesson 5: Direct Variation

• Extra Examples
• Personal Tutor
• Self-Check Quizzes

The resource you requested requires you to enter a username and password below:

Please read our Terms of Use and Privacy Notice before you explore our Web site. To report a technical problem with this Web site, please contact the site producer .

Personal Math Trainer

Exit Ticket

Module Quiz 3: B (PDF)

Module Quiz 3: D (PDF)

Unit Test 2: A (PDF)

Unit Test 2: B (PDF)

Unit Test 2: C (PDF)

Unit Test 2: D (PDF)

●      In a direct variation, the ratio between the variables stays constant. Does the ratio between y and x remain constant for this table?

●      In the equation for this relationship, y = kx, what is the value of k? -1.5

●      Write the equation. y = -1.5x

●      In which quadrant will the graph of this equation be? IV

Challenge Worksheet

Chapter 4, Lesson 2: Slope and Direct Variation

• Extra Examples
• Personal Tutor
• Self-Check Quizzes

The resource you requested requires you to enter a username and password below:

Please read our Terms of Use and Privacy Notice before you explore our Web site. To report a technical problem with this Web site, please contact the site producer .