linear equation problems with solution

Linear Equations Word Problems Worksheet with Solutions

The first equation family that many students learn about is linear equations. Linear equations have many applications in the real-world, which can make for a really great set of word problems! 

As a student studying algebra, you will encounter many linear equations word problems. That’s why I have put together this linear equations word problems worksheet with solutions!

My hope is that this linear equation word problems worksheet and answer key help you deepen your understanding of linear equations and linear systems!

What Are Linear Equations?

A linear equation is an  algebraic equation  where the highest power on the variable is one. When graphed, a linear equation will produce a straight line.

There are a few ways that we can write linear equations, with two of the most common being slope-intercept form and standard form .

Slope-intercept form is best way to identify the slope of the line and the y-intercept of the line. In general, the equation of a line in slope-intercept form is written as:

In this form,  a  represents the slope of the line and  b  represents the y-intercept of the line.

Equations of lines in standard form are easy to recognize because it is a uniformly recognized form of a line. Standard form allows for easy comparison of coefficients. When two linear equations are in standard form, you can quickly compare the coefficients of x and y.

In general, the standard form of a line is written as:

$$Ax+By=C$$

Note that A and B do not represent the slope of the line or the y-intercept in this form. Instead, A and B are simply constants.

Solving Linear Equations

Any set of word problems relating to linear equations will ask you to solve an equation of some sort. However, there are many different types of solving equations problems that you will encounter as you explore linear equations word problems.

Let’s take a look at a few different types to make sure you know what to expect when you check out the linear equation word problems worksheet with solutions below.

Solving Two-Step Equations and Multi-Step Equations

One of the simplest equation problems that you can solve is a two-step equation. A two-step equation requires you to perform just two steps in order to determine the unique solution to the linear equation.

The first step is to identify the side of the equation with the unknown variable. Your goal will be to isolate this variable (or get it by itself). Consider the following example:

In this example, the variable is on the right-hand side of the equation. To isolate x, we “undo” the operations on the right-hand side of the equation using inverse operations. This just means doing whatever the opposite operation is.

We can apply  order of operations  in reverse to start with the subtraction and then deal with the multiplication. Adding 5 to both sides and then dividing by 2 will result in:

$$\begin{split} 9+5&=2x-5+5 \\ \\ 14 &= 2x \\ \\ \frac{14}{2} &= \frac{2x}{2} \\ \\ 7 &= x \end{split} $$

This shows that the value of the unknown variable here is x = 7. This is a unique solution that will satisfy the equation.

If you want to learn more about finding the solution of linear equations and explore multi-step equations that use the distributive property, check out  these equation solving worksheets !

Systems of Linear Equations

Systems of linear equations are another type of problem that you will see on the linear equations word problems worksheet linked below. A system of linear equations involves two (or more!) linear equations that intersect in some way. 

There are a few different ways that linear equations can intersect :

• Once  at a single point of intersection
• Never  as a result of the lines being parallel 
• Always  as a result of the lines being on top of one another

When solving a system of linear equations, your goal is to determine both unknown variables. If the lines intersect, the solution to the system will be the point of intersection for the lines.

When given a linear equation, we can find the point of intersection between it and a second equation using a few different methods. I made a  video on the substitution method  and a  video on the elimination method  to help you understand these strategies for solving systems before you apply them to word problems involving systems of equations.

What Are Linear Equation Word Problems?

A linear equation word problem involves a real-world situation or scenario that can be solved by setting up and solving linear equations. The equations that are used model the relationships between different quantities in the real-world scenario. 

The topics of these problems vary, ranging from applications in science and physics (ie. calculate the speed of the boat) to business applications (ie. how many sales are required to break even?). The problems that you encounter will also vary in depth and difficulty. 

In my teaching experience, students tend to struggle with word problems because it isn’t always immediately clear what is being asked.  I have seen many students feel very confident in their equation solving skills, yet they still struggle when it comes to solving linear equation word problems.

One reason for this is that you aren’t always given equations from the start while solving word problems.

Tips for Solving Linear Equation Word Problems

During my time as a high school math teacher, I have come across a few tips that I think will help you solve linear equation word problems successfully.

To begin, the first step should always be to define two variables. Read the question carefully and think about the quantities involved. Use variables to represent these quantities.

The second step should be writing an equation that models the scenario. Depending on the problem, you may need to write a second equation as well.

Lastly, think about what the problem is asking you to find. 

For example, are you looking for the values of two unknown variables? If so, you are likely going to be setting up and solving a system of linear equations.

​If you are being asked for the value of a single variable, the chances are you will be solving a single linear equation.

Now that you have a basic understanding of the concepts involved in solving linear equations word problems, it’s time to try a few!

My goal here is to provide you with a worksheet that you can use to practice and feel confident that you understand linear equations word problems!

While I was writing this worksheet, I made sure to include a wide variety of problems that range in difficulty. You will see a few simpler problems involving a two-step equation or multi-step equations, but you will also see a few problems that involve systems of linear equations.

After solving each word problem, be sure to check the answer key to verify that you fully understand the process used to set up the problem and solve it. Reflecting on your understanding is an important part of developing comfort with any given math concept!

Click below to download the linear equations word problems worksheet with solutions!

Using This Linear Equation Word Problems Worksheet

Being able to read a  real-world algebra problem  and set up a linear equation (or a system of linear equations) to solve it is a very challenging skill. In my experience as a math teacher, many students struggle with this concept, even if they fully understand the mathematics that the problem requires.

This is the main reason that I put together this linear equation word problems worksheet with solutions. My goal is to provide you with a set of word problems that you can use to check your understanding of solving linear equations in the real-world.

I hope you found this practice worksheet helpful as you continue your studies of algebra and linear equations!

If you are looking for more linear equations math worksheets in PDF formats, check out my collection of  solving linear inequalities worksheets  and this  linear inequality word problems worksheet .

Did you find this linear equation word problems worksheet with solutions helpful? Share this post and subscribe to Math By The Pixel on YouTube for more helpful mathematics content!

RECOMMENDED FOR YOU

Examples of One Solution Equations, Zero, and Infinite

Free Linear Inequalities Word Problems Worksheet

Solving Linear Equations

Solving linear equations means finding the value of the variable(s) given in the linear equations. A linear equation is a combination of an algebraic expression and an equal to (=) symbol. It has a degree of 1 or it can be called a first-degree equation. For example, x + y = 4 is a linear equation. Sometimes, we may have to find the values of variables involved in a linear equation. When we are given two or more such linear equations, we can find the values of each variable by solving linear equations. There are a few methods to solve linear equations. Let us discuss each of these methods in detail.

Solving Linear Equations in One Variable

A linear equation in one variable is an equation of degree one and has only one variable term. It is of the form 'ax+b = 0', where 'a' is a non zero number and 'x' is a variable. By solving linear equations in one variable, we get only one solution for the given variable. An example for this is 3x - 6 = 0. The variable 'x' has only one solution, which is calculated as 3x - 6 = 0 3x = 6 x = 6/3 x = 2

For solving linear equations with one variable, simplify the equation such that all the variable terms are brought to one side and the constant value is brought to the other side. If there are any fractional terms then find the LCM ( Least Common Multiple ) and simplify them such that the variable terms are on one side and the constant terms are on the other side. Let us work out a small example to understand this.

4x + 8 = 8x - 10. To find the value of 'x', let us simplify and bring the 'x' terms to one side and the constant terms to another side.

4x - 8x = -10 - 8 -4x = -18 4x = 18 x = 18/4 On simplifying, we get x = 9/2.

Solving Linear Equations by Substitution Method

The substitution method is one of the methods of solving linear equations. In the substitution method , we rearrange the equation such that one of the values is substituted in the second equation. Now that we are left with an equation that has only one variable, we can solve it and find the value of that variable. In the two given equations, any equation can be taken and the value of a variable can be found and substituted in another equation. For solving linear equations using the substitution method, follow the steps mentioned below. Let us understand this with an example of solving the following system of linear equations. x + y = 6 --------------(1) 2x + 4y = 20 -----------(2)

Step 1: Find the value of one of the variables using any one of the equations. In this case, let us find the value of 'x' from equation (1). x + y = 6 ---------(1) x = 6 - y Step 2: Substitute the value of the variable found in step 1 in the second linear equation. Now, let us substitute the value of 'x' in the second equation 2x + 4y = 20.

x = 6 - y Substituting the value of 'x' in 2x + 4y = 20, we get,

2(6 - y) + 4y = 20 12 - 2y + 4y = 20 12 + 2y = 20 2y = 20 - 12 2y = 8 y = 8/2 y = 4 Step 3: Now substitute the value of 'y' in either equation (1) or (2). Let us substitute the value of 'y' in equation (1).

x + y = 6 x + 4 = 6 x = 6 - 4 x = 2 Therefore, by substitution method, the linear equations are solved, and the value of x is 2 and y is 4.

Solving Linear Equations by Elimination Method

The elimination method is another way to solve a system of linear equations. Here we make an attempt to multiply either the 'x' variable term or the 'y' variable term with a constant value such that either the 'x' variable terms or the 'y' variable terms cancel out and gives us the value of the other variable. Let us understand the steps of solving linear equations by elimination method . Consider the given linear equations: 2x + y = 11 ----------- (1) x + 3y = 18 ---------- (2) Step 1: Check whether the terms are arranged in a way such that the 'x' term is followed by a 'y' term and an equal to sign and after the equal to sign the constant term should be present. The given set of linear equations are already arranged in the correct way which is ax+by=c or ax+by-c=0.

Step 2: The next step is to multiply either one or both the equations by a constant value such that it will make either the 'x' terms or the 'y' terms cancel out which would help us find the value of the other variable. Now in equation (2), let us multiply every term by the number 2 to make the coefficients of x the same in both the equations. x + 3y = 18 ---------- (2) Multiplying all the terms in equation (2) by 2, we get,

2(x) + 2(3y) = 2(18). Now equation (2) becomes, 2x + 6y = 36 -----------(2)

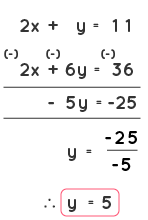
Therefore, y = 5. Step 4: Using the value obtained in step 3, find out the value of another variable by substituting the value in any of the equations. Let us substitute the value of 'y' in equation (1). We get, 2x + y = 11 2x + 5 = 11 2x = 11 - 5 2x = 6 x = 6/2 x = 3

Therefore, by solving linear equations, we get the value of x = 3 and y = 5.

Graphical Method of Solving Linear Equations

Another method for solving linear equations is by using the graph. When we are given a system of linear equations, we graph both the equations by finding values for 'y' for different values of 'x' in the coordinate system. Once it is done, we find the point of intersection of these two lines. The (x,y) values at the point of intersection give the solution for these linear equations. Let us take two linear equations and solve them using the graphical method.

x + y = 8 -------(1)

y = x + 2 --------(2)

Let us take some values for 'x' and find the values for 'y' for the equation x + y = 8. This can also be rewritten as y = 8 - x.

Let us take some values for 'x' and find the values for 'y' in the equation y = x + 2.

Plotting these points on the coordinate plane, we get a graph like this.

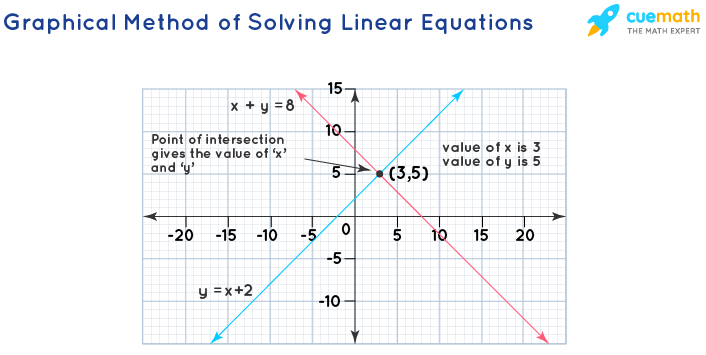
Now, we find the point of intersection of these lines to find the values of 'x' and 'y'. The two lines intersect at the point (3,5). Therefore, x = 3 and y = 5 by using the graphical method of solving linear equations .

This method is also used to find the optimal solution of linear programming problems. Let us look at one more method of solving linear equations, which is the cross multiplication method.

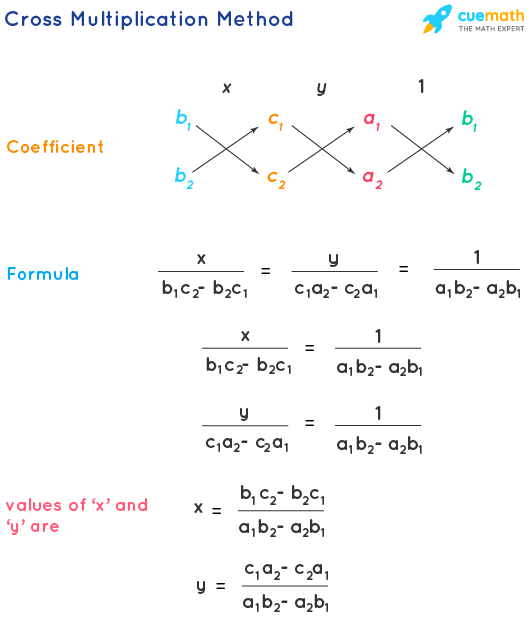
Cross Multiplication Method of Solving Linear Equations

The cross multiplication method enables us to solve linear equations by picking the coefficients of all the terms ('x' , 'y' and the constant terms) in the format shown below and apply the formula for finding the values of 'x' and 'y'.

Topics Related to Solving Linear Equations

Check the given articles related to solving linear equations.

• Linear Equations
• Application of Linear Equations
• Two-Variable Linear Equations
• Linear Equations and Half Planes
• One Variable Linear Equations and Inequations

Solving Linear Equations Examples

Example 1: Solve the following linear equations by the substitution method.

3x + y = 13 --------- (1) 2x + 3y = 18 -------- (2)

By using the substitution method of solving linear equations, let us take the first equation and find the value of 'y' and substitute it in the second equation.

From equation (1), y = 13-3x. Now, substituting the value of 'y' in equation (2), we get, 2x + 3 (13 - 3x) = 18 2x + 39 - 9x = 18 -7x + 39 = 18 -7x = 18 - 39 -7x = -21 x = -21/-7 x = 3 Now, let us substitute the value of 'x = 3' in equation (1) and find the value of 'y'. 3x + y = 13 ------- (1) 3(3) + y = 13 9 + y = 13 y = 13 - 9 y = 4

Therefore, by the substitution method, the value of x is 3 and y is 4.

Example 2: Using the elimination method of solving linear equations find the values of 'x' and 'y'.

3x + y = 21 ------ (1) 2x + 3y = 28 -------- (2)

By using the elimination method, let us make the 'y' variable to be the same in both the equations (1) and (2). To do this let us multiply all the terms of the first equation by 3. Therefore equation (1) becomes,

3(3x) + 3(y) = 63 9x + 3y = 63 ---------- (3) The second equation is, 2x + 3y = 28 Now let us cancel the 'y' terms and find the value of 'x' by subtracting equation (2) from equation (3). This is done by changing the signs of all the terms in equation (2).

Example 3: Using the cross multiplication method of solving linear equations, solve the following equations.

x + 2y - 16 = 0 --------- (1) 4x - y - 10 = 0 ---------- (2)

Compare the given equation with \(a_{1}\)x + \(b_{1}\)y + \(c_{1}\) = 0, and \(a_{2}\)x+\(b_{2}\)y+\(c_{2}\) = 0. From the given equations,

\(a_{1}\) = 1, \(a_{2}\) = 4, \(b_{1}\) = 2, \(b_{2}\) = -1, \(c_{1}\) = -16, and \(c_{2}\) = -10.

By cross multiplication method,

x = \(b_{1}\)\(c_{2}\) - \(b_{2}\)\(c_{1}\)/\(a_{1}\)\(b_{2}\) - \(a_{2}\)\(b_{1}\) y = \(c_{1}\)\(a_{2}\) - \(c_{2}\)\(a_{1}\) / \(a_{1}\)\(b_{2}\) - \(a_{2}\)\(b_{1}\)

Substituting the values in the formula we get,

x = ((2)(-10)) - ((-1)(-16)) / ((1)(-1)) - ((4)(2)) x = (-20-16)/(-1-8) x = -36/-9 x = 36/9 x = 4 y = ((-16)(4)) - ((-10)(1)) / ((1)(-1)) - ((4)(2)) y = (-64 + 10) / (-1 - 8) y = -54 / -9 y = 54/9 y = 6 Therefore, by the cross multiplication method, the value of x is 4 and y is 6.

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Solving Linear Equations

Faqs on solving linear equations, what does it mean by solving linear equations.

An equation that has a degree of 1 is called a linear equation. We can have one variable linear equations , two-variable linear equations , linear equations with three variables, and more depending on the number of variables in it. Solving linear equations means finding the values of all the variables present in the equation. This can be done by substitution method, elimination method, graphical method, and the cross multiplication method . All these methods are different ways of finding the values of the variables.

How to Use the Substitution Method for Solving Linear Equations?

The substitution method of solving equations states that for a given system of linear equations, find the value of either 'x' or 'y' from any of the given equations and then substitute the value found of 'x' or 'y' in another equation so that the other unknown value can be found.

How to Use the Elimination Method for Solving Linear Equations?

In the elimination method of solving linear equations, we multiply a constant or a number with one equation or both the equations such that either the 'x' terms or the 'y' terms are the same. Then we cancel out the same term in both the equations by either adding or subtracting them and find the value of one variable (either 'x' or 'y'). After finding one of the values, we substitute the value in one of the equations and find the other unknown value.

What is the Graphical Method of Solving Linear Equations?

In the graphical method of solving linear equations, we find the value of 'y' from the given equations by putting the values of x as 0, 1, 2, 3, and so on, and plot a graph in the coordinate system for the line for various values of 'x' for both the system of linear equations. We will see that these two lines intersect at a point. This point is the solution for the given system of linear equations. If there is no intersection point between two lines, then we consider them as parallel lines , and if we found that both the lines lie on each other, those are known as coincident lines and have infinitely many solutions.

What are the Steps of Solving Linear Equations that has One Variable?

A linear equation is an equation with degree 1. To solve a linear equation that has one variable we bring the variable to one side and the constant value to the other side. Then, a non-zero number may be added, subtracted, multiplied, or divided on both sides of the equation. For example, a linear equation with one variable will be of the form 'x - 4 = 2'. To find the value of 'x', we add the constant value '4' to both sides of the equation. Therefore, the value of 'x = 6'.

What are the Steps of Solving Linear Equations having Three Variables?

To solve a system of linear equations that has three variables, we take any two equations and variables. We then take another pair of linear equations and also solve for the same variable. Now that, we have two linear equations with two variables, we can use the substitution method or elimination method, or any other method to solve the values of two unknown variables. After finding these two variables, we substitute them in any of the three equations to find the third unknown variable.

What are the 4 Methods of Solving Linear Equations?

The methods for solving linear equations are given below:

• Substitution method
• Elimination method
• Cross multiplication method
• Graphical method

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 3: Linear equations and inequalities

About this unit.

We will now equate two algebraic expressions and think about how it might constrain what value the variables can take on. The algebraic manipulation you learn here really is the heart of algebra.

One-step equations

• One-step addition & subtraction equations (Opens a modal)
• One-step addition equation (Opens a modal)
• One-step division equations (Opens a modal)
• One-step multiplication equations (Opens a modal)
• One-step multiplication & division equations (Opens a modal)
• One-step addition & subtraction equations Get 5 of 7 questions to level up!
• One-step multiplication & division equations Get 5 of 7 questions to level up!

Two-steps equations

• Intro to two-step equations (Opens a modal)
• Two-step equations intuition (Opens a modal)
• Worked example: two-step equations (Opens a modal)
• Two-step equation word problem: computers (Opens a modal)
• Two-step equation word problem: garden (Opens a modal)
• Two-step equation word problem: oranges (Opens a modal)
• Two-step equations Get 5 of 7 questions to level up!
• Two-step equations word problems Get 3 of 4 questions to level up!

Multi-step equations

• Why we do the same thing to both sides: Variable on both sides (Opens a modal)
• Intro to equations with variables on both sides (Opens a modal)
• Equations with variables on both sides: 20-7x=6x-6 (Opens a modal)
• Equations with parentheses (Opens a modal)
• Equations with variables on both sides Get 3 of 4 questions to level up!
• Equations with parentheses Get 3 of 4 questions to level up!

One-step inequalities

• One-step inequalities examples (Opens a modal)
• One-step inequalities: -5c ≤ 15 (Opens a modal)
• One-step inequality word problem (Opens a modal)
• One-step inequalities review (Opens a modal)
• One-step inequalities Get 5 of 7 questions to level up!

Two-step inequalities

• Two-step inequalities (Opens a modal)
• Two-step inequality word problem: apples (Opens a modal)
• Two-step inequality word problem: R&B (Opens a modal)
• Two-step inequalities Get 5 of 7 questions to level up!
• Two-step inequality word problems Get 3 of 4 questions to level up!

Multi-step inequalities

• Inequalities with variables on both sides (Opens a modal)
• Inequalities with variables on both sides (with parentheses) (Opens a modal)
• Multi-step inequalities (Opens a modal)
• Multi-step linear inequalities Get 3 of 4 questions to level up!

Writing & solving proportions

• Worked example: Solving proportions (Opens a modal)
• Solving tricky proportions (Opens a modal)
• Writing proportions example (Opens a modal)
• Proportion word problem: cookies (Opens a modal)
• Proportion word problem: hot dogs (Opens a modal)
• Solving proportions Get 5 of 7 questions to level up!
• Solving proportions 2 Get 5 of 7 questions to level up!
• Writing proportions Get 3 of 4 questions to level up!
• Proportion word problems Get 3 of 4 questions to level up!

4.1 Solve Systems of Linear Equations with Two Variables

Learning objectives.

By the end of this section, you will be able to:

• Determine whether an ordered pair is a solution of a system of equations
• Solve a system of linear equations by graphing
• Solve a system of equations by substitution
• Solve a system of equations by elimination
• Choose the most convenient method to solve a system of linear equations

Be Prepared 4.1

Before you get started, take this readiness quiz.

For the equation y = 2 3 x − 4 , y = 2 3 x − 4 , ⓐ Is ( 6 , 0 ) ( 6 , 0 ) a solution? ⓑ Is ( −3 , −2 ) ( −3 , −2 ) a solution? If you missed this problem, review Example 3.2 .

Be Prepared 4.2

Find the slope and y -intercept of the line 3 x − y = 12 . 3 x − y = 12 . If you missed this problem, review Example 3.16 .

Be Prepared 4.3

Find the x- and y -intercepts of the line 2 x − 3 y = 12 . 2 x − 3 y = 12 . If you missed this problem, review Example 3.8 .

Determine Whether an Ordered Pair is a Solution of a System of Equations

In Solving Linear Equations , we learned how to solve linear equations with one variable. Now we will work with two or more linear equations grouped together, which is known as a system of linear equations .

System of Linear Equations

When two or more linear equations are grouped together, they form a system of linear equations .

In this section, we will focus our work on systems of two linear equations in two unknowns. We will solve larger systems of equations later in this chapter.

An example of a system of two linear equations is shown below. We use a brace to show the two equations are grouped together to form a system of equations.

A linear equation in two variables, such as 2 x + y = 7 , 2 x + y = 7 , has an infinite number of solutions. Its graph is a line. Remember, every point on the line is a solution to the equation and every solution to the equation is a point on the line.

To solve a system of two linear equations, we want to find the values of the variables that are solutions to both equations. In other words, we are looking for the ordered pairs ( x , y ) ( x , y ) that make both equations true. These are called the solutions of a system of equations .

Solutions of a System of Equations

The solutions of a system of equations are the values of the variables that make all the equations true. A solution of a system of two linear equations is represented by an ordered pair ( x , y ) . ( x , y ) .

To determine if an ordered pair is a solution to a system of two equations, we substitute the values of the variables into each equation. If the ordered pair makes both equations true, it is a solution to the system.

Example 4.1

Determine whether the ordered pair is a solution to the system { x − y = −1 2 x − y = −5 . { x − y = −1 2 x − y = −5 .

ⓐ ( −2 , −1 ) ( −2 , −1 ) ⓑ ( −4 , −3 ) ( −4 , −3 )

Determine whether the ordered pair is a solution to the system { 3 x + y = 0 x + 2 y = −5 . { 3 x + y = 0 x + 2 y = −5 .

ⓐ ( 1 , −3 ) ( 1 , −3 ) ⓑ ( 0 , 0 ) ( 0 , 0 )

Determine whether the ordered pair is a solution to the system { x − 3 y = −8 − 3 x − y = 4 . { x − 3 y = −8 − 3 x − y = 4 .

ⓐ ( 2 , −2 ) ( 2 , −2 ) ⓑ ( −2 , 2 ) ( −2 , 2 )

Solve a System of Linear Equations by Graphing

In this section, we will use three methods to solve a system of linear equations. The first method we’ll use is graphing.

The graph of a linear equation is a line. Each point on the line is a solution to the equation. For a system of two equations, we will graph two lines. Then we can see all the points that are solutions to each equation. And, by finding what the lines have in common, we’ll find the solution to the system.

Most linear equations in one variable have one solution, but we saw that some equations, called contradictions, have no solutions and for other equations, called identities, all numbers are solutions.

Similarly, when we solve a system of two linear equations represented by a graph of two lines in the same plane, there are three possible cases, as shown.

Each time we demonstrate a new method, we will use it on the same system of linear equations. At the end of the section you’ll decide which method was the most convenient way to solve this system.

Example 4.2

How to solve a system of equations by graphing.

Solve the system by graphing { 2 x + y = 7 x − 2 y = 6 . { 2 x + y = 7 x − 2 y = 6 .

Solve the system by graphing: { x − 3 y = −3 x + y = 5 . { x − 3 y = −3 x + y = 5 .

Solve the system by graphing: { − x + y = 1 3 x + 2 y = 12 . { − x + y = 1 3 x + 2 y = 12 .

The steps to use to solve a system of linear equations by graphing are shown here.

Solve a system of linear equations by graphing.

• Step 1. Graph the first equation.
• Step 2. Graph the second equation on the same rectangular coordinate system.
• Step 3. Determine whether the lines intersect, are parallel, or are the same line.
• If the lines intersect, identify the point of intersection. This is the solution to the system.
• If the lines are parallel, the system has no solution.
• If the lines are the same, the system has an infinite number of solutions.
• Step 5. Check the solution in both equations.

In the next example, we’ll first re-write the equations into slope–intercept form as this will make it easy for us to quickly graph the lines.

Example 4.3

Solve the system by graphing: { 3 x + y = − 1 2 x + y = 0 . { 3 x + y = − 1 2 x + y = 0 .

We’ll solve both of these equations for y y so that we can easily graph them using their slopes and y -intercepts.

Solve the system by graphing: { − x + y = 1 2 x + y = 10 . { − x + y = 1 2 x + y = 10 .

Solve the system by graphing: { 2 x + y = 6 x + y = 1 . { 2 x + y = 6 x + y = 1 .

In all the systems of linear equations so far, the lines intersected and the solution was one point. In the next two examples, we’ll look at a system of equations that has no solution and at a system of equations that has an infinite number of solutions.

Example 4.4

Solve the system by graphing: { y = 1 2 x − 3 x − 2 y = 4 . { y = 1 2 x − 3 x − 2 y = 4 .

Solve the system by graphing: { y = − 1 4 x + 2 x + 4 y = − 8 . { y = − 1 4 x + 2 x + 4 y = − 8 .

Solve the system by graphing: { y = 3 x − 1 6 x − 2 y = 6 . { y = 3 x − 1 6 x − 2 y = 6 .

Sometimes the equations in a system represent the same line. Since every point on the line makes both equations true, there are infinitely many ordered pairs that make both equations true. There are infinitely many solutions to the system.

Example 4.5

Solve the system by graphing: { y = 2 x − 3 − 6 x + 3 y = − 9 . { y = 2 x − 3 − 6 x + 3 y = − 9 .

If you write the second equation in slope-intercept form, you may recognize that the equations have the same slope and same y -intercept.

Solve the system by graphing: { y = − 3 x − 6 6 x + 2 y = − 12 . { y = − 3 x − 6 6 x + 2 y = − 12 .

Try It 4.10

Solve the system by graphing: { y = 1 2 x − 4 2 x − 4 y = 16 . { y = 1 2 x − 4 2 x − 4 y = 16 .

When we graphed the second line in the last example, we drew it right over the first line. We say the two lines are coincident . Coincident lines have the same slope and same y- intercept.

Coincident Lines

Coincident lines have the same slope and same y- intercept.

The systems of equations in Example 4.2 and Example 4.3 each had two intersecting lines. Each system had one solution.

In Example 4.5 , the equations gave coincident lines, and so the system had infinitely many solutions.

The systems in those three examples had at least one solution. A system of equations that has at least one solution is called a consistent system.

A system with parallel lines, like Example 4.4 , has no solution. We call a system of equations like this inconsistent. It has no solution.

Consistent and Inconsistent Systems

A consistent system of equations is a system of equations with at least one solution.

An inconsistent system of equations is a system of equations with no solution.

We also categorize the equations in a system of equations by calling the equations independent or dependent . If two equations are independent, they each have their own set of solutions. Intersecting lines and parallel lines are independent.

If two equations are dependent, all the solutions of one equation are also solutions of the other equation. When we graph two dependent equations, we get coincident lines.

Let’s sum this up by looking at the graphs of the three types of systems. See below and Table 4.1 .

Example 4.6

Without graphing, determine the number of solutions and then classify the system of equations.

ⓐ { y = 3 x − 1 6 x − 2 y = 12 { y = 3 x − 1 6 x − 2 y = 12 ⓑ { 2 x + y = − 3 x − 5 y = 5 { 2 x + y = − 3 x − 5 y = 5

ⓐ We will compare the slopes and intercepts of the two lines.

A system of equations whose graphs are parallel lines has no solution and is inconsistent and independent.

ⓑ We will compare the slope and intercepts of the two lines.

A system of equations whose graphs are intersect has 1 solution and is consistent and independent.

Try It 4.11

ⓐ { y = −2 x − 4 4 x + 2 y = 9 { y = −2 x − 4 4 x + 2 y = 9 ⓑ { 3 x + 2 y = 2 2 x + y = 1 { 3 x + 2 y = 2 2 x + y = 1

Try It 4.12

ⓐ { y = 1 3 x − 5 x − 3 y = 6 { y = 1 3 x − 5 x − 3 y = 6 ⓑ { x + 4 y = 12 − x + y = 3 { x + 4 y = 12 − x + y = 3

Solving systems of linear equations by graphing is a good way to visualize the types of solutions that may result. However, there are many cases where solving a system by graphing is inconvenient or imprecise. If the graphs extend beyond the small grid with x and y both between −10 −10 and 10, graphing the lines may be cumbersome. And if the solutions to the system are not integers, it can be hard to read their values precisely from a graph.

Solve a System of Equations by Substitution

We will now solve systems of linear equations by the substitution method.

We will use the same system we used first for graphing.

We will first solve one of the equations for either x or y . We can choose either equation and solve for either variable—but we’ll try to make a choice that will keep the work easy.

Then we substitute that expression into the other equation. The result is an equation with just one variable—and we know how to solve those!

After we find the value of one variable, we will substitute that value into one of the original equations and solve for the other variable. Finally, we check our solution and make sure it makes both equations true.

Example 4.7

How to solve a system of equations by substitution.

Solve the system by substitution: { 2 x + y = 7 x − 2 y = 6 . { 2 x + y = 7 x − 2 y = 6 .

Try It 4.13

Solve the system by substitution: { − 2 x + y = −11 x + 3 y = 9 . { − 2 x + y = −11 x + 3 y = 9 .

Try It 4.14

Solve the system by substitution: { 2 x + y = −1 4 x + 3 y = 3 . { 2 x + y = −1 4 x + 3 y = 3 .

Solve a system of equations by substitution.

• Step 1. Solve one of the equations for either variable.
• Step 2. Substitute the expression from Step 1 into the other equation.
• Step 3. Solve the resulting equation.
• Step 4. Substitute the solution in Step 3 into either of the original equations to find the other variable.
• Step 5. Write the solution as an ordered pair.
• Step 6. Check that the ordered pair is a solution to both original equations.

Be very careful with the signs in the next example.

Example 4.8

Solve the system by substitution: { 4 x + 2 y = 4 6 x − y = 8 . { 4 x + 2 y = 4 6 x − y = 8 .

We need to solve one equation for one variable. We will solve the first equation for y .

Try It 4.15

Solve the system by substitution: { x − 4 y = −4 − 3 x + 4 y = 0 . { x − 4 y = −4 − 3 x + 4 y = 0 .

Try It 4.16

Solve the system by substitution: { 4 x − y = 0 2 x − 3 y = 5 . { 4 x − y = 0 2 x − 3 y = 5 .

Solve a System of Equations by Elimination

We have solved systems of linear equations by graphing and by substitution. Graphing works well when the variable coefficients are small and the solution has integer values. Substitution works well when we can easily solve one equation for one of the variables and not have too many fractions in the resulting expression.

The third method of solving systems of linear equations is called the Elimination Method. When we solved a system by substitution, we started with two equations and two variables and reduced it to one equation with one variable. This is what we’ll do with the elimination method, too, but we’ll have a different way to get there.

The Elimination Method is based on the Addition Property of Equality. The Addition Property of Equality says that when you add the same quantity to both sides of an equation, you still have equality. We will extend the Addition Property of Equality to say that when you add equal quantities to both sides of an equation, the results are equal.

For any expressions a, b, c, and d .

To solve a system of equations by elimination, we start with both equations in standard form. Then we decide which variable will be easiest to eliminate. How do we decide? We want to have the coefficients of one variable be opposites, so that we can add the equations together and eliminate that variable.

Notice how that works when we add these two equations together:

The y ’s add to zero and we have one equation with one variable.

Let’s try another one:

This time we don’t see a variable that can be immediately eliminated if we add the equations.

But if we multiply the first equation by −2 , −2 , we will make the coefficients of x opposites. We must multiply every term on both sides of the equation by −2 . −2 .

Then rewrite the system of equations.

Now we see that the coefficients of the x terms are opposites, so x will be eliminated when we add these two equations.

Once we get an equation with just one variable, we solve it. Then we substitute that value into one of the original equations to solve for the remaining variable. And, as always, we check our answer to make sure it is a solution to both of the original equations.

Now we’ll see how to use elimination to solve the same system of equations we solved by graphing and by substitution.

Example 4.9

How to solve a system of equations by elimination.

Solve the system by elimination: { 2 x + y = 7 x − 2 y = 6 . { 2 x + y = 7 x − 2 y = 6 .

Try It 4.17

Solve the system by elimination: { 3 x + y = 5 2 x − 3 y = 7 . { 3 x + y = 5 2 x − 3 y = 7 .

Try It 4.18

Solve the system by elimination: { 4 x + y = − 5 − 2 x − 2 y = − 2 . { 4 x + y = − 5 − 2 x − 2 y = − 2 .

The steps are listed here for easy reference.

Solve a system of equations by elimination.

• Step 1. Write both equations in standard form. If any coefficients are fractions, clear them.
• Decide which variable you will eliminate.
• Multiply one or both equations so that the coefficients of that variable are opposites.
• Step 3. Add the equations resulting from Step 2 to eliminate one variable.
• Step 4. Solve for the remaining variable.
• Step 5. Substitute the solution from Step 4 into one of the original equations. Then solve for the other variable.
• Step 6. Write the solution as an ordered pair.
• Step 7. Check that the ordered pair is a solution to both original equations.

Now we’ll do an example where we need to multiply both equations by constants in order to make the coefficients of one variable opposites.

Example 4.10

Solve the system by elimination: { 4 x − 3 y = 9 7 x + 2 y = −6 . { 4 x − 3 y = 9 7 x + 2 y = −6 .

In this example, we cannot multiply just one equation by any constant to get opposite coefficients. So we will strategically multiply both equations by different constants to get the opposites.

Try It 4.19

Solve the system by elimination: { 3 x − 4 y = − 9 5 x + 3 y = 14 . { 3 x − 4 y = − 9 5 x + 3 y = 14 .

Try It 4.20

Solve each system by elimination: { 7 x + 8 y = 4 3 x − 5 y = 27 . { 7 x + 8 y = 4 3 x − 5 y = 27 .

When the system of equations contains fractions, we will first clear the fractions by multiplying each equation by the LCD of all the fractions in the equation.

Example 4.11

Solve the system by elimination: { x + 1 2 y = 6 3 2 x + 2 3 y = 17 2 . { x + 1 2 y = 6 3 2 x + 2 3 y = 17 2 .

In this example, both equations have fractions. Our first step will be to multiply each equation by the LCD of all the fractions in the equation to clear the fractions.

Try It 4.21

Solve each system by elimination: { 1 3 x − 1 2 y = 1 3 4 x − y = 5 2 . { 1 3 x − 1 2 y = 1 3 4 x − y = 5 2 .

Try It 4.22

Solve each system by elimination: { x + 3 5 y = − 1 5 − 1 2 x − 2 3 y = 5 6 . { x + 3 5 y = − 1 5 − 1 2 x − 2 3 y = 5 6 .

When we solved the system by graphing, we saw that not all systems of linear equations have a single ordered pair as a solution. When the two equations were really the same line, there were infinitely many solutions. We called that a consistent system. When the two equations described parallel lines, there was no solution. We called that an inconsistent system.

The same is true using substitution or elimination. If the equation at the end of substitution or elimination is a true statement, we have a consistent but dependent system and the system of equations has infinitely many solutions. If the equation at the end of substitution or elimination is a false statement, we have an inconsistent system and the system of equations has no solution.

Example 4.12

Solve the system by elimination: { 3 x + 4 y = 12 y = 3 − 3 4 x . { 3 x + 4 y = 12 y = 3 − 3 4 x .

This is a true statement. The equations are consistent but dependent. Their graphs would be the same line. The system has infinitely many solutions.

After we cleared the fractions in the second equation, did you notice that the two equations were the same? That means we have coincident lines.

Try It 4.23

Solve the system by elimination: { 5 x − 3 y = 15 y = − 5 + 5 3 x . { 5 x − 3 y = 15 y = − 5 + 5 3 x .

Try It 4.24

Solve the system by elimination: { x + 2 y = 6 y = − 1 2 x + 3 . { x + 2 y = 6 y = − 1 2 x + 3 .

Choose the Most Convenient Method to Solve a System of Linear Equations

When you solve a system of linear equations in in an application, you will not be told which method to use. You will need to make that decision yourself. So you’ll want to choose the method that is easiest to do and minimizes your chance of making mistakes.

Example 4.13

For each system of linear equations, decide whether it would be more convenient to solve it by substitution or elimination. Explain your answer.

ⓐ { 3 x + 8 y = 40 7 x − 4 y = −32 { 3 x + 8 y = 40 7 x − 4 y = −32 ⓑ { 5 x + 6 y = 12 y = 2 3 x − 1 { 5 x + 6 y = 12 y = 2 3 x − 1

Since both equations are in standard form, using elimination will be most convenient.

Since one equation is already solved for y , using substitution will be most convenient.

Try It 4.25

For each system of linear equations decide whether it would be more convenient to solve it by substitution or elimination. Explain your answer.

ⓐ { 4 x − 5 y = −32 3 x + 2 y = −1 { 4 x − 5 y = −32 3 x + 2 y = −1 ⓑ { x = 2 y − 1 3 x − 5 y = −7 { x = 2 y − 1 3 x − 5 y = −7

Try It 4.26

ⓐ { y = 2 x − 1 3 x − 4 y = − 6 { y = 2 x − 1 3 x − 4 y = − 6 ⓑ { 6 x − 2 y = 12 3 x + 7 y = −13 { 6 x − 2 y = 12 3 x + 7 y = −13

Section 4.1 Exercises

Practice makes perfect.

In the following exercises, determine if the following points are solutions to the given system of equations.

{ 2 x − 6 y = 0 3 x − 4 y = 5 { 2 x − 6 y = 0 3 x − 4 y = 5

ⓐ ( 3 , 1 ) ( 3 , 1 ) ⓑ ( −3 , 4 ) ( −3 , 4 )

{ − 3 x + y = 8 − x + 2 y = −9 { − 3 x + y = 8 − x + 2 y = −9

ⓐ ( −5 , −7 ) ( −5 , −7 ) ⓑ ( −5 , 7 ) ( −5 , 7 )

{ x + y = 2 y = 3 4 x { x + y = 2 y = 3 4 x

ⓐ ( 8 7 , 6 7 ) ( 8 7 , 6 7 ) ⓑ ( 1 , 3 4 ) ( 1 , 3 4 )

{ 2 x + 3 y = 6 y = 2 3 x + 2 { 2 x + 3 y = 6 y = 2 3 x + 2 ⓐ ( −6 , 2 ) ( −6 , 2 ) ⓑ ( −3 , 4 ) ( −3 , 4 )

In the following exercises, solve the following systems of equations by graphing.

{ 3 x + y = −3 2 x + 3 y = 5 { 3 x + y = −3 2 x + 3 y = 5

{ − x + y = 2 2 x + y = −4 { − x + y = 2 2 x + y = −4

{ y = x + 2 y = −2 x + 2 { y = x + 2 y = −2 x + 2

{ y = x − 2 y = −3 x + 2 { y = x − 2 y = −3 x + 2

{ y = 3 2 x + 1 y = − 1 2 x + 5 { y = 3 2 x + 1 y = − 1 2 x + 5

{ y = 2 3 x − 2 y = − 1 3 x − 5 { y = 2 3 x − 2 y = − 1 3 x − 5

{ x + y = −4 − x + 2 y = −2 { x + y = −4 − x + 2 y = −2

{ − x + 3 y = 3 x + 3 y = 3 { − x + 3 y = 3 x + 3 y = 3

{ − 2 x + 3 y = 3 x + 3 y = 12 { − 2 x + 3 y = 3 x + 3 y = 12

{ 2 x − y = 4 2 x + 3 y = 12 { 2 x − y = 4 2 x + 3 y = 12

{ x + 3 y = −6 y = − 4 3 x + 4 { x + 3 y = −6 y = − 4 3 x + 4

{ − x + 2 y = −6 y = − 1 2 x − 1 { − x + 2 y = −6 y = − 1 2 x − 1

{ − 2 x + 4 y = 4 y = 1 2 x { − 2 x + 4 y = 4 y = 1 2 x

{ 3 x + 5 y = 10 y = − 3 5 x + 1 { 3 x + 5 y = 10 y = − 3 5 x + 1

{ 4 x − 3 y = 8 8 x − 6 y = 14 { 4 x − 3 y = 8 8 x − 6 y = 14

{ x + 3 y = 4 − 2 x − 6 y = 3 { x + 3 y = 4 − 2 x − 6 y = 3

{ x = −3 y + 4 2 x + 6 y = 8 { x = −3 y + 4 2 x + 6 y = 8

{ 4 x = 3 y + 7 8 x − 6 y = 14 { 4 x = 3 y + 7 8 x − 6 y = 14

{ 2 x + y = 6 − 8 x − 4 y = −24 { 2 x + y = 6 − 8 x − 4 y = −24

{ 5 x + 2 y = 7 − 10 x − 4 y = −14 { 5 x + 2 y = 7 − 10 x − 4 y = −14

{ y = 2 3 x + 1 − 2 x + 3 y = 5 { y = 2 3 x + 1 − 2 x + 3 y = 5

{ y = 3 2 x + 1 2 x − 3 y = 7 { y = 3 2 x + 1 2 x − 3 y = 7

{ 5 x + 3 y = 4 2 x − 3 y = 5 { 5 x + 3 y = 4 2 x − 3 y = 5

{ y = − 1 2 x + 5 x + 2 y = 10 { y = − 1 2 x + 5 x + 2 y = 10

{ 5 x − 2 y = 10 y = 5 2 x − 5 { 5 x − 2 y = 10 y = 5 2 x − 5

In the following exercises, solve the systems of equations by substitution.

{ 2 x + y = −4 3 x − 2 y = −6 { 2 x + y = −4 3 x − 2 y = −6

{ 2 x + y = −2 3 x − y = 7 { 2 x + y = −2 3 x − y = 7

{ x − 2 y = −5 2 x − 3 y = −4 { x − 2 y = −5 2 x − 3 y = −4

{ x − 3 y = −9 2 x + 5 y = 4 { x − 3 y = −9 2 x + 5 y = 4

{ 5 x − 2 y = −6 y = 3 x + 3 { 5 x − 2 y = −6 y = 3 x + 3

{ − 2 x + 2 y = 6 y = −3 x + 1 { − 2 x + 2 y = 6 y = −3 x + 1

{ 2 x + 5 y = 1 y = 1 3 x − 2 { 2 x + 5 y = 1 y = 1 3 x − 2

{ 3 x + 4 y = 1 y = − 2 5 x + 2 { 3 x + 4 y = 1 y = − 2 5 x + 2

{ 2 x + y = 5 x − 2 y = −15 { 2 x + y = 5 x − 2 y = −15

{ 4 x + y = 10 x − 2 y = −20 { 4 x + y = 10 x − 2 y = −20

{ y = −2 x − 1 y = − 1 3 x + 4 { y = −2 x − 1 y = − 1 3 x + 4

{ y = x − 6 y = − 3 2 x + 4 { y = x − 6 y = − 3 2 x + 4

{ x = 2 y 4 x − 8 y = 0 { x = 2 y 4 x − 8 y = 0

{ 2 x − 16 y = 8 − x − 8 y = −4 { 2 x − 16 y = 8 − x − 8 y = −4

{ y = 7 8 x + 4 − 7 x + 8 y = 6 { y = 7 8 x + 4 − 7 x + 8 y = 6

{ y = − 2 3 x + 5 2 x + 3 y = 11 { y = − 2 3 x + 5 2 x + 3 y = 11

In the following exercises, solve the systems of equations by elimination.

{ 5 x + 2 y = 2 − 3 x − y = 0 { 5 x + 2 y = 2 − 3 x − y = 0

{ 6 x − 5 y = −1 2 x + y = 13 { 6 x − 5 y = −1 2 x + y = 13

{ 2 x − 5 y = 7 3 x − y = 17 { 2 x − 5 y = 7 3 x − y = 17

{ 5 x − 3 y = −1 2 x − y = 2 { 5 x − 3 y = −1 2 x − y = 2

{ 3 x − 5 y = −9 5 x + 2 y = 16 { 3 x − 5 y = −9 5 x + 2 y = 16

{ 4 x − 3 y = 3 2 x + 5 y = −31 { 4 x − 3 y = 3 2 x + 5 y = −31

{ 3 x + 8 y = −3 2 x + 5 y = −3 { 3 x + 8 y = −3 2 x + 5 y = −3

{ 11 x + 9 y = −5 7 x + 5 y = −1 { 11 x + 9 y = −5 7 x + 5 y = −1

{ 3 x + 8 y = 67 5 x + 3 y = 60 { 3 x + 8 y = 67 5 x + 3 y = 60

{ 2 x + 9 y = −4 3 x + 13 y = −7 { 2 x + 9 y = −4 3 x + 13 y = −7

{ 1 3 x − y = −3 x + 5 2 y = 2 { 1 3 x − y = −3 x + 5 2 y = 2

{ x + 1 2 y = 3 2 1 5 x − 1 5 y = 3 { x + 1 2 y = 3 2 1 5 x − 1 5 y = 3

{ x + 1 3 y = −1 1 3 x + 1 2 y = 1 { x + 1 3 y = −1 1 3 x + 1 2 y = 1

{ 1 3 x − y = −3 2 3 x + 5 2 y = 3 { 1 3 x − y = −3 2 3 x + 5 2 y = 3

{ 2 x + y = 3 6 x + 3 y = 9 { 2 x + y = 3 6 x + 3 y = 9

{ x − 4 y = −1 − 3 x + 12 y = 3 { x − 4 y = −1 − 3 x + 12 y = 3

{ − 3 x − y = 8 6 x + 2 y = −16 { − 3 x − y = 8 6 x + 2 y = −16

{ 4 x + 3 y = 2 20 x + 15 y = 10 { 4 x + 3 y = 2 20 x + 15 y = 10

In the following exercises, decide whether it would be more convenient to solve the system of equations by substitution or elimination.

ⓐ { 8 x − 15 y = −32 6 x + 3 y = −5 { 8 x − 15 y = −32 6 x + 3 y = −5 ⓑ { x = 4 y − 3 4 x − 2 y = −6 { x = 4 y − 3 4 x − 2 y = −6

ⓐ { y = 7 x − 5 3 x − 2 y = 16 { y = 7 x − 5 3 x − 2 y = 16 ⓑ { 12 x − 5 y = −42 3 x + 7 y = −15 { 12 x − 5 y = −42 3 x + 7 y = −15

ⓐ { y = 4 x + 9 5 x − 2 y = −21 { y = 4 x + 9 5 x − 2 y = −21 ⓑ { 9 x − 4 y = 24 3 x + 5 y = −14 { 9 x − 4 y = 24 3 x + 5 y = −14

ⓐ { 14 x − 15 y = −30 7 x + 2 y = 10 { 14 x − 15 y = −30 7 x + 2 y = 10 ⓑ { x = 9 y − 11 2 x − 7 y = −27 { x = 9 y − 11 2 x − 7 y = −27

Writing Exercises

In a system of linear equations, the two equations have the same intercepts. Describe the possible solutions to the system.

Solve the system of equations by substitution and explain all your steps in words: { 3 x + y = 12 x = y − 8 . { 3 x + y = 12 x = y − 8 .

Solve the system of equations by elimination and explain all your steps in words: { 5 x + 4 y = 10 2 x = 3 y + 27 . { 5 x + 4 y = 10 2 x = 3 y + 27 .

Solve the system of equations { x + y = 10 x − y = 6 { x + y = 10 x − y = 6

ⓐ by graphing ⓑ by substitution ⓒ Which method do you prefer? Why?

After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

If most of your checks were:

…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.

…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Whom can you ask for help?Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?

…no - I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction

• Authors: Lynn Marecek, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Intermediate Algebra 2e
• Publication date: May 6, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/intermediate-algebra-2e/pages/4-1-solve-systems-of-linear-equations-with-two-variables

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Objective 2

Classify solutions to linear equations (one, no, or infinite solutions), learning objectives.

• Solve equations that have one solution, no solution, or an infinite number of solutions

Introduction

There are three cases that can come up as we are solving linear equations. We have already seen one, where an equation has one solution. Sometimes we come across equations that don’t have any solutions, and even some that have an infinite number of solutions. The case where an equation has no solution is illustrated in the next examples.

Equations with no solutions

Solve for x . [latex]12+2x–8=7x+5–5x[/latex]

Combine like terms on both sides of the equation.

[latex] \displaystyle \begin{array}{l}12+2x-8=7x+5-5x\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,2x+4=2x+5\end{array}[/latex]

Isolate the x term by subtracting 2 x from both sides.

[latex]\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,2x+4=2x+5\\\,\,\,\,\,\,\,\,\underline{-2x\,\,\,\,\,\,\,\,\,\,-2x\,\,\,\,\,\,\,\,}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4= \,5\end{array}[/latex]

This false statement implies there are no solutions to this equation. Sometimes, we say the solution does not exist, or DNE for short.

This is not a solution! You did not find a value for x . Solving for x the way you know how, you arrive at the false statement [latex]4=5[/latex]. Surely 4 cannot be equal to 5!

This may make sense when you consider the second line in the solution where like terms were combined. If you multiply a number by 2 and add 4 you would never get the same answer as when you multiply that same number by 2 and add 5. Since there is no value of x that will ever make this a true statement, the solution to the equation above is “no solution.”

Be careful that you do not confuse the solution [latex]x=0[/latex] with “no solution.” The solution [latex]x=0[/latex] means that the value 0 satisfies the equation, so there is a solution. “No solution” means that there is no value, not even 0, which would satisfy the equation.

Also, be careful not to make the mistake of thinking that the equation [latex]4=5[/latex] means that 4 and 5 are values for x that are solutions. If you substitute these values into the original equation, you’ll see that they do not satisfy the equation. This is because there is truly no solution —there are no values for x that will make the equation [latex]12+2x–8=7x+5–5x[/latex] true.

Think About It

Try solving these equations. How many steps do you need to take before you can tell whether the equation has no solution or one solution?

a) Solve [latex]8y=3(y+4)+y[/latex]

Use the textbox below to record how many steps you think it will take before you can tell whether there is no solution or one solution.

Solve [latex]8y=3(y+4)+y[/latex]

First, distribute the 3 into the parentheses on the right-hand side.

[latex]8y=3(y+4)+y=8y=3y+12+y[/latex]

Next, begin combining like terms.

[latex]8y=3y+12+y = 8y=4y+12[/latex]

Now move the variable terms to one side. Moving the [latex]4y[/latex] will help avoid a negative sign.

[latex]\begin{array}{l}\,\,\,\,8y=4y+12\\\underline{-4y\,\,-4y}\\\,\,\,\,4y=12\end{array}[/latex]

Now, divide each side by [latex]4y[/latex].

[latex]\begin{array}{c}\frac{4y}{4}=\frac{12}{4}\\y=3\end{array}[/latex]

Because we were able to isolate y on one side and a number on the other side, we have one solution to this equation.

b) Solve [latex]2\left(3x-5\right)-4x=2x+7[/latex]

Solve [latex]2\left(3x-5\right)-4x=2x+7[/latex].

First, distribute the 2 into the parentheses on the left-hand side.

[latex]\begin{array}{r}2\left(3x-5\right)-4x=2x+7\\6x-10-4x=2x+7\end{array}[/latex]

Now begin simplifying. You can combine the x terms on the left-hand side.

[latex]\begin{array}{r}6x-10-4x=2x+7\\2x-10=2x+7\end{array}[/latex]

Now, take a moment to ponder this equation. It says that [latex]2x-10[/latex] is equal to [latex]2x+7[/latex]. Can some number times two minus 10 be equal to that same number times two plus seven?

Let’s pretend [latex]x=3[/latex].

Is it true that [latex]2\left(3\right)-10=-4[/latex] is equal to [latex]2\left(3\right)+7=13[/latex]. NO! We don’t even really need to continue solving the equation, but we can just to be thorough.

Add [latex]10[/latex] to both sides.

[latex]\begin{array}{r}2x-10=2x+7\,\,\\\,\,\underline{+10\,\,\,\,\,\,\,\,\,\,\,+10}\\2x=2x+17\end{array}[/latex]

Now move [latex]2x[/latex] from the right hand side to combine like terms.

[latex]\begin{array}{l}\,\,\,\,\,2x=2x+17\\\,\,\underline{-2x\,\,-2x}\\\,\,\,\,\,\,\,0=17\end{array}[/latex]

We know that [latex]0\text{ and }17[/latex] are not equal, so there is no number that x could be to make this equation true.

This false statement implies there are no solutions to this equation, or DNE (does not exist) for short.

Algebraic Equations with an Infinite Number of Solutions

You have seen that if an equation has no solution, you end up with a false statement instead of a value for x . It is possible to have an equation where any value for x will provide a solution to the equation. In the example below, notice how combining the terms [latex]5x[/latex] and [latex]-4x[/latex] on the left leaves us with an equation with exactly the same terms on both sides of the equal sign.

Solve for x . [latex]5x+3–4x=3+x[/latex]

[latex] \displaystyle \begin{array}{r}5x+3-4x=3+x\\x+3=3+x\end{array}[/latex]

Isolate the x term by subtracting x from both sides.

[latex]\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,\,x+3=3+x\\\,\,\,\,\,\,\,\,\underline{\,-x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-x\,}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,3\,\,=\,\,3\end{array}[/latex]

This true statement implies there are an infinite number of solutions to this equation, or we can also write the solution as “All Real Numbers”

You arrive at the true statement “[latex]3=3[/latex].” When you end up with a true statement like this, it means that the solution to the equation is “all real numbers.” Try substituting [latex]x=0[/latex] into the original equation—you will get a true statement! Try [latex]x=-\frac{3}{4}[/latex], and it also will check!

This equation happens to have an infinite number of solutions. Any value for x that you can think of will make this equation true. When you think about the context of the problem, this makes sense—the equation [latex]x+3=3+x[/latex] means “some number plus 3 is equal to 3 plus that same number.” We know that this is always true—it’s the commutative property of addition!

In the following video, we show more examples of attempting to solve a linear equation with either no solution or many solutions.

Solve for x . [latex]3\left(2x-5\right)=6x-15[/latex]

Distribute the 3 through the parentheses on the left-hand side.

[latex] \begin{array}{r}3\left(2x-5\right)=6x-15\\6x-15=6x-15\end{array}[/latex]

Wait! This looks just like the previous example. You have the same expression on both sides of an equal sign.  No matter what number you choose for x , you will have a true statement. We can finish the algebra:

[latex]\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,\,6x-15=6x-15\\\,\,\,\,\,\,\,\,\underline{\,-6x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-6x\,}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-15\,\,=\,\,-15\end{array}[/latex]

This true statement implies there are an infinite number of solutions to this equation.

In this video, we show more examples of solving linear equations with either no solutions or many solutions.

In the following video, we show more examples of solving linear equations with parentheses that have either no solution or many solutions.

We have seen that solutions to equations can fall into three categories:

• One solution
• No solution, DNE (does not exist)
• Many solutions, also called infinitely many solutions or All Real Numbers

And sometimes, we don’t need to do much algebra to see what the outcome will be.

• Revision and Adaptation. Provided by : Lumen Learning. License : Public Domain: No Known Copyright
• Linear Equations with No Solutions or Infinite Solutions. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/iLkZ3o4wVxU . License : Public Domain: No Known Copyright
• Linear Equations with No Solutions of Infinite Solutions (Parentheses). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/EU_NEo1QBJ0 . License : CC BY: Attribution
• Absolute Value Equations with No Solutions. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/T-z5cQ58I_g . License : CC BY: Attribution
• Beginning and Intermediate Algebra. Authored by : Tyler Wallace. Located at : http://wallace.ccfaculty.org/book/book.html . License : CC BY: Attribution
• Unit 10: Solving Equations and Inequalities, from Developmental Math: An Open Program. Provided by : Monterey Institute of Technology and Education. Located at : http://nrocnetwork.org/dm-opentext . License : CC BY: Attribution

Linear Equations in Two Variables Questions

Linear equations in two variables questions presented here cover a variety of questions asked regarding linear equations in two variables with solutions and proper explanations. By practising these questions students will develop problem-solving skills.

Linear equations in two variables are linear polynomials with two unknowns. They are of the general form ax + by + c = 0, where x and y are the two variables, a and b are non-zero real numbers and c is a constant. The graphical representation of a linear equation in two variables is a straight line.

Linear Equations in Two Variables Questions with Solutions

Below are some practice questions on linear equations in two variables with detailed solutions.

Question 1: Solve for x and y:

\(\begin{array}{l}\frac{1}{2x}-\frac{1}{y}=-1,\:\:\frac{1}{x}+\frac{1}{2y}=8\:\:\:(x\neq0,\;y\neq0)\end{array} \)

Put 1/x = u and 1/y = v. The given equations become

u/2 – v = –1 ⇒ u – 2v = – 2 ….(i)

u + v/2 = 8 ⇒ 2u + v = 16 ….(ii)

Multiplying equation (ii) by 2 on both sides and adding (i) and (ii), we get

(u + 4u) + ( –2v + 2v) = –2 + 32

⇒ u = 6 ⇒ x = ⅙ and y = ¼

Question 2: Solve the system of linear equations 2x + 3y = 17 and 3x – 2y = 6 by the cross multiplication method.

By cross multiplication

\(\begin{array}{l}\frac{x}{\left\{ 3\times (-6)-(-2)\times(-17)\right\}}=\frac{y}{\left\{ -17\times 3-(-6)\times 2 \right\}}=\frac{1}{\left\{2\times (-2)-3 \times3\right\}}\end{array} \)

⇒ x/( –52) = y/( –39) = 1/( – 13)

⇒ x = 52/13 = 4 and y = 39/13 = 3

Hence x = 4 and y = 3 is the solution of given equations.

Question 3: Solve the following system of equations by substitution method:

2x + 3y = 0 and 3x + 4y = 5

Given equations,

2x + 3y = 0 ….(i)

3x + 4y = 5 …..(ii)

From (i) we get, y = – 2x/3, substituting value of y in (ii), we get

3x + 4(–2x/3) = 5

⇒ 9x – 8x = 15

Then y = (–2 × 15)/3 = – 10

Therefore, x = 15 and y = – 10 is solution of given system of equations.

Video Lesson on Consistent and Inconsistent Equations

Question 4: Find the value of k for which the given system of equations has infinitely many solutions: x + (k + 1)y = 5 and (k + 1)x + 9y + (1 – 8k) = 0.

The given equations will have infinitely many solutions if a 1 /a 2 = b 1 /b 2 = c 1 /c 2

Hence, 1/(k + 1) = (k + 1)/9 = – 5/(1 – 8k)

Solving the equations we get k = 2.

Question 5: If the lines given by 3x + 2ky = 2 and 2x + 5y + 1 = 0 are parallel. Find the value of k.

If the lines are parallel, then they are inconsistent system of equations and a 1 /a 2 = b 1 /b 2 ≠ c 1 /c 2

Now, it should be 3/2 = 2k/5

Then we have 2k/5 = 30/20 = 3/2, which satisfies the condition of inconsistency.

Question 6: Find the value of k for which the system of equations has a non-zero solution

5x + 3y = 0 and 10x + ky = 0

The given equations are homogenous equations, they will have a non-zero solution if a 1 /a 2 = b 1 /b 2

Then, 5/10 = 3/k

⇒ 1/2 = 3/k

Question7: The monthly incomes of A and B are in the ratio 8:7 and their expenditures are in the ratio 19:16. If each saves ₹ 5000 per month, find the monthly income of each.

Let the monthly incomes of A and B be 8x and 7x rupees respectively, and let their monthly expenditure be 19y and 16y rupees respectively.

Monthly savings of A = 8x – 19y = 5000 ….(i)

Monthly savings of B = 7x – 16y = 5000 ….(ii)

Multiplying (i) 16 and (ii) by 19 and subtracting (ii) from (i) we get

(16 × 8x – 19 × 7x) = 5000 (16 – 19)

⇒ 5x = 15000 ⇒ x = 3000

Monthly income of A is (8 × 3000) = ₹24,000

Monthly income of B is (7 × 3000) = ₹21,000

Question 8: The sum of a two-digit number obtained by reversing the order of its digits is 99. If the digits differ by 3, find the original number.

Let the original number be (10x + y)

According to the question,

(10x + y) + (10y + x) = 99

⇒ 11(x + y) = 99

⇒ x + y = 9 ….(i)

And x – y = 3 ….(ii)

Adding equations (i) and (ii), we get,

Hence the required number is 63.

Question 9: A man’s age is three times the sum of the ages of his two sons. After 5 years, his age will be twice the sum of his two son’s age. Find the age of the man.

Let the age of the man be x and the sum of the ages of his two sons be y.

x = 3y ⇒ x – 3y = 0 ….(i)

And (x + 5) = 2(y + 5 + 5)

⇒ x – 2y = 15 ….(ii)

Subtracting equation (i) from (ii) we get

Y = 15 and from (i) x = 45.

The present age of the man is 45 years.

Question 10: A man can row downstream 20 km in 2 hours, and upstream 4 km in 2 hours, Find his speed of rowing in still water. Also, find the speed of the stream.

Let the speed of the man in still water be x km/hr and let the speed of the current be y kn/hr.

Speed in downstream = (x + y) km/hr

Speed in upstream = (x – y) km/hr

But speed in downstream = 20/2 km/hr = 10 km/hr

And speed in upstream = 4/2 km/hr = 2 km/hr

∴ x + y = 10 and x – y = 2

Solving both the equations we get;

x = 6 and y = 4.

Hence, the speed of the man in still water is 6 km/hr and the speed of the current is 4 km/hr.

Question 11: Find the four angles of a cyclic Quadrilateral ABCD in which ∠A = (2x – 1) o , ∠B = (y + 5) o , ∠C = (2y + 15) o , and ∠D = (4x – 7) o .

We know that sum of opposite angles of a cyclic quadrilateral is 180 o

∴ ∠A + ∠C = 180 o and ∠B + ∠C = 180 o

∠A + ∠C = 180 o ⇒ (2x – 1) + (2y + 15) = 180 o

⇒ x + y = 83 ….(i)

∠B + ∠C = 180 o ⇒ (y + 5) + (4x – 7) = 180 o

⇒ 4x + y = 182 …..(ii)

Subtracting (i) from (ii) we get

3x = 182 – 83 ⇒ x = 33

Substituting in (i), we get y = 50

∴ ∠A = 2 × 33 – 1 = 65 o

∠B = 50 + 5 = 55 o

∠C = 2 × 50 + 15 = 115 o

∠D = 4 × 33 – 7 = 125 o .

Question 12: 8 men and 12 boys can finish a piece of work in 5 days, while 6 men and 8 boys can finish it in 7 days. Find time taken by a man and a boy alone to finish the same work.

Let 1 man can finish the work in x days and let 1 boy can finish the work in y days.

1 man’s one day work = 1/x

1 boy’s one day work = 1/y

8 men’s 1 day’s work + 12 boy’s one day’s work = ⅕

⇒ 8/x + 12/y = ⅕

⇒ 8u + 12v = ⅕ ….(i) where u = 1/x and v = 1/y

Similarly, 6u + 8v = 1/7 ….(ii)

On solving (i) and (ii) we get, x = 70 and y = 140

∴ One man alone can finish the work in 70 days and one boy alone can finish the work in 140 days.

Related Articles:

Practice questions:.

1. Five years ago Anna was three times older than Mira and ten years later Anna will be two times older than Mira. What are the present ages of Anna and Mira?

2. The difference of two numbers is 4 and the difference of their reciprocals is 4/21. Find the numbers.

3. Find the value of k for which the system of equations 5x – 3y = 0, and 2x + ky = 0 has a non-zero solution.

4. Find the value of a and b for which each of the following systems of linear equations

(a – 1)x + 3y = 2 and 6x + (1 – 2b)y = 6 has infinite number of solutions.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

• Share Share

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• \frac{3}{4}x+\frac{5}{6}=5x-\frac{125}{3}
• \sqrt{2}x-\sqrt{3}=\sqrt{5}
• 7y+5-3y+1=2y+2
• \frac{x}{3}+\frac{x}{2}=10
• What is a linear equation?
• A linear equation represents a straight line on a coordinate plane. It can be written in the form: y = mx + b where m is the slope of the line and b is the y-intercept.
• How do you find the linear equation?
• To find the linear equation you need to know the slope and the y-intercept of the line. To find the slope use the formula m = (y2 - y1) / (x2 - x1) where (x1, y1) and (x2, y2) are two points on the line. The y-intercept is the point at which x=0.
• What are the 4 methods of solving linear equations?
• There are four common methods to solve a system of linear equations: Graphing, Substitution, Elimination and Matrix.
• How do you identify a linear equation?
• Here are a few ways to identify a linear equation: Look at the degree of the equation, a linear equation is a first-degree equation. Check if the equation has two variables. Graph the equation.
• What is the most basic linear equation?
• The most basic linear equation is a first-degree equation with one variable, usually written in the form of y = mx + b, where m is the slope of the line and b is the y-intercept.

linear-equation-calculator

• High School Math Solutions – Quadratic Equations Calculator, Part 1 A quadratic equation is a second degree polynomial having the general form ax^2 + bx + c = 0, where a, b, and c...

Please add a message.

Message received. Thanks for the feedback.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.1: Solving Linear Equations and Inequalities

• Last updated
• Save as PDF
• Page ID 48347

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Verify linear solutions.
• Use the properties of equality to solve basic linear equations.
• Clear fractions from equations.
• Identify linear inequalities and check solutions.
• Solve linear inequalities and express the solutions graphically on a number line and in interval notation.

Prerequisite Skills

Before you get started, take this prerequisite quiz.

1. Simplify \(2-6(4-7)^2\) without using a calculator.

If you missed this problem, review here . (Note that this will open a different textbook in a new window.)

2. Evaluate \(6x−4\) when \(x=−2\).

3. Evaluate \(-5x^2−x+9\) when \(x=-3\).

4. Simplify \(7x−1−4x+5\).

\(3x+4\) 

Solving Basic Linear Equations

An equation 129 is a statement indicating that two algebraic expressions are equal. A linear equation with one variable 130 , \(x\), is an equation that can be written in the standard form \(ax + b = 0\) where \(a\) and \(b\) are real numbers and \(a ≠ 0\). For example

\(3 x - 12 = 0\)

A solution 131 to a linear equation is any value that can replace the variable to produce a true statement. The variable in the linear equation \(3x − 12 = 0\) is \(x\) and the solution is \(x = 4\). To verify this, substitute the value \(4\) in for \(x\) and check that you obtain a true statement.

\(\begin{aligned} 3 x - 12 & = 0 \\ 3 ( \color{Cerulean}{4}\color{Black}{ )} - 12 & = 0 \\ 12 - 12 & = 0 \\ 0 & = 0 \:\: \color{Cerulean}{✓} \end{aligned}\)

Alternatively, when an equation is equal to a constant, we may verify a solution by substituting the value in for the variable and showing that the result is equal to that constant. In this sense, we say that solutions “satisfy the equation.”

Example \(\PageIndex{1}\):

Is \(a=2\) a solution to \(−10a+5=−25\)?

Recall that when evaluating expressions, it is a good practice to first replace all variables with parentheses, and then substitute the appropriate values. By making use of parentheses, we avoid some common errors when working the order of operations.

\(\begin{align*} - 10 a + 5 &= -25 \\ - 10 ( \color{Cerulean}{2} \color{Black}{ ) +} 5 & = -25 \\ -20 + 5 & = -25 \\ -15 &\neq 25\:\: \color{red}{✗}\end{align*}\)  

No, \(a=2\) does not satisfy the equation and is therefore not a solution.

Developing techniques for solving various algebraic equations is one of our main goals in algebra. This section reviews the basic techniques used for solving linear equations with one variable. We begin by defining equivalent equations 132 as equations with the same solution set.

\(\left. \begin{aligned} 3 x - 5 & = 16 \\ 3 x & = 21 \\ x & = 7 \end{aligned} \right\} \quad \color{Cerulean}{Equivalent \:equations}\)

Here we can see that the three linear equations are equivalent because they share the same solution set, namely, \(\{7\}\). To obtain equivalent equations, use the following properties of equality 133 . Given algebraic expressions \(A\) and \(B\), where \(c\) is a nonzero number:

Table 1.1.1

Multiplying or dividing both sides of an equation by \(0\) is carefully avoided. Dividing by \(0\) is undefined and multiplying both sides by \(0\) results in the equation \(0 = 0\).

We solve algebraic equations by isolating the variable with a coefficient of 1. If given a linear equation of the form \(ax + b = c\), then we can solve it in two steps. First, use the appropriate equality property of addition or subtraction to isolate the variable term. Next, isolate the variable using the equality property of multiplication or division. Checking the solution in the following examples is left to the reader.

Example \(\PageIndex{2}\):

Solve: \(7x − 2 = 19\).

\(\begin{aligned} 7 x - 2 & = 19 \\ 7 x - 2 \color{Cerulean}{+ 2} & = 19 \color{Cerulean}{+ 2} & & \color{Cerulean}{Add\: 2\: to\: both\: sides.} \\ 7 x & = 21 \\ \frac { 7 x } { \color{Cerulean}{7} } & = \frac { 21 } { \color{Cerulean}{7} } & & \color{Cerulean}{Divide\: both\: sides\: by\: 7.} \\ x & = 3 \end{aligned}\)

The solution is \(3\).

Example \(\PageIndex{3}\):

Solve: \(56 = 8 + 12y\).

When no sign precedes the term, it is understood to be positive. In other words, think of this as \(56 = +8 + 12y\). Therefore, we begin by subtracting \(8\) on both sides of the equal sign.

\(\begin{aligned} 56 \color{Cerulean}{- 8} & = 8 + 12 y \color{Cerulean}{- 8} \\ 48 & = 12 y \\ \frac { 48 } { \color{Cerulean}{12} } & = \frac { 12 y } { \color{Cerulean}{12} } \\ 4 & = y \end{aligned}\)

It does not matter on which side we choose to isolate the variable because the symmetric property 134 states that \(4 = y\) is equivalent to \(y = 4\).

The solution is \(4\).

Example \(\PageIndex{4}\):

Solve: \(\frac { 5 } { 3 } x + 2 = - 8\).

Isolate the variable term using the addition property of equality, and then multiply both sides of the equation by the reciprocal of the coefficient \(\frac{5}{3}\) .

\begin{aligned} \frac { 5 } { 3 } x + 2 & = - 8 \\ \frac { 5 } { 3 } x + 2 \color{Cerulean}{- 2} & = - 8 \color{Cerulean}{- 2}\quad \color{Cerulean}{Subtract\: 2\: on\: both\: sides.} \\ \frac { 5 } { 3 } x & = - 10 \\ \color{Cerulean}{\frac { 3 } { 5 }} \color{Black}{ \cdot} \frac { 5 } { 3 } x & = \color{Cerulean}{\frac { 3 } { \cancel{5} }} \color{Black}{\cdot} ( \overset{-2}{\cancel{-10}} )\quad \color{Cerulean}{Multiply \:both \:sides\: by\: \frac{3}{5}.} \\ 1x & = 3 \cdot ( - 2 ) \\ x & = - 6 \end{aligned}

The solution is \(−6\).

In summary, to retain equivalent equations, we must perform the same operation on both sides of the equation.

Exercise \(\PageIndex{1}\)

Solve: \(\frac { 2 } { 3 } x + \frac { 1 } { 2 } = - \frac { 5 } { 6 }\).

Video Solution: www.youtube.com/v/cQwqXs9AD6M

General Guidelines for Solving Linear Equations

Typically linear equations are not given in standard form, and so solving them requires additional steps. When solving linear equations, the goal is to determine what value, if any, will produce a true statement when substituted in the original equation. Do this by isolating the variable using the following steps:

• Step 1: Simplify both sides of the equation using the order of operations and combine all like terms on the same side of the equal sign.
• Step 2a: Add or subtract as needed to isolate the variable.
• Step 2b: Divide or multiply as needed to isolate the variable.
• Step 3: Check to see if the answer solves the original equation.

We will often encounter linear equations where the expressions on each side of the equal sign can be simplified. If this is the case, then it is best to simplify each side first before solving. Normally this involves combining same-side like terms.

At this point in our study of algebra the use of the properties of equality should seem routine. Therefore, displaying these steps in this text, usually in blue, becomes optional.

Example \(\PageIndex{5}\):

Solve: \(- 4 a + 2 - a = 1\).

First combine the like terms on the left side of the equal sign.

\(\begin{aligned} - 4 a + 2 - a = 1 & \quad \color{Cerulean}{ Combine\: same-side\: like\: terms.} \\ - 5 a + 2 = 1 & \quad\color{Cerulean} { Subtract\: 2\: on\: both\: sides.} \\ - 5 a = - 1 & \quad\color{Cerulean} { Divide\: both\: sides\: by\: - 5.} \\ a = \frac { - 1 } { - 5 } = \frac { 1 } { 5 } \end{aligned}\)

Always use the original equation to check to see if the solution is correct.

\(\begin{aligned} - 4 a + 2 - a & = - 4 \left( \color{OliveGreen}{\frac { 1 } { 5 }} \right) + 2 - \color{OliveGreen}{\frac { 1 } { 5 }} \\ & = - \frac { 4 } { 5 } + \frac { 2 } { 1 } \cdot \color{Cerulean}{\frac { 5 } { 5 }}\color{Black}{ -} \frac { 1 } { 5 } \\ & = \frac { - 4 + 10 + 1 } { 5 } \\ & = \frac { 5 } { 5 } = 1 \:\:\color{Cerulean}{✓} \end{aligned}\)

The solution is \(\frac{1}{5}\) .

Given a linear equation in the form \(ax + b = cx + d\), we begin the solving process by combining like terms on opposite sides of the equal sign. To do this, use the addition or subtraction property of equality to place like terms on the same side so that they can be combined. In the examples that remain, the check is left to the reader.

Example \(\PageIndex{6}\):

Solve: \(−2y − 3 = 5y + 11\).

Subtract \(5y\) on both sides so that we can combine the terms involving y on the left side.

\(\begin{array} { c } { - 2 y - 3 \color{Cerulean}{- 5 y}\color{Black}{ =} 5 y + 11 \color{Cerulean}{- 5 y} } \\ { - 7 y - 3 = 11 } \end{array}\)

From here, solve using the techniques developed previously.

\(\begin{aligned} - 7 y - 3 & = 11 \quad\color{Cerulean}{Add\: 3\: to\: both\: sides.} \\ - 7 y & = 14 \\ y & = \frac { 14 } { - 7 } \quad\color{Cerulean}{Divide\: both\: sides\: by\: -7.} \\ y & = - 2 \end{aligned}\)

The solution is \(−2\).

Solving will often require the application of the distributive property.

Example \(\PageIndex{7}\):

Solve: \(- \frac { 1 } { 2 } ( 10 x - 2 ) + 3 = 7 ( 1 - 2 x )\).

Simplify the linear expressions on either side of the equal sign first.

\(\begin{aligned} - \frac { 1 } { 2 } ( 10 x - 2 ) + 3 = 7 ( 1 - 2 x ) & \quad\color{Cerulean} { Distribute } \\ - 5 x + 1 + 3 = 7 - 14 x & \quad\color{Cerulean} { Combine\: same-side\: like\: terms. } \\ - 5 x + 4 = 7 - 14 x & \quad\color{Cerulean} { Combine\: opposite-side\: like\: terms. } \\ 9 x = 3 & \quad\color{Cerulean} { Solve. } \\ x = \frac { 3 } { 9 } = \frac { 1 } { 3 } \end{aligned}\)

The solution is \(\frac{1}{3}\) .

Example \(\PageIndex{8}\):

Solve: \(5(3−a)−2(5−2a)=3\).

Begin by applying the distributive property.

\(\begin{aligned} 5 ( 3 - a ) - 2 ( 5 - 2 a ) & = 3 \\ 15 - 5 a - 10 + 4 a & = 3 \\ 5 - a & = 3 \\ - a & = - 2 \end{aligned}\)

Here we point out that \(−a\) is equivalent to \(−1a\); therefore, we choose to divide both sides of the equation by \(−1\).

\(\begin{array} { c } { - a = - 2 } \\ { \frac { - 1 a } { \color{Cerulean}{- 1} }\color{Black}{ =} \frac { - 2 } { \color{Cerulean}{- 1} } } \\ { a = 2 } \end{array}\)

Alternatively, we can multiply both sides of \(−a=−2\) by negative one and achieve the same result.

\(\begin{aligned} - a & = - 2 \\ \color{Cerulean}{( - 1 )}\color{Black}{ (} - a ) & = \color{Cerulean}{( - 1 )}\color{Black}{ (} - 2 ) \\ a & = 2 \end{aligned}\)

The solution is \(2\).

Exercise \(\PageIndex{2}\)

Solve: \(6 - 3 ( 4 x - 1 ) = 4 x - 7\).

Video Solution: www.youtube.com/v/NAIAZrFjU-o

The coefficients of linear equations may be any real number, even decimals and fractions. When this is the case it is possible to use the multiplication property of equality to clear the fractional coefficients and obtain integer coefficients in a single step. If given fractional coefficients, then multiply both sides of the equation by the least common multiple of the denominators (LCD).

Example \(\PageIndex{9}\):

Solve: \(\frac { 1 } { 3 } x + \frac { 1 } { 5 } = \frac { 1 } { 5 } x - 1\).

Clear the fractions by multiplying both sides by the least common multiple of the given denominators. In this case, it is the \(LCD (3, 5) = 15\).

\(\begin{aligned} \color{Cerulean}{15}\color{Black}{ \cdot} \left( \frac { 1 } { 3 } x + \frac { 1 } { 5 } \right) & = \color{Cerulean}{15}\color{Black}{ \cdot} \left( \frac { 1 } { 5 } x - 1 \right) \quad \color{Cerulean}{Multiply\: both\: sides\: by\: 15.} \\ \color{Cerulean}{15}\color{Black}{ \cdot} \frac { 1 } { 3 } x + \color{Cerulean}{15}\color{Black}{ \cdot} \frac { 1 } { 5 } & = \color{Cerulean}{15}\color{Black}{ \cdot} \frac { 1 } { 5 } x - \color{Cerulean}{15}\color{Black}{ \cdot} 1\quad\color{Cerulean}{Simplify.} \\ 5 x + 3 & = 3 x - 15\quad\quad\quad\color{Cerulean}{Solve.} \\ 2 x & = - 18 \\ x & = \frac { - 18 } { 2 } = - 9 \end{aligned}\)

The solution is \(−9\).

It is important to know that this technique only works for equations. Do not try to clear fractions when simplifying expressions. As a reminder:

Table 1.1.2

We simplify expressions and solve equations. If you multiply an expression by \(6\), you will change the problem. However, if you multiply both sides of an equation by \(6\), you obtain an equivalent equation.

Table 1.1.3

Applications Involving Linear Equations

Algebra simplifies the process of solving real-world problems. This is done by using letters to represent unknowns, restating problems in the form of equations, and by offering systematic techniques for solving those equations. To solve problems using algebra, first translate the wording of the problem into mathematical statements that describe the relationships between the given information and the unknowns. Usually, this translation to mathematical statements is the difficult step in the process. The key to the translation is to carefully read the problem and identify certain key words and phrases.

Table 1.1.4

When translating sentences into mathematical statements, be sure to read the sentence several times and parse out the key words and phrases. It is important to first identify the variable, “ let x represent… ” and state in words what the unknown quantity is. This step not only makes our work more readable, but also forces us to think about what we are looking for.

Example \(\PageIndex{10}\):

When \(6\) is subtracted from twice the sum of a number and \(8\) the result is \(5\). Represent this as an algebraic equation and find the number.

Let n represent the unknown number.

To understand why we included the parentheses in the set up, you must study the structure of the following two sentences and their translations:

Table 1.1.5

The key was to focus on the phrase “ twice the sum ,” this prompted us to group the sum within parentheses and then multiply by \(2\). After translating the sentence into a mathematical statement we then solve.

\(\begin{aligned} 2 ( n + 8 ) - 6 & = 5 \\ 2 n + 16 - 6 & = 5 \\ 2 n + 10 & = 5 \\ 2 n & = - 5 \\ n & = \frac { - 5 } { 2 } \end{aligned}\)

\(\begin{aligned} 2 ( n + 8 ) - 6 & = 2 \left( \color{Cerulean}{- \frac { 5 } { 2 }}\color{Black}{ +} 8 \right) - 6 \\ & = 2 \left( \frac { 11 } { 2 } \right) - 6 \\ & = 11 - 6 \\ & = 5 \quad\color{Cerulean}{✓}\end{aligned}\)       

The number is \(−\frac{5}{2}\).

General guidelines for setting up and solving word problems follow.

• Step 1: Read the problem several times, identify the key words and phrases, and organize the given information.
• Step 2: Identify the variables by assigning a letter or expression to the unknown quantities.
• Step 3: Translate and set up an algebraic equation that models the problem.
• Step 4: Solve the resulting algebraic equation.
• Step 5: Finally, answer the question in sentence form and make sure it makes sense (check it).

For now, set up all of your equations using only one variable. Avoid two variables by looking for a relationship between the unknowns.

Linear Inequalities

A linear inequality 138 is a mathematical statement that relates a linear expression as either less than or greater than another. The following are some examples of linear inequalities, all of which are solved in this section:

A solution to a linear inequality 139 is a real number that will produce a true statement when substituted for the variable.

Example \(\PageIndex{11}\):

Are \(x=−4\) and \(x=6\) solutions to \(5x+7<22\)?

Substitute the values in for \(x\), simplify, and check to see if we obtain a true statement.

Table 1.1.6

\(x=−4\) is a solution and \(x=6\) is not

Linear inequalities have either infinitely many solutions or no solution. If there are infinitely many solutions, we graph the solution set on a number line and/or express the solution using interval notation.

Expressing Solutions to Linear Inequalities

What number would make the inequality \(x>3\) true? Are you thinking, "\(x\) could be four"? That’s correct, but \(x\) could be 6, too, or 137, or even 3.0001. Any number greater than three is a solution to the inequality \(x>3\). We show all the solutions to the inequality \(x>3\) on the number line by shading in all the numbers to the right of three, to show that all numbers greater than three are solutions. Because the number three itself is not a solution, we put an open parenthesis at three.

We can also represent inequalities using interval notation . There is no upper end to the solution to this inequality. In interval notation, we express \(x>3\) as \((3,\infty)\). The symbol \(\infty\) is read as “ infinity .” It is not an actual number. Figure \(\PageIndex{2}\) shows both the number line and the interval notation.

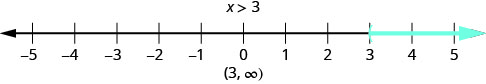
We use the left parenthesis symbol, (, to show that the endpoint of the inequality is not included. The left bracket symbol, [, would show that the endpoint is included.

The inequality \(x\leq 1\) means all numbers less than or equal to one. Here we need to show that one is a solution, too. We do that by putting a bracket at \(x=1\). We then shade in all the numbers to the left of one, to show that all numbers less than one are solutions (Figure \(\PageIndex{3}\)). There is no lower end to those numbers. We write \(x\leq 1x\leq 1 \)in interval notation as \((−\infty,1]\). The symbol \(−\infty\) is read as “negative infinity.”

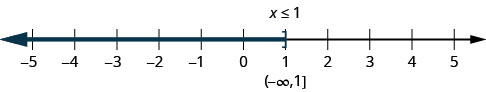
Figure \(\PageIndex{4}\) shows both the number line and interval notation.

INEQUALITIES, NUMBER LINES, AND INTERVAL NOTATION

The notation for inequalities on a number line and in interval notation use the same symbols to express the endpoints of intervals. Notice that \(\infty\) and \(-\infty\) always use parentheses in interval notation, never brackets.

Example \(\PageIndex{12}\)

Graph each inequality on the number line and write in interval notation.

• \(x\geq −3\)
• \(x<2.5\)
• \(x\leq −\frac{3}{5}\)

Exercise \(\PageIndex{3}\)

Graph each inequality on the number line and write in interval notation:

• \(x\leq −4\)
• \(x\geq 0.5\)
• \(x<−\frac{2}{3}\).

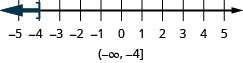
Solving Linear Inequalities

All but one of the techniques learned for solving linear equations apply to solving linear inequalities. You may add or subtract any real number to both sides of an inequality, and you may multiply or divide both sides by any positive real number to create equivalent inequalities. For example:

\[\begin{align*} 10 &> - 5 \\[4pt] 10{\color{Cerulean}{-7}}\,&{\color{Black}{>}} -5{\color{Cerulean}{-7}} & & {\color{Cerulean}{Subtract\: 7\: on\: both\: sides.}}\\[4pt]  3 &> - 12 & & \color{Cerulean}{✓}\quad\color{Cerulean}{True.} \\[20pt] 10 &>-5\\[4pt] \frac{10}{\color{Cerulean}{5}}\,&\color{Black}{>}\frac{-5}{\color{Cerulean}{5}} & & \color{Cerulean}{Divide\: both\: sides\: by\: 5.}\\[4pt] 2 &>-1 & & \color{Cerulean}{✓\:\:True} \end{align*} \]

Subtracting \(7\) from each side and dividing each side by positive \(5\) results in an inequality that is true.

Example \(\PageIndex{13}\):

Solve and graph the solution set: \(5x+7<22\).

\(\begin{array} { c } { 5 x + 7 < 22 } \\ { 5 x + 7 \color{Cerulean}{- 7}\color{Black}{ < 22}\color{Cerulean}{ - 7} } \\ { 5 x < 15 } \\ { \frac { 5 x } {\color{Cerulean}{ 5} } < \frac { 15 } { \color{Cerulean}{5} } } \\ { x < 3 } \end{array}\)

It is helpful to take a minute and choose a few values in and out of the solution set, substitute them into the original inequality, and then verify the results. As indicated, you should expect \(x=0\) to solve the original inequality and that \(x=5\) should not.

Table 1.1.7

Checking in this manner gives us a good indication that we have solved the inequality correctly.

We can express this solution in two ways: using set notation and interval notation.

\(\begin{array} { r } { \{ x | x < 3 \} } &\color{Cerulean}{Set\: notation} \\ { ( - \infty , 3 ) } &\color{Cerulean}{Interval\: notation} \end{array}\)

In this text we will choose to present answers using interval notation.

\((−∞,  3) \)

When working with linear inequalities, a different rule applies when multiplying or dividing by a negative number. To illustrate the problem, consider the true statement \(10 > −5\) and divide both sides by \(−5\).

\(\begin{array} { l } { 10 > - 5 } \\ { \frac { 10 } { \color{Cerulean}{- 5} } \color{Black}{>} \frac { - 5 } { \color{Cerulean}{- 5} } } \quad \color{Cerulean}{Divide\: both\: sides\: by\: -5.} \\ { - 2 \color{red}{>}\color{Black}{ 1} \quad \color{red}{✗} \color{Cerulean}{ False } } \end{array}\)

Dividing by \(−5\) results in a false statement. To retain a true statement, the inequality must be reversed.

\(\begin{array} { l } { 10 \color{OliveGreen}{>}\color{Black}{ - 5} } \\ { \frac { 10 } { \color{Cerulean}{- 5} } \color{Black}{<} \frac { - 5 } { \color{Cerulean}{- 5} } } \quad \color{Cerulean}{Reverse\: the\: inequality.} \\ { - 2 \color{OliveGreen}{<}\color{Black}{ 1} \quad \color{Cerulean}{✓} \color{Cerulean}{ True } } \end{array}\)

The same problem occurs when multiplying by a negative number. This leads to the following new rule: when multiplying or dividing by a negative number, reverse the inequality . It is easy to forget to do this so take special care to watch for negative coefficients. In general, given algebraic expressions \(A\) and \(B\), where \(c\) is a positive nonzero real number, we have the following properties of inequalities 140 :

Table 1.1.8

We use these properties to obtain an equivalent inequality 141 , one with the same solution set, where the variable is isolated. The process is similar to solving linear equations.

Example \(\PageIndex{14}\):

Solve and graph the solution set: \(−2(x+8)+6≥20\).

\(\begin{aligned} - 2 ( x + 8 ) + 6 & \geq 20 \quad\color{Cerulean}{Distribute.} \\ - 2 x - 16 + 6 & \geq 20 \quad\color{Cerulean}{Combine\: like\: terms.} \\ - 2 x - 10 & \geq 20 \quad\color{Cerulean}{Solve\: for\: x.} \\ - 2 x & \geq 30 \quad\color{Cerulean}{Divide\: both\: sides\: by\: -2.} \\ \frac { - 2 x } { \color{Cerulean}{- 2} } & \color{OliveGreen}{\leq} \frac { \color{Black}{30} } { \color{Cerulean}{- 2} } \quad\color{Cerulean}{Reverse\: the\: inequality.} \\ x & \leq - 15 \end{aligned}\)

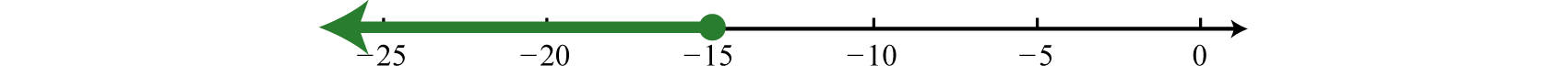
Interval notation \((−∞,  −15] \)

Example \(\PageIndex{15}\):

Solve and graph the solution set: \(−2(4x−5)<9−2(x−2)\).

\(\begin{array} { c } { - 2 ( 4 x - 5 ) < 9 - 2 ( x - 2 ) } \\ { - 8 x + 10 < 9 - 2 x + 4 } \\ { - 8 x + 10 < 13 - 2 x } \\ { - 6 x < 3 } \\ { \frac { - 6 x } { \color{Cerulean}{- 6} } \color{OliveGreen}{>} \frac { \color{Black}{3} } { \color{Cerulean}{- 6} } }\color{Cerulean}{Reverse\:the\:inequality.} \\ { x > - \frac { 1 } { 2 } } \end{array}\)

Interval notation \((−\frac{1}{2}, ∞)\)

Example \(\PageIndex{16}\):

Solve and graph the solution set: \(\frac{1}{2}x−2≥\frac{1}{2}(\frac{7}{4}x−9)+1\).

\(\begin{array} { c } { \frac { 1 } { 2 } x - 2 \geq \frac { 1 } { 2 } \left( \frac { 7 } { 4 } x - 9 \right) + 1 } \\ { \frac { 1 } { 2 } x - 2 \geq \frac { 7 } { 8 } x - \frac { 9 } { 2 } + 1 } \\ { \frac { 1 } { 2 } x - \frac { 7 } { 8 } x \geq - \frac { 7 } { 2 } + 2 } \\ { - \frac { 3 } { 8 } x \geq - \frac { 3 } { 2 } } \\ { \left( \color{Cerulean}{- \frac { 8 } { 3 }} \right) \left(\color{Black}{ - \frac { 3 } { 8 } x} \right) \leq \left( \color{Cerulean}{- \frac { 8 } { 3 }} \right) \left( \color{Black}{-} \frac { 3 } { 2 } \right) \quad \color{Cerulean} { Reverse\: the\: inequality. } } \\ { x \leq 4 } \end{array}\)

Interval notation: \((−∞,  4]\)

Exercise \(\PageIndex{4}\)

Solve and graph the solution set: \(10 - 5 ( 2 x + 3 ) \leq 25\)

\([ - 3 , \infty )\);

Video Solution: www.youtube.com/v/COLLNtwYFm8

Translation of Linear Inequalities

Some of the key words and phrases that indicate inequalities are summarized below:

Table 1.1.9

Key Takeaways

• Solving general linear equations involves isolating the variable, with coefficient \(1\), on one side of the equal sign. To do this, first use the appropriate equality property of addition or subtraction to isolate the variable term on one side of the equal sign. Next, isolate the variable using the equality property of multiplication or division. Finally, check to verify that your solution solves the original equation.
• If solving a linear equation leads to a true statement like \(0 = 0\), then the equation is an identity and the solution set consists of all real numbers, \(ℝ\).
• If solving a linear equation leads to a false statement like \(0 = 5\), then the equation is a contradiction and there is no solution, \(Ø\).
• Clear fractions by multiplying both sides of an equation by the least common multiple of all the denominators. Distribute and multiply all terms by the LCD to obtain an equivalent equation with integer coefficients.
• Simplify the process of solving real-world problems by creating mathematical models that describe the relationship between unknowns. Use algebra to solve the resulting equations.
• Inequalities typically have infinitely many solutions. The solutions are presented graphically on a number line or using interval notation or both.
• All but one of the rules for solving linear inequalities are the same as solving linear equations. If you divide or multiply an inequality by a negative number, reverse the inequality to obtain an equivalent inequality.

129 Statement indicating that two algebraic expressions are equal.

130 An equation that can be written in the standard form \(ax + b = 0\), where \(a\) and \(b\) are real numbers and \(a ≠ 0\).

131 Any value that can replace the variable in an equation to produce a true statement.

132 Equations with the same solution set.

133 Properties that allow us to obtain equivalent equations by adding, subtracting, multiplying, and dividing both sides of an equation by nonzero real numbers.

134 Allows you to solve for the variable on either side of the equal sign, because \(x = 5\) is equivalent to \(5 = x\).

135 Equations that are true for particular values.

136 An equation that is true for all possible values.

137 An equation that is never true and has no solution.