

Solving Absolute Value Equations
Solving absolute value equations is as easy as working with regular linear equations. The only additional key step that you need to remember is to separate the original absolute value equation into two parts: positive and negative ( ± ) components.
Below is the general approach on how to break them down into two equations:
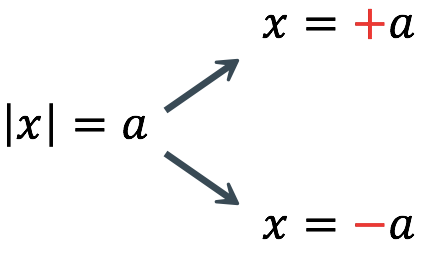
In addition, we also need to keep in mind the following key points regarding the setup above:
Key Points to Remember when Solving Absolute Value Equations
Key Point #1 : The sign of [latex]\left| x \right|[/latex] must be positive. For emphasis, [latex]\left| x \right| \to + \left| x \right|[/latex].
Key Point #2 : The [latex]x[/latex] inside the absolute value symbol, [latex]\left| {\,\,\,\,\,} \right|[/latex], could be any expressions.
Key Point #3 : The [latex]a[/latex] on the right side of the equation must be either a positive number or zero to have a solution.
Key Point #4 : If the [latex]a[/latex] on the right side is a negative number , then it has no solution.
Given the considerations above, there are instances where the right-hand side contains a variable. However, it could also be on the left, provided the opposite side has the absolute value expression.
To solve such cases, we follow the standard procedure, but it’s imperative to validate each solution by plugging it back into the original absolute value equation. If the substitution yields a true statement, the answer we found is included in the solution set. If not, it’s excluded.
See examples #8 and #9 to see the demonstrations of this concept in the practice problems below:
Absolute Value Expressions Practice Problems with Answers
Finally, there is another case that usually shows up when dealing with absolute value equations. That is, the equation contains absolute value expressions on both sides. Here’s the procedure how to work it out.
Suppose we have the absolute value equation
[latex]\left| {ax + b} \right| = \left| {cx + d} \right|[/latex]
Then, the two expressions must either be equal to each other or be negatives of each other.
[latex]ax + b = cx + d[/latex]
[latex]ax + b = – \left( {cx + d} \right)[/latex]
See examples #10 and #11 to see how it works in the practice problems found below:
Examples of How to Solve Absolute Value Equations
Example 1: Solve the absolute value equation [latex]\left| x \right| =\, – 5[/latex] .
The absolute value of any number is either positive or zero. But this equation suggests that there is a number whose absolute value is negative. Can you think of any numbers that can make the equation true? Well, there is none.
Since there’s no value of [latex]x[/latex] that can satisfy the equation, we say that it has no solution .
In fact, the following absolute value equations don’t have solutions as well.
Example 2: Solve the absolute value equation [latex] – \left| x \right| =\, – 5[/latex] .
Don’t be quick to conclude that this equation has no solution. Although the right side of the equation is negative, the absolute value expression itself must be positive. But it is not, right?
What we need is to eliminate first the negative sign of the absolute value symbol before we can proceed.
Observe that the given equation has a coefficient of −1 . Divide both sides of the equation by this value to get rid of the negative sign.
Since the absolute value expression and the number are both positive, we can now apply the procedure to break it down into two equations.
Therefore, the solution to the problem becomes
Therefore, the solution set is [latex]\{- 5,5\}[/latex].
You may verify our answers by substituting them back to the original equation. I’ll leave it to you.
Example 3: Solve the absolute value equation [latex]\left| {x – 5} \right| = 3[/latex] .
This problem is getting interesting since the expression inside the absolute value symbol is no longer just a single variable. Don’t worry; the set-up remains the same. Just be careful when you break up the given absolute value equation into two simpler linear equations, then proceed how you usually solve equations.
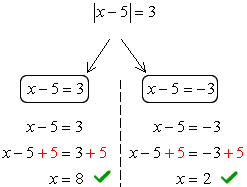
Therefore, the solution set is [latex]\{2,8\}[/latex].
You may check the answers back to the original equation.
Example 4: Solve the absolute value equation [latex]\left| { – 2x + 7} \right| = 25[/latex] .
You may think that this problem is complex because of the [latex]–2[/latex] next to the variable [latex]x[/latex]. However, that shouldn’t intimidate you because the key idea remains the same. We have the absolute value symbol isolated on one side and a positive number on the other. Solving this is just like another day in the park!
Break it up into the [latex]+[/latex] and [latex]-[/latex] components, then solve each equation.

Therefore, the solution set is [latex]\{- 9,16\}[/latex].
Example 5 : Solve the absolute value equation [latex]\left| { – 6x + 3} \right| – 7 = 20[/latex].
This one is not ready just yet to be separated into two components. Why? It is because the absolute value symbol is not by itself on one side of the equation. If you look at it, there is a [latex]-7[/latex] on the left side that must be eliminated first. Once we get rid of that, then we should be okay to proceed as usual.
Eliminate the [latex]-7[/latex] on the left side by adding both sides by [latex]\color{blue}7[/latex].
Now, we have an absolute value equation that can be broken down into two pieces.
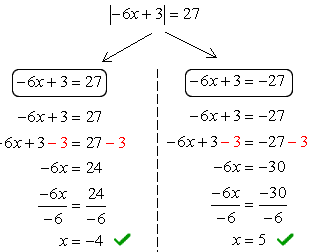
Therefore, the solution set is [latex]\{-4,5\}[/latex].
Example 6 : Solve the absolute value equation [latex] – 7\left| {9\, – 2x} \right| + 9 =\, – 12[/latex].
The absolute value expression is not isolated yet. Eliminate the [latex]+9[/latex] first and then the [latex]-7[/latex] which is currently multiplying the absolute value expression.
Now, let’s split them into two cases, and solve each equation.
Therefore, the solution set is [latex]\{3,6\}[/latex].
Example 7 : Solve the absolute value equation [latex]\left| {{x^2} + 2x – 4} \right| = 4[/latex].
This is an interesting problem because we have a quadratic expression inside the absolute value symbol. I hope you don’t get distracted by how it looks! If you’re faced with a situation in which you’re not sure how to proceed, stick to the basics and things that you already know.
We don’t care about the “stuff” inside the absolute value symbol. As long as it is isolated, and the other side is a positive number, we can definitely apply the rule to split the equation into two cases.
In fact, the only difference between this problem from what you’ve been doing so far is that you will be solving quadratic equations instead of linear equations.
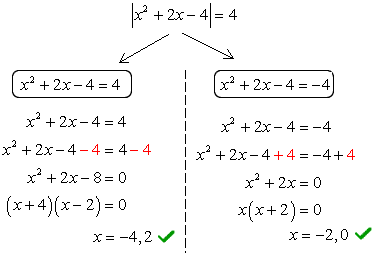
We can verify that our four answers or solutions are [latex]x = – \,4[/latex], [latex]-2[/latex], [latex]0[/latex], and [latex]2[/latex], by graphing the two functions and looking at their points of intersections.
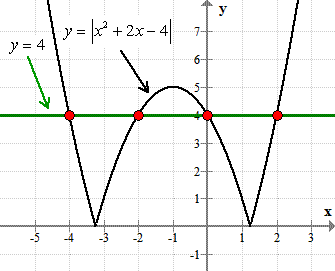
Therefore, the solution set is [latex]\{-4,-2,0,2\}[/latex].
Take a quiz:
Absolute Value Equations Quiz
You may also be interested in these related math lessons or tutorials:
Absolute Value Equations Practice Problems with Answers
Tough Absolute Value Equations
Graphing Absolute Value Functions Solving Absolute Value Inequalities

How to solve absolute value equations
|x + 5| = 3.
Worksheet on Abs Val Equations Abs Val Eqn Solver
The General Steps to solve an absolute value equation are:
- Rewrite the absolute value equation as two separate equations, one positive and the other negative
- Solve each equation separately
- After solving, substitute your answers back into original equation to verify that you solutions are valid
- Write out the final solution or graph it as needed
It's always easiest to understand a math concept by looking at some examples so, check outthe many examples and practice problems below.
You can always check your work with our Absolute value equations solver too
Practice Problems
Example equation.
Solve the equation: | X + 5| = 3
Click here to practice more problems like this one , questions that involve variables on 1 side of the equation.
Some absolute value equations have variables both sides of the equation. However, that will not change the steps we're going to follow to solve the problem as the example below shows:
Solve the equation: |3 X | = X − 21
Solve the following absolute value equation: | 5X +20| = 80
Solve the following absolute value equation: | X | + 3 = 2 X
This first set of problems involves absolute values with x on just 1 side of the equation (like problem 2 ).
Solve the following absolute value equation: |3 X −6 | = 21
Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!
Popular pages @ mathwarehouse.com.

Absolute Value Equation Calculator
What are absolute value equalities, how to use this absolute value equation calculator, how to solve absolute value equations by hand, how to graph absolute value equations, examples of absolute value equations.
Whenever you face absolute value equations, Omni's absolute value equation calculator is here to lend you a hand. With its help, you'll easily deal with all kinds of absolute value equalities , in particular equations where the absolute value is equal to 0. If you want to learn more about this topic, scroll down and learn:
- How to solve absolute value equations by hand ; and
- How to find an absolute value equation from a graph .
Once you're done here, take one step further in your mathematical journey and check out our absolute value inequalities calculator .
Let's briefly recall what the absolute value is, shall we? The absolute value of a real number x is the distance between this number and zero. We denote it by |x| . Algebraically:
- |x| = x if x is non-negative; and
- |x| = -x if x is negative.
For example:
- |0| = 0 ; and
In other words, the absolute value of a non-negative number is exactly this number, while for a negative number you have to throw away the minus sign .
💡 Did you know that absolute value is very popular in statistics? You can learn more via our tools:
- Mean absolute deviation calculator ; and
- Median absolute deviation calculator .
We can now move on and discuss what the absolute value equations are.
Absolute value equalities
In general, any equation involving the absolute value of any expression is an absolute value equality. It can involve, e.g., polynomial expressions, roots, exponents, logarithms, etc.
In school, you're most likely to encounter an absolute value equation of the linear expression bx+c , that is, an equation of the form
a * |bx + c| + d = e ,
where a, b, c, d, e are real coefficients. And here's where our absolute value equation calculator enters the stage!
Omni's absolute value equation calculator can help you solve absolute value equalities of the form a * |bx + c| + d = e . Here's a brief instruction on how to solve them most efficiently:
- Enter the coefficients a, b, c, d, e of your absolute value equality. Remember that neither a nor b can be equal to zero - we don't want x to disappear from the equation!
- Your equation will appear at the bottom of the calculator - verify that
everything is all right. 3. Below the equation, you'll see the solution to your absolute value equation as well! By default, the calculator uses 4 decimal places to display the solution. Click the Advanced mode to adjust the precision . 4. Turn the Show steps? option to Yes to see some intermediate computations performed by our tool. 5. Turn the Show graph? option to Yes to see how to graph your absolute value equation .
If you want to solve by hand an absolute value equation of the form a * |bx + c| + d = e , follow these steps:
- Simplify your equation : transfer d to the right-hand side and divide both sides by a . You'll get |bx + c| = (e - d)/a .
- If (e - d)/a < 0 , then you've got an absolute value equation with no solutions ;
- If (e - d)/a = 0 , then you've got an absolute value equation with one solution , which is equal to -c/b ; and
- If (e - d)/a > 0 , then your equation has two solutions . Let's find them.
- Omitting the absolute value, we have bx + c = (e - d)/a or bx + c = -(e - d)/a . It now suffices to calculate x for each equation.
- Finally, x = (e - d)/(a * b) - c/b or x = (d - e)/(a * b) - c/b .
As you can see, it's not at all hard to solve absolute value equations by hand. Practice a bit with our absolute value equation calculator, and you'll quickly become an expert! As the next step, you may want to learn how to find an absolute value equation from a graph .
Graphing absolute value equations of the form a * |bx + c| + d = e is simple, you only need to remember a few basic rules:
- Start by plotting bx + c . It is a straight line that contains the points (0,c) and (-c/b,0) .
- Reflect the negative part of this line (i.e., where y<0 ) through the horizontal axis to get |bx + c| .
- Multiplying by a is equivalent to changing the slope. Additionally, if a<0 , you have to reflect your plot one more time through the horizontal axis.
- Adding d boils down to moving the plot upwards or downwards, depending on whether d is positive or negative. In any case, you now have the plot of a * |bx + c| + d .
- Draw the line y = e . The points where the two graphs intersect (if there are any) are the solutions of your equations.
Example 1. Solve |2x + 5| = x + 4
We resolve the absolute value on the left-hand side. Clearly 2x + 5 ≥ 0 is equivalent to x ≥ -2.5 Consequently, we obtain -2x - 5 = x + 4 if x < -2.5 and 2x + 5 = x + 4 if x ≥ -2.5
Simplifying, we get -3x = 9 if x < -2.5 and x = 1 if x ≥ -2.5
As a result, we have x = -3 or x = 1 You can use our absolute value solver to graph this solution.
Example 2. Solve |x| = -|x - 1| + 1
1.We resolve the absolute value on the right-hand side: |x| = -x + 1 + 1 if x ≥ 1 and |x| = x - 1 + 1 if x < 1
Simplify: |x| = -x + 2 if x ≥ 1 and |x| = x if x < 1
We will solve the equation |x| = -x + 2 if x ≥ 1 . Resolve the absolute value on the left-hand side:
- x = -x + 2 if x ≥ 1 and x ≥ 0
- -x = -x + 2 if x ≥ 1 and x < 0
Note, that in the second equation we have a contradiction in the conditions. So we ignore this equation and only solve the first one.
Solution of the first equation: 2x = 2 if x ≥ 1 . So x = 1 is indeed a solution.
Next, we will solve the equation |x| = x if x < 1 . Resolve the absolute value on the left-hand side:
- x = x if x < 1 and x ≥ 0
- -x = x if x < 1 and x < 0
- 0 = 0 if 0 ≤ x < 1
- 2x = 0 if x < 0
- All x ∈ [0 , 1) satisfy the equation in question
- x = 0 does not satisfy the condition x < 0 , so this is not a solution.
So all x in the interval [0,1) are solutions to the equation |x| = x if x < 1 .
Final solution: We found that x = 1 and x ∈ [0 , 1) are solutions. Taking all of this together, we see that every x ∈ [0 , 1] is a solution to our problem.
With the help of our absolute value solver, you can train yourself to solve this kind of problem, and become a master of absolute value equations!
How many solutions can an absolute value equation have?
The number of solutions of an absolute value equation of the form a * |bx + c| + d = e depends on the sign of (e - d)/a . Namely, we have:
- Two solutions if (e -d)/a > 0 ;
- One solution if e = d ; and
- No solution if (e -d)/a < 0 .
Can an absolute value be equal to a negative number?
No, absolute values cannot be equal to negative numbers. This follows from the very definition of the absolute value of a number, which is the distance between zero and this number, and distances, as we all know, are always non-negative.
Can an absolute value be equal to 0?
Yes, but in a very special case. Namely, the only situation where the absolute value of a number is zero is when this number is zero: |x| = 0 if and only if x = 0 . A non-zero number will always have its absolute value equal to a positive number!
- Least Common Multiple Calculator
- Interval Notation Calculator
- Least Common Denominator Calculator
- Null Space Calculator
- Trig Identities Calculator
- Partial Fraction Decomposition Calculator
- Unit Rate Calculator
- Exponential Function Calculator
Study Guides > College Algebra
Solve an absolute value equation.
Now that we can graph an absolute value function, we will learn how to solve an absolute value equation. To solve an equation such as [latex]{8}=\left|{2}x - {6}\right|[/latex], we notice that the absolute value will be equal to 8 if the quantity inside the absolute value is 8 or -8. This leads to two different equations we can solve independently.
Knowing how to solve problems involving absolute value functions is useful. For example, we may need to identify numbers or points on a line that are at a specified distance from a given reference point.
An absolute value equation is an equation in which the unknown variable appears in absolute value bars. For example,
A General Note: Solutions to Absolute Value Equations
For real numbers [latex]A[/latex] and [latex]B[/latex], an equation of the form [latex]|A|=B[/latex], with [latex]B\ge 0[/latex], will have solutions when [latex]A=B[/latex] or [latex]A=-B[/latex]. If [latex]B<0[/latex], the equation [latex]|A|=B[/latex] has no solution.
How To: Given the formula for an absolute value function, find the horizontal intercepts of its graph.
- Isolate the absolute value term.
- Use [latex]|A|=B[/latex] to write [latex]A=B[/latex] or [latex]\mathrm{-A}=B[/latex], assuming [latex]B>0[/latex].
- Solve for [latex]x[/latex].
Example 4: Finding the Zeros of an Absolute Value Function
For the function [latex]f\left(x\right)=|4x+1|-7[/latex] , find the values of [latex]x[/latex] such that [latex]\text{ }f\left(x\right)=0[/latex] .
[latex]\begin{cases}0=|4x+1|-7\hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \text{Substitute 0 for }f\left(x\right).\hfill \\ 7=|4x+1|\hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \text{Isolate the absolute value on one side of the equation}.\hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ 7=4x+1\hfill & \text{or}\hfill & \hfill & \hfill & \hfill & -7=4x+1\hfill & \text{Break into two separate equations and solve}.\hfill \\ 6=4x\hfill & \hfill & \hfill & \hfill & \hfill & -8=4x\hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ x=\frac{6}{4}=1.5\hfill & \hfill & \hfill & \hfill & \hfill & \text{ }x=\frac{-8}{4}=-2\hfill & \hfill \end{cases}[/latex]

The function outputs 0 when [latex]x=1.5[/latex] or [latex]x=-2[/latex].
For the function [latex]f\left(x\right)=|2x - 1|-3[/latex], find the values of [latex]x[/latex] such that [latex]f\left(x\right)=0[/latex].
No. We may find one, two, or even no answers. For example, there is no solution to [latex]2+|3x - 5|=1[/latex].
How To: Given an absolute value equation, solve it.
- Use [latex]|A|=B[/latex] to write [latex]A=B[/latex] or [latex]A=\mathrm{-B}[/latex].
Example 5: Solving an Absolute Value Equation
Solve [latex]1=4|x - 2|+2[/latex].
Isolating the absolute value on one side of the equation gives the following.
The absolute value always returns a positive value, so it is impossible for the absolute value to equal a negative value. At this point, we notice that this equation has no solutions.
No. The graphs of [latex]f[/latex] and [latex]g[/latex] would not intersect. This confirms, graphically, that the equation [latex]1=4|x - 2|+2[/latex] has no solution.
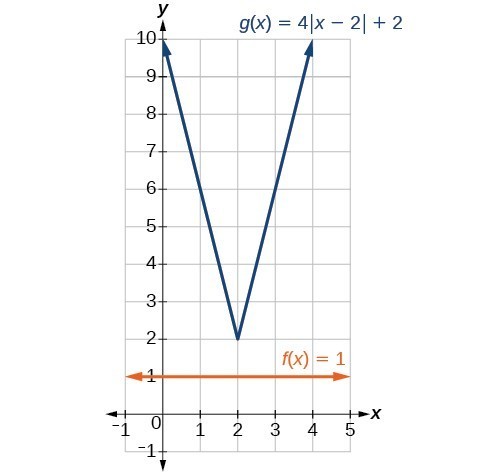
Find where the graph of the function [latex]f\left(x\right)=-|x+2|+3[/latex] intersects the horizontal and vertical axes.
Licenses & Attributions
Cc licensed content, shared previously.
- Precalculus. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution . License terms: Download For Free at : http://cnx.org/contents/ [email protected] ..
Please add a message.
Message received. Thanks for the feedback.

- Mathematicians
- Math Lessons
- Square Roots
- Math Calculators
- Solving Absolute Value Equations – Methods & Examples
JUMP TO TOPIC
What is Absolute Value?
Practice questions, solving absolute value equations – methods & examples.
Solving equations containing an absolute value is as simple as working with regular linear equations . Before we can embark on solving absolute value equations, let’s take a review of what the word absolute value means.
In mathematics, the absolute value of a number refers to the distance of a number from zero, regardless of direction. The absolute value of a number x is generally represented as | x | = a, which implies that, x = + a and -a.
We say that the absolute value of a given number is the positive version of that number . For example, the absolute value of negative 5 is positive 5, and this can be written as: | − 5 | = 5.
Other examples of absolute values of numbers include: |− 9| = 9, |0| = 0, − |−12| = −12 etc. From these examples of absolute values, we simply define absolute value equations as equations containing expressions with absolute value functions.
How to Solve Absolute Value Equations?
The following are the general steps for solving equations containing absolute value functions:
- Isolate the expression containing the absolute value function.
- Get rid of the absolute value notation by setting up the two equations so that in the first equation, the quantity inside absolute notation is positive. In the second equation, it is negative. You will remove the absolute notation and write the quantity with its suitable sign.
- Calculate the unknown value for the positive version of the equation.
- Solve for the negative version of the equation, in which you will first multiply the value on the other side of the equal sign by -1, and then solve.
In addition to the above steps, there are other important rules you should keep in mind when solving absolute value equations.
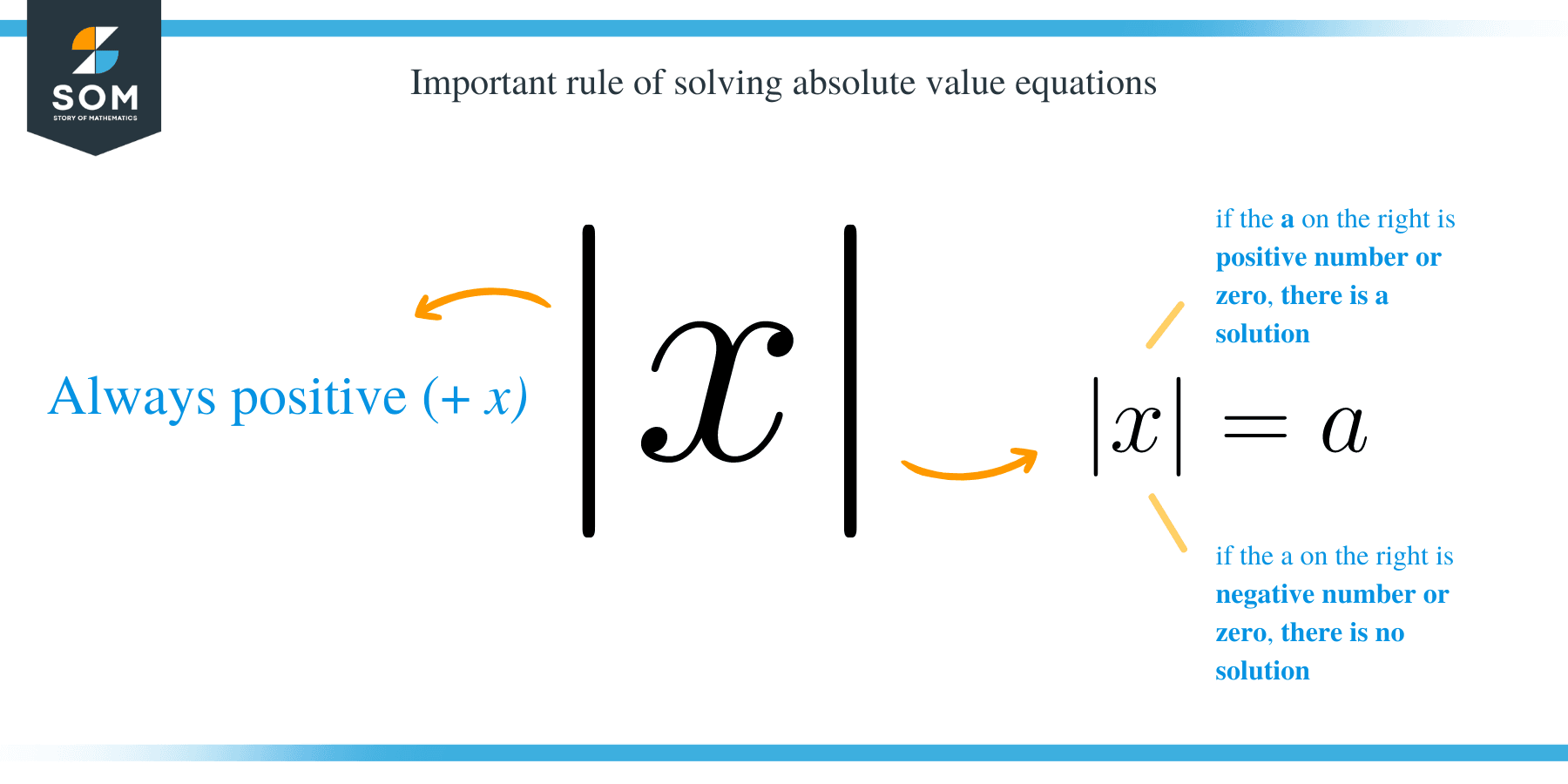
- The ∣x∣is always positive: ∣x∣ → +x.
- In | x| = a, if the a on the right is a positive number or zero, then there is a solution.
Solve the equation for x: |3 + x| − 5 = 4.
- Isolate the absolute value expression by applying the Law of equations. This means, we add 5 to both sides of the equation to obtain;
| 3 + x | − 5 + 5 = 4 + 5
| 3 + x |= 9
- Calculate for the positive version of the equation. Solve the equation by assuming the absolute value symbols.
| 3 + x | = 9 → 3 + x = 9
Subtract 3 from both sides of the equation.
3 – 3 + x = 9 -3
- Now calculate for the negative version of the equation by multiplying 9 by -1.
3 + x | = 9 → 3 + x = 9 × ( −1)
Also subtract 3 from both side to isolate x.
3 -3 + x = – 9 -3
Therefore 6 and -12 are the solutions.
Solve for all real values of x such that | 3x – 4 | – 2 = 3.
- Isolate the equation with absolute function by add 2 to both sides.
= | 3x – 4 | – 2 + 2 = 3 + 2
= | 3x – 4 |= 5
Assume the absolute signs and solve for the positive version of the equation.
| 3x – 4 |= 5→3x – 4 = 5
Add 4 to both sides of the equation.
3x – 4 + 4 = 5 + 4
Divide: 3x/3 =9/3
Now solve for the negative version by multiplying 5 by -1.
3x – 4 = 5→3x – 4 = -1(5)
3x – 4 = -5
3x – 4 + 4 = – 5 + 4
Divide by 3 on both sides.
Therefore, 3 and 1/3 are the solutions.
Solve for all real values of x: Solve | 2 x – 3 | – 4 = 3
Add 4 to both sides.
| 2 x – 3 | -4 = 3 →| 2 x – 3 | = 7
Assume the absolute symbols and solve for the positive version of x.
2 x – 3 = 7
2x – 3 + 3 = 7 + 3
Now solve for the negative version of x by multiplying 7 by -1
2 x – 3 = 7→2 x – 3 = -1(7)
Add 3 to both sides.
2x – 3 + 3 = – 7 + 3
x = – 2
Therefore, x = –2, 5
Solve for all real numbers of x: | x + 2 | = 7
Already the absolute value expression is isolated, therefore assume the absolute symbols and solve.
| x + 2 | = 7 → x + 2 = 7
Subtract 2 from both sides.
x + 2 – 2 = 7 -2
Multiply 7 by -1 to solve for the negative version of the equation.
x + 2 = -1(7) → x + 2 = -7
Subtract by 2 on both sides.
x + 2 – 2 = – 7 – 2
Therefore, x = -9, 5
Previous Lesson | Main Page | Next Lesson
Absolute Value Equation Calculator
What do you want to calculate.
- Solve for Variable
- Practice Mode
- Step-By-Step
Example (Click to try)
About absolute value equations.
- Get the absolve value expression by itself.
- Set up two equations and solve them separately.
Absolute Value Equation Video Lesson
- Khan Academy Video: Absolute Value Equations
Need more problem types? Try MathPapa Algebra Calculator
Clear Absolute Value Equation Calculator »
Reset password New user? Sign up
Existing user? Log in
Absolute Value Equations
Already have an account? Log in here.
- Pranshu Gaba
- Alan Enrique Ontiveros Salazar
- Kai Hsien Boo
- Agnishom Chattopadhyay
- Aditya Virani
- Prince Loomba
- Keshav Ramesh
Absolute value equations are equations involving expressions with the absolute value functions . This wiki intends to demonstrate and discuss problem solving techniques that let us solve such equations.
A very basic example would be as follows:
Find all values of \(x\) satisfying \(|x-2| + |x-4| = 4.\)
Usually, the basic approach is to analyze the behavior of the function before and after the point where they reach 0. For example, for \(|x-a|\) one could analyze the cases where \(x > a\) or \(x < a\), or even \(x = a\) if required. However, these problems are often simplified with a more sophisticated approach like being able to eliminate some of the cases, or graphing the functions. In this wiki, we intend to discuss this techniques along with strategies on when to use which.
Methodology
Technique - squaring both sides, technique - casework, technique - sketching graph, problem solving - miscellaneous.
Introduction to absolute value equations
Methodology to solve absolute value equations: the techniques used to solve absolute value equations and when to use which one
Take an example to describe the following methodology:
1) Understanding absolute value--positive, negative case (or graph approach) 2) Determining possible solutions 3) Verifying solutions
Explain - How do we use this technique to solve absolute value equations?
Remember to verify the possible solutions - why and how?
2-3 examples in increasing order of difficulty - explaining how we squared both sides to solve more difficult problems
Followed by 1-2 TIY problems - relevant to be solved by case work technique
Suppose we have an equation of the form \(\lvert a \rvert = \lvert b \rvert\). Since both sides are positive, we can square them without adding extraneous solutions: \[a^2=b^2.\] Then solve it as an ordinary equation: \[\begin{align} a^2-b^2&=0 \\ (a+b)(a-b)&=0. \end{align}\] So we see that \(a=-b\) or \(a=b\).
Solve the equation \(\lvert 3x+4 \rvert = \lvert 2x-7 \rvert\) for real \(x\). We square both sides to obtain \[(3x+4)^2=(2x-7)^2.\] Here we don't need to expand both sides; just apply the difference of two squares to find the factors: \[\begin{align} (3x+4+2x-7)(3x+4-2x+7)&=0 \\ (5x-3)(x+11)&=0. \end{align} \] The solutions are \(\left\{\frac{3}{5}, -11\right\}. \ _ \square\)
Because absolute value can be defined as piecewise functions, depending on where the value of \(x \) is with respect to the number line, you have to work with a different "piece" of the piecewise function.
General steps:
Using the definition of absolute value as a piecewise function, "undo" the absolute value sign(s) and write cases. For example, we know that the expression in the absolute value sign can either be positive or negative.
Solve each case for \( x\).
Verify the solutions.
Find all real values of \(x\) such that \( | 3x – 4 | – 2 = 3.\) We first isolate the absolute value onto one side: \[\begin{align} | 3x – 4 | – 2 & = 3\\ | 3x – 4 | &= 5. \end{align}\] Now, we "undo" the absolute value signs and split the equation into its two cases, the positive case and the negative case: \[\begin{array}{rlcccrl} (3x – 4) &= 5 &&\text{ or } && –(3x – 4) &= 5\\ 3x – 4 &= 5 &&\text{ or } && –3x + 4 &= 5\\ 3x &= 9 &&\text{ or } && –3x &= 1\\ x &= 3 &&\text{ or } && x &= –\frac{1}{3}. \ _\square \end{array}\]
Find all real values of \(x \) such that \( |x+1| + |2x+3| = 5 \). There are four possible cases, but one will be eliminated due to impossibility: Case 1. If \(x+1 \) and \( 2x+3 \) are both positive, then \[\begin{align} x+1 + 2x+3 &= 5 \\ 3x + 4 &= 5 \\ 3x &= 1 \\ x &= \dfrac{1}{3}. \end{align} \] Case 2. If \( x+1 \) is negative and \( 2x + 3 \) is positive, then \[\begin{align} - x - 1 + 2x + 3 &= 5 \\ x + 2 &= 5 \\ x &= 3. \end{align} \] However, when \( x = 3 \), \( x+1 \) and \( 2x+3 \) are both positive, so this is not a valid solution to the equation. Case 3. If \( x+1 \) and \( 2x+3 \) are both negative, then \[\begin{align} -x - 1 - 2x - 3 &= 5 \\ -3x - 4 &= 5 \\ -3x &= 9 \\ x &= -3. \end{align} \] Case 4. If \( x +1 \) is positive and \( 2x + 3 \) is negative, it is an impossible case. Graph the two lines if you are not convinced. Therefore, the solution set is \(\left \{ -3, \frac{1}{3} \right \}.\ _\square\)
Find all real values of \(x\) such that \[|x+2|+|2x+6|+|3x-3|=12.\] In this problem we are dealing with 3 terms of absolute values. Their turning points (the values of \(x\) such that they change sign) of the three terms are \(x=-2, x=-3, x=1,\) respectively. Hence, we need to check the cases \(-\infty < x \leq -3\), \(-3<x\leq -2\), \(-2 < x \leq 1\), \(1<x<\infty\). Case 1. \(\, -\infty < x \leq -3\) In this case, the three terms will always be negative. Hence, \[\begin{aligned} -(x+2)-(2x+6)-(3x-3)&=12 \\ x &= -\frac{17}{6}. \end{aligned}\] However, \(x=-\frac{17}{6} >-3\) is not within the domain \(-\infty < x \leq -3\). Thus this solution is not valid. Case 2. \(\, -3<x\leq -2\) In this case, the three terms will be negative, positive, and negative, respectively. Hence, \[\begin{aligned} -(x+2)+(2x+6)-(3x-3)&=12 \\ x &= -\frac{5}{2}. \end{aligned}\] \(x=-\frac{5}{2}\) lies between \(-3\) and \(-2\). Thus \(\boxed{x=-\frac{5}{2}}\) is one of the solutions. Case 3. \(\, -2 < x \leq 1\) In this case, the three terms will be positive, positive, and negative, respectively. However, \[\begin{aligned} (x+2)+(2x+6)-(3x-3)=11 \neq 12. \end{aligned}\] Thus there is no solution within this domain. Case 4. \(\, 1<x<\infty\) In this case, the three terms are always positive. Hence, \[\begin{aligned} (x+2)+(2x+6)+(3x-3)&=12 \\ x &= \frac{7}{6}, \end{aligned}\] which lies between \(1\) and \(\infty\). Thus \(\boxed{x=\frac{7}{6}}\) is another solution. In conclusion, \(x=-\frac{5}{2}\) and \(x=\frac{7}{6}\) are the solutions for the given equation. \(_\square\)
Find all real values of \( x \) such that \( |x||x+1| = 2 \). Case 1. \(\, x, x+1 \) both positive \[\begin{align} x(x+1)-2 &= 0 \\ x^2 +x - 2 &= 0 \\ x &= 1, x = -2. \end{align} \] Reject \( x = -2 \) because it does not make both \(x \) and \( x +1 \) positive. Case 2. \(\, x\) negative, \( x + 1 \) positive \[\begin{align} -x(x+1)-2 &= 0 \\ -x^2 - x - 2 &= 0 \\ x^2 + x + 2 &= 0 \\ x &= \dfrac{-1 \pm \sqrt{1 - 4 \cdot 1 \cdot 2 }}{2}. \end{align} \] We only asked for real solutions, so at this point we ignore this case because we're going to get imaginary results. Case 3. \(\, x\) positive, \( x +1 \) negative This is an impossible case (graph the lines and you'll see why), so we can ignore it. Case 4. \(\, x, x+1 \) both negative Because they're both negative, the negatives end up "canceling" and become positive, which was what we had in Case 1. However, the restriction is different from Case 1 (here, both \( x \) and \( x +1 \) have to be negative, not positive ), so instead of rejecting \( x = -2 \), we reject \( x = 1 \) from this case. Basically, in this specific case 4, \( x = 1 \) is not a possible solution, but it does not mean it's not a possible solution for Case 1 because we're simply going piece by piece in this piecewise function--in the end we will take the union of all possible solutions. Thus, the solutions are \( \left \{ -2, 1 \right \} \). \(_\square\)
Sometimes absolute value equations have a ridiculous number of cases and it would take too long to go through every single case. Therefore, we can instead graph the absolute value equations using the definition of absolute value as a piecewise function. To get each piece, you must figure out the domain of each piece. This method is highly beneficial when the question writer asks for the number of solutions instead of the actual solutions. Let's work through some examples to see how this is done.
Find all real solutions to \( |3x-4| = 5 \). To graph this, there are two possible cases: when \( 3x - 4\) is positive, and when \( 3x-4 \) is negative. When is \( 3x-4 \) positive? \[\begin{align} 3x - 4 &> 0 \\ 3x &> 4 \\ x &> \dfrac{4}{3}. \end{align} \] (Also, when \( x < \frac{4}{3} \), \( 3x- 4 \) will be negative.) We know that there will be a "turning point" at \( x = \frac{4}{3} \) for the graph of \( y = |3x-4| \). Finally, using the definition of absolute value, we know that when \( x > \frac{4}{3} \), \( y = 3x - 4 \), and when \( x \leqslant \frac{4}{3} \), \( y = -3x + 4 \). We now just need to graph \( y = 5 \) and look for the intersections. You can see that the solutions are \(\left \{ -\frac{1}{3} , 3 \right \}.\ _\square\). Another benefit of this graphing technique is that you do not need to verify any of the solutions--since we are only graphing the pieces that are actually mathematically possible, we get all the solutions we are looking for, no less and no more. If you could not discern the solutions from the picture, you can simply solve the equation for each case.
Find all real solutions to \( |x+1| + |2x+3| = 5 \). The possible cases are that \(\hspace{0.5cm}\) 1. \( \, x+1, 2x+3 \) are both positive; \(\hspace{0.5cm}\) 2. \( \, x+1 \) is negative and \( 2x+3 \) is positive; \(\hspace{0.5cm}\) 3. \( \, x+1 , 2x + 3 \) are both negative. We need to figure out the domains for which each of these holds. Case 1 holds when \( x > -1 \). Case 2 holds when \( -\frac{3}{2} < x< -1 \). Case 3 holds when \( x < -\frac{3}{2} \). Now, let's write our piecewise function. When \( x > -1 \), we have \( y = x+1 + 2x + 3 = 3x + 4 \). When \( -\dfrac{3}{2} < x< -1 \), we have\( y = -x -1 + 2x + 3 = x + 2 \). When \( x < - \dfrac{3}{2} \), we have \( y = -x - 1 -2x - 3 = -3x -4 \). As you can see in the graph, the solutions for the given equation are \(\left \{ -3, \frac{1}{3} \right \}.\ _\square\) .
Find all real solutions to \( |x||x+1| = 2 \). To graph this, we again only look at the possible cases and when they would occur: \(\hspace{0.5cm}\) 1. \(\, x, x+1 \) both positive \(\hspace{0.5cm}\) 2. \(\, x \) negative, \( x+1 \) positive \(\hspace{0.5cm}\) 3. \(\, x, x+1 \) both negative. Case 1 is true when \( x>0 \). Case 2 is true when \( -1 < x < 0 \). Case 3 is true when \( x<-1 \). When \( x>0 \) and when \( x< -1 \), we have \( y = x(x+1) = x^2 + x \). When \( -1 < x < 0 \), we have \( y = -x(x+1) = -x^2 - x \). It is evident that the solutions are \(\{-2, 1\}.\ _\square\)
Any other technique (fact, definition) you can use to solve the problems? Otherwise move on to the followings.
3-4 examples solved by using a mix of more than one of above techniques
Add guiding text in between. Guiding text means phrasing the section in a way that it keeps on telling the reader what's going on in this section.
3-4 TIY problems - using multiple techniques to solve
What is the sum of all real numbers \(x\) satisfying \[ x^2-\sqrt{x^2} = \lvert x-1 \rvert +5?\] Observe that \(\sqrt{x^2}=\lvert x \rvert.\) Then the given equation becomes \[ x^2-\lvert x \rvert= \lvert x-1 \rvert +5.\] If \(x<0,\) then we rewrite the equation to obtain \[\begin{align} x^2-(-x)&=-(x-1)+5\\ x^2+2x-6&=0\\ x&=-1\pm \sqrt{7}\\ x&=-1-\sqrt{7}. \qquad (\text{since } x<0) \end{align}\] If \(0\le x<1,\) then we rewrite the equation to obtain \[\begin{align} x^2-x&=-(x-1)+5\\ x^2&=6\\ x&=\pm \sqrt{6}, \end{align}\] which do not satisfy the assumption \(0\leq x<1.\) Thus there are no solutions in this interval. If \(x\ge 1,\) then we rewrite the equation to obtain \[\begin{align} x^2-x&=x-1+5\\ x^2-2x-4&=0\\ x&=1\pm \sqrt{5}\\ x&=1+\sqrt{5}. \qquad (\text{since } x\ge 1) \end{align}\] Therefore, the above three cases give two solutions \(x=-1-\sqrt{7}\) and \(x=1+\sqrt{5},\) the sum of which is \(\sqrt{5}-\sqrt{7}.\) \(_\square\)
[IMO 1959/2] Solve the equation \(\sqrt{x+\sqrt{2x-1}}+\sqrt{x-\sqrt{2x-1}}=A\) for real \(x\) (where the square roots are only defined for non-negative values), when \(A=\sqrt{2}\); \(A=1\); \(A=2\). Here we don't see any absolute value involved with the equation. Before doing anything, note that our first restriction for \(x\) is \(x \geq \frac{1}{2}\) and for \(A\) is \(A>0\). Intuitively, we could square both sides to get rid of some square roots: \[\begin{align} x+\sqrt{2x-1}+x-\sqrt{2x-1}+2\sqrt{x^2-(2x-1)}&=A^2 \\ 2x+2\sqrt{(x-1)^2}&=A^2. \end{align}\] Great! We find a perfect square inside the square root, so an absolute value will appear: \[2x+2|x-1|=A^2.\] Now we are going to find the possible cases for \(A\): When \(x-1 > 0\), we have \[\begin{align} 2x+2(x-1)&=A^2 \\ x&=\dfrac{A^2+2}{4}. \end{align}\] Then, by our assumption of \(x-1 > 0\), we get that this solution only works when \(A^2 > 2\). When \(x-1 \leq 0\), something interesting happens: \[\begin{align} 2x-2(x-1)&=A^2 \\ 2&=A^2. \end{align}\] So, when \(A^2=2 (\text{or }A=\sqrt{2})\), the equation becomes independent of \(x\), implying that any value of the interval \(x \in \left[\frac{1}{2},1\right]\) will be a solution for the first point. When \(A=1\), there are no solutions by our restriction of \(A^2 \geq 2\). Finally, when \(A=2\) we have \[x=\dfrac{2^2+2}{4}=\frac{3}{2}.\ _\square\] What happens if we allow the square roots to admit negative values?
Sometimes, in minimization problems, it often helps us to see that the value of an expression inside the absolute value is at least 0.
\[ y = \Big| \big| \small| x - 5 \small| + 5 \big| - 5 \Big| + 5 \]
What is the smallest possible value of \(y\)?
\[\] Notation : \( | \cdot | \) denotes the absolute value function.
Problem Loading...
Note Loading...
Set Loading...
MathBootCamps
Absolute value equations.
Solving absolute value equations is based on the idea that absolute value represents the distance between a point on the number line and zero. In this lesson, we will look at a few examples to understand how to solve these equations and also take a bit of a look at this idea of distance as it relates to solving absolute value equations. Table of Contents
Steps for solving absolute value equations
- Step-by-step examples
- Absolute value equations with no solutions or one solution
- Why does our method work?
Another perspective
[adsenseWide]
When given an absolute value equation, you will first need to isolate the absolute value part of the equation. Then, you will write two equations based on the definition of absolute value (though sometimes, there will end up only being one equation). This sounds complicated, but it is only a step or two more than solving the typical linear equation.

Let’s try these steps out with some examples!
In this first example, the absolute value part of the equation is already isolated, so only step two will apply. Whether or not this first step applies or not, you will always have zero, one, or two solutions to any absolute value equation.
Solve the equation: \(|5x – 2| = 13\)
As mentioned, the absolute value part is already isolated. Therefore, we will solve two equations without the absolute value: one where the 13 is positive and one where 13 is negative.
Equation 1:
\(\begin{align}5x – 2 &= 13\\ 5x &= 15\\ x &= 3\end{align}\)
Equation 2:
\(\begin{align}5x – 2 &= -13\\ 5x &= -11 \\ x &= -\dfrac{11}{5}\end{align}\)
So, there are two solutions to this equation: \(x = \bbox[border: 1px solid black; padding: 2px]{3, -\dfrac{11}{5}}\)
In this next example, there will be a little more work since the absolute value part of the equation is not isolated. In this situation, you will always need to isolate this term before you write your two equations, or you will end up with incorrect answers.
Solve the equation: \(4 + 3|x – 5| = 16\)
Your first step here is to use algebra to isolate the absolute value part of the equation.
\(4 + 3|x – 5| = 16\)
Subtract 4 from both sides.
\(3|x – 5| = 12\)
Divide both sides by 3.
\(|x – 5| = 4\)
Now you can write and solve two equations, one where the 4 is negative and one where the 4 is positive. Remember to drop the absolute value symbol at this step.
\(\begin{align}x – 5 &= 4\\ x &= 9\end{align}\)
\(\begin{align}x – 5 &= -4\\ x &= 1\end{align}\)
Once again, there are two solutions to the equation: \(x = \bbox[border: 1px solid black; padding: 2px]{1, 9}\)

Absolute value equations with one solution or no solutions
In both of our examples above, there were two solutions so you may think that this is always the case. While this is often right, there are cases where there is only one solution and even when there are none. The next two examples will show when this happens.
Example – one solution
Solve the equation: \(6|x – 2| – 1 = -1\)
As usual, we will first isolate the absolute value equation.
\(6|x – 2| – 1 = -1\)
Add 1 to both sides.
\(6|x – 2| = 0\)
Divide both sides by 6.
\(|x – 2| = 0\)
Normally at this stage, we would write two equations without the absolute value bars, but writing 0 with a positive or negative is the same thing. So we only have one equation:
\(x – 2 = 0\)
Adding 2 to both sides then gives the only solution.
\(x = \bbox[border: 1px solid black; padding: 2px]{2}\)
We will look more closely at why this happens, but first let’s look at how you might end up with no solutions.
Example – no solutions
Solve the equation: \(|10x – 1| + 3 = -8\)
To isolate the absolute value, subtract 3 from both sides.
\(|10x – 1| = -11\)
At this step, it can be determined that there are no solutions to the equation. Why? The absolute value of any number is positive. Here, we have the absolute value of something is negative. This is not possible so there are no possible x-values that make this equation true. Therefore, you can write:
Answer : No solutions
The absolute value of any number is always positive. Use this to determine when there are no solutions to an absolute value equation.
Notice that in both examples, the steps were the same as before. You will always follow those two steps when solving any absolute value equation.
Why does this work?
You can think of the absolute value of any number as representing how far it is from zero on the number line. Consider \(|3|\) and \(|–3|\) below.

This is why the absolute value is always positive – it is representing a distance. Now think of an equation where the absolute value part is isolated, such as \(|5x + 1| = 2\). Is the absolute value is 2, then all you know is that \(5x + 1\) is 2 units from zero on the number line. This gives two possibilities:

So this is why we end up with two different equations. In the case of only one solution, you end up with an absolute value expression equal to zero. Since this means that the distance from zero on the number line is zero, you end up with only one equation.
When you study the graphs of absolute value equations, you can see the three cases of one solution, no solution, and two solutions graphically. This is due to the shape of the graph of the absolute value function. This is a bit beyond the scope of this lesson, but in the graph below, you can see the graph of \(y = |x – 1|\) and \(y = 2\). Notice that the two graphs intersect at two points. These represent the two solutions to the equation \(|x – 1| = 2\).
You can probably see how a horizontal line might cross the graph at exactly one point (one solution) or at no points (no solutions). This would be just changing the number on the right hand side of the equation.
Absolute value equations are always solved with the same steps: isolate the absolute value term and then write equations based on the definition of the absolute value. There may end up being two solutions, one solution, or no solutions. To catch when there is no solution, always remember that absolute values must be positive, but remember to apply this idea only after the absolute value term has been isolated.
Share this:
- Click to share on Twitter (Opens in new window)
- Click to share on Facebook (Opens in new window)
Understanding math topics without memorization
Absolute Value: Notation, Expressions, Equations

What Does Absolute Value Mean?
The term “Absolute Value” refers to the magnitude of a quantity without regard to sign. In other words, its distance from zero expressed as a positive number.
The notation used to indicate absolute value is a pair of vertical bars surrounding the quantity, sort of like a straight set of parentheses. These bars mean: evaluate what is inside and, if the final result ( once the entire expression inside the absolute value signs has been evaluated) is negative, change its sign to make it positive and drop the bars; if the final result inside the bars is zero or positive, you may drop the bars without making any changes:
Another example is:
Note that absolute value signs do not instruct you to make “all” quantities inside them positive. Only the final result, after evaluating the entire expression inside the absolute value signs, should be made positive.
Absolute Value expressions that contain variables
Just as with parentheses, absolute value symbols serve as grouping symbols: the expression inside the bars must be evaluated and expressed as either zero or a positive quantity before the bars may be dropped. While this is fairly straightforward when working with constant values, as shown above, what happens when a pair of absolute value signs contains a variable?
In such a case, we don’t know whether the absolute value will have any effect on the quantity until we know whether “x-4” evaluates to a negative value or not. And we won’t know that until we know the value of “x”. Once we do know a value for “x”, if the expression within the bars is not negative, we can drop the bars; if it is negative, we must change its sign (negating it, making it positive) before dropping the absolute value signs.
This same process can be also be used to solve absolute value equations.
Solving Equations Involving Absolute Values
Equations that involve one or more absolute value expressions can be solved by breaking them into piecewise functions . Each “piece” will start and end at a point where an expression inside absolute value bars changes sign. For example, if we are working with:
We can break this equation up into two equations that are part of a single piecewise function, neither of which involves an absolute value sign. The resulting piecewise function will have the exact same graph as the original function. How? By first identifying where the expression(s) inside the absolute value bars change(s) sign.
For this problem, the sign of the result inside the absolute value signs changes at x = 4 (set the expression inside the absolute value signs equal to 0, then solve for x). Let’s consider what effect the absolute value function has when x takes on values around 4.
when x < 4, “x – 4” will be negative, and the absolute value function will change the sign of the result when x = 4, “x – 4” will equal zero, and the absolute value function will not change the result when x > 4, “x – 4” will be positive, and the absolute value function will not change the result
Therefore, we can group the x = 4 and x > 4 situations into a single “piece”, since neither of them will need to change the sign of the result. This analysis is reflected in a piecewise re-definition of the above function shown below. Note that the absolute value signs have been replaced by parentheses below, with a negative sign before the left parentheses in the situation when the sign had to be changed:
This is now a set of equations each of which can be solved using familiar algebra techniques. When that process has been completed, double-check that the solution satisfies the domain restriction (restriction on possible values of x):
So, the first solution to the original problem is x = -2. The second possible solution comes from solving the second “piece”:
So, the second solution is x = 10. If you substitute both of these values, -2 and 10, for x in the original equation that contained the absolute value expression, you can determine for yourself that both values lead to true statements, therefore both are solutions to this equation.
Solving equations involving multiple absolute values
If an equation contains multiple absolute value expressions, each absolute value expression must be considered independently to determine the points at which the piecewise function will change to a different function definition. For example:
The left-hand absolute value above starts/stops having an effect at x = 4, and the right-hand one at x = 2. This problem therefore has three regions we must consider: x less than 2, x between 2 and 4, and x greater than 4. Think carefully about the domain restrictions to ensure that they do not overlap, and also think carefully about whether each expression that was inside absolute value signs needs to be negated for all x values within this domain (or not):
For this problem:
- when x is less than 2 the first absolute value expression will always be negative, and thus must be negated for all x values less than 2. The second absolute value expression will always be positive when x is less than 2, so it never needs to be negated within this domain.
- when x is equal to 2 or 4, one or the other of the absolute value expressions will equal zero. In this case, it will not matter if they are negated or not, as negative zero is still zero. Therefore, we can consider the cases when x equals 2 or 4 at the same time as the cases when x lies between 2 and 4 (below).
- when x is between 2 and 4, the first absolute value expression will still always be negative, and must therefore be negated. However, the second absolute value expression will also always be negative, and thus must also be negated for this “piece” of our piecewise function.
- when x is greater than 4, the first absolute value expression will always be positive, so the absolute value signs can be dropped without negating the expression. The second absolute value expression will always be negative when x is greater than 4, so it must be negated when converting the absolute value signs into parentheses.
We now have three linear equations that can be solved to arrive at the solution to the original equation. In solving these equations, then verifying that the answers satisfy the accompanying domain restrictions, you should find that the answers are 0 and 6. Note that no value of x between 2 and 4 can satisfy the middle equation, which when simplified produces a statement that is always false (such as 6 = 2).
Invalid Solutions
Suppose you are asked to solve an equation such as
If you follow the procedure outlined above, you will end up with:
The solution to the first equation is:
And the solution to the second is:
Note that in this case, both solutions violate their associated domain restrictions, therefore there is no solution to this problem. This makes intuitive sense if you revisit the original problem… if the result of an absolute value expression must always be zero or a positive number, how could that result ever equal a negative two?
Non-linear Absolute Value Equations
Non-linear absolute value equations may be solved using the same approach as outlined above. Some non-linear situations will result in multiple solutions for each equation, each of which should be checked against the domain restriction (or tested by substituting it into the original absolute value equation).
Share this:

- Share on Tumblr
By Whit Ford
Math tutor since 1992. Former math teacher, product manager, software developer, research analyst, etc.
Leave a comment Cancel reply
This site uses Akismet to reduce spam. Learn how your comment data is processed .
- Already have a WordPress.com account? Log in now.
- Subscribe Subscribed
- Copy shortlink
- Report this content
- View post in Reader
- Manage subscriptions
- Collapse this bar
Absolute Value in Algebra
Absolute value means ....
... how far a number is from zero:
"6" is 6 away from zero, and "−6" is also 6 away from zero.
So the absolute value of 6 is 6 , and the absolute value of −6 is also 6
Absolute Value Symbol
To show we want the absolute value we put "|" marks either side (called "bars"), like these examples:
| |−5| = 5 | |7| = 7 |
| The "|" can be found just above the enter key on most keyboards. |
More Formal
More formally we have:
Which says the absolute value of x equals:
- x when x is greater than zero
- 0 when x equals 0
- −x when x is less than zero (this "flips" the number back to positive)
So when a number is positive or zero we leave it alone, when it is negative we change it to positive using −x.
Example: what is |−17| ?
Well, it is less than zero, so we need to calculate "−x":
− ( −17 ) = + 17
(Because two minuses make a plus )
Useful Properties
Here are some properties of absolute values that can be useful:
That makes sense ... |a| can never be less than zero.
Squaring a makes it positive or zero (for a as a Real Number). Then taking the square root will "undo" the squaring, but leave it positive or zero.
Means these are the same:
- the absolute value of (a times b), and
- (the absolute value of a) times (the absolute value of b)
Which can also be useful when solving
Which is often the key to solving most absolute value questions.
Example: Solve |x+2| = 5
Using "|u| = a is the same as u = ±a ":
Which has two solutions:
| x+2 = −5 | x+2 = +5 |
Graphically
Let us graph that example:
It is easier to graph when we have an "=0" equation, so subtract 5 from both sides:
|x+2| − 5 = 0
Now let's plot y=|x+2|−5 and find where it equals zero.
Here is the plot of y=|x+2|−5 , but just for fun let's make the graph by shifting it around :
| Start with | then shift it left to make it | then shift it down to make it |
And the two solutions (circled) are −7 and +3 .
Absolute Value Inequalities
Mixing Absolute Values and Inequalites needs a little care!
There are 4 inequalities:
| < | ≤ | > | ≥ | |
|---|---|---|---|---|
| less than | less than or equal to | greater than | greater than or equal to |
Less Than, Less Than or Equal To
With " < " and " ≤ " we get one interval centered on zero:
Example: Solve |x| < 3
This means the distance from x to zero must be less than 3:
Everything in between (but not including) −3 and 3
It can be rewritten as:
−3 < x < 3
As an interval it can be written as:
The same thing works for "Less Than or Equal To":
Example: Solve |x| ≤ 3
Everything in between and including -3 and 3
How about a bigger example?
Example: Solve |3x-6| ≤ 12
Rewrite it as:
−12 ≤ 3x−6 ≤ 12
−6 ≤ 3x ≤ 18
Lastly, multiply by (1/3). Because we are multiplying by a positive number, the inequalities will not change:
−2 ≤ x ≤ 6
Greater Than, Greater Than or Equal To
This is different ... we get two separate intervals :
Example: Solve |x| > 3
It looks like this:
less than -3 or from 3 onwards
It can be rewritten as
x < −3 or x > 3
(−∞, −3) U (3, +∞)
Note: U means "Union" of the two intervals.
Careful! Do not write it as
Because x cannot be less than -3 and greater than 3 at the same time
It is really:
x is less than −3 or greater than 3
The same thing works for "Greater Than or Equal To":
Example: Solve |x| ≥ 3
Can be rewritten as
x ≤ −3 or x ≥ 3
(−∞, −3] U [3, +∞)
- Isolate the absolute value on one side of the equation.
- Is the number on the other side of the equation negative? If you answered yes, then the equation has no solution. If you answered no, then go on to step 3.
- Write two equations without absolute values. The first equation will set the quantity inside the bars equal to the number on the other side of the equal sign; the second equation will set the quantity inside the bars equal to the opposite of the number on the other side.
- Solve the two equations.
- Write two equations without absolute values. The first equation will set the quantity inside the bars on the left side equal to the quantity inside the bars on the right side. The second equation will set the quantity inside the bars on the left side equal to the opposite of the quantity inside the bars on the right side.
|
| ||
|
|
| |
|
| |
|
|
|
So the only solution to this problem is x = 1/2
Since 3 is included in the set of real numbers, we will just say that the solution to this equation is All Real Numbers

IMAGES
VIDEO
COMMENTS
Solving Absolute Value Equations. Solving absolute value equations is as easy as working with regular linear equations. The only additional key step that you need to remember is to separate the original absolute value equation into two parts: positive and negative (±) components.Below is the general approach on how to break them down into two equations:
Free absolute value equation calculator - solve absolute value equations with all the steps. Type in any equation to get the solution, steps and graph
Learn how to solve equations and inequalities involving absolute value, which represent the distance between two points on a number line. This section covers the basic properties of absolute value, how to isolate the absolute value expression, and how to apply the definition of absolute value to find the solutions. You will also see how to graph absolute value functions and inequalities using ...
The next step is to ditch the absolute value bars and solve the following equations: Positive: 2x-4=2 and Negative: 2x-4=-2. Now you have TWO solutions: x=3 and x=1. STEP THREE: Check Your Answer. The final step is to plug both solutions, x=3 and x=1, into the original equation |2x-4|+8=10 and verify that each solution checks out and you are ...
We're told, solve the absolute value of 3x minus 9 is equal to 0, and graph the solution on a number line. So let's just rewrite the absolute value equation. They told us that the absolute value of 3x minus 9 is equal to 0. So we're told that the absolute value of the something-- in this case the something is 3x minus 9-- is equal to 0.
You get x is equal to 15. To solve this one, add 5 to both sides of this equation. x is equal to negative 5. So our solution, there's two x's that satisfy this equation. x could be 15. 15 minus 5 is 10, take the absolute value, you're going to get 10, or x could be negative 5. Negative 5 minus 5 is negative 10.
The General Steps to solve an absolute value equation are: Rewrite the absolute value equation as two separate equations, one positive and the other negative. Solve each equation separately. After solving, substitute your answers back into original equation to verify that you solutions are valid. Write out the final solution or graph it as needed.
2) The absolute values (besides being the distance from zero) act as grouping symbols. Once you get to the point that you can actually drop the absolute values, if there is a number in front, that number must be distributed. Example: 14 |x+7| = 2 becomes 14 (x+7) = 2 and 14 (x+7) = -2.
Below the equation, you'll see the solution to your absolute value equation as well! By default, the calculator uses 4 decimal places to display the solution. ... Look at the sign on the right-hand side: If (e - d)/a < 0, then you've got an absolute value equation with no solutions;
Now that we can graph an absolute value function, we will learn how to solve an absolute value equation. To solve an equation such as {8}=\left| {2}x - {6}\right| 8 = ∣2x −6∣, we notice that the absolute value will be equal to 8 if the quantity inside the absolute value is 8 or -8. This leads to two different equations we can solve ...
We will now discuss the solutions of the equation \[|x|=a \nonumber \] There are three distinct cases to discuss, each of which depends upon the value and sign of the number a. Case I: a < 0; If a < 0, then the graph of y = a is a horizontal line that lies strictly below the x-axis, as shown in Figure \(\PageIndex{2}\)(a).
To solve an absolute value equation, we first isolate the absolute value expression using the same procedures we used to solve linear equations. Once we isolate the absolute value expression we rewrite it as the two equivalent equations. ... When we take the opposite of a quantity, we must be careful with the signs and to add parentheses where ...
This math video tutorial explains how to solve absolute value equations with variables on both sides. It contains plenty of examples and practice problems.S...
Isolate the absolute value expression to one side of the equal sign. 2. Set the inside of the absolute value equal to + and to - the value on the other side of the equal sign (remove the absolute value bars in this step). 3. If needed, solve for the variable in these 2 new equations. 4. Check your solutions for possible "problems" (extraneous ...
Example 1. Solve the equation for x: |3 + x| − 5 = 4. Solution. Isolate the absolute value expression by applying the Law of equations. This means, we add 5 to both sides of the equation to obtain; | 3 + x | − 5 + 5 = 4 + 5. | 3 + x |= 9. Calculate for the positive version of the equation.
About absolute value equations. Solve an absolute value equation using the following steps: Get the absolve value expression by itself. Set up two equations and solve them separately.
Using the definition of absolute value as a piecewise function, "undo" the absolute value sign(s) and write cases. For example, we know that the expression in the absolute value sign can either be positive or negative. Solve each case for \( x\). Verify the solutions. Find all real values of \(x\) such that \( | 3x - 4 | - 2 = 3.\)
This would be just changing the number on the right hand side of the equation. Summary. Absolute value equations are always solved with the same steps: isolate the absolute value term and then write equations based on the definition of the absolute value. There may end up being two solutions, one solution, or no solutions.
The term "Absolute Value" refers to the magnitude of a quantity without regard to sign. In other words, its distance from zero expressed as a positive number. The notation used to indicate absolute value is a pair of vertical bars surrounding the quantity, sort of like a straight set of parentheses. These bars mean: evaluate what is inside ...
More Formal. More formally we have: Which says the absolute value of x equals: x when x is greater than zero; 0 when x equals 0; −x when x is less than zero (this "flips" the number back to positive); So when a number is positive or zero we leave it alone, when it is negative we change it to positive using −x.
Definition: Absolute Value. Absolute value for linear equations in one variable is given by. If |x| = a, then x = a or x = −a If | x | = a, then x = a or x = − a. where a a is a real number. When we have an equation with absolute value, it is important to first isolate the absolute value, then remove the absolute value by applying the ...
Write two equations without absolute values. The first equation will set the quantity inside the bars equal to the number on the other side of the equal sign; the second equation will set the quantity inside the bars equal to the opposite of the number on the other side. Solve the two equations. Follow these steps to solve an absolute value ...