High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
Free ready-to-use math resources
Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth


15 Venn Diagram Questions And Practice Problems (Middle & High School): Exam Style Questions Included
Beki Christian
Venn diagram questions involve visual representations of the relationship between two or more different groups of things. Venn diagrams are first covered in elementary school and their complexity and uses progress through middle and high school.
This article will look at the types of Venn diagram questions that might be encountered at middle school and high school, with a focus on exam style example questions and preparing for standardized tests. We will also cover problem-solving questions. Each question is followed by a worked solution.
How to solve Venn diagram questions
In middle school, sets and set notation are introduced when working with Venn diagrams. A set is a collection of objects. We identify a set using braces. For example, if set A contains the odd numbers between 1 and 10, then we can write this as:
A = {1, 3, 5, 7, 9}
Venn diagrams sort objects, called elements, into two or more sets.
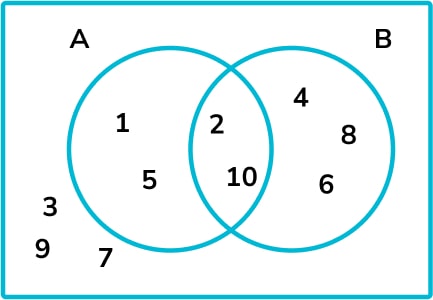
This diagram shows the set of elements
{1,2,3,4,5,6,7,8,9,10} sorted into the following sets.
Set A= factors of 10
Set B= even numbers
The numbers in the overlap (intersection) belong to both sets. Those that are not in set A or set B are shown outside of the circles.
Different sections of a Venn diagram are denoted in different ways.
ξ represents the whole set, called the universal set.
∅ represents the empty set, a set containing no elements.
Venn Diagrams Worksheet
Download this quiz to check your students' understanding of Venn diagrams. Includes 10 questions with answers!
Let’s check out some other set notation examples!
| A \cap B \quad | ^{\prime}\mathrm{A} and B^{\prime} The intersection of \mathrm{A} and \mathrm{B} . The elements in both sets \mathrm{A} and \mathrm{B.} \quad | |
| A \cup B \quad | ^{\prime}\mathrm{A} or B^{\prime} The union of \mathrm{A} or \mathrm{B.} . Any element in set \mathrm{A} or set \mathrm{B.} | |
| A^{\prime} | ‘Not \mathrm{A}^{\prime} The complement of \mathrm{A.} Any element not in \mathrm{A.} |
In middle school and high school, we often use Venn diagrams to establish probabilities.
We do this by reading information from the Venn diagram and applying the following formula.
For Venn diagrams we can say
Middle School Venn diagram questions
In middle school, students learn to use set notation with Venn diagrams and start to find probabilities using Venn diagrams. The questions below are examples of questions that students may encounter in 6th, 7th and 8th grade.
Venn diagram questions 6th grade
1. This Venn diagram shows information about the number of people who have brown hair and the number of people who wear glasses.
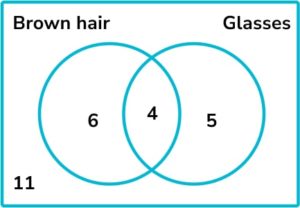
How many people have brown hair and glasses?

The intersection, where the Venn diagrams overlap, is the part of the Venn diagram which represents brown hair AND glasses. There are 4 people in the intersection.
2. Which set of objects is represented by the Venn diagram below?
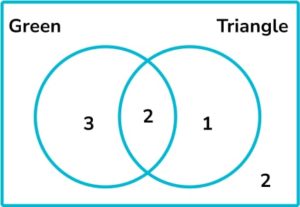
We can see from the Venn diagram that there are two green triangles, one triangle that is not green, three green shapes that are not triangles and two shapes that are not green or triangles. These shapes belong to set D.
Venn diagram questions 7th grade
3. Max asks 40 people whether they own a cat or a dog. 17 people own a dog, 14 people own a cat and 7 people own a cat and a dog. Choose the correct representation of this information on a Venn diagram.
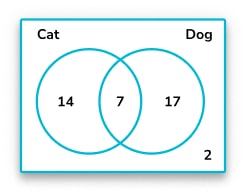
There are 7 people who own a cat and a dog. Therefore, there must be 7 more people who own a cat, to make a total of 14 who own a cat, and 10 more people who own a dog, to make a total of 17 who own a dog.
Once we put this information on the Venn diagram, we can see that there are 7+7+10=24 people who own a cat, a dog or both.
40-24=16 , so there are 16 people who own neither.
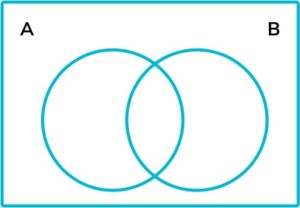
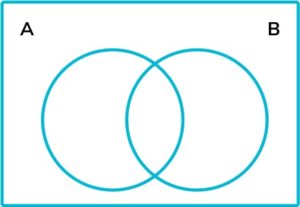
4. The following Venn diagrams each show two sets, set A and set B . On which Venn diagram has A ′ been shaded?
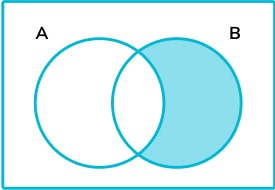
\mathrm{A}^{\prime} means not in \mathrm{A} . This is shown in diagram \mathrm{B.}
Venn diagram questions 8th grade
5. Place these values onto the following Venn diagram and use your diagram to find the number of elements in the set \text{S} \cup \text{O}.
\xi = \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\} \text{S} = square numbers \text{O} = odd numbers
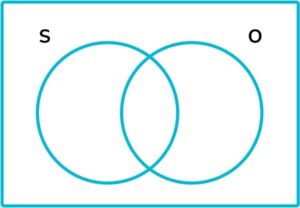
\text{S} \cup \text{O} is the union of \text{S} or \text{O} , so it includes any element in \text{S} , \text{O} or both. The total number of elements in \text{S} , \text{O} or both is 6.
6. The Venn diagram below shows a set of numbers that have been sorted into prime numbers and even numbers.
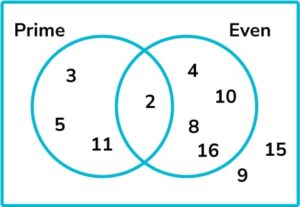
A number is chosen at random. Find the probability that the number is prime and not even.
The section of the Venn diagram representing prime and not even is shown below.
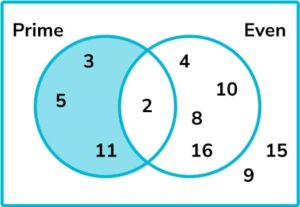
There are 3 numbers in the relevant section out of a possible 10 numbers altogether. The probability, as a fraction, is \frac{3}{10}.
7. Some people visit the theater. The Venn diagram shows the number of people who bought ice cream and drinks in the interval.
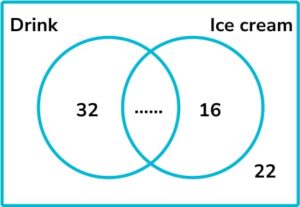
Ice cream is sold for $3 and drinks are sold for $ 2. A total of £262 is spent. How many people bought both a drink and an ice cream?
Money spent on drinks: 32 \times \$2 = \$64
Money spent on ice cream: 16 \times \$3 = \$48
\$64+\$48=\$112 , so the information already on the Venn diagram represents \$112 worth of sales.
\$262-\$112 = \$150 , so another \$150 has been spent.
If someone bought a drink and an ice cream, they would have spent \$2+\$3 = \$5.
\$150 \div \$5=30 , so 30 people bought a drink and an ice cream.
High school Venn diagram questions
In high school, students are expected to be able to take information from word problems and put it onto a Venn diagram involving two or three sets. The use of set notation is extended and the probabilities become more complex.
In advanced math classes, Venn diagrams are used to calculate conditional probability.
Lower ability Venn diagram questions
8. 50 people are asked whether they have been to France or Spain.
18 people have been to France. 23 people have been to Spain. 6 people have been to both.
By representing this information on a Venn diagram, find the probability that a person chosen at random has not been to Spain or France.
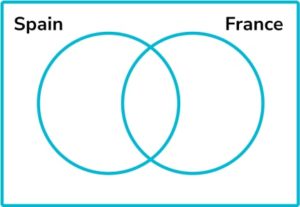
6 people have been to both France and Spain. This means 17 more have been to Spain to make 23 altogether, and 12 more have been to France to make 18 altogether. This makes 35 who have been to France, Spain or both and therefore 15 who have been to neither.
The probability that a person chosen at random has not been to France or Spain is \frac{15}{50}.
9. Some people were asked whether they like running, cycling or swimming. The results are shown in the Venn diagram below.
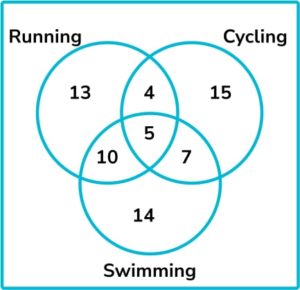
One person is chosen at random. What is the probability that the person likes running and cycling?
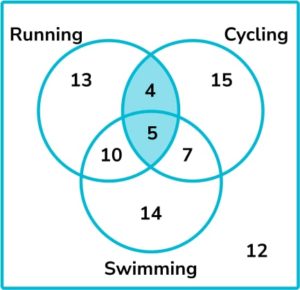
9 people like running and cycling (we include those who also like swimming) out of 80 people altogether. The probability that a person chosen at random likes running and cycling is \frac{9}{80}.
10. ξ = \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16\}
\text{A} = \{ even numbers \}
\text{B} = \{ multiples of 3 \}
By completing the following Venn diagram, find \text{P}(\text{A} \cup \text{B}^{\prime}).
\text{A} \cup \text{B}^{\prime} means \text{A} or not \text{B} . We need to include everything that is in \text{A} or is not in \text{B} . There are 13 elements in \text{A} or not in \text{B} out of a total of 16 elements.
Therefore \text{P}(\text{A} \cup \text{B}^{\prime}) = \frac{13}{16}.
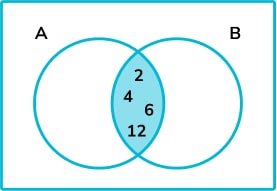
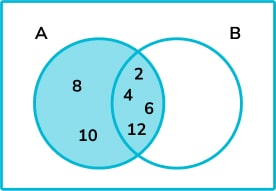
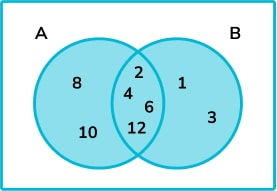
11. ξ = \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12\}
A = \{ multiples of 2 \}
By putting this information onto the following Venn diagram, list all the elements of B.
We can start by placing the elements in \text{A} \cap \text{B} , which is the intersection.
We can then add any other multiples of 2 to set \text{A}.
Next, we can add any unused elements from \text{A} \cup \text{B} to \text{B}.
Finally, any other elements can be added to the outside of the Venn diagram.
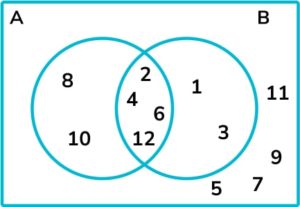
The elements of \text{B} are \{1, 2, 3, 4, 6, 12\}.
Middle ability high school Venn diagram questions
12. Some people were asked whether they like strawberry ice cream or chocolate ice cream. 82% said they like strawberry ice cream and 70% said they like chocolate ice cream. 4% said they like neither.
By putting this information onto a Venn diagram, find the percentage of people who like both strawberry and chocolate ice cream.
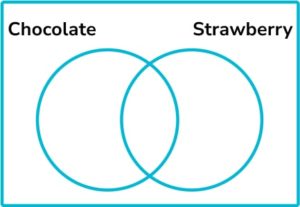
Here, the percentages add up to 156\%. This is 56\% too much. In this total, those who like chocolate and strawberry have been counted twice and so 56\% is equal to the number who like both chocolate and strawberry. We can place 56\% in the intersection, \text{C} \cap \text{S}
We know that the total percentage who like chocolate is 70\%, so 70-56 = 14\%-14\% like just chocolate. Similarly, 82\% like strawberry, so 82-56 = 26\%-26\% like just strawberry.
13. The Venn diagram below shows some information about the height and gender of 40 students.
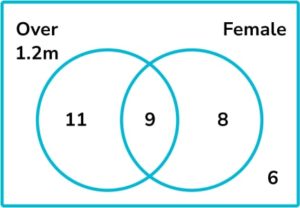
A student is chosen at random. Find the probability that the student is female given that they are over 1.2 m .
We are told the student is over 1.2m. There are 20 students who are over 1.2m and 9 of them are female. Therefore the probability that the student is female given they are over 1.2m is \frac{9}{20}.
14. The Venn diagram below shows information about the number of students who study history and geography.
H = history
G = geography
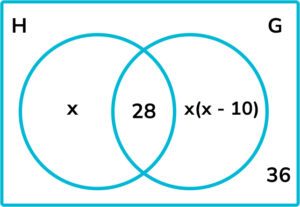
Work out the probability that a student chosen at random studies only history.
We are told that there are 100 students in total. Therefore:
x = 12 or x = -3 (not valid) If x = 12, then the number of students who study only history is 12, and the number who study only geography is 24. The probability that a student chosen at random studies only history is \frac{12}{100}.
15. 50 people were asked whether they like camping, holiday home or hotel holidays.
18\% of people said they like all three. 7 like camping and holiday homes but not hotels. 11 like camping and hotels. \frac{13}{25} like camping.
Of the 27 who like holiday homes, all but 1 like at least one other type of holiday. 7 people do not like any of these types of holiday.
By representing this information on a Venn diagram, find the probability that a person chosen at random likes hotels given that they like holiday homes.
Put this information onto a Venn diagram.
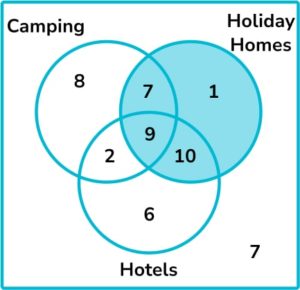
We are told that the person likes holiday homes. There are 27 people who like holiday homes. 19 of these also like hotels. Therefore, the probability that the person likes hotels given that they like holiday homes is \frac{19}{27}.
Looking for more Venn diagram math questions for middle and high school students ?
- Probability questions
- Ratio questions
- Algebra questions
- Trigonometry questions
- Long division questions
- Pythagorean theorem questions
Do you have students who need extra support in math? Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor. Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way. Personalized one-on-one math tutoring programs are available for: – 2nd grade tutoring – 3rd grade tutoring – 4th grade tutoring – 5th grade tutoring – 6th grade tutoring – 7th grade tutoring – 8th grade tutoring Why not learn more about how it works ?
The content in this article was originally written by secondary teacher Beki Christian and has since been revised and adapted for US schools by elementary math teacher Katie Keeton.
Related articles

15 Probability Questions And Practice Problems for Middle and High School: Harder Exam Style Questions Included

9 Algebra Questions And Practice Problems To Do With Your Middle Schoolers

15 Trigonometry Questions And Practice Problems To Do With High Schoolers

Ratio Questions And Practice Problems: Differentiated Practice Questions Included
Solving Inequalities Questions [FREE]
Downloadable skills and applied questions about solving inequalities.
Includes 10 skills questions, 5 applied questions and an answer key. Print and share with your classes to support their learning.
Privacy Overview
Venn Diagram Examples, Problems and Solutions
On this page:
- What is Venn diagram? Definition and meaning.
- Venn diagram formula with an explanation.
- Examples of 2 and 3 sets Venn diagrams: practice problems with solutions, questions, and answers.
- Simple 4 circles Venn diagram with word problems.
- Compare and contrast Venn diagram example.
Let’s define it:
A Venn Diagram is an illustration that shows logical relationships between two or more sets (grouping items). Venn diagram uses circles (both overlapping and nonoverlapping) or other shapes.
Commonly, Venn diagrams show how given items are similar and different.
Despite Venn diagram with 2 or 3 circles are the most common type, there are also many diagrams with a larger number of circles (5,6,7,8,10…). Theoretically, they can have unlimited circles.
Venn Diagram General Formula
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
Don’t worry, there is no need to remember this formula, once you grasp the meaning. Let’s see the explanation with an example.
This is a very simple Venn diagram example that shows the relationship between two overlapping sets X, Y.
X – the number of items that belong to set A Y – the number of items that belong to set B Z – the number of items that belong to set A and B both
From the above Venn diagram, it is quite clear that
n(A) = x + z n(B) = y + z n(A ∩ B) = z n(A ∪ B) = x +y+ z.
Now, let’s move forward and think about Venn Diagrams with 3 circles.
Following the same logic, we can write the formula for 3 circles Venn diagram :
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(C ∩ A) + n(A ∩ B ∩ C)
Venn Diagram Examples (Problems with Solutions)
As we already know how the Venn diagram works, we are going to give some practical examples (problems with solutions) from the real life.
2 Circle Venn Diagram Examples (word problems):
Suppose that in a town, 800 people are selected by random types of sampling methods . 280 go to work by car only, 220 go to work by bicycle only and 140 use both ways – sometimes go with a car and sometimes with a bicycle.
Here are some important questions we will find the answers:
- How many people go to work by car only?
- How many people go to work by bicycle only?
- How many people go by neither car nor bicycle?
- How many people use at least one of both transportation types?
- How many people use only one of car or bicycle?
The following Venn diagram represents the data above:
Now, we are going to answer our questions:
- Number of people who go to work by car only = 280
- Number of people who go to work by bicycle only = 220
- Number of people who go by neither car nor bicycle = 160
- Number of people who use at least one of both transportation types = n(only car) + n(only bicycle) + n(both car and bicycle) = 280 + 220 + 140 = 640
- Number of people who use only one of car or bicycle = 280 + 220 = 500
Note: The number of people who go by neither car nor bicycle (160) is illustrated outside of the circles. It is a common practice the number of items that belong to none of the studied sets, to be illustrated outside of the diagram circles.
We will deep further with a more complicated triple Venn diagram example.
3 Circle Venn Diagram Examples:
For the purposes of a marketing research , a survey of 1000 women is conducted in a town. The results show that 52 % liked watching comedies, 45% liked watching fantasy movies and 60% liked watching romantic movies. In addition, 25% liked watching comedy and fantasy both, 28% liked watching romantic and fantasy both and 30% liked watching comedy and romantic movies both. 6% liked watching none of these movie genres.
Here are our questions we should find the answer:
- How many women like watching all the three movie genres?
- Find the number of women who like watching only one of the three genres.
- Find the number of women who like watching at least two of the given genres.
Let’s represent the data above in a more digestible way using the Venn diagram formula elements:
- n(C) = percentage of women who like watching comedy = 52%
- n(F ) = percentage of women who like watching fantasy = 45%
- n(R) = percentage of women who like watching romantic movies= 60%
- n(C∩F) = 25%; n(F∩R) = 28%; n(C∩R) = 30%
- Since 6% like watching none of the given genres so, n (C ∪ F ∪ R) = 94%.
Now, we are going to apply the Venn diagram formula for 3 circles.
94% = 52% + 45% + 60% – 25% – 28% – 30% + n (C ∩ F ∩ R)
Solving this simple math equation, lead us to:
n (C ∩ F ∩ R) = 20%
It is a great time to make our Venn diagram related to the above situation (problem):
See, the Venn diagram makes our situation much more clear!
From the Venn diagram example, we can answer our questions with ease.
- The number of women who like watching all the three genres = 20% of 1000 = 200.
- Number of women who like watching only one of the three genres = (17% + 12% + 22%) of 1000 = 510
- The number of women who like watching at least two of the given genres = (number of women who like watching only two of the genres) +(number of women who like watching all the three genres) = (10 + 5 + 8 + 20)% i.e. 43% of 1000 = 430.
As we mentioned above 2 and 3 circle diagrams are much more common for problem-solving in many areas such as business, statistics, data science and etc. However, 4 circle Venn diagram also has its place.
4 Circles Venn Diagram Example:
A set of students were asked to tell which sports they played in school.
The options are: Football, Hockey, Basketball, and Netball.
Here is the list of the results:
| Football | Robert, James, John, Mary, Jennifer, William |
| Hockey | Robert, William, Linda, Elizabeth, James |
| Basketball | William, Jayne, Linda, Daniel, Mary |
| Netball | Jessica, William, Linda, Elizabeth, Anthony, Mary |
| None | Dorothy |
The next step is to draw a Venn diagram to show the data sets we have.
It is very clear who plays which sports. As you see the diagram also include the student who does not play any sports (Dorothy) by putting her name outside of the 4 circles.
From the above Venn diagram examples, it is obvious that this graphical tool can help you a lot in representing a variety of data sets. Venn diagram also is among the most popular types of graphs for identifying similarities and differences .
Compare and Contrast Venn Diagram Example:
The following compare and contrast example of Venn diagram compares the features of birds and bats:
Tools for creating Venn diagrams
It is quite easy to create Venn diagrams, especially when you have the right tool. Nowadays, one of the most popular way to create them is with the help of paid or free graphing software tools such as:
You can use Microsoft products such as:
Some free mind mapping tools are also a good solution. Finally, you can simply use a sheet of paper or a whiteboard.
Conclusion:
A Venn diagram is a simple but powerful way to represent the relationships between datasets. It makes understanding math, different types of data analysis , set theory and business information easier and more fun for you.
Besides of using Venn diagram examples for problem-solving and comparing, you can use them to present passion, talent, feelings, funny moments and etc.
Be it data science or real-world situations, Venn diagrams are a great weapon in your hand to deal with almost any kind of information.
If you need more chart examples, our posts fishbone diagram examples and what does scatter plot show might be of help.
About The Author
Silvia Valcheva
Silvia Valcheva is a digital marketer with over a decade of experience creating content for the tech industry. She has a strong passion for writing about emerging software and technologies such as big data, AI (Artificial Intelligence), IoT (Internet of Things), process automation, etc.
Well explained I hope more on this one
WELL STRUCTURED CONTENT AND ENLIGHTNING AS WELL
Leave a Reply Cancel Reply
This site uses Akismet to reduce spam. Learn how your comment data is processed .
Venn Diagram Calculator
More options are available after generating the Venn Diagram, including the ability to change the opacity of the filling and the colors of the borders.
Venn diagram online
Venn diagram example, how to use the venn diagram calculator:, 1. data list:.
- In this case, the " Output " field will appear, and you can choose one of the following options:
2. Number of data items:
- For groups with intersections, you can enter two numbers:
How to solve a Venn diagram problem.
When problem contains numbers of items, when problem contains data lists, calculators.
- + ACCUPLACER Mathematics
- + ACT Mathematics
- + AFOQT Mathematics
- + ALEKS Tests
- + ASVAB Mathematics
- + ATI TEAS Math Tests
- + Common Core Math
- + DAT Math Tests
- + FSA Tests
- + FTCE Math
- + GED Mathematics
- + Georgia Milestones Assessment
- + GRE Quantitative Reasoning
- + HiSET Math Exam
- + HSPT Math
- + ISEE Mathematics
- + PARCC Tests
- + Praxis Math
- + PSAT Math Tests
- + PSSA Tests
- + SAT Math Tests
- + SBAC Tests
- + SIFT Math
- + SSAT Math Tests
- + STAAR Tests
- + TABE Tests
- + TASC Math
- + TSI Mathematics
- + ACT Math Worksheets
- + Accuplacer Math Worksheets
- + AFOQT Math Worksheets
- + ALEKS Math Worksheets
- + ASVAB Math Worksheets
- + ATI TEAS 6 Math Worksheets
- + FTCE General Math Worksheets
- + GED Math Worksheets
- + 3rd Grade Mathematics Worksheets
- + 4th Grade Mathematics Worksheets
- + 5th Grade Mathematics Worksheets
- + 6th Grade Math Worksheets
- + 7th Grade Mathematics Worksheets
- + 8th Grade Mathematics Worksheets
- + 9th Grade Math Worksheets
- + HiSET Math Worksheets
- + HSPT Math Worksheets
- + ISEE Middle-Level Math Worksheets
- + PERT Math Worksheets
- + Praxis Math Worksheets
- + PSAT Math Worksheets
- + SAT Math Worksheets
- + SIFT Math Worksheets
- + SSAT Middle Level Math Worksheets
- + 7th Grade STAAR Math Worksheets
- + 8th Grade STAAR Math Worksheets
- + THEA Math Worksheets
- + TABE Math Worksheets
- + TASC Math Worksheets
- + TSI Math Worksheets
- + AFOQT Math Course
- + ALEKS Math Course
- + ASVAB Math Course
- + ATI TEAS 6 Math Course
- + CHSPE Math Course
- + FTCE General Knowledge Course
- + GED Math Course
- + HiSET Math Course
- + HSPT Math Course
- + ISEE Upper Level Math Course
- + SHSAT Math Course
- + SSAT Upper-Level Math Course
- + PERT Math Course
- + Praxis Core Math Course
- + SIFT Math Course
- + 8th Grade STAAR Math Course
- + TABE Math Course
- + TASC Math Course
- + TSI Math Course
- + Number Properties Puzzles
- + Algebra Puzzles
- + Geometry Puzzles
- + Intelligent Math Puzzles
- + Ratio, Proportion & Percentages Puzzles
- + Other Math Puzzles
How to Solve Problems Using Venn Diagrams
Venn diagrams are visual tools often used to organize and understand sets and the relationships between them. They're named after John Venn, a British philosopher, and logician who introduced them in the 1880s. Venn diagrams are frequently used in various fields, including mathematics, statistics, logic, computer science, etc. They're handy for solving problems involving sets and subsets, intersections, unions, and complements.

A Step-by-step Guide to Solving Problems Using Venn Diagrams
Here’s a step-by-step guide on how to solve problems using Venn diagrams:
Step 1: Understand the Problem
As with any problem-solving method, the first step is to understand the problem. What sets are involved? How are they related? What are you being asked to find?
Step 2: Draw the Diagram
Draw a rectangle to represent the universal set, which includes all possible elements. Each set within the universal set is represented by a circle. If there are two sets, draw two overlapping circles. If there are three sets, draw three overlapping circles, and so forth. Each section in the overlapping circles represents different intersections of the sets.
Step 3: Label the Diagram
Each circle (set) should be labeled appropriately. If you’re dealing with sets of different types of fruits, for example, one might be labeled “Apples” and another “Oranges”.
Step 4: Fill in the Values
Start filling in the values from the innermost part of the diagram (where all sets overlap) to the outer parts. This helps to avoid double-counting elements that belong to more than one set. Information provided in the problem usually tells you how many elements are in each set or section.
Step 5: Solve the Problem
Now, you can use the diagram to answer the question. This might involve counting the number of elements in a particular set or section of the diagram, or it might involve noticing patterns or relationships between the sets.
Step 6: Check Your Answer
Make sure your answer makes sense in the context of the problem and that you’ve accounted for all elements in the diagram.
by: Effortless Math Team about 1 year ago (category: Articles )
Effortless Math Team
Related to this article, more math articles.
- Number Properties Puzzle – Challenge 11
- One-Sided Limits: Everything You need to know
- How to Overcome GED Math Anxiety?
- Full-Length 8th Grade MCAS Math Practice Test
- How to Graph Inverse Trigonometric Functions?
- Geometry Puzzle – Challenge 70
- Pre-Algebra Formulas
- How to Analyze and Understand Rational Functions: A Comprehensive Guide
- FREE 6th Grade Common Core Math Practice Test
- 8th Grade M-STEP Math Worksheets: FREE & Printable
What people say about "How to Solve Problems Using Venn Diagrams - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.
Leave a Reply Cancel reply
You must be logged in to post a comment.
Mastering Grade 6 Math Word Problems The Ultimate Guide to Tackling 6th Grade Math Word Problems
Mastering grade 5 math word problems the ultimate guide to tackling 5th grade math word problems, mastering grade 7 math word problems the ultimate guide to tackling 7th grade math word problems, mastering grade 2 math word problems the ultimate guide to tackling 2nd grade math word problems, mastering grade 8 math word problems the ultimate guide to tackling 8th grade math word problems, mastering grade 4 math word problems the ultimate guide to tackling 4th grade math word problems, mastering grade 3 math word problems the ultimate guide to tackling 3rd grade math word problems.
- ATI TEAS 6 Math
- ISEE Upper Level Math
- SSAT Upper-Level Math
- Praxis Core Math
- 8th Grade STAAR Math
Limited time only!
Save Over 45 %
It was $89.99 now it is $49.99
Login and use all of our services.
Effortless Math services are waiting for you. login faster!
Register Fast!
Password will be generated automatically and sent to your email.
After registration you can change your password if you want.
- Math Worksheets
- Math Courses
- Math Topics
- Math Puzzles
- Math eBooks
- GED Math Books
- HiSET Math Books
- ACT Math Books
- ISEE Math Books
- ACCUPLACER Books
- Premium Membership
- Youtube Videos
Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.
- Bulk Orders
- Refund Policy

- HW Guidelines
- Study Skills Quiz
- Find Local Tutors
- Demo MathHelp.com
- Join MathHelp.com
Select a Course Below
- ACCUPLACER Math
- Math Placement Test
- PRAXIS Math
- + more tests
- 5th Grade Math
- 6th Grade Math
- Pre-Algebra
- College Pre-Algebra
- Introductory Algebra
- Intermediate Algebra
- College Algebra
Venn Diagrams: Exercises
Intro Set Not'n Sets Exercises Diag. Exercises
Venn diagram word problems generally give you two or three classifications and a bunch of numbers. You then have to use the given information to populate the diagram and figure out the remaining information. For instance:
Out of forty students, 14 are taking English Composition and 29 are taking Chemistry.
- If five students are in both classes, how many students are in neither class?
- How many are in either class?
- What is the probability that a randomly-chosen student from this group is taking only the Chemistry class?
Content Continues Below
MathHelp.com

There are two classifications in this universe: English students and Chemistry students.
First I'll draw my universe for the forty students, with two overlapping circles labelled with the total in each:
(Well, okay; they're ovals, but they're always called "circles".)
Five students are taking both classes, so I'll put " 5 " in the overlap:
I've now accounted for five of the 14 English students, leaving nine students taking English but not Chemistry, so I'll put " 9 " in the "English only" part of the "English" circle:
I've also accounted for five of the 29 Chemistry students, leaving 24 students taking Chemistry but not English, so I'll put " 24 " in the "Chemistry only" part of the "Chemistry" circle:
This tells me that a total of 9 + 5 + 24 = 38 students are in either English or Chemistry (or both). This gives me the answer to part (b) of this exercise. This also leaves two students unaccounted for, so they must be the ones taking neither class, which is the answer to part (a) of this exercise. I'll put " 2 " inside the box, but outside the two circles:
The last part of this exercise asks me for the probability that a agiven student is taking Chemistry but not English. Out of the forty students, 24 are taking Chemistry but not English, which gives me a probability of:
24/40 = 0.6 = 60%
- Two students are taking neither class.
- There are 38 students in at least one of the classes.
- There is a 60% probability that a randomly-chosen student in this group is taking Chemistry but not English.
Years ago, I discovered that my (now departed) cat had a taste for the adorable little geckoes that lived in the bushes and vines in my yard, back when I lived in Arizona. In one month, suppose he deposited the following on my carpet:
- six gray geckoes,
- twelve geckoes that had dropped their tails in an effort to escape capture, and
- fifteen geckoes that he'd chewed on a little
In addition:
- only one of the geckoes was gray, chewed-on, and tailless;
- two were gray and tailless but not chewed-on;
- two were gray and chewed-on but not tailless.
If there were a total of 24 geckoes left on my carpet that month, and all of the geckoes were at least one of "gray", "tailless", and "chewed-on", how many were tailless and chewed-on, but not gray?
If I work through this step-by-step, using what I've been given, I can figure out what I need in order to answer the question. This is a problem that takes some time and a few steps to solve.
They've given me that each of the geckoes had at least one of the characteristics, so each is a member of at least one of the circles. This means that there will be nothing outside of the circles; the circles will account for everything in this particular universe.
There was one gecko that was gray, tailless, and chewed on, so I'll draw my Venn diagram with three overlapping circles, and I'll put " 1 " in the center overlap:
Two of the geckoes were gray and tailless but not chewed-on, so " 2 " goes in the rest of the overlap between "gray" and "tailless".
Two of them were gray and chewed-on but not tailless, so " 2 " goes in the rest of the overlap between "gray" and "chewed-on".
Since a total of six were gray, and since 2 + 1 + 2 = 5 of these geckoes have already been accounted for, this tells me that there was only one left that was only gray.
This leaves me needing to know how many were tailless and chewed-on but not gray, which is what the problem asks for. But, because I don't know how many were only chewed on or only tailless, I cannot yet figure out the answer value for the remaining overlap section.
I need to work with a value that I don't yet know, so I need a variable. I'll let " x " stand for this unknown number of tailless, chewed-on geckoes.
I do know the total number of chewed geckoes ( 15 ) and the total number of tailless geckoes ( 12 ). After subtracting, this gives me expressions for the remaining portions of the diagram:
only chewed on:
15 − 2 − 1 − x = 12 − x
only tailless:
12 − 2 − 1 − x = 9 − x
There were a total of 24 geckoes for the month, so adding up all the sections of the diagram's circles gives me: (everything from the "gray" circle) plus (the unknown from the remaining overlap) plus (the only-chewed-on) plus (the only-tailless), or:
(1 + 2 + 1 + 2) + ( x )
+ (12 − x ) + (9 − x )
= 27 − x = 24
Solving , I get x = 3 . So:
Three geckoes were tailless and chewed on but not gray.
(No geckoes or cats were injured during the production of the above word problem.)
For more word-problem examples to work on, complete with worked solutions, try this page provided by Joe Kahlig of Texas A&M University. There is also a software package (DOS-based) available through the Math Archives which can give you lots of practice with the set-theory aspect of Venn diagrams. The program is not hard to use, but you should definitely read the instructions before using.
URL: https://www.purplemath.com/modules/venndiag4.htm
Page 1 Page 2 Page 3 Page 4
Standardized Test Prep
College math, homeschool math, share this page.
- Terms of Use
- About Purplemath
- About the Author
- Tutoring from PM
- Advertising
- Linking to PM
- Site licencing
Visit Our Profiles
Venn Diagram
A Venn diagram is used to visually represent the differences and the similarities between two concepts. Venn diagrams are also called logic or set diagrams and are widely used in set theory, logic, mathematics, businesses, teaching, computer science, and statistics.
Let's learn about Venn diagrams, their definition, symbols, and types with solved examples.
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. | |
| 6. | |
| 7. | |
| 8. |
What is a Venn Diagram?
A Venn diagram is a diagram that helps us visualize the logical relationship between sets and their elements and helps us solve examples based on these sets. A Venn diagram typically uses intersecting and non-intersecting circles (although other closed figures like squares may be used) to denote the relationship between sets.

Venn Diagram Example
Let us observe a Venn diagram example. Here is the Venn diagram that shows the correlation between the following set of numbers.
- One set contains even numbers from 1 to 25 and the other set contains the numbers in the 5x table from 1 to 25.
- The intersecting part shows that 10 and 20 are both even numbers and also multiples of 5 between 1 to 25.

Terms Related to Venn Diagram
Let us understand the following terms and concepts related to Venn Diagram, to understand it better.
Universal Set
Whenever we use a set, it is easier to first consider a larger set called a universal set that contains all of the elements in all of the sets that are being considered. Whenever we draw a Venn diagram:
- A large rectangle is used to represent the universal set and it is usually denoted by the symbol E or sometimes U.
- All the other sets are represented by circles or closed figures within this larger rectangle .
- Every set is the subset of the universal set U.

Consider the above-given image:
- U is the universal set with all the numbers 1-10, enclosed within the rectangle.
- A is the set of even numbers 1-10, which is the subset of the universal set U and it is placed inside the rectangle.
- All the numbers between 1-10, that are not even, will be placed outside the circle and within the rectangle as shown above.
Venn diagrams are used to show subsets. A subset is actually a set that is contained within another set. Let us consider the examples of two sets A and B in the below-given figure. Here, A is a subset of B. Circle A is contained entirely within circle B. Also, all the elements of A are elements of set B.

This relationship is symbolically represented as A ⊆ B. It is read as A is a subset of B or A subset B. Every set is a subset of itself. i.e. A ⊆ A. Here is another example of subsets :
- N = set of natural numbers
- I = set of integers
- Here N ⊂ I, because all-natural numbers are integers .
Venn Diagram Symbols
There are more than 30 Venn diagram symbols. We will learn about the three most commonly used symbols in this section. They are listed below as:
| Venn Diagram Symbols | Explanation |
|---|---|
| The union symbol - ∪ | A ∪ B is read as A union B. Elements that belong to either set A or set B or both the sets. U is the universal set. |
| The intersection symbol - ∩ | A ∩ B is read as A intersection B. Elements that belong to both sets A and B. U is the universal set. |
| The complement symbol - A or A' | A' is read as A complement. Elements that don't belong to set A. U is the universal set. |
Let us understand the concept and the usage of the three basic Venn diagram symbols using the image given below.

| Symbol | It refers to | Total Elements (No. of students) |
|---|---|---|
| A ∪ C | The number of students that prefer either burger or pizza or both. | 1 + 10 + 2 + 2 + 6 + 9 = 30 |
| A ∩ C | The number of students that prefer both burger and pizza. | 2 + 2 = 4 |
| A ∩ B ∩ C | The number of students that prefer a burger, pizza as well as hotdog. | 2 |
| A or A' | The number of students that do not prefer a burger. | 10 + 6 + 9 = 25 |
Venn Diagram for Sets Operations
In set theory, we can perform certain operations on given sets. These operations are as follows,
- Union of Set
- Intersection of set
- Complement of set
- Difference of set
Union of Sets Venn Diagram
The union of two sets A and B can be given by: A ∪ B = {x | x ∈ A or x ∈ B}. This operation on the elements of set A and B can be represented using a Venn diagram with two circles. The total region of both the circles combined denotes the union of sets A and B.
Intersection of Set Venn Diagram
The intersection of sets, A and B is given by: A ∩ B = {x : x ∈ A and x ∈ B}. This operation on set A and B can be represented using a Venn diagram with two intersecting circles. The region common to both the circles denotes the intersection of set A and Set B.
Complement of Set Venn Diagram
The complement of any set A can be given as A'. This represents elements that are not present in set A and can be represented using a Venn diagram with a circle. The region covered in the universal set, excluding the region covered by set A, gives the complement of A.
Difference of Set Venn Diagram
The difference of sets can be given as, A - B. It is also referred to as a ‘relative complement’. This operation on sets can be represented using a Venn diagram with two circles. The region covered by set A, excluding the region that is common to set B, gives the difference of sets A and B.
We can observe the above-explained operations on sets using the figures given below,

Venn Diagram for Three Sets
Three sets Venn diagram is made up of three overlapping circles and these three circles show how the elements of the three sets are related. When a Venn diagram is made of three sets, it is also called a 3-circle Venn diagram. In a Venn diagram, when all these three circles overlap, the overlapping parts contain elements that are either common to any two circles or they are common to all the three circles. Let us consider the below given example:

Here are some important observations from the above image:
- Elements in P and Q = elements in P and Q only plus elements in P, Q, and R.
- Elements in Q and R = elements in Q and R only plus elements in P, Q, and R.
- Elements in P and R = elements in P and R only plus elements in P, Q, and R.
How to Draw a Venn Diagram?
Venn diagrams can be drawn with unlimited circles. Since more than three becomes very complicated, we will usually consider only two or three circles in a Venn diagram. Here are the 4 easy steps to draw a Venn diagram:
- Step 1: Categorize all the items into sets.
- Step 2: Draw a rectangle and label it as per the correlation between the sets.
- Step 3: Draw the circles according to the number of categories you have.
- Step 4: Place all the items in the relevant circles.
Example: Let us draw a Venn diagram to show categories of outdoor and indoor for the following pets: Parrots, Hamsters, Cats, Rabbits, Fish, Goats, Tortoises, Horses.
- Step 1: Categorize all the items into sets (Here, its pets): Indoor pets: Cats, Hamsters, and, Parrots. Outdoor pets: Horses, Tortoises, and Goats. Both categories (outdoor and indoor): Rabbits and Fish.
- Step 2: Draw a rectangle and label it as per the correlation between the two sets. Here, let's label the rectangle as Pets.
- Step 3: Draw the circles according to the number of categories you have. There are two categories in the sample question: outdoor pets and indoor pets. So, let us draw two circles and make sure the circles overlap.

- Step 4: Place all the pets in the relevant circles. If there are certain pets that fit both the categories, then place them at the intersection of sets , where the circles overlap. Rabbits and fish can be kept as indoor and outdoor pets, and hence they are placed at the intersection of both circles.

- Step 5: If there is a pet that doesn't fit either the indoor or outdoor sets, then place it within the rectangle but outside the circles.
Venn Diagram Formula
For any two given sets A and B, the Venn diagram formula is used to find one of the following: the number of elements of A, B, A U B, or A ⋂ B when the other 3 are given. The formula says:
n(A U B) = n(A) + n(B) – n (A ⋂ B)
Here, n(A) and n(B) represent the number of elements in A and B respectively. n(A U B) and n(A ⋂ B) represent the number of elements in A U B and A ⋂ B respectively. This formula is further extended to 3 sets as well and it says:
- n (A U B U C) = n(A) + n(B) + n(C) - n(A ⋂ B) - n(B ⋂ C) - n(C ⋂ A) + n(A ⋂ B ⋂ C)
Here is an example of Venn diagram formula.
Example: In a cricket school, 12 players like bowling, 15 like batting, and 5 like both. Then how many players like either bowling or batting.
Let A and B be the sets of players who like bowling and batting respectively. Then
n(A ⋂ B) = 5
We have to find n(A U B). Using the Venn diagram formula,
n(A U B) = 12 + 15 - 5 = 22.
Applications of Venn Diagram
There are several advantages to using Venn diagrams. Venn diagram is used to illustrate concepts and groups in many fields, including statistics, linguistics, logic, education, computer science, and business.
- We can visually organize information to see the relationship between sets of items, such as commonalities and differences, and to depict the relations for visual communication.
- We can compare two or more subjects and clearly see what they have in common versus what makes them different. This might be done for selecting an important product or service to buy.
- Mathematicians also use Venn diagrams in math to solve complex equations.
- We can use Venn diagrams to compare data sets and to find correlations .
- Venn diagrams can be used to reason through the logic behind statements or equations .
☛ Related Articles:
Check out the following pages related to Venn diagrams:
- Operations on Sets
- Roster Notation
- Set Builder Notation
- Probability
Important Notes on Venn Diagrams:
Here is a list of a few points that should be remembered while studying Venn diagrams:
- Every set is a subset of itself i.e., A ⊆ A.
- A universal set accommodates all the sets under consideration.
- If A ⊆ B and B ⊆ A, then A = B
- The complement of a complement is the given set itself.
Examples of Venn Diagram
Example 1: Let us take an example of a set with various types of fruits, A = {guava, orange, mango, custard apple, papaya, watermelon, cherry}. Represent these subsets using sets notation: a) Fruit with one seed b) Fruit with more than one seed
Solution: Among the various types of fruit, only mango and cherry have one seed.
Answer: a) Fruit with one seed = {mango, cherry} b) Fruit with more than one seed = {guava, orange, custard apple, papaya, watermelon}
Note: If we represent these two sets on a Venn diagram, the intersection portion is empty.
Example 2: Let us take an example of two sets A and B, where A = {3, 7, 9} and B = {4, 8}. These two sets are subsets of the universal set U = {1, 2, 3, 4, 5, 6, 7, 8, 9}. Find A ∪ B.
Solution: The Venn diagram for the above relations can be drawn as:

Answer: A ∪ B means, all the elements that belong to either set A or set B or both the sets = {3, 4, 7, 8, 9}
Example 3: Using Venn diagram, find X ∩ Y, given that X = {1, 3, 5}, Y = {2, 4, 6}.
Given: X = {1, 3, 5}, Y = {2, 4, 6}
The Venn diagram for the above example can be given as,

Answer: From the blue shaded portion of Venn diagram, we observe that, X ∩ Y = ∅ ( null set ).
go to slide go to slide go to slide

Book a Free Trial Class
Venn Diagram Practice Questions
go to slide go to slide
FAQs on Venn Diagrams
What is a venn diagram in math.
In math, a Venn diagram is used to visualize the logical relationship between sets and their elements and helps us solve examples based on these sets.
How do You Read a Venn Diagram?
These are steps to be followed while reading a Venn diagram:
- First, observe all the circles that are present in the entire diagram.
- Every element present in a circle is its own item or data set.
- The intersecting or the overlapping portions of the circles contain the items that are common to the different circles.
- The parts that do not overlap or intersect show the elements that are unique to the different circle.
What is the Importance of Venn Diagram?
Venn diagrams are used in different fields including business, statistics, linguistics, etc. Venn diagrams can be used to visually organize information to see the relationship between sets of items, such as commonalities and differences, and to depict the relations for visual communication.
What is the Middle of a Venn Diagram Called?
When two or more sets intersect, overlap in the middle of a Venn diagram, it is called the intersection of a Venn diagram. This intersection contains all the elements that are common to all the different sets that overlap.
How to Represent a Universal Set Using Venn Diagram?
A large rectangle is used to represent the universal set and it is usually denoted by the symbol E or sometimes U. All the other sets are represented by circles or closed figures within this larger rectangle that represents the universal set.
What are the Different Types of Venn Diagrams?
The different types of Venn diagrams are:
- Two-set Venn diagram: The simplest of the Venn diagrams, that is made up of two circles or ovals of different sets to show their overlapping properties.
- Three-set Venn diagram: These are also called the three-circle Venn diagram, as they are made using three circles.
- Four-set Venn diagram: These are made out of four overlapping circles or ovals.
- Five-set Venn diagram: These comprise of five circles, ovals, or curves. In order to make a five-set Venn diagram, you can also pair a three-set diagram with repeating curves or circles.
What are the Different Fields of Applications of Venn Diagrams?
There are different cases of applications of Venn diagrams: Set theory, logic, mathematics, businesses, teaching, computer science, and statistics.
Can a Venn Diagram Have 2 Non Intersecting Circles?
Yes, a Venn digram can have two non intersecting circles where there is no data that is common to the categories belonging to both circles.
What is the Formula of Venn Diagram?
The formula that is very helpful to find the unknown information about a Venn diagram is n(A U B) = n(A) + n(B) – n (A ⋂ B), where
- A and B are two sets.
- n(A U B) is the number of elements in A U B.
- n (A ⋂ B) is the number of elements in A ⋂ B.
Can a Venn Diagram Have 3 Circles?
Yes, a Venn diagram can have 3 circles , and it's called a three-set Venn diagram to show the overlapping properties of the three circles.
What is Union in the Venn Diagram?
A union is one of the basic symbols used in the Venn diagram to show the relationship between the sets. A union of two sets C and D can be shown as C ∪ D, and read as C union D. It means, the elements belong to either set C or set D or both the sets.
What is A ∩ B Venn Diagram?
A ∩ B (which means A intersection B) in the Venn diagram represents the portion that is common to both the circles related to A and B. A ∩ B can be a null set as well and in this case, the two circles will either be non-intersecting or can be represented with intersecting circles having no data in the intersection portion.
1.3 Understanding Venn Diagrams
Learning objectives.
After completing this section, you should be able to:
- Utilize a universal set with two sets to interpret a Venn diagram.
- Utilize a universal set with two sets to create a Venn diagram.
- Determine the complement of a set.
Have you ever ordered a new dresser or bookcase that required assembly? When your package arrives you excitedly open it and spread out the pieces. Then you check the assembly guide and verify that you have all the parts required to assemble your new dresser. Now, the work begins. Luckily for you, the assembly guide includes step-by-step instructions with images that show you how to put together your product. If you are really lucky, the manufacturer may even provide a URL or QR code connecting you to an online video that demonstrates the complete assembly process. We can likely all agree that assembly instructions are much easier to follow when they include images or videos, rather than just written directions. The same goes for the relationships between sets.
Interpreting Venn Diagrams
Venn diagrams are the graphical tools or pictures that we use to visualize and understand relationships between sets. Venn diagrams are named after the mathematician John Venn, who first popularized their use in the 1880s. When we use a Venn diagram to visualize the relationships between sets, the entire set of data under consideration is drawn as a rectangle, and subsets of this set are drawn as circles completely contained within the rectangle. The entire set of data under consideration is known as the universal set .
Consider the statement: All trees are plants. This statement expresses the relationship between the set of all plants and the set of all trees. Because every tree is a plant, the set of trees is a subset of the set of plants. To represent this relationship using a Venn diagram, the set of plants will be our universal set and the set of trees will be the subset. Recall that this relationship is expressed symbolically as: Trees ⊂ Plants . Trees ⊂ Plants . To create a Venn diagram, first we draw a rectangle and label the universal set “ U = Plants . U = Plants . ” Then we draw a circle within the universal set and label it with the word “Trees.”
This section will introduce how to interpret and construct Venn diagrams. In future sections, as we expand our knowledge of relationships between sets, we will also develop our knowledge and use of Venn diagrams to explore how multiple sets can be combined to form new sets.
Example 1.18
Interpreting the relationship between sets in a venn diagram.
Write the relationship between the sets in the following Venn diagram, in words and symbolically.
The set of terriers is a subset of the universal set of dogs. In other words, the Venn diagram depicts the relationship that all terriers are dogs. This is expressed symbolically as T ⊂ U . T ⊂ U .
Your Turn 1.18
So far, the only relationship we have been considering between two sets is the subset relationship, but sets can be related in other ways. Lions and tigers are both different types of cats, but no lions are tigers, and no tigers are lions. Because the set of all lions and the set of all tigers do not have any members in common, we call these two sets disjoint sets , or non-overlapping sets.
Two sets A A and B B are disjoint sets if they do not share any elements in common. That is, if a a is a member of set A A , then a a is not a member of set B B . If b b is a member of set B B , then b b is not a member of set A A . To represent the relationship between the set of all cats and the sets of lions and tigers using a Venn diagram, we draw the universal set of cats as a rectangle and then draw a circle for the set of lions and a separate circle for the set of tigers within the rectangle, ensuring that the two circles representing the set of lions and the set of tigers do not touch or overlap in any way.
Example 1.19
Describing the relationship between sets.
Describe the relationship between the sets in the following Venn diagram.
The set of triangles and the set of squares are two disjoint subsets of the universal set of two-dimensional figures. The set of triangles does not share any elements in common with the set of squares. No triangles are squares and no squares are triangles, but both squares and triangles are 2D figures.
Your Turn 1.19
Creating venn diagrams.
The main purpose of a Venn diagram is to help you visualize the relationship between sets. As such, it is necessary to be able to draw Venn diagrams from a written or symbolic description of the relationship between sets.
To create a Venn diagram:
- Draw a rectangle to represent the universal set, and label it U = set name U = set name .
- Draw a circle within the rectangle to represent a subset of the universal set and label it with the set name.
If there are multiple disjoint subsets of the universal set, their separate circles should not touch or overlap.
Example 1.20
Drawing a venn diagram to represent the relationship between two sets.
Draw a Venn diagram to represent the relationship between each of the sets.
- All rectangles are parallelograms.
- All women are people.
- The set of rectangles is a subset of the set of parallelograms. First, draw a rectangle to represent the universal set and label it with U = Parallelograms U = Parallelograms , then draw a circle completely within the rectangle, and label it with the name of the set it represents, R = Rectangles R = Rectangles .
In this example, both letters and names are used to represent the sets involved, but this is not necessary. You may use either letters or names alone, as long as the relationship is clearly depicted in the diagram, as shown below.
- The universal set is the set of people, and the set of all women is a subset of the set of people.
Your Turn 1.20
Example 1.21, drawing a venn diagram to represent the relationship between three sets.
All bicycles and all cars have wheels, but no bicycle is a car. Draw a Venn diagram to represent this relationship.
Step 1: The set of bicycles and the set of cars are both subsets of the set of things with wheels. The universal set is the set of things with wheels, so we first draw a rectangle and label it with U = Things with Wheels U = Things with Wheels .
Step 2: Because the set of bicycles and the set of cars do not share any elements in common, these two sets are disjoint and must be drawn as two circles that do not touch or overlap with the universal set.
Your Turn 1.21
The complement of a set.
Recall that if set A A is a proper subset of set U U , the universal set (written symbolically as A ⊂ U A ⊂ U ), then there is at least one element in set U U that is not in set A A . The set of all the elements in the universal set U U that are not in the subset A A is called the complement of set A A , A ' A ' . In set builder notation this is written symbolically as: A ' = { x ∈ U | x ∉ A } . A ' = { x ∈ U | x ∉ A } . The symbol ∈ ∈ is used to represent the phrase, “is a member of,” and the symbol ∉ ∉ is used to represent the phrase, “is not a member of.” In the Venn diagram below, the complement of set A A is the region that lies outside the circle and inside the rectangle. The universal set U U includes all of the elements in set A A and all of the elements in the complement of set A A , and nothing else.
Consider the set of digit numbers. Let this be our universal set, U = { 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 } . U = { 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 } . Now, let set A A be the subset of U U consisting of all the prime numbers in set U U , A = { 2 , 3 , 5 , 7 } . A = { 2 , 3 , 5 , 7 } . The complement of set A A is A ' = { 0 , 1 , 4 , 6 , 8 , 9 } . A ' = { 0 , 1 , 4 , 6 , 8 , 9 } . The following Venn diagram represents this relationship graphically.
Example 1.22
Finding the complement of a set.
For both of the questions below, A A is a proper subset of U U .
- Given the universal set U = { Billie Eilish, Donald Glover, Bruno Mars, Adele, Ed Sheeran} U = { Billie Eilish, Donald Glover, Bruno Mars, Adele, Ed Sheeran} and set A = { Donald Glover, Bruno Mars, Ed Sheeran} A = { Donald Glover, Bruno Mars, Ed Sheeran} , find A ' . A ' .
- Given the universal set U = { d|d is a dog } U = { d|d is a dog } and B = { b ∈ U|b is a beagle } B = { b ∈ U|b is a beagle } , find B ' . B ' .
- The complement of set A A is the set of all elements in the universal set U U that are not in set A . A . A ' = { Billie Eilish, Adele } A ' = { Billie Eilish, Adele } .
- The complement of set B B is the set of all dogs that are not beagles. All members of set B ′ B ′ are in the universal set because they are dogs, but they are not in set B , B , because they are not beagles. This relationship can be expressed in set build notation as follows: B ′ = { All dogs that are not beagles .} B ′ = { All dogs that are not beagles .} , B ′ = { d ∈ U | d is not a beagle .} B ′ = { d ∈ U | d is not a beagle .} , or B ′ = { d ∈ U | d ∉ B } . B ′ = { d ∈ U | d ∉ B } .
Your Turn 1.22
Check your understanding, section 1.3 exercises.
As an Amazon Associate we earn from qualifying purchases.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/contemporary-mathematics/pages/1-introduction
- Authors: Donna Kirk
- Publisher/website: OpenStax
- Book title: Contemporary Mathematics
- Publication date: Mar 22, 2023
- Location: Houston, Texas
- Book URL: https://openstax.org/books/contemporary-mathematics/pages/1-introduction
- Section URL: https://openstax.org/books/contemporary-mathematics/pages/1-3-understanding-venn-diagrams
© Dec 21, 2023 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
Venn Diagram Word Problems
Related Pages Venn Diagrams Intersection Of Two Sets Intersection Of Three Sets More Lessons On Sets More GCSE/IGCSE Maths Lessons
In these lessons, we will learn how to solve word problems using Venn Diagrams that involve two sets or three sets. Examples and step-by-step solutions are included in the video lessons.
What Are Venn Diagrams?
Venn diagrams are the principal way of showing sets in a diagrammatic form. The method consists primarily of entering the elements of a set into a circle or ovals.
Before we look at word problems, see the following diagrams to recall how to use Venn Diagrams to represent Union, Intersection and Complement.
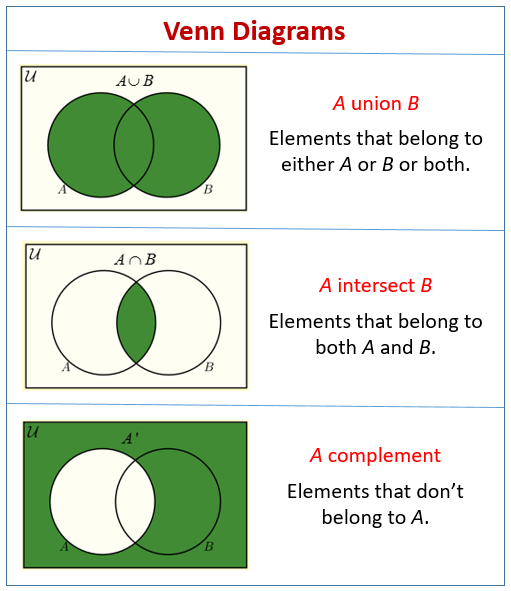
How To Solve Problems Using Venn Diagrams?
This video solves two problems using Venn Diagrams. One with two sets and one with three sets.
Problem 1: 150 college freshmen were interviewed. 85 were registered for a Math class, 70 were registered for an English class, 50 were registered for both Math and English.
a) How many signed up only for a Math Class? b) How many signed up only for an English Class? c) How many signed up for Math or English? d) How many signed up neither for Math nor English?
Problem 2: 100 students were interviewed. 28 took PE, 31 took BIO, 42 took ENG, 9 took PE and BIO, 10 took PE and ENG, 6 took BIO and ENG, 4 took all three subjects.
a) How many students took none of the three subjects? b) How many students took PE but not BIO or ENG? c) How many students took BIO and PE but not ENG?
How And When To Use Venn Diagrams To Solve Word Problems?
Problem: At a breakfast buffet, 93 people chose coffee and 47 people chose juice. 25 people chose both coffee and juice. If each person chose at least one of these beverages, how many people visited the buffet?
How To Use Venn Diagrams To Help Solve Counting Word Problems?
Problem: In a class of 30 students, 19 are studying French, 12 are studying Spanish and 7 are studying both French and Spanish. How many students are not taking any foreign languages?
Probability, Venn Diagrams And Conditional Probability
This video shows how to construct a simple Venn diagram and then calculate a simple conditional probability.
Problem: In a class, P(male)= 0.3, P(brown hair) = 0.5, P (male and brown hair) = 0.2 Find (i) P(female) (ii) P(male| brown hair) (iii) P(female| not brown hair)

Venn Diagrams With Three Categories
Example: A group of 62 students were surveyed, and it was found that each of the students surveyed liked at least one of the following three fruits: apricots, bananas, and cantaloupes.
34 liked apricots. 30 liked bananas. 33 liked cantaloupes. 11 liked apricots and bananas. 15 liked bananas and cantaloupes. 17 liked apricots and cantaloupes. 19 liked exactly two of the following fruits: apricots, bananas, and cantaloupes.
a. How many students liked apricots, but not bananas or cantaloupes? b. How many students liked cantaloupes, but not bananas or apricots? c. How many students liked all of the following three fruits: apricots, bananas, and cantaloupes? d. How many students liked apricots and cantaloupes, but not bananas?
Venn Diagram Word Problem
Here is an example on how to solve a Venn diagram word problem that involves three intersecting sets.
Problem: 90 students went to a school carnival. 3 had a hamburger, soft drink and ice-cream. 24 had hamburgers. 5 had a hamburger and a soft drink. 33 had soft drinks. 10 had a soft drink and ice-cream. 38 had ice-cream. 8 had a hamburger and ice-cream. How many had nothing? (Errata in video: 90 - (14 + 2 + 3 + 5 + 21 + 7 + 23) = 90 - 75 = 15)
Venn Diagrams With Two Categories
This video introduces 2-circle Venn diagrams, and using subtraction as a counting technique.
How To Use 3-Circle Venn Diagrams As A Counting Technique?
Learn about Venn diagrams with two subsets using regions.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
Reset password New user? Sign up
Existing user? Log in
Venn Diagram
Already have an account? Log in here.
- Andrew Hayes
- Suyeon Khim
A Venn diagram is a diagram that shows the relationship between and among a finite collection of sets . If we have two or more sets, we can use a Venn diagram to show the logical relationship among these sets as well as the cardinality of those sets. In particular, Venn Diagrams are used to demonstrate De Morgan's Laws . Venn diagrams are also useful in illustrating relationships in statistics , probability , logic , and more.
Venn diagrams are particularly useful in helping us think carefully about set operations as they give us a visual depiction of the relationships involved.
Basic diagrams
Set notations in venn diagram, more on venn diagrams, example problems.
So what does a Venn diagram look like? To draw a Venn diagram we first draw a rectangle which will contain every item we want to consider. Since it contains every item, we can refer to it as "the universe."
Suppose now we wanted a set \(A\) which is a list of numbers containing 1 up to 5, and a set \(B\) which is a list of numbers containing 6 to 10. To represent each set we use circles:
How about if sets \(A\) and \(B\) have something in common? We can't simply draw two separate circles, as that won't form any logical relationship between the two. As you can see below, the way to show that relationship does indeed exist, where we merge the two circles partially.
In a universal set of all positive integers less than \(10,\) let \(A\) be the set of all positive even integers less than \(10,\) and \(B\) the set of all positive prime integers less than \(10\). Then what will the Venn diagram look like? we \(2\) is the only number that belongs to both sets, so it is found in the intersection point. Also we can see that \(1\) and \(9\) are found outside the circles but inside the rectangle or universal set. \(_\square\)
Venn diagrams are very useful in getting an intuition of set notations. Some common set notations and their respective diagrams are
1) \(A\cap B,\) read as \(A\) intersection \(B,\) is the set of all elements that are common to both \(A\) and \(B.\)
2) \( A\cup B,\) read as the union of \(A\) and \(B,\) is set of all elements found in both sets \(A\) and \(B.\) Observe that \(A \cup B= A + B - A\cap B,\) where we subtracted the intersection to account for the repetition of elements.
3) \(A\Delta B,\) read as symmetric difference of \(A\) and \(B,\) is the set of all elements in both sets excluding the intersection of the sets (\(A\cap B\)).
4) \(A' ,\) read as \(A\) compliment, is the set of all elements in the universal set excluding \(A\) itself. In some books the compliment notation is represented as \(A^{c}\).
The region marked in blue shows where the elements are found.
So far we have seen Venn diagrams showing the relationship between two sets, but that doesn't have to be the case, though the practicality of the diagram is lost after 3 sets.
Consider the above diagram where the number in each region indicates how many elements are there in that region. Then what is \[\] 1) the number of elements in set \(A?\) 2) the number of elements in set \(B?\) 3) the number of elements in sets \(A\) and \(B?\) 4) the number of elements in sets \(B\) and \(C?\) 5) the number of elements in sets \(A\) and \(C?\) 6) the number of elements in sets \(A\), \(B\) and \(C?\) 1) Adding up the numbers in set \(A\) gives \(n(A)=6+5+1+2=14.\) 2) Similarly, adding up the numbers in set \(B\) gives \(n(B)=2+8+1+7=18.\) 3) Ignore \(C\) and add up the elements found inside the intersection of \(A\) and \(B,\) then \(n(A\cap B)= 2 + 1=3.\) 4) Similarly, \(n(B\cap C)= 7+1=8.\) 5) Similarly, \(n(A\cap C)= 5+1=6.\) 6) The region marked in blue is the intersection of all 3 regions, so \(n(A\cap B \cap C)=1.\) \(_\square\)
When given sets and asked to find the relationship among them we see that Venn diagrams make things simpler. So it is advisable to use them when the sets are limited to 3.
Given the Venn diagram above consisting of a total of \(30\) students who study physics, biology, both and neither, if the total number of people studying physics and biology are \(19\) and \(11,\) respectively, what will be the number of people in the region marked "\(?\)" ? The region marked \(?\) is the region common to both physics and biology: \(P \cap B\). We know the total number of students is equal to the number of people in physics and biology \((P\cup B)\), plus the number of people in neither of the sets. Thus, \[\begin{align} \text{Total }&= P \cup B + 4\\ &= (P + B - P\cap B)+4\\ \\ \Rightarrow 30& = (19+11) - ? + 4\\ ?&=34-30 = 4. \ _\square \end{align}\]
Considering the diagram above: What percent of the the student study either biology only or physics only? The question can also be read as the symmetric difference between biology and physics students. So the total number of students studying physics only is \(19-4=15\) and the total number of students studying biology only is \(11-4=7\). This implies \[x=\frac { 22 }{ 30 } \times 100 \text{ (%)}=73.33 \text{ (%)}. \ _\square\]
Problem Loading...
Note Loading...
Set Loading...
Sets and Venn Diagrams
A set is a collection of things.
For example, the items you wear is a set: these include hat, shirt, jacket, pants, and so on.
You write sets inside curly brackets like this:
{hat, shirt, jacket, pants, ...}
You can also have sets of numbers:
- Set of whole numbers : {0, 1, 2, 3, ...}
- Set of prime numbers : {2, 3, 5, 7, 11, 13, 17, ...}
Ten Best Friends
You could have a set made up of your ten best friends:
- {alex, blair, casey, drew, erin, francis, glen, hunter, ira, jade}
Each friend is an "element" (or "member") of the set. It is normal to use lowercase letters for them.

Now let's say that alex, casey, drew and hunter play Soccer :
Soccer = {alex, casey, drew, hunter}
(It says the Set "Soccer" is made up of the elements alex, casey, drew and hunter.)

And casey, drew and jade play Tennis :
Tennis = {casey, drew, jade}
We can put their names in two separate circles:
You can now list your friends that play Soccer OR Tennis .
This is called a "Union" of sets and has the special symbol ∪ :
Soccer ∪ Tennis = {alex, casey, drew, hunter, jade}
Not everyone is in that set ... only your friends that play Soccer or Tennis (or both).
In other words we combine the elements of the two sets.
We can show that in a "Venn Diagram":
A Venn Diagram is clever because it shows lots of information:
- Do you see that alex, casey, drew and hunter are in the "Soccer" set?
- And that casey, drew and jade are in the "Tennis" set?
- And here is the clever thing: casey and drew are in BOTH sets!
All that in one small diagram.
Intersection
"Intersection" is when you must be in BOTH sets.
In our case that means they play both Soccer AND Tennis ... which is casey and drew.
The special symbol for Intersection is an upside down "U" like this: ∩
And this is how we write it:
Soccer ∩ Tennis = {casey, drew}
In a Venn Diagram:
Which Way Does That "U" Go?

Think of them as "cups": ∪ holds more water than ∩ , right?
So Union ∪ is the one with more elements than Intersection ∩
You can also "subtract" one set from another.
For example, taking Soccer and subtracting Tennis means people that play Soccer but NOT Tennis ... which is alex and hunter.
Soccer − Tennis = {alex, hunter}
Summary So Far
- ∪ is Union: is in either set or both sets
- ∩ is Intersection: only in both sets
- − is Difference: in one set but not the other
You can also use Venn Diagrams for 3 sets.
Let us say the third set is "Volleyball", which drew, glen and jade play:
Volleyball = {drew, glen, jade}
But let's be more "mathematical" and use a Capital Letter for each set:
- S means the set of Soccer players
- T means the set of Tennis players
- V means the set of Volleyball players
The Venn Diagram is now like this:
Union of 3 Sets: S ∪ T ∪ V
You can see (for example) that:
- drew plays Soccer, Tennis and Volleyball
- jade plays Tennis and Volleyball
- alex and hunter play Soccer, but don't play Tennis or Volleyball
- no-one plays only Tennis
We can now have some fun with Unions and Intersections ...
S = {alex, casey, drew, hunter}
T ∪ V = {casey, drew, jade, glen}
S ∩ V = {drew}
And how about this ...
- take the previous set S ∩ V
- then subtract T :
(S ∩ V) − T = {}
Hey, there is nothing there!
That is OK, it is just the "Empty Set". It is still a set, so we use the curly brackets with nothing inside: {}
The Empty Set has no elements: {}
Universal Set
The Universal Set is the set that has everything. Well, not exactly everything. Everything that we are interested in now.
Sadly, the symbol is the letter "U" ... which is easy to confuse with the ∪ for Union. You just have to be careful, OK?
In our case the Universal Set is our Ten Best Friends.
U = {alex, blair, casey, drew, erin, francis, glen, hunter, ira, jade}
We can show the Universal Set in a Venn Diagram by putting a box around the whole thing:
Now you can see ALL your ten best friends, neatly sorted into what sport they play (or not!).
And then we can do interesting things like take the whole set and subtract the ones who play Soccer :
We write it this way:
U − S = {blair, erin, francis, glen, ira, jade}
Which says "The Universal Set minus the Soccer Set is the Set {blair, erin, francis, glen, ira, jade}"
In other words "everyone who does not play Soccer".
And there is a special way of saying "everything that is not ", and it is called "complement" .
We show it by writing a little "C" like this:
Which means "everything that is NOT in S", like this:
S c = {blair, erin, francis, glen, ira, jade} (exactly the same as the U − S example from above)
- A c is the Complement of A: everything that is not in A
- Empty Set: the set with no elements. Shown by {}
- Universal Set: all things we are interested in
Venn Diagrams
Until now, we have examined sets using set notation. We know from previous lessons that the following conventions are used with sets:
- Capital letters are used to denote sets.
- Lowercase letters are used to denote elements of sets.
- Curly braces { } denote a list of elements in a set.
Another way to look at sets is with a visual tool called a Venn diagram , first developed by John Venn in the 1880s. In a Venn diagram, sets are represented by shapes; usually circles or ovals. The elements of a set are labeled within the circle. Let’s look at some examples.
Example 1: Given set R is the set of counting numbers less than 7. Draw and label a Venn diagram to represent set R and indicate all elements in the set.
Analysis: Draw a circle or oval. Label it R . Put the elements in R .
Solution:

Notation: R = {counting numbers < 7}
Example 2: Given set G is the set of primary colors. Draw and label a Venn diagram to represent set G and indicate all elements in the set.
Analysis: Draw a circle or oval. Label it G . Put the elements in G.

Notation: G = {primary colors}
Example 3: Given set B is the set of all vowels in the English alphabet. Draw and label a Venn diagram to represent set B and indicate all elements in the set.
Analysis: Draw a circle or oval. Label it B . Put the elements in B.
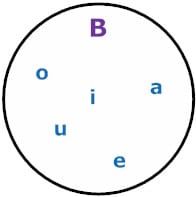
Notation: B = {vowels}
In each example above, we used a Venn diagram to represent a given set pictorially. Venn diagrams are especially useful for showing relationships between sets, as we will see in the examples below. First, we will use a Venn diagram to find the intersection of two sets. The intersection of two sets is all the elements they have in common.
Example 4: Let X = {1, 2, 3} and Let Y = {3, 4, 5}. Draw and label a Venn diagram to show the intersection of sets X and Y.
Analysis: We need to find the elements that are common in both sets. Draw a picture of two overlapping circles. Elements that are common to both sets will be placed in the middle part, where the circles overlap.
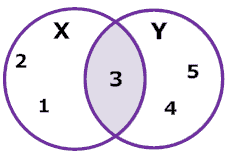
Explanation: The circle on the left represents set X and the circle on the right represents set Y . The shaded section in the middle is what they have in common. That is their intersection.
Example 5: Let X = {1, 2, 3} and Let Y = {3, 4, 5}. Draw and label a Venn diagram to represent the union of these two sets.
Analysis: To find the union of two sets, we look at all the elements in the two sets together.

Explanation: Any element in X , Y , or in their intersection is in their union. So X union Y is {1, 2, 3, 4, 5}. Both circles have been shaded to show the union of these sets.
| written as | ||
| read as | ||
| meaning of | ||
| Look for the | elements in common to both | combine all elements |
The examples in this lesson included simple Venn diagrams. We will explore this topic in more depth in the next few lessons. We will also learn more about intersection and union in this unit.
Summary: We can use Venn diagrams to represent sets pictorially. Venn diagrams are especially useful for showing relationships between sets, such as the intersection and union of overlapping sets.
Directions: Read each question below. Select your answer by clicking on its button. Feedback to your answer is provided in the RESULTS BOX. If you make a mistake, rethink your answer, then choose a different button.
|
| |
| } = {odd numbers between 0 and 10} = {even numbers between 0 and 10} RESULTS BOX: |
|
| |
| } = {hearts, diamonds, clubs, spades} = {jacks, queens, kings, aces} RESULTS BOX: |
|
| |
| = {2, 4, 6, 8, 10} = {6, 9} ∩ RESULTS BOX: |
|
| |
| = {2, 3, 5, 6, 7} = {2, 3, 5, 7, 11} = {2, 3, 5, 7, 11, 15} RESULTS BOX: |
|
| |
| ∪ ∩ = RESULTS BOX: |
- Math Article
- Venn Diagrams
Venn diagrams

Venn diagrams are the diagrams that are used to represent the sets, relation between the sets and operation performed on them, in a pictorial way. Venn diagram, introduced by John Venn (1834-1883), uses circles (overlapping, intersecting and non-intersecting), to denote the relationship between sets. A Venn diagram is also called a set diagram or a logic diagram showing different set operations such as the intersection of sets, union of sets and difference of sets. It is also used to depict subsets of a set.
For example, a set of natural numbers is a subset of whole numbers, which is a subset of integers. The relation between the sets of natural numbers, whole numbers and integers can be shown by the Venn diagram, where the set of integers is the universal set . See the figure below.

Here, W represents whole numbers and N represents natural numbers
The universal set (U) is usually represented by a closed rectangle, consisting of all the sets. The sets and subsets are shown by using circles or oval shapes.
What is a Venn Diagram?
A diagram used to represent all possible relations of different sets. A Venn diagram can be represented by any closed figure, whether it be a Circle or a Polygon (square, hexagon, etc.). But usually, we use circles to represent each set.

In the above figure, we can see a Venn diagram, represented by a rectangular shape about the universal set, which has two independent sets, X and Y. Therefore, X and Y are disjoint sets. The two sets, X and Y, are represented in a circular shape. This diagram shows that set X and set Y have no relation between each other, but they are a part of a universal set.
For example, set X = {Set of even numbers} and set Y = {Set of odd numbers} and Universal set, U = {set of natural numbers}
We can use the below formula to solve the problems based on two sets.
n(X ⋃ Y) = n(X) + n(Y) – n(X ⋂ Y)
Venn Diagram of Three Sets

The formula used to solve the problems on Venn diagrams with three sets is given below:
n(A ⋃ B ⋃ C) = n(A) + n(B) + n(C) – n(A ⋂ B) – n(B ⋂ C) – n(A ⋂ C) + n(A ⋂ B ⋂ C)
Venn Diagram Symbols
The symbols used while representing the operations of sets are:
- Union of sets symbol: ∪
- Intersection of sets symbol: ∩
- Complement of set: A’ or A c
How to draw a Venn diagram?
To draw a Venn diagram, first, the universal set should be known. Now, every set is the subset of the universal set (U). This means that every other set will be inside the rectangle which represents the universal set.
So, any set A (shaded region) will be represented as follows:

Where U is a universal set.
We can say from fig. 1 that
All the elements of set A are inside the circle. Also, they are part of the big rectangle which makes them the elements of set U.
Venn Diagrams of Set operations
In set theory, there are many operations performed on sets, such as:
- Union of Set
- Intersection of set
- Complement of set
- Difference of set
etc. The representations of different operations on a set are as follows:
Complement of a set in Venn Diagram
A’ is the complement of set A (represented by the shaded region in fig. 2). This set contains all the elements which are not there in set A.

It is clear that from the above figure,
A + A’ = U
It means that the set formed with elements of set A and set A’ combined is equal to U.
The complement of a complement set is a set itself.
Properties of Complement of set:
- (A ∪ B)′ = A′ ∩ B′
- (A ∩ B)′ = A′ ∪ B′
Intersection of two sets in Venn Diagram
A intersection B is given by: A ∩ B = {x : x ∈ A and x ∈ B}.
This represents the common elements between set A and B (represented by the shaded region in fig. 3).

Intersection of two Sets
Properties of the intersection of sets operation:
- A ∩ B = B ∩ A
- (A ∩ B) ∩ C = A ∩ (B ∩ C)
- φ ∩ A = φ ; U ∩ A = A
- A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
- A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
Union of Two Sets in Venn Diagram
A union B is given by: A ∪ B = {x | x ∈A or x ∈B} .
This represents the combined elements of set A and B (represented by the shaded region in fig. 4).

Union of two sets
Some properties of Union operation:
- A ∪ B = B ∪ A
- (A ∪ B) ∪ C = A ∪ (B ∪ C)
Complement of Union of Sets in Venn Diagram
(A ∪ B)’ : This is read as complement of A union B . This represents elements which are neither in set A nor in set B (represented by the shaded region in fig. 5).

Complement of A U B
Complement of Intersection of Sets in Venn Diagram
(A ∩ B)’: This is read as complement of A intersection B . This represents elements of the universal set which are not common between set A and B (represented by the shaded region in fig. 6).

Complement of A ∩ B
Difference between Two Sets in Venn Diagram
A – B : This is read as A difference B . Sometimes, it is also referred to as ‘ relative complement ’. This represents elements of set A which are not there in set B(represented by the shaded region in fig. 7).

Difference between Two Sets
Symmetric difference between two sets in Venn Diagram
A ⊝ B: This is read as a symmetric difference of set A and B . This is a set which contains the elements which are either in set A or in set B but not in both (represented by the shaded region in fig. 8).

Symmetric difference between two sets
Related Articles
- Set Theory in Maths
- Set Operations
- Subset And Superset
- Intersection And Difference Of Two Sets
Venn Diagram Example
Example: In a class of 50 students, 10 take Guitar lessons and 20 take singing classes, and 4 take both. Find the number of students who don’t take either Guitar or singing lessons.

Let A = no. of students who take guitar lessons = 10.
Let B = no. of students who take singing lessons = 20.
Let C = no. of students who take both = 4.
Now we subtract the value of C from both A and B. Let the new values be stored in D and E.
D = 10 – 4 = 6
E = 20 – 4 = 16
Now logic dictates that if we add the values of C, D, E and the unknown quantity “X”, we should get a total of 50 right? That’s correct.
So the final answer is X = 50 – C – D – E
X = 50 – 4 – 6 – 16
Venn’s diagrams are particularly helpful in solving word problems on number operations that involve counting. Once it is drawn for a given problem, the rest should be a piece of cake.
Venn Diagram Questions
- Out of 120 students in a school, 5% can play Cricket, Chess and Carroms. If so happens that the number of players who can play any and only two games are 30. The number of students who can play Cricket alone is 40. What is the total number of those who can play Chess alone or Carroms alone?
- Draw the diagram that best represents the relationship among the given classes: Animal, Tiger, Vehicle, Car
- At an overpriced department store, there are 112 customers. If 43 have purchased shirts, 57 have purchased pants, and 38 have purchased neither, how many purchased both shirts and pants?
- In a group, 25 people like tea or coffee; of these, 15 like tea and 6 like coffee and tea. How many like coffee?
Frequently Asked Questions on Venn Diagram
What do you mean by venn diagram, how do venn diagrams work, how do you do venn diagrams in math, what does a ∩ b mean, what are the different types of venn diagrams, what are the four benefits of using venn diagrams.
| MATHS Related Links | |
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.

- Testimonial
- Web Stories
Learning Home

Not Now! Will rate later

Venn Diagram: Concept and Solved Questions
What is a Venn Diagram?
Venn diagram, also known as Euler-Venn diagram is a simple representation of sets by diagrams. The usual depiction makes use of a rectangle as the universal set and circles for the sets under consideration.
In CAT and other MBA entrance exams, questions asked from this topic involve 2 or 3 variable only. Therefore, in this article we are going to discuss problems related to 2 and 3 variables.
Let's take a look at some basic formulas for Venn diagrams of two and three elements.
n ( A ∪ B) = n(A ) + n ( B ) - n ( A∩ B) n (A ∪ B ∪ C) = n(A ) + n ( B ) + n (C) - n ( A ∩ B) - n ( B ∩ C) - n ( C ∩ A) + n (A ∩ B ∩ C )
And so on, where n( A) = number of elements in set A. Once you understand the concept of Venn diagram with the help of diagrams, you don’t have to memorize these formulas.
Venn Diagram in case of two elements
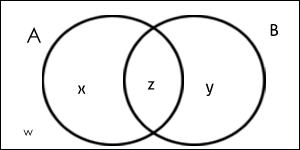
Where; X = number of elements that belong to set A only Y = number of elements that belong to set B only Z = number of elements that belong to set A and B both (AB) W = number of elements that belong to none of the sets A or B From the above figure, it is clear that n(A) = x + z ; n (B) = y + z ; n(A ∩ B) = z; n ( A ∪ B) = x +y+ z. Total number of elements = x + y + z + w
- CAT Admit Card
- CAT Eligibility Criteria
- CAT Exam Pattern
- CAT Preparation
- CAT Registration
- CAT 2019 Analysis
- CAT Study Material
- CAT 2021 Crash Course
- CAT 2023 Analysis
- B-School Application Form
- CAT Percentile Predictor
- MBA College Counselling
- CAT Notification
- CAT Syllabus
- CAT Question Papers
- CAT Sample Papers
- CAT Mock Test
- CAT Test Series
- CAT Cut Off
- CAT Colleges
- CAT Online Coaching
Venn Diagram in case of three elements
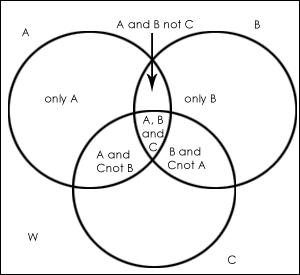
Where, W = number of elements that belong to none of the sets A, B or C
Tip: Always start filling values in the Venn diagram from the innermost value.
Solved Examples
Example 1: In a college, 200 students are randomly selected. 140 like tea, 120 like coffee and 80 like both tea and coffee.
- How many students like only tea?
- How many students like only coffee?
- How many students like neither tea nor coffee?
- How many students like only one of tea or coffee?
- How many students like at least one of the beverages?
Solution: The given information may be represented by the following Venn diagram, where T = tea and C = coffee.
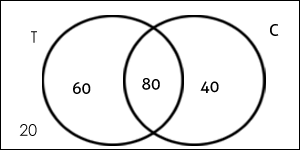
- Number of students who like only tea = 60
- Number of students who like only coffee = 40
- Number of students who like neither tea nor coffee = 20
- Number of students who like only one of tea or coffee = 60 + 40 = 100
- Number of students who like at least one of tea or coffee = n (only Tea) + n (only coffee) + n (both Tea & coffee) = 60 + 40 + 80 = 180
Example 2: In a survey of 500 students of a college, it was found that 49% liked watching football, 53% liked watching hockey and 62% liked watching basketball. Also, 27% liked watching football and hockey both, 29% liked watching basketball and hockey both and 28% liked watching football and basket ball both. 5% liked watching none of these games.
- How many students like watching all the three games?
- Find the ratio of number of students who like watching only football to those who like watching only hockey.
- Find the number of students who like watching only one of the three given games.
- Find the number of students who like watching at least two of the given games.
Solution: n(F) = percentage of students who like watching football = 49% n(H) = percentage of students who like watching hockey = 53% n(B)= percentage of students who like watching basketball = 62% n ( F ∩ H) = 27% ; n (B ∩ H) = 29% ; n(F ∩ B) = 28% Since 5% like watching none of the given games so, n (F ∪ H ∪ B) = 95%. Now applying the basic formula, 95% = 49% + 53% + 62% -27% - 29% - 28% + n (F ∩ H ∩ B) Solving, you get n (F ∩ H ∩ B) = 15%.
Now, make the Venn diagram as per the information given. Note: All values in the Venn diagram are in percentage.
- Number of students who like watching all the three games = 15 % of 500 = 75.
- Ratio of the number of students who like only football to those who like only hockey = (9% of 500)/(12% of 500) = 9/12 = 3:4.
- The number of students who like watching only one of the three given games = (9% + 12% + 20%) of 500 = 205
- The number of students who like watching at least two of the given games=(number of students who like watching only two of the games) +(number of students who like watching all the three games)= (12 + 13 + 14 + 15)% i.e. 54% of 500 = 270.
To know the importance of this topic, check out some previous year CAT questions from this topic:
CAT 2017 Solved Questions:
Solution: It is given that 200 candidates scored above 90th percentile overall in CET. Let the following Venn diagram represent the number of persons who scored above 80 percentile in CET in each of the three sections:
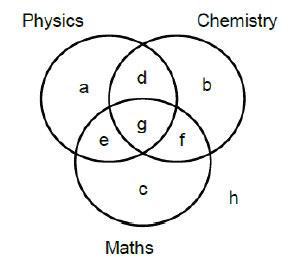
2. From the given condition, g is a multiple of 5. Hence, g = 20. The number of candidates at or above 90th percentile overall and at or above 80th percentile in both P and M = e + g = 60.
3. In this case, g = 20. Number of candidates shortlisted for AET = d + e + f + g = 10 + 40 + 100 + 20 = 170
4. From the given condition, the number of candidates at or above 90th percentile overall and at or above 80th percentile in P in CET = 104. The number of candidates who have to sit for separate test = 296 + 3 = 299.
Another type of questions asked from this topic is based on maxima and minima. We have discussed this type in the other article.
Key Learning:
- It is important to carefully list the conditions given in the question in the form of a Venn diagram.
- While solving such questions, avoid taking many variables.
- Try solving the questions using the Venn diagram approach and not with the help of formulae.
You can also post in the comment section below, any query or explanation for any concept mentioned in the article.
- CAT Logical Reasoning
- CAT Reading Comprehension
- CAT Grammar
- CAT Para Jumbles
- CAT Data Interpretation
- CAT Data Sufficiency
- CAT DI Questions
- CAT Analytical Reasoning
Most Popular Articles - PS

All About the Quantitative Aptitude of CAT

Number System for CAT Made Easy

100 Algebra Questions Every CAT Aspirant Must Solve
Use Creativity to crack CAT

Averages: Finding the Missing Page Number

Strategy for Quant Questions in CAT

Comprehensive Guide for CAT Probability

Comprehensive Guide for CAT Mensuration

Chess Board: How to find Number of Squares and Rectangles
100 Geometry questions every CAT aspirant must solve
Permutation and combination and probability for cat.
Tackle Time, Speed & Distance for CAT
Sequences and Series - Advanced
-thumbnail_0.png?null&itok=Xhd6gz54)
CAT Formulae E-Book

Races and Games

Geometry: Shortcuts and Tricks
-thumbnail.png?null&itok=USokav20)
Number System-Integral Solutions: Shortcuts and Tricks

Permutation and Combination: Advanced

Geometry - Polygons
-thumbnail.png?null&itok=B9Rsz-Xq)
Number System: Integral Solutions and Remainders based on Factorials

How to improve in Geometry & Mensuration

How to improve in Permutation and Combination

Cheat Codes: Permutation and Combination
How to improve in Algebra
Venn Diagram Examples for Problem Solving
Updated on: 13 September 2022
What is a Venn Diagram?
Venn diagrams define all the possible relationships between collections of sets. The most basic Venn diagrams simply consist of multiple circular boundaries describing the range of sets.

The overlapping areas between the two boundaries describe the elements which are common between the two, while the areas that aren’t overlapping house the elements that are different. Venn diagrams are used often in math that people tend to assume they are used only to solve math problems. But as the 3 circle Venn diagram below shows it can be used to solve many other problems.
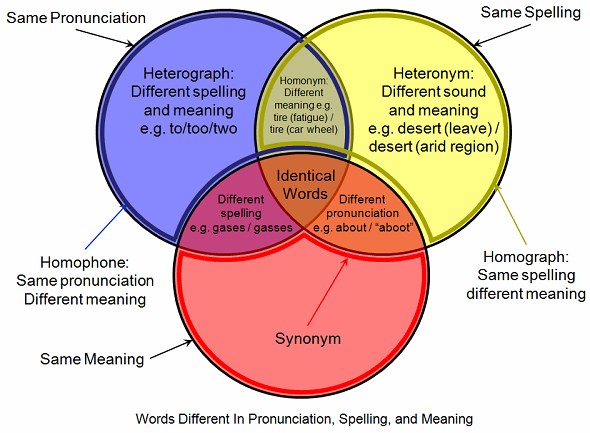
Though the above diagram may look complicated, it is actually very easy to understand. Although Venn diagrams can look complex when solving business processes understanding of the meaning of the boundaries and what they stand for can simplify the process to a great extent. Let us have a look at a few examples which demonstrate how Venn diagrams can make problem solving much easier.
Example 1: Company’s Hiring Process
The first Venn diagram example demonstrates a company’s employee shortlisting process. The Human Resources department looks for several factors when short-listing candidates for a position, such as experience, professional skills and leadership competence. Now, all of these qualities are different from each other, and may or may not be present in some candidates. However, the best candidates would be those that would have all of these qualities combined.

The candidate who has all three qualities is the perfect match for your organization. So by using simple Venn Diagrams like the one above, a company can easily demonstrate its hiring processes and make the selection process much easier.
A colorful and precise Venn diagram like the above can be easily created using our Venn diagram software and we have professionally designed Venn diagram templates for you to get started fast too.
Example 2: Investing in a Location
The second Venn diagram example takes things a step further and takes a look at how a company can use a Venn diagram to decide a suitable office location. The decision will be based on economic, social and environmental factors.

In a perfect scenario you’ll find a location that has all the above factors in equal measure. But if you fail to find such a location then you can decide which factor is most important to you. Whatever the priority because you already have listed down the locations making the decision becomes easier.
Example 3: Choosing a Dream Job
The last example will reflect on how one of the life’s most complicated questions can be easily answered using a Venn diagram. Choosing a dream job is something that has stumped most college graduates, but with a single Venn diagram, this thought process can be simplified to a great extent.
First, single out the factors which matter in choosing a dream job, such as things that you love to do, things you’re good at, and finally, earning potential. Though most of us dream of being a celebrity and coming on TV, not everyone is gifted with acting skills, and that career path may not be the most viable. Instead, choosing something that you are good at, that you love to do along with something that has a good earning potential would be the most practical choice.

A job which includes all of these three criteria would, therefore, be the dream job for someone. The three criteria need not necessarily be the same, and can be changed according to the individual’s requirements.
So you see, even the most complicated processes can be simplified by using these simple Venn diagrams.
Join over thousands of organizations that use Creately to brainstorm, plan, analyze, and execute their projects successfully.

More Related Articles

Great article, and all true, but.. I hate venn diagrams! I don’t know why, they’ve just never seemed to work for me. Frustrating!
Hey thanks for writing. It helped me in many ways Thanks again 🙂
Hi Nishadha,
Nice article! I love Venn Diagrams because nothing comes to close to expressing the logical relationships between different sets of elements that well. With Microsoft Word 2003 you can create fantastic looking and colorful Venn Diagrams on the fly, with as many elements and colors as you need.
Hi Worli, Yes, Venn diagrams are a good way to solve problems, it’s a shame that it’s sort of restricted to the mathematics subject. MS Word do provides some nice options to create Venn diagrams, although it’s not the cheapest thing around.
Leave a comment Cancel reply
Please enter an answer in digits: 20 + eight =
Download our all-new eBook for tips on 50 powerful Business Diagrams for Strategic Planning.

Learn maths at home
How to Solve Venn Diagrams with 3 Circles
Venn diagrams with 3 circles: video lesson, what is the purpose of venn diagrams.
A Venn diagram is a type of graphical organizer which can be used to display similarities and differences between two or more sets. Circles are used to represent each set and any properties in common to both sets will be written in the overlap of the circles. Any property unique to a particular set is written in that circle alone.
For example, here is a Venn diagram comparing and contrasting dogs and cats.
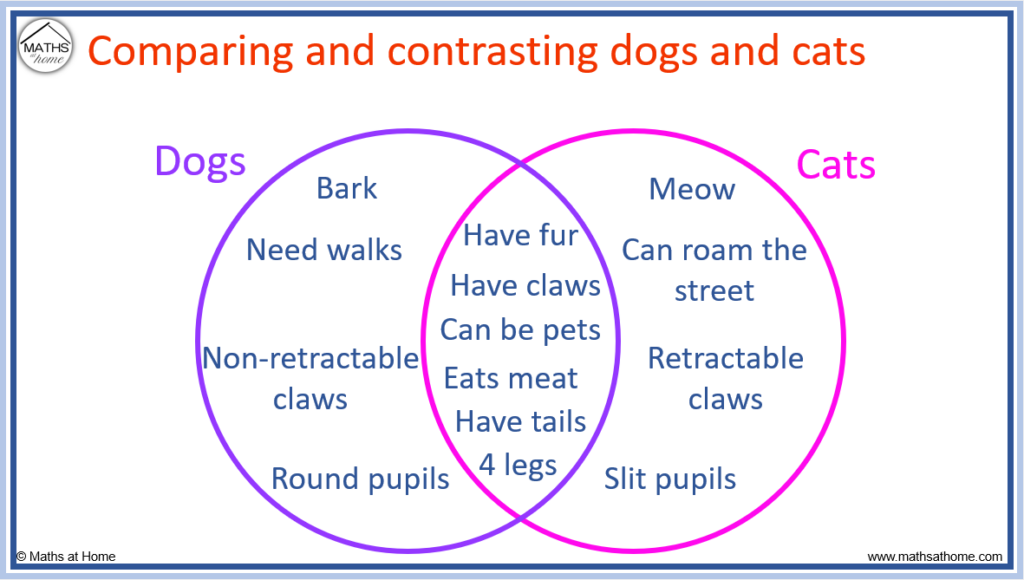
The Venn diagram shows the following information:
- Have non-retractable claws
- Have round pupils
- Roam the street
- Have retractable claws
- Have slit pupils
Both dogs and cats:
- Can be pets
- Have 4 legs
A Venn diagram with three circles is called a triple Venn diagram.
A Venn diagram with three circles is used to compare and contract three categories. Each circle represents a different category with the overlapping regions used to represent properties that are shared between the three categories.
For example, a triple Venn diagram with 3 circles is used to compare dogs, cats and birds.
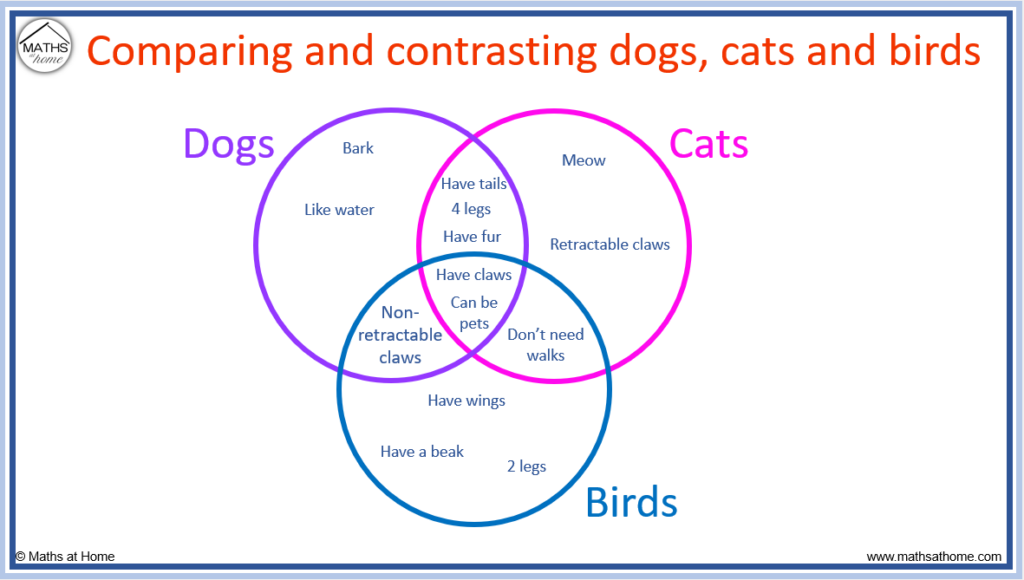
Dogs, cats and birds can all have claws and can also be pets.
Only birds:
- Have a beak
- Have 2 legs
Only both dogs and cats:
Only both dogs and birds:
Only both cats and birds:
- Don’t need walks
How to Make a Venn Diagram with 3 Circles
- Write the number of items belonging to all three sets in the central overlapping region.
- Write the remaining number of items belonging each pair of the sets in their overlapping regions.
- Write the remaining number of items belonging to each individual set in the non-overlapping region of each circle.
Make a Venn Diagram for the following situation:
30 students were asked which sports they play.
- 20 play basketball in total
- 16 play football in total
- 15 play tennis in total
- 10 play basketball and tennis
- 11 play basketball and football
- 9 play football and tennis
- 7 play all three
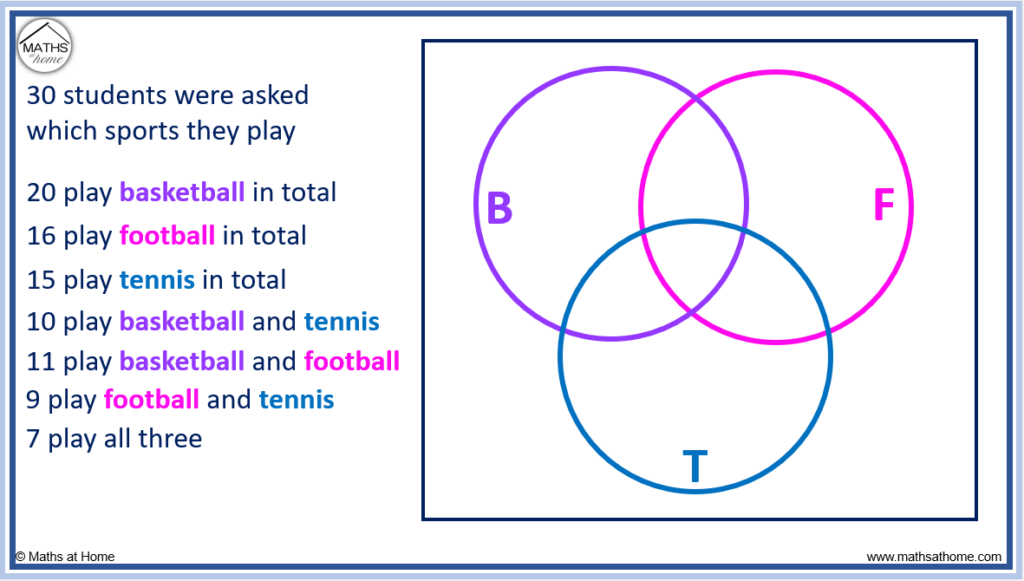
- Write the number of items belonging to all three sets in the central overlapping region
When making a Venn diagram, it is important to complete any overlapping regions first.
In this example, we start with the students that play all three sports. 7 students play all three sports.
The number 7 is placed in the overlap of all 3 circles. The shaded region shown is the overlapping area of all three circles.
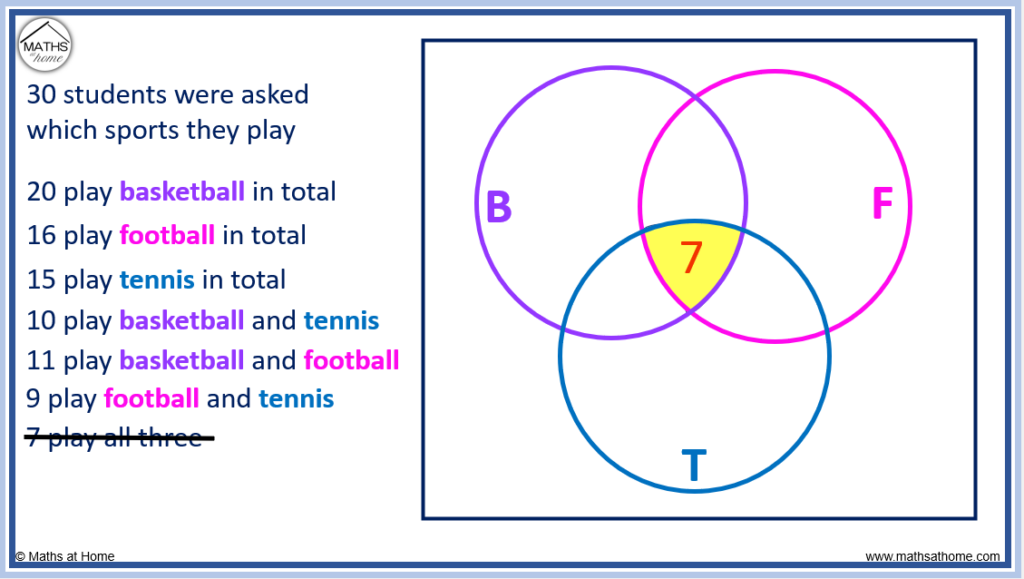
2. Write the remaining number of items belonging each pair of the sets in their overlapping regions
There are 3 regions in which exactly two circles overlap.
There is the overlap of basketball and tennis, basketball and football and then tennis and football.
There are 10 students that play both basketball and tennis. The overlapping region of these two circles is shown below. We already have the 7 students that play all three sports in this region.
Therefore we only need 3 more students who play basketball and tennis but do not play football to make the total of this region add up to 10.
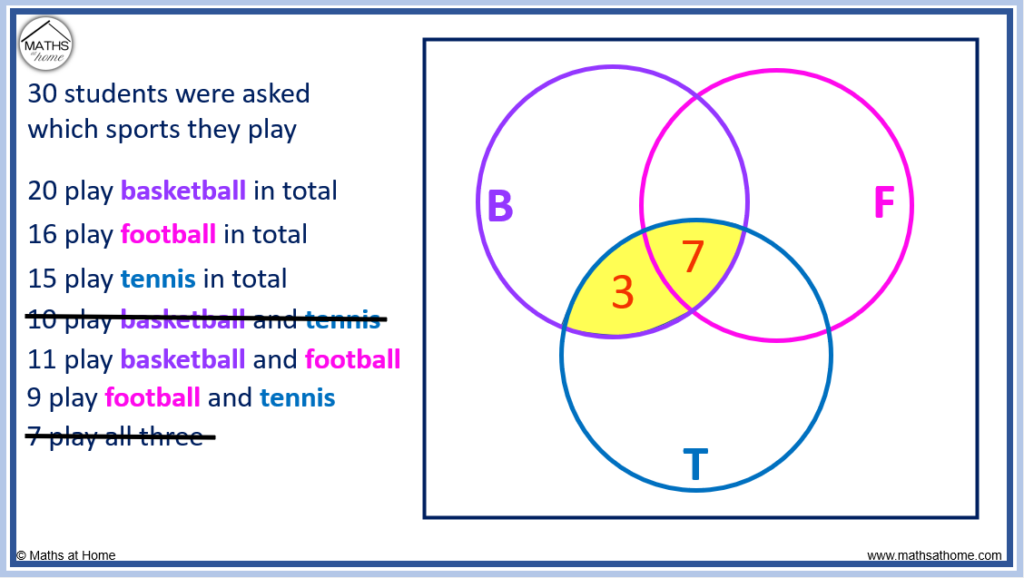
The next overlapping region of two circles is those that play basketball and football. There are 11 students in total that play both.
The overlapping region of the basketball and football circles is shown below.
There are already 7 students who play all three sports and so, a further 4 students must play both basketball and football but not tennis in order to make the total in this shaded region add up to 11 students.
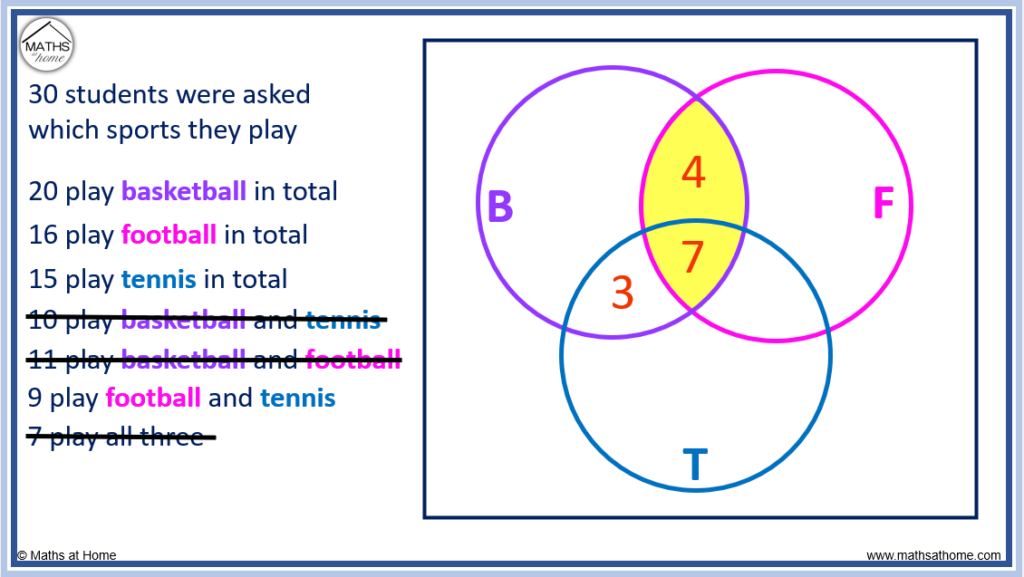
The next overlapping region of two circles is those that play football and tennis. There are 9 students in total that play both.
The overlapping region of the football and tennis circles is shown below.
There are already 7 students who play all three sports and so, a further 2 students must play both football and tennis but not basketball in order to make the total in this shaded region add up to 9 students.
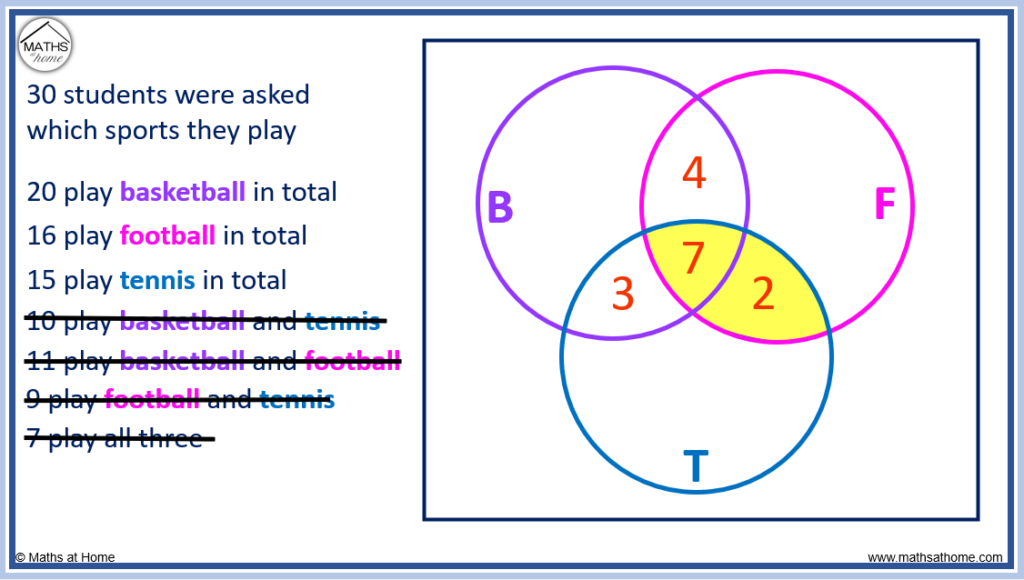
Write the remaining number of items belonging to each individual set in the non-overlapping region of each circle
There are three individual sets which are represented by the three circles. There are those that play basketball, football and tennis.
20 students play basketball in total. These 20 students are shown by the shaded circle below.
We already have 3, 7 and 4 students in the overlapping regions. This is a total of 14 students so far. We need a further 6 students who only play basketball in order for the numbers in this circle to make a total of 20.
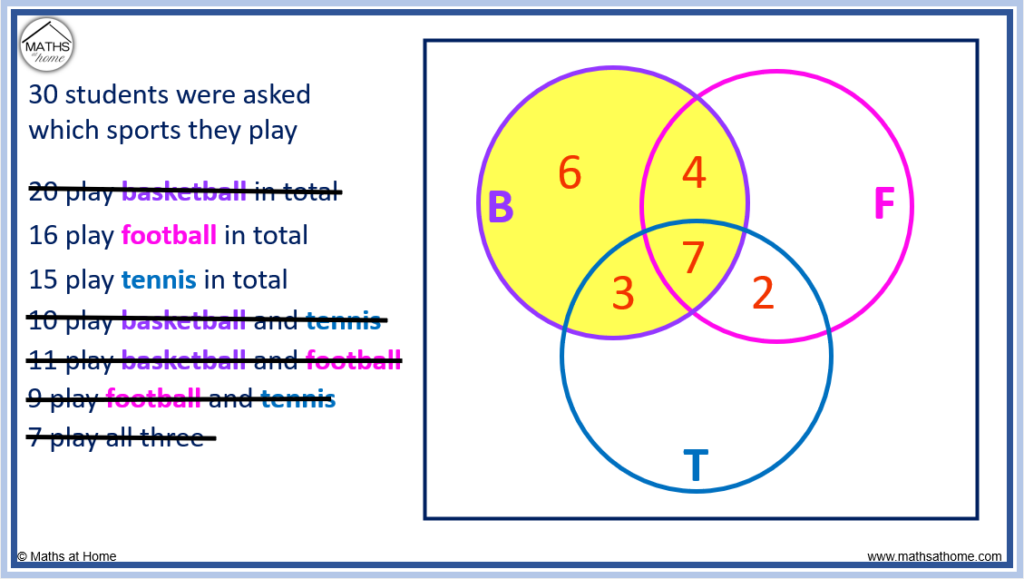
The next individual sport is football. 16 students play football in total.
There are already 4, 7 and 2 students in the overlapping regions. This makes a total of 13 students so far.
3 more students are required to make the circle total up to 16. 3 students play only football and not basketball and tennis.
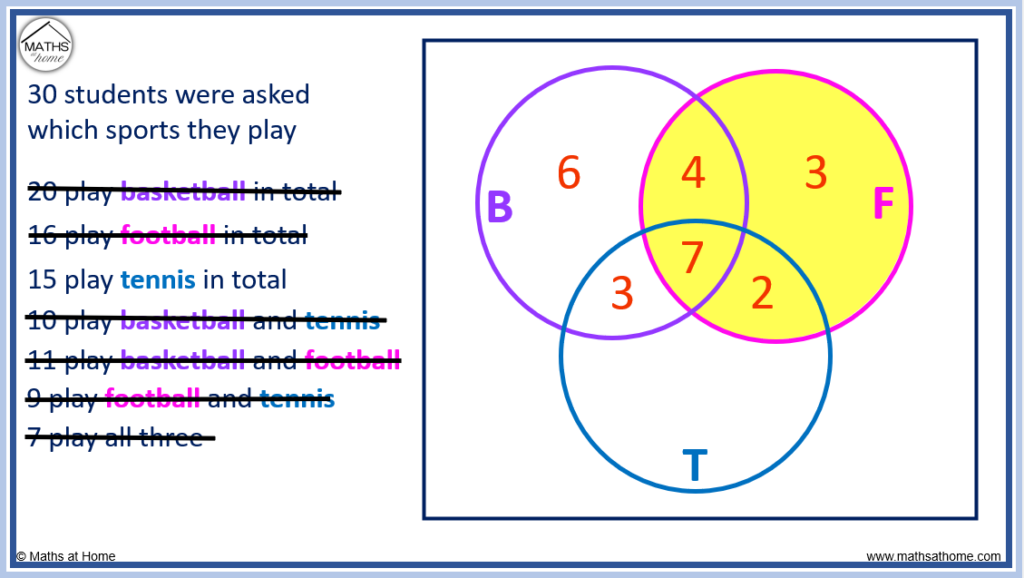
Finally, there are 15 students who play tennis shown by the shaded region below.
There are already 3, 7 and 2 students in the overlapping regions, making a total of 12 students.
A further 3 students are required to make the total of 15 students in this circle.
3 students play tennis but not basketball or football.
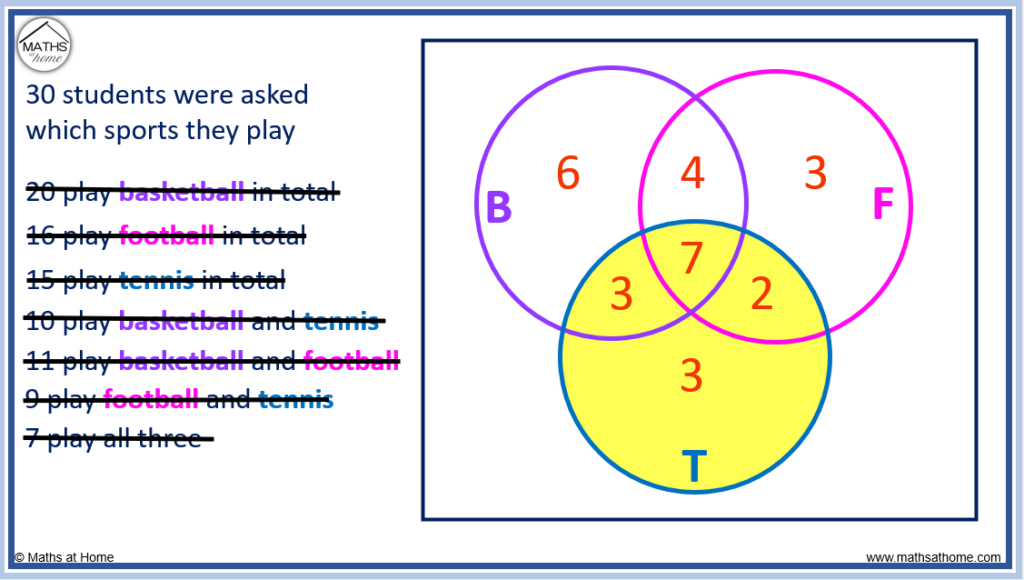
The values in each circle sum to 28 students.
That is 6 + 4 + 3 + 7 + 3 + 2 + 3 = 28.
Since there are 30 students who were asked in total, a further 2 students must play none of these three sports.
How to Solve a Venn Diagram with 3 Circles
To solve a Venn diagram with 3 circles, start by entering the number of items in common to all three sets of data. Then enter the remaining number of items in the overlapping region of each pair of sets. Enter the remaining number of items in each individual set. Finally, use any known totals to find missing numbers.
Venn diagrams are particularly useful for solving word problems in which a list of information is given about different categories. Numbers are placed in each region representing each statement.
100 people were asked which pets they have.
- 32 people in total have a cat
- 18 people in total have a rabbit
- 10 people have just a dog and a rabbit
- 21 people have just a dog and a cat
- 7 people have just a cat and a rabbit
- 3 people own all three pets
How many people just have a dog?
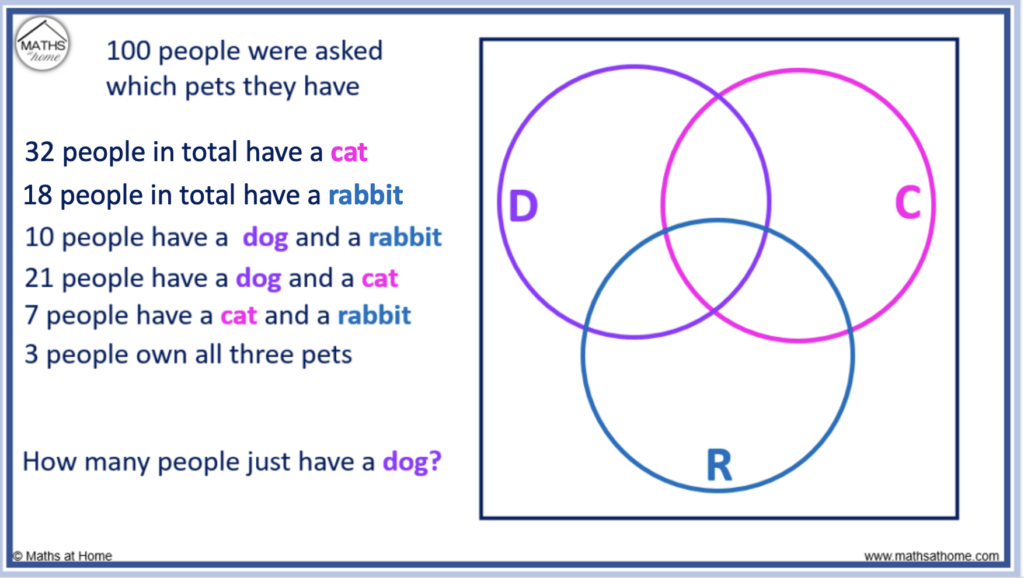
Start by entering the number of items in common to all three sets of data
3 people own all three pets and so, a number 3 is written in the overlapping region of all three circles.
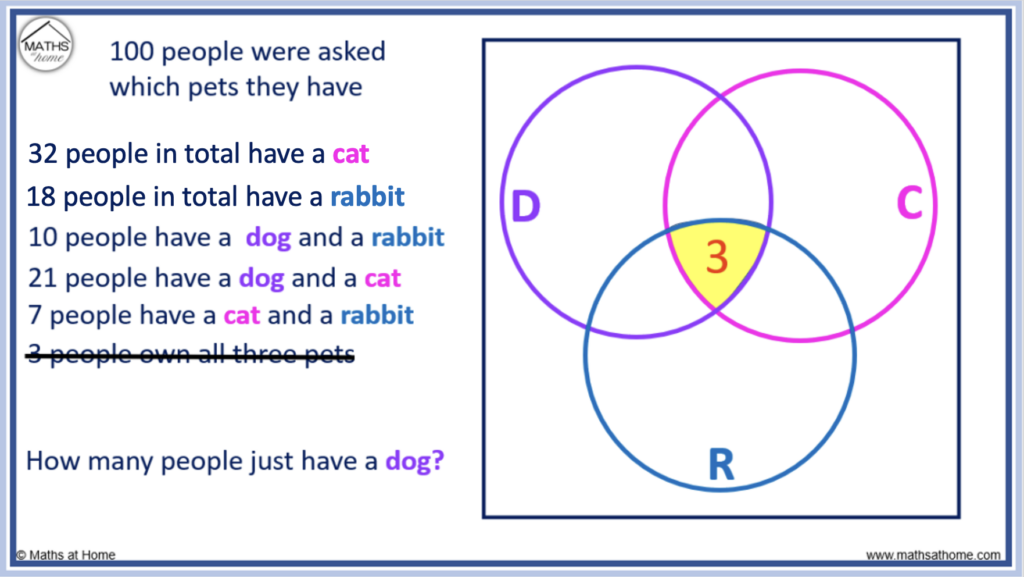
Then enter the remaining number of items in the overlapping region of each pair of sets
10 people have just a dog and a rabbit.
Since 3 people are already in this region, 7 more people are needed.
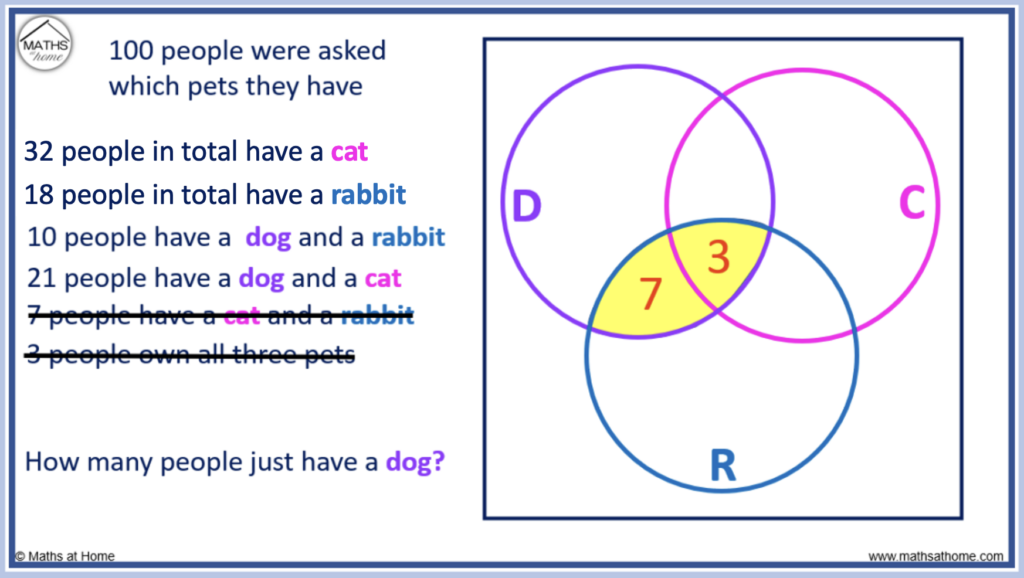
21 people have just a dog and a cat.
Since 3 people are already in this region, 18 more people are needed.
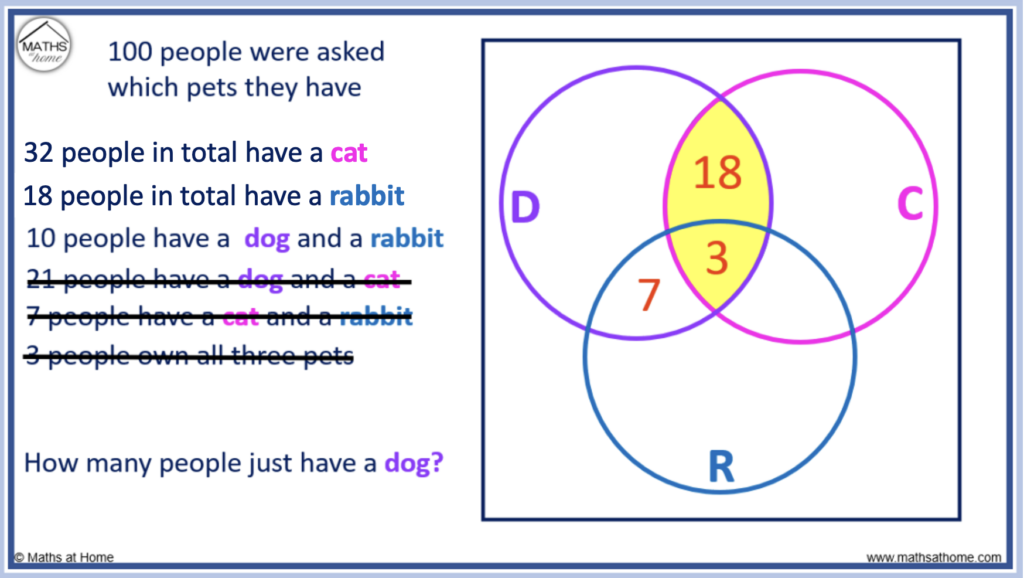
7 people have just a cat and a rabbit.
Since 3 people are already in this region, 4 more people are needed.
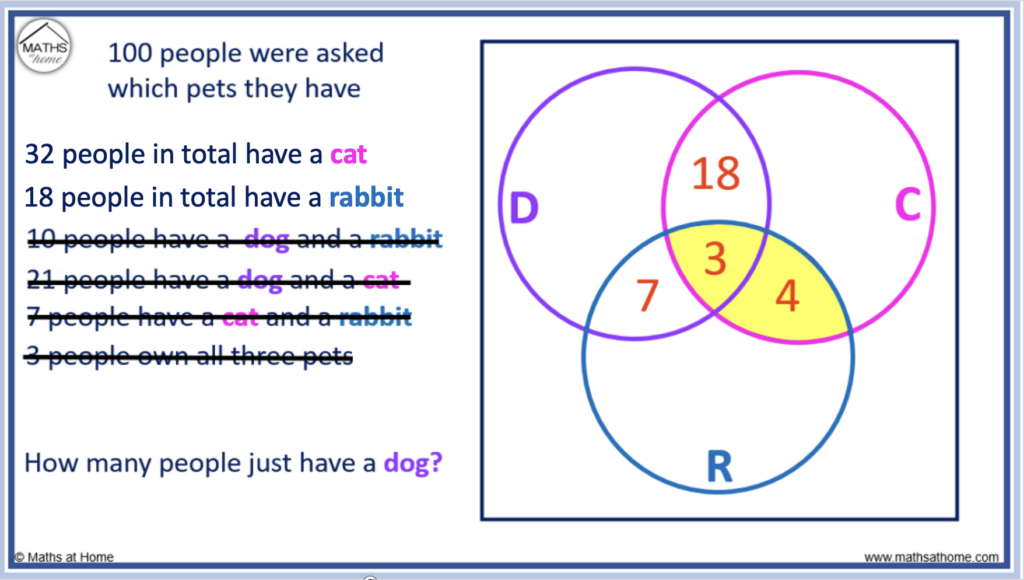
Enter the remaining number of items in each individual set
32 people in total have a cat.
There are already 18 + 3 + 4 = 25 people in this circle.
Therefore a further 7 people are needed in this circle to make 32.
7 people just own a cat and no other pet.
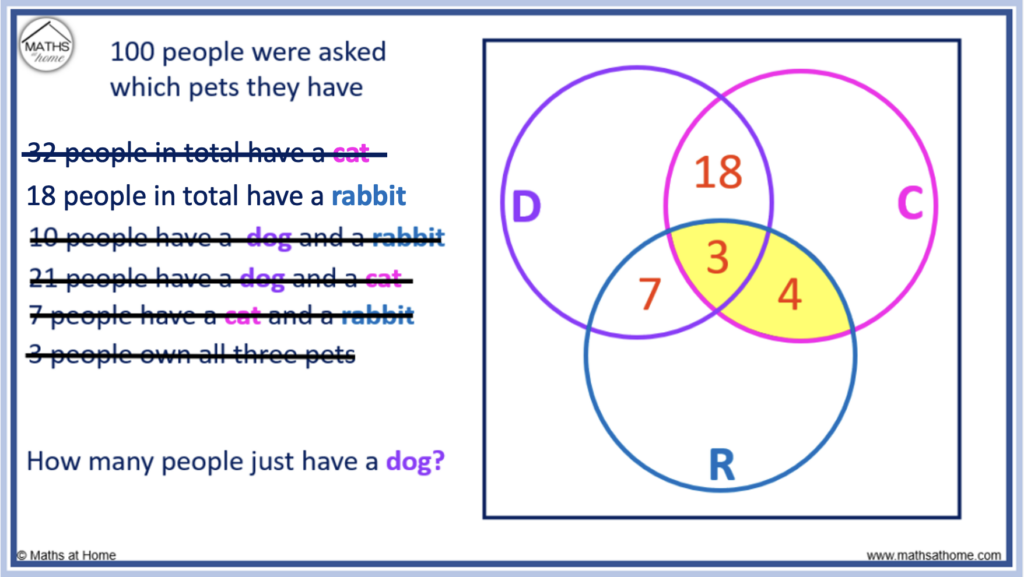
18 people in total have a rabbit.
There are already 7 + 3 + 4 = 14 people in this circle.
Therefore a further 4 people are needed in this circle to make 18.
4 people just own a rabbit and no other pet.
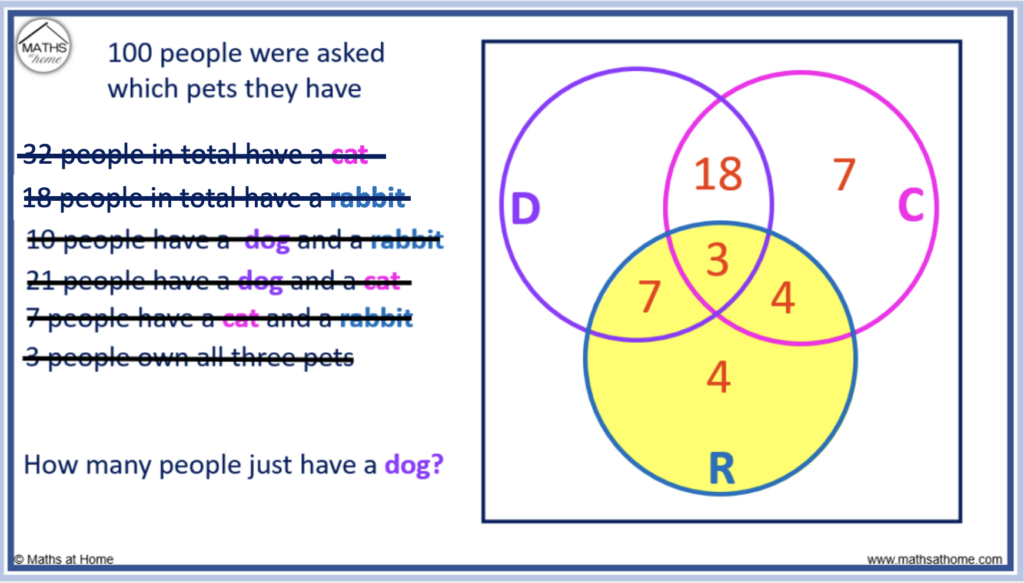
Finally, use any known totals to find missing numbers
We are now told that 25 people own none of these pets. This means that a 25 is written outside of all of the circles but still within the Venn diagram.
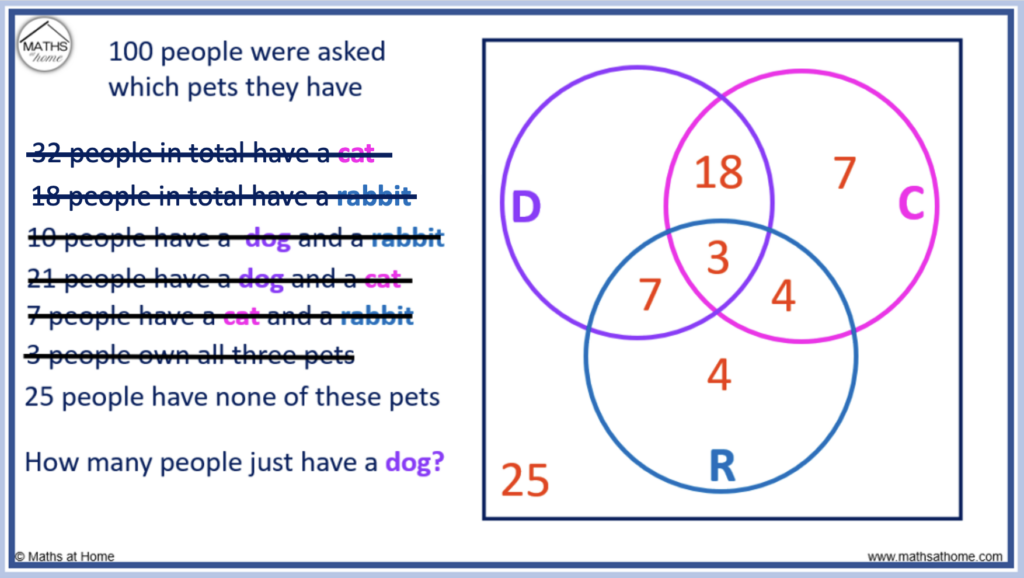
The question requires the number of people who just own a dog.
There are 100 people in total and so, all of the numbers in the complete Venn diagram must add up to 100.

Adding the numbers so far, 3 + 7 + 4 + 18 + 4 + 7 + 25 = 68 people in total.
Since the numbers must add to 100, there must be a further 32 people who own a dog.
Now all of the numbers in the Venn diagram add to 100.
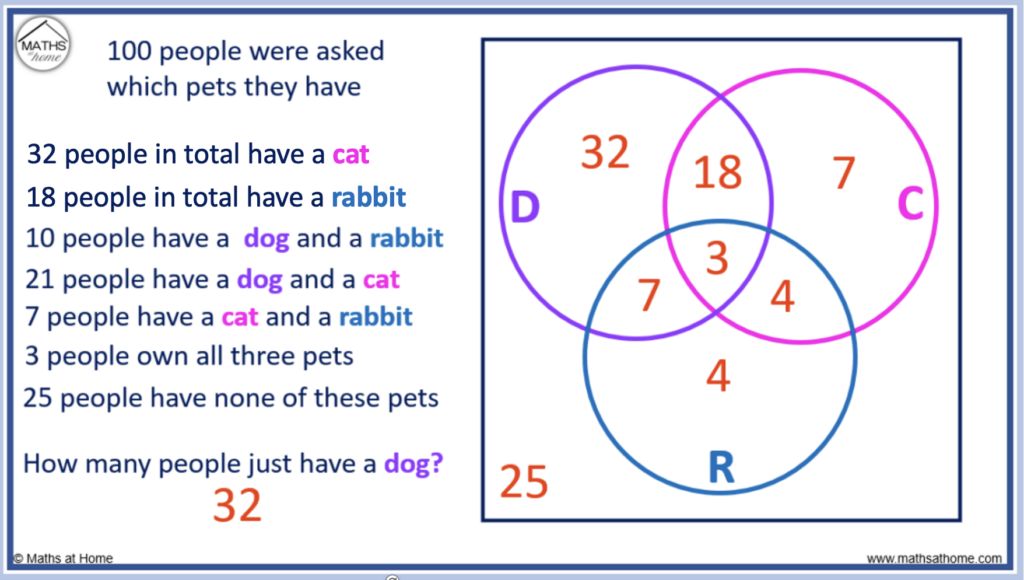
Venn Diagram with 3 Circles Template
Here is a downloadable template for a blank Venn Diagram with 3 circles.
How to Shade a Venn Diagram with 3 Circles
Here are some examples of shading Venn diagrams with 3 sets:
Shaded Region: A
Shaded Region: B
Shaded Region: C
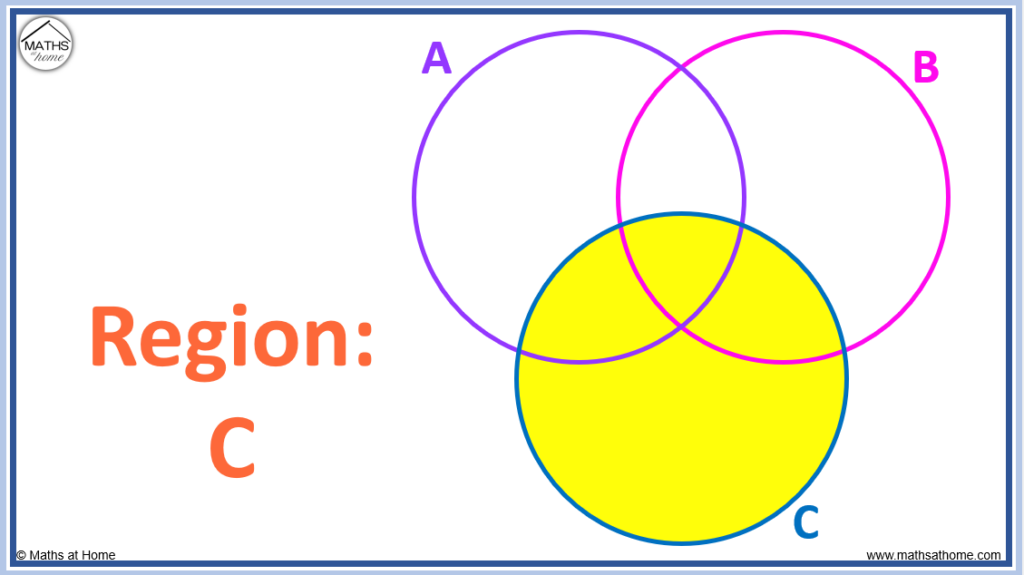
Shaded Region: A∪B
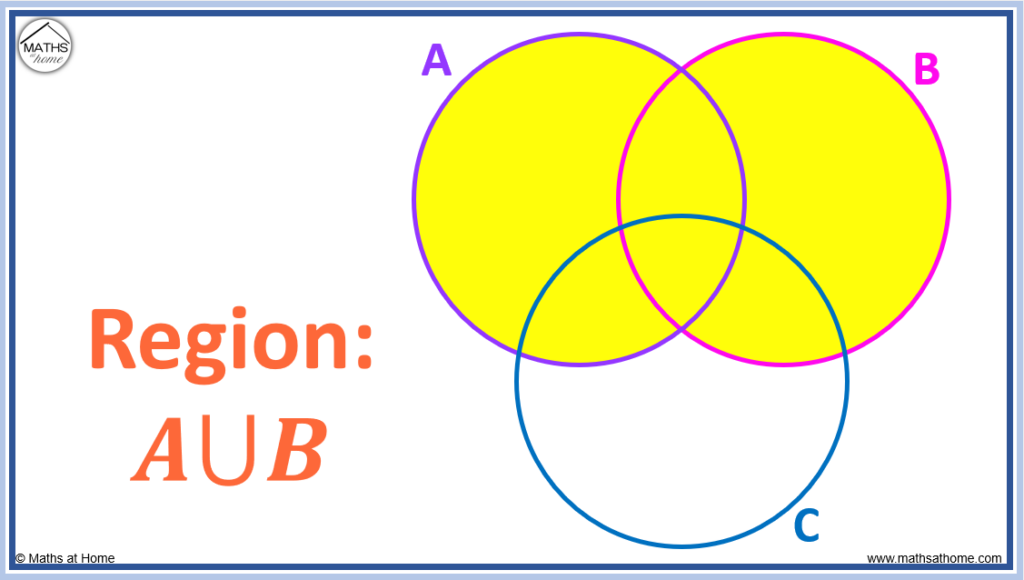
Shaded Region: B∪C
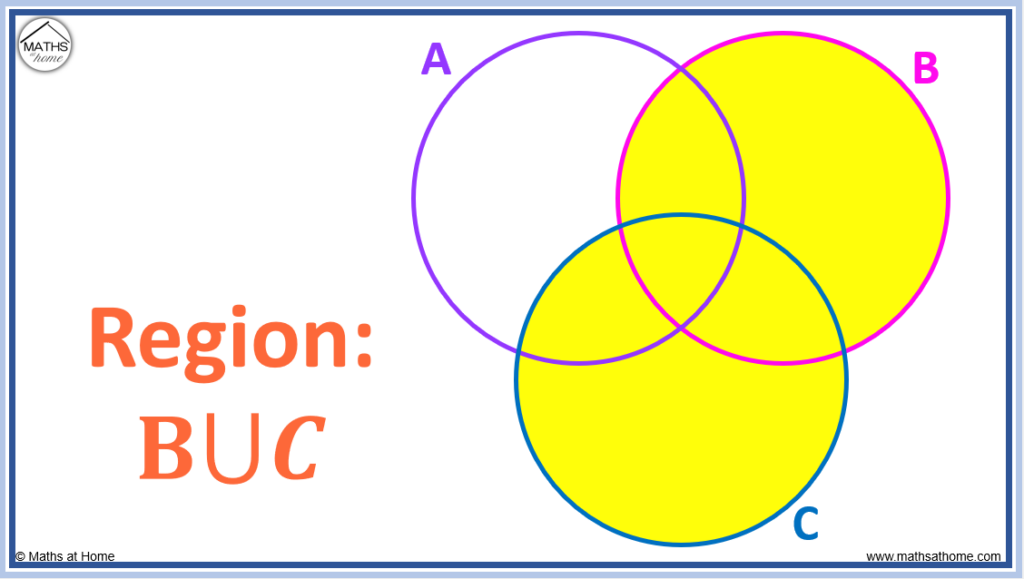
Shaded Region: A∪C
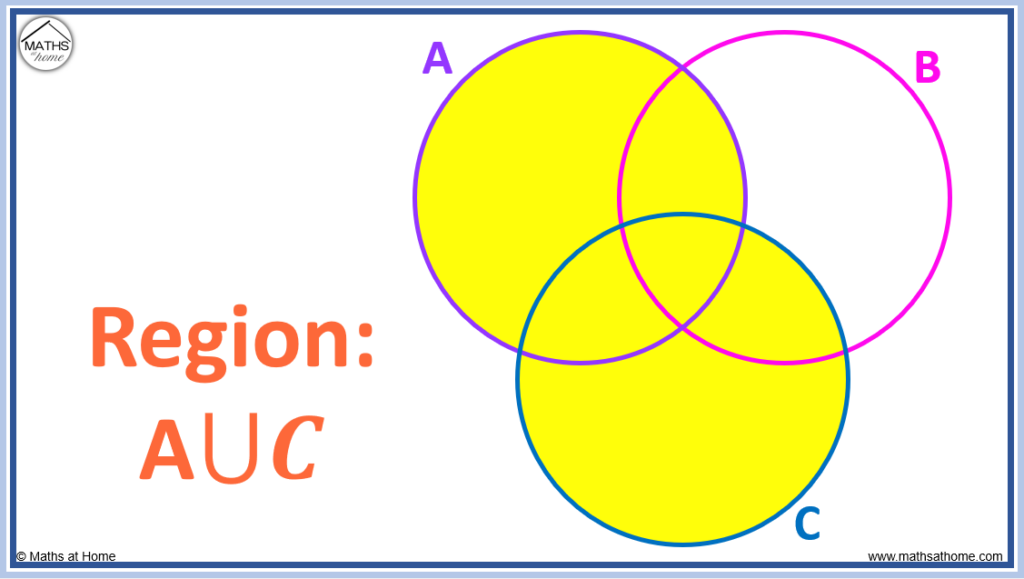
Shaded Region: A∩B
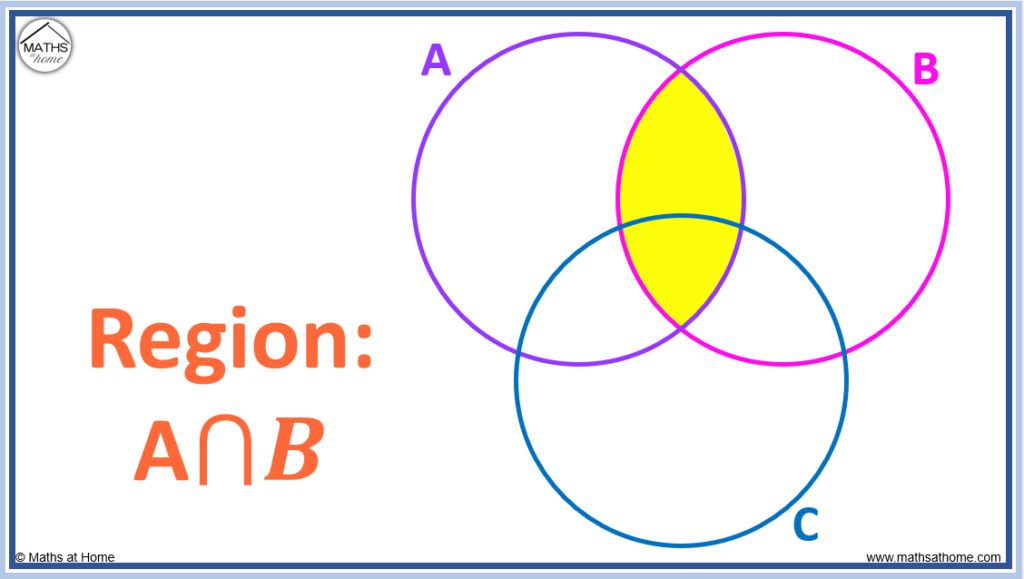
Shaded Region: B∩C
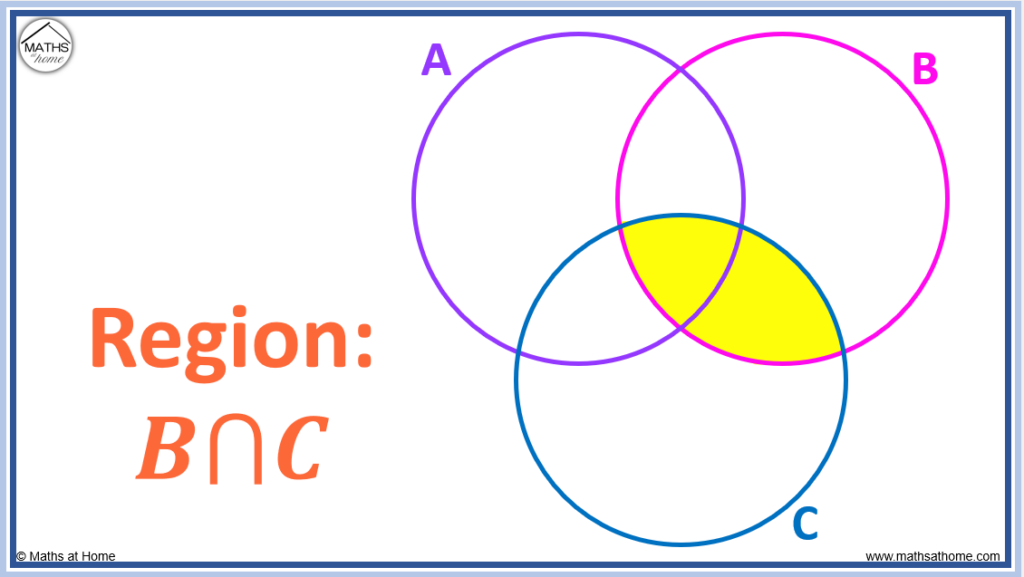
Shaded Region: A∩C
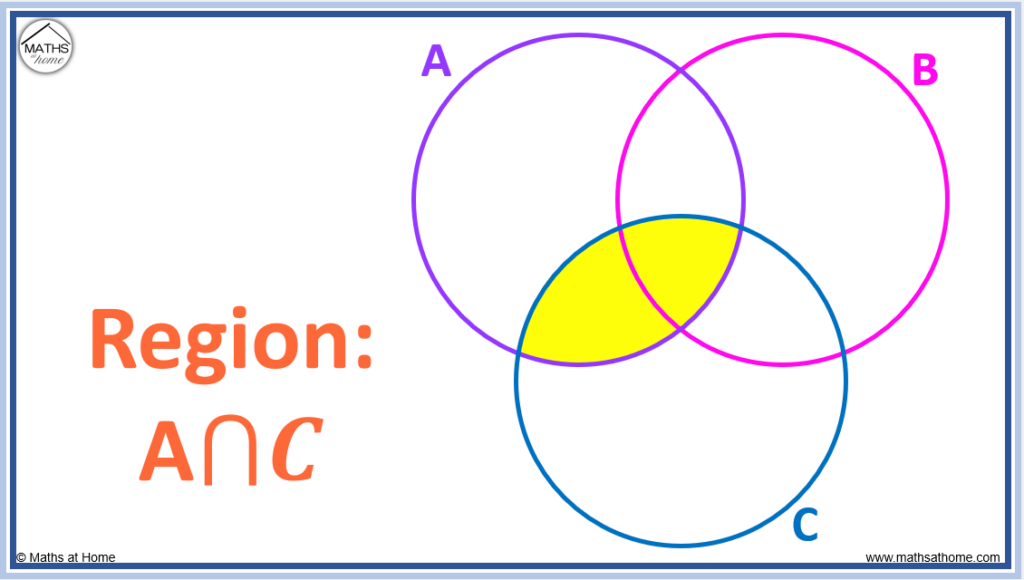
Shaded Region: A∪B∪C
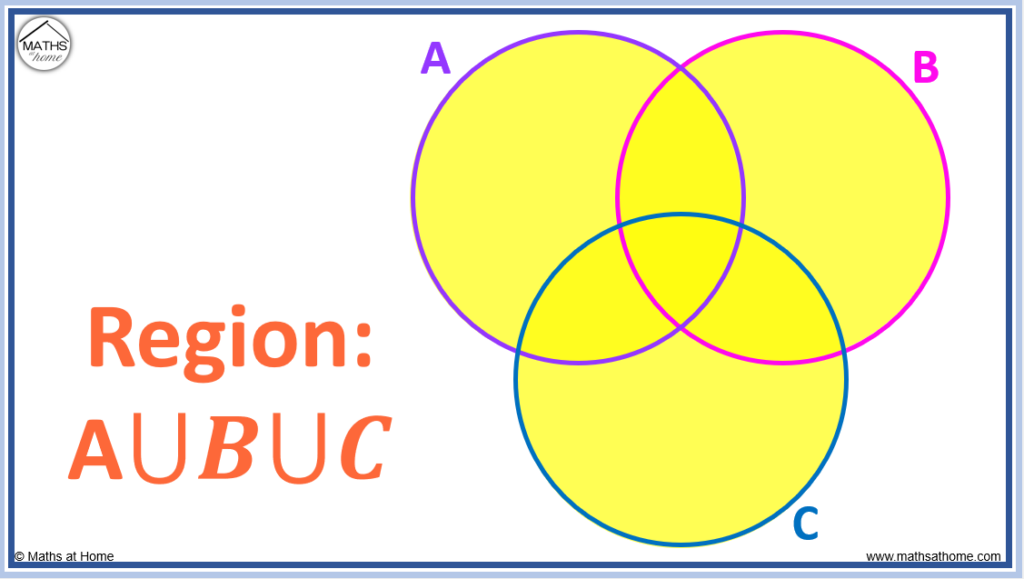
Shaded Region: A∩B∩C
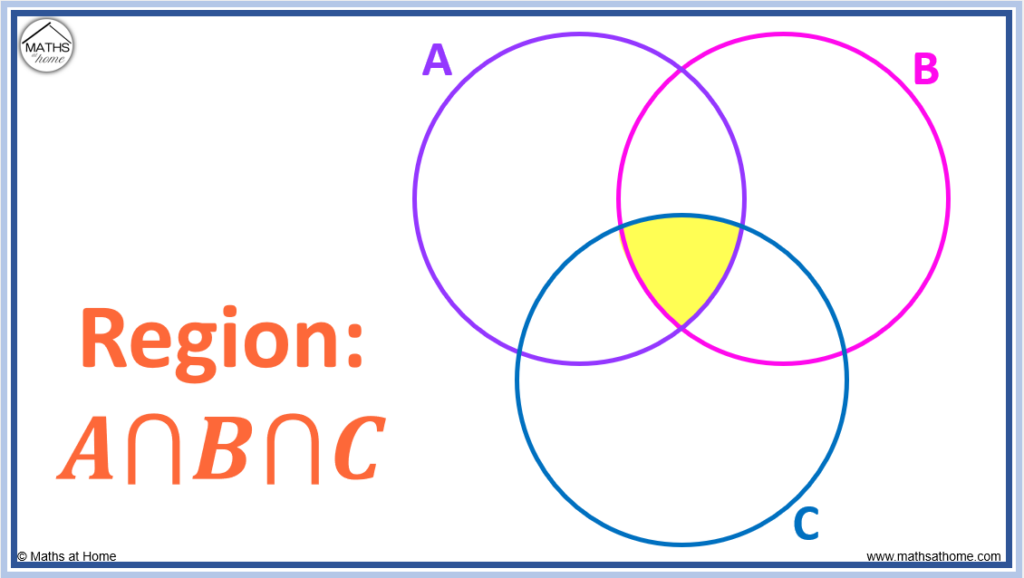
Shaded Region: (A∩B)∪(A∩C)
- Inspiration

COMMENTS
We will also cover problem-solving questions. Each question is followed by a worked solution. How to solve Venn diagram questions ... students learn to use set notation with Venn diagrams and start to find probabilities using Venn diagrams. The questions below are examples of questions that students may encounter in 6th, 7th and 8th grade ...
The best way to explain how the Venn diagram works and what its formulas show is to give 2 or 3 circles Venn diagram examples and problems with solutions. Problem-solving using Venn diagram is a widely used approach in many areas such as statistics, data science, business, set theory, math, logic and etc.
How to use the venn diagram calculator: The Venn diagram calculator, helps you to solve venn diagram problems. To leave the group name or intersection label empty, simply fill in a space. To add a new line to the label, press Enter after first line and continue to the second line. When you enter a value, the Venn diagram calculator will update ...
Venn diagram questions with solutions are given here for students to practice various questions based on Venn diagrams.These questions are beneficial for both school examinations and competitive exams. Practising these questions will develop a skill to solve any problem on Venn diagrams quickly.. Venn diagrams were first introduced by John Venn to represent various propositions in a ...
Information provided in the problem usually tells you how many elements are in each set or section. Step 5: Solve the Problem. Now, you can use the diagram to answer the question. This might involve counting the number of elements in a particular set or section of the diagram, or it might involve noticing patterns or relationships between the sets.
Purplemath. Venn diagram word problems generally give you two or three classifications and a bunch of numbers. You then have to use the given information to populate the diagram and figure out the remaining information. For instance: Out of forty students, 14 are taking English Composition and 29 are taking Chemistry.
Examples of Venn Diagram. Example 1: Let us take an example of a set with various types of fruits, A = {guava, orange, mango, custard apple, papaya, watermelon, cherry}. Represent these subsets using sets notation: a) Fruit with one seed b) Fruit with more than one seed.
This math tutorial video explains Venn diagram problem solving. We show you how to solve Venn diagram survey problems, and we work a few examples (both two ...
GCSE; WJEC; Venn diagrams - WJEC Solving problems using Venn diagrams. Venn diagrams are a useful tool in the world of statistics. Once you have got to grips with these, you will be able to ...
To represent this relationship using a Venn diagram, the set of plants will be our universal set and the set of trees will be the subset. Recall that this relationship is expressed symbolically as: Trees ⊂ Plants. Trees ⊂ Plants. To create a Venn diagram, first we draw a rectangle and label the universal set " U = Plants. U = Plants.
Here is an example on how to solve a Venn diagram word problem that involves three intersecting sets. Problem: 90 students went to a school carnival. 3 had a hamburger, soft drink and ice-cream. 24 had hamburgers. 5 had a hamburger and a soft drink. 33 had soft drinks. 10 had a soft drink and ice-cream. 38 had ice-cream. 8 had a hamburger and ...
These Venn Diagram Worksheets will produce three problems with a maximum of 4 questions for each Venn Diagram for the students to answer. Set Notation Problems Using Three Sets Worksheets These Venn Diagram Worksheets are great for practicing solving set notation problems of different sets, unions, intersections, and complements with three sets.
A Venn diagram is a diagram that shows the relationship between and among a finite collection of sets. If we have two or more sets, we can use a Venn diagram to show the logical relationship among these sets as well as the cardinality of those sets. In particular, Venn Diagrams are used to demonstrate De Morgan's Laws. Venn diagrams are also useful in illustrating relationships in ...
T means the set of Tennis players. V means the set of Volleyball players. The Venn Diagram is now like this: Union of 3 Sets: S ∪ T ∪ V. You can see (for example) that: drew plays Soccer, Tennis and Volleyball. jade plays Tennis and Volleyball. alex and hunter play Soccer, but don't play Tennis or Volleyball. no-one plays only Tennis.
This video solves two problems using Venn Diagrams. One with two sets and one with three sets.Complete Video List at http://www.mathispower4u.com
Example 1: Given set R is the set of counting numbers less than 7. Draw and label a Venn diagram to represent set R and indicate all elements in the set. Analysis: Draw a circle or oval. Label it R. Put the elements in R. Solution: Notation: R = {counting numbers < 7} Example 2: Given set G is the set of primary colors.
Often questions require you to draw a Venn diagram from the information given and calculate one of the value that is missing. E.g. 1 In a group of 24 girls, ... Worksheet Solving problems using Venn diagrams Qu 1-3 9-1 class textbook: p246 M8.7 Qu 1-6 (Look at Qu 2 and 5 in class) A*-G class textbook: No exercise
Venn's diagrams are particularly helpful in solving word problems on number operations that involve counting. Once it is drawn for a given problem, the rest should be a piece of cake. Venn Diagram Questions. Out of 120 students in a school, 5% can play Cricket, Chess and Carroms.
It is important to carefully list the conditions given in the question in the form of a Venn diagram. While solving such questions, avoid taking many variables. Try solving the questions using the Venn diagram approach and not with the help of formulae.
A simple Venn diagram example. The overlapping areas between the two boundaries describe the elements which are common between the two, while the areas that aren't overlapping house the elements that are different. Venn diagrams are used often in math that people tend to assume they are used only to solve math problems.
2.2: Venn Diagrams. Page ID. Julie Harland. MiraCosta College. This is a Venn diagram using only one set, A. This is a Venn diagram Below using two sets, A and B. This is a Venn diagram using sets A, B and C. Study the Venn diagrams on this and the following pages. It takes a whole lot of practice to shade or identify regions of Venn diagrams.
To solve a Venn diagram with 3 circles, start by entering the number of items in common to all three sets of data. Then enter the remaining number of items in the overlapping region of each pair of sets. Enter the remaining number of items in each individual set. Finally, use any known totals to find missing numbers.
Recommendations. Skill plans. IXL plans. Virginia state standards. Textbooks. Test prep. Improve your math knowledge with free questions in "Use Venn diagrams to solve problems" and thousands of other math skills.