solved problems in linear differential equation

• Math Article
• How To Solve Linear Differential Equation

How to Solve Linear Differential Equation

A linear equation or polynomial, with one or more terms, consisting of the derivatives of the dependent variable with respect to one or more independent variables is known as a linear differential equation.

A general first-order differential equation is given by the expression:

dy/dx + Py = Q where y is a function and dy/dx is a derivative.

The solution of the linear differential equation produces the value of variable y.

• dy/dx + 2y = sin x
• dy/dx + y = e x

Linear Differential Equations Definition

A linear differential equation is defined by the linear polynomial equation, which consists of derivatives of several variables. It is also stated as Linear Partial Differential Equation when the function is dependent on variables and derivatives are partial.

A differential equation having the above form is known as the first-order linear differential equation  where P and Q are either constants or functions of the independent variable (in this case x) only.

Also, the differential equation of the form,  dy/dx + Py = Q , is a   first-order linear differential equation where P and Q are either constants or functions of y (independent variable) only.

To find linear differential equations solution, we have to derive the general form or representation of the solution.

Non-Linear Differential Equation

When an equation is not linear in unknown function and its derivatives, then it is said to be a nonlinear differential equation. It gives diverse solutions which can be seen for chaos. 

Solving Linear Differential Equations

For finding the solution of such linear differential equations, we determine a function of the independent variable let us say M(x), which is known as the Integrating factor (I.F).

Multiplying both sides of equation (1) with the integrating factor M(x) we get;

M(x)dy/dx + M(x)Py = QM(x)  …..(2)

Now we chose M(x) in such a way that the L.H.S of equation (2) becomes the derivative of y.M(x)

i.e.    d(yM(x))/dx = (M(x))dy/dx + y (d(M(x)))dx … (Using d(uv)/dx   = v(du/dx)   + u(dv/dx)

⇒ M(x) /(dy/dx) + M(x)Py = M (x) dy/dx + y d(M(x))/dx

⇒ M(x)Py = y dM(x)/dx

⇒ 1/M'(x) = P.dx 

Integrating both sides with respect to x, we get;

\(\begin{array}{l} log M (x) = \int Pdx (As \int \frac {f'(x)}{f(x)} ) = log f(x) \end{array} \)

\(\begin{array}{l} M(x) = e^{\int Pdx}= I.F\end{array} \)

Now, using this value of the integrating factor, we can find out the solution of our first order linear differential equation.

Multiplying both the sides of equation (1) by the I.F. we get

\(\begin{array}{l} e^{\int Pdx}\frac{dy}{dx} + yPe^{\int Pdx} = Qe^{\int Pdx} \end{array} \)

This could be easily rewritten as:

\(\begin{array}{l} \frac {d(y.e^{\int Pdx})}{dx} = Qe^{\int Pdx} (Using \frac{d(uv)}{dx} = v \frac{du}{dx} + u\frac{dv}{dx} ) \end{array} \)

Now integrating both the sides with respect to x, we get:

\(\begin{array}{l} \int d(y.e^{\int Pdx }) = \int Qe^{\int Pdx}dx + c \end{array} \)

\(\begin{array}{l} y = \frac {1}{e^{\int Pdx}} (\int Qe^{\int Pdx}dx + c )\end{array} \)

where C is some arbitrary constant.

How to Solve First Order Linear Differential Equation

Learn to solve the first-order differential equation with the help of steps given below.

• Rearrange the terms of the given equation in the form dy/dx + Py = Q

          where P and Q are constants or functions of the independent variable x only.

• To obtain the integrating factor, integrate P (obtained in step 1) with respect to x and put this integral as a power to e.

\(\begin{array}{l} e^{\int Pdx} = I.F\end{array} \)

• Multiply both the sides of the linear first-order differential equation with the I.F.

\(\begin{array}{l} e^{\int Pdx} \frac{dy}{dx} + yPe^{\int Pdx} = Qe^{\int Pdx} \end{array} \)

• The L.H.S of the equation is always a derivative of y × M (x)

i.e. L.H.S = d(y × I.F)/dx

d(y × I.F)dx = Q × I.F 

• In the last step, we simply integrate both the sides with respect to x and get a constant term C to get the solution.

where C is some arbitrary constant

Similarly, we can also solve the other form of linear first-order differential equation dx/dy +Px = Q using the same steps. In this form P and Q are the functions of y. The integrating factor (I.F) comes out to be  and using this we find out the solution which will be

Now, to get a better insight into the linear differential equation, let us try solving some questions. where C is some arbitrary constant.

Solved Examples

Example 1: Solve the  LDE =   dy/dx = [1/(1+x 3 )] – [3x 2 /(1 + x 2 )]y

The above mentioned equation can be rewritten as   dy/dx + [3x 2 /(1 + x 2 )] y = 1/(1+x 3 )

Comparing it with  dy/dx + Py = O , we get

P = 3x 2 /1+x 3

Q= 1/1 + x 3

Let’s figure out the integrating factor(I.F.) which is,

\(\begin{array}{l} e^{\int Pdx} \end{array} \)

\(\begin{array}{l}I.F  = e^{\int \frac {3x^2}{1 + x^3}} dx = e^{ln (1 + x^3)} \end{array} \)

⇒I.F. = 1 + x 3

Now, we can also rewrite the L.H.S as:

d(y × I.F)/dx, 

⇒ d(y × (1 + x 3 )) dx = [1/(1 +x 3 )] × (1 + x 3 )

Integrating both the sides w. r. t. x, we get,

⇒ y ×  ( 1 + x 3 ) =  x

⇒ y = x/(1 + x 3 )

⇒ y = [ x/(1 + x 3  ) +  C

Solve the following differential equation:  

dy/dx + (sec x)y = 7 

Comparing the given equation with dy/dx + Py = Q 

We see,  P = sec  x, Q = 7

Now lets find out the integrating factor using the formula

\(\begin{array}{l} e^{\int Pdx}= I.F \end{array} \)

\(\begin{array}{l} e^{\int secdx}= I.F. \end{array} \)

\(\begin{array}{l} I.F. = e^{ln |sec x + tan x |} = sec x + tan x  \end{array} \)

Now we can also rewrite the L.H.S as

d(y × I.F)/dx} ,

i.e . d(y × (sec x + tan x ))

⇒ d(y × (sec x + tan x ))/dx = 7(sec x + tan x) 

\(\begin{array}{l}  \int d ( y × (sec x + tan x ))  = \int 7(sec x + tan x) dx \end{array} \)

\(\begin{array}{l} \Rightarrow y × (sec x + tan x) = 7 (ln|sec x + tan x| + log |sec x| ) \end{array} \)

\(\begin{array}{l} y =\frac {7(ln|sec x + tan x| + log|sec x| }{(sec x + tan x)} + c \end{array} \)

A curve is passing through the origin and the slope of the tangent at a point R(x,y) where -1<x<1 is given as ( x 4 + 2xy + 1)/(1 – x 2 ) . What will be the equation of the curve?

We know that the slope of the tangent at (x,y) is,

tanƟ= dy/dx = (x 4 + 2xy + 1)/1 – x 2

Reframing the equation in the form dy/dx  + Py = Q  , we get

dy/dx = 2xy/(1 – x 2 ) + (x 4 + 1)/(1 – x 2 )

⇒ dy/dx – 2xy/(1 – x 2 ) = (x 4 + 1)/(1 – x 2 )

Comparing we get P = -2x/(1 – x 2 )

Q = ( x 4 + 1)/(1 – x 2 )

Now, let’s find out the integrating factor using the formula.

\(\begin{array}{l} e^{\int \frac{-2x}{1-x^2}}dx = e^{ln (1 – x^2)} = 1 – x^2 =I.F \end{array} \)

\(\begin{array}{l} \frac {d(y × I.F)}{dx}, \end{array} \)

\(\begin{array}{l} i.e.,\frac{d(y × (1 – x^2))}{dx} = \frac{x^4 + 1}{1 – x^2} × 1 – x^2 \end{array} \)

Integrating both sides w. r. t. x, we get,

\(\begin{array}{l} \int d(y × (1 – x^2)) = \int \frac{x^4 + 1}{1 – x^2} × (1 – x^2 )dx \end{array} \)

\(\begin{array}{l} \Rightarrow y × (1 – x^2) = \int x^4 + 1 dx …(1) \end{array} \)

 x (1 – x 2 ) = x 5 /5 + x + C

⇒ y =  x 5 /5 + x/(1 – x 2 ) + C 

It is the required equation of the curve. Also as the curve passes through origin; substitute the values as x = 0, y = 0 in the above equation. Thus, C = 0.

Frequently Asked Questions – FAQs

What is a linear differential equation, what is the example of a linear differential equation, how to solve the first order differential equation, what is the difference between linear and nonlinear equations, what is the difference between linear and nonlinear differential equations, leave a comment cancel reply.

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Linear Differential Equation

Linear differential equation is an equation having a variable, a derivative of this variable, and a few other functions. The standard form of a linear differential equation is dy/dx + Py = Q, and it contains the variable y, and its derivatives. The P and Q in this differential equation are either numeric constants or functions of x.

The linear differential equation in an important form of a differential equation and can be solved using a formula. Let us learn the formula and derivation, to find the general solution of a linear differential equation.

What Is a Linear Differential Equation?

The linear differential equation is of the form dy/dx + Py = Q, where P and Q are numeric constants or functions in x. It consists of a y and a derivative of y. The differential is a first-order differentiation and is called the first-order linear differential equation.

This linear differential equation is in y. Similarly, we can write the linear differential equation in x also. The linear differential equation in x is dx/dy + \(P_1\)x = \(Q_1\).

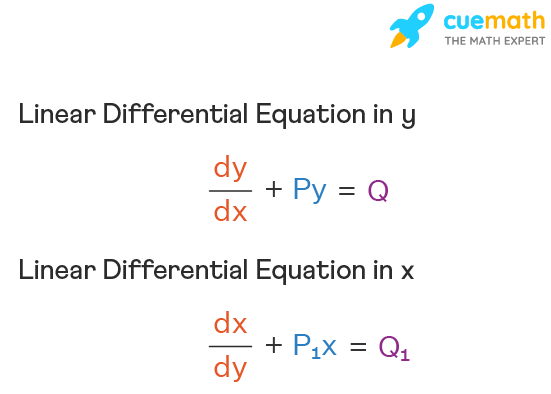
Some of the examples of linear differential equation in y are dy/dx + y = Cosx, dy/dx + (-2y)/x = x 2 .e -x . And the examples of linear differential equation in x are dx/dy + x = Siny, dx/dy + x/y = ey. dx/dy + x/(ylogy) = 1/y.

Derivation for Solution of Linear Differential Equation

The derivation for the general solution for the linear differential equation can be understood through the below sequence of steps. The first-order differential equation is of the form.

dy/dx +Px = Q

Here we multiply both sides of the equation by a function of x, say g(x) . Further, this function is chosen such that the right hand side of the equation is derivative of y.g(x). d/dx(y.g(x)) = y.g(x).

g(x).dy/dx + P.g(x).y = Q.g(x)

Choose g(x) in such a way such that the RHS becomes the derivative of y.g(x).

g(x).dy/dx + P.g(x)y = d/dx(y.g(x)]

The right hand side of the above expression is derived using the derivative formula for the product of functions.

g(x).dy/dx + P.g(x).y = g(x).dy/dx + y.g'(x)

P.g(x) = g'(x)

P = g'(x)/g(x)

Integrating both sides with respect to x, we get

\(\int P.dx= \int \frac{g'(x)}{g(x)}.dx\)

\(\int P.dx= log(g(x))\)

\(g(x)= e^{\int P.dx}\)

This function \(g(x)= e^{\int P.dx}\) is called the Integrating Factor (I.F) of the given linear differential equation. Substituting the value of g(x) in equation linear differential equation, the following expression is obtained.

\(e^{\int P.dx}.\dfrac{dy}{dx} + Pe^{\int P.dx}y = Q.e^{\int P.dx}\)

\(\dfrac{d}{dx}(y.e^{\int P.dx} )= Qe^{\int P.dx}\)

Integrating both sides, with respect to x the following expression is obtained..

\(y.e^{\int P.dx} =\int (Q.e^{\int P.dx}.dx)\)

\(y=e^{-\int P.dx} .\int (Q.e^{\int P.dx}.dx) + C\)

The above expression is the general solution of the linear differential eqution.

Formula for General Solution of Linear Differential Equation

The following are the two important formulas to find the general solution of the linear differential equations.

• The general solution of the differential equation dy/x +Py = Q is as follows. \(y.(I.F)=\int (Q.(I.F).dx)+ C\). Here we have Integrating Factor (I.F) = \(e^{\int P.dx}\).
• Also the general solution of the differential equation dx/y +Px = Q is as follows. \(x.(I.F)=\int (Q.(I.F).dy)+ C\). Here we have Integrating Factor (I.F) = \(e^{\int P.dy}\).

Steps to Solve Linear Differential Equation

The following three simple steps are helpful to write the general solutions of a linear differential equation.

• Step - I: Simplify and write the given differential equation in the form dy/dx + Py = Q, where P and Q are numeric constants or functions in x.
• Step - II: Find the Integrating Factor of the linear differential equation (IF) = \(e^{\int P.dx}\).
• Step-III: Now we can write the solution of the linear differential equation as follows. \(y(I.F) = \int(Q × I.F).dx + C\)

The usage of the above steps can be more clearly understood through the below-solved examples of the linear differential equation.

Related Topics

• Integration Formulas
• Differentiation and Integration Formulas
• Chain Rule Formula
• Differential Equations

Examples on Linear Differential Equation

Example 1: Find the general solution of the differential equation xdy -(y + 2x 2 ).dx = 0

Solution: The give differential equation is xdy - (y + 2x 2 ).dx = 0. This can be simplified to represent the following linear differential equation.

dy/dx - y/x = 2x

Comparing this with the differential equation dy/dx + Py = Q we have the values of P = -1/x and the value of Q = 2x. Hence we have the integration factor as IF = \(e^{\int -\dfrac{1}{x}.dx}\) = \(e^{-\log x}\) = \(\frac{1}{x}\).

Further, the solution of the differential equation is as follows.

y\(\frac{1}{x}\) = \(\int 2x.\frac{1}{y} .dx + c\) \(\frac{y}{x}\) = \(\int 2.dx + c\) \(\frac{y}{x}\) = 2x + c y = 2x 2 + xc Answer: Thus the general solution of the given linear differential equation is y = 2x 2 + xc

Example 2: Find the derivative of dy/dx + Secx.y = Tanx

The given differential equation is dy/dx + Secx.y = Tanx. Comparing this with the linear differential equation dy/dx + Px = Q, we have P = Secx, and Q = Tanx.

Further the integrating factor is I.F = \(e^{\int Secx.dx}

go to slide go to slide

Book a Free Trial Class

Practice Questions on Linear Differential Equation

Faqs on linear differential equation.

The linear differential equation is an equation having a variable, a derivative of this variable, and a few other functions. The standard form of a linear differential equation is dy/dx + Py = Q, and it contains the variable y, and its derivatives. The P and Q in this differential equation are either numeric constants or functions of x.

How Do You Know If a Differential Equation Is a Linear Differential Equation?

A differential equation is said to be a linear differential equation if it has a variable and its first derivative. The linear differential equation in y is of the form dy/dx + Py = Q, Here we have the variable y, the first derivative of the variable y, and we have P, Q which are functions in x. From the name of linear, these differential equations have only the first degree derivatives.

How Do You Solve a Linear Differential Equation?

The solution of a linear differential equation is through three simple steps. First simplify and write the given differential equation in the form dy/dx + Py = Q. For this find the Integrating Factor (IF) = \(e^{\int P.dx}\). Finally the solution of the linear differential equation is \(y(I.F) = \int(Q × I.F).dx + C\)

What Is the Standard Form of Linear Differential Equation in x?

The standard form of the linear differential equation in x is dx/dy + Px = Q, This is a differential equation having a variable x, the first derivative of x, and P, Q represent the functions in y. The linear differential equation in x has first-order derivative of x.

What Is the Formula For the General Solution of Linear Differential Equation

The formula for general solution of the differential equation dy/x +Py = Q is \(y.(I.F)=\int (Q.(I.F).dx)+ C\). Here we have Integrating Factor (I.F) = \(e^{\int P.dx}\). Also the formula for the general solution of the differential equation dx/y +Px = Q is \(x.(I.F)=\int (Q.(I.F).dy)+ C\). Here we have Integrating Factor (I.F) = \(e^{\int P.dy}\).

First Order Linear Differential Equations

You might like to read about Differential Equations and Separation of Variables first!

A Differential Equation is an equation with a function and one or more of its derivatives :

Here we will look at solving a special class of Differential Equations called First Order Linear Differential Equations

First Order

They are "First Order" when there is only dy dx , not d 2 y dx 2 or d 3 y dx 3 etc

A first order differential equation is linear when it can be made to look like this:

dy dx + P(x)y = Q(x)

Where P(x) and Q(x) are functions of x.

To solve it there is a special method:

• We invent two new functions of x, call them u and v , and say that y=uv .
• We then solve to find u , and then find v , and tidy up and we are done!

And we also use the derivative of y=uv (see Derivative Rules (Product Rule) ):

dy dx = u dv dx + v du dx

Here is a step-by-step method for solving them:

• 2. Factor the parts involving v
• 3. Put the v term equal to zero (this gives a differential equation in u and x which can be solved in the next step)
• 4. Solve using separation of variables to find u
• 5. Substitute u back into the equation we got at step 2
• 6. Solve that to find v
• 7. Finally, substitute u and v into y = uv to get our solution!

Let's try an example to see:

  dy dx − y x = 1

First, is this linear? Yes, as it is in the form

dy dx + P(x)y = Q(x) where P(x) = − 1 x and Q(x) = 1

So let's follow the steps:

Step 1: Substitute y = uv , and   dy dx = u dv dx + v du dx

Step 2: Factor the parts involving v

Step 3: Put the v term equal to zero

Step 4: Solve using separation of variables to find u

Step 5: Substitute u back into the equation at Step 2

Step 6: Solve this to find v

Step 7: Substitute into y = uv to find the solution to the original equation.

And it produces this nice family of curves:

What is the meaning of those curves?

They are the solution to the equation   dy dx − y x = 1

In other words:

Anywhere on any of those curves the slope minus y x equals 1

Let's check a few points on the c=0.6 curve:

Estmating off the graph (to 1 decimal place):

Why not test a few points yourself? You can plot the curve here .

Perhaps another example to help you? Maybe a little harder?

  dy dx − 3y x = x

dy dx + P(x)y = Q(x) where P(x) = − 3 x and Q(x) = x

And one more example, this time even harder :

  dy dx + 2xy= −2x 3

dy dx + P(x)y = Q(x) where P(x) = 2x and Q(x) = −2x 3

Let's see ... we can integrate by parts ... which says:

∫ RS dx = R ∫ S dx − ∫ R' ( ∫ S dx ) dx

(Side Note: we use R and S here, using u and v could be confusing as they already mean something else.)

Choosing R and S is very important, this is the best choice we found:

• R = −x 2 and
• S = 2x e x 2

So let's go:

Put in R = −x 2 and S = 2x e x 2

And also R' = −2x and ∫ S dx = e x 2

And we get this nice family of curves:

Browse Course Material

Course info, instructors.

• Prof. Arthur Mattuck
• Prof. Haynes Miller
• Dr. Jeremy Orloff
• Dr. John Lewis

Departments

• Mathematics

As Taught In

• Differential Equations
• Linear Algebra

Learning Resource Types

Problem sets.

You are leaving MIT OpenCourseWare

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Laplace Transform

4.4 Solving Initial Value Problems

Having explored the Laplace Transform, its inverse, and its properties, we are now equipped to solve initial value problems (IVP) for linear differential equations. Our focus will be on second-order linear differential equations with constant coefficients.

Method of Laplace Transform for IVP

General Approach:

1. Apply the Laplace Transform to each term of the differential equation. Use the properties of the Laplace Transform listed in Tables 4.1 and 4.2 to obtain an equation in terms of [asciimath]Y(s)[/asciimath] . The Laplace Transform of the derivatives are

  [asciimath]\mathcal{L}{f'(t)} = sF(s) - f(0)[/asciimath]

  [asciimath]\mathcal{L}{f''(t)\} = s^2F(s) - s f(0) - f'(0)[/asciimath]

2. The transforms of derivatives involve initial conditions at [asciimath]t=0[/asciimath] . Apply the initial conditions.

3. Simplify the transformed equation to isolate  [asciimath]Y(s)[/asciimath] .

4. If needed, use partial fraction decomposition to break down  [asciimath]Y(s)[/asciimath] into simpler components.

5. Determine the inverse Laplace Transform using the tables and linearity property to find [asciimath]y(t)[/asciimath] .

Shortcut Approach:

1. Find the characteristic polynomial of the differential equation [asciimath]p(s)=as^2+bs+c[/asciimath] .

2. Substitute [asciimath]p(s)[/asciimath] , [asciimath]F(s)=\mathcal{L}{f(t)}[/asciimath] , and the initial conditions into the equation

  [asciimath]Y(s)=(F(s)+a(y'(0)+sy(0))+b y(0) )/(p(s))[/asciimath]   (4.4.1)

3. If needed, use partial fraction decomposition to break down [asciimath]Y(s)[/asciimath] into simpler components.

4. Determine the inverse Laplace transform of [asciimath]Y(s)[/asciimath] using the tables and linearity property to find [asciimath]y(t)[/asciimath] .

Solve the initial value problem.

  [asciimath]y''-5y'+6y=4e^(-2t)\ ;[/asciimath]      [asciimath]y(0)=-1, \ y'(0)=2[/asciimath]

Using the General Approach

1. Take the Laplace Transform of both sides of the equation

  [asciimath]\mathcal{L}^-1{ y''}-5\mathcal{L}^-1{ y'}+6\mathcal{L}^-1{y}=4\mathcal{L}^-1{ e^(-2t)}[/asciimath]

Letting [asciimath]Y(s)=\mathcal{L}^-1{y}[/asciimath] , we get

  [asciimath]s^2Y(s)-sy(0)-y'(0)-5(sY(s)-y(0))+6Y(s)=4(1/(s+2))[/asciimath]

2. Plugging in the initial conditions gives

  [asciimath]s^2Y(s)+s-2-5(sY(s)+1)+6Y(s)=4(1/(s+2))[/asciimath]

3. Collecting like terms and isolating [asciimath]Y(s)[/asciimath] , we get

  [asciimath](s^2-5s+6)Y(s)=4/(s+2)-s+7[/asciimath]

  [asciimath]Y(s)[/asciimath]   [asciimath]=(4//(s+2)-s+7)/(s^2-5s+6)[/asciimath]

Multiplying both the denominator and numerator by [asciimath](s+2)[/asciimath] and factoring the denominator yields

  [asciimath]Y(s)=(-s^2+5s+18)/((s+2)(s-3)(s-2))[/asciimath]

4. Using partial fraction expansion, we get

  [asciimath]Y(s)=1/5 (1/(s+2))+24/5 (1/(s-3))-6 (1/(s-2))[/asciimath]

5. From Table 4.1 , we see that

  [asciimath]1/(s-a)[/asciimath]      [asciimath]harr \ \e^(at)[/asciimath]

Taking the inverse, we obtain the solution of the equation

  [asciimath]y(t)=\mathcal{L}^-1{Y(s)}[/asciimath]   [asciimath]=1/5 \ e^(-2t) +24/5 e^(3t)-6 e^(2t)[/asciimath]

  [asciimath]y''+4y=3sin(t) \ ;[/asciimath]      [asciimath]y(0)=1, \ y'(0)=-1[/asciimath]

Using the Shortcut Approach

1. The characteristic polynomial is

  [asciimath]p(s)=s^2+4[/asciimath]

  [asciimath]F(s)=\mathcal{L}^-1{3sin(t)}[/asciimath]   [asciimath]=3/(s^2+1)[/asciimath]

2. Substituting them together with the initial values into Equation 4.4.1 , we obtain

  [asciimath]Y(s)=(3//(s^2+1)+(-1+s(1)))/(s^2+4)[/asciimath] [asciimath]=(3//(s^2+1)+s-1)/(s^2+4)[/asciimath]

Multiplying both the denominator and numerator by [asciimath](s^2+1)[/asciimath]  yields

  [asciimath]Y(s)=(s^3-s^2+s+2)/((s^2+1)(s^2+4))[/asciimath]

3. Using partial fraction expansion, we get

  [asciimath]Y(s)=1/(s^2+1)+(s-2)/(s^2+4)[/asciimath]

[asciimath]\ =1/(s^2+1)+s/(s^2+4)- 2/(s^2+4)[/asciimath]

4. From Table 4.1 ,

  [asciimath]sin(bt)\ harr\ b/(s^2+b^2)[/asciimath]      and    [asciimath]cos(bt)\ harr\ s/(s^2+b^2)[/asciimath]

  [asciimath]y(t)=\mathcal{L}^-1{Y(s)}[/asciimath]   [asciimath]=sin(t)+cos(2t)-sin(2t)[/asciimath]

Section 4.4 Exercises

  [asciimath]y'' +3 y' -10 y = 0, \ quad y(0) = -1, \ quad y'(0) = 2[/asciimath]

[asciimath]y(t)=-3/7 e^(2t)-4/7 e^(-5t)[/asciimath]

  [asciimath]y'' +6 y' + 13 y = 0, \ quad y(0) = 2, \ quad y'(0) = 0[/asciimath]

[asciimath]y(t)=e^(-3t)(2cos(2t)+3sin(2t))[/asciimath]

  [asciimath]y'' - 8 y' +16 y = 0, \ quad y(0) = 1, \ quad y'(0) = -1[/asciimath]

  [asciimath]y(t)=e^(4t)(1-5t)[/asciimath]

Differential Equations Copyright © 2024 by Amir Tavangar is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Differential equations

Course: differential equations   >   unit 1.

• Differential equations introduction
• Verify solutions to differential equations
• Writing a differential equation
• Write differential equations

Worked example: linear solution to differential equation

• Differential equations challenge

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

• School Guide
• Mathematics
• Number System and Arithmetic
• Trigonometry
• Probability
• Mensuration
• Maths Formulas
• Class 8 Maths Notes
• Class 9 Maths Notes
• Class 10 Maths Notes
• Class 11 Maths Notes
• Class 12 Maths Notes

Linear Differential Equations

• Ordinary Differential Equations
• Exact Differential Equations
• Differential Equations
• Separable Differential Equations
• Partial Differential Equations
• Homogeneous Differential Equations
• How to solve Differential Equations?
• Linear Equations
• Order and Degree of Differential Equations
• Particular Solutions to Differential Equations
• Application of Differential Equation
• Difference Between Linear and Non-Linear Equations
• Differentiation and Integration Formula
• Second Order Linear Differential Equations
• Linear Diophantine Equations
• MATLAB - Differentiation
• Euler Method for solving differential equation
• Gill's 4th Order Method to solve Differential Equations
• GRE Algebra | Solving linear Equations

Linear Differential Equations are differential equations where the unknown function and its derivatives appear linearly. In other words, the equation is a linear combination of the function and its derivative, with constant coefficients. Such types of equations have solutions that can be expressed as a sum of particular and homogeneous solutions.

In this article, we will discuss all things linear differential equations, including their order, type, solutions, and applications in various fields of mathematics and science.

Table of Content

What are Linear Differential Equations?

Examples of linear differential equations, order of linear differential equations, formula for general solution of linear differential equations, formula for first-order linear ode, formula for second-order linear ode, first order linear differential equations, how to solve first-order linear differential equation, second-order linear differential equation, how to solve second order linear differential equation, a. for homogeneous second order linear differential equation:, b. for non-homogeneous second order differential equation:, linear differential equation formula, non-linear differential equation, linear vs non-linear differential equation, homogeneous and non homogeneous linear differential equations, examples on linear differential equation, practice questions on linear differential equation.

A linear differential equation is defined as a linear equation or polynomial with one or more terms consisting of derivatives of the dependent variable concerning one or more independent variables.

Equation of form dy/dx + Py = Q , is known as First-Order Differential Equation.

Where P and Q are either constant or function of x.

Equation of form d 2 y/dx 2 + Pdy/dx + Qy = R , is called Second-Order Differential Equation.

Where P, Q and R are functions of x.

• Ordinary Differential Equation
• Order and Degree Of Differential Equations
• dt/dy + y = t 2 + 1
• x log x dy/dx + y = e x
• dx/dy = sin y + x

The order of linear differential equations is determined by the highest derivative present in the differential equation.

• First order linear differential equations involve only the first derivative, dy/dx + Py = Q.
• Second order linear differential equations involve the second derivative, d 2 y/dx 2 + Pdy/dx + Qy = R.
• Continuing like this, the n th order linear differential equations involve the nth derivative in the equation,

a n d n y/dx n + a n-1 d n-1 y/dx n-1 + . . . + a 1 dy/dx + a 0 y = f(x),

Where n represents the order of linear differential equation.

Formula for general solution of linear ODE depends on order and nature of the given equation. Formula for first order and different cases of second order ODE are given as follows:

For any first-order linear ODE of form [Tex]\frac{dy}{dx} + P(x)y = Q(x) [/Tex] , where P(x) and Q(x) functions of x. Then, the general solution to this equation can be found using the following formula:

[Tex]y(x) = \frac{1}{\text{I.F.}} \left( \int Q(x) \cdot \text{I.F.} \, dx + C \right) [/Tex]

Where C is the constant of integration and I.F. (Integration Factor) = e ∫ P ( x ) dx .

For any second-order linear ODE of form [Tex]\frac{d^2y}{dx^2} + P(x) \frac{dy}{dx} + Q(x)y = R(x) [/Tex] , where P(x), Q(x), and R(x) are functions of x. The general solution to this equation depends on the nature of the roots of its associated characteristic equation.

• r 1 and r 2 are the roots of the characteristic equation.
• α and β are the real and imaginary parts of the complex conjugate roots respectively.
• C 1 ​ and C 2 ​ are arbitrary constants determined by initial conditions.

A first-order differential equation involves only the first derivative of the unknown function.

General form first-order linear differential is,

dy/dx +Py = Q

• dx/dy + yx = 1
• dx/dy = tan y – x

Consider the first-order linear differential equation,

dy/dx + Py = Q . . . . . . (1)

Where P and Q are constant or functions of x.

Now, consider a function of x, say, f(x).

Multiply both the sides of the equation (1) by the function f(x), we get

f(x)⋅dy/dx + P⋅f(x)⋅y = Q⋅f(x) . . . . . . (2)

We will choose the function f(x) in such a way that the right-hand side of the equation (2) will becomes derivative of f(x)⋅y.

f(x)⋅dy/dx + P⋅f(x)⋅y = d/dx[f(x)⋅y]

On simplifying, we get

f(x)dy/dx + Pf(x)y = f(x)dy/dx + yf'(x)

⇒ Pf(x)y = yf'(x)

⇒ Pf(x) = f'(x)

⇒ P = f'(x)/f(x)

Now, integrate both the sides with respect to x, we get

∫P⋅dx = ∫ [f'(x)/f(x)] dx

∫P⋅dx = log (f(x))

Taking exponents on both the sides, we get

e ∫P⋅dx = e log (f(x))

⇒ e ∫P⋅dx = f(x) [Since e log x = x]

This function f(x) = e ∫P⋅dx is called i ntegrating factor of given linear differential equation. It is denoted by I.F.

So, I.F = e ∫P⋅dx

Now, multiply both the sides of the linear differential equation (1) by I.F, we get

e ∫P⋅dx dy/dx + Pye ∫P⋅dx = Qe ∫P⋅dx

⇒ d(ye ∫P⋅dx )/dx = Qe ∫P⋅dx (Since d(uv)/dx = udv/dx + vdu/dx)

Integrate both the sides with respect to x, we get

ye ∫P⋅dx = ∫Qe ∫P⋅dx dx + C, where C is integration constant.

⇒ y = e -∫P⋅dx ∫Qe ∫P⋅dx dx + e -∫P⋅dx C

⇒ y × I.F = ∫Q × I.F dt + C

Where I.F is the integrating factor.

Thus, above obtained equation is general solution of the given first order linear differential equation.

A second-order differential equation is the type of differential equation that consists of a function and its second-order derivative.

The equation of the form,

d 2 y/dx 2 + Pdy/dx + Qy = R, is called the second-order differential equation.

Where P, Q and R are the functions of x.

Read more about Second Order Linear Differential Equations .

There are two types of second order linear differential equation, namely homogeneous and non-homogeneous second order linear differential equation.

Consider the homogeneous second order linear differential equation as,

d 2 y/dx 2 + Pdy/dx + Qy = R . . . . . . (1)

Where P, Q and R are constants.

Assume, solution of given linear differential equation be of the form,

y = e λx , where λ is a constant.

Now, we will find the values of λ for which the solution satisfies the given second order differential equation.

So, dy/dx = λe λx and d 2 y/dx 2 = λ 2 e λx

Substitute the values of dy/dx, d 2 y/dx 2 and y in the equation (1), we get

λ 2 e λx + Pλe λx + Qe λx = 0

⇒ e λx (λ 2 + Pλ + Q) = 0

We know that exponent function cannot be negative.

So, λ 2 + Pλ + Q = 0. This equation is known as auxiliary equation or characteristics equation of the given second order linear differential equation.

Observe that auxiliary equation is an quadratic equation which can be easily solved.

Let λ 1 and λ 2 be the roots or zeroes of the quadratic equation.

Case 1: If roots are real and unequal, λ 1 ≠ λ 2 . Then, the solution of the second order differential equation will be,

y = Ae λ1x + Be λ2x , where A, B are constants.

Case 2: If roots are real and equal, λ 1 = λ 2 = λ. Then, the solution of the second order differential equation will be,

y = (A + Bx)e λx , where A, B are constants.

Case 3: If roots are complex, i.e., λ 1 = α+ iβ and λ 2 = α- iβ, Then, the solution of the second order differential equation will be,

y = e αx (A cos βx + B sin βx), where A, B are constants.

Consider the non-homogeneous second order linear differential equation as,

d 2 y/dx 2 + Pdy/dx + Qy = f(x)

Solution of second order linear differential equation is given as,

y = y c + y p , where y c is the complementary function and y p is the particular integral.

Here, y c is the solution of the homogeneous second order linear differential equation.

d 2 y c /dx 2 + Pdy c /dx + Qy c = 0

yc is calculated in the similar way as we have find the solution of homogeneous second order differential equation.

And y p is the solution of the equation,

d 2 y p /dx 2 + Pdy p /dx + Qy p = f(x)

To find y p , we assume the solution of the function f(x). And then substitutes the values of d 2 y/dx 2 , dy/dx, y and f(x).

Then, we compare both the sides to get the values of coefficients and hence the value of particular integral, y p .

Few assumptions, we should know are:

General form of linear differential equation is given by,

a n d n y/dx n + a n-1 d n-1 y/dx n-1 + . . . + a 1 dy/dx + a 0 y = f(x)

where, y is dependent variable, x is independent variable, n is the order of the differential equation, f(x) is given function of x and a n , a n-1 , . . . a 1 , a 0 are the functions of x.

Differential equation in which unknown function and its derivative appear in a non-linear manner. Such types of equations is know as non-linear differential equation. In other words, the differential equation in which the unknown function and its derivative don’t have straight line when plotted on the graph.

Differences between Linear and Non-linear differential equation are as follows:

Homogeneous Linear DE: A linear differential equation is homogeneous if the right-hand side consists only of zeros i.e., there is no term without dependent variable and their derivative.

Non-Homogeneous Linear DE: A linear differential equation is non-homogeneous if the right-hand side is not zero i.e., there are some term without dependent variable and their derivative.

Here are some of the key distinctions between homogeneous and non-homogeneous linear differential equations:

In conclusion, a differential equation is an equation that contains derivatives of one or more dependent variables with respect to one or more independent variables. The derivative of the function is given by dy/dx. The solution of the first order linear differential equation is given by, y × I.F = ∫Q × I.F dt + C, where C is the integration constant and I.F is the integrating factor. The integrating factor is, I.F = e ∫P⋅dx .

Also Check:

• Calculus in Maths
• Chain Rule Formula
• Differentiation Formulas

Example 1: Solve the linear differential equation: x dy/dx + y = x.

Given, x dy/dx + y = x Rearrange the differential equation in the form dy/dx + Py = Q. dy/dx + y/x = 1 Here, P = 1/x and Q = 1. Find the integrating factor, I.F. I.F. = e ∫P⋅dx ⇒ I.F. = e ∫1/x⋅dx ⇒ I.F. = e lnx ⇒ I.F. = x Multiply both the sides of the given differential equation by I.F, we get xdy/dx + y = x ⇒ d(xy)/dx = x Integrate both the sides with respect to x, we get xy = ∫x dx + C ⇒ xy = x 2 /2 + C ⇒ y = x/2 + x -1 C This is the required solution.

Example 2: Find the general solution of the differential equation: (1 + t)dy/dt + y = 1.

Given, (1 + t)dy/dt + y = 1. Rearrange the differential equation in the form dy/dx + Py = Q. dy/dx + 1/(1+t)y = 1/(1+t) Here, P = 1/(1+t) and Q = 1/(1+t). Find the integrating factor, I.F. I.F = e ∫P⋅dx ⇒ I.F. = e ∫1/(1+t)⋅dx ⇒ I.F. = e ln(1+t) ⇒ I.F. = 1+t The general solution of linear differential equation is given by, y × I.F = ∫Q × I.F dt + C ⇒ y(1+t) = ∫1/(1+t) × (1+t) dt + C ⇒ y(1+t) = ∫1 dt + C ⇒ y(1+t) = t + C ⇒ y = t/(1+t) + C/(1+t) This is the required general solution of the given linear differential equation.

Various problems on linear differential equations,

P1: Solve the linear differential equation: dy/dx + ysin x = sin x

P2: Solve: (x + log y)dy + y dx = 0

P3: Solve: dx/dy + 2xy = e -y

Differential Equations Separable Differential Equations Second Order Linear Differential Equations How to solve Differential Equations?

Linear Differential Equations – FAQs

Define linear differential equations..

A linear differential equation refers to an equation that involves a dependent variable and its derivatives. In this type of equation, the linearity property is maintained with respect to the dependent variable and its derivatives.

What is the General Solution of First Order Linear Differential Equations?

General solution of first order linear differential equations is y × I.F = ∫Q × I.F dt + C , where C is the integration constant and I.F is the integrating factor.

How do you Know if its a Linear Differential Equation?

A differential equation is linear if all its terms involving the unknown function and its derivatives are either constants or multiples of the unknown function and its derivatives raised to the power of 1.

What is Integrating Factor?

Integrating factor is a function which is selected in order to solve the given differential equation. If the differential equation is of the form dy/dx + P(x)y = Q(x) then the integrating factor is given by I.F = e ∫P dx .

What is Particular Integral?

Particular integral refers to a specific solution that satisfies the differential equation when combined with the complementary function.

How to Solve Second Order Linear Differential Equations?

Steps to solve a Second Order Linear Differential Equations are: Find the characteristics equation. Solve the Characteristics equation. Apply the initial or boundary conditions.

What are the Differences between Linear and Non-Linear Differential Equation?

Linear differential equations have terms with variables and their derivatives raised to the power of 1, while nonlinear differential equations have terms with variables and their derivatives raised to powers greater than 1.

Please Login to comment...

Similar reads.

• Maths-Class-12
• School Learning

Improve your Coding Skills with Practice

Number Line

• linear\:2y'-y=4\sin(3t)
• linear\:ty'+2y=t^2-t+1
• linear\:ty'+2y=t^2-t+1,\:y(1)=\frac{1}{2}
• linear\:\frac{dv}{dt}=10-2v
• linear\:\frac{dx}{dt}=5x-3

linear-first-order-differential-equation-calculator

• Advanced Math Solutions – Ordinary Differential Equations Calculator, Exact Differential Equations In the previous posts, we have covered three types of ordinary differential equations, (ODE). We have now reached...

Please add a message.

Message received. Thanks for the feedback.

Application of Local Integrated Radial Basis Function Method for Solving System of Fredholm Integro-Differential Equations

• Research Paper
• Published: 05 June 2024

Cite this article

• Yadollah Ordokhani   ORCID: orcid.org/0000-0002-5167-6874 1 &
• Ali Ebrahimijahan 1  

This paper thoroughly examines the Local Integrated Radial Basis Function (LIRBF) method’s performance in addressing linear systems and first- to higher-order Fredholm integro-differential problems. Utilizing a meshless approach with Gauss–Lobatto quadrature points for spatial discretization, we rigorously assess the method’s accuracy and efficiency across various numerical problems from the existing literature. Evaluation criteria, including maximum absolute errors and rates of convergence, validate the method’s effectiveness. To gauge the proposed LIRBF method’s efficacy, we benchmark it against well-established numerical techniques like Multi-Scale-Galerkin’s, Alpert Multiwavelets, Legendre multi-wavelets collocation, Legendre–Galerkin, Legendre polynomial approximation, and variational iteration methods. A comparative analysis based on criterion norms assesses the numerical results obtained by each method. The findings reveal that the proposed method demonstrates a significant reduction in sensitivity to the shape parameter compared to the RBF method. This observation establishes the robustness and stability of the proposed method, highlighting its ability to maintain accuracy and efficiency across diverse conditions. Results from numerical experiments and comparisons with other established techniques affirm the efficiency and accuracy of the LIRBF method in solving Fredholm integro-differential problems. The outcomes demonstrate promising performance, emphasizing the LIRBF method’s potential as a compelling alternative for addressing similar problems with high precision and computational efficiency.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Asady B, Kajani MT, Vencheh AH, Heydari A (2005) Direct method for solving integro differential equations using hybrid Fourier and block-pulse functions. Int J Comput Math 82(7):889–895

Article   MathSciNet   Google Scholar  

Assari P, Dehghan M (2017) A meshless method for the numerical solution of nonlinear weakly singular integral equations using radial basis functions. Eur Phys J Plus 132:1–23

Article   Google Scholar  

Assari P, Adibi H, Dehghan M (2013a) A meshless method for solving nonlinear two-dimensional integral equations of the second kind on non-rectangular domains using radial basis functions with error analysis. J Comput Appl Math 239:72–92

Assari P, Adibi H, Dehghan M (2013b) A numerical method for solving linear integral equations of the second kind on the non-rectangular domains based on the meshless method. Appl Math Model 37(22):9269–9294

Assari P, Adibi H, Dehghan M (2014a) A meshless discrete Galerkin (MDG) method for the numerical solution of integral equations with logarithmic kernels. J Comput Appl Math 267:160–181

Assari P, Adibi H, Dehghan M (2014b) A meshless method based on the moving least squares (MLS) approximation for the numerical solution of two-dimensional nonlinear integral equations of the second kind on non-rectangular domains. Numer Algorithms 67:423–455

Assari P, Adibi H, Dehghan M (2014c) The numerical solution of weakly singular integral equations based on the meshless product integration (MPI) method with error analysis. Appl Numer Math 81:76–93

Assari P, Asadi-Mehregan F, Dehghan M (2019) On the numerical solution of Fredholm integral equations utilizing the local radial basis function method. Int J Comput Math 96(7):1416–1443

Atkinson KE (1997) The numerical solution of integral equations of the second kind, vol 4. Cambridge University Press, Cambridge

Book   Google Scholar  

Aziz I et al (2015) Meshless methods for multivariate highly oscillatory Fredholm integral equations. Eng Anal Bound Elem 53:100–112

Behiry S (2014) Solution of nonlinear Fredholm integro-differential equations using a hybrid of block pulse functions and normalized Bernstein polynomials. J Comput Appl Math 260:258–265

Behiry S, Hashish H (2003) Wavelet methods for the numerical solution of Fredholm integro-differential equations. Int J Appl Math 11(1):27–36

MathSciNet   Google Scholar  

Behiry SH, Mohamed SI (2012) Solving high-order nonlinear Volterra–Fredholm integro-differential equations by differential transform method. Nat Sci 4(8):581–587

Google Scholar  

Bhrawy AH, Tohidi E, Soleymani F (2012) A new bernoulli matrix method for solving high-order linear and nonlinear Fredholm integro-differential equations with piecewise intervals. Appl Math Comput 219(2):482–497

Bildik N, Konuralp A, Yalcinbas S (2010) Comparison of Legendre polynomial approximation and variational iteration method for the solutions of general linear Fredholm integro-differential equations. Comput Math Appl 59(6):1909–1917

Cabre X, Dipierro S, Valdinoci E (2022) The Bernstein technique for integro-differential equations. Arch Ration Mech Anal 243(3):1597–1652

Chen J, Huang Y, Rong H, Wu T, Zeng T (2015) A multiscale Galerkin method for second-order boundary value problems of Fredholm integro-differential equation. J Comput Appl Math 290:633–640

Chen J, He M, Zeng T (2019) A multiscale Galerkin method for second-order boundary value problems of Fredholm integro-differential equation II: efficient algorithm for the discrete linear system. J Vis Commun Image Represent 58:112–118

Chen J, He M, Huang Y (2020) A fast multiscale Galerkin method for solving second order linear Fredholm integro-differential equation with dirichlet boundary conditions. J Comput Appl Math 364:112352

Chen S, Xu M, Zhu X (2022) A cell-based smoothed radial point interpolation method applied to kinematic limit analysis of thin plates. Eng Anal Boundary Elem 143:710–718

Dastjerdi HL, Ghaini FM, Hadizadeh M (2013) A meshless approximate solution of mixed Volterra–Fredholm integral equations. Int J Comput Math 90(3):527–538

Dehghan M, Saadatmandi A (2008) Chebyshev finite difference method for Fredholm integro-differential equation. Int J Comput Math 85(1):123–130

Dzhumabaev DS (2016) On one approach to solve the linear boundary value problems for Fredholm integro-differential equations. J Comput Appl Math 294:342–357

El-Gamel M, Mohamed O (2022) Nonlinear second order systems of Fredholm integro-differential equations. SeMA J 79(2):383–396

Elahi Z, Akram G, Siddiqi SS (2018) Laguerre approach for solving system of linear Fredholm integro-differential equations. Math Sci 12:185–195

Esmaeilbeigi M, Mirzaee F, Moazami D (2017) A meshfree method for solving multidimensional linear Fredholm integral equations on the hypercube domains. Appl Math Comput 298:236–246

Fatahi H, Saberi-Nadjafi J, Shivanian E (2016) A new spectral meshless radial point interpolation (SMRPI) method for the two-dimensional Fredholm integral equations on general domains with error analysis. J Comput Appl Math 294:196–209

Hashemi MS (2021) Numerical study of the one-dimensional coupled nonlinear sine-Gordon equations by a novel geometric meshless method. Eng Comput 37(4):3397–3407

Hashemi MS (2024) A variable coefficient third degree generalized Abel equation method for solving stochastic Schrodinger–Hirota model. Chaos Solitons Fractals 180:114606

Hashemi MS, Darvishi E, Baleanu D (2016) A geometric approach for solving the density-dependent diffusion Nagumo equation. Adv Differ Equ 2016:1–13

Hashemi MS, Hajikhah S (2021) Generalized squared remainder minimization method for solving multi-term fractional differential equations. Nonlinear Anal Model Control 26(1):57–71

Ho PL, Le CV (2020) A stabilized IRBF mesh-free method for quasi-lower bound shakedown analysis of structures. Comput Struct 228:106157

Ho PL, Le CV, Nguyen PH (2021) Kinematic yield design computational homogenization of micro-structures using the stabilized iRBF mesh-free method. Appl Math Model 91:322–334

Hu H-Y, Li Z-C, Cheng AH-D (2005) Radial basis collocation methods for elliptic boundary value problems. Comput Math Appl 50(1–2):289–320

Jalilian R, Tahernezhad T (2020) Exponential spline method for approximation solution of Fredholm integro-differential equation. Int J Comput Math 97(4):791–801

Kajani MT, Vencheh AH (2004) Solving linear integro-differential equation with Legendre wavelets. Int J Comput Math 81(6):719–726

Khan I, Asif M, Amin R, Al-Mdallal Q, Jarad F (2022) On a new method for finding numerical solutions to integro-differential equations based on Legendre multi-wavelets collocation. Alex Eng J 61(4):3037–3049

Khosravifard A, Hematiyan M, Marin L (2011) Nonlinear transient heat conduction analysis of functionally graded materials in the presence of heat sources using an improved meshless radial point interpolation method. Appl Math Model 35(9):4157–4174

Kurt N, Sezer M (2008) Polynomial solution of high-order linear Fredholm integro-differential equations with constant coefficients. J Frankl Inst 345(8):839–850

Liu H, Huang J, Zhang W, Ma Y (2019) Meshfree approach for solving multidimensional systems of Fredholm integral equations via barycentric Lagrange interpolation. Appl Math Comput 346:295–304

Lotfi M, Alipanah A (2020) Legendre spectral element method for solving Volterra-integro differential equations. Results Appl Math 7:100116

Mai-Duy N, Tanner R (2005) Solving high-order partial differential equations with indirect radial basis function networks. Int J Numer Methods Eng 63(11):1636–1654

Mai-Duy N, Tran-Cong T (2006) Solving biharmonic problems with scattered-point discretization using indirect radial-basis-function networks. Eng Anal Bound Elem 30(2):77–87

Mai-Duy N, Khennane A, Tran-Cong T (2007) Computation of laminated composite plates using integrated radial basis function networks. Comput Mater Contin 5(1):63–77

Mirzaee F (2017) Numerical solution of nonlinear Fredholm–Volterra integral equations via bell polynomials. Comput Methods Differ Equ 5(2):88–102

Mirzaee F, Solhi E, Samadyar N (2021) Moving least squares and spectral collocation method to approximate the solution of stochastic Volterra–Fredholm integral equations. Appl Numer Math 161:275–285

Mirzaei D, Dehghan M (2010) A meshless based method for solution of integral equations. Appl Numer Math 60(3):245–262

Ordokhani Y (2010) An application of Walsh functions for Fredholm–Hammerstein integro-differential equations. Int J Contemp Math Sci 5(22):1055–1063

Parand K, Nikarya M (2014) Application of Bessel functions for solving differential and integro-differential equations of the fractional order. Appl Math Model 38(15–16):4137–4147

Pour-Mahmoud J, Rahimi-Ardabili MY, Shahmorad S (2005) Numerical solution of the system of Fredholm integro-differential equations by the tau method. Appl Math Comput 168(1):465–478

Saadatmandi A, Dehghan M (2010) Numerical solution of the higher-order linear Fredholm integro-differential-difference equation with variable coefficients. Comput Math Appl 59(8):2996–3004

Saray BN, Lakestani M, Razzaghi M (2015) Sparse representation of system of Fredholm integro-differential equations by using Alpert multiwavelets. Comput Math Math Phys 55:1468–1483

Sarra SA (2006) Integrated multiquadric radial basis function approximation methods. Comput Math Appl 51(8):1283–1296

Sarra SA (2012) A local radial basis function method for advection–diffusion–reaction equations on complexly shaped domains. Appl Math Comput 218(19):9853–9865

Shidfar A, Molabahrami A, Babaei A, Yazdanian A (2010) A series solution of the nonlinear Volterra and Fredholm integro-differential equations. Commun Nonlinear Sci Numer Simul 15(2):205–215

Tchier F, Dassios I, Tawfiq F, Ragoub L (2021) On the approximate solution of partial integro-differential equations using the pseudospectral method based on Chebyshev cardinal functions. Mathematics 9(3):286

Thieme H (1977) A model for the spatial spread of an epidemic. J Math Biol 4(4):337–351

ul Islam S, Aziz I, Fayyaz M (2013) A new approach for numerical solution of integro-differential equations via Haar wavelets. Int J Comput Math 90(9):1971–1989

Vu TV, Nguyen NT, Nguyen MN, Truong TT, Bui TQ (2022) A meshfree method based on integrated radial basis functions for 2d hyperelastic bodies. In: Modern mechanics and applications: select proceedings of ICOMMA 2020. Springer, pp 990–1003

Wang Q, Wang H (2016) Meshless method and convergence analysis for 2-dimensional Fredholm integral equation with complex factors. J Comput Appl Math 304:18–25

Wazwaz A-M (2011) Linear and nonlinear integral equations, vol 639. Springer, Cham

Xue Q, Niu J, Yu D, Ran C (2018) An improved reproducing kernel method for Fredholm integro-differential type two-point boundary value problems. Int J Comput Math 95(5):1015–1023

Yalcin E, Kurkcu OK, Sezer M (2020) A matched Hermite–Taylor matrix method to solve the combined partial integro-differential equations having nonlinearity and delay terms. Comput Appl Math 39(4):280

Yeganeh S, Ordokhani Y, Saadatmandi A (2012) A sinc-collocation method for second-order boundary value problems of nonlinear integro-differential equation. J Inf Comput Sci 7(2):151–160

Yulan W, Chaolu T, Jing P (2009) New algorithm for second-order boundary value problems of integro-differential equation. J Comput Appl Math 229(1):1–6

Yuzbasi S, Yildirim G (2022) A collocation method to solve the parabolic-type partial integro-differential equations via Pell–Lucas polynomials. Appl Math Comput 421:126956

Download references

Acknowledgements

We would like to thank both reviewers for their insightful and useful comments on how to improve the paper’s quality. Also, we announce that this research was done in the Scientific Computing and Modeling Research Laboratory of Alzahra University.

The authors have not disclosed any funding.

Author information

Authors and affiliations.

Department of Mathematics, Faculty of Mathematical Sciences, Alzahra University, Tehran, Iran

Yadollah Ordokhani & Ali Ebrahimijahan

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Yadollah Ordokhani .

Ethics declarations

Conflict of interest.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Ordokhani, Y., Ebrahimijahan, A. Application of Local Integrated Radial Basis Function Method for Solving System of Fredholm Integro-Differential Equations. Iran J Sci (2024). https://doi.org/10.1007/s40995-024-01654-4

Download citation

Received : 04 February 2024

Accepted : 17 May 2024

Published : 05 June 2024

DOI : https://doi.org/10.1007/s40995-024-01654-4

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Fractional calculus
• Meshless methods
• RBF collocation
• Partition of unity
• Differential quadrature
• Irregular convex domains

Advertisement

• Find a journal
• Publish with us
• Track your research

Help | Advanced Search

Computer Science > Machine Learning

Title: solving differential equations using physics-informed deep equilibrium models.

Abstract: This paper introduces Physics-Informed Deep Equilibrium Models (PIDEQs) for solving initial value problems (IVPs) of ordinary differential equations (ODEs). Leveraging recent advancements in deep equilibrium models (DEQs) and physics-informed neural networks (PINNs), PIDEQs combine the implicit output representation of DEQs with physics-informed training techniques. We validate PIDEQs using the Van der Pol oscillator as a benchmark problem, demonstrating their efficiency and effectiveness in solving IVPs. Our analysis includes key hyperparameter considerations for optimizing PIDEQ performance. By bridging deep learning and physics-based modeling, this work advances computational techniques for solving IVPs, with implications for scientific computing and engineering applications.

Submission history

Access paper:.

• HTML (experimental)
• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.2: Applications Leading to Differential Equations

• Last updated
• Save as PDF
• Page ID 153091

• William F. Trench
• Trinity University

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

In order to apply mathematical methods to a physical or “real life” problem, we must formulate the problem in mathematical terms; that is, we must construct a mathematical model for the problem. Many physical problems concern relationships between changing quantities. Since rates of change are represented mathematically by derivatives, mathematical models often involve equations relating an unknown function and one or more of its derivatives. Such equations are differential equations. They are the subject of this book.

Much of calculus is devoted to learning mathematical techniques that are applied in later courses in mathematics and the sciences; you wouldn’t have time to learn much calculus if you insisted on seeing a specific application of every topic covered in the course. Similarly, much of this book is devoted to methods that can be applied in later courses. Only a relatively small part of the book is devoted to the derivation of specific differential equations from mathematical models, or relating the differential equations that we study to specific applications. In this section we mention a few such applications. The mathematical model for an applied problem is almost always simpler than the actual situation being studied, since simplifying assumptions are usually required to obtain a mathematical problem that can be solved. For example, in modeling the motion of a falling object, we might neglect air resistance and the gravitational pull of celestial bodies other than Earth, or in modeling population growth we might assume that the population grows continuously rather than in discrete steps.

A good mathematical model has two important properties:

• It’s sufficiently simple so that the mathematical problem can be solved.
• It represents the actual situation sufficiently well so that the solution to the mathematical problem predicts the outcome of the real problem to within a useful degree of accuracy. If results predicted by the model don’t agree with physical observations,the underlying assumptions of the model must be revised until satisfactory agreement is obtained.

We will now give examples of mathematical models involving differential equations. We willreturn to these problems at the appropriate times, as we learn how to solve the various types of differential equations that occur in the models. All the examples in this section deal with functions of time, which we denote by \(t\). If \(y\) is a function of \(t\), \(y'\) denotes the derivative of \(y\) with respect to \(t\); thus,

\[y' = \dfrac{dy}{dt}.\nonumber \]

Population Growth and Decay

Although the number of members of a population (people in a given country, bacteria in a laboratory culture, wildflowers in a forest, etc.) at any given time t is necessarily an integer, models that use differential equations to describe the growth and decay of populations usually rest on the simplifying assumption that the number of members of the population can be regarded as a differentiable function \(P = P(t)\). In most models it is assumed that the differential equation takes the form

\[P' = a(P)P \label{1.1.1}\]

where \(a\) is a continuous function of \(P\) that represents the rate of change of population per unit time per individual. In the Malthusian model , it is assumed that \(a(P)\) is a constant, so Equation \ref{1.1.1} becomes

\[P' = aP. \label{1.1.2}\]

(When you see a name in blue italics, just click on it for information about the person.) This model assumes that the numbers of births and deaths per unit time are both proportional to the population. The constants of proportionality are the birth rate (births per unit time per individual) and the death rate (deaths per unit time per individual); a is the birth rate minus the death rate. You learned in calculus that if \(c\) is any constant then

\[P = ce^{at} \label{1.1.3}\]

satisfies Equation \ref{1.1.2}, so Equation \ref{1.1.2} has infinitely many solutions. To select the solution of the specific problem that we are considering, we must know the population \(P_0\) at an initial time, say \(t = 0\). Setting \(t = 0\) in Equation \ref{1.1.3} yields \(c = P(0) = P_0\), so the applicable solution is

\[P(t) = P_0e^{at}.\nonumber \]

This implies that

\[\lim_{t\to\infty}P(t)=\left\{\begin{array}{cl}\infty&\mbox{ if }a>0,\\ 0&\mbox{ if }a<0; \end{array}\right.\nonumber\]

that is, the population approaches infinity if the birth rate exceeds the death rate, or zero if the death rate exceeds the birth rate.

To see the limitations of the Malthusian model, suppose we are modeling the population of a country, starting from a time \(t = 0\) when the birth rate exceeds the death rate (so \(a > 0\)), and the country’s resources in terms of space, food supply, and other necessities of life can support the existing population. Then the prediction \(P = P_0e^{at}\) may be reasonably accurate as long as it remains within limits that the country’s resources can support. However, the model must inevitably lose validity when the prediction exceeds these limits. (If nothing else, eventually there will not be enough space for the predicted population!) This flaw in the Malthusian model suggests the need for a model that accounts for limitations of space and resources that tend to oppose the rate of population growth as the population increases.

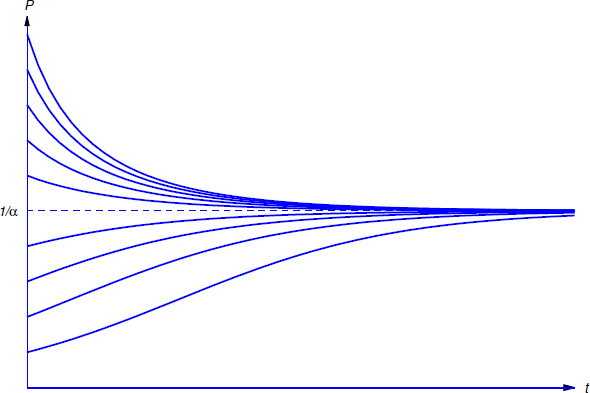
Perhaps the most famous model of this kind is the Verhulst model , where Equation \ref{1.1.2} is replaced by

\[\label{eq:1.1.4} P'=aP(1-\alpha P),\]

where \(\alpha\) is a positive constant. As long as \(P\) is small compared to \(1/\alpha\), the ratio \(P'/P\) is approximately equal to \(a\). Therefore the growth is approximately exponential; however, as \(P\) increases, the ratio \(P'/P\) decreases as opposing factors become significant.

Equation \ref{eq:1.1.4} is the logistic equation . You will learn how to solve it in Section 1.2. (See Exercise 2.2.28 .) The solution is

\[P={P_0\over\alpha P_0+(1-\alpha P_0)e^{-at}},\nonumber \]

where \(P_0=P(0)>0\). Therefore \(\displaystyle \lim_{t\to\infty}P(t)=1/\alpha\), independent of \(P_0\).

Figure 1.1.1 shows typical graphs of \(P\) versus \(t\) for various values of \(P_0\).

Newton’s Law of Cooling

According to Newton’s law of cooling , the temperature of a body changes at a rate proportional to the difference between the temperature of the body and the temperature of the surrounding medium. Thus, if \(T_m\) is the temperature of the medium and \(T = T(t)\) is the temperature of the body at time \(t\), then

\[T' = −k(T −T_m) \label{1.1.5}\]

where \(k\) is a positive constant and the minus sign indicates; that the temperature of the body increases with time if it is less than the temperature of the medium, or decreases if it is greater. We will see in Section 4.2 that if \(T_m\) is constant then the solution of Equation \ref{1.1.5} is

\[T = T_m + (T_0 −T_m)e^{−kt} \label{1.1.6}\]

where \(T_0\) is the temperature of the body when \(t = 0\). Therefore

\[\lim_{t→∞} T(t) = T_m \nonumber\]

independent of \(T_0\) (Common sense suggests this. Why?).

Figure 1.1.2 shows typical graphs of \(T\) versus \(t\) for various values of \(T_0\).

Assuming that the medium remains at constant temperature seems reasonable if we are considering a cup of coffee cooling in a room, but not if we are cooling a huge cauldron of molten metal in the same room. The difference between the two situations is that the heat lost by the coffee isn’t likely to raise the temperature of the room appreciably, but the heat lost by the cooling metal is. In this second situation we must use a model that accounts for the heat exchanged between the object and the medium. Let \(T = T(t)\) and \(T_m = T_m(t)\) be the temperatures of the object and the medium respectively, and let \(T_0\) and \(T_m0\) be their initial values. Again, we assume that T and Tm are related by Equation \ref{1.1.5}. We also assume that the change in heat of the object as its temperature changes from \(T_0\) to \(T\) is \(a(T −T_0)\) and the change in heat of the medium as its temperature changes from \(T_{m0}\) to \(T_m\) is \(a_m(T_m−T_{m0})\), where a and am are positive constants depending upon the masses and thermal properties of the object and medium respectively. If we assume that the total heat of the in the object and the medium remains constant (that is, energy is conserved), then

\[a(T −T_0) + a_m(T_m −T_{m0}) = 0. \nonumber\]

Solving this for \(T_m\) and substituting the result into Equation \ref{1.1.6} yields the differential equation

\[T ^ { \prime } = - k \left( 1 + \frac { a } { a _ { m } } \right) T + k \left( T _ { m 0 } + \frac { a } { a _ { m } } T _ { 0 } \right) \nonumber\]

for the temperature of the object. After learning to solve linear first order equations, you’ll be able to show ( Exercise 4.2.17 ) that

\[T = \frac { a T _ { 0 } + a _ { m } T _ { m 0 } } { a + a _ { m } } + \frac { a _ { m } \left( T _ { 0 } - T _ { m 0 } \right) } { a + a _ { m } } e ^ { - k \left( 1 + a / a _ { m } \right) t }\nonumber \]

Glucose Absorption by the Body

Glucose is absorbed by the body at a rate proportional to the amount of glucose present in the blood stream. Let \(λ\) denote the (positive) constant of proportionality. Suppose there are \(G_0\) units of glucose in the bloodstream when \(t = 0\), and let \(G = G(t)\) be the number of units in the bloodstream at time \(t > 0\). Then, since the glucose being absorbed by the body is leaving the bloodstream, \(G\) satisfies the equation

\[G' = −λG. \label{1.1.7}\]

From calculus you know that if \(c\) is any constant then

\[G = ce^{−λt} \label{1.1.8}\]

satisfies Equation (1.1.7), so Equation \ref{1.1.7} has infinitely many solutions. Setting \(t = 0\) in Equation \ref{1.1.8} and requiring that \(G(0) = G_0\) yields \(c = G_0\), so

\[G(t) = G_0e^{−λt}.\nonumber \]

Now let’s complicate matters by injecting glucose intravenously at a constant rate of \(r\) units of glucose per unit of time. Then the rate of change of the amount of glucose in the bloodstream per unit time is

\[G' = −λG + r \label{1.1.9}\]

where the first term on the right is due to the absorption of the glucose by the body and the second term is due to the injection. After you’ve studied Section 2.1, you’ll be able to show that the solution of Equation \ref{1.1.9} that satisfies \(G(0) = G_0\) is

\[G = \frac { r } { \lambda } + \left( G _ { 0 } - \frac { r } { \lambda } \right) e ^ { - \lambda t }\nonumber \]

Graphs of this function are similar to those in Figure 1.1.2 . (Why?)

Spread of Epidemics

One model for the spread of epidemics assumes that the number of people infected changes at a rate proportional to the product of the number of people already infected and the number of people who are susceptible, but not yet infected. Therefore, if \(S\) denotes the total population of susceptible people and \(I = I(t)\) denotes the number of infected people at time \(t\), then \(S −I\) is the number of people who are susceptible, but not yet infected. Thus, \[I' = rI(S −I)\nonumber \], where \(r\) is a positive constant. Assuming that \(I(0) = I_0\), the solution of this equation is

\[I =\dfrac{SI_0}{I_0 + (S −I_0)e^{−rSt}}\nonumber \]

( Exercise 2.2.29 ). Graphs of this function are similar to those in Figure 1.1.1. (Why?) Since \(\displaystyle\lim_{t→∞} I(t) = S\), this model predicts that all the susceptible people eventually become infected.

Newton’s Second Law of Motion

According to Newton’s second law of motion , the instantaneous acceleration a of an object with constant mass \(m\) is related to the force \(F\) acting on the object by the equation \(F = ma\). For simplicity, let’s assume that \(m = 1\) and the motion of the object is along a vertical line. Let \(y\) be the displacement of the object from some reference point on Earth’s surface, measured positive upward. In many applications, there are three kinds of forces that may act on the object:

• A force such as gravity that depends only on the position \(y,\) which we write as \(−p(y)\), where \(p(y) > 0\) if \(y ≥ 0\).
• A force such as atmospheric resistance that depends on the position and velocity of the object, which we write as \(−q(y,y')y'\), where \(q\) is a nonnegative function and we’ve put \(y'\) “outside” to indicate that the resistive force is always in the direction opposite to the velocity.
• A force \(f = f(t)\), exerted from an external source (such as a towline from a helicopter) that depends only on \(t\).

In this case, Newton’s second law implies that

\[y'' = −q(y,y')y' −p(y) + f(t), \nonumber\]

which is usually rewritten as

\[y'' + q(y,y')y' + p(y) = f(t). \nonumber\]

Since the second (and no higher) order derivative of \(y\) occurs in this equation, we say that it is a second order differential equation.

Interacting Species: Competition

Let \(P=P(t)\) and \(Q=Q(t)\) be the populations of two species at time \(t\), and assume that each population would grow exponentially if the other did not exist; that is, in the absence of competition we would have

\[\label{eq:1.1.10} P'=aP \quad \text{and} \quad Q'=bQ,\]

where \(a\) and \(b\) are positive constants. One way to model the effect of competition is to assume that the growth rate per individual of each population is reduced by an amount proportional to the other population, so Equation \ref{eq:1.1.10} is replaced by

\[\begin{align*} P' &= aP-\alpha Q\\[4pt] Q' &= -\beta P+bQ,\end{align*}\]

where \(\alpha\) and \(\beta\) are positive constants. (Since negative population doesn’t make sense, this system works only while \(P\) and \(Q\) are both positive.) Now suppose \(P(0)=P_0>0\) and \(Q(0)=Q_0>0\). It can be shown ( Exercise 10.4.42 ) that there’s a positive constant \(\rho\) such that if \((P_0,Q_0)\) is above the line \(L\) through the origin with slope \(\rho\), then the species with population \(P\) becomes extinct in finite time, but if \((P_0,Q_0)\) is below \(L\), the species with population \(Q\) becomes extinct in finite time. Figure 1.1.3 illustrates this. The curves shown there are given parametrically by \(P=P(t), Q=Q(t),\ t>0\). The arrows indicate direction along the curves with increasing \(t\).