- FOR INSTRUCTOR
- FOR INSTRUCTORS

1.4.5 Solved Problems: Conditional Probability
In die and coin problems, unless stated otherwise, it is assumed coins and dice are fair and repeated trials are independent.
You purchase a certain product. The manual states that the lifetime $T$ of the product, defined as the amount of time (in years) the product works properly until it breaks down, satisfies $$P(T \geq t)=e^{-\frac{t}{5}}, \textrm{ for all } t \geq 0.$$ For example, the probability that the product lasts more than (or equal to) $2$ years is $P(T \geq 2)=e^{-\frac{2}{5}}=0.6703$. I purchase the product and use it for two years without any problems. What is the probability that it breaks down in the third year?
| $P(B)$ | $=P(T \geq 2)$ |
| $=e^{-\frac{2}{5}}$. |
| $P(A)$ | $=P(2 \leq T \leq 3)$ |
| $=P(T \geq 2)-P(T \geq 3)$ | |
| $=e^{-\frac{2}{5}}-e^{-\frac{3}{5}}$. |
| $P(A|B)$ | $=\frac{P(A \cap B)}{P(B)}$ |
| $=\frac{P(A)}{P(B)}$ | |
| $=\frac{e^{-\frac{2}{5}}-e^{-\frac{3}{5}}}{e^{-\frac{2}{5}}}$ | |
| $=0.1813$ |
- What is the probability of three heads, $HHH$?
- What is the probability that you observe exactly one heads?
- Given that you have observed at least one heads, what is the probability that you observe at least two heads?
- $P(HHH)=P(H)\cdot P(H) \cdot P(H)=0.5^3=\frac{1}{8}$.
| $P(\textrm{One heads})$ | $=P(HTT \cup THT \cup TTH)$ |
| $=P(HTT)+P(THT)+P(TTH)$ | |
| $=\frac{1}{8}+\frac{1}{8}+\frac{1}{8}$ | |
| $=\frac{3}{8}$. |
| $P(A_2|A_1)$ | $=\frac{P(A_2 \cap A_1)}{P(A_1)}$ |
| $=\frac{P(A_2)}{P(A_1)}$ | |
| $=\frac{4}{8}.\frac{8}{7}=\frac{4}{7}$. |
- $A$ and $C$ are independent,
- $B$ and $C$ are independent,
- $A$ and $B$ are disjoint,
- $P(A \cup C)=\frac{2}{3}, P(B \cup C)=\frac{3}{4}, P(A \cup B\cup C)=\frac{11}{12}$
We can use the Venn diagram in Figure 1.26 to better visualize the events in this problem. We assume $P(A)=a, P(B)=b$, and $P(C)=c$. Note that the assumptions about independence and disjointness of sets are already included in the figure.
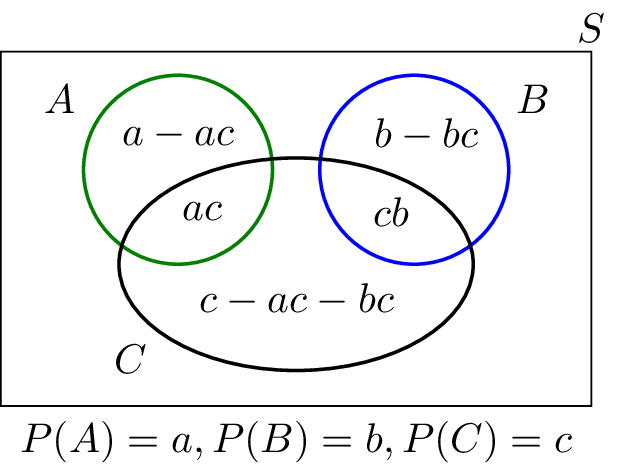
Now we can write $$P(A \cup C)= a+c-ac=\frac{2}{3};$$ $$P(B \cup C)=b+c-bc=\frac{3}{4};$$ $$P(A \cup B\cup C)=a+b+c-ac-bc=\frac{11}{12}.$$ By subtracting the third equation from the sum of the first and second equations, we immediately obtain $c=\frac{1}{2}$, which then gives $a=\frac{1}{3}$ and $b=\frac{1}{2}$.
- $A$ and $B$ are conditionally independent given $C_i$, for all $i \in \{1,2,\cdots,M\}$;
- $B$ is independent of all $C_i$'s.
| $P(A \cap B)$ | $=\sum_{i=1}^{M} P(A \cap B|C_i)P(C_i)$ | |
| $=\sum_{i=1}^{M} P(A|C_i)P(B|C_i)P(C_i) \hspace{10pt}$ | $\textrm{ ($A$ and $B$ are conditionally independent)}$ | |
| $=\sum_{i=1}^{M} P(A|C_i)P(B)P(C_i)$ | $\textrm{ ($B$ is independent of all $C_i$'s)}$ | |
| $=P(B) \sum_{i=1}^{M} P(A|C_i)P(C_i)$ | ||
| $=P(B) P(A)$ | $\textrm{ (law of total probability).}$ |
- What is the probability that it's not raining and there is heavy traffic and I am not late?
- What is the probability that I am late?
- Given that I arrived late at work, what is the probability that it rained that day?
Let $R$ be the event that it's rainy, $T$ be the event that there is heavy traffic, and $L$ be the event that I am late for work. As it is seen from the problem statement, we are given conditional probabilities in a chain format. Thus, it is useful to draw a tree diagram. Figure 1.27 shows a tree diagram for this problem. In this figure, each leaf in the tree corresponds to a single outcome in the sample space. We can calculate the probabilities of each outcome in the sample space by multiplying the probabilities on the edges of the tree that lead to the corresponding outcome.
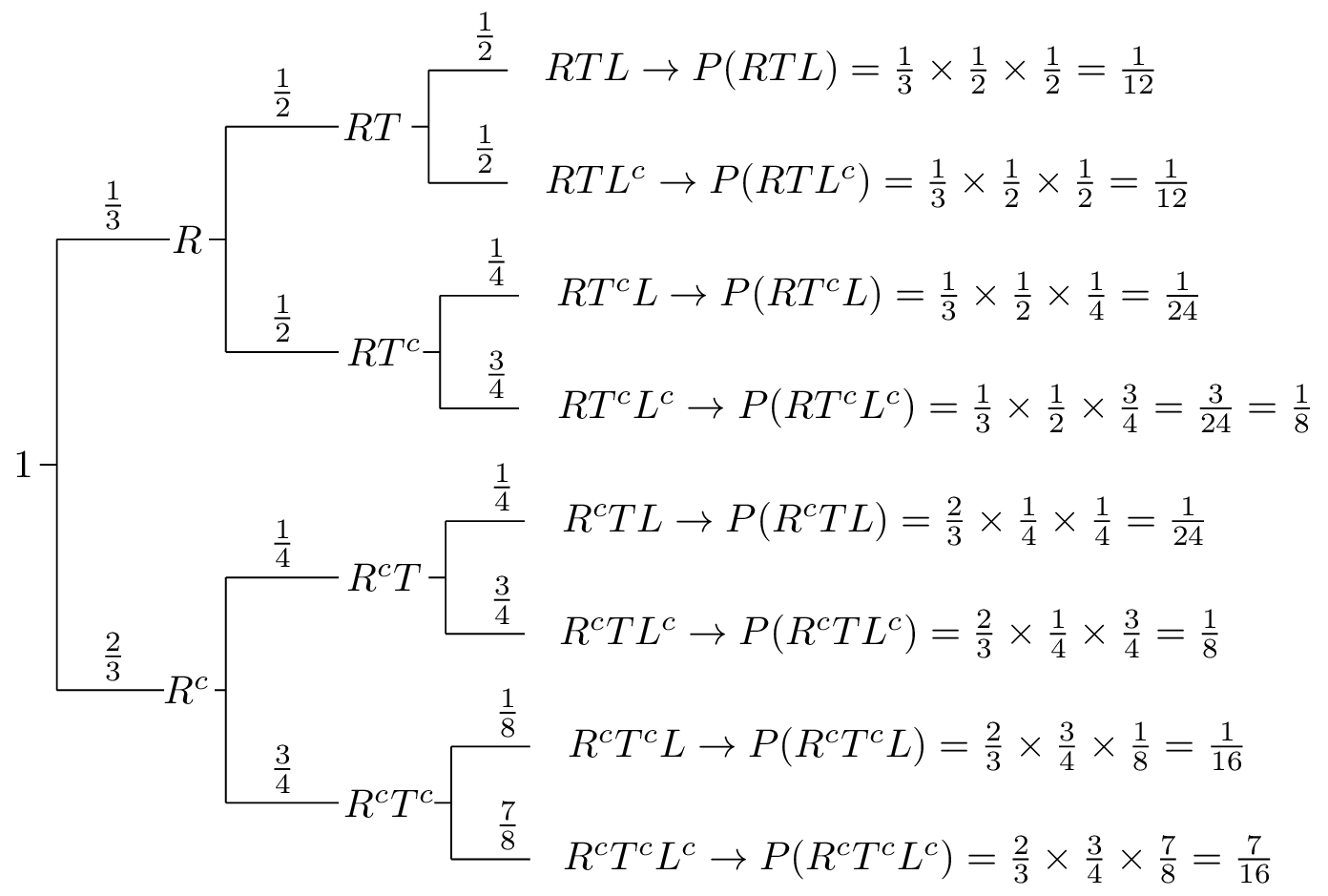
| $P(R^c \cap T \cap L^c)$ | $= P(R^c)P(T|R^c)P(L^c|R^c \cap T)$ |
| $=\frac{2}{3} \cdot \frac{1}{4} \cdot \frac{3}{4}$ | |
| $=\frac{1}{8}$. |
| $P(L)$ | $ = P(R,T,L)+P(R,T^c,L)+P(R^c,T,L)+P(R^c,T^c,L)$ |
| $=\frac{1}{12}+\frac{1}{24}+\frac{1}{24}+\frac{1}{16}$ | |
| $= \frac{11}{48}$. |
| $P(R \cap L)$ | $ = P(R,T,L)+P(R,T^c,L)$ |
| $=\frac{1}{12}+\frac{1}{24}$ | |
| $= \frac{1}{8}$. |
| $P(R|L)$ | $ = \frac{P(R \cap L)}{P(L)}$ |
| $=\frac{1}{8}. \frac{48}{11}$ | |
| $= \frac{6}{11}$. |
- You pick a coin at random and toss it. What is the probability that it lands heads up?
- You pick a coin at random and toss it, and get heads. What is the probability that it is the two-headed coin?
| $P(H)$ | $=P(H|C_1)P(C_1)+P(H|C_2)P(C_2)$ |
| $= \frac{1}{2}. \frac{2}{3} + 1 . \frac{1}{3}$ | |
| $=\frac{2}{3}$. |
| $P(C_2|H)$ | $=\frac{P(H|C_2)P(C_2)}{P(H)}$ |
| $=\frac{1 . \frac{1}{3}}{\frac{2}{3}}$ | |
| $=\frac{1}{2}$. |
Here is another variation of the family-with-two-children problem [1] [7] . A family has two children. We ask the father, "Do you have at least one daughter named Lilia?" He replies, "Yes!" What is the probability that both children are girls? In other words, we want to find the probability that both children are girls, given that the family has at least one daughter named Lilia. Here you can assume that if a child is a girl, her name will be Lilia with probability $\alpha \ll 1$ independently from other children's names. If the child is a boy, his name will not be Lilia. Compare your result with the second part of Example 1.18 .
| $P(GG|L)$ | $=\frac{P(L|GG)P(GG)}{P(L)}$ |
| $= \frac{P(L|GG)P(GG)}{P(L|GG)P(GG)+P(L|GB)P(GB)+P(L|BG)P(BG)+P(L|BB)P(BB)}$ | |
| $= \frac{(2 \alpha-\alpha^2)\frac{1}{4}}{(2 \alpha-\alpha^2)\frac{1}{4}+ \alpha \frac{1}{4}+ \alpha \frac{1}{4}+0.\frac{1}{4}}$ | |
| $= \frac{2-\alpha}{4-\alpha}\approx \frac{1}{2}$. |
Let's compare the result with part (b) of Example 1.18. Amazingly, we notice that the extra information about the name of the child increases the conditional probability of $GG$ from $\frac{1}{3}$ to about $\frac{1}{2}$. How can we explain this intuitively? Here is one way to look at the problem. In part (b) of Example 1.18, we know that the family has at least one girl. Thus, the sample space reduces to three equally likely outcomes: $GG, GB, BG$, thus the conditional probability of $GG$ is one third in this case. On the other hand, in this problem, the available information is that the event $L$ has occurred. The conditional sample space here still is $GG, GB, BG$, but these events are not equally likely anymore. A family with two girls is more likely to name at least one of them Lilia than a family who has only one girl ($P(L|BG)=P(L|GB)=\alpha$, $ P(L|GG)=2 \alpha-\alpha^2$), thus in this case the conditional probability of $GG$ is higher. We would like to mention here that these problems are confusing and counterintuitive to most people. So, do not be disappointed if they seem confusing to you. We seek several goals by including such problems.
First, we would like to emphasize that we should not rely too much on our intuition when solving probability problems. Intuition is useful, but at the end, we must use laws of probability to solve problems. Second, after obtaining counterintuitive results, you are encouraged to think deeply about them to explain your confusion. This thinking process can be very helpful to improve our understanding of probability. Finally, I personally think these paradoxical-looking problems make probability more interesting.
| $P(GG|G_r)$ | $=\frac{P(G_r|GG)P(GG)}{P(G_r)}$ |
| $= \frac{P(G_r|GG)P(GG)}{P(G_r|GG)P(GG)+P(G_r|GB)P(GB)+P(G_r|BG)P(BG)+P(G_r|BB)P(BB)}$ | |
| $= \frac{1.\frac{1}{4}}{1. \frac{1}{4}+ \frac{1}{2} \frac{1}{4}+ \frac{1}{2} \frac{1}{4}+0.\frac{1}{4}}$ | |
| $= \frac{1}{2}$. |
So the answer again is different from the second part of Example 1.18. This is surprising to most people. The two problem statements look very similar but the answers are completely different. This is again similar to the previous problem (please read the explanation there). The conditional sample space here still is $GG, GB, BG$, but the point here is that these are not equally likely as in Example 1.18. The probability that a randomly chosen child from a family with two girls is a girl is one, while this probability for a family who has only one girl is $\frac{1}{2}$. Thus, intuitively, the conditional probability of the outcome $GG$ in this case is higher than $GB$ and $BG$, and thus this conditional probability must be larger than one third.
Okay, another family-with-two-children problem. Just kidding! This problem has nothing to do with the two previous problems. I toss a coin repeatedly. The coin is unfair and $P(H)=p$. The game ends the first time that two consecutive heads ($HH$) or two consecutive tails ($TT$) are observed. I win if $HH$ is observed and lose if $TT$ is observed. For example if the outcome is $HTH\underline{TT}$, I lose. On the other hand, if the outcome is $THTHT\underline{HH}$, I win. Find the probability that I win.
| $W$ | $=P(\{HH, HTHH, HTHTHH,\cdots \})+P(\{THH, THTHH, THTHTHH,\cdots \})$ |
| $=p^2+p^3q+ p^4q^2+\cdots+p^2q+p^3q^2+ p^4q^3+\cdots$ | |
| $=p^2(1+pq+(pq)^2+(pq)^3+\cdots)+p^2q(1+pq+(pq)^2+(pq)^3+\cdots)$ | |
| $=p^2(1+q)(1+pq+(pq)^2+(pq)^3+\cdots)$ | |
| $=\frac{p^2(1+q)}{1-pq}, \hspace{10pt}\textrm{ Using the geometric series formula}$ | |
| $=\frac{p^2(2-p)}{1-p+p^2}$. |
The print version of the book is available on . |
|
Reset password New user? Sign up
Existing user? Log in
Conditional Probability - Problem Solving
Already have an account? Log in here.
Recommended Course
Applied probability.
A framework for understanding the world around us, from sports to science.
This wiki is incomplete.
A lot of difficult probability problems involve conditional probability . These can be tackled using tools like Bayes' Theorem , the principle of inclusion and exclusion , and the notion of independence .
Two standard dice with 6 sides are thrown and the faces are recorded. Given that the sum of the two faces equals to 10, what is the probability that the first throw equals to 5? Let \(A\) denote the event for which the two faces sums to 10, and \(B\) the event for which the first throw equals 5. Then the sample space for \(A\) is \( \{ (5,5),(4,6),(6,4) \} \). The sample space for \(B\) is \( \{ (5,1),(5,2),(5,3),(5,4),(5,5),(5,6) \} \). Therefore, \(A \cap B = \{(5,5)\} \) and \(P(B|A) = \frac{P(A\cap B)}{P(A)} = \frac{1/36}{3/36} = \frac13. \ _\square \)
A bag contains a number of coins, one of which is a two-headed coin and the rest are fair coins. A coin is selected at random and tossed. If the probability that the toss results in a head is \(\frac {7}{12} \), then how many fair coins are in the bag ?
Details and Assumptions: A two-headed coin is a coin which has head on both sides; a fair coin means it has tail on one side and head on the other.
Horace turns up at school either late or on time. He is then either shouted at or not. The probability that he turns up late is \(0.4.\) If he turns up late, the probability that he is shouted at is \(0.7\). If he turns up on time, the probability that he is still shouted at for no particular reason is \(0.2\).
You hear Horace being shouted at. What is the probability that he was late?
This problem is not original.

Master concepts like these
Learn more in our Applied Probability course, built by experts for you.
Problem Loading...
Note Loading...
Set Loading...
Conditional Probability
How to handle Dependent Events
Life is full of random events! You need to get a "feel" for them to be a smart and successful person.
Independent Events
Events can be " Independent ", meaning each event is not affected by any other events.
Example: Tossing a coin.
Each toss of a coin is a perfect isolated thing.
What it did in the past will not affect the current toss.
The chance is simply 1-in-2, or 50%, just like ANY toss of the coin.
So each toss is an Independent Event .
Dependent Events
But events can also be "dependent" ... which means they can be affected by previous events ...
Example: Marbles in a Bag
2 blue and 3 red marbles are in a bag.
What are the chances of getting a blue marble?
The chance is 2 in 5
But after taking one out the chances change!
So the next time:
This is because we are removing marbles from the bag.
So the next event depends on what happened in the previous event, and is called dependent .
Replacement
Note: if we replace the marbles in the bag each time, then the chances do not change and the events are independent :
- With Replacement: the events are Independent (the chances don't change)
- Without Replacement: the events are Dependent (the chances change)
Dependent events are what we look at here.
Tree Diagram
A Tree Diagram is a wonderful way to picture what is going on, so let's build one for our marbles example.
There is a 2/5 chance of pulling out a Blue marble, and a 3/5 chance for Red:
We can go one step further and see what happens when we pick a second marble:
If a blue marble was selected first there is now a 1/4 chance of getting a blue marble and a 3/4 chance of getting a red marble.
If a red marble was selected first there is now a 2/4 chance of getting a blue marble and a 2/4 chance of getting a red marble.
Now we can answer questions like "What are the chances of drawing 2 blue marbles?"
Answer: it is a 2/5 chance followed by a 1/4 chance :
Did you see how we multiplied the chances? And got 1/10 as a result.
The chances of drawing 2 blue marbles is 1/10
We love notation in mathematics! It means we can then use the power of algebra to play around with the ideas. So here is the notation for probability:
P(A) means "Probability Of Event A"
In our marbles example Event A is "get a Blue Marble first" with a probability of 2/5:
And Event B is "get a Blue Marble second" ... but for that we have 2 choices:
- If we got a Blue Marble first the chance is now 1/4
- If we got a Red Marble first the chance is now 2/4
So we have to say which one we want , and use the symbol "|" to mean "given":
P(B|A) means "Event B given Event A"
In other words, event A has already happened, now what is the chance of event B?
P(B|A) is also called the "Conditional Probability" of B given A.
And in our case:
P(B|A) = 1/4
So the probability of getting 2 blue marbles is:
And we write it as
"Probability of event A and event B equals the probability of event A times the probability of event B given event A "
Let's do the next example using only notation:
Example: Drawing 2 Kings from a Deck
Event A is drawing a King first, and Event B is drawing a King second.
For the first card the chance of drawing a King is 4 out of 52 (there are 4 Kings in a deck of 52 cards):
P(A) = 4/52
But after removing a King from the deck the probability of the 2nd card drawn is less likely to be a King (only 3 of the 51 cards left are Kings):
P(B|A) = 3/51
P(A and B) = P(A) x P(B|A) =(4/52)x (3/51) = 12/2652 = 1/221
So the chance of getting 2 Kings is 1 in 221, or about 0.5%
Finding Hidden Data
Using Algebra we can also "change the subject" of the formula, like this:
| Start with: | P(A and B) = P(A) x P(B|A) | |
| Swap sides: | P(A) x P(B|A) = P(A and B) | |
| Divide by P(A): | P(B|A) = P(A and B) / P(A) |
And we have another useful formula:
"The probability of event B given event A equals the probability of event A and event B divided by the probability of event A "
Example: Ice Cream
70% of your friends like Chocolate, and 35% like Chocolate AND like Strawberry.
What percent of those who like Chocolate also like Strawberry?
P(Strawberry|Chocolate) = P(Chocolate and Strawberry) / P(Chocolate)
50% of your friends who like Chocolate also like Strawberry

Big Example: Soccer Game
You are off to soccer, and want to be the Goalkeeper, but that depends who is the Coach today:
- with Coach Sam the probability of being Goalkeeper is 0.5
- with Coach Alex the probability of being Goalkeeper is 0.3
Sam is Coach more often ... about 6 out of every 10 games (a probability of 0.6 ).
So, what is the probability you will be a Goalkeeper today?
Let's build a tree diagram . First we show the two possible coaches: Sam or Alex:
The probability of getting Sam is 0.6, so the probability of Alex must be 0.4 (together the probability is 1)
Now, if you get Sam, there is 0.5 probability of being Goalie (and 0.5 of not being Goalie):
If you get Alex, there is 0.3 probability of being Goalie (and 0.7 not):
The tree diagram is complete, now let's calculate the overall probabilities. Remember that:
P(A and B) = P(A) x P(B|A)
Here is how to do it for the "Sam, Yes" branch:
(When we take the 0.6 chance of Sam being coach times the 0.5 chance that Sam will let you be Goalkeeper we end up with an 0.3 chance.)
But we are not done yet! We haven't included Alex as Coach:
With 0.4 chance of Alex as Coach, followed by the 0.3 chance gives 0.12
And the two "Yes" branches of the tree together make:
0.3 + 0.12 = 0.42 probability of being a Goalkeeper today
(That is a 42% chance)
One final step: complete the calculations and make sure they add to 1:
0.3 + 0.3 + 0.12 + 0.28 = 1
Yes, they add to 1 , so that looks right.
Friends and Random Numbers
Here is another quite different example of Conditional Probability.
4 friends (Alex, Blake, Chris and Dusty) each choose a random number between 1 and 5. What is the chance that any of them chose the same number?
Let's add our friends one at a time ...
First, what is the chance that Alex and Blake have the same number?
Blake compares his number to Alex's number. There is a 1 in 5 chance of a match.
As a tree diagram :
Note: "Yes" and "No" together makes 1 (1/5 + 4/5 = 5/5 = 1)
Now, let's include Chris ...
But there are now two cases to consider:
- If Alex and Blake did match, then Chris has only one number to compare to.
- But if Alex and Blake did not match then Chris has two numbers to compare to.
And we get this:
For the top line (Alex and Blake did match) we already have a match (a chance of 1/5).
But for the "Alex and Blake did not match" there is now a 2/5 chance of Chris matching (because Chris gets to match his number against both Alex and Blake).
And we can work out the combined chance by multiplying the chances it took to get there:
Following the "No, Yes" path ... there is a 4/5 chance of No, followed by a 2/5 chance of Yes:
Following the "No, No" path ... there is a 4/5 chance of No, followed by a 3/5 chance of No:
Also notice that when we add all chances together we still get 1 (a good check that we haven't made a mistake):
(5/25) + (8/25) + (12/25) = 25/25 = 1
Now what happens when we include Dusty?
It is the same idea, just more of it:
OK, that is all 4 friends, and the "Yes" chances together make 101/125:
Answer: 101/125
But here is something interesting ... if we follow the "No" path we can skip all the other calculations and make our life easier:
The chances of not matching are:
(4/5) × (3/5) × (2/5) = 24/125
So the chances of matching are:
1 - (24/125) = 101/125
(And we didn't really need a tree diagram for that!)
And that is a popular trick in probability:
It is often easier to work out the "No" case (and subtract from 1 for the "Yes" case)
(This idea is shown in more detail at Shared Birthdays .)
Conditional Probability
In these lessons, we will learn what is conditional probability and how to use the formula for conditional probability.
Related Pages Dependent Events More Lessons On Probability Probability Tree Diagrams
The following diagram shows the formula for conditional probability. Scroll down the page for more examples and solutions on finding the conditional probability.

What Is Conditional Probability?
The probability of an event occurring given that another event has already occurred is called a conditional probability .
Recall that when two events, A and B, are dependent , the probability of both occurring is:
P(A and B) = P(A) × P(B given A) or P(A and B) = P(A) × P(B | A)
If we divide both sides of the equation by P(A) we get the Formula for Conditional Probability
How To Find The Conditional Probability From A Word Problem?
Step 1: Write out the Conditional Probability Formula in terms of the problem Step 2: Substitute in the values and solve.
Example: Susan took two tests. The probability of her passing both tests is 0.6. The probability of her passing the first test is 0.8. What is the probability of her passing the second test given that she has passed the first test?
Example: A bag contains red and blue marbles. Two marbles are drawn without replacement. The probability of selecting a red marble and then a blue marble is 0.28. The probability of selecting a red marble on the first draw is 0.5. What is the probability of selecting a blue marble on the second draw, given that the first marble drawn was red?
Solution: What is the probability that the total of two dice will be greater than 9, given that the first die is a 5?
Solution: Let A = first die is 5 Let B = total of two dice is greater than 9
Possible outcomes for A and B: (5, 5), (5, 6)
How To Use Real World Examples To Explain Conditional Probability?
Conditional probability is about narrowing down the set of possible circumstances so that the statistics can be measured more accurately.
How To Define Conditional Probability?
This video introduces the basic definition of conditional probability as it is defined in standard probability theory.
How To Calculate Conditional Probability?
Tutorial on how to calculate conditional probability for two events P(A), P(B), P(B|A) with two examples.
- Example 1: What is the probability of rolling a dice and its value is less than 4 knowing that the value is an odd number?
- Example 2: What is the probability of rolling a dice and its value is 1 knowing that the value is an odd number?
How To Determine The Conditional Probability From The Given Word Problems?
- You roll one 6-sided die, what is the probability of a 3 given you know the number is odd?
- At P-Town High School, the probability that a student takes Computer Programming and Spanish is 0.15. The probability that a student takes Computer Programming is 0.4. What is the probability that a student takes Spanish given that the student is taking Computer Programming?
- Here are the results of a survey completed with adult parents with children. What is the probability a person thinks college is too expensive given they have a child in college?
- Two cards are drawn without replacement in succession. What is the probability that the second card drawn is an ace, given that the first can drawn was an ace?
- Two cards are drawn without replacement. What is the probability the second card is a red face card given the first card is a ref face card?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
7.9 Conditional Probability and the Multiplication Rule
Learning objectives.
After completing this section, you should be able to:
- Calculate conditional probabilities.
- Apply the Multiplication Rule for Probability to compute probabilities.
Back in Example 7.18 , we constructed the following table ( Figure 7.38 ) to help us find the probabilities associated with rolling two standard 6-sided dice:
For example, 3 of these 36 equally likely outcomes correspond to rolling a sum of 10, so the probability of rolling a 10 is 3 36 = 1 12 3 36 = 1 12 . However, if you choose to roll the dice one at a time, the probability of rolling a 10 will change after the first die comes to rest. For example, if the first die shows a 5, then the probability of rolling a sum of 10 has jumped to 1 6 1 6 —the event will occur if the second die also shows a 5, which is 1 of 6 equally likely outcomes for the second die. If instead the first die shows a 3, then the probability of rolling a sum of 10 drops to 0—there are no outcomes for the second die that will give us a sum of 10.
Understanding how probabilities can shift as we learn new information is critical in the analysis of our second type of compound events: those built with “and.” This section will explain how to compute probabilities of those compound events.
Conditional Probabilities
When we analyze experiments with multiple stages, we often update the probabilities of the possible final outcomes or the later stages of the experiment based on the results of one or more of the initial stages. These updated probabilities are called conditional probabilities .
In other words, if O O is a possible outcome of the first stage in a multistage experiment, then the probability of an event E E conditional on O O (denoted P ( E | O ) P ( E | O ) , read “the probability of E E given O O ”) is the updated probability of E E under the assumption that O O occurred.
In the example that opened this section, we might consider rolling two dice as a multistage experiment: rolling one, then the other. If we define E E to be the event “roll a sum of 10,” O O to be the event “first die shows 5,” and Q Q to be the event “first die shows 3,” then we computed P ( E ) = 1 12 P ( E ) = 1 12 , P ( E | O ) = 1 6 P ( E | O ) = 1 6 , and P ( E | Q ) = 0 P ( E | Q ) = 0 .
Example 7.31
Computing conditional probabilities.
- April is playing a coin-flipping game with Ben. She will flip a coin 3 times. If the coin lands on heads more than tails, April wins; if it lands on tails more than heads, Ben wins. Let A A be the event “April wins,” H H be “first flip is heads,” and T T be “first flip is tails.” Compute P ( A ) P ( A ) , P ( A | H ) P ( A | H ) , and P ( A | T ) P ( A | T ) .
- You are about to draw 2 cards without replacement from a deck containing only these 10 cards: A ♡ A ♡ , A ♠ A ♠ , A ♣ A ♣ , A ♢ A ♢ , K ♠ K ♠ , K ♣ K ♣ , Q ♡ Q ♡ , Q ♠ Q ♠ , J ♡ J ♡ , J ♠ J ♠ . We’ll define the following events: F F is “both cards are the same rank,” A A is “first card is an ace,” and K K is “first card is a king.” Compute P ( F | A ) P ( F | A ) and P ( F | K ) P ( F | K ) .
- Jim’s sock drawer contains 5 black socks and 3 blue socks. To avoid waking his partner, Jim doesn’t want to turn the lights on, so he puts on 2 socks at random. Let M M be the event “Jim’s 2 socks match,” let K K be the event “the sock on Jim’s left foot is black,” and let L L be the event “the sock on Jim’s left foot is blue.” Compute P ( M ) P ( M ) , P ( M | K ) P ( M | K ) , and P ( M | L ) P ( M | L ) .
Step 1. The sample space is {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}. The event A A consists of the first 4 of those outcomes: HHH, HHT, HTH, and THH. Thus, P ( A ) = 4 8 = 1 2 P ( A ) = 4 8 = 1 2 .
Step 2. Now, let’s compute P ( A | H ) P ( A | H ) . We are assuming the result of the first flip is heads. That leaves us with 4 possible outcomes: HHH, HHT, HTH, and HTT. Of those, April wins 3 (HHH, HHT, HTH) and loses one (HTT). So, P ( A | H ) = 3 4 P ( A | H ) = 3 4 .
Step 3. If the result of the first flip is instead tails, the 4 possible outcomes are THH, THT, TTH, and TTT. Of those, April wins 1 (THH) and loses 3 (THT, TTH, TTT). So, P ( A | T ) = 1 4 P ( A | T ) = 1 4 .
Step 1. If the event A A happens, then 1 of the 4 aces is drawn first; the remaining cards in the deck are 3 aces, 2 kings, 2 queens, and 2 jacks. In order for the event F F to occur, the second card drawn has to be an ace. Since there are 3 aces among the remaining 9 cards, P ( F | A ) = 3 9 = 1 3 P ( F | A ) = 3 9 = 1 3 .
Step 2. If the event K K happens instead, then the first card drawn is a king. That leaves 4 aces, 1 king, 2 queens, and 2 jacks in the deck. Under the assumption that the first card is a king, the event F F will occur only if the second card is also a king. Since only one of the remaining 9 cards is a king, we have P ( F | K ) = 1 9 P ( F | K ) = 1 9 .
Step 1. We can view the event M M as a compound event using “or”: both socks are blue or both socks are black. Let’s compute the probability that both socks are blue using combinations. We’re choosing 2 socks from a group of 8; 3 of the 8 are blue. So, P ( both socks blue ) = 3 C 2 8 C 2 = 3 28 P ( both socks blue ) = 3 C 2 8 C 2 = 3 28 . Similarly, P ( both socks black ) = 5 C 2 8 C 2 = 10 28 P ( both socks black ) = 5 C 2 8 C 2 = 10 28 . Therefore, since these events are mutually exclusive, we can use the Addition Rule: P ( M ) = P ( both socks blue ) + P ( both socks black ) = 3 28 + 10 28 = 13 28 P ( M ) = P ( both socks blue ) + P ( both socks black ) = 3 28 + 10 28 = 13 28 .
Step 2. If the sock on Jim’s left foot is black (i.e., K K occurred), then there are 4 remaining black socks of the 7 in the drawer. So, P ( M | K ) = 4 7 P ( M | K ) = 4 7 .
Step 3. If the sock on Jim’s left foot is blue ( L L occurred), then there are 2 blue socks among the 7 remaining in the drawer. So, P ( M | L ) = 2 7 P ( M | L ) = 2 7 .
Your Turn 7.31
In Tree Diagrams, Tables, and Outcomes , we introduced the concept of dependence between stages of a multistage experiment. We stated at the time that two stages were dependent if the result of one stage affects the other stage. We explained that dependence in terms of the sample space, but sometimes that dependence can be a little more subtle; it’s more properly understood in terms of conditional probabilities. Two stages of an experiment are dependent if P ( E | F ) ≠ P ( E | F ′ ) P ( E | F ) ≠ P ( E | F ′ ) for some outcome of the second stage E E and outcome of the first stage F F .
Protecting Bombers in World War II
In his book How Not to Be Wrong , Jordan Ellenberg recounts this anecdote: During World War II, the American military wanted to add additional armor plating to bomber aircraft, in order to reduce the chances that they get shot down. So, they collected data on planes after returning from missions. The data showed that the fuselage, wings, and fuel system had many more bullet holes (per unit area) than the engine compartments, so the military brass wanted to add additional armor to the parts of the plane that were hit most often. Luckily, before they added the armor to the planes, they asked for a second opinion. Abraham Wald, a Jewish mathematician who had fled the rising Nazi regime, pointed out that it was far more important that the armor plating be added to areas where there were fewer bullet holes. Why? The planes they were studying had already completed their missions, so the military was essentially looking at conditional probabilities: the probability of suffering a bullet strike, given that the plane made it back safely. More bullet holes in an area on the plane indicated that was a region that wasn’t as important for the plane’s survival!
Compound Events Using “And” and the Multiplication Rule
For multistage experiments, the outcomes of the experiment as a whole are often stated in terms of the outcomes of the individual stages. Commonly, those statements are joined with “and.” For example, in the sock drawer example just above, one outcome might be “the left sock is black and the right sock is blue.” As with “or” compound events, these probabilities can be computed with basic arithmetic.
Multiplication Rule for Probability: If E E and F F are events associated with the first and second stages of an experiment, then P ( E and F ) = P ( E ) × P ( F | E ) P ( E and F ) = P ( E ) × P ( F | E ) .
In The Addition Rule for Probability , we considered probabilities of events connected with “and” in the statement of the Inclusion/Exclusion Principle. These two scenarios are different; in the statement of the Inclusion/Exclusion Principle, the events connected with “and” are both events associated with the same single-stage experiment (or the same stage of a multistage experiment). In the Multiplication Rule, we’re looking at events associated with different stages of a multistage experiment.
Example 7.32
Using the multiplication rule for probability.
You are president of a club with 10 members: 4 seniors, 3 juniors, 2 sophomores, and 1 first-year. You need to choose 2 members to represent the club on 2 college committees. The first person selected will be on the Club Awards Committee and the second will be on the New Club Orientation Committee. The same person cannot be selected for both. You decide to select these representatives at random.
- What is the probability that a senior is chosen for both positions?
- What is the probability that a junior is chosen first and a sophomore is chosen second?
- What is the probability that a sophomore is chosen first and a senior is chosen second?
- We need the probability that a senior is chosen first and a senior is chosen second. These are two stages of a multistage experiment, so we’ll apply the Multiplication Rule for Probability: P ( senior chosen first and senior chosen second ) = P ( senior chosen first ) × P ( senior chosen second | senior chosen first ) . P ( senior chosen first and senior chosen second ) = P ( senior chosen first ) × P ( senior chosen second | senior chosen first ) . Since there are 4 seniors among the 10 members, P ( senior chosen first ) = 4 10 = 2 5 P ( senior chosen first ) = 4 10 = 2 5 . Next, assuming a senior is chosen first, there are 3 seniors among the 9 remaining members. So, P ( senior chosen second | senior chosen first ) = 3 9 = 1 3 P ( senior chosen second | senior chosen first ) = 3 9 = 1 3 . Putting this all together, we get P ( senior chosen first and senior chosen second ) = 2 5 × 1 3 = 2 15 P ( senior chosen first and senior chosen second ) = 2 5 × 1 3 = 2 15 .
- There are 3 juniors among the 10 members, so P ( junior chosen first ) = 3 10 P ( junior chosen first ) = 3 10 . Assuming a junior is chosen first, there are 2 sophomores among the remaining 9 members, so P ( sophomore chosen second | junior chosen first ) = 2 9 P ( sophomore chosen second | junior chosen first ) = 2 9 . Thus, using the Multiplication Rule for Probability, we have P ( junior chosen first and sophomore chosen second ) = 3 10 × 2 9 = 1 15 P ( junior chosen first and sophomore chosen second ) = 3 10 × 2 9 = 1 15 .
- The probability that a sophomore is chosen first is 2 10 = 1 5 2 10 = 1 5 , and the probability that a senior is chosen second given that a sophomore was chosen first is 4 9 4 9 . Thus, using the Multiplication Rule for Probability, we have: P ( sophomore chosen first and senior chosen second ) = 1 5 × 4 9 = 4 45 P ( sophomore chosen first and senior chosen second ) = 1 5 × 4 9 = 4 45 .
Your Turn 7.32
Work it out, the birthday problem.
One of the most famous problems in probability theory is the Birthday Problem, which has to do with shared birthdays in a large group. To make the analysis easier, we’ll ignore leap days, and assume that the probability of being born on any given date is 1 365 1 365 . Now, if you have 366 people in a room, we’re guaranteed to have at least one pair of people who share a single birthday. Imagine filling the room by first admitting someone born on January 1, then someone born on January 2, and so on… The 365th person admitted would be born on December 31. If you add one more person to the room, that person’s birthday would have to match someone else’s.
Let’s look at the other end of the spectrum. If you choose two people at random, what is the probability that they share a birthday? As with many probability questions, this is best addressed by find out the probability that they do not share a birthday. The first person’s birthday can be anything (probability 1), and the second person’s birthday can be anything other than the first person’s birthday (probability 364 365 364 365 ). The probability that they have different birthdays is 1 × 364 365 = 364 365 1 × 364 365 = 364 365 . So, the probability that they share a birthday is 1 − 364 365 = 1 365 1 − 364 365 = 1 365 .
What if we have three people? The probability that they all have different birthdays can be obtained by extending our previous calculation: The probability that two people have different birthdays is 364 365 364 365 , so if we add a third to the mix, the probability that they have a different birthday from the other two is 363 365 363 365 . So, the probability that all three have different birthdays is 364 365 × 363 365 ≈ 0.9918 364 365 × 363 365 ≈ 0.9918 , and thus the probability that there’s a shared birthday in the group is 1 − 0.9918 ≈ 0.0082 1 − 0.9918 ≈ 0.0082 .
The big question is this: How many people do we need in the room to have the probability of a shared birthday greater than 1 2 1 2 ? Make a guess, then with a partner keep adding hypothetical people to the group and computing probabilities until you get there!
It is often useful to combine the rules we’ve seen so far with the techniques we used for finding sample spaces. In particular, trees can be helpful when we want to identify the probabilities of every possible outcome in a multistage experiment. The next example will illustrate this.
Example 7.33
Using tree diagrams to help find probabilities.
The board game Clue uses a deck of 21 cards: 6 suspects, 6 weapons, and 9 rooms. Suppose you are about to draw 2 cards from this deck. There are 6 possible outcomes for the draw: 2 suspects, 2 weapons, 2 rooms, 1 suspect and 1 weapon, 1 suspect and 1 room, or 1 weapon and 1 room. What are the probabilities for each of these outcomes?
Step 1: Let’s start by building a tree diagram that illustrates both stages of this experiment. Let’s use S, W, and R to indicate drawing a suspect, weapon, and room, respectively ( Figure 7.39 ).
Step 2: We want to start computing probabilities, starting with the first stage. The probability that the first card is a suspect is 6 21 = 2 7 6 21 = 2 7 . The probability that the first card is a weapon is the same: 2 7 2 7 . Finally, the probability that the first card is a room is 9 21 = 3 7 9 21 = 3 7 .
Step 3: Let’s incorporate those probabilities into our tree: label the edges going into each of the nodes representing the first-stage outcomes with the corresponding probabilities ( Figure 7.40 ).
Note that the sum of the probabilities coming out of the initial node is 1; this should always be the case for the probabilities coming out of any node!
Step 4: Let’s look at the case where the first card is a suspect. There are 3 edges emanating from that node (leading to the outcomes SS, SW, and SR). We’ll label those edges with the appropriate conditional probabilities, under the assumption that the first card is a suspect. First, there are 5 remaining suspect cards among the 20 left in the deck, so P ( second is suspect | first is suspect ) = 5 20 = 1 4 P ( second is suspect | first is suspect ) = 5 20 = 1 4 . Using similar reasoning, we can compute P ( second is weapon | first is suspect ) = 6 20 = 3 10 P ( second is weapon | first is suspect ) = 6 20 = 3 10 and P ( second is room | first is suspect ) = 9 20 P ( second is room | first is suspect ) = 9 20 .
Step 5: Checking our work, we see that the sum of these 3 probabilities is again equal to 1. Let’s add those to our tree ( Figure 7.41 ).
Step 6: Let’s continue filling in the conditional probabilities at the other nodes, always checking to make sure the sum of the probabilities coming out of any node is equal to 1 ( Figure 7.42 ).
Step 7: We can compute the probability of landing on any final node by multiplying the probabilities along the path we would take to get there. For example, the probability of drawing a suspect first and a weapon second (i.e., ending up on the node labeled “SW”) is 2 7 × 3 10 = 3 35 2 7 × 3 10 = 3 35 , as illustrated in Figure 7.43 .
Step 8: Let’s fill in the rest of the probabilities ( Figure 7.44 ).
Step 9: A helpful feature of tree diagrams is that the final outcomes are always mutually exclusive, so the Addition Rule can be directly applied. For example, the probability of drawing one suspect and one room (in any order) would be P ( S R ) + P ( R S ) = 9 70 + 9 70 = 9 35 P ( S R ) + P ( R S ) = 9 70 + 9 70 = 9 35 . We can find the probabilities of the other outcomes in a similar fashion, as shown in the following table:
| Outcome | Probability |
|---|---|
| 2 suspects | |
| 2 weapons | |
| 2 rooms | |
| 1 suspect and 1 weapon | |
| 1 suspect and 1 room | |
| 1 weapon and 1 room |
Checking once again, the sum of these 6 probabilities is 1, as expected.
Your Turn 7.33
The monty hall problem.
On the original version of the game show Let’s Make a Deal , originally hosted by Monty Hall and now hosted by Wayne Brady, one contestant was chosen to play a game for the grand prize of the day (often a car). Here’s how it worked: On the stage were three areas concealed by numbered curtains. The car was hidden behind one of the curtains; the other two curtains hid worthless prizes (called “Zonks” on the show). The contestant would guess which curtain concealed the car. To build tension, Monty would then reveal what was behind one of the other curtains, which was always one of the Zonks (Since Monty knew where the car was hidden, he always had at least one Zonk curtain that hadn’t been chosen that he could reveal). Monty then turned to the contestant and asked: “Do you want to stick with your original choice, or do you want to switch your choice to the other curtain?” What should the contestant do? Does it matter?
With a partner or in a small group, simulate this game. You can do that with a small candy (the prize) hidden under one of three cups, or with three playing cards (just decide ahead of time which card represents the “Grand Prize”). One person plays the host, who knows where the prize is hidden. Another person plays the contestant and tries to guess where the prize is hidden. After the guess is made, the host should reveal a losing option that wasn’t chosen by the contestant. The contestant then has the option to stick with the original choice or switch to the other, unrevealed option. Play about 20 rounds, taking turns in each role and making sure that both contestant strategies (stick or switch) are used equally often. After each round, make a note of whether the contestant chose “stick” or “switch” and whether the contestant won or lost. Find the empirical probability of winning under each strategy. Then, see if you can use tree diagrams to verify your findings.
Check Your Understanding
Section 7.9 exercises.
- P ( tile shows A )
- P ( tile shows A | tile shows a vowel )
- P ( tile shows a vowel )
- P ( tile shows a vowel | tile shows a letter that comes after M alphabetically )
| Class Year | ||||||
|---|---|---|---|---|---|---|
| First-Year | Sophomore | Junior | Senior | Totals | ||
| 138 | 121 | 148 | 132 | 539 | ||
| 258 | 301 | 275 | 283 | 1117 | ||
| 142 | 151 | 130 | 132 | 555 | ||
| 175 | 197 | 203 | 188 | 763 | ||
| 713 | 770 | 756 | 735 | 2974 | ||
In the following exercises deal with the game “Punch a Bunch,” which appears on the TV game show The Price Is Right . In this game, contestants have a chance to punch through up to 4 paper circles on a board; behind each circle is a card with a dollar amount printed on it. There are 50 of these circles; the dollar amounts are given in this table:
| Dollar Amount | Frequency |
|---|---|
| $25,000 | 1 |
| $10,000 | 2 |
| $5,000 | 4 |
| $2,500 | 8 |
| $1,000 | 10 |
| $500 | 10 |
| $250 | 10 |
| $100 | 5 |
Contestants are shown their selected dollar amounts one at a time, in the order selected. After each is revealed, the contestant is given the option of taking that amount of money or throwing it away in favor of the next amount. (You can watch the game being played in the video Playing “Punch a Bunch.” ) Jeremy is playing “Punch a Bunch” and gets 2 punches.
As an Amazon Associate we earn from qualifying purchases.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/contemporary-mathematics/pages/1-introduction
- Authors: Donna Kirk
- Publisher/website: OpenStax
- Book title: Contemporary Mathematics
- Publication date: Mar 22, 2023
- Location: Houston, Texas
- Book URL: https://openstax.org/books/contemporary-mathematics/pages/1-introduction
- Section URL: https://openstax.org/books/contemporary-mathematics/pages/7-9-conditional-probability-and-the-multiplication-rule
© Dec 21, 2023 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
Conditional Probability
Analysis: This problem describes a conditional probability since it asks us to find the probability that the second test was passed given that the first test was passed. In the last lesson, the notation for conditional probability was used in the statement of Multiplication Rule 2.
Multiplication Rule 2: When two events, A and B, are dependent, the probability of both occurring is:
The formula for the Conditional Probability of an event can be derived from Multiplication Rule 2 as follows:
Now we can use this formula to solve the problem at the top of the page.
Problem: A math teacher gave her class two tests. 25% of the class passed both tests and 42% of the class passed the first test. What percent of those who passed the first test also passed the second test?
| P(Second|First) | = | = | = | 0.60 | = | 60% | ||
| P(First) | 0.42 |
Let’s look at some other problems in which we are asked to find a conditional probability.
Example 1: A jar contains black and white marbles. Two marbles are chosen without replacement. The probability of selecting a black marble and then a white marble is 0.34, and the probability of selecting a black marble on the first draw is 0.47. What is the probability of selecting a white marble on the second draw, given that the first marble drawn was black?
| P(White|Black) | = | = | = | 0.72 | = | 72% | ||
| P(Black) | 0.47 |
Example 2: The probability that it is Friday and that a student is absent is 0.03. Since there are 5 school days in a week, the probability that it is Friday is 0.2. What is the probability that a student is absent given that today is Friday?
| P(Absent|Friday) | = | = | = | 0.15 | = | 15% | ||
| P(Friday) | 0.2 |
Example 3: At Kennedy Middle School, the probability that a student takes Technology and Spanish is 0.087. The probability that a student takes Technology is 0.68. What is the probability that a student takes Spanish given that the student is taking Technology?
Solution:
| P(Spanish|Technology) | = | = | = | 0.13 | = | 13% | ||
| P(Technology) | 0.68 |
Summary: The conditional probability of an event B in relationship to an event A is the probability that event B occurs given that event A has already occurred. The notation for conditional probability is P(B|A), read as the probability of B given A . The formula for conditional probability is:
The Venn Diagram below illustrates P(A), P(B), and P(A and B). What two sections would have to be divided to find P(B|A)? Answer
Directions: Read each question below. Select your answer by clicking on its button. Feedback to your answer is provided in the RESULTS BOX. If you make a mistake, choose a different button. Answer choices have been rounded to the nearest percent.
| RESULTS BOX: |
Solved Problems of Conditional Probability
Conditional probability.
In this article, you will learn what is conditional probability and how to solve the questions related to this concept. So, let us get started.

There are two types of events that occur randomly in our lives:
a) Independent events
These events are not affected by other events. For example, rolling the dice on the floor. This event is not influenced by any other event; therefore it is termed as an independent event. In mathematics, we have notations for everything. We denote the simple probability as:
b) Dependent events
These events are dependent on other events, i.e. they are affected by other events.
Suppose that you choose a ball from a set of 8 colored balls and do not replace it. Next time, you choose another ball from the set. The second time the probability changes because, in the beginning, the total number of balls was 8, but the next time, 7 balls were left. Therefore, the second event is dependent on the first one. However, if there is a condition that the ball is replaced each time it is picked, then the events will be independent.
A conditional probability is finding the probability of an event that is dependent on another event.
The mathematical notation of conditional probability is:
It is read as the probability of event A given event B . The formula for finding the conditional probability of two events A and B is given below:

We can also swap the sides of this formula according to the question like this:

Now, we will solve some examples of conditional probability to understand the concept better.
What is the probability of selecting two queen cards from the deck of 52 cards?
To solve the problems related to the cards in a deck, you should know which types of cards are present in each deck. The properties of a deck are given below:
- There are four suits in a deck
- Two suits have black cards and two of them are red
- In each suit, there are 13 cards. These 13 cards include a queen, a king a jack, ace, 2, 3, 4, 5, 6, 7, 8, 9, and 10.
In a deck of 52 cards, there are 4 queen cards. Since we need to select the two cards from the deck, hence, first, we will find the probability of selecting the first card from the deck.
Number of queen cards in a deck = 4
Total number of cards in a deck = 52

Now, we will compute the probability of picking up the second card from the deck.
Number of queen cards left in a deck = 3
Total number of cards left in a deck = 51

In this example, we need to tell the probability of picking up two queen cards, therefore we will multiply the probabilities above:

What is the probability of selecting two black cards from the deck of 52 cards?
Refer to the types of cards that are present in a deck. Out of 52 cards in a deck, two suits have black cards and two of them are red. A deck is divided into 4 suits and each suit has 13 cards.
In a deck of 52 cards, there are 26 black cards. Since we need to select the two cards from the deck, hence, first, we will find the probability of selecting the first card from the deck.
Number of black cards in a deck = 26

Number of black cards left in a deck = 25

In this example, we have to tell the probability that both cards selected are black. Hence, we will multiply the probabilities like this:

There are 12 balls in the pool. 6 balls are blue and the rest are red. Two of the balls are picked up from the pool without replacement. What is the probability of selecting two red balls from the pool?
We will calculate the probability of the first ball.
Total number of balls in the pool = 12

Now, we will compute the probability of the second ball.
Total number of balls left in the pool = 11
Number of red balls left in the pool = 5

There are 8 blue, 7 green, and 6 red-colored pens in a packet. Suppose you draw 2 pens at random from the packet and do not replace them. You then draw another pen. What is the probability that two pens drawn are green and one is red?
First, we will find the probability of drawing one green pen from the packet.
Number of green pens in the packet = 7
Total number of pens in the packet = 21

Now, we will compute the probability of drawing a green pen the second time.
Number of green pens left in the packet = 6
Total number of pens left in the packet = 20

We have to select three pens. Hence, we will also compute the probability of picking up a red pen from the packet after two green pens were selected.
Number of red pens in the packet = 6
Total number of pens in the packet left = 19

In a class, 35% of the students study science and history. 65% of the students study science. What is the probability of a student studying history given he/she is already studying science?
Percentage of the students studying science and history = 35%
Probability of students studying science and history = P(S and H) = 0.35
Percentage of students studying science = 65%
The probability of students studying science = P(S) = 0.65

Did you like this article? Rate it!

I am passionate about travelling and currently live and work in Paris. I like to spend my time reading, gardening, running, learning languages and exploring new places.
Solved Problem of Probabilty 8
Measures of central tendency, position and dispersion, solved problems of simple and compound probability, confidence interval, solved problem of probabilty 1, solved problem of probabilty 13, solved problem of probabilty 15, confidence interval for the mean, contingency tables, multiplication rule, standard normal table, solved problem of probabilty 10, solved problem of probabilty 14, solved problem of probabilty 6, combinatorics and probability, confidence interval for the proportion, normal distribution, percentiles, conditional probability word problems, using the z table, normal approximation, probability properties, solved problem of probability 18, solved problem of probabilty 5, solved problem of probability 2, tree diagrams, probability theory, bayes’ theorem, standard normal distribution, law of total probability, solved problems of probability 4, solved problems of probability 11, solved problems of probability 17, solved problems of probability 16, solved problems of probability 3, solved problem of probabilty 9, s1 and s2 distributions cheat sheet, probability formulas, arithmetic mean worksheet, confidence interval problems, arithmetic mean problems, median worksheet, normal distribution word problems, mode worksheet, standard deviation problems, probability worksheet, probability word problems, cancel reply.
Your comment
Current ye@r *
Leave this field empty
Using facebook account,conduct a survey on the number of sport related activities your friends are involvedin.construct a probability distribution andbcompute the mean variance and standard deviation.indicate the number of your friends you surveyed
this page has a lot of advantage, those student who are going to be statitian
I’m a junior high school,500 students were randomly selected.240 liked ice cream,200 liked milk tea and 180 liked both ice cream and milktea
A box of Ping pong balls has many different colors in it. There is a 22% chance of getting a blue colored ball. What is the probability that exactly 6 balls are blue out of 15?
Where is the answer??
ere is a 60% chance that a final years student would throw a party before leaving school ,taken over 50 student from a total of 150 .calculate for the mean and the variance
There are 4 white balls and 30 blue balls in the basket. If you draw 7 balls from the basket without replacement, what is the probability that exactly 4 of the balls are white?
- Math Formulas
Conditional Probability Formula

Conditional probability formula gives the measure of the probability of an event given that another event has occurred. If the event of interest is A and the event B is known or assumed to have occurred, “the conditional probability of A given B”, or “the probability of A under the condition B”. The events are usually written as P(A|B), or sometimes P B(A). The formula for conditional probability for both the conditions i.e. “the probability of A under the condition B” and “the probability of B under the condition A” are stated below.
Formula for Conditional Probability
| Conditional Probability of A given B | P (A|B) = P(A ∩ B)⁄P(B) |
| Conditional Probability of B given A | P (B|A) = P(B ∩ A)⁄P(A) |
Solved Examples Using Conditional Probability Formula
Question 1:
The probability that it is Friday and that a student is absent is 0.03. Since there are 5 school days in a week, the probability that it is Friday is 0.2. What is the probability that a student is absent given that today is Friday?
The formula of Conditional probability Formula is:
P (B|A) = P(A ∩ B)⁄P(A)
P(Absent | Friday)= P (Absent and Friday)⁄P(Friday)
Question 2: A teacher gave her students of the class two tests namely maths and science. 25% of the students passed both the tests and 40% of the students passed the maths test. What percent of those who passed the maths test also passed the science test?
Solution: Given, Percentage of students who passed the maths test = 40% Percentage of students who passed both the tests = 25% Let A and B be the events of the number of students who passed maths and science tests. According to the given, P(A) = 40% = 0.40 P(A ⋂ B) = 25% = 0.25 Percent of students who passed the maths test also passed the science test = Condition probability of B given A = P(B|A) = P(A ⋂ B)/P(A) = 0.25/0.40 = 0.625 = 62.5%
Question 3: A bag contains green and yellow balls. Two balls are drawn without replacement. The probability of selecting a green ball and then a yellow ball is 0.28. The probability of selecting a green ball on the first draw is 0.5. Find the probability of selecting a yellow ball on the second draw, given that the first ball drawn was green.
Solution: Let A and B be the events of drawing a green in the first draw and yellow ball in the second draw respectively. From the given, P(A) = 0.5 P(A ⋂ B) = 0.28 Probability of selecting a yellow ball on the second draw, given that the first ball drawn was green = Conditional of B given A = P(B|A) = P(A ⋂ B)/P(A) = 0.28/0.5 = 0.56
| FORMULAS Related Links | |
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
Amazing but still i would like to have more examples
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
Conditional Probability
The conditional probability , as its name suggests, is the probability of happening an event that is based upon a condition. For example, assume that the probability of a boy playing tennis in the evening is 95% (0.95) whereas the probability that he plays given that it is a rainy day is less which is 10% (0.1). Then the former case is just normal probability whereas the latter case is the conditional probability. In this example, we represent the two probabilities as P(Play tennis) = 0.95 and P(Play tennis | Rainy day) = 0.1.
Let us learn more about conditional probability along with its formula, examples, and practice questions.
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. |
What Is Conditional Probability?
Conditional probability is one of the important concepts in probability and statistics . The "probability of A given B" (or) the "probability of A with respect to the condition B" is denoted by the conditional probability P(A | B) (or) P (A / B) (or) P\(_B\)(A). Thus, P(A | B) represents the probability of A which happens after event B has happened already. the probability of an event may alter if there is a condition given.
Definition of Conditional Probability
If A and B are two events associated with the same sample space of a random experiment, the conditional probability of event A given that B has occurred is given by P(A/B) = P( A ∩ B)/ P (B) , provided P(B) ≠ 0.
Let us understand conditional probability with an example. Let us find the conditional probability of getting at least two tails given that it is a head on the first toss when 3 coins are tossed. The sample space, S (the list of all outcomes) when 3 coins are tossed is given as follows:

Let us assume the two events A and B as follows:
- A = the event of getting at least two tails
- B = the event of getting a head on the first toss
Then, A = {HTT, THT, TTH, TTT} and B = {HHH, HHT, HTH, HTT}.
Then P(A) = 4/8 = 1/2 and P(B) = 4/8 = 1/2.
We have to find the probability of getting at least two tails given that it is a head on the first toss. It means, out of all elements of B, we have to choose only the ones with two tails. We can see that among the elements of B, there is only one element (which is HTT) with two tails. Thus, the required probability is P(A | B) = 1/4 (only 1 outcome of B is favorable to A out of 4 outcomes of B).
Conditional Probability Formula
In the above example, we have got P(A | B) = 1/4, here 1 represents the element HTT which is present both in "A and B" and 4 represents the total number of elements in B. Using this, we can derive the formula of conditional probability as follows.
P(A | B) = P(A ∩ B) / P(B) (Note that P(B) ≠ 0 here)
Similarly, we can define P(B | A) as follows:
P(B | A) = P(A ∩ B) / P(A) (Note that P(A) ≠ 0 here)
These formulas are also known as the "Kolmogorov definition" of conditional probability.

- P(A | B) = The probability of A given B (or) the probability of A which happens after B
- P(B | A) = The probability of B given A (or) the probability of B which happens after A
- P(A ∩ B) = The probability of happening of both A and B
- P(A) = The probability of A
- P(B) = The probability of B
Derivation of Conditional Probability
Note that the elements of B which favor the event A are the common elements of A and B. i.e. the sample points of A ∩ B.
Thus P(A/B) = Number of events favorable to A ∩ B ÷ Number of events favorable to B.
P(A/B) = \(\dfrac{\dfrac{n(A ∩ B)}{n(S)}}{\dfrac{n(B)}{n(S)}}\)
Thus P(A | B) = P(A ∩ B) / P(B)
Properties of Conditional Probability
Here are some properties of conditional probability along with their proofs (derivations) which we may need to use while solving the problems. All these properties depend on the conditional probability formula (which is mentioned in the previous section).
Let S be the sample space of an experiment and A be any event. Then P(S | A) = P(A | A) = 1.
By the formula of conditional probability,
P(S | A) = P(S ∩ A) / P(A) = P(A) / P(A) = 1
P(A | A) = P(A ∩ A) / P(A) = P(A) / P(A) = 1
Hence property 1 is proved.
Let S be the sample space of an experiment and A and B be any two events. Let E be any other event such that P(E) ≠ 0. Then P((A ⋃ B) | E) = P(A | E) + P(B | E) - P((A ∩ B) | E).
P((A ⋃ B) | E) = [P((A ⋃ B) ∩ E)] / P(E)
= [ P(A ∩ E) ⋃ P(B ∩ E) ] / P(E) (using a property of sets )
= [P(A ∩ E) + P(B ∩ E) - P(A ∩ B ∩ E)] / P(E) (using addition theorem of probability )
= P(A ∩ E) / P(E) + P(B ∩ E) / P(E) - P(A ∩ B ∩ E) / P(E)
= P(A | E) + P(B | E) - P((A ∩ B) | E) (By conditional probability formula)
Hence property 2 is proved.
P(A' | B) = 1 - P(A | B), where A' is the complement of the set A.
By Property 1, we have P(S | B) = 1.
We know that S = A ⋃ A'. Thus by the above property,
P( A ⋃ A' | B) = 1
Since A and A' are disjoint events,
P(A | B) + P(A' | B) = 1
- P(A' | B) = 1 - P(A | B)
Hence property 3 is proved.
Dependent and Independent Events
The definition of independent and dependent events is connected to conditional probability. Let us see the definitions of independent and dependent events along with their formulas.
- Dependent Events
Dependent events , as the name suggests, are any two events in which the happening of one event depends on the happening of the other event.
- If A depends on B, then the probability of A is P(A | B).
- If B depends on A, then the probability of B is P(B | A).
By the conditional probability formulas,
P(A | B) = P(A ∩ B) / P(B) ⇒ P(A ∩ B) = P(A | B) · P(B)
P(B | A) = P(A ∩ B) / P(A) ⇒ P(A ∩ B) = P(B | A) · P(A)
Thus, two event A and B are said to be dependent events if one of the conditions is satisfied.
- P(A ∩ B) = P(A | B) · P(B) (or)
- P(A ∩ B) = P(B | A) · P(A)
- Independent Events
Independent events , as the name suggests, are any two events in which the happening of one event does not depend on the happening of the other event. i.e., if A and B are independent then P(A | B) = P(A) and P(B | A) = P(B). Thus, to get the formula of independent events, we just need to replace P(A | B) with P(A) (or P(B | A) with P(B)) in one of the above (dependent events) formulas. Hence, two events are said to be independent if
P(A ∩ B) = P(A) · P(B)
This is also called as multiplication rule of probability.
☛ Also Check:
- Probability
- Addition Theorem of Probability
Important Notes:
- The probability of A given B is called the conditional probability and it is calculated using the formula P(A | B) = P(A ∩ B) / P(B).
- The events that are part of conditional probability are dependent events. For example, if we have P(A | B) anywhere in the problem, then it means that A and B are dependent.
- If two events A and B are independent, then P(A | B) = P(A) and P(B | A) = P(B).
- For any two events A and B, P(A ∩ B) = P(A) · P(B). This is called the multiplication theorem of probability.

Examples of Conditional Probability
Example 1: The table below shows the occurrence of diabetes in 100 people. Let D and N be the events where a randomly selected person "has diabetes" and "not overweight". Then find P(D | N).
| Diabetes (D) | No Diabetes (D') | |
| Not overweight (N) | 5 | 45 |
| Overweight (N') | 17 | 33 |
From the given table, P(N) = (5+45) / 100 = 50/100.
P(D ∩ N) = 5/100.
By the conditional probability formula,
P(D | N) = P(D ∩ N) / P(N)
= (5/100) / (50/100)
Answer: P(D | N) = 1/10.
Example 2: The probability that it will be sunny on Friday is 4/5. The probability that an ice cream shop will sell ice creams on a sunny Friday is 2/3 and the probability that the ice cream shop sells ice creams on a non-sunny Friday is 1/3. Then find the probability that it will be sunny and the ice cream shop sells the ice creams on Friday.
Let us assume that the probabilities for a Friday to be sunny and for the ice cream shop to sell ice creams be S and I respectively. Then,
P(S) = 4/5.
P(I | S) = 2/3.
P(I | S') = 1/3.
We have to find P(S ∩ I).
We can see that S and I are dependent events. By using the dependent events' formula of conditional probability,
P(S ∩ I) = P(I | S) · P(S) = (2/3) · (4/5) = 8/15.
Answer: The required probability = 8/15.
Example 3: If a fair die is rolled twice, observe the numbers that face up. Find the conditional probability that the sum of the numbers is 7, given that the first number is 2.
Let us determine the sample space of rolling a die twice. S = {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,1), (2,2), (2,3), (2,4), (2,5), (2,6), (3,1), (3,2), (3,3), (3,4), (3,5), (3,6)(4,1), (4,2), (4,3), (4,4), (4,5), (4,6), (5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (6,1), (6,2), (6,3), (6,4), (6,5), (6,6) }
Considering events A and B as given: we have
A : the sum of the numbers is 7. Thus set A = {(1,6),(2,5), (3,4), (4,3), (5,2),(6,1) }
B: the first number is 2. Thus set B = {(2,1), (2,2), (2,3), (2,4), (2,5), (2,6)}
A ∩ B: {(2,5)}
By the conditional probability, we know that P(A ) = P(A ∩ B) / P(B)
P(A ) = \(\dfrac{\dfrac{1}{36}}{\dfrac{6}{36}}\)
P(A ) = 1/6
Answer: The conditional probability that the sum of the numbers is 7, given that the first number is 2 is 1/6
go to slide go to slide go to slide

Book a Free Trial Class
Practice Questions on Conditional Probability
Faqs on conditional probability.
The conditional probability is the probability of happening of an event of A given that another event B has already occurred. It is denoted by P(A | B) and it is calculated by the formula P(A | B) = P(A ∩ B) / P(B).
What Is Conditional Probability Formula?
The conditional probability of A given B is given as P(A | B) = P(A ∩ B) / P(B) and the conditional probability of B given A is P(B | A) = P(A ∩ B) / P(A).
What Are the Properties of Conditional Probability?
Here are the important properties of conditional probability. In all the properties, assume that S is the sample space and A, B, and E are the events.
- P(S | A) = P(A | A) = 1.
- P((A ⋃ B) | E) = P(A | E) + P(B | E) - P((A ∩ B) | E)
Which Example Does Best describe Conditional Probability?
Assume that there are 100 blood donors available in a hospital. Among them, a non-diabetic person has to be chosen given that his blood group is O + . This situation best describes conditional probability. If N and O are the events of selecting a non-diabetic person and a person with the blood group O + respectively, then the conditional probability representing the above situation is P(N | O) and is calculated using the formula, P(N | O) = P(N ∩ O) / P(O).
Which Theorem Best Explains Conditional Probability and Independence?
The multiplication theorem of probability (which is derived from conditional probability) best describes the independent events. According to this, two events A and B are said to be independent if P(A ∩ B) = P(A) · P(B).
How To Read Conditional Probability P(A | B)?
The conditional probability P(A | B) is read as "the probability of A given B" (or) "the probability of A after B has happened". P(A | B) can also be written as P(A/B) (or) P\(_B\)(A).
Why Is Conditional Probability Important?
The conditional probability is important when we have to find the probability of an event that depends on another event. If event A depends on another event B (i.e., event A happens after B has happened), then the probability of event A is denoted by the conditional probability P(A | B) and is calculated using the formula P(A/B) = P(A ∩ B)/P(B).
CONDITIONAL PROBABILITY PROBLEMS WITH SOLUTIONS
Problem 1 :
A problem in Mathematics is given to three students whose chances of solving it are 1/3, 1/4 and 1/5 (i) What is the probability that the problem is solved? (ii) What is the probability that exactly one of them will solve it?
Let "A", "B" and "C" be the events of solving problems by each students respectively.
P(A) = 1/3, P(B) = 1/4 and P(C) = 1/5
(i) What is the probability that the problem is solved?
P(Problem solved) = P(At least one solving)
= 1 - P(None solving the problem)
= 1 - P(A' n B' n C')
= 1 - P(A') ⋅ P(B') ⋅ P(C')
| P(A') = 1 - P(A) = 1-(1/3) P(A') = 2/3 | P(B') = 1 - P(B) = 1-(1/4) P(B') = 3/4 | P(C') = 1 - P(C) = 1-(1/5) P(C') = 4/5 |
= 1 - (2/3) (3/4) (4/5)
= 1 - (2/5)
= (5 - 2) / 5
P(Problem solved) = 3/5
(ii) What is the probability that exactly one of them will solve it
P( exactly one of them will solve it)
= P(A' n B' n c) + P(A' n B n c') + P(A n B' n c')
= P(A') P(B') P(C) + P(A') P(B) P(C') + P(A) P(B') P(C')
= (2/3)(3/4)(1/5) + (2/3)(1/4)(4/5) + (1/3)(3/4)(4/5)
= (6/60) + (8/60) + (12/60)
= (6 + 8 + 12)/60
= 26/60
P(exactly one of them will solve it) = 13/30
Problem 2 :
The probability that a car being filled with petrol will also need an oil change is 0.30; the probability that it needs a new oil filter is 0.40; and the probability that both the oil and filter need changing is 0.15.
(i) If the oil had to be changed, what is the probability that a new oil filter is needed?
(ii) If a new oil filter is needed, what is the probability that the oil has to be changed?
Let "A" and "B" the event of changing oil and new oil filter respectively.
P(A) = 0.30, P(B) = 0.40, P(AnB) = 0.15
Here we have to find the probability that a new oil filter is needed, if the oil had to be changed.
The event B depends on A.
P(B/A) = P(AnB)/P(A)
= 0.15 / 0.30
= 1/2
P(B/A) = 0.5
The event A depends on B.
P(A/B) = P(AnB)/P(B)
= 0.15 / 0.40
= 3/8
P(A/B) = 0.375
Kindly mail your feedback to [email protected]
We always appreciate your feedback.
© All rights reserved. onlinemath4all.com
- Sat Math Practice
- SAT Math Worksheets
- PEMDAS Rule
- BODMAS rule
- GEMDAS Order of Operations
- Math Calculators
- Transformations of Functions
- Order of rotational symmetry
- Lines of symmetry
- Compound Angles
- Quantitative Aptitude Tricks
- Trigonometric ratio table
- Word Problems
- Times Table Shortcuts
- 10th CBSE solution
- PSAT Math Preparation
- Privacy Policy
- Laws of Exponents
Recent Articles
Problems on angles (part -2).
Jul 23, 24 02:00 AM
Problems on Angles (Part - 1)
Jul 23, 24 01:53 AM
SAT Math Resources (Videos, Concepts, Worksheets and More)
Jul 22, 24 07:58 PM
Conditional Probability Calculator
Conditional probability definition - what is conditional probability, how do i calculate conditional probability, conditional probability examples and solutions.
The conditional probability calculator helps you to determine the probability of an event occurring, provided it is conditional on another event .
Read further and we explain:
- What conditional probability is;
- How to calculate conditional probability ; and
- In addition, we show you a real-life conditional probability example where you can also learn how to find it in practice.
If you would like to discover the connection between conditional probability and Bayes' theorem, you may check our Bayes' theorem calculator .
In probability theory, conditional probability quantifies the probability (or likelihood) of an event occurring given that another event has already occurred . This requires that probability of the second event occurring is affected by the first event happening. It is computed by multiplying the probability of the first event by the updated probability of the second, or conditional, event.
Which situations involve conditional probability? Keep reading the article to find it out!
You need the take the following steps to compute the conditional probability of P(A|B):
Determine the total probability of a given final event, B:
P(B) = P(A∩B) + P(Ā∩B) = P(A) * P(B|A) + P(Ā) * P(B|Ā)
Compute the probability of that event :
P(A∩B) = P(A) * P(B|A)
Divide the two numbers :
P(A|B) = P(A∩B) / P(B)
Let's consider a real-life example to demonstrate how to find conditional probability and show the relevance of conditional probability .
Assume that in a population, 5 percent are affected by a disease (denoted by D D D ). A test is available to check if a given person is infected.
The test's sensitivity (also known as the true positive rate ) is 91% , meaning that if the person is infected , the probability for a negative test result (denoted by □ \Box □ ) is 0.09 . On the other hand, the test's specificity (or true negative rate ) is 95% , implying that the probability of having a positive test result (assigned by ⊕ \oplus ⊕ ) when the person doesn't have the disease is 0.05 .
Now, let's consider a random person from the population taking the test and receiving a positive result. How do you find the conditional probability that the person really does have the disease ? We formulate it as P ( D ∩ ⊕ ) P(D \cap \oplus) P ( D ∩ ⊕ ) , that you read as the conditional probability of being infected given that the person has a positive test result .
We can summarize the above problem with the following conditional probability tree diagram :

Translating into mathematical formulas, we can obtain the following equations explaining how to find conditional probability:
So, how to solve conditional probability in this situation?
You need to take the following steps :
- Compute the total probability of having a positive result:
- Compute the probability of an event when the random person is infected and the test result is positive. You can use the conditional probability definition:
- Divide the two numbers , taking into account the conditional probability rules:
Thus, the conditional probability that a random person is infected that has a positive test result is 0.4892 , which is almost fifty percent - nearly analogical to tossing a fair coin. You can try to verify the result with our conditional probability calculator if you want.
Note, that the above-described situation may represent the early stages of the COVID pandemic. Even though only a tiny portion of the population has been infected (thus having antibodies), some countries strongly supported wide-range testing based on antibodies with nearly the same parameters. Therefore, it is particularly important to consider the entire clinical state of a patient with signs and symptom before taking the test, as they may present a positive result without being infected. Taking these steps increases the accuracy of the test result.
Which situations involve conditional probability?
There are many real-life situations where conditional probability matters. For example, the probability of winning the second round of a game given that you won the first round . Or the probability that it will rain given that it is cloudy.
What is the conditional probability rule?
Conditional probability measures the chances that an event occurs, given that another event has also occurred . Typically, it is stated as P(B|A) (read as the probability of B given A), where the probability of B depends on the probability of A's occurrence.
Can the conditional probability be zero?
Yes. If the probability of a given final event is zero, the conditional probability of a previous event given that final event is zero.
- Sum of Squares Calculator
- Midrange Calculator
- Coefficient of Variation Calculator
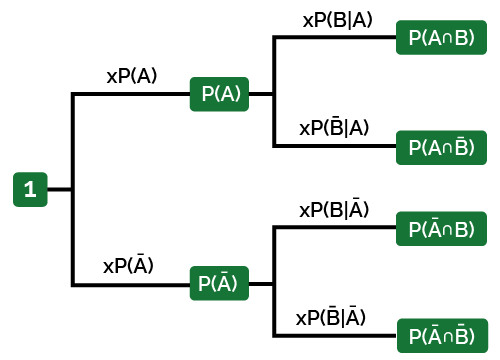
Roulette payout
Steps to calories.
- Biology (101)
- Chemistry (100)
- Construction (148)
- Conversion (302)
- Ecology (31)
- Everyday life (262)
- Finance (588)
- Health (442)
- Physics (513)
- Sports (108)
- Statistics (184)
- Other (185)
- Discover Omni (40)
- School Guide
- Mathematics
- Number System and Arithmetic
- Trigonometry
- Probability
- Mensuration
- Maths Formulas
- Class 8 Maths Notes
- Class 9 Maths Notes
- Class 10 Maths Notes
- Class 11 Maths Notes
- Class 12 Maths Notes
- Probability in Maths
- Events in Probability
Types of Event
- Types of Events in Probability
- Mutually Exclusive Events
Probability Based on Coin
- Tossing a Coin Probability Formula
- What are all the possible outcomes if a coin is tossed?
- How many possible outcomes would be there if three coins were tossed once?
- How to calculate Dice Probabilities?
- What is the probability of not picking a king if you choose randomly from a pack of 52 cards?
- Find the probability that if one card drawn from a well-shuffled pack of 52 playing cards is a face card?
- What is the probability of getting either a red card or King card?
- What is the probability of drawing a black card from a well-shuffled deck of 52 cards?
- Axiomatic Approach to Probability
- Addition Rule for Probability
Conditional Probability
- Bayes' Theorem
- Multiplication Theorem
- Dependent and Independent Events
- Discrete Random Variable
- Probability Distribution - Function, Formula, Table
- Measures of Dispersion | Types, Formula and Examples
- Expected Value
- Bernoulli Trials and Binomial Distribution
- Binomial Distribution in Probability
- What is Binomial Probability Distribution with Example?
- Probability Distribution Function
Conditional probability is one type of probability in which the possibility of an event depends upon the existence of a previous event. As this type of event is very common in real life, conditional probability is often used to determine the probability of such cases.
Conditional probability is the likelihood of an outcome occurring based on a previous outcome in similar circumstances. In probability notation, this is denoted as A given B, expressed as P(A|B), indicating that the probability of event A is dependent on the occurrence of event B.
To know about conditional probability, we need to be familiar with independent events and dependent events. Let’s understand conditional probability, and its formula with solved examples in this article.

Table of Content
What is Conditional Probability?
Conditional probability definition, conditional probability formula, how to find probability of one event given another, conditional probability of independent events, conditional probability vs joint probability vs marginal probability, conditional probability and bayes’ theorem, conditional probability examples, tossing a coin, drawing cards, properties of conditional probability , multiplication rule of probability, how to apply the multiplication rule, applications of conditional probability, conditional probability questions, resources related to conditional probability:.
Conditional probability is the probability that depends on a previous result or event . Due to this fact, they help us understand how events are related to each other. Simply put, conditional probability tells us the likelihood of the occurrence of an event based on the occurrence of some previous outcome.
With the help of conditional probability, we can tell apart dependent and independent events . When the probability of one event happening doesn’t influence the probability of any other event, then events are called independent, otherwise dependent events.
Conditional Probability is defined as the probability of any event occurring when another event has already occurred. In other words, it calculates the probability of one event happening given that a certain condition is satisfied . It is represented as P (A | B) which means the probability of A when B has already happened.
For Example, let’s consider the case of rolling two dice, sample space of this event is as follows:
{(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
Now, consider an event A = getting 3 on the first die and B = getting a sum of 9.
Then the probability of getting 9 when on the first die it’s already 3 is P(B | A),
which can be calculated as follows:
All the cases for the first die as 3 are (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6).
In all of these cases, only one case has a sum of 9.
Thus, P (B | A) = 1/36.
In case, we have to find P (A | B),
All cases where the sum is 9 are (3, 6), (4, 5), (5, 4), and (6, 3).
In all of these cases, only one case has 3 on the first die i.e., (3, 6)
Thus, P(A | B) = 1/36.
As we can calculate the Conditional Probability of simple cases without any formula, just as we have seen in the above heading but for complex cases, we need a Conditional Probability Equation as we can’t possibly count all the cases for those. Let’s consider two events A and B, then the formula for conditional probability of A when B has already occurred is given by:
P(A|B) = P (A ∩ B) / P(B) Where, P (A ∩ B) represents the probability of both events A and B occurring simultaneously. P(B) represents the probability of event B occurring.
In other words, the conditional probability of A given B has already occurred is equal to the probability of the intersection of A and B divided by the probability of event B.
To calculate the conditional probability, we can use the following step-by-step method:
Step 1: I dentify the Events. Let’s call them Event A and Event B. Step 2: Determine the Probability of Event A i.e., P(A) Step 3: Determine the Probability of Event B i.e., P(B) Step 4: Determine the Probability of Event A and B i.e., P(A∩B). Step 5: Apply the Conditional Probability Formula and calculate the required probability.
When two events are independent, those conditional probability is the same as the probability of the event individually i.e., P (A | B) is the same as P(A) as there is no effect of event B on the probability of event A. For independent events, A and B, the conditional probability of A and B with respect to each other is given as follows:
- P(B|A) = P(B)
- P(A|B) = P(A)
Check, Probability Formulas
The difference between Conditional Probability, Joint Probability , and Marginal Probability is given in the following table:
| Parameter | Conditional Probability | Joint Probability | Marginal Probability |
|---|---|---|---|
| The probability of an event occurring given. that another event has already occurred. | The probability of two or more events occurring simultaneously. | The probability of an event occurring without considering any other events. | |
| P (A | B) | P (A ∩ B) | P(A) | |
| Two or more events | Two or more events | Single event. |
Bayes’ Theorem is a fundamental concept in probability theory named after the Reverend Thomas Bayes . It provides a mathematical framework for updating beliefs or hypotheses in light of new evidence or information. This theorem is extensively used in various fields, including statistics, machine learning, and artificial intelligence.
At its core, Bayes’ Theorem enables us to calculate the probability of a hypothesis being true given observed evidence. The theorem is expressed mathematically as follows:
P(A∣B) = (P(B∣A) × P(A)) / P(B)
- P(A∣B) is the posterior probability of hypothesis A given evidence B .
- P(B∣A) is the likelihood of observing evidence B given that hypothesis A is true.
- P(A) is the prior probability of hypothesis A before observing any evidence.
- P(B) is the probability of observing evidence B regardless of the truth of hypothesis A .
Here’s a breakdown of how Bayes’ Theorem works:
Prior Probability P(A): This represents our initial belief in the likelihood of hypothesis A being true before considering any new evidence. Likelihood P(B∣A): This indicates the probability of observing the evidence B given that hypothesis A is true. It quantifies how well the evidence supports the hypothesis. Evidence P(B): This term serves as a normalization factor and represents the total probability of observing the evidence B across all possible hypotheses. Posterior Probability P(A∣B) : This is the updated probability of hypothesis A being true after taking into account the observed evidence B . It’s what we’re ultimately interested in determining.
Bayes’ Theorem is particularly powerful because it allows us to incorporate new evidence incrementally, refining our beliefs as more data becomes available . This iterative process of updating beliefs with new evidence forms the basis of Bayesian inference, which is widely used in fields such as medical diagnosis, spam filtering, weather forecasting, and many others.
Bayes’ Theorem provides a principled approach for reasoning under uncertainty, making it a cornerstone of probabilistic reasoning and decision-making in diverse domains.
Read in Detail: Bayes’s Theorem for Conditional Probability
There are various examples of conditional probability as in real life all the events are related to each other and happening any event affects the probability of another event. For example , if it rains, the probability of road accidents increases as roads have less friction. Let’s consider some problem-based examples here:
Let’s consider two events in tossing two coins be,
- A: Getting a head on the first coin.
- B: Getting a head on the second coin.
Sample space for tossing two coins is:
S = {HH, HT, TH, TT}
Conditional probability of getting a head on the second coin (B) given that we got a head on the first coin (A) is = P(B|A)
Since the coins are independent (one coin’s outcome does not affect the other), P(B|A) = P(B) = 0.5 (50%), which is the probability of getting a head on a single coin toss.
In a deck of 52 cards where two cards are being drawn, then let’s consider the events be.
- A: Drawing a red card on the first draw, and
- B: Drawing a red card on the second draw.
Conditional probability of drawing a red card on the second draw (B) given that we drew a red card on the first draw (A) is = P(B|A)
After drawing a red card on the first draw, there are 25 red cards and 51 cards remaining in the deck. So, P(B|A) = 25/51 ≈ 0.49 (approximately 49%).
Some of the common properties of conditional property are:
Property 1: Let’s consider an event A in any sample space S of an experiment.
P(S|A) = P(A|A) = 1
Property 2: For any two events A and B of a sample space S, and an event X such that P(X) ≠ 0,
P((A ∪ B)|X) = P(A|X) + P(B|X) – P((A ∩ B)|X)
Property 3: The order of set or events is important in conditional probability, i.e.,
P(A|B) ≠ P(B|A)
Property 4: The complement formula for probability only holds conditional probability if it is given in the context of the first argument in conditional probability i.e.,
P(A’|B)=1-P(A|B) P(A|B’) ≠ 1-P(A|B)
Property 5: For any two or three independent events, the intersection of events can be calculated using the following formula:
- For the intersection of two events A and B,
P(A ⋂ B) = P(A) P(B)
- For the intersection of three events A, B, and C,
P (A ⋂ B ⋂ C) = P(A) P(B) P(C)
Multiplication Rule of Probability , when applied in the context of conditional probability, helps us calculate the probability of the intersection of two events when the probability of one event depends on the occurrence of the other event. This rule is crucial in understanding the joint probability of events under specific conditions.
In the context of conditional probability, the Multiplication Rule is often stated as follows:
P(A∩B) = P(A) × P(B∣A)
Here’s what each term represents :
- P(A∩B) : This denotes the probability that both events A and B occur simultaneously.
- P(A) : This represents the probability of event A happening.
- P(B∣A) : This is the conditional probability of event B occurring given that event A has already occurred.
To apply the Multiplication Rule in the context of conditional probability, we can use the following steps:
- First we calculate the probability of event A occurring.
- Then, we compute the probability of event B occurring given that event A has occurred.
- Multiplying these probabilities together gives us the joint probability of both events happening under the specified conditions.
- This rule is particularly useful when dealing with events that are not independent, meaning that the occurrence of one event affects the probability of the other event.
Various applications of conditional probability are,
Finance and Risk Management
- Example: Assessing the probability of default for a borrower given certain financial indicators.
- Application: Banks and financial institutions use conditional probability to evaluate the risk associated with loans and investments.
Healthcare and Diagnostics
- Example: Determining the probability of a patient having a specific disease given the results of diagnostic tests.
- Application: Conditional probability is crucial in medical diagnoses and decision-making, helping healthcare professionals make informed decisions based on test results.
Marketing and Customer Relationship Management (CRM)
- Example: Predicting the probability of a customer making a purchase based on their past buying behavior.
- Application: Businesses use conditional probability to tailor marketing strategies, optimize customer experiences, and personalize product recommendations.
Machine Learning and Artificial Intelligence
- Example: Predicting the likelihood of a user clicking on a particular ad based on their online behavior.
- Application: Conditional probability is fundamental in machine learning algorithms for tasks such as classification, recommendation systems, and natural language processing.
Weather Forecasting
- Example: Estimating the probability of rain tomorrow given today’s weather conditions.
- Application: Meteorologists use conditional probability to make weather predictions based on historical data and current atmospheric conditions.
|
| |
|---|---|
|
|
|
|
|
|
|
|
|
Question 1: A bag contains 5 red balls and 7 blue balls. Two balls are drawn without replacement. What is the probability that the second ball drawn is red, given that the first ball drawn was red?
Let the events be, Event A: The first ball drawn is red. Event B: The second ball drawn is red. P(A) = 5/12 and P(B) = 4/11 (as first ball drawn is already red, thus only 4 red balls remain in the bag) Therefore, probability of the second ball drawn being red given that the first ball drawn was red is 4/11.
Question 2: A box contains 5 green balls and 3 yellow balls. Two balls are drawn without replacement. What is the probability that both balls are green?
Let events be: Event A: The first ball drawn is green, and Event B: The second ball drawn is green. P(A) = 5/8 P(B) = 4/7 (as there are 4 green balls left out of 7) Thus, probability that both balls drawn are green is (5/8) × (4/7) = 20/56 = 5/14.
Question 3: In a bag, there are 8 red marbles, 4 blue marbles, and 3 green marbles. If one marble is randomly drawn, what is the probability that it is not blue?
Let the events be: Event A: The marble drawn is not blue, and Event B: The marble drawn is blue. As A and B are complementary Events, we know P(A) = 1 – P(B) ⇒ P(A) = 1 – 4/15 ⇒ P(A) = (15 – 4)/15 ⇒ P(A) = 11/15 Thus, probability of drawing a marble out of bag which is not blue is 11/15.
Question 4: In a survey among a group of students, 70% play football, 60% play basketball, and 40% play both sports. If a student is chosen at random and it is known that the student plays basketball, what is the probability that the student also plays football?
Let’s assume there are 100 students in the survey. Number of students who play football = n(A) = 70 Number of students who play basketball = n(B) = 60 Number of students who play both sports = n(A ∩ B) = 40 To find the probability that a student plays football given that they play basketball, we use the conditional probability formula : P(A|B) = n(A ∩ B) / n(B) Substituting the values, we get: P(A|B) = 40 / 60 = 2/3 Therefore, probability that a randomly chosen student who plays basketball also plays football is 2/3.
Question 5: In a deck of 52 playing cards, 4 cards are drawn without replacement. What is the probability that all 4 cards are aces, given that the first card drawn is an ace?
Let the events be, Event A: The first card drawn is an ace, Event B: The second card drawn is an ace, Event C: The third card drawn is an ace, and Event D: The fourth card drawn is an ace. P(A) = 4/52 (there are 4 ace out of 52) P(B | A) = 3/51 (one is already drawn, thus 3 ace left) P(C | A and B) = 2/50 (two is already drawn, thus 2 ace left) P(D | A and B and C) = 1/49 (three is already drawn, thus 1 ace left) To find the probability that all four cards are aces, we multiply the probabilities of the individual events. P(A and B and C and D) = P(A) × P(B|A) × P(C|A and B) × P(D|A and B and C) = (4/52) × (3/51) × (2/50) × (1/49) = 1/270725 Therefore, probability that all 4 cards drawn are aces, given that the first card drawn is an ace, is 1/270725 .
Question 6: In a certain city, it rains 30% of the days. A weather forecaster correctly predicts rain 80% of the time when it actually rains, and correctly predicts no rain 90% of the time when it doesn’t rain. If the forecast predicts rain, what is the probability that it will actually rain?
Let R be the event that it rains, and F be the event that rain is forecast. P(R|F) = P(F|R) × P(R) / P(F) P(F) = P(F|R) × P(R) + P(F|not R) × P(not R) = 0.8 × 0.3 + 0.1 × 0.7 = 0.31 P(R|F) = (0.8 × 0.3) / 0.31 = 0.7059
Question 7: A fair die is rolled twice. Given that the sum of the two rolls is even, what is the probability that the first roll was an even number?
There are 18 ways to get an even sum (out of 36 total outcomes). 12 of these 18 ways have an even number on the first roll. P(First even | Sum even) = 12/18 = 2/3
Question 8: A diagnostic test for a disease has a false positive rate of 2% and a false negative rate of 3%. The disease occurs in 1% of the population. If a person tests positive, what is the probability that they actually have the disease?
Let D be the event of having the disease, and T be the event of testing positive. P(D|T) = P(T|D) × P(D) / P(T) P(T) = P(T|D) × P(D) + P(T|not D) × P(not D) = 0.97 × 0.01 + 0.02 × 0.99 = 0.0293 P(D|T) = (0.97 × 0.01) / 0.0293 = 0.3305
Question 9: In a bag, there are 4 red balls and 6 blue balls. Two balls are drawn without replacement. What is the probability that the second ball is red, given that the first ball drawn was blue?
After drawing a blue ball, there are 3 red balls and 5 blue balls left. P(Second is red | First was blue) = 3 / (3 + 5) = 3/8 = 0.444
Question 10: A software company has two development teams: Team A and Team B. Team A completes 60% of all projects, while Team B handles the rest. Team A has a 95% success rate, while Team B has an 85% success rate. If a project is successful, what is the probability that it was handled by Team A?
Let S be the event that a project is successful, and A be the event that Team A handled the project. P(A|S) = P(S|A) × P(A) / P(S) P(S) = P(S|A) × P(A) + P(S|B) × P(B) = 0.95 × 0.6 + 0.85 × 0.4 = 0.91 P(A|S) = (0.95 × 0.6) / 0.91 = 0.6316
Practice Problems on Conditional Probability
P1. A card is drawn at random from a standard 52-card deck. Given that the card drawn is a face card (Jack, Queen, or King), what is the probability that it’s a heart?
P2. In a class of 30 students, 18 play basketball and 12 play football. If 6 students play both sports, what is the probability that a randomly selected student plays basketball, given that they play football?
P3. A bag contains 5 red marbles, 3 blue marbles, and 2 green marbles. Two marbles are drawn without replacement. What is the probability that the second marble is blue, given that the first marble drawn was red?
P4. A manufacturing process produces 5% defective items. The quality control system detects 98% of defective items and 3% of non-defective items are incorrectly identified as defective. If an item is identified as defective by the quality control system, what is the probability that it is actually defective?
P5. A family has two children. Given that at least one of the children is a boy, what is the probability that both children are boys? Assume that the probability of having a boy or a girl is equal.
P6. In a certain population, 10% of people have a particular disease. A test for this disease correctly identifies 95% of people who have the disease (true positives) and 90% of people who don’t have the disease (true negatives). If a person tests positive, what is the probability that they actually have the disease?
P7. A software has three modules: A, B, and C. The probabilities of a bug being in these modules are 0.3, 0.4, and 0.3 respectively. If a bug is found in module A, the probability of it affecting module B is 0.2 and module C is 0.1. What is the probability that a bug affects both modules A and B?
P8. In a group of 100 people, 60 speak English, 40 speak French, and 20 speak both languages. If a person is selected at random and is known to speak French, what is the probability that they also speak English?
P9. A student has to answer 3 out of 5 questions on an exam. The student knows the answers to 3 questions for sure, has a 50% chance of answering the 4th question correctly, and doesn’t know the answer to the 5th question at all. If the student answers a question correctly, what is the probability that it was one of the questions they knew for sure?
P10. A biased coin has a 60% chance of landing heads. It is flipped twice. Given that at least one of the flips resulted in heads, what is the probability that both flips resulted in heads?
Probability Class 12 Notes Probability Class 12 NCERT Solutions
Summary – Conditional Probability
Conditional probability is a fundamental concept in probability theory that quantifies the likelihood of an event occurring given that another event has already occurred. Expressed as P(A|B), it represents the probability of event A happening under the condition that event B has occurred. This concept is crucial in various fields such as statistics, finance, and machine learning, where understanding the relationship between events and their outcomes is essential for making informed decisions. Conditional probability allows us to assess the impact of one event on the occurrence of another, providing valuable insights into probabilistic relationships and dependencies.
FAQs on Conditional Probability
What is conditional probability.
Conditional probability is a measure of the probability of an event occurring given that another event has already occurred or is known to have occurred. It is denoted as P(A|B), which reads as “the probability of event A given event B” .
What is difference between conditional probability and joint probability?
Conditional probability focuses on the probability of one event given that another event has already occurred while Joint probability focuses on the probability of multiple events occurring simultaneously.
What are some real-world examples of conditional probability?
The probability of a person having a specific disease given that they tested positive. The probability of it raining today given that it is cloudy. The probability of a student passing an exam given that they studied.
How is conditional probability calculated?
Conditional Probability Equation is calculated using the formula: P(A|B) = P(A ∩ B) / P(B)
What is the difference between conditional probability and regular probability?
Regular probability , often referred to as unconditional probability, calculates the likelihood of an event occurring without any prior information and is the basic probability of an event in isolation. Conditional probability takes into account additional information or the occurrence of another event to calculate the probability of a particular event.
Can conditional probability be greater than 1?
No, conditional probability cannot be greater than 1 as the conditional probability is a type of probability. It can only be between 0 and 1.
Can conditional probability be used in Bayesian inference?
Yes, conditional probability plays a crucial role in Bayesian inference, where prior beliefs are updated based on observed evidence using Bayes’ theorem.
What is the relationship between conditional probability and independence?
Two events A and B are considered independent if the occurrence of one event does not affect the probability of the other event. In terms of conditional probability , if events A and B are independent, then P(A|B) = P(A), and similarly, P(B|A) = P(B). In other words, the conditional probability of A given B is equal to the unconditional probability of A, and vice versa.
Can conditional probability be negative?
No, conditional probability cannot be negative as probabilities are always non-negative values between 0 and 1.
What is the interpretation of conditional probability?
Conditional probability measures the likelihood of one event occurring, given that another event has already occurred. It helps in updating probabilities based on new information.
What is conditional probability with an example?
Conditional probability , denoted P(A|B), assesses the likelihood of event A happening, given that event B has already occurred. For example, in a medical test scenario, it calculates the chance of having a disease when the test result is positive. It’s a key concept in probability theory, helping us understand real-world situations where one event depends on another.
What are the applications of conditional probability?
Conditional probability has diverse applications across fields such as f inance, medicine, genetics, marketing, weather forecasting, manufacturing, sports analytics, criminal justice, and environmental science.
What are the types of conditional probability?
Various types of conditional probability includes: Simple Conditional Probability Joint Probability Marginal Probability Conditional Probability Distribution Posterior Probability Prior Probability Sequential Conditional Probability Time Series Analysis Markov Chains
Please Login to comment...
Similar reads.
- Engineering Mathematics
- School Learning
- Maths-Class-12
Improve your Coding Skills with Practice
What kind of Experience do you want to share?
- AI technologies
What is Bayes' theorem?

- Olivia Wisbey, Associate Site Editor
Bayes' theorem is a mathematical formula used in probability theory to calculate conditional probability, i.e., the revised likelihood of an outcome occurring given the knowledge of a related condition or previous outcome. It enables the updating of predictions as new data becomes available, finding posterior probability by incorporating prior probability.
Sometimes called Bayes' rule or Bayes' law, the theorem is named after Thomas Bayes, an 18th-century English mathematician and Presbyterian minister. Bayes documented the theorem in his paper "An Essay Toward Solving a Problem in the Doctrine of Chances," published posthumously in 1763.
Bayes' work also laid the foundation for Bayesian statistics , a branch of philosophy focused on statistics and how they should be calculated. Bayesian statistics is closely related to the subjectivist approach to epistemology, which emphasizes the role of probability in empirical learning, and has been influential within the disciplines of probability and machine learning ( ML ).
Bayes' theorem's real-world applications are diverse. For example, it could help an anthropologist determine the likelihood of someone enjoying soccer given that they grew up in England; assist a scientist in calculating the probability of a patient having a specific disease given a diagnostic test's accuracy rate; or enable an analyst to estimate the likelihood of a financial downfall in a hypothetical future scenario.
Understanding conditional probability and Bayes' theorem
Bayes' theorem hinges on the principles of conditional probability. To illustrate, consider a simple card game where winning requires picking a queen from a full deck of 52 cards. The probability of picking a queen from the deck is calculated by dividing the number of queens (4) by the total number of cards (52). Thus, the probability of winning by picking a queen is approximately 7.69%.
Now, imagine picking a card and placing it face down. The dealer then says that the chosen card is a face card. This new condition influences the probability of winning. To calculate this conditional probability, use the equation P(A|B) = P(A ∩ B) / P(B), where P represents probability, | represents "given that," A represents the event of interest and B represents the known condition.
Here, the probability of A (picking a queen) given B (the card is a face card) equals the probability of the card being both a queen and a face card (4/52) divided by the probability of the card being a face card (12/52). This simplifies to approximately 33.33%, as there are 4 queens among the 12 face cards.
Bayes' theorem extends this concept to situations where direct probabilities are unknown. It helps calculate conditional probability in complex scenarios by using inverse probabilities, which are often easier to determine. The theorem is expressed as follows:

Here's how it applies to the card game example:
- A is the event of drawing a queen card.
- B is the event of drawing a face card.
- P(A) is the probability of drawing a queen (7.69%).
- P(B) is the probability of drawing a face card (23.08%).
- P(A|B) is the probability of drawing a queen given that the chosen card is a face card.
- P(B|A) is the probability of drawing a face card given that the chosen card is a queen (100%).
Inputting these numbers into Bayes' theorem results in the following:
P(A|B) = (7.69% * 100%) / 23.08% = 33.33%
While this particular calculation could have been simplified with basic conditional probability, real-world scenarios are often more complex. For instance, in medical diagnostics, patient statistics are often estimated across thousands of cases. Similarly, determining how many people in England are soccer fans would involve numerous variables. Bayes' theorem provides a structured method for deriving conditional probabilities in these types of multifaceted real-world circumstances.
Deriving the formula for Bayes' theorem
We know that Bayes' theorem is P(A|B) = (P(A) * P(B|A)) / P(B). But how did we get there?
To derive the formula, start with the definition of conditional probability:
P(A|B) = P(A ∩ B) / P(B)
Solve for P(A ∩ B) by multiplying both sides by P(B):
P(A ∩ B) = P(A|B) * P(B)
Similarly, the conditional probability P(B|A) is defined as follows:
P(B|A) = P(B ∩ A) / P(A)
Because P(B ∩ A) is the same as P(A ∩ B), we can write:
P(A ∩ B) = P(A) * P(B|A)
Now, we have two expressions for P(A ∩ B), which we can therefore set equal to each other:
P(B) * P(A|B) = P(A) * P(B|A)
To find the conditional probability P(A|B), solve for P(A|B) by dividing both sides by P(B):
P(A|B) = (P(A) * P(B|A)) / P(B)
You have now derived Bayes' theorem. Note that if you wanted to solve for the probability of B given A, you can rearrange the formula to divide both sides by P(A):
P(B|A) = (P(A|B) * P(B)) / P(A)
Real-world applications of Bayes' theorem
Bayes' theorem has diverse applications across various industries. The following are some example use cases:
- Business. Bayes' theorem can help businesses ascertain the probability of events given prior information. For example, it could be used to estimate supply chain losses due to a worker shortage, product exportation impacts from currency rate exchange changes, or revenue increases from a new product or marketing plan.
- Finance. Bayes' theorem can come in handy for many financial evaluations. For instance, lenders can evaluate the risk a potential borrower might pose based on prior information. It could also be used to hypothesize future financial situations, such as a company's potential stock market losses given situations like a stock market crash or major world event.
- Insurance. Similar to financial evaluations, Bayes' theorem is useful in insurance for calculating risk probabilities, such as the likelihood of natural disasters, in light of known information. For example, insurers can estimate flood probabilities by considering factors such as property location, time of year and past weather patterns.
- AI and machine learning. In ML, Bayes' theorem underpins algorithms that help models form relationships between input data and predictive output. This leads to more accurate models that can better adapt to new and changing data.
- Medicine. Bayes' theorem is applicable in many medical contexts. For example, the theorem can help evaluate the accuracy of a patient's test results given other health factors or test accuracy. It is also used in pharmaceutical drug testing and assessing disease risk levels.
- Theory and statistics. In research, Bayes' theorem helps create more accurate and realistic hypotheses and predictions. Therefore, it aids statisticians, anthropologists and other researchers in data-driven analyses and forecasts.
How is Bayes' theorem used in machine learning?
In ML, Bayes' theorem enhances classification and decision-making by providing accurate predictions based on learned data. It helps ML systems establish relationships between data and output, enabling revised predictions that result in more accurate decisions and actions, even with uncertain or incomplete data. However, it should be noted that the more data is collected, the more accurate a model will be.
The Bayesian approach in ML assigns a probability distribution to all elements, including model parameters and variables. It is often used in probabilistic models and provides a foundation for multiple ML algorithms and techniques, including the following:
- Naïve Bayes classifier. This common ML algorithm is used for classification tasks. It relies on Bayes' theorem to make classifications based on given information and assumes that different features are conditionally independent given the class.
- Bayes optimal classifier. This is a type of theoretical model that finds the most optimal, or probable, prediction by averaging over all possible models weighted by their posterior probabilities based on training data.
- Bayesian optimization. This sequential design strategy searches for optimal outcomes based on prior knowledge. It is particularly useful for objective functions that are complex or noisy.
- Bayesian networks. Sometimes referred to as Bayesian belief networks, Bayesian networks are probabilistic graphical models that depict relationships among variables via conditional dependencies.
- Bayesian linear regression. This conditional modeling technique finds posterior probability through a linear regression model, where the mean of one variable is described by the linear combination of other variables.
- Bayesian neural networks. An extension of traditional neural networks , these models help control overfitting by incorporating uncertainty in weights through posterior distributions, informing a model's output with predictions based on historical data.
- Bayesian model averaging. This approach averages predictions from different models to make predictions about new observations, with each considered model weighted by its model probability.
Bayesian ML 's ability to improve prediction accuracy using data makes it useful for many ML tasks , such as fraud detection, spam filtering, medical diagnostics , weather predictions, forensic analysis, robot decision-making and more.
Bayes' theorem advantages and disadvantages
Bayes' theorem has significant benefits for calculating conditional probability in complex scenarios, but it also presents some challenges due to its complexity and reliance on prior probabilities.
Advantages of Bayes' theorem include the following:
- Combines information in an accessible and interpretable way.
- Improves the accuracy of predictions and hypotheses.
- Accounts for unknowns and uncertainties in the data.
- Produces more realistic and reliable predictions.
- Allows for data adjustments, increasing flexibility.
Disadvantages or challenges associated with Bayes' theorem include the following:
- Requires a prior probability, which can sometimes be subjective or difficult to determine.
- Focuses narrowly on finding posterior probability given prior probability.
- Is computationally complex, which can result in high compute costs, especially in ML use cases with large volumes of data and numerous parameters.
Continue Reading About What is Bayes' theorem?
- Machine learning benefits for businesses
- Supervised learning techniques that aid value predictions
- Overcoming struggles to define algorithmic fairness in healthcare
Related Terms
Dig deeper on ai technologies.

25 machine learning interview questions with answers

Compare and assess 4 top small-business NAS devices

Iconic Singapore hotel caught up in major data breach

SSD form factor

Augmented analytics tools play a crucial role in providing users of all technical skills levels access to AI and analytics daily....
Following and understanding the five steps of the business intelligence lifecycle is the foundation of a successful and effective...
The partnership provides the data management and analytics vendor's users with more choice so that they can develop advanced ...
For many employees, poorly executed digital transformation projects lead to fatigue. Learn effective methods for maintaining ...
The next U.S. president will set the tone on tech issues such as AI regulation, data privacy and climate tech. This guide breaks ...
Countries including South Korea and Taiwan are taking a cautious approach to tech regulation and assessing the impact of existing...
IoT devices generate and collect data from points all over the network. Organizations must apply general data management best ...
Organizations that want a data fabric architecture should consider how six top vendors use their suite of tools to support a ...
The longtime BI vendor's new integration platform aims to deliver trust in the information users work with to inform analytics ...
As supply chain attacks continue, ERP security is more important than ever. Learn some best practices to get started protecting ...
GenAI and other tech is being used to tackle supply chain challenges such as high costs and disruption, but organizations are ...
Wars and pandemics offer stark evidence of how global supply chains can break apart. Effective supply chain management can ...
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Statistics and probability
Course: statistics and probability > unit 7.
- Calculating conditional probability
Conditional probability explained visually
- Conditional probability using two-way tables
- Calculate conditional probability
- Conditional probability tree diagram example
- Tree diagrams and conditional probability
- Conditional probability and independence
- Analyzing event probability for independence
- Dependent and independent events
- • Current transcript segment: 0:02 - [Instructor] Consider the following story.
- • 0:05 Bob is in a room and he has two coins.
- • 0:07 One fair coin and one double sided coin.
- • 0:13 He picks one at random, flips it,
- • 0:19 and shouts the result.
- • 0:21 - [Bob] Heads.
- • 0:23 - [Instructor] Now what is the probability
- • 0:24 that he flipped the fair coin?
- • 0:27 To answer this question, we need
- • 0:29 only rewind and grow a tree.
- • 0:32 The first event, he picks one of two coins,
- • 0:35 so our tree grows two branches,
- • 0:38 leading to equally likely outcomes, fair or unfair.
- • 0:42 The next event, he flips the coin.
- • 0:45 We grow again, if he had the fair coin,
- • 0:47 we know this flip can result in two equally likely outcomes,
- • 0:50 heads and tails, while the unfair coin
- • 0:53 results in two outcomes, both heads.
- • 0:56 Our tree is finished, and we see it has four leaves,
- • 0:59 representing four equally likely outcomes.
- • 1:02 The final step, new evidence, he says.
- • 1:06 - [Bob] Heads.
- • 1:07 - [Instructor] Whenever we gain evidence,
- • 1:09 we must trim our tree.
- • 1:11 We cut any branch leading to tails
- • 1:13 because we know tails did not occur,
- • 1:15 and that is it, so the probability that
- • 1:18 he chose the fair coin is the one fair outcome
- • 1:22 leading to heads divided by the three possible outcomes
- • 1:25 leading to heads, or one third.
- • 1:30 What happens if he flips again and reports?
- • 1:32 - [Bob] Heads.
- • 1:34 - [Instructor] Remember, after each event, our tree grows.
- • 1:37 The fair coin leaves result in two equally likely outcomes,
- • 1:41 heads and tails, the unfair coin leaves
- • 1:44 result in two equally likely outcomes, heads and heads.
- • 1:49 After we hear the second.
- • 1:51 - [Bob] Heads.
- • 1:53 - [Instructor] We cut any branches leading to tails.
- • 1:56 Therefore the probability the coin is fair
- • 1:59 after two heads in a row, is the one
- • 2:01 fair outcome leading to heads divided
- • 2:03 by all possible outcome leading to heads, or one fifth.
- • 2:11 Notice our confidence in the fair coin is dropping
- • 2:14 as more heads occur, though realize
- • 2:16 that we'll never reach zero.
- • 2:19 No matter how many flips occur,
- • 2:20 we can never be 100% certain the coin is unfair.
- • 2:26 In fact, all conditional probability questions
- • 2:29 can be solved by growing trees.
- • 2:32 Let's do one more to be sure.
- • 2:35 Bob has three coins, two are fair,
- • 2:43 one is biased, which is weighted to land heads
- • 2:46 two thirds of the time and tails one third.
- • 2:50 He chooses a coin at random and flips it.
- • 2:57 - [Bob] Heads.
- • 2:58 - [Instructor] Now what is the probability
- • 3:00 he chose the biased coin?
- • 3:04 Let's rewind and build a tree.
- • 3:07 The first event, choosing the coin,
- • 3:10 can lead to three equally likely outcomes,
- • 3:13 fair coin, fair coin, and unfair coin.
- • 3:16 The next event, the coin is flipped.
- • 3:21 Each fair coin leads to two equally
- • 3:23 likely leaves, heads and tails.
- • 3:28 The biased coin leads to three equally likely leaves,
- • 3:32 two representing heads, and one representing tails.
- • 3:37 Now the trick is to always make sure our tree is balanced,
- • 3:40 meaning an equal amount of leaves
- • 3:42 growing out of each branch.
- • 3:44 To do this, we simply scale up the number
- • 3:47 of branches to the least common multiple.
- • 3:50 For two and three, this is six.
- • 4:01 And finally, we label our leaves.
- • 4:03 The fair coin now splits into six
- • 4:05 equally likely leaves, three heads and three tails.
- • 4:09 For the biased coin, we now have two tail leaves
- • 4:11 and four head leaves, and that is it.
- • 4:16 When Bob shouts the result.
- • 4:18 - [Bob] Heads.
- • 4:19 - [Instructor] This new evidence allows us
- • 4:21 to trim all branches leading to tails
- • 4:24 since tails did not occur, so the probability
- • 4:27 that he chose the biased coin given heads occurred,
- • 4:33 well four leaves can come from the biased coin
- • 4:35 divided by all possible leaves.
- • 4:39 Four divided by 10, or 40%.
- • 4:43 When it doubt, it's always possible
- • 4:45 to answer conditional probability questions
- • 4:48 by Bayes Theorem, it tells us the probability
- • 4:51 of event A given some new evidence B,
- • 4:55 though if you forgot it, no worries.
- • 4:57 You need only how to grow stories with trimmed trees.
Want to join the conversation?
- Upvote Button navigates to signup page
- Downvote Button navigates to signup page
- Flag Button navigates to signup page

Video transcript

IMAGES
VIDEO
COMMENTS
1.4.5 Solved Problems: Conditional Probability. In die and coin problems, unless stated otherwise, it is assumed coins and dice are fair and repeated trials are independent. Problem. You purchase a certain product. The manual states that the lifetime T T of the product, defined as the amount of time (in years) the product works properly until ...
Let us solve some questions based on conditional probability with detailed solutions. Question 1: Ten numbered cards are there from 1 to 15, and two cards a chosen at random such that the sum of the numbers on both the cards is even. Find the probability that the chosen cards are odd-numbered. Solution:
This page titled 3.2: Problems on Conditional Probability is shared under a CC BY 3.0 license and was authored, remixed, and/or curated by Paul Pfeiffer via source content that was edited to the style and standards of the LibreTexts platform.
Calculate conditional probability. Google Classroom. Microsoft Teams. Pedro observed what customers ordered at his ice cream shop and found the following probabilities: P ( vanilla) = 0.3 P ( sundae) = 0.2 P ( vanilla and sundae) = 0.15. Find the probability that a customer ordered vanilla ice cream given they ordered a sundae.
Probability of B given A times probability of A. But we know probability of A. We know that that is 0.6. We know that this is 0.6. So just like that, we've set up a situation, an equation, where we can solve for the probability of B given A. The probability of B given A. Notice, let me just rewrite it right over here.
A card is drawn from a deck. Find the conditional probability of \(P\)(a queen | a face card). A card is drawn from a deck. Find the conditional probability of \(P\)(a queen | a club). A die is rolled. Find the conditional probability that it shows a three if it is known that an odd number has shown.
This is the symbolism that is used in most conditional probability problems: P E E 21 The symbol asks us to find the probability that event E 2 occurs given event E 1 has occurred. (The vertical line stands for the words ^given that.) There are two formulas we will use to solve conditional probability problems. Here is the first conditional ...
What is conditional probability and how does it relate to independence? Learn how to use formulas and tables to calculate conditional probabilities and check if two events are independent. Khan Academy is a free online learning platform that covers various topics in math, science, and more.
A lot of difficult probability problems involve conditional probability. These can be tackled using tools like Bayes' Theorem, the principle of inclusion and exclusion, and the notion of independence. Submit your answer A bag contains a number of coins, one of which is a two-headed coin and the rest are fair coins. A coin is selected at random and tossed. If the probability that the toss ...
Example 5.5.1 5.5. 1 Conditional Probability for Drawing Cards without Replacement. Two cards are drawn from a well shuffled deck of 52 cards without replacement. Find the following probabilities: The probability that the second card is a heart given that the first card is a spade. The probability that the first card is a face card and the ...
Divide by P (A): P (B|A) = P (A and B) / P (A) And we have another useful formula: "The probability of event B given event A equals. the probability of event A and event B divided by the probability of event A". Example: Ice Cream. 70% of your friends like Chocolate, and 35% like Chocolate AND like Strawberry.
Step 1: Write out the Conditional Probability Formula in terms of the problem. Step 2: Substitute in the values and solve. Example: Susan took two tests. The probability of her passing both tests is 0.6. The probability of her passing the first test is 0.8.
The Birthday Problem. One of the most famous problems in probability theory is the Birthday Problem, which has to do with shared birthdays in a large group. To make the analysis easier, we'll ignore leap days, and assume that the probability of being born on any given date is 1 365 1 365. Now, if you have 366 people in a room, we're ...
Divide both sides of equation by P (A). Cancel P (A)s on right-hand side of equation. Commute the equation. We have derived the formula for conditional probability. Now we can use this formula to solve the problem at the top of the page. Problem: A math teacher gave her class two tests. 25% of the class passed both tests and 42% of the class ...
However, the reason why we can calculate P(F ∩ A) as P(F) × P(A) in this case is because of the given structure of the problem. The conditional probability formula, P(A ∣ B) = P(A ∩ B) / P(B), can still be used here, but because we have the direct probabilities for P(F ∩ A) and P(A), we can simply multiply P(F) and P(A) to find P(F ∩ ...
Now, we will solve some examples of conditional probability to understand the concept better. Example 1. What is the probability of selecting two queen cards from the deck of 52 cards? Solution. To solve the problems related to the cards in a deck, you should know which types of cards are present in each deck. The properties of a deck are given ...
Learn how to solve problems using the formula for conditional probability at BYJU'S. Login. Study Materials. NCERT Solutions. NCERT Solutions For Class 12. ... Solved Examples Using Conditional Probability Formula. Question 1: The probability that it is Friday and that a student is absent is 0.03. Since there are 5 school days in a week, the ...
Here are some properties of conditional probability along with their proofs (derivations) which we may need to use while solving the problems. All these properties depend on the conditional probability formula (which is mentioned in the previous section). Property 1. Let S be the sample space of an experiment and A be any event.
P(exactly one of them will solve it) = 13/30. Problem 2 : The probability that a car being filled with petrol will also need an oil change is 0.30; the probability that it needs a new oil filter is 0.40; and the probability that both the oil and filter need changing is 0.15.
In probability theory, conditional probability quantifies the probability (or likelihood) of an event occurring given that another event has already occurred.This requires that probability of the second event occurring is affected by the first event happening. It is computed by multiplying the probability of the first event by the updated probability of the second, or conditional, event.
This two-way table displays data for the sample of students who responded to the survey: A student will be chosen at random. Find the probability that the student chose to fly as their superpower. Find the probability that the student was male. Find the probability that the student was male, given the student chose to fly as their superpower.
Conditional Probability is defined as the probability of any event occurring when another event has already occurred. In other words, it calculates the probability of one event happening given that a certain condition is satisfied. It is represented as P (A | B) which means the probability of A when B has already happened.
Bayes' theorem helps calculate conditional probability. Learn how to derive the formula, its use cases and use in machine learning, and its pros and cons. ... Bayes documented the theorem in his paper "An Essay Toward Solving a Problem in the Doctrine of Chances," published posthumously in 1763.
• 2:26 In fact, all conditional probability questions • 2:29 can be solved by growing trees. • 2:32 Let's do one more to be sure. • 2:35 Bob has three coins, two are fair, • 2:43 one is biased, which is weighted to land heads • 2:46 two thirds of the time and tails one third. • 2:50 He chooses a coin at random and flips it. • 2: ...