High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
Free ready-to-use math resources
Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth


20 Effective Math Strategies To Approach Problem-Solving
Katie Keeton
Math strategies for problem-solving help students use a range of approaches to solve many different types of problems. It involves identifying the problem and carrying out a plan of action to find the answer to mathematical problems.
Problem-solving skills are essential to math in the general classroom and real-life. They require logical reasoning and critical thinking skills. Students must be equipped with strategies to help them find solutions to problems.
This article explores mathematical problem solving strategies, logical reasoning and critical thinking skills to help learners with solving math word problems independently in real-life situations.
What are problem-solving strategies?
Problem-solving strategies in math are methods students can use to figure out solutions to math problems. Some problem-solving strategies:
- Draw a model
- Use different approaches
- Check the inverse to make sure the answer is correct
Students need to have a toolkit of math problem-solving strategies at their disposal to provide different ways to approach math problems. This makes it easier to find solutions and understand math better.
Strategies can help guide students to the solution when it is difficult ot know when to start.

The ultimate guide to problem solving techniques
Download these ready-to-go problem solving techniques that every student should know. Includes printable tasks for students including challenges, short explanations for teachers with questioning prompts.
20 Math Strategies For Problem-Solving
Different problem-solving math strategies are required for different parts of the problem. It is unlikely that students will use the same strategy to understand and solve the problem.
Here are 20 strategies to help students develop their problem-solving skills.
Strategies to understand the problem
Strategies that help students understand the problem before solving it helps ensure they understand:
- The context
- What the key information is
- How to form a plan to solve it
Following these steps leads students to the correct solution and makes the math word problem easier .
Here are five strategies to help students understand the content of the problem and identify key information.
1. Read the problem aloud
Read a word problem aloud to help understand it. Hearing the words engages auditory processing. This can make it easier to process and comprehend the context of the situation.
2. Highlight keywords
When keywords are highlighted in a word problem, it helps the student focus on the essential information needed to solve it. Some important keywords help determine which operation is needed. For example, if the word problem asks how many are left, the problem likely requires subtraction. Ensure students highlight the keywords carefully and do not highlight every number or keyword. There is likely irrelevant information in the word problem.
3. Summarize the information
Read the problem aloud, highlight the key information and then summarize the information. Students can do this in their heads or write down a quick summary. Summaries should include only the important information and be in simple terms that help contextualize the problem.
4. Determine the unknown
A common problem that students have when solving a word problem is misunderstanding what they are solving. Determine what the unknown information is before finding the answer. Often, a word problem contains a question where you can find the unknown information you need to solve. For example, in the question ‘How many apples are left?’ students need to find the number of apples left over.
5. Make a plan
Once students understand the context of the word problem, have dentified the important information and determined the unknown, they can make a plan to solve it. The plan will depend on the type of problem. Some problems involve more than one step to solve them as some require more than one answer. Encourage students to make a list of each step they need to take to solve the problem before getting started.
Strategies for solving the problem
1. draw a model or diagram.
Students may find it useful to draw a model, picture, diagram, or other visual aid to help with the problem solving process. It can help to visualize the problem to understand the relationships between the numbers in the problem. In turn, this helps students see the solution.

Similarly, you could draw a model to represent the objects in the problem:

2. Act it out
This particular strategy is applicable at any grade level but is especially helpful in math investigation in elementary school . It involves a physical demonstration or students acting out the problem using movements, concrete resources and math manipulatives . When students act out a problem, they can visualize and contectualize the word problem in another way and secure an understanding of the math concepts. The examples below show how 1st-grade students could “act out” an addition and subtraction problem:
| The problem | How to act out the problem |
| Gia has 6 apples. Jordan has 3 apples. How many apples do they have altogether? | Two students use counters to represent the apples. One student has 6 counters and the other student takes 3. Then, they can combine their “apples” and count the total. |
| Michael has 7 pencils. He gives 2 pencils to Sarah. How many pencils does Michael have now? | One student (“Michael”) holds 7 pencils, the other (“Sarah”) holds 2 pencils. The student playing Michael gives 2 pencils to the student playing Sarah. Then the students count how many pencils Michael is left holding. |
3. Work backwards
Working backwards is a popular problem-solving strategy. It involves starting with a possible solution and deciding what steps to take to arrive at that solution. This strategy can be particularly helpful when students solve math word problems involving multiple steps. They can start at the end and think carefully about each step taken as opposed to jumping to the end of the problem and missing steps in between.
For example,

To solve this problem working backwards, start with the final condition, which is Sam’s grandmother’s age (71) and work backwards to find Sam’s age. Subtract 20 from the grandmother’s age, which is 71. Then, divide the result by 3 to get Sam’s age. 71 – 20 = 51 51 ÷ 3 = 17 Sam is 17 years old.
4. Write a number sentence
When faced with a word problem, encourage students to write a number sentence based on the information. This helps translate the information in the word problem into a math equation or expression, which is more easily solved. It is important to fully understand the context of the word problem and what students need to solve before writing an equation to represent it.
5. Use a formula
Specific formulas help solve many math problems. For example, if a problem asks students to find the area of a rug, they would use the area formula (area = length × width) to solve. Make sure students know the important mathematical formulas they will need in tests and real-life. It can help to display these around the classroom or, for those who need more support, on students’ desks.
Strategies for checking the solution
Once the problem is solved using an appropriate strategy, it is equally important to check the solution to ensure it is correct and makes sense.
There are many strategies to check the solution. The strategy for a specific problem is dependent on the problem type and math content involved.
Here are five strategies to help students check their solutions.
1. Use the Inverse Operation
For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7. As good practice, encourage students to use the inverse operation routinely to check their work.
2. Estimate to check for reasonableness
Once students reach an answer, they can use estimation or rounding to see if the answer is reasonable. Round each number in the equation to a number that’s close and easy to work with, usually a multiple of ten. For example, if the question was 216 ÷ 18 and the quotient was 12, students might round 216 to 200 and round 18 to 20. Then use mental math to solve 200 ÷ 20, which is 10. When the estimate is clear the two numbers are close. This means your answer is reasonable.
3. Plug-In Method
This method is particularly useful for algebraic equations. Specifically when working with variables. To use the plug-in method, students solve the problem as asked and arrive at an answer. They can then plug the answer into the original equation to see if it works. If it does, the answer is correct.

If students use the equation 20m+80=300 to solve this problem and find that m = 11, they can plug that value back into the equation to see if it is correct. 20m + 80 = 300 20 (11) + 80 = 300 220 + 80 = 300 300 = 300 ✓
4. Peer Review
Peer review is a great tool to use at any grade level as it promotes critical thinking and collaboration between students. The reviewers can look at the problem from a different view as they check to see if the problem was solved correctly. Problem solvers receive immediate feedback and the opportunity to discuss their thinking with their peers. This strategy is effective with mixed-ability partners or similar-ability partners. In mixed-ability groups, the partner with stronger skills provides guidance and support to the partner with weaker skills, while reinforcing their own understanding of the content and communication skills. If partners have comparable ability levels and problem-solving skills, they may find that they approach problems differently or have unique insights to offer each other about the problem-solving process.
5. Use a Calculator
A calculator can be introduced at any grade level but may be best for older students who already have a foundational understanding of basic math operations. Provide students with a calculator to allow them to check their solutions independently, accurately, and quickly. Since calculators are so readily available on smartphones and tablets, they allow students to develop practical skills that apply to real-world situations.
Step-by-step problem-solving processes for your classroom
In his book, How to Solve It , published in 1945, mathematician George Polya introduced a 4-step process to solve problems.
Polya’s 4 steps include:
- Understand the problem
- Devise a plan
- Carry out the plan
Today, in the style of George Polya, many problem-solving strategies use various acronyms and steps to help students recall.
Many teachers create posters and anchor charts of their chosen process to display in their classrooms. They can be implemented in any elementary, middle school or high school classroom.
Here are 5 problem-solving strategies to introduce to students and use in the classroom.

How Third Space Learning improves problem-solving
Resources .
Third Space Learning offers a free resource library is filled with hundreds of high-quality resources. A team of experienced math experts carefully created each resource to develop students mental arithmetic, problem solving and critical thinking.
Explore the range of problem solving resources for 2nd to 8th grade students.
One-on-one tutoring
Third Space Learning offers one-on-one math tutoring to help students improve their math skills. Highly qualified tutors deliver high-quality lessons aligned to state standards.
Former teachers and math experts write all of Third Space Learning’s tutoring lessons. Expertly designed lessons follow a “my turn, follow me, your turn” pedagogy to help students move from guided instruction and problem-solving to independent practice.
Throughout each lesson, tutors ask higher-level thinking questions to promote critical thinking and ensure students are developing a deep understanding of the content and problem-solving skills.

Problem-solving
Educators can use many different strategies to teach problem-solving and help students develop and carry out a plan when solving math problems. Incorporate these math strategies into any math program and use them with a variety of math concepts, from whole numbers and fractions to algebra.
Teaching students how to choose and implement problem-solving strategies helps them develop mathematical reasoning skills and critical thinking they can apply to real-life problem-solving.
READ MORE : 8 Common Core math examples
There are many different strategies for problem-solving; Here are 5 problem-solving strategies: • draw a model • act it out • work backwards • write a number sentence • use a formula
Here are 10 strategies of problem-solving: • Read the problem aloud • Highlight keywords • Summarize the information • Determine the unknown • Make a plan • Draw a model • Act it out • Work backwards • Write a number sentence • Use a formula
1. Understand the problem 2. Devise a plan 3. Carry out the plan 4. Look back
Some strategies you can use to solve challenging math problems are: breaking the problem into smaller parts, using diagrams or models, applying logical reasoning, and trying different approaches.
Related articles

Why Student Centered Learning Is Important: A Guide For Educators

13 Effective Learning Strategies: A Guide to Using them in your Math Classroom

Differentiated Instruction: 9 Differentiated Curriculum And Instruction Strategies For Teachers

5 Math Mastery Strategies To Incorporate Into Your 4th and 5th Grade Classrooms
Ultimate Guide to Metacognition [FREE]
Looking for a summary on metacognition in relation to math teaching and learning?
Check out this guide featuring practical examples, tips and strategies to successfully embed metacognition across your school to accelerate math growth.
Privacy Overview

In order to continue enjoying our site, we ask that you confirm your identity as a human. Thank you very much for your cooperation.
Math Problem Solving Strategies
In these lessons, we will learn some math problem solving strategies for example, Verbal Model (or Logical Reasoning), Algebraic Model, Block Model (or Singapore Math), Guess & Check Model and Find a Pattern Model.
Related Pages Solving Word Problems Using Block Models Heuristic Approach to Problem-Solving Algebra Lessons
Problem Solving Strategies
The strategies used in solving word problems:
- What do you know?
- What do you need to know?
- Draw a diagram/picture
Solution Strategies Label Variables Verbal Model or Logical Reasoning Algebraic Model - Translate Verbal Model to Algebraic Model Solve and Check.
Solving Word Problems
Step 1: Identify (What is being asked?) Step 2: Strategize Step 3: Write the equation(s) Step 4: Answer the question Step 5: Check
Problem Solving Strategy: Guess And Check
Using the guess and check problem solving strategy to help solve math word problems.
Example: Jamie spent $40 for an outfit. She paid for the items using $10, $5 and $1 bills. If she gave the clerk 10 bills in all, how many of each bill did she use?
Problem Solving : Make A Table And Look For A Pattern
- Identify - What is the question?
- Plan - What strategy will I use to solve the problem?
- Solve - Carry out your plan.
- Verify - Does my answer make sense?
Example: Marcus ran a lemonade stand for 5 days. On the first day, he made $5. Every day after that he made $2 more than the previous day. How much money did Marcus made in all after 5 days?
Find A Pattern Model (Intermediate)
In this lesson, we will look at some intermediate examples of Find a Pattern method of problem-solving strategy.
Example: The figure shows a series of rectangles where each rectangle is bounded by 10 dots. a) How many dots are required for 7 rectangles? b) If the figure has 73 dots, how many rectangles would there be?
| Rectangles | Pattern | Total dots |
| 1 | 10 | 10 |
| 2 | 10 + 7 | 17 |
| 3 | 10 + 14 | 24 |
| 4 | 10 + 21 | 31 |
| 5 | 10 + 28 | 38 |
| 6 | 10 + 35 | 45 |
| 7 | 10 + 42 | 52 |
| 8 | 10 + 49 | 59 |
| 9 | 10 + 56 | 66 |
| 10 | 10 + 63 | 73 |
a) The number of dots required for 7 rectangles is 52.
b) If the figure has 73 dots, there would be 10 rectangles.
Example: Each triangle in the figure below has 3 dots. Study the pattern and find the number of dots for 7 layers of triangles.
| Layers | Pattern | Total dots |
| 1 | 3 | 3 |
| 2 | 3 + 3 | 6 |
| 3 | 3 + 3 + 4 | 10 |
| 4 | 3 + 3 + 4 + 5 | 15 |
| 5 | 3 + 3 + 4 + 5 + 6 | 21 |
| 6 | 3 + 3 + 4 + 5 + 6 + 7 | 28 |
| 7 | 3 + 3 + 4 + 5 + 6 + 7 + 8 | 36 |
The number of dots for 7 layers of triangles is 36.
Example: The table below shows numbers placed into groups I, II, III, IV, V and VI. In which groups would the following numbers belong? a) 25 b) 46 c) 269
| I | 1 | 7 | 13 | 19 | 25 |
| II | 2 | 8 | 14 | 20 | 26 |
| III | 3 | 9 | 15 | 21 | 27 |
| IV | 4 | 10 | 16 | 22 | |
| V | 5 | 11 | 17 | 23 | |
| VI | 6 | 12 | 18 | 24 |
Solution: The pattern is: The remainder when the number is divided by 6 determines the group. a) 25 ÷ 6 = 4 remainder 1 (Group I) b) 46 ÷ 6 = 7 remainder 4 (Group IV) c) 269 ÷ 6 = 44 remainder 5 (Group V)
Example: The following figures were formed using matchsticks.
a) Based on the above series of figures, complete the table below.
| Number of squares | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Number of triangles | 4 | 6 | 8 | 10 | ||||
| Number of matchsticks | 12 | 19 | 26 | 33 |
b) How many triangles are there if the figure in the series has 9 squares?
c) How many matchsticks would be used in the figure in the series with 11 squares?
| Number of squares | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Number of triangles | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
| Number of matchsticks | 12 | 19 | 26 | 33 | 40 | 47 | 54 | 61 |
b) The pattern is +2 for each additional square. 18 + 2 = 20 If the figure in the series has 9 squares, there would be 20 triangles.
c) The pattern is + 7 for each additional square 61 + (3 x 7) = 82 If the figure in the series has 11 squares, there would be 82 matchsticks.
Example: Seven ex-schoolmates had a gathering. Each one of them shook hands with all others once. How many handshakes were there?
| A | B | C | D | E | F | G | |
| A | |||||||
| B | ● | ||||||
| C | ● | ● | |||||
| D | ● | ● | ● | ||||
| E | ● | ● | ● | ● | |||
| F | ● | ● | ● | ● | ● | ||
| G | ● | ● | ● | ● | ● | ● | |
| HS | 6 | 5 | 4 | 3 | 2 | 1 |
Total = 6 + 5 + 4 + 3 + 2 + 1 = 21 handshakes.
The following video shows more examples of using problem solving strategies and models. Question 1: Approximate your average speed given some information Question 2: The table shows the number of seats in each of the first four rows in an auditorium. The remaining ten rows follow the same pattern. Find the number of seats in the last row. Question 3: You are hanging three pictures in the wall of your home that is 16 feet wide. The width of your pictures are 2, 3 and 4 feet. You want space between your pictures to be the same and the space to the left and right to be 6 inches more than between the pictures. How would you place the pictures?
The following are some other examples of problem solving strategies.
Explore it/Act it/Try it (EAT) Method (Basic) Explore it/Act it/Try it (EAT) Method (Intermediate) Explore it/Act it/Try it (EAT) Method (Advanced)
Finding A Pattern (Basic) Finding A Pattern (Intermediate) Finding A Pattern (Advanced)

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
Problem Solving in Mathematics
- Math Tutorials
- Pre Algebra & Algebra
- Exponential Decay
- Worksheets By Grade
The main reason for learning about math is to become a better problem solver in all aspects of life. Many problems are multistep and require some type of systematic approach. There are a couple of things you need to do when solving problems. Ask yourself exactly what type of information is being asked for: Is it one of addition, subtraction, multiplication , or division? Then determine all the information that is being given to you in the question.
Mathematician George Pólya’s book, “ How to Solve It: A New Aspect of Mathematical Method ,” written in 1957, is a great guide to have on hand. The ideas below, which provide you with general steps or strategies to solve math problems, are similar to those expressed in Pólya’s book and should help you untangle even the most complicated math problem.
Use Established Procedures
Learning how to solve problems in mathematics is knowing what to look for. Math problems often require established procedures and knowing what procedure to apply. To create procedures, you have to be familiar with the problem situation and be able to collect the appropriate information, identify a strategy or strategies, and use the strategy appropriately.
Problem-solving requires practice. When deciding on methods or procedures to use to solve problems, the first thing you will do is look for clues, which is one of the most important skills in solving problems in mathematics. If you begin to solve problems by looking for clue words, you will find that these words often indicate an operation.
Look for Clue Words
Think of yourself as a math detective. The first thing to do when you encounter a math problem is to look for clue words. This is one of the most important skills you can develop. If you begin to solve problems by looking for clue words, you will find that those words often indicate an operation.
Common clue words for addition problems:
Common clue words for subtraction problems:
- How much more
Common clue words for multiplication problems:
Common clue words for division problems:
Although clue words will vary a bit from problem to problem, you'll soon learn to recognize which words mean what in order to perform the correct operation.
Read the Problem Carefully
This, of course, means looking for clue words as outlined in the previous section. Once you’ve identified your clue words, highlight or underline them. This will let you know what kind of problem you’re dealing with. Then do the following:
- Ask yourself if you've seen a problem similar to this one. If so, what is similar about it?
- What did you need to do in that instance?
- What facts are you given about this problem?
- What facts do you still need to find out about this problem?
Develop a Plan and Review Your Work
Based on what you discovered by reading the problem carefully and identifying similar problems you’ve encountered before, you can then:
- Define your problem-solving strategy or strategies. This might mean identifying patterns, using known formulas, using sketches, and even guessing and checking.
- If your strategy doesn't work, it may lead you to an ah-ha moment and to a strategy that does work.
If it seems like you’ve solved the problem, ask yourself the following:
- Does your solution seem probable?
- Does it answer the initial question?
- Did you answer using the language in the question?
- Did you answer using the same units?
If you feel confident that the answer is “yes” to all questions, consider your problem solved.
Tips and Hints
Some key questions to consider as you approach the problem may be:
- What are the keywords in the problem?
- Do I need a data visual, such as a diagram, list, table, chart, or graph?
- Is there a formula or equation that I'll need? If so, which one?
- Will I need to use a calculator? Is there a pattern I can use or follow?
Read the problem carefully, and decide on a method to solve the problem. Once you've finished working the problem, check your work and ensure that your answer makes sense and that you've used the same terms and or units in your answer.
- Critical Thinking Definition, Skills, and Examples
- Converting Cubic Meters to Liters
- 2nd Grade Math Word Problems
- The Horse Problem: A Math Challenge
- 2020-21 Common Application Essay Option 4—Solving a Problem
- How to Use Math Journals in Class
- The Frayer Model for Math
- Algorithms in Mathematics and Beyond
- "Grandpa's Rubik's Cube"—Sample Common Application Essay, Option #4
- Math Stumper: Use Two Squares to Make Separate Pens for Nine Pigs
- Graphic Organizers in Math
- College Interview Tips: "Tell Me About a Challenge You Overcame"
- Christmas Word Problem Worksheets
- Solving Problems Involving Distance, Rate, and Time
- Innovative Ways to Teach Math
- Study Tips for Math Homework and Math Tests
Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
32 Mathematical Ideas: Problem-Solving Techniques
Jenna Lehmann
Solving Problems by Inductive Reasoning
Before we can talk about how to use inductive reasoning, we need to define it and distinguish it from deductive reasoning.
Inductive reasoning is when one makes generalizations based on repeated observations of specific examples. For instance, if I have only ever had mean math teachers, I might draw the conclusion that all math teachers are mean. Because I witnessed multiple instances of mean math teachers and only mean math teachers, I’ve drawn this conclusion. That being said, one of the downfalls of inductive reasoning is that it only takes meeting one nice math teacher for my original conclusion to be proven false. This is called a counterexample . Since inductive reasoning can so easily be proven false with one counterexample, we don’t say that a conclusion drawn from inductive reasoning is the absolute truth unless we can also prove it using deductive reasoning. With inductive reasoning, we can never be sure that what is true in a specific case will be true in general, but it is a way of making an educated guess.
Deductive reasoning depends on a hypothesis that is considered to be true. In other words, if X = Y and Y = Z, then we can deduce that X = Z. An example of this might be that if we know for a fact that all dogs are good, and Lucky is a dog, then we can deduce that Lucky is good.
Strategies for Problem Solving
No matter what tool you use to solve a problem, there is a method for going about solving the problem.
- Understand the Problem: You may need to read a problem several times before you can conceptualize it. Don’t become frustrated, and take a walk if you need to. It might take some time to click.
- Devise a Plan: There may be more than one way to solve the problem. Find the way which is most comfortable for you or the most practical.
- Carry Out the Plan: Try it out. You may need to adjust your plan if you run into roadblocks or dead ends.
- Look Back and Check: Make sure your answer gives sense given the context.
There are several different ways one might go about solving a problem. Here are a few:
- Tables and Charts: Sometimes you’ll be working with a lot of data or computing a problem with a lot of different steps. It may be best to keep it organized in a table or chart so you can refer back to previous work later.
- Working Backward: Sometimes you’ll be given a word problem where they describe a series of algebraic functions that took place and then what the end result is. Sometimes you’ll have to work backward chronologically.
- Using Trial and Error: Sometimes you’ll know what mathematical function you need to use but not what number to start with. You may need to use trial and error to get the exact right number.
- Guessing and Checking: Sometimes it will appear that a math problem will have more than one correct answer. Be sure to go back and check your work to determine if some of the answers don’t actually work out.
- Considering a Similar, Simpler Problem: Sometimes you can use the strategy you think you would like to use on a simpler, hypothetical problem first to see if you can find a pattern and apply it to the harder problem.
- Drawing a Sketch: Sometimes—especially with geometrical problems—it’s more helpful to draw a sketch of what is being asked of you.
- Using Common Sense: Be sure to read questions very carefully. Sometimes it will seem like the answer to a question is either too obvious or impossible. There is usually a phrasing of the problem which would lead you to believe that the rules are one way when really it’s describing something else. Pay attention to literal language.
This chapter was originally posted to the Math Support Center blog at the University of Baltimore on November 6, 2019.
Math and Statistics Guides from UB's Math & Statistics Center Copyright © by Jenna Lehmann is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book
- Our Mission
6 Tips for Teaching Math Problem-Solving Skills
Solving word problems is tougher than computing with numbers, but elementary teachers can guide students to do the deep thinking involved.

A growing concern with students is the ability to problem-solve, especially with complex, multistep problems. Data shows that students struggle more when solving word problems than they do with computation , and so problem-solving should be considered separately from computation. Why?
Consider this. When we’re on the way to a new destination and we plug in our location to a map on our phone, it tells us what lane to be in and takes us around any detours or collisions, sometimes even buzzing our watch to remind us to turn. When I experience this as a driver, I don’t have to do the thinking. I can think about what I’m going to cook for dinner, not paying much attention to my surroundings other than to follow those directions. If I were to be asked to go there again, I wouldn’t be able to remember, and I would again seek help.
If we can switch to giving students strategies that require them to think instead of giving them too much support throughout the journey to the answer, we may be able to give them the ability to learn the skills to read a map and have several ways to get there.
Here are six ways we can start letting students do this thinking so that they can go through rigorous problem-solving again and again, paving their own way to the solution.
1. Link problem-solving to reading
When we can remind students that they already have many comprehension skills and strategies they can easily use in math problem-solving, it can ease the anxiety surrounding the math problem. For example, providing them with strategies to practice, such as visualizing, acting out the problem with math tools like counters or base 10 blocks, drawing a quick sketch of the problem, retelling the story in their own words, etc., can really help them to utilize the skills they already have to make the task less daunting.
We can break these skills into specific short lessons so students have a bank of strategies to try on their own. Here's an example of an anchor chart that they can use for visualizing . Breaking up comprehension into specific skills can increase student independence and help teachers to be much more targeted in their problem-solving instruction. This allows students to build confidence and break down the barriers between reading and math to see they already have so many strengths that are transferable to all problems.
2. Avoid boxing students into choosing a specific operation
It can be so tempting to tell students to look for certain words that might mean a certain operation. This might even be thoroughly successful in kindergarten and first grade, but just like when our map tells us where to go, that limits students from becoming deep thinkers. It also expires once they get into the upper grades, where those words could be in a problem multiple times, creating more confusion when students are trying to follow a rule that may not exist in every problem.
We can encourage a variety of ways to solve problems instead of choosing the operation first. In first grade, a problem might say, “Joceline has 13 stuffed animals and Jordan has 17. How many more does Jordan have?” Some students might choose to subtract, but a lot of students might just count to find the amount in between. If we tell them that “how many more” means to subtract, we’re taking the thinking out of the problem altogether, allowing them to go on autopilot without truly solving the problem or using their comprehension skills to visualize it.
3. Revisit ‘representation’
The word “representation” can be misleading. It seems like something to do after the process of solving. When students think they have to go straight to solving, they may not realize that they need a step in between to be able to support their understanding of what’s actually happening in the problem first.
Using an anchor chart like one of these ( lower grade , upper grade ) can help students to choose a representation that most closely matches what they’re visualizing in their mind. Once they sketch it out, it can give them a clearer picture of different ways they could solve the problem.
Think about this problem: “Varush went on a trip with his family to his grandmother’s house. It was 710 miles away. On the way there, three people took turns driving. His mom drove 214 miles. His dad drove 358 miles. His older sister drove the rest. How many miles did his sister drive?”
If we were to show this student the anchor chart, they would probably choose a number line or a strip diagram to help them understand what’s happening.
If we tell students they must always draw base 10 blocks in a place value chart, that doesn’t necessarily match the concept of this problem. When we ask students to match our way of thinking, we rob them of critical thinking practice and sometimes confuse them in the process.
4. Give time to process
Sometimes as educators, we can feel rushed to get to everyone and everything that’s required. When solving a complex problem, students need time to just sit with a problem and wrestle with it, maybe even leaving it and coming back to it after a period of time.
This might mean we need to give them fewer problems but go deeper with those problems we give them. We can also speed up processing time when we allow for collaboration and talk time with peers on problem-solving tasks.
5. Ask questions that let Students do the thinking
Questions or prompts during problem-solving should be very open-ended to promote thinking. Telling a student to reread the problem or to think about what tools or resources would help them solve it is a way to get them to try something new but not take over their thinking.
These skills are also transferable across content, and students will be reminded, “Good readers and mathematicians reread.”
6. Spiral concepts so students frequently use problem-solving skills
When students don’t have to switch gears in between concepts, they’re not truly using deep problem-solving skills. They already kind of know what operation it might be or that it’s something they have at the forefront of their mind from recent learning. Being intentional within their learning stations and assessments about having a variety of rigorous problem-solving skills will refine their critical thinking abilities while building more and more resilience throughout the school year as they retain content learning in the process.
Problem-solving skills are so abstract, and it can be tough to pinpoint exactly what students need. Sometimes we have to go slow to go fast. Slowing down and helping students have tools when they get stuck and enabling them to be critical thinkers will prepare them for life and allow them multiple ways to get to their own destination.
You are using an outdated browser. Please upgrade your browser to improve your experience.
Math Problem Solving Strategies That Make Students Say “I Get It!”

Even students who are quick with math facts can get stuck when it comes to problem solving.
As soon as a concept is translated to a word problem, or a simple mathematical sentence contains an unknown, they’re stumped.
That’s because problem solving requires us to consciously choose the strategies most appropriate for the problem at hand . And not all students have this metacognitive ability.
But you can teach these strategies for problem solving. You just need to know what they are.
We’ve compiled them here divided into four categories:
Strategies for understanding a problem
Strategies for solving the problem, strategies for working out, strategies for checking the solution.
Get to know these strategies and then model them explicitly to your students. Next time they dive into a rich problem, they’ll be filling up their working out paper faster than ever!
Before students can solve a problem, they need to know what it’s asking them. This is often the first hurdle with word problems that don’t specify a particular mathematical operation.
Encourage your students to:
Read and reread the question
They say they’ve read it, but have they really ? Sometimes students will skip ahead as soon as they’ve noticed one familiar piece of information or give up trying to understand it if the problem doesn’t make sense at first glance.
Teach students to interpret a question by using self-monitoring strategies such as:
- Rereading a question more slowly if it doesn’t make sense the first time
- Asking for help
- Highlighting or underlining important pieces of information.
Identify important and extraneous information
John is collecting money for his friend Ari’s birthday. He starts with $5 of his own, then Marcus gives him another $5. How much does he have now?
As adults looking at the above problem, we can instantly look past the names and the birthday scenario to see a simple addition problem. Students, however, can struggle to determine what’s relevant in the information that’s been given to them.
Teach students to sort and sift the information in a problem to find what’s relevant. A good way to do this is to have them swap out pieces of information to see if the solution changes. If changing names, items or scenarios has no impact on the end result, they’ll realize that it doesn’t need to be a point of focus while solving the problem.
Schema approach
This is a math intervention strategy that can make problem solving easier for all students, regardless of ability.
Compare different word problems of the same type and construct a formula, or mathematical sentence stem, that applies to them all. For example, a simple subtraction problems could be expressed as:
[Number/Quantity A] with [Number/Quantity B] removed becomes [end result].
This is the underlying procedure or schema students are being asked to use. Once they have a list of schema for different mathematical operations (addition, multiplication and so on), they can take turns to apply them to an unfamiliar word problem and see which one fits.
Struggling students often believe math is something you either do automatically or don’t do at all. But that’s not true. Help your students understand that they have a choice of problem-solving strategies to use, and if one doesn’t work, they can try another.
Here are four common strategies students can use for problem solving.
Visualizing
Visualizing an abstract problem often makes it easier to solve. Students could draw a picture or simply draw tally marks on a piece of working out paper.
Encourage visualization by modeling it on the whiteboard and providing graphic organizers that have space for students to draw before they write down the final number.
Guess and check
Show students how to make an educated guess and then plug this answer back into the original problem. If it doesn’t work, they can adjust their initial guess higher or lower accordingly.
Find a pattern
To find patterns, show students how to extract and list all the relevant facts in a problem so they can be easily compared. If they find a pattern, they’ll be able to locate the missing piece of information.
Work backward
Working backward is useful if students are tasked with finding an unknown number in a problem or mathematical sentence. For example, if the problem is 8 + x = 12, students can find x by:
- Starting with 12
- Taking the 8 from the 12
- Being left with 4
- Checking that 4 works when used instead of x
Now students have understood the problem and formulated a strategy, it’s time to put it into practice. But if they just launch in and do it, they might make it harder for themselves. Show them how to work through a problem effectively by:
Documenting working out
Model the process of writing down every step you take to complete a math problem and provide working out paper when students are solving a problem. This will allow students to keep track of their thoughts and pick up errors before they reach a final solution.
Check along the way
Checking work as you go is another crucial self-monitoring strategy for math learners. Model it to them with think aloud questions such as:
- Does that last step look right?
- Does this follow on from the step I took before?
- Have I done any ‘smaller’ sums within the bigger problem that need checking?
Students often make the mistake of thinking that speed is everything in math — so they’ll rush to get an answer down and move on without checking.
But checking is important too. It allows them to pinpoint areas of difficulty as they come up, and it enables them to tackle more complex problems that require multiple checks before arriving at a final answer.
Here are some checking strategies you can promote:
Check with a partner
Comparing answers with a peer leads is a more reflective process than just receiving a tick from the teacher. If students have two different answers, encourage them to talk about how they arrived at them and compare working out methods. They’ll figure out exactly where they went wrong, and what they got right.
Reread the problem with your solution
Most of the time, students will be able to tell whether or not their answer is correct by putting it back into the initial problem. If it doesn’t work or it just ‘looks wrong’, it’s time to go back and fix it up.
Fixing mistakes
Show students how to backtrack through their working out to find the exact point where they made a mistake. Emphasize that they can’t do this if they haven’t written down everything in the first place — so a single answer with no working out isn’t as impressive as they might think!
Need more help developing problem solving skills?
Read up on how to set a problem solving and reasoning activity or explore Mathseeds and Mathletics, our award winning online math programs. They’ve got over 900 teacher tested problem solving activities between them!
Get access to 900+ unique problem solving activities
You might like....
- PRINT TO PLAY
- DIGITAL GAMES

Problem-Solving Strategies
October 16, 2019
There are many different ways to solve a math problem, and equipping students with problem-solving strategies is just as important as teaching computation and algorithms. Problem-solving strategies help students visualize the problem or present the given information in a way that can lead them to the solution. Solving word problems using strategies works great as a number talks activity and helps to revise many skills.
Problem-solving strategies
1. create a diagram/picture, 2. guess and check., 3. make a table or a list., 4. logical reasoning., 5. find a pattern, 6. work backward, 1. create a diagram/draw a picture.
Creating a diagram helps students visualize the problem and reach the solution. A diagram can be a picture with labels, or a representation of the problem with objects that can be manipulated. Role-playing and acting out the problem like a story can help get to the solution.
Alice spent 3/4 of her babysitting money on comic books. She is left with $6. How much money did she make from babysitting?
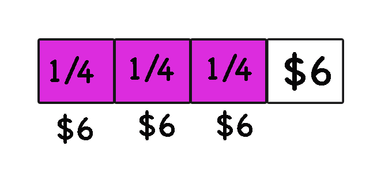
2. Guess and check
Teach students the same strategy research mathematicians use.
With this strategy, students solve problems by making a reasonable guess depending on the information given. Then they check to see if the answer is correct and they improve it accordingly. By repeating this process, a student can arrive at a correct answer that has been checked. It is recommended that the students keep a record of their guesses by making a chart, a table or a list. This is a flexible strategy that works for many types of problems. When students are stuck, guessing and checking helps them start and explore the problem. However, there is a trap. Exactly because it is such a simple strategy to use, some students find it difficult to consider other strategies. As problems get more complicated, other strategies become more important and more effective.
Find two numbers that have sum 11 and product 24.
Try/guess 5 and 6 the product is 30 too high
adjust to 4 and 7 with product 28 still high
adjust again 3 and 8 product 24
3. Make a table or a list
Carefully organize the information on a table or list according to the problem information. It might be a table of numbers, a table with ticks and crosses to solve a logic problem or a list of possible answers. Seeing the given information sorted out on a table or a list will help find patterns and lead to the correct solution.
To make sure you are listing all the information correctly read the problem carefully.
Find the common factors of 24, 30 and 18

Logical reasoning is the process of using logical, systemic steps to arrive at a conclusion based on given facts and mathematic principles. Read and understand the problem. Then find the information that helps you start solving the problem. Continue with each piece of information and write possible answers.
Thomas, Helen, Bill, and Mary have cats that are black, brown, white, or gray. The cats’ names are Buddy, Lucky, Fifi, and Moo. Buddy is brown. Thoma’s cat, Lucky, is not gray. Helen’s cat is white but is not named Moo. The gray cat belongs to Bill. Which cat belongs to each student, and what is its color?
A table or list is useful in solving logic problems.
| Thomas | Lucky | Not gray, the cat is black |
| Helen | Not Moo, not Buddy, not Lucky so Fifi | White |
| Bill | Moo | Gray |
| Mary | Buddy | Brown |
Since Lucky is not gray it can be black or brown. However, Buddy is brown so Lucky has to be black.
Buddy is brown so it cannot be Helen’s cat. Helen’s cat cannot be Moo, Buddy or Lucky, so it is Fifi.
Therefore, Moo is Bill’s cat and Buddy is Mary’s cat.
5. Find a pattern.
Finding a pattern is a strategy in which students look for patterns in the given information in order to solve the problem. When the problem consists of data like numbers or events that are repeated then it can be solved using the “find a pattern” problem-solving strategy. Data can be organized in a table or a list to reveal the pattern and help discover the “rule” of the pattern.
The “rule” can then be used to find the answer to the question and complete the table/list.
Shannon’s Pizzeria made 5 pizzas on Sunday, 10 pizzas on Monday, 20 pizzas on Tuesday, and 40 pizzas on Wednesday. If this pattern continues, how many pizzas will the pizzeria make on Saturday?
| Sunday | 5 |
| Monday | 10 |
| Tuesday | 20 |
| Wednesday | 40 |
| Thursday | |
| Friday | |
| Saturday |
6. Working backward
Problems that can be solved with this strategy are the ones that list a series of events or a sequence of steps .
In this strategy, the students must start with the solution and work back to the beginning. Each operation must be reversed to get back to the beginning. So if working forwards requires addition, when students work backward they will need to subtract. And if they multiply working forwards, they must divide when working backward.
Mom bought a box of candy. Mary took 5 of them, Nick took 4 of them and 31 were given out on Halloween night. The next morning they found 8 pieces of candy in the box. How many candy pieces were in the box when mom bought it.
For this problem, we know that the final number of candy was 8, so if we work backward to “put back” the candy that was taken from the box we can reach the number of candy pieces that were in the box, to begin with.
The candy was taken away so we will normally subtract them. However, to get back to the original number of candy we need to work backward and do the opposite, which is to add them.
8 candy pieces were left + the 31 given out + plus the ones Mary took + the ones Nick took
8+31+5+4= 48 Answer: The box came with 48 pieces of candy.
Selecting the best strategy for a problem comes with practice and often problems will require the use of more than one strategies.
Print and digital activities
I have created a collection of print and digital activity cards and worksheets with word problems (print and google slides) to solve using the strategies above. The collection includes 70 problems (5 challenge ones) and their solution s and explanations.
sample below

How to use the activity cards
Allow the students to use manipulatives to solve the problems. (counters, shapes, lego blocks, Cuisenaire blocks, base 10 blocks, clocks) They can use manipulatives to create a picture and visualize the problem. They can use counters for the guess and check strategy. Discuss which strategy/strategies are better for solving each problem. Discuss the different ways. Use the activities as warm-ups, number talks, initiate discussions, group work, challenge, escape rooms, and more.
Ask your students to write their own problems using the problems in this resource, and more, as examples. Start with a simple type. Students learn a lot when trying to compose a problem. They can share the problem with their partner or the whole class. Make a collection of problems to share with another class.
For the google slides the students can use text boxes to explain their thinking with words, add shapes and lines to create diagrams, and add (insert) tables and diagrams.
Many of the problems can be solved faster by using algebraic expressions. However, since I created this resource for grades 4 and up I chose to show simple conceptual ways of solving the problems using the strategies above. You can suggest different ways of solving the problems based on the grade level.
Find the free and premium versions of the resource below. The premium version includes 70 problems (challenge problems included) and their solutions
There are 2 versions of the resource
70 google slides with explanations + 70 printable task cards
70 google slides with explanations + 11 worksheets
You might also like
Multiplying fractions/mixed numbers/simplifying
Adding and subtracting fractions
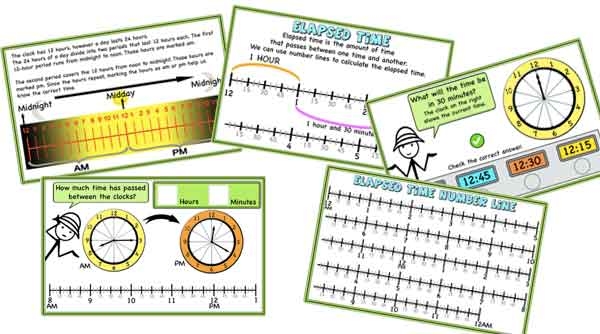
AM/PM, 24-hour clock, Elapsed Time – ideas, games, and activities
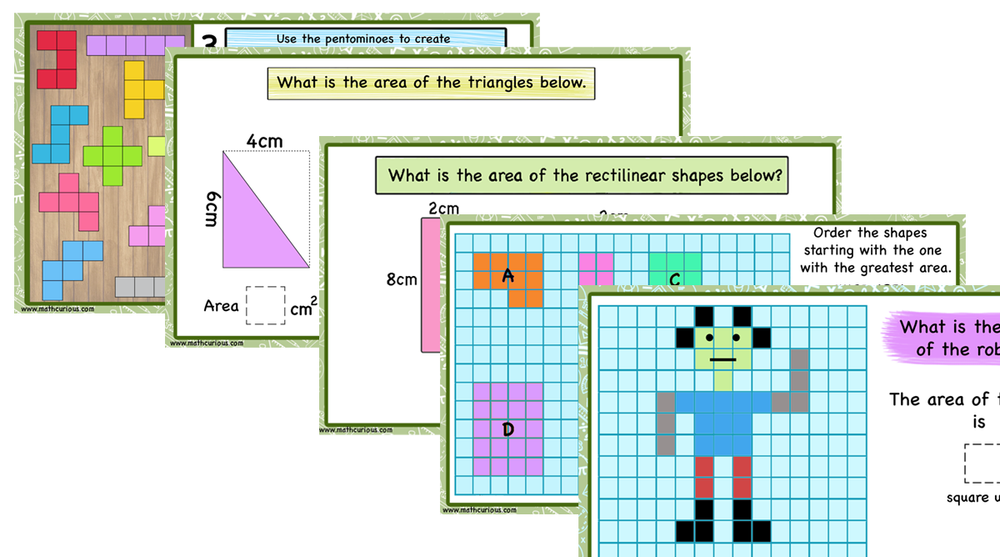
Teaching area, ideas, games, print, and digital activities
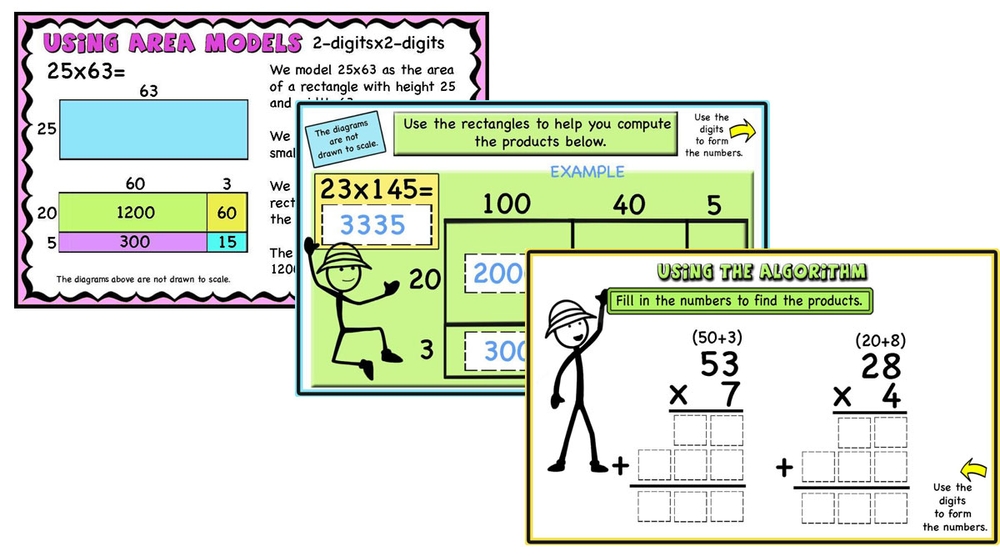
Multi-Digit Multiplication, Area model, Partial Products algorithm, Puzzles, Word problems
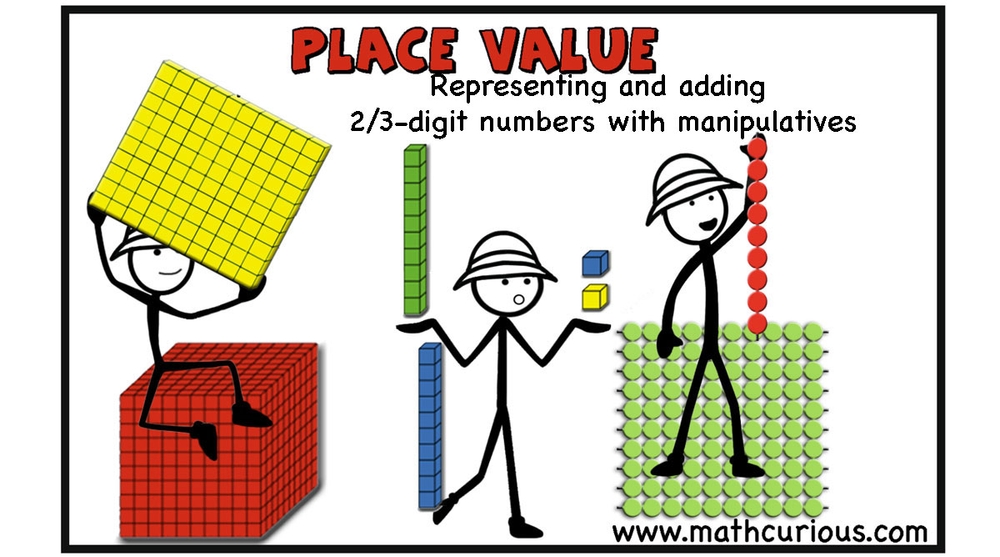
Place Value – Representing and adding 2/3 digit numbers with manipulatives

Multiplication Mission – arrays, properties, multiples, factors, division
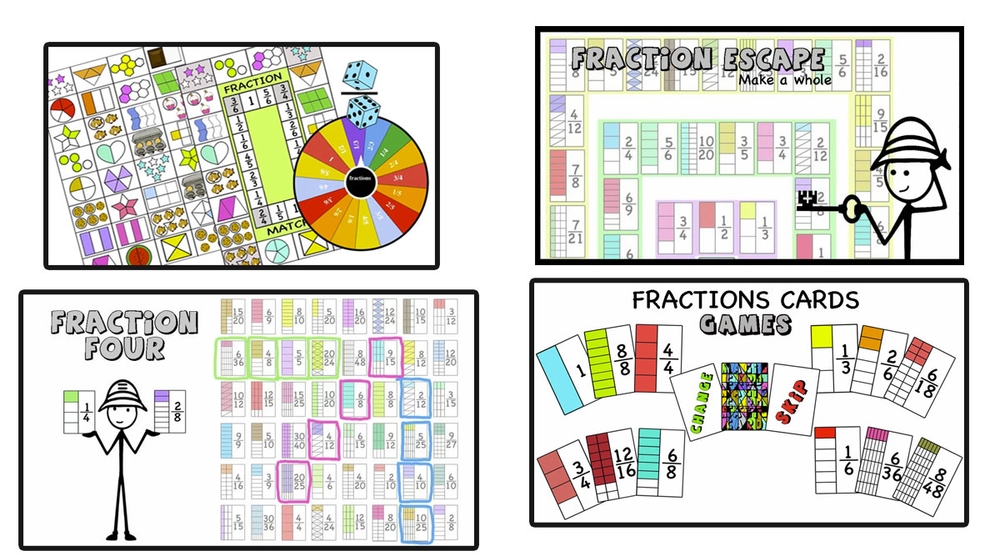
Fractions Games and activities – Equivalence, make 1, compare, add, subtract, like, unlike
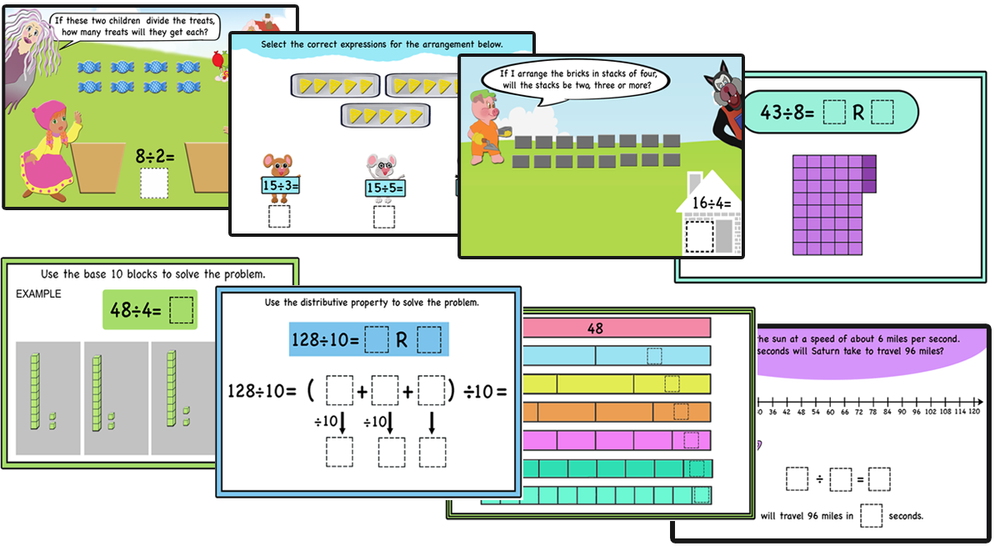
Diving into Division -Teaching division conceptually

Expressions with arrays
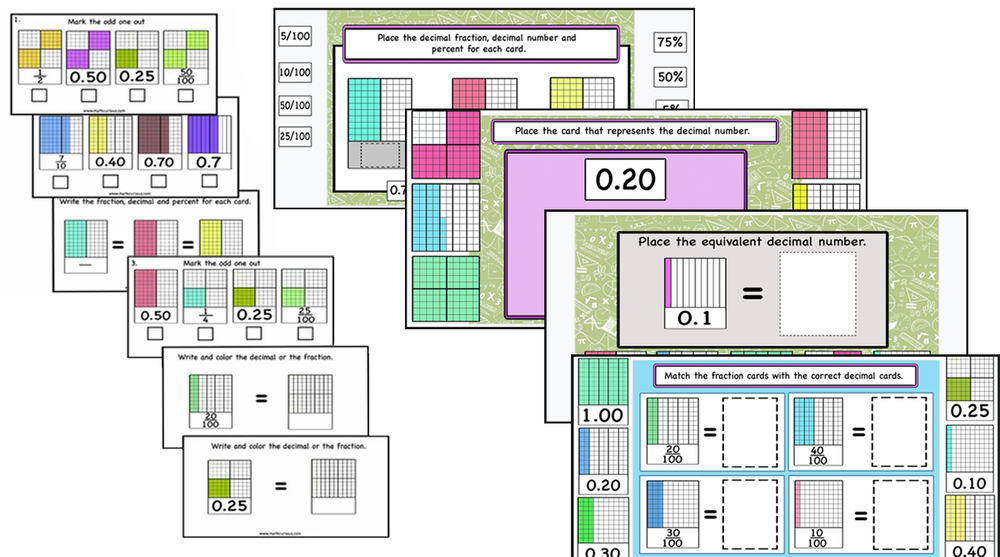
Decimals, Decimal fractions, Percentages – print and digital
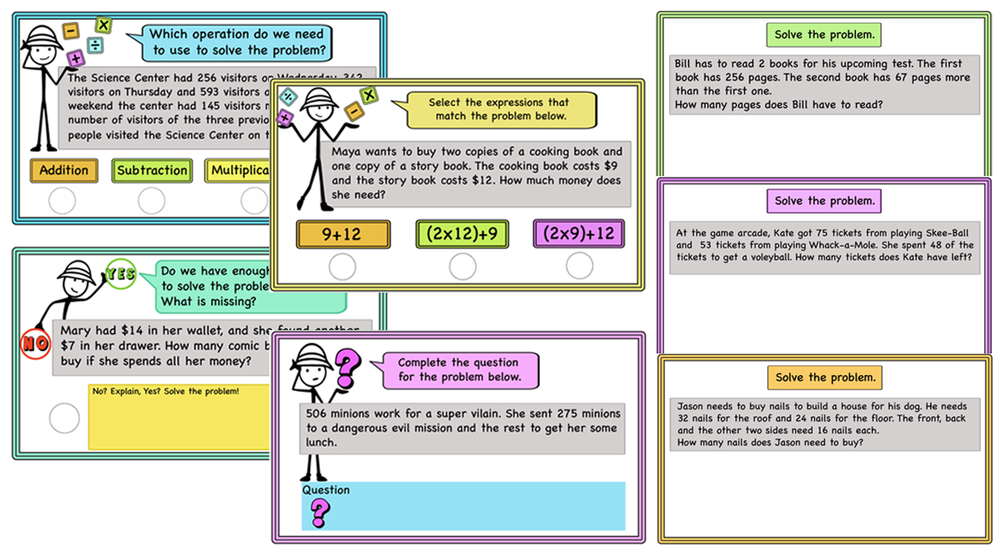
Solving Word Problems- Math talks-Strategies, Ideas and Activities-print and digital
Check out our best selling card games now available at amazon.com and amazon.ca.

Chicken Escape
A multiplayer card game that makes mental math practice fun! Chicken Escape is a fast-paced multiplayer card game. While playing…

Dragon Times – A math Adventure card game
Dragon Times is an educational fantasy card game that aims to motivate children to practice multiplication and division facts while…

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
5 Teaching Mathematics Through Problem Solving
Janet Stramel

In his book “How to Solve It,” George Pólya (1945) said, “One of the most important tasks of the teacher is to help his students. This task is not quite easy; it demands time, practice, devotion, and sound principles. The student should acquire as much experience of independent work as possible. But if he is left alone with his problem without any help, he may make no progress at all. If the teacher helps too much, nothing is left to the student. The teacher should help, but not too much and not too little, so that the student shall have a reasonable share of the work.” (page 1)
What is a problem in mathematics? A problem is “any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method” (Hiebert, et. al., 1997). Problem solving in mathematics is one of the most important topics to teach; learning to problem solve helps students develop a sense of solving real-life problems and apply mathematics to real world situations. It is also used for a deeper understanding of mathematical concepts. Learning “math facts” is not enough; students must also learn how to use these facts to develop their thinking skills.
According to NCTM (2010), the term “problem solving” refers to mathematical tasks that have the potential to provide intellectual challenges for enhancing students’ mathematical understanding and development. When you first hear “problem solving,” what do you think about? Story problems or word problems? Story problems may be limited to and not “problematic” enough. For example, you may ask students to find the area of a rectangle, given the length and width. This type of problem is an exercise in computation and can be completed mindlessly without understanding the concept of area. Worthwhile problems includes problems that are truly problematic and have the potential to provide contexts for students’ mathematical development.
There are three ways to solve problems: teaching for problem solving, teaching about problem solving, and teaching through problem solving.
Teaching for problem solving begins with learning a skill. For example, students are learning how to multiply a two-digit number by a one-digit number, and the story problems you select are multiplication problems. Be sure when you are teaching for problem solving, you select or develop tasks that can promote the development of mathematical understanding.
Teaching about problem solving begins with suggested strategies to solve a problem. For example, “draw a picture,” “make a table,” etc. You may see posters in teachers’ classrooms of the “Problem Solving Method” such as: 1) Read the problem, 2) Devise a plan, 3) Solve the problem, and 4) Check your work. There is little or no evidence that students’ problem-solving abilities are improved when teaching about problem solving. Students will see a word problem as a separate endeavor and focus on the steps to follow rather than the mathematics. In addition, students will tend to use trial and error instead of focusing on sense making.
Teaching through problem solving focuses students’ attention on ideas and sense making and develops mathematical practices. Teaching through problem solving also develops a student’s confidence and builds on their strengths. It allows for collaboration among students and engages students in their own learning.
Consider the following worthwhile-problem criteria developed by Lappan and Phillips (1998):
- The problem has important, useful mathematics embedded in it.
- The problem requires high-level thinking and problem solving.
- The problem contributes to the conceptual development of students.
- The problem creates an opportunity for the teacher to assess what his or her students are learning and where they are experiencing difficulty.
- The problem can be approached by students in multiple ways using different solution strategies.
- The problem has various solutions or allows different decisions or positions to be taken and defended.
- The problem encourages student engagement and discourse.
- The problem connects to other important mathematical ideas.
- The problem promotes the skillful use of mathematics.
- The problem provides an opportunity to practice important skills.
Of course, not every problem will include all of the above. Sometimes, you will choose a problem because your students need an opportunity to practice a certain skill.
Key features of a good mathematics problem includes:
- It must begin where the students are mathematically.
- The feature of the problem must be the mathematics that students are to learn.
- It must require justifications and explanations for both answers and methods of solving.

Problem solving is not a neat and orderly process. Think about needlework. On the front side, it is neat and perfect and pretty.

But look at the b ack.
It is messy and full of knots and loops. Problem solving in mathematics is also like this and we need to help our students be “messy” with problem solving; they need to go through those knots and loops and learn how to solve problems with the teacher’s guidance.
When you teach through problem solving , your students are focused on ideas and sense-making and they develop confidence in mathematics!
Mathematics Tasks and Activities that Promote Teaching through Problem Solving

Choosing the Right Task
Selecting activities and/or tasks is the most significant decision teachers make that will affect students’ learning. Consider the following questions:
- Teachers must do the activity first. What is problematic about the activity? What will you need to do BEFORE the activity and AFTER the activity? Additionally, think how your students would do the activity.
- What mathematical ideas will the activity develop? Are there connections to other related mathematics topics, or other content areas?
- Can the activity accomplish your learning objective/goals?

Low Floor High Ceiling Tasks
By definition, a “ low floor/high ceiling task ” is a mathematical activity where everyone in the group can begin and then work on at their own level of engagement. Low Floor High Ceiling Tasks are activities that everyone can begin and work on based on their own level, and have many possibilities for students to do more challenging mathematics. One gauge of knowing whether an activity is a Low Floor High Ceiling Task is when the work on the problems becomes more important than the answer itself, and leads to rich mathematical discourse [Hover: ways of representing, thinking, talking, agreeing, and disagreeing; the way ideas are exchanged and what the ideas entail; and as being shaped by the tasks in which students engage as well as by the nature of the learning environment].
The strengths of using Low Floor High Ceiling Tasks:
- Allows students to show what they can do, not what they can’t.
- Provides differentiation to all students.
- Promotes a positive classroom environment.
- Advances a growth mindset in students
- Aligns with the Standards for Mathematical Practice
Examples of some Low Floor High Ceiling Tasks can be found at the following sites:
- YouCubed – under grades choose Low Floor High Ceiling
- NRICH Creating a Low Threshold High Ceiling Classroom
- Inside Mathematics Problems of the Month
Math in 3-Acts
Math in 3-Acts was developed by Dan Meyer to spark an interest in and engage students in thought-provoking mathematical inquiry. Math in 3-Acts is a whole-group mathematics task consisting of three distinct parts:
Act One is about noticing and wondering. The teacher shares with students an image, video, or other situation that is engaging and perplexing. Students then generate questions about the situation.
In Act Two , the teacher offers some information for the students to use as they find the solutions to the problem.
Act Three is the “reveal.” Students share their thinking as well as their solutions.
“Math in 3 Acts” is a fun way to engage your students, there is a low entry point that gives students confidence, there are multiple paths to a solution, and it encourages students to work in groups to solve the problem. Some examples of Math in 3-Acts can be found at the following websites:
- Dan Meyer’s Three-Act Math Tasks
- Graham Fletcher3-Act Tasks ]
- Math in 3-Acts: Real World Math Problems to Make Math Contextual, Visual and Concrete
Number Talks
Number talks are brief, 5-15 minute discussions that focus on student solutions for a mental math computation problem. Students share their different mental math processes aloud while the teacher records their thinking visually on a chart or board. In addition, students learn from each other’s strategies as they question, critique, or build on the strategies that are shared.. To use a “number talk,” you would include the following steps:
- The teacher presents a problem for students to solve mentally.
- Provide adequate “ wait time .”
- The teacher calls on a students and asks, “What were you thinking?” and “Explain your thinking.”
- For each student who volunteers to share their strategy, write their thinking on the board. Make sure to accurately record their thinking; do not correct their responses.
- Invite students to question each other about their strategies, compare and contrast the strategies, and ask for clarification about strategies that are confusing.
“Number Talks” can be used as an introduction, a warm up to a lesson, or an extension. Some examples of Number Talks can be found at the following websites:
- Inside Mathematics Number Talks
- Number Talks Build Numerical Reasoning

Saying “This is Easy”
“This is easy.” Three little words that can have a big impact on students. What may be “easy” for one person, may be more “difficult” for someone else. And saying “this is easy” defeats the purpose of a growth mindset classroom, where students are comfortable making mistakes.
When the teacher says, “this is easy,” students may think,
- “Everyone else understands and I don’t. I can’t do this!”
- Students may just give up and surrender the mathematics to their classmates.
- Students may shut down.
Instead, you and your students could say the following:
- “I think I can do this.”
- “I have an idea I want to try.”
- “I’ve seen this kind of problem before.”
Tracy Zager wrote a short article, “This is easy”: The Little Phrase That Causes Big Problems” that can give you more information. Read Tracy Zager’s article here.
Using “Worksheets”
Do you want your students to memorize concepts, or do you want them to understand and apply the mathematics for different situations?
What is a “worksheet” in mathematics? It is a paper and pencil assignment when no other materials are used. A worksheet does not allow your students to use hands-on materials/manipulatives [Hover: physical objects that are used as teaching tools to engage students in the hands-on learning of mathematics]; and worksheets are many times “naked number” with no context. And a worksheet should not be used to enhance a hands-on activity.
Students need time to explore and manipulate materials in order to learn the mathematics concept. Worksheets are just a test of rote memory. Students need to develop those higher-order thinking skills, and worksheets will not allow them to do that.
One productive belief from the NCTM publication, Principles to Action (2014), states, “Students at all grade levels can benefit from the use of physical and virtual manipulative materials to provide visual models of a range of mathematical ideas.”
You may need an “activity sheet,” a “graphic organizer,” etc. as you plan your mathematics activities/lessons, but be sure to include hands-on manipulatives. Using manipulatives can
- Provide your students a bridge between the concrete and abstract
- Serve as models that support students’ thinking
- Provide another representation
- Support student engagement
- Give students ownership of their own learning.
Adapted from “ The Top 5 Reasons for Using Manipulatives in the Classroom ”.
any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method
should be intriguing and contain a level of challenge that invites speculation and hard work, and directs students to investigate important mathematical ideas and ways of thinking toward the learning
involves teaching a skill so that a student can later solve a story problem
when we teach students how to problem solve
teaching mathematics content through real contexts, problems, situations, and models
a mathematical activity where everyone in the group can begin and then work on at their own level of engagement
20 seconds to 2 minutes for students to make sense of questions
Mathematics Methods for Early Childhood Copyright © 2021 by Janet Stramel is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.
Share This Book
Solving Equations
What is an equation.
An equation says that two things are equal. It will have an equals sign "=" like this:
That equations says:
what is on the left (x − 2) equals what is on the right (4)
So an equation is like a statement " this equals that "
What is a Solution?
A Solution is a value we can put in place of a variable (such as x ) that makes the equation true .
Example: x − 2 = 4
When we put 6 in place of x we get:
which is true
So x = 6 is a solution.
How about other values for x ?
- For x=5 we get "5−2=4" which is not true , so x=5 is not a solution .
- For x=9 we get "9−2=4" which is not true , so x=9 is not a solution .
In this case x = 6 is the only solution.
You might like to practice solving some animated equations .
More Than One Solution
There can be more than one solution.
Example: (x−3)(x−2) = 0
When x is 3 we get:
(3−3)(3−2) = 0 × 1 = 0
And when x is 2 we get:
(2−3)(2−2) = (−1) × 0 = 0
which is also true
So the solutions are:
x = 3 , or x = 2
When we gather all solutions together it is called a Solution Set
The above solution set is: {2, 3}
Solutions Everywhere!
Some equations are true for all allowed values and are then called Identities
Example: sin(−θ) = −sin(θ) is one of the Trigonometric Identities
Let's try θ = 30°:
sin(−30°) = −0.5 and
−sin(30°) = −0.5
So it is true for θ = 30°
Let's try θ = 90°:
sin(−90°) = −1 and
−sin(90°) = −1
So it is also true for θ = 90°
Is it true for all values of θ ? Try some values for yourself!
How to Solve an Equation
There is no "one perfect way" to solve all equations.
A Useful Goal
But we often get success when our goal is to end up with:
x = something
In other words, we want to move everything except "x" (or whatever name the variable has) over to the right hand side.
Example: Solve 3x−6 = 9
Now we have x = something ,
and a short calculation reveals that x = 5
Like a Puzzle
In fact, solving an equation is just like solving a puzzle. And like puzzles, there are things we can (and cannot) do.
Here are some things we can do:
- Add or Subtract the same value from both sides
- Clear out any fractions by Multiplying every term by the bottom parts
- Divide every term by the same nonzero value
- Combine Like Terms
- Expanding (the opposite of factoring) may also help
- Recognizing a pattern, such as the difference of squares
- Sometimes we can apply a function to both sides (e.g. square both sides)
Example: Solve √(x/2) = 3
And the more "tricks" and techniques you learn the better you will get.
Special Equations
There are special ways of solving some types of equations. Learn how to ...
- solve Quadratic Equations
- solve Radical Equations
- solve Equations with Sine, Cosine and Tangent
Check Your Solutions
You should always check that your "solution" really is a solution.
How To Check
Take the solution(s) and put them in the original equation to see if they really work.
Example: solve for x:
2x x − 3 + 3 = 6 x − 3 (x≠3)
We have said x≠3 to avoid a division by zero.
Let's multiply through by (x − 3) :
2x + 3(x−3) = 6
Bring the 6 to the left:
2x + 3(x−3) − 6 = 0
Expand and solve:
2x + 3x − 9 − 6 = 0
5x − 15 = 0
5(x − 3) = 0
Which can be solved by having x=3
Let us check x=3 using the original question:
2 × 3 3 − 3 + 3 = 6 3 − 3
Hang On: 3 − 3 = 0 That means dividing by Zero!
And anyway, we said at the top that x≠3 , so ...
x = 3 does not actually work, and so:
There is No Solution!
That was interesting ... we thought we had found a solution, but when we looked back at the question we found it wasn't allowed!
This gives us a moral lesson:
"Solving" only gives us possible solutions, they need to be checked!
- Note down where an expression is not defined (due to a division by zero, the square root of a negative number, or some other reason)
- Show all the steps , so it can be checked later (by you or someone else)
Powerful online learning at your pace

What IS Problem-Solving?
Ask teachers about problem-solving strategies, and you’re opening a can of worms! Opinions about the “best” way to teach problem-solving are all over the board. And teachers will usually argue for their process quite passionately.
When I first started teaching math over 25 years ago, it was very common to teach “keywords” to help students determine the operation to use when solving a word problem. For example, if you see the word “total” in the problem, you always add. Rather than help students become better problem solvers, the use of keywords actually resulted in students who don’t even feel the need to read and understand the problem–just look for the keywords, pick out the numbers, and do the operation indicated by the keyword.
This post contains affiliate links, which simply means that when you use my link and purchase a product, I receive a small commission. There is no additional cost to you, and I only link to books and products that I personally use and recommend.
Another common strategy for teaching problem-solving is the use of acrostics that students can easily remember to perform the “steps” in problem-solving. CUBES is an example. Just as with keywords, however, students often follow the steps with little understanding. As an example, a common step is to underline or highlight the question. But if you ask students why they are underlining or highlighting the question, they often can’t tell you. The question is , in fact, super important, but they’ve not been told why. They’ve been told to underline the question, so they do.
The problem with both keywords and the rote-step strategies is that both methods try to turn something that is inherently messy into an algorithm! It’s way past time that we leave both methods behind.
First, we need to broaden the definition of problem-solving. Somewhere along the line, problem-solving became synonymous with “word problems.” In reality, it’s so much more. Every one of us solves dozens or hundreds of problems every single day, and most of us haven’t solved a word problem in years. Problem-solving is often described as figuring out what to do when you don’t know what to do. My power went out unexpectedly this morning, and I have work to do. That’s a problem that I had to solve. I had to think about what the problem was, what my options were, and formulate a plan to solve the problem. No keywords. No acrostics. I’m using my phone as a hotspot and hoping my laptop battery doesn’t run out. Problem solved. For now.
If you want to get back to what problem-solving really is, you should consult the work of George Polya. His book, How to Solve It , which was first published in 1945, outlined four principles for problem-solving. The four principles are: understand the problem, devise a plan, carry out the plan, and look back. This document from UC Berkeley’s Mathematics department is a great 4-page overview of Polya’s process. You can probably see that the keyword and rote-steps strategies were likely based on Polya’s method, but it really got out of hand. We need to help students think , not just follow steps.
I created both primary and intermediate posters based on Polya’s principles. Grab your copies for free here !

I would LOVE to hear your comments about problem-solving!

Similar Posts

On a Roll: Adding Fractions
Today I have a little freebie for the older kiddos. On a Roll is a simple dice game for practicing adding fractions with like denominators and writing fractions greater than…

Identifying Geometric Attributes
Students begin identifying geometric attributes at a fairly early age. Our 1st Grade teachers introduce vertex, edge, and face. Still, it seems that kids have trouble answering questions about geometric…

Ten Flashing Fireflies: Booklet for the Combinations of Ten
Math practice should be engaging for students, and what could be more engaging than connecting math to a charming children’s book? And while we want math to be engaging, let’s…

Alligators Are for Swamps, Not Comparing Numbers
There, I said it. And while I’m at it, PacMan is soooooooo 70s! It’s time to move past using alligators for comparing numbers. There are really two steps involved in…

Teaching Numeracy, Critical Habits 8 & 9
This week we finish up the final two critical habits. This post contains affiliate links, which simply means that when you use my link and purchase a product, I receive…

Video for Counting Back from 20–Shake Your Groove Thing!
I’m hanging out in one of my Kinder classes, and I’m having a blast! Check out this great video from Have Fun Teaching for counting back from 20. They have…
Do you tutor teachers?
I do professional development for district and schools, and I have online courses.
You make a great point when you mentioned that teaching students to look for “keywords” is not teaching students to become better problem solvers. I was once guilty of using the CUBES strategy, but have since learned to provide students with opportunity to grapple with solving a problem and not providing them with specified steps to follow.
I think we’ve ALL been there! We learn and we do better. 🙂
Love this article and believe that we can do so much better as math teachers than just teaching key words! Do you have an editable version of this document? We are wanting to use something similar for our school, but would like to tweak it just a bit. Thank you!
I’m sorry, but because of the clip art and fonts I use, I am not able to provide an editable version.
Hi Donna! I am working on my dissertation that focuses on problem-solving. May I use your intermediate poster as a figure, giving credit to you in my citation with your permission, for my section on Polya’s Traditional Problem-Solving Steps? You laid out the process so succinctly with examples that my research could greatly benefit from this image. Thank you in advance!
Absolutely! Good luck with your dissertation!
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
Problem solving in mathematics education: tracing its foundations and current research-practice trends
- Original Paper
- Open access
- Published: 30 April 2024
- Volume 56 , pages 211–222, ( 2024 )
Cite this article
You have full access to this open access article

- Manuel Santos-Trigo ORCID: orcid.org/0000-0002-7144-2098 1
1472 Accesses
1 Altmetric
Explore all metrics
In tracing recent research trends and directions in mathematical problem-solving, it is argued that advances in mathematics practices occur and take place around two intertwined activities, mathematics problem formulation and ways to approach and solve those problems. In this context, a problematizing principle emerges as central activity to organize mathematics curriculum proposals and ways to structure problem-solving learning environments. Subjects’ use of concrete, abstract, symbolic, or digital tools not only influences the ways to pose and pursue mathematical problems; but also shapes the type of representation, exploration, and reasoning they engage to work and solve problems. Problem-solving foundations that privilege learners’ development of habits of mathematical practices that involve an inquiry method to formulate conjectures, to look for different ways to represent and approach problems, and to support and communicate results shed light on directions of current research trends and the relevance of rethinking curriculum proposals and extending problem-solving environments in terms of teachers/students’ consistent use of digital tools and online developments.
Similar content being viewed by others
A systematic review of TPACK research in primary mathematics education

Teaching with digital technology

Word problems in mathematics education: a survey
Avoid common mistakes on your manuscript.
1 Introduction and rationale
Mathematical problem solving has been a prominent theme and research area in the mathematics education agenda during the last four decades. Problem-solving perspectives have influenced and shaped mathematics curriculum proposals and ways to support learning environments worldwide (Törner et al., 2007 ; Toh et al., 2023 ). Various disciplinary communities have identified and contributed to connect problem-solving approaches with the students’ learning, construction, and application of mathematical knowledge. The mathematics community recognizes that the formulation and resolution of problems are central activities in the development of the discipline (Halmos, 1980 , Polya, 1945 ). Indeed, the identification and presentation of lists of unsolved mathematical problems have been a tradition that has inspired the mathematics community to approach mathematical problems and to generate mathematical knowledge (Hilbert, 1902 ; Devlin, 2002 ). Thus, mathematical problems, results, and solution attempts provide information regarding what areas and contents were studied at different times during the development of the discipline (Santos-Trigo, 2020a , b ). Cai et al. ( 2023 ) stated that “ …[E]ngaging learners in the activity of problem posing reflects a potentially strong link to the discipline of mathematics” (p. 5). Thurston ( 1994 ) recognized that understanding and applying a mathematical concept implies analysing, coordinating, and integrating diverse meanings (geometric, visual, intuitive, and formal definition) associated with such concept and ways to carry out corresponding procedures and operations in problematic situations.
The centrality of problem-solving in mathematicians’ own work and in their teaching, is incontrovertible. Problem-solving is also a central topic for mathematics educators, who have developed conceptual frameworks to formulate general ideas about problem-solving (as opposed to the specific ideas needed for solving specific problems) (Fried, 2014 ; p.17).
That is, the mathematics education community is interested in analysing and documenting the students’ cognitive and social behaviours to understand and develop mathematical knowledge and problem-solving competencies. “…the idea of understanding how mathematicians treat and solve problems, and then implementing this understanding in instruction design, was pivotal in mathematics education research and practice” (Koichu, 2014 ). In addition, other disciplines such as psychology, cognitive science or artificial intelligence have provided tools and methods to delve into learners’ ways to understand mathematical concepts and to work on problem situations. Thus, members of various communities have often worked in collaboration to identify and relate relevant aspects of mathematical practices with the design and implementation of learning scenarios that foster and enhance students’ mathematical thinking and the development of problem-solving competencies.
2 Methods and procedures
Research focus, themes, and inquiry methods in the mathematical problem-solving agenda have varied and been influenced and shaped by theoretical and methodological developments of mathematics education as a discipline (English & Kirshner, 2016 ; Liljedahl & Cai, 2021 ). Further, research designs and methods used in cognitive, social, and computational fields have influenced the ways in which mathematical problem-solving research are framed. An overarching question to capture shifts and foundations in problem-solving developments was: How has mathematical problem-solving research agenda varied and evolved in terms of ways to frame, pose, and pursue research questions? In addressing this question, it was important to identify and contrast the structure and organization around some published problem-solving reviews (Lester, 1994 ; Törner et al., 2007 ; Rott et al., 2021 ; Liljedahl & Cai, 2021 ; Toh et al., 2023 ) to shed light on a possible route to connect seminal developments in the field with current research trends and perspectives in mathematical problem-solving developments. The goal was to identify common problem-solving principles that have provided a rational and foundations to support recent problem-solving approaches for learners to construct mathematical knowledge and to develop problem-solving competencies. The criteria to select the set of published peer-reviewed studies, to consider in this review, involved choosing articles published in indexed journals (ZDM-Mathematics Education, Educational Studies in Mathematics, Mathematical Thinking and Learning, Journal of Mathematical Behavior, and Journal for Research in Mathematics Education); contributions that appear in International Handbooks in Mathematics Education; and chapters published in recent mathematical problem-solving books. The initial search included 205 publications whose number was reduced to 55, all published in English, based on reviewing their abstracts and conclusions. Around 100 of the initial selection appeared in the references of an ongoing weekly mathematical problem-solving doctoral seminar that has been implemented during the last six years in our department. In addition, some well-known authors in the field were asked to identify their most representative publications to include in the review list. Here, some suggestions were received, but at the end the list of contributions, that appears in the references section, was chosen based on my vision and experience in the field. The goal was to identify main issues or dimensions to frame and analyse recent research trends and perspectives in mathematical problem-solving developments. Thus, seminal reviews in the field (Schoenfeld, 1992 ; Lester, 1994 ; Törner et al., 2007 ) provided directions on ways to structure and select the questions used to analyse the selected contributions. Table 1 shows chosen issues that resemble features of an adjusted framework that Lester ( 1994 ) proposed to organize, summarize, and analyse problem-solving developments in terms of research emphasis (themes and research questions), methodologies (research designs and methods), and achieved results that the problem-solving community addressed during the 1970–1994 period. Furthermore, relevant shifts in the mathematical problem-solving agenda could be identified and explained in terms of what the global mathematics education and other disciplines pursue at different periods.
It is important to mention that the content and structure of this paper involve a narrative synthesis of selected articles that includes contributions related to mathematical problem-solving foundations and those that address recent developments published in the last 9 years that involve the use of digital technologies. Table 1 shows themes, issues, and overarching questions that were used to delve into problem-solving developments.
To contextualize the current state of art in the field, it is important to revisit problem-solving principles and tenets that provide foundations and a rationale to centre and support the design and implementation of learning environments around problem-solving activities (Santos-Trigo, 2020a , b ). The identification of mathematical problem-solving foundations also implies acknowledging what terms, concepts, and language or discourse that the problem-solving community has used to refer to and frame problem-solving approaches. For example, routine and nonroutine tasks, heuristic and metacognitive strategies, students’ beliefs, mathematical thinking and practices, resources, orientations, etc. are common terms used to explain, foster, and characterize students’ problem-solving behaviours and performances. Recently, the consistent use of digital technologies in educational tasks has extended the problem-solving language to include terms such as subjects’ tool appropriation, dynamic models, dragging or moving orderly objects, tracing loci, visual or empirical solution, ChatGPT prompts, etc.
3 On mathematical problem-solving foundations and the problematizing principle
There might be different ways to interpret and implement a problem-solving approach for students to understand concepts and to solve problems (Törner, Schoenfeld, & Reiss, 2007 ; Toh et al., 2023 ); nevertheless, there are common principles or tenets that distinguish and support a problem-solving teaching/learning environment. A salient feature in any problem-solving approach to learn mathematics is a conceptualization of the discipline that privileges and enhance the students’ development of mathematical practices or reasoning habits of mathematical thinking (Cuoco, et, al., 1996 ; Dick & Hollebrands, 2011 ; Schoenfeld, 2022 ). In this context, students need to conceptualize and think of their own learning as a set of dilemmas that are represented, explored, and solved in terms of mathematical resources and strategies (Santos-Trigo, 2023 ; Hiebert et al., 1996 ).
Furthermore, students’ problem-solving experiences and behaviours reflect and become a way of thinking that is consistent with mathematics practices and is manifested in terms of the activities they engage throughout all problem-solving phases. Thus, they privilege the development of mathematics habits such as to always look for different ways to model and explore mathematical problems, to formulate conjectures, and to search for arguments to support them, share problem solutions, defend their ideas, and to develop a proper language to communicate results. In terms of connecting ways of developing mathematical knowledge and the design of learning environments to develop mathematical thinking and problem-solving competencies, Polya ( 1945 ) identifies an inquiry approach for students to understand, make sense, and apply mathematical concepts. He illustrated the importance for students to pose and pursue different questions around four intertwined problem-solving phases: Understanding and making sense of the problem statement (what is the problem about? What data are provided? What is asked to find? etc.), the design of a solution plan (how the problem can be approached? ), the implementation of such plan (how the plan can be achieved? ), and the looking-back phase that involves reviewing the solution process (data used, checking the involved operations, consistency of units, and partial and global solution), generalizing the solution methods and posing new problems. Indeed, the looking-back phase involves the formulation of new or related problems (Toh et al., 2023 ). “For Pólya, mathematics was about inquiry; it was about sense making; it was about understanding how and why mathematical ideas fit together the ways they do” (cited in Schoenfeld, 2020 , p. 1167).
Likewise, the Nobel laureate I. I. Rabi mentioned that, when he came home from school, “while other mothers asked their kids ‘ Did you learn anything today ?’ [my mother] would say, ‘ Izzy, did you ask a good question today ?’” (Berger, 2014 , p.67).
Thus, the problematizing principle is key for students to engage in mathematical problem-solving activities, and it gets activated by an inquiry or inquisitive method that is expressed in terms of questions that students pose and pursue to delve into concepts meaning, representations, explorations, operations, and to work on mathematical tasks (Santos-Trigo, 2020a , b ).
4 The importance of mathematical tasks and the role of tools in problem-solving perspectives
In a problem-solving approach, learners develop a way of thinking to work on different types of tasks that involve a variety of context and aims (Cai & Hwang, 2023 ). A task might require students to formulate a problem from given information, to estimate how much water a family spend in one year, to prove a geometry theorem, to model genetic sequences or to understand the interplay between climate and geography. In this process, students identify mathematical resources, concepts, and strategies to model and explore partial and global solutions, and ways to extend solution methods and results. Furthermore, mathematical tasks or problems are essential for students to engage in mathematical practice and to develop problem-solving competencies. Task statements should be situated in different contexts including realistic, authentic, or mathematical domains, and prompts or questions to solve or respond or even provide information or data for students to formulate and solve their own problems (problem posing). Current events or problematic situations such as climate change, immigration, or pandemics not only are part of individuals concerns; but also, a challenge for teachers and students to model and analyze those complex problems through mathematics and others disciplines knowledge (English, 2023 ). Santos-Trigo ( 2019 ) proposed a framework to transform exercises or routine textbook problems into a series of nonroutine tasks in which students have an opportunity to dynamically model, explore, and extend, the initial problem. Here, the use of technology becomes important to explore the behavior of some elements within the model to find objects’ mathematical relationships. That is, students work on tasks in such a way that even routine problems become a starting point for them to engage in mathematical reflection to extend the initial nature of the task (Santos-Trigo & Reyes-Martínez, 2019 ). Recently, the emergence of tools such as the ChatGPT has confirmed the importance for learners to problematize situations, including complex problems, in terms of providing prompts or inputs that the tool processes and answers. Here, students analyze the tool’ responses and assess its pertinence to work and solve the task. Indeed, a way to use ChatGPT involves that students understand or make sense of the problem statement and pose questions (inputs or prompts) to ask the tool for concept information or ways to approach or solve the task. Then, students analyze the relevance, viability, and consistency of the tool’s answer and introduce new inputs to continue with the solution process or to look for another way to approach the task. Based on the ChatGPT output or task solution, students could always ask whether the tool can provide other ways to solve the task.
5 Main problem-solving research themes and results
In this section the focus will be on identifying certain problem-solving developments that have permeated recent directions of the field. One relates to the importance of extending research designs to analyse and characterize learners’ problem-solving process to work on different types of tasks. Another development involves ways in which theoretical advances in mathematics education have shaped the mathematical problem-solving research agenda and the extent to which regional or national educational systems or traditions influence the developments of conceptual frameworks in the field and ways to implement problem-solving activities within the corresponding system. Finally, research results in the field have provided directions to design and implement curriculum proposals around the world and these proposals have evolved in terms of both content structure and classroom dynamics including the use of digital technologies. Santos-Trigo ( 2023 ) stated that the teachers and students’ systematic use of digital technologies not only expands their ways of reasoning and solving mathematical problems; but also opens new research areas that aim to analyse the integration of several digital tools in curriculum proposals and learning scenarios. The focus of this review will be on presenting problem-solving directions and results in the last 9 years; however, it became relevant to identify and review what principles and tenets provided bases or foundations to support and define current research trends and directions in the field. That is, accumulated research that has contributed to advance and expand the problem-solving research agenda included shifts in the tools used to delve into learners’ problem approaches, the development of conceptual frameworks to explain and characterize students’ mathematical thinking, the tools used to work on mathematical tasks (from paper and pencil, ruler and compass or semiotic tools to digital apps), and in the design of curriculum proposals and the implementation of problem-solving learning scenarios.
5.1 Relevant shifts in problem-solving developments and results
Questions used to analyse important developments in the field include: What research designs and tools are used to foster and analyse learners’ problem-solving performances? How have conceptual frameworks evolved to pose and frame research questions in the field? How have accumulated research results in the field been used to support curriculum proposals and their implementation?
5.1.1 Methodological and research paradigms
Research designs in problem-solving studies have gradually moved from quantitative or statistical paradigms to qualitative perspectives that involve data collection from different sources such as task-based interviews, fieldnotes from observations, students’ written reports, etc. to analyse students’ problem-solving approaches and performances. Trustworthiness of results included triangulating and interpreting data sources from students’ videotapes transcriptions, outside observer notes, class observations, etc. (Stake, 2000 ). Hence, the work of Krutestkii ( 1976 ) was seminal in providing tools to delve into the students’ thinking while solving mathematical tasks. His research program aimed to study the nature and structure of children’ mathematical abilities. His methodological approach involved the use of student’s task-based interviews, teachers, and mathematicians’ questionaries to explore the nature of mathematical abilities, the analysis of eminent mathematicians and physicists regarding their nature and emergence of their talents and case studies of gifted children in mathematics. A major contribution of his research was the variety of mathematical tasks used to explore and analyse the mathematical abilities of school children. Recently, the mathematical problem-posing agenda has been revisited to advance conceptual frameworks to enhance the students’ formulation of problems to learn concepts and to develop problem-solving competencies (Cai et al., 2023 ). In general, the initial qualitative research tendency privileged case studies where individual students were asked to work on mathematical tasks to document their problem-solving performances. Later, research designs include the students’ participation in small groups and the analysis of students’ collaboration with the entire group (Brady et al., 2023 ). Bricolage frameworks that share tenets and information from different fields have become a powerful tool for researchers to understand complex people’ problem-solving proficiency (Lester, 2005 ; English, 2023 ).

5.1.2 Theoretical developments in mathematics education
In mathematics education, the constructivism perspective became relevant to orient and support research programs. Specifically, the recognition that students construct mathematical concepts and ideas through active participation as a part of a learning community that fosters and values what they bring into the classroom (eliciting students’ understanding) and sharing and discussing with peers their ways to work on mathematical activities. Further, it was recognized that students’ learning of mathematics takes place within a sociocultural environment (situated learning) that promotes the students’ interaction in small groups, pairs, and whole group discussions. Thus, problem-solving environments transited from teachers being a main figure to organize learning activities and to model problem-solving behaviours to being centred on students’ active participation to work on a variety of mathematical tasks as a part of a learning community (Lester & Cai, 2016 ). English ( 2023 ) proposed A STEM-based problem-solving framework that addresses the importance of a multidisciplinary approach and experiences to work on complex problems. Here, students develop a system of inquiry that integrates critical thinking, mathematical modelling, and a creative and innovative approach to deal with problematic situations situated in contexts beyond school problems. The STEM-based problem-solving framework enhances and favours the students’ development of multidisciplinary thinking to formulate and approach challenging problematic situations. To this end, they need to problematize information to characterize local and global problems and to collaboratively work on feasible approaches and solutions. It integrates 21st century skills that include an inquiry problem-solving approach to develop and exhibit critical thinking, creativity, and innovative solutions.
5.1.3 Countries or regional education traditions and their influence on the problem-solving agenda
The emergence of problem-solving frameworks takes place within an educational and socio-cultural context that provides conditions for their development and dissemination, but also limitations in their applications inside the mathematics education community. Brady et al. ( 2023 ) pointed out that:
…shifts in the theoretical frameworks of mathematics education researchers favored a widening of the view on problem solving from information-processing theories toward sociocultural theories that encouraged a conception of problem-solving as situated cognition unfolding within a community of practice (p. 34).
In addition, regional or national educational systems and research traditions also shape the problem-solving research and practice agenda. For example, in France, problem-solving approaches and research are framed in terms of two relevant theoretical and practical frameworks: Theory of Didactic Situation and the Anthropological Theory of Didactics (Artigue & Houdement, 2007 ). While, in the Netherlands, problem-solving approaches are situated within the theory of Realistic Mathematics that encourages and supports the students’ construction of meaning of concepts and methods in terms of modelling real-life and mathematical situations (Doorman et al., 2007 ). Ding et al. ( 2022 ) stated that the Chinese educational system refers to problem solving as an instructional goal and an approach to learn mathematics. Here, students deal with different types of problem-solving activities that include finding multiple solutions to one problem, one solution to multiple problems, and one problem multiple changes. Thus, ‘teaching with variation’ is emphasized in Chinese instruction in terms of “variations in solutions, presentations, and conditions/conclusions” (p. 482). Cai and Rott ( 2023 ) proposed a general problem-posing process model that distinguishes four problem-posing phases: Orientation (understanding the situation and what is required or is asked to pose); Connection that involves finding out or generating ideas and strategies to pose problems in different ways such as varying the given situation, or posing new problems; Generation refers to making the posed problem visible for others to understand it; and Reflection involves reflecting on her/his own process to pose the problem including ways to improve problem statements. The challenge in this model is to make explicit how the use of digital technologies can contribute to providing conditions for students to engage in all phases around problem- posing process.
5.1.4 Curriculum proposals and problem-solving teaching/learning scenarios
In the USA, the Common Core State Mathematics Standards curriculum proposal (CCSMS) identifies problem solving as a process standard that supports core mathematical practices that involve reasoning and proof, communication, representation, and connections. Thus, making sense of problems and persevering in solving them, reasoning abstractly and quantitatively, constructing viable arguments and critiquing the reasoning of others, modelling with mathematics, etc. are essential activities for students to develop mathematics proficiency and problem-solving approaches (Schoenfeld, 2023 ). In Singapore, the curriculum proposal identifies problem solving as the centre of its curriculum framework that relates its development with the study of concepts, skills, processes, attitudes, and metacognition (Lee et al., 2019 ). Recently, educational systems have begun to reform curriculum proposals to relate what the use of digital technologies demands in terms of selecting and structuring mathematical contents and ways to extend instructional settings (Engelbrecht & Borba, 2023 ). Indeed, Engelbrecht et al. ( 2023 ) identify what they call a classroom in movement or a distributed classroom - that transforms traditional cubic spaces to study the discipline into a movable setting that might combine remote and face-to-face students work.
It is argued that previous results in mathematical problem-solving research not only have contributed to recognize what is relevant and what common tenets distinguish and support problem-solving approaches; but also have provided bases to identify and pursue current problem-solving developments and directions. Hence, the consistent and coordinated use of several digital technologies and online developments (teaching and learning platforms) has opened new routes for learners to represent, explore, and work on mathematical problems; and to engage them in mathematical discussions beyond formal class settings. How does the students’ use of digital technologies expand the ways they reason and solve mathematical problems? What changes in classroom environments and physical settings are needed to recognize and include students’ face-to-face and remote work? (Engelbrecht et al., 2023 ).
In the next sections, the goal is to characterize the extent to which the consistent use of digital technologies and online developments provides affordances to restructure mathematical curriculum proposals and classrooms or learning settings and to enhance and expand students’ mathematical reasoning.
6 Current mathematical problem-solving trends and developments: the use of digital technologies
Although the use of technologies has been a recurrent theme in research studies, curriculum proposals, and teaching practices in mathematics education; during the COVID-pandemic lockdown, all teachers and students relied on digital technologies to work on mathematical tasks. At different phases, they developed and implemented not only novel paths to present, discuss, and approach teaching/learning activities; but also, ways to monitor and assess students’ problem-solving performances. When schools returned to teachers and students’ face-to-face activities, some questions emerged: What adjustments or changes in school practices are needed to consider and integrate those learning experiences that students developed during the social confinement? What digital tools should teachers and students use to work on mathematical tasks? How should teaching/learning practices reconcile students remote and face-to-face work? To address these questions, recent studies that involve ways to integrate technology in educational practices were reviewed, and their main themes and findings are organized and problematized to shed light on what the use of digital technologies contributes to frame and support learning environments.
6.1 The use of technology to reconceptualize students mathematical learning
There are different studies that document the importance and ways in which the students’ use of tools such as CAS or Excel offers an opportunity for them to think of concepts and problems in terms of different representations to transit from intuitive, visual, or graphic to formal or analytical reasoning (Arcavi et al., 2017 ). Others digital technologies, such as a Dynamic Geometry System Footnote 1 DGS, provide affordances for students to dynamically represent and explore mathematical problems. In students’ use of digital technologies, the problematizing principle becomes relevant to transform the tool into an instrument to work on mathematical tasks. Santos-Trigo ( 2019 ) provides examples where students rely on GeoGebra affordances to reconstruct figures that are given in problem statements; to transform routine problem into an investigation task; to model and explore tasks that involve variational reasoning; and to construct dynamic configurations to formulate and support mathematical relations. In this process, students not only exhibit diverse problem-solving strategies; but also, identify and integrate and use different concepts and resources that are studied in algebra, geometry, and calculus. That is, the use of technology provides an opportunity for students to integrate and connect knowledge from diverse areas or domains. For instance, Sinclair and Ferrara ( 2023 ) used the multi-touch application (TouchCounts) for children to work on mathematical challenging tasks.
6.2 The use of digital technologies to design a didactic route
There is indication, that the use of digital technologies offers different paths for students to learn mathematics (Leung & Bolite-Frant, 2015 ; Leung & Baccaglini-Frank, 2017 ). For instance, in the construction of a dynamic model of a problem, they are required to think of concepts and information embedded in the problem in terms of geometric representation or meaning. Thus, focusing on ways for students to represent and explore concepts geometrically could be the departure point to understand concepts and to solve mathematical problems. In addition, students can explore problems’ dynamic models (dragging schemes) in terms of visual, empirical, and graphic representations to initially identify relations that become relevant to approach and solve the problems. Thus, tool affordances become relevant for students to detect patterns, to formulate conjectures and to transit from empirical to formal argumentation to support problem solutions (Pittalis & Drijvers, 2023 ). Engelbrecht and Borba ( 2023 ) recognized that the prominent use of digital technologies in school mathematics has produced pedagogical shifts in teaching and learning practices to “encourage more active students learning, foster greater engagement, and provide more flexible access to learning’ (p. 1). Multiple use technologies such as internet, communication apps (ZOOM, Teams, Google Meet, etc.) become essential tools for teachers and students to present, communicate, and share information or to collaborate with peers. While tools used to represent, explore, and delve into concepts and to work and solve mathematical problems (Dynamic Geometry Systems, Wolframalpha, etc.) expand the students’ ways of reasoning and solving problems. Both types of technologies are not only important for teachers and students to continue working on school tasks beyond formal settings, but they also provide students with an opportunity to consult online resources such as Wikipedia or KhanAcademy to review or extend their concepts understanding, to analyse solved problems, and to contrast their teachers’ explanation of themes or concepts with those provided in learning platforms.
6.3 Students’ access to mathematics learning
Nowadays, cell phones are essential tools for people or students to interact or to approach diverse tasks and an educational challenge is how teachers/students can use them to work on mathematical tasks. During the COVID-19 social confinement, students relied on communication apps not only to interact with their teachers during class lectures; but also, to keep discussing tasks with peers beyond formal class meetings. That is, students realized that with the use of technology they could expand their learning space to include sharing and discussing ideas and problem solutions with peers beyond class sessions, consulting online learning platforms or material to review or extend their concepts understanding, and to watch videos to contrast experts’ concepts explanations and those provided by their teachers. In this perspective, the use of digital technologies increases the students’ access to different resources and the ways to work on mathematical tasks. Thus, available digital developments seem to extend the students collaborative work in addition to class activities. Furthermore, the flipped classroom model seems to offer certain advantages for students to learn the discipline and this model needs to be analysed in terms of what curriculum changes and ways to assess or monitor students learning are needed in its design and implementation (Cevikbas & Kaiser, 2022 ).
6.4 Changes in curriculum and mathematical assessment
It is recognized that the continuous development and availability of digital technologies is not only altering the ways in which individuals interact and face daily activities; but is also transforming educational practices and settings. Likewise, people’s concerns about multiple events or global problems such climate change, immigration, educational access, renewable resources, or racial conflicts or wars are themes that permeate the educational arena. Thus, curriculum reforms should address ways to connect students’ education with the analysis of these complex problems. English ( 2023 ) stated that:
The ill-defined problems of today, coupled with unexpected disruptions across all walks of life, demand advanced problem-solving by all citizens. The need to update outmoded forms of problem solving, which fail to take into account increasing global challenges, has never been greater (p.5).
In this perspective, mathematics curriculum needs to be structured around essential contents and habits of mathematical thinking for students to understand and make sense of real-world events that lead them to formulate, represent, and deal with a variety of problem situations. “Educators now increasingly seek to emphasise the practical applications of mathematics, such as modelling real-life scenarios and understanding statistical data (Engelbrecht & Borba, 2023 , p. 7). For instance, during the pandemic it was important to problematize the available data to follow, analyze and predict its spread behavior and to propose health measures to reduce people contagion. Thus, exponential functions, graphics, and their interpretations, data analysis, etc. were important mathematics content to understand the pandemic phenomena. Drijvers and Sinclair ( 2023 ) recognized that features of computational thinking share common grounds with mathematical thinking in terms of problem-solving activities that privilege model construction, the use of algorithms, abstraction processes and generalization of results. Thus, “a further integration of computational thinking in the mathematics curriculum is desirable”. In terms of ways to assess and monitor students’ learning, the idea is that with the use of a digital tool (digital wall or log), students could organize, structure, register, and monitor their individual and group work and learning experiences. That is, they could periodically report and share what difficulties they face to understand concepts or to work on a task, what questions they posed, what sources consult, etc. The information that appears in the digital wall is shared within the group and the teacher and students can provide feedback or propose new ideas or solutions (Santos-Trigo et al., 2022 ).
6.5 The integration of technologies and the emergence of conceptual frameworks
Institutions worldwide, in general, are integrating the use of different technologies in their educational practices, and they face the challenge to reconcile previous pandemic models and post confinement learning scenarios. “A pedagogical reason for using technology is to empower learners with extended or amplified abilities to acquire knowledge…technology can empower their cognitive abilities to reason in novice ways (Leung, 2011 , p. 327). Drijvers and Sinclair ( 2023 ) proposed a five-dimensional framework to delve into the rationale and purposes for the mathematics education community to integrate the use of digital technologies in mathematical teaching environments and students learning. The five interrelated categories address issues regarding how teachers and students’ use of digital technology contributes to reconceptualize and improve mathematics learning; to understand and explain how students’ mathematics learning develops; to design environments for mathematics learning; to foster and provide equitable access to mathematics learning; and to change mathematics curricula and teaching and assessment practices (Drijvers & Sinclair, 2023 ). Schoenfeld ( 2022 ) stated that “The challenge is to create robust learning environments that support every student in developing not only the knowledge and practices that underlie effective mathematical thinking, but that help them develop the sense of agency to engage in sense making” (p. 764). Højsted et al. ( 2022 ) argue about the importance of adjusting theoretical frameworks to explicitly integrate the use of digital technologies such as DGS and Computer Algebra Systems (CAS) in teaching practices. They referred to the Danish “Competencies and Mathematical Learning framework” (KOM) that gets articulated through tenets associated with the Theory of Instrumental Orchestration (TIO) and the notion of Justification Mediation (JM). In general terms, the idea is that learners get explicitly involved in a tool’ appropriation process that transforms the artifact into an instrument to understand concepts and to solve mathematical problems. That is, learners’ tool appropriation involves the development of cognitive schemata to rely on technology affordances to work on mathematical tasks. Koichu et al. ( 2022 ) pointed out that the incorporation of problem-solving approaches in instruction should be seen as a specific case of implementing innovation. To this end, they proposed a framework of problem-solving implementation chain that involves “a sequence of actions and interactions beginning with the development of a PS resource by researchers, which teachers then engage with in professional development (PD), and finally, teachers and students make use of in classrooms” (p. 4). In this case, problem-solving resources include the design of problematic situations (tasks) to engage students in mathematical discussions to make sense of problem statements or to ask them to pose a task.
7 Reflections and concluding remarks
Throughout different periods, the research and practice mathematical problem-solving agenda has contributed significantly to understand not only essentials in mathematical practices; but also, the development of conceptual frameworks to explain and document subjects’ cognitive, social, and affective behaviours to understand mathematical concepts and to develop problem-solving competencies. Leikin and Guberman ( 2023 ) pointed out that “…problem-solving is an effective didactical tool that allows pupils to mobilize their existing knowledge, construct new mathematical connections between known concepts and properties, and construct new knowledge in the process of overcoming challenges embedded in the problems” (p. 325). The study of people cognitive functioning to develop multidisciplinary knowledge and to solve problems involves documenting ways in which individuals make decisions regarding ways to organize their subject or disciplinary learning (how to interact with teachers or experts and peers; what material to consult, what tools to use, how to monitor their own learning, etc.) and to engage in disciplinary practices to achieve their learning goals. Both strategic and tactic decisions shape teachers and students’ ways to work on mathematical tasks. Kahneman ( 2011 ) shed light on how human beings make decisions to deal with questions and problematic situations. He argues that individuals rely on two systems to make decisions and engage in thinking processes; system one (fast thinking) that involves automatic, emotional, instinctive reasoning and system two (slow thinking) that includes logical, deliberative, effortful, or conscious reasoning. In educational tasks, the idea is that teachers and students develop experiences based on the construction and activation of system two. Thus, how teachers/students decide what tools or digital developments to use to work on mathematical problems becomes a relevant issue to address in the mathematics education agenda. Recent and consistent developments and the availability of digital technologies open novel paths for teachers and students to represent, explore, and approach mathematical tasks and, provide different tools to extend students and teachers’ mathematical discussions beyond classroom settings. In this perspective, it becomes important to discuss what changes the systematic use of digital technologies bring to the mathematics contents and to the ways to frame mathematical instruction. For example, the use of a Dynamic Geometry System to model and explore calculus, geometry or algebra classic problems dynamically not only offer students an opportunity to connect foundational concepts such as rate of change or the perpendicular bisector concept to geometrically study variational phenomena or conic sections; but also, to engage them in problem-posing activities (Santos-Trigo et al., 2021 ). Thus, teachers need to experience themselves different ways to use digital technologies to work on mathematical tasks and to identify instructional paths for students to internalize the use of digital apps as an instrument to understand concepts and to pose and formulate mathematical problems. Specifically, curriculum proposal should be structured around the development of foundational concepts and problem-solving strategies to formulate and pursue complex problems such as those involving climate changes, wealth distribution, immigration, pollution, mobility, connectivity, etc. To formulate and approach these problems, students need to develop a multidisciplinary thinking and rely on different tools to represent, explore, and share and continuously report partial solutions. To this end, they are encouraged to work with peers and groups as a part of learning community that fosters and values collective problem solutions. Finding multiple paths to solve problems becomes important for students to develop creative and innovative problem solutions (Leikin & Guberman, 2023 ). In this perspective, learning environments should provide conditions for students to transform digital applications in problem-solving tools to work on problematic situations. Online students’ assignments become an important component to structure and organize students and teachers’ face-to-face interactions. Likewise, the use of technology can also provide a tool for students to register and monitor their work and learning experiences. A digital wall or a problem-solving digital notebook (Santos-Trigo et al., 2022 ) could be introduced for students to register and monitor their learning experiences. Here, Students are asked to record on a weekly basis their work, questions, comments, and ideas that include: Questions they pose to understand concepts and problem statements; online resources and platforms they consult to contextualize problems and review and extend their understanding of involved concepts; concepts and strategies used to solve problems through different approaches; the Identification of other problems that can be solved with the methods that were used to solve the problem; digital technologies and online resources used to work on and solve the problem; dynamic models used to solve the problem and strategies used to identify and explore mathematical relations (dragging objects, measuring object attributes, tracing loci, using sliders, etc.; the formulation of new related problems including possible extensions for the initial problem; discussion of solutions of some new problems; and short recorded video presentation of their work and problem solutions. That is, the digital wall becomes an space for learners to share their work and to contrast and reflect on their peers work including extending their problem-solving approaches based on their teachers feedback and peers’ ideas or solutions.
The term Dynamic Geometry System is used, instead of Dynamic Geometry Environment or Dynamic Geometry Software, to emphasize that the app or tool interface encompasses a system of affordances that combines the construction of dynamic models, the use of Computer Algebra Systems and the use spreadsheet programs.
Arcavi, A., Drijvers, P., & Stacy, K. (2017). The learning and teaching of algebra. Ideas, insights, and activities . NY: Routledge. ISBN 9780415743723.
Artigue, M., & Houdement, C. (2007). Problem solving in France: Didactic and curricular perspectives. ZDM Int J Math Educ , 39 (5–6), 365–382. https://doi.org/10.1007/s11858-007-0048-x .
Article Google Scholar
Berger, W. (2014). A more beautiful question . Bloomsbury Publishing. Kindle Edition.
Brady, C., Ramírez, P., & Lesh, R. (2023). Problem posing and modeling: Confronting the dilemma of rigor or relevance. In T. L. Toh et al. (Eds.), Problem Posing and Problem Solving in Mathematics Education, pp: 33–50, Singapore: Springer. https://doi.org/10.1007/978-981-99-7205-0_3 .
Cai, J., & Hwang, S. (2023). Making mathematics challenging through problem posing in classroom. In R. Leikin (Ed.), Mathematical Challenges For All , Research in Mathematics Education, Springer: Switzerland, pp. 115–145, https://doi.org/10.1007/978-3-031-18868-8_7 .
Cai, J., & Rott, B. (2023). On understanding mathematical problem-posing processes. ZDM – Mathematics Education , 56 , 61–71. https://doi.org/10.1007/s11858-023-01536-w .
Cai, J., Hwang, S., & Melville, M. (2023). Mathematical problem-posing research: Thirty years of advances building on the publication of on mathematical problem solving. In J. Cai et al. (Eds.), Research Studies on Learning and Teaching of Mathematics, Research in Mathematics Education, Springer: Switzerland, pp: 1–25. https://doi.org/10.1007/978-3-031-35459-5_1 .
Cevikbas, M., & Kaiser, G. (2022). Can flipped classroom pedagogy offer promising perspectives for mathematics education on pan- demic-related issues? A systematic literature review. ZDM – Math- ematics Education . https://doi.org/10.1007/s11858-022-01388-w .
Cuoco, A., Goldenberg, E. P., & Mark, J. (1996). Habits of mind: An organizing principle for mathematics curricula. Journal of Mathematical Behavior , 15 , 375–402.
Devlin, K. (2002). The millennium problems. The seven greatest unsolved mathematical puzzles of our time . Granta.
Dick, T. P., & Hollebrands, K. F. (2011). Focus in high school mathematics: Technology to support reasoning and sense making . National Council of Teachers of Mathematics, NCTM: Reston Va. ISBN 978-0-87353-641-7.
Ding, M., Wu, Y., Liu, Q., & Cai, J. (2022). Mathematics learning in Chinese contexts. ZDM -Mathematics Education , 54 , 577–496. https://doi.org/10.1007/s11858-022-01385-z .
Doorman, M., Drijvers, P., Dekker, T., Van den Heuvel- Panhuizen, M., de Lange, J., & Wijers, M. (2007). Problem solving as a challenge for mathematics education in the Netherlands. ZDM Int J Math Educ , 39 (5–6), 405–418. https://doi.org/10.1007/s11858-007-0043-2 .
Drijvers, P., & Sinclair, N. (2023). The role of digital technologies in mathematics education: Purposes and perspectives. ZDM-Mathematics Education . https://doi.org/10.1007/s11858-023-01535-x .
Engelbrecht, J., & Borba, M. C. (2023). Recent developments in using digital technology in mathematics education. ZDM -Mathematics Education . https://doi.org/10.1007/s11858-023-01530-2 .
Engelbrecht, J., Borba, M. C., & Kaiser, G. (2023). Will we ever teach mathematics again in the way we used to before the pandemic? ZDM– Mathematics Education , 55 , 1–16. https://doi.org/10.1007/s11858-022-01460-5 .
English, L. D. (2023). Ways of thinking in STEM-based problem solving. ZDM -Mathematics Education . https://doi.org/10.1007/s11858-023-01474-7 .
English, L. D., & Kirshner, D. (Eds.). (2016). Handbook of international research in mathematics education . NY. ISBN: 978-0-203-44894-6 (ebk). https://www.routledge.com/Handbook-of-International-Research-in-Mathematics-Education/English-Kirshner/p/book/9780415832045
Fried, M. N. (2014). Mathematics & mathematics education: Searching for common ground. In M.N. Fried, T. Dreyfus (Eds.), Mathematics & Mathematics Education: Searching for 3 Common Ground , Advances in Mathematics Education, pp: 3–22. https://doi.org/10.1007/978-94-007-7473-5_1 . NY: Springer.
Halmos, P. (1980). The heart of mathematics. American Mathematical Monthly , 87 (7), 519–524.
Hiebert, J., Carpenter, T. P., Fennema, E., Fuson, K., Human, P., Murray, H., et al. (1996). Problem solving as a basis for reform in curriculum and instruction: The case of mathematics. Educational Researcher , 25 (4), 12–21.
Hilbert, D. (1902). Mathematical problems. Bulletin of the American Mathematical Society , 8 , 437–479.
Højsted, I. H., Geranius, E., & Jankvist, U. T. (2022). Teachers’ facilitation of students’ mathematical reasoning in a dynamic geometry environment: An analysis through three lenses. In U. T. Jankvist, & E. Geraniou (Eds.), Mathematical competencies in the Digital era (pp. 271–292). Springer. https://doi.org/10.1007/978-3-031-10141-0_15 .
Kahneman, D. (2011). Thinking, fast and slow . Farrar, Straus and Giroux.
Koichu, B. (2014). Problem solving in mathematics and in mathematics education. In M.N. Fried, T. Dreyfus (Eds.), Mathematics & Mathematics Education: Searching for 113 Common Ground , Advances in Mathematics Education, pp: 113–135. Dordrecht: Springer. https://doi.org/10.1007/978-94-007-7473-5_8 .
Koichu, B., Cooper, J., & Widder, M. (2022). Implementation of problem solving in school: From intended to experienced. Implementation and Replication Studies in Mathematics Education , 2 (1), 76–106. https://doi.org/10.1163/26670127-bja10004 .
Krutestkii, V. A. (1976). The psychology of mathematical abilities in school children . University of Chicago Press, Chicago. ISBN: 0-226-45492-4.
Lee, N. H., Ng, W. L., & Lim, L. G. P. (2019). The intended school mathematics curriculum. In T. L. Toh et al. (Eds.), Mathematics Education in Singapore , Mathematics Education – An Asian Perspective, pp: 35–53. https://doi.org/10.1007/978-981-13-3573-0_3 .
Leikin, R., & Guberman, R. (2023). Creativity and challenge: Task complexity as a function of insight and multiplicity of solutions. R. Leikin (Ed.), Mathematical Challenges For All , Research in Mathematics Education, pp: 325–342. https://doi.org/10.1007/978-3-031-18868-8_17 .
Lester, F. K. Jr. (1994). Musing about mathematical problem-solving research: 1970–1994. Journal for Research in Mathematics Education , 25 (6), 660–675.
Lester, F. K. Jr. (2005). On the theoretical, conceptual, and philosophical foundation for research in mathematics education. Zdm Mathematics Education , 37 (6), 457–467. https://doi.org/10.1007/BF02655854 .
Lester, F. K. Jr., & Cai, J. (2016). Can mathematical problem solving be taught? Preliminary answers from 30 years of research. In P. Felmer, et al. (Eds.), Posing and solving Mathematical problems, Research in Mathematics Education (pp. 117–135). Springer. https://doi.org/10.1007/978-3-319-28023-3_8 .
Leung, A. (2011). An epistemic model of task design in dynamic geometry environment. Zdm , 43 , 325–336. https://doi.org/10.1007/s11858-011-0329-2 .
Leung, A., & Baccaglini-Frank, A. (Eds.). (2017). (Eds.). Digital Technologies in Designing Mathematics Education Tasks, Mathematics Education in the Digital Era 8, https://doi.org/10.1007/978-3-319-43423-0_1 .
Leung, A., & Bolite-Frant, J. (2015). Designing mathematics tasks: The role of tools. In A. Watson, & M. Ohtani (Eds.), Task design in mathematics education (pp. 191–225). New ICMI Study Series. https://doi.org/10.1007/978-3-319-09629-2_6 .
Liljedahl, P., & Cai, J. (2021). Empirical research on problem solving and problem pos- ing: A look at the state of the art. ZDM — Mathematics Education , 53 (4), 723–735. https://doi.org/10.1007/s11858-021-01291-w .
Pittalis, M., & Drijvers, P. (2023). Embodied instrumentation in a dynamic geometry environment: Eleven-year‐old students’ dragging schemes. Educational Studies in Mathematics , 113 , 181–205. https://doi.org/10.1007/s10649-023-10222-3 .
Pólya, G. (1945).; 2nd edition, 1957). How to solve it . Princeton University Press.
Rott, B., Specht, B., & Knipping, C. (2021). A descritive phase model of problem-solving processes. ZDM -Mathematics Education , 53 , 737–752. https://doi.org/10.1007/s11858-021-01244-3 .
Santos-Trigo, M. (2019). Mathematical Problem Solving and the use of digital technologies. In P. Liljedahl and M. Santos-Trigo (Eds.). Mathematical Problem Solving. ICME 13 Monographs , ISBN 978-3-030-10471-9, ISBN 978-3-030-10472-6 (eBook), Springer Nature Switzerland AG. Pp. 63–89 https://doi.org/10.1007/978-3-030-10472-6_4 .
Santos-Trigo, M. (2020a). Problem-solving in mathematics education. In S. Lerman (Ed.), Encyclopedia of mathematics education (pp. 686–693). Springer. https://doi.org/10.1007/978-3-030-15789-0 .
Santos-Trigo, M. (2020b). Prospective and practicing teachers and the use of digital technologies in mathematical problem-solving approaches. In S. Llinares and O. Chapman (Eds.), International handbook of mathematics teacher education , vol 2, pp: 163–195. Boston: Brill Sense, ISBN 978-90-04-41896-7.
Santos-Trigo, M. (Ed.). (2023). Trends and developments of mathematical problem-solving research to update and support the use of digital technologies in post-confinement learning spaces. InT. L. Toh (Eds.), Problem Posing and Problem Solving in Mathematics Education , pp: 7–32. Springer Nature Singapore. https://doi.org/10.1007/978-981-99-7205-0_2 .
Santos-Trigo, M., & Reyes-Martínez, I. (2019). High school prospective teachers’ problem-solving reasoning that involves the coordinated use of digital technologies. International Journal of Mathematical Education in Science and Technology , 50 (2), 182–201. https://doi.org/10.1080/0020739X.2018.1489075 .
Santos-Trigo, M., Barrera-Mora, F., & Camacho-Machín, M. (2021). Teachers’ use of technology affordances to contextualize and dynamically enrich and extend mathematical problem-solving strategies. Mathematics , 9 (8), 793. https://doi.org/10.3390/math9080793 .
Santos-Trigo, M., Reyes-Martínez, I., & Gómez-Arciga, A. (2022). A conceptual framework to structure remote learning scenarios: A digital wall as a reflective tool for students to develop mathematics problem-solving competencies. Int J Learning Technology , 27–52. https://doi.org/10.1504/IJLT.2022.123686 .
Schoenfeld, A. H. (1992). Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics. In D. A. Grows (Ed.), Handbook of research on mathematics teaching and learning (pp. 334–370). Macmillan.
Schoenfeld, A. H. (2020). Mathematical practices, in theory and practice. ZDM Mathematics Education, 52, pp: 1163–1175. https://doi.org/10.1007/s11858-020-01162-w .
Schoenfeld, A. H. (2022). Why are learning and teaching mathematics so difficult? In M. Danesi (Ed.), Handbook of cognitive mathematics (pp. 1–35). Switzerland. https://doi.org/10.1007/978-3-030-44982-7_10-1%23DOI .
Schoenfeld, A. H. (2023). A theory of teaching. In A. K. Praetorius, & C. Y. Charalambous (Eds.), Theorizing teaching (pp. 159–187). Springer. https://doi.org/10.1007/978-3-031-25613-4_6 .
Sinclair, N., & Ferrara, F. (2023). Towards a Socio-material Reframing of Mathematically Challenging Tasks. In R. Leikin (Ed.), Mathematical Challenges For All , Research in Mathematics Education, pp: 307–323. https://doi.org/10.1007/978-3-031-18868-8_16 .
Stake, R. E. (2000). Case studies. In N. K. Denzin, & Y. S. Lincoln (Eds.), Handbook of qualitative research (pp. 435–454). Sage.
Thurston, P. W. (1994). On proof and progress in mathematics. Bull Amer Math Soc , 30 (2), 161–177.
Toh, T. L., Santos-Trigo, M., Chua, P. H., Abdullah, N. A., & Zhang, D. (Eds.). (2023). Problem posing and problem solving in mathematics education: Internationa research and practice trends . Springer Nature Singpore. https://doi.org/10.1007/978-981-99-7205-0 .
Törner, G., Schoenfeld, A. H., & Reiss, K. M. (Eds.). (2007). Problem solving around the world: Summing up the state of the art [Special Issue]. ZDM — Mathematics Education , 39 (5–6). https://doi.org/10.1007/s11858-007-0053-0 .
Download references
Author information
Authors and affiliations.
Centre for Research and Advanced Studies, Mathematics Education Department, Mexico City, Mexico
Manuel Santos-Trigo
You can also search for this author in PubMed Google Scholar
Corresponding author
Correspondence to Manuel Santos-Trigo .
Additional information
Publisher’s note.
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .
Reprints and permissions
About this article
Santos-Trigo, M. Problem solving in mathematics education: tracing its foundations and current research-practice trends. ZDM Mathematics Education 56 , 211–222 (2024). https://doi.org/10.1007/s11858-024-01578-8
Download citation
Accepted : 18 April 2024
Published : 30 April 2024
Issue Date : May 2024
DOI : https://doi.org/10.1007/s11858-024-01578-8
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Mathematical problem solving
- Conceptual frameworks
- Digital and semiotic tools-
- Mathematical reasoning
- Mathematics education developments
- Digital technologies
- Find a journal
- Publish with us
- Track your research
32 Examples of Real-World Math Problems

- • Published: April 23, 2024
- • Last update: June 14, 2024
- • Grades: All grades
Introduction

8th grade algebra problem:
Farmer Alfred has three times as many chickens as cows. In total, there are 60 legs in the barn. How many cows does Farmer Alfred have? [1]
Does this sound like a real-world math problem to you? We’ve got chickens, cows, and Farmer Alfred – it’s a scenario straight out of everyday life, isn’t it?
But before you answer, let me ask you something: If you wanted to figure out the number of cows, would you:
- Count their legs, or
- Simply count their heads ( or even just ask Farmer Alfred, “Hey Alfred, how many cows do you have?” )
Chances are, most people would go with option B.
So, why do our math books contain so many “real-world math problems” like the one above?
In this article, we’ll dive into what truly makes a math problem a real-world challenge.
Understanding 'Problems' in Daily Life and Mathematics
The word “problem” carries different meanings in everyday life and in the realm of mathematics, which can sometimes lead to confusion. In our daily lives, when we say “ I have a problem ,” we typically mean that something undesirable has occurred – something challenging to resolve or with potential negative consequences.
For instance:
- “I have a problem because I’ve lost my wallet.”
- “I have a problem because I forgot my keys at home, and I won’t be able to get into the house when I return from school.”
- “I have a problem because I was sick and missed a few weeks of school, which means I’ll likely fail my math test.”
These are examples of everyday problems we encounter. However, once the problem is solved, it often ceases to be a problem:
- “I don’t have a problem getting into my house anymore because my mom gave me her keys.”
In mathematics, the term “problem” takes on a different meaning. According to the Cambridge dictionary [2], it’s defined as “ a question in mathematics that needs an answer. “
Here are a few examples:
- If x + 2 = 4, what is the value of x?
- How do you find the common denominator for fractions 1/3 and 1/4?
- What is the length of the hypotenuse in a right triangle if two legs are 3 and 4 feet long?
These are all examples of math problems.
It’s important to note that in mathematics, a problem remains a problem even after it’s solved. Math problems are universal, regardless of who encounters them [3]. For instance, both John and Emma could face the same math problem, such as “ If x + 2 = 4, then what is x? ” After they solve it, it still remains a math problem that a teacher could give to somebody else.
Understanding Real-World Math Problems
So, what exactly is a “real-world math problem”? We’ve established that in our daily lives, we refer to a situation as a “problem” when it could lead to unpleasant consequences. In mathematics, a “problem” refers to a mathematical question that requires a mathematical solution.
With that in mind, we can define a real-world math problem as:
A situation that could have negative consequences in real life and that requires a mathematical solution (i.e. mathematical solution is preferred over other solutions).
Consider this example:

Could miscalculating the flour amount lead to less-than-ideal results? Absolutely. Messing up the flour proportion could result in a less tasty cake – certainly an unpleasant consequence.
Now, let’s explore the methods for solving this. While traditional methods, like visually dividing the flour or measuring multiple times, have their place, they may not be suitable for larger-scale events, such as catering for a wedding with 250 guests. In such cases, a mathematical solution is not only preferred but also more practical.
By setting up a simple proportion – 1 1/2 cups of flour for 8 people equals x cups for 20 people – we can quickly find the precise amount needed: 3 3/4 cups of flour. In larger events, like the wedding, the mathematical approach provides even more value, yielding a requirement of nearly 47 cups of flour.
This illustrates why a mathematical solution is faster, more accurate, and less error-prone, making it the preferred method. Coupled with the potential negative consequences of inaccuracies, this makes the problem a real-world one, showcasing the practical application of math in everyday scenarios.
Identifying Non-Real-World Math Problems
Let’s revisit the example from the beginning of this article:
Farmer Alfred has three times as many chickens as cows. In total, there are 60 legs in the barn. How many cows does Farmer Alfred have?
3rd grade basic arithmetic problem:
Noah has $56, and Olivia has 8 times less. How much money does Olivia have?

Once more, in our daily routines, do we handle money calculations this way? Why would one prefer to use mathematical solution ($56 : 8 =$7). More often than not, we’d simply ask Olivia how much money she has. While the problem can theoretically be solved mathematically, it’s much more practical, efficient, and reliable to resolve it by directly asking Olivia.
Examples like these are frequently found in math textbooks because they aid in developing mathematical thinking. However, the scenarios they describe are uncommon in real life and fail to explicitly demonstrate the usefulness of math. In essence, they don’t showcase what math can actually be used for. Therefore, there are two crucial aspects of true real-world math problems: they must be commonplace in real life, and they must explicitly illustrate the utility of math.
To summarize:
Word problems that are uncommon in real life and fail to convincingly demonstrate the usefulness of math are not real-world math problems.
Real-World Math Problems Across Professions
Many professions entail encountering real-world math problems on a regular basis. Consider the following examples:

Nurses often need to calculate accurate drug dosage amounts using proportions, a task solved through mathematical methods. Incorrect dosage calculations can pose serious risks to patient health, leading to potentially harmful consequences.
Construction engineers frequently need to determine whether a foundation will be sturdy enough to support a building, employing mathematical solving techniques and specialized formulas. Errors in these calculations can result in structural issues such as cracks in walls due to foundation deformation, leading to undesirable outcomes.

Marketers often rely on statistical analysis to assess the performance of online advertisements, including metrics like click-through rates and the geographical distribution of website visitors. Mathematical analysis guides decision-making in this area. Inaccurate analyses may lead to inefficient allocation of advertisement budgets, resulting in less-than-optimal outcomes.
These examples illustrate real-world math problems encountered in various professions. While there are numerous instances of such problems, they are often overlooked in educational settings. At DARTEF, we aim to bridge this gap by compiling a comprehensive list of real-world math problems, which we’ll explore in the following section.
32 Genuine Real-World Math Problems
In this section, we present 32 authentic real-world math problems from diverse fields such as safety and security, microbiology, architecture, engineering, nanotechnology, archaeology, creativity, and more. Each of these problems meets the criteria we’ve outlined previously. Specifically, a problem can be classified as a real-world math problem if:
- It is commonly encountered in real-life scenarios.
- It has the potential for undesirable consequences.
- A mathematical solution is preferable over alternative methods.
- It effectively illustrates the practical utility of mathematics.
All these problems stem from actual on-the-job situations, showcasing the application of middle and high school math in various professions.
Math Problems in Biology
Real-world math problems in biology often involve performing measurements or making predictions. Mathematics helps us understand various biological phenomena, such as the growth of bacterial populations, the spread of diseases, and even the reconstruction of ancient human appearances. Here are a couple of specific examples:
1. Reconstructing Human Faces Using Parallel and Perpendicular Lines:

Archeologists and forensic specialists often reconstruct human faces based on skeletal remains. They utilize parallel and perpendicular lines to create symmetry lines on the face, aiding in the recovery of facial features and proportions. Our article, “ Parallel and Perpendicular Lines: A Real-Life Example (From Forensics and Archaeology) ,” provides a comprehensive explanation and illustrates how the shape of the nose can be reconstructed using parallel and perpendicular lines, line segments, tangent lines, and symmetry lines.
2. Measuring Bacteria Size Using Circumference and Area Formulas:

Microbiology specialists routinely measure bacteria size to monitor and document their growth rates. Since bacterial shapes often resemble geometric shapes studied in school, mathematical methods such as calculating circumference or area of a circle are convenient for measuring bacteria size. Our article, “ Circumference: A Real-Life Example (from Microbiology) ,” delves into this process in detail.
Math Problems in Construction and Architecture
Real-world math problems are abundant in architecture and construction projects, where mathematics plays a crucial role in ensuring safety, efficiency, and sustainability. Here are some specific case studies that illustrate the application of math in these domains:
3. Calculating Central Angles for Safe Roadways:

Central angle calculations are a fundamental aspect of roadway engineering, particularly in designing curved roads. Civil engineers use these calculations to determine the degree of road curvature, which significantly impacts road safety and compliance with regulations. Mathematical concepts such as radius, degrees, arc length, and proportions are commonly employed by civil engineers in their daily tasks. Our article, “ How to Find a Central Angle: A Real-Life Example (from Civil Engineering) ,” provides further explanation and demonstrates the calculation of central angles using a real road segment as an example.
4. Designing Efficient Roof Overhang Using Trigonometry

Trigonometry is a powerful tool in architecture and construction, providing a simple yet effective way to calculate the sizes of building elements, including roof overhangs. For example, the tangent function is used to design the optimal length of a roof overhang that blocks the high summer sun while allowing the lower winter sun to enter . Our article, “ Tangent (Trigonometry): A Real-Life Example (From Architecture and Construction) ,” provides a detailed use case with two methods of calculation and also includes a worksheet.
5. Designing Efficient Roofs for Solar Panels Using Angle Geometry:

Mathematics plays a crucial role in architecture, aiding architects and construction engineers in designing energy-efficient building structures. For example, when considering the installation of solar panels on a building’s roof, understanding geometric properties such as adjacent and alternate angles is essential for maximizing energy efficiency . By utilizing mathematical calculations, architects can determine the optimal angle for positioning solar panels and reflectors to capture maximum sunlight. Our article, “ A Real-Life Example of How Angles are Used in Architecture ,” provides explanations and illustrations, including animations.
6. Precision Drilling of Oil Wells Using Trigonometry:

Petroleum engineers rely on trigonometric principles such as sines, cosines, tangents, and right-angle triangles to drill oil wells accurately. Trigonometry enables engineers to calculate precise angles and distances necessary for drilling vertical, inclined, and even horizontal wells. For instance, when drilling at an inclination of 30°, engineers can use trigonometry to calculate the vertical depth corresponding to each foot drilled horizontally. Our article, “ CosX: A Real-Life Example (from Petroleum Engineering) ,” provides examples, drawings of right triangle models, and necessary calculations.
7. Calculating Water Flow Rate Using Composite Figures:

Water supply specialists frequently encounter the task of calculating water flow rates in water canals, which involves determining the area of composite figures representing canal cross-sections . Many canal cross-sections consist of composite shapes, such as rectangles and triangles. By calculating the areas of these individual components and summing them, specialists can determine the total cross-sectional area and subsequently calculate the flow rate of water. Our article, “ Area of Composite Figures: A Real-Life Example (from Water Supply) ,” presents necessary figures, cross-sections, and an example calculation.
Math Problems in Business and Marketing
Mathematics plays a crucial role not only in finance and banking but also in making informed decisions across various aspects of business development, marketing analysis, growth strategies, and more. Here are some real-world math problems commonly encountered in business and marketing:
8. Analyzing Webpage Position in Google Using Polynomials and Polynomial Graphs:

Polynomials and polynomial graphs are essential tools for data analysis. They are useful for a wide variety of people, not only data analysts, but literally everyone who ever uses Excel or Google Sheets. Our article, “ Graphing Polynomials: A Real-World Example (from Data Analysis) ,” describes this and provides an authentic case study. The case study demonstrates how polynomials, polynomial functions of varying degrees, and polynomial graphs are used in internet technologies to analyze the visibility of webpages in Google and other search engines.”
9. Making Informed Business Development Decisions Using Percentages:

In business development, math problems often revolve around analyzing growth and making strategic decisions. Understanding percentages is essential, particularly when launching new products or services. For example, determining whether a startup should target desktop computer, smartphone, or tablet users for an app requires analyzing installation percentages among user groups to gain insights into consumer behavior. Math helps optimize marketing efforts, enhance customer engagement, and drive growth in competitive markets. Check out our article “ A Real-Life Example of Percent Problems in Business ” for a detailed description of this example.
10. Analyzing Customer Preferences Using Polynomials:

Marketing involves not only creative advertising but also thorough analysis of customer preferences and marketing campaigns. Marketing specialists often use simple polynomials for such analysis, as they help analyze multiple aspects of customer behavior simultaneously. For instance, marketers may use polynomials to determine whether low price or service quality is more important to hotel visitors. Smart analysis using polynomials enables businesses to make informed decisions. If you’re interested in learning more, our article “ Polynomials: A Real Life Example (from Marketing) ” provides a real-world example from the hotel industry.
11. Avoiding Statistical Mistakes Using Simpson’s Paradox:

Data gathering and trend analysis are essential in marketing, but a good understanding of mathematical statistics helps avoid intuitive mistakes . For example, consider an advertising campaign targeting Android and iOS users. Initial data may suggest that iOS users are more responsive. However, a careful statistical analysis, as described in our article “ Simpson’s Paradox: A Real-Life Example (from Marketing) ,” may reveal that Android users, particularly tablet users, actually click on ads more frequently. This contradiction highlights the importance of accurate statistical interpretation and the careful use of mathematics in decision-making.
Math Problems in Digital Agriculture
In the modern era, agriculture is becoming increasingly digitalized, with sensors and artificial intelligence playing vital roles in farm management. Mathematics is integral to this digital transformation, aiding in data analysis, weather prediction, soil parameter measurement, irrigation scheduling, and more. Here’s an example of a real-world math problem in digital agriculture:
12. Combatting Pests with Negative Numbers:

Negative numbers are utilized in agriculture to determine the direction of movement, similar to how they’re used on a temperature scale where a plus sign indicates an increase and a minus sign indicates a decrease. In agricultural sensors, plus and minus signs may indicate whether pests are moving towards or away from plants. For instance, a plus sign could signify movement towards plants, while a minus sign indicates movement away from plants. Understanding these directional movements helps farmers combat pests effectively. Our article, “ Negative Numbers: A Real-Life Example (from Agriculture) ,” provides detailed explanations and examples of how negative numbers are applied in agriculture.
Math Problems in DIY Projects
In do-it-yourself (DIY) projects, mathematics plays a crucial role in measurements, calculations, and problem-solving. Whether you’re designing furniture, planning home renovations, crafting handmade gifts, or landscaping your garden, math provides essential tools for precise measurements, material estimations, and budget management. Here’s an example of a real-world math problem in DIY:
13. Checking Construction Parts for Right Angles Using the Pythagorean Theorem:

The converse of the Pythagorean theorem allows you to check whether various elements – such as foundations, corners of rooms, garage walls, or sides of vegetable patches – form right angles. This can be done quickly using Pythagorean triples like 3-4-5 or 6-8-10, or by calculating with square roots. This method ensures the creation of right angles or verifies if an angle is indeed right. Our article, “ Pythagorean Theorem Converse: A Real-Life Example (from DIY) ,” explains this concept and provides an example of how to build a perfect 90° foundation using the converse of the Pythagorean theorem.
Math Problems in Entertainment and Creativity
Mathematics plays a surprisingly significant role in the creative industries, including music composition, visual effects creation, and computer graphic design. Understanding and applying mathematical concepts is essential for producing engaging and attractive creative works. Here’s an example of a real-world math problem in entertainment:
14. Controlling Stage Lamps with Linear Functions:

Linear and quadratic functions are essential components of the daily work of lighting specialists in theaters and event productions. These professionals utilize specialized software and controllers that rely on algorithms based on mathematical functions. Linear functions, in particular, are commonly used to control stage lamps, ensuring precise and coordinated lighting effects during performances. Our article, “ Linear Function: A Real-Life Example (from Entertainment) ,” delves into this topic in detail, complete with animations that illustrate how these functions are applied in practice.
Math Problems in Healthcare
Mathematics plays a crucial role in solving numerous real-world problems in healthcare, ranging from patient care to the design of advanced medical devices. Here are several examples of real-world math problems in healthcare:
15. Calculating Dosage by Converting Time Units:

Nurses frequently convert between hours, minutes, and seconds to accurately administer medications and fluids to patients. For example, if a patient requires 300mL of fluid over 2.5 hours, nurses must convert hours to minutes to calculate the appropriate drip rate for an IV bag. Understanding mathematical conversions and solving proportions are essential skills in nursing. Check out our article, “ Converting Hours to Minutes: A Real-Life Example (from Nursing) ,” for further explanation.
16. Predicting Healthcare Needs Using Quadratic Functions:

Mathematical functions, including quadratic functions, are used to make predictions in public health. These predictions are vital for estimating the need for medical services, such as psychological support following traumatic events. Quadratic functions can model trends in stress symptoms over time, enabling healthcare systems to anticipate and prepare for increased demand. Our article, “ Parabola Equation: A Real-Life Example (from Public Health) ,” provides further insights and examples.
17. Predicting Healthcare Needs Using Piecewise Linear Functions:

Piecewise linear functions are useful for describing real-world trends that cannot be accurately represented by other functions. For instance, if stress symptoms fluctuate irregularly over time, piecewise linear functions can define periods of increased and decreased stress levels. Our article, “ Piecewise Linear Function: A Real-Life Example (From Public Health) ,” offers an example of how these functions are applied.
18. Designing Medical Prostheses Using the Pythagorean Theorem:

The Pythagorean theorem is applied in the design of medical devices , particularly prostheses for traumatic recovery. Components of these devices often resemble right triangles, allowing engineers to calculate movement and placement for optimal patient comfort and stability during rehabilitation. For a detailed explanation and animations, see our article, “ The 3-4-5 Triangle: A Real-Life Example (from Mechatronics) .”
19. Illustrating Disease Survival Rates Using Cartesian Coordinate Plane:

In medicine, Cartesian coordinate planes are utilized for analyzing historical data, statistics, and predictions. They help visualize relationships between independent and dependent variables, such as survival rates and diagnostic timing in diseases like lung cancer. Our article, “ Coordinate Plane: A Real-Life Example (from Medicine) ,” offers a detailed exploration of this concept, including analyses for both non-smoking and smoking patients.
Math Problems in Industry
Mathematics plays a vital role in solving numerous real-world problems across various industries. From designing industrial robots to analyzing production quality and planning logistics, math is indispensable for optimizing processes and improving efficiency. Here are several examples of real-world math problems in industry:
20. Precise Movements of Industrial Robots Using Trigonometry:

Trigonometry is extensively utilized to direct and control the movements of industrial robots. Each section of an industrial robot can be likened to a leg or hypotenuse of a right triangle, allowing trigonometry to precisely control the position of the robot head. For instance, if the robot head needs to move 5 inches to the right, trigonometry enables calculations to ensure each section of the robot moves appropriately to achieve the desired position. For detailed examples and calculations, refer to our article, “ Find the Missing Side: A Real-life Example (from Robotics) .”
21. Measuring Nanoparticle Size via Cube Root Calculation:

Mathematics plays a crucial role in nanotechnology, particularly in measuring the size of nanoparticles. Cube roots are commonly employed to calculate the size of cube-shaped nanoparticles. As nanoparticles are extremely small and challenging to measure directly, methods in nanotechnology determine nanoparticle volume, allowing for the calculation of cube root to determine the size of the nanoparticle cube side. Check out our article, “ Cube Root: A Real-Life Example (from Nanotechnology) ,” for explanations, calculations, and insights into the connection between physics and math.
22. Understanding Human Emotions Using Number Codes for Robots:

Mathematics is employed to measure human emotions effectively, which is essential for building smart robots capable of recognizing and responding to human emotions. Each human emotion can be broken down into smaller features, such as facial expressions, which are assigned mathematical codes to create algorithms for robots to recognize and distinguish emotions. Explore our article, “ Psychology and Math: A Real-Life Example (from Smart Robots) ,” to understand this process and its connection to psychology.
23. Systems of Linear Equations in Self-Driving Cars:

In the automotive industry, mathematics is pivotal for ensuring the safety and efficiency of self-driving cars. Systems of linear equations are used to predict critical moments in road safety, such as when two cars are side by side during an overtaking maneuver. By solving systems of linear equations, self-driving car computers can assess the safety of overtaking situations. Our article, “ Systems of Linear Equations: A Real-Life Example (from Self-Driving Cars) ,” provides a comprehensive explanation, including animated illustrations and interactive simulations, demonstrating how linear functions and equations are synchronized with car motion.
Math Problems in Information Technology (IT)
Mathematics serves as a fundamental tool in the field of information technology (IT), underpinning various aspects of software development, cybersecurity, and technological advancements. Here are some real-world math problems encountered in IT:
24. Selecting the Right Word in Machine Translation Using Mathematical Probability:

Theoretical probability plays a crucial role in AI machine translation systems, such as Google Translate, by aiding in the selection of the most appropriate words. Words often have multiple translations, and theoretical probability helps analyze the frequency of word appearances in texts to propose the most probable translation. Dive deeper into this topic in our article, “ Theoretical Probability: A Real-Life Example (from Artificial Intelligence) .”
25. Creating User-Friendly Music Streaming Websites Using Mathematical Probability:

Probability is utilized in user experience (UX) design to enhance the usability of digital products , including music streaming websites. Recommendation algorithms calculate theoretical probability to suggest songs that users are likely to enjoy, improving their overall experience. Learn more about this application in our article, “ Theoretical Probability: A Real-Life Example (from Digital Design) .”
26. Developing Realistic Computer Games with Vectors:

Mathematics is essential in animating objects and simulating real-world factors in computer games. Vectors enable game developers to incorporate realistic elements like gravity and wind into the gaming environment. By applying vector addition, developers can accurately depict how external forces affect object trajectories, enhancing the gaming experience. Explore this concept further in our article, “ Parallelogram Law of Vector Addition: A Real-Life Example (from Game Development) .”
27. Detecting Malicious Bots in Social Media Using Linear Inequalities:

Mathematical inequalities are valuable tools in cybersecurity for identifying malicious activity on social media platforms. By analyzing behavioral differences between real users and bots—such as friend count, posting frequency, and device usage—cybersecurity experts can develop algorithms to detect and block suspicious accounts. Discover more about this application in our article, “ How to Write Inequalities: A Real-life Example (from Social Media) .”
28. Increasing Computational Efficiency Using Algebraic and Rational Expressions

Algebraic and rational expressions are crucial in computer technology for increasing computational efficiency . Every step in a computer program’s algorithm requires valuable time and energy for execution. This is especially important for programs used in various safety and security systems. Simplifying these expressions helps boost computational performance. Our article, “ Algebraic and Rational Expressions: A Real-Life Example (from Computer Technology) ,” explains this in detail.
Math Problems in Legal Issues
In legal proceedings, mathematics plays a crucial role in analyzing data and making informed decisions. Here’s a real-world math problem encountered in legal work:
29. Proving the Reliability of Technology in Court Using Percentages:

In certain court cases, particularly those involving new technologies like autonomous cars, lawyers may need to employ mathematical methods to justify evidence. Percentage analysis can be utilized to assess the reliability of technology in court. For instance, in cases related to self-driving cars, lawyers may compare the percentage of errors made by autonomous vehicles with those made by human drivers to determine the technology’s safety. Delve deeper into this topic in our article, “ Solving Percent Problems: A Real-Life Example (from Legal) .”
Math Problems in Safety and Security
In the realm of safety and security, mathematics plays a vital role in protecting people, nature, and assets. Real-world math problems in this field can involve reconstructing crime scenes, analyzing evidence, creating effective emergency response plans, and predicting and responding to natural disasters. Here are two examples:
30. Reconstructing a Crime Scene with Inverse Trigonometry:

Forensic specialists rely on mathematical methods, such as inverse trigonometry, to uncover details of crimes long after they’ve occurred. Inverse trigonometric functions like arcsin, arccos, and arctan enable forensic specialists to calculate precise shooting angles or the trajectory of blood drops at crime scenes. Dive into this topic in our article, “ Arctan: A Real-Life Example (from Criminology) .”
31. Responding to Wildfires with Mathematical Variables:

Variables in mathematical language are also prevalent in real-world scenarios like firefighting. For instance, when dealing with wildfires, independent variables like forest type, wind speed and direction, rainfall, and terrain slope influence fire spread speed (dependent variable) . By utilizing specialized formulas incorporating these variables, fire protection specialists can accurately predict fire paths and optimize firefighting efforts. Explore this practical application in our article, “ Dependent and Independent Variables: A Real-Life Example (from Fire Protection) .”
Math Problems in Weather and Climate
In the realm of weather and climate, mathematics is crucial for creating mathematical models of Earth’s atmosphere, making weather forecasts, predicting weather patterns, and assessing long-term climate trends. Here’s an example:
32. Forecasting Thunderstorms with Negative Numbers:

Negative numbers play a significant role in forecasting thunderstorms. The probability of thunderstorms is closely tied to the temperature differences between air masses in the atmosphere. By subtracting negative numbers (representing temperature values) and analyzing the results, meteorologists can forecast the likelihood of thunderstorms based on the temperature differentials. Dive deeper into this concept in our article, “ Subtracting Negative Numbers: A Real-Life Example (from Weather Forecast). “
Conclusions
Many students perceive math as disconnected from the real world, leading them to question its relevance. Admittedly, maintaining this relevance is no easy feat—it requires collective effort. Farmer Alfred can’t tackle this challenge alone. However, introducing more real-world math examples into the school curriculum is a crucial step. Numerous studies have demonstrated that such examples significantly enhance students’ motivation to learn math. Our own pilot tests confirm this, showing that a clear connection between real-world problems and math education profoundly influences how young people view their future careers.
Therefore, to increase the overall relevance of math education and motivate students, we must prioritize the integration of real-world examples into our teaching practices. At DARTEF, we are dedicated to this cause, striving to bring authenticity to mathematics education worldwide.
- Vos, Pauline. ““How real people really need mathematics in the real world”—Authenticity in mathematics education.” Education Sciences 8.4 (2018): 195.
- Cambridge dictionary, Meaning of problem in English.
- Reif, Frederick. Applying cognitive science to education: Thinking and learning in scientific and other complex domains . MIT press, 2008.
Privacy Overview
What real-life math topic interests you.
Interested in seeing how a specific math topic is applied in the real world?
Let us know your preferred topic, and we’ll create a blog post and video showcasing its practical applications.
If you’d like, you can also let us know which real-world domain you’d like us to explore!
Please ensure that your password is at least 8 characters and contains each of the following:
- a special character: @$#!%*?&
Want Better Math Grades?
✅ Unlimited Solutions
✅ Step-by-Step Answers
✅ Available 24/7
➕ Free Bonuses ($1085 value!)
On this page
- Search IntMath
- Math interactives
- About (site info)
- Uses of Trignometry
- ASCIIMath input, KaTeX output
- ASCIIMath input, LaTeX and KaTeX output
- Send Math in emails
- Syntax for ASCIIMathML
- Math Display Experiments
- Scientific Notebook
Math Problem Solver
Related Sections
Math Tutoring
Need help? Chat with a tutor anytime, 24/7.

This tool combines the power of mathematical computation engine that excels at solving mathematical formulas with the power of artificial intelligence large language models to parse and generate natural language answers. This creates a math problem solver that's more accurate than ChatGPT, more flexible than a math calculator, and provides answers faster than a human tutor.
Sign up for free here .
Problem Solver Subjects
Our math problem solver that lets you input a wide variety of math math problems and it will provide a step by step answer. This math solver excels at math word problems as well as a wide range of math subjects.
- Math Word Problems
- Pre-Algebra
- Geometry Graphing
- Trigonometry
- Precalculus
- Finite Math
- Linear Algebra
Here are example math problems within each subject that can be input into the calculator and solved. This list is constanstly growing as functionality is added to the calculator.
Basic Math Solutions
Below are examples of basic math problems that can be solved.
- Long Arithmetic
- Rational Numbers
- Operations with Fractions
- Ratios, Proportions, Percents
- Measurement, Area, and Volume
- Factors, Fractions, and Exponents
- Unit Conversions
- Data Measurement and Statistics
- Points and Line Segments
Math Word Problem Solutions
Math word problems require interpreting what is being asked and simplifying that into a basic math equation. Once you have the equation you can then enter that into the problem solver as a basic math or algebra question to be correctly solved. Below are math word problem examples and their simplified forms.
Word Problem: Rachel has 17 apples. She gives some to Sarah. Sarah now has 8 apples. How many apples did Rachel give her?
Simplified Equation: 17 - x = 8
Word Problem: Rhonda has 12 marbles more than Douglas. Douglas has 6 marbles more than Bertha. Rhonda has twice as many marbles as Bertha has. How many marbles does Douglas have?
Variables: Rhonda's marbles is represented by (r), Douglas' marbles is represented by (d) and Bertha's marbles is represented by (b)
Simplified Equation: {r = d + 12, d = b + 6, r = 2 �� b}
Word Problem: if there are 40 cookies all together and Angela takes 10 and Brett takes 5 how many are left?
Simplified: 40 - 10 - 5
Pre-Algebra Solutions
Below are examples of Pre-Algebra math problems that can be solved.
- Variables, Expressions, and Integers
- Simplifying and Evaluating Expressions
- Solving Equations
- Multi-Step Equations and Inequalities
- Ratios, Proportions, and Percents
- Linear Equations and Inequalities
Algebra Solutions
Below are examples of Algebra math problems that can be solved.
- Algebra Concepts and Expressions
- Points, Lines, and Line Segments
- Simplifying Polynomials
- Factoring Polynomials
- Linear Equations
- Absolute Value Expressions and Equations
- Radical Expressions and Equations
- Systems of Equations
- Quadratic Equations
- Inequalities
- Complex Numbers and Vector Analysis
- Logarithmic Expressions and Equations
- Exponential Expressions and Equations
- Conic Sections
- Vector Spaces
- 3d Coordinate System
- Eigenvalues and Eigenvectors
- Linear Transformations
- Number Sets
- Analytic Geometry
Trigonometry Solutions
Below are examples of Trigonometry math problems that can be solved.
- Algebra Concepts and Expressions Review
- Right Triangle Trigonometry
- Radian Measure and Circular Functions
- Graphing Trigonometric Functions
- Simplifying Trigonometric Expressions
- Verifying Trigonometric Identities
- Solving Trigonometric Equations
- Complex Numbers
- Analytic Geometry in Polar Coordinates
- Exponential and Logarithmic Functions
- Vector Arithmetic
Precalculus Solutions
Below are examples of Precalculus math problems that can be solved.
- Operations on Functions
- Rational Expressions and Equations
- Polynomial and Rational Functions
- Analytic Trigonometry
- Sequences and Series
- Analytic Geometry in Rectangular Coordinates
- Limits and an Introduction to Calculus
Calculus Solutions
Below are examples of Calculus math problems that can be solved.
- Evaluating Limits
- Derivatives
- Applications of Differentiation
- Applications of Integration
- Techniques of Integration
- Parametric Equations and Polar Coordinates
- Differential Equations
Statistics Solutions
Below are examples of Statistics problems that can be solved.
- Algebra Review
- Average Descriptive Statistics
- Dispersion Statistics
- Probability
- Probability Distributions
- Frequency Distribution
- Normal Distributions
- t-Distributions
- Hypothesis Testing
- Estimation and Sample Size
- Correlation and Regression
Finite Math Solutions
Below are examples of Finite Math problems that can be solved.
- Polynomials and Expressions
- Equations and Inequalities
- Linear Functions and Points
- Systems of Linear Equations
- Mathematics of Finance
- Statistical Distributions
Linear Algebra Solutions
Below are examples of Linear Algebra math problems that can be solved.
- Introduction to Matrices
- Linear Independence and Combinations
Chemistry Solutions
Below are examples of Chemistry problems that can be solved.
- Unit Conversion
- Atomic Structure
- Molecules and Compounds
- Chemical Equations and Reactions
- Behavior of Gases
- Solutions and Concentrations
Physics Solutions
Below are examples of Physics math problems that can be solved.
- Static Equilibrium
- Dynamic Equilibrium
- Kinematics Equations
- Electricity
- Thermodymanics
Geometry Graphing Solutions
Below are examples of Geometry and graphing math problems that can be solved.
- Step By Step Graphing
- Linear Equations and Functions
- Polar Equations
Looking for the old Mathway Calculator? We've moved it to here .
Tips, tricks, lessons, and tutoring to help reduce test anxiety and move to the top of the class.
Email Address Sign Up

Problem Solving
Ai generator.
Problem solving is a crucial skill in both personal and professional settings. Whether it’s addressing a personal challenge or drafting a business problem solving proposal , the ability to identify a problem and develop a solution is essential. Writing a problem solving essay helps articulate the issue clearly and systematically outline potential solutions. Effective problem and solution involves critical thinking, creativity, and a structured approach to overcome obstacles and achieve goals.
What is Problem Solving?
Problem solving is the process of identifying a challenge, analyzing its components, and finding an effective solution. It involves critical thinking, creativity, and the application of various techniques and tools.
Examples of Problem Solving

- Analytical Thinking : Breaking down complex problems into manageable parts.
- Creativity : Developing innovative solutions to problems.
- Critical Thinking : Evaluating information and arguments to make a reasoned decision.
- Decision-Making : Choosing the best course of action from various alternatives.
- Research : Gathering relevant information to understand and solve a problem.
- Communication : Clearly conveying ideas and solutions to others.
- Collaboration : Working effectively with others to solve problems.
- Time Management : Prioritizing tasks to efficiently address problems.
- Adaptability : Adjusting strategies as new information or challenges arise.
- Attention to Detail : Ensuring all aspects of a problem are considered.
- Logical Reasoning : Using logic to identify solutions and predict outcomes.
- Empathy : Understanding others’ perspectives to create more effective solutions.
- Negotiation : Finding mutually acceptable solutions through discussion.
- Conflict Resolution : Addressing and resolving disagreements.
- Patience : Remaining calm and persistent when solving complex problems.
- Organization : Structuring tasks and information systematically.
- Leadership : Guiding and motivating a team to solve problems.
- Decision Analysis : Evaluating the potential impact of different solutions.
- Project Management : Planning and executing solutions effectively.
- Technical Skills : Using specialized knowledge to solve technical problems.
- Customer Service : Resolving customer issues effectively and efficiently.
- Risk Management : Identifying and mitigating potential problems.
- Innovation : Implementing new ideas to solve existing problems.
- Strategic Planning : Developing long-term solutions and plans.
- Resourcefulness : Finding quick and clever ways to overcome difficulties.
- Stress Management : Handling pressure while solving problems.
- Observation : Noticing subtle details that could be key to solving a problem.
- Data Analysis : Interpreting data to inform problem-solving decisions.
- Flexibility : Being open to new approaches and changing plans when necessary.
- Self-Assessment : Reflecting on your own problem-solving process to improve future performance.
Problem-Solving Examples for Students
1. math word problems.
Problem: Jane has 3 apples, and she buys 4 more apples from the store. How many apples does she have now?
- Understand the problem: Jane starts with 3 apples and buys 4 more.
- Break it down: 3 apples (initial) + 4 apples (additional).
- Solve: 3 + 4 = 7.
- Answer: Jane has 7 apples.
2. Group Project Coordination
Problem: A group of students needs to complete a science project, but they are having trouble coordinating their schedules.
- Understand the problem: The main issue is scheduling conflicts.
- Break it down: Identify each member’s available times.
- Research: Use tools like Doodle or Google Calendar to find common free times.
- Brainstorm solutions: Propose meeting during lunch breaks or weekends.
- Evaluate: Choose the most convenient and feasible option for everyone.
- Develop an action plan: Set a recurring meeting time and delegate tasks.
- Implement: Start meeting and working on the project according to the plan.
- Monitor and review: Adjust schedules if conflicts arise and keep track of progress.
3. Essay Writing
Problem: A student struggles to start writing an essay on a given topic.
- Understand the problem: The difficulty is starting the essay.
- Break it down: Identify the essay topic, main points, and required structure.
- Research: Gather information and resources related to the topic.
- Brainstorm solutions: Create an outline, jot down ideas, and decide on the thesis statement.
- Evaluate: Choose the most compelling points and organize them logically.
- Develop an action plan: Write a draft based on the outline, then revise and edit.
- Implement: Begin writing the introduction, followed by the body paragraphs and conclusion.
- Monitor and review: Proofread the essay and make necessary corrections.
4. Time Management
Problem: A student has trouble managing time between homework, extracurricular activities, and leisure.
- Understand the problem: The issue is balancing multiple responsibilities.
- Break it down: Identify all tasks and time commitments.
- Research: Look for time management techniques and tools.
- Brainstorm solutions: Use planners, to-do lists, or apps like Trello or Todoist.
- Evaluate: Choose the most effective tool and technique.
- Develop an action plan: Create a weekly schedule, prioritizing tasks by importance and deadlines.
- Implement: Follow the schedule and adjust as necessary.
- Monitor and review: Reflect on the effectiveness of the schedule and make improvements.
5. Conflict Resolution
Problem: Two students have a disagreement over a shared locker space.
- Understand the problem: The conflict is about sharing limited space.
- Break it down: Identify each student’s concerns and needs.
- Research: Look into conflict resolution strategies.
- Brainstorm solutions: Propose solutions like dividing the locker into specific sections or creating a rotation schedule.
- Evaluate: Choose the fairest and most practical solution.
- Develop an action plan: Agree on the solution and set guidelines.
- Implement: Follow the agreed plan and make adjustments if needed.
- Monitor and review: Ensure both students are satisfied with the arrangement and resolve any further issues.
Problem-Solving Examples in Real-life
Example 1: workplace conflict.
Situation : Two team members have a disagreement that affects their productivity.
- Identify the Problem : Understand the root cause of the conflict.
- Analyze : Talk to both parties separately to get their perspectives.
- Generate Solutions : Consider solutions like mediation, reassignment of tasks, or team-building exercises.
- Evaluate : Assess which solution is likely to resolve the conflict without affecting team morale.
- Implement : Arrange a mediation session.
- Review : Follow up to ensure the conflict is resolved and monitor team dynamics.
Example 2: Personal Finance Management
Situation : Struggling to manage monthly expenses and savings.
- Identify the Problem : Determine specific areas where overspending occurs.
- Analyze : Review bank statements and categorize expenses.
- Generate Solutions : Create a budget, reduce unnecessary expenses, and set savings goals.
- Evaluate : Choose a budgeting method that fits your lifestyle.
- Implement : Start tracking expenses and adjust spending habits.
- Review : Regularly review your budget and savings to ensure you are on track.
How to Improve Your Problem-Solving Skills?
Understand the Problem: Before attempting to solve any problem, it’s crucial to fully understand it. Read through the problem statement carefully and make sure you grasp every detail.
Break It Down : Divide the problem into smaller, more manageable parts. This approach, known as decomposition, makes it easier to tackle complex issues by focusing on individual components one at a time.
Research and Gather Information : Collect all relevant information and data that might help in solving the problem. Look for similar problems and their solutions.
Brainstorm Possible Solutions : Generate as many potential solutions as possible. Don’t worry about evaluating them at this stage; the goal is to think creatively and come up with a wide range of ideas.
Evaluate and Select the Best Solution : Assess the feasibility, pros, and cons of each potential solution. Consider factors such as resources, time, and potential risks. Choose the solution that best addresses the problem and is most practical.
Develop an Action Plan : Create a detailed plan for implementing your chosen solution. Outline the steps you need to take, assign tasks if working in a team, and set deadlines to ensure timely progress.
Implement the Solution : Put your plan into action. Stay focused and be prepared to adapt if necessary. Keep track of your progress and make adjustments as needed.
Monitor and Review : After implementing the solution, monitor the results to ensure the problem is resolved. Evaluate the outcome and review the process to learn from any mistakes or successes.
Problem-solving in workplace
- Enhancing Efficiency : Quick and effective problem resolution can streamline processes and reduce downtime.
- Boosting Productivity : Employees who can solve problems independently help maintain workflow and productivity.
- Improving Customer Satisfaction : Solving customer issues promptly can lead to higher satisfaction and loyalty.
- Fostering Innovation : Problem-solving often leads to new ideas and improvements that drive innovation.
- Promoting Employee Development : Encouraging problem-solving helps employees grow and develop their skills.
How To Highlight Problem-Solving Skills?
1. on your resume.
When listing problem-solving skills on your resume, provide concrete examples. Use action verbs and quantify your achievements where possible.
- Resolved a customer service issue that increased customer satisfaction by 20%.
- Developed a new process that reduced production errors by 15%.
2. In a Cover Letter
Your cover letter is a great place to elaborate on your problem-solving abilities. Describe a specific situation where you successfully addressed a challenge.
“In my previous role at XYZ Company, I identified a bottleneck in our production line. I conducted a thorough analysis and implemented a new workflow, which reduced production time by 25% and saved the company $50,000 annually.”
3. During an Interview
Be prepared to discuss your problem-solving skills in depth during an interview. Use the STAR (Situation, Task, Action, Result) method to structure your responses.
Example: “Can you give an example of a time when you solved a difficult problem at work?”
- Situation: Our sales team was struggling with declining numbers.
- Task: I was tasked with identifying the root cause and finding a solution.
- Action: I analyzed sales data, conducted team meetings, and identified a lack of training as the main issue.
- Result: I organized comprehensive training sessions, which led to a 30% increase in sales over the next quarter.
4. On Social Media and Professional Profiles
Highlight problem-solving skills on LinkedIn and other professional profiles. Share posts or articles about your problem-solving experiences and successes.
“I’m thrilled to share that I recently led a project to overhaul our customer service protocol, resulting in a 40% reduction in response time and a significant boost in customer satisfaction!”
5. In Performance Reviews
During performance reviews, make sure to emphasize your problem-solving contributions. Provide specific examples and outcomes.
“In the past year, I resolved three major project roadblocks, enabling our team to meet all deadlines and exceed our performance goals.”
6. Through Projects and Case Studies
If applicable, create case studies or detailed project descriptions that showcase your problem-solving process and results. This can be particularly useful for portfolios or presentations.
Case Study: Improving IT System Efficiency
- Problem: Frequent system downtimes affecting productivity.
- Solution: Implemented a new monitoring system and revised maintenance schedules.
- Outcome: System downtimes were reduced by 50%, significantly improving productivity.
7. By Demonstrating Soft Skills
Problem-solving often involves other soft skills such as communication, creativity, and teamwork. Highlighting these related skills can further emphasize your ability to solve problems effectively.
“By fostering open communication within my team and encouraging creative brainstorming sessions, we were able to devise innovative solutions to our most pressing challenges.”
How to Answer Problem-Solving Interview Questions
- Understand the Question : Make sure you fully understand the problem before you try to solve it. Ask clarifying questions if needed to ensure you have all the relevant information.
- Think Aloud : Demonstrate your thinking process by explaining your thoughts as you work through the problem. This shows your interviewer how you approach problems and organize your thoughts.
- Break It Down : Divide the problem into smaller, manageable parts. This can make a complex issue seem more approachable and allows you to tackle each component systematically.
- Use a Structured Approach : Employ frameworks or methodologies that are relevant to the question. For example, you might use the STAR method (Situation, Task, Action, Result) for behavioral questions, or a simple problem-solving framework like Define, Measure, Analyze, Improve, Control (DMAIC) for process improvements.
- Be Creative : Employers often look for creativity in your answers. Think outside the box and propose innovative solutions when appropriate.
- Prioritize Solutions : If there are multiple potential solutions, discuss the pros and cons of each and explain why you would choose one over the others.
- Stay Calm and Positive : Problem-solving under pressure is part of the test. Maintain a calm and positive demeanor, showing that you can handle stress effectively.
- Summarize Your Steps : After you have worked through the problem, summarize the steps you took and the conclusion you reached. This helps ensure the interviewer followed your process and underscores your methodical approach.
- Ask for Feedback : After presenting your solution, it can be beneficial to ask if there are any additional factors you might consider. This shows openness to learning and adapting.
- Practice Regularly : Like any skill, problem-solving improves with practice. Regularly engage in brain teasers, logic puzzles, or case studies to sharpen your skills.
Why Are Problem-Solving is Important?
- Effective Decision-Making : Problem-solving is essential for making decisions that are logical, informed, and well-considered. This skill helps individuals and organizations make choices that lead to better outcomes.
- Innovation and Improvement : Solving problems effectively often requires innovative thinking. This can lead to new ideas and improvements in processes, products, and services, which are essential for business growth and adaptation.
- Handling Complex Situations : Many roles involve complex situations that are not straightforward to manage. Problem-solving skills enable individuals to dissect these situations and devise effective strategies to deal with them.
- Enhances Productivity : Efficient problem-solving contributes to higher productivity, as it allows for the identification and removal of obstacles that impede workflow and performance.
- Career Advancement : Individuals who are effective problem solvers are often seen as leaders and can advance more quickly in their careers. This skill is valuable because it demonstrates the ability to handle difficult situations and complex challenges.
- Adaptability and Resilience : Problem-solving is key to adapting to new situations and overcoming challenges. Those who can creatively navigate through difficulties are generally more resilient.
- Quality of Life : On a personal level, strong problem-solving skills can improve one’s quality of life by enabling better management of the challenges that come with daily living.
- Team Collaboration : Problem-solving often requires collaboration. Being good at solving problems can improve your ability to work with others, as it involves communication, persuasion, and negotiation skills.
How to Include Problem-Solving in a Job Application
- Resume : Detail specific problem-solving instances in your job descriptions using action verbs like “analyzed” and “implemented”. Mention the positive outcomes achieved.
- Cover Letter : Narrate a specific instance where your problem-solving skills led to a successful outcome, demonstrating initiative and effectiveness.
- Skills Section : Include “problem-solving” in a skills section if the job ad specifically mentions it.
- Quantify Achievements : Use numbers to describe the impact of your solutions, such as cost savings or efficiency improvements.
- Job Interviews : Prepare to discuss specific examples of your problem-solving skills, focusing on the challenge, your action, and the result.
- References : Brief your references about your problem-solving achievements so they can provide specific examples when contacted by employers.
Tips for Enhancing Problem-Solving
- Practice Regularly: Like any skill, problem-solving improves with regular practice. Engage in activities that challenge your thinking, such as puzzles, games, or real-world problem-solving scenarios.
- Learn from Others: Study how others approach and solve problems. This can provide new strategies and perspectives that you can incorporate into your own problem-solving toolkit.
- Stay Calm and Positive: Maintaining a calm and positive mindset can significantly improve your ability to solve problems. Stress and negativity can cloud your judgment and hinder creative thinking.
- Develop Critical Thinking: Sharpen your critical thinking skills by questioning assumptions, analyzing information, and evaluating evidence. This will help you make more informed and logical decisions.
- Collaborate with Others: Working with others can bring new insights and ideas. Collaboration can also help you see the problem from different angles and develop more effective solutions.
- Keep Learning: Continuously expand your knowledge and skills. The more you know, the better equipped you are to tackle a variety of problems.
How can I improve my problem-solving skills?
Practice regularly, learn various problem-solving techniques, and engage in activities that challenge your thinking.
What are common problem-solving techniques?
Common techniques include brainstorming, root cause analysis, the 5 Whys, and SWOT analysis.
What are the steps in the problem-solving process?
Identify the problem, analyze the problem, generate solutions, select a solution, implement, and evaluate.
How do I demonstrate problem-solving skills in an interview?
Discuss specific situations where you effectively solved problems, highlighting your thought process and outcomes.
What’s the difference between critical thinking and problem-solving?
Critical thinking involves analyzing and evaluating information, while problem-solving focuses on finding solutions to problems.
How do problem-solving skills help in leadership?
They enable leaders to manage challenges effectively, inspire innovation, and guide teams through obstacles.
How to measure problem-solving skills?
Assess through scenarios or challenges that require identifying, analyzing, and resolving problems.
What role does creativity play in problem-solving?
Creativity enables out-of-the-box thinking, which can lead to innovative and effective solutions.
How do you use problem-solving in project management?
Apply it to anticipate potential issues, plan solutions, and ensure smooth project execution.
What’s an example of a problem-solving situation?
Resolving customer complaints by identifying the issue, brainstorming solutions, and implementing changes to prevent future complaints.
Text prompt
- Instructive
- Professional
10 Examples of Public speaking
20 Examples of Gas lighting
Student Question Bank: Math Questions
Because each question on the Math section deals with different numbers and mathematical scenarios, it's not as simple as the Reading and Writing section to identify exactly what each question stem will look like. You can still use the descriptions in this section to determine which math domains and skills you want to focus on in the Student Question Bank.
Math Questions
Related topics.
The Hechinger Report
Covering Innovation & Inequality in Education
Why schools are teaching math word problems all wrong

Share this:
- Click to share on LinkedIn (Opens in new window)
- Click to share on Pinterest (Opens in new window)
- Click to share on Reddit (Opens in new window)
- Click to share on WhatsApp (Opens in new window)
- Click to email a link to a friend (Opens in new window)
The Hechinger Report is a national nonprofit newsroom that reports on one topic: education. Sign up for our weekly newsletters to get stories like this delivered directly to your inbox. Consider supporting our stories and becoming a member today.
Get important education news and analysis delivered straight to your inbox
- Weekly Update
- Future of Learning
- Higher Education
- Early Childhood
- Proof Points
CENTRAL FALLS, R.I. — When Natalia Molina began teaching her second grade students word problems earlier this school year, every lesson felt difficult. Most students were stymied by problems such as: “Sally went shopping. She spent $86 on groceries and $39 on clothing. How much more did Sally spend on groceries than on clothing?”

Both Molina, a first-year teacher, and her students had been trained to tackle word problems by zeroing in on key words like “and,” “more” and “total” — a simplistic approach that Molina said too often led her students astray. After recognizing the word “and,” for instance, they might mistakenly assume that they needed to add two nearby numbers together to arrive at an answer.
Some weaker readers, lost in a sea of text, couldn’t recognize any words at all.
“I saw how overwhelmed they would get,” said Molina, who teaches at Segue Institute for Learning, a predominantly Hispanic charter school in this small city just north of Providence.
So, with the help of a trainer doing work in Rhode Island through a state grant, Molina and some of her colleagues revamped their approach to teaching word problems this winter — an effort that they said is already paying off in terms of increased student confidence and ability. “It has been a game changer for them,” Molina said.

Perhaps no single educational task encompasses as many different skills as the word problem. Between reading, executive functioning, problem solving, computation and vocabulary, there are a lot of ways for students to go wrong. And for that reason, students perform significantly worse overall on word problems compared to questions more narrowly focused on computation or shapes (for example: “Solve 7 + _ = 22” or “What is 64 x 3?”).
If a student excels at word problems, it’s a good sign that they’re generally excelling at school. “Word-problem solving in lower grades is one of the better indicators of overall school success in K-12,” said Lynn Fuchs, a research professor at Vanderbilt University. In a large national survey , for instance, algebra teachers rated word-problem solving as the most important among 15 skills required to excel in the subject.
Teacher takeaways
- Don’t instruct students to focus mainly on “key words” in word problems such as “and” or “more”
- Mix question types in any lesson so that students don’t assume they just apply the same operation (addition, subtraction) again and again
- Teach students the underlying structure — or schema — of the word problem
Yet most experts and many educators agree that too many schools are doing it wrong, particularly in the elementary grades. And in a small but growing number of classrooms, teachers like Molina are working to change that. “With word problems, there are more struggling learners than non-struggling learners” because they are taught so poorly, said Nicole Bucka, who works with teachers throughout Rhode Island to provide strategies for struggling learners.
Too many teachers, particularly in the early grades, rely on key words to introduce math problems. Posters displaying the terms — sum, minus, fewer, etc. — tied to operations including addition and subtraction are a staple in elementary school classrooms across the country.
Key words can be a convenient crutch for both students and teachers, but they become virtually meaningless as the problems become harder, according to researchers. Key words can help first graders figure out whether to add or subtract more than half of the time, but the strategy rarely works for the multi-step problems students encounter starting in second and third grade. “With multi-step problems, key words don’t work 90 percent of the time,” said Sarah Powell, a professor at the University of Texas in Austin who studies word problems and whose research has highlighted the inefficacy of key words . “But the average kindergarten teacher is not thinking about that; they are teaching 5-year-olds, not 9-year-olds.”
Many teachers in the youngest grades hand out worksheets featuring the same type of word problem repeated over and over again. That’s what Molina’s colleague, Cassandra Santiago, did sometimes last year when leading a classroom on her own for the first time. “It was a mistake,” the first grade teacher said. “It’s really important to mix them up. It makes them think more critically about the parts they have to solve.”

Another flaw with word problem instruction is that the overwhelming majority of questions are divorced from the actual problem-solving a child might have to do outside the classroom in their daily life — or ever, really. “I’ve seen questions about two trains going on the same track,” said William Schmidt, a University Distinguished Professor at Michigan State University. “First, why would they be going on the same track and, second, who cares?”
Schmidt worked on an analysis of about 8,000 word problems used in 23 textbooks in 19 countries. He found that less than one percent had “real world applications” and involved “higher order math applications .”
“That is one of the reasons why children have problems with mathematics,” he said. “They don’t see the connection to the real world … We’re at this point in math right now where we are just teaching students how to manipulate numbers.”
He said a question, aimed at middle schoolers, that does have real world connections and involves more than manipulating numbers, might be: “Shopping at the new store in town includes a 43% discount on all items which are priced the same at $2. The state you live in has a 7% sales tax. You want to buy many things but only have a total of $52 to spend. Describe in words how many things you could buy.”
Schmidt added that relevancy of word problems is one area where few, if any, countries excel. “No one was a shining star leading the way,” he said.
In her brightly decorated classroom one Tuesday afternoon, Santiago, the first grade teacher, gave each student a set of animal-shaped objects and a sheet of blue paper (the water) and green (the grass). “We’re going to work on a number story,” she told them. “I want you to use your animals to tell me the story.”
“ Once upon a time,” the story began. In this tale, three animals played in the water, and two animals played in the grass. Santiago allowed some time for the ducks, pigs and bears to frolic in the wilds of each student’s desk before she asked the children to write a number sentence that would tell them how many animals they have altogether.
Some of the students relied more on pictorial representations (three dots on one side of a line and two dots on the other) and others on the number sentence (3+2 = 5) but all of them eventually got to five. And Santiago made sure that her next question mixed up the order of operations (so students didn’t incorrectly assume that all they ever have to do is add): “Some more animals came and now there are seven. So how many more came?”
One approach to early elementary word problems that is taking off in some schools, including Segue Institute, has its origins in a special education intervention for struggling math students. Teachers avoid emphasizing key words and ask students instead to identify first the conceptual type of word problem (or schema, as many practitioners and researchers refer to it) they are dealing with: “Total problems,” for instance, involve combining two parts to find a new amount; “change problems” involve increasing or decreasing the amount of something. Total problems do not necessarily involve adding, however.

“The schemas that students learn in kindergarten will continue with them throughout their whole career,” said Powell, the word-problem researcher, who regularly works with districts across the country to help implement the approach.
In Olathe, Kansas — a district inspired by Powell’s work — teachers had struggled for years with word problems, said Kelly Ulmer, a math support specialist whose goal is to assist in closing academic gaps that resulted from lost instruction time during the pandemic. “We’ve all tried these traditional approaches that weren’t working,” she said. “Sometimes you get pushback on new initiatives from veteran teachers and one of the things that showed us how badly this was needed is that the veteran teachers were the most excited and engaged — they have tried so many things” that haven’t worked.
In Rhode Island, many elementary schools initially used the strategy with students who required extra help, including those in special education, but expanded this use to make it part of the core instruction for all, said Bucka. In some respects, it’s similar to the recent, well publicized evolution of reading instruction in which some special education interventions for struggling readers — most notably, a greater reliance on phonics in the early grades — have gone mainstream.
There is an extensive research bas e showing that focusing on the different conceptual types of word problems is an effective way of teaching math, although much of the research focuses specifically on students experiencing difficulties in the subject.
Molina has found asking students to identify word problems by type to be a useful tool with nearly all of her second graders; next school year she hopes to introduce the strategy much earlier.

One recent afternoon, a lesson on word problems started with everyone standing up and chanting in unison: “Part plus part equals total” (they brought two hands together). “Total minus part equals part ” (they took one hand away) .
It’s a way to help students remember different conceptual frameworks for word problems. And it’s especially effective for the students who learn well through listening and repeating. For visual learners, the different types of word problems were mapped out on individual dry erase mats.
The real work began when Molina passed out questions, and the students— organized into the Penguin, Flower Bloom, Red Panda and Marshmallow teams — had to figure out which framework they were dealing with on their own and then work toward an answer. A few months ago, many of them would have automatically shut down when they saw the text on the page, Molina said.
For the Red Pandas, the question under scrutiny was: “The clothing store had 47 shirts. They sold 21, how many do they have now?”
“It’s a total problem,” one student said.
“No, it’s not total,” responded another.
“I think it’s about change,” said a third.
None of the students seemed worried about their lack of consensus, however. And neither was Molina. A correct answer is always nice but those come more often now that most of the students have made a crucial leap. “I notice them thinking more and more,” she said, “about what the question is actually asking.”
This story about word problems was produced by The Hechinger Report , a nonprofit, independent news organization focused on inequality and innovation in education. Sign up for the Hechinger newsletter .
Related articles
The Hechinger Report provides in-depth, fact-based, unbiased reporting on education that is free to all readers. But that doesn't mean it's free to produce. Our work keeps educators and the public informed about pressing issues at schools and on campuses throughout the country. We tell the whole story, even when the details are inconvenient. Help us keep doing that.
Join us today.
Sarah Carr CONTRIBUTING EDITOR
Email:... More by Sarah Carr
Letters to the Editor
At The Hechinger Report, we publish thoughtful letters from readers that contribute to the ongoing discussion about the education topics we cover. Please read our guidelines for more information. We will not consider letters that do not contain a full name and valid email address. You may submit news tips or ideas here without a full name, but not letters.
By submitting your name, you grant us permission to publish it with your letter. We will never publish your email address. You must fill out all fields to submit a letter.
Your email address will not be published. Required fields are marked *
Save my name, email, and website in this browser for the next time I comment.
Sign me up for the newsletter!
More From Forbes
The most rigorous math program you've never heard of.
- Share to Facebook
- Share to Twitter
- Share to Linkedin
Math-M-Addicts students eagerly dive into complex math problems during class.
In the building of the Speyer Legacy School in New York City, a revolutionary math program is quietly producing some of the city's most gifted young problem solvers and logical thinkers. Founded in 2005 by two former math prodigies, Math-M-Addicts has grown into an elite academy developing the skills and mindset that traditional schooling often lacks.
"We wanted to establish the most advanced math program in New York," explains Ruvim Breydo, co-founder of Math-M-Addicts. "The curriculum focuses not just on mathematical knowledge, but on developing a mastery of problem-solving through a proof-based approach aligned with prestigious competitions like the International Mathematical Olympiad."
From its inception, Math-M-Addicts took an unconventional path. What began as an attempt to attract only the highest caliber high school students soon expanded to offer multiple curriculum levels. "We realized we couldn't find enough kids at the most advanced levels," says Breydo. "So we decided to develop that talent from an earlier age."
The program's approach centers on rigor. At each of the 7 levels, the coursework comprises just a handful of fiendishly difficult proof-based math problems every week. "On average, we expect them to get about 50% of the solutions right," explains instructor Natalia Lukina. "The problems take hours and require grappling with sophisticated mathematical concepts."
But it's about more than just the content. Class sizes are small, with two instructors for every 15-20 students. One instructor leads the session, while the other teacher coordinates the presentation of the homework solutions by students. The teachers also provide customized feedback by meticulously reviewing each student's solutions. "I spend as much time analyzing their thought processes as I do teaching new material," admits instructor Bobby Lee.
Netflix’s Best New Show Has A Perfect 100% Critic Score
New chrome security rules—google gives websites until 11/1 to comply, ranked: the 30 most walkable cities in the world, according to a new report.
Lee and the Math-M-Addicts faculty embrace an unconventional pedagogy focused on developing logic, creativity, and a tenacious problem-solving mindset over procedures. "We don't dumb it down for them," says Breydo. "We use technical math language and allow students to struggle through the challenges because that's where real learning happens."
Impressive results of Math-M-addicts students in selective math competitions highlight their ... [+] preparation and dedication.
For the Math-M-Addicts team, finding the right teachers is as essential as shaping brilliant students. Prospective instructors go through a rigorous multi-stage vetting process. "We seek passionate mathematical problem solvers first," says program director Sonali Jasuja. "Teaching experience is great, but first and foremost, we need people who deeply understand and enjoy the reasoning behind mathematics."
Even exceptional instructors undergo extensive training by co-teaching for at least a year alongside veteran Math-M-Addicts faculty before taking the lead role. "Our approach is different from how most US teachers learned mathematics," explains instructor Tanya Gross, the director of Girls Adventures in Math (GAIM) competition. "We immerse them in our unique math culture, which focuses on the 'why' instead of the 'how,' empowering a paradigm shift."
That culture extends to the students as well. In addition to the tools and strategies imparted in class, Math-M-Addicts alumni speak of an unshakable confidence and camaraderie that comes from up to several thousands of hours grappling with mathematics at the highest levels alongside peers facing the same challenges.
As Math-M-Addicts ramps up efforts to expand access through online classes and global partnerships, the founders remain devoted to their core mission. "Math education should not obsess with speed and memorization of math concepts," argues Breydo. "This is not what mathematics is about. To unlock human potential, we must refocus on cognitive reasoning and problem-solving skills. We are seeking to raise young people unafraid to tackle any complex challenge they face"

- Editorial Standards
- Reprints & Permissions
Join The Conversation
One Community. Many Voices. Create a free account to share your thoughts.
Forbes Community Guidelines
Our community is about connecting people through open and thoughtful conversations. We want our readers to share their views and exchange ideas and facts in a safe space.
In order to do so, please follow the posting rules in our site's Terms of Service. We've summarized some of those key rules below. Simply put, keep it civil.
Your post will be rejected if we notice that it seems to contain:
- False or intentionally out-of-context or misleading information
- Insults, profanity, incoherent, obscene or inflammatory language or threats of any kind
- Attacks on the identity of other commenters or the article's author
- Content that otherwise violates our site's terms.
User accounts will be blocked if we notice or believe that users are engaged in:
- Continuous attempts to re-post comments that have been previously moderated/rejected
- Racist, sexist, homophobic or other discriminatory comments
- Attempts or tactics that put the site security at risk
- Actions that otherwise violate our site's terms.
So, how can you be a power user?
- Stay on topic and share your insights
- Feel free to be clear and thoughtful to get your point across
- ‘Like’ or ‘Dislike’ to show your point of view.
- Protect your community.
- Use the report tool to alert us when someone breaks the rules.
Thanks for reading our community guidelines. Please read the full list of posting rules found in our site's Terms of Service.
- Comment Comments
- Save Article Read Later Read Later
AI Reveals New Possibilities in Matrix Multiplication
November 23, 2022
Matrix multiplication is not unlike solving an unthinkably large Rubik’s Cube.
Mahmet Emin Güzel for Quanta Magazine
Introduction
Mathematicians love a good puzzle. Even something as abstract as multiplying matrices (two-dimensional tables of numbers) can feel like a game when you try to find the most efficient way to do it. It’s a little like trying to solve a Rubik’s Cube in as few moves as possible — challenging, but alluring. Except that for a Rubik’s Cube, the number of possible moves at each step is 18; for matrix multiplication, even in relatively simple cases, every step can present more than 10 12 options.
Over the past 50 years, researchers have approached this problem in many ways, all based on computer searches aided by human intuition. Last month, a team at the artificial intelligence company DeepMind showed how to tackle the problem from a new direction, reporting in a paper in Nature that they’d successfully trained a neural network to discover new fast algorithms for matrix multiplication. It was as if the AI had found an unknown strategy for solving a monstrously complex Rubik’s Cube.
“It’s a very neat result,” said Josh Alman , a computer scientist at Columbia University. But he and other matrix multiplication specialists also emphasized that such AI assistance will complement rather than replace existing methods — at least in the near term. “It’s like a proof of concept for something that could become a breakthrough,” Alman said. The result will simply help researchers on their quest.
As if to prove the point, three days after the Nature paper came out, a pair of Austrian researchers illustrated how new and old methods might complement each other. They used a conventional computer-aided search to further improve one of the algorithms that the neural network had discovered.
The results suggest that, like the process of solving a Rubik’s Cube, the path to better algorithms will be full of twists and turns.

Video : DeepMind researchers trained an AI system called AlphaTensor to find new, faster algorithms for matrix multiplication. AlphaTensor quickly rediscovered — and surpassed, for some cases — the reigning algorithm discovered by German mathematician Volker Strassen in 1969.
Christopher Webb Young/ Quanta Magazine ; Emily Zhang for Quanta Magazine
Multiplying Matrices
Matrix multiplication is one of the most fundamental and ubiquitous operations in all of mathematics. To multiply a pair of n -by- n matrices, each with n 2 elements, you multiply and add these elements together in particular combinations to generate the product, a third n -by- n matrix. The standard recipe for multiplying two n -by- n matrices requires n 3 multiplication operations, so a 2-by-2 matrix, for example, requires eight multiplications.
For larger matrices, with thousands of rows and columns, this process quickly becomes cumbersome. But in 1969, the mathematician Volker Strassen discovered a procedure for multiplying a pair of 2-by-2 matrices using seven rather than eight multiplication steps, at the cost of introducing more addition steps.
Strassen’s algorithm is needlessly convoluted if you just want to multiply a pair of 2-by-2 matrices. But he realized it would also work for bigger matrices. That’s because the elements of a matrix can themselves be matrices. For example, a matrix with 20,000 rows and 20,000 columns can be reimagined as a 2-by-2 matrix whose four elements are each 10,000-by-10,000 matrices. Each of these matrices can then be subdivided into four 5,000-by-5,000 blocks, and so on. Strassen could apply his method to multiply 2-by-2 matrices at each level of this nested hierarchy. As the matrix size increases, the savings from fewer multiplications grows.
Strassen’s discovery led to a search for efficient algorithms for matrix multiplication, which has since inspired two distinct subfields. One focuses on a question of principle: If you imagine multiplying two n -by- n matrices and let n run toward infinity, how does the number of multiplication steps in the fastest possible algorithm scale with n ? The current record for the best scaling, n 2.3728596 , belongs to Alman and Virginia Vassilevska Williams , a computer scientist at the Massachusetts Institute of Technology. (A recent unpublished preprint reported a tiny improvement using a new technique.) But these algorithms are of purely theoretical interest, winning out over methods like Strassen’s only for absurdly large matrices.
The second subfield thinks on a smaller scale. Soon after Strassen’s work, the Israeli American computer scientist Shmuel Winograd showed that Strassen had reached a theoretical limit: It’s not possible to multiply 2-by-2 matrices with fewer than seven multiplication steps. But for all other matrix sizes, the minimum number of required multiplications remains an open question. And fast algorithms for small matrices could have an outsize impact, since repeated iterations of such an algorithm might beat Strassen’s algorithm when reasonably sized matrices are being multiplied.
Unfortunately, the sheer number of possibilities is huge. Even for 3-by-3 matrices, “the number of possible algorithms exceeds the number of atoms in the universe,” said Alhussein Fawzi , a DeepMind researcher and one of the leaders of the new work.
Faced with this dizzying menu of options, researchers have made progress by transforming matrix multiplication into what seems like a totally different math problem — one that is easier for computers to handle. It’s possible to represent the abstract task of multiplying two matrices as a specific kind of mathematical object: a three-dimensional array of numbers called a tensor. Researchers can then break this tensor up into a sum of elementary components, called “rank-1” tensors; each of these will represent a different step in the corresponding matrix multiplication algorithm. That means that finding an efficient multiplication algorithm amounts to minimizing the number of terms in a tensor decomposition — the fewer the terms, the fewer the steps involved.
In this way, researchers have discovered new algorithms that multiply n -by- n matrices using fewer than the standard n 3 multiplication steps for many small matrix sizes. But algorithms that outperform not only the standard but also Strassen’s algorithm for small matrices have remained out of reach — until now.
The DeepMind team approached the problem by turning tensor decomposition into a single-player game. They started with a deep learning algorithm descended from AlphaGo — another DeepMind AI that in 2016 learned to play the board game Go well enough to beat the top human players.
All deep learning algorithms are built around neural networks: webs of artificial neurons sorted into layers, with connections that can vary in strength representing how much each neuron influences those in the next layer. The strength of these connections is tweaked over many iterations of a training procedure, during which the neural network learns to transform each input it receives into an output that helps the algorithm accomplish its overall goal.
In DeepMind’s new algorithm, dubbed AlphaTensor, the inputs represent steps along the way to a valid matrix multiplication scheme. The first input to the neural network is the original matrix multiplication tensor, and its output is the rank-1 tensor that AlphaTensor has chosen for its first move. The algorithm subtracts this rank-1 tensor from the initial input, yielding an updated tensor that is fed back into the network as a new input. The process repeats until eventually every element in the starting tensor has been reduced to zero, meaning there are no more rank-1 tensors to take out.
At that point, the neural network has discovered a valid tensor decomposition, since it’s mathematically guaranteed that the sum of all the rank-1 tensors is exactly equal to the starting tensor. And the steps it took to get there can be translated back into steps of the corresponding matrix multiplication algorithm.
Here’s the game: AlphaTensor repeatedly decomposes a tensor to a set of rank-1 components. Each time, AlphaTensor gets rewarded if it finds a way to reduce the number of steps. But shortcuts to victory are not at all intuitive, just as you sometimes must scramble a perfectly ordered face on a Rubik’s Cube before you can solve the whole thing.
The team now had an algorithm that could, theoretically, solve their problem. They just had to train it first.
Like all neural networks, AlphaTensor needs a lot of data to train on, but tensor decomposition is a notoriously hard problem. There were few examples of efficient decompositions that the researchers could feed the network. Instead, they helped the algorithm get started by training it on the much easier inverse problem: adding up a bunch of randomly generated rank-1 tensors.
“They’re using the easy problem to produce more data for the hard problem,” said Michael Littman , a computer scientist at Brown University. Combining this backward training procedure with reinforcement learning, wherein AlphaTensor generated its own training data as it blundered around looking for efficient decompositions, worked much better than either training method on its own.
The DeepMind team trained AlphaTensor to decompose tensors representing the multiplication of matrices up to 12-by-12. It sought fast algorithms for multiplying matrices of ordinary real numbers and also algorithms specific to a more constrained setting known as modulo 2 arithmetic. (This is math based on only two numbers, so matrix elements can only be 0 or 1, and 1 + 1 = 0.) Researchers often start with this more restricted but still vast space, in hopes that algorithms discovered here can be adapted to work on matrices of real numbers.
After training, AlphaTensor rediscovered Strassen’s algorithm within minutes. It then discovered up to thousands of new fast algorithms for each matrix size. These were different from the best-known algorithms but had the same number of multiplication steps.
In a few cases, AlphaTensor even beat existing records. Its most surprising discoveries happened in modulo 2 arithmetic, where it found a new algorithm for multiplying 4-by-4 matrices in 47 multiplication steps, an improvement over the 49 steps required for two iterations of Strassen’s algorithm. It also beat the best-known algorithm for 5-by-5 modulo 2 matrices, reducing the number of required multiplications from the previous record of 98 to 96. (But this new record still lags behind the 91 steps that would be required to beat Strassen’s algorithm using 5-by-5 matrices.)
The new high-profile result created a lot of excitement, with some researchers heaping praise on the AI-based improvement on the status quo. But not everyone in the matrix multiplication community was so impressed. “I felt like it was a little overhyped,” said Vassilevska Williams. “It’s another tool. It’s not like, ‘Oh, the computers beat the humans,’ you know?”
Researchers also emphasized that immediate applications of the record-breaking 4-by-4 algorithm would be limited: Not only is it valid only in modulo 2 arithmetic, but in real life there are important considerations besides speed.
Fawzi agreed that really, this is just the beginning. “There is a lot of room for improvement and research, and that’s a good thing,” he said.
A Final Twist
AlphaTensor’s greatest strength relative to well-established computer search methods is also its greatest weakness: It’s not constrained by human intuition about what good algorithms look like, so it can’t explain its choices. That makes it difficult for researchers to learn from its achievements.
But this may not be as big a drawback as it seems. A few days after the AlphaTensor result, the mathematician Manuel Kauers and his graduate student Jakob Moosbauer , both of Johannes Kepler University Linz in Austria, reported another step forward.

Manuel Kauers tweaked the DeepMind approach to generate further improvements.
Jakob Moosbauer
When the DeepMind paper came out, Kauers and Moosbauer were in the process of searching for new multiplication algorithms using a conventional computer-aided search. But unlike most such searches, which start afresh with a new guiding principle, their method works by repeatedly tweaking an existing algorithm in hopes of squeezing more multiplication savings out of it. Taking AlphaTensor’s algorithm for 5-by-5 modulo 2 matrices as a starting point, they were surprised to find that their method reduced the number of multiplication steps from 96 to 95 after just a few seconds of computation.
AlphaTensor also helped them make another improvement indirectly. Previously, Kauers and Moosbauer hadn’t bothered to explore the space of 4-by-4 matrices, believing that it would not be possible to beat two iterations of Strassen’s algorithm. The AlphaTensor result prompted them to reconsider, and after a week of computation time starting from scratch, their method turned up another 47-step algorithm unrelated to the one AlphaTensor had discovered. “If somebody had told us that there is something to discover for 4-by-4, we could have done that earlier,” said Kauers. “But OK, well, that’s how it works.”
Littman expects more such surprises, likening the situation to the first time a runner finished a mile in under four minutes, a feat that had widely been considered impossible. “People were like, ‘Oh, wait, we can do this,’ and now lots of people can do it,” he said.
Looking forward, Fawzi hopes to generalize AlphaTensor to tackle a broader range of mathematical and computational tasks, just as its ancestor AlphaGo eventually branched out into other games.
Kauers sees this as the true litmus test for the application of machine learning to discovering new algorithms. He points out that the quest for fast matrix multiplication algorithms is a combinatorial problem to which computer searches, with or without human assistance, are well suited. But not all mathematical problems are so easy to pin down. If machine learning can discover a qualitatively new algorithmic idea, he said, “this would then be a game changer.”
Get highlights of the most important news delivered to your email inbox
Comment on this article
Quanta Magazine moderates comments to facilitate an informed, substantive, civil conversation. Abusive, profane, self-promotional, misleading, incoherent or off-topic comments will be rejected. Moderators are staffed during regular business hours (New York time) and can only accept comments written in English.

Next article

IMAGES
VIDEO
COMMENTS
Here are five strategies to help students check their solutions. 1. Use the Inverse Operation. For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7.
Step 1: Understanding the problem. We are given in the problem that there are 25 chickens and cows. All together there are 76 feet. Chickens have 2 feet and cows have 4 feet. We are trying to determine how many cows and how many chickens Mr. Jones has on his farm. Step 2: Devise a plan.
The very first Mathematical Practice is: Make sense of problems and persevere in solving them. Mathematically proficient students start by explaining to themselves the meaning of a problem and looking for entry points to its solution. They analyze givens, constraints, relationships, and goals. They make conjectures about the form and meaning of ...
How do you solve problems and estimate answers in mathematics? This webpage from Mathematics LibreTexts introduces some useful strategies and techniques for problem solving and estimating, such as using diagrams, tables, units, and proportions. You will also find examples and exercises to practice your skills and check your understanding.
Unit test. Level up on all the skills in this unit and collect up to 1,100 Mastery points! There are lots of strategies we can use to solve equations. Let's explore some different ways to solve equations and inequalities. We'll also see what it takes for an equation to have no solution, or infinite solutions.
To solve an algebraic mathematical problem, represent the situation described with an equation. ... In math, a great example of the splitting hairs principle is the use of the terms 'equal' and ...
The following video shows more examples of using problem solving strategies and models. Question 2: The table shows the number of seats in each of the first four rows in an auditorium. The remaining ten rows follow the same pattern. Find the number of seats in the last row. Question 3: You are hanging three pictures in the wall of your home ...
Problem-solving requires practice. When deciding on methods or procedures to use to solve problems, the first thing you will do is look for clues, which is one of the most important skills in solving problems in mathematics. If you begin to solve problems by looking for clue words, you will find that these words often indicate an operation.
Solving algebraic word problems requires us to combine our ability to create equations and solve them. To solve an algebraic word problem: Define a variable. Write an equation using the variable. Solve the equation. If the variable is not the answer to the word problem, use the variable to calculate the answer.
32 Mathematical Ideas: Problem-Solving Techniques Jenna Lehmann. Solving Problems by Inductive Reasoning. ... An example of this might be that if we know for a fact that all dogs are good, and Lucky is a dog, then we can deduce that Lucky is good. Strategies for Problem Solving. No matter what tool you use to solve a problem, there is a method ...
A mathematical problem is a problem that can be represented, analyzed, and possibly solved, with the methods of mathematics.This can be a real-world problem, such as computing the orbits of the planets in the solar system, or a problem of a more abstract nature, such as Hilbert's problems.It can also be a problem referring to the nature of mathematics itself, such as Russell's Paradox.
1. Link problem-solving to reading. When we can remind students that they already have many comprehension skills and strategies they can easily use in math problem-solving, it can ease the anxiety surrounding the math problem. For example, providing them with strategies to practice, such as visualizing, acting out the problem with math tools ...
Schema approach. This is a math intervention strategy that can make problem solving easier for all students, regardless of ability. Compare different word problems of the same type and construct a formula, or mathematical sentence stem, that applies to them all. For example, a simple subtraction problems could be expressed as:
1. Create a Diagram/draw a picture. Creating a diagram helps students visualize the problem and reach the solution. A diagram can be a picture with labels, or a representation of the problem with objects that can be manipulated. Role-playing and acting out the problem like a story can help get to the solution. Example.
Mathematics provides a systematic and logical framework for problem-solving and critical thinking. The study of math helps to develop analytical skills, logical reasoning, and problem-solving abilities that can be applied to many areas of life.By using critical thinking skills to solve math problems, we can develop a deeper understanding of concepts, enhance our problem-solving skills, and ...
Teaching about problem solving begins with suggested strategies to solve a problem. For example, "draw a picture," "make a table," etc. You may see posters in teachers' classrooms of the "Problem Solving Method" such as: 1) Read the problem, 2) Devise a plan, 3) Solve the problem, and 4) Check your work. There is little or no ...
In fact, solving an equation is just like solving a puzzle. And like puzzles, there are things we can (and cannot) do. Here are some things we can do: Add or Subtract the same value from both sides; Clear out any fractions by Multiplying every term by the bottom parts; Divide every term by the same nonzero value; Combine Like Terms; Factoring
Solution. Step 1: Understanding the problem. We are given in the problem that there are 25 chickens and cows. All together there are 76 feet. Chickens have 2 feet and cows have 4 feet. We are trying to determine how many cows and how many chickens Mr. Jones has on his farm. Step 2: Devise a plan.
When I first started teaching math over 25 years ago, it was very common to teach "keywords" to help students determine the operation to use when solving a word problem. For example, if you see the word "total" in the problem, you always add. Rather than help students become better problem solvers, the use of keywords actually resulted ...
In tracing recent research trends and directions in mathematical problem-solving, it is argued that advances in mathematics practices occur and take place around two intertwined activities, mathematics problem formulation and ways to approach and solve those problems. In this context, a problematizing principle emerges as central activity to organize mathematics curriculum proposals and ways ...
• A real-world math problem is a difficult situation in real life where using math to solve it is preferred over other methods. ... Here's an example of a real-world math problem in digital agriculture: 12. Combatting Pests with Negative Numbers: Negative numbers are utilized in agriculture to determine the direction of movement, similar to ...
Free math problem solver answers your algebra homework questions with step-by-step explanations.
Math Word Problem Solutions. Math word problems require interpreting what is being asked and simplifying that into a basic math equation. Once you have the equation you can then enter that into the problem solver as a basic math or algebra question to be correctly solved. Below are math word problem examples and their simplified forms.
Problem solving is the process of identifying a challenge, analyzing its components, and finding an effective solution. It involves critical thinking, creativity, and the application of various techniques and tools. Examples of Problem Solving. Analytical Thinking: Breaking down complex problems into manageable parts.
Domain: Problem-Solving and Data Analysis Skill: Evaluating statistical claims—Observational studies and experiments Solve real-world and mathematical problems about area, perimeter, surface area, or volume of a geometric figure, and use scale factors to calculate changes to length and area.
About the Curricula. A curriculum is how standards, or learning goals, for every grade and subject are translated into day-to-day activities. As part of the NYC Solves initiative, all high schools will use Illustrative Mathematics and districts will choose a comprehensive, evidence-based curricula for middle school math instruction from an approved list.
For example, in this problem you might keep track of how many 1 × 1 squares are on each board, how many 2 × 2 squares on are each board, how many 3 × 3 squares are on each board, and so on. ... Problem Solving Strategy 9 (Find the Math, Remove the Context). Sometimes the problem has a lot of details in it that are unimportant, or at least ...
Between reading, executive functioning, problem solving, computation and vocabulary, there are a lot of ways for students to go wrong. And for that reason, students perform significantly worse overall on word problems compared to questions more narrowly focused on computation or shapes (for example: "Solve 7 + _ = 22" or "What is 64 x 3?").
Ruvim Breydo, founder of Math-M-Addicts, advocates for math education focused on cognitive reasoning and problem-solving to nurture fearless, challenge-ready students.
The team now had an algorithm that could, theoretically, solve their problem. They just had to train it first. New Paths. Like all neural networks, AlphaTensor needs a lot of data to train on, but tensor decomposition is a notoriously hard problem. There were few examples of efficient decompositions that the researchers could feed the network.