solving trig equations by factoring calculator

Trigonometric Equation Calculator

Instructions: Use calculator to solve trigonometric equations you provide, showing all the steps. Please type in the trigonometric equation you want to carry out in the box below.

ABout this Trigonometric Equation Calculator

This calculator will allow you to solve trig equations, showing all the steps of the way. All you need to do is to provide a valid trigonometric equation, with an unknown (x). It could be something simple as 'sin(x) = 1/2', or something more complex like 'sin^2(x) = cos(x) + tan(x)'.

Once you are done typing your equation, just go ahead and click on "Solve" to get all the details of the processes of finding the solutions, if solutions can be found.

Trigonometric properties and rules almost always allow to reduce most trig equations into simpler ones, so this type of equation is one type that often times lead to solutions, but it can be extremely cumbersome at times.

What is a trigonometric Equation?

A trigonometric equation, in the simplest possible terms, is a math equation where the unknown x is inside of a trigonometric expression.

For example, the following expression is a trigonometric eqn:

Why? Simply because x appears inside of trig expression sine. Or for example:

Now, these two are trig eqns, but the difference between the two is that for the first one, x appears ONLY inside of sine, whereas in the second one x appears inside of a trig function (tangent), but it also appears outside. This will usually make it difficult (or impossible) to solve the equation.

How to solve trigonometric equations

• Step 1: Make sure you are dealing with a trigonometric equation. Non-trigonometric equations will likely require a different approach
• Step 2: Make sure that the unknown x is inside of the trigonometric expression , but x does not appear outside a trig expression. If that is the case, it is likely you won't be able to solve the equation with elementary methods
• Step 3: Conduct an appropriate substitution, by first expressing all the trig functions present in the equation into one type (typically sine), and then use a substitution involving sine
• Step 4: With a little luck and if you did the correct substitution, you have reduced the original trigonometric equation into a polynomial equation to solve .

One of the key trig rules you need to use the ability to express all trigonometric functions in terms of any fixed trigonometric function. For example, we can write cosine in terms of sine:

Trigonometric Substitutions

Using trigonometric identities and substitutions is your way to go in this case. For example, suppose you want to solve this:

So we know this is a trig equation, and we know we can write cosine in terms of sine, so we do this:

Now what? Well, we can use the substitution: \(u = \sin x\), so the equation above becomes:

which is a rational equation , which by using simple algebraic manipulation means that we need to solve a polynomial equation in order to solve the original trig equation.

Application of trigonometry

• Step 1: All things mechanical: In manufacturing mechanical parts, circles and trigonometry play a crucial role
• Step 2: Analysis of periodic functions: Many phenomena are tightly related to periodicity, the point at which trigonometry comes to play
• Step 3: Advanced math: Mathematicians love their Fourier Series and Transform, which play a crucial role in spectral analysis

Circles and all their symmetry are so really important in real life, and trigonometry is the language by which we can quantify circles and its relationships. Solving trigonometric equations is at the center of math.

Why would you solve trigonometric equations

Trigonometric equations carry lots of value in practice especially in Engineering. Notable properties such as the period and frequency open a full spectrum of applications.

Circular structures play a crucial role in everything mechanical that we use today. Circles are synonymous of trigonometry, and trigonometric equations are at the center of it.

Example: Solving simple trig equations

Solve: \(\sin(x) = \frac{1}{2}\)

We need to solve the following given trigonometric equation equation:

The following is obtained:

By direct application of the properties of the inverse trigonometric function \( \arcsin(\cdot)\), as well as the properties of the trigonometric function \( \sin\left(x\right)\), we obtain that

Therefore, solving for \(x\) for the given equation leads to the solutions \(x=\frac{5}{6}\pi{}+2\pi{}K_1,\,\,x=\frac{1}{6}\pi{}+2\pi{}K_2\), for \(K_1, K_2\) arbitrary integer constants.

More equation calculators

Our trigonometric equation with steps will come in handy when dealing with equations with specific structure. If you are unsure of the type of equation you are dealing with, you can use our general equation solver , which will figure out the structure of the given equation, and will find a suitable approach.

The main difficulty with solving equations that are not linear equation or polynomial equation is that there is not a specific route to follow, nor there is any guarantee you will find solutions.

Usually, the strategy consists of simplifying expressions as much as possible, and after doing that, it is usually nowhere land, where you need to try whatever feels suitable.

Naturally, the idea is to try to reduce the equation to a simpler equation, by using some kind of substitution and a multi-step process, where you first find solutions of an auxiliary solution, which gives you CANDIDATES to the original equation. You would like to solve a linear equation , or even a quadratic equation , but perhaps the reduction you get will be a bit less generous.

Related Calculators

log in to your account

Reset password.

Game Central

Reciprocals, related concepts.

• Math Lessons
• Math Formulas
• Calculators

Math Calculators, Lessons and Formulas

It is time to solve your math problem

• HW Help (paid service)
• Trigonometry Calculators
• Trigonometric Equations Solver

Trigonometric equation solver

This calculator can solve basic trigonometric equations such as: $\color{blue}{ \sin(x) = \frac{1}{2} }$ or $ \color{blue}{ \sqrt{2} \cos\left(-\frac{3x}{4}\right) - 1 = 0 } $.

The calculator will find exact or approximate solutions on custom range. Solution can be expressed either in radians or degrees.

sin cos tan cot ( · x ) =

• Factoring Polynomials
• Polynomial Roots
• Synthetic Division
• Polynomial Operations
• Graphing Polynomials
• Simplify Polynomials
• Generate From Roots
• Simplify Expression
• Multiplication / Division
• Addition / Subtraction
• Rationalize Denominator
• Simplifying
• Quadratic Equations Solver
• Polynomial Equations
• Solving Equations - With Steps
• Solving (with steps)
• Quadratic Plotter
• Factoring Trinomials
• Equilateral Triangle
• Right Triangle
• Oblique Triangle
• Square Calculator
• Rectangle Calculator
• Circle Calculator
• Hexagon Calculator
• Rhombus Calculator
• Trapezoid Calculator
• Triangular Prism
• Distance calculator
• Midpoint Calculator
• Triangle Calculator
• Graphing Lines
• Lines Intersection
• Two Point Form
• Line-Point Distance
• Parallel/Perpendicular
• Circle Equation
• Circle From 3 Points
• Circle-line Intersection
• Modulus, inverse, polar form
• Vectors (2D & 3D)
• Add, Subtract, Multiply
• Determinant Calculator
• Matrix Inverse
• Characteristic Polynomial
• Eigenvalues
• Eigenvectors
• Matrix Decomposition
• Limit Calculator
• Derivative Calculator
• Integral Calculator
• Arithmetic Sequences
• Geometric Sequences
• Find n th Term
• Degrees to Radians
• Trig. Equations
• Long Division
• Evaluate Expressions
• Fraction Calculator
• Greatest Common Divisor GCD
• Least Common Multiple LCM
• Prime Factorization
• Scientific Notation
• Percentage Calculator
• Dec / Bin / Hex
• Probability Calculator
• Probability Distributions
• Descriptive Statistics
• Standard Deviation
• Z - score Calculator
• Normal Distribution
• T-Test Calculator
• Correlation & Regression
• Simple Interest
• Compound Interest
• Amortization Calculator
• Annuity Calculator
• Work Problems

Hire MATHPORTAL experts to do math homework for you.

Prices start at $3 per problem.

Solve equation $ \sin(2x)=\frac{\sqrt{3}}{2} ~~ \text{for} ~~ 0 \leq x \leq 360^\circ $.

Find all solutions of the equation $ \cos \left( \frac{3x}{2} \right) = -\frac{\sqrt{2}}{2}$. Express the results in degrees.

Find exact solutions of the equation $ \tan \left( -\frac{4x}{3} \right) = 0.4$. Express the results in radians.

Solve $ 2\sin \left( x \right) + \sqrt{2}= 0 ~~ \text{for} ~~ -180^\circ \leq x \leq 180^\circ $. Express the results in degrees.

Welcome to MathPortal. This website's owner is mathematician Miloš Petrović. I designed this website and wrote all the calculators, lessons, and formulas .

If you want to contact me, probably have some questions, write me using the contact form or email me on [email protected]

Email (optional)

Tool / solver to resolve one or more trigonometric equations, equations with unknown variables and cos, sin, tan, etc.

Trigonometric Equation Solver - dCode

Tag(s) : Symbolic Computation

dCode is free and its tools are a valuable help in games, maths, geocaching, puzzles and problems to solve every day! A suggestion ? a feedback ? a bug ? an idea ? Write to dCode !

Please, check our dCode Discord community for help requests! NB: for encrypted messages, test our automatic cipher identifier !

Feedback and suggestions are welcome so that dCode offers the best 'Trigonometric Equation Solver' tool for free! Thank you!

• Trigonometric Equation Solver
• Mathematics
• Symbolic Computation
• Trig Equation Solving

Answers to Questions (FAQ)

• What is a trigonometric equation? (Definition)

A trigonometric equation is a mathematical expression involving an equality involving trigonometric functions such as sine ($ \sin $), cosine ($ \cos $) or tangent ($ \tan $).

Example: $ \cos(x) = sin(\pi) $

Hyperbolic trigonometric functions are also possible $ \cosh() $, $ \sinh() $, etc.

All angles are in radians.

• How to solve a trigonometric equation?

Generally the resolution involves reciprocal trigonometric functions such as arc-sine ($ \arcsin $), arc-cosine ($ \arccos $) or arc-tangent ($ \arctan $).

dCode automatically solves trigonometric equations and calculates the values of the unknowns.

Example: $ \sin(x) = 0 $ returns the solution $ x = 0 $ (radian)

Some equations will have an infinite number of solutions, dCode returns the general solution (modulo $ \pi $ or $ 2\pi $ or with constants $ c_i $)

• How to solve multiple trigonometric equations?

Multiple trig equations with the same variables can be combined with a logical AND operator: && or ⋀ .

Also, any new line return will be considered as a new equation (of trigonometry).

• How to solve a trigonometric equation with Euler's formula?

Sometimes use Euler's formula: $ \exp(i x) = \cos(x) + i \sin(x) $ or its equivalents: $ \cos(x) = \frac{\exp(i x) + \exp(-i x)}{2} $ or $ \sin(x) = \frac{\exp(i x) - \exp(-i x)}{2i} $ can lead to simplifications.

Also use the identity $ \sin^2(x) + \cos^2(x) = 1 $ if possible.

• How to solve a trig equation step by step?

The dCode solver does not display the calculation steps because they do not reflect the steps of a human thinking but to the steps of a machine thinking (bit-by-bit binary calculation operations) far from a hand-held resolution. dCode allows you to check a result.

Source code

dCode retains ownership of the "Trigonometric Equation Solver" source code. Except explicit open source licence (indicated Creative Commons / free), the "Trigonometric Equation Solver" algorithm, the applet or snippet (converter, solver, encryption / decryption, encoding / decoding, ciphering / deciphering, breaker, translator), or the "Trigonometric Equation Solver" functions (calculate, convert, solve, decrypt / encrypt, decipher / cipher, decode / encode, translate) written in any informatic language (Python, Java, PHP, C#, Javascript, Matlab, etc.) and all data download, script, or API access for "Trigonometric Equation Solver" are not public, same for offline use on PC, mobile, tablet, iPhone or Android app! Reminder : dCode is free to use.

The copy-paste of the page "Trigonometric Equation Solver" or any of its results, is allowed (even for commercial purposes) as long as you credit dCode! Exporting results as a .csv or .txt file is free by clicking on the export icon Cite as source (bibliography): Trigonometric Equation Solver on dCode.fr [online website], retrieved on 2024-06-05, https://www.dcode.fr/trig-equation-solver

Need Help ?

Questions / comments.

• Differential Equation Solver
• Inequality Solver
• Equation Solver
• Equality Checker
• Boolean Dual
• Completing the Square
• DCODE'S TOOLS LIST

• About dCode

• calculators
• Simplify Trigonometric Expressions

Simplify Trigonometric Expressions Calculator

Get detailed solutions to your math problems with our simplify trigonometric expressions step-by-step calculator . practice your math skills and learn step by step with our math solver. check out all of our online calculators here .,  example,  solved problems,  difficult problems.

Here, we show you a step-by-step solved example of simplify trigonometric expressions. This solution was automatically generated by our smart calculator:

Applying the trigonometric identity: $\csc\left(\theta \right)^2-1 = \cot\left(\theta \right)^2$

Apply the trigonometric identity: $1-\sin\left(\theta \right)^2$$=\cos\left(\theta \right)^2$

Apply the trigonometric identity: $\cot(x)=\frac{\cos(x)}{\sin(x)}$

Divide fractions $\frac{\cos\left(x\right)^2}{\frac{\cos\left(x\right)^2}{\sin\left(x\right)^2}}$ with Keep, Change, Flip: $a\div \frac{b}{c}=\frac{a}{1}\div\frac{b}{c}=\frac{a}{1}\times\frac{c}{b}=\frac{a\cdot c}{b}$

Simplify the fraction $\frac{\cos\left(x\right)^2\sin\left(x\right)^2}{\cos\left(x\right)^2}$ by $\cos\left(x\right)^2$

 Final answer to the problem

Are you struggling with math.

Access detailed step by step solutions to thousands of problems, growing every day!

 Popular problems

Most popular problems solved with this calculator:

Trigonometric equations online calculator

The general form of trigonometric equation is

f ( trig ( x ) ) = 0

where - some arbitrary function, trig ( x ) - some trigonometric function.

As a rule, to solve trigonometric equation one need to transform it to the simplier form which has a known solution. The transformation can be done by using different trigonometric formulas .

For example, consider the solution of trigonometric equation

By using the cosine double angle formula, transform this equation to the simplier one:

The received equation is the very simple and has known solution. Our online calculator, build on Wolfram Alpha system is able to solve more complex trigonometric equations with step by step solution.

Leave your comment:

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 4: Trigonometric equations and identities

About this unit.

In this unit, you'll explore the power and beauty of trigonometric equations and identities, which allow you to express and relate different aspects of triangles, circles, and waves. You'll learn how to use trigonometric functions, their inverses, and various identities to solve and check equations and inequalities, and to model and analyze problems involving periodic motion, sound, light, and more.

Inverse trigonometric functions

• Intro to arcsine (Opens a modal)
• Intro to arctangent (Opens a modal)
• Intro to arccosine (Opens a modal)
• Restricting domains of functions to make them invertible (Opens a modal)
• Domain & range of inverse tangent function (Opens a modal)
• Using inverse trig functions with a calculator (Opens a modal)
• Inverse trigonometric functions review (Opens a modal)
• Trigonometric equations and identities: FAQ (Opens a modal)
• Evaluate inverse trig functions Get 3 of 4 questions to level up!

Sinusoidal equations

• Solving sinusoidal equations of the form sin(x)=d (Opens a modal)
• Cosine equation algebraic solution set (Opens a modal)
• Cosine equation solution set in an interval (Opens a modal)
• Sine equation algebraic solution set (Opens a modal)
• Solving cos(θ)=1 and cos(θ)=-1 (Opens a modal)
• Solve sinusoidal equations (basic) Get 3 of 4 questions to level up!
• Solve sinusoidal equations Get 3 of 4 questions to level up!

Sinusoidal models

• Interpreting solutions of trigonometric equations (Opens a modal)
• Trig word problem: solving for temperature (Opens a modal)
• Trigonometric equations review (Opens a modal)
• Interpret solutions of trigonometric equations in context Get 3 of 4 questions to level up!
• Sinusoidal models word problems Get 3 of 4 questions to level up!

Angle addition identities

• Trig angle addition identities (Opens a modal)
• Using the cosine angle addition identity (Opens a modal)
• Using the cosine double-angle identity (Opens a modal)
• Proof of the sine angle addition identity (Opens a modal)
• Proof of the cosine angle addition identity (Opens a modal)
• Proof of the tangent angle sum and difference identities (Opens a modal)
• Using the trig angle addition identities Get 3 of 4 questions to level up!

Using trigonometric identities

• Finding trig values using angle addition identities (Opens a modal)
• Using the tangent angle addition identity (Opens a modal)
• Using trig angle addition identities: finding side lengths (Opens a modal)
• Using trig angle addition identities: manipulating expressions (Opens a modal)
• Using trigonometric identities (Opens a modal)
• Trig identity reference (Opens a modal)
• Find trig values using angle addition identities Get 3 of 4 questions to level up!

Challenging trigonometry problems

• Trig challenge problem: area of a triangle (Opens a modal)
• Trig challenge problem: area of a hexagon (Opens a modal)
• Trig challenge problem: cosine of angle-sum (Opens a modal)
• Trig challenge problem: arithmetic progression (Opens a modal)
• Trig challenge problem: maximum value (Opens a modal)
• Trig challenge problem: multiple constraints (Opens a modal)
• Trig challenge problem: system of equations (Opens a modal)

Solving Trigonometric Equations

Solving trigonometric equations is finding the solutions of equations like we did with linear, quadratic, and radical equations, but using trig functions instead. We will mainly use the Unit Circle to find the exact solutions if we can, and we’ll start out by finding the solutions from $ \left[ 0,2\pi \right)$. We can also solve these using a Graphing Calculator , as we’ll see below . Note that we will use Trigonometric Identities to solve trig problems in the Trigonometric Identity section .

Important Note: There is a subtle distinction between finding inverse trig functions and solving for trig functions . If we want $ \displaystyle {{\sin }^{{-1}}}\left( {\frac{{\sqrt{2}}}{2}} \right)$ for example, like in the Inverse Trigonometric Functions section , we only pick the answers from Quadrants I and IV , so we get $ \displaystyle \frac{\pi }{4}$ only. But if we are solving $ \displaystyle \sin \left( x \right)=\frac{{\sqrt{2}}}{2}$ we get $ \displaystyle \frac{\pi }{4}$ and $ \displaystyle \frac{{3\pi }}{4}$ in the interval $ {\left[ {0,2\pi } \right)}$; there are no domain restrictions . In these cases, we want all solutions in the given interval.

Solving Trigonometric Equations Using the Unit Circle

Let’s start out with solving fairly simple trig equations, and getting the solutions from $ \left[ 0,2\pi \right)$, or $ \left[ {0,{{{360}}^{o}}} \right)$. Here is the Unit Circle again so we can “pick off” the answers from it:

Notice that we always isolate the trig function, and some solutions may have none, or more than one solution. If there are multiply angles on the unit circle for that trig function, and an expression is involved, we may have to divide up the equation into two separate equations and solve each, like the example with $ \displaystyle \theta +\frac{\pi }{{18}}$.

If a square is involved, when we take the square root, we have to include both the positive and negative values. (Note that $ {{\left( \cos \theta \right)}^{2}}$  is written as $ {{\cos }^{2}}\theta $, and we can put it in the graphing calculator as $ \boldsymbol{\cos {{\left( x \right)}^{2}}}$ or $ \boldsymbol {{{\left( {\cos \left( x \right)} \right)}^{2}}}$).

Note that sometimes you may have to solve using degrees $ \left[ {0,{{{360}}^{o}}} \right)$ instead of radians. The last problem involves solving a trig inequality .

Solving Trigonometric Equations – General Solutions

Since trig functions go on and on in both directions of the $ x$-axis, we’ll also have to know how to solve trig equations over the set of real numbers ; this is called finding the general solutions for these equations. We still use the Unit Circle to do this, but we have to think about adding and subtracting multiples of $ 2\pi $ for the sin , cos , csc , and sec functions (since $ 2\pi $ is the period for them), and $ \pi $   for the tan and cot functions (since $ \pi $ is the period for them). We can do this by adding $ 2\pi k$ or $ \pi k$ where $ k$ is any integer (positive, negative, or 0 ); sometimes this can be simplified.

We need to be careful about domain restrictions with our answers. For tan , cot , csc , and sec , we have asymptotes, and if our answer happens to fall on an asymptote, we have to eliminate it.

Here are examples; find the general solution, or all real solutions for the following equations. Note that $ k$ represents all integers $ \left( k\in \mathbb{Z} \right)$. Note also that I’m using “fancy” notation; you may not be required to do this.

Note that you can check these in a graphing calculator (radian mode) by putting the left-hand side of the equation into $ {{Y}_{1}}$ and the right-hand side into $ {{Y}_{2}}$ and get the intersection. You won’t get the exact answers, but you can still compare to the exact answers you got above.

Solving Trigonometric Equations with Multiple Angles

We have to be careful when solving trig equations with multiple angles, meaning there is a coefficient before the $ x$   or $ \theta $ (variable). This is because we could have fewer or more solutions in the Unit Circle , and thus for all real solutions when we add the $ 2\pi k$ or $ \pi k$. Thus, when we solve these types of trig problems, we always want to solve for the General Solution first (even if we’re asked to get the solutions between 0 and $ 2\pi k$) and then go back and see how many solutions are on the Unit Circle (between 0 and $ 2\pi k$ ).

When solving trig equations with multiple angles between 0 and $ 2\pi $, we’ll typically get  fewer solutions if the coefficient of the variable is less than 1 , or more solutions if the coefficient of the variable is greater than 1 . As an example, we typically get two solutions for $ \cos \left( \theta \right)$  between 0 and $ 2\pi $, so for  $ \cos \left( 3\theta \right)$, we’ll get 2 times 3 , or 6 solutions. As another example, for $ \displaystyle \cos \left( \frac{\theta }{2} \right)$, we’ll only get one solution instead of the normal two. And always check for extraneous solutions. Note that when we multiply or divide to get the variable by itself, we have to do the same with the “$ +2\pi k$” or “$ +\pi k$”.

Here are some problems: solve the following trig equations for 1) General Solutions , and 2) Solutions between $ \left[ {0,2\pi } \right)$ or $ \left[ {0,360{}^\circ } \right)$:

Factoring to Solve Trigonometric Equations

Note that sometimes we have to factor the equations to get the solutions, typically if they are trig quadratic equations . Then we set all factors to 0 to solve, making sure we test the answers to see if they work. We learned how to factor Quadratic Equations in the Solving Quadratics by Factoring and Completing the Square section.

Here are some general hints when solving advanced trig equations:

• When solving , simplify with identities first, if you can.
• You can square each side, but don’t divide both sides by factors with variables, since you might be missing out on solutions. If you need to cross-multiply, or multiply both sides by what’s in a denominator (even when one side equals 0 ), make sure you’re not missing solutions. (It might be a good idea to see how many solutions there are in a graphing calculator if you can). And always check for extraneous solutions : solutions must work in the original equations , and denominators can’t be 0 .
• If you get answers for any trig function that has asymptotes (like tan ), check for extraneous solutions (solutions that would be asymptotes).

Here are some examples, both solving on the interval 0 to $ 2\pi $ (or $ 360{}^\circ $) and over the reals. In the last problem, the answer ($ \displaystyle \theta = \frac{{\pi k}}{2}$) has to be “thrown out”, because of our domain restriction for cot (it falls on an asymptote); this is an extraneous solution:

Solving Trigonometric Equations Using a Calculator

We already used a calculator to find inverse trig functions   here in the Inverse Trigonometric Functions section . When solving trig equations , however, it’s a little more complicated, since typically we’ll have multiple solutions. We can use a scientific calculator, or graph the functions and find intersections with a graphing calculator (usually easier). Don’t forget to change to the appropriate mode (radians or degrees) using DRG on a TI scientific calculator, or mode on a TI graphing calculator.

If just using a scientific calculator , here are some rules for solving trig problems in the intervals $ \left[ {0,2\pi } \right)$ or $ \left( {-\infty ,\infty } \right)$ in radians (substitute 180° for  if using degrees). Remember these rules, which make sense if you look at the trig functions on the Unit Circle . Remember that $ k$ is any integer, negative, 0 , or positive.

• For $ \displaystyle \sin \theta =A,\,\,\theta ={{\sin }^{{-1}}}A\,\,\left( {+\,2\pi k} \right)$ and also $ \displaystyle \theta =\pi -{{\sin }^{{-1}}}A\,\,\left( {+\,2\pi k} \right)$. (For $ \csc \theta =A$, use $ \displaystyle {{\sin }^{{-1}}}\left( {\frac{1}{A}} \right)$). For example, in the interval $ \left[ {0,2\pi } \right)$, for $ \displaystyle \sin \theta =.5,\,\,\theta ={{\sin }^{{-1}}}\left( {.5\,} \right)\approx .524\,\,\left( {\frac{{\pi }}{6}\,} \right)$, and also $ \displaystyle \theta =\pi -{{\sin }^{{-1}}}\left( {.5\,} \right)\approx 2.618\,\,\left( {\frac{{5\pi }}{6}\,} \right)$.
• For $ \displaystyle \cos \theta =A,\,\theta ={{\cos }^{{-1}}}A\,\,\left( {+\,2\pi k} \right)$, and also $ \displaystyle \theta =2\pi -{{\cos }^{{-1}}}A\,\,\left( {+\,2\pi k} \right)$, which is the same as $ \displaystyle -{{\cos }^{{-1}}}A\,\,\left( {+\,2\pi k} \right)$. (For $ \sec \theta =A$ , use $ \displaystyle {{\cos }^{{-1}}}\left( {\frac{1}{A}} \right)$ ). For example, in the interval $ \left[ {0,2\pi } \right)$, for $ \displaystyle \cos \theta =.5,\,\,\theta ={{\cos }^{{-1}}}\left( {.5} \right)\,\approx 1.047\,\,\left( {\frac{\pi }{3}} \right)$, and also $ \displaystyle \theta =2\pi -{{\cos }^{{-1}}}\left( {.5} \right)\,\approx 5.236\,\,\left( {\frac{{5\pi }}{3}} \right)$.
• For $ \displaystyle \tan \theta =A,\,\,\theta ={{\tan }^{{-1}}}A\,\,\left( {+\,\pi k} \right)$; this will find all the solutions. (For $ \cot \theta =A$, use $ \displaystyle {{\tan }^{{-1}}}\left( {\frac{1}{A}} \right)$, but be careful with the angles $ \displaystyle \frac{\pi }{2}+\pi k$, since the calculator shows undefined, instead of 0 ; you can use $ \displaystyle \cot =\frac{{\cos }}{{\sin }}$ instead). For example, in the interval $ \left[ {0,2\pi } \right)$, for $ \displaystyle \tan \theta =1,\,\,\theta ={{\tan }^{{-1}}}\left( 1 \right)\,\approx .785\,\,\left( {\frac{\pi }{4}} \right)$, and also $ \displaystyle \theta ={{\tan }^{{-1}}}\left( 1 \right)+\pi \,\approx 3.927\,\,\left( {\frac{{5\pi }}{4}} \right)$.

Remember that when the coefficient of the argument of the inverse trig functions isn’t 1 , we need to divide the $ +\,2\pi k$ or $ +\,\pi k$ by this coefficient, since the period changes (see examples below). Typically, the default mode is radian mode , unless problem says “degrees” .

If you have access to a graphing calculator, it’s usually easier to solve trig equations. We can put the left-hand part of the equation in $ {{Y}_{1}}$, the right-hand part of the equation in $ {{Y}_{2}}$, and solve for the intersection(s) between 0 and $ 2\pi $, or whatever the period when finding general solutions. (Use the trace feature and arrow keys to get close to each intersection, and then use the intersect feature ( 2 nd trace, 5 , enter , enter , enter ) to find the intersection.) For the reciprocal functions, take the reciprocal of what’s on the right-hand side, and use the regular trig functions.

For intervals of $ \left[ {0,2\pi } \right)$, use Xmin = 0 , and Xmax = $ 2\pi $. For general solutions (over the reals), use Xmin = 0 and Xmax = the period (such as $ \displaystyle \frac{2\pi }{5}$ when you have $ \sin \left( {5x} \right)$, for example) for general solutions. Then, for your answer, add the appropriate factors of $ \pi k$, $ 2\pi k$, or whatever the period of the function is.

Also remember that $ {{\left( \cos \theta \right)}^{2}}$ is written as $ {{\cos }^{2}}\theta $, and we can put it in the graphing calculator as $ \boldsymbol{\cos {{\left( x \right)}^{2}}}$ or $ \boldsymbol {{{\left( {\cos \left( x \right)} \right)}^{2}}}$.

Here are some examples using both types of calculators:

Solving Trigonometric Systems of Equations

Systems of equations are needed when solving for more than one variable in equations. We learned how to solve systems of equations here in the the Systems of Linear Equations and Word Problems section , and systems of more complicated equations here in the Systems of non-Linear Equations section . Again, use either Substitution  or  Elimination , depending on what’s easier. Once we get the initial solution(s), we’ll can plug in a variable to get the other variable.

Here are some examples of Solving Systems with Trig Equations; solve over the reals :

Solving Trigonometric Inequalities

Sometimes you might be asked to solve a Trig Inequality . (Links to other types of Inequalities are found here ).

We can either solve these inequalities graphically or algebraically ; let’s try one of each. Note that you can also solve these on your graphing calculator , using the Intersect feature, and then see where the inequalities “work”:

Practice these problems, and practice, practice, practice!

Hit Submit (the arrow to the right of the problem) to solve this problem. You can also type in more problems, or click on the 3 dots in the upper right hand corner to drill down for example problems.

For Practice : Use the Mathway  widget below to try a Trig Solving  problem. Click on Submit (the blue arrow to the right of the problem) and click on Solve for x  to see the answer.

You can also type in your own problem, or click on the three dots in the upper right hand corner and click on “Examples” to drill down by topic.

If you click on Tap to view steps , or Click Here , you can register at Mathway for a free trial , and then upgrade to a paid subscription at any time (to get any type of math problem solved!).

On to Trigonometric Identities   – you’re ready! 

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

6.2: Trigonometric Equations

• Last updated
• Save as PDF
• Page ID 72991

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Linear Trigonometric Equations

In Section 5.5, we determined the height of a rider on the London Eye Ferris wheel could be determined by the equation

\(h(t)=-65\cos \left(\dfrac{\pi }{15} t\right)+70. \)

If we wanted to know the length of time during which the rider is more than 100 meters above ground, we would need to solve equations involving trigonometric functions.

Trigonometric equations are, as the name implies, equations that involve trigonometric functions. Although similar in many ways to solving polynomial equations or rational equations, only specific values of the variable will be solutions, if there are solutions at all. Often we will solve a trigonometric equation over a specified interval. However, just as often, we will be asked to find all possible solutions, and as trigonometric functions are periodic, solutions are repeated within each period. In other words, trigonometric equations may have an infinite number of solutions. Additionally, like rational equations, the domain of the function must be considered before we assume that any solution is valid. The period of both the sine function and the cosine function is \(2\pi\). In other words, every \(2\pi\) units, the y- values repeat. If we need to find all possible solutions, then we must add \(2\pi k\), where \(k\) is an integer, to the initial solution. Recall the rule that gives the format for stating all possible solutions for a function where the period is \(2\pi\):

\[\sin \theta=\sin(\theta \pm 2k\pi) \nonumber \]

There are similar rules for indicating all possible solutions for the other trigonometric functions.

• Isolate the trigonometric function (sine, cosine, or tangent) on one side of the equation. The final result for this step should look like \(\sin (x) = y\) or \(\cos (x) = y\) or \(\tan (x) = y\), where \(y\) is a real number or real number expression. If the function is not sine, cosine, or tangent, use a Reciprocal Identity to change it:

\(\sec (t)=\dfrac{1}{\cos (t)}\quad \quad \csc (t)=\dfrac{1}{\sin (t)}\quad \quad \cot (t)=\dfrac{1}{\tan (t)}\)

• Use inverse trigonometric functions to find one solution
• Find a second solution on one cycle, when a second solution exists.  Sine and cosine have 2 solutions per cycle (except when the sine or cosine ratio is 1 or -1) because the period of one cycle is \(P=2\pi\) and they oscillate between \(1\) and \(-1\) and back again. A tangent function just has one solution, because the period \(P=\pi\) for tangent is half the length of that for sine or cosine, and the graph only increases or only decreases within that cycle.
• Find additional solutions if needed, by writing a general solution that involves multiples of the period (use \(k\) to represent any integer). Given a solution \(s\), these general solutions look like

\(x = s + 2\pi k \) for sine or cosine \( \qquad \) or \( \qquad \) \(x = s + \pi k\) for tangent

Solutions that are Special Angles

Simple arguments.

In the last chapter, we learned sine and cosine values at commonly encountered ("special") angles. We can use these to solve sine and cosine equations involving these common angles.

Often the question will ask just for solutions in a given interval.

Example \(\PageIndex{1}\)

A circle of radius \(5\sqrt{2}\) intersects the line \(x = -5\) at two points. Find the angles \(\theta\) on the interval \(0 \le \theta <2\pi\), where the circle and line intersect.

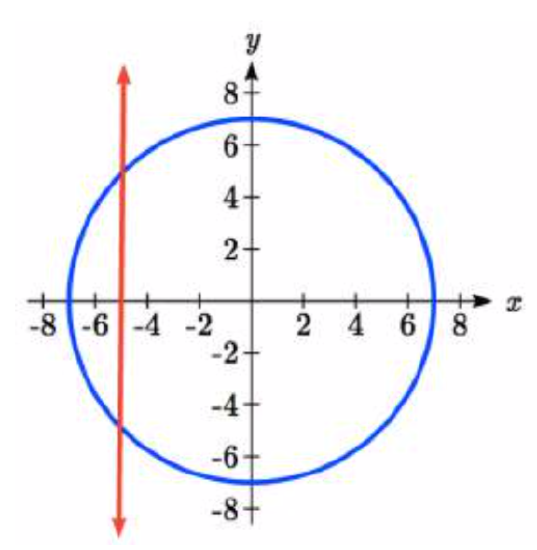
\(\begin{array} {rcll} 5\sqrt{2} \cos \left(\theta \right)   &=&-5 &\text{Isolate the cosine}\\[2pt] \cos \left(\theta \right)  &=& \dfrac{-5}{5\sqrt{2}} = \dfrac{-1}{\sqrt{2} } = \dfrac{-1}{\sqrt{2} } \cdot \dfrac{\sqrt{2}}{\sqrt{2}}  \\[2pt] \cos \left(\theta \right)  &=&  -\dfrac{\sqrt{2}}{2}\\ \end{array}\)

We recognize this as one of our special cosine values. The reference angle is \(\dfrac{\pi}{4}\) because \(\cos \dfrac{\pi}{4} = \dfrac{\sqrt{2} }{2}\), but the desired angles are in Quadrants II and III where the cosine function is negative, as the unit circle diagram suggests. Our solutions are angles

\[\theta =\dfrac{3\pi }{4}\text{ and }\theta =\dfrac{5\pi }{4}\nonumber\]

Example \(\PageIndex{2}\): Solve a Linear Equation Involving Cosine

Solve the equation exactly: \(2 \cos \theta−3=−5\), \(0≤\theta<2\pi\).

Use algebraic techniques to solve the equation.

\[\begin{align*} 2 \cos \theta-3&= -5\\ 2 \cos \theta&= -2\\ \cos \theta&= -1\\ \theta&= \pi \end{align*}\]

Other times, an expression that gives all possible solutions is desired. Two of the solutions are unique; all the others are coterminal with those two solutions. 

Example \(\PageIndex{3}\): Find the General Solution to a Linear Equation Involving Sine

Solve \(\sin \left(t\right)=\dfrac{1}{2}\) for all possible values of \(t\).

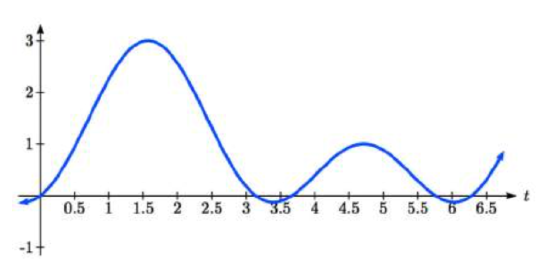
Notice this is asking us to identify all angles, \(t\), that have a sine value of \(\dfrac{1}{2}\). While evaluating a function always produces one result, solving for an input can yield multiple solutions. Two solutions should immediately jump to mind from the last chapter: \(t=\dfrac{\pi }{6}\) and \(t=\dfrac{5\pi }{6}\) because they have the same reference angle and are in quadrants where \(y\) (and thus the sine function) are positive, and because they are the common angles on the unit circle with a sin of \(\dfrac{1}{2}\).

Looking at a graph confirms that there are more than these two solutions. While eight are seen on this graph, there are an infinite number of solutions!

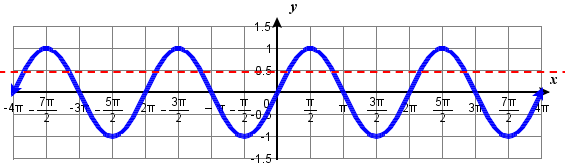
Remember that any coterminal angle will also have the same sine value, so any angle coterminal with these our first two solutions is also a solution. Coterminal angles can be found by adding or subtracting full rotations of 2\(\pi \), so we can write the full set of solutions:

\(t=\dfrac{\pi }{6} +2\pi k\) where k is any integer, and \(t=\dfrac{5\pi }{6} +2\pi k\) where \(k\) is any integer.

Example \(\PageIndex{4}\): Find the General Solution to a Linear Equation Involving Cosine 

Find all possible exact solutions for the equation \(\cos \theta=\dfrac{1}{2}\).

The cosine ratio is positive, so one of the angles is in Quadrant I. We know \( \cos \dfrac{\pi}{3} = \dfrac{1}{2},\) so therefore one of the solutions is \( \dfrac{\pi}{3}\). The other solution is in Quadrant IV, with the same reference angle. Thus the other solution is \(\dfrac{5\pi}{3}\). The same result could be obtained from analysis using the unit circle

These are the solutions in the interval \([ 0,2\pi ]\). All possible solutions are given by

\[\theta=\dfrac{\pi}{3} + 2k\pi \quad \text{and} \quad \theta=\dfrac{5\pi}{3} + 2k\pi \nonumber\]

where \(k\) is any integer.

When we are given equations that involve only one of the six trigonometric functions, their solutions involve using algebraic techniques and solving inverse trigonometric equations. We need to make several considerations when the equation involves trigonometric functions other than sine and cosine. Problems that involve reciprocals of the primary trigonometric functions must first be rewritten in terms of the primary function and then solved.

Example \(\PageIndex{5}\): Solve a Linear Equation Involving Cosecant

Solve the following equation exactly: \(\csc \theta=−2\), \(0≤\theta<4\pi\).

We want all values of \(\theta\) for which \(\csc \theta=−2\) over the interval \(0≤\theta<4\pi\).

\[\begin{align*} \csc \theta&= -2 &&\text{Rewrite as the reciprocal function}\\ \dfrac{1}{\sin \theta}&= -2\\ \sin \theta&= -\dfrac{1}{2} &&\text{The reference angle is \(\dfrac{\pi}{6}\) and solutions are in QIII and QIV}\\ \theta &= \dfrac{7\pi}{6},\space \dfrac{11\pi}{6} &&\text{Solutions in one cycle} \end{align*}\]

Because we are told to find solutions up to \(4\pi\), we must find other solutions that are coterminal to these. This is done by adding \(2\pi\) to each of these answers. Our final result is \(\boxed{\dfrac{7\pi}{6},\space \dfrac{11\pi}{6} ,\space \dfrac{19\pi}{6}, \space \dfrac{23\pi}{6}  } \).

An equation involving the tangent function is slightly different from one containing a sine or cosine function. First, as we know, the period of tangent is \(\pi\), not \(2\pi\). Further, the domain of tangent is all real numbers with the exception of odd integer multiples of \(\dfrac{\pi}{2}\), unless, of course, a problem places its own restrictions on the domain. 

Example \(\PageIndex{6}\): Find the General Solution to a Linear Equation Involving Tangent

Identify all exact solutions to the equation \(2(\tan x+3)=5+\tan x\), \(0≤x<2\pi\).

Isolate the expression \(\tan x\) on the left side of the equals sign. \(\qquad 2 \tan x+6=5+\tan x \rightarrow \tan x = -1.\)

From \(\tan \dfrac{\pi}{4} = 1\) we know the reference angle for the solutions is \( \dfrac{\pi}{4}\).  Because the tangent ratio (\(-1\)) is negative, the solution angles have the same reference angle but are in quadrants QII and QIV.

Therefore the two angles (which could also be derived from using the unit circle) are: \(\qquad x=\dfrac{3\pi}{4}\) and \(x=\dfrac{7\pi}{4}\).

• \(2 \sin x+1=0\) for all exact solutions on the interval \([0,2\pi)\).
• \(\sec x=-2\) for all possible values of \(x\).
• \(\tan \left(t\right)=1\) for all possible values of \(t\).

a. \(x=\dfrac{7\pi}{6},\space \dfrac{11\pi}{6}\)

b.  \(x=\dfrac{2\pi}{3} + 2 \pi k,   \space \dfrac{4\pi}{3}+ 2 \pi k \)

c. From our special angles, we know one answer is \(t=\dfrac{\pi }{4}\). Recall that one cycle for the tangent function is \(\pi\), not \(2\pi\) like for sine and cosine. Tangent equations only have one unique solution per cycle or period, so additional solutions can be found by adding multiples of a full period, \(\pi \). \[t=\dfrac{\pi }{4} +\pi k\nonumber\]

Arguments that are Expressions 

When the argument is an expression, rather than just a simple variable, a substitution approach is helpful.

• Rewrite the equation so it just contains one trigonometric function - sine, cosine, or tangent. Isolate the trigonometric function on one side of the equation. 
• If the argument is an expression, substitute the expression with the variable \(u\).
• Use inverse trigonometric functions to find one solution for \(u\).
• Find a second solution for \(u\) on one cycle, when a second solution exists.  Sine and cosine have 2 solutions (or one if the ratio is \(\pm1\)); tangent just has one solution.
• Find additional solutions for \(u\) if needed by writing a general solution that involves multiples of the period ( use \(k\) to represent any integer).
• Undo the substitution, if one was made in step 2. Replace \(u\) in the solution formula with the expression that was replaced with \(u\) in step 2, and then solve for the original variable.

Example \(\PageIndex{8}\): Solving a Multiple Angle Trigonometric Equation

Solve exactly: \(\cos(2x)=\dfrac{1}{2}\) on \([ 0,2\pi )\).

We can see that this equation is the standard equation with a multiple of an angle. (Replace the argument expression, \(2x\), with \(u\) and find solutions for \(u\) in one cycle of the cosine function.

\(\begin{array} {rcl} \cos(u)=\dfrac{1}{2}  & \text{Substitution made: \( \color{Cerulean}{u=2x} \) }  \\[2pt] u &=    \cos^{-1} \left( \dfrac{1}{2} \right)     & \text{Solutions in QI and QIV with ref. angle \( \dfrac{\pi}{3}\)} \\[2pt] u =    \dfrac{\pi}{3} &\text{   and    } u =    \dfrac{5\pi}{3} \end{array}\)

We saw the solutions to this equation were

\(\begin{array} {c|cl} u =\dfrac{\pi }{3}   & u=\dfrac{5\pi }{3}  \\[2pt] u =\dfrac{\pi }{3} +2\pi k   &     u=\dfrac{5\pi }{3} +2\pi k &\text{General solutions, where \(k\) is any integer}\\[2pt] 2x =\dfrac{\pi }{3} +2\pi k   &    2x=\dfrac{5\pi }{3} +2\pi k &\text{Replace the \(u\) in the solutions with \(2x \) }\\[2pt]  x =\dfrac{\pi }{6} +\pi k     &   x =\dfrac{5\pi }{6} +\pi k  &\text{Solve for \(x\).  }\\[6pt] x =\dfrac{\pi }{6}   &    x =\dfrac{5\pi }{6}      & \qquad \text{solutions when \(k=0\)}\\ x =\dfrac{7\pi }{6}   &    x =\dfrac{11\pi }{6}      &\qquad \text{solutions when \(k=1\) }\\ x =\dfrac{13\pi }{6}   &    x =\dfrac{17\pi }{6}      &\qquad k = 2 \text{ solutions are too big!}\\ \end{array}\)

Our solutions are \(x=\dfrac{\pi}{6}, \space \dfrac{5\pi}{6}, \space \dfrac{7\pi}{6}\), and \(\dfrac{11\pi}{6}\). Note that whenever we solve a problem in the form of \( \sin (nx) =c\), we will get \(n\) times as many solutions as exist in one cycle of the function.

Example  \(\PageIndex{9}\): Multiple Angle Application

The depth of water at a dock rises and falls with the tide, following the equation \(f(t)=4\sin \left(\dfrac{\pi }{12} t\right)+7\), where t is measured in hours after midnight. A boat requires a depth of 9 feet to tie up at the dock. Between what times will the depth be 9 feet or more?

To find when the depth is 9 feet, we need to solve \(f(t) = 9\).

\(\begin{array} {rcl} 4\sin \left(\dfrac{\pi }{12} t\right)+7&=9 & \text{Isolate the sine} \\[2pt] 4\sin \left(\dfrac{\pi }{12} t\right)&=2& \text{Divide by \(4\)} \\[2pt] \sin \left(\dfrac{\pi }{12} t\right)&=\dfrac{1}{2} \end{array}\)

Define  a new temporary variable \(u\) to be \(\color{Cerulean}{u=\dfrac{\pi }{12} t}\), so our equation \(\sin \left(\dfrac{\pi }{12} t\right)=\dfrac{1}{2}\) becomes 

\(\sin \left(u\right)=\dfrac{1}{2}\).

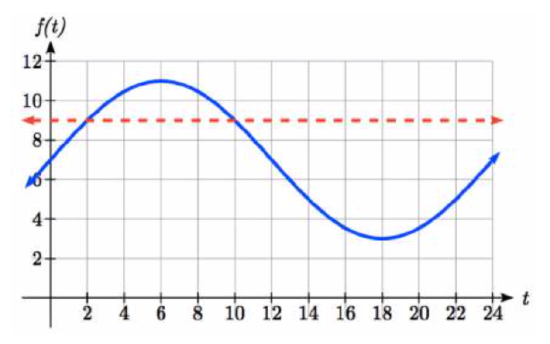
The depth will be 9 feet and the boat will be able to approach the dock between 2 am and 10 am.

Notice how in both scenarios, the 24k shows how every 24 hours the cycle will be repeated.

In the previous example, looking back at the original simplified equation \(\sin \left(\dfrac{\pi }{12} t\right)=\dfrac{1}{2}\), we can use the ratio of the “normal period” to the stretch factor to find the period: \(\dfrac{2\pi }{\left(\dfrac{\pi }{12} \right)} =2\pi \left(\dfrac{12}{\pi } \right)=24\). Notice that the sine function has a period of 24, which is reflected in the solutions: there were two unique solutions on one full cycle of the sine function, and additional solutions were found by adding multiples of a full period.

Example \(\PageIndex{10}\): Multiple Angle Equation Involving Tangent

Solve the equation exactly: \(\tan\left(\theta−\dfrac{\pi}{2}\right)=1\), \(0≤\theta<2\pi\).

The initial substitution is \(u=\theta−\dfrac{\pi}{2}\). Solving the equation \(\tan u = 1\) produces one solution, \(u= \dfrac{\pi}{4}\) .

Recall that the tangent function has a period of \(\pi\). So there is only one solution in one cycle of the tangent function. All others can be obtained from the general form of the solution set, \(u= \dfrac{\pi}{4} + \pi k\), where \(k\) is any integer.

Now we need to solve for our original variable, \(\theta\):    \(\theta−\dfrac{\pi}{2}= \dfrac{\pi}{4} + \pi k\ \rightarrow \theta=\dfrac{3\pi}{4} + \pi k \)

When \(k=0\) we obtain the solution \( \theta=\dfrac{3\pi}{4}\). When \(k=1\) we get \(\theta=\dfrac{7\pi}{4}\). When \(k=2\) the answer we get is \(\dfrac{11\pi}{4}\), which is larger than \(2\pi\), so it must be rejected for this problem.

Over the interval \([ 0,2\pi )\), we have two solutions: \(\theta=\dfrac{3\pi}{4}\) and \(\theta=\dfrac{7\pi}{4}\)

Solve \(4\sin (5t)-1=1\) for all possible values of \(t\).

\(\begin{array} {cl|}   4\sin (5t)-1=1  &  \text{Isolate the cosine}  \\[2pt]       \sin (5t)=\dfrac{1}{2} &  \text{Let \(u=5t\)} \\[2pt]       \sin (u)=\dfrac{1}{2}         \\[2pt] \end{array}\) \(\begin{array} {ccl} u=\dfrac{\pi }{6} +2\pi k  & u=\dfrac{5\pi }{6} +2\pi k   &\text{General solutions}\\[2pt] 5t=\dfrac{\pi }{6} +2\pi k  &   5t = \dfrac{5\pi }{6} +2\pi k  &\text{Solve for \(t\)}   \\[2pt] t=\dfrac{\pi }{30} +\dfrac{2\pi }{5} k  &  t=\dfrac{\pi }{6} +\dfrac{2\pi }{5} k \end{array}\)

Solutions that Require a Calculator

Not all equations involve the “special” values of the trigonometric functions to we have learned. To find solutions to these kind of equations, we need to use an inverse trig function operation on a calculator.

Simple Arguments that need a calculator

Example \(\PageIndex{12}\)

Use the inverse sine function to find one solution to \(\sin \left(\theta \right)=0.8\).

Since this is not a known value, a calculator must be used to find the angle \(\theta =\sin ^{-1} \left(0.8\right)\). The result is an approximate value for this angle. If your calculator is in degree mode, your calculator will give you an angle in degrees as the output. If your calculator is in radian mode, your calculator will give you an angle in radians. In radians, \(\theta =\sin ^{-1} \left(0.8\right)\approx 0.927\), or in degrees, \(\theta =\sin ^{-1} \left(0.8\right)\approx 53.130{}^\circ\).

Always make sure you are using the appropriate mode on your calculator -- degrees or radians. In calculus, we will almost always want to work with radians since they are unit-less.

Notice that the inverse trigonometric functions do exactly what you would expect of any function – for each input they give exactly one output. While this is necessary for these to be a function, it means that to find all the solutions to an equation like \(\sin \left(\theta \right)=0.8\), we need to do more than just evaluate the inverse function.

To find additional solutions, it is good to remember four things:

• The sine is the \(y\)-value of a point on the unit circle
• The cosine is the \(x\)-value of a point on the unit circle
• The tangent is the slope of a line at a given angle
• Other angles with the same \(\sin\)/\(\cos\)/\(\tan\) will have the same reference angle

Example \(\PageIndex{13}\): Find all solutions

Find all solutions to \(\sin \left(\theta \right)=0.8\).

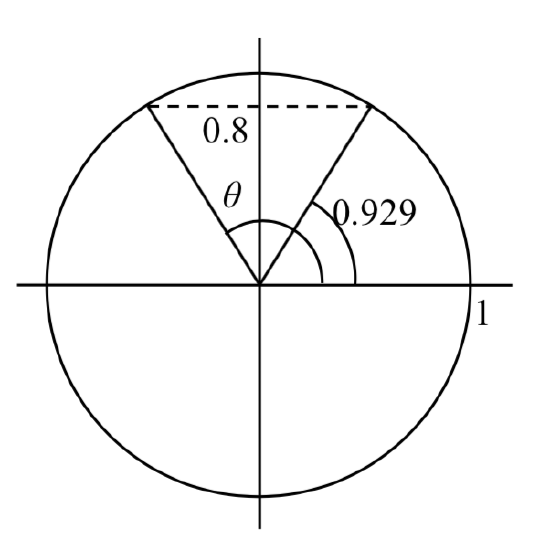
We can think of this as finding all the angles where the y-value on the unit circle is 0.8. Drawing a picture of the circle helps to show in which quadrant another angle with the same \(y\) coordinate would be positioned.

The second angle would have the same reference angle and reside in the second quadrant (where \(y\) coordinates are also positive). This second angle would be located at \(\theta =\pi -\sin ^{-1} (0.8)\), or approximately \(\theta \approx \pi -0.927=2.214\).

To find more solutions we recall that angles coterminal with these two would have the same sine value, so we can add full cycles of 2\(\pi \).

\(\begin{array} {rcll} \theta =\sin ^{-1} (0.8) +2\pi k  &\text{ and } & \theta =\pi -\sin ^{-1} (0.8)+2\pi k \\[2pt] \theta =0.927+ +2\pi k  &\text{ and } & \theta =2.214+2\pi k \\[2pt] \end{array}\) Approximate solutions, where \(k\) is an integer.

Example \(\PageIndex{14}\) 

Find all solutions to \(\sin \left(x\right)=-\dfrac{8}{9}\) on the interval \(0{}^\circ \le x<360{}^\circ\).

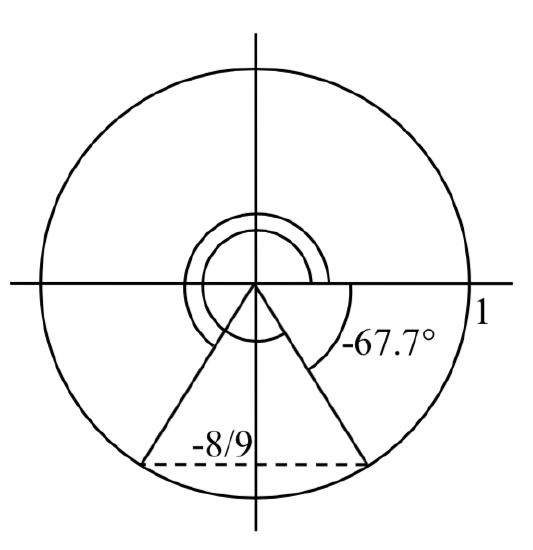
First, we will turn our calculator to degree mode. Using the inverse, we can find one solution \(x=\sin ^{-1} \left(-\dfrac{8}{9} \right)\approx -62.734{}^\circ\). While this angle satisfies the equation, it does not lie in the domain we are looking for. To find the angles in the desired domain, we start looking for additional solutions.

First, an angle coterminal with \(-62.734{}^\circ\) will have the same sine. By adding a full rotation, we can find an angle in the desired domain with the same sine.

\(x=-62.734{}^\circ +360{}^\circ =297.266{}^\circ\)

There is a second angle in the desired domain that lies in the third quadrant. Notice that \(62.734{}^\circ\) is the reference angle for all solutions, so this second solution would be \(62.734{}^\circ\) past \(180{}^\circ\)

\(x=62.734{}^\circ +180{}^\circ =242.734{}^\circ\)

The two solutions on \(0{}^\circ \le x<360{}^\circ\) are \(x\) = \(297.266{}^\circ\) and \(x\) = \(242.734{}^\circ\)

Example \(\PageIndex{15}\)

Find all solutions to \(\tan \left(x\right)=3\) on \(0 \le x<2\pi\).

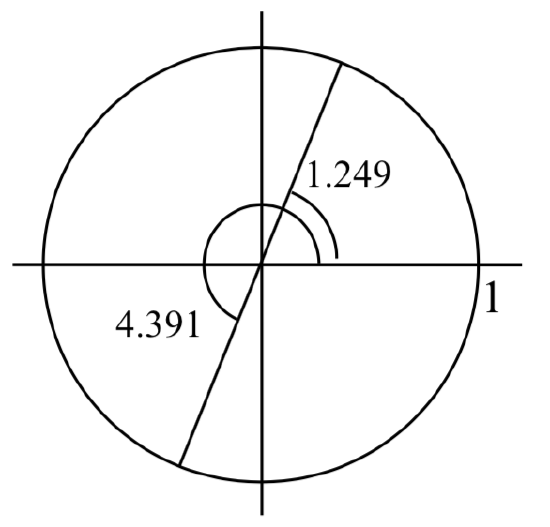
By adding \(\pi \), a full period of tangent function, we can find a second angle with the same tangent value. Notice this gives another angle where the line (along the terminal side of the angle) has the same slope.

If additional solutions were desired, we could continue to add multiples of \(\pi \), so all solutions would take on the form \(x=1.249+k\pi\), however we are only interested in \(0 \le x< 2\pi\).

\(x=1.249+\pi =4.391\)

The two solutions on \(0\le x<2\pi\) are \(x = 1.249\) and \(x = 4.391\).

Find all solutions to \(\tan \left(x\right)=0.7\) on \(0{}^\circ \le x<360{}^\circ\).

The first solution is \(x=\tan ^{-1} (0.7) \approx 34.992{}^\circ\).

For a standard tangent, the second solution can be found by adding a full period, \(180\mathrm{{}^\circ}\), giving \[x=180{}^\circ +34.99{}^\circ =214.992{}^\circ\nonumber\]

Example \(\PageIndex{17}\)

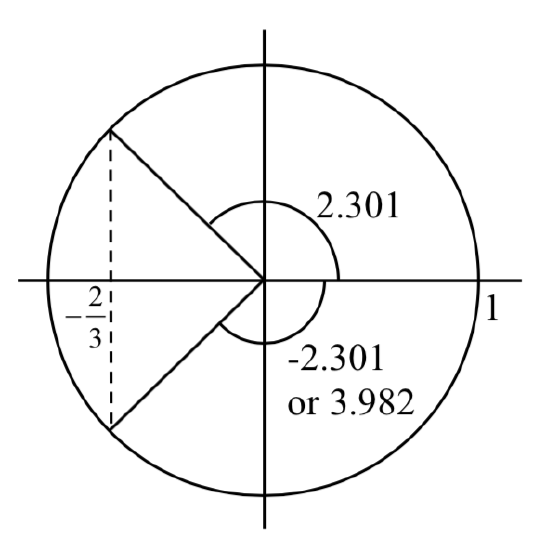
Solve \(3\cos \left(t\right)+4=2\) for all solutions on one cycle, \(0\le t<2\pi\)

\(\begin{array} {rll} 3\cos \left(t\right)+4  &=2   &\text{Isolate the cosine}\\[2pt] 3\cos \left(t\right)  &=-2    \\[2pt] \cos \left(t\right)  &=-\dfrac{2}{3}   &\text{Use the inverse, to find one solution}\\[2pt] t  &=\cos ^{-1} \left(-\dfrac{2}{3} \right)   \\[2pt] t  &\approx 2.301  \end{array}\)

We’re looking for two angles where the \(x\)-coordinate on a unit circle is -2/3. A second angle with the same cosine would be located in the third quadrant. Notice that the location of this angle could be represented as \(t=-2.301\). To represent this as a positive angle we could find a coterminal angle by adding a full rotation.

\[t=-2.301+2\pi = 3.982\nonumber\]

The equation has two solutions between 0 and 2\(\pi \), at \(t = 2.301\) and \(t = 3.982\).

Example \(\PageIndex{18}\): Using a Calculator to Solve a Trigonometric Equation Involving Secant

Use a calculator to solve the equation \( \sec θ=−4, \) giving your answer in radians.

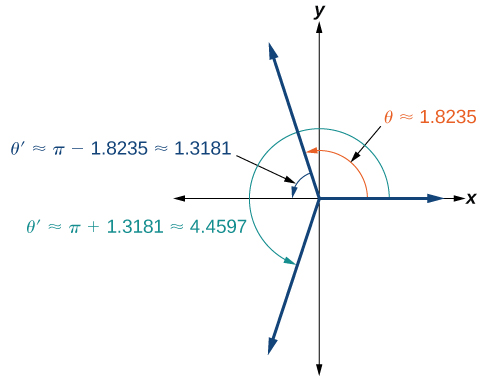
\[\begin{align*} \sec \theta&= -4\\ \dfrac{1}{\cos \theta}&= -4\\ \cos \theta&= -\dfrac{1}{4} \end{align*}\]

Check that the MODE is in radians. Now use the inverse cosine function

\(\begin{align*}{\cos}^{-1}\left(-\dfrac{1}{4}\right) \approx 1.8235\\ \theta \approx 1.8235+2\pi k \end{align*}\)

Since \(\dfrac{\pi}{2}≈1.57\) and \(\pi≈3.14\), and we know \(1.8235\) is between these two numbers, so\(\theta≈1.8235\) is in quadrant II. Cosine is also negative in quadrant III. Note that a calculator will only return an angle in quadrants I or II for the inverse cosine function, since that is the range of the inverse cosine. See the Figure on the right.

So, we also need to find the measure of the angle in quadrant III. In quadrant III, the reference angle is \( \alpha ≈\pi−1.8235≈1.3181\). The other solution in quadrant III is \(\pi + \alpha ≈\pi+1.3181≈4.4597\).

The solutions are \(\theta≈1.8235 + 2\pi k\) and \(\theta≈4.4597 + 2\pi k\).

Solve \(\cos \theta=−0.2\).

\(\theta≈1.7722 + 2\pi k\) and \(\theta≈4.5110 + 2\pi k\)

Arguments that are Expressions that need a calculator

Example \(\PageIndex{20}\)

Solve \(\cos \left(3t\right)=0.2\) for all solutions on two cycles, \(0\le t<\dfrac{4\pi }{3}\).

As before, with a horizontal compression it can be helpful to make a substitution, \(u=3t\) Making this substitution simplifies the equation to a form we have already solved.

\(\begin{array} {c} \cos \left(u\right)  =0.2   \\[2pt]  u   =\cos ^{-1} \left(0.2\right)\approx 1.369 \end{array}\)

A second solution on one cycle would be located in the fourth quadrant with the same reference angle.

\[u\approx 2\pi -1.369=4.914\nonumber\]

In this case, we need all solutions on two cycles, so we need to find the solutions on the second cycle. We can do this by adding a full rotation to the previous two solutions.

\(\begin{array} {r|ll} u = 1.369+2\pi k    &    u=4.914+2\pi  k    &\text{General solutions, \(k\) is any integer} \\[2pt] 3t = 7.653+2\pi k   &    3t=11.197+2\pi k  &\text{Replace \(u\)  with \(3t\)   }  \\[4pt] t = 0.456 +\dfrac{2\pi}{3}k   &    t=1.638+\dfrac{2\pi}{3}k   &\text{General solutions for \(t\)}    \\[2pt] t = \color{Cerulean}{0.456}    &    t=\color{Cerulean}{1.638} &\text{Solutions obtained when \(k=0\) } \\[2pt] t = 0.456... +\dfrac{2\pi}{3}   &    t=1.638....+\dfrac{2\pi}{3}  &\text{Solutions obtained when \(k=1\) } \\[2pt] t = \color{Cerulean}{2.551}   &    t=\color{Cerulean}{3.732}   \\[2pt] \end{array}\)

The question asks for all solutions less than \(\dfrac{4\pi }{3} \approx 4.189 \), so the Solution Set is \( \{  0.456,\;\; 1.638, \;\;  2.551, \;\;  3.732  \} \).

Example \(\PageIndex{21}\)

Solve \(3\sin \left(\pi \, t\right)=-2\) for all solutions.

\(\begin{array} {rlll} 3\sin \left(\pi \, t\right)  &=-2    &\text{Isolate the sine} \\[2pt] \sin \left(\pi \, t\right)   &=-\dfrac{2}{3}    &\text{Make the substitution \(u=\pi \, t\)} \\[2pt] \sin \left(u\right)          &=-\dfrac{2}{3}    &\text{Use the inverse} \\[2pt] u  &=\sin ^{-1} \left(-\dfrac{2}{3} \right)&\text{Find one solution} \\[2pt] u  & \approx -0.730  \end{array}\)

This angle is in the fourth quadrant. A second angle with the same (negative) sine ratio would be in the third quadrant with 0.730 as a reference angle: \(u=\pi +0.730=3.871\). We can write all solutions to the equation \(\sin \left(u\right)=-\dfrac{2}{3}\) as

\(\begin{array} {r|ll} u = -0.730+2\pi k    &    u=3.871+2\pi k    &\text{General solutions, \(k\) is any integer} \\[2pt] \pi t=-0.730+2\pi k   &    \pi t=3.871+2\pi k  &\text{Replace \(u\)  with \(\pi \, t\)   }  \\[2pt] t=-0.232+2 k   &    t=1.232+2 k  &\text{Divide by \(\pi \) to get all (approximate) solutions}  \\[2pt] \end{array}\)

The solutions are \( t=-0.232+2 k \) and \(t=1.232+2 k \), where \(k\) represents any integer.

Solve \(5\sin \left(\dfrac{\pi }{2} t\right)+3=0\) for all solutions on one cycle, \(0 \le t < 4\).

\[\sin \left(\dfrac{\pi }{2} t\right)=-\dfrac{3}{5}\nonumber\]Let \(u=\dfrac{\pi }{2} t\), so this becomes \[\sin \left(u\right)=-\dfrac{3}{5}\nonumber\]

Using the inverse, \(u=\sin ^{-1} \left(-\dfrac{3}{5} \right)\approx -0.6435\). Since we want positive solutions, we can find the coterminal solution by adding a full rotation: \(u=-0.6435+2\pi =5.6397\). Another angle with the same sin would be in the third quadrant with the reference angle 0.6435. \(u=\pi +0.6435=3.7851\).

\(\begin{array} {c|cl} u = 5.6397    &    u= 3.7851    &\text{Solutions for \(u\)} \\[2pt] \dfrac{\pi }{2} t= 5.6397   &   \dfrac{\pi }{2} t=3.7851    &\text{Replace \(u\)  with \(\dfrac{\pi }{2} t\)   } \\[2pt]  t=5.6397\left(\dfrac{2}{\pi } \right)   &    t=3.7851\left(\dfrac{2}{\pi } \right) &\text{Solve for \(t\)   }  \\[2pt] t= 2.4097 &    t = 3.5903  \end{array}\)

The solutions on one cycle are \(t= 2.4097 \) and \( t = 3.5903\).

Applications

We now can return to the question we began the section with.

Example \(\PageIndex{23}\)

The height of a rider on the London Eye Ferris wheel can be determined by the equation \(h(t)=-65\cos \left(\dfrac{\pi }{15} t\right)+70\). How long is the rider more than 100 meters above ground?

\(\begin{array} {rlll} -65\cos \left(\dfrac{\pi }{15} t\right)+70  &=100    &\text{Isolate the cosine} \\[2pt] -65\cos \left(\dfrac{\pi }{15} t\right)     &=30     \\[2pt] \cos \left(\dfrac{\pi }{15} t\right)  &=\dfrac{30}{-65}    &\text{Make the substitution \(u=\dfrac{\pi }{15} t\)  } \\[2pt] \cos (u)   &=  \dfrac{30}{-65}    &\text{Use the inverse} \\[2pt] u  &=\cos ^{-1} \left(\dfrac{30}{-65} \right)   &\text{Find one solution} \\[2pt] u  & \approx 2.051  \end{array}\)

This angle is in the second quadrant. A second angle with the same cosine would be symmetric in the third quadrant. This angle could be represented as u = -2.051, but we need a coterminal positive angle, so we add 2\(\pi \): \(u=2\pi -2.051\approx 4.230\).

Now we can undo the substitution to solve for \(t\)

\(\begin{array} {rcll} u = 2.051    &\text{ and }&   u=4.230    &\text{Solutions for \(u\)} \\[2pt] \dfrac{\pi }{15} t=2.051   &\text{ and }&  \dfrac{\pi }{15} t=4.230    &\text{Replace \(u\)  with \(\dfrac{\pi }{15}\)   } \\[2pt] t = \dfrac{2.051}{\dfrac{\pi }{15}}     &\text{ and }&    t=\dfrac{4.230}{\dfrac{\pi }{15}}      &\text{Solve for \(t\)   }  \\[2pt] t = 9.793 &\text{ and } & t = 20.197 \end{array}\)

A rider will be at 100 meters after 9.793 minutes, and again after 20.197 minutes. From the behavior of the height graph, we know the rider will be above 100 meters between these times. A rider will be above 100 meters for 20.197 - 9.793 = 10.404 minutes of the ride.

Quadratic Trigonometric Equations

At the beginning of this section, we solved linear trigonometric equations. In this section, we explore the techniques needed to solve trigonometric equations that are quadratic in form. Techniques used to solve quadratic trigonometric equations include factoring out a GCF, factoring a difference of squares, using the square root property, factoring a trinomial, and using the Quadratic Formula.

Factor out a GCF

Consider the function \(f(x)=2x^{2} +x\). If you were asked to solve \(f(x)=0\), it requires simple algebra:

\(\begin{align*} x^{2} +x   &=0   &&\text{Factor}  \\ x(2x+1)      &=0     &&\text{Obtain solutions}\\ x = 0\        \text{ or }  &x = -\dfrac{1}{2}\\ \end{align*}\)

We use a similar process on trigonometric equations.

Example \(\PageIndex{24}\): Use GCF Factoring

Solve exactly: \(2 {\sin}^2 \theta+\sin \theta=0;\space 0≤\theta<2\pi\)

This problem should appear familiar as it is similar to a quadratic. Let \(\color{Cerulean}{\sin \theta=s}\). The equation becomes \(2s^2+s=0\). We begin by factoring:

\[\begin{align*} 2s^2+s&= 0\\ s(2s+1)&= 0\qquad \text {Set each factor equal to zero.}\\ \boxed{s= 0} & \quad 2s+1= 0\\        & \quad \boxed{s= -\dfrac{1}{2}} \end{align*}\]

Then, substitute the original expression \(\color{Cerulean}{\sin \theta} \) back for \(\color{Cerulean}{s}\) in each of these solutions. Thus,

\(\begin{array} {c|cl} s=0                &                s= -\dfrac{1}{2}          \\[2pt] \sin \theta= 0            &               \sin \theta = -\dfrac{1}{2}            \\[2pt] \theta= 0,\;\; \theta= \pi      &           \theta= \dfrac{7\pi}{6}, \;\;  \theta= \dfrac{11\pi}{6}    \\[2pt] \end{array}\)

The solutions within the domain \(0≤\theta<2\pi\) are \(\theta=0,\pi,\dfrac{7\pi}{6},\dfrac{11\pi}{6}\).

As one gets more familiar with factoring trig expressions, you may prefer not to substitute, in which case we can solve the equation more directly:

\(\begin{align*} \sin (t)\left(2\sin (t)+1\right)=0 \qquad\\ \sin (t)=0 \quad \text{ or  }   \quad 2\sin (t)+1=0\\\ \end{align*}\)

Solve the quadratic equation \(2 \cos^2 \theta+\cos \theta=0\).

\(\dfrac{\pi}{2}, \space \dfrac{2\pi}{3}, \space \dfrac{4\pi}{3}, \space \dfrac{3\pi}{2}\)

Factor a Difference of Squares

When confronted with two terms that are both perfect squares and one is subtracted from the other, we have what is called a difference of squares. In general, the difference of squares formula is \(a^2−b^2=(a−b)(a+b)\).

Example \(\PageIndex{25}\): Use the Difference of Squares

Solve: \(4{cos}^2 \theta−1 = 0\), \(0≤\theta<2\pi\).

Notice that both the coefficient and the trigonometric expression in the first term are squared, and the square of the number 1 is 1. This is a difference of squares.

\( 4{\cos}^2 \theta-1 = 0 \) \( {(2\cos \theta)}^2-1 = 0 \) \( (2\cos \theta-1)(2\cos \theta+1) = 0 \)

\(\begin{array}{c|c} 2\cos \theta=1 \quad & \quad 2\cos \theta=-1  \\ \cos \theta=\dfrac{1}{2} \quad & \quad \cos \theta=-\dfrac{1}{2}  \\ \theta=\dfrac {\pi}{3},\; \theta=\dfrac {5\pi}{3} \quad & \quad \theta=\dfrac {2\pi}{3},\; \theta=\dfrac {4\pi}{3} \end{array}\)

Solution Set: \( \left\{ \dfrac {\pi}{3},\; \dfrac {5\pi}{3},\; \dfrac {2\pi}{3},\; \dfrac {4\pi}{3} \right\} \)

Solve: \(25−9{\sin}^2 \theta = 0\), \(0≤\theta<2\pi\).

\(25−9{\sin}^2 \theta=(5−3\sin \theta)(5+3\sin \theta) = 0\). Therefore, \( \sin \theta = \pm \dfrac{5}{3} \). However, because it is always true that \( -1 \le \sin \theta \le 1 \), this equation has no solution.

Example \(\PageIndex{26}\): Use the square root property   

Solve the problem exactly: \(2 {\sin}^2 \theta−1=0\), \(0≤\theta<2\pi\).

As this problem is not easily factored, we will solve using the square root property. First, we use algebra to isolate \(\sin \theta\). Then we will find the angles.

\[\begin{align*} 2 {\sin}^2 \theta-1&= 0\\ 2 {\sin}^2 \theta&= 1\\ {\sin}^2 \theta&= \dfrac{1}{2}\\ \sqrt{ {\sin}^2 \theta }&= \pm \sqrt{ \dfrac{1}{2} }= \pm \dfrac{1}{\sqrt{2}}\\ \sin \theta&= \pm \dfrac{\sqrt{2}}{2}\\ \end{align*}\]

Solution Set: \( \dfrac{\pi}{4}, \space \dfrac{3\pi}{4},\space \dfrac{5\pi}{4}, \space \dfrac{7\pi}{4} \)

Factor a Trinomial

Example \(\PageIndex{27}\): Factor a trinomial

Solve: \(2{\cos}^2 \theta+\cos \theta−1\), \(0≤\theta<2\pi\).

Letting \(\cos \theta=c\), we can rewrite a simplified version of the expression as follows:

\(2c^2+c−1 = 0\)

This quadratic expression can be factored as \((2c+1)(c−1)\). Replacing \(c\) with \(\cos \theta\) in this factored form yields

\((2\cos \theta+1)(\cos \theta−1) = 0\)

\(\begin{array}{c|c} 2\cos \theta=-1 \quad & \quad \cos \theta=1  \\ \cos \theta=-\dfrac{1}{2} \quad & \quad \theta=0, \; \theta = \pi  \\ \theta=\dfrac {2\pi}{3},\; \theta=\dfrac {4\pi}{3}  \end{array}\)

Solution Set: \( \left\{ 0, \; \pi, \;  \dfrac {2\pi}{3},\; \dfrac {4\pi}{3} \right\} \)

Example \(\PageIndex{28}\) 

Solve the quadratic in form equation exactly: \(2 {\sin}^2 \theta−3 \sin \theta+1=0\), \(0≤\theta<2\pi\).

We can factor using the AC grouping method or the Reverse Foil method. Initially replacing \(\sin \theta\) with \(s\) may also be helpful. Solution values of \(\theta\) can be found on the unit circle.

\( (2 \sin \theta-1)(\sin \theta-1) = 0 \\[2pt]\) \(\begin{array}{c|c}  2 \sin \theta-1= 0             \quad & \quad  \sin \theta-1= 0 \\ \sin \theta= \dfrac{1}{2}   \quad & \quad      \sin \theta= 1\\[2pt] \theta = \dfrac {\pi}{6}, \dfrac{5\pi}{6}  \quad & \quad \theta=\dfrac{\pi}{2}  \end{array}\)

Solution Set: \( \left\{ \dfrac {\pi}{6}, \;\; \dfrac{5\pi}{6}, \;\; \dfrac{\pi}{2} \right\} \)

Example \(\PageIndex{29}\) 

Solve the equation exactly: \(2 {\sin}^2 \theta−5 \sin \theta+3=0\), \(0≤\theta≤2\pi\).

Using grouping, this quadratic can be factored. Either make the real substitution, \(\sin \theta=u\),or imagine it, as we factor:

\( 2 {\sin}^2 \theta-5 \sin \theta+3   = 0\\ (2 \sin \theta-3)(\sin \theta-1)               = 0  \\[2pt] \) \(\begin{array}{c|c} 2 \sin \theta-3= 0     \quad & \quad    \sin \theta-1= 0 \\ \sin \theta= \dfrac{3}{2} \;\; \text{ Impossible}           \quad & \quad     \sin \theta= 1  \\    \end{array}\)

Solution Set: \( \left\{  \dfrac{\pi}{2}   \right\} \)

Always make sure to check all solutions on the given domain as some factors have no solution.

Example \(\PageIndex{30}\)

Solve \(3\sec ^{2} (t)-5\sec (t)-2=0\) for all solutions with \(0\le t<2\pi\).

If it is easier to for you to consider factoring without the trig function present, consider using a substitution \(u=\sec (t)\), resulting in \(3u^{2} -5u-2=0,\). When factored, this becomes  \(  (3u+1)(u-2)=0 \). Then,

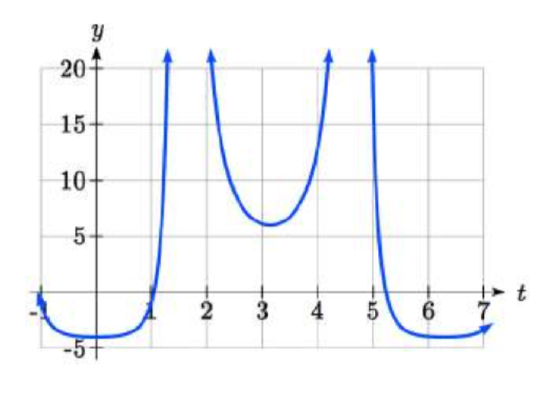
By utilizing technology to graph \(f(t)=3\sec ^{2} (t)-5\sec (t)-2\), a look at a graph confirms there are only two zeros for this function on the interval [0, 2 \(\pi\)), which assures us that we didn’t miss anything.

Solve \(2\sin ^{2} (t)+3\sin (t)+1=0\) for all solutions with \(0\le t<2\pi\).

\(2\sin ^{2} (t)+3\sin (t)+1=0 \\ \left(2\sin (t)+1\right)\left(\sin (t)+1\right)=0 \)

\(\begin{array} {rl|rll} 2\sin (t)+1&=0                &                \sin (t)+1&=0       &\text{Zero factor property}   \\[2pt] \sin (t)&=-\dfrac{1}{2}               &              \sin (t)&=-1            \\[2pt] t=\dfrac{7\pi }{6} ,&\dfrac{11\pi }{6}            &             t&=\dfrac{3\pi }{2}         \end{array}\)

Solution Set: \( \left\{ \dfrac{7\pi }{6} ,\;\; \dfrac{3\pi }{2} ,\;\; \dfrac{11\pi }{6}  \right\} \)

Quadratic Formula

Example \(\PageIndex{32}\): Use the Quadratic Formula

Solve: \({\cos}^2 \theta+3 \cos \theta−1=0\), \(0≤\theta<2\pi\).

We begin by using substitution and replacing \(\cos \theta\) with \(x\). It is not necessary to use substitution, but it may make the problem easier to solve visually. Let \(\cos \theta=x\). We have

\(x^2+3x−1=0\)

The equation cannot be factored, so we will use the quadratic formula: \(x=\dfrac{−b\pm \sqrt{b^2−4ac}}{2a}\).

\(x= \dfrac{ -3\pm \sqrt{ {(-3)}^2-4 (1) (-1) } }{2} = \dfrac{-3\pm \sqrt{13}}{2}\)

Replace \(x\) with \(\cos \theta \) and solve.

\( \cos \theta = \dfrac{-3\pm \sqrt{13}}{2} \)

\( \theta = {\cos}^{-1}\left(\dfrac{-3+\sqrt{13}}{2}\right) \)

Note that only the + sign is used. This is because we get an error when we solve \(\theta={\cos}^{−1}\left(\dfrac{−3−\sqrt{13}}{2}\right)\) on a calculator, since the domain of the inverse cosine function is \([ −1,1 ]\). However, there is a second solution:

\( \theta= {\cos}^{-1}\left(\dfrac{-3+\sqrt{13}}{2}\right) \approx 1.26 \)

This terminal side of the angle lies in quadrant I. Since cosine is also positive in quadrant IV, the second solution is

\( \theta = 2\pi-{\cos}^{-1}\left(\dfrac{-3+\sqrt{13}}{2}\right) \approx 5.02 \)

Use Identities to pre-process an Equation

Before a trigonometric equation can be solved, the equation must usually contain just one trigonometric function and one angle. In cases where there are two different trig functions in the equation, and one is a square of a trigonometric function, it is sometimes helpful apply a Pythagorean Identity to create an equation that has just one trig function in it.  The Pythagorean Identities, as well as some other identities we have learned so far, are listed below.

Definitions: IDENTITIES

Pythagorean Identities

\[\cos ^{2} (t)+\sin ^{2} (t)=1\qquad 1+\cot ^{2} (t)=\csc ^{2} (t)\qquad 1+\tan ^{2} (t)=\sec ^{2} (t) \nonumber \]

Reciprocal and Quotient  Identities

\[\sec (t)=\dfrac{1}{\cos (t)}\qquad \csc (t)=\dfrac{1}{\sin (t)} \qquad \tan (t)=\dfrac{\sin (t)}{\cos (t)} \qquad \cot (t)=\dfrac{1}{\tan (t)} \nonumber \]

Example \(\PageIndex{33}\): Use an Identity

Solve the equation exactly using an identity: \(3 \cos \theta+3=2 {\sin}^2 \theta\), \(0≤\theta<2\pi\).

If we use a Pythagorean Identity to replace \(\sin^2 \theta\) with \(1-\cos^2 \theta \), we can obtain an equation that only has the cosine function in it:

\[\begin{align*} 3 \cos \theta+3&= 2 \color{Cerulean}{{\sin}^2 \theta}\\ 3 \cos \theta+3&= 2\color{Cerulean}{(1-{\cos}^2 \theta)}\\ 3 \cos \theta+3&= 2-2{\cos}^2 \theta\\ 2 {\cos}^2 \theta+3 \cos \theta+1&= 0\\ (2 \cos \theta+1)(\cos \theta+1)&= 0\\ \end{align*}\]

\(\begin{array} {r|ll} 2 \cos \theta+1= 0                &              \cos \theta+1= 0  \\[2pt] \cos (\theta)=-\dfrac{1}{2}               &              \cos \theta=-1            \\[2pt] \theta= \dfrac{2\pi}{3},\space \dfrac{4\pi}{3}            &            \theta= \pi         \end{array}\)

Our solutions are \(\theta=\dfrac{2\pi}{3},\space \dfrac{4\pi}{3},\space \pi\).

Solve \({\sin}^2 \theta=2 \cos \theta+2\), \(0≤\theta≤2\pi\). [Hint: Make a substitution to express the equation only in terms of cosine.]

\(\cos \theta=−1\), \(\theta=\pi\)

The Pythagorean Identities become very useful whenever an equation involves a combination of sine and cosine functions.

Example \(\PageIndex{35}\)

Solve \(2\sin ^{2} (t)-\cos (t)=1\) for all solutions with \(0\le t<2\pi\).

Since this equation has a mix of sine and cosine functions, it becomes more complicated to solve. It is usually easier to work with an equation involving only one trig function. This is where we can use the Pythagorean Identity.

\[\begin{align*} 2 \; {\color{Cerulean}{\sin ^{2} (t)}} -\cos (t)  &=1  &&\text{Use the Pythagorean Identity:  }  \sin ^{2} (\theta )=1-\cos ^{2} (\theta )   \\ 2 \; {\color{Cerulean}{\left(1-\cos ^{2} (t)\right)}} -\cos (t) &=1  &&\text{Distribute the 2}\\ 2-2\cos ^{2} (t)-\cos (t)    &=1\\ \end{align*}\]

Since this is now quadratic in cosine, we rearrange the equation so one side is zero and factor.

\[\begin{align*} -2\cos ^{2} (t)-\cos (t)+1   &=0   &&\text{Multiply by -1 to simplify the factoring}\\ 2\cos ^{2} (t)+\cos (t)-1    &=0   &&\text{Factor}\\ \left(2\cos (t)-1\right)\left(\cos (t)+1\right)    & =0 \end{align*}\]

This product will be zero if either factor is zero, so we can break this into two separate cases and solve each independently.

\(\begin{array} {r|ll} 2\cos (t)-1=0                &              \cos (t)+1=0  \\[2pt]  \cos (t)=\dfrac{1}{2}               &              \cos (t)=-1            \\[2pt]  t=\dfrac{\pi }{3} \text{ or } t=\dfrac{5\pi }{3}            &            t=\pi        \end{array}\)

The solutions are \( t = \dfrac{\pi }{3} ,\; \dfrac{5\pi }{3},\; \pi \). 

Solve \(2\sin ^{2} (t)=3\cos (t)\) for all solutions with \(0\le t<2\pi\).

\[\begin{align*} 2\left(1-\cos ^{2} (t)\right)   &=3\cos (t) \\ 2\cos ^{2} (t)+3\cos (t)-2   &=0 \\ \left(2\cos (t)-1\right)\left(\cos (t)+2\right)   &=0 \end{align*}\]

\(2\cos (t)-1=0\) has two solutions, \(t=\dfrac{\pi }{3} ,\dfrac{5\pi }{3}\). \(\cos (t)+2=0\) has no solutions. 

In addition to the Pythagorean Identity, it is often necessary to rewrite the tangent, secant, cosecant, and cotangent as part of solving an equation.

Example \(\PageIndex{37}\)

Solve \(\tan (x)=3\sin (x)\) for all solutions with \(0\le x<2\pi\).

With a combination of tangent and sine, we might try rewriting tangent

\[\begin{align*} \tan (x)   &=3\sin (x) \\ \dfrac{\sin (x)}{\cos (x)}    &=3\sin (x) &&\text{Multiply both sides by cosine}\\ \sin (x)   &=3\sin (x)\cos (x) \end{align*}\]

At this point, you may be tempted to divide both sides of the equation by sin(\(x\)).

Resist the urge . When we divide both sides of an equation by a quantity, we are assuming the quantity is never zero. In this case, when sin(\(x\)) = 0 the equation is satisfied, so we’d lose those solutions if we divided by the sine.

To avoid this problem, we can rearrange the equation so that one side is zero (You technically can divide by sin( x ), as long as you separately consider the case where sin( x ) = 0. Since it is easy to forget this step, the factoring approach used in the example is recommended.).

\[\begin{align*} \sin (x)-3\sin (x)\cos (x)   &=0 &&\text{Factor out sin(\(x\)) from both parts}\\ \sin (x)\left(1-3\cos (x)\right)   &=0 \\ \end{align*}\]

From here, we can see we get solutions when \(\sin (x)=0\) or \(1-3\cos (x)=0\).

\(\begin{array} {r|ll} \sin (x)=0                &             1-3\cos (x)=0 \\  x=0 \text{ or } x=\pi               &             \cos (x)=\dfrac{1}{3}            \\             &           x=\cos ^{-1} \left(\dfrac{1}{3} \right)\approx 1.231 &\text{First solution (in QI)} \\[2pt]       &            x=2\pi -1.231=5.052  &\text{Second solution in QIV}   \end{array}\)

We have four solutions on \(0 \le x<2\pi\): \(x = 0,\; 1.231,\;  \pi ,\; 5.052\)

Example \(\PageIndex{38}\)

Solve \(\sec (\theta )=2\cos (\theta )\) to find the first four positive solutions.

\[\begin{align*} \dfrac{1}{\cos (\theta )} &=2\cos (\theta )\\ \dfrac{1}{2} &=\cos ^{2} (\theta )\\ \cos (\theta ) &=\pm \sqrt{\dfrac{1}{2} } =\pm \dfrac{\sqrt{2} }{2} \end{align*}\]

Solutions are: \(\theta =\dfrac{\pi }{4} ,\dfrac{3\pi }{4} ,\dfrac{5\pi }{4} ,\dfrac{7\pi }{4}\)

Example \(\PageIndex{39}\)

Solve \(\dfrac{4}{\sec ^{2} (\theta )} +3\cos \left(\theta \right)=2\cot \left(\theta \right)\tan \left(\theta \right)\) for all solutions with \(0\le \theta <2\pi\).

\[\begin{align*} \dfrac{4}{\sec ^{2} (\theta )} +3\cos \left(\theta \right)   &=2\cot \left(\theta \right)\tan \left(\theta \right)\  &&\text{Use the reciprocal identities} \\ 4\cos ^{2} (\theta )+3\cos (\theta )   &=2\dfrac{1}{\tan (\theta )} \tan (\theta )  &&\text{Simplify}\\ 4\cos ^{2} \left(\theta \right)+3\cos \left(\theta \right)   &=2  &&\text{Subtract 2 from each side}\\ 4\cos ^{2} \left(\theta \right)+3\cos \left(\theta \right)-2   &=0\\ \end{align*}\]

This does not appear to factor nicely so we use the quadratic formula, remembering that we are solving for \( \cos(\theta) \).

\[\cos (\theta )=\dfrac{-3\pm \sqrt{3^{2} -4(4)(-2)} }{2(4)} =\dfrac{-3\pm \sqrt{41} }{8}\nonumber\]

\(\begin{array} {r|ll} \cos (\theta )=\dfrac{-3-\sqrt{41} }{8}                &             \cos (\theta )=\dfrac{-3+\sqrt{41} }{8} \\[2pt]  \cos (\theta )=-1.175               &             \cos (\theta )=0.425           \\[2pt]           \text{No solution }  &           \theta =\cos ^{-1} \left(0.425\right)=1.131 &\text{First solution (in QI)} \\[2pt]       &            \theta =2\pi -1.131=5.152  &\text{Second solution in QIV}\\[2pt]   \end{array}\)

Solutions are: \(\theta =1.131,\;  5.152\)

We will now apply these ideas to problems involving periodic behavior.

Example \(\PageIndex{40}\): Modeling an Equation and Sketching a Sinusoidal Graph to Fit Criteria

The average monthly temperatures for a small town in Oregon are given in Table \(\PageIndex{1}\). Find a sinusoidal function of the form \(y=A \sin (Bt−C)+D\) that fits the data (round to the nearest tenth) and sketch the graph.

Recall that amplitude is found using the formula

\[A=\dfrac{\text{largest value −smallest value}}{2} \nonumber\]

Thus, the amplitude is

\( |A|  = \dfrac{69−42.5}{2} =13.25 \)

The data covers a period of 12 months, so \(\frac{2π}{B}=12\) which gives \(B=\frac{2π}{12}=\frac{π}{6}\).

The vertical shift is found using the following equation.

\[D=\dfrac{\text{highest value+lowest value}}{2} \nonumber \]

\[\begin{align*} D &= \dfrac{69+42.5}{2} &=55.8 \end{align*}\]

So far, we have the equation \(y=13.3 \sin (\frac{π}{6}x−C)+55.8\).

To find the horizontal shift, we input the \(x\) and \(y\) values for the first month and solve for \(C\).

\[\begin{align*} 42.5 & =13.3 \sin (\frac{π}{6}(1)−C)+55.8 \\ −13.3 & =13.3 \sin (\frac{π}{6}−C) \\ −1 & =\sin (\frac{π}{6}−C) \;\;\;\;\;\;\;\; \sin θ=−1→ θ=−\frac{π}{2} \\ \frac{π}{6}−C=−\frac{π}{2} \\ \frac{π}{6}+\frac{π}{2} & =C \\ C &=\frac{2π}{3} \end{align*}\]

We have the equation \(y=13.3 \sin (\frac{π}{6}x−\frac{2π}{3})+55.8\). See the graph in Figure \(\PageIndex{9}\).

 Important Topics of This Section

• Solving trig equations using known values
• Using substitution to solve equations
• Finding answers in one cycle or period vs. finding all possible solutions
• Methods for solving trig equations

Precalculus by Richard Wright

Previous Lesson Table of Contents Next Lesson

Are you not my student and has this helped you?

This book is available to download as an epub.

He gives strength to the weary and increases the power of the weak. Isaiah 40:29 NIV

5-04 Solve Trigonometric Equations

Summary: In this section, you will:

• Solve simple trigonometric equations.
• Solve trigonometric equations by factoring.
• Solve trigonometric equations using identities.

SDA NAD Content Standards (2018): PC.6.3

In American Football, the quarterback tries to throw the ball to a wide receiver. The equation to model this is \(R = \frac{v^2 \sin 2θ}{32}\) where R is the distance in feet, v is the speed the ball is thrown in feet/second, and θ is the angle above the horizontal that the ball is thrown. If the distance to the receiver and the speed of the throw are known, then the angle that the quarterback has to throw the ball can be calculated.

Solve Trigonometric Equations

The general method to solve trigonometric equations is to isolate a trigonometric expression. This can be done by factoring, using trigonometric identities, or other problem solving techniques.

Several methods to isolate the trigonometric expression are:

• If only one trigonometric expression is present, move everything else to the other side of the equation.
• Factor, then set each factor equal to zero.
• Use trigonometric identities to simplify complex trigonometric expressions.
• If two trigonometric expressions are present and they are related by a Pythagorean identity, then have one expression on each side of the equation and square both sides. Then use the Pythagorean identity to simplify the resulting equation.

After the trigonometric expression is isolated, find the angles that satisfy the trigonometric expression. Remember that each trigonometric function is positive in two quadrants and negative in two quadrants, so there are usually at least two solutions for each trigonometric equation. Because trigonometric functions are periodic, there are an infinite number of solutions that can be found by adding the period of the function.

Find the Solutions of Trigonometric Equations

After the trigonometric expression is isolated, find the angles that satisfy the trigonometric expression. If the results are on the unit circle,

• Think of which angles on the unit circle are solutions to the equation. There are usually two solutions.
• If the solutions are not evenly spaced, add 2 πn for sine and cosine or πn for tangent.
• If the solutions are evenly spaced around the unit circle, just put the first solution plus the spacing times n such as \(\frac{πn}{3}\).
• If the problem asks for all the solution on the interval [0, 2 π ), substitute values for n starting with 0 to find all the solution between 0 and 2 π .

Solve a Simple Trigonometric Equation

Find all solutions of 2 sin x − 1 = 0.

There is only one trigonometric function, so isolate it and solve.

2 sin x − 1 = 0

2 sin x = 1

$$\sin x = \frac{1}{2}$$

Think of the angles on the unit circle where \(\sin x = \frac{1}{2}\).

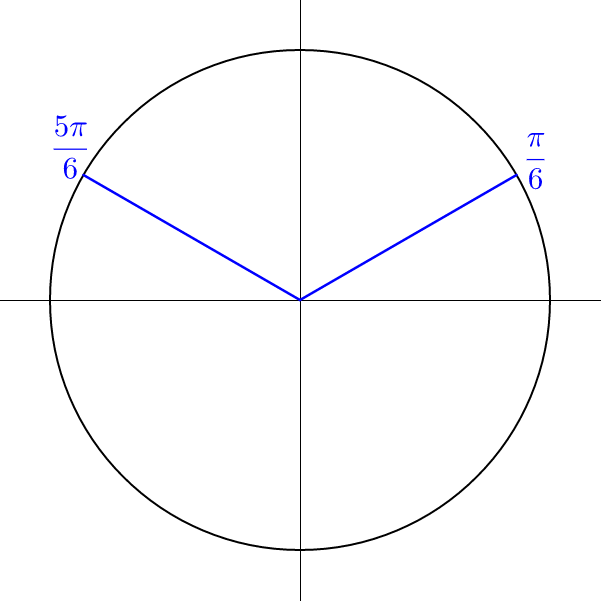
The angles are \(x = \frac{π}{6}, \frac{5π}{6}\). These are not spaced evenly, so add the period times n .

All the solutions are \(x = \frac{π}{6} + 2πn\) and \(\frac{5π}{6} + 2πn\).

Solve \(2 \cos α + \sqrt{2} = 0\).

\(\frac{3π}{4} + 2πn, \frac{5π}{4} + 2πn\)

Solve a Trigonometric Equation by Factoring

Find all solutions of sin x tan x + sin x = 0.

Begin by factoring out the common factor, sin x .

sin x tan x + sin x = 0

sin x (tan x + 1) = 0

Apply the zero product property and set each factor equal to zero and solve.

The solutions are \(x = πn, \frac{3π}{4} + πn\).

Solve tan x sec x − tan x = 0.

Find all solutions of 2 cos 2 α + cos α − 1 = 0.

This is a quadratic type equation, so factor it as you would quadratic trinomial.

2 cos 2 α + cos α − 1 = 0

(2 cos α − 1)(cos α + 1) = 0

Set each factor equal to zero and solve.

These solutions are evenly spaced around the unit circle with \(\frac{2π}{3}\) between each angle, so the solutions can be written as \(α = \frac{π}{3} + \frac{2πn}{3}\).

Solve 2 sin 2 x − sin x − 1 = 0.

\(\frac{π}{2} + \frac{2πn}{3}\)

Solve a Trigonometric Equation Using an Identity

Find all the solutions on the interval [0, 2 π ) of sec 2 β + tan 2 β = 7.

A Pythagorean identity allows the substitution of tan 2 β + 1 for sec 2 β .

sec 2 β + tan 2 β = 7

tan 2 β + 1 + tan 2 β = 7

2 tan 2 β + 1 = 7

2 tan 2 β = 6

tan 2 β = 3

$$\tan β = ±\sqrt{3}$$

$$β = \frac{π}{3}, \frac{2π}{3}, \frac{4π}{3}, \frac{5π}{3}$$

$$β = \frac{π}{3} + πn, \frac{2π}{3} + πn$$

Since only solutions between 0 and 2 π are asked for, the solutions can be found by plugging in integers for n starting with 0 until the results are 2 π or larger. This gives solutions of \(β = \frac{π}{3}, \frac{2π}{3}, \frac{4π}{3}, \frac{5π}{3}\).

Solve on the interval [0, 2π): sin 2 x − cos 2 x = 0.

• \(\frac{π}{4}, \frac{3π}{4}, \frac{5π}{4}, \frac{7π}{4}\)

Find all the solutions on the interval [0, 2π) of sec 2 θ cot 2 θ = 1.

Because the trigonometric expressions do not equal 0, we cannot use the zero product property, so the expression will have to be simplified. Try rewriting the expression in terms of sine and cosine.

sec 2 θ cot 2 θ = 1

$$\frac{1}{\cos 2θ} \frac{\cos 2θ}{\sin 2θ} = 1$$

$$\frac{1}{\sin 2θ} = 1$$

1 = sin 2 θ

The angle in the equation is 2 θ .

$$2θ = \frac{π}{2} + 2πn$$

$$θ = \frac{π}{4} + πn$$

Plug in integers starting with 0 for n until the results are 2 π or higher.

$$θ = \frac{π}{4}, \frac{5π}{4}$$

Solve on the interval [0, 2π): \(2\cos 3x = \sqrt{3}\).

\(\frac{π}{18}\) \(\frac{11π}{18}\), \(\frac{13π}{18}\), \(\frac{23π}{18}\), \(\frac{25π}{18}\), \(\frac{35π}{18}\)

Solve a Trigonometric Equation by Squaring Both Sides

Find all the solutions on the interval [0, 2 π ) of csc 3 x + cot 3 x = 1.

Cosecant, cotangent, and 1 are related with a Pythagorean identity, but the problem does not have squares on the trigonometric functions. To fix this, move the cotangent to other side of the equation and square both sides.

csc 3 x + cot 3 x = 1

csc 3 x = 1 − cot 3 x

csc 2 3 x = (1 − cot 3 x ) 2

csc 2 3 x = 1 − 2 cot 3 x + cot 2 3 x

Apply the Pythagorean identity for cosecant and cotangent to the csc 2 3 x . That way cotangent will be the only trigonometric function in the equation.

1 + cot 2 3 x = 1 − 2 cot 3 x + cot 2 3 x

Subtract 1 and cot 2 3 x from both sides.

0 = −2 cot 3 x

0 = cot 3 x

The angle in the equation is 3 x .

$$3x = \frac{π}{2} + πn$$

$$x = \frac{π}{6} + \frac{πn}{3}$$

$$x = \frac{π}{6}, \frac{π}{2}, \frac{5π}{6}, \frac{7π}{6}, \frac{3π}{2}, \frac{11π}{6}$$

Because both sides were squared earlier in this process, extraneous solutions were introduced. Thus, all the solutions need to be checked. Substitute each of the solutions into the original equation to see if both sides are equal. Of the possible solutions, only the following are actually solutions after checking.

$$x = \frac{π}{6}, \frac{5π}{6}, \frac{3π}{2}$$

Solve on the interval [0, 2π): cos 2 x – sin 2 x = 1.

0, \(\frac{3π}{4}\), π, \(\frac{7π}{4}\)

Solve a Trigonometric Equation by Graphing

Use a graphing utility to find all the solutions in the interval [0, 2π) to three decimal places of tan x = csc x .

Make the equation equal 0, tan x − csc x = 0. Then graph the expression. Use the calculate zero feature to find the x -intercepts.

On a TI graphing calculator, press o and type in the expression. To enter csc x , type \(\frac{1}{\sin x}\). Then press q and choose ZTrig from the menu. This gives a nice graph on the interval [−2π, 2π]. To find the x -intercepts, press y / and choose zero from the menu. Use the left and right arrow keys to move the cursor to the left of an intercept and press enter. Then move the cursor to the right of the intercept and press enter. Finally move the cursor to the approximate intercept to make a guess and press enter. The intercept will be displayed on the bottom of the screen.

On a NumWorks calculator, choose Grapher from the Home screen. Enter the equation after it is solved for 0, tan x − csc x = 0. Enter csc x as \(\frac{1}{\sin x}\). Go to the Graph tab. Press O . Select Find, then Zeros. Use the left and right arrow keys to see all the zeros.

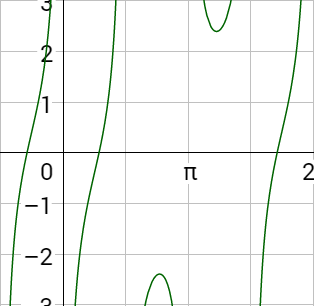
The x -intercepts and solutions are x = 0.905 and x = 5.379.

Solve on the interval [0, 2π) using a graphing utility: sin 2 x + sin x = 0.

0, 3.142, 4.712

Lesson Summary

Helpful videos about this lesson.

• Mr. Wright Teaches the Lesson (https://youtu.be/qitxhDKGgNc)  
• Solving Trigonometric Equations I (http://openstaxcollege.org/l/solvetrigeqI)
• Solving Trigonometric Equations II (http://openstaxcollege.org/l/solvetrigeqII)
• Solving Trigonometric Equations III (http://openstaxcollege.org/l/solvetrigeqIII)
• Solving Trigonometric Equations IV (http://openstaxcollege.org/l/solvetrigeqIV)
• Solving Trigonometric Equations V (http://openstaxcollege.org/l/solvetrigeqV)
• Solving Trigonometric Equations VI (http://openstaxcollege.org/l/solvetrigeqVI)

Practice Exercises

• Describe how to find all solutions in the interval [0, 2π) when the angle is 3θ.
• Find all solutions of the following equations.
• \(2 \cos x - \sqrt{2} = 0\)
• csc x − 2 = 0
• 9 tan 2 x − 3 = 0
• sin x cos x + sin x = 0
• cos x − cos 2 x = 0
• csc 2 x − 3 csc x + 2 = 0
• Find all solutions in the interval [0, 2π).
• 2 sin 2 3 x − sin 3 x − 1 = 0
• csc 2 x + cot 2 x = 3
• \(2 \sin 2x \cot 2x = \sqrt{3}\)
• \(\cot^2 \left(\frac{π}{2} - 2x\right) = 3\)
• sin x + cos x = 1
• Use a graphing utility to find the solutions in the interval [0, 2π) to three decimal places.
• sin x + cos 2 x = 0
• sec 2 x + sec x − 2 = 0
• Problem Solving
• When the initial height and final height of a projectile are equal, then the distance, or range, of the projectile is modeled by \(R = \frac{v^2 \sin 2θ}{32}\) where R is the range in feet, v is the initial speed in feet per second, and θ is the launch angle. If a football receiver is 20 yards away from the quarterback and the ball is thrown at 50 ft/s, at what angle should the ball be thrown?
• Mixed Review
• (5-03) Verify \(\cos\left(-x\right)\sec\left(\frac{π}{2} - x\right) = \cot x\).
• (5-03) Verify sin 3 x − sin x = −cos 2 x sin x .
• (5-02) Simplify using identities: (3 − 3 sin x )(3 + 3 sin x ).
• (5-01) Use the given values to evaluate all six trigonometric functions: \(\sin x = \frac{7}{25}, \tan x < 0\).
• (4-09) Find the exact value, if possible, without a calculator: \(\sin \left(\cos^{−1} \frac{5}{13}\right)\).
• Find the expression for all the solutions and then plug in values for n starting with 0 until the angle is greater than 2π.
• \(\frac{π}{4} + 2πn, \frac{7π}{4} + 2πn\)
• \(\frac{π}{6} + 2πn, \frac{5π}{6} + 2πn\)
• \(\frac{π}{6} + πn\)
• \(\frac{π}{2} + πn, 2πn\)
• \(\frac{π}{6} + 2πn, \frac{5π}{6} + 2πn, \frac{π}{2} + 2πn\)
• \(\frac{π}{6}, \frac{7π}{18}, \frac{11π}{18}, \frac{5π}{6}, \frac{19π}{18}, \frac{23π}{18}, \frac{3π}{2}, \frac{31π}{18}, \frac{35π}{18}\)
• \(\frac{π}{12}, \frac{11π}{12}, \frac{13π}{12}, \frac{23π}{12}\)
• \(\frac{π}{6}, \frac{π}{3}, \frac{2π}{3}, \frac{5π}{6}, \frac{7π}{6}, \frac{4π}{3}, \frac{5π}{3}, \frac{11π}{6}\)
• \(0, \frac{π}{2}\)
• 3.808, 5.617
• 0, 2.094, 4.189
• 25.1°, 64.9°
• \(\cos\left(-x\right)\sec\left(\frac{π}{2}-x\right)\) \(= \cos x \csc x\) \(= \frac{\cos x}{\sin x}\) \(= \cot x\)
• \(\sin^3 x - \sin x\) \(= \sin x\left(\sin^2 x - 1\right)\) \(= \sin x \left(1 - \cos^2 x - 1\right)\) \(= \sin x\left(-\cos^2 x\right)\) \(= -\cos^2 x \sin x\)
• \(\cos x = -\frac{24}{25}\), \(\tan x = -\frac{7}{24}\), \(\csc x = \frac{25}{7}\), \(\sec x = -\frac{25}{24}\), \(\cot x = -\frac{24}{7}\)
• \(\frac{12}{13}\)

Solving Trigonometric Equations using Factoring

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Factoring Calculator

What do you want to calculate.

• Solve for Variable
• Practice Mode
• Step-By-Step

Example (Click to try)

How to factor expressions.

• Add up to 5
• Multiply together to get 4

Current calculator limitations

• Doesn't support multivariable expressions
• If you have an expression that you want the calculator to support in the future, please contact us

Number Line

• x^4-5x^2+4=0
• \sqrt{x-1}-x=-7
• \left|3x+1\right|=4
• \log _2(x+1)=\log _3(27)
• 3^x=9^{x+5}
• What is the completing square method?
• Completing the square method is a technique for find the solutions of a quadratic equation of the form ax^2 + bx + c = 0. This method involves completing the square of the quadratic expression to the form (x + d)^2 = e, where d and e are constants.
• What is the golden rule for solving equations?
• The golden rule for solving equations is to keep both sides of the equation balanced so that they are always equal.
• How do you simplify equations?
• To simplify equations, combine like terms, remove parethesis, use the order of operations.
• How do you solve linear equations?
• To solve a linear equation, get the variable on one side of the equation by using inverse operations.

equation-calculator

• High School Math Solutions – Exponential Equation Calculator Solving exponential equations is pretty straightforward; there are basically two techniques: <ul> If the exponents...

Please add a message.

Message received. Thanks for the feedback.