teaching problem solving strategies in mathematics

Teaching Problem Solving in Math

• Freebies , Math , Planning

Every year my students can be fantastic at math…until they start to see math with words. For some reason, once math gets translated into reading, even my best readers start to panic. There is just something about word problems, or problem-solving, that causes children to think they don’t know how to complete them.

Every year in math, I start off by teaching my students problem-solving skills and strategies. Every year they moan and groan that they know them. Every year – paragraph one above. It was a vicious cycle. I needed something new.

I put together a problem-solving unit that would focus a bit more on strategies and steps in hopes that that would create problem-solving stars.

The Problem Solving Strategies

First, I wanted to make sure my students all learned the different strategies to solve problems, such as guess-and-check, using visuals (draw a picture, act it out, and modeling it), working backward, and organizational methods (tables, charts, and lists). In the past, I had used worksheet pages that would introduce one and provide the students with plenty of problems practicing that one strategy. I did like that because students could focus more on practicing the strategy itself, but I also wanted students to know when to use it, too, so I made sure they had both to practice.

I provided students with plenty of practice of the strategies, such as in this guess-and-check game.

There’s also this visuals strategy wheel practice.

I also provided them with paper dolls and a variety of clothing to create an organized list to determine just how many outfits their “friend” would have.

Then, as I said above, we practiced in a variety of ways to make sure we knew exactly when to use them. I really wanted to make sure they had this down!

Anyway, after I knew they had down the various strategies and when to use them, then we went into the actual problem-solving steps.

The Problem Solving Steps

I wanted students to understand that when they see a story problem, it isn’t scary. Really, it’s just the equation written out in words in a real-life situation. Then, I provided them with the “keys to success.”

S tep 1 – Understand the Problem.   To help students understand the problem, I provided them with sample problems, and together we did five important things:

• read the problem carefully
• restated the problem in our own words
• crossed out unimportant information
• circled any important information
• stated the goal or question to be solved

We did this over and over with example problems.

Once I felt the students had it down, we practiced it in a game of problem-solving relay. Students raced one another to see how quickly they could get down to the nitty-gritty of the word problems. We weren’t solving the problems – yet.

Then, we were on to Step 2 – Make a Plan . We talked about how this was where we were going to choose which strategy we were going to use. We also discussed how this was where we were going to figure out what operation to use. I taught the students Sheila Melton’s operation concept map.

We talked about how if you know the total and know if it is equal or not, that will determine what operation you are doing. So, we took an example problem, such as:

Sheldon wants to make a cupcake for each of his 28 classmates. He can make 7 cupcakes with one box of cupcake mix. How many boxes will he need to buy?

We started off by asking ourselves, “Do we know the total?” We know there are a total of 28 classmates. So, yes, we are separating. Then, we ask, “Is it equal?” Yes, he wants to make a cupcake for EACH of his classmates. So, we are dividing: 28 divided by 7 = 4. He will need to buy 4 boxes. (I actually went ahead and solved it here – which is the next step, too.)

Step 3 – Solving the problem . We talked about how solving the problem involves the following:

• taking our time
• working the problem out
• showing all our work
• estimating the answer
• using thinking strategies

We talked specifically about thinking strategies. Just like in reading, there are thinking strategies in math. I wanted students to be aware that sometimes when we are working on a problem, a particular strategy may not be working, and we may need to switch strategies. We also discussed that sometimes we may need to rethink the problem, to think of related content, or to even start over. We discussed these thinking strategies:

• switch strategies or try a different one
• rethink the problem
• think of related content
• decide if you need to make changes
• check your work
• but most important…don’t give up!

To make sure they were getting in practice utilizing these thinking strategies, I gave each group chart paper with a letter from a fellow “student” (not a real student), and they had to give advice on how to help them solve their problem using the thinking strategies above.

Finally, Step 4 – Check It.   This is the step that students often miss. I wanted to emphasize just how important it is! I went over it with them, discussing that when they check their problems, they should always look for these things:

• compare your answer to your estimate
• check for reasonableness
• check your calculations
• add the units
• restate the question in the answer
• explain how you solved the problem

Then, I gave students practice cards. I provided them with example cards of “students” who had completed their assignments already, and I wanted them to be the teacher. They needed to check the work and make sure it was completed correctly. If it wasn’t, then they needed to tell what they missed and correct it.

To demonstrate their understanding of the entire unit, we completed an adorable lap book (my first time ever putting together one or even creating one – I was surprised how well it turned out, actually). It was a great way to put everything we discussed in there.

Once we were all done, students were officially Problem Solving S.T.A.R.S. I just reminded students frequently of this acronym.

Stop – Don’t rush with any solution; just take your time and look everything over.

Think – Take your time to think about the problem and solution.

Act  – Act on a strategy and try it out.

Review – Look it over and see if you got all the parts.

Wow, you are a true trooper sticking it out in this lengthy post! To sum up the majority of what I have written here, I have some problem-solving bookmarks FREE to help you remember and to help your students!

You can grab these problem-solving bookmarks for FREE by clicking here .

You can do any of these ideas without having to purchase anything. However, if you are looking to save some time and energy, then they are all found in my Math Workshop Problem Solving Unit . The unit is for grade three, but it  may work for other grade levels. The practice problems are all for the early third-grade level.

• freebie , Math Workshop , Problem Solving

FIND IT NOW!

Check me out on tpt.

CHECK THESE OUT

5th Grade Math Workshop Growing Bundle- 9 Units

Three Types of Rocks and Minerals with Rock Cycle Circle Book

Want to save time?

COPYRIGHT © 2016-2024. The Owl Teacher | Privacy page | Disclosure Page | Shipping | Returns/Refunds

BOGO on EVERYTHING!

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

5 Teaching Mathematics Through Problem Solving

Janet Stramel

In his book “How to Solve It,” George Pólya (1945) said, “One of the most important tasks of the teacher is to help his students. This task is not quite easy; it demands time, practice, devotion, and sound principles. The student should acquire as much experience of independent work as possible. But if he is left alone with his problem without any help, he may make no progress at all. If the teacher helps too much, nothing is left to the student. The teacher should help, but not too much and not too little, so that the student shall have a reasonable share of the work.” (page 1)

What is a problem  in mathematics? A problem is “any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method” (Hiebert, et. al., 1997). Problem solving in mathematics is one of the most important topics to teach; learning to problem solve helps students develop a sense of solving real-life problems and apply mathematics to real world situations. It is also used for a deeper understanding of mathematical concepts. Learning “math facts” is not enough; students must also learn how to use these facts to develop their thinking skills.

According to NCTM (2010), the term “problem solving” refers to mathematical tasks that have the potential to provide intellectual challenges for enhancing students’ mathematical understanding and development. When you first hear “problem solving,” what do you think about? Story problems or word problems? Story problems may be limited to and not “problematic” enough. For example, you may ask students to find the area of a rectangle, given the length and width. This type of problem is an exercise in computation and can be completed mindlessly without understanding the concept of area. Worthwhile problems  includes problems that are truly problematic and have the potential to provide contexts for students’ mathematical development.

There are three ways to solve problems: teaching for problem solving, teaching about problem solving, and teaching through problem solving.

Teaching for problem solving begins with learning a skill. For example, students are learning how to multiply a two-digit number by a one-digit number, and the story problems you select are multiplication problems. Be sure when you are teaching for problem solving, you select or develop tasks that can promote the development of mathematical understanding.

Teaching about problem solving begins with suggested strategies to solve a problem. For example, “draw a picture,” “make a table,” etc. You may see posters in teachers’ classrooms of the “Problem Solving Method” such as: 1) Read the problem, 2) Devise a plan, 3) Solve the problem, and 4) Check your work. There is little or no evidence that students’ problem-solving abilities are improved when teaching about problem solving. Students will see a word problem as a separate endeavor and focus on the steps to follow rather than the mathematics. In addition, students will tend to use trial and error instead of focusing on sense making.

Teaching through problem solving  focuses students’ attention on ideas and sense making and develops mathematical practices. Teaching through problem solving also develops a student’s confidence and builds on their strengths. It allows for collaboration among students and engages students in their own learning.

Consider the following worthwhile-problem criteria developed by Lappan and Phillips (1998):

• The problem has important, useful mathematics embedded in it.
• The problem requires high-level thinking and problem solving.
• The problem contributes to the conceptual development of students.
• The problem creates an opportunity for the teacher to assess what his or her students are learning and where they are experiencing difficulty.
• The problem can be approached by students in multiple ways using different solution strategies.
• The problem has various solutions or allows different decisions or positions to be taken and defended.
• The problem encourages student engagement and discourse.
• The problem connects to other important mathematical ideas.
• The problem promotes the skillful use of mathematics.
• The problem provides an opportunity to practice important skills.

Of course, not every problem will include all of the above. Sometimes, you will choose a problem because your students need an opportunity to practice a certain skill.

Key features of a good mathematics problem includes:

• It must begin where the students are mathematically.
• The feature of the problem must be the mathematics that students are to learn.
• It must require justifications and explanations for both answers and methods of solving.

Problem solving is not a  neat and orderly process. Think about needlework. On the front side, it is neat and perfect and pretty.

But look at the b ack.

It is messy and full of knots and loops. Problem solving in mathematics is also like this and we need to help our students be “messy” with problem solving; they need to go through those knots and loops and learn how to solve problems with the teacher’s guidance.

When you teach through problem solving , your students are focused on ideas and sense-making and they develop confidence in mathematics!

Mathematics Tasks and Activities that Promote Teaching through Problem Solving

Choosing the Right Task

Selecting activities and/or tasks is the most significant decision teachers make that will affect students’ learning. Consider the following questions:

• Teachers must do the activity first. What is problematic about the activity? What will you need to do BEFORE the activity and AFTER the activity? Additionally, think how your students would do the activity.
• What mathematical ideas will the activity develop? Are there connections to other related mathematics topics, or other content areas?
• Can the activity accomplish your learning objective/goals?

Low Floor High Ceiling Tasks

By definition, a “ low floor/high ceiling task ” is a mathematical activity where everyone in the group can begin and then work on at their own level of engagement. Low Floor High Ceiling Tasks are activities that everyone can begin and work on based on their own level, and have many possibilities for students to do more challenging mathematics. One gauge of knowing whether an activity is a Low Floor High Ceiling Task is when the work on the problems becomes more important than the answer itself, and leads to rich mathematical discourse [Hover: ways of representing, thinking, talking, agreeing, and disagreeing; the way ideas are exchanged and what the ideas entail; and as being shaped by the tasks in which students engage as well as by the nature of the learning environment].

The strengths of using Low Floor High Ceiling Tasks:

• Allows students to show what they can do, not what they can’t.
• Provides differentiation to all students.
• Promotes a positive classroom environment.
• Advances a growth mindset in students
• Aligns with the Standards for Mathematical Practice

Examples of some Low Floor High Ceiling Tasks can be found at the following sites:

• YouCubed – under grades choose Low Floor High Ceiling
• NRICH Creating a Low Threshold High Ceiling Classroom
• Inside Mathematics Problems of the Month

Math in 3-Acts

Math in 3-Acts was developed by Dan Meyer to spark an interest in and engage students in thought-provoking mathematical inquiry. Math in 3-Acts is a whole-group mathematics task consisting of three distinct parts:

Act One is about noticing and wondering. The teacher shares with students an image, video, or other situation that is engaging and perplexing. Students then generate questions about the situation.

In Act Two , the teacher offers some information for the students to use as they find the solutions to the problem.

Act Three is the “reveal.” Students share their thinking as well as their solutions.

“Math in 3 Acts” is a fun way to engage your students, there is a low entry point that gives students confidence, there are multiple paths to a solution, and it encourages students to work in groups to solve the problem. Some examples of Math in 3-Acts can be found at the following websites:

• Dan Meyer’s Three-Act Math Tasks
• Graham Fletcher3-Act Tasks ]
• Math in 3-Acts: Real World Math Problems to Make Math Contextual, Visual and Concrete

Number Talks

Number talks are brief, 5-15 minute discussions that focus on student solutions for a mental math computation problem. Students share their different mental math processes aloud while the teacher records their thinking visually on a chart or board. In addition, students learn from each other’s strategies as they question, critique, or build on the strategies that are shared.. To use a “number talk,” you would include the following steps:

• The teacher presents a problem for students to solve mentally.
• Provide adequate “ wait time .”
• The teacher calls on a students and asks, “What were you thinking?” and “Explain your thinking.”
• For each student who volunteers to share their strategy, write their thinking on the board. Make sure to accurately record their thinking; do not correct their responses.
• Invite students to question each other about their strategies, compare and contrast the strategies, and ask for clarification about strategies that are confusing.

“Number Talks” can be used as an introduction, a warm up to a lesson, or an extension. Some examples of Number Talks can be found at the following websites:

• Inside Mathematics Number Talks
• Number Talks Build Numerical Reasoning

Saying “This is Easy”

“This is easy.” Three little words that can have a big impact on students. What may be “easy” for one person, may be more “difficult” for someone else. And saying “this is easy” defeats the purpose of a growth mindset classroom, where students are comfortable making mistakes.

When the teacher says, “this is easy,” students may think,

• “Everyone else understands and I don’t. I can’t do this!”
• Students may just give up and surrender the mathematics to their classmates.
• Students may shut down.

Instead, you and your students could say the following:

• “I think I can do this.”
• “I have an idea I want to try.”
• “I’ve seen this kind of problem before.”

Tracy Zager wrote a short article, “This is easy”: The Little Phrase That Causes Big Problems” that can give you more information. Read Tracy Zager’s article here.

Using “Worksheets”

Do you want your students to memorize concepts, or do you want them to understand and apply the mathematics for different situations?

What is a “worksheet” in mathematics? It is a paper and pencil assignment when no other materials are used. A worksheet does not allow your students to use hands-on materials/manipulatives [Hover: physical objects that are used as teaching tools to engage students in the hands-on learning of mathematics]; and worksheets are many times “naked number” with no context. And a worksheet should not be used to enhance a hands-on activity.

Students need time to explore and manipulate materials in order to learn the mathematics concept. Worksheets are just a test of rote memory. Students need to develop those higher-order thinking skills, and worksheets will not allow them to do that.

One productive belief from the NCTM publication, Principles to Action (2014), states, “Students at all grade levels can benefit from the use of physical and virtual manipulative materials to provide visual models of a range of mathematical ideas.”

You may need an “activity sheet,” a “graphic organizer,” etc. as you plan your mathematics activities/lessons, but be sure to include hands-on manipulatives. Using manipulatives can

• Provide your students a bridge between the concrete and abstract
• Serve as models that support students’ thinking
• Provide another representation
• Support student engagement
• Give students ownership of their own learning.

Adapted from “ The Top 5 Reasons for Using Manipulatives in the Classroom ”.

any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method

should be intriguing and contain a level of challenge that invites speculation and hard work, and directs students to investigate important mathematical ideas and ways of thinking toward the learning

involves teaching a skill so that a student can later solve a story problem

when we teach students how to problem solve

teaching mathematics content through real contexts, problems, situations, and models

a mathematical activity where everyone in the group can begin and then work on at their own level of engagement

20 seconds to 2 minutes for students to make sense of questions

Mathematics Methods for Early Childhood Copyright © 2021 by Janet Stramel is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

• Grades 6-12
• School Leaders

Get our FREE 'Meet the Teacher' bundle!

21 Essential Strategies in Teaching Math

Even veteran teachers need to read these.

We all want our kids to succeed in math. In most districts, standardized tests measure students’ understanding, yet nobody wants to teach to the test. Over-reliance on test prep materials and “drill and kill” worksheets steal instructional time while also harming learning and motivation. But sound instruction and good test scores aren’t mutually exclusive. Being intentional and using creative approaches to your instruction can get students excited about math. These essential strategies in teaching mathematics can make this your class’s best math year ever!

1. Raise the bar for all

WeAreTeachers

For math strategies to be effective, teachers must first get students to believe that they can be great mathematicians. Holding high expectations for all students encourages growth. As early as second grade, girls have internalized the idea that math is not for them . It can be a challenge to overcome the socially acceptable thought, I’m not good at math , says Sarah Bax, a math teacher at Hardy Middle School in Washington, D.C.

Rather than success being a function of how much math talent they’re born with, kids need to hear from teachers that anyone who works hard can succeed. “It’s about helping kids have a growth mindset ,” says Bax. “Practice and persistence make you good at math.” Build math equity and tell students about the power and importance of math with enthusiasm and high expectations.

(Psst … you can snag our growth mindset posters for your math classroom here. )

2. Don’t wait—act now!

Look ahead to the specific concepts students need to master for annual end-of-year tests, and pace instruction accordingly. Think about foundational skills they will need in the year ahead.

“You don’t want to be caught off guard come March thinking that students need to know X for the tests the next month,” says Skip Fennell, project director of Elementary Mathematics Specialists and Teacher Leaders Project and professor emeritus at McDaniel College in Westminster, Maryland. Know the specific standards and back-map your teaching from the fall so students are ready, and plan to use effective math strategies accordingly.

[contextly_auto_sidebar]

3. Create a testing pathway

You may not even see the results of standardized tests until next school year, but you have to prepare students for it now. Use formative assessments to ensure that students understand the concepts. What you learn can guide your instruction and determine the next steps, says Fennell. “I changed the wording because I didn’t want to suggest that we are in favor of ‘teaching to the test.'”

Testing is not something separate from your instruction. It should be integrated into your planning. Instead of a quick exit question or card, give a five-minute quiz, an open-ended question, or a meaningful homework assignment to confirm students have mastered the math skill covered in the day’s lesson. Additionally, asking students to explain their thinking orally or in writing is a great way to determine their level of understanding. A capable digital resource, designed to monitor your students in real-time, can also be an invaluable tool, providing actionable data to inform your instruction along the way.

4. Observe, modify, and reevaluate

Sometimes we get stuck in a mindset of “a lesson a day” in order to get through the content. However, we should keep our pacing flexible, or kids can fall behind. Walk through your classroom as students work on problems and observe the dynamics. Talk with students individually and include “hinge questions” in your lesson plans to gauge understanding before continuing, suggests Fennell. In response, make decisions to go faster or slower or put students in groups.

5. Read, read, read!

Although we don’t often think of reading as a math strategy, there’s almost nothing better to get students ready to learn a new concept than a great read-aloud. Kids love to be read to, and the more we show students how math is connected to the world around us, the more invested they become. Reading books with math connections helps children see how abstract concepts connect to their lives.

6. Personalize and offer choice

When students are given the opportunity to choose how they learn and demonstrate their understanding of a concept, their buy-in and motivation increase. It gives them the chance to understand their preferred learning style, provides agency over their own learning, and allows for the space to practice different strategies to solve math problems. Give students a variety of options, such as timed exercises, projects, or different materials , to show that they’ve mastered foundational skills. As students show what they’ve learned, teachers can track understanding, figure out where students need additional scaffolding or other assistance, and tailor lessons accordingly.

7. Plant the seeds!

Leave no child inside! A school garden is a great way to apply math concepts in a fun way while instilling a sense of purpose in your students. Measurement, geometry, and data analysis are obvious topics that can be addressed through garden activities, but also consider using the garden to teach operations, fractions, and decimals. Additionally, garden activities can help promote character education goals like cooperation, respect for the earth, and, if the crops are donated to organizations that serve those in need, the value of giving to others.

8. Add apps appropriately

The number of apps (interactive software used on touch-screen devices) available to support math instruction has increased rapidly in recent years. Kids who are reluctant to practice math facts with traditional pencil-and-paper resources will gladly do essentially the same work as long as it’s done on a touch screen. Many apps focus on practice via games, but there are some that encourage children to explore the content at a conceptual level.

9. Encourage math talk

Communicating about math helps students process new learning and build on their thinking. Engage students during conversations and have them describe why they solved a problem in a certain way. “My goal is to get information about what students are thinking and use that to guide my instruction, as opposed to just telling them information and asking them to parrot things back,” says Delise Andrews, who taught math (K–8) and is now a grade 3–5 math coordinator in the Lincoln Public Schools in Nebraska.

Instead of seeking a specific answer, Andrews wants to have deeper discussions to figure out what a student knows and understands. “True learning happens a lot around talking and doing math—not just drilling,” she says. Of course, this math strategy not only requires students to feel comfortable expressing their mathematical thinking, but also assumes that they have been trained to listen respectfully to the reasoning of their classmates.

Learn more: Free Let’s Talk Math Poster

10. The art of math

Almost all kids love art, and visual learners need a math strategy that works for them too, so consider integrating art and math instruction for one of the easiest strategies in teaching mathematics. Many concepts in geometry, such as shapes, symmetry, and transformations (slides, flips, and turns), can be applied in a fun art project. Also consider using art projects to teach concepts like measurement, ratios, and arrays (multiplication/division).

11. Seek to develop understanding

Meaningful math education goes beyond memorizing formulas and procedures. Memorization does not foster understanding. Set high goals, create space for exploration, and work with the students to develop a strong foundation. “Treat the kids like mathematicians,” says Andrews. Present a broad topic, review various strategies for solving a problem, and then elicit a formula or idea from the kids rather than starting with the formula. This creates a stronger conceptual understanding and mental connections with the material for the student.

12. Give students time to reflect

Sometimes teachers get so caught up in meeting the demands of the curriculum and the pressure to “get it all done” that they don’t give students the time to reflect on their learning. Students can be asked to reflect in writing at the end of an assignment or lesson, via class or small group discussion, or in interviews with the teacher. It’s important to give students the time to think about and articulate the meaning of what they’ve learned, what they still don’t understand, and what they want to learn more about. This provides useful information for the teacher and helps the student monitor their own progress and think strategically about how they approach mathematics.

13. Allow for productive struggle

When giving students an authentic problem, ask a big question and let them struggle to figure out several ways to solve it, suggests Andrews. “Your job as a teacher is to make it engaging by asking the right questions at the right time. So you don’t take away their thinking, but you help them move forward to a solution,” she says.

Provide as little information as possible but enough so students can be productive. Effective math teaching supports students as they grapple with mathematical ideas and relationships. Allow them to discover what works and experience setbacks along the way as they adopt a growth mindset about mathematics.

14. Emphasize hands-on learning

WeAreTeachers; Teacher Created Resources

In math, there’s so much that’s abstract. Hands-on learning is a strategy that helps make the conceptual concrete. Consider incorporating math manipulatives whenever possible. For example, you can use LEGO bricks to teach a variety of math skills, including finding area and perimeter and understanding multiplication.

15. Build excitement by rewarding progress

Students—especially those who haven’t experienced success—can have negative attitudes about math. Consider having students earn points and receive certificates, stickers, badges, or trophies as they progress. Weekly announcements and assemblies that celebrate the top players and teams can be really inspiring for students. “Having that recognition and moment is powerful,” says Bax. “Through repeated practice, they get better, and they are motivated.” Through building excitement, this allows for one of the best strategies in teaching mathematics to come to fruition.

16. Choose meaningful tasks

Kids get excited about math when they have to  solve real-life problems. For instance, when teaching sixth graders how to determine area, present tasks related to a house redesign, suggests Fennell. Provide them with the dimensions of the walls and the size of the windows and have them determine how much space is left for the wallpaper. Or ask them to consider how many tiles they would need to fill a deck. You can absolutely introduce problem-based learning, even in a virtual world.

17. Play math games

Life Between Summers/Shape Guess Who via lifebetweensummers.com; 123 Homeschool 4 Me/Tic-Tac-Toe Math Game via 123homeschool4me.com; WeAreTeachers

Student engagement and participation can be a challenge, especially if you’re relying heavily on worksheets. Games, like these first grade math games , are an excellent way to make the learning more fun while simultaneously promoting strategic mathematical thinking, computational fluency , and understanding of operations. Games are especially good for kinesthetic learners and foster a home-school connection when they’re sent home for extra practice.

18. Set up effective math routines

Students generally feel confident and competent in the classroom when they know what to do and why they’re doing it. Establishing routines in your math class and training kids to use them can make math class efficient, effective, and fun! For example, consider starting your class with a number sense routine. Rich, productive small group math discussions don’t happen by themselves, so make sure your students know the “rules of the road” for contributing their ideas and respectfully critiquing the ideas of others.

19. Encourage teacher teamwork and reflection

You can’t teach in a vacuum. Collaborate with other teachers to improve your math instruction skills. Start by discussing the goal for the math lesson and what it will look like, and plan as a team to use the most effective math strategies. “Together, think through the tasks and possible student responses you might encounter,” says Andrews. Reflect on what did and didn’t work to improve your practice.

Learn With Play at Home/Plastic Bottle Number Bowling via learnwithplayathome.com; Math Geek Mama/Skip-Counting Hopscotch via mathgeekmama.com; WeAreTeachers

Adding movement and physical activity to your instruction might seem counterintuitive as a math strategy, but asking kids to get out of their seats can increase their motivation and interest. For example, you could ask students to:

• Make angles with their arms
• Create a square dance that demonstrates different types of patterns
• Complete a shape scavenger hunt in the classroom
• Run or complete other exercises periodically and graph the results

The possibilities of these strategies in teaching mathematics are limited only by your imagination and the math concepts you need to cover. Check out these active math games .

21. Be a lifelong learner

Generally, students will become excited about a subject if their teacher is excited about it. However, it’s hard to be excited about teaching math if your understanding hasn’t changed since you learned it in elementary school. For example, if you teach how to divide fractions by fractions and your understanding is limited to following the “invert and multiply” rule, take the time to understand why the rule works and how it applies to the real world. When you have confidence in your own mathematical expertise, then you can teach math confidently and joyfully to best apply strategies in teaching mathematics.

What do you feel are the most important strategies in teaching mathematics? Share in the comments below.

Want more articles like this be sure to subscribe to our newsletters ., learn why it’s important to honor all math strategies in teaching math . plus, check out the best math websites for teachers ..

You Might Also Like

24 Creative Ways to Use Math Manipulatives in Your Classroom

Students learn better when they’re engaged, and manipulatives in the classroom make it easy for kids to get excited. We Continue Reading

Copyright © 2024. All rights reserved. 5335 Gate Parkway, Jacksonville, FL 32256

Problem Solving Activities: 7 Strategies

• Critical Thinking

Problem solving can be a daunting aspect of effective mathematics teaching, but it does not have to be! In this post, I share seven strategic ways to integrate problem solving into your everyday math program.

In the middle of our problem solving lesson, my district math coordinator stopped by for a surprise walkthrough. 

I was so excited!

We were in the middle of what I thought was the most brilliant math lesson– teaching my students how to solve problem solving tasks using specific problem solving strategies. 

It was a proud moment for me!

Each week, I presented a new problem solving strategy and the students completed problems that emphasized the strategy. 

Genius right? 

After observing my class, my district coordinator pulled me aside to chat. I was excited to talk to her about my brilliant plan, but she told me I should provide the tasks and let my students come up with ways to solve the problems. Then, as students shared their work, I could revoice the student’s strategies and give them an official name. 

What a crushing blow! Just when I thought I did something special, I find out I did it all wrong. 

I took some time to consider her advice. Once I acknowledged she was right, I was able to make BIG changes to the way I taught problem solving in the classroom. 

When I Finally Saw the Light

To give my students an opportunity to engage in more authentic problem solving which would lead them to use a larger variety of problem solving strategies, I decided to vary the activities and the way I approached problem solving with my students. 

Problem Solving Activities

Here are seven ways to strategically reinforce problem solving skills in your classroom. 

Seasonal Problem Solving

Many teachers use word problems as problem solving tasks. Instead, try engaging your students with non-routine tasks that look like word problems but require more than the use of addition, subtraction, multiplication, and division to complete. Seasonal problem solving tasks and daily challenges are a perfect way to celebrate the season and have a little fun too!

Cooperative Problem Solving Tasks

Go cooperative! If you’ve got a few extra minutes, have students work on problem solving tasks in small groups. After working through the task, students create a poster to help explain their solution process and then post their poster around the classroom. Students then complete a gallery walk of the posters in the classroom and provide feedback via sticky notes or during a math talk session.

Notice and Wonder

Before beginning a problem solving task, such as a seasonal problem solving task, conduct a Notice and Wonder session. To do this, ask students what they notice about the problem. Then, ask them what they wonder about the problem. This will give students an opportunity to highlight the unique characteristics and conditions of the problem as they try to make sense of it. 

Want a better experience? Remove the stimulus, or question, and allow students to wonder about the problem. Try it! You’ll gain some great insight into how your students think about a problem.

Math Starters

Start your math block with a math starter, critical thinking activities designed to get your students thinking about math and provide opportunities to “sneak” in grade-level content and skills in a fun and engaging way. These tasks are quick, designed to take no more than five minutes, and provide a great way to turn-on your students’ brains. Read more about math starters here ! 

Create your own puzzle box! The puzzle box is a set of puzzles and math challenges I use as fast finisher tasks for my students when they finish an assignment or need an extra challenge. The box can be a file box, file crate, or even a wall chart. It includes a variety of activities so all students can find a challenge that suits their interests and ability level.

Calculators

Use calculators! For some reason, this tool is not one many students get to use frequently; however, it’s important students have a chance to practice using it in the classroom. After all, almost everyone has access to a calculator on their cell phones. There are also some standardized tests that allow students to use them, so it’s important for us to practice using calculators in the classroom. Plus, calculators can be fun learning tools all by themselves!

Three-Act Math Tasks

Use a three-act math task to engage students with a content-focused, real-world problem! These math tasks were created with math modeling in mind– students are presented with a scenario and then given clues and hints to help them solve the problem. There are several sites where you can find these awesome math tasks, including Dan Meyer’s Three-Act Math Tasks and Graham Fletcher’s 3-Acts Lessons . 

Getting the Most from Each of the Problem Solving Activities

When students participate in problem solving activities, it is important to ask guiding, not leading, questions. This provides students with the support necessary to move forward in their thinking and it provides teachers with a more in-depth understanding of student thinking. Selecting an initial question and then analyzing a student’s response tells teachers where to go next. 

Ready to jump in? Grab a free set of problem solving challenges like the ones pictured using the form below. 

Which of the problem solving activities will you try first? Respond in the comments below.

Shametria Routt Banks

• Assessment Tools
• Content and Standards
• Differentiation
• Math & Literature
• Math & Technology
• Math Routines
• Math Stations
• Virtual Learning
• Writing in Math

You may also like...

2 Responses

This is a very cool site. I hope it takes off and is well received by teachers. I work in mathematical problem solving and help prepare pre-service teachers in mathematics.

Thank you, Scott! Best wishes to you and your pre-service teachers this year!

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed .

©2024 The Routty Math Teacher.   All Rights Reserved.  Designed by Ashley Hughes.

Privacy overview, grade level.

Making Sense of Mathematics

Teaching Mathematics through Problem Solving- An Upside-Down Approach

By inviting children to solve problems in their own ways, we are initiating them into the community of mathematicians who engage in structuring and modeling their “lived worlds” mathematically.

 Fosnot and Jacob, 2007

Teaching mathematics through problem solving requires you to think about the types of tasks you pose to students, how you facilitate discourse in your classroom, and how you support students use of a variety of representations as tools for problem solving, reasoning, and communication.

This is a different approach from “do-as-I-show-you” approach where the teacher shows all the mathematics, demonstrates strategies to solve a problem, and then students just have to practice that exact same skill/strategy, perhaps using a similar problem.

Teaching mathematics through problem solving means that students solve problems to learn new mathematics through real contexts, problems, situations, and strategies and models that allow them to build concept and make connections on their own.

The main difference between the traditional approach “I-do-you-do” and teaching through problem solving, is that the problem is presented at the beginning of the lesson, and the skills, strategies and ideas emerge when students are working on the problem. The teacher listens to students’ responses and examine their work, determining the moment to extend students’ thinking and providing targeted feedback.

Here are the 4 essential moves in a math lesson using a student-centered approach or problem-solving approach:

• Number Talk (5-8 min) (Connection)

The mini-lesson starts with a Number Talk. The main purpose of a Number Talk is:

*to build number sense, and 

*to provide opportunities for students to explain their thinking and respond to the mathematical thinking of others.

Please refer to the document Int§roducing Number Talks . Or watch this video with Sherry Parrish to gain understanding about how Number Talks can build fluency with your students.

Here are some videos of Number Talks so you can observe some of the main teaching moves.

The role of the teacher during a number talk is crucial. He/she needs to listen carefully to the way student is explaining his/her reasoning, then use a visual representation of what the student said. Other students also share their strategies, and the teacher represents those strategies as well. Students then can visualize a variety of strategies to solve a problem. They learn how to use numbers flexibly, there is not just one way to solve a problem. When students have a variety if strategies in their math tool box, they can solve any problem, they can make connections with mathematical concepts.

There are a variety of resources that can be used for Math Talks. Note : the main difference between Number Talks and Math Talks, is that one allows students to use numbers flexibly leading them to fluency, develop number sense, and opportunities to communicate and reason with mathematics; the other allows for communicating and reasoning, building arguments to critique the reasoning of others, the use of logical thinking, and the ability to recognize different attributes to shapes and other figures and make sense of the mathematics involved.

• 2. Using problems to teach (5-8 min) Mini Lesson

Problems that can serve as effective tasks or activities for students to solve have common features. Use the following points as a guide to assess if the problem/task has the potential to be a genuine problem:

*Problem should be appropriate to their current understanding, and yet still find it challenging and interesting.

*The main focus of the problem should allow students to do the mathematics they need to learn, the emphasis should be on making sense of the problem, and developing the understanding of the mathematics. Any context should not overshadow the mathematics to be learned.

*Problems must require justification, students explain why their solution makes sense. It is not enough when the teacher tells them their answer is correct.

*Ideally, a problem/task should have multiple entries. For example “find 3 factors whose product is 108”, instead of just “multiplying 3 numbers. “

The most important part of the mini-lesson is to avoid teaching tricks or shortcuts, or plain algorithms. Our goal is always to help guide students to understand why the math works (conceptual understanding). And most importantly how different mathematical concepts/ideas are connected! “Math is a connected subject”  Jo Boaler’s video

“Students can learn mathematics through exploring and solving contextual and mathematical problems vs. students can learn to apply mathematics only after they have mastered the basic skills.” By Steve Leinwand author of Principles to Action .

• 3. Active Engagement (20-30 min)

This is the opportunity for students to work with partners or independently on the problem, making connections of what they know, and trying to use the strategy that makes sense to them. Always making sure to represent the problem with a visual representation. It can be any model that helps student understand what the problem is about.

The job of the teacher during this time, is to walk around asking questions to students to guide them in the right direction, but without telling too much. Allowing students to come up with their own solutions and justifications.

• Teacher can clarify any questions around the problem, not the solution.
• Teacher emphasizes reasoning to make sense of the problem/task.
• Teacher encourages student-student dialogue to help build a sense of self.

Some lessons will include a rich task, or a project based learning, or a number problem (find 3 numbers whose product is 108). There are a variety of learning target tasks to choose from, for each grade level on the Assessment Live Binders website created by Erma Anderson and Project AERO.

Again, keep in mind that some lessons will follow a different structure depending on the learning target for that day. Regardless of instructional design, the teacher should not be doing the thinking, reasoning, and connection building; it must be the students who are engaged in these activities

• 4. Share (8-12 min) (Link)

The most crucial part of the lesson is here. This is where the teaching/learning happens, not only learning from teacher, but learning from peers reaching their unique “zone of proximal development” (Vygotsky, 1978).

We bring back our students to share how they solved their problem. Sometimes they share with a partner first, to make sure they are using the right vocabulary, and to make sure they make sense of their answer. Then a few of them can share with the rest of the class. But sharing with a partner first is helpful so everyone has the opportunity to share.

“Talk to each other and the teacher about ideas – Why did I choose this method? Does it work in other cases? How is the method similar or different to methods other people used?” Jo Boaler’s article “How Students Should Be Taught Mathematics.”

Students make sense of their solution. The teacher listens and makes connections between different strategies that students are sharing. Teacher paraphrases the strategy student described, perhaps linking it with an efficient strategy.

“It is a misperception that student-centered classrooms don’t include any lecturing. At times it’s essential the teacher share his or her expertise with the larger group. Students could drive the discussion and the teacher guides and facilitates the learning.” Trevor MacKenzie

If the target for today’s lesson was to introduce the use a number line, for example, this is where the teacher will share that strategy as another possible way to solve today’s problem!

This could also be a good time for any formative assessment, using See Saw, using exit slips, or any kind of evidence of what they learned today.

References.

“Teaching Student-Centered Mathematics” Table 2.1 page 26 , Van de Walle, Karp, Lovin, Bay-Williams

“Number Talks” , Sherry Parrish

“How Students Should be Taught Mathematics: Reflections from Research and Practice” Jo Boaler

“Erma Anderson, Project AERO Assessments live binders

“Principles to Action” , Steve Leinwand

“ Turning Teaching Upside Down “, by Cathy Seeley

“Four Inquiry Qualities At The Heart of Student-Centered Teaching”

By Trevor MacKenzie

“The Zone of Proximal Development” Vygotsky, 1978

*** Here is a link to my favorite places to plan Math padlet, you will find a variety of resources, videos, articles, etc. By Caty Romero

***One more padlet for many resources to plan, teach, and assess mathematics that make sense: Making Sense of Mathematics Padlet.

Share this:

• learning math
• making sense of math
• number sense

Published by Caty Romero - Math Specialist

Passionate about learning and making sense of mathematics. Teacher, Math Learning Specialist, K-8 Math Consultant, and Instructional Coach. Student-Centered-Learning is my approach! Contact me at [email protected] or follow me on Twitter @catyrmath View all posts by Caty Romero - Math Specialist

Leave a comment Cancel reply

• Already have a WordPress.com account? Log in now.
• Subscribe Subscribed
• Copy shortlink
• Report this content
• View post in Reader
• Manage subscriptions
• Collapse this bar

Teaching problem-solving strategies in mathematics

• Eva Fülöp University of Gothenburg

This study uses the methodology of design-based research in search of ways to teach problem-solving strategies in mathematics in an upper secondary school. Educational activities are designed and tested in a class for four weeks. The design of the activities is governed by three design principles, which are based on variation theory. This study aims to contribute to an understanding of how the teaching of problem-solving strategies and strategy thinking in mathematics can be organized in a regular classroom setting and how this affects students´ learning in mathematics. We start by discussing the nature of the concept strategy in relation to the concepts of method and algorithm. Using pre- and post-tests, we compare the development of the students´ conceptual and procedural abilities with a control group. In addition, we use the post-test to investigate the students´ use of problem-solving strategies. The results suggest that these designed activities improve students’ ability to use problem-solving strategies. Moreover, significant differences were found in conceptual and procedural abilities in mathematics, the experimental group improving more than the control groups.

How to Cite

• Endnote/Zotero/Mendeley (RIS)

Make a Submission

Information.

• For Readers
• For Authors
• For Librarians

editoriportal

Usage Statistics Information

We log anonymous usage statistics. Please read the privacy information for details.

LUMAT: International Journal on Math, Science and Technology Education Published by the University of Helsinki, Finland and LUMA Centre Finland. Follow LUMAT on LinkedIn and Twitter via #lumatjournals . ISSN: 2323-7112

You are using an outdated browser. Upgrade your browser today or install Google Chrome Frame to better experience this site.

• Professional learning

Teach. Learn. Grow.

Teach. learn. grow. the education blog.

6 tips for supporting   problem-based learning in your math classroom

Most math teachers have been here before. We’ve all transposed the names of our own students for those in a word problem. We’ve all used our school community goings-on as fodder for plot lines: “If 89 middle schoolers are traveling on buses to Outdoor School, and each bus can transport 35 students and four chaperones.…” But how “real world” are we really getting?

We—Kailey Rhodes and Kristen Tsutsui, math teachers and authors of this blog post—wanted to know teachers’ experience with real-world problem-solving, what’s going well, and what’s in their way. So we surveyed some. In this post, we’ll walk you through what we asked, learned, and think as we move forward—and we’ll also share the resources our teachers shared with us. But first, let us introduce you to an official definition of real-world context in the math classroom.

The PISA Mathematics Framework

PISA is an international assessment administered to 15-year-olds globally. In their 2022 Mathematics Framework , PISA explains the underpinnings of their assessment as it relates to math literacy, reasoning, and problem-solving. It also stipulates that to uplift these underpinnings, mathematics problems should be presented in real-world contexts: personal, occupational, societal, and scientific.

Educators, take a moment to read the descriptions of these contexts . As you read, ask yourself the question we asked in our survey: “Which do you naturally find yourself gravitating toward in your classroom?”

• Personal: “Problems classified in the personal context category focus on activities of one’s self, one’s family, or one’s peer group. Personal contexts include (but are not limited to) those involving food preparation, shopping, games, personal health, personal transportation, sports, travel, personal scheduling, and personal finance.”
• Occupational: “Problems classified in the occupational context category are centered on the world of work. Items categorized as occupational may involve (but are not limited to) such things as measuring, costing, and ordering materials for building, payroll/accounting, quality control, scheduling/inventory, design/architecture, and job-related decision-making. Occupational contexts may relate to any level of the workforce, from unskilled work to the highest levels of professional work, although items in the PISA survey must be accessible to 15-year-old students.”
• Societal: “Problems classified in the societal context category focus on one’s community (whether local, national, or global). They may involve (but are not limited to) such things as voting systems, public transport, government, public policies, demographics, advertising, national statistics, and economics. Although individuals are involved in all of these things in a personal way, in the societal context category, the focus of problems is on the community perspective.”
• Scientific: “Problems classified in the scientific category relate to the application of mathematics to the natural world and issues and topics related to science and technology. Particular contexts might include (but are not limited to) such areas as weather or climate, ecology, medicine, space science, genetics, measurement, and the world of mathematics itself. Items that are intra-mathematical, where all the elements involved belong in the world of mathematics, fall within the scientific context.”

Which context did you most resonate with? If you were to focus on one context per quarter, how would you order them? What is your biggest struggle with real-world context and problem-based learning? How do you bring the “real world” inside your classroom?

We surveyed a focus group of math teachers, from kindergarten to IB, to see what they thought.

Survey says!

When we asked our teachers, “Which do you naturally find yourself gravitating toward in your classroom?” personal and scientific contexts were the winners, with societal coming in fourth. Our guess for this is that societal is not only ever-changing but is also often politically adjacent, something educators can, understandably, be wary of approaching.

Naturally, personal real-world math context offers an entry point into students’ interests, which is paramount in the math classroom. One teacher said, “Good projects that connect to the curriculum and also interest the students are worth their weight in gold. I really wish publishers did a better job of planning good projects; in most books I’ve used, the projects, if they exist at all, are an afterthought and poorly done.”

When it comes to other contexts, like societal, the bullseye of curriculum connection, student interest level, and math teacher time is a hard one to hit. As one teacher said, “With more time I would like to start new math topics with ‘real world problems’ and have the students brainstorm what knowledge would be useful to solve them, building resilience in the face of complex problems. However, these kinds of freeform explorations take time that I often feel like I don’t have in my class.”

This theme of “not enough time” appeared often, with teachers expressing a desire for more real-world presence, including cross-collaboration with other colleagues. A teacher said, “I have tried to coordinate with science classes to talk about the mathematical aspects of science concepts they are learning, but it can be hard to coordinate and map those kinds of things onto my own curriculum.”

This was echoed in the teachers’ comments, along with many wishful statements about what they “would do…if.”

With all the time and resources, what would teachers do?

We asked teachers to describe their dream scenario: what they would do if they had more resources, time, and permission. In most responses, what stood out was teachers’ love for math’s interconnectedness and innate curiosity. Some dreamed big:

• “An interdisciplinary project across all subjects that would allow students to see how math applies to all facets of the world”
• “Something like ‘a history of mathematical thought,’ bringing history, culture, psychology, ecology, science, and engineering into the curriculum”
• “Students being given the opportunity to explore a problem they are passionate about and explore ways that mathematics can be used to help solve it”
• “Students working alongside professionals in various math-related fields so they can see, firsthand, how the math they are learning is currently being used”

It’s clear that teachers want to provide classroom experiences that both underscore math’s omnipresence in the world around us and ignite students’ interests. It’s also clear that when your survey takers have to type qualifiers like, “But this would take a lot of time” and “We don’t have the resources for this,” the “real world” is actually what’s in the way. So, what can be done?

From ideal to real: Helpful tips & a relaxing thought on problem-based learning

No one knows better than math teachers that you can’t add time to your school day.  But, through our interactions with teachers, we walked away with some resources and tips to share with you. Here are the gems:

• Split it into quadrants. Most teachers surveyed would order their quarters and contexts like this: first quarter, personal; second quarter, societal; third quarter, scientific; fourth quarter, occupational.
• Switch with science. One teacher said this: “Actually switch classes with a science teacher to reiterate how what they are learning in science is related to what we do in math. And then they can come to my class to do the same so they can really understand the connection.”
• Draw a parallel. “Have a project that seems like it might belong in an arts classroom, like creating a piece of clothing,” another teacher suggested. “They have to use multiple modes of mathematical knowledge to do this, like unit conversions (centimeters to inches to yards), spatial constraints (if fabric is a certain size, can I fit my pattern in it? How big do the pieces have to be to fit on the body?), and area (how much fabric do I need?).”
• Estimate. “I use Estimation 180 , but I gamify it to address average, mean, median, and mode. I have students secretly record their estimations, and I write them all on the board. We discuss the average classroom guess and how close our range is. Estimation is everywhere.”
• Level up. “I’ve been using Skew the Script to heighten engagement for all my students and teach them about larger global issues affecting society. Their After The AP Data Science Challenge aims to solve the real (unsolved) problem of finding a model to predict the best and worst colleges for conquering student debt.”
• Build the roster: “Try to arrange a handful of yearly speakers and field trips you can count on to bring the math to life. My husband is a civil engineer and uses the Pythagorean theorem. You’d be surprised how many folks would love to come in and talk to a math class—with your teacher guidance and enthusiasm, of course.”

And now for the relaxing thought: Start small. As with any endeavor in the classroom, no matter the discipline, the key is to work incrementally. We already know how important increments are, right, math teachers?

What is “real,” anyway?

Let’s return to the age-old question of, “When will we ever use this?” It plagues math teachers perhaps more than any other discipline, and the task of “real-world” problem-solving often feels like a “gotcha” moment. The fact is, sometimes, we math teachers don’t have a great real-world example of dividing negative fractions in our back pocket. But does that mean that it isn’t worth learning? Must every concept in math be nested perfectly within the “real” world?

In one particular mic-drop moment, one of our teachers shared, “I think the label ‘real-world’ has been used extensively in math education, and I’ve found it a bit frustrating. In many regards, math is the least ‘real’ discipline we teach children. It is, largely, the art of abstraction! That it is ‘real’ is in many ways the least interesting and important thing about it as a system of thinking, and this is often lost when continually looked at with the question ‘When will we ever use this?’”

Maybe when we’ll “use this” is when we’re thinking through a problem with many facets and variables. Math is, after all, less of a “what” and more of a “how.” How should we go about solving this? How do we use computational thinking to solve problems? How do we spiral what we already know with what we don’t?

We’re teaching kids how to think —and isn’t that the most real-world skill we can possibly teach?

To learn more about how NWEA can support you in teaching math, visit our website .

Recommended for you

7 tips for encouraging student discourse about math with number talks

3 non-negotiables for differentiation in the math classroom

4 ways to engage students with writing in math class

Reading differentiation made easy

MAP Reading Fluency now includes Coach, a virtual tutor designed to help students strengthen reading skills in as little as 30 minutes a week.

Helping students grow

Students continue to rebound from pandemic school closures. NWEA® and Learning Heroes experts talk about how best to support them here on our blog, Teach. Learn. Grow.

See the post

Put the science of reading into action

The science of reading is not a buzzword. It’s the converging evidence of what matters and what works in literacy instruction. We can help you make it part of your practice.

Get the guide

Support teachers with PL

High-quality professional learning can help teachers feel invested—and supported—in their work.

Read the article

STAY CURRENT by subscribing to our newsletter

You are now signed up to receive our newsletter containing the latest news, blogs, and resources from nwea..

Teaching Mathematics Through Problem Solving

By Tom McDougal, Akihiko Takahashi

What do your students do when faced with a math problem they don't know how to solve? Most students give up pretty quickly. At best, they seek help from another student or the teacher. At worst, they shut down, seeing their failure as more evidence that they just aren't good at math. Neither of these behaviors will serve students in the long run. Inevitably, someday, every one of your students will encounter problems that they will not have explicitly studied in school and their ability to find a solution will have important consequences for them.

In the Common Core State Standards for Mathematics, the very first Standard for Mathematical Practice is that students should “understand problems and persevere in solving them.”1 Whether you are beholden to the Common Core or not, this is certainly something you would wish for your students. Indeed, the National Council of Teachers of Mathematics (NCTM) has been advocating for a central role for problem solving at least since the release of Agenda for Action in 1980, which said, “Problem solving [must] be the focus of school mathematics… .”2 

The common instructional model of “I do, we do, you do,” increases student dependence on the teacher and decreases students’ inclination to persevere. How, then, can teachers develop perseverance in problem solving in their students?

First we should clarify what we mean by “problem solving.” According to NCTM, “Problem solving means engaging in a task for which the solution is not known in advance.”3 A task does not have to be a word problem to qualify as a problem — it could be an equation or calculation that students have not previously learned to solve. Also, the same task can be a problem or not, depending on when it is given. Early in the year, before students learn a particular skill, the task could be a problem; later, it becomes an exercise, because now they know how to solve it.

In Japan, math educators have been thinking about how to develop problem solving for several decades. They studied George Polya's How to Solve It ,4 NCTM's Agenda for Action , and other documents, and together, using a process called lesson study , they began exploring what it would mean to make problem solving “the focus of school mathematics.” And they succeeded. Today, most elementary mathematics lessons in Japan are organized around the solving of one or a very few problems, using an approach known as “teaching through problem solving.”

“Teaching through problem solving” needs to be clearly distinguished from “teaching problem solving.” The latter, which is not uncommon in the United States, focuses on teaching certain strategies — guess-and-check, working backwards, drawing a diagram, and others. In a lesson about problem solving, students might work on a problem and then share with the class how using one of these strategies helped them solve the problem. Other students applaud, the students sit down, and the lesson ends. These lessons are usually outside the main flow of the curriculum; indeed, they are purposely independent of any curriculum.

In “teaching through problem solving,” on the other hand, the goal is for students to learn precisely that mathematical idea that the curriculum calls for them to learn next.

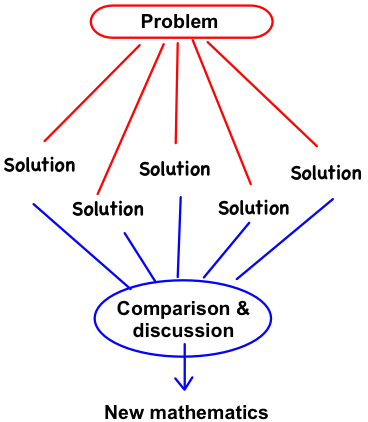
A “teaching through problem solving” lesson would begin with the teacher setting up the context and introducing the problem. Students then work on the problem for about 10 minutes while the teacher monitors their progress and notes which students are using which approaches. Then the teacher begins a whole-class discussion. Similar to a “teaching problem solving” lesson, the teacher may call on students to share their ideas, but, instead of ending the lesson there, the teacher will ask students to think about and compare the different ideas — which ideas are incorrect and why, which ideas are correct, which ones are similar to each other, which ones are more efficient or more elegant. Through this discussion, the lesson enables students to learn new mathematical ideas or procedures. This approach is represented in Figure 1.

Let's illustrate this with an example from a hypothetical fifth-grade lesson based on the most popular elementary mathematics textbook in Japan. (This textbook has been translated into English as Mathematics International and is available at http://GlobalEdResources.com . 5) During most Japanese lessons, the textbook is closed, but the textbook shows how the authors think the lesson might play out.

When the lesson begins, the blackboard is completely empty. The teacher starts by displaying, either with a poster or using a projector, the picture from the textbook of four different rabbit cages, shown in Figure 2 (it is not uncommon for Japanese elementary students to care for rabbits in several rabbit hutches, so this is a familiar context).

Figure 2 (Mathematics International, Grade 5, p. A93)

“What do you notice about the cages?” the teacher asks. Some students notice that some of the cages are different sizes. The teacher then asks, “Should each cage have the same number of rabbits?” No, say the students, smaller cages should have fewer rabbits, so the rabbits aren't too crowded.

The teacher then displays the pictures in Figure 3. “What do you think?” the teacher asks, as he puts them up one at a time for dramatic effect. “Are these equally crowded, or do you think some cages are more crowded than others?” There is some discussion about the rabbits in cage B, and students decide that just because they are bunched together right now, they probably won't stay that way. Students recognize that cages A and B are the same size, and since cage A has more rabbits (9 vs. 8), it is more crowded. The teacher writes that observation on the board: “When two cages are the same size, the one with more rabbits is more crowded.”

Figure 3 (Mathematics International, Grade 5, p. A93)

“What about the others?” he asks. “How can we decide which are more crowded?” This last question becomes the key mathematical question of the lesson, and the teacher writes it on the board: “Let's think about how to compare crowdedness.” Students copy this problem in their notebooks while he writes.

The teacher gives students a piece of paper with the pictures from Figure 3 to glue in their notebooks and gives them 5 minutes to think about the problem. Several students take a ruler and begin measuring. “Why are you doing that?” the teacher quietly asks one of them. “I want to figure out the area,” the student says. “Oh! You think the area might be important. Write that idea in your notebook.” Other students count the rabbits and decide that B and C are equally crowded because they look like they are the same size, but they are unsure about D.

The teacher stops the students and asks for ideas. He first calls on a student who thinks that B and C are the same size. He records her idea on the board: “Arthi says B and C look like they are the same size and have the same number of rabbits, so they are equally crowded.” A student who found the areas says that they are not. The teacher records this idea on the board: “Karen thinks you need to know the area.” He turns to the first student. “Arthi, what do you think?” he asks. She and other students agree. The teacher posts a table with the areas of the four cages (Figure 4). “Let's copy this table into our notebooks, and think about the problem some more.”

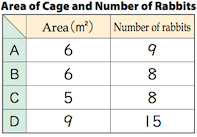
Figure 4 (Mathematics International, Grade 5, p. A94)

Students work independently for another 5 minutes while the teacher monitors their progress, encourages them to keep thinking, and reminds them to record their ideas in their notebook. He anticipates the following five ideas and notes which students are using them:

Idea 1: B and C have the same number of rabbits, but C has a smaller area, so C is more crowded. Unsure about A vs. C. 

Idea 2: If you make 5 copies of A and 6 copies of C, they would have the same area (30 m2). A would then have 45 rabbits while C would have 48 rabbits, so C is more crowded. 

Idea 3: If you make 8 copies of A and 9 copies of C, they would have the same number of rabbits (72). A would have an area of 48 m2 while C would have an area of 45 m2, so B is more crowded. 

Idea 4: Divide: (area) ÷ (# of rabbits) = amount of area per rabbit 

Idea 5: Divide: (# of rabbits) ÷ (area) = number of rabbits per unit area

The teacher invites students to explain their ideas to the class, selecting students based on the order above, while he records each idea on the blackboard. He asks students to compare Idea 1 to the thinking used to compare A and B. He writes on the board: “If either the area or the number of rabbits is the same, it's easy to compare.” The student with Idea 2 says, “I found a way to make the area the same,” and explains. This prompts the student with Idea 3 to say, “I used kind of the same approach to make the number of rabbits the same.”

When a student with Idea 4 comes up, she begins, “I decided to divide the area by the number of rabbits.” The teacher stops her. He writes: “(area) ÷ (# of rabbits).” Then he asks the class, “Why is she doing this? Who can explain her thinking?” Another student says, “That gives the amount of area for each rabbit.” He lets the student finish her idea:

A: 9÷6 = 1.5 C: 8÷5 = 1.6

The teacher asks the class to clarify what the 1.5 and 1.6 mean (m2 per rabbit) and what that says about the crowdedness of each cage.

He then invites a student to explain Idea 5: “I divided the other way…”

A: 6÷9 = 0.66… C: 5÷8 = 0.625

“Why is he doing this?” the teacher asks the class. “What does this 0.66… mean? What does 0.625 mean?” (“Rabbits per square meter,” the students answer.)

The teacher then asks the class to look for similarities across the five ideas, which are all visible on the blackboard. Some students note that Ideas 2 and 3 use multiplication while Ideas 4 and 5 use division, a superficial similarity. But some students notice the more significant connection that 2 and 5 are both about making the area the same, while 3 and 4 are both about making the number of rabbits the same.

“We haven't talked about cage D yet,” the teacher points out. “How shall we compare A, C, and D? Please try using one of these ideas.”

Students work in their notebooks for a few minutes. Students who try using multiplication (Idea 2 or 3) discover that the method is cumbersome. The teacher invites students who used Ideas 4 and 5 to share their calculations, adding them to the lists from before: Idea 4:

A: 9÷6 = 1.5 C: 8÷5 = 1.6 D: 15÷9 = 1.66… (m2/rabbit) Idea 5: A: 6÷9 = 0.66… C: 5÷8 = 0.625 D: 9÷15 = 0.6 (rabbits/m2)

“What do you think about these ideas?” asks the teacher, and students respond, “They are easy!” So the teacher writes a summary on the board, “Using division, it is easy to compare crowdedness.” He asks the students to write a reflection in their notebooks. One student who used multiplication writes, “I tried using multiplication, but dividing is easier. Next time I want to try that.” And the lesson ends.

In the students’ previous experience with comparing quantities, a single quantity was important, such as the number of apples or kilograms or square meters. Their prior experience with division was about finding a missing multiplier or multiplicand, which was itself a single quantity. This problem presented students for the first time with a situation in which two numbers needed to be considered. So by working on a problem about rabbits and cages, students learn that division can be used to compute a new type of quantity, a per unit quantity, that expresses the relationship between rabbits and area and can be used to compare crowdedness. In subsequent lessons, students will see how division can be used to compute other types of per unit quantities, such as the productivity of two farms in crops grown per acre of land or the cost per pencil.

What was the teacher's role in helping students learn this new mathematical idea? He never explained anything to the students, but the task had to be carefully constructed, and the teacher had to be very deliberate in how he directed the lesson, or the lesson wouldn't have worked.

The task was accessible to all students in the beginning by the fact that two cages had the same area (A and B) and two cages had the same number of rabbits (B and C), but since it wasn't clear whether B and C were the same size, students were pushed to think formally about area. And, while using multiplication was feasible for comparing cages A and C, the area of cage D was such that multiplication was cumbersome for comparing all three cages. Students who might have been happy with using multiplication and uncomfortable with the decimal values that result from division were pushed by cage D to appreciate the efficiency of using division.

The teacher's role in the lesson can be compared to the role of a film director, who carefully stages each scene and makes cuts between cameras to create the desired effect. Early in the lesson, the teacher highlighted the idea, raised by students, that equal areas or equal numbers of rabbits made comparisons easier. This was the foundation for the idea of dividing to find a “per unit quantity,” square meters per one rabbit or rabbits per one square meter. By starting with a discussion of incorrect or partially correct ideas and writing them on the board, the teacher valued those ideas. This encourages students to try: Even if they can’t solve the whole problem, they might come up with something to contribute. When a student first suggested the idea of dividing, the teacher asked other students to explain the thinking behind it. This enabled students who did not themselves think of dividing to make the idea their own. And by carefully organizing student ideas on the board (Figure 5), the teacher made it easier for students to compare those ideas with each other and to follow the flow of learning in the lesson.

Figure 5 (includes items from Mathematics International, Grade 5, pp. A93-94)

Although the lesson vignette above is fictional, videos of lessons like it can be found at http://tinyurl.com/kuwb4bg . The grade 3 lesson “Multiplication Algorithm” and the grade 5 lesson “Do I Have a Window Seat or an Aisle Seat?” are particularly good, both for the quality of the lessons and for the quality of the videos themselves.

Japanese educators believe that regular lessons that teach through problem solving, interspersed with occasional practice days, help their students learn mathematics more thoroughly than didactic instruction coupled with a greater amount of practice. Certainly Japanese students have performed very well on the TIMSS and PISA international studies of mathematics achievement. But perhaps more important, teaching through problem solving habituates students to being confronted with unfamiliar problems, to struggling at length with those problems, and to learning from those problems. This is a way to cultivate perseverance in problem solving.

Reading this article and watching videos, however, will not equip most teachers to incorporate teaching through problem solving into their practice. The teacher who wishes to do so is faced with several challenges. The first challenge is that few curricula are designed to support such lessons; most are designed to support fairly direct instruction by the teacher. The second problem is that students are not used to learning this way and may resist. And the third problem is that teaching this way is hard. It requires ways of thinking about a lesson that are unfamiliar to almost all U.S. teachers. One needs to be absolutely clear about what the mathematical goal of the lesson is; that goal is never for students to simply solve a problem. One needs to anticipate the various solutions, correct and incorrect, that are likely to come from students, as well as the ways students will get stuck. One needs to plan how the discussion around the various student ideas will address misconceptions and build toward the mathematical goal of the lesson. One needs to think about how the ideas will be organized on the board so that students can easily compare them.

Japanese teachers certainly did not learn to teach this way by reading articles or watching videos. They learned it — and continue to learn it — by trying it, together, one lesson at a time through a process called lesson study .6,7 A full treatment of lesson study would be another article in itself, but U.S. teachers who are interested in learning to teach through problem solving can find more information about lesson study at http://LessonStudyGroup.net  and at http://LSAlliance.org . Lesson Study Alliance organizes the annual Chicago Lesson Study Conference, which features live lessons by teachers who are working to incorporate teaching through problem solving into their practice.

1. National Governors Association Center for Best Practices, Council of Chief State School Officers, Common Core State Standards for Mathematics (Washington, DC: National Governors Association Center for Best Practices, Council of Chief State School Officers, 2010); online at www.corestandards.org/math/ . 2. National Council of Teachers of Mathematics, An Agenda for Action: Recommendations for School Mathematics of the 1980s (Washington, DC: NCTM, 1980); online at www.nctm.org/standards/content.aspx?id=17278 .  3. National Council of Teachers of Mathematics, Principles and Standards for School Mathematics (Washington, DC: NCTM, 2000); online at http://www.nctm.org/standards/content.aspx?id=16909 . 4. George Polya, How to Solve It: A New Aspect of Mathematical Method (Princeton, NJ: Princeton University Press, 1945).  5. T. Fujii and S. Iitaka, Mathematics International , Grades 1-6 (Tokyo: Tokyo Shoseki Co., Ltd., 2012).  6. Akihiko Takahashi, “Implementing Lesson Study in North American Schools and School Districts” (no date); online at http://hrd.apec.org/images/a/ae/51.2.pdf .  7. Akihiko Takahashi and Makoto Yoshida, “Ideas for Establishing Lesson-Study Communities.” Teaching Children Mathematics , May 2004.

Tom McDougal is executive director of Lesson Study Alliance in Chicago, a nonprofit organization that promotes and supports Lesson Study. He taught middle and high school mathematics and was an elementary math specialist.

Akihiko Takahashi is associate professor of mathematics education at DePaul University in Chicago. He taught students in grades 1-6 for 19 years in Japan, where he helped lead the national shift to teaching mathematics through problem solving.

How School Leaders Can Address the Israel-Hamas War

An educator offers suggestions for schools to handle antisemitism amid the ongoing conflict as they plan for the coming school year..

Read the Post

• DOI: 10.31129/LUMAT.V3I1.1050
• Corpus ID: 56303245

Teaching problem-solving strategies in mathematics

• Published 28 February 2015
• Mathematics, Education

Ask This Paper

By using this feature, you agree to AI2's terms and conditions and that you will not submit any sensitive or confidential info.

AI2 may include your prompts and inputs in a public dataset for future AI research and development. Please check the box to opt-out.

Ask a question about " "

Supporting statements, figures and tables from this paper.

13 Citations

Developing problem-solving abilities by learning problem-solving strategies: an exploration of teaching intervention in authentic mathematics classes.

• Highly Influenced

Learning to solve problems that you have not learned to solve: Strategies in mathematical problem solving

Evaluation of preservice teachers’ skills in solving non-routine mathematical problems through various strategies, investigation of secondary school students' strategies for solving routine and non-routine problems, a comparison of problem solving strategies of primary school 3rd and 4th graders, how does the degree of guidance support students’ metacognitive and problem solving skills in educational robotics, the use of an emerging framework to explore students’ cognitive competency, evaluating the impact of the curriculum structure on group metacognition during collaborative problem-solving using educational robotics, enablers and obstacles in teaching and learning of mathematics, investigation of the relationship between problem-solving achievement and perceptions of students, 55 references, learning theory as teaching resource: enhancing students’ understanding of economic concepts, context problems in realistic mathematics education: a calculus course as an example, instructional tasks, classroom discourse, and students’ learning in second-grade arithmetic, building bridges within mathematics education: teaching, research, and instructional design☆, problem‐based learning and action research in postgraduate teaching: the interdisciplinary core, formative research : a methodology for creating and improving design theories, design experiments: theoretical and methodological challenges in creating complex interventions in c, adding it up: helping children learn mathematics, design research: what we learn when we engage in design, issues in education research: problems and possibilities., related papers.

Showing 1 through 3 of 0 Related Papers

• Our Mission

Setting Small Goals to Achieve High-Impact Math Gains

Prioritizing key concepts can help teachers design instructional strategies that accelerate learning.

 A well-designed Multi-Tiered System of Support (MTSS) for elementary math supports teachers in effectively meeting students’ diverse needs by prioritizing high-quality, universal instruction that is inclusive and engaging for all students. 

In an MTSS, students have access to intervention focused on high-impact math concepts that support grade-level learning. In order to accelerate learning, we need to prioritize math concepts that have the most impact across a grade level. As elementary educators, we are often unsure which concepts to prioritize. When designing instruction for intervention, teachers should start by asking the following questions: What is the current high-priority grade-level math content? What is the most critical content that students need in this grade level in order to access next year’s grade-level learning? These questions can guide the design of high-impact instruction.

designing high-quality math intervention

High-leverage concepts are the key understandings identified at each grade level that help focus math instruction by identifying the big ideas at each grade level that will support success in the next grade. We know that this growth is not necessarily linear. However, this resource allows teachers to understand the key prerequisite understandings along the way toward mastery. When designing for Tier 2 and Tier 3 layers of support in an MTSS, it is critical to prioritize the most impactful math content if the goal is to accelerate learning.

Once teachers have identified the highest-impact math concepts at their grade level, they need to consider the small goals related to that math concept that will indicate progress toward understanding. Teachers should ask themselves these questions: What evidence will I see to indicate understanding? What models do I expect students to use? What strategies do I expect students will apply? 

These learning progressions are a resource to break down these larger concepts into small goals along the way. The idea is to identify and monitor the developing stages along the continuum of critical math concepts, including models and strategies that students should explore. When designing for intervention, teachers intentionally plan lessons based on what a student already knows and understands to help move them forward in their understanding. This process highlights an asset-based approach for instruction. It may be necessary to start on the concepts from one or two grade levels prior that largely impact the current grade-level math content.

Finally, teachers must consider the learning opportunity that includes both teaching and assessing students’ understanding. They need to consider the high-cognitive-demand tasks that students can engage with during intervention that will allow them to show their understanding of these critical concepts. Beyond straight calculation, we need to know the models and strategies that students are using and whether or not those strategies are increasing in complexity. When we look for small gains in strategy use, we are able to increase our impact on student learning while feeling a sense of efficacy in the implementation of our instructional design. 

High-quality Instruction in Practice 

I recently worked with a group of special educators in Illinois to hone their skill set in designing intervention that promotes the acceleration of math learning. Here are the steps we followed.

1. Identify the high-priority grade-level math content to prioritize. The small group of students we planned for were in second grade. The high-priority grade-level math content in second grade is addition and subtraction The Common Core State Standard (CCSS) states the following: Use addition and subtraction within 100 to solve one- and two-step word problems involving situations of adding to, taking from, putting together, taking apart, and comparing, with unknowns in all positions. This group of students was still working on understanding number values and sequences to 20. The concept is critical for addition and subtraction, as students must be able to identify both the name and the total value of a given number in order to add and subtract whole numbers within 100. As a group, we lined up the kindergarten and grades one and two high-leverage progressions documents to identify where instruction should start based on this goal. We identified counting, comparing, and composing/decomposing within 10 on the kindergarten document.

2. Identify the critical strategies and small goals to achieve as an outcome of this intervention. Using the kindergarten and first-grade high-leverage concepts, we discussed our expectation for students to be able to count within 20 both forward and backward and compare quantities within 10. We identified the critical strategy of composing and decomposing quantities using models, specifically a tens frame. We also expected to see evidence of counting by ones, subitizing, organizing, and tracking. 

3. Identify the strategy for teaching and assessing student understanding. Students are much more relaxed and able to show their thinking when playing. We decided to play a simple dice game involving counters or bingo chips, blank printed tens frames, and six-sided dice. In this game, each student rolls a die and answers these questions: How many dots are there? Who has more dots? How do you know? How many chips will you need? How close are you to 10? Students then place that many chips on the tens frame. When all chips are placed, we discuss answers to these questions: How many chips do we have altogether? How do you know? How are your strategies for counting the same, how are they different? 

As we play this game, we are looking for the following:

• Evidence of subitizing
• One-to-one correspondence
• Strategies for counting and cardinality
• Sums to 10 using the tens as a thinking tool and strategies beyond 10 if the situation arises

Following this process, we were able to focus on high-impact math content at the current grade level. We were able to deconstruct the small goals along the way that help us understand student growth toward this concept. Finally, we could design a learning opportunity that was focused on a specific, small learning goal. 

With a small learning goal, we are able to monitor progress toward understanding because we are crystal-clear about what we are looking for. The goal here is for us to set small goals so we know exactly when students know and understand a concept and are ready for the next instructional step on the progression. 

Every small goal we move toward is focused on math concepts that are critical for understanding current grade-level concepts, so that we begin to see impact on grade-level learning at a much faster rate. Through high-quality Tier 1 instruction and high-impact Tier 2 and Tier 3 layers of instruction, we are more readily able to accelerate student learning of key mathematical concepts.

• Student Login
• Educator Login
• Parent Login
• Educators: Sign up for a free trial
• Home Users: Available at Time4MathFacts

How Fact Fluency Boosts Math Success for Students

Teaching Strategies

Compare the two: a student learning a new language and a student learning math facts. As a child masters vocabulary and verb tenses in French, they become more equipped to converse and think in that new language. But without the building blocks of the language, a student is stuck when it comes time to ask for directions to the Eiffel Tower, form a unique sentence, or produce complex thinking or opinions.

The same is true with math facts. When students achieve fact fluency, they propel their present and future math success forward by freeing up working memory space.

What is fact fluency in math?

What are math facts? Math facts are simple calculations performed across addition, subtraction, multiplication, and division. But what does fluency mean regarding math facts?

Math fact fluency is the quick and effortless recall of basic math facts in all four operations. When students can retrieve math fact solutions from their long-term memory without conscious effort (or counting on their fingers!), they achieve automaticity with math facts.

For example, a student with multiplication math fact fluency would automatically know that the product of 6 x 7 is 42 without using tally marks, drawing area models, or punching the numbers into a calculator. By understanding this fluently, the child can solve a more advanced problem, such as 5(6 x 7) + 250 , with greater accuracy and speed.

Why is fluency important in math?

Fact fluency is important because it frees up students’ working memory. When students can retrieve math facts with little effort, they can learn new skills and devote more time to advanced problem-solving.

Extensive research has uncovered the vital role of fact fluency , both in elementary school and beyond. Fact retrieval speed is a strong predictor of standardized test performance, along with students’ ability to solve word problems and tasks related to data interpretation, mathematical reasoning, and concept problems.

The benefits of building fact fluency

Building math fact fluency in the elementary classroom has many benefits.

Why is it important for students to have a quick recall of basic facts?

In addition to freeing up space in working memory, math fact fluency can increase student confidence . Students who are confident about math can enjoy the subject with less intimidation or math anxiety . Math fact fluency also helps students make fewer mistakes on classwork and tests.

When teachers know their students share an understanding of math facts , they can take their teaching to the next level without having to stop and reteach basic calculations. Mathematical fluency allows teachers to stay closer aligned to their scope and sequence and lesson planning needs. It also gives teachers more autonomy and flexibility to assign complex problem-solving tasks, like group work, word problems, or project-based learning, knowing their students have the foundational fluency skills required for advanced calculations.

How fact fluency enhances math skills and problem-solving abilities

Fact fluency also prepares students for more complex fact-solving. For example, to master their multiplication facts, students first need a firm grasp of addition and subtraction facts. When students know their multiplication and division facts fluently, they can take on advanced math and math skills in later elementary school in addition to middle and high school math.

Practical strategies to improve math fact fluency

Fluency matters, but how can teachers develop it in the classroom?

Effective techniques for building fact fluency

One effective way to build fluency is by using fact families . When students can learn related math facts (or fact families) together, problems become more accessible for them to solve. Fact families also help students understand the nature of inverse operations. See the image below for an example of a math fact family.

Teachers can use hands-on manipulatives, classroom whiteboard practice, skip counting, math centers, game-based technology , and more to build fact fluency.

How Reflex helps students achieve math fact fluency

ExploreLearning Reflex is an adaptive and game-based system that helps students build math fact fluency. Built on a math fact family approach, Reflex continuously monitors each student’s performance to help them build fluency at their own pace, while fun games and rewards boost motivation and confidence. Reflex includes advanced reporting features so teachers and administrators can monitor and celebrate fact fluency progress.

2nd-grade students who scored two or more years below grade level math improved by an average of 11 percentile points when they frequently used Reflex , compared to 5 percentile points with non-users. The students who used Reflex were also significantly more likely to meet or exceed on-grade-level proficiency by the end of second grade than non-users (16% vs 9%).

Are you ready to boost fluency in your classroom?

Start a Reflex Trial

  Learn About Reflex Grants

You might also like these stories...

Educational Trends

Mathematics teaching, learning, and assessment in the digital age

• Survey Paper
• Open access
• Published: 10 July 2024

Cite this article

You have full access to this open access article

• Hans-Georg Weigand   ORCID: orcid.org/0000-0001-6099-1318 1 ,
• Jana Trgalova 2 &
• Michal Tabach 3  

601 Accesses

1 Altmetric

Explore all metrics

The role of teaching, learning, and assessment with digital technology has become increasingly prominent in mathematics education. This survey paper provides an overview of how technology has been transforming teaching, learning, and assessment in mathematics education in the digital age and suggests how the field will evolve in the coming years. Based on several decades of research and educational practices, we discuss and anticipate the multifaceted impact of technology on mathematics education, thus laying the groundwork for the other papers in this issue. After a brief introduction discussing the motivations for this issue, we focus our attention on three lines of research: teaching mathematics with technology, learning mathematics with technology, and assessment with technology. We point to new research orientations that address the issue of teaching with technology, specifically describing attempts to conceptualise teachers’ mathematical and digital competencies, perspectives that view teachers as designers of digital resources, and the design and evaluation of long-term initiatives to support teachers as they develop innovative teaching practices enhanced by digital technologies. Our examination shows that learning with technology is still marked by new conceptualizations raised by researchers that can further our understanding of this complex issue. These conceptualizations support the recognition that multiple resources, ranging from paper and pencil to augmented reality, participate in the learning process. Finally, assessment with technology, especially in the formative sense, offers new possibilities for offering individualised support for learners that can benefit from adaptive systems, though more tasks for conceptual understanding need to be developed.

Similar content being viewed by others

Contemporary Framing of Technology in Mathematics Teaching

The Use of Digital Technologies in Teaching and Assessment

Uses of Technology in K–12 Mathematics Education: Concluding Remarks

Avoid common mistakes on your manuscript.

1 Introduction

The widespread availability of digital educational technologies and resources will increasingly influence mathematics teaching and learning in the coming years. How will this growing influence affect teachers and students of mathematics? Which digital and analogue resources will be used in the classroom? How will the use of digital technology affect the theory of mathematics education and the implementation of ideas in the classroom? And finally, what are the consequences for ongoing and final classroom assessments? These questions have been discussed extensively over the last decades in diverse mathematics education journals (see especially ZDM issues 55(1), 2023; 52(7), 2020; 52(5), 2020; 49(5), 2017; 44(6), 2012; 42(7), 2010; 41(4), 2009; 34(3), 2002) and at many conferences, especially the biennial Congress of the European Society for Research in Mathematics Education (CERME), which began in 1999. In 2018, a group of participants who were deeply involved in the CERME Thematic Working Groups on Technology took the initiative to launch the ERME Topic Conference for Mathematics Education in the Digital Age (MEDA). This conference sought to expand discussion of theoretical and practical knowledge and experience in the context of digital technologies and to look ahead at how mathematics education ought to be shaped in the coming years. The articles in this issue are significantly influenced by the three MEDA conferences and in particular are based on papers given at the 2022 MEDA3 conference held in Nitra, Slovakia (Weigand et al., 2022 ).

We begin by explaining the terminology we use in this article, followed by our methodological considerations. The literature uses various terms and expressions to refer to digital devices and digital content for mathematics teaching and learning, the most common of which are digital tools, digital technology, digital resources, and digital media. Because these terms are often used interchangeably, here we discuss each of them briefly to support our decision regarding the terms we use in this paper. Monaghan et al. ( 2016 ) broadly define a tool as “something you use to do something” (p. 5), thus distinguishing a tool from an artefact, defined as an object (material or symbolic) made by humans for a specific purpose. According to these authors, “an artefact becomes a tool when it is used by an agent, usually a person, to do something” (ibid., p. 6). Hence, according to the instrumental approach a tool is called an instrument (Rabardel, 2002 ) in that it cannot be conceived without considering a user and a purpose. The term digital technology usually refers both to tangible devices such as computers or tablets and to intangible means such as software. In the previous conceptualization, digital technology was considered an artefact or a tool when someone used it to achieve a given goal. In the last decade, researchers have begun referring to resources available for teachers and students rather than to technology: “Resources might be software, computers, interactive white-boards, online resources, but also traditional geometry tools and textbooks” (Trgalová et al., 2018 , p. 146). The term resource was conceptualized by Adler ( 2000 ), who suggested thinking of it “as the verb re-source, to source again or differently” (p. 207). This perspective emphasizes the user-resource relationship in which the user’s activity is nourished by the resource and, in turn, the resource can be modified and adapted by the user. Yet another perspective views mathematical knowledge as mediated by artefacts (Vygotsky, 1978 ). To stress the mediating role of a digital artefact, some researchers use the term digital media . Borba et al. ( 2023 ) suggest considering media in a broad sense; for them “computers, videos, paper-and-pencil, regular classrooms, homes, and libraries are examples of media” (p. 2). According to the theoretical construct of “humans-with-media”, digital technologies are thought “to be coparticipants in the production of mathematical knowledge” (ibid., p. 3).

In this paper, we use the term digital technology to refer to hardware or software. Furthermore, in referring to other objects used in mathematics education, such as videos, e-textbooks, and interactive whiteboards, we have chosen to adopt the term resources (whether digital or non-digital) that is widely used in mathematics education research.

After defining our terminology, we can now explain our methodological approach to the topics of teaching, learning, and assessment in the digital age. Like any survey, this survey paper must set the boundaries of what to retain and what to omit. In setting these boundaries, we have adopted two guiding principles. On the one hand, we have attempted to avoid repeating information from recent publications. One example is the chapter on “Technology and Resources in Mathematics Education” (Trgalová et al., 2018 ) in the book Developing Research in Mathematics Education (Dreyfus et al., 2018 ), released to celebrate the 20th anniversary of the European Society for Research in Mathematics Education (ERME) and its tenth congress (CERME). The chapter reviews the last 20 years of technology use in research and practice, describing the development of technology and resources and the design and implementation of digital mathematical tasks and theories and approaches concerning technology and resources. Another example is the book Mathematics Education in the Digital Age (Clark-Wilson et al., 2021 ), which emerged from the intense communication and collaboration during and after the MEDA1 conference. Finally, the recently published handbook on Digital Resources in Mathematics Education (Pepin et al., 2023 ) “presents the state-of-the art scholarship on theoretical frames, mathematical content, learning environments, pedagogic practices, teacher professional learning, and policy issues related to the development and use of digital resources in mathematics education” (p. 2). On the other hand, we have sought to be sensitive to the contributions appearing in this special issue. These two considerations reflect our view of the purpose of this paper: to position the contributions of the special issue in the broader context of the field. We categorised these contributions into three topics inspired by the recent MEDA3 conference: teaching, learning, and assessment with technology. These contributions propose new theoretical developments for tackling emergent issues and employ a variety of research methods, leading to further methodological elaborations: case studies and other qualitative methods; quantitative studies; and mixed methods. In the survey we have also taken into consideration publications from the last five years in journal papers and at leading conferences such as CERME, ICTMT, and MEDA.

Despite highlighting these three main aspects—teaching, learning, and assessment with technology—we are aware of other fields of interest related to technology in mathematics education. While we do not explicitly refer to these, we do touch upon them when relevant to this issue, e.g., technology and curriculum design, technology in instruction processes, technology and embodiment, and technology and beliefs of teachers and students. Moreover, many published studies have focused on young students working with digital technology, especially with tablets and special apps (e.g., Cavalletti et al., 2023 ; Kortenkamp et al., 2020 ) using Scratch or TouchCount (Bakos, 2023 ). In this issue, we concentrate on the use of digital resources in secondary education as all the papers in this special issue address this school level.

We begin our discussion with an overview of recent developments in teaching with technology , with specific emphasis on teachers’ digital competencies in using technology effectively in the classroom and on the role of teachers as designers of digital resources. The section on learning with technology begins with an overview of the use of multiple resources while learning mathematics and then discusses new developments such as augmented reality and video technology. The section on assessment with technology emphasizes the meaning of formative and summative assessment and discusses automatic feedback and adaptive assessment, conceptual understanding, and task design in the development of assessment profiles. In discussing each of these topics, we anticipate the possible future developments emerging from the present state of research to provide further perspective on the use of digital resources in the digital age.

2 Teaching with technology

In a recent survey paper on teaching mathematics with digital technology, Clark-Wilson et al. ( 2020 ) noted that in the last two decades, the focus of research studies has shifted from how technology can foster students’ learning to “how teachers can make practical use of different types of digital technology to provide students with activities that will enhance their mathematical learning” (p. 1223). This shift reflects researchers’ acknowledgement of the fact that “of all the factors influencing student activity it is the teacher who most influences learning” (ibid.).

Topics that address teaching with digital technology and resources include the investigation of obstacles and levers to digital technology integration (e.g., Thomas & Palmer, 2014 ), teachers’ knowledge, beliefs, and competences and the way these influence their digital practices (e.g., Remillard et al., 2024 ), digital task design to support teachers’ use of technology (Mariotti et al., 2023 ), design and evaluation of teacher education, and professional development programs (e.g., Thurm et al., 2024 ).

In this section we provide an overview of three ‘hot’ research topics in the area of teaching mathematics with digital technology that are also the focus of papers in this special issue: teachers’ digital competencies, teachers as designers, and innovative teaching practices leveraged by digital technology.

2.1 Teachers’ digital competencies

The belief that teachers are one of the most important factors influencing student learning when it comes to integrating digital technology in mathematics classrooms led researchers to studying teachers’ practices (e.g., Hennessy et al., 2005 ; Haspekian, 2014 ), knowledge, and skills needed for effective use of digital technology (e.g., Niess et al., 2009 ; Rocha, 2013 ), obstacles to technology integration (e.g., Jones, 2004 ), and affective aspects such as beliefs or personal orientations (e.g., Thomas & Palmer, 2014 ). Considering both cognitive (knowledge) and non-cognitive dimensions (e.g., affective, motivational) underscores the need to focus on teachers’ competencies, as Carr ( 1993 ) points out:

It is argued that we need teachers who are not just knowledgeable or well-informed about education , but whose knowledge and understanding is expressed or exhibited in their abilities - teachers, in short, who are competent by virtue of the intelligent application of their knowledge and understanding in effective practice (p. 254, author’s emphasis).

Hence, the notion of digital competency emerged in the context of digital technology. Various frameworks are available that describe this competency, mostly in institutional documents such as the European Commission Digital Competence Framework for Educators (Redecker & Punie, 2017 ) or the UNESCO ICT Competency Framework for Teachers (Butcher, 2018 ) at the international level. These frameworks Footnote 1 are general and apply to any subject matter and school level.

In their recent literature review of teachers’ professional digital competence (TPDC), Skantz-Åberg et al. ( 2022 ) point to the scarcity of conceptualizations, stating that almost 75% of papers reviewed do not provide a clear definition of the terms they use. The authors express regret that the view of technological competence as “a set of basic technological skills” or “something that applies mainly to teachers’ handling of digital technology” (p. 10) is the most prominent pedagogical view and that its development is considered to be the responsibility of individual teachers. The authors conclude by claiming that

the conceptualisation of TPDC needs to be directed away from the strong focus on the technological competence and basic hands-on skills of individual teachers to a focus on a collective responsibility and accountability for TPDC (p. 16).

In a similar study that examines teachers’ digital competencies in higher education, Basilotta Gómez‑Pablos et al. ( 2022 ) note that the various conceptualizations in the literature converge in “the need for teachers to have didactic and technological knowledge that allow them to make use of digital technologies in their professional practice” (p. 2). The authors call attention to emerging lines of research, among them the necessity “to rely on frameworks and theoretical reference models that identify the dimensions and components of digital competence” (p. 8, authors’ emphasis) and to develop methods for assessing teachers’ digital competencies, since currently most methods are based on “teachers’ self-perception” (p. 9).

Gonscherowski and Rott ( 2023 ) also recently noted that self-assessment is a dominant instrument for assessing teachers’ digital competencies. Indeed, at CERME12 (Clark-Wilson et al., 2022 ) mathematics teachers’ digital competences emerged as one of the “hot” topics in the field of research on teaching mathematics with digital technology and resources. Conceptualising these competences requires considering relevant theoretical frameworks to provide an operational definition of their dimensions and components and to elaborate research methods for capturing and assessing them.

Recent mathematics education research includes initiatives toward defining teachers’ digital competencies that consider specificities related to teaching mathematics. Based on the assumption that the distinction between students’ mathematical and digital competencies tends to fade away, Geraniou and Jankvist ( 2020 ) contend that mathematical and digital competencies must be articulated for teaching as well. These authors use a network of four theoretical frameworks—the Danish KOM framework of mathematics teachers’ competencies (Niss & Højgaard, 2011 ), mathematics knowledge for teaching (Ball et al., 2008 ), TPACK (Mishra & Koehler, 2006 ), and instrumental orchestration (Trouche, 2004 )—to conceptualise mathematical digital competencies for teaching (MDCT). According to Geraniou et al. ( 2022 ), MDCT are “the competencies teachers need (or have) to select and implement technology in their practice in pedagogically productive ways” (p. 167). In this issue, Geraniou et al. ( 2024 ) further elaborate on these competencies by drawing on the concept of mathematics digital competence for students (Geraniou & Jankvist, 2019 ). They rely on the theory of instrumental orchestration, the KOM framework, and the documentational approach to didactics (Gueudet & Trouche, 2009 ; Trouche et al., 2018 ), illustrating their arguments with the case of an experienced teacher.

Dilling et al. ( 2024 , this issue) adopt a different approach. Extending the TPACK framework (Mishra & Koehler, 2006 ), these authors propose the media, pedagogy and content model (MPC) to describe mathematics teachers’ professional media competencies, which they define as “competencies that enable a teacher to evaluate and select digital technologies and use them in the mathematics classroom effectively”. Although these two conceptualizations—MDCT and MPC model—draw on different theoretical frameworks, they share the view that digital competencies allow teachers to identify the affordances and limits of digital tools and consequently select the appropriate ones to be used in support of students’ mathematics learning.

2.2 Teachers as designers

Many researchers have acknowledged the importance of tasks in mathematics teaching and learning. Sierpinska ( 2004 ) considers “the design, analysis and empirical testing of mathematical tasks, whether for the purposes of research or teaching, as one of the most important responsibilities of mathematics education” (p. 10). Watson et al. ( 2013 ) claim that “task design is core to effective teaching” (p. 8). In relation to digital technology, tasks appear even more critical, as “some of the key affordances arising from technology use emanate from the tasks we use with it” (Thomas & Lin, 2013 , p. 109). The introduction to the proceedings of the ICMI study 22, which is devoted to task design in mathematics education , define a task as follows:

anything that a teacher uses to demonstrate mathematics, to pursue interactively with students, or to ask students to do something. Task can also be anything that students decide to do for themselves in a particular situation. Tasks, therefore, are the mediating tools for teaching and learning mathematics (Watson et al., 2013 , p. 10).

Teaching thus includes the selection, adaptation, design, enactment, and evaluation of tasks (ibid.). Acknowledging that interactions with tasks are an important facet of teachers’ professional activity led researchers to consider teachers as designers or partners in task design, rather than merely as task implementers (Brown, 2009 ; Jones & Pepin, 2016 ). Hence, teaching design is gaining increased interest in mathematics education research.

Two emerging research trends can be observed in recent research studies in relation to teachers as designers of their instruction. On the one hand, researchers’ attempts to understand and describe the requirements of designing and using (digital) tasks in terms of teachers’ competencies have led to a focus on teacher design capacity. On the other hand, the emergence of communities engaged in collective task design, such as communities of practice (Wenger, 1998 ), communities of inquiry (Jaworski, 2014 ), or teacher design teams (Handelzalts, 2009 ), has initiated a new research field in teachers’ collaborative work that may be accompanied and supported by facilitators.

Teacher design capacity. During the last two decades, researchers have begun exploring teachers’ interactions with curricular materials, for example by considering teaching as a design process (Brown, 2009 ) and by viewing curriculum materials as resources supporting such a process. Researchers agree on the existence of a mutual influence between teachers and resources, such that resources affect teacher practice and teachers modify resources to adapt them to their own context and needs. Examining such teacher-resource interactions necessitates understanding “pedagogical design capacity”, defined as a teacher’s “skill in perceiving the affordances of the materials and making decisions about how to use them to craft instructional episodes that achieve her goals” (Brown, 2009 , p. 29). Pepin et al. ( 2017 ) further conceptualised Brown’s pedagogical design capacity as “teacher design capacity” that incorporates three main components: (1) an orientation or a goal for the design, (2) a set of design principles, and (3) “reflection-in-action” (p. 802). Building on existing conceptualisations of teacher design capacity, Trgalová and Tabach ( 2024 , this issue) propose a framework that incorporates the specificities of mathematics and the use of digital technology, yielding a definition of teachers’ digital resource design capacity (DRDC). The authors then elaborate a conceptualisation of mathematics teachers’ DRDC, which they illustrate using two case studies from a course for pre-service mathematics teachers aimed at developing participants’ design capacity based on the DRDC conceptualization.

Teacher design teams . In their ICME13 survey paper, Robutti et al. ( 2016 ) claim that “the notion of mathematics teachers’ working and learning through collaboration … gains increasingly more attention in educational research and practice” (p. 651, authors’ emphasis). They point to “ever-increased interest in exploring and examining different activities, processes, and the nature of differing collaborations through which mathematics teachers work and learn” (p. 652). Their paper provides three emblematic examples to illustrate various forms of mathematics teachers’ collaboration: (1) a school-based collaborative lesson study in Japan that relies on iterative teacher processes of planning, teaching, lesson observation, and post-lesson discussion and reflection; (2) collaborative teacher projects in England involving schools and an “expert other” (p. 655), aimed at producing resources, planning, implementing, and evaluating an intervention, and providing professional development for other teachers; (3) mathematics learning communities in Norway involving teams of researchers and teacher educators in partnership with schools and based on “three layers of inquiry” (p. 656): in students’ mathematical activity, in mathematics teaching, and in the research process during the collaboration.

The 25th ICMI study devoted to teachers of mathematics working and learning in collaborative groups (Borko & Potari, 2020 ) confirms the growing interest in this topic. The emergence of new theoretical frameworks during the last decade has allowed researchers to address collective aspects in teachers’ professional activities and to consider how these aspects have affected teachers’ learning and professional development. Examples include the documentational approach to didactics (Gueudet et al., 2013 ) and the meta-didactical transposition theory (Arzarello et al., 2014 ) of collaboration between two communities: teachers and researchers or teacher educators. Most research studies focus on in-service mathematics teachers engaged in collaborative work. Other examples include the collective design of e-textbooks by an association of teachers (Sabra, 2016 ), the documentation workmates initiative in which a pair of teachers designed new resources for teaching algorithms and programming (Wang, 2018 ), and collaborative work on scenario design to consider possible enactments of classroom activities within a professional development programme (Cusi et al., 2020 ). Yet very little research has considered collaboration among pre-service and in-service teachers. To fill this gap, Dilling et al. ( 2024 , this issue) report on a collaborative project between pairs of teachers made up of an in-service teacher and a pre-service teacher trained to assist the in-service teacher in integrating digital technology in the classroom. The paper highlights the importance of a sound distribution of responsibilities within the teacher pairs so as to divide the workload.

2.3 Innovative teaching practices leveraged by digital resources

In the current digital age, mathematics teachers are provided with a profusion of digital resources, mainly available through the Internet. Consequently, much research in mathematics education has focused on teachers’ interactions with resources. Indeed, these interactions are thought to form the core of their professional activity (Remillard, 2005 ; Gueudet & Trouche, 2009 ). As noted above, the consensus is that teachers’ interactions with resources have the potential to affect both the resources themselves as they are modified and combined with other resources and the teachers’ practices that are shaped by the resource use. Hence, it is legitimate to expect that innovative digital resources will lead to innovative teaching practices. Indeed, as Clark-Wilson ( 2017 ) notes, digital resources have the potential to offer learners an environment in which they can explore mathematical ideas:

The advent of dynamic mathematical digital resources in the early 1990s promised a transformation of the teaching and learning mathematics as the technology enabled teachers and learners to experience and explore difficult mathematical ideas in more tangible ways.

Yet Clark-Wilson also notes that despite their potential, such technologies remain underused, mostly because of the complexity of integrating them into teachers’ practices. Research projects examining teachers’ professional development have sought to help teachers overcome barriers to technology use. One of these is the UK Cornerstone Maths project, which aimed to exploit the dynamic and visual affordances of digital technology and provide students an environment in which “to explore and solve problems within structured activities” (Clark-Wilson et al., 2013 , p. 13). Teachers’ appropriation of specifically designed resources was accompanied by professional development programs. Likewise, Naftaliev and Barabash ( 2024 , this issue) orchestrate teachers’ interactions with a specific type of digital resources known as technology-based interactive resources to foster the evolution of in-service teachers’ practices toward teaching experimental mathematics.

Digital technology has also been explored as a vehicle for the development of creativity, which is considered a 21st century skill, for example in the book Creativity and Technology in Mathematics Education (Freiman & Tassel, 2018 ). The European MC2-Mathematical creativity squared project demonstrated that digital technology can support social creativity in the design of digital resources (Kynigos et al., 2020 ) and at the same time can foster students’ creative mathematical thinking (Trgalová et al., 2018b ; Kolovou & Kynigos, 2017 ). Ye et al. ( 2024 , this issue) observe and analyse the mathematical creative actions of in-service teachers engaged in problem solving activities with Scratch, alongside their development of mathematics and programming knowledge.

To summarize, the above survey demonstrates several emerging trends and research evolutions in teaching mathematics with digital technology, which are further discussed in the concluding section: a shift from reporting on the complexity of digital technology integration in mathematics classrooms to exploring what teachers need to use digital tools effectively in terms of mathematical and digital competencies ; viewing teachers as designers of (digital) resources rather mere resource implementers; development of innovative teaching practices enhanced by digital technologies; and the need for long(er) term support for teachers in integrating digital technology in their classrooms.

3 Learning with technology

In her paper “Solid Findings in Mathematics Education: The Influence of the Use of Digital Technology on the Teaching and Learning of Mathematics in Schools”, Hoyles ( 2014 ) stated: “Digital tools have the potential for transforming teaching and learning mathematics in ways not possible with other tools” (p. 50). Indeed, according to Drijvers ( 2019 ), learning mathematics with technology was found to be beneficial for student learning, though the average effect size was small to moderate. At the same time, Hoyles stated:

In order for the potential for transforming mathematical practice through the use of digital technologies for the benefit of all learners to be realised, teachers, teachers’ practice and their beliefs about learning must form part of the process ( 2014 , p. 50).

Taken together, these quotations tell the story of integrating technology in the mathematics classroom and student learning: on the one hand, a clear vision of new opportunities that are realised to some extent, and on the other hand acknowledgment of the practical complexity involved in “making good use” of these opportunities for the benefit of all students.

The issue of student learning with technology raises many questions. For example, what do we know about learning with technology in different mathematical domains? Does learning algebra differ from learning geometry? How does learning algebra in a CAS environment differ from learning algebra in a graphical environment? What is the influence of tasks provided to students which use the same technological tools? How does learning mathematics in technological environments in elementary school differ from high school? Some of these questions are discussed in depth in the chapters of the newly published handbook titled Digital Resources in Mathematics Education (Pepin et al., 2023 ). For example, Leung et al. ( 2023 ) explore how digital technology enhances geometric skills, Haspekian et al. ( 2023 ) study algebra education with digital resources, and Biehler et al. ( 2023 ) question the impact of digitalization on content and goals of statistics education.

In the following concise review, we were guided by the issues emerging from the papers in this issue. We chose two themes that on the one hand go beyond mathematical topics and on the other hand are linked to recent developments in our field. We begin by discussing the use of multiple resources while learning mathematics—a conceptualization that may shed new light on our understanding of learning with resources. We then refer to a new adoption of technologies for learning mathematics that is influenced by developments in hardware, software, and accompanying pedagogy. In each subsection we first describe the topic based on the literature and then refer to the papers in this issue.

3.1 Learning with multiple resources

It is clear today that digital resources do not replace paper and pencil resources, but rather are used alongside them. Acknowledging the fact that learning mathematics takes place both with analogue and with digital resources, Geraniou et al. ( 2023 ) asked

how students (and subsequently teachers) conceptualise mathematics as they make transitions when using digital resources, involving different mathematical representations and different semiotic systems that may be using ‘new’ representations of mathematical concepts? (p. 1).

According to these authors, the use of graphs, symbolic expressions and numerical data can be considered as dynamic realisations of the same mathematical idea or as a dynamic and connected means of bridging between virtual concrete-like phenomena and their abstract counterparts. The authors further define transitions while working with digital and other resources using the words “within, beyond and across” (ibid., p. 1).

A transition is considered “within” a resource if several different representations of the same mathematical object or concept are available for students, who need to make sense of them. Bach ( 2023 ), for example, examines pairs of students who interacted with a dynamic geometry environment and were also asked to report individually in a paper environment. Bach noted:

‘Transitions within a digital tool’ concern the coordination of representations presented in a digital tool, which may be related to different content areas. ‘Transitions beyond a digital tool’ include the coordination of digital tool representations to paper-based representations. Such a transition may be evident even when it is not undertaken (p. 344).

Thus, observing learners as they interact with resources can shed light on transitions, as can researchers’ expectations regarding whether such transitions will take place, which may be absent in students’ work. For example, while working with a spreadsheet, students need to write expressions using such Excel-cell notations as 2*A2, whereas in a paper environment they would use 2*x, 2x or 2*A.

A transition is considered to be “across” resources when the opportunity is provided to navigate between two or more digital resources. In such cases, mathematical knowledge about a concept or an object is learned with one resource and then used with a different resource, possibly also with different representations. For example, Panorkou et al. ( 2023 ) studied students’ covariation thinking while using several resources (simulation, table, and graph) and described their transition across the resources as “messy”. Specifically, the researchers “provide an insight into the nature of the synergy of artefacts that offers a constructive space for students to shape and reorganise their meanings about covarying quantities” (p. 131).

Four papers in this issue describe cases of transitions within, across, and beyond resources. Radmehr and Turgut ( 2024 , this issue) analyse online video resources for studying the topic of derivation. The authors look for representations [realisations in their terminology] of mathematical objects in the video. These representations provide learners opportunities to make transitions within the video resource for the same mathematical object.

Jaber et al. ( 2024 , this issue) studied students working in an augmented reality environment in the mathematical context of covariational change. The authors offer learners the possibility to make transitions across carefully designed physical phenomena and their mathematical representations (tables and graphs).

Brnic et al. ( 2024 , this issue) studied students’ transitions across resources such as digital textbooks, dynamic visualisations, feedback formats, and digital tools, while they learned about conditional probability. The authors also studied students’ transition beyond resources by analysing students’ work on a paper and pencil test. They compared the achievements of students who learned with non-digital resources to those who learned with the digital resources and also compared gender differences.

Finally, Bach et al. ( 2024 , this issue) studied students’ transition beyond resources, moving from working with dynamic geometry resources to oral and written communication concerning the dynamic aspects of the mathematical objects observed.

3.2 Technological developments adopted for school mathematics

A different line of research examining students’ learning with digital resources is related to technological hardware and software developments and their influence on the uses of innovative technologies for teaching and learning mathematics. For example, augmented reality (AR) was first introduced by the US Air force in the early 1990s. AR can be defined as a system that incorporates three basic features: real and virtual worlds, real-time interaction, and accurate 3D registration of virtual and real objects (Wu et al., 2013 ). For mathematics education, AR is “a mixed reality technology that contains virtual objects that are implemented or ‘augmented’ with the real world” (Ahmad & Junaini, 2020 , p. 107). That is, AR technology facilitates design in which virtual elements can be added for the viewer while looking at real world objects such as tables or graphs.

In a systematic review of the use of AR in mathematics education, Palancı and Turan ( 2021 ) found an increased number of reports since 2010 that mainly used qualitative research methods. The researchers note that the use of AR

supported learning and motivation and enhanced the spatial abilities of students. Additionally, the most frequent disadvantages of AR in mathematics education were that it caused technical inconveniences and it is difficult to develop materials through AR (p. 89).

As this AR example shows, it is less accurate to speak about “new” and “old” technologies. Rather, we look for technological developments accompanied by new ways of exploiting hardware and software that have the potential to benefit students’ mathematics learning (Hoyles & Lagrange, 2010 ).

Another example is the use of video technology to capture live images by electronic means. This technology was first developed for commercial television in the early 1950s to capture live images by electronic means. As is the case with other technical tools, these videos were adopted for educational purposes. Specifically, video recordings were adopted for professional teacher development in that the instruction of actual teachers in the classroom was recorded as a basis for discussions and reflections at a professional development meeting (Jaworski, 1990 ). Teacher educators who are also mathematics education researchers used recordings of professional development meetings as an opportunity to reflect on their own practice and research (Coles, 2014 ; Tirosh et al., 2014 ). Video technology was also adopted as part of learning while engaging with (serious) video games (e.g., dragonbox algebra Footnote 2 for learning to solve linear equations, see Kapon et al., 2019 ). Indeed, it is hard to imagine flipped classrooms or MOOCs without the use of videos (Lo et al., 2017 ).

Kay ( 2012 ) identified two main factors that facilitated a tremendous increase in the use of instructional videos for learning aims: one is the YouTube platform, launched in 2005, that allowed users to upload and watch videos with ease; the other is the increasing size and availability of bandwidth, influencing the quality of what one might learn by watching such media. Kay and Kletskin ( 2012 ) identify two kinds of videos for use in mathematics higher education—algorithm presentations and problem-based demonstrations—claiming that problem-based demonstrations were less prevalent in our field. There is still no consensus regarding how to design an instructional video or how to measure its effectiveness (Netzer & Tabach, 2023 ). Some researchers use indirect methods such as students’ course grades, course dropout rate, and student feedback, while others examine the actual way in which learners use the video (Kim et al., 2014 ).

Three papers in this issue describe cases of using AR or video technology.

As noted above, Jaber et al. ( 2024 , this issue) designed special software that students could use to experiment with a physical phenomenon: while a cube slid down an inclined plane (Galileo experiment) students observed the covariation of time-distance in a table and in graph representations. They also observed the elongation of a physical spring under various masses, where the stiffness of the spring served as a parameter (Hooke’s Law). The AR technology enabled juxtaposing the view of the physical experiment and the mathematical representations, allowing students to discuss and make sense of these covariation phenomena.

Radmehr and Turgut ( 2024 , this volume) took advantage of the YouTube platform to identify online instructional video on derivation by using the number of views for the video they chose to analyse as an inclusion criteria (more than 3.2 million views!). The starting point of the analysis was that this highly observed resource provides learning opportunities for the students who watch it.

Finally, Wirth and Greefrath ( 2024 , this issue) designed a video resource that students worked on in pairs to learn how to handle modelling problems. The authors made use of our knowledge as a research community regarding the use of written examples and implemented this knowledge in their instructional video. This video was shown to 18 pairs of students without prior experience in modelling; each pair worked individually with the video to make sense of the modelling process. The authors examine the students’ perceived advantages and pitfalls following this experience.

In summary, although learning with technology has already been examined for several decades, the above survey provides evidence that the field is far from reaching stability. It is still characterised by new conceptualizations that researchers have raised to further our understanding of this complex issue. It is interesting to note how much time it is taking the education system to adopt technological innovations for research purposes, not to mention how much time it is taking for these innovations to be implemented in mathematics classrooms as an everyday reality.

4 Assessment with technology

Digital assessment also offers new types of affordances for assessment, such as automated scoring, feedback, and adaptivity. These affordances provide new opportunities with respect to developed tasks and assessment problems as well as styles of performing tasks and means of solving problems (e.g., see Drijvers & Sinclair, 2023 ). Interactive software such as Computer Algebra Systems (CAS), Dynamic Geometry Systems (DGS), and spreadsheets offer opportunities for carrying out interactive and dynamic tasks that are not possible using paper and pencil means, as do films, animations, and simulations. Assessment can be individualised in that feedback can be adapted to individual learners. Nevertheless, problems and difficulties associated with digital assessment must be considered. One such problem is the possibility that problems will become more complex due to a greater variety in representations. Another is the need to assess conceptual knowledge in addition to procedural knowledge, a form of assessment that is generally thought to be more difficult. Moreover, media use in the classroom and on examinations can change many or even all aspects of assessment.

There are new possibilities for the ways in which tasks are selected for use in assessments, in the way they are presented to students, in the ways that students operate while responding to the task, in the ways in which evidence generated by students is identified , and how evidence is accumulated across tasks. (Stacey & Wiliam, 2013 , p. 722)

In the following section, we begin with some general observations on the use of digital technologies in formative and summative assessment. We then discuss specific aspects we expect to be more important in the coming years: automatic feedback and adaptive assessment, assessment of conceptual understanding, and task development for digital assessment.

4.1 Digital technologies in formative and summative assessment

Assessment in mathematics education is characterised by a well-accepted duality between large-scale or summative assessment on the one hand and classroom or formative assessment on the other. Summative assessment refers to the assessment of learning that is associated with evaluation of student knowledge and learning at the end of a course or teaching unit, quite often with the aim of assessing students’ proficiency level. In contrast, formative assessment is assessment for learning that entails gathering information about a student’s current state of knowledge and learning to guide teachers and students in subsequent teaching and learning (e.g., Stacey & Wiliam, 2013 ). Digital technology has been and will continue to be used to enhance both summative and formative assessments.

Assessment is further marked by another duality: assessment with digital technologies and assessment through digital technologies (Stacey & Wiliam, 2013 ). Footnote 3 Assessment with digital technologies is characterised by traditional paper-based learning methods in which learners have access to digital learning opportunities such as software and videos (Drijvers et al., 2016 ; Fahlgren et al., 2021 ). In many countries today, especially in the West, handheld technology is allowed to be used or is even mandatory in examinations. In contrast, in assessment through technology or technology-based assessment (TBA), technology serves as a testing environment.

Computer-based tests and (final) examinations have been in use for many years at the university level, e.g., in medicine and engineering studies (Iannone, 2020 ). Recently, computer-based examinations have begun to be introduced in school mathematics. Computer-based versions of the PISA test have been offered since 2012; by 2015, PISA’s primary mode of assessment of students’ skills was computer-based and tasks were coded automatically (Jerrim, 2016 ). One part of the national assessment of 18-year-old high school students in Finland is a computer-based test using the Abitti system. In this system, students work in an environment isolated from the digital world yet still have access to mathematical tools like GeoGebra, Maxima, Casio ClassPad or TI-Nspire (Drijvers, 2018 ). The Dutch Ministry of Education developed a diagnostic test for 15-year-old students used on final examinations in lower secondary mathematics education (ibid.).

In addition to summative assessment, in recent years formative assessment has gained importance in assessing classroom work and supporting the learning process, especially while using digital technologies (Aldon et al., 2017 ; Dalby & Swan, 2019 ; Olsher, 2019 ; Cusi & Morselli, 2024 ). In 2009, Black and Wiliam ( 2009 ) provided a widely accepted specification of formative assessment:

Formative assessment (FA) is conceived as a method of teaching in which evidence about student achievement is elicited, interpreted, and used by teachers, learners, or their peers, to make decisions about the next steps in instruction that are likely to be better, or better founded, than the decisions they would have taken in the absence of the evidence that was elicited (p. 7).

In addition to the key areas and moments in which formative assessment is used, the European Formative Assessment in Science and Mathematics Education project ( FaSMEd , Aldon et al., 2017 ) emphasises three main elements or technology functionalities of formative assessment: sending and displaying ; processing and analysing ; and providing an interactive environment (Cusi, 2022 ). These functionalities should be integrated into the whole teaching and learning process. They are especially represented in classroom communication (e.g., with systems like MOODLE or ILIAS), in feedback (e.g., with systems like STACK), and in interactive work with digital technology (e.g., with systems like GeoGebra). In this ZDM-issue, two contributions refer to specific questions concerning formative assessment. Cusi and Morselli ( 2024 , this issue) investigate the specific roles played by teachers when making conscious in-the-moment decisions during classroom discussions to foster the development of effective formative assessment processes. Hershkovitz et al. ( 2024 , this issue) evaluate the use of feedback on the topic of reflective symmetry in digital learning environments among 9- to 12-year-old elementary school students.

4.2 Automatic feedback and adaptive assessment

Feedback is perhaps the most important aspect of teaching and learning (Hattie & Clarke, 2018 ). Feedback with digital technologies, and particularly computer algebra systems like GeoGebra-CAS, Mathematica or STACK, are best suited for algorithmic calculations. When these technologies are used for learning, two types of use-software interactions are important: system input and system output. In the case of input, users must be confident with the question to be answered and its representation in the technical input scripts. In the case of output, users must to be able to interpret the system feedback and validate it with respect to the posed problem. Even though the calculations are done automatically, the feedback system developer, the task designer or the teacher must construct the kind of feedback required in advance. For example, STACK generates automatic differentiated feedback from student solutions. For each task, the designer must define relevant and possible outputs in advance, which will then be checked vis-à-vis the task or problem solution. Various forms of feedback can provide verbal, numerical, graphical or algebraic information about students’ answers (Pinkernell et al., 2019 ). Students in technical and science fields use the interactive adaptive assessment system OPTES (or its follow-up system DigikoS) as supplementary materials to repeat school mathematics in the introductory phase of their studies (see Roos et al., 2019 ). In OPTES, STACK tasks are used to develop an adaptive learning and training system (Wankerl et al., 2019 ), making it possible to select appropriate exercises for individual learners. These kinds of adaptive systems will become increasingly meaningful in the coming years.

An important issue in current research is how to help teachers make productive use of the results of digital learning assessments in the classroom (Dalby & Swan, 2019 ). Klingbeil et al. ( 2024 , this ZDM-issue) describe the development and evaluation of the online formative assessment system SMART, which is designed improve mathematics learning among upper primary and junior secondary school students. The system provides teachers an informative diagnosis of students’ conceptual understanding (Stacey et al., 2009 ; Haspekian, 2020 ; Fahlgren et al., 2021 ). Each SMART test is individually evaluated and identifies students’ understanding, misconceptions, and knowledge gaps. Further, it provides teachers useful information about possible future steps, tasks to solve, or instructions to improve. In SMART, only the teacher receives the results of the test because the teacher is considered the initiator of the developmental process.

Individualisation of the learning process requires more than individual feedback on solutions and solution processes. Indeed, the problems of the next learning step must also be individualised and individual learning trajectories must be adaptive. Since the time teaching and learning machines were first introduced, adaptive assessment was always an important aspect of individual learning (Olsher et al., 2023 ). OPTES, for example, categorises a special mathematical field, e.g., algebra or calculus, based on a didactical reference model concerned with particular aspects of knowledge. Problems in one category are more closely related than problems from different categories. All problems in this field are arranged in a graph with special transformation probabilities. If a learner does not solve a problem, the probability of getting a similar problem is higher than if the problem is solved correctly. The transformation probabilities are calculated in a training process with a large number of users (Wankerl et al., 2019 ).

4.3 Digital assessment and conceptual understanding

Competency assessment is a central but demanding task for which digital technologies are increasingly being used in different contexts. In assessing procedural knowledge—i.e., knowing how to use procedures like transformations of terms, how to solve equations with formulas or how to calculate square roots with the Heron algorithm—computer algebra systems such Mathematica or STACK are adequate tools that allow the development of fully automated examination evaluation and grading. The assessment of conceptual understanding is far more complex for it entails assessing the understanding of mathematical concepts and the adequate application of mathematical concepts in internal and external mathematical problem-solving situations. This assessment is best accomplished by oral tests, interviews or any kind of project work. Concerning digital assessment, Olsher et al. ( 2023 ) note the risk that this kind of assessment “is not commonly testing competencies that match what it means to ‘do mathematics’ in the 21st century” (p. 21). Hoogland and Tout ( 2018 ) even see “mathematics education… at risk of focusing too much on assessment of lower order goals, such as the reproduction of procedural, calculation based, knowledge and skills” (p. 675). Nevertheless, in the context of the increasing importance of digital assessment, means must also be developed for assessing conceptual understanding.

The so-called Basic Mental Models (in German “Grundvorstellungen”) (vom Hofe & Blum, 2016 ) can serve as a good basis for the development of conceptual understanding. A Basic Mental Model (BMM) of a mathematical concept is a conceptual interpretation that gives it meaning. Yet BMMs still need to be developed and empirically validated (Greefrath et al., 2021 ), as do appropriate assessment tasks.

Some empirically based suggestions for the use of digital technologies in developing conceptual understanding have already been proposed. Weigand and Günster ( 2022 ) used digital tools (GeoGebra) to develop the dynamic view of functions on these levels of understanding. Ruchniewicz and Barzel ( 2019 ) developed a digital tool for student self-diagnostics as they work with different representations of functions. Yerushalmy and Olsher ( 2020 ) and Popper and Yerushalmy ( 2022 ) developed a digital tool for the development of reasoning while working with and classifying quadrilaterals.

4.4 Task design for digital assessment

Task design is a crucial element in mathematics education (Watson et al., 2013 ; Watson & Ohtani, 2021 ). Digital assessment raises a number of questions concerning task design: What new kinds of questions do digital tests allow (e.g., how to integrate films, simulations or interactive applets into the questions)? How do working styles in digital tests differ from those of paper-and-pencil tests (e.g., doing preliminary considerations and sketches on paper alongside the digital test, using interactive programs like GeoGebra or hand-held-technology in addition to the digital test)? How do the test questions influence the general classroom work (e.g., does the use laptops, hand-held devices or computer programs in examinations influence the need for hand calculations with paper-and-pencil)?

Concerning the development of tasks in digital assessment systems, four aspects need to be taken into consideration: (1) the task representation; (2) the way students or learners should work (in relation to software functionality); (3) the evaluation of students’ work and answers, and (4) the feedback on students’ solutions. A major theory has evolved regarding principles of designing assessment tasks for both summative and formative assessment. Suurtamm et al. ( 2016 ) believe that the principles underlying these two forms of assessment are similar because “large-scale and classroom assessment interact with one another in different ways” (p. 25). Still of major importance is the emphasis in the NCTM assessment standards ( 1995 ) “that both large-scale and classroom assessment should take into account not only content but also mathematical practices, processes, proficiencies, or competencies” (p. 5). Yet many questions concerning task design in digital environments still remain: Who designs the problems? Who has control over the assessment platforms (e.g., to what extent can individual teachers write their own assessments)? Which tools are allowed? (e.g., Nortvedt & Buchholtz, 2018 ).

Questions with verbal answers are clearly better suited for assessing higher order mathematics skills than multiple choice tests, as these questions enable students to express themselves more freely. Yet assessing handwritten questions is often challenging. Moons et al. ( 2024 , this issue) developed a “checkbox grading system” that (human) assessors can use to assess handwritten mathematics exams as “atomic feedback”. The idea is to combine pre-defined answers for test problems by using a list of checkboxes for classification. The system then automatically calculates the grade and provides individualised feedback to students.

A great deal of experience has accumulated regarding assessment with technology, especially using CAS-systems. For example, CAS-supported examinations have been in use in Great Britain, France, Germany and the Scandinavian countries for many years (Bach, 2023 ). Leigh-Lancaster and Stacey ( 2022 ) give an overview of the 20 years in which CAS-calculators were used in Australia, showing that the availability of sophisticated digital technologies does not necessarily make assessment easy.

One reason for digital assessment is pragmatic: it offers an effective means of designing and implementing tests and examinations. Moreover, the use of digital technologies in tests and examinations is known for allowing enhanced experimental and heuristic work in problem-solving phases and for providing opportunities for realistic modelling tasks (Fahlgren et al., 2021 ). Yet this experimentation requires sufficient time to try out different methods and pursue them thoroughly, which is very difficult to implement within the confines of the time-limited tests that have been the predominant form of examination up to now. Yet, aligning learning activities in the instructional learning process with assessment activities is a crucial part of the learning process: “Any course needs to be designed so that the learning activities and assessment tasks are aligned with the learning outcomes that are intended in the course. This means that the system is consistent” (Hattie, 2009 , p. 6). The issue of the use of digital media in examinations must therefore also be accompanied by a discussion of alternative forms of examination, such as portfolios, individual studies, and project work (Ball et al., 2018 ).

In summary, in the coming years assessment with and through technologies will play an important and increasing role in formative and summative assessment. During the pandemic, many teachers were exposed to new possibilities for digital assessment (e.g., online quizzes or digital interactive learning trajectories) and later adapted some of these in their traditional teaching (Cusi et al., 2023 ; Engelbrecht & Borba, 2023 ). Some current developments will surely influence assessment in the coming years. Inputting symbolic expressions using a formula editor is still not very convenient and “limits the expressivity of ideas due to the efforts of communicating them. Here technological developments such as optical character recognition (OCR) may provide useful solutions” (Olsher et al., 2023 , p. 22). Furthermore, the issue of how to use Virtual and Augmented Reality not only in the classroom but also in assessment situations remains an open question (Wu, 2013 ; Palancı & Turan, 2021 ).

5 Conclusion

Teaching, learning, and assessment are closely related in learning environments, especially in mathematics classrooms. Hence, they must be oriented towards goals in terms of mathematical knowledge and general competencies. On the one hand, digital technologies and resources must be selected with a view to achieving these goals, while on the other hand, digital technologies and resources also influence the way in which these goals are achieved. This interrelationship, along with new developments in digital resources such as artificial intelligence products (e.g., adaptive digital learning systems or generative artificial intelligence systems like chatbots) make planning for the future very difficult or even impossible. In the digital age, all stakeholders in the educational system—politicians, school administrators, teachers, and students alike—must be flexible and prepared for continuous adaptations and corrections in the educational process. Moreover, in view of the diversity of educational systems, together with different national and regional peculiarities and traditions and diverse convictions and emphases, it is unlikely that generally accepted strategies for dealing with digital technologies and resources in mathematics education will emerge.

Nevertheless, based on the experience of the last decades and on the discussion in the above sections about teaching, learning, and assessment with technologies, we can still make some comments, suggestions, and recommendations regarding the use of digital technologies and resources in the digital age:

Despite major expectations on the part of the public, the use of digital technologies is not an end in itself. Rather, these technologies must be critically evaluated in the context of the intended goals of mathematics learning.

Digital technologies for new curriculum developments, task design, and the development of new problems and tasks for teaching, learning, and assessing are continually being explored.

Current digital technologies should be integrated into all levels of pre- and in-service teacher education. Nevertheless, this integration must be flexible and open to further technical developments and must not focus on special hardware or software.

As we show in the section devoted to teaching with digital technology, the mathematics education research community has demonstrated growing interest in conceptualising mathematics teachers’ professional competencies, with the goal of using digital artefacts in classrooms effectively. The current lack of consensual conceptualization highlights the diverse opinions regarding what makes mathematics teachers competent users of digital artefacts in their instruction.

As discussed in the section on assessment with digital technology, formative assessment could benefit from the potential offered by digital technologies, especially concerning individual feedback as a crucial element of mathematics learning and teaching.

The development of digital technologies for tests, examinations, and summative assessment should be intensified, especially concerning conceptual understanding. The fact that examination problems set standards for learning and teaching in the classroom is well-known.

Most recent research studies, including those in this volume, highlight the need for networking theories to address complex issues related to the use of digital artefacts in mathematics teaching, learning, and assessment. Likewise, the field requires large-scale studies using quantitative methods to complement the qualitative research methodologies dominating the research field.

Embodiment and embodied cognition, especially in connection with virtual and augmented reality, will become increasingly important. Hence, research on this topic as well as adequate classroom examples that go beyond the equipment debate need to be developed.

Finally, it is reasonable to assume that Artificial Intelligence will exert a major influence on educational systems. For the time being, the topic of how language generation models such as ChatGPT will influence teaching, learning, and assessment remains an open question.

Despite the ubiquity of digital technology and resources, this issue demonstrates that old but still relevant themes require further theoretical and methodological investigation.

An analysis of these frameworks can be found in (Tabach & Trgalová, 2019 ).

https://dragonbox.com/about .

The use of the word “with” in this paper has a narrower interpretation than the word “with” in the rest of this paragraph.

Adler, J. (2000). Conceptualising resources as a theme for teacher education. Journal of Mathematics Teacher Education , 3 , 205–224. https://doi.org/10.1023/A:1009903206236

Article   Google Scholar  

Ahmad, N. I. N., & Junaini, S. N. (2020). Augmented reality for learning mathematics: A systematic literature review. International Journal of Emerging Technologies in Learning (iJET) , 15 (16), 106–122. https://doi.org/10.3991/ijet.v15i16.14961

Aldon, G., Cusi, A., Morselli, F., Panero, M., & Sabena, C. (2017). Formative assessment and technology: reflections developed through the collaboration between teachers and researchers. In G. Aldon, F. Hitt, L. Bazzini & U. Gellert (Ed.), Mathematics and technology: A CIEAEM source book (pp. 551–578). Springer. https://doi.org/10.1007/978-3-319-51380-5_25

Arzarello, F., Robutti, O., Sabena, C., Cusi, A., Garuti, R., Malara, N., & Martignone, F. (2014). Meta-didactical transposition: A theoretical model for teacher education programmes. In A. Clark-Wilson, O. Robutti, & N. Sinclair (Eds.), The mathematics teacher in the digital era (pp. 347–372). Springer. https://doi.org/10.1007/978-94-007-4638-1_15

Bach, C. C. (2023). Adapting profiles for CAS to students’ use of DGE: Through a transition perspective. Digital Experiences in Mathematics Education , 9 (2), 343–371. https://doi.org/10.1007/s40751-022-00123-0

Bach, C. C., Bergqvist, E., & Jankvist, U. T. (2024). Students’ dynamic communication while transforming mathematical representations in a dynamic geometry environment. ZDM - Mathematics Education , 56 (4).

Bakos, S. (2023). Sociocultural influences while implementing TouchTimes. In P. Drijvers, C. Csapodi, H. Palmér, K. Gosztonyi, & E. Kónya (Eds.), Proceedings of the Thirteenth Congress of the European Society for Research in Mathematics Education (CERME13) (pp. 2598–2605). Alfréd Rényi Institute of Mathematics and ERME.

Ball, D. L., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching: What makes it special? Journal of Teacher Education , 59 (5), 389–407. https://doi.org/10.1177/0022487108324554

Ball, L., Drijvers, P., Ladel, S., Siller, H. S., Tabach, M., & Vale, C. (Eds.). (2018). Uses of technology in primary and secondary Mathematics Education . Springer. https://doi.org/10.1007/978-3-319-76575-4

Basilotta Gómez-Pablos, V., Matarranz, M., Casado-Aranda, L. A., et al. (2022). Teachers’ digital competencies in higher education: A systematic literature review. International Journal of Educational Technology in Higher Education , 19 . https://doi.org/10.1186/s41239-021-00312-8

Biehler, R., Frischemeier, D., Gould, R., & Pfannkuch, M. (2023). Impacts of digitalization on content and goals of Statistics Education. In B. Pepin, G. Gueudet, & J. Choppin (Eds.), Handbook of Digital Resources in Mathematics Education . Springer. https://doi.org/10.1007/978-3-030-95060-6_20-1

Black, P., & William, D. (2009). Developing the theory of formative assessment. Educational Assessment Evaluation and Accountability , 21 , 5–31. https://doi.org/10.1007/s11092-008-9068-5

Borba, M. C., Souto, D. L. P., Cunha, J. F. T., & Domingues, N. S. (2023). Humans-with-Media: Twenty-five years of a theoretical construct in Mathematics Education. In B. Pepin, G. Gueudet, & J. Choppin (Eds.), Handbook of Digital Resources in Mathematics Education . Springer. https://doi.org/10.1007/978-3-030-95060-6_7-1

Borko, H., & Potari, D. (Eds.). (2020). Teachers of Mathematics Working and Learning in Collaborative Groups. Proceedings of the Twenty-Fifth ICMI Study . National and Kapodistrian University of Athens. https://www.mathunion.org/fileadmin/ICMI/Publications/ICMI Study 25/updated DD/201114 ICMI25Proceedings6.13.2020.pdf

Brnic, M., Greefrath, G., & Reinhold, F. (2024). Working with digital textbooks or printed materials: A study with boys and girls on conditional probability. ZDM - Mathematics Education , 56 (4). https://doi.org/10.1007/s11858-023-01543-x

Brown, M. W. (2009). The teacher-tool relationship: Theorizing the design and use of curriculum materials. In J. T. Remillard, et al. (Eds.), Mathematics teachers at work: Connecting curriculum materials and classroom instruction (pp. 17–36). Routledge.

Butcher, N. (2018). UNESCO ICT competency framework for teachers . UNESCO. https://unesdoc.unesco.org/ark:/48223/pf0000265721

Carr, D. (1993). Question of competence. British Journal of Educational Studies , 41 (3), 253–271. https://doi.org/10.2307/3122287

Cavalletti, S., Manzoni, V., Bolondi, G., Cazzaniga, P., & Giberti, C. (2023). Mathematical discussion in problem solving activities supported by technology: An achievable goal in primary school. In P. Drijvers, C. Csapodi, H. Palmér, K. Gosztonyi, & E. Kónya (Eds.), Proceedings of the Thirteenth Congress of the European Society for Research in Mathematics Education (CERME13) (pp. 2903–2910). Alfréd Rényi Institute of Mathematics and ERME.

Clark-Wilson, A. (2017). Transforming mathematics teaching with digital technologies: A community of practice perspective. In Marcus-Quinn, A., Hourigan, T. (Eds.), Handbook on Digital Learning for K-12 Schools (pp. 45–57). Springer. https://doi.org/10.1007/978-3-319-33808-8_4

Clark-Wilson, A., Hoyles, C., & Noss, R. (2013). CornerstoneMath: Designing for scale. In C. Smith (Ed.), Proceedings of the British Society for Research into Learning Mathematics 33(2) (pp. 13–18). Sheffield Hallam University, UK.

Clark-Wilson, A., Robutti, O., & Thomas, M. (2020). Teaching with digital technology. Zdm Mathematics Education , 52 (7), 1223–1242. https://doi.org/10.1007/s11858-020-01196-0

Clark-Wilson, A., Donevska-Todorova, A., Faggiano, E., Trgalová, J., & Weigand, H. G. (2021). Mathematics education in the digital age - learning, practice and theory . Routledge.

Clark-Wilson, A., Robutti, O., Turgut, M., Bozkurt, G., & Thurm, D. (2022). Introduction to the papers of TWG 15. Teaching mathematics with technology and resources. In J. Hodgen, E. Geraniou, G. Bolondi, & F. Ferretti (Eds.), Proceedings of the Twelfth Congress of the European Society for Research in Mathematics Education (CERME12) (pp. 2472–2479). Free University of Bozen-Bolzano, Italy and ERME.

Coles, A. (2014). Mathematics teachers learning with video: The role, for the didactician, of a heightened listening. Zdm , 46 (2), 267–278. https://doi.org/10.1007/s11858-013-0541-3

Cusi, A. (2022). Formative assessment in mathematics in the digital age: teacher’s practices and roles. In H-G. Weigand et al. (Eds.), MEDA3 Mathematics Education in the Digital Age 3: Proceedings of the 13th ERME Topic Conference (ETC3) (pp. 161–168). Constantine the Philosopher University of Nitra. 2–11. https://hal.science/hal-03925304v1/

Cusi, A., & Morselli, F. (2024). The key-roles of the expert during classroom discussions aimed at fostering formative assessment processes through the use of digital technologies. ZDM - Mathematics Education , 56 (4). https://doi.org/10.1007/s11858-024-01572-0

Cusi, A., Faggiano, E., Swidan, O., & Prodromou, T. (2020). The collaborative work on scenario design as a tool to foster teachers’ professional development. In H. Borko & D. Potari (Eds.), Teachers of Mathematics Working and Learning in Collaborative Groups. Proceedings of the Twenty-Fifth ICMI Study (pp. 605–612). National and Kapodistrian University of Athens.

Cusi, A., Schacht, F., Aldon, G., & Swidan, O. (2023). Assessment in mathematics: A study on teachers’ practices in times of pandemic. ZDM– Mathematics Education , 55 , 221–233. https://doi.org/10.1007/s11858-022-01395-x

Cusi, A., Aldon, G., Barzel, B., & Olsher, S. (2024). Rethinking teachers’ formative assessment practices within technology-enhanced classrooms. In B. Pepin, G. Gueudet, & J. Choppin (Eds.), Handbook of Digital Resources in Mathematics Education . Springer. https://doi.org/10.1007/978-3-030-95060-6_29-1

Dalby, D., & Swan, M. (2019). Using digital technology to enhance formative assessment in mathematics classrooms: Using digital technology in formative assessment. British Journal of Educational Technology , 50 (2), 832–845. https://doi.org/10.1111/bjet.12606

Dilling, F., Schneider, R., Weigand, H. G., & Witzke, I. (2024a). Describing the digital competencies of mathematics teachers: Theoretical and empirical considerations on the importance of experience and reflection. ZDM - Mathematics Education , 56 (4). https://doi.org/10.1007/s11858-024-01560-4

Dilling, F., Witzke, I., Hörnberger, K., & Trgalová, J. (2024b). Co-designing teaching with digital technologies: A case study on mixed pre-service and in-service mathematics teacher design teams. ZDM - Mathematics Education , 56 (4).

Dreyfus, T., Artigue, M., Potari, D., Prediger, S., & Ruthven, K. (Eds.). (2018). Developing research in mathematics education. Twenty years of communication, cooperation and collaboration in Europe . Routledge.

Drijvers, P. (2018). Digital assessment of mathematics: Opportunities, issues and criteria. Mesure et évaluation en éducation , 41 (1), 41–66. https://doi.org/10.7202/1055896ar

Drijvers, P. (2019). Embodied instrumentation: Combining different views on using digital technology in mathematics education. In U. T. Jankvist, Van den M. Heuvel-Panhuizen, & M. Veldhuis (Eds.), Eleventh Congress of the European Society for Research in Mathematics Education (pp. 8–28). Freudenthal Group & Freudenthal Institute, Utrecht University and ERME.

Drijvers, P., & Sinclair, N. (2023). The role of digital technologies in mathematics education: Purposes and perspectives. ZDM - Mathematics Education . https://doi.org/10.1007/s11858-023-01535-x

Drijvers, P., Ball, L., Barzel, B., Heid, M. K., Cao, Y., & Maschietto, M. (2016). Uses of technology in lower secondary mathematics education . A concise topical survey. Springer. https://doi.org/10.1007/978-3-319-33666-4

Engelbrecht, J., & Borba, M. C. (2023). Recent developments in using digital technology in mathematics. ZDM– Mathematics Education . https://doi.org/10.1007/s11858-023-01530-2

Fahlgren, M., Brunström, M., Dilling, F., Kristinsdóttir, B., Pinkernell, G., & Weigand, H. G. (2021). Technology-rich assessment in mathematics education. In A. Clark-Wilson, A. Donevska-Todorova, E. Faggiano, Trgalová, & H. G. Weigand (Eds.), Mathematics Education in the Digital Age (pp. 69–83). Routledge.

Freiman, V., & Tassell, J. L. (Eds.). (2018). Creativity and technology in mathematics education . Springer. https://doi.org/10.1007/978-3-319-72381-5

Geraniou, E., & Jankvist, U. T. (2019). Towards a definition of mathematical digital competency. Educational Studies in Mathematics , 102 , 29–45. https://doi.org/10.1007/s10649-019-09893-8

Geraniou, E., & Jankvist, U. T. (2020). Mathematical digital competencies for teaching from a networking of theories perspective. In B. Barzel, R. Bebernik, L. Göbel, M. Pohl, H. Ruchniewicz, F. Schacht, & D. Thurm (Eds.), Proceedings of the 14th International Conference on Technology in Mathematics Teaching– ICTMT 14 (pp. 368–375). https://doi.org/10.17185/duepublico/70775

Geraniou, E., Jankvist, U. T., Elicer, R., Tamborg, A. L., & Misfeldt, M. (2022). On mathematical digital competency for teaching: The case of an expert teacher. In H-G. Weigand et al. (Eds.), MEDA3 Mathematics Education in the Digital Age 3: Proceedings of the 13th ERME Topic Conference (ETC3) (pp. 161–168). Constantine the Philosopher University of Nitra. https://hal.science/hal-03925304v1/ .

Geraniou, E., Baccaglini-Frank, A., Finesilver, C., et al. (2023). Introduction to the special issue supporting transitions within, across and beyond digital experiences for the teaching and learning of mathematics. Digital Experiences in Mathematics Education , 9 (1), 1–4. https://doi.org/10.1007/s40751-023-00125-6

Geraniou, E., Jankvist, U. T., Elicer, R., Tamborg, A. L., & Misfeldt, M. (2024). Towards a definition of mathematical digital competency for teaching. ZDM - Mathematics Education , 56 (4).

Gonscherowski, P., & Rott, B. (2023). Selecting digital technology: a review of TPACK instruments. In M. Ayalon, B. Koichu, R. Leikin, L. Rubel & M. Tabach (Eds.), Proceedings of the 46th Conference of the International Group for the Psychology of Mathematics Education (Vol. 2, pp. 379–386). PME 46.

Greefrath, G., Oldenburg, R., Siller, S., Ulm, V., & Weigand, H. G. (2021). Basic mental models of integrals: Theoretical conception, development of a test instrument, and first results. ZDM - Mathematics Education , 53 , 649–661. https://doi.org/10.1007/s11858-020-01207-0

Gueudet, G., & Trouche, L. (2009). Towards new documentation systems for mathematics teachers? Educational Studies in Mathematics , 71 (3), 199–218. https://doi.org/10.1007/s10649-008-9159-8

Gueudet, G., Pepin, B., & Trouche, L. (2013). Collective work with resources: An essential dimension for teacher documentation. Zdm , 45 (7), 1003–1016. https://doi.org/10.1007/s11858-013-0527-1

Handelzalts, A. (2009). Collaborative curriculum development in teacher design teams . Doctoral dissertation, University of Twente, The Netherlands. http://doc.utwente.nl/67385/1/thesis_A_Handelzalts.pdf

Haspekian, M. (2014). Teachers practices and professional geneses with ICT. Research Journal of Mathematics & Technology , 3 , 96–105.

Google Scholar  

Haspekian, M. (2020). Teaching practices in digital era: some theoretical and methodological perspectives. In Donevska-Todorova, D., Faggiano, E., Trgalová, J., Lavicza, Z., Weinhandl, R., Clark-Wilson, A., & Weigand, H.-G. (Eds.), Proceedings of the 2nd MEDA-conference (pp. 3–10). https://hal.archives-ouvertes.fr/hal-02932218

Haspekian, M., Kieran, C., Drijvers, P., Bråting, K., & Tabach, M. (2023). Algebra education and digital resources: A long-distance relationship? In B. Pepin, G. Gueudet, & J. Choppin (Eds.), Handbook of Digital Resources in Mathematics Education . Springer. https://doi.org/10.1007/978-3-030-95060-6_16-1

Hattie, J. (2009). Visible learning– a synthesis of over 800 meta-analyses relating to achievement . Routledge.

Hattie, J., & Clarke, S. (2018). Visible learning: Feedback . Taylor & Francis.

Hennessy, S., Ruthven, K., & Brindley, S. (2005). Teacher perspectives on integrating ICT into subject teaching: Commitment, constraints, caution, and change. Journal of Curriculum Studies , 37 (2), 155–192. https://doi.org/10.1080/0022027032000276961

Hershkovitz, A., Noster, N., Siller, S., & Tabach, M. (2024). Learning analytics in mathematics education: The case of feedback use in a digital classification task on reflective symmetry. Zdm , 56 (4). https://doi.org/10.1007/s11858-024-01551-5

Hoogland, K., & Tout, D. (2018). Computer-based assessment of mathematics into the twenty-first century: Pressures and tensions. Zdm Mathematics Education , 50 , 675–686. https://doi.org/10.1007/s11858-018-0944-2

Hoyles, C. (2014). Solid findings in mathematics education: the influence of the use of digital technology on the teaching and learning of mathematics in schools. EMS Newsletter , 91 , 49–51.

Hoyles, C., & Lagrange, J. B. (2010). Mathematics education and technology - rethinking the terrain . Springer. https://doi.org/10.1007/978-1-4419-0146-0

Iannone, P. (2020). Assessment of mathematics in the digital age: The case of university mathematics. In A. Donevska-Todorova, E. Faggiano, J. Trgalová, Z. Lavicza, R. Weinhandl, et al. (Eds.), Proceedings of the 10th ERME Topic Conference Mathematics Education in the Digital Age (MEDA) (pp. 11–18).

Jaber, O., Bagossi, S., Fried, M. N., & Swidan, O. (2024). Conceptualizing functional relationships in an AR environment: Connecting real and virtual worlds. ZDM - Mathematics Education , 56 (4).

Jaworski, B. (1990). Video as a tool for teachers’ professional development. Journal of In-Service Education , 16 (1), 60–65. https://doi.org/10.1080/0305763900160112

Jaworski, B. (2014). Communities of inquiry in mathematics teacher education. In Lerman, S. (Ed.). Encyclopedia of mathematics education (pp. 76–87). Springer. https://doi.org/10.1007/978-94-007-4978-8_24

Jerrim, J. (2016). PISA 2012: How do results for the paper and computer tests compare? Assessment in Education : Principles . Policy & Practice , 23 (4), 495–518. https://doi.org/10.1080/0969594X.2016.1147420

Jones, A. (2004). A review of the research literature on barriers to the uptake of ICT by teachers . British Educational Communications and Technology Agency (BECTA). http://dera.ioe.ac.uk/1603/1/becta_2004_barrierstouptake_litrev.pdf

Jones, K., & Pepin, B. (2016). Research on mathematics teachers as partners in task design. Journal of Mathematics Teacher Education , 19 (2/3), 105–121. https://doi.org/10.1007/s10857-016-9345-z

Kapon, S., Hallun, A., & Tabach, M. (2019). Incorporating a digital game into the formal instruction of algebra. Journal of Research in Mathematics Education , 50 (5), 555–591. https://doi.org/10.5951/jresematheduc.50.5.0555

Kay, R. H. (2012). Exploring the use of video podcasts in education: A comprehensive review of the literature. Computers in Human Behavior , 28 (3), 820–831. https://doi.org/10.1016/j.chb.2012.01.011

Kay, R., & Kletskin, I. (2012). Evaluating the use of problem-based video podcasts to teach mathematics in higher education. Computers & Education , 59 (2), 619–627. https://doi.org/10.1016/j.compedu.2012.03.007

Kim, J., Guo, P. J., Seaton, D. T., Mitros, P., Gajos, K. Z., & Miller, R. C. (2014). Understanding in-video dropouts and interaction peaks in online lecture videos. In Proceedings of the first ACM conference on Learning @ scale conference (L@S’ 14) (pp. 31–40). ACM Press. https://doi.org/10.1145/2556325.2566237

Klingbeil, K., Rösken, F., Barzel, B., Schacht, F., Stacey, K., Steinle, V., & Thurm, D. (2024). Validity of multiple-choice digital formative assessment for assessing students’ (mis)conceptions: Evidence from a mixed-methods study in algebra. ZDM - Mathematics Education , 56 (4). https://doi.org/10.1007/s11858-024-01556-0

Kolovou, A., & Kynigos, C. (2017). Teachers designing e-books to foster creative mathematical thinking: the case of curvature. In T. Dooley & G. Gueudet (Eds.), Proceedings of the Tenth Congress of the European Society for Research in Mathematics Education ( CERME 10) (pp. 2423–2429). Institute of Education, Dublin City University, Ireland, and ERME.

Kortenkamp, U., Etzold, H., Larkin, K., Ladel, S., & Abt, L. (2020). Impact of place value chart app on students’ understanding of bundling and unbundling: Mathematics education in the digital age. In A. Donevska-Todorova, E. Faggiano, J. Trgalová, Z. Lavicza, R. Weinhandl, A. Clark-Wilson, & H.-G. Weigand (Eds.), Proceedings of MEDA 2020 (pp. 231–238). https://hal.science/hal-02932218v1

Kynigos, C., Essonnier, N., & Trgalová, J. (2020). Social creativity in the education sector: The case of collaborative design of digital resources in mathematics. Creativity Research Journal , 32 (1), 17–29. https://doi.org/10.1080/10400419.2020.1712166

Leigh-Lancaster, D., & Stacey, K. (2022). Evolution over two decades of CAS-active senior secondary mathematics curriculum and assessment. Mathematics , 10 (13), 2333. https://doi.org/10.3390/math10132333

Leung, A., Baccaglini-Frank, A., Mariotti, M. A., & Miragliotta, E. (2023). Enhancing geometric skills with digital technology: The case of dynamic geometry. In B. Pepin, G. Gueudet, & J. Choppin (Eds.), Handbook of Digital Resources in Mathematics Education . Springer. https://doi.org/10.1007/978-3-030-95060-6_15-1

Lo, C. K., Hew, K. F., & Chen, G. (2017). Toward a set of design principles for mathematics flipped classrooms: A synthesis of research in mathematics education. Educational Research Review , 22 , 50–73. https://doi.org/10.1016/j.edurev.2017.08.002

Mariotti, M. A., Trgalová, J., Maracci, M., & Højsted, I. H. (2023). Resources promoting digital tools integration: Design principles. In B. Pepin, G. Gueudet, & J. Choppin (Eds.), Handbook of Digital Resources in Mathematics Education . Springer. https://doi.org/10.1007/978-3-030-95060-6_38-1

Mishra, P., & Koehler, M. J. (2006). Technological pedagogical content knowledge: A framework for integrating technology in teachers’ knowledge. Teachers College Record , 108 (6), 1017–1054. https://doi.org/10.1111/j.1467-9620.2006.00684.x

Monaghan, J., Trouche, L., & Borwein, J. M. (2016). Tools and mathematics . Springer. https://doi.org/10.1007/978-3-319-02396-0

Moons, F., Iannone, P., & Vandervieren, E. (2024). Checkbox grading of handwritten mathematics exams with multiple assessors: How do students react to the resulting atomic feedback? A mixed-method study. ZDM - Mathematics Education , 56 (4). https://doi.org/10.1007/s11858-024-01550-6

Naftaliev, E., & Barabash, M. (2024). Teachers’ professional development for inclusion of experimental mathematics and interactive resources in the classroom. ZDM - Mathematics Education , 56 (4).

NCTM - National Council of Teachers of Mathematics. (1995). Assessment standards for school mathematics . National Council of Teachers of Mathematics.

Netzer, E., & Tabach, M. (2023). Instructional short videos in calculus: The mathematical didactical structures and watching patterns. In M. Ayalon, B. Koichu, R. Leikin, L. Rubel & M. Tabach (Eds.). Proceedings of the 46th conference of the International Group for the Psychology of Mathematics Education (Vol. 3, pp. 397–404). University of Haifa, Israel: PME.

Niess, M. L., Ronau, R. N., Shafer, K. G., Driskell, S. O., Harper, S. R., Johnston, C., Browning, C., Özgün-Koca, S. A., & Kersaint, G. (2009). Mathematics teacher TPACK standards and development model. Contemporary Issues in Technology & Teacher Education , 9 (1), 4–24. https://citejournal.org/volume-9/issue-1-09/mathematics/mathematics-teacher-tpack-standards-and-development-model

Niss, M., & Højgaard, T. (Eds.). (2011). Competencies and mathematical learning ideas and inspiration for the development of mathematics teaching and learning in Denmark . IMFUFA tekst no. 485. Roskilde University. https://www.researchgate.net/publication/270585013_Competencies_and_Mathematical_Learning_Ideas_and_inspiration_for_the_development_of_mathematics_teaching_and_learning_in_Denmark

Nortvedt, G-A., & Buchholtz, N. (2018). Assessment in mathematics education: Responding to issues regarding methodology, policy, and equity. Zdm Mathematics Education , 50 , 555–570. https://doi.org/10.1007/s11858-018-0963-z

Olsher, S. (2019). Making good practice common using computer-aided formative assessment. In G. Aldon & J. Trgalová (Eds.), Technology in Mathematics Teaching (pp. 31–47). Springer. https://doi.org/10.1007/978-3-030-19741-4_2

Olsher, S., Chazan, D., Drijvers, P., Sangwin, C. J., & Yerushalmy, M. (2023). Digital assessment and the machine. In B. Pepin, G. Gueudet, & J. Choppin (Eds.), Handbook of digital resources in mathematics education . Springer. https://doi.org/10.1007/978-3-030-95060-6_44-1

Palancı, A., & Turan, Z. (2021). How does the use of the augmented reality technology in mathematics education affect learning processes? A systematic review. International Journal of Curriculum and Instructional Studies , 11 (1), 89–110. https://doi.org/10.31704/ijocis.2021.005

Panorkou, N., York, T., & Germia, E. (2023). Examining the messiness of transitions between related artifacts. Digital Experiences in Mathematics Education , 9 (1), 131–162. https://doi.org/10.1007/s40751-022-00112-3

Pepin, B., Gueudet, G., & Choppin, J. (Eds.). (2023). Handbook of digital resources in mathematics education . Springer. https://doi.org/10.1007/978-3-030-95060-6

Pepin, B., Gueudet, G., & Trouche, L. (2017). Refining teacher design capacity: Mathematics teachers’ interactions with digital curriculum resources. Zdm Mathematics Education , 49 , 999–812. https://doi.org/10.1007/s11858-017-0870-8

Pinkernell, G., Gulden, L., & Kalz, M. (2019). Automated feedback at task level: Error analysis or worked out examples. Which type is more effective? In B. Barzel et al. (Eds.), Proceedings of the 14th International Conference on Technology in Mathematics Teaching– ICTMT 14 (pp. 221–228). Essen.

Popper, P., & Yerushalmy, M. (2022). Online example-based assessment as a resource for teaching about quadrilaterals. Educational Studies in Mathematics , 110 , 83–100. https://doi.org/10.1007/s10649-021-10109-1

Rabardel, P. (2002). People and technology: a cognitive approach to contemporary instruments . Université Paris 8. https://hal.science/hal-01020705/file/people_and_technology.pdf

Radmehr, F., & Turgut, M. (2024). Learning more about derivative: Leveraging online resources for varied realizations. ZDM - Mathematics Education , 56 (4). https://doi.org/10.1007/s11858-024-01564-0

Redecker, C., & Punie, Y. (2017). European framework for the digital competence of educators: DigCompEdu . Publications Office of the European Union. https://doi.org/10.2760/178382

Remillard, J. T. (2005). Examining key concepts in research on teachers’ use of mathematics curricula. Review of Educational Research , 75 (2), 211–246. https://doi.org/10.3102/00346543075002211

Remillard, J., Cusi, A., Clark-Wilson, A., & Van Steenbrugge, H. (2024). Research on the relationships between mathematics teachers’ practices, knowledge, and skills and the use of digital resources. In B. Pepin, G. Gueudet, & J. Choppin (Eds.), Handbook of digital resources in mathematics education . Springer. https://doi.org/10.1007/978-3-030-95060-6_27-1

Robutti, O., Cusi, A., Clark-Wilson, A., Jaworski, B., Chapman, O., Goos, M., Isoda, M., Joubert, M., & Esteley, C. (2016). ICME international survey on teachers working and learning through collaboration: June 2016. Zdm , 48 (5), 651–690. https://doi.org/10.1007/s11858-016-0797-5

Rocha, H. (2013). Knowledge for Teaching Mathematics with Technology—A new framework of teacher knowledge. In A. Lindmeier & A. Heinze (Eds.), Proceedings of the 37th PME (Vol. 4, pp. 105–112). PME.

Roos, A. K., Götz, G., Weigand, H. G., & Wörler, J. (2019). OPTES+–A Mathematical Bridging Course for Engineers. In U. T. Jankvist, M. Van den Heuvel-Panhuizen & M. Veldhuis (Eds.), Proceedings of the 11th Congress of the European Society for Research in Mathematics Education (pp. 2642–2643). Utrecht University, the Netherlands.

Ruchniewicz, H., & Barzel, B. (2019). Technology supporting student self-assessment in the field of functions—A design-based research study. In G. Aldon & J. Trgalová (Eds.), Technology in mathematics teaching (pp. 49–74). Springer. https://doi.org/10.1007/978-3-030-19741-4_3

Sabra, H. (2016). L’étude Des rapports entre documentations individuelle et collective: Incidents, connaissances et ressources mathématiques. Recherches en Didactique des Mathématiques , 36 (1), 49–95. https://revue-rdm.com/2016/l-etude-des-rapports-entre/

Sierpinska, A. (2004). Research in mathematics education through a keyhole: Task problematization. For the Learning of Mathematics , 24 (2), 7–15.

Skantz-Åberg, E., Lantz-Andersson, A., Lundin, M., & Williams, P. (2022). Teachers’ professional digital competence: An overview of conceptualisations in the literature. Cogent Education , 9 (1). https://doi.org/10.1080/2331186X.2022.2063224

Stacey, K., & Wiliam, D. (2013). Technology and assessment in mathematics. In M. Clements, A. Bishop, C. Keitel, J. Kilpatrick, & F. Leung (Eds.), Third International Handbook of Mathematics Education (Vol. 27, pp. 721–752). Springer, Springer. https://doi.org/10.1007/978-1-4614-4684-2_23 . International Handbooks of Education.

Stacey, K., Price, B., Steinle, V., Chick, H., & Gvozdenko, E. (2009). SMART assessment for learning. In Papers from the Conference of the International Society for Design and Development in Education, ISDDE2009 (pp. 1–11). International Society for Design and Development in Education. http://www.isdde.org/isdde/cairns/pdf/papers/isdde09_stacey.pdf

Suurtamm, C., Thompson, D. R., Kim, R. Y., Moreno, L. D., Sayac, N., Schukajlow, S., et al. (Eds.). (2016). Assessment in mathematics education: Large-scale assessment and classroom assessment . Springer. https://doi.org/10.1007/978-3-319-32394-7

Tabach, M., & Trgalová, J. (2019). The knowledge and skills that mathematics teachers need for ICT integration: The issue of standards. In Aldon, G., Trgalová, J. (Eds.), Technology in Mathematics Teaching. Mathematics Education in the Digital Era (Vol 13, pp. 183–203). Springer. https://doi.org/10.1007/978-3-030-19741-4_8

Thomas, M. O. J., & Lin, C. (2013). Designing tasks for use with digital technology. In Margolinas, C. (Ed.), Task Design in Mathematics Education. Proceedings of ICMI Study 22 (pp. 109–117). ICMI.

Thomas, M. O. J., & Palmer, J. (2014). Teaching with digital technology: Obstacles and opportunities. In A. Clark-Wilson, O. Robutti, & N. Sinclair (Eds.), The mathematics teacher in the digital era: An international perspective on technology focused professional development (pp. 71–89). Springer. https://doi.org/10.1007/978-94-007-4638-1_4

Thurm, D., Bozkurt, G., Barzel, B., Sacristán, A. I., & Ball, L. (2024). A review of research on professional development for teaching mathematics with digital technology. In B. Pepin, G. Gueudet, & J. Choppin (Eds.), Handbook of Digital Resources in Mathematics Education . Springer. https://doi.org/10.1007/978-3-030-95060-6_49-1

Tirosh, D., Tsamir, P., Levenson, E., et al. (2014). Using video as a tool for promoting inquiry among preschool teachers and didacticians of mathematics. Zdm , 46 (2), 253–266. https://doi.org/10.1007/s11858-013-0563-x

Trgalová, J., & Tabach, M. (2024). Pre-service teachers’ development of digital resource design capacity. ZDM - Mathematics Education , 56 (4). https://doi.org/10.1007/s11858-024-01554-2

Trgalová, J., Clark-Wilson, A., & Weigand, H. G. (2018a). Technology and resources in mathematics education. In T. Dreyfus, M. Artigue, D. Potari, S. Prediger, & K. Ruthven (Eds.). Developing Research in Mathematics Education (pp. 142–161), Routledge. ISBN 9781315113562.

Trgalová, J., El-Demerdash, M., Labs, O., & Nicaud, J. F. (2018b). Design of digital resources for promoting creative mathematical thinking. In L., Ball, P., Drijvers, S., Ladel, H-S., Siller, M., Tabach, & C., Vale, (Eds.), Uses of technology in primary and secondary mathematics education (pp. 289–300). Springer. https://doi.org/10.1007/978-3-319-76575-4_15

Trouche, L. (2004). Managing the complexity of human/machine interactions in computerized learning environments: Guiding students’ command process through instrumental orchestrations. International Journal of Computers for Mathematical Learning , 9 , 281–307. https://doi.org/10.1007/s10758-004-3468-5

Trouche, L., Gueudet, G., & Pepin, B. (2018). Documentational approach to didactics. In S. Lerman (Ed.), Encyclopedia of Mathematics Education . Springer. https://doi.org/10.1007/978-3-319-77487-9_100011-1

vom Hofe, R., & Blum, W. (2016). Grundvorstellungen as a category of subject-matter didactics. Journal für Mathematik-Didaktik , 37 (S1), 225–254. https://doi.org/10.1007/s13138-016-0107-3

Vygotsky, L. S. (1978). Mind in society: The development of higher psychological processes . Harvard University Press.

Wang, C. (2018). Mathematics teachers’ expertise in resources work and its development in collectives. A French and a Chinese Cases. In Fan, L., Trouche, L., Rezat, S., Qi, C., & Visnovska, J. (Eds.), Research on Mathematics Textbooks and Teachers’ Resources: Advances and issues (pp. 193–213). Springer. https://doi.org/10.1007/978-3-319-73253-4_9

Wankerl, S., Götz, G., & Hotho, A. (2019). Solving mathematical exercises: prediction of students’ success. In Jäschke, R. & Weidlich, M. (Eds.), Proceedings of the Conference on „Lernen, Wissen, Daten, Analysen (Vol. 2454, pp. 190–194). Humboldt-Universität zu Berlin. http://ceur-ws.org/Vol-2454/paper_84.pdf

Watson, A., & Ohtani, M. (Eds.). (Eds., 2021). Task design in mathematics education: An ICMI study 22 . Springer. https://doi.org/10.1007/978-3-319-09629-2

Watson, A., Ohtani, M., Ainley, J. (2013). Introduction. In Margolinas, C. (Ed.), Task design in mathematics education. Proceedings of ICMI Study 22 (pp. 7–13). ICMI.

Weigand, H. G., Donevska-Todorova, A., Faggiano, E., Iannone, P., & Medová, J. (Eds.). (2022). MEDA3 Mathematics Education in Digital Age 3. Proceedings of the 13th ERME Topic Conference (ETC13) (pp. v-viii). Constantine the Philosopher University in Nitra. https://hal.science/hal-03925304

Weigand, H. G., & Günster, S. (2022). Digital technologies and the development of the dynamic view of functional thinking. In C. Fernándes, S. Llinares, A. Gutiérrez, & N. Planas (Eds.), Proceedings of the 45th PME (Vol. 4, pp. 139–146). Universidad de Alicante.

Wenger, E. (1998). Communities of practice: Learning, meaning, and identity . Cambridge University Press.

Wirth, L., & Greefrath, G. (2024). Working with an instructional video on mathematical modeling: Upper-secondary students’ perceived advantages and challenges. ZDM - Mathematics Education , 56 (4). https://doi.org/10.1007/s11858-024-01546-2

Wu, H. K., Lee, W. Y., Chang, S., H-Y., & Liang, J. C. (2013). Current status, opportunities and challenges of augmented reality in education. Computers & Education , 62 , 41–49. https://doi.org/10.1016/j.compedu.2012.10.024

Ye, H., Ng, O. L., & Leung, A. (2024). Examining mathematics teachers’ creative actions in programming-based mathematical activities. ZDM - Mathematics Education , 56 (4).

Yerushalmy, M., & Olsher, S. (2020). Online assessment of students’ reasoning when solving example-eliciting tasks: Using conjunction and disjunction to increase the power of examples. ZDM - Mathematics Education , 52 , 1033–1049. https://doi.org/10.1007/s11858-020-01134-0

Download references

Open Access funding enabled and organized by Projekt DEAL.

Author information

Authors and affiliations.

University of Wuerzburg, Würzburg, Germany

Hans-Georg Weigand

Haute École Pédagogique, Lausanne, Switzerland

Jana Trgalova

Tel-Aviv University, Tel-Aviv, Israel

Michal Tabach

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Hans-Georg Weigand .

Additional information

Publisher’s note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Weigand, HG., Trgalova, J. & Tabach, M. Mathematics teaching, learning, and assessment in the digital age. ZDM Mathematics Education (2024). https://doi.org/10.1007/s11858-024-01612-9

Download citation

Accepted : 30 June 2024

Published : 10 July 2024

DOI : https://doi.org/10.1007/s11858-024-01612-9

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Teaching with technology
• Learning with technology
• Assessment with technology
• Mathematics education
• Find a journal
• Publish with us
• Track your research

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Free ready-to-use math resources

Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth

28 7th Grade Math Problems With Answers And Worked Examples

Linda Bortnick

7th grade math problems build on students’ reasoning skills and understanding of key mathematical concepts.

We’ve created 28 7th grade math problems for your classroom, suitable for use as additional practice before an assessment, as a Do Now activity, or for an Exit Slip to check for understanding after a lesson. Math teachers designed these problems to build on students’ math skills and help to prepare them for the rigor expected ahead in 8th grade and in high school courses like Algebra, Geometry, and Statistics.

What are 7th grade math problems?

7th grade math problems combine 7th grade math concepts with grade-level appropriate reasoning and problem solving skills.

7th grade math content includes computing with all rational numbers in all four operations, using the correct order of operations  to simplify expressions, solving problems involving percentages, using proportional reasoning, solving 1 and 2 step equations, multi-step inequalities and extending knowledge of geometry.

Why focus on problem solving in 7th grade?

Excelling at computation is great; excelling at computation but not understanding application is pointless. The purpose of mathematics is to learn to reason, find patterns, and use logic, so solving math problems  that are rich, deep, and complex is necessary to meet those purposes.

Mathematics today has advanced beyond just computation and evolved into a marriage of numbers and words – not only do students need to get to a numerical answer they also need to be able to communicate their thinking and processes along the way. They need repeated practice in reasoning, perseverance, and rational thinking to solve problems throughout their lives.

7th grade is a perfect time to extend problem solving activities in the classroom. The curriculum moves away from much of the memorization required in elementary school of basic addition facts and times tables , and builds on 6th grade content to focus on making connections between mathematical reasoning , logic, and numbers.

Math Games For 7th Grade

13 fun math games and activities for 7th grade students to complete independently or with a partner. Includes ready to go math games with minimal prep required. The perfect lesson starter or finisher.

The 7th grade math curriculum

This article focuses on problems for 7th grade students, especially concepts taught in pre-algebra. Pre-algebra includes concepts of proportional relationships, algebraic expressions, equivalent expressions, equations, rational numbers, graphs, and extension of knowledge of the number system, including whole numbers and mixed numbers. The problems align with common core standards.

Seventh grade math can be considered a turning point in mathematics. It bridges the concepts taught in elementary school, including the foundations of arithmetic and number sense, with the rigor expected ahead in high school courses like Algebra, Geometry, and Statistics.

7th grade math problems

We’ve designed 28 7th grade math problems to use as a whole class or in a Tier 2  or Tier 3 intervention  to help develop and secure students’ mathematical knowledge.  

7th grade math problems: Four operations

• Solve -4 + 10. Use the number line.

Solution:        6

2. Solve: -8 – 12. Use the number line.

Solution:         -20

3. Solve: 4(-3)(-2)

Solution:          24

4. Bill said the answer to -3 – 12 is 9. What mistake did he make? What is the correct answer?

Solution: Bill knows that the opposite of subtraction is addition, but he forgot to take the opposite of 12, so he re-wrote the problem as -3 + 12. Since we are subtracting 12 from -3, the answer is the same as -3+-12, which is -15.

7th grade math problems: Order of operations

5. Solve: 2(10-8) ÷ 2 + 4

    Solution: 2(10-8) ÷ 2 + 4

                    2(2) ÷ 2 + 4

                    4  ÷ 2 + 4

                    2 + 4

                    6

6. Solve: (3 + 10 ÷ 2 – 6) x 6

    Solution: (3 + 10 ÷ 2 – 6) x 6

                    (3 + 5 – 6) x 6

                    (8 – 6) x 6

                     2 x 6

                     12

7. Solve: -5(8) ÷ 2 + 6

   Solution: -5(8) ÷ 2 + 6

                    -40 ÷ 8

                     -5

8. Solve: (-2)3 – 2 + 6 ÷ 3

    Solution: (-2)3 – 2 + 6 ÷ 3

                     -8  – 2 + 6 ÷ 3

                     -8 – 2 + 2

                     -10 + 2

                     -8

7th grade math problems: Percentages

9. Isabella got 16 out of 40 questions wrong on her quiz. What percent did she get correct?

Solution : \frac{16}{40} can be simplified to \frac{2}{5} , which is equivalent to \frac{40}{100} or 40%. If Isabella got 40% incorrect, she got 60% correct (100-40=60).

10. Without doing any computation, explain whether \frac{38}{72} is greater than or less than 50%.

Solution: \frac{38}{72} is greater than 50%. \frac{36}{72} is equivalent to \frac{1}{2} , which is equivalent to 50%. Since 38 is a little greater than 36, \frac{38}{72} is a little greater than 50%.

11. Put the following in order from least to greatest: \frac{3}{4} , 76%, 0.68, \frac{3}{5} , \frac{35}{50} , 0.702

Solution: \frac{3}{5} , 0.68, \frac{35}{50} , 0.702, \frac{3}{4} , 76%

12. A store marked all shoes on sale for 30% off. What percent will Sam pay for shoes? Explain your answer.

Solution: Sam will pay 70% for shoes. The full price is 100%, so if 30% is saved, the remaining 70% will be the sales price.

7th grade math problems: Proportional relationships

13. \frac{5}{6}  = \frac{x+2}{15}

      Solution: 6( x +2) = 5(15)

                     6 x + 12 = 75

                  -12   -12

                    \frac{6x}{6} = \frac{63}{6}

      x =   10.5

14. Three out of every five students are wearing jeans. If there are 20 students in total, how many are wearing jeans?

Solution: \frac{3}{5}  = \frac{x}{20}

                3 (20) = 5 x

                60 = 5 x

                12 = x

15. Three out of every five students are wearing jeans. If there are 20 students in all, how many are not wearing jeans?

Solution: From the last problem, we saw that \frac{3}{5} is the same as the 12 students wearing jeans. If there are 20 students total, we can subtract the 12 wearing jeans from the 20 total to find that 8 are not wearing jeans. We could also set up this proportion and solve to get 8.

                \frac{2}{5}  = \frac{x}{20}

16. A museum requires 12 chaperones for the 60 students attending the field trip. How many students are assigned to each chaperone?

         \frac{12}{60} = \frac{1}{x}

        12 x = 60(1)

        12 x = 60

          x = 5

Each chaperone will have a group of 5 students.

7th grade math problems: One-step equations and two-step equations

17. Solve: x + 7.1 = 15.9

         Solution:   x + 7.1 = 15.9

                           -7.1      -7.1

                         x = 8.8

18. Solve: x – 63 = 106.75

         Solution: x – 63 = 106.75

                       +63     +63

                         x  = 169.75

 19. Solve: 6( x + 3) = -6

         Solution: 6 x + 18 = -6

                     – 18    -18

                          \frac{6x}{6} = \frac{-24}{6}

                         x = -24

20. Solve: 0.5 x + 10 = 36

         Solution: 0.5 x + 10 = 36

                           -10    -10

                        0.5 x = 26

                        x = 52

7th grade math problems: Geometry

21. Madison measured this angle with her protractor and said “It is 60°.”

Without measuring the angle, Bella said she could tell Madison’s answer was incorrect. How did Bella know this?

Solution: Bella knew this angle could not be 60° because this angle is obtuse

but a 60° angle is acute.

22. Find the circumference of the circle.

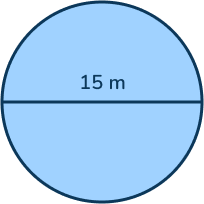
Solution: C = πd

            C =  15π

23. Use the figure to fill in the blanks:

Angles A and B are _________________ angles so their measures are _______________________________.

Solution: Angles A and B are vertical  angles so their measures are equal.

24. Find the value of x .

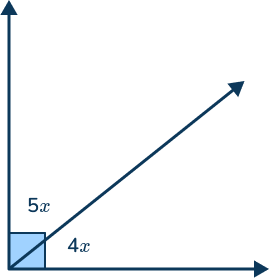
         Solution: 5 x + 4 x =90

                      9 x = 90

                        x = 10

7th grade math problems: Math word problems

25. The 7th Graders at Marxville Middle School voted for their student council representatives. There were 200 votes cast in all. How many votes did the winner get?

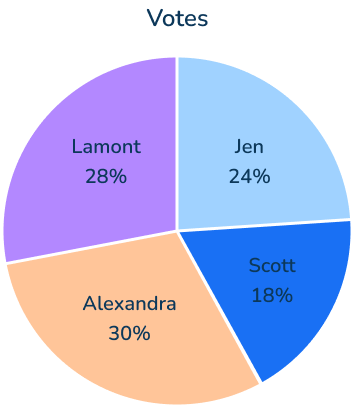
Solution: Alexandra won the election with 30% of the votes. To find 30% of the 200 total votes, we can multiply 0.3 (200) to discover that she got 60 votes in all.

26. Brian runs every 12 days and Stella every 8 days. Both Brian and Stella ran today. How many days will it be before they both run on the same day again?

Solution: This is a Least Common Multiple problem. Brian runs on days 12, 24, 36, 48… and Stella runs on days 8, 16, 24, 32…, so they will both run again on Day 24.

27. Mr. Orlando is planting his vegetable garden this summer. He plants \frac{3}{4} of the garden with peppers and \frac{1}{4} with tomatoes. Of the peppers, \frac{1}{3} are red peppers. What fraction of the entire garden will be red peppers?

Solution: Red peppers will make up \frac{1}{3} of \frac{3}{4} (the pepper section) of the garden. \frac{1}{3} x \frac{3}{4} = \frac{1}{4} , so \frac{1}{4} of the entire garden will consist of red peppers.

28. Will the product of -45(96) be positive or negative? Without solving, how do you know?

Solution: The answer will be negative. Multiplying a negative number by a positive one always leads to a negative product.

Challenges in teaching 7th grade mathematics

Let’s face it, most 7th graders don’t wake up every morning excited to get to math class that day to expand on their mathematical knowledge and thinking! Often, there are much more pressing matters in the mind of a 12 year old. However, with the right mindset and classroom climate, we can support our students to help them put forth their best effort every day.

• Praise effort:  Developing a growth mindset in the classroom  is key. Even if a student struggles to come to an answer, it is critical to praise the effort. We must make the thinking part of mathematics something to treasure rather than solely focus on correct numerical answers.
• Include low threshold high ceiling activities: These go a long way in piquing the interest level of most students.
• Have fun:  Don’t be afraid to have some fun math activities  and silliness in your lessons, whether that’s through funny estimation activities  or videos to get students interested, engaged and willing to try.

How can Third Space Learning help with 7th grade math?

STEM-specialist tutors help close learning gaps and address misconceptions for struggling 7th grade math students. One-on-one online math tutoring sessions help students deepen their understanding of the math curriculum and keep up with difficult math concepts. Each student works with a private tutor who adapts instruction and math lesson content in real-time according to the student’s needs to accelerate learning.

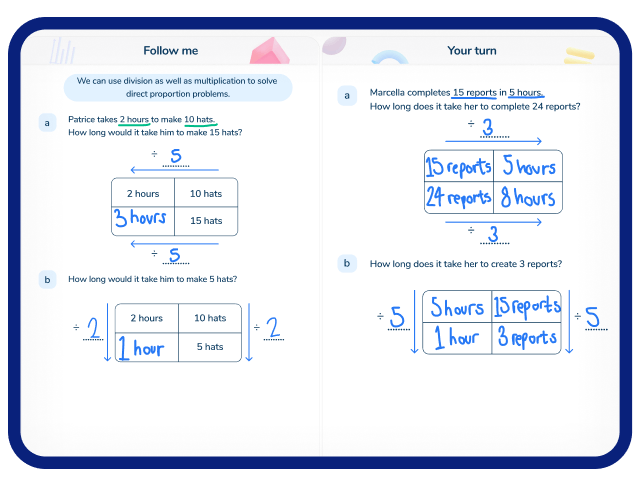
4 top tips for teaching 7th grade math problems

Here are some teaching tips to overcome common challenges and support problem solving in your classroom:

• Focus on effort, not accuracy:  Students come into 7th grade with many ideas about math. Many of these ideas are likely negative and may result in some math anxiety . They’ve heard math is hard, you’re never going to use it, it’s confusing. Be excited about what you’re teaching and learning! Praise kids for trying their best, not for always being correct. Consider establishing effort-based reward systems, such as publicly nominating students for Mathematician of the Month.
• Check for understanding:  Be sure students understand questions before they attempt to answer them. Have them rephrase the question or explain what they’re looking for to solve the problem.
• Ask for wrong answers: Students may feel a lack of confidence in math but if you ask them for a wrong answer, they may feel more inclined to answer. It can also prompt students to engage with and make sense of the information given in the problem in a less pressured environment.

Alternatively, as teachers, you can give some suggestions. For example, “3/10 of students got an A on the last test. There are 20 students in the class. How many got an A?” Could 20 of the students have gotten an A? No? Why not? Could 8.5 of the students have gotten an A? Why not? Then get more specific. Did more or less than 10 of the students get an A? How do you know?

• Use relatable, real-world problems:  Sometimes, problem solving uses questions about gas mileage or building fences that kids either don’t relate to or don’t care about. Find out what your students’ interests are and incorporate that into your math instruction. Alternatively, use seasonal and relatable contexts such as Thanksgiving math activities , summer math  or mardi gras math .

7th grade math worksheets

Looking for more resources? Please see our selection of seventh grade math worksheets covering 7th grade key math topics and more. Each includes printable resources and step-by-step answer keys:

• Surface Area Of Rectangular Prisms Worksheet
• Fraction to Decimal Worksheet
• Adding and Subtracting Integers Worksheet
• Adding and Subtracting Scientific Notation Worksheet
• Distributing Exponents Worksheet
• Simplifying Expressions Worksheet

READ MORE :

• 25 Fun Math Problems For Elementary School
• Math Questions For 5th Graders
• 4th Grade Math Problems

7th grade math problems FAQ

What math should a 7th grader know?

A 7th grader should be able to compute using all four operations with positive and negative rational numbers. They should be able to simplify expressions, solve one- and two- step equations, and solve proportions. Additionally, 7th graders can work with probability of simple and compound events, as well as study concepts of geometry, including finding angle measurements and solving for area and perimeter of regular and irregular polygons and circles.

What does 7th grade math focus on?

Seventh grade math focuses on working with positive and negative rational numbers in simplifying expressions and equations as well as solving one- and two-step equations. Additionally, extensive work is done in solving proportions and ratios.

Is 7th grade math hard?

Seventh grade math is always achievable! Students who find it hard usually come into the grade without having mastered basic concepts and facts. Be sure students are automatic with facts across addition, subtraction, multiplication, and division and have the ability to work with fractions and decimals. It will make the new concepts in 7th grade easier to learn.

Related articles

15 Venn Diagram Questions And Practice Problems (Middle & High School): Exam Style Questions Included

15 Probability Questions And Practice Problems for Middle and High School: Harder Exam Style Questions Included

9 Algebra Questions And Practice Problems To Do With Your Middle Schoolers

15 Trigonometry Questions And Practice Problems To Do With High Schoolers

Solving Inequalities Questions [FREE]

Downloadable skills and applied questions about solving inequalities.

Includes 10 skills questions, 5 applied questions and an answer key. Print and share with your classes to support their learning.

Privacy Overview

• Multi-Tiered System of Supports Build effective, district-wide MTSS
• School Climate & Culture Create a safe, supportive learning environment
• Positive Behavior Interventions & Supports Promote positive behavior and climate
• Family Engagement Engage families as partners in education
• Platform Holistic data and student support tools
• Integrations Daily syncs with district data systems and assessments
• Professional Development Strategic advising, workshop facilitation, and ongoing support

• Success Stories
• Surveys and Toolkits
• Product Demos
• Events and Conferences

18 Research-Based MTSS Interventions

Download step-by-step guides for intervention strategies across literacy, math, behavior, and SEL.

• Connecticut
• Massachusetts
• Mississippi
• New Hampshire
• North Carolina
• North Dakota
• Pennsylvania
• Rhode Island
• South Carolina
• South Dakota
• West Virginia
• Testimonials
• About Panorama
• Data Privacy
• Leadership Team
• In the Press
• Request a Demo

• Popular Posts
• Multi-Tiered System of Supports
• Family Engagement
• Social-Emotional Well-Being
• College and Career Readiness

Show Categories

5 Research-Based Math Interventions for Your MTSS/RTI

Leah Allen-Manning

While overhauls to reading curricula headline the news across the country, its academic counterpart—math—has been somewhat forgotten, despite equally shocking data from the National Assessment of Educational Progress (NAEP) Report . In fact, the most recent data revealed the sharpest decline in math scores since the assessment's inception in 1990.

To counter declining math scores, educators need effective strategies to incorporate into math instruction. When combined with a solid foundation of core instruction , research-based mathematics interventions enable districts to strengthen their tiered systems of support to help all students learn.

Download our toolkit of 12 research-based math interventions.

How Math Interventions Fit Into an MTSS

A core component of an MTSS (multi-tiered system of supports) or RTI (Response to Intervention) framework is interventions: research-based strategies to support students across three levels, called tiers. Math intervention activities teach mathematics topics at a student’s individual level to meet their needs.

• Tier 1 math interventions are included in universal, core instruction provided to all students. These strategies are effective best practices to establish a solid foundation for math success.
• Tier 2 math interventions offer targeted support in small-group instruction for students who need additional resources on top of core instruction.
• Tier 3 math interventions involve intensive, one-on-one instruction and highly individualized support for students who have received both Tier 1 instruction and Tier 2 interventions.

Below are 5 research-based and evidence-based math interventions to share with school teams and add to your district’s intervention menu . These interventions have been selected from Playbook , Panorama’s professional learning library for K-12 educators.

RTI/MTSS Math Interventions:

Math with pals, draw a picture, explore before explain, concrete representational abstract (cra) approach.

Math Songs use rhyme, rhythm, patterns, and repetition to help students remember math concepts, skills, or basic facts. The use of songs helps students retain information in long-term memory.

• Focus Area: Fluency
• Developmental Stage: Lower Elementary, Upper Elementary, Middle School
• MTSS/RTI Tiers: Tier 1

Preparation:

• Consider which topics would benefit from the inclusion of a math song.
• Find math songs about the relevant topic that your students would enjoy. Websites like YouTube, Teachers Pay Teachers, and  GoNoodle offer a variety of math songs. Teachers can search for songs on specific topics such as multiplication tables, fractions, or geometry.
• Print out lyrics or display lyrics for students to read along as they sing (as appropriate for the grade level).

Instructions:

• Play or sing math songs at any point during the learning of a math topic, whether as an introduction or throughout the course of study.
• Consider asking students to create their own math song or write their own lyrics to a familiar tune. This will provide an engaging way for students to interact with the topic and take authentic ownership of their understanding.

Math with PALS (Peer-Assisted Learning Strategy) is an intervention that supports student growth through collaboration, discussion, and practice. Students work in pairs of tutor and tutee to support one another’ s understanding of a previously taught math skill.

• Focus Area: Problem-Solving
• MTSS/RTI Tiers: Tier 1, Tier 2

Preparation :

• Choose stu dents who know how to use the skill or strategy in a problem set.
• Pair students ahead of time in heterogeneous pairings. One partner should be stronger in the math skill (tutor), and the other can be a student who needs some support to improve (tutee). 
• Create a practice worksheet for students to complete while working in pairs. For younger students, consider adding these coaching questions to the worksheet.

Instructions :

• Pair students and provide worksheets or work materials. 
• Allow 20–40 minutes for pairs to work based on grade level and age group.
• The “tutor” partner will support the other partner’s work through questions and modeling. Prompts or questions can be provided for the tutor partner to use.
• If the “tutee” makes a mistake, the tutor should address it and explain their thinking in a respectful way.
• After the pairs complete half of the worksheet, the students switch roles to complete the rest of the worksheet.
• Once the partner work time is complete, students should work individually to complete additional problems, then exchange worksheets and review their partner’s work. 

This strategy asks students to make a drawing of an applied problem. Drawing a picture can support student understanding of the problem itself as well as how to solve the problem. Additionally, this strategy can pinpoint misconceptions students may have about how to set up or solve the problem.

• Focus Area: Comprehension
• Developmental Stage: Lower Elementary, Upper Elementary, Middle School, High School
• Analyze the word problems that students will be asked to solve. 
• Choose a word problem to model how to draw a picture to help solve it. 
• Choose one or two to use as guided practice. Students can then work independently using a drawing.

Explicit Instruction:

• Choose a word problem to display and ensure students have a copy.
• Model reading the problem aloud carefully. 
• Talk through the thought process for how to draw a picture to represent the problem. This may include what you notice, what values you are starting with, and what you will do. 
• Draw the picture as you explain, and ask students to do it along with you.

Guided Practice:

• Provide students with a selected word problem.
• Ask students what information is provided in the problem.
• Guide students to draw a picture to represent the problem. Facilitate student thinking with your own thinking aloud and with guiding questions.

Explore Before Explain is a learning environment where students explore real-life situations as they relate to a concept before an explanation of the concept occurs. Activities to practice a concept are not introduced until students have had time to gain meaning through exploration.

Explore Before Explain helps avoid the question “When will I ever have to use this?” Making connections between math concepts and the real world will help students be more engaged and remember what they’ve learned

• Focus Area: Comprehension   
• MTSS/RTI Tiers: Tier 1, Tier 2, Tier 3
• Think about student experiences that can relate to the math concept in consideration. Consider how students could explore an experience to discover useful information about the concept. This might include a demonstration, using the classroom environment describing a relatable scenario, or watching a video
• In elementary school, this might be a great time to bring in a guest expert—a parent or other relative of one of the students who uses this concept in their work or daily lives.
• Engage students in the context. Provide expectations of the task at hand. Do not formally introduce the math concept at this stage.
• Allow students to explore a common experience related to the concept.
• Explain how the exploration connects to the formal concept.
• Have students elaborate on the concept by applying the concept to a new scenario or using follow-up practice questions.
• Evaluate student understanding of the formal math concept.

Students begin the CRA process by using concrete models to represent math concepts. Next, students transition to the use of drawings to represent the same concepts. Finally, students translate model representations to abstract representations using numbers and symbols.

• Focus Area: Computation  
• Gather concrete manipulatives (counters, blocks, cups, algebra tiles, etc.) that can be used to model the math concept being discussed.
• Choose problems that avoid complicated calculations.
• Download the CRA worksheet .

Concrete : Students work with actual objects to solve the math problem.

• Hand out the manipulatives to each student or pair. Give the students a few minutes to explore the manipulatives.
• Demonstrate how the concrete materials connect to the problem. Allow students to see you “think through” some sample problems. 
• Using a whole-class approach, work through a few more problems together. Check for understanding. If needed, work through additional examples.
• Finally, give students a few problems to work through individually or in pairs.

Representational : Students draw or sketch representations of the objects to model problems.

• Using the same math problems from the concrete examples, transition students to pictorial models.
• Ask for suggestions from students of different ways they can represent the concept on paper instead of with objects.
• Have students practice using pictorial models individually or in pairs.

Abstract : Students write symbolic representations using numbers and symbols.

• Continue with the same math problems. Review previous methods using concrete objects and pictorial representations. Transition students from representational models to abstract displays using math notations.
• Have students practice solving problems using only symbolic notations. Provide additional support, if needed. 

Identify Students & Administer Math Interventions With Panorama

District and school users can identify students who score below benchmark on math assessments—such as iReady, FastBridge, STAR, and NWEA MAP—and create support plans in Panorama Student Success . With all student data in one platform, educators can easily take action with intervention planning workflows, collaboration tools, and evidence-based strategies .

These interventions not only enhance comprehension and problem-solving skills, but they also foster a deeper understanding of mathematical concepts across all tiers of support.

By incorporating research-based and evidence-based math interventions into an MTSS or RTI framework, school and district leaders ensure all students receive the support they need. 

Download these and other research-based strategies in our Math Interventions Toolkit.

Related Articles

The 4 Biggest Challenges of MTSS/RTI During Remote Learning: How Districts Are Adapting

Learn how schools and districts are adapting to support students virtually through MTSS and RTI frameworks during the COVID-19 public health crisis.

The 5 Biggest Challenges of MTSS: How Districts Are Responding

Learn how schools and districts are addressing the five biggest challenges of MTSS (Multi-Tiered System of Supports) to support students.

Val Verde Unified's MTSS Tiers: Measure, Understand, and Act on Data

Learn how Val Verde Unified School District in California is integrating social-emotional learning (SEL) into its MTSS tiers to support the whole child.

Featured Resource

Math interventions toolkit.

Strategies share with your school and district teams.

Join 90,000+ education leaders on our weekly newsletter.