- School Liberty University - Lynchburg, VA
- Course Title EDUC 701 - Advanced Learning Theory and Research
- Uploaded By MissEve
Is there anything else you׳d like to ask? Our top-rated tutors can help you.

Students also viewed
- Applied Sciences
- Architecture and Design
- Business & Finance
- Computer Science
- Engineering
- Environmental science
- Human Resource Management
- Information Systems
- Mathematics
- Political Science
- Social Science
- Liberty University
- New Hampshire University
- Strayer University
- University Of Phoenix
- Walden University
- Homework Answers
Teaching Problem Solving in Math
- Freebies , Math , Planning
Every year my students can be fantastic at math…until they start to see math with words. For some reason, once math gets translated into reading, even my best readers start to panic. There is just something about word problems, or problem-solving, that causes children to think they don’t know how to complete them.
Every year in math, I start off by teaching my students problem-solving skills and strategies. Every year they moan and groan that they know them. Every year – paragraph one above. It was a vicious cycle. I needed something new.

I put together a problem-solving unit that would focus a bit more on strategies and steps in hopes that that would create problem-solving stars.
The Problem Solving Strategies
First, I wanted to make sure my students all learned the different strategies to solve problems, such as guess-and-check, using visuals (draw a picture, act it out, and modeling it), working backward, and organizational methods (tables, charts, and lists). In the past, I had used worksheet pages that would introduce one and provide the students with plenty of problems practicing that one strategy. I did like that because students could focus more on practicing the strategy itself, but I also wanted students to know when to use it, too, so I made sure they had both to practice.
I provided students with plenty of practice of the strategies, such as in this guess-and-check game.

There’s also this visuals strategy wheel practice.

I also provided them with paper dolls and a variety of clothing to create an organized list to determine just how many outfits their “friend” would have.

Then, as I said above, we practiced in a variety of ways to make sure we knew exactly when to use them. I really wanted to make sure they had this down!

Anyway, after I knew they had down the various strategies and when to use them, then we went into the actual problem-solving steps.
The Problem Solving Steps
I wanted students to understand that when they see a story problem, it isn’t scary. Really, it’s just the equation written out in words in a real-life situation. Then, I provided them with the “keys to success.”
S tep 1 – Understand the Problem. To help students understand the problem, I provided them with sample problems, and together we did five important things:
- read the problem carefully
- restated the problem in our own words
- crossed out unimportant information
- circled any important information
- stated the goal or question to be solved
We did this over and over with example problems.

Once I felt the students had it down, we practiced it in a game of problem-solving relay. Students raced one another to see how quickly they could get down to the nitty-gritty of the word problems. We weren’t solving the problems – yet.

Then, we were on to Step 2 – Make a Plan . We talked about how this was where we were going to choose which strategy we were going to use. We also discussed how this was where we were going to figure out what operation to use. I taught the students Sheila Melton’s operation concept map.

We talked about how if you know the total and know if it is equal or not, that will determine what operation you are doing. So, we took an example problem, such as:
Sheldon wants to make a cupcake for each of his 28 classmates. He can make 7 cupcakes with one box of cupcake mix. How many boxes will he need to buy?
We started off by asking ourselves, “Do we know the total?” We know there are a total of 28 classmates. So, yes, we are separating. Then, we ask, “Is it equal?” Yes, he wants to make a cupcake for EACH of his classmates. So, we are dividing: 28 divided by 7 = 4. He will need to buy 4 boxes. (I actually went ahead and solved it here – which is the next step, too.)
Step 3 – Solving the problem . We talked about how solving the problem involves the following:
- taking our time
- working the problem out
- showing all our work
- estimating the answer
- using thinking strategies
We talked specifically about thinking strategies. Just like in reading, there are thinking strategies in math. I wanted students to be aware that sometimes when we are working on a problem, a particular strategy may not be working, and we may need to switch strategies. We also discussed that sometimes we may need to rethink the problem, to think of related content, or to even start over. We discussed these thinking strategies:
- switch strategies or try a different one
- rethink the problem
- think of related content
- decide if you need to make changes
- check your work
- but most important…don’t give up!
To make sure they were getting in practice utilizing these thinking strategies, I gave each group chart paper with a letter from a fellow “student” (not a real student), and they had to give advice on how to help them solve their problem using the thinking strategies above.

Finally, Step 4 – Check It. This is the step that students often miss. I wanted to emphasize just how important it is! I went over it with them, discussing that when they check their problems, they should always look for these things:
- compare your answer to your estimate
- check for reasonableness
- check your calculations
- add the units
- restate the question in the answer
- explain how you solved the problem
Then, I gave students practice cards. I provided them with example cards of “students” who had completed their assignments already, and I wanted them to be the teacher. They needed to check the work and make sure it was completed correctly. If it wasn’t, then they needed to tell what they missed and correct it.

To demonstrate their understanding of the entire unit, we completed an adorable lap book (my first time ever putting together one or even creating one – I was surprised how well it turned out, actually). It was a great way to put everything we discussed in there.

Once we were all done, students were officially Problem Solving S.T.A.R.S. I just reminded students frequently of this acronym.
Stop – Don’t rush with any solution; just take your time and look everything over.
Think – Take your time to think about the problem and solution.
Act – Act on a strategy and try it out.
Review – Look it over and see if you got all the parts.

Wow, you are a true trooper sticking it out in this lengthy post! To sum up the majority of what I have written here, I have some problem-solving bookmarks FREE to help you remember and to help your students!
You can grab these problem-solving bookmarks for FREE by clicking here .
You can do any of these ideas without having to purchase anything. However, if you are looking to save some time and energy, then they are all found in my Math Workshop Problem Solving Unit . The unit is for grade three, but it may work for other grade levels. The practice problems are all for the early third-grade level.
- freebie , Math Workshop , Problem Solving

FIND IT NOW!
Check me out on tpt.

CHECK THESE OUT

Three Types of Rocks and Minerals with Rock Cycle Circle Book

Partitioning Shapes Equal Share Fractions Halves, Thirds, Fourths Math Puzzles
Want to save time?
COPYRIGHT © 2016-2024. The Owl Teacher | Privacy page | Disclosure Page | Shipping | Returns/Refunds
BOGO on EVERYTHING!
- Our Mission
6 Ways to Help Students Understand Math
Help students better understand math by presenting multiple examples, encouraging collaboration on alternative solutions, and framing the class with a clear agenda and effective summary.

The ultimate goals of mathematics instruction are students understanding the material presented, applying the skills, and recalling the concepts in the future. There's little benefit in students recalling a formula or procedure to prepare for an assessment tomorrow only to forget the core concept by next week. It's imperative for teachers to focus on making sure that the students understand the material and not just memorize the procedures.
Here are six ways to teach for understanding in the mathematics classroom:
1. Create an effective class opener.
The first five minutes of the class period set the tone for the entire lesson. Ideally, teachers would start by sharing the agenda for the class period so that students will know the expectations for what will be occurring. Next, teachers could post and articulate the learning objective or essential question to the class so that students know the purpose and, at the end of the lesson, can self-assess whether the objective has been met for them. Finally, the opener might include one or more warm-up problems as a way to review and assess students' prior knowledge in preparation for exposure to the new material. This video shows a class opener for a seventh-grade lesson on rectangular prisms:
2. Introduce topics using multiple representations.
The more types of representations that you can present to students addressing their different learning styles, the more likely they will truly understand the concept being presented. Different representations could include using manipulatives, showing a picture, drawing out the problem, and offering a symbolic representation. For example, when presenting linear relationships with one unknown, illustrate to students the same problem as an equation, on a number line, in words, and with pictures. Students who are exposed to and can recognize the same relationship posed in the different representational modes are more likely to have conceptual understanding of the relationship and perform better on assessments (PDF).
3. Solve the problems many ways.
In the best classroom environment, the teacher is able to show different ways to solve the same problem and encourage the students to come up with their own creative ways to solve them. The more strategies and approaches that students are exposed to, the deeper their conceptual understanding of the topic becomes. Empowering students to create their own problem-solving methods can make the teacher nervous. What if we don't follow their logic? What if they're incorrect? However, it's worth the risk to have them explore. After an individual, pair, or small group of students finish solving the class problem using a single method, encourage them to look for alternate ways to come up with the same correct solution. Having students develop their own methods and then share the correct steps with the class is a very powerful learning experience. The video below shows how a teacher encourages students more than one way to solve the same problem on rectangular prisms:
4. Show the application.
In a perfect world, we would always be able to demonstrate how every concept can be applied to the real world -- and when that's possible, it helps improve the students' understanding. When a concept cannot be applied in that manner, we can still share how it might be applied within mathematics or another subject area . Another option is showing how the concept was developed through the history of math. Consider taking a minute out of each lesson to show your students where or how the math can be seen or used in life outside of the classroom.
5. Have students communicate their reasoning.
Students need to explain their reasoning when solving problems. In order for a teacher to determine if every student truly understands the objective for the class period, it's necessary for each student to communicate both orally and in writing. By giving the class ten minutes to discuss their reasoning with each other while exploring multiple ways of solving the problems, you'll promote excellent engagement and learning. It's not always easy to get students talking in class, but there are ways to encourage them (PDF).
6. Finish class with a summary.
Everyone can get lost in the class period, and it's easy to lose track of time until the bell rings and class is over. The final seven minutes might be the most critical in making sure that students have understood the day's learning objective. You can use this time to accomplish three very important things:
- A quick formative assessment to determine how much was learned, such as students self-rating their comfort with the concept on a 1-5 scale
- Reviewing the objective for the class period and brief discussion as to where the lesson will go next time
- Previewing the homework together to avoid any confusion
These are just some of the activities for the close of a lesson. There are at least 22 additionally powerful closure activities . This video shows the summary phase of the same lesson:
In the comments section below, please share your own tips and tricks for helping students understand math.

Think back to the first problem in this chapter, the ABC Problem . What did you do to solve it? Even if you did not figure it out completely by yourself, you probably worked towards a solution and figured out some things that did not work.
Unlike exercises, there is never a simple recipe for solving a problem. You can get better and better at solving problems, both by building up your background knowledge and by simply practicing. As you solve more problems (and learn how other people solved them), you learn strategies and techniques that can be useful. But no single strategy works every time.
Pólya’s How to Solve It
George Pólya was a great champion in the field of teaching effective problem solving skills. He was born in Hungary in 1887, received his Ph.D. at the University of Budapest, and was a professor at Stanford University (among other universities). He wrote many mathematical papers along with three books, most famously, “How to Solve it.” Pólya died at the age 98 in 1985. [1]
In 1945, Pólya published the short book How to Solve It , which gave a four-step method for solving mathematical problems:
- Understand the problem.
- Devise a plan.
- Carry out the plan.
- Looking back.
This is all well and good, but how do you actually do these steps?!?! Steps 1. and 2. are particularly mysterious! How do you “make a plan?” That is where you need some tools in your toolbox, and some experience to draw upon.
Much has been written since 1945 to explain these steps in more detail, but the truth is that they are more art than science. This is where math becomes a creative endeavor (and where it becomes so much fun). We will articulate some useful problem solving strategies, but no such list will ever be complete. This is really just a start to help you on your way. The best way to become a skilled problem solver is to learn the background material well, and then to solve a lot of problems!
We have already seen one problem solving strategy, which we call “Wishful Thinking.” Do not be afraid to change the problem! Ask yourself “what if” questions:
- What if the picture was different?
- What if the numbers were simpler?
- What if I just made up some numbers?
You need to be sure to go back to the original problem at the end, but wishful thinking can be a powerful strategy for getting started.
This brings us to the most important problem solving strategy of all:
Problem Solving Strategy 2 (Try Something!). If you are really trying to solve a problem, the whole point is that you do not know what to do right out of the starting gate. You need to just try something! Put pencil to paper (or stylus to screen or chalk to board or whatever!) and try something. This is often an important step in understanding the problem; just mess around with it a bit to understand the situation and figure out what is going on.
And equally important: If what you tried first does not work, try something else! Play around with the problem until you have a feel for what is going on.
Problem 2 (Payback)
Last week, Alex borrowed money from several of his friends. He finally got paid at work, so he brought cash to school to pay back his debts. First he saw Brianna, and he gave her 1/4 of the money he had brought to school. Then Alex saw Chris and gave him 1/3 of what he had left after paying Brianna. Finally, Alex saw David and gave him 1/2 of what he had remaining. Who got the most money from Alex?
Think/Pair/Share
After you have worked on the problem on your own for a while, talk through your ideas with a partner (even if you have not solved it). What did you try? What did you figure out about the problem?
This problem lends itself to two particular strategies. Did you try either of these as you worked on the problem? If not, read about the strategy and then try it out before watching the solution.
Problem Solving Strategy 3 (Draw a Picture). Some problems are obviously about a geometric situation, and it is clear you want to draw a picture and mark down all of the given information before you try to solve it. But even for a problem that is not geometric, like this one, thinking visually can help! Can you represent something in the situation by a picture?
Draw a square to represent all of Alex’s money. Then shade 1/4 of the square — that’s what he gave away to Brianna. How can the picture help you finish the problem?
After you have worked on the problem yourself using this strategy (or if you are completely stuck), you can watch someone else’s solution.
Problem Solving Strategy 4 (Make Up Numbers). Part of what makes this problem difficult is that it is about money, but there are no numbers given. That means the numbers must not be important. So just make them up!
You can work forwards: Assume Alex had some specific amount of money when he showed up at school, say $100. Then figure out how much he gives to each person. Or you can work backwards: suppose he has some specific amount left at the end, like $10. Since he gave Chris half of what he had left, that means he had $20 before running into Chris. Now, work backwards and figure out how much each person got.
Watch the solution only after you tried this strategy for yourself.
If you use the “Make Up Numbers” strategy, it is really important to remember what the original problem was asking! You do not want to answer something like “Everyone got $10.” That is not true in the original problem; that is an artifact of the numbers you made up. So after you work everything out, be sure to re-read the problem and answer what was asked!
Problem 3 (Squares on a Chess Board)
How many squares, of any possible size, are on a 8 × 8 chess board? (The answer is not 64… It’s a lot bigger!)
Remember Pólya’s first step is to understand the problem. If you are not sure what is being asked, or why the answer is not just 64, be sure to ask someone!

Think / Pair / Share
After you have worked on the problem on your own for a while, talk through your ideas with a partner (even if you have not solved it). What did you try? What did you figure out about the problem, even if you have not solved it completely?
It is clear that you want to draw a picture for this problem, but even with the picture it can be hard to know if you have found the correct answer. The numbers get big, and it can be hard to keep track of your work. Your goal at the end is to be absolutely positive that you found the right answer. You should never ask the teacher, “Is this right?” Instead, you should declare, “Here’s my answer, and here is why I know it is correct!”
Problem Solving Strategy 5 (Try a Simpler Problem). Pólya suggested this strategy: “If you can’t solve a problem, then there is an easier problem you can solve: find it.” He also said: “If you cannot solve the proposed problem, try to solve first some related problem. Could you imagine a more accessible related problem?” In this case, an 8 × 8 chess board is pretty big. Can you solve the problem for smaller boards? Like 1 × 1? 2 × 2? 3 × 3?
Of course the ultimate goal is to solve the original problem. But working with smaller boards might give you some insight and help you devise your plan (that is Pólya’s step (2)).
Problem Solving Strategy 6 (Work Systematically). If you are working on simpler problems, it is useful to keep track of what you have figured out and what changes as the problem gets more complicated.
For example, in this problem you might keep track of how many 1 × 1 squares are on each board, how many 2 × 2 squares on are each board, how many 3 × 3 squares are on each board, and so on. You could keep track of the information in a table:
| 1 | 0 | 0 | 0 | ||
| 4 | 1 | 0 | 0 | ||
| 9 | 4 | 1 | 0 | ||
Problem Solving Strategy 7 (Use Manipulatives to Help You Investigate). Sometimes even drawing a picture may not be enough to help you investigate a problem. Having actual materials that you move around can sometimes help a lot!
For example, in this problem it can be difficult to keep track of which squares you have already counted. You might want to cut out 1 × 1 squares, 2 × 2 squares, 3 × 3 squares, and so on. You can actually move the smaller squares across the chess board in a systematic way, making sure that you count everything once and do not count anything twice.
Problem Solving Strategy 8 (Look for and Explain Patterns). Sometimes the numbers in a problem are so big, there is no way you will actually count everything up by hand. For example, if the problem in this section were about a 100 × 100 chess board, you would not want to go through counting all the squares by hand! It would be much more appealing to find a pattern in the smaller boards and then extend that pattern to solve the problem for a 100 × 100 chess board just with a calculation.
If you have not done so already, extend the table above all the way to an 8 × 8 chess board, filling in all the rows and columns. Use your table to find the total number of squares in an 8 × 8 chess board. Then:
- Describe all of the patterns you see in the table.
- Can you explain and justify any of the patterns you see? How can you be sure they will continue?
- What calculation would you do to find the total number of squares on a 100 × 100 chess board?
(We will come back to this question soon. So if you are not sure right now how to explain and justify the patterns you found, that is OK.)
Problem 4 (Broken Clock)
This clock has been broken into three pieces. If you add the numbers in each piece, the sums are consecutive numbers. ( Consecutive numbers are whole numbers that appear one after the other, such as 1, 2, 3, 4 or 13, 14, 15.)
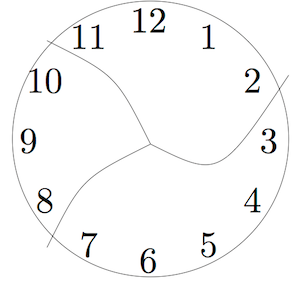
Can you break another clock into a different number of pieces so that the sums are consecutive numbers? Assume that each piece has at least two numbers and that no number is damaged (e.g. 12 isn’t split into two digits 1 and 2.)
Remember that your first step is to understand the problem. Work out what is going on here. What are the sums of the numbers on each piece? Are they consecutive?
After you have worked on the problem on your own for a while, talk through your ideas with a partner (even if you have not solved it). What did you try? What progress have you made?
Problem Solving Strategy 9 (Find the Math, Remove the Context). Sometimes the problem has a lot of details in it that are unimportant, or at least unimportant for getting started. The goal is to find the underlying math problem, then come back to the original question and see if you can solve it using the math.
In this case, worrying about the clock and exactly how the pieces break is less important than worrying about finding consecutive numbers that sum to the correct total. Ask yourself:
- What is the sum of all the numbers on the clock’s face?
- Can I find two consecutive numbers that give the correct sum? Or four consecutive numbers? Or some other amount?
- How do I know when I am done? When should I stop looking?
Of course, solving the question about consecutive numbers is not the same as solving the original problem. You have to go back and see if the clock can actually break apart so that each piece gives you one of those consecutive numbers. Maybe you can solve the math problem, but it does not translate into solving the clock problem.
Problem Solving Strategy 10 (Check Your Assumptions). When solving problems, it is easy to limit your thinking by adding extra assumptions that are not in the problem. Be sure you ask yourself: Am I constraining my thinking too much?
In the clock problem, because the first solution has the clock broken radially (all three pieces meet at the center, so it looks like slicing a pie), many people assume that is how the clock must break. But the problem does not require the clock to break radially. It might break into pieces like this:
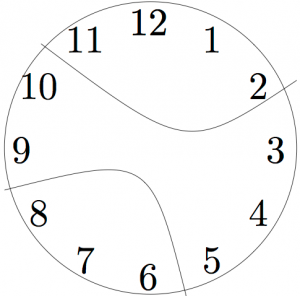
Were you assuming the clock would break in a specific way? Try to solve the problem now, if you have not already.
- Image of Pólya by Thane Plambeck from Palo Alto, California (Flickr) [CC BY 2.0 (http://creativecommons.org/licenses/by/2.0)], via Wikimedia Commons ↵
Mathematics for Elementary Teachers Copyright © 2018 by Michelle Manes is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book
Please ensure that your password is at least 8 characters and contains each of the following:
- a special character: @$#!%*?&
Explaining Your Math: Unnecessary at Best, Encumbering at Worst
Common Core-era rules that force kids to diagram their thought processes can make the equations a lot more confusing than they need to be.

At a middle school in California, the state testing in math was underway via the Smarter Balanced Assessment Consortium (SBAC) exam. A girl pointed to the problem on the computer screen and asked “What do I do?” The proctor read the instructions for the problem and told the student: “You need to explain how you got your answer.”
The girl threw her arms up in frustration and said, “Why can’t I just do the problem, enter the answer and be done with it?”
The answer to her question comes down to what the education establishment believes “understanding” to be, and how to measure it. K-12 mathematics instruction involves equal parts procedural skills and understanding. What “understanding” in mathematics means, however, has long been a topic of debate. One distinction popular with today’s math-reform advocates is between “knowing” and “doing.” A student, reformers argue, might be able to “do” a problem (i.e., solve it mathematically) without understanding the concepts behind the problem-solving procedure. Perhaps he or she has simply memorized the method without understanding it and is performing the steps by “rote.”
The Common Core math standards, adopted in 42 states and the District of Columbia and reflected in Common Core-aligned tests like the SBAC and the Partnership for Assessment of Readiness for College and Careers (PARCC), take understanding to a whole new level. “Students who lack understanding of a topic may rely on procedures too heavily,” states the Common Core website . “But what does mathematical understanding look like?” And how can teachers assess it?
One way is to ask the student to justify, in a way that is appropriate to the student’s mathematical maturity, why a particular mathematical statement is true, or where a mathematical rule comes from.
The underlying assumption here is that if a student understands something, he or she can explain it—and that deficient explanation signals deficient understanding. But this raises yet another question: What constitutes a satisfactory explanation?
While the Common Core leaves this unspecified, current practices are suggestive. Consider a problem that asks how many total pencils there are if five people have three pencils each. In the eyes of some educators, explaining why the answer is 15 by stating, simply, that 5 x 3 = 15 is not satisfactory. To show they truly understand why 5 x 3 is 15, and why this computation provides the answer to the given word problem, students must do more. For example, they might draw a picture illustrating five groups of three pencils. (And in some instances , as was the case recently in a third-grade classroom, a student would be considered to not understand if he or she drew three groups of five pencils.)
Consider now a problem given in a pre-algebra course that involves percentages: “A coat has been reduced by 20 percent to sell for $160. What was the original price of the coat?”
A student may show the solution as follows:
x = original cost of coat in dollars 100% – 20% = 80% 0.8x = $160 x = $200
Clearly, the student knows the mathematical procedure necessary to solve the problem. In fact, for years students were told not to explain their answers, but to show their work, and if presented in a clear and organized manner, the math contained in this work was considered to be its own explanation. But the above demonstration might, through the prism of the Common Core standards, be considered an inadequate explanation. That is, inspired by what the standards say about understanding, one could ask “Does the student know why the subtraction operation is done to obtain the 80 percent used in the equation or is he doing it as a mechanical procedure—i.e., without understanding?”
In a middle school observed by one of us, the school’s goal was to increase student proficiency in solving math problems by requiring students to explain how they solved them. This was not required for all problems given; rather, they were expected to do this for two or three problems in class per week, which took up to 10 percent of total weekly class time. They were instructed on how to write explanations for their math solutions using a model called “Need, Know, Do.” In the problem example given above, the “Need” would be “What was the original price of the coat?” The “Know” would be the information provided in the problem statement, here the price of the discounted coat and the discount rate. The “Do” is the process of solving the problem.
Students were instructed to use “flow maps” and diagrams to describe the thinking and steps used to solve the problem, after which they were to write a narrative summary of what was described in the flow maps and elsewhere. They were told that the “Do” (as well as the flow maps) explains what they did to solve the problem and that the narrative summary provides the why. Many students, though, had difficulty differentiating the “Do” section from the final narrative. But in order for their explanation to qualify as “high level,” they couldn’t simply state “100% – 20% = 80%”; they had to explain what that means. For example, they might say, “The discount rate subtracted from 100 percent gives the amount that I pay.”
An example of a student’s written explanation for this problem is shown in Figure 1:
For problems at this level, the amount of work required for explanation turns a straightforward problem into a long managerial task that is concerned more with pedagogy than with content. While drawing diagrams or pictures may help some students learn how to solve problems, for others it is unnecessary and tedious. As the above example shows, the explanations may not offer the “why” of a particular procedure.
Under the rubric used at the middle school where this problem was given, explanations are ranked as “high,” “middle,” or “low.” This particular explanation would probably fall in the “middle” category since it is unlikely that the statement “You need to subtract 100- 20 to get 80” would be deemed a “purposeful, mathematically-grounded written explanation.”
The “Need” and “Know” steps in the above process are not new and were advocated by George Polya in the 1950s in his classic book How to Solve It . The “Need” and “Know” aspect of the explanatory technique at the middle school observed is a sensible one. But Polya’s book was about solving problems, not explaining or justifying how they were done. At the middle school, problem solving and explanation were intertwined, in the belief that the process of explanation leads to the solving of the problem. This conflation of problem solving and explanation arises from a complex history of educational theories. One theory holds that being aware of one’s thinking process—called “metacognition ”—is part and parcel to problem solving. Other theories that feed the conflation predate the Common Core standards and originated during the Progressive era in the early part of the 20th Century when “conceptual understanding” began to be viewed as a path to, and thus more important than, procedural fluency.
Despite the goal of solving a problem and explaining it in one fell swoop, in many cases observed at the middle school, students solved the problem first and then added the explanation in the required format and rubric. It was not evident that the process of explanation enhanced problem solving ability. In fact, in talking with students at the school, many found the process tedious and said they would rather just “do the math” without having to write about it.
Recommended Reading

When Parents Are the Ones Getting Schooled by the Common Core

The Long-Forgotten Flight That Sent Boeing Off Course

A Biblical Mystery at Oxford
In general, there is no more evidence of “understanding” in the explained solution, even with pictures, than there would be in mathematical solutions presented in a clear and organized way. How do we know, for example, that a student isn’t simply repeating an explanation provided by the teacher or the textbook, thus exhibiting mere “rote learning” rather than “true understanding” of a problem-solving procedure?
Math learning is a progression from concrete to abstract. The advantage to the abstract is that the various mathematical operations can be performed without the cumbersome attachments of concrete entities—entities like dollars, percentages, groupings of pencils. Once a particular word problem has been translated into a mathematical representation, the entirety of its mathematically relevant content is condensed onto abstract symbols, freeing working memory and unleashing the power of pure mathematics. That is, information and procedures that have been become automatic frees up working memory. With working memory less burdened, the student can focus on solving the problem at hand . Thus, requiring explanations beyond the mathematics itself distracts and diverts students away from the convenience and power of abstraction. Mandatory demonstrations of “mathematical understanding,” in other words, can impede the “doing” of actual mathematics.
Explaining the solution to a problem comes when students can draw on a strong foundation of content relevant to the topic currently being learned. As students find their feet and establish a larger repertoire of mastered knowledge and methods, the more articulate they can become in explanations. Children in elementary and middle school who are asked to engage in critical thinking about abstract ideas will, more often than not, respond emotionally and intuitively, not logically and with “understanding.” It is as if the purveyors of these practices are saying: “If we can just get them to do things that look like what we imagine a mathematician does, then they will be real mathematicians.” That may be behaviorally interesting, but it is not mathematical development and it leaves them behind in the development of their fundamental skills.
The idea that students who do not demonstrate their strategies in words and pictures or by multiple methods don’t understand the underlying concepts is particularly problematic for certain vulnerable types of students. Consider students whose verbal skills lag far behind their mathematical skills—non-native English speakers or students with specific language delays or language disorders, for example. These groups include children who can easily do math in their heads and solve complex problems, but often will be unable to explain—whether orally or in written words—how they arrived at their answers.
Most exemplary are children on the autism spectrum. As the autism researcher Tony Attwood has observed, mathematics has special appeal to individuals with autism: It is, often, the school subject that best matches their cognitive strengths. Indeed, writing about Asperger’s Syndrome (a high-functioning subtype of autism), Attwood in his 2007 book The Complete Guide to Asperger’s Syndrome notes that “the personalities of some of the great mathematicians include many of the characteristics of Asperger’s syndrome.”
And yet, Attwood added, many children on the autism spectrum, even those who are mathematically gifted, struggle when asked to explain their answers. “The child can provide the correct answer to a mathematical problem,” he observes, “but not easily translate into speech the mental processes used to solve the problem.” Back in 1944, Hans Asperger, the Austrian pediatrician who first studied the condition that now bears his name, famously cited one of his patients as saying that, “I can’t do this orally, only headily.”
Writing from Australia decades later, a few years before the Common Core took hold in America, Attwood added that it can “mystify teachers and lead to problems with tests when the person with Asperger’s syndrome is unable to explain his or her methods on the test or exam paper.” Here in Common Core America, this inability has morphed into an unprecedented liability.
Is it really the case that the non-linguistically inclined student who progresses through math with correct but unexplained answers—from multi-digit arithmetic through to multi-variable calculus—doesn’t understand the underlying math? Or that the mathematician with the Asperger’s personality, doing things headily but not orally, is advancing the frontiers of his field in a zombie-like stupor?
Or is it possible that the ability to explain one’s answers verbally, while sometimes a sufficient criterion for proving understanding, is not, in fact, a necessary one? And, to the extent that it isn’t a necessary criterion, should verbal explanation be the way to gauge comprehension?
Measuring understanding, or learning in general, isn’t easy. What testing does is measure “markers” or byproducts of learning and understanding. Explaining answers is but one possible marker.
Another, quite simply, are the answers themselves. If a student can consistently solve a variety of problems, that student likely has some level of mathematical understanding. Teachers can assess this more deeply by looking at the solutions and any work shown and asking some spontaneous follow-up questions tailored to the child’s verbal abilities. But it’s far from clear whether a general requirement to accompany all solutions with verbal explanations provides a more accurate measurement of mathematical understanding than the answers themselves and any work the student has produced along the way. At best, verbal explanations beyond “showing the work” may be superfluous; at worst, they shortchange certain students and encumber the mathematics for everyone.
As Alfred North Whitehead famously put it about a century before the Common Core standards took hold:
It is a profoundly erroneous truism … that we should cultivate the habit of thinking of what we are doing. The precise opposite is the case. Civilization advances by extending the number of important operations which we can perform without thinking about them.
Developing Flexibility in Math Problem Solving
- Posted December 4, 2008
- By Amy Magin Wong

A central claim of the current reform movement in mathematics education is that students benefit from comparing and contrasting multiple solution methods. Cognitive science research supports the value of using comparison and contrast to promote general learning: identifying similarities and differences in multiple examples has proven to be a critical and fundamental pathway to flexible, transferable knowledge.
However, few experimental studies have been conducted to demonstrate the value of this approach in math classrooms. Research in mathematics education shows the benefits of a variety of practices advocated by reformers, but we don't know which of these practices are the most effective for student learning.
In his current research, Harvard Graduate School of Education Associate Professor Jon Star , who is also a former middle and high school math teacher, is examining the value of comparing, reflecting on, and discussing multiple solution methods. In a series of experimental studies in middle school classrooms, Star has found that comparing and contrasting solution methods — as opposed to studying one method at a time — does in fact promote greater learning.
Star and his team of researchers traveled to a private, urban school in Tennessee, where they spent four days in seventh-grade mathematics classrooms, specifically to evaluate the effectiveness of comparing multiple solution methods on learning to solve linear equations. A total of 70 students (36 girls, 34 boys) participated in the study, in two regular and two advanced classes.
Star hypothesized that this approach would promote three critical components of mathematical competence: procedural knowledge; procedural flexibility, the abilities to generate, recognize, and evaluate multiple solution methods for the same problem; and conceptual knowledge, students' verbal and nonverbal knowledge of algebra concepts, such as maintaining equivalence, and the meaning of variables.
“We decided to pull out this one practice in math and subject it to more rigorous testing,” says Star. “Is there a benefit to contrasting and comparing multiple examples? We wanted to demonstrate that this is a better method.”
Study procedures
On the first day of the study, students were given 30 minutes to complete a pretest. Then, for the next two days, Star's experimental curriculum replaced the normal materials on solving linear equations. A member of the team or the teacher began the class each day by conducting a ten-minute lesson, and then students worked with a partner on a packet of algebra problems for the remainder of the period.
Students were randomly assigned to a partner, and then partners were randomly assigned to one of two groups. The “compare” group was given a packet of 12 equations, each solved in two different ways, with the solutions side by side on the same page. These worked examples typically illustrated a conventional method for solving an equation, and then a shortcut method that reduced the number of computations and steps needed to solve the equation.
The other group studied sequentially presented solutions. In their packets, the same solution methods were presented as in the compare condition, but each worked example was shown on a separate sheet — one per page. (View a sample of the worked examples in the “compare” and “sequential” packets.)
When studying the worked examples, students had to describe each solution to their partner and answer accompanying questions, first verbally and then in writing. Tape recorders were placed on the desks to record the students' discussions. “We were interested in the process by which they were making sense of it all,” says Star, “and comparing what they were saying to how these methods work.”
To assess the effectiveness of the compare presentation as opposed to the sequential, Star gave the students a posttest on the fourth day. The teacher first provided a brief summary lesson, and then students were given 30 minutes to complete the posttest, which was identical to the pretest.
The team found that comparing and contrasting alternative solution methods led to greater gains in procedural knowledge and flexibility, and comparable gains in conceptual knowledge, as opposed to studying multiple methods sequentially.
- Procedural knowledge: Comparison helped students become better at solving linear equations. This effect was found on problems similar to those in the study packets, and on transfer problems which differed from those the students had already seen.
- Flexibility: The students in the compare group were able to generate multiple solutions to the same problem. These students were also more likely to use the demonstrated shortcuts during the posttest.
- Conceptual knowledge: The compare and sequential groups did not differ in their knowledge of the big ideas of equation solving — such as the concept of equivalence — but students in both groups showed improvements from pretest to posttest.
Further evidence of the benefits of comparison emerged from the process data Star collected. In their written explanations, students in the compare group almost always referenced multiple methods, focused on the solution method, and judged the efficiency or accuracy of the methods. In contrast, those in the sequential groups were much less likely to do so.
“We found that the two examples per page format, combined with questions that asked the student to look at similarities and differences between the two, had a big impact on students' ability to solve math problems correctly, and on their ability to use multiple strategies,” says Star. “Both groups saw the same strategies, but the student who saw them side by side remembered how to use them, and then used them more later on.”
Star and his team have replicated and extended these findings in several additional studies, conducted in public and private schools in Michigan, Tennessee, and Massachusetts. However, this research has also raised a number of interesting questions that Star continues to explore. For example, in a math classroom there are many different things that can be compared: teachers could compare the same problem, solved in two different ways (as was done in Tennessee study); two different problems, each solved the same way; or two very similar problems, each solved the same way (as is typically seen in math texts).
Is one of these types of comparison optimal for student learning? Star's investigation into the role of comparison in students' learning of math continues — with the goal of discovering how teachers can learn to harness the power of comparison most effectively in their math classrooms.
For more information on this research:
Rittle-Johnson, B, & Star, J.R. (2007). Does comparing solution methods facilitate conceptual and procedural knowledge? An experimental study on learning to solve equations. Journal of Educational Psychology , 99(3), 561-574.

Usable Knowledge
Connecting education research to practice — with timely insights for educators, families, and communities
Related Articles

Multiple Methods

How Algebra Is Taught Can Make a Difference

Making Math “Almost Fun”
Alum develops curriculum to entice reluctant math learners
- Solve equations and inequalities
- Simplify expressions
- Factor polynomials
- Graph equations and inequalities
- Advanced solvers
- All solvers
- Arithmetics
- Determinant
- Percentages
- Scientific Notation
- Inequalities
What can QuickMath do?
QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students.
- The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and cancelling common factors within a fraction.
- The equations section lets you solve an equation or system of equations. You can usually find the exact answer or, if necessary, a numerical answer to almost any accuracy you require.
- The inequalities section lets you solve an inequality or a system of inequalities for a single variable. You can also plot inequalities in two variables.
- The calculus section will carry out differentiation as well as definite and indefinite integration.
- The matrices section contains commands for the arithmetic manipulation of matrices.
- The graphs section contains commands for plotting equations and inequalities.
- The numbers section has a percentages command for explaining the most common types of percentage problems and a section for dealing with scientific notation.
Math Topics
More solvers.
- Add Fractions
- Simplify Fractions

Just one more step to access this resource!
Get your free sample task today.
Ready to explore Exemplars rich performance tasks? Sign up for your free sample now.
Mathematical Practice and Problem Solving: How to Support Your Teachers
By: Ross Brewer, Ph.D., Exemplars President
The Common Core State Standards – Mathematics is divided into two parts: Content Standards, and Standards for Mathematical Practice. A major focus of the Standards for Mathematical Practice is on using problem solving to reinforce important concepts and skills and to demonstrate a student’s mathematical understanding.
To fully implement the Common Core, teachers must have an understanding of what problem solving is, why it is important and how to go about implementing it. For many, the successful teaching of problem solving will require real pedagogical shifts. What do teachers need to know?
To help answer this question and prepare your staff, you might turn to findings in the recent report, Improving Mathematical Problem Solving in Grades 4 Through 8 , published in May 2012 under the aegis of the What Works Clearinghouse (NCEE 2012-4055, U.S. Department of Education, available online from the Institute of Education Sciences ). This report provides educators with “specific, evidence-based recommendations that address the challenge of improving mathematical problem solving.”
In the Introduction, the panel that authored the report makes the following points:
- Problem solving is important.
“Students who develop proficiency in mathematical problem solving early are better prepared for advanced mathematics and other complex problem-solving tasks.” The panel recommends that problem solving be part of each curricular unit.
- Instruction in problem solving should begin in the earliest grades.
“Problem solving involves reasoning and analysis, argument construction, and the development of innovative strategies. These should be included throughout the curriculum and begin in kindergarten.”
- The teaching of problem solving should not be isolated.
“… instead, it can serve to support and enrich the learning of mathematics concepts and notation.”
- Despite its importance, problem solving is given short shrift in most classrooms.
To address these points and improve the teaching of problem solving, the panel offers five recommendations.
Recommendation 1
Prepare problems and use them in whole-class instruction.
In selecting or creating problems, it is critical that the language used in the problem and the context of the problem are not barriers to a student’s being able to solve the problem. The same is true for a student’s understanding of the mathematical content necessary to solve the problem.
Recommendation 2
Assist students in monitoring and reflecting on the problem-solving process.
“Students learn mathematics and solve problems better when they monitor their thinking and problem-solving steps as they solve problems.”
Recommendation 3
Teach students how to use visual representations.
Students who learn to visually represent the mathematical information in problems prior to writing an equation are more effective at problem solving.
Recommendation 4
Expose students to multiple problem-solving strategies.
Students who are taught multiple strategies approach problems with “greater ease and flexibility.”
Recommendation 5
Help students recognize and articulate mathematical concepts and notation.
When students have a strong understanding of mathematical concepts and notation, they are better able to recognize the mathematics present in the problem, extend their understanding to new problems, and explore various options when solving problems. Building from students’ prior knowledge of mathematical concepts and notation is instrumental in developing problem-solving skills.
The panel also identifies two specific “roadblocks” to implementing these recommendations:
Roadblock 1
“Traditional textbooks often do not provide students rich experiences in problem solving. Textbooks are dominated by sets of problems that are not cognitively demanding …”
Exemplars was started precisely to meet this need — to provide the rich problem-solving tasks that teachers and students lacked in traditional texts.
Roadblock 2
Lack of time/opportunity to do problem solving in the classroom.
The panel notes that in addition to spending time solving problems, research shows that students benefit by studying already solved problems.
Exemplars annotated anchor papers help meet this need.
As president and founder of Exemplars, it is validating to see the fundamental elements of our material affirmed in this rich research-based report. So much of what is discussed is at the core of what Exemplars math material is all about and has been since we began publishing 19 years ago:
- The importance of success with problem solving
- The critical role formative assessment plays in the classroom
- Students’ use of representations in making the link between the problem and the underlying mathematics
- Students’ ability to communicate their thinking
- Students’ application of appropriate mathematical language and notation
- Helping teachers instruct students in mathematical understanding and allowing students to demonstrate that understanding.
We believe all of these factors should play a critical role in instruction, assessment and professional development.
As teachers are asked to implement more problem solving in their classrooms in support of the Common Core Standards for Mathematical Practice, Exemplars math tasks provide a valuable resource. The tasks are also an effective tool for staff development.
Learn more about Exemplars >>

COMMENTS
Roxana_Colon1 Teacher. Created 2 years ago. Share. Share. Students also viewed. EDU 320 Chapter 5. ... The teacher demonstrated to Kelly how to solve the math problem. Then the teacher stepped back and offered support only as needed. ... this is the stage in which a child uses symbols such as language and math notation to express abstract ...
Final answer: In the provided scenario, the teacher is using the 'Guided Practice' teaching method, where after initial demonstration, students are given independence to solve similar problems with support available as needed. Explanation: The scenario where the teacher demonstrated solving a math problem to the student (Kelly) and then provided support only when needed represents an ...
The teacher demonstrated to Kelly how to solve the math . problem. Then the teacher stepped back and offered support . only as needed. This would best be described as ... symbols such as language and math notation to express . abstract concepts. ...
2.5 / 2.5 pts Question 8 The teacher demonstrated to Kelly how to solve the math problem. Then the teacher stepped back and offered support only as needed. This would best be described as scaffolding. conditioning facilitation discovery learning. Good work 2.5 / 2.5 pts. Question 9 Keeping the processes of accommodation and assimilation ...
Then, I provided them with the "keys to success.". Step 1 - Understand the Problem. To help students understand the problem, I provided them with sample problems, and together we did five important things: read the problem carefully. restated the problem in our own words. crossed out unimportant information.
3. Solve the problems many ways. In the best classroom environment, the teacher is able to show different ways to solve the same problem and encourage the students to come up with their own creative ways to solve them. The more strategies and approaches that students are exposed to, the deeper their conceptual understanding of the topic becomes.
Problem Solving Strategy 9 (Find the Math, Remove the Context). Sometimes the problem has a lot of details in it that are unimportant, or at least unimportant for getting started. The goal is to find the underlying math problem, then come back to the original question and see if you can solve it using the math.
Problem Solving Strategy 9 (Find the Math, Remove the Context). Sometimes the problem has a lot of details in it that are unimportant, or at least unimportant for getting started. The goal is to find the underlying math problem, then come back to the original question and see if you can solve it using the math.
mathematical problem-solving skills, and effect/role of assessments on students' mathematical problem-solving skills' as keywords, 63 studies were obtained. With a deep analysis of the collected data, 32 studies were related to teaching strategies in enhancing problem-solving skills, and these studies were filtered out, while
Free math problem solver answers your algebra homework questions with step-by-step explanations. Mathway. Visit Mathway on the web. Start 7-day free trial on the app. Start 7-day free trial on the app. Download free on Amazon. Download free in Windows Store. Take a photo of your math problem on the app. get Go. Algebra. Basic Math.
Clearly, the student knows the mathematical procedure necessary to solve the problem. In fact, for years students were told not to explain their answers, but to show their work, and if presented ...
For years problem-solving has been an aspect of the American school mathematics curriculum. But for most children— contacts with math educators around the country suggest 80 to 90 per cent of children—problem solving is limited to "word problems", i.e. computational exercises couched in words.
Flexibility: The students in the compare group were able to generate multiple solutions to the same problem. These students were also more likely to use the demonstrated shortcuts during the posttest. Conceptual knowledge: The compare and sequential groups did not differ in their knowledge of the big ideas of equation solving — such as the ...
Question 1 2.5 out of 2.5 points The teacher demonstrated to Kelly how to solve the math problem. Then the teacher stepped back and offered support only as needed. This would best be described as
Study with Quizlet and memorize flashcards containing terms like students in a fourth grade class are working with geoboards. the teacher shows the student how to add the squares. this activity would best promote the students understanding of which of the following geometry concepts, the teacher could best help the students understand that the triangle is equivalent to half a square by showing ...
QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students. The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and ...
Math classes are alive with rich conversations about both concepts and problem-solving approaches—a shift from how U.S. math classes traditionally operate, where teachers demonstrate a process or skill and students spend time practicing and repeating it. ... Eighth-grade math teacher DeQuaz Humphries acknowledges that getting used to the new ...
The teaching of problem solving should not be isolated. "… instead, it can serve to support and enrich the learning of mathematics concepts and notation." Despite its importance, problem solving is given short shrift in most classrooms. To address these points and improve the teaching of problem solving, the panel offers five recommendations.
Question 3 2.5 / 2.5 pts The teacher demonstrated to Kelly how to solve the math problem. Then the teacher stepped back and offered support only as needed. ... Good work Question 12 25 25 pts The teacher demonstrated to Kelly how to solve from EDU... Liberty Uni. EDUC 701 Quiz 2 Behaviorism.docx. Americus Sumter County High South. EDUC 701.
9. The teacher demonstrated to Kelly how to solve the math problem. Then the teacher stepped back and offered support only as needed. This would best be described as a scaffolding 10. According to Bruner, this is the stage in which an object can be directly manipulated by the child. This is the stage of representation in which an object can be directly manipulated, but without an internal ...
The teacher's approach where he/she demonstrated the solution and then stepped back, providing help only when needed, is referred to as 'guided practice'. Explanation: The teacher's approach with Kelly, where she demonstrated the solution to the problem, then stepped back and provided assistance only when necessary, is best described as ...
Good work. Zone of Proximal Development . Question 12 2.5 / 2.5 pts The teacher demonstrated to Kelly how to solve the math problem. Then the teacher stepped back and offered support only as needed. This would best be described as scaffolding conditioning facilitation. discovery learning Good work.
Answer: Scaffolding. Explanation: There are several definitions for scaffolding, but support is the primary one.. Scaffolding is a method that teachers use to help students temporarily and let them become more independent as their help decreases.; A person is standing on a support scaffold to clean the windows of this huge building.