how to solve dp problems

Follow these steps to solve any Dynamic Programming interview problem

by Nikola Otasevic

Despite having significant experience building software products, many engineers feel jittery at the thought of going through a coding interview that focuses on algorithms. I’ve interviewed hundreds of engineers at Refdash , Google, and at startups I’ve been a part of, and some of the most common questions that make engineers uneasy are the ones that involve Dynamic Programming (DP).

Many tech companies like to ask DP questions in their interviews. While we can debate whether they’re effective in evaluating someone’s ability to perform in an engineering role, DP continues to be an area that trips engineers up on their way to finding a job that they love.

Dynamic Programming — Predictable and Preparable

One of the reasons why I personally believe that DP questions might not be the best way to test engineering ability is that they’re predictable and easy to pattern match. They allow us to filter much more for preparedness as opposed to engineering ability.

These questions typically seem pretty complex on the outside, and might give you an impression that a person who solves them is very good at algorithms. Similarly, people who may not be able to get over some mind-twisting concepts of DP might seem pretty weak in their knowledge of algorithms.

The reality is different, and the biggest factor in their performance is preparedness. So let’s make sure everyone is prepared for it. Once and for all.

7 Steps to solve a Dynamic Programming problem

In the rest of this post, I will go over a recipe that you can follow to figure out if a problem is a “DP problem”, as well as to figure out a solution to such a problem. Specifically, I will go through the following steps:

• How to recognize a DP problem
• Identify problem variables
• Clearly express the recurrence relation
• Identify the base cases
• Decide if you want to implement it iteratively or recursively
• Add memoization
• Determine time complexity

Sample DP Problem

For the purpose of having an example for abstractions that I am going to make, let me introduce a sample problem. In each of the sections, I will refer to the problem, but you could also read the sections independently of the problem.

Problem statement:

In this problem, we’re on a crazy jumping ball, trying to stop, while avoiding spikes along the way.

Here are the rules:

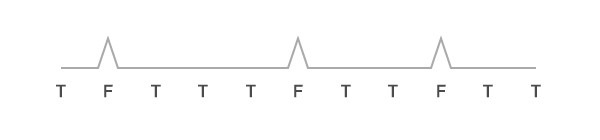
1) You’re given a flat runway with a bunch of spikes in it. The runway is represented by a boolean array which indicates if a particular (discrete) spot is clear of spikes. It is True for clear and False for not clear.

Example array representation:

2) You’re given a starting speed S. S is a non-negative integer at any given point, and it indicates how much you will move forward with the next jump.

3) Every time you land on a spot, you can adjust your speed by up to 1 unit before the next jump.

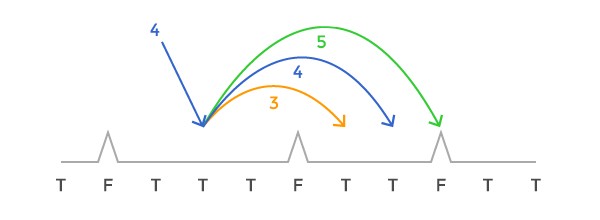
4) You want to safely stop anywhere along the runway (does not need to be at the end of the array). You stop when your speed becomes 0. However, if you land on a spike at any point, your crazy bouncing ball bursts and it’s game over.

The output of your function should be a boolean indicating whether we can safely stop anywhere along the runway.

Step 1: How to recognize a Dynamic Programming problem

First, let’s make it clear that DP is essentially just an optimization technique. DP is a method for solving problems by breaking them down into a collection of simpler subproblems, solving each of those subproblems just once, and storing their solutions. The next time the same subproblem occurs, instead of recomputing its solution, you simply look up the previously computed solution. This saves computation time at the expense of a (hopefully) modest expenditure in storage space.

Recognizing that a problem can be solved using DP is the first and often the most difficult step in solving it. What you want to ask yourself is whether your problem solution can be expressed as a function of solutions to similar smaller problems.

In the case of our example problem, given a point on the runway, a speed, and the runway ahead, we could determine the spots where we could potentially jump next. Furthermore, it seems that whether we can stop from the current point with the current speed depends only on whether we could stop from the point we choose to go to next.

That is a great thing, because by moving forward, we shorten the runway ahead and make our problem smaller. We should be able to repeat this process all the way until we get to a point where it is obvious whether we can stop.

Recognizing a Dynamic Programming problem is often the most difficult step in solving it. Can the problem solution be expressed as a function of solutions to similar smaller problems?

Step 2: Identify problem variables

Now we have established that there is some recursive structure between our subproblems. Next, we need to express the problem in terms of the function parameters and see which of those parameters are changing.

Typically in interviews, you will have one or two changing parameters, but technically this could be any number. A classic example of a one-changing-parameter problem is “determine an n-th Fibonacci number”. Such an example for a two-changing-parameters problem is “Compute edit distance between strings”. If you’re not familiar with these problems, don’t worry about it.

A way to determine the number of changing parameters is to list examples of several subproblems and compare the parameters. Counting the number of changing parameters is valuable to determine the number of subproblems we have to solve. It’s also important in its own right in helping us strengthen the understanding of the recurrence relation from step 1.

In our example, the two parameters that could change for every subproblem are:

• Array position (P)

One could say that the runway ahead is changing as well, but that would be redundant considering that the entire non-changing runway and the position (P) carry that information already.

Now, with these 2 changing parameters and other static parameters, we have the complete description of our sub-problems.

Identify the changing parameters and determine the number of subproblems.

Step 3: Clearly express the recurrence relation

This is an important step that many rush through in order to get into coding. Expressing the recurrence relation as clearly as possible will strengthen your problem understanding and make everything else significantly easier.

Once you figure out that the recurrence relation exists and you specify the problems in terms of parameters, this should come as a natural step. How do problems relate to each other? In other words, let’s assume that you have computed the subproblems. How would you compute the main problem?

Here is how we think about it in our sample problem:

Because you can adjust your speed by up to 1 before jumping to the next position, there are only 3 possible speeds, and therefore 3 spots in which we could be next.

More formally, if our speed is S, position P, we could go from (S, P) to:

• (S, P + S) ; # if we do not change the speed
• (S — 1, P + S — 1) ; # if we change the speed by -1
• (S + 1, P + S + 1) ; # if we change the speed by +1

If we can find a way to stop in any of the subproblems above, then we can also stop from (S, P). This is because we can transition from (S, P) to any of the above three options.

This is typically a fine level of understanding of the problem (plain English explanation), but you sometimes might want to express the relation mathematically as well. Let’s call a function that we’re trying to compute canStop. Then:

canStop(S, P) = canStop(S, P + S) || canStop(S — 1, P + S — 1) || canStop(S + 1, P + S + 1)

Woohoo, it seems like we have our recurrence relation!

Recurrence relation: Assuming you have computed the subproblems, how would you compute the main problem?

Step 4: Identify the base cases

A base case is a subproblem that doesn’t depend on any other subproblem. In order to find such subproblems, you typically want to try a few examples, see how your problem simplifies into smaller subproblems, and identify at what point it cannot be simplified further.

The reason a problem cannot be simplified further is that one of the parameters would become a value that is not possible given the constraints of the problem.

In our example problem, we have two changing parameters, S and P. Let’s think about what possible values of S and P might not be legal:

• P should be within the bounds of the given runway
• P cannot be such that runway[P] is false because that would mean that we’re standing on a spike
• S cannot be negative, and a S==0 indicates that we’re done

Sometimes it can be a little challenging to convert assertions that we make about parameters into programmable base cases. This is because, in addition to listing the assertions if you want to make your code look concise and not check for unnecessary conditions, you also need to think about which of these conditions are even possible.

In our example:

• P < 0 || P >= length of runway seems like the right thing to do. An alternative could be to consider m aking P == end of runway a base case. However, it is possible that a problem splits into a subproblem which goes beyond the end of the runway, so we really need to check for inequality.
• This seems pretty obvious. We can simply check if runway[P] is false .
• Similar to #1, we could simply check for S < 0 and S == 0. However, here we can reason that it is impossible for S to be < 0 because S decreases by at most 1, so it would have to go through S == 0 case beforehand. Ther efore S == 0 is a sufficient base case for the S parameter.

Step 5: Decide if you want to implement it iteratively or recursively

The way we talked about the steps so far might lead you to think that we should implement the problem recursively. However, everything that we’ve talked about so far is completely agnostic to whether you decide to implement the problem recursively or iteratively. In both approaches, you would have to determine the recurrence relation and the base cases.

To decide whether to go iteratively or recursively, you want to carefully think about the trade-offs .

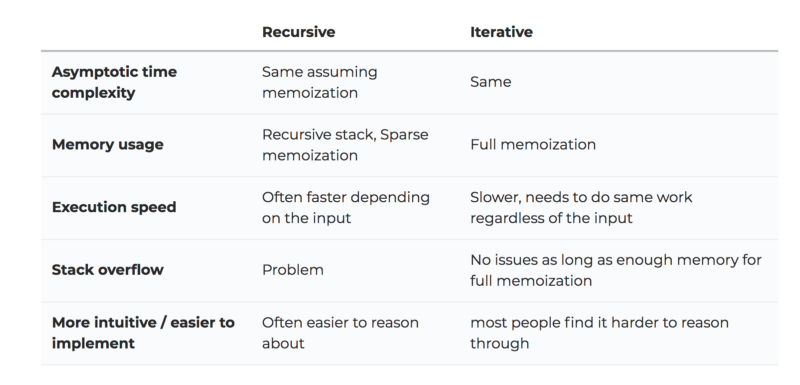
Stack overflow issues are typically a deal breaker and a reason why you would not want to have recursion in a (backend) production system. However, for the purposes of the interview, as long as you mention the trade-offs, you should typically be fine with either of the implementations. You should feel comfortable implementing both.

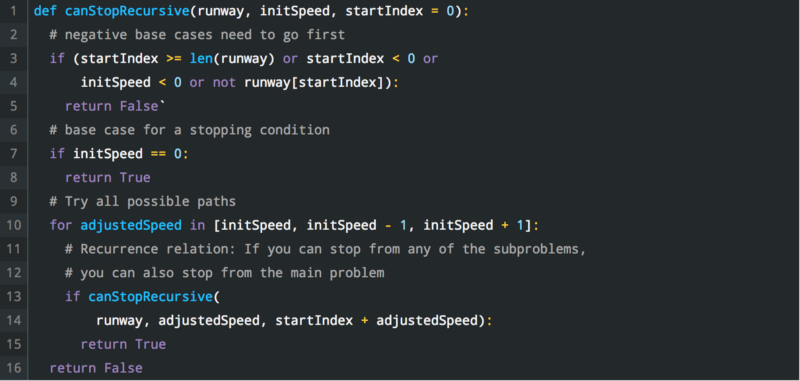
In our particular problem, I implemented both versions. Here is python code for that: A recursive solution: (original code snippets can be found here )

An iterative solution: (original code snippets can be found here )

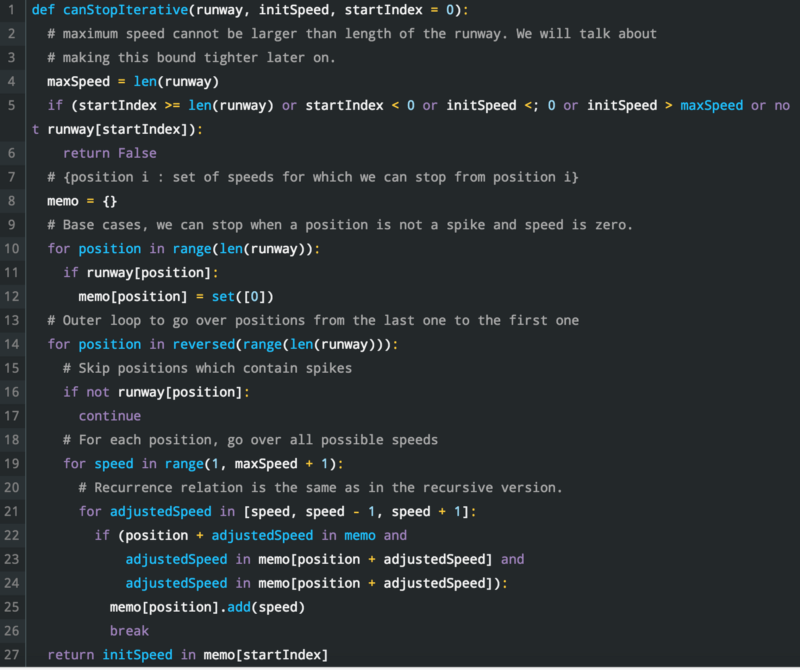
Step 6: Add memoization

Memoization is a technique that is closely associated with DP. It is used for storing the results of expensive function calls and returning the cached result when the same inputs occur again.

Why are we adding memoization to our recursion? We encounter the same subproblems which, without memoization, are computed repeatedly. Those repetitions very often lead to exponential time complexities.

In recursive solutions, adding memoization should feel straightforward. Let’s see why. Remember that memoization is just a cache of the function results. There are times when you want to deviate from this definition in order to squeeze out some minor optimizations, but treating memoization as a function result cache is the most intuitive way to implement it.

This means that you should:

• Store your function result into your memory before every return statement
• Look up the memory for the function result before you start doing any other computation

Here is the code from above with added memoization (added lines are highlighted): (original code snippets can be found here )

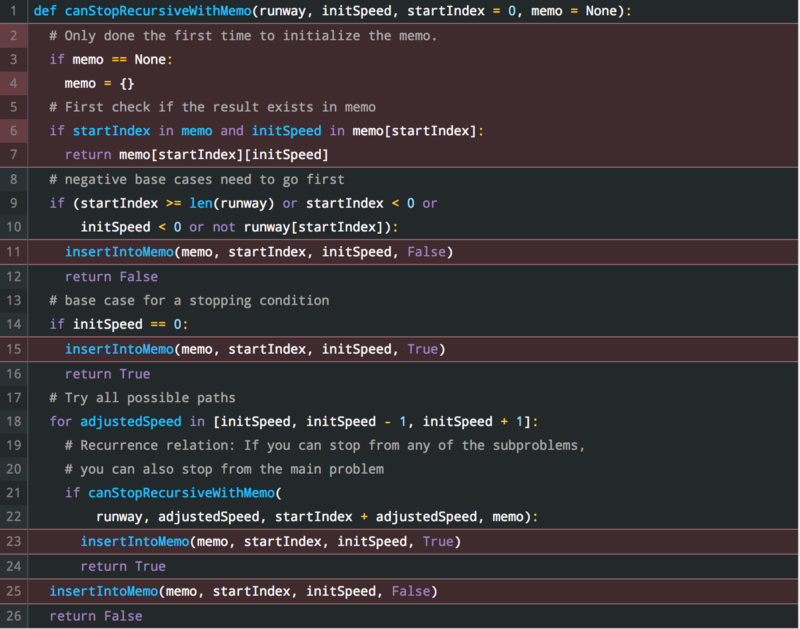
In order to illustrate the effectiveness of memoization and different approaches, let’s do some quick tests. I will stress test all three methods that we have seen so far. Here is the set up:

• I created a runway of length 1000 with spikes in random places (I chose to have a probability of a spike being in any given spot to be 20%)
• initSpeed = 30
• I ran all functions 10 times and measured the average time of execution

Here are the results (in seconds):

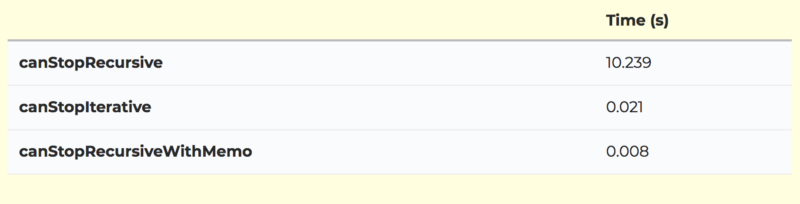
You can see that the pure recursive approach takes about 500x more time than the iterative approach and about 1300x more time than the recursive approach with memoization. Note that this discrepancy would grow rapidly with the length of the runway. I encourage you to try running it yourself.

Step 7: Determine Time complexity

There are some simple rules that can make computing time complexity of a dynamic programming problem much easier. Here are two steps that you need to do:

• Count the number of states — this will depend on the number of changing parameters in your problem
• Think about the work done per each state. In other words, if everything else but one state has been computed, how much work do you have to do to compute that last state?

In our example problem, the number of states is |P| * |S|, where

• P is the set of all positions (|P| indicates the number of elements in P)
• S is the set of all speeds

The work done per each state is O(1) in this problem because, given all other states, we simply have to look at 3 subproblems to determine the resulting state.

As we noted in the code before, |S| is limited by length of the runway (|P|), so we could say that the number of states is |P|² and because work done per each state is O(1), then the total time complexity is O(|P|²).

However, it seems that |S| can be further limited, because if it were really |P|, it is very clear that stopping would not be possible because you would have to jump the length of the entire runway on the first move.

So let’s see how we can put a tighter bound on |S|. Let’s call maximum speed S. Assume that we’re starting from position 0. How quickly could we stop if we were trying to stop as soon as possible and if we ignore potential spikes?

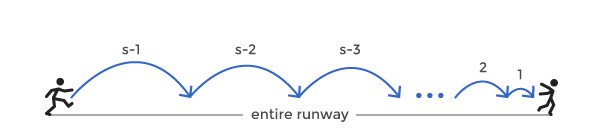
In the first iteration, we would have to come at least to the point (S-1), by adjusting our speed at zero by -1. From there we would at a minimum go by (S-2) steps forward, and so on.

For a runway of length L , the following has to hold:

=> (S-1) + (S-2) + (S-3) + ….+ 1 < L

=> S*(S-1) / 2 < L

=> S² — S — 2L < 0

If you find roots of the above function, they will be:

r1 = 1/2 + sqrt(1/4 + 2L) and r2 = 1/2 — sqrt(1/4 + 2L)

We can write our inequality as:

(S — r1) * (S — r2) < ; 0

Considering that S — r2 > 0 for any S > 0 and L > 0, we need the following:

S — 1/2 — sqrt(1/4 + 2L) < ; 0

=> S < 1/2 + sqrt(1/4 + 2L)

That is the maximum speed that we could possibly have on a runway of a length L. If we had a speed higher than that, we could not stop even theoretically, irrespective of the position of the spikes.

That means that the total time complexity depends only on the length of the runway L in the following form:

O(L * sqrt(L)) which is better than O(L²)

O(L * sqrt(L)) is the upper bound on the time complexity

Awesome, you made it through! :)

The 7 steps that we went through should give you a framework for systematically solving any dynamic programming problem. I highly recommend practicing this approach on a few more problems to perfect your approach.

Here are some next steps that you can take

• Extend the sample problem by trying to find a path to a stopping point. We solved a problem that tells you whether you can stop, but what if you wanted to also know the steps to take in order to stop eventually along the runway? How would you modify the existing implementation to do that?
• If you want to solidify your understanding of memoization, and understand that it is just a function result cache, you should read about decorators in Python or similar concepts in other languages. Think about how they would allow you to implement memoization in general for any function that you want to memoize.
• Work on more DP problems by following the steps we went through. You can always find a bunch of them online (ex. LeetCode or GeeksForGeeks ). As you practice, keep in mind one thing: learn ideas, don’t learn problems. The number of ideas is significantly smaller and it’s an easier space to conquer which will also serve you much better.

When you feel like you’ve conquered these ideas, check out Refdash where you are interviewed by a senior engineer and get a detailed feedback on your coding, algorithms, and system design.

Originally published at Refdash blog . Refdash is an interviewing platform that helps engineers interview anonymously with experienced engineers from top companies such as Google, Facebook, or Palantir and get a detailed feedback. Refdash also helps engineers discover amazing job opportunities based on their skills and interests.

If this article was helpful, share it .

Learn to code for free. freeCodeCamp's open source curriculum has helped more than 40,000 people get jobs as developers. Get started

Reset password New user? Sign up

Existing user? Log in

Dynamic Programming

Already have an account? Log in here.

• Karleigh Moore
• Norbert Madarász

Dynamic programming refers to a problem-solving approach, in which we precompute and store simpler, similar subproblems, in order to build up the solution to a complex problem. It is similar to recursion , in which calculating the base cases allows us to inductively determine the final value. This bottom-up approach works well when the new value depends only on previously calculated values.

An important property of a problem that is being solved through dynamic programming is that it should have overlapping subproblems. This is what distinguishes DP from divide and conquer in which storing the simpler values isn't necessary.

To show how powerful the technique can be, here are some of the most famous problems commonly approached through dynamic programming:

• Backpack Problem : Given a set of treasures with known values and weights, which of them should you pick to maximize your profit whilst not damaging your backpack which has a fixed capacity?
• Egg Dropping : What is the best way to drop \(n\) eggs from an \(m\)-floored building to figure out the lowest height from which the eggs when dropped crack?
• Longest Common Subsequence : Given two sequences, which is the longest subsequence common to both of them?
• Subset Sum Problem : Given a set and a value \(n,\) is there a subset the sum of whose elements is \(n?\)
• Fibonacci Numbers : Is there a better way to compute Fibonacci numbers than plain recursion?

In a contest environment, dynamic programming almost always comes up (and often in a surprising way, no matter how familiar the contestant is with it).

Motivational Example: Change of Coins

Recursion with memoization, bidimensional dynamic programming: example, example: maximum paths.

What is the minimum number of coins of values \(v_1,v_2, v_3, \ldots, v_n\) required to amount a total of \(V?\) You may use a denomination more than once.

Optimal Substructure

The most important aspect of this problem that encourages us to solve this through dynamic programming is that it can be simplified to smaller subproblems.

Let \(f(N)\) represent the minimum number of coins required for a value of \(N\).

Visualize \(f(N)\) as a stack of coins. What is the coin at the top of the stack? It could be any of \(v_1,v_2, v_3, \ldots, v_n\). In case it were \(v_1\), the rest of the stack would amount to \(N-v_1;\) or if it were \(v_2\), the rest of the stack would amount to \(N-v_2\), and so on.

How do we decide which is it? Sure enough, we do not know yet. We need to see which of them minimizes the number of coins required.

Going by the above argument, we could state the problem as follows:

\[f(V) = \min \Big( \big\{ 1 + f(V - v_1), 1 + f(V-v_2), \ldots, 1 + f(V-v_n) \big \} \Big). \]

Because the coin at the top of the stack also counts as one coin, and then we can look at the rest.

Overlapping Subproblems

It is easy to see that the subproblems could be overlapping.

For example, if we are trying to make a stack of $11 using $1, $2, and $5, our look-up pattern would be like this: \[\begin{align} f(11) &= \min \Big( \big\{ 1+f(10),\ 1+ f(9),\ 1 + f(6) \big\} \Big) \\ &= \min \Big ( \big \{ 1+ \min {\small \left ( \{ 1 + f(9), 1+ f(8), 1+ f(5) \} \right )},\ 1+ f(9),\ 1 + f(6) \big \} \Big ). \end{align} \] Clearly enough, we'll need to use the value of \(f(9)\) several times.

One of the most important aspects of optimizing our algorithms is that we do not recompute these values. To do this, we compute and store all the values of \(f\) from 1 onwards for potential future use.

The recursion has to bottom out somewhere, in other words, at a known value from which it can start.

For this problem, we need to take care of two things:

Zero : It is clear enough that \(f(0) = 0\) since we do not require any coins at all to make a stack amounting to 0.

Negative and Unreachable Values : One way of dealing with such values is to mark them with a sentinel value so that our code deals with them in a special way. A good choice of a sentinel is \(\infty\), since the minimum value between a reachable value and \(\infty\) could never be infinity.

The Algorithm

Let's sum up the ideas and see how we could implement this as an actual algorithm:

We have claimed that naive recursion is a bad way to solve problems with overlapping subproblems. Why is that? Mainly because of all the recomputations involved.

Another way to avoid this problem is to compute the data first time and store it as we go, in a top-down fashion.

Let's look at how one could potentially solve the previous coin change problem in the memoization way. 1 2 3 4 5 6 7 8 9 10 11 12 def coinsChange ( V , v ): memo = {} def Change ( V ): if V in memo : return memo [ V ] if V == 0 : return 0 if V < 0 : return float ( "inf" ) memo [ V ] = min ([ 1 + Change ( V - vi ) for vi in v ]) return memo [ V ] return Change ( V )

Dynamic Programming vs Recursion with Caching

There are \(k\) types of brackets each with its own opening bracket and closing bracket. We assume that the first pair is denoted by the numbers 1 and \(k+1,\) the second by 2 and \(k+2,\) and so on. Thus the opening brackets are denoted by \(1, 2, \ldots, k,\) and the corresponding closing brackets are denoted by \(k+1, k+2, \ldots, 2k,\) respectively.

Some sequences with elements from \(1, 2, \ldots, 2k\) form well-bracketed sequences while others don't. A sequence is well-bracketed if we can match or pair up opening brackets of the same type in such a way that the following holds:

• Every bracket is paired up.
• In each matched pair, the opening bracket occurs before the closing bracket.
• For a matched pair, any other matched pair lies either completely between them or outside them.

In this problem, you are given a sequence of brackets of length \(N\): \(B[1], \ldots, B[N]\), where each \(B[i]\) is one of the brackets. You are also given an array of Values: \(V[1],\ldots, V[N] \).

Among all the subsequences in the Values array, such that the corresponding bracket subsequence in the B Array is a well-bracketed sequence, you need to find the maximum sum.

Task: Solve the above problem for this input.

Input Format

One line, which contains \((2\times N + 2)\) space separate integers. The first integer denotes \(N.\) The next integer is \(k.\) The next \(N\) integers are \(V[1],..., V[N].\) The last \(N\) integers are \(B[1],..., B[N].\)

Constraints

• \(1 \leq k \leq 7\)
• \(-10^6 \leq V[i] \leq 10^6\), for all \(i\)
• \(1 \leq B[i] \leq 2k\), for all \(i\)

Illustrated Examples

For the examples discussed here, let us assume that \(k = 2\). The sequence 1, 1, 3 is not well-bracketed as one of the two 1's cannot be paired. The sequence 3, 1, 3, 1 is not well-bracketed as there is no way to match the second 1 to a closing bracket occurring after it. The sequence 1, 2, 3, 4 is not well-bracketed as the matched pair 2, 4 is neither completely between the matched pair 1, 3 nor completely outside of it. That is, the matched pairs cannot overlap. The sequence 1, 2, 4, 3, 1, 3 is well-bracketed. We match the first 1 with the first 3, the 2 with the 4, and the second 1 with the second 3, satisfying all the 3 conditions. If you rewrite these sequences using [, {, ], } instead of 1, 2, 3, 4 respectively, this will be quite clear.

Suppose \(N = 6, k = 3,\) and the values of \(V\) and \(B\) are as follows: Then, the brackets in positions 1, 3 form a well-bracketed sequence (1, 4) and the sum of the values in these positions is 2 (4 + (-2) =2). The brackets in positions 1, 3, 4, 5 form a well-bracketed sequence (1, 4, 2, 5) and the sum of the values in these positions is 4. Finally, the brackets in positions 2, 4, 5, 6 form a well-bracketed sequence (3, 2, 5, 6) and the sum of the values in these positions is 13. The sum of the values in positions 1, 2, 5, 6 is 16 but the brackets in these positions (1, 3, 5, 6) do not form a well-bracketed sequence. You can check the best sum from positions whose brackets form a well-bracketed sequence is 13.

We'll try to solve this problem with the help of a dynamic program, in which the state , or the parameters that describe the problem, consist of two variables.

First, we set up a two-dimensional array dp[start][end] where each entry solves the indicated problem for the part of the sequence between start and end inclusive.

We'll try to think what happens when we run across a new end value, and need to solve the new problem in terms of the previously solved subproblems. Here are all the possibilities:

• When end <= start , there are no valid subsequences.
• When b[end] <= k , i.e, the last entry is an open bracket, no valid subsequence can end with it. Effectively, the result is the same if we hadn't included the last entry at all.
• When b[end] > k , i.e, the last entry is a closing bracket, one has to find the best match for it, or simply ignore it, whichever maximizes the sum.

Can you use these ideas to solve the problem?

Very often, dynamic programming helps solve problems that ask us to find the most profitable (or least costly) path in an implicit graph setting. Let us try to illustrate this with an example.

You are supposed to start at the top of a number triangle and chose your passage all the way down by selecting between the numbers below you to the immediate left or right. Your goal is to maximize the sum of the elements lying in your path. For example, in the triangle below, the red path maximizes the sum.

To see the optimal substructures and the overlapping subproblems , notice that everytime we make a move from the top to the bottom right or the bottom left, we are still left with smaller number triangle, much like this:

We could break each of the sub-problems in a similar way until we reach an edge-case at the bottom:

In this case, the solution is a + max(b,c) .

A bottom-up dynamic programming solution is to allocate a number triangle that stores the maximum reachable sum if we were to start from that position . It is easy to compute the number triangles from the bottom row onward using the fact that the

\[\text{best from this point} = \text{this point} + \max(\text{best from the left, best from the right}).\]

Let me demonstrate this principle through the iterations. Iteration 1: 1 8 5 9 3 Iteration 2: 1 2 10 13 15 8 5 9 3 Iteration 3: 1 2 3 20 19 10 13 15 8 5 9 3 Iteration 4: 1 2 3 4 23 20 19 10 13 15 8 5 9 3 So, the effective best we could do from the top is 23, which is our answer.

Problem Loading...

Note Loading...

Set Loading...

LTCWM > Blog > Resources > Technical guides > How to Solve Any Dynamic Programming Problem

How to Solve Any Dynamic Programming Problem

Updated on April 12th, 2020 | Sign up for learn to code tips

If you’re aiming for a top-tier tech job, you have to face the coding interview —and come out on top. And one sure-fire way to impress is to have dynamic programming down pat.

In today’s special guest post, Sam Gavis-Hughson guides us through his formula for solving any dynamic programming problem.

Take it away, Sam!

Disclosure: I’m an affiliate for Sam's courses. While the resources mentioned in this post are free, I may get a small commission if you click the links below and later buy one of his products. Thanks!

When it comes to coding interviews , not all topics are created equal.

Some are relatively easy. For example, even the hardest linked list problems don’t tend to be that difficult because the concept is on the simpler side.

But then there are some topics where even the easiest variations strike fear into the hearts of interviewees everywhere.

One such topic is dynamic programming —an optimization technique programmers can use to speed up our code when we are repeatedly solving the same problem.

Dynamic programming has truly become the defacto hard topic that your interviewer can ask you. If they want to really put you through your paces, that’s what they’ll ask about.

This means that if you’re interviewing for any top tech company , dynamic programming should be at the top of your list of topics to prepare.

What is Dynamic Programming?

Essentially, dynamic programming is a way of making a recursive algorithm more efficient by making sure it doesn’t have to solve the same subproblem twice. 

When you use dynamic programming, it stores the results of subproblems so you don’t have to re-compute those results next time they’re needed. It’s an alternative to plain recursion, which requires repeating the solution process every time the subproblem is encountered. 

This Stack Overflow answer words it well: “Dynamic programming is when you use past knowledge to make solving a future problem easier.”

Some benefits of dynamic programming are that it saves you coding time, reduces lines of code, and speeds up an algorithm’s processing time.

Now, here’s the crazy thing…

Dynamic Programming Doesn’t Have to Be Hard

The real challenge with dynamic programming is that it is counterintuitive. When you’re trying to solve dynamic programming problems, all the obvious steps that you would normally take actually pull you further away from the correct solution:

• Want to find the optimal solution? You actually need to start with the brute force approach.
• Want to find an iterative solution? You have to start with recursion.
• Want to solve the problem as quickly as possible? You need to slow it down and go step by step.

Click To Tweet

So if dynamic programming is so counterintuitive, how are we ever supposed to solve these problems effectively?

To start, let’s look at how most people prepare for their coding interviews:

They focus on memorizing solutions.

Rather than being strategic and understanding the underlying techniques, most people focus on simply memorizing as many solutions as they can.

Memorizing gives you a quick and easy win. But the problem is that it ultimately handicaps you.

When you focus on memorizing, your interview prep strategy becomes very simple: just go through as many problems as you can. When you go into an interview, you hope that you see a problem that you’ve studied before.

But this approach quickly leads to diminishing returns. There’s only so much that you can actually memorize, and the number of problems that you could be asked is very large.

Not to mention that this approach prevents you from actually being able to connect the dots.

Imagine learning a new language (let’s say French). You decide that you are going to create a massive deck of flashcards and simply memorize individual words. This is your plan to get to fluency.

So you start memorizing. Here’s one sample set of words:

“suis”, “es”, “est”, “sommes”, “êtez”, “sont”

What is the connection between these words (if you already know French, pretend you don’t for a sec)?

On the surface, it’s not obvious. So if you were just memorizing, you would be memorizing 6 discrete words.

However, there actually is a very close connection between these words: They’re all different conjugations of the verb “to be.”

If we look at the translations, we see:

• “Je suis” – “I am”
• “Tu es” – “You are”
• “Elle est” – “She is”
• “Nous sommes” – “We are”
• “Vous êtez” – “You all are”
• “Ils sont” – “They are”

Notice how much easier this is now that we’ve connected them all in some way that is meaningful to us? Yes we still need to memorize the specifics, but now we can see what connects them.

So what if we could do the same thing with dynamic programming?

Well, it’s never going to happen if we just try to memorize solutions to different problems. The issue is that the similarity between these different problems ISN’T in the solution itself.

The similarity between all dynamic programming problems is in the process.

For the rest of this post, I’m going to show you the exact strategy that you can use to solve any dynamic programming problem, even if you’ve never seen the problem before.

The remainder of this post is excerpted from my free ebook, Dynamic Programming for Interviews, which you can download here .

How to Solve Dynamic Programming Problems Using the Fast Method

What is the most important characteristic of any successful interviewee?

They have a repeatable strategy.

That’s exactly what the FAST Method is. It’s a repeatable strategy for solving any dynamic programming problem, whether you’ve seen the problem before or not.

The FAST Method is an acronym for the 4 steps you need to solve any dynamic programming problem:

• F ind the First Solution
• A nalyze the First Solution
• Identify the S ubproblems
• T urn around the solution

By following these 4 steps, you’ll be able to find the optimal dynamic programming solution for any problem.

Start coding now

Stop waiting and start learning! Get my 10 tips on teaching yourself how to code.

Success! Now check your email to confirm your subscription.

There was an error submitting your subscription. Please try again.

1. Find the First Solution

The first step for any dynamic programming problem (and the step that most people skip) is to find an initial brute-force solution to the problem.

The goal here is to just get something down on paper without any concern for efficiency. To be honest, this should be the first step for any problem you might solve, but it is particularly important for dynamic programming.

There are several keys to think about while doing this step that you’ll want to keep in mind:

• The solution should be recursive. If not, the problem probably isn’t a good candidate for dynamic programming. For a lot more info on effectively coming up with a recursive solution, look here .
• Each recursive call must be self-contained. This means that you cannot store your results to a global variable or pass a results variable into your function. I often refer to the required approach as “building up as you return” and you can learn more about that here .
• It is important that we minimize the number of variables that we are passing into our recursive function. Dynamic programming solutions rely on there being multiple recursive calls with the same input, and the more variables there are, the less the inputs will overlap.

With these basic rules in mind, you will have no trouble using this brute force solution in the FAST Method.

Check out Dynamic Programming for Interviews for detailed walkthroughs of 5 of the most popular dynamic programming problems.

2. Analyze the First Solution

This is the step where we decide whether we can actually use dynamic programming to solve a problem. To do this, we’re going to look at a couple of specific things.

First off, we should be sure to determine what the actual time complexity of our code is currently. One mistake that I see fairly often is attempting to optimize something that doesn’t need to be optimized. If our solution is already efficient, spending a lot of time optimizing is a real waste of time.

With most of our recursive functions, we can use a pretty simple heuristic to compute the runtime. We simply look at the branching factor of our recursive function raised to the depth.

For example, if we were finding all combinations of an input, that would give us a time complexity of `O(2n)`. You can read a lot more about this here .

Next up, if our solution is in fact inefficient (we’re most likely looking for something that is exponential time or worse as being inefficient), we want to see if we can optimize it using dynamic programming.

Dynamic programming actually requires us to meet 2 specific criteria. If we don’t, then it is not possible for us to optimize our problem using dynamic programming. However, if we do, we will likely see a major improvement.

These are the criteria that we need to look for:

Optimal Substructure

The first criterion is that our problem must have optimal substructure. Technically speaking, this means that we must be able to find an optimal solution to a problem by solving for its subproblems. An easier way to think about this is simply that we must be able to solve the problem recursively. If we already found a recursive problem in the previous step, then we can safely assume we have optimal substructure.

Overlapping Subproblems

This is where the actual optimization comes in. If our problem has overlapping subproblems, that means that we are calling the same function with the exact same inputs multiple times. So we’re doing repetitive work for no reason. If we were to cache (or “memoize”) the results, we would be able to save a lot of time.

If we meet these two criteria, then we know that we can optimize our solution using dynamic programming.

3. Identify the Subproblems

If we find that we are able to use dynamic programming, the next step is to clearly identify the subproblems. Defining the subproblem in plain English is going to make it much easier for us to understand everything that is going on.

To approach this step, we are going to specifically look at our recursive code and see what recursive calls are being made. We then want to define in plain English what the actual meaning of that recursive call is.

For example, if we are computing the nth Fibonacci number, we have 2 recursive calls, fib(n-1) and fib(n-2). To define these in plain English, the function simply returns the nth Fibonacci number. Pretty simple.

Once we’ve identified what the subproblems are, we can also memoize our recursive solution to make it more efficient. All this means is that we are going to add an array or HashMap that stores all of the values that we’ve previously computed.

Each time we make a function call, we will look in our array to see if a result has already been computed for the current inputs. If so, then we can return it without actually computing anything. If not, we compute it and then save it into our array.

For full code and example problems, download Dynamic Programming for Interviews .

4. Turn Around the Solution

If you’ve ever spent any serious time studying dynamic programming solutions in the past, you may have noticed that the vast majority of them are iterative, not recursive. And yet up to this point in the FAST Method, we have only generated recursive solutions.

In this optional final step of the process, we will take our recursive solution and make it into an iterative solution.

When doing dynamic programming, we really have two different options:

• A top-down (memoized) solution
• A bottom-up (tabular) solution

A top-down solution is the recursive solution that we found in the previous step. We call this top-down because we are starting with the goal result that we’re trying to get (ie. fib(5)) and then repeatedly split it into smaller subproblems until we reach our base case.

Bottom-up is simply the opposite of that. Rather than starting with our target input, we start with the base cases. We iteratively compute larger and larger subproblems until we reach our target result.

Both of these approaches will give us the same worst case complexity. However, many people prefer the bottom-up approach because recursive code tends to execute slower than iterative code that does the same work, given that it requires additional overhead.

The key to turning around the solution and finding a bottom-up solution is to look at what the smallest subproblems are. This is why we needed to carefully identify and define the subproblems in the previous step.

We can start with computing our base case. Then we need to determine how to compute a given subproblem, assuming all the smaller subproblems have already been computed. We’ll save all of these subproblem solutions into an array so that we can easily look them up.

See examples of exactly how to do this in my free ebook, Dynamic Programming for Interviews .

At the end of the day, dynamic programming is a challenging topic. It’s not something that you can magically become a master at overnight.

However, it also isn’t something you have to be afraid of. If you nail down your recursion skills and understand the FAST Method, even the most challenging dynamic programming problems can be easily solved during your interview.

Next Steps : Where to Learn More About Dynamic Programming

Want to learn more about dynamic programming? Check out these online courses:

• Intro To Dynamic Programming – Coding Interview Preparation (Udemy): Specifically designed to help you gain foundational knowledge for your software engineering coding interview
• Dynamic Programming – I (Udemy): Also intro-level and geared toward coding interview basics
• Master the Art of Dynamic Programming (Udemy): In-depth theory and practice of dynamic programming
• Learn Dynamic Programming Using Python (Udemy): Hones in specifically on dynamic programming in the Python programming language
• Greedy Algorithms, Minimum Spanning Trees, and Dynamic Programming (Coursera): A course offered by Stanford about dynamic programming and other algorithm-related topics
• Dynamic Programming: Applications in Machine Learning and Genomics (edX): Learn about two interesting applications of dynamic programming that meld science and technology, from UC San Diego

About the Author

Sam Gavis-Hughson, founder of Byte by Byte, helps software engineers successfully interview for jobs at top tech companies. He is the author of Dynamic Programming for Interviews , the ebook that shows anyone how to succeed at dynamic programming interviews.

The complete beginners guide to dynamic programming 

Dynamic programming isn't about design patterns; it's a way of thinking that breaks down a problem into individual components.

If you've been programming for long enough, you've probably heard the term dynamic programming. Often a key subject in technical interviews , the idea will also come up in design review meetings or regular interactions with fellow developers. This essay will examine what dynamic programming is and why you would use it. I'll be illustrating this concept with specific code examples in Swift, but the concepts I introduce can be applied to your language of choice. Let's begin!

A way of thinking

Unlike specific coding syntax or design patterns, dynamic programming isn't a particular algorithm but a way of thinking . Therefore, the technique takes many forms when it comes to implementation.

The main idea of dynamic programming is to consider a significant problem and break it into smaller, individualized components. When it comes to implementation, optimal techniques rely on data storage and reuse to increase algorithm efficiency. As we'll see, many questions in software development are solved using various forms of dynamic programming. The trick is recognizing when optimal solutions can be devised using a simple variable or require a sophisticated data structure or algorithm.

For example, code variables can be considered an elementary form of dynamic programming. As we know, a variable's purpose is to reserve a specific place in memory for a value to be recalled later.

While addNumbersMemo above does provide a simple introduction, the goal of a dynamic programming solution is to preserve previously seen values because the alternative could either be inefficient or could prevent you from answering the question. This design technique is known as memoization .

Code challenge—Pair of numbers

Over the years, I've had the chance to conduct mock interviews with dozens of developers preparing for interviews at top companies like Apple, Facebook, and Amazon. Most of us would be happy to skip the realities of the dreaded whiteboard or take-home coding project. However, the fact is that many of these brain-teaser questions are designed to test for a basic understanding of computer science fundamentals. For example, consider the following:

As developers, we know there are usually multiple ways to arrive at a solution. In this case, the goal is knowing which numbers should be paired to achieve the expected result. As people, it's easy for us to quickly scan the sequence of numbers and promptly come up with the pair of 9 and 2. However, an algorithm will need to either check and compare each value in the sequence or develop a more streamlined solution to help us find the values we are seeking. Let's review both techniques.

A brute force approach

Our first approach involves looking at the first value, then reviewing each subsequent value to determine if it will provide the difference needed to solve the question. For example, once our algorithm checks the value of the first array item, 8, it will then scan the remaining values for 3 (e.g., 11 - 8 = 3). However, we can see the value of 3 doesn't exist, so the algorithm will repeat the same process for the next value (in our case, 10) until it finds a successful matching pair. Without going into the details of big-O notation, we can assume this type of solution would have an average runtime of O(n ^ 2)time or greater, mainly because our algorithm works by comparing each value with every other value. In code, this can be represented as follows:

A memoized approach

Next, let's try a different approach using the idea of memoization. Before implementing our code, we can brainstorm how storing previously seen values will help streamline the process. While using a standard array is feasible, a set collection object (also referred to as a hash table or hash map) could provide an optimized solution.

Using a memoized approach, we've improved the algorithm's average run time efficiency to O(n + d) by adding previously seen values to a set collection object. Those familiar with hash-based structures will know that item insert and retrieval occurs in O(1) - constant time. This further streamlines the solution, as the set is designed to retrieve values in an optimized way regardless of size.

The Fibonacci sequence

When learning various programming techniques, one topic that comes to mind is recursion. Recursive solutions work by having a model that refers to itself. As such, recursive techniques are implemented through algorithms or data structures. A well-known example of recursion can be seen with the Fibonacci sequence—a numerical sequence made by adding the two preceding numbers (0, 1, 1, 2, 3, 5, 8, 13, 21, etc):

When examined, our code is error-free and works as expected. However, notice a few things about the performance of the algorithm:

Positions (n) fibRec() - Number of times called214510109151219

As shown, there's a significant increase in the number of times our function is called. Similar to our previous example, the algorithm's performance decreases exponentially based on the input size. This occurs because the operation does not store previously calculated values. Without access to stored variables, the only way we can obtain the required (preceding) values is through recursion. Assuming this code is used in a production setting, the function could introduce bugs or performance errors. Let's refactor the code to support a memoized approach:

This revised solution now supports memoization through the use of stored variables. Notice how the refactored code no longer requires a recursive technique. The two most previous values are added to a result, which is appended to the main array sequence. Even though the algorithm's performance still depends on the sequence size, our revisions have increased algorithmic efficiency to O(n) - linear time. In addition, our iterative solution should be easier to revise, test and debug since a single function is added to the call stack, thus reducing complexities with memory management and object scope.

We've learned that dynamic programming isn't a specific design pattern as it is a way of thinking. Its goal is to create a solution to preserve previously seen values to increase time efficiency. While examples include basic algorithms, dynamic programming provides a foundation in almost all programs. This includes the use of simple variables and complex data structures.

Learn C practically and Get Certified .

Popular Tutorials

Popular examples, reference materials, learn c interactively, dsa introduction.

• What is an algorithm?
• Data Structure and Types
• Why learn DSA?
• Asymptotic Notations

Master Theorem

Divide and Conquer Algorithm

Data Structures (I)

• Types of Queue
• Circular Queue
• Priority Queue

Data Structures (II)

• Linked List
• Linked List Operations
• Types of Linked List
• Heap Data Structure
• Fibonacci Heap
• Decrease Key and Delete Node Operations on a Fibonacci Heap

Tree based DSA (I)

• Tree Data Structure
• Tree Traversal
• Binary Tree
• Full Binary Tree
• Perfect Binary Tree
• Complete Binary Tree
• Balanced Binary Tree
• Binary Search Tree

Tree based DSA (II)

• Insertion in a B-tree
• Deletion from a B-tree
• Insertion on a B+ Tree
• Deletion from a B+ Tree
• Red-Black Tree
• Red-Black Tree Insertion
• Red-Black Tree Deletion

Graph based DSA

• Graph Data Structure
• Spanning Tree
• Strongly Connected Components
• Adjacency Matrix
• Adjacency List
• DFS Algorithm
• Breadth-first Search
• Bellman Ford's Algorithm

Sorting and Searching Algorithms

• Bubble Sort
• Selection Sort
• Insertion Sort
• Counting Sort
• Bucket Sort
• Linear Search
• Binary Search

Greedy Algorithms

Greedy Algorithm

• Ford-Fulkerson Algorithm
• Dijkstra's Algorithm
• Kruskal's Algorithm
• Prim's Algorithm
• Huffman Coding

Dynamic Programming

• Floyd-Warshall Algorithm
• Longest Common Sequence

Other Algorithms

Backtracking Algorithm

• Rabin-Karp Algorithm

DSA Tutorials

• What is an Algorithm?
• Longest Common Subsequence

Dynamic Programming is a technique in computer programming that helps to efficiently solve a class of problems that have overlapping subproblems and optimal substructure property.

If any problem can be divided into subproblems, which in turn are divided into smaller subproblems, and if there are overlapping among these subproblems, then the solutions to these subproblems can be saved for future reference. In this way, efficiency of the CPU can be enhanced. This method of solving a solution is referred to as dynamic programming.

Such problems involve repeatedly calculating the value of the same subproblems to find the optimum solution.

• Dynamic Programming Example

Let's find the fibonacci sequence upto 5th term. A fibonacci series is the sequence of numbers in which each number is the sum of the two preceding ones. For example, 0,1,1, 2, 3 . Here, each number is the sum of the two preceding numbers.

We are calculating the fibonacci sequence up to the 5th term.

• The first term is 0.
• The second term is 1.
• The third term is sum of 0 (from step 1) and 1(from step 2), which is 1.
• The fourth term is the sum of the third term (from step 3) and second term (from step 2) i.e. 1 + 1 = 2 .
• The fifth term is the sum of the fourth term (from step 4) and third term (from step 3) i.e. 2 + 1 = 3 .

Hence, we have the sequence 0,1,1, 2, 3 . Here, we have used the results of the previous steps as shown below. This is called a dynamic programming approach .

• How Dynamic Programming Works

Dynamic programming works by storing the result of subproblems so that when their solutions are required, they are at hand and we do not need to recalculate them.

This technique of storing the value of subproblems is called memoization. By saving the values in the array, we save time for computations of sub-problems we have already come across.

Dynamic programming by memoization is a top-down approach to dynamic programming. By reversing the direction in which the algorithm works i.e. by starting from the base case and working towards the solution, we can also implement dynamic programming in a bottom-up manner.

• Recursion vs Dynamic Programming

Dynamic programming is mostly applied to recursive algorithms. This is not a coincidence, most optimization problems require recursion and dynamic programming is used for optimization.

But not all problems that use recursion can use Dynamic Programming. Unless there is a presence of overlapping subproblems like in the fibonacci sequence problem, a recursion can only reach the solution using a divide and conquer approach.

That is the reason why a recursive algorithm like Merge Sort cannot use Dynamic Programming, because the subproblems are not overlapping in any way.

• Greedy Algorithms vs Dynamic Programming

Greedy Algorithms are similar to dynamic programming in the sense that they are both tools for optimization.

However, greedy algorithms look for locally optimum solutions or in other words, a greedy choice, in the hopes of finding a global optimum. Hence greedy algorithms can make a guess that looks optimum at the time but becomes costly down the line and do not guarantee a globally optimum.

Dynamic programming, on the other hand, finds the optimal solution to subproblems and then makes an informed choice to combine the results of those subproblems to find the most optimum solution.

Different Types of Dynamic Programming Algorithms

Table of contents.

• Introduction
• Different Types of Greedy Algorithm

Sorry about that.

Related Tutorials

DS & Algorithms

• Prep Courses
• Coding Questions
• Behavioral Questions
• Build Your Portfolio
• Goal-Setting
• Productivity
• Start a Blog
• Software Engineer
• Game Development
• Blockchain Developer
• Cloud Computing
• Web3 Developer
• The Complete Software Developer’s Career Guide
• 10 Steps to Learn Anything Quickly
• How to Market Yourself as a Software Developer
• Create a Blog That Boosts Your Career
• 10 Ways to Make Money From Your Blog
• Best Coding Hardware
• Blockchain Languages

The Ultimate Guide to Dynamic Programming

Written By Sam Gavis-Hughson

Did you feel a little shiver when you read that?

Imagine it again with those spooky Goosebumps letters.

Dynamic programming.

When I talk to students of mine over at Byte by Byte , nothing quite strikes fear into their hearts like dynamic programming.

And I can totally understand why. Dynamic programming (DP) is as hard as it is counterintuitive. Most of us learn by looking for patterns among different problems. But with dynamic programming, it can be really hard to actually find the similarities.

Even though the problems all use the same technique, they look completely different.

However, there is a way to understand dynamic programming problems and solve them with ease. And in this post I’m going to show you how to do just that.

What Is Dynamic Programming?

Before we get into all the details of how to solve dynamic programming problems, it’s key that we answer the most fundamental question:

What is dynamic programming?

Simply put, dynamic programming is an optimization technique that we can use to solve problems where the same work is being repeated over and over. You know how a web server may use caching? Dynamic programming is basically that.

However, dynamic programming doesn’t work for every problem. There are a lot of cases in which dynamic programming simply won’t help us improve the runtime of a problem at all. If we aren’t doing repeated work, then no amount of caching will make any difference.

To determine whether we can optimize a problem using dynamic programming, we can look at both formal criteria of DP problems. I’ll also give you a shortcut in a second that will make these problems much quicker to identify.

Let’s start with the formal definition.

A problem can be optimized using dynamic programming if it:

• has an optimal substructure.
• has overlapping subproblems.

If a problem meets those two criteria, then we know for a fact that it can be optimized using dynamic programming.

Optimal Substructure

Optimal substructure is a core property not just of dynamic programming problems but also of recursion in general. If a problem can be solved recursively, chances are it has an optimal substructure.

Optimal substructure simply means that you can find the optimal solution to a problem by considering the optimal solution to its subproblems.

For example, if we are looking for the shortest path in a graph, knowing the partial path to the end (the bold squiggly line in the image below), we can compute the shortest path from the start to the end, without knowing any details about the squiggly path.

What might be an example of a problem without optimal substructure?

Consider finding the cheapest flight between two airports. According to Wikipedia :

“Using online flight search, we will frequently find that the cheapest flight from airport A to airport B involves a single connection through airport C, but the cheapest flight from airport A to airport C involves a connection through some other airport D.”

While there is some nuance here, we can generally assume that any problem that we solve recursively will have an optimal substructure.

Overlapping Subproblems

Overlapping subproblems is the second key property that our problem must have to allow us to optimize using dynamic programming. Simply put, having overlapping subproblems means we are computing the same problem more than once.

Imagine you have a server that caches images. If the same image gets requested over and over again, you’ll save a ton of time. However, if no one ever requests the same image more than once, what was the benefit of caching them?

This is exactly what happens here. If we don’t have overlapping subproblems, there is nothing to stop us from caching values. It just won’t actually improve our runtime at all. All it will do is create more work for us.

For an example of overlapping subproblems, consider the Fibonacci problem. Here is a tree of all the recursive calls required to compute the fifth Fibonacci number:

Notice how we see repeated values in the tree. The number 3 is repeated twice, 2 is repeated three times, and 1 is repeated five times. Each of those repeats is an overlapping subproblem. There is no need for us to compute those subproblems multiple times because the value won’t change. If we cache it, we can save ourselves a lot of work.

When Should I Use Dynamic Programming?

To be absolutely certain that we can solve a problem using dynamic programming , it is critical that we test for optimal substructure and overlapping subproblems. Without those, we can’t use dynamic programming.

However, we can use heuristics to guess pretty accurately whether or not we should even consider using DP. This quick question can save us a ton of time.

All we have to ask is: Can this problem be solved by solving a combination problem?

Consider a few examples:

• Find the smallest number of coins required to make a specific amount of change . Look at all combinations of coins that add up to an amount, and count the fewest number.
• Find the most value of items that can fit in your knapsack . Find all combinations of items and determine the highest value combination.
• Find the number of different paths to the top of a staircase . Enumerate all the combinations of steps.

While this heuristic doesn’t account for all dynamic programming problems, it does give you a quick way to gut-check a problem and decide whether you want to go deeper.

Solve Any DP Problem Using the FAST Method

After seeing many of my students from Byte by Byte struggling so much with dynamic programming, I realized we had to do something. There had to be a system for these students to follow that would help them solve these problems consistently and without stress.

It was this mission that gave rise to The FAST Method .

The FAST Method is a technique that has been pioneered and tested over the last several years. As I write this, more than 8,000 of our students have downloaded our free e-book and learned to master dynamic programming using The FAST Method.

So how does it work?

FAST is an acronym that stands for F ind the first solution, A nalyze the solution, identify the S ubproblems, and T urn around the solution. Let’s break down each of these steps.

Find the First Solution

The first step to solving any dynamic programming problem using The FAST Method is to find the initial brute force recursive solution.

Your goal with Step One is to solve the problem without concern for efficiency. We just want to get a solution down on the whiteboard. This gives us a starting point (I’ve discussed this in much more detail here ).

There are a couple of restrictions on how this brute force solution should look:

• Each recursive call must be self-contained . If you are storing your result by updating some global variable, then it will be impossible for us to use any sort of caching effectively. We want to have a result that is completely dependent on the inputs of the function and not affected by any outside factors.
• Remove unnecessary variables. The fewer variables you pass into your recursive function, the better. We will be saving our cached values based on the inputs to the function, so it will be a pain if we have extraneous variables.

Let’s consider two examples here. We’ll use these examples to demonstrate each step along the way.

The first problem we’re going to look at is the Fibonacci problem. In this problem, we want to simply identify the n-th Fibonacci number. Recursively we can do that as follows:

It is important to notice here how each result of fib(n) is 100 percent dependent on the value of “n.” We have to be careful to write our function in this way. For example, while the following code works, it would NOT allow us to do DP.

While this may seem like a toy example, it is really important to understand the difference here. This second version of the function is reliant on result to compute the result of the function and result is scoped outside of the fibInner() function.

You can learn more about the difference here.

The second problem that we’ll look at is one of the most popular dynamic programming problems: 0-1 Knapsack Problem. For this problem, we are given a list of items that have weights and values, as well as a max allowable weight. We want to determine the maximum value that we can get without exceeding the maximum weight.

Here is our brute force recursive code:

With these brute force solutions, we can move on to the next step of The FAST Method.

Note: I’ve found that many people find this step difficult. It is way too large a topic to cover here, so if you struggle with recursion, I recommend checking out this monster post on Byte by Byte .

Analyze the First Solution

Now that we have our brute force solution, the next step in The FAST Method is to analyze the solution. In this step, we are looking at the runtime of our solution to see if it is worth trying to use dynamic programming and then considering whether we can use it for this problem at all.

We will start with a look at the time and space complexity of our problem and then jump right into an analysis of whether we have optimal substructure and overlapping subproblems. Remember that those are required for us to be able to use dynamic programming.

Let’s go back to our Fibonacci example.

Example 1 (Fibonacci):

For this problem, our code was nice and simple, but unfortunately our time complexity sucks. The easiest way to get a handle on what is going on in your code is to sketch out the recursive tree. Here’s the tree for fib(4) :

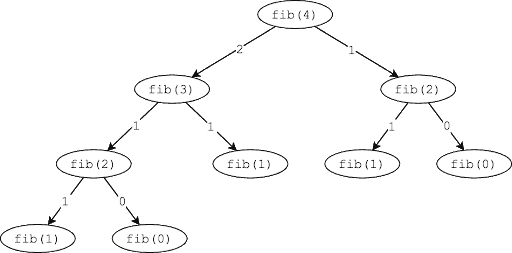
What we immediately notice here is that we essentially get a tree of height n . Yes, some of the branches are a bit shorter, but our Big Oh complexity is an upper bound. Therefore, to compute the time complexity, we can simply estimate the number of nodes in the tree.

For any tree, we can estimate the number of nodes as branching_factorheight , where the branching factor is the maximum number of children that any node in the tree has. That gives us a pretty terrible runtime of O(2n) .

So it would be nice if we could optimize this code, and if we have optimal substructure and overlapping subproblems, we could do just that.

In this case, we have a recursive solution that pretty much guarantees that we have an optimal substructure. We are literally solving the problem by solving some of its subproblems.

We also can see clearly from the tree diagram that we have overlapping subproblems. Notice fib(2) getting called two separate times? That’s an overlapping subproblem. If we drew a bigger tree, we would find even more overlapping subproblems.

Given that we have found this solution to have an exponential runtime and it meets the requirements for dynamic programming, this problem is clearly a prime candidate for us to optimize.

Example 2 (0-1 Knapsack):

The code for this problem was a little bit more complicated, so drawing it out becomes even more important. When we sketch out an example, it gives us much more clarity on what is happening ( see my process for sketching out solutions ).

Here’s what our tree might look like for the following inputs:

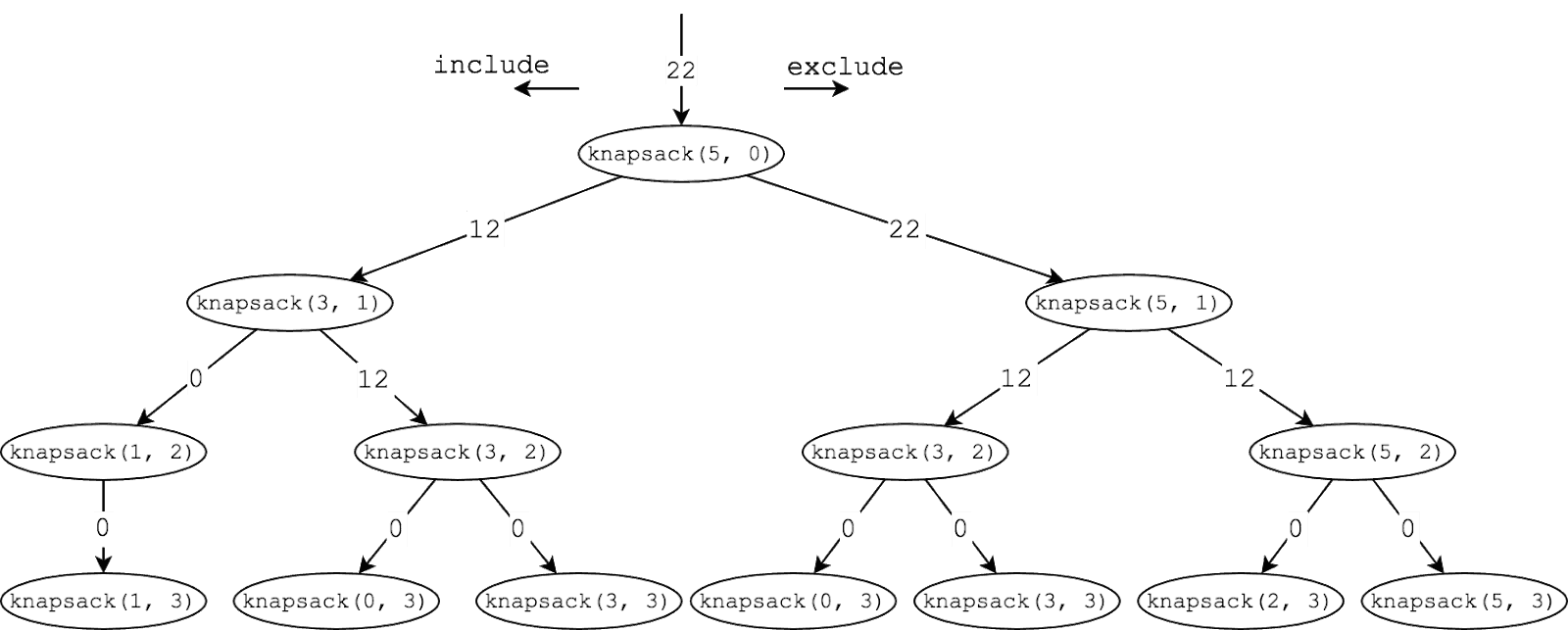
Note the two values passed into the function in this diagram are the maxWeight and the current index in our items list.

So with our tree sketched out, let’s start with the time complexity. Similar to our Fibonacci problem, we see that we have a branching tree of recursive calls where our branching factor is 2. This gives us a time complexity of O(2n) .

Do we have optimal substructure? Yep. Again, the recursion basically tells us all we need to know on that count.

And overlapping subproblems? Since we’ve sketched it out, we can see that knapsack(3, 2) is getting called twice, which is a clearly overlapping subproblem.

This also looks like a good candidate for DP.

Identify the Subproblems

The third step of The FAST Method is to identify the subproblems that we are solving. This is where we really get into the meat of optimizing our code.

We are going to start by defining in plain English what exactly our subproblem is. I’m always shocked at how many people can write the recursive code but don’t really understand what their code is doing. Understanding is critical.

Once we understand the subproblems, we can implement a cache that will memoize the results of our subproblems, giving us a top-down dynamic programming solution.

Memoization is simply the strategy of caching the results. We can use an array or map to save the values that we’ve already computed to easily look them up later.

We call this a top-down dynamic programming solution because we are solving it recursively. Essentially we are starting at the “top” and recursively breaking the problem into smaller and smaller chunks. This is in contrast to bottom-up , or tabular , dynamic programming, which we will see in the last step of The FAST Method.

So what is our subproblem here? This problem is quite easy to understand because fib(n) is simply the nth Fibonacci number. Since our result is only dependent on a single variable, n , it is easy for us to memoize based on that single variable.

Consider the code below. By adding a simple array, we can memoize our results. Notice the differences between this code and our code above:

See how little we actually need to change? Once we understand our subproblem, we know exactly what value we need to cache.

Now that we have our top-down solution, we do also want to look at the complexity. In this case, our code has been reduced to O(n) time complexity. We can pretty easily see this because each value in our dp array is computed once and referenced some constant number of times after that. This is much better than our previous exponential solution.

This problem starts to demonstrate the power of truly understanding the subproblems that we are solving. Specifically, not only does knapsack() take in a weight, it also takes in an index as an argument. So if you call knapsack(4, 2) what does that actually mean? What is the result that we expect? Well, if you look at the code, we can formulate a plain English definition of the function:

Here, “ knapsack(maxWeight, index) returns the maximum value that we can generate under a current weight only considering the items from index to the end of the list of items.”

With this definition, it makes it easy for us to rewrite our function to cache the results (and in the next section, these definitions will become invaluable):

Again, we can see that very little change to our original code is required. All we are doing is adding a cache that we check before computing any function. If the value in the cache has been set, then we can return that value without recomputing it.

In terms of the time complexity here, we can turn to the size of our cache. Each value in the cache gets computed at most once, giving us a complexity of O(n*W) .

Turn Around the Solution

The final step of The FAST Method is to take our top-down solution and “turn it around” into a bottom-up solution. This is an optional step, since the top-down and bottom-up solutions will be equivalent in terms of their complexity. However, many prefer bottom-up due to the fact that iterative code tends to run faster than recursive code.

With this step, we are essentially going to invert our top-down solution. Instead of starting with the goal and breaking it down into smaller subproblems, we will start with the smallest version of the subproblem and then build up larger and larger subproblems until we reach our target. This is where the definition from the previous step will come in handy.

To start, let’s recall our subproblem: fib(n) is the nth Fibonacci number.

Remember that we’re going to want to compute the smallest version of our subproblem first. That would be our base cases, or in this case, n = 0 and n = 1 .

Once we have that, we can compute the next biggest subproblem. To get fib(2) , we just look at the subproblems we’ve already computed. Once that’s computed we can compute fib(3) and so on.

So how do we write the code for this? Well, our cache is going to look identical to how it did in the previous step; we’re just going to fill it in from the smallest subproblems to the largest, which we can do iteratively.

Easy peasy lemon squeezy.

Another nice perk of this bottom-up solution is that it is super easy to compute the time complexity. Unlike recursion, with basic iterative code it’s easy to see what’s going on.

And that’s all there is to it. One note with this problem (and some other DP problems) is that we can further optimize the space complexity , but that is outside the scope of this post.

As is becoming a bit of a trend, this problem is much more difficult. However, you now have all the tools you need to solve the Knapsack problem bottom-up.

Recall our subproblem definition: “ knapsack(maxWeight, index) returns the maximum value that we can generate under a current weight only considering the items from index to the end of the list of items.”

To make things a little easier for our bottom-up purposes, we can invert the definition so that rather than looking from the index to the end of the array, our subproblem can solve for the array up to, but not including, the index.

With this, we can start to fill in our base cases. We’ll start by initializing our dp array. Whenever the max weight is 0, knapsack(0, index) has to be 0. Referring back to our subproblem definition, that makes sense. If the weight is 0, then we can’t include any items, and so the value must be 0.

The same holds if index is 0. Since we define our subproblem as the value for all items up to, but not including, the index, if index is 0 we are also including 0 items, which has 0 value.

From there, we can iteratively compute larger subproblems, ultimately reaching our target:

Again, once we solve our solution bottom-up, the time complexity becomes very easy because we have a simple nested for loop.

Dynamic Programming Doesn’t Have to Be Hard!

While dynamic programming seems like a scary and counterintuitive  topic, it doesn’t have to be. By applying structure to your solutions, such as with The FAST Method, it is possible to solve any of these problems in a systematic way.

Interviewers love to test candidates on dynamic programming because it is perceived as such a difficult topic, but there is no need to be nervous. Follow the steps and you’ll do great.

If you want to learn more about The FAST Method, check out my free e-book, Dynamic Programming for Interviews .

2-Strings DP Problems

• Black Friday Sale: Use coupon code THANKSGIVING to get 50% OFF on all our courses. If you already have a subscription and still interested in taking advantage of this offer, you can buy now and apply in your future subscriptions. This offer is also valid on GIFTS. Click here to get this offer.
• Our one-of-a-kind Low Level Design course is now released for General Availability. Go check it out.
• New Product Launch: We are delighted to announce the launch of our official site of our new product Low Level Design course: LowLevelDesign.io . To celebrate this auspicious milestone, we are offering 30% discount to our first 1000 subscribers starting December 10, 2021. Use coupon code EARLYBIRD . Offer ends on December 31, 2021. Happy Holidays! Happy Christmas!
• Algorithms and Data Structures: TheAlgorist.com
• System Design: www.System.Design
• Low Level Design: LowLevelDesign.io
• Frontend Engineering: FrontendEngineering.io
• Customer Support: [email protected]
• Feedback Form: https://www.thealgorists.com/Feedback .

The above content is written by:

Instructor:.

Abhishek Dey

Senior sde | chief architect, aws | microsoft | university of florida.

• Announcement: We are looking for Campus Ambassadors . If you are a student or professional and want to represent "The Algorists" in your school / college / university / community / institution, fill this form out at https://thealgorists.com/CampusAmbassador and we will be in touch with you shortly. You'd be a good fit if you believe in our mission of democratizing access to high quality and authoritative content to everyone who strives hard to become a better problem solver and achieve their dreams, so that anyone's financial condition does not become a barrier to access content that would help them better prepare for getting an A+ in exams, or prepare for competitive programming or campus interviews or industry hire tech interviews, or just improve overall problem solving skill. Spread the word about the existence of this platform, so that "The Algorists" can touch lives of many more people and help them become a better problem solver without burning a hole in their pocket. I know how it feels when you are a student and in tight budget, from my first-hand experience during my first year as grad student while pursuing my Masters in University of Florida. Time to give back to the community.

• Interview Problems on DP
• Practice DP
• Tutorial on Dynamic Programming
• Optimal Substructure
• Overlapping Subproblem
• Memoization
• Tabulation vs Memoization
• 0/1 Knapsack
• Unbounded Knapsack
• Coin Change
• Egg Dropping Puzzle
• Matrix Chain Multiplication
• Palindrome Partitioning
• DP on Arrays
• DP with Bitmasking
• DP on Trees
• DP on Graph

Memoization (1D, 2D and 3D)

• Memoization using decorators in Python
• Emulating a 2-d array using 1-d array
• What is memoization? A Complete tutorial
• 2D and 2.5D Memory organization
• JavaScript Memoization
• AIM-1 | 2024 | Question 12
• What is Memoization in React ?
• Numpy Reshape 2D To 3D Array
• Lodash _.memoize() Method
• Difference between 2D and 3D Shapes
• Mensuration in Maths | Formulas for 2D and 3D Shapes, Examples
• Explain Implement a memoization helper function
• GATE | GATE-CS-2000 | Question 12
• C | Dynamic Memory Allocation | Question 1
• 3D Array Interpolation MATLAB
• Difference between 2-D and 3-D animation
• NumPy - 3D matrix multiplication
• GATE | GATE CS Mock 2018 | Set 2 | Question 38

Most of the Dynamic Programming problems are solved in two ways:  

• Tabulation: Bottom Up
• Memoization: Top Down

One of the easier approaches to solve most of the problems in DP is to write the recursive code at first and then write the Bottom-up Tabulation Method or Top-down Memoization of the recursive function. The steps to write the DP solution of Top-down approach to any problem is to:  

• Write the recursive code
• Memoize the return value and use it to reduce recursive calls.

1-D Memoization The first step will be to write the recursive code. In the program below, a program related to recursion where only one parameter changes its value has been shown. Since only one parameter is non-constant, this method is known as 1-D memoization. E.g., the Fibonacci series problem to find the N-th term in the Fibonacci series. The recursive approach has been discussed here . Given below is the recursive code to find the N-th term:  

Time Complexity: O(2^n)

As at every stage we need to take 2 function calls and the height of the tree will be of the order of n.

Auxiliary Space: O(n)

The extra space is used due to recursion call stack.

A common observation is that this implementation does a lot of repeated work (see the following recursion tree). So this will consume a lot of time for finding the N-th Fibonacci number if done.  

The following problem has been solved using the Tabulation method.  In the program below, the steps to write a Top-Down approach program have been explained. Some modifications in the recursive program will reduce the complexity of the program and give the desired result. If fib(x) has not occurred previously, then we store the value of fib(x) in an array term at index x and return term[x] . By memoizing the return value of fib(x) at index x of an array, reduce the number of recursive calls at the next step when fib(x) has already been called. So without doing further recursive calls to compute the value of fib(x), return term[x] when fib(x) has already been computed previously to avoid a lot of repeated work as shown in the tree.  Given below is the memoized recursive code to find the N-th term.  

Time Complexity: O(n)

As we have to calculate values for all function calls just once and there will be n values of arguments so the complexity will reduce to O(n).

If the recursive code has been written once, then memoization is just modifying the recursive program and storing the return values to avoid repetitive calls of functions that have been computed previously.  

2-D Memoization In the above program, the recursive function had only one argument whose value was not constant after every function call. Below, an implementation where the recursive program has two non-constant arguments has been shown.  For e.g., Program to solve the standard Dynamic Problem LCS problem when two strings are given. The general recursive solution of the problem is to generate all subsequences of both given sequences and find the longest matching subsequence. The total possible combinations will be 2 n . Hence, the recursive solution will take O(2 n ) . The approach to writing the recursive solution has been discussed here.  Given below is the recursive solution to the LCS problem: 

Considering the above implementation, the following is a partial recursion tree for input strings “AXYT” and “AYZX”   

In the above partial recursion tree, lcs(“AXY”, “AYZ”) is being solved twice . On drawing the complete recursion tree, it has been observed that there are many subproblems that are solved again and again. So this problem has Overlapping Substructure property and recomputation of same subproblems can be avoided by either using Memoization or Tabulation. The tabulation method has been discussed here.   A common point of observation to use memoization in the recursive code will be the two non-constant arguments M and N in every function call. The function has 4 arguments, but 2 arguments are constant which does not affect the Memoization. The repetitive calls occur for N and M which have been called previously. So use a 2-D array to store the computed lcs(m, n) value at arr[m-1][n-1] as the string index starts from 0. Whenever the function with the same argument m and n are called again, we do not perform any further recursive call and return arr[m-1][n-1] as the previous computation of the lcs(m, n) has already been stored in arr[m-1][n-1], hence reducing the recursive calls that happen more than once.  Below is the implementation of the Memoization approach of the recursive code.  

3-D Memoization

In the above program, the recursive function had only two arguments whose values were not constant after every function call. Below, an implementation where the recursive program has three non-constant arguments is done.  For e.g., Program to solve the standard Dynamic Problem LCS problem for three strings. The general recursive solution of the problem is to generate all subsequences of both given sequences and find the longest matching subsequence. The total possible combinations will be 3 n . Hence, a recursive solution will take O(3 n ) .  Given below is the recursive solution to the LCS problem:  

The tabulation method has been shown here . On drawing the recursion tree completely, it has been noticed that there are many overlapping sub-problems which are been calculated multiple times. Since the function parameter has three non-constant parameters, hence a 3-D array will be used to memorize the value that was returned when lcs(x, y, z, m, n, o) for any value of m, n, and o was called so that if lcs(x, y, z, m, n, o) is again called for the same value of m, n, and o then the function will return the already stored value as it has been computed previously in the recursive call. arr[m][n][o] stores the value returned by the lcs(x, y, z, m, n, o) function call. The only modification that needs to be done in the recursive program is to store the return value of (m, n, o) state of the recursive function. The rest remains the same in the above recursive program.  Below is the implementation of the Memoization approach of the recursive code:  

Note: The array used to Memoize is initialized to some value (say -1) before the function call to mark if the function with the same parameters has been previously called or not.  

Please Login to comment...

Similar reads.

• Dynamic Programming

Improve your Coding Skills with Practice

What kind of Experience do you want to share?