how to solve olympiad geometry problems

AlphaGeometry: An Olympiad-level AI system for geometry

Trieu Trinh and Thang Luong

Copy link ×

Abstract neon geometric shapes and figures against a blue, space-like background.

Our AI system surpasses the state-of-the-art approach for geometry problems, advancing AI reasoning in mathematics

Reflecting the Olympic spirit of ancient Greece, the International Mathematical Olympiad is a modern-day arena for the world's brightest high-school mathematicians. The competition not only showcases young talent, but has emerged as a testing ground for advanced AI systems in math and reasoning.

In a paper published today in Nature , we introduce AlphaGeometry, an AI system that solves complex geometry problems at a level approaching a human Olympiad gold-medalist - a breakthrough in AI performance. In a benchmarking test of 30 Olympiad geometry problems, AlphaGeometry solved 25 within the standard Olympiad time limit. For comparison, the previous state-of-the-art system solved 10 of these geometry problems, and the average human gold medalist solved 25.9 problems.

Graph chart showing a set of 30 Olympiad geometry problems (IMO-AG-30), compiled from the Olympiads from 2000 to 2022.

In our benchmarking set of 30 Olympiad geometry problems (IMO-AG-30), compiled from the Olympiads from 2000 to 2022, AlphaGeometry solved 25 problems under competition time limits. This is approaching the average score of human gold medalists on these same problems. The previous state-of-the-art approach, known as “Wu’s method”, solved 10.

AI systems often struggle with complex problems in geometry and mathematics due to a lack of reasoning skills and training data. AlphaGeometry’s system combines the predictive power of a neural language model with a rule-bound deduction engine, which work in tandem to find solutions. And by developing a method to generate a vast pool of synthetic training data - 100 million unique examples - we can train AlphaGeometry without any human demonstrations, sidestepping the data bottleneck.

With AlphaGeometry, we demonstrate AI’s growing ability to reason logically, and to discover and verify new knowledge. Solving Olympiad-level geometry problems is an important milestone in developing deep mathematical reasoning on the path towards more advanced and general AI systems. We are open-sourcing the AlphaGeometry code and model , and hope that together with other tools and approaches in synthetic data generation and training, it helps open up new possibilities across mathematics, science, and AI.

It makes perfect sense to me now that researchers in AI are trying their hands on the IMO geometry problems first because finding solutions for them works a little bit like chess in the sense that we have a rather small number of sensible moves at every step. But I still find it stunning that they could make it work. It's an impressive achievement.

Ngô Bảo Châu, Fields Medalist and IMO gold medalist

AlphaGeometry adopts a neuro-symbolic approach

AlphaGeometry is a neuro-symbolic system made up of a neural language model and a symbolic deduction engine, which work together to find proofs for complex geometry theorems. Akin to the idea of “ thinking, fast and slow ”, one system provides fast, “intuitive” ideas, and the other, more deliberate, rational decision-making.

Because language models excel at identifying general patterns and relationships in data, they can quickly predict potentially useful constructs, but often lack the ability to reason rigorously or explain their decisions. Symbolic deduction engines, on the other hand, are based on formal logic and use clear rules to arrive at conclusions. They are rational and explainable, but they can be “slow” and inflexible - especially when dealing with large, complex problems on their own.

AlphaGeometry’s language model guides its symbolic deduction engine towards likely solutions to geometry problems. Olympiad geometry problems are based on diagrams that need new geometric constructs to be added before they can be solved, such as points, lines or circles. AlphaGeometry’s language model predicts which new constructs would be most useful to add, from an infinite number of possibilities. These clues help fill in the gaps and allow the symbolic engine to make further deductions about the diagram and close in on the solution.

Figure showing the process of AlphaGeometry solving a simple problem.

AlphaGeometry solving a simple problem: Given the problem diagram and its theorem premises (left), AlphaGeometry (middle) first uses its symbolic engine to deduce new statements about the diagram until the solution is found or new statements are exhausted. If no solution is found, AlphaGeometry’s language model adds one potentially useful construct (blue), opening new paths of deduction for the symbolic engine. This loop continues until a solution is found (right). In this example, just one construct is required.

Illustration of AlphaGeometry solving an Olympiad problem.

AlphaGeometry solving an Olympiad problem: Problem 3 of the 2015 International Mathematics Olympiad (left) and a condensed version of AlphaGeometry’s solution (right). The blue elements are added constructs. AlphaGeometry’s solution has 109 logical steps.

See the full solution.

Generating 100 million synthetic data examples

Geometry relies on understanding of space, distance, shape, and relative positions, and is fundamental to art, architecture, engineering and many other fields. Humans can learn geometry using a pen and paper, examining diagrams and using existing knowledge to uncover new, more sophisticated geometric properties and relationships. Our synthetic data generation approach emulates this knowledge-building process at scale, allowing us to train AlphaGeometry from scratch, without any human demonstrations.

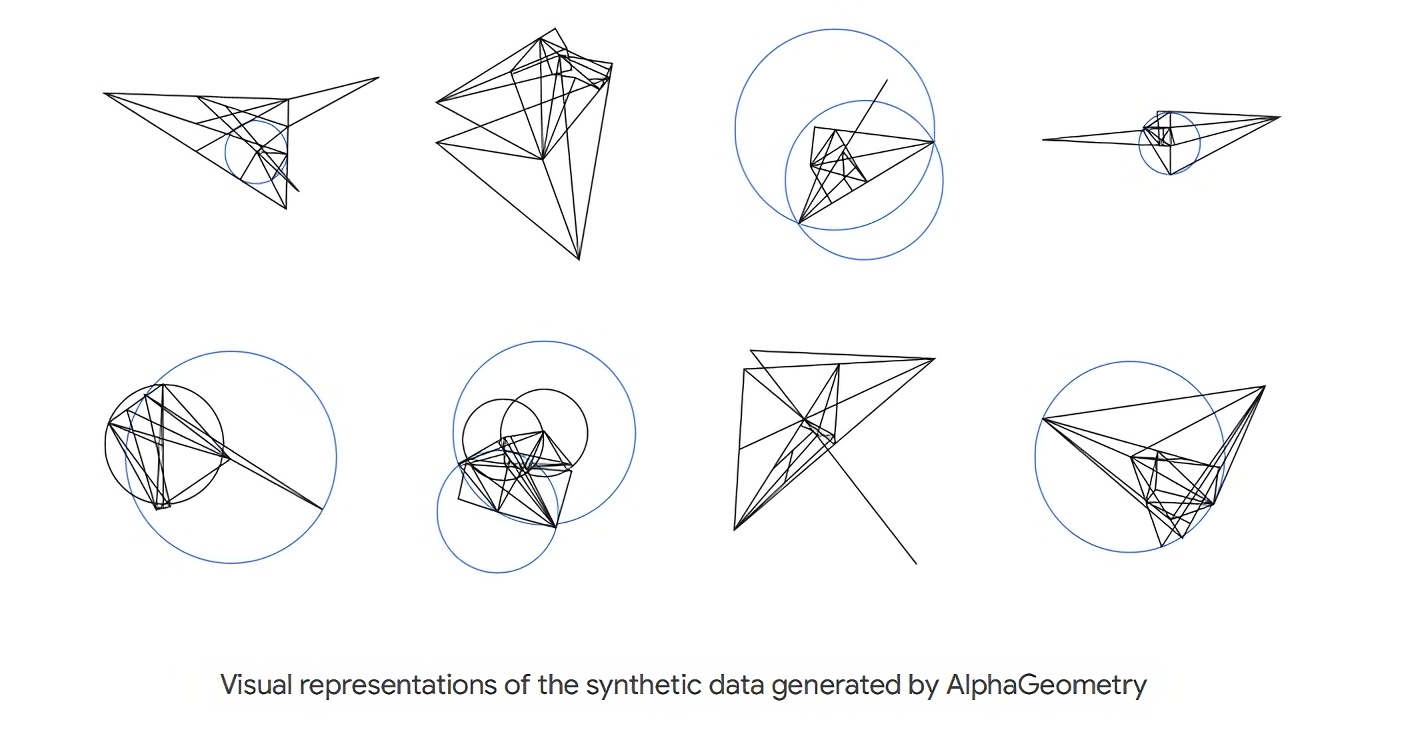
Using highly parallelized computing, the system started by generating one billion random diagrams of geometric objects and exhaustively derived all the relationships between the points and lines in each diagram. AlphaGeometry found all the proofs contained in each diagram, then worked backwards to find out what additional constructs, if any, were needed to arrive at those proofs. We call this process “symbolic deduction and traceback”.

Visual representations of the synthetic data generated by AlphaGeometry

That huge data pool was filtered to exclude similar examples, resulting in a final training dataset of 100 million unique examples of varying difficulty, of which nine million featured added constructs. With so many examples of how these constructs led to proofs, AlphaGeometry’s language model is able to make good suggestions for new constructs when presented with Olympiad geometry problems.

Pioneering mathematical reasoning with AI

The solution to every Olympiad problem provided by AlphaGeometry was checked and verified by computer. We also compared its results with previous AI methods, and with human performance at the Olympiad. In addition, Evan Chen, a math coach and former Olympiad gold-medalist, evaluated a selection of AlphaGeometry’s solutions for us. Chen said: “AlphaGeometry's output is impressive because it's both verifiable and clean. Past AI solutions to proof-based competition problems have sometimes been hit-or-miss (outputs are only correct sometimes and need human checks). AlphaGeometry doesn't have this weakness: its solutions have machine-verifiable structure. Yet despite this, its output is still human-readable. One could have imagined a computer program that solved geometry problems by brute-force coordinate systems: think pages and pages of tedious algebra calculation. AlphaGeometry is not that. It uses classical geometry rules with angles and similar triangles just as students do.”

AlphaGeometry's output is impressive because it's both verifiable and clean…It uses classical geometry rules with angles and similar triangles just as students do.

Evan Chen, math coach and Olympiad gold medalist

As each Olympiad features six problems, only two of which are typically focused on geometry, AlphaGeometry can only be applied to one-third of the problems at a given Olympiad. Nevertheless, its geometry capability alone makes it the first AI model in the world capable of passing the bronze medal threshold of the IMO in 2000 and 2015.

In geometry, our system approaches the standard of an IMO gold-medalist, but we have our eye on an even bigger prize: advancing reasoning for next-generation AI systems. Given the wider potential of training AI systems from scratch with large-scale synthetic data, this approach could shape how the AI systems of the future discover new knowledge, in math and beyond.

AlphaGeometry builds on Google DeepMind and Google Research’s work to pioneer mathematical reasoning with AI – from exploring the beauty of pure mathematics to solving mathematical and scientific problems with language models . And most recently, we introduced FunSearch , which made the first discoveries in open problems in mathematical sciences using Large Language Models.

Our long-term goal remains to build AI systems that can generalize across mathematical fields, developing the sophisticated problem-solving and reasoning that general AI systems will depend on, all the while extending the frontiers of human knowledge.

An illustration featuring a gold medal with a blue and white and red ribbon, with the medal covered in computer circuits, with colorful geometric shapes making up the background.

A.I.’s Latest Challenge: the Math Olympics

Watch out, nerdy high schoolers, AlphaGeometry is coming for your mathematical lunch.

Credit... Christian Gralingen

Supported by

Share full article

By Siobhan Roberts

Reported from Stanford, Calif.

Published Jan. 17, 2024 Updated Jan. 22, 2024

For four years, the computer scientist Trieu Trinh has been consumed with something of a meta-math problem: how to build an A.I. model that solves geometry problems from the International Mathematical Olympiad, the annual competition for the world’s most mathematically attuned high-school students.

Last week Dr. Trinh successfully defended his doctoral dissertation on this topic at New York University; this week, he described the result of his labors in the journal Nature. Named AlphaGeometry , the system solves Olympiad geometry problems at nearly the level of a human gold medalist.

While developing the project, Dr. Trinh pitched it to two research scientists at Google, and they brought him on as a resident from 2021 to 2023. AlphaGeometry joins Google DeepMind’s fleet of A.I. systems, which have become known for tackling grand challenges. Perhaps most famously, AlphaZero , a deep-learning algorithm, conquered chess in 2017. Math is a harder problem, as the number of possible paths toward a solution is sometimes infinite; chess is always finite.

“I kept running into dead ends, going down the wrong path,” said Dr. Trinh, the lead author and driving force of the project.

The paper’s co-authors are Dr. Trinh’s doctoral adviser, He He, at New York University; Yuhuai Wu, known as Tony, a co-founder of xAI (formerly at Google) who in 2019 had independently started exploring a similar idea; Thang Luong, the principal investigator, and Quoc Le, both from Google DeepMind.

Dr. Trinh’s perseverance paid off. “We’re not making incremental improvement,” he said. “We’re making a big jump, a big breakthrough in terms of the result.”

“Just don’t overhype it,” he said.

The big jump

A group portrait of four researchers posing causally outside a Google campus building on an overcast day.

Dr. Trinh presented the AlphaGeometry system with a test set of 30 Olympiad geometry problems drawn from 2000 to 2022. The system solved 25; historically, over that same period, the average human gold medalist solved 25.9. Dr. Trinh also gave the problems to a system developed in the 1970s that was known to be the strongest geometry theorem prover ; it solved 10.

Over the last few years, Google DeepMind has pursued a number of projects investigating the application of A.I. to mathematics . And more broadly in this research realm, Olympiad math problems have been adopted as a benchmark; OpenAI and Meta AI have achieved some results. For extra motivation, there’s the I.M.O. Grand Challenge , and a new challenge announced in November, the Artificial Intelligence Mathematical Olympiad Prize , with a $5 million pot going to the first A.I. that wins Olympiad gold.

The AlphaGeometry paper opens with the contention that proving Olympiad theorems “represents a notable milestone in human-level automated reasoning.” Michael Barany, a historian of mathematics and science at the University of Edinburgh, said he wondered whether that was a meaningful mathematical milestone. “What the I.M.O. is testing is very different from what creative mathematics looks like for the vast majority of mathematicians,” he said.

Terence Tao , a mathematician at the University of California, Los Angeles — and the youngest-ever Olympiad gold medalist, when he was 12 — said he thought that AlphaGeometry was “nice work” and had achieved “surprisingly strong results.” Fine-tuning an A.I.-system to solve Olympiad problems might not improve its deep-research skills, he said, but in this case the journey may prove more valuable than the destination.

As Dr. Trinh sees it, mathematical reasoning is just one type of reasoning, but it holds the advantage of being easily verified. “Math is the language of truth,” he said. “If you want to build an A.I., it’s important to build a truth-seeking, reliable A.I. that you can trust,” especially for “safety critical applications.”

Proof of concept

AlphaGeometry is a “neuro-symbolic” system. It pairs a neural net language model (good at artificial intuition, like ChatGPT but smaller) with a symbolic engine (good at artificial reasoning, like a logical calculator, of sorts).

And it is custom-made for geometry. “Euclidean geometry is a nice test bed for automatic reasoning, since it constitutes a self-contained domain with fixed rules,” said Heather Macbeth, a geometer at Fordham University and an expert in computer-verified reasoning. (As a teenager, Dr. Macbeth won two I.M.O. medals.) AlphaGeometry “seems to constitute good progress,” she said.

The system has two especially novel features. First, the neural net is trained only on algorithmically generated data — a whopping 100 million geometric proofs — using no human examples. The use of synthetic data made from scratch overcame an obstacle in automated theorem-proving: the dearth of human-proof training data translated into a machine-readable language. “To be honest, initially I had some doubts about how this would succeed,” Dr. He said.

Second, once AlphaGeometry was set loose on a problem, the symbolic engine started solving; if it got stuck, the neural net suggested ways to augment the proof argument. The loop continued until a solution materialized, or until time ran out (four and a half hours). In math lingo, this augmentation process is called “auxiliary construction.” Add a line, bisect an angle, draw a circle — this is how mathematicians, student or elite, tinker and try to gain purchase on a problem. In this system, the neural net learned to do auxiliary construction, and in a humanlike way. Dr. Trinh likened it to wrapping a rubber band around a stubborn jar lid in helping the hand get a better grip.

“It’s a very interesting proof of concept,” said Christian Szegedy, a co-founder at xAI who was formerly at Google. But it “leaves a lot of questions open,” he said, and is not “easily generalizable to other domains and other areas of math.”

Dr. Trinh said he would attempt to generalize the system across mathematical fields and beyond. He said he wanted to step back and consider “the common underlying principle” of all types of reasoning.

Stanislas Dehaene , a cognitive neuroscientist at the Collège de France who has a research interest in foundational geometric knowledge, said he was impressed with AlphaGeometry’s performance. But he observed that “it does not ‘see’ anything about the problems that it solves” — rather, it only takes in logical and numerical encodings of pictures. (Drawings in the paper are for the benefit of the human reader.) “There is absolutely no spatial perception of the circles, lines and triangles that the system learns to manipulate,” Dr. Dehaene said. The researchers agreed that a visual component might be valuable; Dr. Luong said it could be added, perhaps within the year, using Google’s Gemini, a “multimodal” system that ingests both text and images.

Soulful solutions

In early December, Dr. Luong visited his old high school in Ho Chi Minh City, Vietnam, and showed AlphaGeometry to his former teacher and I.M.O. coach, Le Ba Khanh Trinh. Dr. Lê was the top gold medalist at the 1979 Olympiad and won a special prize for his elegant geometry solution. Dr. Lê parsed one of AlphaGeometry’s proofs and found it remarkable yet unsatisfying, Dr. Luong recalled: “He found it mechanical, and said it lacks the soul, the beauty of a solution that he seeks.”

Dr. Trinh had previously asked Evan Chen, a mathematics doctoral student at M.I.T. — and an I.M.O. coach and Olympiad gold medalist — to check some of AlphaGeometry’s work. It was correct, Mr. Chen said, and he added that he was intrigued by how the system had found the solutions.

“I would like to know how the machine is coming up with this,” he said. “But, I mean, for that matter, I would like to know how humans come up with solutions, too.”

Explore Our Coverage of Artificial Intelligence

News and Analysis

News Corp, the Murdoch-owned empire of publications like The Wall Street Journal and The New York Post, announced that it had agreed to a deal with OpenAI to share its content to train and service A.I. chatbots.

The Silicon Valley company Nvidia was again lifted by sales of its A.I. chips , but it faces growing competition and heightened expectations.

Researchers at the A.I. company Anthropic claim to have found clues about the inner workings of large language models, possibly helping to prevent their misuse and to curb their potential threats.

The Age of A.I.

D’Youville University in Buffalo had an A.I. robot speak at its commencement . Not everyone was happy about it.

A new program, backed by Cornell Tech, M.I.T. and U.C.L.A., helps prepare lower-income, Latina and Black female computing majors for A.I. careers.

Publishers have long worried that A.I.-generated answers on Google would drive readers away from their sites. They’re about to find out if those fears are warranted, our tech columnist writes .

A new category of apps promises to relieve parents of drudgery, with an assist from A.I. But a family’s grunt work is more human, and valuable, than it seems.

DeepMind AI solves hard geometry problems from mathematics olympiad

AlphaGeometry scores almost as well as the best students on geometry questions from the International Mathematical Olympiad

By Alex Wilkins

17 January 2024

Geometrical problems involve proving facts about angles or lines in complicated shapes

Google DeepMind

An AI from Google DeepMind can solve some International Mathematical Olympiad (IMO) questions on geometry almost as well as the best human contestants.

How does ChatGPT work and do AI-powered chatbots “think” like us?

“The results of AlphaGeometry are stunning and breathtaking,” says Gregor Dolinar, the IMO president. “It seems that AI will win the IMO gold medal much sooner than was thought even a few months ago.”

The IMO, aimed at secondary school students, is one of the most difficult maths competitions in the world. Answering questions correctly requires mathematical creativity that AI systems have long struggled with. GPT-4, for instance, which has shown remarkable reasoning ability in other domains, scores 0 per cent on IMO geometry questions, while even specialised AIs struggle to answer as well as average contestants.

This is partly down to the difficulty of the problems, but it is also because of a lack of training data. The competition has been run annually since 1959, and each edition consists of just six questions. Some of the most successful AI systems, however, require millions or billions of data points. Geometrical problems in particular, which make up one or two of the six questions and involve proving facts about angles or lines in complicated shapes, are particularly difficult to translate to a computer-friendly format.

Thang Luong at Google DeepMind and his colleagues have bypassed this problem by creating a tool that can generate hundreds of millions of machine-readable geometrical proofs. When they trained an AI called AlphaGeometry using this data and tested it on 30 IMO geometry questions, it answered 25 of them correctly, compared with an estimated score of 25.9 for an IMO gold medallist based on their scores in the contest.

Sign up to our The Daily newsletter

The latest science news delivered to your inbox, every day.

“Our [current] AI systems are still struggling with the ability to do things like deep reasoning, where we need to plan ahead for many, many steps and also see the big picture, which is why mathematics is such an important benchmark and test set for us on our quest to artificial general intelligence,” Luong told a press conference.

AlphaGeometry consists of two parts, which Luong compares to different thinking systems in the brain: a fast, intuitive system and a slower, more analytical one. The first, intuitive part is a language model, similar to the technology behind ChatGPT, called GPT-f. It has been trained on the millions of generated proofs and suggests which theorems and arguments to try next for a problem. Once it suggests a next step, a slower but more careful “symbolic reasoning” engine uses logical and mathematical rules to fully construct the argument that GPT-f has suggested. The two systems then work in tandem, switching between one another until a problem has been solved.

While this method is remarkably successful at solving IMO geometry problems, the answers it constructs tend to be longer and less “beautiful” than human proofs, says Luong. However, it can also spot things that humans miss. For example, it discovered a better and more general solution to a question from the 2004 IMO than was listed in the official answers.

The future of AI: The 5 possible scenarios, from utopia to extinction

Solving IMO geometry problems in this way is impressive, says Yang-Hui He at the London Institute for Mathematical Sciences, but the system is inherently limited in the mathematics it can use because IMO problems should be solvable using theorems taught below undergraduate level. Expanding the amount of mathematical knowledge AlphaGeometry has access to might improve the system or even help it make new mathematical discoveries, he says.

It would also be interesting to see how AlphaGeometry copes with not knowing what it needs to prove, as mathematical insight can often come from exploring theorems with no set proof, says He. “If you don’t know what your endpoint is, can you find within the set of all [mathematical] paths whether there is a theorem that is actually interesting and new?”

Last year, algorithmic trading company XTX Markets announced a $10 million prize fund for AI maths models, with a $5 million grand prize for the first publicly shared AI model that can win an IMO gold medal, as well as smaller progress prizes for key milestones.

“Solving an IMO geometry problem is one of the planned progress prizes supported by the $10 million AIMO challenge fund,” says Alex Gerko at XTX Markets. “It’s exciting to see progress towards this goal, even before we have announced all the details of this progress prize, which would include making the model and data openly available, as well as solving an actual geometry problem during a live IMO contest.”

DeepMind declined to say whether it plans to enter AlphaGeometry in a live IMO contest or whether it is expanding the system to solve other IMO problems not based on geometry. However, DeepMind has previously entered public competitions for protein folding prediction to test its AlphaFold system .

Journal reference:

Nature DOI: 10.1038/s41586-023-06747-5

mathematics /

Sign up to our weekly newsletter

Receive a weekly dose of discovery in your inbox! We'll also keep you up to date with New Scientist events and special offers.

More from New Scientist

Explore the latest news, articles and features

DeepMind AI with built-in fact-checker makes mathematical discoveries

Crystal-hunting deepmind ai could help discover new wonder materials, game-playing deepmind ai can beat top humans at chess, go and poker, deepmind ai can beat the best weather forecasts - but there is a catch, popular articles.

This AI just figured out geometry — is this a step towards artificial reasoning?

Download the Nature Podcast 27 January 2024

In this episode:

0:55 The AI that deduces solutions to complex maths problems

Researchers at Google Deepmind have developed an AI that can solve International Mathematical Olympiad-level geometry problems, something previous AIs have struggled with. They provided the system with a huge number of random mathematical theorems and proofs, which it used to approximate general rules of geometry. The AI then applied these rules to solve the Olympiad problems and show its workings for humans to check. The researchers hope their system shows that it is possible for AIs to ‘learn’ basic principles from large amounts of data and use them to tackle complex logical challenges, which could prove useful in fields outside mathematics.

Research article: Trinh et al.

09:46 Research Highlights

A stiff and squishy ‘hydrospongel’ — part sponge, part hydrogel — that could find use in soft robotics, and how the spread of rice paddies in sub-Saharan Africa helps to drive up atmospheric methane levels.

Research Highlight: Stiff gel as squishable as a sponge takes its cue from cartilage

Research Highlight: A bounty of rice comes at a price: soaring methane emissions

12:26 The food-web effects of mass predator die-offs

Mass mortality events, sometimes called mass die-offs, can result in huge numbers of a single species perishing in a short period of time. But there’s not a huge amount known about the effects that events like these might be having on wider ecosystems. Now, a team of researchers have built a model ecosystem to observe the impact of mass die-offs on the delicate balance of populations within it.

Research article: Tye et al.

20:53 Briefing Chat

An update on efforts to remove the stuck screws on OSIRIS-REx’s sample container, the ancient, fossilized skin that was preserved in petroleum, and a radical suggestion to save the Caribbean’s coral reefs.

OSIRIS-REx Mission Blog: NASA’s OSIRIS-REx Team Clears Hurdle to Access Remaining Bennu Sample

Nature News: This is the oldest fossilized reptile skin ever found — it pre-dates the dinosaurs

Nature News: Can foreign coral save a dying reef? Radical idea sparks debate

Subscribe to Nature Briefing, an unmissable daily round-up of science news, opinion and analysis free in your inbox every weekday.

Never miss an episode. Subscribe to the Nature Podcast on Apple Podcasts , Google Podcasts , Spotify or your favourite podcast app. An RSS feed for the Nature Podcast is available too.

Shamini Bundell

Welcome back to the Nature Podcast, this week: an AI that’s figured out geometry…

Benjamin Thompson

…and how mass predator die-offs might affect ecosystems. I’m Benjamin Thompson.

And I’m Shamini Bundell.

<Music>

First up on the show, reporter Nick Petrić Howe has been learning about an AI that can logically deduce solutions to complex mathematical problems. Here’s Nick.

Nick Petrić Howe

You might think that computers are pretty good at maths. When I have a mathematical conundrum for instance I will often reach for a calculator or a trusty spreadsheet. But fundamentally a lot of maths is about logic — deducing what makes sense from the information you have. Meaning that a lot of mathematical problems are really just complicated puzzles. In fact, there is a competition known as the Mathematical Olympiad where high school students are given challenges, where they need to figure out solutions to such puzzles. They’ll be given a series of statements like “x + y = this” and also “5 to the power y equals that” etc and then they’ll have to use these to figure out the solution to a puzzle, like “what could x be?” Challenges like this are difficult though for computers and AIs, as Thang Luong, deep learning researcher and former Mathematical Olympiad competitor, explains.

Thang Luong

Let's say if I give you two basket, each have like 10 balls, how many balls do I have in total. So these actually machine can solve pretty well. But for problem by Mathematical Olympiad, it will involve very deep reasoning. So the model have to think for many, many, many steps before it can arrive at a solution. That's actually what makes it so interesting.

In fact, tackling these Mathematical Olympiad problems has been of interest to AI researchers for decades and it’s been a tough nut to crack. The best AIs still fare worse than the average International Mathematical Olympiad competitor. The thing that makes these lympiad challenges so well… challenging is that there is essentially an infinitely large number of ways you could try and tackle a problem. Where do you even start? Arguably, you have to reason — logically draw conclusions from what is given to you. In other words, if this is true, then this should also be true. This is something that we normally input into our machines, they don’t normally work it out for themselves from scratch.

So that would require, you know, a lot of thinking ahead, and sometimes creativity as well. So the machine needs to be creative. It needs to think for a long time.

Now the way that many Ais solve challenging problems is by scouring through a lot of data and ‘learning’ from it certain rules about how one thing applies to another. This is how Large Language Models, like ChatGPT, are built for example. But for would-be Mathematical Olympiad Ais there’s a snag here.

Large language models, like ChatGPT can read the entire internet, you know, it understand all kinds of knowledge from Wikipedia, from Reddit. But then for Mathematical Olympiad problems, these kinds of data to teach machine is so limited. There’s not many material on the Internet, there are a few forums, but that’s not enough data to really teach the machine.

But despite this lack of training data , Thang and a team of researchers are demonstrating an AI, known as AlphaGeometry in Nature this week. And unlike previous attempts their system can reach the top levels of human performance on geometry problems from the Maths Olympiad. But for the AI to solve these problems, the team had to solve their own — what to do about the lack of data? Well, they made it themselves.

We leveraged a large amount of computation at Google to synthesise a large amount of training data for the machine to learn from scratch. So, in total, we was able to generate 100 millions of theorem and proof so that the machine can learn all of these by itself. And then it can learn to generalise the new problems.

This huge volume of random mathematical theorems and proofs — statements and the relevant logical argument that back them up — were given to AlphaGeometry, which used them to work out general rules of geometry. With that in place, it was ready to take on the Mathematical Olympiad. AlphaGeometry was fed the olympiad problems, which it worked on using a two-part system, a neural network and a symbolic system, two different kinds of AIs that each operate at a different pace. They worked together, to solve the problems

So the neural network you can think of it like system one, because neural network can think very fast. It can be creative, it can suggest interesting lines and points to help unlock a solution. And then we have a symbolic system, which is system two, it’s reliable, but it's slow.

The symbolic system was the one that was trying to use logic to solve the puzzle — it did the heavy lifting, using the geometry rules it ‘learned’ from the synthetic data to solve the problem. And you might think that system would be enough, but actually you need the creative system one as well. As often the slow symbolic system gets stuck and so it needs a bit of creative juice to get its cogs turning. For example, if the symbolic system is working on a problem involving triangles and gets stuck, the creative system one neural network can suggest maybe splitting the triangle in two and thinking about those two ‘new’ triangles instead. The problem would be the same, but, if you'll pardon the phrase, it would be able to think about it in a different way. The systems then go back and forward like this until the problem is solved. Together they would create a proof, essentially showing how it solved the problem, which humans could then check. And this is exactly what happened. The system was given a series of Maths Olympiad problems, and it figured out ways to solve them and wrote out its solutions. Thang and the team then sent the AI’s solutions to pupils of the Maths Olympiad and the US coach who were then able to verify them. Overall, Thang was pleased with how their AlphaGeometry theoretically would have performed, if it was in an International Mathematical Olympiad.

We were very happy that for the year 2000, 2015 AlphaGeometry was able to solve all the geometry problem in that year. So, you can think of it like an AI for the first time achieved the bronze medal.

The AI would win bronze as it only focused on geometry, whereas the actual competition involves other kinds of maths as well. But, if you did just look at geometry problems then AlphaGeometry was almost at the gold-medallist level — solving 25 out of 30 problems where gold medallists solve on average 25.9. However, in years other than 2000 and 2015 the AI wasn’t able to solve all the geometry problems, which could perhaps be down to certain geometry theories not being part of the synthetic data that the AI was using. Another issue was that the solutions that AlphaGeometry came up with were very long, which may be down to much the same reason. Effectively, the AI only knew the very basic rules of geometry, whereas humans are able to use other theorems and even other mathematical notations to shorten their explanations. So in the future Thang would like to make the solutions a bit more… elegant .

The solution from AlphaGeometry for the year 2015, it’s a long list of steps, it’s 109 steps in the solution. This is something that we're not optimised for actually, so far we only optimised to get the solution, but it can also be in the future, we might want to optimise for some beauty, you know, because with 109 steps, it will be a lot of work for people to actually read the proof.

Beautiful or not though, Thang believes that AlphaGeometry shows that it’s possible to build AIs which can ‘learn’ basic principles from large amounts of data and apply them to other situations. For some researchers, this could be a step towards building AIs that could ‘reason’ and potentially come up with solutions even in fields outside mathematics.

It really tells that we can actually build AI to learn from scratch. And then in the future, hopefully AI can discover new knowledge from other domains.

That was Thang Luong, from Google DeepMind. He’s based in the US. For more on that story, check out the show notes for a link to the paper.

Coming up, how researchers built their own ecosystem to find out what happens when a large number of predators die off in a short period. Right now though, it’s time for the Research Highlights, with Dan Fox.

A new material dubbed a ‘hydrospongel’ could find uses in soft robotics by mimicking living tissue. Tissue, like cartilage, can withstand heavy loads and hold large quantities of water, which is helpful in biological systems. But this combination is a challenge for synthetic materials. Hydrogels, for instance, are good at holding lots of water, but they tend to irreversibly deform when squashed. Sponges are resilient to heavy loads springing back after being deformed, but this lack of stiffness means they are too soft for many uses, and drain their liquid contents too readily. Now, researchers have designed a new material made from a network of Kevlar polymer fibres enriched with nitrogen atoms. The interwoven polymers — similar to those used in bulletproof vests — made the gel-like substance stiff, while creating nanoscale pores that trapped water and allowed it to diffuse. Under high compression, the spaghetti like network released water and got squashed before springing back. The material held more than 5,000 times its own weight in water and was 22 times stiffer than comparable water-rich gels. The authors say it could be used in drug delivery, or to build scaffolds for tissue engineering. You can soak up the rest of that research in Nature Materials .

The level of methane in the atmosphere is rising, and scientists have attributed much of that rise to emissions from tropical Africa. And new research puts a large percentage of the continent’s increased emissions down to rice production. Like cattle and natural wetlands, flooded rice paddies can host micro-organisms that emit methane. Between 2008 and 2018, rice production in sub-Saharan Africa doubled. And so a team of researchers recalculated emissions to take this into account. The new number suggests that rice growing in Africa accounted for nearly a third of the increase in the continent’s methane emissions between 2006 and 2017, and for 7% of the global increase in the same period. With aims for rice production in the region to double again between 2019 and 2030, multinational goals of reducing methane emissions by 30% will require deep reductions elsewhere to compensate. You could read that research in full in Nature Climate Change .

<music>

Ecosystems are all about balance. For example — take a super simplified, three-stage food web — plants, herbivores, carnivores. The nutrients in the system feed the plants, which feed herbivores which feed the carnivores. And so the quantity of nutrients impacts the rest of the system from the bottom up . At the same time, the carnivores eat the herbivores and keep their numbers in check, which reduces the number of plants eaten and so allows more plants to grow and so the system is regulated from the top down . Top down and bottom-up effects like these exist in constant, shifting, complex balance, but what happens when that balance is interrupted? Mass Mortality Events, sometimes called mass die-offs, can result in huge numbers of a single species dying off in a short period of time. Events like these have been seen in a variety of different animals: fish, birds, antelope the list goes on. And the numbers of animals that perish can be staggering, in some cases estimates range into the millions or even billions. But there’s not a huge amount known about the effects that events like these might be having on wider ecosystems. Well, that is something that Adam Siepielski from the University of Arkansas and his colleagues have been studying. I gave Adam a call.

Adam Siepielski

I mean, what we wanted to do was, in part, test some of the theory that we had been developing, and we really wanted to know, could you take these really wonderful classic ideas in community ecology, top-down effects where predators have an important role in affecting primary producers like plants, or algae and ecosystems and bottom-up effects, where nutrients are the important factor regulating primary producers and ecosystems and could we combine them. And then use those combinations to make a prediction about how a system would actually respond when predators die, decompose for these nutrients and generate that bottom-up effect.

So obviously, if you want to test this hypothesis and work out what's happening during a mass die-off, you have to study an ecosystem, right? But you can't go into the wild and cause a mass die-off, of course. So what you've done, then you've actually built your own freshwater ecosystem, a series of artificial ecosystems to test what a predator mass die-off might do. How do you go about making these ecosystems and what does one look like?

So, we did take this classic approach in ecology, and generally these little, they're called mesocosms, they're sort of like a smaller version of like a complex lake-ecosystem. What do they look like? If you ever go out to like a farm or something and see a big barrel of water that cattle are drinking water from, that's what those things are, there's nothing special about them we fill them up with water and then we just sort of start seeding it. A lot of the basic things of the food web naturally kind of come in like some of the bacteria will get in there. But you know, we put some like leaf litter in there to start to decompose that releases nutrients that allows algae, phytoplankton the base of this food web to start to grow in the system. We went out to a local lake and we collected zooplankton, the things that eat all the phytoplankton, so the algae and the diatoms, that sort of thing. And then we eventually stocked it with fish, bluegill, which are really common game fish, and really one of the most important predator species of zooplankton in the part of the lake that we were looking at. So basically, we just established like, three different trophic levels that naturally occur in lakes.

And so you had these artificial ecosystems then, and you treated them in different ways. Some of them you just left as they were, some of them, you removed the fish manually. And some of them you used electricity, in part, to cause a mass die-off of the fish. What did you see? What was the difference between the ecosystems? How do they compare?

Yeah, so after we, you know, induced this mass mortality event, we compared a number of different features of the remaining food levels that were present. And if you remove the fish, one of the things that happens is that the zooplankton become more abundant, because the predators that ate them are now gone. And when they become more abundant, the phytoplankton — the things that the zooplankton eat — start to go down. But one of the unique facets though, was that because in a mass mortality event, when the fish are dying and then decomposing, the zooplankton aren't able to simply consume all of the phytoplankton up and cause the system to sort of collapse. What happens is that because those fish die, and decompose and release those nutrients, that kind of causes a fertilisation effect, that allows for the primary producers, the phytoplankton to stay abundant, even though there's this increase in the zooplankton herbivores in a system. What that actually looks like is that it becomes very similar to the control system where everything is being like, nicely regulated. And so it kind of looks a little bit more just like an intact ecosystem,

And how does this fit then with ideas of what might happen?

I mean, so we had developed some mathematical theory where we had tried to make predictions for what would happen, and some of those predictions that we had actually sort of generated a few possibilities, because one thing that we have sort of surmised could happen, and does sometimes happened during a possible like, mortality event, is that the death of those predators could sort of have almost like a toxifying-like effect, and that they could decompose and cloudy the water like so much, that the primary producers become a little bit light limited. And they couldn't even begin to proliferate. Alternatively, and what we found, though, was that, that doesn't really seem to happen, those predators do go to the bottom, they decomposed to release those nutrients, like nitrogen and phosphorus and causes those producers to increase. So it matched very well. Like I remember, when we first got the data, we were like, holy cow, that looks exactly like what we thought it was going to look like. And that was really reassuring for, you know, community ecologists to be able to say that, you know, we've got this beautiful, messy, complex ecosystem that has all these things going on, we can simplify it into this little body of a couple of differential equations, sort of make these projections for how these things should look. But then when you actually get the empirical data based on, you know, experiments from these mesocosms, it was amazing. I was like, this is so cool. It's like we were able to, you know, kind of predict these things.

I mean, what does this result mean, Adam? Because naively one can make the argument that a mass die-off event of predators isn't that much of an impact to an ecosystem, because as you've shown, the ecosystem will continue. But presumably, it's much more complicated than that.

Oh, yeah. I mean, the experiment that we were able to do wasn't in a natural lake, or anything like that, which is, you know, inherently much more complicated. But I think this is important, because it should give us some reassurance about our understanding of how nature is working. Because, again, like we're able to take decades old work and combine it to make reasonably good predictions about how an ecosystem might respond to an event like a mass mortality event or some sort of ecological catastrophe.

And in previous work, you've suggested that mass die-offs are happening more frequently. How does this work fit into that do you think? In terms of our knowledge of what's causing these things or how they can be prevented, for example.

These predator die-offs are happening because of extreme climatic events, disease outbreaks, human disturbances, that sort of thing. So I don't know that the paper can really tell us much about necessarily preventing those as much as it can tell us about the sort of signal of one of these events having happened. And it can also, I think, it informs us though that, you know, maybe reporting these events is an important thing to do. They are still, I think, relatively rare events. So even though you know, the data does suggest that they may be increasing in frequency, we may be observing them more often. I think that we can only continue to understand them better — what the causes of them are, and the effects of them are in ecological systems, if we can continue to get data and monitor these sorts of events from actually happening in nature. And I think citizens that are going out to lakes, and they observe, you know, a large number of animals dying, reporting that to their local authority would be really, really valuable. Just the document that hey, you know, this did happen.

That was Adam Siepielski from the University of Arkansas in the US. To read his paper about the research, which is out this week in Nature , head over to the show notes for a link.

And finally on the show, it's time for the Briefing Chat, where we discuss a couple of articles that have been highlighted in the Nature Briefing . So Ben, tell us what you've been reading this week.

Well, actually, I've got a quick update on a story we covered last week on the podcast and listeners might remember me and Noah and Flora talking about NASA's problems opening the OSIRIS-REx’s containment canister, right. And they were trying to get to the samples of the Bennu asteroid that were inside. Now there was two screws that they couldn't figure out how to open. And we come up with some, frankly, terrible ideas of how they could have gone about that. And Noah asked Flora, like what's the timeframe for this? And she said, I don't know quite what's going to happen. And the answer is, it happened the day after the podcast came out–

–oh, great–

–and NASA have released these two screws and announced that they've got them undone.

Do you think it's a coincidence that you guys put forward some suggestions, and then the very next day, they actually managed to solve it?

I don't Shamini, let’s be honest. But back in the real world, of course–

–okay, so NASA had to design some special tools to fit into the sealed box that the container is currently in. This is quite a small thing. And they've made essentially a very fancy screwdriver, which is not really like any screwdriver that I've seen before.

Yeah, what does it look like the fancy screwdriver?

It's got a lot of right angles, Shamini, I'll say that. But check out the show notes for a link where listeners can have a look at it. And I will say that all this info has come from NASA's OSIRIS REx blog. But we're not quite there yet. Okay, they managed to loosen these two screws, and there's a few more stages yet until they can get actually into the canister proper and look at the rocks and the dust inside. And I think what's going to happen is they're gonna open it up, then take a load of super high-res photos to see what they've got and then start kind of weighing it out and parcelling it out. And some of the previous stuff that was collected has already gone out to researchers. And presumably this will be eventually too.

I presume it's gonna take more than a week, this time for us to have another update on this story while they all analyse the samples.

I'm hoping that tomorrow–

–tomorrow, yes!–

–yeah, and then next week, we can talk about that too. But it is kind of exciting, and hats off to them for doing it. And it's hoped, of course, that these samples will tell us a huge amount about the origins of the solar system and how you know, the things we see around us came to be because some of these samples will have dated back maybe four and a half billion years, estimates suggest. But I've got another story today as well and I'm gonna keep going, which is also pretty old. Not quite that old I have to say, only 289 million years old.

Is that all? Yeah, pretty recent, yeah.

I mean a snip really, let's be honest. And it's a story that I read about in Nature , and it's about a few shreds of fossilised skin that had been discovered and described in a paper in Current Biology .

Ooh, so whose skin is it from 200 and whatever it was million years ago?

Well, that's a great question. And it seems to have come from a lizard-like animal known as Captorhinus aguti . But these skin fragments are only a few millimetres across, but they are the oldest skin ever found from a group of animals collectively known as amniotes. Okay, this includes reptiles and birds and mammals like me and you, basically all terrestrial vertebrates, except amphibians. And so yeah, quite a big find. And this one is the oldest by quite some distance.

And we've definitely talked about dinosaur skin before, which is always exciting thinking about sort of what dinosaurs looked like and stuff, but this is even older than that?

Oh, millions of years older than that, before the rise of dinosaurs at all. And what's interesting is, in many cases, I think what researchers look at is the imprint of skin on rock, right? So we have the kind of pressing, but this is something different, this is actual skin, 3D, fossilised skin, and and it's very rare to find soft tissues, okay, because usually they decompose which is why we only ever find bones. But this is kind of one of those culmination of a bunch of different factors which has led to this discovery. So this skin was found in a cave in Oklahoma, and this cave has kind of got lots of conditions suitable for preserving soft tissues, right. And one of them in particular is that during the fossilisation process, there was oil seeping in from the walls of this cave, right? And this is brilliant line in the article over at nature.com and it's essentially that this skin was pickled in petroleum, like it's almost jet black. But it's completely infused with hydrocarbons and that's one of the reasons that it's in such good nick. And I will say it kind of looks a bit like crocodile skin, right, it's got those bumps on it as well. But because it's so well preserved, the researchers could actually look at the layers within it, which is kind of amazing right, you can see the dermis, and you can see the epidermis and these different kind of bits that are making it up.

And is this being so ancient tell us something about the evolution of these kinds of soft tissues that we don't usually get to see.

Interesting one, I don't know if it gives any definitive answers. But as I said, like finding soft tissue is so rare. And the development of skin was kind of a big evolutionary step for animals moving from living in water to living on land, because of course, the skin is an amazing barrier that keeps the outside out and the inside, in. And so knowing more about when this happened, I think it's such an interesting one is such a key step in evolution of amniotes. And hopefully, they'll be more findings like this. So we can maybe get things even further back in the evolutionary timeline, because much of what we know about how the Tree of Life exists is from studying bones, because that's all that ever is preserved.

Yeah, it sounds like it was quite a sort of unique situation with a very oily cave. So we're going to take a lot more searching to find even more of this rarely preserved, soft tissue. So that's very cool. I do like these fossil stories. I'm going to bring us back to the modern day about the future. It's a climate-change related story, I've got an it's quite an unusual one. So it's an article in Nature but it's not based on a paper, it's based on a presentation that a researcher gave at the Society for Integrative and Comparative Biology annual meeting at the beginning of January. And he's basically got quite a sort of radical proposal to deal with the massive problem of corals in the Caribbean, dying off and really, really suffering and struggling with climate change and other issues.

Of course, a serious problem with the oceans warming up. And I think we've covered on the show before, there's a bunch of different ways that people have been looking to maybe overcome or reverse this issue, you know, growing coral in a lab and transplanting it, dropping big blocks of concrete down for coral to grow on that sort of thing, right? I mean, presumably, if this is a radical solution, this is maybe not those.

Yeah, in a way more radical than those. But yeah, exactly as you've said, like there's all these things that people have been trying, and people are suggesting, because it's a really urgent problem. The corals in this area have been dying off for decades, loads of them are bleached. The coral reefs themselves are really important because they protect against coastal erosion. There's obviously all the sort of young fish and the ecosystem around them. And once you've got the sort of bleaching effects, like for example, there was a massive heatwave last summer, so that had a really, really bad impact. And each time these kinds of things happen, you've got the sort of remaining bleached bit of the reefs that are more likely to erode or collapse. And then it's harder to do things like as you said, transplant new baby corals from the lab and try and plant them there. Which, by the way, it was sort of noted in this article that planting all these young native corals hasn't really worked. It's not great, hence, more radical solution being proposed or being at least introduced into the discussion. The question is, what if instead of growing these native coral species and trying to transplant them, and help them grow, what if we just give up on the native species and get in species from other reefs that are inherently hardier, tougher and might thrive in the Caribbean? So, for example, corals from the Indo Pacific.

I mean, that’s an interesting one, because we had a long read podcast a few weeks ago, about assisted migration, which was moving endangered species away from habitats that are under threat because of climate change, to new habitats, and kind of controversial, right? Kind of considered to be a last resort–

–absolutely–

–and there were concerns about, you know, the threats that the introduced species might bring diseases or upset an ecosystem. And as we heard earlier in the podcast, these things are very finely balanced. I mean, this is kind of the opposite of that, right is taking a healthy species to an endangered habitat.

Yeah, and you’re absolutely right, this both controversial and last resort. So one environmentalist quoted in this article describes it as “unpopular and painful”. Basically, this goes against all of the sort of principles that environmentalists, conservationists usually try and maintain, which is to protect native species and not just bring in other species from outside and the guy who proposed this, his name is Mikhail Matz, I hope I'm pronouncing that right. And there's a quote from him that says “it's an 11 th -hour solution. And it's now 11.45”. He wouldn't be suggesting this — I think is the implication there — unless, you know, we weren't in such a dire situation. And predicting dire situations into the future as well like, there are predictions that this coming summer the heatwaves in the Caribbean could be too just as bad or worse as they were last year.

And so as you say this was described in a talk, this isn't in a peer-reviewed journal. Is this purely theoretical? Or is this based on some experiments? What are we talking about?

Yeah this is theoretical at this stage. And it's also, at this point, it's so against all the principles that you'd have a really hard time even trying to push anything like this through. And the sort of intention here, I think, is to actually start this conversation and say, like, look, we're not in a good state, we have to talk about this. And there are suggestions for experiments that could be done. You know you’ve mentioned some of the obvious downsides earlier, like, there could be diseases that you've introduced from one reef halfway across the world into another one. So would growing the little transplanted corals in a lab helped to reduce the disease risk. Are there sort of areas where you could do a trial of this kind of thing of introducing these hardier corals from elsewhere, in places where if they were to sort of take over and spread, they wouldn't be able to spread out to then other regions, and you know, absolutely might not work. So, the Caribbean corals are struggling with the heat and with the pollution there. And also, there are obviously diseases specific to Caribbean corals. So who knows what happens when you bring in these other corals. Will they even survive? But the tone from a lot of people quoted in this article is just one of we have to try something. So one biologist sort of talking about the things that have been tried so far, and that haven't worked, says we either do something else, or we lose the corals.

Hmm an interesting one, and I'm sure a lot of people have got a lot of opinions on it. So we will follow that one closely I'm sure over the next months, and potentially years. But let's leave it there for this week's Briefing Chat, Shamini. And listeners, if you want to know more about the stories we discussed, or how to get more like them delivered direct to your inbox by signing up to the Nature Briefing , look out for links in the show notes.

And that's all for this episode then. If you want to get in touch with us, then you can. We’re on X, @NaturePodcast, or you can send us an email to [email protected]'m Shamini Bundell.

And I'm Benjamin Thompson. See you next time.

doi: https://doi.org/10.1038/d41586-024-00145-1

Climate change
Materials science
Mathematics and computing

A tiny killer is making an entire region’s sea urchins disintegrate

Research Highlight 23 MAY 24

Save the forest to save the tiger — why vegetation conservation matters

News & Views 21 MAY 24

China's Yangtze fish-rescue plan is a failure, study says

News 20 MAY 24

Singapore Airlines turbulence: why climate change is making flights rougher

News Explainer 22 MAY 24

Why role-playing games can spur climate action

World View 22 MAY 24

Why babies in South Korea are suing the government

Metals strengthen with increasing temperature at extreme strain rates

Article 22 MAY 24

Strain-invariant stretchable radio-frequency electronics

Combined cement and steel recycling could cut CO2 emissions

News & Views 22 MAY 24

Professor, Division Director, Translational and Clinical Pharmacology

Cincinnati Children’s seeks a director of the Division of Translational and Clinical Pharmacology.

Cincinnati, Ohio

Cincinnati Children's Hospital & Medical Center

Data Analyst for Gene Regulation as an Academic Functional Specialist

The Rheinische Friedrich-Wilhelms-Universität Bonn is an international research university with a broad spectrum of subjects. With 200 years of his...

53113, Bonn (DE)

Rheinische Friedrich-Wilhelms-Universität

Recruitment of Global Talent at the Institute of Zoology, Chinese Academy of Sciences (IOZ, CAS)

The Institute of Zoology (IOZ), Chinese Academy of Sciences (CAS), is seeking global talents around the world.

Beijing, China

Institute of Zoology, Chinese Academy of Sciences (IOZ, CAS)

Full Professorship (W3) in “Organic Environmental Geochemistry (f/m/d)

The Institute of Earth Sciences within the Faculty of Chemistry and Earth Sciences at Heidelberg University invites applications for a FULL PROFE...

Heidelberg, Brandenburg (DE)

Universität Heidelberg

Postdoctoral scholarship in Structural biology of neurodegeneration

A 2-year fellowship in multidisciplinary project combining molecular, structural and cell biology approaches to understand neurodegenerative disease

Umeå, Sweden

Umeå University

Quick links

Explore articles by subject
Guide to authors
Editorial policies

DeepMind’s latest AI can solve geometry problems

DeepMind, the Google AI R&D lab, believes that the key to more capable AI systems might lie in uncovering new ways to solve challenging geometry problems.

To that end, DeepMind today unveiled AlphaGeometry — a system that the lab claims can solve as many geometry problems as the average International Mathematical Olympiad gold medalist. AlphaGeometry, the code for which was open sourced this morning, solves 25 Olympiad geometry problems within the standard time limit, beating the previous state-of-the-art system’s 10.

“Solving Olympiad-level geometry problems is an important milestone in developing deep mathematical reasoning on the path toward more advanced and general AI systems,” Trieu Trinh and Thang Luong, Google AI research scientists, wrote in a blog post published this morning. “[We] hope that … AlphaGeometry helps open up new possibilities across mathematics, science and AI.”

Why the focus on geometry? DeepMind asserts that proving mathematical theorems, or logically explaining why a theorem (e.g. the Pythagorean theorem) is true, requires both reasoning and the ability to choose from a range of possible steps toward a solution. This problem solving approach could — if DeepMind’s right — turn out to be useful in general-purpose AI systems someday.

“Demonstrating that a particular conjecture is true or false stretches the abilities of even the most advanced AI systems today,” read DeepMind press materials shared with TechCrunch. “Toward that goal, being able to prove mathematical theorems … is an important milestone as it showcases the mastery of logical reasoning and the ability to discover new knowledge.”

But training an AI system to solve geometry problems poses unique challenges.

Owing to the complexities of translating proofs into a format machines can understand, there’s a dearth of usable geometry training data. And many of today’s cutting-edge generative AI models, while exceptional at identifying patterns and relationships in data, lack the ability to reason logically through theorems.

DeepMind’s solution was twofold.

In designing AlphaGeometry, the lab paired a “neural language” model — a model architecturally along the lines of ChatGPT — with a “symbolic deduction engine,” an engine that leverages rules (e.g. mathematical rules) to infer solutions to problems. Symbolic engines can be inflexible and slow, especially when dealing with large or complicated datasets. But DeepMind mitigated these issues by having the neural model “guide” the deduction engine through possible answers to given geometry problems.

In lieu of training data, DeepMind created its own synthetic data, generating 100 million “synthetic theorems” and proofs of varying complexity. The lab then trained AlphaGeometry from scratch on the synthetic data — and evaluated it on Olympiad geometry problems

Olympiad geometry problems are based on diagrams that need “constructs” to be added before they can be solved, such as points, lines or circles. Applied to these problems, AlphaGeometry’s neural model predicts which constructs might be useful to add — predictions that AlphaGeometry’s symbolic engine uses to make deductions about the diagrams to identify like solutions.

“With so many examples of how these constructs led to proofs, AlphaGeometry’s language model is able to make good suggestions for new constructs when presented with Olympiad geometry problems,” Trinh and Luong write. “One system provides fast, ‘intuitive’ ideas, and the other more deliberate, rational decision-making.”

The results of AlphaGeometry’s problem solving, which were published in a study in the journal Nature this week, are likely to fuel the long-running debate over whether AI systems should be built on symbol manipulation — that is, manipulating symbols that represent knowledge using rules — or the ostensibly more brain-like neural networks.

Proponents of the neural network approach argue that intelligent behavior — from speech recognition to image generation — can emerge from nothing more than massive amounts of data and compute. As opposed to symbolic systems, which solve tasks by defining sets of symbol-manipulating rules dedicated to particular jobs (like editing a line in word processor software), neural networks try to solve tasks through statistical approximation and learning from examples.

Neural networks are the cornerstone of powerful AI systems like OpenAI’s DALL-E 3 and GPT-4. But, claim supporters of symbolic AI, they’re not the end-all be-all; symbolic AI might be better positioned to efficiently encode the world’s knowledge, reason their way through complex scenarios and “explain” how they arrived at an answer, these supporters argue.

As a hybrid symbolic-neural network system akin to DeepMind’s AlphaFold 2 and AlphaGo, AlphaGeometry perhaps demonstrates that the two approaches — symbol manipulation and neural networks — combined is the best path forward in the search for generalizable AI. Perhaps.

“Our long-term goal remains to build AI systems that can generalize across mathematical fields, developing the sophisticated problem-solving and reasoning that general AI systems will depend on, all the while extending the frontiers of human knowledge,” Trinh and Luong write. “This approach could shape how the AI systems of the future discover new knowledge, in math and beyond.”

More TechCrunch

Get the industry’s biggest tech news, techcrunch daily news.

Every weekday and Sunday, you can get the best of TechCrunch’s coverage.

Startups Weekly

Startups are the core of TechCrunch, so get our best coverage delivered weekly.

TechCrunch Fintech

The latest Fintech news and analysis, delivered every Sunday.

TechCrunch Mobility

TechCrunch Mobility is your destination for transportation news and insight.

Startups Weekly: Drama at Techstars. Drama in AI. Drama everywhere.

Welcome to Startups Weekly — Haje‘s weekly recap of everything you can’t miss from the world of startups. Sign up here to get it in your inbox every Friday. Well,…

From Plaid to Figma, here are the startups that are likely — or definitely — not having IPOs this year

Last year’s investor dreams of a strong 2024 IPO pipeline have faded, if not fully disappeared, as we approach the halfway point of the year. 2024 delivered four venture-backed tech…

Feds add nine more incidents to Waymo robotaxi investigation

Federal safety regulators have discovered nine more incidents that raise questions about the safety of Waymo’s self-driving vehicles operating in Phoenix and San Francisco. The National Highway Traffic Safety Administration…

Pitch Deck Teardown: Terra One’s $7.5M Seed deck

Terra One’s pitch deck has a few wins, but also a few misses. Here’s how to fix that.

Women in AI: Chinasa T. Okolo researches AI’s impact on the Global South

Chinasa T. Okolo researches AI policy and governance in the Global South.

Disrupt 2024 early-bird tickets fly away next Friday

TechCrunch Disrupt takes place on October 28–30 in San Francisco. While the event is a few months away, the deadline to secure your early-bird tickets and save up to $800…

Big tech companies are plowing money into AI startups, which could help them dodge antitrust concerns

Another week, and another round of crazy cash injections and valuations emerged from the AI realm. DeepL, an AI language translation startup, raised $300 million on a $2 billion valuation;…

Harlem Capital is raising a $150 million fund

If raised, this new fund, the firm’s third, would be its largest to date.

US pharma giant Cencora says Americans’ health information stolen in data breach

About half a million patients have been notified so far, but the number of affected individuals is likely far higher.

Last day to vote for TC Disrupt 2024 Audience Choice program

Attention, tech enthusiasts and startup supporters! The final countdown is here: Today is the last day to cast your vote for the TechCrunch Disrupt 2024 Audience Choice program. Voting closes…

Signal’s Meredith Whittaker on the Telegram security clash and the ‘edge lords’ at OpenAI

Among other things, Whittaker is concerned about the concentration of power in the five main social media platforms.

Lucid Motors slashes 400 jobs ahead of crucial SUV launch

Lucid Motors is laying off about 400 employees, or roughly 6% of its workforce, as part of a restructuring ahead of the launch of its first electric SUV later this…

Google invests $350 million in Indian e-commerce giant Flipkart

Google is investing nearly $350 million in Flipkart, becoming the latest high-profile name to back the Walmart-owned Indian e-commerce startup. The Android-maker will also provide Flipkart with cloud offerings as…

Jio Financial unit to buy $4.32B of telecom gear from Reliance Retail

A Jio Financial unit plans to purchase customer premises equipment and telecom gear worth $4.32 billion from Reliance Retail.

Foursquare just laid off 105 employees

Foursquare, the location-focused outfit that in 2020 merged with Factual, another location-focused outfit, is joining the parade of companies to make cuts to one of its biggest cost centers –…

Using memes, social media users have become red teams for half-baked AI features

“Running with scissors is a cardio exercise that can increase your heart rate and require concentration and focus,” says Google’s new AI search feature. “Some say it can also improve…

ESA prepares for the post-ISS era, selects The Exploration Company, Thales Alenia to develop cargo spacecraft

The European Space Agency selected two companies on Wednesday to advance designs of a cargo spacecraft that could establish the continent’s first sovereign access to space. The two awardees, major…

Expressable brings speech therapy into the home

Expressable is a platform that offers one-on-one virtual sessions with speech language pathologists.

The biggest French startups in 2024 according to the French government

The French Secretary of State for the Digital Economy as of this year, Marina Ferrari, revealed this year’s laureates during VivaTech week in Paris. According to its promoters, this fifth…

Spotify to shut off Car Thing for good, leading users to demand refunds

Spotify is notifying customers who purchased its Car Thing product that the devices will stop working after December 9, 2024. The company discontinued the device back in July 2022, but…

X should bring back stars, not hide ‘likes’

Elon Musk’s X is preparing to make “likes” private on the social network, in a change that could potentially confuse users over the difference between something they’ve favorited and something…

$6M fine for robocaller who used AI to clone Biden’s voice

The FCC has proposed a $6 million fine for the scammer who used voice-cloning tech to impersonate President Biden in a series of illegal robocalls during a New Hampshire primary…

Tesla lobbies for Elon and Kia taps into the GenAI hype

Welcome back to TechCrunch Mobility — your central hub for news and insights on the future of transportation. Sign up here for free — just click TechCrunch Mobility! Is it…

App developer Crowdaa raises €1.2M and plans a US expansion

Crowdaa is an app that allows non-developers to easily create and release apps on the mobile store.

Canva launches a proper enterprise product — and they mean it this time

Back in 2019, Canva, the wildly successful design tool, introduced what the company was calling an enterprise product, but in reality it was more geared toward teams than fulfilling true…

2 days left to vote for Disrupt Audience Choice

TechCrunch Disrupt 2024 isn’t just an event for innovation; it’s a platform where your voice matters. With the Disrupt 2024 Audience Choice Program, you have the power to shape the…

Ticketmaster antitrust lawsuit could give new hope to ticketing startups

The United States Department of Justice and 30 state attorneys general filed a lawsuit against Live Nation Entertainment, the parent company of Ticketmaster, for alleged monopolistic practices. Live Nation and…

‘Pro-competition’ rules for Big Tech make it through UK’s pre-election wash-up

The U.K. will shortly get its own rulebook for Big Tech, after peers in the House of Lords agreed Thursday afternoon to pass the Digital Markets, Competition and Consumer bill…

Spotify experiments with an AI DJ that speaks Spanish

Spotify’s addition of its AI DJ feature, which introduces personalized song selections to users, was the company’s first step into an AI future. Now, Spotify is developing an alternative version…

Arc Search’s new Call Arc feature lets you ask questions by ‘making a phone call’

Call Arc can help answer immediate and small questions, according to the company.

DeepMind AI solves hard geometry problems from mathematics olympiad

By Alex Wilkins

An AI from Google DeepMind can solve some International Mathematical Olympiad (IMO) questions on geometry almost as well as the best human contestants.

How does ChatGPT work and do AI-powered chatbots “think” like us?

"The results of AlphaGeometry are stunning and breathtaking," says Gregor Dolinar, the IMO president. "It seems that AI will win the IMO gold medal much sooner than was thought even a few months ago."

This is partly down to the difficulty of the problems, but it is also because of a lack of training data. The competition has been run annually since 1959, and each edition consists of just six questions. Some of the most successful AI systems, however, require millions or billions of data points. Geometrical problems in particular, which make up two of the six questions and involve proving facts about angles or lines in complicated shapes, are particularly difficult to translate to a computer-friendly format.

The future of AI: The 5 possible scenarios, from utopia to extinction

It would also be interesting to see how AlphaGeometry copes with not knowing what it needs to prove, as mathematical insight can often come from exploring theorems with no set proof, says He. “If you don't know what your endpoint is, can you find within the set of all [mathematical] paths whether there is a theorem that is actually interesting and new?”

“Solving an IMO geometry problem is one of the planned progress prizes supported by the $10 million AIMO challenge fund,” says Alex Gerko at XTX Markets. “It's exciting to see progress towards this goal, even before we have announced all the details of this progress prize, which would include making the model and data openly available, as well as solving an actual geometry problem during a live IMO contest.”

Journal reference:

Nature DOI: 10.1038/s41586-023-06747-5

DeepMind AI solves hard geometry problems from mathematics olympiad

January 17, 2024

AI Does Math as Well as Math Olympians

Until now computers have failed to solve mathematical problems. But the AI program AlphaGeometry has succeeded in finding proofs for dozens of theorems from the International Mathematical Olympiad

By Manon Bischoff

A man sitting at a desk, facing a geometric shape

Kenn Brown/MondoWorks

T he International Mathematical Olympiad (IMO) is probably the most prestigious competition for preuniversity students. Every year students from around the world compete for its coveted bronze, silver and gold medals. Soon artificial-intelligence programs could be competing with them, too.

In January a team led by Trieu H. Trinh of Google DeepMind and New York University unveiled a new AI program called AlphaGeometry in the journal Nature. The researchers reported that the program was able to solve 25 out of 30 geometry problems from past IMOs—a success rate similar to that of human gold medalists. The AI also found a more general solution to a problem from the 2004 IMO that had escaped the attention of experts.

Over two days students competing in the IMO must solve six problems from different mathematical domains. Some of the problems are so complicated that even experts cannot solve them. They usually have short, elegant solutions but require a lot of creativity, which makes them particularly interesting to AI researchers.

On supporting science journalism

If you're enjoying this article, consider supporting our award-winning journalism by subscribing . By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

Translating a mathematical proof into a programming language that computers know is a difficult task. There are formal programming languages specifically developed for geometry, but they make little use of methods from other areas of mathematics—so if a proof requires an intermediate step that involves, say, complex numbers, programming languages specialized for geometry cannot be used.

To solve this problem, Trinh and his colleagues created a data set that doesn’t require the translation of human-generated proofs into a formal language. They first had an algorithm generate a set of geometric “premises,” or starting points: for example, a triangle with some of its measurements drawn in and additional points marked along its sides. The researchers then used a deductive algorithm to infer further properties of the triangle, such as which angles matched and which lines were perpendicular to each other. By combining the premises with the derived properties, the researchers created a training data set consisting of theorems and corresponding proofs. For example, a problem could involve proving a certain characteristic of a triangle—say, that two of its angles were equal. The corresponding solution would then consist of the steps that led the deductive algorithm to it.

To solve problems at the level of an IMO, however, AlphaGeometry needed to go further. “The key missing piece is generating new proof terms,” Trinh and his team wrote in their paper. For example, to prove something about a triangle, you might need to introduce new points and lines that weren’t mentioned in the problem—and that is something large language models (LLMs) are well suited to do.

LLMs generate text by calculating the probability of one word following another. Trinh and his team were able to use their database to train AlphaGeometry on theorems and proofs in a similar way. An LLM does not learn the deductive steps involved in solving a problem; that work is still done by other specialized algorithms.Instead the AI model concentrates on finding points, lines, and other useful auxiliary objects.

When AlphaGeometry is given a problem, a deductive algorithm first derives a list of statements about it. If the statement to be proved is not included in that list, the AI gets involved. It might decide to add a fourth point X to a triangle ABC, for example, so that ABCX represents a parallelogram—something that the program learned to do from previous training. In doing so, the AI gives the deductive algorithm new information to work with. This process can be repeated until the AI and the deductive program reach the desired conclusion. “The method sounds plausible and in some ways similar to the training of participants in the International Mathematical Olympiad,” says Fields Medalist Peter Scholze, who has won the gold medal at the IMO three times.

To test AlphaGeometry, the scientists selected 30 geometric problems that have appeared in the IMO since 2000. The program previously used to solve geometric problems, called Wu’s algorithm, managed to solve only 10 correctly, and GPT-4 failed on all of them, but AlphaGeometry solved 25. According to the researchers, the AI outperformed most IMO participants, who solved an average of 15.2 out of 30 problems. (Gold-medal winners solved an average of 25.9 problems correctly.)

When the researchers looked through the AI-generated proofs, they noticed that in the process of solving one problem, the program hadn’t used all the information provided—meaning that AlphaGeometry set out on its own and found a solution to a related but more general theorem. It was also apparent that complicated tasks—those in which IMO participants performed poorly—generally required longer proofs from the AI. The machine, it seems, struggles with the same challenges as humans.

AlphaGeometry can’t yet take part in the IMO, because geometry is only one third of the competition, but Trinh and his colleagues have emphasized that their approach could be applied to other mathematical subdisciplines, such as combinatorics. Who knows—maybe in a few years a nonhuman participant will take part in the IMO for the first time. Maybe it will even win gold.

Power Overwhelming

blog.evanchen.cc

Writing Olympiad Geometry Problems

You can use a wide range of wild, cultivated or supermarket greens in this recipe. Consider nettles, beet tops, turnip tops, spinach, or watercress in place of chard. The combination is also up to you so choose the ones you like most.

— Y. Ottolenghi. Plenty More

In this post I’ll describe how I come up with geometry proposals for olympiad-style contests. In particular, I’ll go into detail about how I created the following two problems, which were the first olympiad problems which I got onto a contest. Note that I don’t claim this is the only way to write such problems, it just happens to be the approach I use, and has consistently gotten me reasonably good results.

${ABC}$

1. General Procedure

Here are the main ingredients you’ll need.

The ability to consistently solve medium to hard olympiad geometry problems. The intuition you have from being a contestant proves valuable when you go about looking for things.
In particular, a good eye: in an accurate diagram, you should be able to notice if three points look collinear or if four points are concyclic, and so on. Fortunately, this is something you’ll hopefully have just from having done enough olympiad problems.
Geogebra, or some other software that will let you quickly draw and edit diagrams.

With that in mind, here’s the gist of what you do.

${B}$

Start playing around, adding in points and so on to see if anything interesting happens. You might be guided by some actual geometry constructions: for example, if you know that the starting configuration has a harmonic bundle in it, you might project this bundle to obtain the new points to play with.
Keep going with this until you find something unexpected: three points are collinear, four points are cyclic, or so on. Perturb the diagram to make sure your conjecture looks like it’s true in all cases.
Figure out why this coincidence happened. This will probably add more points to you figure, since you often need to construct more auxiliary points to prove the conjecture that you have found.
Repeat the previous two steps to your satisfaction.
Once you are happy with what you have, you have a nontrivial statement and probably several things that are equivalent to it. Pick the one that is most elegant (or hardest), and erase auxiliary points you added that are not needed for the problem statement.
Look for other ways to reduce the number of points even further, by finding other equivalent formulations that have fewer points.

Or shorter yet: build up, then tear down.

None of this makes sense written this abstractly, so now let me walk you through the two problems I wrote.

2. The December TST Problem

In this narrative, the point names might be a little strange at first, because (to make the story follow-able) I used the point names that ended up in the final problem, rather than ones I initially gave. Please bear with me!

${DT}$

So, I now had the following picture.

This was pretty cool, though not yet interesting enough to be a contest problem. So I looked for most things that might be true.

${AI}$

Now, I could not see quickly at all why this was true. So I started trying to prove it, but initially failed: however, I managed to show (via angle chasing) that

$\displaystyle D, P, E \text{ collinear} \iff \angle PQE = 90^\circ.$

So, at least I had an interesting equivalent statement.

And that was it!

3. The Taiwan TST Problem

How could I use this to get a nice result?

${KL}$

Click to share on Facebook (Opens in new window)
Click to share on Twitter (Opens in new window)
Click to share on Reddit (Opens in new window)
Click to email a link to a friend (Opens in new window)
Click to print (Opens in new window)
Click to share on LinkedIn (Opens in new window)

Published by Evan Chen (陳誼廷)

I am a math olympiad coach and a PhD student at MIT. View all posts by Evan Chen (陳誼廷)

1 thought on “Writing Olympiad Geometry Problems”

Great Post! You could have also seen the 90 degree angle on the first problem by applying spiral similarity on the tangent case.

DeepMind Trains AlphaGeometry Model to Solve Olympiad Geometry Problems

21 January 2024
State-of-the-Art

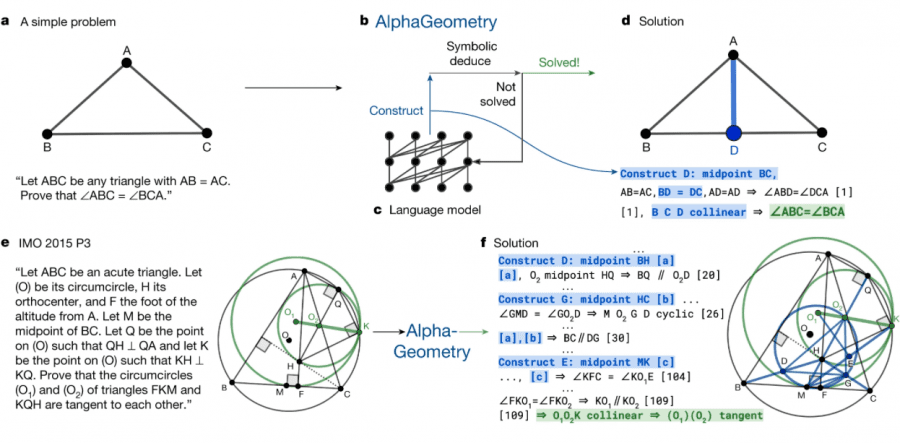
DeepMind has unveiled AlphaGeometry – a model capable of solving geometric problems at the level of International Mathematical Olympiad winners. AlphaGeometry solved 25 out of 30 Olympiad problems, while on average, Olympiad winners solve 25.9 problems, and the previous model only solved 10.

Existing language models often struggle to solve complex mathematical problems due to insufficient training data and the inability to generate error-free, lengthy logical chains. When solving problems, AlphaGeometry combines deduction based on geometric laws with the execution of additional geometric constructions that are most likely to lead to the answer.

Based on the geometric drawing of the problem and its conditions, the model deduces new statements about the relationships between objects until it solves the problem. If a solution is not found, AlphaGeometry performs an additional construction and generates new statements based on it. This cycle continues until a solution is found.

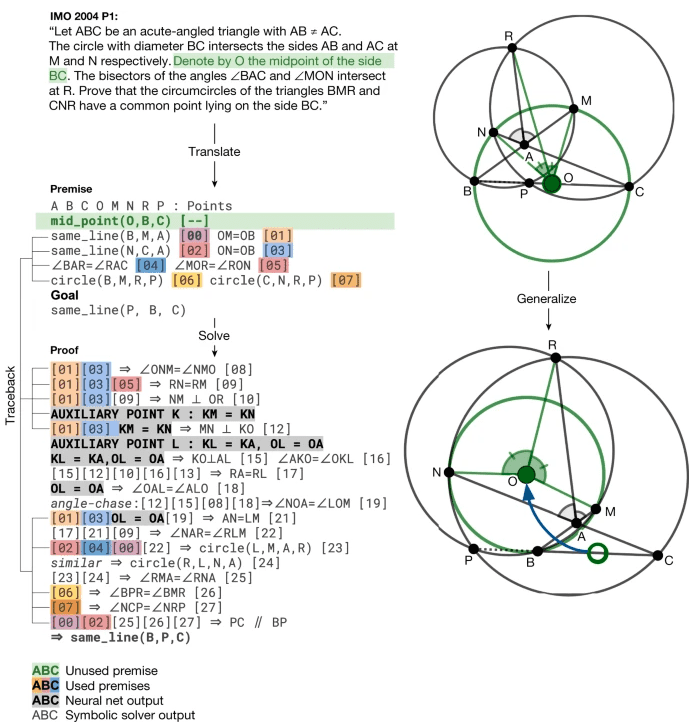
To train the model, approximately one billion random geometric drawings were generated, and all relationships between objects on them were formed. Then the model was trained to understand which additional constructions allowed finding the relationship between each pair of objects. This approach at DeepMind is called “backtracing.” After filtering similar drawings, there were 100 million examples left with labeled object relationships. Thus, only synthetic data without real geometric problems were used to train the model.

The AlphaGeometry code has been released open-source .

More from Neurohive

Google RecurrentGemma: Next-Gen Local Language Model

Gretel: The Largest Open Text-to-SQL Dataset

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Publications
Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

Advanced Search
Journal List
Nature Portfolio
PMC10794143

Solving olympiad geometry without human demonstrations

Trieu h. trinh.

1 Google Deepmind, Mountain View, CA USA

2 Computer Science Department, New York University, New York, NY USA

Thang Luong

Associated data.

The data supporting the findings of this work are available in the Extended Data and the Supplementary Information . Source data are provided with this paper.

Our code and model checkpoint is available at https://github.com/google-deepmind/alphageometry .

Proving mathematical theorems at the olympiad level represents a notable milestone in human-level automated reasoning 1 – 4 , owing to their reputed difficulty among the world’s best talents in pre-university mathematics. Current machine-learning approaches, however, are not applicable to most mathematical domains owing to the high cost of translating human proofs into machine-verifiable format. The problem is even worse for geometry because of its unique translation challenges 1 , 5 , resulting in severe scarcity of training data. We propose AlphaGeometry, a theorem prover for Euclidean plane geometry that sidesteps the need for human demonstrations by synthesizing millions of theorems and proofs across different levels of complexity. AlphaGeometry is a neuro-symbolic system that uses a neural language model, trained from scratch on our large-scale synthetic data, to guide a symbolic deduction engine through infinite branching points in challenging problems. On a test set of 30 latest olympiad-level problems, AlphaGeometry solves 25, outperforming the previous best method that only solves ten problems and approaching the performance of an average International Mathematical Olympiad (IMO) gold medallist. Notably, AlphaGeometry produces human-readable proofs, solves all geometry problems in the IMO 2000 and 2015 under human expert evaluation and discovers a generalized version of a translated IMO theorem in 2004.

A new neuro-symbolic theorem prover for Euclidean plane geometry trained from scratch on millions of synthesized theorems and proofs outperforms the previous best method and reaches the performance of an olympiad gold medallist.

Proving theorems showcases the mastery of logical reasoning and the ability to search through an infinitely large space of actions towards a target, signifying a remarkable problem-solving skill. Since the 1950s (refs. 6 , 7 ), the pursuit of better theorem-proving capabilities has been a constant focus of artificial intelligence (AI) research 8 . Mathematical olympiads are the most reputed theorem-proving competitions in the world, with a similarly long history dating back to 1959, playing an instrumental role in identifying exceptional talents in problem solving. Matching top human performances at the olympiad level has become a notable milestone of AI research 2 – 4 .

Theorem proving is difficult for learning-based methods because training data of human proofs translated into machine-verifiable languages are scarce in most mathematical domains. Geometry stands out among other olympiad domains because it has very few proof examples in general-purpose mathematical languages such as Lean 9 owing to translation difficulties unique to geometry 1 , 5 . Geometry-specific languages, on the other hand, are narrowly defined and thus unable to express many human proofs that use tools beyond the scope of geometry, such as complex numbers (Extended Data Figs. Figs.3 3 and and4). 4 ). Overall, this creates a data bottleneck, causing geometry to lag behind in recent progress that uses human demonstrations 2 – 4 . Current approaches to geometry, therefore, still primarily rely on symbolic methods and human-designed, hard-coded search heuristics 10 – 14 .

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Fig9_ESM.jpg

This is a harder problem (average human score = 1.05/7), with a large number of objects in the problem statements, resulting in a very crowded diagram. Left, the human solution uses complex numbers. With a well-chosen coordinate system, the problem is greatly simplified and a solution follows naturally through algebraic manipulation. Right, AlphaGeometry solution involves two auxiliary constructions and more than 100 deduction steps, with many low-level steps that are extremely tedious to a human reader. This is a case in which the search-based solution is much less readable and much less intuitive than coordinate bashing. A more structural organization, that is, a high-level proof outline, can improve readability of the AlphaGeometry solution substantially. Again, this suggests building into AlphaGeometry many higher-level deduction rules to encapsulate large groups of low-level deductions into fewer proof steps.

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Fig10_ESM.jpg

This is one out of five unsolved problems by AlphaGeometry. Left, the human solution uses both auxiliary constructions and barycentric coordinates. With a well-chosen coordinate system, a solution becomes available through advanced algebraic manipulation. Right, AlphaGeometry solution when provided with the ground-truth auxiliary construction for a synthetic proof. This auxiliary construction can be found quickly with the knowledge of Reim’s theorem, which is not included in the deduction rule list used by the symbolic engine during synthetic data generation. Including such high-level theorems into the synthetic data generation can greatly improve the coverage of synthetic data and thus improve auxiliary construction capability. Further, higher-level steps using Reim’s theorem also cut down the current proof length by a factor of 3.

We present an alternative method for theorem proving using synthetic data, thus sidestepping the need for translating human-provided proof examples. We focus on Euclidean plane geometry and exclude topics such as geometric inequalities and combinatorial geometry. By using existing symbolic engines on a diverse set of random theorem premises, we extracted 100 million synthetic theorems and their proofs, many with more than 200 proof steps, four times longer than the average proof length of olympiad theorems. We further define and use the concept of dependency difference in synthetic proof generation, allowing our method to produce nearly 10 million synthetic proof steps that construct auxiliary points, reaching beyond the scope of pure symbolic deduction. Auxiliary construction is geometry’s instance of exogenous term generation, representing the infinite branching factor of theorem proving, and widely recognized in other mathematical domains as the key challenge to proving many hard theorems 1 , 2 . Our work therefore demonstrates a successful case of generating synthetic data and learning to solve this key challenge. With this solution, we present a general guiding framework and discuss its applicability to other domains in Methods section ‘AlphaGeometry framework and applicability to other domains’.

We pretrain a language model on all generated synthetic data and fine-tune it to focus on auxiliary construction during proof search, delegating all deduction proof steps to specialized symbolic engines. This follows standard settings in the literature, in which language models such as GPT-f (ref. 15 ), after being trained on human proof examples, can generate exogenous proof terms as inputs to fast and accurate symbolic engines such as nlinarith or ring 2 , 3 , 16 , using the best of both worlds. Our geometry theorem prover AlphaGeometry, illustrated in Fig. Fig.1, 1 , produces human-readable proofs, substantially outperforms the previous state-of-the-art geometry-theorem-proving computer program and approaches the performance of an average IMO gold medallist on a test set of 30 classical geometry problems translated from the IMO as shown in Fig. Fig.2 2 .

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Fig1_HTML.jpg

The top row shows how AlphaGeometry solves a simple problem. a , The simple example and its diagram. b , AlphaGeometry initiates the proof search by running the symbolic deduction engine. The engine exhaustively deduces new statements from the theorem premises until the theorem is proven or new statements are exhausted. c , Because the symbolic engine fails to find a proof, the language model constructs one auxiliary point, growing the proof state before the symbolic engine retries. The loop continues until a solution is found. d , For the simple example, the loop terminates after the first auxiliary construction “D as the midpoint of BC”. The proof consists of two other steps, both of which make use of the midpoint properties: “BD = DC” and “B, D, C are collinear”, highlighted in blue. The bottom row shows how AlphaGeometry solves the IMO 2015 Problem 3 (IMO 2015 P3). e , The IMO 2015 P3 problem statement and diagram. f , The solution of IMO 2015 P3 has three auxiliary points. In both solutions, we arrange language model outputs (blue) interleaved with symbolic engine outputs to reflect their execution order. Note that the proof for IMO 2015 P3 in f is greatly shortened and edited for illustration purposes. Its full version is in the Supplementary Information .

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Fig2_HTML.jpg

The test benchmark includes official IMO problems from 2000 to the present that can be represented in the geometry environment used in our work. Human performance is estimated by rescaling their IMO contest scores between 0 and 7 to between 0 and 1, to match the binary outcome of failure/success of the machines. For example, a contestant’s score of 4 out of 7 will be scaled to 0.57 problems in this comparison. On the other hand, the score for AlphaGeometry and other machine solvers on any problem is either 0 (not solved) or 1 (solved). Note that this is only an approximate comparison with humans on classical geometry, who operate on natural-language statements rather than narrow, domain-specific translations. Further, the general IMO contest also includes other types of problem, such as geometric inequality or combinatorial geometry, and other domains of mathematics, such as algebra, number theory and combinatorics.

Source Data

Synthetic theorems and proofs generation

Our method for generating synthetic data is shown in Fig. Fig.3. 3 . We first sample a random set of theorem premises, serving as the input to the symbolic deduction engine to generate its derivations. A full list of actions used for this sampling can be found in Extended Data Table Table1. 1 . In our work, we sampled nearly 1 billion of such premises in a highly parallelized setting, described in Methods . Note that we do not make use of any existing theorem premises from human-designed problem sets and sampled the eligible constructions uniformly randomly.

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Fig3_HTML.jpg

a , We first sample a large set of random theorem premises. b , We use the symbolic deduction engine to obtain a deduction closure. This returns a directed acyclic graph of statements. For each node in the graph, we perform traceback to find its minimal set of necessary premise and dependency deductions. For example, for the rightmost node ‘HA ⊥ BC’, traceback returns the green subgraph. c , The minimal premise and the corresponding subgraph constitute a synthetic problem and its solution. In the bottom example, points E and D took part in the proof despite being irrelevant to the construction of HA and BC; therefore, they are learned by the language model as auxiliary constructions.

Extended Data Table 1

List of actions to construct the random premises

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Tab1_ESM.jpg

These actions include constructions to create new points that are related to others in a certain way, for example, collinear, incentre/excentre etc., and constructions that take a number as its parameter.

Next we use a symbolic deduction engine on the sampled premises. The engine quickly deduces new true statements by following forward inference rules as shown in Fig. Fig.3b. 3b . This returns a directed acyclic graph of all reachable conclusions. Each node in the directed acyclic graph is a reachable conclusion, with edges connecting to its parent nodes thanks to the traceback algorithm described in Methods . This allows a traceback process to run recursively starting from any node N , at the end returning its dependency subgraph G ( N ), with its root being N and its leaves being a subset of the sampled premises. Denoting this subset as P , we obtained a synthetic training example (premises, conclusion, proof) = ( P , N , G ( N )).

In geometry, the symbolic deduction engine is deductive database (refs. 10 , 17 ), with the ability to efficiently deduce new statements from the premises by means of geometric rules. DD follows deduction rules in the form of definite Horn clauses, that is, Q ( x ) ← P 1 ( x ),…, P k ( x ), in which x are points objects, whereas P 1 ,…, P k and Q are predicates such as ‘equal segments’ or ‘collinear’. A full list of deduction rules can be found in ref. 10 . To widen the scope of the generated synthetic theorems and proofs, we also introduce another component to the symbolic engine that can deduce new statements through algebraic rules (AR), as described in Methods . AR is necessary to perform angle, ratio and distance chasing, as often required in many olympiad-level proofs. We included concrete examples of AR in Extended Data Table Table2. 2 . The combination DD + AR, which includes both their forward deduction and traceback algorithms, is a new contribution in our work and represents a new state of the art in symbolic reasoning in geometry.

Extended Data Table 2

Three examples of algebraic reasoning (AR) in geometry theorem proving, with AR proof steps between the two tags <AR></AR>

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Tab2_ESM.jpg

In AlphaGeometry, the engine AR can execute all three examples efficiently, under a unified procedure of Gaussian elimination.

Generating proofs beyond symbolic deduction

So far, the generated proofs consist purely of deduction steps that are already reachable by the highly efficient symbolic deduction engine DD + AR. To solve olympiad-level problems, however, the key missing piece is generating new proof terms. In the above algorithm, it can be seen that such terms form the subset of P that N is independent of. In other words, these terms are the dependency difference between the conclusion statement and the conclusion objects. We move this difference from P to the proof so that a generative model that learns to generate the proof can learn to construct them, as illustrated in Fig. Fig.3c. 3c . Such proof steps perform auxiliary constructions that symbolic deduction engines are not designed to do. In the general theorem-proving context, auxiliary construction is an instance of exogenous term generation, a notable challenge to all proof-search algorithms because it introduces infinite branching points to the search tree. In geometry theorem proving, auxiliary constructions are the longest-standing subject of study since inception of the field in 1959 (refs. 6 , 7 ). Previous methods to generate them are based on hand-crafted templates and domain-specific heuristics 8 – 12 , and are, therefore, limited by a subset of human experiences expressible in hard-coded rules. Any neural solver trained on our synthetic data, on the other hand, learns to perform auxiliary constructions from scratch without human demonstrations.

Training a language model on synthetic data

The transformer 18 language model is a powerful deep neural network that learns to generate text sequences through next-token prediction, powering substantial advances in generative AI technology. We serialize ( P , N , G ( N )) into a text string with the structure ‘<premises><conclusion><proof>’. By training on such sequences of symbols, a language model effectively learns to generate the proof, conditioning on theorem premises and conclusion.

Combining language modelling and symbolic engines

On a high level, proof search is a loop in which the language model and the symbolic deduction engine take turns to run, as shown in Fig. 1b,c . Proof search terminates whenever the theorem conclusion is found or when the loop reaches a maximum number of iterations. The language model is seeded with the problem statement string and generates one extra sentence at each turn, conditioning on the problem statement and past constructions, describing one new auxiliary construction such as “construct point X so that ABCX is a parallelogram”. Each time the language model generates one such construction, the symbolic engine is provided with new inputs to work with and, therefore, its deduction closure expands, potentially reaching the conclusion. We use beam search to explore the top k constructions generated by the language model and describe the parallelization of this proof-search algorithm in Methods .

Empirical evaluation

An olympiad-level benchmark for geometry.

Existing benchmarks of olympiad mathematics do not cover geometry because of a focus on formal mathematics in general-purpose languages 1 , 9 , whose formulation poses great challenges to representing geometry. Solving these challenges requires deep expertise and large research investment that are outside the scope of our work, which focuses on a methodology for theorem proving. For this reason, we adapted geometry problems from the IMO competitions since 2000 to a narrower, specialized environment for classical geometry used in interactive graphical proof assistants 13 , 17 , 19 , as discussed in Methods . Among all non-combinatorial geometry-related problems, 75% can be represented, resulting in a test set of 30 classical geometry problems. Geometric inequality and combinatorial geometry, for example, cannot be translated, as their formulation is markedly different to classical geometry. We include the full list of statements and translations for all 30 problems in the Supplementary Information . The final test set is named IMO-AG-30, highlighting its source, method of translation and its current size.

Geometry theorem prover baselines

Geometry theorem provers in the literature fall into two categories. The first category is computer algebra methods, which treats geometry statements as polynomial equations of its point coordinates. Proving is accomplished with specialized transformations of large polynomials. Gröbner bases 20 and Wu’s method 21 are representative approaches in this category, with theoretical guarantees to successfully decide the truth value of all geometry theorems in IMO-AG-30, albeit without a human-readable proof. Because these methods often have large time and memory complexity, especially when processing IMO-sized problems, we report their result by assigning success to any problem that can be decided within 48 h using one of their existing implementations 17 .

AlphaGeometry belongs to the second category of solvers, often described as search/axiomatic or sometime s ‘synthetic’ methods. These methods treat the problem of theorem proving as a step-by-step search problem using a set of geometry axioms. Thanks to this, they typically return highly interpretable proofs accessible to human readers. Baselines in this category generally include symbolic engines equipped with human-designed heuristics. For example, Chou et al. provided 18 heuristics such as “If OA ⊥ OB and OA = OB, construct C on the opposite ray of OA such that OC = OA ” , besides 75 deduction rules for the symbolic engine. Large language models 22 – 24 such as GPT-4 (ref. 25 ) can be considered to be in this category. Large language models have demonstrated remarkable reasoning ability on a variety of reasoning tasks 26 – 29 . When producing full natural-language proofs on IMO-AG-30, however, GPT-4 has a success rate of 0%, often making syntactic and semantic errors throughout its outputs, showing little understanding of geometry knowledge and of the problem statements itself. Note that the performance of GPT-4 performance on IMO problems can also be contaminated by public solutions in its training data. A better GPT-4 performance is therefore still not comparable with other solvers. In general, search methods have no theoretical guarantee in their proving performance and are known to be weaker than computer algebra methods 13 .

Synthetic data generation rediscovers known theorems and beyond

We find that our synthetic data generation can rediscover some fairly complex theorems and lemmas known to the geometry literature, as shown in Fig. Fig.4, 4 , despite starting from randomly sampled theorem premises. This can be attributed to the use of composite actions described in Extended Data Table Table1, 1 , such as ‘taking centroid’ or ‘taking excentre’, which—by chance—sampled a superset of well-known theorem premises, under our large-scale exploration setting described in Methods . To study the complexity of synthetic proofs, Fig. Fig.4 4 shows a histogram of synthetic proof lengths juxtaposed with proof lengths found on the test set of olympiad problems. Although the synthetic proof lengths are skewed towards shorter proofs, a small number of them still have lengths up to 30% longer than the hardest problem in the IMO test set. We find that synthetic theorems found by this process are not constrained by human aesthetic biases such as being symmetrical, therefore covering a wider set of scenarios known to Euclidean geometry. We performed deduplication as described in Methods , resulting in more than 100 millions unique theorems and proofs, and did not find any IMO-AG-30 theorems, showing that the space of possible geometry theorems is still much larger than our discovered set.

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Fig4_HTML.jpg

Of the generated synthetic proofs, 9% are with auxiliary constructions. Only roughly 0.05% of the synthetic training proofs are longer than the average AlphaGeometry proof for the test-set problems. The most complex synthetic proof has an impressive length of 247 with two auxiliary constructions. Most synthetic theorem premises tend not to be symmetrical like human-discovered theorems, as they are not biased towards any aesthetic standard.

Language model pretraining and fine-tuning

We first pretrained the language model on all 100 million synthetically generated proofs, including ones of pure symbolic deduction. We then fine-tuned the language model on the subset of proofs that requires auxiliary constructions, accounting for roughly 9% of the total pretraining data, that is, 9 million proofs, to better focus on its assigned task during proof search.

Proving results on IMO-AG-30

The performance of ten different solvers on the IMO-AG-30 benchmark is reported in Table Table1, 1 , of which eight, including AlphaGeometry, are search-based methods. Besides prompting GPT-4 to produce full proofs in natural language with several rounds of reflections and revisions, we also combine GPT-4 with DD + AR as another baseline to enhance its deduction accuracy. To achieve this, we use detailed instructions and few-shot examples in the prompt to help GPT-4 successfully interface with DD + AR, providing auxiliary constructions in the correct grammar. Prompting details of baselines involving GPT-4 is included in the Supplementary Information .

Main results on our IMO-AG-30 test benchmark

We compare AlphaGeometry to other state-of-the-art methods (computer algebra and search approaches), most notably Wu’s method. We also show the results of DD + AR (our contribution) and its variants, resulting in the strongest baseline DD + AR + human-designed heuristics. Finally, we include ablation settings for AlphaGeometry without pretraining and fine-tuning.

AlphaGeometry achieves the best result, with 25 problems solved in total. The previous state of the art (Wu’s method) solved ten problems, whereas the strongest baseline (DD + AR + human-designed heuristics) solved 18 problems, making use of the algebraic reasoning engine developed in this work and the human heuristics designed by Chou et al. 17 . To match the test time compute of AlphaGeometry, this strongest baseline makes use of 250 parallel workers running for 1.5 h, each attempting different sets of auxiliary constructions suggested by human-designed heuristics in parallel, until success or timeout. Other baselines such as Wu’s method or the full-angle method are not affected by parallel compute resources as they carry out fixed, step-by-step algorithms until termination.

Measuring the improvements made on top of the base symbolic deduction engine (DD), we found that incorporating algebraic deduction added seven solved problems to a total of 14 (DD + AR), whereas the language model’s auxiliary construction remarkably added another 11 solved problems, resulting in a total of 25. As reported in Extended Data Fig. Fig.6, 6 , we find that, using only 20% of the training data, AlphaGeometry still achieves state-of-the-art results with 21 problems solved. Similarly, using less than 2% of the search budget (beam size of 8 versus 512) during test time, AlphaGeometry can still solve 21 problems. On a larger and more diverse test set of 231 geometry problems, which covers textbook exercises, regional olympiads and famous theorems, we find that baselines in Table Table1 1 remain at the same performance rankings, with AlphaGeometry solving almost all problems (98.7%), whereas Wu’s method solved 75% and DD + AR + human-designed heuristics solved 92.2%, as reported in Extended Data Fig. Fig.6b 6b .

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Fig12_ESM.jpg

a , The effect of reducing training data on AlphaGeometry performance. At 20% of training data, AlphaGeometry still solves 21 problems, outperforming all other baselines. b , Evaluation on a larger set of 231 geometry problems, covering a diverse range of sources outside IMO competitions. The rankings of different machine solvers stays the same as in Table Table1, 1 , with AlphaGeometry solving almost all problems. c , The effect of reducing beam size during test time on AlphaGeometry performance. At beam size 8, that is, a 64 times reduction from its full setting, AlphaGeometry still solves 21 problems, outperforming all other baselines. d , The effect of reducing search depth on AlphaGeometry performance. At depth 2, AlphaGeometry still solves 21 problems, outperforming all other baselines.

Notably, AlphaGeometry solved both geometry problems of the same year in 2000 and 2015, a threshold widely considered difficult to the average human contestant at the IMO. Further, the traceback process of AlphaGeometry found an unused premise in the translated IMO 2004 P1, as shown in Fig. Fig.5, 5 , therefore discovering a more general version of the translated IMO theorem itself. We included AlphaGeometry solutions to all problems in IMO-AG-30 in the Supplementary Information and manually analysed some notable AlphaGeometry solutions and failures in Extended Data Figs. Figs.2 2 – 5 . Overall, we find that AlphaGeometry operates with a much lower-level toolkit for proving than humans do, limiting the coverage of the synthetic data, test-time performance and proof readability.

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Fig5_HTML.jpg

Left, top to bottom, the IMO 2004 P1 stated in natural language, its translated statement and AlphaGeometry solution. Thanks to the traceback algorithm necessary to extract the minimal premises, AlphaGeometry identifies a premise unnecessary for the proof to work: O does not have to be the midpoint of BC for P, B, C to be collinear. Right, top, the original theorem diagram; bottom, the generalized theorem diagram, in which O is freed from its midpoint position and P still stays on line BC. Note that the original problem requires P to be between B and C, a condition where the generalized theorem and solution does not guarantee.

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Fig8_ESM.jpg

Both the AlphaGeometry and human solutions recognize the axis of symmetry between M and N through O. AlphaGeometry constructs point K to materialize this axis, whereas humans simply use the existing point R for the same purpose. This is a case in which proof pruning itself cannot remove K and a sign of similar redundancy in our synthetic data. To prove five-point concyclicity, AlphaGeometry outputs very lengthy, low-level steps, whereas humans use a high-level insight (OR is the symmetrical axis of both LN and AM) to obtain a broad set of conclusions all at once. For algebraic deductions, AlphaGeometry cannot flesh out its intermediate derivations, which is implicitly carried out by Gaussian elimination, therefore leading to low readability. Overall, this comparison points to the use of higher-level tools to improve the synthetic data, proof search and readability of AlphaGeometry. Note that in the original IMO 2004 P1, the point P is proven to be between B and C. The generalized version needs further contraints on the position of O to satisfy this betweenness requirement.

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Fig11_ESM.jpg

This is an unsolved problem by AlphaGeometry and also the hardest one among all 30 problems, with an average human score of only 0.28/7. This human proof uses four auxiliary constructions (diameters of circles W1 and W2) and high-level theorems such as the Pitot theorem and the notion of homothety. These high-level concepts are not available to our current version of the symbolic deduction engine both during synthetic data generation and proof search. Supplying AlphaGeometry with the auxiliary constructions used in this human proof also does not yield any solution. There is also no guarantee that a synthetic solution exists for AlphaGeometry, across all possible auxiliary constructions, without enhancing its symbolic deduction with more powerful rules. Again, this suggests that enhancing the symbolic engine with more powerful tools that IMO contestants are trained to use can improve both the synthetic data and the test-time performance of AlphaGeometry.

Human expert evaluation of AlphaGeometry outputs

Because AlphaGeometry outputs highly interpretable proofs, we used a simple template to automatically translate its solutions to natural language. To obtain an expert evaluation in 2000 and 2015, during which AlphaGeometry solves all geometry problems and potentially passes the medal threshold, we submit these solutions to the USA IMO team coach, who is experienced in grading mathematical olympiads and has authored books for olympiad geometry training. AlphaGeometry solutions are recommended to receive full scores, thus passing the medal threshold of 14/42 in the corresponding years. We note that IMO tests also evaluate humans under three other mathematical domains besides geometry and under human-centric constraints, such as no calculator use or 4.5-h time limits. We study time-constrained settings with 4.5-h and 1.5-h limits for AlphaGeometry in Methods and report the results in Extended Data Fig. Fig.1 1 .

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Fig7_ESM.jpg

Each problem has a different running time resulting from their unique size of the deduction closure. We observed that running time does not correlate with the difficulty of the problem. For example, IMO 2019 P6 is much harder than IMO 2008 P1a, yet it requires far less parallelization to reach a solution within IMO time limits.

Learning to predict the symbolic engine’s output improves the language model’s auxiliary construction

In principle, auxiliary construction strategies must depend on the details of the specific deduction engine they work with during proof search. We find that a language model without pretraining only solves 21 problems. This suggests that pretraining on pure deduction proofs generated by the symbolic engine DD + AR improves the success rate of auxiliary constructions. On the other hand, a language model without fine-tuning also degrades the performance but not as severely, with 23 problems solved compared with AlphaGeometry’s full setting at 25.

Hard problems are reflected in AlphaGeometry proof length

Figure Figure6 6 measures the difficulty of solved problems using public scores of human contestants at the IMO and plots them against the corresponding AlphaGeometry proof lengths. The result shows that, for the three problems with the lowest human score, AlphaGeometry also requires exceptionally long proofs and the help of language-model constructions to reach its solution. For easier problems (average human score > 3.5), however, we observe no correlation ( p = −0.06) between the average human score and AlphaGeometry proof length.

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Fig6_HTML.jpg

Among the solved problems, 2000 P6, 2015 P3 and 2019 P6 are the hardest for IMO participants. They also require the longest proofs from AlphaGeometry. For easier problems, however, there is little correlation between AlphaGeometry proof length and human score.

AlphaGeometry is the first computer program to surpass the performance of the average IMO contestant in proving Euclidean plane geometry theorems, outperforming strong computer algebra and search baselines. Notably, we demonstrated through AlphaGeometry a neuro-symbolic approach for theorem proving by means of large-scale exploration from scratch, sidestepping the need for human-annotated proof examples and human-curated problem statements. Our method to generate and train language models on purely synthetic data provides a general guiding framework for mathematical domains that are facing the same data-scarcity problem.

Geometry representation

General-purpose formal languages such as Lean 31 still require a large amount of groundwork to describe most IMO geometry problems at present. We do not directly address this challenge as it requires deep expertise and substantial research outside the scope of theorem-proving methodologies. To sidestep this barrier, we instead adopted a more specialized language used in GEX 10 , JGEX 17 , MMP/Geometer 13 and GeoLogic 19 , a line of work that aims to provide a logical and graphical environment for synthetic geometry theorems with human-like non-degeneracy and topological assumptions. Examples of this language are shown in Fig. 1d,f . Owing to its narrow formulation, 75% of all IMO geometry problems can be adapted to this representation. In this type of geometry environment, each proof step is logically and numerically verified and can also be evaluated by a human reader as if it is written by IMO contestants, thanks to the highly natural grammar of the language. To cover more expressive algebraic and arithmetic reasoning, we also add integers, fractions and geometric constants to the vocabulary of this language. We do not push further for a complete solution to geometry representation as it is a separate and extremely challenging research topic that demands substantial investment from the mathematical formalization community.

Sampling consistent theorem premises

We developed a constructive diagram builder language similar to that used by JGEX 17 to construct one object in the premise at a time, instead of freely sampling many premises that involve several objects, therefore avoiding the generation of a self-contradicting set of premises. An exhaustive list of construction actions is shown in Extended Data Table Table1. 1 . These actions include constructions to create new points that are related to others in a certain way, that is, collinear, incentre/excentre etc., as well as constructions that take a number as its parameter, for example, “construct point X such that given a number α , ∠ABX = α ”. One can extend this list with more sophisticated actions to describe a more expressive set of geometric scenarios, improving both the synthetic data diversity and the test-set coverage. A more general and expressive diagram builder language can be found in ref. 32 . We make use of a simpler language that is sufficient to describe problems in IMO-AG-30 and can work well with the symbolic engine DD.

The symbolic deduction engine

The core functionality of the engine is deducing new true statements given the theorem premises. Deduction can be performed by means of geometric rules such as ‘If X then Y’, in which X and Y are sets of geometric statements such as ‘A, B, C are collinear’. We use the method of structured DD 10 , 17 for this purpose as it can find the deduction closure in just seconds on standard non-accelerator hardware. To further enhance deduction, we also built into AlphaGeometry the ability to perform deduction through AR. AR enable proof steps that perform angle/ratio/distance chasing. Detailed examples of AR are shown in Extended Data Table Table2. 2 . Such proof steps are ubiquitous in geometry proofs, yet not covered by geometric rules. We expand the Gaussian elimination process implemented in GeoLogic 19 to find the deduction closure for all possible linear operators in just seconds. Our symbolic deduction engine is an intricate integration of DD and AR, which we apply alternately to expand the joint closure of known true statements until expansion halts. This process typically finishes within a few seconds to at most a few minutes on standard non-accelerator hardware.

Algebraic reasoning

There has not been a complete treatment for algebraic deduction in the literature of geometry theorem proving. For example, in iGeoTutor 12 , Z3 (ref. 33 ) is used to handle arithmetic inferences but algebraic manipulations are not covered. DD (ref. 17 ) handles algebraic deductions by expressing them under a few limited deduction rules, therefore, it is unable to express more complex manipulations, leaving arithmetic inferences not covered. The most general treatment so far is a process similar that in ref. 34 for angle-only theorem discovery and implemented in GeoLogic 19 for both angle and ratios. We expanded this formulation to cover all reasoning about angles, ratios and distances between points and also arithmetic reasoning with geometric constants such as ‘pi’ or ‘1:2’. Concrete examples of algebraic reasoning are given in Extended Data Table Table2 2 .

On a high level, we first convert the input linear equations to a matrix of their coefficients. In particular, we create a coefficient matrix A ∈ R M × N in which N is the number of variables and M is the number of input equations. In geometry, any equality is of the form a − b = c − d ⇔ a − b − c + d = 0. For example, the angle equality ∠ABC = ∠XYZ is represented as s (AB) − s (BC) = s (XY) − s (YZ), in which s (AB) is the angle between AB and the x-direction, modulo pi. Similarly, ratios AB:CD = EF:GH are represented as log(AB) − log(CD) = log(EF) − log(GH), in which log(AB) is the log of the length of segment AB. For distances, each variable is a (point, line) pair, representing a specific point on a specific line.

Because all equalities are of the form ‘ a − b − c + d = 0’, we populate the row for each equality with values +1, −1, −1, +1 at columns corresponding to variables a , b , c and d . Running Gaussian elimination on A returns a new matrix with leading 1s at each of the columns, essentially representing each variable as a unique linear combination of all remaining variables. As an example, suppose we have ‘ a − b = b − c ’, ‘ d − c = a − d ’ and ‘ b − c = c − e ’ as input equalities, running the Gaussian elimination process (denoted GE in the following equation) returns the following result:

From this result, we can deterministically and exhaustively deduce all new equalities by checking if x 1 = x 2 or x 1 − x 2 = x 2 − x 3 or x 1 − x 2 = x 3 − x 4 , in which { x 1 , x 2 , x 3 , x 4 } is any 4-permutation of all variables. In the above Gaussian Elimination, for example, AR deduced that b = d from the three input equalities. To handle geometric constants such as ‘0.5 pi’ or ‘5:12’, we included ‘pi’ and ‘1’ as default variables to all coefficient matrices.

Deductive database implementation

Unlike the original implementation of DD, we use a graph data structure to capture the symmetries of geometry, rather than using strings of canonical forms. With a graph data structure, we captured not only the symmetrical permutations of function arguments but also the transitivity of equality, collinearity and concyclicity. This graph data structure bakes into itself some deduction rules explicitly stated in the geometric rule list used in DD. These deduction rules from the original list are therefore not used anywhere in exploration but implicitly used and explicitly spelled out on-demand when the final proof is serialized into text.

Traceback to find minimal proofs

Each deduction step needs to be coupled with a traceback algorithm, which returns the minimal set of immediate ancestor statements that is necessary to deduce the conclusion statement of the step. This is the core building block for extracting proof graphs and minimal premises described in the main text. A minimal-premise-extraction algorithm is necessary to avoid superfluous auxiliary constructions that contribute to the proof through unnecessary transitivity. For example, ‘ a = b ’ and ‘ b = c ’ might not be necessary if ‘ a = c ’ can be obtained directly through other reasoning chains.

Traceback for geometric-rule deduction

To do this, we record the equality transitivity graph. For example, if ‘ a = b ’, ‘ b = c ’, ‘ c = d ’ and ‘ a = d ’ are deduced, which results in nodes a , b , c and d being connected to the same ‘equality node’ e , we maintain a graph within e that has edges [( a , b ), ( b , c ), ( c , d ), ( a , d )]. This allows the traceback algorithm to perform a breadth-first search to find the shortest path of transitivity of equality between any pair of variables among a , b , c and d . For collinearity and concyclicity, however, the representation is more complex. In these cases, hypergraphs G ( V , E ) with 3-edges or 4-edges are used as the equality transitivity graph. The traceback is now equivalent to finding a minimum spanning tree (denoted MST in the following equation) for the target set S of nodes (three collinear nodes or four concyclic nodes) whose weight is the cardinality of the union of its hyperedges e ′:

Such optimization is NP-hard, as it is a reduction from the decision version of vertex cover. We simply use a greedy algorithm in this case to find a best-effort minimum spanning tree.

Traceback for algebraic deduction

Traceback through Gaussian elimination can be done by recognizing that it is equivalent to a mixed integer linear programming problem. Given the coefficient matrix of input equations A constructed as described in the previous sections and a target equation with coefficients vector b ∈ R N , we determine the minimal set of premises for b by defining non-negative integer decision vectors x , y ∈ Z M and solve the following mixed-integer linear programming problem:

The minimum set of immediate parent nodes for the equality represented by b will be the i th equations ( i th rows in A ) whose corresponding decision value ( x i − y i ) is non-zero.

Integrating DD and AR

DD and AR are applied alternately to expand their joint deduction closure. The output of DD, which consists of new statements deduced with deductive rules, is fed into AR and vice versa. For example, if DD deduced ‘AB is parallel to CD’, the slopes of lines AB and CD will be updated to be equal variables in AR’s coefficient matrix A , defined in the ‘Algebraic reasoning’ section. Namely, a new row will be added to A with ‘1’ at the column corresponding to the variable slope(AB) and ‘−1’ at the column of slope(CD). Gaussian elimination and mixed-integer linear programming is run again as AR executes, producing new equalities as inputs to the next iteration of DD. This loop repeats until the joint deduction closure stops expanding. Both DD and AR are deterministic processes that only depend on the theorem premises, therefore they do not require any design choices in their implementation.

Proof pruning

Although the set of immediate ancestors to any node is minimal, this does not guarantee that the fully traced back dependency subgraph G ( N ) and the necessary premise P are minimal. Here we define minimality to be the property that G ( N ) and P cannot be further pruned without losing conclusion reachability. Without minimality, we obtained many synthetic proofs with vacuous auxiliary constructions, having shallow relation to the actual proof and can be entirely discarded. To solve this, we perform exhaustive trial and error, discarding each subset of the auxiliary points and rerunning DD + AR on the smaller subset of premises to verify goal reachability. At the end, we return the minimum proof obtainable across all trials. This proof-pruning procedure is done both during synthetic data generation and after each successful proof search during test time.

Parallelized data generation and deduplication

We run our synthetic-data-generation process on a large number of parallel CPU workers, each seeded with a different random seed to reduce duplications. After running this process on 100,000 CPU workers for 72 h, we obtained roughly 500 million synthetic proof examples. We reformat the proof statements to their canonical form (for example, sorting arguments of individual terms and sorting terms within the same proof step, etc.) to avoid shallow deduplication against itself and against the test set. At the end, we obtain 100 million unique theorem–proof examples. A total of 9 million examples involves at least one auxiliary construction. We find no IMO-AG-30 problems in the synthetic data. On the set of geometry problems collected in JGEX 17 , which consists mainly of problems with moderate difficulty and well-known theorems, we find nearly 20 problems in the synthetic data. This suggests that the training data covered a fair amount of common knowledge in geometry, but the space of more sophisticated theorems is still much larger.

Language model architecture and training

We use the Meliad library 35 for transformer training with its base settings. The transformer has 12 layers, embedding dimension of 1,024, eight heads of attention and an inter-attention dense layer of dimension 4,096 with ReLU activation. Overall, the transformer has 151 million parameters, excluding embedding layers at its input and output heads. Our customized tokenizer is trained with ‘word’ mode using SentencePiece 36 and has a vocabulary size of 757. We limit the maximum context length to 1,024 tokens and use T5-style relative position embedding 37 . Sequence packing 38 , 39 is also used because more than 90% of our sequences are under 200 in length. During training, a dropout 40 rate of 5% is applied pre-attention and post-dense. A 4 × 4 slice of TPUv3 (ref. 41 ) is used as its hardware accelerator. For pretraining, we train the transformer with a batch size of 16 per core and a cosine learning-rate schedule that decays from 0.01 to 0.001 in 10,000,000 steps. For fine-tuning, we maintain the final learning rate of 0.001 for another 1,000,000 steps. For the set-up with no pretraining, we decay the learning rate from 0.01 to 0.001 in 1,000,000 steps. We do not perform any hyperparameter tuning. These hyperparameter values are either selected to be a large round number (training steps) or are provided by default in the Meliad codebase.

Parallelized proof search

Because the language model decoding process returns k different sequences describing k alternative auxiliary constructions, we perform a beam search over these k options, using the score of each beam as its value function. This set-up is highly parallelizable across beams, allowing substantial speed-up when there are parallel computational resources. In our experiments, we use a beam size of k = 512, the maximum number of iterations is 16 and the branching factor for each node, that is, the decoding batch size, is 32. This is the maximum inference-time batch size that can fit in the memory of a GPU V100 for our transformer size. Scaling up these factors to examine a larger fraction of the search space might improve AlphaGeometry results even further.

For each problem, we used a pool of four GPU workers, each hosting a copy of the transformer language model to divide the work between alternative beams, and a pool of 10,000 CPU workers to host the symbolic solvers, shared across all beams across all 30 problems. This way, a problem that terminates early can contribute its share of computing power to longer-running problems. We record the running time of the symbolic solver on each individual problem, which—by design—stays roughly constant across all beams. We use this and the language model decoding speed to infer the necessary parallelism needed for each problem, in isolation, to stay under different time limits at the IMO in Extended Data Fig. Fig.1 1 .

The effect of data and search

We trained AlphaGeometry on smaller fractions of the original training data (20%, 40%, 60% and 80%) and found that, even at 20% of training data, AlphaGeometry still solves 21 problems, more than the strongest baseline (DD + AR + human-designed heuristics) with 18 problems solved, as shown in Extended Data Fig. Fig.6a. 6a . To study the effect of beam search on top of the language model, we reduced the beam size and search depth separately during proof search and reported the results in Extended Data Fig. 6c,d . We find that, with a beam size of 8, that is, a 64 times reduction from the original beam size of 512, AlphaGeometry still solves 21 problems. A similar result of 21 problems can be obtained by reducing the search depth from 16 to only two, while keeping the beam size constant at 512.

Evaluation on a larger test set

We evaluated AlphaGeometry and other baselines on a larger test set of 231 geometry problems, curated in ref. 17 . This set covers a wider range of sources outside IMO competitions: textbook examples and exercises, regional olympiads and famous geometry theorems; some are even more complex than typical IMO problems, such as the five circles theorem, Morley’s theorem or Sawayama and Thébault’s theorem. The results are reported in Extended Data Fig. Fig.6b. 6b . The overall rankings of different approaches remained the same as in Table Table1, 1 , with AlphaGeometry solving almost all problems (98.7%). The strongest baseline DD + AR + human-designed heuristics solves 92.2%, whereas the previous state of the art solves 75%.

AlphaGeometry framework and applicability to other domains

The strength of AlphaGeometry’s neuro-symbolic set-up lies in its ability to generate auxiliary constructions, which is an important ingredient across many mathematical domains. In Extended Data Table Table3, 3 , we give examples in four other mathematical domains in which coming up with auxiliary constructions is key to the solution. In Extended Data Table Table4, 4 , we give a line-by-line comparison of a geometry proof and an inequality proof for the IMO 1964 Problem 2, highlighting how they both fit into the same framework.

Extended Data Table 3

Examples of auxiliary constructions in four different domains

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Tab3_ESM.jpg

In these examples, the construction is key to the proof, whereas the remaining proof is relatively more mechanical. In AlphaGeometry, the mechanical portion is efficiently handled by the symbolic engine DD + AR.

Extended Data Table 4

A comparison between a geometry proof and an IMO inequality proof through the lens of the AlphaGeometry framework

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Tab4_ESM.jpg

We assume AM-GM to be a symbolic engine capable of (1) algebraic rewrites and simplification and (2) applying the inequality rule of arithmetic means–geometric means. With the original premises, directly applying AM-GM fails to deliver a solution, which is similar to the geometry example, for which DD + AR fails to solve the simple problem. Some correct auxiliary constructions are necessary for both symbolic engines (DD + AR in the case of geometry and AM-GM in the case of inequality) to succeed, as shown in the last two rows of the table. Note that there are ten more common inequalities typically used at mathematical olympiads besides AM-GM, just as DD + AR itself encapsulates more than 50 different deduction rules for geometry commonly used at the olympiads.

Our paper shows that language models can learn to come up with auxiliary constructions from synthetic data, in which problem statements and auxiliary constructions are randomly generated together and then separated using the traceback algorithm to identify the dependency difference. Concretely, the AlphaGeometry framework requires the following ingredients:

An implementation of the domain’s objects and definitions.
A random premise sampler.
The symbolic engine(s) that operate within the implementation (1).
A traceback procedure for the symbolic engine.

Using these four ingredients and the algorithm described in the main text, one can generate synthetic data for any target domain. As shown in our paper, there are non-trivial engineering challenges in building each ingredient. For example, current formalizations of combinatorics are very nascent, posing challenges to (1) and (2). Also, building powerful symbolic engines for different domains requires deep domain expertise, posing challenges to (3) and (4). We consider applying this framework to a wider scope as future work and look forward to further innovations that tackle these challenges.

Transformer in theorem proving

Research in automated theorem proving has a long history dating back to the 1950s (refs. 6 , 42 , 43 ), resulting in highly optimized first-order logic solvers such as E (ref. 44 ) or Vampire 45 . In the 2010s, deep learning matured as a new powerful tool for automated theorem proving, demonstrating great successes in premise selection and proof guidance 46 – 49 , as well as SAT solving 50 . On the other hand, transformer 18 exhibits outstanding reasoning capabilities across a variety of tasks 51 – 53 . The first success in applying transformer language models to theorem proving is GPT-f (ref. 15 ). Its follow up extensions 2 , 16 further developed this direction, allowing machines to solve some olympiad-level problems for the first time. Innovation in the proof-search algorithm and online training 3 also improves transformer-based methods, solving a total of ten (adapted) IMO problems in algebra and number theory. These advances, however, are predicated on a substantial amount of human proof examples and standalone problem statements designed and curated by humans.

Geometry theorem proving

Geometry theorem proving evolves in an entirely separate space. Its literature is divided into two branches, one of computer algebra methods and one of search methods. The former is largely considered solved since the introduction of Wu’s method 21 , which can theoretically decide the truth value of any geometrical statement of equality type, building on specialized algebraic tools introduced in earlier works 54 , 55 . Even though computer algebra has strong theoretical guarantees, its performance can be limited in practice owing to their large time and space complexity 56 . Further, the methodology of computer algebra is not of interest to AI research, which instead seeks to prove theorems using search methods, a more human-like and general-purpose process.

Search methods also started as early as the 1950s (refs. 6 , 7 ) and continued to develop throughout the twentieth century 57 – 60 . With the introduction of DD 10 , 17 , area methods 61 and full-angle methods 30 , geometry solvers use higher-level deduction rules than Tarski’s or Hilbert’s axioms and are able to prove a larger number of more complex theorems than those operating in formal languages. Geometry theorem proving of today, however, is still relying on human-designed heuristics for auxiliary constructions 10 – 14 . Geometry theorem proving falls behind the recent advances made by machine learning because its presence in formal mathematical libraries such as Lean 31 or Isabelle 62 is extremely limited.

Synthetic data in theorem proving

Synthetic data has long been recognized and used as an important ingredient in theorem proving 63 – 66 . State-of-the-art machine learning methods make use of expert iteration to generate a curriculum of synthetic proofs 2 , 3 , 15 . Their methods, however, only generate synthetic proofs for a fixed set of predefined problems, designed and selected by humans. Our method, on the other hand, generates both synthetic problems and proofs entirely from scratch. Aygun et al. 67 similarly generated synthetic proofs with hindsight experience replay 68 , providing a smooth range of theorem difficulty to aid learning similar to our work. AlphaGeometry, however, is not trained on existing conjectures curated by humans and does not learn from proof attempts on the target theorems. Their approach is thus orthogonal and can be used to further improve AlphaGeometry. Most similar to our work is Firoiu et al. 69 , whose method uses a forward proposer to generate synthetic data by depth-first exploration and trains a neural network purely on these synthetic data. Our work, on the other hand, uses breadth-first exploration, necessary to obtain the minimal proofs and premises, and uses a traceback algorithm to identify auxiliary constructions, thus introducing new symbols and hypotheses that the forward proposer cannot propose.

Online content

Any methods, additional references, Nature Portfolio reporting summaries, source data, extended data, supplementary information, acknowledgements, peer review information; details of author contributions and competing interests; and statements of data and code availability are available at 10.1038/s41586-023-06747-5.

Supplementary information

Supplementary Sections 1 and 2. Section 1 contains GPT-4 prompting details and includes prompting for two scenarios: (1) GPT-4 producing full proofs in natural language and (2) GPT-4 interfaces with DD + AR. Section 2 contains AlphaGeometry solutions for problems in IMO-AG-30. It lists the 30 problem statements, their diagrams to aid understanding and AlphaGeometry solution (if any) sequentially.

Source data

Acknowledgements.

This project is a collaboration between the Google Brain team and the Computer Science Department of New York University. We thank R. A. Saurous, D. Zhou, C. Szegedy, D. Hutchins, T. Kipf, H. Pham, P. Veličković, E. Lockhart, D. Dwibedi, K. Cho, L. Pinto, A. Canziani, T. Wies, H. He’s research group, E. Chen (the USA’s IMO team coach), M. Olsak and P. Bak.

Extended data figures and tables

Author contributions.

T.H.T. conceived the project, built the codebase, carried out experiments, requested manual evaluation from experts and drafted the manuscript. Y.W. advocated for the neuro-symbolic setting and advised on data/training/codebase choices. Q.V.L. advised on scientific methodology and revised the manuscript. H.H. advised on scientific methodology, experimental set-ups and the manuscript. T.L. is the PI of the project, advised on model designs/implementations/experiments and helped with manuscript structure and writing.

Peer review

Peer review information.

Nature thanks the anonymous reviewers for their contribution to the peer review of this work.

Data availability

Code availability, competing interests.

The following US patent is related to this work: “Training language model neural networks using synthetic reasoning data”, filed in the United States Patent and Trademark Office (USPTO) on 1 May 2023 as application no. 63/499,469.

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Change history

A Correction to this paper has been published: 10.1038/s41586-024-07115-7

Contributor Information

Trieu H. Trinh, Email: moc.elgoog@ueirtht .

Thang Luong, Email: moc.elgoog@gnoulgnaht .

Extended data

is available for this paper at 10.1038/s41586-023-06747-5.

The online version contains supplementary material available at 10.1038/s41586-023-06747-5.

Help | Advanced Search

Computer Science > Computational Geometry

Title: automatically building diagrams for olympiad geometry problems.

Abstract: We present a method for automatically building diagrams for olympiad-level geometry problems and implement our approach in a new open-source software tool, the Geometry Model Builder (GMB). Central to our method is a new domain-specific language, the Geometry Model-Building Language (GMBL), for specifying geometry problems along with additional metadata useful for building diagrams. A GMBL program specifies (1) how to parameterize geometric objects (or sets of geometric objects) and initialize these parameterized quantities, (2) which quantities to compute directly from other quantities, and (3) additional constraints to accumulate into a (differentiable) loss function. A GMBL program induces a (usually) tractable numerical optimization problem whose solutions correspond to diagrams of the original problem statement, and that we can solve reliably using gradient descent. Of the 39 geometry problems since 2000 appearing in the International Mathematical Olympiad, 36 can be expressed in our logic and our system can produce diagrams for 94% of them on average. To the best of our knowledge, our method is the first in automated geometry diagram construction to generate models for such complex problems.

Submission history

Access paper:.

Other Formats

References & Citations

Google Scholar
Semantic Scholar

DBLP - CS Bibliography

Bibtex formatted citation.

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

Stack Exchange Network

Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.

Automatically solving olympiad geometry problems

Warning: I am only an amateur in the foundations of mathematics.

My understanding of this Wikipedia page about Tarski's axiomatization of plane geometry (and especially the discussion about decidability) is that "plane geometry is decidable".

The 2019 International Maths Olympiad happened recently, and there were two plane geometry questions in it (problems 2 and 6). Their solutions look really intimidating! However even as a student I felt that one should be able to solve these questions, in theory, by just "writing down coordinates of everything and doing the algebra". Tarski's work, which I will freely confess that I do not understand fully, might even vindicate my view.

The question: Is there an algorithm for solving these kinds of questions, or have I misunderstood? If so, is this algorithm actually feasible to run in practice nowadays (on a computer say) for IMO-level problems? In other words -- are there computer programs which will take as input a planar geometry question of "olympiad level" (for example problems 2 and 6 in this year's IMO) and actually output a solution?

Currently I am not too bothered about whether the solution is human-readable -- it could just be a formal proof in some kind of type theory or something, but the output would be some object that some expert could coherently argue was a solution of some sort.

The reason I'm asking is that I was talking to some computer scientists about various goals in the long-term project of getting computers to do mathematics "better than humans", and having a computer program which could solve IMO problems by itself was a suggested milestone.

euclidean-geometry
proof-assistants

12 $\begingroup$ Essentially all the usual Euclidean geometry questions could be reformulated as first-order sentences in the language of Tarski's geometry. And thus be solved by a decision algorithm for this theory. The exceptions are problems that talk about polygons with arbitrary amount of vertices rather than configurations that could be described by fixed amount of points. The decision problem is known to be NExpTime-hard. However, it doesn't mean that it is impossible to make algorithm that in practice solves some reasonable class of problems, although I am not aware of any practical algorithms here. $\endgroup$ – Fedor Pakhomov Aug 3, 2019 at 17:45
7 $\begingroup$ My question is whether there is currently a feasible algorithm (and also whether I had misunderstood Tarski's work). I am more than happy to be told my question is not on topic, and would not be offended if it gets bumped to MSE or closed. I am looking for answers, I am not looking to cause trouble. I completely take your point about a 1 rep user. I built my rep up here talking about number theory but I am now interested in other things which are definitely of more marginal interest to the community here. $\endgroup$ – Kevin Buzzard Aug 3, 2019 at 18:13
5 $\begingroup$ Tarski's method gives a way of translating a problem in Elementary Plane Geometry (in the technical sense made precise by his axioms for geometry) into a problem about real-closed fields, and the first-order theory of real-closed field is decidable, using the Tarski-Seidenberg theorem which allows for quantifier elimination. (Presumably the statements you have in mind about properties picking out one of the two points of circle intersections are statements expressible in terms of field ordering.) But algorithms for eliminating quantifiers have complexity unbounded by stacks of exponentials. $\endgroup$ – Todd Trimble ♦ Aug 4, 2019 at 0:13
14 $\begingroup$ @KevinBuzzard Just de-lurking to say that I, for one, would be more than happy to see you ask questions like these and get answers. I can't see the comments you're responding to but I hope that their deletion indicates that the authors thought twice $\endgroup$ – Yemon Choi Aug 4, 2019 at 0:15
12 $\begingroup$ While the time complexity of Tarski's algorithm was not bounded by any stack of exponentials, the modern way of eliminating quantifiers for real-closed fields is cylindrical algebraic decomposition , which is only double exponential. Mathematica has an implementation of this. Apparently, there is also an algorithm for eliminating existential quantifiers (projecting a semialgebraic set) that only takes exponential time, but this is not available in Mathematica or any other major CAS, and the only implementation I could find of it hit a bug on every nontrivial example I tried. $\endgroup$ – Robert Furber Aug 4, 2019 at 2:12

2 Answers 2

Arguably, the so-called " area method " of Chou, Gao and Zhang represents the state of the art in the field of machine proofs of Olympiad-style geometry problems. Their book Machine Proofs in Geometry features over 400 theorems proved by their computer program. Many of the proofs are human-readable, or nearly so.

The area method is less powerful than Tarski–Seidenberg quantifier elimination in the sense that not every statement provable by the latter is provable by the area method, but the area method has the advantage of staying closer to the "synthetic" nature of (the vast majority of) Olympiad problems.

EDIT (February 2022): OpenAI has announced some success with solving (some) formal math olympiad problems . They did not restrict themselves to geometry problems.

EDIT (January 2024): DeepMind has published Solving olympiad geometry without human demonstrations in Nature . On geometry problems, they claim performance close to that of an Olympiad gold medalist, though I would add some caveats. Their "AlphaGeometry" program does not have natural language processing capability, and is not parsing the Olympiad problem in the natural-language form that a human contestant would be presented with. On 30 selected problems, AlphaGeometry with pre-training and fine-tuning solves 25. They compare this with Wu's method , which they say solves 10 problems. There is no direct comparison with the area method of Chou, Gao, and Zhang, although the line "DD+AR+human-designed heuristics" in Table 1 seems to make some use of the area method, and reportedly solves 18 problems.

$\begingroup$ Ah this is great! From 1993 though? Does a link to the prover exist? The suggestion at mathforum.org/kb/message.jspa?messageID=1095436 is also dead. cs.wichita.edu/~ye looks promising but I don't know about whether the prover can be run on your own problems. PS interesting last para in the foreward (p4 of the pdf). $\endgroup$ – Kevin Buzzard Aug 6, 2019 at 17:43
1 $\begingroup$ Patrick Massot pointed me to dpt-info.u-strasbg.fr/~narboux/area_method.html ! $\endgroup$ – Kevin Buzzard Aug 6, 2019 at 19:30
$\begingroup$ @KevinBuzzard : Not sure if you tried clicking on the "area method" hyperlink that Matt F. added? $\endgroup$ – Timothy Chow Aug 6, 2019 at 20:21
1 $\begingroup$ There are some doubts about the axiom system behind DeepMind on the issue tracker . I am also worried, based on the description (I haven't dug into the code) about how Gaussian elimination should work with full angles (= oriented angles modulo 180°), seeing that they live in a $\mathbb{Z}$-module with torsion (i.e., $2\alpha = 2\beta$ does not entail $\alpha = \beta$). But the idea of combining AI guesswork with a symbolic proof checker is a good one and I would love to see this become a finished product. $\endgroup$ – darij grinberg Jan 21 at 1:09

There is a pretty general method (although not always sufficient) to apply your intuition that one could translate everything into algebra and then solve it there.

Essentially, you introduce coordinates for your points, encode all your hypothesis as polynomial equalities between coordinates, do the same for the thesis, and then try to prove that the thesis is in the ideal generated by the hypotheses (or even its radical) using Gröbner bases. Of course, the issue here is that the classical Nullstellensatz does not hold for $\mathbb{R}$ , so the thesis may hold even if it does not lie in the radical of the ideal generated by the hypotheses. Using the real Nullstellensatz, it may be possible to adapt the technique, but I did not give it much thought.

To make a concrete example, say you want to prove Heron's formula. Let $T$ be a triangle with side length $a, b, c$ and area $s$ . You choose coordinates for the vertices of $T$ so that they are $(0, 0), (a, 0), (x, y)$ (this particular nice choice of coordinates is not necessary on a computer but simplifies the discussion for humans). Then the hypotheses are:

$b^2 = x^2 + y^2$
$c^2 = (a - x)^2 + y^2$
$2s = a y$ .

The thesis is Heron's formula $16 s^2 = (a + b - c)(c + a - b)(b + c - a)(a + b + c)$ .

What you do is consider the ideal $I \subset \mathbb{R}[a, b, c, x, y, s]$ generated by $b^2 - x^2 - y^2$ , $c^2 - (a - x)^2 - y^2$ and $2s - ay$ , and use Gröbner bases to check that $16 s^2 - (a + b - c)(c + a - b)(b + c - a)(a + b + c) \in \sqrt{I}$ .

In fact, since the thesis does not involve $x, y$ , one can compute $I \cap \mathbb{R}[a, b, c, s]$ - again using Gröbner bases - and discover that it is generated by the equation expressing Heron's formula.

The above can actually be implemented very efficiently. I used rings , an efficient Scala library to perform polynomial computations, and the following

gave the answer true is about a second on my laptop.

$\begingroup$ Looks like there should be lot more identities. $\endgroup$ – Turbo Aug 7, 2019 at 10:59
1 $\begingroup$ I have a gut feeling that some olympiad problems will not be solvable in this way because they might involve assertions about only some roots. (a+b-c)(c+a-b)(b+c-a)(a+b+c) is a polynomial function of a^2, b^2 and c^2, so issues of sign do not show up. What about an analogous question where it's essential that b is chosen to be the positive square root, and where the claimed equation does not hold if the negative one is chosen? I think that's why Groebner bases are not sufficient here but I do not know a good toy example. $\endgroup$ – Kevin Buzzard Aug 7, 2019 at 11:34
2 $\begingroup$ For what it’s worth, this can also be done easily enough by hand. We have $2ax=a^2+b^2-c^2$, so $(2ab)^2=(2ax)^2+(2ay)^2=(a^2+b^2-c^2)^2+16s^2$, and the result follows by rearranging and factoring the differences of squares. $\endgroup$ – user44143 Aug 7, 2019 at 12:51
1 $\begingroup$ We need a better toy example. $\endgroup$ – Kevin Buzzard Aug 7, 2019 at 18:03
1 $\begingroup$ Another easy one is Apollonius theorem: let ABC be a triangle right in A. The midpoints of the three sides and the foot of the altitude drawn from A to BC all lie on one circle. But again, it may be too easy... $\endgroup$ – Andrea Ferretti Aug 8, 2019 at 12:15

Your Answer

Required, but never shown

By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .

Not the answer you're looking for? Browse other questions tagged lo.logic euclidean-geometry proof-assistants or ask your own question .

Featured on Meta
Testing a new version of Stack Overflow Jobs
What deliverables would you like to see out of a working group?

DeepMind AI solves hard geometry problems from mathematics olympiad

AlphaGeometry scores almost as well as the best students on geometry questions from the International Mathematical Olympiad

By Alex Wilkins

17 January 2024

Geometrical problems involve proving facts about angles or lines in complicated shapes

Google DeepMind

An AI from Google DeepMind can solve some International Mathematical Olympiad (IMO) questions on geometry almost as well as the best human contestants.

How does ChatGPT work and do AI-powered chatbots “think” like us?

Sign up to our The Daily newsletter

The latest science news delivered to your inbox, every day.

The future of AI: The 5 possible scenarios, from utopia to extinction

Journal reference:

Nature DOI: 10.1038/s41586-023-06747-5

mathematics /

Sign up to our weekly newsletter

Receive a weekly dose of discovery in your inbox! We'll also keep you up to date with New Scientist events and special offers.

More from New Scientist

Explore the latest news, articles and features

DeepMind AI with built-in fact-checker makes mathematical discoveries

Crystal-hunting DeepMind AI could help discover new wonder materials

Game-playing DeepMind AI can beat top humans at chess, Go and poker

DeepMind AI can beat the best weather forecasts - but there is a catch

COMMENTS

AlphaGeometry: An Olympiad-level AI system for geometry
Our AI system surpasses the state-of-the-art approach for geometry problems, advancing AI reasoning in mathematics. Reflecting the Olympic spirit of ancient Greece, the International Mathematical Olympiad is a modern-day arena for the world's brightest high-school mathematicians. The competition not only showcases young talent, but has emerged as a testing ground for advanced AI systems in ...
Solving olympiad geometry without human demonstrations
As reported in Extended Data Fig. 6, we find that, using only 20% of the training data, AlphaGeometry still achieves state-of-the-art results with 21 problems solved. Similarly, using less than 2% ...
A.I.'s Latest Challenge: the Math Olympics
Dr. Trinh presented the AlphaGeometry system with a test set of 30 Olympiad geometry problems drawn from 2000 to 2022. The system solved 25; historically, over that same period, the average human ...
Category:Olympiad Geometry Problems
1972 USAMO Problems/Problem 5. 1973 IMO Problems/Problem 1. 1973 IMO Problems/Problem 2. 1973 IMO Problems/Problem 6. 1973 IMO Shortlist Problems/Bulgaria 1. 1973 USAMO Problems/Problem 1. 1974 IMO Problems/Problem 3. 1974 IMO Problems/Problem 4. 1974 IMO Problems/Problem 6.
DeepMind AI solves geometry problems at star-student level
When tested on a set of 30 geometry problems from the International Mathematical Olympiad (IMO), AlphaGeometry could solve 25. This is approaching the performance of the competitions' gold ...
DeepMind AI solves hard geometry problems from mathematics olympiad
17 January 2024. Geometrical problems involve proving facts about angles or lines in complicated shapes. Google DeepMind. An AI from Google DeepMind can solve some International Mathematical ...
This AI just figured out geometry
Researchers at Google Deepmind have developed an AI that can solve International Mathematical Olympiad-level geometry problems, something previous AIs have struggled with. They provided the system ...
DeepMind's latest AI can solve geometry problems
AlphaGeometry, the code for which was open sourced this morning, solves 25 Olympiad geometry problems within the standard time limit, beating the previous state-of-the-art system's 10.
DeepMind AI solves hard geometry problems from mathematics olympiad
An AI from Google DeepMind can solve some International Mathematical Olympiad (IMO) questions on geometry almost as well as the best human contestants. How does ChatGPT work and do AI-powered ...
Geometry/Olympiad
Euclidean Geometry In Mathematical Olympiads by Evan Chen; Geometry Revisited-- A classic. Geometry of Complex Numbers by Hans Schwerdtfeger. Geometry: A Comprehensive Course by Dan Pedoe. Projective Geometry by H.S.M. Coxeter. See math books for additional texts. Classes. The Olympiad Geometry class, an Olympiad level course over geometry.
Olympiad Geometry Online Math Course
Olympiad Geometry Covers numerous topics of geometry useful for Olympiad-level geometric proofs, including similar triangles, cyclic quadrilaterals, power of a point, homothety, inversion, transformations, collinearity, concurrence, construction, locus, and three-dimensional geometry. 12 weeks
Some Advice for Olympiad Geometry
In this article I try to describe how I come up which such solutions. 1. The Three Reductions. Very roughly, there are three different ways I try to make progress on a geometry problem. (I) The standard synthetic techniques; angle chasing, cyclic quadrilaterals, homothety, radical axis / power of a point, etc.
AI Matches the Abilities of the Best Math Olympians
To solve problems at the level of an IMO, however, AlphaGeometry needed to go further. "The key missing piece is generating new proof terms," Trinh and his team wrote in their paper.
PDF arXiv:2012.02590v2 [cs.CG] 1 May 2021
for olympiad-level geometry problems and implement our approach in a new open-source software tool, the Geometry Model Builder (GMB). Central to our method is a new domain-speci c language, the Geometry Model-Building Language (GMBL), for specifying geometry problems along with additional metadata useful for building diagrams. A GMBL
PDF Advanced Geometry Problems For Mathematical Olympiads
Solving Problems in Geometry Kim Hoo Hang,Haibin Wang,2017 This new volume of the Mathematical Olympiad Series focuses on the topic of geometry. Basic and advanced theorems commonly seen in Mathematical Olympiad are introduced and illustrated with plenty of examples. Special techniques in solving various types of geometrical problems are
Writing Olympiad Geometry Problems
The ability to consistently solve medium to hard olympiad geometry problems. The intuition you have from being a contestant proves valuable when you go about looking for things. In particular, a good eye: in an accurate diagram, you should be able to notice if three points look collinear or if four points are concyclic, and so on.
DeepMind's AlphaGeometry: Mastering Olympiad Geometry
DeepMind has unveiled AlphaGeometry - a model capable of solving geometric problems at the level of International Mathematical Olympiad winners. AlphaGeometry solved 25 out of 30 Olympiad problems, while on average, Olympiad winners solve 25.9 problems, and the previous model only solved 10. Existing language models often struggle to solve ...
Solving olympiad geometry without human demonstrations
To solve olympiad-level problems, however, the key missing piece is generating new proof terms. ... On the set of geometry problems collected in JGEX 17, which consists mainly of problems with moderate difficulty and well-known theorems, we find nearly 20 problems in the synthetic data. This suggests that the training data covered a fair amount ...
Automatically Building Diagrams for Olympiad Geometry Problems
We present a method for automatically building diagrams for olympiad-level geometry problems and implement our approach in a new open-source software tool, the Geometry Model Builder (GMB). Central to our method is a new domain-specific language, the Geometry Model-Building Language (GMBL), for specifying geometry problems along with additional metadata useful for building diagrams. A GMBL ...
Solving (some) formal math olympiad problems
We built a neural theorem prover for Lean (opens in a new window) that learned to solve a variety of challenging high-school olympiad problems, including problems from the AMC12 (opens in a new window) and AIME (opens in a new window) competitions, as well as two problems adapted from the IMO (opens in a new window). A The prover uses a language model to find proofs of formal statements.
Automatically solving olympiad geometry problems
Looks like there should be lot more identities. - Turbo. 1. I have a gut feeling that some olympiad problems will not be solvable in this way because they might involve assertions about only some roots. (a+b-c) (c+a-b) (b+c-a) (a+b+c) is a polynomial function of a^2, b^2 and c^2, so issues of sign do not show up.
DeepMind AI solves hard geometry problems from mathematics olympiad
Geometrical problems involve proving facts about angles or lines in complicated shapes. Google DeepMind. An AI from Google DeepMind can solve some International Mathematical Olympiad (IMO) questions on geometry almost as well as the best human contestants.
Geometry Problems And Solutions From Mathematical Olympiads (2023
Geometry Problems And Solutions From Mathematical Olympiads Mathematics via Problems: Part 2: Geometry 2021-08-24 Alexey A. Zaslavsky This book is a translation from Russian of Part II of the book Mathematics Through Problems: From Olympiads and Math Circles to Profession. Part I, Algebra, was recently published in the same series.

AlphaGeometry: An Olympiad-level AI system for geometry

AlphaGeometry adopts a neuro-symbolic approach

Generating 100 million synthetic data examples

A.I.’s Latest Challenge: the Math Olympics

The big jump

Proof of concept

Soulful solutions

Explore Our Coverage of Artificial Intelligence

DeepMind AI solves hard geometry problems from mathematics olympiad

Sign up to our The Daily newsletter

Sign up to our weekly newsletter

More from New Scientist

DeepMind AI with built-in fact-checker makes mathematical discoveries

This AI just figured out geometry — is this a step towards artificial reasoning?

0:55 The AI that deduces solutions to complex maths problems

09:46 Research Highlights

12:26 The food-web effects of mass predator die-offs

20:53 Briefing Chat

Related Articles

Professor, Division Director, Translational and Clinical Pharmacology

Data Analyst for Gene Regulation as an Academic Functional Specialist

Recruitment of Global Talent at the Institute of Zoology, Chinese Academy of Sciences (IOZ, CAS)

Full Professorship (W3) in “Organic Environmental Geochemistry (f/m/d)

Postdoctoral scholarship in Structural biology of neurodegeneration

Quick links

DeepMind’s latest AI can solve geometry problems

More TechCrunch

Startups Weekly

TechCrunch Fintech

TechCrunch Mobility

Startups Weekly: Drama at Techstars. Drama in AI. Drama everywhere.

From Plaid to Figma, here are the startups that are likely — or definitely — not having IPOs this year

Feds add nine more incidents to Waymo robotaxi investigation

Pitch Deck Teardown: Terra One’s $7.5M Seed deck

Women in AI: Chinasa T. Okolo researches AI’s impact on the Global South

Disrupt 2024 early-bird tickets fly away next Friday

Big tech companies are plowing money into AI startups, which could help them dodge antitrust concerns

Harlem Capital is raising a $150 million fund

US pharma giant Cencora says Americans’ health information stolen in data breach

Last day to vote for TC Disrupt 2024 Audience Choice program

Signal’s Meredith Whittaker on the Telegram security clash and the ‘edge lords’ at OpenAI

Lucid Motors slashes 400 jobs ahead of crucial SUV launch

Google invests $350 million in Indian e-commerce giant Flipkart

Jio Financial unit to buy $4.32B of telecom gear from Reliance Retail

Foursquare just laid off 105 employees

Using memes, social media users have become red teams for half-baked AI features

ESA prepares for the post-ISS era, selects The Exploration Company, Thales Alenia to develop cargo spacecraft

Expressable brings speech therapy into the home

The biggest French startups in 2024 according to the French government

Spotify to shut off Car Thing for good, leading users to demand refunds

X should bring back stars, not hide ‘likes’

$6M fine for robocaller who used AI to clone Biden’s voice

Tesla lobbies for Elon and Kia taps into the GenAI hype

App developer Crowdaa raises €1.2M and plans a US expansion

Canva launches a proper enterprise product — and they mean it this time

2 days left to vote for Disrupt Audience Choice

Ticketmaster antitrust lawsuit could give new hope to ticketing startups

‘Pro-competition’ rules for Big Tech make it through UK’s pre-election wash-up

Spotify experiments with an AI DJ that speaks Spanish

Arc Search’s new Call Arc feature lets you ask questions by ‘making a phone call’

DeepMind AI solves hard geometry problems from mathematics olympiad

AI Does Math as Well as Math Olympians

On supporting science journalism

Writing Olympiad Geometry Problems

1. General Procedure

2. The December TST Problem

3. The Taiwan TST Problem

Published by Evan Chen (陳誼廷)

1 thought on “Writing Olympiad Geometry Problems”

Leave a comment Cancel reply

DeepMind Trains AlphaGeometry Model to Solve Olympiad Geometry Problems

More from Neurohive

Google RecurrentGemma: Next-Gen Local Language Model

Gretel: The Largest Open Text-to-SQL Dataset

Solving olympiad geometry without human demonstrations

Thang Luong

Synthetic theorems and proofs generation

Extended Data Table 1

Extended Data Table 2

Generating proofs beyond symbolic deduction