linear equations practice test answer key

Practice Test on Linear Equations

In math equations, students can practice test on linear equations in one variable showing step-by-step solution using addition, subtraction, multiplication and division. While practicing this sheet keep in mind the basic concept on linear equations.

Notes to practice test on linear equations:  An equation which involves only one variable whose highest power is 1 is known as linear equation in that variable.  We can add or subtract the same number to both sides of the equation.  We can divide or multiply both sides of the equation by the same non-zero integer.  Transposition is a process in which any term in an equation can be shifted to the other side of equal to sign by simply changing the sign from (+ to -) ,  (- to +) ,  (× to ÷) , and  (÷ to ×) . The process of multiplying the numerator on L.H.S. with denominator on R.H.S. and multiplying denominator on L.H.S. with numerator on R.H.S. is called cross multiplication. 

Solve the following equations:  

(a) 5x - 11 = 3x + 9 (b) 3y + 4 = 7 - 2y (c) 9 - 2(x - 5) = x + 10 (d) 5(y - 1) = 3(2y - 5) - (1 - 3y) (e) 2(x - 1) - 6x = 10 - 2(x - 4) (f) x/3 - (x - 2)/2 = 7/3 (g) (x - 3)/4 + (x - 1)/5 - (x - 2)/3 = 1 (h) (3y - 2)/3 + (2y + 3)/3 = (y + 7)/6 (i) (8x - 5)/(7x + 1) = -4/5 (j) (5 - 7x)/(2 + 4x) = -8/7 (k) (x - 2)/(x - 3) = (x - 1)/(x + 1) (l) (2x - 5)/(3x - 1) = (2x - 1)/(3x + 2) (m) (3 - 7x)/(15 + 2x) = 0 (n) (0.4y - 3)/(1.5y + 9) = -7/5 (o) 2/(3x - 1) + 3/(3x + 1) = 5/3x (p) 2/(x - 3) + 1/(x - 1) = 5/(x - 1) - 2/(x - 2) (q) 15(x - y) - 3(x - 9) + 5(x + 6) = 0 (r) y/2 - 1/2 = y/3 + 1/4 (s) (0.5y - 9)/0.25 = 4y - 3 (t) [17(2 - y) - 5(y + 12)]/(1 - 7y) = 8

Answers for the practice test on linear equations in one variable are given below to check the exact answers of the equations.

(b) 3/5 (c) 3 (d) 11/4 (e) -10 (f) -8 (g) 11 (h) 5/9 (i) 21/68 (j) 3 (k) 5/3 (l) -11/6 (m) 3/7 (n) - 96/25 (o) 5/3 (p) 7/3 (q) -1/6 (r) 9/2 (s) -16.5 (t) 1

●   Equations

What is an Equation?

What is a Linear Equation?

How to Solve Linear Equations?

Solving Linear Equations

Problems on Linear Equations in One Variable

Word Problems on Linear Equations in One Variable

Practice Test on Word Problems on Linear Equations

●   Equations - Worksheets

Worksheet on Linear Equations

Worksheet on Word Problems on Linear Equation

7th Grade Math Problems 8th Grade Math Practice   From Practice Test on Linear Equations to HOME PAGE

Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

New! Comments

• Preschool Activities
• Kindergarten Math
• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• 9th Grade Math
• 10th Grade Math
• 11 & 12 Grade Math
• Concepts of Sets
• Probability
• Boolean Algebra
• Math Coloring Pages
• Multiplication Table
• Cool Maths Games
• Math Flash Cards
• Online Math Quiz
• Math Puzzles
• Binary System
• Math Dictionary
• Conversion Chart
• Homework Sheets
• Math Problem Ans
• Free Math Answers
• Printable Math Sheet
• Funny Math Answers
• Employment Test
• Math Patterns
• Link Partners
• Privacy Policy

Recent Articles

Numbers | Notation | Numeration | Numeral | Estimation | Examples

May 12, 24 06:28 PM

Face Value and Place Value|Difference Between Place Value & Face Value

May 12, 24 06:23 PM

Patterns in Numbers | Patterns in Maths |Math Patterns|Series Patterns

May 12, 24 06:09 PM

Worksheet on Bar Graphs | Bar Graphs or Column Graphs | Graphing Bar

May 12, 24 04:59 PM

Worksheet on Pictographs | Picture Graph Worksheets | Pictograph Works

May 12, 24 04:31 PM

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

ⓐ yes ⓑ yes ⓒ no ⓓ yes ⓔ no

ⓐ no ⓑ yes ⓒ yes ⓓ no ⓔ no

2 · 2 · 2 · 2 · 5 2 · 2 · 2 · 2 · 5

2 · 2 · 3 · 5 2 · 2 · 3 · 5

ⓐ 9 ⓑ 64 ⓒ 40

ⓐ 216 ⓑ 64 ⓒ 185

10 x 2 + 16 x + 17 10 x 2 + 16 x + 17

12 y 2 + 9 y + 7 12 y 2 + 9 y + 7

ⓐ 14 x 2 − 13 14 x 2 − 13 ⓑ 12 x ÷ 2 12 x ÷ 2 ⓒ z + 13 z + 13 ⓓ 8 x − 18 8 x − 18

ⓐ 17 y 2 + 19 17 y 2 + 19 ⓑ 7 y 7 y ⓒ x + 11 x + 11 ⓓ 11 a − 14 11 a − 14

ⓐ 4 ( p + q ) 4 ( p + q ) ⓑ 4 p + q 4 p + q

ⓐ 2 x − 8 2 x − 8 ⓑ 2 ( x − 8 ) 2 ( x − 8 )

w − 7 w − 7

l − 6 l − 6

4 q − 8 4 q − 8

7 n + 3 7 n + 3

ⓐ = = ⓑ > > ⓒ < < ⓓ = =

ⓐ > > ⓑ = = ⓒ > > ⓓ < <

ⓐ −6 −6 ⓑ 2 ⓒ −2 −2

ⓐ −7 −7 ⓑ 3 ⓒ −3 −3

ⓐ 2 ⓑ −2 −2 ⓒ −10 −10 ⓓ 10

ⓐ 3 ⓑ −3 −3 ⓒ −11 −11 ⓓ 11

ⓐ 8 , 8 8 , 8 ⓑ −18 , −18 , −18 −18 ⓒ 19 , 19 19 , 19 ⓓ −4 , −4 , −4 −4

ⓐ 8 , 8 8 , 8 ⓑ −22 , −22 , −22 −22 ⓒ 23 , 23 23 , 23 ⓓ 3 , 3 3 , 3

ⓐ 23 ⓑ 60 ⓒ −63 −63 ⓓ −9 −9

ⓐ 39 ⓑ 39 ⓒ −28 ⓓ −7

ⓐ 81 ⓑ −81 −81

ⓐ 49 ⓑ −49 −49

( 9 + ( −16 ) ) + 4 ; − 3 ( 9 + ( −16 ) ) + 4 ; − 3

( −8 + ( −12 ) ) + 7 ; − 13 ( −8 + ( −12 ) ) + 7 ; − 13

The difference in temperatures was 45 degrees.

The difference in temperatures was 9 degrees.

− 23 40 − 23 40

− 5 8 − 5 8

−33 a −33 a

−26 b −26 b

3 4 b 3 4 b

79 60 79 60

103 60 103 60

ⓐ 27 a − 32 36 27 a − 32 36 ⓑ 2 a 3 2 a 3

ⓐ 24 k − 5 30 24 k − 5 30 ⓑ 2 k 15 2 k 15

− 1 2 − 1 2

ⓐ 6.58 6.58 ⓑ 6.6 6.6 ⓒ 7

ⓐ 15.218 15.218 ⓑ 15.22 15.22 ⓒ 15.2 15.2

ⓐ −16.49 −16.49 ⓑ −0.42 −0.42

ⓐ −23.593 −23.593 ⓑ −12.58 −12.58

−27.4815 −27.4815

−87.6148 −87.6148

ⓐ 25.8 ⓑ 258 ⓒ 2,580

ⓐ 142 ⓑ 1,420 ⓒ 14,200

587.3 587.3

34.25 34.25

ⓐ 117 500 117 500 ⓑ −0.875 −0.875

ⓐ 3 125 3 125 ⓑ −0.375 −0.375

ⓐ 0.09, 0.87, 0.039 ⓑ 17%, 175%, 8.25%

ⓐ 0.03, 0.91, 0.083 ⓑ 41%, 225%, 9.25%

ⓐ 6 ⓑ 13 ⓒ −15 −15

ⓐ 4 ⓑ 14 ⓒ −10 −10

ⓐ 4 , 49 4 , 49 ⓑ −3 , 4 , 49 −3 , 4 , 49 ⓒ −3 , 0. 3 – , 9 5 , 4 , 49 −3 , 0. 3 – , 9 5 , 4 , 49 ⓓ − 2 − 2 ⓔ −3 , − 2 , 0. 3 – , 9 5 , 4 , 49 −3 , − 2 , 0. 3 – , 9 5 , 4 , 49

ⓐ 6 , 121 6 , 121 ⓑ − 25 , −1 , 6 , 121 − 25 , −1 , 6 , 121 ⓒ − 25 , − 3 8 , −1 , 6 , 121 − 25 , − 3 8 , −1 , 6 , 121 ⓓ 2.041975.. . 2.041975.. . ⓔ − 25 , − 3 8 , −1 , 6 , 121 , 2.041975.. . − 25 , − 3 8 , −1 , 6 , 121 , 2.041975.. .

32 r + 29 s 32 r + 29 s

41 m + 6 n 41 m + 6 n

1 7 15 1 7 15

1 2 9 1 2 9

−48 a −48 a

−92 x −92 x

11 25 11 25

ⓐ 0 ⓑ undefined

4 x + 8 4 x + 8

6 x + 42 6 x + 42

5 y + 3 5 y + 3

4 n + 9 4 n + 9

70 + 15 p 70 + 15 p

4 + 35 d 4 + 35 d

−10 + 15 a −10 + 15 a

−56 + 105 y −56 + 105 y

− z + 11 − z + 11

− x + 4 − x + 4

3 − 3 x 3 − 3 x

2 x − 20 2 x − 20

5 x − 66 5 x − 66

7 x − 13 7 x − 13

Section 1.1 Exercises

Divisible by 2, 3, 6

Divisible by 2

Divisible by 3, 5

2 · 43 2 · 43

5 · 7 · 13 5 · 7 · 13

2 · 2 · 2 · 2 · 3 · 3 · 3 2 · 2 · 2 · 2 · 3 · 3 · 3

ⓐ 64 ⓑ 16 ⓒ 7

10 x + 6 10 x + 6

22 a + 1 22 a + 1

17 x 2 + 20 x + 16 17 x 2 + 20 x + 16

ⓐ 5 x 2 − 6 x y 5 x 2 − 6 x y ⓑ 6 y 2 5 x 6 y 2 5 x ⓒ y 2 + 21 y 2 + 21 ⓓ 81 x 2 − 6 x 81 x 2 − 6 x

ⓐ 4 a b 2 + 3 a 2 b 4 a b 2 + 3 a 2 b ⓑ 20 x y 2 20 x y 2 ⓒ m + 15 m + 15 ⓓ 121 x 2 − 9 x 121 x 2 − 9 x

ⓐ 8 ( y − 9 ) 8 ( y − 9 ) ⓑ 8 y − 9 8 y − 9

ⓐ 5 ( 3 x + y ) 5 ( 3 x + y ) ⓑ 15 x + y 15 x + y

2 c + 14 2 c + 14

3 n − 7 3 n − 7

Answers will vary.

Section 1.2 Exercises

ⓐ > > ⓑ > > ⓒ > > ⓓ > >

ⓐ = = ⓑ = = ⓒ > > ⓓ = =

ⓐ −11 −11 ⓑ −3 −3 ⓒ 3 3

ⓐ 6 ⓑ −6 −6 ⓒ −20 −20 ⓓ 20 20

ⓐ −32 −32 ⓑ −65 −65 ⓒ −4 −4 ⓓ 13 13

ⓐ −4 −4 ⓑ −12 −12 ⓒ −39 −39 ⓓ 14 14

ⓐ 64 64 ⓑ −64 −64

ⓐ −47 −47 ⓑ 16 16

( 3 + ( −15 ) ) + 7 ; − 5 ( 3 + ( −15 ) ) + 7 ; − 5

ⓐ 10 − ( −18 ) ; 28 10 − ( −18 ) ; 28 ⓑ −25 − 11 ; − 36 −25 − 11 ; − 36

−6 a + b −6 a + b

− $ 28 − $ 28

Section 1.3 Exercises

− 12 7 − 12 7

10 21 10 21

2 x 2 3 y 2 x 2 3 y

− 21 a 2 11 b 2 − 21 a 2 11 b 2

− 21 50 − 21 50

11 30 11 30

33 4 x 33 4 x

− 4 9 − 4 9

10 u 9 v 10 u 9 v

− 1 16 − 1 16

− 10 9 − 10 9

− 2 5 − 2 5

2 m 3 n 2 m 3 n

29 24 29 24

17 105 17 105

− 53 40 − 53 40

4 x + 3 12 4 x + 3 12

ⓐ 5 6 5 6 ⓑ 4 4

ⓐ 25 n 16 25 n 16 ⓑ 25 n − 16 30 25 n − 16 30

ⓐ −8 x − 15 18 −8 x − 15 18 ⓑ − 10 k 27 − 10 k 27

ⓐ −5 ( a + 1 ) 3 −5 ( a + 1 ) 3 ⓑ a a

49 25 49 25

−28 − 15 y 60 −28 − 15 y 60

33 64 33 64

23 24 23 24

ⓐ 1 5 1 5 ⓑ 6 5 6 5

− 1 9 − 1 9

− 5 11 − 5 11

Section 1.4 Exercises

ⓐ 5.78 ⓑ 5.8 ⓒ 6

ⓐ 0.30 ⓑ 0.3 ⓒ 0

ⓐ 63.48 ⓑ 63.5 ⓒ 63

−40.91 −40.91

−7.22 −7.22

−27.5 −27.5

102.212 102.212

51.31 51.31

−4.89 −4.89

−1200.47982 −1200.47982

337.8914 337.8914

1.305 1.305

$ 2.44 $ 2.44

19 200 19 200

−12.4 −12.4

0.393 0.393

156 % 156 %

6.25 % 6.25 %

ⓐ 0 , 36 , 9 0 , 36 , 9 ⓑ −8 , 0 , 36 , 9 −8 , 0 , 36 , 9 ⓒ −8 , 0 , 12 5 , 36 , 9 −8 , 0 , 12 5 , 36 , 9 ⓓ 1.95286... , 1.95286... , ⓔ −8 , 0 , 1.95286... , 12 5 , 36 , 9 −8 , 0 , 1.95286... , 12 5 , 36 , 9

ⓐ none ⓑ − 100 , −7 , −1 − 100 , −7 , −1 ⓒ − 100 , −7 , − 8 3 , −1 , 0.77 , 3 1 4 − 100 , −7 , − 8 3 , −1 , 0.77 , 3 1 4 ⓓ none ⓔ − 100 , −7 , − 8 3 , −1 , 0.77 , 3 1 4 − 100 , −7 , − 8 3 , −1 , 0.77 , 3 1 4

Section 1.5 Exercises

27 m + ( −21 n ) 27 m + ( −21 n )

5 4 g + 1 2 h 5 4 g + 1 2 h

2.43 p + 8.26 q 2.43 p + 8.26 q

1 5 6 1 5 6

14.88 14.88

49 11 49 11

32 y + 72 32 y + 72

6 c − 78 6 c − 78

3 4 q + 3 3 4 q + 3

5 y − 3 5 y − 3

3 + 8 r 3 + 8 r

36 d + 90 36 d + 90

r s − 18 r r s − 18 r

y p + 4 p y p + 4 p

−28 p − 7 −28 p − 7

−3 x + 18 −3 x + 18

−3 x + 7 −3 x + 7

−3 y − 8 −3 y − 8

−33 c + 26 −33 c + 26

− a + 19 − a + 19

4 m − 10 4 m − 10

72 x − 25 72 x − 25

22 n + 9 22 n + 9

6 c + 34 6 c + 34

12 y + 63 12 y + 63

Review Exercises

Divisible by 2 , 3 , 5 , 6 , 10 2 , 3 , 5 , 6 , 10

6 x 2 − x + 5 6 x 2 − x + 5

ⓐ 11 ( y − 2 ) 11 ( y − 2 ) ⓑ 11 y − 2 11 y − 2

ⓐ 8 ⓑ −8 −8 ⓒ −22 −22 ⓓ 22

ⓐ −3 −3 ⓑ −15 −15 ⓒ −56 −56 ⓓ 17

( −4 + ( −9 ) ) + 23 ; 10 ( −4 + ( −9 ) ) + 23 ; 10

− 15 x 3 11 y 2 − 15 x 3 11 y 2

8 x 15 y 8 x 15 y

31 36 31 36

ⓐ 11 8 11 8 ⓑ 5 6 5 6

− 1 6 − 1 6

− 1 5 − 1 5

96.978 96.978

− 48 5 − 48 5

1. 27 ¯ 1. 27 ¯

4.75 % 4.75 %

no real number

3 4 x + y 3 4 x + y

1 11 15 1 11 15

8 b + 10 8 b + 10

x p − 5 p x p − 5 p

−6 x − 6 −6 x − 6

6 y + 16 6 y + 16

Practice Test

7 n + 7 7 n + 7

−8 − 11 ; − 19 −8 − 11 ; − 19

( −8 − ( −3 ) ) + 5 ; 0 ( −8 − ( −3 ) ) + 5 ; 0

ⓐ 28.15 28.15 ⓑ 28.146 28.146

15 17 15 17

− 5 3 − 5 3

− 7 6 − 7 6

−65.4 −65.4

1 8 13 1 8 13

13 y − 3 13 y − 3

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction

• Authors: Lynn Marecek, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Intermediate Algebra 2e
• Publication date: May 6, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/intermediate-algebra-2e/pages/chapter-1

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.1: Solving Linear Equations and Inequalities

• Last updated
• Save as PDF
• Page ID 48347

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Verify linear solutions.
• Use the properties of equality to solve basic linear equations.
• Clear fractions from equations.
• Identify linear inequalities and check solutions.
• Solve linear inequalities and express the solutions graphically on a number line and in interval notation.

Prerequisite Skills

Before you get started, take this prerequisite quiz.

1. Simplify \(2-6(4-7)^2\) without using a calculator.

If you missed this problem, review here . (Note that this will open a different textbook in a new window.)

2. Evaluate \(6x−4\) when \(x=−2\).

3. Evaluate \(-5x^2−x+9\) when \(x=-3\).

4. Simplify \(7x−1−4x+5\).

\(3x+4\) 

Solving Basic Linear Equations

An equation 129 is a statement indicating that two algebraic expressions are equal. A linear equation with one variable 130 , \(x\), is an equation that can be written in the standard form \(ax + b = 0\) where \(a\) and \(b\) are real numbers and \(a ≠ 0\). For example

\(3 x - 12 = 0\)

A solution 131 to a linear equation is any value that can replace the variable to produce a true statement. The variable in the linear equation \(3x − 12 = 0\) is \(x\) and the solution is \(x = 4\). To verify this, substitute the value \(4\) in for \(x\) and check that you obtain a true statement.

\(\begin{aligned} 3 x - 12 & = 0 \\ 3 ( \color{Cerulean}{4}\color{Black}{ )} - 12 & = 0 \\ 12 - 12 & = 0 \\ 0 & = 0 \:\: \color{Cerulean}{✓} \end{aligned}\)

Alternatively, when an equation is equal to a constant, we may verify a solution by substituting the value in for the variable and showing that the result is equal to that constant. In this sense, we say that solutions “satisfy the equation.”

Example \(\PageIndex{1}\):

Is \(a=2\) a solution to \(−10a+5=−25\)?

Recall that when evaluating expressions, it is a good practice to first replace all variables with parentheses, and then substitute the appropriate values. By making use of parentheses, we avoid some common errors when working the order of operations.

\(\begin{align*} - 10 a + 5 &= -25 \\ - 10 ( \color{Cerulean}{2} \color{Black}{ ) +} 5 & = -25 \\ -20 + 5 & = -25 \\ -15 &\neq 25\:\: \color{red}{✗}\end{align*}\)  

No, \(a=2\) does not satisfy the equation and is therefore not a solution.

Developing techniques for solving various algebraic equations is one of our main goals in algebra. This section reviews the basic techniques used for solving linear equations with one variable. We begin by defining equivalent equations 132 as equations with the same solution set.

\(\left. \begin{aligned} 3 x - 5 & = 16 \\ 3 x & = 21 \\ x & = 7 \end{aligned} \right\} \quad \color{Cerulean}{Equivalent \:equations}\)

Here we can see that the three linear equations are equivalent because they share the same solution set, namely, \(\{7\}\). To obtain equivalent equations, use the following properties of equality 133 . Given algebraic expressions \(A\) and \(B\), where \(c\) is a nonzero number:

Table 1.1.1

Multiplying or dividing both sides of an equation by \(0\) is carefully avoided. Dividing by \(0\) is undefined and multiplying both sides by \(0\) results in the equation \(0 = 0\).

We solve algebraic equations by isolating the variable with a coefficient of 1. If given a linear equation of the form \(ax + b = c\), then we can solve it in two steps. First, use the appropriate equality property of addition or subtraction to isolate the variable term. Next, isolate the variable using the equality property of multiplication or division. Checking the solution in the following examples is left to the reader.

Example \(\PageIndex{2}\):

Solve: \(7x − 2 = 19\).

\(\begin{aligned} 7 x - 2 & = 19 \\ 7 x - 2 \color{Cerulean}{+ 2} & = 19 \color{Cerulean}{+ 2} & & \color{Cerulean}{Add\: 2\: to\: both\: sides.} \\ 7 x & = 21 \\ \frac { 7 x } { \color{Cerulean}{7} } & = \frac { 21 } { \color{Cerulean}{7} } & & \color{Cerulean}{Divide\: both\: sides\: by\: 7.} \\ x & = 3 \end{aligned}\)

The solution is \(3\).

Example \(\PageIndex{3}\):

Solve: \(56 = 8 + 12y\).

When no sign precedes the term, it is understood to be positive. In other words, think of this as \(56 = +8 + 12y\). Therefore, we begin by subtracting \(8\) on both sides of the equal sign.

\(\begin{aligned} 56 \color{Cerulean}{- 8} & = 8 + 12 y \color{Cerulean}{- 8} \\ 48 & = 12 y \\ \frac { 48 } { \color{Cerulean}{12} } & = \frac { 12 y } { \color{Cerulean}{12} } \\ 4 & = y \end{aligned}\)

It does not matter on which side we choose to isolate the variable because the symmetric property 134 states that \(4 = y\) is equivalent to \(y = 4\).

The solution is \(4\).

Example \(\PageIndex{4}\):

Solve: \(\frac { 5 } { 3 } x + 2 = - 8\).

Isolate the variable term using the addition property of equality, and then multiply both sides of the equation by the reciprocal of the coefficient \(\frac{5}{3}\) .

\begin{aligned} \frac { 5 } { 3 } x + 2 & = - 8 \\ \frac { 5 } { 3 } x + 2 \color{Cerulean}{- 2} & = - 8 \color{Cerulean}{- 2}\quad \color{Cerulean}{Subtract\: 2\: on\: both\: sides.} \\ \frac { 5 } { 3 } x & = - 10 \\ \color{Cerulean}{\frac { 3 } { 5 }} \color{Black}{ \cdot} \frac { 5 } { 3 } x & = \color{Cerulean}{\frac { 3 } { \cancel{5} }} \color{Black}{\cdot} ( \overset{-2}{\cancel{-10}} )\quad \color{Cerulean}{Multiply \:both \:sides\: by\: \frac{3}{5}.} \\ 1x & = 3 \cdot ( - 2 ) \\ x & = - 6 \end{aligned}

The solution is \(−6\).

In summary, to retain equivalent equations, we must perform the same operation on both sides of the equation.

Exercise \(\PageIndex{1}\)

Solve: \(\frac { 2 } { 3 } x + \frac { 1 } { 2 } = - \frac { 5 } { 6 }\).

Video Solution: www.youtube.com/v/cQwqXs9AD6M

General Guidelines for Solving Linear Equations

Typically linear equations are not given in standard form, and so solving them requires additional steps. When solving linear equations, the goal is to determine what value, if any, will produce a true statement when substituted in the original equation. Do this by isolating the variable using the following steps:

• Step 1: Simplify both sides of the equation using the order of operations and combine all like terms on the same side of the equal sign.
• Step 2a: Add or subtract as needed to isolate the variable.
• Step 2b: Divide or multiply as needed to isolate the variable.
• Step 3: Check to see if the answer solves the original equation.

We will often encounter linear equations where the expressions on each side of the equal sign can be simplified. If this is the case, then it is best to simplify each side first before solving. Normally this involves combining same-side like terms.

At this point in our study of algebra the use of the properties of equality should seem routine. Therefore, displaying these steps in this text, usually in blue, becomes optional.

Example \(\PageIndex{5}\):

Solve: \(- 4 a + 2 - a = 1\).

First combine the like terms on the left side of the equal sign.

\(\begin{aligned} - 4 a + 2 - a = 1 & \quad \color{Cerulean}{ Combine\: same-side\: like\: terms.} \\ - 5 a + 2 = 1 & \quad\color{Cerulean} { Subtract\: 2\: on\: both\: sides.} \\ - 5 a = - 1 & \quad\color{Cerulean} { Divide\: both\: sides\: by\: - 5.} \\ a = \frac { - 1 } { - 5 } = \frac { 1 } { 5 } \end{aligned}\)

Always use the original equation to check to see if the solution is correct.

\(\begin{aligned} - 4 a + 2 - a & = - 4 \left( \color{OliveGreen}{\frac { 1 } { 5 }} \right) + 2 - \color{OliveGreen}{\frac { 1 } { 5 }} \\ & = - \frac { 4 } { 5 } + \frac { 2 } { 1 } \cdot \color{Cerulean}{\frac { 5 } { 5 }}\color{Black}{ -} \frac { 1 } { 5 } \\ & = \frac { - 4 + 10 + 1 } { 5 } \\ & = \frac { 5 } { 5 } = 1 \:\:\color{Cerulean}{✓} \end{aligned}\)

The solution is \(\frac{1}{5}\) .

Given a linear equation in the form \(ax + b = cx + d\), we begin the solving process by combining like terms on opposite sides of the equal sign. To do this, use the addition or subtraction property of equality to place like terms on the same side so that they can be combined. In the examples that remain, the check is left to the reader.

Example \(\PageIndex{6}\):

Solve: \(−2y − 3 = 5y + 11\).

Subtract \(5y\) on both sides so that we can combine the terms involving y on the left side.

\(\begin{array} { c } { - 2 y - 3 \color{Cerulean}{- 5 y}\color{Black}{ =} 5 y + 11 \color{Cerulean}{- 5 y} } \\ { - 7 y - 3 = 11 } \end{array}\)

From here, solve using the techniques developed previously.

\(\begin{aligned} - 7 y - 3 & = 11 \quad\color{Cerulean}{Add\: 3\: to\: both\: sides.} \\ - 7 y & = 14 \\ y & = \frac { 14 } { - 7 } \quad\color{Cerulean}{Divide\: both\: sides\: by\: -7.} \\ y & = - 2 \end{aligned}\)

The solution is \(−2\).

Solving will often require the application of the distributive property.

Example \(\PageIndex{7}\):

Solve: \(- \frac { 1 } { 2 } ( 10 x - 2 ) + 3 = 7 ( 1 - 2 x )\).

Simplify the linear expressions on either side of the equal sign first.

\(\begin{aligned} - \frac { 1 } { 2 } ( 10 x - 2 ) + 3 = 7 ( 1 - 2 x ) & \quad\color{Cerulean} { Distribute } \\ - 5 x + 1 + 3 = 7 - 14 x & \quad\color{Cerulean} { Combine\: same-side\: like\: terms. } \\ - 5 x + 4 = 7 - 14 x & \quad\color{Cerulean} { Combine\: opposite-side\: like\: terms. } \\ 9 x = 3 & \quad\color{Cerulean} { Solve. } \\ x = \frac { 3 } { 9 } = \frac { 1 } { 3 } \end{aligned}\)

The solution is \(\frac{1}{3}\) .

Example \(\PageIndex{8}\):

Solve: \(5(3−a)−2(5−2a)=3\).

Begin by applying the distributive property.

\(\begin{aligned} 5 ( 3 - a ) - 2 ( 5 - 2 a ) & = 3 \\ 15 - 5 a - 10 + 4 a & = 3 \\ 5 - a & = 3 \\ - a & = - 2 \end{aligned}\)

Here we point out that \(−a\) is equivalent to \(−1a\); therefore, we choose to divide both sides of the equation by \(−1\).

\(\begin{array} { c } { - a = - 2 } \\ { \frac { - 1 a } { \color{Cerulean}{- 1} }\color{Black}{ =} \frac { - 2 } { \color{Cerulean}{- 1} } } \\ { a = 2 } \end{array}\)

Alternatively, we can multiply both sides of \(−a=−2\) by negative one and achieve the same result.

\(\begin{aligned} - a & = - 2 \\ \color{Cerulean}{( - 1 )}\color{Black}{ (} - a ) & = \color{Cerulean}{( - 1 )}\color{Black}{ (} - 2 ) \\ a & = 2 \end{aligned}\)

The solution is \(2\).

Exercise \(\PageIndex{2}\)

Solve: \(6 - 3 ( 4 x - 1 ) = 4 x - 7\).

Video Solution: www.youtube.com/v/NAIAZrFjU-o

The coefficients of linear equations may be any real number, even decimals and fractions. When this is the case it is possible to use the multiplication property of equality to clear the fractional coefficients and obtain integer coefficients in a single step. If given fractional coefficients, then multiply both sides of the equation by the least common multiple of the denominators (LCD).

Example \(\PageIndex{9}\):

Solve: \(\frac { 1 } { 3 } x + \frac { 1 } { 5 } = \frac { 1 } { 5 } x - 1\).

Clear the fractions by multiplying both sides by the least common multiple of the given denominators. In this case, it is the \(LCD (3, 5) = 15\).

\(\begin{aligned} \color{Cerulean}{15}\color{Black}{ \cdot} \left( \frac { 1 } { 3 } x + \frac { 1 } { 5 } \right) & = \color{Cerulean}{15}\color{Black}{ \cdot} \left( \frac { 1 } { 5 } x - 1 \right) \quad \color{Cerulean}{Multiply\: both\: sides\: by\: 15.} \\ \color{Cerulean}{15}\color{Black}{ \cdot} \frac { 1 } { 3 } x + \color{Cerulean}{15}\color{Black}{ \cdot} \frac { 1 } { 5 } & = \color{Cerulean}{15}\color{Black}{ \cdot} \frac { 1 } { 5 } x - \color{Cerulean}{15}\color{Black}{ \cdot} 1\quad\color{Cerulean}{Simplify.} \\ 5 x + 3 & = 3 x - 15\quad\quad\quad\color{Cerulean}{Solve.} \\ 2 x & = - 18 \\ x & = \frac { - 18 } { 2 } = - 9 \end{aligned}\)

The solution is \(−9\).

It is important to know that this technique only works for equations. Do not try to clear fractions when simplifying expressions. As a reminder:

Table 1.1.2

We simplify expressions and solve equations. If you multiply an expression by \(6\), you will change the problem. However, if you multiply both sides of an equation by \(6\), you obtain an equivalent equation.

Table 1.1.3

Applications Involving Linear Equations

Algebra simplifies the process of solving real-world problems. This is done by using letters to represent unknowns, restating problems in the form of equations, and by offering systematic techniques for solving those equations. To solve problems using algebra, first translate the wording of the problem into mathematical statements that describe the relationships between the given information and the unknowns. Usually, this translation to mathematical statements is the difficult step in the process. The key to the translation is to carefully read the problem and identify certain key words and phrases.

Table 1.1.4

When translating sentences into mathematical statements, be sure to read the sentence several times and parse out the key words and phrases. It is important to first identify the variable, “ let x represent… ” and state in words what the unknown quantity is. This step not only makes our work more readable, but also forces us to think about what we are looking for.

Example \(\PageIndex{10}\):

When \(6\) is subtracted from twice the sum of a number and \(8\) the result is \(5\). Represent this as an algebraic equation and find the number.

Let n represent the unknown number.

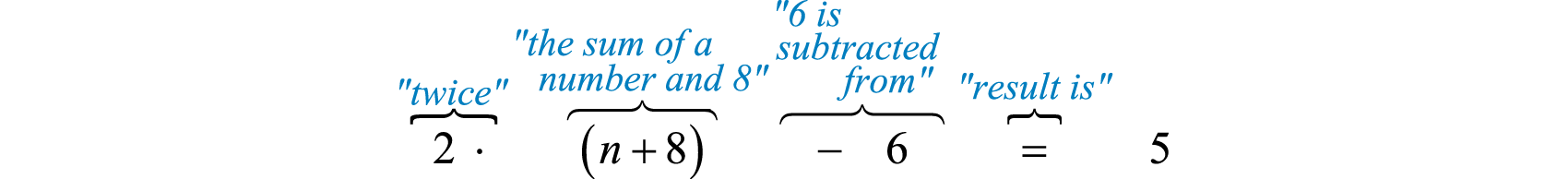
To understand why we included the parentheses in the set up, you must study the structure of the following two sentences and their translations:

Table 1.1.5

The key was to focus on the phrase “ twice the sum ,” this prompted us to group the sum within parentheses and then multiply by \(2\). After translating the sentence into a mathematical statement we then solve.

\(\begin{aligned} 2 ( n + 8 ) - 6 & = 5 \\ 2 n + 16 - 6 & = 5 \\ 2 n + 10 & = 5 \\ 2 n & = - 5 \\ n & = \frac { - 5 } { 2 } \end{aligned}\)

\(\begin{aligned} 2 ( n + 8 ) - 6 & = 2 \left( \color{Cerulean}{- \frac { 5 } { 2 }}\color{Black}{ +} 8 \right) - 6 \\ & = 2 \left( \frac { 11 } { 2 } \right) - 6 \\ & = 11 - 6 \\ & = 5 \quad\color{Cerulean}{✓}\end{aligned}\)       

The number is \(−\frac{5}{2}\).

General guidelines for setting up and solving word problems follow.

• Step 1: Read the problem several times, identify the key words and phrases, and organize the given information.
• Step 2: Identify the variables by assigning a letter or expression to the unknown quantities.
• Step 3: Translate and set up an algebraic equation that models the problem.
• Step 4: Solve the resulting algebraic equation.
• Step 5: Finally, answer the question in sentence form and make sure it makes sense (check it).

For now, set up all of your equations using only one variable. Avoid two variables by looking for a relationship between the unknowns.

Linear Inequalities

A linear inequality 138 is a mathematical statement that relates a linear expression as either less than or greater than another. The following are some examples of linear inequalities, all of which are solved in this section:

A solution to a linear inequality 139 is a real number that will produce a true statement when substituted for the variable.

Example \(\PageIndex{11}\):

Are \(x=−4\) and \(x=6\) solutions to \(5x+7<22\)?

Substitute the values in for \(x\), simplify, and check to see if we obtain a true statement.

Table 1.1.6

\(x=−4\) is a solution and \(x=6\) is not

Linear inequalities have either infinitely many solutions or no solution. If there are infinitely many solutions, we graph the solution set on a number line and/or express the solution using interval notation.

Expressing Solutions to Linear Inequalities

What number would make the inequality \(x>3\) true? Are you thinking, "\(x\) could be four"? That’s correct, but \(x\) could be 6, too, or 137, or even 3.0001. Any number greater than three is a solution to the inequality \(x>3\). We show all the solutions to the inequality \(x>3\) on the number line by shading in all the numbers to the right of three, to show that all numbers greater than three are solutions. Because the number three itself is not a solution, we put an open parenthesis at three.

We can also represent inequalities using interval notation . There is no upper end to the solution to this inequality. In interval notation, we express \(x>3\) as \((3,\infty)\). The symbol \(\infty\) is read as “ infinity .” It is not an actual number. Figure \(\PageIndex{2}\) shows both the number line and the interval notation.

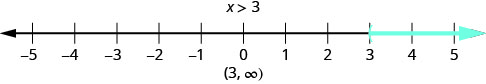
We use the left parenthesis symbol, (, to show that the endpoint of the inequality is not included. The left bracket symbol, [, would show that the endpoint is included.

The inequality \(x\leq 1\) means all numbers less than or equal to one. Here we need to show that one is a solution, too. We do that by putting a bracket at \(x=1\). We then shade in all the numbers to the left of one, to show that all numbers less than one are solutions (Figure \(\PageIndex{3}\)). There is no lower end to those numbers. We write \(x\leq 1x\leq 1 \)in interval notation as \((−\infty,1]\). The symbol \(−\infty\) is read as “negative infinity.”

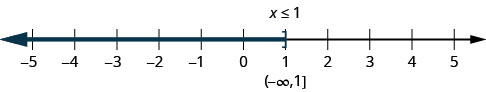
Figure \(\PageIndex{4}\) shows both the number line and interval notation.

INEQUALITIES, NUMBER LINES, AND INTERVAL NOTATION

The notation for inequalities on a number line and in interval notation use the same symbols to express the endpoints of intervals. Notice that \(\infty\) and \(-\infty\) always use parentheses in interval notation, never brackets.

Example \(\PageIndex{12}\)

Graph each inequality on the number line and write in interval notation.

• \(x\geq −3\)
• \(x<2.5\)
• \(x\leq −\frac{3}{5}\)

Exercise \(\PageIndex{3}\)

Graph each inequality on the number line and write in interval notation:

• \(x\leq −4\)
• \(x\geq 0.5\)
• \(x<−\frac{2}{3}\).

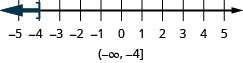
Solving Linear Inequalities

All but one of the techniques learned for solving linear equations apply to solving linear inequalities. You may add or subtract any real number to both sides of an inequality, and you may multiply or divide both sides by any positive real number to create equivalent inequalities. For example:

\[\begin{align*} 10 &> - 5 \\[4pt] 10{\color{Cerulean}{-7}}\,&{\color{Black}{>}} -5{\color{Cerulean}{-7}} & & {\color{Cerulean}{Subtract\: 7\: on\: both\: sides.}}\\[4pt]  3 &> - 12 & & \color{Cerulean}{✓}\quad\color{Cerulean}{True.} \\[20pt] 10 &>-5\\[4pt] \frac{10}{\color{Cerulean}{5}}\,&\color{Black}{>}\frac{-5}{\color{Cerulean}{5}} & & \color{Cerulean}{Divide\: both\: sides\: by\: 5.}\\[4pt] 2 &>-1 & & \color{Cerulean}{✓\:\:True} \end{align*} \]

Subtracting \(7\) from each side and dividing each side by positive \(5\) results in an inequality that is true.

Example \(\PageIndex{13}\):

Solve and graph the solution set: \(5x+7<22\).

\(\begin{array} { c } { 5 x + 7 < 22 } \\ { 5 x + 7 \color{Cerulean}{- 7}\color{Black}{ < 22}\color{Cerulean}{ - 7} } \\ { 5 x < 15 } \\ { \frac { 5 x } {\color{Cerulean}{ 5} } < \frac { 15 } { \color{Cerulean}{5} } } \\ { x < 3 } \end{array}\)

It is helpful to take a minute and choose a few values in and out of the solution set, substitute them into the original inequality, and then verify the results. As indicated, you should expect \(x=0\) to solve the original inequality and that \(x=5\) should not.

Table 1.1.7

Checking in this manner gives us a good indication that we have solved the inequality correctly.

We can express this solution in two ways: using set notation and interval notation.

\(\begin{array} { r } { \{ x | x < 3 \} } &\color{Cerulean}{Set\: notation} \\ { ( - \infty , 3 ) } &\color{Cerulean}{Interval\: notation} \end{array}\)

In this text we will choose to present answers using interval notation.

\((−∞,  3) \)

When working with linear inequalities, a different rule applies when multiplying or dividing by a negative number. To illustrate the problem, consider the true statement \(10 > −5\) and divide both sides by \(−5\).

\(\begin{array} { l } { 10 > - 5 } \\ { \frac { 10 } { \color{Cerulean}{- 5} } \color{Black}{>} \frac { - 5 } { \color{Cerulean}{- 5} } } \quad \color{Cerulean}{Divide\: both\: sides\: by\: -5.} \\ { - 2 \color{red}{>}\color{Black}{ 1} \quad \color{red}{✗} \color{Cerulean}{ False } } \end{array}\)

Dividing by \(−5\) results in a false statement. To retain a true statement, the inequality must be reversed.

\(\begin{array} { l } { 10 \color{OliveGreen}{>}\color{Black}{ - 5} } \\ { \frac { 10 } { \color{Cerulean}{- 5} } \color{Black}{<} \frac { - 5 } { \color{Cerulean}{- 5} } } \quad \color{Cerulean}{Reverse\: the\: inequality.} \\ { - 2 \color{OliveGreen}{<}\color{Black}{ 1} \quad \color{Cerulean}{✓} \color{Cerulean}{ True } } \end{array}\)

The same problem occurs when multiplying by a negative number. This leads to the following new rule: when multiplying or dividing by a negative number, reverse the inequality . It is easy to forget to do this so take special care to watch for negative coefficients. In general, given algebraic expressions \(A\) and \(B\), where \(c\) is a positive nonzero real number, we have the following properties of inequalities 140 :

Table 1.1.8

We use these properties to obtain an equivalent inequality 141 , one with the same solution set, where the variable is isolated. The process is similar to solving linear equations.

Example \(\PageIndex{14}\):

Solve and graph the solution set: \(−2(x+8)+6≥20\).

\(\begin{aligned} - 2 ( x + 8 ) + 6 & \geq 20 \quad\color{Cerulean}{Distribute.} \\ - 2 x - 16 + 6 & \geq 20 \quad\color{Cerulean}{Combine\: like\: terms.} \\ - 2 x - 10 & \geq 20 \quad\color{Cerulean}{Solve\: for\: x.} \\ - 2 x & \geq 30 \quad\color{Cerulean}{Divide\: both\: sides\: by\: -2.} \\ \frac { - 2 x } { \color{Cerulean}{- 2} } & \color{OliveGreen}{\leq} \frac { \color{Black}{30} } { \color{Cerulean}{- 2} } \quad\color{Cerulean}{Reverse\: the\: inequality.} \\ x & \leq - 15 \end{aligned}\)

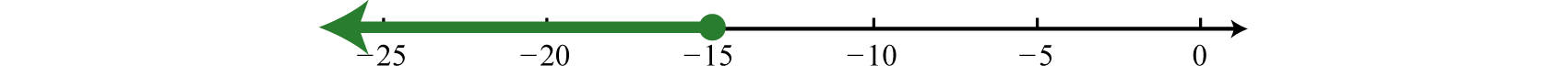
Interval notation \((−∞,  −15] \)

Example \(\PageIndex{15}\):

Solve and graph the solution set: \(−2(4x−5)<9−2(x−2)\).

\(\begin{array} { c } { - 2 ( 4 x - 5 ) < 9 - 2 ( x - 2 ) } \\ { - 8 x + 10 < 9 - 2 x + 4 } \\ { - 8 x + 10 < 13 - 2 x } \\ { - 6 x < 3 } \\ { \frac { - 6 x } { \color{Cerulean}{- 6} } \color{OliveGreen}{>} \frac { \color{Black}{3} } { \color{Cerulean}{- 6} } }\color{Cerulean}{Reverse\:the\:inequality.} \\ { x > - \frac { 1 } { 2 } } \end{array}\)

Interval notation \((−\frac{1}{2}, ∞)\)

Example \(\PageIndex{16}\):

Solve and graph the solution set: \(\frac{1}{2}x−2≥\frac{1}{2}(\frac{7}{4}x−9)+1\).

\(\begin{array} { c } { \frac { 1 } { 2 } x - 2 \geq \frac { 1 } { 2 } \left( \frac { 7 } { 4 } x - 9 \right) + 1 } \\ { \frac { 1 } { 2 } x - 2 \geq \frac { 7 } { 8 } x - \frac { 9 } { 2 } + 1 } \\ { \frac { 1 } { 2 } x - \frac { 7 } { 8 } x \geq - \frac { 7 } { 2 } + 2 } \\ { - \frac { 3 } { 8 } x \geq - \frac { 3 } { 2 } } \\ { \left( \color{Cerulean}{- \frac { 8 } { 3 }} \right) \left(\color{Black}{ - \frac { 3 } { 8 } x} \right) \leq \left( \color{Cerulean}{- \frac { 8 } { 3 }} \right) \left( \color{Black}{-} \frac { 3 } { 2 } \right) \quad \color{Cerulean} { Reverse\: the\: inequality. } } \\ { x \leq 4 } \end{array}\)

Interval notation: \((−∞,  4]\)

Exercise \(\PageIndex{4}\)

Solve and graph the solution set: \(10 - 5 ( 2 x + 3 ) \leq 25\)

\([ - 3 , \infty )\);

Video Solution: www.youtube.com/v/COLLNtwYFm8

Translation of Linear Inequalities

Some of the key words and phrases that indicate inequalities are summarized below:

Table 1.1.9

Key Takeaways

• Solving general linear equations involves isolating the variable, with coefficient \(1\), on one side of the equal sign. To do this, first use the appropriate equality property of addition or subtraction to isolate the variable term on one side of the equal sign. Next, isolate the variable using the equality property of multiplication or division. Finally, check to verify that your solution solves the original equation.
• If solving a linear equation leads to a true statement like \(0 = 0\), then the equation is an identity and the solution set consists of all real numbers, \(ℝ\).
• If solving a linear equation leads to a false statement like \(0 = 5\), then the equation is a contradiction and there is no solution, \(Ø\).
• Clear fractions by multiplying both sides of an equation by the least common multiple of all the denominators. Distribute and multiply all terms by the LCD to obtain an equivalent equation with integer coefficients.
• Simplify the process of solving real-world problems by creating mathematical models that describe the relationship between unknowns. Use algebra to solve the resulting equations.
• Inequalities typically have infinitely many solutions. The solutions are presented graphically on a number line or using interval notation or both.
• All but one of the rules for solving linear inequalities are the same as solving linear equations. If you divide or multiply an inequality by a negative number, reverse the inequality to obtain an equivalent inequality.

129 Statement indicating that two algebraic expressions are equal.

130 An equation that can be written in the standard form \(ax + b = 0\), where \(a\) and \(b\) are real numbers and \(a ≠ 0\).

131 Any value that can replace the variable in an equation to produce a true statement.

132 Equations with the same solution set.

133 Properties that allow us to obtain equivalent equations by adding, subtracting, multiplying, and dividing both sides of an equation by nonzero real numbers.

134 Allows you to solve for the variable on either side of the equal sign, because \(x = 5\) is equivalent to \(5 = x\).

135 Equations that are true for particular values.

136 An equation that is true for all possible values.

137 An equation that is never true and has no solution.

• Number Charts
• Multiplication
• Long division
• Basic operations
• Telling time
• Place value
• Roman numerals
• Fractions & related
• Add, subtract, multiply,   and divide fractions
• Mixed numbers vs. fractions
• Equivalent fractions
• Prime factorization & factors
• Fraction Calculator
• Decimals & Percent
• Add, subtract, multiply,   and divide decimals
• Fractions to decimals
• Percents to decimals
• Percentage of a number
• Percent word problems
• Classify triangles
• Classify quadrilaterals
• Circle worksheets
• Area & perimeter of rectangles
• Area of triangles & polygons
• Coordinate grid, including   moves & reflections
• Volume & surface area
• Pre-algebra
• Square Roots
• Order of operations
• Scientific notation
• Proportions
• Ratio word problems
• Write expressions
• Evaluate expressions
• Simplify expressions
• Linear equations
• Linear inequalities
• Graphing & slope
• Equation calculator
• Equation editor
• Elementary Math Games
• Addition and subtraction
• Math facts practice
• The four operations
• Factoring and number theory
• Geometry topics
• Middle/High School
• Statistics & Graphs
• Probability
• Trigonometry
• Logic and proof
• For all levels
• Favorite math puzzles
• Favorite challenging puzzles
• Math in real world
• Problem solving & projects
• For gifted children
• Math history
• Math games and fun websites
• Interactive math tutorials
• Math help & online tutoring
• Assessment, review & test prep
• Online math curricula

Worksheets for simplifying expressions

Worksheets for evaluating expressions with variables

Worksheets for writing expressions with variables from verbal expressions

Worksheets for linear inequalities

Key to Algebra Workbooks

Key to Algebra offers a unique, proven way to introduce algebra to your students. New concepts are explained in simple language, and examples are easy to follow. Word problems relate algebra to familiar situations, helping students to understand abstract concepts. Students develop understanding by solving equations and inequalities intuitively before formal solutions are introduced. Students begin their study of algebra in Books 1-4 using only integers. Books 5-7 introduce rational numbers and expressions. Books 8-10 extend coverage to the real number system.

UNIT 5 - LINEAR RELATIONS & EQUATIONS

Part 1 - Graphing Linear Relations (Ch 6)

Part 2 - Solving Linear Equations (Ch 6)

• Unit 5 Notes Package •

6.0 - ALGEBRA (REVIEW)

6.1 - representing patterns.

PG 183   #1-5, 8, 11, 13, 16 , 19

6.2 (1) - GRAPHING LINEAR RELATIONS

6.2 (2) - graphing linear relations (cont...).

PG 194  #1-9, 12, 15

6.2 (3) - GRAPHING LINEAR RELATIONS (CONT...)

6.3 (1) - modelling equations to solve.

PG 204   #1- 4

6.3 ( 2 ) - USING ALGEBRA TO SOLVE EQUATIONS

6. 4 (1) - solving equations with more than 1 step, 6.4 (2) - the distributive property, 6.4 (2) - cont..., 6.4 (3) - variables on both sides, 6.4 (4) - word problems, unit 5 review.

GRAPHING REVIEW

WORKSHEET     ANSWER KEY

SOLVING EQUATIONS REVIEW

GENERAL REVIEW

Textbook - PG 215

UNIT 5 TEST

THURSDAY, MAY 2nd

• Texas Go Math
• Big Ideas Math
• Engageny Math
• McGraw Hill My Math
• enVision Math
• 180 Days of Math
• Math in Focus Answer Key
• Math Expressions Answer Key
• Privacy Policy

Practice Test on Linear Equations | Linear Equations Questions Word Problems

Students who are looking for the practice material on linear equations can stay tuned to this page. Here, we are giving several problems on linear equations. Interested students can solve them by using addition, subtraction, multiplication, and division operation. You can also find the step by step solution guide for each and every question. While practicing this Linear Equations Word Problems just have a look at the important notes mentioned below.

How to Solve Linear Equations?

Go through the below steps on solving linear equations. Follow them and arrive at the solutions easily. They are listed as under

• A linear equation in one variable is one that contains only one variable and its highest power is 1.
• One can add or subtract the same number to both sides of the equation.
• One can divide or multiply by both sides of the equation by the same non-zero integer.
• The process in which any term in the equation can be moved to the other side of the equal symbol by changing its sign from (+ to -), (- to +), (x to ÷), and (÷ to x) is called the transposition.
• Cross multiplication means the process of multiplying the numerator of L.H.S with the denominator of the R.H.S and multiplying the denominator of L.H.S with the numerator of R.H.S.

Linear Equations Questions and Answers

Solve the following linear equations.

(a) (3 – 7x)/(15 + 2x) = 1

(b) 8x + 9 – 3x = 8 + 4x + 1

(c) 3x – 12 = 0

Multiply both sides by (15 + 2x).

(3 – 7x) = 1(15 + 2x)

3 – 7x = 15 + 2x

Transfer – 7x to R.H.S becomes 7x

3 = 15 + 2x + 7x

3 = 15 + 9x

Transfer 15 from R.H.S to L.H.s becomes -15.

3 – 15 = 9x

Divide both sides by 9

9x / 9 = -12/9

Therefore required solution is x = -4/3.

5x + 9 = 9 + 4x

Transfer 4x from R.H.S to L.H.S becomes -4x

5x – 4x + 9 = 0

Subtract both sides from -9

x + 9 – 9 = 0 – 9

Therefore, required solution set is x = -9.

Divide both sides of the equation by 3.

3x/3 = 12/3

Therefore, required solution set is x = 4.

Solve the following equations and represent them on a graph.

(a) (3y – 2)/3 + (2y + 3)/3 = (y + 7)/6

(b) 5x – 11 = 3x + 9

(c) (0.5y – 9)/0.25 = 4y – 3

[(3y – 2) + (2y + 3)] / 3 = (y + 7) / 6

(5y + 1) = (y + 7) / 2

Multiply both sides by 2.

2(5y + 1) = (y+7) / 2 x 2

10y + 2 = y + 7

Transferring y from R.H.S to L.H.S becomes -y, 2 from L.H.S to R.H.S becomes -2.

10y – y = 7 – 2

Therefore, the required solution set is y = 5/9.

Transferring 3x from R.H.S to L.H.S becomes -3x, -11 from L.H.S to R.H.S becomes 11.

5x – 3x = 9 + 11

Divide both sides by 2.

2x/2 = 20/2

Therefore, the required solution set is x = 10

Multiply both sides by 0.25.

(0.5y – 9)/0.25 x 0.25 = (4y – 3)0.25

0.5y – 9 = y – 0.75

Transferring 0.5y from L.H.S to R.H.S becomes -0.5y, -0.75 from R.h.s to L.H.S becomes 0.75.

-9 + 0.75 = y – 0.5y

-8.25 = 0.5y

Divide both sides by 0.5.

0.5y/0.5 = -8.25/0.5

Therefore, the required solution set is y = -16.5

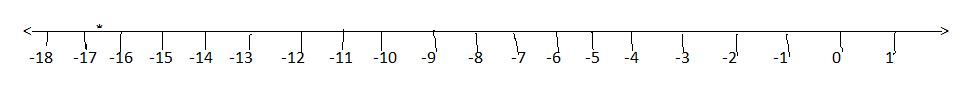
Solve the equations and verify them.

(a) (x – 3)/4 + (x – 1)/5 – (x – 2)/3 = 1

(b) y/2 – 1/2 = y/3 + 1/4

L.C.M of 4, 5, 3 is 60.

[15(x – 3) + 12(x – 1) – 20(x – 2)] / 60 = 1

Multiply both sides of the equation by 60.

[15(x – 3) + 12(x – 1) – 20(x – 2)] / 60 x 60 = 1 x 60

[15(x – 3) + 12(x – 1) – 20(x – 2)] = 60

15x – 45 + 12x – 12 – 20x + 40 = 60

27x – 20x – 57 + 40 = 60

7x – 17 = 60

7x = 60 + 17

Therefore, the required solution set is x = 11.

Verification:

L.H.S = (x – 3)/4 + (x – 1)/5 – (x – 2)/3

Substitute x = 11

L.H.S = (11 – 3)/4 + (11 – 1)/5 – (11 – 2)/3

= 8/4 + 10/5 – 9/3

= 2 + 2 – 3

= 4 – 3 = 1

Hence, L.H.S = R.H.S

(y – 1)/2 = (4y + 3)/12

Cross multiply the fractions.

12(y – 1) = 2(4y + 3)

12y – 12 = 8y + 6

12y – 8y = 6 + 12

L.H.S = y/2 – 1/2

Substitute y = 4.5

L.H.S = 4.5/2 – 1/2

= (4.5 – 1)/2

= 3.5/2 = 1.75

R.H.S = y/3 + 1/4

R.H.S = 4.5/3 + 1/4

= (4.5 x 4 + 3) / 12

= (18 + 3) / 12

= 21/12 = 1.75

Solve the below-mentioned linear equations.

(a) 8a – (4a + 32) = 16

(b) 4(x + 5) = 3(x – 2) – 2(x + 2)

8a – 4a – 32 = 16

4a – 32 = 16

Transferring -32 from L.H.S to R.H.S becomes +32.

4a = 16 + 32

Divide both sides of the equation by 4.

4a/4 = 48/4

Therefore, the required solution set a = 12.

4x + 20 = 3x – 6 – 2x – 4

4x + 20 = x – 10

Transferring x from R.H.S to L.H.S becomes -x, 20 from L.H.S to R.H.S becomes -20.

4x – x = -10 – 20

Divide both sides by 3.

3x/3 = -30/3

Therefore, the required solution set x = -10.

Solve the following equations and verify them.

(a) ⅓ (21 – 3x) = ½ (8 – 4x)

(b) (0.4y – 3)/(1.5y + 9) = -7/5

Cross-multiply the fractions.

2(21 – 3x) = 3(8 – 4x)

42 – 6x = 24 – 12x

Transferring -12x from R.H.S to L.H.S becomes 12x, 42 from L.H.S to R.H.S becomes -42.

-6x + 12x = 24 – 42

Divide both sides by 6.

6x/6 = -18/6

L.H.S = ⅓ (21 – 3x)

L.H.S = ⅓ (21 – 3(-3))

= ⅓ (21 + 9)

R.H.S = ½ (8 – 4x)

R.H.S = ½ (8 – 4(-3))

= ½ (8 + 12)

L.H.S = R.H.S

Hence proved.

5(0.4y – 3) = -7(1.5y + 9)

2y – 15 = -10.5y – 63

Transferring -10.5y from R.H.S to L.H.S becomes 10.5y, -15 from L.H.S to R.H.S becomes 15.

2y + 10.5y = 15 – 63

12.5y = -48

Divide both sides by 12.5

12.5y/12.5 = -48/12.5

L.H.S = (0.4y – 3)/(1.5y + 9)

Substitute y = -3.84

L.H.S = (0.4(-3.84) – 3) / (1.5(-3.84) + 9)

= (-1.536 – 3) / (-5.76 + 9)

= -4.536 / 3.24

R.H.S = -7/5

L.H.S = R.H.S.

Leave a Comment Cancel Reply

You must be logged in to post a comment.