Reset password New user? Sign up
Existing user? Log in

Solving Mixture Problems
Already have an account? Log in here.
Mixture problems involve combining two or more things and determining some characteristic of either the ingredients or the resulting mixture. For example, we might want to know how much water to add to dilute a saline solution, or we might want to determine the percentage of concentrate in a jug of orange juice.
Introduction to Mixtures
Using a table to problem solve, practice problems.
We can use fractions, ratios, or percentages to describe quantities in mixtures.
If 200 grams of a saline solution has 40 grams of salt, what percentage of the solution is salt? Answer \(\frac{40}{200} = 0.20 = 20\%\) of the solution is salt.
If each can of orange juice concentrate contains the same amount of concentrate, which recipe will make the drink that is most orangey?
There is a general strategy for solving these mixture problems that uses simple algebra organized with a chart.
How much 40% rubbing alcohol do we need to add to 90% rubbing alcohol to make a 50% solution of rubbing alcohol? We could organize the data we are given in the following chart: Solution Type Concentration Amount of Solution Amount of Pure Alcohol 40% rubbing alcohol 0.4 ? liters ? liters 90% rubbing alcohol 0.9 ? liters ? liters 50% rubbing alcohol 0.5 10 liters \(0.5(10) = 5\) liters In general, the rows of the chart are the mixture types that you have. The columns describe the amount of each compound you have and the concentration of that component in each mixture (represented as a decimal). When you don't have some of the information needed to fill in the cart, use a variable instead. Solution Type Concentration Amount of Solution Amount of Pure Compound 40% rubbing alcohol 0.4 \(x\) \(0.4(x)\) 90% rubbing alcohol 0.9 \(10-x\) \(0.9(10-x)\) 50% rubbing alcohol 0.5 10 \(0.5(10) = 5\) The amount of 40% solution that we'll need is unknown (so make it \(x\)). The amount of 90% solution that we'll need is also unknown, but must be \(10-x\) liters so that we'll, in total, make 10 liters of the final solution. The amount of alcohol that each part of the mixture adds to the final result is equal to the amount of each solution mixed in, times the fraction of alcohol that that solution is made from. To use this chart to solve the problem, we will use the fourth column as an equation to solve for \(x.\) The 10 liters of our final mixture must have a total volume of 5 liters of alcohol in it in order to be 50% alcohol. Those 5 liters must come from a combination of the amount of 40% solution we mix in and the amount of 90% solution. If the volume (in liters) of 40% solution that we mix in is \(x,\) then \(0.4x\) will be the volume (in liters) of the amount of alcohol contributed. Similarly, \(0.9(10-x)\) will be the amount of alcohol contributed by the \(10-x\) liters of 90% alcohol solution that we add. Therefore, in total, \(0.4x + 0.9(10-x)\) must be equal to the 5 total liters we'll need in the final solution to make it 50% alcohol. Solving the equation, \[\begin{align} 0.4x + (9 - 0.9x) &= 5\\ -0.5x + 9 &= 5\\ 0.5x &= 4\\ \Rightarrow x &= \frac{4}{0.5}= 8. \end{align}\] Therefore, we need \(x = 8\) liters of the 40% solution.
How many grams of pure water must be added to 40 grams of a 10% saline solution to make a saline solution that is 5% salt? Answer Let's set up a table to solve this problem, using \(x\) to represent the number of grams of water that must be added. Solution Type Concentration Amount of Solution Total Amount of Salt water 0 \(x\) 0 10% solution 0.1 40 \((0.1)(40)\) 5% solution 0.05 40+\(x\) \((0.05)(40+x)\) Because the total amount of salt remains the same after we add the water, we can set up and solve the following equation: \[\begin{align} (0.1)(40)&=(0.05)(40+x) \\ 4 &= 2 + 0.05x \\ x&=40.\end{align}\] We need to add \(40 \) grams of pure water to create the solution that is \(5\%\) salt.
I have a 100 ml mixture that is 20% isopropyl alcohol (80 ml of water and 20 ml of isopropyl alcohol).
How much more alcohol do I need to add to make the mixture 25% alcohol?
There is a 40 litre solution of milk and water in which the concentration of milk is 72%. How much water must be added to this solution to make it a solution in which the concentration of milk is 60% ?
Let's practice using the strategies from above on a variety of problems.
Jill mixes 100 liters of A-beverage that contains 45% juice with 200 liters of B-beverage. The resulting C-beverage is 30% fruit juice. What is the percent of fruit juice in the 200 liters of the B-beverage? Answer Let's begin by making a table to show what we know. Beverage Liters of Beverage Concentration Liters of Juice Beverage A 100 0.45 \((0.45)(100) = 45\) Beverage B 200 \(x\) \(200x\) Beverage C 300 0.30 \((0.30)(300)=90\) The total number of liters of juice in Beverages A and B must equal 90, so \[\begin{align} 45 + 200x &= 90 \\ 200x &= 45 \\ 0.225 &= x.\end{align}\] The concentration of juice in Beverage B is 22.5%.
Unequal amounts of 40% and 10% acid solutions were mixed and the resulting mixture was 30% concentrated. However, the required concentration is 25%, so the Chemist added 300 cubic meters of 20% acid solution in order to get the required concentration. What was the original amount of 40% acid solution?
Write only the quantity without the units (cubic meters).
Legend: wt = weight
Strawberries contain about 15 wt% solids and 85 wt% water. To make strawberry jam, crushed strawberries and sugar are mixed in a 45:55 mass ratio, and the mixture is heated to evaporate water until the residue contains one-third water by mass.
Question: 1.) Calculate how many pounds of strawberries are needed to make a pound of jam.
In a mixture of 60 litres, the ratio of milk and water 2 : 1. If this ratio is to be 1 : 2, then the quanity of water to be further added is:
Problem Loading...
Note Loading...
Set Loading...

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
Chapter 6: Polynomials
6.8 Mixture and Solution Word Problems
Solving mixture problems generally involves solving systems of equations. Mixture problems are ones in which two different solutions are mixed together, resulting in a new, final solution. Using a table will help to set up and solve these problems. The basic structure of this table is shown below:
| Name | Amount | Value | Equation |
|---|---|---|---|
The first column in the table (Name) is used to identify the fluids or objects being mixed in the problem. The second column (Amount) identifies the amounts of each of the fluids or objects. The third column (Value) is used for the value of each object or the percentage of concentration of each fluid. The last column (Equation) contains the product of the Amount times the Value or Concentration.
Example 6.8.1
Jasnah has 70 mL of a 50% methane solution. How much of a 80% solution must she add so the final solution is 60% methane? Find the equation.
- The solution names are 50% (S 50 ), 60% (S 60 ), and 80% (S 80 ).
- The amounts are S 50 = 70 mL, S 80 , and S 60 = 70 mL + S 80 .
- The concentrations are S 50 = 0.50, S 60 = 0.60, and S 80 = 0.80.
| Name | Amount | Value | Equation |
|---|---|---|---|
| S | 70 mL | 0.50 | 0.50 (70 mL) |
| S | S | 0.80 | 0.80 (S ) |
| S | 70 mL + S | 0.60 | 0.60 (70 mL + S ) |
The equation derived from this data is 0.50 (70 mL) + 0.80 (S 80 ) = 0.60 (70 mL + S 80 ).
Example 6.8.2
Sally and Terry blended a coffee mix that sells for [latex]\$2.50[/latex] by mixing two types of coffee. If they used 40 mL of a coffee that costs [latex]\$3.00,[/latex] how much of another coffee costing [latex]\$1.50[/latex] did they mix with the first?
| Name | Amount | Value | Equation |
|---|---|---|---|
| C | C | [latex]\$1.50[/latex] | [latex]\$1.50[/latex] (C ) |
| C | 40 mL | [latex]\$3.00[/latex] | [latex]\$3.00[/latex] (40 mL) |
| C | 40 mL + C | [latex]\$2.50[/latex] | [latex]\$2.50[/latex] (40 mL + C ) |
The equation derived from this data is:
[latex]\begin{array}{ccccccc} 1.50(C_{1.50})&+&3.00(40)&=&2.50(40&+&C_{1.50}) \\ 1.50(C_{1.50})&+&120&=&100&+&2.50(C_{1.50}) \\ -2.50(C_{1.50})&-&120&=&-120&-&2.50(C_{1.50}) \\ \hline &&-1.00(C_{1.50})&=&-20&& \\ \\ &&(C_{1.50})&=&\dfrac{-20}{-1}&& \\ \\ &&C_{1.50}&=&20&& \end{array}[/latex]
This means 20 mL of the coffee selling for [latex]\$1.50[/latex] is needed for the mix.
Example 6.8.3
Nick and Chloe have two grades of milk from their small dairy herd: one that is 24% butterfat and another that is 18% butterfat. How much of each should they use to end up with 42 litres of 20% butterfat?
| Name | Amount | Value | Equation |
|---|---|---|---|
| B | B | 0.24 | 0.24 (B ) |
| B | 42 L − B | 0.18 | 0.18 (42 L − B ) |
| B | 42 L | 0.20 | 0.20 (42 L) |
The equation derived from this data is:
[latex]\begin{array}{rrrrrrr} 0.24(B_{24})&+&0.18(42&- &B_{24})&=&0.20(42) \\ 0.24(B_{24})&+&7.56&-&0.18(B_{24})&=&8.4 \\ &-&7.56&&&&-7.56 \\ \hline &&&&0.06(B_{24})&=&0.84 \\ \\ &&&&B_{24}&=&\dfrac{0.84}{0.06} \\ \\ &&&&B_{24}&=&14 \end{array}[/latex]
This means 14 litres of the 24% buttermilk, and 28 litres of the 18% buttermilk is needed.
Example 6.8.4
In Natasha’s candy shop, chocolate, which sells for [latex]\$4[/latex] a kilogram, is mixed with nuts, which are sold for [latex]\$2.50[/latex] a kilogram. Chocolate and nuts are combined to form a chocolate-nut candy, which sells for [latex]\$3.50[/latex] a kilogram. How much of each are used to make 30 kilograms of the mixture?
| Name | Amount | Value | Equation |
|---|---|---|---|
| Chocolate | C | [latex]\$4.00[/latex] | [latex]\$4.00[/latex] (C) |
| Nuts | 30 kg − C | [latex]\$2.50[/latex] | [latex]\$2.50[/latex] (30 kg − C) |
| Mix | 30 kg | [latex]\$3.50[/latex] | [latex]\$3.50[/latex] (30 kg) |
[latex]\begin{array}{rrrrrrl} 4.00(C)&+&2.50(30&-&C)&=&3.50(30) \\ 4.00(C)&+&75&-&2.50(C)&=&105 \\ &-&75&&&&-75 \\ \hline &&&&1.50(C)&=&30 \\ \\ &&&&C&=&\dfrac{30}{1.50} \\ \\ &&&&C&=&20 \end{array}[/latex]
Therefore, 20 kg of chocolate is needed for the mixture.
With mixture problems, there is often mixing with a pure solution or using water, which contains none of the chemical of interest. For pure solutions, the concentration is 100%. For water, the concentration is 0%. This is shown in the following example.
Example 6.8.5
Joey is making a a 65% antifreeze solution using pure antifreeze mixed with water. How much of each should be used to make 70 litres?
| Name | Amount | Value | Equation |
|---|---|---|---|
| Antifreeze (A) | A | 1.00 | 1.00 (A) |
| Water (W) | 70 L − A | 0.00 | 0.00 (70 L − A) |
| 65% Solution | 70 L | 0.65 | 0.65 (70 L) |
[latex]\begin{array}{rrrrl} 1.00(A)&+&0.00(70-A)&=&0.65(0.70) \\ &&1.00A&=&45.5 \\ &&A&=&45.5 \\ \end{array}[/latex]
This means the amount of water added is 70 L − 45.5 L = 24.5 L.
For questions 1 to 9, write the equations that define the relationship.
- A tank contains 8000 litres of a solution that is 40% acid. How much water should be added to make a solution that is 30% acid?
- How much pure antifreeze should be added to 5 litres of a 30% mixture of antifreeze to make a solution that is 50% antifreeze?
- You have 12 kilograms of 10% saline solution and another solution of 3% strength. How many kilograms of the second should be added to the first in order to get a 5% solution?
- How much pure alcohol must be added to 24 litres of a 14% solution of alcohol in order to produce a 20% solution?
- How many litres of a blue dye that costs [latex]\$1.60[/latex] per litre must be mixed with 18 litres of magenta dye that costs [latex]\$2.50[/latex] per litre to make a mixture that costs [latex]\$1.90[/latex] per litre?
- How many grams of pure acid must be added to 40 grams of a 20% acid solution to make a solution which is 36% acid?
- A 100-kg bag of animal feed is 40% oats. How many kilograms of pure oats must be added to this feed to produce a blend of 50% oats?
- A 20-gram alloy of platinum that costs [latex]\$220[/latex] per gram is mixed with an alloy that costs [latex]\$400[/latex] per gram. How many grams of the [latex]\$400[/latex] alloy should be used to make an alloy that costs [latex]\$300[/latex] per gram?
- How many kilograms of tea that cost [latex]\$4.20[/latex] per kilogram must be mixed with 12 kilograms of tea that cost [latex]\$2.25[/latex] per kilogram to make a mixture that costs [latex]\$3.40[/latex] per kilogram?
Solve questions 10 to 21.
- How many litres of a solvent that costs [latex]\$80[/latex] per litre must be mixed with 6 litres of a solvent that costs [latex]\$25[/latex] per litre to make a solvent that costs [latex]\$36[/latex] per litre?
- How many kilograms of hard candy that cost [latex]\$7.50[/latex] per kg must be mixed with 24 kg of jelly beans that cost [latex]\$3.25[/latex] per kg to make a mixture that sells for [latex]\$4.50[/latex] per kg?
- How many kilograms of soil supplement that costs [latex]\$7.00[/latex] per kg must be mixed with 20 kg of aluminum nitrate that costs [latex]\$3.50[/latex] per kg to make a fertilizer that costs [latex]\$4.50[/latex] per kg?
- A candy mix sells for [latex]\$2.20[/latex] per kg. It contains chocolates worth [latex]\$1.80[/latex] per kg and other candy worth [latex]\$3.00[/latex] per kg. How much of each are in 15 kg of the mixture?
- A certain grade of milk contains 10% butterfat and a certain grade of cream 60% butterfat. How many litres of each must be taken so as to obtain a mixture of 100 litres that will be 45% butterfat?
- Solution A is 50% acid and solution B is 80% acid. How much of each should be used to make 100 cc of a solution that is 68% acid?
- A paint that contains 21% green dye is mixed with a paint that contains 15% green dye. How many litres of each must be used to make 600 litres of paint that is 19% green dye?
- How many kilograms of coffee that is 40% java beans must be mixed with coffee that is 30% java beans to make an 80-kg coffee blend that is 32% java beans?
- A caterer needs to make a slightly alcoholic fruit punch that has a strength of 6% alcohol. How many litres of fruit juice must be added to 3.75 litres of 40% alcohol?
- A mechanic needs to dilute a 70% antifreeze solution to make 20 litres of 18% strength. How many litres of water must be added?
- How many millilitres of water must be added to 50 millilitres of 100% acid to make a 40% solution?
- How many litres of water need to be evaporated from 50 litres of a 12% salt solution to produce a 15% salt solution?
Answer Key 6.8
Intermediate Algebra Copyright © 2020 by Terrance Berg is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book

- HW Guidelines
- Study Skills Quiz
- Find Local Tutors
- Demo MathHelp.com
- Join MathHelp.com
Select a Course Below
- ACCUPLACER Math
- Math Placement Test
- PRAXIS Math
- + more tests
- 5th Grade Math
- 6th Grade Math
- Pre-Algebra
- College Pre-Algebra
- Introductory Algebra
- Intermediate Algebra
- College Algebra
Examples of Setting Up "Mixture" Word Problems
Explanation Examples
The solutions to mixture problems tend to be generated by linear equations; that is, solving the set-up for mixture exercises tends to be pretty easy. It's the set-up that can be a bear.
What follows are some examples showing that set-up.
Content Continues Below
MathHelp.com
Mixture Word Problems
These examples demonstrate how to take the information you've been given, and how to use that to pick variables, create a table to organize everything, and then create the equations. In the exercises below are a few more problems, together with their grids (but not their solutions; I've left that part for you to do).
Advertisement
- How many liters of a 70% alcohol solution must be added to 50 liters of a 40% alcohol solution to produce a 50% alcohol solution?
You will be mixing a stronger solution with a weaker solution. The number of liters of the stronger solution is currently unknown; I'll use s to stand for the number of liters of the stronger solution. Then the number of liters of the mixture you're making will be s + 50 .
Make a table, with the columns showing the numbers of liters of solutions, the percentage of alcohol in each solution (this is your "rate"), and the number of liters of actual alcohol in each solution.
| liters sol'n | percent alcohol | total liters alcohol | |
|---|---|---|---|
| 70% sol'n | 0.70 | 0.70 | |
| 40% sol'n | 50 | 0.40 | 0.40(50) = 20 |
| 50% sol'n | + 50 | 0.50 | 0.50( + 50) |
From the last column, you get the equation:
0.7 s + 20 = 0.50( s + 50)
Solve for the value of the variable. Remember to put appropriate units (in this case, "liters") on your hand-in answer .
Forty percent is closer to 50% than is 70% . So you would logically expect that you'll end up using fewer liters of 70% solution than the 50 liters of 40% solution.
- How many ounces of pure water must be added to 50 ounces of a 15% saline solution to make a saline solution that is 10% salt?
I'll use w to stand for the number of ounces of water that are needed. And, since pure water has no salt in it, then the percentage of water that is salt is zero, and the number of ounces of salt is also zero.
| ounces liquid | percent salt | ounces salt | |
|---|---|---|---|
| water | 0 | 0 | |
| 15% sol'n | 50 | 0.15 | 0.15(50) = 7.5 |
| 10% sol'n | 50 + | 0.10 | 0.10(50 + ) |
7.5 = 0.10(50 + w )
Solve for the value of w . Remember to put the appropriate units (in this case, "ounces") on your hand-in answer .
Note: This exercise is typical of algebra courses, and is used to teach problem-solving skills in algebra classes. But, in real life, the actual process is different. ( Example ) If you're in a chemistry lab, expect the measuring and mixing to work in a different way.

- Find the selling price per pound of a coffee mixture made from 8 pounds of coffee that sells for $9.20 per pound and 12 pounds of coffee that costs $5.50 per pound.
This exercise asks us to make the implicit assumption that the selling price of the mix is based only on the selling price (and amounts) of the inputs. Of course, in real life, the selling price of the mix would be a markup on the cost of the mix, and the cost of the mix would be related to the costs of the inputs, plus the extra costs involved in mixing and re-bagging. But this is algebra, not real life.
The price per pound is the "rate" for this exercise. The sum of the prices of the inputs is assumed to be equal to the total price for the mixture.
| pounds of coffee | cost per pound | total cost of coffee | |
|---|---|---|---|
| pricy | 8 | 9.20 | 8(9.20) = 73.60 |
| cheapo | 12 | 5.50 | 12(5.50) = 66 |
| mixture | 8 + 12 = 20 | ? | 73.60 + 66 = 139.60 |
From the last row, you see that you have 20 pounds of coffee mixture. This mixture will sell for $139.60 . To find the selling price per pound of the mixture, divide ( $139.60 ) by ( 20 pounds). Simplify the division to find the unit rate.
Remember to put appropriate units (in this case, "dollars per pound") on your hand-in answer.
Note that, in this case, no variable was actually necessary. But if you'd picked a variable to replace the query-mark (that is, the " ? " in the bottom row), this would also have been fine.
- How many pounds of lima beans that cost $0.90 per pound must be mixed with 16 pounds of corn that costs $0.50 per pound to make a mixture of vegetables that costs $0.65 per pound?
The cost per pound is the "rate" for this exercise.
You are given the number of pounds of corn, but not the number of pounds of beans. I'll use b to stand for this amount.
| pounds of veggies | cost per pound | total cost of veggies | |
|---|---|---|---|
| beans | 0.90 | 0.90 | |
| corn | 16 | 0.50 | 16(0.50) = 8 |
| mix | + 16 | 0.65 | ( + 16)(0.65) |
The cost of the inputs add to the cost of the mix, which (from the far right column) gives the equation:
0.90 b + 8 = 0.65( b + 16)
Solve for the value of the variable. Remember to put the appropriate units (in this case, "pounds") on your hand-in answer .
- Two hundred liters of a punch that contains 35% fruit juice is mixed with 300 liters (L) of another punch. The resulting fruit punch is 20% fruit juice. Find the percent of fruit juice in the 300 liters of punch.
The percentage of the punch that comes from actual fruit is the "rate" for this exercise. Since the exercise is asking for a percentage, I will use the variable f .
| punch, L | % juice | juice, L | |
|---|---|---|---|
| 35% juice | 200 | 0.35 | 0.35(200) = 70 |
| other juice | 300 | 300 | |
| mixture | 200 + 300 = 500 | 0.20 | 0.20(500) = 100 |
The sum of the input amounts of juice will equal the total amount of juice in the mixture. You can use the last column to create the equation:
70 + 300 p = 100
Or you can just eyeball the amounts and notice that 300 p must equal 30 . Either way, do the division to find the value of the variable. Remember that you're looking for a percentage, so you'll need to convert the decimal solution into percentage form.
- Ten grams of sugar are added to a 40 -g serving of a breakfast cereal that is 30% sugar. What is the percent concentration of sugar in the resulting mixture?
Note that, because sugar is 100% sugar, the percentage of sugar in what is added to the bowl, in decimal form, is 1.00 .
I will use the variable s to stand for the percentage of sugar in the mixture.
| grams in bowl | percent sugar | grams sugar | |
|---|---|---|---|
| sugar | 10 | 1.00 | 10(1.00) = 10 |
| cereal | 40 | 0.30 | 40(0.30) = 12 |
| mixture | 10 + 40 = 50 | 10 + 12 = 22 |
From the bottom row, you see that there are 22 grams of sugar in the 50 grams in the bowl, or 22 / 50 . Convert the decimal value to percentage form .
As it turns out in this case, the variable wasn't actually necessary. But there's no harm in developing the habit of defining one.
URL: https://www.purplemath.com/modules/mixture2.htm
Page 1 Page 2
Standardized Test Prep
College math, homeschool math, share this page.
- Terms of Use
- Privacy / Cookies
- About Purplemath
- About the Author
- Tutoring from PM
- Advertising
- Linking to PM
- Site licencing
Visit Our Profiles
Pardon Our Interruption
As you were browsing something about your browser made us think you were a bot. There are a few reasons this might happen:
- You've disabled JavaScript in your web browser.
- You're a power user moving through this website with super-human speed.
- You've disabled cookies in your web browser.
- A third-party browser plugin, such as Ghostery or NoScript, is preventing JavaScript from running. Additional information is available in this support article .
To regain access, please make sure that cookies and JavaScript are enabled before reloading the page.

In order to continue enjoying our site, we ask that you confirm your identity as a human. Thank you very much for your cooperation.
- Anatomy & Physiology
- Astrophysics
- Earth Science
- Environmental Science
- Organic Chemistry
- Precalculus
- Trigonometry
- English Grammar
- U.S. History
- World History
... and beyond
- Socratic Meta
- Featured Answers

- Mixture Problems
Key Questions
Let's try to think about the general form of a word problem involving mixtures.
In general, we have the following scenario:
- a merchant sells two kinds of products (coffee, sweets, etc).
we know the unit prices for both kinds of products and for the final mixture #p_1# US dollars per pound for the first kind of product, #p_2# US dollars per pound for the second kind of product #p_m# US dollars per pound for the mixture
we know the total quantity formed by the mixture of the two products ( #q# pounds)
- we have to find out the quantities of each product needed to form the mixture (here we have the variables : #x# denoting the quantity of the first kind of product and #y# denoting the quantity of the second kind of product)
Now, we have sufficient information to work out the equations.
First, we know that the sum of the two quantities is #q# pounds, which gives us the first equation : #x+y=q#
Second, we know that the sale price is the product of quantity and unit price, which gives us the second equation : #p_1 x + p_2 y = p_m*q#
Now, we have a system of two linear equations that can be easily solved by substitution.

Consider the following question:
How many pints of 20% acid solution and 70% acid solution must be mixed to obtain 40 pints of 50% acid solution?
First, I'll set up my table. I'll fill in the unknowns with variables #x# and #y# .
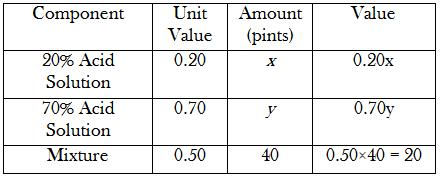
From this, we can easily set up the two equations.
Sum of values of two acids = Value of mixture
Therefore, #0.20x + 0.70y = 20#
For convenience, we'll multiply the entire equation by 10,
#2x + 7y=200#
This is equation (1)
Setting up the second equation,
Sum of amounts of each acid = Amount of mixture
To make at least one term of this equation identical to a term of equation (1), we'll multiply the entire equation by 2,
This is equation (2)
Subtracting equation (2) from (1) ,
#(+) 2x + 7y=200# #(-)2x+2y=80# #--------# #(=)0+5y=120#
Thus, #5y=120#
#y=120/5=24#
Substituting #y=24# in (2) ,
#2x+2(24)=80# #2x+48=80# #2x=80-48=32# #x=32/2=16#
So, we have #x=16# and #y=24#
We can conclude that 16 pints of 20% acid solution must be mixed with 24 pints of 70% solution to obtain 40 pints of 50% solution.
I hope your question was answered.

Free Mathematics Tutorials
Mixture problems with solutions.
Mixture problems and their solutions are presented along with their solutions. Percentages are also used to solve these types of problems.
Problem 1: How many liters of 20% alcohol solution should be added to 40 liters of a 50% alcohol solution to make a 30% solution?
Solution to Problem 1: Let x be the quantity of the 20% alcohol solution to be added to the 40 liters of a 50% alcohol. Let y be the quantity of the final 30% solution. Hence x + 40 = y We shall now express mathematically that the quantity of alcohol in x liters plus the quantity of alcohol in the 40 liters is equal to the quantity of alcohol in y liters. But remember the alcohol is measured in percentage term. 20% x + 50% * 40 = 30% y Substitute y by x + 40 in the last equation to obtain. 20% x + 50% * 40 = 30% (x + 40) Change percentages into fractions. 20 x / 100 + 50 * 40 / 100= 30 x / 100 + 30 * 40 / 100 Multiply all terms by 100 to simplify. 20 x + 50 * 40 = 30 x + 30 * 40 Solve for x. x = 80 liters 80 liters of 20% alcohol is be added to 40 liters of a 50% alcohol solution to make a 30% solution.
Problem 2: John wants to make a 100 ml of 5% alcohol solution mixing a quantity of a 2% alcohol solution with a 7% alcohol solution. What are the quantities of each of the two solutions (2% and 7%) he has to use?
Solution to Problem 2: Let x and y be the quantities of the 2% and 7% alcohol solutions to be used to make 100 ml. Hence x + y = 100 We now write mathematically that the quantity of alcohol in x ml plus the quantity of alcohol in y ml is equal to the quantity of alcohol in 100 ml. 2% x + 7% y = 5% 100 The first equation gives y = 100 - x. Substitute in the last equation to obtain 2% x + 7% (100 - x) = 5% 100 Multiply by 100 and simplify 2 x + 700 - 7 x = 5 * 100 Solve for x x = 40 ml Substitute x by 40 in the first equation to find y y = 100 - x = 60 ml
Problem 3: Sterling Silver is 92.5% pure silver. How many grams of Sterling Silver must be mixed to a 90% Silver alloy to obtain a 500g of a 91% Silver alloy?
Solution to Problem 3: Let x and y be the weights, in grams, of sterling silver and of the 90% alloy to make the 500 grams at 91%. Hence x + y =500 The number of grams of pure silver in x plus the number of grams of pure silver in y is equal to the number of grams of pure silver in the 500 grams. The pure silver is given in percentage forms. Hence 92.5% x + 90% y = 91% 500 Substitute y by 500 - x in the last equation to write 92.5% x + 90% (500 - x) = 91% 500 Simplify and solve 92.5 x + 45000 - 90 x = 45500 x = 200 grams. 200 grams of Sterling Silver is needed to make the 91% alloy.
Problem 4: How many Kilograms of Pure water is to be added to 100 Kilograms of a 30% saline solution to make it a 10% saline solution.
Solution to Problem 4: Let x be the weights, in Kilograms, of pure water to be added. Let y be the weight, in Kilograms, of the 10% solution. Hence x + 100 = y Let us now express the fact that the amount of salt in the pure water (which 0) plus the amount of salt in the 30% solution is equal to the amount of salt in the final saline solution at 10%. 0 + 30% 100 = 10% y Substitute y by x + 100 in the last equation and solve. 30% 100 = 10% (x + 100) Solve for x. x = 200 Kilograms.
Problem 5: A 50 ml after-shave lotion at 30% alcohol is mixed with 30 ml of pure water. What is the percentage of alcohol in the new solution?
Solution to Problem 5: The amount of the final mixture is given by 50 ml + 30 ml = 80 ml The amount of alcohol is equal to the amount of alcohol in pure water ( which is 0) plus the amount of alcohol in the 30% solution. Let x be the percentage of alcohol in the final solution. Hence 0 + 30% 50 ml = x (80) Solve for x x = 0.1817 = 18.75%
Problem 6: You add x ml of a 25% alcohol solution to a 200 ml of a 10% alcohol solution to obtain another solution. Find the amount of alcohol in the final solution in terms of x. Find the ratio, in terms of x, of the alcohol in the final solution to the total amount of the solution. What do you think will happen if x is very large? Find x so that the final solution has a percentage of 15%.
Solution to Problem 6: Let us first find the amount of alcohol in the 10% solution of 200 ml. 200 * 10% = 20 ml The amount of alcohol in the x ml of 25% solution is given by 25% x = 0.25 x The total amount of alcohol in the final solution is given by 20 + 0.25 x The ratio of alcohol in the final solution to the total amount of the solution is given by [ ( 20 + 0.25 x ) / (x + 200)] If x becomes very large in the above formula for the ratio, then the ratio becomes close to 0.25 or 25% (The above function is a rational function and 0.25 is its horizontal asymptote). This means that if you increase the amount x of the 25% solution, this will dominate and the final solution will be very close to a 25% solution. To have a percentage of 15%, we need to have [ ( 20 + 0.25 x ) / (x + 200)] = 15% = 0.15 Solve the above equation for x 20 + 0.25 x = 0.15 * (x + 200) x = 100 ml
Popular Pages
- Math Problems, Questions and Online Self Tests
- Work Rate Problems with Solutions
- Geometry Problems with Answers and Solutions - Grade 10
- Percent Math Problems
- Free Algebra Questions and Problems with Answers
Resource Links
Share with us.
©2024 analyzemath.com
- Privacy Policy
5.5 Solve Mixture Applications with Systems of Equations
Learning objectives.
By the end of this section, you will be able to:
- Solve mixture applications
- Solve interest applications
Be Prepared 5.5
Before you get started, take this readiness quiz.
- Multiply 4.025 (1,562). 4.025 (1,562). If you missed this problem, review Example 1.98 .
- Write 8.2% as a decimal. If you missed this problem, review Example 1.106 .
- Earl’s dinner bill came to $32.50 and he wanted to leave an 18% tip. How much should the tip be? If you missed this problem, review Example 3.15 .
Solve Mixture Applications
When we solved mixture applications with coins and tickets earlier, we started by creating a table so we could organize the information. For a coin example with nickels and dimes, the table looked like this:
Using one variable meant that we had to relate the number of nickels and the number of dimes. We had to decide if we were going to let n be the number of nickels and then write the number of dimes in terms of n , or if we would let d be the number of dimes and write the number of nickels in terms of d .
Now that we know how to solve systems of equations with two variables, we’ll just let n be the number of nickels and d be the number of dimes. We’ll write one equation based on the total value column, like we did before, and the other equation will come from the number column.
For the first example, we’ll do a ticket problem where the ticket prices are in whole dollars, so we won’t need to use decimals just yet.
Example 5.45
Translate to a system of equations and solve:
The box office at a movie theater sold 147 tickets for the evening show, and receipts totaled $1,302. How many $11 adult and how many $8 child tickets were sold?
| the problem. | We will create a table to organize the information. |
| what we are looking for. | We are looking for the number of adult tickets and the number of child tickets sold. |
| what we are looking for. | Let the number of adult tickets. the number of child tickets |
| A table will help us organize the data. We have two types of tickets: adult and child. | Write and for the number of tickets. |
| Write the total number of tickets sold at the bottom of the Number column. | Altogether 147 were sold. |
| Write the value of each type of ticket in the Value column. | The value of each adult ticket is $11. The value of each child tickets is $8. |
| The number times the value gives the total value, so the total value of adult tickets is , and the total value of child tickets is | |
| Altogether the total value of the tickets was $1,302. | Fill in the Total Value column. |
| into a system of equations. | |
| The Number column and the Total Value column give us the system of equations. We will use the elimination method to solve this system. | |
| Multiply the first equation by −8. | |
| Simplify and add, then solve for . | |
| Substitute = 42 into the first equation, then solve for . | |
| the answer in the problem. 42 adult tickets at $11 per ticket makes $462 105 child tickets at $8 per ticket makes $840. The total receipts are $1,302.✓ | |
| the question. | The movie theater sold 42 adult tickets and 105 child tickets. |
Try It 5.89
The ticket office at the zoo sold 553 tickets one day. The receipts totaled $3,936. How many $9 adult tickets and how many $6 child tickets were sold?
Try It 5.90
A science center sold 1,363 tickets on a busy weekend. The receipts totaled $12,146. How many $12 adult tickets and how many $7 child tickets were sold?
In Example 5.46 we’ll solve a coin problem. Now that we know how to work with systems of two variables, naming the variables in the ‘number’ column will be easy.
Example 5.46
Priam has a collection of nickels and quarters, with a total value of $7.30. The number of nickels is six less than three times the number of quarters. How many nickels and how many quarters does he have?
| the problem. | We will create a table to organize the information. |
| what we are looking for. | We are looking for the number of nickels and the number of quarters. |
| what we are looking for. | Let the number of nickels. the number of quarters |
| A table will help us organize the data. We have two types of coins, nickels and quarters. | Write and for the number of each type of coin. |
| Fill in the Value column with the value of each type of coin. | The value of each nickel is $0.05. The value of each quarter is $0.25. |
| The number times the value gives the total value, so, the total value of the nickels is (0.05) = 0.05 and the total value of quarters is (0.25) = 0.25 . Altogether the total value of the coins is $7.30. | |
| into a system of equations. | |
| The Total value column gives one equation. | |
| We also know the number of nickels is six less than three times the number of quarters. Translate to get the second equation. | |
| Now we have the system to solve. | |
| the system of equations We will use the substitution method. Substitute = 3 − 6 into the first equation. Simplify and solve for . | |
| To find the number of nickels, substitute = 19 into the second equation. | |
| the answer in the problem. | |
| the question. | Priam has 19 quarters and 51 nickels. |
Try It 5.91
Matilda has a handful of quarters and dimes, with a total value of $8.55. The number of quarters is 3 more than twice the number of dimes. How many dimes and how many quarters does she have?
Try It 5.92
Juan has a pocketful of nickels and dimes. The total value of the coins is $8.10. The number of dimes is 9 less than twice the number of nickels. How many nickels and how many dimes does Juan have?
Some mixture applications involve combining foods or drinks. Example situations might include combining raisins and nuts to make a trail mix or using two types of coffee beans to make a blend.
Example 5.47
Carson wants to make 20 pounds of trail mix using nuts and chocolate chips. His budget requires that the trail mix costs him $7.60 per pound. Nuts cost $9.00 per pound and chocolate chips cost $2.00 per pound. How many pounds of nuts and how many pounds of chocolate chips should he use?
| the problem. | We will create a table to organize the information. |
| what we are looking for. | We are looking for the number of pounds of nuts and the number of pounds of chocolate chips. |
| what we are looking for. | Let the number of pound of nuts. the number of pounds of chips |
| Carson will mix nuts and chocolate chips to get trail mix. Write in and for the number of pounds of nuts and chocolate chips. There will be 20 pounds of trail mix. Put the price per pound of each item in the Value column. Fill in the last column using | |
| Number · Value = Total Value | |
| into a system of equations. We get the equations from the Number and Total Value columns. | |
| Solve the system of equations We will use elimination to solve the system. | |
| Multiply the first equation by −2 to eliminate . | |
| Simplify and add. Solve for . | |
| To find the number of pounds of chocolate chips, substitute = 16 into the first equation, then solve for . | |
| the answer in the problem. | |
| the question. | Carson should mix 16 pounds of nuts with 4 pounds of chocolate chips to create the trail mix. |
Try It 5.93
Greta wants to make 5 pounds of a nut mix using peanuts and cashews. Her budget requires the mixture to cost her $6 per pound. Peanuts are $4 per pound and cashews are $9 per pound. How many pounds of peanuts and how many pounds of cashews should she use?
Try It 5.94
Sammy has most of the ingredients he needs to make a large batch of chili. The only items he lacks are beans and ground beef. He needs a total of 20 pounds combined of beans and ground beef and has a budget of $3 per pound. The price of beans is $1 per pound and the price of ground beef is $5 per pound. How many pounds of beans and how many pounds of ground beef should he purchase?
Another application of mixture problems relates to concentrated cleaning supplies, other chemicals, and mixed drinks. The concentration is given as a percent. For example, a 20% concentrated household cleanser means that 20% of the total amount is cleanser, and the rest is water. To make 35 ounces of a 20% concentration, you mix 7 ounces (20% of 35) of the cleanser with 28 ounces of water.
For these kinds of mixture problems, we’ll use percent instead of value for one of the columns in our table.

Example 5.48
Sasheena is a lab assistant at her community college. She needs to make 200 milliliters of a 40% solution of sulfuric acid for a lab experiment. The lab has only 25% and 50% solutions in the storeroom. How much should she mix of the 25% and the 50% solutions to make the 40% solution?
| the problem. | A figure may help us visualize the situation, then we will create a table to organize the information. |
| Sasheena must mix some of the 25% solution and some of the 50% solution together to get 200 ml of the 40% solution. | |
| what we are looking for. | We are looking for how much of each solution she needs. |
| what we are looking for. | Let number of ml of 25% solution. number of ml of 50% solution |
| A table will help us organize the data. She will mix ml of 25% with ml of 50% to get 200 ml of 40% solution. We write the percents as decimals in the chart. We multiply the number of units times the concentration to get the total amount of sulfuric acid in each solution. | |
| into a system of equations. We get the equations from the Number column and the Amount column. | |
| Now we have the system. | |
| the system of equations. We will solve the system by elimination. Multiply the first equation by −0.5 to eliminate . | |
| Simplify and add to solve for . | |
| To solve for , substitute = 80 into the first equation. | |
| the answer in the problem. | |
| the question. | Sasheena should mix 80 ml of the 25% solution with 120 ml of the 50% solution to get the 200 ml of the 40% solution. |
Try It 5.95
LeBron needs 150 milliliters of a 30% solution of sulfuric acid for a lab experiment but only has access to a 25% and a 50% solution. How much of the 25% and how much of the 50% solution should he mix to make the 30% solution?
Try It 5.96
Anatole needs to make 250 milliliters of a 25% solution of hydrochloric acid for a lab experiment. The lab only has a 10% solution and a 40% solution in the storeroom. How much of the 10% and how much of the 40% solutions should he mix to make the 25% solution?
Solve Interest Applications
The formula to model interest applications is I = Prt . Interest, I , is the product of the principal, P , the rate, r , and the time, t . In our work here, we will calculate the interest earned in one year, so t will be 1.
We modify the column titles in the mixture table to show the formula for interest, as you’ll see in Example 5.49 .
Example 5.49
Adnan has $40,000 to invest and hopes to earn 7.1% interest per year. He will put some of the money into a stock fund that earns 8% per year and the rest into bonds that earns 3% per year. How much money should he put into each fund?
| the problem. | A chart will help us organize the information. |
| what we are looking for. | We are looking for the amount to invest in each fund. |
| what we are looking for. | Let the amount invested in stocks. the amount invested in bonds. |
| Write the interest rate as a decimal for each fund. Multiply: Principal · Rate · Time to get the Interest. | |
| into a system of equations. We get our system of equations from the Principal column and the Interest column. | |
| the system of equations Solve by elimination. Multiply the top equation by −0.03. | |
| Simplify and add to solve for . | |
| To find , substitute = 32,800 into the first equation. | |
| the answer in the problem. | We leave the check to you. |
| the question. | Adnan should invest $32,800 in stock and $7,200 in bonds. |
Did you notice that the Principal column represents the total amount of money invested while the Interest column represents only the interest earned? Likewise, the first equation in our system, s + b = 40,000, represents the total amount of money invested and the second equation, 0.08 s + 0.03 b = 0.071(40,000), represents the interest earned.
Try It 5.97
Leon had $50,000 to invest and hopes to earn 6.2 % interest per year. He will put some of the money into a stock fund that earns 7% per year and the rest in to a savings account that earns 2% per year. How much money should he put into each fund?
Try It 5.98
Julius invested $7,000 into two stock investments. One stock paid 11% interest and the other stock paid 13% interest. He earned 12.5% interest on the total investment. How much money did he put in each stock?
Example 5.50
Rosie owes $21,540 on her two student loans. The interest rate on her bank loan is 10.5% and the interest rate on the federal loan is 5.9%. The total amount of interest she paid last year was $1,669.68. What was the principal for each loan?
| the problem. | A chart will help us organize the information. |
| what we are looking for. | We are looking for the principal of each loan. |
| what we are looking for. | Let the principal for the bank loan. the principal on the federal loan |
| The total loans are $21,540. | |
| Record the interest rates as decimals in the chart. | |
| Multiply using the formula = Pr to get the Interest. | |
| into a system of equations. The system of equations comes from the Principal column and the Interest column. | |
| the system of equations We will use substitution to solve. Solve the first equation for . | |
| Substitute = − + 21,540 into the second equation. | |
| Simplify and solve for . | |
| To find , substitute = 12,870 into the first equation. | |
| the answer in the problem. | We leave the check to you. |
| the question. | The principal of the bank loan is $12,870 and the principal for the federal loan is $8,670. |
Try It 5.99
Laura owes $18,000 on her student loans. The interest rate on the bank loan is 2.5% and the interest rate on the federal loan is 6.9 %. The total amount of interest she paid last year was $1,066. What was the principal for each loan?
Try It 5.100
Jill’s Sandwich Shoppe owes $65,200 on two business loans, one at 4.5% interest and the other at 7.2% interest. The total amount of interest owed last year was $3,582. What was the principal for each loan?
Access these online resources for additional instruction and practice with solving application problems with systems of linear equations.
- Cost and Mixture Word Problems
- Mixture Problems
Section 5.5 Exercises
Practice makes perfect.
In the following exercises, translate to a system of equations and solve.
Tickets to a Broadway show cost $35 for adults and $15 for children. The total receipts for 1650 tickets at one performance were $47,150. How many adult and how many child tickets were sold?
Tickets for a show are $70 for adults and $50 for children. One evening performance had a total of 300 tickets sold and the receipts totaled $17,200. How many adult and how many child tickets were sold?
Tickets for a train cost $10 for children and $22 for adults. Josie paid $1,200 for a total of 72 tickets. How many children’s tickets and how many adult tickets did Josie buy?
Tickets for a baseball game are $69 for Main Level seats and $39 for Terrace Level seats. A group of sixteen friends went to the game and spent a total of $804 for the tickets. How many of Main Level and how many Terrace Level tickets did they buy?
Tickets for a dance recital cost $15 for adults and $7 for children. The dance company sold 253 tickets and the total receipts were $2,771. How many adult tickets and how many child tickets were sold?
Tickets for the community fair cost $12 for adults and $5 dollars for children. On the first day of the fair, 312 tickets were sold for a total of $2,204. How many adult tickets and how many child tickets were sold?
Brandon has a cup of quarters and dimes with a total value of $3.80. The number of quarters is four less than twice the number of dimes. How many quarters and how many dimes does Brandon have?
Sherri saves nickels and dimes in a coin purse for her daughter. The total value of the coins in the purse is $0.95. The number of nickels is two less than five times the number of dimes. How many nickels and how many dimes are in the coin purse?
Peter has been saving his loose change for several days. When he counted his quarters and dimes, he found they had a total value $13.10. The number of quarters was fifteen more than three times the number of dimes. How many quarters and how many dimes did Peter have?
Lucinda had a pocketful of dimes and quarters with a value of $ $6.20. The number of dimes is eighteen more than three times the number of quarters. How many dimes and how many quarters does Lucinda have?
A cashier has 30 bills, all of which are $10 or $20 bills. The total value of the money is $460. How many of each type of bill does the cashier have?
A cashier has 54 bills, all of which are $10 or $20 bills. The total value of the money is $910. How many of each type of bill does the cashier have?
Marissa wants to blend candy selling for $1.80 per pound with candy costing $1.20 per pound to get a mixture that costs her $1.40 per pound to make. She wants to make 90 pounds of the candy blend. How many pounds of each type of candy should she use?
How many pounds of nuts selling for $6 per pound and raisins selling for $3 per pound should Kurt combine to obtain 120 pounds of trail mix that cost him $5 per pound?
Hannah has to make twenty-five gallons of punch for a potluck. The punch is made of soda and fruit drink. The cost of the soda is $1.79 per gallon and the cost of the fruit drink is $2.49 per gallon. Hannah’s budget requires that the punch cost $2.21 per gallon. How many gallons of soda and how many gallons of fruit drink does she need?
Joseph would like to make 12 pounds of a coffee blend at a cost of $6.25 per pound. He blends Ground Chicory at $4.40 a pound with Jamaican Blue Mountain at $8.84 per pound. How much of each type of coffee should he use?
Julia and her husband own a coffee shop. They experimented with mixing a City Roast Columbian coffee that cost $7.80 per pound with French Roast Columbian coffee that cost $8.10 per pound to make a 20 pound blend. Their blend should cost them $7.92 per pound. How much of each type of coffee should they buy?
Melody wants to sell bags of mixed candy at her lemonade stand. She will mix chocolate pieces that cost $4.89 per bag with peanut butter pieces that cost $3.79 per bag to get a total of twenty-five bags of mixed candy. Melody wants the bags of mixed candy to cost her $4.23 a bag to make. How many bags of chocolate pieces and how many bags of peanut butter pieces should she use?
Jotham needs 70 liters of a 50% alcohol solution. He has a 30% and an 80% solution available. How many liters of the 30% and how many liters of the 80% solutions should he mix to make the 50% solution?
Joy is preparing 15 liters of a 25% saline solution. She only has 40% and 10% solution in her lab. How many liters of the 40% and how many liters of the 10% should she mix to make the 25% solution?
A scientist needs 65 liters of a 15% alcohol solution. She has available a 25% and a 12% solution. How many liters of the 25% and how many liters of the 12% solutions should she mix to make the 15% solution?
A scientist needs 120 liters of a 20% acid solution for an experiment. The lab has available a 25% and a 10% solution. How many liters of the 25% and how many liters of the 10% solutions should the scientist mix to make the 20% solution?
A 40% antifreeze solution is to be mixed with a 70% antifreeze solution to get 240 liters of a 50% solution. How many liters of the 40% and how many liters of the 70% solutions will be used?
A 90% antifreeze solution is to be mixed with a 75% antifreeze solution to get 360 liters of a 85% solution. How many liters of the 90% and how many liters of the 75% solutions will be used?
Hattie had $3,000 to invest and wants to earn 10.6% interest per year. She will put some of the money into an account that earns 12% per year and the rest into an account that earns 10% per year. How much money should she put into each account?
Carol invested $2,560 into two accounts. One account paid 8% interest and the other paid 6% interest. She earned 7.25% interest on the total investment. How much money did she put in each account?
Sam invested $48,000, some at 6% interest and the rest at 10%. How much did he invest at each rate if he received $4,000 in interest in one year?
Arnold invested $64,000, some at 5.5% interest and the rest at 9%. How much did he invest at each rate if he received $4,500 in interest in one year?
After four years in college, Josie owes $65,800 in student loans. The interest rate on the federal loans is 4.5% and the rate on the private bank loans is 2%. The total interest she owed for one year was $2,878.50. What is the amount of each loan?
Mark wants to invest $10,000 to pay for his daughter’s wedding next year. He will invest some of the money in a short term CD that pays 12% interest and the rest in a money market savings account that pays 5% interest. How much should he invest at each rate if he wants to earn $1,095 in interest in one year?
A trust fund worth $25,000 is invested in two different portfolios. This year, one portfolio is expected to earn 5.25% interest and the other is expected to earn 4%. Plans are for the total interest on the fund to be $1150 in one year. How much money should be invested at each rate?
A business has two loans totaling $85,000. One loan has a rate of 6% and the other has a rate of 4.5%. This year, the business expects to pay $4650 in interest on the two loans. How much is each loan?
Everyday Math
Laurie was completing the treasurer’s report for her son’s Boy Scout troop at the end of the school year. She didn’t remember how many boys had paid the $15 full-year registration fee and how many had paid the $10 partial-year fee. She knew that the number of boys who paid for a full-year was ten more than the number who paid for a partial-year. If $250 was collected for all the registrations, how many boys had paid the full-year fee and how many had paid the partial-year fee?
As the treasurer of her daughter’s Girl Scout troop, Laney collected money for some girls and adults to go to a three-day camp. Each girl paid $75 and each adult paid $30. The total amount of money collected for camp was $765. If the number of girls is three times the number of adults, how many girls and how many adults paid for camp?
Writing Exercises
Take a handful of two types of coins, and write a problem similar to Example 5.46 relating the total number of coins and their total value. Set up a system of equations to describe your situation and then solve it.
In Example 5.50 we solved the system of equations { b + f = 21,540 0.105 b + 0.059 f = 1669.68 { b + f = 21,540 0.105 b + 0.059 f = 1669.68 by substitution. Would you have used substitution or elimination to solve this system? Why?
After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
After looking at the checklist, do you think you are well-prepared for the next section? Why or why not?
As an Amazon Associate we earn from qualifying purchases.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/elementary-algebra/pages/1-introduction
- Authors: Lynn Marecek, MaryAnne Anthony-Smith
- Publisher/website: OpenStax
- Book title: Elementary Algebra
- Publication date: Feb 22, 2017
- Location: Houston, Texas
- Book URL: https://openstax.org/books/elementary-algebra/pages/1-introduction
- Section URL: https://openstax.org/books/elementary-algebra/pages/5-5-solve-mixture-applications-with-systems-of-equations
© Feb 9, 2022 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

- Derivation of Formulas
- Engineering Economy
- General Engineering
- Spherical Trigonometry
- Solid Geometry
- Analytic Geometry
- Integral Calculus
- Differential Equations
- Advance Engineering Mathematics
- Strength of Materials
- Structural Analysis
- CE Board: Math
- CE Board: Hydro Geo
- CE Board: Design
- Timber Design
- Reinforced Concrete
- Geotechnical Engineering
- Basic Engineering Math
- General Discussions
Breadcrumbs
Mixture-related problems.
There are four common types of mixture in verbal problems of Algebra.
Solutions Solution is a homogeneous mixture formed by dissolving a substance (solute) in another substance (solvent). A common example is the salt as solute and water as solvent forming into one phase called brine or saline water.
Alloys An alloy is a solid solution formed by fusing two or more metallic elements. A common alloy is bronze which is the product of fusing iron and copper.
Blends Blended product is a result of mixing two or more grades of items of the same class. Example is a coffee of grade A mixed to coffee of grade B which will result to a blended coffee.
Assortments Assorted mixture is a combination of distinct items which can be resorted easily back to its original components. Example is assorted candies in a pack.
Solving mixture-related problems The following example will illustrate how to solve mixture problems.
Problem How many liters of 10% salt solution must be added to 20% salt solution in order to obtain 10 liters of 12% salt solution?
$10x + 20(10 - x) = 12(10)$
$x = 8 \, \text{ liters}$ answer
- Log in to post comments
Book navigation
- Laws of Exponents and Radicals
- Logarithm and Other Important Properties in Algebra
- Quadratic Equations in One Variable
- Special Products and Factoring
- Arithmetic, geometric, and harmonic progressions
- Binomial Theorem
- System of Equations
- Variation / Proportional
- Age-related Problems
- Clock-related Problems
- Digit-Related Problems
- Geometry-related Problems
- 01 - Example of Mixture Related Problem
- Money-related Problems
- Motion-related Problems
- Number-related Problems
- Work-related Problems
- Probability and Statistics
Lesson Mixture problems
Mixture Problems - Algebra
These lessons, with videos, examples and step-by-step solutions, help Algebra students learn about mixture problems.
Related Pages Mixture Word Problems More Lessons for Grade 9 Math Math Worksheets
How to solve mixture word problems for example, adding two acid solutions together, or adding water to a sugar solution?
Solving a Mixture problem with Algebra
Example: How many liters of a 10% salt solution should be added to 80 liters of a 35% salt solution to obtain a mixture that is 30% salt solution?
Mixture Word Problems - Algebra Help
Example: How many gallons of pure alcohol should be added to 20 gallons of a 15% alcohol solution to obtain a mixture that is 25% alcohol?
Mixture Problems
- Imagine you have 6 gallons of fruit punch. It is 25% soda and 75% juice. If you wanted to contain only 60% juice, how much soda would you have to add?
- A restaurant has come pancake batter that is too thin. It weighs 12 kilograms and contains 85% flour. How many kilograms of flour should be added so that the mixture is 90% flour?
- A scientist needs 120 oz of a solution that is 52% acid. She must use existing solutions of 60% acid and 36% acid. How much of each should be mixed together to obtain her 20 oz of 53% acid?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

- Advanced Search
Robust optimization for a steel production planning problem with uncertain demand and product substitution
New citation alert added.
This alert has been successfully added and will be sent to:
You will be notified whenever a record that you have chosen has been cited.
To manage your alert preferences, click on the button below.
New Citation Alert!
Please log in to your account
Information & Contributors
Bibliometrics & citations, view options, recommendations, models and solution techniques for production planning problems with increasing byproducts.
We consider a production planning problem where the production process creates a mixture of desirable products and undesirable byproducts. In this production process, at any point in time the fraction of the mixture that is an undesirable byproduct ...
Optimal production planning in a petrochemical industry using multiple levels
Proposed mixed integer programming formulation for production planning.Proposed formulation incorporates production through multiple levels.Proposed formulation is expressive and can be solved to global optimality.Proposed formulation overcomes the ...
Production planning method for seru production systems under demand uncertainty
- Seru production systems under demand uncertainty are addressed.
The seru production system is a new-type manufacturing system arising from Japanese production practices that can simultaneously achieve high efficiency, flexibility, and responsiveness. In this paper, a worker and production quantity ...
Information
Published in.
Elsevier Science Ltd.
United Kingdom
Publication History
Author tags.
- Steel Industry
- Production Planning
- Product Substitution
- Robust Optimization
- Benders Decomposition.
- Research-article
Contributors
Other metrics, bibliometrics, article metrics.
- 0 Total Citations
- 0 Total Downloads
- Downloads (Last 12 months) 0
- Downloads (Last 6 weeks) 0
View options
Login options.
Check if you have access through your login credentials or your institution to get full access on this article.
Full Access
Share this publication link.
Copying failed.
Share on social media
Affiliations, export citations.
- Please download or close your previous search result export first before starting a new bulk export. Preview is not available. By clicking download, a status dialog will open to start the export process. The process may take a few minutes but once it finishes a file will be downloadable from your browser. You may continue to browse the DL while the export process is in progress. Download
- Download citation
- Copy citation
We are preparing your search results for download ...
We will inform you here when the file is ready.
Your file of search results citations is now ready.
Your search export query has expired. Please try again.

IMAGES
VIDEO
COMMENTS
Solve the equation using good algebra techniques. Check the answer in the problem and make sure it makes sense. Answer the question with a complete sentence. Example \(\PageIndex{2}\) ... Solve Mixture Word Problems. Now we'll solve some more general applications of the mixture model. Grocers and bartenders use the mixture model to set a fair ...
To use this chart to solve the problem, we will use the fourth column as an equation to solve for \ (x.\) The 10 liters of our final mixture must have a total volume of 5 liters of alcohol in it in order to be 50% alcohol. Those 5 liters must come from a combination of the amount of 40% solution we mix in and the amount of 90% solution.
Mixture Problems Solving Mixture Word Problems Using Algebra More Algebra Lessons. What Are Mixture Problems? Mixture problems are word problems where items or quantities of different values are mixed together. Sometimes different liquids are mixed together changing the concentration of the mixture as shown in example 1, example 2 and example 3.
6.8 Mixture and Solution Word Problems. Solving mixture problems generally involves solving systems of equations. Mixture problems are ones in which two different solutions are mixed together, resulting in a new, final solution. Using a table will help to set up and solve these problems. The basic structure of this table is shown below: Example ...
0.30 (10 − w) mixture. 10. 0.15. 0.15 (10) = 1.5. When the problem is set up like this, we can usually use the last column to write our equation. In this case, the liters of acid within the 10% solution, plus the liters of acid within the 30% solution, must add up to the liters of acid within the 15% solution.
This math video tutorial explains how to solve mixture problems that can be found in a typical algebra or a chemistry course. This video contains plenty of ...
The solutions to mixture problems tend to be generated by linear equations; that is, solving the set-up for mixture exercises tends to be pretty easy. ... Note: This exercise is typical of algebra courses, and is used to teach problem-solving skills in algebra classes. But, in real life, the actual process is different. ...
Solution: Set up a table for water. The water is removed from the original. Mixture Problems. Some word problems using systems of equations involve mixing two quantities with different prices. To solve mixture problems, knowledge of solving systems of equations. is necessary. Most often, these problems will have two variables, but more advanced ...
Solution: Set up a table for alcohol. The alcohol is replaced i.e. removed and added. Mixture Problems. Some word problems using systems of equations involve mixing two quantities with different prices. To solve mixture problems, knowledge of solving systems of equations. is necessary. Most often, these problems will have two variables, but ...
Solve mixture word problems. Solve uniform motion applications. Before you get started, take this readiness quiz. Simplify: 0.25x + 0.10(x + 4) 0.25 x + 0.10 ( x + 4). If you missed this problem, review [link]. The number of adult tickets is three more than twice the number of children tickets. Let c represent the number of children tickets.
Here are some examples for solving mixture problems. Example 1. Coffee worth $1.05 per pound is mixed with coffee worth 85¢ per pound to obtain 20 pounds of a mixture worth 90¢ per pound. How many pounds of each type are used?
To solve mixture problems in algebra, we follow these four steps. 1.) Represent the unknown quantity with a variable. 2.) Create an equation involving that variable. 3.) Solve the equation for the ...
Solve Mixture Word Problems. Now we'll solve some more general applications of the mixture model. Grocers and bartenders use the mixture model to set a fair price for a product made from mixing two or more ingredients. Financial planners use the mixture model when they invest money in a variety of accounts and want to find the overall ...
Let's try to think about the general form of a word problem involving mixtures. In general, we have the following scenario: a merchant sells two kinds of products (coffee, sweets, etc).; we know the unit prices for both kinds of products and for the final mixture #p_1# US dollars per pound for the first kind of product, #p_2# US dollars per pound for the second kind of product
Courses on Khan Academy are always 100% free. Start practicing—and saving your progress—now: https://www.khanacademy.org/math/algebra-home/alg-basic-eq-ineq/...
Step 4. Translate into a system of equations. The Total value column gives one equation. We also know the number of nickels is six less. than three times the number of quarters. Translate to get the second equation. Now we have the system to solve. Step 5. Solve the system of equations.
Mixture Problems With Solutions. Mixture problems and their solutions are presented along with their solutions. Percentages are also used to solve these types of problems.. Problem 1: How many liters of 20% alcohol solution should be added to 40 liters of a 50% alcohol solution to make a 30% solution? Solution to Problem 1: Let x be the quantity of the 20% alcohol solution to be added to the ...
To solve mixture problems, knowledge of solving systems of equations. is necessary. Most often, these problems will have two variables, but more advanced problems have systems of equations with three variables. ... Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your ...
3.1 Use a Problem-Solving Strategy; 3.2 Solve Percent Applications; 3.3 Solve Mixture Applications; 3.4 Solve Geometry Applications: Triangles, Rectangles, and the Pythagorean Theorem; 3.5 Solve Uniform Motion Applications; 3.6 Solve Applications with Linear Inequalities
01 - Example of Mixture Related Problem. There are four common types of mixture in verbal problems of Algebra. Solutions Solution is a homogeneous mixture formed by dissolving a substance (solute) in another substance (solvent). A common example is the salt as solute and water as solvent forming into one phase called brine or saline water.
For a complete lesson on mixture problems, go to https://www.MathHelp.com - 1000+ online math lessons featuring a personal math teacher inside every lesson! ...
The Mixture problems of the different type are presented in the lesson More Mixture problems in this module. The way to solve that problems is to reduce them to the linear system of two equations in two unknowns. Problem 1. Add water to the Salt solution. How much water should be added to 200 milliliters of a 10% salt solution to get a 2% salt ...
Mixture Word Problems More Lessons for Grade 9 Math Math Worksheets. How to solve mixture word problems for example, adding two acid solutions together, or adding water to a sugar solution? Solving a Mixture problem with Algebra. Example: How many liters of a 10% salt solution should be added to 80 liters of a 35% salt solution to obtain a ...
To tackle the model, we propose an enhanced Benders decomposition algorithm that incorporates a problem-specific method for generating valid inequalities to strengthen the master problem, and a hybrid strategy that combines approximate and exact methods to solve the non-convex slave problem.