solving problems involving quadratic equations definition

Module 10: Quadratic Equations and Functions

10.3 – applications of quadratic functions, learning objectives, objects in free fall.

• Determining the width of a border

Finding the maximum and minimum values of a quadratic function

(10.3.1) – solve application problems involving quadratic functions.

Quadratic equations are widely used in science, business, and engineering. Quadratic equations are commonly used in situations where two things are multiplied together and they both depend on the same variable. For example, when working with area, if both dimensions are written in terms of the same variable, you use a quadratic equation. Because the quantity of a product sold often depends on the price, you sometimes use a quadratic equation to represent revenue as a product of the price and the quantity sold. Quadratic equations are also used when gravity is involved, such as the path of a ball or the shape of cables in a suspension bridge.

A very common and easy-to-understand application is the height of a ball thrown at the ground off a building. Because gravity will make the ball speed up as it falls, a quadratic equation can be used to estimate its height any time before it hits the ground. Note: The equation isn’t completely accurate, because friction from the air will slow the ball down a little. For our purposes, this is close enough.

A ball is thrown off a building from 200 feet above the ground. Its starting velocity (also called initial velocity ) is [latex]−10[/latex] feet per second. (The negative value means it’s heading toward the ground.)

The equation [latex]h=-16t^{2}-10t+200[/latex] can be used to model the height of the ball after [latex]t[/latex] seconds. About how long does it take for the ball to hit the ground?

When the ball hits the ground, the height is 0. Substitute 0 for [latex]h[/latex].

[latex]\begin{array}{c}h=-16t^{2}-10t+200\\0=-16t^{2}-10t+200\\-16t^{2}-10t+200=0\end{array}[/latex]

This equation is difficult to solve by factoring or by completing the square, so solve it by applying the Quadratic Formula, [latex] x=\frac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}[/latex]. In this case, the variable is [latex]t[/latex] rather than [latex]x[/latex]. [latex]a=−16,b=−10[/latex], and [latex]c=200[/latex].

[latex]\displaystyle t=\frac{-(-10)\pm \sqrt{{{(-10)}^{2}}-4(-16)(200)}}{2(-16)}[/latex]

Simplify. Be very careful with the signs.

[latex]\large \begin{array}{l}t=\frac{10\pm \sqrt{100+12800}}{-32}\\\,\,=\frac{10\pm \sqrt{12900}}{-32}\end{array}[/latex]

Use a calculator to find both roots.

[latex]t[/latex] is approximately [latex]−3.86[/latex] or [latex]3.24[/latex].

Consider the roots logically. One solution, [latex]−3.86[/latex], cannot be the time because it is a negative number. The other solution, [latex]3.24[/latex] seconds, must be when the ball hits the ground.

The ball hits the ground approximately [latex]3.24[/latex] seconds after being thrown.

In the next video we show another example of how the quadratic equation can be used to find the time it takes for an object in free fall to hit the ground.

Here are some more similar objects in free fall examples.

Example: Applying the Vertex and [latex] x[/latex] -Intercepts of a Parabola

A ball is thrown upward from the top of a 40 foot high building at a speed of 80 feet per second. The ball’s height above ground can be modeled by the equation [latex]H\left(t\right)=-16{t}^{2}+80t+40[/latex].

a. When does the ball reach the maximum height?

b. What is the maximum height of the ball?

c. When does the ball hit the ground?

[latex]\large \begin{array}{c} h=-\frac{80}{2\left(-16\right)} \text{ }=\frac{80}{32}\hfill \\ \text{ }=\frac{5}{2}\hfill \\ \text{ }=2.5\hfill \end{array}[/latex]

The ball reaches a maximum height after 2.5 seconds.

b. To find the maximum height, find the y  coordinate of the vertex of the parabola.

[latex]\large \begin{array}{c}k=H\left(-\frac{b}{2a}\right)\hfill \\ \text{ }=H\left(2.5\right)\hfill \\ \text{ }=-16{\left(2.5\right)}^{2}+80\left(2.5\right)+40\hfill \\ \text{ }=140\hfill \end{array}[/latex]

The ball reaches a maximum height of 140 feet.

c. To find when the ball hits the ground, we need to determine when the height is zero, [latex]H\left(t\right)=0[/latex].

We use the quadratic formula.

[latex]\large \begin{array}{c} t=\frac{-80\pm \sqrt{{80}^{2}-4\left(-16\right)\left(40\right)}}{2\left(-16\right)}\hfill \\ \text{ }=\frac{-80\pm \sqrt{8960}}{-32}\hfill \end{array}[/latex]

Because the square root does not simplify nicely, we can use a calculator to approximate the values of the solutions.

[latex]\large \begin{array}{c}t=\frac{-80-\sqrt{8960}}{-32}\approx 5.458\hfill & \text{or}\hfill & t=\frac{-80+\sqrt{8960}}{-32}\approx -0.458\hfill \end{array}[/latex]

The second answer is outside the reasonable domain of our model, so we conclude the ball will hit the ground after about 5.458 seconds.

A rock is thrown upward from the top of a 112-foot high cliff overlooking the ocean at a speed of 96 feet per second. The rock’s height above ocean can be modeled by the equation [latex]H\left(t\right)=-16{t}^{2}+96t+112[/latex].

a. When does the rock reach the maximum height?

b. What is the maximum height of the rock?

c. When does the rock hit the ocean?

a. 3 seconds

b. 256 feet

c. 7 seconds

Applications of quadratic functions: determining the width of a border

The area problem below does not look like it includes a Quadratic Formula of any type, and the problem seems to be something you have solved many times before by simply multiplying. But in order to solve it, you will need to use a quadratic equation.

Bob made a quilt that is 4 ft [latex]\times[/latex] 5 ft. He has 10 sq. ft. of fabric he can use to add a border around the quilt. How wide should he make the border to use all the fabric? (The border must be the same width on all four sides.)

Sketch the problem. Since you don’t know the width of the border, you will let the variable [latex]x[/latex] represent the width.

In the diagram, the original quilt is indicated by the red rectangle. The border is the area between the red and blue lines.

Since each side of the original 4 by 5 quilt has the border of width x added, the length of the quilt with the border will be [latex]5+2x[/latex], and the width will be [latex]4+2x[/latex].

(Both dimensions are written in terms of the same variable, and you will multiply them to get an area! This is where you might start to think that a quadratic equation might be used to solve this problem.)

You are only interested in the area of the border strips. Write an expression for the area of the border.

Area of border = Area of the blue rectangle minus the area of the red rectangle

Area of border[latex]=\left(4+2x\right)\left(5+2x\right)–\left(4\right)\left(5\right)[/latex]

There are 10 sq ft of fabric for the border, so set the area of border to be 10.

[latex]10=\left(4+2x\right)\left(5+2x\right)–20[/latex]

Multiply [latex]\left(4+2x\right)\left(5+2x\right)[/latex].

[latex]10=20+8x+10x+4x^{2}–20[/latex]

[latex]10=18x+4x^{2}[/latex]

Subtract 10 from both sides so that you have a quadratic equation in standard form and can apply the Quadratic Formula to find the roots of the equation.

[latex]\begin{array}{c}0=18x+4x^{2}-10\\\\\text{or}\\\\4x^{2}-10\\\\2\left(2x^{2}+9x-5\right)=0\end{array}[/latex]

Factor out the greatest common factor, 2, so that you can work with the simpler equivalent equation, [latex]2x^{2}+9x–5=0[/latex].

[latex]\large \begin{array}{r}2\left(2x^{2}+9x-5\right)=0\\\\\frac{2\left(2x^{2}+9x-5\right)}{2}=\frac{0}{2}\\\\2x^{2}+9x-5=0\end{array}[/latex]

Use the Quadratic Formula. In this case, [latex]a=2,b=9[/latex], and [latex]c=−5[/latex].

[latex]\large \begin{array}{l}x=\frac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}\\\\x=\frac{-9\pm \sqrt{{{9}^{2}}-4(2)(-5)}}{2(2)}\end{array}[/latex]

[latex]\displaystyle x=\frac{-9\pm \sqrt{121}}{4}=\frac{-9\pm 11}{4}[/latex]

Find the solutions, making sure that the [latex]\pm[/latex] is evaluated for both values.

[latex]\large \begin{array}{c}x=\frac{-9+11}{4}=\frac{2}{4}=\frac{1}{2}=0.5\\\\\text{or}\\\\x=\frac{-9-11}{4}=\frac{-20}{4}=-5\end{array}[/latex]

Ignore the solution [latex]x=−5[/latex], since the width could not be negative.

The width of the border should be 0.5 ft.

Here is a video which gives another example of using the quadratic formula for a geometry problem involving the border around a quilt.

There are many real-world scenarios that involve finding the maximum or minimum value of a quadratic function, such as applications involving area and revenue.

Find two numbers [latex]x[/latex] and [latex]y[/latex] whose difference is 100 and whose product is a minimum.

We are trying to find the minimum of the product [latex]P=xy[/latex] of two numbers, such that their difference is 100: [latex]y-x=100[/latex]. First, we rewrite one variable in terms of the other:

[latex]y-x=100 \rightarrow y=100+x[/latex]

Next, we plug in the above relationship between the variables into the first equation:

[latex]P=xy=x(100+x) = 100x+x^2 = x^2+100x[/latex]

As a result, we get a quadratic function [latex]P(x)=x^2+100x[/latex]. The graph of this quadratic function opens upwards, and its vertex is the minimum, So if we find the vertex of this parabola, we will find the minimum product. The vertex is:

[latex]\displaystyle \displaystyle \left(-\frac{b}{2a}, P\left(-\frac{b}{2a}\right)\right) = \left(-\frac{(100)}{2(1)}, P\left(-\frac{(100)}{2(1)}\right)\right) = (-50,-2,500)[/latex]

Thus the minimum of the parabola occurs at [latex]x=-50[/latex], and is [latex]-2,500[/latex]. So one of the numbers is [latex]x=-50[/latex], the other we obtain by plugging in [latex]x=-50[/latex] in to [latex]y-x=100[/latex]:

[latex]\begin{array}{cc}y-(-50)&=&100 \\ y+50 &=& 100 \\ y &=& 50\end{array}[/latex]

[latex]x=-50[/latex] and [latex]y=50[/latex]

Example: Finding the Maximum Value of a Quadratic Function

A backyard farmer wants to enclose a rectangular space for a new garden within her fenced backyard. She has purchased 80 feet of wire fencing to enclose three sides, and she will use a section of the backyard fence as the fourth side.

• Find a formula for the area enclosed by the fence if the sides of fencing perpendicular to the existing fence have length [latex]L[/latex].
• What dimensions should she make her garden to maximize the enclosed area?

Let’s use a diagram such as the one above to record the given information. It is also helpful to introduce a temporary variable, W , to represent the width of the garden and the length of the fence section parallel to the backyard fence.

1)  We know we have only 80 feet of fence available, and [latex]L+W+L=80[/latex], or more simply, [latex]2L+W=80[/latex]. This allows us to represent the width, [latex]W[/latex], in terms of [latex]L[/latex].

[latex]W=80 - 2L[/latex]

Now we are ready to write an equation for the area the fence encloses. We know the area of a rectangle is length multiplied by width, so

[latex]\begin{array}{l}\text{ }A&=&LW=L\left(80 - 2L\right)\hfill \\ A\left(L\right)&=&80L - 2{L}^{2}\hfill \end{array}[/latex]

This formula represents the area of the fence in terms of the variable length [latex]L[/latex]. The function, written in general form, is

[latex]A\left(L\right)=-2{L}^{2}+80L[/latex].

2) The quadratic has a negative leading coefficient, so the graph will open downward, and the vertex will be the maximum value for the area. In finding the vertex, we must be careful because the equation is not written in standard polynomial form with decreasing powers. This is why we rewrote the function in general form above. Since [latex]a[/latex] is the coefficient of the squared term, [latex]a=-2,b=80[/latex], and [latex]c=0[/latex].

To find the vertex:

[latex]\large \begin{array}{l}h=-\frac{80}{2\left(-2\right)}\hfill & \hfill & \hfill & \hfill & k=A\left(20\right)\hfill \\ \text{ }=20\hfill & \hfill & \text{and}\hfill & \hfill & \text{ }=80\left(20\right)-2{\left(20\right)}^{2}\hfill \\ \hfill & \hfill & \hfill & \hfill & \text{ }=800\hfill \end{array}[/latex]

The maximum value of the function is an area of 800 square feet, which occurs when [latex]L=20[/latex] feet. When the shorter sides are 20 feet, there is 40 feet of fencing left for the longer side. To maximize the area, she should enclose the garden so the two shorter sides have length 20 feet and the longer side parallel to the existing fence has length 40 feet.

Analysis of the Solution

This problem also could be solved by graphing the quadratic function. We can see where the maximum area occurs on a graph of the quadratic function below.

How To: Given an application involving revenue, use a quadratic equation to find the maximum.

• Write a quadratic equation for revenue.
• Find the vertex of the quadratic equation.
• Determine the [latex]y[/latex]-value of the vertex.

Example: Finding Maximum Revenue

The unit price of an item affects its supply and demand. That is, if the unit price goes up, the demand for the item will usually decrease. For example, a local newspaper currently has 84,000 subscribers at a quarterly charge of $30. Market research has suggested that if the owners raise the price to $32, they would lose 5,000 subscribers. Assuming that subscriptions are linearly related to the price, what price should the newspaper charge for a quarterly subscription to maximize their revenue?

Revenue is the amount of money a company brings in. In this case, the revenue can be found by multiplying the price per subscription times the number of subscribers, or quantity. We can introduce variables, [latex]p[/latex] for price per subscription and [latex]Q[/latex] for quantity, giving us the equation [latex]\text{Revenue}=pQ[/latex].

Because the number of subscribers changes with the price, we need to find a relationship between the variables. We know that currently [latex]p=30[/latex] and [latex]Q=84,000[/latex]. We also know that if the price rises to $32, the newspaper would lose 5,000 subscribers, giving a second pair of values, [latex]p=32[/latex] and [latex]Q=79,000[/latex]. From this we can find a linear equation relating the two quantities. The slope will be

[latex]\large \begin{array}{c}m=\frac{79,000 - 84,000}{32 - 30}\hfill \\ \text{ }=\frac{-5,000}{2}\hfill \\ \text{ }=-2,500\hfill \end{array}[/latex]

This tells us the paper will lose 2,500 subscribers for each dollar they raise the price. We can then solve for the y -intercept.

[latex]\begin{array}{c}\text{ }Q=-2500p+b\hfill & \text{Substitute in the point }Q=84,000\text{ and }p=30\hfill \\ 84,000=-2500\left(30\right)+b\hfill & \text{Solve for }b\hfill \\ \text{ }b=159,000\hfill & \hfill \end{array}[/latex]

This gives us the linear equation [latex]Q=-2,500p+159,000[/latex] relating cost and subscribers. We now return to our revenue equation.

[latex]\begin{array}{c}\text{Revenue}=pQ\hfill \\ \text{Revenue}=p\left(-2,500p+159,000\right)\hfill \\ \text{Revenue}=-2,500{p}^{2}+159,000p\hfill \end{array}[/latex]

We now have a quadratic function for revenue as a function of the subscription charge. To find the price that will maximize revenue for the newspaper, we can find the vertex.

[latex]\large \begin{array}{c}h=-\frac{159,000}{2\left(-2,500\right)}\hfill \\ \text{ }=31.8\hfill \end{array}[/latex]

The model tells us that the maximum revenue will occur if the newspaper charges $31.80 for a subscription. To find what the maximum revenue is, we evaluate the revenue function.

[latex]\begin{array}{c}\text{maximum revenue}&=&-2,500{\left(31.8\right)}^{2}+159,000\left(31.8\right)\hfill \\ \text{ }&=&2,528,100\hfill \end{array}[/latex]

This could also be solved by graphing the quadratic. We can see the maximum revenue on a graph of the quadratic function.

A coordinate grid has been superimposed over the quadratic path of a basketball in the picture below. Find an equation for the path of the ball. Does the shooter make the basket?

(credit: modification of work by Dan Meyer)

The path passes through the origin and has vertex at [latex]\left(-4,\text{ }7\right)[/latex], so [latex]\left(h\right)x=-\frac{7}{16}{\left(x+4\right)}^{2}+7[/latex]. To make the shot, [latex]h\left(-7.5\right)[/latex] would need to be about 4 but [latex]h\left(-7.5\right)\approx 1.64[/latex]; he doesn’t make it.

• Quadratic Formula Application - Time for an Object to Hit the Ground. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/RcVeuJhcuL0 . License : CC BY: Attribution
• Quadratic Formula Application - Determine the Width of a Border. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/Zxe-SdwutxA . License : CC BY: Attribution
• College Algebra. Authored by : Abramson, Jay, et al.. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:1/Preface . License : CC BY: Attribution . License Terms : Download for free at : http://cnx.org/contents/[email protected]:1/Preface
• Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution

• Math Article

Quadratics or Quadratic Equations

Quadratics   can be defined as a polynomial equation of a second degree, which implies that it comprises a minimum of one term that is squared. It is also called quadratic equations . The general form of the quadratic equation is: 

ax² + bx + c = 0

where x is an unknown variable and a, b, c are numerical coefficients. For example, x 2 + 2x +1 is a quadratic or quadratic equation. Here, a ≠ 0 because if it equals zero then the equation will not remain quadratic anymore and it will become a linear equation, such as: 

Thus, this equation cannot be called a quadratic equation.

The terms a, b and c are also called quadratic coefficients. 

The solutions to the quadratic equation are the values of the unknown variable x, which satisfy the equation. These solutions are called roots or zeros of quadratic equations . The roots of any polynomial are the solutions for the given equation.

What is Quadratic Equation?

The polynomial equation whose highest degree is two is called a quadratic equation or sometimes just quadratics. It is expressed in the form of:

where x is the unknown variable and a, b and c are the constant terms.

Standard Form of Quadratic Equation

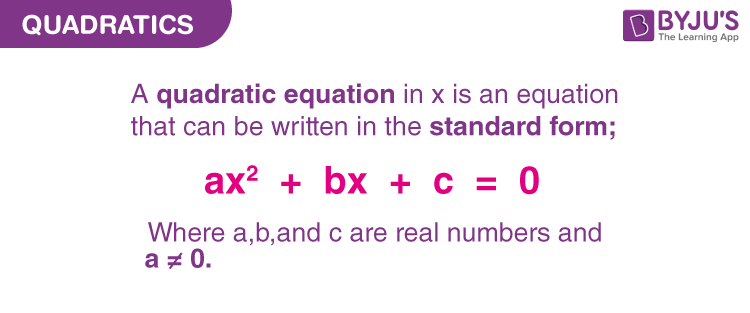
Since the quadratic includes only one unknown term or variable, thus it is called univariate. The power of variable x is always non-negative integers. Hence the equation is a polynomial equation with the highest power as 2.

The solution for this equation is the values of x, which are also called zeros. Zeros of the polynomial are the solution for which the equation is satisfied. In the case of quadratics, there are two roots or zeros of the equation. And if we put the values of roots or x on the left-hand side of the equation, it will equal to zero. Therefore, they are called zeros.

Quadratics Formula

The formula for a quadratic equation is used to find the roots of the equation. Since quadratics have a degree equal to two, therefore there will be two solutions for the equation. Suppose ax² + bx + c = 0 is the quadratic equation, then the formula to find the roots of this equation will be:

x = [-b±√(b 2 -4ac)]/2a

The sign of plus/minus indicates there will be two solutions for x. Learn in detail the quadratic formula here.

Examples of Quadratics

Beneath are the illustrations of quadratic equations of the form (ax² + bx + c = 0)

• x² –x – 9 = 0
• 5x² – 2x – 6 = 0
• 3x² + 4x + 8 = 0
• -x² +6x + 12 = 0

Examples of a quadratic equation with the absence of a ‘ C ‘- a constant term.

• -x² – 9x = 0
• x² + 2x = 0
• -6x² – 3x = 0
• -5x² + x = 0
• -12x² + 13x = 0
• 11x² – 27x = 0

Following are the examples of a quadratic equation in factored form

• (x – 6)(x + 1) = 0  [ result obtained after solving is x² – 5x – 6 = 0]
• –3(x – 4)(2x + 3) = 0  [result obtained after solving is -6x² + 15x + 36 = 0]
• (x − 5)(x + 3) = 0  [result obtained after solving is x² − 2x − 15 = 0]
• (x – 5)(x + 2) = 0  [ result obtained after solving is x² – 3x – 10 = 0]
• (x – 4)(x + 2) = 0  [result obtained after solving is x² – 2x – 8 = 0]
• (2x+3)(3x – 2) = 0  [result obtained after solving is 6x² + 5x – 6]

Below are the examples of a quadratic equation with an absence of linear co – efficient ‘ bx’

• 2x² – 64 = 0
• x² – 16 = 0
• 9x² + 49 = 0
• -2x² – 4 = 0
• 4x² + 81 = 0
• -x² – 9 = 0

How to Solve Quadratic Equations?

There are basically four methods of solving quadratic equations. They are:

• Completing the square

Using Quadratic Formula

• Taking the square root

Factoring of Quadratics

• Begin with a equation of the form ax² + bx + c = 0
• Ensure that it is set to adequate zero.
• Factor the left-hand side of the equation by assuming zero on the right-hand side of the equation.
• Assign each factor equal to zero.
• Now solve the equation in order to determine the values of x.

Suppose if the main coefficient is not equal to one then deliberately, you have to follow a methodology in the arrangement of the factors.

(2x+3)(x-2)=0

Learn more about the factorization of quadratic equations here.

Completing the Square Method

Let us learn this method with example.

Example: Solve 2x 2 – x – 1 = 0.

First, move the constant term to the other side of the equation.

2x 2 – x = 1

Dividing both sides by 2.

x 2 – x/2 = ½

Add the square of half of the coefficient of x, (b/2a) 2 , on both the sides, i.e., 1/16

x 2 – x/2 + 1/16 = ½ + 1/16

Now we can factor the right side,

(x-¼) 2 = 9/16 = (¾) 2

Taking root on both sides;

X – ¼ = ±3/4

Add ¼ on both sides

X = ¼ + ¾ = 4/4 = 1

X = ¼ – ¾ = -2/4 = -½ 

To learn more about completing the square method, click here .

For the given Quadratic equation of the form, ax² + bx + c = 0

Therefore the roots of the given equation can be found by:

\(\begin{array}{l}x = \frac{-b \pm \sqrt{b^{2}-4ac}}{2a}\end{array} \)

where ± (one plus and one minus) represent two distinct roots of the given equation.

Taking the Square Root

We can use this method for the equations such as:

x 2 + a 2 = 0

Example: Solve x 2 – 50 = 0.

x 2 – 50 = 0

Taking the roots both sides

√x 2 = ±√50

x = ±√(2 x 5 x 5)

Thus, we got the required solution.

Related Articles

Video lesson on quadratic equations, range of quadratic equations.

Solved Problems on Quadratic Equations

Applications of quadratic equations.

Many real-life word problems can be solved using quadratic equations. While solving word problems, some common quadratic equation applications include speed problems and Geometry area problems.

• Solving the problems related to finding the area of quadrilateral such as rectangle, parallelogram and so on
• Solving Word Problems involving Distance, speed, and time, etc.,

Example: Find the width of a rectangle of area 336 cm2 if its length is equal to the 4 more than twice its width. Solution: Let x cm be the width of the rectangle. Length = (2x + 4) cm We know that Area of rectangle = Length x Width x(2x + 4) = 336 2x 2 + 4x – 336 = 0 x 2 + 2x – 168 = 0 x 2 + 14x – 12x – 168 = 0 x(x + 14) – 12(x + 14) = 0 (x + 14)(x – 12) = 0 x = -14, x = 12 Measurement cannot be negative. Therefore, Width of the rectangle = x = 12 cm

Practice Questions

• Solve x 2 + 2 x + 1 = 0.
• Solve 5x 2 + 6x + 1 = 0
• Solve 2x 2 + 3 x + 2 = 0.
• Solve x 2 − 4x + 6.25 = 0

Frequently Asked Questions on Quadratics

What is a quadratic equation, what are the methods to solve a quadratic equation, is x 2 – 1 a quadratic equation, what is the solution of x 2 + 4 = 0, write the quadratic equation in the form of sum and product of roots., leave a comment cancel reply.

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Thanks a lot ,This was very useful for me

x=√9 Squaring both the sides, x^2 = 9 x^2 – 9 = 0 It is a quadratic equation.

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Quadratic Equation

Quadratic equations are second-degree algebraic expressions and are of the form ax 2 + bx + c = 0. The term "quadratic" comes from the Latin word "quadratus" meaning square, which refers to the fact that the variable x is squared in the equation. In other words, a quadratic equation is an “equation of degree 2.” There are many scenarios where a quadratic equation is used. Did you know that when a rocket is launched, its path is described by a quadratic equation? Further, a quadratic equation has numerous applications in physics, engineering, astronomy, etc.

Quadratic equations have maximum of two solutions, which can be real or complex numbers. These two solutions (values of x) are also called the roots of the quadratic equations and are designated as (α, β). We shall learn more about the roots of a quadratic equation in the below content.

What is Quadratic Equation?

A quadratic equation is an algebraic equation of the second degree in x. The quadratic equation in its standard form is ax 2 + bx + c = 0, where a and b are the coefficients, x is the variable, and c is the constant term. The important condition for an equation to be a quadratic equation is the coefficient of x 2 is a non-zero term (a ≠ 0). For writing a quadratic equation in standard form, the x 2 term is written first, followed by the x term, and finally, the constant term is written.

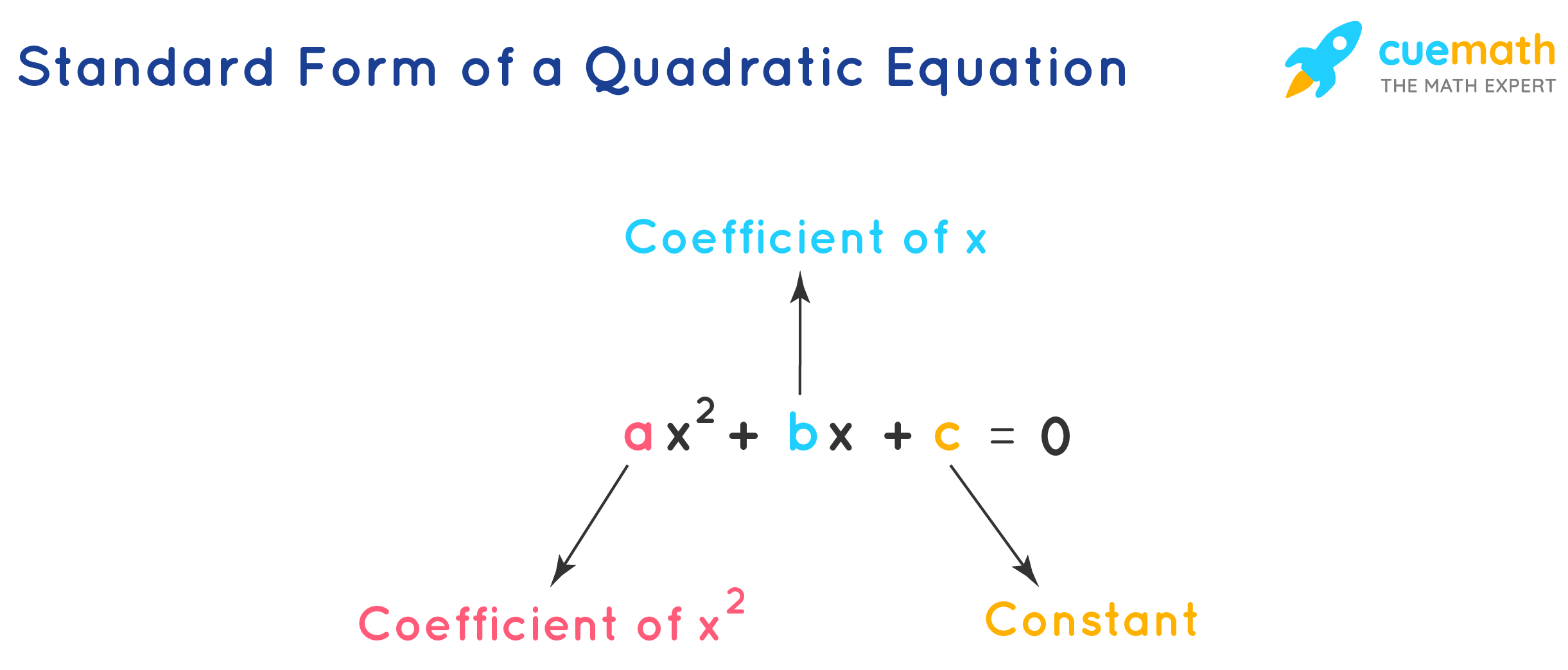
Further, in real math problems the quadratic equations are presented in different forms: (x - 1)(x + 2) = 0, -x 2 = -3x + 1, 5x(x + 3) = 12x, x 3 = x(x 2 + x - 3). All of these equations need to be transformed into standard form of the quadratic equation before performing further operations.

Roots of a Quadratic Equation

The roots of a quadratic equation are the two values of x, which are obtained by solving the quadratic equation. These roots of the quadratic equation are also called the zeros of the equation. For example, the roots of the equation x 2 - 3x - 4 = 0 are x = -1 and x = 4 because each of them satisfies the equation. i.e.,

• At x = -1, (-1) 2 - 3(-1) - 4 = 1 + 3 - 4 = 0
• At x = 4, (4) 2 - 3(4) - 4 = 16 - 12 - 4 = 0

There are various methods to find the roots of a quadratic equation. The usage of the quadratic formula is one of them.

Quadratic Formula

Quadratic formula is the simplest way to find the roots of a quadratic equation . There are certain quadratic equations that cannot be easily factorized, and here we can conveniently use this quadratic formula to find the roots in the quickest possible way. The two roots in the quadratic formula are presented as a single expression. The positive sign and the negative sign can be alternatively used to obtain the two distinct roots of the equation.

Quadratic Formula: The roots of a quadratic equation ax 2 + bx + c = 0 are given by x = [-b ± √(b 2 - 4ac)]/2a.

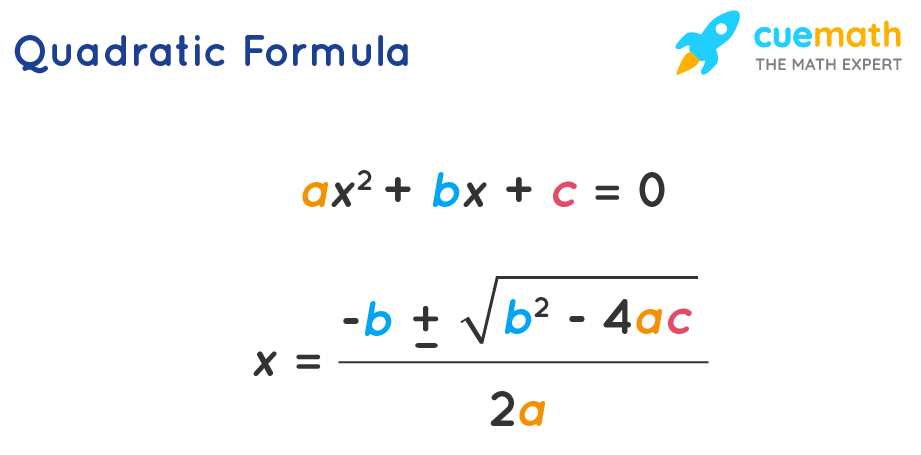
This formula is also known as the Sridharacharya formula .

Example: Let us find the roots of the same equation that was mentioned in the earlier section x 2 - 3x - 4 = 0 using the quadratic formula.

a = 1, b = -3, and c = -4.

x = [-b ± √(b 2 - 4ac)]/2a = [-(-3) ± √((-3) 2 - 4(1)(-4))]/2(1) = [3 ± √25] / 2 = [3 ± 5] / 2 = (3 + 5)/2 or (3 - 5)/2 = 8/2 or -2/2 = 4 or -1 are the roots.

Proof of Quadratic Formula

Consider an arbitrary quadratic equation: ax 2 + bx + c = 0, a ≠ 0

To determine the roots of this equation, we proceed as follows:

ax 2 + bx = -c ⇒ x 2 + bx/a = -c/a

Now, we express the left-hand side as a perfect square , by introducing a new term (b/2a) 2 on both sides:

• x 2 + bx/a + (b/2a) 2 = -c/a + (b/2a) 2

The left-hand side is now a perfect square:

(x + b/2a) 2 = -c/a + b 2 /4a 2 ⇒ (x + b/2a) 2 = (b 2 - 4ac)/4a 2

This is good for us, because now we can take square roots to obtain:

x + b/2a = ±√(b 2 - 4ac)/2a

x = (-b ± √(b 2 - 4ac))/2a

Thus, by completing the squares, we were able to isolate x and obtain the two roots of the equation.

Nature of Roots of the Quadratic Equation

The roots of a quadratic equation are usually represented to by the symbols alpha (α), and beta (β). Here we shall learn more about how to find the nature of roots of a quadratic equation without actually finding the roots of the equation.

The nature of roots of a quadratic equation can be found without actually finding the roots (α, β) of the equation. This is possible by taking the discriminant value, which is part of the formula to solve the quadratic equation. The value b 2 - 4ac is called the discriminant of a quadratic equation and is designated as 'D'. Based on the discriminant value the nature of the roots of the quadratic equation can be predicted.

Discriminant: D = b 2 - 4ac

• D > 0, the roots are real and distinct
• D = 0, the roots are real and equal.
• D < 0, the roots do not exist or the roots are imaginary .

Now, check out the formulas to find the sum and the product of the roots of the equation.

Sum and Product of Roots of Quadratic Equation

The coefficient of x 2 , x term, and the constant term of the quadratic equation ax 2 + bx + c = 0 are useful in determining the sum and product of the roots of the quadratic equation. The sum and product of the roots of a quadratic equation can be directly calculated from the equation, without actually finding the roots of the quadratic equation. For a quadratic equation ax 2 + bx + c = 0, the sum and product of the roots are as follows.

• Sum of the Roots: α + β = -b/a = - Coefficient of x/ Coefficient of x 2
• Product of the Roots: αβ = c/a = Constant term/ Coefficient of x 2

Writing Quadratic Equations Using Roots

The quadratic equation can also be formed for the given roots of the equation. If α, β, are the roots of the quadratic equation, then the quadratic equation is as follows.

x 2 - (α + β)x + αβ = 0

Example: What is the quadratic equation whose roots are 4 and -1?

Solution: It is given that α = 4 and β = -1. The corresponding quadratic equation is found by:

x 2 - (α + β)x + αβ = 0 x 2 - (α + β)x + αβ = 0 x 2 - (4 - 1)x + (4)(-1) = 0 x 2 - 3x - 4 = 0

Formulas Related to Quadratic Equations

The following list of important formulas is helpful to solve quadratic equations.

• The quadratic equation in its standard form is ax 2 + bx + c = 0
• For D > 0 the roots are real and distinct.
• For D = 0 the roots are real and equal.
• For D < 0 the real roots do not exist, or the roots are imaginary.
• The formula to find the roots of the quadratic equation is x = [-b ± √(b 2 - 4ac)]/2a.
• The sum of the roots of a quadratic equation is α + β = -b/a.
• The product of the Root of the quadratic equation is αβ = c/a.
• The quadratic equation whose roots are α, β, is x 2 - (α + β)x + αβ = 0.
• The condition for the quadratic equations a 1 x 2 + b 1 x + c 1 = 0, and a 2 x 2 + b 2 x + c 2 = 0 having the same roots is (a 1 b 2 - a 2 b 1 ) (b 1 c 2 - b 2 c 1 ) = (a 2 c 1 - a 1 c 2 ) 2 .
• When a > 0, the quadratic expression f(x) = ax 2 + bx + c has a minimum value at x = -b/2a.
• When a < 0, the quadratic expression f(x) = ax 2 + bx + c has a maximum value at x = -b/2a.
• The domain of any quadratic function is the set of all real numbers.

Methods to Solve Quadratic Equations

A quadratic equation can be solved to obtain two values of x or the two roots of the equation. There are four different methods to find the roots of the quadratic equation. The four methods of solving the quadratic equations are as follows.

• Factorizing of Quadratic Equation
• Using quadratic formula (which we have seen already)

Method of Completing the Square

• Graphing Method to Find the Roots

Let us look in detail at each of the above methods to understand how to use these methods, their applications, and their uses.

Solving Quadratic Equations by Factorization

Factorization of quadratic equation follows a sequence of steps. For a general form of the quadratic equation ax 2 + bx + c = 0, we need to first split the middle term into two terms, such that the product of the terms is equal to the constant term. Further, we can take the common terms from the available term, to finally obtain the required factors as follows:

• x 2 + (a + b)x + ab = 0
• x 2 + ax + bx + ab = 0
• x(x + a) + b(x + a)
• (x + a)(x + b) = 0

Here is an example to understand the factorization process.

• x 2 + 5x + 6 = 0
• x 2 + 2x + 3x + 6 = 0
• x(x + 2) + 3(x + 2) = 0
• (x + 2)(x + 3) = 0

Thus the two obtained factors of the quadratic equation are (x + 2) and (x + 3). To find its roots, just set each factor to zero and solve for x. i.e., x + 2 = 0 and x + 3 = 0 which gives x = -2 and x = -3. Thus, x = -2 and x = -3 are the roots of x 2 + 5x + 6 = 0.

Further, there is another important method of solving a quadratic equation. The method of completing the square for a quadratic equation is also useful to find the roots of the equation.

The method of completing the square in a quadratic equation is to algebraically square and simplify, to obtain the required roots of the equation. Consider a quadratic equation ax 2 + bx + c = 0, a ≠ 0. To determine the roots of this equation, we simplify it as follows:

• ax 2 + bx + c = 0
• ax 2 + bx = -c
• x 2 + bx/a = -c/a

Now, we express the left-hand side as a perfect square, by introducing a new term (b/2a) 2 on both sides:

• (x + b/2a) 2 = -c/a + b 2 /4a 2
• (x + b/2a) 2 = (b 2 - 4ac)/4a 2
• x + b/2a = + √(b 2 - 4ac)/2a
• x = - b/2a + √(b 2 - 4ac)/2a
• x = [-b ± √(b 2 - 4ac)]/2a

Here the '+' sign gives one root and the '-' sign gives another root of the quadratic equation. Generally, this detailed method is avoided, and only the quadratic formula is used to obtain the required roots.

Graphing a Quadratic Equation

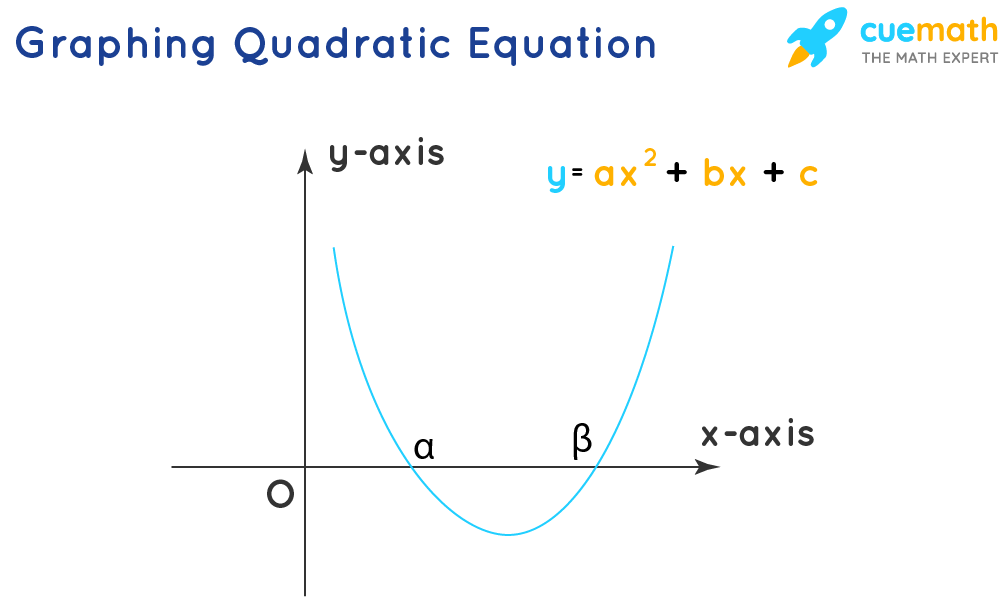
The point(s) where the graph cuts the horizontal x-axis (typically the x-intercepts ) is the solution of the quadratic equation. These points can also be algebraically obtained by equalizing the y value to 0 in the function y = ax 2 + bx + c and solving for x.

Quadratic Equations Having Common Roots

Consider two quadratic equations having common roots a 1 x 2 + b 1 x + c 1 = 0, and a 2 x 2 + b 2 x + c 2 = 0. Let us solve these two equations to find the conditions for which these equations have a common root. The two equations are solved for x 2 and x respectively.

(x 2 )(b 1 c 2 - b 2 c 1 ) = (-x)/(a 1 c 2 - a 2 c 1 ) = 1/(a 1 b 2 - a 2 b 1 )

x 2 = (b 1 c 2 - b 2 c 1 ) / (a 1 b 2 - a 2 b 1 )

x = (a 2 c 1 - a 1 c 2 ) / (a 1 b 2 - a 2 b 1 )

Hence, by simplifying the above two expressions we have the following condition for the two equations having the common root.

(a 1 b 2 - a 2 b 1 ) (b 1 c 2 - b 2 c 1 ) = (a 2 c 1 - a 1 c 2 ) 2

Maximum and Minimum Value of Quadratic Expression

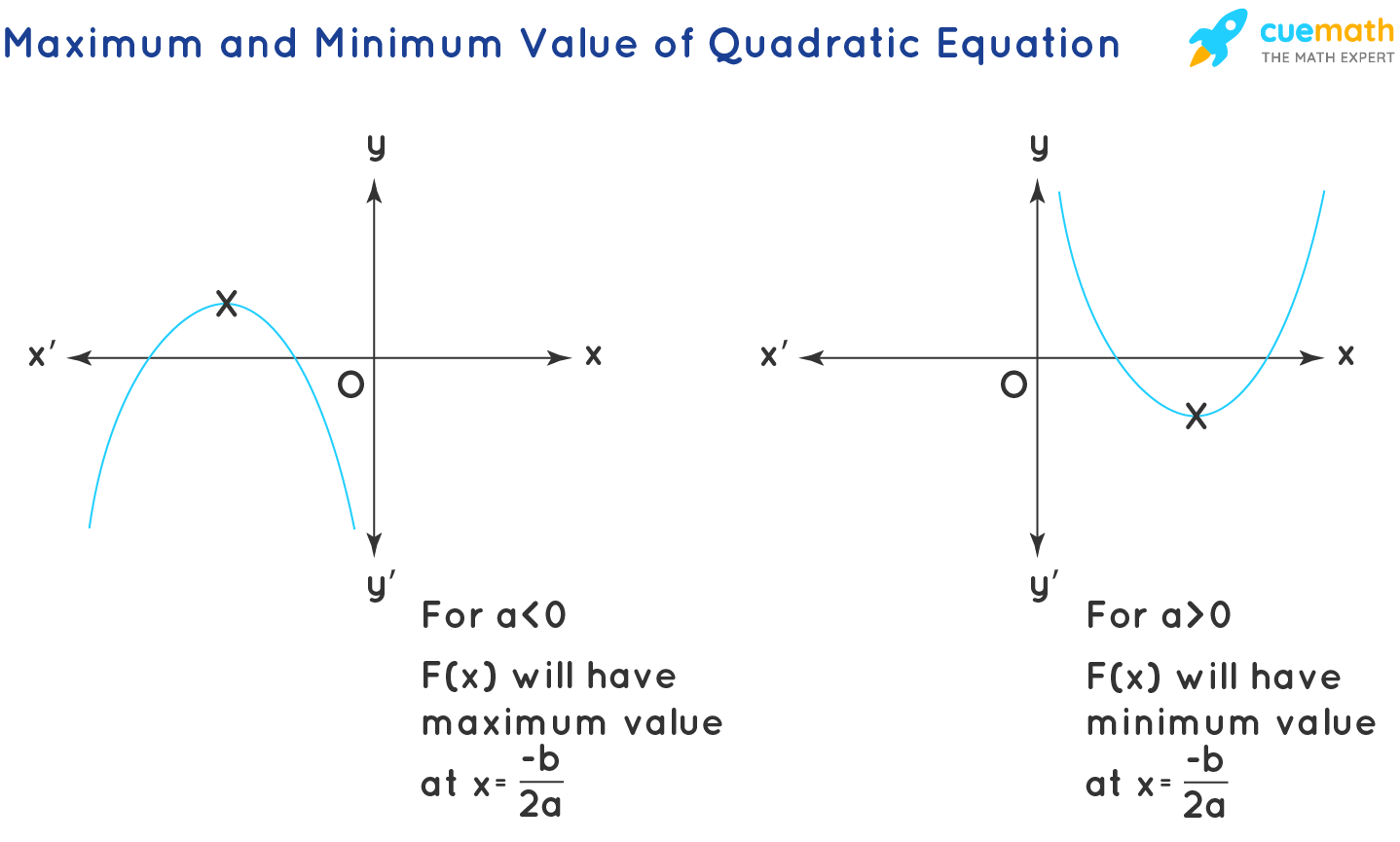
The maximum and minimum values of the quadratic expressions are of further help to find the range of the quadratic expression: The range of the quadratic expressions also depends on the value of a. For positive values of a( a > 0), the range is [ F(-b/2a), ∞), and for negative values of a ( a < 0), the range is (-∞, F(-b/2a)].

• For a > 0, Range: [ f(-b/2a), ∞)
• For a < 0, Range: (-∞, f(-b/2a)]

Note that the domain of a quadratic function is the set of all real numbers, i.e., (-∞, ∞).

Tips and Tricks on Quadratic Equation:

Some of the below-given tips and tricks on quadratic equations are helpful to more easily solve quadratic equations.

• The quadratic equations are generally solved through factorization. But in instances when it cannot be solved by factorization, the quadratic formula is used.
• The roots of a quadratic equation are also called the zeroes of the equation.
• For quadratic equations having negative discriminant values, the roots are represented by complex numbers.
• The sum and product of the roots of a quadratic equation can be used to find higher algebraic expressions involving these roots.

☛Related Topics:

• Roots Calculator
• Quadratic Factoring Calculator
• Roots of Quadratic Equation Calculator

Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12 . Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.

Quadratic Equations Examples

Example 1: James is a fitness enthusiast and goes for a jog every morning. The park where he jogs is rectangular in shape and measures 12m × 8m. An environmentalist group plans to revamp the park and decides to build a pathway surrounding the park. This would increase the total area to 140 sq m. What will be the width of the pathway?

Let’s denote the width of the pathway by x.

Then, the length and breadth of the outer rectangle is (12+2x) m and (8+2x) m.

Given that, area = 140

(12 + 2x)(8 + 2x) = 140

2(6 + x) 2(4 + x) = 140

(6 + x)(4 + x) = 35

24 + 6x + 4x + x 2 = 35

x 2 + 10x -11 = 0

x 2 + 11x - x - 11 = 0

x(x + 11) - 1(x + 11) = 0

(x + 11)(x - 1) = 0

(x + 11) =0 and (x - 1) = 0

x = -11 and x = 1

Since length can’t be negative, we take x = 1.

Answer: Therefore the width of the pathway is 1 m.

Example 2: Rita throws a ball upwards from a platform that is 20m above the ground. The height of the ball from the ground at a time 't', is denoted by 'h'. Suppose h = -4t 2 + 16t + 20. Find the maximum height attained by the ball.

We can rearrange the terms of the quadratic equation

h = -4t 2 + 16t + 20

in such a way that it is easy to find the maximum value of this equation.

= -4t 2 + 16t + 20

= -4(t 2 - 4t - 5)

= -4((t - 2) 2 - 9)

= -4(t - 2) 2 + 36

We should keep the value of (t - 2) 2 minimum in order to find the maximum value of h.

So, the minimum value (t - 2) 2 can take is 0.

Answer: Therefore the maximum height attained is 36m.

Example 3: Find the quadratic equation having the roots 5 and 8 respectively.

The quadratic equation having the roots α, β, is x 2 - (α + β)x + αβ = 0.

Given α = 5, and β = 8.

Therefore the quadratic equation is:

x 2 - (5 + 8)x + 5×8 = 0

x 2 - 13x + 40 = 0

Answer: Hence the required quadratic equation is x 2 - 13x + 40 = 0

Example 4: The quad equation 2x 2 + 9x + 7 = 0 has roots α, β. Find the quadratic equation having the roots 1/α, and 1/β.

The quadratic equation having roots that are reciprocal to the roots of the equation ax 2 + bx + c = 0, is cx 2 + bx + a = 0.

The given quadratic equation is 2x 2 + 9x + 7 = 0.

Hence the required equation having reciprocal roots is 7x 2 + 9x + 2 = 0.

Method 2: From the given equation,

α + β = -9/2 and α β = 2/7.

The new equation should have its roots to be 1/α and 1/β.

Their sum = 1/α + 1/β = (α + β) / α β = -9/7 Their product = 1/α β = 2/7 Thus, the required equation is, x 2 - (1/α + 1/β)x + 1/α β = 0 x 2 - (-9/7)x + 2/7 = 0 Multiplying both sides by 7, 7x 2 + 9x + 2 = 0

Answer: Therefore the equation is 7x 2 + 9x + 2 = 0.

go to slide go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Quadratic Equation

go to slide go to slide

FAQs on Quadratic Equation

What is the definition of a quadratic equation.

A quadratic equation in math is a second-degree equation of the form ax 2 + bx + c = 0. Here a and b are the coefficients, c is the constant term, and x is the variable. Since the variable x is of the second degree, there are two roots or answers for this quadratic equation. The roots of the quadratic equation can be found by either solving by factorizing or through the use of the quadratic formula.

What is the Quadratic Formula?

The quadratic equation formula to solve the equation ax 2 + bx + c = 0 is x = [-b ± √(b 2 - 4ac)]/2a. Here we obtain the two values of x, by applying the plus and minus symbols in this formula. Hence the two possible values of x are [-b + √(b 2 - 4ac)]/2a, and [-b - √(b 2 - 4ac)]/2a.

How do You Solve a Quadratic Equation?

There are several methods to solve quadratic equations, but the most common ones are factoring, using the quadratic formula, and completing the square.

• Factoring involves finding two numbers that multiply to equal the constant term, c, and add up to the coefficient of x, b.
• The quadratic formula is used when factoring is not possible, and it is given by x = [-b ± √(b 2 - 4ac)]/2a.
• Completing the square involves rewriting the quadratic equation in a different form that allows you to easily solve for x.

What is Determinant in Quadratic Formula?

The value b 2 - 4ac is called the discriminant and is designated as D. The discriminant is part of the quadratic formula. The discriminants help us to find the nature of the roots of the quadratic equation, without actually finding the roots of the quadratic equation.

What are Some Real-Life Applications of Quadratic Equations?

Quadratic equations are used to find the zeroes of the parabola and its axis of symmetry . There are many real-world applications of quadratic equations.

• They can be used in running time problems to evaluate the speed, distance or time while traveling by car, train or plane.
• Quadratic equations describe the relationship between quantity and the price of a commodity.
• Similarly, demand and cost calculations are also considered quadratic equation problems.
• It can also be noted that a satellite dish or a reflecting telescope has a shape that is defined by a quadratic equation.

How are Quadratic Equations Different From Linear Equations?

A linear degree is an equation of a single degree and one variable, and a quadratic equation is an equation in two degrees and a single variable. A linear equation is of the the form ax + b = 0 and a quadratic equation is of the form ax 2 + bx + c = 0. A linear equation has a single root and a quadratic equation has two roots or two answers. Also, a quadratic equation is a product of two linear equations.

What Are the 4 Ways To Solve A Quadratic Equation?

The four ways of solving a quadratic equation are as follows.

• Factorizing method
• Roots of Quadratic Equation Formula Method
• Method of Completing Squares
• Graphing Method

How to Solve a Quadratic Equation by Completing the Square?

The quadratic equation is solved by the method of completing the square and it uses the formula (a + b)^2 = a 2 + 2ab + b 2 (or) (a - b)^2 = a 2 - 2ab + b 2 .

How to Find the Value of the Discriminant?

The value of the discriminant in a quadratic equation can be found from the variables and constant terms of the standard form of the quadratic equation ax 2 + bx + c = 0. The value of the discriminant is D = b 2 - 4ac, and it helps to predict the nature of roots of the quadratic equation, without actually finding the roots of the equation.

How Do You Solve Quadratic Equations With Graphing?

The quadratic equation can be solved similarly to a linear equal by graphing. Let us take the quadratic equation ax 2 + bx + c = 0 as y = ax 2 + bx + c . Here we take the set of values of x and y and plot the graph. The two points where this graph meets the x-axis, are the solutions of this quadratic equation.

How Important Is the Discriminant of a Quadratic Equation?

The discriminant is very much needed to easily find the nature of the roots of the quadratic equation. Without the discriminant, finding the nature of the roots of the equation is a long process, as we first need to solve the equation to find both the roots. Hence the discriminant is an important and needed quantity, which helps to easily find the nature of the roots of the quadratic equation.

Where Can I Find Quadratic Equation Solver?

To get the quadratic equation solver, click here . Here, we can enter the values of a, b, and c for the quadratic equation ax 2 + bx + c = 0, then it will give you the roots along with a step-by-step procedure.

What is the Use of Discriminants in Quadratic Formula?

The discriminant (D = b 2 - 4ac) is useful to predict the nature of the roots of the quadratic equation. For D > 0, the roots are real and distinct, for D = 0 the roots are real and equal, and for D < 0, the roots do not exist or the roots are imaginary complex numbers . With the help of this discriminant and with the least calculations, we can find the nature of the roots of the quadratic equation.

How do you Solve a Quadratic Equation without Using the Quadratic Formula?

There are two alternative methods to the quadratic formula. One method is to solve the quadratic equation through factorization, and another method is by completing the squares. In total there are three methods to find the roots of a quadratic equation.

How to Derive Quadratic Formula?

The algebra formula (a + b) 2 = a 2 + 2ab + b 2 is used to solve the quadratic equation and derive the quadratic formula. This algebraic formula is used to manipulate the quadratic equation and derive the quadratic formula to find the roots of the equation.

Real World Examples of Quadratic Equations

A Quadratic Equation looks like this:

Quadratic equations pop up in many real world situations!

Here we have collected some examples for you, and solve each using different methods:

• Factoring Quadratics
• Completing the Square
• Graphing Quadratic Equations
• The Quadratic Formula
• Online Quadratic Equation Solver

Each example follows three general stages:

• Take the real world description and make some equations
• Use your common sense to interpret the results

Balls, Arrows, Missiles and Stones

When you throw a ball (or shoot an arrow, fire a missile or throw a stone) it goes up into the air, slowing as it travels, then comes down again faster and faster ...

... and a Quadratic Equation tells you its position at all times!

Example: Throwing a Ball

A ball is thrown straight up, from 3 m above the ground, with a velocity of 14 m/s. when does it hit the ground.

Ignoring air resistance, we can work out its height by adding up these three things: (Note: t is time in seconds)

Add them up and the height h at any time t is:

h = 3 + 14t − 5t 2

And the ball will hit the ground when the height is zero:

3 + 14t − 5t 2 = 0

Which is a Quadratic Equation !

In "Standard Form" it looks like:

−5t 2 + 14t + 3 = 0

It looks even better when we multiply all terms by −1 :

5t 2 − 14t − 3 = 0

Let us solve it ...

There are many ways to solve it, here we will factor it using the "Find two numbers that multiply to give ac , and add to give b " method in Factoring Quadratics :

ac = −15 , and b = −14 .

The factors of −15 are: −15, −5, −3, −1, 1, 3, 5, 15

By trying a few combinations we find that −15 and 1 work (−15×1 = −15, and −15+1 = −14)

The "t = −0.2" is a negative time, impossible in our case.

The "t = 3" is the answer we want:

The ball hits the ground after 3 seconds!

Here is the graph of the Parabola h = −5t 2 + 14t + 3

It shows you the height of the ball vs time

Some interesting points:

(0,3) When t=0 (at the start) the ball is at 3 m

(−0.2,0) says that −0.2 seconds BEFORE we threw the ball it was at ground level. This never happened! So our common sense says to ignore it.

(3,0) says that at 3 seconds the ball is at ground level.

Also notice that the ball goes nearly 13 meters high.

Note: You can find exactly where the top point is!

The method is explained in Graphing Quadratic Equations , and has two steps:

Find where (along the horizontal axis) the top occurs using −b/2a :

• t = −b/2a = −(−14)/(2 × 5) = 14/10 = 1.4 seconds

Then find the height using that value (1.4)

• h = −5t 2 + 14t + 3 = −5(1.4) 2 + 14 × 1.4 + 3 = 12.8 meters

So the ball reaches the highest point of 12.8 meters after 1.4 seconds.

Example: New Sports Bike

You have designed a new style of sports bicycle!

Now you want to make lots of them and sell them for profit.

Your costs are going to be:

• $700,000 for manufacturing set-up costs, advertising, etc
• $110 to make each bike

Based on similar bikes, you can expect sales to follow this "Demand Curve":

Where "P" is the price.

For example, if you set the price:

• at $0, you just give away 70,000 bikes
• at $350, you won't sell any bikes at all
• at $300 you might sell 70,000 − 200×300 = 10,000 bikes

So ... what is the best price? And how many should you make?

Let us make some equations!

How many you sell depends on price, so use "P" for Price as the variable

Profit = −200P 2 + 92,000P − 8,400,000

Yes, a Quadratic Equation. Let us solve this one by Completing the Square .

Solve: −200P 2 + 92,000P − 8,400,000 = 0

Step 1 Divide all terms by -200

Step 2 Move the number term to the right side of the equation:

Step 3 Complete the square on the left side of the equation and balance this by adding the same number to the right side of the equation:

(b/2) 2 = (−460/2) 2 = (−230) 2 = 52900

Step 4 Take the square root on both sides of the equation:

Step 5 Subtract (-230) from both sides (in other words, add 230):

What does that tell us? It says that the profit is ZERO when the Price is $126 or $334

But we want to know the maximum profit, don't we?

It is exactly half way in-between! At $230

And here is the graph:

The best sale price is $230 , and you can expect:

• Unit Sales = 70,000 − 200 x 230 = 24,000
• Sales in Dollars = $230 x 24,000 = $5,520,000
• Costs = 700,000 + $110 x 24,000 = $3,340,000
• Profit = $5,520,000 − $3,340,000 = $2,180,000

A very profitable venture.

Example: Small Steel Frame

Your company is going to make frames as part of a new product they are launching.

The frame will be cut out of a piece of steel, and to keep the weight down, the final area should be 28 cm 2

The inside of the frame has to be 11 cm by 6 cm

What should the width x of the metal be?

Area of steel before cutting:

Area of steel after cutting out the 11 × 6 middle:

Let us solve this one graphically !

Here is the graph of 4x 2 + 34x :

The desired area of 28 is shown as a horizontal line.

The area equals 28 cm 2 when:

x is about −9.3 or 0.8

The negative value of x make no sense, so the answer is:

x = 0.8 cm (approx.)

Example: River Cruise

A 3 hour river cruise goes 15 km upstream and then back again. the river has a current of 2 km an hour. what is the boat's speed and how long was the upstream journey.

There are two speeds to think about: the speed the boat makes in the water, and the speed relative to the land:

• Let x = the boat's speed in the water (km/h)
• Let v = the speed relative to the land (km/h)

Because the river flows downstream at 2 km/h:

• when going upstream, v = x−2 (its speed is reduced by 2 km/h)
• when going downstream, v = x+2 (its speed is increased by 2 km/h)

We can turn those speeds into times using:

time = distance / speed

(to travel 8 km at 4 km/h takes 8/4 = 2 hours, right?)

And we know the total time is 3 hours:

total time = time upstream + time downstream = 3 hours

Put all that together:

total time = 15/(x−2) + 15/(x+2) = 3 hours

Now we use our algebra skills to solve for "x".

First, get rid of the fractions by multiplying through by (x-2) (x+2) :

3(x-2)(x+2) = 15(x+2) + 15(x-2)

Expand everything:

3(x 2 −4) = 15x+30 + 15x−30

Bring everything to the left and simplify:

3x 2 − 30x − 12 = 0

It is a Quadratic Equation!

Let us solve it using the Quadratic Formula :

Where a , b and c are from the Quadratic Equation in "Standard Form": ax 2 + bx + c = 0

Solve 3x 2 - 30x - 12 = 0

Answer: x = −0.39 or 10.39 (to 2 decimal places)

x = −0.39 makes no sense for this real world question, but x = 10.39 is just perfect!

Answer: Boat's Speed = 10.39 km/h (to 2 decimal places)

And so the upstream journey = 15 / (10.39−2) = 1.79 hours = 1 hour 47min

And the downstream journey = 15 / (10.39+2) = 1.21 hours = 1 hour 13min

Example: Resistors In Parallel

Two resistors are in parallel, like in this diagram:

The total resistance has been measured at 2 Ohms, and one of the resistors is known to be 3 ohms more than the other.

What are the values of the two resistors?

The formula to work out total resistance "R T " is:

1 R T   =   1 R 1 + 1 R 2

In this case, we have R T = 2 and R 2 = R 1 + 3

1 2   =   1 R 1 + 1 R 1 +3

To get rid of the fractions we can multiply all terms by 2R 1 (R 1 + 3) and then simplify:

Yes! A Quadratic Equation!

Let us solve it using our Quadratic Equation Solver .

• Enter 1, −1 and −6
• And you should get the answers −2 and 3

R 1 cannot be negative, so R 1 = 3 Ohms is the answer.

The two resistors are 3 ohms and 6 ohms.

Quadratic Equations are useful in many other areas:

For a parabolic mirror, a reflecting telescope or a satellite dish, the shape is defined by a quadratic equation.

Quadratic equations are also needed when studying lenses and curved mirrors.

And many questions involving time, distance and speed need quadratic equations.

Quadratic Functions Problems with Solutions

quadratic functions problems with detailed solutions are presented along with graphical interpretations of the solutions.

Review Vertex and Discriminant of Quadratic Functions

f(x) = a x 2 + b x + c

If a > 0 , the vertex is a minimum point and the minimum value of the quadratic function f is equal to k. This minimum value occurs at x = h. If a < 0 , the vertex is a maximum point and the maximum value of the quadratic function f is equal to k. This maximum value occurs at x = h. The quadratic function f(x) = a x 2 + b x + c can be written in vertex form as follows:

f(x) = a (x - h) 2 + k

Problems with Solutions

Problem 1 The profit (in thousands of dollars) of a company is given by.

P(x) = 5000 + 1000 x - 5 x 2

• Function P that gives the profit is a quadratic function with the leading coefficient a = - 5. This function (profit) has a maximum value at x = h = - b / (2a) x = h = -1000 / (2(-5)) = 100
• The maximum profit Pmax, when x = 100 thousands is spent on advertising, is given by the maximum value of function P k = c - b 2 / (4 a) b)
• The maximum profit Pmax, when x = 100 thousands is spent on advertising, is also given by P(h = 100) P(100) = 5000 + 1000 (100) - 5 (100) 2 = 55000.
• When the company spends 100 thousands dollars on advertising, the profit is maximum and equals 55000 dollars.

Problem 2 An object is thrown vertically upward with an initial velocity of V o feet/sec. Its distance S(t), in feet, above ground is given by

• S(t) is a quadratic function and the maximum value of S(t)is given by k = c - b 2 /(4 a) = 0 - (v o ) 2 / (4(-16))
• This maximum value of S(t) has to be 300 feet in order for the object to reach a maximum distance above ground of 300 feet. - (v o ) 2 / (4(-16)) = 300
• we now solve - (v o ) 2 / (4(-16)) = 300 for v o v o = 64*300 = 80 √3 feet/sec.

Problem 3 Find the equation of the quadratic function f whose graph passes through the point (2 , -8) and has x intercepts at (1 , 0) and (-2 , 0). Solution to Problem 3

• Since the graph has x intercepts at (1 , 0) and (-2 , 0), the function has zeros at x = 1 and x = - 2 and may be written as follows. f(x) = a (x - 1)(x + 2)
• The graph of f passes through the point (2 , -8), it follows that f(2) = - 8
• which leads to - 8 = a (2 - 1)(2 + 2)
• expand the right side of the above equation and group like terms -8 = 4 a
• Solve the above equation for a to obtain a = - 2
• The equation of f is given by f(x) = - 2 (x - 1)(x + 2)
• Check answer f(1) = 0 f(-2) = 0 f(2) = - 2 (2 - 1)(2 + 2) = -8

Problem 4 Find values of the parameter m so that the graph of the quadratic function f given by

• To find the points of intersection, you need to solve the system of equations y = x 2 + x + 1 y = m x
• Substitute m x for y in the first equation to obtain mx = x 2 + x + 1
• Write the above quadratic equation in standard form. x 2 + x (1 - m) + 1 = 0
• Find the discriminant D of the above equation. D = (1 - m) 2 - 4(1)(1) D = (1 - m) 2 - 4 a)
• For the graph of f and that of the line to have 2 points of intersection, D must be positive, which leads to (1 - m) 2 - 4 > 0
• Solve the above inequality to obtain solution set for m in the intervals (- ∞ , -1) U (3 , + ∞) b)
• For the graph of f and that of the line to have 1 point of intersection, D must be zero, which leads to (1 - m) 2 - 4 = 0
• Solve the above equation to obtain 2 solutions for m. m = -1 m = 3 c)
• For the graph of f and that of the line to have no points of intersection, D must be negative, which leads to (1 - m) 2 - 4 < 0

Problem 5 The quadratic function C(x) = a x 2 + b x + c represents the cost, in thousands of Dollars, of producing x items. C(x) has a minimum value of 120 thousands for x = 2000 and the fixed cost is equal to 200 thousands. Find the coefficients a,b and c. Solution to Problem 5

• Function C is a quadratic function. Its minimum point, which is given as (2000,120) is the vertex of the graph of C. Hence we can write C(x) in vertex form as follows C(x) = a (x - 2000) 2 + 120
• The fixed cost is the value of C(x) when x = 0. Hence C(0) = a (0 - 2000) 2 + 120 = 200
• Solve for a a = 80 / 2000 2 = 0.00002
• We expand C(x) and identify the coefficients a, b and c. C(x) = 0.00002 (x - 2000) 2 + 120 = 0.00002 x 2 - 0.08 x + 200 a = 0.00002 , b = -0.08 and c = 200.

Problem 6 Find the equation of the tangent line to the the graph of f(x) = - x 2 + x - 2 at x = 1. Solution to Problem 6

• There are at least two methods to solve the above question. Method 1
• Let the equation of the tangent line be of the form y = m x + b
• and we therefore need to find m and b. The tangent line passes through the point (1 , f(1)) = (1 , -2)
• Hence the equation in m and b - 2 = m (1) + b or m + b = -2
• To find the point of tangency of the line and the graph of the quadratic function, we need to solve the system y = m x + b and y = - x 2 + x - 2
• Substitute y by m x + b in the second equation of the system to obtain m x + b = - x 2 + x - 2
• Write the above equation in standard form - x 2 + x (1 - m) - 2 - b = 0
• For the line to be tangent to the graph of the quadratic function, the discriminant D of the above equation must be equal to zero. Hence D = b 2 - 4 a c = (1 - m) 2 - 4 (-1) (- 2 - b) = 0
• which gives (1 - (- 2 - b) ) 2 + 4 (- 2 - b) = 0
• Expand, simplify and write the above equation in standard form b 2 2 b + 1 = 0 (b + 1) 2 = 0
• Solve for b b = - 1
• Find m m = - 2 - b = -1

Questions with Solutions

Find the equation of the quadratic function f whose graph has x intercepts at (-1 , 0) and (3 , 0) and a y intercept at (0 , -4).

Question 2 Find values of the parameter c so that the graphs of the quadratic function f given by f(x) = x 2 + x + c and the graph of the line whose equation is given by y = 2 x have: a) 2 points of intersection, b) 1 point of intersection, c) no points of intersection.

Solutions to the Above Questions

Solution to Question 1

• The x intercepts of the graph of f are the zero of f(x). Hence f(x) is of the form f(x) = a (x + 1)(x - 3)
• We now need to find coefficient a using the y intercept f(0) = a(0 + 1)(0 - 3) = - 4
• Solve for a a = 4 / 3
• Hence f(x) = (4 / 3) (x + 1)(x - 3)

Solution to Question 2

• To find the coordinates of the point of intersections of the graphs of f(x) = x 2 + x + c and y = 2 x, we need to solve the system y = x 2 + x + c and y = 2 x
• which by substitution , gives the equation x 2 + x + c = 2x
• Rewrite the above equation in standard form x 2 - x + c = 0
• Find the discriminant D D = 1 - 4 c
• Conclusion If D is positive or c < 1 / 4 , the two graphs intersect at two points. If D is equal to 0 or c = 1 / 4 , the two graphs intersect (touch) at 1 point. If D is negative or c > 1 / 4 , the two graphs have no point of intersection.

More References and Links to Quadratic Functions

• Math Questions With Answers (13): Quadratic Functions.
• Vertex and Intercepts Parabola Problems.
• Find Vertex and Intercepts of Quadratic Functions - Calculator: An applet to solve calculate the vertex and x and y intercepts of the graph of a quadratic function.
• Quadratic functions (general form).
• Quadratic functions (standard form).
• Graphing quadratic functions.
• Solver to Analyze and Graph a Quadratic Function

Procedure Steps, Example Solved Problem - Solving Problems Involving Quadratic Equations | 10th Mathematics : UNIT 3 : Algebra

Chapter: 10th mathematics : unit 3 : algebra.

Solving Problems Involving Quadratic Equations

Steps to solve a problem

Step 1 Convert the word problem to a quadratic equation form

Step 2 Solve the quadratic equation obtained in any one of the above three methods.

Step 3 Relate the mathematical solution obtained to the statement asked in the question.

Example 3.37

The product of Kumaran’s age (in years) two years ago and his age four years from now is one more than twice his present age. What is his present age?

Let the present age of Kumaran be x years. 

Two years ago, his age = ( x − 2)  years.

Four years from now, his age = ( x + 4)  years.

( x − 2)( x + 4)  = 1 +2 x

x 2 + 2 x − 8 = 1 +2 x gives ( x − 3)( x + 3) = 0 then, x = ± 3

Therefore, x = 3 (Rejecting −3 as age cannot be negative)

Kumaran’s present age is 3 years.

Example 3.38

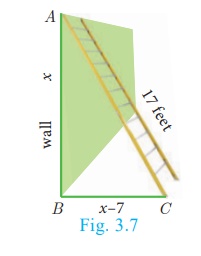
A ladder 17 feet long is leaning against a wall. If the ladder, vertical wall and the floor from the bottom of the wall to the ladder form a right triangle, find the height of the wall where the top of the ladder meets if the distance between bottom of the wall to bottom of the ladder is 7 feet less than the height of the wall?

Let the height of the wall AB = x feet

As per the given data BC = ( x –7) feet

In the right triangle ABC , AC =17 ft, BC = ( x –7) feet

By Pythagoras theorem, AC 2 = AB 2 + BC 2

(17) 2   = x 2   + ( x − 7) 2 ; 289 = x 2 + x 2 − 14 x + 49

x 2 − 7 x −120 = 0 hence,   ( x − 15)( x + 8) = 0 then, x = 15 (or) −8

Therefore, height of the wall AB = 15 ft (Rejecting −8 as height cannot be negative)

Example 3.39

A flock of swans contained x 2 members. As the clouds gathered, 10 x went to a lake and one-eighth of the members flew away to a garden. The remaining three pairs played about in the water. How many swans were there in total?

As given there are x 2 swans.

As per the given data x 2 − 10 x – (1/8) x 2 = 6 we get, 7 x 2 − 680 x − 48 = 0

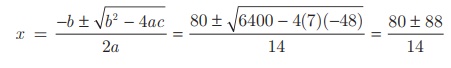
Therefore, x = 12, -4/7

Here x = 4/7 is not possible as the number of swans cannot be negative.

Hence, x = 12. Therefore total number of swans is x 2 = 144.

Example 3.40

A passenger train takes 1 hr more than an express train to travel a distance of 240 km from Chennai to Virudhachalam. The speed of passenger train is less than that of an express train by 20 km per hour. Find the average speed of both the trains.

Let the average speed of passenger train be x km/hr.

Then the average speed of express train will be ( x + 20) km/hr

Time taken by the passenger train to cover distance of 240 km = 240/ x hr

Time taken by express train to cover distance of 240 km = 240 / ( x +20) hr

x 2 + 20 x – 4800 = 0 gives, ( x + 80)( x − 60) = 0 we get, x = –80 or 60.

Therefore x = 60 (Rejecting -80 as speed cannot be negative)

Average speed of the passenger train is 60 km/hr

Average speed of the express train is 80 km/hr.

Related Topics

Privacy Policy , Terms and Conditions , DMCA Policy and Compliant

Copyright © 2018-2024 BrainKart.com; All Rights Reserved. Developed by Therithal info, Chennai.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

2.7.8: Solving Quadratic Equations

• Last updated
• Save as PDF
• Page ID 74493

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

By the end of this section, you will be able to:

• Solve quadratic equations using the Quadratic Formula
• Use the discriminant to predict the number and type of solutions of a quadratic equation
• Identify the most appropriate method to use to solve a quadratic equation

Before you get started, take this readiness quiz.

• Evaluate \(b^{2}-4 a b\) when \(a=3\) and \(b=−2\). If you missed this problem, review Example 1.21.
• Simplify: \(\sqrt{108}\). If you missed this problem, review Example 8.13.
• Simplify: \(\sqrt{50}\). If you missed this problem, review Example 8.76.

Solve Quadratic Equations Using the Quadratic Formula

When we solved quadratic equations in the last section by completing the square, we took the same steps every time. By the end of the exercise set, you may have been wondering ‘isn’t there an easier way to do this?’ The answer is ‘yes’. Mathematicians look for patterns when they do things over and over in order to make their work easier. In this section we will derive and use a formula to find the solution of a quadratic equation.

We have already seen how to solve a formula for a specific variable ‘in general’, so that we would do the algebraic steps only once, and then use the new formula to find the value of the specific variable. Now we will go through the steps of completing the square using the general form of a quadratic equation to solve a quadratic equation for \(x\) .

We start with the standard form of a quadratic equation and solve it for \(x\) by completing the square.

The final equation is called the "Quadratic Formula."

Definition \(\PageIndex{1}\): Quadratic Formula

The solutions to a quadratic equation of the form \(a x^{2}+b x+c=0\), where \(a≠0\) are given by the formula:

\[x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \label{quad}\]

To use the Quadratic Formula , we substitute the values of \(a,b\), and \(c\) from the standard form into the expression on the right side of the formula. Then we simplify the expression. The result is the pair of solutions to the quadratic equation.

Notice the Quadratic Formula (Equation \ref{quad}) is an equation. Make sure you use both sides of the equation.

Example \(\PageIndex{1}\) How to Solve a Quadratic Equation Using the Quadratic Formula

Solve by using the Quadratic Formula: \(2 x^{2}+9 x-5=0\).

HowTo: Solve a Quadratic Equation Using the Quadratic Formula

• Write the quadratic equation in standard form, \(a x^{2}+b x+c=0\). Identify the values of \(a,b\), and \(c\).
• Write the Quadratic Formula. Then substitute in the values of \(a,b\), and \(c\).
• Check the solutions.

If you say the formula as you write it in each problem, you’ll have it memorized in no time! And remember, the Quadratic Formula is an EQUATION. Be sure you start with “\(x=\)”.

Example \(\PageIndex{2}\)

Solve by using the Quadratic Formula: \(x^{2}-6 x=-5\).

When we solved quadratic equations by using the Square Root Property, we sometimes got answers that had radicals. That can happen, too, when using the Quadratic Formula . If we get a radical as a solution, the final answer must have the radical in its simplified form.

Example \(\PageIndex{3}\)

Solve by using the Quadratic Formula: \(2 x^{2}+10 x+11=0\).

When we substitute \(a, b\), and \(c\) into the Quadratic Formula and the radicand is negative, the quadratic equation will have imaginary or complex solutions. We will see this in the next example.

Example \(\PageIndex{4}\)

Solve by using the Quadratic Formula: \(3 p^{2}+2 p+9=0\).

Remember, to use the Quadratic Formula, the equation must be written in standard form, \(a x^{2}+b x+c=0\). Sometimes, we will need to do some algebra to get the equation into standard form before we can use the Quadratic Formula.

Example \(\PageIndex{5}\)

Solve by using the Quadratic Formula: \(x(x+6)+4=0\).

Our first step is to get the equation in standard form.

When we solved linear equations, if an equation had too many fractions we cleared the fractions by multiplying both sides of the equation by the LCD. This gave us an equivalent equation—without fractions— to solve. We can use the same strategy with quadratic equations.

Example \(\PageIndex{6}\)

Solve by using the Quadratic Formula: \(\dfrac{1}{2} u^{2}+\dfrac{2}{3} u=\dfrac{1}{3}\).

Our first step is to clear the fractions.

Think about the equation \((x-3)^{2}=0\). We know from the Zero Product Property that this equation has only one solution, \(x=3\).

We will see in the next example how using the Quadratic Formula to solve an equation whose standard form is a perfect square trinomial equal to \(0\) gives just one solution. Notice that once the radicand is simplified it becomes \(0\), which leads to only one solution.

Example \(\PageIndex{7}\)

Solve by using the Quadratic Formula: \(4 x^{2}-20 x=-25\).

Did you recognize that \(4 x^{2}-20 x+25\) is a perfect square trinomial. It is equivalent to \((2 x-5)^{2}\)? If you solve \(4 x^{2}-20 x+25=0\) by factoring and then using the Square Root Property, do you get the same result?

Use the Discriminant to Predict the Number and Type of Solutions of a Quadratic Equation

When we solved the quadratic equations in the previous examples, sometimes we got two real solutions, one real solution, and sometimes two complex solutions. Is there a way to predict the number and type of solutions to a quadratic equation without actually solving the equation?

Yes, the expression under the radical of the Quadratic Formula makes it easy for us to determine the number and type of solutions. This expression is called the discriminant .

Definition \(\PageIndex{2}\)

Discriminant

Let’s look at the discriminant of the equations in some of the examples and the number and type of solutions to those quadratic equations.

Using the Discriminant \(b^{2}-4ac\), to Determine the Number and Type of Solutions of a Quadratic Equation

For a quadratic equation of the form \(ax^{2}+bx+c=0\), \(a \neq 0\),

• If \(b^{2}-4 a c>0\), the equation has \(2\) real solutions.
• if \(b^{2}-4 a c=0\), the equation has \(1\) real solution.
• if \(b^{2}-4 a c<0\), the equation has \(2\) complex solutions.

Example \(\PageIndex{8}\)

Determine the number of solutions to each quadratic equation.

\(3 x^{2}+7 x-9=0\)

\(5 n^{2}+n+4=0\)

\(9 y^{2}-6 y+1=0\)

To determine the number of solutions of each quadratic equation, we will look at its discriminant.

The equation is in standard form, identify \(a, b\), and \(c\).

\(a=3, \quad b=7, \quad c=-9\)

Write the discriminant.

\(b^{2}-4 a c\)

Substitute in the values of \(a, b\), and \(c\).

\((7)^{2}-4 \cdot 3 \cdot(-9)\)

\(49+108\) \(157\)

Since the discriminant is positive, there are \(2\) real solutions to the equation.

\(a=5, \quad b=1, \quad c=4\)

\((1)^{2}-4 \cdot 5 \cdot 4\)

\(1-80\) \(-79\)

Since the discriminant is negative, there are \(2\) complex solutions to the equation.

\(a=9, \quad b=-6, \quad c=1\)

\((-6)^{2}-4 \cdot 9 \cdot 1\)

\(36-36\) \(0\)

Since the discriminant is \(0\), there is \(1\) real solution to the equation.

Identify the Most Appropriate Method to Use to Solve a Quadratic Equation

We summarize the four methods that we have used to solve quadratic equations below.

Methods for Solving Quadratic Equations

• Square Root Property
• Completing the Square
• Quadratic Formula

Given that we have four methods to use to solve a quadratic equation, how do you decide which one to use? Factoring is often the quickest method and so we try it first. If the equation is \(ax^{2}=k\) or \(a(x−h)^{2}=k\) we use the Square Root Property. For any other equation, it is probably best to use the Quadratic Formula. Remember, you can solve any quadratic equation by using the Quadratic Formula, but that is not always the easiest method.

What about the method of Completing the Square? Most people find that method cumbersome and prefer not to use it. We needed to include it in the list of methods because we completed the square in general to derive the Quadratic Formula. You will also use the process of Completing the Square in other areas of algebra.

Identify the Most Appropriate Method to Solve a Quadratic Equation

• Try Factoring first. If the quadratic factors easily, this method is very quick.
• Try the Square Root Property next. If the equation fits the form \(ax^{2}=k\) or \(a(x−h)^{2}=k\), it can easily be solved by using the Square Root Property.
• Use the Quadratic Formula . Any other quadratic equation is best solved by using the Quadratic Formula.

The next example uses this strategy to decide how to solve each quadratic equation.

Example \(\PageIndex{9}\)

Identify the most appropriate method to use to solve each quadratic equation.

• \(5 z^{2}=17\)

\(4 x^{2}-12 x+9=0\)

\(8 u^{2}+6 u=11\)

\(5z^{2}=17\)

Since the equation is in the \(ax^{2}=k\), the most appropriate method is to use the Square Root Property.

We recognize that the left side of the equation is a perfect square trinomial, and so factoring will be the most appropriate method.

Put the equation in standard form.

\(8 u^{2}+6 u-11=0\)

While our first thought may be to try factoring, thinking about all the possibilities for trial and error method leads us to choose the Quadratic Formula as the most appropriate method.

Problems Involving the Quadratic Formula

First comes the quadratic equation, then comes the quadratic formula. The quadratic formula is the solution to the quadratic equation:

\[ax^2+bx+c=0\]

x is the variable whose value is sought, and a, b, and c are constants

The goal is to find the value of x that makes the left side 0. That value is given by the quadratic formula:

\[x=\dfrac{-b\pm\sqrt {b^2-4ac}}{2a}\]

to be read/said:

‘x’ equals minus ‘b’, plus-or-minus the square root of ‘b’ squared minus four ‘a’ ‘c’, all over two ‘a’.

So, how do you know when you have to use the quadratic formula? There is a good chance that you need it when the square of the variable for which you are solving, appears in the equation you are solving. When that is the case, carry out the algebraic steps needed to arrange the terms as they are arranged in equation 1-8 above. If this is impossible, then the quadratic formula is not to be used. Note that in the quadratic equation you have a term with the variable to the second power, a term with the variable to the first power, and a term with the variable to the zeroth power (the constant term). If additional powers also appear, such as the one-half power (the square root), or the third power, then the quadratic formula does not apply. If the equation includes additional terms in which the variable whose value is sought appears as the argument of a special function such as the sine function or the exponential function, then the quadratic formula does not apply. Now suppose that there is a square term and you can get the equation that you are solving in the form of equation 1-8 above but that either b or c is zero. In such a case, you can use the quadratic formula, but it is overkill. If b in equation 1-8 above is zero then the equation reduces to:

\[ax^2+bx=0\]

The easy way to solve this problem is to recognize that there is at least one x in each term, and to factor the x out. This yields:

\[(ax+b)x=0\]

Then you have to realize that a product of two multiplicands is equal to zero if either multiplicand is equal to zero. Thus, setting either multiplicand equal to zero and solving for x yields a solution. We have two multiplicands involving x, so, there are two solutions to the equation. The second multiplicand in the expression \((ax+b)x=0\) is x itself, so

is a solution to the equation. Setting the first term equal to zero gives:

\[x=-\dfrac{b}{a}\]

Now suppose the b in the quadratic equation \(ax^2+bx+c=0\), equation 1-8, is zero. In that case, the quadratic equation reduces to:

\[ax^2+c=0\]

which can easily be solved without the quadratic formula as follows:

\[ax^2=-c\]

\[x^2=-\dfrac{c}{a}\]

\[x=\pm\sqrt {-\dfrac{c}{a}}\]

where we have emphasized the fact that there are two square roots to every value by placing a plus-or-minus sign in front of the radical.

Now, if upon arranging the given equation in the form of the quadratic equation (equation 1-8):\[ax^2+bx+c=0\]

you find that a, b, and c are all non-zero, then you should use the quadratic formula. Here we present an example of a problem whose solution involves the quadratic formula:

Example \(\PageIndex{1}\): Quadratic Formula Example Problem

Given \[3+x=\dfrac{24}{x+1}\] find x.

At first glance, this one doesn’t look like a quadratic equation, but as we begin isolating x, as we always strive to do in solving for x, (hey, once we have x all by itself on the left side of the equation, with no x on the right side of the equation, we have indeed solved for x—that’s what it means to solve for x) we quickly find that it is a quadratic equation. Whenever we have the unknown in the denominator of a fraction, the first step in isolating that unknown is to multiply both sides of the equation by the denominator. In the case at hand, this yields:

\[(x+1)(x+3)=24\]

Multiplying through on the left we find

\[3x+3+x^2+x=24\]

At this point it is pretty clear that we are dealing with a quadratic equation so our goal becomes getting it into the standard form of the quadratic equation, the form of equation 1-8, namely: \(ax^2+bx+c=0\). Combining the terms involving x on the left and rearranging we obtain \[x^2+4x+3=24\]

Subtracting 24 from both sides yields:

\[x^2+4x-21=0\]

which is indeed in the standard quadratic equation form. Now we just have to use inspection to identify which values in our given equation are the a, b, and c that appear in the standard quadratic equation (equation 1-8) \(ax^2+bx+c=0\). Although it is not written, the constant multiplying the x 2 , in the case at hand, is just 1. So we have a = 1, b = 4, and c = −21.

Substituting these values into the quadratic formula (equation 1-9):\[x=\dfrac{-b\pm\sqrt {b^2-4ac}}{2a}\]

\[x=\dfrac{-4\pm\sqrt {4^2-4(1)(21)}}{2(1)}\]

which results in x=3,x=-7

as the solutions to the problem. As a quick check we substitute each of these values back into the original equation:

\[3+x=\dfrac{24}{x+1}\]

and find that each substitution leads to an identity. (An identity is an equation whose validity is trivially obvious, such as 6 = 6.)

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• ax^2+bx+c=0
• x^2+2x+1=3x-10
• 2x^2+4x-6=0
• How do you calculate a quadratic equation?
• To solve a quadratic equation, use the quadratic formula: x = (-b ± √(b^2 - 4ac)) / (2a).
• What is the quadratic formula?
• The quadratic formula gives solutions to the quadratic equation ax^2+bx+c=0 and is written in the form of x = (-b ± √(b^2 - 4ac)) / (2a)
• Does any quadratic equation have two solutions?
• There can be 0, 1 or 2 solutions to a quadratic equation. If the discriminant is positive there are two solutions, if negative there is no solution, if equlas 0 there is 1 solution.
• What is quadratic equation in math?
• In math, a quadratic equation is a second-order polynomial equation in a single variable. It is written in the form: ax^2 + bx + c = 0 where x is the variable, and a, b, and c are constants, a ≠ 0.
• How do you know if a quadratic equation has two solutions?
• A quadratic equation has two solutions if the discriminant b^2 - 4ac is positive.

quadratic-equation-calculator

• High School Math Solutions – Quadratic Equations Calculator, Part 3 On the last post we covered completing the square (see link). It is pretty strait forward if you follow all the...

Please add a message.

Message received. Thanks for the feedback.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

6.5: Solving Quadratic Inequalities

• Last updated
• Save as PDF
• Page ID 6272

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Check solutions to quadratic inequalities with one variable.
• Understand the geometric relationship between solutions to quadratic inequalities and their graphs.
• Solve quadratic inequalities.

Solutions to Quadratic Inequalities

A quadratic inequality 15 is a mathematical statement that relates a quadratic expression as either less than or greater than another. Some examples of quadratic inequalities solved in this section follow.

A solution to a quadratic inequality is a real number that will produce a true statement when substituted for the variable.

Example \(\PageIndex{1}\):

Are \(-3\), \(-2\), and \(-1\) solutions to \(x^{2}-x-6 \leq 0 \)?

Substitute the given value in for \(x\) and simplify.

\(\begin{array} {r | r | r} {x^{2}-x-6\leq0}&{x^{2}-x-6\leq0}&{x^{2}-x-6\leq0} \\ {(\color{OliveGreen}{-3}\color{black}{)}^{2}-(\color{OliveGreen}{-3}\color{black}{)}-6\leq0}&{(\color{OliveGreen}{-2}\color{black}{)}^{2}-(\color{OliveGreen}{-2}\color{black}{)}-6\leq0}&{(\color{OliveGreen}{-1}\color{black}{)}^{2}-(\color{OliveGreen}{-1}\color{black}{)}-6\leq0} \\ {9+3-6\leq0}&{4+2-6\leq0}&{1+1-6\leq0} \\ {6\leq0\:\:\color{red}{✗}}&{0\leq0\:\:\color{Cerulean}{✓}}&{-4\leq0\:\:\color{Cerulean}{✓}} \end{array}\)

\(-2\) and \(-1\) are solutions and \(-3\) is not.

Quadratic inequalities can have infinitely many solutions, one solution, or no solution. If there are infinitely many solutions, graph the solution set on a number line and/or express the solution using interval notation. Graphing the function defined by \(f (x) = x^{2} − x − 6\) found in the previous example we have

The result of evaluating for any \(x\)-value will be negative, zero, or positive.

\(\begin{aligned} f(-3)&=6 &\color{Cerulean}{Positive \:f(x)>0} \\ f(-2)&=0 &\color{Cerulean}{Zero \:f(x)\:=0} \\f(-1)&=-4 &\color{Cerulean}{Negative \:f(x)<0} \end{aligned}\)

The values in the domain of a function that separate regions that produce positive or negative results are called critical numbers 16 . In the case of a quadratic function, the critical numbers are the roots, sometimes called the zeros. For example, \(f (x) = x^{2} − x − 6 = (x + 2) (x − 3)\) has roots \(−2\) and \(3\). These values bound the regions where the function is positive (above the \(x\)-axis) or negative (below the \(x\)-axis).

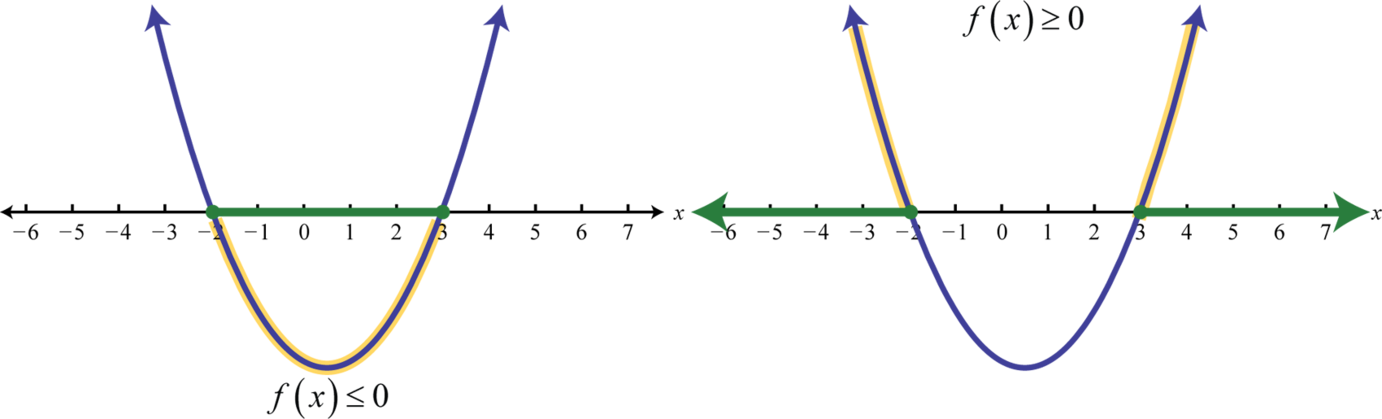
Therefore \(x^{2} − x − 6 ≤ 0\) has solutions where \(−2 ≤ x ≤ 3\), using interval notation \([−2, 3]\). Furthermore, \(x^{2} − x − 6 ≥ 0\) has solutions where \(x ≤ −2\) or \(x ≥ 3\), using interval notation \((−∞, −2] ∪ [−3, ∞)\).

Example \(\PageIndex{2}\):

Given the graph of \(f\) determine the solutions to \(f(x)>0\):

Because of the strict inequality, the solution set is shaded with an open dot on each of the boundaries. This indicates that these critical numbers are not actually included in the solution set. This solution set can be expressed two ways,

\(\begin{aligned}\{x |-4<&x<2\} &\color{Cerulean} { Set\: Notation } \\ (-4,&2) &\color{Cerulean} { Interval\: Notation }\end{aligned}\)

In this textbook, we will continue to present answers in interval notation.

Exercise \(\PageIndex{1}\)

Given the graph of \(f\) determine the solutions to \(f (x) < 0\):

\((-\infty,-4) \cup(2, \infty)\)

www.youtube.com/v/kkBaoM8buBo

Solving Quadratic Inequalities

Next we outline a technique used to solve quadratic inequalities without graphing the parabola. To do this we make use of a sign chart 17 which models a function using a number line that represents the \(x\)-axis and signs \((+\) or \(−)\) to indicate where the function is positive or negative. For example,

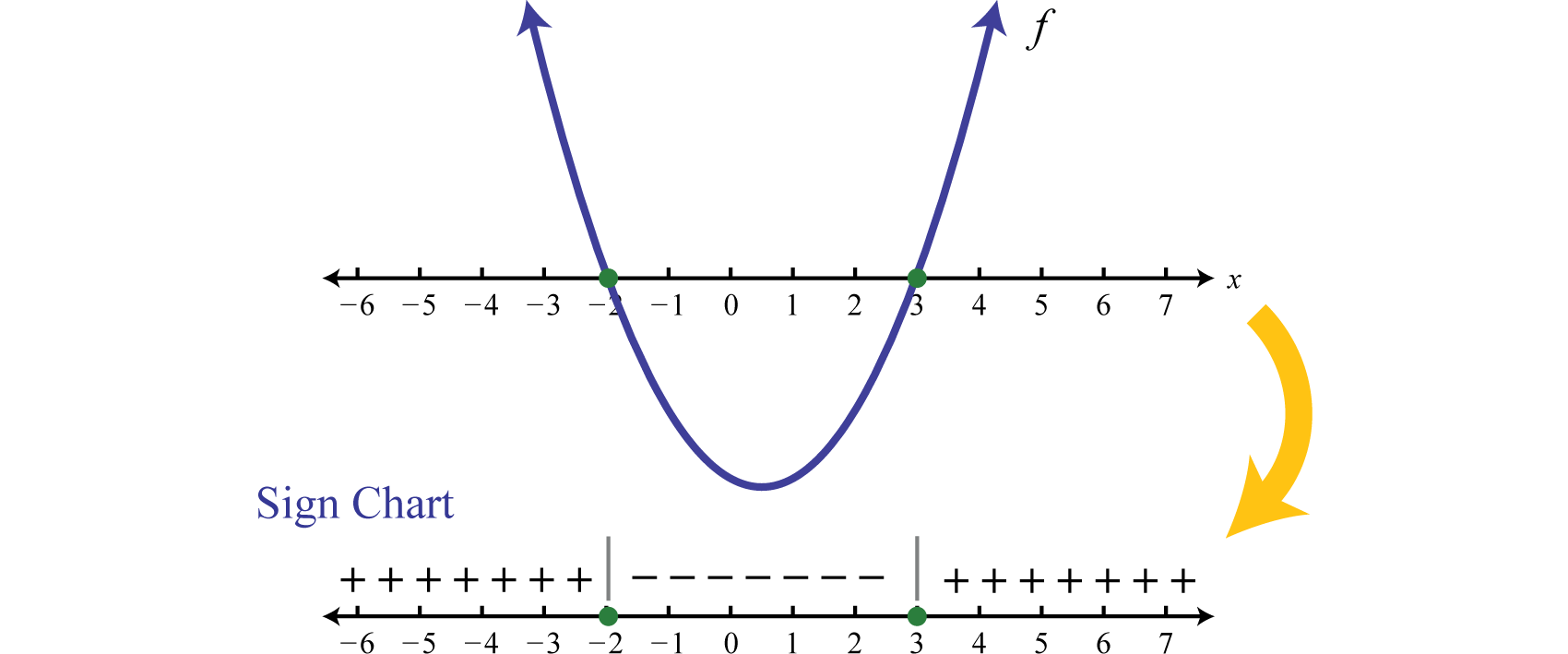
The plus signs indicate that the function is positive on the region. The negative signs indicate that the function is negative on the region. The boundaries are the critical numbers, \(−2\) and \(3\) in this case. Sign charts are useful when a detailed picture of the graph is not needed and are used extensively in higher level mathematics. The steps for solving a quadratic inequality with one variable are outlined in the following example.

Example \(\PageIndex{3}\):

Solve: \(-x^{2}+6 x+7 \geq 0\).

It is important to note that this quadratic inequality is in standard form, with zero on one side of the inequality.

Step 1 : Determine the critical numbers. For a quadratic inequality in standard form, the critical numbers are the roots. Therefore, set the function equal to zero and solve.

\(-x^{2}+6 x+7=0 \) \(-\left(x^{2}-6 x-7\right)=0 \) \(-(x+1)(x-7)=0 \)

\(\begin{aligned}x+1&=0 \:\:\:\:\text { or } &x-7=0 \\ x&=-1 &x=7\end{aligned}\)

The critical numbers are \(-1\) and \(7\).

Step 2 : Create a sign chart. Since the critical numbers bound the regions where the function is positive or negative, we need only test a single value in each region. In this case the critical numbers partition the number line into three regions and we choose test values \(x = −3, x = 0\), and \(x = 10\).

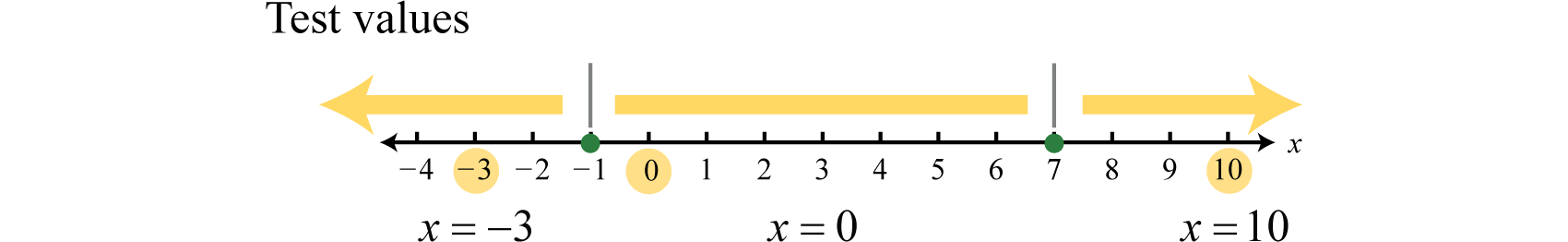
Test values may vary. In fact, we need only determine the sign \((+\) or \(−)\) of the result when evaluating \(f (x) = −x^{2} + 6x + 7 = − (x + 1) (x − 7)\). Here we evaluate using the factored form.

\(\begin{aligned} f(\color{OliveGreen}{-3}\color{black}{)}&=-(\color{OliveGreen}{-3}\color{black}{+}1)(\color{OliveGreen}{-3}\color{black}{-}7) =-(-2)(-10)&=-\color{Cerulean} {Negative} \\ f(\color{OliveGreen}{0}\color{black}{)}&=-(\color{OliveGreen}{0}\color{black}{+}1)(\color{OliveGreen}{0}\color{black}{-}7) =-(1)(-7)&=+\color{Cerulean} { Positive } \\ f(\color{OliveGreen}{10}\color{black}{)}&=-(\color{OliveGreen}{10}\color{black}{+}1)(\color{OliveGreen}{10}\color{black}{-}7) =-(11)(3)&=-\color{Cerulean} {Negative} \end{aligned}\)

Since the result of evaluating for \(−3\) was negative, we place negative signs above the first region. The result of evaluating for \(0\) was positive, so we place positive signs above the middle region. Finally, the result of evaluating for \(10\) was negative, so we place negative signs above the last region, and the sign chart is complete.

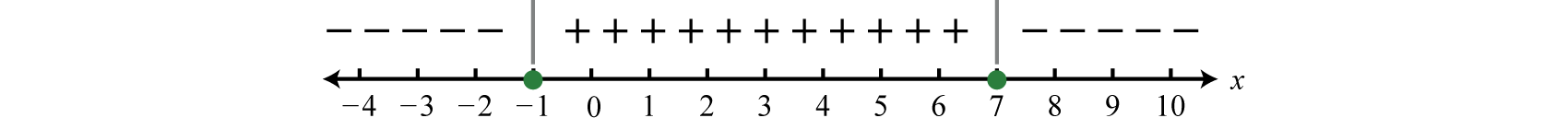
Step 3 : Use the sign chart to answer the question. In this case, we are asked to determine where \(f (x) ≥ 0\), or where the function is positive or zero. From the sign chart we see this occurs when \(x\)-values are inclusively between \(−1\) and \(7\).

Using interval notation, the shaded region is expressed as \([−1, 7]\). The graph is not required; however, for the sake of completeness it is provided below.

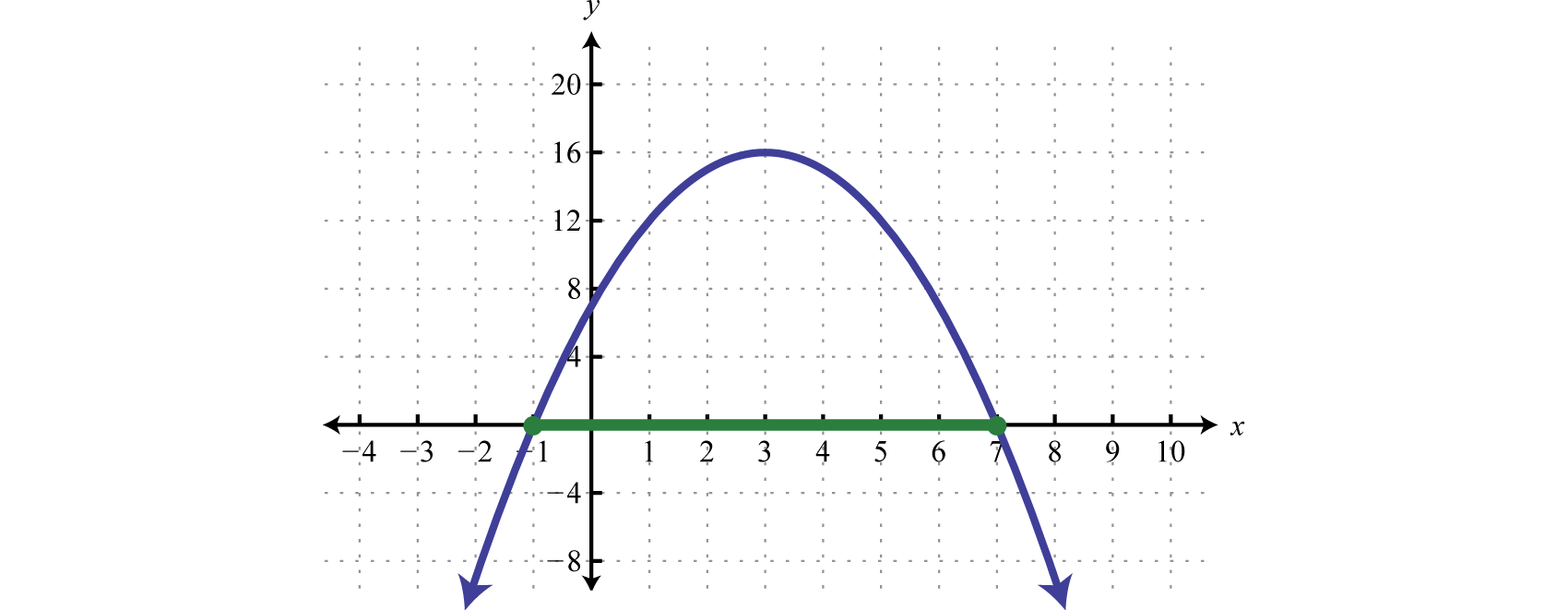
Indeed the function is greater than or equal to zero, above or on the \(x\)-axis, for \(x\)-values in the specified interval.

Example \(\PageIndex{4}\):

Solve: \(2 x^{2}-7 x+3>0\).

Begin by finding the critical numbers, in this case, the roots of \(f(x)=2 x^{2}-7 x+3\).

\(\begin{aligned}2 x^{2}-7 x+3&=0 \\ (2 x-1)(x-3)&=0\end{aligned}\)

\(\begin{aligned} 2 x-1 &=0 \:\:\:\:\:\text { or }& x-3=0 \\ 2 x &=1 \quad &x=3 \\ x &=\frac{1}{2} \end{aligned}\)

The critical numbers are \(\frac{1}{2}\) and \(3\). Because of the strict inequality > we will use open dots.

Next choose a test value in each region and determine the sign after evaluating \(f (x) = 2x^{2} − 7x + 3 = (2x − 1) (x − 3)\). Here we choose test values \(−1, 2\), and \(5\).

\(\begin{aligned} f(\color{OliveGreen}{-1}\color{black}{)} &=[2(\color{OliveGreen}{-1}\color{black}{)}-1](\color{OliveGreen}{-1}\color{black}{-}3)&=(-)(-)=+\\ f(\color{OliveGreen}{2}\color{black}{)} &=[2(\color{OliveGreen}{2}\color{black}{)}-1](\color{OliveGreen}{2}\color{black}{-}3)&=(+)(-)=-\\ f(\color{OliveGreen}{5}\color{black}{)} &=[2(\color{OliveGreen}{5}\color{black}{)}-1](\color{OliveGreen}{5}\color{black}{-}3)&=(+)(+)=+\end{aligned}\)

And we can complete the sign chart.

The question asks us to find the \(x\)-values that produce positive results (greater than zero). Therefore, shade in the regions with a \(+\) over them. This is the solution set.

\(\left(-\infty, \frac{1}{2}\right) \cup(3, \infty)\)

Sometimes the quadratic function does not factor. In this case we can make use of the quadratic formula.

Example \(\PageIndex{5}\):

Solve: \(x^{2}-2 x-11 \leq 0\)

Find the critical numbers.

\(x^{2}-2 x-11=0\)

Identify \(a, b\), and \(c\) for use in the quadratic formula. Here \(a = 1, b = −2\), and \(c = −11\). Substitute the appropriate values into the quadratic formula and then simplify.

\(\begin{aligned} x &=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \\ &=\frac{-(\color{OliveGreen}{-2}\color{black}{)} \pm \sqrt{(\color{OliveGreen}{-2}\color{black}{)}^{2}-4(\color{OliveGreen}{1}\color{black}{)}(\color{OliveGreen}{-11}\color{black}{)}}}{2(\color{OliveGreen}{1}\color{black}{)}} \\ &=\frac{2 \pm \sqrt{48}}{2} \\ &=\frac{2 \pm 4 \sqrt{3}}{2} \\ &=1 \pm 2 \sqrt{3} \end{aligned}\)

Therefore the critical numbers are \(1-2 \sqrt{3} \approx-2.5\) and \(1+2 \sqrt{3} \approx 4.5\). Use a closed dot on the number to indicate that these values will be included in the solution set.

Here we will use test values \(−5, 0\), and \(7\).

\(\begin{aligned} f(\color{OliveGreen}{-5}\color{black}{)}&=(\color{OliveGreen}{-5}\color{black}{)}^{2}-2(\color{OliveGreen}{-5}\color{black}{)}-11 =25+10-11&=+\\ f(\color{OliveGreen}{0}\color{black}{)}&=(\color{OliveGreen}{0}\color{black}{)}^{2}-2(\color{OliveGreen}{0}\color{black}{)}-11 =0+0-11&=-\\ f(\color{OliveGreen}{7}\color{black}{)}&=(\color{OliveGreen}{7}\color{black}{)}^{2}-2(\color{OliveGreen}{7}\color{black}{)}-11 =49-14-11&=+\end{aligned}\)

After completing the sign chart shade in the values where the function is negative as indicated by the question \((f (x) ≤ 0)\).

\([1-2 \sqrt{3}, 1+2 \sqrt{3}]\)

Exercise \(\PageIndex{2}\)

Solve: \(9-x^{2}>0\).

www.youtube.com/v/7gMJ8gUvASw

It may be the case that there are no critical numbers.

Example \(\PageIndex{6}\):

Solve: \(x^{2}-2 x+3>0\).

To find the critical numbers solve,

\(x^{2}-2 x+3=0\)

Substitute \(a = 1, b = −2\), and \(c = 3\) into the quadratic formula and then simplify.

\(\begin{aligned} x &=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \\ &=\frac{-(\color{OliveGreen}{-2}\color{black}{)} \pm \sqrt{(\color{OliveGreen}{-2}\color{black}{)}^{2}-4(\color{OliveGreen}{1}\color{black}{)}(\color{OliveGreen}{3}\color{black}{)}}}{2(\color{OliveGreen}{1}\color{black}{)}} \\ &=\frac{2 \pm \sqrt{-8}}{2} \\ &=\frac{2 \pm 2 i \sqrt{2}}{2} \\ &=1+i \sqrt{2} \end{aligned}\)

Because the solutions are not real, we conclude there are no real roots; hence there are no critical numbers. When this is the case, the graph has no \(x\)-intercepts and is completely above or below the \(x\)-axis. We can test any value to create a sign chart. Here we choose \(x = 0\).

\(f(0)=(0)^{2}-2(0)+3=+\)

Because the test value produced a positive result the sign chart looks as follows:

We are looking for the values where \(f (x) > 0\); the sign chart implies that any real number for \(x\) will satisfy this condition.

\((-\infty, \infty)\)

The function in the previous example is graphed below.

We can see that it has no \(x\)-intercepts and is always above the \(x\)-axis (positive). If the question was to solve \(x^{2} − 2x + 3 < 0\), then the answer would have been no solution. The function is never negative.

Exercise \(\PageIndex{3}\)

Solve: \(9 x^{2}-12 x+4 \leq 0\)

One solution, \(\frac{2}{3}\).

www.youtube.com/v/E7VcOYVV_Ds

Example \(\PageIndex{7}\):

Find the domain: \(f(x)=\sqrt{x^{2}-4}\).

Recall that the argument of a square root function must be nonnegative. Therefore, the domain consists of all real numbers for \(x\) such that \(x^{2} − 4\) is greater than or equal to zero.

\(x^{2}-4 \geq 0\)

It should be clear that \(x^{2} − 4 = 0\) has two solutions \(x = ±2\); these are the critical values. Choose test values in each interval and evaluate \(f (x) = x^{2} − 4\).

\(\begin{aligned} f(-3) &=(-3)^{2}-4=9-4=+\\ f(0) &=(0)^{2}-4=0-4=-\\ f(3) &=(3)^{2}-4=9-4=+\end{aligned}\)

Shade in the \(x\)-values that produce positive results.

Domain: \((-\infty,-2] \cup[2, \infty)\)

Key Takeaways

• Quadratic inequalities can have infinitely many solutions, one solution or no solution.
• We can solve quadratic inequalities graphically by first rewriting the inequality in standard form, with zero on one side. Graph the quadratic function and determine where it is above or below the \(x\)-axis. If the inequality involves “less than,” then determine the \(x\)-values where the function is below the \(x\)-axis. If the inequality involves “greater than,” then determine the \(x\)-values where the function is above the \(x\)-axis.
• We can streamline the process of solving quadratic inequalities by making use of a sign chart. A sign chart gives us a visual reference that indicates where the function is above the \(x\)-axis using positive signs or below the \(x\)-axis using negative signs. Shade in the appropriate x-values depending on the original inequality.
• To make a sign chart, use the function and test values in each region bounded by the roots. We are only concerned if the function is positive or negative and thus a complete calculation is not necessary.

Exercise \(\PageIndex{4}\)

Determine whether or not the given value is a solution.

• \(x^{2}-x+1<0 ; x=-1\)
• \(x^{2}+x-1>0 ; x=-2\)
• \(4 x^{2}-12 x+9 \leq 0 ; x=\frac{3}{2}\)
• \(5 x^{2}-8 x-4<0 ; x=-\frac{2}{5}\)
• \(3 x^{2}-x-2 \geq 0 ; x=0\)
• \(4 x^{2}-x+3 \leq 0 ; x=-1\)
• \(2-4 x-x^{2}<0 ; x=\frac{1}{2}\)
• \(5-2 x-x^{2}>0 ; x=0\)
• \(-x^{2}-x-9<0 ; x=-3\)
• \(-x^{2}+x-6 \geq 0 ; x=6\)

Exercise \(\PageIndex{5}\)

Given the graph of \(f\) determine the solution set.

1. \(f(x) \leq 0\);

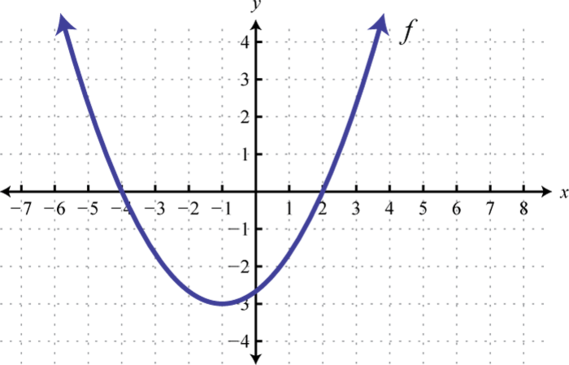
2. \(f(x) \geq 0\);

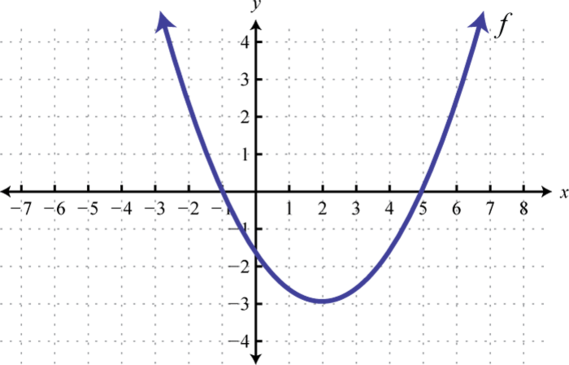
3. \(f(x) \geq 0\);

4. \(f(x) \leq 0\);

5. \(f(x)>0\);

6. \(f(x)<0\);

7. \(f(x)>0\);

8. \(f(x)<0\);

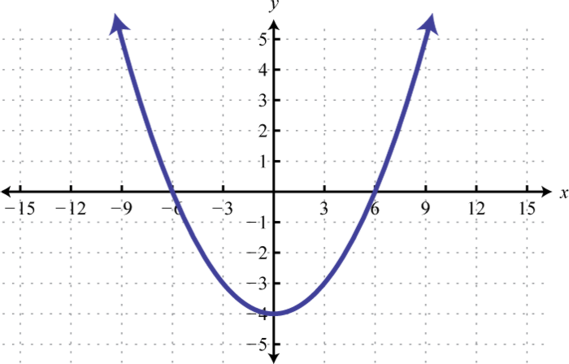
9. \(f(x) \geq 0\);

10. \(f(x)<0\);

1. \([-4,2]\)

3. \([-1,3]\)

5. \((-\infty, \infty)\)

7. \((-\infty, 4) \cup(8, \infty)\)

9. \(\{-10\}\)

Exercise \(\PageIndex{6}\)

Use the transformations to graph the following and then determine the solution set.

• \(x^{2}-1>0\)
• \(x^{2}+2>0\)
• \((x-1)^{2}>0\)
• \((x+2)^{2} \leq 0\)
• \((x+2)^{2}-1 \leq 0\)
• \((x+3)^{2}-4>0\)
• \(-x^{2}+4 \geq 0\)
• \(-(x+2)^{2}>0\)
• \(-(x+3)^{2}+1<0\)
• \(-(x-4)^{2}+9>0\)

1. \((-\infty,-1) \cup(1, \infty)\)

3. \((-\infty, 1) \cup(1, \infty)\)

5. \([-3,-1]\)

7. \([-2,2]\)

9. \((-\infty,-4) \cup(-2, \infty)\)

Exercise \(\PageIndex{7}\)

Use a sign chart to solve and graph the solution set. Present answers using interval notation.

• \(x^{2}-x-12>0\)
• \(x^{2}-10 x+16>0\)
• \(x^{2}+2 x-24<0\)
• \(x^{2}+15 x+54<0\)
• \(x^{2}-23 x-24 \leq 0\)
• \(x^{2}-12 x+20 \leq 0\)
• \(2 x^{2}-11 x-6 \geq 0\)
• \(3 x^{2}+17 x-6 \geq 0\)
• \(8 x^{2}-18 x-5<0\)
• \(10 x^{2}+17 x+6>0\)
• \(9 x^{2}+30 x+25 \leq 0\)
• \(16 x^{2}-40 x+25 \leq 0\)
• \(4 x^{2}-4 x+1>0\)
• \(9 x^{2}+12 x+4>0\)
• \(-x^{2}-x+30 \geq 0\)
• \(-x^{2}-6 x+27 \leq 0\)
• \(x^{2}-64<0\)
• \(x^{2}-81 \geq 0\)
• \(4 x^{2}-9 \geq 0\)
• \(16 x^{2}-25<0\)
• \(25-4 x^{2} \geq 0\)
• \(1-49 x^{2}<0\)
• \(x^{2}-8>0\)
• \(x^{2}-75 \leq 0\)
• \(2 x^{2}+1>0\)
• \(4 x^{2}+3<0\)
• \(x-x^{2}>0\)
• \(3 x-x^{2} \leq 0\)
• \(x^{2}-x+1<0\)
• \(x^{2}+x-1>0\)
• \(4 x^{2}-12 x+9 \leq 0\)
• \(5 x^{2}-8 x-4<0\)
• \(3 x^{2}-x-2 \geq 0\)
• \(4 x^{2}-x+3 \leq 0\)
• \(2-4 x-x^{2}<0\)
• \(5-2 x-x^{2}>0\)
• \(-x^{2}-x-9<0\)
• \(-x^{2}+x-6 \geq 0\)
• \(-2 x^{2}+4 x-1 \geq 0\)
• \(-3 x^{2}-x+1 \leq 0\)

1. \((-\infty,-3) \cup(4, \infty)\)

3. \((-6,4)\)

5. \([-1,24]\)

7. \(\left(-\infty,-\frac{1}{2}\right] \cup[6, \infty)\)

9. \(\left(-\frac{1}{4}, \frac{5}{2}\right)\)

11. \(-\frac{5}{3}\)

13. \(\left(-\infty, \frac{1}{2}\right) \cup\left(\frac{1}{2}, \infty\right)\)

15. \([-6,5]\)

17. \((-8,8)\)

19. \(\left(-\infty,-\frac{3}{2}\right] \cup\left[\frac{3}{2}, \infty\right)\)

21. \(\left[-\frac{5}{2}, \frac{5}{2}\right]\)

23. \((-\infty,-2 \sqrt{2}) \cup(2 \sqrt{2}, \infty)\)

25. \((-\infty, \infty)\)

27. \((0,1)\)

29. \(\emptyset\)

31. \(\frac{3}{2}\)

33. \(\left(-\infty,-\frac{2}{3}\right] \cup[1, \infty)\)

35. \((-\infty,-2-\sqrt{6}) \cup(-2+\sqrt{6}, \infty)\)

37. \((-\infty, \infty)\)

39. \(\left[\frac{2-\sqrt{2}}{2}, \frac{2+\sqrt{2}}{2}\right]\)

Exercise \(\PageIndex{8}\)

Find the domain of the function.

• \(f(x)=\sqrt{x^{2}-25}\)
• \(f(x)=\sqrt{x^{2}+3 x}\)
• \(g(x)=\sqrt{3 x^{2}-x-2}\)
• \(g(x)=\sqrt{12 x^{2}-9 x-3}\)
• \(h(x)=\sqrt{16-x^{2}}\)
• \(h(x)=\sqrt{3-2 x-x^{2}}\)
• \(f(x)=\sqrt{x^{2}+10}\)
• \(f(x)=\sqrt{9+x^{2}}\)
• A robotics manufacturing company has determined that its weekly profit in thousands of dollars is modeled by \(P (n) = −n^{2} + 30n − 200\) where \(n\) represents the number of units it produces and sells. How many units must the company produce and sell to maintain profitability. (Hint: Profitability occurs when profit is greater than zero.)
• The height in feet of a projectile shot straight into the air is given by \(h (t) = −16t^{2} + 400t\) where \(t\) represents the time in seconds after it is fired. In what time intervals is the projectile under \(1,000\) feet? Round to the nearest tenth of a second.

1. \((-\infty,-5] \cup[5, \infty)\)

3. \(\left(-\infty,-\frac{2}{3}\right] \cup[1, \infty)\)

5. \([-4,4]\)

7. \((-\infty, \infty)\)

9. The company must produce and sell more than \(10\) units and fewer than \(20\) units each week.

Exercise \(\PageIndex{9}\)

• Does the sign chart for any given quadratic function always alternate? Explain and illustrate your answer with some examples.
• Research and discuss other methods for solving a quadratic inequality.
• Explain the difference between a quadratic equation and a quadratic inequality. How can we identify and solve each? What is the geometric interpretation of each?

1. Answer may vary

3. Answer may vary

15 A mathematical statement that relates a quadratic expression as either less than or greater than another.

16 The values in the domain of a function that separate regions that produce positive or negative results.

17 A model of a function using a number line and signs \((+\) or \(−)\) to indicate regions in the domain where the function is positive or negative.

Mathematics 9 Quarter 1-Module 9: Solving Problems Involving Quadratic Equations (Week 4 Learning Code – M9AL-1e-1)

In the previous lessons, you learned about the different ways in solving quadratic equations, the concepts of the “nature of its roots” and the relationship of its roots and coefficients. Your mastery of the lessons is an important tool to solve many real-world problems related to quadratic equations. In this module, you will learn how to solve word problems that involves quadratic equations.

LEARNING COMPETENCY

The learners will be able to:

• solve problems involving quadratic equations. M9AL-1e-1

Can't Find What You'RE Looking For?

We are here to help - please use the search box below.

Leave a Comment Cancel reply

• Texas Go Math
• Big Ideas Math
• Engageny Math
• McGraw Hill My Math
• enVision Math
• 180 Days of Math
• Math in Focus Answer Key
• Math Expressions Answer Key
• Privacy Policy

Solving Quadratic Equations – Definition, Formula, Tricks, Examples | What are the 4 Ways to Solve a Quadratic Equation?

Before going to learn about Solving Quadratic Equations, first recall a few facts about the quadratic equations. The word quadratic originated from the word quad and its meaning is “square”. It means that the quadratic equation has a variable raised to 2 as the greatest power term. The standard form of a quadratic equation is given by the equation ax2 + bx + c = 0, where a ≠ 0.

We saw that quadratic equations can represent many real-life situations. Now that we know what quadratic equations are, let us learn about the definition of solving quadratic equations, and the different methods to solve them. Here we will try to develop the Quadratic Equation Formula and other methods of solving the quadratic equations. But the solving quadratic equations by factoring is the most popular method. You learn all the methods in detail here along with all 10th Grade Math Concepts all here.

Also, Read:

• Introduction to Quadratic Equations
• Formation of Quadratic Equation in one variable

What is meant by Solving of Quadratic Equations | Solving of Quadratic Equations-Definition

It is defined as, that any value(s) of x that satisfies the equation is known as a solution (or) root of the equation, and the process of finding the values of x which satisfy the equation ax2 + bx + c = 0 is known as solving quadratic equations.

Methods of Solving a Quadratic Equation | How to Solve Quadratic Equations?

Solving quadratic equations means finding a value (or) values of the variable which satisfies the equation. The value that satisfies the quadratic equation is called its roots (or) solutions (or) zeros. Hence the degree of the quadratic equation is 2, it can have a maximum of 2 roots. But how do find them if they are not given? The different methods of solving quadratic equations are:

1. Solving quadratic equations by factoring 2. Solving quadratic equations by using completing the square 3. Solving quadratic equations by graphing 4. Solving quadratic equations by quadratic formula

Solving Quadratic Equations by Factoring

This method is one of the most famous and simplest methods used to solve a quadratic equation and certain quadratic equations can be factorized. If we have done correctly will give get two linear equations in x. Hence, from that equations, we will get the value of x. The step-by-step process of solving quadratic equations by factoring is explained below along with an example we will solve the equation is x 2 -3x + 2 = 0.

• Step 1: First, we get the equation into a standard form.
• Step 2: Then factorize the quadratic equation.
• Step 3: By zero product property, set each of the factors to zero.
• Step 4: Now, solve each of the above equations.

Example: Solve the equation step by step using the factoring method. The equation is x 2 -3x + 2 = 0. Solution: Given that,

• Step1: Get the equation into standard form. i.e., Get all the terms to one side (usually to the left side) of the equation such that the other side will be 0. The equation x2 – 3x + 2 = 0 is already in standard form.
• Step 2: Factor the quadratic expression. Then we will get as (x – 1) (x – 2) = 0.
• Step 3: In zero product property, set each of the factors will be zero that is  x – 1 = 0 (or) x – 2 = 0
• Step 4: Solve each of the above equations. x = 1 (or) x = 2

Thus, the solutions of the quadratic equation x 2 – 3x + 2 = 0 are 1 and 2. This method is only applicable when the quadratic expression is factorable. If it is not factorable, then we can use one of the other methods. Similar to the quadratic equations we have a solution for linear equations, which are used to solve linear programming problems.

Solving Quadratic Equations by using Completing the Square

In this method, Completing the square means to write the quadratic expression as ax 2 +bx+c into the form a(x – h) 2 + k (it is also known as vertex form), where h = -b/2a and ‘k’ can be obtained by substituting x = h in ax 2 + bx + c. The step-by-step process of solving the quadratic equations by completing the square is given below, along with an example where we are going to find the solutions of the equation 2x 2 + 8x = -3.

• Step 2: Now, complete the square on the left side.
• Step 3: Solve it now, we get the value of x.

Example: Solve the equation using the complete square method. The equation is 2x 2 +8x = -3. Solution: Given that the equation is 2x 2 +8x = -3

Step 1: Initially, we get the equation into standard form. Now adding 3 on both sides, we get 2x 2 + 8x + 3 = 0.

Step 2: Complete the square on the left side, then we get 2(x + 2) 2 -5 = 0.

Step 3: Now, Solve it for x. (We will take the square root on both sides along the way). Next, Adding 5 on both sides, that is 2 (x + 2) 2 = 5. Dividing both sides by 2, (x + 2) 2 = 5/2 Taking square root on both sides, x + 2 = √(5/2) = √5/√2 · √2/√2 = √10/2 Let Subtracte 2 from both sides, x = -2 ± (√10/2) = (-4 ± √10) / 2 Thus, the roots of the quadratic equation 2x 2 +8x = -3 are (-4 + √10)/2 and (-4 – √10)/2.

Solving Quadratic Equations by Graphing

To solve the quadratic equations by using graphing, first, we have to graph the quadratic expression (when the equation is in the standard form) either manually or by using a graphing calculator. Then the x-intercepts of the graph (the point(s) where the graph cuts the x-axis) are nothing but the roots of the quadratic equation. The process of solving quadratic equations by graphing is explained in steps along with an example, and we are going to solve the equation 3x 2 + 5 = 11x.

• Step 1: Initially, we get the equation into the standard form.
• Step 2: Graph the quadratic expression which is on the right side.
• Step 3: Identify the X-intercepts.
• Step 4: Next, the x-coordinates of the x-intercepts are nothing but the roots of the quadratic equation.

Example: Solve the equation is  3x 2 + 5 = 11x. Solution:

Given that,

Step 1: Initially, we get the equation into the standard form. First, subtracting 11x from both sides, 3x 2 – 11x + 5 = 0.

Step 2: Graph the quadratic expression which is on the left side. Graph the quadratic function y = 3x 2 – 11x + 5 either manually or using a graphing calculator (GDC).

Step 3: Identify the x-intercepts. For solving quadratic equations by graphing, the quadratic expression has to be graphed and identify the x-intercepts.

Step 4: Now, the x-coordinates of the x-intercepts are nothing but the roots of the quadratic equation. Thus, the solutions of the quadratic equation 3x 2 + 5 = 11x are 0.532 and 3.135. By observing the above example, we can see that the graphing method of solving quadratic equations may not give the exact solutions (i.e., it gives only the decimal approximations of the roots if they are irrational}. i.e., if we solve the same equation using completing the square, we get x = (11 + √61) / 6 and x = (11 – √61) / 6.

But we will not get the exact roots by the graphing method. If the graph does not intersect the x-axis at all, it means that the quadratic equation has two complex roots that is the graphing method is not useful to find the roots if they are complex numbers. We can use the quadratic formula to find any type of the root’s value (it will be explained in the next section)

Solving Quadratic Equations by Quadratic Formula

As we have already seen, the previous methods for solving the quadratic equations have some limitations such as the factoring method is useful only when the quadratic expression is factorable, the graphing method is useful only when the quadratic equation has real roots, etc.

But solving quadratic equations by quadratic formula overcomes all these limitations and is useful to solve any type of quadratic equation. Here is the step-by-step explanation of solving quadratic equations by quadratic formula along with an example where we will be finding the solutions of the quadratic 2x 2 = 3x – 5.

• Step 2: Now, compare the equation with ax 2 +bx+c=0 and then find the values of a,b and c.
• Step 3: Substitute the values into the quadratic formula which says x = [-b ± √(b² – 4ac)] / (2a).
• Step 4: Now, simplify it, we get the x value.

Solve the equation using the quadratic formula. The equation is 2x 2  – 3x + 5 = 0.

As given in the question. the equation is 2x 2  – 3x + 5 = 0.

• Step 1: Get into the standard form. Then the above equation becomes 2x 2 – 3x + 5 = 0.
• Step 2:  Compare the equation with ax 2 + bx + c = 0 and find the values of a, b, and c. Then we get the value of a is 2, b is -3. and c is 5.
• Step 3:  Substitute the values into the quadratic formula which says x = [-b ± √(b² – 4ac)] / (2a). Then we get x = [-(-3) ± √((-3)² – 4(2)(5))] / (2(2)
• Step – 4:  Simplify it, then the value of x is x = [ 3 ± √(9 – 40) ] / 4 = [ 3 ± √(-31) ] / 4 = [ 3 ± i√(31) ] / 4 Thus, the roots of the quadratic equation 2x 2 = 3x – 5 are [ 3 + i√(31) ] / 4 and [ 3 – i√(31) ] / 4. In a quardratic formula, the expression of b² – 4ac is called as discriminant (which is denoted by D). i.e., D = b² – 4ac. This will used to determine the nature of roots of the quadratic equation.

Nature of Roots Using Discriminant

• If D > 0, then the equation ax 2  + bx + c = 0 has two real and distinct roots.
• If D = 0, then the equation ax 2  + bx + c = 0 has only one real root.
• If D < 0, then the equation ax 2  + bx + c = 0 has two distinct complex roots.

Thus, using the discriminant, we can find the number of solutions to quadratic equations without actually solving them. Apart from these methods, there are a few other methods that are used only in specific cases i.e., when the quadratic equation has missing terms like that, the below explained:

Solving Quadratic Equations Missing b In a quadratic equation ax^2 + bx + c = 0, if the term with b is missing then the equation becomes ax^2 + c = 0. Now, we can solve this by taking square root on both sides. The below explained the process with examples. The equation is x^2 – 4 = 0 ⇒ x^2 = 4 ⇒ x = ±√4 ⇒ x = ± 2 So, the equation roots are 2 and -2. The another example is, x^2 + 36 = 0 ⇒ x^2 = -36 ⇒ x = ±√(-36) ⇒ x = ± 6i Thus, the roots of the equation are 6i and -6i (note that these are imaginary numbers (or) complex numbers).

Solving Quadratic Equations Missing c In a quadratic equation ax^2 + bx + c = 0, if the term with c is missing then the equation becomes ax^2 + bx = 0. To solve this type of equation, we simply factor x out from the left side, set each of the factors to zero, and solve them. The process will explained in below with examples: The equation is x^2 – 5x = 0 ⇒ x (x – 5) = 0 ⇒ x = 0; x – 5 = 0 ⇒ x = 0; x = 5 So, the equation roots are 0 and 5. Next, the equation is x^2 + 11x = 0 ⇒ x (x + 11) = 0 ⇒ x = 0; x + 11 = 0 ⇒ x = 0; x = -11 Hence, the roots of the equations are 0 and -11.

Solving Quadratic Equations Examples with Answers

Problem 1:  The length of a park is 5 ft less than twice its width. If its area is 250 square feet, find the dimensions of the park?

Solution: The data is as given in the question, Assume that, the width of the park is x ft. Then the length of the park is (2x – 5) ft. The area of a park is 250 sq. ft So, the length × width is 250. Substitute the values, it will be (2x – 5)x = 250. 2x^2 – 5x – 250 = 0. So, this is a word problem that is related to solving quadratic equations. Now, let us solve this quadratic equation by using the factoring method. In this, the value of a is 2, b is -5, and c is -250. So, a x c is 2(-250) = -500. Next, the two numbers whose sum is -5 and whose product is -500 are -25 and 20. So we can split the middle term using these two numbers. 2x^2 – 25x + 20x – 250 = 0 x(2x – 25) + 10 (2x – 25) = 0 (2x – 25) (x + 10) = 0 2x – 25 = 0 i.e., x + 10 = 0 The value of x is x = 25/2 = 12.5 (or) x = -10. x = 12.5, x value cannot be in negative. So the width is 12.5 ft and the length is (2x – 5) ft = 2(12.5)-5 = 20 ft. Thus, the dimensions of the park are 20 ft × 12.5.

Problem 2: Let the two positive consecutive numbers is 156. Find the value of two numbers?

Solution: Given that, The two positive consecutive numbers product is 156. Now, we will find the values of two numbers. Assume that the two consecutive numbers be x and x + 1. Then the equation is, x (x + 1) = 156 x^2 + x – 156 = 0 Now, solve this quadratic equation by the factoring method. In this a = 1, b = 1 and c = -156. So, the ac is 1(-156) = -156. The two numbers whose sum is 1 and whose product is -156 are 13 and -12. So we can split the middle term using these two numbers. i.e., x^2 + 13x – 12x – 156 = 0 x (x + 13) – 12 (x + 13) = 0 (x + 13) (x – 12) = 0 The value of x + 13 = 0, and  x – 12 = 0 Therefore, x = -13 (or) x = 12 we know, x is positive, x cannot be in negative i.e.,-13. So the value of x is 12. Thus, the required consecutive numbers are 12 and 13 (12 + 1).

FAQs on Solving Quadratic Equations

1. What is a quadratic equation?

We Simply say that a quadratic equation is an equation of degree 2, which means that the highest exponent of this function is 2. Moreover, the standard quadratic equation is ax^2 + bx + c, where a, b, and c are just numbered and ‘a’ cannot be 0. An example of quadratic equation is 3x^2 + 2x + 1.

2. What are the different methods by which you can solve quadratic equations?

There are various methods by which you can solve a quadratic equation such as factorization, completing the square, quadratic formula, and graphing. All these are the four general methods that we can use to solve a quadratic equation.

3. What are the three forms of a quadratic function?

The three functions are listed below which can be written as: 1. Standard Form: y = ax2 + bx + c, where a, b, and c are just numbers. 2. Factored Form: y = (ax + c) (bx + d) where a, b, and c are just numbers. 3. Vertex Form: y = a (x + b)2 + c, and here also a, b, and c are numbers.

4. What is the formula for solving quadratic equations?

The general quadratic equation formula is “ax2 + bx + c”. In this formula, a, b, and c numbers, are the numerical coefficient of the quadratic equation, and ‘a’ is not zero a 0.

5. How is the Factored Form Helpful in Solving Quadratic Equations? If the quadratic expression that is in the standard form of quadratic expression in it is factorable, then we can just set each factor to zero, and solve them. Thus, the solutions are nothing but the roots of a quadratic equation.

Leave a Comment Cancel Reply

You must be logged in to post a comment.