how to solve absolute value equations inequalities

Absolute Value Inequality

How to solve absolute value inequalities, general formula.

In the picture below, you can see generalized example of absolute value equation and also the topic of this web page: absolute value inequalities .

The diagram below illustrated the difference between an absolute value equation and two absolute value inequalities

Absolute Value Inequality Calculator

Enter any values for A,b and c for any absolute value equation |A x + b| = c into the text boxes below and this solver will calculate your answer and show all of the steps!

Practice Problems

Solve the absolute value inequality below: $$| x -1 | \ge 2 $$

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

Absolute-Value Inequalities

There are many opportunities for mistakes with absolute-value inequalities, so let's cover this topic slowly and look at some helpful pictures along the way. When we're done, I hope you will have a good picture in your head of what is going on, so you won't make some of the more common errors.

Content Continues Below

MathHelp.com

Absolute Value Inequalities

Once you catch on to how these inequalities work, this stuff really isn't so bad.

(Note: This lesson covers linear absolute-value inequalities only.)

What are absolute values?

Recall the original definition of absolute values as distance: " |  x  | is the distance of x from zero." For instance, both −2 and +2 are two units from zero, as you can see in the image below:

This means that their absolute values will both be 2 ; that is, we have:

| −2 | = | +2 | = 2

With this definition and picture in mind, let's look at some absolute value inequalities.

How do you solve "less than" absolute-value inequalities?

To solve a "less than" absolute-value inequality, we use the definition of the absolute value to restate the inquality as a three-part inequality; that is, given |  mx  +  b  | <  c , convert this to:

− c < mx + b < + c

Then solve the resulting three-part linear inequality to get the variable by itself in the middle.

Solve |  x  | < 3 , and graph its solution.

This is an inequality. Where the solution to an absolute-value equation is points (like in the graphic above), the solution to an absolute-value inequality (or "inequation") is going to be intervals.

In this inequality, they're asking me to find all the x -values that are less than three units away from zero in either direction , so the solution is going to be the set of all the points that are less than three units away from zero. First, I'll draw a number line:

Advertisement

Looking at the inequality, I see that the number 1 will work as a solution, as will −1 , because each of these is less than three units from zero. The number 2 will work, as will −2 . But 4 will not work, and neither will −4 , because they are too far away from zero. Even 3 and −3 won't work (though they're right on the edge), because this is a "less than" (but not equal to) inequality.

However, the number 2.99 will work, as will −2.99 . In other words, all the points between −3 and 3 , but not actually including −3 or 3 , will work as solutions to this inequality. So, graphically, the solution looks like this:

Translating this picture into algebraic symbols, I get the following solution:

−3 < x < 3

This pattern for "less than" absolute-value inequalities always holds:

Given an inequality in the form |  x  | <  a , the solution will always be of the form − a  <  x  <  a .

By the way, the correct conjunction for "less than" absolute-value inequalities is "and". Why? Because the variable is contained within one interval. In the example above, x was both "more than −3 " and also "less than +3 ". The x is in the interval that satisfied both inequalities at the same time. So "and" is the correct conjuction.

Even when the exercises get more complicated, the above pattern will still hold.

Solve | 2 x  + 3 | < 6 .

Since this is a "less than" absolute-value inequality, my first step is to clear the absolute value according to the "less than" pattern. Then I'll solve the linear inequality .

| 2 x + 3 | < 6

−6 < 2 x + 3 < 6

This is the pattern for "less than". Continuing, I'll subtract 3 from all three "sides" of the inequality:

−6 − 3 < 2 x + 3 − 3 < 6 − 3

−9 < 2 x < 3

−9/2 < x < 3/2

The solution to the original absolute-value inequality, | 2 x  + 3 | < 6 , is this interval:

The other case for absolute value inequalities is the "greater than" case.

How do you solve "greater than" absolute-value inequalities?

To solve "greater than" absolute-value inequalities, use the definition of the absolute value to split the inequality into two cases; that is, for |  mx  +  b  | >  c , split the inequality into its two cases:

1. mx + b > c

2. mx + b < − c

Then solve the two linear inequalities separately.

Solve |  x  | > 2 , and graph.

First, I'll start with a number line.

The solution to the given inequality will be the set of all points that are more than two units away from zero. For instance, −3 will work, as will +3 ; −4 will work, as will +4 . But −1 will not work, and neither will +1 , because they're too close to zero. Even −2 will not work, and neither will +2 (although they're right on the edge), because this is a "greater than" (but not equal to) inequality.

However, +2.01 will work, as will −2.01 . In other words, the solution will be two separate sections : one section being all the points more than two units from zero off to the left , and the other section being all the points more than two units from zero off to the right . The solution, in graphical terms, looks like this:

Translating this graphical solution into symbols, I get:

x < −2 or x > 2

Take careful note! The solution to this "greater than" absolute-value inequality is TWO regular inequalities, not one. DO NOT try to write this as one inequality. If you try to write this solution as " −2 >  x  > 2 ", your answer be counted wrong. Why? Because, if you take out the x in the middle, you'll see that you would be saying " −2 > 2 ", which certainly is not true. Take the extra half a second, and write the solution correctly.

This pattern for "greater than" absolute-value inequalities always holds:

Given the inequality |  x  | >  a , the solution always starts by splitting the inequality into two pieces: x  < − a or x  >  a .

And, by the way, the correct conjunction is "or", not "and". Why? Because the variable cannot be in both of the solution intervals and the same time. In the example above, x cannot be both "less than −2 " and also "greater than +2 " at the same time . Therefore, we use "or" for these types of solutions.

Even when the inequalities are more complicated, the above pattern still holds.

Solve | 2 x  − 3 | > 5 .

The first thing I need to do is clear the absolute-value bars by splitting the inequality into two pieces. Then I'll solve the two regular inequalities.

| 2 x − 3 | > 5

2 x − 3 < −5 or 2 x − 3 > 5

This is the pattern for "greater than" absolute-value inequalites.

2 x < −2 or 2 x > 8

x < −1 or x > 4

This PAIR of inequalities is the solution to the original absolute-value inequality.

What is the take-away for solving linear absolute-value inequalities?

• If "less than", drop the absolute-value bars, restate as a three-part inequality, and solve with an "and" statement. Example: | x  − 3| < 5 becomes −5 < ( x  − 3) < +5
• If "greater than", drop the absolute-value bars, split the inequality into its two cases, and solve the two inequalities separately with an "or" statement. Example: | x  − 3| > 5 becomes ( x  − 3) < −3 or ( x  − 3) > 3

There is another situation you might encounter: You'll be given a pair of inequalities, and you'll be asked to find the corresponding absolute-value inequality. This process can feel a bit weird, so I'll give a couple examples of how it works.

Find the absolute-value inequality statement that corresponds to −2 <  x  < 4 .

To figure this out, I first look at the endpoints. Minus two and plus four are six units apart. Half of six is three. This tells me that I want to adjust this inequality so that it relates to −3 and +3 , instead of to −2 and +4 . To accomplish this, I see that I can adjust the values at the left- and right-hand ends by subtracting 1 from all three "sides" of the inequality:

−2 < x < 4

−2 − 1 < x − 1 < 4 − 1

−3 < x − 1 < 3

Since the last line above is in the "less than" format for absolute-value inequalities, my solution inequality will be of the form "absolute value of (something) is less than 3". The (something) is the piece in the middle, where the variable is. So I can convert my last line above to the following:

| x − 1 | < 3

Find the absolute-value inequality statement that corresponds to the inequalities x ≤ 19 or x ≥ 24

What they've given me is in two pieces, joined with an "or", so I know that this will be a "greater than" absolute-value inequality.

To start, I look at the endpoints. Nineteen and 24 are five units apart. Half of five is 2.5 . So I want to adjust the inequality so it relates to −2.5 and +2.5 , instead of relating to +19 and +24 . Since 19 − (−2.5) = 21.5 and 24 − 2.5 = 21.5 , I see that I need to subtract 21.5 all around:

x ≤ 19 or x ≥ 24

x − 21.5 ≤ 19 − 21.5 or x − 21.5 ≥ 24 − 21.5

x − 21.5 ≤ −2.5 or x − 21.5 ≥ 2.5

Since the last line above is the "greater than" format, the absolute-value inequality will be of the form "absolute value of (something) is greater than or equal to 2.5 ". The (something) will be the part with the variable in it. So I can convert my last line above to:

| x − 21.5 | ≥ 2.5

Warning: There is one "trick" type of question for this kind of problem, where they'll try to trip you up on homework or tests. They'll ask you to solve something like " |  x  + 2 | < −1 ". But can an absolute value ever be negative, let alone be less than a negative? No! So there is no solution to this inequality; it doesn't even make sense. Don't waste a lot of time trying to "solve" this; just write down "no solution".

Similarly, if you're given something like " |  x  − 2 | > −3 ", the first thing to note is that all absolute values are zero or positive. In particular, they're never negative. They're asking you for the x -values that will make the absolute-value expression greater than a negative number. Since the absolute value will always be greater than any negative number, the solution must be "all x " or "all real numbers".

You can use the Mathway widget below to practice solving absolute-value inequalities. Try the entered exercise, or type in your own exercise. Then click the button and select "Solve for x" to compare your answer to Mathway's.

Please accept "preferences" cookies in order to enable this widget.

(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)

URL: https://www.purplemath.com/modules/absineq.htm

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• Privacy / Cookies
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles

Module 6: Inequalities

6.3 – equations and inequalities with absolute value, learning objectives, equations with one absolute value, equations with two absolute values.

• Recognize when a linear equation that contains absolute value does not have a solution

(6.3.2) – Solve inequalities containing absolute values

(6.3.1) – solve equations containing absolute values.

Next, we will learn how to solve an absolute value equation . To solve an equation such as [latex]|2x - 6|=8[/latex], we notice that the absolute value will be equal to 8 if the quantity inside the absolute value bars is [latex]8[/latex] or [latex]-8[/latex]. This leads to two different equations we can solve independently.

Knowing how to solve problems involving absolute value functions is useful. For example, we may need to identify numbers or points on a line that are at a specified distance from a given reference point.

A General Note: Absolute Value Equations

The absolute value of x is written as [latex]|x|[/latex]. It has the following properties:

For real numbers [latex]A[/latex] and [latex]B[/latex], an equation of the form [latex]|A|=B[/latex], with [latex]B\ge 0[/latex], will have solutions when [latex]A=B[/latex] or [latex]A=-B[/latex]. If [latex]B<0[/latex], the equation [latex]|A|=B[/latex] has no solution.

An absolute value equation in the form [latex]|ax+b|=c[/latex] has the following properties:

How To: Given an absolute value equation, solve it.

• Isolate the absolute value expression on one side of the equal sign.
• If [latex]c>0[/latex], write and solve two equations: [latex]ax+b=c[/latex] and [latex]ax+b=-c[/latex].

In the next video, we show examples of solving a simple absolute value equation.

Example: Solving Absolute Value Equations

Solve the following absolute value equations:

• [latex]|6x+4|=8[/latex]
• [latex]|3x+4|=-9[/latex]
• [latex]|3x - 5|-4=6[/latex]
• [latex]|-5x+10|=0[/latex]

Write two equations and solve each:

[latex]\begin{array}{ll}6x+4\hfill&=8\hfill& 6x+4\hfill&=-8\hfill \\ 6x\hfill&=4\hfill& 6x\hfill&=-12\hfill \\ x\hfill&=\frac{2}{3}\hfill& x\hfill&=-2\hfill \end{array}[/latex]

The two solutions are [latex]x=\frac{2}{3}[/latex], [latex]x=-2[/latex].

b. [latex]|3x+4|=-9[/latex]

There is no solution as an absolute value cannot be negative.

c. [latex]|3x - 5|-4=6[/latex]

Isolate the absolute value expression and then write two equations.

There are two solutions: [latex]x=5[/latex], [latex]x=-\frac{5}{3}[/latex].

d. [latex]|-5x+10|=0[/latex]

The equation is set equal to zero, so we have to write only one equation.

There is one solution: [latex]x=2[/latex].

In the two videos that follow, we show examples of how to solve an absolute value equation that requires you to isolate the absolute value first using mathematical operations.

Solve the absolute value equation: [latex]|1 - 4x|+8=13[/latex].

Some of our absolute value equations could be of the form [latex]|u|=|v|[/latex] where [latex]u[/latex] and [latex]v[/latex] are algebraic expressions. For example, [latex]|x-3|=|2x+1|[/latex].

How would we solve them? If two algebraic expressions are equal in absolute value, then they are either equal to each other or negatives of each other. The property for absolute value equations says that for any algebraic expression, [latex]u[/latex], and a positive real number, [latex]a[/latex], if [latex]|u|=a[/latex], then [latex]u=a[/latex] or [latex]u=-a[/latex].

This leads us to the following property for equations with two absolute values:

Equations with Two Absolute Values

For any algebraic expressions, [latex]u[/latex] and [latex]v[/latex], if [latex]|u|=|v|[/latex], then:

[latex]u=v[/latex] or [latex]u=-v[/latex].

When we take the opposite of a quantity, we must be careful with the signs and to add parentheses where needed.

Solve: [latex]|5x-1|=|2x+3|[/latex].

[latex]\begin{array}{cccc} 5x-1 &=& 2x+3 &or& \,\,\,\, 5x-1 &=& -(2x+3) \\ 5x-1 &=& 2x+3 &or& \,\,\,\, 5x-1 &=& -2x-3 \\ 3x-1 &=& 3 &or& \,\,\,\, 7x-1 &=& -3 \\ 3x &=& 4 &or& \,\,\,\, 7x &=& -2 \\ x &=& \large \frac{4}{3} &or& \,\,\,\, x &=& \large -\frac{2}{7}\end{array}[/latex]

The two solutions are [latex] x=\frac{4}{3}[/latex] and [latex]x=-\frac{2}{7}[/latex]

Absolute value equations with no solutions

As we are solving absolute value equations it is important to be aware of special cases. An absolute value is defined as the distance from 0 on a number line, so it must be a positive number. When an absolute value expression is equal to a negative number, we say the equation has no solution, or DNE. Notice how this happens in the next two examples.

Solve for [latex]x[/latex]. [latex]7+\left|2x-5\right|=4[/latex]

[latex]\begin{array}{r}7+\left|2x-5\right|=4\,\,\,\,\\\underline{\,-7\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-7\,}\\\left|2x-5\right|=-3\end{array}[/latex]

Result of absolute value is negative! The result of an absolute value must always be positive, so we say there is no solution to this equation, or DNE.

Solve for [latex]x[/latex]. [latex]-\frac{1}{2}\left|x+3\right|=6[/latex]

[latex]\begin{array}{r}-\frac{1}{2}\left|x+3\right|=6\,\,\,\,\,\,\,\,\,\,\,\,\\\,\,\,\,\,\,\,\,\left(-2\right)-\frac{1}{2}\left|x+3\right|=\left(-2\right)6\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left|x+3\right|=-12\,\,\,\,\,\end{array}[/latex]

Again, we have a result where an absolute value is negative!

There is no solution to this equation, or DNE.

In this last video, we show more examples of absolute value equations that have no solutions.

Let’s apply what you know about solving equations that contain absolute values and what you know about inequalities to solve inequalities that contain absolute values. Let’s start with a simple inequality.

[latex]\left|x\right|\leq 4[/latex]

This inequality is read, “the absolute value of [latex]x[/latex]   is less than or equal to 4.” If you are asked to solve for [latex]x[/latex], you want to find out what values of [latex]x[/latex]   are 4 units or less away from 0 on a number line. You could start by thinking about the number line and what values of [latex]x[/latex]   would satisfy this equation.

4 and [latex]−4[/latex] are both four units away from 0, so they are solutions. 3 and [latex]−3[/latex] are also solutions because each of these values is less than 4 units away from 0. So are 1 and [latex]−1[/latex], 0.5 and [latex]−0.5[/latex], and so on—there are an infinite number of values for [latex]x[/latex] that will satisfy this inequality.

The graph of this inequality will have two closed circles, at 4 and [latex]−4[/latex]. The distance between these two values on the number line is colored in blue because all of these values satisfy the inequality.

The solution can be written this way:

Inequality: [latex]-4\leq x\leq4[/latex]

Interval: [latex]\left[-4,4\right][/latex]

The situation is a little different when the inequality sign is “greater than” or “greater than or equal to.” Consider the simple inequality [latex]\left|x\right|>3[/latex]. Again, you could think of the number line and what values of [latex]x[/latex] are greater than 3 units away from zero. This time, 3 and [latex]−3[/latex] are not included in the solution, so there are open circles on both of these values. 2 and [latex]−2[/latex] would not be solutions because they are not more than 3 units away from 0. But 5 and [latex]−5[/latex] would work, and so would all of the values extending to the left of [latex]−3[/latex] and to the right of 3. The graph would look like the one below.

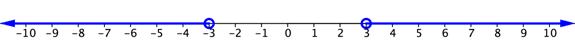
The solution to this inequality can be written this way:

Inequality : [latex]x<−3[/latex] or [latex]x>3[/latex].

Interval: [latex]\left(-\infty, -3\right)\cup\left(3,\infty\right)[/latex]

In the following video, you will see examples of how to solve and express the solution to absolute value inequalities involving both AND and OR.

Writing Solutions to Absolute Value Inequalities

For any positive value of [latex]a[/latex]   and [latex]x[/latex] ,  a single variable, or any algebraic expression:

Let’s look at a few more examples of inequalities containing absolute values.

Solve for [latex]x[/latex]. [latex]\left|x+3\right|\gt4[/latex]

Since this is a “greater than” inequality, the solution can be rewritten according to the “greater than” rule.

[latex] \displaystyle x+3<-4\,\,\,\,\,\,\,\text{or}\,\,\,\,\,\,\,x+3>4[/latex]

Solve each inequality.

[latex]\begin{array}{r}x+3<-4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x+3>4\\\underline{\,\,\,\,-3\,\,\,\,\,-3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{\,\,\,\,\,\,-3\,\,-3}\\x\,\,\,\,\,\,\,\,\,<-7\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,>1\\\\x<-7\,\,\,\,\,\,\,\text{or}\,\,\,\,\,\,x>1\,\,\,\,\,\,\,\end{array}[/latex]

Check the solutions in the original equation to be sure they work. Check the end point of the first related equation, [latex]−7[/latex] and the end point of the second related equation, 1.

[latex] \displaystyle \begin{array}{r}\,\,\,\left| x+3 \right|>4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| x+3 \right|>4\\\left| -7+3 \right|=4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| 1+3 \right|=4\\\,\,\,\,\,\,\,\left| -4 \right|=4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| 4 \right|=4\\\,\,\,\,\,\,\,\,\,\,\,\,4=4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4=4\end{array}[/latex]

Try [latex]−10[/latex], a value less than [latex]−7[/latex], and 5, a value greater than 1, to check the inequality.

[latex] \displaystyle \begin{array}{r}\,\,\,\,\,\left| x+3 \right|>4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| x+3 \right|>4\\\left| -10+3 \right|>4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| 5+3 \right|>4\\\,\,\,\,\,\,\,\,\,\,\left| -7 \right|>4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| 8 \right|>4\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,7>4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,8>4\end{array}[/latex]

Both solutions check!

Inequality: [latex] \displaystyle x<-7\,\,\,\,\,\text{or}\,\,\,\,\,x>1[/latex]

Interval: [latex]\left(-\infty, -7\right)\cup\left(1,\infty\right)[/latex]

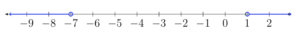
Solve for [latex]y[/latex] .  [latex] \displaystyle 3\left|2y+6\right|-9<27[/latex]

Begin to isolate the absolute value by adding 9 to both sides of the inequality.

[latex] \displaystyle \begin{array}{r}3\left| 2y+6 \right|-9<27\\\underline{\,\,+9\,\,\,+9}\\3\left| 2y+6 \right|\,\,\,\,\,\,\,\,<36\end{array}[/latex]

Divide both sides by 3 to isolate the absolute value.

[latex]\begin{array}{r}\underline{3\left| 2y+6 \right|}\,<\underline{36}\\3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,3\,\\\,\,\,\,\,\,\,\,\,\left| 2y+6 \right|<12\end{array}[/latex]

Write the absolute value inequality using the “less than” rule. Subtract 6 from each part of the inequality.

[latex]\begin{array}{r}-12<2y+6<12\\\underline{\,\,-6\,\,\,\,\,\,\,\,\,\,\,\,\,-6\,\,\,-6}\\-18\,<\,2y\,\,\,\,\,\,\,\,\,<\,\,6\,\end{array}[/latex]

Divide by 2 to isolate the variable.

[latex]\begin{array}{r}\underline{-18}<\underline{2y}<\underline{\,6\,}\\2\,\,\,\,\,\,\,\,\,\,\,2\,\,\,\,\,\,\,\,\,\,2\,\,\\-9<\,\,y\,\,\,\,<\,3\end{array}[/latex]

Inequality: [latex] \displaystyle -9<\,\,y\,\,<3[/latex]

Interval: [latex]\left(-9,3\right)[/latex]

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• \left|3+2x\right|\le 7
• \frac{\left|3x+2\right|}{\left|x-1\right|}>2
• \left|3x-5\right|<-4
• \left|a-8\right|\ge \:3
• 4\left|x+10\right|\ge 8
• \left|7x-4\right|\ge -3
• How do you solve inequalities with absolute value bars?
• To solve an inequality that contains absolute value bars isolate the absolute value expression on one side of the inequality. Then, divide the inequality into two separate cases, one for each possible value of the absolute value expression, positive or negative, and solve each case separately.
• What does absolute value inequality mean in math?
• An absolute value inequality is an inequality that involves an absolute value expression.
• What is the difference between and and or in an absolute inequality?
• In an absolute value inequality, 'and' and 'or' are used to combine the solutions of two inequalities. When 'and' is used, both inequalities must be satisfied for the solution to be valid. When 'or' is used, at least one of the inequalities must be satisfied for the solution to be valid.

absolute-inequalities-calculator

• High School Math Solutions – Inequalities Calculator, Absolute Value Inequalities Part I Last post, we learned how to solve rational inequalities. In this post, we will learn how to solve absolute value...

Please add a message.

Message received. Thanks for the feedback.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.7: Solve Absolute Value Inequalities

• Last updated
• Save as PDF
• Page ID 29041

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

By the end of this section, you will be able to:

• Solve absolute value equations
• Solve absolute value inequalities with “less than”
• Solve absolute value inequalities with “greater than”
• Solve applications with absolute value

Before you get started, take this readiness quiz.

• Evaluate: \(−|7|\). If you missed this problem, review [link] .
• Fill in \(<,>,<,>,\) or \(=\) for each of the following pairs of numbers. ⓐ \(|−8|\text{___}−|−8|\) ⓑ \(12\text{___}−|−12|\) ⓒ \(|−6|\text{___}−6\) ⓓ \(−(−15)\text{___}−|−15|\) If you missed this problem, review [link] .
• Simplify: \(14−2|8−3(4−1)|\). If you missed this problem, review [link] .

Solve Absolute Value Equations

As we prepare to solve absolute value equations, we review our definition of absolute value .

ABSOLUTE VALUE

The absolute value of a number is its distance from zero on the number line.

The absolute value of a number n is written as \(|n|\) and \(|n|\geq 0\) for all numbers.

Absolute values are always greater than or equal to zero.

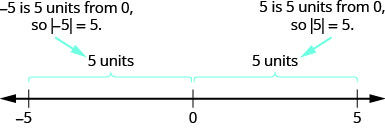
We learned that both a number and its opposite are the same distance from zero on the number line. Since they have the same distance from zero, they have the same absolute value. For example:

• \(−5\) is 5 units away from 0, so \(|−5|=5\).
• \(5\) is 5 units away from 0, so \(|5|=5\).

Figure \(\PageIndex{1}\) illustrates this idea.

For the equation |x|=5,|x|=5, we are looking for all numbers that make this a true statement. We are looking for the numbers whose distance from zero is 5. We just saw that both 5 and −5−5 are five units from zero on the number line. They are the solutions to the equation.

\(\begin{array} {ll} {\text{If}} &{|x|=5} \\ {\text{then}} &{x=−5\text{ or }x=5} \\ \end{array}\)

The solution can be simplified to a single statement by writing \(x=\pm 5\). This is read, “ x is equal to positive or negative 5”.

We can generalize this to the following property for absolute value equations.

ABSOLUTE VALUE EQUATIONS

For any algebraic expression, u , and any positive real number, a ,

\[\begin{array} {ll} {\text{if}} &{|u|=a} \\ {\text{then}} &{u=−a \text{ or }u=a} \\ \nonumber \end{array}\]

Remember that an absolute value cannot be a negative number.

Example \(\PageIndex{1}\)

• \(|y|=−6\)

\(\begin{array} {ll} {} &{|x|=8} \\ {\text{Write the equivalent equations.}} &{x=−8 \text{ or } x=8} \\ {} &{x=\pm 8} \\ \end{array}\)

\(\begin{array} {ll} {} &{|y|=−6} \\ {} &{\text{No solution}} \\ \end{array}\) Since an absolute value is always positive, there are no solutions to this equation.

\(\begin{array} {ll} {} &{|z|=0} \\ {\text{Write the equivalent equations.}} &{z=−0\text{ or }z=0} \\ {\text{Since }−0=0,} &{z=0} \\ \end{array}\) Both equations tell us that z=0z=0 and so there is only one solution.

EXERCISE \(\PageIndex{2}\)

• \(|y|=−4\)

no solution

EXERCISE \(\PageIndex{3}\)

• \(|y|=−5\)

To solve an absolute value equation , we first isolate the absolute value expression using the same procedures we used to solve linear equations. Once we isolate the absolute value expression we rewrite it as the two equivalent equations.

How to Solve Absolute Value Equations

Example \(\pageindex{4}\).

Solve \(|5x−4|−3=8\).

EXERCISE \(\PageIndex{5}\)

Solve: \(|3x−5|−1=6\).

\(x=4, \space x=−\frac{2}{3}\)

EXERCISE \(\PageIndex{6}\)

Solve: \(|4x−3|−5=2\).

\(x=−1,\space x=\frac{5}{2}\)

The steps for solving an absolute value equation are summarized here.

SOLVE ABSOLUTE VALUE EQUATIONS.

• Isolate the absolute value expression.
• Write the equivalent equations.
• Solve each equation.
• Check each solution.

Example \(\PageIndex{7}\)

Solve \(2|x−7|+5=9\).

Exercise \(\PageIndex{8}\)

Solve: \(3|x−4|−4=8\).

\(x=8,\space x=0\)

Exercise \(\PageIndex{9}\)

Solve: \(2|x−5|+3=9\).

\(x=8,\space x=2\)

Remember, an absolute value is always positive!

Example \(\PageIndex{10}\)

Solve: \(|\frac{2}{3}x−4|+11=3\).

\(\begin{array} {ll} {} &{|\frac{2}{3}x−4|=−8} \\ {\text{Isolate the absolute value term.}} &{|\frac{2}{3}x−4|=−8} \\ {\text{An absolute value cannot be negative.}} &{\text{No solution}} \\ \end{array}\)

Exercise \(\PageIndex{11}\)

Solve: \(|\frac{3}{4}x−5|+9=4\).

No solution

Exercise \(\PageIndex{12}\)

Solve: \(|\frac{5}{6}x+3|+8=6\).

Some of our absolute value equations could be of the form \(|u|=|v|\) where u and v are algebraic expressions. For example, \(|x−3|=|2x+1|\).

How would we solve them? If two algebraic expressions are equal in absolute value, then they are either equal to each other or negatives of each other. The property for absolute value equations says that for any algebraic expression, u , and a positive real number, a , if \(|u|=a\), then \(u=−a\) or \(u=a\).

This tell us that

\(\begin{array} {llll} {\text{if}} &{|u|=|v|} &{} &{} \\ {\text{then}} &{|u|=v} &{\text{or}} &{|u|=−v} \\ {\text{and so}} &{u=v \text{ or } u = −v} &{\text{or}} &{u=−v \text{ or } u = −(−v)} \\ \end{array}\)

This leads us to the following property for equations with two absolute values.

EQUATIONS WITH TWO ABSOLUTE VALUES

For any algebraic expressions, u and v ,

\[\begin{array} {ll} {\text{if}} &{|u|=|v|} \\ {\text{then}} &{u=−v\text{ or }u=v} \\ \nonumber \end{array}\]

When we take the opposite of a quantity, we must be careful with the signs and to add parentheses where needed.

Example \(\PageIndex{13}\)

Solve: \(|5x−1|=|2x+3|\).

\(\begin{array} {ll} {} &{} &{|5x−1|=|2x+3|} &{} \\ {} &{} &{} &{} \\ {\text{Write the equivalent equations.}} &{5x−1=−(2x+3)} &{\text{or}} &{5x−1=2x+3} \\ {} &{5x−1=−2x−3} &{\text{or}} &{3x−1=3} \\ {\text{Solve each equation.}} &{7x−1=−3} &{} &{3x=4} \\ {} &{7x=−2} &{} &{x=43} \\ {} &{x=−27} &{\text{or}} &{x=43} \\ {\text{Check.}} &{} &{} &{} \\ {\text{We leave the check to you.}} &{} &{} &{} \\ \end{array}\)

Exercise \(\PageIndex{14}\)

Solve: \(|7x−3|=|3x+7|\).

\(x=−\frac{2}{5}, \space x=\frac{5}{2}\)

Exercise \(\PageIndex{15}\)

Solve: \(|6x−5|=|3x+4|\).

\(x=3, x=19\)

Solve Absolute Value Inequalities with “Less Than”

Let’s look now at what happens when we have an absolute value inequality . Everything we’ve learned about solving inequalities still holds, but we must consider how the absolute value impacts our work. Again we will look at our definition of absolute value. The absolute value of a number is its distance from zero on the number line. For the equation \(|x|=5\), we saw that both 5 and \(−5\) are five units from zero on the number line. They are the solutions to the equation.

\[\begin{array} {lll} {} &{|x|=5} &{} \\ {x=−5} &{\text{or}} &{x=5} \\ \nonumber \end{array}\]

What about the inequality \(|x|\leq 5\)? Where are the numbers whose distance is less than or equal to 5? We know \(−5\) and 5 are both five units from zero. All the numbers between \(−5\) and 5 are less than five units from zero (Figure \(\PageIndex{2}\)).

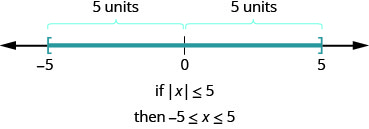
In a more general way, we can see that if \(|u|\leq a\), then \(−a\leq u\leq a\) (Figure \(\PageIndex{3}\)).

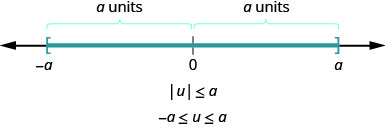
This result is summarized here.

ABSOLUTE VALUE INEQUALITIES WITH \(<\) OR \(\leq\)

\[ \text{if} \quad |u|<a, \quad \text{then} \space −a<u<a \\ \text{if} \quad |u|\leq a, \quad \text{then} \space−a\leq u\leq a \nonumber\]

After solving an inequality, it is often helpful to check some points to see if the solution makes sense. The graph of the solution divides the number line into three sections. Choose a value in each section and substitute it in the original inequality to see if it makes the inequality true or not. While this is not a complete check, it often helps verify the solution.

Example \(\PageIndex{16}\)

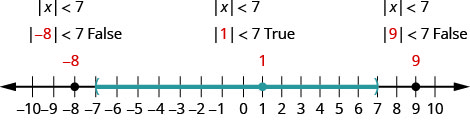
Solve \(|x|<7\). Graph the solution and write the solution in interval notation.

To verify, check a value in each section of the number line showing the solution. Choose numbers such as −8,−8, 1, and 9.

EXERCISE \(\PageIndex{17}\)

Graph the solution and write the solution in interval notation: \(|x|<9\).

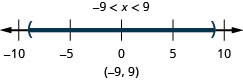
EXERCISE \(\PageIndex{18}\)

Graph the solution and write the solution in interval notation: \(|x|<1\).

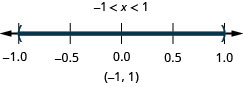
Example \(\PageIndex{19}\)

Solve \(|5x−6|\leq 4\). Graph the solution and write the solution in interval notation.

EXERCISE \(\PageIndex{20}\)

Solve \(|2x−1|\leq 5\). Graph the solution and write the solution in interval notation:

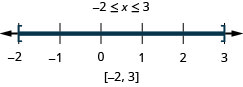
EXERCISE \(\PageIndex{21}\)

Solve \(|4x−5|\leq 3\). Graph the solution and write the solution in interval notation:

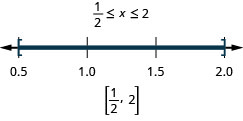
SOLVE ABSOLUTE VALUE INEQUALITIES WITH \(<\) OR \(\leq\)

\[\begin{array} {lll} {|u|<a} &{\quad \text{is equivalent to}} &{−a<u<a} \\ {|u|\leq a} &{\quad \text{is equivalent to}} &{−a\leq u\leq a} \\ \nonumber \end{array}\]

• Solve the compound inequality.
• Graph the solution
• Write the solution using interval notation.

Solve Absolute Value Inequalities with “Greater Than”

What happens for absolute value inequalities that have “greater than”? Again we will look at our definition of absolute value. The absolute value of a number is its distance from zero on the number line.

We started with the inequality \(|x|\leq 5\). We saw that the numbers whose distance is less than or equal to five from zero on the number line were \(−5\) and 5 and all the numbers between \(−5\) and 5 (Figure \(\PageIndex{4}\)).

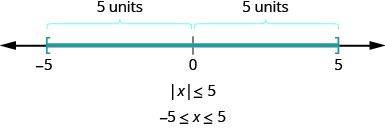
Now we want to look at the inequality \(|x|\geq 5\). Where are the numbers whose distance from zero is greater than or equal to five?

Again both \(−5\) and 5 are five units from zero and so are included in the solution. Numbers whose distance from zero is greater than five units would be less than \(−5\) and greater than 5 on the number line (Figure \(\PageIndex{5}\)).

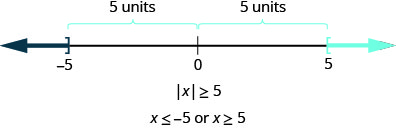
In a more general way, we can see that if \(|u|\geq a\), then \(u\leq −a\) or \(u\leq a\). See Figure .

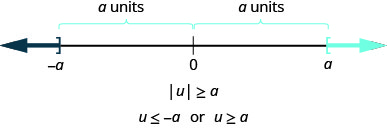
ABSOLUTE VALUE INEQUALITIES WITH \(>\) OR \(\geq\)

\[\begin{array} {lll} {\text{if}} &{\quad |u|>a,} &{\quad \text{then } u<−a \text{ or } u>a} \\ {\text{if}} &{\quad |u|\geq a,} &{\quad \text{then } u\leq −a \text{ or } u\geq a} \\ \nonumber \end{array}\]

Example \(\PageIndex{22}\)

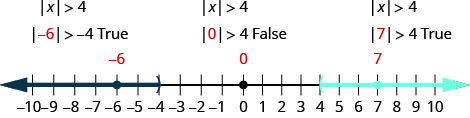
Solve \(|x|>4\). Graph the solution and write the solution in interval notation.

To verify, check a value in each section of the number line showing the solution. Choose numbers such as −6,−6, 0, and 7.

EXERCISE \(\PageIndex{23}\)

Solve \(|x|>2\). Graph the solution and write the solution in interval notation.

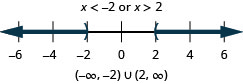
EXERCISE \(\PageIndex{24}\)

Solve \(|x|>1\). Graph the solution and write the solution in interval notation.

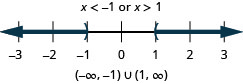
Example \(\PageIndex{25}\)

Solve \(|2x−3|\geq 5\). Graph the solution and write the solution in interval notation.

EXERCISE \(\PageIndex{26}\)

Solve \(|4x−3|\geq 5\). Graph the solution and write the solution in interval notation.

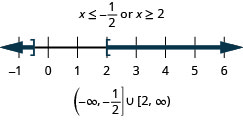
EXERCISE \(\PageIndex{27}\)

Solve \(|3x−4|\geq 2\). Graph the solution and write the solution in interval notation.

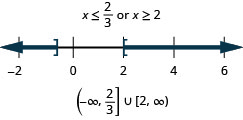
SOLVE ABSOLUTE VALUE INEQUALITIES WITH \(>\) OR \(\geq\).

\[\begin{array} {lll} { |u| >a } &{\quad \text{is equivalent to}} &{ u<−a \quad \text{ or } \quad u>a} \\ { |u| \geq a } &{\quad \text{is equivalent to}} &{ u\leq −a \quad \text{ or } \quad u\geq a} \\ { |u| >a } &{\quad \text{is equivalent to}} &{ u<−a \quad \text{ or } \quad u>a} \\ { |u| \geq a } &{\quad \text{is equivalent to}} &{ u\leq −a \quad \text{ or } \quad u\geq a} \\ \nonumber \end{array}\]

Solve Applications with Absolute Value

Absolute value inequalities are often used in the manufacturing process. An item must be made with near perfect specifications. Usually there is a certain tolerance of the difference from the specifications that is allowed. If the difference from the specifications exceeds the tolerance, the item is rejected.

\[|\text{actual-ideal}|\leq \text{tolerance} \nonumber\]

Example \(\PageIndex{28}\)

The ideal diameter of a rod needed for a machine is 60 mm. The actual diameter can vary from the ideal diameter by \(0.075\) mm. What range of diameters will be acceptable to the customer without causing the rod to be rejected?

\(\begin{array} {ll} {} &{\text{Let }x=\text{ the actual measurement}} \\ {\text{Use an absolute value inequality to express this situation.}} &{|\text{actual-ideal}|\leq \text{tolerance}} \\ {} &{|x−60|\leq 0.075} \\ {\text{Rewrite as a compound inequality.}} &{−0.075\leq x−60\leq 0.075} \\ {\text{Solve the inequality.}} &{59.925\leq x\leq 60.075} \\ {\text{Answer the question.}} &{\text{The diameter of the rod can be between}} \\ {} &{59.925 mm \text{ and } 60.075 mm.} \\ \end{array}\)

ExERCISE \(\PageIndex{29}\)

The ideal diameter of a rod needed for a machine is 80 mm. The actual diameter can vary from the ideal diameter by 0.009 mm. What range of diameters will be acceptable to the customer without causing the rod to be rejected?

The diameter of the rod can be between 79.991 and 80.009 mm.

ExERCISE \(\PageIndex{30}\)

The ideal diameter of a rod needed for a machine is 75 mm. The actual diameter can vary from the ideal diameter by 0.05 mm. What range of diameters will be acceptable to the customer without causing the rod to be rejected?

The diameter of the rod can be between 74.95 and 75.05 mm.

Access this online resource for additional instruction and practice with solving linear absolute value equations and inequalities.

• Solving Linear Absolute Value Equations and Inequalities

Key Concepts

• Absolute Value The absolute value of a number is its distance from 0 on the number line. The absolute value of a number n is written as \(|n|\) and \(|n|\geq 0\) for all numbers. Absolute values are always greater than or equal to zero.
• Absolute Value Equations For any algebraic expression, u , and any positive real number, a , \(\begin{array} {ll} {\text{if}} &{\quad |u|=a} \\ {\text{then}} &{\quad u=−a \text{ or } u=a} \\ \end{array}\) Remember that an absolute value cannot be a negative number.
• Equations with Two Absolute Values For any algebraic expressions, u and v , \(\begin{array} {ll} {\text{if}} &{\quad |u|=|v|} \\ {\text{then}} &{\quad u=−v \text{ or } u=v} \\ \end{array}\)
• Absolute Value Inequalities with \(<\) or \(\leq\) For any algebraic expression, u , and any positive real number, a , \(\begin{array} {llll} {\text{if}} &{\quad |u|=a} &{\quad \text{then}} &{−a<u<a} \\ {\text{if}} &{\quad |u|\leq a} &{\quad \text{then}} &{−a\leq u\leq a} \\ \end{array}\)
• Write the equivalent compound inequality. \(\begin{array} {lll} {|u|<a} &{\quad \text{is equivalent to}} &{\quad −a<u<a} \\ {|u|\leq a} &{\quad \text{is equivalent to}} &{\quad −a\leq u\leq a} \\ \end{array}\)
• Write the solution using interval notation
• Absolute Value Inequalities with \(>\) or \(\geq\) For any algebraic expression, u , and any positive real number, a , \(\begin{array} {lll} {\text{if}} &{\quad |u|>a,} &{\text{then } u<−a\text{ or }u>a} \\ {\text{if}} &{\quad |u|\geq a,} &{\text{then } u\leq −a\text{ or }u\geq a} \\ \end{array}\)
• Write the equivalent compound inequality. \(\begin{array} {lll} {|u|>a} &{\quad \text{is equivalent to}} &{\quad u<−a\text{ or }u>a} \\ {|u|\geq a} &{\quad \text{is equivalent to}} &{\quad u\leq −a\text{ or }u\geq a} \\ \end{array}\)

Absolute Value Equation Calculator

What do you want to calculate.

• Solve for Variable
• Practice Mode
• Step-By-Step

Example (Click to try)

About absolute value equations.

• Get the absolve value expression by itself.
• Set up two equations and solve them separately.

Absolute Value Equation Video Lesson

• Khan Academy Video: Absolute Value Equations

Need more problem types? Try MathPapa Algebra Calculator

Clear Absolute Value Equation Calculator »

• School Guide
• Mathematics
• Number System and Arithmetic
• Trigonometry
• Probability
• Mensuration
• Maths Formulas
• Class 8 Maths Notes
• Class 9 Maths Notes
• Class 10 Maths Notes
• Class 11 Maths Notes
• Class 12 Maths Notes
• Solving Absolute Value Equations
• Absolute Value
• Linear Inequalities
• Real-Life Applications of Absolute Value
• Compound Inequalities
• Inequalities
• Mean Absolute Deviation
• Absolute Value of a Complex Number
• Quadratic Inequalities
• Inequalities in LaTeX
• Ruby | BigDecimal absolute value
• Get the absolute values in Pandas
• Ruby | BigDecimal class absolute value
• Python | Absolute value of list elements
• Python - Absolute Tuple Summation
• GRE Algebra | Solving Linear Inequalities
• Program to find absolute value of a given number
• Getting square of absolute value in Julia - abs2() Method
• Minimize the maximum value of the absolute difference

Absolute Value Inequalities

Inequalities that involve algebraic expressions with absolute value symbols and inequality symbols are called Absolute Value Inequality. In this article, we will discuss inequalities and absolute value inequalities and others in detail.

Table of Content

What is Inequalities?

What is absolute value inequalities, solving absolute value inequalities, types of absolute value inequalities, intersection and union in absolute value inequalities, examples on absolute value inequalities.

Inequalities can be understood as the complement of equations. Inequalities are used to establish a relationship between two or more mathematical values based on the unequal relationship between them. Let us look at an example

• 5 + x > y + 10
• x > y + 5

The above relationship indicates that x is not equal to y+5 rather it is greater than the value of y after 5 is added to it.

Absolute Value Inequalities are a subcategory of inequalities that compare absolute values of mathematical quantities. These usually include symbols like >, < which denote unequal relationships.

What is Absolute Value?

Let us see the formal definition

An absolute value inequality is an expression that uses absolute value expression and variables to denote the relationship between quantities.

We can categorize the inequality into two major types:

• Lesser Than or Equal To
• Greater Than or Equal To
• Compound Inequalities with Absolute Values

Each of the given types is denoted using different symbols which will be discussed later.

Example of Absolute Value Inequalities

Here are some examples to understand the Absolute Value Inequalities

• |x + 5| < 8
• -13 < x < 3

We use number line approach to solve an inequality and follow the steps added below:

Step 1: Write down the inequality and assume it to be an equality making it an equation instead of inequation. Step 2: Draw a number line depending on the intervals and represent the equation on the number line. Step 3: From each interval, select a number and check if it satisfies the inequality. Step 4: Perform step 3 for every interval and the intervals for which a random number satisfies the inequality will be included in your final answer. Step 5: Take the union of all the intervals to get the answer.

Graphical Representation of Inequalities

We can use a graph to plot the inequalities and find the corresponding solution for the inequalities. Let us see how we can use the graph to plot the solution

Note: Open dot ◌ is used for representing an open interval whereas a closed dot ⚈ is used to represent a closed interval in the graph.

Here is the representation of different cases:

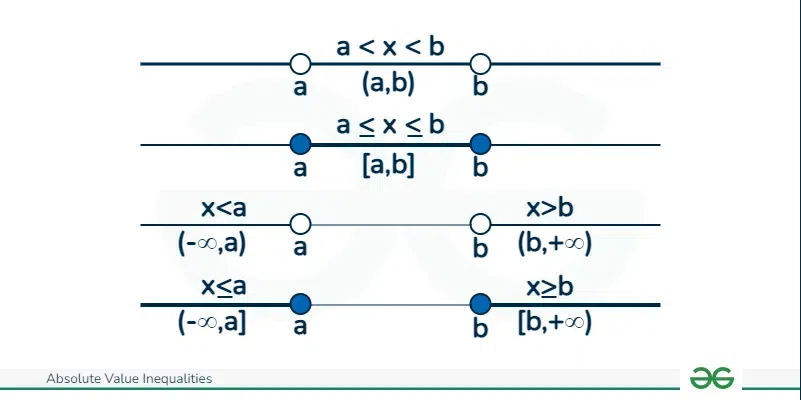
Representation of Inequalities

Depending on the type of sign in the inequality, there are different types of inequalities which are mentioned below:

Inequalities with Greater Than Condition

Inequalities with less than condition, compound inequalities involving absolute values.

These inequalities generally use a greater than sign i.e. the number is greater than the value of some other mathematical value. Here are some examples of such inequalities

• x+ y > 7 + 3y
• 65y > x + 22

These inequalities generally use a less-than sign i.e. the number is less than the value of some other mathematical value. Here are some examples of such inequalities

• x + y < 89
• 5y + 6x < 0

As the name suggests, Compound Inequalities involve both greater than and less than cases i.e. the number is less than and greater than the value of some other mathematical value. These inequalities use the absolute value. Here are some examples of such inequalities

• |x – 5| < 7
• |x + 6y| > 89
• |4x + 2| <= 24

Let us understand how we can take Intersection and Union in Absolute Value Inequalities.

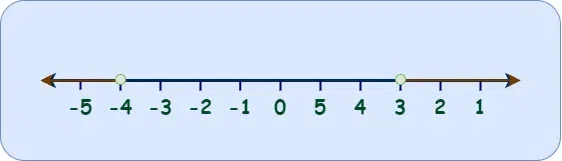
Union of Inequalities

For a given set of values, if the inequality is x>=a or x<b then we need to find the union of the values of x which can be given by

Case 1: x >= a or x < b

{x: x < b U x ≥ a}

Case 2: x < a or x >= b

{x: x <a U x ≥ b} = {x: x < a}∪{x: x ≥ b}.

The solution i.e. the union can be calculated using graph. Consider the example x <= 3 || x >= -4 , then the union of the inequalities will give an overlapping interval which will include all real numbers as shown below.

Intersection of Inequalities

For a given set of values, if the inequality is x >= a and x < b then we need to find the intersection of the values of x which can be given by

Case 1: a <= x < b

{x: a≤x < b}

Case 2: a <= x U b > x

{x: a ≤ x U x < b}

The solution i.e. the intersection can be calculated using graph. Consider the example x <= 4 U x >= -5 , then the intersection of the inequalities will give an interval which will include all real numbers from -5 and 4 as shown below.

Triangle Inequality Compound Inequalities Word Problems of Linear Inequalities

Example 1: Solve for inequality |x+24|>-5 using the formula-based approach.

Given Inequality |x + a| > b -∞ < x + a < -b b < x + a < +∞ Solving both of them individually Case 1: -∞ < x < -a – b Case 2: b – a < x < ∞ x ⋿ (-∞,-a-b) ⋃ (b-a, ∞)

Example 2: Solve this less than equal to absolute inequality |y + 5| <= 3y

Given Inequality |y + 5| <= 3y Case 1: y + 5 <= 3y 5 <= 2y 5/2 <= y y ϵ [5/2, ∞)…(i) Case 2: -3y <= y + 5 -4y <= 5 y >= -1.25 y ϵ (-∞, -5/4]…(ii) From eq. (i) and eq. (ii) y ϵ [5/2, -5/4]

Practice Problems on Absolute Value Inequalities

P1. Use the union and intersection method to find the solution for x given |x+7|<1001 and |x+2|>24.

P2. Use the graphical representation method to find the solution of |2x+5|+y>7x

P3. Solve the inequality ∣2x + 3∣ < 5.

P4. Find all values of such that ∣x − 4∣ ≥ 2.

FAQs Absolute Value Inequalities

When do we use curved and square brackets while writing the solution of inequality.

Curved bracket i.e. ( ) is used to denote a quantity that is not included in the range of possible values of the variable whereas the square bracket i.e. [ ] is used when the number is included in the range of values of the variable.

What are the equivalents of curved and square brackets in graphical representation?

Open dot denotes the curved bracket. Closed dot is used instead of the square bracket.

When is the sign switched from negative to positive and vice-versa in an inequality?

Sign in an inequality changes when we multiply the quantity on both sides of the equation by a negative sign or divide the quantity on both sides by a negative value.

Can an absolute value inequality be negative?

No, absolute value inequality can never be negative.

Please Login to comment...

Similar reads.

• linear algebra
• School Learning

Improve your Coding Skills with Practice

What kind of Experience do you want to share?